
C
ALCOLATRICE
CIENTIFICA
UIDA PER L’UTENTE
CALCOLATRICE
C
GUIDA PER L’UTENTE
GUIDA PER L’UTENTE
ALCOLATRICE
SCIENTIFICA
SCIENTIFICA
<Write View>

INDICE
ISTRUZIONI PER L’USO
Prima di iniziare a usare la calcolatrice
Disposizione dei tasti 2
Tasto di ripristino/Indicatori del display 3
Formato di visualizzazione e impostazione del sistema decimale 3-4
Visualizzazione esponenziale 4
Unità angolari 5
Funzioni e utilizzo dei tasti
Tasti di accensione, spegnimento,
cancellazione e correzione 6
Tasti per l’immissione dei dati 7
Tasto Random 8
Tasto di modifica 9
Tasti aritmetici di base e parentesi 10
Percentuali 11
Inverso, quadrato, cubo, y elevato a x, radice
quadrata, radice cubica, radice x-esima di y 12
10 elevato a x, logaritmo comune e
logaritmo di x in base a
e elevato a x e logaritmo naturale 14
Fattoriali 15
Permutazioni e combinazioni 16
Calcolo degli angoli e del tempo 17
Calcoli frazionari 18
Calcoli con la memoria 19
Memoria dell’ultimo risultato 20
Funzioni definite dall'utente 21
Valore assoluto 22
Funzioni trigonometriche 23
Funzioni trigonometriche inverse 24
Funzioni iperboliche 25
Conversione delle coordinate 26
13
~
~
Operazioni con numeri binari, pentali,
ottali, decimali ed esadecimali (in base N) 27
FUNZIONI STATISTICHE
Immissione e correzione dei dati 28
Tasti “ANS” per le statistiche a una variabile 29
Correzione dei dati 30-32
Tasti “ANS” per le statistiche a due variabili 33
1
Istruzioni per l’uso
≈
Prima di iniziare a usare la calcolatrice
La presente guida per l’utente fa riferimento ai modelli EL-W531, EL-W531G ed EL-W531H.
Alcune funzioni descritte in questa guida non sono presenti in altri modelli. Le operazioni con i
tasti e i simboli visualizzati sul display potrebbero, inoltre, variare a seconda del modello.
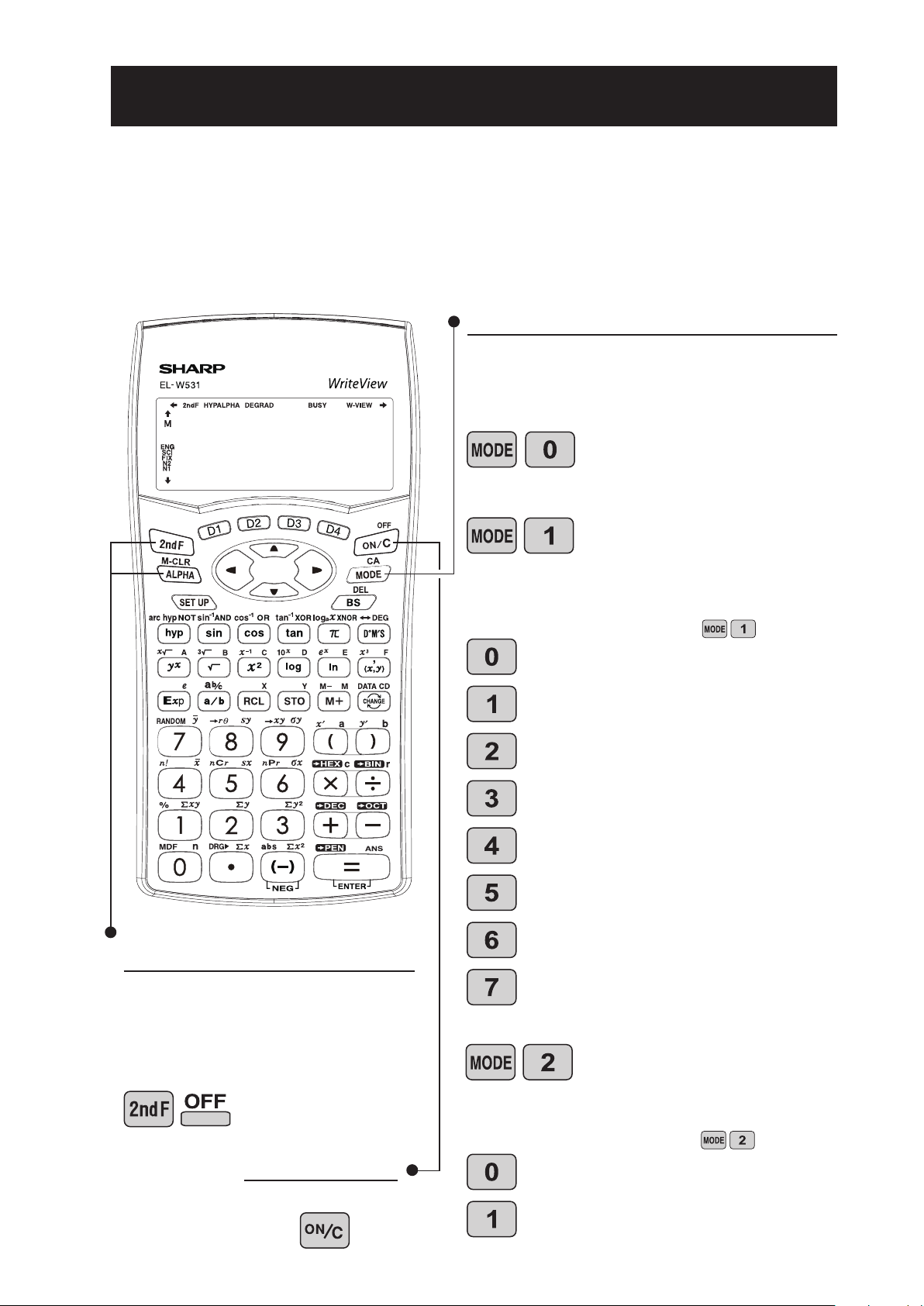
1. DISPOSIZIONE DEI TASTI
Tasto MODE
Questa calcolatrice può funzionare in tre diverse
modalità.
<Esempio>
[Modalità normale]
•Modalità = 0; Modalità
normale per l’esecuzione delle
normali operazioni aritmetiche
e dei calcoli con le funzioni.
[Modalità STAT]
•Modalità = 1; Modalità per
l’esecuzione dei calcoli statistici a
una o due variabili. Per
selezionare la sottomodalità
statistica, premere il tasto del
numero corrispondente dopo
aver premuto .
≈
Tasto 2ndF (seconda funzione)
e tasto ALPHA
Premendo questi tasti, si abilitano le
funzioni indicate in arancione (2ndF) o
in verde (ALPHA) al di sopra dei tasti
della calcolatrice.
Seconda funzione
Indicata in arancione al di
sopra del tasto ON/C
<Spegnimento>
Tasto ON/C, OFF
(SD): Calcolo statistico a variabile singola.
(LINE): Calcolo di regressione lineare.
(QUAD): Calcolo di regressione quadratica.
(E_EXP):
di Eulero.
(LOG): Calcolo di regressione logaritmica.
(POWER):
(INV): Calcolo di regressione inversa.
(EXP): Calcolo di regressione esponenziale.
[Modalità Esercitazione]
(MATH): Esercizi di matematica.
Calcolo della regressione esponenziale
Calcolo di regressione con potenze.
•Modalità = 2; Modalità per
l’esecuzione degli esercizi. Per
selezionare la sottomodalità di
esercitazione, premere il tasto
del numero corrispondente dopo
aver premuto .
Funzione diretta
<Accensione>
(TABLE): Esercizi con la tabella di
moltiplicazione.
2
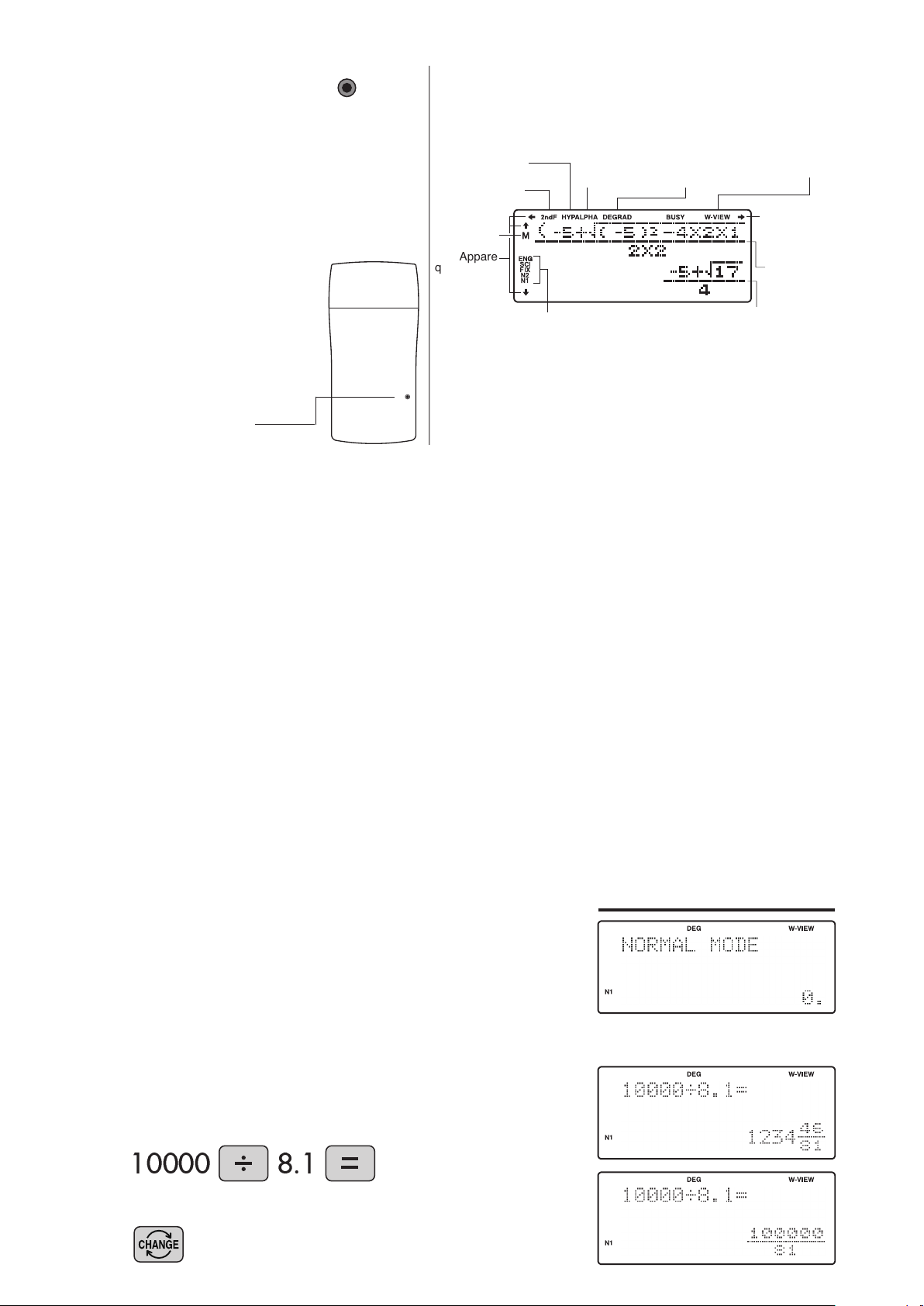
2.
TASTO DI
RESET
3.
DISPLAY PATTERN
RIPRISTINO
In caso di funzionamento anomalo della
calcolatrice, premere il tasto di
ripristino (reset) posizionato sul retro
per reinizializzare l’unità. Il formato di
visualizzazione e la modalità di calcolo
verranno ripristinati alle impostazioni
iniziali.
NOTA:
Premendo il tasto di
ripristino si cancellano tutti i
dati immagazzinati in
memoria.
RESET
Tasto di ripristino
quando non
visualizzata
Simbolo
iperbolico (HYP)
Simbolo
seconda
funzione
Simbolo
memoria
Appare
può essere
lʼintera
equazione
Indicatore formato visualizzazione
(ENG, SCI, FIX, N2, N1)
Simbolo
alfabeto
(ALPHA)
Indicatore unità
angolare
(DEG/RAD/GRAD)
Il display effettivo non si presenta in questo modo.
Questa figura ha un mero scopo illustrativo.
4. FORMATO DI VISUALIZZAZIONE E
IMPOSTAZIONE DEL SISTEMA DECIMALE
Modalità
WriteView
(visualizza le
espressioni
di calcolo
così come
si scrivono)
Appare quando
non può essere
visualizzata
lʼintera
equazione
Visualizzazione
equazione
Visualizzazione
risultato
Per comodità e facilità d'uso, questo modello può essere utilizzato in cinque diverse
modalità di visualizzazione. Il formato di visualizzazione selezionato è indicato nell’angolo
inferiore sinistro del display (Indicatore di formato).
Nota: Nel caso in cui siano visualizzati più 0 (zeri) di quelli necessari quando si preme il
tasto ON/C, verificare il formato di visualizzazione impostato:
• Formato decimale in virgola mobile 1/2 (viene visualizzato il simbolo N1 o N2).
I valori validi che non rientrano nell’intervallo massimo sono visualizzati sotto forma di
mantissa (10 cifre) ed esponente (2 cifre).
• Formato decimale in virgola fissa (viene visualizzato il simbolo FIX).
Visualizza la parte frazionaria del risultato del calcolo in base al numero di cifre decimali
specificate.
• Notazione scientifica (viene visualizzato il simbolo SCI).
Utilizzata spesso nel campo scientifico per eseguire calcoli con numeri estremamente
piccoli o grandi.
• Notazione tecnica (viene visualizzato il simbolo ENG).
Utile per la conversione tra unità diverse.
<Esempio>
(specifica la modalità normale)
Vediamo come appare il risultato di
[10000 ÷ 8.1 =] in ciascun formato di
visualizzazione.
Visualizzazione iniziale
Nota: I numeri in virgola mobile possono essere visualizzati
secondo due diverse modalità: NORM1 (modalità
predefinita) e NORM2. In ciascuna modalità, il numero viene
visualizzato automaticamente in notazione scientifica, nel
caso in cui non rientri nell’intervallo predefinito:
• NORM1: 0.000000001 ≤ x ≤ 9999999999
• NORM2: 0.01 ≤ x ≤ 9999999999
10000 8.1
3
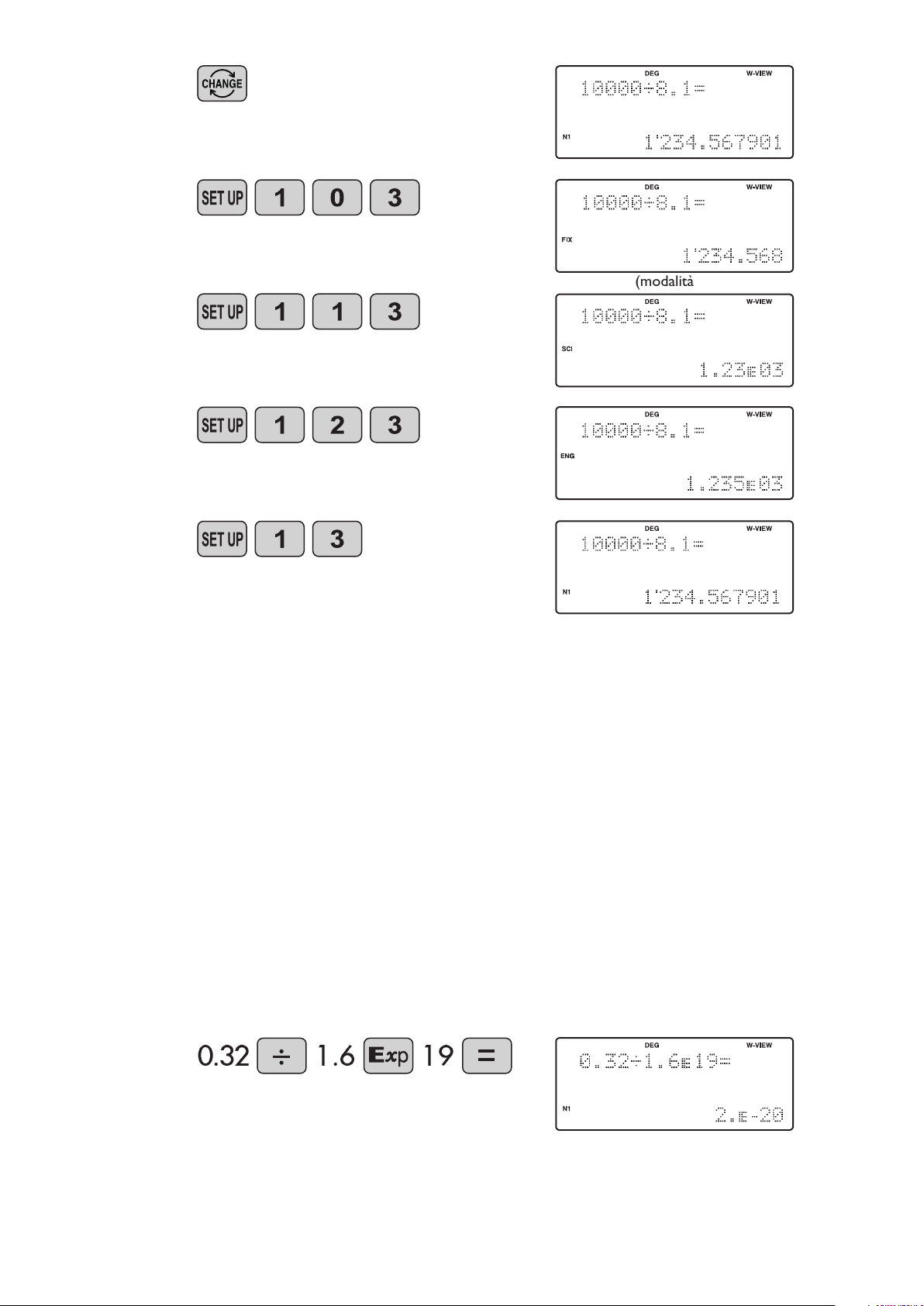
(modalità FIX - TAB = 3)
5. VISUALIZZAZIONE ESPONENZIALE
(modalità SCI)
(modalità ENG)
(modalità normale)
La distanza tra la terra e il sole è di circa 150.000.000 (1,5 x 108) km. Valori con
molti zeri come questi vengono utilizzati spesso nei calcoli scientifici, ma
l’inserimento, uno alla volta, degli zeri richiede tempo e può indurre facilmente in
errore. In questi casi, i valori numerici vengono suddivisi in mantissa ed esponente per
poi essere visualizzati e calcolati.
<Esempio>
Considerato che la carica di un singolo elettrone è pari a
1,6 x 10
-19
coulomb, qual è il numero di elettroni che
scorrono in un conduttore quando la carica elettrica che
attraversa una determinata sezione trasversale è di 0,32
coulomb?
0.32 191.6
4
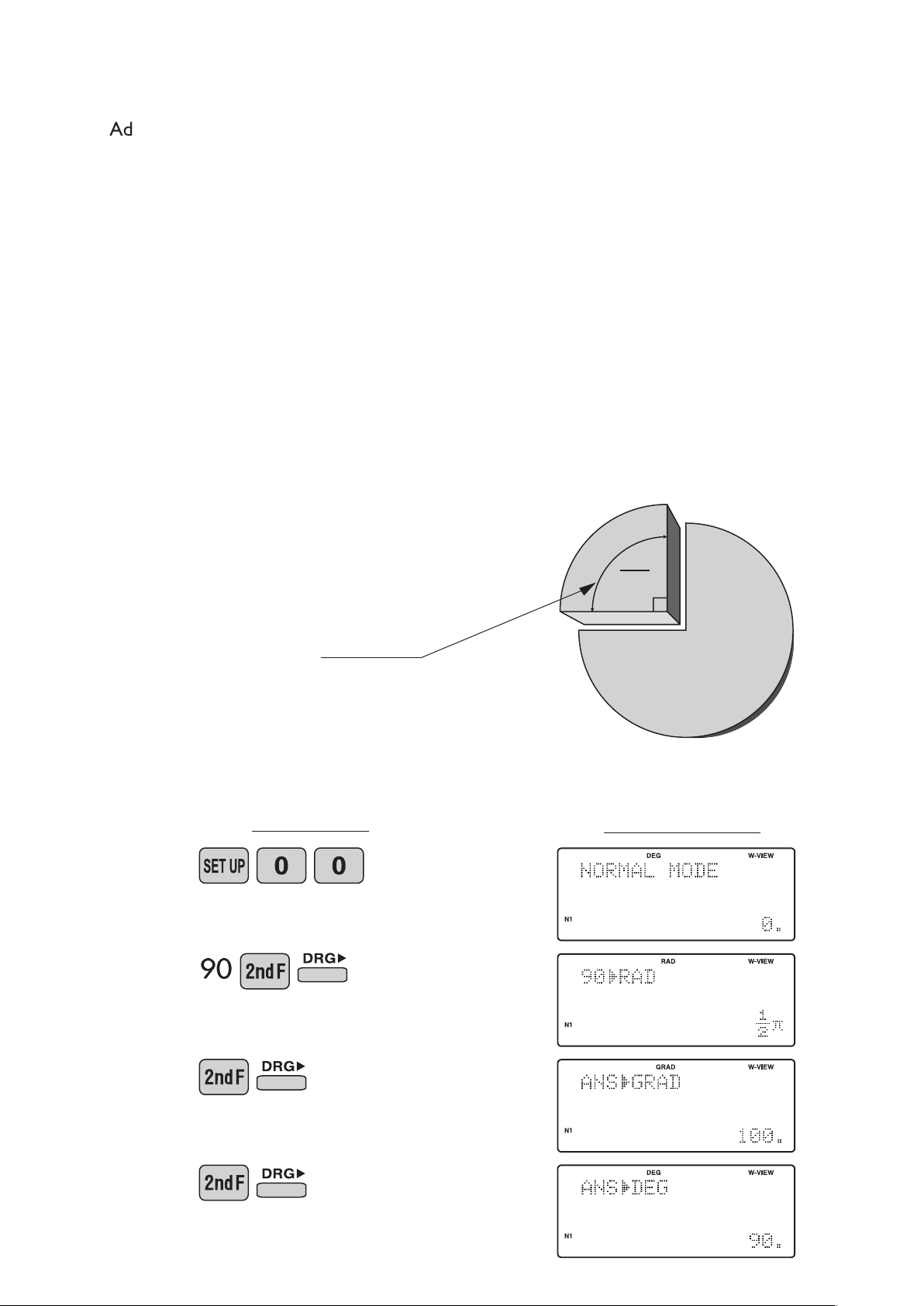
6. UNITÀ ANGOLARI
Ad ogni pressione del tasto DRG. i valori angolari vengono convertiti da DEG a RAD e a
GRAD. Questa funzione viene utilizzata quando si eseguono calcoli che hanno a che fare
con le funzioni trigonometriche o con le conversioni geometriche delle coordinate.
Gradi sessagesimali
(in cima al display appare il simbolo DEG)
Un’unità che viene utilizzata comunemente per la misurazione degli angoli. La
misura angolare di un cerchio viene espressa come 360°.
Radianti (in cima al display appare il simbolo RAD)
I radianti differiscono dai gradi ed esprimono gli angoli in base alla circonferenza di
un cerchio. 180° equivalgono a π radianti. Ne deriva che la misura angolare di un
cerchio è pari a 2π radianti.
Gradi centesimali
(in cima al display appare il simbolo GRAD)
I gradi centesimali sono un’unità di misura angolare che viene utilizzata in Europa e
soprattutto in Francia. 90 gradi sessagesimali equivalgono a 100 gradi centesimali.
I rapporti tra i tre tipi di unità angolari
possono essere espressi come segue:
90˚ (DEG) =
π/2 (RAD) =
100 (GRAD) =
<Esempio>
Operazione
Verificare che 90 gradi sessagesimali equivalgano a π/2
radianti e a100 gradi centesimali. (π=3,14159...)
90
π
2
Visualizzazione
5
≈
Funzioni e utilizzo dei tasti
Tasti di accensione,
spegnimento, cancellazione
e correzione
Accende la calcolatrice o cancella i dati. Cancella anche il contenuto del display
della calcolatrice e annulla qualsiasi comando. Tuttavia, i coefficienti delle
statistiche e delle equazioni lineari a tre variabili, così come i valori
immagazzinati nella memoria indipendente in modalità normale, non vengono
cancellati.
Spegne la calcolatrice.
≈
Cancella tutti i valori interni, compreso l’ultimo risultato (ANS) e le statistiche. I
valori immagazzinati nella memoria in modalità normale non vengono cancellati.
Questi tasti cursore sono utili per la riproduzione multiriga e
consentono di scorrere uno ad uno i vari passaggi dei calcoli.
Questi tasti sono utili per la modifica delle equazioni. Il tasto sposta
il cursore a sinistra, mentre il tasto sposta il cursore a destra.
Il tasto elimina il simbolo/numero a sinistra del cursore, mentre il
tasto elimina il simbolo/numero a destra del cursore.
6

Tasti per l’immissione
dei dati
0 - 9
Tasti numerici per l’immissione dei valori.
Tasto del punto (virgola) decimale. Inserisce un punto decimale.
Inserisce il simbolo della sottrazione.
Il tasto della sottrazione non viene utilizzato per l’immissione dei numeri
negativi.
Premendo il tasto π viene immesso automaticamente il valore di π
(3,14159...).
La costante π, utilizzata spesso nei calcoli con le funzioni, è il rapporto tra la
circonferenza di un cerchio e il suo diametro.
Premendo questo tasto, si passa all’immissione dei dati in notazione
scientifica.
<Esempio>
Considerato che la terra si muove intorno al sole in un'orbita
circolare, quanti chilometri percorre in un anno?
8
* La distanza media tra la terra e il sole è di 1,496 x 10
La circonferenza è uguale al diametro x π, e, di conseguenza,
la risposta si ottiene come segue 1.496 x 10
Operazione
8
x 2 x π.
Visualizzazione
km.
21.496 8
7
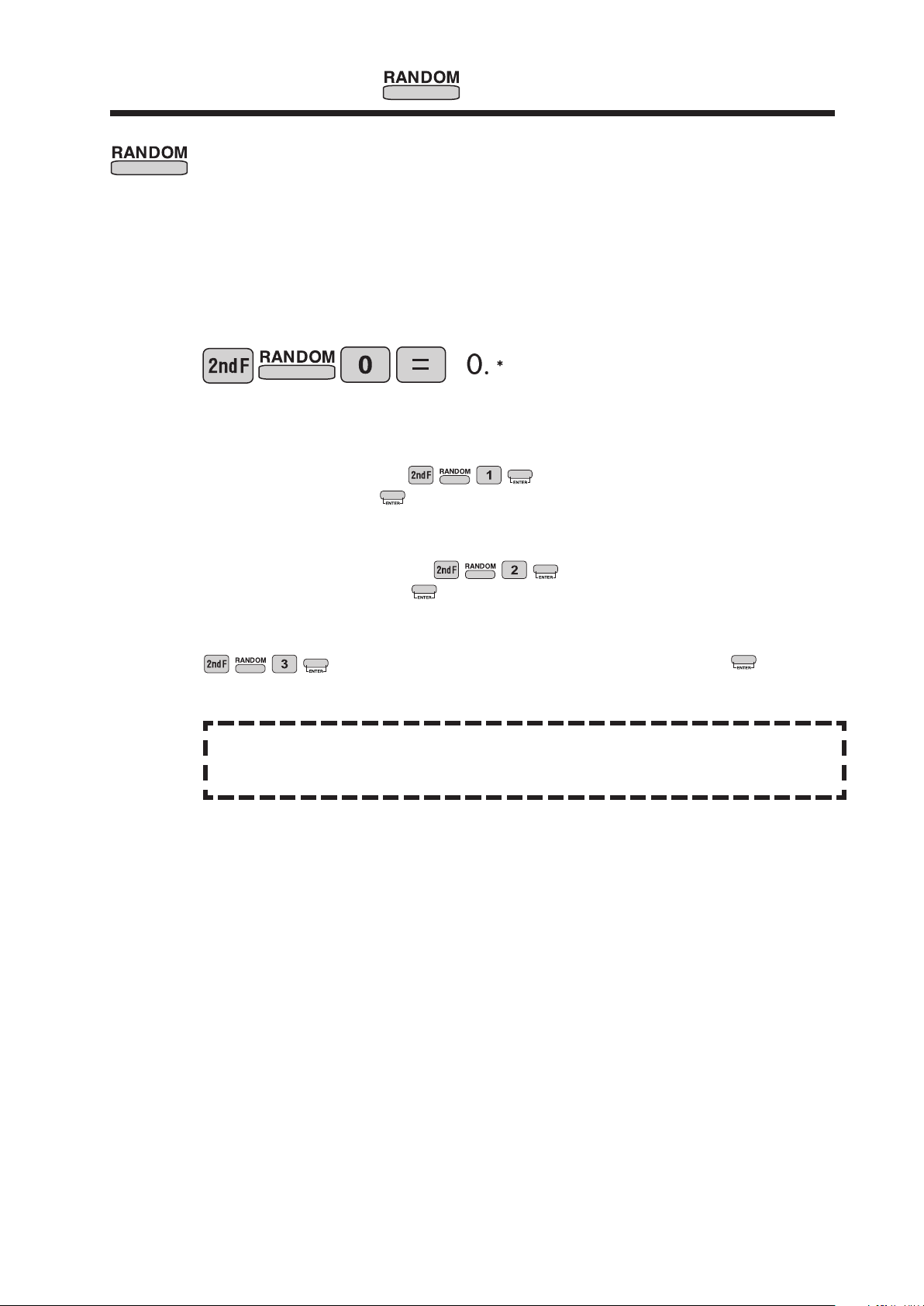
Tasto Random
Genera dei numeri casuali.
I numeri casuali sono valori con tre cifre decimali compresi tra 0,000 e 0,999. L’uso
di questa funzione consente di ottenere dati campionari non distorti ricavati dai
valori casuali generati dalla calcolatrice. È preferibile utilizzare la modalità riga,
poiché, in modalità W-View, i numeri vengono generati mediante frazioni.
<Esempio>
[Dado casuale]
Per simulare il lancio di un dado, un intero casuale compreso tra 1 e 6 può essere
generato premendo i tasti . Per generare il successivo numero di
dado casuale, premere .
[Monetina casuale]
Per simulare il lancio di una monetina, lo 0 (testa) e l’1 (croce) possono essere generati
casualmente premendo i tasti . Per generare il successivo numero di
monetina casuale, premere .
0.
*** (Viene generato un numero casuale.)
[Intero casuale]
Un intero compreso tra 0 e 99 può essere generato casualmente premendo i tasti
. Per generare il successivo intero casuale, premere .
APPLICAZIONI:
Costruire degli insiemi campionari a fini statistici o di ricerca.
8
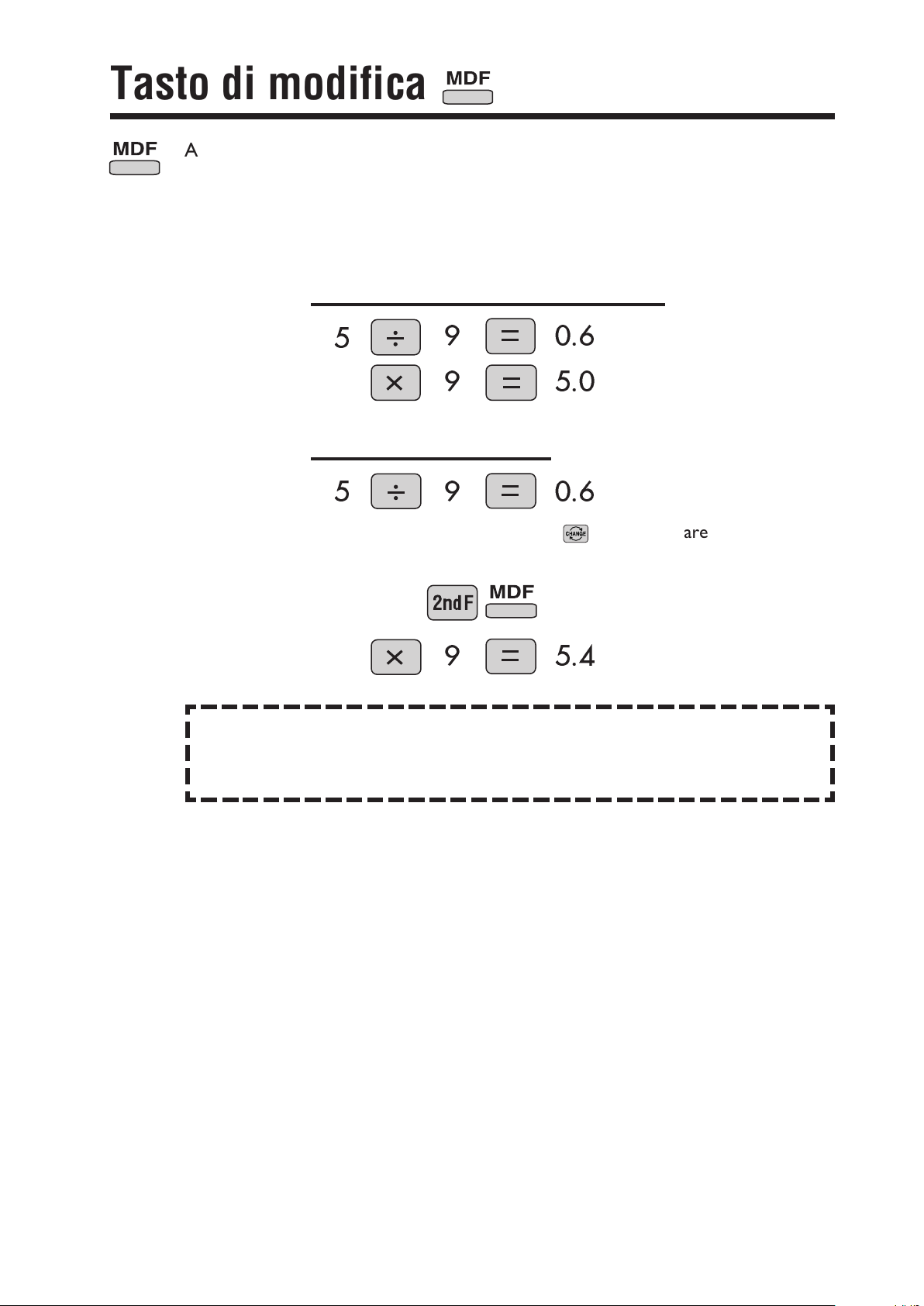
Tasto di modifica
Arrotonda i risultati dei calcoli.
Anche dopo aver impostato il numero di decimali sul display, la calcolatrice esegue i
calcoli utilizzando un numero di decimali maggiore di quelli che vengono visualizzati.
Utilizzando questa funzione, i calcoli interni verranno eseguiti utilizzando soltanto il
valore visualizzato.
<Esempio>
APPLICAZIONI:
Questa funzione viene utilizzata spesso nel campo scientifico, nel campo
tecnico e nel campo commerciale per eseguire dei calcoli a catena.
Modalità FIX - TAB = 1 (calcolo normale)
5
9
9
Calcolo arrotondato (MDF)
59
(in modalità V-View, premere per visualizzare il risultato in
decimali)
9
0.6
5.0
0.6
(internamente, 0.6)
5.4
(internamente, 0.5555...)
(internamente, 0.5555...)
9

Tasti aritmetici di base
e parentesi
I quattro operatori fondamentali, che si usano allo stesso modo in cui
vengono utilizzati in una calcolatrice normale:
(addizione), – (sottrazione), x (moltiplicazione), e ÷ (divisione).
+
Trova il risultato allo stesso modo in cui viene trovato in una calcolatrice
normale.
Vengono utilizzati per specificare la precedenza di determinate
operazioni. Per far sì che delle operazioni di addizione e sottrazione
abbiano la precedenza sulla moltiplicazione e sulla divisione, basta
racchiuderle tra parentesi.
10

Percentuali
Consente di calcolare le percentuali. I quattro metodi utilizzati per il
calcolo delle percentuali sono i seguenti:
1) Aggiunta
Esempio: aggiunta del 10% a $125 = 137,5
125
2) Detrazione
Esempio: detrazione del 20% da $125 = 100
125
10
20
3) Percentuale
Esempio: 15% di $125 = 18,75
125
4) Proporzione
Esempio: Se $125 sono il 5% di X, X è pari a 2.500
15
125 5
11

Inverso, quadrato, cubo,
y
elevato a x, radice quadrata,
radice cubica e
radice x-esima di
Calcola l’inverso del valore visualizzato sul display.
Eleva al quadrato il valore visualizzato sul display.
Eleva al cubo il valore visualizzato sul display.
Calcola i valori esponenziali.
Calcola la radice quadrata del valore visualizzato sul display.
Calcola la radice cubica del valore visualizzato sul display.
Calcola la radice x-esima di y.
y
<Esempio>
Operazione Visualizzazione
2 2 2 2
24
416
12

10 elevato a x,
logaritmo comune e,
logaritmo di x in base
Calcola il valore di 10 elevato alla x-esima potenza.
Calcola il logaritmo, ossia l’esponente della potenza cui va elevato 10 per
ottenere il valore dato.
Calcola il logaritmo di x in base a.
<Esempio>
Operazione
3
a
Visualizzazione
1000
345
13

e
elevato a
x
e logaritmo naturale
Calcola le potenze in base alla costante e (2,718281828).
Calcola il valore del logaritmo naturale, ossia l'esponente della potenza
cui va elevato e per ottenere il valore dato.
<Esempio>
Operazione Visualizzazione
5
10
14

Fattoriali
Il simbolo n! indica il fattoriale di n, ovvero il prodotto di tutti gli interi
positivi inferiori o uguali ad n.
<Esempio>
APPLICAZIONI:
Questa funzione è utilizzata in statistica e in matematica. In statistica,
viene usata nei calcoli relativi alle combinazioni e alle permutazioni.
Operazione Visualizzazione
7
c.f
n! = 1 x 2 x 3 x …xn
15

Permutazioni e combinazioni
Questa funzione consente di trovare ciascuno dei possibili
raggruppamenti di n elementi presi r per volta e che differiscono soltanto
per l’ordine in cui ogni elemento compare. Per esempio, ci sono sei
diversi modi di ordinare le lettere ABC in gruppi di tre lettere: ABC,
ACB, BAC, BCA, CAB e CBA.
L'equazione di calcolo è la seguente
Questa funzione consente di trovare ciascuno dei possibili
raggruppamenti non ordinati di r elementi tra n disponibili. Per esempio,
dall’insieme delle lettere ABC, è possibile estrarre tre gruppi di due
lettere: AB, AC e CB.
L'equazione di calcolo è
3C2
.
<Esempio>
Operazione Visualizzazione
64
= 3 x 2 x 1 = 6 (modi).
3P3
64
APPLICAZIONI:
Queste funzioni vengono utilizzate in statistica (calcolo delle probabilità)
e nelle ipotesi di simulazione formulate nei settori della medicina, della
farmacia e della fisica. Possono essere usate anche per determinare le
possibilità di vincita a una lotteria.
16

Calcolo degli angoli e del tempo
Converte un valore sessagesimale (gradi, minuti e secondi) in valore
decimale e viceversa.
Immette i valori in notazione sessagesimale (gradi, minuti e secondi).
<Esempio>
Convertire 24° 28’ 35" (24 gradi, 20 minuti e 35 secondi)
in notazione decimale. Convertire quindi 24,476° in
notazione sessagesimale.
Operazione Visualizzazione
24 28 35
Convertire in notazione decimale
Premere nuovamente per tornare alla precedente visualizzazione.
APPLICAZIONI:
Queste funzioni vengono utilizzate in fisica per il calcolo degli angoli e
della velocità angolare e, in geografia, per il calcolo della latitudine e
della longitudine.
17

Calcoli frazionari
Inserisce frazioni proprie e improprie formate da un numeratore e da un
denominatore.
Inserisce una frazione mista.
<Esempio>
312
57
Sommare 3 a , e convertire in notazione decimale.
Operazione Visualizzazione
1
5
2
7
Convertire in frazione impropria
Convertire in notazione decimale
APPLICAZIONI:
Le applicazioni di questa funzione sono numerose, perché le frazioni
rappresentano una parte fondamentale della matematica. La funzione
è, ad esempio, utile per i calcoli relativi alla resistenza dei circuiti
elettrici.
18

Calcoli con la memoria
Immagazzina i valori visualizzati nelle memorie A~F, X, Y ed M.
Richiama i valori immagazzinati nelle memorie A~F, X, Y ed M.
Aggiunge il valore visualizzato al valore presente nella memoria indipendente M.
Sottrae il valore visualizzato dal valore presente nella memoria indipendente M.
Memorie temporanee
~
Memoria indipendente
~
<Esempio 1>
Operazione Visualizzazione
0
(Immettere 0 per M)
25 27
73
<Esempio 2>
Calcola $/¥ al tasso di cambio prestabilito.
$1 = ¥110
¥26.510 = $?
$2.750 = ¥?
Operazione
Visualizzazione
110
265
275
10
0
19

Memoria dell’ultimo risultato
Richiama automaticamente l’ultimo risultato ottenuto premendo
<Esempio>
Operazione Visualizzazione
23
4
Calcolare prima x e poi y utilizzando x.
y = 4 ÷ xandx = 2 + 3
20

Funzioni definite dall’utente
~
~
Richiama una funzione definita dall’utente.
<Esempio>
Operazione Visualizzazione
26
APPLICAZIONI:
Le funzioni predefinite dall’utente, tra cui le seconde funzioni
attivate mediante la combinazione del tasto con gli altri tasti,
possono essere immagazzinate nelle memorie D1 ~ D4 per un
uso futuro, riducendo il tempo di immissione dei dati.
21

Valore assoluto
Restituisce un valore assoluto.
<Esempio>
Operazione
Ð4
Visualizzazione
3
22

Funzioni trigonometriche
Le funzioni trigonometriche determinano il rapporto tra i
tre lati di un triangolo rettangolo. Le combinazioni fra i tre
lati sono seno, coseno e tangente e i relativi tasti della
calcolatrice sono i seguenti:
Calcola il seno di un angolo.
Calcola il coseno di un angolo.
Calcola la tangente di un angolo.
sinθ =
cosθ =
tanθ =
b
a
c
a
b
c
<Esempio>
L’angolo che si viene a formare tra un
punto che si trova a 15 metri da un
edificio e il piano più alto dell’edificio è
di 45°. Quanto è alto l’edificio?
Punto di vista 1,5 m
a
b
θ
c
[Modalità DEG]
Operazione Visualizzazione
45 15
1
Punto di vista
5
APPLICAZIONI:
Le funzioni trigonometriche sono utili in matematica e in vari calcoli di
ingegneria. Vengono utilizzate spesso nelle osservazioni astronomiche,
nell’ingegneria civile e nei calcoli relativi ai circuiti elettrici, così come in
fisica per il calcolo, ad esempio, del movimento parabolico e del
movimento ondulatorio.
23

Funzioni trigonometriche
inverse
Le funzioni trigonometriche inverse vengono utilizzate
per determinare un angolo in base ai rapporti che
intercorrono tra i lati di un triangolo rettangolo. Le
combinazioni fra i tre lati sono sin
relativi tasti della calcolatrice sono i seguenti:
(arcoseno) Determina un angolo in base al seno,
ovvero il rapporto tra il lato b e il lato a di un
triangolo rettangolo.
(arcocoseno) Determina un angolo in base al
coseno, ovvero il rapporto tra il lato c e il lato a di
un triangolo rettangolo.
(arcotangente) Determina un angolo in base alla
tangente, ovvero il rapporto tra il lato b e il lato
c di un triangolo rettangolo.
-1
, cos-1 e tan-1 e i
θ
a
c
= sin
θ
= cos
θ
= tan
θ
b
b
-1
a
c
-1
a
b
-1
c
<Esempio>
A quale inclinazione dovrebbe salire un
aeroplano per raggiungere un dislivello di 80
metri percorrendo 100 metri in orizzontale?
[Modalità DEG]
Operazione Visualizzazione
80
100
24

Funzioni iperboliche
La funzione iperbolica viene definita utilizzando esponenti naturali nelle
funzioni trigonometriche.
Le funzioni iperboliche inverse vengono definite utilizzando logaritmi
naturali nelle funzioni trigonometriche.
APPLICAZIONI:
Le funzioni iperboliche e iperboliche inverse sono molto utili in fisica
e in ingegneria elettrica.
25

Conversione delle coordinate
Converte le coordinate cartesiane in coordinate polari (x, y → r, )
Converte le coordinate polari in coordinate cartesiane (r, → x, y)
Suddivide i valori utilizzati per l'immissione di dati a due variabili.
y
Coordinate cartesiane
y
o
<Esempio>
P (x,y)
x
Determinare le coordinate polari (r, ) sapendo che le
coordinate cartesiane del punto P sono (x = 7, y = 3).
x
y
Coordinate polari
r
θ
o
θ
P (r,
θ
θ
θ
)
x
[Modalità DEG]
Operazione Visualizzazione
73
7.6 23.2
APPLICAZIONI:
La conversione delle coordinate viene utilizzata spesso in matematica e in
ingegneria, soprattutto per il calcolo dell’impedenza in elettronica e
ingegneria elettrica.
26

Operazioni con numeri binari,
pentali, ottali, decimali
ed esadecimali (in base N)
Questa calcolatrice può convertire i numeri in valori binari, pentali, ottali, decimali ed
esadecimali. Può, inoltre, eseguire le quattro operazioni aritmetiche fondamentali, i calcoli con
le parentesi e i calcoli con la memoria utilizzando i numeri binari, pentali, ottali, decimali ed
esadecimali. Può, infine, eseguire le operazioni logiche AND, OR, NOT, NEG, XOR e XNOR
con numeri binari, pentali, ottali ed esadecimali.
Converte in numero binario.
Appare “BIN”.
Converte in numero pentale.
Appare “PEN”.
Converte in numero ottale.
Appare “OCT”.
La conversione del valore visualizzato viene eseguita mediante la pressione di questi tasti.
<Esempio 1>
HEX(1AC) gBIN gPEN gOCT gDEC
Operazione Visualizzazione
Converte in numero esadecimale.
Appare “HEX”.
Converte in numero decimale. “BIN”,
“PEN”, “OCT” ed “HEX” scompaiono
dal display.
1AC
<Eesempio 2>
Operazione Visualizzazione
101
1011 AND 101 = (BIN)
1011
27
gDEC

Funzioni statistiche
La funzione statistica è molto utile per analizzare gli aspetti qualitativi di un evento.
Benché sia utilizzata principalmente in ingegneria e in matematica, la funzione viene
applicata in quasi tutti i campi, comprese l'economia e la medicina.
IMMISSIONE E CORREZIONE DEI DATI
Inserisce i dati per i calcoli statistici.
Cancella i dati immessi.
Suddivide i valori utilizzati per l’immissione di dati a due variabili
(si utilizza per i calcoli statistici a due variabili).
<Esempio 1>
Tabella di dati 1
Numero
Punteggio
Numero di
alunni
Operazione Visualizzazione
Selezionare la modalità statistica
a una variabile
La seguente tabella contiene i risultati di un esame.
Immettere questi dati per analizzarli.
1 2 3 4 5 6 7 8
30 40 50 60 70 80 90 100
2 4 5 7 12 10 8 2
30 2
.
.
.
100 2
28

TASTI “ANS” PER LE STATISTICHE A UNA
VARIABILE
Calcola il valore medio dei dati (dati campionari x).
Calcola la deviazione standard dei dati (dati campionari x).
Calcola la deviazione standard di una popolazione di dati (dati campionari x).
Visualizza il numero dei dati immessi (dati campionari x).
Calcola la somma dei dati (dati campionari x).
Calcola la somma dei dati (dati campionari x) elevati al quadrato.
NOTA:
1. I dati campionari sono rappresentati dai valori selezionati casualmente
all’interno della popolazione.
2. La deviazione standard del campione è rappresentata dallo scarto tra
i dati campionari e il valore medio.
3. La deviazione standard della popolazione è rappresentata dalla
deviazione standard, quando il campione viene considerato una
popolazione (dati completi).
Controlliamo i risultati in base ai dati precedenti.
69 (valore medio)
17.75686128 (deviazione standard)
17.57839583 (deviazione standard della popolazione)
50 (numero complessivo dei dati)
3450 (totale)
29

CORREZIONE DEI DATI
Correzione prima della pressione del tasto dopo l’inserimento dei dati:
Eliminare i dati errati con , quindi immettere i dati corretti.
Correzione dopo la pressione del tasto :
Servirsi dei tasti per visualizzare i dati immessi in precedenza.
Premere per visualizzare i dati in ordine ascendente (il più vecchio
prima). Per invertire l’ordine di visualizzazione in discendente (il più
recente prima), premere il tasto .
Ogni dato viene visualizzato con “X:”, “Y:” o “F:” (n è il numero
sequenziale dell’insieme di dati).
Visualizzare il dato per modificarlo e immettere il valore corretto,
quindi premere . Usando , è possibile correggere subito e tutti in
una volta i valori dell’insieme di dati.
• Quando appare il simbolo o , significa che è possibile scorrere più dati
premendo i tasti o .
• Per eliminare un insieme di dati, visualizzare un dato dell’insieme da
eliminare, quindi premere . L’insieme di dati viene eliminato.
• Per aggiungere un nuovo insieme di dati, premere e immettere i valori,
quindi premere .
<Esempio 2>
Tabella di dati 2
X: 30, 40, 40, 50
X: 30, 45, 45, 45, 60
Operazione Visualizzazione
Selezionare la modalità statistica
a una variabile
30
40 2
50
30

Operazione Visualizzazione
45 3
60
APPLICAZIONI:
I calcoli statistici a una variabile vengono utilizzati in numerosi
campi, tra cui l’ingegneria, l’economia e il mondo degli affari. Nella
maggior parte dei casi, vengono applicati alle analisi eseguite
nell’ambito delle osservazioni atmosferiche e degli esperimenti
fisici, nonché per il controllo qualità effettuato negli stabilimenti
industriali.
31

<Esempio 3>
Tabella di dati 3
La seguente tabella elenca i giorni di aprile in cui sbocciano i
fiori di ciliegio e la temperatura media di marzo nella stessa
area. Servirsi della tabella di dati per determinare le quantità
statistiche base relative ai dati X e ai dati Y.
Anno
x Temperatura media
y Giorni in cui sbocciano
i fiori di ciliegio
Operazione Visualizzazione
Selezionare la modalità statistica a due variabili e il calcolo di regressione
lineare nella sottomodalità.
1998 1999 2000 2001 2002 2003 2004 2005
6,2 7,0 6,8 8,7 7,9 6,5 6,1 8,2
13 9 11 5 7 12 15 7
6.2 13
.
.
.
6.1 15
8.2 7
32

TASTI “ANS” PER LE STATISTICHE A DUE VARIABILI
La calcolatrice consente di eseguire non solo dei calcoli statistici a una variabile, ma anche
dei calcoli statistici a due variabili. I tasti relativi a questi ultimi sono i seguenti:
Calcola la somma del prodotto dei dati campionari x e dei dati campionari y.
Calcola la somma dei dati (dati campionari y).
Calcola la somma dei dati (dati campionari y) elevati al quadrato.
Calcola il valore medio dei dati (dati campionari y).
Calcola la deviazione standard dei dati (dati campionari y).
Calcola la deviazione standard di una popolazione di dati (dati campionari y).
NOTA:
I codici delle quantità statistiche base dei dati campionari x e il loro significato
sono gli stessi di quelli relativi ai calcoli statistici a una variabile.
Controlliamo i risultati in base ai dati precedenti:
7.175 (Valore medio dei dati x)
0.973579551 (Deviazione standard dei dati x)
0.91070028 (Deviazione standard della popolazione per i dati x)
9.875 (Valore medio dei dati y)
3.440826313 (Deviazione standard dei dati y)
3.218598297 (Deviazione standard della popolazione per i dati y)
8 (Numero complessivo dei dati)
57.4 (Somma dei dati x)
418.48 (Somma dei dati x elevati al quadrato)
544.1 (Somma del prodotto dei dati x e dei dati y)
79 (Somma dei dati y)
863 (Somma dei dati y elevati al quadrato)
33

©SHARP CORP. (MAR. '07)
 Loading...
Loading...