Sentry CA756 Instruction Manual

GRAPHIC SCIENTIFIC CALCULATOR

• The contents of this manual are subject to change without notice.

• No part of this manual may be reproduced in any form without the express written consent of the manufacturer.

• In no event will the manufacturer and its suppliers being liable to you or any other person for any damages,

expenses, lost profits, lost savings or any other damages arising out of use of or inability to use this calculator or manual.

• In no event will the manufacturer and its suppliers being liable to you or any other person for any damages,

expenses, lost profits, lost savings or any other damages arising out of loss of data and/or formulas caused by use of this calculator or manual.

• Due to limitations imposed by printing processes, the

displays shown in this manual are only approximations and may differ somewhat from actual displays.

Introduction

Thank you for purchasing the Graphic Scientific Calculation. This unit is a totally new type of advanced programmable calculator. Besides versatile scientific functions, graph functions also make it possible to produce a wide variety of useful graphs. Manual calculations can be easily performed following written formulas (true algebraic logic). A replay function is provided that allows confirmation or correction when key operation errors occur. Programs can also be input by following true algebraic logic, so repeat and/or complex calculations are simplified. All of this power built into a compact configuration that folds up to slip right into your pocket. Be sure to carefully read this manual and keep it handy for future reference.

Important–Reset your calculator before using it for the first time!––––––––––––––

Important––Always back up data!––––––

This product features electronic memory that is capable of storing large volumes of data. You must also remember

S6600G-ENG-A 8/30/04, 11:05 AMPage 1 Adobe PageMaker 6.5C/PPC

that your data is safely stored as long as power is being supplied to the memory. Data stored in memory will be irreparably damaged or lost entirely if you let battery power become too low, if you make a mistake while replacing batteries, or if power is cut off. Data can also be damaged by strong impact or electrostatic charge, or by environmental extremes. Once data is damaged or lost, it cannot be recovered, so we strongly recommend that you back up all important data.

Contents

About the Power Supply ................................ 7

Battery replacement ..............................................................7

Auto Power Off function ......................................................... 7

Reset operation ...................................................................... 7

Handling Precautions ................................................ 8

1.General Guide ............................................... 9

1-1 Key Markings ............................................................... 9

1-2 How to Read the Display ........................................... 9

Display indicators ......................................................... 9

About the display layout ...............................................10

Exponential display ...................................................... 11

Special display formats ................................................12

1-3 Key Operations ...........................................................13

Special operation keys ................................................ 13

Numeric/Decimal point/Exponent input keys ............18

Calculation keys ................................................. 19

Graph keys ........................................................ 21

Function keys ..................................................... 21

Contrast adjustment ............................................ 25

1-4 Before Beginning Calculations .....................26

Calculation priority sequence .............................. 26

Number of stacks .............................................. 27

Calculation modes ............................................. 28

Number of input/output digits and Calculation

digits ................................................................ 29

Overflow and errors ........................................... 30

Number of input characters ................................. 31

Graphic and text displays .......................................... 31

Corrections ....................................................... 32

Memory ............................................................ 33

Memory expansion ............................................ 35

2. Manual Calculations ................................ 37

2-1 Basic Calculations ............................................ 37

Arithmetic operations .......................................... 37

Parenthesis calculations ..................................... 38

Memory calculations .......................................... 39

Specifying the number of decimal places, the number of significant digits and the exponent

display ................................................................ 40

S6600G-ENG-A 8/30/04, 11:05 AMPage 2-3 Adobe PageMaker 6.5C/PPC

2-2 Special Functions ............................................ 42

Answer (Ans) function ........................................ 42

Continuous calculation function ........................... 44

Replay function.................................................. 45

Error position display function .............................. 46

Multistatement function .......................................46

2-3 Functional calculations ............................... 47

Angular measurement units ............................... 47

Trigonometric functions and inverse

trigonometric functions ....................................... 49

Logarithmic and exponential functions .................. 50

Hyperbolic functions and inverse hyperbolic

functions .......................................................... 51

Coordinate transformation .................................. 52

Other functions ................................................. 53

Fractions ......................................................... 55

2-4 Binary, Octal, Decimal, Hexadecimal Calculations 57

Binary, octal, decimal, hexadecimal conversions .... 59

Negative expressions ......................................... 59

Basic arithmetic operations using binary, octal,

decimal and hexadecimal values ........................ 60

Logical operations ............................................ 61

2-5 Statistical Calculations ............................... 62

Standard deviation ............................................ 62

Regression calculation ....................................... 64

Linear regression .............................................. 66

Logarithmic regression ...................................... 67

Exponential regression ...................................... 69

Power regression ............................................. 70

3. Graphs .............................................. 71

3-1 Built-in Function Graphs ............................. 71

Overdrawing built-in function graphs .................... 71

3-2 User Generated Graphs .............................. 72

Range parameters ............................................ 72

User generated function graphs .......................... 77

Function graph overdraw ................................... 77

Zoom function .................................................. 78

Trace function .................................................. 81

Plot function ..................................................... 84

Line function .................................................... 84

Graph scroll function ......................................... 86

3-3 Some Graphing Examples .......................... 88

4. Program Calculations .......................... 89

4-1 What is a Program? ..................................... 89

Formulas .......................................................... 89

Programming .................................................... 89

Program storage ................................................ 90

Program execution .............................................92

4-2 Program Checking and Editing .................... 93

(Correction, Addition, Deletion) ............................ 93

Formulas .......................................................... 94

Programming .................................................... 94

Program editing ................................................. 94

Program execution ............................................. 95

4-3 Program Debugging(Correcting Errors) ....... 97

Debugging when an error message is generated ....97

Error messages ................................................. 97

Checkpoints for each type of error ........................ 98

4-4 Counting the Number of Steps ........................99

4-5 Program Areas and Calculation Modes ...... 100

Program area and calculation mode specification

in the WRT mode ..............................................101

Cautions concerning the calculation modes ...........102

4-6 Erasing Programs ......................................102

Erasing a single program .................................. 102

Erasing all programs ........................................ 103

4-7 Convenient Program Commands ............... 104

Jump commands ............................................. 104

Unconditional jump ........................................... 104

Conditional jumps ........................................... 105

Count jumps .................................................... 108

Summary ........................................................ 111

Subroutines ..................................................... 112

4-8 Array-Type Memories ................................ 114

Using array-type memories ............................... 115

Cautions when using array-type memories .......... 115

Application of the array-type memories ............... 117

4-9 Displaying Alpha-Numeric Characters and

Symbols .........................................................119

Alpha-numeric characters and symbols ................119

4-10 Using the Graph Function in Programs ..... 121

Function Reference .................................123

Error Message Table ................................130

S6600G-ENG-A 8/30/04, 11:05 AMPage 4-5 Adobe PageMaker 6.5C/PPC

Input Ranges of Functions ....................... 132

Specifications ....................................... 135

Battery Replacement

If the display becomes dim, replace the battery with new one according to the following procedures.

Battery: CR2032 x 1

1. Turn off the Graphic Scientific Calculator.

2. With a screwdriver, remove the screws of back cover.

3. Remove the old battery and insert the new one immediately (+ side must be UP).

4. Replace the back cover.

Auto Power Off function

The power of the unit is automatically switched off approximately 6 minutes after the last key operation (except during program calculations). Once this occurs, power can be restored by pressing the key. (Numeric values in the memories, programs or calculation modes are unaffected when power is switched off.)

Reset operation

• Strong external electrostatic charges can cause this

calculator to malfunction. Should this happen, perform the following procedure to reset the calculator.

The following procedure clears all data from the memory of the calculator and cannot be undone! To avoid the loss of important data, be sure to always keep written backup copies.

1.Press the RESET button on the back of the calculator with a thin, pointed object.

Following the reset procedure described above, the calculator is initialized as follows:

1.RUN mode

2.COMP mode

3.DEG mode

4.NORM1 mode

5.Decimal mode (for BASE-N calculations)

6.Variable memories cleared

7.Defm 0 (400 program steps)

8.Answer memory clear

S6600G-ENG-A 8/30/04, 11:05 AMPage 6-7 Adobe PageMaker 6.5C/PPC

9.Program clear

10.Input buffer clear

11.Replay memory clear

* Never press the RESET button while internal

operations are being performed. Doing so can cause irreparable damage to the memory of your calculator.

Handling precautions

• Avoid dropping your calculator and subjecting it to other strong impacts.

• Do not store the calculator or leave it in areas exposed to high temperatures, or humidity, or large amounts of dust. when exposed to low temperatures, the calculator may require more time to display results and may even fail to operate. Correct operation will resume once the calculator is brought back to normal temperature.

• The display will go blank and keys will not operate during calculations. When you are operating the keyboard, be sure to watch the display to make sure that all your key operations are being performed correctly.

• Avoid using volatile liquids such as thinner or benzine to clean the unit. Wipe it with a soft, dry cloth, or with a cloth that has been dipped in a solution of water and a neutral detergent and wrung out.

• Be sure that the power is off when replacing batteries.

• If the calculator is exposed to a strong electrostatic charge, its memory contents may be damaged or the keys may stop working. In such a case, perform the Reset operation to clear the memory and restore normal key operation.

• Note that strong vibration or impact during program execution can cause execution to stop or can damage the calculator's memory contents.

• Before assuming malfunction of the unit, be sure to carefully reread this manual and ensure that the problem is not due to insufficient battery power, programming or operational errors.

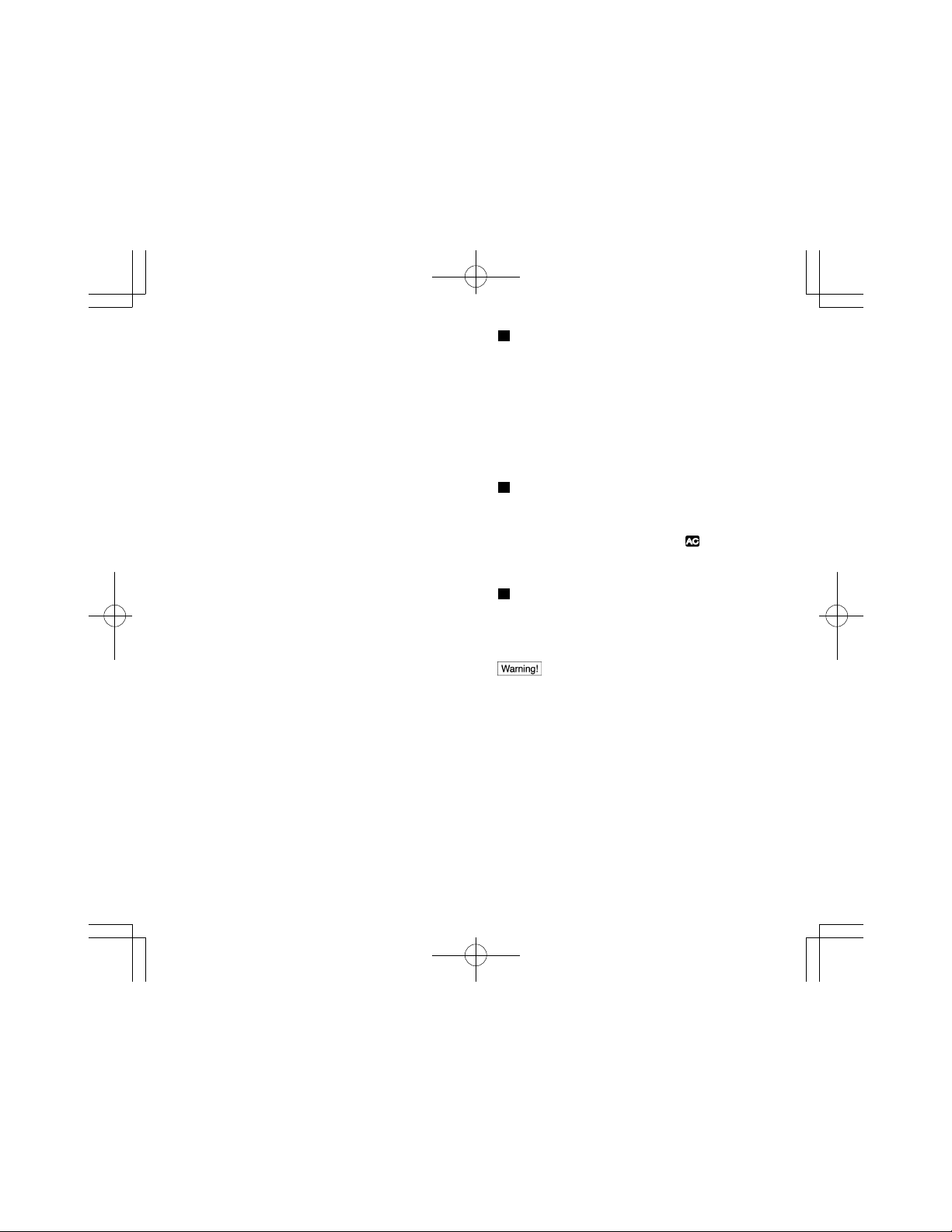
The keys of this unit perform a number of different functions. The key illustrated below, for example, is used to perform 4 different functions:x-1, x!, A, /A.

Note the following, concerning the key illustrated above.

The keys of this calculator can perform a number of different functions. The keyboard is color-coded to help you quickly determine the key sequence you have to perform for each function.

Display indicators

The following indicators appear on the display to show you the current status of the calculator at a glance.

: key pressed.

S6600G-ENG-A 8/30/04, 11:05 AMPage 8-9 Adobe PageMaker 6.5C/PPC

: key pressed.

: key pressed. Sci: Number of significant digits specified. Fix: Number of decimal places specified.

hyp: key pressed.

: Degrees specified at the unit of angular

measurement.

: Radians specified at the unit of angular

measurement.

: Grads specified at the unit of angular

measurement. WRT : Program write mode ( ) specified. PCL : Program clear mode ( ) specified. X= : Indicates current x-and y-coordinate location of

Trace function pointer.

: Indicates display consists of more than 12 characters " " indicates extra characters run off left side of display, " " indicates characters

run off right side.

: Indicates displayed value is intermediate result.

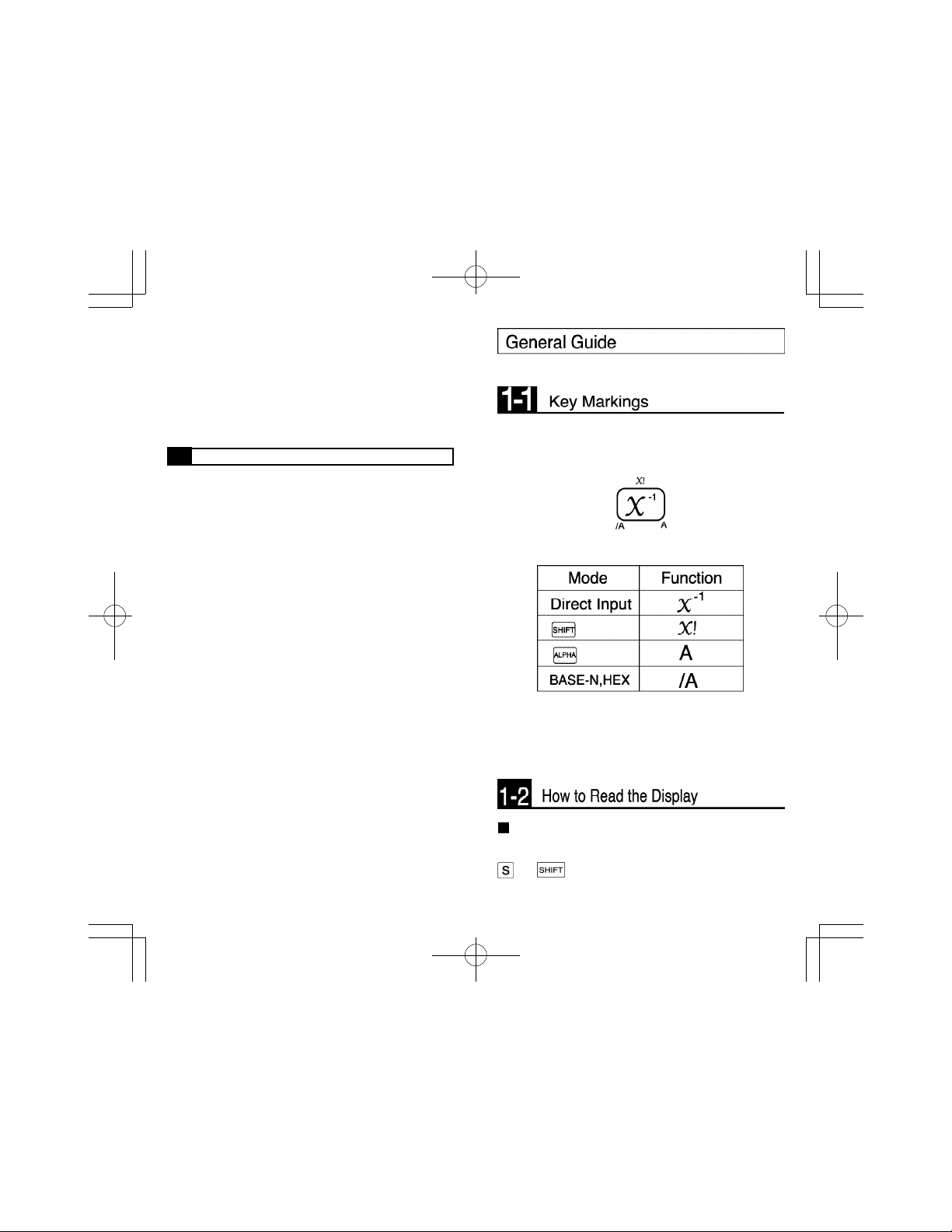
About the display layout

The display consists of a dot area for graphing, as well as an area for indicators and characters. You can monitor the status of the calculator and programs by viewing the display.

Graph Display

Program WRTT mode

Exponential display

During normal calculation, this unit is capable of displaying up to 10 digits. Values that exceed this limit, however, are automatically displayed in exponential format. You can choose between 2 different types of exponential display formats.

NORM 1 mode: 10-2(0.01)> , 10 NORM 2 mode: 10-9(0.000000001)> , 10

Selection of these modes can be carried out by pressing

when no specification has been made for the number of decimal places or significant digits. The present status is not displayed, so it is necessary to perform the following procedure to specify either display format:

Calculation Display

(All of the examples in this manual show calculation results using the NORM 1 mode.) How to interpret exponential format

Mode Status Display

S6600G-ENG-A 8/30/04, 11:05 AMPage 10-11 Adobe PageMaker 6.5C/PPC

111

1.2x10

. 120,000,000,000

1.211 indicates that the result is equivalent to 1.2x1011. This means that you should move the decimal point in 1.2 eleven places to the right, since the exponent is positive. This results in the value 120,000,000,000.

1.2x10-3. 0.0012

-03

1.2

indicates that the result is equivalent to 1.2x10-3. This means that you should move the decimal point in 1.2 three places to left, since the exponent is negative. This results in the value 0.0012.

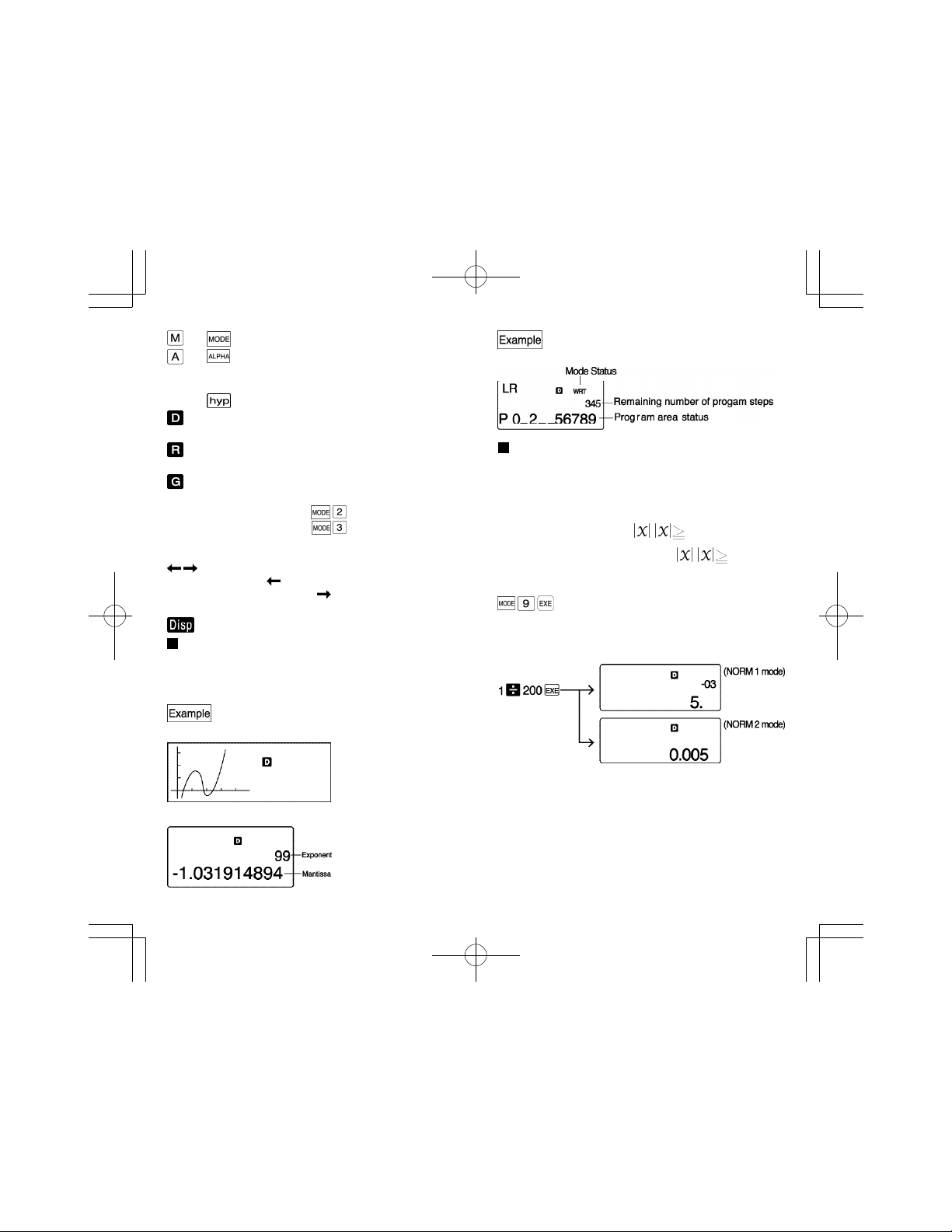
Special display formats

Special display formats are used for the representation of fraction, hexadecimal, and sexagesimal values.

• Fraction value display

• Hexadecimal value display

• Sexagesimal value display

Special operation keys

Shift key

An will blink on the display to indicate that has

been pressed. Pressing again will cause the to disappear form the display and the unit to return to the status it was in before was originally pressed.

Mode key

Use the key in combination with through

, , , , and to specify the calculation

mode and the unit of angular measurement.

...For manual calculations and program

execution (RUN mode). ...WRT displayed. For writing or checking programs. ... PCL displayed. For clearing programs.

... displayed. If is pressed, unit of

S6600G-ENG-A 8/30/04, 11:05 AMPage 12-13 Adobe PageMaker 6.5C/PPC

angular measurement is specified as degrees.

... displayed. If is pressed, unit of

angular measurement is specified as radians.

... displayed. If is pressed, unit of

angular measurement is specified as grads.

... Fix displayed. Entering a value from 0 to 9

followed by will specify the number of decimal places according to the value entered.

Ex. 3 Three decimal places

... Sci displayed. Entering a value from 0 to 9

followed by will specify the number of significant digits from 1 to 10.

Ex. 5 5 significant digits 0 10 significant digits

... Pressing will cancel the specified number

of decimal places or the specified number of significant digits.

* If you have not specified the number of decimal places or

the number of significant digits, you can press

and then change the range of the exponential

display. (NORM 1/NORM 2)

* With the exception of the BASE-N mode, modes ~

can be used in combination with the manual

calculation modes.

* The mode last selected is retained in memory when the

unit's power is switched off.

... Defm displayed. Entering a value followed by

will specify the number of memories available.

Ex. 10 Number of memories

available increased by 10.

If is pressed without entering a value, the current number of memories available and remaining steps will be

displayed .

... Specifies COMP mode for arithmetic

calculation or function calculation (program execution possible).

... For binary, octal or hexadecimal calculations/

conversions (BASE-N mode).

... For standard deviation calculations (SD mode). ... For regression calculations (LR mode).

...Pressed after a numeric value

representing degrees (0) is input.

...Pressed after a numeric value

representing radians (r) is input.

...Pressed after a numeric value

representing grads (g) is input.

Alphabet key

Press to input alphabetic characters or special characters. Pressing displays and allows the input of only

one character. After that, the unit returns to the status it was in before the key was originally pressed.

Pressing followed by will lock the until in this mode and allow consecutive input of alphabetic characters

until is pressed agian.

M-26 S-320

S6600G-ENG-A 8/30/04, 11:05 AMPage 14-15 Adobe PageMaker 6.5C/PPC

Program/Goto key

Press , enter a value from 0 to 9 and then press to execute a program.

Ex. 1 Execution of Program 1 begins

Pressing followed by will cause Goto to appear on the display. This is a jump command used in

programs.

pressing displays it from the end. This allows the formula to be executed again by changing the values.

Pressing followed by displays the insert cursor ( ). Entering a value while the insert cursor is displayed

inserts the value in the position immediately preceding the insert cursor location.

Pressing followed by enters the "Lbl" (Label) command.

Pressing followed by makes it possible to produce line graphs or regression lines.

After you draw a graph, press to display a value that shows the x-coordinate for the current location of the

pointer on the graph. You can switch between display of the x-coordinate and the y-coordinate by pressing

Delete key

Press to delete the character at the current position of the cursor. When the character is deleted, everything to the right of the cursor position will shift one space to the left.

Pressing will clear the memory contents.

Cursor/Replay keys

All clear/Power ON/Power OFF key

Press to clear all input characters or formulas. You can also

The key moves the cursor (blinking "_" ) to the left

moves the cursor to the right. In the Plot function, the key moves the pointer up, and moves the

pointer down. Once a formula or numeric value is input and

is pressed, the key and key become

"replay" keys. In this case, pressing displays the formula or numeric value from the beginning, while

use this key to clear the Error message from the display. Press to switch the power of the calculator on (even if power was switched off by the Auto Power Off function).

Pressing switches the power of the calculator off. Note that mode setting and memory contents are

protected even when power is turned off.

Execute key

Press to obtain the result of a calculation or to draw a graph. pressed after data input for a programmed

S6600G-ENG-A 8/30/04, 11:05 AMPage 16-17 Adobe PageMaker 6.5C/PPC

calculation or to advance to the next execution after a calculation result is obtained.

Answer/Minus key

Pressing followed by will recall the last calculation result. When used during program execution, the last result

calculated is recalled. Press following key to entering a numeric value to

make that value negative. Ex. -123 123

Press following key to input a space.

Numeric/Decimal point/Exponent input keys

Calculation keys

When entering numeric values, enter the number in order. Press the key to enter the decimal point in the desired

position. To input 1.23x10-6, press 1 23 6.

key combinations for the various modes are as

follows:

operation keys

For addition, subtraction, multiplication and division, enter the calculation as it reads. key combinations for the

various modes are as follows:

COMP mode

Arithmetic

, ... Following , this key causes the

graph currently shown on the display to be enlarged or reduced in accordance with the factor setting.

COMP mode or SD mode

... Coordinate transformation

LR mode

...Estimated value calculation of x and y

...Coordinate transformation

S6600G-ENG-A 8/30/04, 11:05 AMPage 18-19 Adobe PageMaker 6.5C/PPC

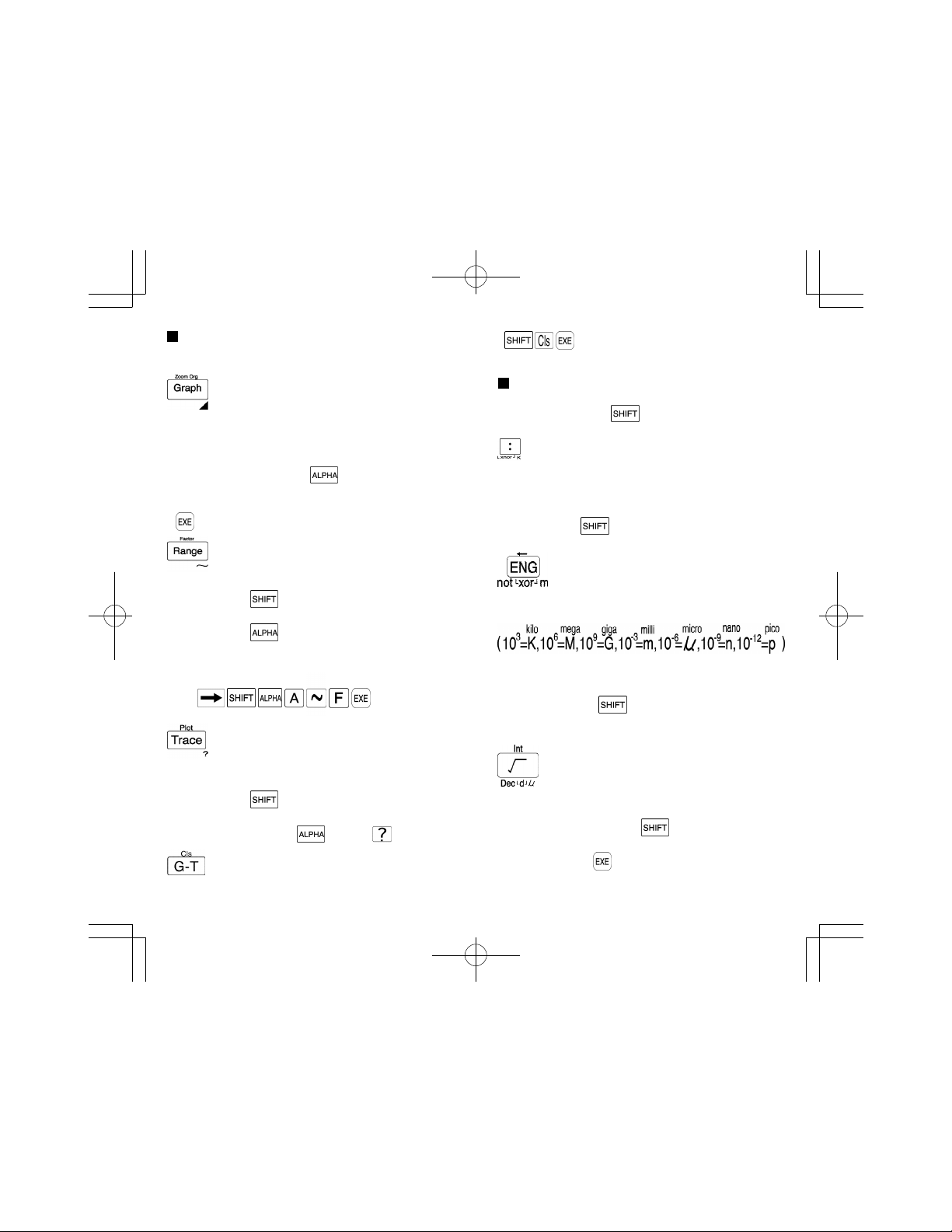
Graph keys

Used to produce a variety of graphs. These keys cannot be used in the BASE-N mode.

Graph/Original zoom key

• Press before entering a formula to be used for a graph ("Graph Y = " appears on the display).

• Press to return an enlarged or reduced graph to its original size.

• When pressed following the key, the results of each section of the programmed calculations or consecutive

calculations are sequentially displayed with each press of

Range/Factor key

• Used to confirm or set the range and size of graphs.

• Press following to magnify or reduce the upper and lower ranges of graphs.

• Press following in order to assign the same value to more than one memory.

Ex. To store the value 456 to memories A through F.

456

Trace/Plot key

• Used to trace over an existing graph and display the x or y coordinate value.

• Press following to plot a point on the graph screen.

• To indicate data input within a programmed calculation or repeat calculation, press and then .

Graph-text/Clear screen key

• Switches between the graph display and text display .

• clears the graph display (" done" is displayed).

Function keys

Press for functional calculation. Various uses are available in combination with the key, and/or depending on the

mode being used.

Multistatement key

• Press to separate formulas or commands in programmed calculations or consecutive calculations. The result of such combinations is known as a multistatement .

• Press following in the BASE-N mode to enter the

logical operation for negation of logical sums (xnor).

Engineering/Negation key

• Press to convert a calculation result to an exponential display whose exponent is a multiple of three.

• When obtaining logical negation for a value in the BASEN mode , press prior to entering the value.

• Press following the key in the BASE-N mode to obtain the exclusive logical sum.

Square root/Integer key

• Press prior to entering a numeric value to obtain the square root of the value.

• When pressed following the key, the integer portion of a value can be obtained.

• Press followed by in the BASE-N mode to specify the decimal calculation mode.

S6600G-ENG-A 8/30/04, 11:05 AMPage 20-21 Adobe PageMaker 6.5C/PPC

• When pressed following the key in the BASE-N mode, the subsequently entered value is specified as a

decimal value.

• When pressed following the key in the BASE-N mode,the subsequently entered value is specified as an

octal value.

Square/Fraction key

• Press after a numeric value is entered to obtain the square of that value.

• Press following key prior to inputting number in order to obtain fraction part of that number.

• Press followed by in the BASE-N mode to specify the hexadecimal calculation mode.

• When pressed following the key in the BASE-N mode, the subsequently entered value is specified as a

hexadecimal value.

Common logarithm/Antilogarithm key

• Press prior to entering a value to obtain the common logarithm of that value.

• When pressed following the key, the subsequently entered value becomes an exponent of 10.

• Press followed by in the BASE-N mode to specity the binary calculation mode.

• When pressed following the key in the BASE-N mode,the subsequently entered value is specified as a binary value.

Natural logarithm/Exponential key

• Press prior to entering a value to obtain the natural logarithm of that value.

• When pressed following the key, the subsequently entered value becomes an exponent of e.

• Press followed by in the BASE-N mode to specify the octal calculation mode.

Reciprocal/Factorial key

• Press after entering a value to obtain the reciprocal of that value.

• When pressed following the key, the factorial of a previously entered value can be obtained.

• Press in the BASE-N mode to enter A (10 hexadecimal value.

) of a

Degree/minute/second key (decimal

sexagesimal key)

• Press to enter sexagesimal value (degree/minute/second or hour/minute/second).

Ex. 78°45'12" 78 45 12

• When pressed following the key, a decimal based value can be displayed in degrees/minutes/seconds (hours/ minutes/seconds).

• Press in the BASE-N mode to enter B (1110) of a hexadecimal value.

Hyperbolic key

• Pressing , and then , ,or prior to entering a value produces the respective hyperbolic

function (sinh, cosh, tanh) for the value.

• Pressing , then , and then, , , or

prior to entering a value produces the respective

inverse hyperbolic function (sinh-1, cosh-1, tanh-1) for the value.

S6600G-ENG-A 8/30/04, 11:05 AMPage 22-23 Adobe PageMaker 6.5C/PPC

• Press in the BASE-N mode to enter C (1210) of a hexadecimal value.

Trigonometric function/

Inverse trigonometric function keys .

• Press one of these keys prior to entering a value to obtain the respective trigonometric function for the value.

• Press and then one of these keys prior to entering a value to obtain the respective inverse trigonometric function for the value.

• Press in the BASE-N mode to enter D, E, F (1310,1410,

1510) of a hexadecimal value.

Fraction/Negative key

• Use this key for input of simple fractions and mixed fractions.

Ex. To input 23/45: 23 45

Parenthesis keys

• Press the open parenthesis key and the closed parenthesis key at the position required in a formula.

• When pressed following the key, a comma or semicolon can be inserted to separate the arguments in coordinate transformation or consecutive calculations.

Power/Absolute value key

• Enter x (any number), press this key and then enter y (any number) to compute x to the power of y. In the SD or LR mode, this function is only available after pressing the

key.

• Press following the key to obtain the absolute value of a subsequently entered numeric value.

• Press in the BASE-N mode to obtain a logical product ("and").

• Press in the SD or LR mode to delete input data.

To input 2-3/4: 2 3 4

• For improper fractions, press this key following (indicated by in this manual).

• Press in the BASE-N mode prior to entering a value to obtain the negative of that value. The negative number is the two's complement of the value entered.

Assignment key

• Press prior to entering a memory to assign the result of a calculation to that memory.

Ex. To assign the result of 12 + 45 to memory A: 12

45 .

• Press this key following to clear all data from the statistical memories.

S6600G-ENG-A 8/30/04, 11:05 AMPage 24-25 Adobe PageMaker 6.5C/PPC

Root/Cube root key

• Enter x, press this key and then enter y to calculate the xth root of y. In the SD or LR mode, this function is only

available after pressing the key.

• Press following the key to obtain the cube root of a subsequently entered numeric value.

• Press in the BASE-N mode to obtain a logical sum ("or").

• Used as a data input key in the SD or LR mode.

Contrast adjustment

Pressing the or key following the key adjusts the contrast of the display. Pressing makes the screen lighter, while makes it darker.

Pressing any other key besides , , or (as well as , ) cancels contrast adjustment.

* If the display becomes dim and difficult to read, even if

you increase contrast, it probably means that battery power is getting low. In such a case, replace batteries as soon as possible.

* Contrast adjustment is impossible during range display

using the key or during factor display using the key .

Calculation priority sequence

This calculator employs true algebraic logic to calculate the parts of a formula in the following order:

Coordinate transformation

Pol (x,y), Rec (r, ) Type A functions With these functions, the value is entered and then the function key is pressed.

x2, x-1, x!, º , r, g,

Power/root

xy,

Fractions

b/c

Abbreviated multiplication format in front of π, memory or

parenthesis 2π, 4R, etc.

Type B functions

With these functions, the function key is pressed and then the value is entered. √, 3√ , log, In, ex, 10x,sin, cos, tan, sin-1, cos-1, tan-1, sinh, cosh, tanh, sinh-1, cosh-1, tanh-1, (-), Abs, Int, Frac, parenthesis, (following in BASE-N calculations only) d, h,b, o, Neg, Not

Abbreviated multiplication format in front of Type B

functions

2√3, A log2, etc. x, ÷ +, –

and or, xor, xnor

BASE-N calculations only.

Relational operators < , > , = , ≠ , ≤ , ≥

* When functions with the same priority are used in series,

execution is performed from right to left. exIn√120 ex {In(√120)}

Otherwise, execution is from left to right. * Compound functions are executed from right to left. * Anything contained within parentheses receives highest

priority.

2 + 3 x (log sin2π 2 + 6.8)=22.07101691 (in the

"Rad" mode)

Number of stacks This calculator uses a memory known as a "stack" for temporary storage of low priority numeric values and commands (functions, etc.). The numeric value stack has 10 levels, while the command stack has 24. If a formula exceeds the stack space available, a stack error (Stk ERROR) message appears on the display.

S6600G-ENG-A 8/30/04, 11:05 AMPage 26-27 Adobe PageMaker 6.5C/PPC

Binary, octal, decimal, hexadecimal conversion and calculations, as well as logical operations. Function calculations and graph drawing cannot be performed.

3.SD mode

Standard deviation calculation (single-variable statistics).

4. LR mode

Regression calculation (paired-variable statistics). With so many modes available, calculations should always be performed after confirming which mode is active. * IMPORTANT: When the power of the unit is switched off

(including Auto Power Off), the current system mode is

cancelled, and the unit will be set to the RUN mode when

switched on again. However, the calculation mode,

number of decimal place setting ( n), number

of significant digits( n), and angle unit (Deg,

Rad, Gra) will be retained in memory. * To return to standard operation ( initialized state) press

* Calculations are performed in sequence, with the highest

(COMP mode) (RUN mode)

priority operation first. Once a calculation is executed, it is cleared from the stack.

Calculation modes

This unit features modes for manual calculations, storing programs, and modes for general as well as statistical calculations. The proper mode to suit calculational requirements should be employed.

• Operation modes

There are a total of three operation modes.

(Norm mode).

Number of input/output digits and calculation digits

• The allowable input/output range (number of digits) of this

unit is 10 digits for a mantissa and 2 digits for an

exponent. Calculations, however, are internally

performed with a range of 12 digits for a mantissa and 2

digits for an exponent.

3 x 105 ÷ 7 =

1. RUN mode

Graph production as well as manual calculations and program executions.

2. WRT mode

Program storage and editing.

3. PCL mode

Deletion of stored programs.

• Calculation modes

There are a total of six calculation modes which are employed according to the type of calculation.

1. COMP mode

* Calculation results greater than 1010 ( 10 billion) or less than 10-2 (0.01) are automatically displayed in exponential form.

123456789 x 9638 =

General calculations, including functional calculations.

2. BASE-N mode

S6600G-ENG-A 8/30/04, 11:05 AMPage 28-29 Adobe PageMaker 6.5C/PPC

Once a calculation is completed, the mantissa is rounded off to

10 digits and displayed. And the displayed mantissa can be used for the next calculation.

3 x 10 5 ÷ 7 =

* Values are stored in memory with 12 digits for the

mantissa and 2 digits for the exponent.

Overflow and errors If the calculation range of the unit is exceeded, or incorrect inputs are made, an error message will appear on the display window and subsequent operation will be impossible. This is the error check function. The following operations will result in errors: (1) The answer, whether intermediate or final, or any value in memory exceeds the value of ±9.999999999x1099. (2) An attempt is made to perform functional calculations that exceed the input range. (3) Improper operation during statistical calculations.

(Ex. Attempting to obtain X or xÓn without data input.)

(4) The capacity of the numeric value stack or the

command stack is exceeded.

(Ex. Entering 23 successive 's followed by 2 3 4

)

(5) Even though memory has not been expanded, a

memory name such as Z [2] is used.

(6) Input errors are made.

(Ex.5 3 )

(7) When improper arguments are used in commands or functions that require arguments. (i.e. Input of an

argument outside of the range of 0 ~ 9 for Sci or Fix.) The following error messages will be displayed for the operations noted above:

(1) ~ (3) Ma ERROR (4) Stk ERROR

S6600G-ENG-A 8/30/04, 11:05 AMPage 30 Adobe PageMaker 6.5C/PPC

(5) Mem ERROR (6) Syn ERROR

(7) Arg ERROR Besides these, there are a "Ne ERROR" (nesting error) and a "Go ERROR". These errors mainly occur when using programs.

Number of input characters

This unit features a 127-step area for calculation execution. One function comprises one step. Each press of numeric or

, , and keys comprise one step. Though

such operations as require two key operations, they actually comprise only one function and, therefore,

only one step. These steps can be confirmed using the cursor. With each press of the or key the

cursor is moved one step. Input characters are limited to 127-steps. Usually the cursor is represented by a blinking "_", but once the 121st step is reached the cursor changes to a blinking " " . If the " " appears during a calculation, the calculation should be divided at some point and performed in two parts. * When numeric values or calculation commands are input,

they appear on the display window from the left. Calculational results, however, are displayed from the right.

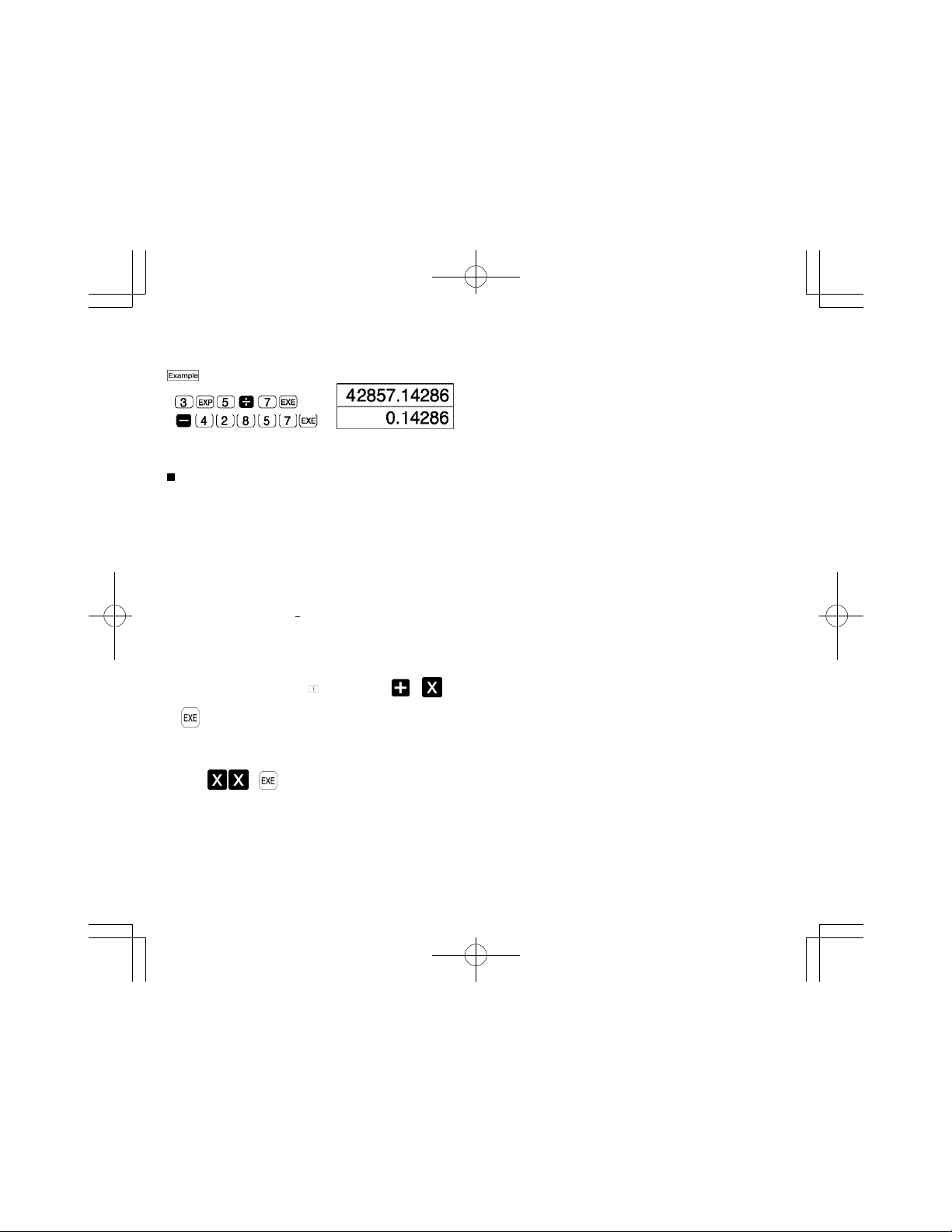
Graphic and text displays This unit has a graph display for production of graphs, as well as a text display for production of formulas and commands. These two types of display contents are stored independently of each other. Switching between graph and text diplays is performed

using the key. Each press of switches from the current type of display to the other.

Operations to clear the display depend upon the type of display being shown:

Graphs: Text:

Pressing the key causes a cleared text display to appear if pressed during a graph display.

Corrections

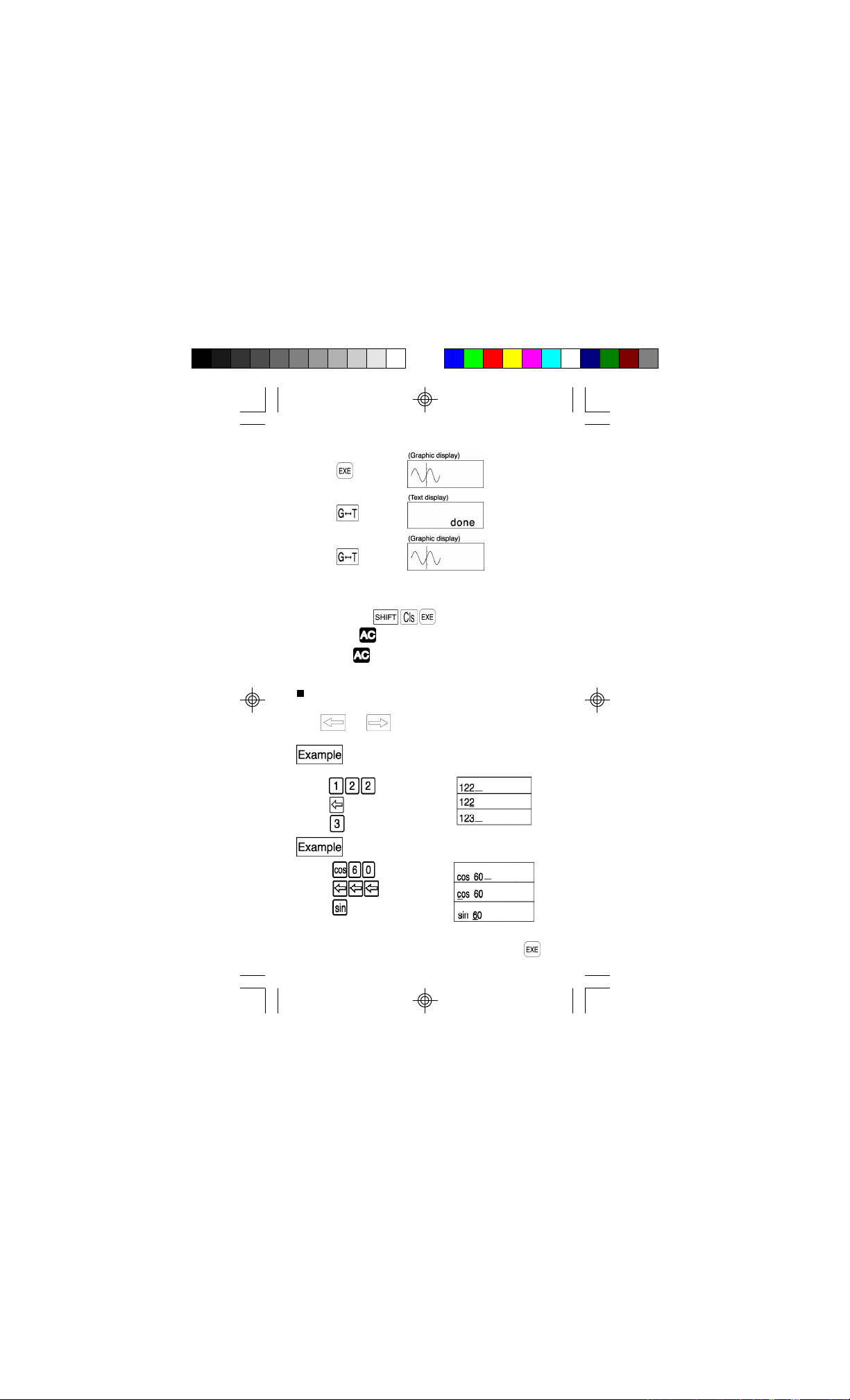
• To make corrections in a formula that is being input, use

the and keys to move to the position of the

error and press the correct keys.

To change an input of 122 to 123:

To change an input of cos60 to sin60:

* If, after making corrections, input of the formula is

complete, the answer can be obtained by pressing .

If, However, more is to be added to the formula, advance

the cursor using the key to the end of the formula

for input.

• If an unnecessary character has been included in a

formula, use the and keys to move to the

position of the error and press the key. Each press

of will delete one command (one step).

To correct an input of 369 x x 2 to 369 x 2:

* If a character has been omitted from a formula, use the

and keys to move to the position where the

character should have been input, and press

followed by the key. Press and insertions

can be subsequently performed as desired.

To correct an input of 2.362 to sin2.362:

* When are pressed, the letter at the insertion

position is surrounded by " " and blinks.The insert

function is activated until you press , , or

or until you perform again.

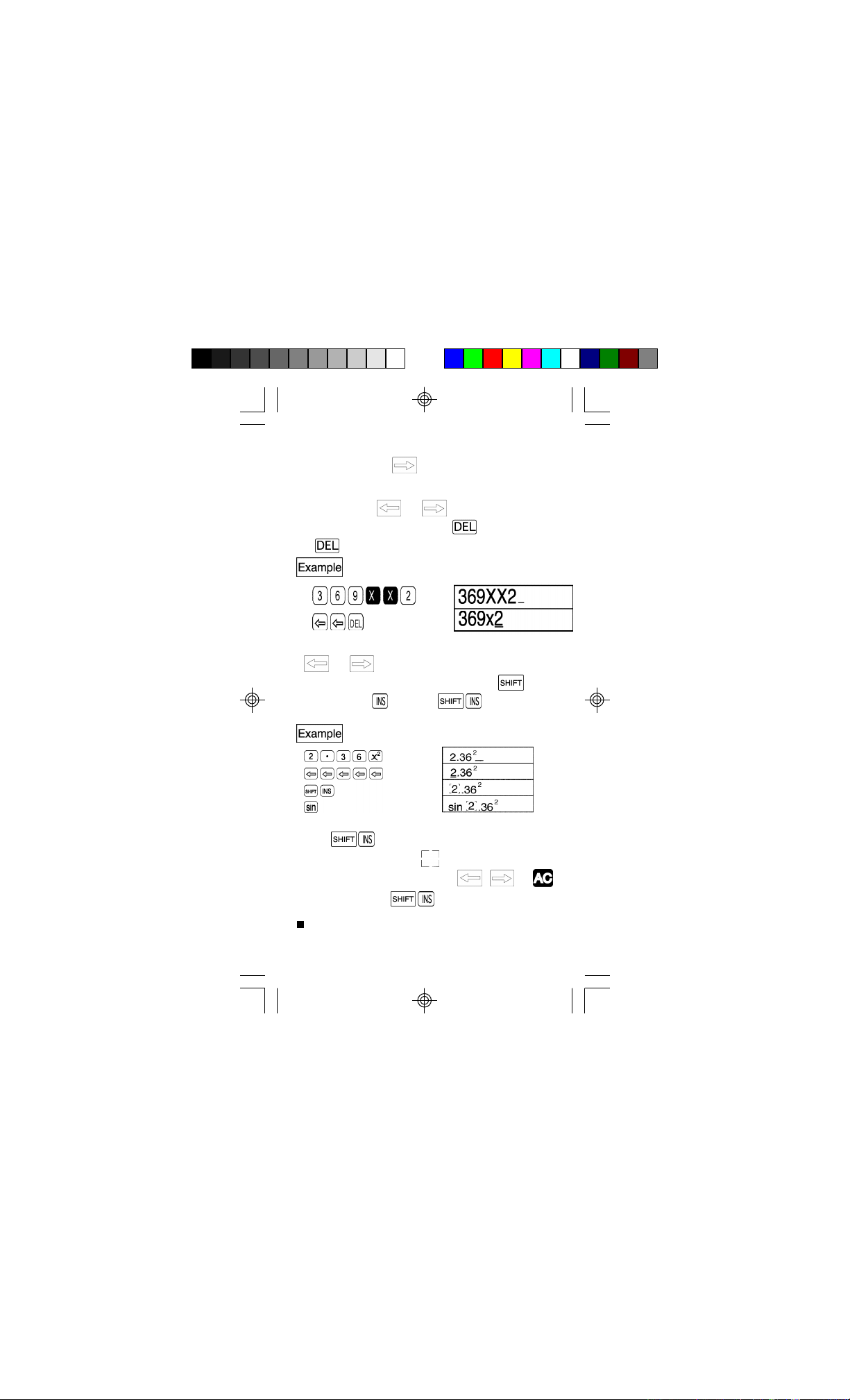
Memory

This unit contains 26 standard memories. Memory names are composed of the 26 letters of the alphabet. Numeric

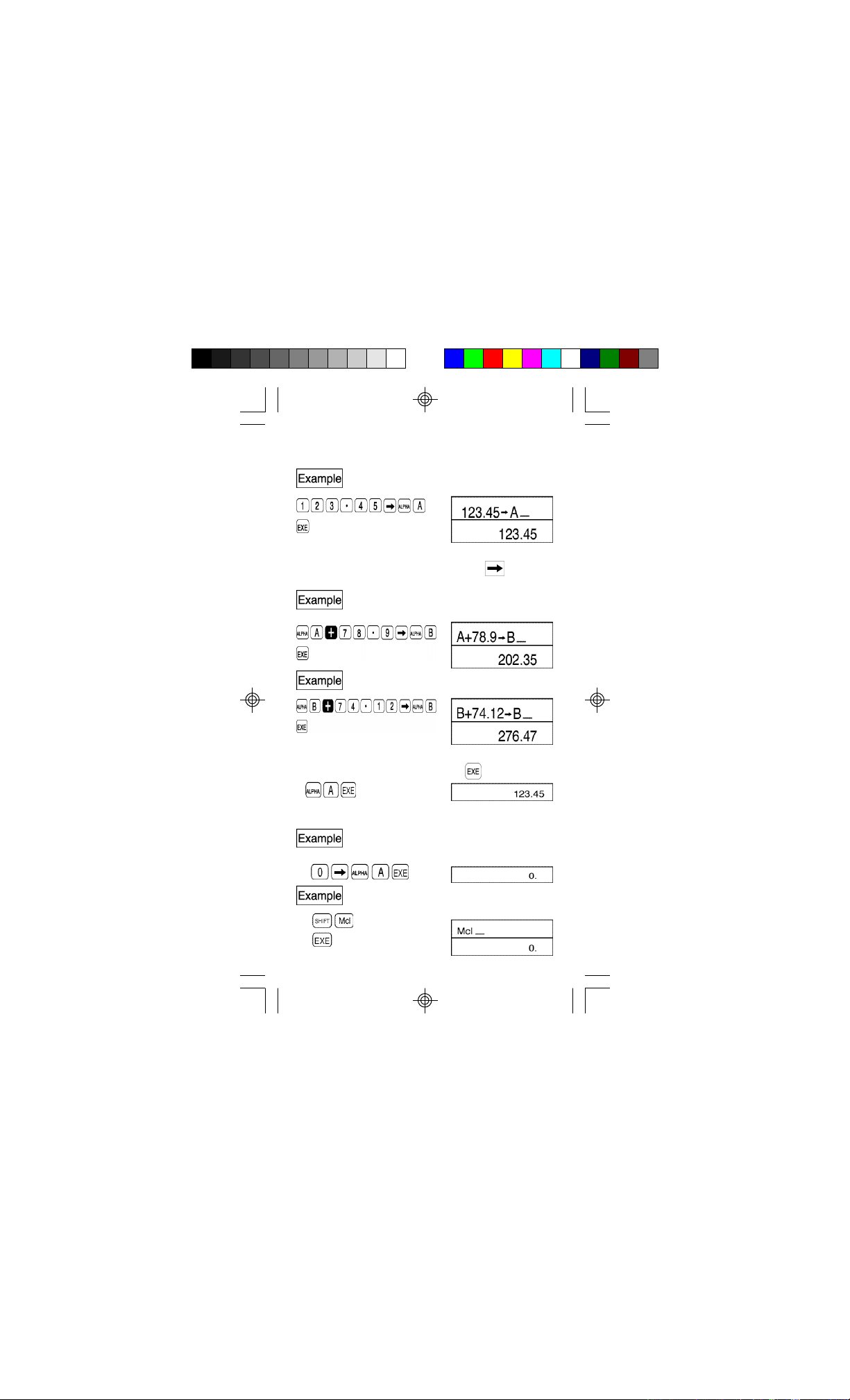
values with 12 digits for a mantissa and 2 digits for an exponent can be stored.

To store 123.45 in memory A :

Values are assigned to a memory using the key followed by the memory name.

To store the sum of memory A + 78.9 in

memory B :

TO add 74.12 to memory B :

•To check the contents of a memory , press the name of the memory to be checked followed by .

•To clear the contents of a memory (make them 0), proceed

as follows:

To clear the contents of memory A only:

To clear the contents of all the memories:

• To store the same numeric value to multiple memories,

press followed by .

To store a value of 10 in memories A through

Memory expansion

Though there are 26 standard memories, they can be expanded by changing program storage steps to memory. Memory expansion is performed by converting 8 steps to one memory.

Memory is expanded in units of one. A maximun of 50 memories can be added for a maximum total of 76 (26+50).

Expansion is performed by pressing , followed by , a value representing the size of the expansion, and then ..

To expand the number of memories by 30 to bring

the total to 56:

The number of memories and number of remaining steps are displayed. The number of remaining steps indicates the current unused area, and will differ according to the size of the program stored. To check the current number of

memories, press ,followed by ,and then .

To initialize the number of memories (to return the number to 26), enter a zero for the value in the memory expansion sequence outlined above.

* Though a maximum of 50 memories can be added, if a

program has already been stored and the number of

remaining steps is less than the desired expansion, an

error will be generated. The size of the memory

expansion must be equal to or less than the number of

steps remaining. * The expansion procedure ( expansion value) can

also be stored as a program.

Using expanded memories

•

Expanded memories are used in the same manner as standard memories, and are referred to as Z[1], Z[2], etc. The letter Z followed by a value in brackets indicating the sequential position of the memory is used as the memory

name. (Brackets are formed by for "[" and for "]".) After the number of memories has been expanded by 5, memories Z[1] through Z[5] are available. The use of these memories is similar to that of a standard computer

array, with a subscript being appended to the name.

Manual Calculations

Arithmetic operations

• Arithmetic operations are performed by pressing the keys

in the same sequence as in the formula.

• For negative values, press before entering the value.

• For mixed arithmetic operations, multiplication and division are given priority over addition and subtraction.

Parenthesis calculations

Memory calculations

• The contents of memories are not erased when power is

off. They are cleared by pressing followed by

and then

Specifying the number of decimal places, the

number of significant digits and the exponent

display

• To specify the number of decimal places, press

followed by , a value indicating the number of

places (0-9) and then .

• To specify the number of significant digits, press

followed by , a value indicating the number of

significant digits (0-9 to set from 1 to 10 digits) and then

• Pressing the key or followed by will cause

the exponent display for the number being displayed to

change in multiples of 3.

• The specified number of decimal places or number of

significant digits will not be cancelled until another value

or is specified using the sequence: , ,

.(Specified values are not cancelled even if power is

switched off or another mode (besides ) is

specified.)

• Even if the number of decimal places and number of

significant digits are specified, internal calculations are

performed in 12 digits for a mantissa, and the displayed

value is stored in 10 digits. To convert these values to the

specified number of decimal places and significant digits,

press followed by and then . * You cannot specify the display format (Fix, Sci) while the

calculator is in the BASE-N mode. Such specifications

can only be made if you first exit the BASE-N mode.

Answer function

The Answer function stores the result of the most recent calculation. Once a numeric value or numeric expression is

entered and is pressed, the result is stored by this function.

To recall the stored value, press the key. When is pressed, "Ans" appears on the display along with the Answer function value. The value can be used in subsequent calculations. * Since the "Ans" function works just like any other

memory,it will be referred to as "Ans memory" throughout

this manual.

123+456 = 579

789-579 = 210

Numeric values with 12 digits for a mantissa and 2 digits for an exponent can be stored in the Ans memory. The Ans memory is not cleared even if the power of the unit is

turned off. Each time is pressed, the value in the Ans memory is replaced with the value produced by the new calculation. When execution of a calculation results in an

error, however, the Ans memory retains its current value. When a value is stored to another memory using the

key, that value is not stored in the Ans memory.

Perform calculation 78 + 56 = 134, then store the

value 123 to memory A:

The Ans memory can be used in the same manner as the other memories, thus making it possible to use it in

calculation formulas. In multiplication operations, the immediately before can be omitted.

15x3=45

78x45 -23=3487

Continuous calculation function

Even if calculations are concluded with the key, the result obtained can be used for further calculations. Such

calculations are performed with 10-digit mantissa of the displayed value.

To calculate ÷ 3.14 after 3 x 4 = 12:

To calculate 1 ÷ 3 x 3 =:

This function can be used with memory and Type A functions ( x2, x-1, x!, °’ ”, °, r, g, ), +, –, xy, and x.

To store the result of 12 x 45 in memory C:

To square the result of 78 ÷ 6 = 13:

Replay function

This function stores the latest formula executed. After execution is complete, pressing either the or

key will display the formula. Pressing will display the formula from the beginning,

with the cursor located under the first character. Pressing

will display the formula from the end, with the cursor

located at the space following the last character. After this, use and to move the cursor, to check the

formula. You can edit numeric values or commands for subsequent execution.

* As with the number of input steps, the replay function can

accept input of up to 127 steps.

Error position display function

When an ERROR message appears, press or to display the calculation with the cursor located at the step

that caused the error. You can also clear an error by pressing and then reenter the values and formulas from the beginning.

14 ÷ 0 x 2.3 mistakenly input instead of 14 ÷ 10

x 2.3:

Multistatement function

• The multistatement function available in program calculations can also be used in manual calculations.

• With the multistatement function, multiple statements are linked together with a colon ( ) separating them.

• Pressing the key after a multistaterment is entered causes the entire chain of statements to be executed

from left to right.

• Using " " ( ) in place of a colon display the calculation result up to the point that " " is encountered.

6.9 x 123 = 848.7 123 ÷ 3.2 = 38.4375

* The final result of a multistatement is always displayed, regardless of whether a " " symbol is input at the end of the last statement in the chain. * Consecutive calculations contained in multistatements cannot be performed.

Angular measurement units

• The unit of angular measurement (degrees, radians,

grads) is set by pressing followed by a value from 4 through 6 and then .

• The numeric value from 4 through 6 specifies degrees,

radians and grads respectively.

• Once a unit of angular measurement is set, it remains in

effect until a new unit is set. Settings are not cleared

when power is off.

• You cannot specify the unit of angular measurement

(degrees, radians, grads) while the calculator is in the

BASE-N mode. Such specifications can only be made if

you first exit the BASE-N mode.

Trigonmetric functions and inverse trigonometric functions

• Be sure to set the unit of angular measurement before

performing trigonometric function and inverse

trigonometric function calculations.

• The operations noted below cannot be performed in the

BASE-N mode.

Logarithmic and exponential functions

• The operations noted below cannot be performed in the

BASE-N mode.

Hyperbolic funcitions and inverse hyperbolic

functions

• The operations noted below cannot be performed in the

BASE-N mode.

Coordinate transformation

• Your calculator lets you convert between rectangular

coordinates and polar coordinates.

•Rectangular coordinates •Polar coordinates

• Calculation results are stored in variable memory I and

variable memory J. Contents of variable memory I are

displayed first. To display contents of memory J, press

• With polar coordinates, can be calculated within a range

of -180° < 180°. The calculation range is the same for radians and grads.

• The operations noted below cannot be performed in the

BASE-N mode.

Other functions ( ,x2 , x

-1

,x! ,3 ,Ran# , Abs, Int ,

Frac )

• The operations noted below cannot be performed in the BASE-N mode.

Fractions

• Fractions are input and displayed in the following order : integer, numerator,denominator.

• Binary, octal, decimal and hexadecimal calculations,

conversions and logical operations are performed in the

BASE-N mode (press ).

• The number system (2,8,10,16) is set by respectively

pressing or followed by . AA

corresponding symbol "b", "o", "d", or "h" appears on the

display.

• Number systems are specified for specific values by

pressing , then the number system designator (b,

o, d,or h), immediately followed by the value.

• General function calculations cannot be performed in the

BASE-N mode.

• Only integers can be handled in the BASE-N mode. If a

calculation produces a result that includes a decimal

value, the decimal portion is cut off.

• The total range of numbers handled in this mode is 0, 1,

2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. If values are not

valid for the particular number system to be used, attach

the corresponding designator (b, o, d or h), or an error

message will appear.

• Negative numbers in binary, octal and hexadecimal are

expressed as two's complements.

• To distinguish the A, B, C, D, E and F used in the

hexadecimal system from standard letters, they appear

as shown in the chart below.

Binary Positive : 1111111111 x 0

Negative : 1111111111 x 1000000000

Octal Positive : 777777777 x 0

Negative: 7777777777 x 4000000000 Decimal 2147483647 x -2147483648

Hexadecimal Positive : 7FFFFFF x 0

Negative: FFFFFFFF x 80000000

• You cannot specify the unit of angular measurement

(degrees, radians, grads) or the display format (Fix,

Sci) while the calculator is in the BASE-N mode. Such

specifications can only be made if you first exit the

BASE-N mode.

Binary, octal, decimal, hexadecimal

conversions

Negative expressions

Basic arithmetic operations using binary,

octal,decimal and hexadecimal values

Logical operations

Logical operations are performed through logical products (and), logical sums (or), negation (Not), exclusive logic sums (xor), and negation of exclusive logical sums (xnor).

Standard deviation

• Standard deviation calculations are performed in the SD mode ( ). "SD" appears on the display.

• Before beginning calculations, the statistical memories are cleared by pressing followed by and then

• Individual data are input using .

• Multiple data of the same value can be input either by repeatedly pressing or by entering the data, pressing

,followed by , that represents the number of

times the data is repeated, and then .

• Standard Deviation

• Mean

* The values for n, ∑x, and ∑x2 are stored in memories W,

V, and U respectively, and can be obtained by pressing

followed by the memory name and then (i.e.

* Erroneous data clearing/correction I (Correct data operation: 51 )

If 50 is entered, enter correct data after pressing .

If 49 was input a number of entries previously, enter correct data after pressing 49 .

* Erroneous data clearing/correction II (correct data operation: 130 31 )

If 120 is entered, enter correct data after pressing .

If 120 31 is entered, enter correct data after pressing .

If 120 30 is entered, enter correct data after pressing . If 120 30 was entered previously, enter

correct data after pressing 120 30 .

Regression calculation

• Regression calculations are performed in the LR mode (

). "LR" appears on the display.

• Before beginning calculations, the tabulation memories

are cleared by pressing followed by and then .

• Individual data are entered as x data y data

• Multiple data of the same value can be entered by

repeatedly pressing . This operation can also be performed by entering x data y data

followed by a value representing the number of times the data is repeated, and then .

• If only x data is repeated (x data having the same value), enter y data or y data

followed by a value representing the number of times the data is repeated, and then .

• If only y data is repeated (y data having the same value), enter x data or x data followed by a

value representing the total number of times the data is repeated, and then .

• Regression

The following are the formulas the unit uses to calculate constant term A and regression coefficient B for the regression formula y = A + Bx.

• Estimated value , and based on the regression formula can be calculated using the following formulas:

(To obtain the estimated value , is used, and to obtain estimated value , is used.)

• The correlation coefficient r for input data can be calculated using the following formula:

* The values for n, ∑x, ∑x2, ∑xy,∑y, and ∑y2 are stored in

memories W, V, U, R, Q and P respectively, and can be obtained by pressing followed by the memory

name and then (i.e. ).

Linear regression

* Erroneous data clearing/correction ( correct data operation: 10 1003 )

If 11 1003 is entered, enter correct data after pressing . If 11 1003 is entered, enter correct data after pressing . If 11 1003 was entered previously, enter correct data after pressing 11 1003 .

Logarithmic regression

• The regression formula is y = A + B•Inx. Enter the x data

as the logarithm (In) of x, and the y data inputs the same as that for linear regression.

• Estimated values ,and based on the regression

formula can be calculated using the following formulas:

• The same operation as with linear regression can be used

to obtain the regression coefficient and for making corrections. To obtain the estimated value , x

, Is used, and to obtain estimated value , y , is used.

Furthermore, ∑x, ∑x2 and ∑xy are obtained by ∑Inx, ∑ (Inx)2, and ∑lnx•y respectively.

Exponential regression

• The regression formula is y = A•e

B•x

(Iny = InA + Bx). Enter the y data as the logarithm of y(ln), and the x data the same as that for linear regression.

• Estimated values , and based on the regression formula can be calculated using the following formulas:

• Correction is performed the same as in linear regression. Constant term A is obtained by , estimated value is obtained by x

, and estimated value is obtained by y . ∑y, ∑y2 and ∑xy are obtained by ∑Iny, ∑(Iny)

and ∑x•Iny respectively.

Power regression

• The regression formula is y=A•xB (lny=InA + BInx). Enter both data x and y as logarithms (In).

• Estimated values , and based on the regression formula can be calculated using the following formulas:

• Correction is performed the same as in linear regression. Constant term A is obtained by ,

estimated value is obtained by x

and estimated value is obtained by

y ,∑x,∑x2, ∑y, ∑y2 and ∑xy are obtained by ∑Inx, ∑(Inx)2, ∑Iny, ∑ (Iny)2 and ∑Inx•Iny

respectively.

3 Graphs

The COMP mode of the RUN mode should be used when graphing functions. Some graphs can be produced in the SD and LR modes, but certain graphs cannot be produced in these modes. The BASE-N mode cannot be used for graphs. This unit contains a total of 20 built-in graphs making it possible to produce the graphs of basic functions.

Any time a built-in graph is executed, the ranges are automatically set to their optimum values, and any graph previously on the display is cleared.

Overdrawing built-in function graphs

Two or more different built-in function graphs can be drawn together on the same display. Since the range for the first graph is automatically set, all subsequent graphs on the same display are produced according to

the range of the first graph. The first graph is produced by using the previously mentioned operation ( function

key] ). Subsequent graphs are produced using the

variable X in the operation [function key] By inputting after the function key, the range is

unchanged and the next graph is produced without clearing the existing display.

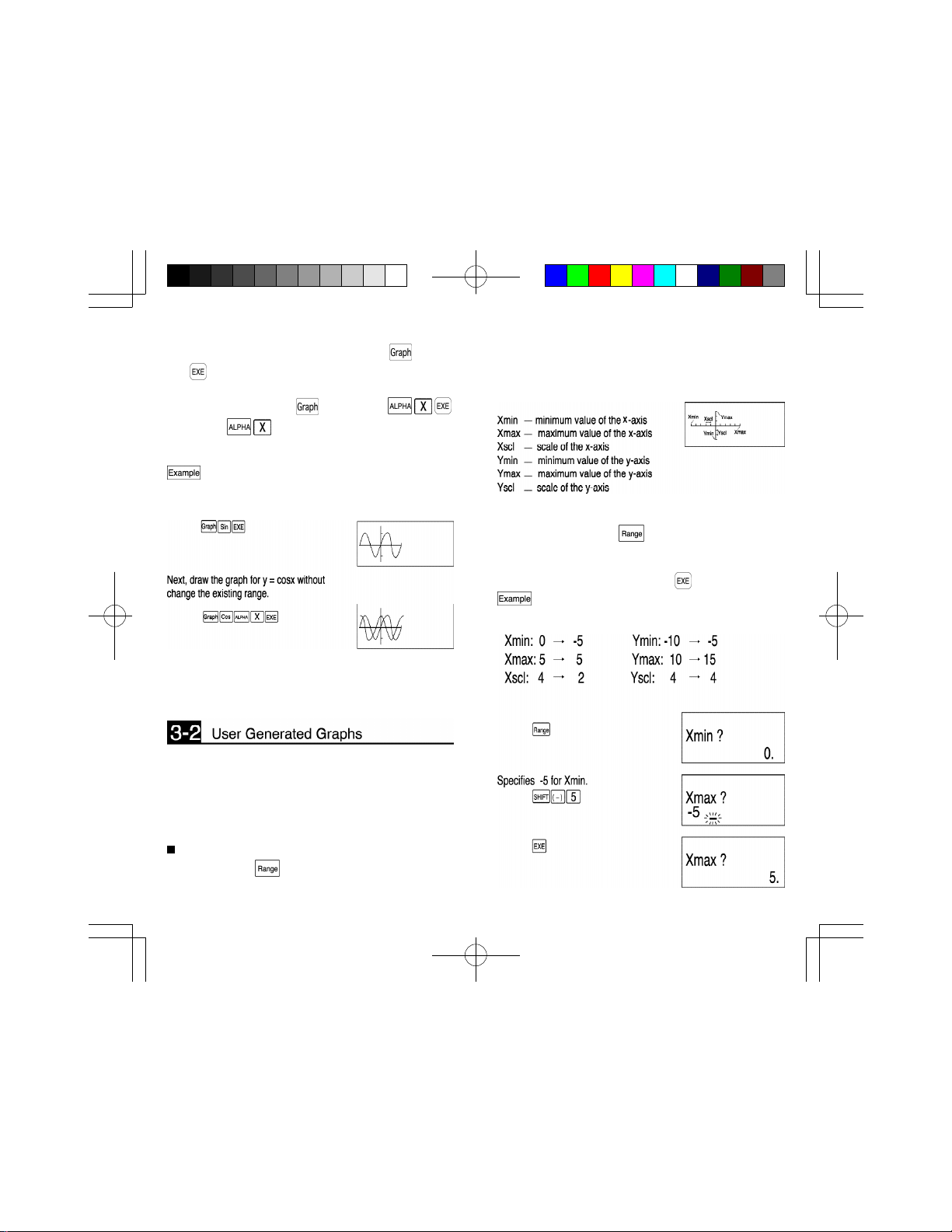
Overdraw the graph for y=cos x on the graph for

y=sin x.

First, draw the graph for y=sin x.

(Note)

Built-in function graphs cannot be used in multistatements and cannot be written into programs.

Built-in function graphs can also be used in combination with each other. Graphing a formula such as y=2x2 + 3x -5 makes it possible to visually represent the solution. Unlike built-in functions, the ranges of user generated graphs are not set automatically, so graphs produced outside of the display range do not appear on the display.

each axis, as well as their scales (distance between hash marks). Before drawing a graph, you should first specify range parameters to set the size of the graph.

• Range parameter types

Range parameters consist of the following:

•Specifying range parameters

Whenever you press the key (except in the BASE-N mode), the range parameter setting screen appears on the display. Enter the value you want to specify for the

displayed parameter and then press .

Change the range parameters on the left to

those on the right.

Range parameters

After pressing the key, you can look up and specify the range parameters for the x- and y- coordinates. Range parameters consist of maximum and minimum values for

Press to return to the display that was shown before entering the range display.

• Checking range parameters

Press the key and the range parameter setting screen appears on the display. Press to scroll

through the range parameter settings without changing them.

Press to return to the display that was shown before entering the range display.

You can input range parameters as expressions (such as 2π) and these expressions are automatically converted to the values.

* The input range for graph ranges is -9.999999999E + 97 through 9.999999999E + 97. * If you enter a value that is outside the allowable range or if you try to perform some other illegal operation, an error message appears on the display. When this happens,

press or to display the place in the calculation that caused the error (Replay function) and make the necessary corrections. * Inputting 0 for Xscl or Yscl does not set any scale. * Inputting a maximum value that is less than the minimum value will reverse the respective axis.

* If the maximum and minimum values of an axis are equal, and error (Ma ERROR) will be generated when an attempt is made to produce a graph. * When a range setting is used that does not allow display of the axes, the scale for the y-axis is indicated on either the left or right edge of the display, while that for the x axis is indicated on either the top or bottom edge. (In both cases, the location of the scale is the edge which is closest to the origin (0,0)). * When range values are changed (reset), the graph display is cleared and the newly set axes only are displayed. * Range settings may cause irregular scale spacing. * If the range is set too wide, the graph produced may not fit on the display. * Points of deflection sometimes exceed the capabilities of the display with graphs that change drastically as they approach the point of deflection. * An Ma ERROR is generated when ranges are extremely narrow.

• Range reset

Range values are reset to their initial values by pressing

during range display.

The initial values are as follows.

Xmin: -3.8 Ymin: -2.2 Xmax: 3.8 Ymax :2.2 Xscl :1 Yscl: 1

(Reference)

Range settings are performed within programs using the following format:

Xmin value, Xmax value, Xscl value, Ymin value,

Ymax value, Yscl value. Up to six data items are programmed after the command. When less than six

items are programmed, range setting is performed in the order from the beginning of the above format.

User generated function graphs

After performing range settings, user generated graphs can be drawn simply by entering the function (formula) after

pressing . Here, let's try drawing a graph for y=2x2 + 3x -4. Set the ranges to the values shown below.

Xmin: -5 Ymin: -10 Xmax: 5 Ymax :10 Xscl: 2 Yscl: 4

Input the functional formula after pressing the key.

The result produces a visual representation of the formula.

Function graph overdraw

Two or more function graphs can be overdrawn, which makes it easy to determine intersection points and solutions that satisfy all the equations.

Here, let's find the intersection points of the

previously used

y=2x2 +3x -4 and y=2x + 3.

First, clear the graph screen in preparation for the first graph.

In this way it can be easily seen that there are two intersections for the two function graphs. The approximate coordinates for these two intersections can be found using the Zoom function and the Trace function described in the following section.

* Be sure to input variable X ( ) into the formula when using built-in graphs for overdraw. If variable X is not included in the second formula, the second graph is produced after clearing the first graph.

Zoom function

This function lets you enlarge or reduce the x - and y-coordinates. If you use the Trace or Plot function to locate the pointer at a specific point on the graph, the enlargement/reduction is performed using the pointer location as the center point.

•Enlarging a graph

To enlarge the graph for y=sinx by a factor of 1.5

on the x-axis and 2.0 on the y-axis. Use the following range parameters for the original graph.

Xmin: -360 Ymin: -1.6 Xmax: 360 Ymax : 1.6 Xscl:180 Yscl: 1

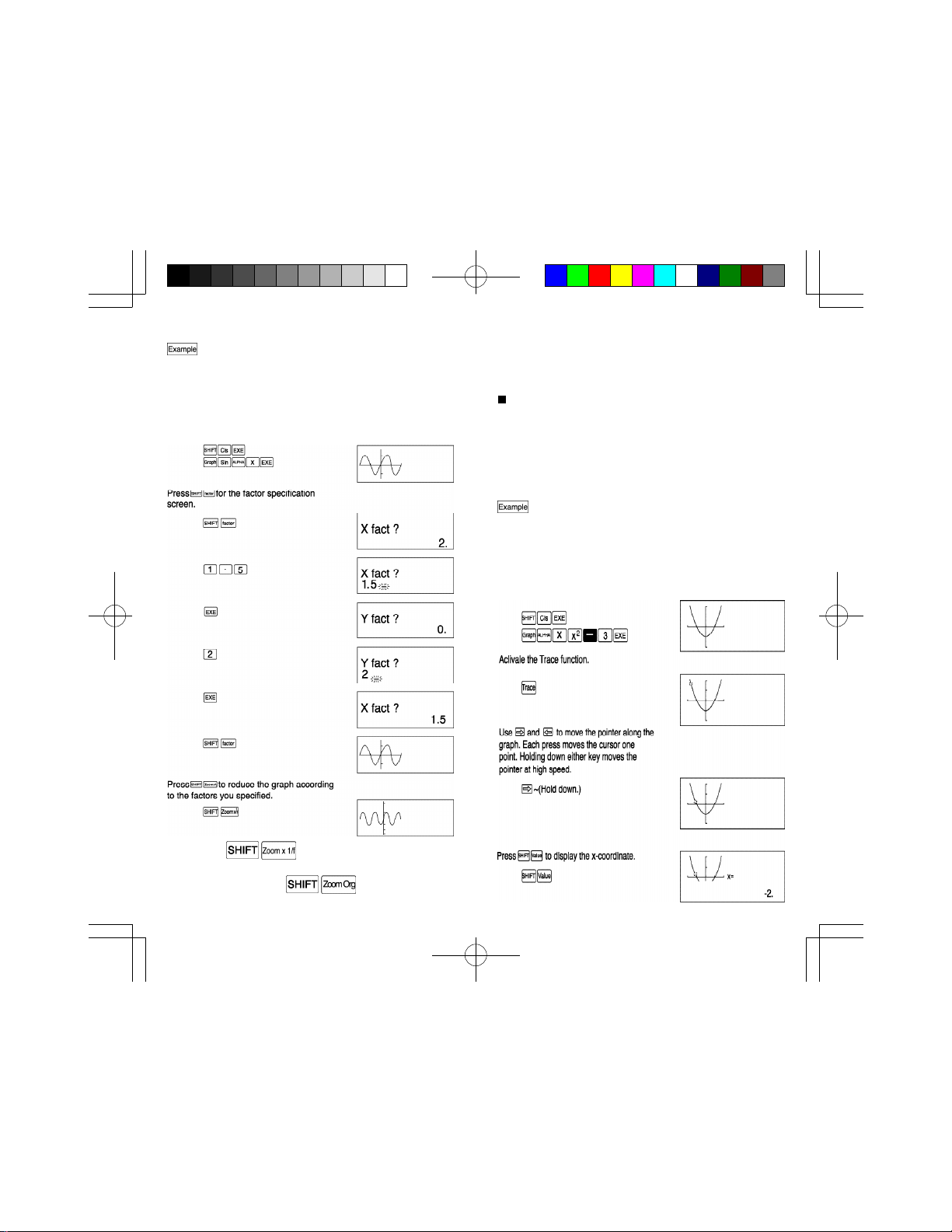
• Reducing a graph

To reduce the graph for y=sinx by a factor of 1.5 on

the x-axis and 2.0 on the y-axis. Use the following range parameters for the original graph.

Xmin: -360 Ymin: -1.6 Xmax: 360 Ymax : 1.6 Xscl:180 Yscl: 1

After specifying the range parameters, graph y=sinx.

• To specify the zoom factors within a program

Use the following formal to specify the zoom factors in a program. Factor (Xfactor), (Yfactor)

Trace function

This function lets you move a pointer around a graph and display the x- and y- coordinates of the current pointer location. You enlarge or reduce the x- and y-coordinates. You can display the coordinates using either seven digits or eleven digits (including negative sign).

•Using the trace function

To use the Trace function in combination with the

Zoom function to analyze the graph for y=x2-3. Use the following range parameters for the original graph.

Xmin: -4 Ymin: -8 Xmax: 4 Ymax : 8 Xscl:2 Yscl: 4

After specifying the range parameters, graph y=x2-3.

If you press again, the graph is reduced once more by the factors you specified. To return the graph

to its original size. press .

first

As you can see above, the Trace and Zoom functions can be used to locate the pointer at an approximate point, and

then produces a readout of the coordinates. To return the graph to its original size, press

(Important)

The pointer does not move at fixed intervals. It follows the dots on the display. Because of this, the values provided for coordinates are approximate.

* The Trace function can only be used immediately after a graph is drawn. This function cannot be used if other

calculations or operations (except and have been employed after a graph has been drawn.

* The Trace function cannot be written into a program. * When the format: " formula formula " is executed and a graph is drawn by pressing directly

after executing the Trace function during halt status, the previous coordinate value remains on the display. After the Trace function is executed and the text display is

brought up using the key, pressing causes the next graph to appear and the coordinate value to clear.

Examine the above using 2 5.

Plot function

The Plot function is used to mark a point on the screen of a graph display. The point can be moved left, right, up and down using the cursor keys, and the coordinates for the graph displayed can be read. Two points can also be connected by a straight line .

Press and specify the x-and y-coordinates after the "Plot" message.

Line function

The Line function makes it possible to connect two points

(including the blinking pointer ) created with the Plot function with a straight line. With this function, user generated lines can be added to graphs to make them easier to read.

Draw perpendiculars from point (2,0) on the x-

axis to its intersection with the graph for y=3x.

Then draw a line from the point of intersection

to the y-axis.

The range values for the graph are as follows:

Xmin: -2 Ymin: -2

Xmax: 5 Ymax : 10 Xscl: 1 Yscl: 2 Clear the graph display and draw the graph for y=3x .

Next, a perpendicular will be drawn from the same point on the graph to the y-axis. First, plot the point on the graph

and use the cursor key ( ) to move the pointer to the yaxis. This can be accomplished using Plot X,Y since the x-y

coordinates of the point on the graph are stored in the X and Y memories.

* The Line function can only be used to draw lines between the blinking pointer and a fixed point created using the Plot function.

Graph scroll function

Immediately after you have drawn a graph,you can scroll it on the display.Use the cursor keys to scroll the graph left, right,up and down.

•To scroll the graph on the display To draw the graph for y=0.25(x+2)(2x+1)(2x-5)

and then scroll it.

Xmin : -5 Ymin : -8 Xmax : 5 Ymax : 8 Xscl : 1 Yscl : 2

• Press to return the graph to its original position after scroll operations.

The following examples are presented to show you some ways that the graphing functions can be used effectively.

To graph the function y=x3-9x2+27x+50

Use the following range parameters.

Xmin : -5 Ymin : -30 Xmax : 10 Ymax : 150 Xscl : 2 Yscl : 20

Program Calculations

This unit has a built-in program feature that facilitates repeat calculations. The program feature is used for the consecutive execution of formulas in the same way as the "multistatement" feature is used in manual calculations. Programs will be discussed here with the aid of illustrative

To graph the function y=x4+4x3-36x2-160x+300

and determine its minimum and maximum

Use the following range parameters.

Xmin : -10 Ymin : -600 Xmax : 10 Ymax : 600 Xscl : 2 Yscl : 200

Find the surface area and volume of a regular octahedron when the length of one side is given.

Formulas

For a surface area S,volume V and one side A,S and V for a regular octahedron are defined as:

Programming

Creating a program based on calculation formulas is known as "programming".Here a program will be created based upon the formulas given above.The basis of a program is manual calculation,so first of all,consider the operational method used for manual calculation.

Surface area (s):2 3 Numeric value A A

Volume (V ): 2 3 Numeric value A A 3 In the above example,numeric value A is used twice,so it

should make sense to store it in memory A before the calculations.

Numeric value A

With this unit,the operations performed for manual calculations can be used as they are in a program.Once program execution starts,it will continue in order without stopping.Therefore,commands are required to request the input of data and to display results.The command to

request data input is "?",while that to display results is " " . A "?" within a program will cause execution to stop temporarily and a "?" to appear on the display as the unit waits for data input.This command cannot be used independently,and is

used together with as memory name". To store a numeric value in memory A,for example:

? A

When "?" is displayed,calculation commands and numeric values can be input within 127 steps.

The command causes program execution to stop temporarily and the latest formula result or alphanumeric characters and symbols to be displayed. This command is used to mark positions in formulas where results are to be displayed. Since programs are ended and their final results displayed automatically,this command can be omitted at the end of program.However,if the BASE-N mode is specified for base conversion during a program,do

not omit final " ". Here these two commands will be used in the previously presented procedure:

Now the program is complete.

Program storage

The storage of programs is performed in the WRT mode which is specified by pressing .

When are pressed,the system mode changes to the WRT mode.Then,the number of remaining steps is indicated.The number of remaining steps is decreased when programs are input or when memories are expanded. If no programs have been input and the number of memories equals 26(the number of memories at initialization),the number of usable steps should equal 400. The larger figures located below indicate the program areas .If the letter "p" is followed by the numbers 0 through 9,it indicates that there are no programs stored in areas P0 through P9.The blinking zero here indicates the current program area is P0. Areas into which programs have already been stored are indicated by"_" instead of numbers.

Here the previously mentioned program will be stored to program area P0 (indicated by the blinking zero):

After these operations are complete,the program is stored. *After the program is stored,press to return to the

RUN mode.

Program execution

Programs are executed in the RUN mode .The program area to be executed is specified using the

key.

To execute P0: 0 To execute P3: 3

To execute P8: 8 Here the sample program that has been stored will be executed.The surface (S) and volume (V) for the regular octahedron in the sample problem are calculated as:

* Program calculations are performed automatically with each press of when it is pressed after data is input or after the result is read. * Directly after a program in P0 is executed by pressing 0 as in this example,the Prog 0 command is stored by the replay function.Therefore,subsequent executions of the same program can be performed by simply pressing . Operation 0 (P0 program execution)

10 (Input 10 for A) (Display V when A = 10) (Reexecute) 7 (Input 7 for A ) (Display V when A = 7 )

. . .

Recalling a stored program can be performed in order to verify its contents.After specifying the desired program

area using or in the WRT mode ( ),the program contents will be displayed by pressing the key. Once the program is displayed,the (or ) key is

used to advance the program one step at a time for verification. When the program has been improperly stored,editing can also be performed by adding to it or erasing portions.Here a new program will be created by checking and editing the previous sample program (the surface area and volume of a regular octahedron).

Find the surface area and volume of a regular tetrahedron when the length of one side is given.

Formulas

For a surface area S,volume V and one side A, S and V for a regular tetrahedron are defined as:

Programming

As with the previous example,the length of one side is stored in memory A and the program then constructed.

Numeric value A

The octahedron program can be changed to a tetrahedron program by deleting the parts marked with wavy lines,and changing those that are marked with straight lines. In actual practice,this would be performed as follows:

Program editing First, a comparison of the two programs would be helpful.

Program execution

Now this program will be executed.

< Summary >

After a program has been created and input,it will sometimes generate error messages when it is executed,or it will produce unexpected results.This indicates that there is an error somewhere within the program that needs to be corrected. Such programming errors are referred to as "bugs", while correcting them is called "debugging".

Debugging when an error message is generated

An error message is displayed as follows:

The error message informs the operator of the program area (P0 to P9) in which the error was generated. It also states the type of error,which gives an idea of the proper countermeasure to be taken.

Error messages

There are a total of seven error messages.

Syn ERROR (Syntax error)

Indicates a mistake in the formula or a misuse of program commands.

Ma ERROR (Mathematical error)

Indicates the calculation result of a numeric expression exceeds 10 zero), or the input of an argument that exceeds the input range of the function.

100

, an illogical operation (e.g. division by

Go ERROR (Jump error)

Indicates a missing Lbl for the Goto command , or that the program area for the Prog command does not contain a program.

Ne ERROR (Nesting error)

Indicates a subroutine nesting overflow by the Prog command .

Stk ERROR (Stack error)

Indicates the calculation performed exceeds the capacity of the stack for numeric values or for commands

Mem ERROR (memory error)

Indicates the attempt to use a memory name such as Z [5] without having expanded memories.

Arg ERROR ( Argument error) Indicates the argument of a command or specification in

a program exceeds the input range (e.g. Sci 10, Goto 11) Further operation will become impossible when an error message is displayed.

Press , or to cancel the error. Pressing cancels the error and new key input becomes

possible. With this operation, the RUN mode is maintained.

Pressing or cancels the error and changes the system mode to the WRT mode. The cursor is positioned at the location where the error was generated to allow modification of the program to eliminate the error.

Checkpoints for each type of error

The following are checkpoints for each type of error:

Syn ERROR

Verify again that there are no errors in the program.

Ma ERROR

For calculations that require use of the memories, check to see that the numeric values in the memories do not exceed the range of the arguments. This type of error often occurs with division by 0 or the calculation of negative square roots.

Go ERROR

Check to see that there is a corresponding Lbl n when Goto n is used. Also check to see that the program in P n has been correctly input when Prog n is used.

Ne ERROR

Check to ensure that the Prog command is not used in the branched program area to return execution to the original program area.

Stk ERROR

Check to see that the formula is not too long thus causing a stack overflow. If this is the case ,the formula should be divided into two or more parts.

Mem ERROR

Check to see that memories were properly expanded using " n (Defm). When using array-type

memories , check to see that the subscripts are correct.

Arg ERROR

Check whether values specified by (Sci) or (Fix) are within the range of 0~9. Also check whether

values specified by Goto, Lbl, or Prog commands are within 0-9.Also ensure that memory expansion using (Defm) is performed within the remaining number of

steps and that the value used for expansion is not negative.

The program capacity of this unit consists of a total of 400 steps. The number of steps indicates the amount of storage space available for programs, and it will decrease as programs are input. The number of remaining steps will also be decreased when steps are converted to memories. There are two methods to determine the current number of remaining steps:

When are pressed in the RUN mode, the number of remaining steps will be displayed together with the number of memories.

Specify the WRT mode ( ), and the number of remaining steps will appear. At this time the status of the

program areas can also be determined.

Basically, one function requires a single step, but there are some commands where one function requires two steps.

• One function/one step: sin, cos, tan, log,(,). :, A, B, 1, 2, 3, etc.

• One function/two steps: Lbl 1, Goto 2, Prog 8, etc. Each step can be verified by the movement of the cursor:

At this time, each press of a cursor key or will cause the cursor to move to the next sequential step, For example:

This unit contains a total of 10 program areas (P0 through P9) for the storage of programs. These program areas are all utilized in the same manner, and 10 independent programs can be input .One main program (main routine) and a number of secondary programs(subroutines) can also be stored. The total number of steps available for storage in program areas P0 through P9 is 400 maximum. Specification of a program area is performed as follows:

RUN mode: Press any key from 0 through 9 after pressing

the key. Then press . P0 P8

* In this mode, program execution begins when is pressed.

WRT mode: Use or to move the cursor under the program area to be specified and press .

Only the numbers of the program areas that do not yet contain programs will be displayed. "-" symbols indicate program areas which already contain programs.

100

Program area and calculation mode

specification in the WRT mode

Besides normal function calculations, to perform binary, octal, decimal and hexadecimal calculations and conversions, standard deviation calculations, and regression calculations in a program, a calculation mode must be specified. Program mode specification and program area specification are performed at the same time.

First the WRT mode is specified ( ), and then a calculation mode is specified. Next, the program area is

specified, and, when is pressed, the calculation mode is memorized in the program area. Henceforth, stored programs will be accompanied with the calculation mode.

Memorizing the BASE-N mode in P2

As shown above, the calculation mode will be memorized into a program area.

101

Cautions concerning the calculation modes

All key operations available in each calculation mode can be stored as programs, but, depending on the calculation mode, certain commands of functions cannot be used.

BASE-N mode

• Function calculations cannot be performed.

• Units of angular measurement cannot be specified.

• All program commands can be used.

• Be sure to include a " " at the final result output to return to the previous calculation mode when a program execution is terminated. Failure to do so may result in a decimal display or an error.

SD mode

• Among the functions, Abs and

√ cannot be used.

• Among the program commands, Dsz, > and < cannot be used.

LR mode

• Among the functions, Abs and 3√ cannot be used.

• Among the program commands, , =, ≠, lsz, ≥, ≤, Dsz, > and < cannot be used.

Erasing of programs is performed in the PCL mode. Press

to specify the PCL mode . There are two

methods used to erase programs: erasing a program located in a single program area, and erasing all programs.

Erasing a single program

To erase a program in a single program area, specify the PCL mode and press the key after specifying the

program area.

Erase the program in P3 only.

Erasing all programs

To erase all programs stored in program areas 0 through 9, specify the PCL mode and press and then .

Erase the programs stored in P0 , P4 , P8 , and P9.

102

103

The programs for this unit are made based upon manual calculations. Special program commands, however, are available to allow the selection of the formula, and repetitive execution of the same formula. Here, some of these commands will be used to produce more convenient programs.

Jump commands

Jump commands are used to change the flow of program execution. Programs are executed in the order that they are input (from the lowest step number first ) until the end of the program is reached. This system is not very convenient when there are repeat calculations to be performed or when it is desirable to transfer execution to another formula. It is in these cases, however, that the jump commands are very effective. There are three types of jump commands: a simple unconditional jump to a branch destination, conditional jumps that decide the branch destination by whether a certain condition is true or not, and count jumps that increase or decrease a specific memory by one and then decide the branch destination after checking whether the value stored equals zero or not.

Unconditional jump

The unconditional jump is composed of “Goto “ and “Lbl” . When program execution reaches the statement “ Goto n ” (where n is a number from 0 through 9),execution then jumps to “Lbl n”(n is the same value as Goto n ). The unconditional jump is often used in simple programs to return execution to the beginning for repetitive calculations, or to repeat calculations from a point within a program . Unconditional jumps are also used in combination with conditional and count jumps,

The previously presented program to find the surface area and volume of a regular

tetrahedron will be rewritten using “Goto 1” and “Lbl 1 ” to allow repeat calculations.

The previous program contained:

?, , A , : ,√ , 3 , x, A,x

2 ,

√ , 2, ÷ , 1, 2, x , A , xy ,3 19 steps

104

* Hereinafter, commas (,) will be used to separate steps for the sake of clarity, Add “Goto 1” to the end of the program, and add “Lbl 1”to the beginning of program as the branch destination. If this is simply left the way it is , however, the volume will not be displayed and execution will move immediately to the input of one side at the beginning, To prevent this situation , insert a display command " " in front of the “Goto 1”. The complete program with the unconditional jump added should look like this : Lbl , 1, : ,?, , A , : ,√ , 3 , x, A,x √ ,2, ÷ , 1, 2, x , A , x

y ,

3 , ,Goto , 1 25 steps

2 ,

Now let’s try executing this program. * Henceforth , the displays will only show calculation result output.

Since the program is in an endless loop, it will continue execution, To terminate execution, press .

Besides the beginning of the program , branch destinations can be designated at any point within the program.

105

Calculate y=ax+b when the value for x changes each time , while a and b can also

change depending upon the calculation.

?, , A , : ,?, ,B, : ,Lbl, 1,: ,?, , X,:,

A ,x, X, +, B , Goto , 1 23 steps When this program is executed, the values for a and b are stored in memories A and B respectively. After that, only the value for x can be changed . In this way an unconditional jump is made in accordance with “Goto “and “Lbl”, and the flow of program execution is changed. When there is no “Lbl n “ to correspond to a “Goto n “ , an error (Go ERROR) is generated.

Conditional jumps

The conditional jumps compare a numeric value in memory with a constant or a numeric value in another memory. If the condition is true, the statement following the is executed, and if the condition is not true, execution skips the statement and continues following the next “:” or “ ”, Conditional jumps take on the following form :

Relational

Left side

operator

Right side Statement { }* Statement

* Anyone can be used. One memory name (alphabetic character from A through Z ), constant numeric values or calculation formulas (Ax2, DE, etc.) are used for “left side “ and “right side “, The relational operator is a comparison symbol. There are 6 types of relational operators: = , ≠ , ≥ , ≤ , > , < . Left side = right side (left side equals right side ) Left side ≠ right side (left side does not equal right side ) Left side ≥ right side (left side is greater than or equal

to right side )

Left side ≤ right side (left side is less than or equal to right

side ) Left side > right side (left side is greater than right side ) Left side < right side (left side is less than right side )

The “ ” is displayed when are pressed. If the

106

condition is true, execution advances to the statement following following

If the condition is not true,the statement

is skipped and execution jumps to the

statement following the next “ : ” or “ ”.

A statement is a calculation formula ( sin A x 5, etc.) or a program command (Goto ,prog, etc.), and everything up to the next “ : ” or “ ” is rgarded as one statement.

If an input numeric value is greater than or equal to zero, calculate the square root of

that value. If the input value is less than zero, reinput another value.

Program

Lbl , 1, : ,?, , A , : ,A , ≥ , 0, ,√ , A , ,Goto , 1 16 steps In this program, the input numeric value is stored in

memory A , and then it is tested to determine whether it is greater than, equal to or less than zero. If the contents of memory A are greater than or equal to 0 (not less than zero ), the statement (calculation formula) located between “ ” and “ ” will be executed, and then Goto 1 returns execution to Lbl 1. If the contents of memory A are less than zero, execution will skip the following statement to the next “ ” and return to Lbl 1 by Goto 1.

Calculate the sum of input numeric values. If a 0 is input, the total should be displayed.

Program

0, ,B,: , Lbl , 1, : ,? ,A , : ,A , = , 0, ,Goto , 2,:, A,+,B, ,B,:,Goto,1,:, Lbl ,2 ,:,B 31 steps

In this program, a 0 is first stored in memory B to clear it for calculation of the sum. Next, the value input by “? A ” is stored in memory A by “A=0 ” and it is determined whether or not the value stored in memory A equals zero. If A = 0 , Goto 2 causes execution to jump to Lbl 2. If memory A does not equal 0 , Goto 2 will be skipped and the command A+ B B which follows “:” is executed, and

107

then Goto 1 returns execution to Lbl 1. Execution from Lbl 2 will display the sum that has been stored in memory B. Actually, the display command “ ” is inserted following B , but here it can be omitted. The following illustration shows the flow of the program:

Count jumps

The count jumps cause the value in a specified memory to be increased or decreased by 1. If the value does equal 0, the following statement is skipped, and the statement following the next “:” or “ ” is executed. The “lsz” command is used to increase the value in memory by 1 and decide the subsequent execution, while the “Dsz” command is used to decrease the value by 1 and decide.

lsz

Dsz

Increase memory A by one............Isz AA

Decrease memory B by one ..........Dsz B

Determine the average of 10 input

numeric values.

Program

1,0, ,A,:, 0 , ,C,:, Lbl, 1,:,?, ,B,:,B,+,C, ,C,:,

Dsz, A,:,Goto,1,:,C,÷,1,0 32 steps In this program, first 10 is stored in memory A , and 0 is stored in memory C . Memory A is used as the “counter” and countdown is performed the specified number of times by the Dsz commmand. Memory C is used to store the sum of the inputs, and so first must be cleared by inputting a 0. The numeric value input in response to “ ? ” is stored in memory B, and then the sum of the input values is stored in memory C by “ B+C C”. The statement Dsz A then decreases the value stored in memory A by 1. If the result does not equal 0 , the following statement, Goto 1 is executed. If the result equals 0, the following Goto 1 is skipped and “C ÷ 10” is executed.

108

109

Determine the altitude at one-second intervals of a ball thrown into the air at an initial

velocity of Vm/ sec and an angle of S °. The formula is expressed as: h=Vsin t-1/2gt2, with g=9.8, with the effects of air resistance being disregarded.

Program

Deg , : ,0, , T ,: , ? , ,V,: ,?, , S, :, Lbl , 1, : ,lsz , T, : ,V , x ,sin , S, x, T,-, 9,•,8,x,T,x2, ÷, 2, ,Goto, 1 38 steps

In this program the unit of angular measurement is set and memory T is first initialized (cleared).Then the initial velocity and angle are input into memories V and S respectively. Lbl 1 is used at the beginning of the repeat calculations. The numeric value stored in memory T is counted up (increased by 1) by Isz T . In this case, the Isz command is used only for the purpose of increasing the value stored in memory T, and the subsequent jump does not depend upon any comparison or decision. The Isz command can also be used in the same manner as seen with the Dsz command for jumps that require decisions, but, as can be seen here, it can also be used to simply increase values. If, in place of the Isz command, another method such as “T+ 1 T “ is used, five steps are required instead of the two for the(Isz T ) method shown here. Such commands are convenient ways of conserving memory space. Each time memory T is increased, calculation is performed according to the formula, and the altitude is displayed. It should be noted that this program is endless, so when the required

value is obtained, are pressed to terminate the program.

110

111

Subroutines

A program contained in a single program area is called a “ main routine” . Often used program segments stored in other program areas are called “ subroutines”. Subroutines can be used in a variety of ways to help make calculations easier. They can be used to store formulas for repeat calculations as one block to be jumped to each time , or to store often used formulas or operations for call up as required.

The subroutine command is “ Prog “ followed by a number from 0 through 9 which indicates the program area.

Prog 0 .......... Jump to program area 0

Prog 2 .......... Jump to program area 2

After the jump is performed using the Prog command, execution continues from the beginning of the program stored in the specified program area. After execution reaches the end of the subroutine, the program returns to the statement following the Prog n command in the original program area. Jumps can be performed from one subroutine to another, and this procedure is known as “nesting “, Nesting can be performed to a maximum of 10 levels, and attempts to exceed this limit will cause an error (Ne ERROR) to be generated. Attempting to use Prog to jump to a program area in which there is no program stored will also result in an error (Go ERROR). *A Goto n contained in a subroutine will jump to the corresponding Lbl n contained in that program area.

112

Simultaneously execute the two previously

presented programs to calculate the surface

areas and volumes of a regular octahedron

and tetrahedron.

Express the result in three decimal places.

This example employs two previously explained programs, and the first step is to input the specified number of

decimal places ( 3 ). Now let’s review the two original programs.

Regular octahedron

P0 Fix, 3 ,: ,?, ,A,:,2,x,√ ,3,x,A,x2, ,

√ , 2 ,÷ ,3,x,A ,xy ,3 23 steps

Regular tetrahedron

P1 Fix, 3 ,: ,?, ,A,: ,√ ,3,x,A,x

2 ,

√ , 2 ,÷ , 1,2 ,x,A ,xy ,3 22 steps

Total 45 steps If the two programs are compared, it is evident that the underlined portions are identical. If these portions are incorporated into a common subroutine, the programs are simplified and the number of steps required is decreased. Furthermore, the portions indicated by the wavy line are not identical as they stand, but if P1 is modified to: √ , 2, ÷ ,

3 , x, A, x

, 3 , ÷ , 4 , the two portions become identical. Now the portions underlined by the straight line will be stored as an independent routine in P9 and those underlined with the wavy line will be stored in P8. P9 Fix , 3 , : , ? , , A , : , √ , 3 , x , A ,x2 12 steps P8 √ , 2 , ÷ , 3 ,x , A , xy , 3 8 steps After the common segments have been removed, the remainder of the regular octahedron formula is stored in P0, and that of the regular tetrahedron is stored in P1 Of course, the “Prog 9” and “Prog 8” must be added to jump to subroutines P9 and P8. P0 Prog, 9, :, Ans, x , 2, , Prog, 8 9 steps P1 Prog, 9, , Prog, 8, :, Ans, ÷, 4 9 steps

Total 38 steps With this configuration execution jumps to program P9 at the beginning of programs P0 and P1, three decimal places are specified, the value for one side is entered, and the surface area of the tetrahedron is calculated. The expression “2x “ of the original octahedron formula was omitted in P9, so when execution returns to P0 , “Ans x 2” is used to obtain the surface of the octahedron. In the case

113

of P1, the result of P9 needs no further modification and so is immediately displayed upon return to P1. Calculation of the volumes is also performed in a similar manner. After a jump is made to P8 for calculation, execution returns to the main routines, In P0, the program ends after the volume of the octahedron is displayed . In P1 , however, the result calculated in P8 is divided by four to obain the volume of the tetrahedron. By using subroutines in this manner, steps can be shortened and programs become neat and easy to read. The following illustration shows the flow of the program just presented.

By isolating the common portions of the two original programs and storing them in separate program areas, steps are shortened and programs take on a clear configuration.

Using array-type memories

Up to this point all of the memories used have been referred to by single alphabetic characters such as A, B, X, or Y. With the array-type memory introduced here, a memory name (one alphabetic character from A through Z ) is appended with a subscript such as [1] or [2].

Brackets are input by and .

Standard memory Array-type memory

A A[0] C [-2] B A[1] C [-1] C A[2] C [0] D A[3] C [1] E A[4] C [2]

114

Proper utilization of subscripts shortens programs and makes them easier to use. Negative values used as subscripts are counted in relation to memory zero as shown above.

Input the numbers 1 through 10 into

memories A through J .

Using standard memories

1, ,A,:,2 , ,B,: ,3 , ,C , : , 4 , ,D, : , 5, ,E,:,6 , ,F,: ,7 , ,G , : , 8 , ,H, : , 9, ,I,:,1 ,0, ,J, 40 steps

Using array-type memories

0, ,Z,:,Lbl ,1 ,: ,Z ,+,1 , ,A , [ , Z, ] , : , Lsz,Z ,:,Z ,<,1,0 , ,Goto, 1 26 steps In the case of using standard memories, inputting values into memories one by one is both inefficient and time consuming. What happens, if we want to see a value stored in a specific memory ?

Using standard memories

Lbl , 1 , : , ? , , Z , : , Z, = , 1 , , A , , Z , = , 2 , , B , , Z, = , 3 , , C , , Z , = , 4 , , D , , Z, = , 5 , , E , , Z , = , 6 , , F , , Z, = , 7 , , G , , Z , = , 8 , , H , , Z, = , 9 , , I, , Z , = , 1 , 0 , , J , , 70 steps

Goto, 1 Using array-type memories

Lbl , 1 , : , ? , , Z , : , A , [ , Z , - , 1 , ] , , Goto, 1 16 steps The difference is readily apparent. When using the standard memories, the input value is compared one by one with the value assigned to each memory (e.g.A=1 B = 2,..) . With the array-type memories, the input value is immediately stored in the proper memory determined by “ [Z-1], Formulas (Z-1 ,A+10, etc.) can even be used for the subscript.

Cautions when using array-type memories

When using array-type memories, a subscript is appended to an alphabetic character that represents a standard memory from A through Z. Therefore, care must be taken to prevent overlap of memories. The relation is as follows:

115

A [0] A[1] A[2] A[3] A[4] A[5] A[6] A [23] A[24] A[25] A[26] A[27] B[-1] B [0] B[1] B[2] B[3] B[4] B[5] B[22] B[23] B[24] B[25] B[26] C[-2] C[-1]C[0] C[1] C[2] C[3] C[4] C[21] C[22] C[23] C[24] C[25]

G[-6] G[-5] G[-4] G[-3] G[-2] G[-1] G[0] G[17] G[18] G[19] G20] G[21]

. . . . . .

. .

. X [0] X[1] X[2] X[3] X[4] Y[-1] Y [0] Y[1] Y[2] Y[3] Z[-2] Z[-1] Z [0] Z[1] Z[2]

The following shows a case in which array-type memories overlap with standard format memories. This situation should always be avoided.

Store the numeric values from 1 through 5 in memories A[1] though A [5] respectively.

5, , C , : , Lbl, 1 , : , C , , A , [ , C , ] , : , Dsz , C , : , Goto , 1 , : , A , [ , 1 , ] , , A , [ , 2 , ] , , A , [ , 3 , ] , , A , [ , 4 , ] , , A , [ , 5 , ] 44 steps In this program, the values 1 through 5 are stored in the array-type memories A[1] through A [5] , and memory C is used as a counter memory. When this program is executed, the following results are obtained:

As can be seen, the second displayed value (which should be 2) in A[2] is incorrect. This problem has occurred because memory A[2] is the same as memory C.

116

A B C D E F A[1] A[2] A[3] A[4] A[5]

The content of memory C (A[2]) is decreased from 5 to 0 in steps of 1. Therefore, the content of memory A[2] is displayed as 0.

Application of the array-type memories

It is sometimes required to treat two different types of data as a single group. In this case, memories for data processing and those for data storage should be kept separate.

Store data x and y in memories. When a x

value is input, the corresponding y value is displayed . There will be a total of 15 pieces of data. Example program 1

Memory A is used as the data control memory, and memory B is used for temporary storage of the x data. The x data are stored in memories C[1] (memory D) through C [15] (memory R), and the y data are stored in memories C[16] (memory S) through C[30] (memory Z (7)). 1, , A , : , Defm , 7 , : , Lbl , 1 , : , ? , , C , [ , A , ] , : , ? , , C , [ , A ,+ ,1 ,5, ] , : , Lsz , A , : , A , = , 1 , 6 , , Goto ,2 , : ,Goto , 1 , : , Lbl, 2 , : ,1 , 5 , , A , : , ? , , B , : , B , = , 0 , , Goto , 5 ,: , Lbl , 3, :, B . = , C , [ , A , ] , , , Goto , 4 , :, Dsz, A , : , Goto , 3 , : , Goto , 2 , : , Lbl , 4 , : ,C, [ , A , + , 1 , 5 , ], , Goto , 2 ,: , Lbl , 5 98 steps In this program, memories are used as follows :

x data

C[1] C[2] C[3] C[4] C[5] C[6] C[7] C[8] D E F G H I J K C[9] C[10] C[11] C[12] C[13] C[14] C[15] L M N O P Q R

y data

C[16] C[17] C[18] C[19] C[20] C[21] C[22] C[23] S T U V W X Y Z C[24] C[25] C[26] C[27] C[28] C[29] C[30] Z(1) Z(2) Z(3) Z(4) Z(5) Z(6) Z(7)

117

Example program 2

The same memories are used as in Example 1, but two types of memory names are used and the x and y data kept separate. 1, , A , : , Defm , 7 , : , Lbl , 1 , : , ? , , C , [ , A , ] , : , ? , , R , [ , A , ] , : , Lsz , A , : , A , = , 1 , 6 , , Goto ,2 , : ,Goto , 1 , : , Lbl, 2 , : ,1 , 5 , , A , : , ? , , B , : , B , = , 0 , , Goto , 5 ,: , Lbl , 3, :, B , = , C , [ , A , ] , , , Goto , 4 , :, Dsz, A , : , Goto , 3 , : , Goto , 2 , : , Lbl , 4 , : , R , [ , A , ] , , Goto , 2 ,: , Lbl , 5 92 steps Memories are used as follows:

x data

C[1] C[2] C[3] C[4] C[5] C[6] C[7] C[8] D E F G H I J K C[9] C[10] C[11] C[12] C[13] C[14] C[15] L M N O P Q R

y data

R[1] R[2] R[3] R[4] R[5] R[6] R[7] R[8] S T U V W X Y Z R[9] R[10] R[11] R[12] R[13] R[14] R[15] Z(1) Z(2) Z(3) Z(4) Z(5) Z(6) Z(7)

In this way, the memory names can be changed. However, since memory names are restricted to the letters from A

through Z , the expanded memories ( ) can only be used as array-type memories.

The memory expansion command (Defm) can be used in a program.

Expand the number of memories by 14 to make a total of 40 available.

Defm, 1, 4, :, ......

118

Alphabetic characters, numbers, calculation command symbols, etc, can be displayed as messages. They are

enclosed in quotation marks ( ).

Alphanumeric characters and symbols

• Characters and symbols displayed when pressed following :

[,], k , m, , n, p, f, space, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P , Q, R, S, T, U, V, W, X, Y, Z

•Other numbers, symbols, calculation commands, program commands

0 1, 2, 3, 4, 5, 6, 7, 8, 9, (,), √, E, +, -, X, ÷, ... sin, cos, tan, log, ln, ... =, ≠, ≥, ≤, >, <, ...

/A , IB, , ID, , , d, h, b, o Neg, Not, and, or , xor

, , , ......

º ( ), r ( ) ,g ( )

*All of the above noted characters can be used in the same manner as the alphabetic characters.

In the preceding example requiring an input of two types of data (x,y ), the prompt “ ? ” does not give any information concerning the type of input expected. A message can be inserted before the “ ? ”, to verify the type of data required for input. Lbl, 1, : ,?, ,X,:,?, ,Y,:,... The message “ x =” and “ y=” will be inserted into this program. Lbl, 1, :,",X,=,",?, ,X,:, ",Y,=,",?, ,Y,:,... If messages are included as shown here, the display is as follows: (Assuming that the program is sorted in P1)

119

Messages are also convenient when displaying result in program calculations .

Lbl, 0, : , " , N , = , " , ? , , B , ~ , C , : ,

0 , ,A , : , Lbl , 1 , : ,C , ÷ , 2 , , C ,: ,Frac ,C ,≠ ,0 , ,Goto ,3 , : , Isz , A , : ,C ,= ,1 , ,Goto ,2 ,: ,Goto , 1 ,: , Lbl , 2 , : , " , X ,= ," , , A , , Goto ,0 ,: , Lbl , 3 ,: ," ,N ,O , " , , Goto , 0 , 70 steps

This program calculates the x power of 2. A prompt of “N =? ” appears for data input. The result is displayed by pressing while “x=” is displayed . When an input data is not the x power of 2, the display “ NO “ appears and execution returns to the beginning for reinput .

Always follow a message with a whenever a formula follows the message. Assuming that the program is stored in P2:

The display is capable of showing up to 12 alpha characters at one time. For messages that are longer than 12 characters, use (Disp) to divide the message.

Using the graph function within programs makes it possible to graphically represent long. complex equations and to overwrite graphs repeatedly. All graph commands (except the trace function) can be included in programs. Range values can also be written into the program. Generally, manual graph operations can be used in programs without modification.

Graphically determine the number of

solutions (real roots) that satisfy both of the following two equations.

y=x4 - x3-24x2+4x+80 y=10x -30

The range values are as follows. Xmin : -10 Ymin : -120 Xmax : 10 Ymax : 150 Xscl : 2 Yscl : 50

120

121

Program the equation for the first graph. Graph, X, Xy,4, -, X, xy,3,-,2,4,X,x2,+, 4, X, +,8,0 Finally program the equation for the second graph. Graph, 1, 0, X, -,3, 0 Total 27 steps

When inputting this program, press after input of the first equation.

The following should appear on the display when the program is executed:

A “ ” can be input after the first equation to suspend execution after the first graph is produced. To continue

execution to the next graph, press . The procedure outlined above can be used to produce a

wide variety of graphs.The library of this manual includes a number of examples of graph programming.

Function Reference

Manual Calculations

122

123

124

125

126

127

Program Calculations

128

129

Error Message Table

130

131

Input Ranges of Functions

132

133

Errors may be cumulative with internal continuous calculations such as x

y , x

√y ,x! ,3√x ,sometimes affecting

accuracy .

Specifications

Graph functions

Built-in function (20 types) sin, cos, tan, sin-1, graphs: cos-1, tan-1, sinh, cosh, tanh,

sinh-1, cosh-1, tanh-1, log, In, 10x, ex, x2, √, 3√, x-1.

Types of graphs: User generated function graphs

Rectangular coordinates

Graph functions: Range specification, Overdraw,

Trace, Zoom (xf,x1/f , factor, original (resume)), plot, Line, Scroll

Calculations

Basic calculation functions:

Built-in scientific functions:

• Statistics: Standard deviation - number of

Negative numbers, exponents, parenthetical addition/subtraction/ multiplication/division(with priority sequence judgement function true algebraic logic). Trigonometric/inverse trigonometric functions (units of angular measurement: degrees, radians, grads), hyperbolic/inverse hyperbolic functions, logarithmic/ exponential functions, reciprocals, factorials, square roots, cube roots, powers, roots, squares, decimal-sexagesimal conversions, binary-octalhexadecimal calculations, coordinate transformations, π, random numbers,absolute values, integers, fractions.

data, sum, sum of squares, mean, standard deviation .

134

135

Linear regression - number of data, sum of x , sum of y, sum of squares of x, sum of squares of y, mean of x, mean of y, standard deviation of x , standard deviation of y , constant term, regression coefficient, correlation coefficient, estimated value of x, estimated value of y.

Special functions: Insert, delete, replay functions,

substitution (=), multistatement (: and ).

Memories: 26 standard (maximum 76), Ans Calculation range: ±1 x 10

-99

~9.999999999 x 10

memory.

and 0. Internal operation uses 12digit mantissa.

Rounding: performed according to the

specified number of significant digits or the number of specified decimal places.

Exponential display:Norm 1 - 10

Norm 2 - 10

-2

> , 10

-9

> , 10

Program function

Number of steps: 400 maximum

Jump functions: Unconditional jump (Goto), 10

maximum Conditional jump (=, ≠, >, <, , , ) Count jumps (Isz, Dsz)

Subroutines: 9 levels Number of stored programs: 10 maximum (p0 to p9) Check functions: program checking, debugging,

deletion, addition, insertion, etc.

General

Power supply: lithium battery (CR2032) Auto power off: Power is automatically switched off

Ambient temperature range: 0°C ~ 40ºC (32ºF~104ºF)

approximately 6 minutes after last operation.

136

137

Sentry CA756 Instruction Manual

Specifications and Main Features

Frequently Asked Questions

User Manual