
application brief AB20-5
replaces AN1149-5
Secondary Optics Design
Considerations for SuperFlux LEDs
Secondary optics are those optics which exist outside of the LED package, such as reflector
cavities, Fresnel lenses, and pillow lenses. Secondary optics are used to create the desired
appearance and beam pattern of the LED signal lamp.
The following section details the optical characteristics and optical model creation for Lumileds
SuperFlux LEDs. In addition, simple techniques to aid in the design of collimating reflectors,
collimating lenses, and pillow lenses are discussed.
Table of Contents
Optical Characteristics of SuperFlux LEDs 2
LED Light Output 2
SuperFlux LED Radiation Patterns 2
Optical Modeling of SuperFlux LEDs 3
Point Source Optical Model 3
Detailed Optical Models 4
Secondary Optics 5
Pillow Lens Design 9
Design Case—Pillow Design for an LED CHMSL 9
Non-symmetric Pillow Lenses 11
Selecting the Size of the Pillow Optic 11
Recommended Pillow Lens Prescriptions 12
Other Diverging Optics 13
Reflector Design 14
Design Case—Reflector for a CHMSL Application 14
Reflector Cavities with Linear Profiles 15
Reflector Cavities with Square and Rectangular Exit Apertures 15
Other Reflector Design Techniques 16
Collimating Lens Design 17
Fresnel Lens Design 18
Design Case—Collimator Lens 19
Other Lens Design Options 19
Appendix 5A 21

Optical Characteristics of
SuperFlux LEDs
LED Light Output
The light output of an LED is typically described
by two photometric measurements, flux and
intensity.
In simple terms, flux describes the rate at which
light energy is emitted from the LED. Total flux
from an LED is the sum of the flux radiated in all
directions. If the LED is placed at the center of a
sphere, the total flux can be described as the
sum of the light incident over the entire inside
surface of the sphere. The symbol for
photometric for flux is Φv, and the unit of
measurement is the lumen (lm).
In simple terms, intensity describes the flux
density at a position in space. Intensity is the
flux per unit solid angle radiating from the LED
source. The symbol for photometric intensity is
Iv, and the unit of measurement is the candela
(cd).
SuperFlux LED Radiation Patterns
The radiation pattern of an LED describes
how the flux is distributed in space. This is
accomplished by defining the intensity of the
LED as a function of angle from the optical axis.
Since the radiation pattern of most LEDs is
rotationally symmetric about the optical axis, it
can be described by a simple, two-axis graph of
intensity versus angle from the optical axis.
Intensity is normalized in order to describe the
relative intensity at any angle. By normalizing
Solid angle is used to describe the amount of
angular space subtended. Angular space is
described in terms of area on a sphere. If a solid
angle ω, with its apex at the center of a sphere of
radius r, subtends an area A on the surface of
that sphere, then ω = A/r
angle are steradians (sr).
To put some of these concepts into perspective,
consider the simple example of a candle. A
candle has an intensity of approximately one
candela. A candle placed in the center of a
sphere radiates light in a fairly uniform manner
over the entire inner surface (ω = A/ r
4π steradians). With this information, the flux from
a candle can be calculated as shown below:
intensity, the radiation pattern becomes a
description of how the flux is distributed,
independent of the amount of flux produced.
Figure 5.1 shows a graph of the radiation pattern
for an HPWA-Mx00 LED.
An attribute of the radiation pattern that is of
common interest is known as the full-width, half-
max, or 2θ
angular width of the radiation pattern at the half
power, or half maximum intensity point. Looking
1
/2. This attribute describes the full
2
. The units for solid
2
= 4π r
2
2
/ r
=
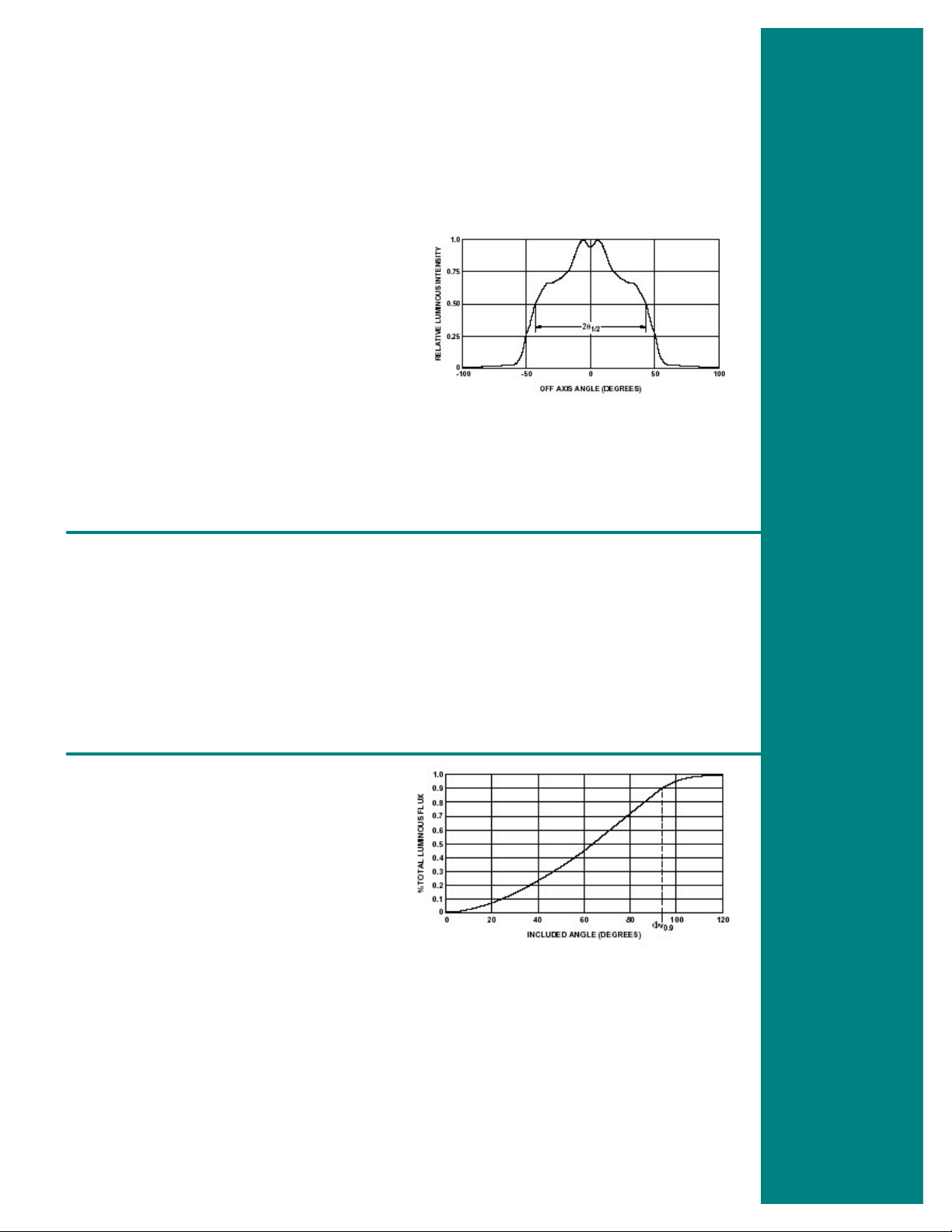
at Figure 5.1, the 2θ
is approximately 90°.
Another attribute that is of common interest is
the total included angle, or θ
describes the cone angle within which 90% of
the total flux is radiated. Using Figure 5.1, the
percent of total flux versus included angle can
be calculated and graphed. (The derivation of
this graph is shown in Appendix 5A.) This graph
is included in the data sheet of SuperFlux LEDs
and is shown in Figure 5.2 for the HPWA-Mx00
LED.
1
/2 of the HPWA-Mx00 LED
. This attribute
v 0.9
Looking at Figure 5.2, the total included angle is
approximately 95°. This implies that 90% of the
flux produced by an HPWA-Mx00 LED is emitted
within a 95° cone centered on the optical axis.
Figure 5.1 Graph of the radiation pattern for an
HPWA-MxOO LED.
Optical Modeling of SuperFlux LEDs
An optical model of the LED is useful when
designing secondary optic elements such as
reflector cavities and pillow lenses. The optical
output of an LED can be approximated as a
point source of light passing through an
aperture, but modeling errors may be
Point Source Optical Model
The internal structure of a SuperFlux LED is
shown in Figure 5.3. Light is produced in the
LED chip. A portion of this light goes directly
from the chip and is refracted by the epoxy
dome (refracted-only light). The remainder of
the light is reflected by the reflector cup and
then refracted by the epoxy dome (reflected-
refracted light).
The light that is refracted appears to come from
a certain location within the LED, while the light
which is reflected and refracted appears to
come from a different location. In addition,
because the LED chip itself has physical size
unacceptable when lenses or reflectors are
placed within 25 mm of the SuperFlux LED. A
more accurate technique involves using an
optical model, which takes into account the
extended source size of the LED.
Figure 5.2 Percent total flux vs. included angle for
an HPWA-MxOO LED.
and is not a point source, the refracted-only light
does not appear to come from a single location,
but a range of locations or a focal smear. This is
true for the reflected-refracted light as well.
3
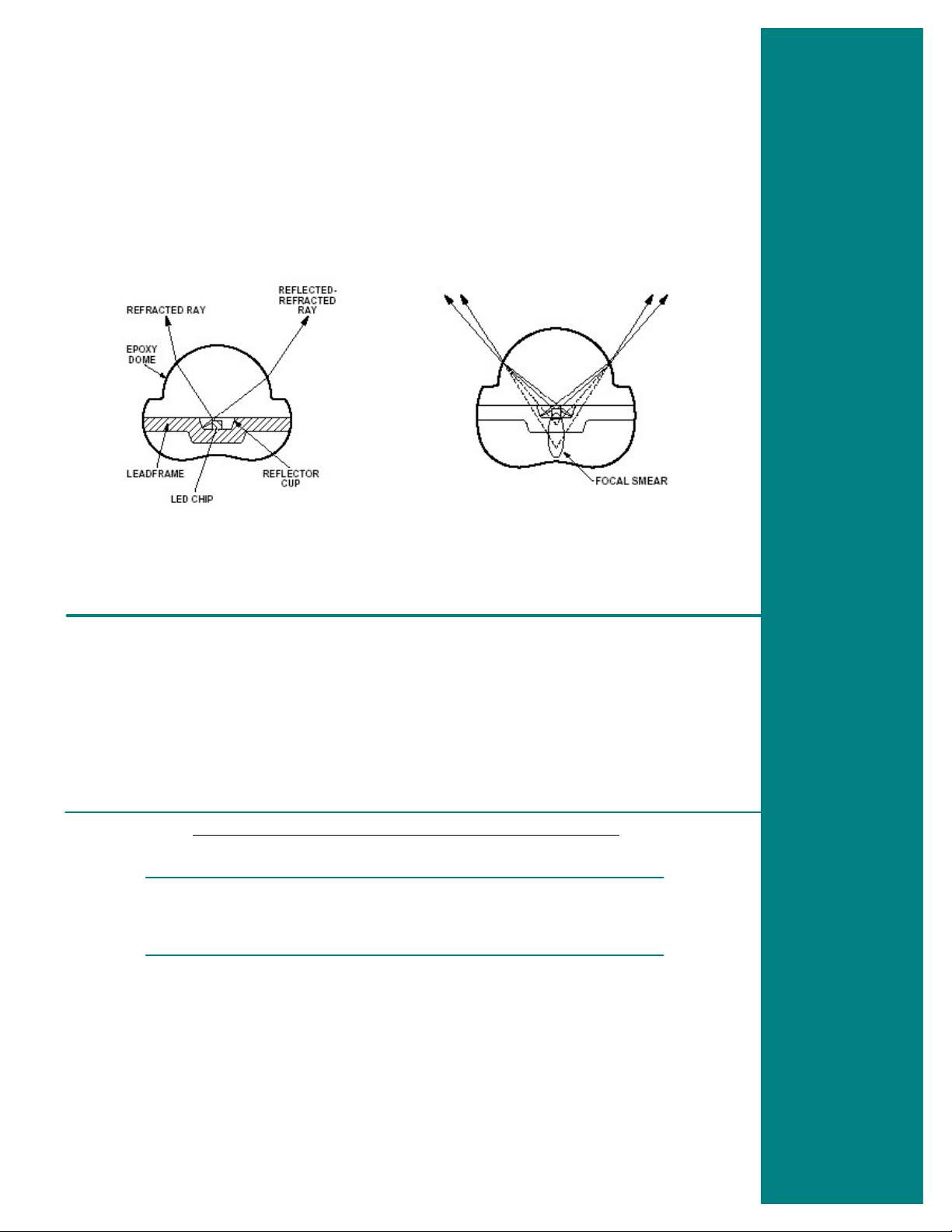
These focal smears overlap, creating an
elongated focal smear as shown in Figure 5.4.
To create the best approximation using a point
source model, the center point of the focal
smears should be chosen as the location of the
points source; and the aperture size should be
equal to that of the epoxy dome at its base as
shown in Figure 5.5.
The optimal position of the point source for each
SuperFlux LED is shown in Table 5.1.
Figure 5.3 Internal structure of a SuperFlux
LED.
Figure 5.4 Focal smear produced by reflected
and reflected-refracted light.
Detailed Optical Models
Detailed optical models of LEDs include all
the internal optical structures within the LED
including the chip, the reflector, and the dome.
In order to accurately construct such a model,
detailed information about the chip, the reflector
surface, and the epoxy encapsulant must be
known. The process usually involves a tedious
trial and error technique of changing parameters
in the model until empirical measurements are
matched.
Table 5.1
HPWA-MxOO 1.03
HPWA-Dx00 1.13
HPWT-Mx00 0.99
HPWT-DxOO 1.17
Due to the complexity of this process, Lumileds
Lighting provides customers with rayset files for
SuperFlux LEDs. The raysets contain spacial
and angular information on a set of rays exiting
the device at the dome surface. These raysets
Position of Point Source for SuperFlux LEDs
SuperFlux LED
Part Number
Position of Point Source
“Z” (mm)
can be used by many optical-modeling software
packages. Contact your local Lumileds
Applications Engineer for more information and
copies of the raysets.
4

Secondary Optics
Figure 5.6 Cross section of an LED signal
This section contains practical design tools for
secondary optic design. More accurate and
sophisticated techniques exist which are beyond
the scope of this application note. The design
methods discussed here are proven, but no
analytical technique can completely replace
empirical testing. Designs should always be
prototyped and tested as early in the design
process as possible.
Secondary optics are used to modify the output
beam of the LED such that the output beam of
the finished signal lamp will efficiently meet the
desired photometric specification. In addition,
secondary optics serve an aesthetic purpose by
determining the lit and unlit appearance of the
signal lamp. The primary optic is included in the
LED package, and the secondary optics are part
of the finished signal lamp. There are two
primary categories of secondary optics used,
those that spread the incoming light (diverging
optics), and those that gather the incoming light
into a collimated beam (collimating optics).
The most common type of diverging optic used
in automotive signal lamp applications is the
pillow lens. The pillow lens spreads the incoming
light into a more divergent beam pattern, and it
breaks up the appearance of the source
resulting in a more uniform appearance. A cross
section of an LED signal lamp with a pillow lens
is shown in Figure 5.6.
Figure 5.5 Point source model of a SuperFlux
LED.
lamp with a pillow lens.
Figure 5.7 Cross section of an LED
signal lamp with a reflector cavity and
pillow lens.
5
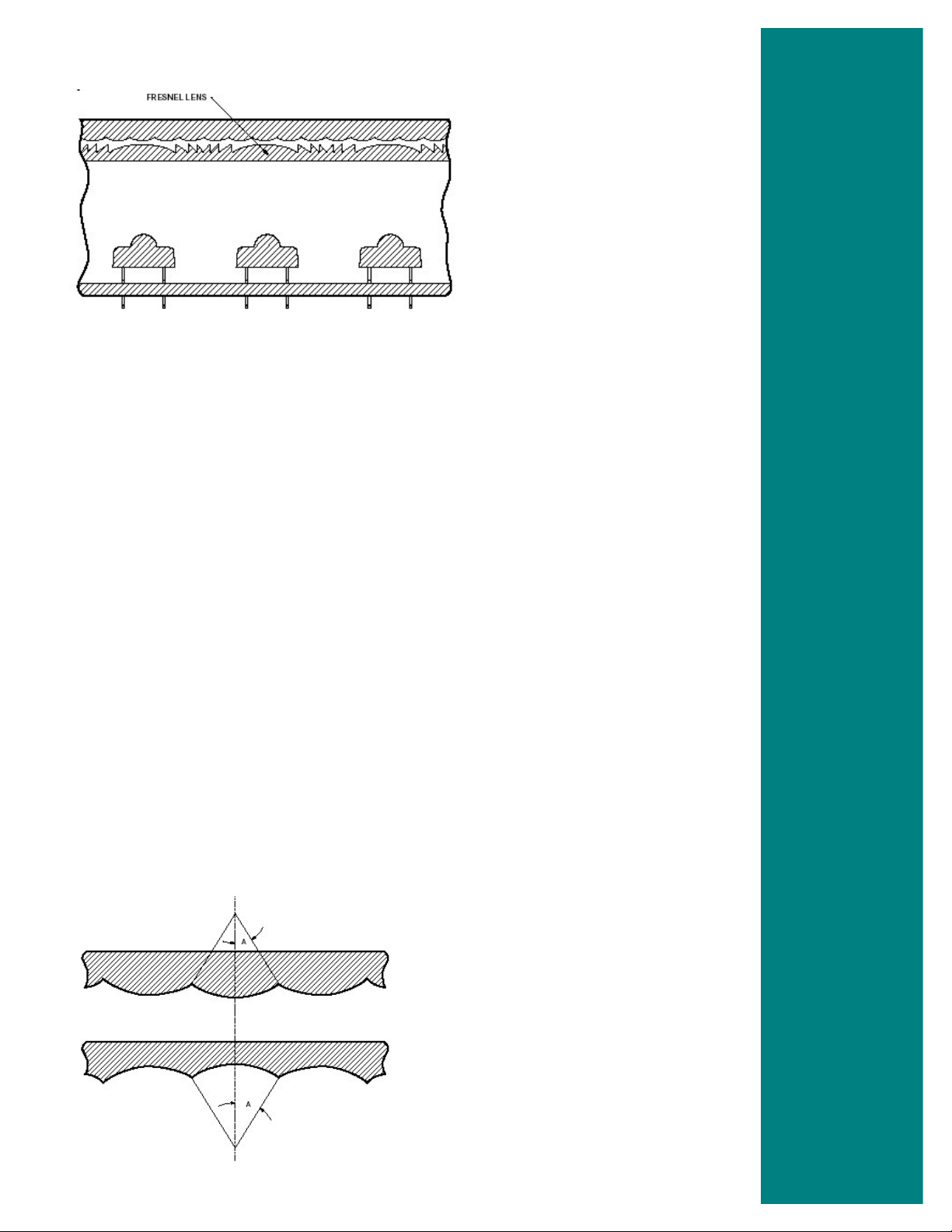
Figure 5.8 Cross section of an LED signal
As the spacing between the pillow and the
LEDs is increased, each LED will illuminate a
larger area of the pillow lens. As the spot
illuminated by each LED grows and as the
adjacent spots begin to overlap, the lens will
appear more evenly illuminated. The trade-off
between lamp depth and lit uniformity is a
common consideration in LED design, where
both unique appearance and space-saving
packages are desired.
Collimating optics come in two main varieties:
reflecting and refracting. Reflecting elements are
typically metalized cavities with a straight or
parabolic profile. A cross section of an LED
signal lamp with a reflector cavity and a pillow
lens is shown in Figure 5.7.
Refracting, collimating optics typically used in
LED signal lamp applications include plano-
convex, dualconvex, and collapsed plano-
convex (Fresnel) lenses. A cross section of an
lamp with Fresnel and pillow lenses.
LED signal lamp with a Fresnel lens and a pillow
lens is shown in Figure 5.8.
In general, designs that use collimating
secondary optics are more efficient, and produce
a more uniform lit appearance than designs
utilizing only pillow or other non-collimating
optics. Fresnel lenses are a good choice for thin
lamp designs and produce a very uniform lit
appearance. Reflectors are a good choice for
thicker lamp designs and are more efficient than
Fresnel lenses at illuminating non-circular areas.
This is because reflectors gather all of the light,
which is emitted as a circular pattern for most
SuperFlux LEDs, and redirect it into the desired
shape. In addition, reflectors can be used to
create a unique, “jeweled” appearance in both
the on and off states.
The dependency of reflector height on reflector
efficiency will be covered later in this section.
Figure 5.9 Half-angle subtended by an individual
pillow (A) for convex (upper) and concave (lower)
pillow lenses.
6
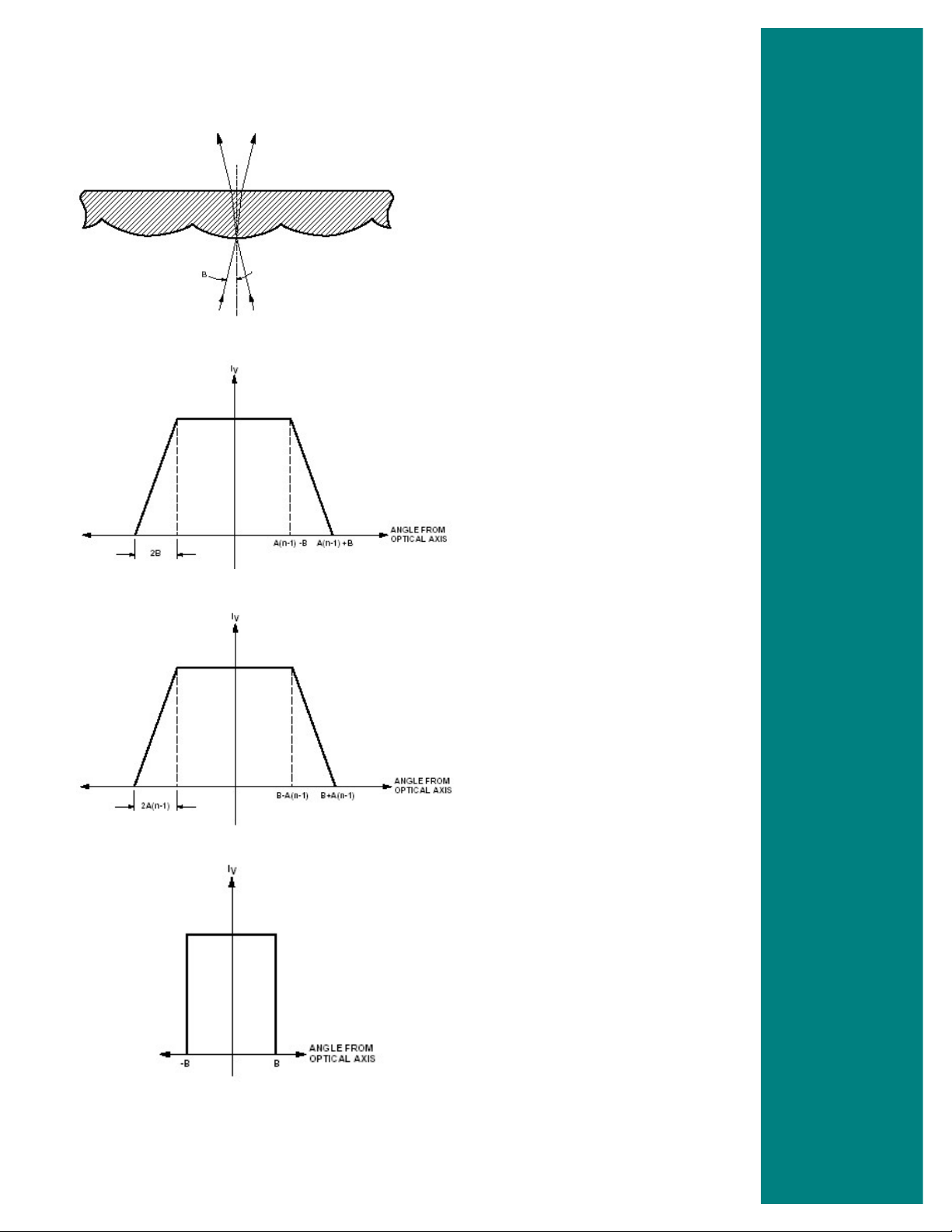
A(n
A(n
Figure 5.10 Half-angle divergence of the
input beam (B).
Figure 5.11 Ideal radiation pattern
produced by a pillow optic where
-1) > B.
7
Figure 5.12 Ideal radiation pattern
produced by a pillow optic where
-1) < B.
Figure 5.13 Ideal input beam with halfangle divergence B.
 Loading...
Loading...