Sas BASIC ANALYSIS AND GRAPHING RELEASE 9 User Manual

Download

Basic Analysis

and Graphing

Get the Most from JMP

Whether you are a first-time or a long-time user, there is always something to learn about JMP.

Visit JMP.com and to find the following:

• live and recorded Webcasts about how to get started with JMP

• video demos and Webcasts of new features and advanced techniques

• schedules for seminars being held in your area

• success stories showing how others use JMP

• a blog with tips, tricks, and stories from JMP staff

• a forum to discuss JMP with other users

http://www.jmp.com/getstarted/

Release 9

Basic Analysis

and Graphing

“The real voyage of discovery consists not in seeking new

landscapes, but in having new eyes.”

Marcel Proust

JMP, A Business Unit of SAS SAS Campus Drive Cary, NC 27513

The correct bibliographic citation for this manual is as follows: SAS Institute Inc. 2009. JMP® 9 Basic Analysis and Graphing. Cary, NC: SAS Institute Inc.

JMP

9 Basic Analysis and Graphing,

ISBN 978-1-60764-596-2

For a hard-copy book: No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, or otherwise, without the prior written permission of the publisher, SAS Institute Inc.

For a Web download or e-book: Your use of this publication shall be governed by the terms established by the vendor at the time you acquire this publication.

U.S. Government Restricted Rights Notice: Use, duplication, or disclosure of this software and related documentation by the U.S. government is subject to the Agreement with SAS Institute and the restrictions set forth in FAR 52.227-19, Commercial Computer Software-Restricted Rights (June 1987).

SAS Institute Inc., SAS Campus Drive, Cary, North Carolina 27513.

1st printing, September 2010

JMP®, SAS® and all other SAS Institute Inc. product or service names are registered trademarks or trademarks of SAS Institute Inc. in the USA and other countries. ® indicates USA registration.

Other brand and product names are registered trademarks or trademarks of their respective companies.

1 Preliminaries

Introducing JMP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

Prerequisites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

JMP Terminology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Learning about JMP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

About JMP Documentation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Use JMP Help . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

Use Tutorials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

Access Sample Data Tables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

Learn About Statistical and JSL Terms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

Learn JMP Tips and Tricks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Access Resources on the Web . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Conventions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Use JMP Platforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8

Work with Multiple Data Tables and Platforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

How JMP Platforms Are Designed . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Process for Analyzing Data Using Platforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Contents

JMP Basic Analysis and Graphing

Common Features Throughout Platforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

Launch Window Features . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

Script Menus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

Automatic Recalc Feature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

2 Performing Univariate Analysis

Using the Distribution Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

Overview of the Distribution Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

Categorical Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

Continuous Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

Example of the Distribution Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

Launch the Distribution Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

The Distribution Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

Histograms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

Resize Histogram Bars for Continuous Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

Highlight Bars and Select Rows . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

Specify Your Selection in Multiple Histograms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

Initial Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

The Frequencies Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

The Quantiles Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

The Moments Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

Distribution Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

Options for Categorical Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

Display Options for Categorical Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

Histogram Options for Categorical Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

Mosaic Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35

Test Probabilities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

Confidence Intervals for Categorical Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

Save Commands for Categorical Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

Options for Continuous Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

Display Options for Continuous Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

Histogram Options for Continuous Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

Normal Quantile Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42

Outlier Box Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43

Quantile Box Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45

Stem and Leaf . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

CDF Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

Tes t M e a n . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48

Tes t S t d D e v . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50

Confidence Intervals for Continuous Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51

Save Commands for Continuous Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52

Prediction Intervals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .54

Tolerance Intervals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .55

Capability Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .57

Fit Distributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61

Example of Fitting a Lognormal Distribution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61

Continuous Fit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62

Discrete Fit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69

Fit Distribution Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71

Statistical Details . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77

Statistical Details for Quantiles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77

Statistical Details for Prediction Intervals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78

Statistical Details for Tolerance Intervals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78

Statistical Details for Capability Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79

3 Introduction to the Fit Y by X Platform

Performing Four Types of Analyses . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83

Overview of the Fit Y by X Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85

Launch the Fit Y by X Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85

Launch Specific Analyses from the JMP Starter Window . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86

4 Performing Bivariate Analysis

Using the Fit Y by X or Bivariate Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87

Example of Bivariate Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

Launch the Bivariate Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

Example of a Bivariate Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90

iii

Overview of Fitting Commands and General Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91

Fitting Command Categories . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92

Fit the Same Command Multiple Times . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93

Fit Mean . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93

Fit Mean Menu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94

Fit Mean Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94

Fit Line and Fit Polynomial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95

Linear Fit and Polynomial Fit Menus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95

Linear Fit and Polynomial Fit Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96

Fit Special . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

Fit Special Reports and Menus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105

Fit Spline . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106

Smoothing Spline Fit Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107

Smoothing Spline Fit Menu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108

Fit Each Value . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108

Fit Each Value Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108

Fit Each Value Menu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109

Fit Orthogonal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109

Fit Orthogonal Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109

Example of a Scenario Using the Fit Orthogonal Command . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111

Orthogonal Regression Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112

Orthogonal Fit Ratio Menu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112

Density Ellipse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112

Correlation Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113

Bivariate Normal Ellipse Menu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114

Nonpar Density . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114

Nonparametric Bivariate Density Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115

Quantile Density Contours Menu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115

Histogram Borders . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116

Group By . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116

Example of Group By Using Density Ellipses . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116

Example of Group By Using Regression Lines . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117

Fitting Menus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118

Fitting Menu Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119

Statistical Details . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .122

Fit Line . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122

Fit Spline . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123

Fit Orthogonal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123

5 Performing Oneway Analysis

Using the Fit Y by X or Oneway Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125

Overview of Oneway Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127

Example of Oneway Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127

Launch the Oneway Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129

The Oneway Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129

Oneway Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130

Display Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134

Quantiles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136

Example of the Quantiles Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 136

Means/Anova and Means/Anova/Pooled t . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138

Examples of the Means/Anova and the Means/Anova/Pooled t Options . . . . . . . . . . . . . . . . . . . . 138

The Summary of Fit Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 139

The t-test Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 140

The Analysis of Variance Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 142

The Means for Oneway Anova Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143

The Block Means Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144

Mean Diamonds and X-Axis Proportional . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144

Mean Lines, Error Bars, and Standard Deviation Lines . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145

Analysis of Means Methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146

Compare Means . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147

Compare Standard Deviations (or Variances) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147

Analysis of Means Charts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148

Analysis of Means Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149

Compare Means . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 150

Using Comparison Circles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151

Each Pair, Student’s t . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153

All Pairs, Tukey HSD . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155

With Best, Hsu MCB . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157

With Control, Dunnett’s . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 159

Compare the Four Tests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 160

Compare Means Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161

Nonparametric . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162

Nonparametric Report Descriptions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 164

Unequal Variances . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 167

Example of the Unequal Variances Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 168

Equivalence Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172

Example of an Equivalence Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172

Power . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173

Example of the Power Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173

Normal Quantile Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176

Example of a Normal Quantile Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 176

CDF Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177

Example of a CDF Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177

Densities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178

Example of the Densities Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178

Matching Column . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 180

Example of the Matching Column Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 180

Statistical Details . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .182

Comparison Circles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 182

Power . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183

6 Performing Contingency Analysis

Using the Fit Y by X or Contingency Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 185

Example of Contingency Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 187

Launch the Contingency Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 188

The Contingency Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 188

Contingency Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 189

Mosaic Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191

Context Menu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192

Te s t s . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 195

Fisher’s Exact Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 197

Analysis of Means for Proportions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 197

Example of Analysis of Means for Proportions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 197

Correspondence Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 199

Understanding Correspondence Analysis Plots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 199

Example of Correspondence Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 199

Correspondence Analysis Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201

The Details Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 202

Additional Example of Correspondence Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 204

Cochran-Mantel-Haenszel Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206

Example of a Cochran Mantel Haenszel Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206

Agreement Statistic . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 207

Example of the Agreement Statistic Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 207

Relative Risk . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209

Example of the Relative Risk Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 209

Two Sample Test for Proportions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 211

Example of a Two Sample Test for Proportions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 211

Measures of Association . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 212

Example of the Measures of Association Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 213

Cochran Armitage Trend Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 214

Example of the Cochran Armitage Trend Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 214

Exact Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 215

Statistical Details for the Agreement Statistic Option . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 216

7 Performing Simple Logistic Regression

Using the Fit Y by X or Logistic Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 219

Overview of Logistic Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 221

Nominal Logistic Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 221

Ordinal Logistic Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 221

Example of Nominal Logistic Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 221

Launch the Logistic Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223

Logistic Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223

Logistic Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 225

Iterations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 225

Whole Model Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 225

Parameter Estimates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 227

Logistic Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 228

ROC Curves . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 229

Save Probability Formula . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231

Inverse Prediction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231

vii

Example of Ordinal Logistic Regression . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 233

Additional Example of a Logistic Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 235

8 Comparing Paired Data

Using the Matched Pairs Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239

Overview of the Matched Pairs Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 241

Example of Comparing Matched Pairs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 241

Launch the Matched Pairs Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 242

Multiple Y Columns . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 243

The Matched Pairs Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 243

Difference Plot and Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 244

Across Groups . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 244

Matched Pairs Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 245

Example of Comparing Matched Pairs Across Groups . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 246

viii

Statistical Details . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 247

Graphics for Matched Pairs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 247

Correlation of Responses . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249

Comparison of Matched Pairs Analysis to Other t-Tests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249

9 Interactive Data Visualization

Using Graph Builder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 253

Overview of Graph Builder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255

Example Using Graph Builder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255

Launch Graph Builder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 261

The Graph Builder Window . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 262

Platform Buttons . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264

Graph Builder Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264

Graph Builder Right-Click Menus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264

Add Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268

Example of Adding Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 268

Move Grouping Variable Labels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270

Separate Variables into Groups . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270

Change Variable Roles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 271

Use the Swap Command . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 271

Use the Clicking and Dragging Method to Change Variable Roles . . . . . . . . . . . . . . . . . . . . . . . . 272

Remove Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .272

Use the Remove Command . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 272

Use the Clicking and Dragging Method to Remove Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . 273

Add Multiple Variables to the X or Y Zone . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 274

Example of Adding Multiple Variables to the X or Y Zone . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 275

Merge Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 276

Order Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 277

Replace Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 280

Create a Second Y Axis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 280

Add Multiple Variables to Grouping Zones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 282

Example of Adding Multiple Variables to Grouping Zones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 282

Replace Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 284

Order Grouping Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 285

Modify the Legend . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 285

Create Map Shapes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 286

Example of Creating Map Shapes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 286

Built-in Map Files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 287

Create Custom Map Files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 288

Additional Examples Using Graph Builder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 289

Measure Global Oil Consumption and Production . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 289

Analyze Popcorn Yield . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 296

Examine Diamond Characteristics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 301

10 Creating Summary Charts

Using the Chart Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 305

Example of the Chart Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 307

Launch the Chart Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 309

Plot Statistics for Y Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 312

Use Categorical Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 313

Use Grouping Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 314

Adding Error Bars . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 316

The Chart Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 317

Legends . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 317

Ordering . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 318

Coloring Bars in a Chart . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 318

Chart Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 319

General Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 319

Y Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 321

Examples of Charts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 321

Plot a Single Statistic . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 322

Plot Multiple Statistics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 322

Plot Counts of Variable Levels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 323

Plot Multiple Statistics with Two X Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 325

Create a Stacked Bar Chart . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 326

Create a Pie Chart . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 327

Create a Range Chart . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 329

Create a Chart with Ranges and Lines for Statistics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 330

11 Creating Overlay Plots

Using the Overlay Plot Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 333

Example of an Overlay Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335

Launch the Overlay Plot Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 336

The Overlay Plot Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 337

Overlay Plot Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 338

General Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 338

Y Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 341

Additional Examples of Overlay Plots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 342

Function Plots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 342

Plotting Two or More Variables with a Second Y-axis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 343

Grouping Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 345

12 Creating Three-Dimensional Scatterplots

Using the Scatterplot 3D Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 347

Example of a 3D Scatterplot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 349

Launch the Scatterplot 3D Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 350

The Scatterplot 3D Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 351

Spin the 3D Scatterplot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 352

Change Variables on the Axes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 352

Adjust the Axes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 353

Assign Colors and Markers to Data Points . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 354

Assign Colors and Markers in the Data Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 354

Scatterplot 3D Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 355

Normal Contour Ellipsoids . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 357

Nonparametric Density Contours . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 359

Context Menu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 364

13 Creating Contour Plots

Using the Contour Plot Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 367

Example of a Contour Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 369

Launch the Contour Plot Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 369

The Contour Plot Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 371

Contour Plot Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 371

Fill Areas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 372

Contour Specification . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 373

Contour Plot Save Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 375

Use Formulas for Specifying Contours . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 375

14 Creating Bubble Plots

Using the Bubble Plot Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 377

Example of a Dynamic Bubble Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 379

Launch the Bubble Plot Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 380

Interact with the Bubble Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 382

Control Animation for Dynamic Bubble Plots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 383

Specify a Time or ID Variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 384

Select Bubbles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 388

Use the Brush Tool . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 389

Bubble Plot Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 389

Show Roles . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 390

Additional Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 392

Example of a Static Bubble Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 392

Example of a Bubble Plot with a Categorical Y Variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 396

15 Creating Cell-Based Plots

Using the Parallel and Cell Plot Platforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 399

Example of a Parallel Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 401

Launch the Parallel Plot Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 402

The Parallel Plot Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 403

Interpreting Parallel Plots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 404

Parallel Plot Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 405

Additional Examples of Parallel Plots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 406

Examine Iris Measurements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 406

Examine Student Measurements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 407

Example of a Cell Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 409

Launch the Cell Plot Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 410

The Cell Plot Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 410

Cell Plot Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 411

Context Menu for Cell Plots . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 412

Additional Example of a Cell Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 413

16 Creating Tree Maps

Using the Tree Map Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 415

Example of Tree Maps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 417

xii

Launch the Tree Map Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 419

Categories . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 420

Sizes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 421

Ordering . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 422

Coloring . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 424

Tree Map Report Window . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 426

Tree Map Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 427

Context Menu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 428

Additional Tree Map Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 428

Examine Pollution Levels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 428

Examine Causes of Failure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 430

Examine Patterns in Car Safety . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 431

17 Creating Scatterplot Matrices

Using the Scatterplot Matrix Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 435

Example of a Scatterplot Matrix . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 437

Launch the Scatterplot Matrix Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 437

Change the Matrix Format . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 439

The Scatterplot Matrix Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 440

Scatterplot Matrix Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 441

Example Using a Grouping Variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 442

Create a Grouping Variable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 444

18 Creating Ternary Plots

Using the Ternary Plot Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 445

Example of a Ternary Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 447

Launch the Ternary Plot Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 449

The Ternary Plot Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 450

Mixtures and Constraints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 450

Ternary Plot Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 451

Example of Using a Contour Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 452

Index

Basic Analysis and Graphing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 465

Credits and Acknowledgments

Origin

JMP was developed by SAS Institute Inc., Cary, NC. JMP is not a part of the SAS System, though portions of JMP were adapted from routines in the SAS System, particularly for linear algebra and probability calculations. Version 1 of JMP went into production in October 1989.

Credits

JMP was conceived and started by John Sall. Design and development were done by John Sall, Chung-Wei Ng, Michael Hecht, Richard Potter, Brian Corcoran, Annie Dudley Zangi, Bradley Jones, Craige Hales, Chris Gotwalt, Paul Nelson, Xan Gregg, Jianfeng Ding, Eric Hill, John Schroedl, Laura Lancaster, Scott McQuiggan, Melinda Thielbar, Clay Barker, Peng Liu, Dave Barbour, Jeff Polzin, John Ponte, and Steve Amerige.

In the SAS Institute Technical Support division, Duane Hayes, Wendy Murphrey, Rosemary Lucas, Win LeDinh, Bobby Riggs, Glen Grimme, Sue Walsh, Mike Stockstill, Kathleen Kiernan, and Liz Edwards provide technical support.

Nicole Jones, Kyoko Keener, Hui Di, Joseph Morgan, Wenjun Bao, Fang Chen, Susan Shao, Yusuke Ono, Michael Crotty, Jong-Seok Lee, Tonya Mauldin, Audrey Ventura, Ani Eloyan, Bo Meng, and Sequola McNeill provide ongoing quality assurance. Additional testing and technical support are provided by Noriki Inoue, Kyoko Takenaka, and Masakazu Okada from SAS Japan.

Bob Hickey and Jim Borek are the release engineers.

The JMP books were written by Ann Lehman, Lee Creighton, John Sall, Bradley Jones, Erin Vang, Melanie Drake, Meredith Blackwelder, Diane Perhac, Jonathan Gatlin, Susan Conaghan, and Sheila Loring, with contributions from Annie Dudley Zangi and Brian Corcoran. Creative services and production was done by SAS Publications. Melanie Drake implemented the Help system.

Jon Weisz and Jeff Perkinson provided project management. Also thanks to Lou Valente, Ian Cox, Mark Bailey, and Malcolm Moore for technical advice.

Thanks also to Georges Guirguis, Warren Sarle, Gordon Johnston, Duane Hayes, Russell Wolfinger, Randall Tobias, Robert N. Rodriguez, Ying So, Warren Kuhfeld, George MacKensie, Bob Lucas, Warren Kuhfeld, Mike Leonard, and Padraic Neville for statistical R&D support. Thanks are also due to Doug Melzer, Bryan Wolfe, Vincent DelGobbo, Biff Beers, Russell Gonsalves, Mitchel Soltys, Dave Mackie, and Stephanie Smith, who helped us get started with SAS Foundation Services from JMP.

Acknowledgments

We owe special gratitude to the people that encouraged us to start JMP, to the alpha and beta testers of JMP, and to the reviewers of the documentation. In particular we thank Michael Benson, Howard

xiv

Yetter (d), Andy Mauromoustakos, Al Best, Stan Young, Robert Muenchen, Lenore Herzenberg, Ramon Leon, Tom Lange, Homer Hegedus, Skip Weed, Michael Emptage, Pat Spagan, Paul Wenz, Mike Bowen, Lori Gates, Georgia Morgan, David Tanaka, Zoe Jewell, Sky Alibhai, David Coleman, Linda Blazek, Michael Friendly, Joe Hockman, Frank Shen, J.H. Goodman, David Iklé, Barry Hembree, Dan Obermiller, Jeff Sweeney, Lynn Vanatta, and Kris Ghosh.

Also, we thank Dick DeVeaux, Gray McQuarrie, Robert Stine, George Fraction, Avigdor Cahaner, José Ramirez, Gudmunder Axelsson, Al Fulmer, Cary Tuckfield, Ron Thisted, Nancy McDermott, Veronica Czitrom, Tom Johnson, Cy Wegman, Paul Dwyer, DaRon Huffaker, Kevin Norwood, Mike Thompson, Jack Reese, Francois Mainville, and John Wass.

We also thank the following individuals for expert advice in their statistical specialties: R. Hocking and P. Spector for advice on effective hypotheses; Robert Mee for screening design generators; Roselinde Kessels for advice on choice experiments; Greg Piepel, Peter Goos, J. Stuart Hunter, Dennis Lin, Doug Montgomery, and Chris Nachtsheim for advice on design of experiments; Jason Hsu for advice on multiple comparisons methods (not all of which we were able to incorporate in JMP); Ralph O’Brien for advice on homogeneity of variance tests; Ralph O’Brien and S. Paul Wright for advice on statistical power; Keith Muller for advice in multivariate methods, Harry Martz, Wayne Nelson, Ramon Leon, Dave Trindade, Paul Tobias, and William Q. Meeker for advice on reliability plots; Lijian Yang and J.S. Marron for bivariate smoothing design; George Milliken and Yurii Bulavski for development of mixed models; Will Potts and Cathy Maahs-Fladung for data mining; Clay Thompson for advice on contour plotting algorithms; and Tom Little, Damon Stoddard, Blanton Godfrey, Tim Clapp, and Joe Ficalora for advice in the area of Six Sigma; and Josef Schmee and Alan Bowman for advice on simulation and tolerance design.

For sample data, thanks to Patrice Strahle for Pareto examples, the Texas air control board for the pollution data, and David Coleman for the pollen (eureka) data.

Translations

Trish O'Grady coordinates localization. Special thanks to Noriki Inoue, Kyoko Takenaka, Masakazu Okada, Naohiro Masukawa and Yusuke Ono (SAS Japan); and Professor Toshiro Haga (retired, Tokyo University of Science) and Professor Hirohiko Asano (Tokyo Metropolitan University) for reviewing our Japanese translation; Professors Fengshan Bai, Xuan Lu, and Jianguo Li at Tsinghua University in Beijing, and their assistants Rui Guo, Shan Jiang, Zhicheng Wan, and Qiang Zhao; and William Zhou (SAS China) and Zhongguo Zheng, professor at Peking University, for reviewing the Simplified Chinese translation; Jacques Goupy (consultant, ReConFor) and Olivier Nuñez (professor, Universidad Carlos III de Madrid) for reviewing the French translation; Dr. Byung Chun Kim (professor, Korea Advanced Institute of Science and Technology) and Duk-Hyun Ko (SAS Korea) for reviewing the Korean translation; Bertram Schäfer and David Meintrup (consultants, StatCon) for reviewing the German translation; Patrizia Omodei, Maria Scaccabarozzi, and Letizia Bazzani (SAS Italy) for reviewing the Italian translation. Finally, thanks to all the members of our outstanding translation teams.

Past Support

Many people were important in the evolution of JMP. Special thanks to David DeLong, Mary Cole, Kristin Nauta, Aaron Walker, Ike Walker, Eric Gjertsen, Dave Tilley, Ruth Lee, Annette Sanders, Tim Christensen, Eric Wasserman, Charles Soper, Wenjie Bao, and Junji Kishimoto. Thanks to SAS Institute quality assurance by Jeanne Martin, Fouad Younan, and Frank Lassiter. Additional testing for Versions 3 and 4 was done by Li Yang, Brenda Sun, Katrina Hauser, and Andrea Ritter.

Also thanks to Jenny Kendall, John Hansen, Eddie Routten, David Schlotzhauer, and James Mulherin. Thanks to Steve Shack, Greg Weier, and Maura Stokes for testing JMP Version 1.

Thanks for support from Charles Shipp, Harold Gugel (d), Jim Winters, Matthew Lay, Tim Rey, Rubin Gabriel, Brian Ruff, William Lisowski, David Morganstein, Tom Esposito, Susan West, Chris Fehily, Dan Chilko, Jim Shook, Ken Bodner, Rick Blahunka, Dana C. Aultman, and William Fehlner.

Technology License Notices

WARRANTIES WITH REGARD TO THIS SOFTWARE, INCLUDING ALL IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS, IN NO EVENT SHALL NEIL HODGSON BE LIABLE FOR ANY SPECIAL, INDIRECT OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.

TO THIS SOFTWARE, INCLUDING ALL IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS, IN NO EVENT SHALL KEITH PACKARD BE LIABLE FOR ANY SPECIAL, INDIRECT OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.

KEITH PACKARD DISCLAIMS ALL WARRANTIES WITH REGARD

NEIL HODGSON DISCLAIMS ALL

xvi

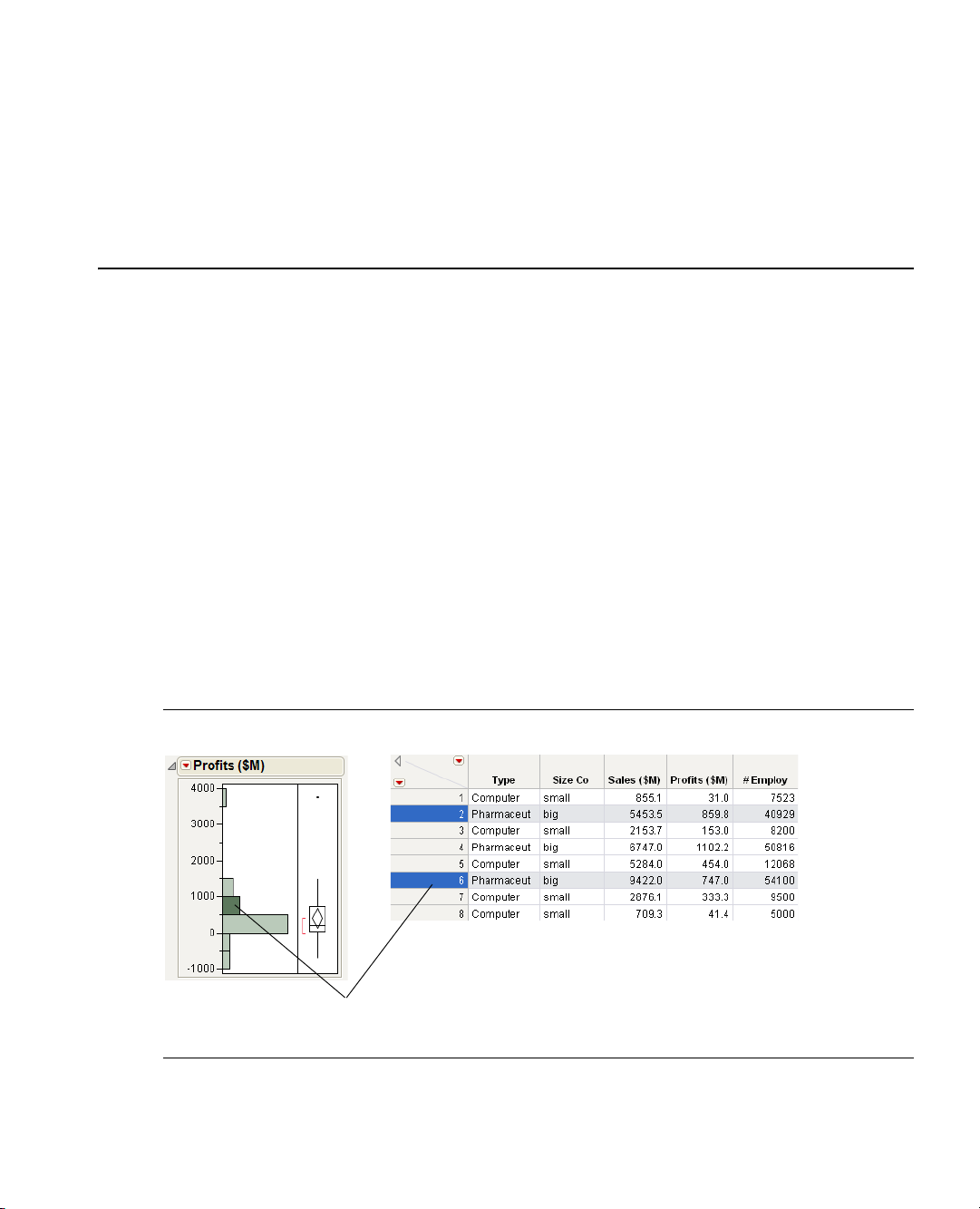
Chapter 1

Clicking on a histogram bar highlights the corresponding data in the associated data table.

Preliminaries

Introducing JMP

Using JMP statistical software, you can interact with your graphs and data to do the following:

Discover Using graphics, you can see patterns and relationships in your data, and find data that does

not fit identifiable patterns.

Interact Using JMP interactive features, you can follow up on clues and try different approaches. The

more approaches you try, the more you likely you are to discover trends in your data.

Understand Using graphics, you can see how the data and the model work together to produce the

statistics. Because JMP is a progressively disclosed system, you learn statistics methods in the right context.

Here are just a few of the things you can do with JMP:

• Interact with data tables and reports.

• Compute values using the Formula Editor.

• Design experiments.

• Use scripting features to automate frequently used processes.

• Open SAS data sets, run stored processes, and submit SAS code.

Figure 1.1 Interacting with JMP

Contents

Prerequisites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

JMP Terminology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Learning about JMP . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

About JMP Documentation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

Use JMP Help . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

Use Tutorials . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

Access Sample Data Tables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

Learn About Statistical and JSL Terms. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

Learn JMP Tips and Tricks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Access Resources on the Web. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Conventions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Use JMP Platforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Work with Multiple Data Tables and Platforms. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

How JMP Platforms Are Designed . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Process for Analyzing Data Using Platforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Common Features Throughout Platforms. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

Launch Window Features . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

Script Menus. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

Automatic Recalc Feature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .17

Chapter 1 Preliminaries 3

Prerequisites

Before you begin using JMP, note the following information:

• You can use many JMP features, such as data manipulation, graphs, and scripting features, without any statistical knowledge.

• A basic understanding of central statistical concepts, such as mean and variation, is recommended.

• Analytical features require statistical knowledge appropriate for the feature.

JMP Terminology

• You can enter, view, edit, and manipulate data using data tables. In a data table, each variable is a column, and each observation is a row.

• You can access a platform from the that you can use to analyze data and work with graphs.

• Platforms use these windows:

– Launch windows where you set up and run your analysis.

– Report windows showing the output of your analysis.

• Report windows normally contain the following items:

– A graph of some type (such as a scatterplot or a chart).

–Specific reports that you can show or hide using the disclosure button .

–Platform options that are located within red triangle menus .

Analyze and Graph menus. Platforms contain interactive windows

For more about platforms, see “Use JMP Platforms,” p. 8.

Learning about JMP

JMP provides numerous resources to help you learn about the software. Most of them can be found within the

Help menu. You can also access context-sensitive Help from within JMP.

Note: For further information about all of the options in the Help menu, see Using JMP.

About JMP Documentation

You can view the JMP documentation suite by selecting Help > Books.

Table 1.1 describes documents in the JMP documentation suite and the purpose of each document.

4 Preliminaries Chapter 1

Learning about JMP

Ta bl e 1 .1 About JMP Documentation

Document Who Should Read This

Document

Discovering JMP If you are not familiar with

JMP, start here.

Using JMP If you want to understand

JMP data tables and how to perform basic operations in JMP, start here.

Basic Analysis and Graphing

If you want to perform basic analysis and graphing functions.

What this Document Covers

Introduces you to JMP and gets you started using JMP

• General JMP concepts and features that span across all of JMP

• Material in these JMP Starter categories: File, Tables, and SAS

• These Analyze platforms:

– Distribution

–Fit Y by X

–Matched Pairs

• Many basic graphing platforms

• Material in these JMP Starter categories: Basic and Graph

Chapter 1 Preliminaries 5

Learning about JMP

Ta bl e 1 .1 About JMP Documentation (Continued)

Document Who Should Read This

Document

Modeling and Multivariate Methods

If you want to perform modeling or multivariate methods

What this Document Covers

• These Analyze platforms:

–Fit Model

– Screening

–Nonlinear

–Neural

– Gaussian Process

– Partition

– Time Series

– Categorical

– Choice

– Multivariate

– Cluster

– Principal Components

– Discriminant

– PLS (Partial Least Squares)

–Item Analysis

• These Graph platforms:

–Profilers

–Surface Plot

• Material in these JMP Starter categories: Model, Multivariate, and Surface

6 Preliminaries Chapter 1

Learning about JMP

Ta bl e 1 .1 About JMP Documentation (Continued)

Document Who Should Read This

Document

Quality and Reliability Methods

If you want to perform quality control or reliability engineering

Design of Experiments If you want to design

experiments

What this Document Covers

• Life Distribution

• Fit Life by X

•Recurrence Analysis

• Degradation

• Survival

• Fit Parametric Survival

• Fit Proportional Hazards

• These Graph platforms:

– Variability/Gauge Chart

– Control Charts

– Capability

– Pareto Plot

– Diagram (Ishikawa)

• Material in these JMP Starter window categories: Reliability, Measure, and Control

• Everything related to the

DOE menu

• Material in this JMP Starter window category: DOE

Scripting Guide If you want to use the JMP

In addition, the New Features document is available at http://jmp.com/support/downloads/

documentation.shtml.

Note: The Books menu also contains two reference cards: The JMP Menu Card describes JMP menus, and the JMP Quick Reference Card describes JMP keyboard shortcuts. You can print these for ease of use.

Use JMP Help

You can access JMP Help in two ways:

• Access the context-sensitive Help by selecting the Help tool from the tool anywhere in a data table or report window to see the Help for that area.

• Within a window, click on the

A reference guide for using JSL commands

Scripting Language (JSL)

Tools menu. Place the Help

Help button.

Chapter 1 Preliminaries 7

Learning about JMP

Search and view JMP Help using the Help > Contents, Search, and Index options.

Use Tutorials

You can access JMP tutorials by selecting Help > Tutorials. The first item on the Tutorials menu is the

Tutorials Directory. This opens a new window with all the tutorials grouped by category.

If you are not familiar with JMP, then start with the interface and explains the basics of using JMP.

The rest of the tutorials help you with specific aspects of JMP, such as creating a pie chart, using Graph Builder, and so on.

Access Sample Data Tables

All of the examples in the JMP documentation suite use sample data. To access JMP’s sample data tables, select

Help > Sample Data. From here, you can do the following:

• Open the sample data directory.

• Open an alphabetized list of all sample data tables.

• Find a sample data table within a category.

Alternatively, the sample data tables are installed in the following directory:

On Windows:

C:\Program Files\SAS\JMP\9\Support Files <language>\Sample Data

On Macintosh: \Library\Application Support\JMP\9\<language>\Sample Data

Learn About Statistical and JSL Terms

The Help menu contains the following indexes:

Ta bl e 1 .2 Descriptions of Help Menu Indexes

Beginners Tutorial. It steps you through the JMP

Statistics Index

JSL Functions

Object Scripting

Provides definitions of statistical terms.

Provides definitions of JSL functions.

Provides a list of JSL scriptable objects and the messages that can be sent to those objects.

DisplayBox Scripting

Provides a list of the JSL objects that comprise a JMP report.

For more details about these indexes, see Using JMP.

8 Preliminaries Chapter 1

Conventions

Learn JMP Tips and Tricks

When you first start JMP, you see the Tip of the Day window.

To turn off the Tip of the Day, clear the

Help > Tip of the Day. Or, you can turn it off using the Preferences window. See the Using JMP book.

You can use the JMP Quick Reference Card to learn more advanced commands in JMP. View this document by selecting

Help > Books > JMP Quick Reference Card.

Access Resources on the Web

To access JMP resources on the Web, select Help > JMP.com or Help > JMP User Community.

The

JMP.com option takes you to the JMP Web site, and the JMP User Community option takes you to

JMP online user forums.

Conventions

The following conventions help you relate written material to information that you see on your screen.

• Most open data table names that are used in examples appear in

Animals.jmp) in this document. References to variable names in data tables and items in reports also

appear in

• Note: Special information, warnings, and limitations are noted as such in boldface.

• Reference to menu names (

• Words or phrases that are important or have definitions specific to JMP are in italics the first time they occur in the text. For example, the word platform is in italics the first time you see it. Most words in italics are defined when they are first used unless clear in the context of use.

Helvetica according to the way they appear on the screen or in the documentation.

File menu) or menu items (Save option) appear in Helvetica bold.

Show tips at startup check box. To view it again, select

Helvetica font (Animals or

Use JMP Platforms

JMP uses many statistical methods that are organized and consolidated into the platforms within the

Analyze and Graph menus.

Work with Multiple Data Tables and Platforms

As mentioned earlier, platforms use interactive windows that help you analyze data and work with graphs. You can have any number of data tables open at the same time and any number of platforms open for each data table. If you have several data tables open, then the platform that you launch analyzes the current data table. The current data table is either the active data table window or the table corresponding to the current report window.

Chapter 1 Preliminaries 9

Use JMP Platforms

How JMP Platforms Are Designed

Before you use JMP’s statistical platforms, note the following design aspects of JMP:

• JMP implements general methods that are consistent with its key concepts. Although platforms produce a variety of results that handle many situations, all platforms are consistent in their treatment of data and statistical concepts.

• JMP methods are generic. They adapt themselves to the context at hand. The principal concept that drives analyses is modeling type. For details, see “Assign Mod e ling Type s , ” p. 9. For example, JMP automatically analyzes a variable with nominal values differently than it analyzes a variable with continuous values.

• JMP platforms give you almost everything that you need at once. If this is more information than you want, you can conceal the reports or graphs that you do not need. The advantage is that there is less need to search for statistical commands.

Process for Analyzing Data Using Platforms

To begin analyzing your data, proceed as follows:

1. With your data table open, assign or change modeling types, as needed. See “Assign Modeling Types,”

p. 9.

2. Choose an analysis and launch the corresponding platform. See “Choose an Analysis and Launching a

Platform,” p. 11.

3. Complete the launch window. See “Complete a Launch Window,” p. 11.

4. View the report window. See “View a Report Window,” p. 11.

Assign Modeling Types

Note: For more details about working with modeling types, see Using JMP.

The modeling type of a variable can be one of the following types, shown with its corresponding icon:

• Continuous

•Ordinal

• Nominal

When you import data into JMP, it predicts which modeling types to use. Character data is considered nominal, and numeric data is considered continuous. However, you might want to change the modeling type, depending on which type of analysis you are performing.

To change the modeling type, click on the modeling type icon next to the variable and make your selection.

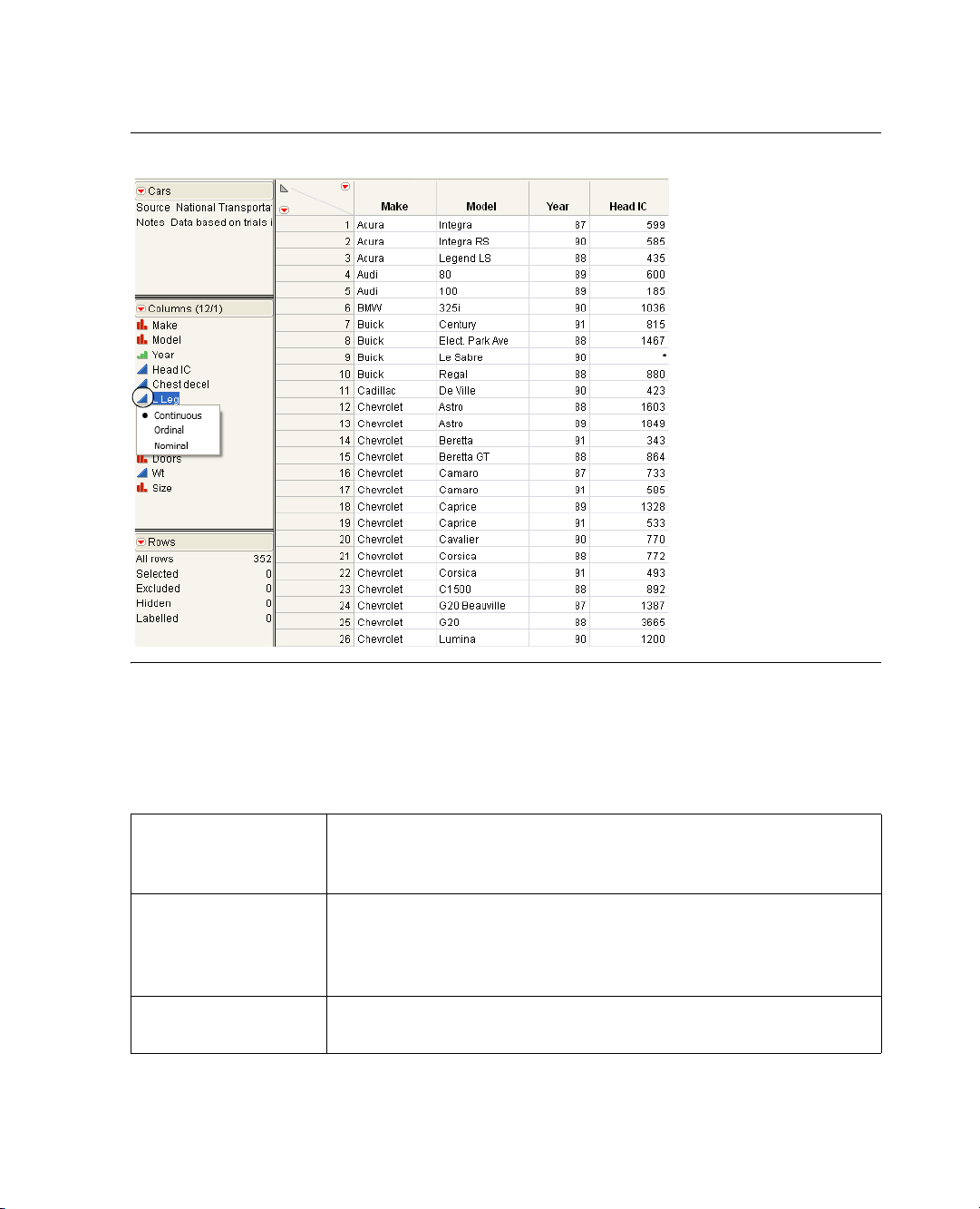
10 Preliminaries Chapter 1

Use JMP Platforms

Figure 1.2 Changing Modeling Type

About Modeling Types

The modeling type tells JMP how to treat its values during analyses. Changing the modeling type lets you look at a variable in different ways in an analysis.

Ta bl e 1 .3 Descriptions of Modeling Types

Continuous

Columns can contain only numeric data types. Continuous values are treated as continuous measurement values. JMP uses the numeric values directly in computations.

Ordinal

Columns can contain either numeric or character data types. JMP analyses treat ordinal values as discrete categorical values that have an order. If the values are numbers, the order is the numeric magnitude. If the values are character, the order is the sorting sequence.

Nominal

Columns can contain either numeric or character data types. All values are treated in JMP analyses as if they are discrete values with no implicit order.

Chapter 1 Preliminaries 11

Use JMP Platforms

Choose an Analysis and Launching a Platform

Choose the analysis that you want to perform. You can launch a platform from the (or from the JMP Starter window).

Table 1.4 provides just a few examples of choosing an analysis and launching the corresponding platform. For a full list of the platforms available within the

Ta bl e 1 .4 Examples of Choosing an Analysis and Launching a Platform

Purpose Analysis

Analyze a distribution of values

Analyze the relationship between two variables

Graph continuous X and Y variables

Animate points on a scatterplot over time

Complete a Launch Window

After you launch a platform, the launch window appears. See Figure 1.3. Use the launch window to set up your analysis by moving columns into roles.

Figure 1.3 The Launch Window (Distribution Platform)

Analyze or Graph menu

Analyze and Graph menus, see Using JMP.

Analyze > Distribution

Analyze > Fit Y by X

Graph > Overlay Plot

Graph > Bubble Plot

For more details about the launch window, see “Launch Window Features,” p. 13.

View a Report Window

Once you have completed the launch window (which runs the analysis) you see a report window. For example, see Figure 1.4. You can use the output in the report window to interpret your data.

12 Preliminaries Chapter 1

Use JMP Platforms

Figure 1.4 Example of a Report Window (Distribution Platform)

• (Windows only) The JMP main menu bar is hidden by default. To see the JMP main menu bar, hover over the bar below the window title. Alternatively, you can always show the main menu bar by changing the Auto-hide menu and toolbars option in

File > Preferences > Windows Specific.

For more general information about using report windows, see Using JMP.

• For detailed information about a specific platform’s report window, see the chapter for that platform in this book, or in one of these books:

– Modeling and Multivariate Methods

– Quality and Reliability Methods

Chapter 1 Preliminaries 13

Use JMP Platforms

Common Features Throughout Platforms

All platforms share certain specific features, documented in these sections:

• “Launch Window Features,” p. 13

• “Script Menus,” p. 15

• “Automatic Recalc Feature,” p. 17

Note: Platforms have additional shared features that are not covered here, such as linked graphs, red triangle menus, and hierarchical report organization. See Using JMP.

Launch Window Features

Each analysis platform prompts you with a launch window. Table 1.5 describes three panes that all launch windows have in common.

Ta bl e 1 .5 Descriptions of Common Panes in Launch Windows

Select Columns

Lists all of the variables in your current data table. For details about the red triangle menu, see “Columns Filter

Menu,” p. 14.

Cast Selected Columns into Roles

Moves selected columns into roles (such as Y, X, and so on.) You cast a column into the role of a variable (like an actor is cast into a role). See “Cast Selected Columns

into Roles Buttons,” p. 13.

This pane does not exist in the Graph Builder platform.

Action

Cancel stops the analysis and quits the launch window.

Remove deletes any selected variables from a role.

Recall populates the launch window with the last

analysis that you performed.

Help takes you to the Help for the launch window.

Cast Selected Columns into Roles Buttons

Table 1.6 describes buttons that appear frequently throughout launch windows. Buttons that are specific to certain platforms are described in the chapter for the platform.

performs the analysis.

14 Preliminaries Chapter 1

Use JMP Platforms

Ta bl e 1 .6 Descriptions of Common Buttons in Launch Windows

Weight

Freq

Columns Filter Menu

In most of the platform launch windows there is a Column Filter menu. This menu appears as a red triangle within the Select Columns panel.

Figure 1.5 Example of the Columns Filter Menu

Identifies a column as a response or dependent variable whose distribution is to be studied.

Identifies a column as an independent, classification, or explanatory variable whose values divide the rows into sample groups.

Identifies the data table column whose variables assign weight (such as importance or influence) to the data.

Identifies the data table column whose values assign a frequency to each row. This option is useful when a frequency is assigned to each row in summarized data.

Identifies a column that creates a report consisting of separate analyses for each level of the variable.

Ta bl e 1 .7 Options within the Columns Filter Menu

Reset

Sort by Name

Continuous

Ordinal

Nominal

Resets the columns to its original list.

Sorts the columns in alphabetical order by name.

Shows or hides columns whose modeling type is continuous.

Shows or hides columns whose modeling type is ordinal.

Shows or hides columns whose modeling type is nominal.

Chapter 1 Preliminaries 15

Use JMP Platforms

Ta bl e 1 .7 Options within the Columns Filter Menu

Numeric

Character

Match case

Name Contains

Name Starts With

Name Ends With

Script Menus

The red triangle menu at the top level of every JMP report contains a Script menu.

Figure 1.6 The Script menu

Shows or hides columns whose data type is numeric.

Shows or hides columns whose data type is character.

(Only applicable to the Name options below) Makes your search case-sensitive.

Searches for column names containing specified text. To remove the text box, select

Reset.

Searches for column names that begin with specified text. To remove the text box, select

Reset.

Searches for column names that end with specified text. To remove the text box, select

Reset.

Most of these options are the same throughout JMP. A few platforms add extra options that are described in the specific platform chapters. Table 1.8 lists the Script menu options that are common to all platforms.

Ta bl e 1 .8 Descriptions of Script Options

Redo Analysis

If the values in the data table that was used to produce the report have changed, this option duplicates the analysis based on the new data. The new analysis appears in a new report window.

16 Preliminaries Chapter 1

Use JMP Platforms

Ta bl e 1 .8 Descriptions of Script Options (Continued)

Relaunch Analysis

Automatic Recalc

Copy Script

Save Script to Data Table

Save Script to Journal

Save Script to Script Window

Save Script to Report

Save Script for All Objects

Save Script to Project

Opens the platform Launch window and recalls the settings used to create the report.

Automatically updates analyses and graphics when data table values change. See “Automatic Recalc Feature,” p. 17.

Places the script that reproduces the report on the clipboard so that it can be pasted elsewhere.

Saves the script to the data table that was used to produce the report.

Saves a button that runs the script in a journal. The script is added to the current journal.

Opens a script editor window and adds the script to it. If you have already saved a script to a script window, additional scripts are added to the bottom of the same script window.

Adds the script to the top of the report window.

If you have By groups or similar multiple reports, a script for each object is saved to the script window. Otherwise, this option is the same as

Save Script to Script Window.

Saves the script in a project. If you have a project open that contains the report, the script is added to that project. If you do not have a project that contains the report, a new project is created and the script is added to it.

Data Table Window

Brings the data table that was used to create the report to the front and makes it the active window.

If you have specified a By variable in the platform launch window, the Script All By-Groups menu also appears.

Figure 1.7 Example of the Script All By-Groups Menu

Chapter 1 Preliminaries 17

Use JMP Platforms

If you specified a By variable, the script options in Table 1.8 apply to a report for a single level of a By variable. The

Ta bl e 1 .9 Descriptions of Script All By-Groups Options

Script All By-Groups options apply to the reports for all the levels of the By variable.

Redo Analysis

Relaunch Analysis

Copy Script

Save Script to Data Table

Save Script to Journal

Save Script to Script Window

Automatic Recalc Feature

The Automatic Recalc feature immediately reflects changes that you make to the data table in the corresponding report window. You can make any of the following data table changes:

• exclude or unexclude data table rows

• delete or add data table rows

If the values in the data table that was used to produce the reports have changed, this option duplicates the analysis based on the new data and produces new reports.

Opens the platform Launch window and recalls the settings used to create the reports.

Places the script that reproduces the reports on the clipboard so that it can be pasted elsewhere.

Saves the script to the data table that was used to produce the reports.

Saves a button that runs the script in a journal. The script is added to the current journal.

Opens a script editor window and adds the script to it. If you have already saved a script to a script window, additional scripts are added to the bottom of the same script window.

This powerful feature immediately reflects these changes to the corresponding analyses, statistics, and graphs that are located in a report window.

To t ur n o n

Script > Automatic Recalc. See Figure 1.6. To turn it off, deselect the same option. You can also turn on Automatic Recalc using JSL.

Automatic Recalc for a report window, click on the platform red triangle menu and select

Note the following:

• By default, platforms in the

Chart > Run Chart

•For some platforms, the

Automatic Recalc is turned off for platforms in the Analyze menu and turned on for

Graph menu. The exceptions are the Capability, Variability/Gauge Chart, and Control

platforms.

Automatic Recalc feature is not appropriate, and therefore is not supported.

These platforms include the following: DOE, Profilers, Choice, Partition, Nonlinear, Neural, Neural Net, Partial Least Squares, Fit Model (REML, GLM, Log Variance), Gaussian Process, Item Analysis, Cox Proportional Hazard, and Control Charts (except Run Chart).

18 Preliminaries Chapter 1

Use JMP Platforms

Chapter 2

Performing Univariate Analysis

Using the Distribution Platform

The Distribution platform describes the distribution of variables using histograms, additional graphs, and reports. You can examine the distribution of several variables at once. The report content for each variable varies, depending on whether the variable is categorical (nominal or ordinal) or continuous.

The Distribution report window is interactive. Clicking on a histogram bar highlights the corresponding data in any other histograms and in the data table. See Figure 2.1.

Figure 2.1 Example of the Distribution Platform

Contents

Overview of the Distribution Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21

Example of the Distribution Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .21

Launch the Distribution Platform . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .23

The Distribution Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

Histograms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

Initial Reports . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

The Frequencies Report. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

The Quantiles Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

The Moments Report . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32

Distribution Platform Options . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .34

Options for Categorical Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .34

Mosaic Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .35

Test Probabilities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .36

Confidence Intervals for Categorical Variables. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .39

Options for Continuous Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .39

Normal Quantile Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42

Outlier Box Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .43

Quantile Box Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .45

Stem and Leaf . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

CDF Plot . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

Tes t M e a n . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 48

Tes t S t d D e v . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50

Confidence Intervals for Continuous Variables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51

Prediction Intervals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .54

Tolerance Intervals. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .55

Capability Analysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .57

Fit Distributions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .61

Example of Fitting a Lognormal Distribution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .61

Statistical Details. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77

Chapter 2 Performing Univariate Analysis 21

Overview of the Distribution Platform

The treatment of variables in the Distribution platform is different, depending on the modeling type of variable, which can be categorical (nominal or ordinal) or continuous.

Categorical Variables

For categorical variables, the initial graph that appears is a histogram. The histogram shows a bar for each level of the ordinal or nominal variable. You can also add a divided (mosaic) bar chart.

The reports show counts and proportions. You can add confidence intervals and test the probabilities.

Continuous Variables

For numeric continuous variables, the initial graphs show a histogram and an outlier box plot. The histogram shows a bar for grouped values of the continuous variable. The following options are also available:

• quantile box plot

• normal quantile plot

• stem and leaf plot

•CDF plot

• overlaid nonparametric smoothing curve

The reports show selected quantiles and moments. Report options are available for the following:

• saving ranks, probability scores, normal quantile values, and so on, as new columns in the data table

• testing the mean and standard deviation of the column against a constant you specify

• fitting various distributions

• performing a capability analysis for a quality control application

• confidence intervals, prediction intervals, and tolerance intervals

Example of the Distribution Platform

Suppose that you have data on 40 students, and you want to see the distribution of age and height among the students.

1. Open the

2. Select

3. Select

4. Click

Big Class.jmp sample data table.

Analyze > Distribution.

age and height and click Y, Co l u mn s .

OK.

22 Performing Univariate Analysis Chapter 2

Example of the Distribution Platform

Figure 2.2 Example of the Distribution Platform

From the histograms, you notice the following:

• The ages are not uniformly distributed.

• For height, there are two points with extreme values (that might be outliers).

Click on the bar for 50 in the height histogram to take a closer look at the potential outliers.

• The corresponding ages are highlighted in the age histogram. The potential outliers are age 12.

• The corresponding rows are highlighted in the data table. The names of the potential outliers are Lillie and Robert.

Add labels to the potential outliers in the height histogram.

1. Select both outliers.

2. Right-click on one of the outliers and select

Row Label.

Label icons are added to these rows in the data table.

3. (Optional) Resize the box plot wider to see the full labels.

Chapter 2 Performing Univariate Analysis 23

Example of the Distribution Platform

Figure 2.3 Potential Outliers Labeled

Launch the Distribution Platform

Launch the Distribution platform by selecting Analyze > Distribution.

Figure 2.4 The Distribution Launch Window

Ta bl e 2 .1 Description of the Distribution Launch Window

Y, C o lu m n s

Assigns the variables that you want to analyze. A histogram and associated reports appear for each variable.

Weight

Assigns a variable to give the observations different weights. Any moment that is based on the Sum Wgts is affected by weights (including the Mean, Std Err Mean, and Upper and Lower 95% Mean).

24 Performing Univariate Analysis Chapter 2

The Distribution Report

Ta bl e 2 .1 Description of the Distribution Launch Window (Continued)

Freq

Histograms Only

The Distribution Report

Follow the instructions in “Example of the Distribution Platform,” p. 21 to produce the report shown in Figure 2.5.

The Distribution report window is divided into variables. For each variable, the initial Distribution report contains a histogram and reports.

Assigns a frequency variable to this role. This is useful if you have summarized data. In this instance, you have one column for the Y values and another column for the frequency of occurrence of the Y values. The sum of this variable is included in the overall count appearing in the Moments report (represented by deviation, and so on) are also affected by the

N). All other moment statistics (mean, standard

Freq variable.

Produces a separate report for each level of the By variable. If more than one

By variables is assigned, a separate report is produced for each possible

combination of the levels of the

By variables.

Removes everything except the histograms from the report window, which includes the following:

• Quantiles and Moments reports for continuous variables

• Frequencies report for nominal and ordinal variables

• Outlier box plot

Chapter 2 Performing Univariate Analysis 25

The Distribution Report

Figure 2.5 The Initial Distribution Report Window

Ta bl e 2 .2 Descriptions of Distribution Report Window Objects

Platform options The red triangle menu next to Distributions contains options that affect all

of the variables. See “Distribution Platform Options,” p. 34.

Variable options The red triangle menu next to each variable contains options that affect only

that variable. See “Options for Categorical Variables,” p. 34 or “Options for

Continuous Variables,” p. 39.

Note: If you hold down the CTRL key and select a variable option, the option applies to all of the variables that have the same modeling type.

Histograms Histograms visually display your data. See “Histograms,” p. 26.

26 Performing Univariate Analysis Chapter 2

Histograms

Ta bl e 2 .2 Descriptions of Distribution Report Window Objects (Continued)

Reports Each variable contains at least initial reports. Continuous variables contain a

Quantiles and a Moments report; categorical variables contain a Frequencies report. See “Initial Reports,” p. 29. Variable options can create additional reports.

Histograms

Histograms visually display your data. For categorical (nominal or ordinal) variables, the histogram shows a bar for each level of the ordinal or nominal variable. For continuous variables, the histogram shows a bar for grouped values of the continuous variable.

Ta bl e 2 .3 Interacting with the Histogram

Highlighting data Click on a histogram bar or an outlying point in the graph. The

corresponding rows are highlighted in the data table, and corresponding sections of other histograms are also highlighted, if applicable. See “Highlight Bars and Select Rows,” p. 27.

Creating a subset Double-click on a histogram bar, or right-click on a histogram bar and

select

Subset. A new data table is created that contains only the

selected data.

Resizing the entire histogram Hover over the histogram borders until you see a double-sided arrow.

Then click and drag the borders. For more details, see the Using JMP book.

Rescaling the axis (Continuous variables only) Click and drag on an axis to rescale it.

Alternatively, hover over the axis until you see a hand. Then, double-click on the axis and set the parameters in the Axis Specification window.

Resizing histogram bars (Continuous variables only) There are multiple options to resize

histogram bars. See “Resize Histogram Bars for Continuous Variables,”

p. 27.

Specifying your selection Specify the data that you select in multiple histograms. See “Specify

Your Selection in Multiple Histograms,” p. 28.

To see additional options for the histogram or the associated data table:

• Right-click on a histogram. See the Using JMP book.

• Click on the red triangle next to the variable, and select

Histogram Options. Options are slightly

different depending on the variable modeling type. See “Histogram Options for Categorical Variables,”

p. 35 or “Histogram Options for Continuous Variables,” p. 40.

Chapter 2 Performing Univariate Analysis 27

Histograms

Resize Histogram Bars for Continuous Variables

Resize histogram bars for continuous variables by using the following:

• the Grabber (hand) tool

• the Set Bin Width option

• the Increment option

Use the Grabber Tool

The Grabber tool is a quick way to explore your data.

1. Select

Tools > Grabber.

Note: (Windows only) To see the menu bar, you might need to hover over the bar below the window title.

You can also change this setting in File > Preferences > Windows Specific.

2. Place the grabber tool anywhere in the histogram.

3. Click and drag the histogram bars.

Think of each bar as a bin that holds a number of observations:

• Moving the hand to the left increases the bin width and combines intervals. The number of bars decreases as the bar size increases.

• Moving the hand to the right decreases the bin width, producing more bars.

• Moving the hand up or down shifts the bin locations on the axis, which changes the contents and size of each bin.

Use the Set Bin Width Option

The Set Bin Width option is a more precise way to set the width for all bars in a histogram. To use the Set Bin Width option, from the red triangle menu for the variable, select Change the bin width value.

Use the Increment Option

The Increment option is another precise way to set the bar width. To use the Increment option, double-click on the axis, and change the Increment value.

Histogram Options > Set Bin Width.

Highlight Bars and Select Rows

Clicking on a histogram bar highlights the bar and selects the corresponding rows in the data table. The appropriate portions of all other graphical displays also highlight the selection. Figure 2.6 shows the results of highlighting a bar in the

Note: To deselect histogram bars, press the CTRL key and click on the highlighted bars.

height histogram. The corresponding rows are selected in the data table.

28 Performing Univariate Analysis Chapter 2

Select a bar to highlight rows and parts of other output.

Histograms

Figure 2.6 Highlighting Bars and Rows

Specify Your Selection in Multiple Histograms

Extend or narrow your selection in histograms as follows:

• To extend your selection, hold down the SHIFT key and select another bar. This is the equivalent of

using an or operator.

• To narrow your selection, hold down the ALT key and select another bar. This is the equivalent of using

an and operator.

Example of Selecting Data in Multiple Histograms

1. Open the

2. Select

3. Select

Companies.jmp sample data table.

Analyze > Distribution.

Ty pe and Size Co and click Y, C o lu m ns .

4. Click OK.

You want to see the type distribution of companies that are small.

5. Click on the bar next to small.

You can see that there are more small computer companies than there are pharmaceutical companies. To broaden your selection, add medium companies.

6. Hold down the SHIFT key. In the Size Co histogram, click on the bar next to medium.

You can see the type distribution of small and medium sized companies. See Figure 2.7 at left. To narrow down your selection, you want to see the small and medium pharmaceutical companies only.

7. Hold down the ALT key. In the Type histogram, click in the Pharmaceutical bar.

You can see how many of the small and medium companies are pharmaceutical companies. See Figure 2.7 at right.

Chapter 2 Performing Univariate Analysis 29

Broaden the selection using the SHIFT key.

Narrow the selection using the ALT key.

Initial Reports

Figure 2.7 Selecting Data in Multiple Histograms

Initial Reports

When you complete the Distribution launch window, the following reports appear automatically (unless other preferences are in effect):

• “The Frequencies Report,” p. 29

• “The Quantiles Report,” p. 31

• “The Moments Report,” p. 32

The Frequencies Report

For nominal and ordinal variables, the Frequencies report lists the levels of the variables, along with the associated frequency of occurrence and probabilities.

Example of a Frequencies Report

1. Open the

2. Select

3. Select

4. Click OK.

VA Lung Cancer.jmp sample data table.

Analyze > Distribution.

Cell Type and click Y, C o l u mn s .

30 Performing Univariate Analysis Chapter 2

Initial Reports

Figure 2.8 Example of a Frequencies Report

For each level of a categorical (nominal or ordinal) variable, the Frequencies report contains the information described in Table 2.4. Missing values are omitted from the analysis.

Ta bl e 2 .4 Description of the Frequencies Report

Level Lists each value found for a response variable.

Count Lists the number of rows found for each level of a response variable. If you

use a Freq variable (see Figure 2.4), the Count is the sum of the Freq variables for each level of the response variable.

Prob Lists the probability (or proportion) of occurrence for each level of a

response variable. The probability is computed as the count divided by the total frequency of the variable, shown at the bottom of the table.

StdErr Prob Lists the standard error of the probabilities. This column might be hidden.

To show the column, right-click in the table and select

Prob

Columns > StdErr

Cum Prob Contains the cumulative sum of the column of probabilities. This column

might be hidden. To show the column, right-click in the table and select

Columns > Cum Prob.

Chapter 2 Performing Univariate Analysis 31

Initial Reports

The Quantiles Report

For continuous variables, the Quantiles report lists the values of selected quantiles (sometimes called percentiles).

Example of a Quantiles Report

1. Open the

2. Select

3. Select

4. Click

Figure 2.9 Example of a Quantiles Report

Cities.jmp sample data table.

Analyze > Distribution.

OZONE and click Y, C o l um n s.

OK.

For details about how quantiles are computed, see “Statistical Details for Quantiles,” p. 77.

32 Performing Univariate Analysis Chapter 2

Initial Reports

The Moments Report

For continuous variables, the Moments report displays the mean, standard deviation, and other summary statistics.

Example of a Moments Report

1. Open the

2. Select

3. Select

4. Click

Figure 2.10 Example of a Moments Report

Cities.jmp sample data table.

Analyze > Distribution.

OZONE and click Y, C o l um n s.

OK.

Ta bl e 2 .5 Description of the Moments Report

Mean Estimates the expected value of the underlying distribution for the response

variable, which is the arithmetic average of the column’s values. It is the sum of the nonmissing values divided by the number of nonmissing values. If you assigned a Weight or Freq variable, the mean is computed by JMP as follows:

1. Each column value is multiplied by its corresponding weight or freq

2. These values are added and divided by the sum of the weights or freqs.

Chapter 2 Performing Univariate Analysis 33

ss2 where =

wiyiyw–()

N 1–

-----------------------------

i 1=



weighed mean=

Initial Reports

Ta bl e 2 .5 Description of the Moments Report (Continued)

Std Dev Measures the spread of a distribution around the mean. It is often denoted as

s and is the square root of the sample variance, denoted s

The normal distribution is mainly defined by the mean and standard deviation. These parameters provide an easy way to summarize data as the sample becomes large:

• 68% of the values are within one standard deviation of the mean

• 95% of the values are within two standard deviations of the mean

• 99.7% of the values are within three standard deviations of the mean

Std Err Mean The standard error of the mean, which estimates the standard deviation of

the distribution of the mean.

Std Err Mean is computed by dividing the

sample standard deviation, s, by the square root of N. In the launch window, if you specified a column for Weight or Freq, then the denominator is the square root of the sum of the weights or frequencies.

Upper 95% Mean and Lower 95% Mean

Are 95% confidence limits about the mean. They define an interval that is very likely to contain the true population mean. If many random samples are drawn from the same population and each 95% confidence interval is determined, you expect 95% of the confidence intervals computed to contain the true population mean.

N Is the total number of nonmissing values.

If you select Display Options > More Moments, additional statistics appear. See “Display Options for

Continuous Variables,” p. 39.

34 Performing Univariate Analysis Chapter 2

Distribution Platform Options

The red triangle menu next to Distributions contains options that affect all of the reports and graphs in the Distribution platform.

Ta bl e 2 .6 Descriptions of Distribution Platform Options

Uniform Scaling

Stack Changes the orientation of the histogram and the reports to horizontal and

Save for Adobe Flash platform (.SWF)

Script This menu contains options that are available to all platforms. They enable

Scales all axes with the same minimum, maximum, and intervals so that the

distributions can be easily compared.

stacks the individual distribution reports vertically. Deselect this option to return the report window to its original layout.

Saves the histograms as .SWF files that are Adobe Flash player compatible. Use these files in presentations and in web pages. An HTML page is also saved that shows you the correct code for using the resulting .SWF file.

For more information about this option, go to http://www.jmp.com/

support/swfhelp/en.

you to redo the analysis or save the JSL commands for the analysis to a window or a file. See “Script Menus,” p. 15 in the “Preliminaries” chapter.

Options for Categorical Variables

The red triangle menus next to each variable in the report window contain additional options that apply to the variable. This section describes the options that are available for categorical (nominal or ordinal) variables.

Note: To see the options that are available for continuous variables, see “Options for Continuous

Variables , ” p . 39.

Display Options for Categorical Variables

Use the Display Options for categorical variables to show or hide the Frequency report and change the orientation of the report.

Ta bl e 2 .7 Descriptions of Display Options for Categorical Variables

Frequencies

Horizontal Layout Changes the orientation of the histogram and the reports to vertical or

Shows or hides the Frequencies report. See “The Frequencies Report,” p. 29.

horizontal.

Chapter 2 Performing Univariate Analysis 35

npi1 pi–()

Options for Categorical Variables

Histogram Options for Categorical Variables

Use the Histogram Options for categorical variables to change various aspects of the histogram, such as orientation, color, size, and so on.

Ta bl e 2 .8 Descriptions of Histogram Options for Categorical Variables

Histogram

Vertical Changes the orientation of the histogram from a vertical to a horizontal

Shows or hides the histogram. See “Histograms,” p. 26.

orientation.

Std Error Bars Draws the standard error bar on each level of the histogram using the

standard error where p

Separate Bars Separates the histogram bars.

Histogram Color Changes the color of the histogram bars.

Count Axis Adds an axis that shows the frequency of column values represented by the

i=ni

/n.

histogram bars.

Note: If you resize the histogram bars, the count axis also resizes.

Prob Axis Adds an axis that shows the proportion of column values represented by

histogram bars.

Note: If you resize the histogram bars, the probability axis also resizes.

Density Axis The density is the length of the bars in the histogram. Both the count and

probability are based on the following calculations:

prob = (bar width)*density

count = (bar width)*density*(total count)

Mosaic Plot

Note: If you resize the histogram bars, the density axis remains constant.

Show Percents Labels the percent of column values represented by each histogram bar.

Show Counts Labels the frequency of column values represented by each histogram bar.

The Mosaic Plot option displays a mosaic bar chart for each nominal or ordinal response variable. A mosaic plot is a stacked bar chart where each segment is proportional to its group’s frequency count.

36 Performing Univariate Analysis Chapter 2

Options for Categorical Variables

Example of a Mosaic Plot

1. Open the

2. Select

3. Select

4. Click

VA Lung Cancer.jmp sample data table.

Analyze > Distribution.

Cell Type and click Y, C o l u mn s .

OK.

5. From the red triangle menu for Cell Type, select

Figure 2.11 Example of a Mosaic Plot

Mosaic Plot.

For a description of the options that appear when you right-click the mosaic plot, see the Using JMP book.

Test Probabilities

Use the Test Probabilities option to enter hypothesized probabilities. The Test Probabilities report contains slightly different options, depending on whether your variable has more than two levels, or exactly two levels. See Figure 2.12.

Examples of the Test Probabilities Option

Initiate a test probability report for a variable with more than two levels:

1. Open the

2. Select Analyze > Distribution.

VA Lung Cancer.jmp sample data table.

Chapter 2 Performing Univariate Analysis 37

report options for a variable with exactly two levels

report options for a variable with more than two levels

Options for Categorical Variables

3. Select Cell Type and click Y, Co l u mn s .

4. Click

5. From the red triangle menu next to Cell Type, select

OK.

Test Probabilities.

See Figure 2.12 at left.

Initiate a test probability report for a variable with exactly two levels:

1. Open the

2. Select

3. Select

4. Click

Penicillin.jmp sample data table.

Analyze > Distribution.

Response and click Y, Co l u mns .

OK.

5. From the red triangle menu next to Response, select

See Figure 2.12 at right.

Figure 2.12 Examples of Test Probabilities Options

Test Probabilities.

The Test Probabilities option scales the hypothesized values that you type, so that the probabilities sum to one. The easiest way to test that all of the probabilities are equal is to type a one in each field. If you want to test a subset of the probabilities, then do not enter a value for any levels that are not involved. JMP substitutes estimated probabilities.

38 Performing Univariate Analysis Chapter 2

Options for Categorical Variables

Generate the Test Probabilities Report

To generate a test probabilities report for a variable with more than two levels:

1. Refer to Figure 2.12 at left. Type 0.25 in all four Hypoth Prob fields.

2. Click the

3. Click

Fix hypothesized values, rescale omitted button.

Done.

Likelihood Ratio and Pearson Chi-square tests are calculated. See Figure 2.13 at left.

To generate a test probabilities report for a variable with exactly two levels:

1. Refer to Figure 2.12 at right. Type 0.5 in both Hypoth Prob fields.

2. Click the

3. Click

probability less than hypothesized value button.

Done.

Exact probabilities are calculated for the binomial test. See Figure 2.13 at right.

Figure 2.13 Examples of Test Probabilities Reports

Chapter 2 Performing Univariate Analysis 39

Options for Continuous Variables

Confidence Intervals for Categorical Variables

Confidence Interval options compute score confidence intervals. The score confidence interval is recommended because it tends to have better coverage probabilities (1 - α), especially with smaller sample sizes (Agresti and Coull 1998).

Save Commands for Categorical Variables

Use the Save options for categorical variables to add level numbers to the data table, and use the Script to log command.

Ta bl e 2 .9 Descriptions of Save Options for Categorical Variables

Level Numbers

Script to log

Creates a new column in the data table called Level <colname>. The level number of each observation corresponds to the histogram bar that contains the observation. The histogram bars are numbered from low to high (or alphabetically) beginning with 1.

In the log window, this option displays the script commands to generate the current report. To see this option, you must have the log window open. Select

View > Log to see the log window.

Options for Continuous Variables

Advanced options for continuous variables are covered in the following sections:

• “Prediction Intervals,” p. 54

• “Tolerance Intervals,” p. 55

• “Capability Analysis,” p. 57

• “Fit Distributions,” p. 61

Note: To see the options that are available for categorical (nominal and ordinal) variables, see “Options for

Categorical Variables,” p. 34.

Display Options for Continuous Variables

Use the Display Options for continuous variables to show, hide, or add reports, or to change the orientation of the report.

40 Performing Univariate Analysis Chapter 2

3 2

-- -

N 1–()N 2–()

------------------------------------



xix–

------------

nn 1+()

n 1–()n 2–()n 3–()

-------------------------------------------------- -

xix–

------------







3 n 1–()

n 2–()n 3–()

--------------------------------- -

–

i 1=



Options for Continuous Variables

Ta bl e 2 .1 0 Descriptions of Display Options for Continuous Variables

Quantiles

Moments

More Moments

Shows or hides the Quantiles report. See “The Quantiles Report,” p. 31.

Shows or hides the Moments report. See “The Moments Report,” p. 32.

An extension of the Moments report that adds the following statistics:

Sum Wgt is the sum of a column assigned to the role of Weight (in the

launch window). Sum Wgt is used in the denominator for computations of the mean instead of N.

Sum is the sum of the response values.

Variance is the sample variance, and the square of the sample

standard deviation.

Skewness measures sidedness or symmetry. It is based on the third

moment about the mean and is computed as follows:

where

is a weight term (= 1 for equally weighted items)

and w

Kurtosis measures peakedness or heaviness of tails. It is based on the

fourth moment about the mean and is computed as follows:

Horizontal Layout

Histogram Options for Continuous Variables

Use the Histogram Options for continuous variables to change various aspects of the histogram, such as orientation, color, size, and so on.

Changes the orientation of the histogram and the reports to vertical or horizontal.

where w

CV is the percent coefficient of variation. It is computed as the

is a weight term (= 1 for equally weighted items)

standard deviation divided by the mean and multiplied by 100. The coefficient of variation can be used to assess relative variation, for example when comparing the variation in data measured in different units or with different magnitudes.

N Missing is the number of missing observations.

Chapter 2 Performing Univariate Analysis 41

Options for Continuous Variables

Ta bl e 2 .1 1 Descriptions of Histogram Options for Continuous Variables

Histogram

Shadowgram

Vertical

Std Error Bars

Set Bin Width

Histogram Color

Shows or hides the histogram. See “Histograms,” p. 26.

Replaces the histogram with a shadowgram. To understand a shadowgram, consider that if the bin width of a histogram is changed, the appearance of the histogram changes. A shadowgram overlays smoothed histograms across a range of bin widths. Dominant features of a distribution are less transparent on the shadowgram.

Note that the following options are not available for shadowgrams:

• Std Error Bars

•Show Counts

•Show Percents

Changes the orientation of the histogram from a vertical to a horizontal orientation.

Draws the standard error bar on each level of the histogram using the standard error. The standard error bar adjusts automatically when you adjust the number of bars with the hand tool (see “Resize Histogram Bars for

Continuous Variables,” p. 27.

Changes the bin width of the histogram bars. See “Resize Histogram Bars for

Continuous Variables,” p. 27.

Changes the color of the histogram bars.

Count Axis

Prob Axis

Adds an axis that shows the frequency of column values represented by the histogram bars.

Note: If you resize the histogram bars, the count axis also resizes.

Adds an axis that shows the proportion of column values represented by histogram bars.

Note: If you resize the histogram bars, the probability axis also resizes.

42 Performing Univariate Analysis Chapter 2

Options for Continuous Variables

Ta bl e 2 .1 1 Descriptions of Histogram Options for Continuous Variables (Continued)

Density Axis

The density is the length of the bars in the histogram. Both the count and probability are based on the following calculations:

When looking at density curves that are added by the Fit Distribution option, the density axis shows the point estimates of the curves.

Note: If you resize the histogram bars, the density axis remains constant.

Show Percents

Show Counts

Labels the proportion of column values represented by each histogram bar.

Labels the frequency of column values represented by each histogram bar.

Normal Quantile Plot

Use the Normal Quantile Plot option to visualize the extent to which the variable is normally distributed. If a variable is normally distributed, the normal quantile plot approximates a diagonal straight line. This type of plot is also called a quantile-quantile plot, or Q-Q plot.

The normal quantile plot also shows Lilliefors confidence bounds (Conover 1980) and probability and normal quantile scales. See Figure 2.14.

Example of a Normal Quantile Plot

prob = (bar width)*density

count = (bar width)*density*(total count)

1. Open the

2. Select

3. Select

4. Click

Cities.jmp sample data table.

Analyze > Distribution.

OZONE and click Y, C o l um n s.

OK.

5. From the red triangle menu next to OZONE, select Normal Quantile Plot.

Chapter 2 Performing Univariate Analysis 43

normal quantile scale

probability scale

Lilliefors confidence bounds

N 1+

-------------

1–

N 1+

-------------





Options for Continuous Variables

Figure 2.14 Example of a Normal Quantile Plot

Note the following information:

•The y-axis shows the column values.

•The x-axis shows the empirical cumulative probability for each value, computed as follows:

where r

is the rank of the ith observation, and N is the number of nonmissing (and nonexcluded)

observations.

• The normal quantile values are computed as follows:

where Φ is the cumulative probability distribution function for the normal distribution.

These normal quantile values are Van Der Waerden approximations to the order statistics that are expected for the normal distribution.

Outlier Box Plot

Use the outlier box plot (also called a Tukey outlier box plot) to see the distribution and identify possible outliers. Generally, box plots show selected quantiles of continuous distributions.

44 Performing Univariate Analysis Chapter 2

median sample value

confidence diamond

1st quartile

3rd quartile

whisker

shortest half

Options for Continuous Variables

Example of an Outlier Box Plot

1. Open the

2. Select

3. Select

4. Click

Figure 2.15 Example of an Outlier Box Plot

Candy Bars.jmp sample data table.

Analyze > Distribution.

Tot a l fa t g and click Y, C o l umn s .

OK.

Note the following aspects about outlier box plots (see Figure 2.15):

• The vertical line within the box represents the median sample value.

• The confidence diamond contains the mean and the upper and lower 95% of the mean. If you drew a line through the middle of the diamond, you would have the mean. The top and bottom points of the diamond represent the upper and lower 95% of the mean.

• The ends of the box represent the 25th and 75th quantiles, also expressed as the 1st and 3rd quartile, respectively.

• The difference between the 1st and 3rd quartiles is called the interquartile range.

• The box has lines that extend from each end, sometimes called whiskers. The whiskers extend from the ends of the box to the outermost data point that falls within the distances computed as follows:

1st quartile - 1.5*(interquartile range)

3rd quartile + 1.5*(interquartile range)

If the data points do not reach the computed ranges, then the whiskers are determined by the upper and lower data point values (not including outliers).

• The bracket outside of the box identifies the shortest half, which is the most dense 50% of the observations (Rousseuw and Leroy 1987).

Chapter 2 Performing Univariate Analysis 45

90%

10%

Options for Continuous Variables

Remove Objects from the Outlier Box Plot

To remove the confidence diamond or the shortest half, proceed as follows:

1. Right-click on the outlier box plot and select

2. Click

Box Plot.

3. Deselect the check box next to

For more details about the Customize Graph window, see the Using JMP book.

Quantile Box Plot

The Quantile Box Plot displays specific quantiles from the Quantiles report. If the distribution is symmetric, the quantiles in the box plot are approximately equidistant from each other. At a glance, you can see if the distribution is symmetric. For example, if the quantile marks are grouped closely at one end, but have greater spacing at the other end, the distribution is skewed toward the end with more spacing. See Figure 2.16.

Example of a Quantile Box Plot

1. Open the

2. Select

3. Select

4. Click

5. From the red triangle menu next to Total fat g, deselect

Candy Bars.jmp sample data table.

Analyze > Distribution.

Tot a l fa t g and click Y, C o l umn s .

OK.

Customize.

Confidence Diamond or Shortest Half.

Outlier Box Plot, and select Quantile Box Plot.

Figure 2.16 Example of a Quantile Box Plot

46 Performing Univariate Analysis Chapter 2

Options for Continuous Variables

Quantiles are values where the pth quantile is larger than p% of the values. For example, 10% of the data lies below the 10th quantile, and 90% of the data lies below the 90th quantile.

Stem and Leaf

The Stem and Leaf option constructs a plot that is a variation on the histogram.

Example of a Stem and Leaf Plot

1. Open the

2. Select

3. Select

4. Click

Candy Bars.jmp sample data table.

Analyze > Distribution.

Tot a l fa t g and click Y, C o l umn s .

OK.

5. From the red triangle menu next to Total fat g, select

Figure 2.17 Example of a Stem and Leaf Plot

Stem and Leaf.

Chapter 2 Performing Univariate Analysis 47

Options for Continuous Variables

Each line of the plot has a Stem value that is the leading digit of a range of column values. The Leaf values are made from the next-in-line digits of the values. You can see the data point by joining the stem and leaf. In some cases, the numbers on the stem and leaf plot are rounded versions of the actual data in the table. The stem-and-leaf plot actively responds to clicking and the brush tool.

CDF Plot

The CDF Plot option creates a plot of the empirical cumulative distribution function. Use the CDF plot to determine the percent of data that is at or below a given value on the x-axis. See Figure 2.18.

Example of a CDF Plot

1. Open the

2. Select

3. Select

4. Click

Candy Bars.jmp sample data table.

Analyze > Distribution.

Tot a l fa t g and click Y, C o l umn s .

OK.

5. From the red triangle menu next to Total fat g, select

Figure 2.18 Example of a CDF Plot

CDF Plot.

48 Performing Univariate Analysis Chapter 2

Options for Continuous Variables

For example, use the crosshair tool and position it at 10 on the x-axis. You can see that about 0.2778 percent of the data is at or below the value of 10.

Test Mean

Use the Test M e an option to perform a one-sample test for the mean. If you type a value for the standard deviation, a z-test is performed. Otherwise, the sample standard deviation is used to perform a t-test. You can also request the nonparametric Wilcoxon Signed-Rank test.

Example of Test Mean

1. Open the

2. Select

3. Select

4. Click

5. From the red triangle next to Total fat g, select

Candy Bars.jmp sample data table.

Analyze > Distribution.

Tot a l fa t g and click Y, C o l umn s .

OK.

Test M e an.

6. In the Test Mean window, type 12 next to Specify Hypothesized Mean.

7. Click

Figure 2.19 Example of the Test Mean Option

OK.

Chapter 2 Performing Univariate Analysis 49

n 20≤

Options for Continuous Variables

Use the Test M e an option repeatedly to test different values. Each time you test the mean, a new Test Mean report appears.

Ta bl e 2 .1 2 Description of the Test Mean Report

Statistics that are calculated for Test Mean

t Test (or z Test) Lists the value of the test statistic and the p-values for the two-sided and

one-sided alternatives.

Signed-Rank (Only appears for the Wilcoxon Signed-Rank test) Lists the value of the

Wilcoxon signed-rank statistic followed by the p-values for the two-sided and one-sided alternatives. The test assumes only that the distribution is symmetric. The Wilcoxon signed-rank test uses average ranks for ties. The p-values are exact for where n is the number of values not equal to the hypothesized value. For n > 20 a Student’s t approximation given by Iman (1974) is used.

Probability values

Prob>|t| The probability of obtaining an absolute t-value by chance alone that is greater

than the observed t-value when the population mean is equal to the hypothesized value. This is the p-value for observed significance of the two-tailed t-test.

Prob>t The probability of obtaining a t-value greater than the computed sample t ratio

by chance alone when the population mean is not different from the hypothesized value. This is the p-value for an upper-tailed test.

Prob<t The probability of obtaining a t-value less than the computed sample t ratio by

chance alone when the population mean is not different from the hypothesized value. This is the p-value for a lower-tailed test.

Red triangle options for Test Mean

PValue animation

Starts an interactive visual representation of the p-value. Enables you to change the hypothesized mean value while watching how the change affects the p-value.

Power animation

Starts an interactive visual representation of power and beta. Enables you to change the hypothesized mean and sample mean while watching how the changes affect power and beta.

Remove Test

Removes the mean test.

50 Performing Univariate Analysis Chapter 2

Options for Continuous Variables

Test Std Dev

Use the Test S t d D e v option to perform a one-sample test for the standard deviation (details in Neter, Wasserman, and Kutner 1990).

Example of Test Std Dev

1. Open the

2. Select

3. Select

4. Click

5. From the red triangle next to Total fat g, select

Candy Bars.jmp sample data table.

Analyze > Distribution.

Tot a l fa t g and click Y, C o l umn s .

OK.

Test S t d De v.

6. In the Test Standard Deviation window, type 4 next to Specify Hypothesized Standard Deviation.

7. Click

Figure 2.20 Example of the Test Std Dev Option

OK.

Use the Test S t d D e v option repeatedly to test different values. Each time you test the standard deviation, a new Test Standard Deviation report appears.

Chapter 2 Performing Univariate Analysis 51

n 1–()s

---------------------

Options for Continuous Variables

Ta bl e 2 .1 3 Description of the Test Std Dev Report

Test Statistic Here is the formula for calculating the Test Statistic:

The Test Statistic is distributed as a Chi-square variable with n - 1 degrees of freedom when the population is normal.

Min PValue The probability of obtaining a greater Chi-square value by chance alone

when the population standard deviation is not different from the hypothesized value. This is the p-value for observed significance of the two-tailed test.

Prob>ChiSq The probability of obtaining a Chi-square value greater than the

computed sample Chi-square by chance alone when the population standard deviation is not different from the hypothesized value. This is the p-value for observed significance of a one-tailed t-test.

Prob<ChiSq The probability of obtaining a Chi-square value less than the computed

sample Chi-square by chance alone when the population standard deviation is not different from the hypothesized value. This is the p-value for observed significance of a one-tailed t-test.

Confidence Intervals for Continuous Variables

The Confidence Interval options display confidence intervals for the mean and standard deviation. The

0.90, 0.95, and 0.99 options compute two-sided confidence intervals for the mean and standard deviation.

Use the confidence intervals. You can also type a known sigma. If you use a known sigma, the confidence interval for the mean is based on z-values rather than t-values.

Example of Confidence Intervals for Continuous Variables

1. Open the

2. Select

3. Select

4. Click

5. From the red triangle next to Total fat g, select

Confidence Interval > Other option to select a confidence level, and select one-sided or two-sided

Candy Bars.jmp sample data table.

Analyze > Distribution.

Tot a l fa t g and click Y, C o l umn s .

OK.

Confidence Interval > 0.95.

52 Performing Univariate Analysis Chapter 2

Options for Continuous Variables

Figure 2.21 Example of a Confidence Interval Report

The Confidence Intervals report shows the mean and standard deviation parameter estimates with upper and lower confidence limits for 1 - α.

Save Commands for Continuous Variables

Use the Save menu commands to save information about continuous variables. Each Save command generates a new column in the current data table. The new column is named by appending the variable name (denoted <

Select the circumstances, such as before and after combining histogram bars. If you use a times, the column name is numbered (name1, name2, and so on) to ensure unique column names.

Ta bl e 2 .1 4 Descriptions of the Save Commands

Command Column Added

Level Numbers

Level Midpoints

colname> in the following definitions) to the Save command name. See Table 2.14.

Save commands repeatedly to save the same information multiple times under different

Description

to Data Table

Level <

colname> The level number of each observation corresponds to the

histogram bar that contains the observation. The histogram bars are numbered from low to high, beginning with 1.

Midpoint <

colname>

The midpoint value for each observation is computed by adding half the level width to the lower level bound.

Save command multiple

Chapter 2 Performing Univariate Analysis 53

1–

N 1+

-------------





XX–

------------

Options for Continuous Variables

Ta bl e 2 .1 4 Descriptions of the Save Commands (Continued)

Command Column Added

to Data Table

Ranks

Ranks Averaged

Prob Scores

Normal Quantiles

Ranked <

colname>

RankAvgd <

colname>

Prob <

colname> For N nonmissing scores, the probability score of a value is

N-Quantile <

colname>

Description

Provides a ranking for each of the corresponding column’s values starting at 1. Duplicate response values are assigned consecutive ranks in order of their occurrence in the data table.

If a value is unique, then the averaged rank is the same as the rank. If a value occurs k times, the average rank is computed as the sum of the value’s ranks divided by k.

computed as the averaged rank of that value divided by N + 1. This column is similar to the empirical cumulative distribution function.

The normal quantile values are computed as follows:

where:

• is the cumulative probability distribution function for the normal distribution

• r

is the rank of the ith observation

• N is the number of nonmissing observations

Standardized

Std <

colname> Creates standardized values for numeric columns with the

formula editor, using the following formula:

where:

• X is the original column

• is the mean of column X

• S

is the standard deviation of column X

Spec Limits

(none) Stores the specification limits applied in a capability analysis

as a column property of the corresponding column in the current data table. Automatically retrieves and displays the specification limits when you repeat the capability analysis.

Script to Log

(none) Prints the script to the log window. Run the script to recreate

the analysis.

54 Performing Univariate Analysis Chapter 2

Prediction Intervals

Prediction intervals concern a single observation, or the mean and standard deviation of the next randomly selected sample. The calculations assume that the given sample is selected randomly from a normal distribution. Select one-sided or two-sided prediction intervals.

When you select the

Prediction Interval option for a variable, the Prediction Intervals window appears. See

Figure 2.22.

Example of Prediction Intervals

1. Open the

2. Select

3. Select

4. Click

Cities.jmp sample data table.

Analyze > Distribution.

OZONE and click Y, C o l um n s.

OK.

5. From the red triangle next to OZONE, select

Figure 2.22 The Prediction Intervals Window

Prediction Interval.

6. In the Prediction Intervals window, type 10 next to Enter number of future samples.

7. Click

OK.

Chapter 2 Performing Univariate Analysis 55

Tolerance Intervals

Figure 2.23 Example of a Prediction Interval Report

In this example, you can be 95% confident about the following:

• Each of the next 10 observations will be between .013755 and .279995.

• The mean of the next 10 observations will be between .115596 and .178154.

• The standard deviation of the next 10 observations will be between .023975 and .069276.

For details about how prediction intervals are computed, see “Statistical Details for Prediction Intervals,”

p. 78.

Tolerance Intervals

A tolerance interval contains at least a specified proportion of the population. It is a confidence interval for a specified proportion of the population, not the mean, or standard deviation. Complete discussions of tolerance intervals are found in Hahn and Meeker (1991) and in Tamhane and Dunlop (2000).

When you select the Figure 2.24. The calculations are based on the assumption that the given sample is selected randomly from a normal distribution. JMP can produce one-sided or two-sided tolerance intervals.

Tolerance Interval option for a variable, the Tolerance Intervals window appears. See

56 Performing Univariate Analysis Chapter 2

Tolerance Intervals

Example of Tolerance Intervals

1. Open the

2. Select

3. Select

4. Click

5. From the red triangle menu next to

Figure 2.24 The Tolerance Intervals Window

Cities.jmp sample data table.

Analyze > Distribution.

OZONE and click Y, C o l um n s.

OK.

OZONE, select Tolerance Interval.

6. Keep the default selections, and click OK.

Figure 2.25 Example of a Tolerance Interval Report

Chapter 2 Performing Univariate Analysis 57

Capability Analysis

In this example, you can be 95% confident that at least 90% of the population lie between .057035 and .236715, based on the Lower TI (tolerance interval) and Upper TI values.

For details about how tolerance intervals are computed, see “Statistical Details for Tolerance Intervals,”

p. 78.

Capability Analysis

The Capability Analysis option measures the conformance of a process to given specification limits. When you select the Figure 2.26.

Example of Capability Analysis

Capability Analysis option for a variable, the Capability Analysis window appears. See

1. Open the

2. Select

3. Select

4. Click

Cities.jmp sample data table.

Analyze > Distribution.

OZONE and click Y, C o l um n s.

OK.

5. From the red triangle menu next to OZONE, select

Figure 2.26 The Capability Analysis Window

6. Type 0 for the Lower Spec Limit.

7. Type 1 for the Targ et .

8. Type 2 for the

9. Keep the rest of the default selections, and click

Upper Spec Limit.

OK.

Capability Analysis.

58 Performing Univariate Analysis Chapter 2

Capability Analysis

Figure 2.27 Example of the Capability Analysis Report

Note: To save the specification limits to the data table as a column property, select Save > Spec Limits. When you repeat the capability analysis, the saved specification limits are automatically retrieved.

The Capability Analysis report is organized into two sections: Capability Analysis and the distribution type (Long Term Sigma, Specified Sigma, and so on).

Capability Analysis Descriptions

Capability Analysis descriptions appear as follows:

• Table 2.15 describes the Capability Analysis window.

• Table 2.16 describes the Capability Analysis report.

• Table 2.17 describes the Capability Analysis red triangle options.

Chapter 2 Performing Univariate Analysis 59

Capability Analysis

Ta bl e 2 .1 5 Description of the Capability Analysis Window

<Distribution type> By default, the normal distribution is assumed when calculating the

capability statistics and the percent out of the specification limits. To perform a capability analysis on non-normal distributions, see the description of Spec Limits under “Fit Distribution Options,” p. 71.

Long Term Sigma

Specified Sigma

Moving Range, Range Span

Short Term Sigma, Group by Fixed Subgroup Size

Ta bl e 2 .1 6 Description of the Capability Analysis Report

Capability Analysis

Calculates capability indices using different estimates for sigma (σ). See “Statistical Details for Capability Analysis,” p. 79.

Specification Lists the specification limits.

Value Lists the values that you specified for each specification limit and the

target.

Portion and % Actual Portion labels describe the numbers in the % Actual column, as follows:

• Below LSL gives the percentage of the data that is below the lower specification limit.

• Above USL gives the percentage of the data that is above the upper specification limit.

• Total Outside gives the total percentage of the data that is either below LSL or above USL.

Capability Type of process capability indices. See Table 2.22 “Descriptions of

Capability Index Names and Formulas,” p. 80.

Note: There is a preference for Capability called Ppk Capability

Labeling

the Preference window (

Distribution to see this preference.

that labels the long-term capability output with Ppk labels. Open

File > Preferences), then select Platforms >

Index Process capability index values.

Upper CI Upper confidence interval.

Lower CI Lower confidence interval.

60 Performing Univariate Analysis Chapter 2

Sigma Quality Normal Quantile 1

Expected # defects()

----------------------------------------------- -

–





1.5+=

Capability Analysis

Ta bl e 2 .1 6 Description of the Capability Analysis Report (Continued)

Portion and Percent Portion labels describe the numbers in the Percent column, as follows:

• Below LSL gives the percentage of the fitted distribution that is below the lower specification limit.

• Above USL gives the percentage of the fitted distribution that is above the upper specification limit.

• Total Outside gives the total percentage of the fitted distribution that is either below LSL or above USL.

PPM (parts per million) The PPM value is the

Percent column multiplied by 10,000.

Sigma Quality Sigma Quality is frequently used in Six Sigma methods, and is also

referred to as the process sigma.

For example, if there are 3 defects in n=1,000,000 observations, the formula yields 6.03, or a 6.03 sigma process. The above and below columns do not sum to the total column because Sigma Quality uses values from the normal distribution, and is therefore not additive.

Ta bl e 2 .1 7 Descriptions of the Capability Analysis Options

Z Bench

Shows the values (represented by Index) of the Benchmark Z statistics. According to the AIAG Statistical Process Control manual, Z represents the number of standard deviation units from the process average to a value of interest such as an engineering specification. When used in capability assessment, Z USL is the distance to the upper specification limit and Z LSL is the distance to the lower specification limit. Here are the Benchmark Z formulas:

Z USL = (USL-Xbar)/sigma = 3 * CPU

Z LSL = (Xbar-LSL)/sigma = 3 * CPL

Z Bench = Inverse Cumulative Prob(1 - P(LSL) - P(USL))

where

P(LSL) = Prob(X < LSL) = 1 - Cum Prob(Z LSL)

P(USL) = Prob(X > USL) = 1 - Cum Prob(Z USL)

Capability Animation

Interactively change the specification limits and the process mean to see the effects on the capability statistics. This option is available only for capability analyses based on the Normal distribution.

Chapter 2 Performing Univariate Analysis 61

Fit Distributions

Use the Continuous or Discrete Fit options to fit a distribution to a continuous or discrete variable.

Example of Fitting a Lognormal Distribution

1. Open the Lipid Data.jmp sample data table.

2. Select

3. Select

4. Click

5. (Optional) Rotate the histogram vertically. From the red triangle menu next to Cholesterol, select

6. From the red triangle menu next to Cholesterol, select

Figure 2.28 Example of a Continuous Fit

Analyze > Distribution.

Cholesterol and click Y, Co l um n s .

OK.

Histogram Options > Vertical.

Continuous Fit > LogNormal.

A curve is overlaid on the histogram, and a Parameter Estimates report is added to the report window. A red triangle menu contains additional options. See “Fit Distribution Options,” p. 71.

Note: The Life Distribution platform also contains options for distribution fitting that might use different parameterizations and allow for censoring. See the Quality and Reliability Methods book.

62 Performing Univariate Analysis Chapter 2

μ 0=

σ 1=

2πσ

-----------------

x μ–()

2σ

-------------------

–exp

∞– x ∞<<

∞– μ∞<<

XY()ln=

σ 2π

--------------

x()log μ–()–2[]exp 2σ2⁄

-------------------------------------------------------------- -

0 x≤

∞– μ∞<<

μσ22⁄+()exp

2 μσ

+()()exp 2μσ

+()exp–

Fit Distributions

Continuous Fit

Use the Continuous Fit options to fit a distribution (such as Normal, Lognormal, or Weibull) to a continuous variable.

Normal

The

Normal fitting option estimates the parameters of the normal distribution. The normal distribution is

often used to model measures that are symmetric with most of the values falling in the middle of the curve. Select the

The parameters for the normal distribution are as follows:

• μ (the mean) defines the location of the distribution on the x-axis

• σ (standard deviation) defines the dispersion or spread of the distribution

The standard normal distribution occurs when and . The Parameter Estimates table shows estimates of μ and σ, with upper and lower 95% confidence limits.

Normal fitting for any set of data and test how well a normal distribution fits your data.

pdf: for ; ; 0 < σ

E(x) = μ

Var( x) = σ

LogNormal

The lognormal distribution. A variable Y is lognormal if and only if is normal. The data must be greater than zero.

Weibull, Weibull with threshold, and Extreme Value

The Weibull distribution has different shapes depending on the values of α (scale) and β (shape). It often provides a good model for estimating the length of life, especially for mechanical devices and in biology. The Weibull option is the same as the Weibull with threshold option, with a threshold (θ) parameter of zero. For the Weibull with threshold option, JMP estimates the threshold as the minimum value. If you know what the threshold should be, set it by using the

The pdf for the Weibull with threshold is as follows:

LogNormal fitting option estimates the parameters μ (scale) and σ (shape) for the two-parameter

pdf: for ; ; 0 < σ

E(x) =

Var( x) =

Fix Parameters option. See “Fit Distribution Options,” p. 71.

Chapter 2 Performing Univariate Analysis 63

------ -

x θ–()

β 1–

x θ–

-----------





–exp

θ x<

θαΓ1

-- -





α2Γ 1

-- -





Γ21

-- -





–







Γ.)(

---

x σ⁄–()exp

0 x≤

Γα()σ

------------------- -

x θ–()

α 1–

x θ–()– σ⁄()exp

θ x≤

Fit Distributions

pdf: for α,β > 0;

E(x) =

Var( x) =

where is the Gamma function.

The Extreme Value distribution is a two parameter Weibull (α, β) distribution with the transformed parameters δ =1/β and λ =ln(α).

Exponential

The exponential distribution is especially useful for describing events that randomly occur over time, such as survival data. The exponential distribution might also be useful for modeling elapsed time between the occurrence of non-overlapping events, such as the time between a user’s computer query and response of the server, the arrival of customers at a service desk, or calls coming in at a switchboard.

The Exponential distribution is a special case of the two-parameter Weibull when β = 1 and α = σ, and also a special case of the Gamma distribution when α = 1.

pdf: for 0 < σ;

E(x) = σ

Var( x) = σ

Devore (1995) notes that an exponential distribution is memoryless. Memoryless means that if you check a component after t hours and it is still working, the distribution of additional lifetime (the conditional probability of additional life given that the component has lived until t) is the same as the original distribution.

Gamma

The

Gamma fitting option estimates the gamma distribution parameters, α >0 and σ > 0. The parameter

α, called alpha in the fitted gamma report, describes shape or curvature. The parameter σ, called sigma, is

the scale parameter of the distribution. A third parameter, θ, called the parameter. It is set to zero by default, unless there are negative values. You can also set its value by using the

Fix Parameters option. See “Fit Distribution Options,” p. 71.

pdf: for ; 0 < α,σ

E(x) = ασ + θ

Var( x) = ασ

Threshold, is the lower endpoint

64 Performing Univariate Analysis Chapter 2

ν()

α 1≤

α 1>

θ x θσ+()≤≤

B αβ,()σ

αβ1–+

-------------------------------------------

x θ–()

α 1–

θσx–+()

β 1–

θ x θσ+≤≤

θσ

αβ+

------------ -

σ2αβ

αβ+()

αβ1++()

------------------------------------------------ -

B.)(

---- -

x μ

–

-------------







i 1=



i 1=



Fit Distributions

•The standard gamma distribution has σ = 1. Sigma is called the scale parameter because values other than 1 stretch or compress the distribution along the x-axis.

• The Chi-square distribution occurs when σ =2, α = ν/2, and θ =0.

• The exponential distribution is the family of gamma curves that occur when α =1 and θ =0.

The standard gamma density function is strictly decreasing when . When , the density function begins at zero, increases to a maximum, and then decreases.

Beta

The standard beta distribution is useful for modeling the behavior of random variables that are constrained to fall in the interval 0,1. For example, proportions always fall between 0 and 1. The

Beta fitting option

estimates two shape parameters, α >0 and β > 0. There are also θ and σ, which are used to define the lower threshold as θ, and the upper threshold as θ + σ. The beta distribution has values only for the interval defined by . The θ is estimated as the minimum value, and σ is estimated as the range. The standard beta distribution occurs when θ = 0 and σ =1.

Set parameters to fixed values by using the than or equal to the maximum data value, and the lower threshold must be less than or equal to the minimum data value. For details about the Fix Parameters option, see “Fit Distribution Options,” p. 71.

pdf: for ; 0 < σ,α,β

E(x) =

Var( x) =

where is the Beta function.

Normal Mixtures

The

Normal Mixtures option fits a mixture of normal distributions. This flexible distribution is capable of

fitting multi-modal data.

Fit a mixture of two or three normal distributions by selecting the options. Alternatively, you can fit a mixture of k normal distributions by selecting the separate mean, standard deviation, and proportion of the whole is estimated for each group.

pdf:

Fix Parameters option. The upper threshold must be greater

Normal 2 Mixture or Normal 3 Mixture

Other option. A

E(x) =

Chapter 2 Performing Univariate Analysis 65

+()

i 1=



i 1=









–

φ.)(

Z γδfy()+=

fy() Y 1 Y2++





ln Y

1–

sinh==

X θ–

------------

= ∞– X ∞<<

fY()

1 Y–

----------- -





ln=

X θ–

------------

= θ X θσ+<<

Fit Distributions

Var( x) =

where μ

, σi, and πi are the respective mean, standard deviation, and proportion for the ith group, and

is the standard normal pdf.

Smooth Curve

The

Smooth Curve option fits a smooth curve using nonparametric density estimation (kernel density

estimation). The smooth curve is overlaid on the histogram and a slider appears beneath the plot. Control the amount of smoothing by changing the kernel standard deviation with the slider. The initial estimate is formed by summing the normal densities of the kernel standard deviation located at each data point.

Johnson Su, Johnson Sb, Johnson Sl

The Johnson system of distributions contains three distributions that are all based on a transformed normal distribution. These three distributions are the Johnson Su, which is unbounded for Y; the Johnson Sb, which is bounded on both tails (0 < Y < 1); and the Johnson Sl, leading to the lognormal family of distributions.

Note: The S refers to system, the subscript of the range. Although we implement a different method, information about selection criteria for a particular Johnson system can be found in Slifker and Shapiro (1980).

Johnson distributions are popular because of their flexibility. In particular, the Johnson distribution system is noted for its data-fitting capabilities because it supports every possible combination of skewness and kurtosis.

Kernel Std

If Z is a standard normal variate, then the system is defined as follows:

where, for the Johnson Su:

where, for the Johnson Sb:

66 Performing Univariate Analysis Chapter 2

σ 1±=

fY() Y()ln=

X θ–

------------

θ X ∞ if σ<< 1= ∞– X θ if σ<< 1–=

---

x θ–

-----------





2+1– 2⁄

φγ δ

x θ–

-----------





sinh

1–

∞– x θγ,, ∞<<

φγ δ

x θ–

σ x θ–()–

------------------------- -





ln+

δσ

x θ–()σx θ–()–()

-----------------------------------------------





x θ–

--------------

φγ δ

x θ–

-----------





ln+

φ.)(

---

2λ2

------------------------------ -





log μ–







xx2λ2++

σ x

2λ2

xx2λ2+++()

----------------------------------------------------------

0 λ≤

∞– μ∞<<

Fit Distributions

and for the Johnson Sl, where .

Johnson Su

pdf: for ; 0 < θ,δ

Johnson Sb

pdf: for θ < x < θ+σ; 0 < σ

Johnson Sl

pdf: for θ < x if σ = 1; θ > x if σ = -1

where is the standard normal pdf. The E(x) and Var(x) are not given for any of the Johnson distributions due to the complexity of finding a closed-form solution.

Note: The parameter confidence intervals are hidden in the default report. Parameter confidence intervals are not very meaningful for Johnson distributions, because they are transformations to normality. To show parameter confidence intervals, right-click in the report and select

95%.

Generalized Log (Glog)

This distribution is useful for fitting data that are rarely normally distributed and often have non-constant variance, like biological assay data. The Glog distribution is described with the parameters μ (location), σ (scale), and λ (shape).

pdf:

for ; 0 < σ;

The E(x) and Var(x) are not given due to the complexity of finding a closed-form solution.

Columns > Lower 95% and Upper

Chapter 2 Performing Univariate Analysis 67

---

xx2λ2++

------------------------------ -





log μ–

Fit Distributions

The Glog distribution is a transformation to normality, and comes from the following relationship:

If z = ~ N(0,1), then x ~ Glog(μ,σ,λ).

When λ = 0, the Glog reduces to the LogNormal (μ,σ).

Note: The parameter confidence intervals are hidden in the default report. Parameter confidence intervals are not very meaningful for the GLog distribution, because it is a transformation to normality. To show parameter confidence intervals, right-click in the report and select

95%.

Columns > Lower 95% and Upper

All

The

All option fits all applicable continuous distributions to a variable. The Compare Distributions report

contains statistics about each fitted distribution. Use the check boxes to show or hide a fit report and overlay curve for the selected distribution. By default, the best fit distribution is selected. See Figure 2.29.

Example of the All Option

1. Open the

2. Select

3. Select

4. Click

Lipid Data.jmp sample data table.

Analyze > Distribution.

Cholesterol and click Y, Co l um n s .

OK.

5. From the red triangle menu next to Cholesterol, select

Continuous Fit > All.

68 Performing Univariate Analysis Chapter 2

-2logL 2ν

2νν 1+()

n ν 1+()–

------------------------- -

Fit Distributions

Figure 2.29 Example of the All Option

The ShowDistribution list is sorted by AICc in ascending order. The formula for AICc is as follows:

AICc =

where:

– logL is the logLikelihood

– n is the sample size

– ν is the number of parameters

Chapter 2 Performing Univariate Analysis 69

eλ–λ

------------- -

0 λ∞<≤





1 p–()

nx–

0 p 1≤≤

Fit Distributions

If your data has negative values, the ShowDistribution list does not include those distributions that require data with positive values. If your data has non-integer values, the list of distributions does not include discrete distributions. Distributions with threshold parameters, like Beta and Johnson Sb, are not included in the list of possible distributions.

Discrete Fit

Use the Discrete Fit options to fit a distribution (such as Poisson or Binomial) to a discrete variable.

Poisson

The Poisson distribution has a single scale parameter λ >0.

pdf: for ; x = 0,1,2,...

E(x) = λ

Var( x) = λ

Since the Poisson distribution is a discrete distribution, the overlaid curve is a step function, with jumps occurring at every integer.

Binomial

The

Binomial option accepts data in two formats: a constant sample size, or a column containing sample

sizes.

pdf: for ; x = 0,1,2,...,n

E(x) = np

Var( x) = np(1-p)

where n is the number of independent trials.

Note: The confidence interval for the binomial parameter is a Score interval. See Agresti (1998).

Gamma Poisson

This distribution is useful when the data is a combination of several Poisson(λ) distributions, each with a different λ. One example is the overall number of accidents combined from multiple intersections, when the mean number of accidents (λ) varies between the intersections.

The Gamma Poisson distribution results from assuming that x|λ follows a Poisson distribution, while λ follows a Gamma(α,β). The Gamma Poisson has parameters λ=αβ and σ=β+1. The σ is a dispersion parameter. If σ > 1, there is overdispersion, meaning there is more variation in x than explained by the Poisson alone. If σ = 1, x reduces to Poisson(λ).

70 Performing Univariate Analysis Chapter 2

Γ x

σ 1–

------------





Γ x 1+()Γ

σ 1–

------------





------------------------------------------ -

σ 1–

------------





σ 1–

------------

–

0 λ<

1 σ≤

Γ.)(

βˆσˆ1–=

-- -

py()

yr1–+





1 p–()

0 y≤

n 2≥





-- -

1–





Γ xp

-- -

1–





+ Γ nx– 1 p–()

-- -

1–





Γ p

-- -

1–





Γ 1 p–()

-- -

1–





Γ n

-- -

1–+





-------------------------------------------------------------------------------------------------------------------------- -

0 p 1≤≤

max

np– 1–

--------------------

–

1 p–

n 2– p+

-------------------- -

–(,)δ 1≤≤

Fit Distributions

pdf: for ; ; x = 0,1,2,...

E(x) = λ

Var( x) = λσ

where is the Gamma function.

Remember that x|λ ~ Poisson(λ), while λ ~ Gamma(α,β). The platform estimates λ=αβ and σ = β+1. To obtain estimates for α and β, use the following formulas:

If the estimate of σ is 1, the formulas do not work. In that case, the Gamma Poisson has reduced to the Poisson(λ), and is the estimate of λ.

If the estimate for α is an integer, the Gamma Poisson is equivalent to a Negative Binomial with the following pdf:

with r = α and (1-p)/p = β.

Beta Binomial

This distribution is useful when the data is a combination of several Binomial(p) distributions, each with a different p. One example is the overall number of defects combined from multiple manufacturing lines, when the mean number of defects (p) varies between the lines.

The Beta Binomial distribution results from assuming that x|p follows a Binomial(n,p) distribution, while p follows a Beta(α,β). The Beta Binomial has parameters p = α/(α+β) and δ =1/(α+β+1). The δ is a dispersion parameter. When δ > 0, there is overdispersion, meaning there is more variation in x than explained by the Binomial alone. When δ < 0, there is underdispersion. When δ =0, x is distributed as Binomial(n,p). The Beta Binomial only exists when .

pdf:

for ; ; x = 0,1,2,...,n

E(x) = np

for

Chapter 2 Performing Univariate Analysis 71

Γ.)(

αˆp

1 δˆ–

-----------





1 pˆ–()

1 δˆ–

-----------





Fit Distributions

Var( x) = np(1-p)[1+(n-1)δ]

where is the Gamma function.

Remember that x|p ~ Binomial(p), while p ~ Beta(α,β). The parameters p = α/(α+β) and δ =1/(α+β+1) are estimated by the platform. To obtain estimates of α and β, use the following formulas:

If the estimate of δ is 0, the formulas do not work. In that case, the Beta Binomial has reduced to the Binomial(p), and is the estimate of p.

The confidence intervals for the Beta Binomial parameters are profile likelihood intervals.

Fit Distribution Options

Each fitted distribution report has a red triangle menu that contains additional options.

Ta bl e 2 .1 8 Descriptions of Fitted Distribution Options

Diagnostic Plot

Density Curve

Goodness of Fit

Fix Parameters

Quantiles

Creates a quantile or a probability plot. See “Diagnostic Plot,” p. 73.

Uses the estimated parameters of the distribution to overlay a density curve on the histogram.

Computes the goodness of fit test for the fitted distribution. See

“Goodness of Fit,” p. 75.

Enables you to enter parameters. The Fixed Parameters report reflects the parameter values that you entered. An Adequacy LR (likelihood ratio) Test report also appears, which tests your parameters to determine whether they fit the data. Any parameters that remain non-fixed are re-estimated considering the fixed constraints, and confidence limits for non-fixed parameters are recomputed based on the fixed parameters. The null hypothesis for the Adequacy LR Test is that the new restricted parameterization adequately describes the data. This means that small p-values reject this hypothesis and conclude that the fixed parameters are not adequate.

Returns the unscaled and uncentered quantiles for the specific upper and lower probability values that you specify.

72 Performing Univariate Analysis Chapter 2

Fit Distributions

Ta bl e 2 .1 8 Descriptions of Fitted Distribution Options (Continued)

Set Spec Limits for K Sigma

Spec Limits

Use this option when you do not know the specification limits for a process and you want to use its distribution as a guideline for setting specification limits. Usually specification limits are derived using engineering considerations. If there are no engineering considerations, and if the data represents a trusted benchmark (well behaved process), then quantiles from a fitted distribution are often used to help set specification limits.

Type a K value and select one-sided or two-sided for your capability analysis. Tail probabilities corresponding to K standard deviations are computed from the Normal distribution. The probabilities are converted to quantiles for the specific distribution that you have fitted. The resulting quantiles are used for specification limits in the capability analysis. This option is similar to the

Quantiles option, but

you provide K instead of probabilities. K corresponds to the number of standard deviations that the specification limits are away from the mean.

For example, for a Normal distribution, where K=3, the 3 standard deviations below and above the mean correspond to the 0.00135 quantile and 0.99865 limit is set at the 0.00135 is set at the 0.99865

quantile, respectively. The lower specification

quantile, and the upper specification limit

quantile of the fitted distribution. A capability

analysis is returned based on those specification limits.

Computes generalizations of the standard capability indices, based on the specification limits and target you specify. See “Spec Limits,”

p. 76.

Save Fitted Quantiles

Save Density Formula

Save Spec Limits

Saved Transformed

Remove Fit

Saves the fitted quantile values as a new column in the current data table. For details about how the quantiles are computed, see the Diagnostic Plot section on p. 74.

Creates a new column in the current data table that contains fitted values that have been computed by the density formula. The density formula uses the estimated parameter values.

Saves the specification limits as a column property.

Creates a new column and saves a formula. The formula can transform the column to normality using the fitted distribution. This option is available only when one of the Johnson distributions or the Glog distribution is fit.

Removes the distribution fit from the report window.

Chapter 2 Performing Univariate Analysis 73

Fit Distributions

Diagnostic Plot

The

Diagnostic Plot option creates a quantile or a probability plot. Depending on the fitted distribution,

the plot is one of four formats.

Ta bl e 2 .1 9 Descriptions of Plot Formats

Plot Format Applicable Distributions

The fitted quantiles versus the data • Weibull with threshold

• Gamma (see Figure 2.30)

•Beta

• Poisson

• GammaPoisson

• Binomial

• BetaBinomial

The fitted probability versus the data • Normal (see Figure 2.30)

• Normal Mixtures

•Exponential

The fitted probability versus the data on log scale • Weibull (see Figure 2.30)

•LogNormal

• Extreme Value

The fitted probability versus the standard normal quantile • Johnson Sl

• Johnson Sb (see Figure 2.30)

• Johnson Su

• Glog

Examples of Diagnostic Plots

1. Open the

2. Select

Lipid Data.jmp sample data table.

Analyze > Distribution.

3. Select Cholesterol and click Y, C ol u mn s .

4. Click

OK.

To create the Gamma Quantile plot in Figure 2.30

1. From the red triangle menu next to Cholesterol, select

2. From the red triangle menu next to Fitted Gamma, select

Continuous Fit > All.

Diagnostic Plot.

74 Performing Univariate Analysis Chapter 2

Fit Distributions

To create the Normal Probability plot in Figure 2.30:

1. From the red triangle menu next to Cholesterol, select

2. From the red triangle menu next to Fitted Normal, select

Continuous Fit > Normal.

Diagnostic Plot.

To create the Weibull 2 Parameter Probability plot in Figure 2.30

1. From the red triangle menu next to Cholesterol, select

Continuous Fit > Weibull.

2. From the red triangle menu next to Fitted 2 parameter Weibull, select

To create the Johnson Sb Probability plot in Figure 2.30

1. From the red triangle menu next to Cholesterol, select

2. From the red triangle menu next to Fitted Johnson Sb, select

Figure 2.30 Examples of Diagnostic Plots

Continuous Fit > Johnson Sb.

Diagnostic Plot.

The fitted quantiles in the Diagnostic Plot and the fitted quantiles saved with the Save Fitted Quantiles command are formed using the following method:

Chapter 2 Performing Univariate Analysis 75

Fit Distributions

1. The data are sorted and ranked. Ties are assigned different ranks.

2. Compute the percentile

3. Compute the quantile

= rank

[i]

= Quantiled(percentile

[i]

/(n+1).

[i]

) where Quantiled is the quantile function for the

[i]

specific fitted distribution, and i = 1,2,...,n.

Table 2.20 describes the options in the red triangle menu next to Diagnostic Plot.

Ta bl e 2 .2 0 Descriptions of Diagnostic Plot Options

Rotate

Confidence Limits

Line of Fit

Median Reference Line

Goodness of Fit

The Goodness of Fit option computes the goodness of fit test for the fitted distribution. The goodness of fit tests are not Chi-square tests, but are EDF (Empirical Distribution Function) tests. EDF tests offer advantages over the Chi-square tests, including improved power and invariance with respect to histogram midpoints.

• For Normal distributions, the Shapiro-Wilk test for normality is reported when the sample size is less than or equal to 2000, and the KSL test is computed for samples that are greater than 2000.

• For Poisson distributions that have sample sizes less than or equal to 30, the Goodness of Fit test is formed using two one-sided exact Kolmogorov tests combined to form a near exact test. For details, see Conover 1972. For sample sizes greater than 30, a Pearson Chi-squared goodness of fit test is performed.

Reverses the x- and y-axes.

Draws Lilliefors 95% confidence limits for the Normal Quantile plot, and 95% equal precision bands with a = 0.001 and b = 0.99 for all other quantile plots (Meeker and Escobar (1998)).

Draws the straight diagonal reference line. If a variable fits the selected distribution, the values fall approximately on the reference line.

Draws a horizontal line at the median of the response.

Ta bl e 2 .2 1 Descriptions of JMP Goodness of Fit Tests

Distribution Parameters Goodness of Fit Test

Normal

μ and σ are unknown Shapiro-Wilk (for n ≤ 2000)

Kolmogorov-Smirnov-Lillefors (for n > 2000)

μ and σ are both known Kolmogorov-Smirnov-Lillefors

either μ or σ is known (none)

LogNormal μ and σ are known or

Kolmogorov's D

unknown

76 Performing Univariate Analysis Chapter 2

0.5

LSL–

0.5P0.00135

–

------------------------------------ -

Fit Distributions

Ta bl e 2 .2 1 Descriptions of JMP Goodness of Fit Tests (Continued)

Distribution Parameters Goodness of Fit Test

Weibull α and β known or unknown Cramer von Mises W

Weibull with threshold α, β and θ known or unknown Cramer von Mises W

Extreme Value α and β known or unknown Cramer von Mises W

Exponential σ is known or unknown Kolmogorov's D

Gamma α and σ are known Cramer von Mises W

either α or σ is unknown (none)

Beta α and β are known Kolmogorov's D

either α or β is unknown (none)

Binomial ρ is known or unknown and n

Pearson χ

is known

Beta Binomial ρ and δ known or unknown Kolmogorov's D (for n ≤ 30)

Poisson λ known or unknown Kolmogorov's D (for n ≤ 30)

Gamma Poisson λ or σ known or unknown Kolmogorov's D (for n ≤ 30)

Spec Limits

The generalizations of the standard capability indices. This is done using the fact that for the normal distribution, 3σ is both the distance from the lower 0.135 percentile to median (or mean) and the distance from the median (or mean) to the upper 99.865 percentile. These percentiles are estimated from the fitted distribution, and the appropriate percentile-to-median distances are substituted for 3σ in the standard formulas.

Writing T for the target, LSL, and USL for the lower and upper specification limits, and P percentile, the generalized capability indices are as follows:

Pearson χ

a. For the three Johnson distributions and the Glog distribution, the data are transformed to Normal, then the appropriate test of normality is performed.

Spec Limits option launches a window requesting specification limits and target, and then computes

(for n > 30)

for the 100th

Chapter 2 Performing Univariate Analysis 77

USL P

0.5

–

0.99865P0.5

–

------------------------------------ -

USL LSL–

0.99865P0.00135

–

-----------------------------------------------

min

0.5

LSL–

0.5P0.00135

–

------------------------------------ -

USL P

0.5

–

0.99865P0.5

–

------------------------------------ -







K 2

1 2

-- -

USL LSL+()P

0.5

–

USL LSL–

------------------------------------------------------ -

×=

min

TLSL–

0.5P0.00135

–

------------------------------------ -

USL T–

0.99865P0.5

–

------------------------------------ -





μ T–

------------ -





-------------------------------------------------------------------------------------------

1 f–()yif()y

i 1+

Statistical Details

If the data are normally distributed, these formulas reduce to the formulas for standard capability indices. See Table 2.22.

Statistical Details

This section contains the following information:

• “Statistical Details for Quantiles,” p. 77

• “Statistical Details for Prediction Intervals,” p. 78

• “Statistical Details for Tolerance Intervals,” p. 78

• “Statistical Details for Capability Analysis,” p. 79

Statistical Details for Quantiles

This section describes how quantiles are computed.

To compute the pth quantile of N nonmissing values in a column, arrange the N values in ascending order and call these column values y

• If the result is an integer, the pth quantile is that rank’s corresponding value.

• If the result is not an integer, the pth quantile is found by interpolation. The pth quantile, denoted q computed as follows:

where:

– n is the number of nonmissing values for a variable

, y2,...,yN. Compute the rank number for the pth quantile as p /100(N +1).

, is

78 Performing Univariate Analysis Chapter 2

100

-------- -

15 1+()12=

100

-------- -

15 1+()14.4=

,[]X 1

-- -

+ t

1 α 2m⁄– n 1–;()

× s×±=

m 1≥

YlYu,[]Xt

1 α 2⁄ n 1–,–()

--- -

-- -

+ s××±=

m 1≥

slsu,[]s

1 α 2⁄ n 1 m 1–,–();–()

--------------------------------------------------------× sF

1 α 2⁄ m 1 n 1–,–();–()

×,=

m 2≥

xg's+

xg' s–

Statistical Details

– y1, y

– y

n+1

represents the ordered values of the variable

2, ..., yn

is taken to be y

– i is the integer part and f is the fractional part of (n+1)p.

–(n + 1)p = i + f

For example, suppose a data table has 15 rows and you want to find the 75th and 90th quantile values of a continuous column. After the column is arranged in ascending order, the ranks that contain these quantiles are computed as follows:

and

The value y 14th and 15th ranked values as y

is the 75th quantile. The 90th quantile is interpolated by computing a weighted average of the

=0.6y14+0.4y15.

Statistical Details for Prediction Intervals

The formulas that JMP uses for computing prediction intervals are as follows:

•For m future observations:

• For the mean of m future observations:

for

Statistical Details for Tolerance Intervals

for .

• For the standard deviation of m future observations:

for

where m = number of future observations, and n = number of points in current analysis sample.

• The one-sided intervals are formed by using 1-α in the quantile functions.

For references, see Hahn and Meeker (1991), pages 61-64.

One-Sided Interval

The one-sided interval is computed as follows:

Upper Limit =

Lower Limit =

where

Chapter 2 Performing Univariate Analysis 79

t 1 α– n 1– Φ1–p() n⋅,,()n⁄

1–

,[]xg

1 α 2⁄ pLn,;–()

s – xg

1 α 2⁄ pUn,;–()

+ s,[]=

1 α 2⁄ p, n;–()

xgsμ–+

----------------------





xgs– μ–

--------------------- -





–

P Φ

Xgsμ–+

-----------------------





Xgs– μ–

---------------------- -





– 1 γ–≥







1 α–=

x–()

n 1–

------------------- -

i 1=



Statistical Details

= from Table 1 of Odeh and Owen (1980).

t is the quantile from the non-central t-distribution, and is the standard normal quantile.

Tw o - Si d e d I n t e r v a l

The two-sided interval is computed as follows:

where

s = standard deviation and is a constant that can be found in Table 4 of Odeh and Owen

1980).

To d et er mi ne g, consider the fraction of the population captured by the tolerance interval. Tamhane and Dunlop (2000) give this fraction as follows:

where Φ denotes the standard normal c.d.f. (cumulative distribution function). Therefore g solves the following equation:

where 1-γ is the fraction of all future observations contained in the tolerance interval.

More information is given in Tables A.1a, A.1b, A.11a, and A.11b of Hahn and Meeker (1991).

Statistical Details for Capability Analysis

All capability analyses use the same formulas. Options differ in how sigma (σ) is computed:

•

Long-term uses the overall sigma. This option is used for P

Note: There is a preference for Distribution called Ppk Capability Labeling that labels the long-term

capability output with P Distribution.

•

Specified Sigma enables you to type a specific, known sigma used for computing capability analyses.

Sigma is user-specified, and is therefore not computed.

labels. This option is found using File > Preferences, then select Platforms >

statistics, and computes sigma as follows:

80 Performing Univariate Analysis Chapter 2

n()

-------------

xi.–()

i 1=



nr–

------------------------------------ -=

α 2⁄ n 1–,

n 1–

------------------------- -

1 α 2⁄– n 1–,

n 1–

--------------------------------- -

1 Φ1–1 α 2⁄–()

--------------- -

2 n 1–()

------------------- -

+–

1 Φ1–1 α 2⁄–()

--------------- -

2 n 1–()

------------------- -

Statistical Details

• Moving Range enables you to enter a range span, which computes sigma as follows:

where

is the average of the moving ranges

(n) is the expected value of the range of n independent normally distributed variables with unit

standard deviation.

Short Term Sigma, Group by Fixed Subgroup Size if r is the number of subgroups and each ith

• subgroup is defined by the order of the data, sigma is computed as follows:

This formula is commonly referred to as the Root Mean Square Error, or RMSE.

Table 2.22 describes capability indices and gives computational formulas.

Ta bl e 2 .2 2 Descriptions of Capability Index Names and Formulas

Index Index Name Formula

CP process capability

CIs for CP Lower CI on CP

CPK (PPK for AIAG)

CIs for CPK

See Bissell (1990)

ratio, C

Upper CI on CP

process capability index, C

Lower CI

Upper CI

(USL - LSL)/6s where:

• USL is the upper spec limit

• LSL is the lower spec limit

min(CPL, CPU)

Sas BASIC ANALYSIS AND GRAPHING RELEASE 9 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Preliminaries

Prerequisites

JMP Terminology

Learning about JMP

About JMP Documentation

Use JMP Help

Use Tutorials

Access Sample Data Tables

Learn About Statistical and JSL Terms

Conventions

Learn JMP Tips and Tricks

Access Resources on the Web

Use JMP Platforms

Work with Multiple Data Tables and Platforms

How JMP Platforms Are Designed

Process for Analyzing Data Using Platforms

Assign Modeling Types

Choose an Analysis and Launching a Platform

Complete a Launch Window

View a Report Window

Common Features Throughout Platforms

Launch Window Features

Cast Selected Columns into Roles Buttons

Columns Filter Menu

Script Menus

Automatic Recalc Feature

Performing Univariate Analysis

Overview of the Distribution Platform

Categorical Variables

Continuous Variables

Example of the Distribution Platform

Launch the Distribution Platform

The Distribution Report

Histograms

Resize Histogram Bars for Continuous Variables

Use the Grabber Tool

Use the Set Bin Width Option

Use the Increment Option

Highlight Bars and Select Rows

Specify Your Selection in Multiple Histograms

Example of Selecting Data in Multiple Histograms

Initial Reports

The Frequencies Report

Example of a Frequencies Report

The Quantiles Report

Example of a Quantiles Report

The Moments Report

Example of a Moments Report

Distribution Platform Options

Options for Categorical Variables

Display Options for Categorical Variables

Histogram Options for Categorical Variables

Mosaic Plot

Example of a Mosaic Plot

Test Probabilities

Examples of the Test Probabilities Option

Options for Continuous Variables

Confidence Intervals for Categorical Variables

Save Commands for Categorical Variables

Display Options for Continuous Variables

Histogram Options for Continuous Variables

Normal Quantile Plot

Example of a Normal Quantile Plot

Outlier Box Plot

Example of an Outlier Box Plot

Quantile Box Plot

Example of a Quantile Box Plot

Stem and Leaf

Example of a Stem and Leaf Plot

CDF Plot

Example of a CDF Plot

Test Mean

Example of Test Mean

Test Std Dev

Example of Test Std Dev

Confidence Intervals for Continuous Variables