RSA Security Crypto-C User Manual

Download

RSA BSAFE

Crypto-C

Cryptographic Components for C

Developer’s Guide

Version 5.2.2

RSA Security Inc. 20 Crosby Drive Bedford, MA 01730 USA Tel (US) 1 877 RSA 4900, +1 781 301 5000 Fax +1 781 301 5170 www.rsasecurity.com

RSA Security Ireland Limited Bay 127, Shannon Free Zone Shannon, County Clare, Ireland Tel +353 61 72 5100 Fax +353 61 72 5110 www.rsasecurity.ie

See our Web Site for regional Customer Service telephone and fax numbers.

Trademarks

ACE/Server, BSAFE, Genuine RSA Encryption Engine, Keon, RC2, RC4, RC5, RSA, RSA SecurPC, SecurCare, SecurID, SoftID, and WebID are registered trademarks, and RC6, RSA Security, RSA Secured, SecurSight, and The Most Trusted Name in e-Security are trademarks, of RSA Security Inc.

Other product and company names mentioned herein may be the trademarks of their respective owners.

License agreement

This software and the associated documentation are proprietary and confidential to RSA Security, are furnished under license, and may be used and copied only in accordance with the terms of such license and with the inclusion of the copyright below. This software and any copies thereof may not be provided or otherwise made available to any other person.

Note on encryption technologies

This product may contain encryption technology. Many countries prohibit or restrict the use, import, or export of encryption technologies, and current use, import, and export regulations should be followed when exporting this product.

Distribution

Limit distribution of this document to trusted personnel.

RSA Security notice

The RC5® Block Encryption Algorithm With Data-Dependent Rotations is protected by U.S. Patent #5,724,428 and #5,835,600.

The RC6™ Encryption Algorithm is the subject of pending U.S. and foreign patent applications.

The DES implementation in this product contains code based on the "libdes" package written by Eric A. Young (eay@pobox.com) and is included with his permission.

Compaq MultiPrime™ technology is protected by United States patent 5,848,159 and is the subject of patent applications in other countries.

Preface xv

What’s New in Version 5.2.2? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xvi

Organization of This Manual . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .xvii

Conventions Used in This Manual. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xviii

Terms and Abbreviations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xix

Related Documents . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .xx

How to Contact RSA Security . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .xxii

Improved performance. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .xvi

Hardware support . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .xvi

MultiPrime RSA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .xvi

Serialization for algorithm objects performing RC4, Diffie Hellman key exchange . . . . .xvi

Advanced Encryption Standard (AES) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xvii

RSA Security Web Site . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xxii

Getting Support and Service . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xxii

SecurCare® Online . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xxii

Technical Support Telephone Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xxii

Call Handling and Escalation Process . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . xxii

Chapter 1 Introduction 1

The Crypto-C Toolkit. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

Symmetric Ciphers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

Message Digests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2

Message Authentication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

Random-Number Generation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2

Public-Key Algorithms. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3

Digital Signatures. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3

Elliptic Curve Public-Key Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3

Secret Sharing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3

Hardware Support . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3

iii

Cryptographic Standards and Crypto-C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

PKCS Standards and Crypto-C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

NIST Standards and Crypto-C. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

PKCS Compared with NIST. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

ANSI X9 Standards and Crypto-C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

Chapter 2 Quick Start 7

The Six-Step Sequence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

Introductory Example . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Saving the Object State (optional). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

Putting It All Together. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

Decrypting the Introductory Example. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

Multiple Updates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

Summary of the Six Steps . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

Chapter 3

Cryptography 35

Cryptography Overview . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

Symmetric-Key Cryptography . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

Ciphers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36

Block Ciphers. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

Padding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

Ciphers in Crypto-C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

DES. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

Triple DES. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

DESX . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

RC2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

RC5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

RC6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

AES. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

Modes of Operation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41

Stream Ciphers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

Message Digests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

Message Digests and Pseudo-Random Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . 48

Hash-Based Message Authentication Codes (HMAC) . . . . . . . . . . . . . . . . . . . . . . 49

Password-Based Encryption. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49

Public-Key Cryptography. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50

The RSA Algorithm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51

Digital Envelopes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

iv RSA BSAFE Crypto-C Developer’s Guide

Optimal Asymmetric Encryption Padding (OAEP). . . . . . . . . . . . . . . . . . . . . . . . . . .55

Authentication and Digital Signatures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

Digital Signature Algorithm (DSA) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .60

Digital Certificates . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .61

Diffie-Hellman Public Key Agreement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .62

Elliptic Curve Cryptography . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .65

Elliptic Curve Parameters. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .66

The Finite Field . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .66

The Point P and its Order . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .69

Summary of Elliptic Curve Terminology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .71

Representing Fields of Even Characteristic . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .72

Elliptic Curve Key Pair Generation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72

Creating the Key Pair . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .73

ECDSA Signature Scheme. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .73

Signing a Message. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .73

Verifying a Signature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .74

The Math. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .74

Elliptic Curve Authenticated Encryption Scheme (ECAES) . . . . . . . . . . . . . . . . . . . . . . . . 75

Encrypting a Message Using the Public Key . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .76

Decrypting a Message Using the Private Key . . . . . . . . . . . . . . . . . . . . . . . . . . . . .77

Elliptic Curve Diffie-Hellman Key Agreement. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .77

Phase 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .78

Phase 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .78

The Math. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .79

Secret Sharing. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .80

Working with Keys. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .81

Key Generation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .81

Key Management . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .82

Key Escrow . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82

ASCII Encoding and Decoding. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .83

Applications of Cryptography. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83

Local Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .83

Point-to-Point Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .84

Client/Server Applications. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .85

Peer-to-Peer Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .86

Choosing Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87

Public-Key vs. Symmetric-Key Cryptography. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .87

Stream vs. Block Symmetric-Key Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .87

Block Symmetric-Key Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .88

Key Agreement vs. Digital Envelopes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .88

Secret Sharing and Key Escrow. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

Contents v

Elliptic Curve Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

Interoperability. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90

Elliptic Curve Standards. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91

Security Considerations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91

Handling Private Keys. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91

Temporary Buffers. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92

Pseudo-Random Numbers and Seed Generation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92

Choosing Passwords. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93

Initialization Vectors and Salts. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94

DES Weak Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 94

Stream Ciphers. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95

Timing Attacks and Blinding. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95

Choosing Key Sizes. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97

RSA Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98

Diffie-Hellman Parameters and DSA Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99

RC2 Effective Key Bits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99

RC4 Key Bits. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99

RC5 Key Bits and Rounds. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99

Triple DES Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99

Elliptic Curve Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100

Chapter 4 Using Crypto-C 101

Algorithms in Crypto-C. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101

Information Formats Provided by Crypto-C. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102

Basic Algorithm Info Types . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102

BER-Based Algorithm Info Types . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102

PEM-Based Algorithm Info Types . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

BSAFE1 Algorithm Info Types . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

Summary of AIs. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

Keys In Crypto-C. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113

Summary of KIs. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113

System Considerations In Crypto-C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116

Algorithm Choosers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116

An Encryption Algorithm Chooser . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116

An RSA Algorithm Chooser . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117

The Surrender Context . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118

A Sample Surrender Function . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119

Saving State. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120

When to Allocate Memory . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121

vi RSA BSAFE Crypto-C Developer’s Guide

Memory-Management Routines . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122

Memory-Management Routines and Standard C Libraries . . . . . . . . . . . . . . . . . .122

Memory Allocation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .123

Binary Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .123

BER/DER Encoding. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .123

Input and Output . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 126

Symmetric Block Algorithms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .126

The RSA Algorithm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .127

General Considerations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .128

Key Size . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .129

DES Keys. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .129

RSA Keys. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .129

Using Cryptographic Hardware . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 132

Interfacing with a BHAPI Implementation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .132

PKCS #11 Support . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .134

Using a PKCS #11 Device with Crypto-C. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .135

PKCS #11 Support for DSA Key Pair Generation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .144

Advanced PKCS #11. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .147

Random Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148

Hardware Issues . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .148

Chapter 5 Non-Cryptographic Operations 151

Message Digests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 152

Creating a Digest. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .152

BER-Encoding the Digest. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .155

Saving the State of a Digest Algorithm Object. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .156

Saved State. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .156

Hash-Based Message Authentication Code (HMAC) . . . . . . . . . . . . . . . . . . . . . . . 161

Generating Random Numbers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165

Generating Random Numbers with SHA1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 165

Generating Independent Streams of Randomness . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 170

Converting Data Between Binary and ASCII . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 172

Encoding Binary Data To ASCII . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .172

Decoding ASCII-Encoded Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174

Contents vii

Chapter 6 Symmetric-Key Operations 177

Block Ciphers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178

DES with CBC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 178

Decrypting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 183

The RC2 Cipher. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 184

Decrypting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 190

The RC5 Cipher. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 190

Decrypting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 196

The RC6 Cipher. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 196

Decrypting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201

The AES Cipher . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 201

Password-Based Encryption . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 206

Decrypting . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 211

Chapter 7 Public-Key Operations 213

Performing RSA Operations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 214

Generating a Key Pair. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 214

MultiPrime . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 218

What is MultiPrime?. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 218

How Many Primes?. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 219

Sample . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 220

Generating an RSA MultiPrime Key . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 222

Distributing an RSA Public Key. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 223

Crypto-C Format. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 224

BER/DER Encoding. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 224

RSA Public-Key Encryption . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 226

RSA Private-Key Decryption. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 229

Optimal Asymetric Encryption Padding (OAEP) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231

Raw RSA Encryption and Decryption . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231

RSA Digital Signatures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 233

Computing a Digital Signature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 233

Verifying a Digital Signature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 236

Performing DSA Operations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239

Generating DSA Parameters. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239

Generating a DSA Key Pair. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 242

DSA Signatures. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 243

Computing a Digital Signature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 244

Verifying a Digital Signature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 246

viii RSA BSAFE Crypto-C Developer’ s Guide

Performing Diffie-Hellman Key Agreement. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 249

Generating Diffie-Hellman Parameters. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .249

Distributing Diffie-Hellman Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .253

Crypto-C Format . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .253

BER Format . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .254

Diffie-Hellman Key Agreement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .256

Saving the Object State . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .259

Performing Elliptic Curve Operations. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 260

Generating Elliptic Curve Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .260

Retrieving Elliptic Curve Parameters. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .264

Generating an Elliptic Curve Key Pair . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .268

Retrieving an Elliptic Curve Key. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .271

Generating Acceleration Tables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .273

Generating a Generic Acceleration Table. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .273

Generating a Public-Key Acceleration Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . .277

Performing EC Diffie-Hellman Key Agreement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .280

Performing ECDSA in Compliance with ANSI X9.62. . . . . . . . . . . . . . . . . . . . . . . . . . . .284

Generating EC Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .285

Generating an EC Key Pair . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .285

Computing a Digital Signature. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .286

Verifying a Digital Signature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .289

Performing ECDSA with X9.62-Compliant BER . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .291

Generating EC Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .291

Generating an EC Key Pair . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .293

Computing a Digital Signature. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .293

Verifying a Digital Signature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .296

Using ECAES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .297

Using Elliptic Curve Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .298

Using an EC Key Pair. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .298

ECAES Public-Key Encryption . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .298

ECAES Private-Key Decryption . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .302

Chapter 8 Secret Sharing Operations 305

Secret Sharing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 305

Generating Shares. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .305

Reconstructing the Secret . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .309

Chapter 9 Putting It All Together: An X9.31 Example 313

The X9.31 Sample Program . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 314

Contents ix

Appendix A Command-Line Demos 327

Overview of the Demos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 327

Command-Line Demo User’s Guide . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 328

BDEMO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 328

Starting BDEMO. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 328

Specifying User Keys. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 329

Using BDEMO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 329

BDEMODSA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 332

Running BDEMODSA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 332

Using BDEMODSA. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 332

BDEMOEC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 334

Running BDEMOEC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 334

Using BDEMOEC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 334

File Reference . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335

BSLite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 336

Glossary 339

Index 349

x RSA BSAFE Crypto-C Developer’ s Guide

List of Figures

Figure 3-1 Symmetric-Key Encryption and Decryption . . . . . . . . . . . . . . . . . . . . 36

Figure 3-2 Triple DES Encryption as Implemented in Crypto-C. . . . . . . . . . . . . . 38

Figure 3-3 Electronic Codebook (ECB) Mode . . . . . . . . . . . . . . . . . . . . . . . . . . . 42

Figure 3-4 Cipher-Block Chaining (CBC) Mode . . . . . . . . . . . . . . . . . . . . . . . . . . 43

Figure 3-5 Cipher Feedback (CFB) Mode. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

Figure 3-6 Output Feedback Mode (OFB) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

Figure 3-7 RC4 Encryption or Decryption . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47

Figure 3-8 DES Key and IV Generation for Password Based Encryption . . . . . . 50

Figure 3-9 Public-Key Cryptography . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51

Figure 3-10 Digital Envelope. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56

Figure 3-11 RSA Digital Signature . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59

Figure 3-12 The Diffie-Hellman Key Agreement Protocol . . . . . . . . . . . . . . . . . . 63

Figure 3-13 Elliptic Curve Diffie-Hellman Key Agreement . . . . . . . . . . . . . . . . . . 79

Figure 3-14 Secret Sharing — Key Share Assignment . . . . . . . . . . . . . . . . . . . . 81

Figure 3-15 Secret Sharing — Full Key Generation From Shares . . . . . . . . . . . . 81

Figure 4-1 Algorithm Object in a Software Implementation . . . . . . . . . . . . . . 132

Figure 4-2 Algorithm Object in a Hardware Implementation . . . . . . . . . . . . . . 133

xii RSA BSAFE Crypto-C Developer’s Guide

List of Tables

Table 3-1 Calculation of 827 mod 55. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54

Table 3-2 Elliptic Curve Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71

Table 3-3 DES Weak and Semi-Weak Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . 94

Table 3-4 Summary of Recommended Key Sizes . . . . . . . . . . . . . . . . . . . . . . . 98

Table 4-1 Message Digests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

Table 4-2 Message Authentication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104

Table 4-3 ASCII Encoding. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104

Table 4-4 Pseudo-Random Number Generation . . . . . . . . . . . . . . . . . . . . . . . 104

Table 4-5 Symmetric Stream Ciphers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104

Table 4-6 Symmetric Block Ciphers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105

Table 4-7 RSA Public-Key Cryptography . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107

Table 4-8 DSA Public-Key Cryptography . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109

Table 4-9 Diffie-Hellman Key Agreement . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110

Table 4-10 Elliptic Curve Public-Key Cryptography . . . . . . . . . . . . . . . . . . . . . . 110

Table 4-11 Bloom-Shamir Secret Sharing. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111

Table 4-12 Hardware Interface . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111

Table 4-13 Advanced Encryption Standard (AES) . . . . . . . . . . . . . . . . . . . . . . . 112

Table 4-14 Generic Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113

Table 4-15 Block Cipher Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113

Table 4-16 RSA Public and Private Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114

Table 4-17 DSA Public and Private Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114

Table 4-18 Elliptic Curve Keys . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115

Table 4-19 Token Keys. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115

Table 4-20 Input Limits for RSA PKCS Encryption . . . . . . . . . . . . . . . . . . . . . . . 127

Table 5-1 Code Sample: DigestDataSavedState() . . . . . . . . . . . . . . . . . . . . . 159

Table A-1 Demo Program Source Files . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 335

xiii

xiv RSA BSAFE Crypto-C Developer’s Guide

Preface

Dear Crypto-C Developer: Congratulations on your purchase of RSA BSAFE®

the-art in cryptographic software toolkits. Crypto-C provides developers with the most important privacy, authentication, and data integrity routines. Crypto-C contains a full palette of popular cryptographic algorithms. This software development kit enables you to develop applications for a wide range of purposes, including electronic commerce, home banking, Webcasting, and enterprise security.

RSA BSAFE® software for enabling applications to share encrypted information, verify the correspondent’s authenticity, and confirm data integrity. RSA Security’s generalpurpose cryptography software has the flexibility to suit a wide variety of security applications or services. This robust, fully supported product is from the most trusted name in e-security: RSA Security.

Crypto-C is written in C and is intended to be completely portable. It is available on a number of platforms and can be ported to most platforms with a minimum of effort. Crypto-C is a toolkit, not an application; it is intended to be integrated into operating systems, communications systems, and other applications. Therefore, you have a modest amount of work ahead of you. We have tried to make this task as clear as possible without limiting your options. This User’s Manual, with its code samples and tutorials, is the best place to start.

Crypto-C 5.2.2 is the latest version of RSA Security’s cryptographic

Crypto-C (Crypto-C), the state-of-

Thanks, and welcome to the RSA Security family. Sincerely, The Crypto-C Development Team

RSA Security

What’s New in Version 5.2.2?

Following is a list of RSA BSAFE Crypto-C features that are new in version 5.2.2:

Improved performance

With the new performance improvements, you’ll be able to use RSA BSAFE CryptoC’s algorithms at unprecedented levels of speed and throughput across a wide range of hardware platforms. RSA BSAFE Crypto-C’s support for the Intel Itanium™ and Pentium™4 processors will allow developers the ability to take advantage of benefits of these powerful processors. Also, RSA Security’s implementation of Compaq’s patented MultiPrime technology is designed to process encryption/decryption tasks more than two times faster than previous methods. Typical tasks where customers will experience these performance enhancements are for SSL transactions (signing on the server or client side) and non-repudiation operations (verifying on the client side).

Hardware support

RSA BSAFE Crypto-C products include PKCS #11 hardware support to allow communication with hardware like smart cards (for secure key storage) and cryptographic accelerator cards (for performance improvements). PKCS #11 support is in addition to the BHAPI hardware support offered in previous versions of CryptoC.

MultiPrime RSA

MultiPrime RSA functionality has been added to Crypto-C v5.2. Use this new function to generate RSA public/private key pairs. RSA MultiPrime key generation follows the same steps as standard RSA key generation with two exceptions: the use of a different AI, AI_RSAMultiPrimeKeyGen, and a different AM must be passed in during the B_GenerateInit call: AM_RSA_MULTI_PRIME_KEY_GEN.

Serialization for algorithm objects performing RC4, Diffie Hellman key exchange

A new algorithm information type, AI_RC4Serialize, has been added to Crypto-C

xvi RSA BSAFE Crypto-C Developer’s Guide

Organization of This Manual

V5.2. Use this AI to save the internal state of an RC4 encryption or decryption object, or to create a new object from the saved state of a previous RC4 object.

Advanced Encryption Standard (AES)

Crypto-C includes basic AES support for the cutting edge in processor technology: Intel Itanium and Pentium 4.

Organization of This Manual

This manual is organized as follows:

• Chapter 1, “Introduction,” introduces the Crypto-C toolkit. It lists the algorithms,

cryptographic standards, NIST standards, and ANSI X9 standards used in Crypto-C.

• Chapter 2, “Quick Start,” uses a code example to describe the basic encryption

and decryption operations in Crypto-C.

• Chapter 3, “Cryptography,” presents a brief outline of the basic cryptographic

principles and terminology that are used in this manual.

• Chapter 4, “Using Crypto-C,” presents a brief description of the Crypto-C

algorithm info types and key info types by functionality. It also covers system considerations when using Crypto-C.

• Chapters 5-8 present sample code for the major Crypto-C operations.

• Chapter 9, “Putting it all Together: An X9.31 Example,” presents sample code for

the steps involved in creating and verifying RSA digital signatures in accordance with the X9.31 standard.

• Appendix A, “Command-Line Demos,” describes the three Crypto-C command

line demo applications: BDEMO, BDEMODSA, and BDEMOEC.

• Glossary

• Index

Preface xvii

Conventions Used in This Manual

The following typographical conventions are used in this manual. Italic is used for:

• new terms where they are introduced

• the names of manuals and books

Lucida Typewriter Sans is used for:

• anything that appears literally in a C program, such as the names of structures

and functions supplied by Crypto-C: for example,

B_DecodeInit

Lucida Typewriter Sans Italic

is used for:

• function parameters and placeholders that indicate that an item is replaced by

some actual value in your own program: for example,

Lucida Typewriter Bold

is used for:

randomAlgorithm

• text the user types in command line demos and text that is printed to the screen

by the demos (Appendix A only)

Structures and routines defined by Crypto-C are boxed. Direct quotes from the RSA BSAFE Crypto-C Reference Manual are also boxed:

/* Structures defined by Crypto-C */

Crypto-C procedures to use with algorithm object:

B_EncryptInit, B_EncryptUpdate, B_EncryptFinal;

Application code and samples are displayed in a box with a shaded outline:

/* Application code and samples */

Some Crypto-C functions are only available when used with a hardware application that has a BSAFE Hardware API interface (BHAPI). These functions are marked with the icon of a hammer.

xviii RSA BSAFE Crypto-C Developer’s Guide

Terms and Abbreviations

The following table lists terms and abbreviations used in this document. Refer to the Glossary for a list of security and cryptographic terms and abbreviations, along with their definitions, that are used throughout the RSA BSAFE Crypto-C documentation set.

Term or Abbreviation Definition

Crypto-C RSA BSAFE Crypto-C: Cryptographic software development kit developers

use to develop secure applications.

.doc (file) Word for Windows, version 6.x or version 7.x files.

.htm (file) Hypertext Markup Language formatted files used for releasing documents on

the RSA Security internet site.

.pdf (file) Portable Document Format created by Adobe Acrobat Distiller and read by

using Adobe Acrobat Reader.

.rtf (file) Rich Text Format files that are compatable with Microsoft Word for Windows.

.txt (file) Unformatted, cross-platform text files.

PKI The Public Key Infrastructure that combines private key, trust, and certificate

databases for the reserve of needed private keys and certificates for signing or encrypting messages.

Public Client API The default application programming interface between PKI services and the

developer's application.

SPI Service provider interfaces that enable customized implementation to

augment or replace the default Cert-J functionality.

User Interface Any interface that the end user sees or accesses. This includes any HTML

browser-based interfaces

Preface xix

How to Contact RSA Security

RSA Security Web Site

You can visit the RSA Security Web site at http://www.rsasecurity.com. It contains the latest RSA Security news, security bulletins, and information about coming events.

RSA BSAFE product information is available at

products/bsafe http://www.rsasecurity.com/rsalabs/faq.

. RSA Laboratories’ Cryptography FAQ can also be found at

http://www.rsasecurity.com/

Getting Support and Service

You can get technical support as follows:

SecurCare® Online

www.rsasecurity.com/securcare/index.html

Technical Support Telephone Numbers

www.rsasecurity.com/support/news/tollfree.html

Call Handling and Escalation Process

www.rsasecurity.com/support/news/escproc.html

xxii RSA BSAFE Crypto-C Developer’s Guide

Chapter 1

Introduction

This chapter introduces the Crypto-C toolkit. It lists the algorithms, cryptographic standards, NIST standards, and ANSI X9 standards used in Crypto-C. This chapter is organized as follows:

• The Crypto-C Toolkit

- Algorithms

- Hardware Support

• Cryptographic Standards and Crypto-C

- PKCS Standards and Crypto-C

- NIST Standards and Crypto-C

-PKCS Compared with NIST

- ANSI X9 Standards and Crypto-C

The Crypto-C Toolkit

Crypto-C provides developers with a state-of-the-art implementation of the most important privacy, authentication, and data integrity routines.

Algorithms

The following algorithms are implemented in Crypto-C:

Symmetric Ciphers

• AES

• DES

• Triple DES

• DESX

• RC2® block cipher

• RC4® stream cipher

• RC5™ block cipher

• RC6™ block cipher

Message Digests

• MD

• MD2

• MD5

• SHA1

Message Authentication

• HMAC

Random-Number Generation

• MD2

• MD5

• SHA1

• X931

2 RSA BSAFE Crypto-C Developer’s Guide

Public-Key Algorithms

• RSA Public Key Cryptosystem

• Diffie-Hellman Key Agreement

Digital Signatures

• DSA

• RSA Digital Signatures

Elliptic Curve Public-Key Algorithms

• Elliptic Curve Digital Signature Algorithm (ECDSA)

• Elliptic Curve Diffie-Hellman Key Agreement

• Elliptic Curve Authenticated Encryption Scheme (ECAES)

Secret Sharing

• Bloom-Shamir Secret Sharing

The Crypto-C Toolkit

Hardware Support

In addition to the cryptographic algorithms listed here, Crypto-C offers a hardware interface that allows vendors of cryptographic hardware to support the Crypto-C API. One such vendor is Intel®, whose Intel hardware security primitives include the Intel Random Number Generator.

For information on using the Intel hardware (when present) with Crypto-C, see the Intel Security Hardware User’s Guide, included on the Crypto-C CD-ROM. For information about using Crypto-C with other cryptographic hardware, contact the specific hardware vendor.

Chapter 1 Introduction 3

Cryptographic Standards and Crypto-C

PKCS Standards and Crypto-C

Crypto-C is a general-purpose programming tool that developers can use to write a wide variety of applications. Crypto-C was built to help developers implement the Public-Key Cryptography Standards (PKCS), a series of documents that specify a standard way of performing basic cryptographic operations. Several higher-level standards, such as S/MIME, SET, IPSec, and SSL, require implementation of various PKCS standards. Since Crypto-C complies with PKCS standards, developers should find it fairly easy to integrate Crypto-C into software that implements the PKCS standards.

For copies of the PKCS documents, see the PKCS section of RSA Security’s Web site at

http://www.rsasecurity.com/rsalabs/pkcs, or contact our sales department for a

PKCS diskette.

NIST Standards and Crypto-C

Certain Crypto-C releases may be used to produce applications that are compliant with the Federal Information Processing Standards. Compliance with the FIPS standards is often required by government agencies and contractors. The National Institute of Standards and Technologies (NIST) establishes the FIPS standards, and certifies FIPS-compliant applications.

As changes are made in a new release, RSA Security may need to reapply for NIST certification. If you need to verify whether or not a specific release is compliant with FIPS, contact your sales representative.

NIST Approval and Windows 32-bit Platforms

If you require NIST approval for your Windows 32-bit applications, you may benefit from using the FIPS-compliant Crypto-C algorithms listed following this paragraph. NIST may approve the use of these algorithms in your application without requiring further algorithm-level testing of your application, based on the algorithm certificates issued to Crypto-C. For more information, see the algorithm compliance Web site provided by NIST.

Crypto-C includes the following FIPS-compliant algorithms:

4 RSA BSAFE Crypto-C Developer’s Guide

Cryptographic Standards and Crypto-C

• Secure Hash Algorithm (SHA1), as specified in FIPS PUB 180-1, Secure Hash

Standard (SHS)

• RSA Digital Signatures (rDSA), as specified in FIPS PUB 186-2

• Digital Signature Algorithm (DSA), as specified in FIPS PUB 186, Digital

Signature Standard (DSS)

• Data Encryption Standard (DES), as specified in FIPS PUB 46-2

• DES Modes of Operation, as specified in FIPS PUB 81

NIST Approval and Windows NT Platforms

If you require NIST approval for your Windows NT applications, you may benefit from using the “Crypto-C Cryptographic Services Module,” a DLL that is compliant with the FIPS 140-1 standard. NIST may approve the use of this module in your application without requiring further testing of your application, based on the NIST certification issued to the Crypto-C module. For more information, see the \FIPS140 folder on the Crypto-C CD-ROM for Windows NT.

PKCS Compared with NIST

In some cases, such as the RSA algorithm, the PKCS standards differ from the NIST standards. In such cases, the standard you choose depends primarily on the scope of your application and how it will be deployed.

As mentioned previously, the PKCS standards, many of which have been in place for a long time, have widespread acceptance and are used as the base for many other higher-level standards (for example, S/MIME, SET, IPSec, and SSL). Therefore, if you are implementing one of these higher-level standards, or if you want compatibility with other applications that use the PKCS standards, you should use the PKCS-based implementation.

However, the United States government may have specific standards requirements for certain government agencies and for government contractors. These are usually the standards as defined by NIST. If you are creating applications for U.S. government use, you should ensure that you are in compliance with any required protocols.

Chapter 1 Introduction 5

Cryptographic Standards and Crypto-C

ANSI X9 Standards and Crypto-C

Crypto-C also complies with a number of standards established by the X9 Financial Services Industry committee of the American National Standards Institute (ANSI). If you are writing a financial or government application that must comply with one of the X9 standards, you may benefit by using Crypto-C. This release is fully compliant with the following ANSI X9 standards:

• The ANSI X9.31 Standard, which specifies an implementation of RSA Digital

Signatures (rDSA). (Note that this implementation also complies with the NIST standard for rDSA, specified in FIPS PUB 186-2, as mentioned previously.)

• The ANSI X9.62 Standard, which specifies an implementation of the Elliptic

Curve Digital Signature Algorithm (ECDSA).

For more information, see the X9 Web site at

http://www.x9.org.

6 RSA BSAFE Crypto-C Developer’s Guide

Chapter 2

Quick Start

This chapter provides an introduction to using Crypto-C. You are first presented with the Crypto-C model and then you are presented an introductory example. This chapter is organized as follows:

• The Six-Step Sequence

• Introductory Example

• Decrypting the Introductory Example

• Multiple Updates

• Summary of the Six Steps

The Six-Step Sequence

The Crypto-C model generally follows a six-step sequence:

1. Create

2. Set

3. Init

4. Update

5. Final

6. Destroy

In addition, for every application, you must include the necessary header files; we will call this Step 0.

The six-step sequence makes it easier to maintain your code. For example, if you have implemented a message digest routine using MD2 and wish to use SHA1 instead, you simply need to make changes in Steps 2 and 3, Set and Init. The rest of your code can be reused. Similarly, if you originally programmed a routine under the assumption that it would get all the data from a single buffer, and you want to modify it to take data from multiple buffers, you can simply change Step 4, Update.

Note: In some cases, an algorithm may not require an Update step. The sections in this chapter show the following:

• A six-step encryption example

• A six-step decryption example

• An example using multiple Updates

• A summary of the six-step process

8 RSA BSAFE Crypto-C Developer’s Guide

Introductory Example

The CD containing the Crypto-C library distribution also includes sample source code to accompany this Developer’s Guide. One of the files on that CD, example of converting the Introductory Example into a program. Later in this manual are instructions on writing code for many Crypto-C operations. There are sample programs on the CD to accompany all the topics covered.

With the RSA BSAFE Crypto-C Reference Manual handy, we will encrypt the sentence, “Encrypt this sentence.” To do this, we will use what is called a stream cipher, that is, an encryption method that encrypts data one character at a time, in a single stream. The cipher we will use is called the RC4 cipher. This cipher can take a key size from 1 to 256 bytes. The RC4 cipher creates a “key stream” based on the key and XORs the stream of data with the key stream to create ciphertext.

introex.c, is an

The example in this section corresponds to the file

introex.c.

Step 0: Include Files

You must include the following header file and the Crypto-C library in every application you write using Crypto-C:

#include “bsafe.h”

When writing a Crypto-C application, include DEMO_ALGORITHM_CHOOSER, see

15. In addition, you must compile and link in management functions called by the Crypto-C library.

Note: For backward compatibility, the BSAFE 2.x

bsafe2.h, are still valid. If your source code contains the older names, you

should not have any problems.

Selecting an Algorithm Chooser on page

bsafe.h. If you want to use the

tstdlib.c, which contains the memory

include file names, global.h and

Step 1: Creating an Algorithm Object

Whatever operation Crypto-C performs, it does so from an algorithm object. An algorithm object is used to hold information about an algorithm’s parameters and to keep a context during a cryptographic operation such as encryption or decryption. For our example, we will build an algorithm object that performs encryption.

You build an algorithm object in Steps 1 to 3. As you go through these steps, you

Chapter 2 Quick Start 9

Introductory Example

specify the type of algorithm that is being used, supply any special information or parameters that the algorithm requires, and generate or supply a key for algorithms that need one.

In Step 1, we simply create the object. We do this by declaring a variable to be an algorithm object and calling

B_CreateAlgorithmObject.

In this case, we name our algorithm object

B_ALGORITHM_OBJ rc4Encrypter = (B_ALGORITHM_OBJ)NULL_PTR;

The data type

B_ALGORITHM_OBJ is defined in bsafe.h:

typedef POINTER B_ALGORITHM_OBJ;

rc4Encrypter

and declare it as follows:

where POINTER is defined in aglobal.h:

typedef unsigned char *POINTER;

and NULL_PTR is also defined in aglobal.h:

#define NULL_PTR ((POINTER)0)

So our variable, object is destroyed, it is a good idea to initialize it to

To create an algorithm object, we call

rc4Encrypter

, is a pointer. To prevent problems when the algorithm

NULL_PTR. See Step 6 for details.

B_CreateAlgorithmObject. Chapter 4 of the

Reference Manual gives the function prototypes and descriptions of all the Crypto-C calls. For

int B_CreateAlgorithmObject ( B_ALGORITHM_OBJ *algorithmObject /* new algorithm object */ );

Because argument, we have to pass the address of

B_CreateAlgorithmObject, we find:

B_CreateAlgorithmObject takes a pointer to a B_ALGORITHM_OBJ as its

rc4Encrypter

. The return value is an int. Most Crypto-C calls return either a 0 (zero), which indicates success, or a non-zero error code. After the call, look at the return value: if it is 0, continue; if not, stop. At RSA Security, the tradition is to name the return value

status

10 RSA BSAFE Crypto-C Developer’s Guide

Introductory Example

int status; do { if ((status = B_CreateAlgorithmObject (&rc4Encrypter)) != 0) break;

. . .

} while (0);

Standard RSA Security coding practices use the above do-while construct to make it easy to break out of a sequence when encountering an error. If a Crypto-C function returns a non-zero value,

break will exit the do-while, and further code dependent on

the offending call will not be executed. However, any clean-up code, such as overwriting sensitive memory with zeroes (see Step 6), can follow the

do-while and

will always execute, whether or not there was an error.

Step 2: Setting the Algorithm Object

The variable

rc4Encrypter

is now an algorithm object, but we have not yet determined what type of operations it can perform. In Step 2, we associate the algorithm object with an algorithm and supply any special information or parameters the algorithm requires. We do this with

B_SetAlgorithmInfo. Chapter 4 of the Reference Manual

gives this function’s prototype and description:

int B_SetAlgorithmInfo ( B_ALGORITHM_OBJ algorithmObject, /* algorithm object */ B_INFO_TYPE infoType, /* type of algorithm information */ POINTER info /* algorithm information */ );

The first argument is

rc4Encrypter

. The second argument is an algorithm info type, or AI. In Crypto-C, you specify the type of operation an algorithm object performs by setting the object to a particular AI. Chapter 2 of the Reference Manual describes the available AIs. Each AI description also lists the information that must accompany that AI when setting an algorithm object. That accompanying information is the third argument of

B_SetAlgorithmInfo.

For our example, we want to choose a stream cipher AI. A stream cipher processes data in a stream of arbitrary length. This is in contrast to another common type of cipher, the block cipher, which processes data in blocks of a fixed size. In Crypto-C,

Chapter 2 Quick Start 11

Introductory Example

there is a single stream cipher, the RC4 cipher, and a number of AIs that can be used to implement it. For this example we will use argument to

B_SetAlgorithmInfo.

AI_RC4; we pass this as the second

The third argument is information that is specific to the AI we chose. For complex algorithms, this is input that is required by the algorithm, including parameters for algorithms that require them, “salt” and the desired number of iterations for password-based encryption, or an “initialization vector” for block ciphers. In our example, in Chapter 2 of the Reference Manual states that the format of the

B_SetAlgorithmInfo is NULL_PTR.

AI_RC4 is a simple algorithm that does not require any parameters; its entry

info

supplied to

Thus, we can make the call to B_SetAlgorithmInfo:

if ((status = B_SetAlgorithmInfo (rc4Encrypter, AI_RC4, NULL_PTR)) != 0) break;

Note: Once you have set an algorithm object, do not set it again. If you need an

algorithm object to perform another type of operation, create a new one.

Step 3: Init

Now that we have created and set our algorithm object, encrypt. Actually, since we haven’t called

B_EncryptInit, it is ready to decrypt as

well. In Step 3, we choose the operations our algorithm object can perform by supplying the desired function pointers to the Crypto-C library; we also create and set a key object that will supply the key data the algorithm needs.

Note: An algorithm object can be used for either encryption or decryption, but not

for both. You should create separate algorithm objects to handle each case.

Look at the entry for

AI_RC4 in Chapter 2 of the Reference Manual:

Crypto-C procedures to use with algorithm object:

B_EncryptInit, B_EncryptUpdate, B_EncryptFinal;

and

B_DecryptInit, B_DecryptUpdate, and B_DecryptFinal.

You may pass

From this, you can see that

(B_ALGORITHM_OBJ)NULL_PTR for all randomAlgorithm arguments.

AI_RC4 can be used with encryption or decryption

procedures; that is, it can be used to encrypt or to decrypt. We want to encrypt, so in Step 3, we will call

B_EncryptInit to initialize our algorithm object to perform

encryption. This call will also associate a key with the algorithm object.

12 RSA BSAFE Crypto-C Developer’s Guide

rc4Encrypter

, it is ready to

Introductory Example

See the description and prototype in Chapter 4 of the Reference Manual for

B_EncryptInit:

int B_EncryptInit ( B_ALGORITHM_OBJ algorithmObject, /* algorithm object */ B_KEY_OBJ keyObject, /* key object */ B_ALGORITHM_CHOOSER algorithmChooser, /* algorithm chooser */ A_SURRENDER_CTX *surrenderContext /* surrender context */ );

As in Step 2, the first argument is the algorithm object; once again, we use

rc4Encrypter

. The next three arguments are new.

Step 3a: Creating a Key Object

The second argument is a key object, which is used to hold any key-related information, such as the RC4 key, and to supply this information to functions that require it. Before we can pass a key object as an argument, we must create and set it. Creating a key object is similar to creating an algorithm object. We name our key object

rc4Key

and declare it as follows:

B_KEY_OBJ rc4Key = (B_KEY_OBJ)NULL_PTR;

where

B_KEY_OBJ is defined in bsafe.h:

typedef POINTER B_KEY_OBJ;

Chapter 4 of the Reference Manual gives the description and prototype of

B_CreateKeyObject:

int B_CreateKeyObject ( B_KEY_OBJ *keyObject /* new key object */ );

For our example, we use:

if ((status = B_CreateKeyObject (&rc4Key)) != 0) break;

Step 3b: Setting a Key Object

We have a key object, but it is not yet distinguished as an RC4 key. To distinguish the

Chapter 2 Quick Start 13

Introductory Example

object as an RC4 key, we need to use B_SetKeyInfo. See Chapter 4 of the Reference Manual for this function’s description and prototype:

int B_SetKeyInfo ( B_KEY_OBJ keyObject, /* key object */ B_INFO_TYPE infoType, /* type of key information */ POINTER info /* key information */ );

This function is similar to just created,

rc4Key

. The second argument is a key info type (KI), and the third

B_SetAlgorithmInfo. The first argument is the key object

argument is information that must accompany the given KI. We want to use a KI compatible with RC4 encryption, so we return to the entry for our AI,

AI_RC4, in

Chapter 2 of the Reference Manual:

Key info types for keyObject in B_EncryptInit or B_DecryptInit:

KI_Item that gives the address and length of the RC4 key.

Key info types are described in Chapter 3 of the Reference Manual. Under the entry for

KI_ITEM we find that the format of ITEM structure:

typedef struct { unsigned char *data; unsigned int len; } ITEM;

len

is the length of the key in bytes. The RC4 cipher takes key sizes of 1 to 256 bytes. A

10-byte key is generally sufficient for most applications.

info

supplied to B_SetKeyInfo is a pointer to an

data

is the key data. A real application would use a random number generator to produce 10 bytes for the key (see “Generating Random Numbers” on page 165). For this example, we can simply use:

14 RSA BSAFE Crypto-C Developer’s Guide

Introductory Example

static unsigned char rc4KeyData[] = { 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x10 };

ITEM rc4KeyItem; rc4KeyItem.data = rc4KeyData; rc4KeyItem.len = sizeof(rc4keyData);

Now we can complete the call to B_SetKeyInfo:

if ((status = B_SetKeyInfo (rc4Key, KI_Item, (POINTER)&rc4KeyItem)) != 0) break;

As with algorithm objects, once you have set a key object, you should not set it again. If you need another key object, you should create a new one.

Note: In a real application, for security reasons, you might want to zeroize and free

your key data immediately after setting the key.

Now that we have created and set our key object, argument to

B_EncryptInit.

rc4Key

, we can pass it as the second

Selecting an Algorithm Chooser

The third argument to B_EncryptInit is an algorithm chooser; this is a structure that specifies which algorithm methods to link in. An algorithm method (AM) is the underlying code that actually performs the cryptographic operation. Because many AIs can perform more than one cryptographic function (for example, perform encryption and decryption), an application often has a choice of which underlying algorithm methods need to be linked in.

An algorithm chooser lists all the AMs the application will use; only these AMs will be linked in. Crypto-C comes with a demonstration application containing the algorithm chooser

DEMO_ALGORITHM_CHOOSER. You can use this algorithm chooser in

any Crypto-C application as long as the module which defines it ( compiled and linked in. However,

DEMO_ALGORITHM_CHOOSER will link in all the

algorithm methods available, even though an application might use only two or three. A developer can write an algorithm chooser for the specific application to make the

executable image smaller. See “Algorithm Choosers” on page 116 in this manual for

Chapter 2 Quick Start 15

AI_RC4 can

choosc.c) is

Introductory Example

instructions on writing an algorithm chooser. For the purposes of our example, we see that the Reference Manual entry for AI_RC4 states that we should use AM_RC4_ENCRYPT in our chooser. Include the following algorithm methods in your chooser:

AM_RC4_ENCRYPT for encryption B_ALGORITHM_METHOD*rc4EncryptChooser[]={ & AM_RC4_ENCRYPT, NULL};

Surrender Context

The fourth argument of B_EncryptInit is a surrender context, which controls when and how the application surrenders control during time-consuming operations. The application developer can put together an surrender function and other information. Crypto-C applications call this surrender function at regular intervals.

The surrender function can simply print out information to the user that indicates that the Crypto-C operation is currently executing, or it can provide the user with a means of halting the operation if it is taking too much time. A surrender context is not required; if none is desired, simply pass a properly cast Context” on page 118 for a more detailed description of the structure. For this example, we will use

A_SURRENDER_CTX structure containing a

NULL_PTR. See “The Surrender

A_SURRENDER_CTX

(A_SURRENDER_CTX *)NULL_PTR.

We can now complete our call to

if ((status = B_EncryptInit (rc4Encrypter, rc4Key, rc4EncryptChooser, (A_SURRENDER_CTX *)NULL_PTR)) != 0) break;

B_EncryptInit:

Saving the Object State (optional)

This step is optional. Refer to “Saving State” on page 120 for information on how to receive a buffer that contains all of the data necessary to reconstruct the object, using the call

B_SetAlgorithmState, to the state it was in at the time of calling the Get

routine. This can be done after B_EncryptInit and B_EncryptUpdate, or B_DecryptInit and B_DecryptUpdate.

Step 4: Update

In Steps 1 through 3, we created our algorithm object and initialized it with the

16 RSA BSAFE Crypto-C Developer’s Guide

Introductory Example

information that it needs to perform RC4 encryption. In Step 4, we can enter the data to encrypt with the

B_EncryptUpdate function. Chapter 4 of the Reference Manual

provides the following description and prototype:

int B_EncryptUpdate ( B_ALGORITHM_OBJ algorithmObject, /* algorithm object */ unsigned char *partOut, /* output data buffer */ unsigned int *partOutLen, /* length of output data */ unsigned int maxPartOutLen, /* size of output data buffer */ unsigned char *partIn, /* input data */ unsigned int partInLen, /* length of input data */ B_ALGORITHM_OBJ randomAlgorithm, /* random byte source */ A_SURRENDER_CTX *surrenderContext /* surrender context */ );

The first argument is our algorithm object,

rc4Encrypter

The other arguments call for the plaintext input and encrypted output. Because the output depends on the input, we start with the fifth and sixth arguments, which describe the input.

We name our input

static char dataToEncrypt[] = “Encrypt this sentence.”;

Crypto-C needs to know how many bytes our input is, so we use

unsigned int dataToEncryptLen; dataToEncryptLen = (unsigned int)strlen (dataToEncrypt) + 1;

If your data is not a string — that is, if it does not end with a character — do not use

dataToEncrypt

strlen to determine its length.

and declare it as follows:

strlen:

NULL-terminating

The output is described by the second, third, and fourth arguments. The second argument is described in the prototype as

does not mean you simply declare a variable to be

unsigned char *partOut. This

unsigned char * and pass it as the

argument. The output argument that you pass is a pointer to a buffer of allocated memory. This is an important point; see “Algorithm Choosers” on page 116 for a detailed discussion of this topic.

Chapter 2 Quick Start 17

Introductory Example

For now, we declare:

unsigned char *encryptedData = NULL_PTR;

For a stream cipher, the length of the encrypted (output) data is equal to the length of the input data. So we allocate

encryptedData = T_malloc (dataToEncryptLen); if ((status = (encryptedData == NULL_PTR)) != 0) break;

dataToEncryptLen

bytes with T_malloc:

The previous code sample uses the Crypto-C routine

T_malloc. Crypto-C supplies its

own memory management routines to increase code portability and to meet the special requirements of handling encrypted data. The Crypto-C memory management routines reside in the file

tstdlib.c; make sure this file is compiled and

linked in. These routines are described in Chapter 4 of the Reference Manual and in “Memory-Management Routines” on page 122 of this manual.

In our example, the

T_malloc routine from tstdlib.c returns a pointer to the

allocated memory. If, for some reason, it cannot allocate memory (for example, when there is not enough memory available), imperative to always check the return value of only a small number of bytes.

T_malloc also sets an unsigned char * variable; it is a

good idea to initialize this variable to

T_malloc will return NULL_PTR. It is

T_malloc, even if you are allocating

NULL_PTR. See “Step 6: Destroy” on page 20 for

more information. The third argument to

B_EncryptUpdate returns a value indicating how many bytes it placed into the output

buffer. It will place this value at the address specified by the pointer to the

. Make the proper declaration:

int

unsigned int outputLenUpdate;

Crypto-C might not encrypt all the input data during a call to

B_EncryptUpdate is a pointer to an unsigned int.

unsigned

B_EncryptUpdate. Any

unprocessed data will be saved in a buffer inside the algorithm object created by Crypto-C and encrypted during a subsequent call to Update (see “Multiple Updates” on page 29) or during the call to

B_EncryptFinal (see “Step 5: Final” on page 19). This

is why it is important to keep track of how many bytes Crypto-C wrote to the output buffer.

The fourth argument to

18 RSA BSAFE Crypto-C Developer’s Guide

B_EncryptUpdate is the size of the output buffer. The Update

Introductory Example

function must know the size of the buffer. The Update function will not attempt to place data into unallocated memory; instead, it returns an error if it needs to place more bytes into the buffer than are allocated. In our example, we will use

dataToEncryptLen

as our output data size.

The seventh argument is a random algorithm. Recall that in Chapter 2 of the Reference Manual, the description of

AI_RC4 states:

You may pass

(B_ALGORITHM_OBJ)NULL_PTR for all

randomAlgorithm

arguments.

That is exactly what we will supply in our example. For the eighth argument, once again we pass a properly cast

NULL_PTR as the

surrender context. When we put this all together, our Update call is:

if ((status = B_EncryptUpdate (rc4Encrypter, encryptedData, &outputLenUpdate, dataToEncryptLen, dataToEncrypt, dataToEncryptLen, (B_ALGORITHM_OBJ)NULL_PTR, (A_SURRENDER_CTX *)NULL_PTR)) != 0) break;

encryptedDataLen = outputLenUpdate + outputLenFinal

Note the warning in the Reference Manual Chapter 2 entry for

AI_RC4:

Due to the nature of the RC4 algorithm, security is compromised if multiple data blocks are encrypted with the same RC4 key. Therefore, called after

B_EncryptFinal. This is because after a call to B_EncryptFinal and

B_EncryptUpdate cannot be

B_DecryptFinal, the state of the algorithm object is reset to the state in which it was following the call to B_EncryptInit and B_DecryptInit. To begin an encryption operation for a new data block, you must call

B_EncryptInit and supply a new key.

This simply means that you should not use the same key for two different encryption sessions.

Step 5: Final

B_EncryptFinal finalizes the encryption process by encrypting any data that B_EncryptUpdate could not. See Chapter 4 of the Reference Manual for the function’s

description and prototype:

Chapter 2 Quick Start 19

Introductory Example

int B_EncryptFinal ( B_ALGORITHM_OBJ algorithmObject, /* algorithm object */ unsigned char *partOut, /* output data buffer */ unsigned int *partOutLen, /* length of output data */ unsigned int maxPartOutLen, /* size of output data buffer */ B_ALGORITHM_OBJ randomAlgorithm, /* random byte source */ A_SURRENDER_CTX *surrenderContext /* surrender context */ );

For our example, the first argument is

rc4Encrypter

The second argument is a pointer to the output buffer that we created for

B_EncryptUpdate. However, B_EncryptUpdate has already placed some data into that

buffer, so we must pass the address of the next byte that is available after the already filled bytes to the number of bytes that

The third argument is a pointer to an

unsigned int to the number of bytes it encrypted.

The fourth argument is the size of the buffer available to

B_EncryptUpdate has already written to part of the buffer, this value will be the total

size of the buffer minus the number of bytes

dataToEncryptLen-outputLenUpdate

B_EncryptFinal. That is the address of the beginning of the buffer plus

B_EncryptUpdate filled, or

unsigned int; B_EncryptFinal will set that

encryptedData

B_EncryptFinal. Because

B_EncryptUpdate has used, or

outputLenUpdate

Once again, we can pass properly cast null pointers for the fifth and sixth arguments, which are the random algorithm and surrender context.

Then, for our example, we have:

if ((status = B_EncryptFinal (rc4Encrypter, encryptedData + outputLenUpdate, &outputLenFinal, dataToEncryptLen - outputLenUpdate, (B_ALGORITHM_OBJ)NULL_PTR, (A_SURRENDER_CTX *)NULL_PTR)) != 0) break;

Step 6: Destroy

When you are done with an algorithm or key object, you must destroy it. The Destroy function frees up any memory that was allocated by Crypto-C and zeroizes any sensitive memory. Because you will always want to destroy the objects, place these

20 RSA BSAFE Crypto-C Developer’s Guide

Introductory Example

function calls after the do-while construct. That way, even if there is an error somewhere and the program breaks out of the within the

do-while, the Destroy functions will execute. In case the error occurs

before an object has been created, it is a good idea to initialize objects to an object is

NULL_PTR, the Destroy function does nothing.

do-while before executing all the calls

NULL_PTR. If

Chapter 4 of the Reference Manual gives the description and prototype of the Destroy functions:

void B_DestroyKeyObject ( B_KEY_OBJ *keyObject /* pointer to key object */ ); void B_DestroyAlgorithmObject ( B_ALGORITHM_OBJ *algorithmObject /* pointer to algorithm object */ );

For our example, we use the following:

B_DestroyKeyObject (&rc4Key); B_DestroyAlgorithmObject (&rc4Encrypter);

Note: Following these calls, rc4Key and rc4Encrypter will be set to NULL if the

objects were disposed of properly.

In addition to destroying any objects that you created, any memory you allocated must be freed when you are done with it. This means that each corresponding

T_free. Placing the T_free after the do-while guarantees that it will be

T_malloc must have a

called even if there is an error somewhere. However, there is a concern that if there is an error before the memory is allocated, then That is why it is important to initialize the pointer to

T_free is NULL_PTR, the extra call to T_free does nothing.

See Chapter 4 of the Reference Manual for the

void T_free ( POINTER block /* block address */ );

Chapter 2 Quick Start 21

T_malloc and the program breaks out of the do-while before

T_free will be called without a corresponding T_malloc.

NULL_PTR. If the argument to

T_free prototype:

Introductory Example

For this example, call T_free as follows:

T_free (encryptedData);

Note: Using

T_free means you can no longer access the data at that address. Do not

free a buffer until you no longer need the data it contains. If you will need the data later, you might want to save it to a file first.

You may want to zeroize any sensitive data before you free it. To do this, duplicate the following sequence after the

do-while. If there is an error inside the do-while

before you zeroize and free, these important tasks will still be performed:

if (rc4KeyItem.data != NULL_PTR) { T_memset (rc4KeyItem.data, 0, rc4KeyItem.len); T_free (rc4KeyItem.data); rc4KeyItem.data = NULL_PTR; rc4KeyItem.len = 0; }

Putting It All Together

Now we can put Steps 0 through 6 into a program. This program can be found in the file

introex.c:

#include "bsafe.h"

void PrintBuf PROTO_LIST ((unsigned char *, unsigned int));

void main() { B_KEY_OBJ rc4Key = (B_KEY_OBJ)NULL_PTR; B_ALGORITHM_OBJ rc4Encrypter = (B_ALGORITHM_OBJ)NULL_PTR;

/* The RC4 key is hard-coded in this example. In a real application, use a random number generator to produce the key. */ unsigned char rc4KeyData[10] = { 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x10 };

22 RSA BSAFE Crypto-C Developer’s Guide

Introductory Example

static char dataToEncrypt[] = "Encrypt this sentence."; unsigned char *encryptedData = NULL_PTR; unsigned int dataToEncryptLen, encryptedDataLen; unsigned int outputLenUpdate, outputLenFinal; int status;

do { dataToEncryptLen = strlen (dataToEncrypt) + 1;

/* Step 1: Create an algorithm object. */ if ((status = B_CreateAlgorithmObject (&rc4Encrypter)) != 0) break;

/* Step 2: Set the algorithm to a type that does rc4 encryption. AI_RC4 will do. */ if ((status = B_SetAlgorithmInfo (rc4Encrypter, AI_RC4, NULL_PTR)) != 0) break;

/* Step 3a: Create a key object. */ if ((status = B_CreateKeyObject (&rc4Key)) != 0) break;

/* Step 3b: Set the key object with the 10-byte key. */ rc4KeyItem.data = rc4KeyData; rc4KeyItem.len = rc4KeyDataLen;

if ((status = B_SetKeyInfo (rc4Key, KI_Item, (POINTER)&rc4KeyItem)) != 0) break;

if (rc4KeyItem.data != NULL_PTR) { T_memset (rc4KeyItem.data, 0, rc4KeyItem.len); T_free (rc4KeyItem.data); rc4KeyItem.data = NULL_PTR; rc4KeyItem.len = 0; }

/* Step 3: Init */ if ((status = B_EncryptInit (rc4Encrypter, rc4Key, DEMO_ALGORITHM_CHOOSER, (A_SURRENDER_CTX *)NULL_PTR)) != 0) break;

Chapter 2 Quick Start 23

Introductory Example

/* Step 4: Update */ encryptedData = T_malloc (dataToEncryptLen); if ((status = (encryptedData == NULL_PTR)) != 0) break;

if ((status = B_EncryptUpdate (rc4Encrypter, encryptedData, &outputLenUpdate, dataToEncryptLen, (unsigned char *)dataToEncrypt, dataToEncryptLen, (B_ALGORITHM_OBJ)NULL_PTR, (A_SURRENDER_CTX *)NULL_PTR)) != 0) break;

/* Step 5: Final */ if ((status = B_EncryptFinal (rc4Encrypter, encryptedData + outputLenUpdate, &outputLenFinal, dataToEncryptLen - outputLenUpdate, (B_ALGORITHM_OBJ)NULL_PTR, (A_SURRENDER_CTX *)NULL_PTR)) != 0) break;

encryptedDataLen = outputLenUpdate + outputLenFinal; printf ("Encrypted data (%u bytes):\n", encryptedDataLen); PrintBuf (encryptedData, encryptedDataLen);

} while (0);

/* Done with the key and algorithm objects, so destroy them. */ B_DestroyKeyObject (&rc4Key); B_DestroyAlgorithmObject (&rc4Encrypter);

/* Free up any memory allocated, save it to a file or print it out first if you need to save it. */ if (rc4KeyItem.data != NULL_PTR) { T_memset (rc4KeyItem.data, 0, rc4KeyItem.len); T_free (rc4KeyItem.data); rc4KeyItem.data = NULL_PTR; rc4KeyItem.len = 0; }

24 RSA BSAFE Crypto-C Developer’s Guide

Introductory Example

if (encryptedData != NULL_PTR){ T_memset (encryptedData, 0, dataToEncryptLen); T_free (encryptedData); encryptedData = NULL_PTR; }

} /* end main */

You may find it a useful exercise to compile and link this program. Also, it could also be instructive to add some print statements. For instance, what are the values of

outputLenUpdate

and

outputLenFinal

While it is possible to print the any kind of string, because there is no

encryptedData

NULL-terminating character. The encrypted data

, it will not be an ASCII string — it is not

is binary data, so it may be more useful to print out the result byte-by-byte in hexASCII strings. For an example of a function that does this, see the RSA_ routine in

samples/common/source/demoutil.c. In addition, note that when writing

PrintBuf()

Crypto-C output to (and reading it from) files, it is usually more useful (in some cases, even necessary) to open the files in binary mode.

To run this exercise, first compile the

samples/make directory. Then link the object files with bsafe.lib or the

introex.c and tstdlib.c. You can find makefiles in

equivalent platform-specific library.

Chapter 2 Quick Start 25

Decrypting the Introductory Example

Decrypting data is similar to encrypting. The RC4 cipher uses symmetric-key encryption, which means the key that was used to encrypt will be the key needed for decryption.

The example in this section corresponds to the file

dintroex.c.

Step 1: Creating an Algorithm Object

First create the algorithm object.

B_ALGORITHM_OBJ rc4Decrypter = (B_ALGORITHM_OBJ)NULL_PTR;

if ((status = B_CreateAlgorithmObject (&rc4Decrypter)) != 0) break;

Step 2: Setting the Algorithm Object

Use the same AI and parameters as for encryption:

if ((status = B_SetAlgorithmInfo (rc4Decrypter, AI_RC4, NULL_PTR)) != 0) break;

Step 3: Init

Use the same key data as for encryption. Once again, we must create and set the key object.

Step 3a: Creating the Key Object

As before, we name our key object

B_KEY_OBJ rc4Key = (B_KEY_OBJ)NULL_PTR;

Then we allocate space for the key object using

if ((status = B_CreateKeyObject (&rc4Key)) != 0) break;

26 RSA BSAFE Crypto-C Developer’s Guide

rc4Key

and declare it as follows:

B_CreateKeyObject:

Decrypting the Introductory Example

Step 3b: Setting the Key Object

We need to fill our key with the same 10 bytes of data we used for encryption. We must make sure that we use the same key as we used to encrypt. For our sample application, we can simply re-create the key data we had before:

static unsigned char rc4KeyData[] = { 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x10 };

Now we can complete the call to

if ((status = B_SetKeyInfo (rc4Key, KI_Item, (POINTER)&rc4KeyData)) != 0) break;

B_SetKeyInfo:

Step 4: Update

Here, we must set the buffer that will store the decrypted data; for the RC4 cipher, it should be the same size as the encrypted data’s buffer:

unsigned char *decryptedData = NULL_PTR;

decryptedData = T_malloc (encryptedDataLen); if ((status = (decryptedData == NULL_PTR)) != 0) break;

if ((status = B_DecryptUpdate (rc4Decrypter, decryptedData, &decryptedLenUpdate, encryptedDataLenTotal, encryptedData, outputLenTotal, (B_ALGORITHM_OBJ)NULL_PTR, (A_SURRENDER_CTX *)NULL_PTR)) != 0) break;

Chapter 2 Quick Start 27

Decrypting the Introductory Example

Step 5: Final

if ((status = B_DecryptFinal (rc4Decrypter, decryptedData + decryptedLenUpdate, &decryptedLenFinal, encryptedDataLen - decryptedLenUpdate, (B_ALGORITHM_OBJ)NULL_PTR, (A_SURRENDER_CTX *)NULL_PTR)) != 0) break;

In the “Introductory Example” on page 9, the plaintext was a string. Therefore, we can compute the sum of many characters make up the decryption.

Note: For some algorithms, the decrypted data may not be a string — for example,

when the want to print the decrypted data, you will not be able to because the data is in binary form, not ASCII. You could print the binary data using

RSA_PrintBuf(), or you can convert the decrypted data. Crypto-C offers

encoding and decoding functions to convert between binary and ASCII. See “Converting Data Between Binary and ASCII” on page 172 for more information.

decryptedLenUpdate

NULL-terminating character was not encrypted. In these cases, if you

and

decryptedLenFinal

to determine how

Step 6: Destroy

Always destroy objects when you no longer need them:

B_DestroyAlgorithmObject (&rc4Decrypter);

if (decryptedData != NULL_PTR) { T_memset (decryptedData, 0, encryptedDataLen); T_free (decryptedData); decryptedData = NULL_PTR; }

28 RSA BSAFE Crypto-C Developer’s Guide

Multiple Updates

An application can do multiple updates before the Final call. For example, suppose you have data from three different files that you want to encrypt into a single buffer. You could do this in three steps: read the contents of the first file into a buffer; read the next file, appending the contents to the end of the existing buffer; then append the contents of the third. But that would be clumsy if the contents of the three files are already in three buffers.

You do not have to put data together into a single buffer to encrypt it. Instead, call

B_EncryptUpdate with the first buffer, call it a second time with the second buffer, and

one last time with the third buffer. Then call finished all Updates. Similarly, you can call blocks of encrypted data.

Multiple updates can also be useful for encrypting or decrypting large amounts of data. If you need to process a one-megabyte file, you could allocate a megabyte of memory, put the entire file into that memory buffer, and call Update once. But using such a large amount of memory is impractical or even impossible in some situations. An application is more robust if it allocates a smaller buffer — say, 64, 128 or 1024 bytes — transfers data from the file in increments, and processes each unit with a separate call to Update. Then it can call Final once for all Updates.

B_EncryptFinal once, after you have

B_DecryptUpdate more than once with

Crypto-C does not always encrypt or decrypt an entire block during an Update call. One reason it might not handle the whole block is because of padding. Padding is used with block ciphers to ensure the data satisfies input restrictions and may add bytes to the original data. See “Padding” on page 37 for more information. Padding and pad operations (encrypting or decrypting the padding, or stripping the pad) take place in Final, so Crypto-C may keep the last few bytes of any input to an Update call in a buffer. If there is another call to Update, then the bytes in that buffer were not the last bytes of input, and Crypto-C continues to encrypt or decrypt. If the next call is to Final, the bytes in the buffer are the last bytes of input, so Crypto-C adds the pad and encrypts it, or decrypts the final bytes and strips the pad.

Note: The output of a particular update may be larger than the input, because

Crypto-C may be processing the current input plus some data in the buffer. Hence, an output buffer of an Update call should always be larger than the input length. For block ciphers, for example, the size of the output buffer may be as large as the length of the input plus the block size.

The following example demonstrates multiple updates. It corresponds to the file

multencr.c; a similar example for decryption is in the file multdecr.c. Assume that

the subroutine

Chapter 2 Quick Start 29

GetDataFromFile

gets, at most, a specified number of bytes from a file,

Multiple Updates

places them into the given buffer, and sets a flag indicating whether the bytes returned are the last ones in the file or not. Assume also that the subroutine

AppendDataToFile

called

B_CreateAlgorithmObject, B_SetAlgorithmInfo, and B_EncryptInit:

#define UPDATE_SIZE 64 #define UPDATE_OUTPUT_SIZE (UPDATE_SIZE + 16)

FILE *inputFile = (FILE *)NULL_PTR; FILE *outputFile = (FILE *)NULL_PTR;

unsigned char dataToEncrypt[UPDATE_SIZE]; unsigned char blockOfEncryptedData[UPDATE_OUTPUT_SIZE]; unsigned int dataToEncryptLen, totalBytesSoFar; unsigned int outputLenUpdate, outputLenFinal; unsigned int sizeToUpdate = UPDATE_SIZE; int endFlag, status;

do {

totalBytesSoFar = 0;

while ((status = GetDataFromFile (inputFile, sizeToUpdate, dataToEncrypt, &dataToEncryptLen, &endFlag)) == 0) { printf ("dataToEncryptLen = %i \n", dataToEncryptLen); PrintBuf (dataToEncrypt, dataToEncryptLen); if ((status = B_EncryptUpdate (encryptionObject, blockOfEncryptedData, &outputLenUpdate, UPDATE_OUTPUT_SIZE, dataToEncrypt, dataToEncryptLen, (B_ALGORITHM_OBJ)NULL_PTR, (A_SURRENDER_CTX *)NULL_PTR)) != 0) break;

appends output data to a file. Finally, assume we have already

/* Save the encrypted data. */ if ((status = AppendDataToFile (outputFile, blockOfEncryptedData, outputLenUpdate)) != 0) break;

totalBytesSoFar += outputLenUpdate; if (endFlag == 1) break; } /* end while */

30 RSA BSAFE Crypto-C Developer’s Guide

Multiple Updates

/* If there was an error in the above while loop, break out of the do-while construct. */ if (status != 0) break;

/* Call B_EncryptFinal once after all Updates. */ if ((status = B_EncryptFinal (encryptionObject, blockOfEncryptedData, &outputLenFinal, UPDATE_OUTPUT_SIZE, (B_ALGORITHM_OBJ)NULL_PTR, (A_SURRENDER_CTX *)NULL_PTR)) != 0) break;

/* Save the encrypted data. */ if ((status = AppendDataToFile (outputFile, blockOfEncryptedData, outputLenFinal)) != 0) break;

totalBytesSoFar += outputLenFinal;

} while (0);

/* Free up any memory allocated, save it to a file or print it out first if you need to save it. */ T_memset (dataToEncrypt, 0, sizeof (dataToEncrypt));

In the preceeding code example, we took and passed them to be

dataToEncryptLen

B_EncryptUpdate. The number of bytes of output may or may not

; check

outputLenUpdate

dataToEncryptLen

to see. If fewer than

bytes of data to encrypt

dataToEncryptLen

bytes were output, the as-yet-unencrypted input waits in a buffer. Notice that we did not allocate memory but used the stack; we did this by declaring

our buffers to be arrays of

unsigned char. This means that the operating system will

do the allocating and freeing. Also notice the call to

tstdlib.c. The T_memset routine sets all the bytes of a buffer to a particular value; in

this case, it wrote a 0 to every byte in 4 of the Reference Manual. When memory is freed, whether by a call to

T_memset, another memory management routine from

dataToEncrypt

. T_memset is described in Chapter

T_free or

automatically by the operating system, the data still exists at that location; the operating system has simply marked that area as available for use. For security, overwrite any memory that held sensitive data when you are done with it. This prevents attackers from reconstructing secrets by examining your computer’s memory.

Chapter 2 Quick Start 31

Summary of the Six Steps

A typical implementation uses the six steps as follows:

Step 0: Include

Include the necessary header files. In addition, make sure that:

• Your compiler can locate the Crypto-C header files.

• Your compiler can locate and link in the Crypto-C library.

• You compile and link in the file containing the definitions for the T_ functions; an

example is provided in

Step 1: Create

Create an algorithm object by declaring a variable to be an algorithm object and calling

B_CreateAlgorithmObject.

Step 2: Set

tstdlib.c.

Use B_SetAlgorithmInfo to associate the algorithm object with an algorithm and to supply any special information or parameters the algorithm requires.

Step 3: Init

Choose the operations the algorithm object can perform by supplying the desired algorithm methods from the Crypto-C library. If the algorithm requires a key, create and set a key object that will supply the key data that the algorithm needs.

Step 4: Update

Initiate an action. The action depends on the algorithm. Update is the only step that can be performed more than once on the same object. For example:

• For an encryption or decryption algorithm, an Update step encrypts or decrypts

all or part of the data. You can use multiple Update steps to encrypt or decrypt data.

• For a message digest, the Update step is used to enter the data to digest.

• For a random number generator, the Update step is used to seed the random

number generation.

32 RSA BSAFE Crypto-C Developer’s Guide

Summary of the Six Steps

• For some algorithms, such as generating a public/private key pair, there is no

Update step.

Step 5: Final

Finalize the action initiated in Step 4. Again, the finalization depends on the algorithm; for some algorithms, Final is replaced by Generate. For example:

• For an encryption or decryption algorithm, the Final step encrypts or decrypts the

final portion of the data. For some algorithms, this data may need special handling, such as padding, that is different from the Update step.

• For a message digest, the digest action takes place during Final.

• For a random number generator, the Final (or Generate) step generates the

random bytes.

• For generating a public/private key pair, the key pair generation takes place in

the Generate step.

Step 6: Destroy

Free any memory allocated in the previous steps and overwrite any sensitive memory with zeroes. The Destroy step is crucial to the security of an application.

Chapter 2 Quick Start 33

Chapter 3

Cryptography

This chapter contains a brief outline of the basic cryptographic principles and terminology used throughout this manual and documentation set. Refer to

Abbreviations

this documentation set. The publications listed in “Related Documents” on page xx provide more comprehensive discussions of cryptographic functions and operations. This chapter is organized as follows:

on page xix of the Preface for a list of terms and abbreviations used in

Terms and

• Cryptography Overview

• Applications of Cryptography

• Choosing Algorithms

• Security Considerations

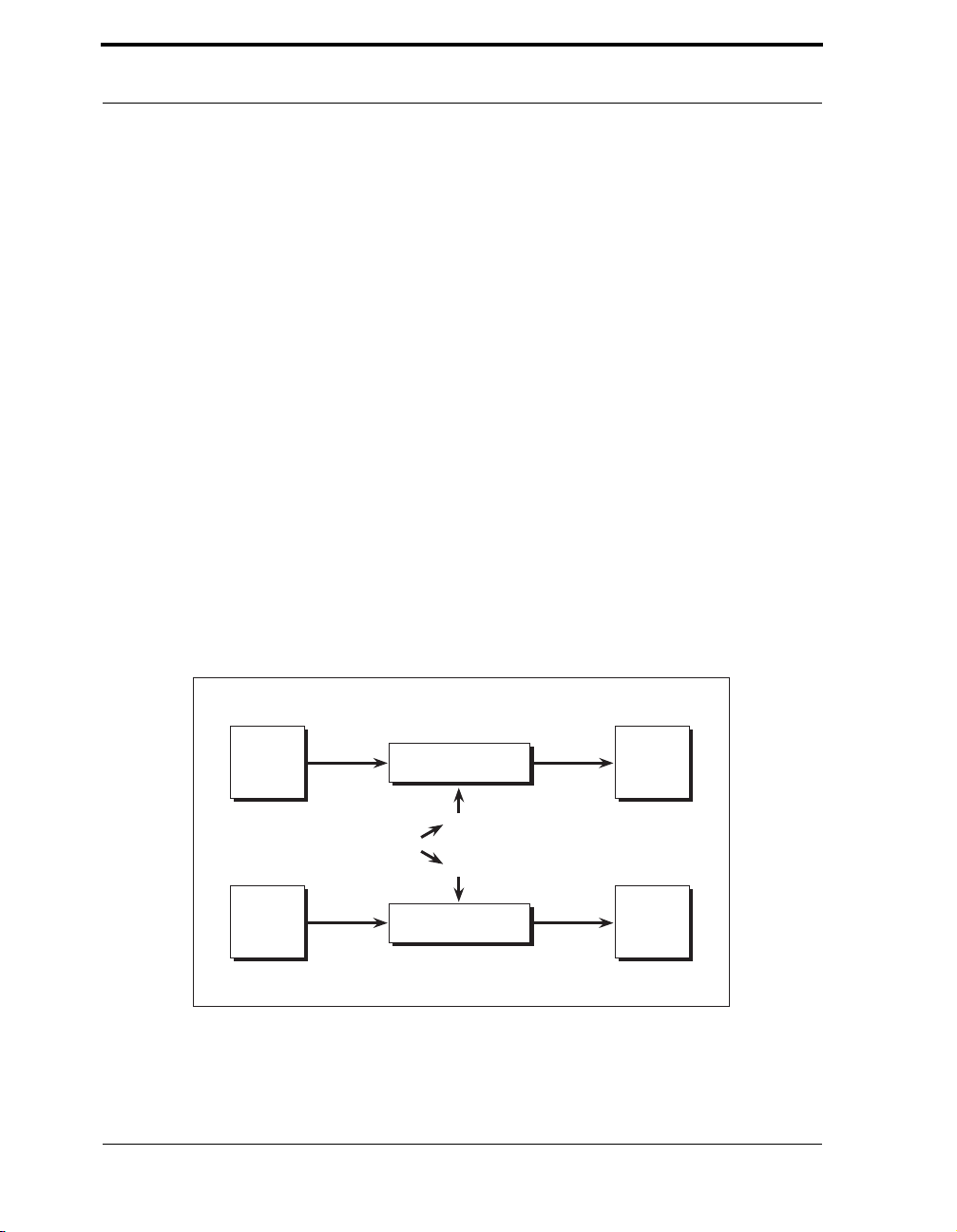
Cryptography Overview

Symmetric-Key Cryptography

In symmetric-key cryptography, as Figure 3-1 shows, the encrypting key is the same as the decrypting key. Using any other key to decrypt will produce incorrect results. Symmetric-key cryptography is also sometimes called secret-key cryptography, because the key used to both encrypt and decrypt must be kept secret.

Ciphers

There are two categories of symmetric encryption algorithms, block ciphers and stream ciphers. As the name implies, a block cipher processes data in blocks. A stream cipher,

on the other hand, processes a unit of data at a time, where a unit is generally a bit or byte. This allows a stream cipher to take in a variable length stream of data, encrypt it, and output a stream of ciphertext the same length as the input. Crypto-C offers the following block ciphers: DES, Triple DES, DESX, the RC2 cipher, the RC5, the RC6 cipher, and theAES cipher. Crypto-C offers the following stream cipher: the RC4 cipher.

Encryption Operation

Original

Message

Key Data

Encrypted

Message

Figure 3-1 Symmetric-Key Encryption and Decryption

36 RSA BSAFE Crypto-C Developer’s Guide

Encryption

Algorithm

Key

Decryption

Algorithm

Decryption Operation

Encrypted

Message

Decrypted

Message

Cryptography Overview

Block Ciphers

Block ciphers encrypt data block-by-block. They can encrypt each block separately as in ECB mode, or they can use other modes to make the cipher less vulnerable to attacks based on regular patterns. A mode of operation usually combines the underlying cipher with feedback and other simple operations. The security remains a function of the cipher and not of the mode. See “Modes of Operation” on page 41 for more information.

Padding

When you encrypt a message using a block cipher, usually your message length will not be a multiple of the block size. Some modes can deal with variable size blocks, but others require the message be a multiple of the block size. For these modes, padding provides a solution to this problem. To pad, you add a regular pattern of bytes to the end of the last block to make it a complete block. With padding, the actual number of bytes encrypted can be as much as one block more than the original data.

Ciphers in Crypto-C

Crypto-C implements the following block ciphers:

• DES

• Triple DES

• DESX

• RC2

• RC5

• RC6

• AES

DES

The Digital Encryption Standard, DES, is a commercial encryption US standard that has been available for over 15 years. The federal standard document FIPS PUB 46-2 describes the algorithm.

For DES, the block size is eight bytes. Therefore, the input must be a multiple of eight bytes, or else it must be padded to be a multiple of eight bytes for DES to operate in CBC or ECB modes properly. The key consists of 56 random bits and 8 parity bits, forming a 64-bit, or 8-byte, key.

Chapter 3 Cryptography 37

Cryptography Overview

Tripl e DES

Triple DES executes DES three times, which triples the number of bits in an encryption key. A number of different methods achieve this function. The technique that Crypto-C uses is depicted in Figure 3-2 on page 38.

This technique is known as EDE, or “Encrypt-Decrypt-Encrypt.” The decryption process in the middle stage of Triple DES encryption provides compatibility with DES. If the three keys are the same, the Triple DES operation is equivalent to a single DES encryption. That way, an application that has only DES capabilities can still communicate with applications that use Triple DES. If the three keys are different, the decryption in the middle will scramble the message further; it will not decrypt the first stage. Triple DES decryption is the inverse operation of the previous sequence, that is, DES decryption followed by DES encryption and then another DES decryption.

24 byte Triple DES key (including parity bits)

8 byte

message

block

First 8 bytes

of the key

DES

encryption

Figure 3-2 Triple DES Encryption as Implemented in Crypto-C

Middle 8 bytes

of the key

DES

decryption

Last 8 bytes

of the key

DES

encryption

8 byte

message

block

DESX

DESX is an RSA Security proprietary extension of the DES encryption algorithm that increases the effective number of key bits from 56 to 120 bits. Crypto-C includes DESX for backward compatibility with BSAFE 1.x versions, or as a faster alternative to Triple DES.

RC2

The RC2 cipher was developed by Ronald Rivest as an alternative to DES encryption;

38 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

it is proprietary to RSA Security. The RC2 cipher has an eight-byte block size. Therefore, the input must be a multiple of eight bytes, or be padded to be a multiple of eight bytes, for the RC2 cipher to operate properly in CBC or ECB modes.

The RC2 input key can be of any length from 1 to 128 bytes. The algorithm uses the input key to generate an effective key that is actually used for encryption purposes. Internally, the algorithm builds a key table based on the bits of the key data; the chosen number of effective key bits limits the number of possible key tables. The effective key size is variable and takes values from one bit up to 1024 bits.

Note: Control over your effective key size benefits you, because you can generate

up to 128 bytes of key data and set the algorithm to use a smaller number of effective bits, such as 80. Then, in the future, if you want to increase the number of effective key bits, you do not have to change the code that generates the key data, only the effective key bit parameter.

RC5

The RC5 cipher was developed by Ronald Rivest as an alternative to DES encryption; it is proprietary to RSA Security. It is a block cipher with the block being either 4 bytes, 8 bytes, or 16 bytes, depending on the word size. The input must be a multiple of the block size, or it must be padded to a multiple of the block size for the RC5 cipher to operate properly. The RC5 cipher’s speed and security are dependent on input parameters determined by the user. These parameters are:

• word size

• rounds

• key size (in bytes)

Word size generally refers to the size of a hardware register. For hardware implementations of the RC5 cipher, developers can take advantage of larger registers to increase speed. On chips with smaller registers, the word size can be emulated in software. Version 1.0 of the RC5 cipher accepts word sizes of 16, 32, or 64 bits. CryptoC accepts a word size of 32 or 64 bits. The block size is twice the word size. For a word size of 32 bits, the block size is 64 bits, or 8 bytes, the same as for DES and the RC2 cipher. For a word size of 64 bits, the block size is 128 bits, or 16 bytes.

The number of rounds is the number of times the operation employs the inner encryption function. Varying the number of rounds allows developers to make a tradeoff between speed and security. The greater the number of rounds, the greater the security, but the slower the execution. The number of rounds can be anywhere from 0 (zero) to 255. For the RC5 cipher with a 32-bit word size, RSA Security recommends at least 16 rounds for applications; while no practical attacks are known

Chapter 3 Cryptography 39

Cryptography Overview

for 12-round RC5-32, recent cryptanalytic work suggests 16 rounds is now a more conservative choice. For the RC5 cipher with a 64-bit word size, RSA Security recommends at least 20 rounds.

The key size can be as little as 0 (zero) and as many as 255 bytes. The RC5 cipher uses the secret key bytes to generate an expanded key table during the Init phase. The key table is then used during encryption or decryption. Therefore, key length will have no appreciable effect on algorithm speed.

The RC5 cipher is more formally described as RC5 w/r/b. For instance, the RC5 cipher with a 32-bit word, 16 rounds, and a 10 byte key would be described as RC5 32/16/10.

RC6

The RC6 cipher was developed by Ronald Rivest and Matthew Robshaw, Ray Sidney, and Lisa Yin of RSA Laboratories West as a candidate for the Advanced Encryption Standard (AES)

The guidelines for the RC6 cipher were aimed at creating a cipher which could take advantage of modern computing power and architecture. These guidelines specify that a submitted algorithm must accept 16-byte blocks (8-byte word). This is in contrast to many previous block ciphers, such as DES and Triple DES, which operate only on 8-byte blocks.

In accordance with these guidelines, RC6 allows a 16-byte block size, which has the following implications:

• When you use RC6 with a feedback mode in Crypto-C, your initialization vector

must be 16 bytes.

• If you use RC6 with padding, the resulting output might be as many as 16 bytes

more than the input.

The full RC6 algorithm also allows you to specify different levels of security by setting the number of rounds. However, the version submitted for the AES specifies 20 rounds. At 20 rounds, RC6 provides an optimal balance between security and speed. The current implementation of Crypto-C only accepts 20 rounds.

Note: At 20 rounds, the fastest known attack on the cipher is a brute-force attack on

the key, and encryption and decryption operations are faster than with a higher number of rounds. While fewer rounds would still offer good security, there are attacks that would be faster than a brute-force attack on the key. More than 20 rounds might offer more security, but the fastest attack would still be a brute-force attack on the key, and the increased rounds number

40 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

would slow down the encryption and decryption operations. In addition, if the 20-round version of RC6 is accepted as submitted to the AES, a round count other than 20 rounds might not be AES.

AES

The National Institute of Standards and Technology (NIST) selected an alogorithm (Rijndael) as the replacement for the Data Encryption Standard (DES) in its Advanced Encryption Standard project. Crypto-C includes basic AES support.

Modes of Operation

When you use a block cipher to encrypt a message of arbitrary length, you can also choose a mode of operation.

Modes of operation can use techniques such as feedback or chaining to make identical plaintext blocks encrypt to different ciphertext blocks. Modes are designed so that they do not weaken the security of the underlying cipher, but they may have properties in addition to those inherent in the basic cipher.

Most of the modes of operation in Crypto-C are feedback modes. Feedback modes use the previous block of output to alter the current block of input before encrypting. In this way, encrypting the same block of plaintext twice will virtually never produce the same ciphertext.

A feedback algorithm requires an initialization vector, or IV, to alter the first block. The IV has no cryptographic significance. It is used to alter the first block of data before any encryption takes place; therefore, it does not need to be secret. It should be random, though, so that the first block of encrypted data is not predictable. In order to start the decryption process, it is necessary to use the IV that was employed in the encryption process.

Four Modes

Crypto-C offers the following four block cipher modes:

• Electronic Codebook (ECB) mode

• Cipher Block Chaining (CBC) mode

• Cipher Feedback (CFB) mode

• Output Feedback (OFB) mode

A brief description of these modes follows. Most cryptography texts, such as Bruce Schneier’s Applied Cryptography [15], provide full descriptions of the various modes.

Chapter 3 Cryptography 41

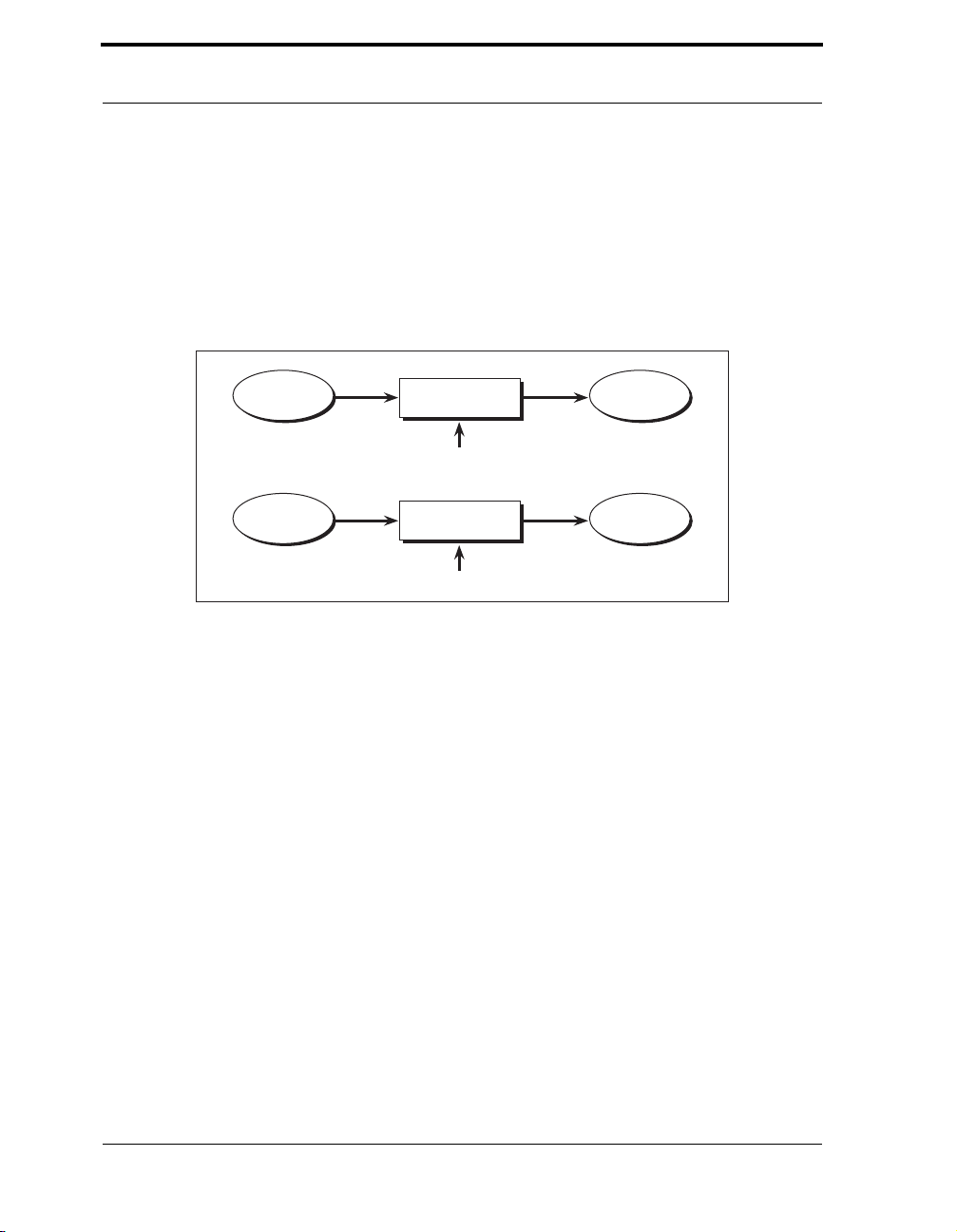
Cryptography Overview

Electronic Codebook (ECB) Mode

ECB is not a feedback mode; it encrypts each block of input independently of all other blocks. Plaintext patterns are not concealed; instead each identical block of plaintext yields an identical block of ciphertext. This could help an eavesdropper break the code. In addition, the plaintext can be easily manipulated by removing, repeating, or interchanging blocks. The speed of each encryption operation is identical to that of the block cipher. ECB mode is as secure as the underlying block cipher.

1st message

block

2nd message

block

Figure 3-3 Electronic Codebook (ECB) Mode

Block Cipher

Key (K)

Block Cipher

Key (K)

1st cipher

block

2nd cipher

block

42 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

Cipher Block Chaining (CBC) Mode

With CBC mode, each plaintext block is XORed with the previous ciphertext block, then encrypted. CBC mode is as secure as the underlying block cipher against standard attacks. In addition, any patterns in the plaintext are concealed by the XORing of the previous ciphertext block with the plaintext block.

The decryptor follows the same sequence of steps to decrypt, using the same (secret) key and initialization vector (IV).

Initialization

Vector (IV)

1st message

block

2nd message

block

Figure 3-4 Cipher-Block Chaining (CBC) Mode

XOR

Block Cipher

Key (K)

Block Cipher

Key (K)

1st cipher

block

2nd cipher

block

An initialization vector is added to the beginning of the plaintext before encryption. This gives you something to XOR the first block with and ensures that identical plaintexts encrypt to different ciphertexts.

Cipher Feedback (CFB) Mode

In cipher feedback (CFB) mode, the cipher object acts as a byte generator. CFB mode encrypts the previous block of ciphertext and XORs the plaintext with this block to produce ciphertext. For the first block, the initialization vector is encrypted. CFB mode is as secure as the underlying cipher against standard attacks. In addition, any patterns in the plaintext are concealed by XORing the previous ciphertext block with the plaintext block.

Chapter 3 Cryptography 43

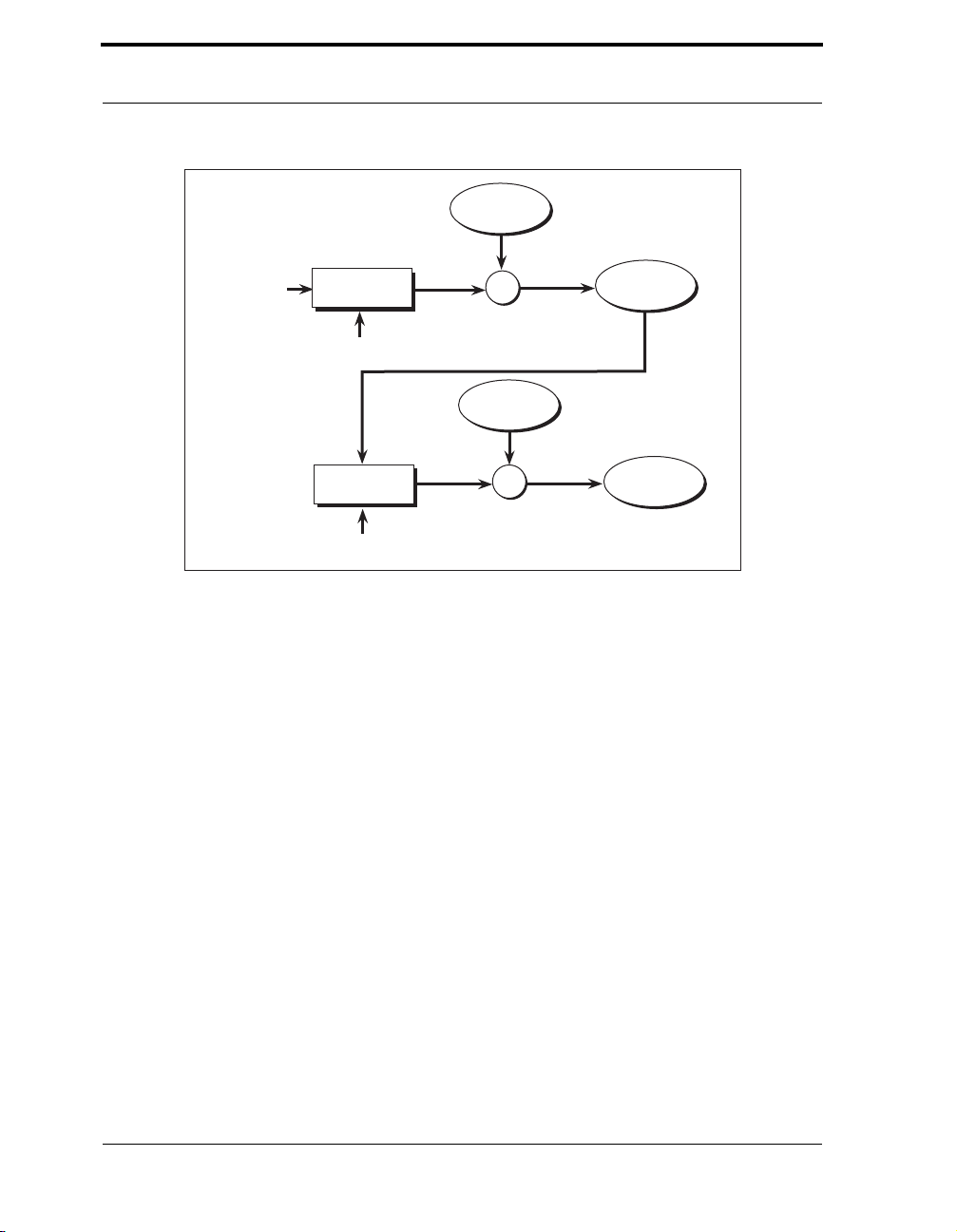
Cryptography Overview

1st message

block

Initialization

Vector (IV)

Block Cipher

Figure 3-5 Cipher Feedback (CFB) Mode

Key (K)

XOR

2nd message block

XOR

To encrypt plaintext using CFB mode:

1. Generate your key and your IV.

2. Encrypt the IV with the key to get a block of output, B

3. XOR B

ciphertext, C

4. Encrypt C

5. XOR B

block of ciphertext, C

6. Repeat Steps 4 and 5 until the entire text is encrypted.

with the first block of your plaintext, P1, to get the first block of

with the key to get the second block of output, B2.

with the second block of your plaintext message, P2, to get the second

1st cipher

block

2nd cipher block

To decrypt the ciphertext, the decryptor uses the same (secret) key and initialization vector and follows the same sequence of steps.

CFB mode does not require padding. If your data length is not a multiple of the block size, simply truncate the final block of output to be the same size as the final segment of the data, and then XOR it. You can use CFB mode to encrypt a stream of data.

44 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

Output Feedback (OFB) Mode

Output feedback mode is similar to CFB mode, except that the quantity XORed with each plaintext block is generated independently of both the plaintext and the ciphertext.

To encrypt a plaintext using OFB, first generate the “output” used for encryption. This is intermediate data that is used in the encryption process. In OFB, the output depends only on the key and the initialization vector.

1. Generate your key and your IV.

2. Encrypt the IV with the key to get a block of output, B

3. Encrypt B

4. Continue encrypting recursively: encrypt B

with the key to get the second block of output, B2.

to get B

This process gives you an arbitrarily long sequence of pseudo-random blocks that you can use to encrypt the data. To use the output to encrypt:

5. XOR your plaintext with the output, block by block. The result of the XOR is the

ciphertext.

OFB does not require padding. If your data length is not a multiple of the block size, simply truncate the final block of the output to be the same size as the final segment of the data, and then XOR it.

i+1

The decryptor can use the same (secret) key and IV to generate the same sequence of output blocks and XOR the sequence with the ciphertext to recover the plaintext.

Chapter 3 Cryptography 45

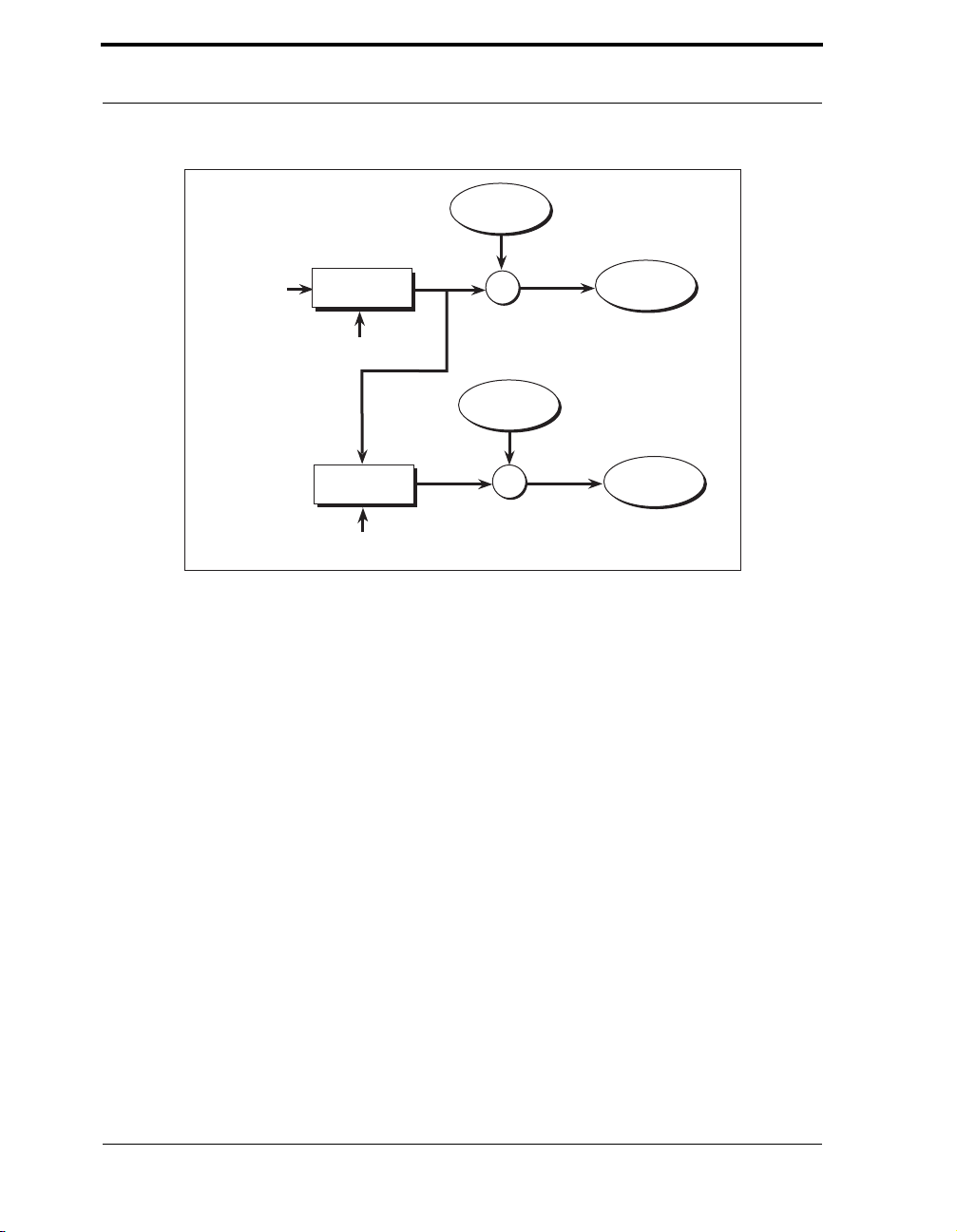
Cryptography Overview

1st message

block

Initialization

Vector (IV)

Block Cipher

Key (K)

Block Cipher

Key (K)

Figure 3-6 Output Feedback Mode (OFB)

XOR

2nd message

block

XOR

1st cipher

block

2nd cipher

block

Stream Ciphers

A stream cipher processes the input data one unit at a time. A unit of data is generally a byte, or sometimes even a bit. In this way, encryption or decryption can execute on a variable length of input. The algorithm does not have to wait for a specified amount of data to be input before processing, nor does it have to append and encrypt extra bytes.

RC4

The RC4 cipher is a symmetric stream-encryption algorithm developed by Ronald Rivest and proprietary to RSA Security. It is actually a keyed pseudo-random sequence. It uses the provided key to produce a pseudo-random number sequence which is then XORed with the input data. This means that the encryption and decryption operations are identical.

The number of key bits is variable and ranges from eight to 2048 bits. Using the RC4 cipher with a key size of less than 40 bits is not recommended.

Because RC4 encryption is an XOR between the message bytes and the pseudorandom byte stream generated from the key, the same key should not be used more than once. Otherwise, if some of the bytes of one input message are known (or easy to

46 RSA BSAFE Crypto-C Developer’s Guide

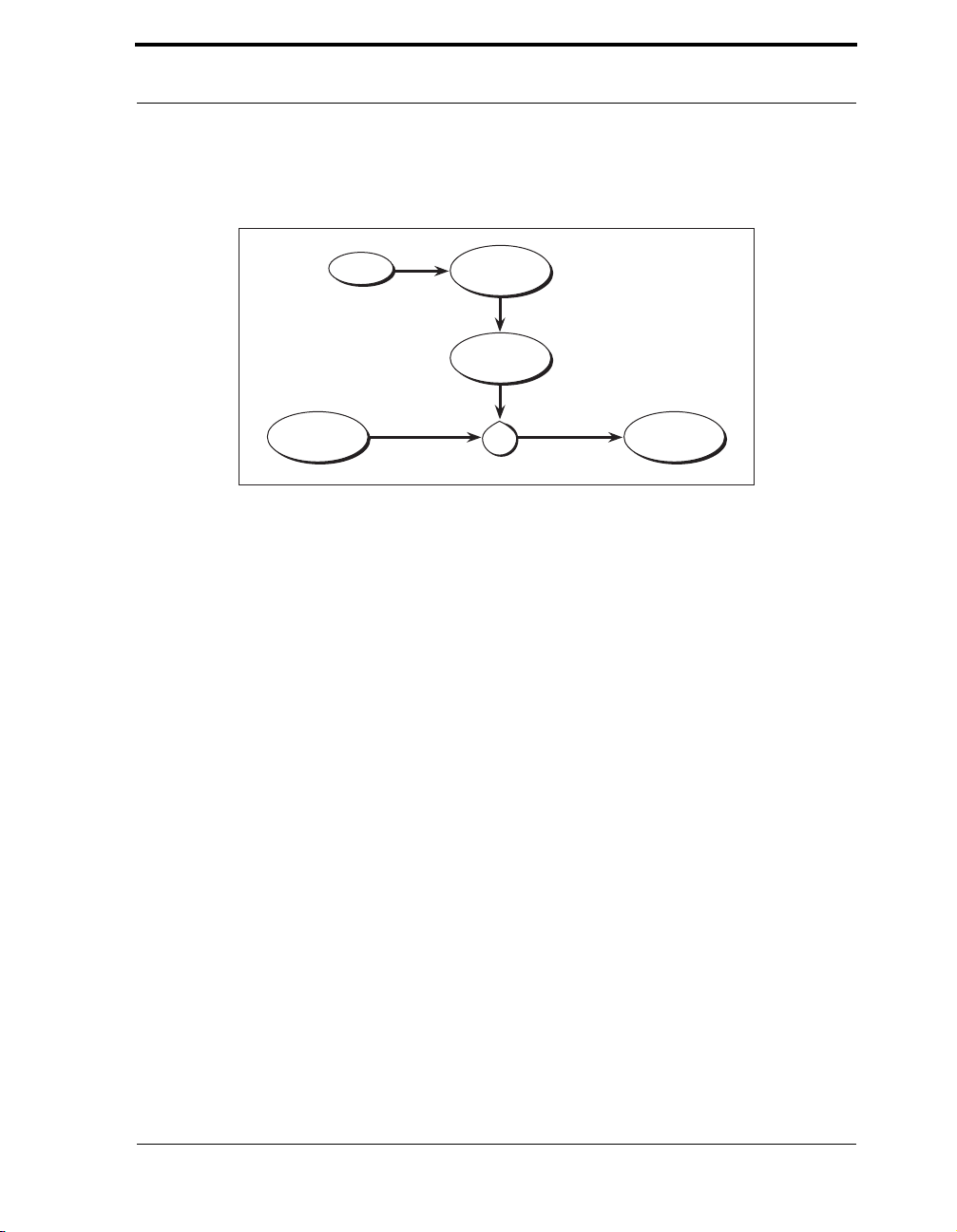
Cryptography Overview

guess), an attacker would be able to determine some of the original message bytes by XORing two sets of cipher bytes.

Key

Mixing

Pseudo-

random

bytes

XOR

Nth cipher

byte

Nth message

byte

Key

Figure 3-7 RC4 Encryption or Decryption

The RC4 algorithm with MAC

The RC4-with-MAC algorithm is an extension of the RC4 cipher. It provides data integrity by using a Message Authentication Code (MAC) with the RC4 encryption algorithm. The authentication code does not provide cryptographic authentication; rather, it provides the equivalent of a checksum that can be used to determine if any errors were introduced within the cipher bytes. The MAC guards against transmission or retrieval errors, but it may not detect deliberate tampering with the data.

Message Digests

A message digest (also sometimes referred to as a one-way hash function) is a fixedlength computationally unique identifier corresponding to a set of data. That is, each unit of data (for example, a file, a string, or a buffer) will map to a particular short block, called a message digest. It is not random: digesting the same unit of data with the same message digest algorithm will always produce the same short block.

A good message digest algorithm possesses the following qualities:

• The algorithm accepts any input data length.

• The algorithm produces a fixed length output for any input data.

Chapter 3 Cryptography 47

Cryptography Overview

• It is computationally infeasible to produce data that has a specific digest. In other

words, given a particular block of the proper size, it will be virtually impossible to determine a unit of data that will digest to that particular block.

• It is computationally infeasible to produce two different units of data that

produce the same digest. In other words, given some data, it is virtually impossible to create different data that will digest to the same block as the first. This quality is also called collision-free.

Message digests have many uses. They can authenticate data, for instance. To create a digest for authentication, digest the data and save the digest. Later, if you need to see if the data has been altered, digest it again and compare the new digest to the old. If the digests are different, the data is different. Although there will exist other sets of data that will digest to the original value, it is virtually impossible to find them. Minor changes in data will produce very different digests.

Crypto-C includes the MD, MD2, MD5, and SHA1 message digest algorithms. MD is included for backward compatibility with BSAFE 1.x. MD, MD2, and MD5 produce a 16-byte digest for any input message; SHA1 produces a 20-byte digest. MD5 is the fastest message digest algorithm implemented in Crypto-C.

Note: Recent cryptanalytic work has discovered a collision in MD2’s internal

compression function, and there is some chance that the attack on MD2 may be extended to the full hash function. The same attack applies to MD. Another attack has been applied to the compression function on MD5, though this has yet to be extended to the full MD5. RSA Security recommends that before you use MD, MD2, or MD5, you should consult the RSA Laboratories Web site at

http://www.rsasecurity.com/rsalabs to be sure that their use is consistent

with the latest information. One bulletin that discusses this issue is Recent Results for MD2, MD4, and MD5; it can be found at

http://www.rsasecurity.com/rsalabs/bulletins/.

Message Digests and Pseudo-Random Numbers

Random number generation (for software implementation, usually pseudo-random number generation) is a key component of cryptographic operations. Random numbers are usually used as cryptographic keys or as a basis for generating keys. Crypto-C uses message digest algorithms with a random seed for generating random numbers. See “Pseudo-Random Numbers and Seed Generation” on page 92 for a discussion of the security considerations of random number generation.

48 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

Hash-Based Message Authentication Codes (HMAC)

A hash-based message authentication code (HMAC) combines a secret key with a message digest to create a message authentication code. This method of creating a MAC makes it possible to update the underlying message digest if a new attack makes the original message digest unsecure. Crypto-C provides an HMAC implementation based on SHA1.

Recall that SHA1 produces a 20-byte digest; in addition, we need to know that SHA1 takes input in 64-byte blocks.

Given a message M and a key k, the HMAC of M is computed as follows:

1. Create two different fixed strings that are used in the calculation:

ipad = the byte opad = the byte

2. Extend k to 64 bytes in length by appending zeros to the end of k. For example, if k

is 25 bytes, append 39 copies of the zero byte k’.

3. Compute the following:

SHA1(k’ XOR opad

where

|| denotes concatenation.

0x36 repeated 64 times

0x5C repeated 64 times

0x00. We will call the extended key

|| SHA1((k’ XOR ipad) || M))

The same key can be used for multiple authentications, but the key should be replaced periodically. For security considerations, the key should be at least as long as the message digest output. For SHA1, this means an HMAC key should be at least 20 bytes. If the key is “weakly random”—that is, if knowing some of the key bits might help an attacker generate other key bits, then a longer key should be used.

Password-Based Encryption

Password-based encryption (PBE) generates a symmetric key from a password, and encrypts data using that generated key. Usually, though, a password will not have enough effective random bits to qualify as a candidate for a key or even a random seed to generate a key. For example, each character of an 8-byte alphanumeric password that also allows case-sensitive letters has the equivalent of slightly less than six bits of randomness. For eight-character passwords, this is far less than the required key size of a block cipher such as DES.

Therefore, a good PBE implementation not only uses the password, but mixes in a random number, known as a salt, to create the key (see Figure 3-8 on page 50).

Chapter 3 Cryptography 49

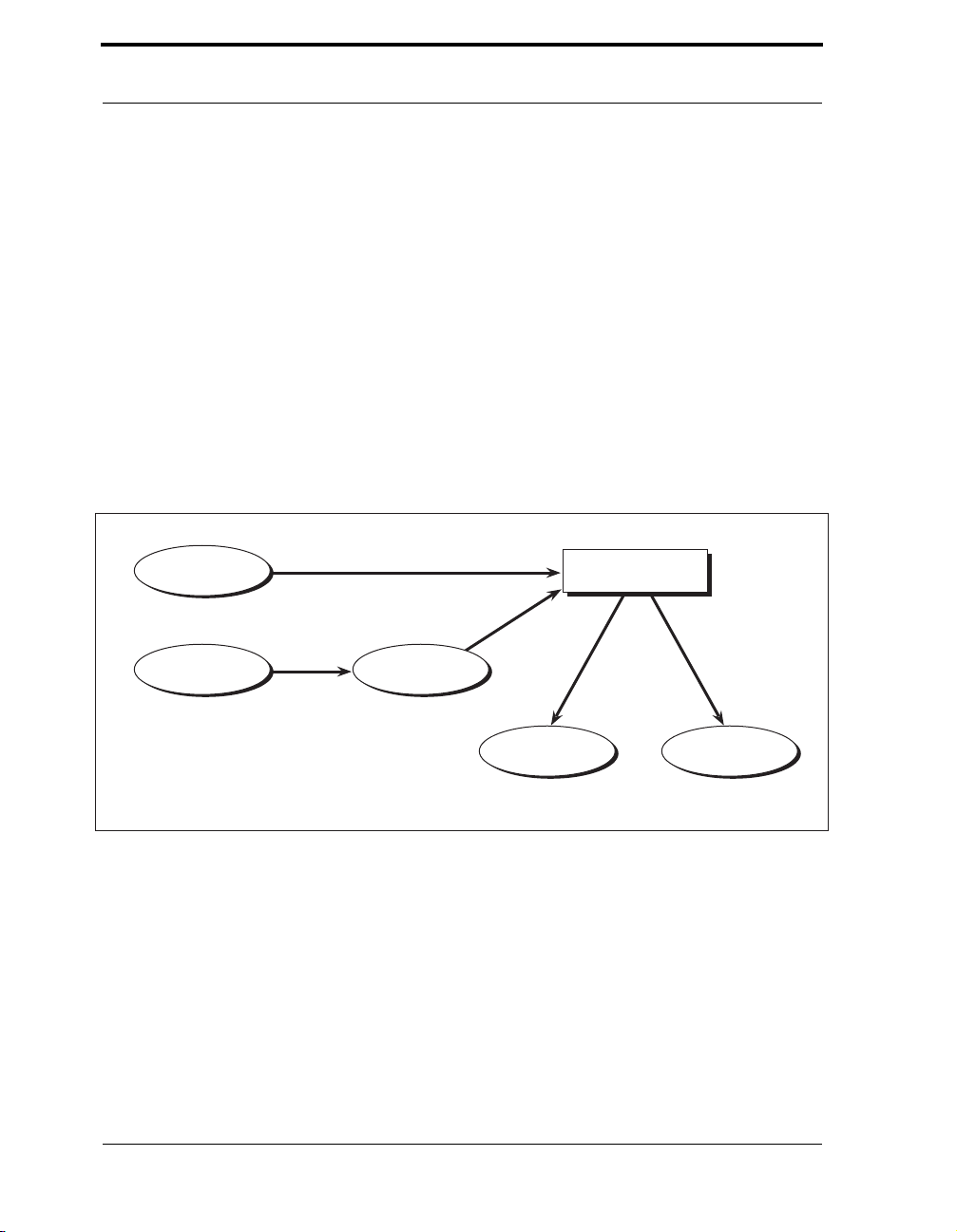
Cryptography Overview

Normally, the mixing is a message digest. This makes the task of getting from password to key very time-consuming for an attacker. Digesting a password with a salt helps thwart dictionary attacks. An attacker could put together a “dictionary” of keys generated from likely passwords, and try out each key on encrypted data. This would greatly reduce the amount of work necessary to find the key and may make it feasible to recover encrypted material. With a salt, the attacker would have to create a dictionary of keys generated from each password, but each password would then have to have a dictionary of each possible salt.

Crypto-C uses the methods described in PKCS v1.5 to implement password-based encryption. The methods use a message digest algorithm with a specific means of padding to increase the search space for dictionary attacks against the key. The applicable Algorithm Information Types (AIs) are: AI_MD2WithDES_*, AI_MD2WithRC2_*, AI_MD5WithDES_*, AI_MD5WithRC2_*, and AI_SHA1WithDES_*.

Password

Pseudo-random

bytes

Figure 3-8 DES Key and IV Generation for Password Based Encryption

Salt

8 bytes

Key

Message digest

I V

8 bytes

Public-Key Cryptography

In 1976, Stanford graduate student Whitfield Diffie and Stanford professor Martin Hellman invented public-key cryptography. In this system, each person owns a pair of keys, called the public key and the private key. The owner of each key pair publishes the public key and keeps the private key secret.

Suppose Alice wants to send a message to Bob. She finds his public key and encrypts

50 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

her message using that public key. Unlike symmetric-key cryptography, the key used for encryption will not decrypt the message. That is, knowledge of Bob’s public key will not help an attacker. To decrypt a message, Bob uses his private key. If Bob wants to respond to Alice, he can encrypt his message using her public key.

To understand this idea, think of taking a number to a power. For instance, given values x and y, compute z=x

1/y

. You end up with the original x, because z

. To recover x, you would not compute zy, but rather

1/y

=(xy)

1/y

= x

y·1/y

= x1= x. You need two values to perform this exercise: a “public key,” y, to compute the encrypted value, and the inverse of the public key, or a “private key,” 1/y, to recover the original value.

This example, of course, is not practical because if you made y public, anyone could easily compute 1/y and know your private key. Therefore, a good public-key cryptosystem relies on a key pair for which it is impossible (or at least intractable) to derive the private key from the public key.

Public Key

Input

Message

Encrypted

Message

The decrypted message is equal to the input message

if the public and private keys form a key pair.

Public Key

Cryptosystem

Encryption Operation

Private Key

Public Key

Cryptosystem

Decryption Operation

Encrypted

Message

Decrypted

Message

Figure 3-9 Public-Key Cryptography

In practice, public-key algorithms are slow compared to symmetric-key algorithms. Therefore, they are more often used for shorter messages, such as encrypting the symmetric key for a message encrypted with a symmetric cipher, or for encrypting a digest.

The RSA Algorithm

The RSA algorithm is a public-key cryptosystem for both encryption and

Chapter 3 Cryptography 51

Cryptography Overview

authentication that MIT professors Ronald L. Rivest, Adi Shamir, and Leonard M. Adleman invented in 1977. It is actually similar to the example in the previous section that takes numbers to a power, except that it works in modular math.

Modular Math

Modular math uses a positive integer as a modulus; the only numbers under consideration are the integers from 0 to one less than the modulus. So for mod n, only the integers from 0 to (n–1) are valid operands, and the results of operations will always be numbers from 0 to (n–1). When an operation such as addition or multiplication would give a result that is greater than the modulus, the remainder of the result after division by n is used instead. Therefore, two numbers are equal mod n if and only if their difference is an even multiple of n.

For example, think of military time where the modulus is 2400. For instance, 2200 hours (10:00 P.M.) plus 4 hours is not 2600, but 0200 hours, or 2:00 in the morning. Likewise, if we start at 0, or midnight, 6 times 5 hours (say six 5-hour shifts) is not 3000, but 0600, or 6:00 A.M. the following day.

Another aspect of modular math is the concept of an inverse. Two numbers are the inverse of each other if their product equals 1. For instance, 7·343 = 2401, but if our modulus is 2400, the result is (7·343) mod 2400 ≡ 2401 – 2400 = 1 mod 2400.

Prime Numbers

The RSA algorithm also employs prime numbers, or primes. A prime number is a number that is evenly divisible by only 1 and itself. For example, 10 is not prime because it is evenly divisible by 1, 2, 5, and 10. But 11 is prime, because its only factors are 1 and 11.

MultiPrime Numbers

MultiPrime RSA functionality was added to Crypto-C V5.1. This new function allows you to generate RSA public/private key pairs. RSA MultiPrime key generation follows the same steps as standard RSA key generation with only a couple of exceptions: the use of a different AI, AI_RSAMultiPrimeKeyGen, and a different AM, AM_RSA_MULTI_PRIME_KEY_GEN, must be passed in during the B_GenerateInit call.

The RSA Algorithm

The RSA algorithm works as follows: take two large primes, p and q, and find their product n = pq; n will be the modulus. Choose a public value, e (also known as the public exponent), that is less than n. There are other constraints on e that are described

52 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

below. To compute ciphertext c from a plaintext message m, find c = me mod n. To decrypt, determine the private key d, the inverse of e, and compute m = c

mod n. The relationship between e and d ensures that the algorithm correctly recovers the original message m, because c

= (me)d = med ≡ m1 = m mod n. Only the entity that knows d can

decrypt. The security of the system relies on the fact that if you know p, q and e, it is easy to

compute d; but if you know only n and e, it is more difficult to determine d. This is due to the following property of the math: the value d is actually not the inverse of e mod n, but rather the inverse of e mod (p–1)(q–1). The value you pick for e must be relatively prime to (p–1)(q–1), which means e and (p–1)(q–1) share no common factors, so that there exists d such that ed ≡ 1 mod (p–1)(q–1). Therefore, you find the private value using a modulus of (p–1)(q–1), but when you apply the RSA algorithm to encryption or decryption, you use a modulus of n = p·q.

Why, if d is the inverse of e mod (p–1)(q–1), does c

= (me)d = med = m1 = m mod n? Aren’t we mixing moduli? That is the quirk of the math; it may seem counterintuitive, but this mixing of moduli is what makes the algorithm work. A complete proof of this fact is beyond the scope of this chapter, so if you want to learn more about the underlying mathematical principle, find a math book that discusses Euler’s phifunction.

Incidentally, in practice, you would generally pick e, the public exponent first, then find the primes p and q, which satisfy the requirement that e be relatively prime to (p–

1)(q–1). Consider the following example with small numbers. Choose public exponent e =3.

Then, let p =5 and q = 11, which means n = 55 and (p–1)(q–1) = 40. This is a valid p and q combination because 3 is relatively prime to 40. The inverse of 3 mod 40 is 27.

(3·27) = 81 81 – (2·40) = 81 – 80 = 1 3·27 = 1 mod 40

Apply the RSA algorithm with these parameters to the “plaintext message” m = 2.

e=23

c = m

=8 mod 55 This yields an encrypted message of 8. To decrypt, raise the message to the power of the inverse of 3, which is 27.

d=827

mod 55

Rather than computing 8

16+8+2+1=816·88·82·81

Chapter 3 Cryptography 53

directly, a shortcut would be to compute:

= 2 mod 55

Cryptography Overview

The calculation is shown in Table 3-1:

Table 3-1 Calculation of 8

· 8

· 82) · 8

· 82 · 88) · 8

mod 55

81 · 81 = 8 · 8 = 64

82 · 82 = 9 · 9 = 81

64 – 55 = 9 9 mod 55

81 – 55 = 26 26 mod 55

84 · 84 = 26 · 26 = 676 676 – (12 · 55) = 16

88 · 88 = 16 · 16 = 256 256 – (4 · 55) = 36

8 · 9 = 72

72 – 55 = 17

17 · 16 = 272 272 – (4 · 55) = 52

52 · 36 = 1872 1872 – (34 · 55) = 2

1 mod 55

8 mod 55

16 mod 55

36 mod 55

52 mod 55

2 mod 55

Summary

Take two large primes, p and q, and find their product n = p · q. Set n to be the modulus. Choose a public exponent, e, less than n and relatively prime to (p–1)(q–1). Find d, the inverse of e mod (p–1)(q–1), that is, ed ≡ 1 mod (p–1)(q–1). The pair (n,e) is the public key; d is the private key (or the private exponent). The primes p and q must be kept secret or destroyed.

To compute ciphertext c from a plaintext message m, find c = m original message, compute m = c

mod n. Only the entity that knows d can decrypt.

mod n. To recover the

Note: In public-key cryptography, it is also possible to encrypt using a private key.

In this case, the sender takes the plaintext input and the private key and follows the same steps need to decrypt an encrypted file. This creates a ciphertext that can be read using the public key; to read it, the recipient follows the same steps needed to encrypt with the public key and restores it to the plaintext. This is used in authentication and digital signatures.

Security

The security of the RSA algorithm relies on the difficulty of factoring large numbers. In theory, it is possible to obtain the private key d from the public key (n,e) by factoring n into p and q. To find d, one must know the product (p–1)(q–1). But to find that value, one must know p and q. For example, in the earlier example, an attacker would know that p · q=55, but what is (p–1)(q–1)? Factoring 55 into its component primes is easy: the answer is 5 and 11.

54 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

However, for very large numbers, factoring is very difficult. The RSA Laboratories publication, Frequently Asked Questions About Today’s Cryptography (the FA Q), describes the state of the art in factoring. Factoring numbers takes a certain number of steps, and the number of steps increases exponentially as the size of the number increases. Even on supercomputers, the time to execute all the steps is so great that for large numbers it could take years to compute. Within a short period of time, the current threshold of general numbers that can be factored will probably rise to 155 digits, approximately the size of a 512-bit RSA modulus. Currently, the limit to the size of an RSA modulus in Crypto-C is 2048 bits.

Digital Envelopes

A digital envelope is a way of combining the advantages of symmetric-key and publickey cryptography. In general, public-key algorithms are slower than symmetric-key ciphers, and for some applications may be too slow to be of practical use, while for symmetric-key ciphers, there is the problem of transmitting the key. A digital envelope provides a solution to this dilemma. The sender encrypts the message using a symmetric-key encryption algorithm, then encrypts the symmetric key using the recipient’s public key. The recipient then decrypts the symmetric key using the appropriate private key and decrypts the message with the symmetric key. In this way, a fast encryption method processes large amounts of data, yet secret information is never transmitted unencrypted.

Optimal Asymmetric Encryption Padding (OAEP)

Optimal Asymmetric Encryption Padding (OAEP) is a general class of methods for constructing digital envelopes from public-key encryption algorithms. OAEP methods have been proposed for the RSA algorithm. OAEP thwarts the Bleichenbacher attack on PKCS #1 digital envelopes.

Recent research by cryptographer Daniel Bleichenbacher of Bell Labs, the research and development arm of Lucent Technologies, indicates that the combination of PKCS #1 and SSL is potentially vulnerable to a class of attacks known as Adaptive Chosen Ciphertext Attacks. Such a potential attack relies on sending a million carefully constructed messages to a target server and observing the variations in the server’s response. The potential attack is detectable by network administrators because of the large number of needed messages. The threat is only against digital envelopes; it does not affect digital signatures.

OAEP is a pre-processing step that is applied to data before it is encrypted and after it is decrypted. OAEP prevents a wide range of attacks on the envelope format and ensures that the attacker must break the underlying cryptographic algorithm in order

Chapter 3 Cryptography 55

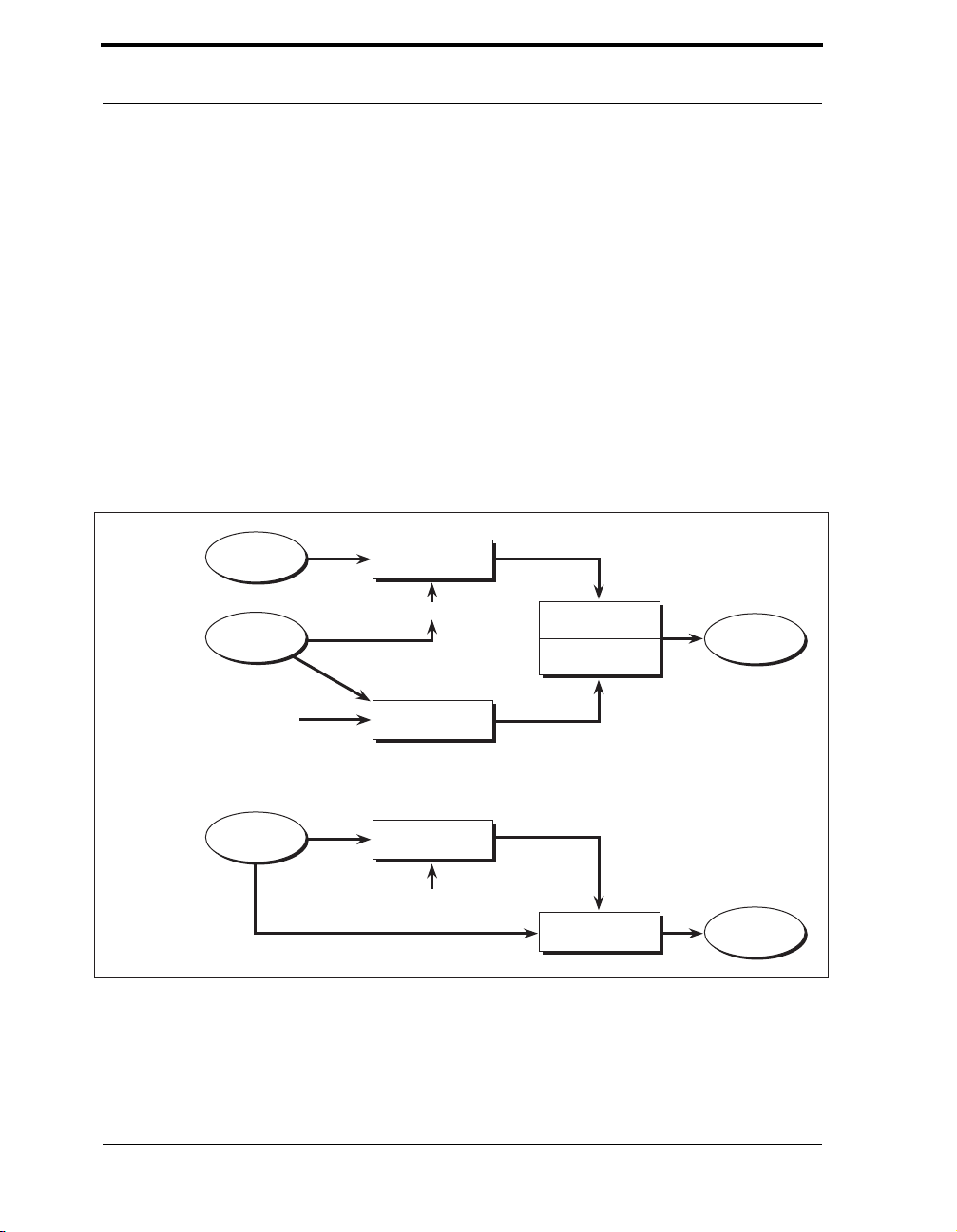
Cryptography Overview

to reveal the contents of a digital envelope. The main features of OAEP are redundancy and randomization. The redundancy feature

makes it difficult for an attacker to create a new derived message from an existing ciphertext message. The recipient of a derived message checks the redundancy after decrypting the message and rejects redundant messages. The PKCS #1 format has only about 16 bits of redundancy, whereas OAEP formats have 64 to 160 bits of redundancy.

The randomization feature makes each bit of the input to the public key operation dependent on each bit of the message and on 64 to 160 bits of randomness. This makes it difficult for chosen input attacks to work, and it causes ciphertext tampering to change many bits in the decrypted message.

Together, redundancy and randomization create verifiable properties for securing digital envelopes.

Sealing Operation

Envelope Open Operation

Message

Symmetric

Key Data

Recipient’s

Public Key

Digital

Envelope

Encrypted

Message

Symmetric-Key

Encryption

Symmetric Key

Public-Key Encryption

Encrypted

Key

Private-Key

Decryption

Private Key

Figure 3-10 Digital Envelope

Encrypted

Message

Encrypted

Data-Encrypting

Key

Symmetric-Key

Decryption

Key

Digital

Envelope

Message

56 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

Authentication and Digital Signatures

Suppose Alice and Bob are disputing a contract. Alice says that Bob must uphold certain obligations because he agreed to them in a contract. Bob says that this is not the contract he signed. He offers as evidence his copy of the contract and sure enough, it differs from Alice’s. One of them has altered their copy of the contract, but who? Or maybe the dispute centers on Bob’s assertion that he never signed a contract, that the signature at the bottom is not his. In that case, either Bob is not telling the truth or Alice forged his signature.

If the contract was signed physically, there are ways to determine the truth. Contracts are often filed with government agencies, so comparing Bob’s and Alice’s copies with the third party’s copy reveals who made alterations. Witnesses may also sign the contract and later testify that both parties did sign it, and the signatures are not forgeries. For electronic documents, there is also a method to determine if a document has been altered or if someone truly did sign it. This method is the digital signature.

There are two types of signature algorithms. The first is a public-key cryptosystem that can perform block encryption, while the second is only capable of digital signatures. The RSA algorithm is an example of the first type. The Digital Signature Algorithm, DSA, is an example of an algorithm of the second type. Crypto-C includes the RSA and DSA signature methods.

A digital signature uses a public/private key pair to sign a document. First the signer digests the document, as described in “Message Digests” on page 47, then encrypts it with their private key. A good digital signature algorithm possesses the following properties:

• Only the owner of a private/public key pair can generate a signature. Knowledge

of the public key does not enable anyone else to forge a signature.

• Knowledge of the public key enables anyone to verify the signature.

• The digital signature guarantees the authenticity of the message and its author.

The digital signature is computationally unique for each message and signer. While a normal signature can be imitated, a digital signature is immune to imitation.

• Any altering of the message renders the signature invalid.

Note: If a digital signature is invalid, you cannot be sure it was a deliberate forgery.

Transmission errors will also produce errors in a digital signature.

For example, to create a digital signature on a contract:

Chapter 3 Cryptography 57

Cryptography Overview

1. Alice and Bob compose a contract in digital format. The file can be in any form,

such as a word processing file or an ASCII file.

2. Each party digests the file and encrypts the digest with their private key.

3. That encrypted digest is their digital signature.

4. The contract now consists of the file and the two copies of the encrypted digest,

one using Alice’s private key, the other using Bob’s private key. Everyone gets copies of this contract.

The digital signature can be used to verify the data at a later time. Suppose that Bob produces a file that is different from Alice’s. To discover which copy has been altered:

1. Digest the new copy.

2. Decrypt each party’s encrypted digest with the corresponding public key.

3. Compare the new digest to the old one.

4. If one of the new digests does not match the old one, that is the altered file.

If a file has been altered, it will produce a different digest, because it is virtually impossible to produce data that will digest to a given value. Even if someone could manipulate the digest, it would be extremely difficult to produce data that has value to anyone.

The digital signature can also be used to verify that a message came from a given person. What if Bob claims Alice forged his digital signature on the original document? He might say her copy of his encrypted digest is not the true version. However, the digest was encrypted using Bob’s private key, to which only Bob has access. Therefore, it is unlikely that Alice forged Bob’s signature.

The following example shows how to verify a message and its signature. Suppose you have the following information:

• A message

• An entity who claims to have sent the message

• A block of data 96 bytes long that purports to be the encrypted digest

To verify the message and the sender:

1. Request the possible sender’s 768-bit (96-byte) RSA public key from a certification

authority.

2. Use that public key to decrypt the 96-byte block of data.

3. If the decryption process results in a 16-byte output, you can say it is a message

digest. There is a message that will digest to those 16 bytes, but you do not yet know what it is.

58 RSA BSAFE Crypto-C Developer’s Guide

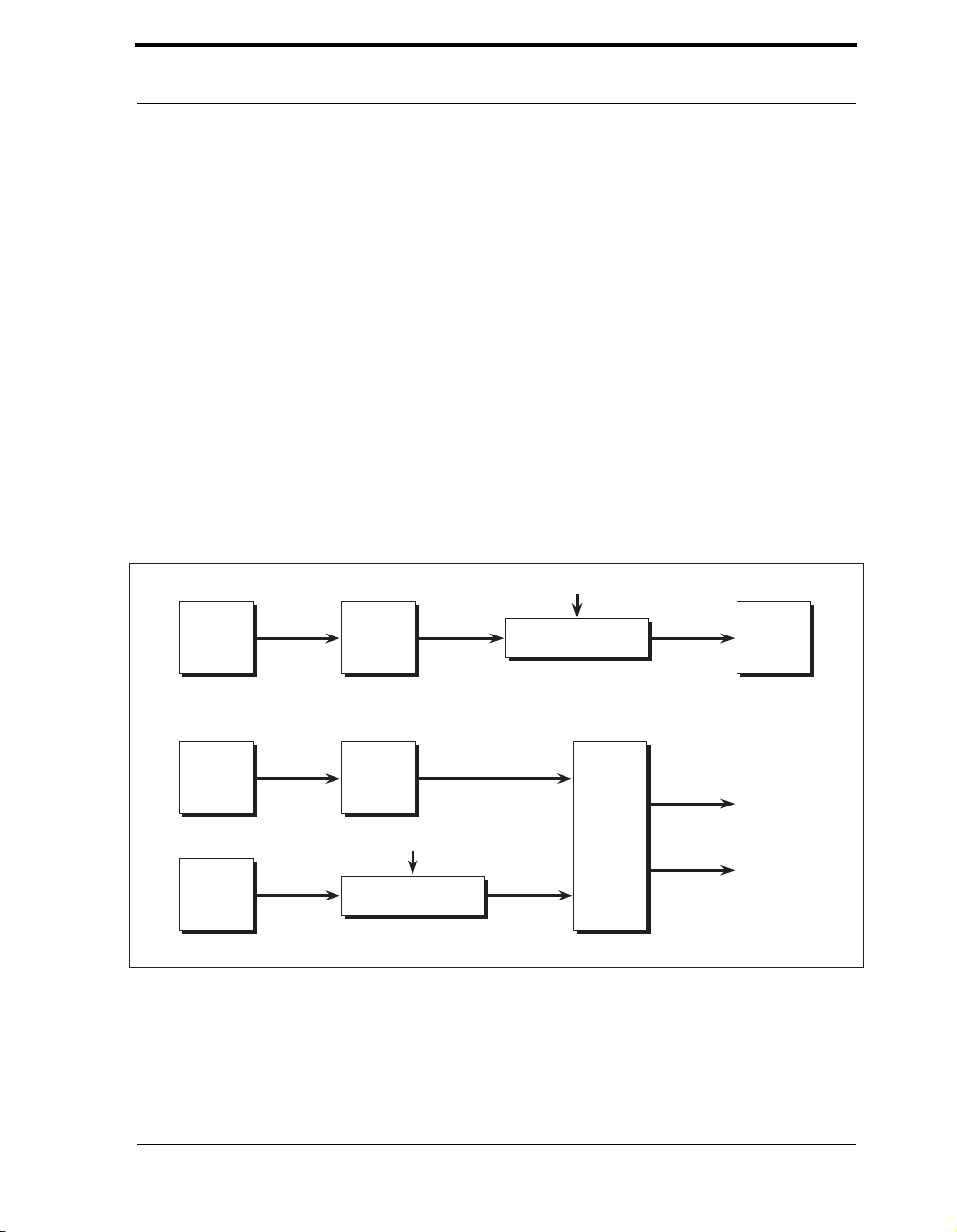
Cryptography Overview

4. Digest the message file.

5. If the digest matches the 16 bytes you obtained from decrypting the original 96-

byte block, the message is verified. That is, you can assume the 96-byte block is the file’s digest encrypted with the RSA private key associated with the public key you used. It would have been computationally infeasible to produce that 96byte block any other way.

There are other uses for a digital signature. Suppose that Bob wishes to buy something from Alice over the Internet. He e-mails her a credit card number. Alice can easily find out from the credit card issuer that the number she received is valid and indeed belongs to Bob. But how does she know that it was Bob who sent the number and not someone posing as Bob? She sends the purchaser a randomly generated message and asks him to digitally sign it with his private key. She then retrieves his public key from a certification authority and verifies the signature. Only the person with access to Bob’s private key will be able to generate a digital signature from the message she generated in such a way that Bob’s public key will verify it properly. In this way, Alice authenticates Bob’s identity.

Private Key

Original

Message

Original

Message

Signature

Message

Digest

Signature Operation

Message

Digest

Public Key

RSA Public

Decryption

Verification Operation

Figure 3-11 RSA Digital Signature

RSA Private

Encryption

EQUAL?

YES

Signature

Valid

Signature

Not Valid

Chapter 3 Cryptography 59

Cryptography Overview

Digital Signature Algorithm (DSA)

The Digital Signature Algorithm (DSA) is part of the Digital Signature Standard (DSS), published by the National Institute of Standards and Technology (NIST), a division of the US Department of Commerce. It is the digital authentication standard of the US government. The DSS specifies the Secure Hash Algorithm (SHA1) as the message digest to use with DSA when generating a digital signature.

To generate a DSA key pair:

1. Find a prime, p, at least 512 bits long.

2. Find a second prime, q, exactly 160 bits long that satisfies the property q|(p–1). q is

called the subprime.

3. Generate a random value, h, the same length as p but less than p.

4. Compute g = h

5. Generate another random value, x, 160 bits long. x is the private value.

6. Compute the public value: y ≡ g

Note: The three values p, q, and g (the prime, subprime, and base, respectively) are

called the DSA parameters. The parameters are public and must be generated before you can sign a message.

(p-1)/q

mod p. g is called the base.

mod p.

To sign a message using DSA:

1. Digest the message using SHA1. This yields a 20-byte (160-bit) digest.

2. Generate a random value, k, 160 bits long and less than q.

3. Find the following values:

= k–1 mod q

inv

r = (g

mod p) mod q xr = (x · r) mod q s = [k

4. Output the signature (r,s).

· (digest + xr)] mod q

inv

To verify a message:

1. Digest the message using SHA1.

2. From the signature (r,s), compute:

= s–1 mod q

inv

= (digest · s

= (r · s

60 RSA BSAFE Crypto-C Developer’s Guide

inv

) mod q

inv

) mod q

Cryptography Overview

a = g

1 mod p

2 mod p

b = y v = (a · b mod p) mod q

3. If v = r, the signature is verified. If v ≠ r, the signature is invalid.

The Math

To see that this is indeed the signature, consider the following. We have the values:

mod p

y = g

and

= r · s

Make the following algebraic substitutions:

a · b mod p = g

u1 + x·u

= g

digest·s

= g

inv

= g

mod q

inv

2 mod p

+ x·r·s

inv

(digest + x·r)

mod p

1 · g

x·u

inv

mod p

2 mod p

Recall that:

mod p) mod q

r = (g

This means that:

v = (a · b mod p) mod q

= (g

mod p) mod q

= r

Digital Certificates

Suppose you own an RSA public/private key pair. You must make your public key public so that others can use it to verify your digital signature or to encrypt session keys when creating an RSA envelope. How do you publicize your key?

Probably the best way is to register public keys with a trusted authority. Then, this trusted authority can certify that a particular public key belongs to a particular entity. Currently, such a public key registration infrastructure exists in the form of digital certificates.

Chapter 3 Cryptography 61

Cryptography Overview

A certificate connects an entity to a public key. For instance, it can list an individual’s name, address, and public key. When people want to use a person’s public key, they look up the certificate associated with that person’s name and address. A certificate can contain a wide variety of information on its owner, such as the person’s organization or job title. This helps differentiate between people who have the same name. The certificate can also contain information on when it was issued or when the public key expires.

For a certificate system to work, there need to be individuals or organizations that issue and maintain the certificates. These are known as a certificate authorities, or CAs. An individual can request a certificate by presenting a CA with a public key and a name and any other identifying information. It is then the CA’s responsibility to verify that the entity making the request is indeed the person identified by the information or is authorized to be associated with that key. The level of trust users place in a CA will depend on the level of verification it performs.

When you ask for an individual’s public key, the CA sends the certificate and signs it with the digest of the certificate encrypted with the CA’s private key. To verify that the certificate is genuine, you must digest the certificate and decrypt the signature using the CA’s public key. Compare the two results: if they are the same, you have a proper certificate.

If the CA you deal with does not have a certificate for the individual in question, that CA can communicate with another CA that might have the right certificate. In fact, to find a particular certificate, a CA may have to go through a chain of CAs until it finds one that possesses the desired certificate.

Names that uniquely distinguish users are necessary for digital certificates to be of real use. The CCITT X.500 series of documents offer more discussion regarding naming conventions and related topics.

Diffie-Hellman Public Key Agreement

The Diffie-Hellman Public Key Agreement, invented by Whitfield Diffie and Martin Hellman in 1976, was the first true public-key algorithm. It provides a method for key agreement; that is, it allows two parties to each compute the same secret key without exchanging secret information. Diffie-Hellman key agreement does not provide encryption or authentication.

The Algorithm

The Diffie-Hellman algorithm is made up of three parts (see Figure 3-12 on page 63):

• Parameter Generation

62 RSA BSAFE Crypto-C Developer’s Guide

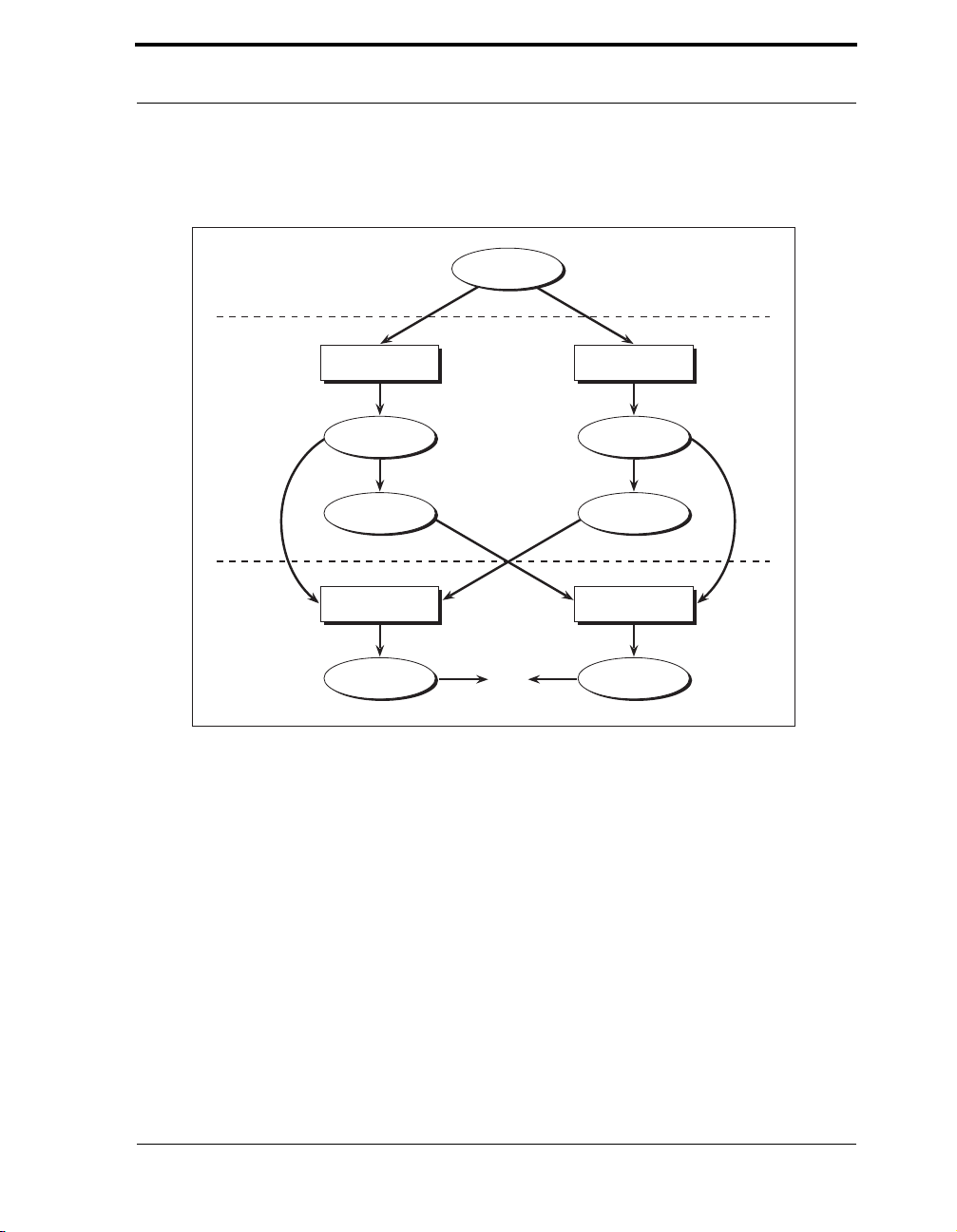
• Phase 1

• Phase 2

Phase 1

Alice

Cryptography Overview

Parameters

Bob

Private value

Public value

Bob

Agreed upon

key

Phase 2

Private value

Public value

Alice

Agreed upon

key

Figure 3-12 The Diffie-Hellman Key Agreement Protocol

Parameter Generation

A central authority selects a prime number p of length k bytes, and an integer g greater than 0 but less than p, called the base. The central authority may optionally select an integer l, the private-value length in bits, that satisfies 2

l–1

≤ p.

Phase 1

Each of the two parties executing the Diffie-Hellman protocol does the following:

1. Each party, i, i = 1 or 2, randomly generates a private value, which is a number, x

greater than 0 but less than the prime. If the central authority has specified the

l–1

= g

≤ xi < 2l.

mod p.

length l, the private value shall satisfy 2

2. Each party computes a public value y

Chapter 3 Cryptography 63

Cryptography Overview

3. The two parties exchange the public values.

These private and public values correspond to the private and public key components of a key pair. The public value is generated in such a way that computing the private value from the public number is computationally infeasible.

Phase 2

Each participant computes the agreed-upon secret key, z, using the other participant’s public value, y', their own private value, x, and the prime, p.

z =(y')

mod p

Even with knowledge of the parameters and both public keys, an outside individual will not be able to determine the secret key. You must have one of the private values to determine the secret key. This means secret information is never sent over unsecure lines.

The Math

Even though the two parties involved are making computations using different private values, they will both end up with the same secret key, as illustrated by the following.

p: prime g: base x

: 1st party’s private value

: 2nd party’s private value

: 1st party’s public value

: 2nd party’s public value

z: secret key

In Phase 1, each party computes a private value, x

= g

mod p

, and a public value, yn:

In Phase 2, the parties trade public values and compute the same secret key:

z = y

mod p

They both compute the same z, because:

= (g

)

= (g

64 RSA BSAFE Crypto-C Developer’s Guide

)

= y

mod p

Cryptography Overview

Security

The security of Diffie-Hellman key agreement relies on the difficulty of computing nth roots modulo a prime number. It takes very little time to exponentiate a number modulo a prime, but it takes a great deal of time to compute its roots. This problem in modular arithmetic is called the discrete logarithm problem. (Recall that, in the real numbers, if you can compute the logarithm of a number, you can easily compute all of its roots.) The RSA Laboratories publication, Frequently Asked Questions About Today’s Cryptography, states, “The best discrete log problems have expected running times similar to that of the best factoring algorithms.” That is, the time it takes to compute discrete logs modulo a prime of a certain length is approximately equivalent to the time it takes to factor a number of that same length. See “The RSA Algorithm” on page 51 for a discussion of factoring.

Multiple-Party Key Agreement

The previous protocol can be extended to more than two parties. For a multiple-party agreement, each individual chooses a private value, then uses the collection of public values from other parties to generate a common secret key.

Elliptic Curve Cryptography

Elliptic curves are mathematical constructs that have been studied by mathematicians for over 100 years. The application of elliptic curves to cryptosystems is more recent; in 1985, Neal Koblitz and Victor Miller independently devised a public-key system using a group of points on an elliptic curve.

The core of elliptic curve cryptosystems rests on the difficulty of a particular type of calculation. For some public-key algorithms, such as Diffie-Hellman key agreement, the security is based in part on the fact that given a modulus n, a number g, and g mod n, it is difficult to determine k. This is called the discrete logarithm problem. Elliptic curve cryptosystems rest on a similar problem: given an elliptic curve E and two points on the curve, P and Q, such that Q = k · P for some number k, it is difficult to determine k. This is called the elliptic curve discrete logarithm problem. (See the next subsection, Elliptic Curve Parameters, for a discussion of these terms.) Many algorithms that are based on the discrete logarithm problem can be translated to analogous algorithms based on the elliptic curve discrete log problem.

Elliptic curves can be used for a variety of public-key cryptosystems. Crypto-C supports the following elliptic curve features:

• Generation of elliptic curve parameters

• Elliptic curve key pair generation

Chapter 3 Cryptography 65

Cryptography Overview

• Elliptic Curve Signature Schemes (ECDSA)

• Elliptic Curve Authenticated Encryption Scheme (ECAES)

• Elliptic Curve Diffie-Hellman key agreement (ECDH)

Crypto-C also allows you to generate precomputed acceleration tables to speed up certain elliptic curve operations. For more information, see the example “Generating a Public-Key Acceleration Table” on page 277.

Elliptic Curve Parameters

A number of parameters are necessary for elliptic curve cryptosystems. These parameters must be generated before you generate a key pair, create an acceleration table, initiate encryption, or perform key agreement with these systems. You can use the same parameters to generate more than one key. These parameters include:

• The finite field, F

• Two elements of F

the coefficients of the curve.

, over which the elliptic curve is defined.

, a and b, which define the elliptic curve; a and b are also called

• A point P of prime order on the elliptic curve E .

• The order, n, of P .

• The cofactor h=#E(F

and #E(F Curve” on page 70 for more information.

Note: In all discussions of elliptic curves, the upper case letters P and Q are used to

The next section discusses these terms in detail. We will try to give enough of the math to give you a feel for what the underlying concepts are without going too deeply into the details. A full discussion of elliptic curve cryptography is far beyond the scope of this manual. For background on elliptic curves, see the book by J. Silverman and J. Tate, Rational Points on Elliptic Curves [20]. For more information on elliptic curves in cryptography, see the ANSI X9.62 and X9.63 standards [13], the IEEE

Standard Specifications for Public-Key Cryptography [14], and A. Menezes’s book, Elliptic Curve Public Key Cryptosystems [19].

) means the number of points in that set. See “The Order of an Elliptic

denote points on an elliptic curve. The lower case letter p is used to denote a prime.

)/n. Here, E(Fq) means the set of points on the elliptic curve

The Finite Field

The elliptic curves used in cryptography are always defined over a finite field, denoted F

. There are two choices for this field:

66 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

• An odd prime field, F

• A field of even characteristic, F

, where p is an odd prime.

For more information about finite fields, see the book by A. Menezes, I. Blake, X. Gao, R. Mullin, S. Vanstone, and T. Yaghoobian, Applications of Finite Fields [18] and also Chapter 2 of Alfred J. Menezes, Paul C. van Oorschot, and Scott A. Vanstone’ s book, Handbook of Applied Cryptography [17].

Odd Prime Fields

The odd prime field Fp is simply Zp, the integers mod p. Modular math is described in the section “The RSA Algorithm” on page 51. Recall that in modular math, we have addition and multiplication, with the additional twist that the numbers loop around, so that, for example, p+1 = 1 mod p.

Although you don’t need it to use the cryptosystem, a little background may help. Because p is prime, F have: except for 0, every number in F number c between 1 and p–1, there is another number d in the same range such that cd = 1 mod p. This is the crucial property that distinguishes F math systems and makes it a field.

Not all moduli will give you a field. For instance, our earlier example, arithmetic mod 55, is not a field. You can see this by looking at the number 5 in this system. The first ten multiples of 5 are: 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50. When we multiply 5 by 11, we get 55, which is just 0 mod 55. Now, when we multiply 5 by 12, we just fall back down to 60 = 60–55 = 5 mod 55. In fact, no matter by what we multiply 5, we will just get a multiple of 5, which will reduce back down to the ten numbers listed above. There is no way we can get to 1 as a multiple of 5 in this particular modular system.

has an interesting property that not all modular math systems

has a multiplicative inverse. That is, given any

from other modular

In fact, the only numbers that will give a field in modular arithmetic are the primes. So you can see that fields are fairly special. The crucial thing to remember is:

An odd prime field, F

, is just modular arithmetic, where the modulus p is prime.

Fields of Even Characteristic

The fields of even characteristic, also known as characteristic 2, are more complicated. If you were looking for a field of that size, you might start with the integers mod 2 However, it turns out that integers mod 2

cannot be a field for any m>1.

Why is this? Remember, we said every element in a field, except 0, has a multiplicative inverse. But, for example, 2

(except for m = 1). To see this, consider the product 2·2

m–1

cannot be invertible in the integers mod

m–1

= 2m≡ 0 mod 2m. If 2

did have an inverse, I, then we would have:

Chapter 3 Cryptography 67

m–1

Cryptography Overview

0=0·I

m–1

)·I mod2

·I)

≡ (2·2 = 2·(2 ≡ 2·1 mod 2

Instead, we create the field F the elements of the finite field F

m in a completely abstract manner. We start by letting

m be the bit strings of bit-length m. Mathematicians

have shown that it is possible to create an addition and a multiplication that make these strings, called m-tuples, into a field.

Addition is easy to define: to add two strings, just XOR them. This is the same as adding them bit by bit, with no carry. Notice that with this field addition rule, for every x in F the integers mod 2

m, we have that x + x = 0. That is already very different from addition in

Note: If you look closely, you will see that we are trying to create a system where 2

can equal 0. In fact, it is because of this property — that the number 1 added to itself two times gives us 0 — that we say this is a field of “characteristic 2” or “even characteristic.”

Multiplication is even more difficult to define. When you multiply two m-tuples, you can’t just multiply them bit-by-bit, or else you would never be able to invert any string that had a 0 in it somewhere. Instead, multiplication in F

m is a complicated

operation involving ordinary multiplication and addition of cross terms. The mathematics underlying the construction of F

m is deep, but it is very well-

understood by mathematicians. For an in-depth discussion of this field, refer to “Related Documents” on page xx.

An elliptic curve, E, can be thought of as a particular type of equation. Elliptic curves look slightly different in the two different cases.

Coefficients Over an Odd Prime Field

An elliptic curve E over an odd prime field Fp is all the pairs of points (x,y) that satisfy the equation:

2=x3

In this equation, x and y are elements of F evaluated over F that is included as well.

The numbers a and b are called the coefficients of the elliptic curve; they are part of the

68 RSA BSAFE Crypto-C Developer’s Guide

+ax+b

, and so are a and b. The whole equation is

. For computational reasons, there is also a “point at infinity”, Ο,

elliptic curve parameters.

Coefficients Over a Field of Even Characteristic

An elliptic curve E over a field of even characteristic F that satisfy the equation:

+ xy = x3+ax2+b

Cryptography Overview

m is all the pairs of points (x,y)

In this equation, x and y are elements of F evaluated over F

m. For computational reasons, there is also a “point at infinity”, Ο,

m, and so are a and b. The whole equation is

that is included as well. The numbers a and b are called the coefficients of the elliptic curve; they are part of the

elliptic curve parameters.

Note: Note that the equation over F

m there is a quadratic term, ax

m is different from the equation over F

, instead of the linear term ax in the odd

. Over

prime case, as well as a new cross-term, xy. The differences in the equation arise because of the differences in arithmetic between the two types of fields.

The Point P and its Order

Obviously, you can’t create a cryptosystem out of just any equation. The elliptic curve equation is important because it has special properties. One of these properties is that it is possible to set up an addition system that lets you add one point on the elliptic curve to another. The addition is complex and non-obvious, but it is possible to set up a system of equations that determine the sum of two points. Adding two points on an elliptic curve involves several operations in the underlying field, F multiplications, additions, and the computation of inverses. The complexity of the addition is what makes elliptic curve cryptosystems work — if you add a point P to itself k times to get kP, there is no known fast way to get k.

To implement an elliptic curve cryptosystem, we need to specify a point P on our curve that has some special properties. To understand these properties, we need some more concepts: the points on a curve, the order of a curve, and the order of a point on the curve.

, including

The Points of an Elliptic Curve

For our field, Fq, and our elliptic curve E, determined by a and b, we can consider all the pairs (x,y) in F point of the elliptic curve. The collection of all the points that satisfy the equation, along with the special point Ο mentioned earlier, is called the points of E over F

Chapter 3 Cryptography 69

that satisfy the elliptic curve equation. Each such pair is called a

; this

Cryptography Overview

is written E(Fq).

The Order of an Elliptic Curve

The addition system that makes the points on the elliptic curve into what is called a group has a number of properties. First, there can only be a finite number of points on the curve. If every possible pair (x,y) were on the curve, there would be only p

m)2

= 22m possibilities of pairs. The total number of points, including the point Ο, is

called the order of the elliptic curve. The order is written as #E(F

The special point Ο plays the role of the additive identity, zero, in the group of the elliptic curve.

The Order of a Point

Given any point on the curve, P, the addition rule lets you add that point to itself. Then you can add your new point to the old point, and so on. When you add a point to itself a number of times, it is called scalar multiplication. Although this is not multiplication in the usual sense — it is an iteration of point addition k times — it still has the usual math properties like commutativity and associativity over addition. Adding a point P to itself k times gives another point denoted kP.

No matter what P is, there is always some n such that nP = Ο. The smallest n that works for a given P is called the order of P. Not only does n exist, but it is always true that n evenly divides the order of the elliptic curve, #E(F

The order n of P is important because it means that when we use P as the starting point of our calculations, we can apply the rules of arithmetic modulo n. That is, we have the following important fact:

r = r’ mod n if and only if rP = r’P

A Point of Prime Order

Now that we have those concepts, we can go on to the next parameter. Given our elliptic curve, E, defined over our finite field, F will be used to mask the private key in a public/private key pair. The properties of P are important to the security of our system. Not just any point will do: we need a point P whose order n is prime; the larger the prime, the more secure the cryptosystem.

Remember, P is of the form P =(x,y) where x and y satisfy the elliptic curve equation. To show that x and y are specific to P, we usually write them as x the special point P gives us two parameters:

• A point P = (x

70 RSA BSAFE Crypto-C Developer’s Guide

) of prime order

P,yP

, we want to fix a special point that

and yP. Therefore,

Cryptography Overview

• The order n of P

P is sometimes called the base point.

The Cofactor

We mentioned previously that the prime number n that is the order of P must evenly divide the order of the elliptic curve. That is, we know that the number h =#E(F an integer. We call h the cofactor, and set it as our last parameter:

)/n is

• The cofactor h =#E(F

)/n

Summary of Elliptic Curve Terminology

Table 3-2 lists the elliptic curve parameters and gives a short description of each parameter. For a brief description,refer to the previous sections in this chapter; for a detailed discussion, see [13], [14], and [19] in “Related Documents” on page xx.

Table 3-2 Elliptic Curve Parameters

Notation Name Description

a, b coefficients of the curve a and b are elements of F

P point of prime order

n order of P The smallest nonzero number such that P added

h cofactor The order of the curve divided by the order of P:

base field Either:

: {0,1,...,p–1} with arithmetic mod p

m : strings of m bits. Addition is bitwise XOR,

multiplication exists, but has no quick description

equation, which depends on the base field:

For F

(x or base point

P,yP

The pair x

to itself n times is the zero point, Ο, on the curve.

n is prime.

#E(F

. They determine an

:y2=x3+ax+b

m:y

+ xy = x3+ax2+b

)

, yP satisfies the curve equation.

)/n

Chapter 3 Cryptography 71

Cryptography Overview

Representing Fields of Even Characteristic

For fields of even characteristic (fields of the form F

m), Crypto-C allows you to choose

how you want the field to be represented. The representation you choose is internal to Crypto-C and affects how field arithmetic is performed. The choice of representation is also one of the formal elliptic curve parameters that must be transmitted along with the public key. Some representations lead to more efficient implementations in hardware or software.

When we talk about representations of F mathematics underlying the construction of F

m, we use the term basis to reflect the original

m. From our point of view, it is most

important to know that a different basis corresponds to a different representation in Crypto-C. Crypto-C offers two types of representation for fields of even characteristic:

• Polynomial basis: this representation closely reflects how the field was originally

constructed by mathematicians. Every field of even characteristic has a polynomial basis representation.

• Optimal normal basis (ONB): this representation is constructed to optimize certain

multiplicative operations. Not all fields have an ONB representation; it can be constructed only for certain values of m.

The difference in the choice of basis shows up most clearly in how multiplication is defined. For example, for any polynomial basis representation, the multiplicative identity is represented as (000…01). For any optimal normal basis, the multiplicative identity is (111…11).

Note: Although arithmetic looks different when you choose a different

representation, the field is still the same. Just as you can represent “normal”arithmetic using a hexadecimal or a decimal system, you can represent F

m inmore than one way.

Elliptic Curve Key Pair Generation

Elliptic curve parameters can be used to generate a public/private key pair. Elliptic curve parameters can either be common to several key pairs or specific to one key pair. The elliptic curve parameters can be public; the security of the system does not rely on these parameters being secret.

72 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

Creating the Key Pair

To compute a public/private key pair:

1. Generate a random value, d, between 1 and n–1.

2. Compute the elliptic curve point dP, that is, P added to itself d times. Call this

point Q; it is a pair of field elements (x

Q,yQ

The key pair is (Q,d): Q is the public key, d is the private key. As previously mentioned, even if you know P and Q, you cannot easily calculate d.

ECDSA Signature Scheme

Once you have generated elliptic curve parameters and created a public/private key pair, you can use this information to create an elliptic curve analogue of the Digital Signature Algorithm (DSA).

Signing a Message

The holder of the private key can sign a message as follows:

1. Digest the outgoing message using SHA1. This yields a 20-byte (160-bit) digest, e.

2. Compute a random value, k, between 1 and n–1.

3. Compute the elliptic curve point kP = (x

4. Currently, the first coordinate, x

, is an element of the finite field. To perform

further calculations, we must convert x follows:

For F

, x1 is an integer α in the range 0 to p–1. Let = α. (Essentially, no

conversion is required.) For F

m, x

is a bit string of length m bits: s1s2...sm. Because F

arithmetic, we need a way to think of its elements as integers. To do this, let the integer

be a weighted sum of the bits of x1:

∑

i1=

1,y1

to an integer, called . We do this as

mi–()

si⋅

m has a very strange

In either case, once you have calculated , set r= . If r is zero, go back to step 2.

Note: Although this lets you take a member of the field F

m and represent it as an

integer, it has some limitations. If you perform any arithmetic operations on

Chapter 3 Cryptography 73

Cryptography Overview

, you will be using regular arithmetic. This is so different from arithmetic in

m that, for example, . However, if you convert two field

x1x2+x1x2+≠

elements and perform operations on them that show they are equal after conversion, then they were equal before conversion.

5. Compute s = k

–1

(e+dr)mod n. Again, you must check that s is nonzero.

The signature for this message is the pair r and s. Notice that, as with DSA, the signature depends on both the message and the private key. This means no one can substitute a different message for the same signature.

Note: The previous equation is merely an outline. For cryptographic purposes, it is

necessary to verify that certain numbers are nonzero, or that they satisfy other conditions. Crypto-C makes the appropriate verifications when it generates your key pair.

Verifying a Signature

When a message is received, the recipient can verify the signature using the received signature values and the signer’s public key, Q. Because the pair (r,s) that has been received may not actually be a valid signature pair, it is customary to call the received pair (r’,s’) instead.

To verify a signature:

1. First verify that r’ and s’ are between 1 and n-1. If they are not, the output is

invalid.

2. Digest the received message using SHA1. This yields a 20-byte (160-bit) digest, e.

3. Compute c = (s’)

-1

. Remember, s’ is an integer mod n, so its inverse is also an

integer mod n.

4. Compute u

5. Compute the elliptic curve point (x

6. Convert x

7. Compute v = mod n

= ec mod n and u2= r’c mod n.

)=u1P +u2Q.

1,y1

to an integer, . See Step 5 on page 74 for details.

If v = r’, the signature is verified. If they are different, the signature is invalid.

The Math

The ECDSA algorithm depends in part on the fact that if r = r’ mod n, then rP = r’P. (See “The Point P and its Order” on page 69.)

74 RSA BSAFE Crypto-C Developer’s Guide

Cryptography Overview

The following calculations are really just a series of substitutions that can be made by looking back at the definition. You may find it more convincing to go through the substitution steps yourself, by glancing back at the preceding sections Creating the Key Pair, Signing a Message, and Verifying a Signature.

If the message has been signed correctly, then s = s’. Expanding the elliptic curve point (x

Recall that Q =dP, so:

Now recall that s = k

)=u1P +u2Q calculated by the recipient, we see that:

1,y1

P +u2Q =es–1P + rs-1Q

–1

(eP +rQ)

P +u2Q =s–1(eP +rQ)

–1

(eP +rdP)

–1

(e + rd)P

–1

(e + dr)P

–1

(e+dr)mod n, so:

P +u2Q =s–1(e + dr)P

–1

=[k

(e+dr)]-1(e + dr)P

–1)–1

= (k = kP

(e+dr)–1(e+dr)P

This is the point calculated by the recipient. But this is also the point generated by the sender. The recipient then checks that the x-coordinate of the calculated point is in fact the x-coordinate that was received.

Elliptic Curve Authenticated Encryption Scheme (ECAES)

You can use elliptic curves to create an authenticated encryption scheme with a public/private key pair.

As always with elliptic curves, we assume that the elliptic curve parameters have been defined in advance. Suppose Bob has a key pair based on these parameters. The pair is (Q,k elliptic curve parameters. The point Q is the public value and the number k private value.

Chapter 3 Cryptography 75

), where Q = k2P, where P is the base point of prime order specified in the

is the

Cryptography Overview

Encrypting a Message Using the Public Key

Anyone who wishes to send Bob an encrypted message can do so using the elliptic curve parameters and Q. To encrypt a message M, where the length (in bytes) of the message is f, another party follows these steps:

1. Compute a random value, k

2. Compute the elliptic curve point Q

, between 1 and n – 1.

= k1P. This will be transmitted along with the

encrypted message.

3. Compute the elliptic curve point S

= k1Q. S1 is a pair (x1,y1). This is the secret

information the sender uses to encode the message.

4. Compute a one time pad, otp, of length f, from x

using a key derivation function

(KDF). otp is a concatenation of a series of hashes; it is constructed using f, x SHA1. otp is described below. The description uses the following notation: (1)

denotes the concatenation of two numbers, (2) for a number a, [a] denotes the integer part of a. In particular, [f/160] denotes the integer part of f/160.

a. Initiate a 32-bit, big-endian bit string counter. In hex, counter is initialized to

00000001

b. For i = 1 to [f/160], create a series of hashes, as follows:

Compute Hash concatenation of x

= SHA1(x1 || counter), that is, the SHA1 hash of the

and counter.

Increment counter. Increment i.

c. We want the length of the pad to be exactly the same as the length, f, of the

message M. If f/160 is not an integer, we need to truncate the last hash to make the lengths equal. Therefore, we define Hash’

[f/160]

as follows:

, and

Hash

Hash’

d. Set otp to be the concatenation of the series of hashes:

otp = Hash

5. Compute M’ = otp XOR M.

76 RSA BSAFE Crypto-C Developer’s Guide

[f/160]

{

the [f/160] – (160 × [f/160]) leftmost bits of Hash

|| Hash2 ||…|| Hash

if f/160 is an integer

[f/160]

if f/160 is not an integer

[f/160]

[f/160]-1

|| Hash’

[f/160]

Cryptography Overview

6. Compute an authentication tag, tag = SHA1 (x

hash of concatenation of the x-coordinate of the secret point k

|| M’). That is, tag is the SHA1

Q and the message

M’. Since tag is an SHA1 hash, tag is 20 bytes long.

7. Transmit the ciphertext c =(Q

,M’,tag). The total length of c in bytes is: 21+2 · (the

length of a field element in bytes) + f.

Decrypting a Message Using the Private Key

A message that had been encrypted in the previous example can be decrypted using the private key as follows:

1. Parse the received ciphertext c =(Q

2. Use the private key k

). If the message was transmitted correctly and encoded with the correct

2,y2

public key, S

3. To v er i fy tha t S

is equal to S1.

to compute the elliptic curve point S2= k2Q1. S2 is a pair

is equal to S1, compute tag' = SHA1 (x2 || M'). If tag' is different

from tag, output an error and stop.

4. Compute a one time pad, otp’, of length f, from x

function outlined in Step 4 on page 76. Use x otp’ = otp.

5. Compute M = otp XOR M’.

,M’,tag) into its components, Q1, M’, and tag.

using the key derivation

instead of x1. Since x1 = x2,

Elliptic Curve Diffie-Hellman Key Agreement

It is possible to construct a version of the Diffie-Hellman key agreement that uses elliptic curves. (For more information on Diffie-Hellman key agreement, see “Diffie- Hellman Public Key Agreement” on page 62.) Like Diffie-Hellman, EC DiffieHellman provides for key agreement, but not encryption or authentication.

The elliptic curve Diffie-Hellman key agreement algorithm provides a method for two parties to each compute the same secret key without exchanging secret information. The algorithm is made up of two parts: Phase 1 and Phase 2. Before they begin, the two parties must agree on the elliptic curve parameters: a base field, an elliptic curve over the base field, and point P of prime order, along with its order n. See the section “Elliptic Curve Parameters” on page 66 for details. See Figure 3-13 on page 79 for an illustration of Elliptic Curve Diffie-Hellman key agreement.

Chapter 3 Cryptography 77

Cryptography Overview

Phase 1

The first party randomly generates a private value, a number k1, greater than 0 but less than n. Similarly, the second party generates a random private value, k

Each party then computes a public value. To do this, they each compute R each party, this is an elliptic curve point. The two parties exchange their public values.

= kiP. For

Phase 2

Each participant computes the agreed-upon secret key, z, from the other’s public value, R curve point S. This is a pair, (x secret value.

Even with knowledge of the parameters and both public keys, an outside individual will not be able to determine the secret key. One must have one of the private values to determine the secret key. This means secret information is never sent over unsecure lines.

, and their own private value, ki. The parties compute kiRj to get the elliptic

). They then use the first coordinate of S, xS, as their

S,yS

78 RSA BSAFE Crypto-C Developer’s Guide

RSA Security Crypto-C User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Contents

Preface

What’s New in Version 5.2.2?

Improved performance

Hardware support

MultiPrime RSA

Serialization for algorithm objects performing RC4, Diffie Hellman key exchange

Organization of This Manual

Advanced Encryption Standard (AES)

Conventions Used in This Manual

Terms and Abbreviations

Related Documents

How to Contact RSA Security

RSA Security Web Site

Getting Support and Service

SecurCare® Online

Technical Support Telephone Numbers

Call Handling and Escalation Process

Introduction

The Crypto-C Toolkit

Algorithms

Symmetric Ciphers

Message Digests

Message Authentication

Random-Number Generation

Public-Key Algorithms

Digital Signatures

Elliptic Curve Public-Key Algorithms

Secret Sharing

Hardware Support

Cryptographic Standards and Crypto-C

PKCS Standards and Crypto-C

NIST Standards and Crypto-C

PKCS Compared with NIST

ANSI X9 Standards and Crypto-C

Quick Start

The Six-Step Sequence

Introductory Example

Saving the Object State (optional)

Putting It All Together

Decrypting the Introductory Example

Multiple Updates

Summary of the Six Steps

Cryptography

Cryptography Overview

Symmetric-Key Cryptography

Ciphers

Block Ciphers

Padding

Ciphers in Crypto-C

Tripl e DES

DESX

Modes of Operation

Stream Ciphers

Message Digests

Message Digests and Pseudo-Random Numbers

Hash-Based Message Authentication Codes (HMAC)

Password-Based Encryption

Public-Key Cryptography

The RSA Algorithm

Digital Envelopes

Optimal Asymmetric Encryption Padding (OAEP)

Authentication and Digital Signatures

Digital Signature Algorithm (DSA)

Digital Certificates

Diffie-Hellman Public Key Agreement

Elliptic Curve Cryptography

Elliptic Curve Parameters

The Finite Field

The Point P and its Order

Summary of Elliptic Curve Terminology

Representing Fields of Even Characteristic

Elliptic Curve Key Pair Generation

Creating the Key Pair

ECDSA Signature Scheme

Signing a Message