Page 1

ICS Regent
I
mportant!
®
PD-6043
Math Package for
W
INTERPRET
Floating Point Math Function Block
(T3833)
Issue 1,
The Math pac
package which allows the user to create Floating Point Math
function blocks for Regent application programs. When
installed on the PC, the math package is seamlessly
integrated with the base WINTERPRET
Floating point math function blocks are used to perform
mathematical calculations that require floating point
precision or use values that exceed the 16-bit signed integer
range (-32768 to +32767) used in ladder logic math
operations. The expressions that can be used in floating point
math function blocks include addition, subtraction, division,
multiplication, exponentiation, logarithms, and square root.
kage for W
INTERPRET
is an add-in software
software.
March, 06
Software Installation
The Math package is installed on the PC running the
W
INTERPRET
package provides the necessary installation software to install
this add-in math package. The math package should be
installed at the same time or after you have installed the
W
INTERPRET
Installation Procedure
The files on the Math package diskette are in compressed
form. You cannot simply copy the files to your hard drive —
they must be decompressed before they will run. You must
have the WINTERPRET base package distribution disk in order
to run the setup procedure to install the Math package.
To install the Math package, use the following sequence:
Industrial Control Services
1
application software. The W
base package.
INTERPRET
base
Page 2

Math Package for
1. Insert the WINTERPRET base package distribution disk into
W
INTERPRET
drive A: or B:
(T3833)
2. Start Windows (if it isn’t already running).
3. Choose Run from the Program Manager’s File menu.
4. Type a:\
W
INTERPRET base package disk in drive B: type
b:\setup.exe
5. In the WINTERPRET Setup dialog box enter the name of the
directory in which you have installed the WINTERPRET
base package (This assumes that you have already
installed WINTERPRET). Choose Continue.
6. In the WINTERPRET Installation dialog box check the Math
package box.
7. Choose OK to have the setup program install the Math
package software.
When the installation is completed, you can run the
W
INTERPRET application and create floating point math
function blocks in you application programs.
setup.exe
.) Choose OK or press ENTER.
in the text box. (if you inserted the
Working with Floating Point Math Function Blocks
Floating point math function blocks are created as part of an
application program which may also contain other types of
function blocks. A single application program is made up of as
many as 50 function blocks of any type or combination.
When you installed the Math package, additional sof
was added to W
point math function blocks. With this additional software you
can create floating point math function blocks by opening a
project, opening a program and opening (or creating) a
function block.
For an overview about Regent application programs and
function blocks and how to create them using WINTERPRET
refer to Section 5, Working with Programs and Function
Blocks in the Regent User’s Guide.
INTERPRET
to allow you to work with floating
tware
,
2
Industrial Control Services
Page 3

Math Package for
W
INTERPRET
(T3833)
Using Floating Point Math Statements
In floating point math function blocks you enter
mathematical equations and expressions in the form of
statements. Each line can contain one statement that
calculates the result of a mathematical equation. For
example, consider the quadratic equation below.
y = 1.6x2 +8x -22.4
Using floating point math the statement representing this
equation would be:
Y = 1.6*X^2 + 8*X - 22.4
You can also enter comments in any line by entering a
semicolon (;) and placing your comments after the semicolon
as shown below.
Y
= 1.6*X^2 + 8*X - 22.4 ; This is a comment.
Floating point math also allows you to create conditional
statements using IF, ELSE, ENDIF, WHILE, ENDW, AND
and OR operations. Below is an example of using IF, ELSE
and ENDIF to calculate the absolute value of the difference
between two variables.
PD-6043
March, 06
IF AI1 > AI2
DIFF = AI1 - AI2
ELSE
DIFF = AI2 - AI1
ENDIF
Using combinations of conditional statements and
mathematical operations allows you to configure floating
point function blocks to meet a wide range
requirements.
Mathematical Operations
of control
The mathematical operators perform arithmetic and
functional operations.
3
Page 4
Math Package for
Operator Operation
^ Exponentiation
* Multiplication
/
Division
+
Addition
- Subtraction
Operator Operation
SQRT(x)
Returns the square root of x
EXP(x)
Raises e to the x power
LOG(x)
Returns the logarithm of x
LN(x)
Returns the natural logarithm of x
Note:
Note:
W
INTERPRET
(T3833)
Arithmetic Operations
Table 1 shows the arithmetic operators recognized by floating
point math listed in their default order of precedence.
Table 1. Arithmetic Operators.
Multiplication and division have equal precedence from
right, as do addition and subtraction.
The exponent, X, in an exponential expression (
Y^X
left to
) is always
evaluated as an integer (fractional portion is truncated). Do
not use the exponentiation operator to perform square root
calculations, instead use the
below.
SQRT(X)
function described
Parentheses may be used to clarify the order of operation:
operations within parenthesis are performed first. Inside the
parentheses, the usual order of precedence is maintained.
Functional Operators
A functional operator is used in an expression to perform a
predetermined operation that is to be performed on one or
more operands. The Regent’s floating point math has four
standard functions that reside in the system as shown in
Table 2.
Table 2. Functional Operators.
In each function you can enter a variable or arithmetic
expression within the parenthesis of the function. For
example the following statement is valid.
4
Industrial Control Services
Page 5

Math Package for
Note:
W
INTERPRET
(T3833)
The exponentiation operator (
integer power X. If you need to calculate
values of X you can use the
shown below.
Conditional Statements
ROOT1 = (-B + SQRT(B^2 - 4*A*C)) / (2*A)
Y^X
) can only raise Y to an
YX for non-integer
LN(X)
and
EXP(X)
functions as
Y_2_THE_X = EXP(X*LN(Y))
The statements available in the floating point math let you
alter program flow base
IF, ELSE, and ENDIF
d on testing of conditions.
The IF statement is used to make a decision regarding
program flow based on the result returned by an expression.
The expression can include mathematical and logical
operators. The use of ELSE within the lines controlled by the
IF statement is optional.
Syntax:
IF expression
•
•
ELSE (optional)
•
•
ENDIF
IF, ELSE, and ENDIF statements must not
the same line.
WHILE and ENDW
be combined on
The WHILE statement executes a series of statements in a
l
oop as long as the expression is true. The expression can
include mathematical and logical operators.
Syntax:
WHILE expression
•
PD-6043
March, 06
•
loop statement
5
Page 6

Math Package for
Operator
Relation Tested
Expression
=
Equality
X = Y
<> Inequality
X <> Y
<
Less than
X < Y
>
Greater than
X > Y
<= Less than or equal to
X <= Y
>= Greater than or equal to
X >= Y
Important!
If the expression is true (not zero), loop statements are
executed until the ENDW statement is encountered. Floating
point math then returns to the WHILE statement and checks
expression. If expression is still true, the process is repeated.
If the expression is not true, execution resumes with the
statement following the ENDW statement.
To avoid infinite loops, the expression must be modified (its
value changed) during repeated execution to make the
expression false and exit the loop.
W
INTERPRET
•
•
ENDW
(T3833)
WHILE and ENDW statements may be nested.
Relational and Logical Operators
Relational and logic operators are often used in the
expressions for IF and WHILE statements to control the
execution of other mathematical statements.
Relational Operators
Relational operators compare two values. The result of the
comparison is either true (1) or false (0
). The result can then
be used to make a decision regarding program flow. The
relational operators are shown in Table 3.
Table 3. Relational Operators.
6
When arithmetic and relational operators are combined in
one expression, the arithmetic is always p
Industrial Control Services
erformed first.
Page 7

Math Package for
Value
A
Value
B
Result
A AND B
Result
A OR B
T T T T
T F F T
F T F T
F F F
F
W
INTERPRET
(T3833)
Logical Operators
Logical operators perform logical, or boolean, operations on
numeric values. Just as the relational operators are usually
used to make decisions regarding program flow, logical
operators are used to connect two or more relations and return
a true or false value to be used in a decision.
A logical operator takes a combination of true/false values and
returns a true or false result. An operand of a logical operator
is considered to be true if it is not equal to zero, or
false if it is
equal to zero. The result of the logical operation is a number
which is, again, true if it is not equal to zero, or false if it is
equal to zero.
In an expression, logical operations are performed after
arithmetic and relational operations.
Table 4. Logical Operators.
Using Variables and Constants
Constants
Constants are static values used by the floating point math
function blocks during execution of your program. All
constants are numeric.
Numeric constants can be either positive or negative.
Numeric constants must not contain commas. For example, if
the number 20,000 is needed as a constant, it should be typed
in the floating point math statement as 20000.
There are two types of numeric constants: integer and floating
point.
PD-6043
March, 06
7
Page 8

Math Package for
W
INTERPRET
(T3833)
Integer Constants
Integer constants are constants entered as whole numbers
that do not contain decimal points or commas. Entering
an
integer constant greater than 7 numerals long is allowed but
the precision of the actual number stored and used in the
Regent is limited to 7 significant digits. For example, the
integer constants 12345678 and 12345679 may result in an
equal values when converted and stored in the Regent.
Floating Point Constants
Floating point constants are positive and negative numbers
represented in exponential form (similar to scientific
notation). A floating point constant consists of an optionally
signed integer or fixed point number (the mantissa) followed
by the letter "E" and an optionally signed integer (the
exponent). The "E" means "times ten to the power of."
For example:
33E-2
Here, 33 is the mantissa, and -2 is the exponent. This number
could be read as "thirty-three times ten to the power of
negative two." You could also write this number as 0.33 in
regular fixed point notation.
8
You can represent any number from -1.175494E-38 to
3.402823E38 as a floating point constant.
Variables
Variables are names representing values used in the float
ing
point math function blocks. All of the variables you use in a
floating point math function block must be shared variables,
I/O points, or local variables used by floating point math
function blocks only. For example, if you scale an analog
input value to a register, the register should be defined as a
shared variable register if you want to use the scaled result in
a floating point function block.
The floating point math compiler assumes that any local
var
iables found in the function block will be local floating
point registers. If a local variable is used in both a floating
point math and other type of function block, a local data
allocation error will be reported when you attempt to load the
Industrial Control Services
Page 9

Math Package for
W
INTERPRET
(T3833)
application program in the Regent. This will prevent the
program from being loaded into the Regent.
For more information about Regent variable types, see
Regent Variable Types and Memory, in Section 4, Working
with Projects, in the Regent User’s Guide.
Floating point math function blocks recognize the following
variable types:
Logical Variables
Logical variables are used for digital output, shared control
relays, and local control relays. Logical values are always 1
(on) or 0 (off).
Analog Variables
Analog variables are used for analog inputs and outputs.
Analog variables must be within the range 0 to 4095.
Thermocouple and RTD inputs are within the range of -16384
and 16383.
Integer Variables
Integer variables are used for shared registers and local
regist
and 32767.
Floating Point Variables
ers. Integer values must be within the range -32768
Floating point variables are used for floating point shared
registers and floating point local registers. Floating point
values must be within the range -1.175494E-38 and
3.402823E38.
PD-6043
March, 06
Coercion (Type Conversion)
Regardless of the variable type, all calculations performed in
floating point math are done using floating point numbers.
When logical, analog, or integer type variables are used, code
is created in the fun
to a floating point number for calculation in the Regent.
ction block to convert the variable value
When storing the result of a calculation, the value is
converted to the type of the destination variable.
When performing variable conversions, the rules in Table
apply:
9
5
Page 10

Math Package for
Logical to analog
False to 0, true to 1.
Logical to integer
False to 0, true to 1.
Logical to floating point
False to 0.0, true to 1.0
Analog to logical
0 to
false, otherwise true.
Analog to integer
Valid for all analog values.
Analog to floating point
Valid for all analog values.
Integer to logical
0 to false, otherwise true.
Integer to analog
Valid for all integers between 0 and
4095 (-16384 to +16384 for T/C and
RTD inputs). Otherwise a conversion
error is reported.
Integer to floating point
Valid for all integers.
Floating point to logical
0.0 to false, otherwise true.
Floating point to analog
Valid for all floating point number
s
between 0.0 and 4095.0 (-16384.0 to
+16384.0 for T/C and RTD inputs).
Otherwise a conversion error is
reported.
Floating point to integer
Valid for all floating point numbers
between -32768.0 and +32767.0.
Otherwise a conversion error is
reported.
W
INTERPRET
(T3833)
Table 5. Conversion Rules.
Error Handling
In a floating point math function block, errors may occur
during floating point calculations as the values used in the
equations change. An example of a math error is the square
root of a negative number. For each function block the us
must define two tag names which are used to report the line
number and error code of the math error. These tag names
may be used in the function block to annunciate errors and
optionally execute user defined actions if math errors occur.
Hold Last Valid Value
When a math error occurs during a calculation, the result of
the equation retains the last valid value.
er
10
For example, consider the equation:
Industrial Control Services
Page 11

Math Package for
Scan B
SQRT(B)
Result, A
1 25 5 5
2 16 4 4
3 2
1.414213
1.414213
4 -7
<error>
1.414213
5 1 1 1
W
INTERPRET
(T3833)
A = SQRT (B)
During execution in the Regent, the value of B may change
from one scan cycle to the ne
xt. Table 6 illustrates the values
of B the result stored in A for a series of scan cycles to
illustrate the effects of a math error (square root of a negative
number).
Table 6. Example of Math Error and Result Values.
During scan 4, the square root of -7 produces an error, and the
result, A, retains its last valid value (1.414213
). In scan 5, the
square root of 1 is valid so the result, A, is updated with the
new value square root of 1 = 1.
User-Supplied Error Handling Logic
Each floating point math function block contains two registers
in which error codes are placed by the Regent during
execution. Error codes indicate what type of error occurred
and the line number on which it occurred. This error
information can be tested in the function block as desired.
Error Code Variable
The error code variable must be assigned a name
. This name
will hold the error code. Four error codes are generated as
shown in Table 7.
PD-6043
March, 06
11
Page 12

Math Package for
Error Code
Description Example
1 Underflow
C = A / B; |A/B| < 1.175494E-38
2 Overflow
C = A * B; A * B > 3.402823E38
C = A/B; B = 0
3
Not a number
C = SQRT A; A < 0
4
Conversion AO = 3000 + 2000
(where AO is an analog output)
Scan AI
AI+300
AO
Comments
1 3000
3300
3300
No error
2 3200
3500
3500
No error
3 3700
4000
4000
No error
4 3900
4200
4000
Error Code 4, last value used
5 4000
4300
4000
Error Code 4, last value used
6 3780
4080
4080
No error
W
INTERPRET
(T3833)
Table 7. Error Codes.
In most floating point equations, the results do not approach
the error limits of floating point math. When equations are
used that can produce floating point errors, the variable on
the left side of the equal sign will not be changed and it will
contain the last valid result. If under error conditions this
last value is not the best answer and a better answer can be
determined by the error code, then the error term should be
examined.
Example:
AO = 300 + AI
where,
AO is analog output (maximum 4095)
AI
is analog input (0 - 4095)
if AI > 3795 then an error will occur.
Table 8. Examp
le of Conversion Error, Error Code 4.
The most desirable answer for scans 4 and 5 would probably
be AO max = 4095, not the last value of 4000. To alter this
value, you may use the error code to examine the error term
to determine a bett
er value.
12
Industrial Control Services
Page 13

Math Package for
Line Equation
Comments
1 LINE = 0
Reset line number variable to 0 to clear
status each scan.
2 ERROR = 0
Reset error code variable to 0 to clear status
each scan.
3 A = EQUATION 1
Equation that generates an error, a better
answer is pre
dictable:
4 IF (ERROR <> 0 AND LINE = 3)
If line 3 produces an error, a better value for
A should be determined.
5 A = BETTER VALUE
Equation that sets A to a better value than
calculated in line 3.
6 ENDIF
7 B = EQUATION 2
Equation not requiring special error handling.
8 C = EQUATION 3
Equation not requiring special error handling.
9 D = EQUATION 4
Equations not requiring special error
handling.
10 E = EQUATION 5
Next equation requiring better error handling.
11 IF (ERROR <> 0 AND LINE = 10)
If line 10 produces an error, a better value
for E should be determined.
12 E = BETTER VALUE
Equation that sets A to a better value than
calculated in line 10.
13 ENDIF
W
INTERPRET
(T3833)
Table 9 shows a general example of how the error variables
can be used in a floating point function block to check for error
conditions and conditionally execute alternate equations that
calculate a more appropriate result than leaving the value at
its last valid value. For example, if our analog output
equation, AO = 300 + AI, was the equation in line 3, we could
use the equation, AO
maximum value for the analog output when AI > 3795.
=
4095, in line 5 to always produce a
Table 9. Using Error Variables.
PD-6043
March, 06
When multiple lines in the function block have math errors,
the error code variable and line number variable will change
during the execution of the function block. For each equation
that you identify a potential for a math error, you must test
for errors before executing any other equations which may
also generate errors. At the end of the scan, the error
variables will have the value of the last math error.
13
Page 14

Math Package for
The Regent does not reset the values of the line number and
error code variables when n
When the error condition ceases, these variables contain the
values for the last error. You should include equations to
reset the error variables (as shown in lines 1 and 2 in Table 9.
Otherwise, once an equation generates an error, the test for
error will remain true for that equation until a different line
number generates a math error.
W
INTERPRET
(T3833)
o more math errors are present.
Using the Floating Point Math Editor
Floating Point Math function blocks are created using the
Add Function Block or Insert Function Block from the
Program Editor. After you have created a new math function
block the Floating Point Math Editor window is opened as
shown in Figure 1.
14
Figure 1. The Floating Point Math Editor Window.
Using the drop-down menus you can select commands to
create floating point math statements, define error variables,
perform cut, copy and paste operations, print the function
block and a host of other configuration operations.
The F
floating point math function blocks. When you create a math
function block you will enter your equations line by line in a
simple text-based editor.
loating Point Math Editor lets you create and edit
Industrial Control Services
Page 15

Math Package for
Note:
W
INTERPRET
(T3833)
The floating point math editor allows you to create up to 6500
lines in a single function block. The size of each compiled
function block is limited to 64 kbytes of code which provides up
to 1300 lines which contain floating point math statements (a
simple statement like A = 1 occupies approximately 50 bytes).
Statement Lines
Each line of the function block may contain up to 72
characters that form a floating point math statement.
Additional comment characters may also be included (see
Comments below). Statements cannot be extended from one
line to the next.
Comments and Blank Lines
In-line comments may be included on any line of the floating
point math function block.
Comments begin with a semicolon (;). Anything following a
semicolon will be interpreted as a comment. All characters to
the right of a
semicolon will be interpreted as comments and
will not be used to generate code that is loaded and executed
in the Regent. A line beginning with a semicolon is
completely a comment line.
Blank lines may be used to make the function block more
easily readable by separating sequential lines from others.
Blank lines and lines that are completely comments do not
generate any executable code, but do require 2 bytes of
function block local data.
PD-6043
March, 06
The editor allows you to enter up to 1024 characters per
line,
however, when the function block is printed only the first 125
characters of each line are printed. Avoid entering lines
longer than 125 characters wide.
An floating point math example which includes comments and
blank lines is shown in Figure 2.
15
Page 16

Math Package for
W
INTERPRET
Figure 2. Example of the Floating Point Math Editor
(T3833)
Window.
File Menu
The File Menu gives you access to the standard function block
file commands which include: Save Function Block, Revert to
Last Saved, Compile, View Error Messages, Edit Function
Block Description, Edit Function Block Details, Print
Function Block, Print Setup, Log Off and Exit. For more
information on all of these commands refer to Commands
Common to all Function Blocks in Section 5 of the Regent
User’s Guide.
Edit Menu
From the Edit Menu the user can select a variety of
commands such as cut, copy and paste of the currently
selected text in the editor.
Undo
Use the Undo command to restore the text in the editor to its
original state before performing a Cut, Copy, Paste or delete.
Cut
16
The Cut command can be used to remove the currently
selected text from the editor. Subsequently the text can be
inserted into the function block using the Paste command.
Industrial Control Services
Page 17

Math Package for
W
INTERPRET
(T3833)
Click and drag the mouse to select the desired text to cut.
Choose Cut from the Edit Menu to remove the selected text.
Copy
The Copy command can be used to copy the currently selected
text to the Windows clipboard. Copied text can later be
inserted into the function block using the
Paste command.
Click and drag the mouse to select the desired text to copy.
Choose Copy from the Edit Menu to copy the selected text to
the clipboard.
Paste
The Paste command is used to insert the current contents of
the clipboard at the currently selected position. Paste is
normally used in conjunction with the Cut and Copy
commands.
After using the Cut or Copy command, place the cursor at the
position that you wish to insert the text. Choose Paste from
the Edit Menu to insert the contents of the c
Note:
lipboard.
The Paste command can be used to replace text in the
function block. Use the mouse to select the range of text that
you wish to replace. Choose Paste from the Edit Menu to
replace the selected text with the text previously selected by
Cut or Copy.
PD-6043
March, 06
Select All
Choose Select All to select all of the lines in the function block.
This performs the same operation as selecting all of the lines
by clicking and dragging the cursor from the start of the first
line to the end of the last line in
Error Variables
the editor.
Use the Error Variables command to define the line number
and error code variable names for floating point math error
reporting. For additional information about error variables
and how they can be used in the function block see Page 10,
Error Handling.
When you select the Error Variables command from the Edit
menu the following dialog box is opened:
17
Page 18

Math Package for
W
INTERPRET
(T3833)
Figure 3. Floating Point Math Error Variables.
Line number va
riable
Enter the tag name for the line number variable. The
variable is used to report line numbers that generate math
errors if they occur during execution in the Regent.
Error code variable
Enter the tag name for the error code variable. The variable is
used to report the error code for math errors if they occur
during execution in the Regent.
Search Menu
Go to Line
The Go to Line command lets you quickly move to different
lines in the floating point math function block. From the
Floating Point Math Editor's Search menu choose Go to Line
(
ALT,S,G
).
18
Figure 4. Floating Point Math: Go to Line.
For your convenience, the dialog displays the number of lines
currently defined in the function block.
Line number
Enter the line number that you want to go to.
Industrial Control Services
Page 19
Go
Math Package for
W
INTERPRET
(T3833)
Choose Go to move to the line number that you entered in the
Line Number text box.
First
Go to the first line in the function block.
Last
Go to the last line in the function block.
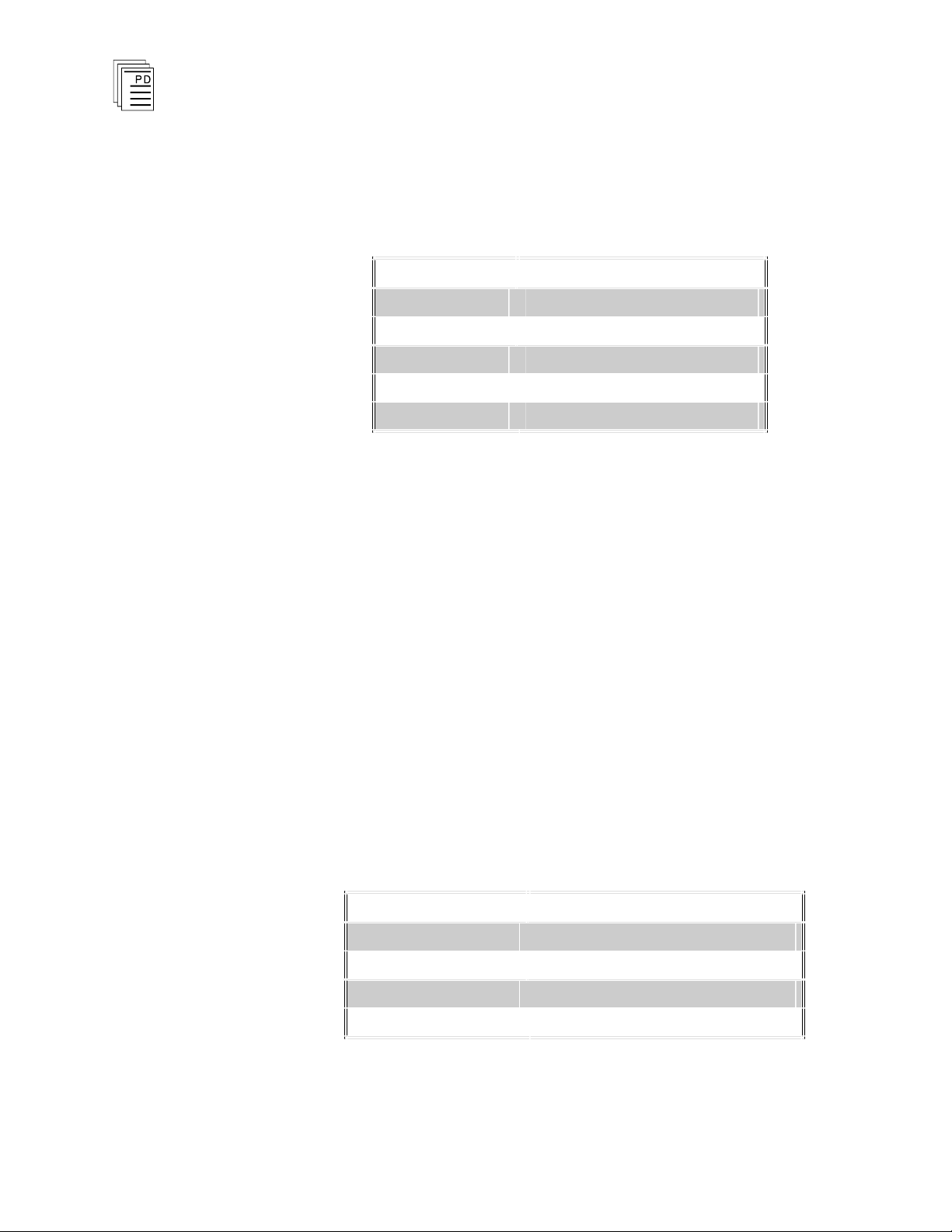
Find
The Find command lets you quickly loca
te text strings in the
floating point math function block. For example, you can
search for a tag name and have the editor locate the line of
the function block where the tag name is used. From the
Floating Point Math Editor's Search menu choose Find
(
ALT,S,F
).
PD-6043
March, 06
Find Next
Figure 5. Floating Point Math: Find.
The Find Next command repeats the last selected Find
operation. From the Floating Point Math Editor's Search
menu choose Find Next (
ALT,S,N
) or simply press F3.
19
Page 20

Math Package for
W
INTERPRET
(T3833)
Window Menu
The Wi
W
Window menu commands see Commands Common to all
W
W
ndow menu commands are standard throughout all
INTERPRET windows. For more information on using the
INTERPRET Windows in Section 3, Installing the
INTERPRET Application of the Regent User’s Guide.
Help Menu
The Help menu commands are standard throughout all
W
INTERPRET windows. For more information on using the
Help menu commands see Commands Common to all
W
INTERPRET Windows in Section 3, Installing the
W
INTERPRET Application of the Regent User’s Guide.
Using the Floating Point Math Monitor
When you have selected a Floating Point Math function block
in the Program Monitor window and choose the Monitor
command from the Control Menu, the Floating Point Math
Monitor window is opened as shown in Figure 6.
20
Figure 6. Floating Point Math Monitor Window.
Industrial Control Services
Page 21

Math Package for
W
INTERPRET
(T3833)
Normally you will use the Floating Point Math Monitor
Window to observe results of the floating point math
calculations. You can also select a single line and d
values of all the variables used in the selected line.
isplay the
File Menu
The File Menu provides access to several commands common
to all function block monitors. These include View Function
Block Details, View Function Block Description, Log Off and
Exit. For descriptions of these commands see Commands
Common to all Function Block Monitors in Section 7, Loading
Monitoring and Testing Application Programs in the Regent
User’s Guide.
Control Menu
The Control Menu provides certain command that are
com
mon to all function block monitors. These include Run,
Stop and Scan commands to control the execution status of
the entire application program. For descriptions of these
commands see Commands Common to all Function Block
Monitors in Section 7, Loading Monitoring and Testing
Application Programs in the Regent User’s Guide.
Additionally the Control Menu provides a Line Details
command used specifically for monitoring floating point math
function blocks.
PD-6043
March, 06
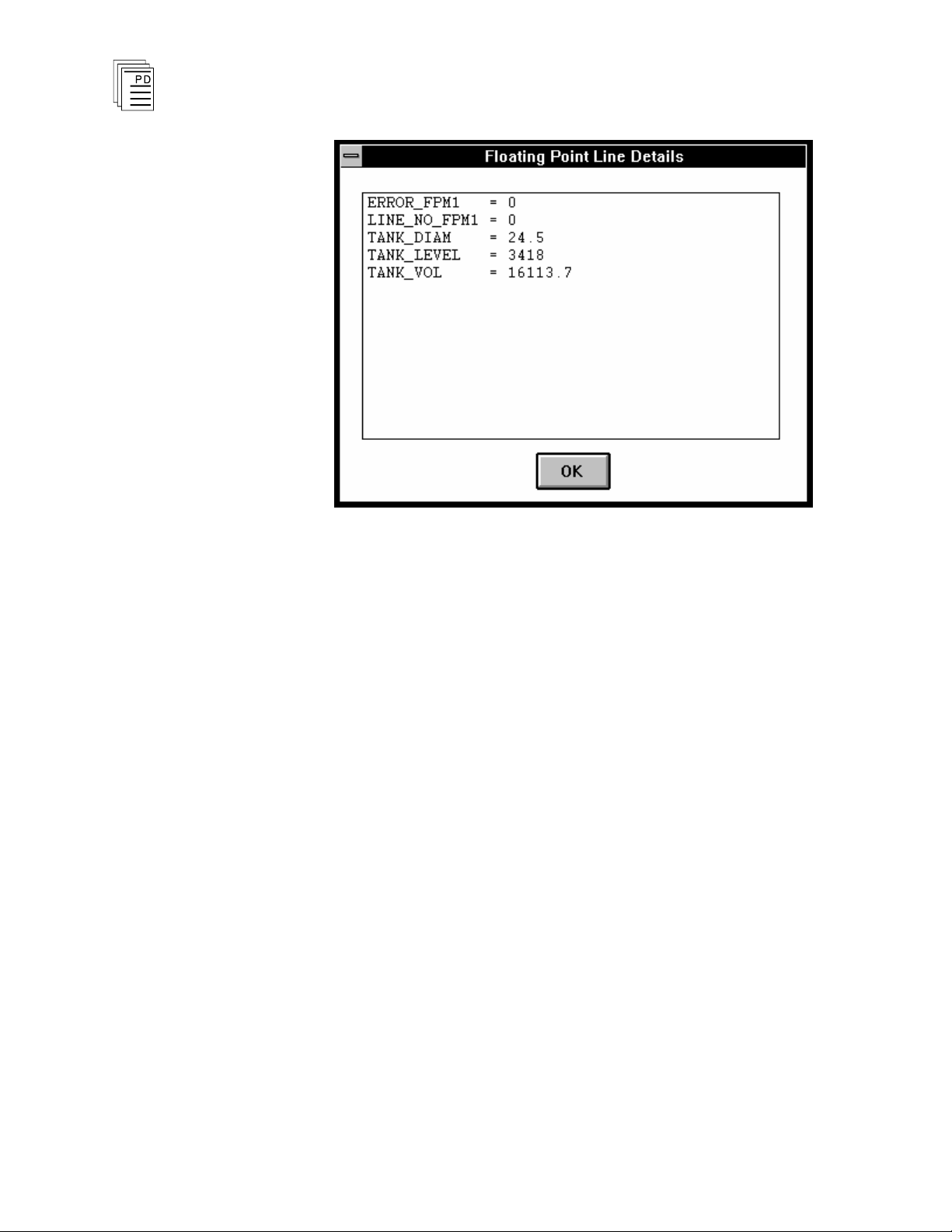
Line Details
This command opens a dialog box which
displays the status of
all variables in the currently selected line. The status of the
error variables are also shown in the Line Details dialog.
21
Page 22
Math Package for
W
INTERPRET
(T3833)
Figure 7. Floating Point Math: Line Details Dialog.
Search Menu
The Search Menu provides commands to locate information in
floating point math function block. You can choose Go to Line
(to move to a particular line number), Find (to search for test
strings) or Find Next (to repeat the last Find selection). More
details about each of these commands are described on Page
18.
Window Menu
The Window menu commands are standard throughout all
W
INTERPRET windows. For more information on using the
Window menu commands see Commands Common to all
W
INTERPRET Windows in Section 3, Installing the
W
INTERPRET Application of the Regent User’s Guide.
Help Menu
22
The Help menu commands are standard throughout all
W
INTERPRET windows. For more information on using the
Help menu commands see Commands Common to all
W
INTERPRET
W
INTERPRET Application of the Regent User’s Guide.
Windows
in Section 3, Installing the
Industrial Control Services
Page 23

Math Package for
W
INTERPRET
(T3833)
Typical Equation Sizes and
Execution Speeds
The following information may be used for estimating the size
and increasing the efficiency of floating point equations. This
is only a guideline. Execution speeds and memory size
requirements will vary for each equation according to the
general rules shown below.
Compiled Function Block Size
As with all types of function blocks, the size of the compiled
function block is repor
compiling the function block (
later). The total size of the function block along with the data
size and code size are reported, where;
Total Size
Data Size
=
=
ted in the Error Messages dialog after
Data Size + Code Size (bytes)
2 bytes per line
(all lines, whether they are blank,
comments only or actual floating point
statements).
W
INTERPRET
version 3.2 or
The code required for actual floating point statements
depends on the types of operations used in the st
the types of variables used in the statements (see Table 10).
A general rule for size considerations when designing floating
point equations for the Regent is: using floating point
variables creates the least amount of code, followed by
constants, shared registers, analogs, and bit-type variables.
The size required for floating point math operations depends
upon the types of variables in the operation. Use the
multipliers below to approximate the size based on the
variable types used.
Code Size
=
52 + Code for Statements
atements and
PD-6043
March, 06
23
Page 24

Math Package for
Operation
Format
Code
Min.
Code
Max.
Add + 8 26
Subtract - 12 30
Multiply * 8 26
Divide / 8 26
Logarithm
LOG(x) 4 4
Natural Log
LN(x) 4 4
Square root
SQRT(x)
4 4
Exponentiation
X^Y 10 18
e raised to the X
EXP(x) 4 4
Equality = 44 82
WHILE statement
98
see note, below
IF statement
94
see note, below
Note
W
INTERPRET
(T3833)
Local and Floating point
Constant
Shared register
Analog
Bit-type
1.0
1.2
1.5
1.8
2.5
The maximum and minimum code sizes for each operation
listed in Table 10 are approximate and will vary according to
use in an equation. Code sizes are shown in bytes. These
numbers should be used only to estimate the size of a function
block. The actual size of the function block can always be
checked by compiling the function block and observing the
actual size reported by the compile operation.
Table 10. Floating Point Operation Sizes.
WHILE and IF statement sizes will vary with the number
and type of equations they contain, use of compare
statements, and use of AND and OR.
Execution Speeds
The execution speeds of each operation listed below were
derived using floating point variables in a floating point math
24
Industrial Control Services
Page 25

Math Package for
Operation
Format
Minimum Speed
(msec.)
Add + 63
Subtract - 87
Multiply * 56
Divide / 56
Logarithm
LOG(x) 45
Natural Log
LN(x) 62
Square root
SQRT(x) 45
Exponentiation
X^Y 90
e raised to the X
EXP(x) 1845
Equality = 15
W
INTERPRET
(T3833)
function block, and will vary according to type of data used
and the complexity of the equation.
Table 11. Execution Speeds.
There are two general rules for creating the most efficient
floating point equations:
1. Simplify equations. Using parentheses will increase the
execution speed of the equation.
2. Store intermediate results in local or shared floating point
registers. Other data types are converted to floating point
prior to equation execution. The fewer times a conversion
is performed, the faster the execution.
Safety Considerations
The floating point math function block is TÜV certified for
Risk Class 5 as non-interfering. These function blocks may
only be used in safety critical applications if they do not
perform any control actions that affect the value of Risk Class
5 safety critical variables.
PD-6043
March, 06
25
Page 26

Math Package for
W
INTERPRET
(T3833)
26
Industrial Control Services
 Loading...
Loading...