PASCO OS-8515C User Manual
®
C
T
NORMAL
Instruction Manual with
Experiment Guide and
Basic Optics System
OS-8515C
Teachers’ Notes
012-09900B
Optics Bench
50
40
60
30
70
20
80
10
0
10
20
30
40
50
60
70
80
COMPONENT
90
90
90
OS-8465
NORMAL
80
80
70
COMPONENT
60
50
BASIC OPTICS
RAY TABLE
40
30
NORMAL
20
10
0
10
20
70
30
60
40
50
Basic Optics System Table of Contents
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
About the Equipment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
Storage Box. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7
About the Experiments. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Experiment 1: Color Addition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
Experiment 2: Prism. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
Experiment 3: Reflection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
Experiment 4: Snell’s Law . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
Experiment 5: Total Internal Reflection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
Experiment 6: Convex and Concave Lenses. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
Experiment 7: Hollow Lens . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
Experiment 8: Lensmaker’s Equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
Experiment 9: Apparent Depth. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
Experiment 10: Reversibility . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
Experiment 11: Dispersion. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
Experiment 12: Focal Length and Magnification of a Thin Lens . . . . . . . . . . . . . . . . . . 33
Experiment 13: Focal Length and Magnification of a Concave Mirror. . . . . . . . . . . . . . 37
Experiment 14: Virtual Images. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
Experiment 15: Telescope. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
Experiment 16: Microscope . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
Experiment 17: Shadows. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
Telescope and Microscope Test Pattern . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
Teacher’s Guide. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
Storage Box. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
Technical Support . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
Basic Optics System
C
NORMAL
OS-8515C
Optics Bench
10
20
30
40
50
60
70
1
3
4
5
2
6
50
40
60
30
70
20
80
10
90
90
OS-8465
0
NORMAL
80
COMPONENT
90
80
80
70
COMPONENT
60
50
BASIC OPTICS
RAY TABLE
40
30
NORMAL
20
10
0
10
20
70
30
60
40
50
7
8
11
a
9
b
c
12
d
e
f
10
13
®
4
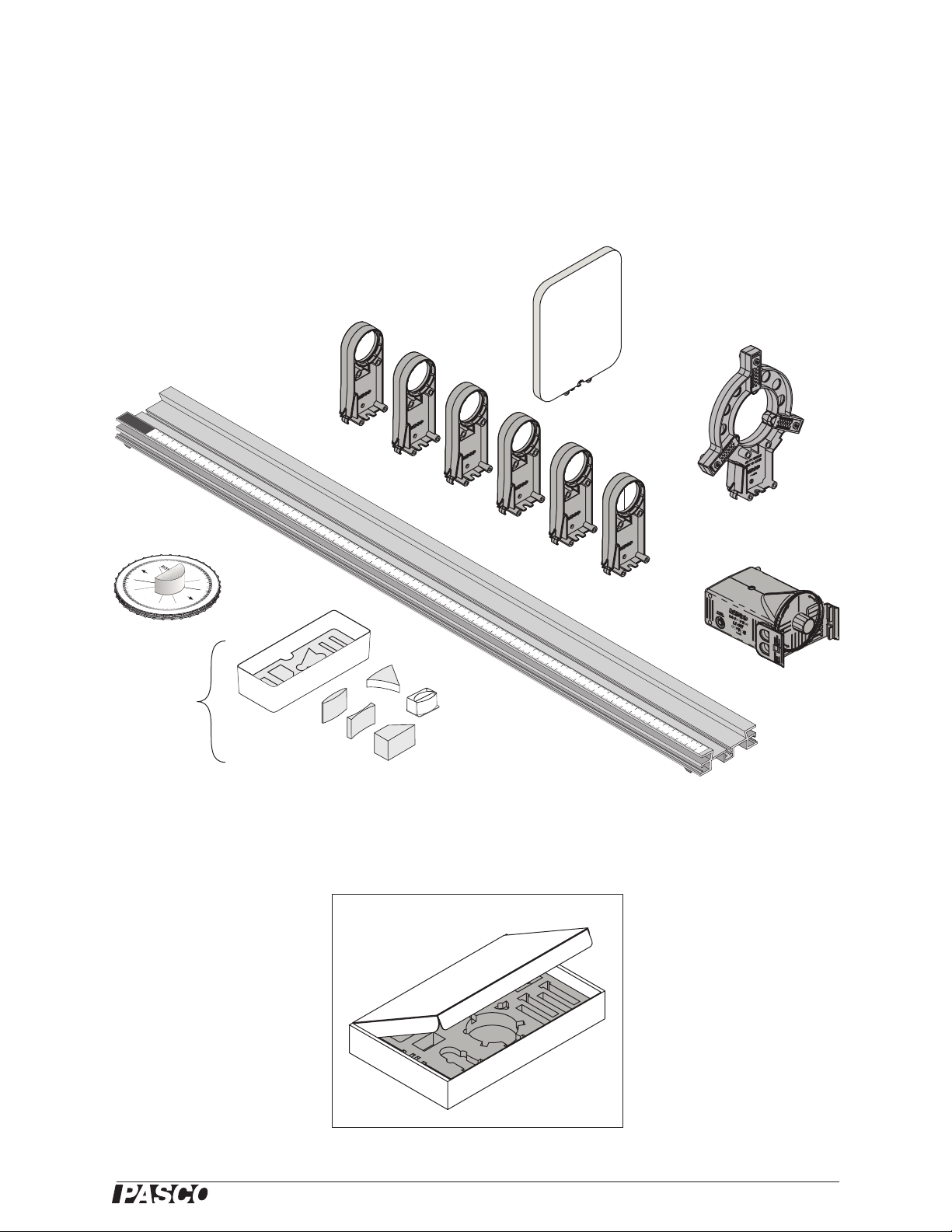
Included Equipment Part Number
1. Viewing Screen OS-8460
2. Adjustable Lens Holder OS-8474
3. +100 mm Mounted Lens
OS-8456
4. +200 mm Mounted Lens
5. +250 mm Mounted Lens
6. −150 mm Mounted Lens
OS-8519
7. Concave/convex Mirror
8. Half-screen
9. Light Source OS-8470
10. 1.2 m Optics Bench OS-8508
11. Ray Tabl e with D-shaped Lens OS-8465
12. Ray Optics Kit with: OS-8516A
13. Storage Box 740-09892
Introduction
OS-8457
a. Storage Box/Water Tank 740-177
b. Mirror 636-05100
c. Hollow Lens OS-8511
d. Convex Lens 636-05501
e. Concave Lens 636-05502
f. Acrylic Trapezoid 636-05611
The PASCO Basic Optics System contains the optics components you will need for a variety of experiments and
demonstrations. This manual includes student instructions and teacher’s notes for 17 typical experiments.
For an even greater variety, you can expand the system with any of the Basic Optics kits and components available from PASCO, including lasers, polarizers, diffraction slits, and light sensors. See the PASCO Physics catalog or visit www.pasco.com for details.
®
5
Basic Optics System About the Equipment
About the Equipment
For detailed information on the Light Source, Ray Table, Adjustable Lens Holder, and Ray Optics
Kit, see the instruction sheets included with those components.
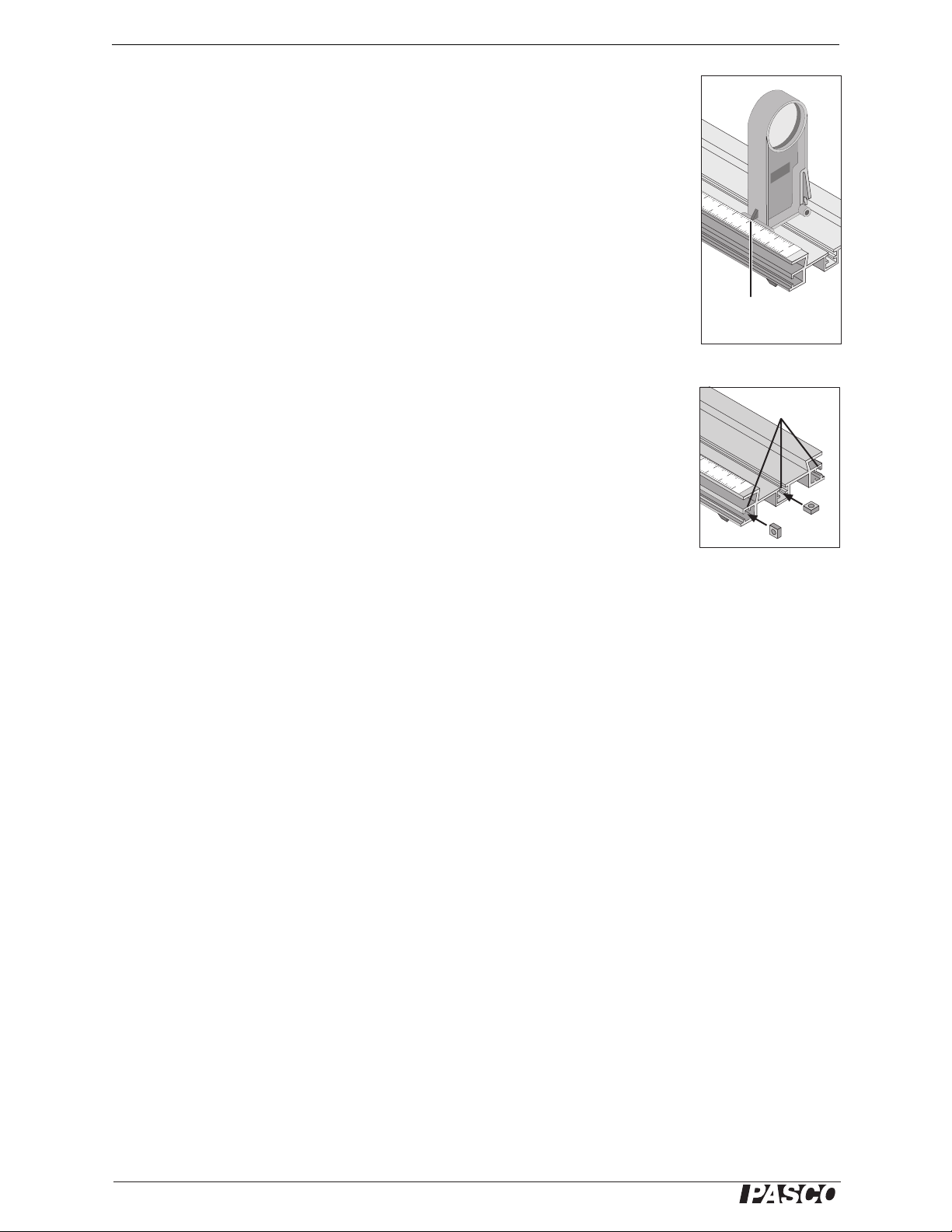
Optics Bench Basic Optics components, such as mounted lenses and the adjustable lens holder, snap into the wide centra l channel of the optics bench. Place the base
of the component on the bench and push down firmly to snap it in place. To move it,
squeeze the tab on base and slide it along the bench.
Components that include a square bolt and a thumb screw are designed to be fasted to
the T -slots on the sides and center of the bench. Slide the bolt into the T -slot, insert the
thumb screw through the component’s mounting hold, thread the screw into the bolt
and tighten it down.
Use the metric scale on the bench to measure the positions of components.
metric scale for
measuring component
positions
Light Source The included light source can be used on a tabletop or mounted on
the bench. It functions as a bright point source, an illuminated crossed-arrow object, a
primary-color source, and a ray box with up to five parallel rays.
Mounted Lenses The Basic Optics System includes four lenses mounted in holders. Use them on the optics bench with the light source, viewing screen, and other
Basic Optics components.
Adjustable Lens Holder To use an unmounted lens on the bench, place it in the
adjustable lens holder. It will hold any round lens between 20 and 75 mm in diameter.
Viewing Screen Mount the screen on the bench to view real images formed by
lenses.
Concave/convex Mirror and Half-screen The mounted mirror is concave on
one side and convex on the other side. The radius of curvature of both surfaces is 200
mm. Use the half-screen to view real images formed by the concave side of the mirror.
Ray Table and D-shaped Lens Use the ray table and D-shaped lens on a tabletop with the light source (in ray-box mode) to study angles of incidence, reflection
and refraction.
Ray Optics Kit The ray optics kit is a set of optics components designed for use
with the light source in ray-box mode. To make the rays easy to see and trace, use the
ray optics components on a white sheet of paper on a flat table top. The transparent
storage box doubles as a water tank for studying lenses under water.
T-slots
6
®
Model No. OS-8515C Storage Box
Storage Box
Use the foam-padded box to store, organize, and protect the system’s components.
Place the components in the fitted compartments as illustrated below. Extra compartments are included for additional components as spare parts. A full-page diagram
appears on page 69. Remove or copy that page and attach it the bo x lid.
Concave/convex
Ray Optics Kit
Viewing
Screen
Light
Source
+100 mm
+200 mm
Lenses
AC
Adapter
D-shaped Lens
+250 mm
-150 mm
Ray Table
and
Adjustable Lens
Holder
About the Experiments
The experiment instructions on the following pages are arranged and categorized
according to which components of the Basic Optics System they use. See the table at
the top of each experiment for a detailed list of required equipment. Teachers’ notes,
including typical data and answers to questions, can be found starting on page 59 .
Mirror
Half-screen
The experiments that call for the light source work best in a dimly lit room.
Ray Optics Kit Experiments These experiments use the Ray Optics Kit, the
Light Source (in ray-box mode), and may require blank white paper, a ruler, protractor, and drawing compass.
1. Color Addition (page 9 ): Expl ore the results of mixing colored light and illumi-
nating colored ink with colored light.
2. Prism (page 11): Show how a prism separates white light into its component col-
ors and show that different colors are refracted at different angles through a
prism.
3. Reflection (page 13): Show how rays are reflected from plane, concave, and con-
vex mirrors.
4. Snell’s Law (page 15): Determine the index of refraction of acrylic by measuring
angles of incidence and refraction of a ray passing through the trapezoid.
5. Total Internal Reflection (page 17): Determine the critical angle at which total
internal reflection occurs in the trapezoid.
®
7
Basic Optics System About the Experiments
6. Convex and Concave Lenses (page 19): Use ray tracing to determine the focal
lengths of lenses.
7. Hollow Lens (page 21): Use the hollow lens and water to explore how the prop-
erties of a lens are related to its shape, its index of refraction, and the index of
refraction of the surrounding medium.
8. Lensmaker’s Equation (page 23): Determine the focal length of a concave lens
by measuring its radius of curvature.
9. Apparent Depth (page 25): Measure the apparent depth of the trapezoid and
determine its index of refraction by comparing the apparent depth to the actual
thickness.
Ray Table Experiments These experiments use the Ray Table with the D-shaped
Lens and the Light Source (in ray-box mode).
10. Reversibility (page 29): Explore how the relationship between the angles of inci-
dence and refraction is related to the direction of propagation.
11. Dispersion (page 31): Show how white light is separated into colors by the
acrylic D-shaped lens and determine the different indices of refraction for red and
blue light.
Optics Bench Experiments These experiments use the Optics Bench, Mounted
Lenses, and Viewing Screen. Experiments 12 and 17 also use the Light Source.
12. Focal Length and Magnification of a Thin Lens (page 33): Determine the
focal length of a converging lens and measure the magnification for a certain
combination of object and image distances.
13. Focal Length and Magnification of a Concave Mirror (page 37): Determine
the focal length of a concave mirror and measure the magnification for a certain
combination of object and image distances.
14. Virtual Images (page 41): Study virtual images formed by a diverging lens and a
convex mirror.
15. Telescope (page 47): Construct a telescope and determin e its magnifi cation.
16. Microscope (page 51): Construct a microscope and determine its magnification.
17. Shadows (page 55): Show the um bra and the penum bra of a shadow.
8
®
Model No. OS-8515C Experiment 1: Color Addition
Experiment 1: Color Addition
Required Equipment from Basic Optics System
Light Source
Convex Lens from Ray Optics Kit
Other Required Equipment
Red, blue, and black pens
Blank white paper
Purpose
In Part 1 of this experiment, you will discover the results of
Light source
mixing red, green, and blue light in different combinations.
In Part 2, you will compare the appearance of red, blue, and
black ink illuminated by red and blue light.
Part 1: Addition of Colored Light
Procedure
1. Turn the wheel on the light source to select the red,
green, and blue color bars. Fold a blank, white sheet of
paper, as shown in Figure 1.1. Lay the paper on a flat
surface and put the light source on it so that the colored
rays are projected along the horizontal part of the paper
and onto the vertical part.
2. Place the convex lens near the ray box so it focuses the rays and causes them to
cross at the vertical part of the paper.
Note: The lens has one flat edge. Place the flat edge on the paper so the lens stands stably
without rocking.
3. What is the resulting color where the three
colors come together? Record your observation in Table 1.1.
4. Now block the green ray with a pencil.
What color results from adding red and blue
light? Record the result in Table 1.1.
red + blue + green
red + blue
red + green
Table 1.1: Results of Colored Light Addition
Colors Added Resulting Color
Convex lens
Folded paper
Red, green,
and blue rays
Combined
colors
Figure 1.1: Color addition
5. Block each color in succession to see the
green + blue
addition of the other two colors and complete Table 1.1.
Questions
1. Is mixing colored light the same as mixing colored paint? Explain.
2. White light is said to be the mixture of all colors. In this experiment, did mixing
red, green, and blue light result in white? Explain.
®
9
Basic Optics System Experiment 1: Color Addition
Part 2: Observing Colored Ink Under Colored Light
Procedure
1. While you look away, have your partner draw two lines—one red and one
black—on a sheet of white paper. One of the lines should be labeled A, and the
other B, but you should not know which is which.
Before you look at the paper, have your partner turn off the room lights and cover
the red and green bars so the paper is illuminated only with blue light.
Now look. What colors do the two lines appear to be? Do they appear to be
different colors? Record your observations in Table 1.2.
Finally, observe the lines under white light and record their actual colors in Table
1.2.
2. Repeat step 1, but this time have your partner draw lines using blue and black ink
(labeled C and D), and observe them under red light.
3. For Trial 2, switch roles and repeat steps 1 and 2 with your partner observing
lines that you have drawn. Record the results in Table 1.2. (For this trial, you may
try to trick your partner by drawing both lines the same color—both red or both
black, for instance.)
Table 1.2: Colored Ink Observed Under Colored Light
Trial 1: Name of observer: ______________________________________
Color of Light Line Apparent Color of Ink Do they look different? Actual Color of Ink
Blue Light
Red Light
Trial 2: Name of observer: ______________________________________
Color of Light Line Apparent Color of Ink Do they look different? Actual Color of Ink
Blue Light
Red Light
A
B
C
D
A
B
C
D
4. Look at red and black lines under red light. Which line is easier to see?
_________________________
Questions
1. What makes red ink appear red? When red ink is illumined by blue light, is most
of the light absorbed or reflected?
2. When illumined with red light, why is red ink on white paper more difficult to
see than black ink?
10
®
Model No. OS-8515C Experiment 2: Prism
Experiment 2: Prism
Required Equipment from Basic Optics System
Light Source
Trapezoid from Ray Optics Kit
Blank white paper
Purpose
Incident ray
The purpose of this experiment is to show how a prism
separates white light into its component colors and to
show that different colors are refracted at different
angles through a prism.
Theory
n
1
n
2
When a monochromatic light ray crosses from one
medium (such as air) to another (such as acrylic), it is
refracted. According to Snell’s Law,
sin θ1 = n2sin θ
n
1
2
Figure 2.1: Refraction of Light
the angle of refraction (θ2) depends on the angle of incidence (θ1) and the indices of
refraction of both media (n
and n2), as shown in Figure 2.1. Because the index of
1
refraction for light varies with the frequency of the light, white light that enters the
material (at an angle other than 0°) will separate into its component colors as each frequency is bent a different amount.
The trapezoid is made of acrylic which has an index of refraction of 1.497 for light of
wavelength 486 nm in a vacuum (blue light), 1.491 for wavelength 589 nm (yellow),
and 1.489 for wavelength 651 nm (red). In general for visible light, index of refraction increases with increasing frequency.
Normal to surface
q
1
Surface
q
2
Refracted ray
(n
> n
)
1
2
Procedure
1. Place the light source in ray-box mode on a sheet of blank white paper. Turn the
wheel to select a single white ray.
Color
spectrum
Single white ray
q
Normal to surface
Figure 2.2
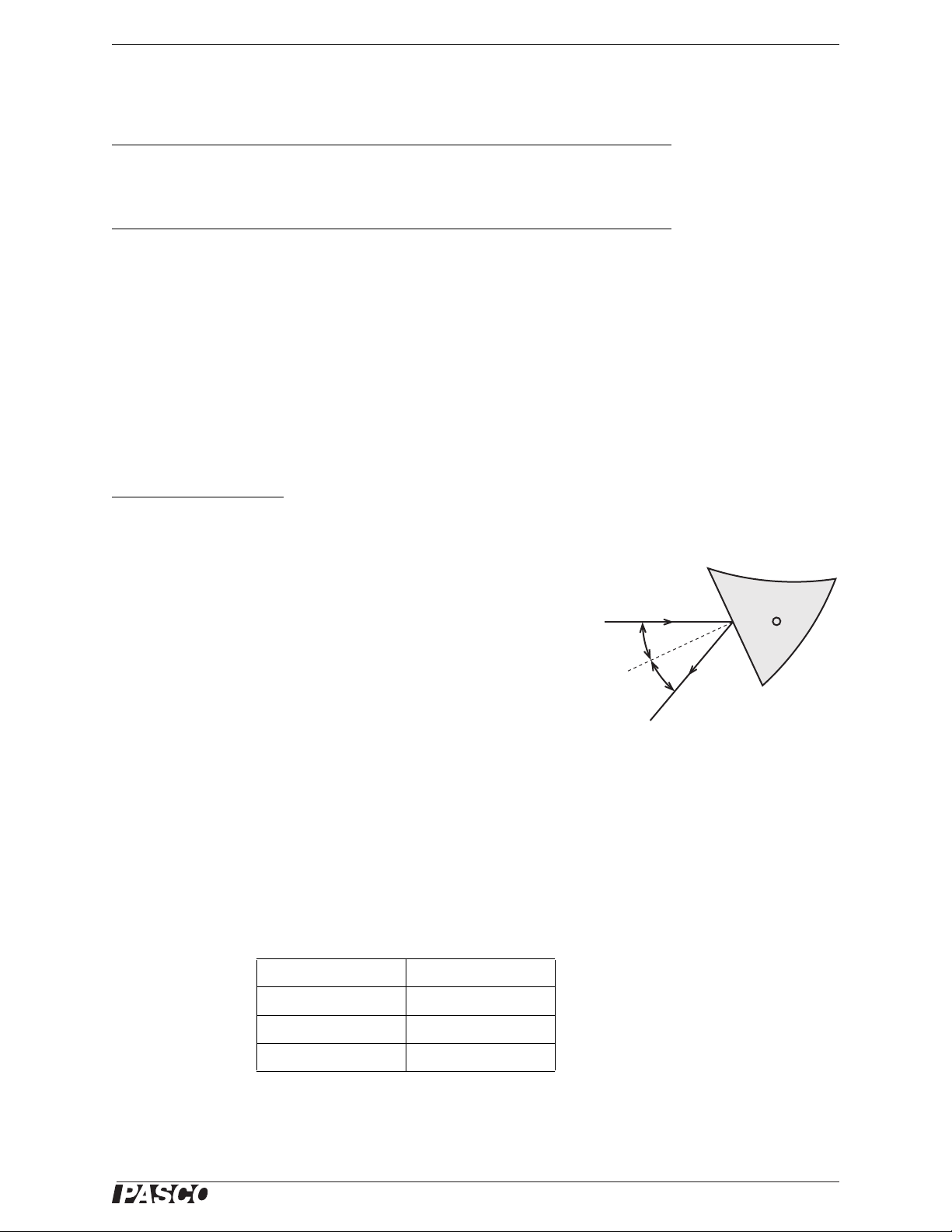
2. Position the trapezoid as shown in Figure 2.2. The acute-angled end of the trape-
zoid is used as a prism in this experiment. Keep the ray near the point of the trapezoid for maximum transmission of the light .
®
11
Basic Optics System Experiment 2: Prism
3. Rotate the trapezoid until the angle (θ) of the emerging ray is as large as possible
and the ray separates into colors.
(a) What colors do you see? In what order are they?
(b) Which color is refracted at the largest angle?
(c) According to Snell’s Law and the information given about the frequency
dependence of the index of refraction for acrylic, which color is predicted to
refract at the largest angle?
4. Without repositioning the light source, turn the wheel to select the three primary
color rays. The colored rays should enter trapezoid at the same angle that the
white ray did. Do the colored rays emerge from the trapezoid parallel to each
other? Why or why not?
12
®
Model No. OS-8515C Experiment 3: Reflection
Experiment 3: Reflection
Required Equipment from Basic Optics System
Light Source
Mirror from Ray Optics Kit
Other Required Equipment
Drawing compass
Protractor
Metric ruler
White paper
Purpose
In this experiment, you will study how rays are reflected from different types of mirrors. You will measure the focal length and determine the radius of curvature of a concave mirror and a convex mirror.
Part 1: Plane Mirror
Procedure
1. Place the light source in ray-box mode on a blank sheet of
white paper. Turn the wheel to select a single ray.
2. Place the mirror on the paper. Position the plane (flat) surface
of the mirror in the path of the incident ray at an angle that
allows you to clearly see the incident and reflected rays.
3. On the paper, trace and label the surface of the plane mirror
and the incident and reflected rays. Indicate the incoming and
the outgoing rays with arrows in the appropriate directions.
4. Remove the light source and mirror from the paper. On the
paper, draw the normal to the surface (as in Figure 3.1).
5. Measure the angle of incidence and the angle of reflection. Measure these angles
from the normal. Record the angles in the first row Table 3.1.
6. Repeat steps 1–5 with a different angle of incidence. Repeat the procedure again
to complete Table 3.1 with three different angles of incidence.
Table 3.1: Plane Mirror Results
Normal to
surface
Incident ray
Reflected ray
Figure 3.1
Angle of Incidence Angle of Reflection
7. Turn the wheel on the light source to select the three primary color rays. Shine
the colored rays at an angle to the plane mirror. Mark the position of the surface
of the plane mirror and trace the incident and reflected rays. Indicate the colors of
®
13
Basic Optics System Experiment 3: Reflection
the incoming and the outgoing rays and mark them with arrows in the appropriate
directions.
Questions
1. What is the relationship between the angles of incidence and reflection?
2. Are the three colored rays reversed left-to-right by the plane mirror?
Part 2: Cylindrical Mirrors
Theory
mirror
A concave cylindrical mirror focuses incoming parallel rays at its focal
point. The focal length ( f) is the distance from the focal point to the center of the mirror surface. The radius of curvature (R) of the mirror is
twice the focal length. See Figure 3.2.
R
f
focal
point
Procedure
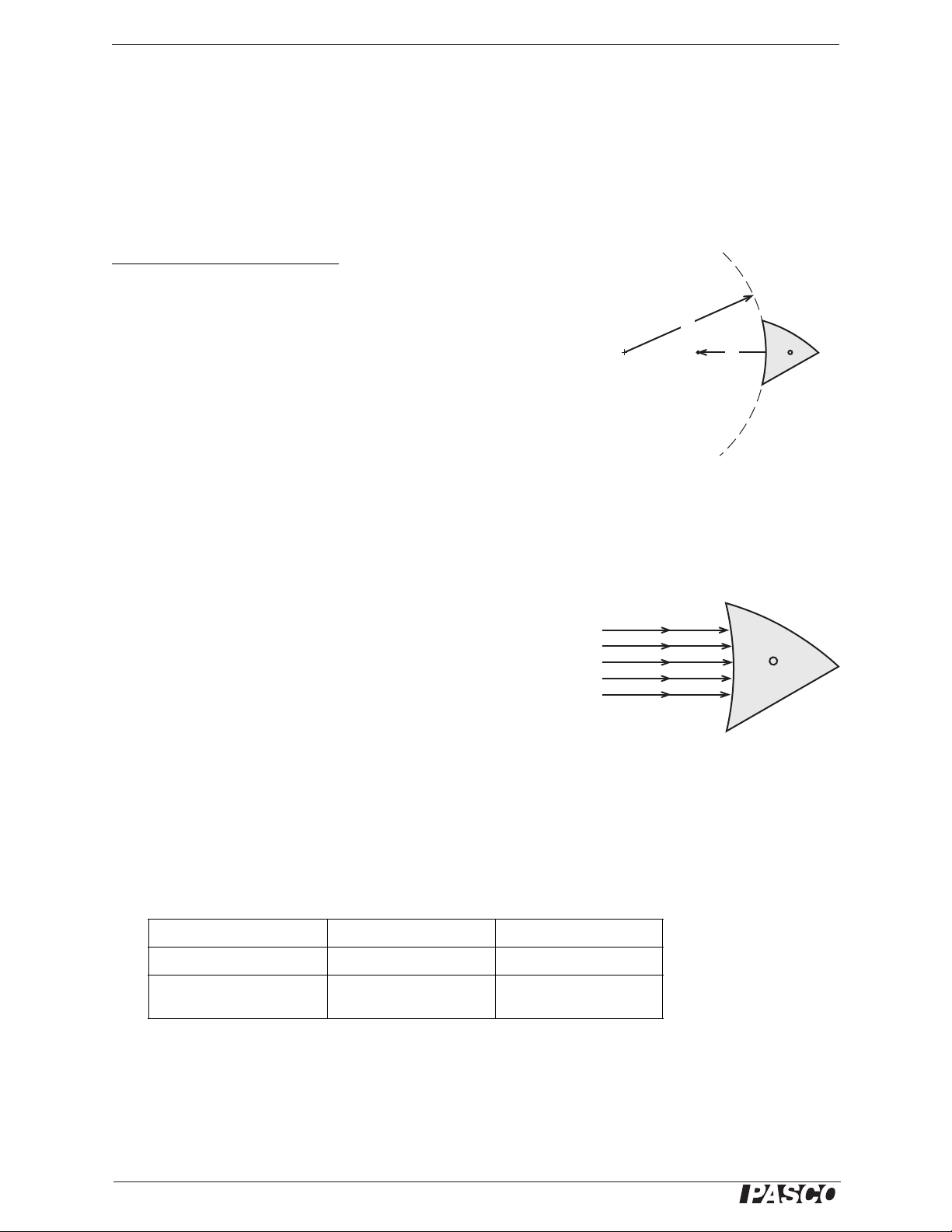
1. Turn the wheel on the light source to select five parallel rays. Shine
the rays straight into the concave mirror so that the light is reflected
back toward the ray box (see Figure 3.3). Trace the surface of the
mirror and the incident and reflected rays. Indicate the incoming
and the outgoing rays with arrows in the appropriate directions.
(You can now remove the light source and mirror from the paper.)
2. The place where the five reflected rays cross each other is the focal
point of the mirror. Mark the focal point.
Incident rays
3. Measure the focal length from the center of the concave mirror sur-
face (where the middle ray hit the mirror) to the focal point. Record
the result in Table 3.2.
4. Use a compass to draw a circle that matches the curvature of the
mirror (you will have to make several tries with the compass set to
different widths before you find the right one). Measure the radius
of curvature and record it in Table 3.2.
5. Repeat steps 1–4 for the convex mirror. Note that in step 3, the reflected rays will
diverge, and they will not cross. Use a ruler to extend the reflected rays back
behind the mirror’s surface. The focal point is where these extended rays cross.
Table 3.2: Cylindrical Mirror Results
Figure 3.2
Figure 3.3
Concave Mirror Convex Mirror
Focal Length
Radius of Curvature
(determined using compass)
Questions
1. What is the relationship between the focal length of a cylindrical mirror and its
radius of curvature? Do your results confirm your answer?
2. What is the radius of curvature of a plane mirror?
14
®
Model No. OS-8515C Experiment 4: Snell’s Law
Experiment 4: Snell’s Law
Required Equipment from Basic Optics System
Light Source
Trapezoid from Ray Optics Kit
Other Required Equipment
Protractor
White paper
Purpose
The purpose of this experiment is to determine the index
of refraction of the acrylic trapezoid. For rays entering
the trapezoid, you will measure the angles of incidence
and refraction and use Snell’s Law to calculate the index
of refraction.
Theory
For light crossing the boundary between two transparent
materials, Snell’s Law states
sin θ1 = n2sin θ
n
1
2
where θ1 is the angle of incidence, θ2 is the angle of
refraction, and n
and n2 are the respective indices of
1
refraction of the materials (see Figure 4.1).
Procedure
1. Place the light source in ray-box mode on a sheet of
white paper. Turn the wheel to select a single ray.
2. Place the trapezoid on the paper and position it so
the ray passes through the parallel sides as shown in
Figure 4.2.
n
1
n
2
Incident ray
Incident ray
q
i
q
1
Figure 4.1
Normal to surface
q
2
Surface
Refracted ray
(n
> n
)
1
2
3. Mark the position of the parallel surfaces of the
Figure 4.2
trapezoid and trace the incident and transmitted
rays. Indicate the incoming and the outgoing rays with arrows in the appropriate
directions. Carefully mark where the rays enter and leave the trapezoid.
4. Remove the trapezoid and draw a line on the paper connecting the points where
the rays entered and left the trapezoid. This line represents the ray inside the trapezoid.
5. Choose either the point where the ray enters the trapezoid or the point where the
ray leaves the trapezoid. At this point, draw the normal to the surface.
6. Measure the angle of incidence (θ
) and the angle of refraction with a protractor.
i
Both of these angles should be measured from the normal. Record the angles in
the first row of Table 4.1.
®
15
Basic Optics System Experiment 4: Snell’s Law
7. On a new sheet of paper, repeat steps 2–6 with a different angle of incidence.
Repeat these steps again with a third angle of incidence. The first two columns of
Table 4.1 should now be filled.
Table 4.1: Data and Results
Angle of Incidence Angle of Refraction Calculated index of refraction of
acrylic
Average:
Analysis
1. For each row of Table 4.1, use Snell’s Law to calculate the index of refraction,
assuming the index of refraction of air is 1.0.
2. Average the three values of the index of refraction. Compare the average to the
accepted value (n = 1.5) by calculating the percent difference.
Question
What is the angle of the ray that leaves the trapezoid relative to the ray that enters it?
16
®
Model No. OS-8515C Experiment 5: Total Internal Reflection
Experiment 5: Total Internal Reflection
Required Equipment from Basic Optics System
Light Source
Trapezoid from Ray Optics Kit
Other Required Equipment
Protractor
White paper
Purpose
In this experiment, you will determine the critical angle at which total internal reflection occurs in the acrylic trapezoid and confirm your result using Snell’s Law.
Theory
For light crossing the boundary between two transparent materials, Snell’s Law states
sin θ1 = n2sin θ
n
1
where θ1 is the angle of incidence, θ2 is the angle of
refraction, and n
and n2 are the respective indices of
1
refraction of the materials (see Figure 5.1).
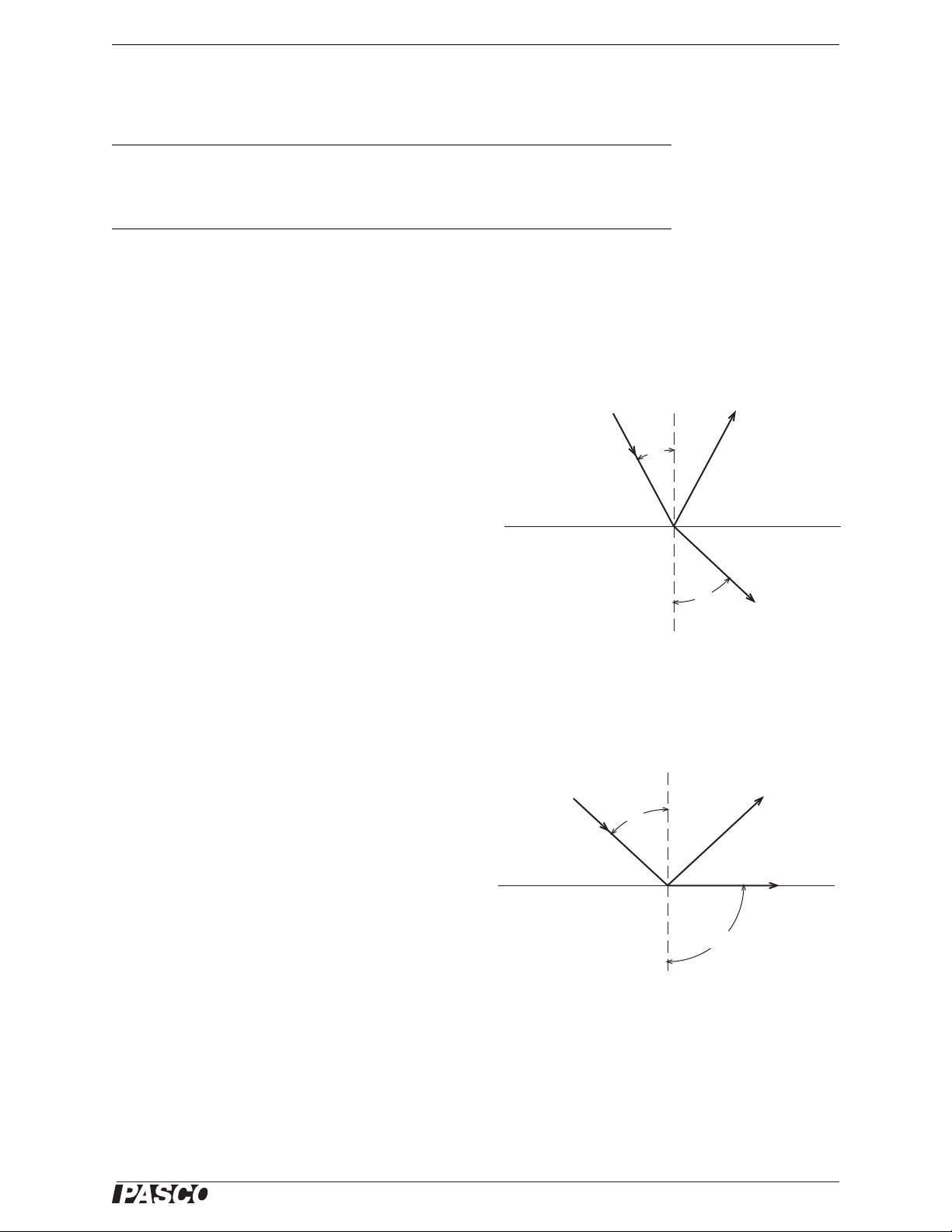
In this experiment, you will study a ray as it passes out
of the trapezoid, from acrylic (n =1.5) to air (n
If the incident angle (θ
angle (θ
), there is no refracted ray and total internal
c
reflection occurs. If θ
) is 90°, as in Figure 5.2.
ray (θ
2
) is greater than the critical
1
= θc, the angle of the refracted
1
In this case, Snell’s Law states:
n sin θc = 1 sin 90°
Solving for the sine of critical angle gives:
sin θ
c
2
1
-- -
=
n
air
=1).
Incident ray
n
1
n
2
Incident ray
n
n
= 1
air
q
1
Figure 5.1
q
c
q
2
90°
Reflected ray
Surface
Refracted ray
(n
> n
1
Reflected ray
Refracted ray
)
2
Figure 5.2
®
17
Basic Optics System Experiment 5: Total Internal Reflection
2q
c
point
Re
po
Procedure
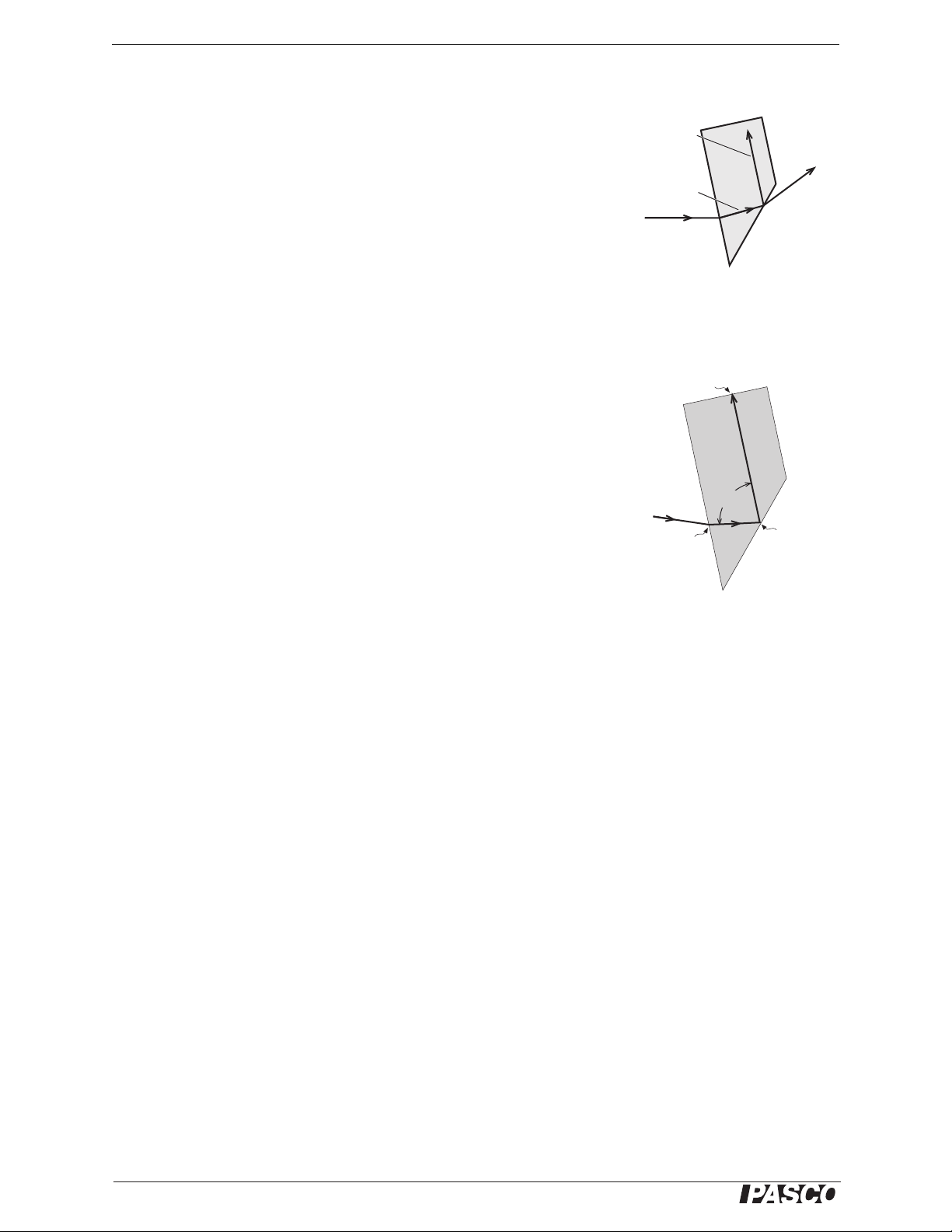
1. Place the light source in ray-box mode on a sheet of white paper. Turn the
wheel to select a single ray.
2. Position the trapezoid as shown in Figure 5.3, with the ray entering the
trapezoid at least 2 cm from the tip.
3. Rotate
the trapezoid until the emerging ray just barely disappears. Just as
it disappears, the ray separates into colors. The trapezoid is correctly positioned if the red has just disappeared.
4. Mark the surfaces of the trapezoid. Mark exactly the point on the surface
where the ray is internally reflected. Also mark the entrance point of the
incident ray and the exit point of the reflected ray.
5. Remove the trapezoid and draw the rays that are incident upon and
reflected from the inside surface of the trapezoid. See Figure 5.4. Measure
the angle between these rays using a protractor. (Extend these rays to
make the protractor easier to use.) Note that this angle is twice the critical
angle because the angle of incidence equals the angle of reflection.
Record the critical angle here:
= _______ (experimental)
θ
c
Reflected
ray
Incident
ray
Exit point
Entrance
point
Figure 5.3
2q
c
Refracted
Ray
Reflection
point
6. Calculate the critical angle using Snell’ s Law and the given index of
refraction for Acrylic (n = 1.5). Record the theoretical value here:
= _______ (theoretical)
θ
c
7. Calculate the percent difference between the measured and theoretical values:
% difference = _______
Questions
1. How does the brightness of the internally reflected ray change when the incident
angle changes from less than θ
2. Is the critical angle greater for red light or violet light? What does this tell you
about the index of refraction?
to greater than θc?
c
Figure 5.4
18
®
Model No. OS-8515C Experiment 6: Convex and Concave Lenses
Experiment 6: Convex and Concave Lenses
Required Equipment from Basic Optics System
Light Source
Convex Lens from Ray Optics Kit
Concave Lens from Ray Optics Kit
Other Required Equipment
Metric ruler
Purpose
In this experiment, you will explore the difference between convex and concave
lenses and determine their focal lengths.
Theory
When parallel light rays pass through a thin lens, they emerge either converging or
diverging. The point where the converging rays (or their extensions) cross is the focal
point of the lens. The focal length of the lens is the distance from the center of the lens
to the focal point. If the rays diverge, the focal length is negative.
Procedure
1. Place the light source in ray-box mode on a white sheet of paper. Turn the wheel
to select three parallel rays. Shine the rays straight into the convex lens (see Figure 6.1).
Note: The lenses used in this experiment have one flat edge. Place the flat edge on the
paper so the lens stands stably without rocking.
2. Trace around the surface of the lens and trace the incident and transmitted rays.
Indicate the incoming and the outgoing rays with arrows in the appropriate directions.
3. The point where the outgoing rays cross is the focal point of the lens. Measure
the focal length from the center of the lens to the focal point. Record the result in
Table 6.1.
Table 6.1: Results
Convex Lens Concave Lens
Focal Length
4. Repeat the procedure with the concave lens. Note that in step 3, the rays leaving
the lens are diverging and do not cross. Use a ruler to extend the outgoing rays
straight back through the lens. The focal point is where these extended rays cross.
(Remember to record the focal length as a negative number.)
Incoming rays
Convex lens
Figure 6.1
®
19
Basic Optics System Experiment 6: Convex and Concave Lenses
5. Nest the convex and concave lenses together and place them in the path of the
parallel rays (see Figure 6.2). Trace the rays. Are the outgoing rays converging,
diverging or parallel? What does this tell you about the relationship between the
focal lengths of these two lenses?
6. Slide the convex and concave lenses apart by a few centimeters and observe the
effect. Then reverse the order of the lenses. T race at leas t one pattern of this type.
What is the effect of changing the distance between the lenses? What is the effect
of reversing their positions?
Figure 6.2
20
®
Model No. OS-8515C Experiment 7: Hollow Lens
Experiment 7: Hollow Lens
Required Equipment from Basic Optics System
Light Source
Hollow Lens from Ray Optics Kit
Box from Ray Optics Kit (with lenses and foam insert removed)
White Plastic Sheet from Ray Optics Kit
Other Equipment
Water
Paper towels
White paper
Small weight (to stop lens from floating)
Eye-dropper (optional, for removing water from the hollow lens)
Purpose
In this experiment you will explore how the properties of a lens are related to its
shape, its index of refraction, and the index of refraction of the surrounding medium.
Background
A conventional lens is made of a material whose index of refraction
is higher than that of the surrounding medium. For instance, the
lenses in a pair of eyeglasses are usually made from glass or plastic
with an index of refraction of 1.5 or higher, while the air surrounding
the lenses has an index of refraction of 1.0. However, a lens can also
have a lower index of refraction than the surrounding medium, as is
the case when a hollow lens is “filled with air” and surrounded by
water. (The index of refraction of water is about 1.3.)
The hollow lens in this experiment has three sections: a plano-concave section and two plano-convex sections. W e will refer to these as
sections 1, 2, and 3 (see Figure 7.1).
You will determine whether each section acts as a converging or
diverging lens when it is a) filled with water and surrounded by air
and b) filled with air and surrounded by water.
Procedure
1
Figure 7.1: The hollow lens
2
3
1. Before you test the hollow lens, make some predictions: For every configuration
in Table 7.1, predict whether incoming parallel rays will converge or diverge
after passing through the lens. Record your predictions in the table.
2. Place the light source in ray-box mode on a white sheet of paper. Turn the wheel
to select five parallel rays.
3. Fill section 1 with water and place the lens in front of the light source so the par-
allel rays enter it through the flat side. Do the rays converge or diverge after passing through the lens? Record your observation in T able 7.1.
®
21
Basic Optics System Experiment 7: Hollow Lens
Repeat this step with water in different section of the lens to complete the first
four rows of Table 7.1.
Table 7.1: Predictions and Observations
Lens
surrounded by:
Air
Water
Section 1
filled with:
Water Air Air
Air Water Air
Air Air Water
Water Air Water
Air Water Water
Water Air Water
Water Water Air
Section 2
filled with:
Section 3
filled with:
Prediction
(converging or diverging)
4. Put the white plastic sheet in the transparent ray-optics box. Put the hollow lens
in the box on top of the sheet as shown in Figure 7.2. Place a small weight on top
of the lens to stop it from floating. Position the light source outside of the box so
that the rays enter the hollow lens through the flat side.
Box
Hollow lens
Incident rays
Observation
(converging or diverging)
Figure 7.2: Hollow lens set up for testing surrounded by water
5. Fill the box with water to just below the top of the lens. Fill sections 2 and 3 of
the lens with water (leaving section 1 “filled” with air). Record your observation
in Table 7.1.
Repeat this step with air in different section of the lens to complete Table 7.1.
Questions
1. Under what conditions is a plano-convex lens converging? Under what condi-
tions is it diverging?
2. If a plano-concave lens of an unknown material is a diverging lens when sur-
rounded by air, is it possible to know whether the lens will be converging or
diverging when placed in water? Explain.
22
®
Loading...