PASCO OS-8500 User Manual

Download

NORMALNORMAL

COMPONENTCOMPONENT

Includes

Teachers Notes

and

Typical

Experiment Results

Instruction Manual and

012-02744K

Experiment Guide for the PASCO scientific Model OS-8500

INTRODUCTORY OPTICS

SYSTEM

COMPONENT

NORMAL

COMPONENT

Introductory Optics System 012-02744K

012-02744K Introductory Optics System

Table of Contents

Section ..........................................................................................................Page

Preface to the Teacher ..................................................................................... iv

Introduction ...................................................................................................... 1

Equipment ........................................................................................................2

Setting Up the Equipment ................................................................................ 3

Copy Ready Experiments ................................................................................ 6

Basic Experiments

Experiment 1: Introduction to Ray Optics ................................................ 7

Experiment 2: The Law of Reflection ...................................................... 9

Experiment 3: Image Formation in a Plane Mirror .................................. 11

Experiment 4: The Law of Refraction ..................................................... 13

Experiment 5: Reversibility ..................................................................... 15

Experiment 6: Dispersion and Total Internal Reflection .......................... 17

Experiment 7: Converging Lens: Image and Object Relationships ......... 19

Experiment 8: Light and Color ................................................................ 21

Experiment 9: Two-Slit Interference ....................................................... 23

Experiment 10: Polarization ..................................................................... 25

Advanced Experiments

Experiment 11: Image Formation with Cylindrical Mirrors ...................... 27

Experiment 12: Image Formation with Spherical Mirrors ........................ 29

Experiment 13: Image Formation with Cylindrical Lenses ...................... 31

Experiment 14: Spherical Lenses—Spherical and Chromatic

Aberration, Aperture Size, and Depth of Field ............................. 33

Experiment 15: The Diffraction Grating .................................................. 35

Experiment 16: Single Slit Diffraction ..................................................... 37

Experiment 17: General Diffraction ......................................................... 39

Optical Instruments

Experiment 18: Introduction ..................................................................... 41

Experiment 19: The Projector .................................................................. 43

Experiment 20: The Magnifier ................................................................. 45

Experiment 21: The Telescope ................................................................. 47

Experiment 22: The Compound Microscope ........................................... 49

Appendix ........................................................................................................ 51

Replacement Parts ........................................................................................... 52

Teacher's Guide ........................................................................................... 52-67

Introductory Optics System 012-02744K

Please—Feel free to duplicate this manual subject to the copyright restrictions below.

The PASCO scientific Model OS-8500 Introductory Optics System manual is copyrighted and all rights reserved. However, permission is granted to nonprofit educational institutions for reproduction of any part of this manual providing the reproductions are used only for their laboratories and are not sold for profit. Reproduction under any other circumstances, without the written consent of PASCO scientific, is prohibited.

Limited Warranty

PASCO scientific warrants this product to be free from defects in materials and workmanship for a period of one year from the date of shipment to the customer. PASCO will repair or replace, at its option, any part of the product which is deemed to be defective in material or workmanship. This warranty does not cover damage to the product caused by abuse or improper use. Determination of whether a product failure is the result of a manufacturing defect or improper use by the customer shall be made solely by PASCO scientific. Responsibility for the return of equipment for warranty repair belongs to the customer. Equipment must be properly packed to prevent damage and shipped postage or freight prepaid. (Damage caused by improper packing of the equipment for return shipment will not be covered by the warranty.) Shipping costs for returning the equipment, after repair, will be paid by PASCO scientific.

Equipment Return

Should this product have to be returned to PASCO scientific, for whatever reason, notify PASCO scientific by letter or phone BEFORE returning the product. Upon notification, the return authorization and shipping instructions will be promptly issued.

➤➤

➤NOTE: NO EQUIPMENT WILL BE AC-

➤➤

CEPTED FOR RETURN WITHOUT AN AUTHORIZATION.

When returning equipment for repair, the units must be packed properly. Carriers will not accept responsibility for damage caused by improper packing. To be certain the unit will not be damaged in shipment, observe the following rules:

➀ The carton must be strong enough for the item

shipped.

➁ Make certain there is at least two inches of packing

material between any point on the apparatus and the inside walls of the carton.

➂ Make certain that the packing material can not shift

in the box, or become compressed, thus letting the instrument come in contact with the edge of the box.

Address: PASCO scientific

10101 Foothills Blvd.

P.O. Box 619011

Credits

This manual authored by: Ed Pitkin

This manual edited by: Dave Griffith

Teacher's guide written by: Eric Ayars

Roseville, CA 95678-9011

Phone: (916) 786-3800

FAX: (916) 786-8905

012-02744K Introductory Optics System

Preface to the Teacher

The PASCO scientific Introductory Optics System is designed to provide a comprehensive introduction to laboratory optics. Of course, textbooks and lab books vary in the areas covered and the degree of complexity taught. To ensure that all essential concepts are covered, the experiments in this guide are based on material presented in several of the most comprehensive physics textbooks, including Modern Physics (Holt, Rinehart, and Winston) and PSSC Physics (Haber-Schaim, Dodge, and Walter). However, even if you do not use one of these textbooks, you should have little problem finding a collection of experiments in this manual that suits your needs.

The experiments are presented in three groups: Basic Experiments, Advanced Experiments, and Optical Instruments. All the experiments are designed as worksheets, to be copied from the manual for student use.

➤NOTE: Each experiment includes a series of questions with blank spaces for students to write their answers. We encourage students not to limit themselves to the space provided, but rather to use as much additional paper as needed to discuss, argue, prove points, etc.

The Advanced Experiments provide more in-depth investigations into some of the areas that were introduced in the Basic Experiments. These experiments are generally longer and more demanding. They should provide ample material for advanced classes and for independent study.

The Optical Instruments section provides an opportunity for students to apply some of the optics theory they have learned. Students can build and investigate a Projector, a Magnifier, a Microscope, and a Telescope. The optical bench and magnetic mounts make the setup easy.

In addition to the equipment provided in the PASCO Optics System, a few common items are needed for some experiments.

Additional Items Needed:

Items Purpose Expts

Pencil, Straightedge, Ray 1, 3, 5,

Protractor, White Paper Tracing 11, 13

Black Construction Circular 17

Paper, Pin Aperture

The Basic Experiments provide all the essentials for a solid introduction to optics.These experiments are designed to give clear presentations of the basic phenomena. The fill-in-the-blank format (used in all the experiments in this manual) provides a structured format and simple evaluation of student progress.

All experiments, except where otherwise stated, are best performed in a semi-darkened room. For optimal conditions, allow just enough light to enable comfortable reading of the lab book.

iii

Introductory Optics System 012-02744K

Notes

012-02744K Introductory Optics System

Introduction

A vast and complicated amount of information comes to us through our eyes. Because of this, the nature of light plays a critical role in our experience. Certainly our view of the world is colored (pun intended) by the nature of the medium which brings us so much information about it.

In our day to day life, we rarely concern ourselves with light, except perhaps when there is too much or not enough of it. We interact with light that has interacted with objects to determine such things as the color, shape, and position of the objects. We use this information to navigate, and to find what we want and what we wish to avoid. But our attention is almost always on the objects, not on the light that brings us the information.

In studying optics we change the focus of our attention. We still gain our information by interacting with light that has interacted with objects. But in studying optics we want to know what our observations tell us, not about the objects, but about light itself.

Before plunging into your experimental investigations of optics, its a good idea to become familiar with the equipment you will be using. The Equipment section of this manual will help you identify each of the components included with your optics system. The section entitled Equipment Setup gives some useful tips for aligning the optical equipment.

Introductory Optics System 012-02744K

Equipment

Figure one shows all the equipment that is included with your OS-8500 Introductory Optics System. The system also includes a fitted box, with cutouts for each component, and of course, this manual. If you wish to order additional components or replacement parts, please see the information at the end of the manual.

Incandescent Light Source

Optics Bench

Slit

Plate

Ray Optics

Mirror

Mask

Cylindrical

Lens

Slit

Parallel

Ray Lens

Crossed

Viewing

Screen

Arrow

Target

Ray Table Base

Ray Table

Ray Table Component Holder

Component Holders (3)

Lenses (3): 75, 150, and –150 mm focal lengths

Spherical Mirror: 50 mm focal length

DIFFRACTION GRATING

5276 LINES/cm

Color Filters:

Red

Green

Blue/Green

Virtual Image

Locators

(2)

Diffraction

Scale

Polarizers

(2)

Variable Aperture

Figure 1: Equipment Included in the OS-8500 Introductory Optics System

For Replacement Parts See Page 52

DIFFRACTION PLATE

A B C D E

. . . . . . . ..

.....................

. . . . . . . ..

.....................

. . . . .. . .

.....................

. . . . .. . . . .

. . . . . . . ..

.....................

. . . . .. . . . .

. . . . . . . ..

.....................

. . . . .. . .

.....................

. . . . .. . .

. . . . .. . . . .

.....................

. . . . . . . ..

. . . . .. . . . .

.....................

. . . . .. . .

.....................

. . . . .. . . . .

.....................

J I H G F DIFFRACTION PLATE

Diffraction Grating

Diffraction Plate

012-02744K Introductory Optics System

Setting Up the Equipment

Optics Bench

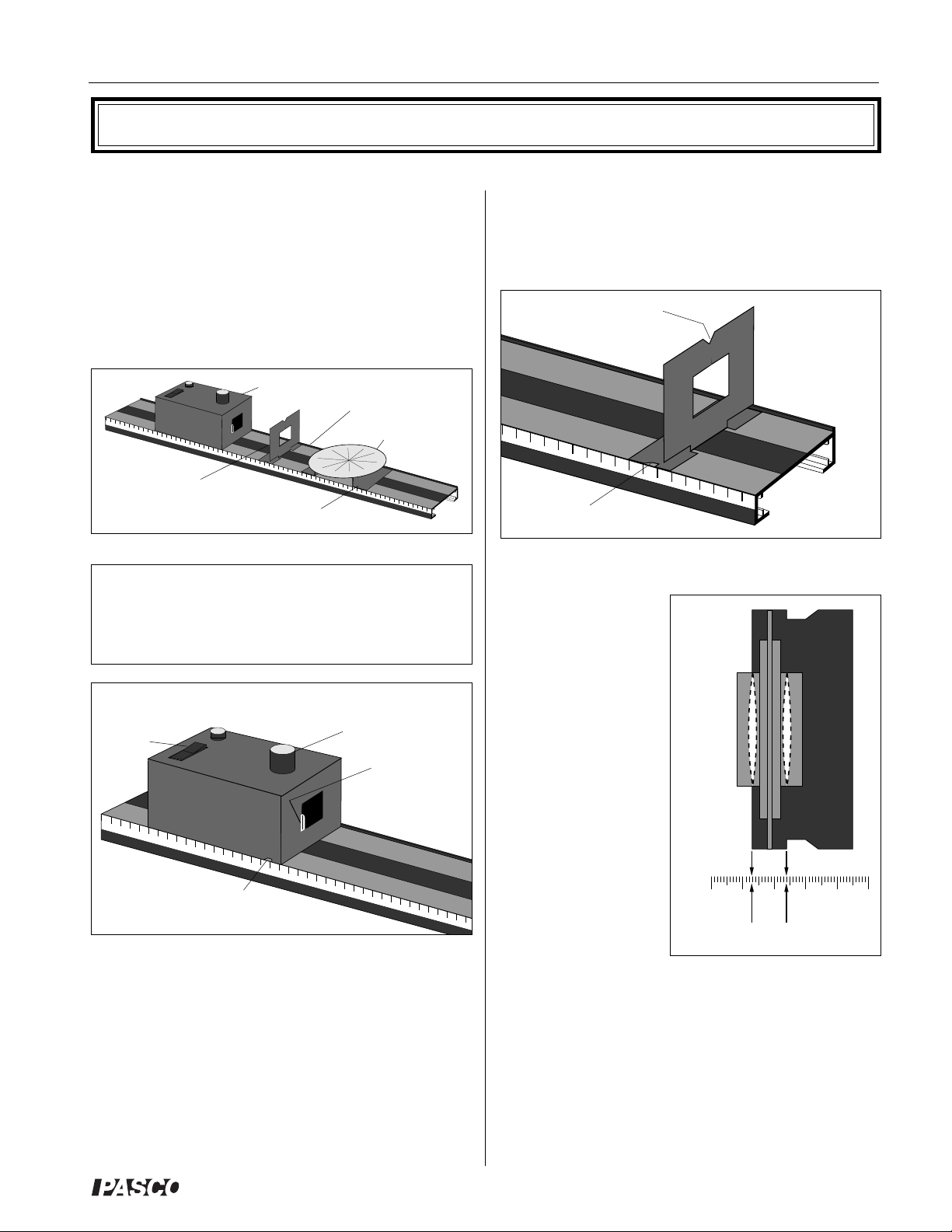
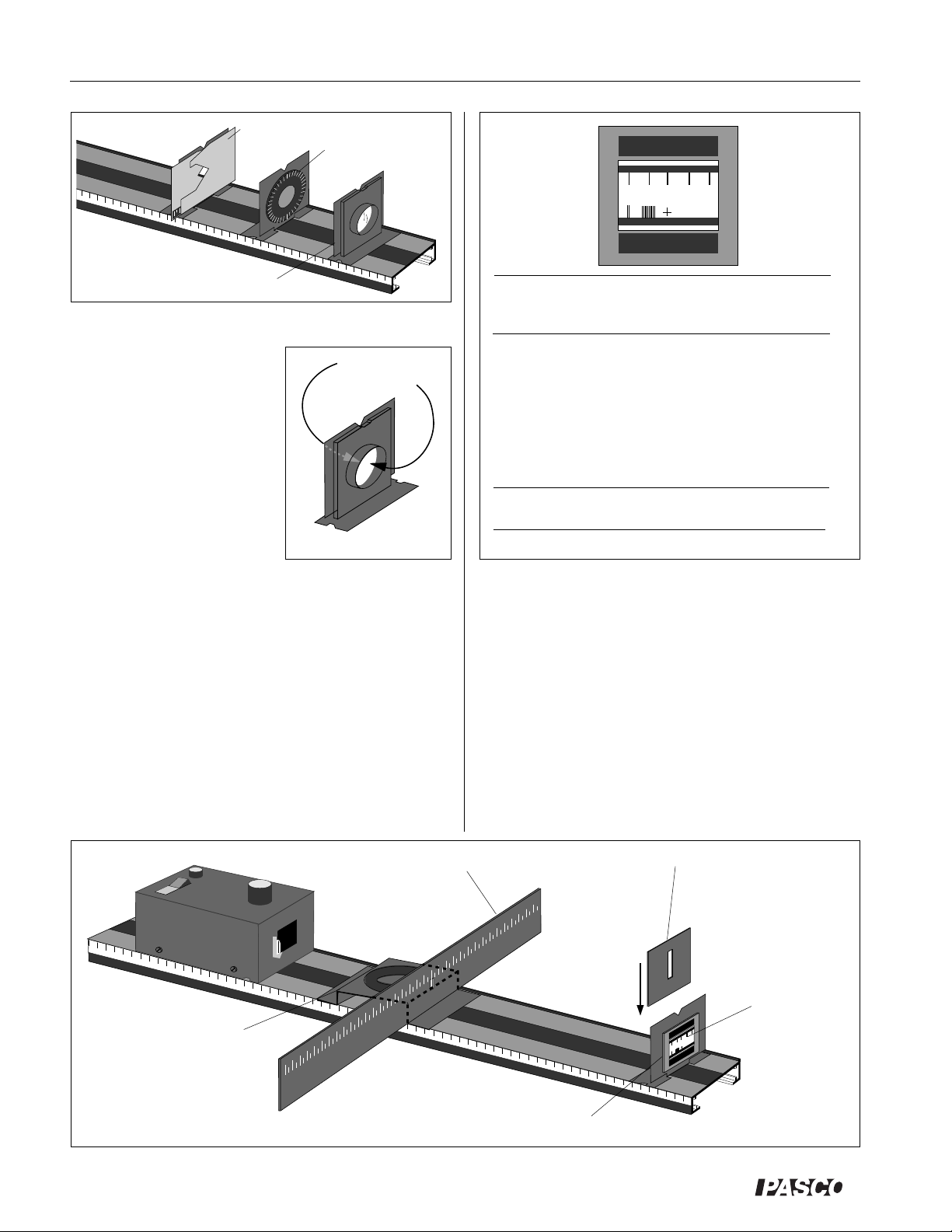
The Optics Bench is shown in Figure 2. The Light Source, Component Holders, and Ray Table Base all attach magnetically to the bench as shown. For proper optical alignment, the edge of each of these components should be mounted flush to the alignment rail, which is the raised edge that runs along one side of the bench.

Light Source

Alignment Rail

Ray Table

Component

Holder

Ray Table Base

Figure 2: Bench

NOTE: Avoid scratching or otherwise abusing the surface of the magnetic pads. If they get dirty, use only soapy water or rubbing alcohol for cleaning. Other solvents may dissolve the magnetic surface.

Switch

Notch Showing Location of

Filament

Figure 3: Using the Light Source

Filament Knob

Light Bulb

Incandescent Light Source

The Light Source is shown in Figure 3. To turn it on, connect the power cord to any grounded 105-125 VAC receptacle, and flip the switch on the top panel to ON. If at any time the light fails to come on, check with your instructor.

The Filament Knob on the top of the unit moves the light bulb from side to side. The notch at the bottom indicates the position of the light bulb filament, so that accurate measurements can be made during experiments.

Centering

Notch

Base Notch

Figure 4: Using the Component Holders

Component Holders and

(Top View)

Components

The Optics set comes with three regular Component Holders and one holder designed for use with the Ray Table. The regular Component Holders attach magnetically to the optics bench, as in Figure 4. The notch at the top of each holder is for centering components on the holder. The notches in the base of the holders are for accurate distance measurements on the metric scale of the bench. These base notches—and also the edge of the component holder base—are positioned so that they align with the vertical axis of a mounted lens or mirror. Accurate measurements of component position can be made as shown in Figure 5.

0 1 2 3 4 5

Vertical Axes of Lens or Mirror

Figure 5: Component

Alignment

Introductory Optics System 012-02744K

. . . . . . . ..

. . . . .. . .

. . . . .. . . . .

. . . . . . . ..

. . . . .. . .

. . . . .. . . . .

. . . . . . . ..

. . . . .. . .

. . . . .. . . . .

. . . . . . . ..

. . . . .. . .

. . . . .. . . . .

. . . . . . . ..

. . . . .. . .

. . . . .. . . . .

.....................

DIFFRACTION PLATE

A B C D E

DIFFRACTION PLATE

J I H G F

Variable Aperture

Polarizer

Lens or Mirror

Figure 6: Using the Component Holders

The Variable Aperture, the Polarizers, and the Lenses attach to the component

Concave Side

Convex Side

holders as shown in Figure 6. Use the centering notch to align the components along the optical axis of the bench and, in the case of the Polarizers, to measure the angle of polarization.

The Spherical Mirror mounts onto the component holders in

Figure 7:

The Spherical Mirror

the same manner as the Lenses. However, the mirror is silvered on both sides, so that, depending on which side you use, it can be a convex or a concave mirror (see Figure 7).

Diffraction Experiments

Set up diffraction experiments as shown in Figure 8. You can use either the Diffraction Plate, which has ten different apertures, or the Diffraction Grating, which has a line spacing of 600 lines/mm. If you are using the Diffraction Plate, place the Slit Mask on the other side of the

Slit Spacing

center-to-center

(mm)

Pattern No. Slits

Slit Width

(mm)

A 1 0.04

B 1 0.08

C 1 0.16

D 2 0.04 0.125

E 2 0.04 0.250

F 2 0.08 0.250

G 10 0.06 0.250

H 2 (crossed) 0.04

I 225 Random Circular Apertures (.06 mm dia.)

J 15 x 15 Array of Circular Apertures (.06 mm dia.)

Figure 9: Diffraction Plate Apertures

component holder and position it so that only a single diffraction aperture is illuminated by the light from the light source.

When you look through the aperture or grating toward the light source, you will see the diffraction pattern superimposed over the Diffraction Scale. You can use the illuminated scale to accurately measure the geometry of the diffraction pattern. Information about analyzing the measurements is provided in experiments 9, 15, 16, and

17. The dimensions of the apertures in the Diffraction Plate are provided in Figure 9.

Ray Table Base

Diffraction Scale

Diffraction Plate or

Diffraction Grating

Figure 8: Setting Up a Diffraction Experiment

Slit Mask: to isolate a

single diffraction aper-

ture (not needed when

using the Diffraction

Grating)

Look through

IFFRACTION PLATE

A B C D E

. . . .

. .

. . .

. .

.. .

. ..

. . .

. . . . . .

. .

. . .

. .

. . .

. .

. . .

. . . .

. .. .

. . . .

. .

. . .

. .

. . . .

. .

. . .. . .

. . .

. . . .

. .

. . . .

. . . . . .

. . . . . . . . . . .

DIFFRACTION PLATE

. . . .

. .

. . . .

J I H G F

here toward

Diffraction

Scale to view (and measure) the diffraction

pattern.

012-02744K Introductory Optics System

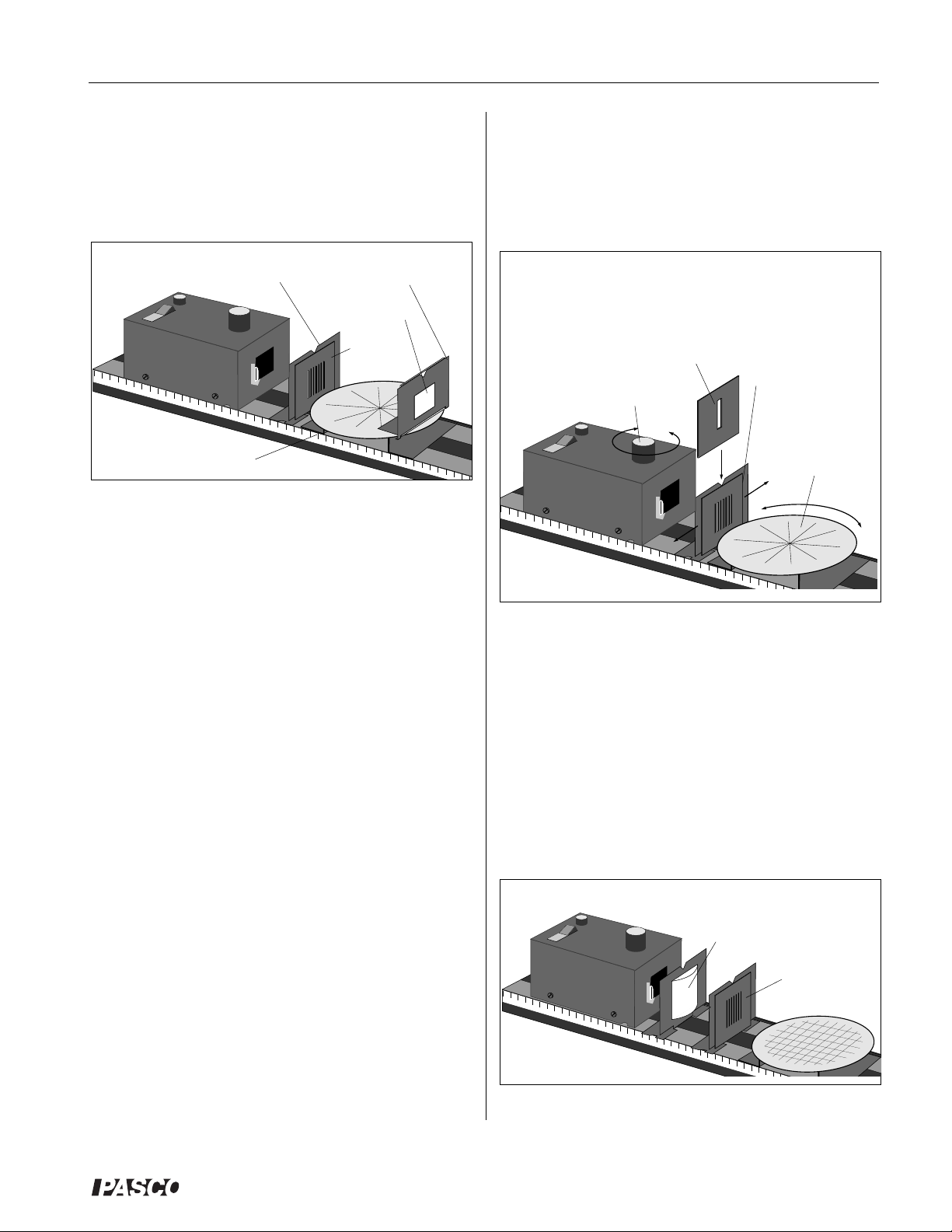
Basic Ray Optics Setup

The basic setup for Ray Optics is shown in Figure 10. The Ray Table Base should be flush against the alignment rail. The Ray Table fits over the pin on the top of the Base.

Component Holder

Ray Table and Base

Figure 10: Basic Ray Optics Setup

Notice that the Ray Table Base is slightly slanted. When mounting the base on the Optics Bench, be sure the Ray Table slants down toward the Light Source. This ensures sharp, bright rays. (In all the experiments described in this manual, the error introduced by this tilt is negligible.)

Ray Table

Component Holder

Viewing

Screen

Slit Plate

➀ the lateral position of the Slit Plate on its Component

Holder,

➁ the position of the light source filament with respect to

the optical axis, and

➂ the rotation of the Ray Table.

To align a single ray:

4. Use the Slit Mask to block all but the desired ray.

2. Adjust the position of the filament.

Figure 11: Single Ray Setup

1. Adjust the lateral position of the Slit Plate.

3. Adjust the rotation angle of the Ray Table.

Either side of the Ray Table may be used. One side has a rotational scale, the other has both a rotational scale and a grid that may be used for linear measurements.

The Slit Plate is attached to a component holder between the Light Source and the Ray Table. The positioning shown in the illustration will give clear, sharp rays in a slightly darkened room. However, the quality of the rays is easily varied by adjusting the distance between the Light Source and the Slit Plate. Narrower, less divergent rays may be obtained by sliding the Light Source farther away from the slits, but there is a corresponding loss of brightness.

The Ray Table Component Holder attaches magnetically to the Ray Table as shown. It may be used to mount the Viewing Screen, the Polarizer, or another component.

Single Ray Setup

Most quantitative ray optics experiments are most easily performed using a single ray. This can be obtained by using the Slit Mask, as shown in Figure 11, to block all but the desired ray.

For accurate measurements using the rotational scale, the incident ray must pass directly through the center of the Ray Table. To accomplish this, alternately adjust:

When one of the rays is aligned in this manner, place the Slit Mask on the other side of the Component Holder to block all but the desired ray.

Parallel Ray Setup

Parallel rays are obtained by positioning the Parallel Ray Lens between the Light Source and the slits, as shown in Figure 12. Use the parallel lines of the Ray Table grid as a reference, and adjust the longitudinal position of the lens until the rays are parallel.

Parallel Ray Lens

Slit Plate

Figure 12: Single Ray Setup

Introductory Optics System 012-02744K

Copy Ready Experiments

The following experiments are written in worksheet form.

Feel free to photocopy them for use in your lab.

➤NOTE: The first paragraph in each experiment lists all the equipment

needed to perform the experiment. Be sure to read this equipment list first, as

the requirements vary with each experiment.

012-02744K Introductory Optics System

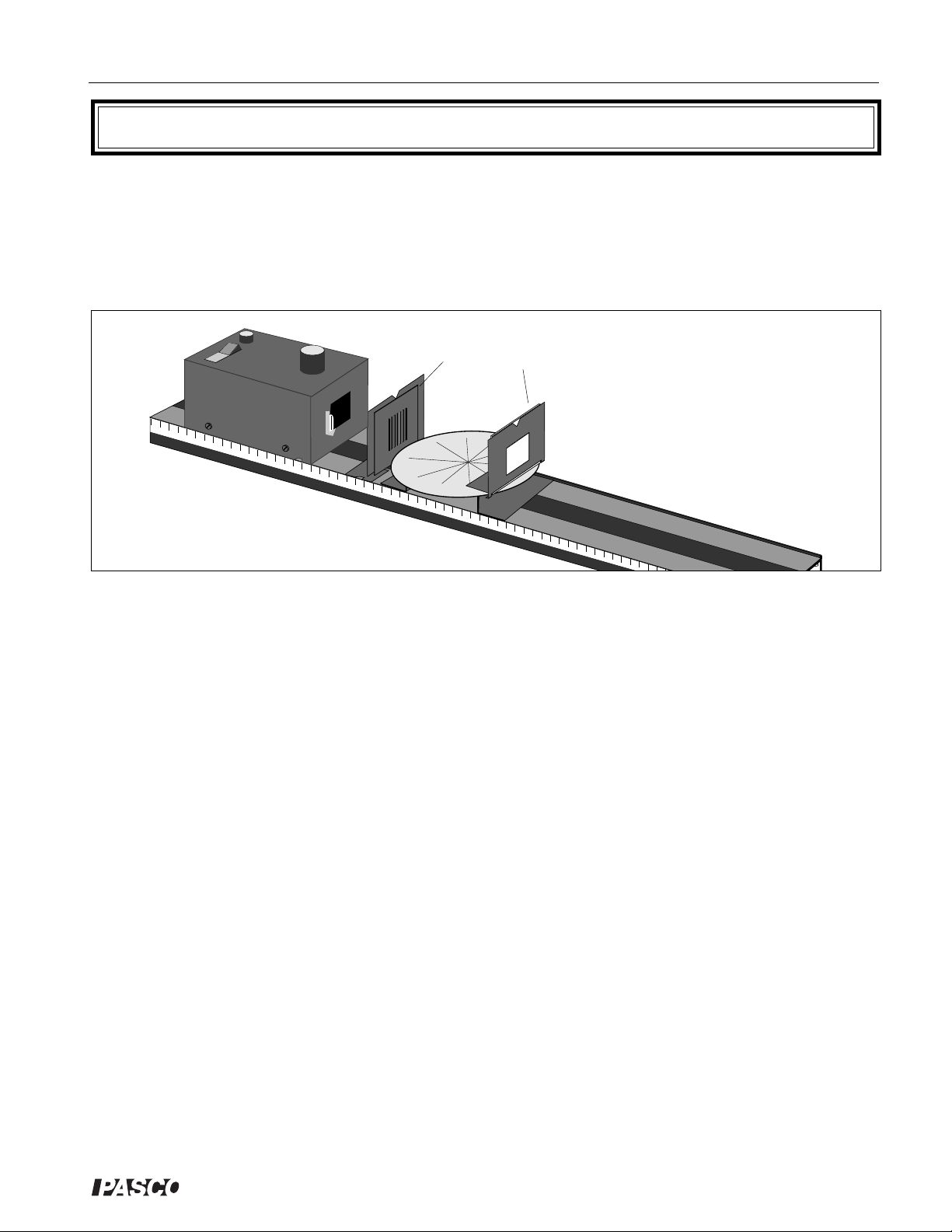
Experiment 1: Introduction to Ray Optics

EQUIPMENT NEEDED:

-Optics Bench, -Light Source,

-Ray Table and Base, -Component Holder,

-Slit Plate, -Ray Table Component Holder,

-Viewing Screen.

Purpose

➀ Observe straight line propagation of light. ➁ Use Ray Tracing to locate an object.

Procedure

Set up the equipment as shown in Figure 1.1, and turn on the Light Source. Darken the room enough so the light rays on the Ray Table are easily visible.

Straight Line Propagation of Light

Observe the light rays on the Ray Table.

Slit Plate

Figure 1.1 Equipment Setup

Viewing Screen

➀ Are the rays straight? _______________________________________________________. ➁ How does the width and distinctness of each ray vary with its distance from the Slit Plate?

_________________________________________________________________________. Set the Viewing Screen and its holder aside for the next step.

➂ Lower your head until you can look along one of the "Rays" of light on the Ray Table. Where does

the light originate? What path did it take going from there to your eye? Try this for several rays. _____________________________________________________________________.

Replace the Viewing Screen as shown in Figure 1.1. Rotate the Slit Plate slowly on the component holder until the slits are horizontal. Observe the slit images on the Viewing Screen.

➃ How does the width and distinctness of the slit images depend on the angle of the Slit Plate?

_________________________________________________________________________.

➄ For what angle of the Slit Plate are the images most distinct? For what angle are the images least

distinct?_________________________________________________________________.

Introductory Optics System 012-02744K

➅ On a separate sheet of paper, explain your observations in terms of the straight line propaga-

tion of light. Include a diagram showing how the width of the slit images depends on the orientation of the Light Bulb filament with respect to the Slit Plate. ____________________________________________________________________________________________.

Ray Tracing: Locating the Filament

Filament

Light Source

Note: The vertical edge of the notch on the side of the Light Source indicates the position of the filament.

Component

Holder

Figure 1.2: Ray Tracing

Slit Plate

Center

You can use the fact that light propagates in a straight line to measure the distance between the Light Source filament and the center of the Ray Table. Figure 1.2 shows how. The rays on the Ray Table all originate from the filament of the Light Source. Since light travels in a straight line, you need only extend the rays backward to locate the filament. (See Step 3 in the first part of this experiment.)

Rays on Ray

Table

Paper

Place a piece of blank white paper on top of the Ray Table, holding it there with a piece of tape. Make a reference mark on the paper at the position of the center of the Ray Table. Using a pencil and straight edge, trace the edges of several of the rays onto the paper.

Remove the paper. Use the pencil and straightedge to extend each of the rays. Trace them back to their common point of intersection. (You may need to tape on an additional sheet of paper.) Label the filament and the center of the Ray Table on your diagram.

➀ Measure the distance between your reference mark and the point of intersection of the rays.

_______________________________________________________________________.

➁ Use the metric scale on the Optics Bench to measure the distance between the filament and

the center of the Ray Table directly (see the note in Figure 1.2). _____________________________________________________________________________________________.

➂ How well do your measurements in Steps 1 and 2 agree? Comment.

________________________________________________________________________________________. One of the key ideas that this experiment illustrates is the ability for us to trace light rays to

their origin or apparent origin. This concept will prove most useful in future experiments.

012-02744K Introductory Optics System

NORMALNORMAL

COMPONENTCOMPONENT

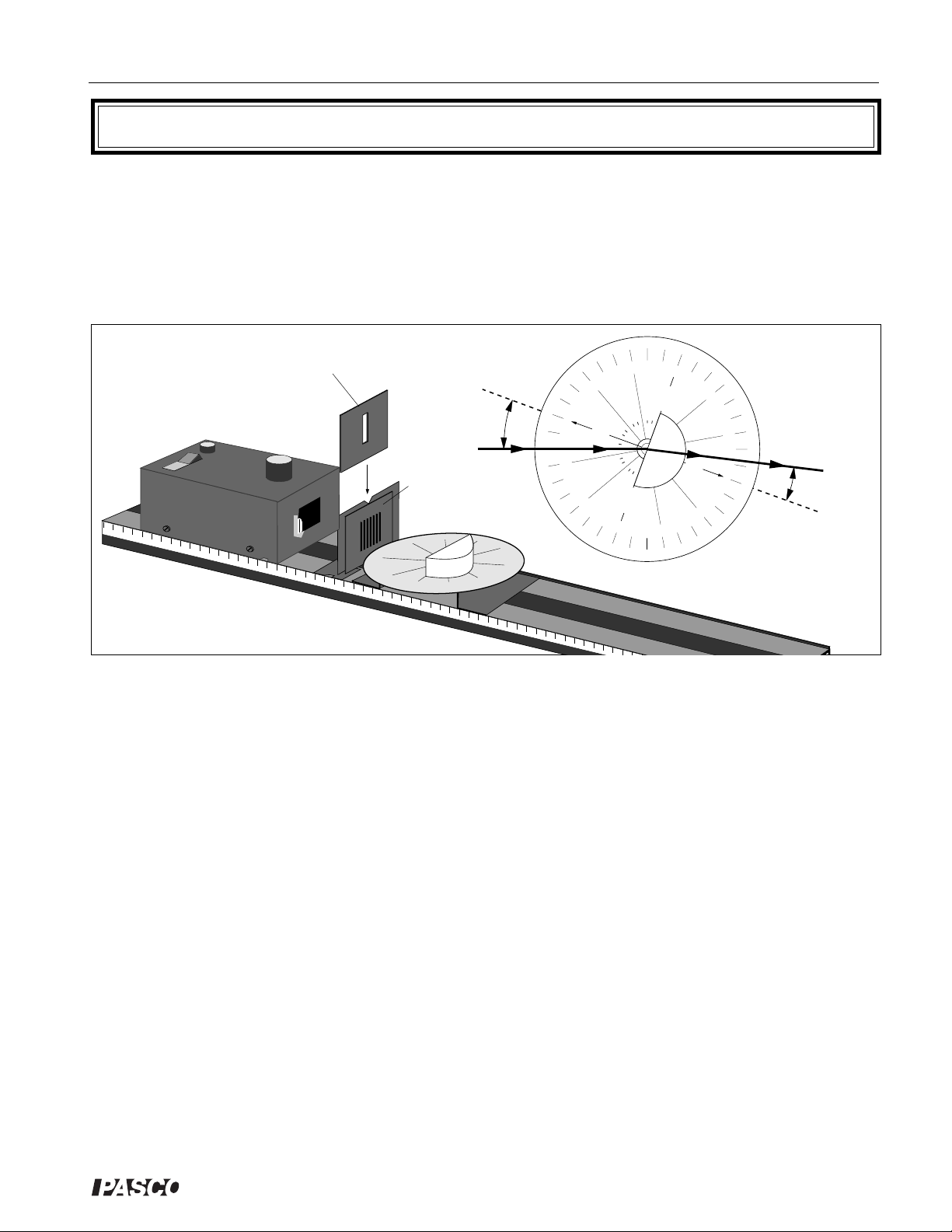
Experiment 2: The Law of Reflection

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-Ray Table and Base -Component Holder

-Slit Plate -Slit Mask

-Ray Optics Mirror.

Slit Mask

COMPONENTCOMPONENT

NORMALNORMAL

Slit Plate

Introduction

The shape and location of the image created by reflection from a mirror of any shape is determined by just a few simple principles. One of these principles you already know: light propagates in a straight line. You will have an opportunity to learn the remaining principles in this experiment.

To determine the basic principles underlying any phenomenon, it is best to observe that phenomenon in its simplest possible form. In this experiment, you will observe the reflection of a single ray of light from a plane mirror. The principles you discover will be applied, in later experiments, to more complicated examples of reflection.

Figure 2.1 Equipment Setup

Angle of

Reflection

Angle of

Incidence

Figure 2.2 Incident and Reflected Rays

Introductory Optics System 012-02744K

Procedure

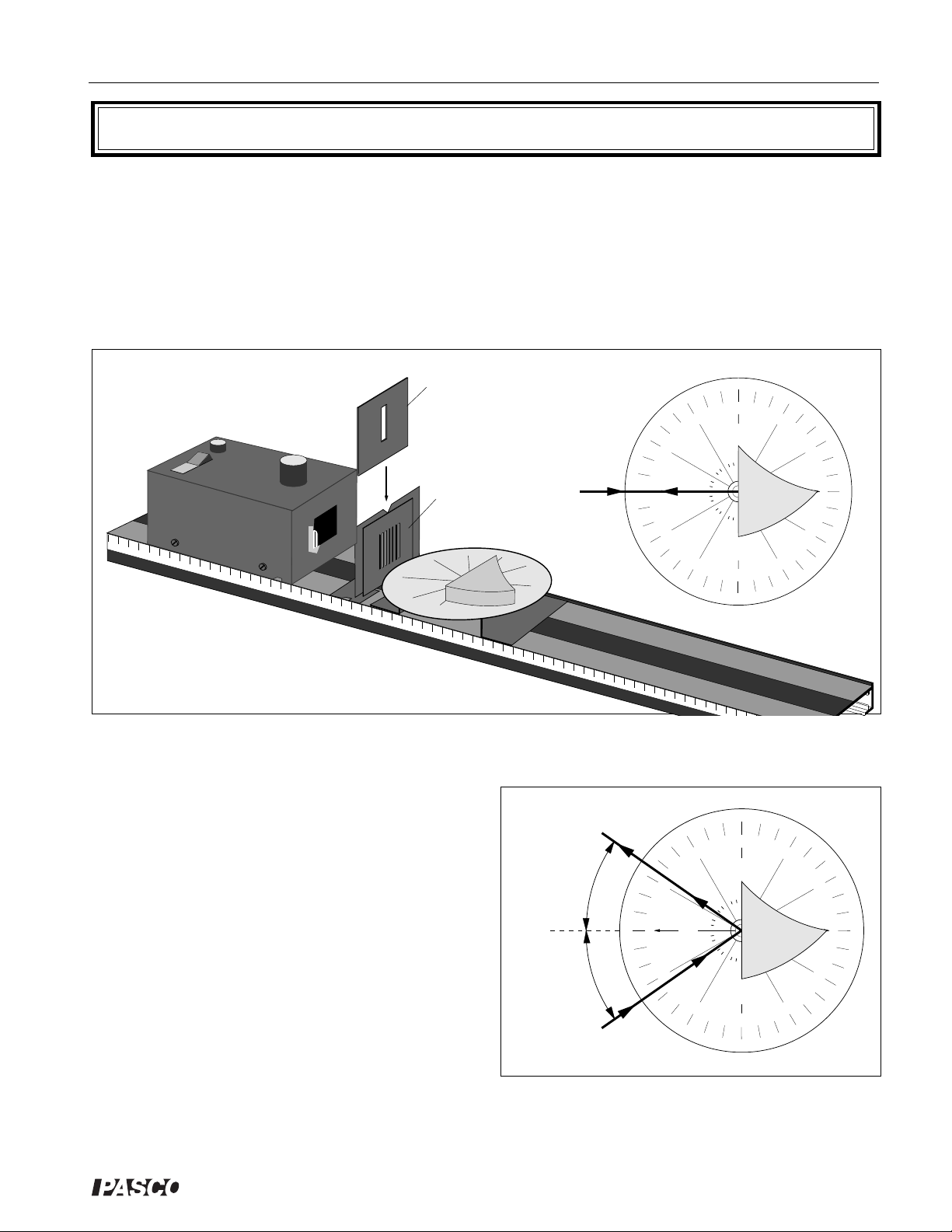
Set up the equipment as shown in Figure 2.1. Adjust the components so a single ray of light is aligned with the bold arrow labeled “Normal” on the Ray Table Degree Scale. Carefully align the flat reflecting surface of the mirror with the bold line labeled “Component” on the Ray Table. With the mirror properly aligned, the bold arrow on the Ray Table is normal (at right angles) to the plane of the reflecting surface.

Rotate the Ray Table and observe the light ray. The angles of incidence and reflection are measured with respect to the normal to the reflecting surface, as shown in Figure 2.2.

By rotating the Ray Table, set the angle of incidence to each of the settings shown in Table

2.1. For each angle of incidence, record the angle of reflection (Reflection measurements with the incident ray coming from the opposite side of the normal (Reflec-

tion

➀ Are the results for the two trials the same? If not, to what do you attribute the differences?

________________________________________________________________________

➁ Part of the law of reflection states that the incident ray, the normal and the reflected ray all lie

in the same plane. Discuss how this is shown in your experiment _____________________________________________________________________________________________.

). Repeat your

➂ What relationship holds between the angle of incidence and the angle of reflection?

______________________________________________________________________________

Additional Questions

➀ The Law of Reflection has two parts. State both

parts.

➁ You were asked to measure the angle of reflection

when the ray was incident on either side of the normal to the surface of the mirror. What advantages does this provide?

➂ Physicists expend a great deal of energy in attempts

to increase the accuracy with which an exact law can be proven valid. How might you test the Law of Reflection to a higher level of accuracy than in the experiment you just performed?

Angle of: Incidence Reflection1 Reflection

Table 2.1 Data

0°

10°

20°

30°

40°

50°

60°

70°

80°

90°

012-02744K Introductory Optics System

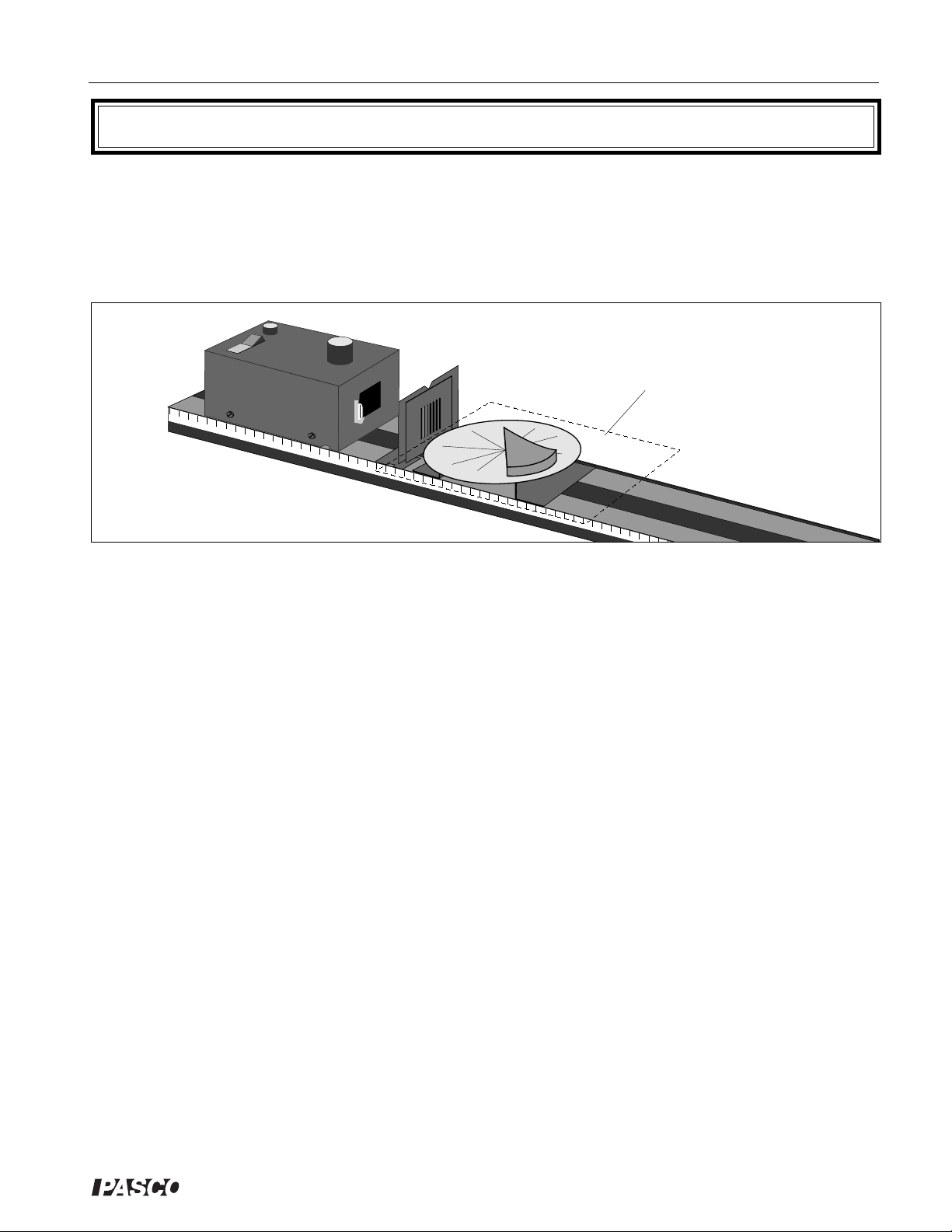
Experiment 3: Image Formation in a Plane Mirror

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-Ray Table and Base -Component Holder

-Slit Plate -Ray Optics Mirror

Paper

Introduction

Figure 3.1 Equipment Setup

Looking into a mirror and seeing a nearly exact image of yourself hardly seems like the result of simple physical principles. But it is. The nature of the image you see in a mirror is understandable in terms of the principles you have already learned: the Law of Reflection and the straight-line propagation of light.

In this experiment you will investigate how the apparent location of an image reflected from a plane mirror relates to the location of the object, and how this relationship is a direct result of the basic principles you have already studied.

Procedure

Set up the equipment as shown in Figure 3.1. Adjust the Slit Plate and Light Source positions for sharp, easily visible rays.

As shown, place a blank, white sheet of paper on top of the Ray Table, and place the Ray Optics Mirror on top of the paper. Position the mirror so that all of the light rays are reflected from its flat surface. Draw a line on the paper to mark the position of the flat surface of the mirror.

Look into the mirror along the line of the reflected rays so that you can see the image of the Slit Plate and, through the slits, the filament of the Light Source. (Rotate the mirror as needed to do this.)

➀ Do the rays seem to follow a straight line into the mirror? ________________________________.

With a pencil, mark two points along one edge of each of the incident and reflected rays. Label the points (r etc.), so you know which points belong to which ray.

1,r2

Remove the paper and reconstruct the rays as shown on the next page (Figure 3.2), using a pencil and straightedge. If you need to, tape on additional pieces of paper. Draw dotted lines to extend the incident and reflected rays. (If this ray tracing technique is unfamiliar to you, review ray tracing in Experiment 1: Introduction to Ray Optics.)

On your drawing, label the position of the filament and the apparent position of its reflected image.

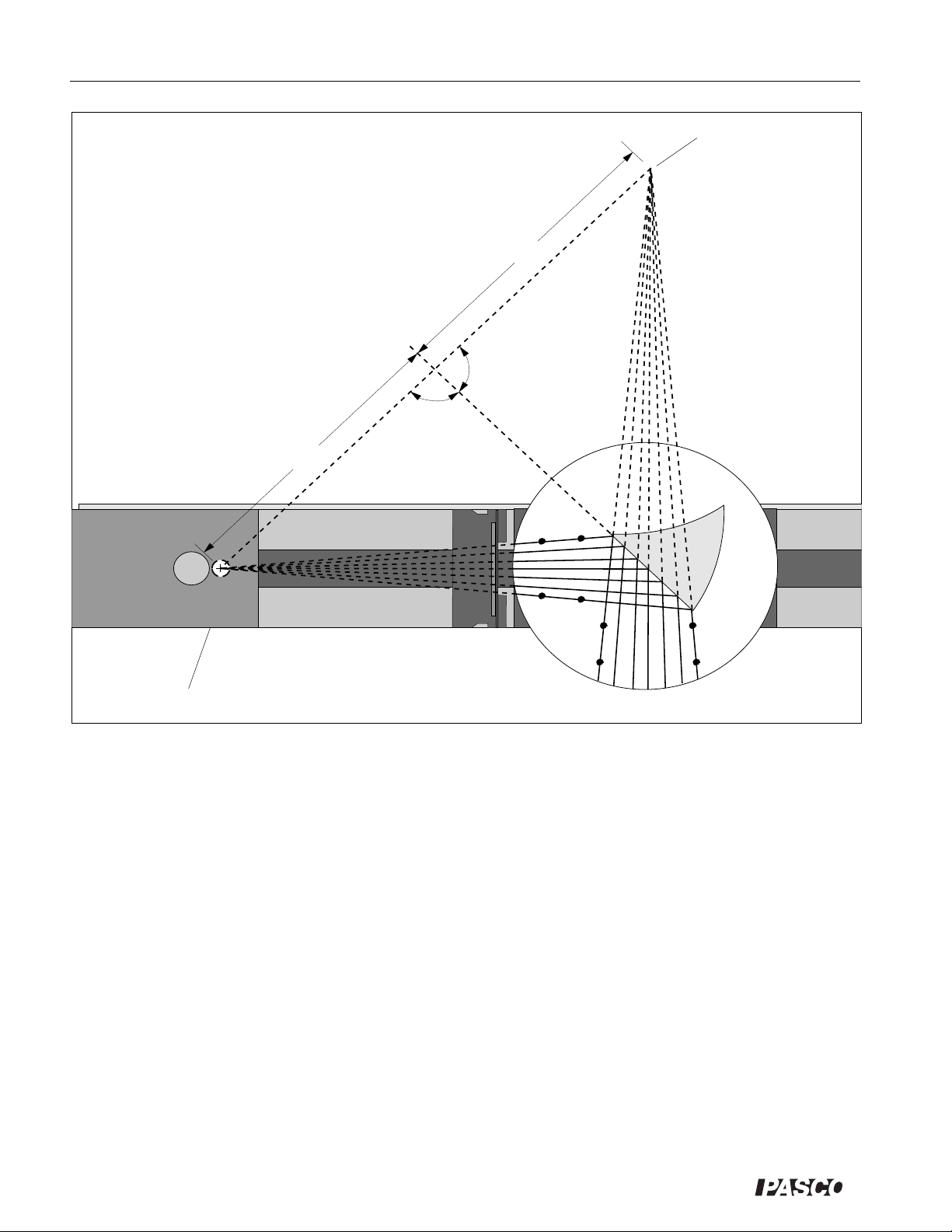
Introductory Optics System 012-02744K

Image of the

Filament

90˚

Filament

Figure 3.2 Ray Tracing

➁ What is the perpendicular distance from the filament to the plane of the mirror (distance d1, as shown in the

Figure 3.2)? ________________________________________________.

➂ What is the perpendicular distance from the image of the filament to the plane of the mirror (distance d

, as

shown in the Figure)? _________________________________________. Change the position of the mirror and the Light Source and repeat the experiment.

➃ What is the relationship between object and image location for reflection in a plane mirror?

________________________________________________________________________.

Additional Questions

➀ If one wall of a room consists of a large, flat mirror, how much larger does the room appear to be than it

actually is?

➁ Make a diagram illustrating why an image of the letter F, reflected from a plane mirror, is inverted. (Treat

each corner on the F as a source of light. Locate the image for each source to construct the image of the F.)

➂ How does the size of the image reflected from a plane mirror relate to the size of the object?

012-02744K Introductory Optics System

NORM

NORMAL

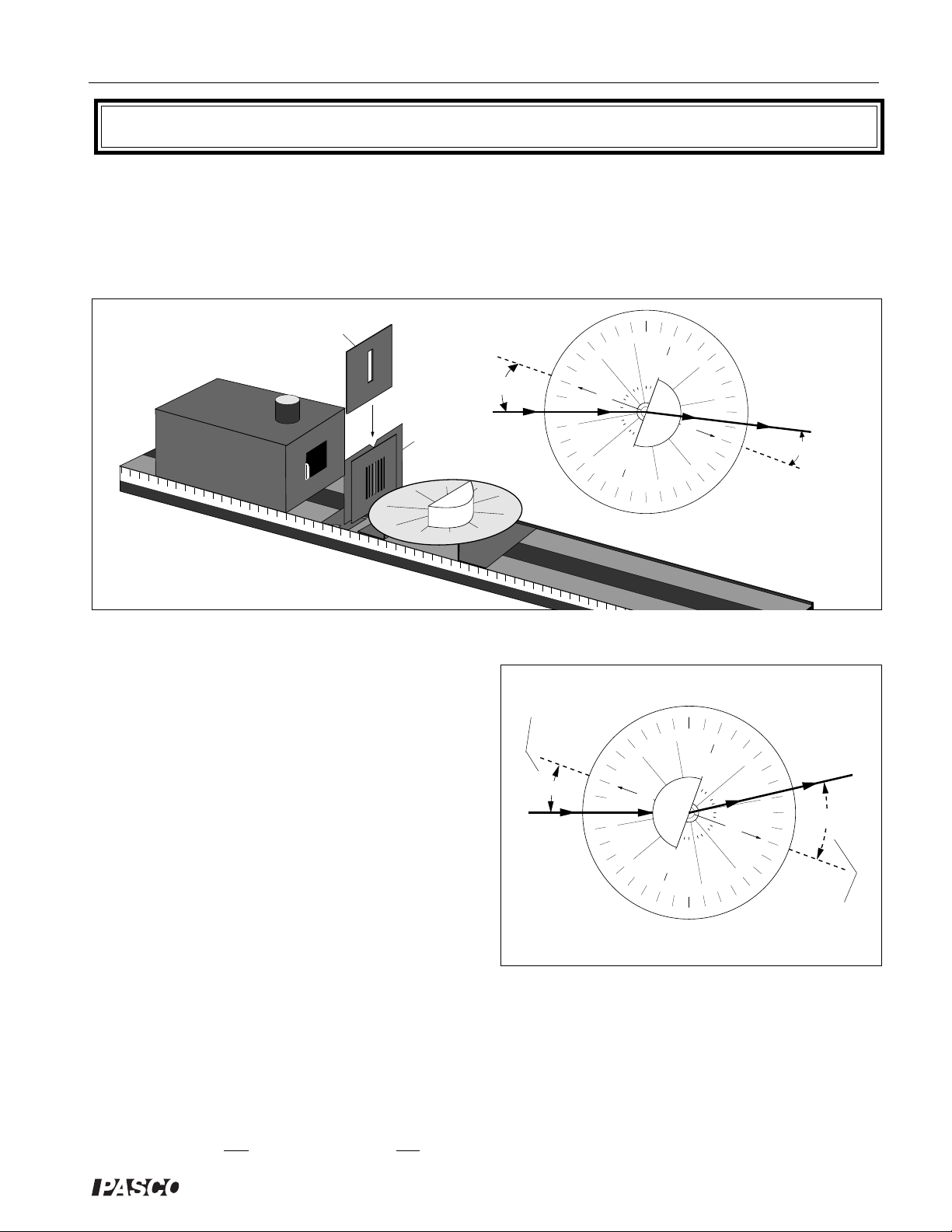
Experiment 4: The Law of Refraction

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-Ray Table and Base -Component Holder

-Slit Plate -Slit Mask

-Cylindrical Lens.

Slit Mask

Angle of

Incidence

Introduction

As you have seen, the direction of light propagation changes abruptly when light encounters a reflective surface. The direction also changes abruptly when light passes across a boundary between two different media of propagation, such as between air and acrylic, or between glass and water. In this case, the change of direction is called Refraction.

As for reflection, a simple law characterizes the behavior of a refracted ray of light. According to the Law of Refraction, also known as Snell’s Law:

The quantities n1 and n2 are constants, called indices of refraction, that depend on the two media through which the light is passing. The angles θ1 and θ2 are the angles that the ray of light makes with the normal to the boundary between the two media (see the inset in Figure 4.1). In this experiment you will test the validity of this law, and also measure the index of refraction for acrylic.

Slit Plate

Figure 4.1 Equipment Setup

sin θ1 = n2 sin θ

Angle of

Refraction

Procedure

Set up the equipment as shown in Figure 4.1. Adjust the components so a single ray of light passes directly through the center of the Ray Table Degree Scale. Align the flat surface of the Cylindrical Lens with the line labeled “Component”. With the lens properly aligned, the radial lines extending from the center of the Degree Scale will all be perpendicular to the circular surface of the lens.

Introductory Optics System 012-02744K

Without disturbing the alignment of the Lens, rotate the Ray Table and observe the refracted ray for various angles of incidence.

➀ Is the ray bent when it passes into the lens perpen-

dicular to the flat surface of the lens? _______________________________________

_______________________________________.

➁ Is the ray bent when it passes out of the lens

perpendicular to the curved surface of the lens? _______________________________________

_______________________________________. By rotating the Ray Table, set the angle of inci-

dence to each of the settings shown in Table 4.1 on the following page. For each angle of incidence, measure the angle of refraction (Refraction

Repeat the measurement with the incident ray striking from the opposite side of the normal (Refraction2).

Angle of: Incidence Refraction1Refraction

0°

10°

20°

30°

40°

50°

60°

70°

80°

90°

➂ Are your results for the two sets of measurements

Table 4.1 Data

the same? If not, to what do you attribute the differences? ___________________________________________________________________

_______________________________________________________________________. On a separate sheet of paper, construct a graph with sin(angle of refraction) on the x-axis

and sin(angle of incidence) on the y-axis. Draw the best fit straight line for each of your two sets of data.

➃ Is your graph consistent with the Law of Refraction? Explain.

_____________________________________________________________________________________________.

➄ Measure the slope of your best fit lines. Take the average of your results to determine the

index of refraction for acrylic (assume that the index of refraction for air is equal to 1.0). n = ________________________________________.

Additional Questions

➀ In performing the experiment, what difficulties did you encounter in measuring the angle of

refraction for large angles of incidence?

➁ Was all the light of the ray refracted? Was some reflected? How might you have used the

Law of Reflection to test the alignment of the Cylindrical Lens?

➂ How does averaging the results of measurements taken with the incident ray striking from

either side of the normal improve the accuracy of the results?

012-02744K Introductory Optics System

Experiment 5: Reversibility

Equipment Needed:

-Optics Bench -Light Source

-Ray Table and Base -Component Holder

-Slit Plate -Slit Mask

-Cylindrical Lens.

Introduction

In Experiment 4, you determined the relationship that exists between the angle of incidence and the angle of refraction for light passing from air into a more optically dense medium (the Cylindrical Lens). An important question remains. Does the same relationship hold between the angles of incidence and refraction for light passing out of a more optically dense medium back into air? That is to say, if the light is traveling in the opposite direction, is the law of refraction the same or different? In this experiment, you will find the answer to this question.

Procedure

Set up the equipment as shown in Figure 5.1. Adjust the components so a single ray of light passes directly through the center of the Ray Table Degree Scale. Align the flat surface of the Cylindrical Lens with the line labeled “Component”. With the lens properly aligned, the radial lines extending from the center of the Degree Scale will all be perpendicular to the circular surface of the lens.

Slit Mask

Incidence

Slit Plate

0 3

Figure 5.1 Equipment Setup

Internal Angle

of Incidence

(Incidence

)

Figure 5.2 Internal Angle of Incidence

0 4

T N

N O P

M O C

T N E

O P M

O C

NORMAL

COMPONENT

4 0

3 0

COMPONENT

NORMAL

Refraction

(Refraction

)

Angle of

Refraction

Without disturbing the alignment of the lens, rotate the Ray Table and set the angle of incidence to the values listed in Table 5.1 on the following page. Enter the corresponding angles of Refraction in the table in

two columns: Refraction1 and Incidence2. (Let Incidence2 = Refraction1).

Introductory Optics System 012-02744K

Table 5.1 Data

Ray Incident on: Flat Surface Curved Surface

Angle of: Incidence

Refraction

Incidence

Refraction

0°

10°

20°

30°

40°

50°

60°

70°

80°

90°

Now let the incident ray strike the curved surface of the lens. (Just rotate the Ray Table 180°.) The internal angle of incidence for the flat surface of the Cylindrical Lens is shown in Figure 5.2. Set this angle of incidence to the values you have already listed in the table (Incidence2). Record the corresponding angles of refraction (Refraction2).

➀ Using your collected values for Incidence

and Refraction1, determine the index of refraction for

the acrylic from which the Cylindrical Lens is made. (As in experiment 4, assume that the index of refraction for air is equal to 1.0.)

______________________________________________________________________.

➁ Using your collected values for Incidence

and Refraction2, redetermine the index of refraction

for the acrylic from which the Cylindrical Lens is made. n

______________________________________________________________________.

➂ Is the Law of Refraction the same for light rays going in either direction between the two

media? ____________________________________________________________________.

➃ On a separate sheet of paper, make a diagram showing a light ray passing into and out of the

Cylindrical Lens. Show the correct angles of incidence and refraction at both surfaces traversed by the ray. Use arrow heads to indicate the direction of propagation of the ray. Now reverse the arrows on the light ray. Show that the new angles of incidence and refraction are still consistent with the Law of Refraction. This is the principle of optical reversibility.

➄ Does the principle of optical reversibility hold for Reflection as well as Refraction? Explain.

_________________________________________________________________________.

012-02744K Introductory Optics System

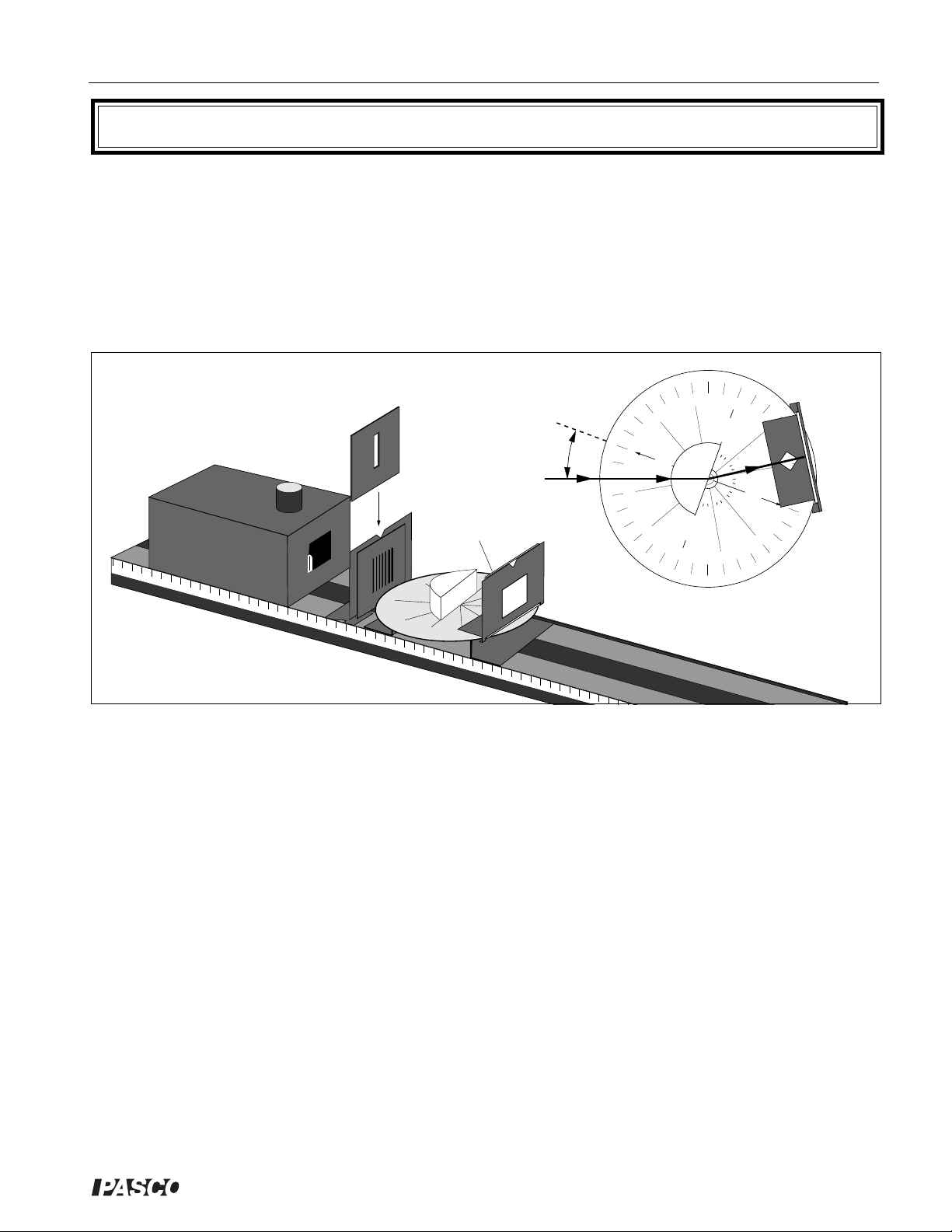
Experiment 6: Dispersion and Total Internal Reflection

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-Ray Plate and Base -Component Holder

-Slit Plate -Slit Mask

-Cylindrical Lens -Ray Table Component Holder

-Viewing Screen.

COMPONENT

Viewing

Screen

Angle of

Incidence

Figure 6.1 Equipment Setup

Introduction

In this experiment you will look at two phenomena related to refraction: Dispersion and Total Internal Reflection. Dispersion introduces a complication to the Law of Refraction, which is that most materials have different indexes of refraction for different colors of light. In Total Internal Reflection, it is found that in certain circumstances, light striking an interface between two transparent media can not pass through the interface.

Procedure

Set up the equipment as shown in Figure 6.1, so a single light ray is incident on the curved surface of the Cylindrical Lens.

Dispersion

Set the Ray Table so the angle of incidence of the ray striking the flat surface of the lens (from inside the lens) is zero-degrees. Adjust the Ray Table Component Holder so the refracted ray is visible on the Viewing Screen.

Slowly increase the angle of incidence. As you do, watch the refracted ray on the Viewing Screen.

➀ At what angle of refraction do you begin to notice color separation in the refracted ray?

Introductory Optics System 012-02744K

➁ At what angle of refraction is the color separation a maximum? ____________________

_______________________________________________________________________.

➂ What colors are present in the refracted ray? (Write them in the order of minimum to maxi-

mum angle of refraction.) __________________________________________________

_______________________________________________________________________.

➃ Measure the index of refraction of acrylic for red and blue light

acrylic

sin θ

acrylic

= n

air

sin θ

air

➤NOTE: In Experiment 4 we said that the index of refraction of a given material is a

constant. That statement was almost accurate, but not quite. As you can see, different colors of light refract to slightly different angles, and therefore have slightly different indexes of refraction.

= ______________________________________.

red

= ______________________________________.

blue

Total Internal Reflection

Without moving the Ray Table or the Cylindrical Lens, notice that not all of the light in the incident ray is refracted. Part of the light is also reflected.

➀ From which surface of the lens does reflection primarily occur? ___________________

________________________________________________________________.

➁ Is there a reflected ray for all angles of incidence? (Use the Viewing Screen to detect faint

rays.) _________________________________________________________________

________________________________________________________________.

➂ Are the angles for the reflected ray consistent with the Law of Reflection? __________

________________________________________________________________.

➃ Is there a refracted ray for all angles of incidence?____________________________

________________________________________________________________.

➄ How do the intensity of the reflected and refracted rays vary with the angle of incidence?

________________________________________________________________.

➅ At what angle of refraction is all the light reflected (no refracted ray)? ______________

________________________________________________________________.

012-02744K Introductory Optics System

Experiment 7: Converging Lens – Image and Object

Relationships

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-75 mm Focal Length Convex Lens -Crossed Arrow Target

-Component Holders (3) -Viewing Screen.

Introduction

Given a lens of any shape and index of refraction, you could determine the shape and location of the images it forms based only on the Law of Refraction. You need only apply the law along with some of the ray tracing techniques you have already used. However, for spherical lenses (and for spherical mirrors as well), there is a more general equation that can be used to determine the location and magnification of an image. This equation is called the Fundamental Lens equation:

where f is the focal length of the lens, and d and object respectively (see Figure 7.1). The magnification of the image is given by the equation:

In this experiment, you will have an opportunity to test and apply these equations.

Crossed Arrow

Target

Figure 7.1: Equipment Setup

f f

Lens

1/d

+ 1/di = 1/f

and di are the distance from the mirror to the image

m = -d

i/do

Viewing Screen

➤➤

➤NOTE: Instead of the above equation, you may have learned the Fundamental Lens Equation

➤➤

= f2, where So and Si are the distances between the principle focus of the lens and the

as S

oSi

object and image, respectively. If so, notice that So = do - f, and Si = di - f (see Figure 7.1). Using these equalities, convince yourself that 1/do + 1/di = 1/f and SoSi = f2 are different expressions of the same relationship.

Procedure

Set up the equipment as shown in Figure 7.1. Turn on the Light Source and slide the lens toward or away from the Crossed Arrow Target, as needed to focus the image of the Target onto the Viewing Screen.

➀ Is the image magnified or reduced? ____________________________________________. ➁ Is the image inverted?______________________________________________________. ➂ Based on the Fundamental Lens Equation, what would happen to d

further?_________________________________________________________________.

if you increased do even

Introductory Optics System 012-02744K

Table 7.1: Data and Calculations

Data Calculations

(mm) d

500

450

400

350

300

250

200

150

100

1/di + 1/d

1/f hi/h

-di/d

➂ What would happen to di if do were very, very large?

______________________________.

➃ Using your answer to question 4, measure the focal length of the lens.

Focal Length = ___________________________________________. Now set d

to the values (in millimeters) listed in the table above. At each setting, locate the

image and measure di. Also measure hi, the height of the image. (ho is the height of the arrow on the crossed arrow target.)

Using the data you have collected, perform the calculations shown in the table.

➄ Are your results in complete agreement with the Fundamental Lens Equation? If not, to what

do you attribute the discrepancies? __________________________________________________________________.

➅ For what values of d

were you unable to focus an image onto the screen? Use the Funda-

mental Lens Equation to explain why. __________________________________________.

Additional Questions

➀ For a lens of focal length f, what value of do would give an image with a magnification of one? ➁ Is it possible to obtain a non-inverted image with a converging spherical lens? Explain. ➂ For a converging lens of focal length f, where would you place the object to obtain an image

as far away from the lens as possible? How large would the image be?

012-02744K Introductory Optics System

Experiment 8: Light and Color

EQUIPMENT NEEDED:

-Optics Bench -Ray Table and Base

-Component Holder -Ray Table Component Holder

-Slit Plate -Slit Mask

-Cylindrical Lens -Viewing Screen

-Colored Filters (3)

N O P

M O C

T N E

O P M

5 0

Viewing

Screen

Angle of

Incidence

0 3

0 5

Introduction

Early investigators assumed that light, in its purest, simplest form is white; and that refractive materials alter the characteristics of the white light to create the various colors. Sir Isaac Newton was the first to show that light, in its simplest form, is colored; and that refractive materials merely separate the various colors which are the natural constituents of white light. He used this idea to help explain the colors of objects.

The Colors of Light

Set up the equipment as shown in Figure 8.1, so that a single ray of light passes through the center of the Ray Table. Slowly rotate the Ray Table to increase the angle of incidence of the light ray. Examine the refracted ray on the Viewing Screen. Notice the color separation at large angles of refraction.

Figure 8.1 Equipment Setup

Red Filter

Viewing

Screen

Red

Green

Blue

Blue/Green Filter

Figure 8.2 Mixing Colored Light

Introductory Optics System 012-02744K

Transmitted

Green Filter

(hold in place by hand)

Figure 8.3 Equipment Setup

Rays

Reflected

Rays

➀ Do your observations support Newton’s theory? Explain. __________________________

____________________________________________________________________. To investigate further, setup the equipment as shown in Figure 8.2. Arrange the Cylindrical Lens so

that the three central light rays (one red, one green, and one blue) intersect at precisely the same point on the Ray Table. Slowly move the Viewing Screen toward this point of intersection (you'll have to remove it from its component holder).

➁ What color of light results when red, green, and blue light are mixed? How does this support

Newton’s theory? ______________________________________________________ ___________________________________________________________________.

The Colors of Objects

Set up the equipment as shown in Figure 8.3. Observe the light rays that are transmitted and reflected from the Green Filter.

➀ What color are the transmitted rays? What color are the reflected rays?

___________________________________________________________________. Place the Red Filter behind the Green Filter (so the light passes first through the Green Filter and

then through the Red Filter). Look into the Green Filter.

➁ What color are the reflected rays now? Which rays are reflected from the front surface of the

Green Filter, and which are reflected from the front surface of the Red Filter? ___________________________________________________________________.

Place the Blue Filter over the Light Source aperture so the incident rays are blue. Let these rays pass through the Green Filter only.

➂ What colors are the reflected rays now?

___________________________________________________________________.

➃ Based on your observations, what makes the Green Filter appear green?

___________________________________________________________________.

012-02744K Introductory Optics System

Experiment 9: Two-Slit Interference

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-Diffraction Plate -Diffraction Scale

-Ray Table Base -Slit Mask

Introduction

What is light? There may be no complete answer to this question. However, in certain circumstances, light behaves exactly as if it were a wave. In fact, in this experiment you will measure the wavelength of light, and see how that wavelength varies with color.

In two-slit interference, light falls on an opaque screen with two closely spaced, narrow slits. As Huygen’s principle tells us, each slit acts as a new source of light. Since the slits are illuminated by the same wave front, these sources are in phase. Where the wave fronts from the two sources overlap, an interference pattern is formed.

Diffraction Scale

Figure 9.1 Equipment Setup

Slot

Slit Mask

Ray Table

Base

IF D B

. . . ..

. . . . ..

. .

. . . .

. . .

. . . . .. . .

. . . ..

.. . . . .

. . . . ..

. . . . .. . . . .

. . . .

. . . .. . .

. . . .

. .

.. . .

. . . . . ..

. . . . . . . . . . .

. . . . ..

. . . .

.. . . . .

. . . . ..

. . . . .

. . . .

R A

C T IO

A T E

Diffraction

Plate

Window

E T

. . . .

. .

. . .

. .

. . . .

J I H D

Procedure

Set up the Equipment as shown in Figure 9.1. The Slit Mask should be centered on the Component Holder. While looking through the Slit Mask, adjust the position of the Diffraction Scale so you can see the filament of the Light Source through the slot in the Diffraction Scale.

Diffraction Scale

nλ

Retina of your

n 2

zeroth

maxima

nth

maxima

Eye

Diffraction Plate

Figure 9.2 Geometry of Two-Slit Interference

Introductory Optics System 012-02744K

Attach the Diffraction Plate to the other side of the Component Holder, as shown. Center pattern D, with the slits vertical, in the aperture of the Slit Mask. Look through the slits. By centering your eye so that you look through both the slits and the window of the Diffraction Plate, you should be able to see clearly both the interference pattern and the illuminated scale on the Diffraction Scale.

Table 9.1 Data and Calculations

Data Calculations

Color n AB X L sin (arctan X/L) = λ

Red

Green

Blue

➤➤

➤NOTE:

➤➤

In this experiment, you look through the narrow slits at the light source, and the diffraction

split

( )

spacing

()

pattern is formed directly on the retina of your eye. You then see this diffraction pattern superimposed on your view of the illuminated diffraction scale. The geometry is therefore slightly more complicated than it would be if the pattern were projected onto a screen, as in most textbook examples. (A very strong light source, such as a laser, is required in order to project a sharp image of a diffraction pattern onto a screen.)

The essential geometry of the experiment is shown in Figure 9.2. At the zeroth maxima, light rays from slits A and B have traveled the same distance from the slits to your eye, so they are in phase and interfere constructively on your retina. At the first order maxima (to the left of the viewer) light from slit B has traveled one wavelength farther than light from slit A, so the rays are again in phase, and constructive interference occurs at this position as well.

At the nth order maxima, the light from slit B has traveled n wavelengths farther than the light from slit A, so again, constructive interference occurs. In the diagram, the line AC is constructed perpendicular to the line PB. Since the slits are very close together (in the experiment, not the diagram), lines AP and BP are nearly parallel. Therefore, to a very close approximation, AP = CP. This means that, for constructive interference to occur at P, it must be true that BC = nλ.

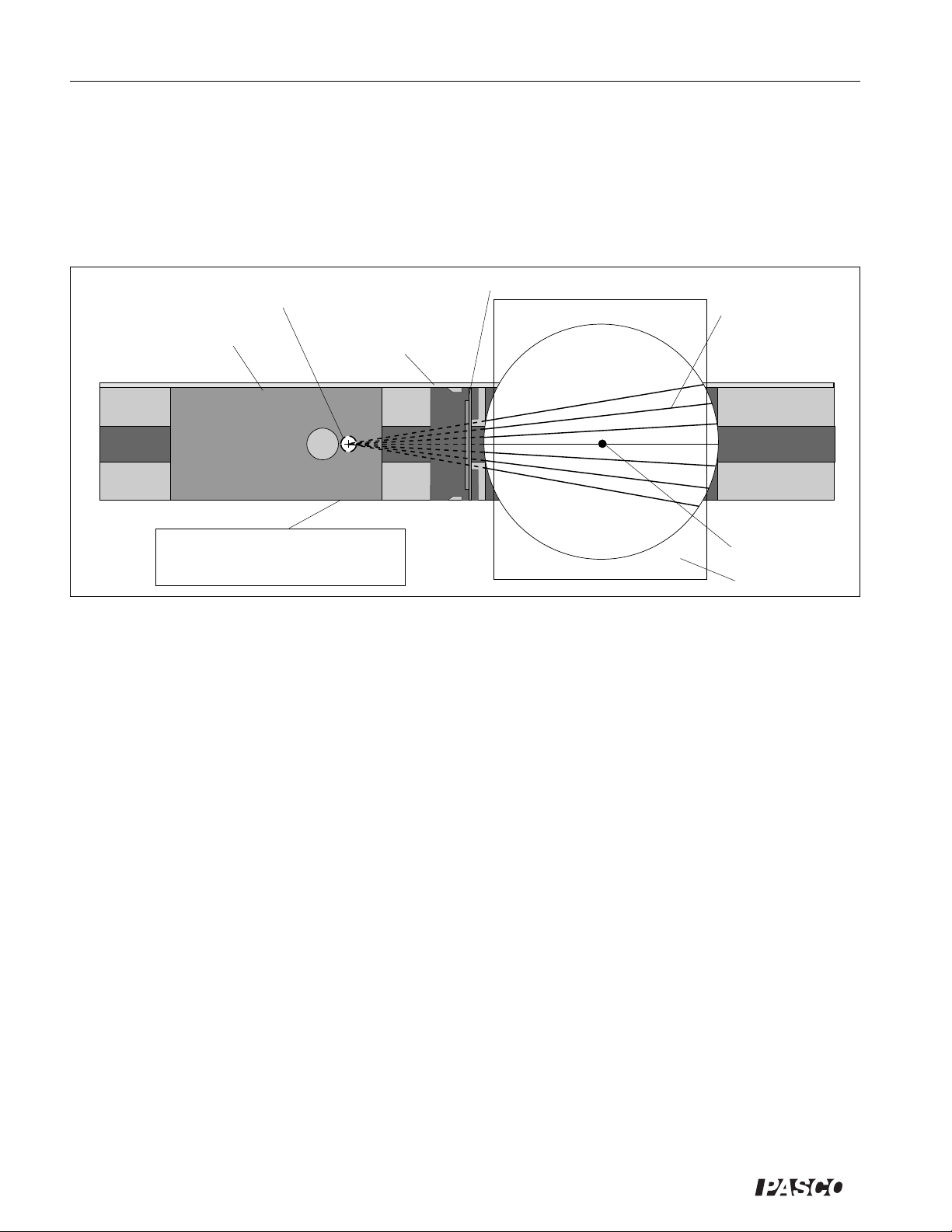
From right triangle ACB, it can be seen that BC = AB sin θ, where A is the distance between the two slits on the Diffraction Plate. Therefore, AB sin θ = nλ. (The spacing between the slits, AB, is listed in the Equipment section of this manual.) Therefore, you need only measure the value of θ for a particular value of n to determine the wavelength of light.

To measure θ, notice that the dotted lines in the illustration show a projection of the interference pattern onto the Diffraction Scale (as it appears when looking through the slits). Notice that θ´ = arctan X/L. It can also be shown from the diagram that, if BP is parallel to AP as we have already assumed, then θ´ = θ. Therefore, θ = arctan X/L; and AB sin (arctan X/L) = nλ.

Looking through the pair of slits (pattern D) at the Light Source filament, make measurements to fill in Table

9.1. Alternately place the Red, Green, and Blue color filters over the Light Source aperture to make the measurements for the different colors of light. If you have time, make measurements with the other two-slit patterns as well (patterns E and F on the Diffraction Plate). Perform the calculations shown to determine the wavelength of Red, Green, and Blue Light.

Additional Questions

➀ Assume, in the diagram showing the geometry of the experiment, that AP and BP are parallel.

Show that θ = θ´.

➁ Suppose the space between the slits was smaller than the wavelength of light you were trying to measure.

How many orders of maxima would you expect to see?

012-02744K Introductory Optics System

Experiment 10: Polarization

EQUIPMENT NEEDED:

-Optical Bench -Light Source

-Polarizers (2) -Component Holders (3)

-Ray Table and Base -Ray Table Component Holder

-Cylindrical Lens -Crossed Arrow Target

-Slit Plate -Slit Mask.

_ E (Electric Field)

90˚

(a) (b) (c)

_ n (direction of

propagation)

90˚

_ B (magnetic Field)

(d)

Introduction

Light is a transverse wave; that is, the electromagnetic disturbances that compose light occur in a direction perpendicular to the direction of propagation (see Figure 10.1a). Polarization, for light, refers to the orientation of the electric field in the electromagnetic disturbance. The magnetic field is always perpendicular to the electric field. Figure 10.1b and 10.1c show vertical and horizontal polarization, respectively. Figure 10.1d depicts random polarization, which occurs when the direction of polarization changes rapidly with time, as it does in the light from most incandescent light sources.

Your optics equipment includes two Polarizers, which transmit only light that is plane polarized along the plane defined by the 0 and 180 degree marks on the Polarizer scales. Light that is polarized along any other plane is absorbed by the polaroid material. Therefore, if randomly polarized light enters the Polarizer, the light that passes through is plane polarized. In this experiment, you will use the Polarizers to investigate the phenomena of polarized light.

Figure 10.1 Polarization of Light

Crossed Arrow Target

Polarizer A

Polarizer B

Figure 10.2 Equipment Setup

Introductory Optics System 012-02744K

Figure 10.3 Equipment Setup

Procedure

Set up the equipment as shown in Figure 10.2. Turn the Light Source on and view the Crossed Arrow Target with both Polarizers removed. Replace Polarizer A on the Component Holder. Rotate the Polarizer while viewing the target.

➀ Does the target seem as bright when looking through the Polarizer as when looking directly at the target? Why?

_______________________________________________________________________

_______________________________________________________________________.

➁ Is the light from the Light Source plane polarized? How can you tell?__________________

____________________________________________________________________. Align Polarizer A so it transmits only vertically polarized light. Replace Polarizer B on the other Component

Holder. Looking through both polarizers, rotate Polarizer B.

➂ For what angles of Polarizer B is a maximum of light transmitted? For what angles is a minimum of light

transmitted?_________________________________________________

____________________________________________________________________.

Polarization by Reflection: Brewster’s Angle

Set up the equipment as shown in Figure 10.3. Adjust the components so a single ray of light passes through the center of the Ray Table. Notice the rays that are produced as the incident ray is reflected and refracted at the flat surface of the Cylindrical Lens. (The room must be reasonably dark to see the reflected ray.)

Rotate the Ray Table until the angle between the reflected and refracted rays is 90°. Arrange the Ray Table Component Holder so it is in line with the reflected ray. Look through the Polarizer at the filament of the light source (as seen reflected from the Cylindrical Lens), and rotate the Polarizer slowly through all angles.

➀ Is the reflected light plane polarized? If so, at what angle from the vertical is the plane of polarization?

____________________________________________________________________ ____________________________________________________________________. Observe the reflected image for other angles of reflection.

➁ Is the light plane polarized when the reflected ray is not at an angle of 90° with respect to the refracted

ray? Explain. ____________________________________________________________________

____________________________________________________________________.

012-02744K Introductory Optics System

(a) (b)

Experiment 11: Image Formation from Cylindrical Mirrors

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-Ray Table and Base -Component Holder (2)

-Slit Plate -Ray Optics Mirror

-Parallel Ray Lens.

Parallel Ray

Lens

F.L.

Optical Axis of

Mirror

Figure 11.1 Equipment Setup

Introduction

Ray tracing techniques can be used to locate the image formed by reflection from any mirror of known shape. Simply think of the object as a collection of point sources of light. For a given point source, light rays diverging from it are reflected from the mirror according to the Law of Reflection. If the reflected rays intersect at a point, a real image is formed at that point. If the reflected rays do not intersect, but would if they were extended back beyond the mirror, a virtual image is formed which appears to be located at the point where the extended rays cross.

In this experiment, you will use the Ray Table to study the properties of image formation from cylindrical surfaces. The properties you will observe have important analogs in image formation from spherical mirrors.

Procedure

Set up the equipment as shown in Figure 11.1. Position the Ray Optics Mirror on the Ray Table so the rays are all reflected from the concave surface of the mirror.

Focal Point

Adjust the position of the Parallel Ray Lens to obtain parallel rays on the Ray Table. Adjust the mirror on the Ray Table so the incident rays are parallel to the optical axis of the mirror.

➀ Measure F.L., the focal length of the concave cylindrical mirror.

F.L. = _______________________________________.

➁ Use ray tracing techniques to measure the focal length of

the convex cylindrical mirror. (Check your textbook if you have doubts about the sign conventions.)

F.L. = _______________________________________. Position the Light Source and the Parallel Ray Lens so the rays cross at a point on the Ray Table, as shown in Figure

11.2a. (A blank, white sheet of paper placed over the Ray Table will help to see the rays.) Since rays diverge from this point of intersection, it can be used as an object.

Figure 11.2 Virtual Object

Introductory Optics System 012-02744K

Place the convex side of the Ray Optics Mirror so that its focal point is coincident with the point where the rays cross, as in Figure 11.2b. Of course, with the mirror in this position, the rays are reflected and don’t actually cross. The point where the rays did cross, though, can be used as a virtual object.

➂ Describe the reflected rays when a virtual object is positioned at the focal point of the convex mirror.

Image Location

Remove the Parallel Ray Lens. Slide the Slit Plate, Ray Table, and mirror along the Optics Bench, as far as possible from the Light Source. Orient the mirror as in Figure 11.1.

➀ Where is the image of the light bulb filament formed? ______________________________. ➁ How is image location affected as you move the mirror closer to the filament? ____________

_________________________________________________________________________.

➂ Is an image still formed when the distance between the filament and mirror is less than the focal length of

the mirror? If so, what kind? _____________________________________.

➃ Using the convex side of the mirror, can you obtain a real image of the Light Source filament? If so,

how? _______________________________________________________________.

Magnification and Inversion

In the plane of the Ray Table, the filament of the Light Source acts as a point source. To observe magnification and inversion, an extended source is needed. As shown in Figure 11.3, two positions of the Light Source filament can be used to define an imaginary arrow, of height ho.

Position the filament of the Light Source first at the tail of the imaginary arrow, then at the tip. For each position, locate the image. The magnification is determined by dividing h

, the height of the image arrow, by ho, the

height of the object arrow.

Measure the magnification for several different distances between the light source and the mirror.

➀ Qualitatively, how does the degree of magnification depend on the distance between the object and the mirror?

____________________________________________________________.

➁ Is the image inverted? Does image inversion depend on object location? ____________________.

________________________________________________________________________________.

Cylindrical Aberration

Cylindrical aberration is the distortion of the reflected image caused by imperfect focusing of the reflected rays. Place a blank sheet of paper over the Ray Table. Arrange the equipment so all the light rays are reflected from the concave surface of the mirror. Block all but two rays and mark the point of intersection. Do this for several pairs of rays.

➀ Are all the rays focused at precisely the same point?________________________________. ➁ How would you alter the shape of the cylindrical lens to reduce the amount of cylindrical aberra-

tion?________________________________________________________________.

For each position of the light source Two positions of the light source filament define an imaginary arrow.

Slit Plate

filament, an image is formed, defining

the image of the imaginary arrow.

Figure 11.3 Magnification and Inversion

012-02744K Introductory Optics System

Experiment 12: Image Formation from Spherical Mirrors

EQUIPMENT NEEDED:

-Optics Bench, Light Source -Component Holder (3)

-50 mm F. L. Spherical Mirror -Viewing Screen

-Crossed Arrow Target.

Spherical Mirror

Introduction

Figure 12.1 Equipment Setup

If you cut a thin strip along any diameter of a spherical mirror, the result is a close approximation to a thin cylindrical mirror. With this in mind, it's not surprising that images formed with spherical mirrors exhibit many of the same properties as those formed with cylindrical mirrors. In this experiment, you will investigate some of these properties.

Procedure

Focal Length

Set up the equipment as shown in Figure 12.1, with the concave side of the mirror facing the Light Source. The Viewing Screen should cover only half the hole in the Component Holder so that light from the filament reaches the mirror.

To verify the focal length of the mirror, position the mirror on the optical bench as far from the Crossed Arrow Target as possible. Vary the position of the Viewing Screen to find where the image of the target is focused.

➀ What is your measured focal length for the concave spherical mirror?

F.L. = ________________________________________________.

➁ How might you determine the focal length more accurately? _______________________.

Image Location, Magnification, and Inversion

In Experiment 7, you tested the validity of the Fundamental Lens Equation: 1/do + 1/di = 1/f, for which the magnification of the image is given by the equation: m = -di/do.

In this experiment you will test the validity of this same equation for image formation in a spherical mirror.

Set the distance between the concave mirror and the Crossed Arrow Target to the values shown in Table

12.1. At each position, place the Viewing Screen so the image of the target is in sharp focus. Use your data to fill in Table 12.1. Perform the calculations shown in the table to determine if the Fundamental Lens Equation is also valid for real images formed from a spherical mirror.

➂ Are your results in complete agreement with the Fundamental Lens Equation? If not, to what do you

attribute the discrepancies? _______________________________________.

Introductory Optics System 012-02744K

Virtual Images

In the previous part of this experiment, you tested the Fundamental Lens Equation only for the concave mirror, and only for those cases in which a real image was focused between the object and the mirror. However, when an object is placed between a concave mirror and its focal point, a virtual image is formed. Virtual images can also be formed using a convex spherical mirror.

In the Appendix of this manual, read the section titled “Locating Virtual Images”. Construct a table similar to Table 12.1 and

Data Calculations

(mm) d

500

450

400

350

300

250

200

150

100

Table 12.1

1/di + 1/d

1/f hi/ho-di/d

use the Image Locators to collect your data. Remember, for a virtual image, d

is negative.

➀ Are your results compatible with the Fundamental Lens Equation? If not, to what do you attribute the

difference? _________________________________________________.

Repeat the procedure with the convex side of the Spherical Mirror.

➁ Does the Fundamental Lens Equation hold for images formed by convex spherical mir-

rors?______________________________________________________________.

Spherical Aberration

Adjust the position of the Light Source and Crossed Arrow Target so the image of the target on the screen is reasonably large and as sharp as possible.

➀ Is the focus of the image sharpest at its center or at its edges? (This is a subtle effect which is easier to

observe in a darkened room.) __________________________________________.

Place the Variable Aperture on the Component Holder as shown in Figure 12.2. The bottom of the V formed by the Aperture plates should be aligned with the notch in the top of the Component Holder.

➁ Vary the size of the aperture. How does this affect

the focus of the image? ____________________

______________________________________.

➂ Explain your observations in terms of spherical

Variable

Aperture

Spherical

Mirror

aberration. ______________________________

_______________________________________.

➃ What aperture size would give the best possible focus

of the image? Why is this size aperture impractical? _________________________________________

______________________________________.

Figure 12.2 Using the Variable Aperture

012-02744K Introductory Optics System

Experiment 13: Image Formation with Cylindrical Lenses

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-Ray Table and Base -Component Holder (2)

-Slit Plate -Cylindrical Lens

-Parallel Ray Lens -Slit Mask

Introduction

You have investigated image formation through reflection. The principles at work in image formation through refraction are analogous. Similar ray tracing techniques can be used to determine the form and location of the image. The important differences are (1) the Law of Refraction replaces the Law of Reflection in determining the change in direction of the incident rays; and (2) the bending of the rays takes place at two surfaces, since the light passes into and then out of the lens.

In this experiment, you will use the Ray Table to study the properties of image formation with cylindrical lenses. The properties you will observe have important analogs in image formation with spherical lenses.

Procedure

Set up the equipment as shown in Figure 13.1. Position the Cylindrical Lens on the Ray Table so the rays are all incident on the flat surface of the lens.

Focal Point

Parallel Ray

Lens

F.L.

Figure 13.1 Equipment Setup

F.L.

Adjust the position of the Parallel Ray Lens to obtain parallel rays on the Ray Table. Adjust the Cylindrical Lens so its flat surface is perpendicular to the incident rays and so the central ray passes through the lens undeflected.

➀ Measure F.L.

F.L.

= __________________________________.

F.L.

= __________________________________.

and F.L.2. (see Figure 13.1).

Remove the Parallel Ray Lens and Component Holder. Remove the Slit Mask from its Component Holder. Set the Holder aside and replace the Slit Mask on the front of the Light Source. Move the Ray Table and Base close enough to the Light Source so the filament of the Light Source is a distance f

from the curved side of the

Cylindrical Lens

➁ Describe the refracted rays.___________________________________________________. ➂ Turn the Cylindrical Lens around and place it on the Ray Table so that its straight side is a distance f

from the

filaments (you may need to move the Ray Table and Base closer to the Light Source).

Describe the refracted rays. __________________________________________________.

Introductory Optics System 012-02744K

Why is one focal length shorter than the other? (Hint: consider the refraction of the light rays at both surfaces of the lens.)____________________________________________________.

Image Location

Remove the Slit Mask from the front of the Light Source. Move the Ray Table and Base so it is as far from the Light Source as possible. Set the Cylindrical Lens on the Ray Table with the straight side toward the Light Source.

➀ Where is the image formed? ___________________________________________________.

➁ What happens to the location of the image as you move the Light Source closer?

_____________________________________________________________________.

➂ Is an image still formed when the Light Source is closer than the focal length of the lens? If so, what

kind? ______________________________________________________________.

Magnification and Inversion

In the plane of the Ray Table, the filament of the Light Source acts as a point source. To observe magnification and inversion, an extended source is needed. As shown below, two positions of the Light Source filament can be used to define an imaginary arrow, of height h

Position the filament of the Light Source first at the tail of the imaginary arrow, then at the tip. At each position, locate the image of the filament. The height of the image arrow, h

, divided by the height of the

object arrow, ho, is the magnification of the image.

Measure the magnification for several different distances between the Light Source and the lens.

➀ Qualitatively, how does the degree of magnification depend on the distance between the object and the

lens?________________________________________________________________.

➁ Is the image inverted? Is it inverted for all object loca-

tions?______________________________________________________________________.

Cylindrical Aberration

Cylindrical aberration is the distortion of the image caused by imperfect focusing of the refracted rays. Place a blank sheet of paper over the Ray Table. Arrange the equipment as in Figure 13.1 so all the light rays are refracted by the Cylindrical Lens. Use the Slit Mask to block all but two rays. Do this for several pairs of rays.

➀ Are all the rays focused at precisely the same point? ________________________________.

➁ How would you alter the shape of the lens to reduce the amount of cylindrical aberration?

_____________________________________________________________________________.

Two positions of the light source filament define an imaginary arrow.

Slit Plate

For each position of the filament, an image is formed, defining the image of the imaginary arrow.

Figure 13.2 Magnification and Inversion

012-02744K Introductory Optics System

Experiment 14: Spherical Lenses—Spherical and Chro-

matic Aberration, Aperture Size, and Depth of Field

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-75 mm Focal Length Convex Lens -Variable Aperture

-Crossed Arrow Target -Viewing Screen

-Component Holders (3)

Crossed Arrow Target

Variable Aperture

75 mm Lens

Viewing Screen

Introduction

No matter how perfectly a spherical lens is formed, there will always be some degree of image distortion. One source of distortion, spherical aberration, could be eliminated by changing the shape of the lens (from spherical to paraboloid). As you will see in this experiment, however, there are simpler ways of reducing, though not eliminating, spherical aberration.

Chromatic aberration arises because lens materials have slightly different indexes of refraction for different colors (wavelengths) of light. Because of this, incident white light is separated by a lens into its constituent colors, and different colored images are formed at slightly different locations. Chromatic aberration can be corrected only with the use of compound lenses in which two or more lenses of different material and shape are combined.

Procedure

Set up the equipment as shown in Figure 14.1. Begin with the Variable Aperture fully open. Vary the distance between the Lens and Viewing Screen until an image of the Crossed Arrow Target is focused on the screen.

Spherical Aberration

Slowly close the Variable Aperture. Be sure that the V formed by the two aperture plates remains centered on the notch at the top of the Component Holder. Observe the image of the Crossed Arrow Target on the screen.

Figure 14.1 Equipment Setup

➀ How is the focus of the image effected by the size of the aperture? ________________________

______________________________________________________________________________.

➁ What size aperture would give the best possible image focus? Why is this aperture size not practical?

_________________________________________________________________________.

Introductory Optics System 012-02744K

Depth of Field

Viewing Screen

Depth of Field

Crossed Arrow

Target

Figure 14.2 Depth of Field

Lens

Variable

Aperture

In addition to spherical aberration, aperture size has an important effect on another variable of image focusing; depth of field. Depth of field is a measure of how much the distance between the lens and screen can be varied while still retaining a well focused image (see Figure 14.2).

To investigate this phenomenon, begin with the Variable Aperture fully open. Measure the depth of field. Now vary the size of the aperture, measuring the depth of field for each size.

➀ How does depth of field depend on aperture size? __________________________________

__________________________________________________________________________.

➁ Why is it not possible to have a depth of field that is infinitely long? ___________________

__________________________________________________________________________.

With the aperture size very small (less than 1 mm), remove the lens from the Component Holder.

➂ Is an image of the Crossed Arrow Target still visible on the screen? ____________________

__________________________________________________________________________.

➃ How do variations in the size of the aperture affect the focus of the image? ______________

__________________________________________________________________________.

➄ How does varying the distance between the Variable Aperture and the Viewing Screen affect the magni-

fication of the image? ________________________________________________.

➅ Why does a very small aperture allow formation of an image without using the lens? (Hint: consider

the role played by the lens in focusing the diverging rays from a point object.)

Chromatic Aberration

Replace the lens and remove the Crossed Arrow Target from the Light Source. Using a small aperture size (2-3 mm), focus the filament of the Light Source onto the screen. Slide the aperture plates slowly to one side, away from the optical axis of the lens, as shown below. Do not change the size of the aperture. Notice the color separation in the image of the filament as the aperture gets sufficiently far from the optical axis of the lens.

➀ Why is chromatic aberration more apparent when the aperture is far from the optical axis of the lens?

__________________________________________________________________.

Variable Aperture Displaced From The Optical Axis

Aperture open 2-3 mm

Figure 14.3 Chromatic Aberration

Lens

Viewing Screen

012-02744K Introductory Optics System

. .

.. .

. .

..........

......

....

.........

....

.......

.........

....

..........

.......

....

........

......

....

.........

....

.......

........

......

....

.........

....

.........

....

.......

.........

....

..........

......

....

......

....

......

....

R A

P L A

Experiment 15: The Diffraction Grating

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-Ray Table Base -Component Holder

-Diffraction Scale -Diffraction Plate

-Diffraction Grating -Slit Mask

-Color Filter (any color). Perform in a well lighted room.

Introduction

Diffraction gratings are used to make very accurate measurements of the wavelength of light. In theory, they function much the same as two slit apertures (see Experiment 9). However, a diffraction grating has many slits, rather than two, and the slits are very closely spaced. By using closely spaced slits, the light is diffracted to large angles, and measurements can be made more accurately. In spreading out the available light to large angles, however, brightness is lost. By using many slits, many sources of light are provided, and brightness is preserved.

Diffraction Scale

Figure 15.1 Equipment Setup

Slot

Slit Mask

Ray Table

Base

Diffraction

Plate

Window

In this experiment you will use a diffraction grating to determine the range of wavelengths for each of the colors in the visible spectrum.

Procedure

Arrange the equipment as shown in Figure 15.1. When looking through the Diffraction Plate window, the filament of the Light Source must be directly visible through the slot in the Diffraction Plate. Look through each of the double slit patterns (Patterns D, E, and F) of the Diffraction Plate at the filament of the Light Source. Qualitatively, compare the spacing of the interference maxima for the different patterns.

➤NOTE: You may find that a blue/green color filter placed behind the Slit Mask will make it easier to distinguish the details of the diffraction patterns.

➀ How does the spacing of the maxima relate to the spacing of the slits on the Diffraction Plate (compare

patterns of equal slit width, but different slit spacing)?

__________________________________________________________.

➁ Look through the 10-slit pattern (Pattern G) at the filament. What effect does the larger number of slits

have on the diffraction pattern?_________________________________.

Introductory Optics System 012-02744K

Table 15.1

Data Calculations

Color A L X

Violet

Blue

Green

Yellow

Orange

Red

Color Image

seen on

Diffraction Scale

X2 green

yellow)

X1 green

blue)

Diffraction

Scale

red

orange

yellow

green

blue

violet

blue

green

yellow

orange

red

Diffraction Grating

λλ

λ = A sin θ = A sin (arctan )

λλ

x L

λλ

A = Slit spacing = 6000 slits/cm

A = 0.00016cm

red

Slits

orange yellow green blue violet

violet blue green yellow orange red

1st

maximum

Zeroth

maximum

1st

maximum

Image on the

Retina of

your eye

Figure 15.2 Measurements with the Diffraction Grating

Remove the Diffraction Plate and the Slit Mask and replace them with the Diffraction Grating. Look through the grating and observe the first order spectrum.

➤NOTE: When looking through the Diffraction Grating avert your eye from looking straight at the filament. Instead, look at a position on the Diffraction Scale about 4 to 5 cm to the right or left of the slit in the scale.

Using Figure 15.2 to identify the variables, fill in the data in Table 15.1. Review Experiment 9, if necessary, to determine the calculations needed to calculate λ

and λ2, the range of

wavelengths corresponding to each particular color of light.

Compare your results with those of other students, or with textbook values.

➀ Are your results in complete agreement? Can you account for any discrepancies?

➁ What advantages are there in using wavelength rather than color to characterize visible light?

012-02744K Introductory Optics System

. .

R A

I H

Experiment 16: Single Slit Diffraction

EQUIPMENT NEEDED:

-Optical Bench -Light Source

-Ray Table Base -Diffraction Scale

-Component Holder -Diffraction Plate

-Slit Mask -Color Filters (Red, Green, Blue/Green). Perform in a well lighted room.

Introduction

If you look closely at a two slit interference pattern, you will notice that the intensity of the fringes varies. This variation in intensity forms an interference pattern of its own that is independent of the number of slits or the separation between the slits. In fact, two slits are not required to see this pattern; it can be seen most clearly when light passes through a single, narrow slit.

Diffraction Scale

Figure 16.1 Equipment Setup

Slot

Slit Mask

Ray Table

Base

Diffraction

Plate

Window

In this experiment you will compare the single slit diffraction pattern with the double slit pattern, and then use the single slit pattern to measure the wavelengths of red, green, and blue light.

Procedure

Setup the equipment as shown in Figure 16.1. Look through each of the three single slit apertures in the Diffraction Plate (Patterns A, B, and C). Examine the diffraction patterns with and without color filters over the aperture of the Light Source.

➀ How does the spacing between fringes vary with the width of the slit?______________________

______________________________________________________________________________.

Compare the single slit patterns with the double slit patterns.

➁ How does a double slit interference pattern differ from a single slit pattern? (Compare patterns of equal

slit widths, such as A

_____________________________________________________________________________.

vs D, or B vs E.)__________________________________________

Introductory Optics System 012-02744K

1st

maximum

1st

minimum

zeroth

maximum

Diffraction

Scale

__ AB = W

Diffraction Grating

Retina of

your eye

Figure 16.2 Geometry of Single Slit Diffraction

The single slit pattern can be explained using Huygen’s theory. When a plane wave front strikes the slit, each point on the slit acts as a point source of light. Figure 16.2 shows a point P, far from the slit, where the distance AP = BP + λ. Since light from point A travels one wavelength farther than light from point B, the light from these two points is in phase at point P. But light reaching point P from the points in between A and B will vary in phase through a full 360°. For any point from which light reaches point P at a particular phase, there will be a point from which light arrives in the exact opposite phase. Because of this, there is complete cancellation at point P, and a minima (dark fringe) will be seen at that point.

1st

maximum

1st

minimum

Zeroth

maximum

1st

minimum

1st

maximum

In the Figure, point P is at an angle q from the center of the slit. We make the assumption that point P is far enough away such that AP and BP are very nearly parallel (this is true in reality, if not in the diagram). As shown in the diagram, angle ABC = θ , also. Therefore W sin θ = λ; where W is the width of the slit (AB). A similar argument can be used to show that a minima will be found at any angle such that W sin θ = nλ , where n is any integer.

Review the two slit interference experiment. Notice the similarity between the equations for single and double slit patterns. To measure the wavelength of light, use the same techniques you used in the two slit experiment (θ = arctan X/L). When measuring the distance to the minima (x) for each color, place the Color Filter on the front of the Light Source. Use your data to fill in Table 16.1, then perform the calculations shown to determine the wavelength of Red, Green, and Blue Light.

➀ If the width of the slit, W, were less than the wavelength of the light being used, how many

maxima would you expect to see in the single slit diffraction pattern? Why?____________

________________________________________________________________________.

Table 16.1

Data Calculations

Color n W X L arctan X/L Wsin (arctan X/L) =

Red

λλ

Green

Blue

012-02744K Introductory Optics System

Experiment 17: General Diffraction

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-Component Holders (2) -Variable Aperture

-Diffraction Plate -Slit Mask

-Color Filter (any color) -Black Construction Paper

-pin.

E T

D O I

R F F

. . . .

. .

. . .

. .

. . .

. .

. . . .

. . . . ..

. . . .

. . . . . . . ..

. . . . .. . .

. . . . .. . . . .

. . . . ..

. . . . . . . ..

. . . . .. . . .

. . . .. . .

. . .

. . . . . . .

. . . . .

. . . . .. . . . .

. . . . .. . .

. . . . .

. . . . .. . . .

F F R

Figure 17.1 Equipment Setup

Introduction

The simplest diffraction patterns are produced by narrow slits. However, any aperture, or collection of apertures, will produce a diffraction pattern if the dimensions of the apertures are of the same order of magnitude as the wavelength of visible light.

The diffraction pattern created by a particular aperture can be determined quantitatively using Huygen’s principle. Simply treat each aperture as a collection of point sources of light (small, closely packed points will give the best approximation of the diffraction pattern). At any position on your viewing screen, determine the phase of the light contributed by each point on the aperture. Finally, use the superposition principle to sum the contributions from all the points on the aperture.

Of course, you must perform this same calculation for each point on your viewing screen to determine the complete diffraction pattern—a time consuming task. In this experiment the approach will be more qualitative. You will use your knowledge of diffraction patterns formed by slits to understand the patterns formed by more complicated apertures.

Procedure

Setup the equipment as shown in Figure 17.1. Begin with the Variable Aperture fully open. Looking through the Diffraction Plate at the Light Source filament, examine the diffraction patterns formed by Patterns H, I, and J.

While looking through Pattern H, slowly close the Variable Aperture. Repeat this with Patterns I and J.

➀ What effect does aperture size have on the clarity of the diffraction patterns?

➁ What affect does aperture size have on the brightness of the diffraction patterns?

Adjust the Variable Aperture to maximize the brightness and clarity of the pattern. Place a color filter over the Light Source Aperture.

➂ In what way does the color filter simplify the diffraction patterns that are formed?

Introductory Optics System 012-02744K

Crossed Slits

Examine the diffraction pattern formed by aperture H, the crossed slits. As you watch the pattern, slowly rotate the Diffraction Plate so first one slit is vertical, then the other.

➀ Describe the diffraction pattern in terms of the patterns formed by each individual slit.

Random Array of Circular Apertures

Examine the diffraction pattern formed by aperture I, the random array of circular apertures. The pattern is similar to that formed by diffraction through a single circular aperture. To verify this, use a pin to poke a small hole in a piece of black construction paper. Look at the Light Source filament through this hole. In the pattern formed by the random array, the patterns from all the circular apertures are superposed, so the combined diffraction pattern is brighter.

In the random array, smaller circles are used than you can produce with a pin.

➀ What effect does the smaller diameter of the circles have on the diffraction pattern?

In observing single slit diffraction, you found that the narrower the slit, the greater the separation between the fringes in the diffraction pattern. This is generally true. For any aperture, diffraction effects are most pronounced in a direction parallel with the smallest dimension of the aperture.

➁ Use the above generalization to explain the symmetry of the diffraction pattern formed

by a circular aperture.

Square Array of Circular Apertures

Examine the diffraction pattern formed by aperture J, the square array of circular apertures.

➀ How is this pattern similar to that formed by the random array? How is it different?

Each circular aperture in the array forms a circular diffraction pattern with maxima and minima appearing at different radii. However, the regularity of the array causes there to be interference between the patterns formed by the individual circles. This is analogous to the way in which the double slit interference pattern creates maxima and minima that are superimposed on the single slit patterns created by the individual slits.

➁ On a separate sheet of paper, draw the diffraction pattern you would expect if there were

no interference between the patterns from the different holes (as in the random array). Clearly indicate the maxima and the minima.

➂ To understand the interference that takes place, consider the array of points as if it were

actually a collection of parallel slits, such as those shown in Figures 17.2a, b, and c. Draw the diffraction patterns that would be created by each of these collections of parallel slits. Clearly label the maxima and minima.

➃ Your drawing from step 2 shows where the light

is diffracted to from each individual circular aperture. To approximate the effect of interference between circular apertures, superimpose a copy of one of your interference patterns from step 3 over your drawing from step 2. Only where maxima overlap, will there be maxima in the combined pattern. Repeat this procedure for each of your interference drawings.

(a) (b) (c)

Figure 17.2 Square Array Interference

012-02744K Introductory Optics System

Experiment 18: Introduction to Optical Instruments

EQUIPMENT NEEDED:

-none

Introduction

The design of high quality optical instruments can be quite complex, involving compound lenses and intricate lens coatings. But the complexity arises primarily from the need to reduce the effects of spherical and chromatic aberration (see Experiment 14). Understanding the basic principles of standard optical instruments is not complex. It requires only an understanding of the Fundamental Lens Equation:

1/d

+ 1/di = 1/f;

for which the magnification of the image is given by the equation:

m = -d

i/do

In Experiments 19-22, you will use the above equations to investigate the workings of a Projector, a Magnifier, a Telescope, and a Compound Microscope. Before beginning, however, it is useful to understand certain generalities that can be made with regard to these equations.

Procedure

Use the Fundamental Lens Equation to complete Table 18.1, on the following page. Show the location (di) and magnification (m) of the image, and whether the image is real or virtual, inverted or uninverted. Notice that do is given in units of f. Your calculated value for di will therefore also be in units of f.

After completing the table, use it to answer the following questions. In each question, assume that f > 0 (as for a converging lens). A negative value for d

➀ For what range of d

(Remember: d

➁ For what range of do values is the image real and magnified?

values is the image virtual and magnified?

dof

= )

- f

indicates that the image is virtual.

➂ For what range of d

➃ For what range of d

values is the image real and reduced in size?

values can the image be focused onto a viewing screen?

Introductory Optics System 012-02744K

Table 18.1: Object/Image Relationships

m Real/Virtual Inverted/Uninverted

Example f/16 -f/15 16/15 Virtual Uninverted

f/8

f/4

f/2

3f/4

7f/8

15f/16

17f/16

9f/8

5f/4

3f/2

7f/4

15f/8

31f/16

33f/16

17f/8

9f/4

5f/2

11f/4

23f/8

10f

100f

012-02744K Introductory Optics System

Experiment 19: The Projector

EQUIPMENT NEEDED:

-Optics Bench -Light Source

-75 mm Focal Length Convex Lens -150 mm Focal Length Convex Lens

-Variable Aperture -Crossed Arrow Target

-Viewing Screen -Component Holders (3).

Introduction

When an object is located between the focal point (f) and twice the focal point (2f) of a converging lens, a real, inverted, magnified image is formed as shown in the diagram of Figure 19.1. If a viewing screen is placed at the location of the image, the image will be focused onto the screen. In this case the lens functions as a projector.

Crossed Arrow Target

Variable Aperture

Figure 19.1 Equipment Setup

75 mm Lens

Viewing Screen

Procedure

Set up a projector as shown in Figure 19.1. Try both the 75 and 150 mm converging lenses.

➀ What happens to the image if d

Why or why not? _______________________________________________________

_____________________________________________________________________________.

➁ What happens to the image if d

Screen? Why or why not? ____________________________________________________

_____________________________________________________________________________.

➂ Are there practical limits to the degree of magnification of the image? If so, what are they?

_____________________________________________________________________________.

Is it possible, using a single lens, to project an image that is uninverted? ___________________

_____________________________________________________________________________.

➃ Can the image formed by a projector be viewed without using a viewing screen? If so, where must the

observer be? _______________________________________________________________

_____________________________________________________________________________.

is less than f? Can the image still be focused onto the Viewing Screen?

is greater than 2f? Can the image now be focused onto the Viewing

Introductory Optics System 012-02744K

Notes

012-02744K Introductory Optics System

Experiment 20: The Magnifier

EQUIPMENT NEEDED:

-Optics Bench -75 mm Focal Length Convex Lens

-150 mm Focal Length Convex Lens -Viewing Screen

-Component Holders (2)

Introduction

When an object is located between a converging lens and its focal point, a virtual, magnified, uninverted image is formed. Since the image is not real, it can not be focused onto a screen. However, it can be viewed directly by an observer.

Procedure

Set up a magnifier as shown in Figure 20.1 First try it with the 75 mm focal length lens, and then with the 150 mm focal length lens. For each lens, adjust the distance between the object (the Viewing Screen) and the lens so the magnification is a maximum and the image is clearly focused.

Figure 20.1 The Magnifier

Examine Table 18.1 from Experiment 18.

➀ Does the Fundamental Lens Equation place any

limit on the magnification, m, that a lens can produce? ______________________________

______________________________________

_____________________________________.

➁ Looking through the lenses, which lens seems to

provide the greater magnification? __________

______________________________________

_____________________________________.

eye of the

observer

eye

Figure 20.2 Angular Magnification

Introductory Optics System 012-02744K

Using each of the lenses as a magnifier, it should be clear that the magnification provided by a converging lens is not unlimited. This does not mean that the equation m = -d

is in error. This

i/do

equation does give the correct ratio between the image size and the object size. However, image size is not the only important variable in determining the magnification of an optical system, such as a magnifier. Equally important is the distance between the observer and the image he is looking at. Just as a distant object appears smaller than the same object up close, an image viewed through an optical system appears larger if the image is close than if it is farther away.

Figure 20.2 shows an object of height h the retina of the observer is proportional to the angle θ which the Fundamental Lens Equation holds), θ

There is an important limitation to the magnitude of θ

, a distance do from the observer. The size of the image on

eye

. For small angles, (the only angles for

eye

= ho/do.

. To see this, hold an object at arms length

eye

and move it slowly toward your eye (with one eye closed). There is a distance—called the near point—at which the image begins to blur, because the rays entering your eye from the object are too divergent for your eye to focus. The near point differs for different people, but the average is approximately 25 cm. Therefore θ

= ho/25 cm, where θ

eye-max

is the maximum value of θ

eye-max

which the eye can focus an image.

When using a magnifier, or any optical system for that matter, the apparent size of the image depends on the size and location of the image rather than on the size and location of the object, so that θ

, the angular magnification for the magnifier, is equal to hi/di. From the Fundamental Lens

mag

Equation hi = mho = (-di/do) ho. Therefore, ignoring the minus sign,

= ho/do, the same as without the magnifier.

mag

This result seems to imply that a magnifier doesn't produce any magnification. However, using a magnifier, the object can be brought closer to the eye than the near point, and yet still be focused by the eye. If the object is placed at the focal point of the magnifier for example, the equation θ = ho/do becomes θ

= ho/f. Therefore, the magnifying power of a magnifier is a function of how

mag

much closer it allows the observer to be to the object. This, in turn, is a function of the focal length of the magnifying lens.

The magnifying power of a lens (called the angular magnification) is calculated as

mag/θeye-max

= 25 cm/f.

➂ Calculate the angular magnification for the 75 mm and 150 mm focal length lenses. Are your

calculated magnifications consistent with your answer to question 1? ____________ ________________________________________________________________________

eye

for

mag

________________________________________________________________________.

➃ Would a converging lens with a 50 cm focal length be useful as a magnifier? Why or why not?

____________________________________________________________________

________________________________________________________________________.

012-02744K Introductory Optics System

Experiment 21: The Telescope

EQUIPMENT NEEDED:

-Optics Bench -75 mm Focal Length Convex Lens

-150 mm Focal Length Convex Lens -Component Holders (2)

(150 mm Lens)

(75 mm Lens)

Line of sight

Introduction

Telescopes are used to obtain magnified images of distant objects. As you can see by looking at Table 18.1 from Experiment 18, the image of a distant object when viewed through a single converging lens will be focused nearly at the focal point of the lens. This image will be real, inverted, and reduced in size. In fact, the greater the distance of the object (with respect to f), the smaller the size of the image.

However, this reduced image is useful. By viewing this image through a second converging lens—used as a magnifier—an enlarged image can be seen.

f1 + f2 = 225 mm

Figure 21.1 The Telescope

f1,f

Figure 21.2 Telescope Magnification

Introductory Optics System 012-02744K

Figure 21.1 shows the setup for a simple telescope. The objective lens, L1, creates a real, inverted image. (You can barely see this image in the diagram. It's very small, just inside the focal point of lens L

.) If the object is sufficiently far away, this image will be located approximately at f1, the

focal point of L1. The eyepiece, L2, then acts as a magnifier, creating a magnified, virtual image which can be viewed by the observer. For maximum magnification, L

is positioned so the virtual

image is just slightly closer than its focal point, f2. Therefore, the distance between the objective lens and the eyepiece of a telescope, when viewing distant objects, is approximately f

+ f2.

The angular magnification (see Experiment 20: The Magnifier) for a telescope can be approximated by assuming the lenses are exactly f object as seen with the naked eye is proportional to the angle q distance from the object to the telescope is large—much larger than is shown in the diagram— θ

+ f2 apart, as shown in Figure 21.2. The height of the

in the lower diagram. If the

= θ1´, to a good approximation. The ray shown in the upper diagram passes through the focal point of the objective lens, comes out parallel to the optical axis of the telescope, and is therefore refracted by the eyepiece through the focal point of the eyepiece. The angle θ2 is therefore proportional to h

, the height of the image seen by the observer.

Procedure

➀ Using Figure 21.2, calculate tan θ1 and tan θ2 as a function of the height of the image, hi, and the

focal lengths of the two lenses, f1 and f2.

tan θ

Assume that θ

= tan θ1´ = ______________________________________________.

= ________________________________________________.

and θ2 are very small, and therefore equal to tan θ1 and tan θ2, respectively.

➁ Calculate the angular magnification of the telescope.

Angular Magnification = θ

= _______________________________________ ______.

2/θ1

Set up a telescope using the 75 mm and 150 mm focal length lenses; the distance between the lenses should be approximately 225 mm. Using the 75 mm lens as the eyepiece, look at some reasonably distant object. Adjust the distance between the lenses as needed to bring the object into sharp focus.

To measure the magnification, look with one eye through the telescope, and with the other eye look directly at the object. Compare the size of the two images. (If a meter stick is used as the object, fairly accurate measurements of magnification can be made.)

➂ What is the magnification of the telescope when using the 75 mm lens as the eyepiece?

________________________________________________________________________

________________________________________________________________________.

➃ What is the magnification of the telescope when using the 150 mm lens as the eyepiece and the 75

mm lens as the objective lens?

________________________________________________________________________

________________________________________________________________________.

➄ Are your answers to questions 3 and 4 in keeping with your answer to question 2?

________________________________________________________________________

________________________________________________________________________.

012-02744K Introductory Optics System

Experiment 22: The Compound Microscope

EQUIPMENT NEEDED:

-Optics Bench, Light Source -75 mm Focal Length Convex Lens

-150 mm Focal Length Convex Lens -Variable Aperture

-Component Holders (2) -Viewing Screen

do 150 mm

Introduction

A compound microscope uses two lenses to provide greater magnification of near objects than is possible using a single lens as a magnifier. The setup is shown in Figure 22.1. The objective lens, L1, functions as a projector. The object is placed just beyond the focal point of L1 so a real, magnified, inverted image is formed. The eyepiece, L2, functions as a magnifier. It forms an enlarged virtual image of the real image projected by L1.

The real image that is projected by L Fundamental Lens Equation. That image is in turn magnified by the eyepiece by a factor of 25 cm/f (see Experiment 20: The Magnifier). The combined magnification is, therefore:

Object

(Objective

Lens)

L2 (Eyepiece)

Figure 22.1 The Compound Microscope

is magnified by an amount m = -di/do, as indicated by the

M = (-d

) (25 cm/f).

i/do

Procedure

Set up the microscope as shown in Figure 22.1. Use the 75 mm focal length lens as the objective lens and the 150 mm focal length lens as the eyepiece. Begin with the objective lens approximately 150 mm away from the object (the Viewing Screen). Adjust the position of the eyepiece until you see a clearly focused image of the Viewing Screen scale.

➀ Is the image magnified? How does the magnification compare to using the 75 mm focal length lens

alone, as a simple magnifier? __________________________________________________________________________

__________________________________________________________________________.

While looking through the eyepiece, slowly move the objective lens closer to the Viewing Screen. Adjust the position of the eyepiece as needed to retain the best possible focus.

Introductory Optics System 012-02744K

➁ Why does the magnification increase as the objective lens is moved closer to the object?

________________________________________________________________________

________________________________________________________________________.

➂ What focusing problems develop as the magnification increases?

_____________________________________________________________________

_____________________________________________________________________.

Use the Variable Aperture to restrict the path of light to the central regions of the objective lens. Vary the size of the aperture and observe the effects on focusing.

➃ What effect does the aperture have on focusing?

_____________________________________________________________________

_____________________________________________________________________.

➄ What effect does the aperture have on the brightness of the image?

_____________________________________________________________________

_____________________________________________________________________.

➅ What advantage would there be in using a 75 mm focal length lens as the eyepiece?

_____________________________________________________________________

_____________________________________________________________________.

012-02744K Introductory Optics System

1 2 3 4

Appendix

Locating Virtual Images

Virtual images can be located using the Virtual Image Locators. The following procedure is for locating virtual images formed by a spherical mirror. The procedure for lenses is similar though, of course, both image locators are placed on the far side of the lens from the observer.

Set up the equipment as shown in Figure A1. Notice that the object must be between the mirror and its focal point, f, in order for a virtual image to be formed. Look through Locator A into the spherical mirror. Move your head from side to side, and notice how the image of the locator arrow moves.

Look through Locator A into the mirror, so your line of sight is at a slight angle from the optical axis of the mirror. The setup should look approximately as in Figure A2a. Align a straightedge with the image of the locator arrow as shown in Figure A2b. Now adjust the position of Locator B until its arrow is aligned with the straightedge in your line of sight. Do this in two steps:

Locator B

50 mm Focal

Length Spherical

Figure A1 Setup for Locating Virtual Images

Mirror

Locator A

➀ Move the Locator laterally (perpendicular to the

optical axis of the bench) to remove half the distance between the straightedge and the arrow as shown in Figure A2b, then;

➁ Move the Locator longitudinally (sliding the Com-

ponent Holder along the optical axis of the bench) to complete the alignment as in A2c.

Locator B

Locator A

Check to be sure that the image of the arrow of Locator A is aligned with the straightedge, and the straightedge is aligned with the arrow of Locator B.

Now move the straightedge to the other side of the arrow of Locator A and repeat the process. Continue changing the straightedge from side to side and aligning the locator arrows until the image of the

Locator B

Straightedge

Locator A

(a)

(b)

(c)

Figure A2 Locating a Virtual Image

Introductory Optics System 012-02744K

arrow of Locator A and the arrow of Locator B remain aligned in your line of sight as you move your head from side to side. When this is the case, the arrow of Locator B is in the apparent position of the virtual image of the arrow of Locator A.

Maintenance

➀ If at any time the Light Source fails to come on,

remove the top cover of the Light Source by removing the four screws as shown in Figure A3, and replace the light bulb. If problems persist, contact PASCO scientific.

➤➤

➤NOTE: The light bulb should be replaced

➤➤

only with the following replacement part: Light Bulb: #211-2 (Available at automotive stores, or from PASCO: part # 526-016.)

➁ To avoid scratching component surfaces, clean

lenses and mirrors only with lens tissue—lens tissue can be purchased at any camera supply store.

Remove screws (4) to lift off cover

Figure A3 Light Source

➂ Care should be taken not to scratch or abuse the

surface of the magnetic pads. Should the surfaces become dirty, use only soapy water or rubbing alcohol for cleaning. Other solvents may dissolve the magnetic surface.

Replacement Parts

The following replacement parts can be ordered from PASCO scientific:

Item PASCO Part No.

Optics Bench 003-02694

Incandescent Light Source 003-07236 Light Bulb-#211-2 - All Units 526-016

Cord Set (U.S.) 516-010

Cord Set (European) 516-006

Power Supply, 12 VDC 2.5 A 540-040

Component Holder 648-02696

Ray Table 003-02702

Ray Table Base 003-02700

Ray Table Component Holder 003-02753

Slit Plate 003-02722

Slit Mask 003-02723

Ray Optics Lens 003-02736

Cylindrical Lens 003-02764

Ray Optics Mirror 003-05101

Viewing Screen 003-02730

Item PASCO Part No.

Red Color Filter 003-02746

Green Color Filter 003-02748

Blue/Green Color Filter 003-02750

75 mm F.L. Convex Lens 003-02710

150 mm F.L. Convex Lens 003-02716

– 150 mm F.L. Concave Lens 003-02713

50 mm F.L. Spherical Mirror 003-02714

Crossed Arrow Target 003-02732

Polarizer 003-02709

Variable Aperture 003-02726

Virtual Image Locator 003-02734

Diffraction Plate 003-02742

Diffraction Grating 003-02756

Diffraction Scale 003-02757

Manual and Experiments Guide 012-02744

012-02744K Introductory Optics System

Teacher's Guide

Exp 1: Introduction to Ray Optics

Straight-Line Propagation of Light

The rays are straight, originating from the lamp filament. Because of this, they widen and become less distinct as the distance to the filament increases.

As the slit plate is rotated from vertical, the slit images become wider and less distinct. This is caused by the greater angle subtended by the filament on the slit.

Slits aligned with filament

Image width

Filament

Slits perpendicular to filament

Filament

Slit

Image width

Slit

Ray Tracing: Locating the Filament

The measurements in steps 1 and 2 should agree very closely. (within a few millimeters)

Exp 2: The Law of Reflection

Suggestions on – Procedure

Make sure that the mirror is set up exactly on the “component” line. Any deviation will affect the accuracy of your results.

angle of: Incidence Reflection 1 Reflection 2

000

10 10 10

20 20 20

30 30 30

40 41 41

50 51 51

60 61 61

70 71 71

80 81 80

90 90 90

➀ The two trials are essentially the same, with a slight

deviation due to improper alignment of the mirror.

➁ The incident ray, reflected ray, and the normal are

all on the ray table, which is a plane.

➂ The two are equal. (This experimental trial shows a

slight deviation due to improper alignment of the mirror.)

Answers to – Questions

➀ The angle of incidence equals the angle of reflec-

tion.

The incident ray, normal, and reflected ray are all in the same plane.

➁ It doubles any error, thus allowing us to see any

error more accurately.

➂ (answers may vary)

Introductory Optics System 012-02744K

Exp 3: Image Formation in a Plane Mirror

Suggestions on – Procedure

➀

The rays seem to follow straight lines into and out of the mirror. The ones coming out of the mirror seem to be coming from a second filament behind the mirror plane.

➁ In the test setup used, the distance from the fila-

ment to the mirror plane was 10.8 cm. The distance from the image of the filament to the mirror plane was 10.3 cm.

➂ The image and object are equidistant from the mir-

ror plane.

Answers to – Questions

➀ The room will appear to be twice its actual size.

➁

➂

The sizes are the same.

mirror

reflection is inverted

Exp 4: The Law of Refraction

Suggestions on – Procedure

➀ The ray is not bent either time it goes through the

surface, as long as it goes through perpendicular to the surface.

Angle of: Incidence Refraction 1 Refraction 2

0 0.0 0.0

10 7.0 6.5

20 13.5 13.5

30 20.0 20.0

40 25.5 25.5

50 31.0 31.0

60 35.5 35.5

70 39.0 39.5

80 41.0 41.0

➁ The results are roughly the same: slight differences

are due to the lens not being centered exactly.

0.9

0.8

0.7

0.6

0.5

0.4

0.3

Sine of incident angle

0.2

0.1

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

Index of Refraction

Sine of refracted angle

slope = 1.504

data set 1 data set 2

012-02744K Introductory Optics System

➂ It is. The graph comes out completely linear, which

means that there is a direct proportionality.

➃ n = 1.50

Answers to – Questions

The beam tends to spread out more on the larger

➀

angles, due to the wider area of incidence on the flat side of the lens.

➁ Some was reflected. This reflected light could be

used to verify that the lens was aligned correctly with the ray table by noting whether the angle of refraction was the same as the angle of incidence on the ray table.

➂ If there is a systematic error, it is likely to be can-

celled by measurements taken on opposite sides.

Exp 5: Reversibility

Suggestions on – Procedure

For best results, make sure that the cylindrical lens is aligned exactly with the ray table.

Angle of:

Incidence1 Refraction1 Incidence2 Refraction2

0 0.0 0.0 1.0

10 7.0 7.0 7.5

20 13.5 13.5 19.5

30 20.0 20.0 30.0

40 25.5 25.5 39.0

50 31.0 31.0 49.0

60 35.5 35.5 59.0

70 39.5 39.5 70.0

80 41.0 41.0 77.0

0.9

0.8

0.7

slope = 1.498

0.6

0.5

0.4

0.3

0.2

Sin (angle of incidence)

0.1

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Sin (angle of refraction)

slope = 0.6662 1/slope = 1.501

Refraction 1

2 Refraction 2

➀ The index of refraction is equal to the slope of the

“Refraction 1” graph. n = 1.498

➁ The slope of data set 2 is 1/n. Thus, n = 1.501.

➂ Yes.

➃ Drawings will vary.

➄ Yes. The angle of incidence equals the angle of

reflection regardless of which side the light is coming from.

Introductory Optics System 012-02744K

Exp 6: Dispersion and Total Internal Reflection

Dispersion

Color separation was first noted at about 40°, al-

➀

though it may be noticeable before then depending on the light in the room.

➁ Maximum separation occurs at about 85°; beyond

that the violet is totally internally reflected.

➂ In order: (although not all colors may be resolvable

depending on the room light) red, orange, yellow, green, cyan, blue, violet.

➃ With an incident angle of 40°, the violet was at 76°

and the red was at 73°.

= 1.488

red

= 1.510

violet

Exp 7: Converging Lens: Image and Object Relationships

Total Internal Reflection

➀ The reflection occurs mainly at the internal flat side

of the lens.

➁ There is a reflected ray for all angles.

➂ The reflected ray is consistent with the law of re-

flection.

➃ There is not a refracted ray for all angles of inci-

dence. Beyond 43°, the light is totally internally reflected.

➄ The intensity of the reflected ray increases with the

angle of incidence; the intensity of the refracted ray decreases.

➅ All the light is reflected when the angle of refrac-

tion reaches 90°. This occurs for an angle of incidence of about 43°.

Suggestions on – Procedure

➀ The image magnification will depend on the rela-

tive placement of the lens. For any target-to-screen distance of more than four times the focal length, there will be two lens positions which will focus the image. One of these positions will enlarge the image, one will reduce it.

➁ The image will be inverted regardless of magnifi-

➂ Increasing d

➃ As d

goes to infinity, di goes to the focal length of

will decrease di.

the lens.

➄ Use the lens to focus an image of a very distant ob-

ject on the screen (d meters - preferably much longer.) Measure the image distance; it will be approximately equal to the focal length of the lens.

should be greater than two

cation.

do (mm) di hi 1/di + 1/do 1/f hi/ho -di/do % f % m

500 87 -3.5 0.01 0.01 -0.18 -0.17 1.19% 5.54%

450 90 -4.0 0.01 0.01 -0.21 -0.20 0.00% 5.00%

400 93 -4.5 0.01 0.01 -0.24 -0.23 -0.61% 1.83%

350 96 -5.5 0.01 0.01 -0.29 -0.27 -0.45% 5.25%

300 100 -6.5 0.01 0.01 -0.34 -0.33 0.00% 2.56%

250 107 -8.0 0.01 0.01 -0.42 -0.43 0.09% -1.65%

200 120 -11.5 0.01 0.01 -0.61 -0.60 -0.00% 0.87%

150 149 -19.0 0.01 0.01 -1.00 -0.99 0.33% 0.67%

100 300 -58.0 0.01 0.01 -3.05 -3.00 0.00% 1.72%

012-02744K Introductory Optics System

➃ There is nearly exact agreement. The average error

in focal length is 0.06%, the average error in magnification is 2.5%. Discrepancies are introduced due to uncertainty in the location of exact focus and uncertainty in measuring the size of the image.

➄ The final two. If the object is located at the focal

point of the lens, then the image will be located at infinity. This was the problem with the 75mm measurement: our optics bench was not long enough to handle this distance. If the object is located inside the focal length of the lens, then the image will be a virtual image on the same side of the lens as the object. Such an image can not be seen on a viewscreen: this was the problem with the 50mm measurement.

Exp 8: Light and Color

Answers to – Questions

➀

➁ Yes, but it will be a virtual image instead of a real

image, and it would be on the same side of the lens as the object.

➂ I would place the object at f. This would give me

an infinitely large image an infinite distance from the lens.

The colors of light

➀ Yes. As you change the angle of the cylindrical

lens, you can see the white light gradually break up into its component colors.

➁ The light where the three colors intersect is white.

This supports Newton’s theory by showing that white light is the combination of the other colors.

The colors of objects

➤➤

➤Note: The best way to verify the colors of the

➤➤

rays is to look directly into the rays, rather than observing them on the ray table. You may dispense with the ray table entirely, if you wish.

➀ The transmitted rays are green. There are two sets

of reflected rays: they reflect from the front and rear surfaces of the filter. The front-surface reflections are white, the rear-surface reflections are green.

➁ Now there are three sets of reflections: one white

and two green. The white comes from the front of the green filter, one green reflection comes from the back of the green filter, and one green reflection comes from the front of the red filter.

➂ The reflected rays are the same color as the inci-

dent light: blue, in this case. (The transmitted rays are a faint green.)

➃ The green filter appears green because it transmits

green light. It reflects whatever color is incident on it, but transmits primarily green. When we look at it, we see mainly the transmitted light.

➤➤

➤Another Note: The second portion of this lab

➤➤

may be slightly misleading. Most objects appear to be whatever color they are because they reflect that color, not because they transmit that color. The filters reflect all colors of incident light because they are highly polished. If they had a matte finish, then they would reflect mainly their own color.

Introductory Optics System 012-02744K

Exp 9: Two-Slit Interference

Suggestions on – Procedure

color n AB (mm) X (mm) L (mm) wavelength (m) average (m)

red 1 0.125 3 450 833e—9 725e—9

2 0.125 5 450 694e—9

3 0.125 7 450 648e—9

green 1 0.125 2 450 555e—9 555e—9

2 0.125 4 450 555e—9

3 0.125 6 450 555e—9

blue 1 0.125 2 450 555e—9 501e—9

2 0.125 3.5 450 486e—9

3 0.125 5 450 462e—9

Actual values obtained will vary due to differences in eyesight, but they should at least be ordered with red longest and blue shortest.

Answers to – Questions

➀ Here AP and BP are drawn parallel to each other.

θ '

a’ + θ’ = 90°

a + θ = 90°

a = a’, since the center line is parallel to AP. therefore, θ = θ’

➁

sin tan

–1

(unless n = 0)

sin tan

but if then

λn

However, sin(x) - 1, so the equation is not valid unless n = 0. Therefore you would expect to see only the zeroth maxima.

012-02744K Introductory Optics System

Exp 10: Polarization

Suggestions on – Procedure

➀

The target is not as bright when you look through the polarizer. This is because half of the light is blocked: the half that is polarized in the wrong direction.

➁ The light source is not polarized. There is no effect

when the polarizer is rotated, so the light source must be randomly polarized.

➂ With polarizer A set at 0°, there is a maximum

when polarizer B is at 0° or 180°. The minimum occurs when B is at 90° or 270°. Note that the minimum is not zero: some light will still be transmitted due to the fact that the polarizers used do not completely polarize the violet or the deep red light.

Brewster’s Angle

➀ The reflected light is plane polarized at 90° from

the vertical.

➁ At other angles of reflection, the light is partially

polarized; with the degree of polarization depending on the angle of incidence.

➤➤

➤Notes: It may be interesting to call attention

➤➤

to the effect of polarizers on digital watches. LCD displays work by having a polarizer just above a liquid crystal cell. When an electric field is applied to the liquid crystal, it polarizes light at 90° to the permanent polarizer, and blocks the light. This is what makes the black numbers seen on the display. If you look at a digital watch through a polarizer, it will be completely black at certain angles.

Another effect that can be tied into the investigation of Brewster’s angle is reflection off water. Such a reflection will be partially polarized, as in section 2 of the Brewster’s angle part of the lab. Polarized sunglasses make use of this; they are polarized in the opposite direction to cut glare.

Exp 11: Image Formation from Cylindrical Mirrors

Focal Point

➀ 58 mm

➁ 59 mm

➂ The reflected rays will be parallel.

Image Location

➀ 65 mm from the mirror

➁ As the mirror moves closer to the filament, the im-

age distance lengthens.

➂ Yes, it is a virtual image located on the opposite

side of the mirror from the filament.

➃ Only if you use the cylindrical lens as well.

Magnification and Inversion

➤➤

➤Note: There are two ways of moving the

➤➤

filament. One is to just slide the entire lamp some distance to the side and measure that distance. Another is to rotate the filament holder so that the filament is even with one edge of the lamp window, then rotate it to the other side. In the second method, ho is just the width of the window.

➀ The amount of magnification decreases with dis-

tance from the object.

➁ The image is inverted, and the inversion does not

depend on distance.

Cylindrical Aberration

➀ The rays do not all focus to the same point.

➁ Make a parabolic mirror instead of a cylindrical

one.

Introductory Optics System 012-02744K

Exp 12: Image Formation from Spherical Mirrors

Focal Length

60 mm

➀

➁ Remove the viewing screen and focus an image of

the crossed arrow target on itself. In this position, the focal length will be half of the distance between the target and the mirror. This method gives a focal length of 49.5 mm

Magnification

f = 50

ho = 19

do (mm) di hi 1/di+1/do 1/f hi/ho -di/do % f % m

500 55 -2.0 0.02 0.02 -0.11 -0.11 0.90% -4.50%

450 56 -2.5 0.02 0.02 -0.13 -0.12 0.40% 5.42%

400 57 -3.0 0.02 0.02 -0.16 -0.14 0.22% 9.75%

350 58 -3.5 0.02 0.02 -0.18 -0.17 0.49% 10.04%

300 60 -4.0 0.02 0.02 -0.21 -0.20 0.00% 5.00%

250 62 -4.5 0.02 0.02 -0.24 -0.25 0.64% -4.71%

200 66 -6.0 0.02 0.02 -0.32 -0.33 0.75% -4.50%

150 76 -10.0 0.02 0.02 -0.53 -0.51 -0.88% 3.73%

100 100 -19.0 0.02 0.02 -1.00 -1.00 0.00% 0.00%

➤➤

➤Note: The final two data points are not

➤➤

available because the image is located on the opposite side of the target from the mirror. In other words, the view of the image is blocked by the object.

➀ The results are in very good agreement with the

fundamental lens equation. The magnifications are not as accurate, due to the difficulty in measuring the size of the image accurately.

f = -50

ho = 32

do (mm) di hi 1/di + 1/d 1/f hi/ho -di/do % f % m

Virtual Images

➤➤

➤Note: It is difficult to accurately locate the

➤➤

virtual images. Because of this difficulty, the accuracy of the second part of this lab does not compare to the accuracy of the first. In addition, the image of the virtual image finder is too small to use at longer distances, so only the shorter ones should be used.

500 N/A N/A N/A N/A N/A N/A N/A N/A

450 N/A N/A N/A N/A N/A N/A N/A N/A

400 N/A N/A N/A N/A N/A N/A N/A N/A

350 N/A N/A N/A N/A N/A N/A N/A N/A

300 -37 3.0 -0.02 -0.02 0.09 0.12 15.59% -31.56%

250 -52 3.5 -0.02 -0.02 0.11 0.21 -31.31% -90.17%

200 -46 4.5 -0.02 -0.02 0.14 0.23 -19.48% -63.56%

150 -35 5.5 -0.02 -0.02 0.17 0.23 8.70% -35.76%

100 -30 7.0 -0.02 -0.02 0.22 0.30 14.29% -37.14%

75 -23 9.5 -0.03 -0.02 0.30 0.31 33.65% -3.30%

50 -21 12.0 -0.03 -0.02 0.38 0.42 27.59% -12.00%

012-02744K Introductory Optics System

Spherical Aberration

The image will be sharpest at the center.

➀

➁ Smaller apertures make the image sharper, but

dimmer.

Exp 13: Image Formation with Cylindrical Lenses

Focal Point

➀

F.L. 1 = 43 mm

F.L. 2 = 31 mm

➁ The refracted rays are parallel when they go

through the center of the lens, but are not parallel when they go through the edges.

➂ Same as #2

➃ Because of the shape of the lens, it bends the light

at only one edge - the curved one. When the lens is rotated 180°, the curved side of the lens is on the opposite side, so the refraction occurs at a different place.

Image Location

➂ Smaller apertures limit the light to the central por-

tion of the mirror. Using a smaller part of the spherical mirror causes smaller amounts of spherical aberration.

➃ The best aperture for maximum sharpness would

be a pinhole. This is not practical, though, because it limits the amount of light entering the mirror and causes diffraction.

➂ Yes, but it is a virtual image located on the oppo-

site side of the lamp from the lens.

Magnification & Inversion

➀ The magnification decreases with object distance.

➁ The image is inverted for all object locations

greater than the focal length of the lens.

Cylindrical Aberration

➀ The rays do not all focus at the same point.

➁ Make it thinner, decrease the curvature, limit the

aperture to include only the center of the lens, change the shape from circular to parabolic. (Answers may vary.)

➀ 57 mm from the lens

➁ As you decrease the object distance, the image dis-

tance increases.

Exp 14: Spherical Lenses-Spherical and Chromatic

Aberration, Aperture Size, and Depth of Field

Spherical Aberration

➀ The focus becomes sharper as the aperture is de-

creased.

➁ The best image focus would be obtained with the

smallest possible aperture. This is not practical, however, because smaller apertures allow less light to enter; and at very small apertures, diffraction degrades the image.

Depth of Field

➤➤

➤Note: The depth of field measured by students

➤➤

will vary, depending on what they consider “good focus”.

➀ The depth of field increases as the aperture is de-

creased.

➁ An infinite depth of field would require an aperture

size of zero.

Introductory Optics System 012-02744K

➂ A slightly blurred image is still visible. (The room

must be fairly dark for this image to be visible.)

➃ The smaller the aperture, the sharper the focus.

➄ The magnification increases with distance.

➅

Aperture

Object

Diverging rays from object

Light radiates from the object in all directions, but a small aperture selects only certain rays of that light. The rays selected by the aperture will be approximately parallel, and form an inverted image as shown.

Image

Chromatic Aberration

Note: This effect is difficult to see unless the room is dark and the magnification is high.

➀ The light that travels through the edge of the lens is

bent more, thus the difference in the amount of bend of the different colors is more visible.

➤➤

➤Notes: Everything in this lab applies directly

➤➤

to photography. It may be interesting to do the experiments described here with a lens from an SLR camera, and compare the amount of distortion.

Exp 15: The Diffraction Grating

➀ Narrower spacing makes wider diffraction patterns

➁ The larger number of slits makes the pattern

brighter, and somewhat sharper.

➂ There will not be complete agreement due to dif-

ferences in eyesight and perception of color.

A = 1.89E—4

L = 44.9

Color X1 (cm) X2 (cm) Wavelength 1 Wavelength 2

Violet 9.5 10.7 392.3e—9 439.3e—9

Blue 10.7 12.3 439.3e—9 500.7e—9

Green 12.3 14.0 500.7e—9 564.1e—9

Yellow 14.0 14.5 564.1e—9 582.4e—9

Orange 14.5 15.0 582.4e—9 600.5e—9

Red 15.0 19.0 600.5e—9 738.6e—9

➃ Color is a very subjective measurement; different

people will see the same wavelengths as being different colors. In addition, different people may not even be able to see some colors. Most people will not see as far into the violet spectrum as this, for example, but they will see farther into the red.

012-02744K Introductory Optics System

W sin tan

±1

= n

sin tan

±1

X L

Exp 16: Single-Slit Diffraction

Suggestions on – Procedure

➀

The spacing between fringes increases with decreasing slit width.

➁ The double-slit patterns are a superposition of a

single-slit pattern and a “bar” pattern. The singleslit pattern goes like this:

0.9

0.8

0.7

0.6

0.5

0.4

Intensity

0.3

0.2

0.1 0

-7-5-3-11357

and the double-slit pattern shows this same intensity pattern superimposed on a finer pattern.

Single-Slit Intensity

Position

W = 0.04

L = 448

n X wavelength

Red 1 9 803.4E—9

2 18 802.9E—9

3 27 802.1E—9

Green 1 8 714.1E—9

2 16 713.8E—9

3 24 713.2E—9

Blue 1 7 624.9E—9

2 14 624.6E—9

3 22 653.9E—9

The wavelengths obtained by this method are consistently higher than expected. This is due to difficulties in measuring the exact position of the minimum, due to the width of that minimum. For a better way of calculating wavelengths, use experiment 15.

➂ You would only see one maxima.

0.9

0.8

0.7

0.6

0.5

0.4

Intensity

0.3

0.2

0.1

X X

X X X

Double-Slit Intensity

X X X

X X

XXX

-7 -5 -3 -1 1 3 5 7 Position

W <

but if

X X

X X X

However, sin(x) - 1; so the equation is not valid unless n = 0. Therefore you would expect to see only the zeroth maxima.

then

(unless n = 0)

Introductory Optics System 012-02744K

Exp 17: General Diffraction

Suggestions on – Procedure

➀ Smaller apertures make the diffraction pattern more

clear.

➁ Smaller apertures make the diffraction pattern less

bright.

➂ White light causes many overlapping diffraction

patterns of different colors and slightly different sizes. Color filters simplify this pattern by limiting the pattern to one color.

Crossed Slits

➀ There are really two diffraction patterns at 90° to

each other, caused by the two slits. This is important for the other parts of the lab; each diffraction pattern is independent of the others.

Random array of Circular Apertures

➀ The diffraction pattern is wider when the holes are

smaller; just as in part 1 of experiment 16.

➁ The diffraction pattern of a point source through a

circular aperture is symmetrical because the aperture itself is symmetrical. Diffraction effects are most pronounced in a direction parallel with the smallest dimension of the aperture; but in a circular aperture, all directions are the same.

Square array of Circular Apertures

➀ This pattern is similar in that there is an overall

“target” pattern. It is different in that the target is made up of a square grid of points, roughly like so:

➁–➃ Drawings will vary.

Exp 18: Introduction to Optical Instruments

➀ A virtual, magnified image is formed for object

distances of less than the focal length of the lens.

➁ A real, magnified image (also inverted) is formed

for object distances between one and two focal lengths from the lens.

➂ A real, reduced image (still inverted) is formed for

object distances greater than twice the focal length of the lens.

➃ Any real image can be focused on the screen, thus

any object distance greater than the focal length of the lens will work.

012-02744K Introductory Optics System

do di m Real/Virtual Inv/Uninv

f/16 -f/15 16/15 Virtual Uninverted

f/8 -f/7 8/7 Virtual Uninverted f/4 -f/3 4/3 Virtual Uninverted

f/2 -f 2 Virtual Uninverted 3f/4 -3f 4 Virtual Uninverted 7f/8 -7f 8 Virtual Uninverted

15f/16 -15f 16 Virtual Uninverted

f No image formed (A.K.A. “Image at Infinity”)

17f/16 17f -16 Real Inverted

9f/8 9f -8 Real Inverted 5f/4 5f -4 Real Inverted 3f/2 3f -2 Real Inverted 7f/4 7f/3 -4/3 Real Inverted

15f/8 15f/7 -8/7 Real Inverted

31f/16 31f/15 -16/15 Real Inverted

2f 2f -1 Real Inverted

33f/16 33f/17 -16/17 Real Inverted

17f/8 17f/9 -8/9 Real Inverted

9f/4 9f/5 -4/5 Real Inverted 5f/2 5f/3 -2/3 Real Inverted

11f/4 11f/7 -4/7 Real Inverted 23f/8 23f/15 -8/15 Real Inverted

3f 3f/2 -1/2 Real Inverted 5f 5f/4 -1/4 Real Inverted

10f 10f/9 -1/9 Real Inverted

100f 100f/99 -1/99 Real Inverted

Exp 19: The Projector

➀ If the object distance is less than the focal length of

the lens, then the image formed is a virtual image, located on the same side of the lens as the object. This can not be focused on a viewing screen.

➁ If the object distance is greater than 2f, then the im-

age will be reduced in size. It will still be a real image, so it may be focused on the screen.

➂ One practical limit to the magnification is the size

of the lens used, another is the amount of light available. Magnified images are dimmer than reduced images, because the same amount of light is spread out over more area. If the image is magnified too much, it may not be visible.

Object Lens Image View from here

➃ It is not possible to project an uninverted image

with one lens. (This is why projector slides must be put in upside down and backwards.)

➄ The image from a projector may be viewed with-

out a screen, but the observer must be looking towards the lens, on the opposite side of the lens from the object.

The observer will see the image floating in space on the near side of the lens. (This is easiest to see when the magnification is about one.) It will be somewhat difficult to focus both eyes on the image at the same time, but when it happens, the effect is startling.

Introductory Optics System 012-02744K

Exp 20: The Magnifier

Suggestions on – Procedure

➀

No. According to the fundamental lens equation the magnification, and the angular magnification, are unlimited. The limit of useful magnification is caused by spherical aberration in the lens.

➁ The 75mm lens provides greater magnification.

➤ Note: As a demonstration that the limit to

useful magnification is caused by spherical aberration, put the variable aperture in position just in front of the 75mm lens. Close the aperture as far as practical without losing the image completely, and then move the lens/aperture set as far from the object as possible without losing focus (about 9-11 cm). While looking through the lens, widen the aperture. The image will become almost completely blurred.

Another Note: The actual angular magnification depends on the distance from the eye to the lens, as well as from the lens to the object.

'= ±

dedo± fdo+ d

distance to the eye.

= 0, then the angular size is the same as if

if d

there were no lens there at all. This is why contact lenses do not change the apparent size of things, although they do affect the focus.

where de is the

➂ Angular magnification = 25 cm/f.

75 mm = 7.5 cm: power = 3.33

150 mm = 15 cm: power = 1.67

➃ Power = 25/50 = 1/2. This would have limited use

as a magnifier; it just wouldn’t be strong enough to make much difference.

Exp 21: The Telescope

Suggestions on – Procedure

➀ The angular magnification of the telescope is 2.

(150/75) If the telescope is looked through backwards, the lenses are reversed in the equation and the magnification becomes 1/2.

➁ About 2.1. One of the best ways of measuring this

is to look at a meter stick with both eyes open (one eye through the telescope). Then you will see both the unmagnified and magnified images at the same time, and you may compare their sizes using the scales on the images. The magnification observed will generally be slightly larger than the theoretical value, since the object you are looking at is not an infinite distance away.

➂ About 1/2, using the same method as in part 2.

➃ Yes.

012-02744K Introductory Optics System

Exp 22: The Compound Microscope

Suggestions on – Procedure

➀

The image is magnified; but at 150mm objective distance, the magnification is not significantly more than when the 75mm lens is used as a magnifier.

➁ The magnification increases dramatically as the

objective lens moves closer to the object. This is because the projected image of the object becomes larger as the distance between object and objective gets closer to the focal length of the lens. (The image will be lost entirely when the objective is 75mm from the object.)

➂ Spherical aberration becomes quite a problem, and

chromatic aberration becomes significant at the very high magnifications.

➃ The smaller the aperture is, the sharper the view

through the microscope. A very small aperture eliminates both chromatic and spherical distortion, and allows higher magnification.

➄ Small apertures make the image quite dim. (You

may want to use the lamp to illuminate the viewscreen.)

➅ The magnification would be higher.

Introductory Optics System 012-02744K

Notes

012-02744J Introductory Optics System

Technical Support

Feed-Back

If you have any comments about this product or this manual please let us know. If you have any suggestions on alternate experiments or find a problem in the manual please tell us. PASCO appreciates any customer feed-back. Your input helps us evaluate and improve our product.

To Reach PASCO

For Technical Support call us at 1-800-772-8700 (tollfree within the U.S.) or (916) 786-3800.

Email: support@pasco.com

Contacting Technical Support

Before you call the PASCO Technical Support staff it would be helpful to prepare the following information:

• If your problem is computer/software related, note:

Title and Revision Date of software.

Type of Computer (Make, Model, Speed).

Type of external Cables/Peripherals.

• If your problem is with the PASCO apparatus, note:

Title and Model number (usually listed on the label).

Approximate age of apparatus.

A detailed description of the problem/sequence of events. (In case you can't call PASCO right away, you won't lose valuable data.)

If possible, have the apparatus within reach when calling. This makes descriptions of individual parts much easier.

• If your problem relates to the instruction manual, note:

Part number and Revision (listed by month and year on the front cover).

Have the manual at hand to discuss your questions.

PASCO OS-8500 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual