PASCO ES-9070 User Manual

Download

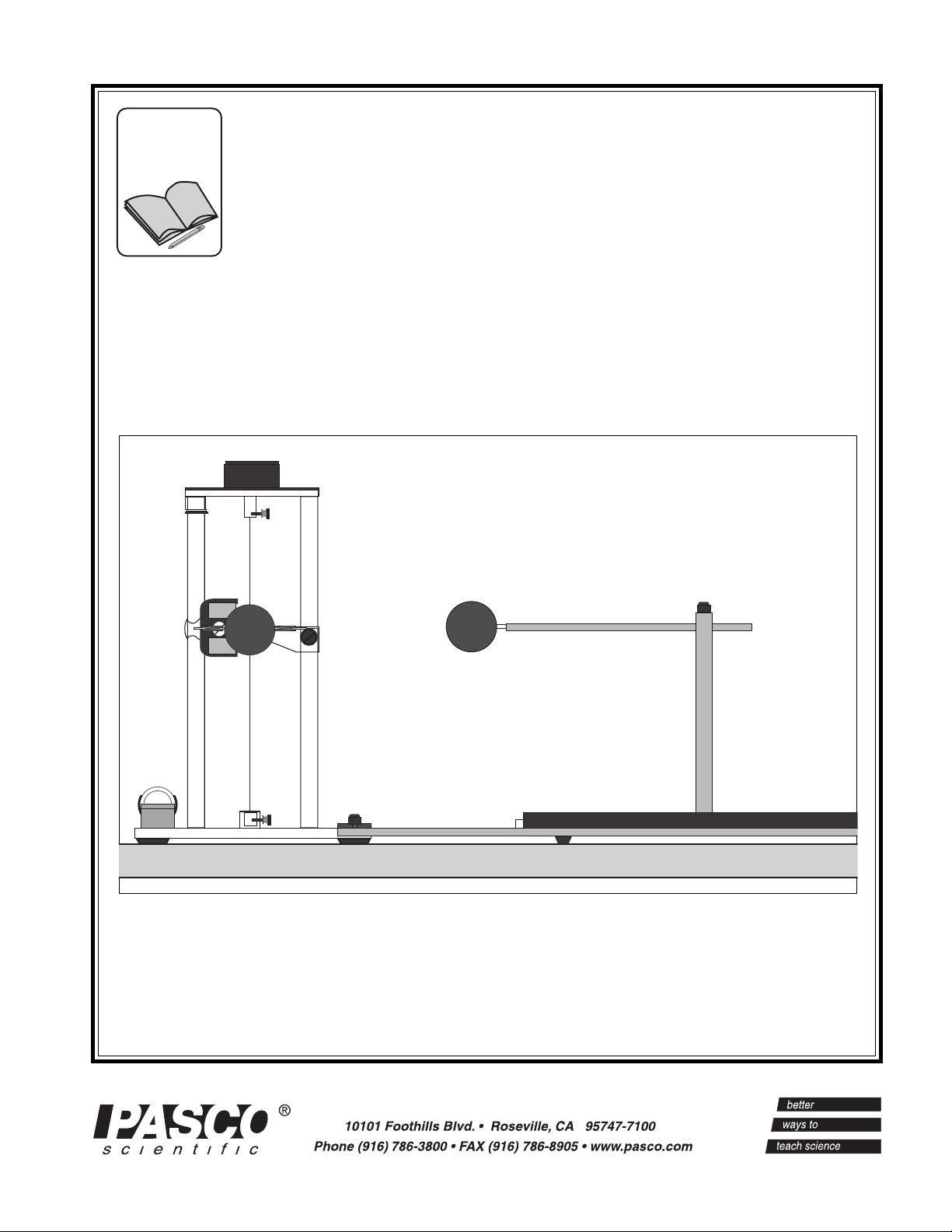
Includes

Teacher's Notes

and

Typical

Experiment Results

COULOMB BALANCE

Instruction Manual and Experiment Guide for the PASCO scientific Model ES-9070

012-03760E

05/99

012-03760E Coulomb Balance

T able of Contents

Section Page

Introduction .....................................................................................................1

Theory ............................................................................................................. 2

Equipment........................................................................................................3

Additional Equipment Recommended: .....................................................3

Tips for Accurate Results ................................................................................ 4

Setup .............................................................................................................5

Experiments:

Part A Force Versus Distance...................................................................7

Part B Force Versus Charge ......................................................................8

Part C The Coulomb Constant...................................................................9

Replacing the Torsion Wire........................................................................... 13

Teacher’s Guide............................................................................................. 15

Technical Support.................................................................Inside Back Cover

Coulomb Balance 012-03760E

Please—Feel free to duplicate this manual subject to the copyright restrictions below.

The PASCO scientific 012-03760E Coulomb Balance manual is copyrighted and all rights reserved. However, permission is granted to nonprofit educational institutions for reproduction of any part of the manual providing the reproductions are used only for their laboratories and are not sold for profit. Reproduction under any other circumstances, without the written consent of PASCO scientific, is prohibited.

Limited Warranty

PASCO scientific warrants the product to be free from defects in materials and workmanship for a period of one year from the date of shipment to the customer. PASCO will repair or replace at its option any part of the product which is deemed to be defective in material or workmanship. The warranty does not cover damage to the product caused by abuse or improper use. Determination of whether a product failure is the result of a manufacturing defect or improper use by the customer shall be made solely by PASCO scientific. Responsibility for the return of equipment for warranty repair belongs to the customer. Equipment must be properly packed to prevent damage and shipped postage or freight prepaid. (Damage caused by improper packing of the equipment for return shipment will not be covered by the warranty.) Shipping costs for returning the equipment after repair will be paid by PASCO scientific.

Equipment Return

Should the product have to be returned to PASCO scientific for any reason, notify PASCO scientific by letter, phone, or fax BEFORE returning the product. Upon notification, the return authorization and shipping instructions will be promptly issued.

NOTE: NO EQUIPMENT WILL BE

ACCEPTED FOR RETURN WITHOUT AN AUTHORIZATION FROM PASCO.

When returning equipment for repair, the units must be packed properly. Carriers will not accept responsibility for damage caused by improper packing. To be certain the unit will not be damaged in shipment, observe the following rules:

➀ The packing carton must be strong enough for the

item shipped.

➁ Make certain there are at least two inches of

packing material between any point on the apparatus and the inside walls of the carton.

➂ Make certain that the packing material cannot shift

in the box or become compressed, allowing the instrument come in contact with the packing carton.

Address: PASCO scientific

10101 Foothills Blvd. Roseville, CA 95747-7100

Credits

Author: Bruce Lee Editor: Dave Griffith

Phone: (916) 786-3800 FAX: (916) 786-3292 email: techsupp@pasco.com web: www.pasco.com

012-03760E Coulomb Balance

Introduction

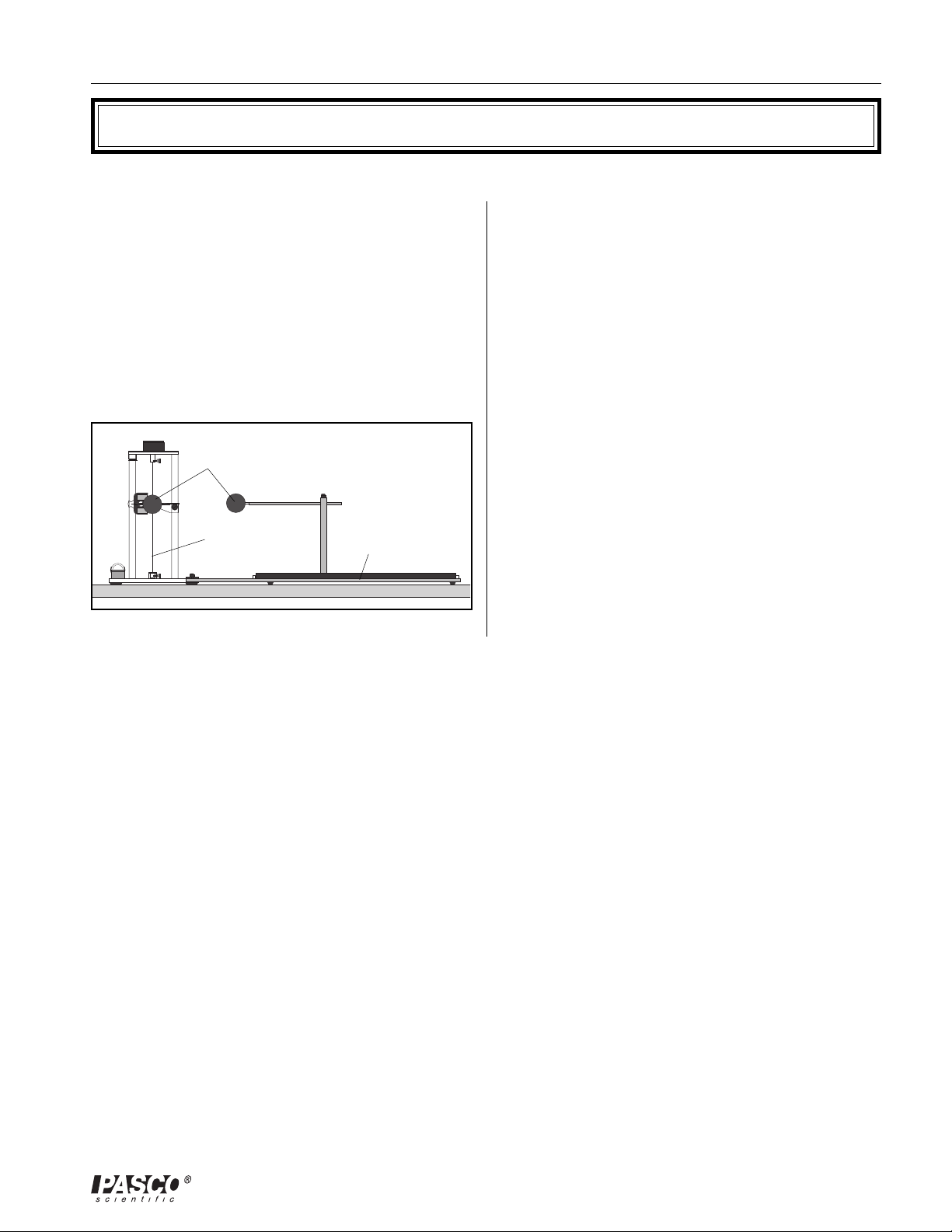
The PASCO Model ES-9070 Coulomb Balance (Figure 1) is a delicate torsion balance that can be used to investigate the force between charged objects. A conductive sphere is mounted on a rod, counterbalanced, and suspended from a thin torsion wire. An identical sphere is mounted on a slide assembly so it can be positioned at various distances from the suspended sphere.

To perform the experiment, both spheres are charged, and the sphere on the slide assembly is placed at fixed

charged spheres

torsion wire

Figure 1. Experimenting with the Coulomb Balance

slide assembly

distances from the equilibrium position of the suspended sphere. The electrostatic force between the spheres causes the torsion wire to twist. The experimenter then twists the torsion wire to bring the balance back to its equilibrium position. The angle through which the torsion wire must be twisted to reestablish equilibrium is directly proportional to the electrostatic force between the spheres.

All the variables of the Coulomb relationship (F = kq

/R2) can be varied and measured using the

1q2

Coulomb Balance. You can verify the inverse square relationship and the charge dependence using the balance and any electrostatic charging source. However, for best results, we recommend you charge the spheres with a stable kilovolt power supply to ensure a reproducible charge throughout the experiment. To determine the Coulomb constant with reasonable accuracy, we recommend you use an electrometer and a Faraday ice pail to accurately measure the charge on the spheres. For more information about accuracy, read the section Tips for Accurate Results.

Coulomb Balance 012-03760E

Theory

Take one gram of protons and place them one meter away from one gram of electrons. The resulting force is equal to

1.5 x 1023 newtonsroughly the force it would take to lift an object from the surface of the Earth that had a mass about 1/5 that of the moonnot a small force.

So, if such small amounts of charge produce such enormous forces, why does it take a very delicate torsion balance to measure the force between charged objects in the laboratory? In a way, the very magnitude of the forces is half the problem. The other half is that the carriers of the electrical forcethe tiny proton and the even tinier electronare so small, and the electrons are so mobile. Once you separate them, how do you keep them separated? The negatively charged electrons are not only drawn toward the positively charged protons; they also repel each other. Moreover, if there are any free electrons or ions between the separated charges, these free charges will move very quickly to reduce the field caused by the charge separation.

So, since electrons and protons stick together with such tenacity, only relatively small charge differentials can be sustained in the laboratory. This is so much the case that, even though the electrostatic force is more than a billion-

billion-billion-billion times as strong as the gravitational force, it takes a very delicate torsion balance to measure the electrical force, whereas we can measure the gravitational force by weighing an object with a spring balance.

NOTE: The torsion balance gives a direct and reasonably accurate measurement of the Coulomb force. The most accurate determinations of Coulomb's law, however, are indirect. It can be shown mathematically that if the inverse square law holds for the electrostatic force, the electric field inside a uniformly charged sphere must be everywhere zero. Measurements of the field inside a charged sphere have shown this to be true with remarkable accuracy. The Coulomb force can be expressed by the formula:

1q2

2+n

F = kq

Using this indirect method, it has been demonstrated

experimentally that n  2 x 10

16

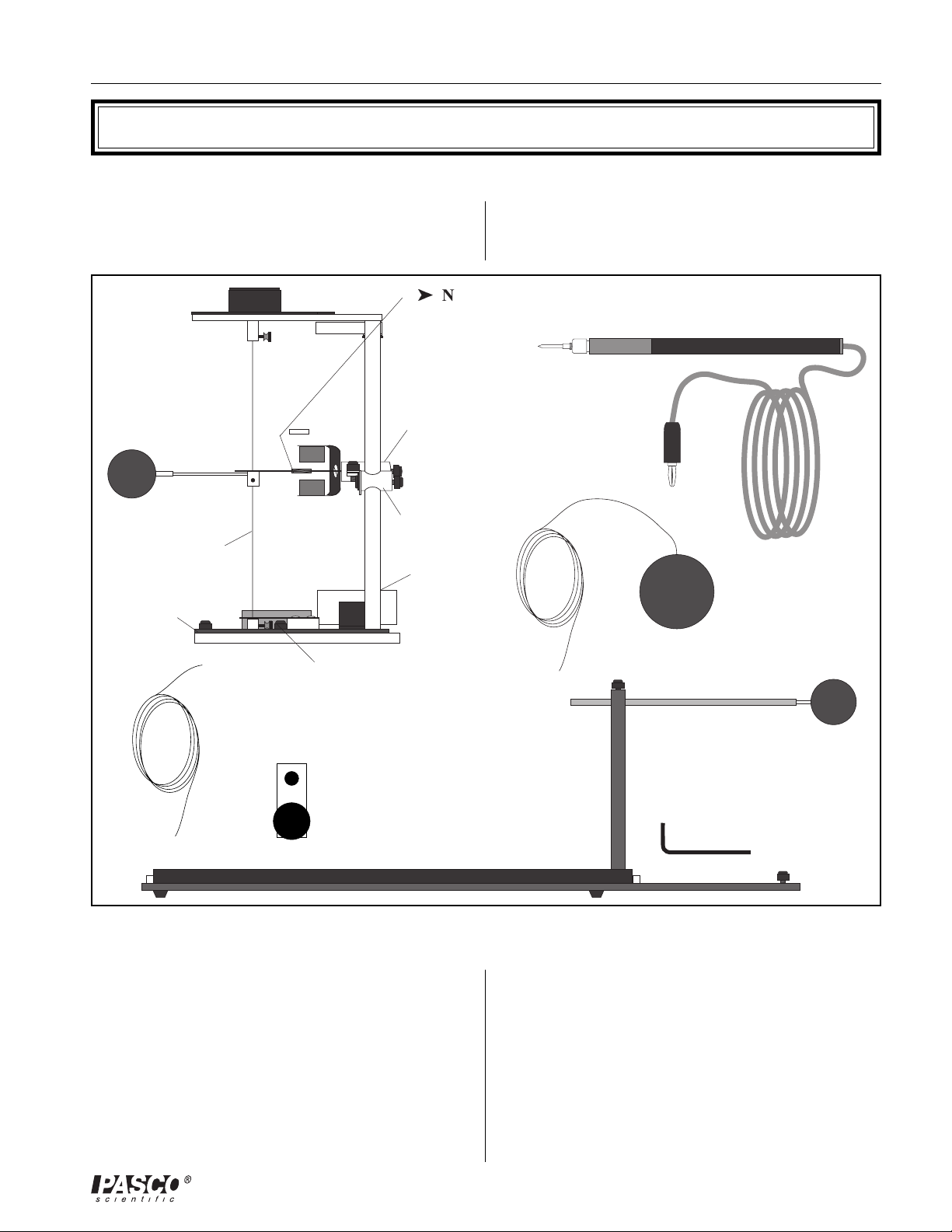
012-03760E Coulomb Balance

Equipment

The Coulomb Balance and the included accessories are shown in Figure 2.

be shipped with the copper rings unattached.

COULOMB

BALANCE

torsion wire (pendulum)

coupling

Plate

retainer

spare torsion wire

(3 meters)

toolbox with: one 50 mg mass two 20 mg masses one hex key

magnetic

damping arm

index arm

calibration

support tube

(The Coulomb Balance and the slide assembly should be shipped with one of the conductive spheres unattached. See the Setup section of this manual.)

NOTE: The balance may

charging probe

conductive sphere on insulating

thread

torsion wire

clamp

Figure 2. The Coulomb Balance

Additional Equipment Recommended:

 A stable kilovolt power supply for charging the

spheresAny electrostatic charger can be used to charge the spheres, but a power supply lets you replenish the charge to a fixed value throughout an experiment. Ideally the supply would have a momentary power on button so that you can conveniently turn it off whenever you are not charging the spheres.

allen wrench for the slide

assembly

slide assembly

 An electrometer and Faraday ice pail (such as

PASCO Models ES-9054A and ES-9058) for accurately measuring the charge on the spheres.

 A spring balance capable of measuring a force of

approximately 4 newtons (400 gram mass). This is not necessary for the experiment itself, but is helpful in setting the tension of the torsion wire.

Coulomb Balance 012-03760E

Tips for Accurate Results

IMPORTANT: If you live in an area where humidity is always high, and if you have no facilities for controlling humidity, the experiment will be difficult, if not impossible, to perform. Static charges are very hard to maintain in a humid atmosphere because of surface conductivity.

Experiments with the Coulomb Balance are straightforward and quite accurate, yet, as with any quantitative electrostatic experiment, frustration lurks just around the corner. A charged shirt sleeve, an open window, an excessively humid dayany of these and more can affect your experiment. However, if you carefully follow the tips listed below, youve got a good start toward a successful experiment.

 Perform the experiment during the time of year when

humidity is lowest.  Perform the experiment in a draft-free room.  The table on which you set up the experiment should

be made of an insulating materialwood, masonite,

plastic, etc. If a metal table is used, image charges

will arise in the table that will significantly affect the

results. (This is also true for insulating materials, but

the effect is significantly reduced.)  Position the torsion balance at least two feet away

from walls or other objects which could be charged

or have a charge induced on them.  When performing experiments, stand directly behind

the balance and at a maximum comfortable distance

from it. This will minimize the effects of static

charges that may collect on clothing.  Avoid wearing synthetic fabrics, because they tend to

acquire large static charges. Short sleeve cotton

clothes are best, and a grounding wire connected to

the experimenter is helpful.

 Use a stable, regulated kilovolt power supply to

charge the spheres. This will help ensure a constant charge throughout an experiment.

 When charging the spheres, turn the power supply

on, charge the spheres, then immediately turn the supply off. The high voltage at the terminals of the supply can cause leakage currents which will affect the torsion balance. A supply with a momentary power on button is ideal.

 When charging the spheres, hold the charging probe

near the end of the handle, so your hand is as far from the sphere as possible. If your hand is too close to the sphere, it will have a capacitive effect, increasing the charge on the sphere for a given voltage. This effect should be minimized so the charge on the spheres can be accurately reproduced when recharging during the experiment.

 If you are using a PASCO Electrometer (Model

ES-9035 or ES9054A) to measure the charge on the spheres, connect the voltage output to a digital multimeter so that values can be measured more accurately. It is also useful to calibrate the electrometer. This is done by applying a calibrating voltage to the input and measuring the electrometer output on the digital multimeter. Your measured values can then be adjusted as necessary.

 Surface contamination on the rods that support the

charged spheres can cause charge leakage. To prevent this, avoid handling these parts as much as possible and occasionally wipe them with alcohol to remove contamination.

 There will always be some charge leakage. Perform

measurements as quickly as possible after charging, to minimize the leakage effects.

 Recharge the spheres before each measurement.

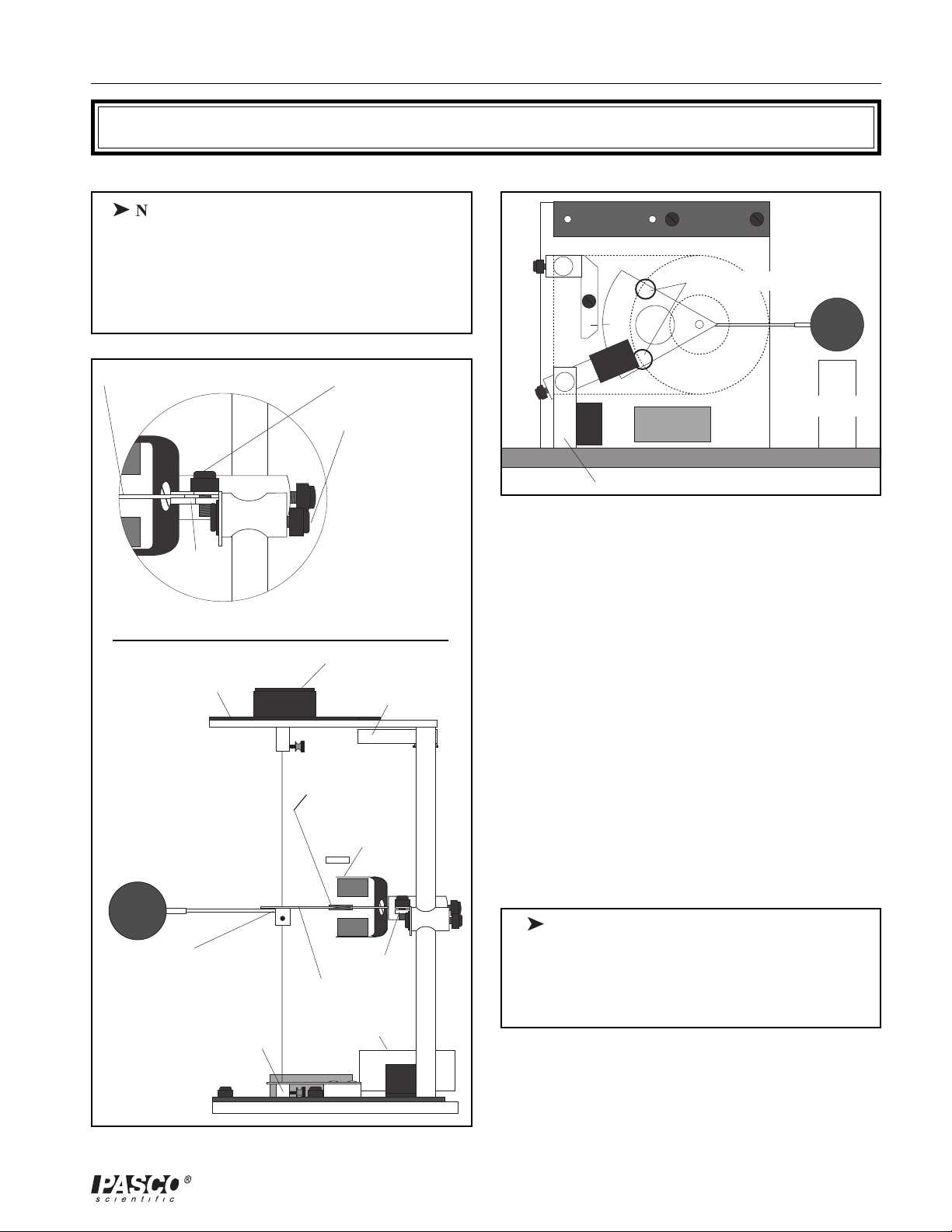
012-03760E Coulomb Balance

Setup

Note  Threading the Torsion Wire: The Torsion Balance is shipped to you with the wire already threaded. However, if it ever breaks, you can thread it using the spare wire that is supplied. See the procedure at the end of this manual.

copper rings

counterweight

vane

degree scale

packing

clamp

Releasing the packing clamp

1. Loosen the top thumbscrew

2. Loosen the side thumbscrew and rotate the index arm so it is parallel with the base of the Coulomb Balance. Then tighten the thumbscrew.

torsion knob

copper rings

magnetic

damping arm

lateral support

bar

support

tube

lateral support bar

Figure 4. Zeroing the Torsion Balance

Torsion Balance Setup

➀ One of the conductive spheres is not attached when the

Coulomb Balance is shipped. To attach it, just slip the stem of the sphere over the fiber glass rod of the pendulum assembly.

➁ Slide the copper rings onto the counterweight vane, as

shown in the bottom of Figure 3. Then release the packing clamp that holds the counterweight vane, as shown in the top of Figure 3. Adjust the position of the copper rings so the pendulum assembly is level.

➂ Reposition the index arm so it is parallel with the base

of the torsion balance and at the same height as the vane.

pendulum assembly

torsion wire retainer

Index arm

counterweight

vane

support tube

Figure 3. Setting Up the Coulomb Balance

Important: When storing the torsion balance, always clamp the counterweight vane to protect the torsion wire. When you do this, be sure to adjust the height and angle of the index arm so that you can clamp the vane without pulling on the torsion wire.

➃ Adjust the height of the magnetic damping arm so the

counterweight vane is midway between the magnets.

➄ Turn the torsion knob until the index line for the degree

scale is aligned with the zero degree mark.

Coulomb Balance 012-03760E

➅ Rotate the bottom torsion wire retainer (do not loosen

or tighten the thumbscrew) until the index line on the counterweight vane aligns with the index line on the index arm.

➆ Carefully turn the torsion balance on its side,

supporting it with the lateral support bar, as shown in Figure 4. Place the support tube under the sphere, as shown.

➇ Adjust the positions of the copper rings on the

counterweight vane to realign the index line on the counterweight with the index line on the index arm.

➈ Place the torsion balance upright.

Slide Assembly Setup

(Refer to Figure 5)

➀ Connect the slide assembly to the torsion balance as

shown in Figure 5, using the coupling plate and thumbscrews to secure it in position.

➁ Align the spheres vertically by adjusting the height of

the pendulum assembly so the spheres are aligned: Use the supplied allen wrench to loosen the screw that anchors the pendulum assembly to the torsion wire. Adjust the height of the pendulum assembly as needed.

Readjust the height of the index arm and the magnetic damping arm as needed to reestablish a horizontal relationship.

➂ Align the spheres laterally by loosening the screw in

the bottom of the slide assembly that anchors the vertical support rod for the sphere, using the supplied allen wrench (the vertical support rod must be moved to the end of the slide assembly, touching the white plastic knob to access the screw). Move the sphere on the vertical rod until it is laterally aligned with the suspended sphere and tighten the anchoring screw.

➃ Position the slide arm so that the centimeter scale

reads 3.8 cm (this distance is equal to the diameter of the spheres).

➄ Position the spheres by loosening the thumbscrew on

top of the rod that supports the sliding sphere and sliding the horizontal support rod through the hole in the vertical support rod until the two spheres just touch. Tighten the thumbscrew.

You're now ready to experiment. The degree scale should read zero, the torsion balance should be zeroed (the index lines should be aligned), the spheres should be just touching, and the centimeter scale on the slide assembly should read 3.8 cm. (This means that the reading of the centimeter scale accurately reflects the distance between the centers of the two spheres.)

side view

top view

Figure 5. Slide Assembly Setup

012-03760E Coulomb Balance

Experiment: (Part A) Force V ersus Distance

Procedure

➀ Set up the Coulomb Balance as described in the

suspended

sphere

previous section.

➁ Be sure the spheres are fully discharged (touch

them with a grounded probe) and move the sliding sphere as far as possible from the suspended sphere. Set the torsion dial to 0×C. Zero the torsion balance by appropriately rotating the bottom torsion wire retainer until the pendulum assembly is at its zero displacement position as indicated by the index marks.

pendulum

assembly

Figure 6. Experimental Setup

➂ With the spheres still at maximum separation, charge both the spheres to a potential of

6-7 kV, using the charging probe. (One terminal of the power supply should be grounded.) Immediately after charging the spheres, turn the power supply off to avoid high voltage leakage effects.

IMPORTANT: Read the section Tips for Accurate Results. It has some helpful hints about

charging the spheres.

➃ Position the sliding sphere at a position of 20 cm. Adjust the torsion knob as necessary to balance

the forces and bring the pendulum back to the zero position. Record the distance (R) and the angle (q) in Table 1.

sliding

sphere

slide assembly

➄ Separate the spheres to their maximum separation, recharge them to the same voltage, then

reposition the sliding sphere at a separation of 20 cm. Measure the torsion angle and record your results again. Repeat this measurement several times, until your result is repeatable to within ± 1 degree. Record all your results.

➅ Repeat steps 3-5 for 14, 10, 9, 8, 7, 6 and 5 cm.

Analysis

NOTE: In this part of the experiment, we are assuming that force is proportional to the torsion angle. If you perform Part C of the experiment, you will test this assumption when you calibrate the torsion balance.

Determine the functional relationship between the force, which is proportional to the torsion angle (q); and the distance (R). This can be done in the following ways:

➀ Plot log q versus log R.

Explanation: If q = bR The slope of the graph of log q versus log R will therefore be a straight line. Its slope will be equal to n and its y  intercept will be equal to log b. Therefore, if the graph is a straight line, the function is determined.

, where b and n are unknown constants, then log q = n log R + log b.

Coulomb Balance 012-03760E

➁ Plot q versus R

Either of these methods will demonstrate that, for relatively large values of R, the force is proportional to 1/R2. For small values of R, however, this relationship does not hold.

Corrections to the data

The reason for the deviation from the inverse square relationship at short distances is that the charged spheres are not simply point charges. A charged conductive sphere, if it is isolated from other electrostatic influences, acts as a point charge. The charges distribute themselves evenly on the surface of the sphere, so that the center of the charge distribution is just at the center of the sphere. However, when two charged spheres are separated by a distance that is not large compared to the size of the spheres, the charges will redistribute themselves on the spheres so as to minimize the electrostatic energy. The force between the spheres will therefore be less than it would be if the charged spheres were actual point charges.

A correction factor B, can be used to correct for his deviation. Simply multiply each value of q by 1/ B, where

where a equals the radius of the spheres and R is the separation between spheres.

To correct your data:

=1–4

;

➀ Calculate the correction factor B for each of the separations R that you used. Record your results in

Table 1.

➁ Multiply each of your collected values of q by 1/B and record your results as q ➂ Reconstruct your graphs relating force and separation, but this time use q

corrected

instead of q. Make your new plot on the same graph as your original plot. How does the correction factor affect your results?

(Part B) Force V ersus Charge

With the sphere separation (R) held at a constant value (choose a value between 7 and 10 cm), charge the spheres to different values and measure the resulting force. Keep the charge on one sphere constant, and vary the charge on the other. Then graph angle versus charge to determine the relationship.

The charge can be varied using either of two methods:

Method I:

If your power supply is adjustable, simply charge the spheres to different potentials, such as 7, 6, 5, 4, and 3 kV. (When charging the spheres, they should always be at their maximum separation.) The charge on the sphere is proportional to the charging potential.

Method II:

If your power supply voltage is not adjustable, the charge can be changed by touching one or both of the spheres with an identical sphere that is discharged. The charge will be shared equally between the charged and discharged sphere. Therefore, touch the charged sphere once to reduce the charge by half, twice to reduce the charge by 1/4, etc.

012-03760E Coulomb Balance

(Part C) The Coulomb Constant

In parts A and B of this lab, you determined (if all went well) that the electrostatic force between two point charges is inversely proportional to the square of the distance between the charges and directly proportional to the charge on each sphere. This relationship is stated mathematically in Coulombs Law:

1q2

where F is the electrostatic force, q

and q2 are the charges, and R is the distance between the charges. In

order to complete the equation, you need to determine the value of the Coulomb constant, k. To accomplish this, you must measure three additional variables: the torsion constant of the torsion wire (K can convert your torsion angles into measurements of force, and the charges, q1 and q2. Then, knowing F, q1, q2, and R, you can plug these values into the Coulomb equation to determine k.

Measuring the Torsion constant, K

F = k

;

), so you

tor

center

line

➀ Carefully turn the Torsion Balance on its side,

supporting it with the lateral support bar, as shown

copper rings

in Figure 7. Place the support tube under the sphere, as shown.

➁ Zero the torsion balance by rotating the torsion

dial until the index lines are aligned. Record the angle of the degree plate in Table 2.

support

tube

➂ Carefully place the 20 mg mass on the center line

of the conductive sphere.

➃ Turn the degree knob as required to bring the

lateral support bar

index lines back into alignment. Read the torsion angle on the degree scale. Record the angle in

Figure 7. Calibrating the Torsion Balance

Table 2.

➄ Repeat steps 3 and 4, using the two 20 mg masses and the 50 mg mass to apply each of the masses shown

in the table. Each time record the mass and the torsion angle.

➅ Complete the table as follows to determine the torsion constant for the wire:

a. Calculate the weight for each set of masses that you used. b. Divide the weight by the torsion angle to determine the torsion constant at each weight. c. Average your measured torsion constants to determine the torsion constant for the wire. Use the

variance in your measured values as an indication of the accuracy of your measurement.

mass

NOTE: A torsion constant for a wire usually expresses the torque required to twist the wire a unit angle, and is normally expressed in newton meters per degree. However, when using the torsion balance, the torque arm is always the same (the distance from the center of the conductive sphere to the torsion wire), so the torsion constant for the balance is more conveniently expressed in newtons per degree.

Coulomb Balance 012-03760E

Measuring the Charges, q1 and q

Method I:

The capacitance of an isolated conductive sphere is given by the equation:

where C is the capacitance, e For a capacitor, charge (q) and charging potential (V) are related by the equation: q = CV. You can

use this equation to determine the charge on the spheres from your applied charging potential. This is the simplest method for determining the charge on the spheres. Unfortunately, the conducting

spheres of the Coulomb Balance are not isolated in this application, so the measured values of q will be only approximate.

NOTE: A capacitor normally consists of two conductors. The charge on one conductor is +q and the charge on the other is q. V is the potential difference between the two conductors. For an isolated sphere with a charge +q, the second conductor is a hypothetical plane at ground potential and with charge q, located at a distance infinitely far from the sphere.

Method II:

The charge on the spheres can be measured more accurately using an electrometer with a Faraday ice pail. The setup for the measurement is shown in Figure 8. The electrometer and ice pail can be modeled as an infinite impedance voltmeter in parallel with a capacitor. A sphere with a charge q is touched against the ice pail. Since the capacitance of the ice pail and electrometer is much greater than that of the sphere, virtually all of the charge q is transferred onto the ice pail. The relationship between the voltage reading of the electrometer and the charge deposited into the system is given by the equation q = CV, where C is the combined capacitance of the electrometer, the ice pail, and the connecting leads. Therefore, in order to determine the charge, you must know the capacitance of the system.

= 8.85 x 10

p e

C = 4

12

F/m, and a = the radius of the sphere.

Conductive sphere on an

insulating thread

Electrometer

Faraday

ice pail

The simplest way to measure the capacitance of the electrometer and ice pail is to use a good capacitance meter connected between the inside and

Figure 8. Measuring the Charge with an

Electrometer and a Faraday Ice Pail

outside conductors of the ice pail (the electrometer must be connected to the ice pail during the measurement). A second method is to charge a precision capacitor with capacitance equal to C on the capacitor is then equal to q inside and outside conductors of the ice pail. The charge q

(³ 250 pF) to a known voltage V

test

= C

. Place the leads of the charged capacitor between the

testVtest

test

(10 - 30 V). The charge

test

is now distributed across two parallel capacitors, the precision capacitor and the capacitance of the ice pail and electrometer system. Therefore: C

testVtest

= (C + C

)V; where C is the capacitance of the electrometer and Faraday ice pail

test

and V is the voltage reading of the electrometer.

012-03760E Coulomb Balance

Therefore C = C

test

- V)/V. Once youve measured the capacitance C, measure the charge of

test

the charged sphere is follows:

➀ Discharge the conducting sphere on the insulating thread, by touching it to a grounded probe. ➁ Holding the sphere by the insulating thread, touch it to the charged sphere, then to the inner

conductor of the ice pail.

➂ The charge on the original charged sphere, q, can now be determined using the equation:

q = 2CV;

where C is the capacitance of the electrometer and ice pail and V is the reading on the electrometer. (The factor of two arises because, in using the test sphere to sample the charge on the original sphere, only half the original charge was transferred.)

Calculations for the Coulomb Constant

The Coulomb constant can now be determined by using any data pair from your force versus distance data.

➀ Convert your torsion angle measurement (q

torsion constant for the torsion wire: F = K

) to a force measurement, using your measured

corrected

torqcorrected

➁ Determine the charge that was on the sphere using Method I or Method II above. If you are using

Method II, you will need to recharge the sphere to the voltage previously used while taking data, so that you can determine the charge using the electrometer and the Faraday ice pail.

➁ Plug your collected data into the Coulomb equation, F = k q

/R2, to determine the value of k.

1q2

Do this for several sets of data. Average your results to determine a value for k.

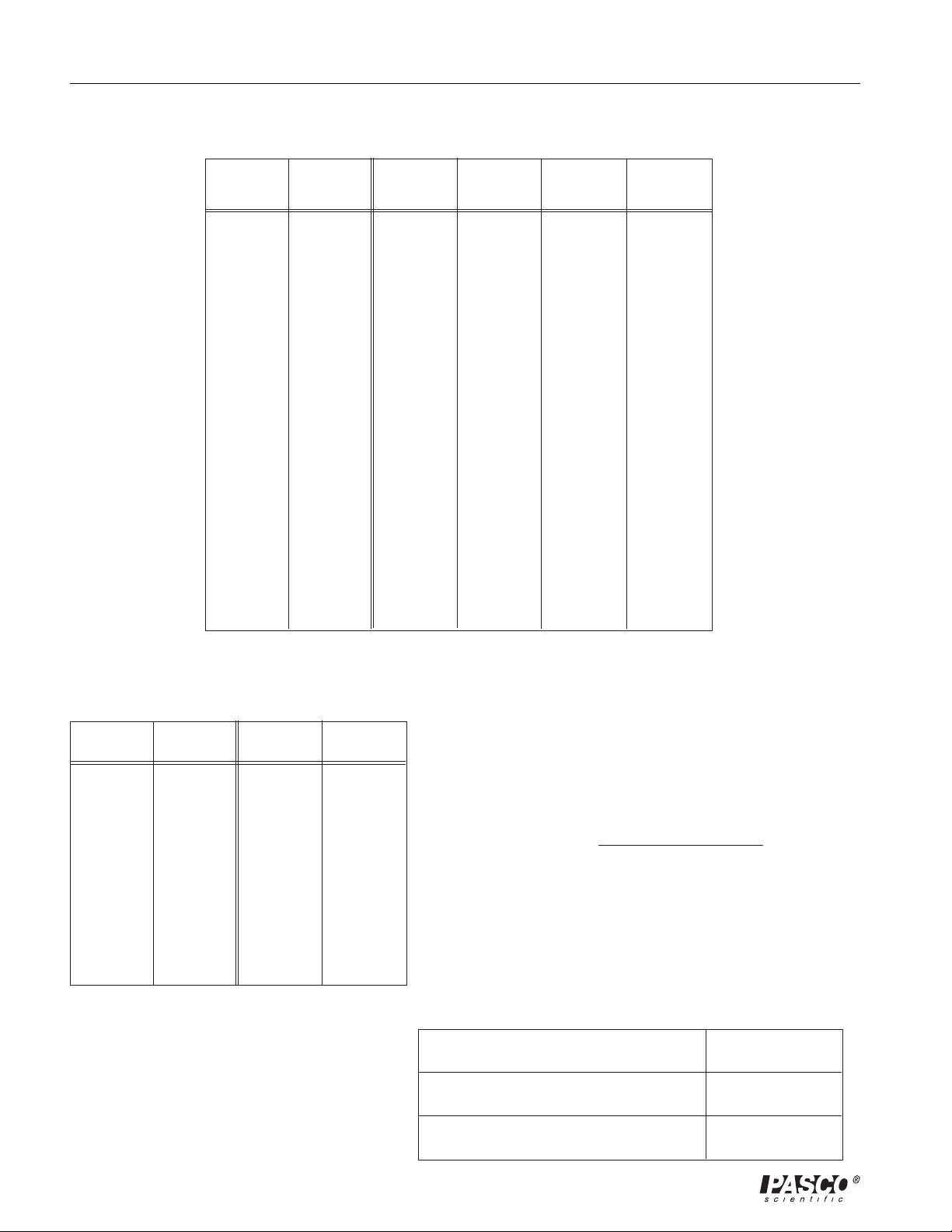
Coulomb Balance 012-03760E

Table 1. Force versus Distance

Data and Calculations

1 - 4a

3/R3

avg

corrected

1/R

0 mg

20 mg

40 mg

50 mg

70 mg

Table 2. Force Calibration

Data and Calculations

mg/q

Torsion constant = K

Table 3. The Charge on the Sphere

tor

C (Capacitance of Electrometer System) =

V (Electrometer Voltage) =

q (Charge on sphere) = 2CV =

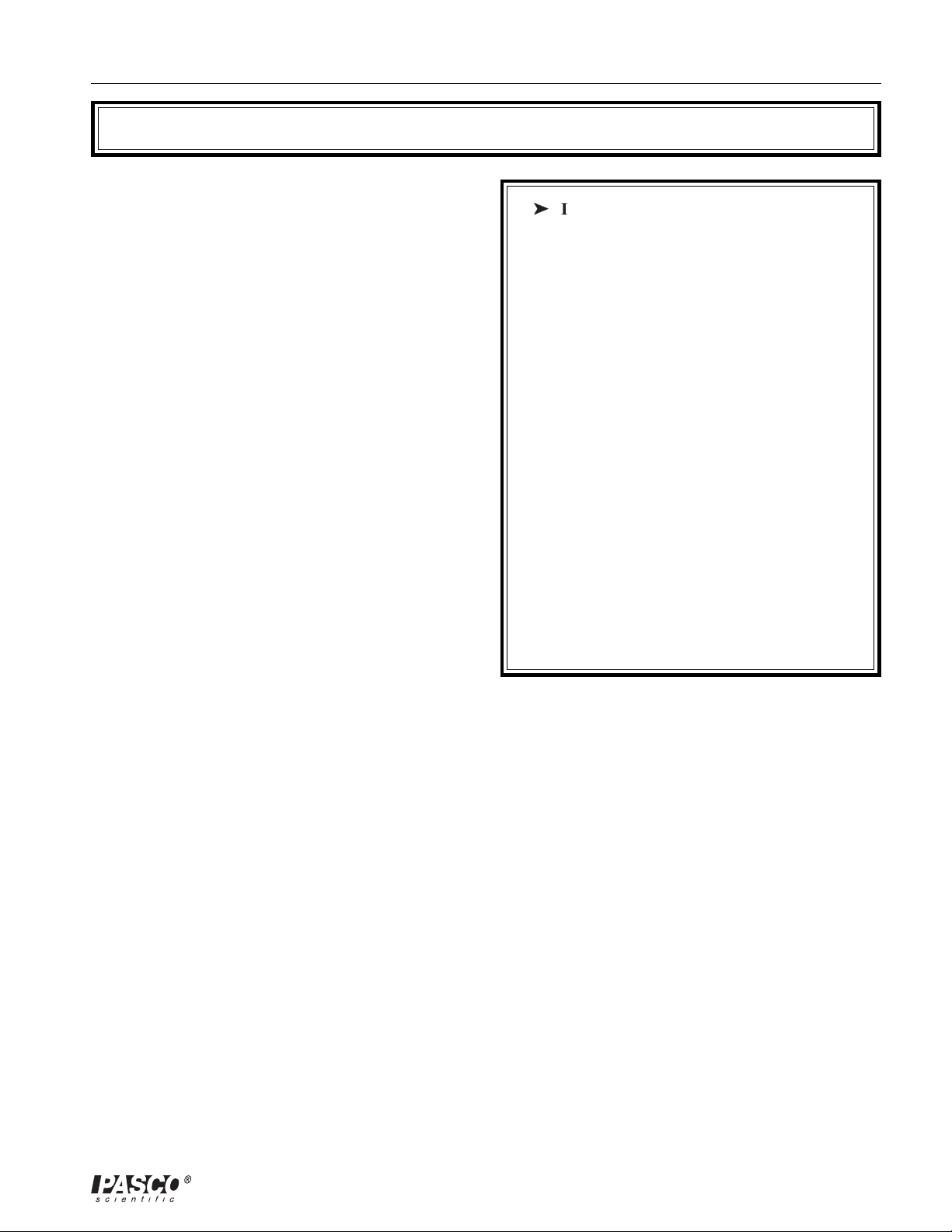
012-03760E Coulomb Balance

Replacing the T orsion Wire

To replace the torsion wire, follow the numbered steps in Figure 9. When you're done, follow the instructions in the Setup section of this manual to balance the pendulum and to zero the torsion balance.

IMPORTANTWhen Replacing the

Wire:

➀ Begin with a length of wire at least 50 cm

long (if you've done this before, you may not need such a long piece).

➁ Be careful not to kink the wire. ➂ As you thread the wire, the end may become

bent or kinked. It will help to clip the end off so it remains straight.

➃ Tighten the screws that hold the torsion wire

gently. Overtightening will break the wire.

➄ The tension on the torsion wire is not a

critical variable, as long as the wire is reasonably taut. The advantage of the spring balance is that it helps you adjust the tension, without pulling too hard and breaking the wire. If you don't have a spring balance, you can adjust the tension by feel. Just take care not to break the wire.

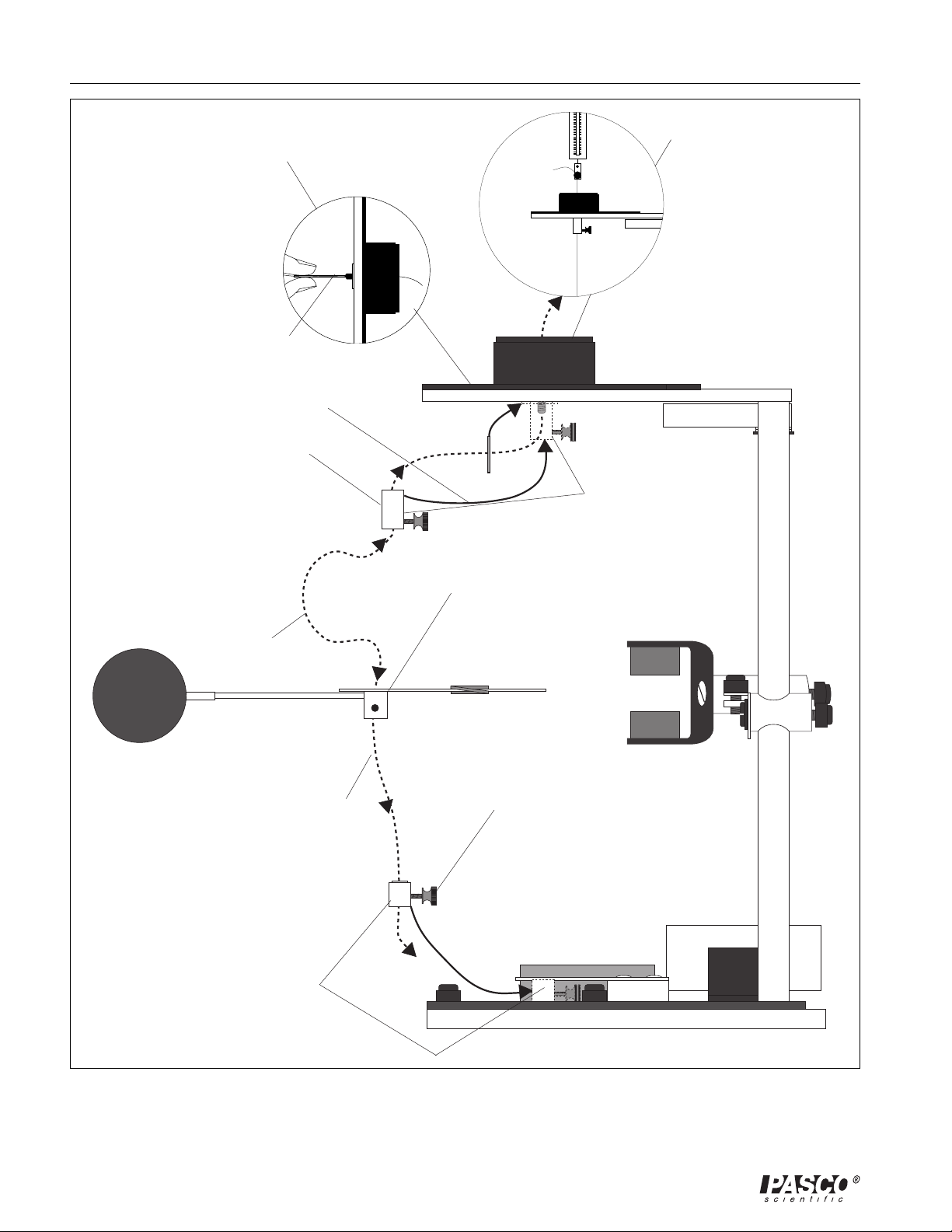
Coulomb Balance 012-03760E

5. a. Carefully lay the torsion

balance on its side.

b. Thread the wire through

the hole in the torsion knob. It is helpful to hold the thread against the small allen wrench, pushing them through together, as shown.

allen wrench

4. Thread the wire

through the washer.

3. a. Remove the wire retainer by

unscrewing it.

b. Loosen the set screw and

thumbscrew one full turn.

c. Thread the wire in the

direction shown.

d. Retighten the set screw, but

do not tighten the thumbscrew. The wire must be able to turn.

Torsion wire

8. a. Using the torsion wire

clamp and a spring balance, pull the wire with a force of approximately 4 newtons (400 gram mass).

b. Tighten the thumb-

screw.

7. Screw the wire

retainer back in place.

9. Adjust the height of

the pendulum assembly, then tighten the set screws with the allen wrench.

1. a. Use the allen wrench to

loosen both set screws one full turn.

b. Thread the wire in the

direction shown.

c. Do not tighten the screws.

6. Put the lower wire retainer

back in position, sliding the wire through the slot in the bottom bracket.

2. a. Using the allen wrench,

loosen the set screw one full turn.

b. Loosen the thumbscrew

one full turn.

c. Thread the wire in the

direction shown.

d. Tighten both screws.

Figure 9. Replacing the Torsion Wire

012-03760E Coulomb Balance

Teacher’s Guide

Experiments: Parts A-C

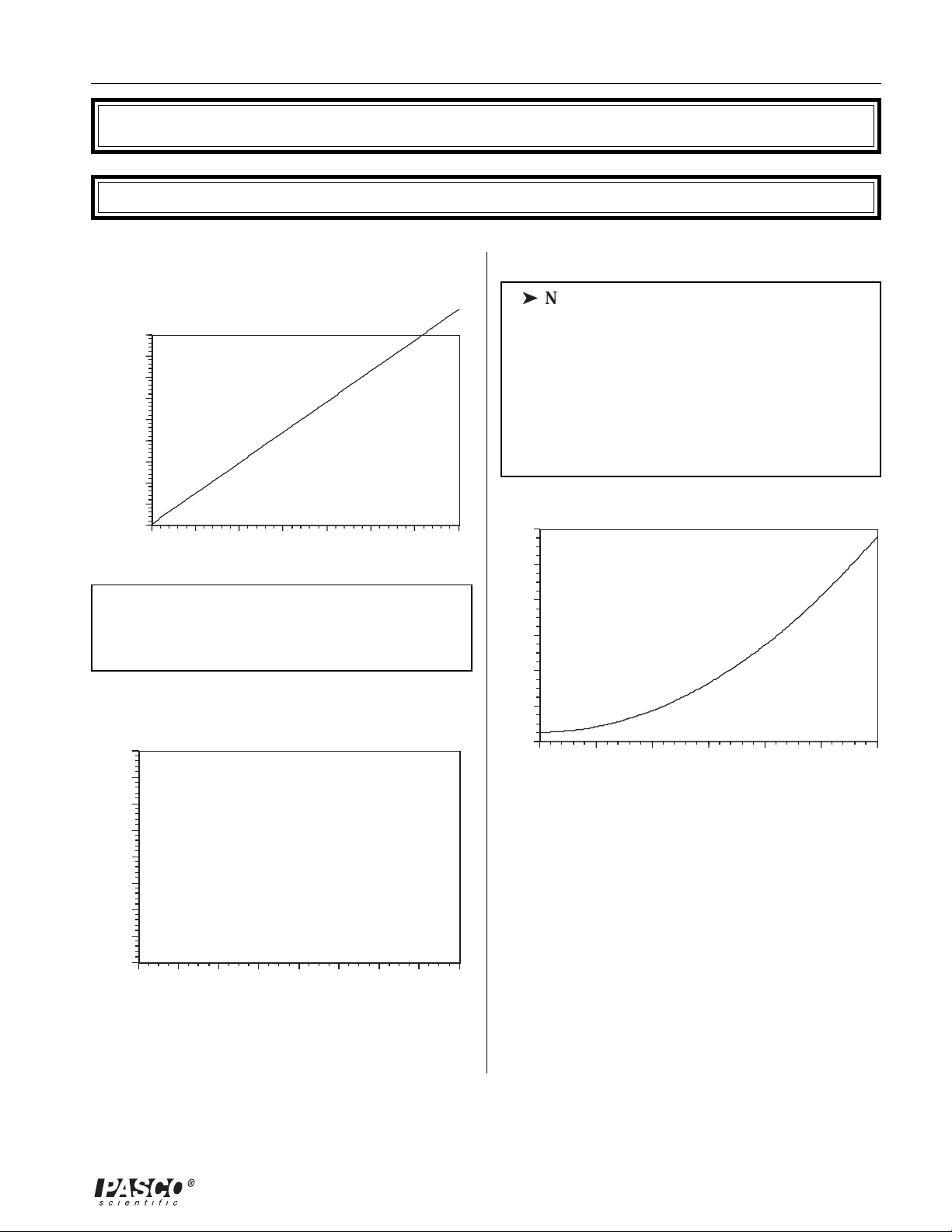
Torsion Wire Calibration

0.0009

0.0008

0.0007

0.0006

0.0005

0.0004

Force (N)

0.0003

0.0002

0.0001

0 100 200 300 400 500 600 700

f(x) = 1.448574E-6*x + 4.496489E-6 R^2 = 9.998832E-1

Angle (degrees)

➤ NOTE: The slope of this curve is dependent on the tension on the wire; thus, it will be slightly different for each unit.

Distance Dependence

Charge Dependence

NOTE: There are two ways of verifying the

dependence of force on charge. You may hold one of the spheres at a constant charge and show that force is linear with the other charge, or you may charge both spheres equally and show that the force is proportional to the square of the charge. The latter method is easier to control with a single voltage supply, and was used for this write-up.

120

f(x) = 1.335407E-5 * (x^1.836206E+0 ) R^2 = 9.954969E-1

100

y= 3.071653E-6*x^2+4.956344E+0; R^2 = 9.967336E-1

Angle (degrees)

400 350 300 250 200

Angle

150 100

0246810121416

f(x) = 3.994733E+3 * (x^-1.749366E+0 ) R^2 = 9.959050E-1

Distance (cm)

A power regression of this data shows that there is an inverse-square dependence, as predicted by theory.

0 1000 2000 3000 4000 5000 6000

Potential (V)

The first equation given here (a power regression) shows that the force is dependent on the square of the charges, as predicted by the equations.

The second curve fit (a programmed least-squares fit), when converted to SI units, gives us a value of

1.05x10 accepted value of 9 x 109. We do not know the

for k. This value is 17% higher than the

reason for this error at the time this is being written. If you have any explanations for this error, or suggestions about how to improve it, please let us know. Call PASCO Technical support at (800) 772-

8700.

Coulomb Balance 012-03760D

Notes

T echnical Support

Feedback

If you have any comments about the product or manual, please let us know. If you have any suggestions on alternate experiments or find a problem in the manual, please tell us. PASCO appreciates any customer feedback. Your input helps us evaluate and improve our product.

To Reach PASCO

For technical support, call us at 1-800-772-8700 (toll-free within the U.S.) or (916) 786-3800.

fax: (916) 786-3292 e-mail: techsupp@pasco.com web: www.pasco.com

Contacting Technical Support

Before you call the PASCO Technical Support staff, it would be helpful to prepare the following information:

➤ If your problem is with the PASCO apparatus, note:

 Title and model number (usually listed on the

label);

 Approximate age of apparatus;  A detailed description of the problem/sequence of

events (in case you can’t call PASCO right away, you won’t lose valuable data);

 If possible, have the apparatus within reach when

calling to facilitate description of individual parts.

➤ If your problem relates to the instruction manual,

note:

 Part number and revision (listed by month and

year on the front cover);

 Have the manual at hand to discuss your

questions.

PASCO ES-9070 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual