PASCO AP-8215 Instruction Manual

Instruction Manual and
Experiment Guide for the

6#7869%67:

##;$%

PASCO scientific
Model AP-8215

GRAVITATIONAL TORSION BALANCE

AP-8215

GRAVITATIONAL
TORSION BALANCE

Attach to

Earth Ground.

!"#$$%"&'()*"+,-./0-1-, 23456

Gravitational Torsion Balance 012–06802B

!"#$%&&!"#$ %"&' #( )* $+ & ,- # . /* #. ") 0 &" ,
)&((",1#./*#2"3+&,-#4*3/$,&04#450.#(*
65227#)$&0*'#",# ("./# 0&'*0# '5)&,­4"%&,-# ")#.)$,08").&,-#./*

9)$%&.$.&",$2# !")0&",#:$2$,3*;

!"#$%&&<$%*#./*#8$3+&,-# 4$.*)&$2#6) "4
./*#&,.*)&")#"6# ./*# 3/$4(*)1#$,'
)*=&,0.$22#./&0#4$.*)&$2#'5)&,-#4"%&,-#")
.)$,08").&,-# ./*#9)$%&.$.&",$2#!")0&",
:$2$,3*;

The exclamation point within an equilateral
triangle is intended to alert the user of the
presence of important operating and
maintenance (servicing) instructions in the
literature accompanying the device.

!"#$!%&!#' ()*+,-*-,./*012.)3,./1'*0*/45

!"#$%#$&

!"#$%&' ()*"

!"#$%&'()*+,-*.+%%+,)$*/,0"%1+)&", 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 &&

/,)%"-34)&", 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222225

!" #$%%&'"()*+,-./01 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 3

673,) 2222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 9

45/$67'0%"8)-)7'%'-9 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 :

673,)*:8)3# 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 ;

;0$%$)&"<'%/6 2222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 :
#'='&$0,"%>'"?-)=$%)%$.0)&"@.-9$.0"()&)0*' 222222222222222222222222222222222222222222222222222222222222222222222 A
B' - % $ * ) & "! 1 C / 9 % 7 '0 % ". D "%> ' "8 ' 0 1 / & / 7 2 2 2 2 2 2 2 2 2 2 2 22 2 2 2 2 2 2 2 2 2 2 2 2 22 2 2 2 2 2 2 2 2 2 2 2 2 22 2 2 2 2 2 2 2 2 2 2 2 2 22 2 2 2 2 2 2 2 2 2 2 2 2 22 2 2 2 2 2 2 2 2 2 2 A
E.%)%$.0)&"!&$,07'0%".D"%>'"8'01/&/7"(.F"!-79"GH'-.$0,I22222222222222222222222222222222222222222222 J
<'%%$0,"/6"D.-"%>'"4K6'-$7'0%2222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 L

<8+=3%&,'*)(8*>%+?&)+)&",+@*!",=)+,) 22222222222222222222222222222222222222222222222222222222222222222222222222222222222222 A

M='-=$'N".D"%>'"4K6'-$7'0% 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 L

<6BCDE*/F* *<8+=3%818,)*G$* H&,+@*E80@84)&", 222222222222222222222222222222222222222222222222222222222222222222 I

@>'.-O 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 P
8-.*'1/-' 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222223Q
!0)&O9$9 22222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 33

<6BCDE*//F**<8+=3%818,)* G$*673&@&G%&31*J"=&)&",= 22222222222222222222222222222222222222222222222222222 5;

@>'.-O 2222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 3:
8-.*'1/-' 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222223:
!0)&O9$9 22222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 3:

<6BCDE*///F* *<8+=3%818,)*G$*K448@8%+)&", 222222222222222222222222222222222222222222222222222222222222222222 5L

@>'.-O 2222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 3A
8-.*'1/-' 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222223R
!0)&O9$9 22222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 3R

<+&,)8,+,48 22222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 5A

B%+,=#"%)&,'*+,-*:)"%&,' 22222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 5I

:+08)$*J%84+3)&", 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 5I

B84(,&4+@*:3##"%) 222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222 /,=&-8*M+4N*! "?8%

!

!"#$%&'()*+, -%%-.)$*+-./+012".)+54)2%.

J@8+=8OY''&"D-''"%."1/6&$*)%'" %>$9"7)0/)&
9/FC'*%"%."%>'"*.6O-$,>%"-'9%-$*%$.09"F' &.N2

Copyright Notice

@>'"8!<SM"9*$'0%$D$*" Q3TUQRPQT!" " ?-)=$%)%$.0)&
@.-9$.0"()&)0*'" 7)0/)&" $9" *.6O-$,>%'1")01")&&"-$,>%9

-'9'-='12"V.N'='-W"6'-7$99$.0" $9",-)0%'1"%."0.0U6-.D$%
'1/*)%$.0)&"$09%$%/%$.09"D.-" -'6-.1/*%$.0" .D")0O"6)-%".D
%>'"7)0/)&"6-.=$1$0,"%>'"-'6-.1/*%$.09" )-'"/9'1".0&O
D.-"%>'$-"&)F.-)%.-$'9")01")-'"0.%"9.&1"D.-"6-.D$%2
E'6-.1/*%$.0"/01'-")0O" .%>'-"*$-*/79%)0*'9W"N$%>./%
%>'"N-$%%'0"*.09'0%".D"8!<SM"9*$'0%$D$*W" $9"6-.>$F$%'12

Limited Warranty

8!<SM"9*$'0%$D$*"N)--)0%9"%>'" 6-.1/*%" %." F'" D-''" D-.7
1'D'*%9"$0" 7)%'-$)&9" )01"N.-+7)09>$6"D.-")" 6'-$.1".D
.0'"O')-" D-.7"%>'"1)%'".D"9>$67'0%"%."%>'"*/9%.7'-2
8!<SM"N$&&"-'6)$-".-"-'6&)*'")%"$%9".6%$.0")0O"6)-%".D
%>'"6-.1/ *%"N>$*>"$9"1''7'1" %."F'"1'D'*%$='"$0" 7)%'-$)&
.-"N.-+7)09>$62" @>'"N)--)0%O"1.'9"0.%"*.='-"1)7),'
%."%>'"6-.1/*%"* )/9'1" FO" )F/9'" .-" $76-.6'-" /9'2
X'%'-7$0)%$.0".D"N>'%>'-" )" 6-.1/*%"D)$&/-'"$9"%>'" -'9/&%
.D")"7)0/D)*%/-$0," 1'D'*%" .-"$76-.6'-"/9'"FO"%>'
*/9%.7'-"9>)&&" F'"7)1'"9.&'&O"FO"8!<SM" 9*$'0%$D$*2
E'96.09$F$&$%O"D.-" %>'" -'%/-0".D"'5/$67'0%"D.-"N)--)0%O

-'6)$-"F'&.0,9" %."%>'"*/9%.7'-2" 45/$67'0%"7/9%"F'
6-.6'-&O"6)*+'1"%."6-'='0%"1)7),'")01"9>$66'1

6.9%),'".-"D-'$,>%"6-'6)$12"GX)7),'"*)/9'1" FO
$76-.6'-"6 )*+$0,".D"%>'"'5/$67'0%" D.-"-'%/-0"9>$67'0%
N$&&"0.%"F'" *.='-'1"FO"%>'"N)--)0%O2I"<>$66$0," *.9%9
D.-"-'%/-0$0,"%>'" '5/$67'0%" )D%'-"-'6)$-"N$&&"F'"6)$1"FO
8!<SM" 9*$'0%$D$*2

Equipment Return

<>./&1"%>'"6-.1/*%">)='" %." F'" -'%/-0'1" %." 8!<SM
9*$'0%$D$*"D.-" ) 0O" -' )9.0W" 0 .%$DO" 8 !<SM"9*$'0%$D$*"FO
&'%%'-W"6>.0'W".-"D)K "(4YM E4"-'%/ -0$0,"%> '"6-.1 /*%2
Z6.0"0.%$D$*)%$.0W"%>'"-'%/-0")/%>.-$[)%$.0")01
9>$66$0," $09%-/*%$.09"N$&&" F'"6-.76%&O" $99/'12

PDB6F""\M"4]Z; 8 ^ 4 \@"_;##"(4
!SS48@4X"YME"E4@ZE\"_;@VMZ@"!\
!Z@VME;H!@;M\"YEM^"8!<SM2

_>'0"-'%/-0$0,"'5/$67'0%"D.-"-'6)$-W"%>'"/0$%9"7/9%" F'

6)*+'1"6-.6'-&O2" S)--$'-9" N $&&" 0.%")**'6%"-'96.09$F$&$%O
D.-"1)7),'"*)/9'1" FO"$76-.6'-"6)*+$0,2"@."F'"*'-%)$0
%>'"/0$%"N$&&"0.%"F'"1)7),'1"$0"9>$67'0%W".F9'-='"%>'
D.&&.N$0,"-/&'9`

➀ @>'"6)*+$0,"*)-%.0" 7/9%"F'"9%-.0,"'0./,>" D.-"%>'"$%'7

9>$66'12

➁ ^)+'"*'-%)$0"%>'-'")-'")%" &')9%" %N." $0*>'9".D" 6)*+$0,

7)%'-$)&"F'%N''0")0O" 6.$0%".0"%>'")66)-)%/9")01"%>'
$09$1'"N)&&9" .D"%>'"*)-%.02

➂ ^)+'"*'-%)$0"%>)%"%>'"6)*+$0," 7)%'-$)&" *)00.%" 9>$D%"$0

%>'" F.K".-" F'*.7' "*.76-'99'1W" )&&.N$0,"%>'
$09%-/7'0%"*.7'"$0"*.0%)*%"N$%>"%>'" 6) *+$0,"*)-%.02

!11-'99` 8!<SM"9*$'0%$D$*

3Q3Q3"Y..%>$&&9"(&=12
E.9'=$&&'W"S!"aJLALUL3QQ

8>.0'` Ga3RI"LPRU:PQQ
Y!b` Ga3RI"LPRU:TaT
'7)$&` %'*>9/66c6)9*.2*.7
N'F` NNN26)9*.2*.7

!!

!"#6!%&!#' ()*+,-*-,./*012.)3,./1'*0*/45

F
m1m

r

head of
torsion ribbon

Introduction

The PASCO scientific AP-8215 Gravitational Torsion Balance
reprises one of the great experiments in the history of physics—
the measurement of the gravitational constant, as performed by
Henry Cavendish in 1798.

The Gravitational Torsion Balance consists of two 38.3 gram
masses suspended from a highly sensitive torsion ribbon and two

1.5 kilogram masses that can be positioned as required. The
Gravitational Torsion Balance is oriented so the force of gravity
between the small balls and the earth is negated (the pendulum is
nearly perfectly aligned vertically and horizontally). The large
masses are brought near the smaller masses, and the gravitational
force between the large and small masses is measured by
observing the twist of the torsion ribbon.

An optical lever, produced by a laser light source and a mirror
affixed to the torsion pendulum, is used to accurately measure the
small twist of the ribbon. Three methods of measurement are
possible: the final deflection method, the equilibrium method, and
the acceleration method.

grounding
wire

large
masses

base with leveling feet

zero adjust
knob

mirror on
pendulum bob

sight for
leveling

A Little Background

The gravitational attraction of all objects toward the Earth is
obvious. The gravitational attraction of every object to every
other object, however, is anything but obvious. Despite the lack
of direct evidence for any such attraction between everyday
objects, Isaac Newton was able to deduce his law of universal
gravitation.

However, in Newton's time, every measurable example of this
gravitational force included the Earth as one of the masses. It was
therefore impossible to measure the constant, G, without first
knowing the mass of the Earth (or vice versa).

The answer to this problem came from Henry Cavendish in 1798,
when he performed experiments with a torsion balance,
measuring the gravitational attraction between relatively small
objects in the laboratory. The value he determined for G allowed
the mass and density of the Earth to be determined. Cavendish's
experiment was so well constructed that it was a hundred years
before more accurate measurements were made.

Figure 1

Assembled Gravitational Torsion Balance,
ready to begin Henry Cavendish’s classic
experiment to determine the gravitational
constant

Newton’s law of universal
gravitation:

2

2

where m

= G

and m2 are the masses of

1

the objects, r is the distance between
them, and
G = 6.67 x 10

-11

Nm2/kg

2

1

()*+,-*-,./*012.)3,./1'*0*/45 !"#6!%&!#'

Equipment

Included:

•Gravitational Torsion Balance

•support base with leveling feet

•1.5 kg lead balls (2)

•plastic plate

•replacement torsion ribbon
(part no. 004-06788)

•2-56 x 1/8 Phillips head screws (4)

•Phillips screwdriver (not shown)

Additional Required:

•laser light source (such as the PASCO OS-9171 He-Ne Laser)

•meter stick

2-56x1/8
Phillips head
screws

torsion ribbon
head

replacement
torsion ribbon

Attach to

Earth Ground.

AP-8215

GRAVITATIONAL
TORSION BALANCE

zero adjust
knob

aluminum
plate

pendulum
mirror

1.5 kg lead
masses

plastic
demonstration
plate

Figure 2

Equipment Included

2

optical grade
glass window

large mass
swivel support

leveling sight

leveling feet

!"#6!%&!#' ()*+,-*-,./*012.)3,./1'*0*/45

Attach to

Earth Ground.

GRAVITATIONAL
TORSION BALA NCE

AP-8215

IMPORTANT NOTES

Equipment Parameters

•Small lead balls
Mass: 38.3 g
Radius: 9.53 mm
Distance from ball center to torsion axis: d = 50 .0 mm

•Large lead balls
Mass: 1500 g
Radius: 31.9 mm

•Distance from the center of mass of the large ball to the

center of mass of the small ball when the large ball is
against the aluminum plate and the small ball is in the
center position within the case: b = 46.5 mm (Tolerances
will vary depending on the accuracy of the horizontal
alignment of the pendulum.)

•Distance from the surface of the mirror to the outer surface

of the glass window: 11.4 mm

•Torsion Ribbon Material: Beryllium Copper
Length: approx. 260 mm
Cross-section: .017 x .150 mm

+ 0.2 g (m2)

+ 10 g (m1)

➤ The Gravitational Torsion Balance
is a delicate instrument. We
recommend that you set it up in a
relatively secure area where it is safe
from accidents and from those who
don’t fully appreciate delicate
instruments.

➤ The first time you set up the
torsion balance, do so in a place
where you can leave it for at least one
day before attempting measurements,
allowing time for the slight elongation
of the torsion band that will occur
initially.

Keep the pendulum bob secured in
the locking mechanisms at all times,
except while setting up and
conducting experiments.

Equipment Setup

Initial Setup

1. Place the support base on a flat, stable table that is located

such that the Gravitational Torsion Balance will be at least
5 meters away from a wall or screen.

Note: For best results, use a very sturdy table, such as an optics

table.

2. Carefully remove the Gravitational Torsion Balance from

the box, and secure it in the base.

3. Remove the front plate by removing the thumbscrews

(Figure 3), and carefully remove the packing foam from the
pendulum chamber.

Note: Save the packing foam, and reinstall it each time the

Gravitational Torsion Balance is transported.

4. Fasten the clear plastic plate to the case with the

thumbscrews.

Do not touch the mirror on the pendulum.

pendulum
chamber

pendulum
bob

aluminum plate

Figure 3

Removing a plate from the chamber box

3

()*+,-*-,./*012.)3,./1'*0*/45 !"#6!%&!#'

torsion ribbon

Leveling the Gravitational Torsion Balance

head

1. Release the pendulum from the locking mechanism by

unscrewing the locking screws on the case, lowering the
locking mechanisms to their lowest positions (Figure 4).

torsion ribbon

!

Turn locking
screws clockwise.

"

pendulum
bob arm

locking
mechanisms

Figure 4

Lowering the locking mechanism to release the pendulum bob arms

2. Adjust the feet of the base until the pendulum is centered in

the leveling sight (Figure 5). (The base of the pendulum will
appear as a dark circle surrounded by a ring of light).

3. Orient the Gravitational Torsion Balance so the mirror on

the pendulum bob faces a screen or wall that is at least 5
meters away.

SIDE,
CUTAWAY
VIEW

pendulum

Pendulum bob
must be

Look through the
sight to view the
reflection of the
pendulum bob in
the mirror.

centered over
the mirror.

mirror

Figure 5

Using the leveling sight to level the
Gravitational Torsion Balance.

Vertical Adjustment of the Pendulum

The base of the pendulum should be flush with the floor of the
pendulum chamber. If it is not, adjust the height of the pendulum:

1. Grasp the torsion ribbon head and

loosen the Phillips retaining screw

Grasp the torsion ribbon head
and loosen the Phillips screw.

(Figure 6a).

2. Adjust the height of the pendulum

by moving the torsion ribbon head
up or down so the base of the
pendulum is flush with the floor of
the pendulum chamber
(Figure 6b).

3. Tighten the retaining (Phillips

head) screw.

Figure 6

Adjusting the height of the pendulum bob

4

The bottom of the pendulum

bob should be flush with the

!

floor of the chamber.

"

!"#6!%&!#' ()*+,-*-,./*012.)3,./1'*0*/45

L

Note: Vertical adjustment is only necessary at initial setup and
when you change the torsion ribbon or if someone has loosened
the retaining screw by mistake; it is not normally done during
each experimental setup.

TOP, CUTAWAY VIEW

Rotational Alignment of the Pendulum Bob Arms
(Zeroing)

The pendulum bob arms must be centered rotationally in the case
— that is, equidistant from each side of the case (Figure 7). To
adjust them:

1. Mount a metric scale on the wall or other projection surface

that is at least 5 meters away from the mirror of the
pendulum.

2. Replace the plastic cover with the aluminum cover.

3. Set up the laser so it will reflect from the mirror to the

projection surface where you will take your measurements
(approximately 5 meters from the mirror). You will need to
point the laser so that it is tilted upward toward the mirror
and so the reflected beam projects onto the projection surface
(Figure 8). There will also be a fainter beam projected off the
surface of the glass window.

The pendulum bob arm
must be centered
rotationally between the
plates.

small mass

case plates

Figure 7

Aligning the pendulum bob rotationally

TOP VIEW

reflected beam
(from mirror)

laser

SIDE VIEW

L

screen with scale

Figure 8

Setting up the optical lever

5

()*+,-*-,./*012.)3,./1'*0*/45 !"#6!%&!#'

3. Rotationally align the case by rotating it until the laser beam

projected from the glass window is centered on the metric
scale (Figure 9).

4. Rotationally align the pendulum arm:

a. Raise the locking mechanisms by turning the locking

screws until both of the locking mechanisms barely
touch the pendulum arm. Maintain this position for a
few moments until the oscillating energy of the
pendulum is dampened.

b. Carefully lower the locking mechanisms slightly so the

pendulum can swing freely. If necessary, repeat the
dampening exercise to calm any wild oscillations of the
pendulum bob.

c. Observe the laser beam reflected from the mirror. In the

optimally aligned system, the equilibrium point of the
oscillations of the beam reflected from the mirror will be
vertically aligned below the beam reflected from the
glass surface of the case (Figure 9).

location of the
projected laser
beam from the glass
window

location of the
projected laser beam
from the mirror

Figure 9

Ideal rotational alignment (zeroing) of the
pendulum

d. If the spots on the projection surface (the laser beam

reflections) are not aligned vertically, loosen the zero
adjust thumbscrew, turn the zero adjust knob slightly to
refine the rotational alignment of the pendulum bob
arms (Figure 10), and wait until the movement of the
pendulum stops or nearly stops.

e. Repeat steps 4a – 4c as necessary until the spots are

aligned vertically on the projection surface.

5. When the rotational alignment is complete, carefully tighten

the zero adjust thumbscrew, being careful to avoid jarring the
system.

Hints for speedier rotational alignments:

•Dampen any wild oscillations of the pendulum bob with the
locking mechanisms, as described;

•Adjust the rotational alignment of the pendulum bob using
small, smooth adjustments of the zero adjust knob;

•Exercise patience and finesse in your movements.

zero adjust knob

zero adjust thumbscrew

Figure 10

Refining the rotational alignment of the
pendulum bob

6

!"#6!%&!#' ()*+,-*-,./*012.)3,./1'*0*/45

IT

B

GRAV
TORSION

Setting up for the Experiment

grounding
screw

Attach to

Earth Ground.

1. Take an accurate measurement of the distance from the

mirror to the zero point on the scale on the projection
surface (L) (Figure 8). (The distance from the mirror surface
to the outside of the glass window is 11.4 mm.)

Note: Avoid jarring the apparatus during this setup procedure.

2. Attach copper wire to the grounding screw (Figure 11), and

ground it to the earth.

3. Place the large lead masses on the support arm, and rotate

the arm to Position I (Figure 12), taking care to avoid
bumping the case with the masses.

4. Allow the pendulum to come to resting equilibrium.

5. You are now ready to make a measurement using one of

three methods: the final deflection method, the equilibrium
method, or the acceleration method.

Note: The pendulum may require several hours to reach resting
equilibrium. To shorten the time required, dampen the oscillation
of the pendulum by smoothly raising the locking mechanisms up
(by turning the locking screws) until they just touch the crossbar,
holding for several seconds until the oscillations are dampened,
and then carefully lowering the locking mechanisms slightly.

copper wire to
earth ground

Figure 11

Attaching the grounding strap to the
grounding screw

Light beam

Large Masses:
Position I

glass
window

case

Mirror

small
mass

Measuring the Gravitational
Constant

Overview of the Experiment

The gravitational attraction between a 15 gram mass and a 1.5 kg
mass when their centers are separated by a distance of
approximately 46.5 mm (a situation similar to that of the
Gravitational Torsion Balance ) is about 7 x 10
doesn’t seem like a small quantity to measure, consider that the
weight of the small mass is more than two hundred million times
this amount.

-10

newtons. If this

Large Masses:
Position II

Figure 12

Moving the large masses into Position I

7

Gravitational Torsion Balance 012–06802B

The enormous strength of the Earth's attraction for the small
masses, in comparison with their attraction for the large masses, is
what originally made the measurement of the gravitational
constant such a difficult task. The torsion balance (invented by
Charles Coulomb) provides a means of negating the otherwise
overwhelming effects of the Earth's attraction in this experiment.
It also provides a force delicate enough to counterbalance the tiny
gravitational force that exists between the large and small masses.
This force is provided by twisting a very thin beryllium copper
ribbon.

The large masses are first arranged in Position I, as shown in
Figure 12, and the balance is allowed to come to equilibrium. The
swivel support that holds the large masses is then rotated, so the
large masses are moved to Position II, forcing the system into
disequilibrium. The resulting oscillatory rotation of the system is
then observed by watching the movement of the light spot on the

➤ Note: 5% accuracy is possible in
Method I if the experiment is set up on a
sturdy table in an isolated location
where it will not be disturbed by
vibration or air movement.

scale, as the light beam is deflected by the mirror.

➤ Note: 5% accuracy is possible in

Any of three methods can be used to determine the gravitational
constant, G, from the motion of the small masses. In Method I,
the final deflection method, the motion is allowed to come to

Method II if the resting equilibrium
points are determined using a graphical
analysis program.

resting equilibrium—a process that requires several hours—and
the result is accurate to within approximately 5%. In method II,
the equilibrium method, the experiment takes 90 minutes or more
and produces an accuracy of approximately 5% when graphical
analysis is used in the procedure. In Method III, the acceleration
method, the motion is observed for only 5 minutes, and the result
is accurate to within approximately 15%.

METHOD I: Measurement by Final Deflection

Setup Time: ~ 45 minutes; Experiment Time: several hours
Accuracy: ~ 5%

Theory

With the large masses in Position I (Figure 13), the gravitational
attraction, F, between each small mass (m
large mass (m

) is given by the law of universal gravitation:

1

F = Gm

where b = the distance between the centers of the two
masses.

8

) and its neighboring

2

2

1m2

/b

(1.1)

d

Figure 13

Origin of variables b and

Large Masses:
Position I

b

Large Masses:
Position II

d

012–06802B Gravitational Torsion Balance

The gravitational attraction between the two small masses and
their neighboring large masses produces a net torque (

grav

) on

the system:

= 2Fd (1.2)

grav

where d is the length of the lever arm of the
pendulum bob crosspiece.

Since the system is in equilibrium, the twisted torsion band

20

T

must be supplying an equal and opposite torque. This torque
(

) is equal to the torsion constant for the band (κ) times the

band

angle through which it is twisted (

band

θ

), or:

= –κθ.(1.3)

Combining equations 1.1, 1.2, and 1.3, and taking into account
that

grav

= –

band

, gives:

κθ

= 2dGm1m2/b

2

s

2

(cm)

S

s

1

Time

(min)

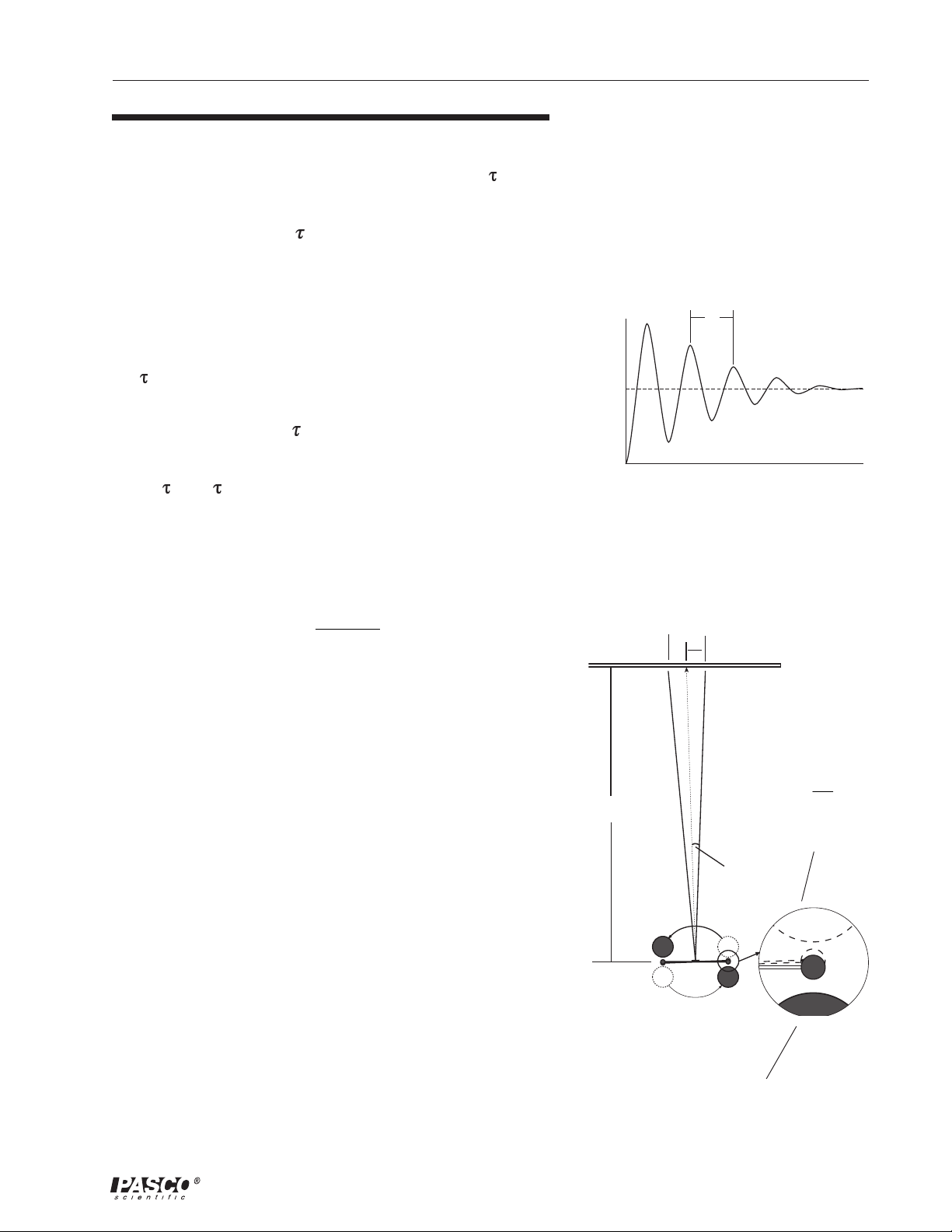
Figure 14

Rearranging this equation gives an expression for G:

Graph of Small Mass Oscillations

60

2

G =

To determine the values of

κθb

2dm1m

θ

and κ — the only unknowns in

2

(1.4)

equation 1.4 — it is necessary to observe the oscillations of the
small mass system when the equilibrium is disturbed. To
disturb the equilibrium (from S

), the swivel support is rotated

1

so the large masses are moved to Position II. The system will
then oscillate until it finally slows down and comes to rest at a
new equilibrium position (S

At the new equilibrium position S
twisted through an angle
twist in Position I, so the total change in angle is equal to 2

) (Figure 14).

2

, the torsion wire will still be

2

θ

, but in the opposite direction of its

θ

.
Taking into account that the angle is also doubled upon
reflection from the mirror (Figure 15):

Δ

S = S2 – S1,

4

θ

= ΔS/L or

θ

= ΔS/4L (1.5)

S

S

1

2

ΔS

2

2θ»tan(2θ)=

L

θ

Position II

ΔS

2L

Position I

Figure 15

Diagram of the experiment showing the
optical lever.

9

Gravitational Torsion Balance 012–06802B

The torsion constant can be determined by observing the period
(T) of the oscillations, and then using the equation:

2

T

= 4

2

π

I/

κ

(1.6)

where I is the moment of inertia of the small mass system.

The moment of inertia for the mirror and support system for the
small masses is negligibly small compared to that of the
masses themselves, so the total inertia can be expressed as:

(1.7)

2

Therefore:

d2+

2

252

r2)

5

252

r

5

2

T

I =2m2(d2+

(1.8)

κ =8π2m

Substituting equations 1.5 and 1.8 into equation 1.4 gives:

G = π2ΔSb

(d2+

2

(1.9)

T

2

m1Ld

5

r2)

252

All the variables on the right side of equation 1.9 are known or
measurable:

r= 9.55 mm

d = 50 mm

b = 46.5 mm

m

= 1.5 kg

1

L = (Measure as in step 1 of the setup.)

By measuring the total deflection of the light spot (
period of oscillation (T ), the value of G can therefore be
determined.

Procedure

1. Once the steps for leveling, aligning, and setup have been

completed (with the large masses in Position I), allow the
pendulum to stop oscillating.

2. Turn on the laser and observe the Position I end point of

the balance for several minutes to be sure the system is at
equilibrium. Record the Position I end point (S
accurately as possible, and indicate any variation over
time as part of your margin of error in the measurement.

Δ

S) and the

) as

1

10

012–06802B Gravitational Torsion Balance

3. Carefully rotate the swivel support so that the large

masses are moved to Position II. The spheres should be
just touching the case, but take care to avoid knocking the
case and disturbing the system.

Note: You can reduce the amount of time the pendulum

requires to move to equilibrium by moving the large
masses in a two-step process: first move the large masses
and support to an intermediate position that is in the
midpoint of the total arc (Figure 16), and wait until the
light beam has moved as far as it will go in the period;
then move the sphere across the second half of the arc
until the large mass support just touches the case. Use a
slow, smooth motion, and avoid hitting the case when
moving the mass support.

4. Immediately after rotating the swivel support, observe the

light spot and record its position (S

).

1

5. Use a stop watch to determine the time required for one

period of oscillation (T). For greater accuracy, include
several periods, and then find the average time required
for one period of oscillation.

Note: The accuracy of this period value (T ) is very

important, since the T is squared in the calculation of G.

6. Wait until the oscillations stop, and record the resting

equilibrium point (S

).

2

Analysis

S

S

1

2

L

Position I

intermediate
position

Position II

Figure 16

Two -step pr ocess of moving the large
masses to reduce the time required to stop
oscillating

1. Use your results and equation 1.9 to determine the value

of G.

2. The value calculated in step 2 is subject to the following

systematic error. The small sphere is attracted not only to
its neighboring large sphere, but also to the more distant
large sphere, though with a much smaller force. The

11

Gravitational Torsion Balance 012–06802B

geometry for this second force is shown in Figure 17 (the
vector arrows shown are not proportional to the actual
forces).

b

F

0

Φ

f

From Figure 17,

f = F0sinΦ

(b

b

2

+4d2)

121

2

The force, F

sinΦ =

is given by the gravitational law, which

0

translates, in this case, to:

Gm

F0=

2m1

(b2+4d2)

and has a component ƒ that is opposite to the direction of
the force F

f =

:

2

(b

+4d2)(b2+4d2)

Gm2m1b

1
2

= βF

This equation defines a dimensionless parameter, b, that is
equal to the ratio of the magnitude of ƒ to that of F. Using
the equation F = Gm

b = b3/(b2+ 4d2)

/b2, it can be determined that:

1m2

3/2

From Figure 17,

d

Figure 17

Correcting the measured value of

F

G

12

Fnet = F - f = F - bF = F(1 - b)

where F

is the value of the force acting on each small

net

sphere from both large masses, and F is the force of
attraction to the nearest large mass only.

Similarly,

G = G

(1 - b)

0

where G is your experimentally determined value for the
gravitational constant, and G

is corrected to account for

0

the systematic error.

Finally,

G

= G/(1 - b)

0

Use this equation with equation 1.9 to adjust your
measured value.

012–06802B Gravitational Torsion Balance

60

S

(cm)

Time

(min)

S

2

S

1

0

20

METHOD II: Measurement by Equilibrium
Positions

Observation Time: ~ 90+ minutes
Accuracy: ~ 5 %

Theory

When the large masses are placed on the swivel support and
moved to either Position I or Position II, the torsion balance
oscillates for a time before coming to rest at a new equilibrium
position. This oscillation can be described by a damped sine
wave with an offset, where the value of the offset represents
the equilibrium point for the balance. By finding the
equilibrium point for both Position I and Position II and taking
the difference, the value of

Δ

S can be obtained. The remainder
of the theory is identical to that described in
Method I.

Note: To obtain an accuracy of 5%

with this method, it is important
to use graphical analysis of the
position and time data to
extrapolate the resting equilibrium
positions, S

and S2.

1

Procedure

1. Set up the experiment following steps 1–3 of Method I.

2. Immediately after rotating the swivel support to Position

II, observe the light spot. Record the position of the light
spot (S) and the time (t) every 15 seconds. Continue
recording the position and time for about 45 minutes.

3. Rotate the swivel support to Position I. Repeat the

procedure described in step 2.

Note: Although it is not imperative that step 3 be performed

immediately after step 2, it is a good idea to proceed with
it as soon as possible in order to minimize the risk that the
system will be disturbed between the two measurements.
Waiting more than a day to perform step 3 is not advised.

Analysis

1. Construct a graph of light spot position versus time for

both Position I and Position II. You will now have a
graph similar to Figure 18.

2. Find the equilibrium point for each configuration by

analyzing the corresponding graphs using graphical
analysis to extrapolate the resting equilibrium points S
and S2 (the equilibrium point will be the center line about
which the oscillation occurs). Find the difference between

1

Figure 18

Typical pendulum oscillation pattern
showing equilibrium positions

13

Gravitational Torsion Balance 012–06802B

the two equilibrium positions and record the result as ΔS.

3. Determine the period of the oscillations of the small mass

system by analyzing the two graphs. Each graph will
produce a slightly different result. Average these results
and record the answer as T.

4. Use your results and equation 1.9 to determine the value

of G.

5. The value calculated in step 4 is subject to the same

systematic error as described in Method I. Perform the
correction procedure described in that section (Analysis,
step 3) to find the value of G

.

0

METHOD III:
Measurement by Acceleration

Observation Time: ~ 5 minutes
Accuracy: ~ 15%

Theory

With the large masses in Position I, the gravitational attraction,
F, between each small mass (m
mass (m

) is given by the law of universal gravitation:

1

F = Gm

This force is balanced by a torque from the twisted torsion
ribbon, so that the system is in equilibrium. The angle of twist,

θ

, is measured by noting the position of the light spot where
the reflected beam strikes the scale. This position is carefully
noted, and then the large masses are moved to Position II. The
position change of the large masses disturbs the equilibrium of
the system, which will now oscillate until friction slows it
down to a new equilibrium position.

Since the period of oscillation of the small masses is long
(approximately 10 minutes), they do not move significantly
when the large masses are first moved from Position I to
Position II. Because of the symmetry of the setup, the large
masses exert the same gravitational force on the small masses
as they did in Position I, but now in the opposite direction.
Since the equilibrating force from the torsion band has not

) and its neighboring large

2

2

1m2

/b

(3.1)

14

012–06802B Gravitational Torsion Balance

changed, the total force (F

) that is now acting to accelerate

total

the small masses is equal to twice the original gravitational
force from the large masses, or:

F

= 2F = 2Gm1m2/b

total

2

(3.2)

Each small mass is therefore accelerated toward its
neighboring large mass, with an initial acceleration (a

) that is

0

expressed in the equation:

m

= 2Gm

2a0

1 m2

/b

2

(3.3)

Of course, as the small masses begin to move, the torsion
ribbon becomes more and more relaxed so that the force
decreases and their acceleration is reduced. If the system is
observed over a relatively long period of time, as in Method I,
it will be seen to oscillate. If, however, the acceleration of the
small masses can be measured before the torque from the
torsion ribbon changes appreciably, equation 3.3 can be used to
determine G. Given the nature of the motion—damped
harmonic—the initial acceleration is constant to within about
5% in the first one tenth of an oscillation. Reasonably good
results can therefore be obtained if the acceleration is measured
in the first minute after rearranging the large masses, and the
following relationship is used:

S

S

1

2

ΔS

2

L

2θ

2

G = b

a0/2m

1

(3.4)

The acceleration is measured by observing the displacement of
the light spot on the screen. If, as is shown in Figure 19:

Δ

s =the linear displacement of the small masses,

d =the distance from the center of mass of the small

masses to the axis of rotation of the torsion
balance,

Δ

S =the displacement of the light spot on the screen,

and

L =the distance of the scale from the mirror of the

balance,

then, taking into account the doubling of the angle on
reflection,

Δ

S = Δs(2L/d ) (3.5)

Using the equation of motion for an object with a constant

Figure 19

Source of data for calculations in
Method III

15

()*+,-*-,./*012.)3,./1'*0*/45 !"#6!%&!#'

acceleration (x = 1/2 at2), the acceleration can be calculated:

a0 = 2Δs/t2 = ΔSd/t2L (3.6)

By monitoring the motion of the light spot over time, the
acceleration can be determined using equation 3.6, and the
gravitational constant can then be determined using equation

3.4.

Procedure

1. Begin the experiment by completing steps 1–3 of the

procedure detailed in Method I.

2. Immediately after rotating the swivel support, observe the

light spot. Record the position of the light spot (S) and the
time (t) every 15 seconds for about two minutes.

Analysis

1. Construct a graph of light spot displacement

(

Δ

S = S - S1) versus time squared (t2), with t2 on the

horizontal axis (Figure 20). Draw a best-fit line through
the observed data points over the first minute of
observation.

2. Determine the slope of your best-fit line.

9

8

7

6

5

Δ S

4

3

2

1

0

900 3600 5625 8100 11025

225 2025

BEST FIT LINE

t2

(sec2)

Figure 20

Sample data and best-fit line

CURVE

THROUGH

DATA

3. Use equations 3.4 and 3.6 to determine the gravitational

constant.

4. The value calculated in step 3 is subject to a systematic

error. The small sphere is attracted not only to its
neighboring large sphere, but also to the more distant
large sphere, although with a much smaller force. Use the
procedure detailed in Method I (Analysis, step 3) to
correct for this force.

16

!"#6!%&!#' ()*+,-*-,./*012.)3,./1'*0*/45

➁ Grasp the

pendulum bob here
to stabilize it.

!

Maintenance

➂ Loosen

the Phillips
screw.

Replacing the Torsion Ribbon Assembly

If the torsion ribbon breaks, replace it as follows:

1. Remove the plates, and raise the locking mechanism using

the locking screws until the pendulum arms are securely
anchored (Figure 21a).

2. Grasp the pendulum bob near the bottom ribbon tab to

stabilize it.

3. Loosen the Phillips screw on the bottom tab of the torsion

ribbon assembly (Figure 21a), and remove the bottom half
of the broken ribbon assembly.

4. Loosen the Phillips screw at the top of the balance

assembly (Figure 21b).

locking
mechanism

5. Grasp the torsion ribbon head and remove the top portion

of the broken torsion ribbon assembly.

6. Attach the top tab of the new torsion ribbon to the torsion

ribbon head using the Phillips screw, being sure the
copper disc on the tab is in contact with the torsion ribbon
head (Figure 22). Align the tab with the face of the torsion
ribbon head.

torsion ribbon head

Attach the tab with
the Phillips screw.

ribbon tab

The copper
disk must
contact the
torsion

torsion
ribbon

ribbon
head.

Figure 22

Attaching the top tab of the torsion ribbon assembly to the torsion
ribbon head

7. Thread the ribbon through the shaft.

8. Using the zero adjust knob, align the bottom tab with the

face of the pendulum bob.

broken
torsion
ribbon

➀ Turn locking screws until

locking mechanism anchors
the pendulum arms.

➄ Grasp the torsion

ribbon head and remove
the top portion of the
broken ribbon assembly.

"

zero adjust
knob

➃ Loosen the

Phillips screw.

Figure 21

Securing the pendulum bob before
removing a broken torsion ribbon, and
loosening the torsion ribbon head

17

Gravitational Torsion Balance 012–06802B

Note: Be sure the ribbon is not twisted.

9. Tighten the Phillips screw on the top of the balance to

secure the torsion ribbon head.

10. Attach the bottom tab of the ribbon to the pendulum bob

using the Phillips screw.

11. Replace the back plate.

12. Level and align the pendulum according to the instructions

in the Equipment Setup section of this manual.

Transporting and Storing

1. To prepare the Gravitational Torsion Balance for

transporting or storing:

a. Remove the front plate.

b. Raise the locking mechanism to securely anchor

the pendulum bob.

Note: To avoid breaking the
torsion ribbon, the locking
mechanism must be fully raised
on both sides during any
moving or transporting of the
Gravitational Torsion Balance.

c. Check to be sure that the torsion ribbon is

hanging straight down the center of the tube. If it
is not, lower the locking mechanisms, be sure the
torsion wire is centered, and raise the locking
mechanisms again. Repeat as necessary until the
ribbon is centered in the tube.

d. Reinstall the packing foam into the chamber to

secure the pendulum bob.

e. Replace the plate.

2. The Gravitational Torsion Balance may be stored flat in

its shipping container.

3. Store in a cool, dry place, and protect the device from any

jarring or rough handling.

Safety Precaution

The small and large masses are made of lead, which is toxic if
ingested. Use appropriate precautions for handling lead,
including hand washing after handling the masses.

18

012–06802B Gravitational Torsion Balance

Technical Support

Feedback

If you have any comments about the product or
manual, please let us know. If you have any
suggestions on alternate experiments or find a
problem in the manual, please tell us. PASCO
appreciates any customer feedback. Your input
helps us evaluate and improve our product.

To Reach PASCO

For technical support, call us at 1-800-772-8700
(toll-free within the U.S.) or [phone].

fax: [phone]

e-mail: [e-mail]

web: www.pasco.com

Contacting Technical Support

Before you call the PASCO Technical Support staff,
it would be helpful to prepare the following
information:

➤ If your problem is with the PASCO apparatus,
note:

- Title and model number (usually listed on the

label);

- Approximate age of apparatus;

- A detailed description of the problem/sequence

of events (in case you can’t call PASCO right
away, you won’t lose valuable data);

- If possible, have the apparatus within reach

when calling to facilitate description of
individual parts.

➤ If your problem relates to the instruction manual,

note:

- Part number and revision (listed by month and

year on the front cover);

- Have the manual at hand to discuss your

questions.

19