Palisade RISKOPTIMIZER 5.7 User Manual

Download

用户指南

RISKOptimizer

Microsoft Excel 的模拟

最优化程序

第 5.7 版

2010 年 7 月

Palisade Corporation 798 Cascadilla St. Ithaca, NY 14850 USA +1-607-277-8000

+1-607-277-8001（传真） http://www.palisade.com（网站） sales@palisade.com（电子邮件）

版权通告

商标确认

Microsoft、Excel 和 Windows 是 Microsoft Corporation 的注册商标。 IBM 是 International Business Machines, Inc. 的注册商标。

Palisade、RISKOptimizer、TopRank、BestFit 和 RISKview 是 Palisade Corporation 的

注册商标。

RISK 是 Tonka Corporation 分部 Parker Brothers 的商标，须获得许可才能使用。

第一章：简介 1

简介.......................................................................................................3

安装说明................................................................................................9

第二章：背景知识 13

什么是 RISKOptimizer？ ...................................................................15

传统最优化与模拟最优化 ....................................................................21

第三章：RISKOptimizer 分步介绍 27

简介.....................................................................................................29

RISKOptimizer 教程 ..........................................................................31

第四章：应用示例 51

简介.....................................................................................................53

预算分配..............................................................................................55

能力规划..............................................................................................57

课程安排程序 ......................................................................................59

期货对冲..............................................................................................61

加工车间日程安排 ...............................................................................63

投资组合平衡 ......................................................................................65

投资组合..............................................................................................67

目录 i

投资组合风险......................................................................................69

推销员问题 .........................................................................................71

收益管理 .............................................................................................73

第五章：RISKOptimizer 参考指南 75

模型定义命令......................................................................................77

“最优化设置”命令 —“常规”选项卡............................................. 97

“最优化设置”命令 —“运行时间”选项卡...................................... 99

“最优化设置”命令 —“视图”选项卡...........................................103

“最优化设置”命令 —“宏”选项卡...............................................105

“开始最优化”命令.........................................................................107

“实用工具”命令.............................................................................109

RISKOptimizer 观察器 ....................................................................113

第六章：最优化 123

简介 .................................................................................................. 125

最优化方法 .......................................................................................125

有关登山算法....................................................................................127

Excel Solver.................................................................................... 129

问题类型 ...........................................................................................131

第七章：遗传算法 135

简介 .................................................................................................. 137

历史 .................................................................................................. 137

生物示例 ...........................................................................................139

数字示例............................................................................................141

第八章：模拟和风险分析 145

简介...................................................................................................147

什么是风险？ ....................................................................................147

在 RISKOptimizer 中为不确定因素建立模型 ...................................151

使用模拟方法分析模型......................................................................153

第九章：RISKOptimizer 附加说明 155

添加约束条件 ....................................................................................157

提高速度............................................................................................165

如何执行 RISKOptimizer 的最优化..................................................167

附录 A：RISKOptimizer 自动化 169

VBA ..................................................................................................169

附录 B：故障排除/问与答 171

故障排除/问与答................................................................................171

附录 C：其他资源 173

其他学习资源 ....................................................................................173

词汇 179

索引 185

目录 iii

第一章：简介

简介.......................................................................................................3

为什么需要 RISKOptimizer？................................................................3

传统最优化问题............................................................................3

不确定模型的最优化 ....................................................................4

建立不确定因素的模型 ................................................................4

使用模拟方法最优化 ....................................................................4

模拟结果........................................................................................5

使用 RISKOptimizer 的自定义应用程序 .....................................5

使用 RISKOptimizer 模拟最优化的实际应用 .........................5

开始之前 .....................................................................................................6

软件包内装物品..........................................................................................6

本版本简介..................................................................................................6

在您的操作环境中使用..............................................................................6

如果需要获得帮助......................................................................................6

打电话之前....................................................................................7

与 Palisade 联系...........................................................................7

学生版............................................................................................8

RISKOptimizer 系统要求........................................................................8

安装说明................................................................................................9

一般安装说明..............................................................................................9

从计算机上移除 RISKOptimizer ..............................................9

DecisionTools Suite.................................................................................9

设置 RISKOptimizer 图标或快捷方式.................................................10

启动时的宏安全警告消息........................................................................10

其他有关 RISKOptimizer 的信息.........................................................11

RISKOptimizer Readme .........................................................11

RISKOptimizer 教程 ................................................................11

学习 RISKOptimizer..............................................................................11

第一章：简介 1

简介

RISKOptimizer 将模拟和最优化功能进行了结合，可以对包含不确定因素的模型进行最优化。通过应用功能强大的基于遗传算法的最优化方法和蒙特卡罗模拟，RISKOptimizer 能够找到标准线性和非线性优化程序 “无法解决”问题的优化解法。RISKOptimizer 结合了 @RISK 的模拟技术、Palisade 的风险分析插件，以及 Palisade 基于遗传算法的求解程序 Evolver。熟悉 @RISK 以及 Evolver 或 Excel 内建 Solver 的用户应当能够轻松使用 RISKOptimizer。

传统最优化问题

您正在阅读的《RISKOptimizer 用户指南介、RISKOptimizer 工作原理以及 RISKOptimizer 的独特遗传算法和模拟技术的几个应用示例。本套手册也可以用作完整索引的参考指南，其中包含有关每种 RISKOptimizer 功能的说明和实例。

》提供 RISKOptimizer 简

为什么需要 RISKOptimizer？

RISKOptimizer 使一系列新问题的最优化成为可能。当问题包含的变量在您的控制范围之外，并且其值未知时，您可以使用 RISKOptimizer 查找优化解法。在模型中输入不确定因素的可能值范围时，目前使用的诸如 Solver（一款 Excel 随附的线性和非线性优化程序）和 Evolver （一款由 Palisade Corporation 开发的基于遗传算法的优化程序）之类的优化程序无法找到优化解法。

使用 Solver 或 Evolver 进行分析且基于 Excel 的传统最优化问题包括：

• 您希望最小化或最大化的输出项或“目标”单元格

• 您能够控制其值的一组输入项或“可调整单元格”

• 一组需要符合的约束条件，此类约束条件通常使用诸如 COSTS<100

或 A11>=0 之类的表达式指定。

在 Solver 或 Evolver 内进行最优化的过程中，可调整单元格在您指定的整个允许范围内变化。针对每组可能的可调整单元格值重新计算模型，并且会生成一个新的目标单元格值。最优化完成后，会找到一个优化解法（或可调整单元格值的组合）。此解法是生成目标单元格最佳（即最小或最大）值，同时符合您输入的约束条件的可调整单元格值的组合。

第一章：简介 3

不确定模型的最优化

但是，如果模型含有不确定因素，Solver 和 Evolver 均无法生成优化解法。过去，很多最优化模型只是忽略不确定因素，使模型不切实际，但却可以进行优化。如果使用模拟方法尝试寻找优化值，则会采用“强力”方法，用迭代方法搜索可能的可调整单元格值。这涉及运行初始模拟、更改一个或多个值、重新运行模拟，并重复该过程，直至找到看似是优化的解法。这是一个冗长的过程，通常如何更改从一次模拟到另一次模拟的值也不清楚。

RISKOptimizer 可以包括模型中的不确定因素，并生成考虑不确定因素的可靠优化解法。RISKOptimizer 利用模拟（通过 @RISK）处理模型中存在的不确定因素，并使用遗传算法（通过 Evolver）生成可调整单元格生成的值。这种“模拟最优化”的结果是可调整单元格值的组合，该组合将目标单元格模拟结果的统计量最小化或最大化。例如，您可能希望确定将目标单元格概率分布平均值最大化或标准差最小化的可调整单元格值的组合。

建立不确定因素的模型

使用模拟方法最优化

为了建立不确定因素的模型，RISKOptimizer 允许您使用 @RISK 中提供的任何概率分布函数描述任何电子表格元素的可能值。例如，电子表格单元格中的值 10 可以用 @RISK 函数 =RiskNormal(10,2) 取代。此函数表示该单元格的可能值用平均值 10 和标准差 2 的概率分布表示。如同在 @RISK 中一样，可以使用诸如 RiskCorrmat 和 DepC 之类的 @RISK 函数使概率分布相关。

在进行最优化时，RISKOptimizer 为基于遗传算法的优化程序生成的每种可能的试验解法运行完整模拟。在试验解法模拟的每次迭代中，对电子表格中的概率分布函数进行抽样，并生成新的目标单元格值。在模拟结束时，试验解法的结果是您希望最小化或最大化的目标单元格分布的统计量。然后，该值返回给优化程序，遗传算法使用该值生成新的和更好的试验解法。对于每种新的试验解法，系统会运行另一次模拟，并生成目标统计量的另一个值。

如同在传统优化程序中一样，可以在 RISKOptimizer 中输入需要符合的约束条件。您可以在模拟的每次迭代时（“迭代”约束条件）或在每次模拟结束时（“模拟”约束条件）检查约束条件。迭代约束条件是典型的传统 Solver 或 Evolver 样式的约束条件，例如 A11>1000。模拟约束条件是引用您指定的模型中任何单元格模拟结果分布统计量的约束条件。典型的模拟约束条件可以是“A11 A11 的模拟结果分布平均值必须大于 1000。如同在 Evolver 中一样，约束条件必须是严格约束条件或宽松约束条件，违反约束条件会导致试验解法被拒绝。

的平均值

> 1000”或者单元格

4 简介

在运行大量模拟时，RISKOptimizer 会使用两种重要的技术，以便最小化运行时间，并尽快生成优化解法。首先，RISKOptimizer 使用收敛监控方法确定何时已经运行足够数量的迭代（但不得过多）。这样可以确保目标单元格概率分布生成的统计量的稳定性，以及来自约束条件引用输出分布的任何统计量的稳定性。其次，RISKOptimizer 使用 Evolver 的遗传算子尽快生成接近优化解法的试验解法。

模拟结果

使用

RISKOptimizer

自定义应用程序

使用

RISKOptimizer

模拟最优化的实际应用

RISKOptimizer 随附一组模拟统计函数，可以用于直接在您的电子表格中返回模拟结果。例如，RiskMean( 布的平均值直接返回工作表单元格或公式。此外，当您希望获得

RISKOptimizer 找到的最佳模型解法的详细图像和统计量时，在 RISKOptimizer 中建立的任何模型可以直接在 Palisade Corporation 为 Excel 设计的风险分析和模拟插件 @RISK 中进行模拟。由于 RISKOptimizer 的模拟基于 @RISK，因此在 @RISK 中进行模拟不需要更改 RISKOptimizer 模型。

RISKOptimizer 随附一套建立使用 RISKOptimizer 功能的自定义应用程序的完整宏语言。RISKOptimizer 的自定义函数可以在 Visual Basic

的

for Applications (VBA) 中用于设置和运行最优化，并显示最优化的结果。有关该编程接口的更多信息，请参见可以通过 RISKOptimizer“帮助”菜单获取的 RISKOptimizer Developer Kit 帮助文档。

最优化不确定模型的功能可以帮助解决很多以前“无法优化的”问题。通常，任何含有不确定因素的模型均可以通过模拟和最优化组合进行优化，其中包括：

♦ 为具有不确定市场条件的新产品选择最佳产量和能力水平 ♦ 确定具有不确定需求的最佳库存水平 ♦ 将风险降至最低的资产组合配置 ♦ 为产品市场具有不同的地理分布且需求水平不确定的工厂确定最佳

产品组合

单元格引用

) 将输入单元格模拟分

♦ 确定对冲买卖中期权购买的最佳水平 ♦ 相同的产品按照不同的价格在不同的限制条件下进行销售的收益管理 ♦ 具有不确定任务时间的日程安排

第一章：简介 5

开始之前

在安装和开始使用 RISKOptimizer 之前，请确保您的 RISKOptimizer 软件包包括所有要求的物品，并确定您的计算机是否符合适当用途的最低要求。

软件包内装物品

RISKOptimizer 与 @RISK 正式版和 DecisionTools Suite 正式版一起提供。除了随 Excel @RISK 正式版提供的 @RISK for Excel 文件外，

@RISK 正式版 CD-ROM 还包含 RISKOptimizer Excel 插件、几个 RISKOptimizer 示例以及完整索引的 RISKOptimizer 在线帮助系统。 DecisionTools Suite 正式版包括以上所有项目，以及附加应用程序。

本版本简介

本 RISKOptimizer 版本可以作为 Microsoft Excel 2000 或更高版本的 32 位程序安装。

在您的操作环境中使用

本《用户指南》假设您掌握了 Windows 操作系统和 Excel 的一般知识。特别是以下知识：

♦

熟悉自己的计算机和鼠标的用法。

♦

熟悉图标、单击、双击、菜单、窗口、命令和目标等术语。

♦

理解目录结构和文件命名之类的基本概念。

如果需要获得帮助

我们向拥有有效维护计划的所有 RISKOptimizer 注册用户免费提供技术支持，或按照每次事件收取服务费。要确保您是 RISKOptimizer 的注册用户，请在以下网站注册：

http://www.palisade.com/support/register.asp。

如果通过电话与我们联系，请准备好您的序列号和《用户指南》。如果您坐在计算机前并作好准备，这将有助于我们为您提供更好的技术支持。

6 简介

打电话之前

在与技术支持部联系之前，请检查以下核对清单：

•

是否已经查阅了在线帮助？

•

是否已经查阅本《用户指南》，并查看了联机多媒体教程？是否已经阅读

•

有关

RISKOptimizer

•

是否是能够始终重复出现的问题？是否是能够在另一台计算机或不

README.WRI

同型号的计算机上重复出现的问题？

•

是否已经在互联网上查阅了我们的网站？我们的网址为：

http://www.palisade.com

文件？该文件包含可能未纳入手册的

的最新信息。

。我们的网站还在“技术支持”部分中

提供最新常见问题解答（可搜索的技术支持问答数据库）和

RISKOptimizer RISKOptimizer

补丁。我们建议您定期访问我们的网站，了解有关

以及其他

Palisade

软件的最新信息。

与 Palisade 联系

Palisade Corporation 欢迎您提出有关 RISKOptimizer 的问题、评论意见或建议。请用以下任何一种方法与我们的技术支持部人员联系：

请发送电子邮件至

•

请在美国东部时间上午

+1-607-277-8000

•

请发送传真至

•

请寄邮件至：

Technical Support Palisade Corporation 798 Cascadilla St. Ithaca, NY 14850 USA

如果您希望与 Palisade 欧洲分部联系：

•

请发送电子邮件至

•

请致电

•

请发送传真至

•

请寄邮件至：

Palisade Europe 31 The Green West Drayton Middlesex UB7 7PN United Kingdom

+44 1895 425050

support@palisade.com。

点至下午

点（星期一至星期五）致电

，并按照提示接通技术支持部。

+1-607-277-8001。

support@palisade-europe.com。

（英国）。

+441895425051

（英国）。

第一章：简介 7

如果您希望与 Palisade 亚太分部联系：

•

请发送电子邮件至

•

请致电

•

请发送传真至

•

请寄邮件至：

Palisade Asia-Pacific Pty Limited Suite 404, L4, 20 Loftus Street Sydney NSW 2000 AUSTRALIA

无论您用何种方法与我们联系，请提供产品名称、版本和序列号。请在 Excel 的 RISKOptimizer 菜单上选择“帮助”命令，查找确切的版本。

+61 2 9929 9799

support@palisade.com.au。

（澳大利亚）。

+61 2 9954 3882

（澳大利亚）。

学生版

不为 RISKOptimizer 学生版提供技术支持。如果需要获得帮助，我们建议您采取以下替代方法：

向您的教授或助教咨询。

♦ ♦

登录以下网站查找常见问题的回答：

♦

通过电子邮件或传真与我们的技术支持部联系。

http://www.palisade.com。

RISKOptimizer 系统要求

RISKOptimizer 系统要求包括：

•

配备硬盘的

• Microsoft Windows 2000 SP4

• Microsoft Excel 2000

Pentium

个人计算机或速度更快的个人计算机。

或更高版本。

8 简介

安装说明

RISKOptimizer 是 Microsoft Excel 的插件程序。通过在 Excel 菜单栏上添加命令，RISKOptimizer 可以增强电子表格程序的功能。

一般安装说明

安装程序会将 RISKOptimizer 系统文件复制到您指定的硬盘目录中去。要在 Windows 2000 或更高版本的系统上运行安装程序：

将

@RISK

的

CD-ROM

正式版或

驱动器中

DecisionTools Suite

正式版的

CD-ROM

插入您

从计算机上移除

RISKOptimizer

依次单击“开始”按钮、“设置”和“控制面板”

双击“添加/删除程序”图标

在“安装/卸载”选项卡上，单击“安装”按钮

按照屏幕上显示的“安装”说明进行安装

如果您在安装 RISKOptimizer 时遇到问题，请确认尝试安装 RISKOptimizer 的驱动器是否有足够的空间。释放足够的空间后，尝试重新运行安装程序。

如果您希望从计算机上移除 RISKOptimizer（以及@RISK 正式版或 DecisionTools Suite 正式版），请使用控制面板的“添加/删除程序” 实用程序，并选择 @RISK 或 DecisionTools Suite 条目。

DecisionTools Suite

RISKOptimizer 可以与 Palisade Corporation 提供的一套风险与决策分析产品 DecisionTools Suite 配合使用。RISKOptimizer 的默认安装程序会将 RISKOptimizer 放入“Program Files\Palisade”主目录的一个子目录内。这与通常将 Excel 安装至“Microsoft Office”目录的一个子目录非常相似。

“Program Files\Palisade”目录的一个子目录将成为 RISKOptimizer 目录（默认名称为 RISKOptimizer5）。该目录包含 RISKOptimizer 插件程序文件 (RISKOPT.XLA)、模型示例以及运行 RISKOptimizer 所需的其他文件。“Program Files\Palisade”的另一个子目录是“SYSTEM” 目录，该目录包含 DecisionTools Suite 中的每个程序所需的文件，包括普通帮助文件和程序库。

第一章：简介 9

设置 RISKOptimizer 图标或快捷方式

在 Windows 中，安装程序会自动在任务栏的“程序”菜单中创建 RISKOptimizer 命令。但是，如果在安装过程中出现问题，或者希望以

后再以手动方式设置，请遵循以下说明：

单击“开始”按钮，然后将光标指向“设置”。

单击“任务栏”，然后单击“开始菜单”选项卡。

单击“添加”，然后单击“浏览”。

找到

RISKOPT.EXE

单击“下一步”，然后双击您希望显示程序的菜单。

键入名称“

RISKOptimizer

文件，并双击此文件。

”，然后单击“完成”。

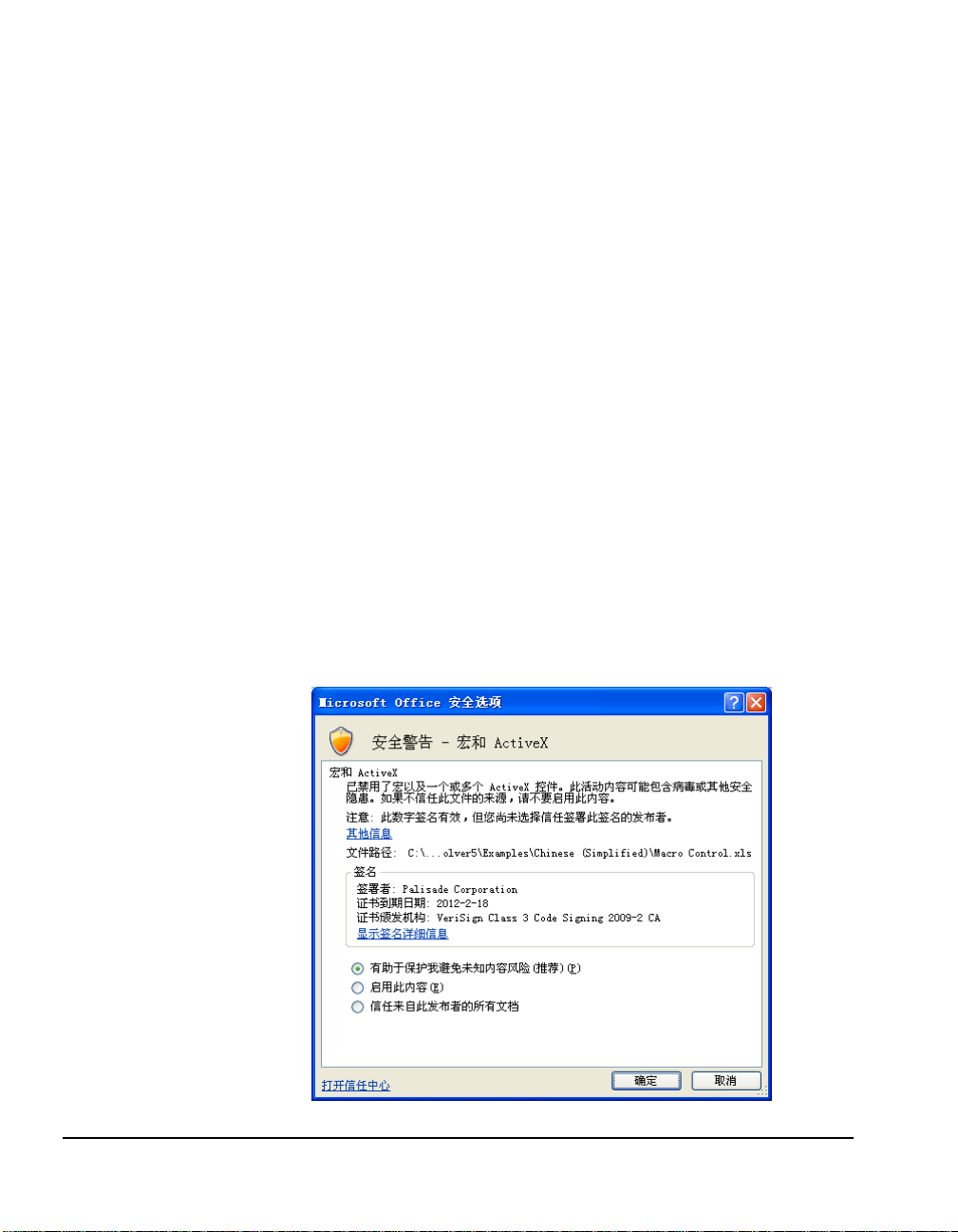
启动时的宏安全警告消息

Microsoft Office 提供几种不同的安全设置，以防不受欢迎的或恶意的宏在 Office 应用程序中运行。除非使用最低安全设置，否则在每次尝试载入带有宏的文件时，系统都会显示一条警告消息。为了防止在每次运行 Palisade 插件时显示此消息，Palisade 以数字方式在所提供的插件文件中签名。因此，一旦将 Palisade Corporation 指定为受信任的发布者，您就可以使用任何 Palisade 插件，而不会再显示警告消息。要进行此操作：

• 在使用 RISKOptimizer 时，如果显示“安全报警”对话框

（例如以下对话框），请单击信任来自此发布者的所有文档。

10 安装说明

其他有关 RISKOptimizer 的信息

用户可在以下来源中查找其他有关 RISKOptimizer 的信息：

RISKOptimizer

Readme

RISKOptimizer

教程

该文件包含 RISKOptimizer 的简单总结，以及有关您的软件最新版本的任何最新新闻或信息。要查看 Readme 文件，请选择 Windows“开始”菜单/“程序”/“Palisade DecisionTools”/“Readmes”，然后单击“RISKOptimizer 5.7 – Readme”。在使用 RISKOptimizer 之前阅读该文件会有帮助。

RISKOptimizer 联机教程向新用户提供有关 RISKOptimizer 和遗传算法的简介。观看该演示只需几分钟时间。请参见以下“学习 RISKOptimizer”一节中有关如何访问教程的信息。

学习 RISKOptimizer

熟悉 RISKOptimizer 的最快方法是使用 RISKOptimizer 联机教程，业界专家会以电影格式引导您观看模型样本。本联机教程是有关 RISKOptimizer 主要功能的多媒体演示。

用户可以通过选择 RISKOptimizer“帮助”菜单的“入门教程”命令，运行联机教程。

第一章：简介 11

第二章：背景知识

什么是 RISKOptimizer？ ...................................................................15

RISKOptimizer 的工作原理？..............................................................16

遗传算法......................................................................................16

概率分布和模拟..........................................................................16

什么是最优化？........................................................................................17

为什么要建立 Excel 模型？ ....................................................................18

在 Exce l 模型中为不确定因素建立模型 ...............................................18

采用模拟方法解释不确定因素................................................................19

为什么要使用 RISKOptimizer？..........................................................19

更准确、更有意义 ......................................................................19

更灵活..........................................................................................19

更便于使用..................................................................................20

传统最优化与模拟最优化 ....................................................................21

传统的电子表格最优化过程....................................................................21

模拟最优化过程........................................................................................22

RISKOptimizer 最优化分步说明..........................................................23

输入概率分布..............................................................................23

输入可调整单元格 ......................................................................24

设置最优化和模拟选项 ..............................................................24

运行最优化..................................................................................25

第二章：背景知识 13

什么是 RISKOptimizer？

RISKOptimizer 软件包向用户提供查找包含不确定因素模型优化解法的简便方法。简言之，RISKOptimizer 可以确定生成所需模拟输出项的最佳输入项。您可以使用 RISKOptimizer 查找变量的适当搭配、顺序或组合，使之生成最高的利润预期值、最低的利润风险（即最小方差）或用最少量的材料生成最高商品预期值。RISKOptimizer 是一款 Microsoft Excel 电子表格程序的插件；用户在 Excel 中建立问题的模型，然后调用 RISKOptimizer 来解决问题。

您必须首先在 Excel 中建立问题的模型，然后在 RISKOptimizer 插件中描述问题。

Excel 为大多数用户创建问题的切合实际的模型提供所需的所有公式、函数、图形和宏功能。RISKOptimizer 查找解法的接口，并提供查找解法的引擎。将 Excel 与 RISKOptimizer 结合，能够找到几乎所有可模型化问题的优化解法。

第二章：背景知识 15

提供描述模型中的不确定因素和要

RISKOptimizer 的工作原理？

遗传算法

概率分布和模拟

RISKOptimizer 使用一组专有

率分布

RISKOptimizer 使用遗传算法确定您模型的最佳解法。遗传算法模拟达尔文的自然选择法则，方法是创建一个允许某个问题的数百种可能解法相互竞争的环境，最后只留下“最适合的”解法。如同生物进化一样，每个解法可以通过“子孙”解法遗传良好的“基因”，因此整个解法群体将继续进化为更好的解法。

您可能已经注意到，在遗传算法中使用的术语通常与生物进化中使用的术语相似。我们会谈到“交叉”功能如何帮助确定查找解法的重点、 “突变”率如何帮助使“基因群”多样化，并且我们会评估整个解法 “群体”或“组织”。要详细了解 RISKOptimizer 遗传算法的工作原理，请参见第七章 — 遗传算法

RISKOptimizer 使用概率分布和模拟方法处理模型变量中存在的不确定因素。Palisade Corporation 为 Excel 设计的风险分析插件 @RISK 提供这些功能。概率分布用于描述模型中不确定因素的可能值范围，并使用概率分布函数输入，例如 RiskTriang(10,20,30)。此分布函数表示您的模型中的一个变量的最小值为 10，最可能值为 20，最大值为 30。然后，通过模拟生成优化程序生成的每个可能试验解法可能结果的分布。

和

模拟

方法处理模型中存在的不确定因素。

遗传算法

。

搜索问题的优化解法，并使用

概

16 什么是 RISKOptimizer？

什么是最优化？

最优化是尝试确定可能有多种可能解法问题的最佳解法的过程。大多数问题涉及众多根据特定公式和约束条件相互作用的变量。例如，一家公司可能有三家制造厂，每家制造厂制造不同数量的不同商品。根据每家制造厂生产每种商品的成本、每家制造厂将商品运送至每家商店的成本和每家制造厂的限制条件，可以在充分满足当地零售店需求的同时，并且将运输成本降至最低的最优方法是什么？这就是最优化工具设计用来回答的一种问题。

最优化经常用于确定从特定资源产生最多产量的组合。

在上例中，每种建议的解法都有一份完整的列表，包括将哪家制造厂生产的哪些商品用什么卡车运送至哪一家零售店的信息。其他最优化问题的示例包括确定如何产生最高利润、最低成本、拯救最多的生命、电路中的噪音最低、在一组城市之间最短的路程或广告媒体采购最有效的组合。最优化问题的一个重要子集涉及日程安排，其目标可以包括在工作班次中最大程度提高效率或尽量减少在不同时间进行团体会议的日程冲突。要详细了解最优化，请参见第六章 — 最优化

。

如果一个问题包括不确定因素，则传统的求解程序就无法解决，因为传统方法没有处理模型中存在的不确定因素的能力。在上例中，如果地方零售商店的需求量不确定，也就是您不知道每一家商店确切地需要多少产品，该如何处理？在传统的求解程序中，您需要为每家商店的需求量假设一个数量。这样才能对模型进行最优化；但是，假设的需求量水平会使您的模型生成对实际情况不确切的描述。在 RISKOptimizer 中，您无需假设需求水平。您使用概率分布描述需求量的可能值，然后使用 RISKOptimizer 的内建模拟功能将所有可能的需求量值包括在最优化结果中。

第二章：背景知识 17

如果使用 RISKOptimizer，优化程序生成的最佳解法就不是您尝试最优化的模型中的目标或“目标单元格”的一个最大值或最小值，而是目标的最大或最小模拟统计量。RISKOptimizer 运行的每次模拟都会为您的目标生成一种可能的结果分布。分布有多个统计量，例如平均值、标准差、最小值等。在上例中，您可能希望找到将利润分布平均值最大化或标准差最小化的输入项组合。

要详细了解模拟，请参见第八章 — 模拟

。

为什么要建立 Excel 模型？

为了提高任何系统的效率，我们必须首先了解系统的行为方式。这就是我们需要构建系统工作模型的原因。在研究复杂系统时，模型是必要的抽象概念，但为了使结果可以应用于“真实的世界”，模型不能将变量之间的因果关系过于简单化。更好的软件和功能日益强大的计算机允许经济学家构建更切合实际的经济模型，允许科学家改善对化学反应的预测，并且允许商界人士提高企业模型的灵敏度。

在过去几年内，计算机硬件和软件程序（例如 Microsoft Excel）取得了巨大的发展，几乎任何拥有个人计算机的人都能为复杂系统创建切合实际的模型。Excel 的内建函数、宏功能和简洁直观的界面使初学者可以对复杂的问题建立模型并进行分析。要详细了解模型的构建，请参见第九章 — RISKOptimizer 附加说明。

在 Exce l 模型中为不确定因素建立模型

变量是您在 Excel 模型中确定为对您的分析十分重要的基本成分。如果您在建立财务状况的模型，您的变量可能是“销售”、“成本”、“收入”或“利润”。如果您在建立地质状况的模型，您的变量可能是“至矿层的深度”、“煤层的厚度”或“多孔性”。每种情况的变量各异，由您自己确定。

在某些情况下，您可能知道在您的模型时段内您的变量值 — 这些是确定变量，统计学家称为“确定性”变量。相反，您也可能不知道这些变量值 — 这些是不确定变量，或“随机”变量。如果您的变量是不确定变量，则需要描述此类变量的不确定性。这需要通过概率分布的方法来完成，概率分布赋予变量可能变化的值范围（从最小值到最大值），以及每个值在该范围内出现的可能性。在 RISKOptimizer 中，不确定变量和单元格值作为概率分布函数输入，例如：

RiskNormal(100,10)

RiskUniform(20,30)

RiskExpon(A1+A2)

RiskTriang(A3/2.01,A4,A5)

如同任何其他 Excel 函数一样，这些“分布”函数可以放在工作表单元格和公式中。

18 什么是 RISKOptimizer？

采用模拟方法解释不确定因素

RISKOptimizer 采用模拟（有时称为“蒙特卡罗模拟”）方法对最优化过程中生成的每个可能的解法进行风险分析。这种意义上的模拟是指用一种方法让计算机反复重新计算您的工作表，并生成可能的结果分布，每次以随机方式选择不同的值组合，获得您的单元格值和公式的概率分布。事实上，计算机在尝试所有有效的输入变量值组合，以模拟所有可能的结果。这如同您同时在工作表中运行数百次或数千次假设分析。

在模拟的每次迭代中，对电子表格中的概率分布函数进行抽样，并生成新的目标单元格值。在模拟结束时，试验解法的结果是您希望最小化或最大化的目标单元格分布的统计量。然后，该值返回给优化程序，遗传算法使用该值生成新的和更好的试验解法。对于每种新的试验解法，系统会运行另一次模拟，并生成目标统计量的另一个值。

为什么要使用 RISKOptimizer？

当您在处理大量相互作用的变量、尝试确定变量的最佳搭配、适当的顺序和最佳组合时，您可能会倾向于只做出“有根据的猜测”。很多人认为除猜测之外的任何类型的模型建立和分析都需要复杂的编程，或令人困惑的统计或数学算法。一种良好的最优化解法可以节约数百万美元、数千加仑稀缺燃料、几个月的时间等。现在，功能强大的台式计算机的价格越来越便宜，并且 Excel 和 RISKOptimizer 之类的软件随手可得，因此我们就没有理由再猜测解法，或以手工方法尝试多种选择方案，而浪费宝贵的时间。

更准确、更有意义

更灵活

第二章：背景知识 19

RISKOptimizer 允许您使用全套 Excel 公式和概率分布来为任何系统创建更切合实际的模型。在使用 RISKOptimizer 时，您无需因为所使用的算法无法处理现实世界的复杂问题而“损害”模型的准确性。传统的“婴儿”求解程序（统计和线性编程工具）强制用户对变量在问题中相互作用的方式做出假设，从而迫使用户建立过于简单且不切实际的问题模型。这些求解程序强制用户假设不确定变量值，因为优化程序无法处理不确定模型成分的可能值。当用户对系统进行简化以使其可以使用这些求解程序时，生成的解法通常因为过于抽象而没有实际价值。无论您尝试将模型设计得多么简单，任何涉及大量变量、非线性函数、查找表、假定陈述、数据库查询或随机元素的问题都无法使用这些方法解决。

有许多求解算法可以解决小型、简单的线性和非线性类型的问题，这些算法包括登山、婴儿求解程序和其他数学方法。即使作为电子表格的插件提供，这些一般用途的优化工具只能进行数字优化。对于更大型或更复杂的问题，您也许能够编写具体的自定义算法，并获得良好的结果，但可能需要进行很多研发工作。即使如此，每当您的模型变化时，都需要对生成的程序进行修改。

RISKOptimizer 不仅能够处理数字问题，而且是世界上唯一一种能够解决大多数组合问题的商用程序。这些是必须将变量打乱（序列改变）或相互组合的问题。例如，为棒球队选择击球顺序是一个组合问题；这是一个交换队员在队列中位置的问题。复杂的日程安排问题也是组合问题。RISKOptimizer 能够解决所有此类型的问题，以及很多任何其他程序无法解决的问题。RISKOptimizer 的独特

遗传算法和模拟

技术允许对

几乎任何类型的模型进行最优化，包括任何大小和任何复杂性的模型。

更便于使用

尽管 RISKOptimizer 明显具有强大功能和灵活优势，但该程序仍然便于使用，因为用户完全没有必要理解 Evovler 使用的复杂遗传算法技术。RISKOptimizer 不关心您问题的“具体细节”；只需要一个能够评估不同选择方案优良程度的电子表格模型。只需选择包含变量的电子表格单元格，并告知 RISKOptimizer 需要查找的内容即可。 RISKOptimizer 以智能方式将困难的技术隐藏起来，自动运行分析问题的“假设分析”过程。

尽管已经开发出许多用于数学编程和模型建立的商用程序，但电子表格仍然是最受欢迎的程序，每个月的销售量都达到数百万套。由于电子表格使用直观的行和列格式，因而比其他专用软件包更容易设置和维护。此外，电子表格与其他程序（例如文字处理程序和数据库）的兼容性更好，并且比任何其他独立软件包提供更多的内建公式、格式化选项、图形绘制和宏功能。由于 RISKOptimizer 是 Microsoft Excel 的插件，因此用户可以使用所有功能和开发工具，方便地为系统建立更切合实际的模型。

20 什么是 RISKOptimizer？

传统最优化与模拟最优化

RISKOptimizer 将模拟和最优化功能进行了结合，从而允许对包含不确定因素的模型进行最优化。此优化程序使用模拟模型连续运行的结果，指导模拟过程搜索更好、更优化的解法。本节提供有关模拟和最优化如何在 RISKOptimizer 中配合使用的背景信息。

传统的电子表格最优化过程

使用最优化插件（例如 Solver 或 Evolver）的传统电子表格优化过程会执行以下步骤：

1) 确定您希望最小化或最大化的输出项或“目标”单元格。

2) 确定一组其值受您控制的输入项或“可调整”单元格，并描述这些

单元格的可能值范围。

3) 一组需要符合的约束条件，此类约束条件通常使用诸如 COSTS<100

或 A11>=0 之类的表达式指定。

4) 运行优化程序，在运行过程中使用可调整单元格的不同可能值连续

多次重新计算电子表格。

5) 在此过程中： a) 每次重新计算为目标单元格生成一个新“答案”或值。 b) 优化程序使用该新目标单元格值选择要尝试的下一组可调整单

元格值。

c) 再次进行重新计算并提供另一个新答案，优化程序可以利用该

新答案找到可调整单元格的一组新值。

此过程在第 5) 步中反复重复，从而使优化程序越来越接近要查找的优化解法，即一组最小化或最大化目标单元格值的可调整单元格值。

第二章：背景知识 21

模拟最优化过程

使用 RISKOptimizer 进行模拟最优化与此处描述的传统电子表格最优化过程的大多数步骤相同。但是，也具有以下不同之处：1) 允许在电子表格中输入不确定因素，以及 2) 使用模拟，而不是简单的电子表格重新计算，提供新的目标单元格“答案”，从而为优化程序提供反馈信息，以便指导优化程序为可调整单元格选择一组新值。

以下是对使用 RISKOptimizer 进行模拟最优化的新过程的描述，与传统电子表格最优化过程的不同之处使用粗体显示：

1) 使用概率分布函数描述模型中不确定因素的可能值范围。

2) 确定输出项或“目标”单元格，选择您希望最小化或最大化的单元

格的模拟统计量（平均值、标准差等）。

3) 确定一组其值受您控制的输入项或“可调整”单元格，并描述这些

单元格的可能值范围。

4) 一组需要符合的约束条件，此类约束条件通常使用诸如 COSTS<100

或 A11>=0 之类的表达式指定。也可以输入基于模拟统计量的附加约束条件（例如，A11>1000

5) 运行优化程序，在运行过程中使用可调整单元格的不同可能值在每

次模拟中连续多次对电子表格进行模拟。在此过程中：

a) 每次模拟为目标单元格生成一个新的可能值的分布。您希望最

小化或最大化的统计量根据此分布计算。

b) 优化程序使用该目标单元格的新统计量选择要尝试的下一组可

调整单元格值。

c) 再次进行模拟并提供另一个新的统计量，优化程序可以利用该

统计量找到可调整单元格的一组新值。

的第 95 百分位数）。

此过程在第 5) 步中反复重复，从而使优化程序越来越接近要查找的优化解法，即一组最小化或最大化目标单元格模拟结果统计量的可调整单元格值。

22 传统最优化与模拟最优化

RISKOptimizer 最优化分步说明

以下是 RISKOptimizer 使用的模拟最优化过程的分步说明：

输入概率分布

RISKOptimizer 使用概率分布描述模型成分中存在的不确定因素。例如，您可以在您的工作表的一个单元格中输入 RiskUniform(10,20)。这表示该单元格值将通过最小值为 10、最大值为 20 的均匀分布生成。该值范围取代 Excel 要求的一个“固定”值。在传统电子表格最优化过程中，无法在模型中增加不确定因素，因此不能使用概率分布。

RISKOptimizer 会为优化程序生成的每种输入值的可能组合运行模型模拟过程。RISKOptimizer 在可能值抽样模拟过程中使用分布函数。模拟的每次迭代使用从您的工作表每个分布函数中抽样的一组新值。然后，使用这些值重新计算工作表，并生成新的目标单元格值。

与 Excel 函数一样，分布函数包含两个元素，函数名称和放在括号中的引数值。以下是一个典型的分布函数：

RiskNormal(100,10)

与 Excel 函数一样，分布函数可以具有引用单元格或表达式的引数。例如：

RiskTriang(B1,B2*1.5,B3)

在此示例中，单元格值将用三角分布表示，其中最小值来自单元格 B1，最可能值通过用单元格 B2 的数值乘以 1.5 计算，最大值来自单元格 B3。

与 Excel 函数一样，分布函数也可以用于单元格公式。例如，单元格公式可以是：

B2: 100+RiskUniform(10,20)+(1.5*RiskNormal(A1,A2))

有关输入概率分布的更多信息，请参见 @ RISK 手册或“帮助”中的参考资料：分布函数。

确定目标单元格和统计量

第二章：背景知识 23

在 RISKOptimizer 和传统电子表格最优化过程中，均要确定一个目标单元格。这是您要尝试将其值最小化或最大化的单元格，或要尝试使其值尽量接近预设值的单元格。通常，这就是您模型的“结果”

总计等

— 但这可以是电子表格中的任何单元格。该单元格中需要有一个

公式，当您的可调整单元格值变化时，该公式可以返回不同的数值。

在 RISKOptimizer 中，您不是最小化或最大化目标单元格中的实际值，而是最小化或最大化与目标单元格模拟结果相关的“统计量”。在优化过程中，RISKOptimizer 将运行连续模拟，每次模拟都有一组不同的可调整单元格值。每次模拟为目标单元格生成一个可能的结果分布。例如，您正在查找一组将目标单元格分布的平均值最大化或标准差最小化的可调整单元格值。

— 利润、模型

在 RISKOptimizer 中，您可以使用更多进行最小化或最大化（

值、标准差、最小值等

相关模拟不只生成一个答案。模拟为目标单元格生成一组完整的可能结果分布，其中包括最小值、最大值、平均值和标准差等。传统最优化过程只为优化程序尝试的每种解法生成一个结果 — 新目标单元格值，该值是最小化或最大化的唯一可能选择。

）的选项，因为对于优化程序尝试的每种解法，

平均

输入可调整单元格

输入约束条件

在传统电子表格最优化和 RISKOptimizer 中，可调整单元格的输入方法很相似。针对在最优化过程中可以更改的每个单元格输入一个最小可能值和一个最大可能值。

由于 RISKOptimizer 使用的优化程序是基于 Evolver，因此 RISKOptimizer 中的可调整单元格输入与 Evolver 中具有相同的选项。这些选项包括突变率、求解方法和遗传算子。有关输入可调整单元格的更多信息，请参见第五章：RISKOptimizer 参考资料

与传统电子表格最优化一样，您可以在 RISKOptimizer 中输入必须符合的严格约束条件。在传统电子表格最优化中，需要针对每种试验解法检验严格约束条件。如果不符合约束条件，则解法则将丢弃。

在 RISKOptimizer 中，为每种试验解法运行完整的模拟过程。每次模拟包括一些迭代，或用来自模型概率分布的新样本对电子表格进行的单独重新计算。可以在以下情况中检测严格约束条件：

♦ 每次模拟的每次迭代（

束条件的值，则模拟将被终止（试验解法将被拒绝），并开始运行下一个试验解法及其相关模拟。

♦ 在模拟结束时（

的模拟统计量表示；例如，A11 模拟结束时评估该约束条件。与迭代约束条件相反，模拟约束条件绝对不会在完成之前使模拟终止。

模拟约束条件）

迭代约束条件

中的

“可调整单元格范围”

）。如果迭代生成违反严格约

。此类约束条件用电子表格单元格

的平均值

>1000。在此示例中，在

一节。

您也可以在 RISKOptimizer 中使用第二种类型的约束条件 —“宽松约束条件”。宽松约束条件生成的惩罚值在模拟结束时计算。任何计算得出的惩罚值将增加到要最小化或最大化的目标统计量，或从目标统计量中减去。

有关输入约束条件的更多信息料中的

设置最优化和模拟选项

24 传统最优化与模拟最优化

与传统电子表格最优化中一样，RISKOptimizer 中有多个选项可以用于控制最优化的运行时间。但是，RISKOptimizer 为控制每个试验解法模拟的运行时间增加了新的选项。

RISKOptimizer 将搜索更好的解法，并且在符合所选的终止选项之前一直运行。您可以将 RISKOptimizer 设为在指定的分钟数内运行，运行至生成指定数目的试验解法或直至目标单元格最佳模拟统计量更改为特定的试验数目。

“约束条件”

一节。

，

请参见第五章：RISKOptimizer 参考资

您还可以指定每次试验解法模拟的运行时间。您可以选择让每次模拟运行指定次数的迭代，或者选择让 RISKOptimizer 确定何时停止每次模拟。当您选择让 RISKOptimizer 确定何时停止每次模拟时，RISKOptimizer 会在为 1) 最优化目标单元格和 2) 模拟约束条件中引用的单元格生成的分布保持稳定且相关统计量收敛时停止模拟。

运行最优化

当 RISKOptimizer 运行最优化时，使用可调整单元格的不同可能值在每次模拟中连续多次对电子表格进行模拟。在此过程中：

1) 优化程序为可调整单元格生成一组值。

2) 对电子表格进行模拟，可调整单元格被设为优化程序生成的

值。在模拟的每次迭代中，对电子表格中的所有分布函数进行抽样，重新计算电子表格，并生成新的目标单元格值。如果在迭代重新计算后没有符合任何迭代约束条件，则停止模拟，而优化程序会生成要模拟的新试验解法。

3) 在每次模拟结束时，会生成新的目标单元格可能值的分布。您

希望最小化或最大化的统计量根据此分布计算。如果没有符合任何模拟约束条件，则试验解法和模拟结果将被丢弃，而优化程序会生成要模拟的新试验解法。

4) 优化程序使用在模拟中计算得出的目标单元格新统计量选择要

尝试的下一组可调整单元格值。

5) 再次进行模拟并提供另一个新的统计量，优化程序可以利用该

统计量找到可调整单元格的一组新值。

此过程反复重复，从而使优化程序越来越接近要查找的优化解法，即一组最小化或最大化目标单元格统计量的可调整单元格值。

第二章：背景知识 25

第三章：RISKOptimizer 分步介绍

简介.....................................................................................................29

RISKOptimizer 教程 ..........................................................................31

启动 RISKOptimizer..............................................................................31

RISKOptimizer 工具栏 ............................................................31

打开示例模型..............................................................................31

描述模型中的不确定因素........................................................................32

RISKOptimizer“模型”对话框...........................................................34

选择目标单元格的统计量........................................................................35

添加可调整单元格范围............................................................................35

输入可调整单元格的取值范围 ..................................................36

选择求解方法..............................................................................37

约束条件 ...................................................................................................38

迭代和模拟约束条件 ..................................................................38

添加约束条件..............................................................................39

简单值范围和公式约束条件 ......................................................39

其他 RISKOptimizer 选项.....................................................................42

最优化停止条件..........................................................................42

模拟停止条件..............................................................................43

记录模拟数据..............................................................................44

运行最优化................................................................................................45

RISKOptimizer 观察器 ............................................................46

停止最优化..................................................................................47

摘要报表......................................................................................48

将结果放在模型中 ......................................................................49

第三章：RISKOptimizer 分步介绍 27

第三章：RISKOptimizer 分步介绍 28

简介

在本章中，我们将逐步向您介绍 RISKOptimizer 的所有最优化设置。如果您没有在硬盘中安装 RISKOptimizer，请在开始本教程之前参见第一章：安装的安装部分并安装 RISKOptimizer。

首先，我们将打开预制的电子表格模型，然后将使用概率分布和

RISKOptimizer 对话框定义 RISKOptimizer 中的问题。最后，当 RISKOptimizer 正在查找解法时，我们将检查 RISKOptimizer 的进

度，并研究“RiskOptimizer 观察器”的多个选项中的部分选项。有关任何特定主题的附加信息，请参见本手册后面的索引或第五章： RISKOptimizer 参考资料。

注：以下所示屏幕来自本，则屏幕上显示的窗口可能与图片稍有不同。

通过一个可以准确表示您的问题的模型，开始问题的求解过程。您的模型必须能够评估一组特定的输入值（可调整单元格），并生成这些输入项在解决问题方面表现的数字评级（评估或“适应度”函数）。您的模型还需要包括描述任何不确定因素的可能值范围的概率分布。当

RISKOptimizer 查找解法时，适应度函数的模拟提供反馈信息，告知 RISKOptimizer 每个猜测好或差的程度，从而使 RISKOptimizer 生成

越来越好的猜测。创建问题的模型时，您必须密切关注适应度函数，因为 RISKOptimizer 将尽一切能力使此单元格的模拟结果最大化（或最小化）。

Excel 2007

。如果您正在使用

Excel

的其他版

第三章：RISKOptimizer 分步介绍 29

RISKOptimizer 教程

启动 RISKOptimizer

RISKOptimizer

工具栏

打开示例模型

您可以选择以下方式启动 RISKOptimizer：1) RISKOptimizer 图标，或者 2) 在 Windows“开始”菜单的“程序” 条目中依次选择 Palisade DecisionTools

上两种方法均可以启动

加载 RISKOptimizer 后，将会在 Excel 中显示一个新的 RISKOptimizer 工具栏或功能导航栏。此工具栏中包含可以用于指定 RISKOptimizer 设置，以及用于启动、暂停和停止最优化的按钮。

要查看 RISKOptimizer 的功能，您需要查看在安装 RISKOptimizer 时所安装的示例模型。要进行此操作：

打开“ 工作表。

RISKOPTIMIZER5\EXAMPLES

Microsoft Excel 和 RISKOptimizer。

单击

Windows

和

RISKOptimizer 5.7

”目录中的

AIRLINES.XLS

桌面上的

。以

第三章：RISKOptimizer 分步介绍 31

此示例工作表包含一个收益管理模型，此模型用于确定在某一特定航班销售的全票价和折扣票价座位的最佳数目。此模型还可以确定可接受的超过可提供座位的最佳预订数目 — 传统的“超额预订”问题。对于这一标准最优化问题只有一种解释 — 模型中的部分估计是不确定或“随机”的。这包括所显示的要登机的实际乘客数，每种票价类别所需的预订座位数，以及超额预订乘客成本（即有时将提供 100 美元的旅行优惠券，而有时有必要提供免费的往返机票）。通常，将单点估计用于这些项目，以允许执行正态最优化。但是，如果您的估计不正确，该如何处理？结果可能是预定的座位太少，使座位空置，或者超额预订过多座位。您可以销售过多的折扣票价座位，但这降低了您的利润。您也可以保留过多的全票价座位，但这会导致飞机上半数座位空置。 RISKOptimizer 将解决这一最优化问题，同时允许您解释您模型中所存在的不确定因素。

以航班为例，您首先将使用概率分布描述模型中存在的不确定因素。然后，您将使用 RISKOptimizer 对话框设置您的最优化问题。最后，运行 RISKOptimizer 以确定全票价座位和折扣票价座位的最佳预订数目，从而将利润最大化，同时将风险保持在可接受水平之内。

描述模型中的不确定因素

在 RISKOptimizer 中，概率分布用于描述您的模型中的不确定因素的可能值范围。概率分布指定不确定因素的最小值和最大值，以及最小值和最大值之间的值的相对概率。

在 RISKOptimizer 中，使用概率分布函数输入概率分布。与标准 Excel 函数一样，您可以在电子表格的单元格和公式中输入这些自定义 RISKOptimizer 函数。例如，函数：

♦ RiskTriang(10,20,30) 指定一个三角分布，其中最小可能值为 10，

最可能值为 20，而最大值为 30。

在航班模型中，共有五个不确定因素，每个均通过概率分布描述。第一个不确定因素是：

♦ “全票价预订需求”（单元格 C8），通过概率分布 RiskTriang(3,7,15)

进行描述。此函数指定所需的全票价预订座位的数目可以低至 3，也可以高达 15，而其最可能值为 7。

32 RISKOptimizer 教程

要输入此概率分布：

选择单元格

C8。

输入公式

采用由整数。（您不会需要

=ROUND(RiskTriang(3,7,15),0)。Excel ROUND

RiskTriang

函数返回的样本，并将其四舍五入为最接近的

5.65

个预订座位！）

函数只

模型中的其他分布已输入“Airlines.XLS”工作表中，如下所示。如果要了解相关情况，可以移动到每个分布所在的单元格进行查看。

♦ “未登机 % — 全票价座位”（单元格 C7）。此分布由 RiskNormal

(.2,.03) 描述，表示航班中平均有 20% 的全票价预订座位空置。按

平均值为 .2 和标准差为 .03 的正态分布的描述，未登机的实际百分比将围绕 20% 上下波动。

♦ “未登机 % — 折扣票价预订”（单元格C11）。此分布由 RiskNormal

(.1,.01) 描述，表示航班中平均有 10% 的折扣票价预订座位空置。

按平均值为 .1 和标准差为 .01 的正态分布的描述，未登机的实际百分比将围绕 10% 上下波动。与全票价预订座位相比，显示了更多的折扣票价预订座位，因为更改折扣票要收取 75 美元的费用，而全价票可全额退款，并且不收取任何费用。

♦ “折扣票价预订需求”（单元格 C12），通过概率分布 RiskTrigen

(12,20,40,10,90)) 进行描述。此函数指定通过三角概率分布描述所需

的折扣票价预定座位的数目，其中第 10 值为 20，而第 90

个百分位数为 40。

♦ “超额预订成本”（单元格 C23），通过概率分布 RiskDiscrete

个百分位数为 12，最可能

({100,150,200,250},{0.1,0.4,0.4,0.1}) 进行描述。此函数指定每名超额预订乘客的成本可以是 100 美元、150 美元、200 美元或 250 美元，因为有时乘客会接受 100 美元的旅行优惠券并自愿离开超额预订的航班，而其他时候有必要提供更多的补偿。

第三章：RISKOptimizer 分步介绍 33

有关此类问题和其他概率分布的更多信息，请参见 @RISK 手册或“帮助”中的参考资料：分布函数

在使用概率分布描述模型中输入的不确定因素后，您现在可以使用 RISKOptimizer 对话框设置最优化。

。

RISKOptimizer“模型”对话框

要设置此工作表的 RISKOptimizer 选项：

单击

RISKOptimizer

具栏的最左侧）。

将会显示以下的 RISKOptimizer“模型”对话框：

工具栏上的

RISKOptimizer

模型

图标

（在工

RISKOptimizer“模型”对话框旨在使用户能够以简单明了的方式描述其问题。在教程示例中，我们要尝试确定应接受的全票价和折扣票价预定座位的数目，从而使总利润最大化。

34 RISKOptimizer 教程

选择目标单元格的统计量

“Airlines.XLS”模型的单元格 C27 中的“利润”就是所说的目标单元格。这是您尝试将模拟统计量最小化或最大化的单元格，或尝试使模拟统计量尽量接近预设值的单元格。要指定目标单元格的模拟统计量：

将“最优化目标”选项设置为“最大值”。

在“单元格”字段中，输入目标单元格

从下拉“统计量”列表中选择“平均值”，从而选择“平均值”作

为要最大化的模拟统计量。

在 RISKOptimizer 对话框字段中输入单元格引用的方法有两种：1) 使用鼠标指针单击字段，并在字段中直接输入引用，或者 2) 将光标放置在选中字段上，然后单击“引用条目”图标，以便用鼠标直接选择工作表单元格。

$C$27。

添加可调整单元格范围

现在，您必须指定包含数值的单元格的位置，RISKOptimizer 可以调整这些数值来查找解法。您可以通过中一次性添加和编辑这些变量。此外，可以在“可调整单元”对话框内输入的单元格的数目视您正在使用的 RISKOptimizer 版本而定。

单击“可调整单元范围”部分中的“添加”按钮。

在

Excel

中选择

C14

作为要作为可调整单元格添加的单元格。

“可调整单元”对话框

在一个单元块

第三章：RISKOptimizer 分步介绍 35

输入可调整单元格的取值范围

在大多数情况下，您需要将可调整单元格范围的可能值限制在一个特定的取值范围内。在 RISKOptimizer 中，将其称为“范围”约束条件。当选择一组要调整的单元格时，您可以快速输入此取值范围。以航班为例，此范围内可接受的预订座位的最小可能值为 19，而最大可能值为 30。要输入此范围约束条件：

在“最小值”单元格中输入

在“值”单元格中，从下拉列表中选择“整数”

接下来，输入要调整的另一个单元格：

单击“添加”，以输入另一个可调整单元格。

选择单元格

输入

C15。

作为“最小值”，而输入

，而在“最大值”单元格中输入

作为“最大值”。

30。

36 RISKOptimizer 教程

这可以指定最后的可调整单元格 C15，其表示将分配至全票价座位的总预定座位所占的百分比。

如果此问题中还存在其他变量，我们将继续添加几组可调整单元格。在 RISKOptimizer 中，您可以创建数量不受限制的可调整单元格组。要添加更多单元格，请再次单击“添加”按钮。

稍后，您可能需要检查可调整单元格或更改其中的一些设置。要执行此操作，只需在表格中编辑取值范围。您也可以选择一组单元格，然后单击“删除”按钮将其删除。

选择求解方法

定义可调整单元格时，您可以指定要使用的

求解方法

。不同的求解方法可以处理不同类型的可调整单元格。设置求解方法以用于可调整单元格组，而且可以通过单击

“组”

按钮和显示可调整单元设置对话框对其进行更改。通常，您将使用默认的“菜单”求解方法；在此求解方法中，每个单元格值可以独立与其他单元格进行更改。由于将其选为默认方法，因此您无需进行更改。

“菜单”和“顺序”求解方法是最常用的方法，而且可以将其结合使用，以解决复杂的组合问题。尤其值得一提的是，“菜单”求解方法将每个变量视为菜单中的基本成分，其通过分别更改每个变量的值来尝试确定“最佳搭配”。与此相反，“顺序”求解方法在变量之间交换值，按不同的方式排列初始值以确定“最佳顺序”。

第三章：RISKOptimizer 分步介绍 37

迭代和模拟约束条件

约束条件

RISKOptimizer 允许您输入约束条件，必须符合这些条件才能使解法有效。在此示例模型中，必须符合两个附加约束条件，才能使

大预订座位数的一组可能值

已为可调整单元格输入的范围约束条件之外的附加约束条件。这三个约束条件如下所示：

♦ 利润必须始终大于 0。 ♦ 利润模拟结果的标准差必须小于 400。

RISKOptimizer 会针对每次为您的模型生成的可能解法运行模拟。每次模拟将涉及成百上千次迭代，或对电子表格的重新计算。在每次迭代中，RISKOptimizer 从模型的每个概率分布中抽样一个值，并使用这些新抽样的值对模型进行重新计算，然后生成新的目标单元格值。在试验解法模拟结束时，使用针对每次迭代计算得出的目标单元格值生成目标单元格的概率分布。

RISKOptimizer 可以在以下情况中检查约束条件：

♦ 在模拟的每次迭代后（“迭代”约束条件） ♦ 在每次模拟结束时（“模拟”约束条件）

和

全票价座位的百分比

有效。这些是除我们

可接受的最

在航班模型中，“利润必须始终大于 0”是迭代约束条件，而“利润模拟结果的标准差必须小于 400”是模拟约束条件。换言之，在模拟的每次迭代后，RISKOptimizer 将检查以确保利润大于 0；如果没有满足此条件，此试验解法将被丢弃。如果模拟成功完成（即所有迭代的利润均大于 0），将会检查利润的概率分布的标准差，以确保其小于 400；如果没有满足此条件，此试验解法将被丢弃。

约束条件显示在 RISKOptimizer“模型”对话框底部的您可以在 RISKOptimizer 中指定两种类型的约束条件：

♦ 严格。必须符合才能使解法有效的条件（例如，严格迭代约束条件

为 C10<=A4；在这种情况下，如果解法为 C10 生成的值比 A4 单元格的值大，则此解法将会被丢弃）

♦ 宽松。我们希望尽可能符合，但可能会为了大大改进适应度或目

标单元格结果而愿意做出让步的条件。（即宽松约束条件可以是 C10<100。在这种情况下，C10 的值可以超过 100，但是，当此情况发生时，为目标单元格计算的值将会根据您输入惩罚函数而减小）。

38 RISKOptimizer 教程

约束条件

部分。

添加约束条件

要添加约束条件：

请单击按钮。

“约束条件设置”对话框将会显示，您可以在其中输入模型的约束条件。

RISKOptimizer

主对话框的“约束条件”部分的“添加”

简单值范围和公式约束条件

可以使用用简单的 <、<=、>、>= 或 = 关系输入约束条件。典型的简单值范围约束条件为 0< A1

值

的运算符。如果使用简单值范围格式的约束条件，您可以只输入一个 “最小”值、一个“最大”值或同时输入二者。

公式约束条件则允许您输入任何有效的 Excel 公式作为约束条件，例如 A19<(1.2*E7)+E8。对于每种可能解法，RISKOptimizer 将检查输入的公式估值是 TRUE 还是 FALSE，以查看解法是否已符合约束条件。如果您希望将工作表单元格中的布尔公式用作约束条件，只需在“约束条件设置”对话框的

第三章：RISKOptimizer 分步介绍 39

简单和公式

框中输入 0，而在

公式

这两种格式输入约束条件。简单值范围格式允许使

的值

<10，其中在

最大值

框中输入 10。可以从下拉列表框中选择所需

字段中引用此单元格。

单元格范围

框中输入 A1，在

最小

要输入航班模型的约束条件，您要指定三个新的严格约束条件。首先，输入

简单值范围

格式的严格约束条件，即“利润 > 0”：

在“描述”框中，输入“利润

在“要约束的范围”框中，输入

在“要约束的范围”框的右侧，选择

清除“最大值”框中的默认值 0。

在“要约束的范围”框的左侧，通过从下拉列表中选择空白来清除

运算符

单击“每次模拟的每一次迭代”，然后单击“确定”。这表示无论

预订座位数是多少，您必须始终确保“利润”大于

> 0

C27。

”。

运算符。

0。

单击“确定”以输入此约束条件。

40 RISKOptimizer 教程

现在，输入模拟约束条件：

单击“添加”以再次显示“约束条件设置”对话框。

在“描述”框中，输入“利润标准差

在“要约束的范围”框中，输入

在“要约束的范围”框的右侧，选择

在“最大值”框中，输入

在“要约束的范围”框的左侧，通过从下拉列表中选择空白来清除

运算符

单击“要约束的统计量”下拉列表，然后选择“标准差”。

单击“确定”。

已完成“约束条件”部分的“模型”对话框应如下所示。

400。

<400

C27。

”。

运算符。

第三章：RISKOptimizer 分步介绍 41

其他 RISKOptimizer 选项

在最优化过程中，可以使用更新显示、随机数种子、最优化停止条件和模拟停止条件之类的选项控制 RISKOptimizer 的运行方式。让我们来指定一些停止条件和更新显示设置。

最优化停止条件

RISKOptimizer 将按照您的要求运行最优化。当处于以下情况时，停止条件允许 RISKOptimizer 自动停止运行：a)

“试验”，进之处，算得出一个错误值

单击

选择“运行时间”选项卡。

已消耗一定数量的时间

已输入的

RISKOptimizer

Excel

。要查看和编辑停止条件：

，c)

公式评估为

工具栏上的“最优化设置”图标。

已检查一定数目的方案或

未在最后

TRUE

，或者

个方案中找到改

目标单元格计

42 RISKOptimizer 教程

在“最优化设置”对话框中，您可以选择这些最优化停止条件的任意组合，或者根本不选择任何停止条件

。如果选择了多个停止条件，当符合所选的任何一个停止条件时，RISKOptimizer 均将停止运行。如果没有选择任何停止条件，RISKOptimizer 将会一直运行，除非按 RISKOptimizer 工具栏中的“停止”按钮，以手动方式将其停止运行。

模拟

此选项设置您希望 RISKOptimizer 运行的“模拟”的数目。RISKOptimizer 运行一整套变量或问题的一种可能解法的模拟。

将分钟数设置为 5，以允许

在已消耗指定数量的时间后， RISKOptimizer 将会停止运行。此数目可以是分数 (4.25)。

时间

RISKOptimizer

进度

此停止条件是最常用的条件，因为它跟踪改进之处，并允许 RISKOptimizer 在改进比率降低之前保持运行。例如，我们已通过了 100 次模拟，而到目前为止，尚未在最佳方案中找到任何改进之处，此时 RISKOptimizer 将会停止运行。

运行五分钟。

公式为真

在模拟中，如果已输入的 Excel 公式评估为 TRUE， RISKOptimizer 将会停止运行。

模拟停止条件

RISKOptimizer 针对其生成的每种试验解法运行模型的完整模拟。您可以使用“模拟停止条件”指定这些模拟中每次模拟的运行时间。您可以让每次模拟运行固定次数的迭代，或者让 RISKOptimizer 确定何时终止每次模拟。

迭代

此选项允许您让每次模拟运行固定次数的迭代。在这种情况下，RISKOptimizer 将就 RISKOptimizer 生成的每种试验解法所执行的每次模拟运行指定数目的迭代（除非由于不符合某个迭代约束条件，而使模拟过早停止）。

将迭代次数设置为行快速模拟。

遇到实际收敛时停止

如果为 1) 最优化目标单元格和 2) 模拟约束条件中引用的单元格生成的分布保持稳定且相关统计量收敛时，此选项指示 RISKOptimizer 停止每次模拟。通过选项设置在统计量标记为 “已收敛”时，统计量中允许存在的变差数量。

500

，以使

如果为 1) 最优化目标单元格和 2) 拟约束条件中引用的单元格生成的分布保持稳定，并且可以在内部进行投影时，此选项指示 RISKOptimizer 停止

公差

每次模拟。RISKOptimizer 基于最优化过程中先前已运行模拟的结果对收敛进行投影。

RISKOptimizer

遇到投影收敛停止

对每种试验解法运

第三章：RISKOptimizer 分步介绍 43

记录模拟数据

RISKOptimizer 可以显示最优化过程中运行的每次模拟的当前描述，包括计算的目标统计量的值，目标单元格值的模拟分布的基本统计量，使用的可调整单元格值，以及是否满足约束条件。要在最优化过程中查看此日志：

单击“查看”选项卡，然后选择“最优化设置”对话框中的“记录所有模拟”。

44 RISKOptimizer 教程

运行最优化

现在，所有要做的事就是最优化此模型，以确定每种票价类别的最高预订数目，从而将利润最大化。要进行此操作：

单击“确定”以退出“最优化设置”对话框。

单击“开始最优化”图标

当 RISKOptimizer 开始研究您的问题时，您将在电子表格中看到可调整单元格的当前最佳值—

分比

。

利润

的最佳平均值以蓝色显示，同时会有一个指向目标单元格的

箭头。

运行期间，“进度”窗口会显示：1) 到目前为止找到的最佳解法，2) RISKOptimizer 开始最优化时，目标单元格中所选的模拟统计量的初始值，3) 对您的模型所执行的模拟次数，以及有效模拟次数；即符合所有约束条件，以及 4) 在最优化过程中已消耗的时间。

在运行期间，您可以随时单击显示 Excel 更新选项图标来查看每次模拟的屏幕的实时更新。

可接受的预定座位总数和全票价预订座位百

第三章：RISKOptimizer 分步介绍 45

RISKOptimizer 观察器

RISKOptimizer 也可以显示针对每种试验解法所执行的模拟的运行日志。当 RISKOptimizer 运行时，会在“RISKOptimizer 观察器”中显示此运行日志。“RISKOptimizer 观察器”在运行时允许您研究和修改问题的多个方面。要查看模拟执行的运行日志：

请单击“进度”窗口中的“观察器”（放大镜）图标，以显示

“

RISKOptimizer

单击“日志”选项卡。

观察器”

此报表显示针对每种试验解法所运行的模拟的结果。您要尝试最大化或最小化的目标单元格的统计量的值 — 在此示例中，为 $C$27 中的“利润”的平均值。

出项最小值和输出项最大值

润”的概率分布。$C$14 和 $C$15 列确定用于可调整单元格的值。

标准差

46 RISKOptimizer 教程

<400 列和

利润

列描述每次模拟计算得出的目标单元格“利

>0 列显示每次模拟是否符合您的约束条件。

输出项平均值、输出项标准差、输

结果

列按模拟显示

利润

停止最优化

五分钟后，RISKOptimizer 将停止最优化。您也可通过以下方式停止最优化：

单击

RISKOptimizer 观察器或进度

窗口中的“停止”图标。

当 RISKOptimizer 进程停止时，RISKOptimizer 会显示“停止选项” 选项卡，此选项卡提供以下选择：

当符合“RISKOptimizer 最优化设置”对话框中设置的任何一个停止条件时，这些相同选项将会自动出现。

第三章：RISKOptimizer 分步介绍 47

摘要报表

RISKOptimizer 可以创建一个最优化摘要报表，其中包含诸如运行日期和时间、使用的最优化设置、计算的目标单元格的值，以及每个可调整单元格的值之类的信息。

对于比较连续最优化的结果，此报表将非常有用。

48 RISKOptimizer 教程

将结果放在模型中

要将航班的十六种任务的新的且已最优化的生产水平组合放在您的工作表中：

请单击“停止”按钮。

确保将“将显示在工作簿中的可调整单元格值更新到”选项设置为

“最佳”

RISKOptimizer 将会返回到“AIRLINES.XLS”电子表格，其中包含创建了最佳解法的所有新变量值。请牢记，最佳解法是“利润”的模拟结果的平均值，而且这与使用了最佳变量值针对“利润”进行的简单重新计算后所显示的值不同。最佳平均值显示在蓝色框中，同时会有一个指向“利润”的箭头。

重要提示：在我们的示例中，尽管您看到生成的总利润为

RISKOptimizer 也可以确定生成的总得分相同的“可接受的最多预订座位”与“按照全票价出售的座位百分比”的不同组合。这些差异由

RISKOptimizer 与所有其他问题求解算法之间的重要区别造成：这是 RISKOptimizer 遗传算法引擎的随机性，它使 RISKOptimizer 能够解决各种不同问题，并找到更佳解法。

第三章：RISKOptimizer 分步介绍 49

2248.96

的解法，但您的结果可能比此结果稍高或稍低。

RISKOptimizer

找到了一个

在您保存已在其上运行过 RISKOptimizer 的任何工作表时（即使在运行 RISKOptimizer 之后“恢复”了工作表中的初始值），RISKOptimizer 对话框中的所有 RISKOptimizer 设置也将随此工作表一起保存。下次打开此工作表时，所有最近的 RISKOptimizer 设置将会自动加载。所有其他示例工作表中已预填充了 RISKOptimizer 设置，并准备进行最优化。

注：如果您要了解已预填充所有最优化设置的航班模型，请打开示例模型

AIRYIELD.XLS

50 RISKOptimizer 教程

第四章：应用示例