PALISADE RISKOPTIMIZER 5.5 User Manual

Download

Guide d’utilisation

RISKOptimizer

Optimisation de simulation pour

Microsoft Excel

Version 5.5

mars, 2009

Palisade Corporation 798 Cascadilla St. Ithaca, NY USA 14850 +1-607-277-8000 +1-607-277-8001 (fax) http://www.palisade.com (site Web) sales@palisade.com (courriel)

Avis de copyright

Marques déposées

Microsoft, Excel et Windows sont des marques déposées de Microsoft, Corporation IBM est une marque déposée d’International Business Machines, Inc. Palisade, RISKOptimizer, TopRank, BestFit et RISKview sont des marques déposées de Palisade Corporation. RISK est une marque commerciale de Parker Brothers, une division de Tonka Corporation, exploitée sous licence.

Table des matières

Chapitre 1 : Introduction 1

Introduction.........................................................................................3

Installation.........................................................................................11

Chapitre 2 : Principes 15

Qu’est-ce que RISKOptimizer ? ......................................................17

Optimisation conventionnelle vs optimisation par simulation....27

Chapitre 3 : RISKOptimizer : Pas à pas 36

Introduction.......................................................................................38

Visite guidée......................................................................................40

Chapitre 4 : Applications types 64

Introduction.......................................................................................66

Allocation budgétaire.......................................................................68

Planification de capacité..................................................................70

Planificateur de classes...................................................................72

Couverture sur contrats à terme.....................................................76

Ordonnancement multigamme........................................................78

Équilibrage de portefeuille...............................................................80

Composition de portefeuille............................................................82

Risque de portefeuille......................................................................84

Table des matières i

Problème de voyageur de commerce ............................................86

Gestion du rendement..................................................................... 88

Chapitre 5 : Guide de référence RISKOptimizer 90

Commande Définition du modèle...................................................92

Commande Paramètres d’optimisation – Onglet Général .........119

Commande Paramètres d’optimisation – Onglet Temps

d’exécution.................................................................................. 123

Commande Paramètres d’optimisation – Onglet Affichage......127

Commande Paramètres d’optimisation – Onglet Macros.......... 129

Commande Démarrer l'optimisation ............................................132

Commandes Utilitaires ..................................................................134

Suivi RISKOptimizer.......................................................................135

Chapitre 6 : Optimisation 150 Chapitre 7 : Algorithmes génétiques 165

Introduction .................................................................................... 167

Histoire............................................................................................ 167

Exemple biologique .......................................................................171

Exemple numérique....................................................................... 173

Chapitre 8 : Simulation et analyse de risque 177

Introduction .................................................................................... 179

Définition du risque........................................................................179

Modélisation de l’incertitude dans RISKOptimizer.....................185

Analyse d’un modèle avec simulation......................................... 189

Chapitre 9 : Et aussi… 191

Ajout de contraintes.......................................................................193

Accélération du processus............................................................203

Mode d’exécution de l’optimisation RISKOptimizer...................205

Annexe A : Automatisation de RISKOptimizer 209 Annexe B : Dépannage / Questions-Réponses 211

Dépannage / Questions-Réponses ...............................................211

Annexe C : Ressources complémentaires 215 Glossaire 221 Index 230

Table des matières iii

Chapitre 1 : Introduction

Introduction .........................................................................................3

Pourquoi RISKOptimizer ?....................................................................3

Problèmes d’optimisation conventionnels............................3

Optimisation de modèles incertains.......................................4

Modéliser l’incertitude..............................................................4

Optimisation par simulation....................................................5

Résultats de la simulation.........................................................6

Applications personnalisées et RISKOptimizer...................6

Applications de l’optimisation par simulation sous

RISKOptimizer...........................................................................6

Avant de commencer ...............................................................................7

Éléments du progiciel..............................................................................7

À propos de cette version........................................................................7

Votre contexte d’exploitation.................................................................8

Si vous avez besoin d’aide......................................................................8

Avant d’appeler...........................................................................8

Contacter Palisade......................................................................9

Versions étudiants....................................................................10

Configuration requise...........................................................................10

Installation.........................................................................................11

Généralités ..............................................................................................11

Désinstallation de RISKOptimizer.......................................11

DecisionTools Suite...............................................................................12

Configuration des icônes ou raccourcis de RISKOptimizer ..........12

Messages d’avertissement de sécurité des macros

au démarrage...........................................................................................13

Renseignements complémentaires .....................................................14

Fichier Lisezmoi de RISKOptimizer.....................................14

RISKOptimizer:Didacticiel ....................................................14

Apprendre RISKOptimizer..................................................................14

Chapitre 1 : Introduction 1

2 Introduction

Introduction

RISKOptimizer combine la simulation et l’optimisation pour permettre l’optimisation de modèles contenant des facteurs incertains. À travers les puissantes techniques d’optimisation par algorithmes génétiques et la simulation Monte Carlo, RISKOptimizer identifie les solutions optimales aux problèmes impossibles à résoudre pour les optimiseurs linéaires et non linéaires. RISKOptimizer combine la technologie de la simulation de @RISK, le compagnon Palisade d’analyse du risque, à celle d’Evolver, le solveur Palisade par algorithmes génétiques. Pour les utilisateurs de @RISK et d’Evolver ou du Solveur Excel, RISKOptimizer n’aura guère de secrets.

Problèmes d’optimisation conventionnels

Ce Guide de l’utilisateur RISKOptimizer au programme et aux principes qui le sous-tendent. Vous y trouverez aussi plusieurs exemples d’application des technologies d’algorithme génétique et de simulation uniques de RISKOptimizer. Ce manuel peut aussi servir de guide de référence complet et pleinement indexé, avec description et illustration de chaque fonctionnalité de RISKOptimizer.

présente une introduction

Pourquoi RISKOptimizer ?

RISKOptimizer permet l’optimisation de tout un éventail de problèmes sinon exclus de la technique. Avec RISKOptimizer, il est possible de trouver des solutions optimales même aux problèmes qui présentent des variables incontrôlables dont les valeurs vous sont inconnues. Les optimiseurs actuels tels que Solveur (optimiseur linéaire et non linéaire intégré à Excel) et Evolver (optimiseur à algorithmes génétiques de Palisade Corporation) sont impuissants face aux plages de valeurs possibles entrées pour les facteurs incertains d’un modèle.

Les problèmes d’optimisation Excel conventionnels analysés à l’aide de Solveur ou d’Evolver se composent des éléments suivants :

• une cellule de sortie ou « cible » à minimiser ou maximiser

• un ensemble de cellules en entrée ou « cellules ajustables » dont

vous contrôlez les valeurs,

• un ensemble de contraintes à respecter, souvent exprimées à

l’aide d’expressions telles que COÛTS<100 ou A11>=0.

Chapitre 1 : Introduction 3

Lors de l’optimisation par Solveur ou Evolver, les cellules ajustables changent de valeur selon les plages admises que vous précisez. Pour chaque ensemble possible de valeurs de cellules ajustables, le modèle se recalcule et une nouvelle valeur est générée pour la cellule cible. En fin d’optimisation, une solution (ou combinaison de valeurs de cellules ajustables) optimale est proposée. Cette solution représente la combinaison des valeurs de cellules ajustables qui produit la valeur optimale (minimum ou maximum) de la cellule cible tout en respectant les contraintes définies.

Optimisation de modèles incertains

Lorsqu’un modèle comporte des éléments incertains, toutefois, Solveur et Evolver sont impuissants. Dans le passé, beaucoup de modèles d’optimisation omettaient simplement l’incertitude. Optimisables, ces modèles perdaient cependant leur caractère réaliste. Le cas échéant, les tentatives de recherche des valeurs optimales par simulation s’effectuaient selon une approche de « force brute », avec recherche de toutes les valeurs de cellules ajustables possibles sur base itérative. Il fallait procéder à une simulation initiale, changer une ou plusieurs valeurs, réexécuter la simulation et répéter le processus jusqu’à trouver ce qui semblait être une solution optimale. Le processus est long, et la manière de changer les valeurs d’une simulation à la suivante n’est généralement pas claire.

RISKOptimizer permet en revanche d’inclure l’incertitude présente dans un modèle et de produire des solutions optimales fiables qui en tiennent compte. RISKOptimizer fait appel à la simulation (de @RISK) pour gérer l’incertitude du modèle et aux algorithmes génétiques (d’Evolver) pour générer les valeurs possibles des cellules ajustables. Le résultat de cette « simulation-optimisation » est la combinaison des valeurs de cellules ajustables qui minimise ou maximise une statistique pour les résultats de simulation de la cellule cible. On peut, par exemple, trouver la combinaison de valeurs de cellules ajustables qui maximise la moyenne de la distribution de probabilités de la cellule cible, ou qui minimise l’écart type.

Modéliser l’incertitude

Pour modéliser l’incertitude, RISKOptimizer permet de décrire les valeurs possibles de tout élément de tableur à l’aide de l’une quelconque des fonctions de distribution de probabilités disponibles sous @RISK. La valeur 10 d’une cellule pourrait par exemple être remplacée par la fonction @RISK =RiskNormal(10;2). Les valeurs possibles de la cellule seraient ainsi décrites par une distribution de probabilités caractérisée par une moyenne de 10 et un écart type de 2. Comme dans @RISK, les distributions de probabilités peuvent être corrélées à l’aide de fonctions @RISK telles que RiskCorrmat et DepC.

4 Introduction

Optimisation par simulation

Lors de l’optimisation, RISKOptimizer exécute une simulation complète de chaque solution itérative possible générée par l’optimiseur AG. À chaque itération de la simulation, les fonctions de distribution de probabilités introduites dans le tableur sont échantillonnées et une nouvelle valeur est générée pour la cellule cible. En fin de simulation, le résultat de la solution itérative représente la statistique de la cellule cible à minimiser ou maximiser. Cette valeur est ensuite renvoyée à l’optimiseur et aux algorithmes génétiques pour la génération de meilleures solutions encore. Pour chaque nouvelle solution itérative, une nouvelle simulation s’exécute, avec génération d’une nouvelle valeur pour la statistique cible.

À l’image des optimiseurs conventionnels, RISKOptimizer gère les contraintes. Les contraintes peuvent être évaluées à chaque itération d’une simulation (contraintes d’« itération ») ou à la fin de chaque simulation (contraintes de « simulation »). Les contraintes d’itération sont généralement des contraintes de style Solveur ou Evolver (A11>1000, par exemple). Celles de simulation font plutôt référence à une statistique de la distribution des résultats de simulation pour une cellule spécifiée du modèle. Une contrainte de simulation type serait, par exemple, « Moyenne de A11>1000 », indiquant que la moyenne de la distribution des résultats de simulation pour la cellule A11 doit être supérieure à 1000. Comme dans Evolver, les contraintes peuvent être fermes ou souples et la violation d’une contrainte ferme donne lieu au rejet d’une solution itérative.

Pour faire face aux grands nombres de simulations exécutées, RISKOptimizer tire parti de deux techniques importantes pour minimiser les temps d’exécution et produire ses solutions optimales aussi rapidement que possible. En premier, RISKOptimizer applique la surveillance de convergence pour déterminer le moment où un nombre suffisant (non excessif) d’itérations a été exécuté. Cette technique assure la stabilité de la statistique résultant de la distribution de probabilités de la cellule cible, de même que celle des statistiques de distributions de sortie éventuellement référencées dans les contraintes. Ensuite, RISKOptimizer fait appel aux opérateurs génétiques d’Evolver pour générer des solutions itératives qui évoluent vers la solution optimale aussi rapidement que possible.

Chapitre 1 : Introduction 5

Résultats de la simulation

RISKOptimizer s’accompagne d’un ensemble de fonctions statistiques de simulation qui renvoient directement les résultats au tableur. Par exemple, la fonction RiskMean(réf. cell.) renverrait la moyenne de la distribution simulée pour la cellule entrée directement à une cellule ou formule de la feuille de calcul. Mieux encore, un modèle élaboré sous RISKOptimizer peut être simulé directement sous @RISK, le compagnon d’analyse du risque et de simulation pour Excel publié par Palisade Corporation, pour la production de graphiques et statistiques détaillés de la meilleure solution identifiée par RISKOptimizer. La simulation sous RISKOptimizer repose sur la méthodologie @RISK : aucune modification ne doit donc être apportée au modèle RISKOptimizer pour le simuler sous @RISK !

Applications personnalisées et RISKOptimizer

Applications de l’optimisation par simulation sous RISKOptimizer

RISKOptimizer est assorti d’un langage macro intégral qui permet l’élaboration d’applications personnalisées tirant parti de ses capacités. Les fonctions personnalisées de RISKOptimizer sont exploitables en VBA pour la configuration et l’exécution d’optimisations et l’affichage de leurs résultats. Pour plus de détails sur cette interface de programmation, voir le document d’aide Kit du développeur RISKOptimizer, accessible à travers le menu d’aide de RISKOptimizer.

La capacité d’optimisation de modèles incertains apporte une solution à de nombreux problèmes jusque là considérés comme « inoptimisables ». En règle générale, la combinaison de la simulation et de l’optimisation permet d’optimiser tous les modèles sujets à l’incertitude. Notamment :

♦ Sélection de niveaux de production et de capacité optimaux pour

les nouveaux produits confrontés à des conditions de marché incertaines.

♦ Identification de niveaux de stocks optimaux face à une demande

incertaine.

♦ Allocation de portefeuille propice à la minimisation du risque. ♦ Identification d’une gamme de production optimale en présence

de marchés géographiquement distincts et de niveaux de demande incertains.

♦ Détermination des niveaux optimaux d’achat d’options dans les

opérations financières de couverture.

♦ Gestion du rendement lorsqu’un même produit est vendu à prix

différents sous restrictions distinctes.

♦ Planification en présence de durées de tâches incertaines.

6 Introduction

Avant de commencer

Avant d’installer et de démarrer RISKOptimizer, vérifiez que votre progiciel contient bien tous les éléments nécessaires et que votre ordinateur satisfait aux exigences de configuration minimales requises.

Éléments du progiciel

RISKOptimizer accompagne la version @RISK Industrial, ainsi que la version DecisionTools Suite Industrial. Outre les fichiers de @RISK pour Excel, le CD-ROM @RISK Industrial contient le compagnon RISKOptimizer pour Excel, plusieurs exemples d’application de RISKOptimizer et un système d’aide RISKOptimizer en ligne indexé. La version DecisionTools Suite Industrial contient tous les éléments ci-dessus et d’autres applications encore.

À propos de cette version

Cette version de RISKOptimizer peut être installée en tant que programme 32 bits pour Microsoft Excel 2000 ou version ultérieure.

Chapitre 1 : Introduction 7

Votre contexte d’exploitation

Les descriptions contenues dans ce guide présupposent une connaissance générale du système d’exploitation Windows et du tableur Excel, notamment :

♦ familiarité avec l’ordinateur et la souris ♦ compréhension des termes icônes, cliquer, double-clic, menu,

fenêtre, commande, objet, etc.

♦ notions élémentaires de structure de répertoires et désignation

des fichiers

Si vous avez besoin d’aide

Un service d’assistance technique est proposé gratuitement à tous les utilisateurs enregistrés de RISKOptimizer dotés d’un plan de maintenance à jour, ou sur forfait à l’incident. Pour assurer que vous êtes bien un utilisateur enregistré de RISKOptimizer, enregistrez- vous en ligne sur http://www.palisade.com/support/register.asp.

Si vous nous contactez par téléphone, soyez prêt à nous communiquer le numéro de série de vos outils et gardez votre guide d’utilisation à portée de main. Nous pourrons vous être d’une meilleure assistance si vous vous trouvez face à votre ordinateur, prêt à exécuter les commandes du programme.

Avant d’appeler

8 Introduction

Avant d’appeler le service d’assistance technique, passez en revue la liste de contrôle suivante :

• Avez-vous consulté l’aide en ligne ?

• Avez-vous consulté ce manuel et passé en revue le didacticiel multimédia

en ligne ?

• Avez-vous consulté le fichier LISEZMOI.WRI ? Il contient des

informations sur RISKOptimizer non disponibles lors de l’impression du manuel.

• Pouvez-vous reproduire le problème de manière constante ? Pouvez-

vous reproduire le problème sur un autre ordinateur ou avec un autre modèle ?

• Avez-vous consulté notre site Web, à l’adresse

http://www.palisade.com ? Vous y trouverez notre dernier fichier FAQ (base de données consultable de questions et réponses techniques) et les correctifs RISKOptimizer dans la section de support technique. Il est utile de consulter régulièrement notre site pour obtenir les dernières informations publiées sur RISKOptimizer et sur les autres logiciels Palisade.

Contacter Palisade

Vos questions, commentaires ou suggestions relatifs à RISKOptimizer sont les bienvenus ! Vous pouvez prendre contact avec notre personnel d’assistance technique par l’une des méthodes suivantes :

• Courriel : support@palisade.com

• Téléphone : +1-607-277-8000, du lundi au vendredi, de 9 à 17 heures,

heure de l’Est des États-Unis. Suivez les instructions données pour joindre l’Assistance technique (Technical Support).

• Fax : +1-607-277-8001

• Adresse postale :

Technical Support Palisade Corporation 798 Cascadilla St. Ithaca, NY 14850 USA

Palisade Europe :

• Courriel : support@palisade-europe.com

• Téléphone : +44 1895 425050 (Royaume-Uni)

• Fax : +44 1895 425051 (Royaume-Uni).

• Adresse postale :

Palisade Europe 31 The Green West Drayton Middlesex UB7 7PN Royaume-Uni

Palisade Asie-Pacifique :

• Courriel : support@palisade.com.au

• Téléphone : +61 2 9929 9799 (Australie)

• Fax : +61 2 9954 3882 (Australie)

• Adresse postale :

Palisade Asia-Pacific Pty Limited Suite 101, Level 1 8 Cliff Street Milsons Point NSW 2061 Australie

Quelle que soit la méthode choisie, veillez à indiquer le nom de votre produit, sa version et son numéro de série. La version exacte de votre produit est indiquée sous la commande Aide, À propos de… du menu RISKOptimizer proposé dans Excel.

Chapitre 1 : Introduction 9

Versions étudiants

L’assistance téléphonique n’est pas disponible pour la version étudiants de RISKOptimizer. Si vous avez besoin d’aide, procédez de l’une des manières suivantes :

♦ Consultez votre professeur ou assistant. ♦ Consultez le fichier FAQ sur http://www.palisade.com ♦ Adressez-vous au service d’assistance technique par courriel ou

par fax.

Configuration requise

RISKOptimizer – Configuration requise

• PC Pentium ou mieux avec disque dur.

• Microsoft Windows 2000 SP4 ou mieux.

• Microsoft Excel, version 2000 ou ultérieure.

10 Introduction

Installation

RISKOptimizer, compagnon de Microsoft Excel, enrichit la fonctionnalité du tableur moyennant l’ajout de commandes à ses barres de menus.

Généralités

Le programme d’installation copie les fichiers système RISKOptimizer dans un répertoire spécifié du disque dur. Sous Windows 2000 ou version ultérieure :

1) Insérez le CD-ROM de la version @RISK Industrial ou DecisionTools

Suite Industrial dans le lecteur CD-ROM.

2) Cliquez sur le bouton Démarrer, puis sur Paramètres et enfin sur

Panneau de configuration.

3) Cliquez deux fois sur l’icône Ajout/Suppression de programmes.

4) Cliquez sur le bouton Installer de l’onglet Installation/désinstallation.

5) Suivez les instructions d’installation affichées à l’écran.

En cas de problème, vérifiez que vous disposez d’un espace suffisant sur le disque prévu pour l’installation. Après avoir libéré l’espace disque requis, essayez de réexécuter l’installation.

Suppression de RISKOptimizer

Chapitre 1 : Introduction 11

Pour désinstaller RISKOptimizer (avec le reste de la version @RISK Industrial ou DecisionTools Suite Industrial), utilisez l’utilitaire Ajout/Suppression de programmes du Panneau de configuration et sélectionnez l’entrée correspondant à @RISK ou DecisionTools Suite.

DecisionTools Suite

RISKOptimizer est compatible avec les outils d’analyse du risque et de décision DecisionTools Suite, de Palisade Corporation. L’installation par défaut de RISKOptimizer place le programme dans un sous-répertoire du répertoire principal « Program Files\Palisade », de la même manière qu’Excel s’installe généralement dans un sousrépertoire du répertoire « Microsoft Office ».

Ce sous-répertoire de Program Files\Palisade devient le répertoire RISKOptimizer (appelé, par défaut, RISKOptimizer5). Ce répertoire contient le fichier programme du compagnon RISKOptimizer (RISKOPT.XLA), plus les modèles types et les autres fichiers nécessaires à l’exécution de RISKOptimizer . Un autre sous-répertoire de Program Files\Palisade, intitulé SYSTEM, reçoit les fichiers nécessaires à tous les programmes de la série DecisionTools Suite, y compris les fichiers d’aide et bibliothèques communs.

Configuration des icônes ou raccourcis de RISKOptimizer

Sous Windows, l’installation crée automatiquement une commande RISKOptimizer dans le menu Programmes de la barre des tâches. Si toutefois vous rencontrez des problèmes en cours d’installation ou que vous désirez exécuter cette opération ultérieurement, procédez comme suit :

1) Cliquez sur le bouton Démarrer et pointez sur Paramètres.

2) Cliquez sur Barre des tâches, puis sur l’onglet Programmes du

menu Démarrer.

3) Cliquez sur Ajouter, puis sur Parcourir.

4) Repérez le fichier RISKOPT.EXE et cliquez deux fois dessus.

5) Cliquez une fois sur Suivant, puis deux fois sur le menu de votre

choix.

6) Tapez le nom « RISKOptimizer » et cliquez sur Terminer.

12 Installation

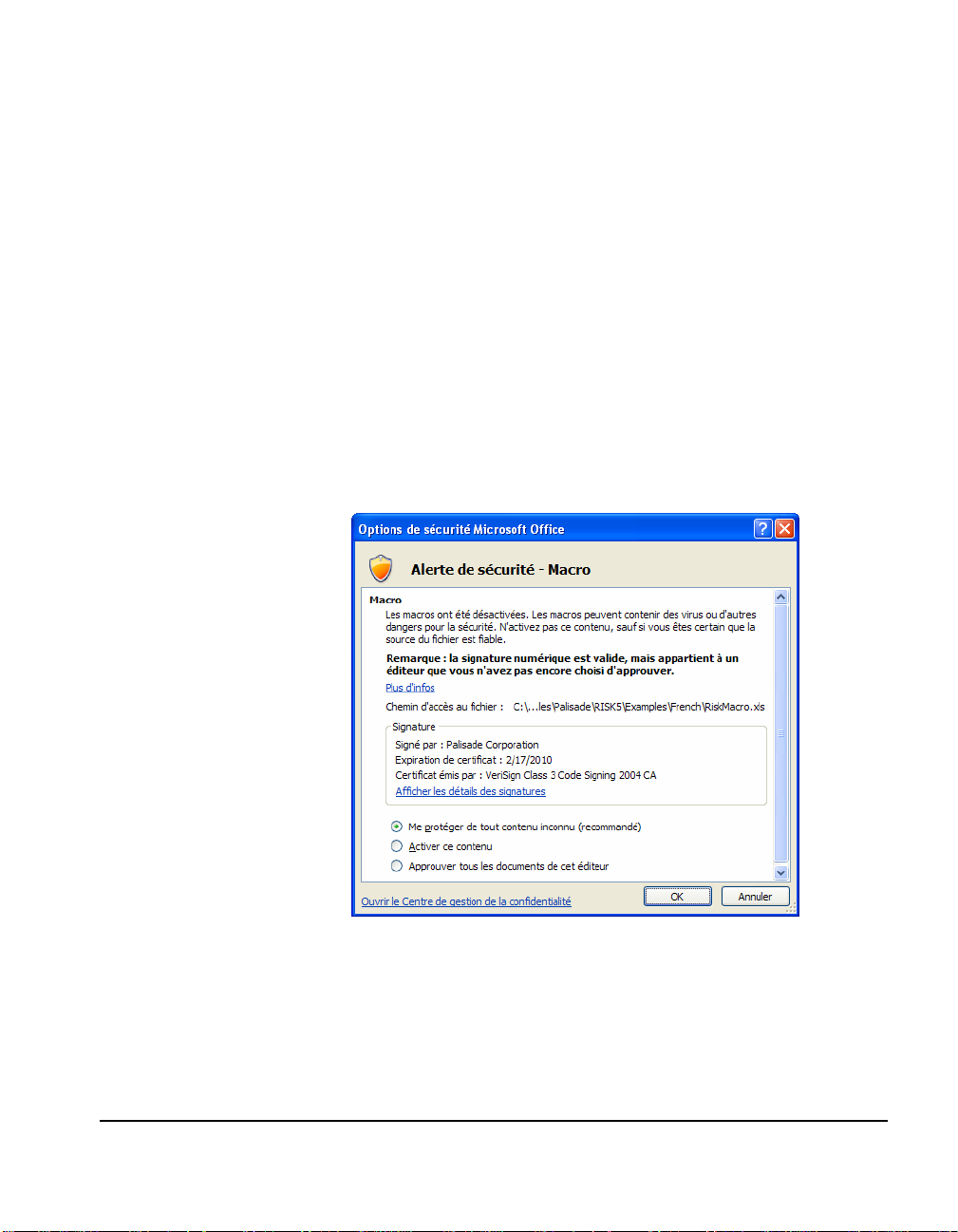
Messages d’avertissement de sécurité des macros au démarrage

Microsoft Office propose plusieurs paramètres de sécurité pour éviter l’exécution de macros indésirables ou hostiles dans vos applications Office. Sauf sous le paramètre de sécurité le plus faible, un message d’avertissement s’affiche à chaque tentative de chargement d’un fichier assorti de macros. Pour éviter l’affichage de ce message à chaque exécution d’un compagnon Palisade, Palisade signe numériquement ses fichiers. Après avoir spécifié Palisade Corporation en tant que source fiable, vous pouvez dès lors ouvrir les compagnons Palisade sans message d’avertissement. Pour ce faire :

• Séléctionnez l’option Approuver tous les documents de cet

éditeur lorsqu’une boîte de dialogue Options de sécurité (telle

que celle illustrée ci-dessous) s’ouvre au démarrage de RISKOptimizer.

Chapitre 1 : Introduction 13

Renseignements complémentaires

Les ressources suivantes peuvent contenir une information complémentaire relative à RISKOptimizer :

Fichier Lisezmoi de RISKOptimizer

RISKOptimizer:Di dacticiel

Ce fichier contient une présentation rapide de RISKOptimizer, ainsi que, éventuellement, l’information de dernière minute publiée sur la dernière version du logiciel. Pour y accéder, choisissez Démarrer/ Programmes/ Palisade DecisionTools/ Readmes et cliquez sur RISKOptimizer 5.5 – Lisezmoi. Il est utile de lire ce fichier avant l’emploi de RISKOptimizer.

Le didacticiel en ligne de RISKOptimizer apporte aux utilisateurs débutants une présentation rapide du logiciel et des algorithmes génétiques. La présentation se limite à quelques minutes seulement. Voir la rubrique Apprendre RISKOptimizer ci-dessous pour tous détails concernant l’accès au didacticiel.

Apprendre RISKOptimizer

Pour vous familiariser rapidement avec RISKOptimizer, suivez le didacticiel en ligne, où des experts du logiciel vous guident à travers différents modèles types en format cinéma présentation multimédia des principales fonctionnalités de RISKOptimizer.

Pour y accéder, choisissez la commande Didacticiel du menu Aide de RISKOptimizer.

. Ce didacticiel est une

14 Installation

Chapitre 2 : Principes

Qu’est-ce que RISKOptimizer ? ......................................................17

Principes fonctionnels de RISKOptimizer........................................18

Algorithmes génétiques ..........................................................18

Distributions de probabilités et simulation........................18

Qu’est-ce que l’optimisation ?.............................................................19

Pourquoi bâtir des modèles Excel ? ....................................................21

Modélisation de l’incertitude dans les modèles Excel ....................22

Recours à la simulation pour gérer l’incertitude..............................23

Pourquoi choisir RISKOptimizer ?.....................................................23

Plus précis et plus utile ...........................................................24

Plus souple.................................................................................24

Plus convivial............................................................................25

Optimisation conventionnelle vs optimisation par simulation....27

Processus d’optimisation conventionnel...........................................27

Processus d’optimisation par simulation...........................................28

Étapes individuelles de l’optimisation sous RISKOptimizer .......29

Entrée des distributions de probabilités..............................29

Cellule cible et statistique.......................................................31

Cellules ajustables....................................................................32

Contraintes.................................................................................32

Options d’optimisation et de simulation.............................33

Exécution de l’optimisation....................................................33



Chapitre 2 : Principes 15

Qu’est-ce que RISKOptimizer ?

Le progiciel RISKOptimizer apporte à l’utilisateur une méthode simple de recherche de solutions optimales aux modèles empreints d’incertitude. En un mot, RISKOptimizer trouve les meilleures entrées pour la production d’une sortie de simulation désirée. Servez-vous-en pour rechercher la combinaison, l’ordre ou le groupement de variables qui produisent la plus haute valeur probable de bénéfices, le moindre risque (variance minimum) ou la plus grande valeur probable de produits au moyen de la plus faible quantité de matériaux. RISKOptimizer est un compagnon destiné au tableur Microsoft Excel : la configuration du problème s’effectue dans Excel, et sa résolution à l’aide de RISKOptimizer.

Commencez par modéliser le problème dans Excel, avant de le décrire au compagnon

Excel apporte toutes les formules, fonctions, graphiques et capacités de macro dont la plupart des utilisateurs ont besoin pour créer des modèles réalistes de leurs problèmes. RISKOptimizer l’interface de description de l’incertitude du modèle et de la cible recherchée, ainsi que les moteurs qui permettent de l’atteindre. Ensemble, ils découvrent les solutions optimales à pratiquement tous les problèmes modélisables.

RISKOptimizer.

apporte

Chapitre 2 : Principes 17

Principes fonctionnels de RISKOptimizer

RISKOptimizer recourt à un ensemble exclusif d’algorithmes génétiques pour rechercher les solutions optimales à un problème. Il

fait aussi appel aux distributions de probabilités et à la simulation pour gérer l’incertitude présente dans le modèle.

Algorithmes génétiques

Distributions de probabilités et simulation

RISKOptimizer fait appel aux algorithmes génétiques pour rechercher la meilleure solution à un modèle Les algorithmes génétiques imitent les principes darwiniens de sélection naturelle en créant un environnement dans lequel des centaines de solutions possibles à un problème rivalisent les unes avec les autres, avec survie de « la plus apte ». Comme dans l’évolution biologique, chaque solution transmet ses bons « gènes » à ses solutions « descendantes », de sorte que la population de solutions tout entière continue à évoluer vers de meilleures solutions.

Vous l’avez compris, la terminologie des algorithmes génétiques est souvent similaire à celle du domaine dont elle est inspirée. Les fonctions de « croisement » aident à concentrer la recherche de solutions ; les taux de « mutation » contribuent à la diversification du « capital génétique » ; et l’évaluation porte sur l’ensemble de la « population » de solutions ou « organismes ». Pour plus de détails sur le fonctionnement des algorithmes génétiques de RISKOptimizer, voir le chapitre 7 – Algorithmes génétiques

RISKOptimizer fait appel aux distributions de probabilités et à la simulation pour gérer l’incertitude présente dans les variables du modèle. Ces capacités sont extraites de @RISK, le compagnon d’analyse du risque pour Excel de Palisade Corporation. Les distributions de probabilités décrivent la plage de valeurs possibles des éléments incertains du modèle. Elle se définissent à l’aide de fonctions de distribution de probabilités telles que RiskTriang(10;20;30). Cette fonction spécifierait qu’une variable du modèle pourrait avoir une valeur minimum de 10, une valeur probable de 20 et une valeur maximum de 30. La simulation sert ensuite à générer une distribution des issues possibles pour chaque solution itérative possible générée par l’optimiseur.

18 Qu’est-ce que RISKOptimizer ?

Qu’est-ce que l’optimisation ?

L’optimisation est le processus qui consiste à rechercher la meilleure solution à un problème présentant de nombreuses solutions possibles. La plupart des problèmes impliquent de nombreuses variables interdépendantes basées sur des formules et des contraintes données. Supposons par exemple une entreprise comptant trois usines, fabriquant chacune des différentes quantités de différents produits. Étant donné le coût de production de chaque produit par chaque usine, les coûts de livraison de chaque usine à chaque débouché des produits et les limitations de chaque usine, quelle est la formule optimale qui permettrait de répondre adéquatement à la demande des magasins de détail locaux tout en minimisant les coûts de transport ? Il s’agit là du type de question auquel les outils d’optimisation sont censés répondre.

L’optimisation consiste souvent à rechercher la

combinaison la plus rentable compte tenu de ressources données.

Dans l’exemple ci-dessus, chaque solution proposée consisterait en une liste complète indiquant quels produits fabriqués par quelle usine sont expédiés dans quel camion vers quel magasin. D’autres problèmes d’optimisation pourraient chercher, par exemple, comment réaliser le plus grand bénéfice, le moindre coût, le plus grand nombre de vies sauvées, le moins de bruit dans un circuit, le chemin le plus court entre différentes villes, ou la combinaison la plus rentable d’achats de médias publicitaires. Un sous-ensemble important de problèmes d’optimisation concerne la planification d’horaires ou de programmes, le but étant de maximiser l’efficacité d’un poste de

Chapitre 2 : Principes 19

travail ou de minimiser les conflits de rencontre de groupes. Pour plus de détails sur l’optimisation, voir le chapitre 6 – Optimisation

En présence d’incertitude, les solveurs classiques échouent car ils sont incapables de gérer cette incertitude. Dans la situation décrite plus haut, que se passerait-il, par exemple, si la demande des magasins de détail locaux était incertaine ? Sous un solveur conventionnel, il faudrait présumer une quantité demandée par chaque magasin. Le modèle pourrait ainsi être optimisé, mais la demande présumée en ferait une représentation inexacte de la réalité. Avec RISKOptimizer, il n’est plus nécessaire de présumer le niveau de la demande. Il suffit de décrire les valeurs possibles de la demande à l’aide d’une distribution de probabilités, puis de laisser les capacités de simulation intégrées de RISKOptimizer inclure toutes les valeurs possibles de la demande dans les résultats de l’optimisation.

Sous RISKOptimizer, la meilleure solution générée par l’optimiseur n’est pas une simple valeur minimum ou maximum de la cellule cible du modèle, mais plutôt une statistique de simulation maximum ou minimum de l’objectif visé. Chaque simulation exécutée par RISKOptimizer génère une distribution des résultats possibles pour l’objectif. Cette distribution comporte différentes statistiques, telles que moyenne, écart type, minimum, etc. Dans l’exemple ci-dessus, on pourrait ainsi rechercher la combinaison d’entrées apte à maximiser la moyenne de la distribution pour le bénéfice ou à minimiser l’écart type.

Pour plus de détails sur la simulation, voir le chapitre 8 – Simulation

20 Qu’est-ce que RISKOptimizer ?

Pourquoi bâtir des modèles Excel ?

Si l’on veut accroître l’efficacité d’un système, il faut d’abord en comprendre le comportement. Là se trouve l’utilité de la construction d’un modèle fonctionnel du système. Les modèles sont les abstractions nécessaires à l’étude de systèmes complexes. Pour que les résultats restent applicables au « monde réel », le modèle doit cependant éviter de simplifier à l’excès les rapports de cause à effet entre ses variables. De meilleurs logiciels et des ordinateurs de plus en plus puissants permettent aux économistes de bâtir des modèles plus réalistes de la conjoncture ; aux scientifiques, d’améliorer leurs prédictions de réactions chimiques et aux gestionnaires, d’accroître la sensibilité de leurs modèles d’entreprise.

Ces dernières années, le matériel informatique et les programmes logiciels tels que Microsoft Excel ont progressé à une telle allure qu’il suffit pour ainsi dire aujourd’hui de disposer d’un ordinateur personnel pour créer des modèles réalistes de systèmes complexes. Les fonctions intégrées d’Excel, ses capacités de macros et son interface rationnelle et intuitive permettent même aux débutants de modéliser et d’analyser des problèmes de haut niveau. Pour plus de détails sur l’élaboration d’un modèle, voir le chapitre 9 – Et aussi…

Chapitre 2 : Principes 21

Modélisation de l’incertitude dans les modèles Excel

Les variables sont les éléments de base des modèles Excel qu’on identifie comme les ingrédients importants de l’analyse. Pour une situation financière, les variables peuvent être, par exemple, le chiffre d’affaires, les coûts, les revenus ou le bénéfice. Pour une situation géologique, il peut s’agir de facteurs tels que la profondeur du gisement, l’épaisseur de la veine de charbon ou la porosité. À chaque situation ses variables propres, qu'il vous revient d'identifier.

Dans les cas où on connaît les valeurs que prendront les variables dans le cadre temporel du modèle, on parle de variables certaines ou, dans le jargon des statisticiens, « déterministes ». Au contraire, si ces valeurs sont inconnues, les variables sont qualifiées d’incertaines, ou « stochastiques ». Il faut alors décrire la nature de leur incertitude. L’opération s’effectue à l’aide de distributions de probabilités, qui indiquent à la fois la plage des valeurs possibles de la variable (du minimum au maximum) et la probabilité de réalisation de chaque valeur. Dans RISKOptimizer, les variables incertaines et les valeurs des cellules se définissent sous forme de fonctions de distribution de probabilités. Par exemple :

RiskNormal(100;10) RiskUniform(20;30) RiskExpon(A1+A2) RiskTriang(A3/2,01;A4;A5)

Ces fonctions de « distribution » se configurent dans les cellules et les formules d’une feuille de calcul comme n’importe quelle autre fonction Excel.

22 Qu’est-ce que RISKOptimizer ?

Recours à la simulation pour gérer l’incertitude

RISKOptimizer recourt à la simulation, parfois appelée simulation Monte Carlo, pour effectuer une analyse de risque sur chaque solution possible générée en cours d’optimisation. En ce sens, la simulation désigne la méthode par laquelle la distribution des issues possibles résulte de l’exécution, par l’ordinateur, de calculs répétés de la feuille de calcul, sur la base, à chaque fois, d’un ensemble de valeurs différentes, sélectionnées au hasard dans les distributions de probabilités introduites dans les valeurs et formules des cellules. L'ordinateur essaie en somme toutes les combinaisons valables des variables en entrée pour simuler toutes les issues possibles, comme si on analysait tout à la fois des centaines ou même des milliers de scénarios hypothétiques !

À chaque itération de la simulation, les fonctions de distribution de probabilités introduites dans le modèle sont échantillonnées et une nouvelle valeur est générée pour la cellule cible. En fin de simulation, le résultat de la solution itérative représente la statistique à minimiser ou maximiser pour la distribution de la cellule cible. Cette valeur est ensuite renvoyée à l’optimiseur et aux algorithmes génétiques pour la génération de meilleures solutions encore. Pour chaque nouvelle solution itérative, une nouvelle simulation s’exécute, avec génération d’une nouvelle valeur pour la statistique cible.

Pourquoi choisir RISKOptimizer ?

En présence de nombreuses variables interactives, il peut être tentant, pour trouver la meilleure combinaison, le meilleur ordre ou le groupement optimal de ces variables, de procéder par « supposition éclairée ». Un nombre surprenant de personnes croient que toute forme de modélisation et d’analyse au-delà de la supposition exige une programmation compliquée ou le recours à de complexes statistiques ou algorithmes mathématiques. Une bonne solution optimisée peut pourtant épargner des millions d’euros, des milliers de litres de combustible rare, des mois de travail inutile, etc. Maintenant que de puissants ordinateurs et logiciels de bureau tels qu’Excel et RISKOptimizer sont à la portée de tous, la simple supposition, ou la perte de temps précieux à essayer différents scénarios, ne se justifient plus.

Chapitre 2 : Principes 23

Plus précis et plus utile

RISKOptimizer admet le recours à toutes les formules et distributions de probabilités, pour l’élaboration de modèles plus réalistes, quel que soit le système. Avec RISKOptimizer, le « compromis » n’est pas nécessaire, car l’algorithme choisi peut gérer les complexités du monde réel. Les « mini-solveurs » conventionnels (outils statistiques et de programmation linéaire) obligent l’utilisateur à supposer l’interaction entre les variables d’un problème, imposant dès lors la création de modèles par trop simplistes et peu réalistes. Ils exigent la supposition des valeurs des variables incertaines car l’optimiseur est impuissant à gérer les plages de valeurs possibles des composants incertains du modèle. Une fois le système suffisamment simplifié pour permettre l’usage de ces solveurs, la solution produite est souvent plus abstraite que pratique. Les problèmes présentant de nombreuses variables, fonctions non linéaires, tables de recherche, déclarations conditionnelles, interrogations de base de données ou éléments stochastiques (aléatoires) sont exclus de ces méthodes, quel que soit le degré de simplification du modèle.

Plus souple

Beaucoup d’algorithmes conviennent à la résolution de simples problèmes linéaires et non linéaires, qu’ils procèdent par escalade, mini-solveur ou autres approches mathématiques. Même proposés sous forme de compagnons de tableur, ces outils d’optimisation universels ne gèrent que l’optimisation numérique. Pour les problèmes plus vastes ou plus complexes, il est parfois possible de formuler des algorithmes personnalisés, au prix de longues opérations de recherche et développement toutefois. Dans cette éventualité même, le programme résultant doit être modifié à chaque changement de modèle !

RISKOptimizer gère en revanche les problèmes numériques et

est le seul programme commercial au monde apte à résoudre la plupart des problèmes combinatoires. Ces problèmes sont ceux où les variables doivent être réorganisées (par permutation) ou combinées les unes avec les autres. Par exemple, choisir l’ordre des joueurs à la batte, pour une équipe de base-ball, est un problème de nature combinatoire, de même que les problèmes complexes de planification. Le seul et même RISKOptimizer peut résoudre tous ces types de problèmes et bien d’autres encore qu’aucun autre programme ne peut aborder. La technologie unique des algorithmes génétiques et de simulation proposée par RISKOptimizer permet d’optimiser pratiquement tous les types de modèles, aussi volumineux et complexes soient-ils.

24 Qu’est-ce que RISKOptimizer ?

Plus convivial

Malgré ses avantages de puissance et de souplesse manifestes, RISKOptimizer reste convivial et simple d’emploi, car il n’est pas nécessaire de comprendre les techniques complexes et les algorithmes génétiques sur lesquelles il repose. RISKOptimizer ne s’inquiète pas des menus détails du problème : il lui faut simplement un modèle apte à évaluer la qualité des différents scénarios. Il suffit donc de sélectionner les cellules qui contiennent les variables et d’indiquer à RISKOptimizer l’objectif recherché. RISKOptimizer masque intelligemment la difficulté de la technologie, présentant comme automatique l’analyse hypothétique du problème.

Beaucoup de programmes commerciaux ont été développés pour la programmation mathématique et l’élaboration de modèles, mais les tableurs sont de loin les plus appréciés et se vendent, littéralement, comme des petits pains. Leur format intuitif en lignes et colonnes les rend plus faciles à configurer et à gérer que les autres progiciels spécialisés. Ils offrent également une meilleure compatibilité avec d’autres programmes, tels que traitements de texte et bases de données, et proposent plus de formules intégrées, options de formatage, capacités graphiques et de macros que les systèmes autonomes. Compagnon de Microsoft Excel, RISKOptimizer donne accès à toute la gamme de fonctions et outils de développement d’Excel, pour une modélisation plus simple et plus réaliste.

Chapitre 2 : Principes 25

Optimisation conventionnelle vs optimisation par simulation

RISKOptimizer combine la simulation et l’optimisation pour permettre l’optimisation de modèles contenant des facteurs incertains. L’optimiseur utilise les résultats d’exécutions successives du modèle de simulation pour guider sa recherche de meilleures solutions optimales. Les paragraphes qui suivent décrivent le contexte du travail combiné de la simulation et de l’optimisation dans RISKOptimizer.

Processus d’optimisation conventionnel

Le processus conventionnel d’optimisation d’une feuille de calcul à l’aide d’un compagnon tel que Solveur ou Evolver suit les étapes suivantes :

1) Une cellule de sortie ou « cible » à minimiser ou maximiser est

identifiée.

2) Un ensemble de cellules en entrée, dites « ajustables », dont on

contrôle les valeurs est identifié, et les plages de valeurs possibles de ces cellules sont décrites.

3) Un ensemble de contraintes à respecter, souvent exprimées à

l’aide d’expressions telles que COÛTS<100 ou A11>=0, est défini.

4) L’optimisation s’exécute, par calculs successifs répétés sous les

différentes valeurs possibles des cellules ajustables.

5) Durant ce processus : a) Chaque recalcul produit une nouvelle « réponse » ou valeur

pour la cellule cible.

b) L’optimiseur utilise cette nouvelle valeur cible pour

sélectionner l’ensemble suivant de valeurs des cellules ajustables à essayer.

c) Un nouveau recalcul s’exécute, produisant une nouvelle

réponse encore dont l’optimiseur se sert pour identifier un nouvel ensemble de valeurs encore pour les cellules ajustables.

L’étape 5) se répète encore et encore, tandis que l’optimiseur se rapproche de la solution optimale, soit l’ensemble de valeurs de

Chapitre 2 : Principes 27

cellules ajustables qui minimise ou maximise la valeur de la cellule cible.

Processus d’optimisation par simulation

L’optimisation par simulation sous RISKOptimizer suit essentiellement les étapes du processus classique décrit ici, si ce n’est qu’elle 1) permet l’introduction de l’incertitude dans la feuille de

calcul et 2) recourt à la simulation, plutôt qu’au simple recalcul de la feuille pour produire la nouvelle « réponse » de cellule cible renvoyée

à l’optimiseur pour la sélection d’un nouvel ensemble de valeurs de cellules ajustables.

Le nouveau processus d’optimisation par simulation sous RISKOptimizer est décrit ci-dessous. Les différences par rapport au processus conventionnel sont imprimées en caractères gras.

1) Des fonctions de distribution de probabilités décrivent la plage

de valeurs possibles des éléments incertains du modèle.

2) Une cellule de sortie, « cible » est identifiée et la statistique de

simulation (moyenne, écart type, etc.) de la cellule à minimiser ou maximiser est sélectionnée.

3) Un ensemble de cellules en entrée, dites « ajustables », dont on

contrôle les valeurs est identifié, et les plages de valeurs possibles de ces cellules sont décrites.

4) Un ensemble de contraintes à respecter, souvent exprimées à

l’aide d’expressions telles que COÛTS<100 ou A11>=0, est défini.

D’autres contraintes, basées sur les statistiques de simulation

(95

centile de A11>1000, par exemple), peuvent aussi être

définies.

5) L’optimisation s’exécute par simulations successives, sous

différentes valeurs possibles des cellules ajustables à chaque simulation. Durant ce processus :

a) Chaque simulation produit une nouvelle distribution des

valeurs possibles de la cellule cible. La statistique à minimiser ou maximiser se calcule au départ de cette distribution.

b) L’optimiseur utilise cette nouvelle statistique de la valeur

cible pour sélectionner l’ensemble suivant de valeurs de cellules ajustables à essayer.

c) Une autre simulation s’effectue, produisant une nouvelle

statistique encore dont l’optimiseur se sert pour identifier un nouvel ensemble de valeurs pour les cellules ajustables.

28 Optimisation conventionnelle vs optimisation par simulation

L’étape 5) se répète encore et encore, tandis que l’optimiseur se rapproche d’une solution optimale, soit l’ensemble de valeurs de cellules ajustables qui minimise ou maximise la statistique des résultats de simulation de la cellule cible.

Étapes individuelles de l’optimisation sous RISKOptimizer

Les étapes individuelles du processus d’optimisation par simulation de RISKOptimizer sont décrites ci-dessous.

Entrée des distributions de probabilités

RISKOptimizer fait appel aux distributions de probabilités pour décrire l’incertitude présente dans les composants d’un modèle. Par exemple, la fonction RiskUniform(10;20), dans une cellule de feuille de calcul, spécifie que les valeurs de la cellule seront générées par une distribution uniforme à valeur minimum de 10 et valeur maximum de

20. Cette plage de valeurs remplace la simple valeur « fixe » requise

par Excel. L’optimisation classique n’admet pas l’introduction d’incertitude dans un modèle, de sorte que les distributions de probabilités n’y figurent pas.

Sous RISKOptimizer, une simulation du modèle s’exécute pour chaque combinaison possible de valeurs en entrée générées par l’optimiseur. RISKOptimizer utilise les fonctions de distribution lors de ces simulations pour échantillonner les ensembles de valeurs possibles. Chaque itération d’une simulation utilise un nouvel ensemble de valeurs échantillonnées dans chaque fonction de distribution de la feuille de calcul. Ces valeurs servent ensuite à recalculer la feuille de calcul et à générer une nouvelle valeur pour la cellule cible.

À l’image des fonctions Excel, les fonctions de distribution se composent de deux éléments : le nom de la fonction et, entre parenthèses, les valeurs d’argument. Une fonction de distribution typique se présente comme suit :

RiskNormal(100;10)

Comme pour les fonctions Excel, les arguments des fonctions de distribution peuvent être des références de cellule ou des expressions. Par exemple :

RiskTriang(B1;B2*1,5;B3)

Dans ce cas, la valeur de la cellule serait spécifiée par une distribution triangulaire à valeur minimum prélevée dans la cellule B1, valeur

Chapitre 2 : Principes 29

probable calculée sur la base de la valeur de la cellule B2 multipliée par 1,5 et valeur maximum prélevée dans la cellule B3.

30 Optimisation conventionnelle vs optimisation par simulation

Les fonctions de distribution sont aussi admises dans les formules de cellule, comme les fonctions Excel. Par exemple :

B2: 100+RiskUniform(10;20)+(1,5*RiskNormal(A1;A2))

Pour plus de détails sur l’entrée de distributions de probabilités, voir Références : Fonctions de distribution

dans le manuel ou l’aide

@RISK.

Cellule cible et statistique

Sous RISKOptimizer comme dans l’optimisation conventionnelle, une cellule cible doit être identifiée. Cette cellule est celle dont la valeur doit être minimisée ou maximisée, ou dont la valeur doit se rapprocher autant que possible d’une valeur prédéfinie. Il s’agit généralement, mais pas nécessairement, du « résultat » du modèle (le bénéfice, le total général du modèle, etc.). La cellule doit contenir la formule qui renverra différentes valeurs suivant la variation des valeurs des cellules ajustables.

RISKOptimizer minimise ou maximise non pas la valeur réelle de la cellule cible, mais une « statistique » associée aux résultats de simulation de la cellule cible. Lors de l’optimisation, RISKOptimizer exécute des simulations successives avec, pour chacune, un ensemble différent de valeurs de cellules ajustables. Chaque simulation produit une distribution des issues possibles pour la cellule cible. L’optimisation recherche, par exemple, la combinaison de valeurs de cellules ajustables qui maximise la moyenne de la distribution de la cellule cible, ou qui minimise l’écart type.

RISKOptimizer élargit les options de minimisation ou de maximisation (moyenne, écart type, minimum, etc.) car, pour chaque solution essayée par l’optimiseur, la simulation correspondante ne produit pas simplement une seule réponse. Elle génère une distribution complète des issues possibles de la cellule cible, avec une valeur minimum, maximum, moyenne, d’écart type, etc. L’optimisation conventionnelle se limite à produire une nouvelle valeur de cellule cible pour chaque solution essayée, et cette valeur devient la seule sélection possible pour la minimisation ou la maximisation.

Chapitre 2 : Principes 31

Cellules ajustables

Les cellules ajustables se définissent de la même manière dans l’optimisation classique ou de RISKOptimizer. Pour chaque cellule dont la valeur peut varier lors de l’optimisation, on entre une valeur minimum possible et une valeur maximum possible.

Comme l’optimiseur de RISKOptimizer repose sur Evolver, les mêmes options sont possibles pour l’entrée des cellules ajustables : taux de mutation, méthode de résolution et opérateurs génétiques. Pour plus de détails sur la définition des cellules ajustables, voir le chapitre 5 : Guide de référence RISKOptimizer

, sous le titre « Plages

de cellules ajustables ».

Contraintes

À l’image de l’optimisation classique, RISKOptimizer gère les contraintes fermes, dont le respect est obligatoire. Les optimiseurs classiques testent ces contraintes pour chaque solution. Si les contraintes ne sont pas satisfaites, la solution est rejetée.

Sous RISKOptimizer, une simulation complète s’exécute pour chaque solution itérative. Chaque simulation compte un certain nombre d’itérations, ou de recalculs individuels du tableur sur base de nouveaux échantillons issus des distributions de probabilités du modèle. Une contrainte ferme peut être testée :

♦ à chaque itération de chaque simulation (contrainte d'itération). Si

une itération produit des valeurs contraires à la contrainte ferme, la simulation s’arrête (et la solution itérative est rejetée) et la recherche de solution itérative suivante, avec simulation correspondante, commence.

♦ en fin de simulation (contrainte de simulation). Ce type de

contrainte se spécifie en tant que statistique de simulation pour une cellule de tableur : Moyenne de A11>1000, par exemple. Dans ce cas, la contrainte est évaluée en fin de simulation. Une contrainte de simulation, par opposition à une contrainte d’itération, ne cause jamais l’arrêt de la simulation avant son exécution complète.

RISKOptimizer reconnaît par ailleurs une seconde forme de contraintes, appelées « contraintes souples ». Les pénalités qui résultent des contraintes souples se calculent en fin de simulation. La pénalité calculée s’ajoute à la statistique cible minimisée ou maximisée (ou s’y soustrait).

Pour plus de détails sur la définition des contraintes, voir le chapitre 5 : Guide de référence RISKOptimizer, sous le titre « Contraintes ».

32 Optimisation conventionnelle vs optimisation par simulation

Options d’optimisation et de simulation

Exécution de l’optimisation

Sous RISKOptimizer, comme dans l’optimisation classique, plusieurs options sont admises pour gérer la durée de l’opération. RISKOptimizer propose en outre des options de configuration de la durée de chaque simulation pour chaque solution itérative.

RISKOptimizer recherche de meilleures solutions et exécute ses simulations jusqu’à satisfaction des options d’arrêt d’optimisation sélectionnées, qu’il s’agisse du nombre de minutes spécifié, de la génération d’un nombre spécifiés de solutions itératives ou de l’accès à une statistique de simulation optimale de cellule cible inchangée sur une nombre donné d’essais.

La durée de simulation de chaque solution itérative peut aussi être spécifiée, sous forme de nombre d’itérations donné ou selon la détermination automatique de RISKOptimizer. Sous cette dernière option, la simulation s’arrête lorsque les distributions générées pour

1) la cellule cible de l’optimisation et

2) les cellules référencées dans les contraintes de simulation sont stables et que les statistiques visées convergent.

RISKOptimizer exécute l’optimisation par simulations successives de la feuille de calcul, sous différentes valeurs possibles des cellules ajustables à chaque simulation. Durant ce processus :

1) L’optimiseur génère un ensemble de valeurs pour les

cellules ajustables.

2) La feuille de calcul se simule en fonction des valeurs de

cellules ajustables générées par l’optimiseur. À chaque itération de la simulation, toutes les fonctions de distribution de la feuille de calcul sont échantillonnées et la feuille se recalcule pour produire une nouvelle valeur pour la cellule cible. Si une contrainte d’itération n’est pas satisfaite à l’issue d’un recalcul d’itération, la simulation s’arrête et l’optimiseur génère la simulation d’une nouvelle solution itérative.

3) Chaque simulation produit une nouvelle distribution des

valeurs possibles de la cellule cible. La statistique à minimiser ou maximiser se calcule d’après cette distribution. Si une contrainte de simulation n’est pas

satisfaite, la solution itérative et les résultats de la simulation sont rejetés et l’optimiseur génère la simulation d’une nouvelle solution itérative.

Chapitre 2 : Principes 33

4) L’optimiseur utilise la nouvelle statistique de la valeur cible

calculée lors de la simulation pour sélectionner l’ensemble suivant de valeurs de cellules ajustables à essayer.

5) Une autre simulation s’effectue, produisant une nouvelle

statistique encore dont l’optimiseur se sert pour identifier un nouvel ensemble de valeurs pour les cellules ajustables.

Le processus se répète encore et encore, tandis que l’optimiseur se rapproche de la solution optimale, soit l’ensemble de valeurs de cellules ajustables qui minimise ou maximise la statistique de la cellule cible.

34 Optimisation conventionnelle vs optimisation par simulation

Chapitre 2 : Principes 35

Chapitre 3 : RISKOptimizer : Pas à pas

Introduction ...................................................................................... 38

Visite guidée.....................................................................................40

Démarrer RISKOptimizer ................................................................... 40

La barre d’outils RISKOptimizer.......................................... 40

Ouverture d’un modèle type ................................................. 40

Décrire l’incertitude dans le modèle ................................................. 42

La boîte de dialogue RISKOptimizer – Modèle.............................. 44

Sélectionner la statistique de la cellule cible................................... 45

Ajouter les plages de cellules ajustables .......................................... 45

Plage Min-Max de cellules ajustables.................................. 45

Méthode de résolution............................................................ 47

Contraintes ............................................................................................. 48

Contraintes d’itération et de simulation.............................. 48

Ajout de contrainte.................................................................. 50

Simple plage de valeurs ou Formule.................................... 50

Autres options RISKOptimizer.......................................................... 53

Conditions d’arrêt d’optimisation........................................ 53

Conditions d’arrêt de simulation.......................................... 55

Journal des données de simulation...................................... 56

Exécuter l’optimisation......................................................................... 57

Suivi RISKOptimizer.............................................................. 58

Arrêt de l’optimisation............................................................ 59

Rapport de synthèse................................................................ 60

Placement des résultats dans le modèle.............................. 61

36 Optimisation conventionnelle vs optimisation par simulation

Chapitre 3 : RISKOptimizer : Pas à pas 37

Introduction

Ce chapitre suit, pas à pas, une optimisation complète sous RISKOptimizer. Si RISKOptimizer n’est pas installé sur votre disque dur, reportez-vous à la section du chapitre 1 : Introduction à l’installation et installez RISKOptimizer avant d’entreprendre ce didacticiel.

Nous commencerons par ouvrir modèle de calcul prédéfini, pour définir le problème à RISKOptimizer à l’aide de distributions de probabilités et des boîtes de dialogue RISKOptimizer. Nous suivrons ensuite la progression de RISKOptimizer dans sa recherche de solutions et nous explorerons quelques-unes des nombreuses options de Suivi RISKOptimizer. Pour plus de détails sur une rubrique abordée ici, voir l’index en fin de manuel ou le chapitre 5 : Guide de référence RISKOptimizer.

REMARQUE : Les écrans illustrés ci-dessous sont extraits d’Excel

2007. Les fenêtres d’autres versions d’Excel seront peut-être légèrement différentes.

Le processus de résolution commence par l’élaboration d’un modèle qui représente précisément le problème. Ce modèle doit pouvoir évaluer un ensemble donné de valeurs en entrée (les cellules ajustables) et produire une cote numérique indicatrice de la qualité de la solution produite sous ces valeurs (évaluation ou fonction de « pertinence »). Le modèle doit aussi inclure des distributions de probabilités qui décrivent la plage de valeurs possibles de ses éléments incertains. Tandis que RISKOptimizer recherche les solutions possibles, la simulation de la fonction de pertinence lui renvoie une indication de la qualité ou non de chaque supposition, permettant ainsi à l’optimiseur d’améliorer en permanence ses suppositions. Lors de la création du modèle d’un problème, la fonction de pertinence revêt une extrême importance en ce RISKOptimizer n’a de cesse de maximiser (ou minimiser) les résultats de la simulation pour cette cellule.

consacrée

38 Introduction

Chapitre 3 : RISKOptimizer : Pas à pas 39

Visite guidée

Démarrer RISKOptimizer

Pour lancer RISKOptimizer : 1) cliquez sur l’icône RISKOptimizer sur le bureau Windows ou 2) choisissez Palisade DecisionTools puis RISKOptimizer 5.5 dans la liste des programmes listés sous le menu Démarrer de Windows. Ces deux méthodes démarrent chacune Microsoft Excel et RISKOptimizer.

La barre d’outils RISKOptimizer

Ouverture d’un modèle type

Lorsque RISKOptimizer est chargé, une nouvelle barre d’outils s’affiche dans Excel. Cette barre contient les boutons de commande de RISKOptimizer, pour la spécification des paramètres et le démarrage, la pause et l’arrêt des optimisations.

Pour passer en revue les fonctionnalités de RISKOptimizer, nous allons examiner un modèle type installé lors de l’installation du programme :

1) Ouvrez la feuille de calcul CIES AERIENNES.XLS proposée dans

le répertoire RISKOPTIMIZER5\EXEMPLES.

40 Visite guidée

Cet exemple présente un modèle de gestion de rendement identifiant le nombre optimal de places à tarif plein et tarif réduit à vendre sur un vol donné. Il identifie également le nombre optimal de réservations à accepter en plus du nombre de sièges disponibles – le problème classique de la surréservation. Le « hic », dans ce problème d’optimisation classique, est que certaines estimations du modèle sont incertaines ou « stochastiques » : le nombre de passagers qui se présenteront effectivement à l’embarquement, le nombre de réservations qui seront demandées dans chaque catégorie tarifaire et le coût de l’embarquement refusé d’un passager (un bon de voyage de 100 euros peut suffire, mais il faut parfois offrir un billet aller-retour gratuit). De simple estimations sont généralement utilisées pour ces facteurs, pour permettre une optimisation ordinaire. Que se passe-t-il pourtant si ces estimations sont erronées ? La compagnie risque d’accepter trop peu de réservations, d’avoir de nombreux sièges vides ou de surréserver à l’excès. Trop de places à tarif réduit pourraient aussi être vendues, au détriment du bénéfice réalisé. Ou bien trop de places seraient proposées à tarif plein, avec le risque d’avions à moitié remplis. Avec RISKOptimizer, il est possible de résoudre ce problème d’optimisation tout en tenant compte de l’incertitude inhérente au modèle !

Dans notre exemple Cies aériennes, nous allons donc commencer par décrire l’incertitude du modèle à l’aide de distributions de probabilités. On configurera ensuite le problème d’optimisation dans les boîtes de dialogue de RISKOptimizer. RISKOptimizer s’exécutera ensuite pour identifier le nombre optimal de réservations à tarif plein et tarif réduit qui permettra de maximiser le bénéfice tout en maintenant le risque dans des limites acceptables.

Chapitre 3 : RISKOptimizer : Pas à pas 41

Décrire l’incertitude dans le modèle

Dans RISKOptimizer, les distributions de probabilités décrivent la plage de valeurs possibles des éléments incertains du modèle. Une distribution de probabilités spécifie les valeurs minimum et maximum d’un facteur incertain et les probabilités relatives de valeurs comprises entre ces deux valeurs.

Pour l’optimisation, ces distributions se définissent à l’aide de fonctions de distribution propres à RISKOptimizer, dans les cellules et formules de la feuille de calcul tout comme les fonctions Excel standard. Par exemple, la fonction

♦ RiskTriang(10;20;30) spécifie une distribution triangulaire à

valeur minimum de 10, valeur probable de 20 et valeur maximum de 30.

Notre modèle Cies aériennes comporte cinq facteurs incertains décrits, chacun, par une distribution de probabilités. La première :

♦ Demande de réservations à tarif plein (cellule C8), décrite par la

distribution de probabilités RiskTriang(3;7;15). Cette fonction spécifie que le nombre de réservations à tarif plein demandées pourrait être compris entre un minimum de 3 et un maximum de 15, avec une valeur probable de 7.

Pour entrer cette distribution de probabilités :

1) Sélectionnez la cellule C8.

2) Entrez-y la formule =ARRONDI(RiskTriang(3;7;15);0). La

fonction ARRONDI d’Excel arrondit simplement l’échantillon renvoyé par la fonction RiskTriang à l’entier le plus proche. (La demande de 5,65 réservations serait en effet absurde !)

42 Visite guidée

Les autres distributions du modèle, telles qu’énumérées ci-dessous, figurent déjà dans le fichier CiesAériennes.XLS. Si vous désirez les examiner de plus près, accédez à la cellule de chacune.

♦ % Passagers défaillants – Réservations tarif plein (cellule C7).

Cette distribution est décrite par la fonction RiskNormal(0,2;0,03), indiquant qu’en moyenne, 20 % des passagers disposant de réservations faites à tarif plein ne se présentent pas à l’embarquement. Le pourcentage effectif de passagers défaillants varie aux alentours de 20 %, comme décrit par une distribution normale à moyenne de 0,2 et écart type de 0,03.

♦ % Passagers défaillants – Réservations tarif réduit (cellule C11).

Cette distribution est décrite par la fonction RiskNormal(0,1;0,01), indiquant qu’en moyenne, 10% des passagers disposant de réservations faites à tarif réduit ne se présentent pas à l’embarquement. Le pourcentage effectif de passagers défaillants varie aux alentours de 10%, comme décrit par une distribution normale à moyenne de 0,1 et écart type de 0,01. Un plus grand nombre de passagers dotés de réservations à tarif réduit se présente à l’embarquement, leur billet étant sujet à une pénalité de changement de €75, alors que les billets à tarif plein sont totalement remboursables, sans pénalité de changement.

♦ Demande de réservations à tarif réduit (cellule C12), décrite par

la distribution de probabilités RiskTrigen(12;20;40;10;90)). Cette fonction spécifie que le nombre de réservations à tarif réduit demandées est décrit par une distribution de probabilités triangulaire dont le 10 probable est 20 et le 90

centile a une valeur de 12, la valeur

centile a une valeur de 40.

♦ Coût d’embarquement refusé (cellule C23), décrit par la

distribution de probabilités RiskDiscrete({100;150;200;250};{0,1;0,4;0,4;0,1}). Cette fonction spécifie que le coût par passager refusé à l’embarquement peut être de €100, €150, €200 ou €250. Certains passagers se portent en effet volontaires pour quitter un vol surréservé moyennant bon de voyage de €100, alors que dans d’autres cas, une plus grande compensation est nécessaire.

Pour plus de détails sur les distributions de probabilités, voir Références : Fonctions de distribution

dans le manuel ou l’aide

@RISK.

Chapitre 3 : RISKOptimizer : Pas à pas 43

Les distributions de probabilités décrivant l’incertitude ainsi définies dans le modèle, il reste maintenant à configurer l’optimisation dans les boîtes de dialogue de RISKOptimizer.

La boîte de dialogue RISKOptimizer – Modèle

Pour configurer les options RISKOptimizer de notre feuille de calcul :

1) Cliquez sur l’icône Modèle de la barre d’outils RISKOptimizer (à

l’extrême gauche).

La boîte de dialogue RISKOptimizer – Modèle illustrée ci-dessous s’ouvre :

Cette boîte est conçue pour permettre à l’utilisateur de décrire le problème de manière simple et directe. Nous cherchons, dans notre exemple, à déterminer le nombre de réservations à tarif plein et à tarif réduit qu’il convient d’accepter pour maximiser le bénéfice total global.

44 Visite guidée

Sélectionner la statistique de la cellule cible

La cellule C27, Bénéfice, du modèle CiesAériennes.XLS est la « cellule cible » : celle dont la statistique de simulation doit être minimisée ou maximisée, ou doit se rapprocher autant que possible d’une valeur prédéfinie. Pour définir la statistique de simulation de la cellule cible :

1) Pour « But d’optimisation », choisissez l’option « Maximum ».

2) Entrez la cellule cible, $C$27, dans le champ « Cellule ».

3) Choisissez « Moyenne » dans la liste déroulante « Statistique »

pour sélectionner la moyenne comme statistique de simulation à maximiser.

Les références de cellule peuvent être entrées dans les champs des boîtes de dialogue RISKOptimizer de deux manières : 1) Cliquez dans le champ et tapez-y directement la référence de la cellule, ou 2) curseur dans le champ sélectionné, cliquez sur l’icône d’entrée de référence pour sélectionner la ou les cellules voulues directement dans la feuille de calcul à l’aide de la souris.

Ajouter les plages de cellules ajustables

L’étape suivante consiste à spécifier l’emplacement des cellules qui contiennent les valeurs que RISKOptimizer peut faire varier, ou « ajuster », dans sa recherche de solutions. Ces variables s’ajoutent et se modifient, un bloc à la fois, dans la boîte de dialogue Cellules ajustables. Le nombre de cellules admis dépend de la version RISKOptimizer utilisée.

1) Cliquez sur le bouton « Ajouter » dans le volet « Plages de cellules

ajustables ».

2) Sélectionnez C14 comme cellule Excel à ajouter comme cellule

ajustable.

Plage Min-Max de cellules ajustables

Chapitre 3 : RISKOptimizer : Pas à pas 45

Il convient, dans la plupart des cas, de restreindre les valeurs possibles d’une plage de cellules ajustables à une plage minimummaximum spécifique. Il s’agit là, en jargon RISKOptimizer, d’une contrainte de « plage ». Cette plage se définit rapidement lors de la sélection de l’ensemble de cellule à ajuster. Dans l’exemple qui nous occupe, la valeur minimum possible de réservations acceptées dans cette plage est 19 et la valeur maximum, 30. Pour définir cette contrainte de plage :

1) Entrez 19 dans la cellule Minimum et 30 dans la cellule

Maximum.

2) Pour la cellule Valeurs, sélectionnez Entiers dans la liste

déroulante.

Entrez maintenant une deuxième cellule à ajuster :

1) Cliquez sur Ajouter.

2) Sélectionnez la cellule C15.

3) Entrez 0 comme Minimum et 1 comme Maximum.

Il s’agit là de notre dernière cellule ajustable, C15, représentant le pourcentage du total de réservations qui sera affecté aux places à tarif plein.

Si le problème comportait d’autres variables encore, on continuerait ainsi à ajouter des cellules ajustables. RISKOptimizer admet un nombre illimité de groupes de cellules ajustables. Il suffit, pour chacun, de cliquer sur le bouton « Ajouter ».

Si vous décidez plus tard de vérifier les cellules ajustables ou d’en changer les paramètres, il suffit de modifier la plage min-max dans ce

46 Visite guidée

tableau. Le bouton « Supprimer » permet aussi de supprimer un ensemble de cellules sélectionné.

Méthode de résolution

La méthode de résolution à utiliser peut être spécifiée lors de la définition des cellules ajustables. Différentes méthodes de résolution gèrent différents types de cellules ajustables. Les méthodes se définissent pour un Groupe de cellules ajustables et se modifient en cliquant sur le bouton « Groupe » pour afficher la boîte de dialogue Paramètres de groupe de cellules ajustables. La méthode par défaut « recette » convient généralement. Cette méthode permet le changement de valeur de chaque cellule indépendamment des autres. Cette méthode est sélectionnée par défaut. Il est donc inutile de la changer ici.

Les méthodes de résolutions « recette » et « ordre » sont les plus courantes et peuvent être utilisées ensemble pour la résolution de problèmes combinatoires compliqués. Plus spécifiquement la méthode « recette » traite chaque variable comme s’il s’agissait d’un ingrédient d’une recette, essayant de trouver la « meilleure combinaison » en changeant indépendamment la valeur de chaque variable. En revanche, la méthode « ordre » permute les valeurs des variables, réorganisant les valeurs originales à la recherche du « meilleur ordre ».

Chapitre 3 : RISKOptimizer : Pas à pas 47

Contraintes

RISKOptimizer admet les contraintes, qui définissent les conditions à remplir pour qu’une solution soit valable. Dans notre exemple, deux autres contraintes doivent être satisfaites pour assurer la validité d’un ensemble possible de valeurs de nombre maximum de réservations acceptées et de % de places à tarif plein. Ces contraintes sont complémentaires à celles de plage définies plus haut pour les cellules ajustables. Elles se définissent comme suit :

♦ Le bénéfice doit toujours être >0. ♦ L’écart type des résultats de simulation du bénéfice doit

être <400.

À chaque génération de solution possible au modèle, RISKOptimizer exécute une simulation de cette solution. Chaque simulation implique des centaines ou même des milliers d’itérations ou de recalculs de la feuille de calcul. À chaque itération, une valeur est échantillonnée dans chaque distribution de probabilités introduite dans le modèle, le modèle est recalculé en fonction des valeurs échantillonnées et une nouvelle valeur est générée pour la cellule cible. La simulation d’une solution itérative produit une distribution de probabilités pour la cellule cible en fonction des valeurs cibles calculées à chaque itération.

Contraintes d’itération et de simulation

RISKOptimizer vérifie les contraintes

♦ après chaque itération de simulation (pour une contrainte dite

« d’itération ») OU

♦ en fin de simulation (pour une contrainte « de simulation »)

Dans notre modèle de compagnie aérienne, « Le bénéfice doit toujours être >0 » est une contrainte d’itération et « L’écart type des résultats de simulation du bénéfice doit être <400 », une contrainte

de simulation. Autrement dit, RISKOptimizer vérifie après chaque itération d’une simulation si le bénéfice est supérieur à 0. S’il ne l’est pas, la solution itérative est rejetée. Si une simulation s’exécute avec succès (avec un bénéfice >0 pour toutes les itérations), l’écart type de la distribution de probabilités du bénéfice est vérifiée pour assurer qu’il est inférieur à 400, sous peine de rejet, aussi, de la solution itérative.

48 Visite guidée

Les contraintes s’affichent au bas du volet Contraintes de la boîte de dialogue RISKOptimizer – Modèle. RISKOptimizer admet deux types de contraintes :

♦ Ferme. Les contraintes fermes sont les conditions qui doivent être

satisfaites pour qu’une solution soit valable. Par exemple, une contrainte d’itération ferme pourrait être exprimée sous la forme C10<=A4, et si une solution générait une valeur C10 supérieure à celle de la cellule A4, la solution serait rejetée.

♦ Souple. Les contraintes souples sont les conditions que l’on veut

respecter autant que possible, mais pour lesquelles on est prêt à accepter le compromis en vue d’une importante amélioration de pertinence ou de résultat de cellule cible. Par exemple, une contrainte souple pourrait être exprimée sous la forme C10<100. Dans ce cas, C10 pourrait dépasser la valeur 100, mais la valeur calculée de la cellule cible serait alors diminuée conformément à la fonction de pénalité définie.

Chapitre 3 : RISKOptimizer : Pas à pas 49

Ajout de contrainte

Pour ajouter une contrainte :

1) Cliquez sur le bouton Ajouter du volet Contraintes, dans la boîte

de dialogue RISKOptimizer principale.

La boîte de dialogue Paramètres de contrainte s’ouvre, pour la définition des contraintes du modèle.

Simple plage de valeurs ou Formule

Les formules peuvent être définies selon deux formats : Simple ou Formule. Le format Simple plage de valeurs permet la définition des

contraintes selon de simples relations <,<=, >, >= ou =. Par exemple : 0<Valeur de A1<10, où A1 s’entre dans la case Plage, 0 dans la case Min et 10 dans la case Max. Les opérateurs désirés se sélectionnent dans les listes déroulantes. Sous une contrainte de format « Simple », on peut entrer une valeur Min, une valeur Max, ou les deux.

Le format Formule permet en revanche l’entrée, pour la contrainte, d’une formule Excel correcte, telle que A19<(1,2*E7)+E8. Pour chaque solution possible, RISKOptimizer vérifie si la formule entrée est VRAIE ou FAUSSE, afin de déterminer le respect ou non de la contrainte. Pour utiliser une formule booléenne de cellule de feuille de travail comme contrainte, il suffit de faire référence à cette cellule dans le champ Formule de la boîte de dialogue Paramètres de contrainte.

50 Visite guidée

Nous allons, pour notre modèle Cies aériennes, spécifier deux nouvelles contraintes. Commencez par configurer une contrainte ferme de style Simple pour Bénéfice Profit > 0 :

1) Entrez « Bénéfice > 0 » comme description.

2) Dans la case Plage sous contrainte, entrez C27.

3) Sélectionnez l’opérateur > à droite de Plage sous contrainte.

4) Acceptez la valeur par défaut 0 de la case Maximum.

5) À gauche de Plage sous contrainte, supprimez l’opérateur en

sélectionnant l’option blanche dans la liste déroulante.

6) Sélectionnez « À chaque itération de chaque simulation » et

cliquez sur OK. Vous avez ainsi spécifié que Bénéfice doit toujours être supérieur à 0, quel que soit le nombre de réservations acceptées.

7) Cliquez sur OK pour valider cette contrainte.

Chapitre 3 : RISKOptimizer : Pas à pas 51

Définissons maintenant la contrainte de simulation :

1) Cliquez sur Ajouter pour rouvrir la boîte de dialogue Paramètres

de contrainte.

2) Entrez « Écart type de bénéfice <400 » dans la zone de description.

3) Dans la case Plage sous contrainte, entrez C27.

4) Sélectionnez l’opérateur < à droite de Plage sous contrainte.

5) Entrez 400 dans la case Max.

6) À gauche de Plage sous contrainte, supprimez l’opérateur en

sélectionnant l’option blanche dans la liste déroulante.

7) Dans la liste déroulante Statistique sous contrainte, sélectionnez

« Écart type ».

8) Cliquez sur OK.

La boîte de dialogue résultante doit se présenter comme suit :

52 Visite guidée

Conditions d’arrêt d’optimisation

Autres options RISKOptimizer

Les options telles qu’Actualiser l’affichage, Racine de nombres aléatoires, Arrêt d’optimisation et Arrêt de simulation permettent de

gérer le fonctionnement de RISKOptimizer en cours d’optimisation. Précisons donc quelques conditions d’arrêt et paramètres d’actualisation de l’affichage.

RISKOptimizer exécute l’optimisation aussi longtemps que vous le désirez. Les conditions d’arrêt gèrent l’arrêt automatique de RISKOptimizer lorsque a) un certain nombre de scénarios ou d’« essais » a

été examiné, b) un certain temps s’est écoulé, c) les n derniers scénarios n’ont produit aucune amélioration, d) la formule Excel entrée est VRAIE ou

e) une valeur d’erreur est calculée pour la cellule cible. Pour afficher et modifier les conditions d’arrêt :

1) Cliquez sur l’icône Paramètres d’optimisation de la barre d’outils

RISKOptimizer.

2) Cliquez sur l’onglet Temps d’exécution.

Chapitre 3 : RISKOptimizer : Pas à pas 53

Dans la boîte de dialogue Paramètres d’optimisation, vous pouvez sélectionner une combinaison quelconque de conditions d’arrêt. Vous pouvez aussi choisir de n’en sélectionner aucune

. Si vous sélectionnez plusieurs conditions d’arrêt, RISKOptimizer s’arrête lorsque l’une d’entre elles est remplie. Si vous ne sélectionnez aucune condition d’arrêt, RISKOptimizer s’exécute indéfiniment, jusqu’à ce que vous l’arrêtiez manuellement en cliquant sur le bouton Arrêter de la barre d’outils.

Simulations

Cette option définit le nombre de simulations à exécuter. RISKOptimizer exécute une simulation par ensemble complet de variables ou solution possible au problème.

RISKOptimizer s’arrête au terme de la durée de temps spécifiée. Cette valeur peut être une fraction (4,25).

Durée

Progression

Cette condition d’arrêt est la plus appréciée car elle suit l’amélioration du processus et permet à RISKOptimizer de continuer jusqu’à ce que le degré d’amélioration se réduise. Par exemple, RISKOptimizer pourrait s’arrêter au bout de 100 simulations si aucune nouvelle amélioration n’est apparue par rapport au dernier scénario optimal.

La formule est

vraie

RISKOptimizer s’arrête si la formule Excel entrée s’avère VRAIE dans une simulation.

1) Paramétrez une durée de 5 minutes pour laisser RISKOptimizer

tourner pendant cinq minutes.

54 Visite guidée

Conditions d’arrêt de simulation

RISKOptimizer exécute une simulation complète du modèle par solution itérative générée. Il est possible de limiter la durée de chaque simulation à l’aide des conditions d’arrêt de simulation. Vous pouvez fixer un nombre d’itérations par simulation ou laisser à RISKOptimizer le soin de déterminer le moment d’arrêter chaque simulation.

Itérations

Cette option vous permet de limiter chaque simulation à un nombre fixe d’itérations. RISKOptimizer exécute le nombre d’itérations spécifié pour chaque simulation de solution itérative (sauf arrêt prématuré en cas de violation de contrainte d’itération).

Arrêt sur convergence

réelle

Sous cette option, la simulation s’arrête lorsque les distributions générées pour 1) la cellule cible de l’optimisation et cellules référencées dans les contraintes de simulation que les statistiques visées convergent. La quantité de variation admise dans une statistique « convergente » est régie par l’option Tolérance.

2) les

sont stables et

Arrêt sur convergence

Sous cette option, RISKOptimizer arrête la simulation lorsqu’il projette que les distributions générées pour 1) la cellule cible de l’optimisation et référencées dans les contraintes de simulation sont stables. RISKOptimizer projette la convergence en fonction des résultats des simulations antérieures de l’optimisation.

projetée

2) les cellules

1) Entrez 500 dans la case Itérations pour que RISKOptimizer

exécute une simulation rapide pour chaque solution itérative.

Chapitre 3 : RISKOptimizer : Pas à pas 55

Journal des données de simulation

RISKOptimizer peut afficher une description continue de chaque exécution de simulation en cours d’optimisation, y compris la valeur de la statistique calculée, les statistiques de base de la distribution simulée des valeurs de la cellule cible, les valeurs des cellules ajustables et la satisfaction ou non des contraintes. Pour afficher ce journal en cours d’optimisation :

1) Cliquez sur l’onglet Affichage et sélectionnez « Tenir un journal

de toutes les simulations » dans la boîte de dialogue Paramètres d’optimisation.

56 Visite guidée

Exécuter l’optimisation

Il ne reste maintenant plus qu’à optimiser notre modèle pour déterminer le nombre maximum de réservations, dans chaque catégorie tarifaire, qui nous permettra de maximiser notre bénéfice. Pour ce faire :

1) Cliquez sur OK pour fermer la boîte de dialogue Paramètres

d’optimisation.

2) Cliquez sur l’icône Démarrer l’optimisation.

Tandis que RISKOptimizer se met au travail, les valeurs optimales courantes de nos cellules ajustables – nombre total de réservations acceptées et % de réservations à tarif plein – s’affichent dans le tableur. La meilleure moyenne de Bénéfice figure en bleu, avec une flèche pointée sur la cellule cible.

La fenêtre de progression suit l’exécution et affiche : 1) la meilleure solution trouvée jusque là, 2) la valeur originale de la statistique de simulation sélectionnée pour la cellule cible en début d’optimisation par RISKOptimizer, 3) le nombre de simulations du modèle exécutées et le nombre de celles valables (où toutes les contraintes ont été satisfaites) et 4) le temps d’optimisation écoulé.

À tout moment pendant l’exécution, l’icône Afficher les options d’actualisation Excel permet de visualiser chaque simulation en direct à l’écran.

Chapitre 3 : RISKOptimizer : Pas à pas 57

Suivi RISKOptimizer

RISKOptimizer peut aussi afficher un journal courant des simulations effectuées pour chaque solution itérative. Ce journal s’affiche dans Suivi RISKOptimizer en cours d’optimisation. Le système Suivi RISKOptimizer vous permet d’explorer et de modifier de nombreux aspects de votre problème en cours d’exécution. Pour afficher le journal courant des simulations effectuées :

1) Cliquez sur l’icône Suivi (loupe) dans la fenêtre de progression.

2) Cliquez sur l’onglet Journal.

Ce rapport présente les résultats de la simulation exécutée pour chaque solution itérative. La colonne Résultat indique, par simulation, la valeur de la statistique de la cellule cible à maximiser ou minimiser – en l’occurrence, la moyenne de Bénéfice dans $C$27. Les colonnes Moyenne sortie, Ec. Type sortie, Min sortie et Max sortie décrivent la distribution de probabilités de la cellule cible Bénéfice calculée à chaque simulation. Les colonnes $C$14 et $C$15 identifient les valeurs utilisées pour les cellules ajustables. Les colonnes Ec. Type Bénéfice<400 et Bénéfice>0 indiquent la satisfaction ou non des contraintes à chaque simulation.

58 Visite guidée

Arrêt de l’optimisation

Au bout de cinq minutes, RISKOptimizer arrête l’optimisation. Vous pouvez aussi arrêter l’optimisation en

1) cliquant sur l’icône Arrêter dans la fenêtre Suivi RISKOptimizer

ou dans celle de progression.

À l’arrêt du processus, RISKOptimizer affiche l’onglet Options d’arrêt. Les choix suivants y sont proposés :

Ces mêmes options s’affichent automatiquement lorsqu’une condition d’arrêt quelconque de la boîte de dialogue Paramètres d’optimisation est remplie.

Chapitre 3 : RISKOptimizer : Pas à pas 59

Rapport de synthèse

RISKOptimizer peut créer un rapport de synthèse d’optimisation faisant état des date et heure de l’exécution, des paramètres d’optimisation utilisés, de la valeur calculée pour la cellule cible et de la valeur de chaque cellule ajustable.

Ce rapport est utile à la comparaison des résultats d’optimisations successives.

60 Visite guidée

Placement des résultats dans le modèle

Pour placer la nouvelle combinaison optimisée de niveaux de production de Cies aériennes à chacune des 16 tâches de la feuille de calcul :

1) Cliquez sur le bouton « Arrêter ».

2) Sélectionnez l’option « Actualiser les valeurs de cellules

ajustables affichées dans le classeur aux valeurs » « Meilleures ».

La feuille de calcul CIES AERIENNES.XLS réapparaît, garnie de toutes les nouvelles valeurs variables à l’origine de la meilleure solution. N’oubliez pas que la meilleure solution représente la

moyenne des résultats de simulation de Bénéfice, différente de la valeur indiquée pour un simple recalcul basé sur les meilleures valeurs variables. La meilleure moyenne figure dans la case bleue,

avec la flèche pointée sur Bénéfice.

Chapitre 3 : RISKOptimizer : Pas à pas 61

REMARQUE IMPORTANTE : Bien que notre exemple ait produit une solution présentant un bénéfice total de 2236,03, votre résultat pourra être supérieur ou inférieur à cette valeur. RISKOptimizer a peut-être

identifié aussi une combinaison différente de Maximum de réservations acceptées et Pourcentage vendu au tarif plein ayant produit une même cote totale. Ces différences s’expliquent par l’importante distinction qui sépare RISKOptimizer de tous les autres algorithmes de résolution de problèmes : c’est la nature aléatoire du moteur d’algorithmes génétiques de RISKOptimizer qui lui permet de résoudre une plus grande variété de problèmes et d’y trouver de meilleures solutions.

Lorsque vous enregistrez une feuille après l’exécution de RISKOptimizer (et même si vous en « rétablissez » les valeurs originales après cette exécution), tous les paramètres RISKOptimizer configurés dans les boîtes de dialogue du programme s’enregistrent avec cette feuille. À l’ouverture suivante de la feuille, tous les paramètres les plus récents de RISKOptimizer se chargent ainsi automatiquement. Tous les autres exemples de feuilles de calcul sont déjà dotés des paramètres RISKOptimizer et sont prêts à être optimisés.

REMARQUE : Si vous désirez consulter le modèle Cies aériennes déjà assorti de tous ses paramètres d’optimisation, ouvrez le fichier d’exemple RENDAERIEN.XLS.

62 Visite guidée

Chapitre 3 : RISKOptimizer : Pas à pas 63

Chapitre 4 : Applications types

Introduction ...................................................................................... 66

Allocation budgétaire.......................................................................68

Planification de capacité .................................................................70

Planificateur de classes ..................................................................72

Couverture sur contrats à terme .................................................... 76

Ordonnancement multigamme.......................................................78

Équilibrage de portefeuille.............................................................. 80

Composition de portefeuille............................................................ 82

Risque de portefeuille...................................................................... 84

Problème de voyageur de commerce ............................................86

Gestion du rendement..................................................................... 88



Chapitre 4 : Applications types 64

Chapitre 4 : Applications types 65

Introduction

Dans ce chapitre, vous trouverez différentes applications de RISKOptimizer. Ces exemples ne couvrent pas nécessairement toutes les fonctionnalités qui vous intéressent. Leur but serait plutôt de servir de modèles et d’éveiller de nouvelles idées. Tous les exemples présentés illustrent la manière dont RISKOptimizer recherche ses solutions sur la base des relations existantes dans la feuille de calcul. Veillez par conséquent à ce que vos modèles représentent précisément le problème à résoudre.

Tous les exemples de feuille de calcul présentés ici se trouvent dans le répertoire RISKOPTIMIZER5, sous-répertoire « EXEMPLES ».

Tous les paramètres RISKOptimizer voulus sont présélectionnés dans chaque exemple : cellule cible, cellules ajustables, méthodes de résolution et contraintes. Ne manquez pas d’examiner ces paramètres dans leur boîte de dialogue avant de lancer l’optimisation. En examinant les formules et en essayant différents paramètres, vous comprendrez et maîtriserez mieux le fonctionnement de RISKOptimizer. Les modèles proposés vous permettent aussi de remplacer les données d’échantillon par vos propres données « utilisateur ». Si vous décidez de modifier ou d’adapter ces feuilles d’exemple, enregistrez-les sous un autre nom pour conserver les versions originales pour référence.

66 Introduction

Chapitre 4 : Applications types 67

Allocation budgétaire

Supposons qu’un haut cadre désire identifier le mode le plus efficace de distribution de fonds entre les différents services de son entreprise pour maximiser le bénéfice. Le modèle ci-dessous représente l’entreprise et son bénéfice projeté pour l’année prochaine. Le modèle estime ce bénéfice en examinant le budget annuel et en supposant, par exemple, la manière dont la publicité affecte les ventes. Les estimations de ventes incertaines incluent des distributions de probabilités reflétant les plages de valeurs possibles. Il s’agit ici d’un modèle simple, mais qui illustre la configuration d’un modèle et le recours à RISKOptimizer pour y identifier la sortie optimale.

Fichier de l’exemple : But :

Méthode de résolution : Problèmes similaires :

budget.xls Affecter le budget annuel entre cinq services

pour maximiser le bénéfice de l’an prochain. budget Affecter des ressources précaires (telles que

main-d’œuvre, argent, carburant, temps) à des postes susceptibles de les utiliser de différentes manières plus ou moins efficientes.

68 Allocation budgétaire

Modèle

Le fichier « budget.xls » modélise les effets du budget d’une entreprise sur ses ventes et bénéfices à venir. Les cellules C4:C8 (les variables) représentent les montants à allouer à chacun des cinq services. La cellule C10 représente le total de ces valeurs, soit le budget annuel total de l’entreprise. Ce budget est défini par l’entreprise et est inchangeable.

Les cellules F6:F10 calculent une estimation de la demande du produit de l’entreprise pour l’année prochaine, en fonction des budgets publicitaires et de marketing. Le montant de ventes réelles représente le minimum de la demande calculée et de l’offre. L’offre dépend des fonds alloués aux services de production et d’exploitation. Les estimations incertaines du modèle sont incluses dans les distributions de probabilités des calculs d’estimation des ventes dans les cellules F6 à F10.

Résolution

On maximise le bénéfice dans la cellule I16 en choisissant la méthode de résolution « budget » pour ajuster les valeurs des cellules C4 :C8. On fixe les plages indépendantes de chacune des cellules ajustables du budget de chaque service pour éviter que RISKOptimizer n’essaie de valeurs négatives ou de chiffres qui ne produiraient pas de solutions budgétaires pertinentes (toute publicité sans production, par exemple).

La méthode de résolution « budget » opère de la même manière que « recette » en ce qu’elle recherche la bonne « combinaison » des variables choisies. La différence est que sous la méthode « budget », on ajoute la contrainte que le total de toutes les variables doit rester égal avant et après l’optimisation.

Chapitre 4 : Applications types 69

Planification de capacité

Ce modèle fait appel à RISKOptimizer pour sélectionner le niveau de capacité d’une nouvelle usine et maximiser les bénéfices. Dans le modèle , l’entreprise ZooCo envisage le lancement d’un nouveau médicament pour hippopotames. Un modèle de simulation ordinaire génère la distribution de VAN pour la production du nouveau médicament. Il faut cependant décider de la capacité de l’usine à construire. Quel est le niveau de capacité qui maximise la VAN ajustée en fonction du risque ?

Fichier de l’exemple : But :

Méthode de résolution : Problèmes similaires :

capacité.xls Maximiser la moyenne de la distribution simulée

pour VAN par variation de la capacité d’usine. recette Analyses de gestion combinant des modèles de

simulation conventionnels à des variables de décision contrôlées par l’utilisateur.

70 Planification de capacité

Modèle

Au début de l’année courante, un million d’hippopotames sont susceptibles d’utiliser le produit, comme indiqué dans la cellule B34. Chaque hippopotame prendra le médicament (ou celui d’un concurrent), au plus, une fois par an. Selon les prévisions, la population d’hippopotames devrait s’accroître, en moyenne, de 5 % par an, et on est sûr, à 95 %, qu’elle s’accroîtra chaque année de 3 % à 7 % (comme modélisé à l’aide des distributions de probabilités des cellules B34 à F34). La consommation du médicament durant la première année est incertaine, mais on imagine qu’elle sera, au pire, de 20 %, le plus probablement, de 40 % et, au mieux, de 70 % (comme modélisé par distribution de probabilités dans la cellule B35). Pour les années suivantes, la proportion des hippopotames qui prendront le médicament (ou celui d’un concurrent) devrait rester la même, mais durant toute année suivant l’arrivée d’un concurrent sur le marché, l’entreprise perdra vraisemblablement 20 % de sa part par concurrent. Une unité de capacité annuelle coûte €3,50 à la construction et €0,30 par an à l’exploitation (que cette capacité soit utilisée ou non pour la production du médicament). Un niveau de capacité compris entre 100 000 et 500 000 unités peut être réalisé.

Résolution

On choisit la méthode de résolution recette pour la cellule I26. On maximise la moyenne simulée de B45.

Chapitre 4 : Applications types 71

Planificateur de classes

Une université doit affecter 25 classes différentes à 6 blocs temps prédéfinis. Comme le programme doit être élaboré avant l’inscription des étudiants, le nombre réel d’étudiants par classe est incertain. La durée de chaque classe est d’exactement un bloc temps. Cela permettrait ordinairement d’aborder le problème par la méthode de résolution « groupement ». La programmation des classes exige cependant la satisfaction de plusieurs contraintes. Par exemple, les cours de biologie et chimie ne doivent pas être programmés en même temps, pour que les étudiants de médicine puissent les suivre la même année. Pour satisfaire à ces contraintes, on choisira donc la méthode de résolution « programmation ». Cette méthode est comparable à celle de « groupement », si ce n’est que certaines tâches doivent (ou ne doivent pas) se produire avant (ou après ou pendant) d’autres.

Fichier de l’exemple : But :

Méthode de résolution : Problèmes similaires :

classes.xls Affecter 25 classes à 6 périodes de temps de

manière à minimiser la moyenne de la distribution simulée pour le nombre d’étudiants qui devront être exclus de certaines classes. Satisfaire aux contraintes d’agencement des classes dans le temps.

programme Tout problème de programmation où toutes les

tâches sont de même longueur et peuvent être affectées à un bloc temps discret quelconque. Tout problème de groupement aussi soumis à des contraintes quant aux groupes auxquels certains éléments peuvent être affectés.

72 Planificateur de classes

Modèle

Le fichier « classes.xls » contient un modèle de problème de programmation type soumis à de nombreuses contraintes. La plage des valeurs possibles de chaque classe est donnée par les distributions de probabilités entrées dans la plage D8:D32 libellée « Taille réelle ». Les cellules C8:C32 affectent les 25 classes aux 6 blocs temps. On ne dispose que de cinq salles de classe. L’affectation de plus de cinq classes par bloc temps impliquerait l’impossibilité de réunion d’au moins une classe.

Les cellules L20:N28 définissent les contraintes. À gauche de ces contraintes figurent leurs descriptions littérales. Vous pouvez utiliser, au choix, le code numérique ou la description littérale de la contrainte. La liste des codes de contrainte des problèmes de programmation figure en détails dans la section du chapitre 5 : Guide de référence RISKOptimizer consacrée aux « Méthodes de résolution ».

Chaque programme possible est évalué en calculant a) le nombre de classes exclues et b) le nombre d’étudiants exclus pour cause de classe saturée. Cette dernière contrainte évite la programmation simultanée de toutes les classes nombreuses. Si une ou deux classes nombreuses seulement se réunissent sur un bloc temps donné, les salles de classe plus vastes peuvent leur être réservées.

Les cellules J11:M11 font appel à la fonction BDNB pour compter le nombre de classes affectées à chaque bloc temps. La section juste audessous des cellules J12:M12 calcule le nombre de classes non affectées à une salle de classe pour le bloc temps correspondant. Toutes les classes sans salle sont totalisées dans la cellule L13.

Chapitre 4 : Applications types 73

Si le nombre de sièges requis pour une classe donnée dépasse le nombre de sièges disponibles, les cellules J15:M15 calculent l’excès et le nombre total d’étudiants sans siège est calculé dans la cellule L16. Dans la cellule G9, ce nombre total d’étudiants sans siège est ajouté à la taille de classe moyenne et multiplié par le nombre de classes sans salle. Une cellule combine ainsi toutes les pénalités, de sorte qu’un nombre inférieur, dans cette cellule, indique toujours un meilleur programme.

Résolution

On minimise la moyenne de la distribution simulée pour les pénalités dans G9 par variation des cellules C8:C32. On choisit la méthode de résolution « programme ». Lorsque cette méthode est sélectionnée, ses options s’affichent dans le volet « options » inférieur de la boîte de dialogue. On fixe le nombre de blocs temps à 6 et les cellules sous contrainte à L20:N28.

74 Planificateur de classes

Chapitre 4 : Applications types 75

Couverture sur contrats à terme

Nous sommes le 8 juin 2000. L’entreprise GlassCo doit acheter 500 000 litres de mazout le 8 novembre 2000. Le cours au comptant actuel est de $0,42 le litre. Le cours du carburant est censé suivre une variable aléatoire normale logarithmique à moyenne = 0,08 et écart type = 0,30. Le taux sans risque est de 6 %. On couvre le risque par un achat de contrats de carburant à terme expirant le 8 décembre 2000. Combien de contrats à terme faut-il acheter ?

Fichier de l’exemple : But :

Méthode de résolution : Problèmes similaires :

mazout.xls Déterminer le nombre de contrats à terme

aptes à protéger contre les fluctuations de cours d’un achat futur.

recette Modèles de minimisation du risque où

l’objectif est de minimiser l’écart type de la cible.

76 Couverture sur contrats à terme

Modèle

Résolution

Le modèle cherche à assurer un coût d’achat, dans cinq mois, de 210 000 litres de mazout à un prix aussi prévisible que possible moyennant l’achat de contrats à terme pour se protéger contre les fluctuations des cours. Les facteurs incertains du modèle sont le prix comptant futur du mazout (cellule B13) et celui des contrats à terme futurs (cellule B15).

On commence par choisir une cellule ajustable. Pour ce modèle, on ajustera la cellule B12 – Nbre de contrats à terme « long » ou achetés – pour minimiser l’écart type du coût total dans la cellule B23. Le nombre de contrats achetés peut être compris entre un minimum de 0 et un maximum de 600 000.

Chapitre 4 : Applications types 77

Ordonnancement multigamme

Un atelier de travail des métaux doit trouver le meilleur moyen de planifier un ensemble de projets à répartir par étapes réalisables sur différentes machines. Chaque projet compte cinq tâches, dont la réalisation doit s’effectuer dans un certain ordre. Chaque tâche doit être accomplie sur une machine particulière, mais sa durée d’exécution est incertaine. Il y a cinq projets et cinq machines.

Le bouton Programme, en haut de la feuille de calcul, retrace le graphique à barres pour indiquer le moment d’exécution prévu de chaque tâche.

Fichier de l’exemple : But :

Méthode de résolution : Problèmes similaires :

atelier de travail.xls Affecter les éléments d’un projet (tâches) à des

machines de manière à minimiser la durée totale de tous les projets.

ordre Problèmes de planification ou gestion de projet

78 Ordonnancement multigamme

Modèle

La durée incertaine de chaque tâche est décrite par les distributions de probabilités des cellules E11 à E35. La cellule D5 calcule le temps écoulé entre le début de la première tâche planifiée et la fin de la dernière tâche planifiée. Ce temps total est l’élément à minimiser. Les cellules G11:G35 contiennent les variables (les tâches) à organiser de différentes manières pour déterminer l’ordre optimal. Les équations calculent le moment auquel chaque tâche peut être exécutée sur la machine nécessaire à sa réalisation.

Résolution

On sélectionne l’ensemble de cellules ajustables G11:G35 et on choisit la méthode de résolution ordre. On minimise la moyenne des résultats de simulation de la cellule D5.

Chapitre 4 : Applications types 79

Équilibrage de portefeuille

Un courtier a une liste de 80 titres de différents types dont la valeur future sera différente et incertaine. Le courtier veut grouper ces titres en cinq ensembles (portefeuilles) dont les valeurs totales respectives seront aussi proches que possible dans un an.

Il s’agit ici d’un exemple relevant d’une classe générale de problèmes dits d’emballage optimal. Le chargement des cales d’un cargo de manière à répartir uniformément de poids en est un autre exemple. S’il y a des millions de petits éléments à « emballer » dans quelques groupes seulement (des grains de blé dans les cales d’un navire, par exemple), une distribution plus ou moins égale peut être estimée sans grande différence de poids. En revanche, plusieurs douzaines de paquets de poids et/ou tailles différents peuvent être disposés de différentes manières, et un emballage efficace peut améliorer l’équilibre qu’on atteindrait manuellement.

Fichier de l’exemple : But :

Méthode de résolution : Problèmes similaires :

équilibrage de portefeuille.xls Répartir une liste de titres en cinq portefeuilles

différents dont les valeurs futurs seront aussi proches que possible les unes des autres.

groupement Formation d’équipes dotées de talents collectifs

plus ou moins équivalents. Chargement de conteneurs dans les cales d’un bateau pour répartir uniformément la charge.

80 Équilibrage de portefeuille

Modèle

Le fichier « équilport.xls » modélise une tâche de groupement typique. La colonne A contient les numéros d’identification de titres spécifiques, et la colonne B identifie la classe de chaque titre (la feuille de calcul TITRES documente chaque classe de titres). Les colonnes C, D et E indiquent la valeur courante en dollars de chaque titre et la moyenne et l’écart type du rapport de l’année suivante (en fonction de la classe du titre). La colonne F calcule la valeur du titre dans un an selon un taux de rendement échantillonné dans une distribution de probabilités utilisant la moyenne et l’écart type indiqués. La colonne G affecte chaque titre à l’un des cinq portefeuilles. Lors de la configuration d’une type de problème à groupement ou emballage optimal avec sélection de la méthode de résolution groupement, on veillera, avant de démarrer RISKOptimizer, à ce que chaque groupe (1-5) soit représenté au moins une fois dans le scénario.

Les cellules J6:J10 utilisent les formules « BDSOMME() » pour calculer la valeur totale de chacun des cinq portefeuilles. Ainsi, par exemple, la cellule J6 calcule la BDSOMME de toutes les valeurs de la colonne F affectées au groupe 5 (dans la colonne G).

La cellule J12 calcule l’écart type des valeurs de portefeuille totales au moyen de la fonction « ECARTYPE() ». On obtient ainsi une mesure de la proximité des valeurs de portefeuille les unes par rapport aux autres. Le graphique représente la valeur totale de chaque portefeuille, avec une ligne de référence marquant la valeur cible s’ils étaient tous égaux.

Résolution

On minimise la moyenne des résultats de simulation de la cellule J12 par variation des cellules G5:C84. On choisit la méthode « groupement » et on assure que les valeurs 1, 2, 3, 4 et 5 figurent chacune au moins une fois dans la colonne G.

Sous la méthode de résolution « groupement », RISKOptimizer dispose les variables en x groupes, où x représente le nombre de valeurs différentes dans les cellules ajustables au début d’une optimisation.

Chapitre 4 : Applications types 81

Composition de portefeuille

Un jeune couple détient des valeurs dans plusieurs types d’investissement différents, présentant chacun leur propre rapport, croissance potentielle et risque. Le but est de sélectionner la combinaison d’investissements apte à maximiser le rapport total tout en maintenant le risque à un niveau acceptable.

Fichier de l’exemple : But :

Méthode de résolution :

composition de portefeuille.xls Trouver la combinaison optimale

d’investissements pour maximiser le bénéfice, compte tenu du rapport risque/besoin de rendement actuel.

budget

82 Composition de portefeuille

Modèle

Cet exemple présente un modèle d’investissement classique cherchant à équilibrer le risque de perte par rapport au rendement. Chaque valeur listée dans la colonne B présente un % de croissance incertain et un rendement fixe. Le rapport total additionne la plus-value et le rendement. L’objectif consiste à maximiser le rendement total tout en gardant l’écart type de la rentabilité du portefeuille à moins de 9 %.

Résolution

Le rapport total, dans la cellule D33, reflète la somme de la plus-value totale et du rendement total. On maximise la moyenne de la distribution simulée pour cette cellule. Une contrainte de simulation ferme spécifie que l’écart type de la cellule D33 doit être inférieur à 0,09.

Chapitre 4 : Applications types 83

Risque de portefeuille

Un investisseur cherche à déterminer le moyen le plus sûr de structurer un portefeuille d’après plusieurs investissements. Les données historiques révèlent une corrélation entre les taux de rendement de l’investissement. L’objectif est de diviser le portefeuille total entre trois investissements disponibles de manière à atteindre le taux de rendement désiré de 12 % tout en minimisant le risque, ou l’écart type, du rendement de portefeuille.

Fichier de l’exemple : But :

Méthode de résolution : Problèmes similaires :

corrmat.xls Minimiser l’écart type du rendement de

portefeuille tout en atteignant le rendement désiré.

budget Tout modèle de minimisation du risque.

84 Risque de portefeuille

Modèle

Chacun des trois investissements disponibles présente un rendement incertain modélisé à l’aide de distributions de probabilités dans les cellules E3 à E5. Pour corréler les rendements des trois investissement, la fonction RiskCorrmat est utilisée, avec matrice de corrélation dans les cellules J9:L11. RISKOptimizer va ajuster le pourcentage du portefeuille affecté à chaque investissement. La méthode de résolution « budget » assure que le % total affecté est toujours de 100 %.

L’objectif est de minimiser l’écart type du rendement de portefeuille total tout en satisfaisant à la contrainte d’un rendement total égal ou supérieur à 12 %.

Résolution

On minimise l’écart type des résultats de simulation de la cellule G6. On définit une contrainte de simulation ferme selon laquelle la moyenne des résultats de la simulation de la cellule G6 doit être supérieure à 0,12.

Chapitre 4 : Applications types 85

Problème de voyageur de commerce

Un voyageur de commerce doit se rendre une fois dans chaque ville de son territoire. Quel est l’itinéraire le plus rapide qui lui permettra de couvrir chaque ville ? Il s’agit ici d’un problème d’optimisation classique présentant un aspect pointu (le temps de route entre chaque ville est incertain), particulièrement difficile à résoudre selon les techniques traditionnelles si le nombre de villes est grand (>50).

La recherche du meilleur ordre d’exécution des tâches dans une usine présenterait un problème similaire. Ainsi, il pourrait être beaucoup plus simple d’appliquer la peinture noire après la blanche plutôt que l’inverse. Sous RISKOptimizer, ces types de problème se résolvent le mieux à l’aide de la méthode ordre.

Fichier de l’exemple : But :

Méthode de résolution : Problèmes similaires :

vendeur.xls Rechercher l’itinéraire le plus rapide entre n villes

dont chacune doit être visitée une fois. ordre Planifier le perçage le plus rapide possible d’une

carte de circuit imprimé.

86 Problème de voyageur de commerce

Modèle

Le fichier « vendeur.xls » calcule le temps de route vers différentes villes en recherchant les durées de voyage sur un tableau. Les temps de route entre deux villes sont décrits par une distribution de probabilités (le tableau en compte 200). La colonne A contient les numéros d’identification des villes. La colonne B contient les noms correspondant à ces numéros (par fonction de recherche). L’ordre dans lequel les villes (et leurs numéros) figurent de haut en bas représentent l’ordre dans lequel elles sont visitées. Par exemple, si on entre « 9 » dans la cellule A3, Ottawa est la première ville visitée. « 6 » (Halifax) dans la cellule A4 désigne Halifax comme deuxième ville.

Les temps de route entre les villes sont représentés par des distributions de probabilités à partir de C25. Ces distributions font référence au tableau des distances de route réelles entre les villes, présenté à partir de la cellule C48. Les distances indiquées dans le tableau sont symétriques (la distance de A à B est identique à celle de B à A). Les modèles plus réalistes peuvent cependant inclure des distances non symétriques pour représenter la difficulté accrue du voyage dans l’une ou l’autre des directions (à cause des péages, moyens de transport disponibles, direction des vents, relief, etc.)

Une fonction doit maintenant être utilisée pour calculer la longueur du trajet entre ces villes. La longueur de route totale se stocke dans la cellule G2, qui représente la cellule à optimiser. On utilise ici la fonction « LongueurRoute ». Il s’agit d’une fonction VBA personnalisée dans Vendeur.xls.

Résolution

On minimise la valeur de la cellule G2 en ajustant les cellules A3:A22. On choisit la méthode « ordre » et on assure que les valeurs 1 à 20 figurent dans les cellules ajustables (A3:A22) avant de démarrer l’optimisation.

Sous la méthode de résolution « ordre », RISKOptimizer réorganise les variables choisies, en essayant différentes permutations des variables existantes.

Chapitre 4 : Applications types 87

Gestion du rendement

Fichier de l’exemple : But :

Méthode de résolution : Problèmes similaires :

rendementoaérien.xls Identifier le nombre maximum de réservations à

accepter dans différentes catégories tarifaires pour maximiser le bénéfice.

recette Tout problème de gestion de rendement où un

même produit est proposé à différents prix.

88 Gestion du rendement

Modèle

Le fichier « rendaérien.xls » représente un modèle tout simple d’application de RISKOptimizer à la gestion du rendement. Des distributions de probabilités sont affectées à une série de facteurs incertains du modèle, y compris la Demande de réservations plein

tarif (cellule C8), le % Passagers défaillants – Réservations tarif plein (cellule C7), le % Passagers défaillants – Réservations tarif réduit (cellule C11), la Demande de réservations à tarif réduit (cellule 12) et le Coût d’embarquement refusé (cellule C23). Le

bénéfice brut du vol est déterminé en calculant le revenu total des réservations dans chaque catégorie, moins le coût des embarquements refusés sur vol surréservé.

Résolution

Dans ce modèle, les variables à ajuster occupent les cellules C14 et C15. Ces cellules contiennent les valeurs du nombre maximum de réservations acceptées et le pourcentage des réservations qui seront affectées aux places plein tarif. « Le bénéfice doit toujours être >0 » est une contrainte d’itération et « L’écart type des résultats de simulation du bénéfice doit être <400 », une contrainte de simulation. L’objectif est de maximiser la moyenne de la distribution simulée pour le bénéfice tout en minimisant le risque comme spécifié par les contraintes définies.

Chapitre 4 : Applications types 89

Chapitre 5 : Guide de référence RISKOptimizer

Commande Définition du modèle...................................................92

Plages de cellules ajustables............................................................... 97

Groupes de cellules ajustables ........................................................... 99

Méthode de résolution « recette »....................................... 101

Méthode de résolution « ordre »......................................... 102

Méthode de résolution « groupement »............................. 102

Méthode de résolution budget............................................ 104

Méthode de résolution « projet »........................................ 104

Méthode de résolution « programme ».............................. 106

Taux de croisement et de mutation ................................... 108

Nombre de blocs temps et cellules sous contrainte ........ 110

Tâches précédentes................................................................ 110

Opérateurs............................................................................... 110

Contraintes ........................................................................................... 113

Ajouter – Ajout de contraintes........................................... 113

Type de contrainte................................................................. 114

Contraintes de simulation.................................................... 115

Format de contrainte Simple ou Formule.......................... 115

Contraintes souples............................................................... 116

Commande Paramètres d’optimisation – Onglet Général .........119

Commande Paramètres d’optimisation – Onglet Temps

d’exécution.................................................................................. 123

Optimisation........................................................................... 124

Simulation............................................................................... 125

Commande Paramètres d’optimisation – Onglet Affichage......127

Commande Paramètres d’optimisation – Onglet Macros.......... 129

Commande Démarrer l'optimisation ............................................132

90 Gestion du rendement

Commandes Utilitaires...................................................................134

Commande Paramètres d’application ..............................................134

Commande Solveur de contraintes...................................................135

Suivi RISKOptimizer.......................................................................138

Suivi RISKOptimizer – Onglet Progression...................................139

Options graphiques................................................................140

Suivi RISKOptimizer – Onglet Synthèse........................................141

Suivi RISKOptimizer – Onglet Journal...........................................142

Suivi RISKOptimizer – Onglet Population ....................................144

Suivi RISKOptimizer – Onglet Diversité........................................145

Suivi RISKOptimizer – Onglet Options d’arrêt.............................146

Chapitre 5 : Guide de référence RISKOptimizer 91

Commande Définition du modèle

Définit le but, les cellules ajustables et les contraintes d’un modèle.

La commande Définition du modèle de RISKOptimizer (ou l’icône Modèle de la barre d’outils de RISKOptimizer) ouvre la boîte de dialogue Modèle.

La boîte de dialogue RISKOptimizer – Modèle sert à spécifier ou décrire un problème d’optimisation à RISKOptimizer. Vide à chaque ouverture de nouveau classeur Excel, cette boîte de dialogue enregistre cependant son information avec chaque classeur. À la réouverture de la feuille de calcul, elle se remplit donc de la même manière. Chaque composant de cette boîte de dialogue est décrit dans cette section.

Chapitre 5 : Guide de référence RISKOptimizer 92

Boîte de dialogue RISKOptimizer – Modèle

Options de la boîte de dialogue Modèle :

• But d’optimisation. L’option But d’optimisation détermine le type

de réponse que RISKOptimizer devra rechercher. Minimum configure la recherche de valeurs variables qui produisent la plus petite valeur possible pour la statistique sélectionnée des résultats de simulation de la cellule cible (jusqu’à –1e300). Maximum configure la recherche de valeurs variables qui produisent la plus grande valeur possible pour la statistique sélectionnée des résultats (jusqu’à +1e300).

Valeur cible configure la recherche de valeurs variables qui produisent pour la statistique sélectionnée une valeur aussi proche que possible de la valeur spécifiée. L’optimisation s’arrête automatiquement lorsque RISKOptimizer trouve une solution qui produit le résultat désiré. Par exemple, si vous configurez la recherche de la moyenne de la distribution de résultats de simulation la plus proche de 14, RISKOptimizer trouvera peutêtre des scénarios produisant une moyenne de 13,7 ou 14,5. Remarquez que 13,7 est plus proche de 14 que 14,5. Peu importe que la valeur de la statistique soit supérieure ou inférieure à celle que vous spécifiez : RISKOptimizer considère strictement la proximité de la valeur.

• Cellule. La cellule ou cellule cible contient la sortie du modèle.

Une distribution de valeurs possibles pour cette cellule cible sera générée (par simulation) pour chaque « solution itérative » produite par RISKOptimizer (c.-à-d. chaque combinaison de valeurs possibles de cellules ajustables). La cellule cible doit contenir une formule qui dépend (directement ou à travers une série de calculs) des cellules ajustables. Cette formule peut faire appel aux formules Excel standard telles que SOMME() ou aux macro-fonctions VBA définies par l’utilisateur. Ces dernières permettent l’évaluation par RISKOptimizer de modèles extrêmement complexes.

Pendant la recherche, RISKOptimizer se réfère à la statistique des résultats de simulation de la cellule cible comme cote ou « fonction de pertinence » pour évaluer la qualité de chaque scénario possible et déterminer les valeurs variables dont il convient de poursuivre le croisement et celles destinées à « mourir ». Dans l’évolution biologique, la mort est la « fonction de pertinence » qui détermine les gènes appelés à survivre et prospérer dans la population. Lors de l’élaboration d’un modèle, la cellule cible doit refléter la pertinence ou la « qualité » d’un

Chapitre 5 : Guide de référence RISKOptimizer 93

scénario donné, de sorte que RISKOptimizer puisse mesurer précisément le progrès de ses calculs.

94 Commande Définition du modèle

PALISADE RISKOPTIMIZER 5.5 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Introduction

Problèmes d’optimisation conventionnels

Optimisation de modèles incertains

Modéliser l’incertitude

Applications personnalisées et RISKOptimizer

Avant d’appeler

Installation

Suppression de RISKOptimizer

Fichier Lisezmoi de RISKOptimizer

RISKOptimizer:Di dacticiel

Qu’est-ce que RISKOptimizer ?

Algorithmes génétiques

Distributions de probabilités et simulation

Plus souple

Optimisation conventionnelle vs optimisation par simulation

Entrée des distributions de probabilités

Cellule cible et statistique

Contraintes

Exécution de l’optimisation

Introduction

Visite guidée

La barre d’outils RISKOptimizer

Ouverture d’un modèle type

Plage Min-Max de cellules ajustables

Méthode de résolution

Contraintes d’itération et de simulation

Simple plage de valeurs ou Formule

Conditions d’arrêt d’optimisation

Introduction

Allocation budgétaire

Planification de capacité

Planificateur de classes

Couverture sur contrats à terme

Résolution

Ordonnancement multigamme

Équilibrage de portefeuille

Composition de portefeuille

Risque de portefeuille

Problème de voyageur de commerce

Gestion du rendement

Commande Définition du modèle