Page 1

Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com 87
Application Notes
100
400
Percent Rated Watts
Percent Current
or Voltage
300
200
100
0
2000
Resistor Selection
R E S I S T O R F A C T S A N D F A C T O R S
A resistor is a device connected into an electrical circuit to
introduce a specified resistance. The resistance is measured in
ohms. As stated by Ohm’s Law, the current through the resistor
will be directly proportional to the voltage across it and inversely
proportional to the resistance.
The passage of current through the resistance produces heat.
The heat produces a rise in temperature of the resistor above
the ambient temperature. The physical ability of the resistor to
withstand, without deterioration, the temperature attained, limits
the operating temperature which can be permitted. Resistors are
rated to dissipate a given wattage without exceeding a specified
standard “hot spot” temperature and the physical size is made
large enough to accomplish this.
Deviations from the standard conditions (“Free Air Watt
Rating”) affect the temperature rise and therefore affect the wattage at which the resistor may be used in a specific application.
S E L E C T I O N R E Q U I R E S 3 S T E P S
Simple short-cut graphs and charts in this catalog permit rapid
determination of electrical parameters. Calculation of each
parameter is also explained. To select a resistor for a specific
application, the following steps are recommended:
1 . (a) Determine the Resistance.
(b) Determine the Watts to be dissipated by the Resistor.
2 . Determine the proper “Watt Size” (physical size) as controlled
by watts, volts, permissible temperatures, mounting conditions and
circuit conditions.
3 . Choose the most suitable kind of unit, including type, terminals
and mounting.
S T E P 1 D E T E R M I N E R E S I S T A N C E A N D W A T T S
Ohm’s Law
(a) R = V or I = V or V = IR
Ohm’s Law, shown in formula form above, enables determination of the resistance when the required voltage and current are
known. When the current and voltage are unknown, or the best
values not decided on, at least two of the three terms in Ohm’s
Law must be measured in a trial circuit.
(b) P = I2R or P = VI or P =
Power in watts, can be determined from the formulas above,
which stem from Ohm’s Law. R is measured in ohms, V in volts,
I in amperes and P in watts.
I R
2
V
R
Why Watts Must Be Accurately Known
Stated non-technically, any change in current or voltage produces a much larger change in the wattage (heat to be dissipated by the resistor). Therefore, the effect of apparently small
increases in current or voltage must be investigated because
the increase in wattage may be large enough to be significant.
Mathematically, the wattage varies as the square of the current, or voltage, as stated in the formulas (b). For example, an
increase of 20% in current or voltage will increase the wattage
44%. Figure 1 below graphically illustrates the square law relation. Hence, the actual current must be used in figuring the wattage and the increase in wattage due to apparently small changes, then determined in order to select the proper size resistor.
Allowance should be made for maximum possible line voltage.
Subscribe to our
New Product Bulletin at
ohmite.com
Fig. 1: Rapid increase of wattage with current or voltage.
86 Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com
Page 2
S T E P 2 P O W E R R A T I N G O R P H Y S I C A L S I Z E O F R E S I S T O R
100
400
Temperature Rise above Ambient Temperature
Resistor Load — Percent Rated Watts
300
200
100
0
0 20 40 60 80 9
010 30 50 70
350
250
150
50
700
600
500
400
300
200
100
0
°F
°C
A
375°C 675°F
B 325°C 585°F
C 300°C 540°F
D 250°C 450°F
Bare Resistor—
NEMA;
Corrib & Powr-rib
U.L.-NEMA Std.
for Resistors
Ind. & Comm. Std.
Mil-R-26: Char. V
EIA: E, H & V
Mil-R-26: Char. U
EIA: Char. G
350
100
Percent Rated Watts
Ambient Temperature, °C
60
20
0
0 100 200 30050 150 250
80
40
U.L.-NEMA Std.
for Resistors
Ind. & Comm. Std.
Mil-R-26: Char. V.
EIA: Char. E, H & V
Mil-R-26: Char. U
EIA: Char. G
25°40°
275° 340°
A resistor operated at a constant wattage will attain a steady temperature which is determined largely by the ratio between the size (surface
area) and the wattage dissipated, The temperature stabilizes when the
sum of the heat loss rates (by radiation, convection and conduction)
equals the heat input rate (proportional to wattage). The greater the
resistor area per watt to be dissipated, the greater the heat loss rate
and therefore the lower the temperature rise. The relation between the
losses varies for different resistors.
Free Air Watt Rating
The wattage rating of resistors, as established under specified standard conditions, is defined as the “Free Air Rating” (“Full Rating” or
“Maximum Power Rating”). Several standard methods of rating are
in use based on different service conditions. The method of both
the “National Electrical Manufacturers Association” (NEMA) and the
“Underwriters’ Laboratories, Inc.” (UL) can be described as follows:
The relation of the “Free Air Watt Rating” of tubular type, vitreous enameled resistors to the physical size, is to be set at such a
figure that when operated at their rated watts, the temperature rise
of the hottest spot shall not exceed 300°C (540°F) as measured by a
thermocouple when the temperature of the surrounding air does not
exceed 40°C (104°F). The temperature is to be measured at the hottest point of a two-terminal resistor suspended in free still air space
with at least one foot of clearance to the nearest object, and with
unrestricted circulation of air.
A slightly different definition of temperature limit used as a basis
for wattage rating, and which results in a slightly higher attained temperature, was originally established in military specification MIL-R-26
for wirewound resistors.
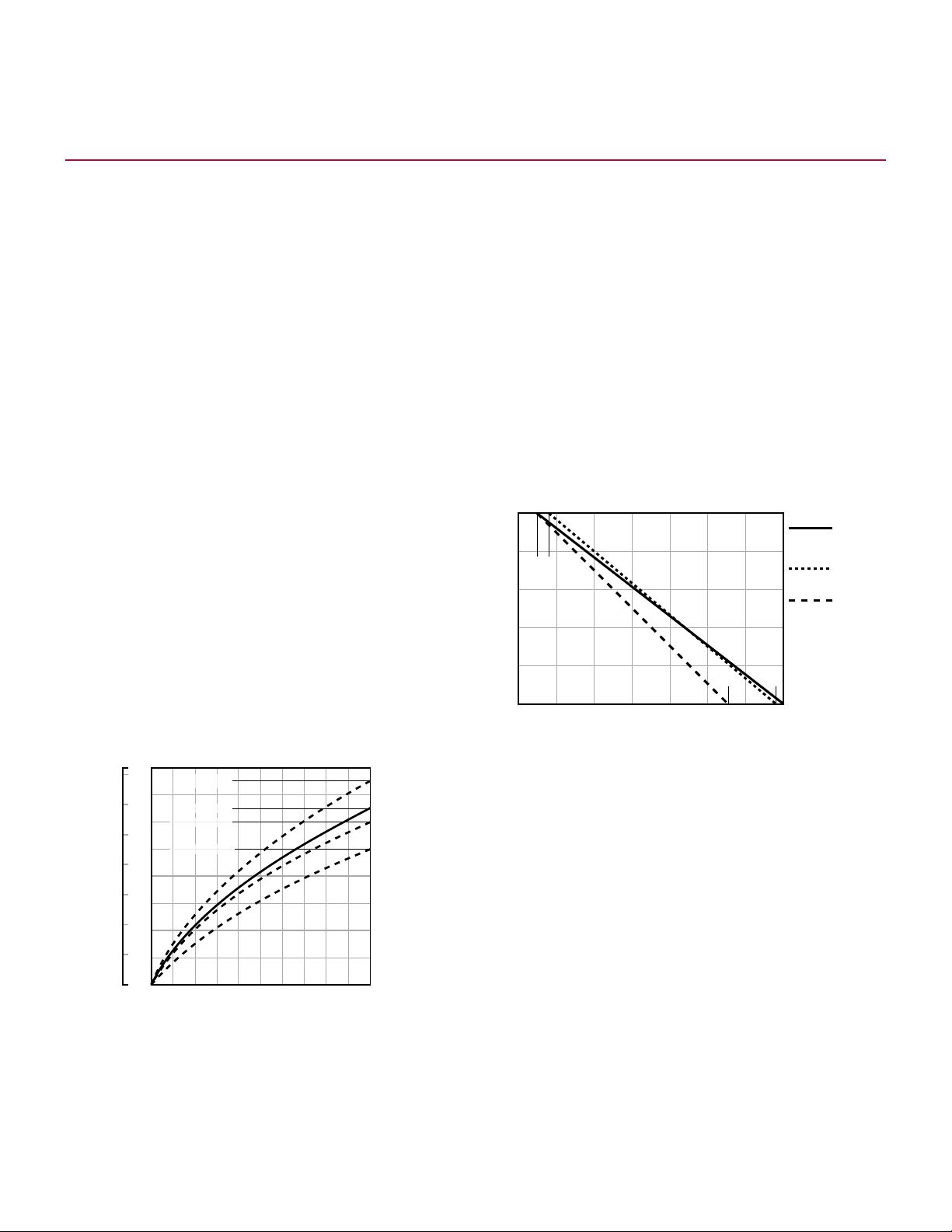
Characteristic V resistors are required to dissipate rated wattage in
an ambient of 25°C without exceeding a maximum operating temperature of 350°C at the hottest spot. This corresponds to a temperature
rise of 325°C in a 25°C ambient. Although MIL-R-26 permits a 25°C
greater temperature rise than NEMA or UL, the reference ambient for
the latter two is 15°C higher. Consequently, the difference in attained
temperature between the two systems is only 10°C. The curves in Fig.
2 show the relation between temperature rise and wattage for various
specifications. Note the differences in the permissible rise for each
specification.
Fig. 2: Approximate hot spot temperature rise of a resistor in free air for various specifications.
The absolute temperature rise for a specific resistor is roughly
related to the area of its radiating surface. It is also dependent upon a
number of other factors, however, such as thermal conductivity of the
core and coating materials, emissivity factor of the outer surfaces, ratio
of length to diameter, heat-sink effect of mountings, and other minor
factors.
The maximum permissible operating temperature for a given resistor is basically determined by the temperature limitations imposed by
Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com 87
Application Notes
Resistor Selection
the materials used in its construction. Generally speaking, these limits
cannot be sharply defined in terms of temperature alone. Other factors
such as resistance stability versus time, deterioration rates of insulation and moisture-resistance characteristics, type and size of resistance wire, all enter into consideration of “acceptable service life.”
For these reasons, the precise temperature limits corresponding to
100% rated wattage are somewhat arbitrary and serve primarily as
design targets. In the last analysis, once a wattage rating has been
assigned on the basis of an empirical hot spot limit, the verification of
its correctness must be established through long term load-life tests
based on performance and stability standards rather than the measurement of hot spot temperature. Maximum limits are stipulated for
parameter changes as a result of various tests, including a 2000 hour
load-life test.
It is also assumed that the temperature rise at a given wattage
is independent of the ambient temperature in which this wattage is
being dissipated. Therefore, for high ambient temperatures, the operating wattage should be limited in accordance with the curves of Fig.
3. Although the assumption that temperature rise is independent of
ambient is not exactly true, the approximation is sufficiently close for
all practical purposes and, therefore, has been adopted for derating
purposes.
Fig. 3: Derating for ambient temperature.
Despite the above variables, figures may be cited in terms of
“watts dissipated per square inch of winding surface” for a given temperature rise. For power type resistors operating at 300°C rise above
ambient, this figure varies between approximately 6.3 watts per
square inch for large resistors (175 watt) to about 9 watts per square
inch for smaller resistors (12 watt). It should also be observed from
Fig. 2 that temperature rise is not directly proportional to wattage dissipated. Note, for example, that at 50% rated wattage, the temperature
rise still remains about 70% of that at full rating.
The wattage ratings used in this catalog, unless otherwise stated for
certain types, are on the basis of a nominal operating temperature of
350°C at full rating. There are two general categories of power resistors for which the 350°C nominal temperature limit does not apply. One
is that class of power-precision resistors where high stability is a salient
feature, in which case the operating temperature is nominally limited to
275°C. The other category includes all exposed ribbon wire resistors
(see description of Corrib® and Powr-Rib®) which are rated for 375°C
(675°F) maximum temperature rise when measured on the wire per
NEMA standards.
Temperature Distribution on a Resistor
The temperature rise varies (following a curve) along the length
of the resistor with the hot spot at the center-top (of a horizontal
tube) and the ends at approximately 60% of the maximum temperature rise. The terminals themselves are still cooler. When the resistor
is vertical, the hot spot shifts upwards a little and the top end is hotter than the bottom. The standard “Free Air Watt Rating,” however, is
used regardless of position.
Page 3

Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com 89
Application Notes
Resistor Selection
S T E P S 3 S E L E C T A R E S I S T O R
Choose the most suitable resistor meeting the requirements of
the application. Standard resistors carried in stock should be
considered first. If a suitable resistor cannot be found in the
standard sizes or resistance values, then select a non-standard
resistor from the range on available sizes (consult factory).
A P P L I C A T I O N W A T T R A T I N G
To allow for the differences between the actual service conditions and the “Free Air Watt Rating” it is a general engineering
practice to operate resistors at more or less than the nominal
rating. The details by which such ratings can be estimated are
given in the following pages. Most thermal calculations, however,
involve so many factors which are usually not accurately known,
that at best they are only approximations.
The most accurate method of determining or checking the
rating is to measure the temperature rise in a trial installation. A
thermocouple (made of #30 B & S gage wire) is recommended
for the measuring element. Even measurements made with a
thermocouple will vary slightly with different samples and techniques. The factors which affect the temperature rise act independently of each other and are summarized as follows:
1. Ambient Temperature
As the maximum permissible operating temperature is a set
amount, any increase in the ambient temperature subtracts from
the permissible temperature rise and therefore reduces the permissible watt load.
2. Enclosure
Enclosure limits the removal of heat by convection currents in
the air and by radiation. The walls of the enclosure also introduce a thermal barrier between the air contacting the resistor
and the outside cooling air. Hence, size, shape, orientation,
amount of ventilating openings, wall thickness, material and finish all affect the temperature rise of the enclosed resistor.
3. Grouping
When resistors are close to each other they will show an
increased hot spot temperature rise for a given wattage
because of the heat received by radiation from each other and
the increased heat per unit volume of air available for convection cooling.
5. Pulse Operation
This is not an environmental condition but a circuit condition.
As a pulse of power, when averaged over the total on and off
time, results in less heat per unit time than for continuous duty,
the temperature rise is affected. This may permit higher power
during the pulses. The conditions must be expertly considered
for conservative rating. The open-wound “Powr-Rib®” resistor
construction is most suitable.
6. Cooling Air
Forced circulation of air over a resistor removes more heat per
unit time than natural convection does and therefore permits an
increased watt dissipation. Liquid cooling and special conduction mountings also can increase the rating.
7. Limited Temperature Rise
It is sometimes desirable to operate a resistor at a fraction of
the Free Air Watt Rating in order to keep the temperature rise
low. This may be to protect adjacent heat sensitive apparatus,
to hold the resistance value very precisely both with changing
load and over long periods of time and to insure maximum life.
8. Other Considerations
High Resistance. High resistance units, which require the use of
very small diameter wire, generally should operate at reduced
temperature for maximum reliability.
High Voltage
A maximum voltage gradient of 500 volts R.M.S. (705 volts
peak) per inch of winding length is recommended under normal conditions. For higher gradients in pulse applications or for
other special conditions such as oil immersion, consult factory.
High Frequency
Non-inductively wound resistors are generally required for use
at high frequencies.
4. Altitude
The amount of heat which air will absorb varies with the density, and therefore with the altitude above sea level. At altitudes
above 100,000 feet, the air is so rare that the resistor loses heat
practically only by radiation.
Military and Other Specifications
The special physical operating and test requirements of the
applicable industrial or military specification must be considered.
Military specification resistors should be ordered by their MIL
numbers.
Our friendly Customer
Service team can be
reached at 866-9-OHMITE
88 Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com
Page 4

Application Notes
7
100
Percent of Single Unit Wattage Rating
Number of Resistors in Group
60
20
0
2 4 61 3 5
80
40
2" (50.8 mm) space
8 9
10 11 12
1" (25.4 mm) space
0.5" (12.7 mm) space
100
300
Percent Rated Load
100
0
0 25 7550
200
Temperature Rise
540
500
400
300
200
100
0
°F
°C
Resistor in
Small Box
Resistor in
Large Box
Box Temp., Small
Box Temp., Large
Resistor
in Free Air
Resistor: 100 watt, 0.75 x 6.5"
(19.05 x 165.10 mm)
In unpainted 0.032"
(0.813 mm)
thick
upainted sheet steel box, no vents
Small box: 3.375 x 3.375 x 8"
(85.725 x 85.725 x 203.20 mm)
Large box: 5.813 x 5.813 x 12.75"
(147.65 x 147.65 x 323.85 mm)
70
100
Percent Rated Watts
Altitude in Thousands of Feet
60
20
0
0 20 40 6
010 30 50
80
40
5000
ft.
1009080
350
100
Percent Rated Watts
Ambient Temperature, °C
60
20
0
0 100 200 30050 150 250
80
40
U.L.-NEMA Std.
for Resistors
Ind. & Comm. Std.
Mil-R-26: Char. V.
EIA: Char. E, H & V
Mil-R-26: Char. U
EIA: Char. G
25°40°
275° 340°
Resistor Selection
E N V I R O N M E N T A L F A C T O R S — E F F E C T O N T H E P O W E R R A T I N G O F C O M P O N E N T S
All the components of an electrical apparatus — resistors, rheostats, capacitors, transformers, chokes, wiring, terminal boards,
rectifiers, transistors, electronic tubes, etc.—have their own
limitations as to the maximum temperature at which they can
reliably operate. The attained temperature in service is the sum
of the ambient temperature plus the temperature rise due to the
heat dissipated in the apparatus.
The temperature rise of a component is affected by a number
of factors. The graphs and discussions which follow, amplify and
supplement the factors on the previous page.
Note that the Multiplying Factors given on the Short Cut
Chart, on page 96 are the reciprocals of the “Percent Load
Ratings” shown on the graphs in this section. The percent figures are, of course, expressed as decimals before finding the
reciprocals.
Ambient Temperature Derating
Fig. 4 shows the percent of full load which power resistors can
dissipate for various high ambient temperatures.
Fig.5: Example of Effect of Size of Enclosure on Temperature
Rise of An Enclosed Resistor.
Fig. 4: Derating of Resistors for High Ambient Temperatures.
Derating Due to Enclosure
The amount of derating required, if any, because of enclosure
is affected by a number of factors, most of which are hard to
determine accurately. The watts per square inch of surface, size,
shape, orientation, wall thickness, material, finish and amount
and location of ventilating openings all play a part. Fig. 5 serves
to indicate for a particular set of conditions how the temperatures
varied with the size of enclosure for a moderate size power
resistor.
Derating Due to Grouping
The temperature rise of a component is affected by the nearby
presence of other heat-producing units, such as resistors, electronic tubes, etc. The curves in Fig. 6 show the power rating for
groups of resistors with various spacings between the closest
points of the resistors, assuming operation at maximum permissible hot spot temperature. If resistors are to be operated at
lower hot spot temperatures, the amount of derating for grouping
can be reduced.
Derating for Altitude
The curve in Fig. 7 shows the proportional watts for various altitudes, assuming standard atmospheric conditions.
Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com 89
Fig.6: Derating of Resistors to Allow for Grouping
Fig. 7: Derating for Altitude
Page 5

Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com 91
Application Notes
1000
Percent of Continuous-duty Wattage Rating
NEMA Duty Cycles
400
600
100
10 15 155 15 15
1200
800
Powr-rib
(low resistance)
0 20 4
010 30 5015 355 25 45
200
1400
100
150
175
200
225
250
275
300
325
350
125
375
70 45 1575 75 30
0.125 x 8.5" Corrib
(28.575 x 215.90 mm)
Powr-rib
(high resistance)
seconds on:
seconds off:
Percent of Continuous-duty Current Rating
Duty Cycle in Percent
700
Percent of Continuous-duty Wattage Rating
“On” Time in Seconds to Reach Rated Temperature
400
500
100
10 30 2005 20 100
800
600
200 watt vitreous enamel
1500 watt Corrib 0.125"
(3.175 mm),
ribbon
Low-resistance Powr-rib, edgewound
300 watt Corrib 0.125"
(3.175 mm),
ribbon
10 & 50 watt vitreous enamel
High-resistance Powr-rib, roundwire
0.1 0.5
40.3 2 100.4 30.2 1 5
200
1000
“On” Time in Minutes to Reach Rated Temperature
20 30
50 300 500 1000 2000
300
000
Resistor Selection
Pulse Operation
Unlike the environmental factors, which result in reduction of
the watt rating, pulse operation may permit higher power in the
pulses than the continuous duty rating.
The NEMA has set up certain standard duty cycles for motor
control resistors and the resistor ratings for some of these conditions are shown in Fig. 8.
The curves in Figures 10,11,12 and 13 illustrate the more
general case of various combinations of on and off time for
specified loads up to 1000% for a continuous series of pulses.
Intermediate loads can be approximated by interpolation. The
“on-time” at which each curve flattens out also indicates the
maximum on-time for single pulses (with enough off-time for
cooling to ambient). Additional data on single pulses is given by
Fig. 9. Resistors will reach about 75% of the rated maximum
temperature rise in approximately 5 to 8 pulses and level off at
maximum rise in another 10 to 20 cycles, depending on percent
load, size, type, etc. Any curve passing above the intersection of
the designated on and off-times indicates a percent load which
can be used. A resistor operated at the rating of an interpolated
curve through the point of intersection would operate at maximum rated temperature rise.
The exact temperature rise, of course, varies with each resistor, depending on size, ohms winding, etc. The curves shown
indicate the approximate rise for typical units only, as a band or
range of values actually exists for each percent load.
Ratings at over 1000% are not recommended except for
Powr-Rib® resistors. Curves for intermediate size resistors can
be roughly estimated by comparison with the sizes given.
Ratings for single pulses in the milli-second range (and up to
1 to 2 seconds) require individual calculation. This is because
the ratings vary greatly with the resistance, or more specifically
with the actual weight and specific heat of the resistance alloy
used. Calculation is based on the assumption that all of the
heat generated in the pulse goes to raise the temperature of the
resistance wire.
Fig. 9: Time Required for Typical Resistors to Reach Rated
Operating Temperatures at Various Watt Loads.
Fig. 8: Percent of Continuous Duty Rating for Resistors for
Typical NEMA Duty Cycles.
90 Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com
Our friendly Customer
Service team can be
reached at 866-9-OHMITE
Page 6

Application Notes
10
“On” Time in Seconds
“Off” Time in Seconds
4
5
1
31 10
7
2
3
2 4
5
7
30 100
20 405070
300 1K
200 400
500
700
3K 10K
2K 4K5K7K
100
40
50
70
20
30
100
40
50
70
20
30
125%
Small Vitreous Enamel Resistors
10 watt
50 watt
150%
200%
500%
1000%
10
“On” Time in Seconds
“Off” Time in Seconds
4
5
1
31 10
7
2
3
2 4
5
7
30 100
20 405070
300 1K
200 400
500
700
3K 10K
2K 4K5K7K
100
40
50
70
20
30
100
40
50
70
20
30
125%
Large Vitreous Enamel Resistors
160 watt shown
150%
200%
500%
1000%
500
400
Percent Rated Watts
Air Velocity, ft./min.
300
200
100
10000 1500
350
250
150
10
“On” Time in Seconds
“Off” Time in Seconds
4
5
1
31 10
7
2
3
2 4
5
7
30 100
20 405070
300 1K
200 400
500
700
3K 10K
2K 4K5K7K
100
40
50
70
20
30
100
40
50
70
20
30
Corrib Resistors
300 watt
1500 watt
200%
500%
1000%
round wire
edgewound
10
“On” Time in Seconds
“Off” Time in Seconds
4
5
1
31 10
7
2
3
2 4
5
7
30 100
20 405070
300 1K
200 400
500
700
3K 10K
2K 4K5K7K
100
40
50
70
20
30
100
40
50
70
20
30
Powr-ribs
round wire
edgewound
200%
500%
1000%
300%
800%
200%
500%
1000%
300%
800%
P U L S E O P E R A T I O N — C O O L I N G — L I M I T E D T E M P E R A T U R E S
Resistor Selection
Fig. 10: 10 Percent of Continuous Duty Rating for Pulse Operation of small to
Medium Size Vitreous Enameled Resistors.
Fig. 11: Percent of Continuous Duty Rating for Pulse Operation of Large Vitreous
Enameled Resistors.
Cooling Air
Resistors can be operated at higher than rated wattage when
cooled by forced circulation of air. A typical curve is illustrated in
Fig 14. The curve tends to level off at higher velocities as excessive hot spots develop where the air flow does not reach all
parts uniformly.
Limited Temperature Rise
When it is desired to operate a resistor at less than maximum
temperature rise, the percent watts for a given rise can be read
from “Temperature Rise vs. Resistor Load” Fig 2 graph on page
91.
Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com 91
Fig.12: Percent of Continuous Duty Rating for Pulse Operation of CORRIB®,
Corrugated Ribbon Resistors.
Fig. 13: Percent of Continuous Duty Rating for Pulse Operation of Powr-Rib®,
Bare Resistors
Fig. 14: Percent of Free Air Rating for Typical Resistor Cooled by Forced Air
Circulation.
Page 7

Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com 93
Application Notes
watts to be
dissipated
factor factor factor factor factor factor factor
Temperature at
installation includes
room temperature
plus temperature
rise due to adjacent
heat sources.
Factors apply
approximately for
average sheet
metal boxes of
dimensions such
that watts per sq.
in. of surface are in
the range of 0.2 to
0.4.
Factors apply to
uniformly spaced
banks of parallel
resistors with
spacing as shown.
Factors apply to
altitudes show. No
derating is required
for altitudes to
5000 ft. above sea
level.
Percent load for
pulse operation
must first be
determined from
graphs and data on
page xx.
Factors are
approximations
only. Effectiveness
of cooling varies
with installation.
Low temperatures
may be desired
because of
adjacent
apparatus,
increased stability
or maximum
reliability.
Record the
watts to be
dissipated as
set by your
circuit
conditions.
Standard
free air
conditions
°C F
1
% F
2
no. F
3
ft. F
4
% F5fpm F
6
°C F
7
300 6.6
3.2
2.7
2.2
1.9
1.6
1.4
1.3
1.2
1.1
1.0
4.1
5.0
200
100
50
25
100 2.0
1.8
1.7
1.6
1.5
1.4
1.3
1.2
1.1
1.0
1.990
80
70
None
60
50
40
30
20
10
3 1.4
1.6
1.5
1.4
1.5
1.3
1.4
1.3
1.2
1.0
1.32
12
8
1
4
12
4
12
8
4
1.32
1.48
1.22
1.12
2" space 1" space 0.5" space std. brackets
100
1.5
1.5
1.4
1.3
1.2
1.1
1.0
90
80
70
0
60
50
40
30
20
10
1.05
1000 0.10
0.50
900
800
700
600
500
400
300
200
100 1.0
0.11
0.12
0.13
0.14
0.15
0.16
0.17
0.18
0.19
0.20
0.25
0.30
0.35
0.40
0.60
0.75
thousands of feet
percent load
1500 0.27
900
800
700
600
500
400
300
200
Still 1.0
0.28
0.29
0.30
0.32
0.35
0.40
0.50
0.60
0.70
0.80
0.90
100
1400
1300
1200
1100
1000
air velocity: feet per minute
40
13.0
300
200
1.0
10.0
8.0
6.0
4.0
3.0
1.75
1.3
1.2
1.1
100
50
7.0
5.0
2.5
2.0
1.5
1.4
Ambient
Temperature Enclosure Grouping Altitude
Pulse
Operation Cooling Air
Limited
Temp. Rise
Application ConditionsWatts
Resistor Selection
S H O R T - C U T C H A R T M E T H O D T O F I N D R E Q U I R E D S I Z E (as affected by application conditions)
1. For each Condition, locate the relevant value on the scales below and
record the corresponding Factor (F1 to F7). Note: The Standard Free
Air Condition Factor is always 1.
2. Multiply the Factors together.
3. Multiply the Watts by the product obtained from 2 above.
Four resistors, each dissipating 115 watts, are to be
mounted in a group. Spacing is to be 2” surface to surface.
Ambient to be 50°C (122°F). Enclosure to be total. Other factors standard. Determine Watt Size required.
92 Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com
E X A M P L E
Operation (1) On Ambient Temperature scale locate 50°C. Note and
record F1 = 1.1 as shown. Locate and record the other factors.
F1 F2 F3 F4 F5 F6 F7
50° 100% 4@2” Standard Conditions
1.1 x 2.0 x 1.2 x 1 x 1 x 1 1
Operation (2) Multiply the factors together = 2.64
Operation (3) 115 Watts x 2.64 = 304 Watts Free Air Watt Size Rating
required for each resistor.
Page 8

T E M P E R A T U R E C O E F F I C I E N T O F R E S I S T A N C E
+5%
Calculated Change in Resistance
Temperature Rise, °C
+2%
+3%
0 +200-100 +100
+6%
+4%
-50 +200+25 +1000 +300
0
+8%
Te
mperature Attained, °C
+300
+1%
+7%
-1%
-3%
-2%
90 ohms
per C.M.F. wire
+380 PPM/°C
675 ohms
per C.M.F. wire
+140 PPM/°C
Range for
294 or 800 ohms
per C.M.F. wire
±20 PPM/°C
Ambient
Temp.
Application Notes
Resistor Selection
The resistance alloys used for all except the lowest ohmic values
show such little change with temperature that in most power
circuits the resistance is considered constant. Actually there may
be changes at full load of -4% to +8% of the initial resistance.
The change is attributed in most part to the “temperature coefficient of resistance” (TCR) which is the change in resistance
expressed as “parts per million per degree centigrade of temperature” (ppm/°C).
For special applications which require very constant resistance, it may be necessary to specify the maximum permissible
TCR for the range of temperature involved. This would limit the
choice of wire to only certain types of resistance alloys. The
commonly known low TCR alloys in the 800 ohms per circularmil-foot class consist largely of nickel and chromium alloyed with
small amounts of aluminum and either copper or iron. Other low
resistivity alloys, 294 ohms per circular-mil-foot, consist primarily
of nickel and copper with only traces of other metals.
Both of these wire classes are rated by the wire manufacturers
as having a TCR of 0±20ppm/°C. The expression “0±20ppm/°C”
implies that, although the nominal value of the TCR is zero, the
actual value may lie anywhere within the tolerance range of
–20ppm/°C to +20ppm/°C.
For other resistance wires such as the widely used nickelchromium-iron, for example, a nominal value of +140ppm/°C is
given. Actually, however, a tolerance of ±30ppm is applicable so
that the TCR may range between the limits of +110 to
+170ppm/°C.
Unfortunately, the TCR of a completed power resistor is generally somewhat different from that of the original wire. This is
because the TCR may be affected by such factors as heat treatment during processing, and materials and methods of construction. Without special controls and precautions, the TCR over the
range of 25°C to 300°C rise may increase to as much as
0±80ppm from the original 0±20ppm for certain types of wire
on vitreous enameled resistors. Theoretical changes in resistance with temperature are shown in Fig. 15.
The circuit designer should carefully consider the actual
needs of the circuit before specifying limits on the TCR of a
desired resistor. Wherever possible it is best to select a resistor
for a critical application so that it operates at a low temperature rise. This will also provide the maximum stability over a
long period. For low TCR (and other) applications, Ohmite can
provide resistors with an “Ohmicone” (silicone-ceramic) coating. “Ohmicone” is processed at much lower temperatures than
vitreous enamel and therefore makes control of TCR and tolerance easier. Data on the TCR and other properties of various
alloys is given on page 98.
Fig. 15: Calculated change in resistance with nominal TC assumed constant.
Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com 93
Our Tech Center is open 10am to
2pm CT Tuesdays and Thursdays,
just call 866-9-OHMITE
Page 9

Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com 95
Application Notes
Resistor Selection
R E S I S T A N C E A L L O Y S A N D U S E S
A number of different resistance alloys are used in winding resistors and rheostats as shown in Fig. 16. The general use for each
alloy is indicated by the column headed, “Resistance Range for
Which Used.” Whether a particular alloy can be used on a specific resistor can be estimated by dividing the given resistance
by the area of the given winding space and determining whether
the quotient falls within the limits given hereafter. The “high resistance” alloys cover the range from approximately 10 to 25,000
ohms per square inch of winding area, the “low to medium”
type from 5 to 400 ohms and the “very low resistance” alloys
from less than an ohm to 250 ohms. It should be noted that the
“Ohms per Square Inch” ranges overlap considerably, indicating
that in many instances a given resistor could use any of several
alloys. Both the upper and lower limits of the ranges are only
approximate and in general can be extended somewhat when
necessary.
The actual temperature coefficient of a complete resistor is
generally greater than the nominal for the wire alone. The approximate change in overall resistance at full load is shown in the table.
ASTM Ohms Mean Temp Temperature Resistance Average ResisAlloy Alloy Composition per Trade Coeff. of Res. Range for Range for tance Change
Class* (Approximate) CMF Names ppm/°C TCR °C Which Used at Full Load**
Nickel base, Evanohm
1a
non-magnetic
Ni 75%, Cr 20% Moleculoy um and up, for to ± 2%
1b
plus Al, Cu, Fe, etc.
Iron base, magnetic
2a
Fe 73%, Cr 22.5%,
Al 4.5% (plus Co
2b
in one alloy)
Chromel A
3a 650 Nichrome V + 80 ± 20
Nickel-Chromium Nikrothal B -65 to + 250 High and + 4 to + 5%
80% — 20% Protoloy A + 60 ± 20 medium
3b 675
Chromel C
Electroloy
4 Nickel-Chromium-Iron 675 Nichrome + 140 ± 30 -65 to + 200 High and + 5 to + 8%
60%—16%—24% Nikrothal 6 medium
Tophet C
Advance
5a
Copel
5b
Neutroloy
Low and low Under
6
7
Midohm
9
Cuprothal 90
*American Society for Testing Materials. Tentative Specification B267-68.
**For resistor with 300°C hot spot rise from 25°C ambient except 54°C rise for Manganin.
Copper-Nickel
55% — 45%
Manganin
13% Mn, 87% Cu
Copper-Nickel
77% — 23%
Copper-Nickel
90% — 10%
300 Cupron -65 to + 150 to medium for ± 1% to ± 2%
Cuprothal 294
290 Manganin 0 ± 15 + 15 to + 35 to medium for ± 1%
180 Alloy
180 Cuprothal 180 + 180 ± 30 -65 to + 150 Very low + 5% to + 8%
90 Alloy
90 95 Alloy + 450 ± 50 -65 to + 150 Very low + 5% to + 10%
800
Karma
800
Nikrothal L
Alloy 815-R
800
Kanthall Dr
Mesaloy
800
Tophet C
low TC near 25°C to ± 2%**
Other Alloys
In addition to the alloys tabulated which show small changes in
resistance with temperature, there are others which sometimes
have to be used for very low resistance units. These alloys have
higher temperature coefficients, which limit their use to applications where the change in resistance with load is not important.
An example is No. 60 alloy, which has a resistance of 60 ohms
per circular-mil-foot and a temperature coefficient of +700ppm/
°C.
Ballast Wire
There are other alloys which are selected especially for
their high temperature coefficient of resistance. These are used
for so-called “ballast” resistors where a large change in resistance is desired with a change in load. A typical ballast wire is
Nickel, which has 58 ohms/cmf and a temperature coefficient of
+4800ppm/°C. Others are “Hytemco” and “Balco” at 120 ohms/
CMF and a TC of +4500pp /°C.
0 ± 20 -65 to + 250
0 ± 10 -65 to + 150
0 ± 20
0 ± 10
0 ± 20
0 ± 40
-65 to + 200 Alternate Under ± 1%
Low and low Under
low temp. coeff.
0 to + 150 for Class 1
Very high, Medi Under ± 1%
low temp. coeff.
sometimes to ± 2%
Fig. 16: Table of Resistance Alloys Generally Used for Resistors and Rheostats.
94 Ohmite Mfg. Co. 1600 Golf Rd., Rolling Meadows, IL 60008 • 1-866-9-OHMITE • Int’l 1-847-258-0300 • Fax 1-847-574-7522 • www.ohmite.com • info@ohmite.com
 Loading...
Loading...