Page 1

GFLIB User's Guide
ARM® Cortex® M7F
Document Number: CM7FGFLIBUG
Rev. 4, 12/2020
Page 2

GFLIB User's Guide, Rev. 4, 12/2020
2 NXP Semiconductors
Page 3

Contents
Section number Title Page
Chapter 1
Library
1.1 Introduction.................................................................................................................................................................... 5
1.2 Library integration into project (MCUXpresso IDE) ....................................................................................................8
1.3 Library integration into project (Keil µVision) ............................................................................................................. 16
1.4 Library integration into project (IAR Embedded Workbench) ..................................................................................... 25
Chapter 2
Algorithms in detail
2.1 GFLIB_Sin..................................................................................................................................................................... 33
2.2 GFLIB_Cos.................................................................................................................................................................... 35
2.3 GFLIB_Tan.................................................................................................................................................................... 37
2.4 GFLIB_Asin...................................................................................................................................................................40
2.5 GFLIB_Acos.................................................................................................................................................................. 42
2.6 GFLIB_Atan...................................................................................................................................................................44
2.7 GFLIB_AtanYX.............................................................................................................................................................46
2.8 GFLIB_Sqrt....................................................................................................................................................................49
2.9 GFLIB_Limit..................................................................................................................................................................51
2.10 GFLIB_LowerLimit....................................................................................................................................................... 53
2.11 GFLIB_UpperLimit........................................................................................................................................................55
2.12 GFLIB_VectorLimit.......................................................................................................................................................56
2.13 GFLIB_VectorLimit1.....................................................................................................................................................60
2.14 GFLIB_Hyst...................................................................................................................................................................63
2.15 GFLIB_Lut1D................................................................................................................................................................ 65
2.16 GFLIB_LutPer1D...........................................................................................................................................................69
2.17 GFLIB_Ramp.................................................................................................................................................................73
2.18 GFLIB_DRamp.............................................................................................................................................................. 77
2.19 GFLIB_FlexRamp..........................................................................................................................................................83
2.20 GFLIB_DFlexRamp.......................................................................................................................................................88
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 3
Page 4

Section number Title Page
2.21 GFLIB_FlexSRamp........................................................................................................................................................95
2.22 GFLIB_Integrator...........................................................................................................................................................108
2.23 GFLIB_CtrlBetaIPpAW.................................................................................................................................................112
2.24 GFLIB_CtrlBetaIPDpAW..............................................................................................................................................119
2.25 GFLIB_CtrlPIpAW........................................................................................................................................................ 127
2.26 GFLIB_CtrlPIDpAW..................................................................................................................................................... 133
GFLIB User's Guide, Rev. 4, 12/2020
4 NXP Semiconductors
Page 5

Chapter 1
Library
1.1 Introduction
1.1.1 Overview
This user's guide describes the General Functions Library (GFLIB) for the family of
ARM Cortex M7F core-based microcontrollers. This library contains optimized
functions.
1.1.2
GFLIB supports several data types: (un)signed integer, fractional, and accumulator, and
floating point. The integer data types are useful for general-purpose computation; they
are familiar to the MPU and MCU programmers. The fractional data types enable
powerful numeric and digital-signal-processing algorithms to be implemented. The
accumulator data type is a combination of both; that means it has the integer and
fractional portions.The floating-point data types are capable of storing real numbers in
wide dynamic ranges. The type is represented by binary digits and an exponent. The
exponent allows scaling the numbers from extremely small to extremely big numbers.
Because the exponent takes part of the type, the overall resolution of the number is
reduced when compared to the fixed-point type of the same size.
The following list shows the integer types defined in the libraries:
• Unsigned 16-bit integer —<0 ; 65535> with the minimum resolution of 1
• Signed 16-bit integer —<-32768 ; 32767> with the minimum resolution of 1
• Unsigned 32-bit integer —<0 ; 4294967295> with the minimum resolution of 1
• Signed 32-bit integer —<-2147483648 ; 2147483647> with the minimum resolution
Data types
of 1
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 5
Page 6

Introduction
• Unsigned 64-bit integer —<0 ; 18446744073709551615> with the minimum
resolution of 1
• Signed 64-bit integer —<-9223372036854775808 ; 9223372036854775807> with
the minimum resolution of 1
The following list shows the fractional types defined in the libraries:
• Fixed-point 16-bit fractional —<-1 ; 1 - 2
• Fixed-point 32-bit fractional —<-1 ; 1 - 2
-15
> with the minimum resolution of 2
-31
> with the minimum resolution of 2
-15
-31
The following list shows the accumulator types defined in the libraries:
• Fixed-point 16-bit accumulator —<-256.0 ; 256.0 - 2-7> with the minimum
resolution of 2
• Fixed-point 32-bit accumulator —<-65536.0 ; 65536.0 - 2
resolution of 2
-7
-15
-15
> with the minimum
The following list shows the floating-point types defined in the libraries:
• Floating point 32-bit single precision —<-3.40282 · 1038 ; 3.40282 · 1038> with the
minimum resolution of 2
1.1.3
API definition
-23
GFLIB uses the types mentioned in the previous section. To enable simple usage of the
algorithms, their names use set prefixes and postfixes to distinguish the functions'
versions. See the following example:
f32Result = MLIB_Mac_F32lss(f32Accum, f16Mult1, f16Mult2);
where the function is compiled from four parts:
• MLIB—this is the library prefix
• Mac—the function name—Multiply-Accumulate
• F32—the function output type
• lss—the types of the function inputs; if all the inputs have the same type as the
output, the inputs are not marked
The input and output types are described in the following table:
Table 1-1. Input/output types
Type Output Input
frac16_t F16 s
Table continues on the next page...
GFLIB User's Guide, Rev. 4, 12/2020
6 NXP Semiconductors
Page 7

Chapter 1 Library
Table 1-1. Input/output types (continued)
Type Output Input
frac32_t F32 l
acc32_t A32 a
float_t FLT f
1.1.4 Supported compilers
GFLIB for the ARM Cortex M7F core is written in C language or assembly language
with C-callable interface depending on the specific function. The library is built and
tested using the following compilers:
• MCUXpresso IDE
• IAR Embedded Workbench
• Keil µVision
For the MCUXpresso IDE, the library is delivered in the gflib.a file.
For the Kinetis Design Studio, the library is delivered in the gflib.a file.
For the IAR Embedded Workbench, the library is delivered in the gflib.a file.
For the Keil µVision, the library is delivered in the gflib.lib file.
The interfaces to the algorithms included in this library are combined into a single public
interface include file, gflib.h. This is done to lower the number of files required to be
included in your application.
1.1.5
Library configuration
GFLIB for the ARM Cortex M7F core is written in C language or assembly language
with C-callable interface depending on the specific function. Some functions from this
library are inline type, which are compiled together with project using this library. The
optimization level for inline function is usually defined by the specific compiler setting. It
can cause an issue especially when high optimization level is set. Therefore the
optimization level for all inline assembly written functions is defined by compiler
pragmas using macros. The configuration header file RTCESL_cfg.h is located in:
specific library folder\MLIB\Include. The optimization level can be changed by
modifying the macro value for specific compiler. In case of any change the library
functionality is not guaranteed.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 7
Page 8

Library integration into project (MCUXpresso IDE)
Similarly as optimization level the High-speed functions execution suppport can be
enable by defined symbol RAM_OPTIM_LOW (RAM_OPTIM_MEDIUM or
RAM_OPTIM_HIGH) or disable by not defining any of these macrors. symbol
RTCESL_MMDVSQ_OFF in project setting described in the High-speed functions
execution suppport cheaper for specific compiler.
1.1.6 Special issues
1. The equations describing the algorithms are symbolic. If there is positive 1, the
number is the closest number to 1 that the resolution of the used fractional type
allows. If there are maximum or minimum values mentioned, check the range
allowed by the type of the particular function version.
2. The library functions that round the result (the API contains Rnd) round to nearest
(half up).
1.2
Library integration into project (MCUXpresso IDE)
This section provides a step-by-step guide on how to quickly and easily include GFLIB
into any MCUXpresso SDK example or demo application projects using MCUXpresso
IDE. This example uses the default installation path (C:\NXP\RTCESL
\CM7F_RTCESL_4.6_MCUX). If you have a different installation path, use that path
instead.
1.2.1
High-speed functions execution suppport
Some RT (or other) platforms contain high-speed functions execution support by
relocating all functions from the default Flash memory location to the RAM location for
much faster code access. The feature is important especially for devices with a slow Flash
interface. This section shows how to turn the RAM optimization feature support on and
off.
1. In the MCUXpresso SDK project name node or on the left-hand side, click Properties
or select Project > Properties from the menu. A project properties dialog appears.
2. Expand the C/C++ Build node and select Settings. See Figure 1-1.
3. On the right-hand side, under the MCU C Compiler node, click the Preprocessor
node. See Figure 1-1.
GFLIB User's Guide, Rev. 4, 12/2020
8 NXP Semiconductors
Page 9
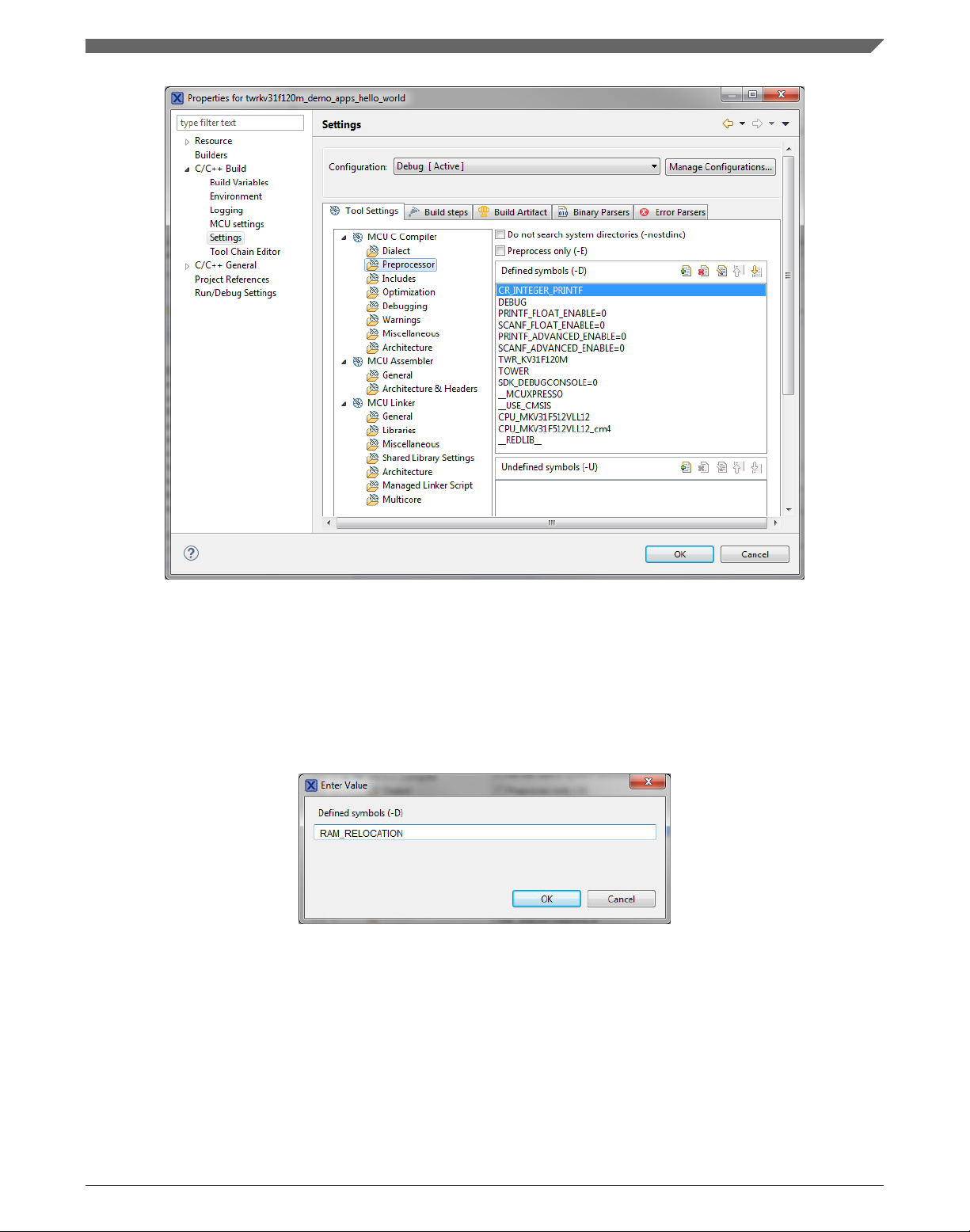
Chapter 1 Library
Figure 1-1. Defined symbols
4. On the right-hand side of the dialog, click the Add... icon located next to the Defined
symbols (-D) title.
5. In the dialog that appears (see Figure 1-2), type the following:
• RAM_RELOCATION — to turn the RAM optimization feature support on
If the define is defined, all RTCEL functions are put to the RAM.
Figure 1-2. Symbol definition
6. Click OK in the dialog.
7. Click OK in the main dialog.
The device reference manual shows how the__RAMFUNC(RAM) atribute works in connection
with your device.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 9
Page 10
Library integration into project (MCUXpresso IDE)
1.2.2 Library path variable
To make the library integration easier, create a variable that holds the information about
the library path.
1. Right-click the MCUXpresso SDK project name node in the left-hand part and click
Properties, or select Project > Properties from the menu. A project properties dialog
appears.
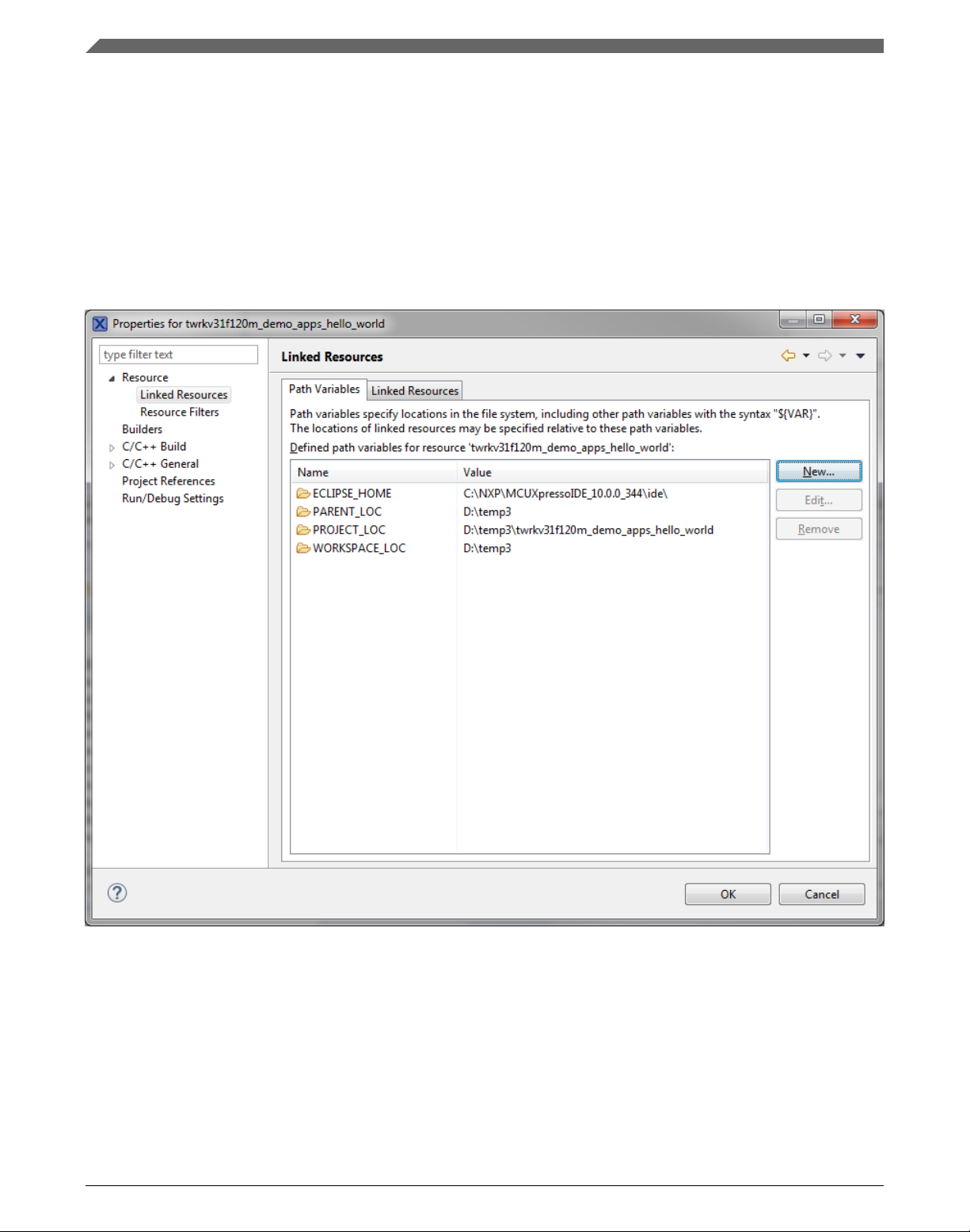
2. Expand the Resource node and click Linked Resources. See Figure 1-3.
Figure 1-3. Project properties
3. Click the New… button in the right-hand side.
4. In the dialog that appears (see Figure 1-4), type this variable name into the Name
box: RTCESL_LOC.
5. Select the library parent folder by clicking Folder…, or just type the following path
into the Location box: C:\NXP\RTCESL\CM7F_RTCESL_4.6_MCUX. Click OK.
GFLIB User's Guide, Rev. 4, 12/2020
10 NXP Semiconductors
Page 11
Chapter 1 Library
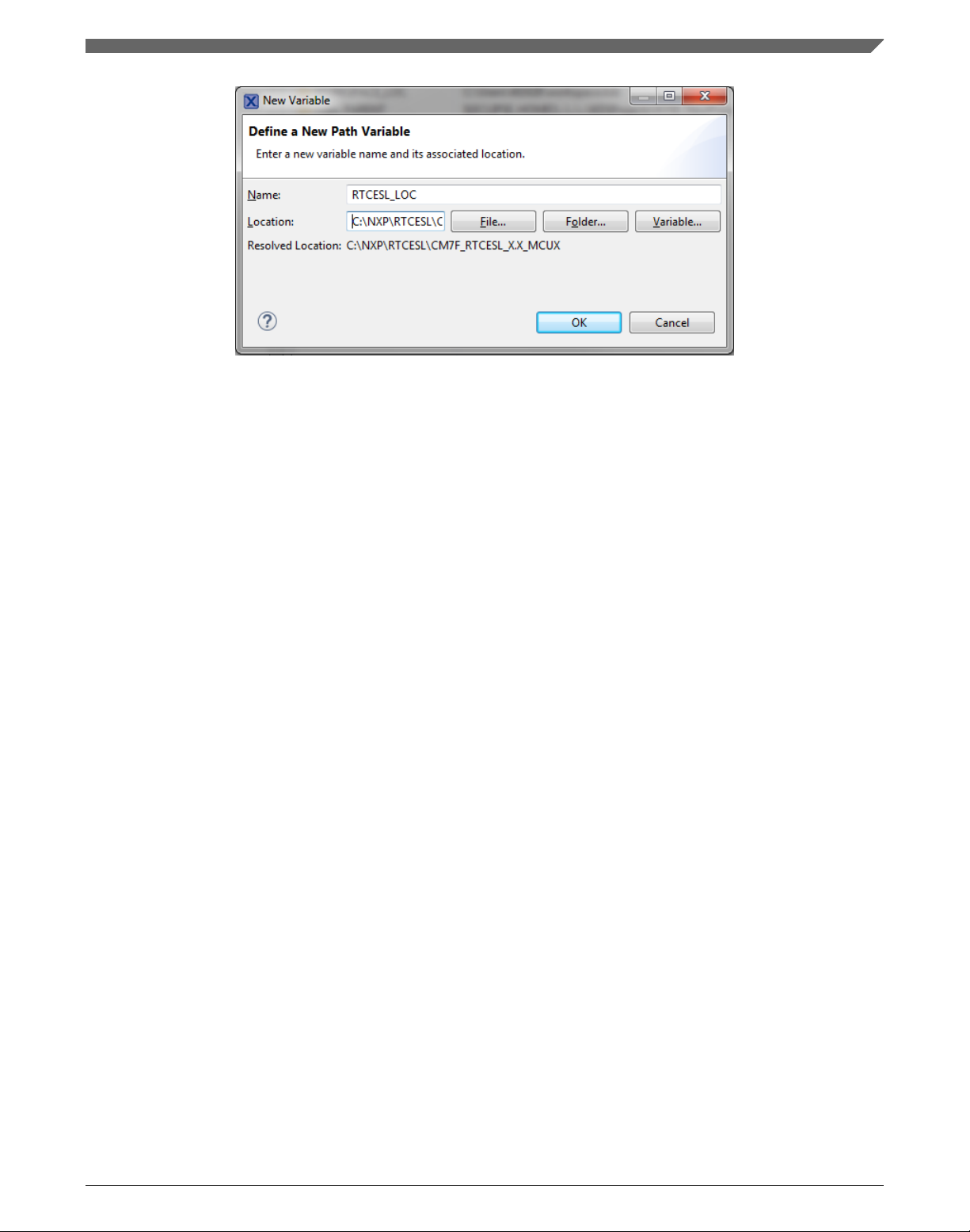
Figure 1-4. New variable
6. Create such variable for the environment. Expand the C/C++ Build node and click
Environment.
7. Click the Add… button in the right-hand side.
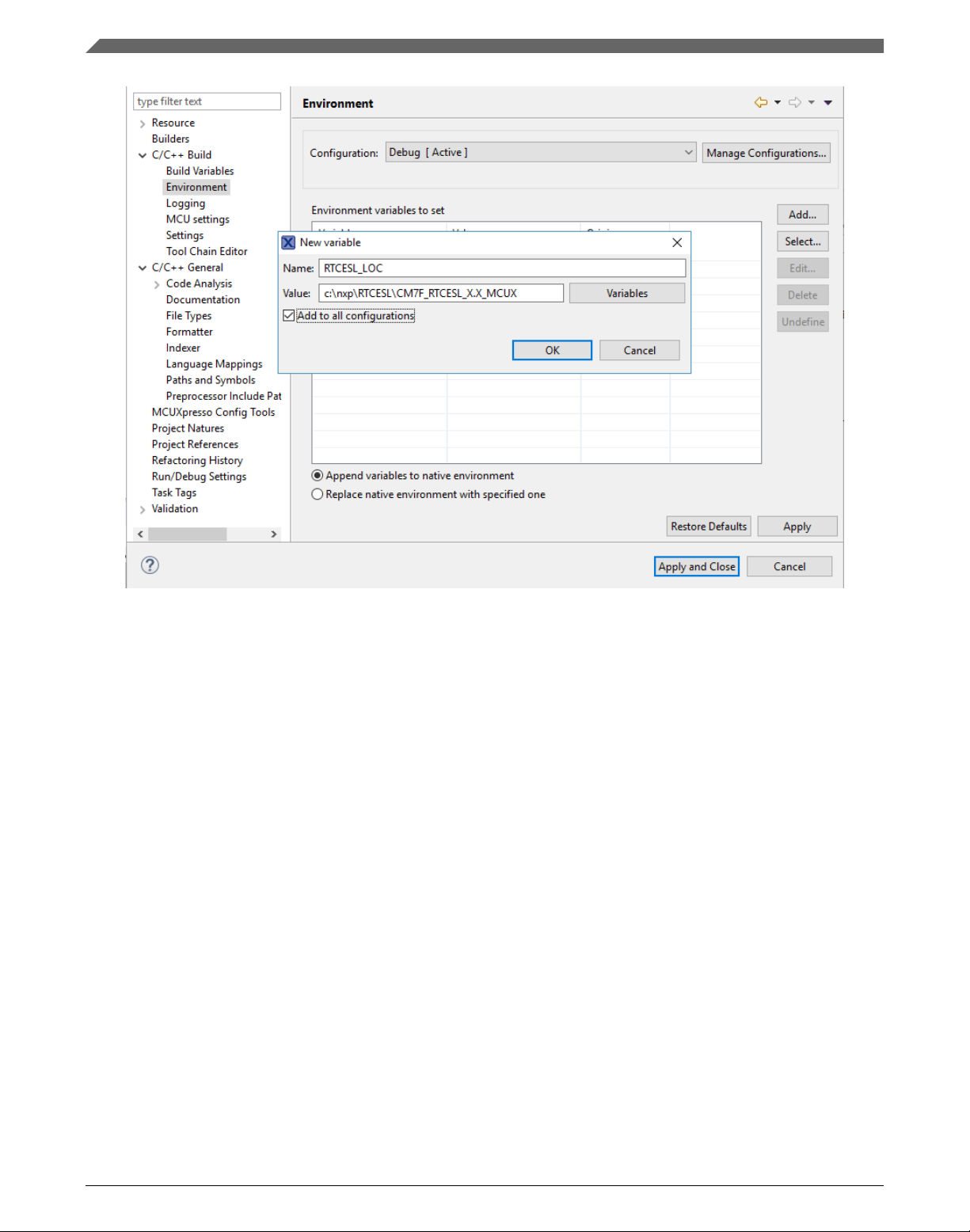
8. In the dialog that appears (see Figure 1-5), type this variable name into the Name
box: RTCESL_LOC.
9. Type the library parent folder path into the Value box: C:\NXP\RTCESL
\CM7F_RTCESL_4.6_MCUX.
10. Tick the Add to all configurations box to use this variable in all configurations. See
Figure 1-5.
11. Click OK.
12. In the previous dialog, click OK.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 11
Page 12
Library integration into project (MCUXpresso IDE)
Figure 1-5. Environment variable
1.2.3
Library folder addition
To use the library, add it into the Project tree dialog.
1. Right-click the MCUXpresso SDK project name node in the left-hand part and click
New > Folder, or select File > New > Folder from the menu. A dialog appears.
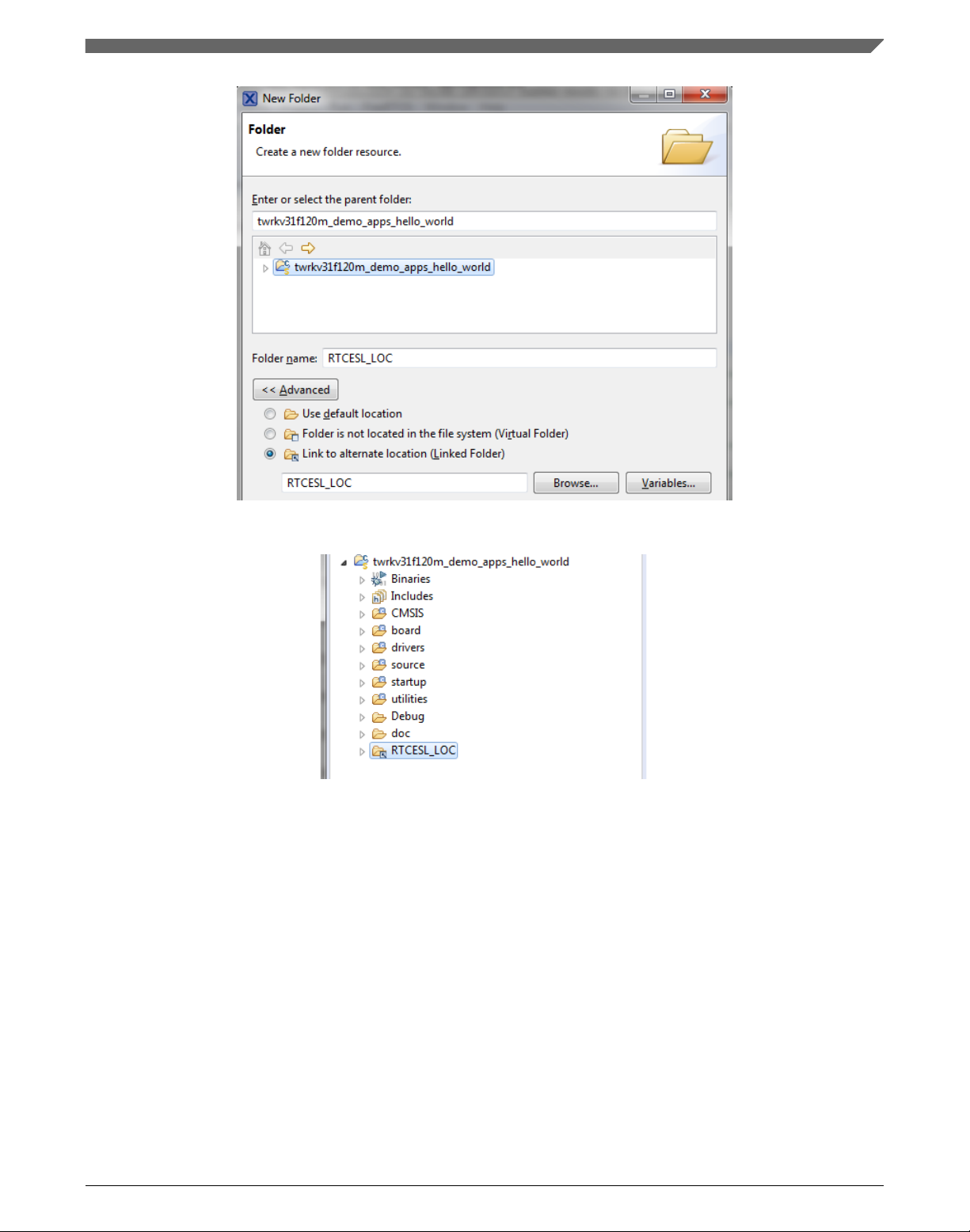
2. Click Advanced to show the advanced options.
3. To link the library source, select the Link to alternate location (Linked Folder)
option.
4. Click Variables..., select the RTCESL_LOC variable in the dialog, click OK, and/or
type the variable name into the box. See Figure 1-6.
5. Click Finish, and the library folder is linked in the project. See Figure 1-7.
GFLIB User's Guide, Rev. 4, 12/2020
12 NXP Semiconductors
Page 13
Chapter 1 Library
Figure 1-6. Folder link
Figure 1-7. Projects libraries paths
1.2.4
Library path setup
GFLIB requires MLIB to be included too. These steps show how to include all dependent
modules:
1. Right-click the MCUXpresso SDK project name node in the left-hand part and click
Properties, or select Project > Properties from the menu. The project properties
dialog appears.
2. Expand the C/C++ General node, and click Paths and Symbols.
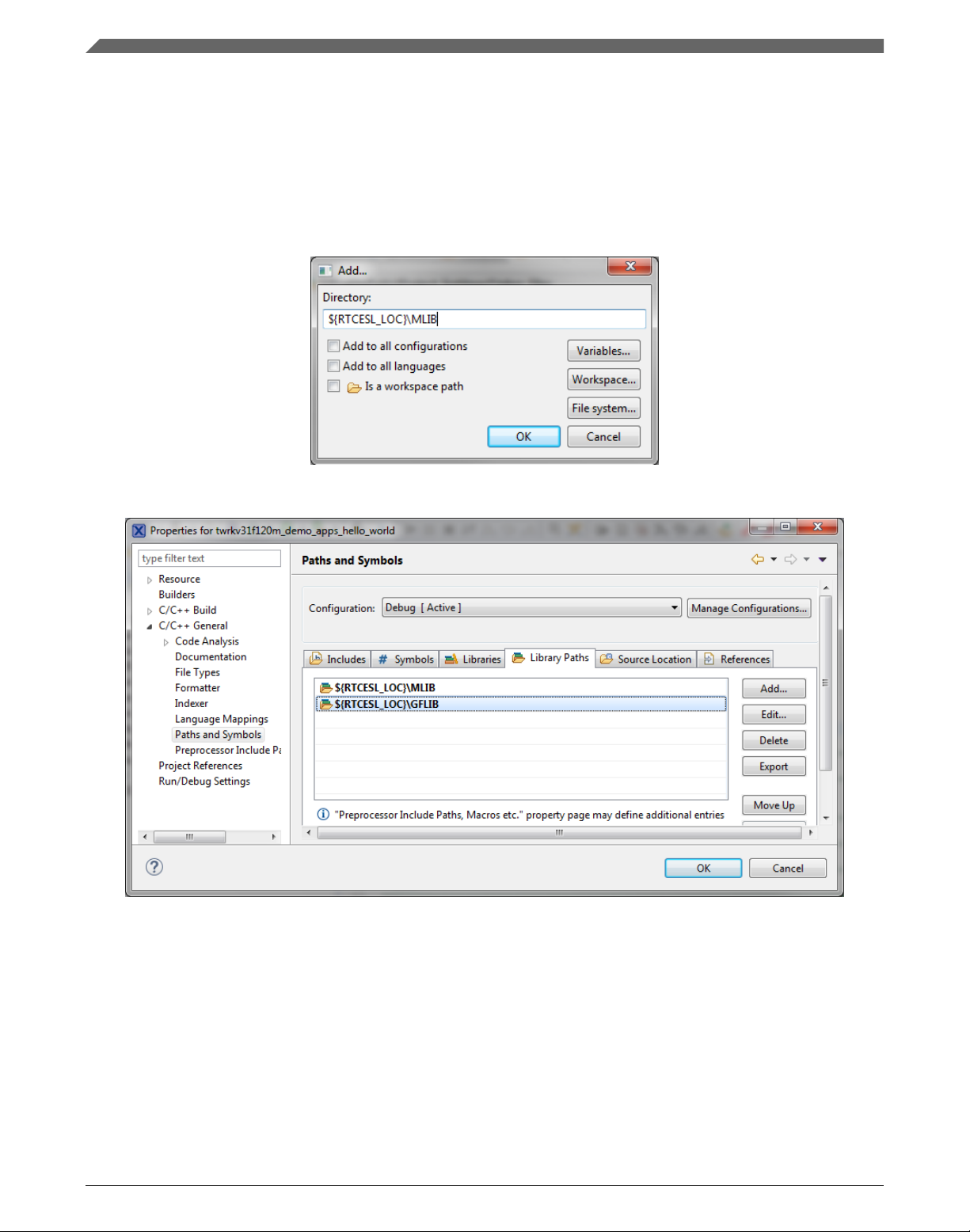
3. In the right-hand dialog, select the Library Paths tab. See Figure 1-9.
4. Click the Add… button on the right, and a dialog appears.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 13
Page 14
Library integration into project (MCUXpresso IDE)
5. Look for the RTCESL_LOC variable by clicking Variables…, and then finish the
path in the box by adding the following (see Figure 1-8): ${RTCESL_LOC}\MLIB.
6. Click OK, and then click the Add… button.
7. Look for the RTCESL_LOC variable by clicking Variables…, and then finish the
path in the box by adding the following: ${RTCESL_LOC}\GFLIB.
8. Click OK, you will see the paths added into the list. See Figure 1-9.
Figure 1-8. Library path inclusion
Figure 1-9. Library paths
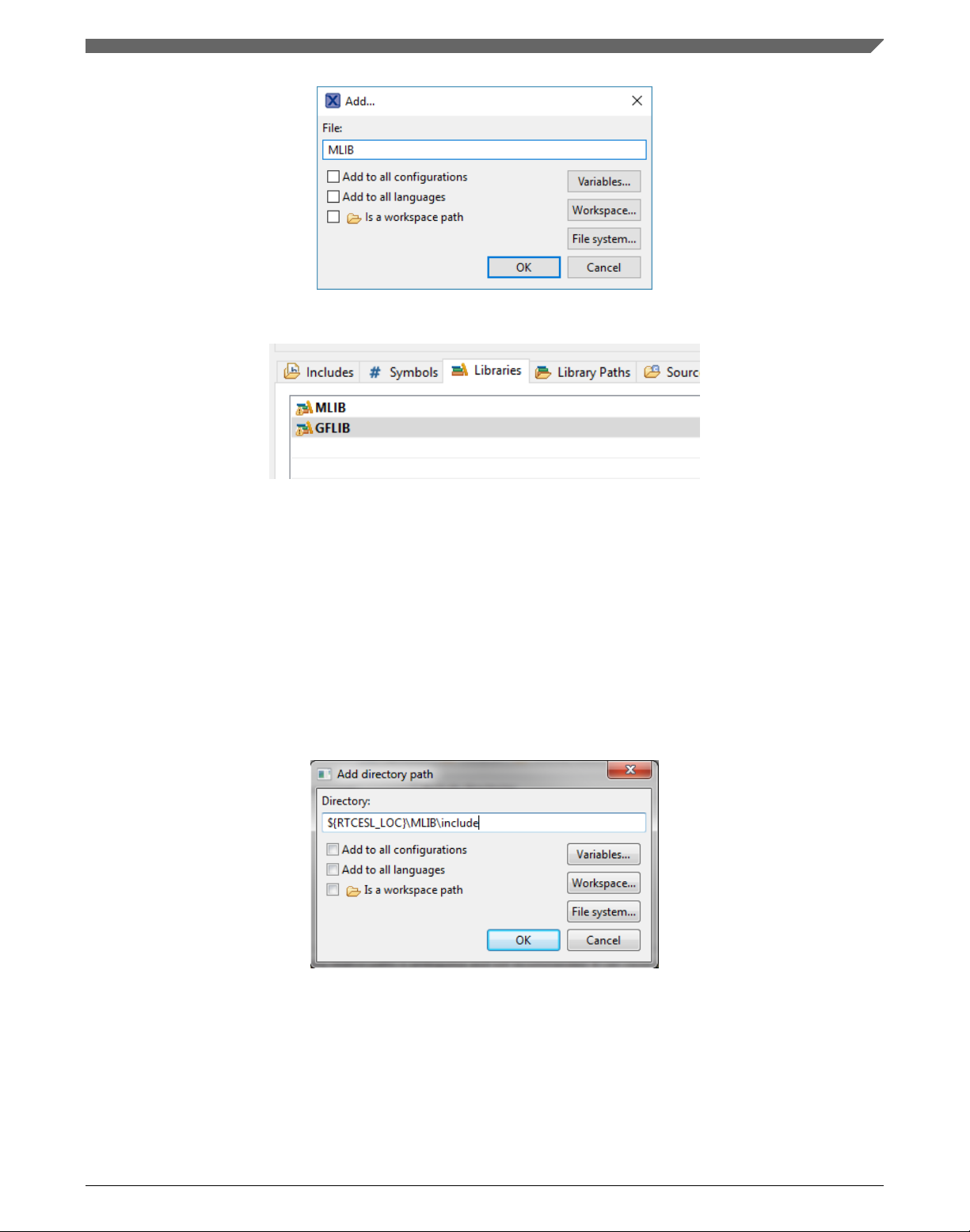
9. After adding the library paths, add the library files. Click the Libraries tab. See
Figure 1-11.
10. Click the Add… button on the right, and a dialog appears.
11. Type the following into the File text box (see Figure 1-10): :mlib.a
12. Click OK, and then click the Add… button.
13. Type the following into the File text box: :gflib.a
14. Click OK, and you will see the libraries added in the list. See Figure 1-11.
GFLIB User's Guide, Rev. 4, 12/2020
14 NXP Semiconductors
Page 15
Chapter 1 Library
Figure 1-10. Library file inclusion
Figure 1-11. Libraries
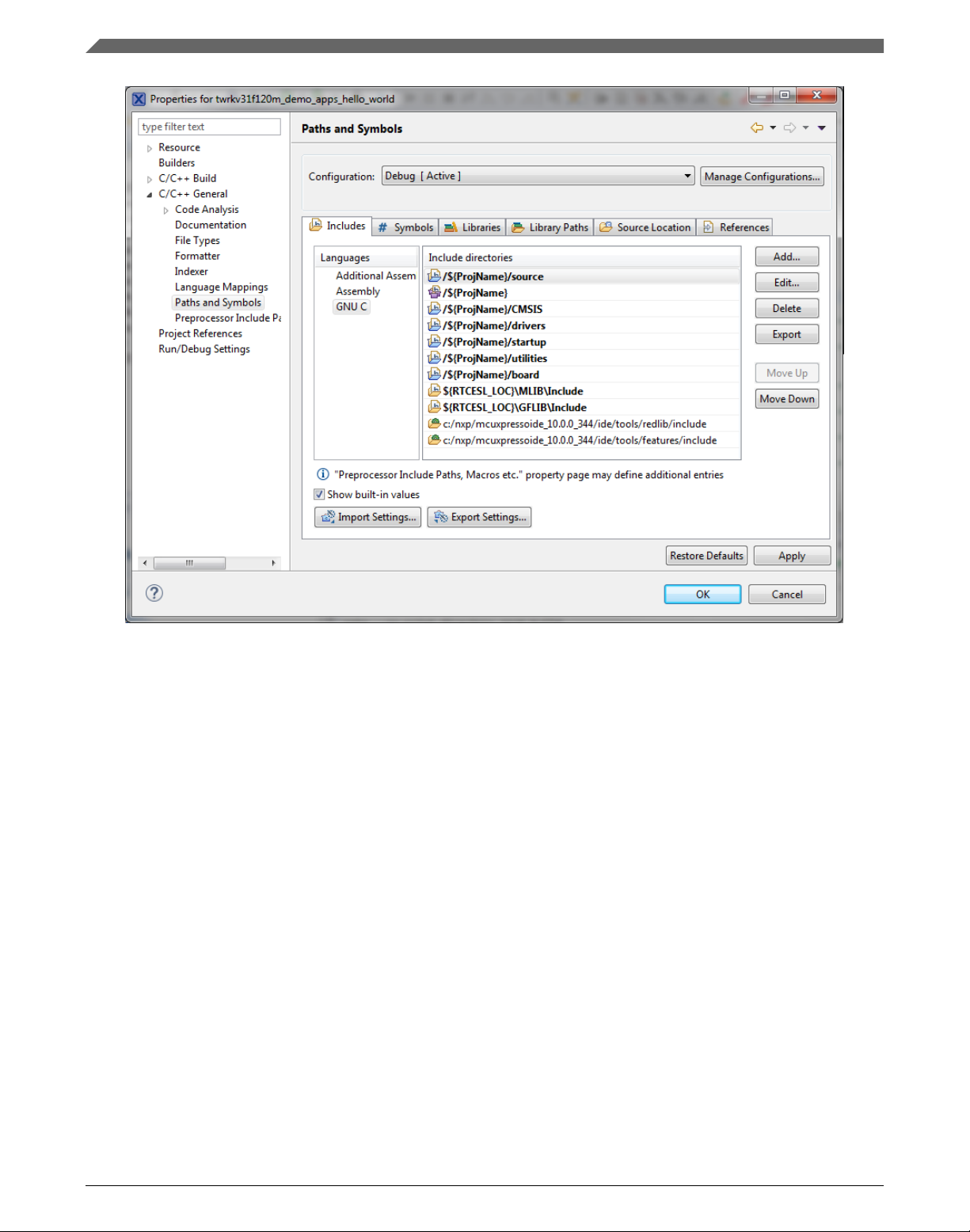
15. In the right-hand dialog, select the Includes tab, and click GNU C in the Languages
list. See Figure 1-13.
16. Click the Add… button on the right, and a dialog appears. See Figure 1-12.
17. Look for the RTCESL_LOC variable by clicking Variables…, and then finish the
path in the box to be: ${RTCESL_LOC}\MLIB\Include
18. Click OK, and then click the Add… button.
19. Look for the RTCESL_LOC variable by clicking Variables…, and then finish the
path in the box to be: ${RTCESL_LOC}\GFLIB\Include
20. Click OK, and you will see the paths added in the list. See Figure 1-13. Click OK.
Figure 1-12. Library include path addition
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 15
Page 16
Library integration into project (Keil µVision)
Figure 1-13. Compiler setting
Type the #include syntax into the code where you want to call the library functions. In
the left-hand dialog, open the required .c file. After the file opens, include the following
lines into the #include section:
#include "mlib_FP.h"
#include "gflib_FP.h"
When you click the Build icon (hammer), the project is compiled without errors.
1.3
Library integration into project (Keil µVision)
This section provides a step-by-step guide on how to quickly and easily include GFLIB
into an empty project or any MCUXpresso SDK example or demo application projects
using Keil µVision. This example uses the default installation path (C:\NXP\RTCESL
\CM7F_RTCESL_4.6_KEIL). If you have a different installation path, use that path
instead. If any MCUXpresso SDK project is intended to use (for example hello_world
project) go to Linking the files into the project chapter otherwise read next chapter.
GFLIB User's Guide, Rev. 4, 12/2020
16 NXP Semiconductors
Page 17
Chapter 1 Library
1.3.1 NXP pack installation for new project (without MCUXpresso
SDK)
This example uses the NXP MKV58F1M0xxx22 part, and the default installation path
(C:\NXP\RTCESL\CM7F_RTCESL_4.6_KEIL) is supposed. If the compiler has never
been used to create any NXP MCU-based projects before, check whether the NXP MCU
pack for the particular device is installed. Follow these steps:
1. Launch Keil µVision.
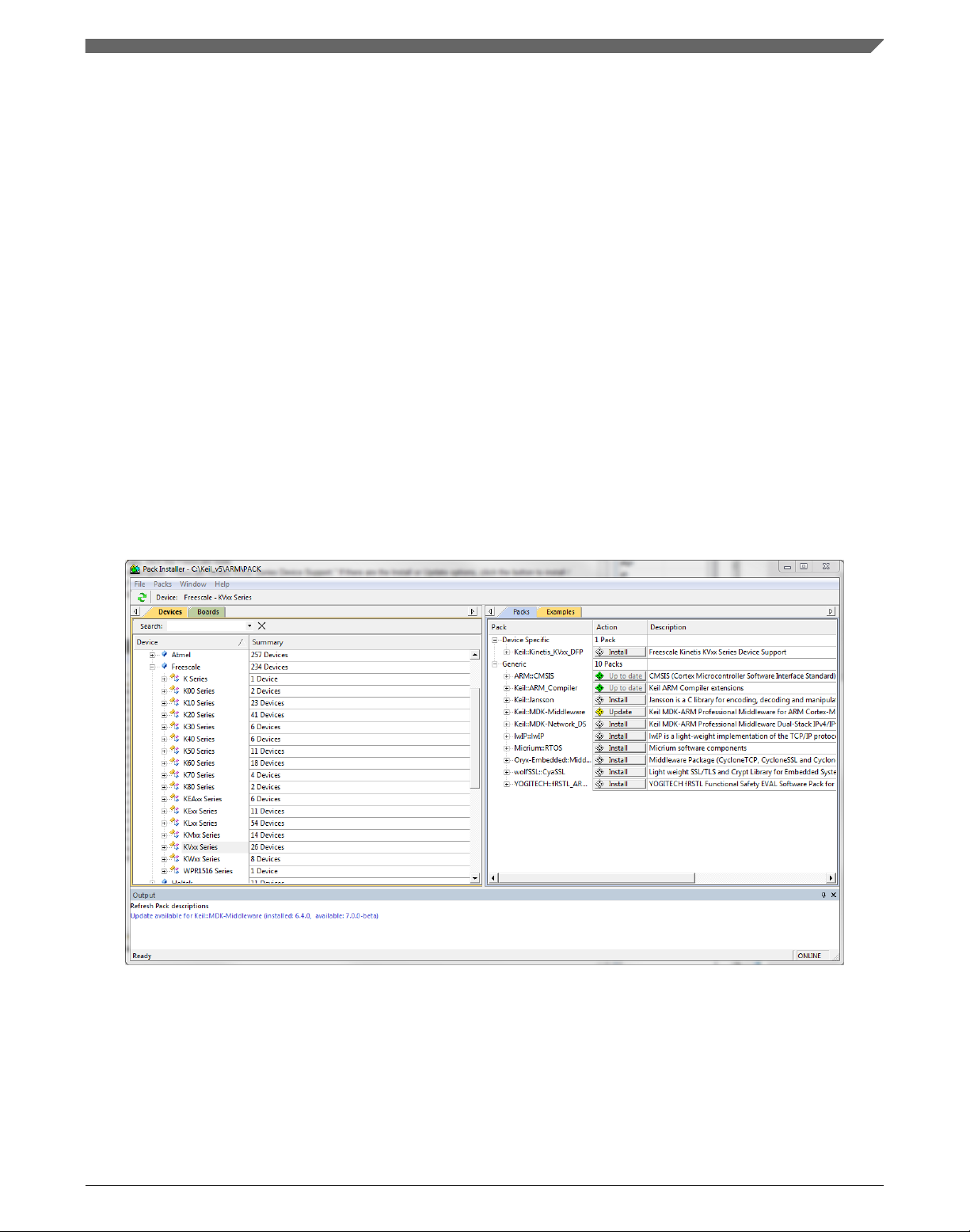
2. In the main menu, go to Project > Manage > Pack Installer….
3. In the left-hand dialog (under the Devices tab), expand the All Devices > Freescale
(NXP) node.
4. Look for a line called "KVxx Series" and click it.
5. In the right-hand dialog (under the Packs tab), expand the Device Specific node.
6. Look for a node called "Keil::Kinetis_KVxx_DFP." If there are the Install or Update
options, click the button to install/update the package. See Figure 1-14.
7. When installed, the button has the "Up to date" title. Now close the Pack Installer.
Figure 1-14. Pack Installer
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 17
Page 18
Library integration into project (Keil µVision)
1.3.2 New project (without MCUXpresso SDK)
To start working on an application, create a new project. If the project already exists and
is opened, skip to the next section. Follow these steps to create a new project:
1. Launch Keil µVision.
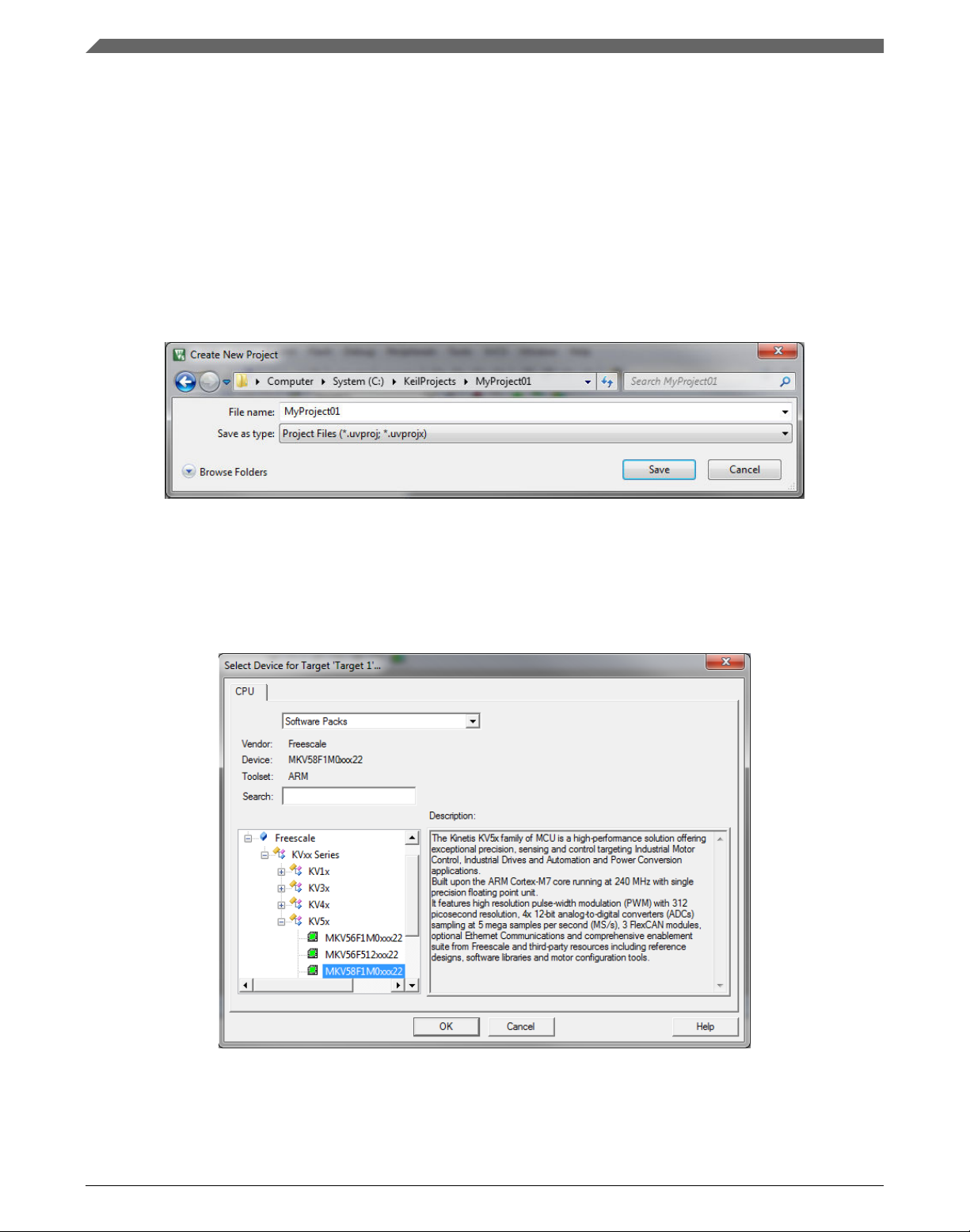
2. In the main menu, select Project > New µVision Project…, and the Create New
Project dialog appears.
3. Navigate to the folder where you want to create the project, for example C:
\KeilProjects\MyProject01. Type the name of the project, for example MyProject01.
Click Save. See Figure 1-15.
Figure 1-15. Create New Project dialog
4. In the next dialog, select the Software Packs in the very first box.
5. Type '' into the Search box, so that the device list is reduced to the devices.
6. Expand the node.
7. Click the MKV58F1M0xxx22 node, and then click OK. See Figure 1-16.
Figure 1-16. Select Device dialog
8. In the next dialog, expand the Device node, and tick the box next to the Startup node.
See Figure 1-17.
GFLIB User's Guide, Rev. 4, 12/2020
18 NXP Semiconductors
Page 19
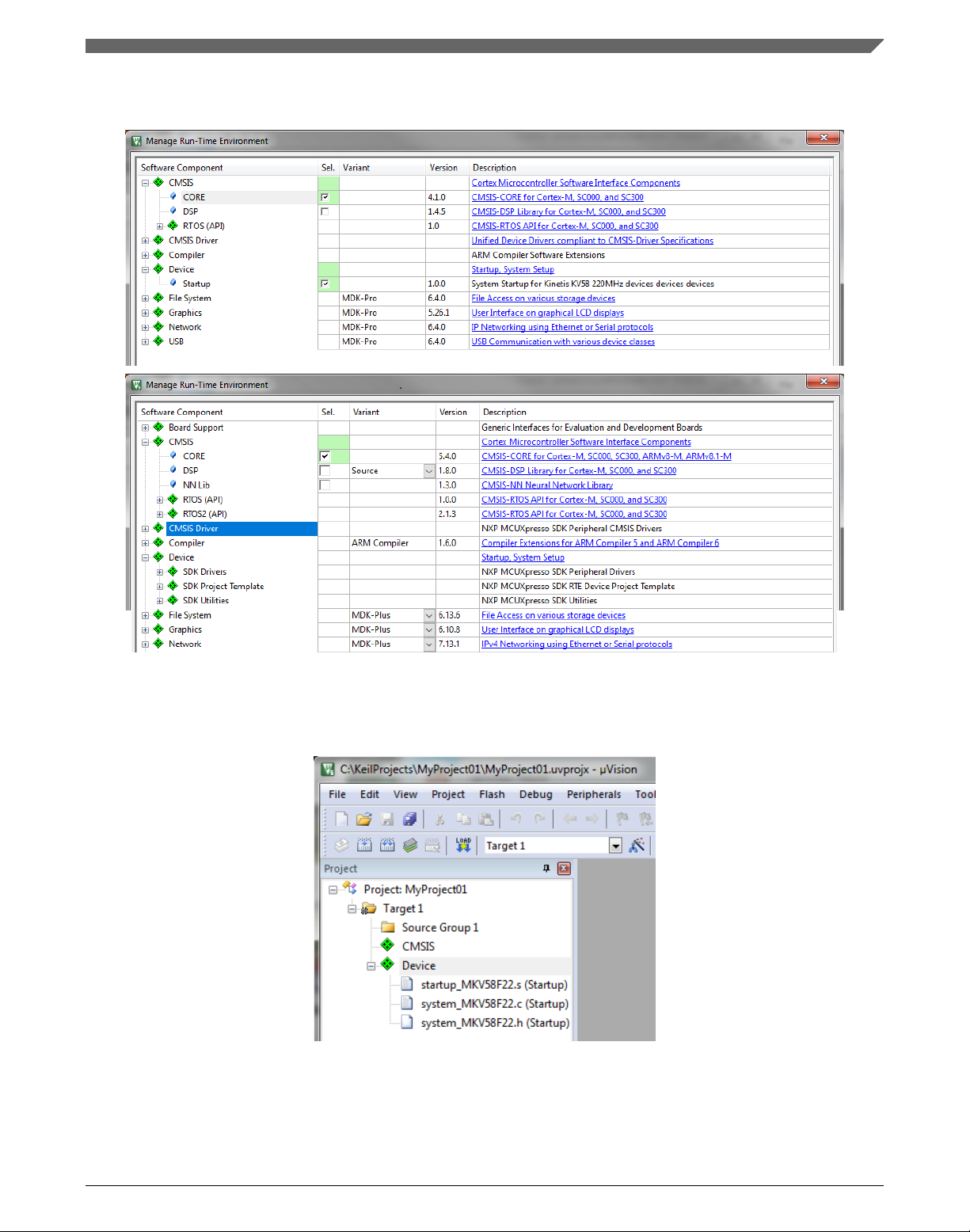
9. Expand the CMSIS node, and tick the box next to the CORE node.
Chapter 1 Library
Figure 1-17. Manage Run-Time Environment dialog
10. Click OK, and a new project is created. The new project is now visible in the lefthand part of Keil µVision. See Figure 1-18.
Figure 1-18. Project
11. In the main menu, go to Project > Options for Target 'Target1'…, and a dialog
appears.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 19
Page 20
Library integration into project (Keil µVision)
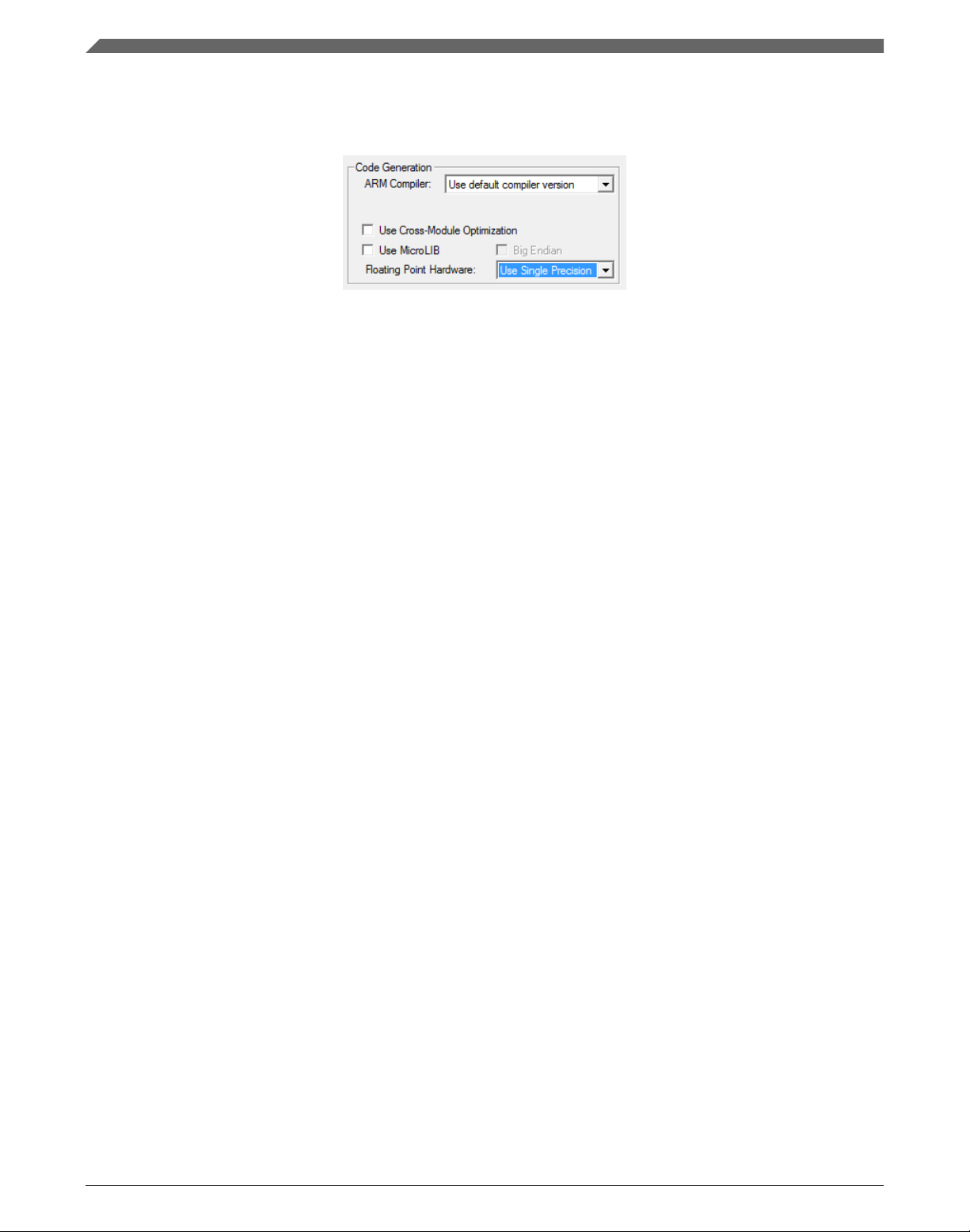
12. Select the Target tab.
13. Select Use Single Precision in the Floating Point Hardware option. See Figure 1-18.
Figure 1-19. FPU
1.3.3
High-speed functions execution support
Some RT (or other) platforms contain high-speed functions execution support by
relocating all functions from the default Flash memory location to the RAM location for
much faster code access. The feature is important especially for devices with a slow Flash
interface. This section shows how to turn the RAM optimization feature support on and
off.
1. In the main menu, go to Project > Options for Target 'Target1'…, and a dialog
appears.
2. Select the C/C++ tab. See .
3. In the Include Preprocessor Symbols text box, type the following:
• RAM_RELOCATION — to turn the RAM optimization feature support on
If the define is defined, all RTCEL functions are put to the RAM.
GFLIB User's Guide, Rev. 4, 12/2020
20 NXP Semiconductors
Page 21
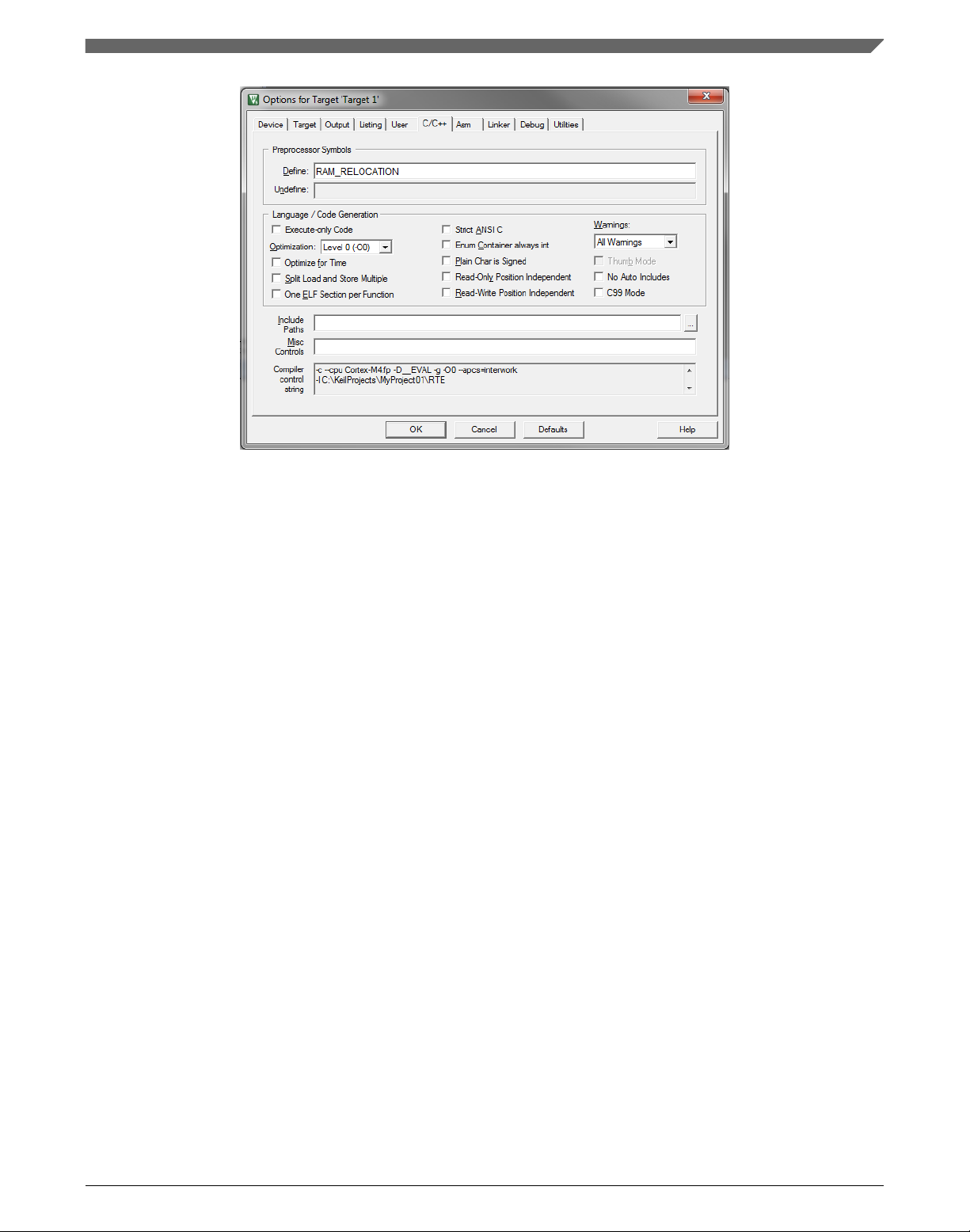
Figure 1-20. Preprocessor symbols
4. Click OK in the main dialog.
Chapter 1 Library
The device reference manual shows how the__attribute__ ((section ("ram"))) atribute
works in connection with your device.
1.3.4
Linking the files into the project
GFLIB requires MLIB to be included too. The following steps show how to include all
dependent modules.
To include the library files in the project, create groups and add them.
1. Right-click the Target 1 node in the left-hand part of the Project tree, and select Add
Group… from the menu. A new group with the name New Group is added.
2. Click the newly created group, and press F2 to rename it to RTCESL.
3. Right-click the RTCESL node, and select Add Existing Files to Group 'RTCESL'…
from the menu.
4. Navigate into the library installation folder C:\NXP\RTCESL
\CM7F_RTCESL_4.6_KEIL\MLIB\Include, and select the mlib_FP.h file. If the file
does not appear, set the Files of type filter to Text file. Click Add. See Figure 1-21.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 21
Page 22
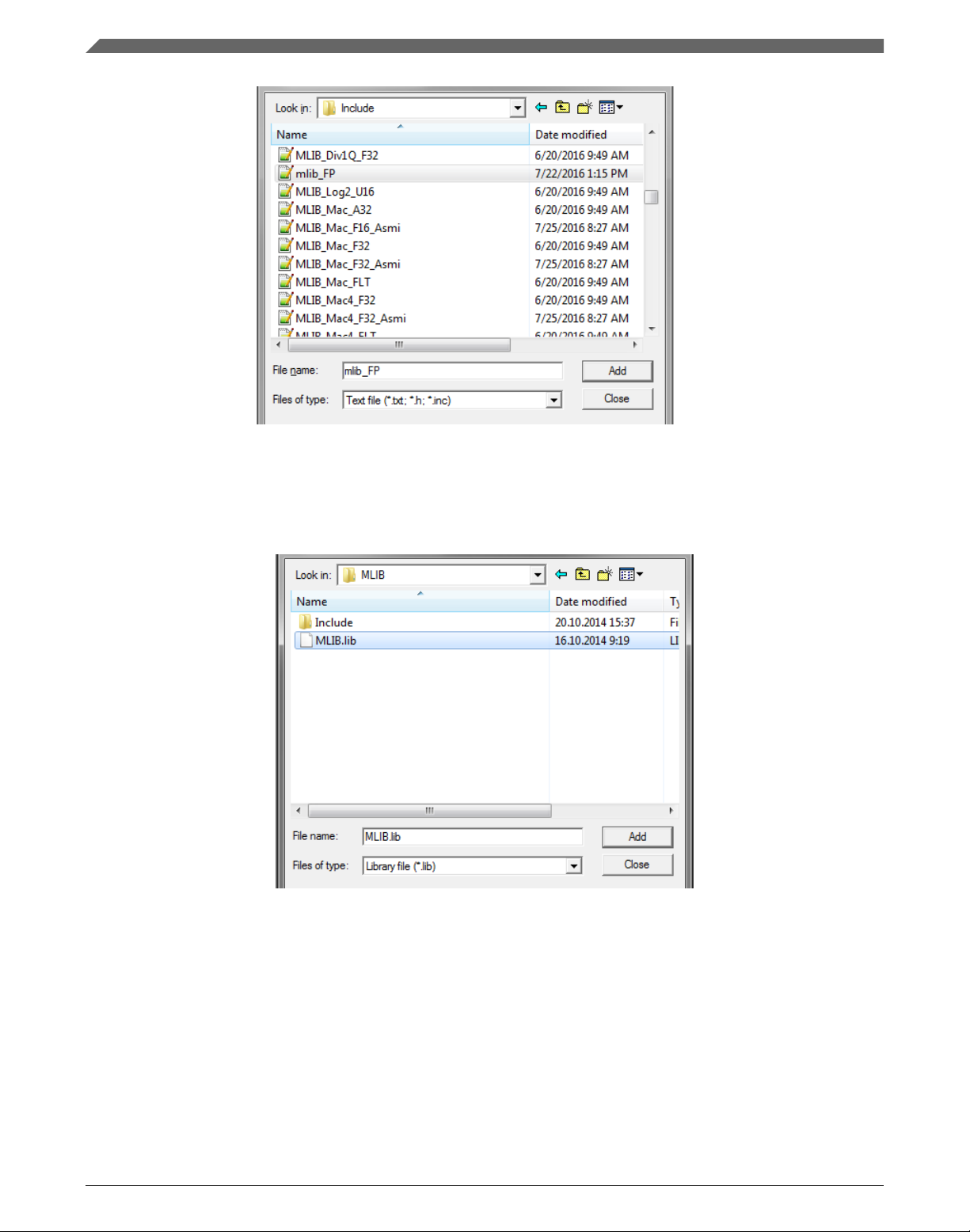
Library integration into project (Keil µVision)
Figure 1-21. Adding .h files dialog
5. Navigate to the parent folder C:\NXP\RTCESL\CM7F_RTCESL_4.6_KEIL\MLIB,
and select the mlib.lib file. If the file does not appear, set the Files of type filter to
Library file. Click Add. See Figure 1-22.
Figure 1-22. Adding .lib files dialog
6. Navigate into the library installation folder C:\NXP\RTCESL
\CM7F_RTCESL_4.6_KEIL\GFLIB\Include, and select the gflib_FP.h file. If the
file does not appear, set the Files of type filter to Text file. Click Add.
7. Navigate to the parent folder C:\NXP\RTCESL\CM7F_RTCESL_4.6_KEIL\GFLIB,
and select the gflib.lib file. If the file does not appear, set the Files of type filter to
Library file. Click Add.
8. Now, all necessary files are in the project tree; see Figure 1-23. Click Close.
GFLIB User's Guide, Rev. 4, 12/2020
22 NXP Semiconductors
Page 23
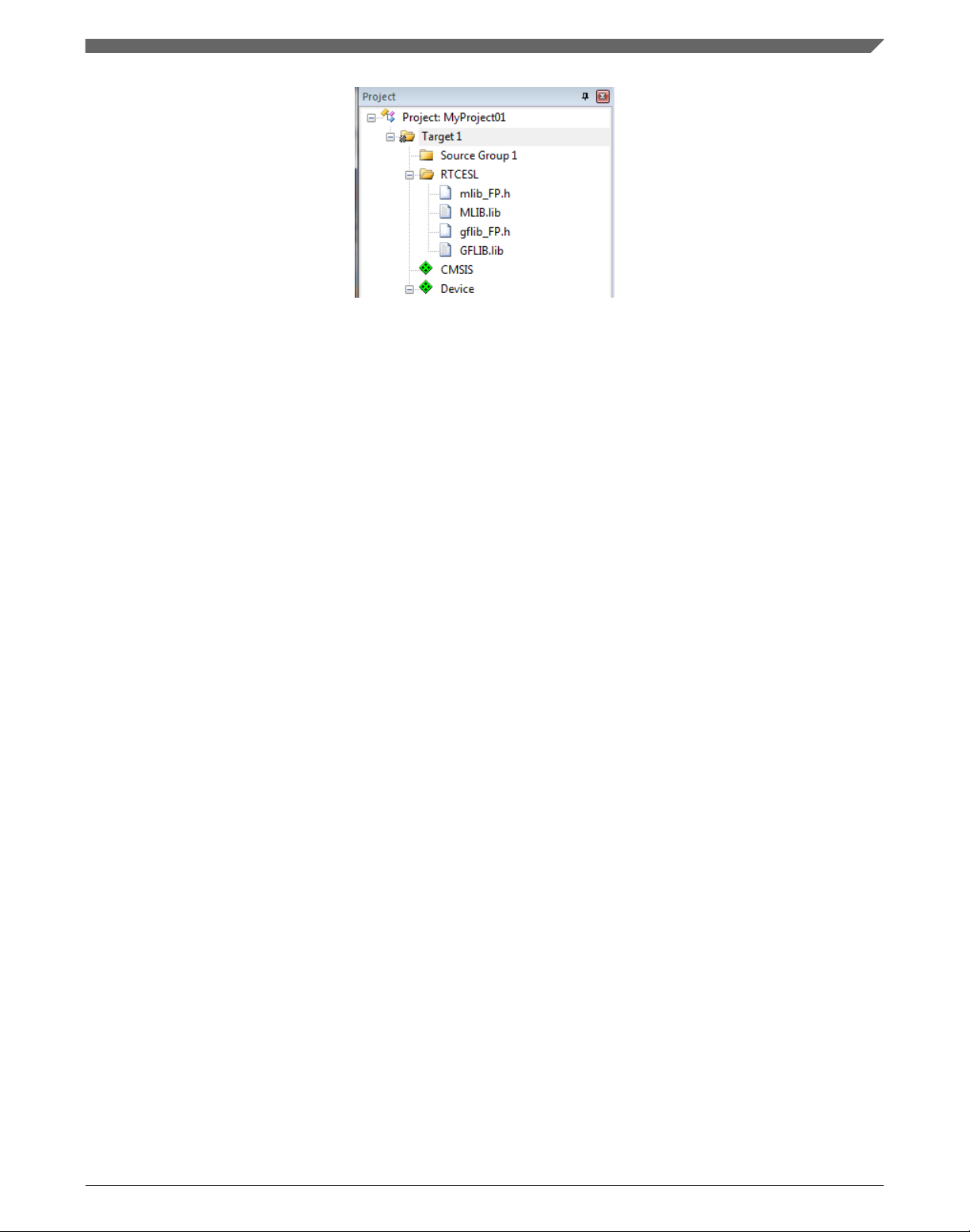
Figure 1-23. Project workspace
Chapter 1 Library
1.3.5
Library path setup
The following steps show the inclusion of all dependent modules.
1. In the main menu, go to Project > Options for Target 'Target1'…, and a dialog
appears.
2. Select the C/C++ tab. See Figure 1-24.
3. In the Include Paths text box, type the following paths (if there are more paths, they
must be separated by ';') or add them by clicking the … button next to the text box:
• "C:\NXP\RTCESL\CM7F_RTCESL_4.6_KEIL\MLIB\Include"
• "C:\NXP\RTCESL\CM7F_RTCESL_4.6_KEIL\GFLIB\Include"
4. Click OK.
5. Click OK in the main dialog.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 23
Page 24
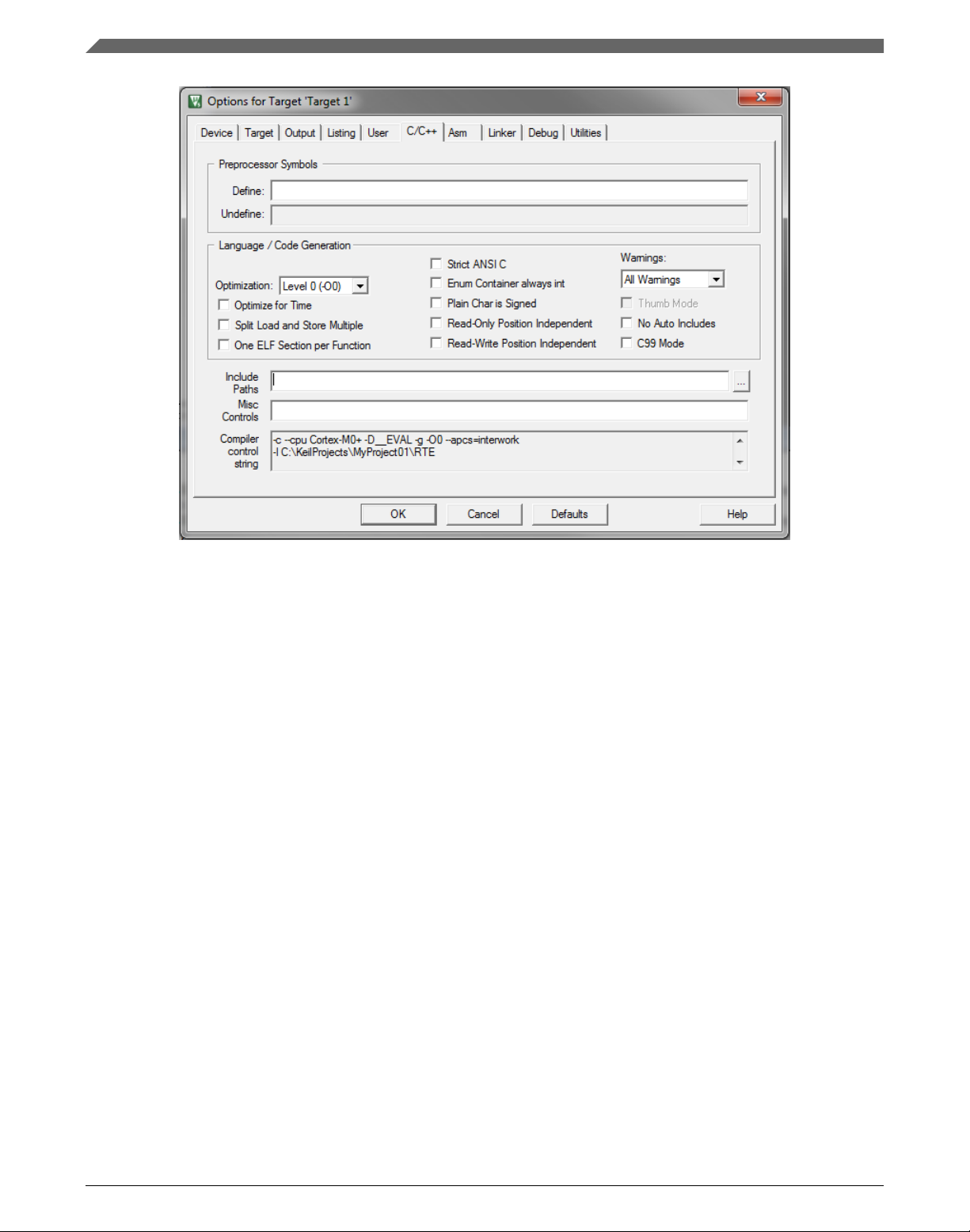
Library integration into project (Keil µVision)
Figure 1-24. Library path addition
Type the #include syntax into the code. Include the library into a source file. In the new
project, it is necessary to create a source file:
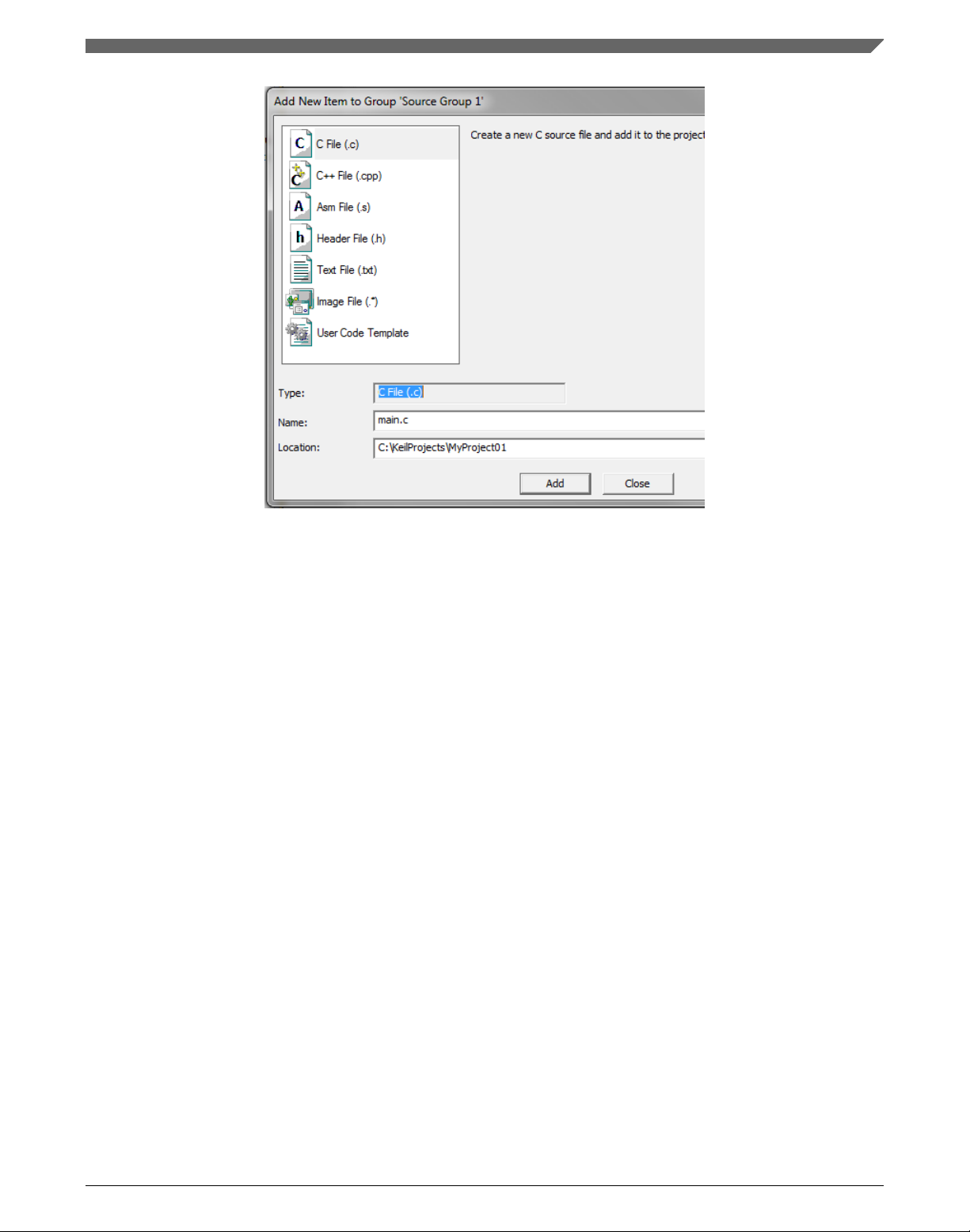
1. Right-click the Source Group 1 node, and Add New Item to Group 'Source Group
1'… from the menu.
2.
Select the C File (.c) option, and type a name of the file into the Name box, for
example 'main.c'. See Figure 1-25.
GFLIB User's Guide, Rev. 4, 12/2020
24 NXP Semiconductors
Page 25
Chapter 1 Library
Figure 1-25. Adding new source file dialog
3. Click Add, and a new source file is created and opened up.
4. In the opened source file, include the following lines into the #include section, and
create a main function:
#include "mlib_FP.h"
#include "gflib_FP.h"
int main(void)
{
while(1);
}
When you click the Build (F7) icon, the project will be compiled without errors.
1.4
Library integration into project (IAR Embedded Workbench)
This section provides a step-by-step guide on how to quickly and easily include the
GFLIB into an empty project or any MCUXpresso SDK example or demo application
projects using IAR Embedded Workbench. This example uses the default installation
path (C:\NXP\RTCESL\CM7F_RTCESL_4.6_IAR). If you have a different installation
path, use that path instead. If any MCUXpresso SDK project is intended to use (for
example hello_world project) go to Linking the files into the project chapter otherwise
read next chapter.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 25
Page 26
Library integration into project (IAR Embedded Workbench)
1.4.1 New project (without MCUXpresso SDK)
This example uses the NXP MKV58F1M0xxx22 part, and the default installation path
(C:\NXP\RTCESL\CM7F_RTCESL_4.6_IAR) is supposed. To start working on an
application, create a new project. If the project already exists and is opened, skip to the
next section. Perform these steps to create a new project:
1. Launch IAR Embedded Workbench.
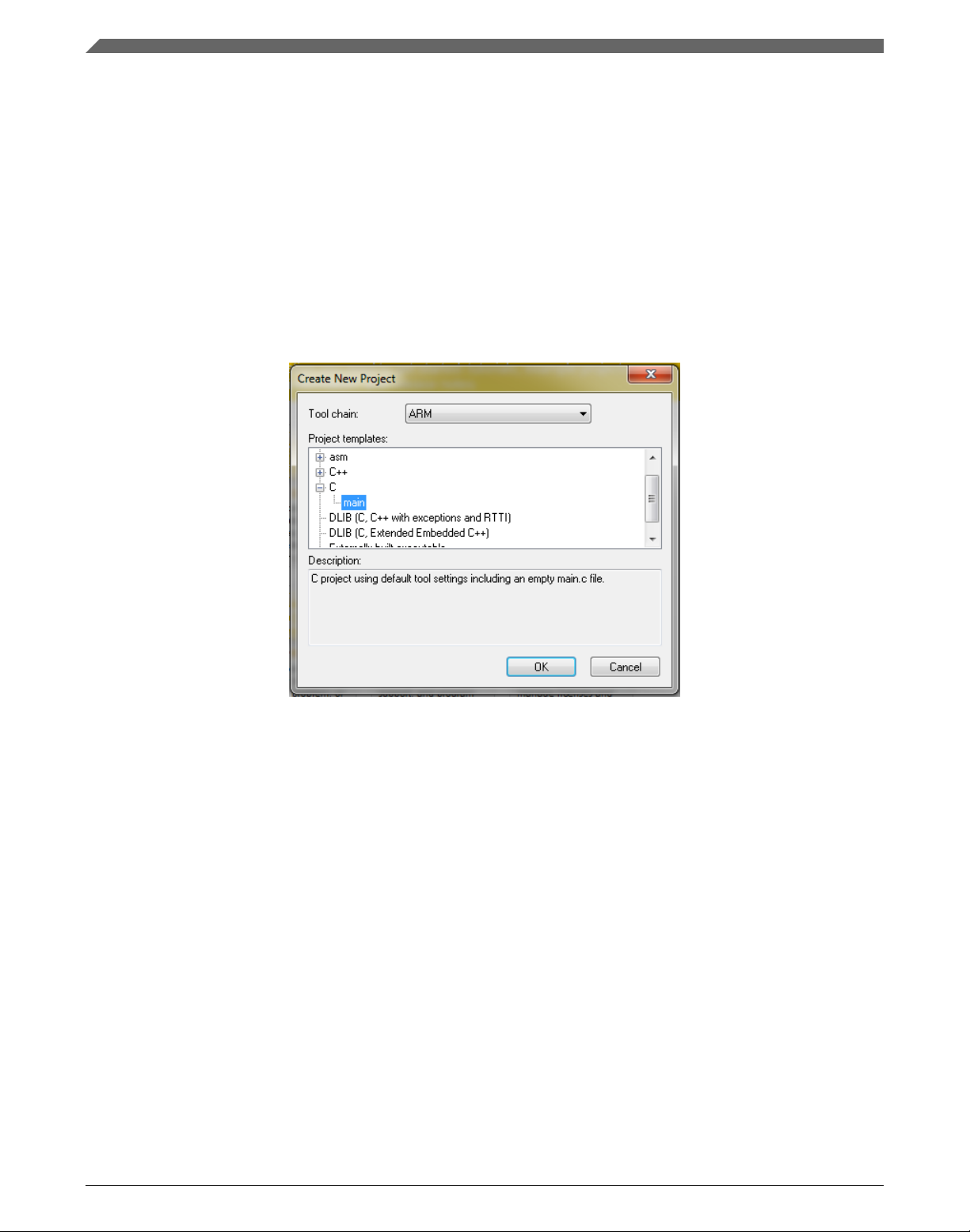
2. In the main menu, select Project > Create New Project… so that the "Create New
Project" dialog appears. See Figure 1-26.
Figure 1-26. Create New Project dialog
3. Expand the C node in the tree, and select the "main" node. Click OK.
4. Navigate to the folder where you want to create the project, for example, C:
\IARProjects\MyProject01. Type the name of the project, for example, MyProject01.
Click Save, and a new project is created. The new project is now visible in the lefthand part of IAR Embedded Workbench. See Figure 1-27.
GFLIB User's Guide, Rev. 4, 12/2020
26 NXP Semiconductors
Page 27
Chapter 1 Library
Figure 1-27. New project
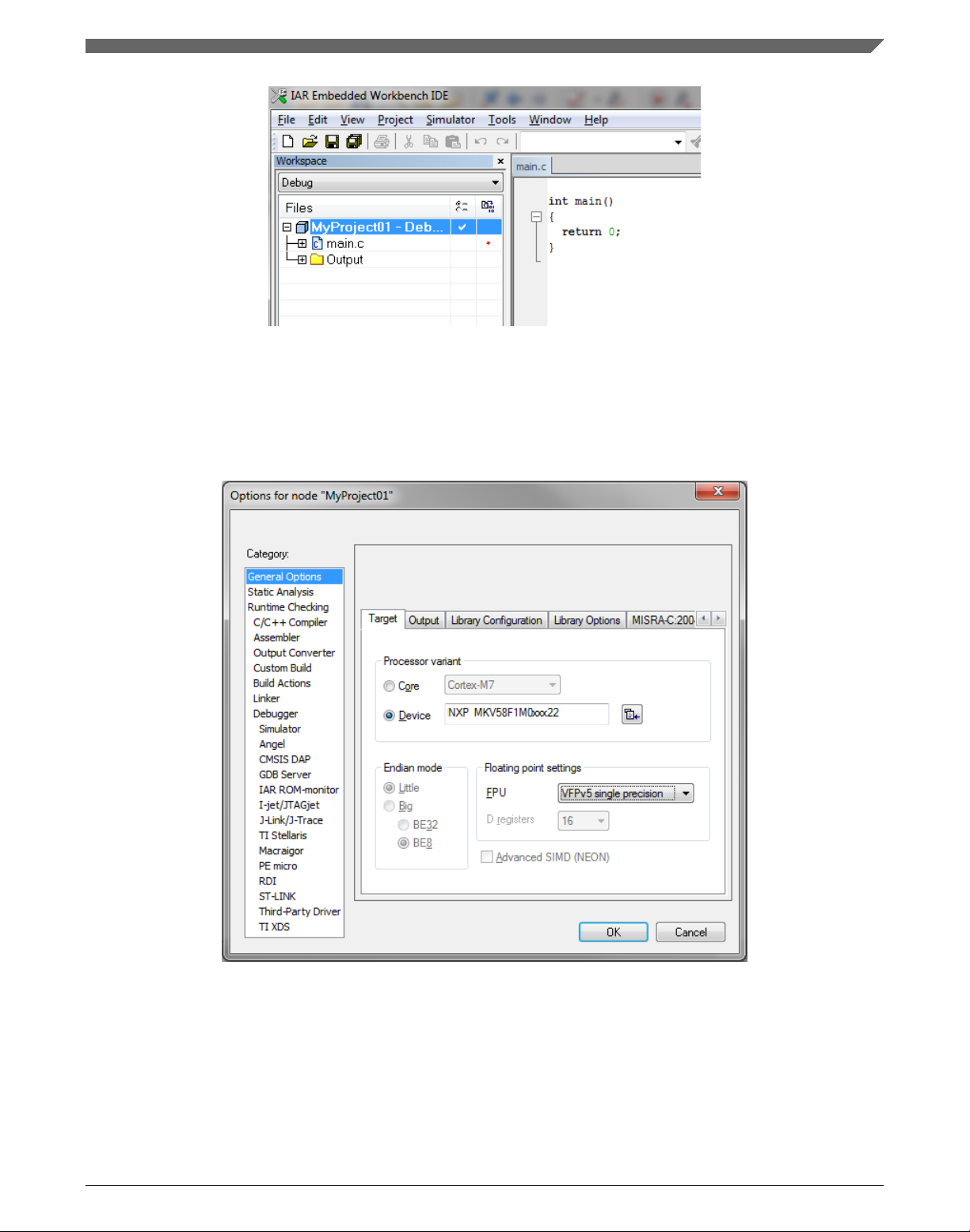
5. In the main menu, go to Project > Options…, and a dialog appears.
6. In the Target tab, select the Device option, and click the button next to the dialog to
select the MCU. In this example, select NXP > KV5x > NXP MKV58F1M0xxx22.
Select VFPv5 single precision in the FPU option. Click OK. See Figure 1-28.
Figure 1-28. Options dialog
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 27
Page 28
Library integration into project (IAR Embedded Workbench)
1.4.2 High-speed functions execution suppport
Some RT (or other) platforms contain high-speed functions execution support by
relocating all functions from the default Flash memory location to the RAM location for
much faster code access. The feature is important especially for devices with a slow Flash
interface. This section shows how to turn the RAM optimization feature support on and
off.
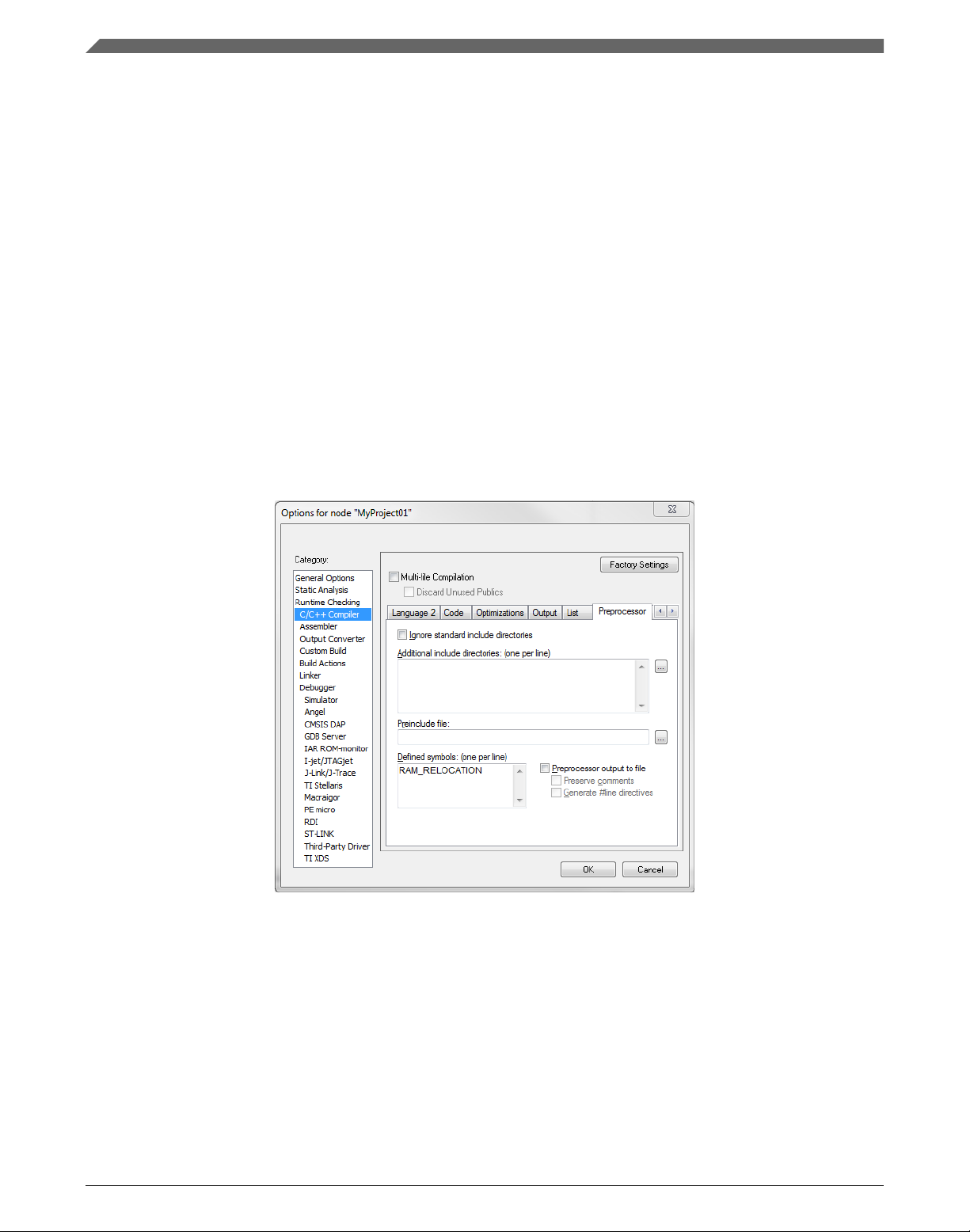
1. In the main menu, go to Project > Options…, and a dialog appears.
2. In the left-hand side column, select C/C++ Compiler.
3. In the right-hand side of the dialog, click the Preprocessor tab (it can be hidden on
the right; use the arrow icons for navigation).
4. In the text box (in Defined symbols: (one per line)), type the following (See Figure
1-29):
• RAM_RELOCATION — to turn the RAM optimization feature support on
If the define is defined, all RTCEL functions are put to the RAM.
Figure 1-29. Defined symbols
5. Click OK in the main dialog.
The device reference manual shows how the __ramfunc atribute works in connection with
your device.
GFLIB User's Guide, Rev. 4, 12/2020
28 NXP Semiconductors
Page 29
Chapter 1 Library
1.4.3 Library path variable
To make the library integration easier, create a variable that will hold the information
about the library path.
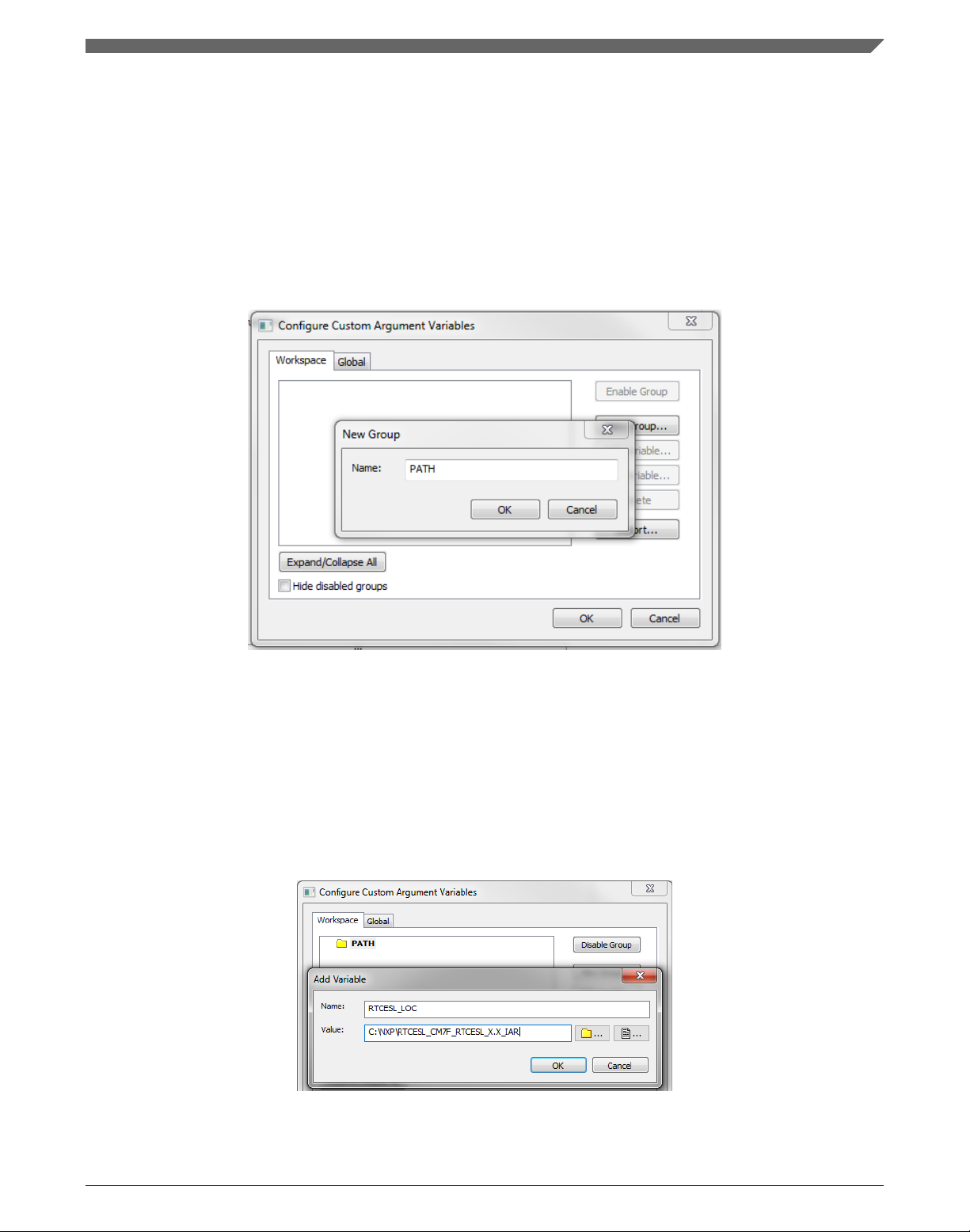
1. In the main menu, go to Tools > Configure Custom Argument Variables…, and a
dialog appears.
2. Click the New Group button, and another dialog appears. In this dialog, type the
name of the group PATH, and click OK. See Figure 1-30.
Figure 1-30. New Group
3. Click on the newly created group, and click the Add Variable button. A dialog
appears.
4. Type this name: RTCESL_LOC
5. To set up the value, look for the library by clicking the '…' button, or just type the
installation path into the box: C:\NXP\RTCESL\CM7F_RTCESL_4.6_IAR. Click
OK.
6. In the main dialog, click OK. See Figure 1-31.
Figure 1-31. New variable
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 29
Page 30

Library integration into project (IAR Embedded Workbench)
1.4.4 Linking the files into the project
GFLIB requires MLIB to be included too. The following steps show the inclusion of all
dependent modules.
To include the library files into the project, create groups and add them.
1. Go to the main menu Project > Add Group…
2. Type RTCESL, and click OK.
3. Click on the newly created node RTCESL, go to Project > Add Group…, and create
a MLIB subgroup.
4. Click on the newly created node MLIB, and go to the main menu Project > Add
Files… See Figure 1-33.
5. Navigate into the library installation folder C:\NXP\RTCESL
\CM7F_RTCESL_4.6_IAR\MLIB\Include, and select the mlib_FP.h file. (If the file
does not appear, set the file-type filter to Source Files.) Click Open. See Figure 1-32.
6. Navigate into the library installation folder C:\NXP\RTCESL
\CM7F_RTCESL_4.6_IAR\MLIB, and select the mlib.a file. If the file does not
appear, set the file-type filter to Library / Object files. Click Open.
Figure 1-32. Add Files dialog
7. Click on the RTCESL node, go to Project > Add Group…, and create a GFLIB
subgroup.
8. Click on the newly created node GFLIB, and go to the main menu Project > Add
Files….
9. Navigate into the library installation folder C:\NXP\RTCESL
\CM7F_RTCESL_4.6_IAR\GFLIB\Include, and select the gflib_FP.h file. (If the file
does not appear, set the file-type filter to Source Files.) Click Open.
10. Navigate into the library installation folder C:\NXP\RTCESL
\CM7F_RTCESL_4.6_IAR\GFLIB, and select the gflib.a file. If the file does not
appear, set the file-type filter to Library / Object files. Click Open.
11. Now you will see the files added in the workspace. See Figure 1-33.
GFLIB User's Guide, Rev. 4, 12/2020
30 NXP Semiconductors
Page 31

Figure 1-33. Project workspace
Chapter 1 Library
1.4.5
Library path setup
The following steps show the inclusion of all dependent modules:
1. In the main menu, go to Project > Options…, and a dialog appears.
2. In the left-hand column, select C/C++ Compiler.
3. In the right-hand part of the dialog, click on the Preprocessor tab (it can be hidden in
the right; use the arrow icons for navigation).
4. In the text box (at the Additional include directories title), type the following folder
(using the created variable):
• $RTCESL_LOC$\MLIB\Include
• $RTCESL_LOC$\GFLIB\Include
5. Click OK in the main dialog. See Figure 1-34.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 31
Page 32

Library integration into project (IAR Embedded Workbench)
Figure 1-34. Library path adition
Type the #include syntax into the code. Include the library included into the main.c file.
In the workspace tree, double-click the main.c file. After the main.c file opens up, include
the following lines into the #include section:
#include "mlib_FP.h"
#include "gflib_FP.h"
When you click the Make icon, the project will be compiled without errors.
GFLIB User's Guide, Rev. 4, 12/2020
32 NXP Semiconductors
Page 33

Chapter 2
Algorithms in detail
2.1 GFLIB_Sin
The
GFLIB_Sin function implements the polynomial approximation of the sine function.
It provides a computational method for the calculation of a standard trigonometric sine
function sin(x), using the 9th order Taylor polynomial approximation. The Taylor
polynomial approximation of a sine function is expressed as follows:
Equation 1.
Equation 2.
where the constants are:
The fractional arithmetic is limited to the range <-1 ; 1), so the input argument can only
be within this range. The input argument is the multiplier of π: sin(π · x), where the user
passes the x argument. Example: if the input is -0.5, it corresponds to -0.5π.
The fractional function sin(π · x) is expressed using the 9th order Taylor polynomial as
follows:
Equation 3.
where:
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 33
Page 34

GFLIB_Sin
2.1.1 Available versions
The function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The result may saturate.
• Floating-point output - the output is the floating-point result within the range <-1.0 ;
1.0>.
• Floating-point output with accumulator input - the output is the floating-point result
within the range <-1.0 ; 1.0>. The input is the accumulator angle in radians divided
by π.
The available versions of the GFLIB_Sin function are shown in the following table:
Table 2-1. Function versions
Function name Input type Result type Description
GFLIB_Sin_F16 frac16_t frac16_t Calculation of the sin(π · x), where the input argument is a 16-bit fractional
value normalized to the range <-1 ; 1) that represents an angle in radians
within the range <-π; π). The output is a 16-bit fractional value within the
range <-1 ; 1).
GFLIB_Sin_FLT float_t float_t Calculation of the sin(x), where the input argument is a 32-bit single
precision floating-point value in radians within the range <-π; π). The output
is a 32-bit single precision floating-point value within the range <-1.0 ; 1.0>.
GFLIB_Sin_FLTa acc32_t float_t Calculation of the sin(π · x), where the input argument is a 32-bit
accumulator value where the fractional part <-1 ; 1) represents the angle
within the range <-π; π). The output is a 32-bit single precision floatingpoint value within the range <-1.0 ; 1.0>.
2.1.2 Declaration
The available GFLIB_Sin functions have the following declarations:
frac16_t GFLIB_Sin_F16(frac16_t f16Angle)
float_t GFLIB_Sin_FLT(float_t fltAngle)
float_t GFLIB_Sin_FLTa(acc32_t a32Angle)
GFLIB User's Guide, Rev. 4, 12/2020
34 NXP Semiconductors
Page 35

Chapter 2 Algorithms in detail
2.1.3 Function use
The use of the GFLIB_Sin function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Result;
static frac16_t f16Angle;
void main(void)
{
f16Angle = FRAC16(0.333333); /* f16Angle = 0.333333 [60°] */
/* f16Result = sin(f16Angle); (π * f16Angle[rad]) = deg * (π / 180) */
f16Result = GFLIB_Sin_F16(f16Angle);
}
Floating-point version:
#include "gflib.h"
static float_t fltResult;
static float_t fltAngle;
void main(void)
{
fltAngle = 1.04719F; /* fltAngle = 1.04719 rad [60°] */
/* fltResult = sin(fltAngle); fltAngle[rad] = deg * (pi / 180) */
fltResult = GFLIB_Sin_FLT(fltAngle);
}
2.2
GFLIB_Cos
The GFLIB_Cos function implements the polynomial approximation of the cosine
function. This function computes the cos(x) using the ninth-order Taylor polynomial
approximation of the sine function, and its equation is as follows:
Equation 4.
Because the fractional arithmetic is limited to the range <-1 ; 1), the input argument can
only be within this range. The input argument is the multiplier of π: cos(π · x), where the
user passes the x argument. For example, if the input is -0.5, it corresponds to -0.5π.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 35
Page 36

GFLIB_Cos
2.2.1 Available versions
This function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The result may saturate.
• Floating-point output - the output is the floating-point result within the range <-1.0 ;
1.0>.
• Floating-point output with accumulator input - the output is the floating-point result
within the range <-1.0 ; 1.0>. The input is the accumulator angle in radians divided
by π.
The available versions of the GFLIB_Cos function are shown in the following table:
Table 2-2. Function versions
Function name Input type Result type Description
GFLIB_Cos_F16 frac16_t frac16_t Calculation of cos(π · x), where the input argument is a 16-bit fractional
value, normalized to the range <-1 ; 1) that represents an angle in radians
within the range <- π; π). The output is a 16-bit fractional value within the
range <-1 ; 1).
GFLIB_Cos_FLT float_t float_t Calculation of cos(x), where the input argument is a 32-bit single precision
floating-point value in radians within the range <-π; π). The output is a 32bit single precision floating-point value within the range <-1.0 ; 1.0>.
GFLIB_Cos_FLTa acc32_t float_t Calculation of the cos(π · x), where the input argument is a 32-bit
accumulator value where the fractional part <-1 ; 1) represents the angle
within the range <-π; π). The output is a 32-bit single precision floatingpoint value within the range <-1.0 ; 1.0>.
2.2.2 Declaration
The available GFLIB_Cos functions have the following declarations:
frac16_t GFLIB_Cos_F16(frac16_t f16Angle)
float_t GFLIB_Cos_FLT(float_t fltAngle)
float_t GFLIB_Cos_FLTa(acc32_t a32Angle)
2.2.3
The use of the GFLIB_Cos function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
36 NXP Semiconductors
Function use
GFLIB User's Guide, Rev. 4, 12/2020
Page 37

static frac16_t f16Result;
static frac16_t f16Angle;
void main(void)
{
f16Angle = FRAC16(0.333333); /* f16Angle = 0.333333 [60°] */
/* f16Result = cos(f16Angle); f16Angle[rad] = deg * (π / 180) */
f16Result = GFLIB_Cos_F16(f16Angle);
}
Floating-point version:
#include "gflib.h"
static float_t fltResult;
static float_t fltAngle;
void main(void)
{
fltAngle = 1.04719F; /* fltAngle = 1.04719 rad [60°] */
/* fltResult = cos(fltAngle); fltAngle[rad] = deg * (π / 180) */
fltResult = GFLIB_Cos_FLT(fltAngle);
}
Chapter 2 Algorithms in detail
2.3
GFLIB_Tan
The GFLIB_Tan function provides a computational method for calculation of a standard
trigonometric tangent function tan(x), using the piece-wise polynomial approximation.
Function tan(x) takes an angle and returns the ratio of two sides of a right-angled triangle.
The ratio is the length of the side opposite the angle divided by the length of the side
adjacent to the angle.
Equation 5.
Because both sin(x) and cos(x) are defined in interval <-π ; π>, the function tan(x) is
equal to zero when sin(x)=0 and is equal to infinity when cos(x)=0. The graph of tan(x) is
shown in the following figure:
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 37
Page 38

GFLIB_Tan
Figure 2-1. Course of the function GFLIB_Tan
The fractional arithmetic is limited to the range <-1 ; 1) so the input argument can only be
within this range. The input argument is the multiplier of π: tan(π · x) where you pass the
x argument. Example: if the input is -0.5, it corresponds to -0.5π. The output of the
function is limited to the range <-1 ; 1) for the fractional arithmetic. For the points where
the function is not defined, the output is fractional -1.
2.3.1
Available versions
The function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The result may saturate.
• Floating-point output - the output is the floating-point result.
• Floating-point output with accumulator input - the output is the floating-point result.
The input is the accumulator angle in radians divided by π.
The available versions of the GFLIB_Tan function are shown in the following table:
Table 2-3. Function versions
Function name Input type Result type Description
GFLIB_Tan_F16 frac16_t frac16_t Calculation of the tan(π · x) where the input argument is a 16-bit fractional
value normalized to the range <-1 ; 1) that represents an angle in radians
within the range <-π ; π). The output is a 16-bit fractional value within the
range <-1 ; 1).
Table continues on the next page...
GFLIB User's Guide, Rev. 4, 12/2020
38 NXP Semiconductors
Page 39

Chapter 2 Algorithms in detail
Table 2-3. Function versions (continued)
Function name Input type Result type Description
GFLIB_Tan_FLT float_t float_t Calculation of the tan(x) where the input argument is a 32-bit single
precision floating-point value in radians within the range <-π ; π). The
output is a 32-bit single precision floating-point value within the full range.
GFLIB_Tan_FLTa acc32_t float_t Calculation of the tan(π · x), where the input argument is a 32-bit
accumulator value where the fractional part <-1 ; 1) represents the angle
within the range <-π ; π). The output is a 32-bit single precision floatingpoint value within the full range.
2.3.2 Declaration
The available GFLIB_Tan functions have the following declarations:
frac16_t GFLIB_Tan_F16(frac16_t f16Angle)
float_t GFLIB_Tan_FLT(float_t fltAngle)
float_t GFLIB_Tan_FLTa(acc32_t a32Angle)
2.3.3
Function use
The use of the GFLIB_Tan function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Result;
static frac16_t f16Angle;
void main(void)
{
f16Angle = FRAC16(0.1); /* f16Angle = 0.1 [18°] */
/* f16Result = tan(f16Angle); (π * f16Angle[rad]) = deg * (π / 180) */
f16Result = GFLIB_Tan_F16(f16Angle);
}
Floating-point version:
#include "gflib.h"
static float_t fltResult;
static float_t fltAngle;
void main(void)
{
fltAngle = 0.1F; /* fltAngle = 0.1 [5.72°] */
/* fltResult = tan(fltAngle); (π * f16Angle[rad]) = deg * (π / 180) */
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 39
Page 40

GFLIB_Asin
fltResult = GFLIB_Tan_FLT(fltAngle);
}
2.4 GFLIB_Asin
The GFLIB_Asin function provides a computational method for calculation of a standard
inverse trigonometric arcsine function arcsin(x), using the piece-wise polynomial
approximation. Function arcsin(x) takes the ratio of the length of the opposite side to the
length of the hypotenuse and returns the angle.
Figure 2-2. Course of the function GFLIB_Asin
The fractional arithmetic is limited by the range <-1;1) so the output can only be within
this range. This range corresponds to the angle <-1;1). Example: if the output is -0.5 it
corresponds to -0.5π.
2.4.1
Available versions
The function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1;1). The result may saturate.
• Floating point output - the output is the floating point result within the range <-π;π>.
GFLIB User's Guide, Rev. 4, 12/2020
40 NXP Semiconductors
Page 41

Chapter 2 Algorithms in detail
The available versions of the GFLIB_Asin function are shown in the following table:
Table 2-4. Function versions
Function name Input type Result type Description
GFLIB_Asin_F16 frac16_t frac16_t Calculation of the arcsin(x) / π where the input argument is a 16-bit
fractional within the range <-1;1). The output is a 16-bit fractional value
within the range <-1;1) that represents an angle in radians within the range
<-π;π).
GFLIB_Asin_FLT float_t float_t Calculation of the arcsin(x) where the input argument is a 32-bit single
precision floating point value within the range <-1;1>. The output is a 32-bit
single precision floating point value within the range <-π;π>.
2.4.2 Declaration
The available GFLIB_Asin functions have the following declarations:
frac16_t GFLIB_Asin_F16(frac16_t f16Val)
float_t GFLIB_Asin_FLT(float_t fltVal)
2.4.3
Function use
The use of the GFLIB_Asin function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Result;
static frac16_t f16Value;
void main(void)
{
f16Value = FRAC16(0.5); /* f16Value = 0.5 */
/* f16Result = arcsin(f16Value); */
f16Result = GFLIB_Asin_F16(f16Value);
}
Floating-point version:
#include "gflib.h"
static float_t fltResult;
static float_t fltValue;
void main(void)
{
fltValue = 1.57F; /* fltValue = 1.57 rad */
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 41
Page 42

GFLIB_Acos
/* fltResult = arcsin(fltValue); */
fltResult = GFLIB_Asin_FLT(fltValue);
}
2.5 GFLIB_Acos
The GFLIB_Acos function provides a computational method for calculation of a standard
inverse trigonometric arccosine function arccos(x), using the piece-wise polynomial
approximation. Function arccos(x) takes the ratio of the length of the adjacent side to the
length of the hypotenuse and returns the angle.
Figure 2-3. Course of the function GFLIB_Acos
The fractional arithmetic is limited by the range <-1;1) so the output can only be within
this range. This range corresponds to the angle <-1;1). Example: if the output is -0.5 it
corresponds to -0.5π.
2.5.1
Available versions
The function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1;1). The result may saturate.
• Floating point output - the output is the floating point result within the range <-π;π>.
GFLIB User's Guide, Rev. 4, 12/2020
42 NXP Semiconductors
Page 43

Chapter 2 Algorithms in detail
The available versions of the GFLIB_Acos function are shown in the following table:
Table 2-5. Function versions
Function name Input type Result type Description
GFLIB_Acos_F16 frac16_t frac16_t Calculation of the arccos(x) / π where the input argument is a 16-bit
fractional within the range <-1;1). The output is a 16-bit fractional value
within the range <-1;1) that represents an angle in radians within the range
<-π;π).
GFLIB_Acos_FLT float_t float_t Calculation of the arccos(x) where the input argument is a 32-bit single
precision floating point value within the range <-1;1>. The output is a 32-bit
single precision floating point value within the range <-π;π>.
2.5.2 Declaration
The available GFLIB_Acos functions have the following declarations:
frac16_t GFLIB_Acos_F16(frac16_t f16Val)
float_t GFLIB_Acos_FLT(float_t fltVal)
2.5.3
Function use
The use of the GFLIB_Acos function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Result;
static frac16_t f16Value;
void main(void)
{
f16Value = FRAC16(0.5); /* f16Value = 0.5 */
/* f16Result = arccos(f16Value); */
f16Result = GFLIB_Acos_F16(f16Value);
}
Floating-point version:
#include "gflib.h"
static float_t fltResult;
static float_t fltValue;
void main(void)
{
fltValue = 1.57F; /* fltValue = 1.57 rad */
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 43
Page 44

GFLIB_Atan
/* fltResult = arccos(fltValue); */
fltResult = GFLIB_Acos_FLT(fltValue);
}
2.6 GFLIB_Atan
The GFLIB_Atan function implements the polynomial approximation of the arctangent
function. It provides a computational method for calculating the standard trigonometric
arctangent function arctan(x), using the piece-wise minimax polynomial approximation.
Function arctan(x) takes a ratio, and returns the angle of two sides of a right-angled
triangle. The ratio is the length of the side opposite to the angle divided by the length of
the side adjacent to the angle. The graph of the arctan(x) is shown in the following figure:
Figure 2-4. Course of the GFLIB_Atan function
The fractional arithmetic version of the GFLIB_Atan function is limited to a certain
range of inputs <-1 ; 1). Because the arctangent values are the same, with just an opposite
sign for the input ranges <-1 ; 0) and <0 ; 1), the approximation of the arctangent function
over the entire defined range of input ratios can be simplified to the approximation for a
ratio in the range <0 ; 1). After that, the result will be negated, depending on the input
ratio.
GFLIB User's Guide, Rev. 4, 12/2020
44 NXP Semiconductors
Page 45

Chapter 2 Algorithms in detail
2.6.1 Available versions
The function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-0.25 ; 0.25), which corresponds to the angle <-π / 4 ; π / 4).
• Floating-point output - the output is the floating-point result within the range <-π /
2 ;π / 2>.
• Accumulator output with floating-point input - the output is the accumulator angle
within the range (-0.5 ; 0.5), which corresponds to the angle (-π / 2 ; π / 2). The input
is the floating-point value.
The available versions of the GFLIB_Atan function are shown in the following table:
Table 2-6. Function versions
Function name Input type Result type Description
GFLIB_Atan_F16 frac16_t frac16_t Input argument is a 16-bit fractional value within the range <-1 ; 1). The
output is the arctangent of the input as a 16-bit fractional value, normalized
within the range <-0.25 ; 0.25), which represents an angle (in radians) in
the range <-π / 4 ; π / 4) <-45° ; 45°).
GFLIB_Atan_FLT float_t float_t Input argument is a 32-bit single precision floating-point value within the
full type's range. The output is the arctangent of the input as a 32-bit single
precision floating-point value in radians.
GFLIB_Atan_A32f float_t acc32_t Input argument is a 32-bit single precision floating-point value within the
full type's range. The output is the arctangent of the input as a 32-bit
accumulator value, normalized within the range (-0.5 ; 0.5), which
represents an angle (in radians) in the range (-π / 2 ; π / 2) (-90° ; 90°).
2.6.2 Declaration
The available GFLIB_Atan functions have the following declarations:
frac16_t GFLIB_Atan_F16(frac16_t f16Val)
float_t GFLIB_Atan_FLT(float_t fltVal)
acc32_t GFLIB_Atan_A32f(float_t fltVal)
2.6.3
The use of the GFLIB_Atan function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
NXP Semiconductors 45
Function use
GFLIB User's Guide, Rev. 4, 12/2020
Page 46

GFLIB_AtanYX
static frac16_t f16Result;
static frac16_t f16Val;
void main(void)
{
f16Val = FRAC16(0.1666666); /* f16Val = 0.1666666 (30°) */
/* f16Result = atan(f16Val); f16Result * 180 => angle[degree] */
f16Result = GFLIB_Atan_F16(f16Val);
}
Floating-point version:
#include "gflib.h"
static float_t fltResult;
static float_t fltVal;
void main(void)
{
fltVal = 0.52359f; /* fltVal = 0.52359 rad (30°) */
/* fltResult = atan(fltVal); fltResult * 180 => angle[degree] */
fltResult = GFLIB_Atan_FLT(fltVal);
}
2.7
GFLIB_AtanYX
The GFLIB_AtanYX function computes the angle, where its tangent is y / x (see the
figure below). This calculation is based on the input argument division (y divided by x),
and the piece-wise polynomial approximation.
GFLIB User's Guide, Rev. 4, 12/2020
46 NXP Semiconductors
Page 47

Chapter 2 Algorithms in detail
Figure 2-5. Course of the GFLIB_AtanYX function
The first parameter Y is the ordinate (the x coordinate), and the second parameter X is the
abscissa (the x coordinate). The counter-clockwise direction is assumed to be positive,
and thus a positive angle is computed if the provided ordinate (Y) is positive. Similarly, a
negative angle is computed for the negative ordinate. The calculations are performed in
several steps. In the first step, the angle is positioned within the correct half-quarter of the
circumference of a circle by dividing the angle into two parts: the integral multiple of 45
(half-quarter), and the remaining offset within the 45o range. Simple geometric properties
of the Cartesian coordinate system are used to calculate the coordinates of the vector with
the calculated angle offset. In the second step, the vector ordinate is divided by the vector
abscissa (y / x) to obtain the tangent value of the angle offset. The angle offset is
computed by applying the GFLIB_Atan function. The sum of the integral multiple of
half-quarters and the angle offset within a single halfquarter form the angle is computed.
o
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 47
Page 48

GFLIB_AtanYX
The function returns 0 if both input arguments equal 0, and sets the output error flag; in
other cases, the output flag is cleared. When compared to the GFLIB_Atan function, the
GFLIB_AtanYX function places the calculated angle correctly within the fractional range
<-π ; π>.
In the fractional arithmetic, both input parameters are assumed to be in the fractional
range <-1 ; 1). The output is within the range <-1 ; 1), which corresponds to the real
range <-π ; π).
2.7.1 Available versions
This function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1), which corresponds to the angle <-π ; π).
• Floating-point output - the output is the floating-point result within the range <- π;
π>.
• Accumulator output with floating-point input - the output is the accumulator angle
within the range <-1 ; 1>, which corresponds to the angle <-π ; π>. The input is the
floating-point value.
The available versions of the GFLIB_AtanYX function are shown in the following table:
Table 2-7. Function versions
Function name Input type Output type Result type
Y X Error flag
GFLIB_AtanYX_F16 frac16_t frac16_t bool_t * frac16_t
The first input argument is a 16-bit fractional value that contains the ordinate of the input vector (y
coordinate). The second input argument is a 16-bit fractional value that contains the abscissa of the
input vector (x coordinate). The result is the arctangent of the input arguments as a 16-bit fractional
value within the range <-1 ; 1), which corresponds to the real angle range <- π; π). The function sets
the boolean error flag pointed to by the output parameter if both inputs are zero; in other cases, the
output flag is cleared.
GFLIB_AtanYX_FLT float_t float_t bool_t * float_t
The first input argument is a 32-bit single precision floating-point value, which contains the ordinate
of the input vector (y coordinate). The second input argument is a 32-bit single precision floatingpoint value, which contains the abscissa of the input vector (x coordinate). The result is the
arctangent of the input arguments as a 32-bit single precision floating-point value within the range
<- π; π>. The function sets the boolean error flag pointed to by the output parameter if both inputs
are zero; in other cases, the output flag is cleared.
GFLIB_AtanYX_A32ff float_t float_t bool_t * acc32_t
The first input argument is a 32-bit single precision floating-point value, which contains the ordinate
of the input vector (y coordinate). The second input argument is a 32-bit single precision floatingpoint value, which contains the abscissa of the input vector (x coordinate). The result is the
arctangent of the input arguments as a 32-bit accumulator value within the range <-1 ; 1>, which
corresponds to the real angle range <- π; π>. The function sets the boolean error flag pointed to by
the output parameter if both inputs are zero; in other cases, the output flag is cleared.
GFLIB User's Guide, Rev. 4, 12/2020
48 NXP Semiconductors
Page 49

Chapter 2 Algorithms in detail
2.7.2 Declaration
The available GFLIB_AtanYX functions have the following declarations:
frac16_t GFLIB_AtanYX_F16(frac16_t f16Y, frac16_t f16X, bool_t *pbErrFlag)
float_t GFLIB_AtanYX_FLT(float_t fltY, float_t fltX, bool_t *pbErrFlag)
acc32_t GFLIB_AtanYX_a32ff(float_t fltY, float_t fltX, bool_t *pbErrFlag)
2.7.3 Function use
The use of the GFLIB_AtanYX function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Result;
static frac16_t f16Y, f16X;
static bool_t bErrFlag;
void main(void)
{
f16Y = FRAC16(0.9); /* f16Y = 0.9 */
f16X = FRAC16(0.3); /* f16X = 0.3 */
/* f16Result = atan(f16Y / f16X); f16Result * 180 => angle [degree] */
f16Result = GFLIB_AtanYX_F16(f16Y, f16X, &bErrFlag);
}
Floating-point version:
#include "gflib.h"
static float_t fltResult;
static float_t fltY, fltX;
static bool_t bErrFlag;
void main(void)
{
fltY = 0.9F; /* fltY = 0.9 */
fltX = 0.3F; /* fltX = 0.3 */
/* fltResult = atan(fltY / fltX); fltResult * 180 / 3.14 => angle [degree] */
fltResult = GFLIB_AtanYX_FLT(fltY, fltX, &bErrFlag);
}
2.8
NXP Semiconductors 49
GFLIB_Sqrt
GFLIB User's Guide, Rev. 4, 12/2020
Page 50

GFLIB_Sqrt
The GFLIB_Sqrt function returns the square root of the input value. The input must be a
non-negative number, otherwise the function returns undefined results. See the following
equation:
Equation 6. Algorithm formula
2.8.1 Available versions
This function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <0 ; 1). The function is only defined for non-negative inputs. The
function returns undefined results out of this condition.
• Floating-point output - the output is the floating-point non-negative result. The
function is only defined for non-negative inputs. The function returns undefined
results out of this condition.
The available versions of the GFLIB_Sqrt function are shown in the following table:
Table 2-8. Function versions
Function name Input
type
GFLIB_Sqrt_F16 frac16_t frac16_t The input value is a 16-bit fractional value, limited to the range <0 ; 1). The
GFLIB_Sqrt_F16l frac32_t frac16_t The input value is a 32-bit fractional value, limited to the range <0 ; 1). The
GFLIB_Sqrt_FLT float_t float_t The input value is a 32-bit single precision floating-point non-negative value.
Result
type
Description
function is not defined out of this range. The output is a 16-bit fractional value
within the range <0 ; 1).
function is not defined out of this range. The output is a 16-bit fractional value
within the range <0 ; 1).
The function is not defined for the negative inputs. The output is a 32-bit single
precision floating-point non-negative value.
2.8.2 Declaration
The available GFLIB_Sqrt functions have the following declarations:
frac16_t GFLIB_Sqrt_F16(frac16_t f16Val)
frac16_t GFLIB_Sqrt_F16l(frac32_t f32Val)
float_t GFLIB_Sqrt_FLT(float_t fltVal)
GFLIB User's Guide, Rev. 4, 12/2020
50 NXP Semiconductors
Page 51

Chapter 2 Algorithms in detail
2.8.3 Function use
The use of the GFLIB_Sqrt function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Result;
static frac16_t f16Val;
void main(void)
{
f16Val = FRAC16(0.5); /* f16Val = 0.5 */
/* f16Result = sqrt(f16Val) */
f16Result = GFLIB_Sqrt_F16(f16Val);
}
Floating-point version:
#include "gflib.h"
static float_t fltResult;
static float_t fltVal;
void main(void)
{
fltVal = 0.5F; /* fltVal = 0.5 */
/* fltResult = sqrt(fltVal) */
fltResult = GFLIB_Sqrt_FLT(fltVal);
}
2.9
GFLIB_Limit
The GFLIB_Limit function returns the value limited by the upper and lower limits. See
the following equation:
Equation 7. Algorithm formula
2.9.1
Available versions
This function is available in the following versions:
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 51
Page 52

GFLIB_Limit
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The result may saturate.
• Floating-point output - the output is the floating-point result within the type's full
range.
The available versions of the GFLIB_Limit functions are shown in the following table:
Table 2-9. Function versions
Function name Input type Result
Input Lower
limit
GFLIB_Limit_F16 frac16_t frac16_t frac16_t frac16_t The inputs are 16-bit fractional values within the range
GFLIB_Limit_F32 frac32_t frac32_t frac32_t frac32_t The inputs are 32-bit fractional values within the range
GFLIB_Limit_FLT float_t float_t float_t float_t The inputs are 32-bit single precision floating-point
Upper
limit
type
<-1 ; 1). The function returns a 16-bit fractional value in
the range <f16LLim ; f16ULim>.
<-1 ; 1). The function returns a 32-bit fractional value in
the range <f32LLim ; f32ULim>.
values within the full range. The function returns a 32bit single precision floating-point value in the range
<fltLLim ; fltULim>.
Description
2.9.2 Declaration
The available GFLIB_Limit functions have the following declarations:
frac16_t GFLIB_Limit_F16(frac16_t f16Val, frac16_t f16LLim, frac16_t f16ULim)
frac32_t GFLIB_Limit_F32(frac32_t f32Val, frac32_t f32LLim, frac32_t f32ULim)
float_t GFLIB_Limit_FLT(float_t fltVal, float_t fltLLim, float_t fltULim)
2.9.3
Function use
The use of the GFLIB_Limit function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Val, f16ULim, f16LLim, f16Result;
void main(void)
{
f16ULim = FRAC16(0.8);
f16LLim = FRAC16(-0.3);
f16Val = FRAC16(0.9);
GFLIB User's Guide, Rev. 4, 12/2020
52 NXP Semiconductors
Page 53

f16Result = GFLIB_Limit_F16(f16Val, f16LLim, f16ULim);
}
Floating-point version:
#include "gflib.h"
static float_t fltVal, fltULim, fltLLim, fltResult;
void main(void)
{
fltULim = 0.8F;
fltLLim = -0.3F;
fltVal = 0.9F;
fltResult = GFLIB_Limit_FLT(fltVal, fltLLim, fltULim);
}
Chapter 2 Algorithms in detail
2.10
GFLIB_LowerLimit
The GFLIB_LowerLimit function returns the value limited by the lower limit. See the
following equation:
Equation 8. Algorithm formula
2.10.1
Available versions
This function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The result may saturate.
• Floating-point output - the output is the floating-point result within the type's full
range.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 53
Page 54

GFLIB_LowerLimit
The available versions of the GFLIB_LowerLimit functions are shown in the following
table:
Table 2-10. Function versions
Function name Input type Result
Input Lower
limit
GFLIB_LowerLimit_F16 frac16_t frac16_t frac16_t The inputs are 16-bit fractional values within the range <-1 ;
GFLIB_LowerLimit_F32 frac32_t frac32_t frac32_t The inputs are 32-bit fractional values within the range <-1 ;
GFLIB_LowerLimit_FLT float_t float_t float_t The inputs are 32-bit single precision floating-point values
type
1). The function returns a 16-bit fractional value in the range
<f16LLim ; 1).
1). The function returns a 32-bit fractional value in the range
<f32LLim ; 1).
within the full range. The function returns a 32-bit single
precision floating-point value greater than or equal to fltLLim.
Description
2.10.2 Declaration
The available GFLIB_LowerLimit functions have the following declarations:
frac16_t GFLIB_LowerLimit_F16(frac16_t f16Val, frac16_t f16LLim)
frac32_t GFLIB_LowerLimit_F32(frac32_t f32Val, frac32_t f32LLim)
float_t GFLIB_LowerLimit_FLT(float_t fltVal, float_t fltLLim)
2.10.3
Function use
The use of the GFLIB_LowerLimit function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Val, f16LLim, f16Result;
void main(void)
{
f16LLim = FRAC16(0.3);
f16Val = FRAC16(0.1);
f16Result = GFLIB_LowerLimit_F16(f16Val, f16LLim);
}
Floating-point version:
GFLIB User's Guide, Rev. 4, 12/2020
54 NXP Semiconductors
Page 55

Chapter 2 Algorithms in detail
#include "gflib.h"
static float_t fltVal, fltLLim, fltResult;
void main(void)
{
fltLLim = 0.3F;
fltVal = 0.1F;
fltResult = GFLIB_LowerLimit_FLT(fltVal, fltLLim);
}
2.11 GFLIB_UpperLimit
The GFLIB_UpperLimit function returns the value limited by the upper limit. See the
following equation:
Equation 9. Algorithm formula
2.11.1
Available versions
This function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The result may saturate.
• Floating-point output - the output is the floating-point result within the type's full
range.
The available versions of the GFLIB_UpperLimit functions are shown in the following
table:
Table 2-11. Function versions
Function name Input type Result
Input Upper
limit
GFLIB_UpperLimit_F16 frac16_t frac16_t frac16_t The inputs are 16-bit fractional values within the range <-1 ;
GFLIB_UpperLimit_F32 frac32_t frac32_t frac32_t The inputs are 32-bit fractional values within the range <-1 ;
GFLIB_UpperLimit_FLT float_t float_t float_t The inputs are 32-bit single precision floating-point values
type
1). The function returns a 16-bit fractional value in the range
<-1 ; f16ULim>.
1). The function returns a 32-bit fractional value in the range
<-1 ; f32ULim>.
within the full range. The function returns a 32-bit single
precision floating-point value, which is lower or equal to
fltULim.
Description
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 55
Page 56

GFLIB_VectorLimit
2.11.2 Declaration
The available GFLIB_UpperLimit functions have the following declarations:
frac16_t GFLIB_UpperLimit_F16(frac16_t f16Val, frac16_t f16ULim)
frac32_t GFLIB_UpperLimit_F32(frac32_t f32Val, frac32_t f32ULim)
float_t GFLIB_UpperLimit_FLT(float_t fltVal, float_t fltULim)
2.11.3 Function use
The use of the GFLIB_UpperLimit function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Val, f16ULim, f16Result;
void main(void)
{
f16ULim = FRAC16(0.3);
f16Val = FRAC16(0.9);
f16Result = GFLIB_UpperLimit_F16(f16Val, f16ULim);
}
Floating-point version:
#include "gflib.h"
static float_t fltVal, fltULim, fltResult;
void main(void)
{
fltULim = 0.3F;
fltVal = 0.9F;
fltResult = GFLIB_UpperLimit_FLT(fltVal, fltULim);
}
2.12
GFLIB_VectorLimit
The GFLIB_VectorLimit function returns the limited vector by an amplitude. This
limitation is calculated to achieve the zero angle error.
GFLIB User's Guide, Rev. 4, 12/2020
56 NXP Semiconductors
Page 57

Chapter 2 Algorithms in detail
Figure 2-6. Input and releated output
The GFLIB_VectorLimit function limits the amplitude of the input vector. The input
vector a, b components, are passed into the function as the input arguments. The resulting
limited vector is transformed back into the a, b components. The limitation is performed
according to the following equations:
Equation 10. Algorithm formulas
Equation 11
where:
• a, b are the vector coordinates
• a*, b* are the vector coordinates after limitation
• lim is the maximum amplitude
The relationship between the input and limited output vectors is obvious from Figure 2-6.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 57
Page 58

GFLIB_VectorLimit
If the amplitude of the input vector is greater than the input Lim value, the function
calculates the new coordinates from the Lim value; otherwise the function copies the
input values to the output.
2.12.1 Available versions
The function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1;1). The result may saturate.
• Floating point output - the output is the floating point result within the type's full
range.
The available versions of the GFLIB_VectorLimit functions are shown in the following
table:
Table 2-12. Function versions
Function name Input type Output type Result
Input Limit
GFLIB_VectorLimit_F16 GFLIB_VECTORLIMIT_T_F16 * frac16_t GFLIB_VECTORLIMIT_T_F16 * void
Limitation of a two-component 16-bit fractional vector within the range <-1;1) with a 16-bit
fractional limitation amplitude. The function returns a two-component 16-bit fractional vector.
GFLIB_VectorLimit_FLT GFLIB_VECTORLIMIT_T_FLT * float_t GFLIB_VECTORLIMIT_T_FLT * void
Limitation of a two-component 32-bit single precision floating point vector within the full range
with a 32-bit single precision floating point limitation amplitude. The function returns a twocomponent 32-bit single precision floating point vector.
type
2.12.2 GFLIB_VECTORLIMIT_T_F16 type description
Variable name Input type Description
f16A frac16_t A-component; 16-bit fractional type.
f16B frac16_t B-component; 16-bit fractional type
2.12.3 GFLIB_VECTORLIMIT_T_FLT type description
Variable name Input type Description
fltA float_t A-component; 32-bit single precision floating point type.
fltB float_t B-component; 32-bit single precision floating point type.
GFLIB User's Guide, Rev. 4, 12/2020
58 NXP Semiconductors
Page 59

Chapter 2 Algorithms in detail
2.12.4 Declaration
The available GFLIB_VectorLimit functions have the following declarations:
frac16_t GFLIB_VectorLimit_F16(const GFLIB_VECTORLIMIT_T_F16 *psVectorIn, frac16_t f16Lim,
GFLIB_VECTORLIMIT_T_F16 *psVectorOut)
float_t GFLIB_VectorLimit_FLT(const GFLIB_VECTORLIMIT_T_FLT *psVectorIn, float_t fltLim,
GFLIB_VECTORLIMIT_T_FLT *psVectorOut)
2.12.5
Function use
The use of the GFLIB_VectorLimit function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static GFLIB_VECTORLIMIT_T_F16 sVector, sResult;
static frac16_t f16MaxAmpl;
void main(void)
{
f16MaxAmpl = FRAC16(0.8);
sVector.f16A = FRAC16(-0.79);
sVector.f16B = FRAC16(0.86);
GFLIB_VectorLimit_F16(&sVector, f16MaxAmpl, &sResult);
}
Floating-point version:
#include "gflib.h"
static GFLIB_VECTORLIMIT_T_FLT sVector, sResult;
static float_t fltMaxAmpl;
void main(void)
{
fltMaxAmpl = 0.8F;
sVector.fltA = -0.79F;
sVector.fltB = 0.86F;
GFLIB_VectorLimit_FLT(&sVector, fltMaxAmpl, &sResult);
}
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 59
Page 60

GFLIB_VectorLimit1
2.13 GFLIB_VectorLimit1
The GFLIB_VectorLimit1 function returns the limited vector by an amplitude. This
limitation is calculated to achieve that the first component remains unchanged (if the
limitation factor allows).
Figure 2-7. Input and releated output
The GFLIB_VectorLimit1 function limits the amplitude of the input vector. The input
vector a, b components are passed to the function as the input arguments. The resulting
limited vector is transformed back into the a, b components. The limitation is performed
according to the following equations:
Equation 12
Equation 13
GFLIB User's Guide, Rev. 4, 12/2020
60 NXP Semiconductors
Page 61

Chapter 2 Algorithms in detail
where:
• a, b are the vector coordinates
• a*, b* are the vector coordinates after limitation
• lim is the maximum amplitude
The relationship between the input and limited output vectors is shown in Figure 2-7.
If the amplitude of the input vector is greater than the input Lim value, the function
calculates the new coordinates from the Lim value; otherwise the function copies the
input values to the output.
2.13.1
Available versions
The function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The result may saturate.
• Floating-point output - the output is the floating-point result within the type's full
range.
The available versions of the GFLIB_VectorLimit1 function are shown in the following
table:
Table 2-13. Function versions
Function name Input type Output type Result
Input Limit
GFLIB_VectorLimit1_F16 GFLIB_VECTORLIMIT_T_F16 * frac16_t GFLIB_VECTORLIMIT_T_F16 * void
Limitation of a two-component 16-bit fractional vector within the range <-1 ; 1) with a 16-bit
fractional limitation amplitude. The function returns a two-component 16-bit fractional vector.
GFLIB_VectorLimit1_FLT GFLIB_VECTORLIMIT_T_FLT * float_t GFLIB_VECTORLIMIT_T_FLT * void
Limitation of a two-component 32-bit single precision floating-point vector within the full range
with a 32-bit single precision floating-point limitation amplitude. The function returns a twocomponent 32-bit single precision floating-point vector.
type
2.13.2 GFLIB_VECTORLIMIT_T_F16 type description
Variable name Input type Description
f16A frac16_t A-component; 16-bit fractional type.
f16B frac16_t B-component; 16-bit fractional type.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 61
Page 62

GFLIB_VectorLimit1
2.13.3 GFLIB_VECTORLIMIT_T_FLT type description
Variable name Input type Description
fltA float_t A-component; 32-bit single precision floating-point type.
fltB float_t B-component; 32-bit single precision floating-point type.
2.13.4 Declaration
The available GFLIB_VectorLimit1 functions have the following declarations:
frac16_t GFLIB_VectorLimit1_F16(const GFLIB_VECTORLIMIT_T_F16 *psVectorIn, frac16_t f16Lim,
GFLIB_VECTORLIMIT_T_F16 *psVectorOut)
float_t GFLIB_VectorLimit1_FLT(const GFLIB_VECTORLIMIT_T_FLT *psVectorIn, float_t fltLim,
GFLIB_VECTORLIMIT_T_FLT *psVectorOut)
2.13.5
Function use
The use of the GFLIB_VectorLimit1 function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static GFLIB_VECTORLIMIT_T_F16 sVector, sResult;
static frac16_t f16MaxAmpl;
void main(void)
{
f16MaxAmpl = FRAC16(0.5);
sVector.f16A = FRAC16(-0.4);
sVector.f16B = FRAC16(0.2);
GFLIB_VectorLimit1_F16(&sVector, f16MaxAmpl, &sResult);
}
Floating-point version:
#include "gflib.h"
static GFLIB_VECTORLIMIT_T_FLT sVector, sResult;
static float_t fltMaxAmpl;
GFLIB User's Guide, Rev. 4, 12/2020
62 NXP Semiconductors
Page 63

Chapter 2 Algorithms in detail
void main(void)
{
fltMaxAmpl = 0.8F;
sVector.fltA = -0.79F;
sVector.fltB = 0.86F;
GFLIB_VectorLimit1_FLT(&sVector, fltMaxAmpl, &sResult);
}
2.14 GFLIB_Hyst
The
GFLIB_Hyst function represents a hysteresis (relay) function. The function switches
the output between two predefined values. When the input is higher than the upper
threshold, the output is high; when the input is lower than the lower threshold, the output
is low. When the input is between the two thresholds, the output retains its value. See the
following figure:
Figure 2-8. GFLIB_Hyst functionality
The four points in the figure are to be set up in the parameters structure of the function.
For a proper functionality, the HystOn point must be greater than the HystOff point.
2.14.1
Available versions
This function is available in the following versions:
• Fractional output - the output is the fractional portion of the result, and the result is
within the range <-1 ; 1).
• Floating-point output - the output is the floating-point result within the type's full
range.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 63
Page 64

GFLIB_Hyst
The available versions of the GFLIB_Hyst function are shown in the following table.
Table 2-14. Function versions
Function name Input
type
GFLIB_Hyst_F16 frac16_t GFLIB_HYST_T_F16 * frac16_t The input is a 16-bit fractional value within
GFLIB_Hyst_FLT float_t GFLIB_HYST_T_FLT * float_t The input is a 32-bit single precision
Parameters Result
type
Description
the range <-1 ; 1). The output is a twostate 16-bit fractional value.
floating-point value within its full range.
The output is a two-state 32-bit single
precision floating-point value.
2.14.2 GFLIB_HYST_T_F16
Variable name Input
type
f16HystOn frac16_t The point where the output sets the output to the f16OutValOn value when the input rises.
Set by the user.
f16HystOff frac16_t The point where the output sets the output to the f16OutValOff value when the input falls.
Set by the user.
f16OutValOn frac16_t The ON value. Set by the user.
f16OutValOff frac16_t The OFF value. Set by the user.
f16OutState frac16_t The output state. Set by the algorithm. Must be initialized by the user.
Description
2.14.3 GFLIB_HYST_T_FLT
Variable name Input
type
fltHystOn float_t The point where the output sets the output to the fltOutValOn value when the input rises.
Set by the user.
fltHystOff float_t The point where the output sets the output to the fltOutValOff value when the input falls.
Set by the user.
fltOutValOn float_t The ON value. Set by the user.
fltOutValOff float_t The OFF value. Set by the user.
fltOutState float_t The output state. Set by the algorithm. Must be initialized by the user.
GFLIB User's Guide, Rev. 4, 12/2020
64 NXP Semiconductors
Description
Page 65

Chapter 2 Algorithms in detail
2.14.4 Declaration
The available GFLIB_Hyst functions have the following declarations:
frac16_t GFLIB_Hyst_F16(frac16_t f16Val, GFLIB_HYST_T_F16 *psParam)
float_t GFLIB_Hyst_FLT(float_t fltVal, GFLIB_HYST_T_FLT *psParam)
2.14.5 Function use
The use of the GFLIB_Hyst function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Result, f16InVal;
static GFLIB_HYST_T_F16 sParam;
void main(void)
{
f16InVal = FRAC16(-0.11);
sParam.f16HystOn = FRAC16(0.5);
sParam.f16HystOff = FRAC16(-0.1);
sParam.f16OutValOn = FRAC16(0.7);
sParam.f16OutValOff = FRAC16(0.3);
sParam.f16OutState = FRAC16(0.0);
f16Result = GFLIB_Hyst_F16(f16InVal, &sParam);
}
Floating-point version:
#include "gflib.h"
static float_t fltResult, fltInVal;
static GFLIB_HYST_T_FLT sParam;
void main(void)
{
fltInVal = -0.11F;
sParam.fltHystOn = 0.5F;
sParam.fltHystOff = -0.1F;
sParam.fltOutValOn = 0.7F;
sParam.fltOutValOff = 0.3F;
sParam.fltOutState = 0.0F;
fltResult = GFLIB_Hyst_FLT(fltInVal, &sParam);
}
2.15
GFLIB_Lut1D
The GFLIB_Lut1D function implements the one-dimensional look-up table.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 65
Page 66

GFLIB_Lut1D
Equation 14.
where:
• y is the interpolated value
• y1 and y2 are the ordinate values at the beginning and end of the interpolating
interval, respectively
• x1 and x2 are the abscissa values at the beginning and end of the interpolating
interval, respectively
• x is the input value provided to the function in the X input argument
Figure 2-9. Algorithm diagram - fractional version
The GFLIB_Lut1D function fuses a table of the precalculated function points. These
points are selected with a fixed step.
The fractional version of the algorithm has a defined interval of inputs within the range
<-1 ; 1>. The last table point is intended for the real value of 1, not the value of 1 from
the fraction numbers, which is lower than the real value of 1. The calculations are based
on the same intervals among the table points. The number of points must be 2n + 1, where
n can range from 1 through to 15.
The floating-point version of the algorithm has a defined interval of inputs within the
range <min ; max>, where the min and max values are the parameters of the algorithms.
The number of points is within the range <2 ; 65535>, where the first point lies at the min
position, and the last point lies at the max position.
GFLIB User's Guide, Rev. 4, 12/2020
66 NXP Semiconductors
Page 67

Chapter 2 Algorithms in detail
The function finds two nearest precalculated points of the input argument, and calculates
the output value using the linear interpolation between these two points.
2.15.1 Available versions
This function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1).
• Floating-point output - the output is the floating-point result within the type's full
range. The input values are defined by the minimum and maximum input parameters
of the GFLIB_Lut1DInit function.
The available versions of the GFLIB_Lut1DInit function are shown in the following
table:
Table 2-15. Init function versions
Function name Input type Parameters Result
Min Max Table size Table
GFLIB_Lut1DInit_FLT float_t float_t uint16_t GFLIB_LUT1D_T_FLT * void
The input arguments are the 32-bit single precision floating-point values that contain the minimum
and maximum x-coordinates of the look-up table. The table size parameter can be in the range <2 ;
65535> and the pointer to the structure that contains the parameters defined in Table 2-16.
type
The available versions of the GFLIB_Lut1D function are shown in the following table:
Table 2-16. Function versions
Function name Input type Parameters Result type
Table Table size
GFLIB_Lut1D_F16 frac16_t frac16_t * uint16_t frac16_t
The input arguments are the 16-bit fractional value that contains the abscissa for which the 1-D
interpolation is performed, the pointer to a table which contains the 16-bit fractional values of the
look-up table, and the size of the look-up table. The table size parameter can be in the range <1 ;
15> (that means the parameter is log2 of the number of points + 1). The output is the interpolated 16bit fractional value computed from the look-up table.
GFLIB_Lut1D_F32 frac32_t frac32_t * uint16_t frac32_t
The input arguments are the 32-bit fractional value that contains the abscissa for which the 1-D
interpolation is performed, the pointer to a table which contains the 32-bit fractional values of the
look-up table, and the size of the look-up table. The table size parameter can be in the range <1 ;
15> (that means the parameter is log2 of the number of points + 1). The output is the interpolated 32bit fractional value computed from the look-up table.
GFLIB_Lut1D_FLT float_t float_t * GFLIB_LUT1D_T_FLT * float_t
Table continues on the next page...
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 67
Page 68

GFLIB_Lut1D
Table 2-16. Function versions (continued)
Function name Input type Parameters Result type
Table Table size
The input arguments are the 32-bit single precision floating-point value that contains the abscissa for
which the 1-D interpolation is performed, the pointer to a table which contains the 32-bit single
precision floating-point values of the look-up table, and the pointer to a structure that contains the
size of the look-up table together with the minimum and maximum borders of the input interval. The
table size parameter can be in the range <2 ; 65535>. The first value of the table is located at the
fltMin position, and the last value of the table is located at the fltMax position. The output is the
interpolated 32-bit single precision floating-point value computed from the look-up table.
2.15.2 GFLIB_LUT1D_T_FLT type description
Variable name Input type Description
fltMin float_t The minimum of the look-up table x-coordinate; a 32-bit single precision floating-point type.
Set by the user in GFLIB_Lut1DInit_FLT.
fltMax float_t The maximum of the look-up table x-coordinate; a 32-bit single precision floating-point
type. Set by the user in GFLIB_Lut1DInit_FLT.
fltIntInv float_t Inverse interval of the look-up table; a 32-bit single precision floating-point type. Set by the
algoritm in GFLIB_Lut1DInit_FLT.
u16TableSize uint16_t Size of the table; a 16-bit unsigned integer type within the range <2 ; 65535>. Set by the
user in GFLIB_Lut1DInit_FLT.
2.15.3 Declaration
The available GFLIB_Lut1D functions have the following declarations:
frac16_t GFLIB_Lut1D_F16(frac16_t f16X, const frac16_t *pf16Table, uint16_t u16TableSize)
void GFLIB_Lut1DInit_FLT(float_t fltMin,float_t fltMax, uint16_t u16TableSize, const
GFLIB_LUT1D_T_FLT *psParam)
float_t GFLIB_Lut1D_FLT(float_t fltX, const float_t *pfltTable, const GFLIB_LUT1D_T_FLT
*psParam)
2.15.4
The use of the GFLIB_Lut1D function is shown in the following examples:
Fixed-point version:
68 NXP Semiconductors
Function use
GFLIB User's Guide, Rev. 4, 12/2020
Page 69

Chapter 2 Algorithms in detail
#include "gflib.h"
static frac16_t f16Result, f16X;
static uint16_t u16TableSize;
static frac16_t f16Table[9] = {FRAC16(0.8), FRAC16(0.1), FRAC16(-0.2), FRAC16(0.7),
FRAC16(0.2), FRAC16(-0.3), FRAC16(-0.8), FRAC16(0.91), FRAC16(0.99)};
void main(void)
{
u16TableSize = 3; /* size of table = 2 ^ 3 + 1 */
f16X = FRAC16(0.625); /* f16X = 0.625 */
/* f16Result = value from look-up table between 7th and 8th position */
f16Result = GFLIB_Lut1D_F16(f16X, f16Table, u16TableSize);
}
Floating-point version:
#include "gflib.h"
static float_t fltResult, fltX;
GFLIB_LUT1D_T_FLT sParam;
static float_t fltTable[9] = {0.8F, 0.1F, -0.2F, 0.7F, 0.2F, -0.3F, -0.8F, 0.9F, 0.99F};
void main(void)
{
fltX = 0.25F; /* fltX = 0.25 */
sParam.fltMin = 0.0F;
sParam.fltMax = 8.0F;
sParam.u16TableSize = 9;
GFLIB_Lut1DInit_FLT(sParam.fltMin, sParam.fltMax, sParam.u16TableSize, &sParam);
}
/* periodically called function */
void Isr()
{
fltResult = GFLIB_Lut1D_FLT(fltX, fltTable, &sParam);
}
2.16
GFLIB_LutPer1D
The GFLIB_LutPer1D function approximates the one-dimensional arbitrary user function
using the interpolation look-up method. It is periodic.
Equation 15.
where:
• y is the interpolated value
• y1 and y2 are the ordinate values at the beginning and end of the interpolating
interval, respectively
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 69
Page 70

GFLIB_LutPer1D
• x1 and x2 are the abscissa values at the beginning and end of the interpolating
interval, respectively
• x is the input value provided to the function in the X input argument
Figure 2-10. Algorithm diagram - fractional version
The GFLIB_LutPer1D fuses a table of the pre-calculated function points. These points
are selected with a fixed step.
The fractional version of the algorithm has a defined interval of inputs within the range
<-1 ; 1>. The last table point is intended for the real value of 1 not the value of 1 from the
fraction numbers, which is lower than the real value of 1. The calculations are based on
the same intervals among the table points. The floating-point version of the algorithm has
a defined interval of inputs within the range <min ; max>, where the min and max values
are the parameters of the algorithms. The number of points is within the range <2 ;
65535>, where the first point lies at the min position, and the last point lies at the max
position.
The function finds two nearest precalculated points of the input argument, and calculates
the output value using the linear interpolation between these two points. This algorithm
serves for periodical functions. That means that when the input argument lies behind the
last pre-calculated point of the function, the interpolation is calculated between the last
and first points of the table.
2.16.1
Available versions
This function is available in the following versions:
GFLIB User's Guide, Rev. 4, 12/2020
70 NXP Semiconductors
Page 71

Chapter 2 Algorithms in detail
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1).
• Floating-point output - the output is the floating-point result within the type's full
range. The input values are defined by the minimum and maximum input parameter
of the GFLIB_LutPer1DInit function.
The available versions of the GFLIB_LutPer1DInit function are shown in the following
table:
Table 2-17. Init function versions
Function name Input type Parameters Result
Min Max Table size Table
GFLIB_LutPer1DInit_FLT float_t float_t uint16_t GFLIB_LUT1D_T_FLT * void
The input arguments are the 32-bit single precision floating-point values that contain the
minimum and maximum x-coordinates of the periodic look-up table. The table size parameter can
be in the range <2 ; 65535> and the pointer to the structure that contains the parameters defined
in .Table 2-18
type
The available versions of the GFLIB_LutPer1D function are shown in the following
table:
Table 2-18. Function versions
Function name Input type Parameters Result type
Table Table size
GFLIB_LutPer1D_F16 frac16_t frac16_t * uint16_t frac16_t
The input arguments are the 16-bit fractional value that contains the abscissa for which the 1-D
interpolation is performed, the pointer to a structure which contains the 16-bit fractional values of
the periodic look-up table, and the size of the look-up table. The table size parameter can be in
the range <1 ; 15> (that means the parameter is log2 of the number of points). The output is the
interpolated 16-bit fractional value computed from the periodic look-up table.
GFLIB_LutPer1D_F32 frac32_t frac32_t * uint16_t frac32_t
The input arguments are the 32-bit fractional value that contains the abscissa for which the 1-D
interpolation is performed, the pointer to a table which contains the 32-bit fractional values of the
periodic look-up table, and the size of the periodic look-up table. The table size parameter can be
in the range <1 ; 15> (that means the parameter is log2 of the number of points). The output is
the interpolated 32-bit fractional value computed from the periodic look-up table.
GFLIB_LutPer1D_FLT float_t float_t * GFLIB_LUT1D_T_FLT * float_t
The input arguments are the 32-bit single precision floating-point value that contains the abscissa
for which the 1-D interpolation is performed, the pointer to a structure which contains the 32-bit
single precision floating-point values of the periodic look-up table, and the pointer a to structure
that contains the size of the periodic look-up table together with the minimum and maximum
borders of the input interval. The table size parameter can be in the range <2 ; 65535>. The first
value of the table is located at the fltMin position, and the last value of the table is located at the
fltMax position. The output is the interpolated 32-bit single precision floating-point value
computed from the periodic look-up table.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 71
Page 72

GFLIB_LutPer1D
2.16.2 GFLIB_LUTPER1D_T_FLT type description
Variable name Input type Description
fltMin float_t The minimum of the periodic look-up table x-coordinate; a 32-bit single precision floating-
point type. Set by the user in GFLIB_LutPer1DInit_FLT.
fltMax float_t The maximum of the periodic look-up table x-coordinate; a 32-bit single precision floating-
point type. Set by the user in GFLIB_LutPer1DInit_FLT.
fltIntInv float_t Inverse interval of the periodic look-up table; a 32-bit single precision floating-point type.
Set by the algorithm in GFLIB_LutPer1DInit_FLT.
u16TableSize uint16_t Size of the table; a 16-bit unsigned integer type within the range <2 ; 65535>. Set by the
user in GFLIB_LutPer1DInit_FLT.
2.16.3 Declaration
The available GFLIB_LutPer1D functions have the following declarations:
frac16_t GFLIB_LutPer1D_F16(frac16_t f16X, const frac16_t *pf16Table, uint16_t u16TableSize)
void GFLIB_LutPer1DInit_FLT(float_t fltMin,float_t fltMax, uint16_t u16TableSize, const
GFLIB_LUTPER1D_T_FLT *psParam)
float_t GFLIB_LutPer1D_FLT(float_t fltX, const float_t *pfltTable, const
GFLIB_LUTPER1D_T_FLT *psParam)
2.16.4
Function use
The use of the GFLIB_LutPer1D function is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16Result, f16X;
static uint16_t u16TableSize;
static frac16_t f16Table[8] = {FRAC16(0.8), FRAC16(0.1), FRAC16(-0.2), FRAC16(0.7),
FRAC16(0.2), FRAC16(-0.3), FRAC16(-0.8), FRAC16(0.91)};
void main(void)
{
u16TableSize = 3; /* size of table = 2 ^ 3 */
f16X = FRAC16(0.25); /* f16X = 0.25 */
/* f16Result = value from periodic look-up table at 6th position */
f16Result = GFLIB_LutPer1D_F16(f16X, f16Table, u16TableSize);
}
GFLIB User's Guide, Rev. 4, 12/2020
72 NXP Semiconductors
Page 73

Chapter 2 Algorithms in detail
Floating-point version:
#include "gflib.h"
static float_t fltResult, fltX;
static float_t fltTable[8] = {0.8F, 0.1F, -0.2F, 0.7F, 0.2F, -0.3F, -0.8F, 0.9F};
GFLIB_LUTPER1D_T_FLT sParam;
void Isr(void);
void main(void)
{
fltX = 0.25F; /* fltX = 0.25 */
sParam.fltMin = 0.0F;
sParam.fltMax = 7.0F;
sParam.u16TableSize = 8;
GFLIB_LutPer1DInit_FLT(sParam.fltMin, sParam.fltMax, sParam.u16TableSize, &sParam);
}
/* periodically called function */
void Isr()
{
fltResult = GFLIB_LutPer1D_FLT(fltX, fltTable, &sParam);
}
2.17
GFLIB_Ramp
The GFLIB_Ramp function calculates the up / down ramp with the defined fixed-step
increment / decrement. These two parameters must be set by the user.
For a proper use, it is recommended that the algorithm is initialized by the
GFLIB_RampInit function, before using the GFLIB_Ramp function. The
GFLIB_RampInit function initializes the internal state variable of the GFLIB_Ramp
algorithm with a defined value. You must call the init function when you want the ramp
to be initialized.
The use of the GFLIB_Ramp function is as follows: If the target value is greater than the
ramp state value, the function adds the ramp-up value to the state output value. The
output will not trespass the target value, that means it will stop at the target value. If the
target value is lower than the state value, the function subtracts the ramp-down value
from the state value. The output is limited to the target value, that means it will stop at the
target value. This function returns the actual ramp output value. As time passes, it is
approaching the target value by step increments defined in the algorithm parameters'
structure. The functionality of the implemented ramp algorithm is explained in the next
figure:
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 73
Page 74

GFLIB_Ramp
Figure 2-11. GFLIB_Ramp functionality
2.17.1
Available versions
This function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The result may saturate.
• Floating-point output - the output is the floating-point result within the type's full
range.
The available versions of the GFLIB_RampInit functions are shown in the following
table:
Table 2-19. Init function versions
Function name Input
type
GFLIB_RampInit_F16 frac16_t GFLIB_RAMP_T_F16 * void Input argument is a 16-bit fractional value that
GFLIB_RampInit_F32 frac32_t GFLIB_RAMP_T_F32 * void Input argument is a 32-bit fractional value that
Parameters Result
type
Description
represents the initialization value. The
parameters' structure is pointed to by a pointer.
The input data value is in the range <-1 ; 1).
represents the initialization value. The
parameters' structure is pointed to by a pointer.
The input data value is in the range <-1 ; 1).
Table continues on the next page...
GFLIB User's Guide, Rev. 4, 12/2020
74 NXP Semiconductors
Page 75

Chapter 2 Algorithms in detail
Table 2-19. Init function versions (continued)
Function name Input
type
GFLIB_RampInit_FLT float_t GFLIB_RAMP_T_FLT * void Input argument is a 32-bit single precision
Parameters Result
type
Description
floating-point value that represents the
initialization value. The parameters' structure is
pointed to by a pointer. The input value is within
the full 32-bit single-point floating-point range.
The available versions of the GFLIB_Ramp functions are shown in the following table:
Table 2-20. Function versions
Function name Input
type
GFLIB_Ramp_F16 frac16_t GFLIB_RAMP_T_F16 * frac16_t Input argument is a 16-bit fractional value that
GFLIB_Ramp_F32 frac32_t GFLIB_RAMP_T_F32 * frac32_t Input argument is a 32-bit fractional value that
GFLIB_Ramp_FLT float_t GFLIB_RAMP_T_FLT * float_t Input argument is a 32-bit single precision floating-
Parameters Result
type
Description
represents the target output value. The
parameters' structure is pointed to by a pointer.
The function returns a 16-bit fractional value,
which represents the actual ramp output value.
The input data value is in the range <-1 ; 1), and
the output data value is in the range <-1 ; 1).
represents the target output value. The
parameters' structure is pointed to by a pointer.
The function returns a 32-bit fractional value,
which represents the actual ramp output value.
The input data value is in the range <-1 ; 1), and
the output data value is in the range <-1 ; 1).
point value that represents the target output value.
The parameters' structure is pointed to by a
pointer. The function returns a 32-bit single
precision floating-point value, which represents
the actual ramp output value. The input and output
values are within the full 32-bit single-point
floating-point range.
2.17.2 GFLIB_RAMP_T_F16
Variable name Type Description
f16State frac16_t Actual value - controlled by the algorithm.
f16RampUp frac16_t Value of the ramp-up increment. The data value is in the range <0 ; 1). Set by the user.
f16RampDown frac16_t Value of the ramp-down increment. The data value is in the range <0 ; 1). Set by the user.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 75
Page 76

GFLIB_Ramp
2.17.3 GFLIB_RAMP_T_F32
Variable name Type Description
f32State frac32_t Actual value - controlled by the algorithm.
f32RampUp frac32_t Value of the ramp-up increment. The data value is in the range <0 ; 1). Set by the user.
f32RampDown frac32_t Value of the ramp-down increment. The data value is in the range <0 ; 1). Set by the user.
2.17.4 GFLIB_RAMP_T_FLT
Variable name Type Description
fltState float_t Actual value - controlled by the algorithm.
fltRampUp float_t Value of the ramp-up increment. The data value is within the full 32-bit single precision
floating point. Set by the user as non- negative value.
fltRampDown float_t Value of the ramp-down increment. The data value is within the full 32-bit single precision
floating point. Set by the user as non- negative value.
2.17.5 Declaration
The available GFLIB_RampInit functions have the following declarations:
void GFLIB_RampInit_F16(frac16_t f16InitVal, GFLIB_RAMP_T_F16 *psParam)
void GFLIB_RampInit_F32(frac32_t f32InitVal, GFLIB_RAMP_T_F32 *psParam)
void GFLIB_RampInit_FLT(float_t fltInitVal, GFLIB_RAMP_T_FLT *psParam)
The available GFLIB_Ramp functions have the following declarations:
frac16_t GFLIB_Ramp_F16(frac16_t f16Target, GFLIB_RAMP_T_F16 *psParam)
frac32_t GFLIB_Ramp_F32(frac32_t f32Target, GFLIB_RAMP_T_F32 *psParam)
float_t GFLIB_Ramp_FLT(float_t fltTarget, GFLIB_RAMP_T_FLT *psParam)
2.17.6
The use of the GFLIB_RampInit and GFLIB_Ramp functions is shown in the following
examples:
Fixed-point version:
Function use
#include "gflib.h"
static frac16_t f16InitVal;
static GFLIB_RAMP_T_F16 sParam;
static frac16_t f16Target, f16Result;
GFLIB User's Guide, Rev. 4, 12/2020
76 NXP Semiconductors
Page 77

void Isr(void);
void main(void)
{
sParam.f16RampUp = FRAC16(0.1);
sParam.f16RampDown = FRAC16(0.02);
f16Target = FRAC16(0.75);
f16InitVal = FRAC16(0.9);
GFLIB_RampInit_F16(f16InitVal, &sParam);
}
/* periodically called function */
void Isr()
{
f16Result = GFLIB_Ramp_F16(f16Target, &sParam);
}
Floating-point version:
#include "gflib.h"
static float_t fltInitVal;
static GFLIB_RAMP_T_FLT psParam;
static float_t fltTarget, fltResult;
Chapter 2 Algorithms in detail
void Isr(void);
void main(void)
{
psParam.fltRampUp = 0.1F;
psParam.fltRampDown = 0.02F;
fltTarget = 0.75F;
fltInitVal = 0.9F;
GFLIB_RampInit_FLT(fltInitVal, &psParam);
}
/* periodically called function */
void Isr()
{
fltResult = GFLIB_Ramp_FLT(fltTarget, &psParam);
}
2.18
GFLIB_DRamp
The GFLIB_DRamp function calculates the up / down ramp with the defined step
increment / decrement. The algorithm approaches the target value when the stop flag is
not set, and/or returns to the instant value when the stop flag is set.
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 77
Page 78

GFLIB_DRamp
Figure 2-12. GFLIB_DRamp functionality
For a proper use, it is recommended that the algorithm is initialized by the
GFLIB_DRampInit function, before using the GFLIB_DRamp function. This function
initializes the internal state variable of GFLIB_DRamp algorithm with the defined value.
You must call this function when you want the ramp to be initialized.
The GFLIB_DRamp function calculates a ramp with a different set of up / down
parameters, depending on the state of the stop flag. If the stop flag is cleared, the function
calculates the ramp of the actual state value towards the target value, using the up or
down increments contained in the parameters' structure. If the stop flag is set, the
function calculates the ramp towards the instant value, using the up or down saturation
increments.
If the target value is greater than the state value, the function adds the ramp-up value to
the state value. The output cannot be greater than the target value (case of the stop flag
being cleared), nor lower than the instant value (case of the stop flag being set).
If the target value is lower than the state value, the function subtracts the ramp-down
value from the state value. The output cannot be lower than the target value (case of the
stop flag being cleared), nor greater than the instant value (case of the stop flag being
set).
If the actual internal state reaches the target value, the reach flag is set.
GFLIB User's Guide, Rev. 4, 12/2020
78 NXP Semiconductors
Page 79

Chapter 2 Algorithms in detail
2.18.1 Available versions
The function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The result may saturate.
• Floating-point output - the output is the floating-point result within the type's full
range.
The available versions of the GFLIB_DRampInit function are shown in the following
table:
Table 2-21. Init function versions
Function name Input
type
GFLIB_DRampInit_F16 frac16_t GFLIB_DRAMP_T_F16 * void Input argument is a 16-bit fractional value
GFLIB_DRampInit_F32 frac32_t GFLIB_DRAMP_T_F32 * void Input argument is a 32-bit fractional value
GFLIB_DRampInit_FLT float_t GFLIB_DRAMP_T_FLT * void Input argument is a 32-bit single precision
Parameters Result
type
Description
that represents the initialization value. The
parameters' structure is pointed to by a
pointer. The input data value is in the range
<-1 ; 1).
that represents the initialization value. The
parameters' structure is pointed to by a
pointer. The input data value is in the range
<-1 ; 1).
floating-point value that represents the
initialization value. The parameters'
structure is pointed to by a pointer. The
input value is within the full 32-bit singlepoint floating-point range.
The available versions of the GFLIB_DRamp function are shown in the following table:
Table 2-22. Function versions
Function name Input type Parameters Result type
Target Instant Stop flag
GFLIB_DRamp_F16 frac16_t frac16_t bool_t * GFLIB_DRAMP_T_F16 * frac16_t
The target and instant arguments are 16-bit fractional values. The parameters' structure is pointed to
by a pointer. The function returns a 16-bit fractional value, which represents the actual ramp output
value. The input data values are in the range of <-1 ; 1), the Stop flag parameter is a pointer to a
boolean value, and the output data value is in the range <-1 ; 1).
GFLIB_DRamp_F32 frac32_t frac32_t bool_t * GFLIB_DRAMP_T_F32 * frac32_t
Table continues on the next page...
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 79
Page 80

GFLIB_DRamp
Table 2-22. Function versions (continued)
Function name Input type Parameters Result type
Target Instant Stop flag
The target and instant arguments are 32-bit fractional values. The parameters' structure is pointed to
by a pointer. The function returns a 32-bit fractional value, which represents the actual ramp output
value. The input data values are in the range <-1 ; 1), the Stop flag parameter is a pointer to a boolean
value, and the output data value is in the range <-1 ; 1).
GFLIB_DRamp_FLT float_t float_t bool_t * GFLIB_DRAMP_T_FLT * float_t
The target and instant arguments are 32-bit single precision floating-point values. The parameters'
structure is pointed to by a pointer. The function returns a 32-bit single precision floating-point value,
which represents the actual ramp output value. The input and output values are within the full 32-bit
single-point floating-point range, the Stop flag parameter is a pointer to a boolean value.
2.18.2 GFLIB_DRAMP_T_F16
Variable name Type Description
f16State frac16_t Actual value - controlled by the algorithm.
f16RampUp frac16_t Value of non-saturation ramp-up increment. The data value is in the range <0 ; 1). Set by
the user.
f16RampDown frac16_t Value of non-saturation ramp-down increment. The data value is in the range <0 ; 1). Set
by the user.
f16RampUpSat frac16_t Value of saturation ramp-up increment. The data value is in the range <0 ; 1). Set by the
user.
f16RampDownSat frac16_t Value of saturation ramp-down increment. The data value is in the range <0 ; 1). Set by the
user.
bReachFlag bool_t If the actual state value reaches the target value, this flag is set, otherwise, it is cleared.
Set by the algorithm.
2.18.3 GFLIB_DRAMP_T_F32
Variable name Type Description
f32State frac32_t Actual value - controlled by the algorithm.
f32RampUp frac32_t Value of non-saturation ramp-up increment. The data value is in the range <0 ; 1). Set by
the user.
f32RampDown frac32_t Value of non-saturation ramp-down increment. The data value is in the range <0 ; 1). Set
by the user.
f32RampUpSat frac32_t Value of saturation ramp-up increment. The data value is in the range <0 ; 1). Set by the
user.
f32RampDownSat frac32_t Value of saturation ramp-down increment. The data value is in the range <0 ; 1). Set by the
user.
Table continues on the next page...
GFLIB User's Guide, Rev. 4, 12/2020
80 NXP Semiconductors
Page 81

Chapter 2 Algorithms in detail
Variable name Type Description
bReachFlag bool_t If the actual state value reaches the target value, this flag is set, otherwise, it is cleared.
Set by the algorithm.
2.18.4 GFLIB_DRAMP_T_FLT
Variable name Type Description
fltState float_t Actual value - controlled by the algorithm.
fltRampUp float_t Value of non-saturation ramp-up increment. The data value is within the full 32-bit single
precision floating point. Set by the user as non- negative value.
fltRampDown float_t Value of non-saturation ramp-down increment. The data value is within the full 32-bit single
precision floating point. Set by the user as non- negative value.
fltRampUpSat float_t Value of saturation ramp-up increment. The data value is within the full 32-bit single
precision floating point. Set by the user as non- negative value.
fltRampDownSat float_t Value of saturation ramp-down increment. The data value is within the full 32-bit single
precision floating point. Set by the user as non- negative value.
bReachFlag bool_t If the actual state value reaches the target value, this flag is set, otherwise, it is cleared.
Set by the algorithm.
2.18.5 Declaration
The available GFLIB_DRampInit functions have the following declarations:
void GFLIB_DRampInit_F16(frac16_t f16InitVal, GFLIB_DRAMP_T_F16 *psParam)
void GFLIB_DRampInit_F32(frac32_t f32InitVal, GFLIB_DRAMP_T_F32 *psParam)
void GFLIB_DRampInit_FLT(float_t fltInitVal, GFLIB_DRAMP_T_FLT *psParam)
The available GFLIB_DRamp functions have the following declarations:
frac16_t GFLIB_DRamp_F16(frac16_t f16Target, frac16_t f16Instant, const bool_t *pbStopFlag,
GFLIB_DRAMP_T_F16 *psParam)
frac32_t GFLIB_DRamp_F32(frac32_t f32Target, frac32_t f32Instant, const bool_t *pbStopFlag,
GFLIB_DRAMP_T_F32 *psParam)
float_t GFLIB_DRamp_FLT(float_t fltTarget, float_t fltInstant, const bool_t *pbStopFlag,
GFLIB_DRAMP_T_FLT *psParam)
2.18.6
The use of the GFLIB_DRampInit and GFLIB_DRamp functions is shown in the
following examples:
Function use
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 81
Page 82

GFLIB_DRamp
Fixed-point version:
#include "gflib.h"
static frac16_t f16InitVal, f16Target, f16Instant, f16Result;
static GFLIB_DRAMP_T_F16 sParam;
static bool_t bStopFlag;
void Isr(void);
void main(void)
{
sParam.f16RampUp = FRAC16(0.05);
sParam.f16RampDown = FRAC16(0.02);
sParam.f16RampUpSat = FRAC16(0.025);
sParam.f16RampDownSat = FRAC16(0.01);
f16Target = FRAC16(0.7);
f16InitVal = FRAC16(0.3);
f16Instant = FRAC16(0.6);
bStopFlag = FALSE;
GFLIB_DRampInit_F16(f16InitVal, &sParam);
}
/* periodically called function */
void Isr()
{
f16Result = GFLIB_DRamp_F16(f16Target, f16Instant, &bStopFlag, &sParam);
}
Floating-point version:
#include "gflib.h"
static float_t fltInitVal, fltTarget, fltInstant, fltResult;
static GFLIB_DRAMP_T_FLT psParam;
static bool_t bStopFlag;
void Isr(void);
void main(void)
{
psParam.fltRampUp = 0.05F;
psParam.fltRampDown = 0.02F;
psParam.fltRampUpSat = 0.025F;
psParam.fltRampDownSat = 0.01F;
fltTarget = 0.7F;
fltInitVal = 0.3F;
fltInstant = 0.6F;
bStopFlag = FALSE;
GFLIB_DRampInit_FLT(fltInitVal, &psParam);
}
/* periodically called function */
void Isr()
{
fltResult = GFLIB_DRamp_FLT(fltTarget, fltInstant, &bStopFlag, &psParam);
}
GFLIB User's Guide, Rev. 4, 12/2020
82 NXP Semiconductors
Page 83

Chapter 2 Algorithms in detail
2.19 GFLIB_FlexRamp
The GFLIB_FlexRamp function calculates the up/down ramp with a fixed-step increment
that is calculated according to the required speed change per a defined duration. These
parameters must be set by the user.
The GFLIB_FlexRamp algorithm consists of three functions that must be used for a
proper functionality of the algorithm:
• GFLIB_FlexRampInit - this function initializes the state variable with a defined
value and clears the reach flag
• GFLIB_FlexRampCalcIncr - this function calculates the increment and clears the
reach flag
• GFLIB_FlexRamp - this function calculates the ramp in the periodically called loop
For a proper use, it is recommended to initialize the algorithm by the
GFLIB_FlexRampInit function. The GFLIB_FlexRampInit function initializes the
internal state variable of the algorithm with a defined value and clears the reach flag. Call
the init function when you want to initialize the ramp.
To calculate the increment, use the GFLIB_FlexRampCalcIncr function. This function is
called at the point when you want to change the ramp output value. This function's inputs
are the target value and duration. The target value is the destination value that you want
to get to. The duration is the time required to change the ramp output from the actual state
to the target value. To be able to calculate the ramp increment, fill the control structure
with the sample time, that means the period of the loop where the GFLIB_FlexRamp
function is called. The structure also contains a variable which determines the maximum
value of the increment. It is necessary to set it up too. The equation for the increment
calculation is as follows:
Equation 16.
where:
• I is the increment
• Vt is the target value
• Vs is the state (actual) value (in the structure)
• T is the duration of the ramp (to reach the target value starting at the state value)
• Ts is the sample time, that means the period of the loop where the ramp algorithm is
called (set in the structure)
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 83
Page 84

GFLIB_FlexRamp
If the increment is greater than the maximum increment (set in the structure), the
increment uses the maximum increment value.
As soon as the new increment is calculated, call the GFLIB_FlexRamp algorithm in the
periodical control loop. The function works as follows: The function adds the increment
to the state value (from the previous step), which results in a new state. The new state is
returned by the function. As the time passes, the algorithm is approaching the target
value. If the new state trespasses the target value, that new state is limited to the target
value and the reach flag is set. The functionality of the implemented algorithm is shown
in this figure:
Figure 2-13. GFLIB_FlexRamp functionality
2.19.1
Available versions
This function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The input parameters are the fractional and accumulator
types.
• Floating-point output - the output is the floating-point result within the type's full
range.
GFLIB User's Guide, Rev. 4, 12/2020
84 NXP Semiconductors
Page 85

Chapter 2 Algorithms in detail
The available versions of the GFLIB_FlexRampInit function are shown in the following
table:
Table 2-23. Init function versions
Function name Input
type
GFLIB_FlexRampInit_F16 frac16_t GFLIB_FLEXRAMP_T_F32 * void The input argument is a 16-bit
GFLIB_FlexRampInit_FLT float_t GFLIB_FLEXRAMP_T_FLT * void The input argument is a 32-bit
Parameters Result
type
Description
fractional value that represents the
initialization value. The
parameters' structure is pointed to
by a pointer. The input data value
is in the range <-1 ; 1).
single precision floating-point
value that represents the
initialization value. The
parameters' structure is pointed to
by a pointer. The input value is
within the full 32-bit single-point
floating-point range.
The available versions of the GFLIB_FlexRamp function are shown in the following
table:
Table 2-24. Increment calculation function versions
Function name Input type Parameters Result
Target Duration
GFLIB_FlexRampCalcIncr_F16 frac16_t acc32_t GFLIB_FLEXRAMP_T_F32 * void
The input arguments are a 16-bit fractional value in the range <-1 ; 1) that represents
the target output value and a 32-bit accumulator value in the range (0 ; 65536.0) that
represents the duration of the ramp (in seconds) to reach the target value. The
parameters' structure is pointed to by a pointer.
GFLIB_FlexRampCalcIncr_FLT float_t float_t GFLIB_FLEXRAMP_T_FLT * void
The input arguments are 32-bit single precision floating-point values that represent
the target output value and the duration of the ramp (in seconds, except zero value)
to reach the target value. The parameters' structure is pointed to by a pointer. The
target argument is within the full range; the duration argument is a non-negative
value.
type
Table 2-25. Function versions
Function name Parameters Result
type
GFLIB_FlexRamp_F16 GFLIB_FLEXRAMP_T_F32 * frac16_t The parameters' structure is pointed to by a
pointer. The function returns a 16-bit fractional
value, which represents the actual ramp
output value. The output data value is in the
range <-1 ; 1).
Table continues on the next page...
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 85
Description
Page 86

GFLIB_FlexRamp
Table 2-25. Function versions (continued)
Function name Parameters Result
type
GFLIB_FlexRamp_FLT GFLIB_FLEXRAMP_T_FLT * float_t The parameters' structure is pointed to by a
pointer. The function returns a 32-bit single
precision floating-point value, which
represents the actual ramp output value. The
output value is within the full 32-bit singlepoint floating-point range.
Description
2.19.2 GFLIB_FLEXRAMP_T_F32
Variable name Type Description
f32State frac32_t The actual value. Controlled by the GFLIB_FlexRampInit_F16 and GFLIB_FlexRamp_F16
algorithms.
f32Incr frac32_t The value of the flex ramp increment. Controlled by the GFLIB_FlexRampCalcIncr_F16
algorithm.
f32Target frac32_t The target value of the flex ramp algorithm. Controlled by the
GFLIB_FlexRampCalcIncr_F16 algorithm.
f32Ts frac32_t The sample time, that means the period of the loop where the GFLIB_FlexRamp_F16
algorithms are periodically called. The data value (in seconds) is in the range (0 ; 1). Set by
the user.
f32IncrMax frac32_t The maximum value of the flex ramp increment. The data value is in the range (0 ; 1). Set
by the user.
bReachFlag bool_t The reach flag. This flag is controlled by the GFLIB_FlexRamp_F16 algorithm. It is cleared
by the GFLIB_FlexRampInit_F16 and GFLIB_FlexRampCalcIncr_F16 algorithms.
2.19.3 GFLIB_FLEXRAMP_T_FLT
Variable name Type Description
fltState float_t The actual value. Controlled by the GFLIB_FlexRampInit_FLT and GFLIB_FlexRamp_FLT
algorithms.
fltIncr float_t The value of the flex ramp increment. Controlled by the GFLIB_FlexRampCalcIncr_FLT
algorithm.
fltTarget float_t The target value of the flex ramp algorithm. Controlled by the
GFLIB_FlexRampCalcIncr_FLT algorithm.
fltTs float_t The sample time, that means the period of the loop where the GFLIB_FlexRamp_FLT
algorithm is periodically called. The data value (in seconds, except zero value) is a nonnegative value. Set by the user.
fltIncrMax float_t The maximum value of the flex ramp increment. The data is a positive value. Set by the
user.
bReachFlag bool_t The reach flag. This flag is controlled by the GFLIB_FlexRamp_FLT algorithm. It is cleared
by the GFLIB_FlexRampInit_FLT and GFLIB_FlexRampCalcIncr_FLT algorithms.
GFLIB User's Guide, Rev. 4, 12/2020
86 NXP Semiconductors
Page 87

Chapter 2 Algorithms in detail
2.19.4 Declaration
The available GFLIB_FlexRampInit functions have the following declarations:
void GFLIB_FlexRampInit_F16(frac16_t f16InitVal, GFLIB_FLEXRAMP_T_F32 *psParam)
void GFLIB_FlexRampInit_FLT(float_t fltInitVal, GFLIB_FLEXRAMP_T_FLT *psParam)
The available GFLIB_FlexRampCalcIncr functions have the following declarations:
void GFLIB_FlexRampCalcIncr_F16(frac16_t f16Target, acc32_t a32Duration,
GFLIB_FLEXRAMP_T_F32 *psParam)
void GFLIB_FlexRampCalcIncr_FLT(float_t fltTarget, float_t fltDuration, GFLIB_FLEXRAMP_T_FLT
*psParam)
The available GFLIB_FlexRamp functions have the following declarations:
frac16_t GFLIB_FlexRamp_F16(GFLIB_FLEXRAMP_T_F32 *psParam)
float_t GFLIB_FlexRamp_FLT(GFLIB_FLEXRAMP_T_FLT *psParam)
2.19.5
Function use
The use of the GFLIB_FlexRampInit, GFLIB_FlexRampCalcIncr, and
GFLIB_FlexRamp functions is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16InitVal;
static GFLIB_FLEXRAMP_T_F32 sFlexRamp;
static frac16_t f16Target, f16RampResult;
static acc32_t a32RampDuration;
void Isr(void);
void main(void)
{
/* Control loop period is 0.002 s; maximum increment value is 0.15 */
sFlexRamp.f32Ts = FRAC32(0.002);
sFlexRamp.f32IncrMax = FRAC32(0.15);
/* Initial value to 0 */
f16InitVal = FRAC16(0.0);
/* Flex ramp initialization */
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 87
Page 88

GFLIB_DFlexRamp
GFLIB_FlexRampInit_F16(f16InitVal, &sFlexRamp);
/* Target value is 0.7 in duration of 5.3 s */
f16Target = FRAC16(0.7);
a32RampDuration = ACC32(5.3);;
/* Flex ramp increment calculation */
GFLIB_FlexRampCalcIncr_F16(f16Target, a32RampDuration, &sFlexRamp);
}
/* periodically called control loop with a period of 2 ms */
void Isr()
{
f16RampResult = GFLIB_FlexRamp_F16(&sFlexRamp);
}
Floating-point version:
#include "gflib.h"
static float_t fltInitVal;
static GFLIB_FLEXRAMP_T_FLT sFlexRamp;
static float_t fltTarget, fltRampResult;
static float_t fltRampDuration;
void Isr(void);
void main(void)
{
/* Control loop period is 0.002 s; maximum increment value is 0.15 */
sFlexRamp.fltTs = 0.002F;
sFlexRamp.fltIncrMax = 0.15F;
/* Initial value to 0 */
fltInitVal = 0.0F;
/* Flex ramp initialization */
GFLIB_FlexRampInit_FLT(fltInitVal, &sFlexRamp);
/* Target value is 0.7 in duration of 5.3 s */
fltTarget = 0.7F;
fltRampDuration = 5.3F;
/* Flex ramp increment calculation */
GFLIB_FlexRampCalcIncr_FLT(fltTarget, fltRampDuration, &sFlexRamp);
}
/* periodically called control loop */
void Isr()
{
fltRampResult = GFLIB_FlexRamp_FLT(&sFlexRamp);
}
2.20
GFLIB_DFlexRamp
GFLIB User's Guide, Rev. 4, 12/2020
88 NXP Semiconductors
Page 89

Chapter 2 Algorithms in detail
The GFLIB_DFlexRamp function calculates the up/down ramp with a fixed-step
increment that is calculated according to the required speed change per a defined
duration.These parameters must be set by the user. The algorithm has stop flags. If none
of them is set, the ramp behaves normally. If one of them is set, the ramp can run in the
opposite direction.
The GFLIB_DFlexRamp algorithm consists of three functions that must be used for a
proper functionality of the algorithm:
• GFLIB_DFlexRampInit - this function initializes the state variable with a defined
value and clears the reach flag
• GFLIB_DFlexRampCalcIncr - this function calculates the increment and clears the
reach flag
• GFLIB_DFlexRamp - this function calculates the ramp in the periodically called
loop
For a proper use, initialize the algorithm by the GFLIB_DFlexRampInit function. The
GFLIB_DFlexRampInit function initializes the internal state variable of the algorithm
with a defined value and clears the reach flag. Call the init function when you want to
initialize the ramp.
To calculate the increment, use the GFLIB_DFlexRampCalcIncr function. Call this
function when you want to change the ramp output value. This function's inputs are the
target value and duration, and the ramp increments for motoring and generating
saturation modes. The target value is the destination value that you want to get to. The
duration is the time required to change the ramp output from the actual state to the target
value. To calculate the ramp increment, fill the control structure with the sample time,
that means the period of the loop where the GFLIB_DFlexRamp funciton is called. The
structure also contains a variable which determines the maximum value of the increment.
It is necessary to set it up too. The equation for the increment calculation is as follows:
Equation 17.
where:
• I is the increment
• Vt is the target value
• Vs is the state (actual) value (in the structure)
• T is the duration of the ramp (to reach the target value starting at the state value)
• Ts is the sample time, that means the period of the loop where the ramp algorithm is
called (set in the structure)
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 89
Page 90

GFLIB_DFlexRamp
If the increment is greater than the maximum increment (set in the structure), the
increment uses the maximum increment value.
The state, target, and instant values must have the same sign, otherwise the saturation
modes don't work properly.
As soon as the new increment is calculated, you can call the GFLIB_DFlexRamp
algorithm in the periodical control loop. If none of the stop flags is set, the function
works as follows: The function adds the increment to the state value (from the previous
step), which results in a new state. The new state is returned by the function. As time
passes, the algorithm is approaching the target value. If the new state trespasses the target
value that new state is limited to, the target value and the reach flag are set. The
functionality of the implemented algorithm is shown in the following figure:
Figure 2-14. GFLIB_DFlexRamp functionality
If the motoring mode stop flag is set and the absolute value of the target value is greater
than the absolute value of the state value, the function uses the increment for the
motoring saturation mode to return to the instant value. Use case: when the application is
in the saturation mode and cannot supply more power to increase the speed, then a
saturation (motoring mode) flag is generated. To get out of the saturation, the ramp
output value is being reduced.
GFLIB User's Guide, Rev. 4, 12/2020
90 NXP Semiconductors
Page 91
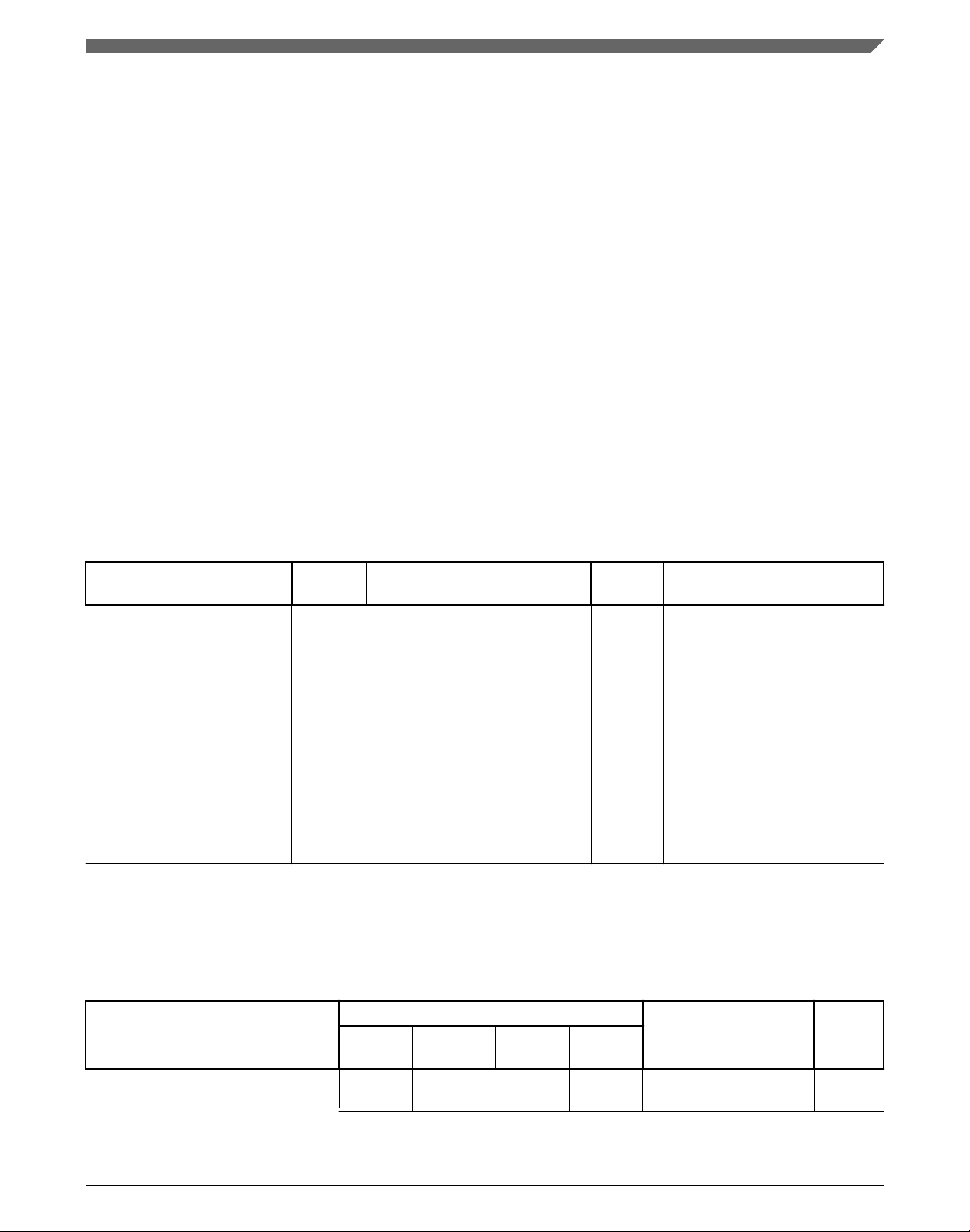
Chapter 2 Algorithms in detail
If the generating mode stop flag is set and the absolute value of the target value is lower
than the absolute value of the state value, the funcion uses the increment for the
generating saturation mode to return to the instant value. Use case: when the application
is braking a motor and voltage increases on the DC-bus capacitor, then a saturation
(generating mode) flag is generated. To avoid trespassing the DC-bus safe voltage limit,
the speed requirement is increasing to disipate the energy of the capacitor.
2.20.1 Available versions
This function is available in the following versions:
• Fractional output - the output is the fractional portion of the result; the result is
within the range <-1 ; 1). The input parameters are the fractional and accumulator
types.
The available versions of the GFLIB_DFlexRampInit functions are shown in the
following table:
Table 2-26. Init function versions
Function name Input
type
GFLIB_FlexRampInit_F16 frac16_t GFLIB_DFLEXRAMP_T_F32 * void The input argument is a 16-bit
GFLIB_FlexRampInit_FLT float_t GFLIB_DFLEXRAMP_T_FLT * void The input argument is a 32-bit
Parameters Result
type
Description
fractional value that represents
the initialization value. The
parameters' structure is pointed
to by a pointer. The input data
value is in the range <-1 ; 1).
single precision floating-point
value that represents the
initialization value. The
parameters' structure is pointed
to by a pointer. The input value is
within the full 32-bit single-point
floating-point range.
The available versions of the GFLIB_DFlexRamp functions are shown in the following
table:
Table 2-27. Increment calculation function versions
Function name Input type Parameters Result
Target Duration Incr. sat-
mot
GFLIB_DFlexRampCalcIncr_F16 frac16_t acc32_t frac32_t frac32_t GFLIB_DFLEXRAMP_T_
Table continues on the next page...
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 91
Incr. sat-
gen
F32 *
type
void
Page 92

GFLIB_DFlexRamp
Table 2-27. Increment calculation function versions (continued)
Function name Input type Parameters Result
Target Duration Incr. sat-
mot
The input arguments are 16-bit fractional values in the range <-1 ; 1) that represent
the target output value and a 32-bit accumulator value in the range (0 ; 65536.0) that
represents the duration (in seconds) of the ramp to reach the target value. The other
two arguments are increments for the saturation mode when in the motoring and
generating modes. The parameters' structure is pointed to by a pointer.
GFLIB_DFlexRampCalcIncr_FLT float_t float_t float_t float_t GFLIB_DFLEXRAMP_T_
The input arguments are 32-bit single precision floating-point values that represent
the target output value and the duration of the ramp (in seconds, except zero value)
to reach the target value. The other two arguments are increments for the saturation
mode when in the motoring and generating modes. The parameters' structure is
pointed to by a pointer. The target argument is within the full range; the duration
argument is a non-negative value.
Incr. sat-
gen
FLT *
type
void
Table 2-28. Function versions
Function name Input type Parameters Result
Instant Stop flag-
mot
GFLIB_DFlexRamp_F16 frac16_t bool_t * bool_t * GFLIB_DFLEXRAMP_T_F32 * frac16_t
The input argument is a 16-bit fractional value in the range <-1 ; 1) that represents
the measured instant value. The stop flags are pointers to the bool_t types. The
parameters' structure is pointed to by a pointer. The function returns a 16-bit
fractional value, which represents the actual ramp output value. The output data
value is in the range <-1 ; 1).
GFLIB_DFlexRamp_FLT float_t bool_t * bool_t * GFLIB_DFLEXRAMP_T_FLT * float_t
The input arguments are 32-bit single precision floating-point values that represent
the measured instant value. The stop flags are pointers to bool_t types. The
parameters' structure is pointed to by a pointer. The function returns a 32-bit single
precision floating-point value, which represents the actual ramp output value. The
output value is within the full 32-bit single-point floating-point range.
Stop flag-
gen
type
2.20.2 GFLIB_DFLEXRAMP_T_F32
Variable name Type Description
f32State frac32_t The actual value. Controlled by the GFLIB_FlexRampInit_F16 and GFLIB_FlexRamp_F16
algorithms.
f32Incr frac32_t The value of the dyn. flex ramp increment. Controlled by the
GFLIB_FlexRampCalcIncr_F16 algorithm.
f32IncrSatMot frac32_t The value of the dyn. flex ramp increment when in the motoring saturation mode.
Controlled by the GFLIB_DFlexRampCalcIncr_F16 algorithm.
Table continues on the next page...
GFLIB User's Guide, Rev. 4, 12/2020
92 NXP Semiconductors
Page 93

Chapter 2 Algorithms in detail
Variable name Type Description
f32IncrSatGen frac32_t The value of the dyn. flex ramp increment when in the generating saturation mode.
Controlled by the GFLIB_DFlexRampCalcIncr_F16 algorithm.
f32Target frac32_t The target value of the flex ramp algorithm. Controlled by the
GFLIB_DFlexRampCalcIncr_F16 algorithm.
f32Ts frac32_t The sample time, that means the period of the loop where the GFLIB_DFlexRamp_F16
algorithm is periodically called. The data value (in seconds) is in the range (0 ; 1). Set by
the user.
f32IncrMax frac32_t The maximum value of the flex ramp increment. The data value is in the range (0 ; 1). Set
by the user.
bReachFlag bool_t Reach flag. This flag is controlled by the GFLIB_DFlexRamp_F16 algorithm. It is cleared
by the GFLIB_DFlexRampInit_F16 and GFLIB_DFlexRampCalcIncr_F16 algorithms.
2.20.3 GFLIB_DFLEXRAMP_T_FLT
Variable name Type Description
fltState float_t The actual value. Controlled by the GFLIB_DFlexRampInit_FLT and
GFLIB_DFlexRamp_FLT algorithms.
fltIncr float_t The value of the flex ramp increment. Controlled by the GFLIB_DFlexRampCalcIncr_FLT
algorithm.
fltIncrSatMot float_t The value of the dyn. flex ramp increment when in the motoring saturation mode.
Controlled by the GFLIB_DFlexRampCalcIncr_FLT algorithm.
fltIncrSatGen float_t The value of the dyn. flex ramp increment when in the generating saturation mode.
Controlled by the GFLIB_DFlexRampCalcIncr_FLT algorithm.
fltTarget float_t The target value of the flex ramp algorithm. Controlled by the
GFLIB_DFlexRampCalcIncr_FLT algorithm.
fltTs float_t The sample time, that means the period of the loop where the GFLIB_DFlexRamp_FLT
algorithm is periodically called. The data value (in seconds, except zero value) is a nonnegative value. Set by the user.
fltIncrMax float_t The maximum value of the flex ramp increment. The data is a positive value. Set by the
user.
bReachFlag bool_t The reach flag. This flag is controlled by the GFLIB_DFlexRamp_FLT algorithm. It is
cleared by the GFLIB_DFlexRampInit_FLT and GFLIB_DFlexRampCalcIncr_FLT
algorithms.
2.20.4 Declaration
The available GFLIB_DFlexRampInit functions have the following declarations:
void GFLIB_DFlexRampInit_F16(frac16_t f16InitVal, GFLIB_DFLEXRAMP_T_F32 *psParam)
void GFLIB_DFlexRampInit_FLT(float_t fltInitVal, GFLIB_DFLEXRAMP_T_FLT *psParam)
The available GFLIB_DFlexRampCalcIncr functions have the following declarations:
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 93
Page 94

GFLIB_DFlexRamp
void GFLIB_DFlexRampCalcIncr_F16(frac16_t f16Target, acc32_t a32Duration, frac32_t
f32IncrSatMot, frac32_t f32IncrSatGen, GFLIB_DFLEXRAMP_T_F32 *psParam)
void GFLIB_DFlexRampCalcIncr_FLT(float_t fltTarget, float_t fltDuration, float_t
f32IncrSatMot, float_t f32IncrSatGen, GFLIB_DFLEXRAMP_T_FLT *psParam)
The available GFLIB_DFlexRamp functions have the following declarations:
frac16_t GFLIB_DFlexRamp_F16(frac16_t f16Instant, const bool_t *pbStopFlagMot, const
bool_t *pbStopFlagGen, GFLIB_DFLEXRAMP_T_F32 *psParam)
float_t GFLIB_DFlexRamp_FLT(float_t fltInstant, const bool_t *pbStopFlagMot, const bool_t
*pbStopFlagGen, GFLIB_DFLEXRAMP_T_FLT *psParam)
2.20.5
Function use
The use of the GFLIB_DFlexRampInit, GFLIB_DFlexRampCalcIncr, and
GFLIB_DFlexRamp functions is shown in the following examples:
Fixed-point version:
#include "gflib.h"
static frac16_t f16InitVal;
static GFLIB_DFLEXRAMP_T_F32 sDFlexRamp;
static frac16_t f16Target, f16RampResult, f16Instant;
static acc32_t a32RampDuration;
static frac32_t f32IncrSatMotMode, f32IncrSatGenMode;
static bool_t bSatMot, bSatGen;
void Isr(void);
void main(void)
{
/* Control loop period is 0.002 s; maximum increment value is 0.15 */
sDFlexRamp.f32Ts = FRAC32(0.002);
sDFlexRamp.f32IncrMax = FRAC32(0.15);
/* Initial value to 0 */
f16InitVal = FRAC16(0.0);
/* Dyn. flex ramp initialization */
GFLIB_FlexRampInit_F16(f16InitVal, &sDFlexRamp);
/* Target value is 0.7 in duration of 5.3 s */
f16Target = FRAC16(0.7);
a32RampDuration = ACC32(5.3);;
/* Saturation increments */
f32IncrSatMotMode = FRAC32(0.000015);
f32IncrSatGenMode = FRAC32(0.00002);
/* Saturation flags init */
bSatMot = FALSE;
bSatGen = FALSE;
/* Dyn. flex ramp increment calculation */
GFLIB_DFlexRampCalcIncr_F16(f16Target, a32RampDuration, f32IncrSatMotMode,
GFLIB User's Guide, Rev. 4, 12/2020
94 NXP Semiconductors
Page 95

Chapter 2 Algorithms in detail
f32IncrSatGenMode, &sDFlexRamp);
}
/* periodically called control loop with a period of 2 ms */
void Isr()
{
f16RampResult = GFLIB_DFlexRamp_F16(f16Instant, &bSatMot, &bSatGen, &sDFlexRamp);
}
Floating-point version:
#include "gflib.h"
static float_t fltInitVal;
static GFLIB_DFLEXRAMP_T_FLT sDFlexRamp;
static float_t fltTarget, fltRampResult, fltInstant;
static float_t fltRampDuration;
static float_t fltIncrSatMotMode, fltIncrSatGenMode;
static bool_t bSatMot, bSatGen;
void Isr(void);
void main(void)
{
/* Control loop period is 0.002 s; maximum increment value is 0.15 */
sDFlexRamp.fltTs = 0.002F;
sDFlexRamp.fltIncrMax = 0.15F;
/* Initial value to 0 */
fltInitVal = 0.0F;
/* Dyn. flex ramp initialization */
GFLIB_DFlexRampInit_FLT(fltInitVal, &sDFlexRamp);
/* Target value is 0.7 in duration of 5.3 s */
fltTarget = 0.7F;
fltRampDuration = 5.3F;
/* Saturation increments */
fltIncrSatMotMode = 0.000015F;
fltIncrSatGenMode = 0.00002F;
/* Saturation flags init */
bSatMot = FALSE;
bSatGen = FALSE;
/* Dyn. flex ramp increment calculation */
GFLIB_DFlexRampCalcIncr_FLT(fltTarget, fltRampDuration, fltIncrSatMotMode,
fltIncrSatGenMode, &sDFlexRamp);
}
/* periodically called control loop with a period of 2 ms */
void Isr()
{
fltRampResult = GFLIB_DFlexRamp_FLT(fltInstant, &bSatMot, &bSatGen, &sDFlexRamp);
}
2.21
GFLIB_FlexSRamp
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 95
Page 96

GFLIB_FlexSRamp
The GFLIB_FlexSRamp function calculates the up/down ramp with a variable increment
that is calculated according to the required speed change per a defined duration. These
parameters must be set by the user. The variable increment is profiled to reach the Sprofile of the resulting ramp.
The GFLIB_FlexSRamp algorithm consists of three functions that must be used for a
proper functionality of the algorithm:
• GFLIB_FlexSRampInit - this function initializes the state variable with a defined
value, resets the accelaration increment to zero, sets the acceleration state to zero,
and clears the reach flag
• GFLIB_FlexSRampCalcIncr - this function calculates the desired acceleraion, two
points of the speed where the acceleration changes from a variable to a constant and
vice-versa, acceleration (derivative) increment, resets the increment to zero, sets the
acceleration state to zero, and clears the reach flag
• GFLIB_FlexSRamp - this function calculates the ramp in the periodically called loop
For a proper use, initialize the algorithm by the GFLIB_FlexSRampInit function. The
GFLIB_FlexSRampInit function initializes the internal state variable of the algorithm
with a defined value, resets the acceleration increment to zero, sets the acceleration state
to zero, and clears the reach flag. This function does not affect the other parameters of the
ramp. Call the init function to initialize the ramp.
To calculate the profile of the ramp, use the GFLIB_FlexSRampCalcIncr function. This
function is called when you want to change the ramp output value. This function's inputs
are the target value and duration. The target value is the destination value that you want
to get to. The duration is the time required to change the ramp output from the actual state
to the target value. To calculate the ramp increment, fill the control structure with the
sample time, that means the period of the loop where the GFLIB_FlexSRamp function is
called. Set up the desirable acceleration derivative that is necessary for the acceleration
and decceleration states. The structure also contains a variable that determines the
maximum value of the increment (acceleration). It is necessary to set it up too. The
equations for the ramp calculation are derived from the following figure:
GFLIB User's Guide, Rev. 4, 12/2020
96 NXP Semiconductors
Page 97

Chapter 2 Algorithms in detail
Figure 2-15. GFLIB_FlexSRamp profile
For the ramp output change in each state, these equations apply:
Equation 18.
Equation 19.
Equation 20.
where:
• x is the ramp output
• Δx1 is the ramp change in state 0
• Δx2 is the ramp change in state 1
• Δx3 is the ramp change in state 2
• T1 is the instant when the desired acceleration is reached and becomes constant
• T2 is the instant when the desired acceleration starts to decrease
To get the full ramp change between the actual state value and the target value, this
equation applies:
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 97
Page 98

GFLIB_FlexSRamp
Equation 21.
The value of the desired accelelarion that is reached by the integration of the acceleration
derivative along the time within state 0 is:
Equation 22.
where:
• a
is the desired acceleration
des
• dA is the derivative of the acceleration
Similarly, the Δx1 and Δx2 values are given by integrating the acceleration in time:
Equation 23.
Equation 24.
Because the ramp is symetrical, time T2 is expressed as:
Equation 25.
where:
• T is the duration of the ramp
Using the equations for a
and T2, Equation 24 on page 98 is rewritten as:
des
Equation 26.
Putting Equation 26 on page 98 and Equation 26 on page 98 into Equation 21 on page 98,
the following equation is reached:
Equation 27.
GFLIB User's Guide, Rev. 4, 12/2020
98 NXP Semiconductors
Page 99

Chapter 2 Algorithms in detail
Having normalized the previous equation, a quadrature equation is reached:
Equation 28.
One root of this quadrature equation is T1:
Equation 29.
Using Equation 22 on page 98, the desired acceleration is expressed as:
Equation 30.
This equation has a solution within the range of real numbers only if the square root
argument is not negative, so this condition must be met:
Equation 31.
If this condition is met and the desired acceleration is not greater than the maximum
increment (set in the structure), the ramp is achievable within the defined duration and
the function's output flag is TRUE. If the acceleration is greater than the maximum
increment, the function uses the maximum increment value and then the ramp is not
achieved on time, the output flag is FALSE.
If the condition given by Equation 31 on page 99 is not met, the ramp is not achievable
within the defined duration and the function returns the flag FALSE. In such case, the
ramp skips state 1 (where the acceleration is constant) and goes directly from state 0 to
state 2. The following figure shows the ramp profile:
GFLIB User's Guide, Rev. 4, 12/2020
NXP Semiconductors 99
Page 100

GFLIB_FlexSRamp
Figure 2-16. GFLIB_FlexSRamp delayed profile
This ramp takes longer time than desirable duration. In this case, Δx1 is exactly a half of
the full ramp change output. The T1 instant is derived from Equation 23 on page 98 as:
Equation 32.
The desired acceleration is given by Equation 22 on page 98 as:
Equation 33.
Similarly to the previous case (when the ramp is achievable within the desired time), the
desired acceleration cannot be greater than the maximum increment, otherwise the
function uses the maximum increment value. If the desired acceleration is trimmed, the
ramp is in state 1 with a constant acceleration.
In both cases, the desired acceleration could have been reduced to the maximum
increment value, therefore it is necessary to adjust the T1 value using Equation 22 on
page 98 :
GFLIB User's Guide, Rev. 4, 12/2020
100 NXP Semiconductors
 Loading...
Loading...