NSC LM2937ET-2.5, LM2937ES-2.5, LM2937ESX-2.5, LM2937IMPX-2.5 Datasheet

LM2937-2.5, LM2937-3.3
400mA and 500mA Voltage Regulators

General Description

The LM2937-2.5 and LM2937-3.3 are positive voltage regu­lators capable of supplying up to 500 mA of load current.
Both regulators are ideal for converting a common 5V logic
supply, orhigherinput supply voltage, to the lower 2.5V and

3.3V supplies to power VLSI ASIC’s and microcontrollers.
Special circuitry has been incorporated to minimize the qui­escent current to typically only 10 mA with a full 500 mAload
current when the input to output voltage differential is greater
than 5V.

The LM2937 requires an output bypass capacitor for stabil­ity. As with most regulators utilizing a PNP pass transistor,
the ESR of this capacitor remains a critical design param­eter, but the LM2937-2.5 and LM2937-3.3 include special
compensation circuitry that relaxes ESR requirements. The
LM2937 is stable for all ESR ratings less than 5Ω. This al­lows the use of low ESR chip capacitors.

The regulators are also suited for automotive applications,
with built in protection from reverse battery connections,

two-battery jumps and up to +60V/−50V load dump tran­sients. Familiar regulator features such as short circuit and
thermal shutdown protection are also built in.

Features

n Fully specified for operation over −40˚C to +125˚C
n Output current in excess of 500 mA (400mA for

SOT-223 package)

n Output trimmed for 5%tolerance under all operating

conditions

n Wide output capacitor ESR range, 0.01Ω up to 5Ω
n Internal short circuit and thermal overload protection
n Reverse battery protection
n 60V input transient protection
n Mirror image insertion protection

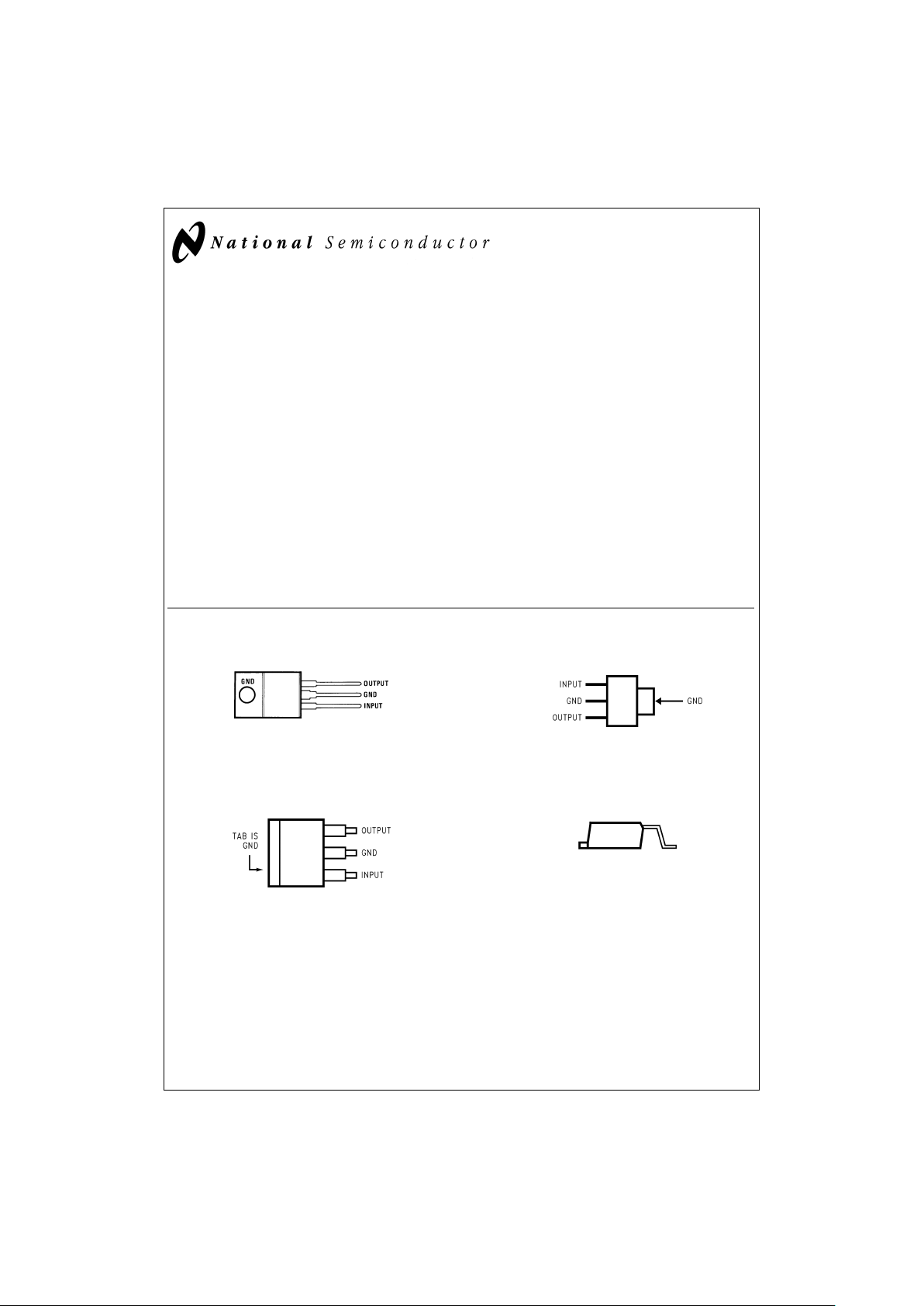
Connection Diagram and Ordering Information

TO-220 Plastic Package

DS100113-24

Front View

Order Number LM2937ET-2.5, LM2937ET-3.3,

See NS Package Number T03B

SOT-223 Plastic Package

DS100113-25

Front View

Order Number LM2937IMP-2.5, LM2937IMP-3.3,

See NS Package Number MA04A

TO-263 Surface-Mount Package

DS100113-26

Top View

DS100113-27

Side View

Order Number LM2937ES-2.5, LM2937ES-3.3,

See NS Package Number TS3B

February 1998

LM2937-2.5, LM2937-3.3 400mA and 500mA Voltage Regulators

© 1998 National Semiconductor Corporation DS100113 www.national.com

Connection Diagram and Ordering Information (Continued)

Temperature

Range

Output Voltage NSC Package

2.5 3.3 Package
Drawing

−40˚C ≤ T

A

≤ 125˚C LM2937ES-2.5 LM2937ES-3.3 TS3B TO-263

LM2937ET-2.5 LM2937ET-3.3 T03B TO-220

−40˚C ≤ T

A

≤ 85˚C LM2937IMP-2.5 LM2937IMP-3.3 MA04A SOT-223

SOT-223 Package
Markings

L68B L69B

The small physical size of the SOT-223 package does not allow sufficient space to provide the complete device part number. The actual devices will be labeled with
the package markings shown.

www.national.com 2

Absolute Maximum Ratings (Note 1)

If Military/Aerospace specified devices are required,
please contact the National Semiconductor Sales Office/
Distributors for availability and specifications.

Input Voltage

Continuous 26V

Transient (t ≤ 100 ms) 60V
Internal Power Dissipation (Note 2) Internally Limited
Maximum Junction Temperature 150˚C
Storage Temperature Range −65˚C to +150˚C
Lead Temperature Soldering

TO-220 (10 seconds) 260˚C

TO-263 (10 seconds) 230˚C

SOT-223 (Vapor Phase, 60 seconds) 215˚C

SOT-223 (Infrared, 15 seconds) 220˚C

ESD Susceptibility (Note 3) 2 kV

Operating Conditions(Note 1)

Temperature Range (Note 2)

LM2937ES, LM2937ET −40˚C ≤ T

A

≤ 125˚C

LM2937IMP −40˚C ≤ T

A

≤ 85˚C

Input Voltage Range 4.75V to 26V

Electrical Characteristics(Note 4)

V

IN

=

V

NOM

+ 5V, I

OUTmax

=

500 mA for the TO-220 and TO-263 packages, I

OUTmax

=

400mA for the SOT-223 package, C

OUT

=

10 µF unless otherwise indicated. Boldface limits apply over the entire operating temperature range, of the indicated

device, all other specifications are for T

A

=

T

J

=

25˚C.

Output Voltage (V

OUT

) 2.5V 3.3V Units

Parameter Conditions Typ Limit Typ Limit

Output Voltage 5 mA ≤ I

OUT

≤ I

OUTmax

2.42 3.20 V (Min)

2.5 2.38 3.3 3.14 V(Min)

2.56 3.40 V(Max)

2.62 3.46 V(Max)

Line Regulation(Note 5) 4.75V ≤ V

IN

≤ 26V, 7.5 25 9.9 33 mV(Max)

I

OUT

=

5mA

Load Regulation 5 mA ≤ I

OUT

≤ I

OUTmax

2.5 25 3.3 33 mV(Max)

Quiescent Current 7V ≤ V

IN

≤ 26V, 2 10 2 10 mA(Max)

I

OUT

=

5mA

V

IN

=

(V

OUT

+ 5V), 10 20 10 20 mA(Max)

I

OUT

=

I

OUTmax

V

IN

=

5V, I

OUT

=

I

OUTmax

66 100125 66 100125 mA(Max)
Output Noise 10 Hz–100 kHz, 75 99 µVrms
Voltage I

OUT

=

5mA
Long Term Stability 1000 Hrs. 10 13.2 mV
Short-Circuit Current 1.0 0.6 1.0 0.6 A(Min)
Peak Line Transient t

f

<

100 ms, R

L

=

100Ω 75 60 75 60 V(Min)
Voltage
Maximum Operational 26 26 V(Min)
Input Voltage
Reverse DC V

OUT

≥ −0.6V, R

L

=

100Ω −30 −15 −30 −15 V(Min)
Input Voltage
Reverse Transient t

r

<

1 ms, R

L

=

100Ω −75 −50 −75 −50 V(Min)

Input Voltage

Note 1: Absolute Maximum Ratings indicate limits beyond which damage to the device may occur. Electrical specifications do not apply when operating the device
outside of its rated Operating Conditions.

Note 2: The maximum allowable power dissipation at any ambient temperature is P

MAX

=

(125 − T

A

)/θJA, where 125 is the maximum junction temperature for op-

eration, T

A

is the ambient temperature, and θJAis the junction-to-ambient thermal resistance. If this dissipation isexceeded,thedietemperaturewillriseabove125˚C
and the electrical specifications do not apply. If the die temperature rises above 150˚C, the regulator will go into thermal shutdown. The junction-to-ambient thermal
resistance θ

JA

is 65˚C/W, for the TO-220 package, 73˚C/W for the TO-263 package, and 174˚C/W for the SOT-223 package. When used with a heatsink, θJAis the

sum of the device junction-to-case thermal resistance θ

JC

of 3˚C/W and the heatsink case-to-ambient thermal resistance. If the TO-263 or SOT-223 packages are
used, the thermal resistancecanbereducedbyincreasingtheP.C.boardcopperareathermallyconnectedtothepackage (see Application Hints for more information
on heatsinking).

Note 3: ESD rating is based on the human body model, 100 pF discharged through 1.5 kΩ.
Note 4: Typicals are at T

J

=

25˚C and represent the most likely parametric norm.

Note 5: The minimum input voltage required for proper biasing of these regulators is 4.75V. Below this level the outputs will fall out of regulation. This effect is not
the normal dropout characteristic where the output falls out of regulation due to the PNP pass transistor entering saturation. If a value for worst case effective input
to output dropout voltage is required in a specification, the values should be 2.37V maximum for the LM2937-2.5 and 1.6V maximum for the LM2937-3.3.

3 www.national.com

Typical Performance Characteristics

Output Voltage vs
Temperature (2.5V)

DS100113-2

Output Voltage vs
Temperature (3.3V)

DS100113-3

Quiescent Current vs
Output Current (2.5V)

DS100113-4

Quiescent Current vs
Output Current (3.3V)

DS100113-5

Quiescent Current vs
Input Voltage (2.5V)

DS100113-6

Quiescent Current vs
Input Voltage (3.3V)

DS100113-7

Line Transient Response

DS100113-8

Load Transient Response

DS100113-9

Ripple Rejection

DS100113-10

www.national.com 4

Typical Performance Characteristics (Continued)

Output Impedance

DS100113-11

Maximum Power
Dissipation (TO-220)

DS100113-12

Maximum Power Dissipation
(TO-263) (Note 2)

DS100113-13

Low Voltage Behavior (2.5V)

DS100113-14

Low Voltage Behavior (3.3)

DS100113-15

Output at Voltage
Extremes

DS100113-16

Output Capacitor ESR

DS100113-17

Peak Output Current

DS100113-18

Typical Application

DS100113-1

* Required if the regulator is located more than 3 inches from the power supply filter capacitors.
*

*

Required for stability. C

out

must be at least 10 µF (over the full expected operating temperature range) and located as close as possible to the regulator. The

equivalent series resistance, ESR, of this capacitor may be as high as 3Ω.

5 www.national.com

Application Hints

EXTERNAL CAPACITORS

The output capacitor is critical to maintaining regulator stabil­ity, and must meet the required conditions for both ESR
(Equivalent Series Resistance) and minimum amount of ca­pacitance.

MINIMUM CAPACITANCE:
The minimum output capacitance required to maintain stabil-

ity is 10 µF (this value may be increased without limit).
Larger values of output capacitance will give improved tran­sient response.

ESR LIMITS:
The ESR of the output capacitor will cause loop instability if

it is too high or too low. The acceptable range of ESR plotted
versus load current is shown in the graph below.

It is essen­tial that the output capacitor meet these requirements,
or oscillations can result.

It is important to note that for most capacitors, ESR is speci­fied only at room temperature. However, the designer must
ensure that the ESR will stay inside the limits shown over the
entire operating temperature range for the design.

For aluminum electrolytic capacitors, ESR will increase by
about 30X as the temperature is reduced from 25˚C to

−40˚C. This type of capacitor is not well-suited for low tem­perature operation.

Solid tantalum capacitors have a more stable ESR over tem­perature, but are more expensive than aluminum electrolyt­ics. A cost-effective approach sometimes used is to parallel
an aluminum electrolytic with a solid Tantalum, with the total
capacitance split about 75/25%with the Aluminum being the
larger value.

If two capacitors are paralleled, the effective ESR is the par­allel of the two individual values. The “flatter” ESR of the Tan­talum will keep the effective ESR from rising as quickly at low
temperatures.

HEATSINKING

A heatsink may be required depending on the maximum
power dissipation and maximum ambient temperature of the
application. Under all possible operating conditions, the junc­tion temperature must be within the range specified under
Absolute Maximum Ratings.

To determine if a heatsink is required, the power dissipated
by the regulator, P

D

, must be calculated.

The figure below shows the voltages and currents which are
present in the circuit, as well as the formula for calculating
the power dissipated in the regulator:

The next parameter which must be calculated is the maxi­mum allowable temperature rise, T

R

(max). This is calcu-

lated by using the formula:

T

R

(max)=TJ(max) − TA(max)

where: T

J

(max) is the maximum allowable junction tem-

perature, which is 125˚C for commercial
grade parts.

T

A

(max) is the maximum ambient temperature

which will be encountered in the applica­tion.

Using the calculated values for T

R

(max) and PD, the maxi­mum allowable value for the junction-to-ambient thermal re­sistance, θ

(J−A)

, can now be found:

θ

(J−A)

=

T

R

(max)/P

D

IMPORTANT: If the maximum allowable value for θ

(J−A)

is
found to be ≥ 53˚C/W for the TO-220 package, ≥ 80˚C/W for
the TO-263 package, or ≥174˚C/W for the SOT-223 pack­age, no heatsink is needed since the package alone will dis­sipate enough heat to satisfy these requirements.

If the calculated value for θ

(J−A)

falls below these limits, a

heatsink is required.

HEATSINKING TO-220 PACKAGE PARTS

The TO-220 can be attached to a typical heatsink, or se­cured to a copper plane on a PC board. If a copper plane is
to be used, the values of θ

(J−A)

will be the same as shown in

the next section for the TO-263.
If a manufactured heatsink is to be selected, the value of

heatsink-to-ambient thermal resistance, θ

(H−A)

, must first be

calculated:

θ

(H−A)

=

θ

(J−A)

− θ

(C−H)

− θ

(J−C)

Where: θ

(J−C)

is defined as the thermal resistance from
the junction to the surface of the case. A
value of 3˚C/W can be assumed for θ

(J−C)

for this calculation.

θ

(C−H)

is defined as the thermal resistance be­tween the case and the surface of the heat­sink. The value of θ

(C−H)

will vary from
about 1.5˚C/W to about 2.5˚C/W (depend­ing on method of attachment, insulator,
etc.). If the exact value is unknown, 2˚C/W
should be assumed for θ

(C−H)

.

When a value for θ

(H−A)

is found using the equation shown,

a heatsink must be selected that has a value that is less than
or equal to this number.

Output Capacitor ESR

DS100113-17

FIGURE 1. ESR Limits

DS100113-19

I

IN

=

I

L

÷

I

G

P

D

=

(V

IN−VOUT)IL

+(VIN)I

G

FIGURE 2. Power Dissipation Diagram

www.national.com 6

θ

(H−A)

is specified numerically by the heatsink manufacturer
in the catalog, or shown in a curve that plots temperature rise
vs power dissipation for the heatsink.

HEATSINKING TO-263 AND SOT-223 PACKAGE PARTS

Both the TO-263 (“S”) and SOT-223 (“MP”) packages use a
copper plane on the PCB and the PCB itself as a heatsink.
To optimize the heat sinking ability of the plane and PCB,
solder the tab of the package to the plane.

Figure 3

shows for the TO-263 the measured values of θ

(J−A)

for different copper area sizes using a typical PCB with 1
ounce copper

and no solder mask over the copper area used

for heatsinking.

As shown in the figure, increasing the copper area beyond 1
square inch produces very little improvement. It should also
be observed that the minimum value of θ

(J−A)

for the TO-263

package mounted to a PCB is 32˚C/W.
As a design aid,

Figure 4

shows the maximum allowable
power dissipation compared to ambient temperature for the
TO-263 device (assuming θ

(J−A)

is 35˚C/W and the maxi-

mum junction temperature is 125˚C).

Figure 5

and

Figure 6

show the information for the SOT-223

package.

Figure 6

assumes a θ

(J−A)

of 74˚C/W for 1 ounce
copper and 51˚C/W for 2 ounce copper and a maximum
junction temperature of 125˚C.

Please see AN1028 for power enhancement techniques to
be used with the SOT-223 package.

SOT-223 SOLDERING RECOMMENDATIONS

It is not recommended to use hand soldering or wave solder­ing to attach the small SOT-223 package to a printed circuit
board. The excessive temperatures involved may cause
package cracking.

Either vapor phase or infrared reflow techniques are pre­ferred soldering attachment methods for the SOT-223 pack­age.

DS100113-20

FIGURE 3. θ

(J−A)

vs Copper (1 ounce) Area for the
TO-263 Package

DS100113-21

FIGURE 4. Maximum Power Dissipation vs T

AMB

for

the TO-263 Package

DS100113-22

FIGURE 5. θ

(J−A)

vs Copper (2 ounce) Area for the

SOT-223 Package

DS100113-23

FIGURE 6. Maximum Power Dissipation vs T

AMB

for

the SOT-223 Package

7 www.national.com

Physical Dimensions inches (millimeters) unless otherwise noted

Plastic Package

Order Number LM2937ET-2.5,

LM2937ET-3.3,

NS Package Number T03B

www.national.com 8

Physical Dimensions inches (millimeters) unless otherwise noted (Continued)

TO-263 3-Lead Plastic Surface Mount Package

Order Number LM2937ES-2.5, LM2937ES-3.3,

NS Package Number TS3B

9 www.national.com

Physical Dimensions inches (millimeters) unless otherwise noted (Continued)

LIFE SUPPORT POLICY

NATIONAL’S PRODUCTS ARE NOT AUTHORIZED FOR USE AS CRITICAL COMPONENTS IN LIFE SUPPORT DE­VICES OR SYSTEMS WITHOUT THE EXPRESS WRITTEN APPROVAL OF THE PRESIDENT OF NATIONAL SEMI­CONDUCTOR CORPORATION. As used herein:

1. Life support devices or systems are devices or sys­tems which, (a) are intended for surgical implant into
the body, or (b) support or sustain life, and whose fail­ure to perform when properly used in accordance
with instructions for use provided in the labeling, can
be reasonably expected to result in a significant injury
to the user.

2. A critical component in any component of a life support
device or system whose failure to perform can be rea­sonably expected to cause the failure of the life support
device or system, or to affect its safety or effectiveness.

National Semiconductor
Corporation

Americas
Tel: [phone]
Fax: [phone]
Email: [e-mail]

www.national.com

National Semiconductor
Europe

Fax: [phone]

Email: [e-mail]
Deutsch Tel: [phone]
English Tel: [phone]
Français Tel: [phone]
Italiano Tel: [phone]

National Semiconductor
Asia Pacific Customer
Response Group

Tel: [phone]
Fax: [phone]
Email: [e-mail]

National Semiconductor
Japan Ltd.

Tel: [phone]
Fax: [phone]

SOT-223 3-Lead Plastic Surface Mount Package

Order Number LM2937IMP-2.5, LM2937IMP-3.3,

NS Package Number MA04A

LM2937-2.5, LM2937-3.3 400mA and 500mA Voltage Regulators

National does not assume any responsibility for use of any circuitry described, no circuit patent licenses are implied and National reserves the right at any time without notice to change said circuitry and specifications.