Noty AN140fa Linear Technology

Application Note 140

October 2013

Basic Concepts of Linear Regulator and Switching
Mode Power Supplies

Henry J. Zhang

ABSTRACT

This article explains the basic concepts of linear regulators
and switching mode power supplies (SMPS). It is aimed
at system engineers who may not be ver

y familiar with
power supply designs and selection. The basic operating
principles of linear regulators and SMPS are explained
and the advantages and disadvantages of each solution
are discussed. The buck step-down converter is used as
an example to further explain the design considerations
of a switching regulator.

INTRODUCTION

Today’s designs require an increasing number of power
rails and supply solutions in electronics systems, with
loads ranging from a few mA for standby supplies to over
100A for ASIC voltage regulators. It is important to choose
the appropriate solution for the targeted application and
to meet specified performance requirements, such as
high efficiency, tight printed circuit board (PCB) space,
accurate output regulation, fast transient response, low
solution cost, etc. Power management design is becoming
a more frequent and challenging task for system designers,
many of whom may not have strong power backgrounds.

A power converter generates output voltage and current
for the load from a given input power source. It needs to
meet the load voltage or current regulation requirement
during steady-state and transient conditions. It also must
protect the load and system in case of a component
failure. Depending on the specific application, a designer
can choose either a linear regulator (LR) or a switching
mode power supply (SMPS) solution. To make the best
choice of a solution, it is essential for designers to be
familiar with the merits, drawbacks and design concerns
of each approach.

This article focuses on nonisolated power supply applica­tions and provides an introduction to their operation and
design basics.

LINEAR REGULATORS

How a Linear Regulator W

orks

Let’s start with a simple example. In an embedded system,
a 12V bus rail is available from the front-end power supply.
On the system board, a 3.3V voltage is needed to power an
operational amplifier (op amp). The simplest approach to
generate the 3.3V is to use a resistor divider from the 12V
bus, as shown in Figure 1. Does it work well? The answer
is usually no. The op amp’s V

pin current may vary under

CC

different operating conditions. If a fixed resistor divider
is used, the IC V

voltage varies with load. Besides, the

CC

12V bus input may not be well regulated. There may be
many other loads in the same system sharing the 12V rail.
Because of the bus impedance, the 12V bus voltage var

-

ies with the bus loading conditions. As a result, a resistor

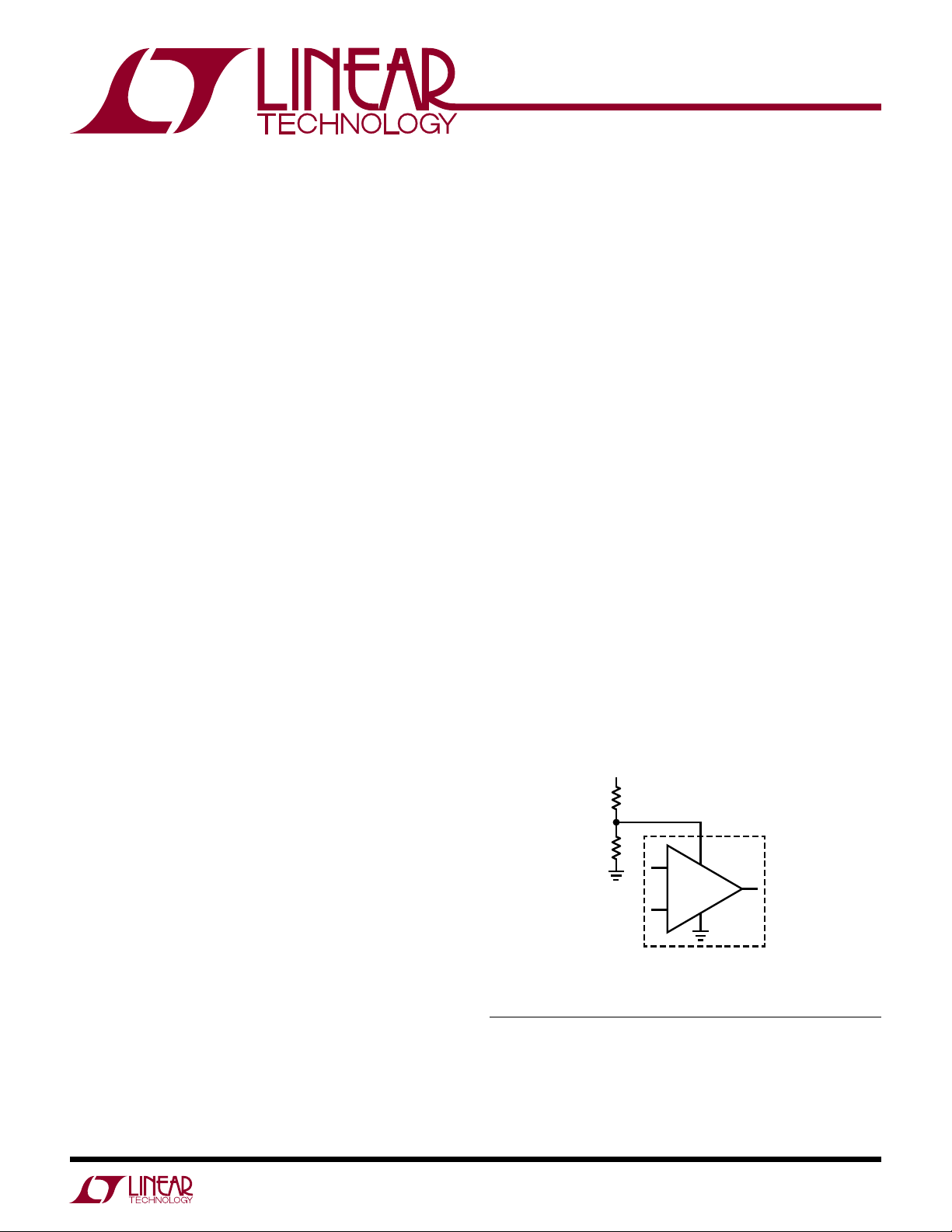
12VDC BUS

R1

3.3V

R2

V

X

Figure 1. Resistor Divider Generates 3.3VDC from 12V Bus Input

L, LT, LTC, LTM, Linear Technology, LTspice, µModule, PolyPhase and the Linear logo are
registered trademarks and LTpowerCAD is a trademark of Linear Technology Corporation. All
other trademarks are the property of their respective owners.

V

CC

LOAD

+

–

AN140 F01

an140fa

AN140-1

Application Note 140

divider cannot provide a regulated 3.3V to the op amp to
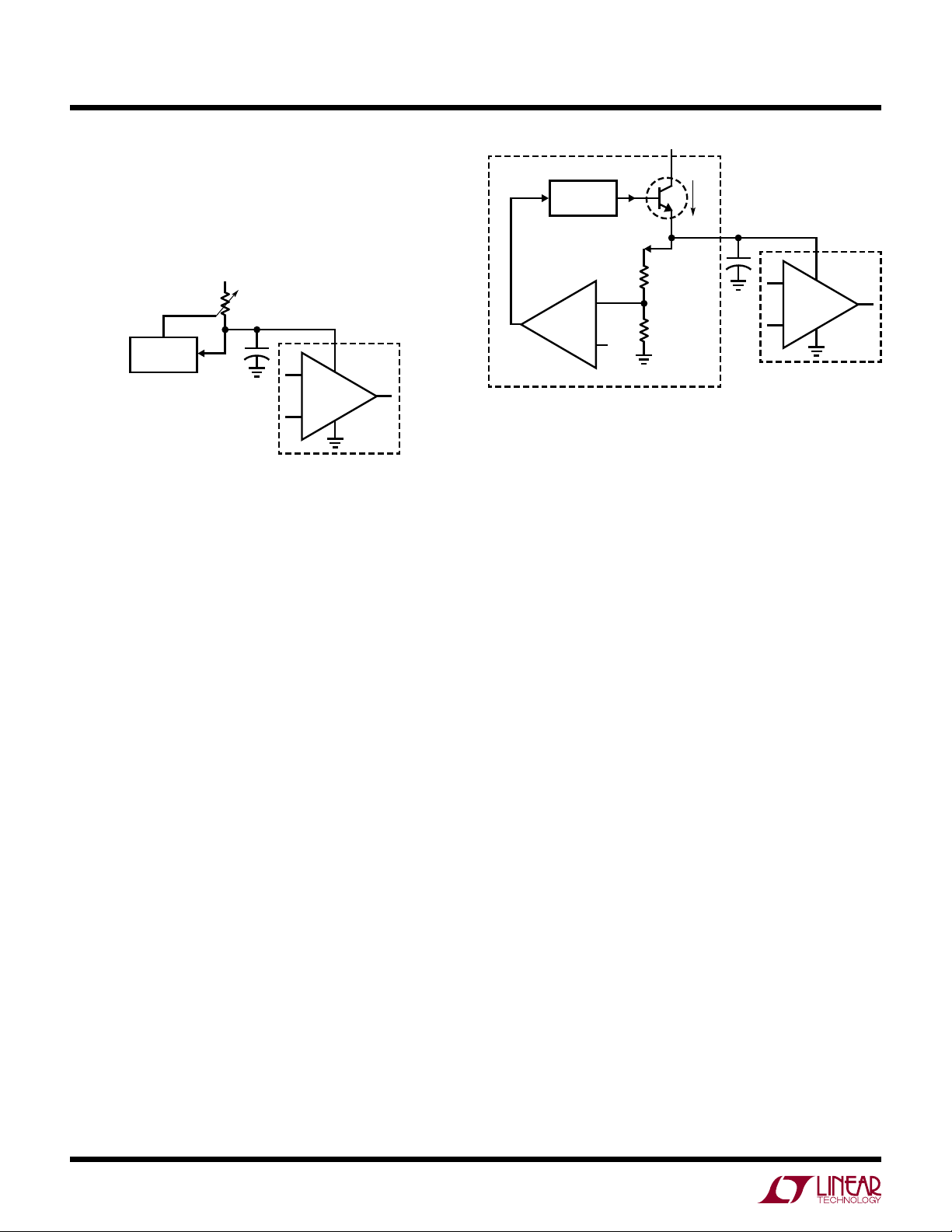
ensure its proper operation. Therefore, a dedicated volt­age regulation loop is needed. As shown in Figure 2, the
feedback loop needs to adjust the top resistor R1 value
to dynamically regulate the 3.3V on V

12V

BUS

R1

3.3V

FEEDBACK

REGULATOR

Figure 2. Feedback Loop Adjusts Series Resistor R1 Value
to Regulate 3.3V

+

V

X

.

CC

V

CC

LOAD

+

–

AN140 F02

This kind of variable resistor can be implemented with a
linear regulator, as shown in Figure 3. A linear regulator
operates a bipolar or field effect power transistor (FET)
in its linear mode. So the transistor works as a variable
resistor in series with the output load. To establish the
feedback loop, conceptually, an error amplifier senses
the DC output voltage via a sampling resistor network R
and R
reference voltage V

, then compares the feedback voltage VFB with a

B

. The error amplifier output voltage

REF

A

drives the base of the series power transistor via a current
amplifier. When either the input V
or the load current increases, the V
down. The feedback voltage V

FB

voltage decreases

BUS

output voltage goes

CC

decreases as well. As a
result, the feedback error amplifier and current amplifier
generate more current into the base of the transistor
Q1. This reduces the voltage drop V
back the V
the other hand, if the V

output voltage, so that V

CC

output voltage goes up, in a

CC

similar way, the negative feedback circuit increases V

and hence brings

CE

equals V

FB

REF

. On

CE

VIN = 12V

LINEAR REGULATOR

CURRENT

AMPLIFIER

ERROR

AMPLIFIER

B

–

+

V

REF

BUS

Q1

C

+

V

CE

–

C

E

R

A

V

FB

R

B

O

VO = 3.3V

+

V

CC

LOAD

+

V

X

–

AN140 F03

Figure 3. A Linear Regulator Implements a Variable Resistor
to Regulate Output Voltage

to ensure the accurate regulation of the 3.3V output. In
summary, any variation of V
regulator transistor’s V

is always constant and well regulated.

V

CC

CE

is absorbed by the linear

O

voltage. So the output voltage

Why Use Linear Regulators?

The linear regulator has been widely used by industry for
a very long time. It was the basis for the power supply
industry until switching mode power supplies became
prevalent after the 1960s. Even today, linear regulators
are still widely used in a wide range of applications.

In addition to their simplicity of use, linear regulators have
other performance advantages. Power management sup

-

pliers have developed many integrated linear regulators.

, V

A typical integrated linear regulator needs only V

IN

OUT

,
FB and optional GND pins. Figure 4 shows a typical 3-pin
linear regulator, the LT1083, which was developed more
than 20 years ago by Linear Technology. It only needs an
input capacitor, output capacitor and two feedback resistors
to set the output voltage. Almost any electrical engineer
can design a supply with these simple linear regulators.

AN140-2

an140fa

P

OUTPUT+PLOSS

VO•I

O

V

IN

1.2V TO 36V

F

5V AT 7.5A

V

≥ 6.5V

AN140 F04

IN

+

10µF

*REQUIRED FOR STABILITY

Application Note 140

work with low headroom (VIN – VO) are called low dropout

LT1083

IN

ADJ

OUT

121Ω
1%

365Ω
1%

+

10µF*
TANTALUM

regulators (LDOs).

It is also clear that a linear regulator or an LDO can only
provide step-down DC/DC conversion. In applications that
require V
negative V

voltage to be higher than VIN voltage, or need

O

voltage from a positive VIN voltage, linear

O

regulators obviously do not work.

Figure 4. Integrated Linear Regulator Example: 7.5A
Linear Regulator with Only Three Pins

One Drawback – A Linear Regulator Can Burn a Lot of
Power

A major drawback of using linear regulators can be the
excessive power dissipation of its series transistor Q1
operating in a linear mode. As explained previously, a lin

­ear regulator transistor is conceptually a variable resistor.
Since all the load current must pass through the series
transistor

. In this case, the efficiency of a linear regulator can be

I

O

, its power dissipation is P

Loss

= (V

– VO) •

IN

quickly estimated by:

ηLR=

P

OUTPUT

=

VO•IO+(VIN– VO)•I

O

O

=

V

(1)

So in the Figure 1 example, when the input is 12V and
output is 3.3V, the linear regulator efficiency is just 27.5%.
In this case, 72.5% of the input power is just wasted and
generates heat in the regulator. This means that the transis

­tor must have the thermal capability to handle its power/
heat dissipation at worst case at maximum V

and full

IN

load. So the size of the linear regulator and its heat sink
may be large, especially when V

is much less than VIN.

O

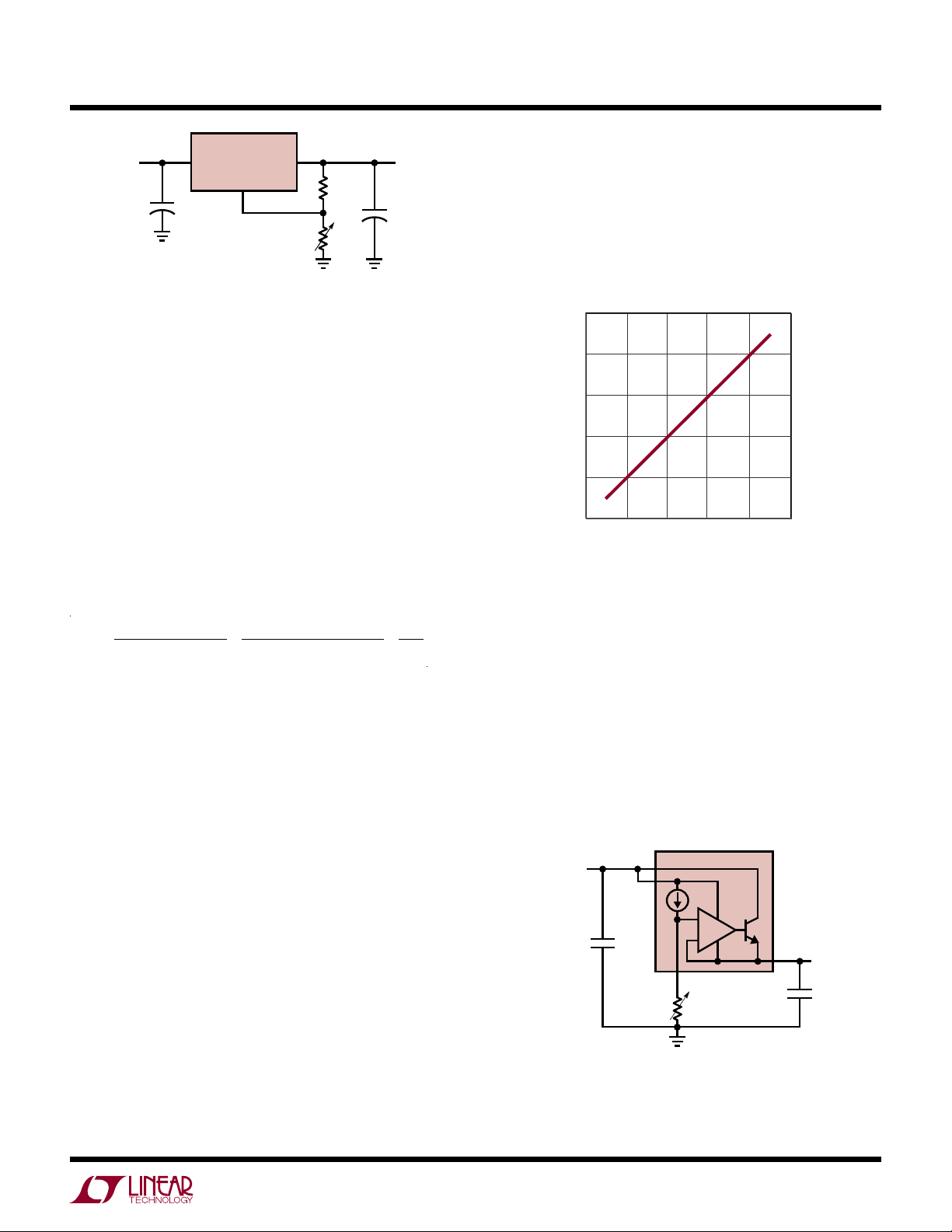
Figure 5 shows that the maximum efficiency of the linear
regulator is proportional to the V

O/VIN

ratio.

On the other hand, the linear regulator can be very efficient

is close to VIN. However, the linear regulator (LR) has

if V

O

another limitation, which is the minimum voltage differ­ence between V

and VO. The transistor in the LR must

IN

be operated in its linear mode. So it requires a certain
minimum voltage drop across the collector to emitter
of a bipolar transistor or drain to source of a FET. When

is too close to VIN, the LR may be unable to regulate

V

O

output voltage anymore. The linear regulators that can

100

80

60

40

EFFICIENCY %

20

0

0

0.40.2
VO/V

IN

0.6

0.8 1

AN140 F05

Figure 5. Maximum Linear Regulator Efficiency
vs, VO/VIN Ratio

Linear Regulator with Current Sharing for High Power [8]

For applications that require more power, the regulator must
be mounted separately on a heat sink to dissipate the heat.
In all-surface-mount systems, this is not an option, so the
limitation of power dissipation (1W for example) limits
the output current. Unfortunately, it is not easy to directly
parallel linear regulators to spread the generated heat.

SET

LT3080

R

SET

V

OUT

+
–

= R

SET

• 10µA

OUT

AN140 F06

V

OUT

2.2µ

an140fa

V

CONTROL

1µF

IN

V

IN

Figure 6. Single Resistor Setting LDO LT3080 with a
Precision Current Source Reference

AN140-3

Application Note 140

4.5V TO 30V

OUT

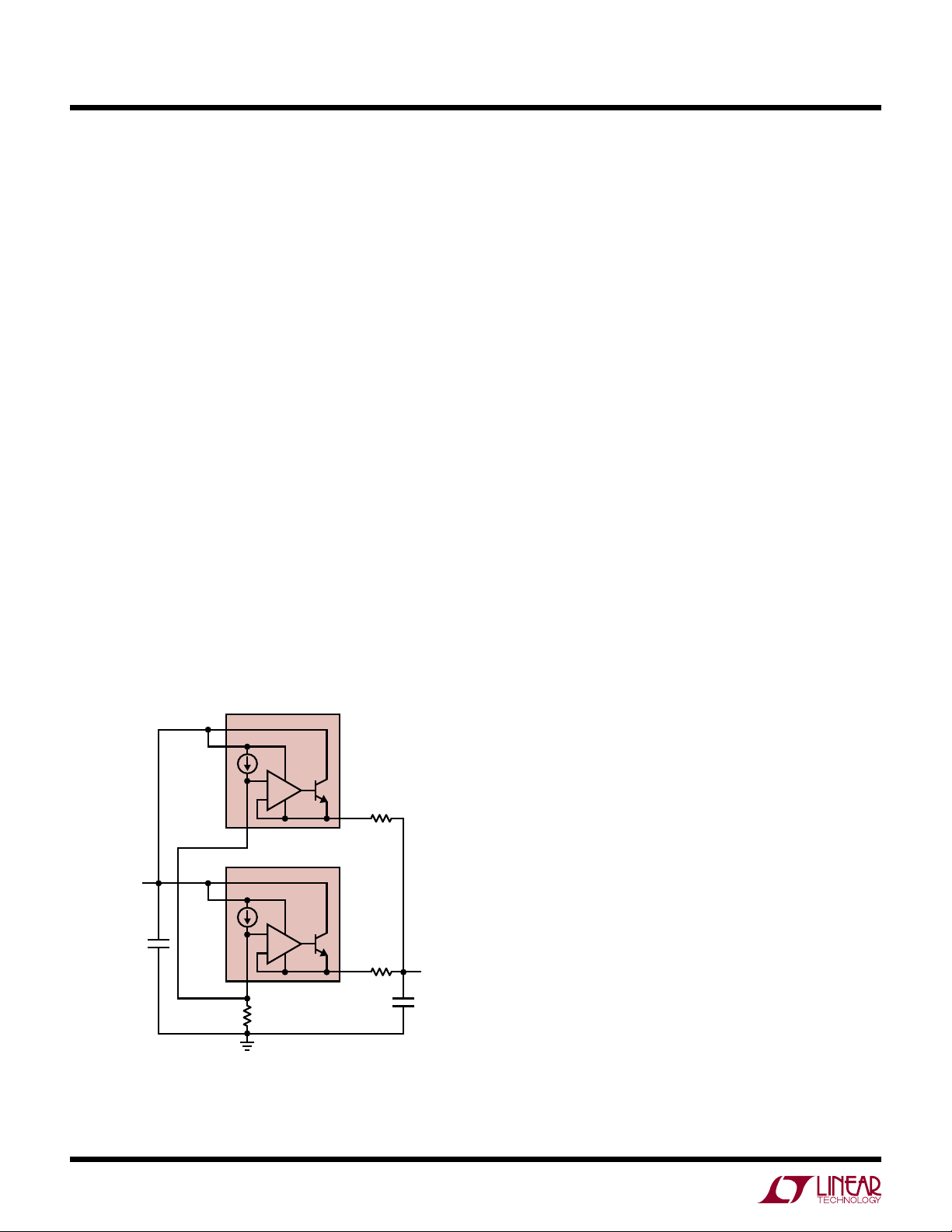
Replacing the voltage reference shown in Figure 3 with
a precision current source, allows the linear regulator to
be directly paralleled to spread the current load and thus
spread dissipated heat among the ICs. This makes it pos

­sible to use linear regulators in high output current, all­surface-mount applications, where only a limited amount
of heat can be dissipated in any single spot on a board.

T3080 is the first adjustable linear regulator that can

The L
be used in parallel for higher current. As shown in Figure 6,
it has a precision zero TC 10µA internal current source
connected to the noninverting input of the operational
amplifier
R

SET

from 0V to (V

. With an external single voltage setting resistor

, the linear regulator output voltage can be adjusted

IN

– V

DROPOUT

).

Figure 7 shows how easy it is to parallel LT3080s for
current sharing. Simply tie the SET pins of the LT3080s
together, the two regulators share the same reference
voltage. Because the operational amplifiers are precisely
trimmed, the offset voltage between the adjustment pin
and the output is less than 2mV. In this case, only 10mΩ
ballast resistance, which can be the sum of a small external
resistor and PCB trace resistance, is needed to balance
the load current with better than 80% equalized sharing.
Need even more power? Even paralleling 5 to 10 devices
is reasonable.

V

IN

LT3080

Applications Where Linear Regulators Are Preferable

There are many applications in which linear regulators or
LDOs provide superior solutions to switching supplies,
including:

1. Simple/low cost solutions. Linear regulator or LDO

solutions are simple and easy to use, especially for
low power applications with low output current where
thermal stress is not critical. No external power inductor
is required.

2. Low noise/low ripple applications. For noise-sensitive

applications, such as communication and radio devices,
minimizing the supply noise is very critical. Linear
regulators have very low output voltage ripple because
there are no elements switching on and off frequently
and linear regulators can have very high bandwidth. So
there is little EMI problem. Some special LDOs, such
as Linear Technology’s LT1761 LDO family, have as low
as 20μV

noise voltage on the output. It is almost

RMS

impossible for an SMPS to achieve this low noise level.
An SMPS usually has mV of output ripple even with
very low ESR capacitors.

3. Fast transient applications. The linear regulator feed

­back loop is usually internal, so no external compensa­tion is required. Typically, linear regulators have wider
control loop bandwidth and faster transient response
than that of SMPS.

V

CONTROL

+
–

SET

V

V

CONTROL

IN

V

IN

1µF

Figure 7. Paralleling of Two LT3080 Linear Regulators for
Higher Output Current

LT3080

+
–

SET

165k

OUT

OUT

10mΩ

10mΩ

AN140 F07

AN140-4

V

3.3V
2A

100µF

Low dropout applications. For applications where

4.
output voltage is close to the input voltage, LDOs may
be more efficient than an SMPS. There are very low
dropout LDOs (VLDO) such as Linear’s LTC1844, LT3020
and LTC3025 with from 20mV to 90mV dropout voltage
and up to 150mA current. The minimum input voltage
can be as low as 0.9V. Because there is no AC switch

­ing loss in an LR, the light load efficiency of an LR or
an LDO is similar to its full load efficiency. An SMPS
usually has lower light load efficiency because of its
AC switching losses. In batter

y powered applications
in which light load efficiency is also critical, an LDO
can provide a better solution than an SMPS.

In summary, designers use linear regulators or LDOs
because they are simple, low noise, low cost, easy to use
and provide fast transient response. If V

is close to VIN,

O

an LDO may be more efficient than an SMPS.

an140fa

Application Note 140

T

S

SWITCHING MODE POWER SUPPLY BASICS

Why Use a Switching Mode Supply?

A quick answer is high efficiency. In an SMPS, the tran

­sistors are operated in switching mode instead of linear
mode. This means that when the transistor is on and
conducting current, the voltage drop across its power path
is minimal. When the transistor is off and blocking high
voltage, there is almost no current through its power path.
So the semiconductor transistor is like an ideal switch. The
power loss in the transistor is therefore minimized. High
efficiency, low power dissipation and high power density
(small size) are the main reasons for designers to use
SMPS instead of linear regulators or LDOs, especially in
high current applications. For example, nowadays a 12V

3.3V

switching mode synchronous buck step-down

OUT

IN

,

supply can usually achieve >90% efficiency vs less than

27.5% from a linear regulator. This means a power loss
or size reduction of at least eight times.

The Most Popular Switching Supply—the Buck
Converter

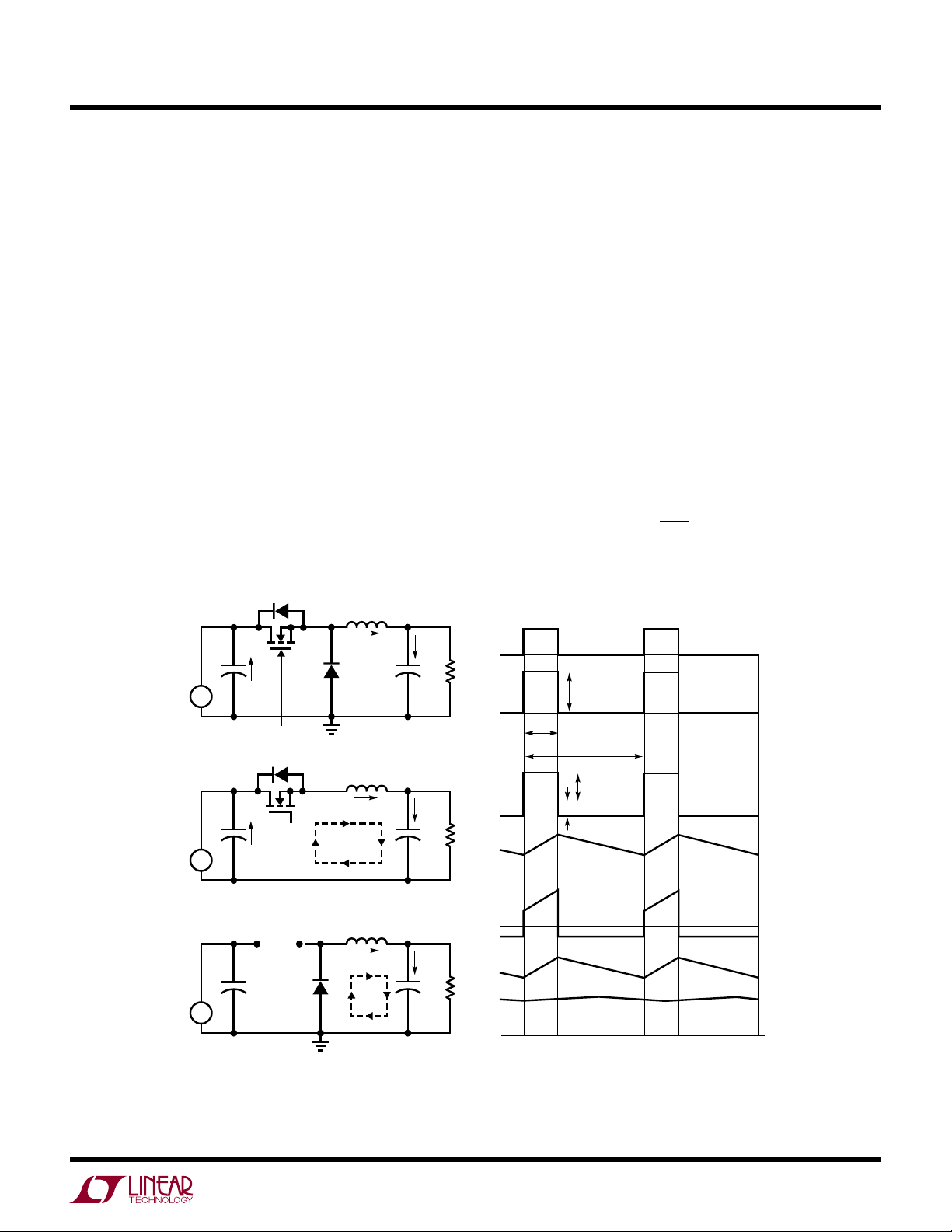
Figure 8 shows the simplest and most popular switching
regulator, the buck DC/DC converter. It has two operating
modes, depending on if the transistor Q1 is turned on or
off. To simplify the discussion, all the power devices are
assumed to be ideal. When switch (transistor) Q1 is turned
on, the switching node voltage V
L current is being charged up by (V

SW

IN

= V

and inductor

IN

– VO). Figure 8(a)
shows the equivalent circuit in this inductor charging
mode. When switch Q1 is turned off, inductor current goes
through the freewheeling diode D1, as shown in Figure
8(b). The switching node voltage V
L current is discharged by the V

= 0V and inductor

SW

load. Since the ideal

O

inductor cannot have DC voltage in the steady state, the
average output voltage V

V

= AVG[VSW]=

O(DC)

can be given as:

O

ON

• V

IN

T

(2)

Q1

I

C(IN)

DUTY

CYCLE

Q1

+

V

GS1

+

+

V

IN

–

+

I

C(IN)

+

V

IN

–

A. INDUCTOR CHARGING MODE

+

+

V

IN

–

B. INDUCTOR DISCHARGING MODE

–

SW

SW

SW

+

–

V

V

L

O

L

I

L

D1

+

–

V

L

I

L

I

L

–

+

V

L

I

L

D1

I

L

I

CO

+

C

V

O

L

I

CO

+

C

V

O

L

I

CO

+

C

V

GS1

LOAD

O

V

SW

V

L

LOAD

O

O

LOAD

I

C(IN)

I

I

L

CO

V

O

D • T

V

IN

S

T

S

VIN – V

O

V

O

AN140 F08

Figure 8. Buck Converter Operating Modes and Typical Waveforms

an140fa

AN140-5

Application Note 140

T

S

P

33W+4.095W

CYCLE

AN140 F09

Q1

where TON is the on-time interval within the switching
period T
D, the output voltage V

When the filter inductor L and output capacitor C
are sufficiently high, the output voltage V

. If the ratio of TON/TS is defined as duty cycle

S

is:

O

V

O(DC)

ON

=

T

• VIN=D• V

IN

(3)

is a DC voltage

O

values

O

with only mV ripple. In this case, for a 12V input buck
supply, conceptually, a 27.5% duty cycle provides a 3.3V
output voltage.

Other than the above averaging approach, there is another
way to derive the duty cycle equation. The ideal inductor
cannot have DC voltage in steady state. So it must maintain
inductor volt-second balance within a switching period.
According to the inductor voltage waveform in Figure 8,
volt-second balance requires:

(V

Hence, V

– VO) • D • TS = VO • (1 – D) • TS (4)

IN

= VIN • D (5)

O

Equation (5) is the same as equation (3). The same volt­second balance approach can be used for other DC/DC
topologies to derive the duty cycle vs V

and VO equations.

IN

Power Losses in a Buck Converter

DC Conduction Losses

With ideal components (zero voltage drop in the ON
state and zero switching loss), an ideal buck converter
is 100% efficient. In reality, power dissipation is always
associated with every power component. There are two
types of losses in an SMPS: DC conduction losses and
AC switching losses.

The conduction losses of a buck converter primarily result
from voltage drops across transistor Q1, diode D1 and

inductor L when they conduct current. To simplify the
discussion, the AC ripple of inductor current is neglected
in the following conduction loss calculation. If a MOSFET
is used as the power transistor, the conduction loss of
the MOSFET equals I

• R

O

• D, where R

DS(ON)

DS(ON)

is

2

the on-resistance of MOSFET Q1. The conduction power
loss of the diode equals I

• VD • (1 – D), where VD is the

O

forward voltage drop of the diode D1. The conduction
loss of the inductor equals I

• R

O

, where R

DCR

DCR

is the

2

copper resistance of the inductor winding. Therefore, the
conduction loss of the buck converter is approximately:

2

= I

P

• R

CON_LOSS

(6)

DCR

O

• R

For example, a 12V input, 3.3V/10A
can use following components: MOSFET R
inductor R

= 2 mΩ, diode forward voltage VD = 0.5V.

DCR

• D + IO • VD • (1 – D) + I

DS(ON)

output buck supply

MAX

DS(ON)

O2

= 10mΩ,

Therefore, the conduction loss at full load is:

P

CON_LOS

= 102 • 10 • 10–3 • 0.275 + 10 • 0.5 •
(1 – 0.275) + 102 • 2 • 10–3(W) = 0.275W + 3.62W
+ 0.2W = 4.095W (7)

Considering only conduction loss, the converter
efficiency is:

η

=

BUCK_CON

3.3V •10A

=

P

OUTPUT

OUTPUT+PCON_LOSS

= 88.96%

(8)

The above analysis shows that the freewheeling diode
consumes 3.62W power loss, which is much higher than
the conduction losses of the MOSFET Q1 and the inductor
L. To further improve efficiency, diode D1 can be replaced
with a MOSFET Q2, as shown in Figure 9. This converter
is referred to as a synchronous buck converter. Q2’s gate
requires signals complementary to the Q1 gate, i.e., Q2

AN140-6

SW

I

C(IN)

+

V

IN

–

DUTY

Figure 9. Synchronous Buck Converter and Its Transistor Gate Signals

V

O

L

I

L

Q2

I

V

CO

C

GSQ1

LOAD

O

V

GSQ2

an140fa

Application Note 140

P

33W+1.2W

AN140 F10

is only on when Q1 is off. The conduction loss of the
synchronous buck converter is:

P

CON_LOSS

+ I

2

R

O

DCR

If a 10mΩ R

2

= I

O

• R

DS1(ON)

• D + I

(9)

MOSFET is used for Q2 as well, the

DS(ON)

O

2

• R

DS2(ON)

• (1– D)

conduction loss and efficiency of the synchronous buck
converter are:

P

CON_LOS

= 102 • 0.01 • 0.275 + 102 • 0.01 •

(1 – 0.275) + 102 • 2 • 10–3(W) = 0.275W + 0.725W +

0.2W = 1.2W (10)

OUTPUT

OUTPUT+PCON_LOSS

= 96.45%

(11)

η

BUCK_CON

3.3V •10A

=

=

P

The above example shows that the synchronous buck is
more efficient than a conventional buck converter, especially
for low output voltage applications where the duty cycle
is small and the conduction time of the diode D1 is long.

AC Switching Losses

In addition to the DC conduction losses, there are other
AC/switching related power losses due to the nonideal
power components:

1. MOSFET switching losses. A real transistor requires

time to be turned on or off. So there are voltage and
current overlaps during the turn-on and turn-off tran

­sients, which generate AC switching losses. Figure 10
shows the typical switching waveforms of the MOSFET

V

∆T

ON

Q1

Q

GD

V

DS

GS

I

DS

∆T

OFF

Q

GD

t

Q1 in the synchronous buck converter. The charging and
discharging of the top FET Q1’s parasitic capacitor C
with charge Q

determine most of the Q1 switching

GD

GD

time and related losses. In the synchronous buck, the
bottom FET Q2 switching loss is small, because Q2 is
always turned on after its body diode conducts and is
turned off before its body diode conducts, while the
voltage drop across the body diode is low. However,
the body diode reverse recovery charge of Q2 can
also increase the switching loss of the top FET Q1 and
can generate switching voltage ringing and EMI noise.
Equation (12) shows that the control FET Q1 switching
loss is proportional to the converter switching frequency

. The accurate calculation of the energy losses EON

f

S

and E

for Q1 is not simple but can be found from

OFF

MOSFET vendors’ application notes.

SW_Q1

= (EON + E

P

2. Inductor core loss P

) • fS (12)

OFF

SW_CORE

. A real inductor also
has AC loss that is a function of switching frequency.
Inductor AC loss is primarily from the magnetic core
loss. In a high frequency SMPS, the core material may
be powdered iron or ferrite. In general, powdered iron
cores saturate softly but have high core loss, while fer

­rite material saturates more sharply but has less core
loss. Ferrites are ceramic ferromagnetic materials that
have a crystalline structure consisting of mixtures of
iron oxide with either manganese or zinc oxide. Core
losses are due mainly to magnetic hysteresis loss. The
core or inductor manufacturer usually provide the core
loss data for power supply designers to estimate the
AC inductor loss.

3. Other AC related losses. Other AC related losses

include the gate driver loss P

• QG • fS, and the dead time (when both top FET

V

DRV

SW_GATE

, which equals

Q1 and bottom FET Q2 are off) body diode conduction
loss, which is equal to (ΔT

ON

+ ΔT

OFF

) • V

D(Q2)

• fS.

In summary, the switching-related loss includes:

E

ON

Figure 10. Typical Switching Waveform and Losses in the Top
FET Q1 in the Buck Converter

E

OFF

P

t

SW_LOSS

= P

Q1_SW

+ P

CORE_SW

+ P

DRV

+ P

DEADTIME

The calculation of switching related losses is usually

not easy. The switching related losses are proportional
to switching frequency f

. In the 12VIN, 3.3VO/10A

S

synchronous buck converter, the AC loss causes about
2% to 5% efficiency loss with 200kHz – 500kHz switch

AN140-7

(13)

MAX

an140fa

-

Application Note 140

(VIN– VO)• VO/ V

S

ing frequency. So the overall efficiency is about 93% at
full load, much better than that of an LR or LDO supply.
The heat or size reduction can be close to 10x.

DESIGN CONSIDERATIONS OF THE SWITCHING
POWER COMPONENTS

Switching Frequency Optimization

In general, higher switching frequency means smaller
size output filter components L and C

. As a result, the

O

size and cost of the power supply can be reduced. Higher
bandwidth can also improve load transient response.
However, higher switching frequency also means higher
AC-related power loss, which requires larger board space
or a heat sink to limit the thermal stress. Currently, for
≥10A output current applications, most step-down sup

­plies operate in the range of 100kHz to 1MHz ~ 2MHz. For
< 10A load

current, the switching frequency can be up to
several MHz. The optimum frequency for each design is
a result of careful trade-offs in size, cost, efficiency and
other performance parameters.

Output Inductor Selection

In a synchronous buck converter, the inductor peak-to­peak ripple current can be calculated as:

ΔI

L(P-P)

=

L • f

IN

(14)

With a given switching frequency, a low inductance gives
large ripple current and results in large output ripple volt­age. Large ripple current also increases MOSFET RMS
current and conduction losses. On the other hand, high
inductance means large inductor size and possible high
inductor DCR and conduction losses. In general, 10%
~ 60% peak-to-peak ripple current is chosen over the
maximum DC current ratio when selecting an inductor. The
inductor vendors usually specify the DCR, RMS (heating)
current and saturation current ratings. It is important to
design the maximum DC current and peak current of the
inductor within the vendor’s maximum ratings.

Power MOSFET Selection

When selecting a MOSFET for a buck converter, first make
sure its maximum VDS rating is higher than the supply
V

IN(MAX)

with sufficient margin. However, do not select a

FET with an excessively high voltage rating. For example,
for a 16V

IN(MAX)

supply, a 25V or 30V rated FET is a good
fit. A 60V rated FET can be excessive, because the FET
on-resistance usually increases with rated voltage. Next,
the FET’s on-resistance R

and gate charge QG (or

DS(ON)

QGD) are two most critical parameters. There is usually a
trade-off between the gate charge QG and on-resistance
R
low QG but high on-resistance R
a large silicon die has low R

. In general, a FET with small silicon die size has

DS(ON)

, while a FET with

DS(ON)

but large QG. In a buck

DS(ON)

converter, the top MOSFET Q1 takes both conduction loss
and AC switching loss. A low QG FET is usually needed for
Q1, especially in applications with low output voltage and
small duty cycle. The lower side synchronous FET Q2 has
small AC loss because it is usually turned on or off when
its VDS voltage is near zero. In this case, low R

DS(ON)

is
more important than QG for synchronous FET Q2. When a
single FET cannot handle the total power, several MOSFETs
can be used in parallel.

Input and Output Capacitor Selection

First, the capacitors should be selected with sufficient
voltage derating.

The input capacitor of a buck converter has pulsating
switching current with large ripple. Therefore, the input
capacitor should be selected with sufficient RMS ripple
current rating to ensure its lifetime. Aluminum electrolytic
capacitors and low ESR ceramic capacitors are usually
used in parallel at the input.

The output capacitor determines not only the output volt­age ripple, but also the load transient performance. The
output voltage ripple can be calculated by Equation (15).
For high performance applications, both the ESR and total
capacitance are important to minimize output ripple volt­age and to optimize load transient response. Usually, low
ESR tantalum, low ESR polymer capacitors and multilayer
ceramic capacitors (MLCC) are good choices.

∆V

OUT

≈ ∆I

L(P-P)



• ESR+



8 • f

1

S•COUT




(15)

Close the Feedback Regulation Loop

There is another important design stage for a switching
mode supply—closing the regulation loop with a negative
feedback control scheme. This is usually a much more
challenging task than using an LR or LDO. It requires good

an140fa

AN140-8

understanding of loop behavior and compensation design

1

to optimize dynamic performance with a stable loop.

Small Signal Model of the Buck Converter

As explained above, a switching converter changes its
operation mode as a function of the switch ON or OFF
state. It is a discrete and nonlinear system. To analyze the
feedback loop with the linear control method, linear small
signal modeling is needed [1]. Because of the output L-C
filter, the linear small signal transfer function of duty cycle
D to output V

is actually a second-order system with two

O

poles and one zero, as shown in Equation (16). There are
double poles located at the resonant frequency of the output
inductor and capacitor. There is a zero determined by the
output capacitance and the capacitor ESR.

S

GDV(s)=



• 1+

V

V

IN

O

=

D

1+

ω

S



S

•Q

O




_

ESR

Z

2

S

+

2

ω

O

(16)

Application Note 140

Where, S

ω

= 2πfWO=

O

Voltage Mode Control vs Current Mode Control

The output voltage can be regulated by a closed loop
system shown in Figure 11. For example, when the output
voltage increases, the feedback voltage V
and the output of the negative feedback error amplifier
decreases. So the duty cycle decreases. As a result, the
output voltage is pulled back to make V
compensation network of the error op amp can be a type I,
type II or type III feedback amplifier network [4]. There is
only one control loop to regulate the output. This scheme
is referred to as voltage mode control. Linear T
LTC3775 and LTC3861 are typical voltage mode buck
controllers.

_ESR

Z

= 2πf

1

L • C

_ESR

Z

O

=

ESR•C

DCR

1+

1+

R

ESR

•

R

,

O

1

≈

L • C

(17)

O

increases

FB

FB

= V

. The

REF

echnology

’s

L

+

D

PWM

+

V

IN

–

D

RAMP

–

+

COMPARATOR

FEEDBACK CONTROL

Figure 11. Block Diagram of a Voltage Mode-Controlled Buck Converter

COMP

V

C

ESR

V

O

R

C

LOAD

O

–

–

+

V

REF

V

C

R2

V

FB

R1

D•T

S

T

D = k • V

S

RAMP

C

AN140 F11

an140fa

AN140-9

Application Note 140

C

5V TO 26V

T

Figure 12 shows a 5V to 26V input, 1.2V/15A output syn­chronous buck supply using the LTC3775 voltage mode
buck controller. Due to the L

TC3775’s leading-edge PWM
modulation architecture and very low (30ns) minimum
on-time, the supply operates well for applications that
converts a high voltage automotive or industrial power
supply down to the 1.2V low voltage required by today’s
microprocessors and programmable logic chips. [9] High
power applications require multiphase buck converters
with current sharing. With voltage mode control, an
additional current sharing loop is required to balance
current among parallel buck channels. A typical current
sharing method for voltage mode control is the master-

®

slave method. The LTC3861 is such a PolyPhase

voltage
mode controller. Its very low, ±1.25mV, current sense offset
makes current sharing between paralleled phases very
accurate to balance the thermal stress. [10]

F

220pF

Current mode control uses two feedback loops: an
outer voltage loop similar to the control loop of voltage
mode-controlled converters, and an inner current loop
that feeds back the current signal into the control loop.
Figure 13 shows the conceptual block diagram of a peak
current mode control buck converter that directly senses
the output inductor current. With current mode control,
the inductor current is determined by the error op amp
output voltage. The inductor becomes a current source.
Therefore, the transfer function from op amp output, V
to supply output voltage V

becomes a single pole system.

O

,

C

This makes loop compensation much easier. The control
loop compensation has less dependency on the output
capacitor ESR zero, so it is possible to use all ceramic
output capacitors.

V

IN

D

B

R

ILIMT

732Ω

R

ILIMB

57.6k

C

VCC

4.7µF

R
10k

C

OUT

: CMDSH4E

D

B

L1: IHLP-4040DZ-ER-R36-M11

: RJK0301DPB-00-J0

Q

B

: RJK0305DPB-00-J0

Q

C

SS

0.01µF

R

39.2k

330pF

R

A

B

10k

C1

4.7k

3.9nF

: SANYO 2R5TPD470M5

SET

C2

R2

I

LIMT

I

LIMB

INTV

SS

FREQ

FB

V

IN

BOOST

CC

LTC3775

MODE/SYNC

RUN/SHDNCOMP

SGND

TG Q

SENSE

SW

BG

PGND

C

0.1µF

R

SENSE

0.003Ω

T

B

L1

0.36µH

Q

B

+

+

AN140 F12

C

IN1

330µF
35V

C

OUT

470µF

2.5V
×2

V

OUT

1.2V
15A

Figure 12. The LTC3775 Voltage Mode Synchronous Buck Supply Offers
a High Step-Down Ratio

an140fa

AN140-10

Application Note 140

AN140 F13

There are many other benefits from current mode control.
As shown in Figure 13, since the peak inductor current is
limited by the op amp V

in a cycle-by-cycle fashion, the

C

current mode-controlled system provides a more accurate
and faster current limit under overload conditions. The
in-rush inductor current is well controlled during start-up,
too. Also, the inductor current does not change quickly
when the input voltage changes, so the supply has good
line transient performance. When multiple converters are
paralleled, with current mode control, it is also very easy
to share current among supplies, which is important for
reliable high current applications using PolyPhase buck
converters. In general, a current mode-controlled converter
is more reliable than a voltage mode-controlled converter.

The current mode control scheme solution needs to sense
the current precisely. The current sensing signal is usu

­ally a small signal at a level of tens of millivolts that is
sensitive to switching noise. Therefore, proper and careful
PCB layout is needed. The current loop can be closed by
sensing the inductor current through a sensing resistor

,
the inductor DCR voltage drop, or the MOSFET conduction
voltage drop. T

ypical current mode controllers include

Linear Technology’s LTC3851A and LTC3855.

Constant Frequency vs Constant On-Time Control

Typical voltage mode and current mode schemes in the
Voltage Mode Control vs Current Mode Control section
have constant switching frequency generated by controller
internal clocks. These constant switching frequency con

­trollers can be easily synchronized, an important feature
for high current, PolyPhase buck controllers. However

, if
the load step-up transient occurs just after the control FET
Q1 gate is turned off, the converter must wait the entire Q1
off-time until the next cycle to respond to the transient. In
applications with small duty cycles, the worst case delay
is close to one switching cycle.

In such low duty cycle applications, constant on-time val

­ley current mode control has shorter latency to respond
to load step-up transients. In steady state operation, the
switching frequency of constant on-time buck converters
is nearly fixed. In the event of a transient, the switching
frequency can var

y quickly to speed up the

transient
response. As a result, the supply has improved transient
performance and output capacitance and its related cost
can be reduced.

However, with constant on-time control, the switching fre

-

quency may vary with line or load. The LTC3833 is a valley

D

PWM

+

V

IN

–

D

COMPARATOR

CURRENT MODE CONTROL

R

L

SEN

ERROR OP AMP

OUTPUT

GATE SIGNAL

SLOPE

COMP

–
–
+

K

I

V

C

ESR

C

I

SIGNAL

L

COMPENSATION

NETWORK

–

+

ERROR
0P AMP

+

V

O

R
LOAD

–

V

REF

SLOPE COMP

INDUCTOR

R2

V

FB

R1

CURRENT

SIGNAL

Figure 13. Block Diagram of a Current Mode-Controlled Buck Converter

TOP FET

~I

OUT

an140fa

AN140-11

Application Note 140

INTV

B

OUT1

330µF

current mode buck controller with a more sophisticated
controlled-on-time architecture—a variant of the constant
on-time control architecture with the distinction that the
on-time is controlled so that the switching frequency
remains constant over steady stage conditions under line
and load. With this architecture, the LTC3833 controller
has 20ns minimum on-time and allows step-down appli
cations from up to 38V

to 0.6VO. The controller can be

IN

-

synchronized to an external clock in the 200kHz to 2MHz

CC

V

IN

CSS 0.1µF

C

ITH1

220pF

R

PGD

100k

C

47pF

ITH2

R

84.5k

ITH

137k

R

T

LTC3833

PGOOD

SENSE

RUN

V

RNG

MODE/PLLIN

EXTV

TRACK/SS

ITH

RT
SGND

C

IN1

C

OUT1

: CENTRAL CMDSH-3

D

SENSE

BOOST

CC

INTV

V
V

: SANYO 16SVP180M

: SANYO 2R5TPE330M9

V

OUT

SW

PGND

OSNS
OSNS

TG

BG

–

+

D

B

CC

C

4.7µF

+
–

frequency range. Figure 14 shows a typical LTC3833 supply
with 4.5V to 14V input and 1.5V/20A output. [11] Figure 15
shows that the supply can respond quickly to sudden,
high slew rate load transients. During the load step-up
transient, the switching frequency increases to provide
faster transient response. During the load step-down
transient, the duty-cycle drops to zero. Therefore only the
output inductor

limits the current slew rate. In addition to

the LTC3833, for multiple outputs or PolyPhase applica

V

IN

C

IN1

180µF
16V

4.5V TO 14V

R

FB2

15k

R

FB1

10k

C

OUT2

100µF
×2

+

C

2.5V
×2

AN140 F14

V

OUT

1.5V
20A

MT

L1

0.47µH

C

B

0.1µF

INTV

CC

VCC

MB

L1: PULSE PA0515.471NLT
MB: RENESAS RJK0330DPB
MT: RENESAS RJK0305DPB

C

IN2

22µF
×2

+

R

SENSE

1.5mΩ

-

I

LOAD

20A/DIV

V

OUT

50mV/DIV

I

L

20A/DIV

VIN = 12V

= 1.5V

V

OUT

LOAD TRANSIENT = 0A TO 20A

AN140-12

Figure 14. Fast, Controlled-On-Time Current Mode Supply Using the LTC3833

50µs/DIV

AN140 F15a

I

LOAD

20A/DIV

V

OUT

50mV/DIV

20A/DIV

I

L

VIN = 12V

= 1.5V

V

OUT

LOAD STEP = 0A TO 20A

5µs/DIV

AN140 F15b

I

LOAD

20A/DIV

V

OUT

50mV/DIV

20A/DIV

I

L

Figure 15. LTC3833 Supply Offers Fast Response During Rapid Load Step Transients

VIN = 12V

= 1.5V

V

OUT

LOAD RELEASE = 20A TO 0A

5µs/DIV

AN140 F15c

an140fa

Application Note 140

tions, the LTC3838 and LTC3839 controllers provide fast
transient, multiphase solutions.

Loop Bandwidth and Stability

A well designed SMPS is quiet, both electrically and acous

­tically. This is not the case with an undercompensated
system, which

tends to be unstable. Typical symptoms of
an undercompensated power supply include: audible noise
from the magnetic components or ceramic capacitors, jitter
in the switching waveforms, oscillation of output voltage,
and so on. An overcompensated system can be very stable
and quiet, but at the cost of a slow transient response.
Such a system has a loop crossover frequency at very
low frequencies, typically below 10kHz. Slow transient
response designs require excessive output capacitance
to meet transient regulation requirements, increasing the
overall supply cost and size. An optimum loop compensa

­tion design is stable and quiet, but is not overcompen­sated, so it also has a fast response to minimize output
capacitance. There are numerous articles that discuss how
to optimize loop compensation networks for both voltage
mode-controlled and current mode-controlled SMPS [2-4].
Small signal modeling and loop compensation design can
be difficult for inexperienced power supply designers.
Linear Technology

’s LTpowerCAD™ design tool handles

the complicated equations and makes loop compensa

®

tion a much simpler task [6]. The LTspice

simulation

-

tool integrates all of Linear Technology’s part models and
provides additional time domain simulations to optimize
the design. However, bench test/verification of loop stabil

­ity and transient performance is usually necessary in the
prototype stage.

In gener
loop is evaluated by two important values: the loop band

al, the performance of the closed voltage regulation

­width and the loop stability margin. The loop bandwidth
is quantified by

the crossover frequency f

, at which the

C

loop gain T(s) equals one (0dB). The loop stability margin
is typically quantified by the phase margin or gain margin.
The loop phase margin Φ

is defined as the difference

m

between the overall T(s) phase delay and –180° at the
crossover frequency. The gain margin is defined by the
difference between T(s) gain and 0dB at the frequency
where overall T(s) phase equals –180°. For a buck con

­verter, typically 45 degree phase margin and 10dB gain

is

margin
Bode plot of loop gain for a current mode LTC3829 12V
to 1V

considered sufficient. Figure 16 shows a typical

/60A 3-phase buck converter. In this example, the

O

IN

crossover frequency is 45kHz and the phase margin is 64
degrees. The gain margin is close to 20dB.

Figure 16. LTpowerCAD Design Tool Provides an Easy Way to Optimize the Loop Compensation and Load Transient
Response (3-Phase, Single-Output LTC3829 Buck Converter Example).

AN140-13

an140fa

Application Note 140

V
6V TO 28V

AN140 F17

PolyPhase Buck Converter for High Current
Applications

As data processing systems become faster and larger,
their processor and memory units demand more current
at ever decreasing voltages. At these high currents, the
demands on power supplies are multiplied. In recent years,
PolyPhase (multiphase) synchronous buck converters
have been widely used for high current, low voltage power
supply solutions, due to their high efficiency and even
thermal distribution. Besides, with interleaved multiple
buck converter phases, the ripple current on both input
and output sides can be significantly reduced, resulting
in reduction of input and output capacitors and related
board space and cost.

In PolyPhase buck converters, precise current sensing and
sharing become extremely important. Good current sharing
ensures even thermal distribution and high system reliabil

-

ity. Because of their inherent current sharing capability in

t

eady state and during transients, current mode-controlled

s
bucks are usually preferred. Linear Technology’s LTC3856
and LTC3829 are typical PolyPhase buck controllers with
precise current sensing and sharing. Multiple controllers
can be connected in a daisy chain fashion for 2-, 3-, 4-,
6- and 12-phase systems with output current from 20A
to over 200A.

Other Requirements of a High Performance Controller

Many other important features are required of a high
performance buck controller. Soft-start is usually needed
to control the inrush current during start-up. Overcurrent
limit and short-circuit latchoff can protect the supply when
the output is overloaded or shorted. Overvoltage protec

­tion safeguards the expensive load devices in the system.
To minimize system EMI noise, sometimes the controller
must be synchronized to an external clock signal. For low
voltage, high current applications, remote differential volt

sensing compensates for the PCB resistance voltage

age

-

drop and accurately regulates output voltage at the remote
load. In a complicated system with many output voltage
rails, sequencing and tracking among different voltage
rails is also necessary

.

PCB Layout

Component selection and schematic design is only half
of the supply design process. Proper PCB layout of a
switching supply design is always critical. In fact, its
importance can not be overstated. Good layout design
optimizes supply efficiency, alleviates thermal stress, and
most importantly, minimizes noise and interactions among
traces and components. To achieve this, it is important
for the designer to understand the current conduction

+

22µF
35V
×3

V

OUT

1.2V
50A

C

OUT

+

470µF
4V
×4

SW3 SW2 SW1

5k

4.7µF

680pF

0.1µF

20k

20k

100k

INTV

CC

BOOST1
BOOST2
BOOST3

FREQ

I

TH

TK/SS

SGND

DIFFOUT

V

FB

DIFFN
DIFFP

V

IN

LTC3829

SW1

PGND

SENSE1
SENSE1

SW2

SENSE2
SENSE2

SW3

SENSE3
SENSE3

TG1

BG1

TG2

BG2

TG3

BG3

+
–

+
–

+
–

0.6µH

0.002Ω

V

IN

0.6µH

0.002Ω

V

IN

0.6µH

0.002Ω

Figure 17. A 3-Phase, Single VO High Current Buck Converter Using the LTC3829

IN

an140fa

AN140-14

Application Note 140

OUT

BOOST CONVERTER

OUT

OUT

OUT

OUT

DUTY

paths and signal flows in the switching power supply. It
usually requires significant effort to gain the necessary
experience. See Linear Technology Application Note 136
for detailed discussions. [7]

Selection of Various Solutions – Discrete, Monolithic
and Integrated Supplies

At the integration level, system engineers can decide
whether to choose a discrete, monolithic or fully integrated
power module solution. Figure 18 shows examples of dis
crete and power module solutions for typical point-of-load
supply applications. The discrete solution uses a controller
IC, external MOSFETs and passive components to build
the power supply on the system board. A major reason
to choose a discrete solution is low component bill of
materials (BOM) cost. However

, this requires good power
supply design skills and relatively long development time.
A monolithic solution uses an IC with integrated power
MOSFETs to further reduce the solution size and component
count. It requires similar design skills and time. A fully
integrated power module solution can significantly reduce
design effort, development time, solution size and design
risk, but usually with a higher component BOM cost.

Other Basic Nonisolated DC/DC SMPS Topologies

This application note uses buck converters as a simple ex
ample to demonstrate the design considerations of SMPS.
However, there are at least five other basic nonisolated
converter topologies (boost, buck/boost, Cuk, SEPIC and
Zeta converters) and at least five basic isolated converter
topologies (flyback, for

ward, push-pull, half-bridge and
full-bridge) which are not covered in this application note.
Each topology has unique properties that make it suited
for specific applications. Figure 19 shows simplified

­schematics for the other nonisolated SMPS topologies.

There are other nonisolated SMPS topologies which
are combinations of the basic topologies. For example,

L

+

C

V

O

LOAD

–

–

V

C

O

+

LOAD

+

–

V

LOAD

O

+

+

+

V

IN

–

DUTY

BUCK/BOOST CONVERTER

+

V

IN

–

DUTY

L1

+

V

IN

–

L

CUK CONVERTER

C

B

+

+

L2

C

-

(a)

(b)

Figure 18. Examples of (a) a Discrete 12VIN to 3.3V/10A LTC3778
Supply; (b) a Fully Integrated 16VIN, Dual 13A or Single 26A
LTM4620 µModule® Step-Down Regulator

Information furnished by Linear Technology Corporation is believed to be accurate and reliable.
However, no responsibility is assumed for its use. Linear Technology Corporation makes no representa­tion that the interconnection of its circuits as described herein will not infringe on existing patent rights.

DUTY

SEPIC CONVERTER

C

L1

+

V

IN

–

DUTY

+

V

IN

–

B

+

ZETA CONVERTER

C

B

+

•

•

+

L2

V

LOAD

+

–

C

O

+

V

LOAD

+

–

C

O

AN140 F19

Figure 19. Other Basic Nonisolated DC/DC Converter Topologies

an140fa

AN140-15

Application Note 140

Figure 20 shows a high efficiency, 4-switch synchronous
buck/boost converter based on the LTC3789 current mode
controller. It can operate with input voltages below, equal,
or above the output voltage. For example, the input can be
in the range of 5V to 36V, and the output can be a regulated
12V. This topology is a combination of a synchronous buck
converter and a synchronous boost converter, sharing a
single inductor. When VIN > V

, switches A and B operate

OUT

as an active synchronous buck converter, while the switch
C is always off and switch D is always on. When V

, switches C and D operate as an active synchronous

V

OUT

IN

<

boost converter, while switch A is always on and switch B
is always off. When VIN is close to V

, all four switches

OUT

operate actively. As a result, this converter can be very
efficient, with up to 98% efficiency for a typical 12V output
application. [12] The LT8705 controller further extends the
input voltage range up to 80V. To simplify the design and
increase power density, the LTM4605/4607/4609 further
integrate a complicated buck/boost converter into a high
density, easy-to-use power module. [13] They can be easily
paralleled with load sharing for high power applications.

4-SWITCH BUCK-BOOST
TOPOLOGY YIELDS HIGH
EFFICIENCY AT HIGH POWER

ONLY ONE INDUCTOR SIMPLIFIES
LAYOUT AND SAVES SPACE

REFERENCES

[1] V. Vorperian, “Simplified Analysis of PWM Converters
Using the Model of the PWM Switch: Parts I and II,” IEEE
Transactions on Aerospace and Electronic Systems, Mar.
1990, Vol. 26, No.2.

[2] R.B. Ridley, B.H.Cho, F.C.Lee, “Analysis and Interpre

­tation of Loop Gains of Multi-Loop-Controlled Switching
Regulators,” IEEE Transactions on Power Electronics,
pp.489-498, Oct. 1988.

[3] J. Seago, “Opti-Loop Architecture Reduces Output Ca

­pacitance and Improves Transient Response,” Application
Note 76, Linear Technology Corp., May 1999.

4] H. Dean Venable, “Optimum Feedback Amplifier Design

[
for Control Systems,” Venable Technical Paper.

[5] Linear Technology Data Sheets at www.linear.com.

[6] LTpowerCAD™ design tool at
www.linear.com/designtools/software.

[7] H. Zhang, “PCB Layout Considerations for Non-Isolated
Switching Power Supplies,” Application Note 136, Linear
Technology Corp., 2012.

L

SW2

V

IN

SINGLE SENSE RESISTOR
KEEPS EFFICIENCY HIGH

Figure 20. High Efficiency 4-Switch Buck-Boost Converter Operates
with Input Voltage Below, Equal or Above the Output Voltage

A D

C

IN

LTC3789

R

SW1

CB

SENSE

SNS

SNS

V

OUT

C

OUT

+

–

+

SNS

–

SNS

R1

R2

AN140 F20

SUMMARY

In summary, linear regulators are simple and easy to use.
Since their series regulation transistors are operated in a
linear mode, supply efficiency is usually low when output
voltage is much lower than input voltage. In general, lin

­ear regulators (or LDOs) have low voltage ripple and fast
transient response. On the other hand, SMPS operate the
transistor

as a switch, and therefore are usually much more
efficient than linear regulators. However, the design and
optimization of SMPS are more challenging and require
more background and experience. Each solution has its
own advantages and drawbacks for specific applications.

Linear Technology Corporation

AN140-16

1630 McCarthy Blvd., Milpitas, CA 95035-7417

[phone] ● FAX: [phone]

●

www.linear.com

[8] R. Dobbkin, “Low Dropout Regulator Can be Directly
Paralleled to Spread the Heat,” LT Journal of Analog In

-

novation, Oct. 2007.

[9] T. Phillips, “Produce High DC/DC Step-Down Ratios
in Tight Spaces with 30ns Minimum On-Time Controller
in 3mm × 3mm QFN,” LT Journal, Dec. 2009.

[10] M. Subramanian, T. Nguyen and T. Phillips, “Sub­Milliohm DCR Current Sensing with Accurate Multiphase
Current Sharing for High Current Power Supplies,” LT
Journal, Jan. 2013.

[11] B. Abesingha, “Fast, Accurate Step-Down DC/DC
Controller Converts 24V Directly to 1.8V at 2MHz,” LT
Journal, Oct. 2011.

[12] T. Bjorklund, “High Efficiency 4-Switch Buck-Boost
Controller Provides Accurate Output Current Limit,” Linear
Technology Design Note 499.

[13] J. Sun, S. Young and H. Zhang, “µModule Regulator
Fits a (Nearly) Complete Buck-Boost Solution in 15mm
× 15mm × 2.8mm for 4.5V-36Vin to 0.8V-34V Vout,” LT
Journal, Mar. 2009.

an140fa

LT 1113 REV A • PRINTED IN USA

 LINEAR TECHNOLOGY CORPORATION 2013