Noty an12fa Linear Technology

Circuit Techniques for Clock Sources

Jim Williams

Application Note 12

October 1985

Almost all digital or communication systems require some form of clock source. Generating accurate and stable clock signals is often a difficult design problem.

Quartz crystals are the basis for most clock sources. The combination of high Q, stability vs time and temperature, and wide available frequency range make crystals a price-performance bargain. Unfortunately, relatively little information has appeared on circuitry for crystals and engineers often view crystal circuitry as a black art, best left to a few skilled practitioners (see box, “About Quartz Crystals”).

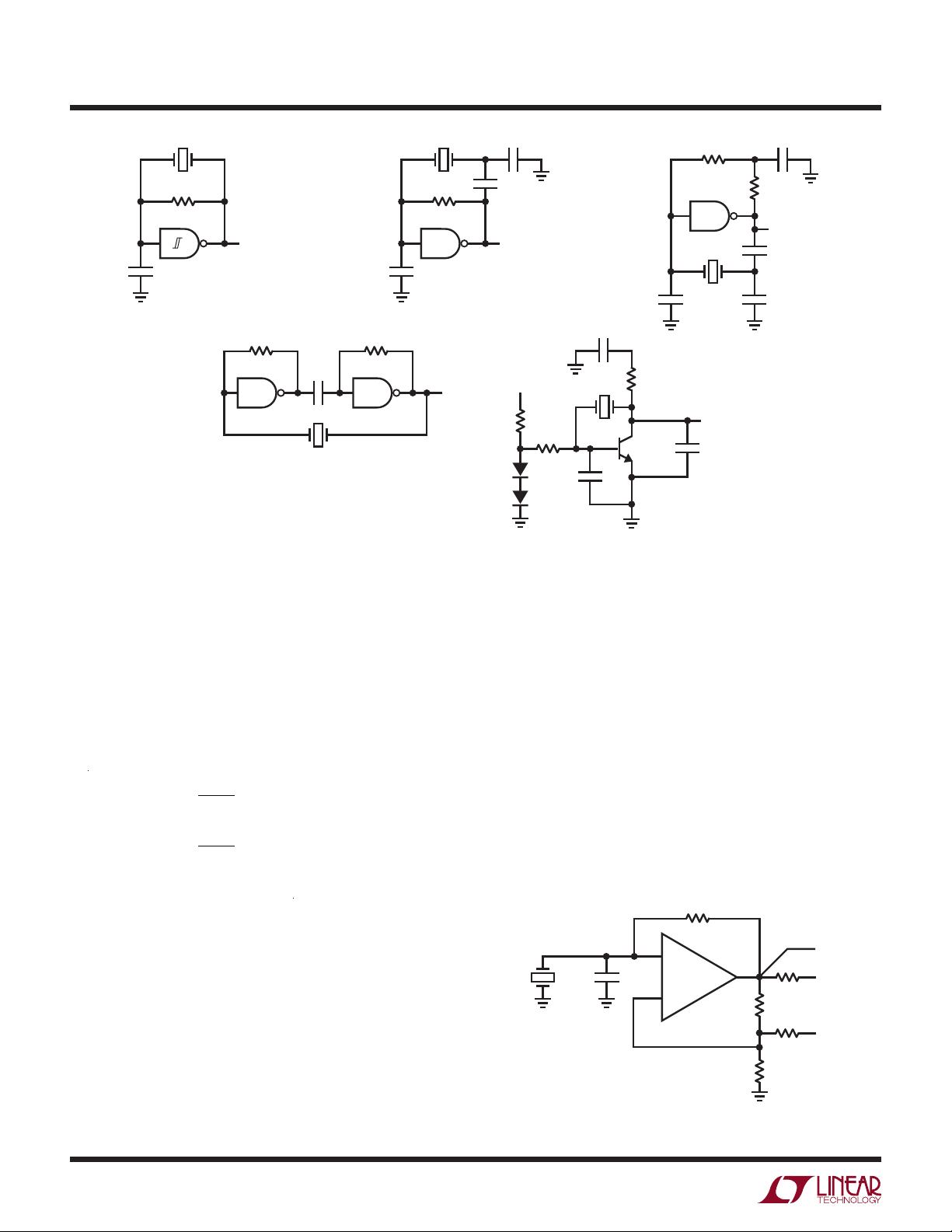
In fact, the highest performance crystal clock circuitry does demand a variety of complex considerations and subtle implementation techniques. Most applications, however, don’t require this level of attention and are relatively easy to serve. Figure 1 shows five (5) forms of simple crystal clocks. Types 1a through 1d are commonly referred to as gate oscillators. Although these types are popular, they are often associated with temperamental operation, spurious modes or outright failure to oscillate. The primary reason for this is the inability to reliably identify the analog characteristics of the gates used as gain elements. It is not uncommon in circuits of this type for gates from different manufacturers to produce markedly different circuit operation. In other cases, the circuit works, but is influenced by the status of other gates in the same package. Other circuits seem to prefer certain gate locations within the package. In consideration of these difficulties, gate oscillators are generally not the best possible choice in a production design; nevertheless, they offer low discrete component count, are used in a variety of situations, and bear mention. Figure 1a shows a CMOS Schmitt trigger biased into its linear region. The capacitor adds phase shift and the circuit oscillates at the crystal resonant frequency. Figure 1b shows a similar version for higher frequencies. The gate gives inverting gain, with the capacitors providing additional phase shift to produce oscillation. In Figure 1c, a TTL gate is used to allow the 10MHz operating frequency. The low input resistance of TTL elements does not allow the high value, single resistor biasing method. The R-C-R

network shown is a replacement for this function. Figure 1d is a version using two gates. Such circuits are particularly vulnerable to spurious operation but are attractive from a component count standpoint. The two linearly biased gates provide 360 degrees of phase shift with the feedback path coming through the crystal. The capacitor simply blocks DC in the gain path. Figure 1e shows a circuit based on discrete components. Contrasted against the other circuits, it provides a good example of the design flexibility and certainty available with components specified in the linear domain. This circuit will oscillate over a wide range of crystal frequencies, typically 2MHz to 20MHz.

The 2.2k and 33k resistors and the diodes compose a pseudo current source which supplies base drive.

At 25°C the base current is:

1.2V –1V

To saturate the transistor, which would stop the oscillator, requires V necessary to do this is:

IC(sat) =

with 18μA of base drive a beta of:

5mA

18µA

At 1mA the DC beta spread of 2N3904’s is 70 to ≅210.

The transistor should not saturate...even at supply voltages below 3V.

In similar fashion, the effects of temperature may also be determined.

vs temperature over 25°C – 70°C is:

–2.2mV/°C • 45° = –99mV.

L, LT, LTC, LTM, Linear Technology and the Linear logo are registered trademarks of Linear Technology Corporation. All other trademarks are the property of their respective owners.

33k

= 18µA

to go to near zero. The collector current

= 5mA

= 278 is required

an12fa

AN12-1

Application Note 12

100kHz

74C14

OUT

43pF

(1a) (1b) (1c)

1k 3k

74LS04 74LS04

ALL CRYSTALS PARALLEL RESONANT AT-CUT TYPES

1200pF

5MHz

4049

68pF

1MHz

6.8M

OUT

68pF

OUT

0.1μF 5V

2.2k

33k

20MHz

100pF

2N3904

(1e)(1d)

Figure 1. Typical Gate Oscillators and the Preferred Discrete Unit

74LS04

10MHz

68pF

OUT

22pF

0.25μF

OUT

68pF

AN-12 F01

The compliance voltage of the current source will move:

2 • –2.2mV/°C • 45°C = –198mV.

Hence, a first order compensation occurs:

–198mV – 99mV = –99mV total shift.

This remaining –99mV over temperature causes a shift in base current:

25°C current =

70°C current =

18µA – 15µA = 3µA

0.6V 33k

0.5V 33k

= 18µA

= 15µA

This 3μA shift (about 16%) provides a compensation for transistor hFE shift with temperature, which moves about 20% from 25°C to 70°C. Thus the circuit’s behavior over temperature is quite predictable. The resistor, diode and

tolerances mean that only first order compensations

for V

and hFE over temperature are appropriate.

to the crystal’s resonance, the crystal “steals” energy from the RC, forcing it to run at the crystal’s frequency. The crystal activity is readily apparent in Trace A of Figure 3,

which is the LT

1011’s “–” input. Trace B is the LT1011’s output. In circuits of this type, it is important to ensure that enough current is available to quickly start the crystal resonating while simultaneously maintaining an RC time constant of appropriate frequency. Typically, the free running frequency should be set 5% to 10% above crystal resonance with a resistor feedback value calculated to allow about 100μA into the capacitor-crystal network. This type of circuit is not recommended for use above a few hundred kHz because of comparator delays.

50k

85kHz

100pF

–

LT1011

10k

0UT

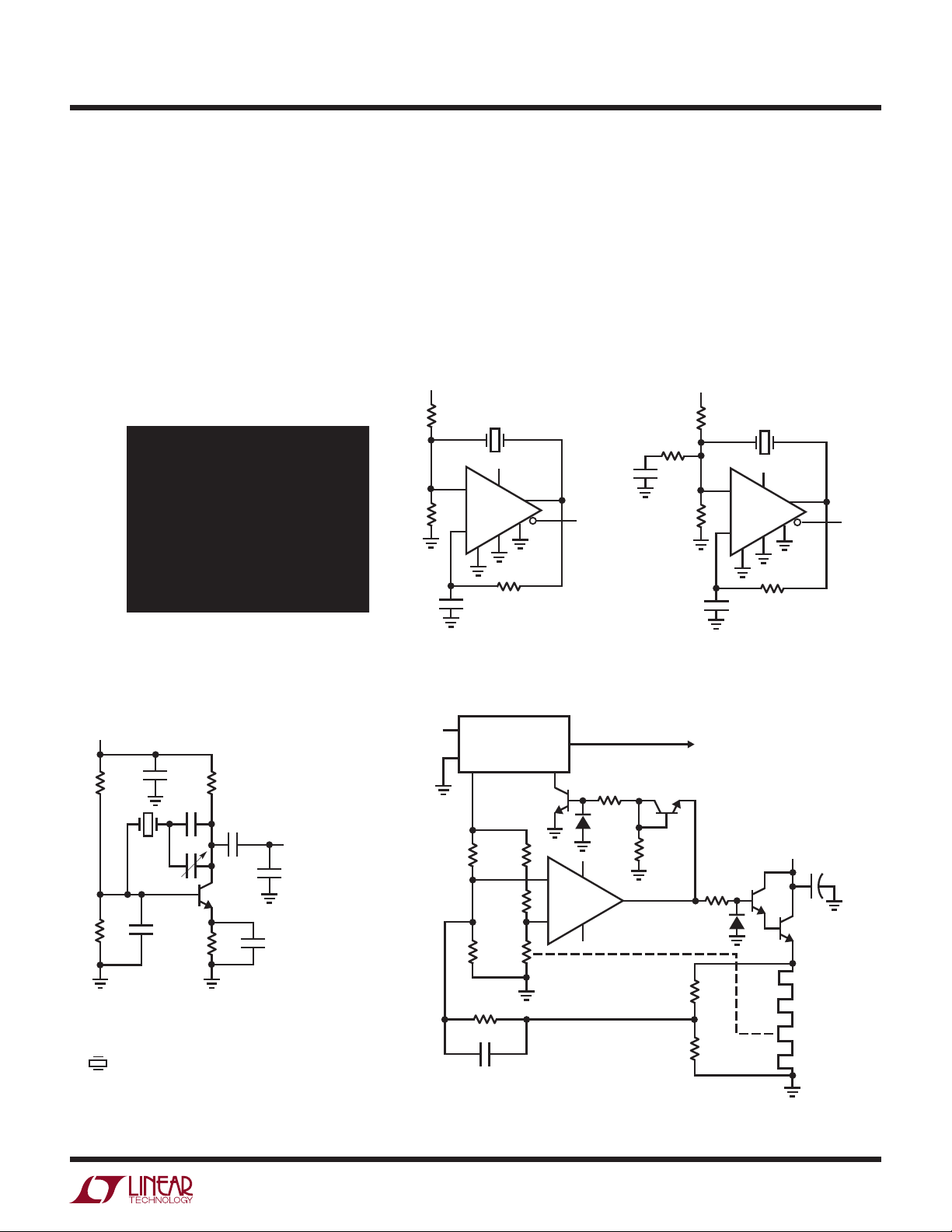
Figure 2 shows another approach. This circuit uses a standard RC-comparator multivibrator circuit with the crystal connected directly across the timing capacitor. Because the free running frequency of the circuit is close

AN12-2

10k

AN-12 F02

Figure 2. Crystal Stabilized Relaxation Oscillator

an12fa

Application Note 12

Figures 4a and 4b use another comparator based approach. In Figure 4a, the LT1016 comparator is set up with DC negative feedback. The 2k resistors set the common mode level at the device’s positive input. Without the crystal, the circuit may be considered as a very wideband (50GHz GBW) unity gain follower biased at 2.5V. With the crystal inserted, positive feedback occurs and oscillation commences. Figure 4a is useful with AT-cut fundamental mode crystals up to 10MHz. Figure 4b is similar, but supports oscillation frequencies to 25MHz. Above 10MHz, AT-cut

1MHz TO 10MHz

A = 1V/DIV

B = 5V/DIV

10μs/DIV

0.068μF

AN-12 F03

–

crystals operate in overtone mode. Because of this, oscillation can occur at multiples of the desired frequency. The damper network rolls off gain at high frequency, insuring proper operation.

All of the preceding circuits will typically provide temperature coefficients of 1ppm/°C with long term (1 year) stability of 5ppm to 10ppm. Higher stability is achievable with more attention to circuit design and control of temperature. Figure 5 shows a Pierce class circuit with fine frequency trimming provided by the paralleled fixed and

10MHz TO 25MHz

22Ω

820pF

200pF

(AT CUT)

LT1016

–

LATCH

GND

OUTPUT

AN-12 F04b

CRYSTAL

LT1016

–

LATCH

GND

OUTPUT

AN-12 F04a

Figure 3. Figure 2’s Waveforms

15V

10k

5.6k

* TRW MAR-6 RESISTOR

= YELLOW SPRINGS INST. #44014 75°C = 35.39k

= BLILEY #BG61AH-55, 75°C TURNING POINT. 5MHz FREQUENCY

0.1μF

330pF

Oscillator

33pF

10pF

5.6k

1000pF

Q1 2N3904

3.3k

OUTPUT (50Ω)

100pF

0.1μF

Figure 4a. 1MHz to 10MHz Crystal Oscillator

15V

AUX OUT 5V

R SELECT

TYPICAL

34.8k

22M

0.01μF

LT1005

34.8k34.8k

600Ω

2N3904

CONTROL

–

LT1001

Oven Control

5V MAIN OUT TO SUPPLY

10k

1N914

15V

–15V

THERMAL FEEDBACK

Figure 4b. 10MHz to 25MHz Crystal Oscillator

“OSCILLATOR READY” AND MAIN 5V POWER

2N3904

100k

1N914

8.2k

15V

8.2μF

2N6387 DARLINGTON

AN-12 F05

Figure 5. Ovenized Oscillator

an12fa

AN12-3

Application Note 12

variable capacitors. The transistor provides 180° of phase shift with the loop components adding another 180°, resulting in oscillation. The LT1005 voltage regulator and the LT1001 op amp are used in a precision temperature servo to control crystal temperature. The LT1001 extracts the differential bridge signal and drives the Darlington stage to power the heater, which is monitored by the thermistor. In practice, the sensor is tightly coupled to the heater. The RC feedback values should be optimized for the thermal characteristics of the oven. In this case, the oven was constructed of aluminum tube stock 3" long × 1" wide × 1/8" thick. The heater windings were distributed around the cylinder and the assembly placed within a small insulating Dewar flask. This allows 75°C setpoint (the zero TC or “turnover” temperature of the crystal specified) control of 0.05°C over 0°C to 70°C. The LT1005 regulator sources bridge drive from its auxiliary output and also keeps system power off until the crystal’s temperature (hence, its frequency) is stabilized. When power is applied the negative TC thermistor is high in value, causing the LT1001 to saturate positive. This turns on zener-connected Q2, biasing Q3. Q3’s collector current pulls the regulator’s control pin low, disabling its output. When the oven arrives at its control point, the LT1001’s output comes out of saturation and servo controls the oven at a point well below Q2’s zener value. This turns off Q3, enabling the regulator to source power to whatever

system the clock is associated with. For the crystal and circuit values specified, this clock will drift less than

–9

1 × 10 10

over 0°C to 70°C with a time drift of 1 part

–9

week.

The oven approach to removing temperature effects of crystal clock frequency is the most effective and in wide use. Ovens do, however, require substantial power and warm-up time. In some situations, this is unacceptable. Another approach to offsetting temperature effects is to measure ambient temperature and insert a scaled compensation factor into the crystal clock’s frequency trimming network. This open loop correction technique relies on matching the clock frequency vs temperature characteristic, which is quite repeatable. Figure 6 shows a temperature compensated crystal oscillator (TXCO) which uses a first order linear fit to correct for temperature. The oscillator is a Colpitts type, with a capacitive tapped tank network. The LT319A picks off the output and the RC network at the LT319’s “–” input provides a signal adaptive trip threshold. The LT1005 regulator’s auxiliary output buffers supply variations and the main regulator output control pin allows the system to be shut down without removing power from the oscillator, aiding overall stability. The ambient temperature is sensed by the linear thermistor network in A1’s feedback loop with A2 used for scaling and offsetting. A2’s voltage output

–15V

6.8k

LT1034

1.2V

3k*

–

LT1055

10.7k*

*1% FILM RESISTOR

= YELLOW SPRINGS INST, CO

THERMISTOR NETWORK #44201

Figure 6. Temperature Compensated Crystal Oscillator (TXCO)

10k*

–

84.5k*

1μF

15V

LT1055

0 – 3.955

100k 100k 100k

MV-209

MAIN OUTPUT

CONTROL

3.5MHz

500k

510pF

GND

LT1005

OUT

AUX

5V AUX OUTPUT

2N2222A

680Ω

20k

56.5mV/°C

5V MAIN OUTPUT TO SYSTEM

1/2 LT319A

–

0.05μF

OUTPUT

AN-12 F06

an12fa

AN12-4

Application Note 12

expresses the ambient temperature information required to compensate the clock. The correction is implemented by biasing the varactor diode (a varactor diode’s capacitance varies with reverse bias) which is in series with the crystal. The varactor’s shift in capacitance is used to pull the crystal’s frequency in a complementary fashion to the circuit’s temperature error. If the thermistor is maintained isothermally with the circuit, compensation is very effective. Figure 7 shows the results. The –40ppm frequency shift over 0°C to 70°C is corrected to within 2ppm. Better compensation is achievable by including 2nd and 3rd order terms in the temperature to voltage conversion to more accurately complement the nonlinear frequency drift characteristic.

Figure 8 is another voltage-varactor tuned circuit but is configured to allow frequency shift instead of opposing it. This voltage controlled crystal oscillator (VXCO) has a

–10

–20

FREQUENCY DEVIATION (ppm)

–30

–40

UNCOMPENSATED

20 40

10 30 50 70

TEMPERATURE (°C)

COMPENSATED

AN-12 G07

clean 20MHz sine wave output (Figure 9) suitable for communications applications. The curve of Figure 10 shows a 7kHz shift from 20MHz over the 10V tuning range. The 25pF trimmer sets the 20MHz zero bias frequency. In many applications, such as phase-locking and narrow bandwidth FM secure communications, the nonlinear response is irrelevant. Improved linearity will require conditioning the tuning voltage or the varactor network’s response. In circuits of this type it is important to remember that the limit on pulling frequency is set by the crystals Q, which is high. Achieving wide dynamic “pull” range without stopping the oscillator or forcing it into abnormal modes is difficult. Typical circuits, such as this one, offer pull ranges of several hundred ppm. Larger shifts (e.g., 2000ppm to 3000ppm) are possible without losing crystal lock, although clock output frequency stability suffers somewhat.

0.01μF

10k

2.7k

24V

12k

2N2369

4.7k 220pF

330pF

OUTPUT

20.0000MHz TO 20.0070MHz

100Ω

20MHz25pF100pF

100k

MV-1405

TUNING VOLTAGE 0V TO 10V

AN-12 F08

A = 100mV/DIV

Figure 7. TXCO Drift Performance

10ns/DIV

AN-12 F09

Figure 9. Figure 8’s Output

Figure 8. Voltage Controlled Crystal Oscillator (VCXO)

7000

6000

5000

4000

3000

2000

FREQUENCY SHIFT (Hz)

1000

TUNING VOLTAGE (V)

6384

10579

AN-12 F10

Figure 10. Figure 8’s Tuning Characteristics

AN12-5

an12fa

Application Note 12

Noncrystal Clock Circuits

Although crystal based circuits are universally applied, they cannot serve all clock requirements. As an example, many systems require a reliable 60Hz line synchronous clock. Zero crossing detectors or simple voltage level detectors are often employed, but have poor noise rejection characteristics. The key to achieving a good line clock under adverse conditions is to design a circuit which takes advantage of the narrow bandwidth of the 60Hz fundamental. Approaches utilizing wide gain bandwidth, even if hysteresis is applied, invite trouble with noise. Figure 11 shows a line synchronous clock which will not lose lock under noisy line conditions. The basic RC multivibrator is tuned to free run near 60Hz, but the AC-line derived synchronizing input forces the oscillator to lock to the line. The circuit derives its noise rejection from the integrator characteristics of the RC network. As Figure 12 shows, noise and fast spiking on the 60Hz input (Trace A, Figure 12) has little effect on the capacitor’s charging characteristics (Trace B, Figure 12) and the circuit’s output (Trace C, Figure 12) is stable.

Figure 13 is another synchronous clock circuit. In this instance, the circuit output locks at a higher frequency than the synchronizing input. Circuit operation is the time domain equivalent of a reset stabilized DC amplifier. The LT1055 and its associated components form a stable oscillator. The LM329 diode bridge and compensating diodes provide a stable bipolar charging source for the RC located at the amplifier’s negative input. The synchronizing pulse (Trace A, Figure 14) is level shifted by the LT1011 comparator to drive the FET. When the synchronizing pulse appears, the FET turns on, grounding the capacitor (Trace B, Figure

14). This interrupts normal oscillator action, but only for a small fraction of a cycle. When the sync pulse falls, the capacitor’s charge cycle, which has been reset to 0V, starts again. This resetting action forces the frequency of the RC charging to be synchronous and stabilized by the sync pulse. The only evidence of this operation at the output is an occasional, slightly enlarged pulse width (Trace C, Figure 14), which is caused by the synchronizing interval. The sync adjust potentiometer should be trimmed so the sync pulse appears when the capacitor is near 0V. This

60Hz

INPUT

SYNC

20k

0.15μF

68k

–

LT1055

60Hz OUTPUT

10k

AN-12 F11

A = 10V/DIV

B = 5V/DIV

C = 5V/DIV

5ms/DIV

Figure 11. Synchronized Oscillator Figure 12. Figure 11’s Waveforms

SYNC

15V

SYNC ADJ

0.05μF

–

15V

12k

–

330k

LT1011

2N4392

3.3k

LT1055

Figure 13. Reset Stabilized Oscillator

10k

7.5k*

620Ω

OUTPUT

LM329

1N4148

AN-12 F13

AN-12 F12

an12fa

AN12-6

Application Note 12

minimizes output waveform width deviation and allows maximum protection against losing lock due to RC drift over time and temperature. The maximum practical output frequency to sync frequency ratio is about 50×.

Pure RC oscillators are a final form of clock circuit. Although this class of circuit cannot achieve the stability of a synchronized or crystal based approach, it offers simplicity, economy and direct low frequency output. As such they are used in baud rate generators and other low frequency applications. The key to designing a stable RC oscillator is to make output frequency insensitive to drift in as many circuit elements as possible. Figure 15 shows an RC clock circuit which depends primarily on the RC elements for stability. All other components contribute very low order error terms, even for substantial shifts. In addition, the RC components have been chosen for opposing temperature coefficients, further aiding stability. The circuit is a standard comparator-multivibrator with parallel CMOS inverters interposed between the comparator output and the feedback resistors. This replaces the relatively large and unstable bipolar V

saturation losses

of the LT1011 output with the superior ON characteristics of MOS. Not only are the MOS switching losses to the rails

low and resistive, but they tend to cancel. The paralleling of inverters further reduces errors to insignificant levels. With this arrangement, the charge and discharge time constant of the capacitor is almost totally immune from supply and temperature shifts. The 10k units need not be precision types, because shifts in them will cancel. In addition, the effect of the comparator’s DC input errors is also negated because of the symmetrical nature of the oscillator. This leaves only the RC network as a significant error term. The nominal—120ppm/°C temperature coefficient of the polystyrene capacitor is partially offset by the opposing positive temperature coefficient designed into the specified resistor. In practice, only a first order compensation is achievable because of the uncertainty of the capacitor’s exact TC. For the test circuit, 0°C to 70°C temperature excursion showed a 15ppm/°C TC with a power supply rejection factor of less than 20ppm/V. In contrast, a clock constructed from the popular 555 timer, using the compensating RC network, showed 95ppm/°C and 1050ppm/V of supply shift. Because of comparator propagation delays, circuits of this type are less stable above a 5kHz to 10kHz operating frequency.

A = 5V/DIV

B = 2V/DIV

C = 50V/DIV

200μs/DIV

Figure 14. Figure 13’s Waveforms

AN-12 F12

0.015μF

LT1011

–

*TRW TYPE MTR-5/+120ppm/°C C = 0.015μF = POLYSTYRENE—

120ppm/°C ±30ppm WESCO TYPE 32-P

Figure 15. Stable RC Oscillator

15V

4.7k

74C04s

10k

OUTPUT

15V

AN-12 F15

an12fa

Information furnished by Linear Technology Corporation is believed to be accurate and reliable. However, no responsibility is assumed for its use. Linear Technology Corporation makes no representation that the interconnection of its circuits as described herein will not infringe on existing patent rights.

AN12-7

Application Note 12

ABOUT QUARTZ CRYSTALS

The frequency stability and repeatability of quartz crystals represent one of nature’s best bargains for the circuit designer. The equivalent circuit of a crystal looks like a series-parallel combination of elements.

Typical Values:

R = 100Ω

L = 500μH

C = 0.01pF

= 5pF

Q = 50,000

is the static capacitance produced by the contact

wires, crystal electrodes and the crystal holder. The RLC term is called the motional arm. C is the mechanical mass. R includes all electrical losses in the crystal and L is the reactive component of the quartz. Different angles of cut from the mother crystal produce different electrical characteristics in individual crystals. Cuts can be optimized for temperature coefficient, frequency range and other parameters. The basic “AT” cut used in most crystals in the 1MHz to 150MHz range is a good compromise between temperature coefficient, frequency

range, ease of manufacture and other considerations. Other factors affecting resonator performance include the method of lead attachment, package sealing method and internal environment (e.g., vacuum, partial pressure, etc.). Some circuit considerations when using crystals include:

Load Capacitance—The reactance the crystal must present to the circuit. Some circuits use the crystal in the parallel resonant mode (e.g., the crystal looks inductive). Other circuits are specified as series resonant and the crystal appears resistive. In this mode, the circuit’s load capacitance, including all parasitics, must be specified. A typical number is around 30pF.

Resistance—The impedance the crystal presents when it is resonating.

Drive Level—How much power may be dissipated in the crystal and still maintain all specifications. 10mW is typical. Excessive levels can fracture the crystal.

Temperature Coefficient/Turning Point—The tempco of the crystal is usually specified near the “turning point.” This is the temperature at which the crystal tempco is zero. Typically the tempco will be below 1ppm/°C over the operating range and the turning point around 75°C, although different cuts can considerably alter these numbers.

Frequency Tolerance—The deviation from ideal frequency when used under specified circuit conditions at a defined temperature. Tolerances vary from 50ppm to less than 1ppm.

AN12-8

Linear Technology Corporation

1630 McCarthy Blvd., Milpitas, CA 95035-7417

(408) 432-1900 ● FAX: (408) 434-0507

●

www.linear.com

an12fa

LT/TP 1101 1.5K REV A • PRINTED IN USA

Noty an12fa Linear Technology

Specifications and Main Features

Frequently Asked Questions

User Manual