National Instruments Xmath Interactive Control Design Module ICDM User Manual

Download

NI MATRIXx

XmathTM Interactive Control Design Module

Xmath Interactive Control Design Module

April 2007 370754C-01

Support

Worldwide Technical Support and Product Information

ni.com

National Instruments Corporate Headquarters

11500 North Mopac Expressway Austin, Texas 78759-3504 USA Tel: 512 683 0100

Worldwide Offices

Australia 1800 300 800, Austria 43 662 457990-0, Belgium 32 (0) 2 757 0020, Brazil 55 11 3262 3599, Canada 800 433 3488, China 86 21 5050 9800, Czech Republic 420 224 235 774, Denmark 45 45 76 26 00, Finland 385 (0) 9 725 72511, France 33 (0) 1 48 14 24 24, Germany 49 89 7413130, India 91 80 41190000, Israel 972 3 6393737, Italy 39 02 413091, Japan 81 3 5472 2970, Korea 82 02 3451 3400, Lebanon 961 (0) 1 33 28 28, Malaysia 1800 887710, Mexico 01 800 010 0793, Netherlands 31 (0) 348 433 466, New Zealand 0800 553 322, Norway 47 (0) 66 90 76 60, Poland 48 22 3390150, Portugal 351 210 311 210, Russia 7 495 783 6851, Singapore 1800 226 5886, Slovenia 386 3 425 42 00, South Africa 27 0 11 805 8197, Spain 34 91 640 0085, Sweden 46 (0) 8 587 895 00, Switzerland 41 56 2005151, Taiwan 886 02 2377 2222, Thailand 662 278 6777, Turkey 90 212 279 3031, United Kingdom 44 (0) 1635 523545

For further support information, refer to the Technical Support and Professional Services appendix. o comment on National Instruments documentation, refer to the National Instruments Web site at ni.com/info and enter the info code feedback.

Important Information

Warranty

The media on which you receive National Instruments software are warranted not to fail to execute programming instructions, due to defects in materials and workmanship, for a period of 90 days from date of shipment, as evidenced by receipts or other documentation. National Instruments will, at its option, repair or replace software media that do not execute programming instructions if National Instruments receives notice of such defects during the warranty period. National Instruments does not warrant that the operation of the software shall be uninterrupted or error free.

A Return Material Authorization (RMA) number must be obtained from the factory and clearly marked on the outside of the package before any equipment will be accepted for warranty work. National Instruments will pay the shipping costs of returning to the owner parts which are covered by warranty.

National Instruments believes that the information in this document is accurate. The document has been carefully reviewed for technical accuracy. In the event that technical or typographical errors exist, National Instruments reserves the right to make changes to subsequent editions of this document without prior notice to holders of this edition. The reader should consult National Instruments if errors are suspected. In no event shall National Instruments be liable for any damages arising out of or related to this document or the information contained in it.

XCEPT AS SPECIFIED HEREIN, NATIONAL INSTRUMENTS MAKES NO WARRANTIES, EXPRESS OR IMPLIED, AND SPECIFICALLY DISCLAIMS ANY WARRANTY OF

MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. CUSTOMER’S RIGHT TO RECOVER DAMAGES CAUSED BY FAULT OR NEGLIGENCE ON THE PART OF NATIONAL

NSTRUMENTS SHALL BE LIMITED TO THE AMOUNT THERETOFORE PAID BY THE CUSTOMER. NATIONAL INSTRUMENTS WILL NOT BE LIABLE FOR DAMAGES RESULTING

FROM LOSS OF DATA, PROFITS, USE OF PRODUCTS, OR INCIDENTAL OR CONSEQUENTIAL DAMAGES, EVEN IF ADVISED OF THE POSSIBILITY THEREOF. This limitation of

the liability of National Instruments will apply regardless of the form of action, whether in contract or tort, including negligence. Any action against National Instruments must be brought within one year after the cause of action accrues. National Instruments shall not be liable for any delay in performance due to causes beyond its reasonable control. The warranty provided herein does not cover damages, defects, malfunctions, or service failures caused by owner’s failure to follow the National Instruments installation, operation, or maintenance instructions; owner’s modification of the product; owner’s abuse, misuse, or negligent acts; and power failure or surges, fire, flood, accident, actions of third parties, or other events outside reasonable control.

Copyright

Under the copyright laws, this publication may not be reproduced or transmitted in any form, electronic or mechanical, including photocopying, recording, storing in an information retrieval system, or translating, in whole or in part, without the prior written consent of National Instruments Corporation.

National Instruments respects the intellectual property of others, and we ask our users to do the same. NI software is protected by copyright and other intellectual property laws. Where NI software may be used to reproduce software or other materials belonging to others, you may use NI software only to reproduce materials that you may reproduce in accordance with the terms of any applicable license or other legal restriction.

Trademarks

MATRIXx™, National Instruments™, NI™, ni.com™, and Xmath™ are trademarks of National Instruments Corporation. Refer to the Terms of Use section on ni.com/legal for more information about National Instruments trademarks.

Other product and company names mentioned herein are trademarks or trade names of their respective companies.

Members of the National Instruments Alliance Partner Program are business entities independent from National Instruments and have no agency, partnership, or joint-venture relationship with National Instruments.

Patents

For patents covering National Instruments products, refer to the appropriate location: Help»Patents in your software, the patents.txt file on your CD, or

ni.com/patents.

WARNING REGARDING USE OF NATIONAL INSTRUMENTS PRODUCTS

(1) NATIONAL INSTRUMENTS PRODUCTS ARE NOT DESIGNED WITH COMPONENTS AND TESTING FOR A LEVEL OF RELIABILITY SUITABLE FOR USE IN OR IN CONNECTION WITH SURGICAL IMPLANTS OR AS CRITICAL COMPONENTS IN ANY LIFE SUPPORT SYSTEMS WHOSE FAILURE TO PERFORM CAN REASONABLY BE EXPECTED TO CAUSE SIGNIFICANT INJURY TO A HUMAN.

(2) IN ANY APPLICATION, INCLUDING THE ABOVE, RELIABILITY OF OPERATION OF THE SOFTWARE PRODUCTS CAN BE IMPAIRED BY ADVERSE FACTORS, INCLUDING BUT NOT LIMITED TO FLUCTUATIONS IN ELECTRICAL POWER SUPPLY, COMPUTER HARDWARE MALFUNCTIONS, COMPUTER OPERATING SYSTEM SOFTWARE FITNESS, FITNESS OF COMPILERS AND DEVELOPMENT SOFTWARE USED TO DEVELOP AN APPLICATION, INSTALLATION ERRORS, SOFTWARE AND HARDWARE COMPATIBILITY PROBLEMS, MALFUNCTIONS OR FAILURES OF ELECTRONIC MONITORING OR CONTROL DEVICES, TRANSIENT FAILURES OF ELECTRONIC SYSTEMS (HARDWARE AND/OR SOFTWARE), UNANTICIPATED USES OR MISUSES, OR ERRORS ON THE PART OF THE USER OR APPLICATIONS DESIGNER (ADVERSE FACTORS SUCH AS THESE ARE HEREAFTER COLLECTIVELY TERMED “SYSTEM FAILURES”). ANY APPLICATION WHERE A SYSTEM FAILURE WOULD CREATE A RISK OF HARM TO PROPERTY OR PERSONS (INCLUDING THE RISK OF BODILY INJURY AND DEATH) SHOULD NOT BE RELIANT SOLELY UPON ONE FORM OF ELECTRONIC SYSTEM DUE TO THE RISK OF SYSTEM FAILURE. TO AVOID DAMAGE, INJURY, OR DEATH, THE USER OR APPLICATION DESIGNER MUST TAKE REASONABLY PRUDENT STEPS TO PROTECT AGAINST SYSTEM FAILURES, INCLUDING BUT NOT LIMITED TO BACK-UP OR SHUT DOWN MECHANISMS. BECAUSE EACH END-USER SYSTEM IS CUSTOMIZED AND DIFFERS FROM NATIONAL INSTRUMENTS' TESTING PLATFORMS AND BECAUSE A USER OR APPLICATION DESIGNER MAY USE NATIONAL INSTRUMENTS PRODUCTS IN COMBINATION WITH OTHER PRODUCTS IN A MANNER NOT EVALUATED OR CONTEMPLATED BY NATIONAL INSTRUMENTS, THE USER OR APPLICATION DESIGNER IS ULTIMATELY RESPONSIBLE FOR VERIFYING AND VALIDATING THE SUITABILITY OF NATIONAL INSTRUMENTS PRODUCTS WHENEVER NATIONAL INSTRUMENTS PRODUCTS ARE INCORPORATED IN A SYSTEM OR APPLICATION, INCLUDING, WITHOUT LIMITATION, THE APPROPRIATE DESIGN, PROCESS AND SAFETY LEVEL OF SUCH SYSTEM OR APPLICATION.

Conventions

The following conventions are used in this manual:

» The » symbol leads you through nested menu items and dialog box options

to a final action. The sequence File»Page Setup»Options directs you to pull down the File menu, select the Page Setup item, and select Options from the last dialog box.

This icon denotes a note, which alerts you to important information.

bold Bold text denotes items that you must select or click in the software, such

as menu items and dialog box options. Bold text also denotes parameter names.

italic Italic text denotes variables, emphasis, a cross-reference, or an introduction

to a key concept. Italic text also denotes text that is a placeholder for a word or value that you must supply.

monospace Text in this font denotes text or characters that you should enter from the

keyboard, sections of code, programming examples, and syntax examples. This font is also used for the proper names of disk drives, paths, directories, programs, subprograms, subroutines, device names, functions, operations, variables, filenames, and extensions.

monospace bold Bold text in this font denotes the messages and responses that the computer

automatically prints to the screen. This font also emphasizes lines of code that are different from the other examples.

monospace italic

Italic text in this font denotes text that is a placeholder for a word or value that you must supply.

Chapter 1 Introduction

Using This Manual.........................................................................................................1-1

Document Organization...................................................................................1-1

Commonly-Used Nomenclature......................................................................1-3

Related Publications ........................................................................................1-3

MATRIXx Help...............................................................................................1-4

ICDM Overview ............................................................................................................1-4

SISO Versus MIMO Design............................................................................1-4

Starting ICDM .................................................................................................1-4

Chapter 2 Introduction to SISO Design

SISO Design Overview..................................................................................................2-1

Basic SISO Terminology.................................................................................2-1

Overview of ICDM .......................................................................................................2-3

ICDM Windows ..............................................................................................2-3

ICDM Main Window ........................................................................2-4

PID Synthesis Window .....................................................................2-4

Root Locus Synthesis Window .........................................................2-4

Pole Place Synthesis Window...........................................................2-4

LQG Synthesis Window ...................................................................2-5

H-Infinity Synthesis Window ...........................................................2-5

History Window................................................................................2-5

Alternate Plant Window....................................................................2-5

Key Transfer Functions and Data Flow in ICDM ...........................................2-5

Summary ...........................................................................................2-6

Origin of the Controller.....................................................................2-6

What the ICDM Main Window Plots Show .....................................2-7

Controller/Synthesis Window Compatibilities ................................................2-7

Using ICDM ....................................................................................................2-9

General Plotting Features ................................................................................2-11

Ranges of Plots and Sliders...............................................................2-11

Zooming ............................................................................................2-12

Data-Viewing Plots ...........................................................................2-12

Interactive Plot Re-ranging ...............................................................2-13

Contents

Graphically Manipulating Poles and Zeros..................................................... 2-13

Editing Poles and Zeros Graphically .............................................................. 2-14

Chapter 3 ICDM Main Window

Window Anatomy ......................................................................................................... 3-1

Communicating with Xmath........................................................................... 3-2

ICDM Plots ..................................................................................................... 3-5

Selecting Plots................................................................................................. 3-5

Selecting a Synthesis or History Window ..................................................................... 3-9

Edit Menu ...................................................................................................................... 3-9

Editing Poles and Zeros.................................................................... 2-13

Complex Poles and Zeros .................................................................2-14

Isolated Real Poles and Zeros...........................................................2-14

Nonisolated Real Poles and Zeros and Almost Real Pairs ............... 2-14

Adding/Deleting Poles and Zeros..................................................... 2-15

Adding/Deleting Pole-Zero Pairs ..................................................... 2-15

Most Common Usage ....................................................................... 3-3

Default Plants ................................................................................... 3-3

Saving and Restoring an ICDM Session .......................................... 3-3

Reading Another Plant into ICDM ................................................... 3-3

Reading a Controller from Xmath into ICDM ................................. 3-4

Writing the Plant Back to Xmath ..................................................... 3-4

Writing the Alternate Plant back to Xmath ...................................... 3-4

Writing a Controller on the History List to Xmath .......................... 3-4

Ranges of Plots ................................................................................. 3-6

Plot Magnify Windows..................................................................... 3-7

Chapter 4 PID Synthesis

Window Anatomy ......................................................................................................... 4-1

PID Controller Terms .................................................................................................... 4-1

Toggling Controller Terms On and Off .......................................................... 4-2

Opening the PID Synthesis Window ..............................................................4-4

Manipulating the Controller Parameters ....................................................................... 4-4

Time Versus Frequency Parameters ............................................................... 4-5

Ranges of Sliders and Plots............................................................................. 4-5

Controller Term Normalizations..................................................................... 4-5

Integral Term Normalization ............................................................ 4-5

Derivative Term Normalization........................................................ 4-6

Rolloff Term Normalization............................................................. 4-6

Xmath Interactive Control Design Module vi ni.com

Chapter 5 Root Locus Synthesis

Overview........................................................................................................................5-1

Window Anatomy..........................................................................................................5-1

Opening the Root Locus Synthesis Window .................................................................5-3

Terminology...................................................................................................................5-3

Plotting Styles ................................................................................................................5-4

Phase Contours ................................................................................................5-5

Magnitude Contours ........................................................................................5-5

Slider and Plot Ranges.....................................................................................5-6

Manipulating the Parameters .........................................................................................5-6

Design ............................................................................................................................5-7

Adding a Pole-Zero Pair..................................................................................5-7

Deleting Pole-Zero Pairs .................................................................................5-7

Interpreting the Nonstandard Contour Plots ....................................................5-8

Chapter 6 Pole Place Synthesis

Window Anatomy..........................................................................................................6-1

Pole Place Modes...........................................................................................................6-2

Normal Mode...................................................................................................6-3

Integral Action Mode ......................................................................................6-4

State-Space Interpretation ...............................................................................6-5

Opening the Pole Place Window.....................................................................6-5

Manipulating the Closed-Loop Poles ............................................................................6-5

Time and Frequency Scaling...........................................................................6-5

Butterworth Configuration ..............................................................................6-6

Editing the Closed-Loop Poles........................................................................6-6

Slider and Plot Ranges.....................................................................................6-6

Contents

Chapter 7 LQG Synthesis

LQG Synthesis Window Anatomy ................................................................................7-1

Synthesis Modes ............................................................................................................7-3

Opening the LQG Synthesis Window .............................................................7-3

Setup and Terminology ...................................................................................7-4

Standard LQG (All Toggle Buttons Off).........................................................7-4

Integral Action.................................................................................................7-5

Exponential Time Weighting ..........................................................................7-5

Output Weight Editing ....................................................................................7-6

State-Space Interpretation ...............................................................................7-7

Contents

Manipulating the Design Parameters.............................................................................7-7

Manipulating the Design Parameters Graphically .......................................... 7-7

Ranges............................................................................................................. 7-8

Chapter 8 H-Infinity Synthesis

H-Infinity Synthesis Window Anatomy........................................................................ 8-1

Opening the Synthesis Window ....................................................................................8-3

Setup and Synthesis Method .........................................................................................8-3

Central H-Infinity Controller ..........................................................................8-4

Output Weight Editing .................................................................................... 8-5

Manipulating the Design Parameters.............................................................................8-6

Manipulating the Weight Transfer Function................................................... 8-6

Infeasible Parameter Values............................................................................8-6

Ranges............................................................................................................. 8-7

Chapter 9 History Window

Saving the Current Controller on the History List ........................................................ 9-1

Opening the History Window........................................................................................9-1

History Window Anatomy ............................................................................................9-1

Selecting the Active Controller ..................................................................................... 9-2

Editing the Comments ................................................................................................... 9-2

Deleting History List Entries......................................................................................... 9-3

To Continue Designing from a Saved Controller.......................................................... 9-3

Cycling Through Designs.............................................................................................. 9-3

Writing a Saved Design to Xmath................................................................................ 9-3

Using the History List ................................................................................................... 9-4

Chapter 10 Alternate Plant Window

Role and Use of Plant and Alternate Plant .................................................................... 10-1

Displaying the Alternate Plant Responses.....................................................................10-1

Alternate Plant Window Anatomy ................................................................................ 10-2

Opening the Alternate Plant Window............................................................................ 10-3

Normalization ................................................................................................................ 10-4

Manipulating the Parameters......................................................................................... 10-4

Using the Alternate Plant Window................................................................................10-5

Robustness to Plant Variations ....................................................................... 10-5

Adding Unmodeled Dynamics........................................................................10-5

Ranges of Sliders and Plot ..............................................................................10-6

Xmath Interactive Control Design Module viii ni.com

Chapter 11 Introduction to MIMO Design

Basic Terminology for MIMO Systems ........................................................................11-1

Feedback System Configuration......................................................................11-1

Transfer Functions .........................................................................................................11-2

Integral Action.................................................................................................11-4

Overview of ICDM for MIMO Design..........................................................................11-5

ICDM MIMO Windows ..................................................................................11-5

Main Window..................................................................................................11-5

MIMO Plot Window........................................................................................11-6

History Window ..............................................................................................11-7

Alternate Plant Window (MIMO Version)......................................................11-7

Chapter 12 LQG/H-Infinity Synthesis

Window Anatomy..........................................................................................................12-1

LQG/H-Infinity Main Window .......................................................................12-1

LQG/H-Infinity Weights Window ..................................................................12-2

Decay Rate Window........................................................................................12-5

H-Infinity Performance Window.....................................................................12-5

Frequency Weights Window ...........................................................................12-6

Synthesis Modes and Window Usage............................................................................12-7

Opening the LQG/H-Infinity Synthesis Window ............................................12-8

Setup and Terminology ...................................................................................12-8

Standard LQG (All Toggle Buttons “Off”) .....................................................12-11

Integral Action.................................................................................................12-11

Exponential Time Weighting ..........................................................................12-12

Weight Editing.................................................................................................12-12

How to Select w, u, y, and z.............................................................................12-13

H-Infinity Solution ..........................................................................................12-14

Manipulating the Design Parameters.............................................................................12-16

Main Window..................................................................................................12-16

Ranges .............................................................................................................12-17

Contents

Chapter 13 Multi-Loop Synthesis

Multi-Loop Window Anatomy...................................................................................... 13-1

Setup and Synthesis Method .........................................................................................13-3

Multi-Loop Versus Multivariable Design....................................................... 13-3

Opening the Multi-Loop Synthesis Window .................................................. 13-7

Designing a Multi-Loop Controller............................................................................... 13-7

Graphical Editor.............................................................................................. 13-7

Selecting and Deselecting Loops .................................................................... 13-7

Editing and Deleting Loops ............................................................................ 13-8

Loop Gain Magnitude and Phase .................................................................... 13-8

Appendix A Using an Xmath GUI Tool

Appendix B Technical Support and Professional Services

Index

Xmath Interactive Control Design Module x ni.com

Introduction

The Xmath Interactive Control Design Module (ICDM) is a complete

library of classical and modern interactive control design functions that

takes full advantage of Xmath’s powerful, object-oriented, graphical

environment. It provides a flexible, intuitive interactive control design

framework. This manual provides an overview of different aspects of linear

systems analysis, describes the Xmath Interactive Control Design function

library, and gives examples of how you can use Xmath to solve problems

rapidly.

Using This Manual

This manual is meant to complement the Xmath Help system. The Xmath

Help system can be used to find answers to specific questions such as, “In

the Root Locus window, how can I add a new pair of complex poles to the

controller?” In contrast, this manual is intended for describing the general

concepts and operation of the ICDM.

Document Organization

This manual includes the following chapters:

• Chapter 1, Introduction, starts with an outline of the manual and some use notes. It also contains an overview of the Interactive Control Design Module.

• Chapter 2, Introduction to SISO Design, outlines the types of linear systems the system object represents and then discusses the implementation of a system within Xmath.

• Chapter 3, ICDM Main Window, describes the use of the ICDM Main Window, which includes communication with Xmath, displaying warning and log messages, displaying a variety of standard plots, selecting a synthesis method for controller design, and controlling auxiliary windows.

• Chapter 4, PID Synthesis, discusses the PID synthesis window. This window is used to synthesize various types of standard classical SISO controllers such as P, PI, PD, PID, lead-lag, and lag-lead.

Chapter 1 Introduction

• Chapter 5, Root Locus Synthesis, describes the user interface, terminology, and parameters used for root locus synthesis.

• Chapter 6, Pole Place Synthesis, discusses the Pole Place synthesis window, which is used to design a SISO controller by assigning the closed-loop poles.

• Chapter 7, LQG Synthesis, discusses the LQG synthesis window which is used to synthesize a linear quadratic Gaussian (LQG) controller for a SISO plant.

• Chapter 8, H-Infinity Synthesis, describes the H∞ synthesis window used for SISO plants. The H∞ synthesis window is used to synthesize a central controller. Such controllers are sometimes called linear exponential quadratic Gaussian (LEQG) or minimum entropy controllers.

• Chapter 9, History Window, describes the History window used for SISO plants. The History window is used to display and manipulate the design history list, which is a list of controllers that have been explicitly saved during the design process.

• Chapter 10, Alternate Plant Window, describes the form of the Alternate Plant window used for SISO design.

• Chapter 11, Introduction to MIMO Design, provides an introduction to MIMO design building on the earlier discussions of SISO design. ICDM automatically switches between SISO and MIMO modes depending on the plant that is read in.

• Chapter 12, LQG/H-Infinity Synthesis, describes the MIMO LQG/H∞ synthesis window. The LQG/H∞ window is used to synthesize both LQG and H∞ controllers. The two design methods have been combined in a single window because of the similarity regarding the use of weights: constant weights, frequency-dependent weights, and integrators.

• Chapter 13, Multi-Loop Synthesis, describes multi-loop synthesis. The multi-loop window is used to synthesize a MIMO controller using PID and Root Locus methods, applying them one loop at a time. In many practical industrial applications, this is the way control systems are designed for complex multivariable plants.

• Appendix A, Using an Xmath GUI Tool, describes the basics of using an Xmath GUI tool. Throughout this manual, extended examples following each function discussion help pinpoint the flexibility and applicability of the Interactive Control Design function library. This appendix describes the basics of using an Xmath GUI tool.

Xmath Interactive Control Design Module 1-2 ni.com

Commonly-Used Nomenclature

This manual uses the following general nomenclature:

• Matrix variables are generally denoted with capital letters; vectors are represented in lowercase.

• G(s) is used to denote a transfer function of a system where s is the Laplace variable. G(q) is used when both continuous and discrete systems are allowed.

• H(s) is used to denote the frequency response, over some range of frequencies of a system where s is the Laplace variable. H(q) is used to indicate that the system can be continuous or discrete.

• A single apostrophe following a matrix variable, for example, x', denotes the transpose of that variable. An asterisk following a matrix variable (for example, A*) indicates the complex conjugate, or Hermitian, transpose of that variable.

Related Publications

For a complete list of MATRIXx publications, refer to Chapter 2,

MATRIXx Publications, Help, and Customer Support, of the MATRIXx Getting Started Guide. The following documents are particularly useful for

topics covered in this manual:

• MATRIXx Getting Started Guide

• Xmath User Guide

• Xmath Control Design Module

• Xmath Interactive Control Design Module

• Xmath Interactive System Identification Module, Part 1

• Xmath Interactive System Identification Module, Part 2

• Xmath Module Reduction Module

• Xmath Optimization Module

• Xmath Robust Control Module

•Xmath X

Module

Chapter 1 Introduction

MATRIXx Help

Interactive Control Design Module function reference information is available in the MATRIXx Help. The MATRIXx Help includes all Interactive Control Design functions. Each topic explains a function’s inputs, outputs, and keywords in detail. Refer to Chapter 2, MATRIXx

Publications, Help, and Customer Support, of the MATRIXx Getting Started Guide for complete instructions on using the MATRIXx Help

feature.

ICDM Overview

This section provides an overview of the Interactive Control Design Module, a tool for interactive design of continuous-time linear time-invariant controllers. ICDM runs under Xmath, using the Xmath Graphical User Interface (GUI).

SISO Versus MIMO Design

Version 2.0 of ICDM handles full multivariable design, that is, design of multi-input multi-output (MIMO) controllers for MIMO plants. Thus ICDM 2.0 operates in two basic modes: SISO design (single input, single output) and MIMO design. The mode is determined automatically by the plant you read into ICDM. The two different modes feature somewhat different plot options, different synthesis options, and so on.

NI has made the notation, conventions, and windows used for MIMO design as similar as possible to those used for SISO design. Therefore a user familiar with version 1.0 of ICDM (which handled only SISO design) should have little trouble using the new MIMO synthesis tools. NI also recommends that the user who wishes to use ICDM for MIMO design start by becoming familiar with its features for SISO design.

Chapters 2 through 10 discuss SISO design. Chapters 11 through 13 discuss MIMO design. The MIMO descriptions have been written for the user who is familiar with SISO design features.

Starting ICDM

To use ICDM, you should:

• Have a user’s understanding of Microsoft Windows or X Windows and the window manager that you use. For example, you should be able to move, resize, and iconify windows; use a pull-down menu; and use a scrollbar.

Xmath Interactive Control Design Module 1-4 ni.com

Chapter 1 Introduction

• Have a user’s understanding of Xmath (enough to create a plant transfer function).

• Know the basics of how to interact with an Xmath GUI application—for example, using a slider to set a parameter value, a variable-edit box for typing in values, data-viewing, and plot zooming.

• Know the basics of classical control system design (for SISO design) and state-space design (for MIMO design).

An introduction to Xmath and a basic introduction to X Windows can be found in the Xmath User Guide. There are several ways you can find out about the basics of interacting with an Xmath GUI application:

• Refer to Appendix A, Using an Xmath GUI Tool.

• Enter

guidemo in the Xmath Command window to start up the GUI

demo applications; this allows you to try out sliders, push buttons, scrollbars, data-viewing, and so on.

After you have mastered the basic mechanics of using an Xmath GUI application, you should be ready to get started.

To start up ICDM, enter

icdm in the Xmath Command window:

Your window manager may require you to position a window that is created using the left or middle mouse button. After the ICDM Main Window appears, the Xmath command prompt will return. You now can use Xmath and ICDM simultaneously.

The user interface for ICDM is designed to be intuitive; that is, things mostly work the way you would assume that they should work, so you should be able to start using ICDM immediately. NI recommends that you read Chapter 2, Introduction to SISO Design, before using the module.

ICDM includes a complete Help system. In the menu bar of every ICDM window there is a Help menu. The Help messages contain detailed descriptions of every feature and function of ICDM. You can get a good overview of the features of ICDM by scanning the entries in the menu bars and reading the Help messages in the various windows.

ICDM function reference material is available in the MATRIXx Help. Refer to Chapter 2, MATRIXx Publications, Help, and Customer Support, of the

MATRIXx Getting Started Guide for additional instructions on using the MATRIXx Help.

Introduction to SISO Design

Xmath provides a structure for system representation called a system object. This object includes system parameters in a data structure designed

to reflect the way these systems are analyzed mathematically. Operations on these systems are likewise defined using operators that mirror as closely as possible the notation control engineers use. This chapter outlines the types of linear systems the system object represents and then discusses the implementation of a system within Xmath. The functions used to create a system object and to extract data from this object are an intrinsic part of the object class and are also described. Finally, this chapter discusses the functions check, discretize, and makecontinuous, which use information stored in the system object to convert systems from one particular representation to another.

SISO Design Overview

This section provides an overview of what ICDM does and how it works, restricting the discussion to SISO design. If your interest is MIMO design, you first should read this chapter and then Chapter 11, Introduction to

MIMO Design.

Basic SISO Terminology

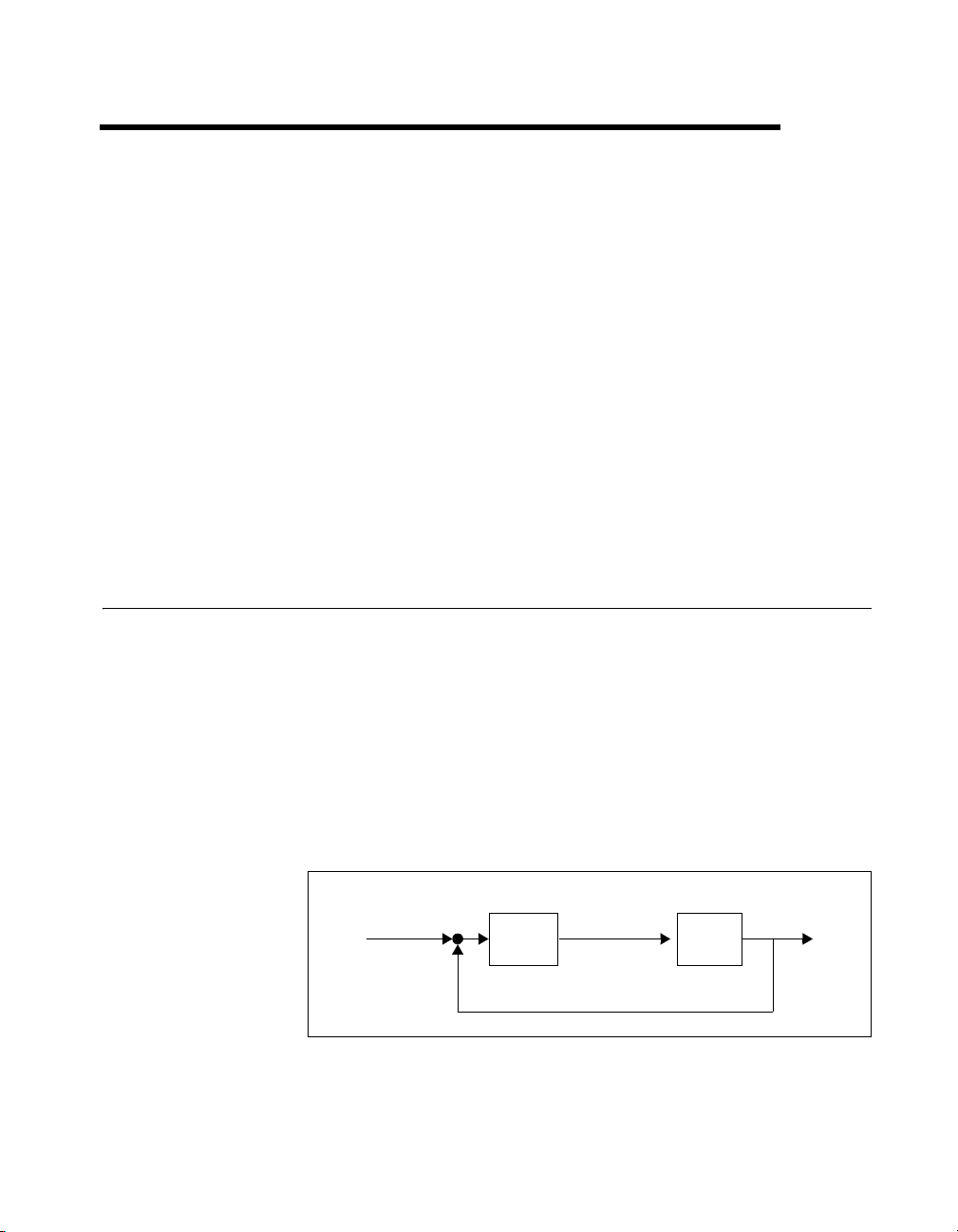
This section describes the basic terminology and notation for SISO plants and controllers used in ICDM and this manual. ICDM uses the standard classical feedback configuration shown in Figure 2-1.

Figure 2-1. Standard Classical Feedback Configuration Used in ICDM

C(s)

–

P(s)

Chapter 2 Introduction to SISO Design

The equations describing this system are as follows:

where y denotes the plant output or sensor signal

In ICDM, the plant and controller transfer function are required to be rational, that is, the ratio of two polynomials:

yPu=

uCe=

ery–=

u denotes the plant input or actuator signal

r denotes the reference or command input signal

e denotes the error signal

P denotes the plant transfer function

C denotes the controller transfer function

Ps()

s()

-----------= Cs() s()

s()

-----------=

s()

where n

, dp, nc, and dc are polynomials called the plant numerator,

plant denominator, controller numerator, and controller denominator, respectively. The symbols n and d are mnemonics for numerator and denominator. The degree of d the degree of d

is the controller order or controller degree.

is the plant order or plant degree. Similarly,

The poles and zeros of these transfer functions are the zeros (roots) of the denominator and numerator polynomials, respectively.

In ICDM, P and C are required to be proper polynomials; that is, they have at least as many poles as zeros. In other words, the degree of n or equal to the degree of d

(which is N) and similarly for nc and dc. In some

is less than

situations, the plant and controller are required to be strictly proper, which means that there are more poles than zeros.

Other important terms include:

• The loop transfer function L is defined as L = PC. The loop gain is the magnitude of the loop transfer function.

• The sensitivity transfer function is denoted as S and given by S =1/(1+PC). The sensitivity transfer function is the transfer function from the reference input r to the error signal e.

Xmath Interactive Control Design Module 2-2 ni.com

• The closed-loop transfer function T is given by T = PC/(1 + PC). T is the transfer function from r to y.

• The characteristic polynomial of the system is defined as X = n plus the order of the controller.

• The closed-loop poles are the zeros of the characteristic polynomial. This definition avoids any problem with unstable pole-zero cancellations between the plant and controller. The closed-loop zeros are the zeros of n

• The output response to a unit step input (or just, the step response), is the step response of the transfer function T; that is, the response of y when the command input r is a unit step.

• The actuator step response is the step response of the transfer function C/(1 + PC), which is the transfer function from r to u.

• Integral action means that the controller C has a pole at s = 0. Roughly speaking, this means that the loop gain is very large at low frequencies. Integral action implies that S(0) = 0, so if r is constant, the error e converges to zero, that is, the output y(t) approaches r as t →∞.

Overview of ICDM

Chapter 2 Introduction to SISO Design

+ dcdp. Its degree is equal to the order of the plant

cnp

This section provides a broad overview of the architecture, concepts, and major functions of ICDM, restricting our discussion to the case of SISO plants and controllers. This section also provides a summary of how ICDM works and what it does.

ICDM Windows

ICDM supports many windows that serve a variety of functions. The most important windows are:

•ICDM Main window

• PID Synthesis window

• Root Locus Synthesis window

• Pole Place Synthesis window

• LQG Synthesis

•H∞ Synthesis

• History window

• Alternate Plant window

window

Chapter 2 Introduction to SISO Design

These are briefly described in the following sections, and in more detail in later chapters. Several of these windows have different forms for SISO and MIMO design. This chapter restricts the discussion to the SISO forms. Refer to Chapter 11, Introduction to MIMO Design, for a discussion of the MIMO forms.

ICDM Main Window

The most important window is the ICDM Main window, which is used to:

• Communicate with Xmath (for example, transfer plants/controllers from/to Xmath).

• Display warning and log messages.

• Display a variety of standard plots.

• Select a synthesis method for controller design.

• Control several auxiliary windows.

PID Synthesis Window

The PID Synthesis window is used to synthesize a PID controller, with up to two additional poles (usually used for high frequency rolloff). Each term can be separately toggled on and off, so the PID synthesize P, PD, PI, PID, lead-lag, and lag-lead controllers. The design parameters can be typed in, manipulated graphically by slider controls, or manipulated graphically on a Bode plot of the controller transfer function.

window can be used to

Root Locus Synthesis Window

The Root Locus window can be used in many ways for synthesis and analysis of controllers. It can display a conventional root locus in near real-time, while the user drags controller poles and zeros. The user can graphically create or destroy controller poles and zeros. The closed-loop poles can be dragged along the root locus plot, which causes the gain parameter to be set automatically. Nonconventional phase and gain contours can be plotted as an aid to controller synthesis or robustness analysis.

Pole Place Synthesis Window

The Pole Place Synthesis window is used to design a controller by assigning the closed-loop poles. The closed-loop poles can be typed in, or dragged on a plot. The closed-loop poles can be scaled in frequency or time by graphical input, or assigned to a Butterworth configuration. The pole place window supports integral action as an option.

Xmath Interactive Control Design Module 2-4 ni.com

Chapter 2 Introduction to SISO Design

LQG Synthesis Window

The LQG Synthesis window synthesizes LQG controllers, and therefore can be used only with strictly proper plants. The user can vary weights for the ratio of control (input) to regulation (output) cost and the ratio of sensor (output) noise power to process (input) noise power. Optionally, the user can specify a guaranteed decay rate and integral time constant. By dragging zeros on a symmetric root locus plot, the user can vary the state weighting or perform LTR design.

There also is a MIMO LQG window, described in Chapter 12,

LQG/H-Infinity Synthesis.

H-Infinity Synthesis Window

The H∞ Synthesis window synthesizes central H∞ controllers (also called minimum entropy, risk sensitive, or LEQG controllers). The user can vary weights for the ratio of control (input) to regulation (output) cost, the ratio of sensor (output) noise power to process (input) noise power, and the risk sensitivity or H∞ bound parameter γ. The user can vary the state weighting, or equivalently, the output weight transfer function, by dragging zeros.

History Window

The History window is used to display and manipulate the design history list, which is a list of controllers that have been explicitly saved during the design process. The History window can be used to rapidly cycle through and compare a subset of the saved designs. Any controller on the history list can be recalled, and the design process continued.

Alternate Plant Window

The Alternate Plant window is used to study the robustness of a controller to variations or changes in the plant. The user can interactively vary the plant gain or dynamics, or add extra parasitic dynamics to the plant, see the effect on the closed-loop system, and compare it to the nominal system.

Key Transfer Functions and Data Flow in ICDM

ICDM has three key transfer functions:

• The plant transfer function P

• The alternate plant transfer function P

• The current controller transfer function C

alt

Chapter 2 Introduction to SISO Design

The plant and the alternate plant have very different uses in ICDM, and therefore different data flow characteristics.

The plant transfer function is read from Xmath into the ICDM Main window, and is then exported to the synthesis windows that need it—Pole Place, LQG, and H∞. In other words, the controllers designed using the Pole Place, LQG, or H∞ Synthesis windows are based on the plant transfer function. You cannot change the plant transfer function in ICDM except by reading in a new plant from Xmath.

The alternate plant transfer function can be read into ICDM from Xmath, or set equal to the plant transfer function. Its properties are very different from the plant transfer function, however:

• Using the Alternate Plant window, the user can graphically manipulate the alternate plant transfer function.

• The alternate plant transfer function is never exported to—that is, used by—the synthesis windows that need to know the plant: Pole Place, LQG, H∞.

The alternate plant transfer function is used to verify a controller design that was based on the plant transfer function. The alternate plant transfer function is used only to show the alternate plant plots in the ICDM Main window. Refer to the What the ICDM Main Window Plots Show section.

Summary

The plant transfer function is used for design; the alternate plant transfer function is used for (robustness) analysis or validation.

The distinction is not so important for PID and root locus design, because the controller does not depend on the plant.

Origin of the Controller

The controller can originate from—that is, be designed by—several possible sources:

• An Open Synthesis window—For example, if the Pole Place Synthesis window is open, then the current controller is determined by the Pole Place Synthesis window. When you interact with the Pole Place window by dragging a closed-loop pole to a new location, you will be changing the current controller transfer function C.

• The History window—If the History window is open, the controller comes from the list of controllers that have been saved on the history

Xmath Interactive Control Design Module 2-6 ni.com

Chapter 2 Introduction to SISO Design

list. The current controller is the active or selected entry on the list of saved controllers.

Only one synthesis window, or the History window, is allowed to be open at any given time, which eliminates any possible confusion over the source of the current controller. Remember the simple rule: If any synthesis window, or the History window, is open, it is the source of the current controller.

What the ICDM Main Window Plots Show

The plots in the ICDM Main window always use the plant and the current controller. For example, the step response plot shows the step response of the closed-loop system formed by the plant transfer function and the current controller transfer function.

Optionally, the plots also can show the response of the alternate plant connected with the current controller. In this case, the responses with the plant and the alternate plant are shown in different line types or colors, and can always be distinguished by data-viewing. Refer to the Data-Viewing

Plots section.

Controller/Synthesis Window Compatibilities

As much as possible, ICDM allows you to switch from one synthesis method to another while keeping the current controller the same. As an example, suppose the LQG Synthesis window is open, so the current controller is an LQG controller. You then can open the Root Locus Synthesis window, which will be initialized with the current (LQG) controller. Moreover, opening the Root Locus window will cause the LQG synthesis window to close. You now can continue the design using the Root Locus

window. For example, you might delete some controller poles and

zeros—that is, do some interactive controller model reduction. When you have deleted some controller poles and zeros, the controller will no longer be an LQG controller, so you cannot expect to be able to open the LQG window and retain the current controller.

There are some restrictions on the controllers that each synthesis window can accept (read):

• The PID Synthesis window can accept any PID controller. The PID Synthesis window is intuitive enough to figure out if a given controller has PID form and, if so, set its parameters appropriately.

• The Root Locus window accepts all controllers, so it can be opened at any time. The current controller will be read into the Root Locus

Chapter 2 Introduction to SISO Design

window. Thus, the Root Locus Synthesis window can be used to interactively tweak or model-reduce a controller designed by another method such as LQG.

• The Pole Place window accepts any controller with the same number of poles as the plant, or one more pole than the plant if it has integral action. In particular, the Pole Place window can accept any LQG or H∞ controller with or without integral action. This allows the user to manually tune the closed-loop poles in a design that was originally LQG or H∞.

• The LQG window only accepts controllers that were generated by the LQG synthesis window.

• The H∞ Synthesis window only accepts controllers that were generated by the H∞ Synthesis window.

• The History window, which can be considered as a synthesis window since it exports a controller to the ICDM Main window, is compatible with all controllers. If the current controller has been saved on the history list, then the History window opens, with the current controller the active controller on the history list. If the current controller has not been saved on the history list, it is first automatically saved on the history list, then the History window opens with the current controller active.

These restrictions are important when you select a new synthesis window or read a controller from Xmath into ICDM. If the controller is not compatible with the synthesis window, the user is warned and given several options about how to proceed. In general, these restrictions on controllers and synthesis windows should be transparent to the user. ICDM is designed to do something sensible whenever a conflict can arise, and to warn the user before any damaging actions are taken.

When the new controller and synthesis window will be compatible, the new synthesis window is initialized with the controller. The user can simply start designing, using the new synthesis window, from the current design. Roughly speaking, ICDM tries to keep the current controller when you select a new synthesis window.

As an example, suppose the LQG

window is used to design an LQG

controller. The user then can open the Pole Place window, which will be initialized with the LQG controller, and continue the design by dragging the closed-loop poles to new locations. At this point, the user cannot expect to import the current controller back into the LQG Synthesis window because the controller is no longer an LQG controller. The user can, however, open the Root Locus window, which will be initialized with the current

Xmath Interactive Control Design Module 2-8 ni.com

Using ICDM

Chapter 2 Introduction to SISO Design

controller. Using the Root Locus window, the user could reduce the controller to a PI controller by deleting poles and zeros, at which point the PID window can be opened, initialized at the current controller.

ICDM can be used in many ways. For example, you might:

• Interactively design a controller.

• Switch synthesis methods and continue designing.

• Review and compare your best designs, and perhaps start designing again from a previous design.

• Analyze the robustness of one or more controllers, with respect to variations in the plant transfer function, export one or more controllers to Xmath, such as for a nonlinear simulation or downloading to an AC-100 for real-time testing.

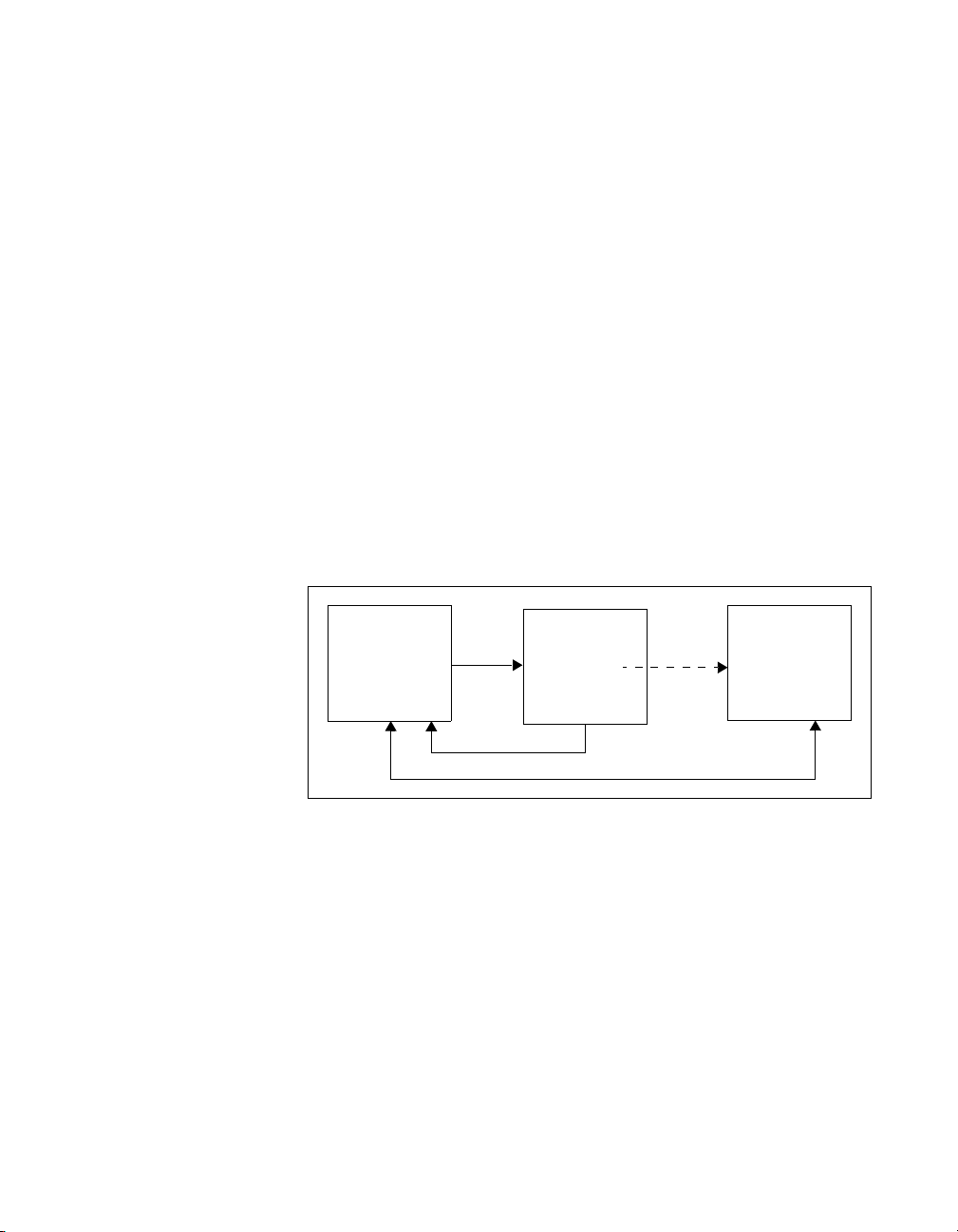
The most common tasks are interactively designing a controller, and interactively studying the robustness of a given controller. Figure 2-2 shows a simplified schematic representation of the interactive design loop.

Designer

ICDM Synthesis

Window

C(s)

ICDM Main

Window

Figure 2-2. Simple Representation of the Interactive Design Loop

The solid lines indicate graphical or alpha-numeric communication. The dashed line shows the automatic export of the controller from the synthesis window to the ICDM Main window. Notice that only one synthesis window can be open at any given time. Also notice that for the purposes of design, the user interacts only with the synthesis window and not with the ICDM Main

window.

Chapter 2 Introduction to SISO Design

Figure 2-3 shows a simplified schematic representation of the interactive robustness analysis loop. Here, the user interacts with the Alternate Plant window, interactively changing the alternate plant transfer function P which is automatically exported to the ICDM Main window for analysis and display. The user receives graphical information from the Alternate Plant window displays and also the ICDM Main window.

Figure 2-3 shows a simplified schematic representation of the interactive design loop.

Figure 2-3. Simple Representation of the Interactive Robustness Analysis

Designer

Alternate

Plant

Window

alt

(s)

ICDM Main

Window

Figure 2-4 shows a simple ICDM session. The ICDM Main window is shown at upper left, and the Pole Place Synthesis window is at lower right. The user can drag the closed-loop poles in the Pole Place window. The controller that is synthesized is automatically exported to the ICDM Main window for analysis and plotting. Notice that the user’s graphical input is mostly through the Pole Place window. The ICDM Main window is used mostly for graphical output.

Xmath Interactive Control Design Module 2-10 ni.com

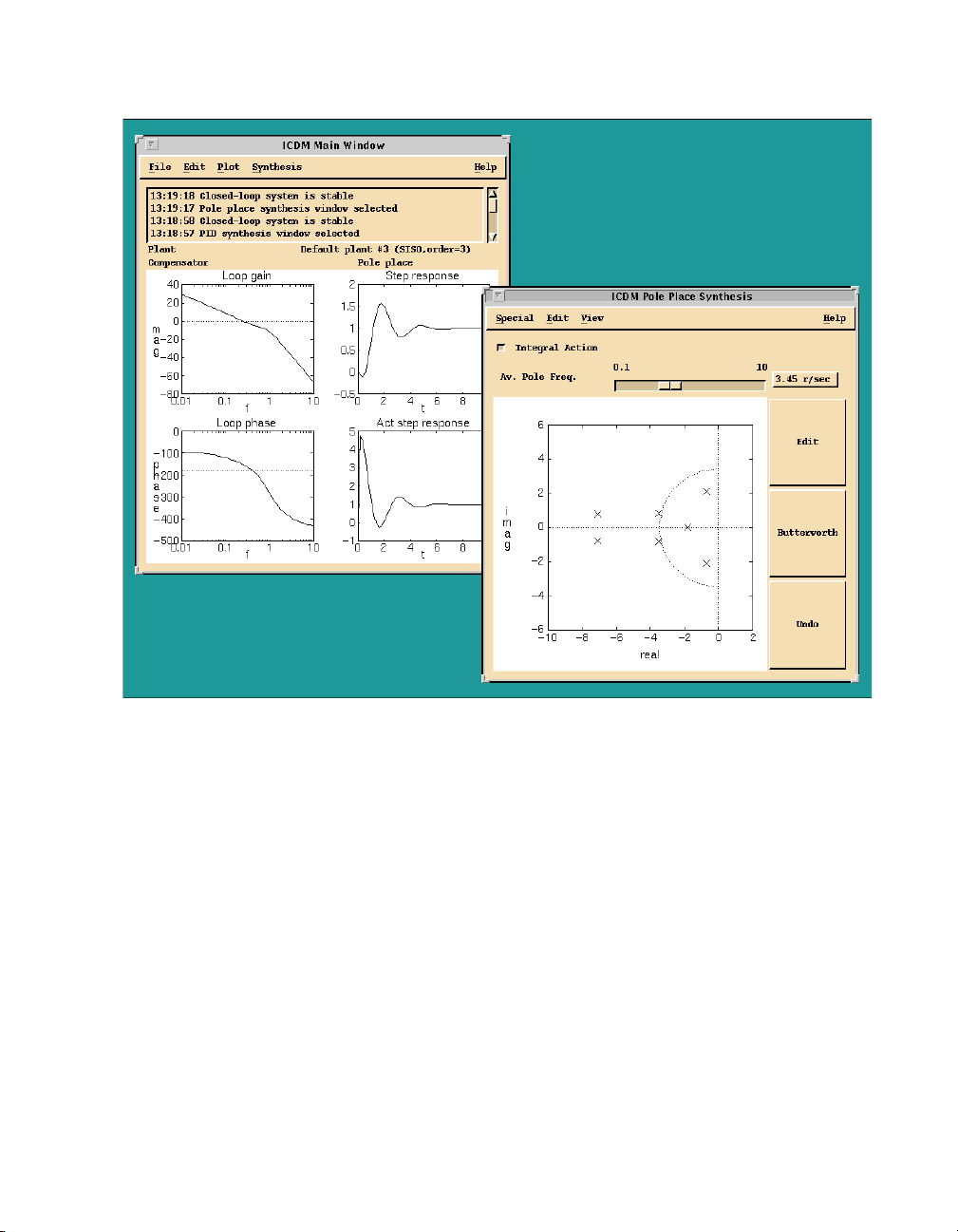
Chapter 2 Introduction to SISO Design

Figure 2-4. Simple ICDM Session

General Plotting Features

All of the plots in the ICDM Main and other windows support several useful features: arbitrary re-ranging, zooming, data-viewing, and interactive (graphical) re-ranging.

Ranges of Plots and Sliders

Every ICDM window has an associated Ranges window that can be used to set the ranges of the sliders and plots appearing in the window, as well as other parameters such as numbers of points plotted. The Ranges window can be opened by selecting Ranges on the View or Plot menu, or by pressing <Ctrl-R>

in the window in question. In addition, every ICDM

Chapter 2 Introduction to SISO Design

window has an autoscale feature, which can be invoked by selecting Autoscale on the View or Plot menu of the window. When you invoke Autoscale, ICDM tries to assign some reasonable values to the slider and plot scales.

Zooming

You can enlarge any portion of an ICDM plot using plot zooming. Clicking the middle mouse button with the cursor anywhere in the plot creates a small box containing a magnified version of the plot near the cursor. The middle mouse button can be held down and dragged, which creates an effect similar to dragging a magnifying glass across the plot.

Pressing <Ctrl> along with the middle mouse the size of the magnified box. Clicking with the middle mouse increases the zoom factor. Pressing <Shift-Ctrl> along with middle mouse button yields a large zoom box with a large magnification factor.

Zooming is a good way to read text in ICDM plots—for example, titles, axis labels, and so on. These were intentionally made small because zooming is easy.

button (on UNIX) increases

button

Data-Viewing Plots

Pointing at or near plotted information within the ICDM windows and clicking the right mouse button causes a small window to appear that identifies the plot and gives the coordinates of the nearest data point (for example, Loop Gain, L(10.1Hz) |=+11.2dB), along with its index. This feature is called data-viewing.

If the right mouse button is clicked and dragged, the selected plot is tracked, even if another plot comes close.

Pressing <Shift> along with the right mouse button allows the user to get values on the piecewise linear plot that interpolates the data values. In this case, index = 45.7 means that the selected plot point is between the 45th and 46th X-coordinate entries.

Because all ICDM plots have extensive data-viewing features, the number of labels used to identify plots are minimal. For example, the Root Locus plot has red and black poles and zeros shown, but no indication or label in the plot saying what these colors mean. On a black-and-white display, you cannot distinguish between the red and black poles/zeros. You can read in the Help file message that the red ones correspond to the plant, and the black ones to the controller. However, the easiest way to find out what the

Xmath Interactive Control Design Module 2-12 ni.com

Chapter 2 Introduction to SISO Design

poles and zeros are (and indeed, the only way on a black-and-white display) is to use data-viewing.

As a general rule: To find out the meaning, purpose, or value of an object (pole, zero, curve, and so on.) in an ICDM plot, use data-viewing.

Most objects in the ICDM Plot windows support data-viewing.

Interactive Plot Re-ranging

The range for any plot can be set in the appropriate Ranges window. Alternatively, the ranges for plots can be interactively changed by grabbing and dragging the axes of the plots. To make the plot range smaller, grab and drag the appropriate axis to the desired location. A dashed line shows what the new plot range will be. To make the plot range larger, click the left mouse

button on the appropriate axis and, while holding the button down,

move the cursor away from the plot axis. In this case you will not see a dashed line showing the new plot range. Instead, a small box will appear that tells you what the new range will be. The new range is given by extrapolation of the cursor position. You can move the cursor over other plots, and even out of the plotting window, while increasing the range of aplot.

If a plot range is symmetric, then the new range also will be symmetric. That is, for a symmetric plot range the minimum and maximum values for X or Y are the same except for sign. Changing the maximum will also change the minimum.

These changes will be exported to the Ranges window.

Graphically Manipulating Poles and Zeros

In many of the ICDM windows, the user can grab and drag poles and zeros graphically. The paradigm of grabbing and dragging poles and zeros is uniform across windows. Remember that you cannot always grab and drag every pole or zero you see in an ICDM plot—for example, in the Root Locus window, you can grab and drag any controller pole or zero, but you cannot grab or drag a plant pole or zero.

Editing Poles and Zeros

If there is a push button labeled Edit near the plotting area, you can use it to edit poles and zeros. If you click the Edit button, the cursor will become a pencil symbol. Select a pole or zero by clicking the left mouse the cursor positioned at the desired pole or zero. A dialog box will open that

button with

Chapter 2 Introduction to SISO Design

contains variable edit boxes for the value of the pole or zero (the real and imaginary part when the pole or zero is complex) and, if appropriate, its multiplicity. After you enter new values, you can select OK, which will make the changes and dismiss the dialog box, or Cancel, which will dismiss the dialog box without making the changes.

The values you type in will not be accepted if they are invalid—for example, a negative multiplicity for a pole or zero.

Editing Poles and Zeros Graphically

The easiest way to change a pole or zero is to grab it by clicking the left mouse button and dragging it to the desired location. You can only drag poles and zeros in “sensible” ways. For example, you cannot drag a single real pole or zero off the real axis to a complex location. More precisely, the dragging of poles and zeros works as described in the following sections.

Complex Poles and Zeros

If the pole or zero that you grab is complex, then the complex conjugate pole or zero will automatically move as required. In this case you can drag the pole or zero in any direction.

Isolated Real Poles and Zeros

If the pole or zero that you grab is real and not very close to another real pole or zero, then the pole or zero motion will be constrained to the real axis. You cannot drag the pole or zero off the real axis.

Nonisolated Real Poles and Zeros and Almost Real Pairs

If a pair of nearby poles or zeros is very near the real axis—that is, two nearby real poles or zeros, or a pair of complex poles and zeros with very small imaginary part—then the dragging motion will depend on how you originally drag the poles or zeros. If you drag it up or down, then the pair acts as a complex pair and there is no constraint on how you can drag it. For example, two real poles that are very close to each other can be split into a complex pair by grabbing either one and dragging it away from the real axis. On the other hand, if you drag the selected pole or zero left or right, then the pair act as a real pair—the selected pole or zero then can be dragged only along the real axis, and the other pole or zero becomes real

Xmath Interactive Control Design Module 2-14 ni.com

Chapter 2 Introduction to SISO Design

(if it was not already) but otherwise does not move. Thus, to make a pair of complex poles real, you first drag one of them near the real axis and release. Then you select one of these poles again, and this time drag it left or right. This will cause the pair to become real.

Adding/Deleting Poles and Zeros

This section describes how you are allowed to add or delete poles or zeros in some windows. Bear in mind that ICDM may not allow you to add or delete a zero or pole in certain cases—for example, if the action would result in a nonproper controller. In this situation, you will be warned with a dialog box which opens.

To add a zero, click the Add Zero button that is near the plotting area, or select the Add Zero entry from the Edit menu. In some cases there is an accelerator for this, such as typing cause the cursor to become a crosshairs symbol. If you click the left mouse button with the cursor very near the real axis, then you will create one real zero. If you click the left mouse button with the cursor farther from the real axis, then you will create a pair of complex conjugate zeros. Creating a pole is similar; typing complex conjugate pole pair. To abort a pole or zero add operation, click the left mouse button with the cursor outside the plot area.

p in the window is the accelerator for creating a pole or

z in the window. These actions will

To delete a pole or zero, press the <Ctrl> key near the plotting area, select the Delete entry from the Edit menu, or enter actions will cause the cursor to become a skull and crossbones symbol. Then click the left mouse button with the cursor near the pole or zero that you want to delete. If the pole or zero is complex, then its complex conjugate also will be destroyed.

You always can select Undo in the Edit menu to restore deleted poles or zeros back, provided you have not made any other changes since deleting. To abort a delete operation, click the left mouse button with the skull and crossbones cursor in a free area of the plot.

d in the window. These

Adding/Deleting Pole-Zero Pairs

When you add (or delete) a pole or zero, you can drastically change the transfer function that you are editing. In some cases, it may be better to add (or delete) a pole-zero pair—that is, a pole and zero in exactly the same location. Adding a pole-zero pair does not change the transfer function at all until the pole and zero are moved apart.

Chapter 2 Introduction to SISO Design

To add a pole-zero pair, click the Add Pair button, select the Add Pair entry on the Edit menu, or press <Ctrl-P> in the window. As with poles and zeros, the pole-zero pair you create will be either real or a complex conjugate pair, depending on how close the cursor is to the real axis when you click the left mouse button.

After the pair is created, you can drag the pole and zero away from each other, which results in a smooth change to the transfer function. By convention, the cursor first grabs the zero in a pole-zero pair.

To delete a pole and zero that are very near each other, click the Delete button, position the cursor near the pole and zero, and click the left mouse button. This will remove the pole and zero but have little effect on the transfer function.

If you want to delete a pole or zero that is very near a zero or pole, respectively, then you may have to first separate them a little bit. Otherwise, the delete command may be interpreted as a delete pair command.

Xmath Interactive Control Design Module 2-16 ni.com

ICDM Main Window

This chapter describes the use of the ICDM Main window, which is used to perform the following functions:

• Communicate with Xmath—for example, transfer plants/controllers from/to Xmath

• Display warning and log messages

• Display a variety of standard plots

• Select a synthesis method for controller design

• Control several auxiliary windows (for example, Ranges, Alternate Plant)

Notice that the ICDM Main window is not directly used to design the controller. It is used to make high level decisions, such as which synthesis method to use, and to view or analyze the response with the current controller.

This chapter is limited to the discussion of SISO design. For MIMO design information, refer to Chapter 11, Introduction to MIMO Design.

Window Anatomy

The ICDM Main window, shown in Figure 3-1, consists of the following elements, from top to bottom:

• A menu bar with File, Edit, Plot, Synthesis, and Help menus.

• A scrolled text area for warnings and messages. You can resize this area independently of the rest of the ICDM Main messages that appear here are meant to give a rough trace of your ICDM design session. It records major actions such as reading a new controller or plant in, opening a new synthesis window, saving controllers to the history list, and so on.

• A line that gives the plant name.

window. The log

Chapter 3 ICDM Main Window

• A line that identifies the type and source of the current controller. The source is either the currently active synthesis window or the history list.

• A plotting area for the various plots.

Figure 3-1. ICDM Main Window

Communicating with Xmath

The File menu is used to communicate with Xmath—that is, to read controllers and/or plants from Xmath into ICDM, and to write controllers and/or plants from ICDM back to Xmath.

Xmath Interactive Control Design Module 3-2 ni.com

Chapter 3 ICDM Main Window

Most Common Usage

In most cases, you will read a plant from Xmath at the beginning of an ICDM design session, and write one or more controllers back to Xmath during or at the end of an ICDM design session. This is done by selecting the appropriate entries in the File menu.

Reading a plant into ICDM is often the first thing you do in a design session. Before a plant is read in, the plots will be empty and you will be unable to open any synthesis windows.

Similarly, writing the ICDM controller back to Xmath is often the last thing you do in an ICDM design session before quitting or exiting. If the current controller has not been written to Xmath and you attempt to exit ICDM, a dialog box will open and ask for confirmation before exiting.

Default Plants

By selecting FileRead Default Plant, a dialog box will open which you can use to read one of three default plants into ICDM. This default plant dialog box is only meant to be used when you are learning how to use ICDM and need a quick way to enter a plant. It saves you the trouble of creating a plant in Xmath and then reading it into ICDM. It has no real use, except in the unlikely event that your plant happens to be one of the default plants.

Saving and Restoring an ICDM Session

The FileSave Tool button saves the entire state of the ICDM tool into an Xmath save file. You can continue the design session at another time or on another computer using the FileRestore Tool button.

Reading Another Plant into ICDM

When you first start ICDM, you can read a plant from Xmath using the FileRead plant from Xmath button. After there is a plant defined in ICDM, you can only read a new plant into ICDM from Xmath when there is no synthesis window and the history window is not open. If you try to read a plant when a synthesis window or the History window is open, a dialog box will notify you that the open synthesis or History closed.

Reading a new plant into ICDM when there already was a defined plant has several important consequences. First, all controllers on the history list that were designed by the Pole Place, LQG, or synthesis windows are converted

window first must be

Chapter 3 ICDM Main Window

to a simple transfer function representation, which means that you cannot read them back into the Pole Place, LQG, or synthesis windows because these types depend on the plant. Also, all synthesis windows will be reset to their initial (default) settings. Because these side effects may be undesired, the user is warned before these actions are taken.

Reading a Controller from Xmath into ICDM

You can read a controller from Xmath into ICDM using the FileRead Controller entry. This requires closing any open synthesis window or the History window. Reading in a new controller will overwrite the current controller in ICDM, so unless there is no current controller or you have saved the current controller to the history list or Xmath, you will be warned and asked for confirmation.

After you have read in the new controller, you can proceed with opening a synthesis window, and the usual rules apply. If the synthesis window is compatible with the current controller that you have just read in, the parameters in the synthesis window will be set appropriately. If the synthesis window is not compatible with the controller, you will be warned that opening the synthesis window will overwrite the controller.

When you read a controller from Xmath, it is represented as a transfer function. This means that you cannot get a controller from Xmath into the LQG or synthesis windows.

Writing the Plant Back to Xmath

Because you cannot change the plant transfer function from inside ICDM, the only reason to write the plant back to Xmath is if you have forgotten what the plant transfer function is or if you fear that you may have changed it in Xmath.

Writing the Alternate Plant back to Xmath

If you want to write the alternate plant transfer function to Xmath, use the Special menu in the Alternate Plant window.

Writing a Controller on the History List to Xmath

If you want to write a controller that has been saved on the history list to Xmath, you first must make it the current controller by opening the History window and selecting it. Then use the FileWrite Controller button to write the current controller to Xmath.

Xmath Interactive Control Design Module 3-4 ni.com

ICDM Plots

Chapter 3 ICDM Main Window

Various plots can be shown at the bottom of the main ICDM window. The Plot menu is used to select which plots are shown, and also to magnify a plot or set the plotting ranges. The user can choose any combination of the following:

• Loop transfer function magnitude

• Loop transfer function phase

• Sensitivity and complementary sensitivity magnitude

• Closed-loop poles and zeros

• Output response to a unit step input

• Actuator response to a unit step input

• Nyquist plot of loop transfer function

• Nichols plot of loop transfer function

Refer to the Basic SISO Terminology section of Chapter 2, Introduction to

SISO Design, for definitions of these terms. The default plots are loop

transfer function magnitude and phase, and output and actuator response to a unit step input.

For more information about other plots available for MIMO design, refer to Chapter 11, Introduction to MIMO Design.

Selecting Plots

Selecting Plot»Plot Choices or pressing <Ctrl-P> in the main ICDM window will cause a plot selection dialog box to appear, as shown in Figure 3-2. The plot selection dialog box that appears is modal, which means that you cannot interact with any other Xmath window until you have dismissed this dialog by clicking Cancel or OK.

Figure 3-2. ICDM Main Window Plot Choices Dialog

Chapter 3 ICDM Main Window

In the ICDM Main window, the Plot Choices dialog box is used to select any combination of the eight plots. This dialog box is modal so you cannot interact with any other Xmath window until you dismiss it.

Ranges of Plots

The ranges for the plots can be set in the Ranges window, shown in Figure 3-3. The Ranges Plot»Ranges or pressing <Ctrl-R> in the ICDM Main window. The Ranges

window also is used to determine the number of points used

in the plots.

ICDM provides two convenient ways to select ranges for the plots. The first is to use the Autoscale feature which can be invoked from the Plot menu or from the Ranges assign sensible ranges to the plots but does not always succeed. The second convenient method for changing the ranges of plots is to use interactive re-ranging, which is described in the General Plotting Features section of Chapter 2, Introduction to SISO Design.

window can be made to appear by selecting

window. When Autoscale is invoked, ICDM tries to

The ICDM Ranges

window, shown in Figure 3-3, is used to set the analysis

ranges and plot ranges for the ICDM Main

window.

Xmath Interactive Control Design Module 3-6 ni.com

Chapter 3 ICDM Main Window

Figure 3-3. ICDM Ranges Window

Plot Magnify Windows

In addition to the standard plotting features (zooming, data-viewing, and interactive re-ranging) described in the General Plotting Features section of Chapter 2, Introduction to SISO Design, the plots in the ICDM Main window support another feature: plot magnify windows.

Selecting Plot»Plot Magnify or pressing <Ctrl-M> or in the ICDM Main window will cause the cursor to change into a crosshairs symbol. Positioning the cursor over an ICDM plot and clicking the left mouse button causes the plot to appear, in a new window called a Plot Magnify window, as shown in Figure 3-4. This window can be resized using the window manager, and can be independently re-ranged. Refer to the Ranges

Chapter 3 ICDM Main Window

of Plots section. If another plot is subsequently selected for magnifying,

it will replace the current plot in the plot magnify window.

The Plot Magnify window is a separate window that shows one of the ICDM main plots. The Plot Magnify window, shown in Figure 3-4, can be independently resized by the window manager. The ranges of the Plot Magnify window can also be independently set.

Figure 3-4. Plot Magnify Window

It also is possible to select a portion of a plot for magnification. Click and drag the left mouse button with the cursor in an ICDM plot. While holding the left mouse button down, you can drag out a box (shown in dashed lines); when you release, the dashed box becomes the range for the magnified plot. You also can drag out a box in the magnified plot itself. This effectively changes the range of the magnified plot.

By selecting Plot»New Plot Magnify or pressing <Ctrl-N> in the ICDM Main window, you can select a plot for magnification. In this case, the new plot will appear in a new Plot Magnify window. When multiple Plot Magnify windows are open, the Plot Magnify command will send the selected plot to the most recently created Plot Magnify window. New Plot Magnify will create a new Plot Magnify window.

Xmath Interactive Control Design Module 3-8 ni.com

Selecting a Synthesis or History Window

The Synthesis menu in the ICDM Main window is used to select which synthesis window will be active. If the current controller is compatible with the requested synthesis window, then the synthesis window opens, and is initialized with the current controller.

If the current controller is not compatible with the Synthesis menu selected, then a dialog box appears that gives the user several options. If the user proceeds in this case, the current controller will be replaced with the previous design in the synthesis window selected. For example, if the Root Locus Synthesis transfer function, and the user requests the LQG Synthesis dialog box will issue a warning that the current design will be overwritten, and give the user the option of cancelling the request, proceeding, or writing the current (Root Locus) controller to the history list before proceeding. If the user proceeds, then the Root Locus the LQG with the controller from the LQG Synthesis

window will open, and the current controller will be overwritten

window is open so that the current controller is a general

window.

Chapter 3 ICDM Main Window

window, a

window will close,

Edit Menu

To open the History controllers are compatible with the History will open with the current controller active. In other words, the current controller will be saved on the history list (if it has not already been saved) and made the active or selected controller on the history list.

The Edit menu has two important entries:

• Selecting EditAdd to History, or typing

will cause the current controller to be saved on the history list. You will be prompted for a comment that will be saved along with the current controller. Refer to Chapter 9, History Window.

• Selecting Edit»Alternate Plant

window to appear. Refer to Chapter 10, Alternate Plant Window.

window, select Synthesis»History. Because all

window, the History window

h in the ICDM Main window,

window causes the Alternate Plant

PID Synthesis

This chapter discusses the PID Synthesis window. This window is used to synthesize various types of standard classical SISO controllers such as P, PI, PD, PID, lead-lag, and lag-lead. However, the controller that is designed by the PID Synthesis window will be referred to as a PID controller even if it has some other form such as PI. Multivariable (MIMO) PID controllers can be synthesized using the Multiloop Synthesis Refer to Chapter 13, Multi-Loop Synthesis.

Window Anatomy

The PID Synthesis window is shown in Figure 4-1. It consists of the following, from top to bottom:

• A menu bar with entries Special, Edit, View, and Help.

• A text area that displays the transfer function of the current PID controller.

• A control panel with five rows, each of which corresponds to one design parameter. A Bode plot of the controller transfer function with handles for graphically manipulating the design.

window.

PID Controller Terms

The overall controller transfer function is given by the product of up to five terms, each of which depends on one parameter. The five parameters and corresponding terms in the controller are shown in Table 4-1, from top to bottom.

Table 4-1. PID Controller Terms and Parameters

Term Parameter Symbol Controller

Proportional (P) Gain K

Integral (I) Integral time constant

Derivative (D) Derivative time constant

int

diff

1+1/(sT

1+sT

diff

)

int

Chapter 4 PID Synthesis

Term Parameter Symbol Controller

Table 4-1. PID Controller Terms and Parameters (Continued)

HF rolloff 1 HF rolloff time 1

HF rolloff 2 HF rolloff time 2

Toggling Controller Terms On and Off

For each parameter, the toggle button at the left of the row is used to toggle the terms on and off. “On” means that the corresponding controller term appears in the overall controller transfer function, and the slider and variable edit box can be used to change the parameter. “Off” means that the controller term does not appear in the overall controller transfer function. In this case, the slider and the variable-edit box are read-only—you cannot drag the slider, and you cannot type in the variable-edit box. When the button is turned on again, the parameter value is restored to its previous value. You can use the buttons to do a quick A/B comparison of a PID controller with or without a given term—for example, to see the effect of a high frequency rolloff term or integral action.

hf1

hf2

1+1/(sT

hf1

hf2

)

Xmath Interactive Control Design Module 4-2 ni.com

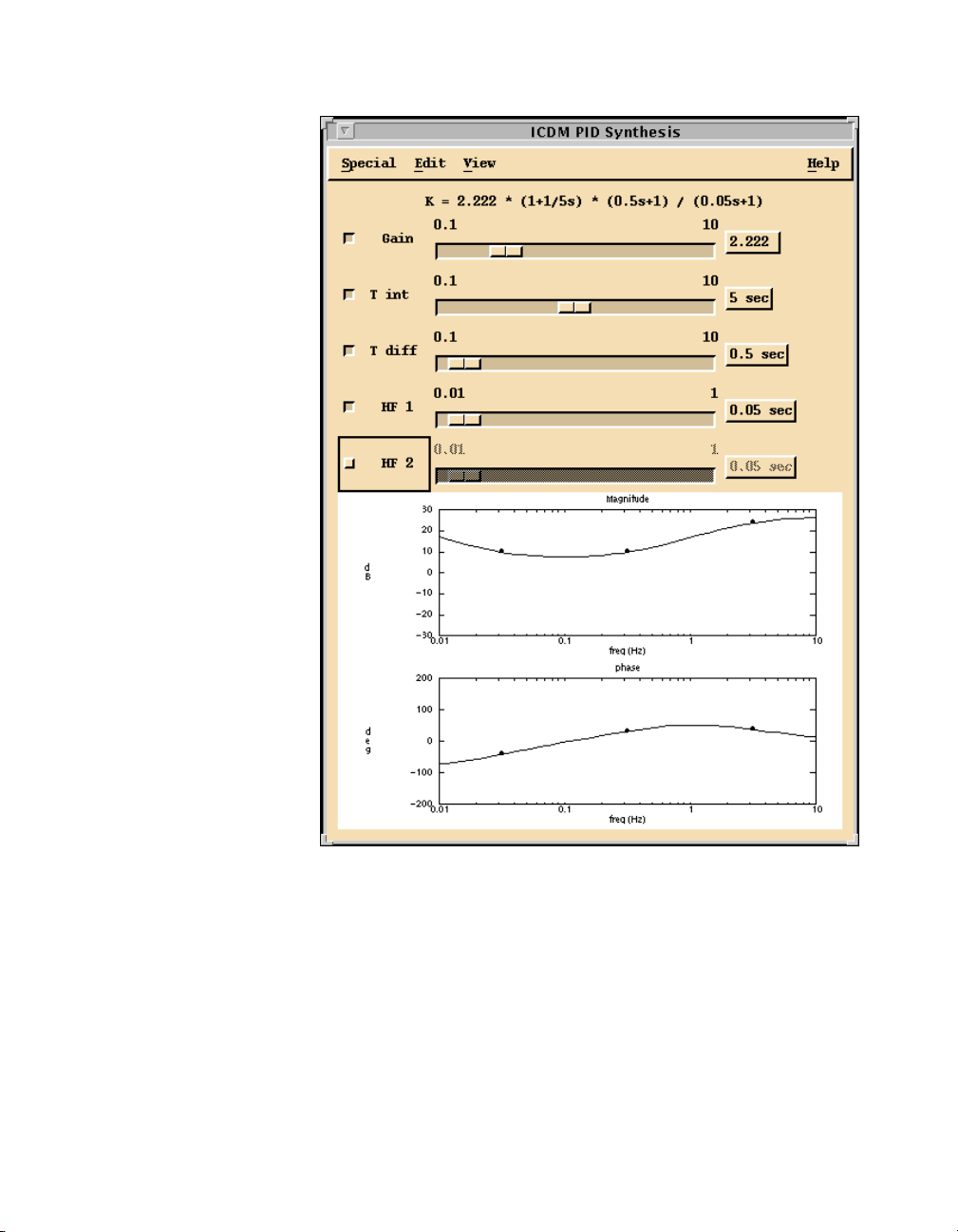
Chapter 4 PID Synthesis

Figure 4-1. PID Synthesis Window

As an example, suppose that the P and I toggle buttons are on, and the D and HF rolloff buttons are off. The controller transfer function will then have the following form:

Cs() K

= 1 sT

⁄()+

int

Chapter 4 PID Synthesis

Notice that there are at least two other commonly used forms for a PID control law that differ from the one used in ICDM:

Cs() K

and

ICDM enforces a proper controller transfer function, that is, a finite high frequency gain. Therefore, if the D term is on, ICDM will require at least one HF rolloff term also to be on.

Opening the PID Synthesis Window

When you select the PID window from the Synthesis menu in the ICDM Main window, the PID transfer function has the form of a PID controller. If it does, then the PID window sets its parameters (including the push buttons) to the values that would yield the current controller, and then opens. In this case the current controller remains unchanged. If the current controller does not have the form of a PID controller, then a dialog box appears and warns the user and offers several alternatives.

= 11+ T

Cs() K

= 1 T

window first decides whether the current controller

int

diff

s+⁄()+

s+⁄+

Manipulating the Controller Parameters

Each parameter can be changed using the slider, variable-edit box, or graphically. To change the sign of the parameter or to change the parameter to a value outside the current slider or plot range, you must use the variable-edit box. Notice that negative values are allowed, but often are not what you want.

The parameters also can be changed graphically by grabbing and dragging the controller Bode plot in the following ways:

• To change the gain, with the gain parameter turned on, grab the magnitude Bode plot anywhere except near the handles (dark circles) on the plot. You now can drag the Bode plot up and down, which changes the gain.

• To change the other parameters, listed in column four of Table 4-1, grab the appropriate handle (dark circle) on either plot and drag it left and right to the desired frequency, which is the inverse of the time parameter. The associated slider and variable-edit box also will be updated as you drag the handle.

Xmath Interactive Control Design Module 4-4 ni.com

Time Versus Frequency Parameters

Notice that the sliders and variable-edit boxes use time parameters, whereas the Bode plot handles use frequencies, that is, the inverses of the time parameters. If you think of integral action as being parameterized by a characteristic time, then you may prefer to use the slider. If you think of integral action as being parameterized by a characteristic frequency (reset rate), then you may prefer to manipulate the Bode plot handle.

Ranges of Sliders and Plots

The ranges for the sliders and plots can be changed in several ways. If you enter a value that lies outside the slider range in the corresponding variable edit box, the range of the slider will automatically adjust to accommodate the new value. You also can change the range of a slider using the Ranges window, which appears when you select View»Ranges or press <Ctrl-R> in the PID window. Selecting View»Auto Scale will cause ICDM to select sensible values for the slider and plot ranges based on the current controller. The ranges for the plots also can be changed interactively. Refer to the

General Plotting Features section of Chapter 2, Introduction to SISO Design.

Chapter 4 PID Synthesis

Controller Term Normalizations

Each of the controller terms is normalized in a way that is convenient for most PID design tasks as described in the following sections.

Integral Term Normalization

The integral term is high-frequency normalized, which means that it is approximately one for frequencies above 1/ T the integral time constant 1/T controller transfer function at high frequencies. For example, you can add integral action to a controller without significantly affecting the stability margins or closed-loop dynamics by adding the integral term with 1/T well below the crossover frequency, that is, 1/T controller will enforce steady-state tracking, but over a time period longer than the closed-loop system dynamics. You then can slowly decrease 1/T until you get a good balance between fast integral action and the degradation of stability margins.

. Therefore, you can adjust

int

without significantly affecting the

int

large. In this case, your

int

Chapter 4 PID Synthesis

Derivative Term Normalization

The derivative term is low-frequency normalized, which means that at low frequencies (below 1/T

) it is nearly one, and so has little effect on the

diff

overall controller transfer function at low frequencies. In particular, the loop transfer function at s = 0 is not affected by the derivative term at all, so static tracking, static actuator effort, and so on are not affected by the derivative term. You can start by making the T

term small and then

diff

gradually increasing it until you get a good balance between better stability margins and excessive actuator effort.

Rolloff Term Normalization

The two HF rolloff terms are low-frequency normalized, so they have little effect at frequencies below T parameters, and then gradually increase them until you start to notice a degradation in stability.

. You can start with small values for these

Xmath Interactive Control Design Module 4-6 ni.com

Root Locus Synthesis

This chapter describes the user interface, terminology, and parameters used for root locus synthesis.

Overview

The Root Locus window performs two main functions:

• Displays selected gain and phase contours in the complex plane of the loop transfer function.

• Allows the user to manipulate the controller transfer function graphically by dragging controller poles and zeros, or dragging the closed-loop poles along the root locus plot.

The Root Locus

Window Anatomy

The Root Locus Synthesis window is shown with the standard (default) contour in Figure 5-1. The branches of the locus connect the zeros and poles of the loop transfer function, which are shown in the plot. The closed-loop poles, which are on the locus, also are shown.

window only works in SISO mode.

Chapter 5 Root Locus Synthesis

Figure 5-1. Root Locus Synthesis Window

The Root Locus Synthesis window consists of, from top to bottom:

• A menu bar with entries Special, Edit, View, and Help.

• A slider and variable edit box for the gain. These controls are used to show and also to change the controller gain. The gain also can be changed graphically by dragging the closed-loop poles along the root locus.

• (Bottom left) The root locus plot. The plot shows selected phase or gain contours of the loop transfer function along with the plant and controller poles and zeros. A more detailed description appears following.

• (Bottom right) Buttons to add/delete/edit poles and/or zeros. Poles, zeros, and pole-zero pairs also can be created and destroyed using the

Xmath Interactive Control Design Module 5-2 ni.com

Chapter 5 Root Locus Synthesis

Edit menu or by typing the accelerators in the Root Locus window. A more detailed description appears following.

The Root Locus Synthesis

window is shown in Figure 5-1 with the standard

(default) 180° contour. The branches of the locus connect the zeros and poles of the loop transfer function, which are shown in the plot. The closed-loop poles, which are on the locus, are also shown.

Opening the Root Locus Synthesis Window

The Root Locus window can accept any type of controller, so it can always be opened. It simply reads the current controller from ICDM. You then can use the Root Locus

window to manipulate the controller poles, zeros, and

gain.

After you have changed the controller using the Root Locus controller loses any special form it may have had—for example, LQG. It is represented by its transfer function. Thus, you can use the Root Locus window to change the zeros, poles, and gain of a controller originally designed using the LQG back into the LQG Synthesis

window, but you then cannot read the controller

window since it is no longer an LQG

controller.

Terminology

The loop transfer function is expressed in the following product form:

window, the

s() K

–()…sz

-----------------------------------------------

–()…sp

–()

where K is called the gain (notice that the gain is high-frequency normalized), the z and the p

values are the poles of the loop transfer function.

values are the zeros of the loop transfer function

Each of these poles and zeros is associated with either the plant or the controller. The Root Locus

window allows you to change the gain, change

or delete any controller pole or zero, or create new controller poles and zeros as long as the controller transfer function remains proper—that is, has finite gain at high frequencies. The Root Locus to change or delete any plant pole or zero. The Alternate Plant

window will not allow you

window can

be used to modify the plant interactively and see the effect on the closed-loop system performance.

Chapter 5 Root Locus Synthesis

Plotting Styles

Selecting View»Locus Select or pressing <Ctrl-L> in the Root Locus window produces a dialog box in which the user can choose one of many possible plotting styles. In all cases, the (open-loop) controller and plant poles and zeros are shown on the plot. On color displays:

• Controller poles and zeros are black

• Plant poles and zeros are red

This serves as a mnemonic: you can manipulate black but not red poles or zeros. On monochrome displays, the plant poles and zeros are lighter than the controller poles and zeros. You can always use data-viewing to obtain more information about a pole or zero. Refer to the Data-Viewing Plots section of Chapter 2, Introduction to SISO Design. Figure 5-2 shows a dialog box for choosing plotting style with standard (default) contours selected.

Figure 5-2. Root Locus Select Dialog for Choosing Plotting Style

Xmath Interactive Control Design Module 5-4 ni.com

Phase Contours

Magnitude Contours

Chapter 5 Root Locus Synthesis

For each of magnitude and phase contours, you can choose one of three possible plotting styles.

• 180°

The plot shows the locus of points where the phase angle of the loop transfer function is 180°. This yields a conventional root locus display. This is the default phase contour plotting style. The plot shows the set of all possible closed-loop pole locations as the gain is swept from 0to∞.

• 160° 200° 10°

The plot shows the loci of points where the phase angle of the loop transfer function is 160°, 170°, 180°, 190°, or 200°. These plots show the set of all possible closed-loop pole locations as the gain is swept from 0 to and there is an additional phase shift of ±20°, ±10° in the loop transfer function.

• None

No phase contours are plotted.

•0 dB

The plot shows the locus of points where the magnitude of the loop transfer function (including the delay, if applicable) is 0 dB.

• –2:2 dB

The plot shows the loci of points where the magnitude of the loop transfer function is –2, –1, 0, +1, and +2 dB, respectively.

• None

No magnitude contours are plotted. This is the default magnitude contour plotting style.

Notice that by selecting None for both phase and magnitude contours, the plot shows only the controller and plant poles and zeros. This is useful for graphically editing the controller poles and zeros.

If any phase contours are plotted, the closed-loop poles are shown (in blue on a color display). They can be dragged along the 180° contour plot.

Chapter 5 Root Locus Synthesis

All of the plots support data viewing: click the right mouse button with the cursor positioned near a pole, zero, or one of the plots. This allows you to find the gain associated with a particular point on a phase contour, for example.

Slider and Plot Ranges

To change the ranges of the Gain slider or the root locus plot, select View»Ranges or press <Ctrl-R> in the Root Locus

The slider range also will be changed automatically if you type a new value which is outside the current range in the corresponding variable edit box. The plot also can be re-ranged interactively by grabbing and dragging the plot axes. Refer to the discussion of plot re-ranging in section s-plots-features.

Selecting View»Auto-scale or pressing <Ctrl-A> in the Root Locus window will cause new ranges to be assigned to the slider and plot, based on the current controller.

Manipulating the Parameters

window.

The Graphically Manipulating Poles and Zeros section of Chapter 2,

Introduction to SISO Design, describes how to graphically manipulate the

controller poles and zeros.

The Root Locus must have at least as many poles as zeros. If you attempt to add one zero or a pair of zeros, that would result in more controller zeros than poles, a warning is issued. Similarly, you cannot delete one or more controller poles, if the deletion would result in an improper controller.

You can select Edit»Undo to restore the deleted pole(s) and/or zero(s), provided you have not made any other changes since deleting. To abort a delete operation, click the left mouse button with the skull and crossbones cursor away from any pole or zero.

Xmath Interactive Control Design Module 5-6 ni.com

window enforces a proper controller; that is, the controller

Design

This section gives short descriptions of how the Root Locus window can be used to design or analyze controllers. This section also provides some interpretations and describes some uses of the nonstandard contour plots.

Adding a Pole-Zero Pair

Adding a pole-zero pair is a good way to add a little lead or lag action to an existing controller. When you first add the pole-zero pair, you will not have changed the controller transfer function. As you grab the zero and drag it away from the pole, you will induce a smooth change in the controller transfer function. By dragging the zero a little closer to the origin, you will add a small amount of lead action to the controller—that is, increase the controller phase for frequencies between the pole and zero, and increase the magnitude at frequencies larger than the pole.

Similarly, by dragging the zero away from the origin, you will create some lag action—that is, decrease the loop phase between the zero and pole, and increase the gain below the pole frequency.

Chapter 5 Root Locus Synthesis

Deleting Pole-Zero Pairs

Deleting a controller pole-zero pair is a good way to do interactive controller model reduction. Suppose that you have synthesized a suitable controller and need to find a lower order controller that has nearly the same performance. Using the Root Locus window, you want to move (stable) controller poles or zeros near each other without sacrificing controller performance. Good candidates are poles and zeros substantially outside the control system bandwidth, or pairs of nearby poles and zeros. After you have moved a controller pole or zero (or both) so that they are near each other—and hopefully, control system performance has not changed too much—then you can delete the pair without severely affecting the controller transfer function. You have just reduced the controller order by one (or two, if you deleted a complex conjugate pair of poles and zeros).

Chapter 5 Root Locus Synthesis

Interpreting the Nonstandard Contour Plots

The Root Locus window can display phase contours other than the standard 180° as well as various magnitude contour plots. The meaning of these curves is simple: if L(s)=a, then s would be a closed-loop pole if the loop transfer function were multiplied by –1/a at the frequency s. For example, a point s labeled ⏐L(s)⏐ = –3 dB on one of the 170° curves would be a closed-loop pole if the loop transfer function at the frequency were to increase in magnitude by 3 dB and increase in phase by 10°.

This simple observation works two ways. Continuing the previous example, to have a pole at s, try to change the current controller to achieve the required phase shift +10° and gain increase (+3 dB) at (for example, by adding an appropriate pole-zero pair).

On the other hand, if the complex number is a poor place for a closed-loop pole (for example, very lightly damped or unstable), then the current compensator is not robust, since only a 10° phase shift along with 3 dB of gain change in loop gain (most likely, the plant) would result in a closed-loop pole at s. In this case, you turn to the problem of synthesizing new compensation which decreases the phase and magnitude of the loop transfer function at the frequency s. This has the effect of making the closed-loop system less likely to have a pole at s when the plant transfer function is changed; that is, it results in a more robust design.

Figure 5-3 shows the Root Locus

window with the phase contours turned

off and the 0 dB magnitude contour turned on. The locus shows the set of all possible closed-loop poles for the modified loop transfer function

L(s)=e

jθ

L(s) as θ varies from zero to 2π. By data-viewing the contour,

you can find the phase shift (value of θ) that corresponds to any point on the locus.

Xmath Interactive Control Design Module 5-8 ni.com

Chapter 5 Root Locus Synthesis

Figure 5-3. Root Locus Synthesis Window with the 0 dB Magnitude Contour

Pole Place Synthesis

This chapter discusses the Pole Place Synthesis window, which is used to design a SISO controller by assigning the closed-loop poles. Pole Place operates in two modes:

• Normal mode (integral action not enforced)

• Integral action mode

The Pole Place Synthesis controllers.

Window Anatomy

The Pole Place window is shown in Figure 6-1. From top to bottom, it consists of:

• A menu bar with entries Special, Edit, View, and Help.

• A toggle button used to set normal or integral action mode.

• A slider and variable-edit box used to time or frequency-scale the

• A plot used to display and manipulate the closed-loop poles.

• Buttons used to manipulate the closed-loop poles.

window cannot be used to design MIMO

closed-loop poles.

Chapter 6 Pole Place Synthesis

Figure 6-1. Pole Place Synthesis Window

Pole Place Modes

In Pole Place, the user selects either closed-loop poles (in normal mode) or 2n + 1 closed-loop poles (in integral action mode). These poles uniquely determine the controller transfer function.

This process can be described in terms of the coefficients of the plant and controller numerators and denominators.

The plant transfer function is given by

P(s)=n

Xmath Interactive Control Design Module 6-2 ni.com

(s)/dp(s)

where

Chapter 6 Pole Place Synthesis

Normal Mode

(s)=sn+ a1s

np(s)=b0sn+ b1s

n–1

+ a2s

n–1

n–2

+...+a

+...+ab

Notice that the order of the plant is n, and allow the possibility that the plant transfer function is not strictly proper; that is, the plant can have as many zeros as poles.

In normal mode, the order (number of poles) of the controller is fixed and equal to n (the order of the plant), so there are a total of 2n closed-loop poles. In this case, the 2n degrees of freedom in the closed-loop poles exactly determine the controller transfer function, which also has 2n degrees of freedom.

In normal mode, the controller transfer function has order n and is strictly proper:

C(s)=n

(s)/dc(s)

where

(s)=sn+ x1s

n–1

+ x2s

n–2

+...+x

nc(s)=y1s

n–1

+ y2s

n–2

+...+2y

Therefore, the closed-loop characteristic polynomial has degree 2n:

χ s() n

where λ

, …, λ

are the closed-loop poles chosen by the user.

s()nps() dcs()dps()+=

–()s λ2–()…s λ2n–()=

s λ

2n 1–

…α2n+++()=

Chapter 6 Pole Place Synthesis

We can write this polynomial equation as follows:

0 … 0

n 1–

… 0 … 0

1b0

2b1

……

n 1–bn 2–

bnb

0 b

00 b

……

00… b

10… 0

1 … 0

2a1

……

n 1–an 2–

nan 1–

0 a

00 a

……

00… a

…

… 0

These 2n linear equations are solved to find the 2n controller parameters x

, ..., xn and y1,...,yn.

Integral Action Mode

The degree (number of poles) of the controller is fixed and equal to n +1, so there are a total of 2n + 1 closed-loop poles. In this case, the 2n +1 degrees of freedom in the closed-loop poles, along with the constraint that the controller must have at least one pole at s = 0, exactly determine the controller transfer function. In fact, the closed-loop poles give a complete parameterization of all controllers with at least one pole at s = 0, and n or fewer other poles.

Equations similar to those shown in the Normal Mode section are used to determine the controller parameters given the closed-loop pole locations.

Xmath Interactive Control Design Module 6-4 ni.com

State-Space Interpretation

In a state-space framework, it is common to classify the closed-loop poles as n “control eigenvalues” and n “estimator eigenvalues.” But, in fact, it makes no difference in the final controller transfer function how you classify the closed-loop poles.

In other words, in a state-space framework, swapping a “control eigenvalue” and an “estimator eigenvalue” will result in different feedback and estimator gains, but the same final controller.

Opening the Pole Place Window

The Pole Place window can accept any controller with n poles, or n +1 poles provided the controller has at least one pole at s =0. The Integral Action toggle button will be properly set. In particular, it accepts all LQG and H∞ controllers. This allows the user to manually tune the closed-loop poles in a design that was, originally, LQG or H∞. In this case, you cannot read the resulting controller back into the LQG or window since the controller no longer has this special form.

Manipulating the Closed-Loop Poles

Chapter 6 Pole Place Synthesis

The closed-loop poles and zeros can be dragged and edited interactively. Refer to the Graphically Manipulating Poles and Zeros section of Chapter 2, Introduction to SISO Design, for a general discussion of manipulating poles graphically.

Time and Frequency Scaling

The slider and variable-edit box show the average value of the closed-loop pole magnitudes, and therefore can be interpreted as, roughly, the bandwidth of the closed-loop system. The average frequency is given by:

= ⏐λ1λ2... λ2n⏐

avg

where λ1, ..., λ geometric.

You can change F box. The effect is that the closed-loop poles are all multiplied by a scale factor in such a way that becomes the requested value. Therefore, by changing F dynamics.

are the closed-loop poles. Notice that the average is

by dragging the slider or typing into the variable edit

avg

, you are time- or frequency-scaling the closed-loop

avg

1/2n

Chapter 6 Pole Place Synthesis

A circle of radius F circle to change F

Butterworth Configuration

Click the Butterworth button to move the poles to a Butterworth configuration, preserving F set to Butterworth.

Editing the Closed-Loop Poles

You can change the closed-loop poles two ways: by editing or by grabbing and dragging them. Both of these methods are described in the General

Plotting Features section of Chapter 2, Introduction to SISO Design.

Slider and Plot Ranges

To change the ranges of the Frequency Scaling slider or the plot of closed-loop poles, select View»Ranges or press <Ctrl-R> in the Pole Place window.

The slider range also will be changed automatically if you type a new value which is outside the current range in the variable edit box. The plot also can be re-ranged interactively by grabbing and dragging the plot axes; refer to the General Plotting Features section of Chapter 2, Introduction to SISO

Design.

also is displayed in the plot. You also can drag the

avg

. The initial pole configuration also is

avg

Selecting View»Auto-scale or pressing <Ctrl-A> in the Root Locus window will cause new ranges to be assigned to the slider and plot, based on the current controller.

Xmath Interactive Control Design Module 6-6 ni.com

LQG Synthesis

This chapter discusses the LQG Synthesis window, which is used to synthesize a linear quadratic Gaussian (LQG) controller for a SISO plant. If you select LQG synthesis with a MIMO plant, you will get the MIMO LQG Synthesis window described in Chapter 12, LQG/H-Infinity

Synthesis.

LQG Synthesis Window Anatomy

The LQG Synthesis window is shown in Figure 7-1. From top to bottom, it contains:

• A menu bar with entries Special, Edit, View, and Help.

• A message area that describes the synthesis mode (type of controller); for example,

• A control panel for changing the four design parameters: – Control cost parameter (ρ) – Sensor noise parameter (υ)

– Integral action time constant (T

– Decay rate or exponential time weighting parameter (a)

LQG with integral action.

)

int

These parameters are described in greater detail later in this chapter.

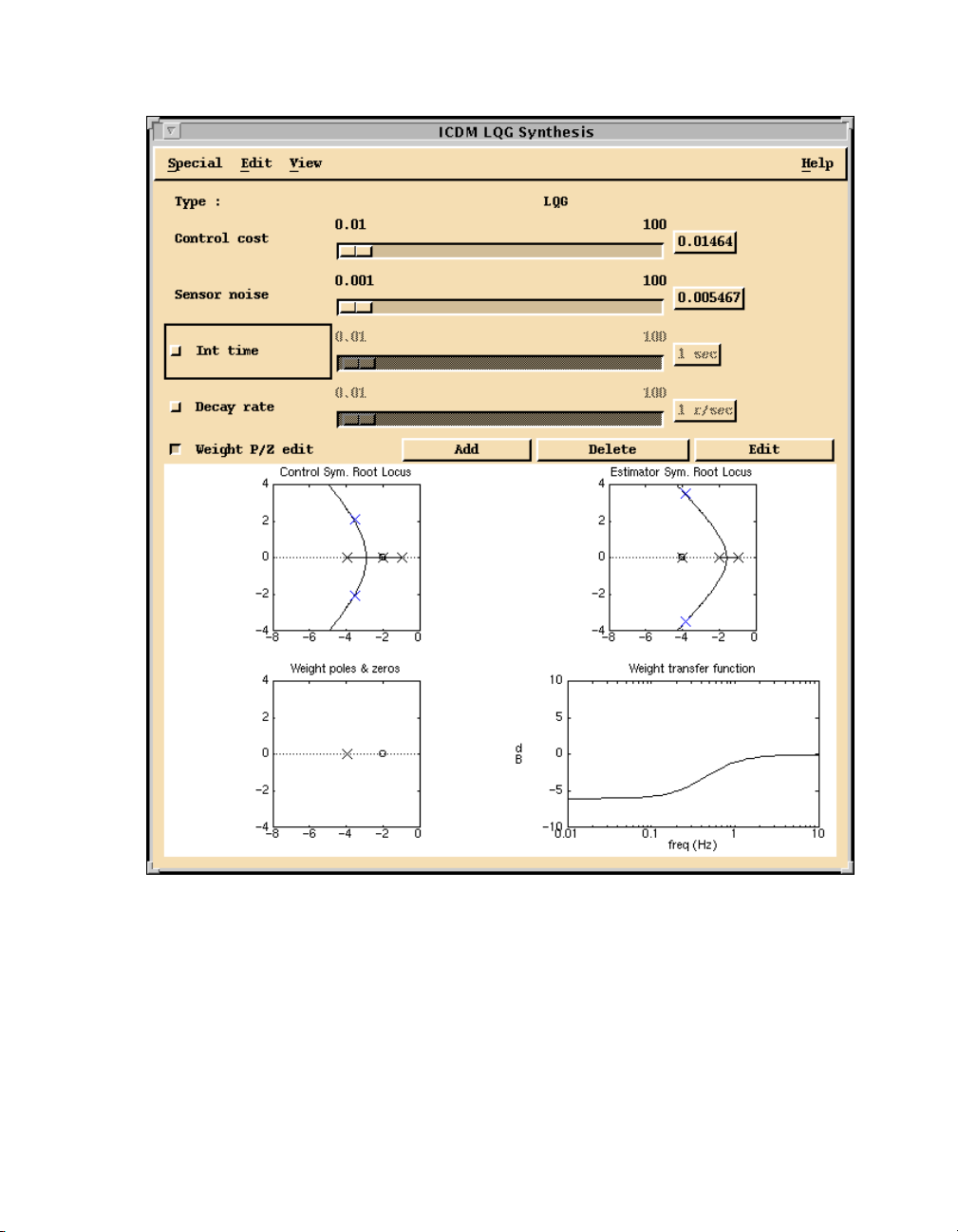
Chapter 7 LQG Synthesis

Figure 7-1. LQG Synthesis Window

• A control panel used to graphically edit the output weight transfer function.

• A plotting area that contains the following plots:

– The symmetric root locus plots of the control and estimator

closed-loop poles. The control cost and sensor noise parameters can be changed by dragging the closed-loop poles along the plot.

Xmath Interactive Control Design Module 7-2 ni.com

Synthesis Modes

In addition to standard LQG synthesis, the LQG Synthesis window supports any combination of three optional features:

• Integral action

• Exponential time weighting (guaranteed decay rate)

• Output weight editing

The synthesis mode is reported in the text at the top of the window. The toggle Int Time (integral action time) button enables and disables integral action. The Decay Rate toggle button controls exponential time weighting. The Weight Zero Edit toggle button enables and disables output weight editing.

Chapter 7 LQG Synthesis

If the decay rate is enabled, it is shown as a vertical line that can be dragged.

– A plot showing the poles and zeros of the output weight transfer

function. If weight zero editing is enabled, the zeros can be edited graphically.

– A plot showing the magnitude of the output weight transfer

function.

Opening the LQG Synthesis Window

The LQG window can only accept LQG controllers. If the current controller is of type LQG (perhaps, from the History window is opened, the current controller is read into the LQG window. That is, the push buttons and parameters are set to the appropriate values.

If the current controller is not of type LQG, and the user attempts to open the LQG Synthesis proceeding with opening the LQG Synthesis current controller with the LQG controller.

The LQG window remembers its parameter settings. When it is opened, the parameters will be exactly as they were when the LQG closed, or it will be set to default values if the LQG opened in this ICDM session.

window, a dialog box appears and warns the user that

window) and the LQG

window will overwrite the

window was last

window has not been

Chapter 7 LQG Synthesis

Setup and Terminology

The different modes are described using the following basic terminology:

r=0

yPuw

+()= uC–()yw

proc

+()= y

sens

Wy=

Figure 7-1 shows a block diagram with the basic setup for LQG synthesis,

where u is the actuator signal (output of the controller)

is an (input referred) process noise

proc

y is the (plant) output signal

is the weighted output signal

is a sensor noise

sens

P is the plant transfer function

C is the controller transfer function

W is the output weight transfer function

The noises w

proc

and w

are white; that is, they have constant power

sens

spectral densities (PSDs). The parameter υ is the ratio of the PSD of w to the PSD of w

C(s)

proc

P(s)

W(s)

sens

Figure 7-2. Block Diagram Showing the Basic Setup for LQG Synthesis

Standard LQG (All Toggle Buttons Off)

In LQG synthesis mode, the controller minimizes a weighted sum of the steady-state actuator and output variance:

lim ρut()2yt()

t ∞→

where E denotes expectation, ρ is the Control cost parameter, and the parameter ν gives the ratio of the intensity of the sensor noise w intensity of the process w

Xmath Interactive Control Design Module 7-4 ni.com

noise (which are assumed to be white).

proc

+()=

to the

sens

Integral Action

Chapter 7 LQG Synthesis

When integral action is enabled, the controller minimizes a variation on the LQG cost:

where

As in the standard mode, the sensor noise parameter ν is the ratio of the sensor noise intensity to the input-referred process noise intensity.

Penalizing the “running integral” of the plant output forces the power spectral density of the plant output to vanish at zero frequency.

In classical control terms, this forces a pole at S = 0 in the loop transfer function, that is, integral control. As with PID design, the parameter T gives the time scale over which the effects of the integral action will take place.

Exponential Time Weighting

When this feature is enabled, the plant is first changed to P(s – a), where a is the Decay Rate parameter. In other words, the plant is made less stable; its poles (and zeros) are shifted to the right by the value a. Then, the LQG controller for this “destabilized” plant is computed. Finally, the poles and zeros of this controller are shifted left by the Decay Rate parameter a.

lim ρut()2yt()2zt()

t ∞→

zt() 1 T

++()=

⁄()y τ()τd

int

∫

int

One effect of this shifting is that the closed-loop poles are guaranteed to have real part less than the Decay Rate parameter a. In other words, the closed-loop time domain responses are guaranteed to decay at least as fast as exp(–at). This is why the parameter is called Decay Rate.

Chapter 7 LQG Synthesis

Output Weight Editing

When Weight Zero Edit is enabled, the LQG controller is based on

y˜W

integral action, the controller minimizes the quantity:

, which is a filtered version of the plant output signal y. Without

lim ρut()2yt()

t ∞→

+()=

and with integral action, the quantity:

lim ρut()2yt()2zt()

t ∞→

++()=

where

zt() 1 T

⁄()y˜τ()τd

int

∫

The transfer function W is the output weighting transfer function. When W = 1, this reduces to the standard LQG controller described previously.

The weighting transfer function is given by:

Ws() n

s()nps()⁄=

Its denominator is fixed and equal to the numerator of the plant transfer function. Its numerator can be manipulated by the user.

The lower left plot shows the poles and zeros of the weight transfer function W. When Weight Zero Edit is enabled, the user can grab and drag the zeros shown, or Add/Delete/Edit zeros using the push buttons.

The lower right plot shows the magnitude of the weight transfer function. When it is flat and equal to 0 dB for all frequencies, you have W =1, that is, standard LQG design based on the plant output y. When, for example, W is larger than 0 dB at low frequencies, this means that the LQG controller is based on a filtered version of y that emphasizes low frequencies, which presumably results in a controller with larger loop gain at low frequencies.

Xmath Interactive Control Design Module 7-6 ni.com

State-Space Interpretation

In LQG theory, the closed-loop poles consist of n “optimal control eigenvalues” and n “estimator (Kalman filter) eigenvalues.” For multivariable systems, the optimal control and the optimal estimator play different roles in the control system. But in the single-actuator, single-sensor case, the roles are completely symmetric.

In particular, swapping the parameters ρ and ν yields the same final LQG controller. This symmetry is broken if you use either output weighting or integral action, however.

Manipulating the Design Parameters

The design parameters ρ and ν can be changed using the associated sliders or the variable edit boxes. If you type in a value that is outside the current slider range, the slider range will automatically adjust. You can change the ranges for the sliders using the Ranges

Chapter 7 LQG Synthesis

window.

The parameters T edit boxes provided the associated toggle button is on. If the toggle button is off, then the slider and variable edit box are insensitive; you cannot drag the slider handle, and you cannot type into the variable edit box.

When the toggle buttons are turned on again, the parameters are restored to their previous (or default) values.

and a can be manipulated using the sliders or variable

int

Manipulating the Design Parameters Graphically

The design parameters also can be manipulated graphically as follows:

• The closed-loop poles are shown on the two symmetric root locus plots. They can be dragged along the root locus plot, which results in setting the parameters ρ or ν appropriately.

•When the Decay Rate toggle button is on, a dashed line appears in the symmetric root locus plots, showing ℜs = a. You can drag this line left and right to set the Decay Rate parameter.

•When Weight Zero Editing is enabled, the user can graphically manipulate the zeros of the weight transfer function W on the plot labeled Weight Poles & Zeros. Refer to the Graphically

Manipulating Poles and Zeros section of Chapter 2, Introduction to SISO Design, for a general discussion of how to move, add, delete,

or edit these zeros graphically.

Chapter 7 LQG Synthesis

Ranges

To change the ranges of the sliders or plots, select View»Ranges or enter

R in the LQG window.

The slider ranges also will be changed automatically if you type a new value which is outside the current range into the corresponding variable edit box. The plot also can be re-ranged interactively by grabbing and dragging the plot axes; refer to the Interactive Plot Re-ranging section of Chapter 2,

Introduction to SISO Design.

Selecting View»Auto-scale or pressing <Ctrl-A> in the LQG

window

causes new ranges to be assigned to the sliders and plots, based on the current controller.

Xmath Interactive Control Design Module 7-8 ni.com

H-Infinity Synthesis

This chapter describes the H∞ Synthesis window used for SISO plants. The H∞ Synthesis controllers are sometimes called linear exponential quadratic Gaussian (LEQG) or minimum entropy controllers. For a description of the MIMO Synthesis window, refer to Chapter 12, LQG/H-Infinity Synthesis.

H-Infinity Synthesis Window Anatomy

The H∞ Synthesis window is shown in Figure 8-1. From top to bottom, it consists of:

• A menu bar with entries Special, Edit, View, and Help.

• A control panel for changing the three design parameters: –H∞ performance level (γ) – Control cost parameter (ρ) – Sensor noise parameter (ν)

These parameters are described in greater detail later in this chapter.

• A control panel used to edit the output weight transfer function (described in the Output Weight Editing section).

• A plotting area that contains four plots:

– A singular value plot of the normalized closed-loop transfer

matrix along with the parameter γ, which can be grabbed and dragged to a new value. If a lower bound on the minimal value of γ is known, it also is displayed.

–A plot that shows the closed-loop poles.

– A plot that shows the poles and zeros of the output weight transfer

function. When Weight Zero Edit is enabled, the user can grab and drag the zeros to new locations.

– A plot that shows the magnitude of the output weight transfer

function.

window is used to synthesize a central controller. Such

Chapter 8 H-Infinity Synthesis

Figure 8-1. H-Infinity Synthesis Window

Xmath Interactive Control Design Module 8-2 ni.com

Opening the Synthesis Window

The H∞ window can only accept H∞ controllers. If the current controller is of type H∞ (perhaps from the History window) and the H∞ window is opened, the current controller is read into the H∞ window; that is, the parameters are set to the appropriate values.

If the current controller is not of type H∞, and the user attempts to open the H∞ Synthesis

window, a dialog box appears and warns the user that

proceeding with opening the synthesis window will overwrite the current controller with the controller.

The H∞ window remembers its parameter settings. When it is opened, the parameters will be exactly as they were when the window was last closed, or they will be set to default values if the H∞ window has not been opened in this ICDM session.

Setup and Synthesis Method

This section describes the closed-loop transfer matrix (refer to Figure 8-2). The H∞ synthesis procedure can be described using the following standard setup:

Chapter 8 H-Infinity Synthesis

yPuw

+()= uC–()y νw

ρu= z

Wy=

+()=

where y is the plant output signal

is a normalized (input-referred process) noise

is a normalized (sensor) noise

is the normalized actuator signal

is the weighted plant output signal

P is the plant transfer function

C is the controller transfer function

W is the output weight transfer function

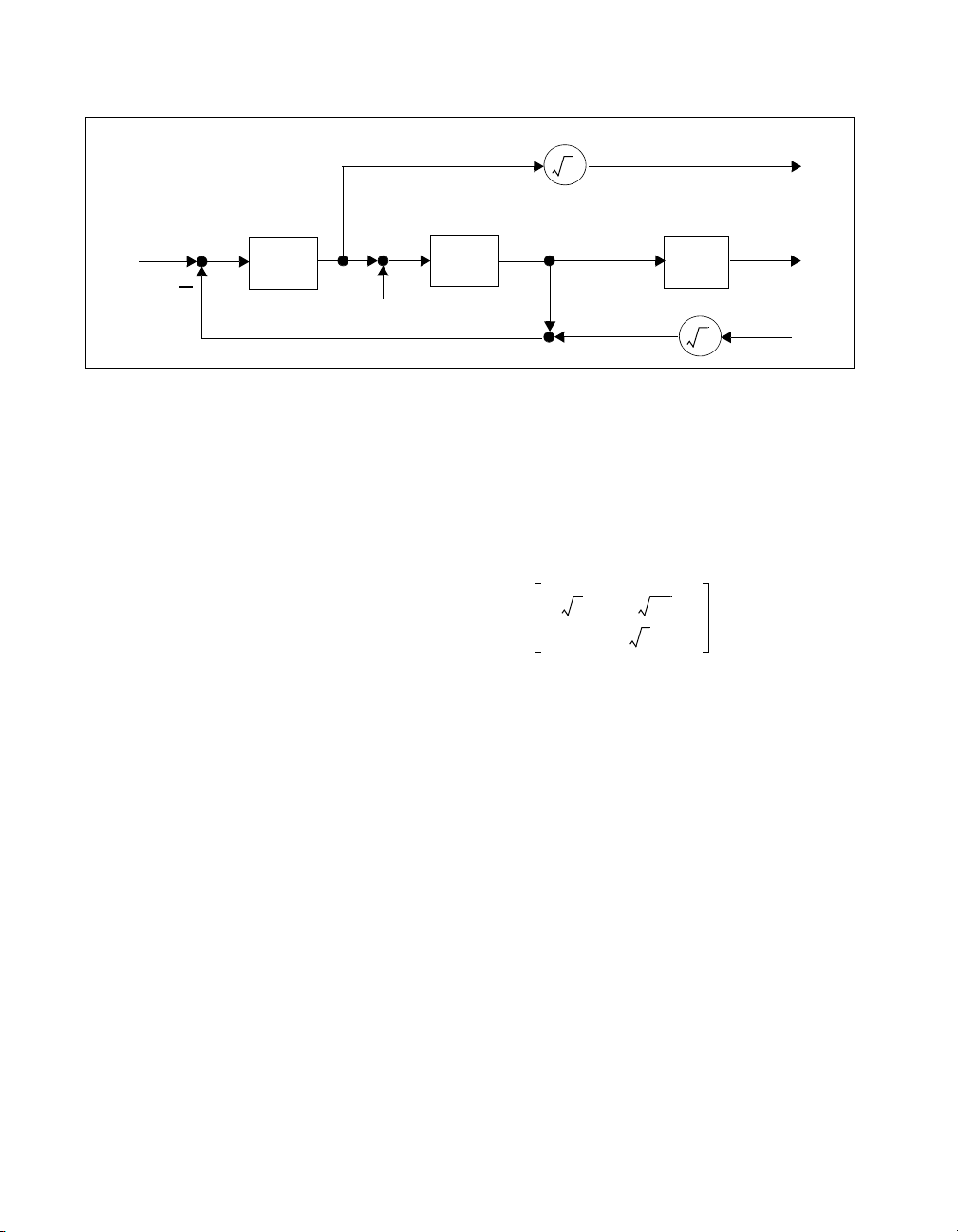
Chapter 8 H-Infinity Synthesis

r=0

C(s)

Figure 8-2. Block Diagram Showing the Basic Setup for H-Infinity Synthesis

P(s)

W(s)

Figure 8-2 shows a block diagram with the basic setup for H∞ synthesis where closed-loop transfer matrix H relates the two exogenous inputs w and w

to the two outputs z1 and z2.

The design is based on H, the closed-loop transfer matrix relating the noises

and w2 to the signals z1 and z2. H is given by the following equation:

-----------------

1 PC+

ρPC– ρυC–

PW νPCW–

The entries of the closed-loop transfer matrix can be interpreted as the (normalized) transfer functions from the process and sensor noises to the actuator and output, respectively.

The singular values of H are shown in the top left plot of the H∞ Synthesis window.

Central H-Infinity Controller

The controller C is chosen to minimize the γ-entropy of the closed-loop transfer matrix H, given by:

∞

⎛⎞

where σ

Xmath Interactive Control Design Module 8-4 ni.com

----

H()

⎜⎟

∫

⎝⎠

and σ2 are the singular values of H(jω).

------------------------------------

ω()γ⁄()

–

1 σ

------------------------------------log+log 1 σ2ω()γ⁄()

–

dω

Chapter 8 H-Infinity Synthesis

If either of these singular values is equal to or exceeds γ, the γ-entropy is defined to be +∞.

In other words, the γ-entropy is finite only for , and rapidly increases to +∞ as becomes close to γ, where the H∞-norm is defined as:

Refer to Chapters 5 and 12 of Linear Controller Design, Boyd and Barratt, Prentice-Hall 1991, for some interpretations of the γ-entropy.

Therefore, the controller designed will always satisfy . For this reason, γ is sometimes called the H∞ performance level. For γ, which is too small, there may be no controller that can achieve the required performance level.

For large γ, the γ-entropy of H is very nearly the same as the LQG cost with the same parameters (ρ and ν), so the H∞ controller will be nearly the same as the LQG controller with the same values of ρ and ν.

Output Weight Editing

When Weight Zero Edit is enabled, the user can graphically edit the output weight transfer function W. The weighting transfer function is given by:

γ<

∞

max σ1Hjω()()=

0 ω∞≤≤

∞

γ<

∞

s()

Ws()

------------=

s()

Its denominator is fixed and equal to the numerator of the plant transfer function; its numerator can be manipulated by the user.

The lower right plot shows the magnitude of the weight transfer function. When it is flat and equal to 0 dB for all frequencies, you have W =1; that is, standard (unweighted) design.

Chapter 8 H-Infinity Synthesis

Manipulating the Design Parameters

The parameters γ, ρ, and ν can be changed using the associated slider or variable edit box. If the user types in a value that is outside the current slider range, the slider range will automatically adjust. The user can change the ranges for the sliders using the Ranges Parameter Values section for what happens when the requested value of γ is infeasible.

The parameter γ also can be changed graphically, by grabbing and dragging the dashed horizontal line in the singular value plot.

Manipulating the Weight Transfer Function

When Weight Zero Editing is enabled, the user can graphically manipulate the zeros of the weight transfer function W on the plot labeled Weight Poles & Zeros. Refer to the Graphically Manipulating Poles and

Zeros section of Chapter 2, Introduction to SISO Design, for a general

discussion of how to move, add, delete, or edit these zeros graphically.

Infeasible Parameter Values

If the user requests an infeasible value for γ, then it will be reset to an approximation of the optimal (that is, smallest possible feasible) value, γ In this case, four (logarithmic) bisection iterations are used to determine γ, a feasible value of γ such that:

window. Refer to the Infeasible

opt

()log γ

new

where γ

is the value that γ is reset to

new

is the optimal (smallest possible feasible) value of γ

opt

is the previous value of γ

is the value of γ requested by the user

req

After the H∞ Synthesis

()log γ

----------------------------------------------------

()log–

opt

window has determined a lower bound on γ

()log–

req

, it is

opt

displayed in the singular value plot. It will disappear if the user changes the control cost, sensor noise, or output weight parameters.

Xmath Interactive Control Design Module 8-6 ni.com

Ranges

Chapter 8 H-Infinity Synthesis

To change the ranges of the sliders or plots, select View»Ranges or press <Ctrl-R> in the H∞ window.

The slider ranges also will be changed automatically if you type a new value which is outside the current range in the corresponding variable edit box. The plot also can be re-ranged interactively by grabbing and dragging the plot axes; refer to the Interactive Plot Re-ranging section of Chapter 2,

Introduction to SISO Design.

Selecting View»Auto-scale or pressing <Ctrl-A> in the H∞ window will cause new ranges to be assigned to the sliders and plots, based on the current controller.

History Window

This chapter describes the History window used for SISO plants. The History window is used to display and manipulate the design history list, which is a list of controllers that have been explicitly saved during the design process. For a description of the History window used for MIMO design, refer to Chapter 11, Introduction to MIMO Design.

Saving the Current Controller on the History List

You can save the current controller on the History list at any time, by selecting the Add to History button in the Edit Menu of the ICDM Main window, or pressing <Ctrl-A> prompted for a comment that is saved along with the design.

Opening the History Window

To make the History window appear, select Synthesis»History Window in the ICDM Main window. This will close any open synthesis window, automatically save the current controller on the history list if it has not already been saved, and make the current controller the active or selected design on the history list.

in the ICDM Main Window. You will be

History Window Anatomy

The History window is shown in Figure 9-1.

From top to bottom, it consists of:

• A menu bar with Special, Edit, and Help menus.

• A scrolled list that shows the designs saved on the history list. Columns show the history number, the date and time the controller was saved, the type of controller, and a comment that was saved with the controller. If the comments run off the visible part of the list, you can scroll left and right, or resize the History

window wider.

Chapter 9 History Window

• A Variable-Edit box which shows which history list entry is active or currently selected. The selected entry is the controller exported to ICDM for plotting.

• Buttons for manipulating the history list.

Selecting the Active Controller

You can type a number in the Variable-Edit box that shows the selected controller, or you can select a controller in the list (which will become highlighted) and then click Select at the bottom of the History

window.

Notice that you can consider the History window, with one simple design parameter: the integer that gives the selected design.

Editing the Comments

window as a type of synthesis

Figure 9-1. History Window

To change the comment stored with a design, select an entry from the list and click Edit.

Xmath Interactive Control Design Module 9-2 ni.com

Chapter 9 History Window

Deleting History List Entries

Any number of designs on the history list can be deleted by selecting them and then clicking Delete. To renumber the remaining designs, you can select Edit»Renumber.

Refer to Appendix A, Using an Xmath GUI Tool, for a discussion of how to select multiple, non-contiguous entries in a list.

To Continue Designing from a Saved Controller

First, select the desired design to make it the ICDM current controller. Then, select an appropriate synthesis window from the Synthesis menu in the ICDM Main with the controller, it will appear, initialized with the current controller, and the History Alternatively, you can select a design on the history list and then click the → Synthesis button at the bottom of the History things: first, it makes that entry active—that is, the current controller—and second, it opens the appropriate synthesis window, which closes the History

window.

Window. If the synthesis window you select is compatible

window will disappear. You now can continue designing.

window. This does two

Cycling Through Designs

The Cycle button is used to quickly compare some of the designs on the history list. First, select several designs from the list and then click the Cycle button. Refer to Appendix A, Using an Xmath GUI Tool, for a discussion of how to select multiple, non-contiguous entries in a list. Clicking Cycle causes the current controller to cycle among the selected entries. Therefore, the Cycle button is used both to select a subset of designs for cycling and to cycle the current controller among the selected designs.

Writing a Saved Design to Xmath

To write a design that has been saved on the history list to Xmath, select it so it becomes the current controller for ICDM, and then save to Xmath by selecting File»Write Controller in the ICDM Main window.

Chapter 9 History Window

Using the History List

The history list can be used in several ways. You can save controllers as “benchmarks” whose performance you want to match with a simpler controller. You also can save any promising designs that you find so you can later use them as the initial conditions for designing.

Xmath Interactive Control Design Module 9-4 ni.com

Alternate Plant Window

This chapter describes the form of the Alternate Plant window used for SISO design; refer to Chapter 11, Introduction to MIMO Design, for the form used for MIMO design.

Role and Use of Plant and Alternate Plant

In addition to the plant P, ICDM can optionally maintain an alternate plant

. These two transfer functions have different uses and purposes:

alt

• The plant is always used for the synthesis windows (that need it). For example, when synthesizing an LQG controller, the LQG synthesis is based on the plant P. In other words, the plant is used for design. In contrast, the alternate plant P

• The alternate plant P turning on the Alternate Plant display (refer to the Displaying the Alternate Plant Responses section) the plots in the ICDM Main Window will show the alternate plant connected with the current controller and the plant connected with the current controller.

• It is not possible to change the plant in ICDM except by reading it from Xmath. In contrast, the alternate plant can be manipulated using the Alternate Plant

window.

is used only for analysis. Specifically, by

alt

is never used by any synthesis method.

alt

You can think of the plant P as the plant model used for control system design, and the alternate plant P system validation.

as the plant model used for control

alt

Displaying the Alternate Plant Responses

The ICDM Main window plots always show the response of the controller connected with the plant. By turning on the Alternate Plant display, the responses of the controller with the alternate plant also are shown in these plots.

You always can use data-viewing to determine which plot corresponds to the plant and which corresponds to the alternate plant.

Chapter 10 Alternate Plant Window

Alternate Plant Window Anatomy

The Alternate Plant window is shown in Figure 10-1. From top to bottom, it consists of:

• A menu bar with Special, Edit, and View menus.

• A toggle button for controlling whether the plots in ICDM main will include the response with the alternate plant.

• A toggle button that is used to display the plant poles and zeros in the plot (refer to Figure 10-1).

• Two toggle buttons that select DC or high frequency normalization (refer to Figure 10-1).

• A slider and variable edit box for the gain of the alternate plant. These controls are used to show and also to change the gain of the alternate plant.

• (Bottom left) A plot for displaying and manipulating the poles and zeros of the alternate plant. Optionally, the poles and zeros of plant can be shown.

• (Bottom right) Buttons to Add/Delete/Edit poles and/or zeros of the alternate plant.

Xmath Interactive Control Design Module 10-2 ni.com

Chapter 10 Alternate Plant Window

Figure 10-1. Alternate Plant Window

Opening the Alternate Plant Window

When the Alternate Plant window is first opened, the alternate plant is initialized to the plant transfer function. This is convenient because in most cases the alternate plant is some sort of variation on the plant. Using the Special menu, you can read the plant from ICDM or any transfer function from Xmath into the alternate plant.

Chapter 10 Alternate Plant Window

Normalization

The form of the transfer function of the alternate plant depends on the normalization selected. With high-frequency normalization, the alternate plant transfer function is:

alt

where K is the gain (shown in the slider and Variable Edit box), are the zeros, and are the poles shown in the plot. The alternate

… p

plant is required to be proper, that is, have at least as many poles as zeros ().

nm≥

For high-frequency normalization there is no restriction on the poles or zeros.

With DC normalization, the alternate plant transfer function is:

s() K

alt

where K is the gain (shown in the slider and Variable Edit box), are the zeros, and are the poles. For DC normalization the poles

… p

and zeros are restricted to be nonzero. If you want the alternate plant to have either poles or zeros at s = 0, you must use high frequency normalization. Notice that with DC normalization the gain is exactly the DC gain of the alternate plant, that is, K = P

Manipulating the Parameters

–()…sz

s() K

-------------------------------------------

–()…sp

⁄–()…1 szm⁄–()

1 sz

---------------------------------------------------------

1 sp

(0).

alt

⁄–()…1 spn⁄–()

–()

… z

The gain K can be changed using the slider or the Variable Edit box. The poles and zeros of P

can be manipulated graphically, using the buttons to

alt

the right of the plot. Refer to the Graphically Manipulating Poles and

Zeros section of Chapter 2, Introduction to SISO Design, for a general

discussion of how to graphically edit poles and zeros.

You cannot add a zero if the addition would result in an improper alternate plant transfer function. Similarly, you cannot delete a pole if the deletion would result in an improper alternate plant transfer function. With DC normalization, you cannot create any poles or zeros at s = 0, and you cannot move existing poles or zeros to s =0.

Xmath Interactive Control Design Module 10-4 ni.com

You can switch between high frequency and DC normalization by clicking the appropriate buttons. If the alternate plant has a pole or zero at s =0, then you cannot switch to DC normalization.

Using the Alternate Plant Window

The Alternate Plant window is used to analyze the robustness of a given controller to changes or unmodeled dynamics in the plant.

Robustness to Plant Variations

The simplest test is to start with the plant (which is the default value of the alternate plant), and then vary the gain and the poles and zeros of the alternate plant. A robust system will not show excessive differences between the responses with the plant and the alternate plant. With this method, you can easily see the effects of plant gain, pole, and zero variations.

With DC normalization, varying the poles and zeros affects at high frequencies but does not change the DC gain. This is appropriate when the plant variations and modeling errors are more pronounced at high frequencies.

Chapter 10 Alternate Plant Window

Adding Unmodeled Dynamics

Starting with P the effects of a little “unmodeled plant dynamics” on the system. Notice that when you add a pole-zero pair, you have not yet changed the alternate plant transfer function. The change occurs smoothly as you drag the zero away from the pole.

• To add a little excess phase and rolloff in the loop, create a real pole-zero pair and separate them a bit, with the pole to the right of the zero. This simulates the effect of unmodeled “diffusion dynamics” in the system.

• To add a little lightly damped dynamics, create a lightly damped pole-zero pair (that is, with small negative real part) and then drag the pole and zero away from each other. This will create a resonance typical of a neglected mode in a mechanical system.

• To simulate the effect of an unmodeled time delay in the loop, create a real pole-zero pair at s = –2/T

= P and then adding a pole-zero pair is a good way to see

alt

and then drag the zero to s =–2/T

del

Chapter 10 Alternate Plant Window

Ranges of Sliders and Plot

To change the ranges of the Gain slider or the pole zero plot, select View»Ranges or press <Ctrl-R>

The slider range also will be changed automatically if you type a new value which is outside the current range into the variable edit box. The plot can also be re-ranged interactively by grabbing and dragging the plot axes; refer to the Interactive Plot Re-ranging section of Chapter 2, Introduction to

SISO Design.

in the Alternate Plant window.

Selecting View»Auto-scale or pressing <Ctrl-A> in the Alternate Plant window will cause new ranges to be assigned to the slider and plot, based on the current alternate plant.

Xmath Interactive Control Design Module 10-6 ni.com

Introduction to MIMO Design

The following chapters describe the use of ICDM for MIMO design. NI assumes the reader is familiar with the use of ICDM for SISO design. In many cases, the texts describe the differences between SISO and MIMO design.

This chapter provides an introduction to MIMO design. ICDM automatically switches between SISO and MIMO modes depending on the plant that is read in. To try out the MIMO features described here and in the next two chapters, you must first either read in a MIMO plant, or select the MIMO plant from the Default Plants submenu in the Read Plant menu.

Basic Terminology for MIMO Systems

The following sections define the basic terminology and notation used to refer to MIMO systems in ICDM, for analysis and plotting. The LQG/H∞ Synthesis window uses additional terminology described in Chapter 12,

LQG/H-Infinity Synthesis.

Feedback System Configuration

ICDM uses the feedback configuration shown in Figure 11-1. The configuration and signal names agree with the standard SISO configuration shown in Figure 2-1, with two differences. Here, all signal paths represent vector signals, whereas in the SISO setup, the signals are scalar. There is also a new signal, d can be thought of as an actuator-referred disturbance signal, an actuator noise, or just a fictitious input that allows you to see the transfer functions from the actuator to various other signals.

The equations describing this system are:

yPud

where, as shown in Figure 11-1:

y denotes the plant output or sensor signal, which is a vector of size n

, that subtracts from the actuator signal. This signal

act

–()= uCe= ery–=

act

Chapter 11 Introduction to MIMO Design

u denotes the plant input or actuator signal, which is a vector of size n

r denotes the reference or command input signal, which is a vector of size n

e denotes the error signal, which is a vector of size n

denotes the actuator disturbance signal, which is a vector of size n

act

P denotes the plant transfer function, which is a matrix of size n

C denotes the controller transfer function, which is a matrix of size n

× n

Figure 11-1 shows standard feedback connections and signals used in ICDM for MIMO design. All of the signals are vectors.

act

–

Figure 11-1. Standard Feedback Connections and Signals for MIMO Design

Transfer Functions

In ICDM, the plant and controller transfer function are required to be strictly proper, that is,

Ps() CsI A–()1–B= Cs() C

contr

sI A

–()

where A, B, and C are matrices stored in the system object corresponding to the plant, and similarly for the controller. The plant order or plant (McMillan) degree is the size of A; that is, the number of plant states. Similarly, the size of A

is the controller order or controller degree.

contr

In ICDM, the multivariable transfer function is required to be strictly proper; that is, have zero feedthrough term D = 0. The controller is required to be proper.

Xmath Interactive Control Design Module 11-2 ni.com

contr

1–

contr

Chapter 11 Introduction to MIMO Design

The standard feedback system has two vector input signals, r and d

act

, and

three vector output signals, e, u, and y. It can therefore be described by the 3 × 2 block matrix that relates the three output vector signals to the two input vector signals:

IPC+()

CI PC+()1–CP I CP+()

PC I PC+()1–P– ICP+()

1–

PI CP+()

1–

act

1–

The entries of this block matrix, that is, the transfer functions from r and

to e, u, and y, have standard names and interpretations (which agree

act

with the standard SISO notation):

• The sensitivity transfer function is denoted S and given by S =(I + PC)

–1

. The sensitivity transfer function is the transfer function

from reference input r to the error signal e.

• The closed-loop transfer function T is given by T = PC(I + PC)

–1

. T is the transfer function from r to y. T can be expressed in several other ways, for example:

TPCICP+()1–IPC+()

• The actuator effort transfer function C(I + PC)

1–

PC I S–===

–1

is the transfer function from r to u, and so is related to the actuator effort required. For example, its step response matrix shows the closed-loop step responses from each reference input signal to each actuator signal.

• The transfer function from d

to e, P(I + CP)–1, is denoted S

act

and called the actuator-referred sensitivity transfer function. The actuator-referred sensitivity transfer function determines the errors generated by actuator-referred disturbances. It also can be expressed as (I + PC) described just above, that is, C(I + PC)

–1

P. Notice that it is “complementary” to the transfer function

–1

, in the sense that the two transfer functions can be obtained from each other by swapping P and C.

• The transfer function from d

to u, CP(I + CP)–1, is called the

act

actuator-referred actuator effort transfer function. Notice that it is related to the closed-loop transfer function by swapping P and C. It can also be expressed as C(I + PC)

• The transfer function from d

–1

to y, (–P)(I +CP)–1, is denoted T

act

and

called the actuator-referred closed-loop transfer function.

Chapter 11 Introduction to MIMO Design

Notice that in the SISO case, these “complementary pairs” of transfer functions (obtained by swapping P and C) are the same. It is important to remember that in the MIMO case they can be different; they even have different dimensions if n

In addition to these transfer functions you encounter two (complementary) open-loop transfer functions:

• The loop transfer function L is defined as L = PC. This is the transfer function of the loop cut at the sensor (or the error e).

• The actuator loop transfer function (or complementary loop transfer function) L loop cut at the actuator.

Integral Action

Integral action can be quite complicated in the MIMO setting. The simplest case occurs when the plant is “square”, that is, n poles at s = 0, and no zeros at s = 0—which in this case means debt P(0) ≠ 0.

Suppose the controller has the form

is defined as L

act

≠ n

= CP. This is the transfer function of the

act

= nu, the plant has no

Cs() 1 s⁄()R

where has no poles at s = 0 and the (constant) matrix is nonsingular

(for example, R

= I). Then you have T(0) = I, so that you have perfect

s()+=

asymptotic decoupling and tracking of constant reference inputs. You also have perfect asymptotic rejection of constant actuator disturbances. The condition on C means the controller has an integrator in each of its channels. In this case the integrators can be thought of as either acting on the sensor signals or acting on the actuator signals.

You often have integrators associated with some of the sensors, or some of the actuators. Then the matrix can be less than full rank, and you generally get the benefits of integral action in only some of the I/O channels; that is, only some of the entries of T(0) are 1 (or 0).

When things get more complicated. The rank of R

ynu

r = max{n

≠

}. If you ask ICDM to insert more than r integrators (say,

ynu

is at most

using an integrator in each sensor channel for a plant with three actuators and five sensors), you will have a closed-loop system that cannot be stabilized—it will have an uncontrollable or unobservable mode at s =0. If this happens, ICDM will warn you. Even if you do not have excess integrators, you should realize that you will get perfect asymptotic tracking

Xmath Interactive Control Design Module 11-4 ni.com

or disturbance rejection only on a subspace of dimension r, so do not be surprised if some (or many) diagonal entries of T are not one, or off diagonal entries are not zero. Finally, unlike a SISO plant, a MIMO plant can have both poles and zeros at s = 0, and such situations will constraint what types of integral action are possible. In all cases, however, ICDM will warn you if the integral action you have selected results in an unstable closed-loop system.

Overview of ICDM for MIMO Design

The following sections provide an overview of ICDM for MIMO Design.

ICDM MIMO Windows

The most important windows for MIMO design are:

•ICDM Main window

• LQG/H∞ window

• Multi-Loop Synthesis window

•History window

• (MIMO) Alternate Plant window

•MIMO Plot window

Chapter 11 Introduction to MIMO Design

Some of windows used for SISO design are not available in MIMO design mode; for example, PID, Root Locus, and Pole Place Synthesis. Some others are very similar or even the same; for example, the Main window and the History window. Others have different forms that depend on the mode; for example, LQG Synthesis, Alternate Plant, and History. Some windows only work in MIMO mode, for example, Multiloop Synthesis and MIMO plot.

Windows that are not available or applicable in the current mode are dimmed in the menus and cannot be selected.

Main Window

The ICDM Main window is almost the same as in SISO mode. The greatest difference is that a different set of plots is available in MIMO mode, and the default plot selections are different. When the user selects Plot Options from the ICDM Main window menu bar, the window shown in Figure 11-2 appears. It shows the Plot Choices window for the MIMO case. This window contains a subset of the complete set of plot options which are the ones most likely to be used. To get access to the complete set of plot

Chapter 11 Introduction to MIMO Design

options, the user clicks the Show all options button after which the plot options window shown in Figure 11-3 opens. From this window, all transfer functions mentioned in the Transfer Functions section can be selected.

Figure 11-2. Plot Choices Window for the MIMO Case

MIMO Plot Window

For a more detailed MIMO transfer function plot, an option labeled MIMO plot is available under the Main window menu bar. This plot will display

MIMO responses in a matrix format, where each element of the transfer function is displayed individually in one element of the plot matrix (Figure 11-4). Figure 11-4 shows the MIMO Plot window with a step response plot of the transfer function, arranged as a matrix.

The MIMO Plot window offers a choice between either:

• Step response

• Frequency response magnitude

• Frequency response phase

The type of transfer function displayed can be selected by clicking one of the buttons at the bottom of the window. When an alternate plant is selected, the MIMO plot will contain two responses in each element of the plot matrix—one for the plant, and one for the alternate plant.

Xmath Interactive Control Design Module 11-6 ni.com

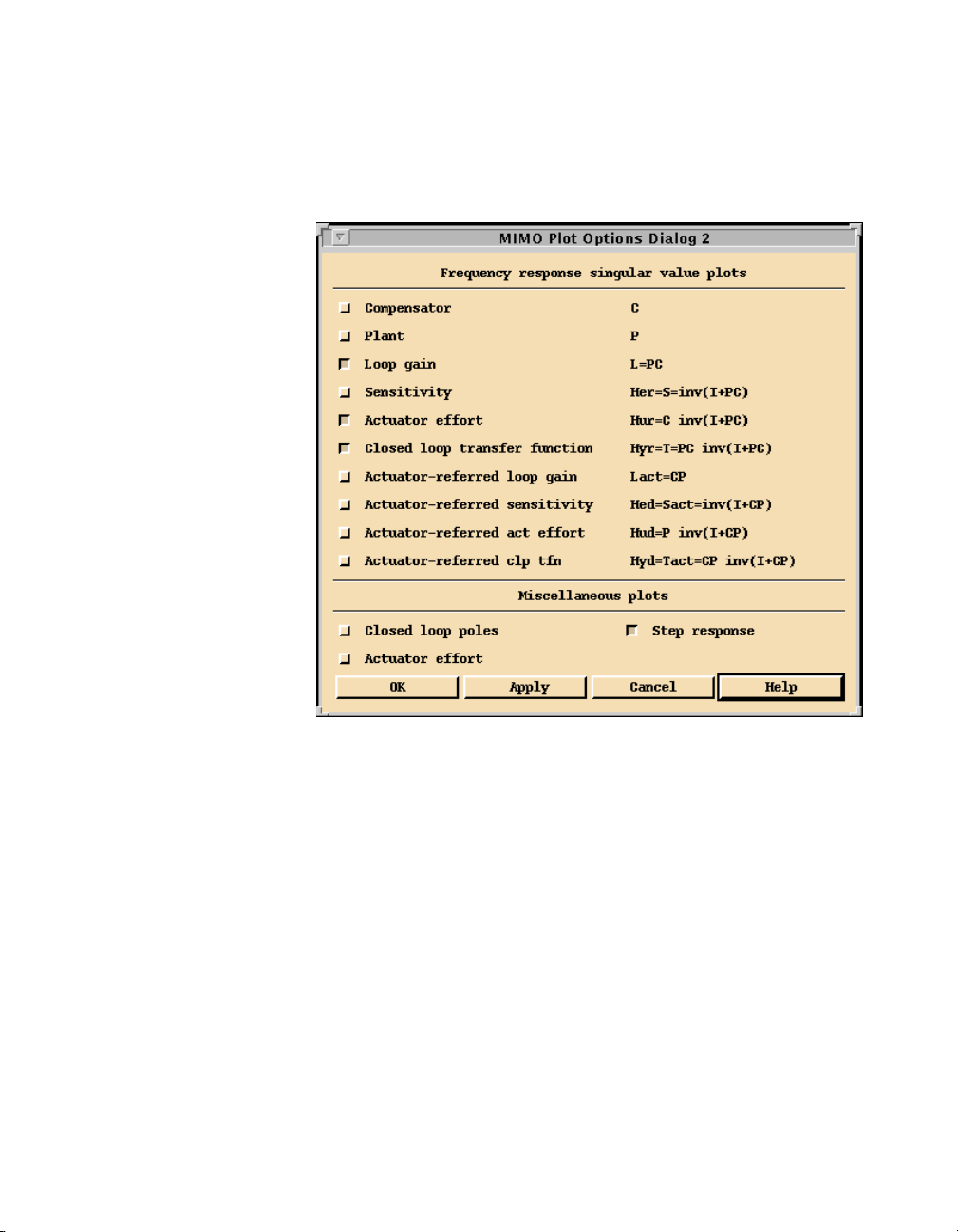
Chapter 11 Introduction to MIMO Design

Notice that having the MIMO Plot window on the screen may increase the required computational response time of ICDM. Closing the window using the Special option of the MIMO Plot menu bar will then result in a speed-up.

Figure 11-3. Complete Set of Plot Choices

History Window

The History window is exactly the same in SISO and MIMO modes.

Alternate Plant Window (MIMO Version)

The MIMO version of the alternate plant window differs from the SISO version. For a MIMO plant there are many parameters that the user might want to vary in a robustness analysis, for example, the gain in each actuator, the gain in each sensor, various poles, zeros, and their residues for each entry of P, and so on. There are so many parameters that the user might want vary in MIMO robustness analysis that no simple user-interface could suffice. Instead, the user manipulates the plant in Xmath in the ways appropriate for the problem at hand, and simply reads in the set of alternate

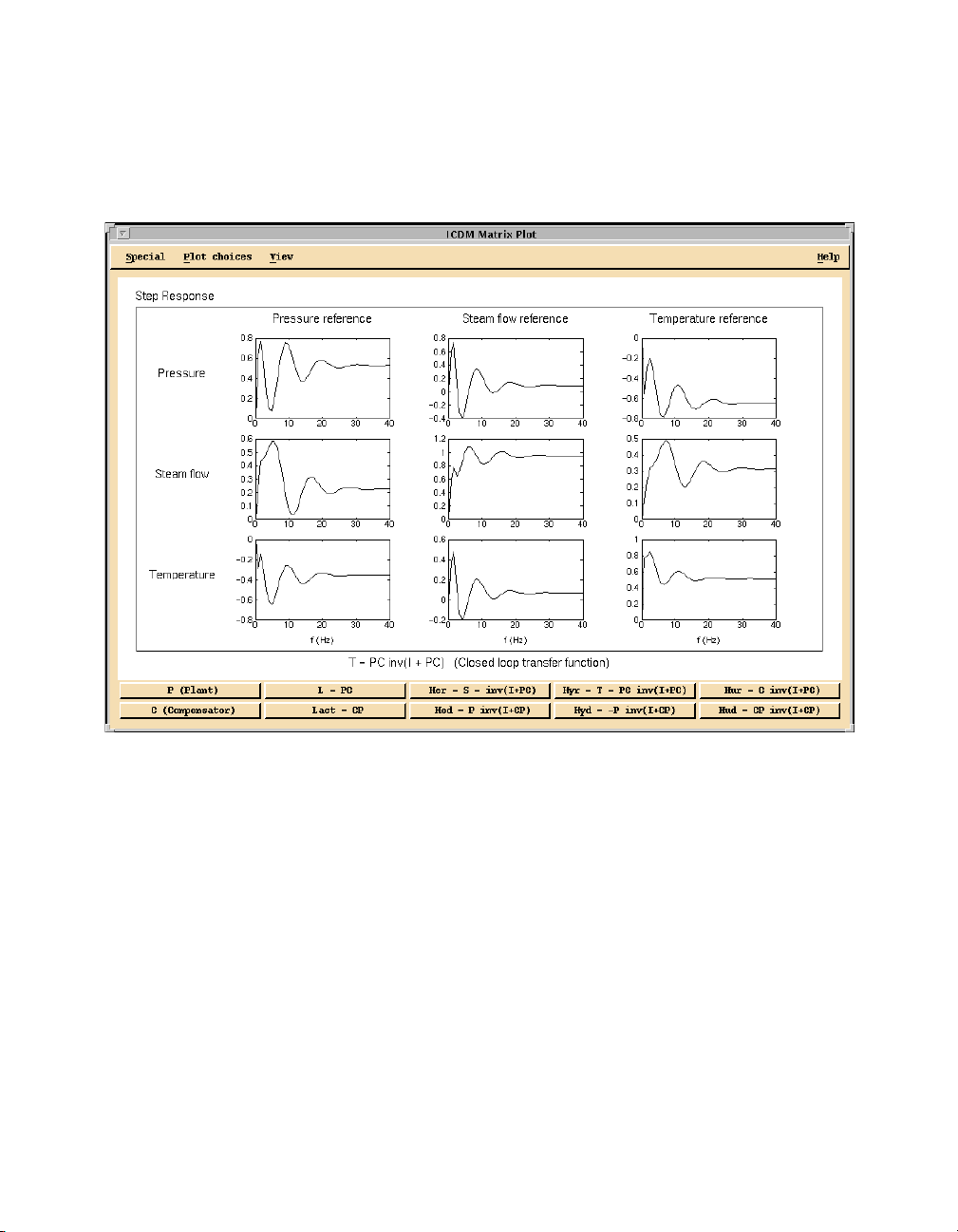
Chapter 11 Introduction to MIMO Design

plants. Therefore, the (MIMO) Alternate Plant window looks very much like the History window—the user can read various alternate plants into a list, and select one as the alternate plant. The semantics of the Alternate Plant window are identical in SISO and MIMO versions.

Figure 11-4. MIMO Plot Window with a Step Response Plot of the Transfer Function

Xmath Interactive Control Design Module 11-8 ni.com

LQG/H-Infinity Synthesis

This chapter describes the MIMO LQG/H∞ Synthesis window. The LQG/H∞ window is used to synthesize both LQG and H∞ controllers. The two design methods have been combined in a single window because of the similarity regarding the use of weights: constant weights, frequency-dependent weights, and integrators.

Window Anatomy

The MIMO LQG/H∞Synthesis window consists of a main window and four auxiliary windows for editing constant weights, frequency-dependent weight functions, decay rate, and performance level.

LQG/H-Infinity Main Window

The LQG/H∞ Main window is shown in Figure 12-1. From top to bottom, it consists of:

• A menu bar with entries Special, Edit, View, and Help.

• A message area that describes the synthesis mode (type of controller), for example, LQG with integral action.

• A control panel for changing the five design parameters: – Control cost parameter (ρ) – Sensor noise parameter (ν)

– Integral action time constant (T

– Decay rate or exponential time weighting parameter (a) –H∞ performance level (γ)

)

int

Chapter 12 LQG/H-Infinity Synthesis

Figure 12-1. LQG/H-Infinity Main Window

• A pull-down menu for frequency-dependent weight selection on inputs:

i 1= … n

,,,

ui,

and outputs:

j 1= … n

,,,

yj,

• A button for recomputing the controller.

These parameters are described in greater detail later in this chapter.

LQG/H-Infinity Weights Window

The Weights window is for defining control cost and noise level parameters and is shown in Figure 12-2.

From top to bottom, the Weights window consists of:

• A menu bar with entries Special, Edit, View, and Help.

• A row with two radio buttons which toggle the contents of the window between control cost and noise level parameters. The following

Xmath Interactive Control Design Module 12-2 ni.com

Chapter 12 LQG/H-Infinity Synthesis

descriptions are for the control cost parameter display. The noise level display is similar in appearance.

• A table with n

rows, having in each row:

– A toggle button to include the input in the set of control inputs

– A toggle button to include the input in the set of costed inputs,

labeled with the signal name

– A slider defining the constant weight factor of the input:

i 1= … n

,,,

ui,

– A variable edit box for the same constant weight factor

Figure 12-2. LQG/H-Infinity Weights Window

• A slider representing the logarithmic average of the input weights (ρ

that is,

-----

log

∑

i1=

ui,

Chapter 12 LQG/H-Infinity Synthesis

• A table with ny rows with, in each row:

• A slider representing the logarithmic average of the weights for each

• A button for entering an Xmath variable name of type matrix of the

– A toggle button to include the output in the set of measured

outputs

– A toggle button to include the output in the set of costed outputs,

labeled with the signal name

– A slider defining the constant weight factor of the output:

i 1= … n

,,,

yj,

– A variable edit box for the same constant weight factor

output (ρ

), that is,

log

-----

log

∑

j1=

yj,

form

xxRxu

RuxR

containing the weights on states and inputs, including cross terms.

The control weight parameter ρ in the main LQG/H∞ window is related to the weights in this window by ρ = ρ

u/ρy

If the radio buttons in the first row are set to select the noise level display, the contents of the window looks almost exactly the same. The leftmost column of toggle buttons has the same meaning, but the second column of toggle buttons is used to enable/disable the noise on selected inputs and outputs.

The sliders represent the noise intensities instead of the control cost. The button is meant to load the noise variance matrix of states and outputs, including cross terms:

xxQxy

QyxQ

Xmath Interactive Control Design Module 12-4 ni.com

Chapter 12 LQG/H-Infinity Synthesis

Decay Rate Window

The weights ρ ν

, ν

, νu,andνy. The noise level parameter in the main LQG/H∞

u, i

y, j

window is related to the noise levels in this window by υ = υ

u, i

, ρ

y, j

, ρu,andρ

are then replaced with noise variances

y/υu

The Decay Rate window is shown in Figure 12-3. From top to bottom, it consists of:

• A menu bar with entries Special, Edit, View, and Help.

• A plotting area that contains two plots:

– A plot of controller poles, and a vertical line indicating the

decay rate.

– A plot of estimator poles, and a vertical line indicating the

decay rate.

Figure 12-3. LQG/H-Infinity Decay Rate Window

H-Infinity Performance Window

The H∞ Performance window, shown in Figure 12-4, consists of, from top to bottom:

• A menu bar with entries Special, Edit, View, and Help.

• A plot area that contains a plot of the closed-loop transfer matrix along

with the parameter γ, which can be grabbed and dragged to a new

Chapter 12 LQG/H-Infinity Synthesis

value. If a lower bound on the minimal value of γ is known, it also is displayed.

Figure 12-4. LQG/H-Infinity Performance Level Window

Frequency Weights Window

The Frequency Weights window is shown in Figure 12-5. From top to bottom, it consists of:

• A menu bar with entries Special, Edit, View, and Help.

• A plot area with two plots:

– A plot that shows the poles and zeros of the selected input or

output weight transfer function. The user can grab and drag the poles and zeros to new locations.

– A plot with the frequency response magnitude of the weight

function.

Xmath Interactive Control Design Module 12-6 ni.com

National Instruments Xmath Interactive Control Design Module ICDM User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Xmath Interactive Control Design Module

Support

Worldwide Technical Support and Product Information

National Instruments Corporate Headquarters

Worldwide Offices

Important Information

Warranty

Copyright

Trademarks

Patents

WARNING REGARDING USE OF NATIONAL INSTRUMENTS PRODUCTS

Conventions

Contents

Using This Manual

Document Organization

Commonly-Used Nomenclature

Related Publications

MATRIXx Help

ICDM Overview

SISO Versus MIMO Design

Starting ICDM

SISO Design Overview

Basic SISO Terminology

Figure 2-1. Standard Classical Feedback Configuration Used in ICDM

Overview of ICDM

ICDM Windows

ICDM Main Window

PID Synthesis Window

Root Locus Synthesis Window

Pole Place Synthesis Window

LQG Synthesis Window

H-Infinity Synthesis Window

History Window

Alternate Plant Window

Key Transfer Functions and Data Flow in ICDM

Summary

Origin of the Controller

What the ICDM Main Window Plots Show

Controller/Synthesis Window Compatibilities

Using ICDM

Figure 2-2. Simple Representation of the Interactive Design Loop

Figure 2-3. Simple Representation of the Interactive Robustness Analysis

Figure 2-4. Simple ICDM Session

General Plotting Features

Ranges of Plots and Sliders

Zooming

Data-Viewing Plots

Interactive Plot Re-ranging

Graphically Manipulating Poles and Zeros

Editing Poles and Zeros

Editing Poles and Zeros Graphically

Complex Poles and Zeros

Isolated Real Poles and Zeros

Nonisolated Real Poles and Zeros and Almost Real Pairs

Adding/Deleting Poles and Zeros

Adding/Deleting Pole-Zero Pairs

Window Anatomy

Figure 3-1. ICDM Main Window

Communicating with Xmath

Most Common Usage

Default Plants

Saving and Restoring an ICDM Session

Reading Another Plant into ICDM

Reading a Controller from Xmath into ICDM

Writing the Plant Back to Xmath

Writing the Alternate Plant back to Xmath

Writing a Controller on the History List to Xmath

ICDM Plots

Selecting Plots

Figure 3-2. ICDM Main Window Plot Choices Dialog

Ranges of Plots

Figure 3-3. ICDM Ranges Window

Plot Magnify Windows

Figure 3-4. Plot Magnify Window

Selecting a Synthesis or History Window

Edit Menu