National Instruments NI MATRIXx Xmath User Manual

Download

NI MATRIXx

XmathTM Model Reduction Module

Xmath Model Reduction Module

April 2007 370755C-01

Support

Worldwide Technical Support and Product Information

ni.com

National Instruments Corporate Headquarters

11500 North Mopac Expressway Austin, Texas 78759-3504 USA Tel: 512 683 0100

Worldwide Offices

Australia 1800 300 800, Austria 43 662 457990-0, Belgium 32 (0) 2 757 0020, Brazil 55 11 3262 3599, Canada 800 433 3488, China 86 21 5050 9800, Czech Republic 420 224 235 774, Denmark 45 45 76 26 00, Finland 385 (0) 9 725 72511, France 33 (0) 1 48 14 24 24, Germany 49 89 7413130, India 91 80 41190000, Israel 972 3 6393737, Italy 39 02 413091, Japan 81 3 5472 2970, Korea 82 02 3451 3400, Lebanon 961 (0) 1 33 28 28, Malaysia 1800 887710, Mexico 01 800 010 0793, Netherlands 31 (0) 348 433 466, New Zealand 0800 553 322, Norway 47 (0) 66 90 76 60, Poland 48 22 3390150, Portugal 351 210 311 210, Russia 7 495 783 6851, Singapore 1800 226 5886, Slovenia 386 3 425 42 00, South Africa 27 0 11 805 8197, Spain 34 91 640 0085, Sweden 46 (0) 8 587 895 00, Switzerland 41 56 2005151, Taiwan 886 02 2377 2222, Thailand 662 278 6777, Turkey 90 212 279 3031, United Kingdom 44 (0) 1635 523545

For further support information, refer to the Technical Support and Professional Services appendix. To comment on National Instruments documentation, refer to the National Instruments Web site at ni.com/info and enter the info code feedback.

Important Information

Warranty

The media on which you receive National Instruments software are warranted not to fail to execute programming instructions, due to defects in materials and workmanship, for a period of 90 days from date of shipment, as evidenced by receipts or other documentation. National Instruments will, at its option, repair or replace soft ware media that do not execute programm in g i nstruct ions if National Instruments receives notice of such defects during the warranty p e riod . N ati on al In struments does not warrant that the operation of the software shall be uninterrupted or error free.

A Return Material Authorization (RMA) number must be obtained from the factory and clearly marked on the outside of the package before any equipment will be accepted for warranty work. National Instruments will pay the shipping costs of returning to the owner parts which are covered by warranty.

National Instruments believes that the information in this document is accurate. The document has been carefully reviewed for technical accuracy. In the event that technical or typographical errors exist, National Instruments reserves the right to make changes to subsequent editions of this document without prior notice to holders of this edition. The reader should consult National Instruments if errors are suspected. In no event shall National Instruments be liable for any damages arising out of or related to this document or the information contained in it.

XCEPT AS SPECIFIED HEREIN, NATIONAL INSTRUMENTS MAKES NO WARRANTIES, EXPRESS OR IMPLIED, AND SPECIFICALLY DISCLAIMS ANY WARRANTY OF

MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. CUSTOMER’S RIGHT TO RECOVER DAMAGES CAUSED BY FAULT OR NEGLIGENCE ON THE PART OF NATIONAL

NSTRUMENTS SHALL BE LIMITED TO THE AMOUNT THERETOFORE PAID BY THE CUSTOMER. NATIONAL INSTRUMENTS WILL NOT BE LIABLE FOR DAMAGES RESULTING

FROM LOSS OF DATA, PROFITS, USE OF P RODUCTS, OR INCIDENTAL OR CONSEQUENTIAL DAMAGES, EVEN IF ADVISED OF THE POSSIBILITY THEREOF. This limitation of

the liability of National Instruments will apply regardless of the form of action, whether in contract or tort, including negligence. Any action against National Instruments must be brought within one year after the cause of action accrues. National Instruments shall not be liable for any delay in performance due to causes beyond its reasonable control. The warranty provided herein does not cover damages, defects, malfunctions, or service failures caused by owner’s failure to follow the National Instruments installation, operation, or maintenance instructions; owner’s modification of the product; owner’s abuse, misuse, or negligent acts; and power failure or surges, fire, flood, accident, actions of third parties, or other events outside reasonable control.

Copyright

Under the copyright laws, this publication may not be reproduced or transmitted in any form, electronic or mechanical, including photocopying, recording, storing in an information retrieval system, or translating, in whole or in part , w itho ut th e prior w r itten con sent of National Instruments Corporation.

National Instruments respects the intellectual property of others, and we ask our users to do the same. NI software is protected by copyright and other intellectual property laws. Where NI software may be used to reproduce software or other materials belonging to others, you may use NI software only to reproduce materials that you may reproduce in accordance with the terms of any applicable license or other legal restriction.

Trademarks

MATRIXx™, National Instruments™, NI™, ni.com™, and Xmath™ are trademarks of National Instruments Corporation. Refer to the Terms of Use section on ni.com/legal for more information about National Instruments trademarks.

Other product and company names mentioned herein are trademarks or trade names of their respective companies. Members of the National Instruments Alliance Partner Program are business entities independent from National Instruments and have no agency,

partnership, or joint-venture relationship with National Instruments.

Patents

For patents covering National Instruments products, refer to the ap prop riate lo cati on: Help»Patents in your software, th e patents.txt file on your CD, or

ni.com/patents.

WARNING REGARDING USE OF NATIONAL INSTRUMENTS PRODUCTS

(1) NATIONAL INSTRUMENTS PRODUCTS ARE NOT DESIGNED WITH COMPONENTS A ND T ESTING FOR A LE VEL OF RELIABILITY SUITABLE FOR USE IN OR IN CONNECTION WITH SURGICAL IMPLANTS OR AS CRITICAL COMPONENTS IN ANY LIFE SUPPORT SYSTEMS WHOSE FAILURE TO PERFORM CAN REASONABLY BE EXPECTED TO CAUSE SIGNIFICANT INJURY TO A HUMAN.

(2) IN ANY APPLICATION, INCLUDING THE ABOVE, RELIABILITY OF OPERATION OF THE SOFTW ARE P RODUCTS C AN BE IMPAIRED BY ADVERSE FACTORS, INCLUDING BUT NOT LIMITED TO FLUCTUATIONS IN ELECTRICAL POWER SUPPLY, COMPUTER HARDWARE MALFUNCTIONS, COMPUTER OPERATING SYSTEM SOFTWARE FITNESS, FITNESS OF COMPILERS AND DEVELOPMENT SOFTWARE USED TO DEVELOP AN APPLICATION, INSTALLATION ERRORS, SOFTWARE AND HARDWARE COMPATIBILITY PROBLEMS, MALFUNCTIONS OR FAILURES OF ELECTRONIC MONITORING OR CONTROL DEVICES, TRANSIENT FAILURES OF ELECTRONIC SYSTEMS (HARDWARE AND/OR SOFTWARE), UNANTICIPATED USES OR MISUSES, OR ERRORS ON THE PART OF THE USER OR APPLICATIONS DESIGNER (ADVERSE FACTORS SUCH AS THESE ARE HEREAFTER COLLECTIVELY TERMED “SYSTEM FAILURES”). ANY APPLICATION WHERE A SYSTEM FAILURE WOULD CREATE A RISK OF HARM TO PROPERTY OR PERSONS (INCLUDING THE RISK OF BO DILY INJURY AND DEATH) SHOULD NOT BE RELIANT SOLELY UPON ONE FORM OF ELECTRONIC SYSTEM DUE TO THE RISK OF SYSTEM FAILURE. TO AVOID DAMAGE, INJURY, OR DEATH, THE USER OR APPLICATION DESIGNER MUST TAKE REASONABLY PRUDENT S TEPS TO PROTECT AGAINST SYSTEM FAILURES, INCLUDING BUT NOT LIMITED TO BACK-UP OR SHUT DOWN MECHANISMS. BECAUSE EACH END-USER SYSTEM IS CUSTOMIZED AND DIFFERS FROM NATIONAL INSTRUMENTS' TESTING PLATFORMS AND BECAUSE A USER OR APPLICATION DESIGNER MAY USE NATIONAL INSTRUMENTS PRODUCTS IN COMBINATION WITH OTHER PRODUCTS IN A MANNER NOT EVALUATED OR CONTEMPLATED BY NATIONAL INSTRUMENTS, THE USER OR APPLICATION DESIGNER IS ULTIMATELY RESPONSIBLE FOR VERIFYING AND VALIDATING THE SUITABILITY OF NATIONAL INSTRUMENTS P RODUCTS W HENEVER NATIONAL INSTRUMENTS PRODUCTS ARE INCORPORATED IN A SYSTEM OR APPLICATION, INCLUDING, WITHOUT LIMITATION, THE APPROPRIATE DESIGN, PROCESS AND SAFETY LEVEL OF SUCH SYSTEM OR APPLICATION.

Conventions

The following conventions are used in this manual:

[ ] Square brackets enclose optional items—for example, [

brackets also cite bibliographic references.

» The » symbol leads you through nested menu items and dialog box options

to a final action. The sequence File»Page Setup»Options directs you to pull down the File menu, select the Page Setup item, and select Options from the last dialog box.

This icon denotes a note, which alerts you to important information.

bold Bold text denotes items that you must select or click in the software, such

as menu items and dialog box options. Bold text also denotes parameter names.

italic Italic text denotes variables, emphasis, a cross-reference, or an introduction

to a key concept. Italic text also denotes text that is a placeholder for a word or value that you must supply.

monospace Text in this font denotes text or characters that you should enter from the

keyboard, sections of code, programming examples, and syntax examples. This font is also used for the proper names of disk drives, paths, directories, programs, subprograms, subroutines, device names, functions, operations, variables, filenames, and extensions.

monospace bold Bold text in this font denotes the messages and responses that the computer

automatically prints to the screen. This font also emphasizes lines of code that are different from the other examples.

response]. Square

monospace italic

Italic text in this font denotes text that is a placeholder for a word or value that you must supply.

Chapter 1 Introduction

Using This Manual.................................................................................................. .......1-1

Document Organization...................................................................................1-1

Bibliographic References ................................................................................1-2

Commonly Used Nomenclature..................................... .................................1-2

Conventions.....................................................................................................1-2

Related Publications........................................................................................1-3

MATRIXx Help...............................................................................................1-3

Overview........................................................................................................................1-3

Functions .........................................................................................................1-4

Nomenclature .................................................................................................1-6

Commonly Used Concepts ........................................................... .................................1-7

Controllability and Observability Grammians ................................................1-7

Hankel Singular Values...................................................................................1-8

Internally Balanced Realizations.....................................................................1-10

Singular Perturbation.......................................................................................1-11

Spectral Factorization......................................................................................1-13

Low Order Controller Design Through Order Reduction .............................................1-15

Chapter 2 Additive Error Reduction

Introduction....................................................................................................................2-1

Truncation of Balanced Realizations.............................................................................2-2

Reduction Through Balanced Realization Truncation...................................................2-4

Singular Perturbation of Balanced Realization..............................................................2-5

Hankel Norm Approximation........................................................................................2-6

balmoore( )..................................................................................................................... 2-8

Related Functions............................................................................................2-11

truncate( ).......................................................................................................................2-11

Related Functions............................................................................................2-11

redschur( )......................................................................................................................2-12

Algorithm ........................................................................................................2-12

Related Functions............................................................................................2-14

ophank( )........................................................................................................................2-14

Restriction........................................................................................................2-14

Algorithm ........................................................................................................2-15

Behaviors.........................................................................................................2-15

Contents

Onepass Algorithm .........................................................................................2-18

Multipass Algorithm ......................................................................................2-20

Discrete-Time Systems ...................................................................................2-21

Impulse Response Error..................................................... .............................2-22

Unstable System Approximation....................................................................2-23

Related Functions............................................................................................2-23

Chapter 3 Multiplicative Error Reduction

Selecting Multiplicative Error Reduction...................................................................... 3-1

Multiplicative Robustness Result.................................................................... 3-2

bst( )...............................................................................................................................3-3

Restrictions...................................................................................................... 3-4

Algorithm........................................................................................................3-4

Algorithm with the Keywords right and left...................................................3-5

Securing Zero Error at DC.............................................................................. 3-8

Hankel Singular Values of Phase Matrix of G

Further Error Bounds ......................................................................................3-9

Reduction of Minimum Phase, Unstable G ....................................................3-9

Imaginary Axis Zeros (Including Zeros at ∞)................................................. 3-10

Related Functions............................................................................................3-14

mulhank( ) ..................................................................................................................... 3-14

Restrictions...................................................................................................... 3-14

Algorithm........................................................................................................3-14

right and left.................................................... ................................................3-15

Consequences of Step 5 and Justification of Step 6........................................ 3-18

Error Bounds...................................................................................................3-20

Imaginary Axis Zeros (Including Zeros at ∞)................................................. 3-21

Related Functions............................................................................................3-24

r................................................3-9

Chapter 4 Frequency-Weighted Error Reduction

Introduction ...................................................................................................................4-1

Controller Reduction......................... ........................................................... ...4-2

Controller Robustness Result............................ ..............................................4-2

Fractional Representations..............................................................................4-5

wtbalance( ) ................................................................................................................... 4-10

Algorithm........................................................................................................4-12

Related Functions............................................................................................4-15

Xmath Model Reduction Module vi ni.com

fracred( ) ........................................................................................................................4-15

Chapter 5 Utilities

hankelsv( )......................................................................................................................5-1

stable( ) ..........................................................................................................................5-2

compare( )......................................................................................................................5-4

Chapter 6 Tutorial

Plant and Full-Order Controller.....................................................................................6-1

Controller Reduction......................................... ........................................................... ..6-5

Contents

Restrictions......................................................................................................4-15

Defining and Reducing a Controller................................................................4-16

Algorithm ........................................................................................................4-18

Additional Background ...................................................................................4-20

Related Functions............................................................................................4-21

Related Functions............................................................................................5-2

Algorithm ........................................................................................................5-2

Related Functions............................................................................................5-4

ophank( )..........................................................................................................6-9

wtbalance.........................................................................................................6-12

fracred..............................................................................................................6-20

Appendix A Bibliography

Appendix B Technical Support and Professional Services

Index

Introduction

This chapter starts with an outline of the manual and some useful notes. It also provides an overview of the Model Reduction Module, describes the functions in this module, and introduces nomenclature and concepts used throughout this manual.

Using This Manual

This manual describes the Model Reduction Module (MRM), which provides a collection of tools for reducing the order of systems.

Readers who are not familiar with Parameter Dependent Matrices (PDMs) should consult the Xmath User Guide before using MRM functions and tools. Although several MRM functions accept both PDMs and matrices as input parameters, PDMs are preferable because they can include additional information that is useful for simulation, plotting, and signal labeling.

Document Organization

This manual includes the following chapters:

• Chapter 1, Introduction, starts with an outline of the manual and some useful notes. It also provides an overview of the Model Reduction Module, describes the functions in this module, and introduces nomenclature and concepts used throughout this manual.

• Chapter 2, Additive Error Reduction, describes additive error reduction including discussions of truncation of, reduction by, and perturbation of balanced realizations.

• Chapter 3, Multiplicative Error Reduction, describes multiplicative error reduction presenting considerations for using multiplicative rather than additive error reduction.

• Chapter 4, Frequency-Weighted Error Reduction, describes frequency-weighted error reduction problems, including controller reduction and fractional representations.

Chapter 1 Introduction

• Chapter 5, Utilities, describes three utility functions: hankelsv( ),

stable( ), and compare( ).

• Chapter 6, Tutorial, illustrates a number of the MRM functions and their underlying ideas.

Bibliographic References

Throughout this document, bibliographic references are cited with bracketed entries. For example, a reference to [VODM1] corresponds to a paper published by Van Overschee and De Moor. For a table of bibliographic references, refer to Appendix A, Bibliography.

Commonly Used Nomenclature

This manual uses the following general nomenclature:

• Matrix variables are generally denoted with capital letters; vectors are represented in lowercase.

• G(s) is used to denote a transfer function of a system where s is the Laplace variable. G(q) is used when both continuous and discrete systems are allowed.

• H(s) is used to denote the frequency response, over some range of frequencies of a system where s is the Laplace variable. H(q) is used to indicate that the system can be continuous or discrete.

• A single apostrophe following a matrix variable, for example, x’, denotes the transpose of that variable. An asterisk following a matrix variable, for example, A*, indicates the complex conjugate, or Hermitian, transpose of that variable.

Conventions

This publication makes use of the following types of conventions: font, format, symbol, mouse, and note. These conventions are detailed in Chapter 2, MATRIXx Publications, Online Help, and Customer Support, of the MATRIXx Getting Started Guide.

Xmath Model Reduction Module 1-2 ni.com

Related Publications

For a complete list of MATRIXx publications, refer to Chapter 2,

MATRIXx Publications, Online Help, and Customer Support, of the MATRIXx Getting Started Guide. The following documents are particularly

useful for topics covered in this manual:

• MATRIXx Getting Started Guide

• Xmath User Guide

• Control Design Module

• Interactive Control Design Module

• Interactive System Identification Module, Part 1

• Interactive System Identification Module, Part 2

• Model Reduction Module

• Optimization Module

• Robust Control Module

•X

MATRIXx Help

Model Reduction Module function reference information is available in the MATRIXx Help. The MATRIXx Help includes all Mode l Reduct ion functions. Each topic explains a function’s inputs, outputs, and keywords in detail. Refer to Chapter 2, MATRIXx Publications, Online Help, and Customer Support, of the MATRIXx Getting Started Guide for complete instructions on using the help feature.

Module

Chapter 1 Introduction

Overview

The Xmath Model Reduction Module (MRM) provides a collection of tools for reducing the order of systems. Many of the functions are based on state-of-the-art algorithms in conjunction with researchers at the Australian National University, who were responsible for the original development of some of the algorithms. A common theme throughout the module is the use of Hankel singular values and balanced realizations, although considerations of numerical accuracy often dictates whether these tools are used implicitly rather than explicitly. The tools are particularly suitable when, as generally here, quality of approximation is measured by closeness of frequency domain behavior.

Chapter 1 Introduction

Functions

As shown in Figure 1-1, functions are provided to handle four broad tasks:

• Model reduction with additive errors

• Model reduction with multiplicative errors

• Model reduction with frequency weighting of an additive error, including controller reduction

• Utility functions

Additive Error

Model Reduction

balmoore redschur ophank truncate balance mreduce

Multiplicative

Model Reduction

bst mulhank

Utility Functions

hankelsv stable compare

Figure 1-1. MRM Function

Frequency Weighted

Model Reduction

wtbalance fracred

Xmath Model Reduction Module 1-4 ni.com

Chapter 1 Introduction

Certain restrictions regarding minimality and stability are required of the input data, and are summarized in Table 1-1.

Table 1-1. MRM Restrictions

balance( )

balmoore ( ) A state-space system must be stable and minimal,

A stable, minimal system

having at least one input, output, and state

bst( ) A state-space system must be linear,

continuous-time, and stable, with full rank along the jω-axis, including infinity

compare( ) Must be a state-space system

fracred( )

hankelsv( ) A system must be linear and stable mreduce( ) A submatrix of a matrix must be nonsingular

A state-space system must be linear and continuous

for continuous systems, and variant for discrete systems

mulhank( )

A state-space system must be linear, continuous-time, stable and square, with full rank along the jω-axis, including infinity

ophank( )

A state-space system must be linear, continuous-time and stable, but can be nonminimal

redschur( ) A state-space system must be stable and linear,

but can be nonminimal

stable ( ) No restriction

truncate( )

wtbalance( )

Any full-order state-space system A state-space system must be linear and

continuous. Interconnection of controller and plant must be stable, and/or weight must be stable.

Documentation of the individual functions sometimes indicates how the restrictions can be circumvented. There are a number of model reduction methods not covered here. These include:

• Padé Approximation

• Methods based on interpolating, or matching at discrete frequencies

Chapter 1 Introduction

Nomenclature

• L2 approximation, in which the L2 norm of impulse response error (or, by Parsev al’ s theorem, the L

norm of the transfer-function error along

the imaginary axis) serves as the error measure

• Markov parameter or impulse response matching, moment matching, covariance matching, and combinations of these, for example, q-COVER approximation

• Controller reduction using canonical interactions, balanced Riccati equations, and certain balanced controller reduction algorithms

This manual uses standard nomenclature. The user should be familiar with the following:

• sup denotes supremum, the least upper bound.

• The acute accent (´) denotes matrix transposition.

• A superscripted asterisk (*) denotes matrix transposition and complex conjugation.

• λ

(A) for a square matrix A denotes the maximum eigenvalue,

max

presuming there are no complex eigenvalues.

•Reλ

(A) and |λi(A)| for a square matrix A denote an arbitrary real part

and an arbitrary magnitude of an eigenvalue of A.

Xjω()

• for a transfer function X(·) denotes:

∞

sup

∞– ω∞<<

X*jω()Xjω()[][]

max

12/

• An all-pass transfer-function W(s) is one where for all ω;

Xjω() 1= to each pole, there corresponds a zero which is the reflection through the jω-axis of the pole, and there are no jω-axis poles.

• An all-pass transfer-function matrix W(s) is a square matrix where W′ jω–()Wjω() I=

P > 0 and P ≥ 0 for a symmetric or hermitian matrix denote positive and nonnegative definiteness.

• P

> P2 and P

– P2 is positive definite and nonnegativ e definite.

≥ P

for symmetric or hermitian P1 and P2 denote

•A superscripted number sign (#) for a square matrix A denotes the

Moore-Penrose pseudo-inverse of A.

Xmath Model Reduction Module 1-6 ni.com

Chapter 1 Introduction

• An inequality or bound is tight if it can be met in practice, for example 1 xx– 0≤log+

is tight because the inequality becomes an equality for x =1. Again, if F(jω) denotes the Fourier transform of some , the

ft() L

∈

Heisenberg inequality states,

ft()

------------------------------------------------------------------------------------------ -

ft()2dt

∫

12⁄

Fjω()2dω

∫

4π≤

12⁄

and the bound is tight since it is attained for f(t) = exp + (–kt

Commonly Used Concepts

This section outlines some frequently used standard concepts.

Controllability and Observability Grammians

Suppose that G(s)=D + C(sI–A)–1B is a transfer-function matrix with

(A)<0. Then there exist symmetric matrices P, Q defined by:

Reλ

PA′ +AP = –BB′

QA + A′Q = –C′C

These are termed the controllability and observability grammians of the realization defined by {A,B,C,D}. (Sometimes in the code, WC is used for P and WO for Q.) They have a number of properties:

• P ≥ 0, with P > 0 if and only if [A,B] is controllable, Q ≥ 0 with Q >0

if and only if [A,C ] is observable.

∞

PeAtBB′e

= Qe

• and

∫

•With vec P denoting the column vector formed by stacking column 1

of P on column 2 on column 3, and so on, and ⊗ denoting Kronecker product

A′ t

IAAI⊗+⊗[]vecP vec(– BB′)=

∞

∫

A′ t

C′CeAtdt

• The controllability grammian can be thought of as measuring the

difficulty of controlling a system. More specifically , if the system is in the zero state initially, the mini mum energy (as measured by the L

is x

P –1x

norm of u) required to bring it to the state x

; so small

eigenvalues of P correspond to systems that are difficult to control, while zero eigenvalues correspond to uncontrollable systems.

Chapter 1 Introduction

• The controllability grammian is also E[x(t)x′(t)] when the system

Ax Bw+=

noise with .

has been excited from time –∞ by zero mean white

Ewt()w′ s()[]Iδ ts–()=

• The observability grammian can be thought of as measuring the information contained in the output concerning an initial state.

If with x(0) = x

Ax= y, Cx=

∞

y′ t()yt()dt

∫

then:

x′0Qx

Systems that are easy to observe correspond to Q with large eigenvalues, and thus large output energy (when unforced).

•

lyapunov(A,B*B') produces P and lyapunov(A',C'*C)

produces Q. For a discrete-time G(z)=D + C(zI-A)

–1

B with |λi(A)|<1, P and Q are:

P – APA′ = BB′

Q – A′QA = C′C

The first dot point above remains valid. Also,

∞

• and

= QA

∑

k 0=

BB′A′

∞

∑

k 0=

C′CA′

with the sums being finite in case A is nilpotent (which is the case if the transfer-function matrix has a finite impulse response).

•[I–A⊗ A] vec P = vec (BB′)

lyapunov( ) can be used to evaluate P and Q.

Hankel Singular Values

If P, Q are the controllability and observability grammians of a transfer-function matrix (in continuous or discrete time), the Hankel Singular Values are the quantities λ

• All eigenvalues of PQ are nonnegati v e, and so are the Hank el singular values.

• The Hankel singular values are independent of the realization used to calculate them: when A,B,C,D are replaced by TAT then P and Q are replaced b y TPT′ and (T

–1

by TPQT

and the eigenvalues are unaltered.

• The number of nonzero Hankel singular values is the order or McMillan degree of the transfer-function matrix, or the state dimension in a minimal realization.

Xmath Model Reduction Module 1-8 ni.com

1/2

(PQ). Notice the following:

–1

)′QT–1; then PQ is replaced

, TB, CT

–1

and D,

Chapter 1 Introduction

• Suppose the transfer-function matrix corresponds to a discrete-time system, with state variable dimension n. Then the infinite Hankel matrix,

CB CAB CA

CAB CA

has for its singular values the n nonzero Hankel singular values, together with an infinite number of zero singular values.

The Hankel singular values of a (stable) all pass system (or all pass matrix) are all 1.

Slightly different procedures are used for calculating the Hankel singular values (and so-called weighted Hankel singular values) in the various functions. These procedures are summarized in Table 1-2.

Table 1-2. Calculating Hankel Singular Values

(balance( ))

balmoore( )

hankelsv( )

ophank( )

redschur( )

bst( ) mulhank( ) wtbalance( ) fracred( )

For a discussion of the balancing algorithm, refer to the Internally Balanced Realizations section; the Hankel singular values are given by

1/2

diag(R

)=HSV

For a discussion of the balancing algorithm, refer to the Internally Balanced Realizations section; the matrix S

diag(SH)

real(sqrt(eig(p*q)))

yields the Hankel singular values through

Calls hankelsv( ) Computes a Schur decomposition of P*Q and then

takes the square roots of the diagonal entries Same as redschur( ) except either P or Q can be

a weighted grammian

Chapter 1 Introduction

Internally Balanced Realizations

Suppose that a realization of a transfer-function matrix has the controllability and observability grammian property that P = Q = Σ for some diagonal Σ. Then the realization is termed internally balanced. Notice that the diagonal entries σ that is, they are the Hankel singular values. Often the entries of Σ are assumed ordered with σ

As noted in the discussion of grammians, systems with small (eigenvalues of) P are hard to control and those with small (eigenvalues of) Q are hard to observe. Now a state transformation T = α I will cause P = Q to be replaced by α expense of difficulty of observation, and conversely . Balanced realizations are those when ease of control has been balanced against ease of observation.

Given an arbitrary realization, there are a number of ways of finding a state-variable coordinate transformation bringing it to balanced form.

A good survey of the available algorithms for balancing is in [LHPW87]. One of these is implemented in the Xmath function

P, α–2Q, implying that ease of control can be obtained at the

of Σ are square roots of the eigenvalues of PQ,

≥ σ

i+1

balance( ).

The one implemented in

balmoore( ) as part of this module is more

sophisticated, but more time consuming. It proceeds as follows:

1. Singular value decompositions of P and Q are defined. Because P and Q are symmetric, this is equivalent to diagonalizing P and Q by orthogonal transformations.

cSc

U′

P=U

Q=UoSo U′

2. The matrix,

12⁄

UHSHV

12⁄

is constructed, and from it, a singular value decomposition is obtained:

′

HSHVH

3. The balancing transformation is given by:

The balanced realization is T

Xmath Model Reduction Module 1-10 ni.com

12⁄–

0S0

–1

AT, T–1B, CT.

UHS

12⁄

Chapter 1 Introduction

This is almost the algorithm set out in Section II of [LHPW87]. The one difference (and it is minor) is that in [LHPW87], lower triangular Cholesky factors of P and Q are used, in place of U

cSc

1/2

and U

1/2

in forming H

OSO

in step 2. The grammians themselves need never be formed, as these Cholesky factors can be computed directly from A, B, and C in both continuous and discrete time; this, however, is not done in

balmoore.

The algorithm has the property that:

1–

PT1–()′ S

T′ QT′ T

Thus the diagonal entries of S The algorithm implemented in

A lower triangular Cholesky factor L Then the symmetric matrix L value decomposition), thus L′ the coordinate basis transformation is given by T = L T′QT = T

Singular Perturbation

A common procedure for approximating systems is the technique of Singular Perturbation. The underlying heuristic reasoning is as follows. Suppose there is a system with the property that the unforced responses of the system contain some modes which decay to zero extremely fast. Then an approximation to the system behavior may be attained by setting state variable derivatives associated with these modes to zero, even in the forced case. The phrase “associated with the modes” is loose: exactly what occurs is shown below. The phrase “even in the forced case” captures a logical flaw in the argument: smallness in the unforced case associated with initial conditions is not identical with smallness in the forced case.

Suppose the system is defined by:

–1

P(T–1)′ = R

are the Hankel singular values.

balance( ) is older, refer to [Lau80].

of P is found, so that L

′QL

is diagonalized (through a singular

= VRU′, with actuall y V = U. Finally,

cQLc

1/2

A11A

A21A

u+=

′ = P.

cLc

–1/4

, resulting in

1C2

Du+=

(1-1)

Chapter 1 Introduction

and also:

(A22)<0 and .

Reλ

–()0<

iA11A12A22

1–

Usually , we e xpect that,

Reλ

()ReλiA11A12A

iA22

–()«

1–

in the sense that the intuitive argument hinges on this, but it is not necessary .

Then a singular perturbation is obtained by replacing by zero; this

means that:

A21x1A22x2B

u++ 0=

1–

A–

A21x1A

1–

u–=

Accordingly,

A11A12A

–()x

1C2A22

1–

=()x

1–

B1A12A

DC2A

–()u+=

1–

(1-2)

Equation 1-2 may be an approximation for Equation 1-1. This means that:

• The transfer-function matrices may be similar.

• If Equation 1-2 is excited by some u(·), with initial condition x

1(to

), and if Equation 1-1 is excited by the same u(·) with initial condition given by,

•x

1(to

then x

) and x2(to) = –A

(·) and y(·) computed from Equation 1-1 and from Equation 1-2

–1

A21x1(to)–A

–1

B2u(to),

should be similar.

• If Equation 1-1 and Equation 1-2 are excited with the same u(·), have the same x

) and Equation 1-1 has arbitrary x2, then x1(·) and y(·)

1(to

computed from Equation 1-1 and Equation 1-2 should be similar after a possible initial transient.

As far as the transfer-function matrices are concerned, it can be verif ied that they are actually equal at DC.

Xmath Model Reduction Module 1-12 ni.com

Chapter 1 Introduction

Similar considerations govern the discrete-time problem, where,

can be approximated by:

mreduce( ) can carry out singular perturbation. For further discussion,

refer to Chapter 2, Additive Error Reduction. If Equation 1-1 is balanced, singular perturbation is provably attractive.

Spectral Factorization

Let W(s) be a stable transfer-function matrix, and suppose a system S with transfer-function matrix W(s) is excited by zero mean unit intensity white noise. Then the output of S is a stationary process with a spectrum Φ(s) related to W(s) by:

k 1+()

k 1+()A

yk()

C1C2IA

x1k()

k()

11A12

A21A

x1k()

1C2

+[]x1k()+=

11A12

+[]uk()

1A12

+[]x1k()+=

+[]uk()

–()

Du k()+=

k()

1–

uk()+=

Φ s() Ws()W′ s–()=

(1-3)

Evidently,

Φ jω() Wjω()W

jω()=

so that Φ(jω) is nonnegative hermitian for all ω; when W(jω) is a scalar, so

is Φ(jω) with Φ( jω)=|W( jω)|

In the matrix case, Φ is singular for some ω only if W does not have full rank there, and in the scalar case only if W has a zero there.

Spectral factorization, as shown in Example 1-1, seeks a W(jω), given Φ(jω). In the rational case, a W(jω) exists if and only if Φ(jω) is

Chapter 1 Introduction

nonnegative hermitian for all ω. If Φ is scalar, then Φ(jω)≥0 for all ω. Normally one restricts attention to Φ(·) with lim

Φ(jω)<∞. A key result

ω→∞

is that, given a rational, nonnegative hermitian Φ(jω) with

Φ(jω)<∞, there exists a rational W(s) where,

lim

ω→∞

• W(∞)<∞.

• W(s) is stable.

• W(s) is minimum phase, that is, the rank of W(s) is constant in Re[s]>0.

In the scalar case, all zeros of W(s) lie in Re[s]≤0, or in Re[s]<0 if Φ(jω)>0 for all ω.

In the matrix case, and if Φ(jω) is nonsingular for some ω, it means that W(s) is square and W is nonsingular for all ω.

Moreover , the particular W(s) pre viously def ined is unique, to within right multiplication by a constant orthogonal matrix. In the scalar case, this means that W(s) is determined to within a ±1 multiplier.

Example 1-1 Example of Spectral Factorization

Suppose:

Then Equation 1-3 is satisfied by , which is stable and minimum phase.

Also, Equation 1-3 is satisfied by and , and , and so forth, but none of these is minimum phase.

bst( ) and mulhank( ) both require execution within the program of

a spectral factorization; the actual algorithm for achieving the spectral factorization depends on a Riccati equation. The concepts of a spectrum and spectral factor also underpin aspects of

–1

(s) has all its poles in Re[s]≤ 0, or in Re[s]<0 if Φ(jω)

Ws()

s 1–

----------s 2+

---------------=

s 1+

-----------

±=

s 2+

s 3–

----------s 2+

wtbalance( ).

s 1–

-----------

s 2+

s 1+

sT–

-----------

s 2+

Φ j ω()

Xmath Model Reduction Module 1-14 ni.com

Chapter 1 Introduction

Low Order Controller Design Through Order Reduction

The Model Reduction Module is particularly suitable for achieving low order controller design for a high order plant. This section explains some of the broad issues involved.

Most modern controller design methods, for example, LQG and H controllers of order roughly comparable with that of the plant. It follows that, to obtain a low order controller using such methods, one must either follow a high order controller design by a controller reduction step, or reduce an initially given high order plant model, and then design a controller using the resulting low order plant, with the understanding that the controller will actually be used on the high order plant. Refer to Figure 1-2.

High Order Plant

Plant

High Order Controller

Controller

∞, yield

Reduction Reduction

Low Order Plant

Figure 1-2. Low Order Controller Design for a High Order Plant

Generally speaking, in any design procedure, it is better to postpone approximation to a late step of the procedure: if approxim atio n is done early, the subsequent steps of the design procedure may have unpredictable effects on the approximation errors. Hence, the scheme based on high order controller design followed by reduction is generally to be preferred.

Low Order Controller

Controller reduction should aim to preserve closed-loop properties as far as possible. Hence the controller reduction procedures advocated in this module reflect the plant in some way . This leads to the frequenc y weighted reduction schemes of Chapter 4, Frequency-Weighted Error Reduction. Plant reduction logically should also seek to preserve closed-loop properties, and thus should involv e the controller. With the controller unknown however, this is impossible. Nevertheless, it can be argued, on the basis of the high loop gain property within the closed-loop bandwidth that is typical of many systems, that

wtbalance( ) and fracred( ), as described in

Chapter 1 Introduction

multiplicative reduction, as described in Chapter 4, Frequency-Weighted

Error Reduction, is a sound approach. Chapter 3, Multiplicative Error Reduction, and Chapter 4, Frequency-Weighted Error Reduction, develop

these arguments more fully.

Xmath Model Reduction Module 1-16 ni.com

Additive Error Reduction

This chapter describes additive error reduction including discussions of truncation of, reduction by, and perturbation of balanced realizations.

Introduction

Additive error reduction focuses on errors of the form,

Gjω()G

where G is the originally given transfer function, or model, and G reduced one. Of course, in discrete-time, one works instead with:

Gejω()Gre

As is argued in later chapters, if one is reducing a plant that will sit inside a closed loop, or if one is reducing a controller, that again is sitting in a closed loop, focus on additive error model reduction may not be appropriate. It is, however, extremely appropriate in considering reducing the transfer function of a filter. One pertinent application comes specif ically from digital filtering: a great many design algorithms lead to a finite impulse response (FIR) filter which can have a very large number of coefficients when poles are close to the unit circle. Model reduction provides a means to replace an FIR design by a much lower order infinite impulse response (IIR) design, with close matching of the transfer function at all frequencies.

jω()–

∞

is the

jω

()–

∞

Chapter 2 Additive Error Reduction

Truncation of Balanced Realizations

A group of functions can be used to achieve a reduction through truncation of a balanced realization. This means that if the original system is

A11A

A21A

u+=

1C2

(2-1)

and the realization is internally balanced, then a truncation is provided by

A11x1B

1x1

u+=

Du+=

The functions in question are:

• balmoore( )

• balance( ) (refer to the Xmath Help)

• truncate( )

• redschur( )

One only can speak of internally balanced realizations for systems which are stable; if the aim is to reduce a transfer function matrix G(s) which contains unstable poles, one must additively decompose it into a stable part and unstable part, reduce the stable part, and then add the unstable part back in. The function

stable( ), described in Chapter 5, Utilities, can be used

to decompose G(s). Thus: G(s) = G G

(s) = found by algorithm (reduction of Gs(s))

(s) + Gu(s)(Gs(s) stable, Gu(s) unstable)

(s) = Gsr(s) + Gu(s) (reduction of G(s))

Xmath Model Reduction Module 2-2 ni.com

Chapter 2 Additive Error Reduction

A very attractive feature of the truncation procedure is the availability of an error bound. More precisely, suppose that the controllability and observability grammians for [Enn84] are

===

PQΣ

with the diagonal entries of Σ in decreasing order, that is, σ

0 Σ

≥ σ

≥ ···. Then

the key result is,

(2-2)

with G, G

Gjω()G

the transfer function matrices of Equation 2-1 and Equation 2-2,

jω()–

2trΣ

≤

∞

respectively. This formula shows that small singular values can, without great cost, be thrown away. It also is valid in discrete time, and can be improved upon if there are repeated Hankel singular values. Provided that the smallest diagonal entry of Σ

, the reduced order system is guaranteed to be stable.

of Σ

strictly exceeds the largest diagonal entry

Several other points concerning the error can be made:

• The error G( jω)–G

( jω) as a function of frequency is not flat; it is zero

at ω = ∞, and may take its largest value at ω = 0, so that there is in general no matching of DC gains of the original and reduced system.

• The actual error may be considerably less than the error bound at all frequencies, so that the error bound formula can be no more than an advance guide. However, the bound is tight when the dimension reduction is 1 and the reduction is of a continuous-time transfer-function matrix.

•With g(·) and g responses of G and G

(·) denoting the impulse responses for impulse

and with Gr of degree k, the following L1 bound

holds [GCP88]

–

This bound also will apply for the L

≤

42k 1+()trΣ

error on the step response.

∞

It is helpful to note one situation where reduction is likely to be difficult (so that Σ will contain few diagonal entries which are, relatively, very small). Suppose G(s), strictly proper, has degree n and has (n – 1) unstable zeros. Then as ω runs from zero to infinity, the phase of G(s) will change by (2n – 1)π/2. Much of this change may occur in the passband. Suppose G

(s)

has degree n–1; it can have no more than (n – 2) zeros, since it is strictly

Chapter 2 Additive Error Reduction

proper. So, e ven if all zeros are unstable, the maximum phase shift when ω moves from 0 to ∞ is (2n–3)π/2. It follows that if G(jω) remains large in magnitude at frequencies when the phase shift has moved past (2n – 3)π/2, approximation of G by G approximation may depend somehow on removing roughly cancelling pole-zeros pairs; when there are no left half plane zeros, there can be no rough cancellation, and so approximation is unsatisfactory.

As a working rule of thumb, if there are p right half plane zeros in the passband of a strictly proper G(s), reduction to a G p + 1 is likely to involve substantial errors. For non-strictly proper G(s), having p right half plane zeros means that reduction to a G than p is likely to involve substantial errors.

An all-pass function exemplifies the problem: there are n stable poles and n unstable zeros. Since all singular values are 1, the error bound formula indicates for a reduction to order n – 1 (when it is not just a bound, but exact) a maximum error of 2.

Another situation where poor approximation can arise is when a highly oscillatory system is to be replaced by a system with a real pole.

will necessarily be poor. Put another way, good

(s) of order less than

(s) of order less

Reduction Through Balanced Realization Truncation

This section briefly describes functions that reduce( ), balance( ),

truncate( ) to achieve reduction.

and

•

balmoore( )—Computes an internally balanced realization of a

system and optionally truncates the realization to form an approximation.

•

balance( )—Computes an internally balanced realization of a

system.

•

truncate( )—This function truncates a system. It allows

examination of a sequence of different reduced order models formed from the one balanced realization.

•

redschur( )—These functions in theory function almost the same

as the two features of state-variable realization of a reduced order model, such that the transfer function matrix of the model could have resulted by truncating a balanced realization of the original full order transfer function matrix. Howe ver, the initially given realizat ion of the ori ginal transfe r function matrix is never actually balanced, which can be a numerically hazardous step. Moreover, the state-v ariable realization of the reduced

Xmath Model Reduction Module 2-4 ni.com

balmoore( ). That is, they produce a

Chapter 2 Additive Error Reduction

order model is not one in general obtainable by truncation of an internally-balanced realization of the full order model.

Figure 2-1 sets out several routes to a reduced-order realization. In continuous time, a truncation of a balanced realization is again balanced. This is not the case for discrete time, but otherwise it looks the same.

Full Order Realization

balmoore

(with both steps)

Balanced Realization of

Reduced Order Model

(in continuous time)

Reduced Order Model Transfer Function

balmoore

(with first step)

truncate

balance redschur

Nonbalanced Realization of

Reduced Order Model

Figure 2-1. Different Approaches for Obtaining the Same Reduced Order Model

Singular Perturbation of Balanced Realization

Singular perturbation of a balanced realization is an attractive way to produce a reduced order model. Suppose G(s) is defined by,

A11A

A21A

u+=

1C2

xDu+=

Chapter 2 Additive Error Reduction

with controllability and observability grammians given by,

in which the diagonal entries of Σ are in decreasing order, that is,

1≥σ2

the first diagonal entry of Σ

Reλ

defined by:

===

PQΣ

0 Σ

≥ ···, and such that the last diagonal entry of Σ1 exceeds

(A11–A

. It turns out that Reλi()<0 and

1–

)< 0, and a reduced order model Gr(s) can be

1–

x·A11A12A

1C2A22

The attractive feature [LiA89] is that the same error bound holds as for balanced truncation. For example,

Although the error bounds are the same, the actual frequency pattern of the errors, and the actual maximum modulus, need not be the same for reduction to the same order. One crucial difference is that balanced truncation provides exact matching at ω = ∞, but does not match at DC, while singular perturbation is exactly the other way round. Perfect matching at DC can be a substantial advantage, especially if input signals are known to be band-limited.

Singular perturbation can be achieved with the two alternative approaches. For both continuous-time and discrete-time reductions, the end result is a balanced realization.

Hankel Norm Approximation

1–

–()xB

–()xDC

Gjω()G

1–

jω()–

– A

+()u+=

–()u+=

2A22

2trΣ

≤

∞

mreduce( ). Figure 2-1 shows

1–

In Hankel norm approximation, one relies on the fact that if one chooses an approximation to exactly minimize one norm (the Hankel norm) then the infinity norm will be approximately minimized. The Hankel norm is defined in the following way. Let G(s) be a (rational) stable transfer

Xmath Model Reduction Module 2-6 ni.com

Chapter 2 Additive Error Reduction

function matrix. Consider the way the associated impulse response maps inputs defined over (–∞,0] in L

into outputs, and focus on the output over

[0,∞). Define the input as u(t) for t < 0, and set v(t)=u(–t). Define the output as y(t) for t > 0. Then the mapping is

∞

yt() CexpAt r+()Bv r()dr

∫

–1

if G(s)=C(sI-A)

norm of G. A key result is that if σ

values of G(s), then .

B. The norm of the associated operator is the Hankel

≥ ···, are the Hankel singular

1≥σ2

T o av oid minor confusion, suppose that all Hankel singular values of G are distinct. Then consider approximating G by some stable of prescribed degree k much that is minimized. It turns out that

–

inf

Gˆof degree k

and there is an algorithm available for obtaining . Further, the optimum which is minimizing does a reasonable job of minimizing , because it can be shown that

–

∞

–

where n =deg G, with this bound subject to the proviso that G and are

–

≤

∞

k 1+

G()=

∑

jk1+=

allowed to be nonzero and different at s = ∞.

The bound on is one half that applying for balanced truncation.

–

However,

• It is actual error that is important in practice (not bounds).

• The Hankel norm approximation does not give zero error at ω = ∞ or at ω = 0. Balanced realization truncation gives zero error at ω = ∞, and singular perturbation of a balanced realization gives zero error at ω =0.

There is one further connection between optimum Hankel norm approximation and L

with stable and of degree k and with F unstable, then:

error. If one seeks to approximate G by a sum + F,

∞

inf

Gˆof degree k and F unstable

– F–

k 1+

G()=

∞

Chapter 2 Additive Error Reduction

balmoore( )

Further, the which is optimal for Hankel norm approximation also is

optimal for this second type of approximation. In Xmath Hankel norm approximation is achieved with

ophank( ).

The most comprehensive reference is [Glo84].

[SysR,HSV,T] = balmoore(Sys,{nsr,bound})

The balmoore( ) function computes an internally-balanced realization of a continuous system and then optionally truncates it to provide a balance reduced order system using B.C. Moore’s algorithm.

balmoore( ) is being used to reduce a system, its objective mirrors

When

redschur( ), therefore, if the same Sys and nsr are used for both

that of algorithms, the reduced order system should have the same transfer function (though in general the state-variable realizations will be different).

balmoore( ) is being used to balance a system, its objective, like

When that of balance, is to generate an internally-balanced state-variable realization. The implementations are not identical.

balmoore( ) only can be applied on systems that have a stable A matrix,

and are controllable and observable, (that is, minimal). Checks, which are rather time-consuming, are included. The computation is intrinsically not well-conditioned if

balmoore( ) serves to find a transformation matrix T such that the

Sys is nearly nonminimal. The first part of

controllability and observability grammians after transformation are equal, and diagonal, with decreasing entries down the diagonal, that is, the system representation is internally balanced. (The condition number of T is a measure of the ill-conditioning of the algorithm. If there is a problem with ill-conditioning,

redschur( ) can be used as an alternative.) If this

common grammian is Σ, then after transformation:

Σ A′

(continuous)

(discrete)

Σ diag σ

1σ2σ3

Singular Values of

Xmath Model Reduction Module 2-8 ni.com

... σ

Sys. In the second part of balmoore( ), a truncation

+ A Σ = –BB

– A Σ A

,,,[]= σ

with with the the Hankel

= –BB

iσi 1+

′Σ

A + A′Σ = –C′C

′Σ

- A

′ Σ

A = –C′C

0>≤σ

Chapter 2 Additive Error Reduction

of the balanced system occurs, (assuming nsr is less than the number of states). Thus, if the state-space representation of the balanced system is

11A12

with A

possessing dimension nsr × nsr, B1 possessing nsr rows and C1

possessing

= B

A21A

nsr columns, the reduced order system SysR is:

(continuous) (discrete)

A11x1B

u+=

xDu+=

The following error formula is relevant:

(continuous)

1–

jω

IA–()

(discrete)

[]C1jωIA

CjωIA–()

k 1+()A

yk() C

2 σ

nsr 1+

1–

BD+[]C

1C2

k() B

11x1

k() Du k()+=

1x1

1–

–()

+++[]≤

nsr 2+

ejωIA

uk()+=

D+()[]–

... σ

–()

∞

1–

D+[]–

∞

2 σ

nsr 1+

+++[]≤

nsr 2+

... σ

It is this error bound which is the basis of the determination of the order of the reduced system when the keyword bound sought is smaller than , then no reduction is possible which is

2σ

consistent with the error bound. If it is larger than , then the constant

bound is specified. If the error

2trΣ

transfer function matrix D achieves the bound. For continuous systems, the actual approximation error depends on

frequency, but is always zero at ω = ∞. In practice it is often greatest at ω = 0; if the reduction of state dimension is 1, the error bound is exact, with the maximum error occurring at DC. The bound also is exact in the special case of a single-input, single-output transfer function which has poles and zero alternating along the negative real axis. It is far from exact when the poles and zeros approximately alternate along the imaginary axis (with the poles stable).

Chapter 2 Additive Error Reduction

The actual approximation error for discrete systems also depends on frequency , and can be lar ge at ω = 0. The error bound is almost never tight, that is, the actual error magnitude as a function of ω almost never attains the error bound, so that the bound can only be a guide to the selection of the reduced system dimension.

In principle, the error bound formula for both continuous and discrete systems can be improved (that is, made tighter or less likely to overestimate the actual maximum error magnitude) when singular values occur with multiplicity greater than one. However, because of errors arising in calculation, it is safer to proceed conservativ ely (that is, work with the error bound above) when using the error bound to select actual error achieved. If this is smaller than required, a smaller dimension for the reduced order system can be selected.

mreduce( ) provides an alternative reduction procedure for a balanced

realization which achieves the same error bound, but which has zero error at ω = 0. For continuous systems there is generally some error at ω = ∞, because the D matrix is normally changed. (This means that normally the approximation of a strictly proper system through strictly proper, in contrast to the situation with systems the D matrix is also normally changed so that, for example, a system which was strictly causal, or guaranteed to contain a delay (that is, D = 0), will be approximated by a system

nsr, and examine the

mreduce( ) will not be

balmoore( ).) For discrete

SysR without this property.

The presentation of the Hankel singular values may suggest a logical

dimension for the reduced order system; thus if , it may be

kσk 1+

sensible to choose nsr = k.

mreduce( ) and a continuous system, the reduced order system

With

SysR is internally balanced, with the grammian , so

diag σ

...,σ

,,[]

1σ2

nsr

that its Hankel Singular Values are a subset of those of the original system

Sys. Provided , SysR also is controllable, observable, and

stable. This is not guaranteed if , so it is highly advisable to

nsrσnsr 1+

nsr

nsr 1+

avoid this situation. Refer to the balmoore( ) section for more on the

balmoore( ) algorithm.

mreduce( ) and discrete systems, the reduced order system SysR is

With not in general balanced (in contrast to singular values are not in general a subset of those of

nsrσsrn 1+

, the reduced order system

observable and stable. This is not guaranteed if , so it is

balmoore( )), and its Hankel

Sys. Provided

SysR also is controllable,

nsr

nsr 1+

highly advisable to avoid this situation. For additional information about

balmoore( ) function, refer to the Xmath Help.

the

Xmath Model Reduction Module 2-10 ni.com

Related Functions

truncate( )

Chapter 2 Additive Error Reduction

balance(), truncate(), redschur(), mreduce()

SysR = truncate(Sys,nsr,{VD,VA})

The truncate( ) function reduces a system Sys by retaining the first

nsr states and throwing away the rest to form a system SysR.

Sys one has,

If for

Related Functions

11A12

= B

A21A

1C2

the reduced order system (in both continuous-time and discrete-time cases) is defined by A approximation of well be used after an initial application of

, B1, C1, and D. If Sys is balanced, then SysR is an

Sys achieving a certain error bound. truncate( ) may

balmoore( ) to further reduce

a system should a larger approximation error be tolerable. Alternatively, it may be used after an initial application of

Sys was calculated from redschur( ) and VA,VD were posed as

If arguments, then

SysR is calculated as in redschur( ) (refer to the

balance( ) or redschur( ).

redschur( ) section).

truncate( ) should be contrasted with mreduce( ), which achieves a

reduction through a singular perturbation calculation. If

Sys is balanced,

the same error bound formulas apply (though not necessarily the same errors),

truncate( ) always ensures exact matching at s = ∞ (in the

continuous-time case), or exacting matching of the first impulse response coefficient D (in the discrete-time case), while matching of DC gains for

Sys and SysR in both the continuous-time and

discrete-time case. For a additional information about the

mreduce( ) ensures

truncate( )

function, refer to the Xmath Help.

balance(), balmoore(), redschur(), mreduce()

Chapter 2 Additive Error Reduction

redschur( )

[SysR,HSV,slbig,srbig,VD,VA] = redschur(Sys,{nsr,bound})

The redschur( ) function uses a Schur method (from Safonov and Chiang) to calculate a reduced version of a continuous or discrete system without balancing.

Algorithm

The objective of redschur( ) is the same as that of balmoore( ) when the latter is being used to reduce a system; this means that if the same and the same transfer function matrix. However, in contrast to

redschur( ) do not initially transform Sys to an internally balanced

realization and then truncate it; nor is there is no balancing offers numerical advantages, especially if nearly nonminimal.

Sys should be stable, and this is checked by the algorithm. In contrast to balmoore( ), minimality of Sys (that is, controllability and

observability) is not required.

Sys

nsr are used for both algorithms, the reduced order system should have

balmoore( ),

SysR in balanced form. The fact that

Sys is

If the Hankel singular values of then those of

SysR in the continuous-time case are .

A restriction of the algorithm is that is required for both

Sys are ordered as ,

nsrσnsr 1+

continuous-time and discrete-time cases. Under this restriction,

1σ2

... σns0≥≥≥ ≥

... σ

nsr

SysR is

0>≥≥≥

guaranteed to be stable and minimal. The algorithms depend on the same algorithm, apart from the calculation

of the controllability and observability grammians W original system. These are obtained as follows:

(continuous)

(discrete)

WcA′ AW

+ BB′–= W

A′– BB′= W

and Wo of the

AA′W

+ C′C=

A′ W

A– C′C=

The maximum order permitted is the number of nonzero eigenvalues of

that are larger than ε.

cWo

Xmath Model Reduction Module 2-12 ni.com

Chapter 2 Additive Error Reduction

Next, Schur decompositions of W

in ascending and descending order. These eigen values are the square

cWo

of the Hankel singular values of

are formed with the eigenvalues of

cWo

Sys, and if Sys is nonminimal, some can

be zero.

asc

des

, S

are upper triangular. Next,

asc

des

The matrices V

V′

AWcWoVA

V′

DWcWoVD

, VD are orthogonal and S

submatrices are obtained as follows:

= V

lbig

nsr

rbig

nsr

and then a singular value decomposition is found:

ebigSebigVebig

V′

lbigVrbig

From these quantities, the transformation matrices used for calculating

SysR are defined:

lbig

rbig

lbigUebigSebig

rbigVebigSebig

12⁄

and the reduced order system is:

′

lbig

rbig

′

lbig

An error bound is available. In the continuous-time case it is as follows. Let G(jω) and G

(jω) be the transfer function matrices of Sys and SysR,

respectively. For the continuous case:

Gjω()G

jω()–

2 σ

∞

nsr 1+

+++()≤

nsr 2+

... σ

Chapter 2 Additive Error Reduction

For the discrete-time case:

Related Functions

ophank( )

Gejω()GRe

{bound} is specified, the error bound just enunciated is used to

When choose the number of states in is as small as possible. If the desired error bound is smaller than 2σ

jω

()–

2 σ

∞

nsr 1+

SysR so that the bound is satisfied and nsr

+++()≤

nsr 2+

... σ

no reduction is made. In the continuous-time case, the error depends on frequency, but is always

zero at ω = ∞. If the reduction in dimension is 1, or the system

Sys is

single-input, single-output, with alternating poles and zeros on the real axis, the bound is tight. It is far from tight when the poles and zeros approximately alternate along the jω-axis. It is not normally tight in the discrete-time case, and for both continuous-time and discrete-time cases, it is not tight if there are repeated singular values.

The presentation of the Hankel singular values may suggest a logical

σkσ

dimension for the reduced order system; thus if , it may be

k 1+

sensible to choose nsr = k.

ophank(), balmoore()

[SysR,SysU,HSV] = ophank(Sys,{nsr,onepass})

The ophank( ) function calculates an optimal Hankel norm reduction

Sys.

Restriction

This function has the following restriction:

• Only continuous systems are accepted; for discrete systems use

makecontinuous( ) before calling bst( ), then discretize the

result.

Sys=ophank(makecontinuous(SysD));

SysD=discretize(Sys);

Xmath Model Reduction Module 2-14 ni.com

Algorithm

Chapter 2 Additive Error Reduction

The algorithm does the following. The system Sys and the reduced order

SysR are stable; the system SysU has all its poles in Re[s] > 0. If

system the transfer function matrices are G(s), G

• G

(s) is a stable approximation of G(s).

• G

(s)+Gu(s) is a more accurate, but not stable, approximation of G(s),

(s) and Gu(s) then:

and optimal in a certain sense.

Of course, the algorithm works with state-space descriptions; that of G(s) can be minimal, while that of G

(s) cannot be.

Behaviors

These statements are explained in the Behaviors section. If specified, reduction is calculated in one pass. If set to 0

{onepass=0}, reduction is calculated in (number of states of

onepass is not called or is

onepass is

Sys - nsr) passes. There seems to be no general rule to suggest which

setting produces the more accurate approximation G

. Therefore, if

accuracy of approximation for a giv en order is critical, both should be tried. As noted previously, if an approximation involving an unstable system is desired, the default

{onepass=1} is specified.

The following explanation deals first with the keyword {onepass}. Suppose that σ

, σ2,..., σns are the Hankel Singular values of S, which has

transfer function matrix G(s). Suppose that the singular values are ordered so that:

=== σ

1σ2

Thus, there are n by n

The order

... σ

equal values, followed b y n2– n1 equal values, followed

...>σ

n11+

m 1–

– n2 equal values, and so forth.

nsr of G

(s) cannot be arbitrary when there are equal Hankel

n11+

... σ

m 1–

...>==

n21+

=σ

()0≥==>

singular values. In fact, the orders sho wn in Table 2-1 for the strictly stable

(all poles in Re[s]<0) and strictly unstable Gu (all poles Re[s]>0) are

possible (and there are no other possibilities).

Chapter 2 Additive Error Reduction

Table 2-1. Orders of G

Order of

nsr

0 ns – n

Order of

nsu

ns – n

Number of

Eliminated States

(Retaining G

– n

)

Number of

Eliminated States

(Discarding G

)

ns – n

⇓ ⇓ ⇓ ⇓

m –1

0 ns – n

m –1

ns – n

m –1

By abuse of notation, when we say that G is reduced to a certain order, this corresponds to the order of G

(s) alone; the unstable part of Gu(s) of the

approximation is most frequently thrown away . The number of eliminate d states (retaining G

(# of states in G) – (# of states in G

) refers to:

) – (# of states in Gu)

This number is always the multiplicity of a Hankel singular value. Thus, when the order of G the multiplicity of σ

For each order n

is n

of Gr(s), it is possible to find Gr and Gu so that:

i –1

the number of eliminated states is ni– n

i –1

+ 1 = σni

i – 1

i –1

Gjω()G

(Choosing i = 1 causes G

to be of order zero; identify n0 = 0.) Actually,

jω()– Gujω()–

≤

∞

among all “approximations” of G(s) with stable part restricted to having degree n can never obtain a lower bound on the approximation error than σ scalar or SISO G(s) case, the G unique, while in the matrix or MIMO G(s) case, the G

and with no restriction on the degree of the unstable part, one

i –1

(s) which achieves the previous bound is

(s) which achieves

; in the

the previous bound may not be unique [Glo84]. The algorithm we use to

(s) and Gu(s) however allows no user choice, and delivers a single

find G

pair of transfer function matrices. The transfer function matrix G

approximation of G( jω). If the D matrix in G

(jω) alone can be regarded as a stable

(jω) is approximately

chosen, (and the algorithm ensures that it is), then:

Gjω()G

Xmath Model Reduction Module 2-16 ni.com

jω()–

+++≤

∞

... σ

i 1+

(2-3)

Chapter 2 Additive Error Reduction

Thus, the penalty for not being allowed to include Gu in the approximation

+ ... +

is an increase in the error bound, by σ

ni + 1

. A number of

theoretical developments hinge on bounding the Hankel singular values of

(s) and Gu(–s) in terms of those of G(s). With Gr(s) of order n

i –1

, there

holds:

)σkG()k≤( 12… n

kGr

,, ,=

i 1–

The transfer function matrix G singular values; however, G

(s), being unstable, does not have Hankel

(–s) (which is stable) does have Hankel

singular values. They satisfy:

kGu

s–()[]σ

nik+

G()≤

In most cases, the Hankel singular values of G(s) are distinct. If, accordingly,

GGr– G

has degree (i –1), Gu has degree ns – i and

then G

–

∞

–

σiσ

+++=

i 1+

∞

... σ

(2-4)

Observe that the bound (Equation 2-3 or Equation 2-4), which is not necessarily obtained, is one half that applying for both balanced truncation (as implemented by also is one half that obtained when applying realization. In general, the D matrices of G and G

G(∞) ≠ G G(0) ≠ G

(∞) (in contrast to balmoore( ) and redschur( )). Similarly ,

(0) in general (in contrast to the result when mreduce is applied

balmoore( ) or, effectively, by redschur( )); it

mreduce to a balanced

are different, that is,

to a balanced realization). The price paid for obtaining a smaller error bound overall through Hankel norm reduction is that one no longer (normally) secures zero error at ω = ∞ or ω = 0.

T wo special cases should be noted. If This constant can be added onto G

nsr = 0 then G

(s), so that G(s) is then being

approximated by a totally unstable transfer function matrix, with error σ

(s) is a constant only .

this type of approximation is known as Nehari approximation. The second special case arises when

nsr = n

singular value has multiplicity 1). In this case, G which can then be lumped in with G

(or NS – 1 if the smallest Hankel

m –1

(s) becomes a constant,

(s), so that G(s), of degree NS, is then

;

Chapter 2 Additive Error Reduction

being approximated by a stable Gr(s) with the actual error (as opposed to just the error bound) satisfying:

Note G

is optimal, that is, there is no other Gr achieving a lower bound.

Onepass Algorithm

Gs() G

s()–

∞

The first steps of the algorithm are to obtain the Hankel singular values of

G(s) (by using G(s) is checked in this process.) If the user has specified

not coincide with one of 0,n all the σ The next step of the algorithm is to calculate the sum G(s)=G following [SCL90]. (A separate function

hankelsv( )) and identify their multiplicities. (Stability of

nsr and this does

, ... an error message is obtained; generally,

are different, so the occurrence of error messages will be rare.

1,n2

(s)+Gu(s),

ophred( ) is called for this

purpose.) The controllability and observability grammians P and Q are found in the usual way.

AP + PA′ = –BB′

QA + A′Q = –C′C

and then a singular value decomposition is obtained of the

QP σ

matrix :

I–

1U2

SB0

′

QP σ

′

I–=

– n

There are precisely n

. Next, the following definitions are made:

of σ

A11A

A21A

C1C

[]CP V1V

Xmath Model Reduction Module 2-18 ni.com

zero singular values, this being the multiplicity

i –1

U1′

= σ

U1′

A′ QAP+()V

′

()

1V2

QB=

′

[]=

and finally:

Chapter 2 Additive Error Reduction

# 22

12–A22

# 21

G˜s()

1–

A11A

1–

B1A

–=

–()=

# 22

A˜S

B˜S

C˜C1C2A

D˜DC2A

These four matrices are the constituents of the system matrix of , where:

G˜s() G

s() G

s()+=

Digression:

This choice is related to the ideas of [Glo84] in the following way; in [Glo84], the complete set is identified of satisfying

Gjω()G

with having a stable part of order n

jω()–

G˜s()

∞

. The set is parameterized in

i –1

terms of a stable transfer function matrix K(s) which has to satisfy

Ks()B

′

+ 0=

IK′ jω–()Kjω()– 0forallω≤

, B2 being two matrices appearing in the course of the algorithm

with C

of [Glo84], and enjoying the property . The particular

′

C2B2B

′

choice

Ks() C

–=

()

2C′2C2

in the algorithm of [Glo84] and flagged in corollary 7.3 of [Glo84] is equivalent to the previous construction, in the sense of yielding the

same , though the actual formulas used here and in [Glo84] for the

construction procedure are quite different. In a number of situations, including the case of scalar (SISO)G(s), this is the only choice.

The next step of the algorithm is to call its stable and unstable parts, call them and , always assign the matrix to , and the final step of the algorithm is

D˜G

stable( ), to separate into

stable( ) will

G˜s()

s()

G˜s()

Chapter 2 Additive Error Reduction

to choose the D matrix of Gr(s), by splitting between Gr(s) and Gu(s). This is done by using a separate function the unstable output of

stable( ), and let K(s)=G

ophiter( ). Suppose G

(–s). By applying the

(s) is

multipass Hankel reduction algorithm, described further below, K(s) is reduced to the constant K

Ks() K

(the approximation), which satisfies,

–

σ1K() ... σσ

∞

σ≤

ni1+

G() ... σ

nsni–

G()++

K()++≤

that is, if it is larger than,

s–()K0–

≤

∞

kni1+=

∑

σkG()

then one chooses:

GrG

This ensures satisfaction of the error bound for G – G

given previously,

because:

–

∞

= KK

G() σ

–– G

––

ni1+

–()+

–

∞

G() ... σ

∞

G()+++≤

Multipass Algorithm

We now explain the multipass algorithm. For simplicity in first explaining the idea, suppose that the Hankel singular values at every stage or pass are distinct.

1. Find a stable order ns – 1 approximation G

Gjω()G

ns 1–

jω–

∞

(This can be achieved by the algorithm alr eady given, and there is no unstable part of the approximation.)

Xmath Model Reduction Module 2-20 ni.com

(s) of G(s) with:

n–1

G()=

Chapter 2 Additive Error Reduction

2. Find a stable order ns – 2 approximation G

ns 1–

jω()G

ns 2–

jω()–

∞

of G

ns –2

()=

ns 1–Gns 1–

ns –1

(s), with

. . .

3. (Step ns–nr): Find a stable order nsr approximation of G

with

Then, because for ,

for , ..., this being a property of the algorithm, there follows:

isi–≤

jω()G

nsr 1+

σiG

Gjω()G

()σ

nsr

jω()–

nsr

ns 1–

iGns 2–

jω()– σ

∞

()σiG

nsr 1+Gnsr 1+

≤

insr1+=

nsr 1+Gnsr 1+

G()≤ ins<

()≤

ns 1–

()... σ

σiG()

∑

nsr +1

()=

++ G()≤

The only difference that arises when singular values have multiplicity in excess of 1 is that the degree reduction at a given step is greater. Thus, if

(G) has multiplicity k, then G(s) is approximated by G

(s) of degree

ns – k

ns – k.

No separate optimization of the D matrix of G

is required. The

nsr

approximation error bound is the same as for the first algorithm. The actual approximation error may be different. Notice that this second algorithm

nsr

jω()– Gujω()–

(s) such that

nsr 1+

∞

does not calculate an unstable G

Gjω()G

Discrete-Time Systems

No special algorithm is presented for discrete-time systems. Any stable discrete-time transfer-function matrix G(z) can be used to define a stable continuous-time transfer-function matrix by a bilinear transformation, thus

α s+

⎛⎞

Hs() G

when α is a positive constant.

------------

⎝⎠

α s–

Chapter 2 Additive Error Reduction

We use sysZ to denote G(z) and define:

bilinsys=makepoly([-1,a]/makepoly([1,a])

as the mapping from the z-domain to the s-domain. The specification is reversed because this function uses backward polynomial rotation. Hankel norm reduction is then applied to H(s), to generate, a stable reduced order approximation H

(s) and unstable Hu(s) such that:

–– σi=

rHu

– σ

+++=

iσni1+

... σ

Here, the s

are the Hankel singular values of both G(z) and H(s); they are

the same:

z 1–

⎛⎞

Grz() Hrα

z() Huα

-----------

⎝⎠

z 1+

z 1–

⎛⎞

-----------

⎝⎠

z 1+

We then implement the s-domain equivalent with:

sysS=subsys(sysZ,bilinsys)

There is no simple rule for choosing α; the choice α = 1 is probably as good as any. The orders of G

and Gu are the same as those of Hr and Hu,

respectively. The error formulas are as follows:

jω

()Gre

jω

()– G

Gejω()Gre

jω

()–

∞

jω

()–

∞σn

++≤

ni1+

...σ

Impulse Response Error

If Gr is determined by the first (single-pass) algorithm, the impulse response error (for t > 0) between the impulse responses of G and G be bounded. As shown in Corollary 9.9 of [Glo84], if G and the multiplicity of the ith larger singular value σ

σjGG

–[]σ

ji– 1+

Xmath Model Reduction Module 2-22 ni.com

G for j≤ 1 2 ... 2i 2 r+–,, ,=

G()for j≤ 2i 1– r ...,ns i 1–+,+=

is of degree i –1

of G is r, then:

can

Chapter 2 Additive Error Reduction

It follows by a result of [BoD87] that the impulse response error for t >0 satisfies:

gt() g

Evidently, Hankel norm approximation ensures some form of approximation of the impulse response too.

Unstable System Approximation

A transfer function G(s) with stable and unstable poles can be reduced by applying

stable( ) to separate G(s) into a stable and unstable part. The

former is reduced and then the unstable part can be added back on. For additional information about the Help.

Related Functions

stable(), redschur(), balmoore()

t()– 122i 2– r+()σ

ophank( ) function, refer to the Xmath

G() σjG()

+≤

∑

ir+

Multiplicative Error Reduction

This chapter describes multiplicative error reduction presenting two reasons to consider multiplicative rather than additive error reduction, one general and one specific.

Selecting Multiplicative Error Reduction

The general reason to use multiplicative error reduction is that many specifications are given using decibels; ±1 db corresponds to a multiplicative error of about 12%. Specifications regarding phase shift also can be regarded as multiplicative error statements: ±0.05 radians of phase shift is like 5% multiplicative error also.

The more specific reason arises in considering the problem of plant approximation, with a high order (possibly very high order) plant being initially prescribed, with no controller having been designed, and with a requirement to provide a simpler model of the plant, possibly to allow controller design. Consider the arrangement of Figure 3-1, controller C(s) designed for G(s)j with G(s) = (I + Δ)G(s).

Figure 3-1. Controller C(s) Designed for Multiplicative Error Reduction

The full order plant is G = (I + Δ)G, and the reduced order model is . Since , this means that Δ is the multiplicative error. Another way one could measure the multiplicative error would be as

–()G

product gives two more possibilities again. The following multiplicative robustness result can be found in [Vid85].

–()G

1–

. In the matrix plant case, interchange of the order of the

1–

Δ=

Chapter 3 Multiplicative Error Reduction

Multiplicative Robustness Result

Suppose C stabilizes , that has no jω-axis poles, and that G has the same number of poles in Re[s] ≥ 0 as . If for all ω,

Δ jω()Gˆjω()Cjω()IG

then C stabilizes G. This result indicates that if a controller C is designed to stabilize a nominal

or reduced order model , satisfaction of Equation 3-1 ensures that the controller also will stabilize the true plant G.

In reducing a model of the plant, there will be concern not just to have this type of stability property, but also concern to have as little error as possible between the designed system (based on ) and the true system (based on G). Extrapolation of the stability result then suggests that the goal should be not just to have Equation 3-1, but to minimize the quantity on the left side of Equation 3-1, or its greatest value:

max Δ jω()Gˆjω()Cjω()IG

However, there are difficulties. The principal one is that if we are reducing the plant without knowledge of the controller, we cannot calculate the measure because we do not know C(jω). Nevertheless, one could presume that, for a well designed system, will be close to I over the operating bandwidth of the system, and have smaller norm than 1 (tending to zero as ω→∞ in fact) outside the operating bandwidth of the system. This suggests that in the absence of knowledge of C, one should carry out multiplicative approximation by seeking to minimize:

Δ GG

–()G

1–

jω()Cjω()+[]

1–

(3-1)

{}

GˆCI G

C+()

jω()Cjω()+[]

1–

max Δ jω() Δj ω()

∞

This is the prime rationale for (unweighted) multiplicative reduction of a plant.

Two other points should be noted. First, because frequencies well beyond the closed-loop bandwidth, will be small, it is in a sense,

GˆCI G

1–

C+()

wasteful to seek to have Δ(jω) small at very high frequencies. The choice

maxωΔ jω()

of as the index is convenient, because it removes a requirement to make assumptions about the controller, but at the same time it does not allow to be made even smaller in the closed-loop

Xmath Model Reduction Module 3-2 ni.com

Δ jω()

Chapter 3 Multiplicative Error Reduction

bandwidth at the expense of being larger outside this bandwidth, which would be preferable.

–()G

Second, the previously used multiplicative error is . In the algorithms that follow, the error appears. It is easy to

δ GG

–()G

1–

check that:

Δ jω()

δ jω()

-------------------------------

≤

∞

1 Δ jω()

–

∞

and

δ jω()

Δ jω()

------------------------------ -

≤

∞

1 δ jω()

–

∞

This means that if either bound is small, so is the other, with the bounds approximately equal.

bst( )

Two algorithms for multiplicative reduction are presented: a mnemonic for balanced stochastic truncation, and Roughly, they relate to one another in the same way that

ophank( ) relate, that is, one focuses on balanced realization

and

bst( ),

mulhank( ).

redschur( )

truncation and the other on Hankel norm approximation. Some of the similarities and differences are as follows:

• When the errors are small, the error bound formula for about one half of that for

•With

bst( ), the actual multiplicative error as a function of frequency

bst( ).

bst( ) is

goes to zero as ω→∞ (or, after using an optional transformation given in the algorithm description, to zero as ω→ 0); with

mulhank( ), the

error tends to be more uniform as a function of frequency.

•

bst( ) can handle nonsquare reduction, while mulhank( ) cannot.

• Both algorithms are restricted to stable G(s); both preserve right half plane zeros, that is, these zeros are copied into the reduced order object; both have difficulties with jω-axis zeros of G(s), but these difficulties are not insuperable.

[SysR,HSV] = bst(Sys,{nsr,left,right,bound,method})

The bst( ) function calculates a balanced stochastic truncation of Sys for the multiplicative case.

Chapter 3 Multiplicative Error Reduction

∞

The objective of the algorithm is to approximate a high-order stable transfer function matrix G(s) by a lower-order G

(g-gr)inv(g) minimized, under the condition that G

prescribed order.

Restrictions

This function has the following restrictions:

• The user must ensure that the input system is stable and nonsingular at s = infinity .

• The algorithm may be problematic if the input system has a zero on the jω-axis.

• Only continuous systems are accepted; for discrete systems use

makecontinuous( ) before calling bst( ), then discretize the

result.

Sys=bst(makecontinuous(SysD));

SysD=discretize(Sys);

Algorithm

The modifications described in this section allow you to circumvent the previous restrictions.

(s) with either inv(g)(g-gr) or

is stable and of the

The objective of the algorithm is to approximate a high order stable transfer function matrix G(s) by a lower order G either or

–()G

under the constraint that G

1–

G1–GG

∞

is stable and of prescribed order nsr. In case

(s) with, in the square G(s) case,

–()

(approximately) minimized,

G is not square but has full row rank, the algorithm seeks to minimize:

–()

GG*()1–GG

Recall that so that when ,

s() X′ s–()= sj

jω() X

–()

jω()=

∞

When G is not square but has full column rank, the algorithm seeks to minimize:

–()G

Xmath Model Reduction Module 3-4 ni.com

G()1–GG

–()

* ∞

Chapter 3 Multiplicative Error Reduction

These cases are secured with the keywords right and left, respecti v ely. If the wrong option is requested for a nonsquare G(s), an error message will result.

The algorithm has the property that right half plane zeros of G(s) remain as right half plane zeros of G zeros in Re[s] > 0, G

zeros in Re[s] > 0 it would not be proper, [Gre88].

(s). This means that if G(s) has order nsr with n+

(s) must have degree at least n+, else, given that it has

The conceptual basis of the algorithm can best be grasped by considering the case of scalar G(s) of degree n. Then one can form a minimum phase,

stable W(s) with |W(jω)|

–1

function) W

(–s) G(s). This all pass function has a mixture of stable and

= |G(jω)|2 and then an all-pass function (the phase

unstable poles, and it encodes the phase of G(jω). Its stable part has n Hankel singular values σ

with σi ≤ 1, and the number of σi equal to 1 is the

same as the number of zeros of G(s) in Re[s] > 0. State-variable realizations

–1

of W,G and the stable part of W and when the stable part of W

(–s)G(s) can be connected in a nice way,

–1

(–s)G(s) has a balanced realization, we say

that the realization of G is stochastically balanced. Truncating the balanced

–1

realization of the stable part of W

(–s)G(s) induces a corresponding truncation in the realization of G(s), and the truncated realization defines an approximation of G. Further, a good approximation of a transfer function encoding the phase of G somehow ensures a good approximation, albeit in a multiplicative sense, of G itself.

Algorithm with the Keywords right and left

The following description of the algorithm with the keyword right is based on ideas of [GrA86] developed in [SaC88]. The procedure is almost the same when algorithm finds an approximation in the same manner as for transposes the approximation to yield the desired G

1. The algorithm checks

• That the system is state-space, continuous, and stable

• That a correct option has been specified if the plant is nonsquare

• That D is nonsingular; if the plant is nonsquare, DD´ must be

left is specified, except the transpose of G(s) is used; the

(s).

nonsingular

right, but

Chapter 3 Multiplicative Error Reduction

2. With G(s)=D + C(sI – A)–1B and stable, with DD´ nonsingular and G(jω) G'(–jω) nonsingular for all ω, part of a state v ariable realization of a minimum phase stable W(s) is determined such that W´(–s)W(s) = G(s)G´(–s) with

Ws() D

WCW

sI A

1–

–()

The state variable matrices in W(s) are obtained as follows. The controllability grammian P associated with G(s) is first found from

AP + PA´ +BB´=0 then A

=A, B

=PC´+BD´.

When G(s) is square, the algorithm checks to see if there is a zero or singularity of G(s) close to the jω-axis (the zeros are given by the eigenvalues of A – BD

schur( )). If one is found, you are warned that results may be

–1

C and are computed reliably with the aid of

unreliable. Next, a stabilizing solution Q is found for the following Riccati equation:

′

QA A

singriccati( ) function is used; failure of the nonsingularity

The

QCB′

–()′DD′()

1–

′

Q–()++ 0=

condition on G(jω)G´(–jω) will normally result in an error message that no stabilizing solution exists. To obtain the best numerical results,

singriccati( ) is invoked with the keyw ord {method="schur"}.

Although D

, CW are not needed for the remainder of the algorithm,

they are simply determined in the square case by

D′C

D1–CB

′

Q–()==

with minor modification in the nonsquare case. The real point of the algorithm is to compute P and Q; the matrix Q satisfies (square or nonsquare case).

′

QA A

′

++ 0=

P, Q are the controllability and observ ability grammians of the transfer function C the strictly proper, stable part of θ(s)=W

(sI – A)–1B. This transfer function matrix, it turns out, is

–T

(–s)G(s), which obeys the matrix all-pass property θ(s)θ´(–s)=I, and is the phase matrix associated with G(s).

3. Compute ordered Schur decompositions of PQ, with the eigenvalues of PQ is ascending and descending order. Obtain the phase matrix Hankel singular values, that is, the Hankel singular values of the

Xmath Model Reduction Module 3-6 ni.com

Chapter 3 Multiplicative Error Reduction

strictly proper stable part of θ(s), as the square roots of the eigenvalues of PQ. Call these quantities ν

. The Schur decompositions are,

where V

′

PQVAS

, VD are orthogonal and S

= V

asc

′

PQVDS

, S

asc

are upper triangular.

des

4. Define submatrices as follows, assuming the dimension of the reduced order system

nsr is known:

= V

lbig

nsr

rbig

nsr

Determine a singular value decomposition,

ebigSebigVebig

′

lbig

rbig

and then define transformation matrices:

lbig

rbig

The reduced order system G

′

lbig

rbig

lbigUebigSebig

rbigVebigSebig

is:

12⁄–

′

lbig

rbig

where step 4 is identical with that used in the matrices P, Q which determine V

, VD and so forth, are the

controllability and observability grammians of C

–1

than of C(sI – A)

B, the controllability grammian of G(s) and the

D=A

redschur( ), except

(sI – A)–1B rather

observability grammian of W(s). The error formula [WaS90] is:

1–

–()

All ν

obey νi ≤ 1. One can only eliminate νi where νi < 1. Hence, if nsr is

chosen so that ν algorithm also checks that

= 1, the algorithm produces an error message. The

nsr + 1

nsr does not exceed the dimension of a minimal

≤

∞

∑

------------ -

1 v

–

(3-2)

Chapter 3 Multiplicative Error Reduction

state-variable representation of G. In this case, the user is effecti vely asking

= G. When the phase matrix has repeated Hankel singular values,

for G

they must all be included or all excluded from the model, that is,

= ν

nsr

is not permitted; the algorithm checks for this.

nsr + 1

The number of ν as mentioned already, these zeros remain as zeros of G

error is specified, then the error bound formula (Equation 3-2) in

If conjunction with the ν For nonsquare G with more columns than rows, the error formula is:

If the user is presented with the ν intelligently choosing be tight, except when nsr = ns –1.

Securing Zero Error at DC

The error G–1(G – Gr) as a function of frequency is always zero at ω = ∞. When the algorithm is being used to approximate a high order plant by a low order plant, it ma y be preferable to secure zero error at ω = 0. A method for doing this is discussed in [GrA90]; for our purposes:

1. We need a bilinear transformation of sys = 1/z. Given G(s) we generate H(s) through:

bilinsys=makepoly([b3,b4]/makepoly([b1,b2])

sys=subsys(sys,bilinsys)

2. Reduce with the previous algorithm:

[sr,nsr,hsv] = bst(sys)

3. Use the bilinear transformation s = 1/z again:

[sr1,nsr1] = bilinear(sr,nsr,[0,1,1,0])

equal to 1 is the number of zeros in Re[s]>0 of G(s), and

(s).

values from step 3 is used to define nsr for step 4.

∑

------------ -

1 v

–

≤

insr1+=

–()

nsr. However, the error bound is not guaranteed to

G*G()1–GG

–()

, the error formula provides a basis for

12⁄ ∞

The νi are the same for G(s) and H(s)=G(s–1). The error bound formula is the same; H is stable and H(jω)H'(–jω) of full rank for all ω including ω = ∞ if and only if G has the same property; right half plane zeros of G are

–1

still preserved by the algorithm. The error G

(G – Gr), though now zero at

ω = 0, is in general nonzero at ω = ∞.

Xmath Model Reduction Module 3-8 ni.com

Chapter 3 Multiplicative Error Reduction

∞

Hankel Singular Values of Phase Matrix of G

The νi, i = 1,2,...,ns have been termed above the Hankel singular values of the phase matrix associated with G. The corresponding quantities for G

, i = 1,..., nsr.

Further Error Bounds

The introduction to this chapter emphasized the importance of the error measures

–()G

1–

for plant reduction, as opposed to or The BST algorithm ensures that in addition to (Equation 3-2), there holds

[WaS90a].

which also means that for a scalar system,

1–

–()

----- -

8.69≤ 2

20log

1–

G1–GG

–()G

∑

------------ -

1 v

–

------------ -

1 v

–

≤

∞

insr1+=

⎛⎞ ⎜⎟ ⎜⎟ ⎝⎠

insr1+=

–()

are

∞

and, if the bound is small:

phase G()phase G

()–

insr1+=

∑

------------ -

1 v

–

radians≤

Reduction of Minimum Phase, Unstable G

For square minimum phase but not necessarily stable G, it also is possible to use this algorithm (with minor modification) to try to minimize (for G of a certain order) the error bound

–()G

r1–∞

Chapter 3 Multiplicative Error Reduction

which also can be relevant in finding a reduced order model of a plant. The procedure requires G again to be nonsingular at ω = ∞, and to hav e no jω-axis poles. It is as follows:

1. Form H = G then H is described by A – BD stable, and of full rank on the jω-axis.

2. Form H

3. Set Gr = H Observe that

–1

. If G is described by state-v ariable matrices A, B, C, D,

of the desired order to minimize approximately:

–1

C, BD–1, –D–1C, D–1. H is square,

1–

–()

∞

H1–HH

–()IH

The reduced order G

will have the same poles in Re[s]>0 as G, and

be minimum phase.

Imaginary Axis Zeros (Including Zeros at ∞)

We shall now explain how to handle the reduction of G(s) which has a rank drop at s = ∞ or on the jω-axis. The key is to use a bilinear transformation, [Saf87]. Consider the bilinear map defined by

-------------------=

-------------- -= bs 1+

–1

where 0 < a < b

and mapping G(s) into through:

G˜s() G

1–

IGG

–=

1–

G–()G

za– bz– 1+

sa+

G˜s()

sa–

⎛⎞

-------------------

⎝⎠

bs– 1+

1–

Gs() G

Xmath Model Reduction Module 3-10 ni.com

⎝⎠

bs 1+

sa+

⎛⎞

-------------- -

Chapter 3 Multiplicative Error Reduction

⎠

⎞

The values of G(s), as shown in Figure 3-2, along the jω-axis are the same as the values of around a circle with diameter defined by

–1

[a – j0, b

+ j 0] on the positive real axis.

G˜s()

1–

Gs()

s()

valuesvalues

Figure 3-2. Bilinear Mapping from G(s) to (Case 1)

Also, the values of , as shown in Figure 3-3, along the jω-axis are

G˜s()

the same as the values of G(s) around a circle with diameter defined by

–1

+ j0, –a + j 0].

[–b

1–

Gs()

-a

G˜s()

valuesvalues

Figure 3-3. Bilinear Mapping from G(s) to (Case 2)

G˜s()

We can implement an arbitrary bilinear transform using the subsys( ) function, which substitutes a given transfer function for the s- or z-domain operator.

sa–

⎛

-------------------

To implement use:

gtildesys=subsys(gsys,makep([-b,1]/makep([1,-a])

To implement use:

gsys=subsys(gtildesys,makep([b,1]/makep([1,a])

G˜s() G

Gs() G

⎝

bs– 1+

sa+

⎛⎞

-----------

⎝⎠

s 1+

Note

The systems substituted in the previous calls to subsys invert the function

specification because these functions use backward polynomial rotation.

Chapter 3 Multiplicative Error Reduction

)

⎠

⎞

Any zero (or rank reduction) on the jω-axis of G(s) becomes a zero (or rank reduction) in Re[s] > 0 of , and if G(s) has a zero (or rank reduction) at infinity, this is shifted to a zero (o r rank reduction) of at the point

–1

, (in Re[s] > 0). If all poles of G(s) are inside the circle of diameter

–1

+ j0, a + j0], all poles of will be in Re[s] < 0, and if G(s) has no

[–b zero (or rank reduction) on this circle, will have no zero (or rank reduction) on the jω-axis, including ω = ∞.

G˜s()

G˜s(

G˜s()

If G(s) is nonsingular for almost all values of s, it will be nonsingular or

–1

have no zero or rank reduction on the circle of diameter [–b

+ j 0, –a + j 0] for almost all choices of a,b. If a and b are chosen small enough, G(s) will have all its poles inside this circle and no zero or rank reduction on it, while

G˜s()

then will have all poles in Re[s] < 0 and no zero or rank reduction on the jω-axis, including s = ∞. The steps of the algorithm, when G(s) has a zero on the jω-axis or at s = ∞, are as follows:

–1

1. For small a,b with 0 < a < b

gtildesys.

2. Reduce to , this being possible because is stable and

G˜s() G

s() G˜s()

, form as shown for

G˜s() G

sa–

⎛

-------------------

⎝

bs– 1+

has full rank on s = jω, including ω = ∞.

sa+

⎛⎞

3. Form as shown for The error will be overbounded by the error

1–

G˜G

–()

s() G

1–

, and G

∞

-------------- -

⎝⎠

bs 1+

–()

∞

will contain the same zeros in Re[s] ≥ 0 as G.

gsys.

If there is no zero (or rank reduction) of G(s) at the origin, one can take

–1

a =0 and b needed, and at the very least b lie in the circle of diameter [–b

= bandwidth over which a good approximation of G(s) is

–1

sufficiently large that the poles of G(s)

–1

+ j 0, –a + j 0]. If there is a zero or rank reduction at the origin, one can replace a =0 by a = b. It is possible to take b too small, or, if there is a zero at the origin, to take a too small. The user will be presented with an error message that there is a jω-axis zero and/or that the Riccati equation solution may be in error. The basic ex planation is that as b → 0, and thus a → 0, the zeros of approach those of G(s). Thus, for sufficiently small b, one or more zeros of may be identified

G˜s()

s()

as lying on the imaginary axis. The remedy is to increase a and/or b above the desirable values.

The procedure for handling jω-axis zeros or zeros at infinity will be deficient if the number of such zeros is the same as the order of G(s)—for example, if G(s) = 1/d(s), for some stable d(s). In this case, it is possible

Xmath Model Reduction Module 3-12 ni.com

Chapter 3 Multiplicative Error Reduction

again with a bilinear transformation to secure multiplicative approximations over a limited frequency band. Suppose that

⎛⎞

G˜s() G

--------------

⎝⎠

εs 1+

Create a system that corresponds to with:

gtildesys=subs(gsys,(makep([-eps,1])/makep([1,-]))

bilinsys=makep([eps,1])/makep([1,0])

sys=subsys(sys,bilinsys)

G˜s()

Under this transformation:

• Values of G(s) along the jω-axis correspond to values of around a circle in the left half plane on diameter (–ε

• Values of along the jω-axis correspond to values of G(s) around

G˜s()

a circle in the right half plane on diameter (0, ε

Multiplicative approximation of (along the jω-axis) corresponds to

G˜s()

–1

+ j 0, 0).

–1

G˜s()

+ j 0).

multiplicative approximation of G(s) around a circle in the right half plane, touching the jω-axis at the origin. For those points on the jω-axis near the circle, there will be good multiplicative approximation of G(jω). If it is desired to have a good approximation of G(s) over an interval [–j Ω, jΩ],

–1

then a choice such as ε

= 5 Ω or 10 Ω needs to be made. Reduction then

proceeds as follows:

1. Form .

2. Reduce through

3. Form with:

G˜s()

bst( ).

s 1 εs–()⁄()–=

G˜s()

s() G

gsys=subsys(gtildesys(gtildesys,

makep([-eps,-1])/makep[-1,-0]))

Notice that the number of zeros of G(s) in the circle of diameter

1–

, j0+()s

0 ε

sets a lower bound on the degree of G plane zeros of , and must be preserved by

G˜s()

(s)—for such zeros become right half

bst( ). Obviously , zeros at

s = ∞ are never in this circle, so a procedure for reducing G(s) = 1/d(s) is available.

Chapter 3 Multiplicative Error Reduction

∞

There is one potential source of failure of the algorithm. Because G(s) is stable, certainly will be, as its poles will be in the left half plane circle on diameter . If acquires a pole outside this circle (but still in the left half plane of course)—and this appears possible in principle—G be encountered, a smaller value of ε should be used.

Related Functions

redschur(), mulhank()

mulhank( )

[SysR,HSV] = mulhank(Sys,{nsr,left,right,bound,method})

The mulhank( ) function calculates an optimal Hankel norm reduction of

Sys for the multiplicative case.

Restrictions

This function has the following restrictions:

• The user must ensure that the input system is stable and nonsingular at s =infinity.

• The algorithm may be problematic if the input system has a zero on the jω-axis.

• Only continuous systems are accepted; for discrete systems use

makecontinuous( ) before calling mulhank( ), then discretize

the result.

Sys=mulhank(makecontinuous(SysD));

SysD=discretize(Sys);

G˜s()

ε– j00,=()G

(s) will then acquire a pole in Re [s] > 0. Should this difficulty

s()

Algorithm

The objective of the algorithm, like bst( ), is to approximate a high order square stable transfer function matrix G(s) by a lower order G

either or (approximately) m ini mized,

–()G

under the constraint that G

1–

G1–GG

–()

∞

is stable and of prescribed order.

The algorithm has the property that right half plane zeros of G(s) are retained as zeros of G zeros in Re[s] > 0, G

zeros in Re[s] > 0 it would not be proper, [GrA89].

has N

Xmath Model Reduction Module 3-14 ni.com

(s). This means that if G(s) has order NS with N+

(s) must have degree at least N+—else, given that it

(s) with

right and left

Chapter 3 Multiplicative Error Reduction

The conceptual basis of the algorithm can best be grasped by considering the case of scalar G(s) of degree n. Then one can form a minimum phase,

stable W(s) with |W(jω)|

–1

function) W

(–s) G(s). This all-pass function has a mixture of stable and

= |G(jω)|2 and then an all-pass function (the phase

unstable poles, and it encodes the phase of G(jω). Its stable part has n Hankel singular values σ

with σi ≤ 1, and the number of σi equal to 1

is the same as the number of zeros of G(s) in Re[s]>0. State-variable

–1

realizations of W,G and the stable part of W

(–s)G(s) can be connected in

a nice way . The algorithm computes an additiv e Hankel norm reduction of

–1

the stable part of W multiplicity of the smallest σ

(–s)G(s) to cause a degree reduction equal to the

. The matrices defining the reduced order

object are then combined in a new way to define a multiplicative approximation to G(s); as it turns out, there is a close connection between

–1

additive reduction of the stable part of W

(–s)G(s) and multiplicative reduction of G(s). The reduction procedure then can be repeated on the new phase function of the just found approximation to obtain a further reduction again in G(s).

A description of the algorithm for the keyword right follows. It is based on ideas of [Glo86] in part developed in [GrA86] and further developed in [SaC88]. The procedure is almost the same when

{left} is specified,

except the transpose of G(s) is used; the following algorithm finds an approximation, then transposes it to yield the desired G

(s).

1. The algorithm checks that G(s) is square, stable, and that the transfer

function is nonsingular at infinity.

2. With G(s) = D + C(sI–A)

rank(d) must equal number of rows in d] and G(jω) nonsingular for

[

–1

B square and stable, with D nonsingular

all finite ω, this step determines a state variable realization of a minimum phase stable W(s) such that,

W´(–s)W(s) = G(s)G´(–s) with: W(s) = D

w+Cw

(sI–Aw)–1B

The various state variable matrices in W(s) are obtained as follo ws. The controllability grammian P associated with G(s) is first found from AP + PA´ + BB´ = 0, then:

=ABw=PC´+BD´Dw=D´

The algorithm checks to see if there is a zero or singularity of G(s) close to the jω-axis. The zeros are determined by calculating the

Chapter 3 Multiplicative Error Reduction

eigenvalues of A – B/D * C with the aid of schur( ). If any real part of the

Next, a stabilizing solution Q is found for the following Riccati equation:

eigenvalues is less than eps, a warning is displayed.

QA A′QCB′

The function

Q–()′DD′()

singriccati( ) is used; failure of the nonsingularity

1–

′

Q–()++ 0=

condition of G(jω) will normally result in an error message. To obtain the best numerical results, keyword

The matrix C

method="schur".

is given by .

Notice that Q satisfies , so that P and Q are

singriccati( ) is invoked with the

D1–CB′

QA A′QC′

++ 0=

wCw

Q–()=

the controllability and observability grammians of

Fs() C

sI A–()1–B=

This strictly proper, stable transfer function matrix is the strictly proper, stable part (under additive decomposition) of

θ(s)=W

–T

(–s)G(s), which obeys the matrix all pass property

θ(s)θ'(–s)=I. It is the phase matrix associated with G(s).

3. The Hankel singular values ν computed, by calling

hankelsv( ). The value of nsr is obtained if

Fs() C

of are

sI A–()1–B=

not prespecified, either by prompting the user or by the error bound formula ([GrA89], [Gre88], [Glo86]).

nsr 1+

G1–GG

≤≤

–()

∞

jnsr1+=

∏

1 v

+()1–

(3-3)

(with ν

i≥νi +1

k, (that is, ν

≥ ⋅⋅⋅ being assumed). If ν

has multiplicity greater than unity), then νk appears once

= ν

k +1

=...=ν

for some

k + r

only in the previous error bound formula. In other words, the number of terms in the product is equal to the number of distinct ν

. There are restrictions on nsr. nsr cannot exceed the dimension

nsr

of a minimal realization of G(s); although ν

> n

nsr

number of ν They must be retained in G be equal to the number of ν

; and while 1 ≥ νi for all i, it is necessary that 1>

nsr+1

equal to 1 is the number of right half plane zeros of G(s).

(s), so the order of Gr(s), nsr, must at least

equal to 1.) The software checks all these

⋅⋅⋅, nsr must obey

i≥i +1

less than

nsr +1

. (The

conditions. The minimum order permitted is the number of Hankel

Xmath Model Reduction Module 3-16 ni.com

Chapter 3 Multiplicative Error Reduction

singular values of F(s) larger than 1– ε (refer to steps 1 through 3 of the

Restrictions section). The maximum order permitted is the number of

nonzero eigenvalues of W

4. Let r be the multiplicity of ν

larger than ε.

cWo

. The algorithm approximates

Fs() C

by a transfer function matrix of order ns – r, using Hankel norm

Fˆs()

sI A–()1–B=

approximation. The procedure is slightly different from that used in

ophank( ).

Construct an SVD of :

= V′ U

I– U

of dimension (ns – r) × (ns – r) and nonsingular. Also, obtain

with Σ

QP v

I–

′

[]

1U2

′

an orthogonal matrix T, satisfying:

B2C′

where and are the last r rows of and , the state variable

C′

matrices appearing in a balanced realization of . It is possible to calculate T without evaluating , as it turns out (refer

T+ 0=

B C

C′

B C

′

sI A–()

1–

to [AnJ]), and the algorithm does this. Now with

Fˆs() D

s() C

sI A

–()B

1–

–() ˆ

there holds:

1–

′

CwPv

1–

v–nsT=

A′ QAP vnsC

′

QB vnsC

+[]=

TB′+()V′=

′T w

′

TB′–+[]V

Chapter 3 Multiplicative Error Reduction

Note The expression is the strictly proper part of . The matrix

1–

when

Fs() F

s()–[]

ophank( ) is used to find a Hankel norm approximation of F(s).

5. The algorith m constructs and , which satisfy,

s() Fˆs()

is all pass; this property is not always secured in the multivariable case

s() Gs() W ′ s–()Fs() Fˆs()–[]–=

and,

Wˆs() Iv

Ws() Fs() F

T′–()IvnsT–()

1–

s()–[]G′– s–()+{}

through the state variable formulas

′

=()

Gˆs() DI v

T–()()DC

UΣ

+[]sI A

–()

and:

T′–()D′ IvnsT′–()IvnsT–()

Wˆs() Iv

sI A

–()

1–

D′ V

′

C′+[]

1–

Continue the reduction procedure, starting with , , and repeating the process till G For example, in the second iteration, is given by:

Gˆs() Gˆs() W

of the desired degree nsr is obtained.

′– s–()F

s()

s() F

GˆWˆF

s()–[]+=

(3-4)

Consequences of Step 5 and Justification of Step 6

A number of properties are true:

• is of order ns – r, with:

Gˆs()

1–

–()

Xmath Model Reduction Module 3-18 ni.com

∞

(3-5)

Chapter 3 Multiplicative Error Reduction

Wˆs() Gˆs

• and stand in the same relation as W(s) and G(s), that is: ˆ

– – With , there holds

′ s–()W

PˆAˆ′

s() Gˆs()G

+ B

′ s–()=

Bˆ′

–=

′

PˆC

′

D′ V

– With there holds

QˆA

C′+ P

+ Cˆ′–

B′WU1Σ

+()′B

′

1–

B′

–()=

T′–()D′+=

1–

T′–()IvnsT–()

–

D′

– is the stable strictly proper part of .

• The Hankel singular values of (and ) are the first as – r Hankel

B′WU1Σ1B

DI v

–()+{}

1–

T–()[]

D′ V

C′+[]′Q

1–

s–()()G

s()

singular values of F,

1–

PˆΣ

QˆV

• has the same zeros in Re[s] > 0 as G(s).

Gˆs

′

QV1V

′

PU1Σ1Σ1U

′

QU1Σ

′

1–

These properties mean that one is immediately positioned to repeat the reduction procedure on , with almost all needed quantities being on

Gˆs

hand.

Chapter 3 Multiplicative Error Reduction

Error Bounds

The error bound formula (Equation 3-3) is a simple consequence of iterating (Equation 3-5). To illustrate, suppose there are three reductions

→→ → , each by degree one. Then,

GGˆG

GˆG

1–

GˆG

1–

ˆ ˆ

–()=

GˆG

1–

–()+

G1–GG

–()G

1–

Also,

1–

1 v

+≤

1–

G–()I+=

Similarly,

1–

1 v

+≤ G

ns 1–

1–

1 v

+≤,

ns 2–

Then:

G1–GG

–()v

1 v

+()1 v

+()v

ns 1–

+()1 v

ns 1–

1 v

++≤

+()= 1–

+()v

ns 1–

ns 2–

The error bound (Equation 3-3) is only exact when there is a single reduction step. Normally, this algorithm has a lower error bound than

bst( ); in particular, if the ν

are all distinct and , the error

nsr 1+

1«

bounds are approximately

for mulhank( ) for bst(

∑

insr1+=

Xmath Model Reduction Module 3-20 ni.com

insr1+=

∑

Chapter 3 Multiplicative Error Reduction

For mulhank( ), this translates for a scalar system into

86.9 v

–

∑

insr1+=

dB 20 log

< G

< dB

G⁄

nsr

8.69 v

∑

insr1+=

and

phase error v

The bounds are double for

bst( ).

The error as a function of frequency is always zero at ω = ∞ for (or at ω = 0 if a transformation s → s property of the error holds for

mulhank( ).

Imaginary Axis Zeros (Including Zeros at ∞)

When G(jω) is singular (or zero) on the jω axis or at ∞, reduction can be handled in the same manner as explained for

The key is to use a bilinear transformation [Saf87]. Consider the bilinear map defined b y

-------------------=

-------------- -= bs 1+

where 0 < a < b

–1

and mapping G(s) into through

radians

∑

insr1+=

–1

is used), whereas no such particular

bst( ).

bst( )

za–

bz– 1+

sa+

G˜s()

sa–

⎛⎞

G˜s() G

Gs() G

-------------------

⎝⎠

bs– 1+

sa+

⎛⎞

-------------- -

⎝⎠

bs 1+

Chapter 3 Multiplicative Error Reduction

⎠

⎞

⎠

⎞

⎠

⎞

The values of G(s) along the jω-axis are the same as the values of around a circle with diameter defined by [a – j 0, b real axis (refer to Figure 3-2). Also, the values of along the jω-axis

–1

+ j 0] on the positive

G˜s()

are the same as the values of G(s) around a circle with diameter defined by

–1

+ j0, –a + j 0].

[–b We can implement an arbitrary bilinear transform using the

function, which substitutes a given transfer function for the s- or z-domain operator, as previously shown.

To implement use:

gtildesys=subsys(gsys,makep([-b,1]/makep([1,-a])

To implement use:

gsys=subsys(gtildesys,makep([b,1]/makep([1,a])

The systems substituted in the previous calls to subsys invert the function

Note

G˜s() G

Gs() G

⎛ ⎝

⎝

bs– 1+

sa+

-------------- -

bs 1+

sa–

⎛

-------------------

specification because these functions use backward polynomial rotation.

Any zero (or rank reduction) on the jω-axis of G(s) becomes a zero (or rank reduction) in Re[s] > 0 of , and if G(s) has a zero (or rank reduction)

G˜s()

at infinity, this is shifted to a zero (o r rank reduction) of at the point

–1

, again in Re[s] > 0. If all poles of G(s) are inside the circle of diameter

–1

+ j0, a + j0], all poles of will be in Re[s] < 0, and if G(s) has no

[–b zero (or rank reduction) on this circle, will have no zero (or rank

G˜s()

reduction) on the jω-axis, including ω = ∞.

G˜s()

subsys( )

G˜s()

If G(s) is nonsingular for almost all values of s, it will be nonsingular or

–1

have no zero or rank reduction on the circle of diameter [–b

+ j0, –a + j 0] for almost all choices of a,b. If a and b are chosen small enough, G(s) will have all its poles inside this circle and no zero or rank reduction on it, while

then will have all poles in Re[s] < 0 and no zero or rank reduction on

G˜s()

the jω-axis, including s = ∞. The steps of the algorithm, when G(s) has a zero on the jω-axis or at s = ∞,

are as follows:

sa–

–1

1. For small a,b with 0 < a < b

gtildesys.

2. Reduce to , this being possible because is stable and

G˜s() G

s() G˜s()

, form as shown for

G˜s() G

⎛

-------------------

⎝

bs– 1+

has full rank on s = jω, including ω = ∞.

sa+

⎛⎞

3. Form as shown for

Xmath Model Reduction Module 3-22 ni.com

s() G

-------------- -

⎝⎠

bs 1+

gsys.

Chapter 3 Multiplicative Error Reduction

1–

–()

1–

G˜G

–()

, and G

∞

will contain the same zeros in Re[s] ≥ 0 as G.

The error will be overbounded by the error

If there is no zero (or rank reduction) of G(s) at the origin, one can take

–1

a =0 and b needed, and at the very least b lie in the circle of diameter [–b

= bandwidth over which a good approximation of G(s) is

–1

sufficiently large that the poles of G(s)

–1

+ j 0, –a + j 0]. If ther e is a zero or rank reduction at the origin, one can replace a =0 by a = b. It is possible to take b too small, or, if there is a zero at the origin, to take a too small. In these cases an error message results, saying that there is a jω-axis zero and/or that the Riccati equation solution may be in error. The basic e xplanation is that as b → 0, and thus a → 0, the zeros of approach those of G(s). Thus, for sufficiently small b, one or more zeros of may be identified as

G˜s()

lying on the imaginary axis. The remedy is to increase a and/or b above the desirable values.

The previous procedure for handling jω-axis zeros or zeros at infinity will be deficient if the number of such zeros is the same as the order of G(s); for example, if G(s) = 1/d(s), for some stable d(s). In this case, it is possible again with a bilinear transformation to secure multiplicative approximations over a limited frequency band. Suppose that

⎛⎞

G˜s() G

Create a system that corresponds to with:

gtildesys=subs(gsys,(makep([-eps,1])/makep([1,-]))

bilinsys=makep([eps,1])/makep([1,0])

sys=subsys(sys,bilinsys)

--------------

⎝⎠

εs 1+

G˜s()

Under this transformation:

• Values of G(s) along the jω-axis correspond to values of around

a circle in the left half plane on diameter (–ε

• Values of along the jω-axis correspond to values of G(s) around

G˜s()

a circle in the right half plane on diameter (0, ε

–1

+ j0, 0).

–1

+ j0).

G˜s()

Chapter 3 Multiplicative Error Reduction

Multiplicative approximation of (along the jω-axis) corresponds to

G˜s()

multiplicative approximation of G(s) around a circle in the right half plane, touching the jω-axis at the origin. For those points on the jω-axis near the circle, there will be good multiplicative approximation of G(jω). If a good approximation of G(s) over an interval [–jΩ, jΩ] it is desired, then

–1

= 5 Ω or 10 Ω are good choices. Reduction then proceeds as follows:

1. Form .

2. Reduce through

3. Form with:

G˜s()

s() G

gsys=subsys(gtildesys(gtildesys,

makep([-eps,-1])/makep[-1,-0]))

bst( ).

s 1 εs–()⁄()–=

Notice that the number of zeros of G(s) in the circle of diameter (0, ε–1 + j 0) sets a lower bound on the degree of G plane zeros of , and must be preserved by

G˜s()

(s)—for such zeros become right half

bst( ). Zeros at s = ∞ are

never in this circle, so a procedure for reducing G(s)=1/d(s) is available. There is one potential source of failure of the algorithm. Because G(s) is

G˜s()

stable, certainly will be, as its poles will be in the left half plane circle on diameter . If acquires a pole outside this circle

1–

ε–

j00,=()

s()

(but still in the left half plane of course)—and this appears possible in principle—G

(s) will then acquire a pole in Re [s] >0. Should this difficulty

be encountered, a smaller value of ε should be used.

Related Functions

singriccati(), ophank(), bst(), hankelsv()

Xmath Model Reduction Module 3-24 ni.com

Frequency-Weighted Error Reduction

This chapter describes frequency-weighted error reduction problems. This includes a discussion of controller reduction and fractional representations.

Introduction

Frequency-weighted error reduction means that the error is measured not, as previously, by

Gjω()G

but rather by

Gjω()G

Wjω()Gjω()G–

where W,V are certain weighting matrices. Their presence reflects a desire that the approximation process be more accurate at certain frequencies (where V or W have large singular values) than at others (where they have small singular values). For scalar G(jω), all the indices above are effectively the same, with the effective weight just |V(jω)|, |W(jω)|, or |W(jω)V(jω)|.

When the system G is processing signals which do not have a flat spectrum, and is to be approximated, there is considerable logic in using a weight. If the signal spectrum is Φ(jω), then taking V(jω) as a stable spectral factor

Wjω()Gjω()G–

jω()Vjω()–

jω()[]Vjω()

jω()–

∞

jω()[]

∞

(4-1)

(4-2)

(4-3)

Chapter 4 Frequency-Weighted Error Reduction

(so that ) is logical. However, a major use of weighting is in

controller reduction, which is now described.

Controller Reduction

Frequency weighted error reduction becomes particularly important in reducing controller dimension. The LQG and design procedures lead to controllers which have order equal to, or roughly equal to, the order of the plant. Very often, controllers of much lower order will result in acceptable performance, and will be desired on account of their greater simplicity.

It is almost immediately evid ent that (unweighted) additiv e approximation of a controller will not necessarily ensure closeness of the behavior of the two closed-loop systems formed from the original and reduced order controller together with the plant. This behavior is dependent in part on the plant, and so one would expect that a procedure for approximating controllers ought in some way to reflect the plant. This can be done several ways as described in the Controller Robustness Result section. The following result is a trivial variant of one in [V id85] dealing with robustness in the face of plant variations.

Controller Robustness Result

Suppose that a controller C stabilizes a plant P, and that C order) approximation to C with the same number of unstable poles. Then

stabilizes P also provided

Φ=

∞

is a (reduced

Cjω()C

jω()–[]Pjω()ICjω()Pjω()+[]

1–

∞

IP+ jω()Cjω()[]

An extrapolation to this thinking [AnM89] suggests that C

1–

Pjω()Cjω()Crjω()[]()

∞

will be a good

approximation to C (from the viewpoint of some form of stability robustness) if

–()PI CP+()

1–

∞

Xmath Model Reduction Module 4-2 ni.com

–()PI CP+()

1–

∞

Chapter 4 Frequency-Weighted Error Reduction

is minimized (and of course is less than 1). Notice that these two error measures are like those of Equation 4-1 and Equation 4-2. The fact that the plant ought to show up in a good formulation of a controller reduction problem is evidenced by the appearance of P in the two weights.

It is instructive to consider the shape of the weighting matrix or function

+ CP)–1. Consider the scalar plant case. In the pass band, |PC| is likely

to be large, and if this is achieved by having |C | large, then |P(

+ CP)–1|

will be (approximately) small. Also outside the plant bandwidth,

+ CP)–1| will be small. This means that it will be most likely to take its

|P( biggest values at frequencies near the unity gain cross-over frequenc y . This means that the approximation C

is being forced to be more accurate near

this frequency than well away from it—a fact very much in accord with classical control, where one learns the importance of good loop shaping round this frequency.

The above measures E stability, and the need for its preservation in approximating C by C

and EOS are advanced after a consideration of

. If one

takes the viewpoint that the important thing to preserve is the closed-loop transfer function matrix, a different error measure arises. With T, T

denoting the closed-loop transfer function matrices,

– PC I PC+()PC

–=

Then, to a first order approximation in C – C

– IPC+()

≈

1–

PC C

–()IPC+()

IPC

+()

, there holds

1–

The natural error measure is then

IPC+()

1–

and this error measure parallels E

PC C

–()IPC+()

in Equation 4-3. Further refinement

1–

∞

(4-4)

again is possible. It may well be that closed-loop transfer function matrices should be better matched at some frequencies than others; if this weighting on the error in the closed-loop transfer function matrices is determined by the input spectrum , then one really wants (T – T

Φ=

)V to be small,

so that Equation 4-4 is replaced by

IPC+()

1–

PC C

–()IPC+()

1–

∞

Chapter 4 Frequency-Weighted Error Reduction

∞

Most of these ideas are discussed in [Enn84], [AnL89], and [AnM89]. The function choices of error measure, namely E V(jω). The first four are specifically for controller reduction, whereas the last is not aimed specifically at this situation.

Several features of the algorithms are:

• Only the stable part of C is really reduced; the unstable part is copied exactly into C

• A modification of balanced realization truncation underpins the algorithms, namely (frequency) weighted balanced truncation, although to avoid numerical problems, the actual construction of a frequency weighted balanced realization of C is avoided.

• Frequency weighted Hankel singular values can be computed, and although no error bound formula is available (in contrast to the unweighted problem), generally speaking there is little damage done in reducing by a number of states equal to the number of (relativ ely) small Hankel singular values.

The error measures themselves deserve certain comments:

• The two stability based measures E sufficiency condition for stability, rather than a necessity and sufficiency condition, and so capture stability a little crudely.

• For any constant nonsingular N, the error measure E by and the robustness result remains

NC C

valid. Use of an N may improve or worsen the quality of the approximation.

•Having T – T impulse and step responses.

• In classical control especially, constraints on the loop gain can be imposed (Minimum value of gain in one band, maximum v alue of gain in another band, for example). None of the methods presented directly addresses the task of retaining satisfaction of these constraints after reduction of a high order acceptable controller. Ho wever , judicious use of a weight V can assist. Suppose that above the closed-loop bandwidth there is an overbound constraint on the loop gain, which is violated when a controller reduction is performed (but not with the original controller). At these frequencies, roughly PC and PC

– PC Cr–()=

frequencies in the region in question will evidently encourage PC better track PC.

wtbalance( ) implements weighted reduction, with five

, EOS, EM, EMS, and E1 with arbitrary

and EOS are derived from a

can be replaced

–()PI CP+()

small normally ensures closeness of the closed-loop

1–N1–

. Introduction of a weight V in E

are small, so that

penalizing

Xmath Model Reduction Module 4-4 ni.com

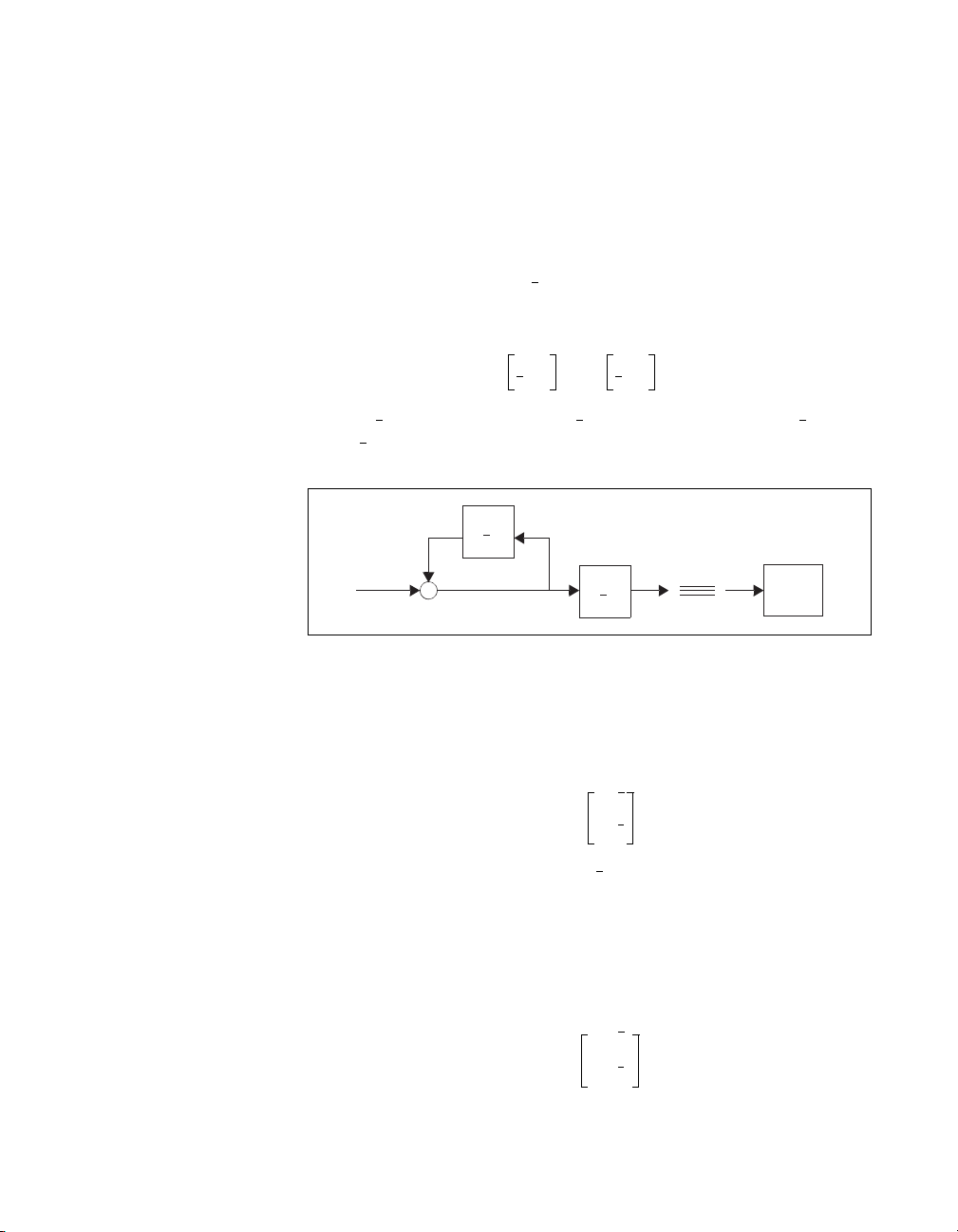
Fractional Representations

The treatment of jω-axis or right half plane poles in the above schemes is crude: they are simply copied into the reduced order controller. A different approach comes when one uses a so-called matrix fraction description (MFD) to represent the controller, and controller reduction procedures based on these representations (only for continuous-time) are found in

fracred( ). Consider first a scalar controller . One

can take a stable polynomial of the same degree as d, and then represent the controller as a ratio of two stable transfer functions, namely

Chapter 4 Frequency-Weighted Error Reduction

Cs() ns() ds()⁄=

ds()

ns()

----------

ds()

nd⁄ dd⁄ dd⁄

Now is the numerator, and the denominator. Write as 1 ed⁄+

. Then we have the equivalence shown in Figure 4-1.

---

ds()

----------

ds()

1–

--d

Figure 4-1. Controller Representation Through Stable Fractions

Cs()

Evidently, C(s) can be formed by completing the following steps:

1. Construction of the one-input, two-output stable transfer function matrix

nd⁄

ed⁄

(which has order equal to that of or ).

d d

2. Interconnection through negative feedback of the second output to the single input.

These observations motivate the reduction procedure:

•Reduce G to G

; notice that G is stable. Let Gr be

dr⁄

Chapter 4 Frequency-Weighted Error Reduction

• Form the reduced controller by interconnecting using negative feedback the second output of G

to the input, that is, set

s()

---------------=

dre

Nothing has been said as to how should be chosen—and the end result of the reduction, C

(s), depends on . Nor has the reduction procedure

been specified. When C(s) has been designed to combine a state estimator with a

stabilizing feedback law, it turns out that there is a natural choice for .

ds()

As for the reduction procedure, one possibility is to use a weight based on the spectrum of the input signals to G—and in case C(s) has been determined by an LQG optimal design, this spectrum turns out to be white, that is, independent of frequency, so that no weight (apart perhaps from scaling) is needed. A second possibility is to use a weight based on a stability robustness measure. These points are now discussed in more detail.

To understand the construction of a natural fractional representation for C(s), suppose that and let K that A – BK

generates an estimate of the feedback control . The controller

Ps() CsI A–()1–B=

and A – KEC are stable. The controller

AxˆBu K

–=

– KRx–

, KE be matrices such

y–()–+=

can be represented as a series compensator

AxˆBK

–=

xˆKECxˆK

y+–+=

(with compensator input y and output u). Allowing for connection with negative feedback, the compensator transfer function matrix is:

Cs() K

Xmath Model Reduction Module 4-6 ni.com

sI A BKRK

++–()

1–

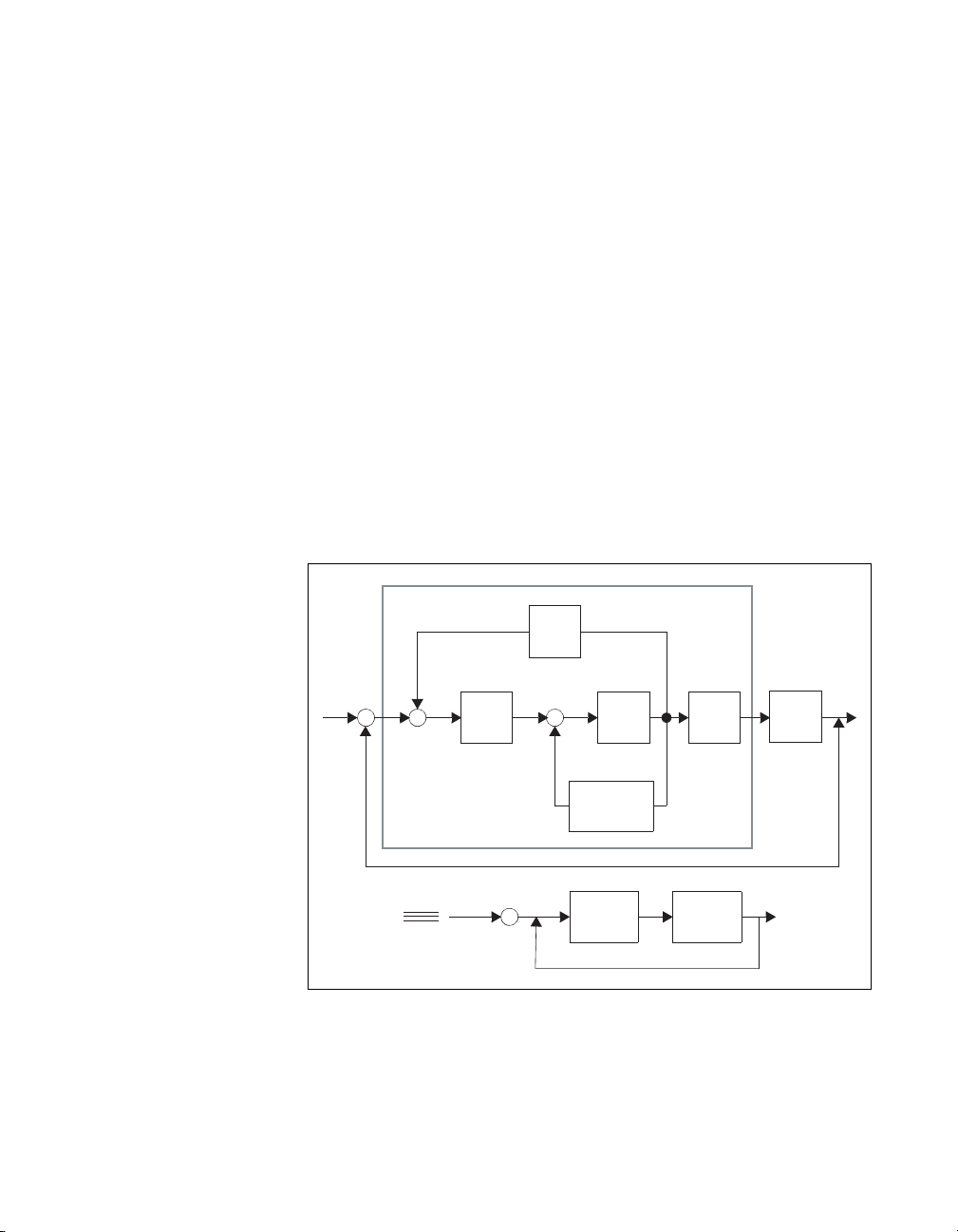
Chapter 4 Frequency-Weighted Error Reduction

Matrix algebra shows that C(s) can be described through a left or right matrix fraction description

with D

Cs() D

, and related values, all stable transfer function matrices.

1–

s()NLs() NRs()D

1–

s()==

In particular:

sI A– KEC+()

LKR

sI A– BK

RKR

ICsIA– BK

sI A– KEC+()

+()

1–

B+=

1–

For matrix C(s), the left and right matrix fraction descriptions are distinct entities. It is the right MFD which corresponds to Figure 4-1; refer to Figure 4-2.

-- -

Ps()

ABK

–

Figure 4-2. C(s) Implemented to Display Right MFD Representation

Cs() Ps()

Chapter 4 Frequency-Weighted Error Reduction

The left MFD corresponds to the setup of Figure 4-3.

Ps()

KrsI A KEC+–()

Figure 4-3. C(s) Implemented to Display Left MFD Representation

1–

The setup of Figure 4-2 suggests approximation of:

= sI A– BK

Gs()

+()

1–

whereas that of Figure 4-3 suggests approximation of:

Hs() K

sI A– KEC+()

In the LQG optimal case, the signal driving K

1–

in Figure 4-2 is white noise

(the innovations process); this motivates the possibility of using no frequency dependent weighting in approximating G(s) [but observe that after approximating, the signal will no longer be white noise, so that argument is questionable]. Simple appeal to duality motivates using no frequency dependent weighting for H(s). These are two of the options offered by

fracred( ).

T w o more

fracred( ) options depend on examining stability robustness

(the options are duals of one another). From the stability point of view, the set-up of Figure 4-3 is identical to that of Figure 4-4, with .

Xmath Model Reduction Module 4-8 ni.com

sI A BK

Figure 4-4. Redrawn; Individual Signal Paths as Vector Paths

It is possible to verify that

Chapter 4 Frequency-Weighted Error Reduction

+–()

Cs() Pˆs()

1–

Ps()I

1–

G+()

CsI A K

ICsI AK

and accordingly the output weight can be used in an

–()

error measure . It turns out that the calculations for frequency

WG G

weighted balanced truncation of G and subsequent construction of C

1–

C+–

B[=

1–

C+()

–()– ]

G+()

1–

(s) are

exceptionally easy using this weight. The second

fracred( ) option is the dual of this. The error measure is

–()V

where:

sI A BK

CsI A BK

+–()

1–

B–

1–

It is possible to argue heuristically the relevance of these error measures from a second point of view. It turns out that:

DLN

– W

V1N

–

2Dr

I 0

0 I

Chapter 4 Frequency-Weighted Error Reduction

(Here, the Wi and Vi are submatrices of W,V.) Evidently,

LNL

VI=

and

Some manipulation shows that trying to preserve these identities after approximation of D

WG G

–()

and . F or further details, refer to

∞

, NL or NR, DR suggests use of the error measures

–()V

∞

[AnM89]

and

[LAL90]. In all four

fracred( ) options, it is possible to construct (weighted)

Hankel singular values, and to use them as a guide to the likely quality of approximation. The patterns tend to be different for the four options.

fracred( ) options are normally different in outcome from the

The

wtbalance( ) options. However, if the controller has been designed

by the loop transfer recovery method and is stable, then one of the

fracred( ) options is essentially the same as one of the wtbalance( )

options, refer to [LiA90]. More precisely, if the LTR design is performed with input noise or process

noise weighting tending to infinity, reduction with

type="left stab", which uses the error measure , leads to

effectiv ely the same reduction as

stab"

. If the LTR design is performed with state or output weighting

wtbalance () with the type="input

fracred( ) and

–()V

tending to infinity (in the index determining the state feedback law), reduction with measure leads to effectively the same reduction as

wtbalance( ) with type="output stab".

fracred( ) and type="right stab" using the error

WG G

–()

∞

wtbalance( )

[SysCR,SysCLR,HSV] = wtbalance(Sys,SysC,type,{nscr,SysV})

The wtbalance( ) function calculates a frequency weighted balanced truncation of a system.

wtbalance( ) has two separate uses:

• Reduce the order of a controller C(s) located in a stable closed-loop, with the plant P(s) known. Frequency-weighted balanced truncation is used, with the weights involving P(s) and being calculated in a predominantly standard way.

Xmath Model Reduction Module 4-10 ni.com

Chapter 4 Frequency-Weighted Error Reduction

• Reduce the order of a transfer function matrix C(s) through frequency-weighted balanced truncation, a stable frequency weight V(s) being prescribed.

The syntax is more accented towards the first use. F or the second use, the user should set S =0, NS = 0. This results in (automatically) SCLR = NSCLR = 0. The user will also select the

spec".

Let C

(s) be the reduced order approximation of C(s) which is being

type="input

sought. Its order is either specified in advance, or the user responds to a prompt after presentation of the weighted Hankel singular values. Then the different types concentrate on (approximately) minimizing certain error measures, through frequency weighted balanced truncation. These are shown in Table 4-1.

Table 4-1. Types versus Error Measures

Type Error Measure

"input stab"

"output stab"

"match"

"match spec"

"input spec"

–[]PI CP+[]

–[]V

1–

PC C

1–

PC C

1–

PC C

∞

IPC+[] IPC+[] IPC+[]

1–

∞

–[]

∞

–[]IPC+[]

1–

∞

1–

∞

These error measures have certain interpretations, as shown in Table 4-2. In case C(s) is not a compensator in a closed-loop and the error measure

Vjω()Cjω()C

is of interest, you can work with

type="input spec" and C', V' in lieu

jω()–[]

∞

of C and V. There is no restriction on the stability of C(s) [or indeed of P(s)] in the

algorithm, though if C(s) is a controller the closed-loop must be stabilizing. Also, V(s) must be stable. Hence all weights (on the left or right of C(jω)–C

(jω) in the error measures) will be stable. The algorithm,

however, treats unstable C(s) in a special way, by reducing only the stable part of C(s) (under additive decomposition) and copying the unstable part

(s).

into C

Chapter 4 Frequency-Weighted Error Reduction

This rather crude approach to the handling of the unstable part of a controller is avoided in

wtbalance( ) for controller reduction, at least for an important family

of controllers.

Table 4-2. Error Measure Interpretation for wtbalance

Type Error Measure Interpretations

fracred( ), which provides an alternative to

"input stab"

"output stab"

"match"

"match spec"

"input spec"

Algorithm

A stability robustness argument, based on breaking the loop at the controller output, indicates that if C is stabilizing for P and the error measure is less than 1, then Cr is stabilizing for P. The smaller the error measure is, the greater the stability robustness.

A similar stability robustness argument, but based on breaking the loop at the controller input, indicates that if C is stabilizing for P and the error measure is less that 1, then C

is stabilizing for P. The smaller the error

measure is, the greater the stability robustness. If T = PC(I + PC)–1 and Tr = PCr(I + PCr)–1 are the two closed-loop transfer

function matrices, then T – T

–1

(I + PC)

P[Cr– C][I + PC]–1, so that the error measure looks at matching

to first order in C – Cr is given by

of the closed-loop transfer function matrix. It may be important to match closed-loop transfer function matrices more

at certain frequencies than others; frequency weighting is achieved by introducing V(s). Frequencies corresponding to larger values of |V(jω)| or V(jω)V*(jω) will be the frequencies at which T(jω) and T

(jω) should have

smaller error. This is the one error measure that is not associated with a plant, or

closed-loop of some kind. It simply allows the user to emphasize certain frequencies in the reduction procedures.

The major steps of the algorithm are as follows:

1. Check dimension, syntax, stability of

SysV, closed-loop stability, and

decomposition of C(s) into the sum of a stable part (poles in Re[s] < 0) and unstable part (poles in Re[s] ≥ 0);

stable( ) is used for this

purpose.

2. Compute input (right) weight and/or output (left) weight as appropriate for the specified type.

Xmath Model Reduction Module 4-12 ni.com

Chapter 4 Frequency-Weighted Error Reduction

3. Compute weighted Hankel Singular Values σi (described in more detail later). If the order of C

(s) is not specified a priori, it must be

input at this time. Certain values may be flagged as unacceptable for various reasons. In particular nscr cannot be chosen so that

= σ

nscr

nscr +1

4. Execute reduction step on stable part of C(s), based on a modification of

redschur( ) to accommodate frequency weighting, and yielding

stable part of C

5. Compute C

6. Check closed-loop stability with C

(s).

(s) by adding unstable part of C(s) to stable part of Cr(s).

(s) introduced in place of C(s),

at least in case C(s) is a compensator.

More details of steps 3 and 4, will be given for the case when there is an input weight only. The case when there is an output weight only is almost the same, and the case when both weights are present is very similar , refer to [Enn84a] for a treatment. Let

Cs() D

s() DwCwsI A

cCc

sI A

1–

–()

1–

–()

be a stable transfer function matrix to be reduced and its stable weight.

–1

Thus, W(s) may be P(I + CP)

, corresponding to "input stab", and will thus have been calculated in step 2; or it maybe an independently specified stable V(s). Then

s()Ws() DcD

CcDcC

sI A

– B

0 sI A

cCw

–

1–

BcD

The controllability grammian P satisfying

′

AcBcC

′

0 A

cDw

++ 0=

′

is written as

ccPcw

′

Chapter 4 Frequency-Weighted Error Reduction

and the observability grammian Q, defined in the obvious way, is written as

ccQcw

′

It is trivial to verify that so that Q observability gramian of C

QccAcA

(s) alone, as well as a submatrix of Q.

′

+ C

The weighted Hankel singular values of C eigenvalues of P singular values because P rather a weighted controllability gramian. The usual controllability gramian can be regarded as when C

. They differ from the usual or unweighted Hankel

ccQcc

is not the controllability gramian of Cs(s) but

′

[]

cxc

The weighted controllability gramian is still , but now C

′

– C

(s) are the square roots of the

(s) is excited by white noise.

′

[]

cxc

is the

(s) is

excited by colored noise, that is, the output of the shaping filter W(s), which is excited by white noise.

Small weighted Hankel singular values are a pointer to the possibility of eliminating states from C

Cjω()C

jω()–[]Wjω()

(s) without incurring a large error in

. No error bound formula is known, however.

∞

The actual reduction procedure is virtually the same as that of

redschur( ), except that P

are formed with the eigenvalues in ascending and descending order

ccQcc

is used. Thus Schur decompositions of

′

PccQccV

′

PccQccV

asc

des

The maximum order permitted is the number of nonzero eigenvalues of

that are larger than ε.

ccQcc

The matrices V

, VD are orthogonal and S

asc

and S

are upper triangular.

des

Next, submatrices are obtained as follows:

= V

lbig

nscr

rbig

nscr

and then a singular value decomposition is fo rmed:

ebigSebigVebig

Xmath Model Reduction Module 4-14 ni.com

′

lbig

rbig

Chapter 4 Frequency-Weighted Error Reduction

From these quantities the transformation matrices used for calculating

(s), the stable part of Cr(s), are defined

Related Functions

fracred( )

12⁄–

lbig

rbig

lbigVebigSebig

rbigVebigSebig

and then

′

= B

RSlbig

= B

RCCSrbig

ACS

rbig

′

CRSlbig

CRDC

Just as in unweighted balanced truncation, the reduced order transfer function matrix is guaranteed stable, the same is guaranteed to be true in weighted balanced truncation when either a left (output) weight or a right (input) weight is used. It is suspected to be true when both input and output weights are present. The overall algorithm is not, however, at risk in this case, since it is stability of the closed-loop system which is the key issue of concern, (except for

type="input spec", but here there is only a single

weight, and so the theory guarantees preservation of stability).

balance(), redschur(), stable(), fracred()

[SysCR,HSV] = fracred(Sys,Kr,Ke,type,{nscr,Qyy})

The fracred( ) function uses fractional representations to calculate a reduction of a continuous-time compensator comprising a state estimator with state feedback law.

Restrictions

1. The closed-loo p syst em (SCLR,NSCLR) is calculated from

sysol=scr*sys # open loop system

syscl=feedback(sysol) # closed loop system

2. Initial state values, state names, and input and output names are not

considered by

fracred( ).

Chapter 4 Frequency-Weighted Error Reduction

3. Only continuous systems are accepted; for discrete systems use

makecontinuous( ) before calling bst( ), then discretize the

result.

Sys=fracred(makecontinuous(SysD));

SysD=discretize(Sys);

Defining and Reducing a Controller

Suppose P(s) = C(sI – A)–1B and A – BKR and A – KEC are stable (where

is a stabilizing state feedback gain and KE a stabilizing observer gain).

A controller for the plant P(s) can be defined by

(with u the plant input and y the plant output). The associated series compensator under unity negative feedback is

AxˆBu K

–=

y–()–+=

Cs() K

sI A BKRK

1–

C++–()

and this may be written as a left or right MFD as follows:

Cs() IK

sI A BK

Cs() K

The reduction procedures

sI A K

+–()

"right perf" and "left perf" have si milar

rationales. We shall describe

1–

C+–()

B+[]

1–

KEICsIABK

"right perf", refer to [AnM89] and

KRsI A K

+[]

+–()

1–

C+–()

1–

(4-5)

(4-6)

1–

[LiA86]. The first rationale involves observing that to red uce C(s), one might as well reduce its numerator and denominator simultaneously, and then form a new fraction C

(s) of lower order than C(s).

This amounts to reducing

Es()

+–()

sI A BK

1–

(4-7)

Xmath Model Reduction Module 4-16 ni.com

to, for example,

Chapter 4 Frequency-Weighted Error Reduction

s()

sI A

–()K

through, for example, balanced truncation, and then defining:

Cs() KRsI A

–()

KRsI A

– KEC+()

1–

IC+ sI Aˆ–()

[]

1–

For the second rationale, consider Figure 4-5.

-- -

ABK

–

1–

Ps()

Figure 4-5. Internal Structure of Controller

Recognize that the controller C(s) (shown within the hazy rectangle in Figure 4-5) can be constructed by implementing

KRsI A BK

+–()

1–

and

CsI A BK

+–()

1–

and then applying an interconnection rule (connect the output of the second transfer function matrix back to the input at point X in Figure 4-5).

Chapter 4 Frequency-Weighted Error Reduction

Controller reduction proceeds by implementing the same connection rule but on reduced versions of the two transfer function matrices.

Algorithm

When K spectrum of the signal driving K

has been defined through Kalman filtering considerations, the

in Figure 4-5 is white, with intensity Qyy.

It follows that to reflect in the multiple input case the different intensities on the different scalar inputs, it is advisable to introduce at some stage a weight into the reduction process.

12⁄

After preliminary checks, the algorithm steps are:

1. Form the observability and weighted (through Q

) controllability

grammians of E(s) in Equation 4-7 by

PA BK

–()′ABK

QA BK

–()ABK

–()P+ K–

–()′Q+ K

′

EQyyKE

′

C′C––=

(4-8)

(4-9)

2. Com pute the square roots of the eigenvalues of PQ (Hankel singular values of the fractional representation of Equation 4-5). The maximum order permitted is the number of nonzero eigenvalues of PQ that are larger than ε.

3. Introduce the order of the reduced-order controller, possibly by displaying the Hankel singular values (HSVs) to the user. Broadly speaking, one can throw away small HSVs but not large ones.

4. Using

redschur( )-type calculations, find a state-variable

description of E

(s). This means that Er(s) is the transfer function

matrix of a truncation of a balanced realization of E(s), but the

redschur( ) type calculations avoid the possibly numerically

difficult step of balancing the initially known realization of E(s). Suppose that:

′

ABK

lbig

–()S

rbig

AˆS

5. Define the reduced order cont roller C

′

ABK

– KEC–()S

lbig

KE, S

(s) by

rbig

′

lbig

(4-10)

so that

s() CCRsI A

Xmath Model Reduction Module 4-18 ni.com

–()

1–

Chapter 4 Frequency-Weighted Error Reduction

6. Check the stability of the closed-loop system with Cr(s). When the

type="left perf" is specified, one works with

Es() K

sI A K

1–

C+–()

(4-11)

which is formed from the numerator and denominator of the MFD in Equation 4-5. The grammian equations (Equation 4-8 and Equation 4-9) are replaced by

PA K

QA K

C–()′AKEC–()P+ BB′– K

C–()AKEC–()′Q+ K

′

–=

redschur( )-type calculations are used to reduce E(s) and Equation 4-10

′

–=

EKE

again yields the reduced-order controller. Notice that the HSVs obtained from Equation 4-10 or the left MFD (Equation 4-5) of C(s) will in general be quite different from those coming from the right MFD (Equation 4-6). It may be possible to reduce much more with the left MFD than with the right MFD (or vice-versa) before closed-loop stability is lost.

As noted in the

"right stab" focus on a stability robustness measure, in conjunction

fracred( ) input listing, type="left stab" and

with Equation 4-5 and Equation 4-6, respectively. Leaving aside for the moment the explanation, the key differe nces in the algorithm computations lie solely in the calculation of the grammians P and Q. For

stab"

, these are given by

type="left

PA BK

–()′ABK

QA K

and for

"right stab",

PA BK

–()′ABK

QA K

C–()AKEC–()′Q+ K

C–()AKEC–()′Q+ C– ′C=

–()P+ BB′–=

–()P+ K

–=

EKE

′

′–=

(4-12)

(4-13)

Chapter 4 Frequency-Weighted Error Reduction

Additional Background

A discussion of the stability robustness measure can be found in [AnM89] and [LAL90]. The idea can be understood with reference to the transfer functions E(s) and E possible to argue (through block diagram manipulation) that

• C(s) stabilizes P(s) when E(s) stabilizes (as a series compensator) with unity negative feedback .

• E

(s) also will stabilize [P(s)I], and then Cr(s) will stabilize P(s),

provided

(s) used in discussing type="right perf". It is

Pˆs()

Ps()I

CjωIA– KEC+()

1–

BICjωIA– KEC+()

–

Ejω()E

jω()–[]

1–

∞

(4-14)

Accordingly, it makes sense to try to reduce E by frequency-weighted balanced truncation. When this is done, the controllability grammian for E(s) remains unaltered, while the observability grammian is altered. (Hence Equation 4-5, at least with Q

= I, and Equation 4-12 are the same while

Equation 4-6 and Equation 4-13 are quite different.) The calculations leading to Equation 4-13 are set out in [LAL90].

The argument for

type="left perf" is dual. Another insight into

Equation 4-14 is provided by relations set out in [NJB84]. There, it is established (in a somewhat broader context) that

CjωIA– KEC+()

× I=

1–

BICjωIA– KEC+()

sI A BK

ICjωIA– BK

–{}

+–()

+()

1–

The left matrix is the weighting matrix in Equation 4-14; the right matrix is the numerator of C(jω) stacked on the denominator, or alternatively

E(jω) +

This formula then suggests the desirability of retaining the weight in the approximation of E( jω) by E

Xmath Model Reduction Module 4-20 ni.com

(jω) .

Chapter 4 Frequency-Weighted Error Reduction

The four schemes all produce different HSVs; it follows that it may be prudent to try all four schemes for a particular controller reduction. Recall again that their relative sizes are only a guide as to what can be thro wn away without incurring much error. There is no simple rule to indicate which of the four schemes will be the most effective at controller reduction.

Two rough rules can, however, be formulated.

• Problems with instability through reduction to too low a controller order are more likely with

"left stab" or "right stab".

"left perf" and "right perf" than

• If the controller has been designed using the loop transfer recovery idea,

"left stab" will probably be attractive if the input noise

covariance is very large, and

"right stab" will probably be

attractive if the output weighting in the performance index is very large, [LiA90]. The reduced controllers will then actually be very similar to those obtained using

"input stab" in the first case and "output stab" in the second

wtbalance( ) with the option

case.

One example gives the HSVs summarized in Table 4-3 for an eighth order controller.

Table 4-3. HSVs for an Eighth Order Controller

1 2 3 4 5 6 7 8

right perf

left perf

right stab

left stab

.0339 .0164 .0128 .0102 .0040 .0037 .0000 .0000

4.9075 4.8742 3.8457 3.7813 1.2255 1.1750 .5055 .0413

3.3081 .7278 .1123 .0783 .0242 .0181 .0107 .0099

1.3914 1.317 1.1269 1.0862 .9638 .5846 .5646 .3144

The most attractive candidate for reducing to second order is

right stab.

This is because the HSVs being discarded (columns 3 to 8) are smaller relative t o those being retained (columns 1 and 2) for

right stab than for

the other three candidates.

Note The relative values count, not the absolute values.

Related Functions

redschur(), wtbalance()

Utilities

This chapter describes three utility functions: hankelsv( ), stable( ),

compare( ).

and

hankelsv( )

The background to values, was presented in Chapter 1, Introduction. Hankel singular values are also calculated in other functions, sometimes by other procedures. A comparison of the procedures is given in the Hankel Singular Values section. The function of an unreduced and a reduced system, from various points of views.

The function stable and unstable parts, that is, given G(s), the function determines G

(s), the first with all poles in Re[s] < 0, the second with all poles in

and G

Re[s] ≥ 0, such that

The function is used within some of the other functions of the Model Reduction Module. It should also be used when reduction of an unstable G(s) is contemplated. The normal reduction functions, for example,

balmoore( ) or redschur( ), require stability of the transfer function

matrix G(s) being reduced. If G(s) is unstable, to generate G

(s) added to the outcome using the + operator, to yield the desired

then G

reduction of G

hankelsv( ), which calculates Hankel singular

compare( ) serves to facilitate the comparisons

stable( ) is used to separate (additively) a system into its

(s)

Gs() G

(s) and Gu(s); reduction of Gs(s) should be performed, and

(s).

s() G

s()+=

stable( ) should be used

[HSV,Wc,Wo] = hankelsv(Sys,{noplot})

The hankelsv( ) function computes the Hankel Singular Values of a stable system (continuous or discrete) and displays them in a bar plot.

Chapter 5 Utilities

The gramian matrices are defined by solving the equations (in continuous time)

Related Functions

stable( )

AA′W

A′+ BB′–=

cWc

+ C ′C–=

and, in discrete time

The computations are effected with

A′– BB′=

A′ W

A– C′C=

lyapunov( ) and stability is checked,

which is time-consuming. The Hankel singular values are the square roots of the eigenvalues of the product.

lyapunov(), dlyapunov()

[SysS,SysU] = stable(Sys,{tol})

The stable( ) function decomposes Sys into its stable (SysS) and unstable(

Continuous systems have unstable poles if real parts >

SysU) parts, such that Sys=SysS+SysU.

–tol.

Discrete systems have unstable poles if magnitudes >

• The direct term (D matrix) is included in

•If

Sys has poles clustered near -tol (or 1-tol), then SysS and SysU

SysS.

might be ill-conditioned. To av oid this problem choose

1-tol.

tol to a value

that is not close to the majority of poles.

Algorithm

The algorithm begins by transforming the A matrix to Schur form, and counting the number of stable and unstable eigenvalues, together with those for which classification is doubtful. Stable eigenvalues are those in either of the following:

• Re[s] < 0 (continuous time)

•|z| < 1 (discrete time)

Xmath Model Reduction Module 5-2 ni.com

Chapter 5 Utilities

Doubtful ones are those for which the real part of the eigenvalue has magnitude less than or equal to

tol for continuous-time, or eigenvalue

magnitude within the following range for discrete time:

1 tol– 1 tol+, A warning is given if doubtful eigenvalues exist. The algorithm then computes a real ordered Schur decomposition of A

so that after transformation

SASU

0 A

where the eigenvalues of A A matrix X satisfying –A the algorithm

sylvester( ). The eigenvalue properties of A

and AU are respectively stable and unstable.

+ XAU+ ASU= 0 is then determined by calling

and AU

guarantee that X exists. If doubtful eigenvalues are present, they are assigned to the unstable part of

Sys. In this circumstance you get the

message,

The system has poles near, or upon, the jw-axis

for continuous systems, and the following for discrete systems:

The system has poles near the unit circle.

If A has eigenvalues clustered near -tol (1–tol in discrete-time), then X is likely

Note

to be ill-conditioned and consequently example, the B matrix of

SysS could contain very small values, while the C matrix could

contain large values. In this case,

SysS and SysU will also be ill-conditioned. (For

SysS would be very weakly controllable and very

strongly observable. This will cause problems when gramians and Hankel singular values are calculated.) To avoid this problem, change

tol to a value that is not close to the

majority of eigenvalues.

A further transformation of A is constructed using X:

→ A

0 I

IX–

0 I

AS0

0 A

Chapter 5 Utilities

After this last transformation, and with

= CC

it follows that

[]=

SCU

Related Functions

compare( )

SysS ASASC

D;[, ]=

and

SysU A

UBUCU

0;[, ]=

By combining the transformation yielding the real ordered Schur form for A with the transformation defined using X, the overall transformation T is readily identified. In case all eigen values of A are stable or all are unstable, this is flagged, and T = I.

stable( ) can be combined with a reduction algorithm such as redschur( ) or balmoore( ) to reduce the order of a system with some

unstable and some stable poles. One uses

stable( ) to separate the stable

and unstable parts, and then, for example, reduces the stable part with

redschur( ); the reduced stable part is added to the original unstable part

to provide the desired system reduction.

sylvester(), schur(), redschur(), balmoore()

[respdiff] = compare(Sys,SysRed,FTvec,{Fmin,Fmax,npts,radians,type})

The compare( ) function provides a number of different graphical tests which can be used to compare two state-space system implementations.

compare( ) can be used as a tool for evaluating a reduced-order system

by comparing it with the original full-order system from which it was obtained. However, it can be used for more general comparisons as well, such as examining the results of different discretization or identification techniques.

Xmath Model Reduction Module 5-4 ni.com

Tutorial

This chapter illustrates a number of the MRM functions and their underlying ideas. A plant and full-order controller are defined, and then the effects of various reduction algorithms are examined. The data for this example is stored in the file To follow the example, start Xmath, and then select File»Load from the Xmath Commands menu, or enter the specification appropriate to your operating system from the Xmath Commands area. For example:

load "$XMATH/demos/mr_disc"

Plant and Full-Order Controller

The plant in question comprises four spinning disks, connected by a flexible shaft. A motor applies torque to the third disk, and the output variable of interest is the angular displacement of the first disk. The plant transfer function, which is nonminimum phase and has a double pole at the origin, is as follows:

mr_disc.xmd in the Xmath demos directory.

load command with the file

Gs()

2ζ0ω0s ω

----------------------------------- -

-------------------------------------------------------------------------------------------------------------------- -

------- -

2ζ2ω2s ω

----------------------------------- -

⋅⋅

ζ1ω1s ω

------------------------------- -

2ζ3ω3s ω

----------------------------------- -

sa+

-----------

⋅⋅

2ζ4ω4s ω

----------------------------------- -

2 4

with:

ζ0=0.02 ω0=1 ζ1=-0.4 ω1=5.65 ζ2=0.02 ω2=0.765 ζ3=0.02 ω3=1.41 ζ4=0.02 ω4=1.85

a=4.84

Chapter 6 Tutorial

Adiag

A minimal realization in modal coordinates is C(sI – A)–1B where:

⎧⎫

⎨⎬

⎩⎭

0.015– 0.765

,,,

0.765– 0.015–

0.028– 1.410

1.410– 0.028–

0.04– 1.85

1.85– 0.04–

0.026

0.251–

0.033

0.886–

C′

4.017–

0.145

3.604

0.280

0.996–

0.105–

0.261

0.009

0.001–

0.043–

0.002

0.026–

The specifications seek high loop gain at low frequencies (for performance) and low loop gain at high frequencies (to guarantee stability in the presence of unstructured uncertainty). More specifically, the loop gain has to lie outside the shaded region shown in Figure 6-1.

40 dB/decade

Loop Gain (dB)

0.3

Frequency (rad/sec)

0.07

40 dB/decade

Figure 6-1. Loop Gain Constraints

Xmath Model Reduction Module 6-2 ni.com

Chapter 6 Tutorial

With a state weighting matrix,

Q = 1e-3*diag([2,2,80,80,8,8,3,3]);

R = 1;

(and unity control weighting), a state-feedback control-gain is determined through a linear-quadratic performance index minimization as:

[Kr,ev] = regulator(sys,Q,R);

A – B × Kr is stable. Next, with an input noise variance matrix Q = W

BBW

where,

DIAG 0.346 0.346 0.024 0.024 0.042 0.042, 0.042 0.042,,,,[]()=

and measurement noise covariance matrix =1, an estimation gain K (so that A – K

Qhat = Wt*b*b'*Wt;

Rhat = 1;

[Ke,ev] = estimator(sys,Qhat,Rhat,{skipChks});

C is stable) is determined:

The keyword skipChks circumvents syntax checking in most functions. It is used here because we know that

Qhat does not fulfill positive

semidefiniteness due to numerics).

sysc=lqgcomp(sys,Kr,Ke);

poles(sysc)

ans (a column vector) =

-0.296674 + 0.292246 j

-0.296674 - 0.292246 j

-0.15095 + 0.765357 j

-0.15095 - 0.765357 j

-0.239151 + 1.415 j

-0.239151 - 1.415 j

-0.129808 + 1.84093 j

-0.129808 - 1.84093 j

The compensator itself is open-loop stable. A brief explanation of how Q and

Wt are chosen is as follows. First, Q is chosen to ensure that the loop

gain (which would be relevant were the state measurable)

jωIA–()

1–

meets the constraints as far as possible. However, it is not possible to obtain a 40 dB per decade roll-off at high frequencies, as LQ design virtually always yields a 20 dB per decade roll-off. Second, a loop transfer recovery

approach to the choice of as for some large ρ is modified through the introduction of the diagonal matrix

ρBB′

Wt. The larger entries of Wt, because

of the modal coordinate system, in effect promote better loop transfer

Chapter 6 Tutorial

recovery at low frequencies; there is consequently a faster roll-off of the loop gain at high frequencies than for , and this is desired.

jωIA–()

1–

Figure 6-2 displays the (magnitudes of the) plant transfer function, the compensator transfer function and the loop gain, as well as the constraints; evidently the compensated plant meets the constraints.

You can enter the following commands to create a plot equivalent to Figure 6-2:

sysol=sys*sysc;

svals=svplot(sys,w,{radians});

svalsc=svplot(sysc,w,{radians});

svalsol=svplot(sysol,w,{radians});

plot(svals,{x_log,!grid,!ylab,

line_width=2,hold})

plot(svalsc,{keep})

plot(svalsol,{keep})

f2=plot(wc,constr,{keep,

legend=["plant","compensator",

"compensated plant","constraint"]})

plot({!hold})

Figure 6-2. Frequency Response for Plant, Compensator, and Compensated Plant

Xmath Model Reduction Module 6-4 ni.com

Controller Reduction

This section contrasts the effect of unweighted and weighted controller reduction. Unweighted reduction is at first examined, through

redschur( ) (using balance( ) or balmoore( ) will give similar

results). The Hankel singular values of the controller transfer function are

6.264×10

1.545×10–2 1.335×10–2 9.467×10–3 9.466×10 A reduction to order 2 is attempted. The ending Hankel singular values, that

is, σ

, σ4, ..., σ8, have a sum that is not particularly small with respect to σ1

and σ

; this is an indication that problems may arise in the reduction.

[syscr,hsv] = redschur(sysc,2);

svalsRol = svplot(sys*syscr,w,{radians});

plot(svalsol, {keep})

f3=plot(wc, constr,{keep,!grid,

legend=["reduced","original","constrained"],

title="Open-Loop Gain Using redschur()"})

–2

4.901×10–2 2.581×10–2 2.474×10

Chapter 6 Tutorial

–2

–3

National Instruments NI MATRIXx Xmath User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Xmath Model Reduction Module

Support

Worldwide Technical Support and Product Information

National Instruments Corporate Headquarters

Worldwide Offices

Important Information

Warranty

Copyright

Trademarks

Patents

WARNING REGARDING USE OF NATIONAL INSTRUMENTS PRODUCTS

Conventions

Contents

Using This Manual

Document Organization

Bibliographic References

Commonly Used Nomenclature

Conventions

Related Publications

MATRIXx Help

Overview

Functions

Figure 1-1. MRM Function

Table 1-1. MRM Restrictions

Nomenclature

Commonly Used Concepts

Controllability and Observability Grammians

Hankel Singular Values

Table 1-2. Calculating Hankel Singular Values

Internally Balanced Realizations

Singular Perturbation

Spectral Factorization

Low Order Controller Design Through Order Reduction

Figure 1-2. Low Order Controller Design for a High Order Plant

Introduction

Truncation of Balanced Realizations

Reduction Through Balanced Realization Truncation

Figure 2-1. Different Approaches for Obtaining the Same Reduced Order Model

Singular Perturbation of Balanced Realization

Hankel Norm Approximation

balmoore( )

Related Functions

truncate( )

Related Functions

redschur( )

Algorithm

Related Functions

ophank( )

Restriction

Algorithm

Behaviors

Table 2-1. Orders of G

Onepass Algorithm

Multipass Algorithm

Discrete-Time Systems

Impulse Response Error

Unstable System Approximation

Related Functions

Selecting Multiplicative Error Reduction

Figure 3-1. Controller C(s) Designed for Multiplicative Error Reduction

Multiplicative Robustness Result

bst( )

Restrictions

Algorithm

Algorithm with the Keywords right and left

Securing Zero Error at DC

Further Error Bounds

Reduction of Minimum Phase, Unstable G

Imaginary Axis Zeros (Including Zeros at ∞)

Related Functions

mulhank( )

Restrictions

Algorithm

right and left

Consequences of Step 5 and Justification of Step 6

Error Bounds