National Instruments 370757C-01 User Manual

NI MATRIXx

XmathTM Robust Control Module

MATRIXx Xmath Robust Control Module

TM

April 2007
370757C-01

Support

Worldwide Technical Support and Product Information

ni.com

National Instruments Corporate Headquarters

11500 North Mopac Expressway Austin, Texas 78759-3504 USA Tel: [phone]

Worldwide Offices

Australia 1800 300 800, Austria 43 662 457990-0, Belgium 32 (0) 2 757 0020, Brazil 55 11 3262 3599,
Canada 800 433 3488, China 86 21 5050 9800, Czech Republic 420 224 235 774, Denmark 45 45 76 26 00,
Finland 385 (0) 9 725 72511, France 33 (0) 1 48 14 24 24, Germany 49 89 7413130, India 91 80 41190000,
Israel 972 3 6393737, Italy 39 02 413091, Japan 81 3 5472 2970, Korea 82 02 3451 3400,
Lebanon 961 (0) 1 33 28 28, Malaysia 1800 887710, Mexico 01 800 010 0793, Netherlands 31 (0) 348 433 466,
New Zealand 0800 553 322, Norway 47 (0) 66 90 76 60, Poland 48 22 3390150, Portugal 351 210 311 210,
Russia 7 495 783 6851, Singapore 1800 226 5886, Slovenia 386 3 425 42 00, South Africa 27 0 11 805 8197,
Spain 34 91 640 0085, Sweden 46 (0) 8 587 895 00, Switzerland 41 56 2005151, Taiwan 886 02 2377 2222,
Thailand 662 278 6777, Turkey 90 212 279 3031, United Kingdom 44 (0) 1635 523545

For further support information, refer to the Technical Support and Professional Services appendix. To comment
on National Instruments documentation, refer to the National Instruments Web site at ni.com/info and enter
the info code feedback.

© 2007 National Instruments Corporation. All rights reserved.

Important Information

Warranty

The media on which you receive National Instruments software are warranted not to fail to execute programming instructions, due to defects
in materials and workmanship, for a period of 90 days from date of shipment, as evidenced by receipts or other documentation. National
Instruments will, at its option, repair or replace software media that do not execute programming instructions if National Instruments receives
notice of such defects during the warranty period. National Instruments does not warrant that the operation of the software shall be
uninterrupted or error free.

A Return Material Authorization (RMA) number must be obtained from the factory and clearly marked on the outside of the package before any
equipment will be accepted for warranty work. National Instruments will pay the shipping costs of returning to the owner parts which are covered by
warranty.

National Instruments believes that the information in this document is accurate. The document has been carefully reviewed for technical accuracy. In
the event that technical or typographical errors exist, National Instruments reserves the right to make changes to subsequent editions of this document
without prior notice to holders of this edition. The reader should consult National Instruments if errors are suspected. In no event shall National
Instruments be liable for any damages arising out of or related to this document or the information contained in it.

XCEPT AS SPECIFIED HEREIN, NATIONAL INSTRUMENTS MAKES NO WARRANTIES, EXPRESS OR IMPLIED, AND SPECIFICALLY DISCLAIMS ANY WARRANTY OF

E

MERCHANTABILITY OR FITNESS FOR A PARTICULAR PURPOSE. C USTOMER’S RIGHT TO RECOVER DAMAGES CAUSED BY FAULT OR NEGLIGENCE ON THE PART OF NATIONAL

NSTRUMENTS SHALL BE LIMITED TO THE AMOUNT THERETOFORE PAID BY THE CUSTOMER. NATIONAL INSTRUMENTS WILL NOT BE LIABLE FOR DAMAGES RESULTING

I

FROM LOSS OF DATA, PROFITS, USE OF PRODUCTS, OR INCIDENTAL OR CONSEQUENTIAL DAMAGES, EVEN IF ADVISED OF THE POSSIBILITY THEREOF. This limitation of

the liability of National Instruments will apply regardless of the form of action, whether in contract or tort, including negligence. Any action against
National Instruments must be brought within one year after the cause of action accrues. National Instruments shall not be liable for any delay in
performance due to causes beyond its reasonable control. The warranty provided herein does not cover damages, defects, malfunctions, or service
failures caused by owner’s failure to follow the National Instruments installation, operation, or maintenance instructions; owner’s modification of the
product; owner’s abuse, misuse, or negligent acts; and power failure or surges, fire, flood, accident, actions of third parties, or other events outside
reasonable control.

Copyright

Under the copyright laws, this publication may not be reproduced or transmitted in any form, electronic or mechanical, including photocopying,
recording, storing in an information retrieval system, or translating, in whole or in part, without the prior written consent of National
Instruments Corporation.

National Instruments respects the intellectual property of others, and we ask our users to do the same. NI software is protected by copyright and other
intellectual property laws. Where NI software may be used to reproduce software or other materials belonging to others, you may use NI software only
to reproduce materials that you may reproduce in accordance with the terms of any applicable license or other legal restriction.

Trademarks

MATRIXx™, National Instruments™, NI™, ni.com™, and Xmath™ are trademarks of National Instruments Corporation. Refer to the Terms of
Use section on ni.com/legal for more information about National Instruments trademarks.

Other product and company names mentioned herein are trademarks or trade names of their respective companies.

Members of the National Instruments Alliance Partner Program are business entities independent from National Instruments and have no agency,
partnership, or joint-venture relationship with National Instruments.

Patents

For patents covering National Instruments products, refer to the appropriate location: Help»Patents in your software, the patents.txt file
on your CD, or

ni.com/patents.

WARNING REGARDING USE OF NATIONAL INSTRUMENTS PRODUCTS

(1) NATIONAL INSTRUMENTS PRODUCTS ARE NOT DESIGNED WITH COMPONENTS AND TESTING FOR A LEVEL OF
RELIABILITY SUITABLE FOR USE IN OR IN CONNECTION WITH SURGICAL IMPLANTS OR AS CRITICAL COMPONENTS IN
ANY LIFE SUPPORT SYSTEMS WHOSE FAILURE TO PERFORM CAN REASONABLY BE EXPECTED TO CAUSE SIGNIFICANT
INJURY TO A HUMAN.
(2) IN ANY APPLICATION, INCLUDING THE ABOVE, RELIABILITY OF OPERATION OF THE SOFTWARE PRODUCTS CAN BE
IMPAIRED BY ADVERSE FACTORS, INCLUDING BUT NOT LIMITED TO FLUCTUATIONS IN ELECTRICAL POWER SUPPLY,
COMPUTER HARDWARE MALFUNCTIONS, COMPUTER OPERATING SYSTEM SOFTWARE FITNESS, FITNESS OF COMPILERS
AND DEVELOPMENT SOFTWARE USED TO DEVELOP AN APPLICATION, INSTALLATION ERRORS, SOFTWARE AND HARDWARE
COMPATIBILITY PROBLEMS, MALFUNCTIONS OR FAILURES OF ELECTRONIC MONITORING OR CONTROL DEVICES,
TRANSIENT FAILURES OF ELECTRONIC SYSTEMS (HARDWARE AND/OR SOFTWARE), UNANTICIPATED USES OR MISUSES, OR
ERRORS ON THE PART OF THE USER OR APPLICATIONS DESIGNER (ADVERSE FACTORS SUCH AS THESE ARE HEREAFTER
COLLECTIVELY TERMED “SYSTEM FAILURES”). ANY APPLICATION WHERE A SYSTEM FAILURE WOULD CREATE A RISK OF
HARM TO PROPERTY OR PERSONS (INCLUDING THE RISK OF BODILY INJURY AND DEATH) SHOULD NOT BE RELIANT SOLELY
UPON ONE FORM OF ELECTRONIC SYSTEM DUE TO THE RISK OF SYSTEM FAILURE. TO AVOID DAMAGE, INJURY, OR DEATH,
THE USER OR APPLICATION DESIGNER MUST TAKE REASONABLY PRUDENT STEPS TO PROTECT AGAINST SYSTEM FAILURES,
INCLUDING BUT NOT LIMITED TO BACK-UP OR SHUT DOWN MECHANISMS. BECAUSE EACH END-USER SYSTEM IS
CUSTOMIZED AND DIFFERS FROM NATIONAL INSTRUMENTS' TESTING PLATFORMS AND BECAUSE A USER OR APPLICATION
DESIGNER MAY USE NATIONAL INSTRUMENTS PRODUCTS IN COMBINATION WITH OTHER PRODUCTS IN A MANNER NOT
EVALUATED OR CONTEMPLATED BY NATIONAL INSTRUMENTS, THE USER OR APPLICATION DESIGNER IS ULTIMATELY
RESPONSIBLE FOR VERIFYING AND VALIDATING THE SUITABILITY OF NATIONAL INSTRUMENTS PRODUCTS WHENEVER
NATIONAL INSTRUMENTS PRODUCTS ARE INCORPORATED IN A SYSTEM OR APPLICATION, INCLUDING, WITHOUT
LIMITATION, THE APPROPRIATE DESIGN, PROCESS AND SAFETY LEVEL OF SUCH SYSTEM OR APPLICATION.

Conventions

The following conventions are used in this manual:

[ ] Square brackets enclose optional items—for example, [

» The » symbol leads you through nested menu items and dialog box options

to a final action. The sequence File»Page Setup»Options directs you to
pull down the File menu, select the Page Setup item, and select Options
from the last dialog box.

This icon denotes a note, which alerts you to important information.

bold Bold text denotes items that you must select or click in the software, such

as menu items and dialog box options. Bold text also denotes parameter
names.

italic Italic text denotes variables, emphasis, a cross-reference, or an introduction

to a key concept. Italic text also denotes text that is a placeholder for a word
or value that you must supply.

monospace Text in this font denotes text or characters that you should enter from the

keyboard, sections of code, programming examples, and syntax examples.
This font is also used for the proper names of disk drives, paths, directories,
programs, subprograms, subroutines, device names, functions, operations,
variables, filenames, and extensions.

monospace bold Bold text in this font denotes the messages and responses that the computer

automatically prints to the screen. This font also emphasizes lines of code
that are different from the other examples.

response].

Contents

Chapter 1
Introduction

Using This Manual......................................................................................................... 1-1

Document Organization...................................................................................1-1

Bibliographic References ................................................................................1-2

Commonly-Used Nomenclature......................................................................1-2

Related Publications ........................................................................................ 1-2

MATRIXx Help...............................................................................................1-3

Overview........................................................................................................................1-3

Chapter 2
Robustness Analysis

Modeling Uncertain Systems.........................................................................................2-1

Stability Margin (smargin).............................................................................................2-3

smargin( ).........................................................................................................2-4

Worst-Case Performance Degradation (wcbode) ..........................................................2-8

wcbode( ).........................................................................................................2-9

Advanced Topics ...........................................................................................................2-10

Stability Margin...............................................................................................2-10

Stability Margin and Structured Singular

Stability Margin Bounds Using Singular Values..............................2-11

Approximation with Scaled Singular Values ....................................2-12

ssv( ) ................................................................................................................2-15

osscale( )..........................................................................................................2-16

pfscale( ) ..........................................................................................................2-16

optscale( ) ........................................................................................................2-17

Reducibility....................................................................................................................2-17

Worst-Case Performance Degradation (wcgain) ...........................................................2-18

Conversion to a Stability Margin Problem ...................................................... 2-18

wcgain( )..........................................................................................................2-19

Values (µ) .......................2-10

© National Instruments Corporation v MATRIXx Xmath Robust Control Module

Contents

Chapter 3
System Evaluation

Singular Value Bode Plots............................................................................................. 3-1

L Infinity Norm (linfnorm)............................................................................................ 3-3

linfnorm( ) ....................................................................................................... 3-4

Singular Value Bode Plots of Subsystems .................................................................... 3-7

perfplots( )....................................................................................................... 3-7

clsys( ) ............................................................................................................. 3-10

Chapter 4
Controller Synthesis

H-Infinity Control Synthesis ......................................................................................... 4-1

Problem Definition.......................................................................................... 4-1

Extended Transfer Matrix ............................................................................... 4-2

Building the Plant Model ................................................................................ 4-3

Weight Selection ............................................................................................. 4-5

Restrictions on the Extended Plant ................................................................. 4-7

hinfcontr( ) ...................................................................................................... 4-8

singriccati( ) .................................................................................................... 4-13

Linear-Quadratic-Gaussian Control Synthesis .............................................................. 4-14

LQG Frequency Shaping ................................................................................ 4-14

fsregu( ) ........................................................................................................... 4-14

fsesti( )............................................................................................................. 4-16

fslqgcomp( ) .................................................................................................... 4-17

Frequency-Shaped Control Design Commands.............................................. 4-17

Loop Transfer Recovery (lqgltr) ................................................................................... 4-22

lqgltr( ) ............................................................................................................ 4-23

Appendix A
Bibliography

Appendix B
Technical Support and Professional Services

Index

MATRIXx Xmath Robust Control Module vi ni.com

Introduction

The Xmath Robust Control Module (RCM) provides a collection of

analysis and synthesis tools that assist in the design of robust control

systems.

This chapter starts with an outline of the manual and some use notes. It

continues with an overview of the Xmath Robust Control Module (RCM)

functions.

Using This Manual

This manual provides complete documentation for all the RCM functions

along with their associated theoretical background, references, and

examples.

Document Organization

This manual includes the following chapters:

• Chapter 1, Introduction, describes the Robust Control Module (RCM)
and shows the RCM function structure.

• Chapter 2, Robustness Analysis, covers the robustness analysis
tools and introduces the concepts of uncertainty, robustness, and
performance degradation in the framework of closed-loop systems.
The Modeling Uncertain Systems section should be read by all those
interested in robustness analysis or performance degradation, which
are explained in the Stability Margin (smargin) section and the

Worst-Case Performance Degradation (wcbode) section. The
Advanced Topics section provides additional information but this

material is not prerequisite to the use of RCM functions.

• Chapter 3, System Evaluation, describes system analysis functions that
create singular value Bode plots, performance plots, and calculate the

L

users.

• Chapter 4, Controller Synthesis, discusses synthesis tools in two
categories, H
of the theory of H

1

norm of a linear system. This chapter should be of interest to all

∞

and H2. This manual does not attempt to explain all

∞

, LQG/LTR, and frequency shaped LQG design

∞

© National Instruments Corporation 1-1 MATRIXx Xmath Robust Control Module

Chapter 1 Introduction

techniques. The general problem setup is explained together with
known limitations; the rest is left to the references.

Bibliographic References

Throughout this document, bibliographic references are cited with
bracketed entries. For example, a reference to [DoS81] corresponds
to a document published by Doyle and Stein in 1981. For a table of
bibliographic references, refer to Appendix A, Bibliography.

Commonly-Used Nomenclature

This manual uses the following general nomenclature:

• Matrix variables are generally denoted with capital letters; vectors are
represented in lowercase.

• G(s) is used to denote a transfer function of a system where s is the
Laplace variable. G(q) is used when both continuous and discrete
systems are allowed.

• H(s) is used to denote the frequency response, over some range of
frequencies of a system where s is the Laplace variable. H(q) is used to
indicate that the system can be continuous or discrete.

• A single apostrophe following a matrix variable, for example, x
denotes the transpose of that variable. An asterisk following a matrix
variable (for example, A*) indicates the complex conjugate, or
Hermitian, transpose of that variable.

'

,

Related Publications

For a complete list of MATRIXx publications, refer to Chapter 2,

MATRIXx Publications, Help, and Online Support, of the MATRIXx
Getting Started Guide. The following documents are particularly useful

for topics covered in this manual:

• MATRIXx Getting Started Guide

• Xmath User Guide

• Xmath Control Design Module

• Xmath Interactive Control Design Module

• Xmath Interactive System Identification Module, Part 1

• Xmath Interactive System Identification Module, Part 2

• Xmath Model Reduction Module

MATRIXx Xmath Robust Control Module 1-2 ni.com

MATRIXx Help

Overview

Chapter 1 Introduction

• Xmath Optimization Module

• Xmath Robust Control Module

• Xmath X

Robust Control Module function reference information is available in the
MATRIXx Help. The MATRIXx Help includes all Robust Control functions.
Each topic explains a function’s inputs, outputs, and keywords in detail.
Refer to Chapter 2, MATRIXx Publications, Help, and Online Support, of
the MATRIXx Getting Started Guide for complete instructions on using the
Help feature.

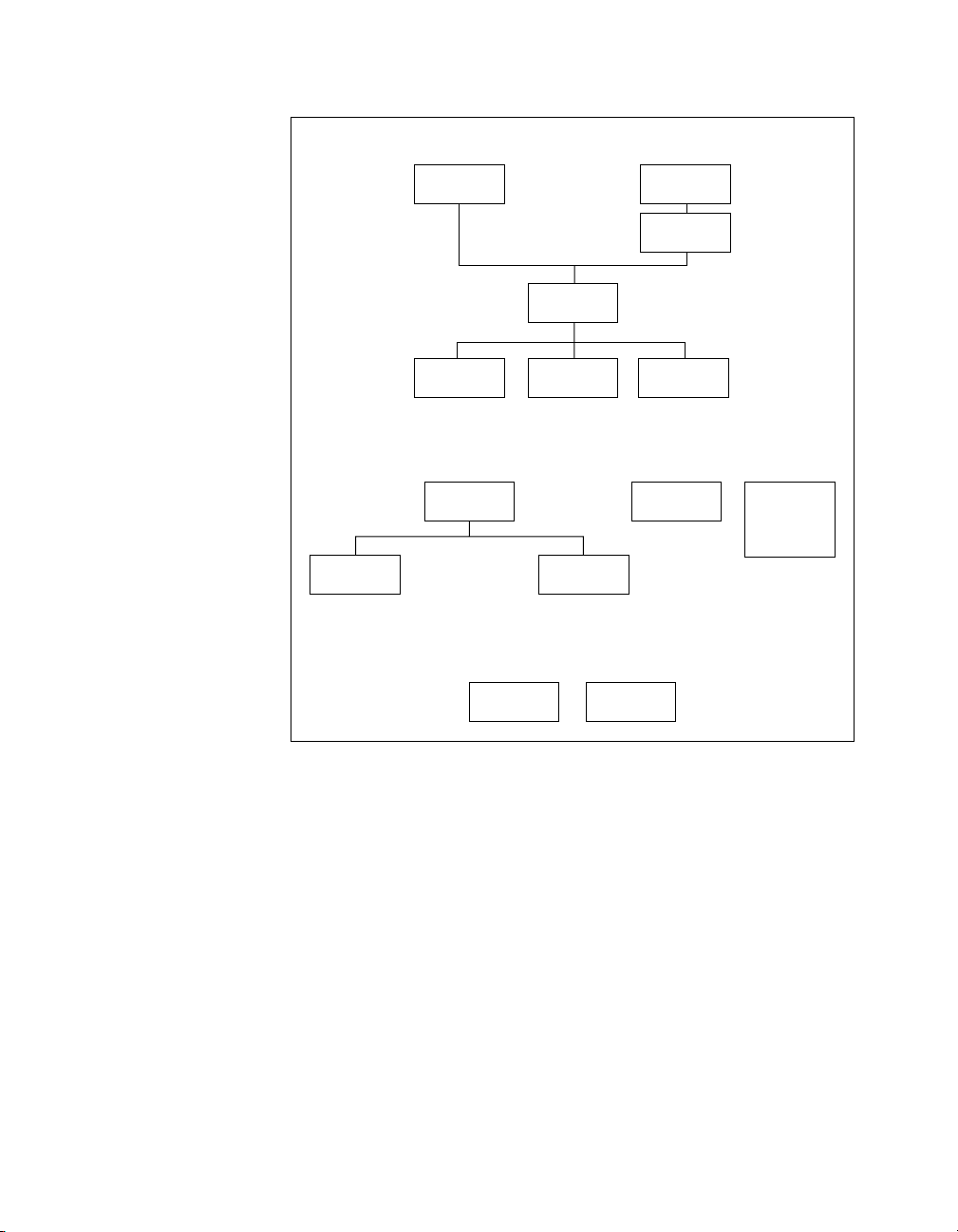
RCM functionality is structured as shown in Figure 1-1.

μ

Module

© National Instruments Corporation 1-3 MATRIXx Xmath Robust Control Module

Chapter 1 Introduction

Analysis Functions

smargin

ssv

pfscale optscale osscale

Synthesis Functions

hinfcontr

singriccati clsys

Utility Functions

wcbode

wcgain

lqgltr

perfplotslinfnorm

fslqgcomp

fsesti

fsregu

Figure 1-1. RCM Function Structure

Many RCM functions are based on state-of-the-art algorithms implemented
in cooperation with researchers at Stanford University. The robustness
analysis functions are based on structured singular value calculations.
The synthesis tools expand on existing LQG (H
and frequency shaping) while adding new H

MATRIXx Xmath Robust Control Module 1-4 ni.com

) techniques (LQG/LTR

2

design functions.

∞

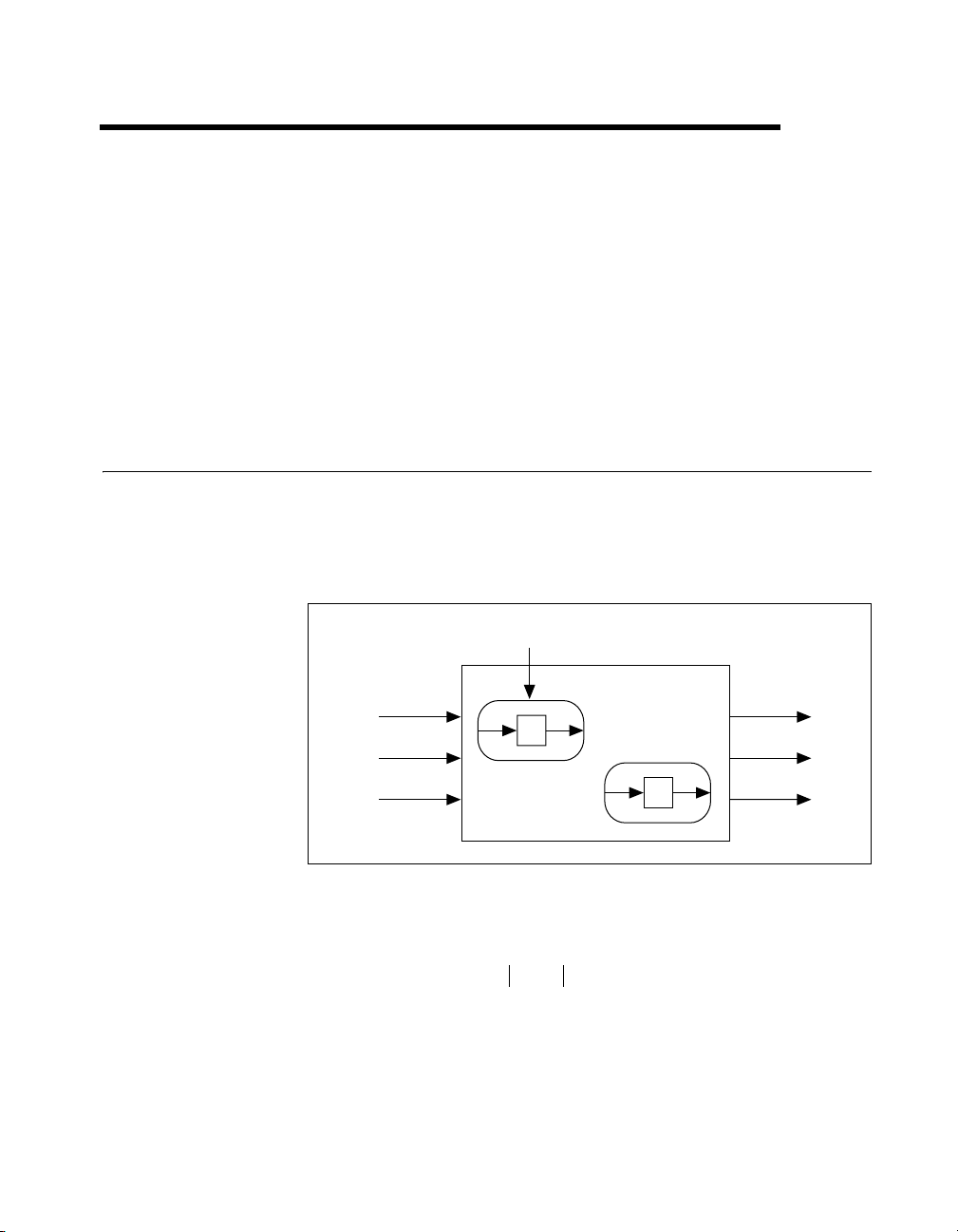
Robustness Analysis

z

This chapter describes RCM tools used for analyzing the robustness
of a closed-loop system. The chapter assumes that a controller has been
designed for a nominal plant and that the closed-loop performance of
this nominal system is acceptable. The goal of robustness analysis is to
determine whether the performance will remain acceptable if the plant
differs from the nominal plant.

Modeling Uncertain Systems

This section describes the method RCM uses to model an uncertain system.
The closed-loop system is modeled as a known or nominal closed-loop
system with input w and output z, together with k unknown or uncertain
transfer functions δ

w

(jω), …, δk(jω), as shown in Figure 2-1.

1

Uncertain Transfer Function

2

Known Nominal

q

r

1

1

δ

1

System

q

r

2

2

δ

2

Figure 2-1. Model of an Uncertain System

The following transfer functions are assumed to be stable:

δijω()lijω()≤

where the l
uncertainty model is known as structured nonparametric uncertainties.
To describe this model, you also must describe the nominal closed-loop

© National Instruments Corporation 2-1 MATRIXx Xmath Robust Control Module

are given non-negative functions of frequency. This type of

i

(2-1)

Chapter 2 Robustness Analysis

system, including how the uncertain transfer functions are connected to the
system and the magnitude bound functions l

(w).

i

To do this, extract the uncertain transfer functions and collect them into a

k-input, k-output transfer matrix Δ, where:

Δ jω() diagonal δ

jω(),...,δkjω()()=

1

(2-2)

The resulting closed-loop system can be viewed as a feedback connection
of the nominal closed-loop system with transfer matrix H(jω) and the
uncertain transfer matrix Δ( jω). You describe your nominal closed-loop
system as a linear system with

w

input and output .

r

Note The signals r and q are not really inputs and outputs of the nominal system; r and q

z

q

show how the uncertain transfer functions connect to your nominal system. The signals r
and q each have k components.

You will partition H into the four submatrices,

H

H

so that H
transfer matrix from r to z, H
and H

is the nominal transfer matrix from w to z, Hzr is the nominal

zw

qw

is the nominal transfer matrix from r to q.

qr

The magnitude bound functions l
with the PDM

delb:

zwHzr

=

HqwH

qr

is the nominal transfer matrix from w to q,

(jω) from Equation 2-1 are described

i

ω

l1ω1()…lkω1()

1

DELB

Thus, a complete description of your system requires the system
to represent H

MATRIXx Xmath Robust Control Module 2-2 ni.com

and the response delb to represent the bounds.

jw

=

,

:

ω

m

::

()…lkωm()

l

1ωm

SysH

Stability Margin (smargin)

Assume that the nominal closed-loop system is stable. That belief raises a
question: Does the system remain stable for all possible uncertain transfer
functions that satisfy the magnitude bounds (Equation 2-1)? If so, the
system is said to be robustly stable. If the magnitude bounds are small
enough, the uncertainties will not destabilize the system; your system will
be robustly stable.

Roughly speaking, the stability margin of your system is defined as the
factor by which you can increase all the magnitude bounds l
maintain stability for all possible uncertain transfer functions δ
number is larger than one (0 dB), then you know that there are no uncertain
transfer functions that satisfy the magnitude bound and destabilize your
system. Moreover, the number tells you how much more uncertainty your
system could tolerate than the given bounds l
one, then there are uncertain transfer functions that satisfy the magnitude
bound (Equation 2-1) and result in an unstable system. In this case, the
margin tells you how much you must reduce the magnitude bounds before
you have robust stability.

More precisely, the stability margin at frequency ω is defined as the
smallest α such that the system can have a pole at jω, with the uncertain
transfer functions satisfying |δ

(jω)| ≤ αli(ω):

i

Chapter 2 Robustness Analysis

and still

i

. If this

i

(ω). If the margin is less than

i

margin(w) = min{ α| systems can have a pole at jω with magnitude bounds αl

(jω)}

i

The stability margin also can be expressed as:

margin(w) = min{ α| det I – H

Note The stability margin only depends on H

jωΔ ≠ 0 such that |Δii|≤αli(α)}

qr

.

qr

The margin often is expressed in dB. If the margin is greater than zero for
all frequencies, then your system is robustly stable. If the margin is less
than zero for some frequencies, then your system is not robustly stable.
In particular, there are uncertain transfer functions that satisfy the
magnitude bound (Equation 2-1) and cause the system to have a pole at
those frequencies where the margin is negative. This does not mean that any

values that satisfy the magnitude bound will destabilize the system: it

δ

i

means that there are some bad δ

values that satisfy the magnitude bounds

i

and destabilize the system.

© National Instruments Corporation 2-3 MATRIXx Xmath Robust Control Module

Chapter 2 Robustness Analysis

z

q

smargin( )

marg = smargin(SysH, delb {scaling, graph})

The smargin( ) function plots an approximation to the stability margin
of the system as a function of frequency. For a full discussion of

smargin( ) syntax, refer to the MATRIXx Help. The approximation is

exact if the number of uncertain transfer functions is less than four and

scaling="OPT" (optimum scaling).

In other cases, the approximation is generally considered to be extremely
good. Refer to the Approximation with Scaled Singular Values section. The
approximation is always conservative.

smargin( ) always will report a

margin that is less than or equal to the actual margin.

smargin( ) function counts the columns in delb to calculate the

The
number of uncertainties k. It then assumes that the last k inputs of

SysH are

signal r in Figure 2-2, and the last k outputs are signal q. To create a Nominal
System, refer to the Creating a Nominal System section.

w

Known Closed-Loop System

r

size

k

Figure 2-2. Nominal Closed-Loop System

H(s)

size

k

Creating a Nominal System

To better understand how to create H(s) in Figure 2-3, you will examine
a SISO tracking system with three uncertainties. δ
actuator uncertainty, while δ

and δ3 are multiplicative sensor uncertainties.

2

is a multiplicative

1

MATRIXx Xmath Robust Control Module 2-4 ni.com

Chapter 2 Robustness Analysis

reference

8

––

reference

+

1

+

1
s

+

= 4

K

1

x

1

1

+

+

K2 = 8

+

–

error

x

2

1
s

2

+

+

Figure 2-3. SISO Tracking System with Three Uncertainties

The H system will have the reference input as input1 and the error output
as output1 (w and z, respectively, in Figure 2-2). Removing the δ values will
create inputs 2 through 4 and outputs 2 through 4 (r and q, respectively, in
Figure 2-2).

1. The A, B, C, D matrices of the state-space system representing H are
as follows:

A=[-4,-8;1,0];

B=[8,1,-4,-8;zeros(1,4)];

C=[0,-1;-4,-8;1,0;0,1];

D=[1,0,0,0;8,0,-4,-8;zeros(2,4)];

H = system(A,B,C,D,{inputNames=["reference",

"r1","r2","r3"],outputNames=["error",

"q1","q2","q3"],stateNames=["x1","x2"]});

2. Specify the uncertainty bounds.

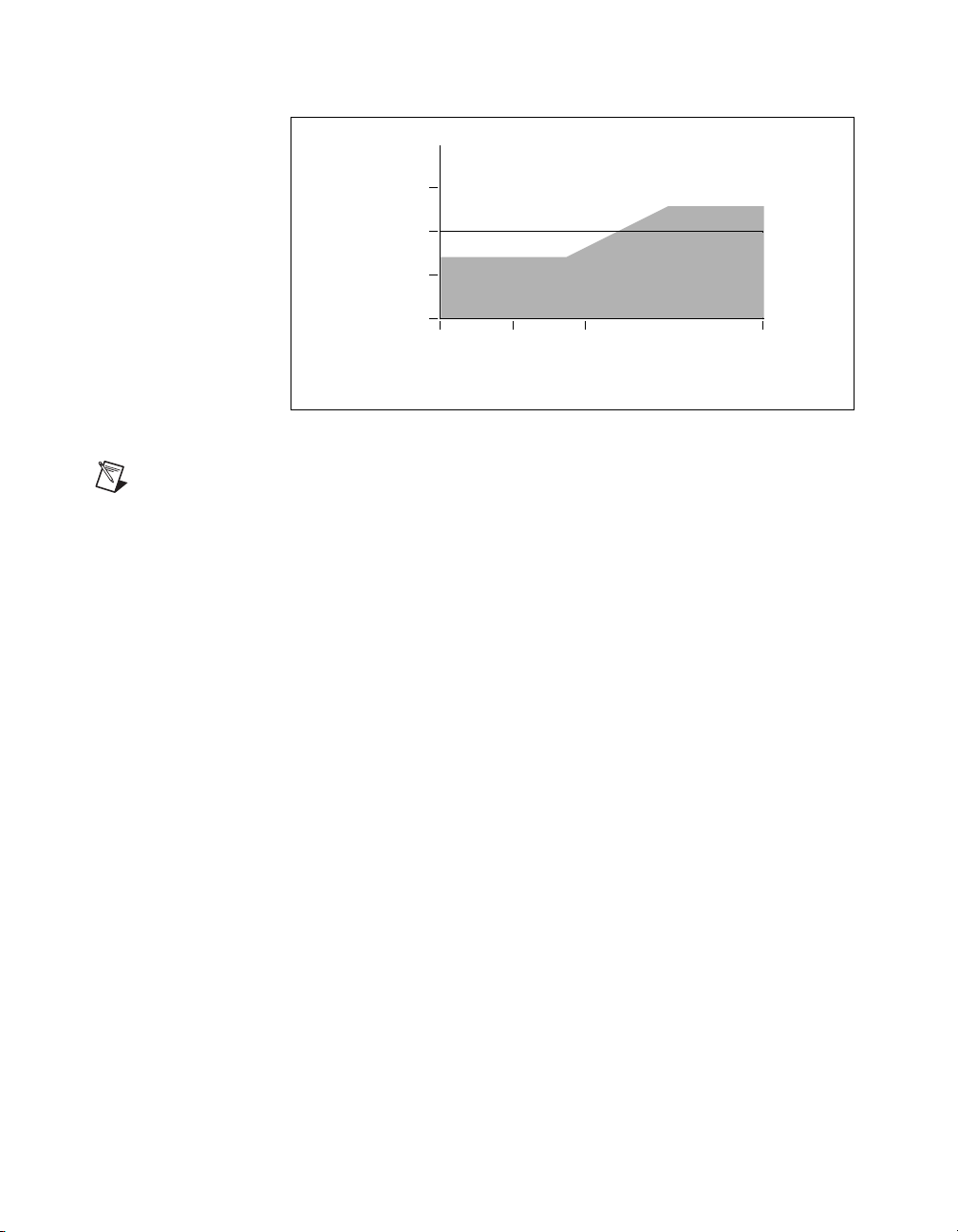
The sensor uncertainty δ
to Equation 2-1. Because the position x

is known to be bounded by l3(w), according

3

sensor model is known to be

2

accurate to 10% up to one radian per second, and very inaccurate at
high frequencies, the l

shown in Figure 2-4 is selected.

3

© National Instruments Corporation 2-5 MATRIXx Xmath Robust Control Module

Chapter 2 Robustness Analysis

dB

10

0

–20

0.1

1

Frequency, Radian/Second

30 100

Figure 2-4. Bound for Sensor Uncertainty

Note

A value of l3 at one radian per second of –20 dB indicates that modeling

uncertainties of up to 10% (–20 dB = 0.1) are allowed.

The actuator and sensor uncertainties δ

and δ2 are bounded by –20 dB

1

at all frequencies. You will use these values to interpolate to obtain l
First, create the bound for δ

L3 = pdm([-20,-20,10,10],[0.1,1,30,100]/2/pi);

in Hz.

3

3. Now interpolate to obtain 30 points:

L3 = interpolate(L3,logspace(0.01,10,30),{xlog});

4. Create L1 and L2 (bounds for and ):

δ

δ

1

2

L1=-20*ones(L3); L2 = L1;

delb = [L1,L2,L3];

5. Calculate the stability margin:

marg=smargin(H,delb);

smargin --> Scaling algorithm is type: PF

smargin --> Margin computation 10% complete

smargin --> Margin computation 50% complete

smargin --> Margin computation 90% complete

The output indicates that Perron-Frobenius scaling (the default) is
used. Refer to the Approximation with Scaled Singular Values section.

The stability margin plot is shown in Figure 2-5. The minimum margin
is about 8 dB at about 1/2 Hz. This implies that all three l
(uncertainty bounds) could be increased (relaxed) simultaneously
by 8 dB, and the system would still remain robustly stable.

values

1

.

3

MATRIXx Xmath Robust Control Module 2-6 ni.com

Chapter 2 Robustness Analysis

Figure 2-5. Stability Margin

Now examine the effect on the stability margin of discretizing H(s) at
100 Hz.

dt = 0.01;

Hd = discretize(H,dt);

margD = smargin(Hd,delb);

smargin --> Scaling algorithm is type: PF

smargin --> Margin computation 10% complete

smargin --> Margin computation 50% complete

smargin --> Margin computation 90% complete

100 Hz is a high discretization frequency for H, so the stability margin
is unchanged in the discrete-time case. The new plot is not much
different from Figure 2-6. Again, minimum margin is about 8 dB
at about 1/2 Hz.

© National Instruments Corporation 2-7 MATRIXx Xmath Robust Control Module

Chapter 2 Robustness Analysis

Worst-Case Performance Degradation (wcbode)

Even if a system is robustly stable, the uncertain transfer functions still can
have a great effect on performance. Consider the transfer function from the
qth input, w
nominal system, and this transfer function is the p,q entry of H
called the nominal transfer function.

, to the pth output, zp. With δ1 = ... = ...δk = 0, you have the

q

. This is

zw

When the δ values are not zero, the transfer function from w
entry of H

given by the formula:

pert

H

HzwHzrΔ IHqrΔ–()

pert

1–

+=

H

to zp is the p,q

q

qw

This is referred to as the perturbed transfer function. The perturbed transfer
function depends on the particular δ

, …, δk.

1

If the magnitude bounds are small enough, then you expect the perturbed
transfer function H

to be close to the nominal transfer function. Roughly

pert

speaking, small perturbations should not significantly alter the closed-loop
transfer function from w

to zp.

q

The worst-case gain is defined as the largest magnitude of the perturbed
transfer function, considering all δ values that satisfy the magnitude bound.
More precisely:

wcgain ω() max H

pert,pq

wcgain(ω) is always larger than the nominal gain, |H

Δ = diagonal δ1,...,δ

()δiliω()≤,{}=

k

(jω)|. This is not

zw,pq

because the uncertain transfer functions only can increase the magnitude of
the transfer function from w

to zq. In fact, it is possible that for a lucky

q

choice of the δ values, the perturbed transfer function actually can be
smaller than the nominal transfer function over all frequencies. But in the
worst-case gain, you consider only the worst possible δ values, and these
always increase the perturbed gain over the nominal gain.

(2-3)

Intuitively, if the stability margin is large, then the uncertain transfer
functions should not greatly effect the gain from w
should be not much larger than the nominal gain |H

to zp, so that wcgain(ω)

q

(jω)|. If the stability

zw,pq

margin is small, however, wcgain(ω) could be much larger than the nominal
gain. An extreme case occurs if the stability margin is negative (in dB) at
the frequency δ. Then you have wcgain(ω) = ∞, although

wcbode( ) clips

the worst-case gain curve so that it never exceeds (the maximum nominal
gain) * 100, or +20 dB. Of course, instability is an extreme form of
performance degradation.

MATRIXx Xmath Robust Control Module 2-8 ni.com

wcbode( )

Chapter 2 Robustness Analysis

[WCMAG, NOMMAG] = wcbode (SysH, delb, {input, output,

graph})

The wcbode( ) function computes and plots the worst-case gain of a
closed-loop transfer function.

This function is useful for checking a system that already has been verified
to be robustly stable using

smargin( ). For example, a system can have a

minimum stability margin of 4 dB, so it is robustly stable. If the worst-case
gain from a function input to the output it commands has a 20 dB peak, then
even though the system is robustly stable, the design is unacceptable. On
the other hand, if you verify that the perturbed closed-loop transfer function
increases only 2 dB over the nominal, then the design is probably
acceptable.

wcbode( ) function computes and plots an approximation to

The
wcgain(ω), the largest possible magnitude of a perturbed closed-loop
transfer function that can be caused by uncertain transfer functions that
satisfy the magnitude bound. The

wcbode( ) function is conservative:

it does not under-report the maximum of the perturbed transfer function.

A large value of

wcbode( ) returns a maximum value of ten times the maximum of

case,

wcbode( ) indicates instability: wcgain(ω) = ∞. In this

the nominal transfer function over all frequencies. Consequently, the
window is clipped at 20 dB above the maximum of the nominal transfer
function over all frequencies.

The wcbode( ) function also plots the

nominal transfer function for reference.

Using wcbode( ) to Analyze Performance Degradation

The wcbode( ) function can be used to analyze performance degradation
for the system you have been using (Figure 2-3). The transfer function,
which should be small, is from reference to error (input 1 to output 1).
Figure 2-6 shows the results of the following function call:

[NOMMAG,WCMAG]=wcbode(H,delb,{input=1,output=1});

The performance degradation due to the uncertainties is small but not
negligible.

© National Instruments Corporation 2-9 MATRIXx Xmath Robust Control Module

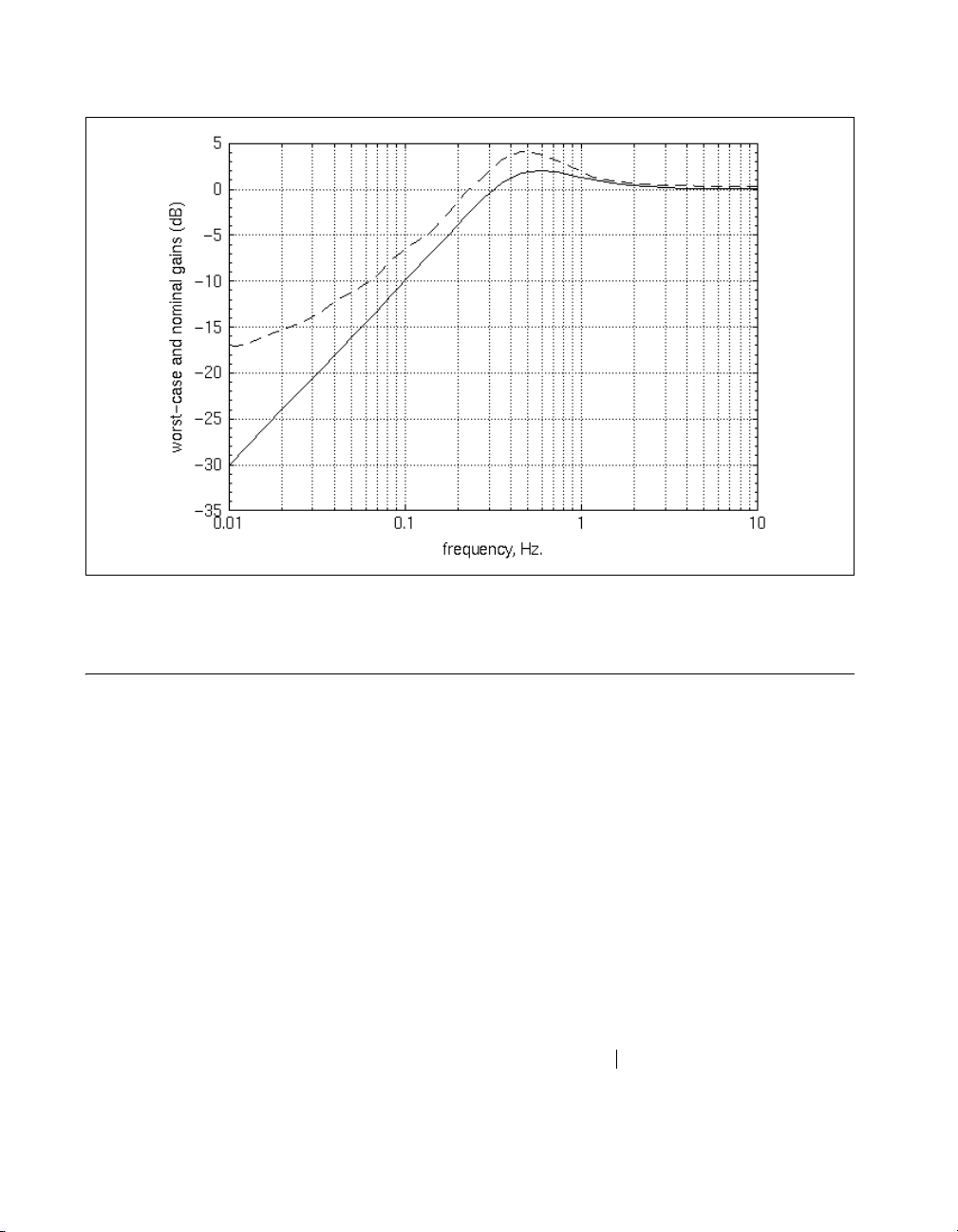
Chapter 2 Robustness Analysis

Figure 2-6. Performance Degradation of the SISO Tracking System

Advanced Topics

This section describes the theoretical background on robustness analysis
and performance degradation.

Stability Margin

This section discusses advanced aspects of computing the stability margin
and the related scaling algorithms.

Stability Margin and Structured Singular Values (μ)

The stability margin was first defined by Safonov in [Saf82]. If you let

MHqrdiagonal l1w()...,lkw(),()=

then you can express the margin at frequency d as

margin ω() max= α det I MΔ–()0≠{

MATRIXx Xmath Robust Control Module 2-10 ni.com

for all diagonal Δ such that

Chapter 2 Robustness Analysis

1

-------------=

μ M()

where μ(

Δiiα≤()}

.

) is the structured singular value, introduced by Doyle in

[Doy82]. Thus, the margin is the inverse of the structured singular value of

diagonally scaled by the magnitude bounds.

H

qr

There is no numerically efficient algorithm that is guaranteed to compute
μ(M), and hence the stability margin. However, it is possible to compute
various good approximations to μ(M). One of these approximations is often
exact.

Stability Margin Bounds Using Singular Values

A popular but conservative method uses singular values:

1

----------------------

margin ω()

Plotting the right side of Equation 2-4 gives a lower bound on the
actual stability margin. To get this plot, specify

scaling="SVD". This approximation can be very conservative, meaning

that the left side can be much larger than the right side. This fact spurred
the study of structured singular values and the other approximations
discussed in the following sections.

≥

σ

max

M()

smargin( ) with

(2-4)

Use of Scaling Example

For this example, you will use the system in Figure 2-3. This time

smargin( ) will be invoked with scaling="SVD", so smargin( )

will calculate Equation 2-4.

margSVD = smargin(H,delb,{scaling="SVD"});

smargin --> Scaling algorithm is type: SVD

smargin --> Margin computation 10% complete

smargin --> Margin computation 50% complete

smargin --> Margin computation 90% complete

© National Instruments Corporation 2-11 MATRIXx Xmath Robust Control Module

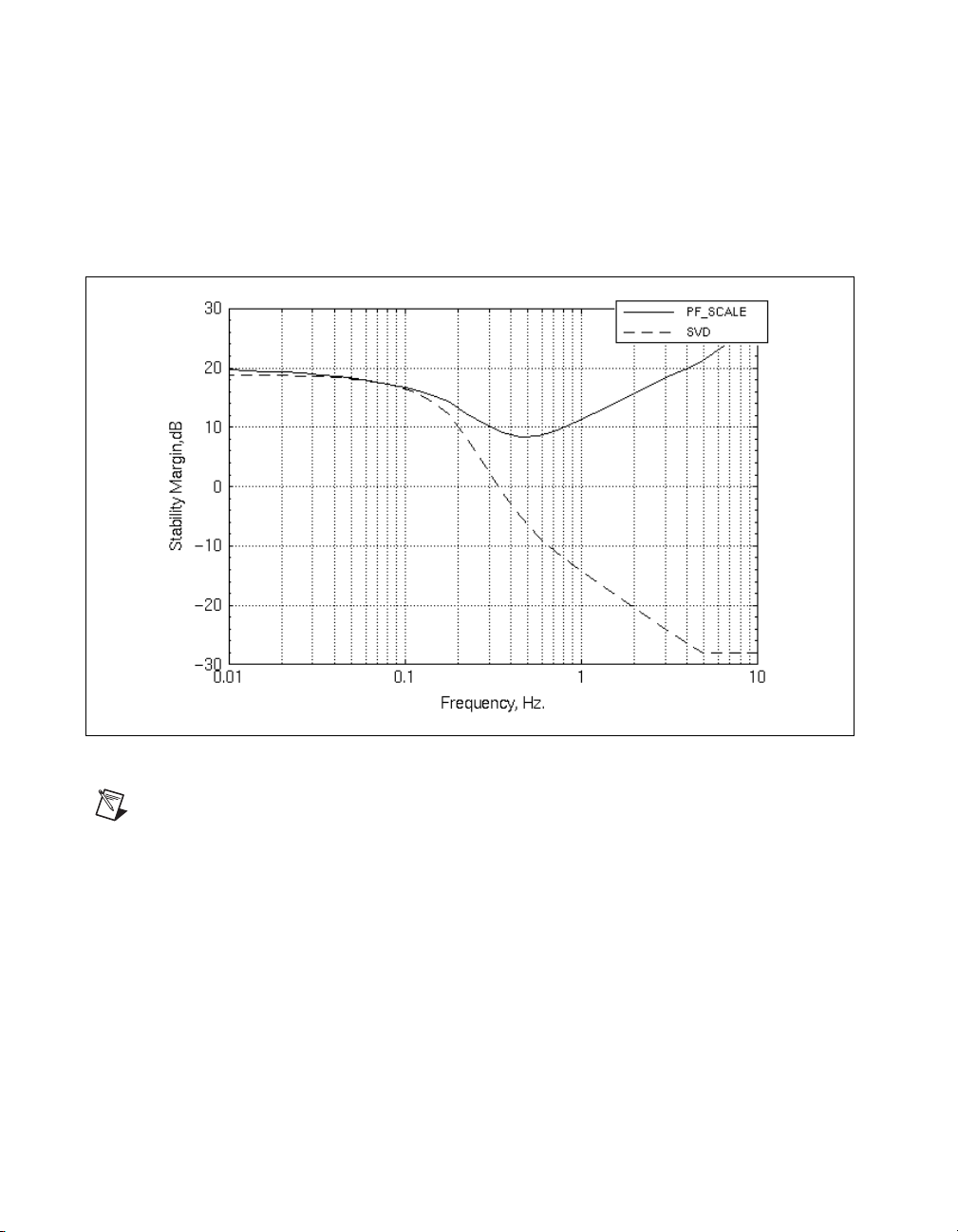
Chapter 2 Robustness Analysis

You can compare this margin to that of the example in the Creating a

Nominal System section; the following inputs produce Figure 2-7.

plot ([marg,margSVD],{xlog}

legend=["PF_SCALE","SVD"],

ylab="Stability Margin,dB",

xlab="Frequency, Hz."})

Figure 2-7. pfscale( ) versus svd Stability Margins

Note

The singular value approach gives results that are too conservative, suggesting that
the uncertainties can destabilize the system. Conversely, you know from the scaled singular
value calculations that the system is robustly stable.

Approximation with Scaled Singular Values

In [Saf82] and [Doy82], the inequality

min σ

D diagonal

()μM()≥

max

is noted. This optimization problem can be shown to be
unimodal—for D>0, an assumption that can be made without loss

MATRIXx Xmath Robust Control Module 2-12 ni.com

DMD

1–

(2-5)

Chapter 2 Robustness Analysis

of generality—so, roughly speaking, it can be solved. [SD83,SD84]
discusses this optimization problem.

Notice that:

M() σDMD

σ

max

()= for D 1=

1–

so you have the following from Equation 2-5:

σ

M()μM()≥

max

This inequality is thought to be nearly an equality, so that the left side is a
good engineering approximation to the right side. No theory supports this
generally held belief, but no example is known where the left side is more
than 15% larger than the right side. Equality can be shown to hold provided
k ≤ 3—for example, if there are three or fewer uncertain transfer functions
[Doy82].

Note The approximation equation of μ(M) (Equation 2-5) is an upper bound. This means

that the stability margin calculated using this approximation is conservative, that is, less
than the actual stability margin. This optimization problem itself can be difficult. Osborne
[Osb60] and Safonov [Saf82] provide two methods for finding good suboptimal scalings
for Equation 2-5.

Both Osborne’s and Safonov’s Perron-Frobenius scalings usually have
been found to be close to the optimum for the optimization problem
equation. The resulting approximations,

ˆ

u

OS

ˆ

u

PF

M() σ

M() σ

maxDOSMDOS

maxDPFMDPF

()=

()=

1–

1–

are thought to be good engineering approximations to μ.

optscale( )

provides an iterative optimization function based on the ellipsoid
algorithm.

© National Instruments Corporation 2-13 MATRIXx Xmath Robust Control Module

Chapter 2 Robustness Analysis

Comparing Scaling Algorithms

Using the system from the first example (Figure 2-3), you can compare
the results of using the three scaling algorithms:

MARG_PF=smargin(H,delb,{scaling="PF",!graph});

MARG_OS=smargin(H,delb,{scaling="OS",!graph});

MARG_OPT=smargin(H,delb,{scaling="OPT",!graph});

plot ([MARG_PF,MARG_OS,MARG_OPT],{xlog,

legend=["PF","OS","OPT"],xlab="Frequency, Hz.",

ylab="Stability margin, dB"})

Figure 2-8 plots the margins produced by the three scaling algorithms.
Notice that in this problem the three scalings yield identical stability
margins.

Figure 2-8. Results of Scaling Algorithm Options

MATRIXx Xmath Robust Control Module 2-14 ni.com

ssv( )

Chapter 2 Robustness Analysis

[v,vD] = SSV(M, {scaling})

The ssv( ) function computes an approximation (and guaranteed upper
bound) to the Scaled Singular Value of a complex square matrix M, where
M can be a reducible matrix. The scaled singular value v(M) is defined by:

vM()= inf σ DMD

nn×

DC

∈ det D()0 dia,≠, gonal

()

1–

Scaling can be accomplished with one of three algorithms:

• Perron-Frobenius—If

{scaling="PF"} Safonov’s

Perron-Frobenius method [Saf82] is used. This method finds the scaled
singular value for non-negative real matrices M. In general, it is
suboptimal if M is complex. This algorithm is the default because
empirical tests show that is the fastest of the three.

• Osborne—If

This method solves the problem of finding D

where D is diagonal and positive, and is the Frobenius norm.

{scaling="OS"}, Osborne’s Method [Osb60] is used.

such that

O

DOMD

1–

O

D diagonal

inf

DMD

⋅

F

1–

F

Thus, the Osborne method minimizes the Frobenius norm, and is
therefore suboptimal.

• Optimal—If

{scaling="OPT"}, Boyd’s ellipsoid algorithm

[BYB89] is used. This algorithm computes the scaled singular value
to a guaranteed accuracy. It is, however, the most computationally
expensive of the three algorithms.

ssv( ) Examples

Consider the complex matrix M:

M = [–1, jay, 0; 0, 2*jay, 1+jay;1, 0, 1];

ssv( ) can return the optimally scaled singular value of M using Osborne,

Perron-Frobenius, or Boyd methods:

VOS=ssv(M,{scaling="OS"})

VOS (a scalar) = 2.56723

VPF=ssv(M,{scaling="PF"})

VPF (a scalar) = 2.45133

© National Instruments Corporation 2-15 MATRIXx Xmath Robust Control Module

Chapter 2 Robustness Analysis

osscale( )

pfscale( )

VOPT=ssv(M,{scaling="OPT"})

VOPT (a scalar) = 2.43952

VSVD = max(svd(M))

VSVD (a scalar) = 2.65886

[v, vD] = osscale(M)

The osscale( ) function scales a matrix using the Osborne Algorithm.
A diagonal scaling D

D

OSMDOS

1–

, which is the square root of the sum of the squares of its
singular values. If M is reducible,
by zero. To avoid this, use

[v,vD]=ssv(M,{scaling="OS"})

[v, vD] = pfscale(M)

is found that minimizes the Frobenius norm of

OS

osscale( ) may encounter a divide

ssv( ) with the Osborne scaling option:

The pfscale( ) function scales a matrix using the Perron-Frobenius
Algorithm. This scaling is optimal for matrices with all positive entries.
The matrix M must be irreducible for this function. If M is reducible,

ssv( ) with the Perron-Frobenius scaling option instead:

use

[v,vD]=ssv(M,{scaling="PF"})

The optimum diagonal scaling is found for M using the Perron-Frobenius
theory of non-negative matrices. This scaling is given by

PF

D

i

p

i

----=

q

i

where p and q are right and left eigenvectors of | associated with its largest
eigenvalue:

Mp λ

MATRIXx Xmath Robust Control Module 2-16 ni.com

p,= MTq λ

max

q,= p 0 q≠≠

max

optscale( )

Reducibility

Chapter 2 Robustness Analysis

[v, vOPTD] = optscale (M, {tol})

The optscale( ) function optimally scales a matrix. An iterative
optimization (ellipsoid) algorithm which calculates upper and lower
bounds on the left side of Equation 2-5 is used. If these bounds are within
a relative accuracy you have specified

optscale( ) also will stop and issue a warning if the maximum number

(tol), optscale( ) stops.

of iterations is reached:

200 rows(M)×

optscale( ) will find a μ(M) no larger than pfscale( ).

In some cases, the uncertain transfer functions can be divided into groups
that do not interact. This is illustrated in Figure 2-9.

δ

1

δ

2

δ

3

δ

4

Figure 2-9. Non-Interacting Uncertain Transfer Functions

As you can see, δ3 does not affect the stability margin at all because there
is no feedback through it. The system in Figure 2-9 can be reduced to the
two separate systems shown in Figure 2-10. The stability margin of
Figure 2-9 is the minimum of the stability margins of the systems in
Figure 2-10.

© National Instruments Corporation 2-17 MATRIXx Xmath Robust Control Module

Chapter 2 Robustness Analysis

δ

1

δ

δ

2

Figure 2-10. Reduction to Separate Systems

4

In terms of the approximations to the margin discussed above, this
reducibility will manifest itself as a problem such as divide-by-zero or
nontermination. It really means that the minimum of the optimization
problem is not achieved by any finite scaling.

A matrix M can be split into its reducible components using the following
technique (refer to[BeP79]):

1. Form the matrix X =(αI + M)–1

radius of M, for example 2 .

2. Form Y = X + X

T

where Y has a positive i,j entry if and only if δi and δj

for any α larger than the spectral

M

are in the same reduced system; otherwise, the entries will be zero.

ssv( ) checks for reducibility before invoking a scaling algorithm. The

margins of each of the reduced systems then can be calculated separately,
and the minimum taken.

Worst-Case Performance Degradation (wcgain)

Conversion to a Stability Margin Problem

In [DWS82], it is shown that a simple relation holds between the
worst-case gain defined in Equation 2-3, and the stability margin. For γ > 0,

wcgain (jw) £ g if and only if m(Hred(jw) diag(g-1,

l1(w),...,lk(w)) £ 1

where H
outputs deleted except the ones of interest (the qth input and the pth output).
This can be interpreted as adding a fictitious uncertain transfer function
from w
additional uncertainty is called a performance loop as described in
reference [BoB91].

MATRIXx Xmath Robust Control Module 2-18 ni.com

is H with the rows and columns corresponding to all inputs and

red

to zp with magnitude bound γ–1 at the given frequency. This

q

wcgain( )

Chapter 2 Robustness Analysis

Using this relation and any of the previously discussed approximations for

.

), you can compute an approximation to wcgain( ). Because the

μ(
approximations to μ(

wcgain( ) also are upper bounds. For speed purposes, wcgain( ) uses

.

) are upper bounds, the resulting approximations to

Perron-Frobenius scaling to calculate the approximation of μ.

gamma = wcgain(H, gammin, gammax, gam0)

The wcgain( ) function estimates the largest possible magnitude from
a given input of the system to a given output, when the other inputs are
connected to the other outputs through uncertain transfer functions
bounded by one.

For a discussion of

wcgain( ) syntax, refer to the Xmath Help. This is a

low-level function that calculates the worst-case gain at a single frequency,
where the magnitude bounds are normalized to one as follows:

l

… lk1===

1

Because it is a lower level function, there is no syntax checking. This
function is called by the

wcbode( ) function.

© National Instruments Corporation 2-19 MATRIXx Xmath Robust Control Module

System Evaluation

This chapter describes system analysis functions that create singular value
Bode plots, performance plots, and calculate the L
system.

Singular Value Bode Plots

The singular value Bode plot is a MIMO generalization of the bode( )
magnitude plot. It is calculated as

where

Hjw()(), i 1…k=

σ

i

3

norm of a linear

∞

kminn

and

H() σ2H() … σkH() 0≥≥≥≥

σ

1

In these equations, σ
system at frequency ω, and σ
gain of the system at frequency ω.

(H(jw)) » σk(H(jw)), then at the frequency ω, the system gain can be

If σ

i

large for some input directions and small for other input directions.

The singular value plot allows you to generalize to the MIMO case notions
such as “the command-to-tracking error transfer function is small” or “the
loop gain is large.” For example:

• If the system represents the command-to-tracking error for a

closed-loop system, then you would hope that σ
σ values, are small over the bandwidth of the system. This means
that the command-to-tracking error is small in all directions at these
frequencies.

• The singular value plot of a certain transfer matrix gives a lower bound
on the stability margin of the system.

(H(jw)) can be thought of as the maximum gain of the

i

(, )()=

inputsnoutputs

(H(jw)) can be thought of as the minimum

k

, and hence all

1

© National Instruments Corporation 3-1 MATRIXx Xmath Robust Control Module

Chapter 3 System Evaluation

Refer to [BoB91] in Appendix A, Bibliography.

Example 3-1 Creating a Singular Value Plot

1. Let a system H be a 2-input/2-output system:

tf=makepoly([1,2],"s")/...

polynomial([0,-2.334,-12],"s")

tf (a transfer function) =

s + 2

--------------------

(s + 2.334)(s + 12)s

System is continuous

H = [tf, 2*tf; tf*tf, tf+3];

[outputs,inputs]=size(H)

outputs (a scalar) = 2

inputs (a scalar) = 2

2. Now plot the singular values of the system between 0.01 and 100 Hz

svplot( ):

using

svplot(H,{Fmin=0.01,Fmax=100})

The result is shown in Figure 3-1. For a discussion of svplot( ) syntax,
refer to the Xmath Help.

MATRIXx Xmath Robust Control Module 3-2 ni.com

L Infinity Norm (linfnorm)

Chapter 3 System Evaluation

Figure 3-1. Singular Value Plot

The L∞ norm of a stable transfer matrix H is defined as:

H

sup σ Hjω()()=

∞

ωℜ∈

where is the maximum singular value and H(jω) is the transfer matrix

σ

under consideration.

The L

norm of a stable transfer matrix is the maximum of the maximum

∞

singular values over frequency. For example, the highest point of its
singular values plot. Observe that the L

norm can be calculated even if H is

∞

not stable.

A simple interpretation of the L

norm of a stable system can be given as:

∞

RMS y()

=

max

--------------------

RMS u()

H

∞

where u and y are the input and output of H, respectively. This means that

H

is the root mean square (RMS) gain of the system: it is the largest

∞

© National Instruments Corporation 3-3 MATRIXx Xmath Robust Control Module

Chapter 3 System Evaluation

factor by which the RMS value of a signal flowing through H can be
increased.

linfnorm( )

By comparison, the H

norm is defined as:

2

∞

k

1

H

------

= dw

2

2π

σ

Hjω()()

i

∑

∫

∞–

i 1=

2

This norm can be interpreted as the RMS value of the output when the input
is unit intensity white noise. It can be computed in Xmath using the

rms( )

function.

For discrete-time systems with a stable H,

H

∞

σ

where is the maximum singular value and H(e

max

ωππ,–()∈

()()=

σ He

jω

jω

) is the transfer matrix

under consideration.

[sigma, vOMEGA] = linfnorm( Sys, {tol,maxiter} )

The linfnorm( ) function computes the L∞ norm of a dynamic system
using a quadratically convergent algorithm. The

linfnorm( ) function

relies on eigenvalue calculations of a Hamiltonian matrix with twice as
many states as
A singular value plot created with

Sys and, consequently, may be unreliable for large systems.

svplot( )can be used as an alternative

in these cases. Refer to the Singular Value Bode Plots section.

• The keyword
is 0.01.

tol controls the required relative accuracy. The default

maxiter is the maximum number of iterations. The default

is 15.

• If the maximum norm is found at ω = ∞,

vOMEGA = Infinity

sigma = gain at infinity.

linfnorm( ) returns:

MATRIXx Xmath Robust Control Module 3-4 ni.com

Chapter 3 System Evaluation

•If A has an imaginary eigenvalue at jω0, linfnorm( ) returns:

vOMEGA =

SIGMA = Infinity

ω

0

where ω0 is one of the imaginary eigenvalues of A.

•Even if H is unstable,

linfnorm( ) returns its maximum singular

value on the jω axis.

For discrete-time systems
norm computation problem to a continuous-time problem using a Cayley
transformation. For example, it maps the unit circle conformally onto the
complex right half plane using a linear fractional transformation. The

linfnorm( ) function then calls itself to solve the continuous-time

problem, and finally converts the solution back to discrete-time.

Example 3-2 Example of linfnorm( )

Sys=system([-0.2,-1;1,0],[1,0]',[0,1],0);

[sigma,omega]=linfnorm(Sys)

sigma (a scalar) = 5.07322

omega (a scalar) = 0.157081

The linfnorm( ) function will return the L∞ norm (sigma) of the transfer
matrix H(jω) described by
where it is achieved.
plotting the singular values of H(jω) as a function of ω (Figure 3-2).

sv=svplot(Sys,{fmin=.01, fmax=1.0});

linfnorm( ) converts a discrete-time L

Sys, and omega is the vector of frequencies

linfnorm( ) computation can be checked by

∞

© National Instruments Corporation 3-5 MATRIXx Xmath Robust Control Module

Chapter 3 System Evaluation

Figure 3-2. Singular Values of H(jω) as a Function of ω

Note sv

10**(max(sv,{channels})/20).

is returned in dBs. Check that sigma is within 0.01 (the default value of tol) of

[sigma,10^(max(sv,{channels})/20)]

ans (a row vector) = 5.07322 4.98731

The linfnorm( ) function also can be used on discrete-time systems.
Consider a state-space system with a sample rate of 10 Hz:

SysD=system([0.5,0.5;0.8,0.5],[0.8,0.5]',

[0,1],0,{dt=0.1})

[sigma,omega]=linfnorm(SysD)

sigma (a scalar) = 5.99267

omega (a scalar) = 0

MATRIXx Xmath Robust Control Module 3-6 ni.com

Singular Value Bode Plots of Subsystems

e

u

r

To evaluate the performance achieved by a given controller rapidly, it is
useful to check four basic maximum singular value plots—for example, the
transfer matrices from process and sensor noises to the error and actuator
signals.

perfplots( )

SV = perfplots ( Sys, nd, ne, { keywords } )

The perfplots( ) function plots the maximum singular value of the
four transfer matrices of the system in the following figure.

d

Sys

n

Chapter 3 System Evaluation

In most applications, the

perfplots( ) function is applied to a system of

the form shown in Figure 3-3, where
controller.

process
noise

d

sensor
noise

n

Figure 3-3. Typical System with Plant and Controller

uy

Sys

P is the plant and K is a proposed

error

P

K

e

actuato

u

© National Instruments Corporation 3-7 MATRIXx Xmath Robust Control Module

Chapter 3 System Evaluation

The four transfer matrices are labeled e/d, e/n, u/d, and u/n in the final plot.
The plots in the top row, consisting of e/d and e/n, show the regulation or
tracking achieved by the controller. If both these quantities are small, then
the disturbance d and the sensor noise n will not make the error signal e
large.

The bottom row of plots, consisting of u/d and u/n, show the actuator effort
used by the controller. If these are both small, then the actuator effort u,
which results from the disturbance d and the sensor noise n will be small.

A classic trade-off in controller design boils down to a choice between
making the top row of a

perfplot( ) small (good regulation/tracking)

and making the bottom row small (low actuator effort). For example, by
varying the design parameter ρ in the

lqgltr( ) regulator design process,

the magnitude of the top two transfer matrices can be traded off against the
magnitude of the bottom two. Increasing ρ makes the top two magnitudes
smaller but makes the bottom two larger.

The columns of a
left column, e/d and u/d, show how sensitive the system is to the process
noise or disturbance d. The plots in the right column, e/n and
sensitive the system is to the sensor noise n. Again, there is a trade-off
between making the magnitudes of the transfer matrices on the left small
(good disturbance rejection) and making the magnitudes of the transfer
matrices on the right small (low sensitivity to sensor noise). In the

lqgltr( ) estimator design, the parameter ρ controls the relative

magnitude of the left and right plots. Increasing ρ makes the left two
magnitudes smaller but makes the right two larger. Refer to Example 3-3.

Example 3-3 Example of perfplots( )

Consider the simple closed-loop system shown in Figure 3-4.

perfplot( ) have a dual interpretation. The plots in the

u/n, show how

noise

disturbance

–

+

n

Figure 3-4. Closed-Loop System

1

s

K

e

+

+

MATRIXx Xmath Robust Control Module 3-8 ni.com

Chapter 3 System Evaluation

The system matrix can be calculated using the afeedback( ) function for
different values of K. Consider two cases: K=1 and K=5.

P = 1/makepoly([1,0],"s")

P (a transfer function) =

1

--

s

System is continuous

K1= 1/makepoly(1,"s")

K1 (a transfer function) =

1

-

1

System is continuous

K5= 5/makepoly(1,"s");

Sys1 = afeedback(P,K1);

Sys5 = afeedback(P,K5);

The effect of the value of K on closed-loop performance can be investigated

perfplots( ).

using

sv1 = perfplots(Sys1,1,1);

Overlap plots:

sv5 = perfplots(Sys5,1,1,{!graph});

for i = 1:4

plot(sv5(1,i),

{graphnumber=i,line_style=2,keep})?

endfor

In Figure 3-5, you can see that over the bandwidth of 0.1 Hz, the controller
K=5 has better regulation (e/d is smaller for K=5 than for K=1, with e/n
about the same for both cases) but uses slightly more actuator effort. Above
the bandwidth of 0.1 Hz, the e/n and u/n show that the K=5 controller is
more sensitive to sensor noise. In classic terms, the K=5 controller has a
higher bandwidth.

© National Instruments Corporation 3-9 MATRIXx Xmath Robust Control Module

Chapter 3 System Evaluation

y

z

Figure 3-5. Perfplots( ) for K = 1 and K =5

clsys( )

SysCL = clsys( Sys, SysC )

The clsys( ) function computes the state-space realization SysCL, of the
closed-loop system from

Figure 3-6. Closed Loop System from w to z

MATRIXx Xmath Robust Control Module 3-10 ni.com

w to z as shown in Figure 3-6.

w
u

Sys

SysC

Chapter 3 System Evaluation

Where SysC=system(Ac,Bc,Cc,Dc), Sys=system(A,B,C,D), and nz
is the dimension of z and nw is the dimension of w:

nw

B

w

B is

B

u

Given the above,

A

=

CL

B

CL

C

CL

D

CL

A+BuIDcD

BcCyBcDyuIDcD

=

=

BwBuIDcD

B

cDywBcDyu

CzDzuIDcD

+ DzuIDcD

DzwDzuIDcD

+=

–()

yu

+ AcBcDyuIDcD

+

+

–()

–()

yu

IDcD

–()

–()

yu

–()

yu

nz

C is

C

z,Cy

SysCL is calculated as shown in Figure 3-7.

1–

DcC

y

1–

DcC

yu

1–

DcC

1–

DcD

1–

DcD

yu

y

yw

1–

DcD

y

yw

D is

BuIDcD

+

yw

–()

nw

D

zwDzu

DywD

yu

–()

yu

1–

C

yu

c

–()

1–

C

c

1–

yu

nz

C

c

Figure 3-7. Calculation of the Closed Loop System (SysCL)

The closed-loop system is assumed to be well-posed—(I – DcDyu) must
be invertible). A well-posed closed-loop system assures that if two given
systems,
represented in state space), then the resulting closed-loop system,

Sys and SysC, are proper (only proper transfer functions can be

SysCL,

also is proper and therefore realizable in state space.

Figure 3-8 is an example of an ill-posed feedback system, where the
closed-loop transfer function is

s+1, which cannot be represented as

a state-space system.

© National Instruments Corporation 3-11 MATRIXx Xmath Robust Control Module

Chapter 3 System Evaluation

Example 3-4 Example of Closed-Loop System

a = 1;

b = [1,0,1];

c = b';

d = [0,0,0;0,0,1;0,1,0];

Sys = SYSTEM(a,b,c,d);

SysC = SYSTEM(-40,2.7,-40,0);

SysCL = clsys(Sys,SysC)

SysCL (a state space system) =

A

1 -40

2.7 -40

B

1 0

0 2.7

C

1 0

0 -40

D

0 0

0 0

X0

0

0

System is continuous

1

+ 1

s

+

+

Figure 3-8. Ill-Posed Feedback System

MATRIXx Xmath Robust Control Module 3-12 ni.com

Controller Synthesis

e

This chapter discusses synthesis tools in two categories, H∞ and H2. This
chapter does not explain all of the theory of H
shaped LQG design techniques. The general problem setup is explained
together with known limitations.

H-Infinity Control Synthesis

Problem Definition

The H∞ control synthesis function hinfcontr( ) finds a stabilizing
multivariable controller K for the plant P, as shown in Figure 4-1.

In the closed-loop system with plant P and controller K, all frequencies ω,

4

, LQG/LTR, and frequency

∞

H

jω()()γ≤

ew

∞

P

K

∞

γ≤

σ

maxHew

where H
specified limit. Equation 4-1 can be expressed in terms of the H

The function hinfcontr( ) is based on the 2-Riccati state space
solutions presented in [GD88,DGKF89]. You can examine these references
for theoretical descriptions.

is the closed-loop transfer matrix from w to e and γ is some

ew

H

ew

w

Figure 4-1. Closed-Loop System with Plant P and Controller K

uy

(4-1)

norm as:

© National Instruments Corporation 4-1 MATRIXx Xmath Robust Control Module

Chapter 4 Controller Synthesis

The function hinfcontr( ) can be used to find an optimal H∞ controller
K that is arbitrarily close to solving:

hinfcontr( ) function description in the hinfcontr( ) section

The
describes how the optimum can be found manually by decreasing γ until
an error condition occurs, or conversely by increasing γ until the error
condition is fixed.

The particular restrictions, required by the 2-Riccati solutions and
summarized in the Restrictions on the Extended Plant section are
those imposed in [GD88,DGKF89].

Extended Transfer Matrix

Referring to Figure 4-1, plant P specifies two groupings of vector inputs
and outputs. Such systems or transfer matrices are referred to as extended
transfer matrices or systems. To enter these in Xmath requires a
modification of your existing system representation. The standard system
has the form y = G(s)u and can be described either in state-space form:

or as a transfer matrix:

min H

K

ew

x' Ax Bu+=

yAxDu+=

γ≤γ

∞

=

opt

(4-2)

Gs() DCsIA–()

1–

B+=

G(s) can be described in Xmath using the state-space system object:

G = system(A,B,C,D)

There is, however, insufficient information in this form to distinguish
the input/output groupings in the extended system P in Figure 4-1.
The state-space form of P is:

x·Ax B

eC

yC

MATRIXx Xmath Robust Control Module 4-2 ni.com

wB2u++=

1

xD11wD12u++=

1

xD21wD22u++=

2

Equivalently, as a transfer matrix:

e

y

Chapter 4 Controller Synthesis

To enter the extended system, you must know the sizes of e and w shown
in Figure 4-1. The extended plant P can be constructed using the Xmath
interconnection functions, as shown in Example 4-1.

Building the Plant Model

The general form of the plant P is shown in Figure 4-2.

The plant consists of three transfer matrices: Win and W
weights, and G which can be interpreted as the system dynamics. Both P
and G distinguish inputs and outputs into two groups of variables.

Plant P

w

u

D

Ps()

11D12

D21D

vz

W

in

Figure 4-2. Construction of Plant P

C

C

22

G

1

sI A–()1–B1B

2

W

out

[]+=

out

2

, referred to as

The input/output variables are organized as follows:

• actuator/sensor variables

u—vector of actuator (control) signals

y—vector of sensor (measured) and other accessible signals

• exogenous inputs

v—vector of commands and disturbance

w—vector of “normalized” commands and disturbances

• performance outputs

z—vector of critical performance signals (regulated variables)

e—vector of “normalized” critical performance signals

© National Instruments Corporation 4-3 MATRIXx Xmath Robust Control Module

Chapter 4 Controller Synthesis

e

y

e

The transfer matrix G can be viewed as a model of the underlying system
dynamics with v and u as generalized forces that produce effects in the
performance signals z and measured signals y.

The weight W

is used to model the exogenous input v by v = Winw.

in

Similarly, the critical performance variables in the vector z are weighted to
form the normal critical variables e = W

In general, the input weight W

can be viewed as a dynamic model of the

in

exogenous inputs and the output weight W

z.

out

as the inverse of the desired

out

performance. As an illustration, consider the plant configuration in
Figure 4-3.

P

W

in

w

w

dist

noise

W

dist

W

noise

w

w

u

G

d

n

y

reg

G

u

dyn

y

W

W

W

sens

out

reg

act

e

reg

e

act

Figure 4-3. Typical Plant Configuration

The exogenous input vectors d and n represent disturbances and sensor
noise, respectively. These are generated by passing normalized
unpredictable signals, ω

W

dist

and W

, respectively. The critical performance variables are some

noise

regulated variables y

and ω

dist

, as well as the actuator commands u. These are

reg

weighed by the transfer matrices W
variables e

reg

and e

. The sensed variables y

act

additive noise n to form the measured signal y. The transfer matrix G
represents the underlying system dynamics. Observe that the transfer
matrix G, as defined in [BBK88], consists of G

, through stable transfer matrices,

noise

and W

reg

to form the normalized error

act

are contaminated by

sens

with some special

dyn

dyn

output/input connections among the variables n and u as depicted in
Figure 4-3. This is in the form of the familiar LQG setup, except that

MATRIXx Xmath Robust Control Module 4-4 ni.com

Chapter 4 Controller Synthesis

⎛⎞

here the weighting matrices are transfer matrices, whereas in the LQG
setup they are constants.

A description of the plant in Figure 4-3 is as follows:

• Dynamical system G

dyn

:

Weight Selection

x·Ax B

y

reg

y

sens

• Measured variables y = y

• Input weight W

• Output weight W

:

in

d

n

W

dist

==

0 W

:

out

e

reg

e

act

W

==

C

reg

C

sens

sens

0

noise

reg

0 W

x=

x=

+ n:

0

act

dB

dist

w

w

noise

dist

y

reg

u

act

u++=

w

dist

W

in

w

noise

y

reg

W

in

u

In the standard LQG formulation, the weighting functions (W
W

, and W

reg

) are all constant matrices. In fact, if Q

act

reg

and Q

definite matrices in the LQ cost, for example,

, W

dist

noise

are positive

act

,

∞

1

---

J

x'Q

⎜⎟

∫

2

⎝⎠

0

xu'Q

reg

act

u+

dt=

then the following apply:

Similarly, if R

proc

W

and R

reg

sens

reg

act

are positive definite matrices corresponding to

12/

Q

= W

12/

Q

=

act

the process and measurement noise intensities, then the following apply:

dist

© National Instruments Corporation 4-5 MATRIXx Xmath Robust Control Module

proc

noise

12/

Q

= W

W

12/

Q

=

sens

Chapter 4 Controller Synthesis

Selecting these weights has much the same effect here. Specifically, let Hzv

d

) from inputs:

γ

be the closed-loop transfer matrix (with u = K

v

=

n

to outputs:

y

reg

z

=

u

Thus,

H

y

dHy

=

reg

HudH

H

zv

reg

un

n

Suppose that the controller u = K

approximates Equation 4-2. Thus,

y

W

outHzvWin

γ

≈

opt

∞

In many cases, this means that the maximum singular value of the
frequency response matrix (W

outHzvWin

)( jω) is constant over all

frequencies. That is,

⎛⎞

W

regHy

⎜⎟

σ

max

⎜⎟

W

⎝⎠

dWdistWregHy

reg

actHudWdist

W

An interpretation is that the weighting filters W
shape of the closed-loop frequency response H

nWnoise

reg

actHjnWnoise

in

zw

jw()

and W

determine the

out

( jω), and γ

≈

γ

opt

determines

opt

the peak value. This observation helps motivate the selection of the weights
so as to shape the closed-loop frequency response matrix H

( jω).

zw

Observe, however, that the elements of the frequency response matrix,
(W

outHzvWin

value of at least one of the four subblocks is within 3 dB of γ

)( jω), need not be constant. Instead, the maximum singular

. For all ω,

opt

M ω() σ

()jω()[]2M ω()≤≤

maxWoutHzvWin

MATRIXx Xmath Robust Control Module 4-6 ni.com

where

Chapter 4 Controller Synthesis

M ω() max m

u(),m12u()m21u()m22u(){}=

11

and

m

σ

11

m

12

m

21

m

22

[]=

maxWregHy

σ

[]=

maxWregHy

σ

[]=

maxWactHudWdist

σ

[]=

maxWactHunWnoise

reg

reg

dWdist

nWnoise

The weights also can be viewed as “design knobs” (for example,
[ONR84]). In this view, the weights are not directly related to specific
disturbance or performance models but rather are used as a vehicle to obtain
a closed-loop transfer matrix, H
every selection of weights W

, from v to z with desired properties. For

zv

and W

in

, the closed-loop system has the

out

following property:

W

inHzvWout

has other properties, both good and bad. To some extent, these all

But H

zv

γ≤

∞

can be affected by varying the weights. An effective way to provide a rapid
evaluation of performance is with the function

perfplots( ), as

described in the perfplots( ) section of Chapter 3, System Evaluation. With
a few trial and error adjustments of the weights,

perfplots( ) will give

a good indication of their effect on performance.

Restrictions on the Extended Plant

Not all choices of weights will result in an extended plant P = W
that will solve Equation 4-1. The following conditions, established in
references [GD88,DGKF89], if satisfied, will result in a solution. If any
are not satisfied, an error condition occurs.

The conditions are:

•(A, B

• rank(D

• rank(D

© National Instruments Corporation 4-7 MATRIXx Xmath Robust Control Module

, C2) can be stabilized and detected

2

) = NU (number of inputs)

12

) = NY (number of outputs)

21

outGWin

Chapter 4 Controller Synthesis

•For all ω ≥ 0,

hinfcontr( )

rank

AjωI– B

C1D

2

NS NU+=

12

•

rank

AjωI– B

C2D

1

NS NY+=

21

Condition 1 is a standard condition to ensure the existence of a stabilizing
controller. Condition 2 ensures that the control signal u is contained in the
normalized error vector e (refer to Figure 4-3). Conversely, condition 3
ensures that some exogenous input (disturbance or noise) affects the
measured signals (refer to Figure 4-3). Conditions 4 and 5 ensure certain
minimal realizations of subblocks of the extended plant ([GD88]).

[SysC,Syszw]= hinfcontr(SysAug,gamma,nw,nz,{method})

The hinfcontr( ) function designs an H∞ controller for an augmented
plant. The augmented plant should satisfy the five restrictions in the

Restrictions on the Extended Plant section. The

hinfcontr( ) function

tests for these restrictions and returns an error if they are violated.

Assuming the restrictions are not violated, a controller satisfying

H

ew

γ≤

will exist if certain low-level conditions also hold. These

∞

involve conditions for the solution of the underlying Riccati equations
and conditions for some other constraints. The details can be found in
[GD88,DGKF89] and are beyond the scope of this manual. If the low-level
conditions are violated, an error statement is displayed:

hinfcontr –>No stabilizing controller meets the spec!

Adjust gamma and try again!

When this occurs it means that the original gamma is too small and a

gamma (for example, a looser spec) is required to eliminate the

larger
error condition. If
is not met, the

gamma is too small, or any other necessary condition

hinfcontr( ) function returns a zero controller and the

closed-loop system is equal to the open-loop system:

SysC = system( [], [], [], 0 ),

Syszw = system(A, B1, C1, D11)

MATRIXx Xmath Robust Control Module 4-8 ni.com

Chapter 4 Controller Synthesis

If no error message occurs, then is guaranteed. However,
this does not preclude the possibility that either or that

γ

opt

For the former case, there are two checks:

•Use the

• Compute the graph versus ω.

If by about 6 dB or more, then you can decrease

H

ew

again.

gamma is very large, the specification (Equation 4-1) is easily

When
met. In this case, the
approximately minimizes the H
Equation 4-2.
transforms the H

optimal controller (with ).

H

∞

Similarly, for a large
with the noise spectra determined by the weights W

gamma, the controller has good worst-case performance for noise

small
spectra that lay below the weights W

Example 4-1 Example of hinfcontr( )

H

Hew∞«

.

linfnorm( ) function to compute .

σ

maxHew

γ«

∞

hinfcontr( ) function returns a controller that

norm of Hew while satisfying

Gamma can be interpreted as a “knob” that smoothly

optimal (LQG) controller, (with gamma large), to a

2

2

gamma γ

gamma, the controller has good RMS performance

γ≤

ew

∞

jω()[]

≈

opt

and W

dist

noise

H

ew

H

.

ew

dist

γ«

∞

∞

gamma and try

and W

noise

. For a

Referring to Figure 4-2, suppose G has the state space description,

x·xd+= u+

yxn+=

where:

x

z

= v

u

d

=

n

1. The extended system matrix for G is:

A = 1;

B1 = [1,0]; B2 = 1; B = [B1,B2];

C1 = [1;0]; C2 = 1; C = [C1;C2];

D11 = zeros(2,2); D12 = [0;1]; D21 = [0,1]; D22 = 0;

D = [D11,D12; D21,D22];

G = system(A,B,C,D);

nw = 2; nz = 2;

© National Instruments Corporation 4-9 MATRIXx Xmath Robust Control Module

Chapter 4 Controller Synthesis

y

y

y

Suppose the input/output weights are as follows:

1

-----------

W

s 1+

0

W

=

in

00.1

out

10

=

00.1

2. Create the four weights:

Wdist = 1/makepoly([1,1],"s")

Wdist (a transfer function) =

1

-----

s + 1

Wnoise = 0.1;

Wreg=1/makepoly(1,"s");

Wact = 0.1;

3. Combine the weights in Win and W

(refer to Figure 4-4):

out

Win = [Wdist,0,0;0,Wnoise,0;0,0,1];

Wout=[Wreg,0,0;0,Wact,0;0,0,1];

The resulting system, P can be obtained by putting in series the plant
G and the two weights:

P = Wout*G*Win;

Before using the hinfcontr( ) function, you must decide on an
initial guess for

gamma.

W

in

u

u

u

1

s + 1

0.1 0.1

1 1

Figure 4-4. Plant and Weights for hinfcontr( )

MATRIXx Xmath Robust Control Module 4-10 ni.com

d

n

u

G

W

out

1

Chapter 4 Controller Synthesis

4. For this example, you will start with gamma=1 as the initial guess and
enter:

[K,Hew] = hinfcontr(P,1,2,2);

No error messages are reported. This means that a stabilizing
controller has been found such that Equation 4-1 holds. That is,

H

ew

1≤

.

∞

The actual H∞ norm is found from:

normHew=linfnorm(Hew)

normHew (a scalar) = 0.211984

The result is that on this first iteration:

gamma = 1 Æ normHew = 0.212

Continuing to iterate for the optimal gamma:

[K,Hew] = hinfcontr(P,.2,2,2);

normHew=linfnorm(Hew)

normHew (a scalar) = 0.173218

[K,Hew] = hinfcontr(P,.15,2,2);

normHew=linfnorm(Hew)

normHew (a scalar) = 0.147418

[K,Hew] = hinfcontr(P,.13,2,2);

normHew=linfnorm(Hew)

normHew (a scalar) = 0.13103

[K,Hew] = hinfcontr(P,.12,2,2);

normHew=linfnorm(Hew)

normHew (a scalar) = 2.02252

hinfcontr --> No stabilizing controller meets the

spec.!!

Adjust gamma and try again

The iterations establish that γ
shows the output of the
system H

[K,Hew] = hinfcontr(P,.13,2,2);

normHew = linfnorm(Hew, {tol=1e-3})

normHew (a scalar) = 0.129863

svHew = perfplots(Hew,1,1,{Fmin=0.01,Fmax=100});

for γ =0.13.

ew

lies between 0.12 and 0.13. Figure 4-5

opt

perfplots function on the closed-loop

© National Instruments Corporation 4-11 MATRIXx Xmath Robust Control Module

Chapter 4 Controller Synthesis

Figure 4-5. Perfplots for H

ew

It also is useful to perform perfplots( ) on the unweighted
closed-loop system, H

, which in this case is the closed-loop transfer

zv

matrix from (d,n) into (x,u).

The following function calls produce Figure 4-6:

Hzv=clsys(G,K);

Hzv=perfplots(Hzv,1,1,{vF=domain(svHew)});

MATRIXx Xmath Robust Control Module 4-12 ni.com

Chapter 4 Controller Synthesis

singriccati( )

Figure 4-6. Perfplots for H

[P, solstat] = singriccati(A,Q,R {method})

zv

The singriccati( ) function solves the Indefinite Algebraic Riccati
Equation (ARE):

A′PPAPRP– Q++0=

The ARE is solved by decomposing the Hamiltonian:

AR–

′

Q– A

–

The required decomposition of the Hamiltonian can be achieved using

method="eig" or method="schur". The Schur decomposition is

slower, but might handle some ill-conditioned problems. After solving the

singriccati( ) calculates the residue (A

ARE,

T

P + PA – PRP + Q).

A warning is displayed if the residue is large. For an example of this
function, refer to the Xmath Help.

© National Instruments Corporation 4-13 MATRIXx Xmath Robust Control Module

Chapter 4 Controller Synthesis

Linear-Quadratic-Gaussian Control Synthesis

The H2 Linear-Quadratic-Gaussian (LQG) control design methods are
based on minimizing a quadratic function of state variables and control
inputs. Conventionally, the problem is specified in the time domain.
By converting the LQG performance index into the frequency domain,
it becomes obvious that the conventional LQG places equal penalty on
states and control inputs at all frequencies. It is possible to realize
significant improvement in robustness and performance by making the
penalty weighting matrices functions of frequency.

LQG Frequency Shaping

Bryson’s rule [BH69] can be extended to initially select a frequency
shaping for a particular problem. For the control design problem, the
frequency-shaped weighting matrices should be large at frequencies where
control inputs are less desirable. For example, a large weighting on control
signals at high frequency would produce less control activity at those
frequencies, leading to a closed-loop system with lower bandwidth. Similar
ideas apply to selection of state weighting in control design and the
development of robust state estimators.

Three functions are available to solve the problem of frequency-shaped cost
functionals:

fsregu( )—frequency-shaped regulator

•

•

fsesti( )—frequency-shaped estimator

•

fslqgcomp( )—frequency-shaped linear-quadratic-gaussian

compensator

fsregu( )

[SysC, SysCC, vEV] = fsregu(SysA, ns, RXXA, RUUA, {RXUA})

The fsregu( ) function computes a frequency-shaped control law.
It assumes you start with:

x·Ax Bu+=

and

∞

1

*

---

=

J

2

MATRIXx Xmath Robust Control Module 4-14 ni.com

jω()Qjω()xjω()u*jω()Rjω()ujω()+[]ωd

x

∫

∞–

Chapter 4 Controller Synthesis

This expression can be converted into the following form [Gu80]:

·

x

x·′

A

11A12

A21A

x′

22

⎧⎪⎨⎪⎩

A

c

u

0 C

⎧⎪⎨⎪⎩

C

x

12

x′

c

If R(jω) is not a function of frequency, then C

Note The system has a new input v and the old input u is now the output of the system.

x

Dv+=

D

12

B

1

v+=

B

2

⎧⎨⎩

B

c

{

c

= 0 and D = I.

This structure is only used for computational convenience.

Define:

x

x

=

A

x'

Thus,

·

x

AcxABcv+=

A

uC

cxADc

∞

1

---

=

J

∫

2

v+=

*

R

xAv*R

x

A

xx

A

uu

v 2x

+ R

A

*

v+()dω

A

xu

A

After the system is put in this form, you are ready to use the
function. For more information on the

fsregu( ) syntax, refer to the

fsregu( )

Xmath Help.

© National Instruments Corporation 4-15 MATRIXx Xmath Robust Control Module

Chapter 4 Controller Synthesis

fsesti( )

[SysF, vEV] = fsesti(SysA, ns, QWWA, QVVA, {QWVA})

The fsesti( ) function computes a frequency-shaped state estimator.
The estimation problem is stated as follows:

x·Ax Bu w++=

yCxDuv++=

The frequency-shaped filter design problem is to minimize,

∞

1

*

---

J

w

= dω

2

Qwwjω()wv*Qvvjω()v+()

∫

∞–

which can be written as:

·

x

= Beuw

AAexA

++

A

or it can be written as:

·

x

x·′

A

11A12

A21A

⎧⎪⎨⎪⎩

A

⎛⎞

u

J

C

1C2

⎝⎠

⎧⎪⎨⎪⎩

C

∞

1

*

---

w

= v

Q

A

∫

2

∞–

For more information on the

MATRIXx Xmath Robust Control Module 4-16 ni.com

x

x′

22

x

A

e

e

w

ww

A

A

fsesti( ) syntax, refer to the Xmath Help.

x·′

B

++=

·

x

*

Q

A

0

⎧⎨⎩

uv

D

e

vv

A

uw

B

e

++=

A

vA2w

A

*

Q

v )dω++

A

wv

A

fslqgcomp( )

[SysCC, vEV] = fslqgcomp(SysF, SysC)

The fslqgcomp( ) function combines filter and control law to compute a
controller from a control law and an estimator. For more information on the

fslqgcomp( ) syntax, refer to the Xmath Help.

Frequency-Shaped Control Design Commands

This extended example uses the previously discussed functions to
demonstrate frequency-shaped control design techniques. A four-state,
poorly damped system is studied to demonstrate how robustness can be
attained using frequency shaping. The control law and filter are designed
on a reduced second order system with and without frequency shaping.

1. Create a full-order system:

a=[0,1,0,0;-1,-.01,0,0;0,0,0,1;0,0,-25,-.05];

b=[0,1,0,1]';

c=[0,1,0,-1]; d=0;

Sys=system(a,b,c,d);

2. Calculate open-loop eigenvalues:

eig(a)

ans (a column vector) =

-0.005 + 0.999987 j

-0.005 - 0.999987 j

-0.025 + 4.99994 j

-0.025 - 4.99994 j

3. Create a reduced order system by selecting only the first mode:

ar=a(1:2,1:2);br=b(1:2);cr=c(1:2);

Sysr=system(ar,br,cr,d);

4. Design an LQG compensator for the reduced-order system, without
using frequency shaping:

qxx=diagonal([0,1]);quu=1;

kr=regu(Sysr,qxx,quu); # Linear-Quadratic-Regulator

ke=esti(Sysr,qxx,quu); # Linear-Quadratic-Estimator

Sysc=lqgcomp(Sysr,kr,ke); # LQG Compensator

Syscl=feedback(Sysr,Sysc); # Reduced-order closed-loop

poles(Syscl)

ans (a column vector) =

-0.500025 + 0.866011 j

-0.500025 - 0.866011 j

Chapter 4 Controller Synthesis

© National Instruments Corporation 4-17 MATRIXx Xmath Robust Control Module

Chapter 4 Controller Synthesis

-0.500025 + 0.866011 j

-0.500025 - 0.866011 j

5. Try the LQG compensator with the full-order system:

[Syscl_fo]=feedback(Sys,Sysc);

poles(Syscl_fo)

ans (a column vector) =

-0.401519 + 0.864869 j

-0.401519 - 0.864869 j

-0.638796 + 0.855861 j

-0.638796 - 0.855861 j

0.0152647 + 4.90994 j

0.0152647 - 4.90994 j

6. Find a stabilizing reduced order controller using frequency shaping.

To stabilize this system, try a frequency-shaped control-law, where the
weighting on the control signal will be 1 + (ω)

4

.

First, form an augmented system, defining two additional states,
μ and

u·.

The augmented system will be:

x

r

d

-----

u

dt

·

u

0001

0000

u

Note The augmented system has two extra states implementing the frequency shaping on

A

rBr

0010

0

x

0

u

·

u

r

x

u

·

u

r

0

0

v+ A

0

1

0()v+ C

axABa

xADav+==

a

v+==

(4-3)

(4-4)

the control system.

aa=[ar,br,[0;0];0,0,0,1;0,0,0,0];

bb=[0,0,0,1]';cc=[0,0,1,0];dd=0;

Sysa=system(aa,bb,cc,dd)

Sysa (a state space system) =

A

0 1 0 0

-1 -0.01 1 0

MATRIXx Xmath Robust Control Module 4-18 ni.com

0 0 0 1

0 0 0 0

B

0

0

0

1

C

0 0 1 0

D

0

X0

0

0

0

0

System is continuous

7. Frequency-weight the control signal.

Transfer the weight on

U from RUU to the third diagonal entry in RXXA.

Chapter 4 Controller Synthesis

Note In Equation 4-3, u is the third state of the augmented system. RUU weighs the new

frequency-shaped control signal v.

Design a frequency-shaped regulator:

rxxa=diagonal([0,1,1,0]);ruua=1;

[Sysfs_sr,,fs_evr]=fsregu(Sysa,2,rxxa,ruua)

Sysfs_sr (a state space system) =

A

0 1

-1.95171 -1.97571

B

0 0

0.951712 -0.228069

C

1 0

D

0 0

X0

0

0

© National Instruments Corporation 4-19 MATRIXx Xmath Robust Control Module

Chapter 4 Controller Synthesis

System is continuous

fs_evr (a column vector) =

-0.645263 + 0.587929 j

-0.645263 - 0.587929 j

-0.347592 + 1.09155 j

-0.347592 - 1.09155 j

8. Calculate the frequency-shaped estimator:

Sysaf=system(ar,br,cr,0);qwwa=qxx;qvva=quu;

[Sysfs_se,fs_eve]=fsesti(Sysaf,2,qwwa,qvva)

Sysfs_se (a state space system) =

A

0 1

-1 -1.00005

B

5.52357e-17 0

0.99005 1

C

1 0

0 1

D

0 0

0 0

X0

0

0

System is continuous

fs_eve (a column vector) =

-0.500025 + 0.866011 j

-0.500025 - 0.866011 j

The compensator should be structured as shown in Figure 4-7.

x

y

Sysfs_se Sysfs_se

A

Figure 4-7. Frequency-Shaped Compensator

u

The fslqgcomp( ) function can be used to develop the compensator.

MATRIXx Xmath Robust Control Module 4-20 ni.com

Chapter 4 Controller Synthesis

9. Design the LQG compensator.

[Sysfs_sc,fs_evc]=fslqgcomp(Sysfs_se,Sysfs_sr)

Sysfs_sc (a state space system) =

A

0 1 0 0

-1 -1.00005 1 0

0 0 0 1

0.951712 -0.228069 -1.95171 -1.97571

B

5.52357e-17

0.99005

0

0

C

0 0 1 0

D

0

X0

0

0

0

0

System is continuous

fs_evc (a column vector) =

-0.373302

-1.17564

-0.713411 + 1.33028 j

-0.713411 - 1.33028 j

Enforce negative feedback:

Sysfs_sc = -Sysfs_sc;

© National Instruments Corporation 4-21 MATRIXx Xmath Robust Control Module

Chapter 4 Controller Synthesis

10. Compute the closed-loop system for the reduced order plant and the
frequency-shaped compensator:

[Sysfs_scl]=feedback(Sysr,Sysfs_sc);

poles(Sysfs_scl)

ans (a column vector) =

-0.645263 + 0.587929 j

-0.645263 - 0.587929 j

-0.500025 + 0.866011 j

-0.500025 - 0.866011 j

-0.347592 + 1.09155 j

-0.347592 - 1.09155 j

11. Compute the closed-loop system for the full-order plant and the
frequency-shaped compensator.

Sysfs_scl_fo = feedback(Sys,Sysfs_sc);

poles(Sysfs_scl_fo)

ans (a column vector) =

-0.690216 + 0.522898 j

-0.690216 - 0.522898 j

-0.419783 + 0.892632 j

-0.419783 - 0.892632 j

-0.381722 + 1.10668 j

-0.381722 - 1.10668 j

-0.0261589 + 5.00027 j

-0.0261589 - 5.00027 j

The full-order closed-loop system is stable. The open-loop eigenvalues
of the unmodelled mode have not moved much, which is a sign of good
robustness. The eigenvalue of the unmodelled mode changed from
–.0250 ± 5j to –0.0262 ± 5j.

Loop Transfer Recovery (lqgltr)

Loop transfer recovery (LTR) is fully described in references [KS72,
DoS79,DoS81,SA88]. The properties of the recovery pertain to the LQG
feedback system as shown in Figure 4-8.

The parameter ρ (
transfer recovery through the regulator (

lqeltr).

(

MATRIXx Xmath Robust Control Module 4-22 ni.com

rho) can be manipulated by the user to obtain loop

lqrltr) or the estimator

y

G(s)

Chapter 4 Controller Synthesis

Plant

lqgltr( )

u

Estimator

K

R

K(s)

Figure 4-8. LQG Feedback System for Loop Transfer Recovery

[SysC,EV,Kr] = lqgltr(Sys,Wx,Wy,K,rho,{keywords})

x

x = Ax + Bu

y = Cx

x = Ax + Bu

ε = y – Cx

+

x

KEε

The lqgltr( ) function designs an estimator or regulator which recovers
loop transfer robustness through the design parameter ρ (

rho). For a

discussion of the syntax and a full listing of keywords, refer to the Xmath
Help.

The keyword

recover specifies whether the recovery should be achieved

through regulator or estimator design.

If the keyword is set to

recover="regulator", the loop-transfer is

recovered by designing a regulator with the following model:

x·Ax w+=

yCxv+=

and the objective function:

J

=

x'Qx u'Ru+()td

∫

2

0

∞

1

---

with:

QR

=

RR

© National Instruments Corporation 4-23 MATRIXx Xmath Robust Control Module

xx

uu

ρC'C+=

Chapter 4 Controller Synthesis

Then ρ is increased so that pointwise in s:

Ks()Gs() K

→ B

sI A–()

R

1–

Regulator recovery is only guaranteed if G(s) is minimum-phase and there
are at least as many control signals u as measurements y.

recover="estimator", the loop-transfer is recovered by designing an

If
estimator with the following model:

x·Ax w+=

yCxv+=

where w and v have noise intensities:

WQ

=

VQ

ρBB'+=

xx

yy

Then ρ is increased so that pointwise in s:

Gs()Ks() CsI A–()

→ K

1–

E

Recovery is only guaranteed if G(s) is minimum-phase and there are at least
as many measurements y as there are control signals u.

graph is on (default) the singular value loop transfer response is plotted.

If
The solid line represents the original loop transfer, and the dashed line
represents the loop transfer after recovery.

MATRIXx Xmath Robust Control Module 4-24 ni.com

A

Bibliography

[BBK88] S. Boyd, V. Balakrishnan, and P. Kabamba. “A bisection method for computing the

norm of a transfer matrix and related problems.” Mathematical Control Signals,

L

∞

Systems Vol. 2, No. 3, pp 207–219, 1989.

[BeP79] A. Berman and R.J. Plemmons. “Nonnegative Matrices in the Mathematical

Sciences.” Computer Science and Applied Mathematics Series, Academic

Press, 1979.

[BoB90] S. Boyd and V. Balakrishnan. “A regularity result for the singular values of a transfer

matrix and a quadratically convergent algorithm for computing its L

Systems Control Letters, Vol. 15, pp 1–7, 1990.

[BoB91] S. Boyd and C. Barratt. Linear Controller Design: Limits of Performance.

Prentice-Hall, 1991.

norm.”

∞

[BH69] A.E. Bryson and Y.C. Ho. Applied Optimal Control, p 149. Blaisdell

Publishing Co., 1969.

[DoS79] J.C. Doyle and G. Stein. “Robustness with Observers.” IEEE Transactions on

Automatic Control, August 1979.

[DoS81] J.C. Doyle and G. Stein. “Multivariable Feedback Design: Concepts for a

Classical/Modern Synthesis.” IEEE Transactions on Automatic Control,
Vol. AC-26, pp 4–16, February 1981.

[Doy82] J.C. Doyle. “Analysis of Feedback Systems with Structured Uncertainties.”

IEEE Proceedings, November 1982.

[DWS82] J.C. Doyle, J.E. Wall, and G. Stein. “Performance and Robustness Analysis for

Structure Uncertainties.” Proceedings IEEE Conference on Decision and Control,
pp 629–636, 1982.

© National Instruments Corporation A-1 MATRIXx Xmath Robust Control Module

Appendix A Bibliography

[FaT88] M.K. Fan and A.L. Tits. “m-form Numerical Range and the Computation of the

Structured Singular Value.” IEEE Transactions on Automatic Control, Vol. 33,
pp 284–289, March 1988.

[FaT86] M.K. Fan and A.L. Tits. “Characterization and Efficient Computation of the

Structured Singular Value.” IEEE Transactions on Automatic Control, Vol. AC-31,
pp 734–743, August 1986.

[Fr87] B. Francis. A Course in L

Control Theory. Springer-Verlag,

∞

Berlin-New York, 1987.

[FPGM87] D.S. Flamm, S. Boyd, G. Stein, and S.K. Mitter. “Tutorial Workshop on L

Control

∞

Theory.” pre-conference workshop, Proceedings 26th IEEE Conference on Decision
and Control, December 1988.

[GD88] K. Glover and J.C. Doyle. “State-space formulae for all stabilizing controllers that

satisfy an L

norm bound and relations to risk sensitivity.” Systems and Control

∞

Letters, Vol. 11, pp 167–172, 1988.

[DGKF89] J.C. Doyle, K. Glover, P.K. Khargonekar, and B. Francis. ‘‘State-space solutions to

standard H

and L∞ control problems.” IEEE Transactions on Automatic Control,

2

Vol. AC-34, No. 8, pp 831–847, August 1989.

[Gu80] N.K. Gupta. “Frequency Shaping of Cost Functionals: An extension of LQG Design

Methods.” AIAA Journal of Guidance and Control, Vol. 3, No. 6, December 1980.

[ONR84] ONR/Honeywell Workshop on Advances in Multivariable Control. Lecture Notes,

Minneapolis, MN, 1984.

[Osb60] E.E. Osborne. “On Preconditioning of Matrices.” JACM, 7:338–345, 1960.

[Saf82] M.G. Safonov. “Stability Margins of Diagonally Perturbed Multivariable Feedback

Systems.” IEEE Proceedings, 129-D:251–256, November 1982.

[SD83] M.G. Safonov and J.C. Doyle. “Optimal Scaling for Multivariable Stability Margin

Singular Value Computation.” Proceedings of MECO/EES 1983, Symposium, 1983.

[SD84] M.G. Safonov and J.C. Doyle. “Minimizing Conservativeness of Robust Singular

Va lu e s. ” Multivariable Control, pp 197–207, S.G. Tzafestas, editor. D. Reidel
Publishing Company, 1984.

[SLH81] M.G. Safonov, A.J. Laub, and G.L. Hartmann. “Feedback Properties of

Multivariable Systems: The Role and Use of the Return Difference Matrix.”
IEEE Transactions on Automatic Control, Vol. AC-26, February 1981.

MATRIXx Xmath Robust Control Module A-2 ni.com

Appendix A Bibliography

[SA88] G. Stein and M. Athans. “The LQG/LTR Procedure for Multivariable Control

Design.” IEEE Transactions on Automatic Control, Vol. AC-32, No. 2, pp 105–114,
February 1987.

[Za81] G. Zames. “Feedback and optimal sensitivity: model reference transformations,

multiplicative semi-norms, and approximate inverses.” IEEE Transactions on
Automatic Control, Vol. AC-26, pp 301–320, 1981.

[KS72] H. Kwakernaak and R. Sivan. Linear Optimal Control Systems. Wiley, 1972.

© National Instruments Corporation A-3 MATRIXx Xmath Robust Control Module

Technical Support and
Professional Services

Visit the following sections of the National Instruments Web site at

ni.com for technical support and professional services:

• Support—Online technical support resources at

include the following:

– Self-Help Resources—For answers and solutions, visit the

award-winning National Instruments Web site for software drivers
and updates, a searchable KnowledgeBase, product manuals,
step-by-step troubleshooting wizards, thousands of example
programs, tutorials, application notes, instrument drivers, and
so on.

– Free Technical Support—All registered users receive free Basic

Service, which includes access to hundreds of Application
Engineers worldwide in the NI Discussion Forums at

ni.com/forums. National Instruments Application Engineers

make sure every question receives an answer.

For information about other technical support options in your
area, visit

ni.com/contact.

• Training and Certification—Visit

self-paced training, eLearning virtual classrooms, interactive CDs,
and Certification program information. You also can register for
instructor-led, hands-on courses at locations around the world.

• System Integration—If you have time constraints, limited in-house

technical resources, or other project challenges, National Instruments
Alliance Partner members can help. To learn more, call your local
NI office or visit

ni.com/services or contact your local office at

ni.com/alliance.

B

ni.com/support

ni.com/training for

If you searched
your local office or NI corporate headquarters. Phone numbers for our
worldwide offices are listed at the front of this manual. You also can visit
the Worldwide Offices section of
office Web sites, which provide up-to-date contact information, support
phone numbers, email addresses, and current events.

© National Instruments Corporation B-1 MATRIXx Xmath Robust Control Module

ni.com and could not find the answers you need, contact

ni.com/niglobal to access the branch

Index

A

Algebraic Riccati Equation (ARE), 4-13

C

clsys( ), 3-10
conventions used in the manual, iv

D

diagnostic tools (NI resources), B-1
documentation

conventions used in the manual, iv
NI resources, B-1

drivers (NI resources), B-1

E

examples (NI resources), B-1
extended transfer matrices, 4-2

F

frequency-shaped

control law, 4-14

filter design, 4-16
fsesti( ), 4-16
fslqgcomp( ), 4-17
fsregu( ), 4-14

H

H∞ control synthesis, 4-1

building the plant model, 4-3

extended transfer matrix, 4-2

problem definition, 4-1
restrictions on extended plant, 4-7
weight selection, 4-5

H

control synthesis, 4-14

2

H

norm, 3-4

2

help, technical support, B-1
hinfcontr( ), 4-2, 4-8

I

instrument drivers (NI resources), B-1

K

KnowledgeBase, B-1

L

L∞ norm, 3-3
linfnorm( ), 3-4
loop transfer recovery, 4-22
LQG frequency shaping, 4-14
lqgltr( ), 4-23

M

MATRIXx Help, 1-3
modeling uncertain systems, 2-1

N

National Instruments support and services, B-1
NI support and services, B-1
nomenclature, 1-2
nominal closed-loop system, 2-2

creating, 2-4

© National Instruments Corporation I-1 MATRIXx Xmath Robust Control Module

Index

nominal transfer function, 2-8
norm

H

, 3-4

2

L∞, 3-3

O

optscale( ), 2-17
osscale( ), 2-16

P

perfplots( ), 3-7
pfscale( ), 2-16
programming examples (NI resources), B-1

R

reducibility, 2-17
robust stability, 2-3

S

scaled singular values, 2-11
scaling

Optimal (Boyd), 2-15
Osborne, 2-15
Perron-Frobenius, 2-15

ssv( ), 2-15
singriccati( ), 4-13
singular value Bode plots, 3-1
singular values, 2-11
smargin( ), 2-4

software (NI resources), B-1
ssv( ), 2-15
stability margin, 2-3, 2-10
structured nonparametric uncertainty, 2-1
structured singular value, 2-11
support, technical, B-1
system

feedback connection, 2-2
nominal closed-loop, 2-1

creating, 2-4
magnitude bounds, 2-2
stability margin, 2-3

T

technical support, B-1
training and certification (NI resources), B-1
transfer function

nominal, 2-8
perturbed, 2-8
uncertain, 2-2

troubleshooting (NI resources), B-1

W

wcbode( ), 2-9
wcgain( ), 2-19
Web resources, B-1
well-posed closed-loop system, 3-11
worst-case gain, 2-8
worst-case performance degradation, 2-8,

2-18

MATRIXx Xmath Robust Control Module I-2 ni.com