MITEL PDSP16116MCGGDR, PDSP16116AA0AC, PDSP16116AB0AC, PDSP16116AB0GG, PDSP16116B0AC Datasheet
...
Supersedes October 1996 version, DS3707 - 4.2 DS3707 - 5.3 October 1997
PDSP16116
16 X 16 Bit Complex Multiplier
FEATURES
■ Complex Number (16116)3(16116) Multiplication
■ Full 32-bit Result
■ 20MHz Clock Rate
■ Block Floating Point FFT Butterfly Support
■ (21)3(21) Trap
■ Two’s Complement Fractional Arithmetic
■ TTL Compatible I/O
■ Complex Conjugation
■ 2 Cycle Fall Through
■ 144-pin PGA or QFP packages
APPLICATIONS
■ Fast Fourier Transforms
■ Digital Filtering
■ Radar and Sonar Processing
■ Instrumentation
■ Image Processing
ORDERING INFORMATION
PDSP16116 MC GGDR 10MHz MIL-883 screened
PDSP16116A B0 AC 20MHz Industrial
PDSP16116A A0 AC 20MHz Military
PDSP16116A B0 GG 20MHz Industrial
PDSP16116A MC GGDR 20MHz MIL-883 screened
PDSP16116B B0 AC 25MHz Industrial
PDSP16116D B0 GG 31·5MHz Industrial
ASSOCIATED PRODUCTS
PDSP16318/A Complex Accumulator
PDSP16112/A (16116)3(12112) Complex Multiplier
PDSP16330/A Pythagoras Processor
PDSP1601/A ALU and Barrel Shifter
PDSP16350 Precision Digital Modulator
PDSP16256 Programmable FIR Filter
PDSP16510 Single Chip FFT Processor
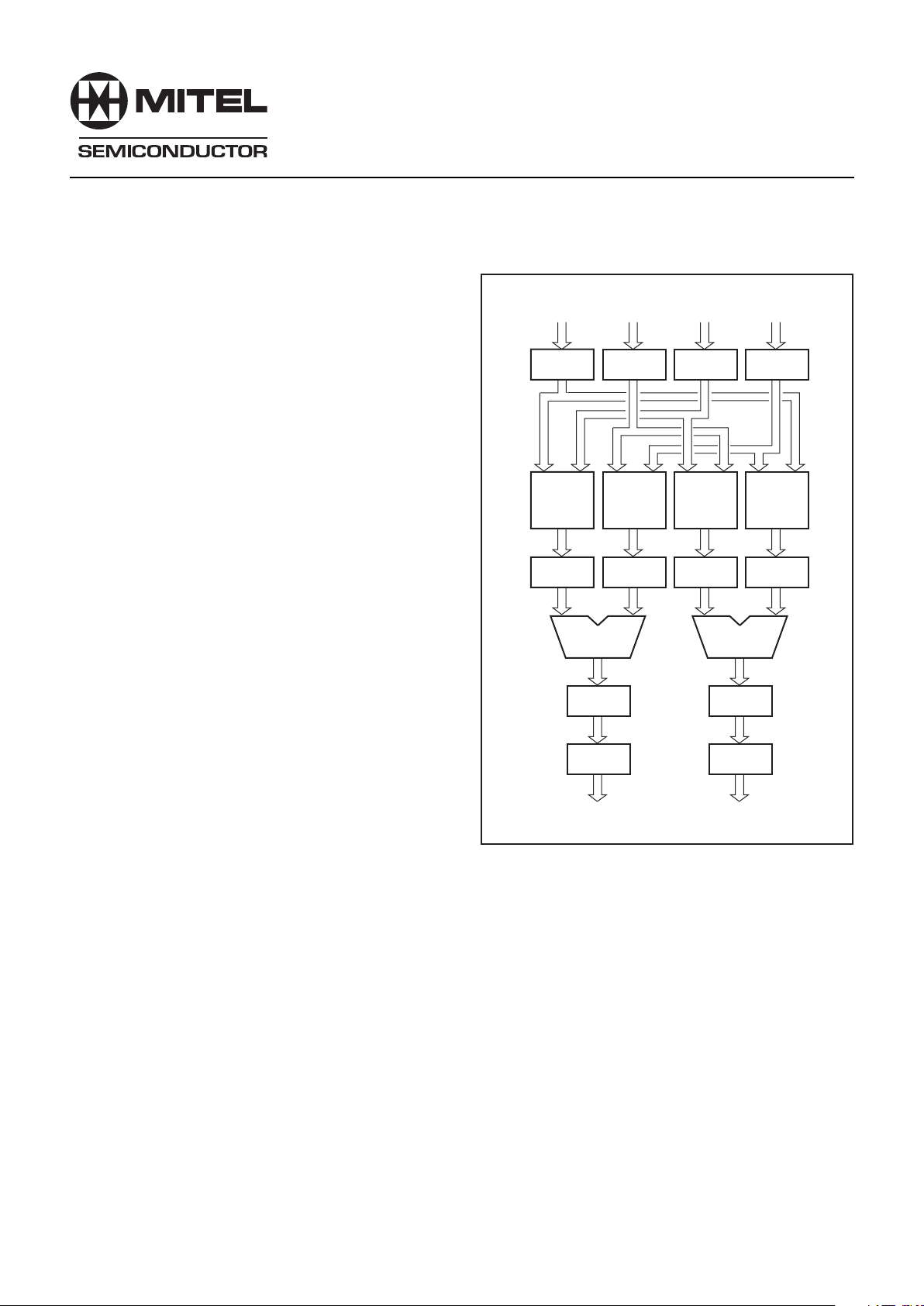
Fig. 1 Simplified block diagram
PR15:0
ADD/SUB
REG
MULT
REG
REG
MULT
REG
REG
MULT
REG
REG
MULT
REG
ADD/SUB
SHIFT
REG
SHIFT
REG
PI15:0
XR15:0 XI15:0 YR15:0 YI15:0
The PDSP16116 contains four 16316 array multipliers, two
32-bit adder/subtractors and all the control logic required to support Block Floating Point Arithmetic as used in FFT applications.
The PDSP16116A variant will multiply two complex (16116)
bit words every 50ns and can be configured to output the complete complex (32132) bit result within a single cycle. The data
format is fractional two’s complement.
In combination with a PDSP16318A, the PDSP16116A forms
a two-chip 20MHz complex multiplier accumulator with 20-bit
accumulator registers and output shifters. The PDSP16116A in
combination with two PDSP16318As and two PDSP1601As
forms a complete 20MHz Radix 2 DIT FFT butterfly solution
which fully supports block floating point arithmetic. The
PDSP16116 has an extremely high throughput that is suited to
recursive algorithms as all calculations are performed with a
single pipeline delay (two cycle fall-through).

PDSP16116
2
SYSTEM FEATURES
The PDSP16116 has a number of features tailored for system applications.
(21)3(21) Trap
In multiply operations using two’s complement fractional notation, the (21)3(21) operation forms an invalid result because
11 is not representable in the fractional number range. The
PDSP16116 eliminates this problem by trapping the (21)3(21)
operation and forcing the multiplier result to become the most
positive representable number.
Complex Conjugation
Many algorithms using complex arithmetic require conjugation of complex data stream. This operation has traditionally required an additional ALU to multiply the imaginary component
by -1. The PDSP16116 eliminates this requirement by offering
on-chip complex conjugation of either of the two incoming complex data words with no loss in throughput.
Easy Interfacing
As with all PDSP family members the PDSP16116 has registered l/O for data and control. Data inputs have independent
clock enables and data outputs have independent three state
output enables.
Signal
XR15:0
Xl15:0
YR15:0
Yl15:0
PR15:0
Pl15:0
CLK
CONX
CONY
ROUND
MBFP
AR15:1 3
Al15:1 3
WTA1:0
WTB1:0
WTOUT1:0
SFTA1:0
SFTR2:0
GWR4:0
OSEL1:0
V
DD
GND
Type
Input
Input
Input
Input
Output
Output
Input
Input
Input
Input
Input
Input
Input
Input
Input
Input
Input
Input
Input
Output
Output
Output
Output
Input
Input
Power
Power
Description
16-bit input for real X data
16-bit input for imaginary X data
16-bit input for real Y data
16-bit input for imaginary Y data
16-bit output for real P data
16-bit output for imaginary P data
Clock; new data is loaded on rising edge of CLK
Clock, enable X-port input register
Clock, enable Y-port input register
Conjugate X data
Conjugate Y data
Rounds the real and imaginary results
Mode select (BFP/Normal)
Start of BFP operations (see Note 1)
End of pass (See Note 1)
3 MSBs from real part of A-word (See Note 1)
3 MSBs from imaginary part of A-word (See Note 1)
Word tag from A-word
Word tag from B-word/shift control (See Note 2)
Word tag output (See Note 1)
Shift control for A-word / overflow flag (See Note 2)
Shift control for accumulator result (See Note 1)
Global weighting register contents (See Note 1)
Selects the desired output configuration
Output enables
15V Supply (See Note 3)
0V Supply (See Note 3)
Normal
mode
configuration
Tie low
Tie low
Tie low
Tie low
Tie low
Tie low
NOTES
1. Used only in BFP mode
2. Performs different functions in BFP/Normal modes
3. All supply pins must be connected
Table 1 Signal descriptions
CEX
CEY
SOBFP
EOPSS
OER, OEI
PDSP16116
3
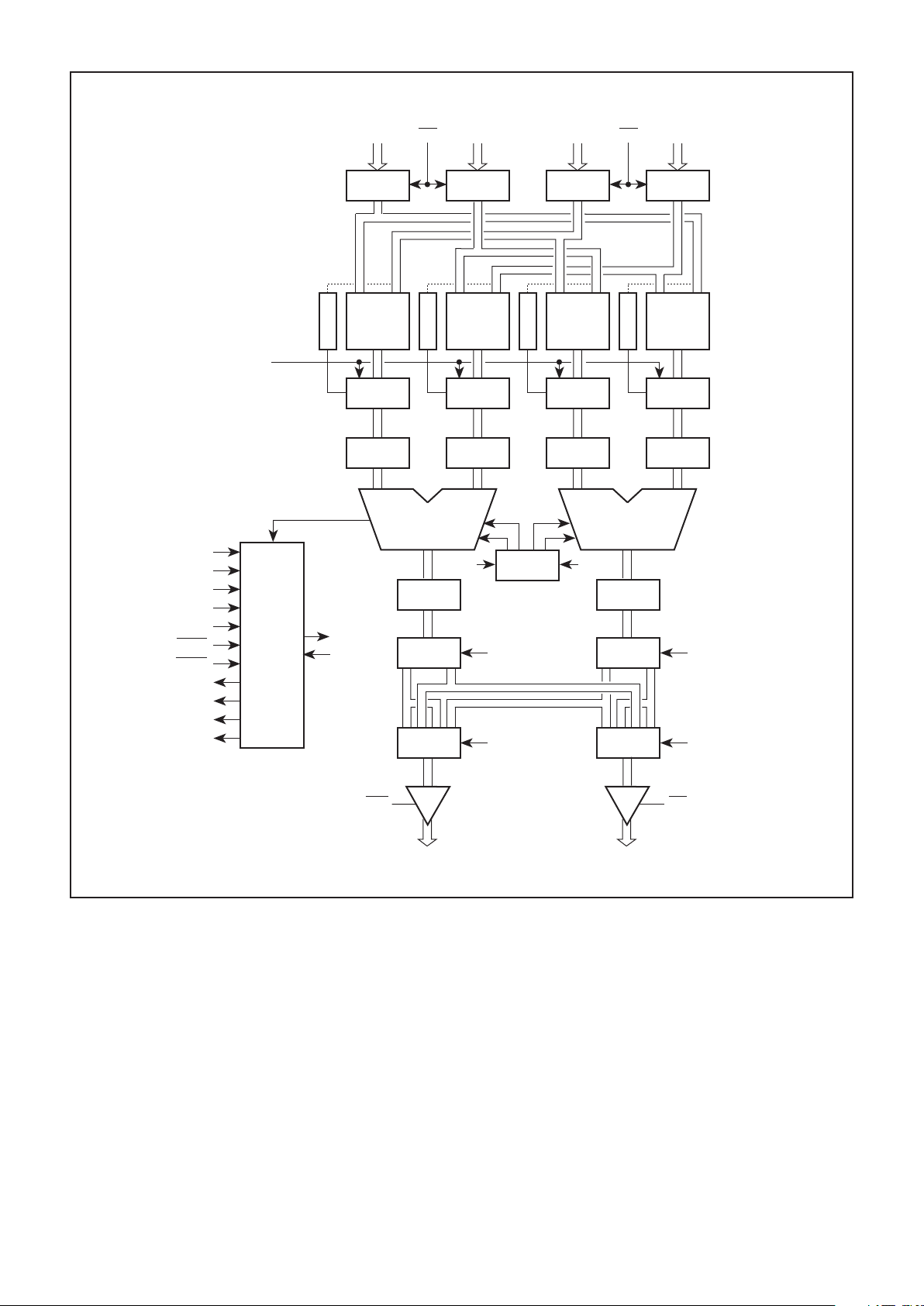
Fig. 2 PDSP16116 Block diagram
ADD/SUB
DECODE
REG
REG
16316
MULT
MUX
XR15:0
C
O
M
P
REG
REG
MUX
XI15:0
C
O
M
P
REG
REG
MUX
YR15:0
C
O
M
P
REG
REG
MUX
YI15:0
C
O
M
P
16316
MULT
16316
MULT
16316
MULT
ADD/SUB
CONX CONY
SHIFT
REG
SHIFT
REG
MUX MUX
OVR
CEYCEX
CONTROL
LOGIC
CLK
WTA
AR15:13
WTB
AI15:13
SOBPF
EOPSS
SFTR
SFTA
GWR4:0
WTOUT
ROUND
OSEL
ROUND
OSEL
OER OEI
PR15:0 PI15:0
INTERNAL
SIGNALS
‘1’
PDSP16116
4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
A B C D E F G H J K L M N P R
PIN 1 IDENT
(SEE NOTE 2)
PIN 144
PIN 1
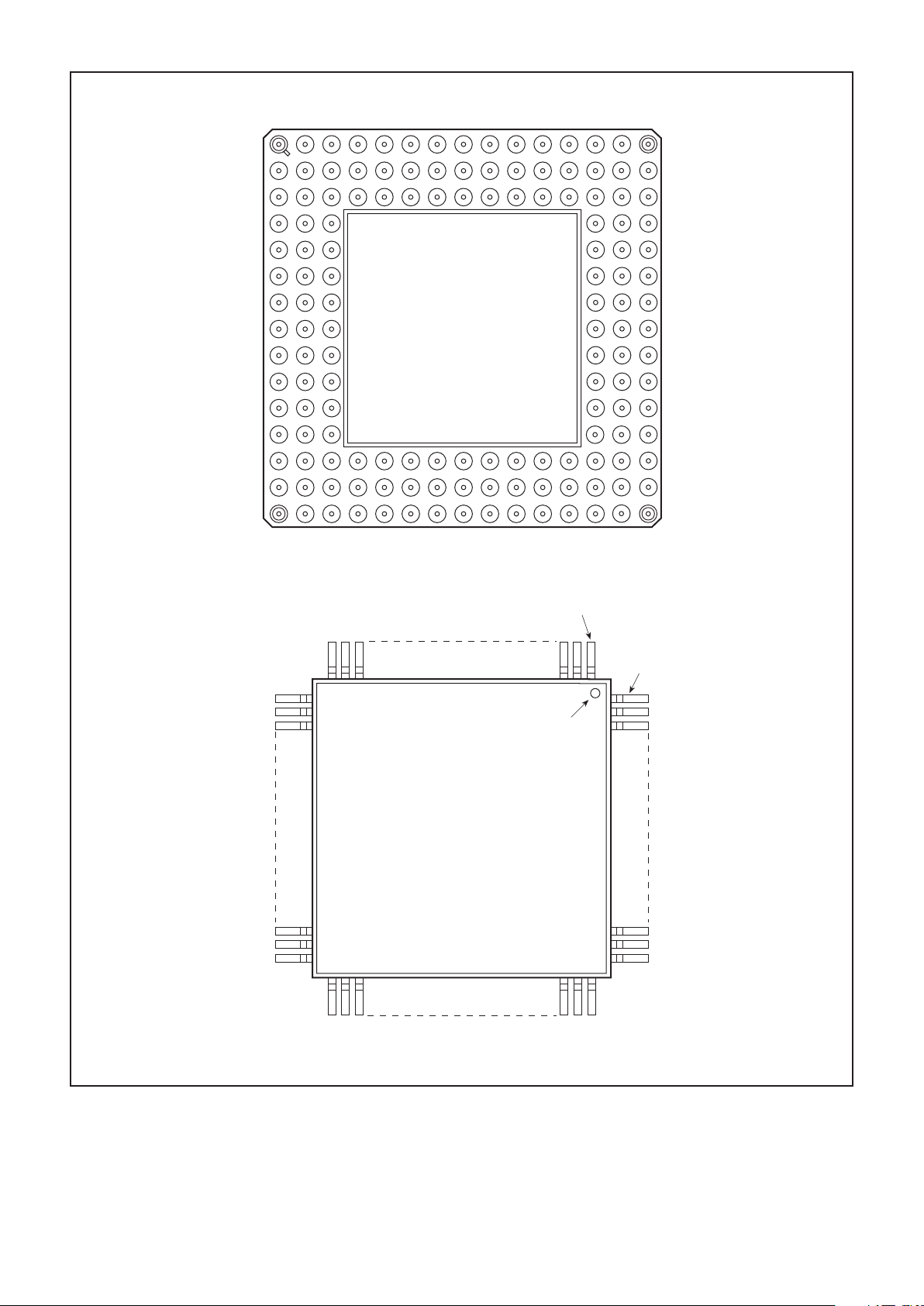
Fig. 3a Pin connections for 144 I/O power pin grid array package (bottom view)
Fig. 3b Pin connections for 144 I/O ceramic quad flatpack (top view)
Fig. 3 Pin connection diagrams (not to scale). See Table 1 for signal descriptions and Table 2 for pinouts.
AC144 (POWER)
GG144

PDSP16116
5
Signal
V
DD
GND
PR13
PR12
PR11
PR10
PR9
PR8
PR7
PR6
PR5
GND
V
DD
PR4
PR3
PR2
PR1
PR0
PI0
PI1
PI2
PI3
PI4
V
DD
PI5
GND
PI6
PI7
PI8
PI9
PI10
PI11
PI12
PI13
GND
V
DD
GG
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
Signal
PI14
PI15
WTOUT1
WTOUT0
SFTR0
SFTR1
SFTR2
OEI
CONY
CONX
ROUND
AI13
AI14
AI15
AR13
AR14
AR15
YI15
YI14
YI13
YI12
YI11
YI10
YI9
YI8
YI7
YI6
YI5
YI4
YI3
YI2
YI1
YI0
XI0
GND
V
DD
AC
D3
C2
B1
D2
E3
C1
E2
D1
F2
F3
E1
G2
G3
F1
G1
H2
H1
H3
J3
J1
K1
J2
K2
K3
L1
L2
M1
N1
M2
L3
N2
P1
M3
N3
B2
A1
GG
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
Signal
XI1
XI2
XI3
XI4
XI5
XI6
XI7
XI8
XI9
XI10
XI11
XI12
XI13
XI14
XI15
CEY
CEX
XR15
XR14
XR13
XR12
XR11
XR10
XR9
XR8
XR7
XR6
XR5
XR4
XR3
XR2
XR1
XR0
YR15
YR14
YR13
AC
N4
P3
R2
P4
N5
R3
P5
R4
N6
P6
R5
P7
N7
R6
R7
P8
R8
N8
N9
R9
R10
P9
P10
N10
R11
P11
R12
R13
P12
N11
P13
R14
N12
N13
P14
R15
GG
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
Signal
GND
V
DD
YR12
YR11
YR10
YR9
YR8
YR7
YR6
YR5
YR4
YR3
YR2
YR1
YR0
EOPSS
V
DD
SOBFP
WTB1
WTB0
WTA1
WTA0
MBFP
CLK
OSEL1
OSEL0
OER
SFTA0
SFTA1
GWR0
GWR1
GWR2
GWR3
GWR4
PR15
PR14
AC
P2
R1
P15
M14
L13
N15
L14
M15
K13
K14
L15
J14
J13
K15
J15
H14
H15
H13
G13
G15
F15
G14
F14
F13
E15
E14
D15
C15
D14
E13
C14
B15
D13
C13
B14
A15
GG
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
AC
N14
M13
A14
B12
C11
A13
B11
A12
C10
B10
A11
B13
C12
A10
A9
B8
A8
C8
C7
A7
A6
B7
B6
C6
A5
B5
A4
A3
B4
C5
B3
A2
C4
C3
B9
C9
NOTE. All GND and VDD pins must be used
Table 2 Pin connections for AC144 (Power) and GG144 packages
PDSP16116
6
NORMAL MODE OPERATION
When the MBFP mode select input is held low the ‘Normal’
mode of operation is selected. This mode supports all complex
multiply operations that do not require block floating point
arithmetic.
Complex two’s complement fractional data is loaded into the
X and Y input registers via the X and Y Ports on the rising edge
of CLK. The X and Y port registers are individually enabled by
the
CEX
and
CEY
signals respectively. If the registers are required to be permanently enabled, then these signals may be
tied to ground.
The Real and Imaginary components of the fractional data
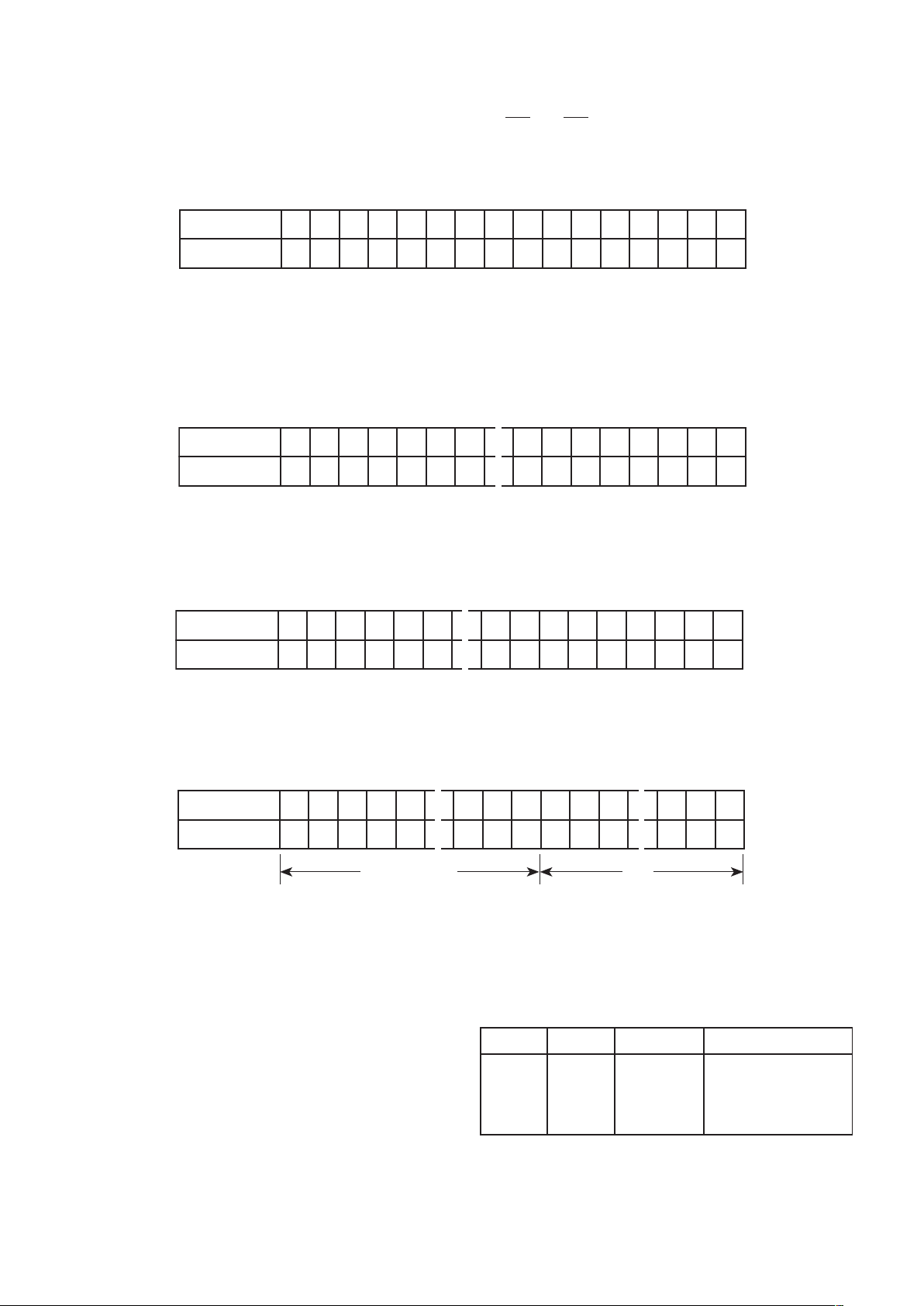
are each assumed to have the following format:
Bit Number
15
Weighting
14131211109 76543210
S
2
–
15
2
–
14
2
–
13
2
–
12
2
–
11
2
–
10
2
–
9
2
–
8
2
–
6
2
–
5
2
–
4
2
–
3
2
–
2
2
–
1
8
2
–
7
Where S = sign bit, which has an effective weighting of 22
0
The value of the 16-bit two’s complement word is (213S)1(bit143221)1(bit133222)1(bit123223) …
Multiplier Stage
On each clock cycle the contents of the input registers are passed
to the four multipliers to start a new complex multiply operation.
Each complex multiply operation requires four partial products
(XR3YR), (XR3YI), (XI3YR), (XI3YI), all of which are calculated
in parallel by the four 16316 multipliers. Only one clock cycle is
required to complete the multiply stage before the multiplier results
are loaded into the multiplier output registers for passing on to the
adder/ subtractors in the next cycle. Each multiplier produces a 31bit result with the duplicate sign bit eliminated. The format of the
output data from the multipliers is:
Bit Number
30
Weighting
292827262524 76543210
≈ ≈ ≈
S
2
–
30
2
–
29
2
–
28
2
–
27
2
–
26
2
–
25
2
–
24
2
–
23
2
–
6
2
–
5
2
–
4
2
–
3
2
–
2
2
–
1
The effective weighting of the sign bit is 22
0
Adder/Subtractor Stage
The 31-bit real and imaginary results from the multipliers
are passed to two 32-bit adder/subtractors. The adder calculates the imaginary result [(XR 3 YI) 1 (XI 3 YR)] and the
Rounding
The ROUND control when asserted rounds the most
significant 16 bits of the full 32-bit result from the shifter. If the
ROUND signal is active (high), then bit 16 is set to ‘1’, rounding
the most significant 16 bits of the shifted result. (The least
significant 16 bits are unaffected). Inserting a ‘1’ ensures that
the rounding error is never greater than 1 LSB and that no DC
bias is introduced as a result of the rounding processes. The
format of the rounded result is:
The effective weighting of the sign bit is 22
1
Bit Number
30
Weighting
29 28 27 17 16 15 14 13 2 1 0
≈ ≈ ≈
S
2
–
30
2
–
29
2
–
28
2
–
17
2
–
16
2
–
15
2
–
14
2
–
13
2
–
3
2
–
2
2
–
1
2
0
31 18
2
–
1
2
≈ ≈ ≈
ROUNDED VALUE
LSBs
The effective weighting of the sign bit is 22
1
Bit Number
30
Weighting
29282726 76543210
≈ ≈ ≈
S
2
–
30
2
–
29
2
–
28
2
–
27
2
–
26
2
–
25
2
–
24
2
–
23
2
–
4
2
–
3
2
–
2
2
–
1
2
0
31 8
2
–
22
subtractor calculates the real result (XR 3 YR) = (XI 3 YI).
Each adder/subtractor produces a 32-bit result with the
following format:
Result Correction
Due to the nature of the fraction two’s complement representation it is possible to represent 21 exactly but not 11. With
conventional multipliers this causes a problem when 21 is multiplied by 21 as the multiplier produces an incorrect result. The
PDSP16116 includes a trap to ensure that the most positive
number (value = 1·2
230
, hex = 7FFFFFFFF) is substituted for
the incorrect result. The multiplier result is therefore always a
correct fractional value. Fig.2 shows the value ‘1’ being multiplexed into the data path controlled by four comparators.
Complex Conjugation
Either the X or Y input data may be complex conjugated by
asserting the CONX or CONY signals respectively. Asserting
either of these signals has the effect of inverting (multiplying
by 21 ) the imaginary component of the respective input. Table 3
shows the effect of CONX and CONY on the X and Y inputs.
Table 3 Conjugate functions
CONYCONX
Low
High
Low
High
Low
Low
High
High
Function
(XR 1 XI)3(YR 1 YI)
(XR 2 XI)3(YR 1 YI)
(XR 1 XI)3(YR 2 YI)
Invalid
Operation
X 3 Y
Conj. X 3 Y
X 3 Conj. Y
Invalid
 Loading...
Loading...