Mathworks FIXED-POINT TOOLBOX 3 user guide

Download

Fixed-Point Toolb

User’s Guide

ox™ 3

How to Contact The MathWorks

www.mathworks. comp.soft-sys.matlab Newsgroup www.mathworks.com/contact_TS.html Technical Support

suggest@mathworks.com Product enhancement suggestions

bugs@mathwo doc@mathworks.com Documentation error reports service@mathworks.com Order status, license renewals, passcodes

info@mathwo

com

rks.com

Web

Bug reports

Sales, prici

ng, and general information

508-647-7000 (Phone)

508-647-7001 (Fax)

The MathWorks, Inc. 3 Apple Hill Drive Natick, MA 01760-2098

For contact information about worldwide offices, see the MathWorks Web site.

Fixed-Point Toolbox™ User’s Guide

The software described in this document is furnished under a license agreement. The software may be used or copied only under the terms of the license agreement. No part of this manual may be photocopied or reproduced in any form without prior written consent from The MathW orks, Inc.

FEDERAL ACQUISITION: This provision applies to all acquisitions of the Program and Documentation by, for, or through the federal government of the United States. By accepting delivery of the Program or Documentation, the government hereby agrees that this software or documentation qualifies as commercial computer software or commercial computer software documentation as such terms are used or defined in FAR 12.212, DFARS Part 227.72, and DFARS 252.227-7014. Accordingly, the terms and conditions of this Agreement and only those rights specified in this Agreement, shall pertain to and govern theuse,modification,reproduction,release,performance,display,anddisclosureoftheProgramand Documentation by the federal government (or other entity acquiring for or through the federal government) and shall supersede any conflicting contractual terms or conditions. If this License fails to meet the government’s needs or is inconsistent in any respect with federal procurement law, the government agrees to return the Program and Docu mentation, unused, to The MathWorks, Inc.

Trademarks

MATLAB and Simulink are registered trademarks of The MathWorks, Inc. See

www.mathworks.com/trademarks for a list of additional trademarks. Other product or brand

names may be trademarks or registered trademarks of their respective holders.

Patents

The MathWorks products are protected by one or more U.S. patents. Please see

www.mathworks.com/patents for more information.

Revision History

June 2004 First printing New for Version 1.0 (Release 14) October 2004 Online only Version 1.1 (Release 14SP1) March 2005 Online only Version 1.2 (Release 14SP2) September 2005 Online only Version 1.3 (Release 14SP3) October 2005 Second printing Version 1.3 March 2006 Online only Version 1.4 (R2006a) September 2006 Third printing Version 1.5 (R2006b) March 2007 Fourth printing Version 2.0 (R2007a) September 2007 Online only Revised for Version 2.1 (R2007b) March 2008 Online only Revised for Version 2.2 (R2008a) October 2008 Online only Revised for Version 2.3 (R2008b) March 2009 Online only Revised for Version 2.4 (R2009a) September 2009 Online only Revised for Version 3.0 (R2009b) March 2010 Online only Revised for Version 3.1 (R2010a)

Getting Started

Product Overview ................................. 1-2

Contents

Licensing

Getting Help

Getting Help in This Document Getting Help at the MATLAB Command Line

Display Settings

Displaying the fimath Properties of fi Objects Hiding the fimath Properties of fi O bjects Shortening the numerictype Display of fi Objects

Demos

......................................... 1-3

...................................... 1-4

...................... 1-4

.......... 1-4

................................... 1-6

.......... 1-7

.............. 1-8

........ 1-9

............................................ 1-10

Fixed-Point Concepts

Fixed-Point Data Types ............................ 2-2

Scaling

........................................... 2-4

Precision and Range

Range Precision

Arithmetic Operations

Modulo Arithmetic Two’s Complement

........................................... 2-5

........................................ 2-6

............................... 2-5

............................. 2-10

................................ 2-10

................................ 2-11

Addition and Subtraction ........................... 2-12

Multiplication Casts

........................................... 2-19

.................................... 2-13

fi Objects Compared to C Integer Data Types

Integer Data Types Unary Conversions Binary Conversions Overflow H a ndling

................................ 2-22

................................ 2-24

................................ 2-25

................................ 2-28

........ 2-22

Working with fi Objects

Constructing fi Objects ............................. 3-2

fi Object Syntaxes Examples of Constructing fi Objects

Casting fi Objects

Overwriting by Assignment Ways to Cast with MATLAB Software

fi Object Properties

Data Propertie s fimath Properties numerictype Properties Setting fi Object Properties

................................. 3-2

.................. 3-3

.................................. 3-12

......................... 3-12

................ 3-12

................................ 3-17

................................... 3-17

................................. 3-17

............................. 3-19

......................... 3-20

vi Contents

fi Object Functions

................................ 3-24

Working with fimath Objects

Constructing fimath Objects ........................ 4-2

fimath Object Syntaxes Building fimath Object Constructors in a GUI

............................. 4-2

.......... 4-4

Working with the Global fimath ..................... 4-6

Configuring the Global fimath Saving the Global fimath Resetting the Global fimath to the Factory Default Using the Global fimath with the Embedded MATLAB

Function Block

................................. 4-10

....................... 4-7

........................... 4-8

...... 4-8

fimath Object Properties

Math, Rounding, and Overflow Properties Setting fimath Object Properties

Using fimath Properties to Perform Fixed-Point

Arithmetic

fimath Rules for Fixed-Point Arithmetic Binary-Point Arithmetic [Slope Bias] Arithmetic

UsingfimathtoSpecifyRoundingandOverflow

Modes

Using fimath t o Share Arithmetic Rules

Using the Global fimath to Share Arithmetic Rules Using fimath Objects to Share Arithmetic Rules

Using fimath ProductMode and SumMode

Example Setup FullPrecision KeepLSB KeepMSB SpecifyPrecision

...................................... 4-16

.......................................... 4-25

................................... 4-30

..................................... 4-31

........................................ 4-32

........................................ 4-33

.................................. 4-34

........................... 4-11

............. 4-11

..................... 4-12

............... 4-16

............................ 4-18

............................. 4-22

............. 4-27

........ 4-28

........... 4-30

..... 4-27

fimath Object Functions

............................ 4-36

Working with fipref Objects

Constructing fipref Objects ......................... 5-2

vii

fipref Object Properties ............................ 5-3

Display, Data Type Override, and Logging Properties Setting fipref Object Properties

...................... 5-3

.... 5-3

Using fipref Objects to Set Display Preferences

Using fipref Objects to Set Logging Preferences

Logging Overflows and Underflows as Warnings Accessing Logged Information with Functions

Using fipref Objects to Set Data Type Override

Preferences

OverridingtheDataTypeoffiObjects Using Data Type Override to Help Set Fixed-Point

Scaling

fipref Object Functions

..................................... 5-12

................ 5-12

........................................ 5-13

............................ 5-15

...... 5-5

...... 5-7

........ 5-7

.......... 5-9

Working with numerictype Objects

Constructing numerictype Objects .................. 6-2

numerictype Object Syntaxes Example: Constructing a numerictype Object with Property

Name and Property Value Pairs Example: Copying a numerictype Object Example: Building numerictype Object Constructors in a

GUI

.......................................... 6-5

........................ 6-2

................... 6-3

.............. 6-4

viii Contents

numerictype Object Properties

Data Type and Scaling Properties Setting numerictype Object Properties

The n umerictype Structure

Valid Values for numerictype Structure Properties Properties That Affect the Slope Stored Intege r Value and Real World Value

..................... 6-7

.................... 6-7

................ 6-8

......................... 6-11

..................... 6-13

...... 6-11

............ 6-13

Using numerictype Objects to Share Data Type and

Scaling Settings of fi objects

Example 1 Example 2

....................................... 6-14

....................................... 6-15

...................... 6-14

numerictype O bject Functions

...................... 6-17

Working with quantizer Objects

Constructing quantizer Objects ..................... 7-2

quantizer Object Properties

Quantizing Data with quantizer Objects

Transformations for Quantized Data

quantizer Object Functions

Working with the Fixed-Point Embedded

........................ 7-3

............. 7-4

................ 7-6

......................... 7-7

MATLAB Subset

What is the Embedded MATLAB Subset? ............. 8-2

Supported Functions and Limitations of the

Fixed-Point Em bedd ed MATLAB Subset

Embedded MATLAB MEX

Using Embedded MATLAB M EX with Fixed-Point

Algorithms

..................................... 8-12

.......................... 8-12

........... 8-3

Speeding Up Fixed-Point Execution with the emlmex

Function Using Data Type Override with Embedded MATLAB

MEX

....................................... 8-12

.......................................... 8-15

Embedded MATLAB Function Block

Composing a MATLAB Language Function in a Simulink

Model Using the Embedded MATLAB Function Block with Data

Type Override Using Fixed-Point Data Types with the Embedded

MATLAB Function Block Example: Implementing a Fixed-Point Direct Form FIR

Using the Embedded MATLAB Function Block

Embedded M ATL AB Coder

Working with Fixed-Point Compilation Reports

Generating the Compilation Report Opening the Compilation Report Viewing Your MATLAB Code Viewing V aria bles in the Variables Tab See Also

......................................... 8-16

.................................. 8-17

......................... 8-18

......................... 8-36

........................ 8-38

......................................... 8-41

................ 8-16

................... 8-37

..................... 8-38

............... 8-40

Interoperability with Other Products

....... 8-26

...... 8-37

x Contents

Using fi Objects with Simulink ...................... 9-2

Reading Fixed-Po int Data from the Workspace Writing Fixed-Point Data to the Workspace Setting the Value and Data Type of Block Parameters Logging Fixed-Point Signals Accessing Fixed-Point Block Data During Simulation

Using the Embedded MATLAB Subset

Using fi Objects with Signal Processing Blockset

Software

........................................ 9-8

......................... 9-6

............... 9-7

......... 9-2

............ 9-2

... 9-6

.... 9-6

Reading Fixed-Point Signals from the Workspace ....... 9-8

Writing Fixed-Point Signals to the Workspace

.......... 9-8

Using fi Objects with Filter Design Toolbox Software

.. 9-13

Index

xii Contents

Getting Started

• “Product Overview” on page 1-2

• “Licensing” on page 1-3

• “Getting Help” on page 1 -4

• “Display Settings” on page 1-6

• “Demos” on page 1-10

1 Gettin g Started

Product Overview

Fixed-Point Toolbox™ provides fixed-point data types and arithmetic in MATLAB syntax and execute them at compiled C-code speed. You can reuse these algorithms in Simulink models, facilitating bit-true simulation, implementation, and analysis and enabling you to generate test sequences for fixed-point software and hardware verification.

Key features of Fixed-Point Toolbox software include:

• Fixed-point data types in MATLAB with word lengths up to 65535 bits

• Global and local settings for performing fixed-point arithmetic

• Logical and bitwise operators and native integers

• Fixed-point data types usable in both MATLAB and Simulink

• Data logging, data-type override, and other tools for floating-to-fixed-point

conversion

• Accelerated execution of fixed-point algorithms in MATLAB

. The toolbox lets you design fixed-point algorithms using MATLAB

and pass fixed-point data to and from Simulink

1-2

Licensing

You can use fi objects with the DataType property set to double without a Fixed-Point Toolbox ™ license when you set the to

off. A Fixed-Point Toolbox license is checked out when you

fipref LoggingMode property

Licensing

• Use any

• Create any

including

• Load a M AT-file that contains any

set to

fi obje ct with any DataType other than double.

fi object with the fipref LoggingMode property set to on,

fi objects with DataType dou ble.

fi object with the DataT ype property

single, boolean, S cale dDouble,orFixed.

You can prevent the checko ut of a F ixed-Point Toolbox™ license when working with Fixed-Point Toolbox ™ code by setting the

fipref DataTypeOverride

property to TrueDoubles.

1-3

1 Gettin g Started

Getting Help

In this section...

“Getting Help in This Document” on page 1-4

“Getting Help at the MATLAB Command Line” on page 1-4

Getting Help in This Document

The following chapters discuss the objects of Fixed-Point Toolbox software:

• Chapter 3, “Working with fi Objects”

• Chapter 4, “Working with fimath Objects”

• Chapter 5, “Working with fipref Objects”

• Chapter 6, “Working with numerictype Objects”

• Chapter 7, “Working with quant izer Objects”

1-4

To get in-depth information about the properties of these objects, refer to the Property Reference.

To get in-depth information about the functions of these objects, refer to the Function Reference.

Getting Help at the MATLAB Command Line

To get command-line help for Fixed-Point T oolbox objects, type

help objectname

For example,

help fi help fimath help fipref help numerictype help quantizer

To get command-line help for Fixed-Point Toolbox functions, type

help embedded.fi/functionname

For example,

help embedded.fi/abs help embedded.fi/bitset help embedded.fi/sqrt

To invoke Help Browser documentation for Fixed-Point Toolbox functions from the MATLAB command line, type

doc fixedpoint/functionname

For example,

doc fixedpoint/int doc fixedpoint/add doc fixedpoint/savefipref doc fixedpoint/quantize

Getting Help

1-5

1 Gettin g Started

Display Settings

In Fixed-Point T oo lbox software, the fipref object determines the display properties of generally show

fi objects. Code examples throughout this User’s Guide

fi objects as they appear with the following fipref object

properties:

•

NumberDisplay — 'RealWorldValue'

• NumericTypeDisplay — 'full'

• FimathDisplay — 'full'

Setting 'FimathDisplay' to 'full' provides a quick and easy way to differentiate between associated with the global fimath. When MATLAB displays MATLAB never displays

fi objects with a local fimath and those that are

'FimathDisplay' is set to 'full',

fimath object properties for fi objects with a local fimath.

fimath object properties for fi objects that are

associated with the global fimath. Because of this display difference, you can tell when a

fi object is associated with the global fimath just by looking at

the output.

1-6

Additionally, unless otherwise specified, examples throughout the Fixed-Point Toolbox d ocumentation use the following configuration of the global fimath:

RoundMode: nearest

OverflowMode: saturate

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

Note If you are using a different global fimath, you may see different results when running the examples.

For more information on display settings, re fe r to Chapter 5, “Working with fipref Objects”.

Display Settings

Displaying the fimath Properties of fi Objects

To see the output as it appears in most Fixed-Point Toolbox code examples, set your

MATLAB returns the following :

fipref properties as follows and create two fi objects:

p = fipref('NumberDisplay', 'RealWorldValue',... 'NumericTypeDisplay', 'full', 'FimathDisplay', 'full'); a = fi(pi,'RoundMode', 'floor', 'OverflowMode', 'wrap') b = fi(pi)

3.1415

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

RoundMode: floor

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

3.1416

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

MATLAB displays fimath o bject properties in the output o f fi object a because a has a local fimath.

MATLAB does not display any

fimath object properties in the output of fi

object b because b associates itself with the global fimath.

1-7

1 Gettin g Started

Hiding the fimath Properties of fi Objects

If you are working with multiple fi objects tha t have local fimaths, you may want to turn off the

•

NumberDisplay — 'RealWorldValue'

• NumericTypeDisplay — 'full'

• FimathDisplay — 'none'

For example,

p = fipref('NumberDisplay', 'RealWorldValue',... 'NumericTypeDisplay', 'full', 'FimathDisplay', 'none')

NumberDisplay: 'RealWorldValue'

NumericTypeDisplay: 'full'

FimathDisplay: 'none'

DataTypeOverride: 'ForceOff'

fimath object display:

LoggingMode: 'Off'

1-8

F = fimath('RoundMode', 'floor', 'OverflowMode', 'wrap'); a = fi(pi, F)

3.1415

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

Although this setting helps decrease the amount of output produced, it also makes it impossible to tell from the output whether a with the globa l fimath. To do so, you can use the

fi object is associated

isfimathlocal function.

For example,

isfimathlocal(a)

Display Settings

ans =

When the i sfim athlocal function returns 1,thefi object has a local fimath. If the function returns

0,thefi object is associated with the global fimath.

For more information on the global fimath, see “Working w ith the Global fimath” on page 4-6 in the Fixed-Point Toolbox User’s Guide.

Shortening the numerictype Display of fi Objects

To reduce the amount of output even further, you can set the

NumericTypeDisplay to 'sh ort'. For example,

p = fipref('NumberDisplay', 'RealWorldValue',... 'NumericTypeDisplay', 'short', 'FimathDisplay', 'full');

a = fi(pi)

3.1416 s16,13

1-9

1 Gettin g Started

Demos

You can find interactive Fixed-Point Toolbox demos in the MATLAB Help browser. Fixed-Point Toolbox software includes the following demos:

• Fixed-Poin t Basics — Demonstrates the basic use of the fixed-point

object

• Number Circle — Illustrates the definitions of unsigned and signed two’s

complement integer and fixed-point numbers

• Binary Point Scaling — Explains binary point-only scaling

• Fixed-Point Data Type Override, Min/Max Logging, and Scaling — Steps

through the workflow of using doubles override and min/max logging in the toolbox to choose appropriate scaling for a fixed-point algorithm

• Fixed-Point C Development — Shows how to use the parameters from a

fixed-point MATLAB program in a fixed-point C program

• Fixed-Point Algorithm Development — Presents the development and

verification of a simple fixed-point algorithm

• Fixed-Point Fast Fourier Transform (FFT) — Provides an example of

converting a textbook Fast F ourie r Transform algorithm into fixed-point MATLAB code and then into fixed-point C code

• Analysis of a Fixed-Point State-Space System with Limit Cycles —

Demonstrates a limit cycle detection routine applied to a state-space system

• Quantization Error — Demonstrates the statistics of the error when signals

are quantized using various rounding methods

• Fixed-Point Lowpass Filtering Using Embedded MATLAB

through generating a C-MEX function from MATLAB code, running the generated C-MEX function, and displaying the results

MEX — Steps

1-10

• Fixed-Point ATAN2 Calculation — Uses the CORDIC algorithm and

polynomial approximation to perform a fixed-point calculation of the four quadrant inverse tangent

• Fixed-Point Sine and Cosine Calculation — Uses the CORDIC

approximation functions to compute the sine and cosine of fixed-point data

To access these demos, click the Demos entry for Fixed-Point Toolbox in the Contents pane of the Help browser, or type demo(’toolbox’,’fixed-point’) at the MATLAB command line.

Demos

1-11

1 Gettin g Started

1-12

Fixed-Point Concepts

• “Fixed-Point Data Types” on page 2-2

• “Scaling” on page 2-4

• “Precision and Range” on page 2-5

• “Arithmetic Operations” on page 2-10

• “fi Objects Compared to C Integer Data Types” on page 2-22

2 Fix e d-Point Concepts

Fixed-Point Data Types

In digital hardware, numbers are stored in binary words. A binary word is a fixed-length sequence of bits (1’s and 0’s). How hardware components or software functions interpret this sequence of 1’s and 0’s is defined by the data type.

Binary numbers are represented as either fixed-point or floating-point data types. This chapter discusses many terms and concepts relating to fixed-point numbers, data types, and mathematics.

A fixed-point data type is characterized by the word length in bits, the position of the binary point, and whether it is signed or unsigned. The position of the binary point is the means by which fixed-point values are scaled and interpreted.

For example, a binary representation of a generalized fixed-point number (either signed or unsigned) is shown below:

2-2

where

• b

is the ithbinary digit.

• wl is the w ord length in bits.

• b

is th e location of the most signif ica nt, or highest, bit (MSB).

wl-1

is the location of the least significant, o r lowest, bit (LSB).

• The binary point is shown four places to the left of the LSB. In this

example, therefore, the number is said to have four fractional bits, o r a fraction length of four.

Fixed-point data types can be either signed or unsigned. Signed binary fixed-point numbers are typically represented in one of three ways:

Fixed-Point Data Types

• Sign/magnitude

• One’s complement

• Two’s complement

Two’s complement is the mos t common representation of signed fixed-point numbers and is the only representation used by Fixed-Point Toolbox documentation. Refer to “Two’s Complement” on page 2-11 for more information.

2-3

2 Fix e d-Point Concepts

Scaling

Fixed-point numbers can be encoded according to the scheme

real world value slope integer bias- =× +()

where the slope can be expressed as

slope fractional slope

=×2

The integer number, in w In Fixed-P often refe

The slope In a numbe number th number i fractio or power

real world value integer

Fixed-Point Toolbox software supports both binary point-only scaling and [Slope Bias] scaling.

is sometimes called the stored integer. Thisistherawbinary

hich the binary point assumed to be at the far right of the word.

oint Toolbox documentation, the negative of the fixed exponent is

rred to as the fraction length.

and bias together represent the scaling of the fixed-point number.

r with zero bias, only the slope affects the scaling. A fixed-point

at is only scaled by binary point position is equivalent to a

n [Slope Bias] representation that has a bias equal to zero and a

nal slope equal to one. T his is referred to as binary point-only scaling

-of-two scaling:

- =×2

- =×

fixed exponent

fraction length

−

2-4

Note For examples of binary point-only scaling, see the Fixed-Point Toolbox Binary-Point Scaling dem o.

Precision and Range

In this section...

“Range” on page 2 -5

“Precision” on page 2-6

Note Youmustpayattentiontotheprecisionandrangeofthefixed-point data types and scalings you choose in order to know whether rounding methods will be invoked or if overflows or underflows will occur.

Range

The range is the span of numbers that a fixed-point data type and scaling can represent. The range of representable numbers for a two’s complement

fixed-po below:

int number of word length

Precision and Range

,scalingSand biasBis illustrated

()

negative numbers positive numbers

For both signed and unsigned fixed-point numbers of any data type, the number of different bit patterns is 2

For example, in two’s com plement, negative numbers must be represented as well as zero, so the maximum value is 2 representation for zero, the re are an unequal number of positive and negative

numbers. This means there is a representation for

wl -1

– 1. Because there is only one

−−2

1wl

but not for

1wl−

For slope = 1 and bias = 0:

negative numbers positive numbers

2-5

2 Fix e d-Point Concepts

Overflow Handling

Because a fixed-point data type represents numbers within a finite range, overflows and underflows can occur if the result of an operation is larger or smaller than the numbers in that range.

Fixed-Point Toolbox software allows you to either saturate or wrap overflows. Saturation represents positive overflows as the largest positive number in the range being used, and negative overflows as the largest negative number in the range being used. Wrapping uses modulo arithmetic to cast an overflow back into the representable range of the data type. Refer to “Modulo Arithmetic” on page 2-10 for more information.

When you create a property of the default global fimath is saturate. You can log overflows and underflows by setting the Refer to “LoggingMode” for more information.

fi object, any overflow s are saturated. The OverflowMode

LoggingMode property of the fipref object to on.

Precision

The precision of a fixed-point number is the difference between successive values representable by its data type and scaling, which is equal to the value of its least significant bit. The value of the least significant bit, and therefore the p recision of the number, is determined by the number of fractional bits. A fixed-point value can be represented to within half of t h e precision of its data type and scaling.

For example, a fixed-point representation with four bits to the right of the binary point has a precision of 2 significant bit. Any number within the range of this data type and scaling can be represented to within (2 an example of representing a number with finite precision.

Rounding Methods

When you represent numbers with finite precision, not every number in the available range can be represented exactly. If a number cannot be represented exactly by the specified data type and scaling, a rounding method is used to cast the value to a representable number. A lthough precision is always lost in the rounding operation, the cost of the operation and the amount of bias that is introduced depends on the rounding method itself. To provide you with

-4

or 0.0625, which is the value of its least

-4

)/2 or 0.03125, which is half the precision. This is

2-6

Precision and Range

greater flexibility in the trade-off between cost and bias, Fixed-Point Toolbox software currently supports the following rounding methods:

•

ceil rounds to the closest representable number in the direction of positive

infinity.

•

convergent rounds to the closest representable number. In the case of

atie,

convergent rounds to the nearest even number. This is the least

biased rounding method provided by the toolbox.

•

fix rounds to the closest representable number in the direction of zero.

floor, which is equivalent to two’s complement truncation, rounds to the

•

closest representable number in the direction of negative infinity.

•

nearest rounds to the closest representable number. In the case of a tie, nearest rounds to the closest representable number in the direction of

positive infinity. This rounding method is the default for and

fi arithmetic.

round rounds to the closest representable number. In the case of a tie,

•

the

round method rounds:

fi object creation

- Positive numbers to the closest representable number in the direction

of positive infinity.

- Negative numbers to the closest representable number in the direction

of negative infinity.

Choosing a Rounding Method. Each rounding method has a set of inherent properties. Depending on the requirements of your design, these properties could make the rounding method more or less desirable to you. By knowing the requirements of your design and understanding the properties of each rounding method, you can determine which is the best fit for your needs. The most important properties to consider are:

• Cost — Independent of the hardware b eing used, how much processing

expense does the rounding method require?

- Low — The method requires few processing cycles.

- Moderate — The method requires a moderate number of processing

cycles.

- High — The method requires more processing cycles.

2-7

2 Fix e d-Point Concepts

Note The cost estimates provided here are hardware independent. Some

processors have rounding modes built-in,soconsidercarefullythehardware you are using before calculating the true co st of each rounding mode.

• Bias — What is the expected value of the rounded values minus the original



−

values:

• Possibility of Overflow — Does the rounding method introduce the

possibility of overflow?

()



−

()



−

()



−

()

< 0

— T he rounding method introduces a negative bias.

— The rounding method is unbiased.

= 0

> 0

— The rounding m ethod introduces a positive bias.

2-8

- Yes — The rounded values may exceed the minimum or maximum

representable value.

- No — The rounded values will never exceed the minimum or maximum

representable value.

Precision and Range

The following table shows a comparison of the different rounding methods available in both Fixed-Point Toolbox and Simulink

Fixed-Point Toolbox Rounding Method

Simulink Fixed Point Rounding Mode

ceil Ceiling

convergent Convergent

fix Zero

floor Floor

nearest Nearest

round Round

Cost

Low

Bias

Large positive

High Unbiased

Low

• Largepositivefor

negative samples

• Unbiased for

samples with evenly distributed positive and negative values

• Largenegativefor

positive samples

Low

Moderate

High

Large negative

Small positive

• Small negative for

negative samples

Fixed Point™ products.

Possibility of Overflow

Yes

N/A

Simplest

(Simulink Fixed Point only)

Low

• Unbiased for

samples with evenly distributed positive and negative values

• Small positive for

positive samples

Depends on the operation

2-9

2 Fix e d-Point Concepts

Arithmetic Operations

In this section...

“Modulo Arithmetic” on page 2-10

“Two’s Complement” on page 2-11

“Addition and Su btra ction ” on page 2-12

“Multiplication” on page 2-13

“Casts” on page 2-19

Note These sections will help you understand what data type and scaling choices result in overflows or a loss of precision.

Modulo Arithmetic

Binary math is based on modulo arithmetic. Modulo arithmetic uses only a finite set of numbers, wrapping the results of any calculations that fall outside the given set back into the set.

2-10

For example, the common everyday clock uses modulo 12 arithmetic. Numbers in this system can only be 1 through 12. Therefore, in the “clock” system, 9 plus 9 equals 6. This can be more easily visualized as a number circle:

9 ... ... plus 9 more ...

Arithmetic Operations

Similarly, binary math can o nly use the numbers 0 and 1, and any arithmetic results that fall outside this range are wrapped “around the circle” to either 0 or 1.

... equals 6.

Two’s Complement

Two’s complement is a way to interpret a binary number. In two’s complement, positive numbers always start with a 0 and negative numbers always start with a 1. If the leading bit of a two’s complement number is 0, the value is obtained by calculating the standard binary value of the number. If the leading bit of a two’s complemen t number is 1, the value is obtained by assuming that the leftmost bit is negative, and then calculating the binary value of the number. For example,

()

01 0 2 1

=+ =

11 2 2 2 1 1

=−

(

To compute the negative of a binary number using two’s complement,

1 Take the one’s complement, or “flip the bits.”

()

=− + =−

()

)

2-11

2 Fix e d-Point Concepts

010010 100

1001 010

1001011 110

18 5

675

11 75

. .

(.) (.) (.)

−

2 Add a 1 using binary math.

3 Discard any bits carried beyond the original word length.

Forexample,considertakingthenegative of 11010 (-6). First, take the one’s complement of the number, or flip the bits:

11010 00101→

Next, add a 1, wrapping all numbers to 0 or 1:

00101

00110 6+()

Addition and Subtraction

The addition of fixed-point numbers requires that the binary points of the addends be aligned. The addition is then performed using binary arithmetic so that no number other than 0 or 1 is used.

2-12

For example, consider the addition of 010010.1 (18.5) with 0110.110 (6.75):

18 5

010010 1

0110 110

011001 010

Fixed-point subtraction is equivalent to adding while using the two’s complement value for any negative values. In subtraction, the addends must be sign-extended to match each other’s length. For example, consider subtracting 0110.110 (6.75) from 010010.1 (18.5):

010010 100

0110 110

. .

(.)

675

(. )

25 25

(.)

18 5

(.)

675

(. )−

twos complement

and sign extension

Carry bit is discarded

Arithmetic Operations

The default global fimath has a value of 1 (true) for the CastBeforeSum property. This casts addends to the sum data type before addition. Therefore, no further shifting is necessary during the addition to line up the binary points.

CastBeforeSum has a value of 0 (false), the adde n ds are added with full

precision maintained. After the addition the sum is then quantized.

Multiplication

The multiplication of two’s complement fixed-point numbers is directly analogous to regular decimal multiplication, with the exception that the intermediate results must be sign-extended so that their left sides align before you add them together.

For example, consider the multiplication of 10.11 (-1.25) with 011 (3):

Multiplication Data Types

ollowing diagrams show the data types used for fixed-point multiplication

The f

g Fixed-Point Toolbox software. The diagrams illustrate the differences

usin

een the data types used for real-real, complex-real, and complex-complex

betw

tiplication.

mul

2-13

2 Fix e d-Point Concepts

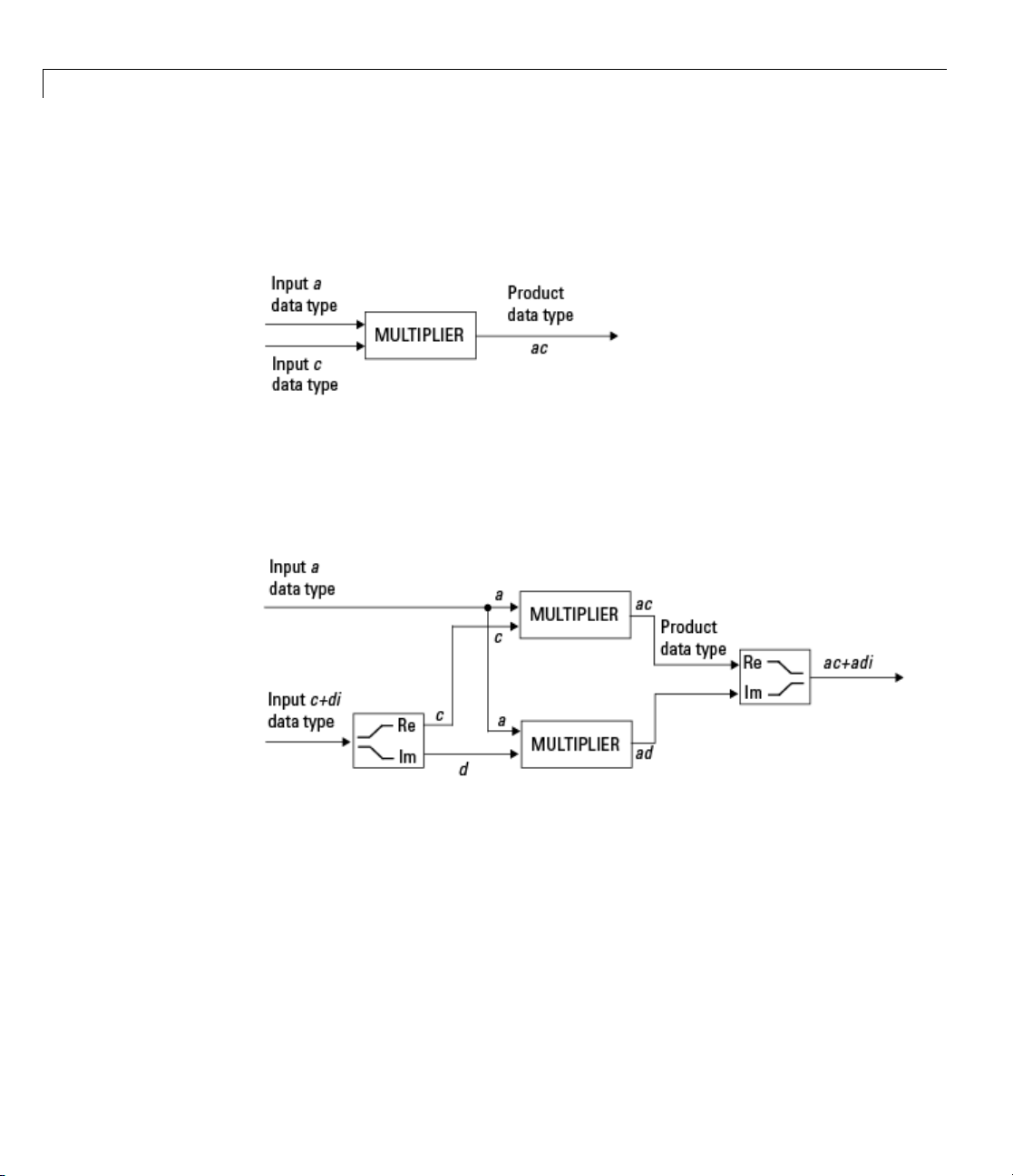
Real-Real Multiplication. The following diagram shows the data types used

by the toolbox in the multiplication of two real numbers. The software returns the output of this operation in the product data type, which is governed by the

fimath object ProductMode property.

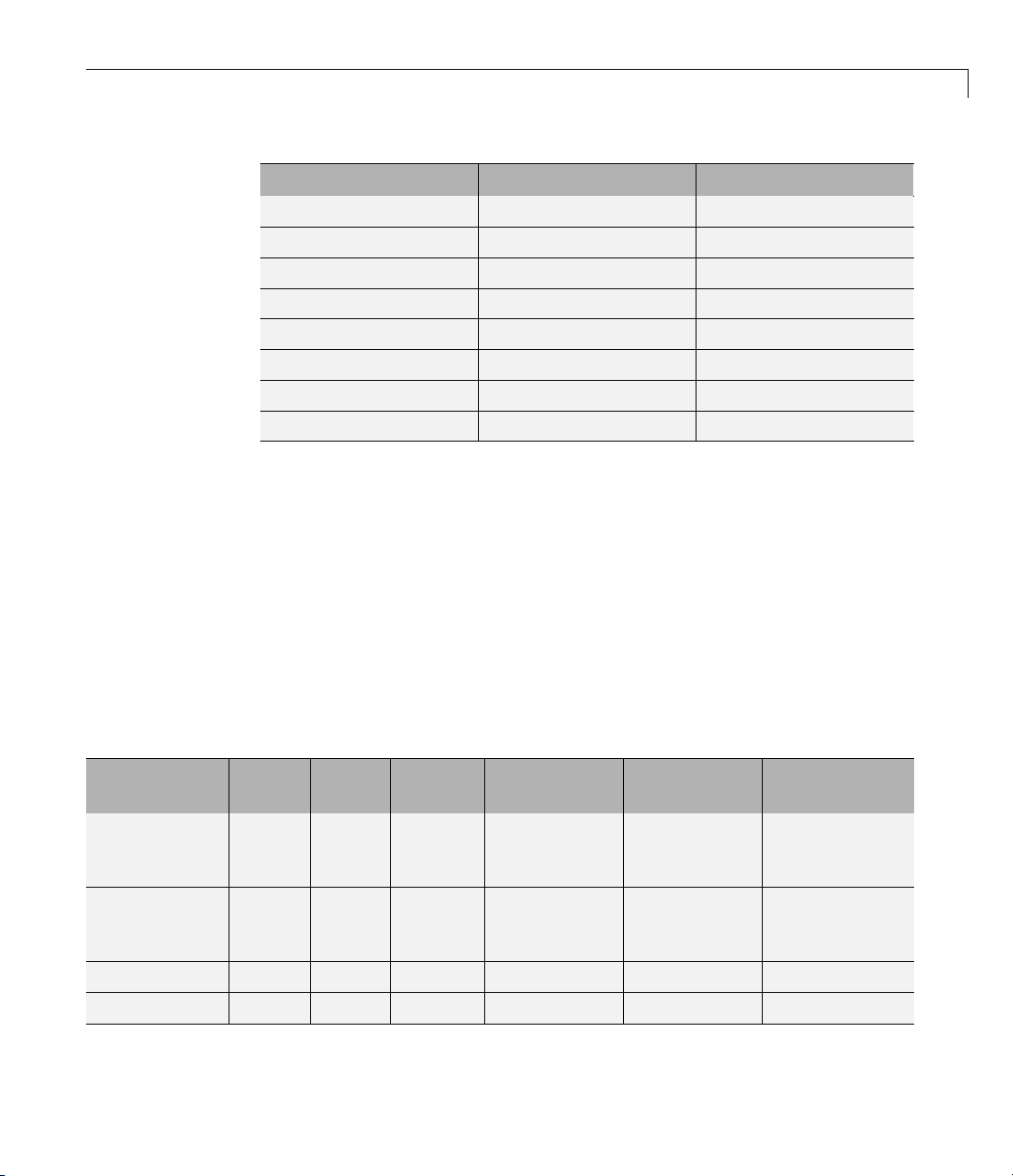
Real-Complex Multipli cation. The following diagram shows the data types used by the toolbox in the multiplication of a real and a complex fixed-point number. Real-complex and complex-real multiplication are equivalent. The software returns the output of this operation in the product data type, which is governed by the

fimath object ProductMode property:

2-14

Complex-Complex Multiplication. The following diagram shows the multiplication of two complex fixed-point numbers. Note that the software returns the output of this operation in the sum data type, which is governed by the determined by the

fimath object SumMode property. The intermediate product data type is

fimath object ProductMode property.

Arithmetic Operations

When th sum dat C code,

acc=ac; acc-=bd;

fimath object CastBeforeSum property is true, the casts to the

a type are prese n t after the multipliers in the preceding diagram. In

this is equivalent to

for the subtractor, and

acc=ad; acc+=bc;

for the adder, where acc is the a ccumulator. When the CastBeforeSum property is false, the casts are not present, and the data remains in the product data type befo re the subtraction and addition operations.

2-15

2 Fix e d-Point Concepts

Multiplication with fimath

In the following examples, let

F = fimath('ProductMode','FullPrecision',... 'SumMode','FullPrecision') T1 = numerictype('WordLength',24,'FractionLength',20) T2 = numerictype('WordLength',16,'FractionLength',10)

Real*Real. Notice that the word length and fraction length of the result z are equal to the sum of the word lengths and fraction lengths, respectively, of the multiplicands. This is because the properties are set to FullPrecision:

P = fipref; P.FimathDisplay = 'none'; x = fi(5, T1, F)

fimath SumMode and ProductMode

2-16

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 24

FractionLength: 20

y = fi(10, T2, F)

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 10

z = x*y

Arithmetic Operations

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 40

FractionLength: 30

Real*Complex. Notice that the word length and fraction length of the result

z areequaltothesumofthewordlengthsand fraction lengths, respectively,

of the multiplicands. This is because the

fimath SumMode and ProductMode

properties are set to FullPrecision:

x = fi(5,T1,F)

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 24

FractionLength: 20

y = fi(10+2i,T2,F)

10.0000 + 2.0000i

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 10

2-17

2 Fix e d-Point Concepts

z = x*y

50.0000 +10.0000i

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 40

FractionLength: 30

Complex*Complex. Complex-complex multiplication involves an addition as well as multiplication, so the word length of the full-precision result has onemorebitthanthesumofthewordlengthsofthemultiplicands:

x = fi(5+6i,T1,F)

2-18

5.0000 + 6.0000i

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 24

FractionLength: 20

y = fi(10+2i,T2,F)

10.0000 + 2.0000i

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 10

Arithmetic Operations

z = x*y

38.0000 +70.0000i

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 41

FractionLength: 30

Casts

The fimath objectallowsyoutospecifythedatatypeandscalingof intermediate sums and products with the properties. It is important to keep in mind the ramifications of each cast when you set the

SumMode and ProductMode properties. Depending upon the

data types you select, overflow and/or rounding might occur. The following two examples demonstrate cases where overflow and rounding can occur.

SumMode and ProductMode

Note For more examples of casting, see “Casting fi Objects” on page 3-12.

Casting from a Shorter Data Type to a Longer Data Type

Consider the cast of a nonzero number, represented by a 4-bit data type with two fractional bits, to an 8-bit data type with seven fractional bits:

2-19

2 Fix e d-Point Concepts

source

destination

This bit from the source data type falls off the high end with the shift up. Overflow might occur. The result will saturate or wrap.

Asthediagramshows,thesourcebitsareshiftedupsothatthebinarypoint matches the destination binary point position. The highest source bit does not fit, so overflow might occur and the result can saturate or wrap. The empty bits at the low end of the destination data type are padded with either 0’s or 1’s:

• If overflow does not occur, the empty bits are padded with 0’s.

• If wrapping occurs, the empty bits are padded with 0’s.

The source bits must be shifted up to match the binary point position of the destination data type.

These bits of the destination data type are padded with 0s or 1s.

2-20

• If saturation occurs,

- The empty bits of a positive number are padded with 1’s.

- The empty bits of a negative number are padded with 0’s.

Youcanseethatevenwithacastfromashorterdatatypetoalongerdata type, overflow can still occur. This canhappenwhentheintegerlengthof the source data type (in this case two) is longer than the integer length of the destination data type (in this case one). Similarly, rounding might be necessary even when casting from a shorter data type to a longer data type, if the destination data type and scaling has fewer fractional bits than the source.

Arithmetic Operations

Casting from a Longer Data Type to a Shorter Data Type

Consider the cast of a nonzero number, represented by an 8-bit data type with seven fractional bits, to a 4-bit data type with two fractional bits:

source

The source bits must be shifted down to match the binary point position of the destination data type.

destination

These bits from the source do not fit into the destination

There is no value for this bit

data type. The result is rounded. from the source, so the result must be sign-extended to fill the destination data type.

As the diagram shows, the source bits are shifted down so that the binary point matches the destination binary po int position. There is no value for the highest bit from the source, so sign extension is used to fill the integer portion of the destination data type. The bottom five bits of the source do not fit into the fraction length of the destination. Therefore, precision can be lost as the result is rounded.

In this case , even though the cast is from a longer data type to a shorter data type, all the integer bits are maintained. Conversely, full precision can be maintained even if you cast to a shorter data type, as long as the fraction length of the destination data type is the same length or longer than the fraction length of the source data type. In that case, however, bits are lost from the high end of the result and overflow can occur.

The worst case occurs when both the integer length and the fraction length of the d estination data type are shorter than those of the source data type and scaling. In that case, both overflow and a loss of precision can occur.

2-21

2 Fix e d-Point Concepts

fi Objects Compared to C Integer Data Types

In this section...

“Integer Data Types” on page 2-22

“Unary Conversions” on page 2-24

“Binary Conversions” on page 2-25

“Overflow Handling” on page 2-28

Note The sections in this topic compare the fi object with fixed-point d ata types and operations in C. In these sections, the information on ANSI C is adapted from Samuel P. Harbison and Guy L. Steele Jr., C: A Reference Manual, 3rd ed., Prentice Hall, 1991.

Integer Data Types

This section compares the numerical range of fi integer data types to the minimum numerical ranges of ANSI C integer data types.

2-22

ANSI C Integer Data Types

The following table shows the minimum ranges of ANSI C integer data types. The integer ranges can be larger than or equal to those shown, but cannot be smaller. The range of a

int, which must be larger than or equal to the range of a short.

Note that the minimum ANSI C ranges are large enough to accommodate one’s complement or sign/magnitude representation, but not two’s complement representation. In the one’s complement and sign/magnitude representations,

a signed integer with n bits has a range from In both of these representations, an equal number of positive and negative numbers are represented, and zero is represented twice.

long must be larger than or equal to the range of an

−

−+

1n−

−

,inclusive.

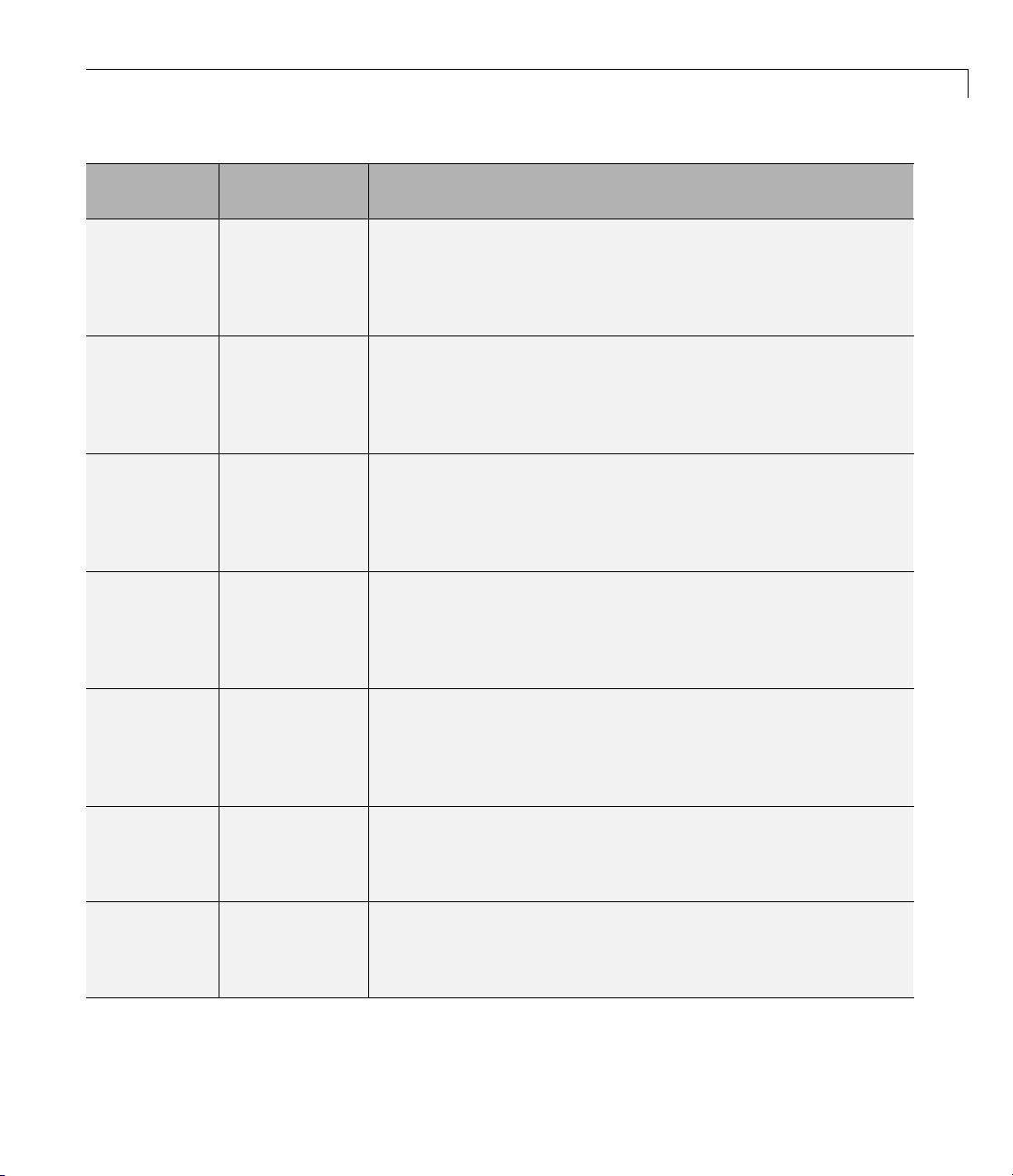
fi Objects Compared to C Integer Data Types

Integer Type Minimum Maximum

signed char

unsigned char

short int

unsigned short

int

unsigned int

long int

unsigned long

–127 127

0255

–32,767 32,767

0 65,535

–32,767 32,767

0 65,535

–2,147,483,647 2,147,483,647

0 4,294,967,295

fi Integer Data Types

The following table lists the numerical ranges of the integer data types of the types. The ranges are large enough to accommodate the two’s complement representation, which is the only signed binary encoding technique supported by Fixe d-Point Toolbox software. In the two’s complement representation, a

signed integer with n bits has a range from

unsigned integer with n bits has a range from 0 to negative side of the range has one more value than the positive side, and zero is represented uniquely.

fi object, in particular those equivalent to the C integer data

−−2

1n−

−

,inclusive. The

,inclusive. An

Constructor

fi(x,1,n,0)

fi(x,0,n,0)

fi(x,1,8,0)

fi(x,0,8,0)

Signed

Yes

Word

Length

Fraction

Length

Minimum Maximum

(2 to 65,535)

−−2

1n−

−

(2 to 65,535)

−

8 0 –128 127

80 0 255

Closest ANSI

CEquivalent

N/A

signed char

unsigned char

2-23

2 Fix e d-Point Concepts

Constructor

fi(x,1,16,0)

fi(x,0,16,0)

fi(x,1,32,0)

fi(x,0,32,0)

Signed

Yes

Word

Length

16 0 –32,768 32,767

16 0 0 65,535

32 0 –2,147,483,648 2,147,483,647

32 0 0 4,294,967,295

Fraction

Length

Minimum Maximum

Unary Conversions

Unary conversions dictate whether and how a single operand is converted before an operation is performed. This section discusses unary convers ions in ANSI C and of

ANSI C Usual Unary Conversions

Unary conversions in ANSI C are automatically applied to the operands of the unary according to the following table:

Original Operand Type ANSI C Conversion

char or short int

unsigned char or unsigned short int or unsigned int

float float

!,–,~,and* operators, and of the binary << and >> operators,

fi objects.

Closest ANSI

CEquivalent

short int

unsigned short

long int

unsigned long

Array of T

Function returning T

2-24

Pointer to T

Pointer to function returning T

If type int cannot represent all the values of the original data type without

overflow, the converted type is

unsigned int.

fi Usual Unary Conversions

The following table shows the fi unary conversions:

C Operator fi Equivalent fi Conversion

!x ~x = not(x)

~x bitcmp(x)

x<<n bitshift(x,n)

No equivalent

positive n

x>>n bitshift(x,-n)

+x +x

-x -x

Result is logical.

Result is same numeric type as operand.

N/A

Result is same numeric type as operand. Round mode is always

floor. Overflow mode is obeyed. 0-valued

bits are shifted in on the right.

Result is same numeric type as operand. Round mode is always

floor. Overflow mode is obeyed. 0-valued

bits are shifted in on the left if the operand is unsigned or signed and positive. 1-valued bits are shifted in on the left if the operand is signed and negative.

Result is same numeric type as operand.

Result is same numeric type as operand. Overflow mode is obeye d. For example, overflow might occur when you negate an unsigned value of a signed

fi Objects Compared to C Integer Data Types

fi or the most negative

fi.

Binary Conversions

This section describes the conversions that occur when the operands of a binary operator are different data types.

ANSI C Usual Binary Conversions

In ANSI C, operands of a binary operator must be of the same type. If they are different, one is converted to the type of the other according to the first applicable conversion in th e following table:

2-25

2 Fix e d-Point Concepts

Type of Ot her

Type of One Ope rand

long double

double

float

unsigned long

long unsigned long or unsigned

long int long

unsigned int or unsigne d unsigned

int int int

Type long is only used if it can represent all values of type unsigned.

Operand ANSI C Conversion

Any

long double

double

float

unsigned long

long

fi Usual Binary Conversions

When one of the operands of a binary operator (+,–,*, .*)isafi object and the other is a MATLAB built-in numeric type, then the nonconverted to a

fi object before the operation is performed, according to the

following table:

fi operand is

Type of One Operand

fi double or

fi int8

2-26

Type o f Othe r Operand

single

Properties of Other Operand After Conversion to a fi Object

• Signed = same as the original fi operand

WordLength = same as the original fi operand

•

FractionLength = set to best precision possible

•

• Signed = 1

• WordLength = 8

• FractionLength = 0

fi Objects Compared to C Integer Data Types

Type of One Operand

fi uint8

fi int16

fi uint16

fi int32

fi uint32

Type o f Othe r Operand

Properties of Other Operand After Conversion to a fi Object

• Signed = 0

• WordLength = 8

• FractionLength = 0

• Signed = 1

• WordLength = 16

• FractionLength = 0

• Signed = 0

• WordLength = 16

• FractionLength = 0

• Signed = 1

• WordLength = 32

• FractionLength = 0

• Signed = 0

• WordLength = 32

• FractionLength = 0

fi int64 • Signed = 1

• WordLength = 64

• FractionLength = 0

fi uint64 • Signed = 0

• WordLength = 64

• FractionLength = 0

2-27

2 Fix e d-Point Concepts

Overflow Handlin g

The following sections co mpare how ANSI C and Fixed-Point Toolbox software handle overflows.

ANSI C Overflow Handling

In ANSI C, the result of signed integer operations is whatever value is produced by the machine instruction used to implement the operation. Therefore, ANSI C has no rules for handling signed integer overflow.

The results of unsigned integer overflows wrap in ANSI C.

fi Overflow Handling

Addition and multiplication with fi objects yield results that can be exactly represented b y a memory on your machine. T his is not true of division, however, because many ratios result in infinite binary expressions. You can perform division with objects using the divide function, which requires you to explicitly specify the numeric type of the result.

fi object, up to word lengths of 65,535 bits or the available

The conditions under which a produced are determined by the associated certain overflow characteristics separately for sums (including differences) and products. Refer to the following table:

fimath Object Properties Related to Overflow Handling Property Value Description

OverflowMode

'saturate'

'wrap'

fi object overflows and the results then

2-28

fimath object. You can specify

Overflows are saturated to the maximum or minimum value in the range.

Overflows wrap using modulo arithmetic if unsigned, two’s complement wrap if signed.

fimath Object Properties Related to Overflow Handling Property Value Description

ProductMode 'FullPrecision'

Full-precision results are kept. Overflow does not occur. An error is thrown if the resulting word length is greater than

MaxProductWordLength.

The rules for computing the resulting product word and fraction lengths are given in “ProductMode” in the Property Reference.

'KeepLSB'

The le ast significant bits of the product are kept. Full precision is kept, but overflow is possible. This behavior models the C language integer operations.

The resulting word length is determined by the

ProductWordLength is greater than is

ProductWordLength property. If

necessary for the full-precision product, then the result is stored in the least significant bits. If less th a n is necessary for the full-precision product, then overflow occurs.

fi Objects Compared to C Integer Data Types

ProductWordLength is

The rule for computing the resulting product fraction length is given in “ProductMode” in the Property Reference.

2-29

2 Fix e d-Point Concepts

fimath Object Properties Related to Overflow Handling Property Value Description

ProductWordLength

MaxProductWordLength

ProductFractionLength

'KeepMSB'

'SpecifyPrecision'

Positive integer

Positive integer The maximum product word length allowed

Integer

The most significant bits of the product are kept. Overflow is prevented, but precision may be lost.

The resulting word length is determined by the

ProductWordLength is greater than is

necessary for the full-precision product, then the result is stored in the most significant bits. If less th a n is necessary for the full-precision product, then rounding occurs.

The rule for computing the resulting product fraction length is given in “ProductMode” in the Property Reference.

You can specify both the word length and the fraction length of the resulting p roduct.

The word length of product results when

ProductMode is 'KeepLSB', 'KeepMSB',or 'SpecifyPrecision'.

when The default is 128 bits. The maximum is 65,535 bits. This property can help ensure that your simulation does not exceed your hardware requirements.

The fraction length of product results when

ProductMode is 'Specify Precision'.

ProductWordLength property. If

ProductWordLength is

ProductMode is 'Full Precision'.

2-30

fimath Object Properties Related to Overflow Handling Property Value Description

SumMode 'FullPrecision'

Full-precision results are kept. Overflow does not occur. An error is thrown if the resulting word length is greater than

MaxSumWordLength.

The rules for computing the resulting sum word and fraction lengths are given in “SumMode” in the Property Reference.

'KeepLSB'

The least significant bits of the sum are kept. Full precision is kept, but overflow is possible. This behavior models the C language integer operations.

The resulting word length is determined by the

SumWordLength is greater than is necessary

SumWordLength property. If

for the full-precision sum, then the result is stored in the least significant bits. If

SumWordLength is less than is necessary

for the full-precision sum, then overflow occurs.

fi Objects Compared to C Integer Data Types

'KeepMSB'

The rule for computing the resulting sum fraction length is given in “SumMode” in the Property Reference.

The most significant bits of the sum are kept. Overflow is prevented, but precision may be lost.

The resulting word length is determined by the

SumWordLength is greater than is necessary

SumWordLength property. If

for the full-precision sum, then the result is stored in the most significant bits. If

SumWordLength is less than is necessary

for the full-precision sum, then rounding occurs.

2-31

2 Fix e d-Point Concepts

fimath Object Properties Related to Overflow Handling Property Value Description

The rule for computing the resulting sum fraction length is given in “SumMode” in the Property Reference.

SumWordLength

MaxSumWordLength

SumFractionLength

'SpecifyPrecision'

Positive integer

Positive integer The maximum sum word length allowed

Integer

You can specify both the word length and the fraction length of the resulting sum.

The word length of sum results when

SumMode is 'KeepLSB', 'KeepMSB',or 'SpecifyPrecision'.

when default is 128 bits. The maximum is 65,535 bits. This property can help ensure that your simulation does not exceed your hardware requirements.

The fraction length of sum results when

SumMode is 'SpecifyPrecision'.

SumMode is 'Fu llPrecision'.The

2-32

Working with fi Objects

• “Constructing fi Objects” on page 3-2

• “Casting fi Objects” on page 3-12

• “fi Object Properties” on page 3-17

• “fi Object Functions” on page 3-24

3 Working with fi Objects

Constructing fi Objects

In this section...

“fi Object S yntaxes” on pa ge 3-2

“Examples of Constructing fi Objects” on page 3-3

fi Object Syntaxes

You can create fi objects using Fixed-Point Toolbox software in any of the following ways:

• You can use the

• You can use any of the

To get started, type

a = fi(0)

to create a fi object with the default data type and a value of 0.

FractionLength: 15

This constructor syntax creates a signed fi object with a value of 0, word length of 16 bits, and fraction length of 15 bits. Because you did not specify any

fimath object properties in the fi constructor, the resulting fi object a

associates itself with the global fimath.

fi constructor function to create a new fi object.

sfi constructor function to create a new signed fi object.

ufi constructor function to create a new unsigned fi object.

fi constructor functions to copy an existing fi object.

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

3-2

Constructing fi Objects

To see all of the fi, sfi,andufi constructor syntaxes, refer to the respective reference pages.

Note For information on the display format of fi objects, refer to “Display Settings” on page 1-6.

Examples of Constructing fi Objects

The following examples show you several different ways to construct fi objects. For other, more basic examples of constructing fi objects, see the Examples section of the following constructor function reference pages:

•

• sfi

• ufi

Constructing a fi Object with Property Name/Property Value Pairs

You can use property name/property value pairs to set fi and fimath object properties when you create the

a = fi(pi, 'roundmode', 'floor', 'overflowmode', 'wrap')

3.1415

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

RoundMode: floor

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

fi object:

3-3

3 Working with fi Objects

MaxSumWordLength: 128

You do not have to specify every fi math object property in the fi constructor. The

fi object inherits all unspecified fimath object properties from the global

fimath.

• If you specify at least one

the

fi object will have a lo cal fimath object. The fi object inherits the

remaining unspecified

• If you do not specify any

constructor, the

fi object associates itself with the global fimath. See

fimath object property in the fi constructor,

fimath o bject properties from the glo bal fimath.

fimath object properties in the fi object

“Working with the Global fimath” onpage4-6formoreinformation.

Constructing a fi Object Using a numerictype Object

You can use a numerictype object to define a fi object:

T = numerictype

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 15

a = fi(pi, T)

3-4

1.0000

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 15

Constructing fi Objects

You can also use a fimath object with a numerictype object to define a fi object:

F = fimath('RoundMode', 'nearest',... 'OverflowMode', 'saturate',... 'ProductMode','FullPrecision',... 'MaxProductWordLength', 128,... 'SumMode','FullPrecision',... 'MaxSumWordLength', 128)

RoundMode: nearest

OverflowMode: saturate

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

a = fi(pi, T, F)

1.0000

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 15

RoundMode: nearest

OverflowMode: saturate

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

3-5

3 Working with fi Objects

Note The syntax a = fi(pi,T,F) is equivalent to a = fi(pi,F ,T).You

can use both statements to de fine a

numerictype object.

fi object using a fimath object and a

Constructing a fi Object Using a fimath Object

You can create a fi object using a specific fimath object. When you do so, a local

fimath object is assigned to the fi object you create. If you do n ot specify

any

numerictype object properties, the word length of the fi object defaults

to 16 bits. The fraction length is determined by best precision scaling:

F = fimath('RoundMode', 'nearest',... 'OverflowMode', 'saturate',... 'ProductMode','FullPrecision',... 'MaxProductWordLength', 128,... 'SumMode','FullPrecision',... 'MaxSumWordLength', 128)

3-6

RoundMode: nearest

OverflowMode: saturate

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

F.OverflowMode = 'wrap'

RoundMode: nearest

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

a = fi(pi, F)

3.1416

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

RoundMode: nearest

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

Constructing fi Objects

You can also create fi objects using a fimath object while specifying various

numerictype properties at creation time:

b = fi(pi, 0, F)

3.1416

DataTypeMode: Fixed-point: binary point scaling

Signedness: Unsigned WordLength: 16

FractionLength: 14

RoundMode: nearest

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

3-7

3 Working with fi Objects

c = fi(pi, 0, 8, F)

3.1406

DataTypeMode: Fixed-point: binary point scaling

Signedness: Unsigned WordLength: 8

FractionLength: 6

RoundMode: nearest

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

3-8

d = fi(pi, 0, 8, 6, F)

3.1406

DataTypeMode: Fixed-point: binary point scaling

Signedness: Unsigned WordLength: 8

FractionLength: 6

RoundMode: nearest

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

Constructing fi Objects

Building fi Object Constructors in a GUI

When you are working with files in MATLAB, you can build your fi object constructors using the Insert fi Constructor dialog box. After specifying the value and properties of the prepopulated

fi object constructor string at a specific location in your file.

fi object in the dialog box, you can insert the

For example, to create a signed

fi object with a value of pi, a word length of

16 bits and a fraction length of 13 bits, perform the following steps:

1 Open the Insert fi Constructor dialog box by selecting

Tools > Fixed-Point Toolbox > Insert fi Constructor from the editor

menu.

2 Use the edit boxes and drop-down menus to specify the following properties

of the

• Value =

fi object:

• Data type mode = Fixed-point: binary point scaling

• Signedness = Signed

• Word length = 16

• Fraction length = 13

3-9

3 Working with fi Objects

3 To insert the fi object constructor string in your file, place your cursor at

the desired location in the file, and click OK on the Insert fi Constructor dialog box. Clicking OK closes the Insert fi Constructor dialog box and automatically populates the

fi object constructor string in your file:

Determining Property Precedence

The value of a property is taken from the last time it is set. For example, create a and a fraction length of

numerictype object with a value of true for the Signed property

14:

T = numerictype('Signed', true, 'FractionLength', 14)

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 14

3-10

Now, create the following fi object in which you specify the numerictype property after the Signed property, so that the resulting fi object is signed:

a = fi(pi,'Signed',false,'numerictype',T)

1.9999

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 14

Contrast the fi object in this code sample with the fi object in the following code sample. The specified before the

numerictype property in the following code sample is

Signed property, so the resulting fi object is unsigned:

Constructing fi Objects

b = fi(pi,'numerictype',T,'Signed',false)

3.1416

DataTypeMode: Fixed-point: binary point scaling

Signedness: Unsigned WordLength: 16

FractionLength: 14

Copying a fi Object

To copy a fi object, simply use assignment, as in the following example:

a = fi(pi)

3.1416

b=a

3.1416

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

3-11

3 Working with fi Objects

Casting fi Objects

In this section...

“Overwriting by Assignment” on page 3-12

“Ways to Cast with MA TLAB Software” on page 3-12

Overwriting by Assignment

BecauseMATLABsoftwaredoesnothave type declarations, an assignment like

A=BreplacesthetypeandcontentofA w ith the type and content of B.If A does not exist at the time of the assignment, MATLAB creates the variable A and assigns it the same type and value as B. Such assignment happens

with all types in MATLAB—objects and built-in types alike—including

double, single, int8, uint8, int16,etc.

fi,

For example, the following code overwrites the value and the value and

A = int8(0); B = int16(32767); A=B

32767

class(A)

ans =

int16

int16 type of B:

int8 type of A with

Ways to Cast with MATLAB Software

You may find it useful to cast data into another type—for example, when you are casting data from an accumulator to memory. There are several ways to cast data in MATLAB. The following sections provide examples of three different methods:

3-12

• CastingbySubscriptedAssignment

• CastingbyConversionFunction

Casting fi Objects

• Casting with the Fixed-Point Toolbox

reinterpretcast Function

Casting by Subscripted Assignment

The following subscripted assignment statement retains the type of A and saturates the value of

A = int8(0); B = int16(32767); A(:) = B

127

class(A)

ans =

int8

Thesameistrueforfi objects:

fipref('NumericTypeDisplay', 'short'); A = fi(0, true, 8, 0); B = fi(32767, true, 16, 0); A(:) = B

B to an int8:

127

s8,0

Note For more information on subscripted assignments, see the subsasgn function.

3-13

3 Working with fi Objects

Casting by Conversion Function

You can convert from one data type to another by using a conversion function. In this example,

B = int16(32767); A = int8(B)

127

class(A)

ans =

int8

Thesameistrueforfi objects:

B = fi(32767, true, 16, 0) A = fi(B, 1, 8, 0)

A doesnothavetobepredefinedbecauseitisoverwritten.

3-14

32767

s16,0

127

s8,0

Using a numerictype Object in the fi Conversion Function. Often a specific

numerictype objects for use in the conversion functions. Predefining these

numerictype is used in many places, and it is convenient to predefine

objects is a good practice because it also put s the data type specification in one place.

T8 = numerictype(1,8,0)

T8 =

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 8

FractionLength: 0

T16 = numerictype(1,16,0)

T16 =

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 0

B = fi(32767,T16)

Casting fi Objects

32767

s16,0

A = fi(B, T8)

127

s8,0

Casting with the reinterpretcast Function

You can convert fixed-point and built-in data types without changing the underlying data. The Fixed-Point Toolbox performs this ty pe of conversion.

In the following example,

B is an unsigned fi object with a w ord length of 8

bits and a fraction length of 5 bits. The into a signed fi object A with a word length of 8 bits and a fraction length of 1

reinterpretcast function

reinterpretcast function converts B

3-15

3 Working with fi Objects

bit. The real-world values of A and B differ, but their binary representations are the same.

B = fi([pi/4 1 pi/2 4], false, 8, 5) T = numerictype(true, 8, 1 ); A = reinterpretcast(B, T)

0.7813 1.0000 1.5625 4.0000

DataTypeMode: Fixed-point: binary point scaling

Signedness: Unsigned WordLength: 8

FractionLength: 5

12.5000 16.0 000 25.0000 -64 .0000

3-16

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 8

FractionLength: 1

To verify that the underlying data has not changed, compare the binary representations of

binary_B = bin(B) binary_A = bin(A)

binary_A =

00011001 001 00000 0011001 0 10000000

binary_B =

00011001 001 00000 0011001 0 10000000

A and B:

fi Object Properties

In this section...

“Data Properties” on page 3-17

“fimath Properties” on page 3-17

“numerictype Properties” on page 3-19

“Setting fi Object Properties” on page 3-20

Data Properties

The data properties of a fi object are always writable.

•

bin —Storedintegervalueofafi object in binary

data — Numeri c al real-world value of a fi object

•

dec — Stored integer value of a fi object in decimal

•

fi Object Properties

double — Real-world value of a fi object, stored as a MATLAB double

•

data type

hex — Stored integer value of a fi object in hexadecimal

•

int —Storedintegervalueofafi object, stored in a built-in MATLAB

•

integer data type. You can also use

uint16, uint32,anduint64 to get the stored integer value of a fi object

in these formats

•

oct — Stored integer value of a fi object in octal

Tolearnmoreabouttheseproperties,see“fiObjectProperties”inthe Fixed-Point Toolbox Reference.

int8, int16, int32, int64, uint8,

fimath Properties

In general, the fimath properties associated with fi objects depend on how you create the

• When you s pecify one or more

constructor, the resulting fi object has a local fimath object.

fi object:

fimath object properties in the fi

3-17

3 Working with fi Objects

• When you do not specify any fimath object properties in the fi constructor,

the resulting created in this way do not have a local

fi object associates itself with the global fim ath . fi objects

fimath object.

To determine whether a

isfimathlocal function.

The

fimath properties associated with fi objects determine how fixed-point

arithmetic is performed. These

fimath object or from the global fimath. To learn more about the relationship

between

fimath objects and the global fimath in fixed-point arithmetic, see

fi object has a local fimath object, use the

fimath properties can come from a local

“fimath Rules for Fixed-Point Arithmetic” on page 4-16.

The following

fimath properties are, by transitivity, also properties of the fi

object. Y ou can set these properties for individual fi objects or, for multiple

fi objects, by configuring the global fimath. The following fimath properties

are always writable.

•

CastBeforeSum — Whether both operands are cast to the sum data type

before addition

Note This property is hidden when the SumMode is set to FullPrecision.

• MaxProductWordLength — Maximum allowable word length for the product

data type

•

MaxSumWordLength — Maximum allowable word length for the sum data

type

3-18

•

OverflowMode —Overflowmode

ProductBias — Bias of the product data type

•

ProductFixedExponent — Fixed exponent of the product data type

•

ProductFractionLength — Fraction length, in bits, of the product data

•

type

•

ProductMode — Defines how the product data type is determined

ProductSlope — Slope of the product data type

•

fi Object Properties

• ProductSlopeAdjustmentFactor — Slope adjustment factor of the product

data type

•

ProductWordLength — Word length, in bits, of the prod uct data type

RoundMode — Rounding mode

•

SumBias —Biasofthesumdatatype

•

SumFixedExponent — Fixed exponent of the sum data type

•

SumFractionLength — Fraction length, in bits, of the sum data type

•

SumMode — Defines how the sum data type is determined

•

SumSlope — Slope of the sum data type

•

SumSlopeAdjustmentFactor — Slope adjustment factor of the sum data

•

type

•

SumWordLength — The word length, in bits, of the sum data type

To learn more about these properties, see the “fimath Object Properties” in the Fixed-Point Too lbox Reference.

To learn more about the global fimath, see “Working with the Global fimath” on page 4-6.

numerictype P roperties

When you create a fi object, a numerictype object is also automatically created as a property of the

numerictype — Object containing all the data type information of a fi object,

Simulink signal or model parameter

The following

fi object. The following properties of the numerictype object become read

numerictype properties are, by transitivity, also properties of a

only after you create the object w ith new values specified for the numerictype properties:

•

Bias —Biasofafi object

DataType — Data type category associated with a fi object

•

fi object:

fi object. H owever, you can create a copy of a fi

3-19

3 Working with fi Objects

• DataTypeMode — Data type and scaling mode of a fi object

FixedExponent — Fixed-point exponent associated with a fi object

•

FractionLength — Fraction lengt h of the stored integer value of a fi

•

object in bits

Scaling — Fixed-point scaling mode of a fi object

•

Signed —Whetherafi object is signed or unsigned

•

Signedness —Whetherafi object is signed or unsigned

•

Note numerictype objects can have a Signedness of Auto,butallfi

objects must be Signed or Unsigned.Ifanumerictype object with Auto

Signedness

object automatically defaults to Signed.

• Slope — Slope associated with a fi object

is used to create a fi object, the Signedness property of the fi

3-20

SlopeAdjustmentFactor — Slope adjustment associated with a fi object

•

WordLength — Word length of the stored integer value of a fi object in bits

•

For further details on these properties, see the Property Reference.

Therearetwowaystospecifypropertiesfor software. Refer to the following sections:

• “Setting Fixed-Point Properties at Object Creation” on page 3-21

• “Using Direct Property Referencing w ith fi” on page 3-21

fi objects in Fixed-Point Toolbox

Setting fi Object Properties

You can set fi object properties in two ways:

• Setting the propertie s when you create the object

• Using direct property refere ncing

fi Object Properties

Setting Fixed-Point Properties at Object Creation

You can set properties of fi objects at the time of object creation by including properties after the arguments of the set the overflow mode to

a = fi(pi, 'OverflowMode' , 'wrap', 'RoundMode', 'convergent')

3.1416

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

RoundMode: convergent

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

MaxSumWordLength: 128

wrap and the rounding mode to convergent,

SumMode: FullPrecision

fi constructor function. For example, to

Using Direct Property Referencing with fi

You can reference directly into a property for setting or retrieving fi object property values using MATLAB structure-like referencing. You do so by using a period to index into a property by name.

For example, to get the

a.DataTypeMode

ans =

Fixed-point: binary point scaling

To set the OverflowMode of a,

DataTypeMode of a,

3-21

3 Working with fi Objects

a.OverflowMode = 'wrap'

3.1416

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

RoundMode: convergent

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

3-22

You can also use direct property referencing to associate fi objects with the global fimath. For example, if you have a

fi object b with a local fimath

object, you can remove the local fimath object and force b to associate itself with the global fimath:

b = fi(pi, 1, 'RoundMode', 'Floor')

3.1415

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

RoundMode: floor

OverflowMode: saturate

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

b.fimath = []

3.1415

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

isfimathlocal(b)

ans =

fi Object Properties

3-23

3 Working with fi Objects

fi Object Functions

You can learn about the functions associated with fi objects in the Function Reference.

The following data-access functions can be also used to ge t the data in a object using dot notation.

•

bin

• data

• dec

• double

• hex

• int

• oct

For example,

a = fi(pi); n = int(a)

25736

a.int

3-24

ans =

25736

h = hex(a)

6488

a.hex

ans =

6488

fi Object Functions

3-25

3 Working with fi Objects

3-26

Working with fimath Objects

• “Constructing fimath Objects” on page 4-2

• “Working with the Global fimath” on page 4-6

• “fimath Object Properties” on page 4-11

• “Using fimath Properties to Perform Fixed-Point Arithmetic” on page 4-16

• “Using fimath to Specify Rounding and Overflow Modes” on page 4-25

• “Using fimath to Share Arithmetic Rules” on page 4-27

• “Using fimath ProductMode and SumM ode” on page 4-30

• “fimath Object Functions” on page 4-36

4 Working with fimath Ob jects

Constructing fimath Objects

In this section...

“fimath Object Syntaxes” on page 4-2

“Building fimath Object Constructors in a GUI” on page 4-4

fimath Object Syntaxes

The arithmetic attributes of fi objects are defined by either a local fimat h object, or the global fimath.

You can create ways:

• You can use the

object.

To get started, type

F = fimath

to create a fimath object. If your global fimath is set to the factory default configuration, you get the following output:

MaxProductWordLength: 128

fimath objects in Fixed-Point Toolbox software in one of two

fimath constructor function to create new fimath objects.

fimath constructor function to copy an existing fimath

RoundMode: nearest

OverflowMode: saturate

ProductMode: FullPrecision

SumMode: FullPrecision

MaxSumWordLength: 128

4-2

To learn how to configure the global fimath, see “Working with the Global fimath” on page 4-6.

Constructing fimath Objects

To copy a fimath object, simply use assignment as in the following example:

F = fimath; G=F; isequal(F,G)

ans =

4-3

4 Working with fimath Ob jects

The syntax

allows you to set properties for a fimath object at object creation with property name/property value pairs. Refer to “Setting fimath Properties at Object Creation” on page 4-12.

Building fimath Object Constructors in a GUI

When you are working with files in MATLAB, you can build your fimath object constructors using the Insert fimath Constructor dialog box. After specifying the properties of the the prepopulated your file.

F = fimath(...'PropertyName',PropertyValue...)

fimath object in the dialog box, you can insert

fimath object constructor string at a specific location in

For example, to create a wraps on overflow, perform the following steps:

1 Open the Insert fimath Constructor dialog box by selecting

Tools > Fixed-Point Toolbox > Insert fimath Constructor from the

editor menu.

2 Use the edit boxes and drop-down menus to specify the following properties

of the

fimath object:

• Round mode =

• Overflow mode = Wrap

• Product mode = FullPrecision

• Maximum product word length = 128

• Sum mode = FullPrecision

• Maximum sum word length = 128

• Cast before sum =Checked

fimath object that uses convergent rounding and

Floor

4-4

Constructing fimath Objects

3 To insert the fimath object constructor string in your file, place your

cursor at the desired location in the file. Then click OK on the Insert fimath Constructor dialog box. Clicking OK closes the Insert fimath Constructor dialog box and automatically populates the

fimath object

constructor string in your file:

4-5

4 Working with fimath Ob jects

Working with the Global fimath

The global fimath is the set of fi math properties that fi objects associate with, and properties in the constructor. If you do not specify any fimath properties in a

fi object constructor, the resulting fi object associates itself with the global

fimath. If you specify one or more constructor, the resulting object properties that you do not specify in a fi or fimath object constructor inherit their values from the global fimath. The factory-default setting of the global fimath has the following properties:

fimath constructors return, when you do not specify any fimath

RoundMode: nearest

OverflowMode: saturate

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

fimath object properties in a fi object

fi object has a local fim ath object. All fimath

4-6

If you create a fi object with a local fimath obje ct, you can use dot notation to change the local remove a local

fi object with the global fimath. For example, if the fi object a has a local fimath object, you can use the syntax a.fimath = [] to remove its local fimath object. When you do so, a becomes associated with the global fimath.

fimath object properties. You can also use dot notation to

fimath object from an existing fi object, and associate that

You can configure your global fimath settings using the Fix ed-Po int Toolbox

globalfimath, saveglobalfimathpref, removeglobalfimathpref,and resetglobalfimath functions. The global fimath allows you to define your

own set of

fimath properties for all fi and fimath o bjects to use as a default.

See the following sections for more information about the Fixed-Point Toolbox global fimath functions:

• “Configuring the Global fimath” on page 4-7

• “Saving the Global fimath” on page 4-8

• “Resetting the Global fimath to the Factory Default” on page 4-8

• “Using the Global fimath with the Embedded MATLAB Function Block”

on page 4-10

Worki n g w ith the G l obal fim ath

For information on how fi objects with local fimath objects interact with fi objects associated with the globa l fimath, see the following section:

“fimath Rules for Fixed-Point Arithmetic” on page 4-16

Configuring the Global fimath

You can configure the global fimath using the globalfimath function. When you provide an output argument, this function returns a handle object to the global fimath. You can then control the global fimath properties through that handle object. The following syntaxes provide you with a handle object to the global fimath:

•

G = globalfimath — Use this syntax when you want to get a handle object

to the global fimath, but do not want to change any of the current global fimath properties. You can modify the properties of the global fimath later using dot notation on the object handle object to the global fimath, and then uses that handle object to change the

RoundMode of the global fimath.

G. For example, the follow i ng code gets a

G = globalfimath; G.RoundMode = 'Floor';

• G = globalfimath(f) — Use this syntax when you want to configure

the global fimath using an existing specifies

G as an output argument, the function returns a handle object to

fimath object f.Becausethissyntax

the global fimath. You can then modify the properties of the global fimath at any time by changing the properties of

f = fimath('RoundMode', 'Floor'); G = globalfimath(f); G.RoundMode = 'Nearest';

G. For example,

• G = globalfimath('RoundMode', 'Floor') — Use this syntax when you

want to set the properties of the global fimath using property name/property value pairs. You can specify as many property name/property value pairs as necessary. All properties that you do not specify values for inherit their values from the current global fimath. As always, you can use the handle object to modify the global fimath properties at a later time.

G = globalfimath('RoundMode', 'Floor', 'OverflowMode', 'Wrap');

4-7

4 Working with fimath Ob jects

The global fimath properties you set with the globalfimath function apply only in your current MATLAB session. To save the global fimath for use in future M ATLA B sessions, use the

Saving the Global fimath

If you want to use the current global fimath in future MATLAB sessions, you must save it as a preference. The current global fimath as a preference, and MATLAB uses that global fimath in all future sessio n s.

To use the current global fimath in all future MATLAB sessions, type

at the MATLAB command line. MATLAB now uses the current global fimath in all of your future MATLAB sessions.

G.OverflowMode = 'Saturate';

saveglobalfimathpref function.

saveglobalfimathpref function saves the

saveglobalfimathpref;

4-8

Resetting the Global fimath to the Factory Default

Therearetwowaystoresettheglobalfimath to the factory default in your current MATLAB session:

• Use the

at the MATLAB command line.

• Use the reset method of the global fimath. If

global fimath, type

at the MATLAB command line.

Unlessyouchoosetoconfiguretheglobal fimath again, MATLAB uses the factory-default setting of the global fimath for the remainder of your MATLAB session. For example, after resetting the global fimath to the factory default, MATLAB returns the following

resetglobalfimath function. Todoso,type

resetglobalfimath;

et(G);

res

fi and fimath objects:

G is a handle object to the

b = fi(pi)

3.1416

DataTypeMode: Fixed-point: binary point scaling

Signedness: Signed WordLength: 16

FractionLength: 13

b.fimath

ans =

RoundMode: nearest

OverflowMode: saturate

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

Worki n g w ith the G l obal fim ath

F1 = fimath

F1 =

RoundMode: nearest

OverflowMode: saturate

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

To reset the global fimath to the factory default for all future MATLAB sessions, remove your global fimath from the MATLAB preferences. To do so, type

removeglobalfimathpref;

at the MATLAB command line. This command sets the global fimath back to its factory-default configuration for all future MATLAB sessions.

4-9

4 Working with fimath Ob jects

Using the Global fimath with the Embedded MATLAB Function Block

For information about using the global fimath with the Embedded MATLAB Function block, se e the following section:

“Using fimath Objects in E mbedded MATLAB Function Blocks” on page 8-20

4-10

fimath Object Properties

In this section...

“Math, Rounding, and Overflow Properties” on page 4-11

“Setting fimath Object Properties” on page 4-12

Math, Rounding, and Overflow Properties

You can always write to the following pro perties of fimath objects:

fimath Object Properties

Property

CastBeforeSum

MaxProductWordLength

MaxSumWordLength

OverflowMode

ProductBias

ProductFixedExponent

ProductFractionLength

ProductMode

ProductSlope

ProductSlopeAdjustmentFactor

ProductWordLength

RoundMode

Description

Whether both operands are cast to the sum data type before addition

Maximum allowable word length for the product data type

Maximum allowable word length for the sum data type

Overflow-handling mode

Bias of the product data type

Fixed exponent of the product data type

Fraction length, in bits, of the product data type

Defines how the product data type is determined

Slope of the product data type

Slope adjustment factor of the product data type

Word length, in bits, of the product data type

Rounding mode

4-11

4 Working with fimath Ob jects

Property

SumBias

SumFixedExponent

SumFractionLength

Description

Bias of the sum data type

Fixed exponent of the sum data type

Fraction length, in bits, of the sum data type

SumMode

Defines how the sum data type is determined

SumSlope

SumSlopeAdjustmentFactor

Slope of the sum data type

Slope adjustment factor of the sum data type

SumWordLength

Word length, in bits, of the sum data type

For details about these properties, refer to the Property Reference. To learn how to specify properties for

fimath objects in Fixed-Point Toolbox software,

refer to “Setting fimath Object Properties” on page 4-12.

Setting fimath Object Properties

• “Setting fimath Properties at Object Creation” on page 4-12

4-12

• “Using Direct Property Referencing with fimath” on page 4-13

• “Setting fimath Properties in the Model Explorer” on page 4-14

Setting fimath Properties at Object Creation

You can set properties of fimath objects at the time of object creation by including properties after the arguments of the

Forexample,tosettheoverflowmodeto

convergent,

F = fimath('OverflowMode','saturate','RoundMode','conver gent ')

fimath constructor function.

saturate and the rounding mode to

fimath Object Properties

RoundMode: convergent

OverflowMode: saturate

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

Using Direct Property Referencing with fimath

You can reference directly into a property for setting or retrieving fimath object property values using MATLAB structure-like referencing. You do so by using a period to index into a property by name.

For example, to get the

F.RoundMode

ans =

convergent

RoundMode of F,

To set the OverflowMode of F,

F.OverflowMode = 'wrap'

RoundMode: convergent

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

4-13

4 Working with fimath Ob jects

Setting fimath Properties in the Model Explorer

You can view and change the properties for a ny fimath object defined in the MATLAB workspace in the Model Explorer. Open the Model Explorer by selecting View > Model Explorer in any Simulink model, or by typing

daexplr at the MATLAB command line.

The following figure shows the Model Explorer when you define the following

fimath objects in the MATLAB workspace:

F = fimath

RoundMode: nearest

OverflowMode: saturate

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

4-14

G = fimath('OverflowMode','wrap')

RoundMode: nearest

OverflowMode: wrap

ProductMode: FullPrecision

MaxProductWordLength: 128

SumMode: FullPrecision

MaxSumWordLength: 128

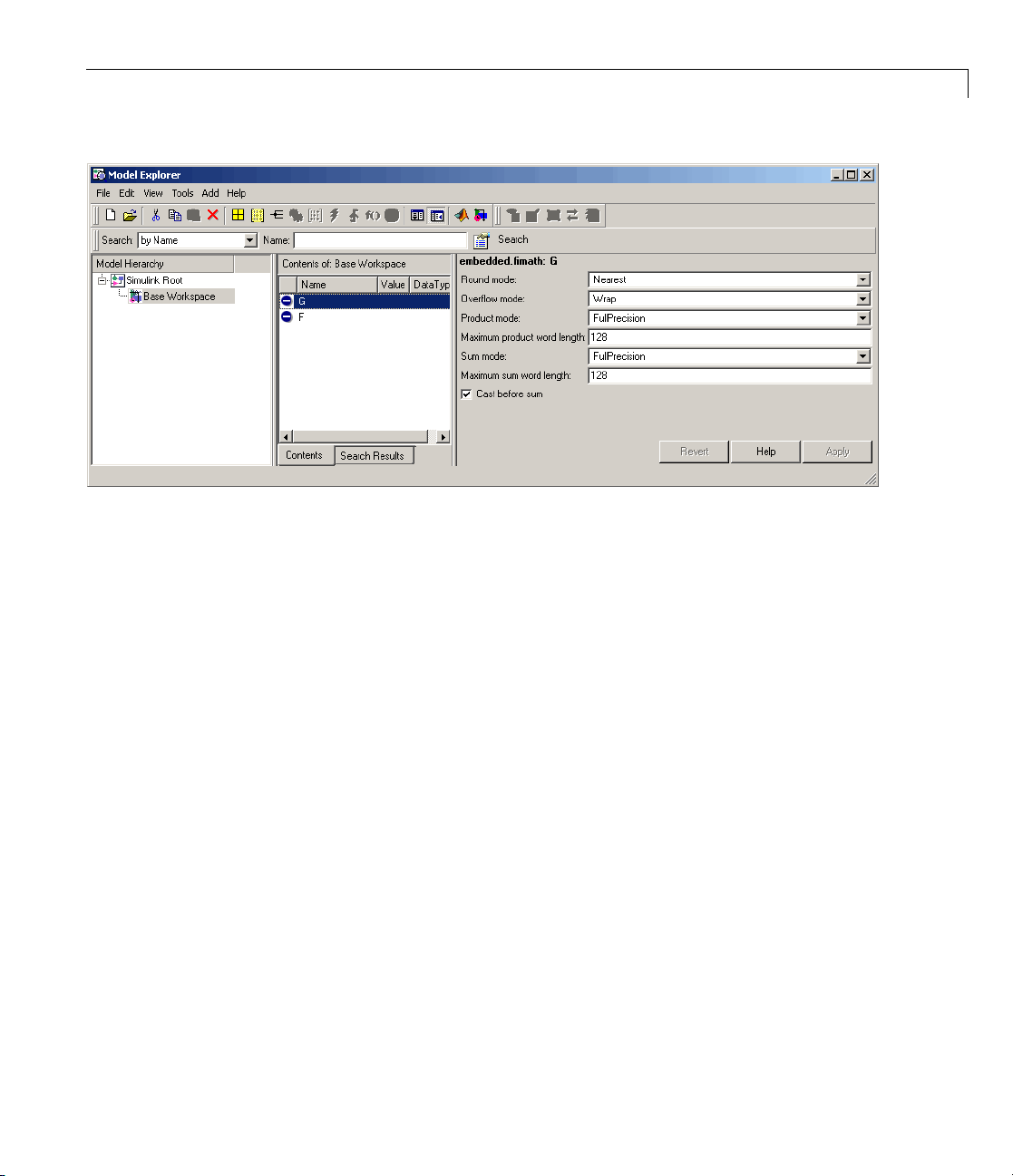
fimath Object Properties

Select the Base Workspace node in the Model Hierarchy pane to view the current objects in the Contents pane. When you select a

fimath obje ct in the

Contents pane, you can view and change its properties in the Dialog pane.

For more information on working with the Model Explorer, see the following sections of the Fixed-Point Toolbox documentation:

• “Specifying Fixed-Point Parameters in the Model Explorer” on page 8-18

• “Sharing Models with Fixed-Point Embedded MATLAB Function Blocks”

on page 8-24

4-15

4 Working with fimath Ob jects

Using fimath Properties to Perform Fixed-Point Arithmetic

In this section...

“fimath Rules for Fixed-Point Arithmetic” on page 4-16

“Binary-Point Arithmetic” on page 4-18

“[Slope Bias] Arithmetic” on page 4-22

fimath Rules for Fixed-Point Arithmetic

fimath properties define the rules for performing arithmetic operations on fi

objects. The fimath properties that govern fixed-point arithmetic o pe ration s can come from a global fimath have the following differences:

fimath object or the global fimath. fimath objects and the

• Individual

fimath object when you specify fimath properties in a fi constructor or

use dot notation to set any

• The global fimath is the set of

associate w ith, and any

fimath properties in the constructor. When you us e the sfi or ufi

constructor or when you fail to specify any fimath properties in the fi constructor, the resulting fi object associates itself with the global fimath. It does not have a local fimath” on page 4-6 for more information.

To determine whether a the global fimath, use the

The following sections discuss how interact wi th

fi objects can h av e a local fimath object. fi objects have a local

fimath object property of a fi object.

fimath properties that fi constructors

fimath constructors return, when you do not specify

fimath object. See “Working with the Global

fi object has a local fimath object or associates with

isfimathlocal function.

fi objects with lo cal fimath objects

fi objects associated with the global f imath.

Binary Operations

In binary fixed-point operations such as c=a+b, the following rules apply:

• If both

global fimath to perform the fixed-point arithmetic. The output also associates with the global fimath.

a and b associate with the global fimath, the ope ration uses the

fi obje ct c

4-16

Using fimath Properties to Perform Fixed-Point Arithmetic

• If either a or b has a local fimath object, the operation uses that fimath

object to perform the fixed-point arithmetic. The output fi object c has the same local

fimath object as the input.

Unary Operations

In unary fixed-point operations such as b = abs(a), the following rules apply:

• If

a associates with the global fimath, the operation uses the global fimath

to perform the fixed-point arithmetic. The output with the global fimath.

• If

a has a local fimath object, the operation uses that fimath object to

perform the fixed-point arithmetic. The output local

fimath object as the input a.

fi object b also associates

fi object b has the same

When you specify a operation, the operation uses the fixed-point arithmetic. For example, when you use a syntax such as

abs(a,F)

or b = sqrt(a,F),theabs and s qrt operations use the fimath

fimath object in the function call of a unary fixed-point

fimath object you specify to perform the

object F to compute intermediate quantities. The output fi object b always associates with the global fimath.

Concatenation Operations

In fixed-point concatenation operations such as c = [a b], c = [a;b] and

c = bitconcat(a,b), the following rule applies:

• The

For e xample, consider the following scenarios for t h e operation

• If

fimath properties of the left-most fi object in the operation determine

the

fimath properties of the o utput fi object c.

d=[abc]:

a is a fi object associated with the global fimath, the output fi object d

also associates with the global fimath.

a has a local fimath object, the output fi object d has the same loca l

fimath object.

a is not a fi object, the output fi object d inherits the fimath properties

of the next left-most

fi object. For example, if b is a fi object with a local

4-17

4 Working with fimath Ob jects

fimath Object Operations: add, mpy, sub

The output of the fimath object operations add, mpy,andsub always associates with the global fimath. The operations use the the function call, but the output

Embedded MATLAB Subset Operations

Fixed-point operations performed with Embedded MATLAB subset functions use the same rules as fixed-point operations performed in MATLAB.

All input signals to the Embedded MATLAB Function block that you treat as

fi objects associate w ith whatever you specify for the Embedded MATLAB

Function block fimath parameter. When you set this parameter to

as MATLAB

the Embedded MATLAB Function block fimath parameter to

other

theEmbeddedMATLABFunctionblocktoassociatewith.Youcanchoose to treat only fixed-point input signals as integer input signals as MATLAB Function Blocks” on page 8-20 for more information.

fimath object, the output fi object d has the same local fimath object as

the input

fi object b.

fimath object you specify in

fi object never has a local fimath object.

Same

,yourfi objects associate with the global fimath. When you set

Specify

, y ou can define your own set of fimath properties for all fi objects in

fi objects or both fixed-point and

fi objects. See “Using fimath Objects in Embedded

4-18

Binary-Point Arithmetic

The fimath object and the global fimath encapsulate the math properties of Fixed-Point Toolbox software.

fi objects only h ave a local fimath object when you explicitly specify fimath

properties in the fi constructor. When you use the sfi or ufi constructor or do not specify any object associates itself with the global fimath.

a = fi(pi)

3.1416

fimath properties in the fi constructor, the resulting fi

DataTypeMode: Fixed-point: binary point scaling

Mathworks FIXED-POINT TOOLBOX 3 user guide

Specifications and Main Features

Frequently Asked Questions

User Manual

Getting Started

Product Overview

Licensing

Getting Help

Getting Help in This Document

Getting Help at the MATLAB Command Line

Display Settings

Displaying the fimath Properties of fi Objects

Hiding the fimath Properties of fi Objects

Shortening the numerictype Display of fi Objects

Demos

Fixed-Point Concepts

Fixed-Point Data Types

Scaling

Precision and Range

Range

Overflow Handling

Precision

Rounding Methods

Arithmetic Operations

Modulo Arithmetic

Two’s Complement

Addition and Subtraction

Multiplication

Multiplication Data Types

Multiplication with fimath

Casts

Casting from a Shorter Data Type to a Longer Data Type

Casting from a Longer Data Type to a Shorter Data Type

fi Objects Compared to C Integer Data Types

Integer Data Types

ANSI C Integer Data Types

fi Integer Data Types

Unary Conversions

ANSI C Usual Unary Conversions

fi Usual Unary Conversions

Binary Conversions

ANSI C Usual Binary Conversions

fi Usual Binary Conversions

Overflow Handlin g

ANSI C Overflow Handling

fi Overflow Handling

Working with fi Objects

Constructing fi Objects

fi Object Syntaxes

Examples of Constructing fi Objects

Constructing a fi Object with Property Name/Property Value Pairs

Constructing a fi Object Using a numerictype Object

Constructing a fi Object Using a fimath Object

Building fi Object Constructors in a GUI

Determining Property Precedence

Copying a fi Object

Casting fi Objects

Overwriting by Assignment

Ways to Cast with MATLAB Software

Casting by Subscripted Assignment

Casting by Conversion Function

Casting with the reinterpretcast Function

fi Object Properties

Data Properties

fimath Properties

numerictype P roperties

Setting fi Object Properties

Setting Fixed-Point Properties at Object Creation

Using Direct Property Referencing with fi

fi Object Functions

Working with fimath Objects

Constructing fimath Objects

fimath Object Syntaxes

Building fimath Object Constructors in a GUI

Working with the Global fimath

Configuring the Global fimath

Saving the Global fimath

Resetting the Global fimath to the Factory Default

Using the Global fimath with the Embedded MATLAB Function Block

fimath Object Properties