Mathworks FILTER DESIGN TOOLBOX 4 Reference Guide

Download

Filter Design Tool

Reference Guide

box™ 4

How to Contact The MathWorks

www.mathworks. comp.soft-sys.matlab Newsgroup www.mathworks.com/contact_TS.html T echnical Support

suggest@mathworks.com Product enhancement suggestions

bugs@mathwo doc@mathworks.com Documentation error reports service@mathworks.com Order status, license renewals, passcodes

info@mathwo

com

rks.com

Web

Bug reports

Sales, prici

ng, and general information

508-647-7000 (Phone)

508-647-7001 (Fax)

The MathWorks, Inc. 3 Apple Hill Drive Natick, MA 01760-2098

For contact information about worldwide offices, see the MathWorks Web site.

Filter Design Toolbox™ Reference Guide

The software described in this document is furnished under a license agreement. The software may be used or copied only under the terms of the license agreement. No part of this manual may be photocopied or reproduced in any form without prior written consent from The MathW orks, Inc.

FEDERAL ACQUISITION: This provision applies to all acquisitions of the Program and Documentation by, for, or through the federal government of the United States. By accepting delivery of the Program or Documentation, the government hereby agrees that this software or documen tation qualifies as commercial computer software or commercial computer software documentation as such terms are used or defined in FAR 12.212, DFARS Part 227.72, and DFARS 252.227-7014. Accordingly, the terms and conditions of this Agreement and only those rights specified in this Agreement, shall pertain to and govern theuse,modification,reproduction,release,performance,display,anddisclosureoftheProgramand Documentation by the federal government (or other entity acquiring for or through the federal government) and shall supersede any conflicting contractual terms or conditions. If this License fails to meet the government’s needs or is inconsistent in any respect with federal procurement law, the government agrees to return the Program and Docu mentation, unused, to The Mat hWorks, Inc.

Trademarks

MATLAB and Simulink are registered trademarks of The MathWorks, Inc. See

www.mathworks.com/trademarks for a list of additional trademarks. Other product or brand

names may be trademarks or registered trademarks of their respective holders.

Patents

The MathWorks products are protected by one or more U.S. patents. Please see

www.mathworks.com/patents for more information.

Revision History

March 2007 Online only New for Version 4.1 (Release 2007a) September 2007 Online only New for Version 4.2 (Release 2007b) March 2008 Online only New for Version 4.3 (Release 2008a) October 2008 Online only New for V ersion 4.4 (Release 2008b) March 2009 Online only New for Version 4.5 (Release 2009a) September 2009 Online only New for Version 4.6 (Release 2009b) March 2010 Online only New for Version 4.7 (Release 2010a)

Function Reference

Adaptive Filters ................................... 1-2

Least Mean Squares Recursive Least Squares Affine Projection Frequency D omain Lattice

.......................................... 1-4

............................... 1-2

............................ 1-3

.................................. 1-3

................................ 1-4

Contents

Discrete-Time Filters

Filter Specifications — Response Types

Filter Specifications — Design Methods

Multirate Filters

GUIs

Filter Analysis

Fixed-Point Filters

Quantized F ilter Analysis

SOS Conversion

Filter Design

.............................................. 1-11

..................................... 1-12

...................................... 1-18

.............................. 1-5

................................... 1-10

................................. 1-15

.......................... 1-16

................................... 1-17

............. 1-7

............. 1-9

Filter Conversion

.................................. 1-19

Functions — Alphabetical List

Reference for the Properties of Filter Objects

Fixed-Point Filter Properties ....................... 3-2

Overview o f Fixed-Point Filters Fixed-Point Objects and Filters Summary — Fixed-Point Filter Properties Property De tails for Fixed-Point Filters

...................... 3-2

............. 3-5

............... 3-18

Adaptive Filter Properties

Property Sum m aries Property De tails for Adaptive Filter Properties

References

Multirate Filter Properties

Property Sum m aries Property De tails for Multirate Filter Properties

References

........................................ 3-115

........................................ 3-132

.......................... 3-102

............................... 3-102

......................... 3-116

............................... 3-116

......... 3-107

......... 3-121

Index

vi Contents

Function Reference

Adaptive Filters (p. 1-2) Design adaptive filters

Discrete-Time F ilters (p. 1-5)

Filter Specifications — Response Types (p. 1-7)

Filter Specifications — Design Methods (p. 1-9)

Multirate Filters (p. 1-10) Design multirate filter objects

GUIs (p. 1-11) Use graphical user interface tools to

Filter Analysis (p. 1-12) Analyze filters and filter objects

Fixed-Point Filters (p. 1-15) Create fixed-point filters

Quantized Filter Analysis (p. 1-16) Analyze fixed-point filters

SOS Conversion (p. 1-17)

Filter Design (p. 1-18) Design filters (not object-based)

Filter Conversion (p. 1-19) Transform filters to other forms,

Design FIR and IIR discrete-time filter objects

Create objects that specify filter responses

Design filter objects from specification objects

design filters

Work with second-order section filters

or use features in filter to develop another filter

1 Function Reference

Adaptive Filters

Least Mean Squares (p. 1-2) Filter w ith LMS techniques

Recursive L east Squares (p. 1-3) Filter with RLS techniques

Affine Projection (p. 1-3) Filter with affine projection

Frequency Domain (p. 1-4) Filter in the frequency domain

Lattice (p. 1-4) Filter with lattice filters

Least Mean Squares

adaptfilt.adjlms

adaptfilt.blms

adaptfilt.blmsfft

adaptfilt.dlms

adaptfilt.filtxlms

adaptfilt.lms

adaptfilt.nlms

adaptfilt.sd

adaptfilt.se

adaptfilt.ss

FIR a da ptive filter that uses adjoint LMS algorithm

FIR adaptive filter that uses BLM S

FIR adaptive filter that uses FFT-based BLMS

FIR adaptive filter that uses delayed LMS

FIR adaptive filter that uses filtered-x LMS

FIR adaptive filter that uses LMS

FIR adaptive filter that uses NLMS

FIR adaptive filter that uses sign-data algorithm

FIR adaptive filter that uses sign-error algorithm

FIR adaptive filter that uses sign-sign algorithm

1-2

Recursive Least Squares

Adaptive Filters

adaptfilt.ftf

adaptfilt.hrls

adaptfilt.hswrls

adaptfilt.qrdrls

adaptfilt.rls

adaptfilt.swftf

adaptfilt.swrls

Affine Projection

adaptfilt.ap

adaptfilt.apru

adaptfilt.bap

Fast transversal LMS adaptive filter

FIR adaptive filter that uses householder (RLS)

FIR adaptive filter that uses householder sliding window RLS

FIR adaptive filter that uses QR-decomposition-based RLS

FIR adaptive filter that uses direct form RLS

FIR adaptive filter that uses sliding window fast transversal least squares

FIR adaptive filter that uses window recursive least squares (RLS)

FIR adaptive filter that uses direct matrix inversion

FIR adaptive filter that uses recursive matrix updating

FIR adaptive filter that uses block affine projection

1-3

1 Function Reference

Frequency Domain

adaptfilt.fdaf

adaptfilt.pbfdaf

adaptfilt.pbufdaf

adaptfilt.tdafdct

adaptfilt.tdafdft

adaptfilt.ufdaf

Lattice

adaptfilt.gal

adaptfilt.lsl

adaptfilt.qrdlsl

FIR adaptive filter that uses frequency-domain with bin step size normalization

FIR adaptive filter that uses PBFDAF with bin step size normalization

FIR adaptive filter that uses PBUFDAF with bin ste p size normalization

Adaptive filter that uses discrete cosine transform

Adaptive filter that uses discrete Fourier transform

FIR adaptive filter that uses unconstrained frequency-domain with quantized step size normalization

FIR adaptive filter that uses gradient lattice

Adaptive filter that uses LSL

Adaptive filter that uses QR-decomposition-based LSL

1-4

Discrete-Time Filters

dfilt

dfilt.allpass

dfilt.calattice

dfilt.calatticepc

dfilt.cascade

dfilt.cascadeallpass

dfilt.cascadewdfallpass

dfilt.delay

dfilt.df1

dfilt.df1sos

dfilt.df1t

dfilt.df1tsos

dfilt.df2

dfilt.df2sos

dfilt.df2t

dfilt.df2tsos

dfilt.dfasymfir

dfilt.dffir

Discrete-time filter

Allpass filter

Coupled-allpass, lattice filter

Coupled-allpass, power-complementary lattice filter

Cascade of discrete-time filters

Cascade of allpass discrete-time filters

Cascade allpass WDF filters to construct allpass WDF

Delay filter

Discrete-time, direct-form I filter

Discrete-time, SOS direct-form I filter

Discrete-time, direct-form I transposed filter

Discrete-time, SOS direct-form I transposed filter

Discrete-time, direct-form II filter

Discrete-time, SOS, direct-form II filter

Discrete-time, direct-form II transposed filter

Discrete-time, SOS direct-form II transposed filter

Discrete-time, direct-form antisymmetric FIR filter

Discrete-time, direct-form FIR filter

1-5

1 Function Reference

dfilt.dffirt

dfilt.dfsymfir

dfilt.farrowfd

dfilt.farrowlinearfd

dfilt.fftfir

dfilt.latticeallpass

dfilt.latticear

dfilt.latticearma

dfilt.latticemamax

dfilt.latticemamin

dfilt.parallel

dfilt.scalar

dfilt.wdfallpass

Discrete-time, direct-form FIR transposed filter

Discrete-time, direct-form symmetric FIR filter

Fractional Delay Farrow filter

Farrow Linear Fractional Delay filter

Discrete-time, overlap-add, FIR filter

Discrete-time, lattice allpass filter

Discrete-time, lattice, autoregressive filter

Discrete-time, lattice, autoregressive, moving-average filter

Discrete-time, lattice, moving-average filter with maximum phase

Discrete-time, lattice, moving-average filter with minimum phase

Discrete-time, parallel structure filter

Discrete-time, scalar filter

Wave digital allpass filter

1-6

Filter Specifications — Response Types

fdesign

fdesign.arbmag

fdesign.arbmagnphase

fdesign.audioweighting

fdesign.bandpass

fdesign.bandstop

fdesign.ciccomp

fdesign.comb

fdesign.decimator

fdesign.differentiator

fdesign.fracdelay

fdesign.halfband

fdesign.highpass

fdesign.hilbert

fdesign.interpolator

fdesign.isinclp

fdesign.lowpass

fdesign.notch

fdesign.nyquist

fdesign.octave

fdesign.parameq

Filter specification object

Arbitrary response magnitude filter specification object

Arbitrary response magnitude and phase filter specification object

Audio weighting filter specification object

Bandpass filter specification object

Bandstop filter specification object

CIC compensator filter specification object

IIR comb filter specification object

Decimator filter specification object

Differentiator filter specification object

Fractional delay filter specification object

Halfband filter specification object

Highpass filter specification object

Hilbert filter specification object

Interpolator filter specificatio n

Inverse-sinc filter specification

Lowpass filter specification

Notch filter specification

Nyquist filter specification

Octave filter specification

Parametric equalizer filter specification

1-7

1 Function Reference

fdesign.peak

fdesign.polysrc

fdesign.pulseshaping

fdesign.rsrc

Peak filter specification

Construct polynomial sample-rate converter (POLYSRC) filter designer

Pulse-shaping filter specification object

Rational-factor sample-rate converter specification

1-8

Filter Specifications — Design Methods

butter

cheby1

cheby2

designmethods

ellip

equiripple

fircls

ifir

iirlinphase

kaiserwin

maxflat

multistage

window

Butterworth IIR filter design using specification object

Chebyshev Type I filter using specification object

Chebyshev Type I I filter using specification object

Methods available for designing filter from specification object

Elliptic filter using specification object

Equiripple single-rate or multirate FIR filter from specification object

FIR Constrained Least Squares filter

Interpolated FIR filter from filter specification

Quasi-linear phase IIR filter from halfband filter specification

Kaiser window filter from specification object

Maxflat FIR filter

Multistage filter from specification object

FIR filter using windowed impulse response

1-9

1 Function Reference

Multirate Filters

mfilt.cascade

mfilt.cicdecim

mfilt.cicinterp

mfilt.farrowsrc

mfilt.fftfirinterp

mfilt.firdecim

mfilt.firfracdecim

mfilt.firfracinterp

mfilt.firinterp

mfilt.firsrc

mfilt.firtdecim

mfilt.holdinterp

mfilt.iirdecim

ilt.iirinterp

mfilt.iirwdfdecim

mfilt.iirwdfinterp

mfilt.linearinterp

Cascade filter objects

Fixed-point CIC decimator

Fixed-point CIC interpolator

Sample rate converter with arbitrary conversion factor

Overlap-add FIR polyphase interpolator

Direct-form FIR polyphase decimator

Direct-form FIR polyphase fractional decimator

Direct-form FIR polyphase fractional interpolator

FIR filter-based interpolator

Direct-form FIR polyphase sample rate converter

Direct-form transposed FIR filter

FIR hold interpolator

decimator

IIR

IIR interpolator

IIR wave digital filter decimator

IIR wave digital f il t er interpolator

Linear interpolator

1-10

GUIs

fdatool

filterbuilder

Open Filter Design and Analysis Tool

GUI-based filter design

1-11

1 Function Reference

Filter Analysis

autoscale

block

coeffs

cost

cumsec

denormalize

designmethods

designopts

disp

doubl

idfactors

eucl

coeffs

fft

ter

fil

ltstates.cic

rtype

reqrespest

freqrespopts

freqsamp

freqz

grpdelay

Automatic dynamic range scaling

Generate block from multirate filter

Coefficients for filters

Cost of using discrete-time or multirate filter

Vector of SOS filters for cumulative sections

Undo filter coefficient and gain changes caused by

normalize

Methods available for designing filter from specification object

Valid input arguments and values for specification object and method

properties and values

Filter

ixed-point filter to use

Cast f

e-precision arithmetic

doubl

id factors for multirate filter

Eucl

uency-domain coefficients

Freq

terdatawithfilterobject

Fil

ore CIC filter states

pe of linear phase FIR filter

stimate fixed-point filter frequency

esponse through filtering

freqrespest

parameters and values

Real or complex frequency-sampled FIR filter from specification object

Frequency response of filter

Filter group delay

1-12

Filter Analysis

help

impz

isfir

islinphase

ismaxphase

isminphase

isreal

isstable

limitcycle

maxstep

measure

msepred

msesim

noisepsd

noisepsdopts

norm

normalize

normalizefreq

Help for design method with filter specification

Filter impulse response

Determine whether filter is FIR

Determine whether filter is linear phase

Determine whether filter is maximum phase

Determine whether filter is minimum phase

Determine whether filter uses real coefficients

Determine whether filter is stable

Response of single-rate, fixed-point IIR filter

Maximum step size for adaptive filter convergence

Measure filter magnitude response

Predicted mean-squared error for adaptive filter

Measured mean-squared error for adaptive filter

Power spectral density of filter output

Options for running filter output noise PSD

P-norm of filter

Normalize filter numerator or feed-forward coefficients

Switch filter specification between normalized frequency and absolute frequency

1-13

1 Function Reference

nstates

order

phasedelay

phasez

polyphase

qreport

realizemdl

reffilter

reorder

reset

scale

scalecheck

set2int

setspecs

specifyall

stepz

validstructures

zerophase

zplane

Number of filter states

Order of fixed-point filter

Phase delay of filter

Unwrapped phase response for filter

Polyphase decomposition of multirate filter

Most recent fixed-point filtering operation report

Simulink®subsystem block for filter

Reference filter for fixed-point or single-precision filter

Rearrange sections in SOS filter

Reset filter properties to initial conditions

Scale sections of SOS filter

Check scaling of SOS filter

Configure filter for integer filtering

Specifications for filter specification object

Fixed-point scaling modes in direct-form FIR filter

Step response for filter

Structures for specification object with design method

Zero-phase response for filter

Zero-pole plot for filter

1-14

To see the full listing of analysis m eth o d s that apply to the or

mfilt objects, enter help adaptfilt, help dfilt,orhelp mfilt at the

MATLAB

prompt.

adaptfilt, dfilt,

Fixed-Point Filters

cell2sos

get

isreal

reset

scale

scalecheck

scaleopts

set

sos

sos2cell

Convert cell array to SOS matrix

Properties of quantized filter

Test if filter coefficients are real

Reset properties of quantized filter to initial values

Scale sections of SOS filters

Check scaling of SOS filter

Scaling options for second-order section scaling

Properties of quantized filter

Convert quantized filter to SOS form, order, and scale

Convert SOS matrix to cell array

1-15

1 Function Reference

Quantized Filter Analysis

freqz

impz

isallpass

isfir

islinphase

ismaxphase

isminphase

isreal

issos

isstable

noisepsd

noisepsdopts

zplane

Frequency response of filter

Filter impulse response

Determine whether filter is allpass

Determine whether filter is FIR

Determine whether filter is linear phase

Determine whether filter is maximum phase

Determine whether filter is minimum phase

Determine whether filter uses real coefficients

Determine whether filter is SOS form

Determine whether filter is stable

Power spectral density of filter output

Options for running filter output noise PSD

Zero-pole plot for filter

1-16

SOS Conversion

cell2sos

sos

sos2cell

Convert a cell array to a second-order sections matrix

Convert a quantized filter to second-order sections form, order, and scale

Convert a second-order sections matrix to a cell array

1-17

1 Function Reference

Filter Design

farrow

fdatool

filterbuilder

fircband

firceqrip

fireqint

firgr

firhalfband

firlpnorm

firls

firminphase

firnyquist

ifir

iircomb

iirgrpdelay

iirlpnorm

iirlpnormc

iirnotch

iirpeak

Farrow filter

Open Filter Design and Analysis Tool

GUI-based filter design

Constrained-band equiripple FIR filter

Constrained, equiripple FIR filter

Equiripple FIR interpolators

Parks-McClellan FIR filter

Halfband FIR filter

Least P-norm optimal FIR filter

Least square linear-phase FIR filter design

Minimum-phase FIR spectral factor

Lowpass Nyquist (Lth-band) FIR filter

Interpolated FIR filter from filter specification

IIR comb notch or peak filter

Optimal IIR filter with prescribed group-delay

Least P-norm optimal IIR filter

Constrained least Pth-norm optimal IIR filter

Second-order IIR notch filter

Second-order IIR peak or resonator filter

1-18

Filter Conversion

ca2tf

cl2tf

convert

firlp2hp

firlp2lp

iirlp2bp

iirlp2bs

iirlp2hp

iirlp2lp

iirpowcomp

set2int

tf2ca

tf2cl

Convert coupled allpass filter to transfer function form

Convert coupled allpass lattice to transfer function form

Convert filter structure of discrete-time or multirate filter

Convert FIR lowpass filter to Type I FIR highpass filter

Convert FIR Type I lowpass to FIR Type 1 lowpass with inverse bandwidth

Transform IIR lowpass filter to IIR bandpass filter

Transform IIR lowpass filter to IIR bandstop filter

Transform lowpass IIR filter to highpass filter

Transform lowpass IIR filter to different lowpass filter

Power complementary IIR filter

Configure filter for integer filtering

Transfer function to coupled allpass

Transfer function to coupled allpass lattice

1-19

1 Function Reference

1-20

Functions — Alphabetical List

adaptfilt

Purpose Adaptive filter

Syntax ha = adaptfilt.algorithm('input1',input2,...)

Description ha = adaptfilt.algorithm('input1',input2,...) returns the

adaptive filter object specified by include an Note that you do n ot enclose the algorithm option in single quotation marks as you do for m ost strings. To construct an adaptive filter object you must supply an although every constructor creates a default adaptive filter when you do not provide input arguments such as syntax.

algorithm. When you construct an a daptive filter object,

algorithm specifier to implement a specific adaptive filter.

Algorithms

For adaptive filter (adaptfilt)objects,thealgorithm string determines which adaptive filter algorithm your implements. Each available algorithm entry appears in one of the tables along with a brief d es cription of the algorithm. Click on the algorithm in the first column to get more information about the associated adaptive filter technique.

ha that uses the adaptive filtering technique

algorithm string — there is no default a lgorithm,

input1 or input2 in the calling

adaptfilt object

2-2

• “Least Mean Squares (LMS) Based FIR Adaptive Filters” on page 2-3

• “Recursive Least Squares (RLS) Based FIR Adaptive Filters” on

page 2-4

• “Affine Projection (AP) FIR Adaptive Filters” on page 2-4

• “FIR Adaptive Filters in the Frequency Domain (FD)” on page 2-5

• “Lattice Based (L) FIR Adaptive Filters” on page 2-5

Least Mean Squares (LMS) Based FIR Adaptive Filters

adaptfilt

adaptfilt.algorithm String

adaptfilt.adjlms

adaptfilt.blms

adaptfilt.blmsfft

adaptfilt.dlms

adaptfilt.filtxlms

adaptfilt.lms

adaptfilt.nlms

adaptfilt.sd

adaptfilt.se

adaptfilt.ss

Algorithm Used to Generate Filter Coefficients

Use the Adjoint LM S FIR adaptive filter algorithm

UsetheBlockLMSFIRadaptivefilter algorithm

Use the FFT-based Block LMS FIR adaptive filter algorithm

Use the delayed LMS FIR adaptive filter algorithm

Use the filtered-x LMS FIR adaptive filter algorithm

Use the LMS FIR adaptive filter algorithm

Use the normalized LMS FIR adaptive filter algorithm

Use the sign-data LMS FIR adaptive filter algorithm

Use the sign-error LMS FIR adaptive filter algorithm

Usethesign-signLMSFIRadaptivefilter algorithm

For further information about an adapting algorithm, refer to the reference page for the algorithm.

2-3

adaptfilt

Recursive Least Squares ( RLS) Based FIR Adaptive Filters

adaptfilt.algorithm String

adaptfilt.ftf

adaptfilt.qrdrls

adaptfilt.hrls

adaptfilt.hswrls

adaptfilt.rls

adaptfilt.swrls

adaptfilt.swftf

For more complete information about an adapting algorithm, refer to the reference page for the algorithm.

Algorithm Used to Generate Filter Coefficients

Use the fast transversal least squares adaptation algorithm

Use the QR-decomposition RLS adaptation algorithm

Use the householder RLS adaptation algorithm

Use the householder SWRLS adaptation algorithm

Use the recursive-least squares (RLS) adaptation algorithm

Use the sliding window (SW) R LS adaptation algorithm

Use the sliding window F TF adaptation algorithm

Affine Projection (AP) FIR Adaptive Filters

2-4

adaptfilt.algorithm String

adaptfilt.ap

adaptfilt.apru

adaptfilt.bap

Algorithm Used to Generate Filter Coefficients

Use the affine projection algorithm that uses direct matrix inversion

Use the affine projection algorithm that uses recursive matrix updating

Usetheblockaffineprojectionadaptation algorithm

adaptfilt

To find more information about an adapting algorithm, refer to the reference page for the algorithm.

FIR Adaptive Filters in the Frequency Domain ( FD)

adaptfilt.algorithm String

adaptfilt.fdaf

adaptfilt.pbfdaf

adaptfilt.pbufdaf

adaptfilt.tdafdct

adaptfilt.tdafdft

adaptfilt.ufdaf

For more information about an adapting algorithm, refer to the reference page for the algorithm.

Algorithm Used to Generate Filter Coefficients

Use the frequency domain adaptation algorithm

Use the partition block version of the FDAF algorithm

Use the partition block unconstrained version of the FDAF algorithm

Use the transform domain adaptation algorithm using DCT

Use the transform domain adaptation algorithm using DFT

Use the unconstrained FDAF algorithm for adaptation

Lattice Based (L) FIR Adaptive Filters

adaptfilt.algorithm String

adaptfilt.gal

adaptfilt.lsl

adaptfilt.qrdlsl

Algorithm Used to Generate Filter Coefficients

Use the gradient adaptive lattice filter adaptation algorithm

Use the least squares lattice adaptation algorithm

Use the QR decomposition least squares lattice adaptation algorithm

2-5

adaptfilt

For more information about an adapting algorithm, refer to the reference page for the algorithm.

Properties for All Adaptive Filter Objects

Each reference page for an algorithm and adaptfilt.algorithm object specifies w hich properties apply to the adapting algorithm and how to use them.

Methods for Adaptive Filter Objects

As is true with all objects, methods enable you to perform various operations on to the object handle that you assigned when you constructed the

adaptfilt object.

adaptfilt objects. To use the methods, you apply them

Most of the analysis methods that apply to

adaptfilt objects. Methods like freqz rely on the filter coefficients in

the

adaptfilt object. Since the coefficients change each time the filter

adapts to data, you should view the results of using a method as an analysis of the filter a t a moment in time for the object. Use caution when you apply an analysis method to your adaptive filter objects — always check that your result approached your expectation.

In particular, the Filter Visualization Tool (FVTool) supports all of the

adaptfilt objects. Analyzing and viewing your adaptfilt objects is

straightforward — use the

fvtool(objectname)

to launch FVTool and work with your object.

Some methods share their names with functions in Signal Processing Toolbox™ software, or even functions in this toolbox. Functions that share names with methods behave in a similar way. Using the same name for more than one function or method is called overloading and is commoninmanytoolboxes.

fvtool method with the name of your object

dfilt objects also work with

2-6

Method Description

adaptfilt/coefficients

Return the instantaneous adaptive filter coefficients

adaptfilt/filter

Apply an adaptfilt object to your signal

adaptfilt/freqz

Plot the instantaneous adaptive filter frequency response

adaptfilt/grpdelay

Plot the instantaneous adaptive filter group delay

adaptfilt/impz

Plot the instantaneous adaptive filter impulse response.

adaptfilt/info

adaptfilt/isfir

Return the adaptive filter information.

Test whether an adaptive filter is an finite impulse response (FIR) filters.

adaptfilt/islinphase

Testwhetheranadaptivefilterislinear phase

adaptfilt/ismaxphase

Test whether an adaptive filter is maximum phase

adaptfilt/isminphase

Test whether an adaptive filter is minimum phase

adaptfilt/isreal

True whether an adaptive filter has real coefficients

adaptfilt/isstable

adaptfilt/maxstep

Test whether an adaptive filter is stable

Return the maximum step size for an adaptive filter

adaptfilt/msepred

adaptfilt/msesim

Return the predicted mean square error

Return the measured mean square error via simulation.

adaptfilt

2-7

adaptfilt

Method Description

adaptfilt/phasez

Plot the instantaneous adaptive filter phase response

adaptfilt/reset

Reset an adaptive filter to initial conditions

adaptfilt/stepz

Plot the instantaneous adaptive filter step response

adaptfilt/tf

Return the instantaneous adaptive filter transfer function

adaptfilt/zerophase

Plot the instantaneous adaptive filter zerophase response

adaptfilt/zpk

Return a matrix containing the instantaneous adaptive filter zero, p o le, and gain values

adaptfilt/zplane

Plot the instantaneous adaptive filter in the Z-plane

2-8

Working with Adaptive Filter Objects

The next sections cover viewing and changing the properties of

adaptfilt objects. Generally, modifying the properties is the same for adaptfilt, dfilt,andmfilt obje cts and most of the same me thods

apply to all.

Viewing Object Properties

As with any object, you can use get to view a adaptfilt object’s properties. To see a specific property, use

get(ha,'property')

To see all properties for an object, use

get(ha)

adaptfilt

Changing Object Properties

To set specific properties, use

set(ha,'property1',value1,'property2',value2,...)

You must use single quotation marks around the property name so MATLABtreatsthemasstrings.

Copying an Object

To create a copy of an object, use copy.

ha2 = copy(ha)

Note Using the syntax ha2 = ha copies only the object handle a nd does not create a new object — change the characteristics of

ha and ha2 are not independent. When you

ha2,thoseofha change as well.

Using Filter States

Two properties control your adaptive filter states.

•

States — stores the current states of the filter. Before the filter is

applied, the states correspond to the initial conditions and after the filter is applied, the states correspond to the final conditions.

•

PersistentMemory — resets the filter before filtering. The default

value is filter, such as specified when you constructed the object, before you use the object to filter data. Setting to retain its current properties between filtering operations, rather than resetting the filter to its property values at construction.

false which causes the properties that are modified by the

coefficients and states,toberesettothevalueyou

PersistentMemory to true allows the object

Examples Construct an LMS adaptive filter object and use it to identify an

unknown system. For this example, use 500 iteration of the adapting process to determine the unknown filter coefficients. Using the LMS

2-9

adaptfilt

algorithm represents one of the most straightforward technique for adaptive filters.

x = randn(1,500); % Input to the filter

b = fir1(31,0.5); % FIR system to be identified

n = 0.1*randn(1,500); % Observation noise signal

d = filter(b,1,x)+n; % Desired signal

mu = 0.008; % LMS step size.

ha = adaptfilt.lms(32,mu);

[y,e] = filter(ha,x,d);

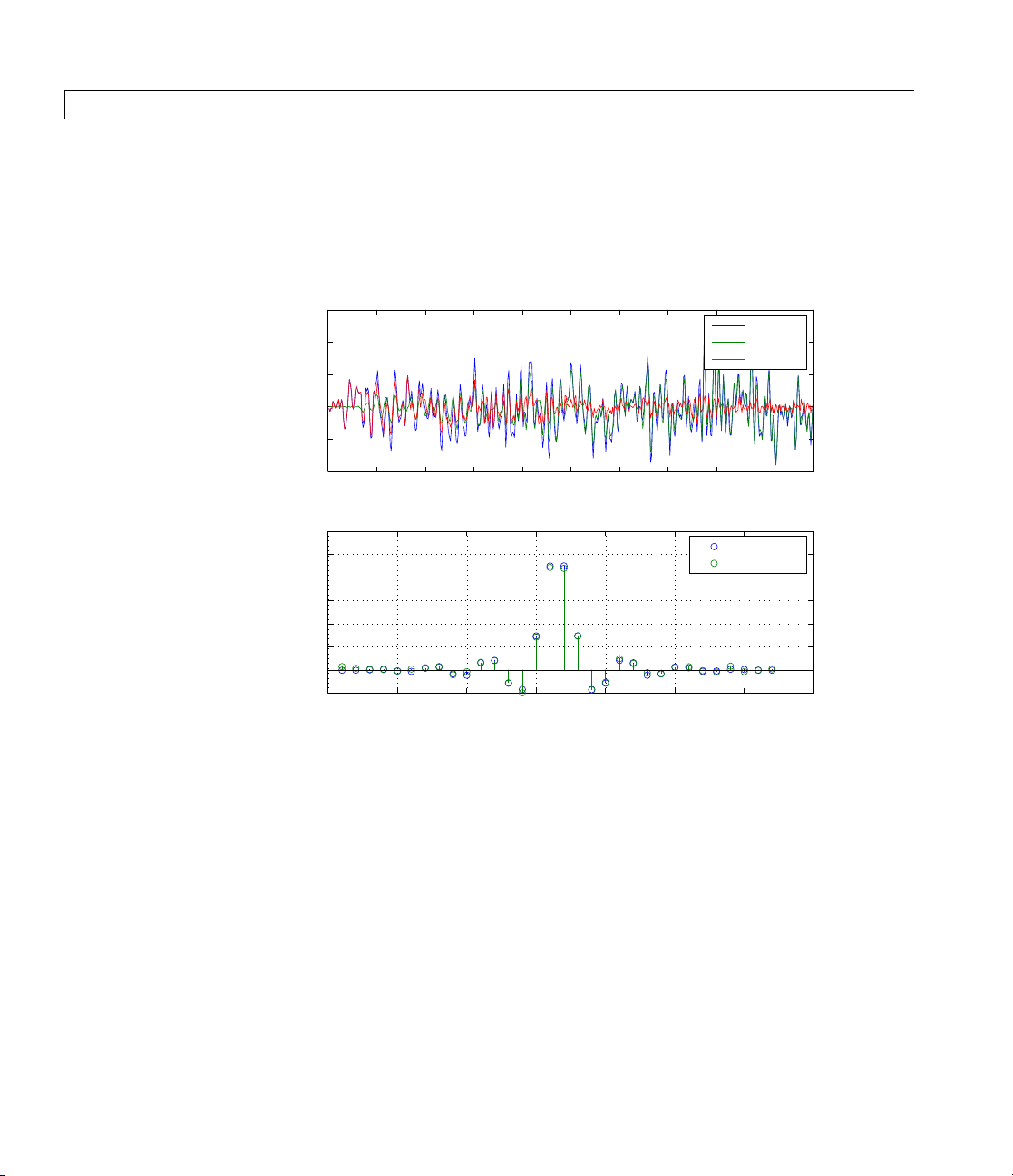
subplot(2,1,1); plot(1:500,[d;y;e]);

title('System Identification of an FIR Filter');

legend('Desired','Output','Error');

xlabel('Time Index'); ylabel('Signal Value');

subplot(2,1,2); stem([b.',ha.coefficients.']);

legend('Actual','Estimated');

xlabel('Coefficient #'); ylabel('Coefficient Value'); grid on;

Glancing at the figure shows you the coefficients after adapting closely match the desired unknown FIR filter.

2-10

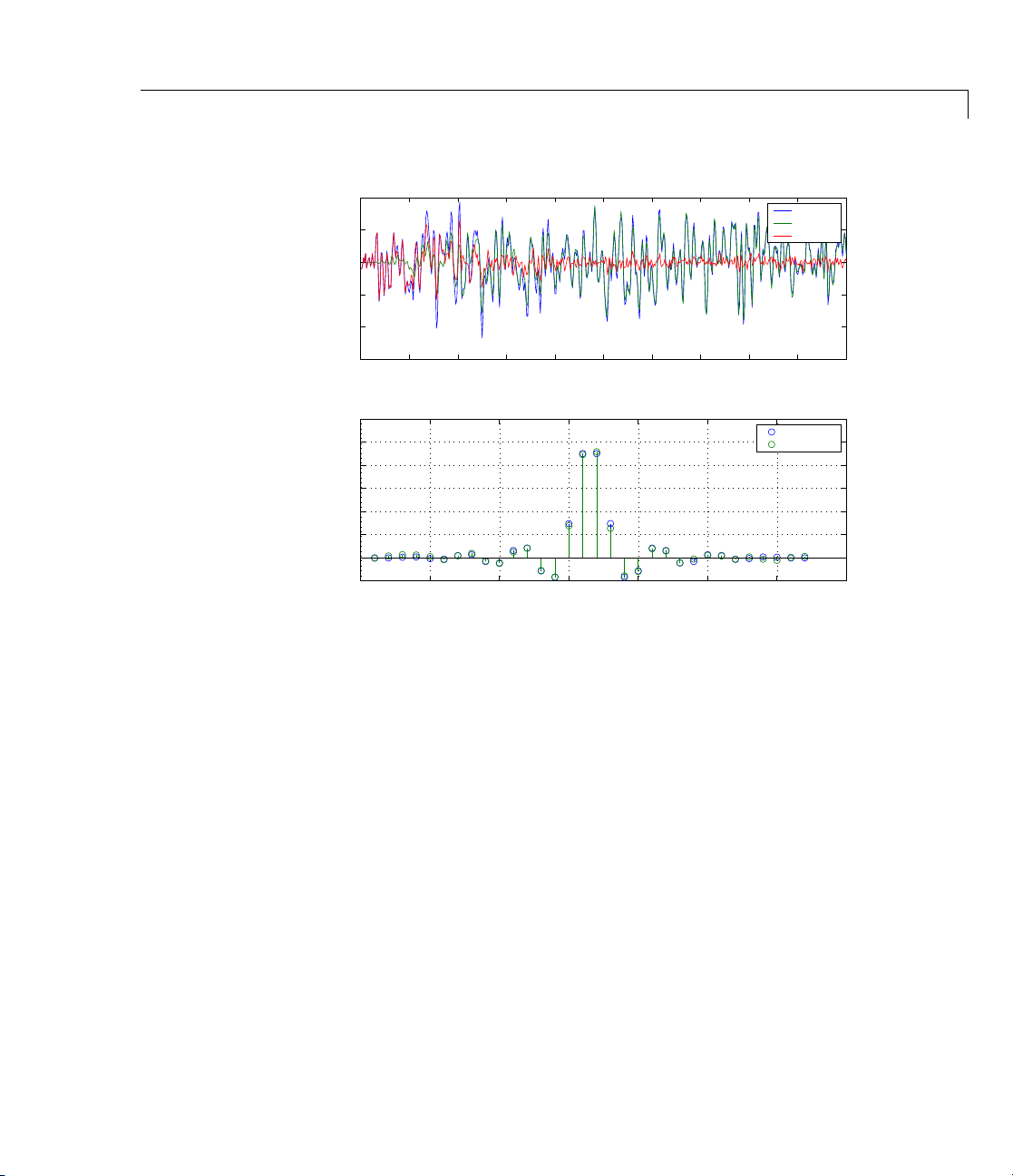
adaptfilt

−1

Signal Value

−2

−3 0 50 100 150 200 250 300 350 400 450 500

0.6

0.5

0.4

0.3

0.2

0.1

Coefficient Value

−0.1 0 5 10 15 20 25 30 35

See Also msesim

In−Phase Components

Time Index

Received Signal Scatter Plot

−2 0 2 Real[x]

Desired Output Error

l the QPSK process at work.

Quadrature Components

Signal Value

−1

−2

−3 0 200 400 600 800 1000

Imag[y]

−1

−2

−3

Time Index

Equalized Signal Scatter Plot

−2 0 2 Real[y]

Desired Output Error

2-21

adaptfilt.ap

References [1] Ozeki, K. and Umeda, T., “An Adaptive Filtering Algorithm Using

an Orthogonal Projection to an Affine Subspace and Its Properties,” Electronics and Communications in Japan, vol.67-A, no. 5, pp. 19-27, May 1984

[2] Maruyama, Y., “A Fast Method of Projection Algorithm,” Proc. 1990 IEICE Spring Conf., B-744

2-22

adaptfilt.apru

Purpose FIR adaptive filter that uses recursive matrix updating

Syntax ha = adaptfilt.apru(l,step,projectord,offset,coeffs,states,

...errstates,epsstates)

Description ha = adaptfilt.apru(l,step,projectord,offset,coeffs,states,

...errstates,epsstates)

filter

ha using recursive matrix updating.

Input Arguments

Entries in the following table describe the input arguments for

adaptfilt.apru.

Input Argument Description

step

projectord

offset

coeffs

Adaptive filter length (the number of coefficients or taps). It must be a positive integer.

Affine projection step size. This is a scalar that should be a value between zero and one. Setting equal to one provides the fastest convergence during adaptation.

Projection order of the affine projection algorithm.

projectord defines the size of the input signal

covariance matrix and defaults to two.

Offset for the input signal covariance matrix. You should initialize the covariance matrix to a diagonal matrix whose diagon al entries are equ a l to the offset you specify. defaults to one.

Vector containing the initial filter coefficients. It must be a length

coeffs defaults to length l vector of zeros when you

do not provide the argument for input.

constructs an affine projection FIR adaptive

l defaults to 10.

step

step defaults to 1.

offset should be positive. offset

l vector, the number of filter coefficients.

2-23

adaptfilt.apru

Input Argument Description

states

errstates

epsstates

Properties Since your adaptfilt.apru filter is an object, it has properties that

define its behavior in operation. Note that many of the properties are also input arguments for creating the properties that apply, this table lists and describes each property for the affine projection filter object.

Vector of the adaptive filter states. states defaults to a vector of zeros which has length equal t o (

projectord -2).

Vector of the adaptive filter error states. errstates defaults to a zero vector with length equal to (

projectord -1).

Vector of the epsilon values of the a daptive filter.

epsstates defaults to a vector of zeros with

(

projectord -1)elements.

adaptfilt.apru objects. To show you

l +

2-24

Name Range Description

Algorithm

None

Defines the adaptive filter algorithm the object uses during adaptation

FilterLength

Any positive integer

Reports the length of the filter, the number of coefficients or taps

ProjectionOrder

1toaslarge as needed.

Projection order of the affine projection algorithm.

ProjectionOrder defines

the size of the input signal covariance matrix and defaults to two.

Name Range Description

OffsetCov

Coefficients

Matrix of values

Vector of elements

Contains the offset covariance matrix

Vector containing the initial filter coefficients. It must be alength

l vector, the number

of filter coefficients. defaults to length l vector of zeros w hen you do not provide the a rgument for input.

States

Vector of elements, data type double

Vector of the adaptive filter states. states defaults to a vector of zeros which has length equal to (

-2).

ErrorStates

Vector of elements

Vector of the adaptive filter error states. defaults to a zero vector with length equal to (

1).

EpsilonStates

Vector of elements

Vector of the epsilon values of the adaptive filter. defaults to a vector of zeros with (

projectord -1)elements.

adaptfilt.apru

coeffs

l + projectord

errstates

projectord -

epsstates

2-25

adaptfilt.apru

Name Range Description

StepSize

PersistentMemory false or true

Example Demonstrate quadrature phase shift keying (QPSK) adaptive

equalization using a 32-coefficient FIR filter. This example runs the adaptation process for 1000 iterations.

Any scalar from zero to one, inclusive

Specifies the step size taken between filter coefficient updates

Determine whether the filter states get restored to their starting values for each filtering operation. The starting values are the values in place when you create the filter.

PersistentMemory

returns to zero any state that the filter changes during processing. States that the filter does not change are not affected. Defaults to

true.

2-26

D = 16; % Number of samples of delay

b = exp(j*pi/4)*[-0.7 1]; % Numerator coefficients of channel

a = [1 -0.7]; % Denominator coefficients of channel

ntr= 1000; % Number of iterations

s = sign(randn(1,ntr+D)) + j*sign(randn(1,ntr+D)); % Baseband

n = 0.1*(randn(1,ntr+D) + j*randn(1,ntr+D)); % Noise signal

r = filter(b,a,s)+n; % Received signal

x = r(1+D:ntr+D); % Input signal (received signal)

d = s(1:ntr); % Desired signal (delayed QPSK signal)

mu = 0.1; % Step size

po = 4; % Projection order

del = 0.05; % Offset

ha = adaptfilt.apru(32,mu,po,offset); [y,e] = filter(ha,x,d);

subplot(2,2,1); plot(1:ntr,real([d;y;e])); title('In-Phase Components');

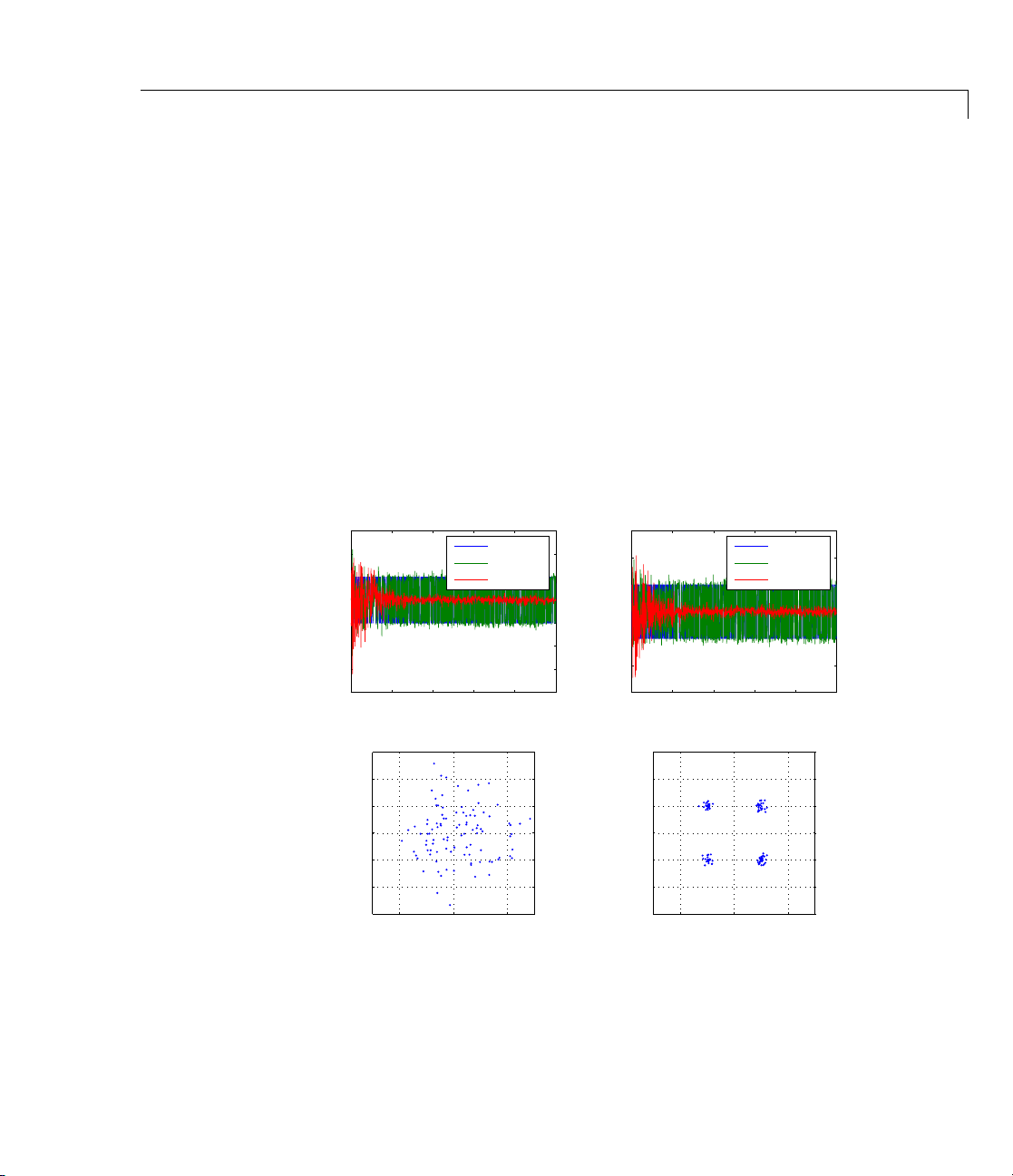
adaptfilt.apru

legend('Desired','Output','Error');

xlabel('Time Index'); ylabel('Signal Value');

subplot(2,2,2); plot(1:ntr,imag([d;y;e])); title('Quadrature Components');

legend('Desired','Output','Error');

xlabel('Time Index'); ylabel('Signal Value');

subplot(2,2,3); plot(x(ntr-100:ntr),'.'); axis([-3 3 -3 3]);

title('Received Signal Scatter Plot');

axis('square'); xlabel('Real[x]'); ylabel('Imag[x]'); grid on;

subplot(2,2,4); plot(y(ntr-100:ntr),'.'); axis([-3 3 -3 3]);

title('Equalized Signal Scatter Plot');

axis('square'); xlabel('Real[y]'); ylabel('Imag[y]'); grid on;

In the following component and scatter plots, you see the results of QPSK equalization.

3 2 1 0

−1

Signal Value

−2

−3

−4

In−Phase Components

Desired Output Error

0 200 400 600 800 1000

Imag[x]

−1

−2

−3

Time Index

Received Signal Scatter Plot

−2 0 2 Real[x]

Quadrature Components

Signal Value

−1

−2

−3 0 200 400 600 800 1000

Imag[y]

−1

−2

−3

Time Index

Equalized Signal Scatter Plot

−2 0 2 Real[y]

Desired Output Error

2-27

adaptfilt.apru

See Also adaptfilt, adaptfilt.ap, adaptfilt.bap

References [1] Ozeki. K., T. Omeda, “An Adaptive Filtering Algorithm Using

an Orthogonal Projection to an Affine Subspace and Its Properties,” Electronics and Communications in Japan, vol. 67-A, no. 5, pp. 19-27, May 1984

[2] Maruyama, Y, “A Fast Method of Projection Algo rithm,” Proceedings 1990 IEICE Spring Conference, B-744

2-28

adaptfilt.bap

Purpose FIR adaptive f ilter that uses block affine pr ojection

Syntax ha = adaptfilt.bap(l,step,projectord,offset,coeffs,states)

Description ha = adaptfilt.bap(l,step,projectord,offset,coeffs,states)

constructs a block affine projection FIR adaptive filter ha.

Input Arguments

Entries in the following table describe the input arguments for

adaptfilt.bap.

Input Argument Description

step

projectord

offset

Adaptive filter length (the number of coefficients or taps) and it must be a positive integer. defaults to 10.

Affine projection step size. This is a scalar that should be a value between zero and one. Setting

step equal to one provides the fastest convergence

during adaptation.

Projection order of the affine projection algorithm.

projectord defines the size of the input signal

covariance matrix and defaults to two.

Offset for the input signal covariance matrix. You should initialize the covariance matrix to a diagonal matrix whose diagonal entries are equal to the offset y ou specify.

offset defaults to one.

step defaults to 1.

offset should be positive.

2-29

adaptfilt.bap

Input Argument Description

coeffs

states

Properties Since your adaptfilt.bap filter is an object, it has properties that

Name Range Description

Algorithm

FilterLength

ProjectionOrder

OffsetCov

Vector containing the initial filter coefficients. It must be a length coefficients. zeros when you do not provide the argument for input.

Vector of the adaptive filter states. states defaults to a vector of zeros which has length equal to ( + projectord -2).

None

Any positive integer

1 to as large as needed.

Matrix of values Contains the offset

l vector, the number of filter

coeffs defaults to length l vector of

adaptfilt.bap objects. To show you

Defines the adaptive filter algorithm the object uses during adaptation

Reports the length of the filter, the number of coefficients or taps

Projection order of the affine projection algorithm.

ProjectionOrder defines

thesizeoftheinputsignal covariance matrix and defaults to two.

covariance matrix

2-30

Name Range Description

Coefficients

Vector of elements

Vector containing the initial filter coefficients. It must be a length number of filter coefficients.

coeffs defaults to length l

vector of zeros when you do not provide the argument for input.

States

Vector of elements, data type double

Vector of the adaptive filter states. states defaults to a vector of zeros which has length equal to (

projectord -2).

StepSize

PersistentMemory false or true

Any scalar from zero to one, inclusive

Specifies the step size taken between filter coefficient updates

Determine whether the filter states get restored to their starting values for each filtering operation. The starting values are the values inplacewhenyoucreatethe filter.

PersistentMemory

returns to zero any state that the filter changes during processing. States that the filter does not change are not affected. Defaults to

adaptfilt.bap

l vector, the

l +

true.

Example Show an example of quadrature phase shift keying (QPSK) adaptive

equalization using a 32-coefficient FIR filter.

D = 16; % delay

2-31

adaptfilt.bap

b = exp(j*pi/4)*[-0.7 1]; % Numerator coefficients

a = [1 -0.7]; % Denominator coefficients

ntr= 1000; % Number of iterations

s = sign(randn(1,ntr+D))+j*sign(randn(1,ntr+D));% Baseband signal

n = 0.1*(randn(1,ntr+D) + j*randn(1,ntr+D)); % Noise signal

r = filter(b,a,s)+n; % Received signal

x = r(1+D:ntr+D); % Input signal (received signal)

d = s(1:ntr); % Desired signal (delayed QPSK signal)

mu = 0.5; % Step size

po = 4; % Projection order

offset = 1.0; % Offset for covariance matrix

ha = adaptfilt.bap(32,mu,po,offset);

[y,e] = filter(ha,x,d); subplot(2,2,1);

plot(1:ntr,real([d;y;e]));

title('In-Phase Components'); legend('Desired','Output','Error');

xlabel('Time Index'); ylabel('Signal Value');

subplot(2,2,2); plot(1:ntr,imag([d;y;e]));

title('Quadrature Components');

legend('Desired','Output','Error');

xlabel('Time Index'); ylabel('Signal Value');

subplot(2,2,3); plot(x(ntr-100:ntr),'.'); axis([-3 3 -3 3]);

title('Received Signal Scatter Plot'); axis('square');

xlabel('Real[x]'); ylabel('Imag[x]'); grid on;

subplot(2,2,4); plot(y(ntr-100:ntr),'.'); axis([-3 3 -3 3]);

title('Equalized Signal Scatter Plot'); axis('square');

xlabel('Real[y]'); ylabel('Imag[y]'); grid on;

2-32

adaptfilt.bap

Signal Value

−2

−4

In−Phase Components

Desired Output Error

0 200 400 600 800 1000

Imag[x]

−1

−2

−3

Time Index

Received Signal Scatter Plot

−2 0 2 Real[x]

−1

Signal Value

−2

−3

−4

Quadrature Components

3 2 1 0

0 200 400 600 800 1000

Imag[y]

−1

−2

−3

Time Index

Equalized Signal Scatter Plot

−2 0 2 Real[y]

Desired Output Error

Using the block affine projection object in QPSK results in the plots shown here.

See Also adaptfilt, adaptfilt.ap, adaptfilt.apru

References [1] Ozeki, K. and T. Omeda, “An Adaptive Filtering Algorithm Using

an Orthogonal Projection to an Affine Subspace and Its Properties,” Electronics and Communications in Japan, vol. 67-A, no. 5, pp. 19-27, May 1984

[2] Montazeri, M. and Duhamel, P, “A S et of Algorithms Linking NLMS and Block RLS Algorithms,” IEEE Transactions Signal Processing, vol. 43, no. 2, pp, 444-453, February 1995

2-33

adaptfilt.blms

Purpose FIR adaptive filter that uses BLMS

Syntax ha = adaptfilt.blms(l,step,leakage,blocklen,coeffs,states)

Description ha = adaptfilt.blms(l,step,leakage,blocklen,coeffs,states)

constructs an FIR block LMS adaptive filter ha,wherel is the adaptive filter length (the number of coefficients or taps) and must be a positive integer.

step is the block LMS step size. You must set step to a nonnegative

scalar. You can use function of step size values for the signals being processed. When unspecified,

step defaults to 0.

leakage is the block LMS leakag e factor. It must be a scalar between 0

and 1 . If you se t leakage to be less than one, you implement the leaky block LMS algorithm. the adapting a lgorithm .

blocklen is the block length used. It must be a positive inte ger and

the signal vectors block lengths result in faster per-sample execution times but with poor adaptation characteristics. When you choose

blocklen + length(coeffs) is a power of 2, use adaptfilt.blmsfft. blocklen defaults to l.

l defaults to 10.

maxstep to determine a reasonable range

leakage defaults to 1 specifying no leakage in

d and x should be divisible by blocklen.Larger

blocklen such that

coeffs is a vector of initial filter coefficients. it must be a length l

vector. coeffs defaults to length l vector of zeros.

states contains a vector of your initial filter states. It must be a length l vector and defaults to a length l vector of zeros when you do not

include it in your calling function.

Properties In the syntax for creating the adaptfilt object, the input options are

properties of the object created. This table lists the propertie s for the adjoint LMS object, their default values, and a brief description of the property.

2-34

Property

Algorithm

FilterLength

Coefficients

States

Leakage

BlockLength

Default Value Description

None

Defines the adaptive filter algorithm the object uses during adaptation

Any positive

Reports the length of the filter, the number o f coefficients or taps

integer

Vector of elements

Vector containing the initial filter coefficients. It must be a length

l vector where l is the number of

filter coefficients. length

l vector of zeros when you do

not provide the argument for input.

Vector of elements

Vector of the adaptive filter states.

states defaults to a vector of zeros

which has length equal to

Vector of length

Size of the blocks of data processed in each iteration

adaptfilt.blms

coeffs defaults to

2-35

adaptfilt.blms

Default

Property

StepSize

PersistentMemory false or

Value Description

0.1

true

Sets the block LMS algorithm step size used for each iteration of the adapting algorithm. Determines both how quickly and how closely the adaptive filter converges to the filter solution. Use

maxstep to determine

the maximum usable step size.

Determine whether the filter states get restored to their starting values for each filtering operation. The starting values are the values in place when you create the filter.

PersistentMemory returns to zero

any state that the filter changes during processing. States that the filter does not change are not affected. Defaults to

false.

Example Use an adaptive filter to identify an unknown 32nd-order FIR filter.

In this example 500 input samples result in 500 iterations of the adaptation process. You see in the plot that follows the example code that the adaptive filter has determined the coefficients of the unknown system under test.

x = randn(1,500); % Input to the filter b = fir1(31,0.5); % FIR system to be identified no = 0.1*randn(1,500); % Observation noise signal d = filter(b,1,x)+no; % Desired signal mu = 0.008; % Block LMS step size n = 5; % Block length ha = adaptfilt.blms(32,mu,1,n); [y,e] = filter(ha,x,d); subplot(2,1,1); plot(1:500,[d;y;e]);

2-36

adaptfilt.blms

title('System Identification of an FIR Filter'); legend('Desired','Output','Error'); xlabel('Time Index'); ylabel('Signal Value'); subplot(2,1,2); stem([b.',ha.coefficients.']); legend('Actual','Estimated'); xlabel('Coefficient #'); ylabel('Coefficient Value'); grid on;

Based on looking at the figures here, the adaptive filter correctly identified the unknown system after 500 iterations, or few er. In the lower plo t, you see the comparison between the actual filter coefficients and those determined by the adaptation process.

Signal Value

−1

−2

−3 0 50 100 150 200 250 300 350 400 450 50

0.6

0.5

0.4

0.3

0.2

0.1

Coefficient Value

−0.1 0 5 10 15 20 25 30 35

System Identification of an FIR filter

Time Index

See Also adaptfilt.blmsfft, adaptfilt.fdaf, adaptfilt.lms

Desired Output Error

Actual Estimated

2-37

adaptfilt.blms

References Shynk, J.J.,“Frequency-Domain and Multirate Adaptive Filtering,”

IEEE

Signal Processing Magazine, vol. 9, no. 1, pp. 14-37, Jan. 1992.

2-38

adaptfilt.blmsfft

Purpose FIR adaptive filter that uses FFT-based BLMS

Syntax ha = adaptfilt.blmsfft(l,step,leakage,blocklen,coeffs,

states)

Description ha = adaptfilt.blmsfft(l,step,leakage,blocklen,coeffs,

states) l istheadaptivefilterlength(thenumberofcoefficientsortaps)and

must be a positive integer. step size. It must be a nonnegative scalar. The function be helpful to determine a reasonable range of step size values for the signals you are processing.

leakage is the block LMS leakage factor. It must also be a

scalar between 0 and 1. When

adaptfilt.blmsfft implem ents a leaky block LMS algorithm. leakage

defaults to 1 (no leakage). blocklen is the block length used. It must be a positive integer such that

constructs an FIR block LMS adaptive filter object ha where

l defaults to 10. step is the block LMS

maxstep may

step defaults to 0.

leakage is less than one, the

blocklen + length(coeffs)

is a power of two; otherwise, an adaptfilt.blms algorithm is used for adapting. Larger block lengths result in faster execution times, with poor adaptation characteristics as the cost of the speed gained.

blocklen defaults to l. Enter your initial filter coefficients in coeffs,a

vector of length all zeros. length you omit the

l vector. states defaults to a length l vector of all zeros when

l. When omitted, coeffs defaults to a length l vector of

states contains a vector of initial filter states; it must be a

states argument in the calling syntax.

Properties In the syntax for creating the adaptfilt object, the input options

are properties of the object you create. This table lists the properties for the block LMS object, their default values, and a brief description of the property.

2-39

adaptfilt.blmsfft

Property

Algorithm

FilterLength

Coefficients

States

Leakage 1

BlockLength

Default Value Description

None

Defines the adaptive filter algorithm the object uses during adaptation

Any positive

Reports the length of the filter, the number of coefficients or taps

integer

Vector of elements

Vector containing the initial filter coefficients. It must be a length

l vector where l is the number of

filter coefficients. defaults to length l vector of zeros when you do not provide the argument for input.

Vector of elements of length

Vector of the adaptive filter states.

states defaults to a vector of zeros

which has length equal to

Vector of length

Size of the blocks of data processed in each iteration

coefficients

2-40

Default

Property

StepSize

PersistentMemory false or

Value Description

0.1

true

adaptfilt.blmsfft

Sets the block LMS algorithm step size used for each iteration of the adapting algorithm. Determines both how quickly and how closely the adaptive filter converges to the filter solution. Use determine the maximum usable step size.

Determine whether the filter states get restored to their starting values for each filtering operation. The starting values are the values in placewhenyoucreatethefilter.

PersistentMemory returns to zero

any state that the filter changes during processing. States that the filter does not change are not affected. Defaults to

maxstep to

false.

Example Identify an unknown FIR filter with 32 coefficients using 512 iterations

of the adapting algorithm.

x = randn(1,512); % Input to the filter b = fir1(31,0.5); % FIR system to be identified no = 0.1*randn(1,512); % Observation noise signal d = filter(b,1,x)+no; % Desired signal mu = 0.008; % Step size n = 16; % Block length ha = adaptfilt.blmsfft(32,mu,1,n); [y,e] = filter(ha,x,d); subplot(2,1,1); plot(1:500,[d(1:500);y(1:500);e(1:500)]); title('System Identification of an FIR Filter'); legend('Desired','Output','Error'); xlabel('Time Index');

2-41

adaptfilt.blmsfft

ylabel('Signal Value'); subplot(2,1,2); stem([b.',ha.coefficients.']); legend('actual','estimated'); grid on; xlabel('Coefficient #'); ylabel('Coefficient Value');

Signal Value

−1

−2 0 50 100 150 200 250 300 350 400 450 500

0.6

0.5

0.4

0.3

0.2

0.1

Coefficient Value

−0.1 0 5 10 15 20 25 30 35

System Identification of an FIR Filter

Desired Output Error

Time Index

actual estimated

Coefficient #

As a result of running the adaptation process, filter object ha now matches the unknown system FIR filter

b, based on comparing the filter

coefficients derived during adaptation.

See Also adaptfilt.blms, adaptfilt.fdaf, adaptfilt.lms, filter

References Shynk, J.J., “Frequency-Domain and Multirate Adaptive Filtering,”

IEEE Signal Processing Magazine, vol. 9, no. 1, pp. 14-37, Jan. 1992.

2-42

adaptfilt.dlms

Purpose FIR adaptive filter that uses delayed LMS

Syntax ha = adaptfilt.dlms(l,step,leakage,delay,errstates,coeffs,

...states)

Description ha = adaptfilt.dlms(l,step,leakage,delay,errstates,coeffs,

...states)

Input Arguments

Entries in the following table describe the input arguments for

adaptfilt.dlms.

Input Argument Description

step

leakage

delay

errstates

constructs an FIR delayed LMS adaptive filter ha.

Adaptive filter length (the number of coefficients or taps) and it must be a positive integer. to 10.

LMS step size. It must be a nonnegative scalar. You can use of step size values for the signals b eing processed.

step defaults to 0.

YourLMSleakagefactor. Itmustbeascalar between 0 and 1. When

adaptfilt.lms implements a leaky LMS algorithm.

When you omit the syntax, it defau lts to 1 providing no leakage in the adapting algorithm.

Update delay given in time samples. This scalar should be a positive integer — negative delays do not work.

Vector of the error states of your adaptive filter. It must have a length equal to the update delay ( in samples. length vector of zeros.

maxstep to determine a reasonable range

leakage is less than one,

leakage property in the calling

delay defaults to 1.

errstates defaults to an appropriate

l defaults

delay)

2-43

adaptfilt.dlms

Input Argument Description

coeffs

states

Properties In the syntax for creating the adaptfilt object, the input options

are properties of the object you create. This table lists the properties for the block LMS object, their default values, and a brief description of the property.

Property

Algorithm

Coefficients

Delay 1

Vector of initial filter coefficients. it must be a length with elements equal to zero.

Vector of initial filter states for the adaptive filter. It must be a length length l-1 vector of zeros.

l vector. coeffs defaults to length l vector

l-1 vector. states defaults to a

Default Val ue Description

None

Vector of elements

Defines the adaptive filter algorithm the object uses during adaptation

Vector containing the initial filter coefficients. It must be a length

l vector where l is the number

of filter coefficients. defaults to length l vector of zeros when you do not provide the argument for input. LMS FIR filter coefficients. Should be initialized with t he initial coefficients for the FIR filter prior to adapting. You need entries in coeffs.

Specifies the update delay for the adaptive algorithm.

coeffs

2-44

Default

Property

ErrorStates

FilterLength

Leakage 1

PersistentMemory false or

Val ue Description

Vector of zeros with the number of elements equal to

delay

Any positive integer

true

adaptfilt.dlms

A vector comprising the error states for the adaptive filter.

Reports the length of the filter, the number of coefficients or taps.

Determine whether the filter states get restored to their starting values for each filtering operation. The starting values are the values in place when you create the filter if you have not changed the filter since you constructed it.

PersistentMemory returns to

zero any state that the filter changes during processing. States that the filter does not change are not affected. Defaults to

false.

2-45

adaptfilt.dlms

Default

Property

StepSize

States

Example System identification of a 32-co effi cient FIR filter. R efer to the figure

that follow s to see the results of the adapting filter process.

x = randn(1,500); % Input to the filter b = fir1(31,0.5); % FIR system to be identified n = 0.1*randn(1,500); % Observation noise signal d = filter(b,1,x)+n; % Desired signal mu = 0.008; % LMS step size. delay = 1; % Update delay ha = adaptfilt.dlms(32,mu,1,delay); [y,e] = filter(ha,x,d); subplot(2,1,1); plot(1:500,[d;y;e]); title('System Identification of an FIR Filter'); legend('Desired','Output','Error'); xlabel('Time Index'); ylabel('Signal Value'); subplot(2,1,2); stem([b.',ha.coefficients.']); legend('Actual','Estimated'); grid on; xlabel('Coefficient #'); ylabel('Coefficient Value');

Val ue Description

0.1

Sets the LMS algorithm step size used for each iteration of the adapting algorithm. D etermines both how quickly and how closely the adaptive filter converges to the filter solution.

Vector of elements, data type double

Vector of the adaptive filter states.

states defaults to a

vector of zeros which has length equal to (

l + projectord -2).

2-46

Using a delayed LM S adaptive filter in the process to identify an unknownfilterappearstoworkasplanned,asshowninthisfigure.

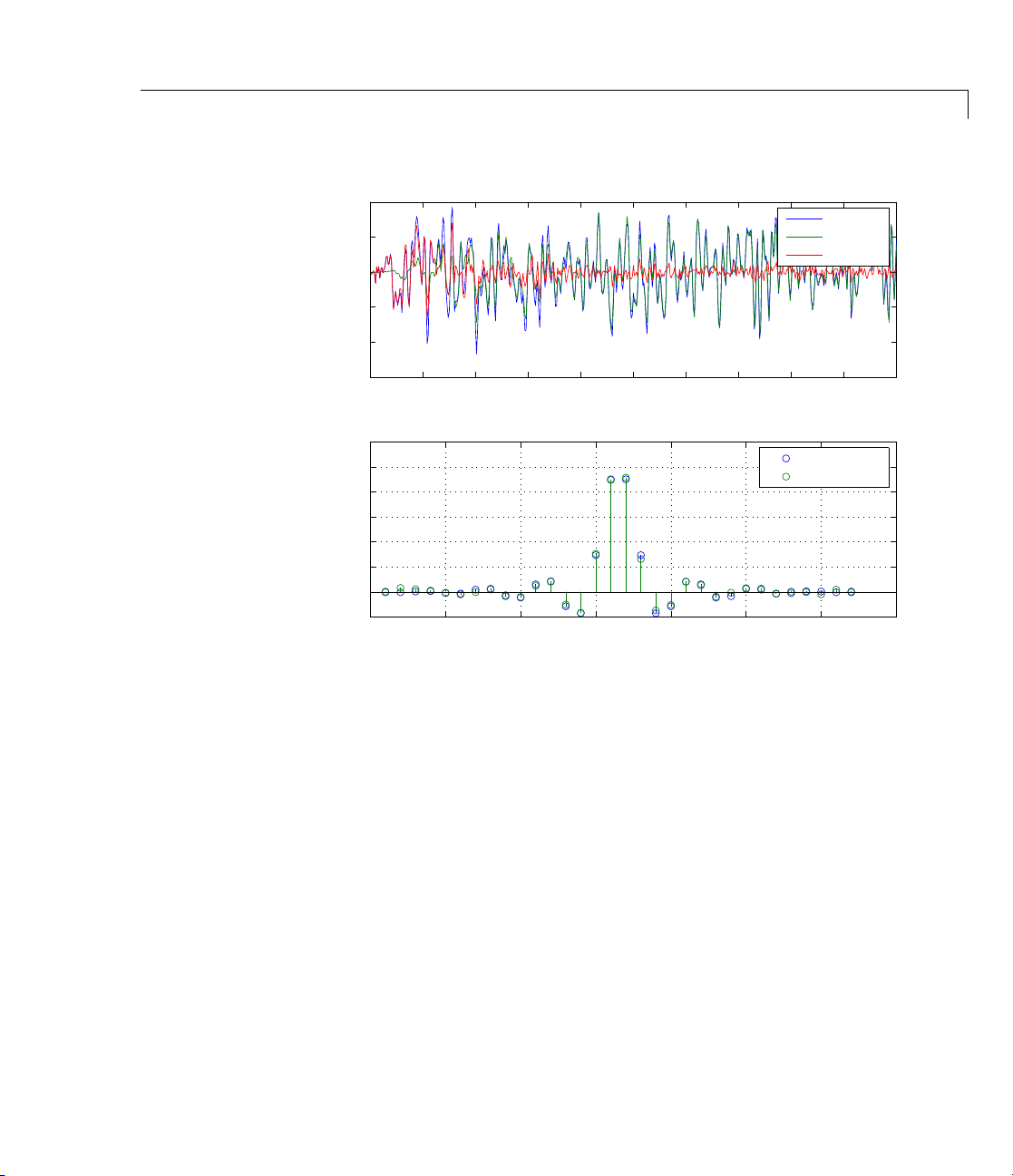
adaptfilt.dlms

−1

Signal Value

−2

−3 0 50 100 150 200 250 300 350 400 450 500

0.6

0.5

0.4

0.3

0.2

0.1

Coefficient Value

−0.1 0 5 10 15 20 25 30 35

System Identification of an FIR Filter

Time Index

Coefficient #

See Also adaptfilt.adjlms, adaptfilt.filtxlms, adaptfilt.lms

Desired Output Error

Actual Estimated

References Shynk, J.J.,“Frequency-Domain and Multirate Adaptive Filtering,”

IEEE Signal Processing Magazine, vol. 9, no. 1, pp. 14-37, Jan. 1992.

2-47

adaptfilt.fdaf

Purpose FIR adaptive filter that uses frequency-domain with bin step size

normalization

Syntax ha = adaptfilt.fdaf(l,step,leakage,delta,lambda,blocklen,

offset,...coeffs,states)

Description ha = adaptfilt.fdaf(l,step,leakage,delta,lambda,blocklen,

offset,...coeffs,states)

adaptive filter inputargumentsyoucreateadefaultobjectwithl=10and

ha with bin step size normalization. If you omit all the

Input Arguments

Entries in the following table describe the input arguments for

adaptfilt.fdaf.

Input Argument Description

step

leakage

delta

lambda

Adaptive filter length (the number of coefficients or taps). l must be a positive integer; it defaults to 10 when you omi t the argument.

Step size of the adaptive filter. This is a scalar and should lie in the range (0,1].

Leakage parameter of the adaptive filter. If this parameter is set to a value between zero and one, you implement a leaky FDAF algorithm. defaults to 1 — no leakage provided in the algorithm.

Initial common value of all of the FFT input signal powers. Its initial value should be positive. defaults to 1.

Specifies the averaging factor used to compute the exponentially-windowed FFT input signal powers for the coefficient updates. (0,1].

lambda defaults to 0.9.

constructs a frequency-domain FIR

step defaults to 1.

lambda should lie in the range

step =1.

leakage

delta

2-48

Input Argument Description

blocklen

offset

coeffs

states

Block length for the coefficient updates. This must be a positive integer. For faster execution, ( l) should be a power of two.

Offset for the normalization terms in the coefficient updates. Usethistoavoiddividebyzerosorbyvery small numbers when any of the FFT input signal powers become very small.

Initial time-domain coefficients of the adaptive filter.

coeff should be a length l vector. The adaptive

filter object uses these coefficients to compute the initial frequency-domain filter coefficients via an FFT computed after zero-padding the time-domain vector by the

The adaptive filter states. states defaults to a zero vector that has length equal to l.

blocklen.

adaptfilt.fdaf

blocklen +

blocklen defaults to l.

offset defaults to zero.

Properties Since your adaptfilt.fdaf filter is an object, it has properties that

define its behavior in operation. Note that many of the properties are also input arguments for creating show you the properties that apply, this table lists and describes each property for the

adaptfilt.fdaf filter object.

adaptfilt.fdaf objects. To

2-49

adaptfilt.fdaf

Name Range Description

Algorithm

None

Defines the adaptive filter algorithm the object uses during adaptation.

AvgFactor

(0, 1] S pecifies the averaging

factor used to compute the exponentially-windowed FFT input signal powers for the coefficient updates. Same as the input argument

BlockLength

Any integer Block length for the coefficient

updates. This must be a positive integer. Forfasterexecution, (

blocklen + l) should be a power

FFTCoefficients

of two.

Stores the discrete Fourier

blocklen defaults to l.

transform of the filter co efficients in

coeffs.

FFTStates

FilterLength

Any positive

States for the FFT operation.

Reports the length of the filter, the number of coefficients or taps.

integer

Leakage

Leakage param eter of the adaptive filter. if this parameter issettoavaluebetweenzeroand one, you implement a leaky FDAF algorithm. 1—noleakageprovidedinthe algorithm.

lambda.

leakage defaults to

2-50

Name Range Description

Offset

PersistentMemory false or

Power

StepSize

Any positive real value

true

Any scalar from zero to one, inclusive

Offset for the normalization terms in the coefficient updates. Use this to avoid dividing by zero or by very small numbers when any of the FFT input signal powers become very small.

offset defaults to zero.

Determine whether the filter states get restored to their starting values for each filtering operation. The starting values are the values in place when you create the filter.

PersistentMemory returns to

zero any state that the filter changes during p rocessing. States that the filter does not change are not affected. Defaults to

false.

Avectorof2*l elements, each initialized with the value from the input arguments. As you filter data, the filter process.

Specifies the step size taken between filter coefficient updates

adaptfilt.fdaf

delta

Power gets updated by

Examples Quadrature Phase Shift Keying (QPSK) adaptive equalization using

1024 iterations of a 32-coefficient FIR filter. After this example code, a figure demonstrates the equalization results.

2-51

adaptfilt.fdaf

D = 16; % Number of samples of delay

b = exp(j*pi/4)*[-0.7 1]; % Numerator coefficients of channel

a = [1 -0.7]; % Denominator coefficients of channel

ntr= 1024; % Number of iterations

s = sign(randn(1,ntr+D))+j*sign(randn(1,ntr+D)); %QPSK signal

n = 0.1*(randn(1,ntr+D) + j*randn(1,ntr+D)); % Noise signal

r = filter(b,a,s)+n; % Received signal

x = r(1+D:ntr+D); % Input signal (received signal)

d = s(1:ntr); % Desired signal (delayed QPSK signal)

del = 1; % Initial FFT input powers

mu = 0.1; % Step size

lam = 0.9; % Averaging factor

ha = adaptfilt.fdaf(32,mu,1,del,lam);

[y,e] = filter(ha,x,d);

subplot(2,2,1); plot(1:ntr,real([d;y;e])); title('In-Phase Components');

legend('Desired','Output','Error');

xlabel('Time Index'); ylabel('signal value');

subplot(2,2,2); plot(1:ntr,imag([d;y;e])); title('Quadrature Components');

legend('Desired','Output','Error');

xlabel('Time Index'); ylabel('signal value');

subplot(2,2,3); plot(x(ntr-100:ntr),'.'); axis([-3 3 -3 3]);

title('Received Signal Scatter Plot'); axis('square');

xlabel('Real[x]'); ylabel('Imag[x]'); grid on;

subplot(2,2,4); plot(y(ntr-100:ntr),'.'); axis([-3 3 -3 3]);

title('Equalized Signal Scatter Plot'); axis('square');

xlabel('Real[y]'); ylabel('Imag[y]'); grid on;

2-52

adaptfilt.fdaf

See Als

signal value

−1

−2 0 500 1000 1500

adaptf adaptf

In−Phase Components

Time Index

Received Signal Scatter Plot

Imag[x]

−1

−2

−3

−2 0 2 Real[x]

ilt.ufdaf ilt.blmsfft

Desired Output Error

1.5 1

0.5 0

−0.5

signal value

−1

−1.5

−2

, adaptfilt.pbfdaf, adaptfilt.blms,

Quadrature Components

Desired Output Error

0 500 1000 1500

Imag[y]

−1

−2

−3

Time Index

Equalized Signal Scatter Plot

−2 0 2 Real[y]

References Shynk, J.J.,“Frequency-Domain and Multirate Adaptive Filtering,”

IEEE Signal Processing Magazine, vol. 9, no. 1, pp. 14-37, Jan. 1992

2-53

adaptfilt.filtxlms

Purpose FIR adaptive filter that uses filtered-x L M S

Syntax ha = adaptfilt.filtxlms(l,step,leakage,pathcoeffs,

pathest,...errstates,pstates,coeffs,states)

Description ha = adaptfilt.filtxlms(l,step,leakage,pathcoeffs,

pathest,...errstates,pstates,coeffs,states)

filtered-x LMS adaptive filter

Input Arguments

Entries in the following table describe the input arguments for

adaptfilt.filtxlms.

Input Argument Description

step

leakage

pathcoeffs

pathest

fstates

Adaptive filter length (the number of coefficients or taps) and it must be a positive integer. to 10.

Filtered LMS step size. it must be a nonnegativ e scalar.

is the filtered-x LMS leakage factor. it must be a scalar between 0 and 1. If it is less than one, a leaky version of

leakage defaults to 1 (no leakage).

is the secondary path filter model. this vector should contain the coefficient values of the secondary path from the output actuator to the error sensor.

is the estimate of the secondary path filter model.

pathest defaults to the values in pathcoeffs.

is a vector of filtered input states of the adaptive filter. equal to (

ha.

step defaults to 0.1.

adaptfilt.filtxlms is implemented.

fstates defaults to a zero vector of leng th

l -1).

constructs an

l defaults

2-54

adaptfilt.filtxlms

Input Argument Description

pstates

coeffs

states

Properties In the syntax for creating the adaptfilt object, the input options are

properties of the object created. This table lists the propertie s for the adjoint LMS object, their default values, and a brief description of the property.

are the secondary path FIR filter states. it must be a vector of length equal to the (

-1).

pstates defaults to a vector of zeros of

length(pathcoeffs)

appropriate length.

is a vector of initial filter coefficients. it must be a length

l vector. coeffs defaults to length l vector

of zeros.

Vector of initial filter states. states defaults to a zero vector of length equal to the larger of (

length(pathcoeffs)-1)and(length(pathest)-1).

Property

Algorithm

Coefficients

Default Value Description

None

Defines the adaptive filter algorithm the object uses during adaptation

Vector of elements

Vector containing the initial filter coefficients. It must be a length where

l is the number of

filter coefficients. defaults to length l vector of zeros when you do not provide the argument for input.

l vector

coeffs

2-55

adaptfilt.filtxlms

Property

FilteredInputStates l-1

FilterLength

States

SecondaryPathCoeffs

SecondaryPathEstimate pathcoeffs

SecondaryPathStates

StepSize

Default Value Description

Vector of filtered input states with length equal to

l -1.

Any positive integer

Reports the length of the filter, the number of coefficients or taps

Vector of elements

Vector of the adaptive filter states.

states

defaults to a vector of zeros which has length equal to (

l + projectord -2)

No default A vector that contains the

coefficient values of your secondary path from the output actuator to the error sensor

An estimate of the

values

secondary path filter model

Vector of size (

length

(pathcoeffs)

The states of the secondary path FIR f ilter — the unknown system

-1) with all elements equal to zero.

0.1

Sets the f iltered-x algorithm step size used for each iteration of the adapting alg orithm. Determines both how quickly and how closely the

2-56

adaptfilt.filtxlms

Default

Property

Example Demonstrate active noise control of a random noise signal over 1000

iterations.

As the figure that follows this code demonstrates, the filtered-x LMS filter successfully controls random noise in this context.

x = randn(1,1000); % Noise source

g = fir1(47,0.4); % FIR primary path system model

n = 0.1*randn(1,1000); % Observation noise signal

d = filter(g,1,x)+n; % Signal to be cancelled

b = fir1(31,0.5); % FIR secondary path system model

mu = 0.008; % Filtered-X LMS step size

ha = adaptfilt.filtxlms(32,mu,1,b);

[y,e] = filter(ha,x,d); plot(1:1000,d,'b',1:1000,e,'r');

title('Active Noise Control of a Random Noise Signal');

legend('Original','Attenuated');

xlabel('Time Index'); ylabel('Signal Value'); grid on;

Value Description

adaptive filter converges to the filter solution.

2-57

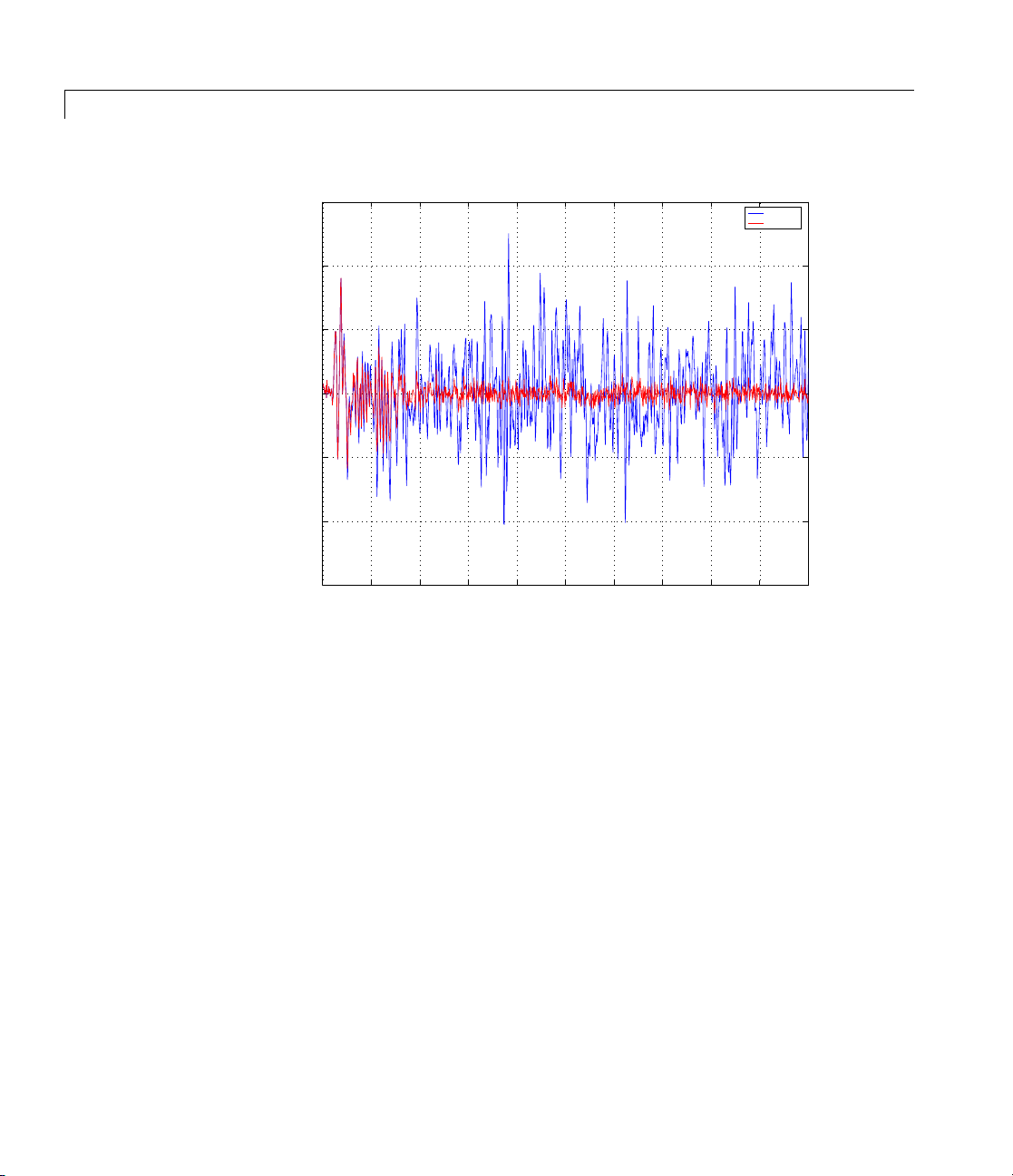
adaptfilt.filtxlms

Signal Value

−1

−2

−3 0 100 200 300 400 500 600 700 800 900 1000

Active Noise Control of a Random Noise Signal

Time Index

Original Attenuated

Mathworks FILTER DESIGN TOOLBOX 4 Reference Guide

Specifications and Main Features

Frequently Asked Questions

User Manual