Mathworks COMMUNICATIONS BLOCKSET 4 Reference

Download

Communications Bl

Reference

ockset™ 4

How to Contact The MathWorks

www.mathworks. comp.soft-sys.matlab Newsgroup www.mathworks.com/contact_TS.html T echnical Support

suggest@mathworks.com Product enhancement suggestions

bugs@mathwo doc@mathworks.com Documentation error reports service@mathworks.com Order status, license renewals, passcodes

info@mathwo

com

rks.com

Web

Bug reports

Sales, prici

ng, and general information

508-647-7000 (Phone)

508-647-7001 (Fax)

The MathWorks, Inc. 3 Apple Hill Drive Natick, MA 01760-2098

For contact information about worldwide offices, see the MathWorks Web site.

Communications Blockset™ Reference

The software described in this document is furnished under a license agreement. The software may be used or copied only under the terms of the license agreement. No part of this manual may be photocopied or reproduced in any form without prior written consent from The MathW orks, Inc.

FEDERAL ACQUISITION: This provision applies to all acquisitions of the Program and Documentation by, for, or through the federal government of the United States. By accepting delivery of the Program or Documentation, the government hereby agrees that this software or documentation qualifies as commercial computer software or commercial computer software documentation as such terms are used or defined in FAR 12.212, DFARS Part 227.72, and DFARS 252.227-7014. Accordingly, the terms and conditions of this Agreement and only those rights specified in this Agreement, shall pertain to and govern theuse,modification,reproduction,release,performance,display,anddisclosureoftheProgramand Documentation by the federal government (or other entity acquiring for or through the federal government) and shall supersede any conflicting contractual terms or conditions. If this License fails to meet the government’s needs or is inconsistent in any respect with federal procurement law, the government agrees to return the Program and Docu mentation, unused, to The MathWorks, Inc.

Trademarks

MATLAB and Simulink are registered trademarks of The MathWorks, Inc. See

www.mathworks.com/trademarks for a list of additional trademarks. Other product or brand

names may be trademarks or registered trademarks of their respective holders.

Patents

The MathWorks products are protected by one or more U.S. patents. Please see

www.mathworks.com/patents for more information.

Revision History

May 2001 Online only New for Version 2.0.1 (Release 12.1) July 2002 Online only Revised for Version 2.5 (Release 13) June 2004 Online only Revised for Version 3.0 (Release 14) October 2004 Online only Revised for Version 3.0.1 (Release 14SP1) March 2005 Online only Revised for Version 3.1 (Release 14SP2) September 2005 Online only Revised for Version 3.2 (Release 14SP3) March 2006 Online only Revised for Version 3.3 (Release 2006a) September 2006 Online only Revised for Version 3.4 (Release 2006b) March 2007 Online only Revised for Version 3.5 (Release 2007a) September 2007 Online only Revised for Version 3.6 (Release 2007b) March 2008 Online only Revised for Version 4.0 (Release 2008a) October 2008 Online only Revised for Version 4.1 (Release 2008b) March 2009 Online only Revised for Version 4.2 (Release 2009a) September 2009 Online only Revised for Version 4.3 (Release 2009b) March 2010 Online only Revised for Version 4.4 (Release 2010a)

Block Reference

Communications Sources ........................... 1-2

Random Data Sources Noise G enerators Sequence Generators

.............................. 1-2

.................................. 1-2

.............................. 1-2

Contents

Communications Sinks

Source Coding

Error Detection and Correction

Block Coding Convolutional Coding Cyclic Redundancy Check Coding

Interleaving

Block Interleaving Convolutional Interleaving

MIMO

Modulation

Digital Baseband AM Sublibrary Digital Baseband PM Sublibrary Digital Baseband FM Sublibrary Digital Baseband CPM Sublibrary Digital Baseband TCM Sublibrary Analog Pa ssb an d Modulation

............................................ 1-8

..................................... 1-3

..................................... 1-4

....................................... 1-6

....................................... 1-8

............................. 1-3

.............................. 1-5

................................. 1-6

.......................... 1-7

........................ 1-11

..................... 1-4

.................... 1-6

..................... 1-8

..................... 1-9

..................... 1-10

.................... 1-10

.................... 1-11

Communications F ilters

Channels

.......................................... 1-12

............................ 1-12

RF Impairments ................................... 1-13

Synchronization

Carrier Phase Recovery Timing Phase Recovery Synchronization Components

Equalizers

Sequence Operations

Utility Blocks

................................... 1-13

............................ 1-14

............................. 1-14

........................ 1-14

........................................ 1-15

.............................. 1-16

..................................... 1-17

Blocks — Alphabetical List

Function Reference

vi Contents

Algorithm Used to Decode BCH and

Reed-Solomon Codes

Errors-only Decoding .............................. A-2

Errors and Erasures Decoding

References

........................................ A-4

...................... A-3

Index

vii

viii Contents

Block Reference

Communications Sources (p. 1-2) Sources of random and nonrandom

data

Communications Sinks (p. 1-3)

Source Coding (p. 1-3) Quantization, companding, and

Error Detection and Correction (p. 1-4)

Interleaving (p. 1-6)

MIMO (p. 1-8) Multiple Input Multiple Output

Modulation (p. 1-8)

Communications Filters (p. 1-12)

Channels (p. 1-12)

RF Impairments (p. 1-13)

Synchronization (p. 1-13)

Equalizers (p. 1-15) Adaptive and MLSE equalizers

Sequence Operations (p. 1-16) Scrambling, puncturing, and other

Error statistics and plotting

differential coding

Block, convolutional, and CRC coding

Block and convolutional interleaving

blocks

Digital baseban d and analog passband modulation

Filtering a nd pulse shaping

Modeling channel impairments

Modeling impairments caused by the radio frequency components

Phase recovery methods and phase-locked loops

operations on sequences

Utility Blocks (p. 1-17)

Miscellaneous relevant blocks

1 Block Reference

Communications Sources

These are the sublibraries of Communications Sources:

Random Data Sources (p. 1-2)

Noise Generators (p. 1-2)

Sequence Generators (p. 1-2)

Random Data Sources

Bernoulli Binary Generator Generate Bernoulli-distributed

Poisson Integer Generator Generate Poisson-distributed

Random Integer Generator Generate integers randomly

random binary numbers

random integers

distributed in range [0, M-1]

1-2

Noise Generators

Gaussian Noise Generator Generate Gaussian distributed noise

with given mean and variance values

Rayleigh Noise Generator Generate Rayleigh distributed noise

Rician Noise Generator Generate Rician distributed noise

Uniform Noise Generator Generate uniformly distributed noise

between upper and lower bounds

Sequence Generators

Barker Code Generator Generate Barker Code

Gold Sequence Generator Generate Gold sequence from set of

sequences

Hadamard Code Generator Generate Hadamard code from

Kasami Se quence Generator Generate Kasami sequence from set

OVSF Code Generator Generate orthogonal variable

PN Sequence Generator Generate pseudonoise sequence

Walsh Code Generator Generate Walsh code from

Communications Sinks

Discrete-Time Eye Diagram Scope Display multiple traces of modulated

Communications Sinks

orthogonal set of codes

of Kasami sequences

spreading factor (OVSF) code from set of orthogonal codes

orthogonal set of codes

signal

Discrete-Time Scatter Plot Scope

Discrete-Time Signal Trajectory Scope

Error Rate Calculation Compute bit error rate or symbol

Source Coding

A-Law Compressor Implement A-law compressor for

A-Law Expander Implement A-law expander for

Display in-phase a nd quadrature components of modulated signal constellation

Plot modulated signal’s in-pha s e component versus its quadrature component

error rate of input data

source coding

1-3

1 Block Reference

Differential Decoder

Differential Encoder

Mu-Law Compressor Implement µ-law compressor for

Mu-Law Expander

Quantizing Decoder

Quantizing Encoder Quantize signal using partition and

Error Detection and Correction

ThesearethesublibrariesofError Detection and Correction:

Block Coding (p. 1-4)

Convolutional Coding (p. 1-5)

Decode binary signal using differential coding

Encode binary s ignal using differential coding

source coding

Implement µ-law expander for source coding

Decode quantization index according to codebook

codebook

1-4

Cyclic Redundancy Check Coding (p. 1-6)

Block Coding

BCH Decoder Decode BCH code to recover binary

vector data

BCH Encoder Create BCH code from binary vector

data

Binary Cyclic Decoder

Decode systematic cyclic code to recover binary vector data

Error Detection and Correction

Binary Cyclic Encoder Create systematic cyclic code from

binary vector data

Binary Linear Decoder Decode linear block code to recover

binary vector data

Binary Linear Encoder

Binary-Input RS Encoder Create Reed-Solomon code from

Binary-Output RS Decoder Decode Reed-Solomon code to recover

Hamming Decoder Decode Hamming code to recover

Hamming Encoder

Integer-Input RS Encoder Create Reed-So lomon code from

Integer-Output RS Decoder Decode Reed-Solomon code to recover

LDPC Decoder

LDPC Encoder

Create linear block code from binary vector data

binary vector data

Create Hamming code from binary vector data

integer vector data

Decode binary low-density parity-check code specified by parity-check matrix

Encode binary low-density parity-check code specified by parity-check matrix

Convolutional Coding

APP Decoder

Convolutional E ncoder Create convolutional code from

Viterbi Decoder Decode convolutionally encoded data

Decode convolutional code using a posteriori probability (APP) method

binary data

using Viterbi al gorithm

1-5

1 Block Reference

Interleaving

Cyclic Redundan

CRC-N Generator Generate CRC bits according to CRC

CRC-N Syndrome Detector Detect errors in input data frames

General CRC Generator Generate CRC bits according to

General CRC Syndrome Detector Detect errors in input data frames

These are the sublibraries of Interleaving:

Block In

Convolu

terleaving (p. 1-6)

tional Interleaving (p. 1-7)

cy Check Coding

methodandappendtoinputdata frames

according to selected CR C method

generator polynomial and append to input data frames

according to generator polynomial

1-6

Block Interleaving

raic Deinterleaver

Algeb

braic Interleaver

Alge

General Block Deinterleaver Restore ordering of symbols in input

General B lock Interleaver

re ordering of input symbols

Resto

algebraically derived

using

tation

permu

Reorder input symbols using algebraically derived permutation table

vector

Reorder symbols in input vector

Interleaving

Matrix Deinterleaver

Matrix Helical Scan Deinterleaver Restore ordering of input symbols by

Matrix Helical Scan Interleaver

Matrix Interleaver

Random Deinterleaver

Random Interleaver Reorder input symbols using random

Permute input symbols by filling matrix by columns and emptying it by rows

filling matrix alon g diagonals

Permute input symbols by selecting matrix elements along diag onals

Permute input symbols by filling matrix by rows and emptying it by columns

Restore ordering of input symbols using random permutation

permutation

Convolutional Interleaving

Convolutional Deinterleaver Restore ordering of symbols that

were permuted using shift registers

Convolutional Interleaver Permute input symbols using set of

shift registers

General Multiplexed Deinterleaver Restore ordering of symbo ls using

specified-delay shift regi sters

General Multiplex ed Interleaver Permute input sy mbols using set of

shift re gi sters with specified delays

Helical Deinterleaver

Helical Interleaver Permute input symbols using helical

Restore ordering of symbols permuted by helical interleaver

array

1-7

1 Block Reference

MIMO

OSTBC Combiner Combine inputs for received signals

and channel estimate according to orthogonal space-time block code (OSTBC)

Modulation

OSTBC Encoder

These are the sublibraries of Modulation:

Digital Baseband AM Sublibrary (p. 1-8)

Digital Baseband PM Sublibrary (p. 1-9)

Digital Baseband FM Sublibrary (p. 1-10)

Digital Baseband CPM Sublibrary (p. 1-10)

Digital Baseband TCM Sublibrary (p. 1-11)

Analog Passband Modulation (p. 1-11)

Encode input message using orthogonal space-time block code (OSTBC)

1-8

Digital Baseband AM Sublibrary

General Q AM De modulator Baseband

General QAM Modulator Baseband

Demodulate QAM-modulated data

Modulate using quadrature amplitude modulation

M-PAM D emodulator Baseband Demodulate PAM-modulated data

Modulation

M-PAM Modulator Baseband

Rectangular QAM Demodulator Baseband

Rectangular QAM Modulator Baseband

Modulate using M-ary pulse amplitude modulation

Demodulate rectangular-QAM-modulated data

Modulate using rectangular quadrature amplitude modulation

Digital Baseband PM Sublibrary

BPSK Demodulator Baseband Demodulate BPSK-modulated data

BPSK Modulator Baseband Modulate using binary phase shift

keying method

DBPSK D emodulator Baseband Demodulate DBPSK-modulated data

DBPSK Modulator Baseband Modulate using differential binary

phase shift keying method

DQPSK Demodulator Baseband Demodulate DQPSK-modulated

data

DQPSK M odulator Baseband Modulate using differential

quaternary phase shift keying method

M-DPSK Demodulator Baseband Demodulate D PSK-modulated data

M-DPSK M odulator Baseband Modulate using M-ary differential

phase shift keying method

M-PSK Demodulator Baseband Demodulate PSK-modulated data

M-PSK Modulator Baseband Modulate using M-ary phase shift

keying method

OQPSK Demodulator Baseband Demodulate OQPSK-modulated

data

OQPSK M odulator Baseband Modulate using offset quadrature

phase shift keying method

1-9

1 Block Reference

QPSK Dem odulator Baseband Demodulate QPSK-modulated data

QPSK Modulator Baseband

Modulate using quaternary phase shift keying method

Digital Baseband F M Sublibrary

M-FSK Demodulator Baseband Demodulate FSK-modulated data

M-FSK M odulator Baseband Modulate using M-ary frequency

shift keying method

Digital Baseband CPM Sublibrary

CPFSK Demodulator Baseband Demodulate CPFSK-modulated data

CPFSK Modulator Baseband

CPM Demodulator Baseband Demodulate CPM-modulated data

CPM Modulator Baseband

GMSK Demodulator Baseband Demodulate GMSK-modulated data

GMSK Modulator Baseband Modulate using Gaussian minimum

Modulate using continuous phase frequency shift keying method

Modulate using continuous phase modulation

shift keying method

1-10

MSK D emodulator Baseband Demodulate MSK-modulated data

MSK Modulator Ba seb an d Modulate using minimum shift

keying method

Modulation

Digital Baseban

General TCM Decoder

General TCM En

M-PSK TCM Dec

M-PSK TCM Encoder Convolutionally encode binary data

Rectangular QA M TCM Decoder

Rectangular QAM TCM Encoder Convolutionally encode binary data

Analog

DSB AM Demodulator Passband Demodulate DSB-AM-modulated

Passband Modulation

dTCMSublibrary

coder

oder

Decode trellisdata, mapped us constellation

Convolutiona data and map us constellati

Decode trellis-coded modulation data, modulated using PSK method

and modulate using PSK method

Decode trellis-coded modulation data, modulated using QAM method

and modulate using QAM method

data

coded modulation

ing arbitrary

lly encode binary

ing arbitrary

late using double-sideband

DSB AM Modulator Passband

SC AM Demodulator Passband

DSB

SC AM Modulator Passband

DSB

FM Demodulator Passband Demodulate FM-modulated data

FM Modulator Passband

PM Demodulator Passband Demodulate PM-modulated data

PM Modulator Passband Modulate using phase modulation

Modu

itude modulation

ampl

odulate DSBSC-AM-modulated

Dem

dat

Modulate using double-sideban d suppressed-carrier amplitude modulation

Modulate using frequency modulation

1-11

1 Block Reference

SSB AM Demodulator Passband Demodulate SSB-AM-modulated

data

SSB AM Modulator Passband

Communications Filters

Gaussian Filter

Ideal Rectangular Pulse Filter

Integrate and Dump Integrate discrete-time signal,

Raised Cosine Receive Filter

Raised Cosine Transmit Filter Upsample and filter input signal

Windowed Integrator

Modulate using single-sideband amplitude modulation

Filter input signal, possibly downsampling, using Gaussian FIR filter

Shape input signal using ideal rectangular pulses

resettingtozeroperiodically

Filter input signal, possibly downsampling, using raised cosine FIR filter

using raised cosine FIR filter

Integrateovertimewindowoffixed length

Channels

1-12

AWGN Channel Add white Gaussian noise to input

signal

Binary Symmetric Channel

Introduce binary errors

Multipath Rayleigh Fading Channel Simulate multipath Rayleigh fading

Multipath Rician Fading Channel Simulate multipath Rician fading

RF Impairments

Free Space Path Loss Reduce amplitude of input signal by

I/Q Imbalance Create complex baseband m odel

RF Impairments

propagation channel

amount specified

of signal impairments caused by imbalances between in-phase and quadrature receiv er components

Memoryless Nonlinearity

Phase Noise

Phase/Frequency Offset Apply phase and frequency offsets to

Receiver Thermal Noise

Synchronization

These are the sublibraries of Synchronization:

Carrier Phase Recovery (p. 1-14)

Timing Phase Recovery (p. 1-14)

Synchronization Components (p. 1-14)

Apply memoryless nonlinearity to complex baseband signal

Apply receiver phase noise to complex baseband signal

complex baseband signal

Apply receiver thermal noise to complex baseband signal

1-13

1 Block Reference

covery

Recover carrier 2P-Power metho

Recover carrier phase using M-Pow er method

phase using d

Carrier Phase Re

CPM Phase Recovery

M-PSK Phase Re

Timing Phase Recover y

Early-Late Gate Timing Recovery

Gardner Timing Recovery

MSK-Type

Mueller-Muller Timing Recovery Recover symbol timing phase using

Squaring Timing Recovery

Signal Timing Recovery

Recover symbol timing phase using early-late gate method

Recover sy Gardner’s

Recover symbol timing phase using fourth-order nonlinearity method

Mueller-Muller method

Recov squar

mbol timing phase using method

er symbol timing phase using

ing method

1-14

Synchronization Components

Baseband PLL Implement baseband phase-locked

loop

Charge Pump PLL

Continuous-Time VCO

Discrete-Time VCO

Implement charge pump phase-locked loop using digital phase detector

mplement voltage-controlled

scillator

Implement voltage-controlled oscillator in discrete time

Equalizers

Linearized B aseband PLL

Phase-Locked Loop Impleme nt phase-locke d loop to

CMA Equalizer

LMS Decisio n Feedback E qualizer Equalize using decision feedback

LMS Linear Equalizer

MLSE Equalizer

Normalized L M S Decision Feedback Equalizer

Implement linearized version of baseband phase-locked loop

recover phase of input signal

Equalize using constant modulus algorithm

equalizer that updates weights with LMS algorithm

Equalize using linear equalizer that updates weights with LMS algorithm

Equalize using Viterbi algorithm

Equalize using decision feedback equalizer that updates weights with normalized LMS algorithm

Normalized LMS Linear Equalizer

RLS Decision Feedback Equalizer Equalize using decision feedback

RLS Linear Equalizer

Sign LMS Decision Feedback Equalizer

Equalize using linear equalizer that updates weights with normalized LMS algorithm

equalizer that updates weights with RLS algorithm

Equalize using linear equalizer that updates weights using RLS algorithm

Equalize using decision feedback equalizer that updates weights with signed LMS algorithm

1-15

1 Block Reference

Sign LMS Linear Equalizer

Variable Step LMS Decision Feedback Equalizer

Variable Step LMS Linear Equalizer

Sequence Operations

Deinterlacer

Derepeat

Descrambler Descramble input signal

Insert Zero

Equalize using linear equalizer that updates weights with signed LMS algorithm

Equalize using decision feedback equalizer that updates weights with variable-step-size LMS algorithm

Equalize using linear equalizer that updates weights with variable-step-size LMS algorithm

Distribute elements of input vector alternately between two output vectors

Reduce sampling rate by averaging consecutive samples

Distribute input elements in output vector

1-16

Interlacer

Puncture

Scrambler Scramble input signal

Alternately select elements from two input vectors to generate output vector

Output elements which correspond to 1s in binary Puncture vector

Utility Blocks

Align Signals Align two signals by finding delay

between them

Bipolar to Unipolar Converter

Bit to Integer Converter Map vector of bits to corre sponding

Complex Phase Difference Output phase difference between

Complex Phase Shift Shift phase of complex input signal

Data Mapper

EVM Measurement

Find De

Integ

MER Measurement

Uni

lay

er to Bit Converter

polar to Bipolar Converter

Map bipolar signal into unipolar signal in range [0, M-1]

vector of integers

two complex input signals

by second input value

Map integer symbols from one coding scheme to another

Calculate vector magnitude difference between ideal reference signal and measured signal

Find de

Map ve bits

Meas in di

Map unipolar signal in range [0, M-1] into bipolar signal

lay betw een two signals

ctor of integers to vector of

ure signal-to-noise ratio (SNR)

gital modulationapplications

1-17

1 Block Reference

1-18

Blocks — Alphabetical List

A-Law Compressor

Purpose Implement A-law compressor for source coding

Library Source Coding

Description The A-Law Compressor block implements an A-law compressor for the

input signal. The formula for the A-law compressor is

⎧ ⎪

log

⎪

⎨

VAxV

log( / )

()

⎪ ⎪

⎩

where A is the A-law parameter of the compressor, V is the peak signal magnitude for x, log is the natural logarithm, and sgn is the signum function (

The most commonly used A value is 87.6.

The input can have any shape or frame status. This block processes each vector element independently.

sgn( )

log

sgn( )

software).

for

≤≤

<<≤

2-2

Dialog Box

A value

The A-law parameter of the compressor.

A-Law Compressor

Peak signal m agnitude

The peak value of the input signal. This is also the peak value of the output signal.

Supported Data Type

Port

Out

Supported Data Types

• double

Pair Block A-Law Expander

See Also General Block Interleaver

References [1] Heegard, Chris and Stephe n B. Wicker. Turbo Coding.Boston:

Kluwer Academic Publishers, 1999.

[2]Takeshita,O.Y.andD.J.Costello,Jr. "NewClassesOfAlgebraic Interleavers for Turbo-Codes." Proc. 1998 IEEE International Symposium on Information Theory, Boston, Aug. 16-21, 1998. 419.

Welch-Costas.

2-11

Align Signals

Purpose Align two signals by finding delay between them

Library Utility Blocks

Description The Align Signals block aligns a signal with a delayed, and possibly

distorted, version of itself. The block is particularly useful when you want to compare a transmitted and received signal to find the bit error rate, but do not know the delay in the received signal.

The input port labeled port labeled signals must have the same sample times. The block calculates the delay between the two signal, and then

• Delays the first signal,

through the port labeled

• Outputs the second signal

labeled

• Outputs the delay value through the port labeled

See “Computing Delays” in the Communications Blockset™ online documentation for more information about signal delays.

The block’s Correlation window length parameter specifies how many samples of the signals the block uses to calculate the cross-correlation. The delay output is a nonnegative integer less than the Correlation window length.

As the Correlation window length is increased, the reliability of the computed delay also increases. However, the processing time to compute the delay increases as well.

You can make the Align Signals block stop updating the delay after it computes the same delay value for a specified number of samples. To do so, select the Disable recurring updates check box, and enter a positive integer in the Num ber of constant delay outputs to disable

updates field. For example, if you set Number of constant delay outputs to disable updates to

s2 receives the delayed version of the signal. The two input

s2.

s1 receives the original signal, while the input

s1, by the calculated value, and outputs it

s1 del.

s2 without change through the port

delay.

20, the block will stop recalculating

2-12

Align Signals

and updating the delay after it calculates the same value 20 times in succession. Disabling recurring updates causes the simulation to run faster after the target number of constant delays occurs.

Tips for Using the Block Effectively

• Set the Correlation window length parameter sufficiently large so

that the computed delay eventually stabilizes at a constant value. If the computed delay is not constant, you should increase Correlation

window length. If the increased value of Correlation window length ex ceeds the duratio n of the simulation, then you should also

increase the duration of the simulation accordingly.

• If the cross-correlation between the two signals is broad, then

Correlation window length should be much larger than the expected delay, or else the algorithm might stabilize at an incorrect value. For example, a CPM signal has a broad autocorrelation, so it has a broad cross-correlation with a delayed version of itself. In this case, the Correlation window length value should be much larger than the expected delay.

• If the block calculates a delay that is greater than 75 percent of

Correlation window length,thesignal relative to the signal lines leading into the two input ports.

• If you use the Align Signals block with the Error Rate Calculation

block, you should set the Receive delay parameter of the Error Rate Calculation block to for the delay. Also, you might want to set the Error Rate Calculation block’s Computation delay parameter to a nonzero value to account for the possibility that the Align Signals block takes a nonzero amount of time to stabilize on the correct amount by which to delay one of the signals.

s2. Inthiscase,youshouldswitchthesignal

0 because the Align Signals block compensates

s1 is probably delayed

Examples See the“Computing Delays” section of Communications Blockset User’s

Guide for an example that uses the Align Signals block in conjunction

with the Error Rate Calculation block.

2-13

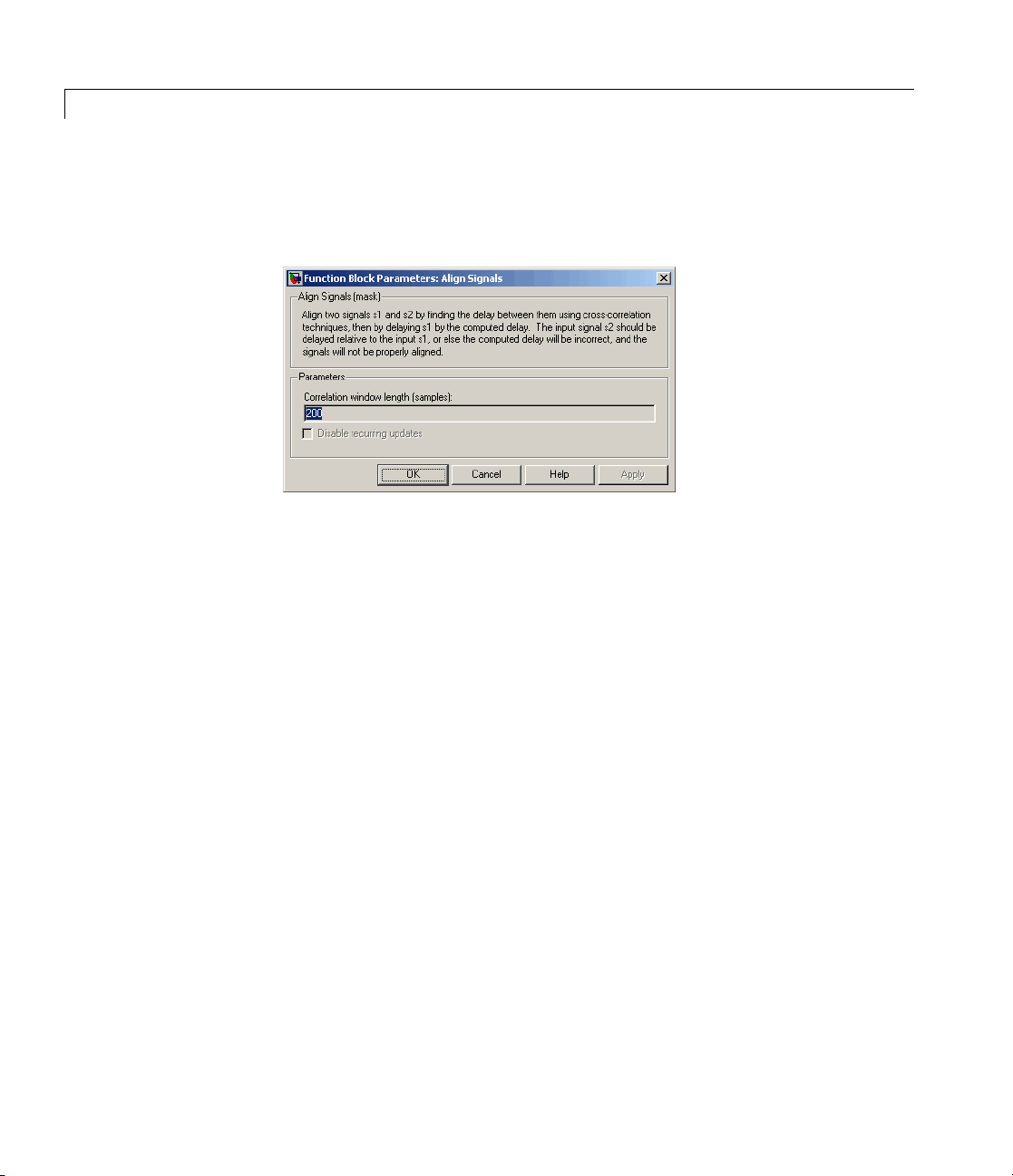
Align Signals

Dialog Box

See S etting the Correlation Window Length, on the reference page for the Find Delay block, for an example that illustrates how to set the correlation window length properly.

Correlati

Disable r

Number o

on window length

The number cross-co

ecurring updates

Selectin after it of sampl

f constant delay outputs to disable updates

Aposit comput appear

of samples the block uses to calculate the

rrelations of the two signals.

g this option causes the block to stop computing the delay

computes the same delay value for a specified number

es.

ive integer specifying how many times the block must

e the same delay before ceasing to update. This field

sonlyifDisable recurring updates is selected.

Algorithm The Align Signals block finds the delay by calculatin g the

cross-correlations of the first signal with time-shifted versions of the second signal, and then finding the index at which the cross-correlation is maximized.

See Also Find Delay, Error Rate Calculation

2-14

APP Decoder

Purpose Decode convolutional code using a posteriori probability (APP) method

Library Convolutional sublibrary of Channel Coding

Description The APP Decoder block performs a posteriori probability (APP) decoding

of a convolutional code.

Inputs and Outputs

The input L(u) represents the sequence of log-likelihoods of encoder input bits, while th e input L(c) r epresents the sequence of log-likelihoods of code bits. The outputs L(u) and L(c) are updated versions of these sequences, based on information about the encoder.

If the convolutional code uses an alphabet of 2 this block’s L(c) vectors have length Q*n for some positive integer Q. Similarly, if the decoded data uses an alphabet of 2 symbols, then this block’s L(u) vectors have length Q* k.TheintegerQ is the number of frames that the block processes in each step.

The inputs can be either

possible symbols,

possible output

• Sample-based vectors having the same dimension and orientation,

with Q = 1

• Frame-based column vectors with any positive integer for Q

If you only need the input L(c) and output L(u), you can attach a Simulink Ground block to the input L(u) and a Simulink Terminator block to the output L(c).

This block accepts however, must be of the s am e type. The output data type is the same as the input data type.

single and double data types. Both inputs,

Specifying the Encoder

To define the convolutional encoder that produced the coded input, use the Trellis structure parameter. This parameter is a MATLAB structure whose format is described in “Trellis Description

2-15

APP D ecoder

of a Convolutional Encoder” in the Communications Toolbox™ documentation. You can use this parameter field in two ways:

• IfyouhaveavariableintheMATLAB workspace that contains the

trellis structure, enter its name as the Trellis structure parameter. This way is preferable because it causes Simulink

to spend less time updating the diagram at the beginning of each simulation, compared to the usage described next.

• If you want to specify the encoder using its constraint length,

generator polynomials, and possibly feedback connection polynomials, use a

poly2trellis command within the Trellis structure field.

For example, to use an encoder with a constraint length of 7, code generator polynomials of 171 and 133 (in octal numbers), and a feedback connection of 171 (in octal), set the Trellis structure parameter to

poly2trellis(7,[171 133],171)

To indicate how the encoder treats the trellis a t the beginning and end of each frame, set the Termination method parameter to either

Truncated or Terminated.TheTruncated option indicates that the

encoder resets to the all-zeros state at the beginning of each frame. The

Terminated option indicates that the encoder forces the trellis to end

each frame in the all-zeros state. If you use the Convolutional Encoder block w ith the Operation mode parameter set to

every frame)

,usetheTruncated option in this block. If you use the

Truncated (reset

Convolutional Encoder block with the Operation mode parameter set to

Terminate trellis by appending tail bits,usetheTerminated

option in this block.

2-16

Specifying Details of the Algorithm

You can control part of the decoding algorithm using the Algorithm parameter. The

True APP option implements a posteriori probability

decoding as per equations 20–23 in section V of [1]. To gain speed, both the

Max* and Max options approximate expressions like

APP Decoder

Dialog Box

log exp( )a

∑

by other quantities. The Max option uses max(ai) as the approximation, while the

ln( exp( ))11+−−

Max* option enables the Scaling bits parameter in the dialog box.

The This parameter is the number of bits by which the block scales the data it processes internally (multiplies the input by (2^ divides the pre-output by the same factor). Use this parameter to avoid losing precision during the computations.

Max* option uses max(a

−

[3].

) plus a correction term given by

numScalingBits)and

Trellis structure

MATLAB structure that contains the trellis description of the convolutional encoder.

Termination method

Either the convolutional encoder treats the trellis at the beginning and end of frames.

Truncated or Terminated. This parameter indicates how

2-17

APP D ecoder

Algorithm

Either

Number of scaling bits

An integer between 0 and 8 that indicates by how many bits the decoder scales data in order to avoid losing precision. This field is active only when Algorithm is set to

See Also Viterbi Decoder, Convolutional Encoder;poly2trellis

References [1] Benedetto, S., G. Montorsi, D. Divsalar, and F. Polla ra , “A S of t-In p ut

Soft-Output Maximum A Posterior (MAP) Module to Decode Parallel and Serial Concatenated Codes,” JPL TDA P rogress Report, Vol. 42-127, November 1996.

[2] Benedetto, Sergio and Guido Montorsi, “Performance of Continuous and Blockwise Decoded Turbo Codes.” IEEE Communications Letters, Vol. 1, May 1997, 77–79.

[3] Viterbi, Andrew J., “An Intuitive Justification and a Simplified Implementation of the MAP Decoder for Convolutional Codes,” IEEE Journal on Selected Areas in Communications, Vol. 16, February 1998, 260–264.

True APP, Max*,orMax.

Max*.

2-18

AWGN Channel

Purpose Add white Gaussian noise to input signal

Library Channels

Description TheAWGNChannelblockaddswhiteGaussiannoisetoarealor

complex input signal. When the input signal is real, this block adds real Gaussian noise and produces a real output signal. When the input signal is complex, this block adds complex Gaussian noise an d produces a complex output signal. This block inherits its sample time from the input signal.

This block uses the Signal Processing Blockset™ Random Source block to generate the noise. Random numbers are generated using the Ziggurat method, which is the same method used by the MATLAB

randn function. The Initial seed parameter in this block initializes the

noise generator. Initial seed canbeeitherascalaroravectorwhose length matches the number of channels in the input signal. For details on Initial seed, see the Random Source block reference page in the Signal Processing Blockset documentation set.

The signal inputs can only be of type types are inherited from the signals that drive the block.

Note All values of pow er assume a nominal impedance of 1 ohm.

single or double. The port data

Frame-Based Processing and Input Dimensions

This block can process multichannel signals that are frame-based or sample-based. The guidelines below in dicate how the block interprets your data, depending on the data’s shape and frame status:

• If your input is a sample-based scalar, then the block adds scalar

Gaussian noise to your signal.

• If your input is a sample-based vector or a frame-based row vector,

then th e block adds independent Gaussian noise to each channel.

2-19

AWGN Channel

• If your input is a frame-based column vector, then the block adds a

• If your input is a frame-based m-by-n m atrix, then the block adds

The input cannot be a sample-based m-by-n matrix if both m and n are greater than 1.

Specifying the Variance Directly or Indirectly

You can specify the variance of the noise generated by the AWGN Channel block using one of these modes:

•

frame of Gaussian noise to your single-channel signal.

a length-m frame of Gaussian noise independently to each of the n channels.

Signal to noise ratio (Eb/No), where the block calculates the

variance from these quantities that you specify in the dialog box:

- Eb/No, the ratio of bit energy to noise power spectral density

- Number of bits per symbol

2-20

- Input signal power, the actual power of the symbols at the input

of the block

- Symbol period

Signal to noise ratio (Es/No), where the block calculates the

•

variance from these quantities that you specify in the dialog box:

- Es/No, the ratio of signal energy to noise power spectral density

- Input signal power, the actual power of the symbols at the input

of the block

- Symbol period

Signal to noise ratio (SNR), where the block calculates the

•

variance from these quantities that you specify in the dialog box:

- SNR, the ratio of signal power to noise power

- Input signal power, the actual power of the samples at the input

of the block

AWGN Channel

• Variance from mask, where you specify the variance in the dialog

box. The value must be positive.

•

Variance from port, where you provide the variance as an input

to the block. The variance input must be positive, and its sampling rate must equal that of the input signal. If the first input signal is sample-based, then the variance input must be sample-based. If the first input signal is frame-based, then the variance input can be either fram e-based with exactly one row, or sample-based.

Changing the symbol period in the

AWGN Channel block affects the

variance of the noise added per sample, which also causes a change in the final error rate.

NoiseVariance

SignalPower S ymbolPeriod

SampleTime

Es No

×10

A good rule of thumb for selecting the Sym b ol period value is to setittobewhatyoumodelasthesymbolperiodinthemodel. The value would depend upon what constitutes a symbol and what the oversampling applied to it is (e.g., a symbol could have 3 bits and be oversampled by 4).

In both

Variance from mask mode and Variance from port mode,

these rules describe how the block interprets the variance:

• If the variance is a scalar, then all signal channels are uncorrelated

but share the same variance.

• Ifthevarianceisavectorwhoselengthisthenumberofchannelsin

the input signal, then each element represents the variance of the corresponding signal channel.

2-21

AWGN Channel

Relationship Among Eb/No, Es/No, and SNR Modes

Note If you apply complex input signals to the AWGN Channel

block, then it adds complex zero-mean Gaussian noise with the calculated or specified variance. T he variance of each of the quadrature components of the complex noise is half of the calculated or specified value.

For complex input signals, the AWGN Channel block relates Eb/N

Es/N0, and SNR according to the following equations:

=(T

s/N0

s/N0=Eb/N0

sym/Tsamp

)·SNR

+10log10(k) in dB

where

• E

= Signal energy (Joules)

= Bit energy (Joules)

• E

= Noise power spectral density (Watts/Hz)

• N

• T

is the Symbol period parameter o f the block in Es/No mode

sym

• k is the number of information bits per input symbol

• T

For real signal inputs, the AWGN Channel block relates E

is the inherited sample time of the block, in seconds

samp

s/N0

and S NR

according to the following equation:

s/N0

=0.5(T

sym/Tsamp

)·SNR

Note that the e quation for the real case differs from the corresponding equation for the complex case by a factor of 2. This is so because the block uses a noise power spectral density of N signals, versus N

Watts/Hz for complex signals.

/2 Watts/Hz for real input

2-22

AWGN Channel

For more information about t hes e quantities, see “Describing the Noise Level of an AWGN Channel” in the Communications Toolbox documentation.

Tunable Block Parameters

The following table indicates which parameters are tunable, for different block modes.

Mode Tunable Parameters

Eb/No

Es/No

SNR

Variance from mask

You can tune parameters in normal mode, Accelerator mode and the Rapid Accelerator mode.

If you use the Re al-Time Workshop® rapid simulation (RSI M) target to build an RSIM executable, then you can tune the parameters listed in the previous table without recompiling the model. This is useful for Monte Carlo simulations in which you run the simulation multiple times (perhaps on multiple computers) with different amounts of noise.

Eb/No, In put signal power

Es/No, Input signal power

SNR, Inpu t signal power

Variance

2-23

AWGN Channel

2-24

Dialog Box

Initial seed

The seed for the Gaussian noise generator.

Mode

The mode by which you specify the noise variance:

noise ratio (Eb/No) Signal to noise ratio (SNR), Variance from mask,or Variance from port.

Eb/No (dB)

The ratio of bit energy per symbol to noise power spectral density, in decibels. This field appears only if Mode is set to

Es/No (dB)

The ratio of signal energy per symbol to noise power spectral density, in decibels. This field appears only if Mode is set to

Es/No.

, Signal to noise ratio (Es/No),

Signal to

Eb/No.

AWGN Channel

SNR (dB)

The ratio of signal power to noise power, in decibels. This field appears only if Mode is set to

Number of bits per symbol

The number of bits in each input symbol. This field appears only if Mode is set to

Input signal power, referenced to 1 ohm (watts)

The mean square power of the input symbols (if Mode is or Es/No) or input samples (if Mode is SNR), in watts. This field appears only if Mode is set to

Symbol period (s)

The duration of a channel symbol, in seconds. This field appears only if Mode is set to

Variance

ThevarianceofthewhiteGaussiannoise. This field appears only if Mode is set to

Eb/No.

Eb/No or Es/No.

Variance from mask.

SNR.

Eb/No, Es/No,orSNR.

Eb/No

Examples Many demonstration models and documentation examples use this

block, including:

• Gray Coded 8-PSK demo,

• Phase Noise Effects in 256-QAM demo,

• “Building a Frequency-Shift Keying Model” (

• “Example: Using Raised C osine Filters” (

• Discrete Multitone Signaling Demo,

mode)

commgraycode (EbNo mode)

commphasenoise (EsNo mode)

EsNo mode)

SNR mode)

commdmt (Variance from mask

See Also Random Source (Signal Processing Blockset documentation)

Reference [1] Proakis, John G., Digital Communications, 4th Ed., McGraw - Hill,

2001.

2-25

Barker Code Generator

Purpose Generate Barker Code

Library Sequence Generators sublibrary of Comm Sources

Description Barker codes, which are subsets of PN sequences, are commonly used

for frame synchro n iza t ion in digital communication systems. Barker codes have length at most 13 and have low correlation sidelobes. A correlation sidelobe is the correlation of a codeword with a time-shifted version of itself. The correlation sidelobe, C N-bit code sequence, {X

−

CXX

kjjk

∑

}, is given by

where Xjis an individual code symbol taking values +1 or -1 for j=1, 2, 3,..., N, and the adjace n t symbols are assumed to be zero.

The Barker Code Generator block provide s the codes listed in the following table:

, for a k-symbol shift of an

2-26

Code length Barker Code

1[-1]

2[-11];

3 [-1 -1 1]

4 [-1 -1 1 -1]

5 [-1 -1 -1 1 -1]

7 [-1 -1 -1 1 1 -1 1]

11 [-1-1-1111-111-11]

13 [-1-1-1-1-111-1-11-11-1]

Dialog Box

Barker Code Generator

Opening this dialog box causes a running simulation to pause. See “ Changing Source Block Param eters ” in the online Simulink documentation for details.

Code length

The length of the Barker code.

Sample time

Period of each element of the output signal.

Frame-based outputs

Determines whether the block’s output is frame-based or sample-based.

Samples per frame

The number of samples in a frame-based output signal. This field appears if you select the Frame-based outputs check box.

Output data type

The output type of the block can be specified as an By default, the block sets this to

See Also PN Sequence Generator

int8 or double.

double.

2-27

Baseband PLL

Purpose Implement baseband phase-locked loop

Library Components sublibrary of Synchronization

Description The Baseband PLL (phase-locked loop) block is a feedback control

system that automatically adjusts the phase of a locally generated signal to match the phase of an input signal. Unlike thePhase-Locked Loop block, this block uses a baseband method and does not depend on a carrier frequency.

This PLL has these three components:

• An integrator used as a phase detector.

• A filter. You s pecify the filter’s transfer function using the Lowpass

filter numerator and Lowpass filter denominator parameters. Each is a vector that gives the respective polynomial’s coefficients in order of descending powers of s.

To design a filter, you can use the Signal Processing Toolbox™ functions II filter whose transfer function arises from the command below .

cheby1,andcheby2. The default filter is a Chebyshev type

2-28

[num, den] = cheby2(3,40,100,'s')

• A voltage-controlled oscillator (VCO). You specify the sensitivity

of the VCO signal to its input using the VCO input sensitivity parameter. This parameter, measured in Hertz per volt, is a scale factor that determines how much the VCO shifts from its quiescent frequency.

The input signal represents the received signal. The input must be a sample-based scalar signal. The three output ports produce:

• The output of the filter

• The output of the phase detector

• The output of the VCO

Dialog Box

Baseband PLL

This model is nonlinear; for a linearized version, use theLinearized Baseband PLL block.

Lowpass filter numerator

The numerator of the lowpass filter’s transfer function, represented as a vector that lists the coefficients in order of descending powers of s.

Lowpass filter denominator

The denominator of the lowpass filter’s transfer function, represented as a vector that lists the coefficients in order of descending powers of s.

VCO input sensitivity (Hz/V)

This value scales the input to the VCO and, consequently, the shift from the VCO’s quiescent frequency.

See Also Linearized Baseband PLL, Phase-Locked Loop

Refe

rences

ore information about phase-locked loops, see the works listed

For m

elected Bibliography for Synchronization” in Communications

in “S

kset User’s Guide.

Bloc

2-29

BCH Decoder

Purpose Decode BCH code to recover binary vector d ata

Library Block sublibrary of Channel Coding

Description The BCH Decoder block recovers a binary message vector from a binary

BCH codeword ve ctor. For proper decoding, the first two parameter values in this block should match the parameters in the corresponding BCH Encoder block.

The input must be a frame-based column vector with an integer multiple of (N - the number of punctures) elements. Each group of N input elements represents one codeword to be decoded. The values of (N + shortening length) and (K + shortening length) must produce a valid narrow-sense BCH code.

If the decoder is processing multiple codewords per frame, then the same puncture pattern holds for all codewords.

For a given codeword length N,onlyspecificmessagelengthsK are validforaBCHcode. ForafulllengthBCHcode,N must be of the

form 2 that the code has been shortened by length 2 greaterthanorequalto2 to appropriately set the value of M.

-1, where

316≤≤M

.IfN is less than 2M-1, the block a ssumes

M-1

, Primitive polynomial must be specified

M -1

- N. However, if N is

2-30

No known analytic formula describes the relationship among the codeword length, message length, and error-correction capability. For a list of some valid values of K corresponding to values of N up to 511, see the documentation.

The primitive and generator polynomials may be specified in their respective fields, which appear after selecting their corresponding check boxes.

To have the block output error information, select Output number of corrected errors. Selecting this option causes a second output port to appear. The second output is the number of errors detected during

bchenc reference page in the Communications Toolbox

BCH Decoder

decoding of the codeword. A negative integer indicates that the block detected more errors than it could correct using the coding scheme.

Inthecaseofadecoderfailure,themessage portion of the decoder input is returned unchanged as the decoder output.

The sample times of all input and output signals are equal.

For i nformation about the data types each block port supports, see the “Supported D ata Type” on page 2-34 table on this page.

Punctured Codes

This block supports puncturing when you select the Punctured code parameter. This selection enables the Puncture vector parameter, which takes in a binary vector to specify the puncturing pattern. For a puncture vector,

0 means that the data symbol is punctured (i.e., removed) from the data

stream. This convention is carried for both the encoder and the decoder. For more information, see “Shortening, Puncturing, and Erasures”.

Note 1sand0s have precisely opposite meanings for the puncture and erasure vectors. For an erasure vector, is to be replaced with an erasure symbol, and symbol is passed unaltered. This convention is carried for both the encoder and the decoder.

1 means that the data symbol is passed unaltered, and

1 means that the data symbol

0 means that the data

2-31

BCH Decoder

Dialog Box

2-32

Codeword length, N

The codeword length.

Message length, K

The message length.

BCH Decoder

Specify primitive polynomial

Selecting this check box enables the field Primitive polynomial.

Primitive polynomial

A row vector that represents the binary coefficients of the primitive polynomial in order of descending powers.

This field defaults to

'left-msb')

This field appears only when you select Specify primitive polynomial.

Specify generator polynomial

Selecting this check box enables the field Generator polynomial.

Generator polynomial

A row vector that represents the binary coefficients of the generator polynomial in order of descending powers.

The length of the Generator polynomial must be N-K+1.

This field defaults to

This field appears only when you select Specify generator

polynomial.

Disable generator polynomial checking

This check box appears only when you select Specify generator polynomial.

Each time a model initializes, the block performs a polynomial check. This check verifies that X user-defined generator polynomial, where N represents the full code word length. Selecting this check box disables the polynomial check. For larger codes, dis abling the check speeds up the simulation process. You should always run the check at least once before disabling this feature.

, corresponding to a (15,5) code.

de2bi(primpoly(4, 'nodisplay'),

bchgenpoly(15,5).

+1isdivisiblebythe

2-33

BCH Decoder

Puncture code

Selecting this check box enables the field Puncture vector.

Puncture vector

This field is available onl y when Puncture code is selected.

Supported Data Type

A column vector of length N-K.Avalueof vector corresponds to a bit that is not punctured, and a corresponds to a bit that is punctured.

The default value is

Enable erasures input port

Selecting this check box will open the

Through the vectorthesamesizeasthecodewordinput.

Erasure values of in the codeword, and values of

Output number of corrected errors

Selecting this check box gives the block an additional output port, Err, which indicates the number of errors the block corrected in the input codeword.

Port

Era port, you can input a frame-based binary column

[ones(8,1); zeros(2,1)].

1 correspond to erased bits in the same position

0 correspond to nonerased bits.

Supported Data Types

• Double-precision floating point

• Single-precision floating point

1 in the Puncture

Era port.

2-34

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

BCH Decoder

Port

Out • Double-precision floating point

Era

Err

Pair Block BCH Encoder

Supported Data Types

• Single-precision floating point

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

• Double-precision floating point

• Boolean

• Double-precision floating point

• Single-precision floating point

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

References [1] Wicker, Stephen B., Error Control Systems for Digital

Communication and Storage, Upper Saddle River, N.J., Prentice Ha ll,

1995.

[2] Berlekamp, Elwyn R., Algebraic Coding Theory,NewYork, McGraw-Hill, 1968.

[3] Clark, George C., Jr., and J . Bibb Cain, Error-Correction Coding for Digital Communications, New York, Plenum Press, 1981.

2-35

BCH Decoder

See Also bchdec (in Communications Toolbox documentation)

2-36

BCH Encoder

Purpose Create BCH code from binary vector data

Library Block sublibrary of Channel Coding

Description This block supports punctures (“Shortening, Puncturing, and Erasures”

provides a tutorial).

The BCH Encoder block creates a BCH code with message length K and codeword length (N - number of punctures). You specify both N and K directly in the dialog box.

The input must be a frame-based column vector with an integer multiple of K elements. Each group of K input elements represents one message word to be encoded.

If the encoder is processing multiple codewords per frame, then the same puncture pattern holds for all codewords.

For a given codeword length N,onlyspecificmessagelengthsK are validforaBCHcode. ForafulllengthBCHcode,N must be of the

form 2 that the code has been shortened by length 2 greaterthanorequalto2 to appropriately set the value of M.

-1, where

316≤≤M

.IfN is less than 2M-1, the block a ssumes

M-1

, Primitive polynomial must be specified

M -1

- N. However, if N is

The primitive and generator polynomials may be specified in their respective fields, which appear after selecting their corresponding check boxes.

For i nformation about the data types each block port supports, see the “Supported D ata Type” on page 2-41 table on this page.

bchenc reference page in the Communications Toolbox

2-37

BCH Encoder

Puncture Codes

This block supports puncturing when you select the Puncture code parameter. This selection enables the Puncture vector parameter, which takes in a binary vector to specify the puncturing pattern. For a puncture vector,

0 means that the data symbol is punctured (i.e., removed) from the data

stream. This convention is carried for both the encoder and the decoder. For more information, see “Shortening, Puncturing, and Erasures”.

1 means that the data symbol is passed unaltered, and

1 means that the data symbol

0 means that the data

2-38

Dialog Box

BCH Encoder

Codeword length, N

The codeword length.

Message length, K

The message length.

Specify primitive polynomial

Selecting this check box enables the field Primitive polynomial.

Primitive polynomial

A row vector that represents the binary coefficients of the primitive polynomial in order of descending powers.

2-39

BCH Encoder

This field defaults to de2bi(primpoly(4, 'nodisplay'),

'left-msb')

This field is available only when you select Specify primitive polynomial.

Specify generator polynomial

Selecting this check box enables the field Generator polynomial.

Generator polynomial

A row vector that represents the binary coefficients of the generator polynomial in order of descending powers.

The length of the Generator polynomial must be N-K+1.

, corresponding to a (15,5) code.

This field defaults to

This field appears only when you select Specify generator

polynomial.

Disable generator polynomial checking

This check box appears only when you select Specify generator polynomial.

Puncture code

Selecting this check box enables the field Puncture vector.

Puncture vector

A column vector of length N-K.Avalueof vector corresponds to a bit that is not punctured, and a corresponds to a bit that is punctured.

bchgenpoly(15,5).

+1isdivisiblebythe

1 in the Puncture

2-40

BCH Encoder

The field defaults to [ones(8,1); zeros(2,1)].

This field appears only when you select Puncture code.

Supported Data Type

Port

Out • Double-precision floating point

Supported Data Types

• Double-precision floating point

• Single-precision floating point

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

• Single-precision floating point

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

Pair Block BCH Decoder

References [1] Clark, George C., Jr., and J. Bibb Cain, Error-Correction Coding for

Digital Communications, New York, Plenum Press, 1981.

See Also bchenc (in Communications Toolbox documentation)

2-41

Bernoulli Binary Generator

Purpose Generate Bernoulli-distributed random binary numbers

Library Random Data Sources sublibrary of Comm Sources

Description The Bernoulli Binary Generator block generates random binary

numbers using a Bernoulli distribution. The Bernoulli distribution with parameter p produces zero with probability p and one with probability 1-p. The Bernoulli distribution has mean value 1-p and variance p(1-p). The Probability of a zero parameter specifies p, and can be any real number between zero and one.

Attributes of Output Signal

The output signal can be a frame-based matrix, a sample-based row or column vector, or a sample-based one-dimensional array. These attributes are controlled by the Frame-based outputs, Samples per frame,andInterpret vector parameters as 1-D parameters. See “Signal Attribute Parameters for Random Sources” in Communications Blockset User’s Guide for more details.

The number of elements in the Initial seed and Probability of a zero parameters becomes the number of columns in a frame-based output or the number of elements in a sample-based vector output. Also, the shape (row or column) of the Initial seed and Probability of a zero parameters becomes the shape of a sample-based two-dimensional output signal.

2-42

Dialog Box

Bernoulli Binary G en erator

Opening this dialog box causes a running simulation to pause. See “Changing Source Block Parameters” in the online Simulink documentation for details.

Probability of a zero

The probability with which a zero output occurs.

Initial seed

The initial seed value for the random number generator. The seed canbeeitheravectorofthesamelengthastheProbability of

azeroparameter, or a scalar.

Sample time

The period of each sample-based vector or each row of a frame-based matrix.

Frame-based outputs

Determines whether the output is frame-based or sample-based. This box is active only if Interpret vector parameters as 1-D is unchecked.

2-43

Bernoulli Binary Generator

Samples per frame

The number of samples in each column of a frame-based output signal. This field is active only if Frame-based outputs is checked.

Interpret vector parameters as 1-D

If this box is checked, then the output is a one-d imensional signal. Otherwise, the output is a two-dimensional signal. This box is active only if Frame-based outputs is unchecked.

Output data type

The output type of the block can be specified as a

uint8, int16, uint16, int32, uint32, single,ordouble.By

default, the block sets this to to different results when compared with double outputs for the same set of parameters.

double.Singleoutputsmaylead

See Also Random Integer Generator, Binary Symmetric Channel; randint (in

Communications Toolboxdocumentation), function)

rand (built-in M ATLAB

boolean, int8,

2-44

Binary Cyclic Deco der

Purpose Decode systematic cyclic code to recover binary vector d ata

Library Block sublibrary of Channel Coding

Description The Binary Cyclic Decoder block recovers a messag e vector from

a codeword vector of a binary systematic cyclic code. For proper decoding, the parameter values in this block should match those in the correspondingBinary Cyclic Encoder block.

If the cyclic code has message length K and codeword length N, then N must have the form 2

The input must contain exactly N elements. If it is frame-based, then it must be a column vector. The output is a vector of length K.

You can determine the systematic cyclic coding schem e in one of two ways:

• To create an [N,K] code, enter N and K as the first and second

dialog parameters, respectively. The block computes an appropriate generator polynomial, namely,

• To create a code with codeword length N and a particular

degree-(N-K) binary generator polynomial, enter N as the first parameter and a binary vector as the second parameter. The vector represents the generator polynomial by listing its coefficients in order of ascending exponents. You can create cyclic generator polynomials using the Communications Toolbox

For i nformation about the data types each block port supports, see the “Supported D ata Type” on page 2-46 table on this page.

-1 for some integer M greater than or equal to 3.

cyclpoly(N,K,'min').

cyclpoly function.

2-45

Binary Cyclic Decoder

Dialog Box

Codeword length N

The codew ord length N, which is also the input vector length.

Message length K, or generator polynomial

Either the message length, which is also the output vector length; or a binary vector that represents the generator polynomial for the code.

Supported Data Type

2-46

Port

Out • Double-precision floating point

Supported Data Types

• Double-precision floating point

• Single-precision floating point

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

• Fixed-point

• Single-precision floating point

Binary Cyclic Deco der

Port

Pair Block Binary Cyclic Encoder

See Also cyclpoly (Communications Toolbox)

Supported Data Types

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

• Fixed-point

2-47

Binary Cyclic Encoder

Purpose Create systematic cyclic code from binary vector data

Library Block sublibrary of Channel Coding

Description The Binary Cyclic Encoder block creates a system atic cyclic code with

message length K and codeword length N. The number N must have the form 2

The input must contain exactly K elements. If it is frame-based, then it must be a column vector. The output is a vector of length N.

You can determine the systematic cyclic coding schem e in one of two ways:

• To create an [N,K] code, enter N and K as the first and second

• To create a code with codeword length N and a particular

-1, w he re M is an integer greater than or equal to 3.

dialog parameters, respectively. The block computes an appropriate generator polynomial, namely,

cyclpoly(N,K,'min').

cyclpoly function.

2-48

For i nformation about the data types each block port supports, see the “Supported D ata Type” on page 2-49 table on this page.

Dialog Box

Binary Cyclic En co der

Codeword length N

The codew ord length, w hich is also the output vector length.

Message length K, or generator polynomial

Either the message length, which is also the input vector length; or a binary vector that represents the generator polynomial for the code.

Supported Data Type

Port

Out • Double-precision floating point

Supported Data Types

• Double-precision floating point

• Single-precision floating point

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

• Fixed-point

• Single-precision floating point

2-49

Binary Cyclic Encoder

Port

Pair Block Binary Cyclic Decoder

See Also cyclpoly (in the Communications Toolbox documentation)

Supported Data Types

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

• Fixed-point

2-50

Binary-Input RS Encoder

Purpose Create Reed-Solomon code from binary vector data

Library Block sublibrary of Channel Coding

Description The Binary-Input RS Encoder block creates a Reed-Solomon code with

message length, K, and codeword length, (N - number of punctures). You specify both N and K directly in the dialog box. The symbols for the code are binary sequences of length M, corresponding to elements of the Galois field GF(2 significant bit. Restrictions on M and N are given in “Restrictions on the M and the Codeword Length N” on page 2-52 below. The difference N-Kmustbeaneveninteger.

This block can output shortened codewords when N and K are appropriately specified. To specify output codewords that are shortened by a length S, N and K must be specified in the dialog box as N and K

code. If

the value of N

–S,whereN

full

<+()12

full

polynomial must be specified in order to properly define the e xtension field for the code.

full

), where the first bit in each sequence is the most

full

and K

are the N and K of an unshortened

full

, the encoder can automatically determine

and K

. However, if

full

≥+()12

full

, Primitive

full

–S

The input and output are binary-valued signals that represent messages and codew ords, respectively. The i nput must be a frame-based column vector whose leng th is an integer multiple of M*K. The output is a frame-based column vector whose length is the same integer multiple of M*(N - number of punctures), and whose data type is inherited from the input. For information about the data types each block port supports, see the “Supported Data Type” on page 2-56 table on this page.

For m ore information o n representing data for R eed-So lom on codes, see the section “Integer Format (Reed-Solomon Only)” in Communications Blockset User’s Guide.

If the encoder is processing multiple codewords per frame, then the same puncture pattern holds for all codewords.

2-51

Binary-Input RS Encoder

The default val u e of M is the smallest integer that is greater than or equal to log2(N+1), that is, valueofMfromthedefaultbyspecifyingtheprimitivepolynomialfor

GF(2

), as described in “Specifying the Primitive Polynomial” on pag e 2-52 below. If N is less than 2 been shortened by length 2

Each M*K input bits represent K integers between 0 and 2 Similarly, each M*(N - number of punctures) output bits represent N integers between 0 and 2 of the Galois field GF(2

ceil(log2(N+1)). You can change the

-1, the block assumes that the code has

M-1

-N.

-1.

-1. These integers in turn represent elements

An (N,K) Reed-Solomon code can correct up to

floor((N-K)/2) symbol

errors (not bit errors) in each codeword.

Specifying the Primitive Polynomial

You can specify the primitive polynomia l tha t defi nes the finite field GF(2

), corresponding to the integers that form messages and codewords. To do so, first select Specify primitive polynomial. Then, set Primitive polynomial to a binary row vector that represents a primitive polynomial over GF(2) of degree M, in descending order of powers. For example, to specify the polynomial x

[1 0 1 1].

+x+1, enter the vector

If you do not select Specify primitive polynomial,the block uses the default primitive polynomial of degree M = ceil(log2(N+1)). You can display the defa u lt polynomial by entering

primpoly(ceil(log2(N+1))) at the MATLAB prompt.

Restrictions on the M and the Codeword Length N

The restrictions on the degree M of the primitive polynomial a nd the codeword length N are as follows:

• If you do not select Specify primitive polynomial,Nmustliein

the range 3 < N < 2

–1.

• If you do select Specify primitive polynomial,Nmustlieinthe

range 3 ≤ N<2

–1 and M must lie in the range 3 ≤ M ≤ 16.

2-52

Binary-Input RS Encoder

Specifying the Generator Polynomial

You can specify the generator polynomial for the Reed-Solomon code. To do so, first select Specify generator polynomial. Then, in the Generator polynomial field, enter an integer row vector whose entries are between 0 and 2 in descending order of powers, whose coefficients are elements of

GF(2

) represented in integer format. See the section “Integer Format (Reed-Solomon Only)” for more information about integer format. The generator polynomial must be equal to a polynomial with a factored form

g(x) = (x+A

)(x+A

b+1

where A is the primiti ve element of the Galois field over which the input message is defined, and b is a non-negative integer.

If you do not select Specify generator polynomial, the block uses the default g enerator polynomial, corresponding to b=1, for Reed-Solomon encoding. You can display the default generator polynomial by entering

rsgenpoly(N1,K1),whereN1=2^M-1 and K1=K+(N1-N),atthe

MATLAB prompt, if you are using the default primitive polynomial. If the Specify primitive polynomial box is selected, and you specify the primitive polynomial specified as polynomial is

rsgenpoly(N1,K1,poly).

)(x+A

-1. The vector represents a polynomial,

b+2

)...(x+A

b+N-K-1

)

poly, the default generator

Puncture Codes

The block supports puncturing when you select the Puncture code parameter. This enables the Puncture vector parameter, which takes in a binary vector to specify the puncturing pattern. For a puncture vector, a 1 means that the data symbol is passed unaltered, and a 0 means that the data symbol is punctured (i.e., removed) from the data stream. This convention is carried for both the encoder and the decoder. For more information, see “Shortening, Puncturing, and Erasures”.

Examples Suppose M = 3, N = 2

vector of length 15 that represents 5 three-bit integers. A corresponding codeword is a binary vector of length 21 that represents 7 three-bit integers. The following figure shows the codeword that w ould result

-1 = 7, and K = 5. Then a message is a binary

2-53

Binary-Input RS Encoder

from a particular message word. The integer format equivalents illustrate that the highest order bit is at the left.

Dialog Box

Message input:

Code output: ]001000001011011 [

[0111110

[]0111110

Binary-Input RS Encoder with N = 7, K = 5

01000001 ][

37101

in integer format

37101 ]33

in integer format

2-54

Binary-Input RS Encoder

Codeword length N

The codeword length. The output has vector length NC*M*(N NP), where NC is the number of codewords being output, and NP is the number of punctures per codeword.

Message length K

The message length. The input has vector length NM*M*K, where NM is the number of messages per frame being input.

Specify primitive polynomial

Selecting this check box enables the field Primitive polynomial.

Primitive polynomial

This field is available only when Specify primitive polynomial is selected.

Binary row vector representing the primitive polynomial in descending order o f powers.

Specify generator polynomial

Selecting this check box enables the field Generator polynomial.

Generator polynomial

This field is available only w hen Specify generator polynomial is selected.

Integer row vector, whose entries are in the range from 0 to

-1, representing the generator polynomial in descending order

of powers.

Puncture code

Selecting this check box enables the field Puncture vector.

Puncture vector

This field is available onl y when Puncture code is selected.

A column vector of length N-K. A value of vector corresponds to an M-bit symbol that is not punctured, and a

0 corresponds to an M-bit symbol that is punctured.

1 in the Puncture

2-55

Binary-Input RS Encoder

The default value is [ones(2,1); zeros(2,1)].

Output data type

The output type of the block can be specified as

boolean,ordouble. By default, the block sets this to Same as

input

Same as input,

Supported Data Type

Port

Out • Double-precision floating point

Supported Data Types

• Double-precision floating point

• Single-precision floating point

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

• 1-bit unsigned integer (ufix(1))

• Single-precision floating point

• Boolean

• 8-, 16-, and 32-bit signed

integers

• 8-, 16-, and 32-bit unsigned

integers

• 1-bit unsigned integer (ufix(1))

Pair Block Binary-Output RS Decoder

Mathworks COMMUNICATIONS BLOCKSET 4 Reference

Specifications and Main Features

Frequently Asked Questions

User Manual