LOGIC L2330QC25, L2330QC20 Datasheet

DEVICES INCORPORATED

L2330

Coordinate Transformer

L2330

DEVICES INCORPORATED

FEATURES DESCRIPTION

❑❑

❑ Rectangular-to-Polar or Polar-to-

❑❑

Rectangular at 50 MHz

❑❑

❑ Performs Direct Digital Synthesis

❑❑

(DDS) functions along with PM and FM Modulation

❑❑

❑ 24-Bit Polar Phase Angle Accuracy

❑❑ ❑❑

❑ Replaces Fairchild TMC2330A

❑❑ ❑❑

❑ 120-pin PQFP

❑❑

The L2330 is a coordinate transformer that converts bidirectionally between Rectangular and Polar coordinates.

When in Rectangular-to-Polar mode, the L2330 is able to retrieve phase and magnitude information or backward map from a rectangular raster display to a radial data set.

When in Polar-to-Rectangular mode, the L2330 is able to execute direct digital waveform synthesis and modulation. Real-time image-space conversions are achieved from radially-generated images, such as RADAR, SONAR, and ultrasound to raster display formats.

Functional Description

The L2330 converts bidirectionally between Rectangular (Cartesian) and Polar (Phase and Magnitude) coordinates. The user selects the numeric format. A valid transformed result is

Coordinate T ransformer

seen at the output after 22 clock cycles and will continue upon every clock cycle thereafter.

When in Rectangular-to-Polar mode, the user inputs a 16-bit Rectangular coordinate and the output generates a Polar transformation with 16-bit magnitude and 16-bit phase. The user may select the data format to be either two’s complement or sign-andmagnitude Cartesian data format. Polar Magnitude data is always in magnitude format only. Polar Phase Angle data is modulo 2π so it may be regarded as either unsigned or two’s complement format.

When in Polar-to-Rectangular mode, the user inputs 16-bit Polar Magnitude and 32-bit Phase data and the output generates a 16-bit Rectangular coordinate. The use may select the data format to be either two’s complement or sign-and-magnitude Cartesian data format.

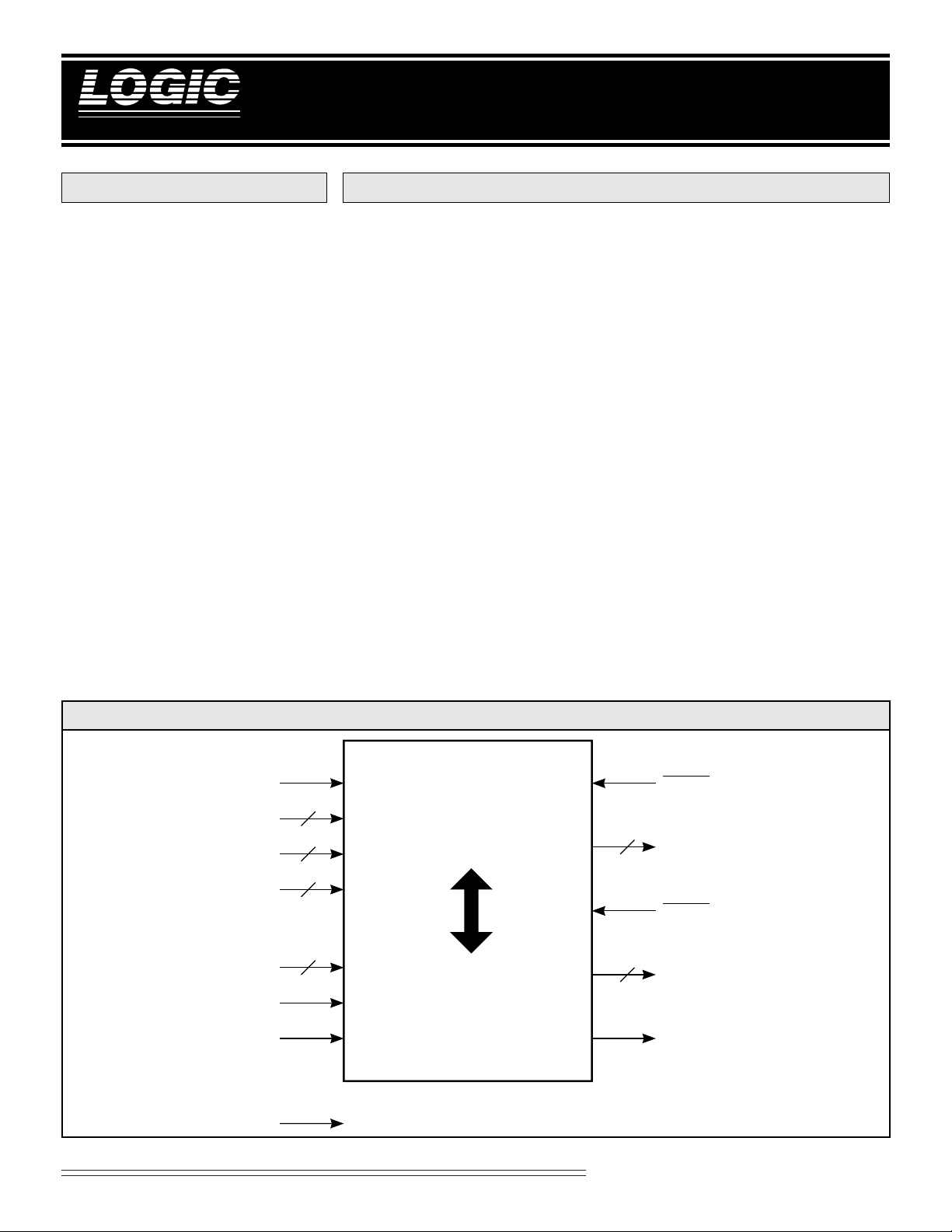
L2330 BLOCK DIAGRAM

ENXR

XRIN

ENYP

YPIN

ACC

TCXY

RTP

CLK

15-0

1-0

31-0

1-0

16

32

OERX

2

POLAR

RECTANGULAR

16

RXOUT

OEPY

PYOUT

OVF

15-0

Special Arithmetic Functions

1

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

L2330

Coordinate T ransf ormer

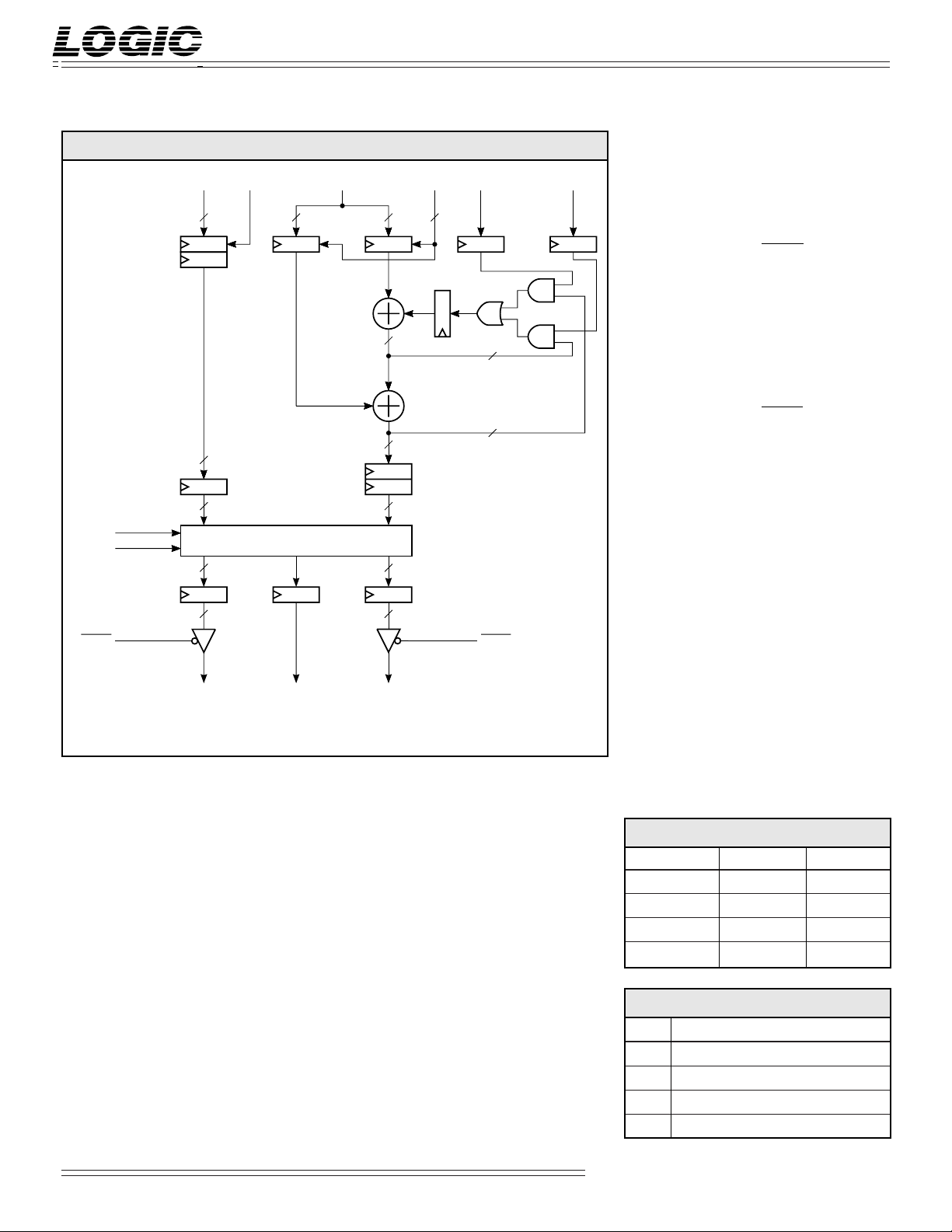
L2330 FUNCTIONAL BLOCK DIAGRAM

15-0

XRIN

16

TCXY

RTP

16

OERX

ENXR ENYP

AM

TRANSFORM

*

PROCESSOR

YPIN

32

MC

31-0

Outputs

RXOUT15-0 — x-coordinate/Magnitude

1-0

ACC

1

32

2

ACC

0

Data Output

RXOUT15-0 is the 16-bit Cartesian x-coordinate/Polar Magnitude Data output port. When OERX is HIGH, RXOUT15-0 is forced into the highimpedance state.

32

PM

32

PYOUT15-0 — y-coordinate/Phase Angle

Data Output

PYOUT15-0 is the 16-bit Cartesian y-coordinate/Polar Phase Angle Data

FM

**

n

**

n

32

output port. When OEPY is HIGH, PYOUT15-0 is forced into the highimpedance state.

Controls

ENXR — x-coordinate/Magnitude Data

Input Enable

16

When ENXR is HIGH, XRIN is latched into the input register on the rising

16

edge of clock. When ENXR is LOW, the value stored in the register is

OEPY

unchanged.

RXOUT

15-0

REQUIRES 18 CYCLES TO COMPLETE AND IS FULLY PIPELINED* WHEN RTP IS HIGH ’n’ IS 16-BITS, WHEN RTP IS LOW ’n’ IS 24-BITS**

OVF

SIGNAL DEFINITIONS

Power

VCC and GND

+5V power supply. All pins must be connected.

Clock

CLK — Master Clock

The rising edge of CLK strobes all enabled registers.

PYOUT

15-0

Inputs

XRIN15-0 — x-coordinate/Magnitude

Data Input

XRIN15-0 is the 16-bit Cartesian x-coordinate/Polar Magnitude Data input port. XRIN15-0 is latched on the rising edge of CLK.

YPIN31-0 — y-coordinate/Phase Angle

Data Input

YPIN31-0 is the 32-bit Cartesian y-coordinate/Polar Phase Angle Data input port. When RTP is HIGH, the input accumulators should not be used. When ACC is LOW, the upper 16 bits of YPIN are the input port and the lower 16 bits become “don’t cares”. YPIN31-0 is latched on the rising edge of CLK.

ENYP1-0 — y-coordinate/Phase Angle

Data Input Control

ENYP1-0 is the 2-bit y-coordinate/ Phase Angle Data Input Control that determines four modes as shown in

TABLE 1. REGISTER OPERATION

ENYP1-0 MC

0 0 Hold Hold 0 1 Load Hold 1 0 Hold Load 1 1 Clear Load

TABLE 2. ACCUMULATOR CONTROL

ACC1-0 Configuration

0 0 No accumulation (normal operation) 0 1 PM accumulator path enabled 1 0 FM accumulator path enabled 1 1 Logical OR of PM and FM (Nonsensical)

Special Arithmetic Functions

2

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

L2330

Coordinate Transformer

Table 1. ‘M’ is the Modulation Register and ‘C’ is the Carrier Register as shown in the Functional Block Diagram.

RTP — Rectangular-to-Polar

When RTP is HIGH, Rectangular-toPolar conversion mode is selected. When RTP is LOW, Polar-to-Rectangular conversion mode is selected.

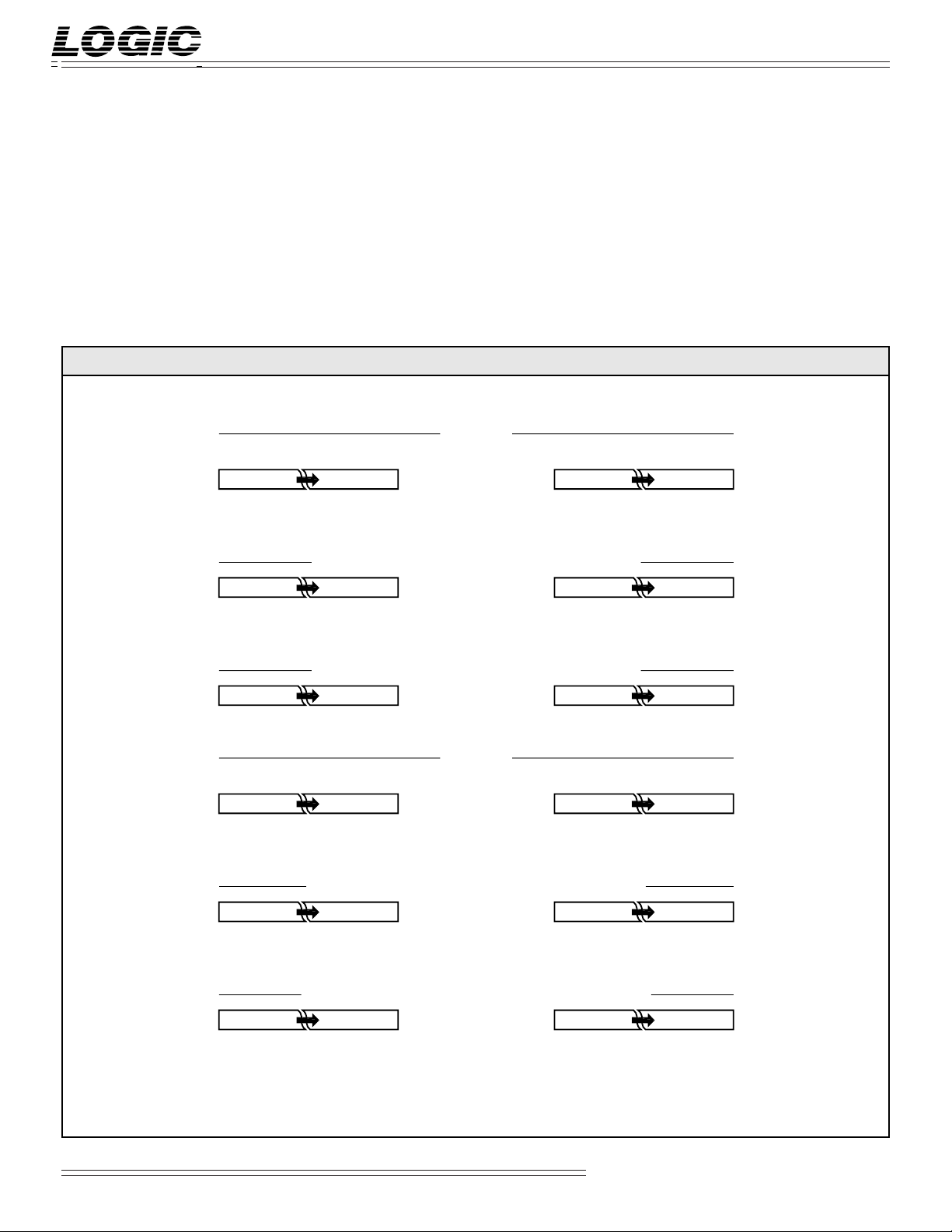
FIGURE 1A.INPUT FORMATS

XRIN YPIN

15 14 13 2 1 0 2152142

15 14 13 2 1 0

NS 2142

13

ACC1-0 — Accumulator Control

ACC1-0 is the 2-bit accumulator control that determines four modes as shown in Table 2. Changing of the internal phase Accumulator structure is very useful when RTP is LOW allowing for waveform synthesis and modulation. ACC1-0 set to ‘00’ is most commonly used when RTP is HIGH

(RTP = 0)

Fract. Unsigned Mag./Two's Comp.Integer Unsigned Magnitude

22212

0

Integer Signed Magnitude (RTP = 1, TCXY = 0)

22212

0

31 30 29 2 1 0

*±202–12

–2

31 30 29 18 17 16

NS 2142

13

unless performing backward mapping from Cartesian to Polar coordinates.

TCXY — Data Input/Output Format

Select

When TCXY is HIGH, two’s complement format is selected. When TCXY is LOW, sign-and-magnitude format is selected.

–292–302–31

2

22212

0

Integer Two's Complement (RTP = 1, TCXY = 1)

15 14 13 2 1 0

–2152142

13

22212

0

31 30 29 18 17 16

–2152142

13

22212

(RTP = 0)

Fractional Unsigned Magnitude

15 14 13 2 1 0

202–12

–2

–132–142–15

2

Fract. Unsigned Mag./Two's Comp.

31 30 29 2 1 0

*±202–12

–2

–292–302–31

2

Fractional Signed Magnitude (RTP = 1, TCXY = 0)

15 14 13 2 1 0

NS 2–12

–2

–132–142–15

2

31 30 29 18 17 16

NS 2–12

–2

–132–142–15

2

Fractional Two's Complement (RTP = 1, TCXY = 1)

15 14 13 2 1 0

–202–12

*±20 denotes two's complement sign or highest magnitude bit. Since phase angles are modulo 2π and phase accumulator is modulo 232, this bit may be regarded as ±π. NS denotes negative sign. (i.e. '1' negates the number)

–2

–132–142–15

2

31 30 29 18 17 16

–202–12

–2

–132–142–15

2

0

Special Arithmetic Functions

3

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

L2330

Coordinate T ransf ormer

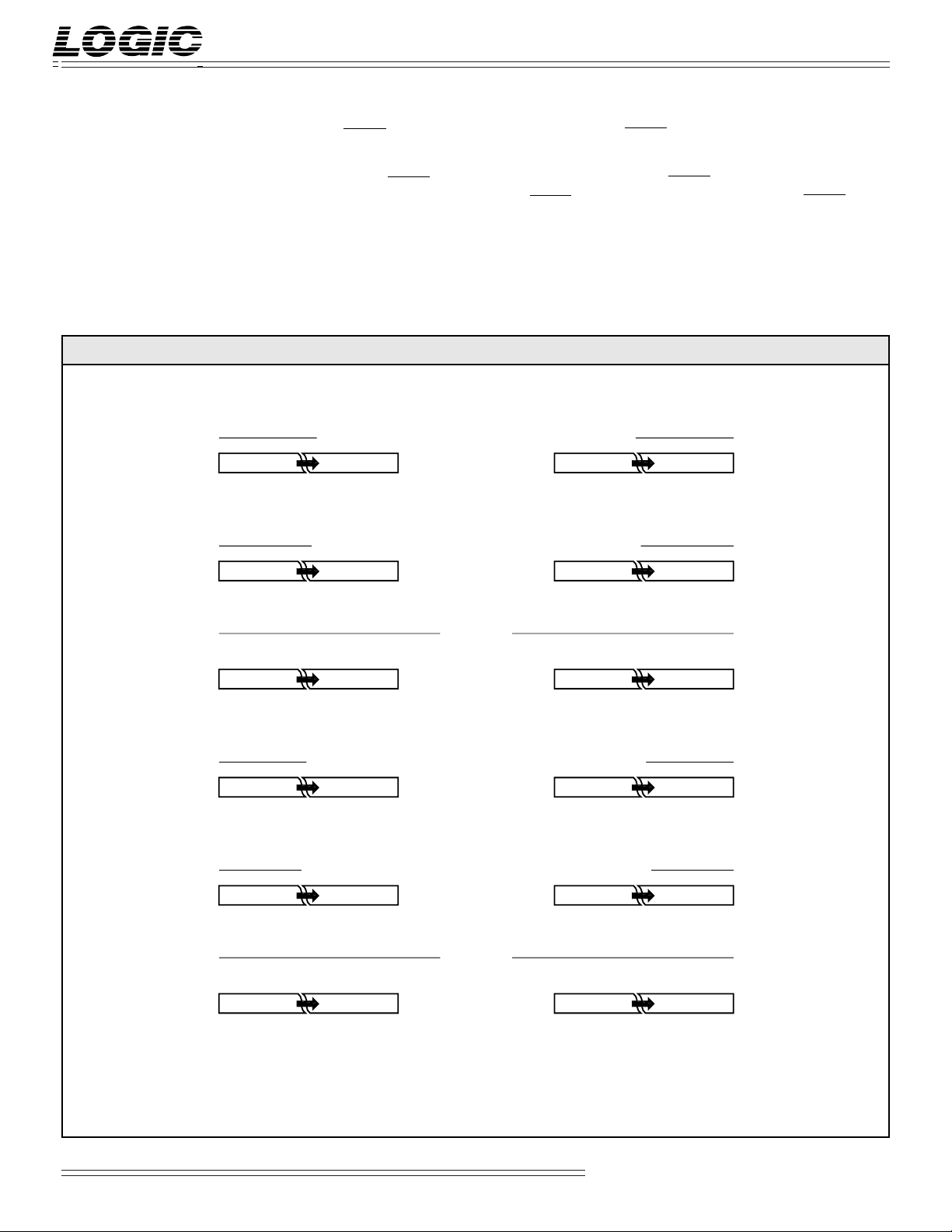
OVF — Overflow Flag

OVF will go HIGH on the clock the magnitude of either of the current Cartesian coordinate outputs exceed the maximum range. OVF will return LOW on the clock that the Cartesian output value(s) return within range. An overflow condition can only occur when RTP is LOW.

FIGURE 1B.OUTPUT FORMATS

RXOUT PYOUT

15 14 13 2 1 0

NS 2142

15 14 13 2 1 0

–2152142

13

OERX — x-coordinate/Magnitude Data

Output Enable

When OERX is LOW, RXOUT15-0 is enabled for output. When OERX is HIGH, RXOUT15-0 is placed in a high-impedance state.

Integer Signed Magnitude (RTP = 0, TCXY = 0)

22212

0

Integer Two's Complement (RTP = 0, TCXY = 1)

22212

0

15 14 13 2 1 0

NS 2142

13

15 14 13 2 1 0

–2152142

13

OEPY — y-coordinate/Phase Angle Data

Output Enable

When OEPY is LOW, PYOUT15-0 is enabled for output. When OEPY is HIGH, PYOUT15-0 is placed in a high-impedance state.

22212

0

(RTP = 1)

Fract. Unsigned Mag./Two's Comp.Integer Unsigned Magnitude

15 14 13 2 1 0 2152142

13

22212

0

15 14 13 2 1 0

*±202–12

–2

–132–142–15

2

Fractional Signed Magnitude (RTP = 0, TCXY = 0)

15 14 13 2 1 0

NS 2–12

–2

–132–142–15

2

15 14 13 2 1 0

NS 2–12

–2

–132–142–15

2

Fractional Two's Complement (RTP = 0, TCXY = 1)

15 14 13 2 1 0

–202–12

–2

–132–142–15

2

15 14 13 2 1 0

–202–12

–2

–132–142–15

2

(RTP = 1)

Fract. Unsigned Mag./Two's Comp.Fractional Unsigned Magnitude

15 14 13 2 1 0

202–12

*±20 denotes two's complement sign or highest magnitude bit. Since phase angles are modulo 2π and phase accumulator is modulo 232, this bit may be regarded as ±π NS denotes negative sign. (i.e. '1' negates the number)

–2

–132–142–15

2

15 14 13 2 1 0

*±202–12

–2

–132–142–15

2

.

Special Arithmetic Functions

4

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

L2330

Coordinate Transformer

Conversion Ranges

The L2330 supports 16-bit unsigned radii and 16-bit signed Cartesian coordinates. Since the 16-bit rectangular coordinate space does not completely cover the polar space defined by 16-bit radii, certain values of “r” will not map correctly. This condition is indicated by the overflow (OVF) flag.

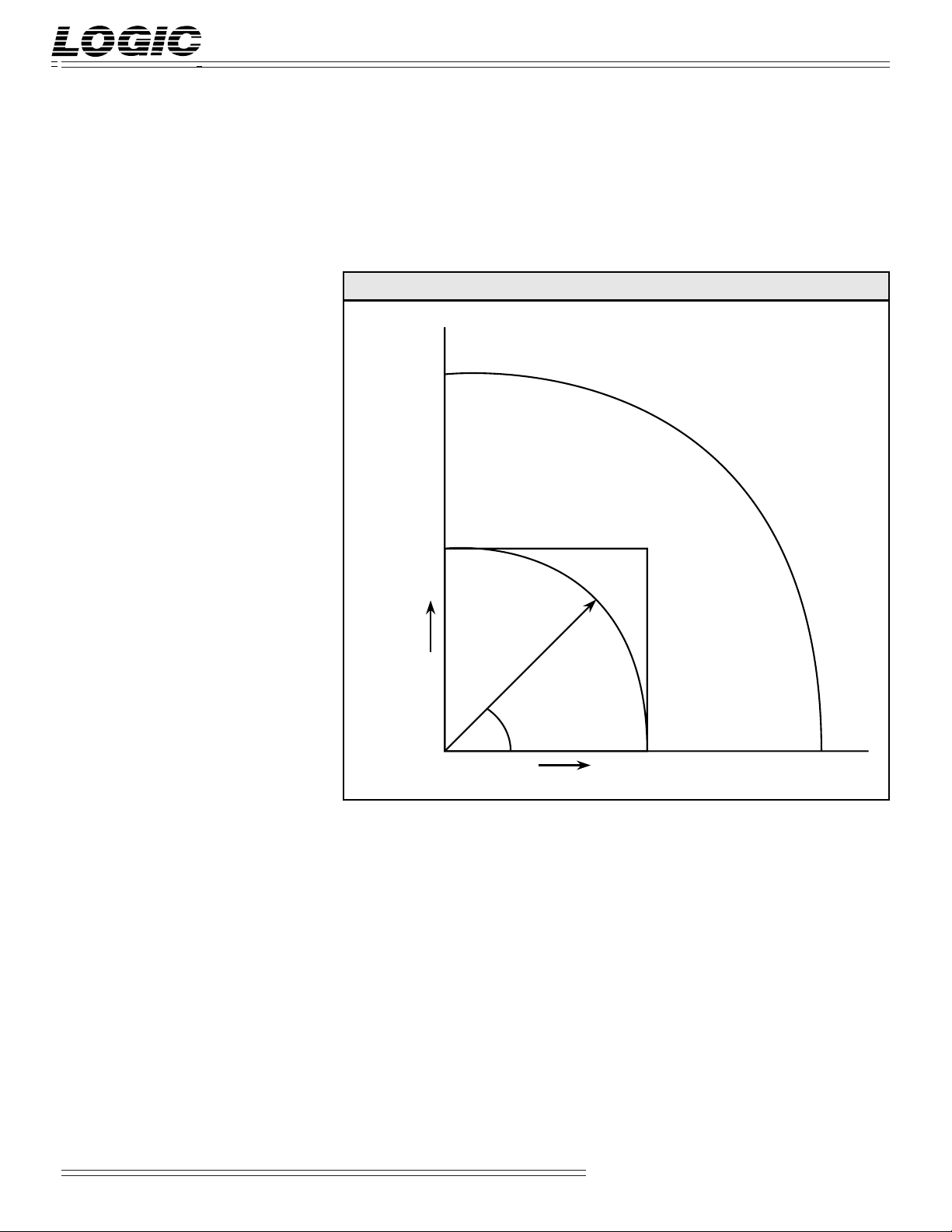
In Polar-to-Rectangular conversions, no overflow occurs for r ≤ 32767 (7FFFH). Overflow will always occur when r > 46341 (B505H). Note that in signed magnitude mode r = 46340 (B504H) will also cause an overflow. For 32767 ≤ r ≤ 46340, overflow may occur depending on the exact values of r and θ. Figure 2 shows, for the first quadrant, these three regions: A = no overflow (correct conversion), B = possible overflow, C = overflow. The other quadrants are mapped in a similar manner.

complement number system is not symmetric about zero. For example, if the X or Y component of the input is –32768 (8000H), no overflow occurs. But if the X or Y component of the input is +32768, overflow does occur.

FIGURE 2. CONVERSION RANGES

π/2

65535

32767

When converting from Rectangular-toPolar, if both inputs are zero the radius is zero but the angle is not defined. The L2330 will output 4707H in this case. Since the angle is not defined for a zero length vector, this is not an error.

C

B

When in signed magnitude mode, the overflows on the other three quadrants are the same as in the first. This occurs because the signed magnitude number system is symmetric about zero. For example, if a given r and angle θ cause an overflow, the same r will cause an overflow for the angles -θ, π+θ , π-θ.

However, when in two’s complement mode, the overflows aren’t quite the same. This occurs because the two’s

A

y

r

θ

x

32767

65535

Special Arithmetic Functions

5

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

L2330

Coordinate T ransf ormer

Internal Precision

When performing a coordinate transformation, inaccuracies are introduced by a combination of quantization and approximation errors. The accuracy of a coordinate transformer is dependent on the word length used for the input variables, the word length used for internal calculations, as well as the number of iterations or steps performed. Truncation errors are due to the finite word length, and approximation errors are due to the finite number of iterations. For example, in the case of performing a polar-to-rectangular transformation, the accuracy of the rotation will be determined by how closely the input rotation angle was approximated by the summation of sub-rotation angles.

In this study, we examine the effectiveness of 16-bit internal precision versus 24-bit internal precision. 10,000 random Rectangular coordinates were converted to Polar and back to Rectangular. The resulting Rectangular coordinates from this double conversion were then compared to the original

Rectangular coordinates input to the device. These vectors, with maximum word width of 16-bits, were sent through a 16-bit internal processor versus a 24-bit internal processor. The Rectangular coordinates were limited to the following conditions:

–32769<x<32768 –32769<y<32768

Using the 16-bit internal processor, the resulting Rectangular coordinates were compared to the original Rectangular coordinates (see Table 3). Using the 24bit internal processor, the resulting

Rectangular coordinates were compared to the original Rectangular coordinates (see Table 3). By way of comparison between the 16-bit internal processor and the 24-bit internal processor, we find that the 24-bit internal processor is significantly more accurate. This accuracy is due to internal word length. During coordinate transformation, the number of bits truncated within a 24-bit internal processor are much smaller than in a 16-bit internal processor resulting in smaller error.

TABLE 3. DOUBLE CONVERSION ERROR

Error Internal 16-bit Internal 24-bit

Mean Error (X) 0.0216 –0.0118 Mean Error (Y) –0.0036 –0.0028 Mean Absolute Error (X) 1.5736 0.5116 Mean Absolute Error (Y) 1.0756 0.5160 Root Mean Square Error (X) 2.0168 0.7664 Root Mean Square Error (Y) 1.4356 0.7738 Max Error (X) 6.0/–7.0 3.0/–3.0 Max Error (Y) 5.0/–5.0 3.0/–3.0 Standard Deviation of Error (X) 2.0168 0.7664 Standard Deviation of Error (Y) 1.4357 0.7739

Special Arithmetic Functions

6

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

L2330

Coordinate Transformer

Circle Test

When performing a polar-to-rectangular transformation, a 24-bit internal processor proves to be significantly more accurate than a 16-bit internal processor.

In this study, we compare how accurately a coordinate transformer with a 16-bit internal processor versus a 24-bit internal processor can calculate all the coordinates of a circle. By setting the radius to 7FFFH (maximum before overflow), θ is incremented using the accumulator of the L2330 in steps of 0000 4000H until all the points of a full circle are calculated into rectangular coordinates.

The resulting rectangular coordinates were plotted and graphed. A graphical representation of the resulting vectors for both 16-bit and 24-bit internal processors are compared near 45°. Theoretically, a perfect circle is the desired output but when the resulting vectors from a coordinate transformer with 16-bit internal processor are graphed and displayed as shown in Figure 3, we see significant errors due to the inherent properties of a digital coordinate transformation system. In comparison, the 24-bit internal processor proves to be significantly more accurate than a 16-bit internal processor due to minimization of truncation errors. In many applications, this margin of error is of great significance especially when being used in applications such as medical ultrasound or modulation techniques.

step resolution on a 24-bit internal processor is 1 unit in the x and y thus resulting in greater accuracy.

The minimum theoretical angle resolution that could be produced is 0.00175° when x = 7FFFH and y = 1H. A 16-bit internal processor can produce a minimum angle resolution of only

0.00549° and will not be able to properly calculate the theoretical minimum angle resolution. On the other hand, a 24-bit internal processor can produce a minimum angle resolution of 0.00002° and could therefore properly calculate the theoretical minimum angle resolution.

FIGURE 3. CIRCLE TEST RESULT NEAR 45° (16-BIT INTERNAL PROCESSOR)

23200

23190

23180

23170

Y

23160

23150

23140

23140 23150 23160 23170 23180 23190 23200

X

FIGURE 4. CIRCLE TEST RESULT NEAR 45° (24-BIT INTERNAL PROCESSOR)

23200

23190

23180

23170

Y

23160

Data values for Figure 3 and Figure 4 are shown in Table 4. By looking at these values, we observe the step resolution on a 16-bit internal processor is not 1 unit in the x and y. In most cases, the minimum step resolution is 2 units in the x and y. On the other hand,

23150

23140

23140 23150 23160 23170 23180 23190 23200

X

Special Arithmetic Functions

7

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

TABLE 4. R ESULTANT DATA VALUES OF CIRCLE TEST NEAR 45°

16-bit Internal Processor 24-bit Internal Processor

x x (HEX) y y (HEX) x x (HEX) y y (HEX)

23201 5AA1 23139 5A63 23199 5A9F 23140 5A64 23199 5A9F 23141 5A65 23198 5A9E 23141 5A65 23199 5A9F 23141 5A65 23198 5A9E 23141 5A65 23199 5A9F 23141 5A65 23197 5A9D 23142 5A66 23199 5A9F 23141 5A65 23197 5A9D 23142 5A66 23197 5A9D 23143 5A67 23196 5A9C 23143 5A67 23197 5A9D 23143 5A67 23196 5A9C 23143 5A67 23197 5A9D 23143 5A67 23195 5A9B 23144 5A68 23197 5A9D 23143 5A67 23194 5A9A 23145 5A69 23195 5A9B 23145 5A69 23194 5A9A 23145 5A69 23195 5A9B 23145 5A69 23194 5A9A 23145 5A69 23195 5A9B 23145 5A69 23193 5A99 23146 5A6A 23195 5A9B 23145 5A69 23192 5A98 23147 5A6B 23192 5A98 23148 5A6C 23191 5A97 23148 5A6C 23192 5A98 03148 5A6C 23191 5A97 23148 5A6C 23192 5A98 23148 5A6C 23191 5A97 23148 5A6C 23192 5A98 23148 5A6C 23190 5A96 23149 5A6D 23190 5A96 23150 5A6E 23189 5A95 23150 5A6E 23190 5A96 23150 5A6E 23189 5A95 23150 5A6E 23190 5A96 23150 5A6E 23189 5A95 23150 5A6E 23190 5A96 23150 5A6E 23188 5A94 23151 5A6F 23187 5A93 23152 5A70 23187 5A93 23152 5A70 23187 5A93 23152 5A70 23186 5A92 23153 5A71 23187 5A93 23152 5A70 23186 5A92 23153 5A71 23187 5A93 23152 5A70 23186 5A92 23153 5A71 23185 5A91 23154 5A72 23185 5A91 23154 5A72 23185 5A91 23154 5A72 23184 5A90 23155 5A73 23185 5A91 23154 5A72 23184 5A90 23155 5A73 23185 5A91 23154 5A72 23184 5A90 23155 5A73 23183 5A8F 23156 5A74 23183 5A8F 23156 5A74

L2330

Coordinate T ransf ormer

Special Arithmetic Functions

8

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

L2330

Coordinate Transformer

MAXIMUM RATINGS

Storage temperature ........................................................................................................... –65°C to +150°C

Operating ambient temperature........................................................................................... –55°C to +125°C

VCC supply voltage with respect to ground............................................................................ –0.5 V to +7.0V

Input signal with respect to ground ............................................................................... –0.5 V to VCC + 0.5 V

Signal applied to high impedance output ...................................................................... –0.5 V to VCC + 0.5 V

Output current into low outputs............................................................................................................. 25 mA

Latchup current ............................................................................................................................... > 400 mA

OPERATING CONDITIONS

Active Operation, Commercial 0°C to +70°C 4.75 V ≤ VCC ≤ 5.25 V Active Operation, Military –55°C to +125°C 4.50 V ≤ VCC ≤ 5.50V

ELECTRICAL CHARACTERISTICS

Above which useful life may be impaired (Notes 1, 2, 3, 8)

To meet specified electrical and switching characteristics

Mode Temperature Range (Ambient) Supply Voltage

Over Operating Conditions (Note 4)

Symbol Parameter Test Condition Min Typ Max Unit

VOH Output High Voltage VCC = Min., IOH = –2.0 mA 2.4 V VOL Output Low Voltage VCC = Min., IOL = 4.0 mA 0.4 V VIH Input High Voltage 2.0 VCC V VIL Input Low Voltage (Note 3) 0.0 0.8 V IIX Input Current Ground ≤ VIN ≤ VCC (Note 12) ±10 µA IOZ Output Leakage Current Ground ≤ VOUT ≤ VCC (Note 12) ±10 µA ICC1 VCC Current, Dynamic (Notes 5, 6) 95 mA ICC2 VCC Current, Quiescent (Note 7) 5mA CIN Input Capacitance TA = 25°C, f = 1 MHz 10 pF COUT Output Capacitance TA = 25°C, f = 1 MHz 10 pF

Special Arithmetic Functions

9

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

4

6

4

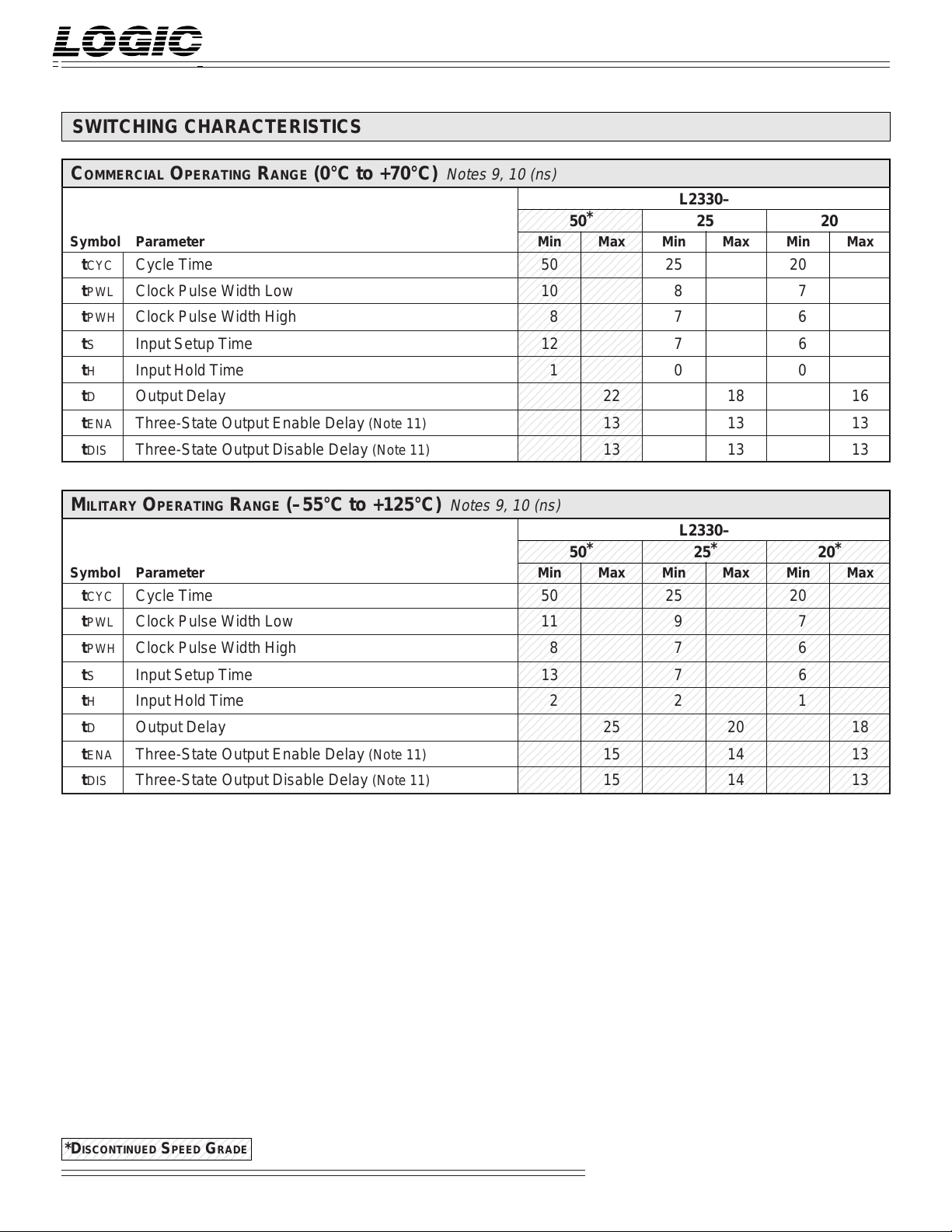
SWITCHING CHARACTERISTICS

L2330

Coordinate T ransf ormer

COMMERCIAL OPERATING RANGE (0°C to +70°C)

Symbol Parameter Min Max Min Max Min Max

tCYC Cycle Time 50 25 20 tPWL Clock Pulse Width Low 10 8 7 tPWH Clock Pulse Width High 8 7 6 tS Input Setup Time 12 7 6 tH Input Hold Time 1 0 0 tD Output Delay 22 18 16 tENA Three-State Output Enable Delay (Note 11) 13 13 13 tDIS Three-State Output Disable Delay (Note 11) 13 13 13

MILITARY OPERATING RANGE (–55°C to +125°C)

Symbol Parameter Min Max Min Max Min Max

tCYC Cycle Time 50 25 20 tPWL Clock Pulse Width Low 11 9 7 tPWH Clock Pulse Width High 8 7 6 tS Input Setup Time 13 7 6 tH Input Hold Time 2 2 1 tD Output Delay 25 20 18 tENA Three-State Output Enable Delay (Note 11) 15 14 13 tDIS Three-State Output Disable Delay (Note 11) 15 14 13

Notes 9, 10 (ns)

23456789012345

Notes 9, 10 (ns)

23456789012345678901234567890121234567890123

50

L2330–

*

25 20

L2330–

*

25

*

20

*

2345678901234567890123

*DISCONTINUED SPEED GRADE

10

Special Arithmetic Functions

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

SWITCHING WAVEFORMS:NO ACCUMULATION

L2330

Coordinate Transformer

01232223

CLK

t

H

t

RTP

S

TCXY

ACC

ENXR

ENYP XRIN

YPIN

RXOUT PYOUT

1-0

15-0 31-0

15-0 15-0

00 00 00

EN EN EN

A B C

SWITCHING WAVEFORMS:PHASE MODULATION

CLK

RTP, TCXY

ACC

ENXR

1-0

0123422

00 01

01 01

24

t

PWL

CYC

t

PWH

D

t

f(A) f(B)

23

01

24 25

XRIN

ENYP

YPIN

RXOUT

PYOUT

15-0

31-0

15-0 15-0

R

1-0

10

C

01 01 01

I J K

01

L

C + I 2C + J 3C + K 4C + L

Special Arithmetic Functions

11

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

S1

I

OH

I

OL

V

TH

C

L

DUT

OE

0.2 V

t

DIS

t

ENA

0.2 V

1.5 V 1.5 V

3.5V Vth

1

Z

0

Z

1

Z

0

1.5 V

0V Vth

VOL*

V

OH

*

V

OL

*

V

OH

*

Measured V

OL

with IOH = –10mA and IOL = 10mA

Measured V

OH

with IOH = –10mA and IOL = 10mA

NOTES

L2330

Coordinate T ransf ormer

1. Maximum Ratings indicate stress specifications only. Functional operation of these products at values beyond those indicated in the Operating Conditions table is not implied. Exposure to maximum rating conditions for extended periods may affect reliability.

2. The products described by this specification include internal circuitry designed to protect the chip from damaging substrate injection currents and accumulations of static charge. Nevertheless, conventional precautions should be observed during storage, handling, and use of these circuits in order to avoid exposure to excessive electrical stress values.

3. This device provides hard clamping of transient undershoot and overshoot. Input levels below ground or above

VCC will be clamped beginning at –

0.6 V and VCC + 0.6 V. The device can withstand indefinite operation with inputs in the range of –0.5 V to +7.0 V. Device operation will not be adversely affected, however, input current levels will be well in excess of 100 mA.

9. AC specifications are tested with input transition times less than 3 ns, output reference levels of 1.5 V (except

tDIS test), and input levels of nominally

0 to 3.0 V. Output loading may be a resistive divider which provides for specified IOH and IOL at an output voltage of VOH min and VOL max respectively. Alternatively, a diode bridge with upper and lower current sources of IOH and IOL respectively, and a balancing voltage of 1.5 V may be used. Parasitic capacitance is 30 pF minimum, and may be distributed.

This device has high-speed outputs capable of large instantaneous current pulses and fast turn-on/turn-off times. As a result, care must be exercised in the testing of this device. The following measures are recommended:

a. A 0.1 µF ceramic capacitor should be installed between VCC and Ground leads as close to the Device Under Test (DUT) as possible. Similar capacitors should be installed between device VCC and the tester common, and device ground and tester common.

11. For the tENA test, the transition is measured to the 1.5 V crossing point with datasheet loads. For the tDIS test, the transition is measured to the ±200mV level from the measured steady-state output voltage with ±10mA loads. The balancing voltage, VTH, is set at 3.5 V for Z-to-0 and 0-to-Z tests, and set at 0 V for Zto-1 and 1-to-Z tests.

12. These parameters are only tested at the high temperature extreme, which is the worst case for leakage current.

FIGURE A. OUTPUT LOADING CIRCUIT

FIGURE B. THRESHOLD LEVELS

4. Actual test conditions may vary from those designated but operation is guaranteed as specified.

5. Supply current for a given application can be accurately approximated by:

2

NCV F

where

4

N = total number of device outputs C = capacitive load per output V = supply voltage F = clock frequency

6. Tested with all outputs changing every cycle and no load, at a 20 MHz clock rate.

7. Tested with all inputs within 0.1 V of

VCC or Ground, no load.

8. These parameters are guaranteed but not 100% tested.

b. Ground and VCC supply planes must be brought directly to the DUT socket or contactor fingers.

c. Input voltages should be adjusted to compensate for inductive ground and VCC noise to maintain required DUT input levels relative to the DUT ground pin.

10. Each parameter is shown as a minimum or maximum value. Input requirements are specified from the point of view of the external system driving the chip. Setup time, for example, is specified as a minimum since the external system must supply at least that much time to meet the worst-case requirements of all parts. Responses from the internal circuitry are specified from the point of view of the device. Output delay, for example, is specified as a maximum since worst-case operation of any device always provides data within that time.

12

Special Arithmetic Functions

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

ORDERING INFORMATION

120-pin

PYOUT5PYOUT6GND

PYOUT7PYOUT8PYOUT9GND

PYOUT10PYOUT11PYOUT12VCCPYOUT13PYOUT14PYOUT15GND

OVF

RXOUT0RXOUT1VCCRXOUT2RXOUT3RXOUT4GND

Coordinate Transformer

RXOUT5RXOUT6RXOUT7GND

RXOUT8RXOUT9V

CC

L2330

V PYOUT PYOUT

GND PYOUT PYOUT PYOUT

V

OEPY

GND

RTP CLK

GND

TCXY

ENYP

GND

ENYP

ACC ACC

V YPIN YPIN YPIN YPIN YPIN YPIN YPIN

GND YPIN YPIN

120

119

118

117

116

115

114

113

112

111

110

109

108

107

106

105

104

CC

1

4

2

3

3 4

2

5 6

1

7

0

8

CC

9 10 11 12 13 14 15

0

16 17

1

18

0

19

1

20

CC

21

0

22

1

23

2

24

3

25

4

26

5

27

6

28 29

7

30

8

3132333435363738394041424344454647484950515253545556575859

9

10

CC

V

GND

YPIN

YPIN11YPIN12YPIN13YPIN14YPIN15YPIN16YPIN

17

CC

V

Top

View

YPIN18YPIN19YPIN

103

20

21

GND

YPIN22YPIN

YPIN

999897969594939291

102

101

100

23

CC

V

YPIN24YPIN25YPIN26YPIN27YPIN28YPIN29YPIN30YPIN

31

60

0

ENXR

XRIN

90

RXOUT RXOUT GND RXOUT RXOUT RXOUT V

CC

RXOUT GND OERX

CC

V XRIN XRIN XRIN GND XRIN XRIN XRIN XRIN XRIN XRIN XRIN GND XRIN XRIN XRIN GND XRIN XRIN V

CC

10 11

12 13 14

15

15 14 13

12 11 10 9 8 7 6

5 4 3

2 1

89 88 87 86 85 84 83 82 81 80 79 78 77 76 75 74 73 72 71 70 69 68 67 66 65 64 63 62 61

Speed

25 ns 20 ns

Plastic Quad Flatpack

(Q1)

0°C to +70°C — COMMERCIAL SCREENING

L2330QC25 L2330QC20

Special Arithmetic Functions

13

09/27/2001–LDS.2330-E

DEVICES INCORPORATED

1

ORDERING INFORMATION

23456789012345678901234567890121234567890123456789012345678901212345678901234567890123456789012

120-pin

23456789012345678901234567890121234567890123456789012345678901212345678901234567890123456789012

Speed

0°C to +70°C — COMMERCIAL SCREENING

–55°C to +125°C — COMMERCIAL SCREENING

–55°C to +125°C — MIL-STD-883 COMPLIANT

12345

A

PYO

7

PYO

5

B

PYO

4

PYO

3

C

PYO

2

PYO

1

V

D

PYO

0

OEPY

GND

E

GND

V

RTP

F

GND

CLK

TCXY

G

GND

0

1

ENYP

H

V

ACC

1

0

J

YPI

1

YPI

0

YPI

K

YPI

4

YPI

2

GND

L

GND

YPI

7

5

M

YPI

9

6

N

YPI

10

YPI

8

YPI

CC

6

7 8 9 10 11

PYO

10

PYO

12

PYO

14

8

PYO

9

PYO

6

GND

PYO

V

CC

OVF

13

GND

11

KEY

Top View

Through Package

(i.e., Component Side Pinout)

3

CC

14

V

CC

YPI

GND

18

YPI

19

YPI

V

YPI

13

YPI

11

YPI

12

16

15

YPI

17

Discontinued Package

Ceramic Pin Grid Array

(G4)

14

L2330

Coordinate T ransf ormer

12 13

15

RXO

0

RXO

2

RXO

4

RXO

6

RXO

8

RXO

10

RXO

1

RXO

3

RXO

5

RXO

7

RXO

9

RXO

12

V

CC

GND

V

CC

RXO

11

RXO

13

GND

RXO

14

RXO

15

V

CC

GND

OERX

XRI

YPI

XRI

15

14

12

XRI

13

10

XRI

11

7

XRI

8

5

XRI

6

3

XRI

4

1

XRI

2

30

XRI

0

09/27/2001–LDS.2330-E

V

CC

GND

XRI

9

GND

V

CC

27

YPI

20

YPI

23

YPI

25

21

YPI

22

YPI

24

YPI

V

31

CC

28

ENXR

YPI

26

29

Special Arithmetic Functions

LOGIC L2330QC25, L2330QC20 Datasheet

Specifications and Main Features

Frequently Asked Questions

User Manual