Page 1

Littelfuse Varistors - Basic Properties,
Terminology and Theory
What Is A Littelfuse Varistor?
Varistors are voltage dependent, nonlinear devices which
have an electrical behavior similar to back-to-back zener
diodes. The symmetrical, sharp breakdown characteristics
shown in Figure 1 enable the varistor to provide excellent
transient suppression performance. When exposed to high
voltage transients the varistor impedance changes many
orders of magnitude from a near open circuit to a highly
conductive level, thus clamping the transient voltage to a
safe level. The potentially destructive energy of the incoming
transient pulse is absorbed by the varistor, thereby
protecting vulnerable circuit components.
PER VERT
DIV 1mA
PER HORIZ
DIV 50V
I
PER STEP
gm PER DIV
9991 yluJetoN noitacilppA
Littelfuse Varistors are available with AC operating voltages
from 2.5V to 6000V. Higher voltages are limited only by
packaging ability. Peak current handling exceeds 70,000A
and energy capability extends beyond 10,000J for the larger
units. Package styles include the tiny multilayer surface
mount suppressors, tubular devices for use in connectors,
and progress in size up to the rugged industrial device line.
AN9767.1
Physical Properties
Introduction
An attractive property of the metal oxide varistor, fabricated
from zinc oxide (ZnO), is that the electrical characteristics
are related to the bulk of the device. Each ZnO grain of the
ceramic acts as if it has a semiconductor junction at the
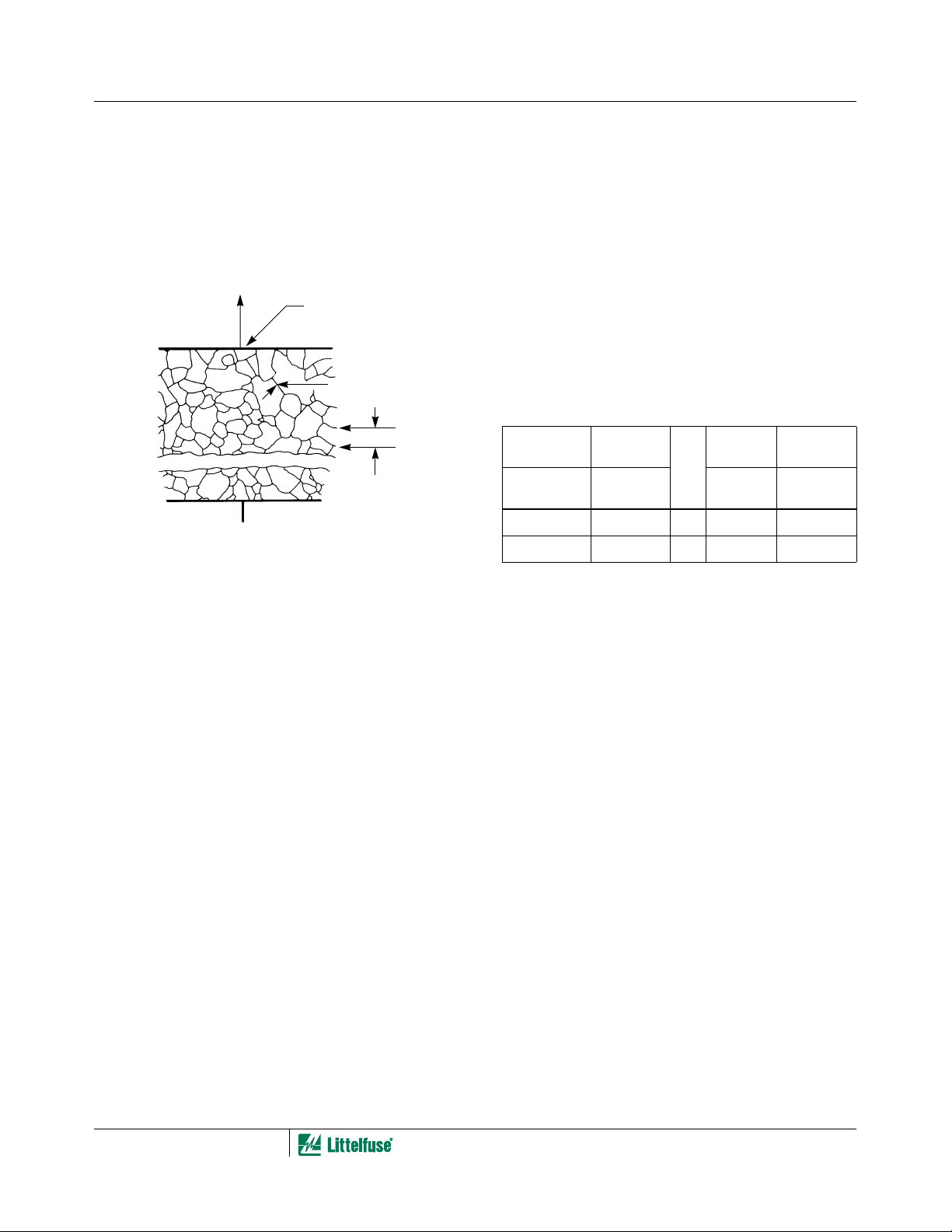
grain boundary. A cross-section of the material is shown in
Figure 2, which illustrates the ceramic microstructure. The
ZnO grain boundaries can be clearly observed. Since the
nonlinear electrical behavior occurs at the boundary of each
semiconducting ZnO grain, the varistor can be considered a
“multi-junction” device composed of many series and parallel
connections of grain boundaries. Device behavior may be
analyzed with respect to the details of the ceramic
microstructure. Mean grain size and grain size distribution
play a major role in electrical behavior.
V
FIGURE 1. TYPICAL VARISTOR V-I CHARACTERISTIC
The varistor is composed primarily of zinc oxide with small
additions of bismuth, cobalt, manganese and other metal
oxides. The structure of the body consists of a matrix of
conductive zinc oxide grains separated by grain boundaries
providing P-N junction semiconductor characteristics. These
boundaries are responsible for blocking conduction at low
voltages and are the source of the nonlinear electrical
conduction at higher voltages.
Since electrical conduction occurs, in effect, between zinc
oxide grains distributed throughout the bulk of the device, the
Littelfuse Varistor is inherently more rugged than its single PN junction counterparts, such as zener diodes. In the
varistor, energy is absorbed uniformly throughout the body of
the device with the resultant heating spread evenly through
its volume. Electrical properties are controlled mainly by the
physical dimensions of the varistor body which is sintered in
various form factors such as discs, chips and tubes. The
energy rating is determined by volume, voltage rating by
thickness or current ow path length, and current capability
by area measured normal to the direction of current ow.
100µ
FIGURE 2. OPTICAL PHOTOMICROGRAPH OF A POLISHED
AND ETCHED SECTION OF A VARISTOR
10-89
1-800-999-9445 or 1-847-824-1188 | Copyright © Littelfuse, Inc. 1999
Page 2
Application Note 9767
Varistor Microstructure
Varistors are fabricated by forming and sintering zinc
oxide-based powders into ceramic parts. These parts are
then electroded with either thick film silver or arc/flame
sprayed metal. The bulk of the varistor between contacts is
comprised of ZnO grains of an average size “d” as shown in
the schematic model of Figure 3. Resistivity of the ZnO is
<0.3 Ω -cm.
CURRENT
FIGURE 3. SCHEMATIC DEPICTION OF THE
MICROSTRUCTURE OF A METAL-OXIDE
VARISTOR. GRAINS OF CONDUCTING ZnO
(AVERAGE SIZE d) ARE SEPARATED BY
INTERGRANULAR BOUNDARIES
Designing a varistor for a given nominal varistor voltage, V
is basically a matter of selecting the device thickness such
that the appropriate number of grains, n, are in series
between electrodes. In practice, the varistor material is
characterized by a voltage gradient measured across its
thickness by a specific volts/mm value. By controlling
composition and manufacturing conditions the gradient
remains fixed. Because there are practical limits to the range
of thicknesses achievable, more than one voltage gradient
value is desired. By altering the composition of the metal
oxide additives it is possible to change the grain size “d” and
achieve the desired result.
A fundamental property of the ZnO varistor is that the
voltage drop across a single interface “junction” between
grains is nearly constant. Observations over a range of
compositional variations and processing conditions show a
fixed voltage drop of about 2V-3V per grain boundary
junction. Also, the voltage drop does not vary for grains of
different sizes.
It follows, then, that the varistor voltage will be determined by
the thickness of the material and the size of the ZnO grains.
The relationship can be stated very simply as follows:
ELECTRODES
INTERGRANULAR
BOUNDARY
d
N
Varistor Voltage, V
Where, n = average number of grain boundaries
and, varistor thickness, D = (n + 1)d
where, d = average grain size
The varistor voltage, V
(DC) = (3V)n
N
between electrodes
VNd×
-----------------
≈
3
, is defined as the voltage across a
N
varistor at the point on its V-I characteristic where the transition
is complete from the low-level linear region to the highly
nonlinear region. For standard measurement purposes, it is
arbitrarily defined as the voltage at a current of 1mA.
Some typical values of dimensions for Littelfuse Varistors are
given in Table 1.
TABLE 1.
VARISTOR
VOLTAGE
VOLTS MICRONS
150V
RMS
25V
RMS
NOTE: Low voltage formulation.
AVERAGE
GRAIN SIZE
20 75 150 1.5
80 (Note) 12 39 1.0
GRADIENT
V/mm AT
n
1mA mm
DEVICE
THICKNESS
Theory of Operation
,
Because of the polycrystalline nature of metal-oxide
semiconductor varistors, the physical operation of the device
is more complex than that of conventional semiconductors.
Intensive measurement has determined many of the device’s
electrical characteristics, and much effort continues to better
define the varistor's operation. In this application note we will
discuss some theories of operation, but from the user’s
viewpoint this is not nearly as important as understanding
the basic electrical properties as they relate to device
construction.
The key to explaining metal-oxide varistor operation lies in
understanding the electronic phenomena occurring near the
grain boundaries, or junctions between the zinc oxide grains.
While some of the early theory supposed that electronic
tunneling occurred through an insulating second phase layer
at the grain boundaries, varistor operation is probably better
described by a series-parallel arrangement of
semiconducting diodes. In this model, the grain boundaries
contain defect states which trap free electrons from the
n-type semiconducting zinc oxide grains, thus forming a
space charge depletion layer in the ZnO grains in the region
adjacent to the grain boundaries [6].
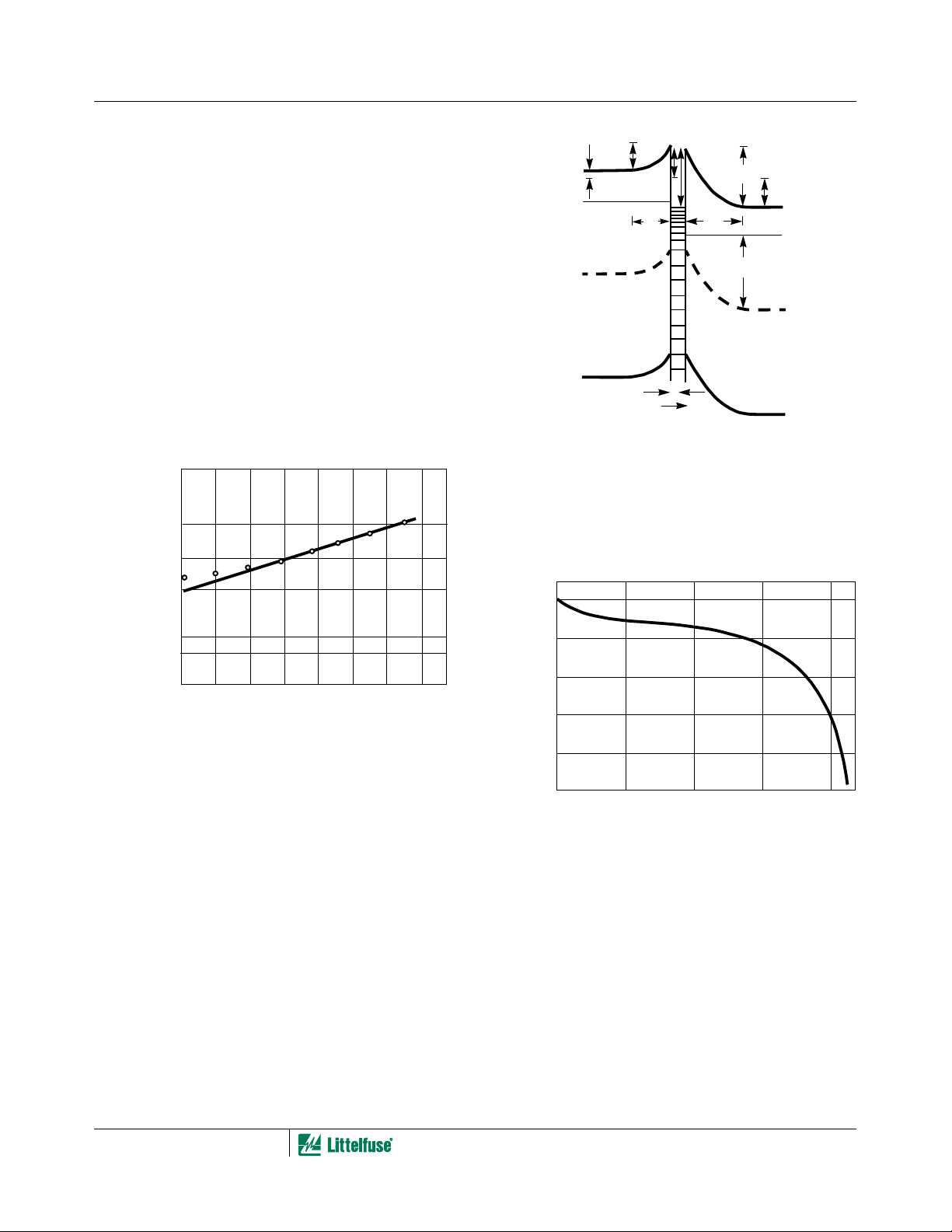
Evidence for depletion layers in the varistor is shown in
Figure 4 where the inverse of the capacitance per
boundary squared is plotted against the applied voltage per
boundary [7]. This is the same type of behavior observed
10-90
Page 3
Application Note 9767
for semiconductor abrupt P-N junction diodes. The
relationship is:
2V
1
-------
2
C
Where V
V+()
b
--------------------------=
qε sN
is the barrier voltage, V the applied voltage, q the
b
electron charge, ε s the semiconductor permittivity and N is
the carrier concentration. From this relationship the ZnO
carrier concentration, N, was determined to be about
2 x 10
17
per cm
3
[7]. In addition, the width of the depletion
layer was calculated to be about 1000 Angstrom units.
Single junction studies also support the diode model [9].
It is these depletion layers that block the free flow of carriers
and are responsible for the low voltage insulating behavior in
the leakage region as depicted in Figure 5. The leakage current
is due to the free flow of carriers across the field lowered
barrier, and is thermally activated, at least above about 25
(1014)
/cm
4
4
3
2
0 0.4 0.8 1.2
V
PER BOUNDARY
A
VARISTOR RESEMBLES A SEMICONDUCTOR
ABRUPT-JUNCTION REVERSED BIASED DIODE
Nd ~ 2 x 10
17
3
/cm
1
-------------
2n2
c
FIGURE 4. CAPACITANCE-VOLTAGE BEHAVIOR OF
o
C.
Figure 5 shows an energy band diagram for a ZnO-grain
boundary-ZnO junction [10].
biased, V
, and the right side is reverse biased to V
L
depletion layer widths are X
barrier heights are φ
is φ
. As the voltage bias is increased, φ
O
φ
is increased, leading to a lowering of the barrier and an
R
L
The left-hand grain is forward
and X
L
and φ
. The zero biased barrier height
R
, and the respective
R
is decreased and
L
. The
R
increase in conduction.
The barrier height φ
of a low voltage varistor was measured
L
as a function of applied voltage [11], and is presented in
Figure 6. The rapid decrease in the barrier at high voltage
represents the onset of nonlinear conduction [12].
φ
φ
B
0
V
E
C
E
E
E
V
FIGURE 5. ENERGY BAND DIAGRAM OF A
LφL
f
X
L
I
δ
ZnO-GRAINBOUNDARY-ZnO JUNCTION
φR
V
X
R
φ
F
0
R
Transport mechanisms in the nonlinear region are very
complicated and are still the subject of active research. Most
theories draw their inspiration from semiconductor transport
theory and the reader is referred to the literature for more
information [3, 5, 13, 14, 15]
o
φ
1.0
⁄
L
φ
0.8
0.6
0.59=
o
0.4
φ
0.2
0
NORMALIZED THERMAL BARRIER
0
FIGURE 6. THERMAL BARRIER vs APPLIED VOLTAGE
.
4
8
VOLTAGE (V)
12
16
Turning now to the high current upturn region in Figure 10,
we see that the V-I behavior approaches an ohmic
characteristic. The limiting resistance value depends upon
the electrical conductivity of the body of the semiconducting
ZnO grains, which have carrier concentrations in the range
17
of 10
to 10
18
per cm
3
. This would put the ZnO resistivity
below 0.3 Ω cm.
Varistor Construction
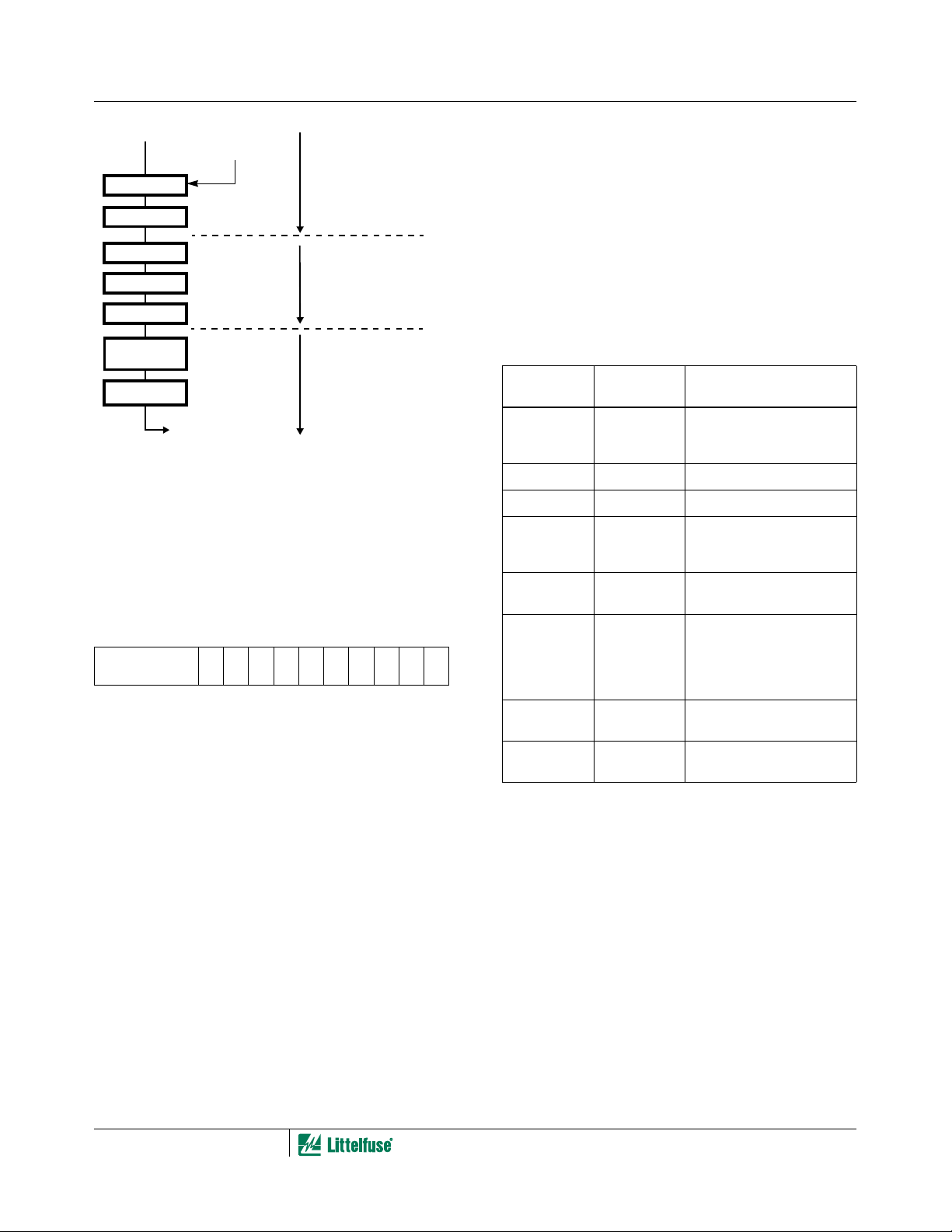
The process of fabricating a Littelfuse Varistor is illustrated in
the flow chart of Figure 7. The starting material may differ in
the composition of the additive oxides, in order to cover the
voltage range of product.
10-91
Page 4
Application Note 9767
ZnO
MIXING
POWDER
PRESS
SINTER
ELECTRODE
MECHANICAL
ASSEMBLY
ENCAPSULATE
FIGURE 7. SCHEMATIC FLOW DIAGRAM OF LITTELFUSE
ADDITIVE OXIDES
(MAINLY BL
FINAL PRODUCT TO
ELECTRICAL TEST
VARISTOR FABRICATION
203
)
POWDER PREPARATION
FORM CERAMIC BODY
PACKAGE AS/IF REQUIRED
Device characteristics are determined at the pressing
operation. The powder is pressed into a form of
predetermined thickness in order to obtain a desired value of
nominal voltage. To obtain the desired ratings of peak
current and energy capability, the electrode area and mass
of the device are varied. The range of diameters obtainable
in disc product offerings is listed here:
Nominal Disc
Diameter - mm
3 5 7 10 14 20 32 34 40 62
Of course, other shapes, such as rectangles, are also
possible by simply changing the press dies. Other ceramic
fabrication techniques can be used to make different shapes.
For example, rods or tubes are made by extruding and
cutting to length. After forming, the green (i.e., unfired) parts
are placed in a kiln and sintered at peak temperatures in
excess of 1200
o
825
C, assisting in the initial densification of the
o
C. The bismuth oxide is molten above
polycrystalline ceramic. At higher temperatures, grain growth
occurs, forming a structure with controlled grain size.
Radials are also available with phenolic coatings applied
using a wet process. The PA series package consists of
plastic molded around a 20mm disc subassembly. The RA,
DA, and DB series devices are all similar in that they all are
composed of discs or chips, with tabs or leads, encased in a
molded plastic shell filled with epoxy. Different package
styles allow variation in energy ratings, as well as in
mechanical mounting. Figures 8 and 9 illustrate several
package forms.
Figure 9 shows construction details of some packages.
Dimensions of the ceramic, by package type, are given in
Table 2.
TABLE 2. BY-TYPE CERAMIC DIMENSIONS
PACKAGE
TYPE SERIES CERAMIC DIMENSIONS
Leadless
Surface Mount
Connector Pin CP Series 22, 20, 16 ID Gauge Tube
Axial Leaded MA Series 3mm Diameter Disc
Radial
Leaded
Boxed, Low
Profile
Industrial
Packages
Industrial Discs CA, NA Series 32mm, 40mm, 60mm
Arrester AS Series 32mm, 42mm, 60mm
Littelfuse multilayer suppressor technology devices.
†
CH, AUML
ML
†
MLN
ZA, LA, “C” III,
UltraMOV™
Series
RA Series 5mm x 8mm, 10mm x 16mm,
PA Series
HA Series
HB Series
DA, DB Series
BA, BB Series
, MLE
Series
†
,
5mm x 8mm Chip, 0603, 0805,
†
1206, 1210, 1812, 2220
†
5mm, 7mm, 10mm, 14mm,
20mm Diameter Discs
14 x 22 Chips
20mm Diameter Disc
32mm, 40mm Diameter Disc
34mm Square Disc
40mm Diameter Disc
60mm Diameter Disc
Diameter Discs, 34mm Square
Diameter Discs
Electroding is accomplished, for radial and chip devices, by
means of thick film silver fired onto the ceramic surface. Wire
leads or strap terminals are then soldered in place. A
conductive epoxy is used for connecting leads to the axial
3mm discs. For the larger industrial devices (40mm and
60mm diameter discs) the contact material is arc sprayed
aluminum, with an overspray of copper if necessary to give a
solderable surface.
Many encapsulation techniques are used in the assembly of
the various Littelfuse Varistor packages. Most radials and
some industrial devices (HA Series) are epoxy coated in a
fluidized bed, whereas epoxy is “spun” onto the axial device.
10-92
Page 5

Application Note 9767
DA
BA
RA
AS
PA
CA
BB
DB
HA
MA
CP/CS CH AUML
FIGURE 8. PACKAGE FORMS
10-93
UltraMOV/LA/ ZA
ML
Page 6

Application Note 9767
PA SERIES
FIGURE 9A. CROSS-SECTION OF MA
PACKAGE
DB SERIES
FIGURE 9B. CROSS-SECTION OF
RADIAL LEAD PACKAGE
DA SERIES
FIGURE 9C. PICTORIAL VIEW OF
POWER MOV PACKAGE
BA/BB SERIES
FIGURE 9D. PICTORIAL VIEW OF HIGH ENERGY PACKAGES, DA, DB, AND BA/BB SERIES
Electrical Characterization
Varistor VI Characteristics
Varistor electrical characteristics are conveniently displayed
using log-log format in order to show the wide range of the
V-I curve. The log format also is clearer than a linear
representation which tends to exaggerate the nonlinearity
in proportion to the current scale chosen. A typical V-I
10-94
characteristic curve is shown in Figure 10. This plot shows a
wider range of current than is normally provided on varistor
data sheets in order to illustrate three distinct regions of
electrical operation.
Page 7

Application Note 9767
Ω
1000
500
200
100
50
VOLTAGE (V)
20
10
-8
10
LEAKAGE
REGION
Ω
9
0
1
=
R
10
-6
NORMAL VARISTOR
SLOPE =
-4
10
CURRENT (A)
OPERATION
1
---
α
(TYPICAL V130LA20A)
-2
10
0
10
I = kV
UPTURN
REGION
Ω
α
= 1 - 10
R
2
10
10
FIGURE 10. TYPICAL VARISTOR V-I CURVE PLOTTED ON
LOG-LOG SCALE
Equivalent Circuit Model
An electrical model for the varistor can be represented by
the simplified equivalent circuit of Figure 11.
(LEAD
L
INDUCTANCE)
(TYPICAL V130LA20A)
capacitance abruptly decreases. Capacitance remains nearly
constant with frequency change up to 100kHz. Similarly, the
change with temperature is small, the 25
capacitance being well within ± 10% from -40
o
C value of
o
C to 125
o
C.
The temperature effect of the V-I characteristic curve in the
leakage region is shown in Figure 13. A distinct temperature
dependence is noted.
100
80
60
50
C (%)
o
4
40
30
VALUE AT 25
20
NOM
V
VARISTOR VOLTAGE IN PERCENT OF
10
10
-8
-9
10
25 50 100
75
-7
10
VARISTOR CURRENT (A
SPECIMEN V130LA10A
125oC
-6
10
-5
10
10-410-310
)
DC
FIGURE 13. TEMPERATURE DEPENDENCE OF THE
CHARACTERISTIC CURVE IN THE LEAKAGE
REGION
-2
C
(0.002µF)
V
R
x
(0 TO ∞)
RON
(1Ω)
R
OFF
(1000MΩ)
FIGURE 11. VARISTOR EQUIVALENT CIRCUIT MODEL
Leakage Region of Operation
At low current levels, the V-I Curve approaches a linear
(ohmic) relationship and shows a significant temperature
dependence. The varistor is in a high resistance mode
(approaching 10
nonlinear resistance component, R
because R
insignificant compared to R
FIGURE 12. EQUIVALENT CIRCUIT AT LOW CURRENTS
For a given varistor device, capacitance remains
approximately constant over a wide range of voltage and
frequency in the leakage region. The value of capacitance
drops only slightly as voltage is applied to the varistor. As the
voltage approaches the nominal varistor voltage, the
9
) and appears as an open circuit. The
, can be ignored
OFF
X
.
L
R
OFF
in parallel will predominate. Also, R
OFF
C
ON
will be
The relation between the leakage current, I, and
temperature, T, is:
-V
/kT
B
I = IO ε
where:
I
= constant
O
k = Boltzmann’s Constant
V
= 0.9eV
B
The temperature variation, in effect, corresponds to a
change in R
resistance value even at elevated temperatures. For
example, it is still in the range of 10M Ω to 100M Ω at 125
Although R
. However, R
OFF
is a high resistance it varies with frequency.
OFF
remains at a high
OFF
o
C.
The relationship is approximately linear with inverse
frequency.
1
OFF
---
~
f
and C is
OFF
R
However, the parallel combination of R
predominantly capacitive at any frequency of interest. This is
because the capacitive reactance also varies approximately
linearly with 1/f.
At higher currents, at and above the milliamp range,
temperature variation becomes minimal. The plot of the
temperature coefficient (DV/DT) is given in Figure 14. It
should be noted that the temperature coefficient is negative
and decreases as current rises. In the clamping voltage range
of the varistor (I > 1A), the temperature dependency
approaches zero.
10-95
Page 8

Application Note 9767
NORMAL
OPERATION
0
10
10
10
2
1
10
0.1
C)
o
SAMPLE TYPE
V130LA10A
0
-0.1
-0.2
-0.3
-0.4
-0.5
TEMPERATURE COEFFICIENT (%/
10
V22ZA3
-4
-5
10
LEAKAGE REGION
-2
-3
10
10
CURRENT (A)
-1
10
NOTE: Typical Temperature Coefficient of Voltage vs Current, 14mm
Size, 55oC to 125oC.
FIGURE 14. RELATION OF TEMPERATURE COEFFICIENT
DV/DT TO VARISTOR CURRENT
Normal Varistor Region of Operation
The varistor characteristic follows the equation I = kVα,
where k is a constant and the exponent α defines the degree
of nonlinearity. Alpha is a figure of merit and can be
determined from the slope of the V-I curve or calculated from
the formula:
I
⁄()log
-------------------------------=
-------------------------------
.
ON
V
1
V
2I1
⁄()log
2V1
⁄()log
2V1
for I
⁄ 1==
2I1
ON
and R
will
. RX becomes many
OFF
but remains larger than
OFF
X
α
In this region the varistor is conducting and R
predominate over C, R
orders of magnitude less than R
R
Plots of typical resistance values vs current, I, are given in
Figure 16.
500
100
50
10
5
1
0.5
STATIC RESISTANCE
3
0.1
0.05
Ω PER RATED RMS INPUT VOLT)
(
0.01
0.01 0.1 1 10010
PEAK CURRENT (A)
FIGURE 16A. RX STATIC VARISTOR RESISTANCE FIGURE
5
1
0.5
0.01
0.05
0
.01
DYNAMIC RESISTANCE
0.005
Ω PER RATED RMS INPUT VOLT)
(
0.001
0.01 0.1 1.0 10 100
PEAK CURRENT (A)
FIGURE 16B. ZX DYNAMIC VARISTOR RESISTANCE
L
R
X
FIGURE 15. EQUIVALENT CIRCUIT AT VARISTOR CONDUCTION
During conduction the varistor voltage remains relatively
constant for a change in current of several orders of
magnitude. In effect, the device resistance, R
, is changing
X
in response to current. This can be observed by examining
the static or dynamic resistance as a function of current. The
static resistance is defined by:
V
R
----=
X
I
and the dynamic resistance by:
dv
Z
------ V αI⁄ R
X
di
α⁄== =
X
10-96
Upturn Region of Operation
At high currents, approaching the maximum rating, the varistor
approximates a short-circuit. The curve departs from the
nonlinear relation and approaches the value of the material bulk
resistance, about 1Ω-10Ω. The upturn takes place as R
approaches the value of R
. Resistor RON represents the
ON
bulk resistance of the zinc oxide grains. This resistance is linear
(which appears as a steeper slope on the log plot) and occurs
at currents 50A to 50,000A, depending on the varistor size.
L
R
ON
FIGURE 17. EQUIVALENT CIRCUIT AT VARISTOR UPTURN
X
Page 9

Application Note 9767
Speed of Response and Rate Effects
The varistor action depends on a conduction mechanism
similar to that of other semiconductor devices. For this
reason, conduction occurs very rapidly, with no apparent
time lag - even into the nanosecond range. Figure 18 shows
a composite photograph of two voltage traces with and
without a varistor inserted in a very low inductance impulse
generator. The second trace (which is not synchronized with
the first, but merely superimposed on the oscilloscope
screen) shows that the voltage clamping effect of the varistor
occurs in less than one nanosecond.
TRACE 1
LOAD
VOLTAGE
WITHOUT
VARISTOR
100V/DIV.
TRACE 2
LOAD
VOLTAGE
CLAMPED BY
VARISTOR
500ps/DIV.
FIGURE 18. RESPONSE OF A ZnO VARISTOR TO A FAST
RISE TIME (500ps) PULSE
In the conventional lead-mounted devices, the inductance of
the leads would completely mask the fast action of the
varistor; therefore, the test circuit for Figure 18 required
insertion of a small piece of varistor material in a coaxial line
to demonstrate the intrinsic varistor response.
Tests made on lead mounted devices, even with careful
attention to minimizing lead length, show that the voltages
induced in the loop formed by the leads contribute a
substantial part of the voltage appearing across the
terminals of a varistor at high current and fast current rise.
Fortunately, the currents which can be delivered by a
transient source are invariably slower in rise time than the
observed voltage transients. The applications most
frequently encountered for varistors involve current rise
times longer than 0.5µs.
Voltage rate-of-rise is not the best term to use when
discussing the response of a varistor to a fast impulse (unlike
spark gaps where a finite time is involved in switching from
nonconducting to conducting state). The response time of
the varistor to the transient current that a circuit can deliver is
the appropriate characteristic to consider.
The V-I characteristic of Figure 19A shows how the response
of the varistor is affected by the current waveform. From
such data, an “overshoot” effect can be defined as being the
relative increase in the maximum voltage appearing across
the varistor during a fast current rise, using the conventional
8/20µs current wave as the reference. Figure 19B shows
typical clamping voltage variation with rise time for various
current levels.
140
1000
CLAMPING VOLTAGE (V)
DEVICE: V130LA20A
(LEAD AREA <1cm
800
600
400
200
10
20 10040 60 200 400 600 1000 2000
2
) (NOTE)
PEAK CURRENT (A)
WAVESHAPE
0.5/1.5µs
1/3µs
8/20µs
FIGURE 19A. V-I CHARACTERISTICS FOR VARIOUS CURRENT
RISE TIMES
1000A/cm
130
120
110
100
% OF CLAMPING VOLTAGE AT 8µs
90
0.2 0.4 0.6 0.8 1 2 4 6 8 10
FIGURE 19B. OVERSHOOT DEFINED WITH REFERENCE TO
THE BASIC 8/20µs CURRENT PULSE
2
(2.5kA)
2
100A/cm
(250A)
2
10A/cm
(25A)
PULSE RISE TIME (µs)
NOTE: Refer to the Maximum Clamping Voltage section of DB450, Transient Voltage Suppression Devices.
FIGURE 19. RESPONSE OF LEAD-MOUNTED VARISTORS TO CURRENT WAVEFORM
10-97
DEVICE: V130LA20A
(LEAD AREA <1cm
2
) (NOTE)
100%
AT
8µs
Page 10

Application Note 9767
Varistor Terminology
The following tabulation defines the terminology used in
varistor specifications. Existing standards have been
followed wherever possible.
Definitions (IEEE Standard C62.33, 1982)
A characteristic is an inherent and measurable property of a
device. Such a property may be electrical, mechanical, or
thermal, and can be expressed as a value for stated
conditions.
A rating is a value which establishes either a limiting
capability or a limiting condition (either maximum or
minimum) for operation of a device. It is determined for
specified values of environment and operation. The ratings
indicate a level of stress which may be applied to the device
without causing degradation or failure. Varistor symbols are
defined on the linear V-I graph illustrated in Figure 20.
I
P
I
X
Test Waveform
At high current and energy levels, varistor characteristics are
measured, of necessity, with an impulse waveform. Shown in
Figure 21 is the ANSI Standard C62.1 waveshape, an
exponentially decaying waveform representative of lightning
surges and the discharge of stored energy in reactive
circuits.
The 8/20µs current wave (8µs rise and 20µs to 50% decay of
peak value) is used as a standard, based on industry
practices, for the characteristics and ratings described. One
exception is the energy rating (W
waveform of 10/1000µs is used. This condition is more
representative of the high energy surges usually
experienced from inductive discharge of motors and
transformers. Varistors are rated for a maximum pulse
energy surge that results in a varistor voltage (V
less than ±10% from initial value.
100
90
50
), where a longer
TM
) shift of
N
CURRENT (A)
I
N(DC)
I
PM
I
1000
V
N(DC)
VOLTAGE (V)
D
10
-6
10
V
M(DC)
VOLTAGE (V)
I
N(DC)
CURRENT (A)
V
PM
VARISTOR
SYMBOL
V
N(DC)VXVC
o
10
FIGURE 20. I-V GRAPH ILLUSTRATING SYMBOLS AND
DEFINITIONS
10
VIRTUAL START OF WAVE
CURRENT IN PERCENT OF PEAK VALUE
IMPULSE DURATION
VIRTUAL FRONT DURATION
= 1.25 x RISETIME FROM 10% TO 90%
PEAK CURRENT(A)
FIGURE 21. DEFINITION OF PULSE CURRENT WAVEFORM
10-98
Page 11

Application Note 9767
TABLE 3. VARISTOR CHARACTERISTICS (IEEE STANDARD C62.33-1982 SUBSECTION 2.3 AND 2.4)
TERMS AND DESCRIPTIONS SYMBOL
Clamping Voltage. Peak voltage across the varistor measured under conditions of a specified peak VC pulse current and specified
waveform. NOTE: Peak voltage and peak currents are not necessarily coincidental in time.
Rated Peak Single Pulse Transient Currents (Varistor). Maximum peak current which may be applied for a single 8/20µs im-
pulse, with rated line voltage also applied, without causing device failure.
Lifetime Rated Pulse Currents (Varistor). Derated values of ITM for impulse durations exceeding that of an 8/20µs waveshape,
and for multiple pulses which may be applied over device rated lifetime.
Rated RMS Voltage (Varistor). Maximum continuous sinusoidal RMS voltage which may be applied. V
Rated DC Voltage (Varistor). Maximum continuous DC voltage which may be applied. V
DC Standby Current (Varistor). Varistor current measured at rated voltage, V
For certain applications, some of the following terms may be useful.
Nominal Varistor Voltage. Voltage across the varistor measured at a specified pulsed DC current, I
I
of specific duration. I
N(DC)
is specified by the varistor manufacturer.
N(DC)
Peak Nominal Varistor Voltage. Voltage across the varistor measured at a specified peak AC current, I
I
is specified by the varistor manufacturer.
N(AC)
Rated Recurrent Peak Voltage (Varistor). Maximum recurrent peak voltage which may be applied for a specified duty cycle and
waveform.
Rated Single Pulse Transient Energy (Varistor). Energy which may be dissipated for a single impulse of maximum rated current
at a specified waveshape, with rated RMS voltage or rated DC voltage also applied, without causing device failure.
Rated Transient Average Power Dissipation (Varistor). Maximum average power which may be dissipated due to a group of
pulses occurring within a specified isolated time period, without causing device failure.
Varistor Voltage. Voltage across the varistor measured at a given current, IX. V
Voltage Clamping Ratio (Varistor). A figure of merit measure of the varistor clamping effectiveness as defined by the symbols
VC/V
M(AC)
, VC/V
M(DC)
.
Nonlinear Exponent. A measure of varistor nonlinearity between two given operating currents, I1 and I2, as described by I = kV
where k is a device constant, I
α
12
I2I1⁄log
--------------------------=
V
⁄log
2V1
≤ I ≤ I2, and
1
.I
M(DC)
, of specific duration.
N(DC)
, of specific duration.
N(AC)
V
V
W
P
T(AV)M
------------
V
α
V
C
I
TM
-
M(AC
M(DC)
D
N(DC)
N(AC)
V
PM
TM
X
V
C
PM
α
)
Dynamic Impedance (Varistor). A measure of small signal impedance at a given operating point as defined by: Z
dV
X
-----------=
Z
X
dI
X
Resistance (Varistor). Static resistance of the varistor at a given operating point as defined by: R
V
X
R
-------=
X
I
X
Capacitance (Varistor). Capacitance between the two terminals of the varistor measured at C specified frequency and bias. C
AC Standby Power (Varistor). Varistor AC power dissipation measured at rated RMS voltage V
Voltage Overshoot (Varistor). The excess voltage above the clamping voltage of the device for a given current that occurs when
.P
M(AC)
V
current waves of less than 8µs virtual front duration are applied. This value may be expressed as a % of the clamping voltage (VC)
for an 8/20 current wave.
Response Time (Varistor). The time between the point at which the wave exceeds the clamping voltage level (VC) and the peak
of the voltage overshoot. For the purpose of this definition, clamping voltage as defined with an 8/20µs current waveform of the
same peak current amplitude as the waveform used for this response time.
Overshoot Duration (Varistor). The time between the point voltage level (VC) and the point at which the voltage overshoot has
decayed to 50% of its peak. For the purpose of this definition, clamping voltage is defined with an 8/20µs current waveform of the
same peak current amplitude as the waveform used for this overshoot duration.
10-99
X
X
D
OS
-
-
Page 12

Application Note 9767
How to Connect a Littelfuse Varistor
Transient suppressors can be exposed to high currents for
short durations in the nanoseconds to millisecond time
frame.
Littelfuse Varistors are connected in parallel to the load, and
any voltage drop in the leads to the varistor will reduce its
effectiveness. Best results are obtained by using short leads
that are close together to reduce induced voltages and a low
ohmic resistance to reduce I • R drops.
Electrical Connections
Single Phase
LINE
1
NEUTRAL
3 2
GND
FIGURE 22.
This is the most complete protection one can select, but in
many cases only Varistor 1 or Varistor 1 and 2 are selected.
LINE
SINGLE PHASE
2 WIRE 110V
SINGLE PHASE
2 WIRE 240V
SINGLE PHASE
3 WIRE 120V/240V
LINE
GND OR
NEUTRAL
LINE
FIGURE 23.
GND
LINE
GND
110V
240V
120V
240V
120V
3 Phase
SUPPRESSOR
CONNECTION
1
3
8
0
V
220V
4
23
110V
220V
23
SUPPRESSOR
CONNECTION
220V
FIGURE 24A. 3 PHASE 220V/380V,
UNGROUNDED
LOWER
VOLTAGE
1
220V 220V
4
110V
FIGURE 24D. 3 PHASE 220V
1 - 4
2 - 4
3 - 4
1 - 3
1 - 2
2 - 4
3 - 4
SUPPRESSOR
CONNECTION
1 - 2
2 - 3
(3
8
0
V
)
1
220V 220V
220V
3 - 1
23
FIGURE 24B. 3 PHASE 220V OR 380V,
UNGROUNDED
SUPPRESSOR
CONNECTION
21
2
0
8
2
110V
8
0
V
110V
V
3
110V
208V
1 - 2
1 - 3
3 - 2
1 - GND
2 - GND
3 - GND
If only 3 suppressor use 1-GND, 2-GND,
3-GND
FIGURE 24E. 3 PHASE 120V/208V, 4-WIRE
SUPPRESSOR
CONNECTION
1 - 2
2 - 3
1
220V 220V
220V
1 - 3
23
FIGURE 24C. 3 PHASE 220V, ONE PHASE
GND
SUPPRESSOR
CONNECTION
21
4
1
5
240V
1
4
V
240V
V
5
240V
3
1 - 2
1 - 3
3 - 2
1 - GND
4
1
5
V
2 - GND
3 - GND
If only 3 suppressor use 1-GND, 2-GND,
3-GND
FIGURE 24F. 3 PHASE 240V/415V
For higher voltages use same connections, but select varistors for the appropriate voltage rating.
10-100
Page 13

Application Note 9767
DC Applications
DC applications require connection between plus and minus
or plus and ground and minus and ground.
For example, if a transient towards ground exists on all
3 phases (common mode transients) only transient
suppressors connected phase to ground would absorb
energy. Transient suppressors connected phase to phase
would not be effective.
COMMON
MODE
TRANSIENT
FIGURE 25A. INCORRECT
FIGURE 25. COMMON MODE TRANSIENT AND CORRECT
SOLUTION
On the other hand if a differential mode of transient (phase to
phase) exists then transient suppressors connected phase
to phase would be the correct solution.
DIFFERENTIAL
MODE
TRANSIENT
FIGURE 26A. INCORRECT
FIGURE 26. DIFFERENTIAL MODE TRANSIENT AND CORRECT
SOLUTION
This is just a selection of some of the more important
variations in connecting transient suppressors.
The logical approach is to connect the transient suppressor
between the points of the potential difference created by the
transient. The suppressor will then equalize or reduce these
potentials to lower and harmless levels.
FIGURE 25B. CORRECT
FIGURE 26B. CORRECT
References
For Littelfuse documents available on the web, see
http://www.littelfuse.com/
[1] Harnden, J.D., F.D. Martzloff, W.G. Morris and F.B.
Golden, “The GEMOV® Varistor - The Super Alpha
Varistor” Electronics, Vol. 45, No. 21,1972, p. 91.
[2] Morris, W.G., “Electrical Properties of ZnO-Bi
Ceramics,” Journal of the Am. Ceram. Soc., Vol. 56,
1973.
[3] Matsuoka, M., “Non-Ohmic Properties of Zinc Oxide
Ceramics,” Japanese Jnl. Appl. Phys., Vol. 10,1971, p.
736.
[4] Mahan, G., L. Levinson and H. Philipp, “Single Grain
Junction Studies at ZnO Varistors Theory &
Experiment,” Report #78CRF160, General Electric,
Schenectady, N.Y., 1978. Forthcoming in Applied
Physics Letters.
[5] Mahan, G., L. Levinson and H. Philipp, “Theory of
Conduction in ZnO Varistors,” Journal of Applied
Physics (in press).
[6] Levine, J.D., “Theory of Varistor Electronic Properties,”
Critical Review of Solid State Science, 5,1975, pp.
597-608.
[7] May, J.E., “Carrier Concentration and Depletion Layer
Model of Zinc Oxide Varistors,” Bulletin of the American
Ceramic Society, Vol. 57, No. 3, 1978, p. 335.
[8] Sze, S.M., “Physics of Semiconductor Devices,” John
Wiley & Sons, New York, N.Y., 1969.
[9] Einzinger, R., “Microcontact Measurement of ZnO
Varistors,” Ber. Dt. Keram, Vol. 52, 1975, pp. 244-245.
[10] Lou, L.F., “Current- Voltage Characteristics of ZnO-
Bi
Heterojunction,” Journal of Applied Physics,
2O3
Vol. 50, 1979, p. 555.
[11] Lou, L.F. “Semiconducting Properties of ZnO-Grain
Boundary-ZnO Junctions in Ceramic Varistors,” Appl.
Phys. Letters, Vol. 36, 1980, pp. 570-572.
[12] Lou, L.F., and J.E. May, Unpublished Research,
General Electric, Syracuse, N.Y., 1981.
[13] Morris, W., “Physical Properties of the Electrical
Barriers in Varistors,” J. Vac. Sci. Technol., 13,1976,
pp. 926-931.
[14] Bernasconi, J., S. Strassler, B. Knecht, H. Klein and A.
Menth, Solid State Communication, Vol. 21,1977,
pp. 867-869.
[15] Pike, G. and C. Seager, “The DC Voltage Dependence
of Semiconductor Grain-Boundary Resistance,” Journal
of Appl. Phys., Vol. 50, 1979, pp. 3414-3422
2O3
10-101
 Loading...
Loading...