LINEAR TECHNOLOGY LTC1968 Technical data

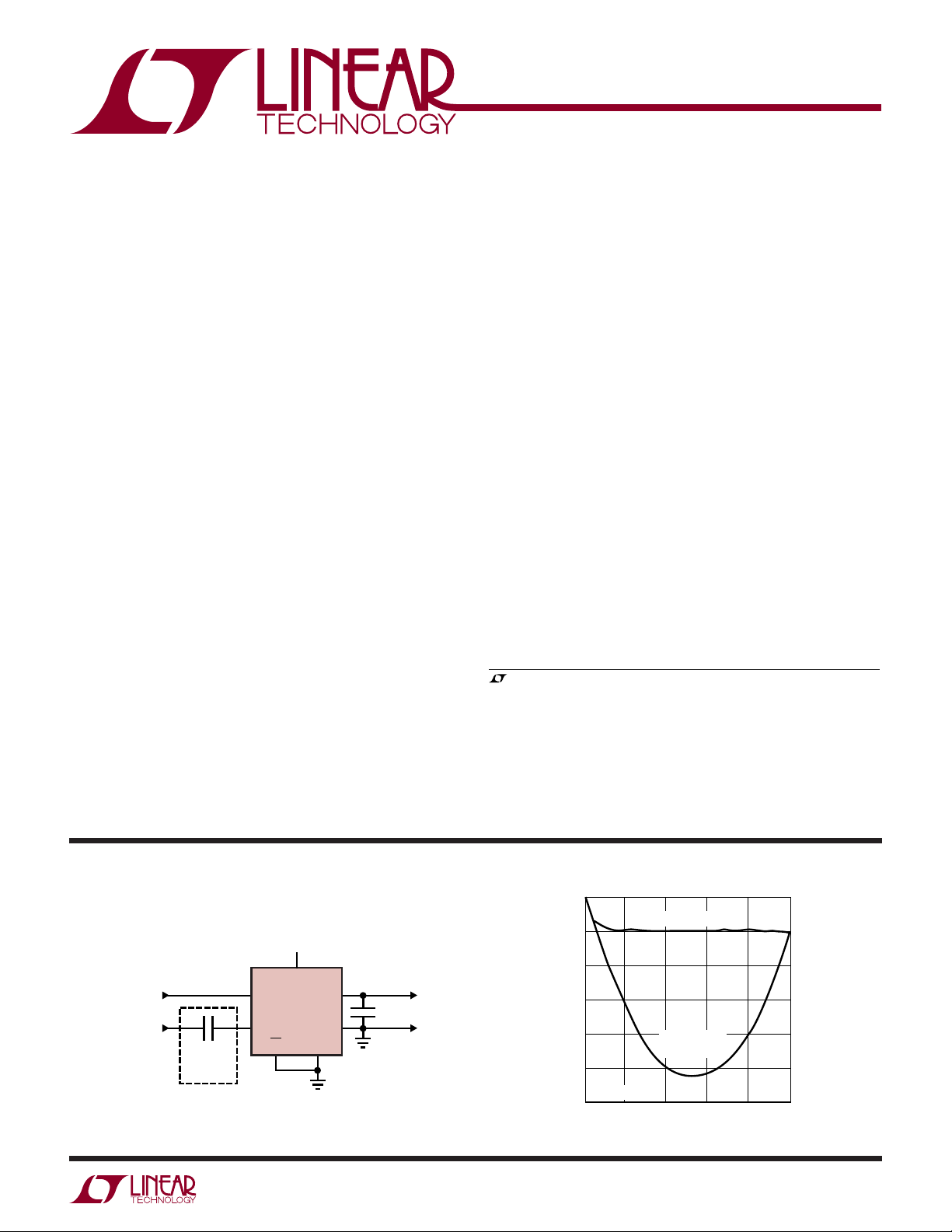
FEATURES

■

High Linearity:

0.02% Linearity Allows Simple System Calibration

■

Wide Input Bandwidth:

Bandwidth to 1% Additional Gain Error: 500kHz
Bandwidth to 0.1% Additional Gain Error: 150kHz
3dB Bandwidth Independent of Input Voltage
Amplitude

■

No-Hassle Simplicity:

True RMS-DC Conversion with Only One External
Capacitor
Delta Sigma Conversion Technology

■

Ultralow Shutdown Current:

0.1µA

■

Flexible Inputs:

Differential or Single Ended
Rail-to-Rail Common Mode Voltage Range
Up to 1V

■

Flexible Output:

Differential Voltage

PEAK

Rail-to-Rail Output
Separate Output Reference Pin Allows Level Shifting

■

Small Size:

Space Saving 8-Pin MSOP Package

U

APPLICATIO S

LTC1968

Precision Wide Bandwidth,

RMS-to-DC Converter

U

DESCRIPTIO

The LTC®1968 is a true RMS-to-DC converter that uses an
innovative delta-sigma computational technique. The ben­efits of the LTC1968 proprietary architecture, when com­pared to conventional log-antilog RMS-to-DC converters,
are higher linearity and accuracy, bandwidth independent
of amplitude and improved temperature behavior.

The LTC1968 operates with single-ended or differential in­put signals and accurately supports crest factors up to 4.
Common mode input range is rail-to-rail. Differential in­put range is 1V
LTC1968 allows hassle-free system calibration at any in­put voltage.

The LTC1968 has a rail-to-rail output with a separate out­put reference pin providing flexible level shifting; it oper­ates on a single power supply from 4.5V to 5.5V. A low power
shutdown mode reduces supply current to 0.1µA.

The LTC1968 is packaged in the space-saving MSOP pack­age, which is ideal for portable applications.

, LTC and LT are registered trademarks of Linear Technology Corporation.

Protected under U.S. Patent Numbers 6,359,576, 6,362,677 and 6,516,291

, and offers unprecedented linearity. The

PEAK

■

True RMS Digital Multimeters and Panel Meters

■

True RMS AC + DC Measurements

U

TYPICAL APPLICATIO

Single Supply RMS-to-DC Converter

4.5V TO 5.5V

+

V

OUTPUT

DIFFERENTIAL

INPUT

0.1µF

OPT. AC

COUPLING

IN1

LTC1968

IN2

EN GND

OUT RTN

1968 TA01

C

AVE

10µF

)

0.2

RMS

mV AC

IN

–0.2

mV DC – V

+

V

OUT

–

–0.4

OUT

–0.6

–0.8

–1.0

LINEARITY ERROR (V

Linearity Performance

0

60Hz SINEWAVE

0

LTC1968, ∆Σ

CONVENTIONAL

100 200 300 400

VIN (mV AC

LOG/ANTILOG

RMS

500

1968 TA01b

)

1968f

1

LTC1968

1
2
3
4

GND

IN1
IN2

NC

8
7
6
5

ENABLE
V

+

OUT RTN
V

OUT

TOP VIEW

MS8 PACKAGE

8-LEAD PLASTIC MSOP

WWWU

ABSOLUTE AXI U RATI GS

(Note 1)

Supply Voltage

+

V

to GND ............................................................. 6V

Input Currents (Note 2) ..................................... ±10mA

Output Current (Note 3) ..................................... ±10mA

ENABLE Voltage ......................................... –0.3V to 6V

OUT RTN Voltage........................................ –0.3V to V

Operating Temperature Range (Note 4)

LTC1968C/LTC1968I ......................... – 40°C to 85°C

Specified Temperature Range (Note 5)

LTC1968C/LTC1968I ......................... – 40°C to 85°C

Maximum Junction Temperature ......................... 150°C

Storage Temperature Range ................ –65°C to 150°C

Lead Temperature (Soldering, 10 sec)................. 300°C

ELECTRICAL CHARACTERISTICS

temperature range, otherwise specifications are TA = 25°C. V+ = 5V, V
unless otherwise noted.

+

The ● denotes specifications which apply over the full operating

UU

W

PACKAGE/ORDER I FOR ATIO

ORDER PART

NUMBER

LTC1968CMS8
LTC1968IMS8

MS8 PART MARKING

T

= 150°C, θJA = 220°C/ W

JMAX

Consult LTC Marketing for parts specified with wider operating temperature ranges.
The temperature grade (I or C) is indicated on the shipping container.

OUTRTN

= 2.5V, C

= 10µF, VIN = 200mV

AVE

RMS

LTAFG

, V

ENABLE

= 0.5V

SYMBOL PARAMETER CONDITIONS MIN TYP MAX UNITS

Conversion Accuracy

G

ERR

V

OOS

∆V

/∆T Output Offset Voltage Drift (Note 11) ● 210µV/°C

OOS

LIN

ERR

PSRRG Power Supply Rejection (Note 9) ±0.02 ±0.20 %/V

V

IOS

∆V

/∆T Input Offset Voltage Drift (Note 11) ● 210µV/°C

IOS

Additional Error vs Crest Factor (CF)

Input Characteristics

V

IMAX

I

VR

Z

IN

CMRRI Input Common Mode Rejection (Note 13) ● 50 400 µV/V

V

IMIN

PSRRI Power Supply Rejection (Note 9) ● 250 700 µV/V

Low Frequency Gain Error 50Hz to 20kHz Input (Notes 6, 7) ±0.1 ±0.3 %

● ±0.4 %

Output Offset Voltage (Notes 6, 7) 0.2 0.75 mV

Linearity Error 50mV to 350mV (Notes 7, 8) ● ±0.02 ±0.15 %

● ±0.25 %/V

Input Offset Voltage (Notes 6, 7, 10) 0.4 1.5 mV

CF = 3 60Hz Fundamental, 200mV

CF = 5 60Hz Fundamental, 200mV

Maximum Peak Input Swing Accuracy = 1% (Note 14) ● 1 1.05 V

Input Voltage Range ● 0V
Input Impedance Average, Differential (Note 12) 1.2 MΩ

Average, Common Mode (Note 12) 100 MΩ

Minimum RMS Input ● 5mV

RMS

RMS

● 0.2 mV

● 5mV

+

V

2

1968f

LTC1968

ELECTRICAL CHARACTERISTICS

temperature range, otherwise specifications are TA = 25°C. V+ = 5V, V

The ● denotes specifications which apply over the full operating

OUTRTN

= 2.5V, C

= 10µF, VIN = 200mV

AVE

RMS

, V

ENABLE

= 0.5V

unless otherwise noted.

SYMBOL PARAMETER CONDITIONS MIN TYP MAX UNITS
Output Characteristics

OVR Output Voltage Range ● 0V
Z

OUT

Output Impedance (Note 12) ● 10 12.5 16 kΩ

CMRRO Output Common Mode Rejection (Note 13) ● 50 250 µV/V
V

OMAX

Maximum Differential Output Swing Accuracy = 1%, DC Input (Note 14) 1.0 1.05 V

● 0.9 V

PSRRO Power Supply Rejection (Note 9) ● 250 1000 µV/V

Frequency Response

f

1P

f

–3dB

1% Additional Gain Error (Note 15) 500 kHz
±3dB Frequency (Note 15) 15 MHz

Power Supplies

+

V
I

S

Supply Voltage ● 4.5 5.5 V
Supply Current IN1 = 20mV, IN2 = 0V ● 2.3 2.7 mA

IN1 = 200mV, IN2 = 0V 2.4 mA

Shutdown Characteristics

I

SS

I

IH

I

IL

V

TH

V

HYS

Supply Current V
ENABLE Pin Current High V
ENABLE Pin Current Low V

= 4.5V ● 0.1 10 µA

ENABLE

= 4.5V ● –1 –0.1 µA

ENABLE

= 0.5V ● –3 –0.5 –0.1 µA

ENABLE

ENABLE Threshold Voltage 2.1 V
ENABLE Threshold Hysteresis 0.1 V

+

V

Note 1: Absolute Maximum Ratings are those values beyond which the life
of a device may be impaired.

Note 2: The inputs (IN1, IN2) are protected by shunt diodes to GND and

+

. If the inputs are driven beyond the rails, the current should be limited

V
to less than 10mA.

Note 3: The LTC1968 output (V

) is high impedance and can be

OUT

overdriven, either sinking or sourcing current, to the limits stated.
Note 4: The LTC1968C/LTC1968I are guaranteed functional over the

operating temperature range of –40°C to 85°C.
Note 5: The LTC1968C is guaranteed to meet specified performance from

0°C to 70°C. The LTC1968C is designed, characterized and expected to
meet specified performance from –40°C to 85°C but is not tested nor QA
sampled at these temperatures. The LTC1968I is guaranteed to meet
specified performance from –40°C to 85°C.

Note 6: High speed automatic testing cannot be performed with

= 10µF. The LTC1968 is 100% tested with C

C

AVE

AVE

= 47nF.

Note 7: The LTC1968 is 100% tested with DC and 10kHz input signals.
Measurements with DC inputs from 50mV to 350mV are used to calculate

, V

, V

the four parameters: G

ERR

OOS

and linearity error. Correlation tests

IOS

have shown that the performance limits can be guaranteed with the
additional testing being performed to guarantee proper operation of all
internal circuitry.

Note 8: The LTC1968 is inherently very linear. Unlike older log/antilog
circuits, its behavior is the same with DC and AC inputs, and DC inputs are
used for high speed testing.

Note 9: The power supply rejections of the LTC1968 are measured with
DC inputs from 50mV to 350mV. The change in accuracy from V+ = 4.5V
to V+ = 5.5V is divided by 1V.

Note 10: Previous generation RMS-to-DC converters required nonlinear
input stages as well as a nonlinear core. Some parts specify a “DC reversal
error,” combining the effects of input nonlinearity and input offset voltage.
The LTC1968 behavior is simpler to characterize and the input offset
voltage is the only significant source of “DC reversal error.”

Note 11: Guaranteed by design.
Note 12: The LTC1968 is a switched capacitor device and the input/output

impedance is an average impedance over many clock cycles. The input
impedance will not necessarily lead to an attenuation of the input signal
measured. Refer to the Applications Information section titled “Input
Impedance” for more information.

Note 13: The common mode rejection ratios of the LTC1968 are measured
with DC inputs from 50mV to 350mV. The input CMRR is defined as the
change in V
V+, divided by V+. The output CMRR is defined as the change in V

measured with the input common mode voltage at 0V and

IOS

OOS

measured with OUT RTN = 0V and OUT RTN = V+ – 350mV divided by
V+ – 350mV.

Note 14: The LTC1968 input and output voltage swings are limited by
internal clipping. However, its ∆Σ topology is relatively tolerant of
momentary internal clipping.

Note 15: The LTC1968 exploits oversampling and noise shaping to reduce
the quantization noise of internal 1-bit analog-to-digital conversions. At
higher input frequencies, increasingly large portions of this noise are
aliased down to DC. Because the noise is shifted in frequency, it becomes
a low frequency rumble and is only filtered at the expense of increasingly
long settling times. The LTC1968 is inherently wideband, but the output
accuracy is degraded by this aliased noise.

1968f

3

LTC1968

UW

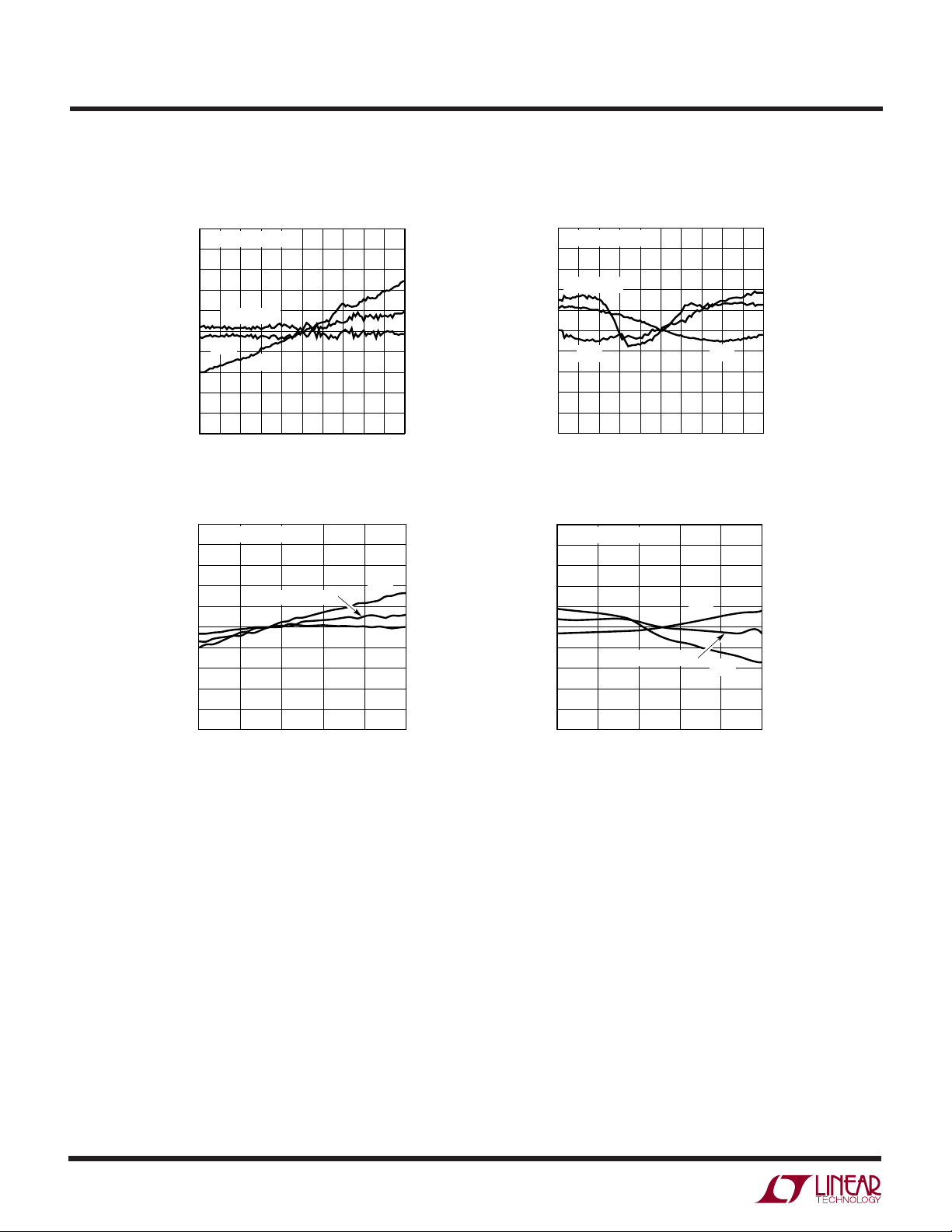
TYPICAL PERFOR A CE CHARACTERISTICS

Gain and Offset
vs Input Common Mode Voltage

0.5

50mV ≤ VIN ≤ 350mV

0.4

0.3

0.2

0.1
GAIN ERROR

0

V

OOS

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

0

V

IOS

0.5 1.5

1.0

INPUT COMMON MODE VOLTAGE (V)

2.0

3.5

2.5 5.04.5

3.0

Gain and Offset vs Supply Voltage

0.5

50mV ≤ VIN ≤ 350mV

0.4

0.3

0.2

0.1

0

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

4.5

GAIN ERROR

4.8

5.1

SUPPLY VOLTAGE (V)

V

5.4

IOS

4.0

5.7

V

OOS

1968 G01

1968 G03

1.0

0.8

0.6

OFFSET VOLTAGE (mV)

0.4

0.2

0

–0.2

–0.4

–0.6

–0.8

–1.0

1.0

0.8

0.6

OFFSET VOLTAGE (mV)

0.4

0.2

0

–0.2

–0.4

–0.6

–0.8

–1.0

6.0

Gain and Offset
vs Output Common Mode Voltage

0.5

50mV ≤ VIN ≤ 350mV

0.4

0.3
GAIN ERROR

0.2

0.1

0

–0.1

V

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

OOS

0.5 1.5

1.0

0

OUTPUT COMMON MODE VOLTAGE (V)

2.0

3.5

2.5 5.04.5

3.0

Gain and Offset vs Temperature

0.5

50mV ≤ VIN ≤ 350mV

0.4

0.3

0.2

0.1

0

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

–40

–15

GAIN ERROR

10

TEMPERATURE (°C)

V

IOS

35

1.0

0.8

0.6

OFFSET VOLTAGE (mV)

0.4

0.2

0

1968 G02

1968 G04

–0.2

–0.4

–0.6

–0.8

–1.0

0.5

0.4

0.3

OFFSET VOLTAGE (mV)

0.2

0.1

0

–0.1

–0.2

–0.3

–0.4

–0.5

85

V

IOS

4.0

V

OOS

60

4

1968f

UW

TEMPERATURE (°C)

–55

2.30

SUPPLY CURRENT (mA)

2.32

2.36

2.38

2.40

–15

25

45 125

1968 G10

2.34

–35 5

65

85

105

2.44

2.42

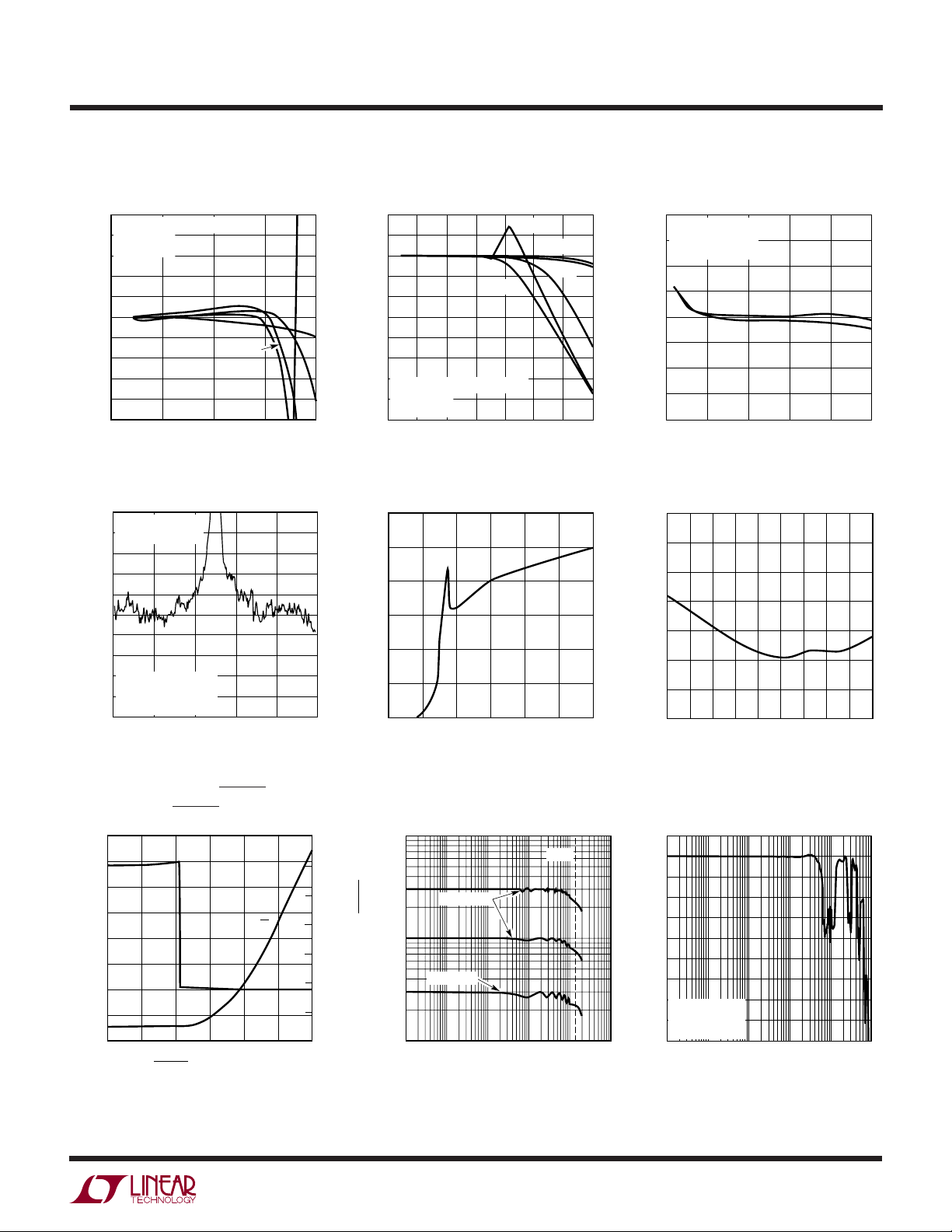
TYPICAL PERFOR A CE CHARACTERISTICS

LTC1968

Performance vs Crest Factor

201.0
200mV

200.8

C
O.1%/DIV

200.6

200.4

200.2

200.0

199.8

199.6

OUTPUT VOLTAGE (mV DC)

199.4

199.2

199.0

1

SCR WAVEFORMS

RMS

= 10µF

AVE

23

CREST FACTOR

DC Linearity

0.10
C

= 10µF

AVE

0.08

0.06

0.04

|} (mV)

0.02

INDC

– |V

–0.02

OUTDC

–0.04

{V

–0.06

–0.08

–0.10

= MIDSUPPLY

V

IN2

0

EFFECT OF OFFSETS
MAY BE POSITIVE OR
NEGATIVE AT V

–300

–500

IN

–100

= 0V

V

IN1

10kHz

(mV)

100

60Hz

1kHz

4

20Hz

300

1968 G05

1968 G08

500

220

210

200

190

180

170

160

150

OUTPUT VOLTAGE (mV DC)

140

130

5

120

3.0

2.5

2.0

1.5

1.0

SUPPLY CURRENT (mA)

0.5

0

Performance vs Large Crest Factor

20Hz

10kHz

40kHz

200mV
C
5%/DIV

1

SCR WAVEFORMS

RMS

= 10µF

AVE

23 5

CREST FACTOR

60Hz

4

1kHz

678

1968 G06

Supply Current vs Supply Voltage

0

234

1

SUPPLY VOLTAGE (V)

56

1968 G09

AC Linearity

0.20
SINEWAVES

= 10µF

C

AVE

0.15

)

RMS

0.10

0.05

(mV AC

IN

–0.05

(mV DC) – V

–0.10

OUT

V

–0.15

–0.20

= MIDSUPPLY

V

IN2

0

0

100 200 300 500

V

(mV AC

IN1

Supply Current vs Temperature

RMS

60Hz

40kHz

400

)

1968 G07

3.0

2.5

2.0

1.5

1.0

0.5

SUPPLY CURRENT (mA)

0

–0.5

–1.0

0

Power Supply and ENABLE Pin
Current vs ENABLE Voltage

I

S

I

EN

46

12

ENABLE PIN VOLTAGE (V)

35

1968 G11

300

200

100

0

–100

–200

–300

–400

1000

ENABLE PIN CURRENT (nA)

100

OUTPUT DC VOLTAGE (mV)

10

Input Signal Bandwidth
vs RMS Value

1% ERROR

1% ERROR

1k 10k

100k 1M 10M 100M

INPUT SIGNAL FREQUENCY (Hz)

–3dB

1968 G12

Input Signal Bandwidth

202

200

198

196

194

192

190

188

OUTPUT DC VOLTAGE (mV)

186

1%/DIV

= 10µF

C

184

AVE

= 200mV

V

182

IN

100

RMS

1k 10k 100k 1M 10M

INPUT SIGNAL FREQUENCY (Hz)

1968 G13

1968f

5

LTC1968

UW

TYPICAL PERFOR A CE CHARACTERISTICS

Bandwidth to 500kHz

202

0.5%/DIV
= 10µF

C

AVE

201

= 200mV

V

IN

200

199

198

197

OUTPUT VOLTAGE (mV)

196

195

0

RMS

100 200 300 500

INPUT FREQUENCY (kHz)

Output Accuracy
vs Signal Amplitude

10

1% ERROR

5

)} (mV)

RMS

0

(mV

IN

–5

–1% ERROR

–10

(mV DC) – V

OUT

–15

{V

–20

0

0.5 1 1.5

400

1968 G14

V

= MIDSUPPLY

IN2

DC

AC – 60Hz
SINEWAVE

2

V

(V

)

IN1

RMS

1967 G17

DC Transfer Function Near Zero

40

V

= MIDSUPPLY

IN2

THREE REPRESENTATIVE UNITS

35

30

25

20

15

(mV DC)

10

OUT

V

5

0

–5

–10

–30

–20

–10

V

010

(mV DC)

IN1

Output Noise vs Input Frequency

1

PEAK NOISE MEASURED
IN 10 SECOND PERIOD

C

= 1µF

0.1

0.01

PEAK OUTPUT NOISE (% OF READING)

0.001
10k

AVE

C

= 10µF

AVE

INPUT FREQUENCY (Hz)

C

AVE

100k 1M

20

= 100µF

1968 G15

1967 G18

Input Common Mode Rejection
Ratio vs Frequency

90

80

70

60

50

40

30

INPUT CMRR (dB)

4.5V COMMON

20

MODE INPUT

10

CONVERSION
TO DC OUTPUT

30

0

100

10

10k 100k

1k

INPUT FREQUENCY (Hz)

1M

10M

1967 G16

Output Noise vs Device

1

LTC1966

= 1µF

C

AVE

0.1

LTC1967

= 1.5µF

C

AVE

PEAK OUTPUT NOISE (% OF READING)

0.01
1k

AVE CAPACITOR CHOSEN FOR EACH DEVICE

TO GIVE A 1 SECOND, 0.1% SETTLING TIME

10k 100k 1M

INPUT FREQUENCY (Hz)

LTC1968

= 6.8µF

C

AVE

1968 G19

6

1968f

LTC1968

U

UU

PI FU CTIO S

GND (Pin 1): Ground. The power return pin.

IN1 (Pin 2): Differential Input. DC coupled (polarity is

irrelevant).

IN2 (Pin 3): Differential Input. DC coupled (polarity is
irrelevant).

V

(Pin 5): Output Voltage. Pin 5 is high impedance. The

OUT

RMS averaging is accomplished with a single shunt ca­pacitor from Pin 5 to OUT RTN. The transfer function is
given by:

V OUT RTN Average IN IN

––

()

OUT

=

⎡

21

()

⎢

⎣

2

⎤
⎥

⎦

WUUU

APPLICATIO S I FOR ATIO

RMS-TO-DC CONVERSION

OUT RTN (Pin 6): Output Return. The output voltage is

created relative to this pin. The V

and OUT RTN pins

OUT

are not balanced and this pin should be tied to a low
impedance, both AC and DC. Although Pin 6 is often tied
to GND, it can also be tied to any arbitrary voltage:

GND < OUT RTN < (V+ – Max Output)

V+ (Pin 7): Positive Voltage Supply. 4.5V to 5.5V.

ENABLE (Pin 8): An Active-Low Enable Input. LTC1968 is

debiased if open circuited or driven to V+. For normal
operation, pull to GND.

Alternatives to RMS

Definition of RMS

RMS amplitude is the consistent, fair and standard way to
measure and compare dynamic signals of all shapes and
sizes. Simply stated, the RMS amplitude is the heating
potential of a dynamic waveform. A 1V

AC waveform

RMS

will generate the same heat in a resistive load as will 1V DC.

Mathematically, RMS is the “Root of the Mean of the
Square”:

VV

RMS

2

=

+

R1V DC

–

1V AC

RMS

R

R1V (AC + DC) RMS

Figure 1

SAME
HEAT

1968 F01

Other ways to quantify dynamic waveforms include peak
detection and average rectification. In both cases, an
average (DC) value results, but the value is only accurate
at the one chosen waveform type for which it is calibrated,
typically sine waves. The errors with average rectification
are shown in Table 1. Peak detection is worse in all cases
and is rarely used.

Table 1. Errors with Average Rectification vs True RMS

AVERAGE

RECTIFIED

WAVEFORM V

Square Wave 1.000 1.000 11%

Sine Wave 1.000 0.900 *Calibrate for 0% Error

Triangle Wave 1.000 0.866 –3.8%

SCR at 1/2 Power, 1.000 0.637 –29.3%
Θ = 90°

SCR at 1/4 Power, 1.000 0.536 –40.4%
Θ = 114°

RMS

(V) ERROR*

The last two entries of Table 1 are chopped sine waves as
is commonly created with thyristors such as SCRs and
Triacs. Figure 2a shows a typical circuit and Figure 2b
shows the resulting load voltage, switch voltage and load

1968f

7

LTC1968

WUUU

APPLICATIO S I FOR ATIO

currents. The power delivered to the load depends on the
firing angle, as well as any parasitic losses such as switch
“ON” voltage drop. Real circuit waveforms will also typi­cally have significant ringing at the switching transition,
dependent on exact circuit parasitics. For the purposes of
this data sheet, “SCR Waveforms” refers to the ideal
chopped sine wave, though the LTC1968 will do faithful
RMS-to-DC conversion with real SCR waveforms as well.

The case shown is for Θ = 90°, which corresponds to 50%
of available power being delivered to the load. As noted in
Table 1, when Θ = 114°, only 25% of the available power
is being delivered to the load and the power drops quickly
as Θ approaches 180°.

With an average rectification scheme and the typical
calibration to compensate for errors with sine waves, the
RMS level of an input sine wave is properly reported; it is
only with a non-sinusoidal waveform that errors occur.
Because of this calibration, and the output reading in
V

, the term True-RMS got coined to denote the use of

RMS

an actual RMS-to-DC converter as opposed to a calibrated
average rectifier.

V

LOAD

–

MAINS

+

I

LOAD

+

AC

V

LINE

CONTROL

–

+

V

–

1968 F02a

THY

the lowpass filter. The input to the LPF is the calculation
from the multiplier/divider; (VIN)2/V

. The lowpass

OUT

filter will take the average of this to create the output,
mathematically:

2

⎛

V

=

⎜

OUT

⎜
⎝

Because V is DC,

2

⎛
⎜

⎜
⎝

⎞

V

()

IN

⎟
⎟

V

OUT

⎠

⎛
⎝

=

V

OUT

22

VVor

()

OUT IN

V V RMS V

OUT IN IN

=

=

V

⎞

V

()

IN

,

⎟
⎟

V

OUT

⎠

OUT

2

⎛
⎝

=

V

()

IN

V

OUT

()

()=()

IN

⎞

V

()

IN

⎠

,

,

so

and

V

2

OUT

⎞
⎠

,

2

÷×

2

V

()

IN

V

OUT

LPF

1968 F03

V

OUT

Figure 2a

V

LINE

Θ

V

LOAD

V

THY

I

LOAD

1968 F02b

Figure 2b

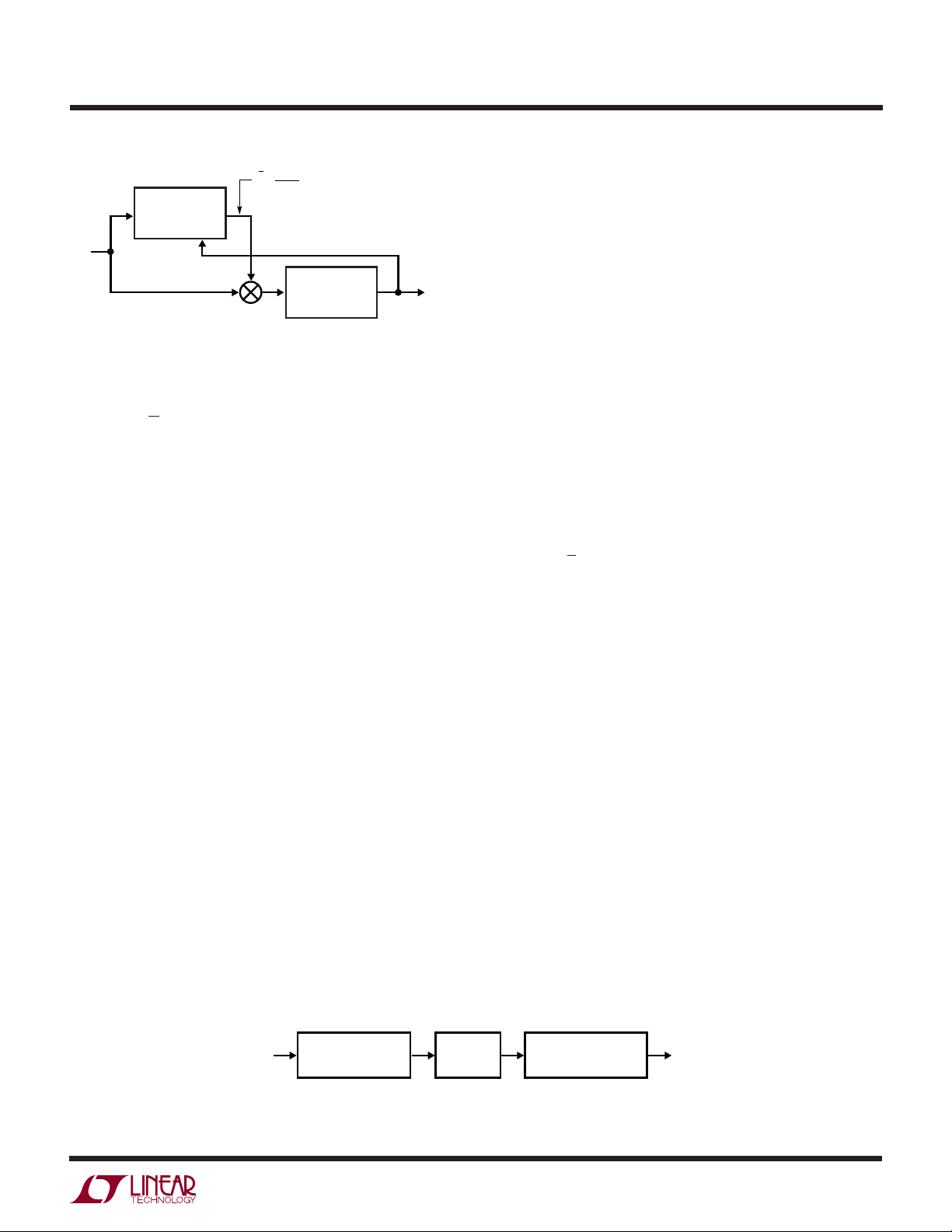
How an RMS-to-DC Converter Works

Monolithic RMS-to-DC converters use an implicit compu­tation to calculate the RMS value of an input signal. The
fundamental building block is an analog multiply/divide
used as shown in Figure 3. Analysis of this topology is
easy and starts by identifying the inputs and the output of

8

Figure 3. RMS-to-DC Converter with Implicit Computation

Unlike the prior generation RMS-to-DC converters, the
LTC1968 computation does NOT use log/antilog circuits,
which have all the same problems, and more, of log/
antilog multipliers/dividers, i.e., linearity is poor, the band­width changes with the signal amplitude and the gain drifts
with temperature.

How the LTC1968 RMS-to-DC Converter Works

The LTC1968 uses a completely new topology for RMS-to­DC conversion, in which a ∆Σ modulator acts as the
divider, and a simple polarity switch is used as the multi­plier1 as shown in Figure 4.

1

Protected by multiple patents.

1968f

WUUU

APPLICATIO S I FOR ATIO

V

IN

D

α

V

OUT

∆-Σ

REF

V

IN

±1

LPF

1968 F04

Figure 4. Topology of LTC1968

The ∆Σ modulator has a single-bit output whose average
duty cycle (D) will be proportional to the ratio of the input
signal divided by the output. The ∆Σ is a 2nd order
modulator with excellent linearity. The single-bit output is
used to selectively buffer or invert the input signal. Again,
this is a circuit with excellent linearity, because it operates
at only two points: ±1 gain; the average effective multipli­cation over time will be on the straight line between these
two points. The combination of these two elements again
creates a lowpass filter input signal equal to (VIN)2/V
which, as shown above, results in RMS-to-DC conversion.

The lowpass filter performs the averaging of the RMS
function and must be a lower corner frequency than the
lowest frequency of interest. For line frequency measure­ments, this filter is simply too large to implement on-chip,
but the LTC1968 needs only one capacitor on the output
to implement the lowpass filter. The user can select this
capacitor depending on frequency range and settling time
requirements, as will be covered in the Design Cookbook
section to follow.

This topology is inherently more stable and linear than log/
antilog implementations primarily because all of the signal
processing occurs in circuits with high gain op amps
operating closed loop.

More detail of the LTC1968 inner workings is shown in the
Simplified Schematic towards the end of this data sheet.

V

OUT

OUT

,

LTC1968

Note that the internal scalings are such that the ∆Σ output
duty cycle is limited to 0% or 100% only when VIN exceeds
±4 • V

Linearity of an RMS-to-DC Converter

Linearity may seem like an odd property for a device that
implements a function that includes two very nonlinear
processes: squaring and square rooting.

However, an RMS-to-DC converter has a transfer func­tion, RMS volts in to DC volts out, that should ideally have
a 1:1 transfer function. To the extent that the input to
output transfer function does not lie on a straight line, the
part is nonlinear.

A more complete look at linearity uses the simple model
shown in Figure 5. Here an ideal RMS core is corrupted by
both input circuitry and output circuitry that have imper­fect transfer functions. As noted, input offset is introduced
in the input circuitry, while output offset is introduced in
the output circuitry.

Any nonlinearity that occurs in the output circuity will
corrupt the RMS in to DC out transfer function. A nonlin­earity in the input circuitry will typically corrupt that
transfer function far less simply because with an AC input,
the RMS-to-DC conversion will average the nonlinearity
from a whole range of input values together.

But the input nonlinearity will still cause problems in an
RMS-to-DC converter because it will corrupt the accuracy
as the input signal shape changes. Although an RMS-to­DC converter will convert any input waveform to a DC
output, the accuracy is not necessarily as good for all
waveforms as it is with sine waves. A common way to
describe dynamic signal wave shapes is Crest Factor. The
crest factor is the ratio of the peak value relative to the RMS
value of a waveform. A signal with a crest factor of 4, for
instance, has a peak that is four times its RMS value.

OUT

.

INPUT CIRCUITRY

INPUT OUTPUT

• V

IOS

• INPUT NONLINEARITY

Figure 5. Linearity Model of an RMS-to-DC Converter

IDEAL

RMS-TO-DC

CONVERTER

OUTPUT CIRCUITRY

• V

OOS

• OUTPUT NONLINEARITY

1968 F05

1968f

9