Lecroy 93XXC-OM-E21 User Manual

&

$SSHQGL[&)DVW)RXULHU7UDQVIRUP))7

:KHQDQG+RZWR8VH))7

The WP02 Spectral Analysis package, with FFT (Fast Fourier
Transform), reveals signal characteristics not visible in t he
time domain and adds the power of frequency domain
analysis to your oscilloscope. FFT converts a time domain
waveform into frequency domain spectra similar to those of
a spectrum analyzer, but with important differences and
added benefits.

:K\8VH))7" For a large class of signals, greater insight can be gained by

looking at spectral representation rather than time description.
Signals encountered in the frequency response of amplifiers,
oscillator phase noise and those in mechanic al vibration analysis

— to mention just som e applications — are easier to observe in
the frequency domain.

If sampling is done at a rate f ast enough to f aithfully approxim ate
the original waveform (usually five times the highest frequency
component in the signal), the resulting discrete data series will
uniquely describe the analog signal.

This is of particular value when dealing with transient signals
because, unlike FFT, conventional swept spectrum analyzers
cannot handle them.

7KHRU\%HKLQG))7 Spectral analysis theory assumes that the signal for

transformation be of infinite duration. Since no physical signal
can meet this condition, a useful assumption for reconciling
theory and practice is to view the signal as consisting of an
infinite series of replica of itself . Thes e replica are m ultiplied by a
rectangular window (the display grid) that is zero outside of the
observation grid.

À

For an explanation of FFT terms: see the Glossary

on page C–17

À

Using FFT Functions: see page C–9

À

FFT Algorithms: page C–14

&²

$SSHQGL[&

Figure C–1 shows spectra of a swept triangular wave.
Discontinuities at the edges of the wave produce leakage, an
effect clearly visible in Trace A, which was computed with a
rectangular window, but less pronounced in the Von Hann
window in Trace B (

explanations

first harmonic.

). Histogramming in Trace C tracks the spread of the

see below for leakage and window-type

Figure C–1

Slicing the waveform in the fashion described above is
tantamount to diluting the spectral energy in an infinite number of
side lobes, which correspond to multiples of the frequency
resolution ∆f (
T determines the frequency resolution of the FFT (∆f=1/T).
Whereas the sampling period and the record length set the
maximum frequency span that can be obtained (f

Fig. C–2

&²

). The observation window or capture time

=∆f*N/2).

Nyq

Figure C–2

8VLQJ))7

An FFT operation on an N point time-dom ain signal may thus be
compared to passing the signal through a comb f ilter consisting
of a bank of N/2 filters. All the filter s have the same shape and
width and are centered at N/2 discrete frequencies. Each filter
collects the signal energy that falls into the immediate
neighborhood of its center frequency. Thus it can be said that
there are N/2 frequency bins. The distance in Hz between the
center frequencies of two neighboring bins is always the same:

∆

f.

3RZHU'HQVLW\6SHFWUXP Because of the linear scale used to show magnitudes, lower

amplitude components are often hidden by larger com ponents . In
addition to the functions offering magnitude and phase
representations, the FFT option offers power density and power

spectrum density functions, selec ted from the “FFT result” m enu
shown in the figures. These latter functions are even better
suited for characterizing spectra. The power spectr um (V

2

) is the
square of the magnitude spectrum (0 dB m corresponds to
voltage equivalent to 1 mW into 50 Ω.) This is the representation

&²

$SSHQGL[&

of choice for signals containing isolated peaks — periodic
signals, for instance.

2

The power density spectrum (V
divided by the equivalent noise bandwidth of the filter in Hz
associated with the FFT calculation. This is best employed for
characterizing broad-band signals such as noise.

0HPRU\IRU))7 The amount of acquisition memory available will determine the

maximum range (Nyquist frequency) over which signal
components can be observed. Consider the problem of
determining the length of the observation window and the size of
the acquisition buffer if a Nyquist rate of 500 MHz and a
resolution of 10 kHz are required. To obtain a resolution of 10
kHz, the acquisition time must be at least:

T = 1/∆f = 1/10 kHz = 100 µs.

For a digital oscilloscope with a memory of 100 k, the highest
frequency that can be analyzed is:

∆f ×

N/2 = 10 kHz × 100 k/2 = 500 MHz.

/Hz) is the power spectrum

))73LWIDOOVWR$YRLG Take care to ensure that signals are correctly acquired: im proper

waveform positioning within the observation window produces a
distorted spectrum. T he most com mon distortions can be trac ed
to insufficient sampling, edge discontinuities, windowing or the
“picket fence” effect.

Because the FFT acts like a bank of bandpass filters c entered at
multiples of the frequency resolution, components that are not
exact multiples of that frequency will fall within two consecutive
filters. This results in an attenuation of the true amplitude of
these components.

3LFNHW)HQFHDQG6FDOORS The highest point in the spectrum c an be 3.92 dB lower when the

source frequency is halfway between two discrete frequencies.
This variation in spectrum magnitude is the picket fence effect.
And the corresponding attenuation loss is ref erred to as scallop
loss. LeCroy scopes automatically correc t for the scallop effect,
ensuring that the magnitude of the spectra lines correspond to
their true values in the time domain.

&²

8VLQJ))7

If a signal contains a frequency component above Nyquist, the
spectrum will be aliased, meaning that the frequencies will be
folded back and spurious. Spotting aliased frequencies is of ten
difficult, as the aliases may ride on top of real harmonics. A
simple way of checking is to modify the sample rate and verify
whether the frequency distribution changes.

/HDNDJH FFT assumes that the signal contained within the time grid is

replicated endlessly outside the observation window. Therefore if
the signal contains discontinuities at its edges, pseudo­frequencies will appear in the spectral dom ain, distorting the real
spectrum. W hen the start and end phas e of the signal differ, the
signal frequency falls within two frequency cells broadening the
spectrum.

This effect is illustrated in Figure C–1. Bec ause the display does
not contain an integral number of periods, the spectrum
displayed in Trace B does not reveal sharp frequency
components. Intermediate components exhibit a lower and
broader peak. The broadening of the base, stretching out in
many neighboring bins, is termed leakage. Cures for this are to
ensure that an integral number of periods is contained within the
display grid or that no discontinuities appear at the edges.
Another is to use a window function to smooth the edges of the
signal.

&KRRVLQJD:LQGRZ The choice of a spectral window is dictated by the signal’s

characteristics. Weighting functions control the filter response
shape and affect noise bandwidth as well as side-lobe levels.
Ideally, the main lobe should be as narrow and flat as possible to
effectively discriminate all spectral components, while all side
lobes should be infinitely attenuated.

Chosen from the “with window” menu, the window type defines
the bandwidth and shape of the equivalent filter to be used in the
FFT processing.

In the same way as one would choose a particular camera lens
for taking a picture, s ome experimenting is generally necessary
to determine which window is most suitable. However, the
following general guidelines should help (

window types

).

&²

see page C–11 for

$SSHQGL[&

Rectangular windows provide the highest frequency resolution
and are thus useful for estim ating the type of harm onics pres ent
in the signal. Because the rectangular window decays as a sinx/x
function in the spectral domain, slight attenuation will be induced.

Alternative functions with less attenuation — Flat-top and
Blackman-Harr is — provide maximum amplitude at the expense
of frequency resolution. Whereas, Hamming and von Hann are
good for general purpose use with continuous waveforms.

,PSURYLQJ'\QDPLF5DQJH Enhanced resolution (

technique that can potentially provide for three additional bits
(18 dBs) if the signal noise is uniformly distributed (white). Low
pass filtering should be considered when high frequency
components are irrelevant. A distinct advantage of this technique
is that it works for both repetitive and transient signals. The SNR
increase is conditioned by the cut-off frequency of the Eres low
pass filter and the noise shape (frequency distribution).

LeCroy digital oscilloscopes employ FIR digital filters so that a
constant phase shift is maintained. The phase information is
therefore not distorted by the filtering action.

6SHFWUDO3RZHU$YHUDJLQJ Even greater dynamic-range im provem ent is obtained on signals

showing periodicity. Moreover, the range can be increased
without sacrificing frequency response. T he LeCroy oscilloscope
being used is equipped with accumulation buffers 32 bits wide to
prevent overflows.

Spectral power averaging is useful when the signal var ies in tim e
and the mean power of the signal needs to be estim ated. T ypical
applications include noise and pseudo- random noise. Whereas
time averaging ignores phase information, spectral averaging
tracks magnitude as well as phase information. It is thus a
superior estimator. And the improvement is typically proportional
to the square root of the number of averages. For instance,
averaging white noise at full scale over 10 sweeps yields a typical
improvement of nearly 20 dBs.

see Appendix B

) uses a low pass f iltering

&²

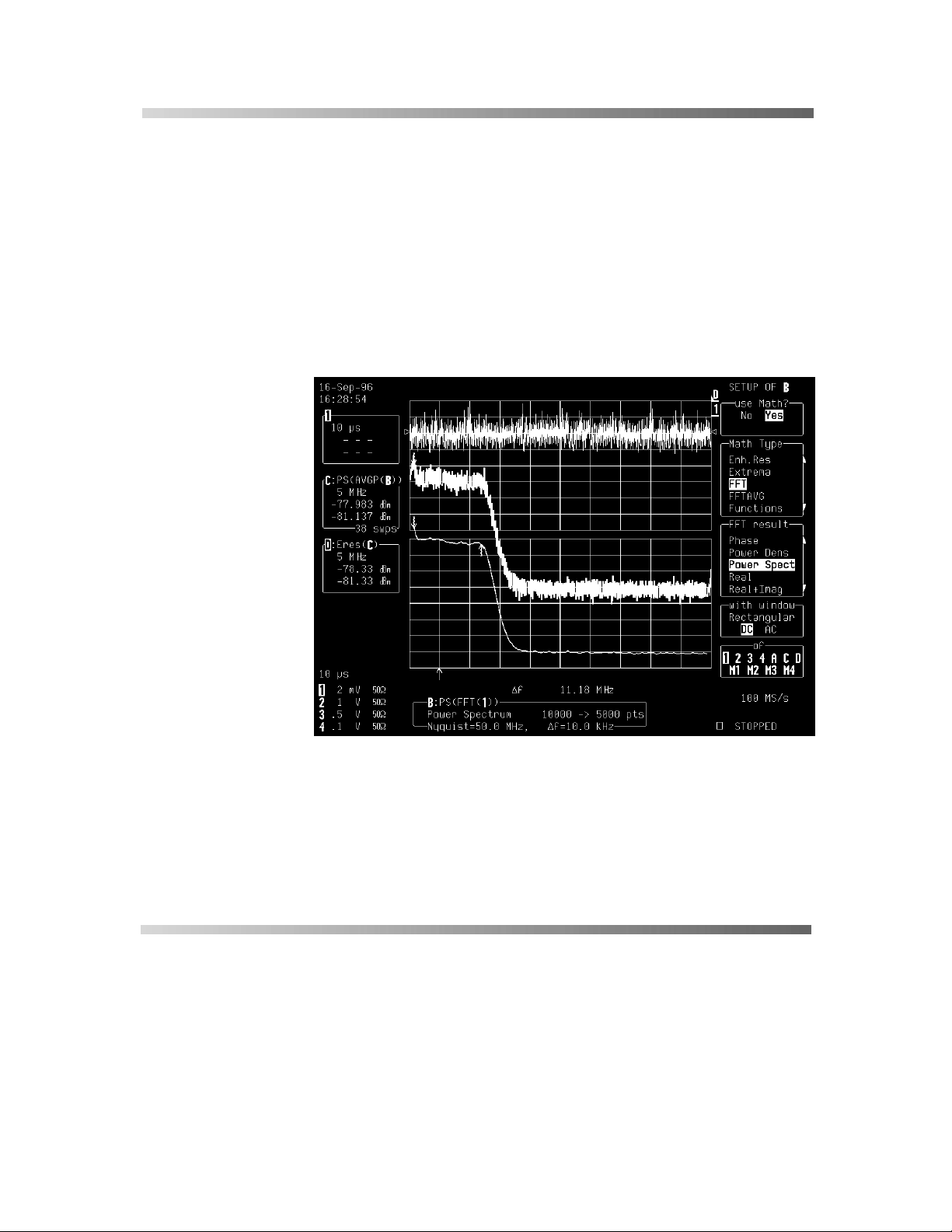
8VLQJ))7

Spectral power averaging is the technique of choice when
determining the frequency response of passive network s suc h as
filters. Figures 3 and 4 show the transfer functions of a low pass
filter with a 3 dB cutoff o1 11 MHz obtained by exciting the filter
with a white noise source (
(

Fig. C–4

The choice of method is governed by the availability of an
adequate generating source.

The spectra of single tim e-domain waveforms can be computed
and displayed to obtain power averages obtained over as many
as 50 000 spectra.

). Both techniques give substantially the same results.

Fig. C–3

) and a sine swept generator

&²

Figure C–3

$SSHQGL[&

Figure C–4

2YHUDOO« Because of its versatility, FFT analysis has become a popular

analysis tool. However, some care must be taken with it. In most
instances, incorrect positioning of the signal within the display
grid will significantly alter the spectrum. Eff ects such as leakage
and aliasing that distort the spectrum must be understood if
meaningful conclusions are to be arrived at when using FFT.

An effective way to reduce these effects is to maximize the
acquisition record length. Record length directly conditions the
effective sampling rate of the scope and therefore determines the
frequency resolution and span at which spectral analysis can be
carried out.

&²

8VLQJ))7)XQFWLRQV

8VLQJ))7

Select “FFT” from the “Math Type” menu (

for a full description of math and waveform processing
menus

running from zero to the Nyquist frequency are shown at the
right-hand edge of the trace. The frequency scale factors
(Hz/div) are in a 1–2–5 sequence.

The processing equation is displayed at the bottom of the screen,
together with the three key parameters that characterize an FFT
spectrum. These are:

1. Transform Size N (number of input points)

2. Nyquist frequency (= ½ sample rate), and

3. Frequency Increment, ∆f, between two successive points of

These parameters are related as:

Where: ∆f = 1/T, and where T is the duration of the input
waveform record (10 ∗ time/div). The num ber of output points is
equal to N/2.

). Spectra displayed with a linear frequency axis

the spectrum.

Nyquist frequency = ∆f ∗ N/2.

see Chapter 10

1RWHRQ0D[LPXP3RLQWV

over the entire source time-domain waveform. This limits
the number of points used for FFT processing. If the
input waveform contains more points than the selected

maximum (in “for Math use max points”, they are
decimated before FFT processing. But if it has fewer, all
points are used.

&²

FFT spectra are computed

$SSHQGL[&

The following selections can be made using the “FFT result”
menu.

3KDVH

Measured with respect to a cosine whose maximum occurs at
the left-hand edge of the screen, at which point it has 0 °.
Similarly, a positive-going sine starting at the left-hand edge of
the screen has a –90 ° phase. (Displayed in degrees.)

3RZHU'HQVLW\

The signal power normalized to the bandwidth of the equivalent
filter associated with the FFT calculation. The power density is
suitable for characterizing broad-band noise. (It is displayed on a
logarithmic vertical axis calibrated in dBm.)

3RZHU6SHFWUXP

The signal power (or magnitude) represented on a logarithmic
vertical scale: 0 dBm corresponds to the voltage (0.316 V peak )
which is equivalent to 1 mW into 50 Ω. The power spectrum is
suitable for characterizing spectra which contain isolated peaks.
(dBm.)

0DJQLWXGH

The peak signal am plitude represented on a linear scale. ( Same
units as input signal.)

5HDO5HDO,PDJLQDU\,PDJLQDU\

These represent the complex result of the FFT processing.
(Same units as input signal.)

&²

8VLQJ))7

:LQGRZV Chosen using the “with window” menu, the window type defines the

bandwidth and shape of the filter to be used in the FFT processing

see the table on page C–17 for these filters’ parameters

(
“AC” is selected from the same m enu, the DC com ponent of the
input signal is forced to zero prior to the FFT processing. This
improves the amplitude r esolution, especially when the input has
a large DC component.

Window Type Applications and Limitations

Normally used when the signal is transient — completely contained
in the time-domain window — or known to have a fundamental

Rectangular

Hanning (Von Hann)

Hamming

Flat Top

Blackman–Harris

frequency component that is an integer multiple of the fundamental
frequency of the window. Signals other than these types will show
varying amounts of spectral leakage and scallop loss, corrected by
selecting another type of window.

Reduce leakage and improve amplitude accuracy. However,
frequency resolution is also reduced.

Reduce leakage and improve amplitude accuracy. However,
frequency resolution is also reduced.

This window provides excellent amplitude accuracy with moderate
reduction of leakage, but also at the loss of frequency resolution.

It reduces the leakage to a minim um, but again along with reduc ed
frequency resolution.

). When

))73RZHU$YHUDJH A function can be defined as the power average of FFT spectra

computed by another function (

“FFTAVG” from the “Math Type” Menu, and “Power Spect” from
“FFT Result”.

&²

see page C–6

). Choose

$SSHQGL[&

$GGLWLRQDO3URFHVVLQJ Other waveform processing functions, such as Averaging and

Arithmetic, can be applied to waveform s before FFT processing
is performed. Tim e-domain averaging prior to FFT, for ex ample,
can be used if a stable trigger is available to reduce random
noise in the signal.

1RWH

À

To increase the FFT frequency range, the Nyquist
frequency, raise the effective sampling frequency by
increasing the maximum number of points or using a
faster time base.

À

To increase the FFT frequency resolution, increase the
length of the time-domain waveform record by using a
slower time base.

0HPRU\6WDWXV When FFT is used, the field beneath the grid displays

parameters of the waveform descriptor, including number of
points, horizontal and vertical scale factors and units.

8VLQJ&XUVRUVZLWK))7 For reading the amplitude and frequency of a data point, the

Absolute Time cursor can be m oved into the frequency domain by
going beyond the right-hand edge of a time-domain waveform.

The Relative Time cursors can be moved into the frequency
domain to simultaneously indicate the frequency difference and
the amplitude difference between two points on each frequency­domain trace.

The Absolute Voltage cursor reads the absolute value of a point
in a spectrum in the appropriate units, and the
cursors indicate the difference between two levels on each trace

&²

Relative Voltage

8VLQJ))7

(UURU0HVVDJHV One of these FFT-related error messages may be displayed at

the top of the screen.

(UURU0HVVDJHV

Message Meaning

“Incompatible input record type”

“Horizontal units don't match” FFT of a frequency-domain waveform is not available.

“FFT source data zero filled” If there are invalid data points in the source waveform (at

“FFT source data over/underflow” The source waveform data has been clipped in

“Circular computation” A function definition is circular (i.e. the function is its own

FFT power average is defined only on a function defined
as FFT.

the beginning or at the end of the record), these are
replaced by zeros before FFT processing.

amplitude, either in the acquisition — gain too high or
inappropriate offset — or in previous processing. The
resulting FFT contains harmonic components which
would not be present in the unclipped waveform. The
settings defining the acquisition or processing should be
changed to eliminate the over/underflow condition.

source, indirectly via another function or expansion).
One of the definitions should be changed.

&²

))7$OJRULWKPV

e

j

N

π

/

$SSHQGL[&

A summary of the algorithms used in the oscilloscope’s FFT
computation is given here in the form of seven steps:

1. If the maximum number of points is smaller than the source

number of points, the source waveform data are decimated
prior to the FFT. These decim ated data extend over the full
length of the source waveform. The resulting sampling
interval and the actual transform size selected provide the

frequency scale factor in a 1–2–5 sequence.

2. The data are multiplied by the selected window function.

3. FFT is computed, using a fast implementation of the DFT

(Discrete Fourier Transform):

=−

1

kN

1

where:

X

=×

nk

N

x

is a complex array whose real part is the m odified

k

∑

=

k

0

xW

source time domain wavef orm, and whose imaginary part is

X

is the resulting complex frequency-domain waveform ;

0;

n

−

2

; and

N

W

=

is the number of points in

The generalized FFT algorithm, as im plemented her e, works

not

on N, which need

be a power of 2.

nk

,

x

and

X

k

.

n

X

4. The resulting com plex vector

is divided by the coherent

n

gain of the window function, in order to compensate for the
loss of the signal energy due to windowing. This
compensation provides accurate amplitude values for
isolated spectrum peaks.

X

5. The real part of

is symmetric around the Nyquist

n

frequency, i.e.

Rn = R

N-n

,

while the imaginary part is asymmetric, i.e.

In = –I

N-n

.

&²

))7$OJRULWKPV

The energy of the signal at a frequency n is distributed equally
between the first and the second halves of the spec trum; the
energy at frequency 0 is completely contained in the 0 term.

The first half of the spectrum (Re, Im) , from 0 to the Nyquist
frequency is kept for further processing and doubled in
amplitude:

R’n = 2  R

= 2  I

I’

n

n

n

0 ≤ n < N/2
0 ≤ n < N/2.

6. The resultant waveform is computed for the spectrum type

selected.

If “Real”, “Imaginary”, or “Real + Imaginary” is selected, no
further computation is needed. The appropriate part of the

R’

or

I’

or

R’

+

jI’

complex result is given as the re sult (

n

n

, as

n

n

defined above).
If “Magnitude” is selected, the magnitude of the complex

vector is computed as:

MRI

nnn

22

=+’’

.

Steps 1–6 lead to the following result:
An AC sine wave of amplitude 1.0 V with an integral number of

periods Np in the time window, transformed with the rectangular
window, results in a fundamental peak of 1.0 V m agnitude in the
spectrum at frequency Np × ∆f. However, a DC component of 1.0
V, transformed with the rectangular window, results in a peak of

2.0 V magnitude at 0 Hz.
The waveforms for the other available spectrum types are

computed as follows:

Phase: angle = arctan (

angle = 0

&²

In/R

n

)

Mn > M
Mn ≤ M

min
min

.

$SSHQGL[&

Where

M

is the minimum magnitude, fixed at about 0.001 of

min

the full scale at any gain setting, below which the angle is not well
defined.

dBm Power Spectrum:

The

2



where



M

n



dBm PS

M

ref

=×

10 20

log log

10

= 0.316 V (that is, 0 dBm is defined as a sine wave of



M

ref



2



=×









M

n



10



M





ref

0.316 V peak or 0.224 V RMS, giving 1.0 mW into 50Ω).
The dBm Power Spectrum is the same as dBm Magnitude, as

suggested in the above formula.
dBm Power Density:

dBmPD dBmPS ENBW f

where

ENBW

corresponding to the selected window, and

=−× ×1010log ∆

()

is the equivalent noise bandwidth of the filter

∆

f

is the current

frequency resolution (bin width).

7. The FFT Power Average takes the complex frequency-

R’n

and

I’n

domain data

for each spectrum generated in Step

5, and computes the square of the magnitude:

2

2

M

n

= R’

2

+ I’

n

,

n

then sums

2

M

and counts the accumulated spectra. The

n

total is normalized by the number of spectra and converted to
the selected result type using the same formulae as are us ed
for the Fourier Transform.

&²

))7*ORVVDU\

*ORVVDU\

Defines the terms frequently used in FFT spectrum analysis
and relates them to the oscilloscope.

$OLDVLQJ If the input signal to a sampling acquisition system contains

components whose frequency is greater than the Nyquist
frequency (half the sampling fr equency), ther e will be less than
two samples per signal period. The r esult is that the contribution
of these components to the sampled waveform is
indistinguishable from that of components below the Nyquist
frequency. This is aliasing.

The timebase and transform -size should be selected so that the
resulting Nyquist frequency is higher than the highest significant
component in the time-domain record.

&RKHUHQW*DLQ The normalized coherent gain of a filter corresponding to each

window function is 1.0 (0 dB) for a rectangular window and less
than 1.0 for other windows. It defines the loss of signal energy
due to the multiplication by the window function. This loss is
compensated in the oscilloscope. This table lists the values for
the implemented windows.

:LQGRZ)UHTXHQF\'RPDLQ3DUDPHWHUV

Highest Side

Window Type

Rectangular –13 3.92 1.0 0.0
von Hann
Hamming –43 1.78 1.37 –5.35
Flat Top

Blackman–Harris

Lobe

(dB)

–32 1.42 1.5 – 6.02

–44 0.01 2.96 –11.05
–67 1.13 1.71 –7.53

Scallop Loss

(dB)

ENBW

(bins)

Coherent Gain

(dB)

&²

$SSHQGL[&

(1%: Equivalent Noise BandWidth (ENBW) is the bandwidth of a

rectangular filter (sam e gain at the center frequency), equivalent
to a filter associated with each frequency bin, which would collect
the same power from a white noise signal. In the table on the
previous page, the ENBW is listed for each window function
implemented and is given in bins.

)LOWHUV Computing an N-point FFT is equivalent to passing the time-

domain input signal through N/2 filters and plotting their outputs
against the frequency. The spacing of f ilters is ∆f = 1/T while the
bandwidth depends on the window function used (see Frequency
bins).

)UHTXHQF\ELQV The FFT algorithm takes a discrete source waveform, defined

over N points, and computes N complex Fourier coefficients,
which are interpreted as harmonic components of the input
signal.

For a real source waveform (imaginary part equals 0), there are
only N/2 independent harmonic components.

An FFT corresponds to analyzing the input signal with a bank of
N/2 filters, all having the same shape and width, and centered at
N/2 discrete frequencies. Each filter collects the signal energy
that falls into the immediate neighborhood of its center

frequency, and thus it can be said that there are N/2 “frequency
bins”.

The distance in hertz between the center frequencies of two
neighboring bins is always:

∆

f = 1/T,
where T is the duration of the time-domain record in seconds.
The width of the main lobe of the filter centered at each bin

depends on the window function used. The rectangular window
has a nominal width at 1.0 bin. Other windows have wider main
lobes (

see table

).

)UHTXHQF\5DQJH The range of frequencies computed and displayed is 0 Hz

(displayed at the left-hand edge of the screen) to the Nyquist
frequency (at the rightmost edge of the trace).

&²

))7*ORVVDU\

)UHTXHQF\5HVROXWLRQ In a simple sense, the frequency resolution is equal to the bin

width ∆f. That is, if the input signal changes its frequency by ∆f,
the corresponding spectrum peak will be displaced by ∆f. For
smaller changes of frequency, only the shape of the peak will
change.

However, the effective frequency resolution (i.e. the ability to
resolve two signals whose frequencies are alm ost the same) is
further limited by the use of window functions. T he ENBW value
of all windows other than the rectangular is greater than ∆f and
the bin width.

the implemented windows.

/HDNDJH In the power spectrum of a sine wave with an integral num ber of

periods in the (rectangular) time window (i.e. the source
frequency equals one of the bin frequencies), the spectrum
contains a sharp component whose value accurately reflects the
source waveform’s amplitude. For intermediate input frequencies
this spectral component has a lower and broader peak.

The broadening of the base of the peak , str etching out into m any
neighboring bins is termed
side lobes of the filter associated with each frequency bin.

The filter side lobes and the r esulting leakage are reduced when
one of the available window functions is applied. The best

reduction is provided by the Blackman–Harris and Flat Top
windows. However, this reduction is offset by a broadening of the
main lobe of the filter.

The table on page C–17 lists the ENBW values for

leakage

. It is due to the relatively high

1XPEHURI3RLQWV FFT is computed over the number of points (Transform Size)

whose upper bounds are the source number of points, and by the
maximum number of points selected in the menu. FFT generates
spectra of N/2 output points.

1\TXLVW)UHTXHQF\ The Nyquist frequency is equal to one half of the effective

sampling frequency (after the decimation): ∆f × N/2.

3LFNHW)HQFH(IIHFW If a sine wave has a whole number of periods in the time dom ain

record, the power spectrum obtained with a rectangular window
will have a sharp peak, corresponding exactly to the frequency
and amplitude of the sine wave. Otherwise the spectrum peak
with a rectangular window will be lower and broader.

The highest point in the power spectrum can be 3.92 dB lower
(1.57 times) when the source f requency is halfway between two

&²

$SSHQGL[&

discrete bin frequencies. This variation of the spectrum
magnitude is called the

picket fence effect

scallop loss).
All window functions compensate this loss to some extent, but

the best compensation is obtained with the Flat Top window.

2

3RZHU6SHFWUXP The power spectrum (V

) is the square of the magnitude

spectrum.
The power spectrum is displayed on the dBm scale, with 0 dBm

corresponding to:

2

= (0.316 Vpeak)2,

Vref

where Vref is the peak value of the sinusoidal voltage, which is
equivalent to 1 mW into 50 Ω.

2

3RZHU'HQVLW\6SHFWUXP The power density spectrum (V

/Hz) is the power spectrum
divided by the equivalent noise bandwidth of the filter in hertz.
The power density spectrum is displayed on the dBm scale, with

2

0 dBm corresponding to (Vref

/Hz).

6DPSOLQJ)UHTXHQF\ The time-domain records are acquired at sampling frequencies

dependent on the selected time base. Before the FFT
computation, the time-domain record may be decimated. If the
selected maximum number of points is lower than the source
number of points, the effective sampling frequency is reduced.
The effective sampling frequency equals twice the Nyquist
frequency.

(the loss is called the

6FDOORS/RVV Loss associated with the picket fence effect.
:LQGRZ)XQFWLRQV All available window functions belong to the sum of cosines

family with one to three non-zero cosine terms:

=−

1

mM

Wa

=

km

∑

=

0

m

where:

M = 3

is the maximum number of terms,
coefficients of the terms,
decimated source waveform, and

k

2

p






N

is the number of points of the



mkN





N

k

is the time index.

≤<

0cos

a

are the

m

,

&²

))7*ORVVDU\

The following table lists the coefficients
functions seen in the time domain are symmetric around the
point k = N/2.

&RHIILFLHQWV2I:LQGRZ)XQFWLRQV

Window Type a0 a1 a2

Rectangular 1.0 0.0 0.0
von Hann 0.5 –0.5 0.0
Hamming 0.54 –0.46 0.0
Flat-Top 0.281 –0.521 0.198
Blackman-Harris 0.423 –0.497 0.079

$SSHQGL[&5HIHUHQFHV Bergland, G.D.,

IEEE Spectrum, July 1969, pp. 41–52.
A general introduction to FFT theory and applications.

am.

The window

A Guided Tour of the Fast Fourier Transform

,

Brigham, E.O.,

The Fast Fourier Transform

, Prentice Hall, Inc.,
Englewood Cliffs, N.J., 1974.
Theory, applications and implementation of FFT. Includes
discussion of FFT algorithms for N not a power of 2.

Harris, F.J.,

the Discrete Fourier Transform

On the Use of Windows for Har monic Analysis with

, Proceedings of the IEEE, vol. 66,
No. 1, January 1978, pp. 51–83.
Classic paper on window functions and their figures of mer it, with
many examples of windows.

Ramirez, R.W.,

The FFT Fundamentals and Concepts

, Prentice
Hall, Inc., Englewood Cliffs, N.J., 1985.
Practice-oriented, many examples of applications.

&²