John Wiley & Sons TI-83, TI-84 User Manual

TI-83, TI-83 Plus and the TI-84

GRAPHING CALCULATOR MANUAL

James A. Condor

Manatee Community College

to accompany

Introductory Statistics

Sixth Edition

Prem S. Mann

Eastern Connecticut State University

JOHN WILEY & SONS, INC.

Contents

Preface 3

1 Introduction 4

2 Organizing Data 11

3 Numerical Descriptive Measures 17

4 Probability 27

5 Discrete Random Variables 32

6 Continuous Random Variables 39

7 Sampling Distributions 46

8 Estimation of the Mean and Proportion 50

9 Hypothesis Tests: Mean and Proportion 55

10 Two Populations 61

11 Chi-Square Tests 69

12 Analysis of Variance 74

13 Simple Linear Regression 78

14 Nonparametric Methods 84

Preface

Statistics is an important field of study, now more so than ever. We are surrounded by statistical information in work and in our everyday lives. Many of us work in professions that require us to understand statistical summaries, and some of us work in areas that require us to produce statistical information.

The art of teaching statistics has changed dramatically in recent years, with computational software eliminating the need for many of the previously taught techniques. The answers to many of the complex computations come easier and faster students with today’s calculators performing most of the work in elementary statistical analysis. The challenge to the instructor is to get the student to acquire a greater understanding of what (s)he is doing, with the calculator tending to the details of the computations.

The TI-83, TI-83 Plus, and TI-84 Plus calculators, by Texas Instruments, are leading examples of the progress in statistical technology. Texas Instruments has provided us with advanced devices at an affordable price that are capable of powerful statistical work and yet is still easy to use.

This text will run through the statistical capabilities of the TI-83, TI-83 Plus, and TI-84 Plus calculators. The calculators are almost identical with regards to the type of statistical functions they will perform and the keystrokes needed to call those functions.

This text will follow the order of topics presented in Mann’s Introductory Statistics, sixth edition, published by John Wiley & Sons, Inc., but should also prove useful with other texts. It will not explain the underlying statistics but instead focus on how best to use the TI-83, TI-83 Plus, and TI-84 Plus calculators in computing them.

Chapter

Introduction

Use of Technology

Statistics is a field that deals with sets of data. After the data is collected it needs to be organized and interpreted. There is a limit to how much of the work can be done effectively without the help of some type of technology. The use of technology, such as a calculator with enhanced statistical functions can take care of most of the details of our work so that we can spend more time focusing on what we are doing and how to interpret the results.

Technology can help us not only to store and manipulate data, but also to visualize what the data is trying to tell us. As we work with a calculator, we will be able to:

• Enter, revise, and store data.

• Perform statistical computations on stored data or entered statistics.

• Draw pictures, based on the data to help us to understand what useful information can be inferred from that data.

Advantages of Using a Calculator

There are many good statistical software packages available, such as MINITAB, SAS, and SPSS. Excel also contains many statistical built-in functions as well as supporting plug-in’s for statistical work. Still, for the student starting to learn statistics, it’s hard to beat the advantages of using a powerful hand-held calculator.

• It is portable and easy to use in many different work environments.

• It has battery power that lasts far longer than that of a laptop computer.

• It is less expensive than a computer.

• It is less expensive than a statistical software package.

Advantages to Using the TI-83, TI-83 Plus, and TI-84 Plus

This calculator manual will focus on how to get the most out of using the TI-83, TI-83 Plus, and the TI-84 Plus calculators by Texas Instruments. The TI-83 was first released in 1996, improving upon its predecessors the TI-81 and TI-82 with the addition of many advanced statistical and financial functions. The TI-83 Plus and the TI-84 Plus have essentially the same features as the TI-83, but with increased memory capacity and a few extra statistical features. They are powerful calculators with advanced functions, but at the same time easy to use.

• Most complicated statistical computations are handled through menus which prompt you for the necessary input.

• Data entry and revision is handled through a Stat List Editor that is similar to a spreadsheet in how it is used.

• Statistical graphs are handled through menus and important parts of the graph can be read by tracing along with the arrow keys.

• The calculators are built sturdily, and can withstand many falls off of student desks.

Entering and Revising Data

This chapter focuses on getting numbers into your calculator and storing them for the organization, interpretation, and analysis part of statistics. When you are not given the necessary statistics to perform calculations, you will need to enter data into the calculator to generate the statistics. We will learn how to do statistical calculations with the calculator in future chapters.

Using the Stat List Editor

The Stat List Editor in the TI-83, TI-83 Plus, and TI-84 Plus calculators provides a convenient way to enter numbers and review them. Numbers from a data set can be stored in a list in the calculator so that we can keep numbers that are related to each other together.

Example: Weights

Suppose that you have ten people in a room, with the following weights in pounds:

131, 114, 167, 180, 126, 134, 188, 175, 133, 130

If we want to do any sort of analysis on these numbers, we will need to get them into the calculator and keep them together as a group.

Press the STAT key.

To input data or to make changes to an existing set of data values use the Edit function. (number one under the EDIT list).

Press the number 1 key.

If your stat list editor does not show the columns labeled L1, L2, and L3 you can set up the Editor by selecting SetUpEditor on the previous screen.

Press the STAT key. Press the 5 key. Press the ENTER key.

If you set up the editor then return to the Edit function. Go ahead and type the ten weights in under the column labeled L1. Press the ENTER key when you are done with one number and ready to move on to the next number.

Type in 131 and press the ENTER key. Type in 114 and press the ENTER key. Type in 167 and press the ENTER key.

…continue until all the data values have been entered.

Use the up and down arrow keys to go back and forth between the numbers. Try changing the value of one of the entries by typing in a new weight.

Clearing a List of Data Values

After a list of data values is no longer needed you can delete the values by using one of the following methods.

1. You can highlight each data value and use the DEL key. This method is slow and clears

the list one data value at a time.

2. You can highlight the list name, for example L1 at the top of the column, and press the

CLEAR key and then press the ENTER key.

3. You can go to the EDIT menu and press the number 4 key to clear list.

Press the STAT key. Press the number 4 key. Press the 2

key and then press the 1 key to get L1.

Press the ENTER key.

Entering Lists Directly

The home screen is where you do most of your calculator work that doesn’t involve menus. Wherever you are on your calculator, you can always get back to the home screen by pressing

the 2

key and then the MODE key to access the QUIT function. From the home screen, you can enter data into a list by typing it between a set of braces { and }, and separating the numbers by commas:

{131, 114, 167, 180, 126, 134, 188, 175, 133, 130}

Once you’ve typed the numbers in, you will want to save them. Use the store button STO► followed by L1, L2 or any other list. ( L1 – L6 are above the 1–6 keys.) When you press the STO► key, the screen will display an arrow going to the right.

{131, 114, 167, 180, 126, 134, 188, 175, 133, 130} → L1

Once you’ve entered a list from the Stat List Editor, you can see the list by typing its name. For example, if you stored the weights in L1, typing L1 on the home screen will display the list’s contents. (You will need to use the left and right arrow keys to see all of the list’s contents.)

You can also store data to a name that you create. From the home screen, you can save a list to a name by using the STO► key.

{131, 114, 167, 180, 126, 134, 188, 175, 133, 130} → WEIGH

If you type in WEIGH on the home screen and press the ENTER key the list of numbers will be displayed across the screen.

Next we will learn how to create a different name for a list rather than using L1, L2, and so on.

Working with Named Lists

The lists L1 through L6 are good places to work with data if you won’t be needing to save the data. If, on the other hand, you think that you may need the data later on and don’t want to accidentally over-write it, you can give the data a name. A list can be named with 1–5 characters. The first character must be a letter or the angle symbol θ “theta”. The other characters can be a letter, a θ, or a number.

To get letters from the keyboard, press the ALPHA key before each letter that appears above and to the right of most of the keys. If you are typing several letters in a row, press A-LOCK (above the ALPHA key), type the letters, and then press the ALPHA key again to release the lock.

To create a different name for a list within the Stat List Editor,

Press the STAT key. Press the number 1 key. Press the ▲ key to highlight the name at the top of one of the columns. Press the 2

key and then the DEL key to get to the INS (insert) function. Type in the name of your new list (note that the A-LOCK is already turned on for you, so you don’t need to press the ALPHA key before each letter), Press the ENTER key.

You are now ready to begin entering data into the newly named list.

Getting the Names of Lists

Some of the commands needed later in this book will require you to type in the name of a list. If it is one of L1–L6, then you can type it quickly from the keyboard above the 1–6 keys.

On the other hand, you cannot just type the name of a named list from the keyboard using the ALPHA key. List names on the TI-83, TI-83 Plus, and TI-84 Plus calculators are distinguished from the names of other variables by a small L to the left of the name. To see this, go into the

LIST menu, and choose one of the list names there by using the arrow keys and then press the ENTER key.

In general, when you need to supply the name of a list to a command or a menu, use the LIST page and the NAMES list.

Choosing Lists to Edit

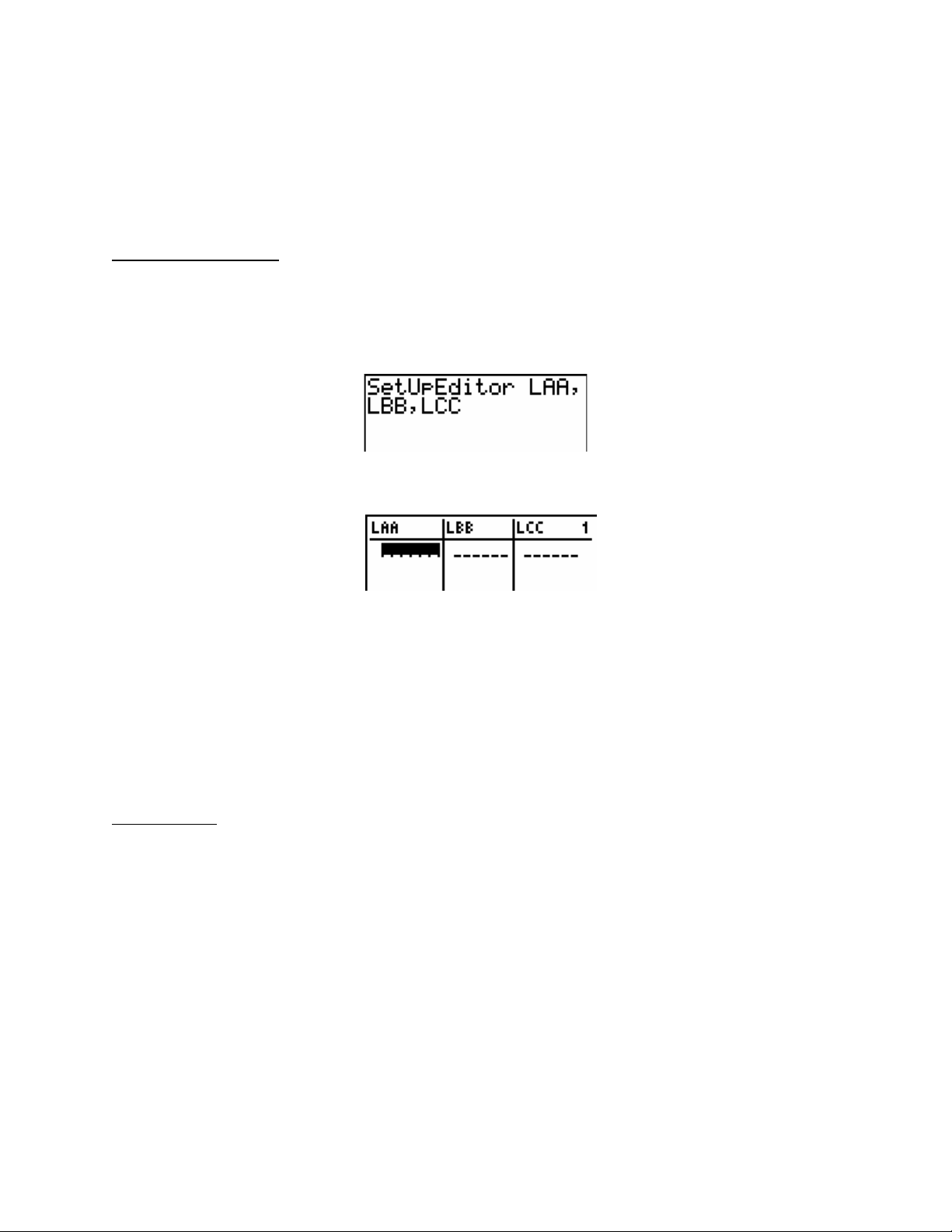
There are several ways to control which lists are displayed in the Stat List Editor. If you press the STAT key and then the number 5 key to get to SetUpEditor, you can use that command with a series of list names separated by columns. For example,

will configure the Stat List Editor to display lists LAA, LBB, and LCC.

As we saw above, if you enter the command SetUpEditor without any list names the Editor goes back to showing L1–L6 by default. If you are already in the Stat List Editor, you can use the arrow keys to highlight the names of lists. If you press INS for insert, you can insert new or existing lists. If you press the DEL key for delete you delete the list from the editor.

This does not erase the contents list. If you wish to do that, highlight the name of the list and press the CLEAR button and then the ENTER key. This will leave the list name in the editor and clear its entries.

Deleting Lists

If you store many lists, programs, etc. on your calculator, it is possible that you may start to run out of memory. If that should happen go into the MEM menu (above the + key) and follow the sub-menus for deleting items from your calculator. This is one of the few places where the steps differ between the TI-83, TI-83 Plus, and TI-84 Plus calculators. Just follow the instructions on the screen.

Exercises

1. Store the following numbers into the list L2:

11, 23, 35, 47, 59

2. Store the following numbers into the list ABC:

2, 3, 5, 7, 11, 13

3. Configure the Stat List Editor to display lists L2, ABC, and L5.

4. Save the following data in a storage location labeled TIME.

23, 45, 56, 32, 42, 22

Solutions

1. Go to the STAT page and select Edit. If L2 is not one of the lists displayed, use the up arrow to highlight one of the column titles, press INS for insert and press the ENTER key. Use the down arrow key to go back down into the column. Type in the numbers, pressing the ENTER key after each one. If you make a typo, use the arrow keys to highlight the entry and enter it again.

2. Press the STAT key and select Edit. Use the up arrow to highlight one of the column titles, press INS for insert. Type ABC and press the ENTER key. Use the down arrow key to go back down into the column. Type in the numbers, pressing ENTER after each one. If you make a typo, use the arrow keys to highlight the entry and enter it again.

3. Go to SetUpEditor and type in L2, ABC, L5. You will need to go to the LIST page and the NAMES list to get the name ABC. The names will appear as the column labels.

4. Go to the home page and type in {23, 45, 56, 32, 42, 22}→TIME

Chapter

Organizing Data

After the data has been input into the calculator one of the tasks of the statistician is to try to make sense of that data by organizing it. As a consumer of statistics, you are presented with tables and graphical displays of data on a daily basis. This chapter focuses on ways of organizing data on the TI-83, TI-83 Plus, and TI-84 Plus calculators.

Frequency Distributions

One of the simplest ways of organizing data is to group together similar values. Once we’ve grouped them together we can count how many elements there are in each group. Since the TI83, TI-83 Plus, and TI-84 plus calculators work only with numerical data, we will be trying to group numbers together.

To get some idea of how the numbers are distributed, we will split them into intervals or classes, all of the same width, and count how many are in each class. Listing the classes and their

frequencies provide us with information to create a frequency distribution. The calculators do

not provide us directly with a frequency distribution, but it will construct a frequency histogram for us which helps us create the frequency distribution.

Example: Home Runs

The following table lists the number of home runs hit by major league baseball teams during the 2002 season. Enter the number of home runs into a list labeled RUNS. By inspection we can see that the values go from 124 to 230. This gives us a range of 230 − 124 = 106. To find the class width we divide the range by the number of classes we desire. We will construct the frequency distribution with five classes. Dividing the range 106 by 5 the number of classes gives us a class width of 22.

Team Home Runs Team Home Runs

Anaheim 152 Milwaukee 139 Arizona 165 Minnesota 167 Atlanta 164 Montreal 162 Baltimore 165 New York Mets 160 Boston 177 New York Yankees 223 Chicago Cubs 200 Oakland 205 Chicago White Sox 217 Philadelphia 165 Cincinnati 169 Pittsburgh 142 Cleveland 192 St. Louis 175 Colorado 152 San Diego 136 Detroit 124 San Francisco 198 Florida 146 Seattle 152 Houston 167 Tampa Bay 133 Kansas City 140 Texas 230 Los Angeles 155 Toronto 187

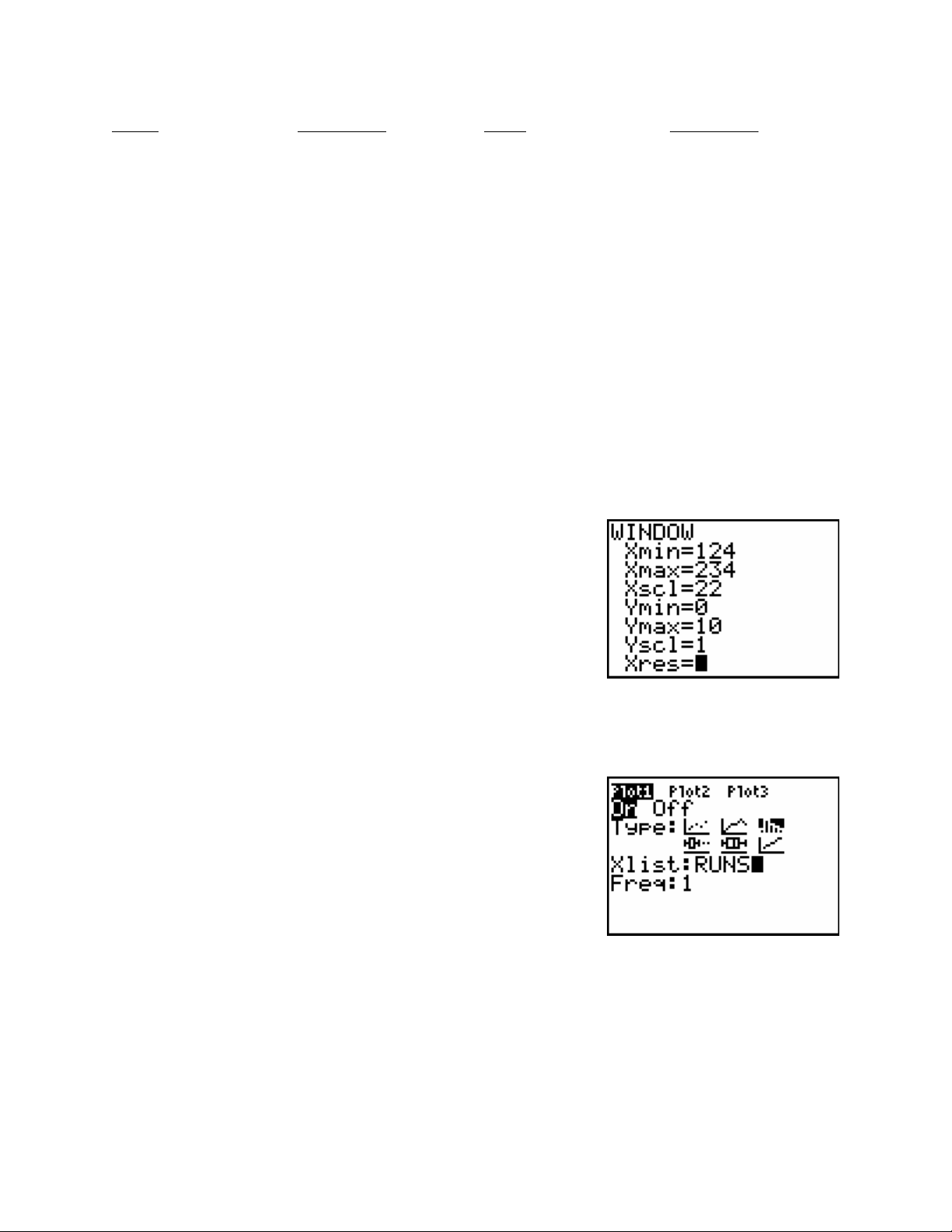
Press the WINDOW key. Set Xmin to 124 and Xmax to 234. Set Xscl to our class width 22. Set Ymin to 0 and Ymax to 15.

Now that we have told the calculator how to split the data up into classes, we need to tell it that we want a frequency histogram.

Press the 2

key. Press the Y= key to get to STAT PLOT. Press the ENTER key.

With the flashing cursor over On, Press the ENTER key to turn the plot On. Use the arrow keys to select the histogram.

Enter the name of our list RUNS for Xlist. Leave Freq at 1, since each of our data values represents only one point.

Finally, we need to tell the calculator to draw the graph.

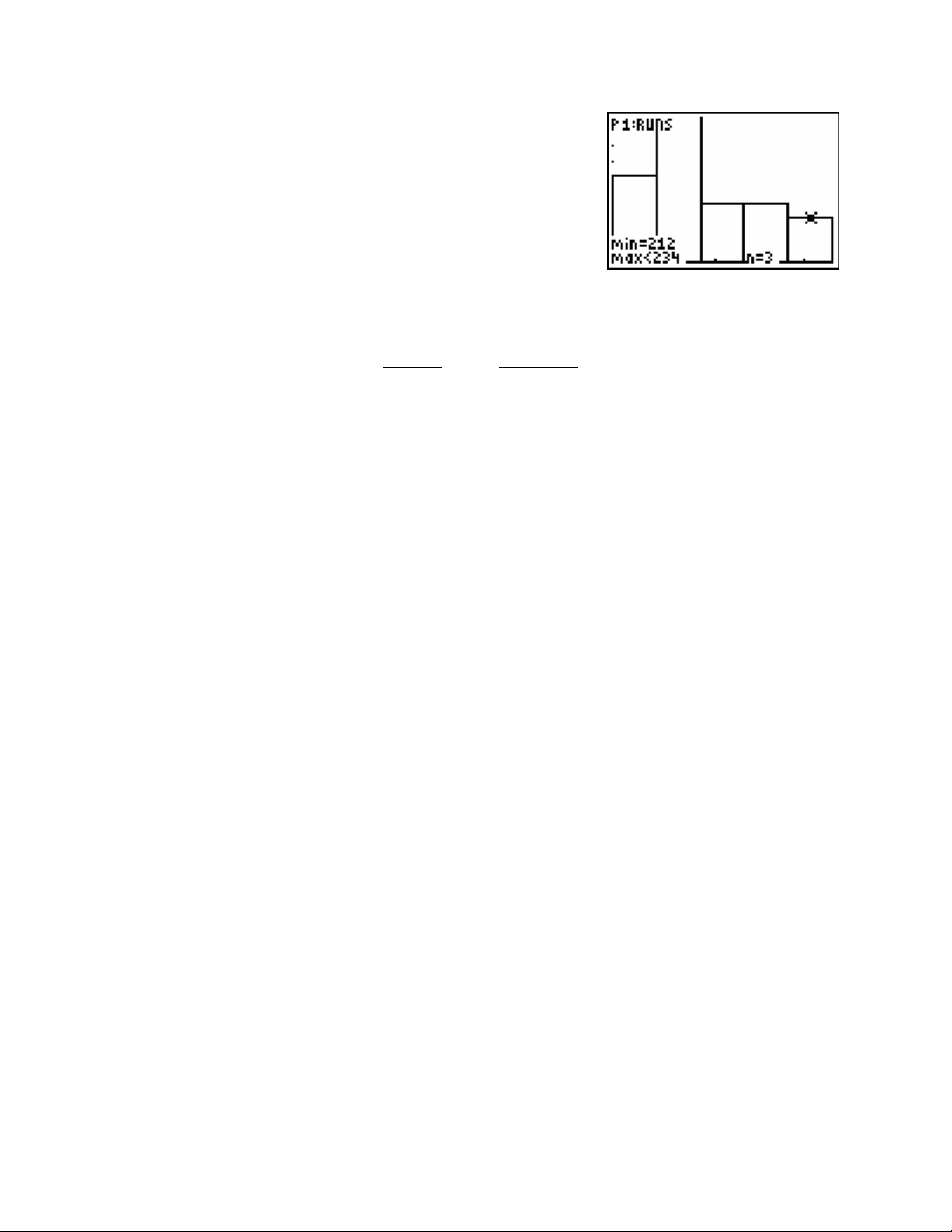
Press the GRAPH key. Press the TRACE key.

Use the arrow keys to move from one bar to the other. (this will supply information on the frequency in each category and the range of values in each category).

The histogram provides us with the following information.

_Class_ Frequency 124-145 6 146-167 13 168-189 4 190-212 4 213-234 3

Lets review the steps for creating a histogram.

1. Enter the data into a list.

2. Determine the range of values for your data, as well as your desired class width.

3. Press the WINDOW key and set Xmin, Xmax, Xscl to the range of values and class width. Set Ymin to 0 and Ymax to a value large enough for the tallest box in the histogram. (You may need to come back and revise this to get it correct.)

4. Press the 2

key and then the Y= key to get to STAT PLOT. Make sure that at most one

plot is turned on, and select the plot.

5. Turn the plot On by pressing the ENTER key and select the third figure in the first row. Enter the name of your data list in Xlist, and leave Freq as 1.

6. Press the GRAPH key.

Example: Travel Time to Work

Here we have some data on average travel time (in minutes) to work for the fifty states.

22.4 18.2 23.7 19.8 26.7 23.4 23.5 22.5 24.3 26.7

24.2 19.7 27.0 21.7 17.6 17.7 22.5 23.7 21.2 29.2

26.1 22.7 21.6 21.9 23.2 16.0 16.1 22.3 24.4 28.7

19.9 31.2 22.6 15.4 22.1 19.6 21.4 23.8 21.9 21.9

15.6 22.7 23.6 20.8 21.1 25.4 24.9 25.5 20.1 17.1

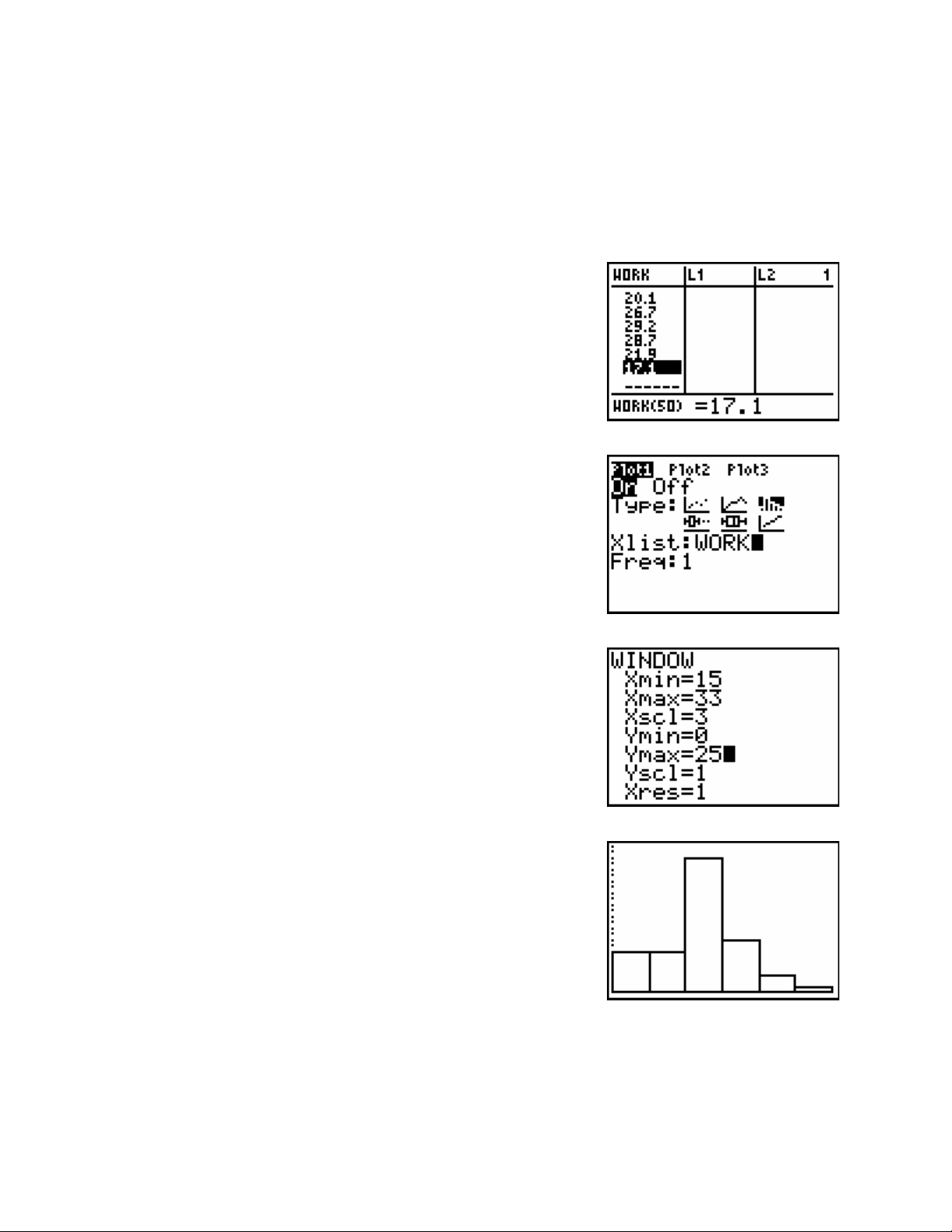
We’re going to construct a frequency histogram from the data. The data ranges from 15.4 to 31.2 so we will have our classes go from 15 to 33. That is a range of 33 − 15 = 18, so we will construct six classes of width 3.

Go into the Stat List Editor and create a new list called WORK. Enter the times.

Press the STAT key. Press the number 1 key. Press the 2

key and then the DEL key to get to INS. Type in WORK and then press the ENTER key. Enter the data values.

Press the 2

key and then the Y= key to get to the STAT PLOT page. Make sure that only one statistic plot is turned on and go into that plot. Turn the plot On. Select the third icon in the first row for Type. Type WORK for Xlist. Leave Freq as 1.

Press the WINDOW key. Set Xmin to 15 and Xmax to 33. Set Xscl to 3. Set Ymin to 0 and Ymax to 25.

Press the GRAPH key.

To get the class and frequency information to appear press the TRACE key.

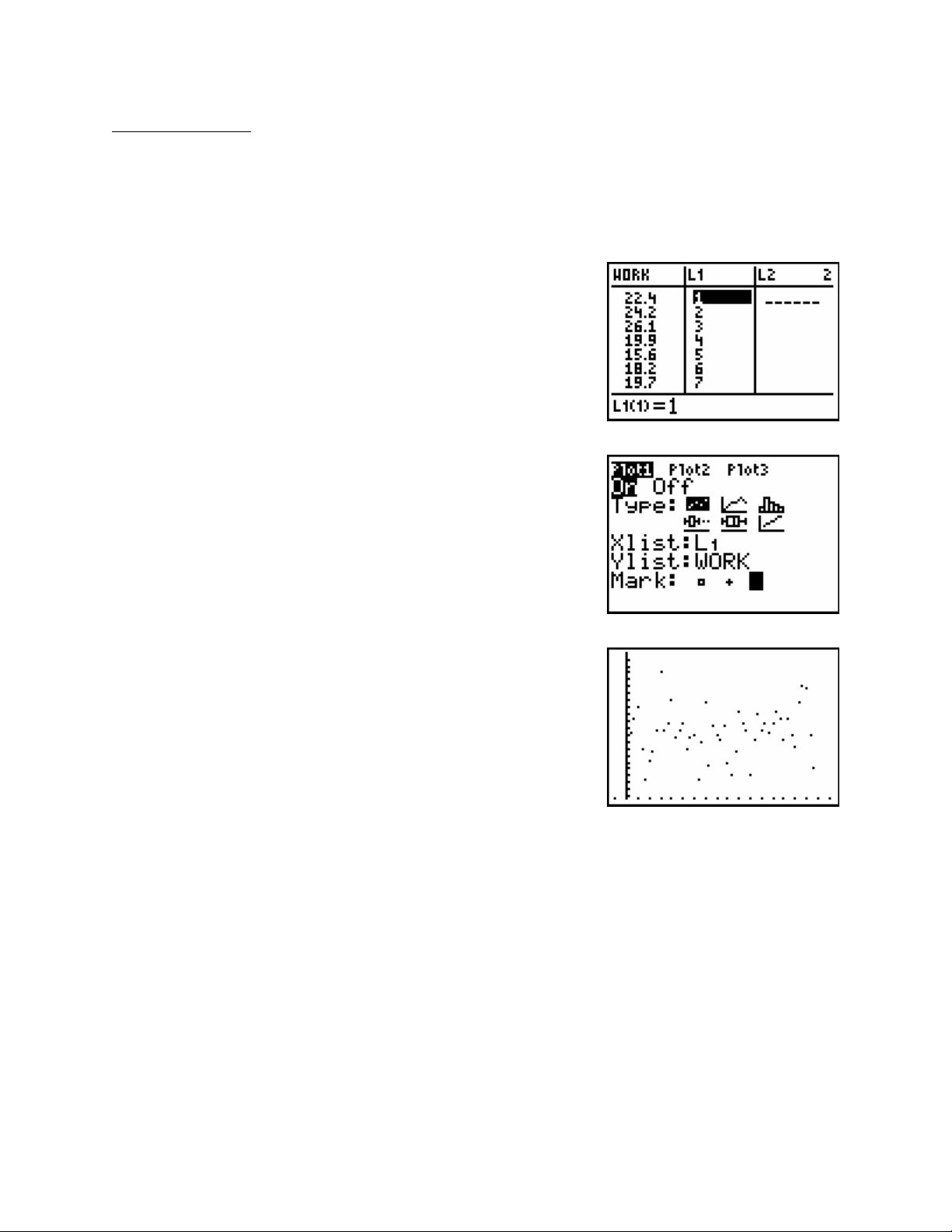
Creating a Dotplot

You can create a Dotplot by using the scatterplot option under STATPLOT. The steps to create the dotplot are very similar to those needed to create the histogram. We will use the data stored under the label WORK that we used to create the histogram in the previous example.

Press the STAT key. Press the number 1 key. Type in the numbers 1 through 50 in the L1 column. Press the 2

key and then the Y= key to get to STATPLOT. Press the number 1 key.

Turn Plot1 On and highlight the scatterplot under Type. Type L1 in for the Xlist: Type WORK for the Ylist: Select the period under Mark:

Press the Zoom Key. Press the number 9 key to get to ZoomStat.

The Xlist values 1-50 are used only to spread out the data values. The distribution of the numbers stored in the WORK list can be seen in the variability of the Ylist or on the vertical axis.

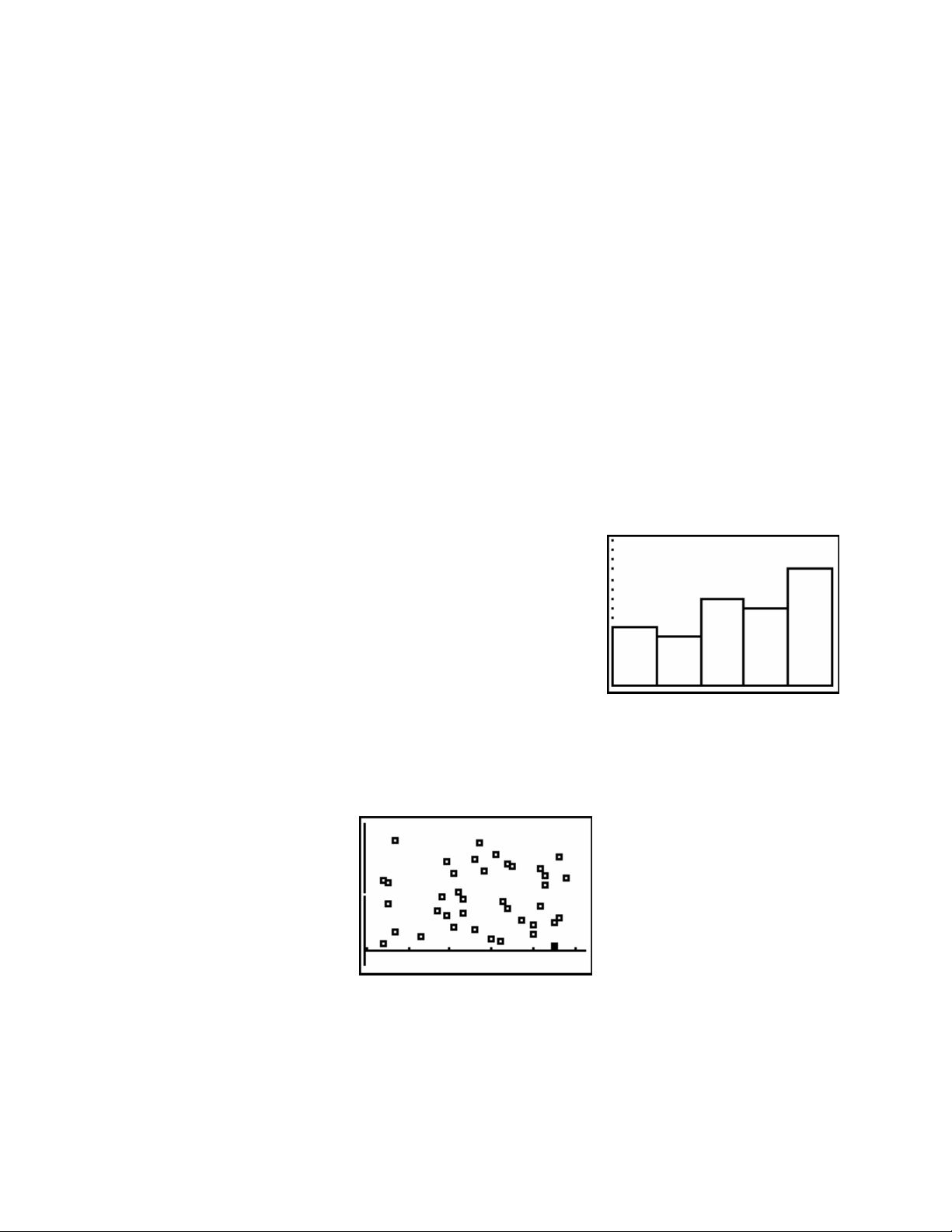
Exercises

1. Take the following statistics exam scores and construct a frequency histogram for them with classes from 50 to 59, from 60 to 69, from 70 to 79, from 80 to 89, and from 90 to 99.

95 80 76 87 67 83 77 54 78 69 95 63 71 96 84 73 57 98 92 76 54 90 90 69 92 68 93 93 85 96 82 57 95 73 55 72 55 71 84 81

2. Create a dot plot using the above data values.

Solutions

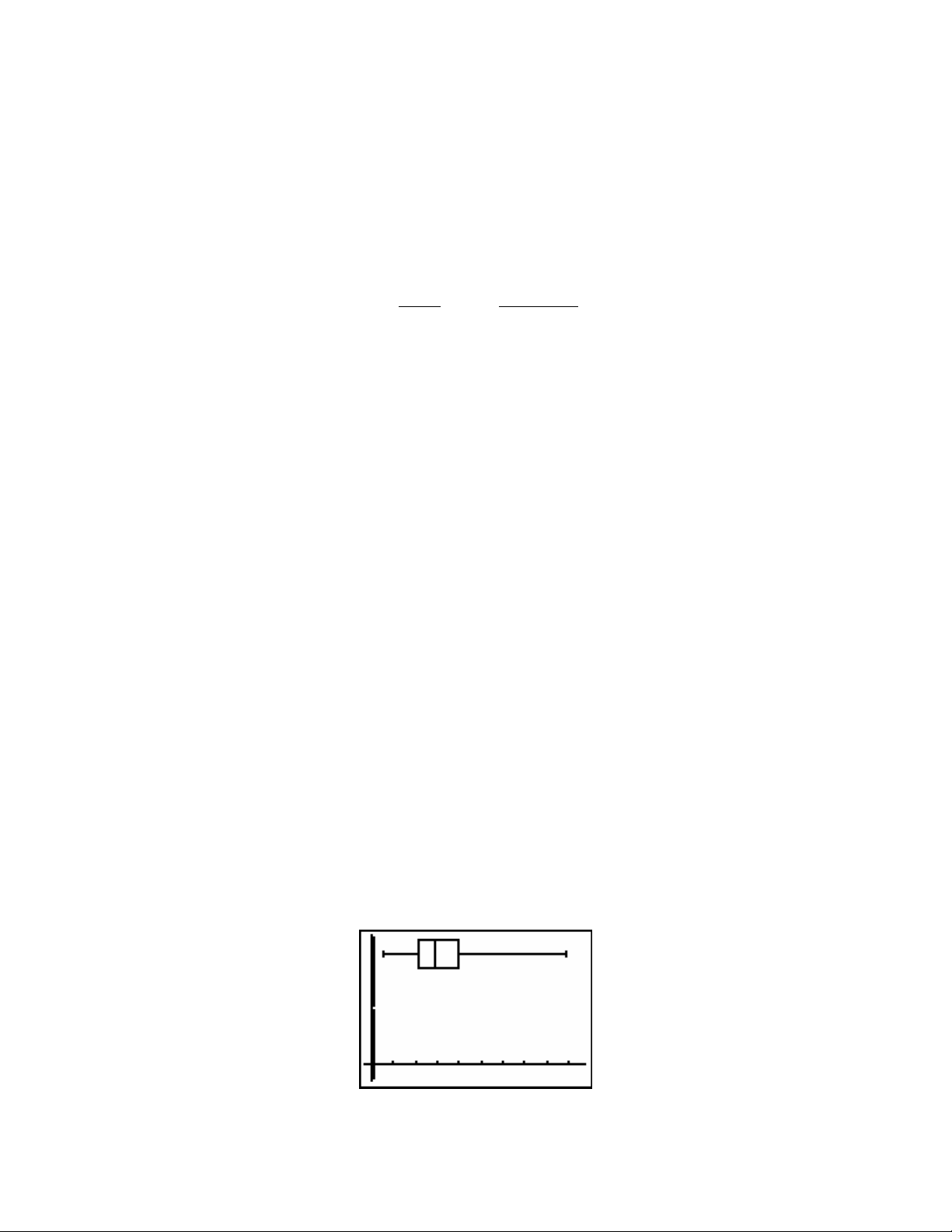
1. Enter the data into a list. In STAT PLOT turn one of the plots on, and choose a frequency histogram as the type. Enter the name of your list for Xlist.

In WINDOW, set Xmin to 50, Xmax to 100, Xscl to 10, Ymin to 0, and Ymax to 15. Press GRAPH. Your graph should look like this:

2. The data is stored in L1. Type in the numbers 1-40 in L2. In STAT PLOT turn one of the plots on, and choose a dotplot as the type. Press the ZOOM key. Press the number 9 key.

Chapter

Numerical Descriptive

Measures

After data is collected and organized the next step is usually to generate descriptive statistics. Descriptive statistics helps you describe the contents of the data set. The two most common measures are measures of central tendency and measures of variability. These measures tell you where the data is centered and how spread out it is. The center of the data can be described by such statistics as the mean and the median, while the spread of the data can be described by the standard deviation, the range, and the interquartile range.

You may also want to describe where one number is with respect to all the other numbers in a large set of numerical data. You can use percentiles to say what percent of the data lies below a given number. After learning about percentiles, another visual display can be created called the box-and-whisker plot.

On the TI-83, TI-83 Plus, and TI-84 Plus calculators, many numerical descriptive statistics for one variable are gathered together into one command called 1-Var Stats. There are two ways of using this command: with ungrouped data and with grouped data.

Generating Descriptive Statistics

Ungrouped Data

Ungrouped data sets are sets where each value is counted as occurring only once. Thus if the list {2, 3, 5, 7} is considered as ungrouped data, it merely consists of the four numbers 2, 3, 5, and 7. Grouped data, as we shall see later, lists the data values and how many times each of those values show up in the data set. The starting point for generating numerical descriptive statistics is getting the data into a list and then using the 1-Var Stats function to get the statistics.

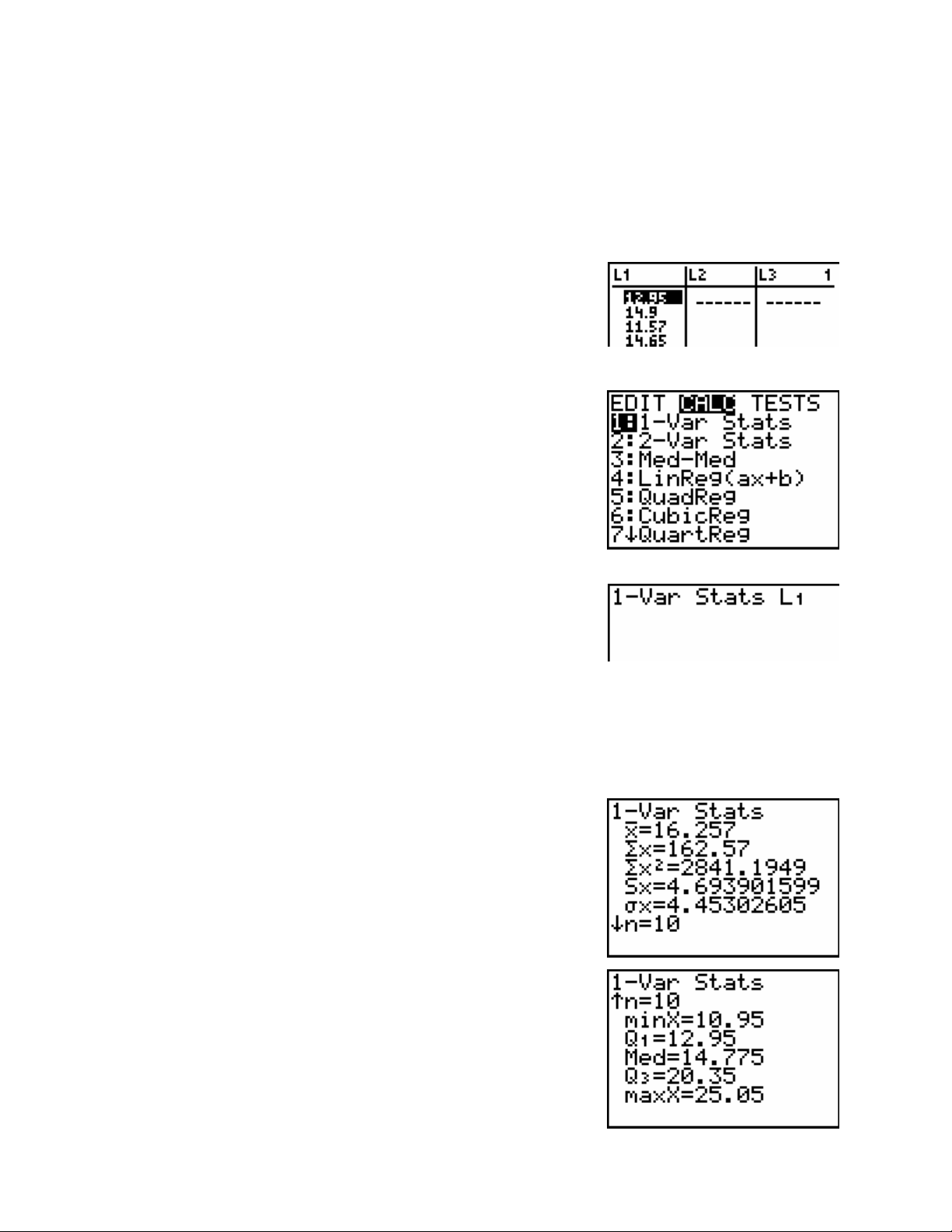
Example: Prices of CDs.

The following data values are the prices of the same popular CD sold from ten different discount stores.

12.95, 14.90, 11.57, 14.65, 17.95, 21.25, 12.95, 20.35, 10.95, 25.05

Press the STAT key. Press the number 1 key. Enter the data values into L1.

Press the STAT key. Press the ► key to highlight CALC.

Press the number 1 key to select 1-Var Stats. Press the 2

key and then the number 1 key to get L1.

Press the ENTER key.

You have to tell the calculator which list you want to use for the computations. If you omit the name of the list, 1-Var Stats uses L1 as its default.

The output screen contains many results. You will need to use the down arrow key to see all of them. Let’s go through the output line by line.

• Ë is the sample mean of the data.

• Σx is the sum of the values in the data set.

• Σx

is the sum of the squares of the values.

• Sx is the sample standard deviation.

• σx is the population standard deviation.

• n is the number of values in the data set.

• minX is the smallest value in the data set.

• Q

is the first quartile.

• Med is the median of the data set.

• Q

is the third quartile.

• maxX is the largest value in the data set.

The last five numbers (minimum, first quartile, median, third quartile, and maximum) are collectively known as the five-number summary of the data. From the five-number-summary we can compute the range, which is the difference between maxX and minX, and the interquartile range, which is the difference between Q3 and Q1.

Example: Average Payroll

The following list of data values lists the 2002 total payroll for five Major League Baseball teams. Let’s analyze the five payrolls.

MLB Team

2002 Total Payroll

(millions of dollars)

Anaheim Angels 62 Atlanta Braves 93

New York Yankees 126

St. Louis Cardinals 75 Tampa Bay Devil Rays 34

First store the data as a list labeled MLB.

Press the STAT key. Press the ► key to highlight CALC.

Press the number 1 key. Press the 2

key and then the STAT key to get to the LIST page. MLB is stored under the NAMES list.

Select MLB

Press the ENTER key.

The first line displays the sample mean, Ë = 78 million dollars. The fourth line displays the

sample standard deviation, Sx = 34.4 million dollars. Use the down arrow key to see that the median payroll is 75 million dollars. The interquartile range is found by subtracting the two quartiles Q3−Q1 = 109.5 − 48 = 61.5 million dollars. The range is maxX − minX = 126 − 34 = 92 million dollars.

Example: Concert Revenues

The following table contains the top twelve concert revenues of all time. Let’s describe the center and spread of these revenues.

Total Revenue Tour Artist (millions of dollars)____

Steel Wheels, 1989 The Rolling Stones 98.0 Magic Summer, 1990 New Kids on the Block 74.1 Voodoo Lounge, 1994 The Rolling Stones 121.2 The Division Bell, 1994 Pink Floyd 103.5 Hell Freezes Over, 1994 The Eagles 79.4 Bridges to Babylon, 1997 The Rolling Stones 89.3 Popmart, 1997 U2 79.9 Twenty-Four Seven, 2000 Tina Turner 80.2 No Strings Attached, 2000 ‘N-Sync 76.4 Elevation, 2001 U2 109.7 Popodyssey, 2001 ‘N-Sync 86.8 Black and Blue, 2001 The Backstreet Boys 82.1

First enter the data into a list labeled CON.

Use 1-Var Stats CON.

The sample mean Ë is 90.05 million dollars and the

sample median Med is 84.45 million dollars.

The population standard deviation is σ =

14.23 million dollars, the range is maxX − minX =

121.2 − 74.1 = 47.1 million dollars, and the interquartile range is Q3 − Q1 = 100.75 − 79.65 = 21.10 million dollars.

Grouped Data

Sometimes a set of data values has many numbers that show up over and over again. Instead of typing those numbers in over and over again you can save time by typing in the numbers that repeat along with how many times it repeats.

Example: Multiple Frequencies

The following is a list of data values that are ungrouped.

5, 7, 8, 8, 5, 3, 4, 5, 3, 3, 5, 7, 8, 8, 8, 7, 5, 4, 3, 6, 5, 4, 5, 9

The following table shows the same set of data values by showing each different value and how many times the value appears in the data set. This is called a grouped data set.

Value Frequency

3 4 4 2 5 7 6 1 7 3 8 5 9 1

The number 5 appears 4 times in the data set. The number 7 appears 3 time in the data set and so on. If you add up the frequencies, there are 23 numbers in our data set. Data with a frequency count of repeated values is known as grouped data. If the values are stored in L1, and the frequencies are stored in L2, we can call the 1-Var Stats command by typing 1-Var Stats L1, L2 and then pressing the ENTER key.

Example: Commuting Time

The following table lists the frequency classes for the length in minutes of the commute for all 32 employees of a company. We’ll use 1-Var Stats to describe the center and spread of the data.

Daily Commuting Time in minutes for Employees.

Time Frequency

5 4 7 2 8 11

9 7 12 4 15 3 17 1

Press the STAT key. Press the number 1 key. Enter the times in L1. Enter the frequencies in L2.

Press the STAT key. Press the ► key to Highlight CALC.

Press the ENTER key. Type in L1, L2.

Press the ENTER key.

The sample mean and median are 9.22 and 8 minutes, respectively. The sample standard deviation is 3.1 minutes, the range is 12 minutes, and the interquartile range is 2.5 minutes.

Measures of Position

Percentiles

The TI-83, TI-83 Plus, and TI-84 Plus do not perform percentile calculations directly, but do simplify them tremendously by helping us to sort data with the command SortD( . Once the data is sorted, the kth percentile is found by counting up to the kth position in the sorted data and dividing by the number of data values in the data set. After the number is divided, you multiply by 100 to get the percentile. The command SortD( is on the STAT page under the EDIT list and is found by pressing the STAT key and then pressing the number 3 key.

Example: Final Exam Scores

Use the following data set containing Elementary Statistics final exam scores from 16 students. Store the values in a list labeled FINAL.

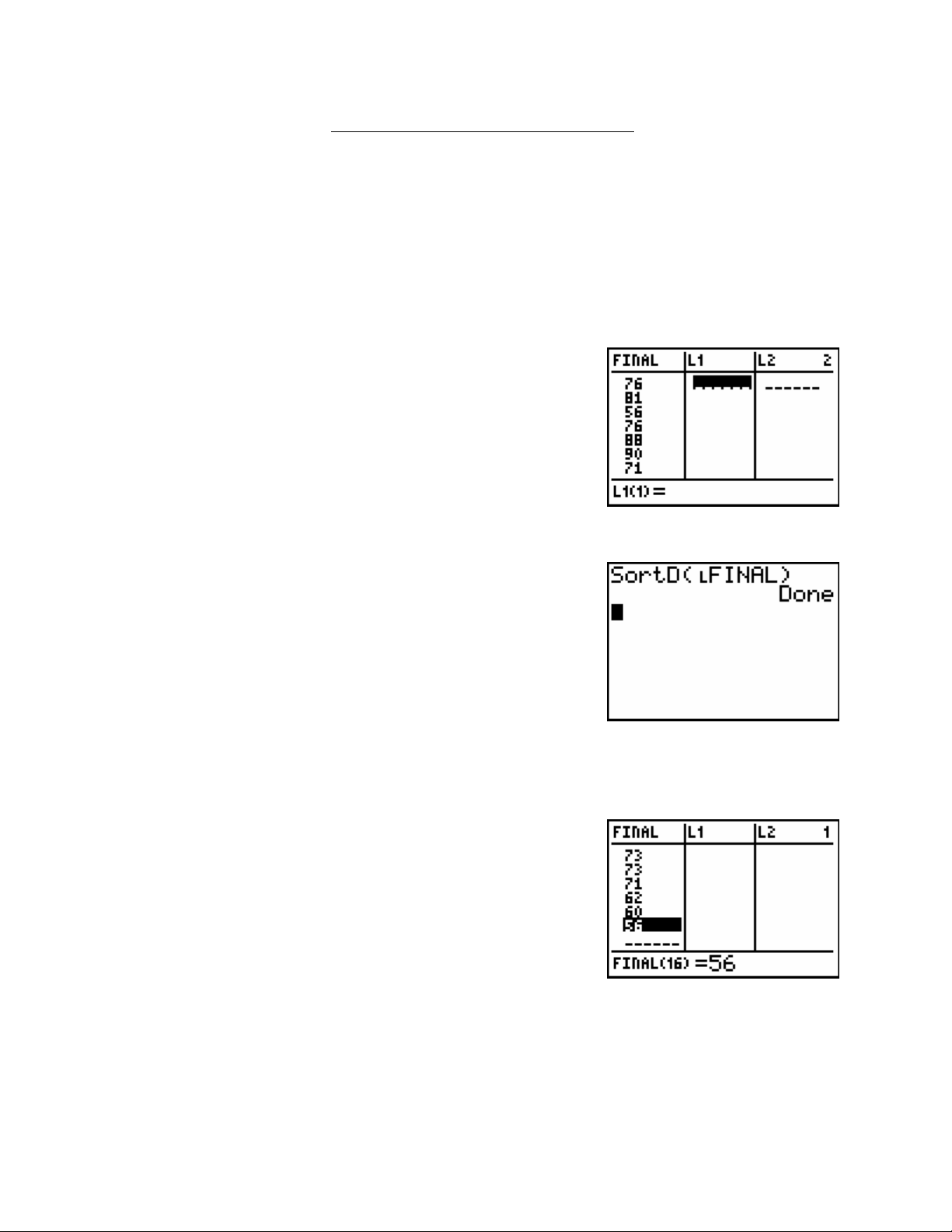
Elementary Statistics Final Exam Scores

76 88 94 73 81 90 62 94 56 71 77 85 76 60 84 73

Enter the exam scores into a list with the name FINAL.

Press the STAT key. Press the number 1 key. Press the ▲ key to highlight L1. Press the 2

key and then the DEL key to get to INS. Type in FINAL for the name of the new list. Type in the exam scores.

Press the STAT key. Press the number 3 key to get the function SortD( . Press the 2

key and then the STAT key to get to LIST. Select FINAL from the list and press the ENTER key. Press the ENTER key again.

The data values in the FINAL list are now sorted from highest to lowest. Each data value has an associated percentile or rank. The percentile tells how each data value is ordered with respect to the other data values. Let’s compute the percentile for the data value 88.

Press the STAT key. Press the number 1 key. Press the ▼ key until you get to the bottom of the data set. Press the ▲ key until you get to the data value 88 and be certain to count the number of places you go up from the bottom number.

The number 88 is 13 numbers up from the bottom. To compute the percentile take 13 divided by 16 which is the total number of numbers in the data set. The percentile is (13/16) X 100 =

81.25. Percentiles are usually rounded to the nearest whole number so you get the 81

percentile.

Box-and-Whisker Plot

The TI-83, TI-83 Plus, and TI-84 Plus calculators will take a list of data and automatically draw a box-and-whisker plot for that data. Since there are a number of different types of plots available on the calculator, it is important to make sure that all other plots are turned off before you begin or you graph will be cluttered with several unrelated plots being graphed at the same time. Even worse, it is possible for previous plots to become invalid or the data sets that were used before are changed or deleted, causing an error whenever you try to graph anything new. Before you begin any plotting:

• Press the Y= key at the top left of the keyboard, and delete or deselect any equations being plotted there.

• Press STAT PLOT (above the Y= key) and choose 4 to turn off any other statistical plots.

There are three stages to creating a box-and-whisker plot.

1. Enter the data into a list as before.

2. Tell the calculator what kind of plot you want.

3. Tell the calculator what size to draw the window for the plot.

Example: Household Incomes

The following numbers represent household incomes in thousands of dollars for twelve households:

35 29 44 72 34 64 41 50 54 104 39 58

We’ll use this data to construct a box-and-whisker plot. First store the data in the list L1.

Press the 2 STATPLOT. Press the number 1 key. Move the cursor to On and press the ENTER key. Use the arrow keys and highlight the box-and-whisker plot picture. Type L1 in for Xlist:

key and then press the Y= key to get to

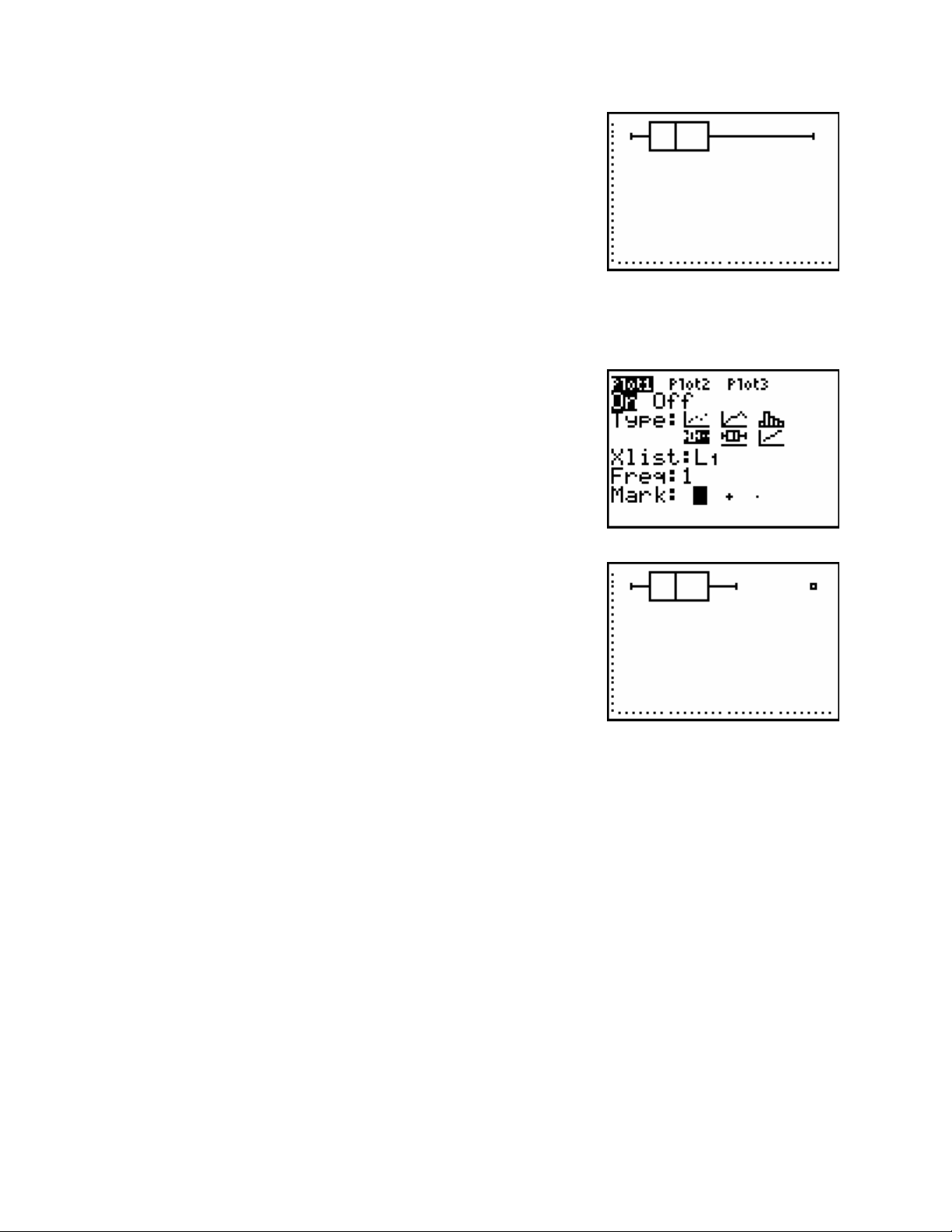
Set the Freq: to 1. Press the ZOOM key. Press the number 9 key.

We have two different types of box-and-whisker plots to select from. One will separate outliers from the maximum or minimum value and the other will include the outliers in to whiskers.

If you select the picture that shows two dots after the maximum on the plot, the outliers will be shown outside of the whiskers.

Exercises

1. Find the mean and sample standard deviation for the following data:

34 23 55 91 23 34 12 34 98 23

2. Find the median and interquartile range for the following grouped data:

Score Frequency

34 9 27 11 84 4 72 14 86 8 59 12 22 9

3. What is the percentile rank of 82 in the following data?

68 89 77 71 57 90 97 82 58 69

4. Create a box-and-whisker plot for the following data:

71 23 19 34 42 21 5 11 32 89 38 39 25 24

Solutions

1. The sample mean Ë = 42.7. The sample standard deviation sx = 29.58.

2. The median is 59. The interquartile range is 45.

3. The number 82 is the 70

percentile.

Chapter

Probability

Generating Random Numbers

When working with probabilities, it is sometimes useful to generate numbers that you can’t predict, but at the same time follow some standard rules. Computer simulations are a common example of the need for random occurrences within a structured setting. These numbers are called pseudo-random numbers since they are not totally random. Your calculator can generate these types of random numbers. The numbers that will appear on your calculator screen are hard to predict, but you will be able to attach probabilities to them. For each kind of pseudo-random number, we will be able to say what the probability is that it will occur next.

Generating Random Numbers Between 0 and 1

Suppose that you would like to generate a number between 0 and 1. You want the number to be unpredictable, but you want every number between 0 and 1 to have an equally likely chance of being generated.

A list of these types of numbers that are generated with the random number function on your calculator will be very similar to those found in the random number table in an Elementary Statistics textbook. The function is on the MATH page and can found in the PRB list.

Press the MATH key. Press the ► key until PRB is highlighted.

+ 62 hidden pages