Jbl Professional Sound System Service Manual

Sound System Design Reference Manual

Table of Contents

Preface ............................................................................................................................................. i

Chapter 1: Wave Propagation........................................................................................................ 1-1

Wavelength, Frequency, and Speed of Sound ................................................................................. 1-1

Combining Sine Waves .................................................................................................................... 1-2

Combining Delayed Sine Waves ...................................................................................................... 1-3

Diffraction of Sound .......................................................................................................................... 1-5

Effects of Temperature Gradients on Sound Propagation ................................................................ 1-6

Effects of Wind Velocity and Gradients on Sound Propagation........................................................ 1-6

Effect of Humidity on Sound Propagation......................................................................................... 1-7

Chapter 2: The Decibel................................................................................................................... 2-1

Introduction....................................................................................................................................... 2-1

Power Relationships......................................................................................................................... 2-1

Voltage, Current, and Pressure Relationships.................................................................................. 2-2

Sound Pressure and Loudness Contours......................................................................................... 2-4

Inverse Square Relationships........................................................................................................... 2-6

Adding Power Levels in dB............................................................................................................... 2-7

Reference Levels.............................................................................................................................. 2-7

Peak, Average, and RMS Signal Values........................................................................................... 2-8

Chapter 3: Directivity and Angular Coverage of Loudspeakers ................................................ 3-1

Introduction....................................................................................................................................... 3-1

Some Fundamentals ........................................................................................................................ 3-1

A Comparison of Polar Plots, Beamwidth Plots, Directivity Plots, and Isobars ................................ 3-3

Directivity of Circular Radiators ........................................................................................................ 3-4

The Importance of Flat Power Response ......................................................................................... 3-6

Measurement of Directional Characteristics..................................................................................... 3-7

Using Directivity Information............................................................................................................. 3-8

Directional Characteristics of Combined Radiators .......................................................................... 3-8

Chapter 4: An Outdoor Sound Reinforcement System............................................................... 4-1

Introduction....................................................................................................................................... 4-1

The Concept of Acoustical Gain ....................................................................................................... 4-2

The Influence of Directional Microphones and Loudspeakers on System Maximum Gain .............. 4-3

How Much Gain is Needed?............................................................................................................. 4-4

Conclusion........................................................................................................................................ 4-5

Chapter 5: Fundamentals of Room Acoustics............................................................................. 5-1

Introduction....................................................................................................................................... 5-1

Absorption and Reflection of Sound ................................................................................................. 5-1

The Growth and Decay of a Sound Field in a Room ........................................................................ 5-5

Reverberation and Reverberation Time............................................................................................ 5-7

Direct and Reverberant Sound Fields .............................................................................................. 5-12

Critical Distance................................................................................................................................ 5-14

The Room Constant ......................................................................................................................... 5-15

Statistical Models and the Real World.............................................................................................. 5-20

Sound System Design Reference Manual

Table of Contents (cont.)

Chapter 6: Behavior of Sound Systems Indoors ......................................................................... 6-1

Introduction....................................................................................................................................... 6-1

Acoustical Feedback and Potential System Gain............................................................................. 6-2

Sound Field Calculations for a Small Room ..................................................................................... 6-2

Calculations for a Medium-Size Room ............................................................................................. 6-5

Calculations for a Distributed Loudspeaker System......................................................................... 6-8

System Gain vs. Frequency Response ............................................................................................ 6-9

The Indoor Gain Equation ................................................................................................................ 6-9

Measuring Sound System Gain........................................................................................................ 6-10

General Requirements for Speech Intelligibility................................................................................ 6-11

The Role of Time Delay in Sound Reinforcement ............................................................................ 6-16

System Equalization and Power Response of Loudspeakers .......................................................... 6-17

System Design Overview ................................................................................................................. 6-19

Chapter 7: System Architecture and Layout................................................................................ 7-1

Introduction....................................................................................................................................... 7-1

Typical Signal Flow Diagram ............................................................................................................ 7-1

Amplifier and Loudspeaker Power Ratings ...................................................................................... 7-5

Wire Gauges and Line Losses ......................................................................................................... 7-5

Constant Voltage Distribution Systems (70-volt lines)...................................................................... 7-6

Low Frequency Augmentation—Subwoofers ................................................................................... 7-6

Case Study A: A Speech and Music System for a Large Evangelical Church.................................. 7-9

Case Study B: A Distributed Sound Reinforcement System for a Large Liturgical Church .............. 7-12

Case Study C: Specifications for a Distributed Sound System Comprising a Ballroom,

Small Meeting Space, and Social/Bar Area ............................................................................... 7-16

Bibliography

Sound System Design Reference Manual

Preface to the 1999 Edition:

This third edition of JBL Professional’s Sound System Design Reference Manual is presented in a new graphic format that makes for easier reading and study. Like its predecessors, it presents in virtually their original 1977 form George Augspurger’s intuitive and illuminating explanations of sound and sound system behavior in enclosed spaces. The section on systems and case studies has been expanded, and references to JBL components have been updated.

The fundamentals of acoustics and sound system design do not change, but system implementation improves in its effectiveness with ongoing developments in signal processing, transducer refinement, and front-end flexibility in signal routing and control.

As stated in the Preface to the 1986 edition: The technical competence of professional dealers and sound contractors is much higher today than it was when the Sound Workshop manual was originally introduced. It is JBL’s feeling that the serious contractor or professional dealer of today is ready to move away from simply plugging numbers into equations. Instead, the designer is eager to learn what the equations really mean, and is intent on learning how loudspeakers and rooms interact, however complex that may be. It is for the student with such an outlook that this manual is intended.

John Eargle

January 1999

Sound System Design Reference Manual

Chapter 1: Wave Propagation

Sound System Design Reference Manual

Wavelength, Frequency, and Speed of Sound

Sound waves travel approximately 344 m/sec (1130 ft/sec) in air. There is a relatively small velocity dependence on temperature, and under normal indoor conditions we can ignore it. Audible sound covers the frequency range from about 20 Hz to 20 kHz. The wavelength of sound of a given frequency is the distance between successive repetitions of the waveform as the sound travels through air. It is given by the following equation:

wavelength = speed/frequency

or, using the common abbreviations of c for speed, f for frequency, and l for wavelength:

l = c/f

Period (T) is defined as the time required for

one cycle of the waveform. T = 1/f.

For f = 1 kHz, T = 1/1000, or 0.001 sec, and

l = 344/1000, or .344 m (1.13 ft.)

The lowest audible sounds have wavelengths on the order of 10 m (30 ft), and the highest sounds have wavelengths as short as 20 mm (0.8 in). The range is quite large, and, as we will see, it has great bearing on the behavior of sound.

The waves we have been discussing are of course sine waves, those basic building blocks of all speech and music signals. Figure 1-1 shows some of the basic aspects of sine waves. Note that waves of the same frequency can differ in both amplitude and in phase angle. The amplitude and phase angle relationships between sine waves determine how they combine, either acoustically or electrically.

Figure 1-1. Properties of sine waves

1-1

Sound System Design Reference Manual

Combining Sine Waves

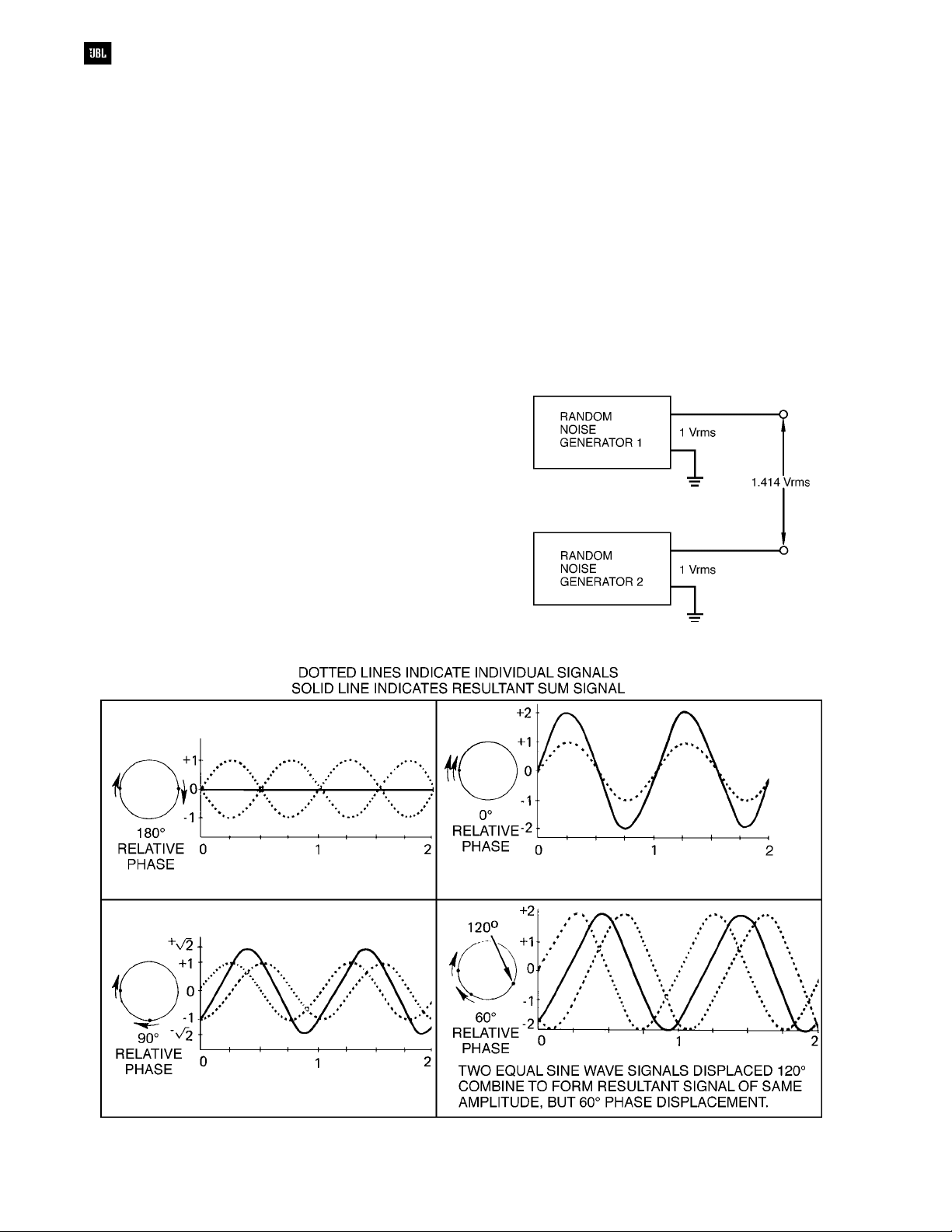
Referring to Figure 1-2, if two or more sine wave signals having the same frequency and amplitude are added, we find that the resulting signal also has the same frequency and that its amplitude depends upon the phase relationship of the original signals. If there is a phase difference of 120°, the resultant has exactly the same amplitude as either of the original signals. If they are combined in phase, the resulting signal has twice the amplitude of either original. For phase differences between l20° and 240°, the resultant signal always has an amplitude less than that of either of the original signals. If the two signals are exactly 180° out of phase, there will be total cancellation.

In electrical circuits it is difficult to maintain identical phase relationships between all of the sine components of more complex signals, except for the special cases where the signals are combined with a 0° or 180° phase relationship. Circuits which maintain some specific phase relationship (45°, for example) over a wide range of frequencies are fairly complex. Such wide range, all-pass phase-shifting networks are used in acoustical signal processing.

When dealing with complex signals such as music or speech, one must understand the concept of coherence. Suppose we feed an electrical signal through a high quality amplifier. Apart from very small amounts of distortion, the output signal is an exact

replica of the input signal, except for its amplitude. The two signals, although not identical, are said to be highly coherent. If the signal is passed through a poor amplifier, we can expect substantial differences between input and output, and coherence will not be as great. If we compare totally different signals, any similarities occur purely at random, and the two are said to be non-coherent.

When two non-coherent signals are added, the rms (root mean square) value of the resulting signal can be calculated by adding the relative powers of the two signals rather than their voltages. For example, if we combine the outputs of two separate noise generators, each producing an rms output of 1 volt, the resulting signal measures 1.414 volts rms, as shown in Figure 1-3.

Figure 1-3. Combining two random noise generators

1-2

Figure 1-2. V ector addition of two sine waves

Sound System Design Reference Manual

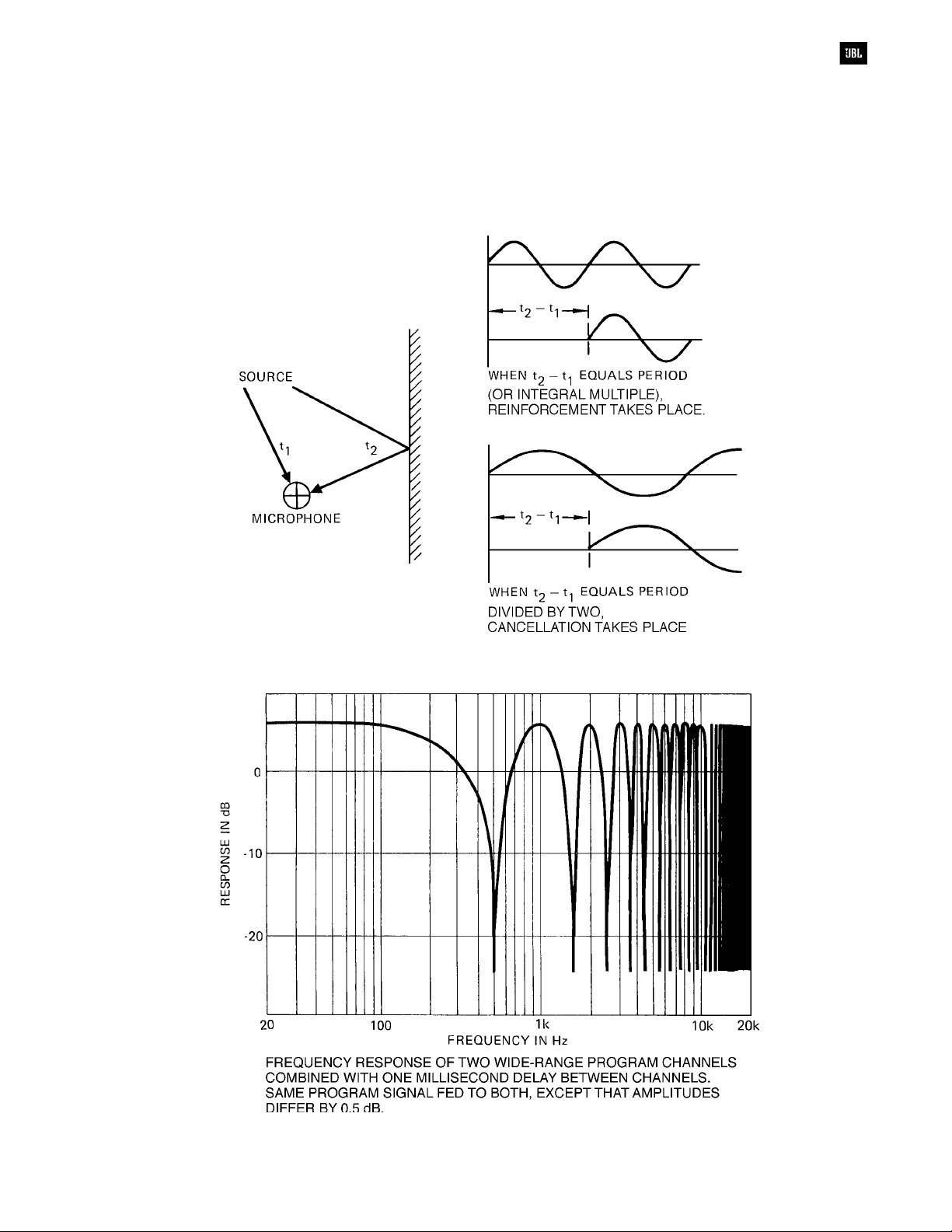
Combining Delayed Sine Waves

If two coherent wide-range signals are combined with a specified time difference between them rather than a fixed phase relationship, some frequencies will add and others will cancel. Once the delayed signal arrives and combines with the original signal, the result is a form of “comb filter,” which

alters the frequency response of the signal, as shown in Figure 1-4. Delay can be achieved electrically through the use of all-pass delay networks or digital processing. In dealing with acoustical signals in air, there is simply no way to avoid delay effects, since the speed of sound is relatively slow.

Figure 1-4A. Combining delayed signals

Figure 1-4B. Combining of coherent signals with constant time delay

1-3

Sound System Design Reference Manual

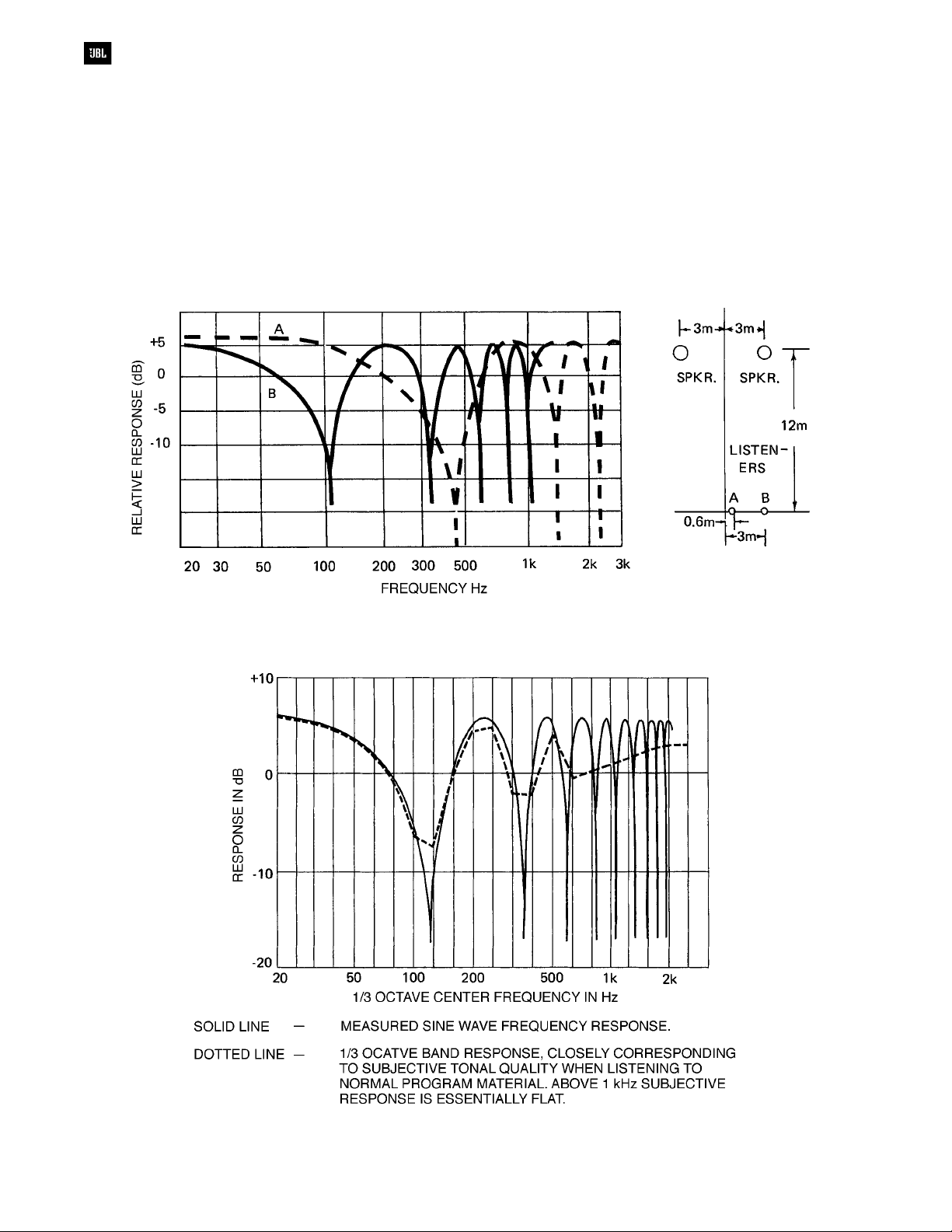
A typical example of combining delayed coherent signals is shown in Figure 1-5. Consider the familiar outdoor PA system in which a single microphone is amplified by a pair of identical separated loudspeakers. Suppose the loudspeakers in question are located at each front corner of the stage, separated by a distance of 6 m (20 ft). At any distance from the stage along the center line, signals from the two loudspeakers arrive simultaneously. But at any other location, the distances of the two loudspeakers are unequal, and sound from one must

arrive slightly later than sound from the other. The illustration shows the dramatically different frequency response resulting from a change in listener position of only 2.4 m (8 ft). Using random noise as a test signal, if you walk from Point B to Point A and proceed across the center line, you will hear a pronounced swishing effect, almost like a siren. The change in sound quality is most pronounced near the center line, because in this area the response peaks and dips are spread farther apart in frequency.

Figure 1-5. Generation of interference effects (comb filter response) by a split array

1-4

Figure 1-6. Audible effect of comb filters shown in Figure 1-5

Sound System Design Reference Manual

Subjectively, the effect of such a comb filter is not particularly noticeable on normal program material as long as several peaks and dips occur within each one-third octave band. See Figure 1-6. Actually, the controlling factor is the “critical bandwidth.” In general, amplitude variations that occur within a critical band will not be noticed as such. Rather, the ear will respond to the signal power contained within that band. For practical work in sound system design and architectural acoustics, we can assume that the critical bandwidth of the human ear is very nearly one-third octave wide.

In houses of worship, the system should be suspended high overhead and centered. In spaces which do not have considerable height, there is a strong temptation to use two loudspeakers, one on either side of the platform, feeding both the same program. We do not recommend this.

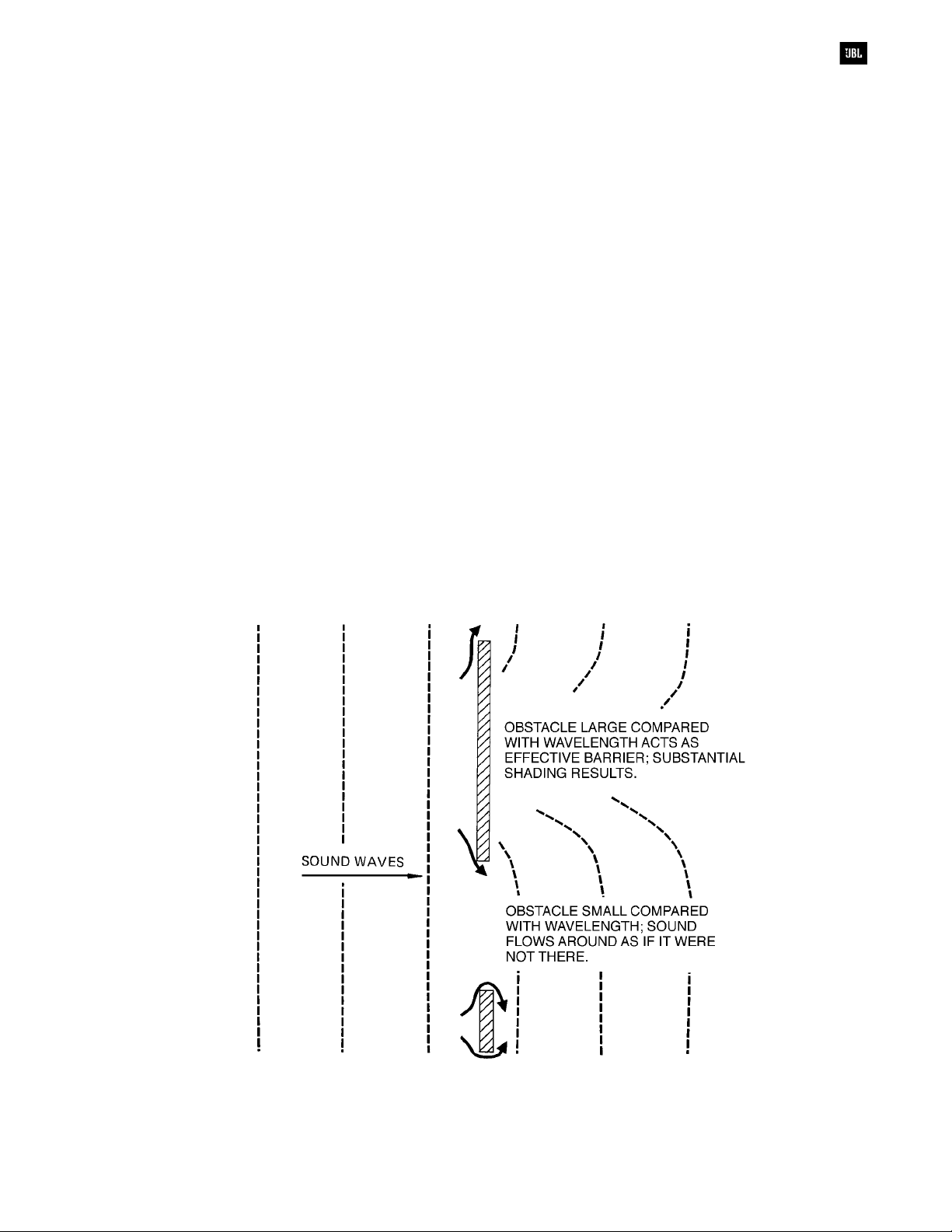
Diffraction of Sound

Diffraction refers to the bending of sound waves as they move around obstacles. When sound strikes a hard, non-porous obstacle, it may be reflected or

diffracted, depending on the size of the obstacle relative to the wavelength. If the obstacle is large compared to the wavelength, it acts as an effective barrier, reflecting most of the sound and casting a substantial “shadow” behind the object. On the other hand, if it is small compared with the wavelength, sound simply bends around it as if it were not there. This is shown in Figure 1-7.

An interesting example of sound diffraction occurs when hard, perforated material is placed in the path of sound waves. So far as sound is concerned, such material does not consist of a solid barrier interrupted by perforations, but rather as an open area obstructed by a number of small individual objects. At frequencies whose wavelengths are small compared with the spacing between perforations, most of the sound is reflected. At these frequencies, the percentage of sound traveling through the openings is essentially proportional to the ratio between open and closed areas.

At lower frequencies (those whose wavelengths are large compared with the spacing between perforations), most of the sound passes through the openings, even though they may account only for 20 or 30 percent of the total area.

Figure 1-7. Diffraction of sound around obstacles

1-5

Sound System Design Reference Manual

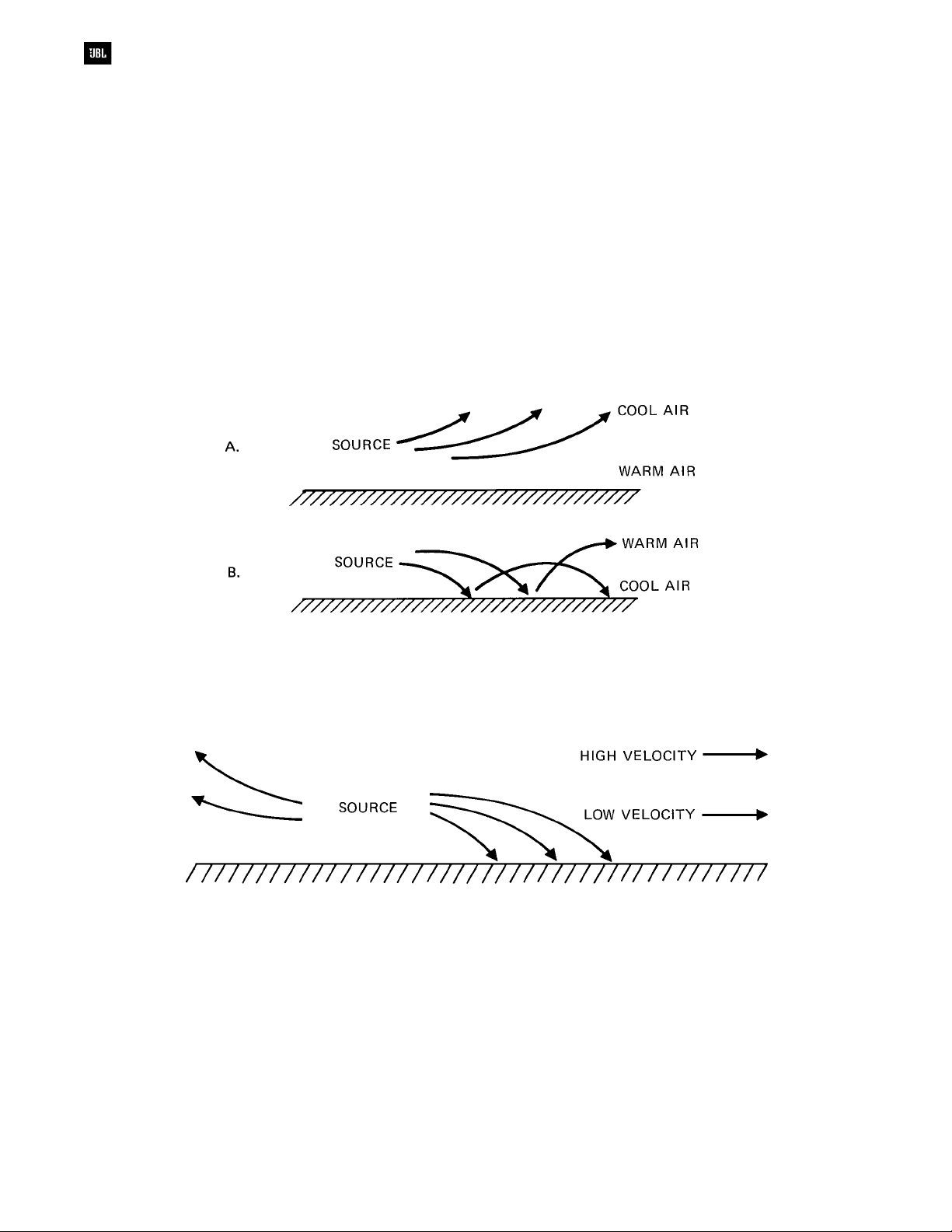
Effects of Temperature Gradients on Sound Propagation

If sound is propagated over large distances out of doors, its behavior may seem erratic. Differences (gradients) in temperature above ground level will affect propagation as shown in Figure 1-8. Refraction of sound refers to its changing direction as its velocity increases slightly with elevated temperatures. At Figure 1-8A, we observe a situation which often occurs at nightfall, when the ground is still warm. The case shown at B may occur in the morning, and its “skipping” characteristic may give rise to hot spots and dead spots in the listening area.

Effects of Wind Velocity and Gradients on Sound Propagation

Figure 1-9 shows the effect wind velocity gradients on sound propagation. The actual velocity of sound in this case is the velocity of sound in still air plus the velocity of the wind itself. Figure 1-10 shows the effect of a cross breeze on the apparent direction of a sound source.

The effects shown in these two figures may be evident at large rock concerts, where the distances covered may be in the 200 - 300 m (600 - 900 ft) range.

Figure 1-8. Effects of temperature gradients on sound propagation

Figure 1-9. Effect of wind velocity gradients on sound propagation

1-6

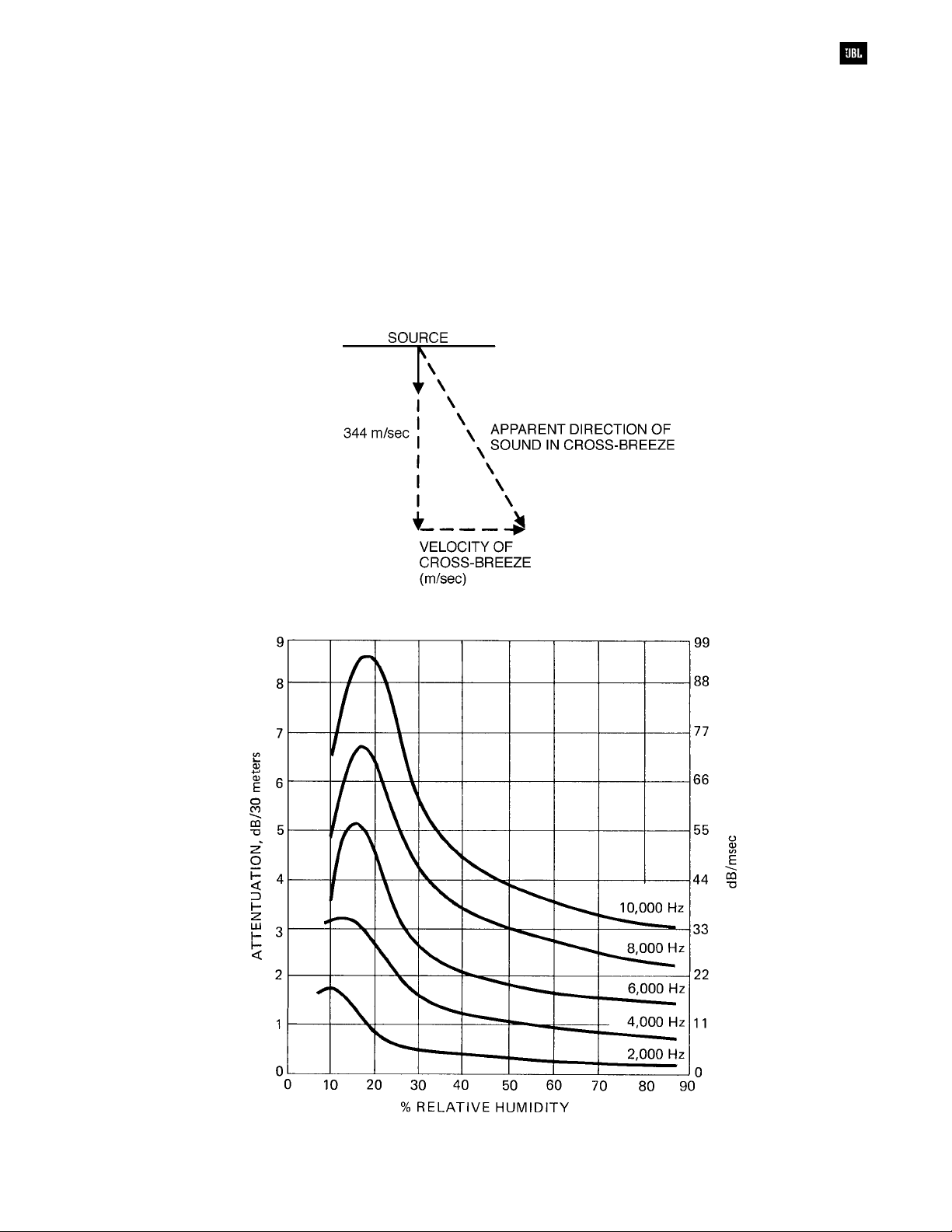
Effects of Humidity on Sound Propagation

Contrary to what most people believe, there is more sound attenuation in dry air than in damp air. The effect is a complex one, and it is shown in Figure 1-11. Note that the effect is significant only at frequencies above 2 kHz. This means that high frequencies will be attenuated more with distance than low frequencies will be, and that the attenuation will be greatest when the relative humidity is 20 percent or less.

Sound System Design Reference Manual

Figure 1-10. Effect of cross breeze on apparent direction of sound

Figure 1-1 1. Absorption of sound in air vs. relative humidity

1-7

Sound System Design Reference Manual

Chapter 2: The Decibel

Sound System Design Reference Manual

Introduction

In all phases of audio technology the decibel is used to express signal levels and level differences in sound pressure, power, voltage, and current. The reason the decibel is such a useful measure is that it enables us to use a comparatively small range of numbers to express large and often unwieldy quantities. The decibel also makes sense from a psychoacoustical point of view in that it relates directly to the effect of most sensory stimuli.

Power Relationships

Fundamentally, the bel is defined as the common logarithm of a power ratio:

bel = log (P1/P0)

For convenience, we use the decibel, which is simply one-tenth bel. Thus:

decibel = 10 log (P1/P0)

The following tabulation illustrates the usefulness of the concept. Letting P0 = 1 watt:

signal. The convenience of using decibels is apparent; each of these power ratios can be expressed by the same level, 10 dB. Any 10 dB level difference, regardless of the actual powers involved, will represent a 2-to-1 difference in subjective loudness.

We will now expand our power decibel table:

P1 (watts) Level in dB

1.25 1

1.60 2 23

2.5 4

3.15 5 46 57

6.3 8 89

10 10

This table is worth memorizing. Knowing it, you can almost immediately do mental calculations, arriving at power levels in dB above, or below, one watt.

P1 (watts) Level in dB

10 10

100 20

1000 30 10,000 40 20,000 43

Note that a 20,000-to-1 range in power can be expressed in a much more manageable way by referring to the powers as levels in dB above one watt. Psychoacoustically, a ten-times increase in power results in a level which most people judge to be “twice as loud.” Thus, a 100-watt acoustical signal would be twice as loud as a 10-watt signal, and a 10-watt signal would be twice as loud as a 1-watt

Here are some examples:

1. What power level is represented by 80 watts? First, locate 8 watts in the left column and note that the corresponding level is 9 dB. Then, note that 80 is 10 times 8, giving another 10 dB. Thus:

9 + 10 = 19 dB

2. What power level is represented by 1 milliwatt? 0.1 watt represents a level of minus 10 dB, and 0.01 represents a level 10 dB lower. Finally,

0.001 represents an additional level decrease of 10 dB. Thus:

–10 – 10 – 10 = –30 dB

2-1

Sound System Design Reference Manual

3. What power level is represented by 4 milliwatts? As we have seen, the power level of 1 milliwatt is –30 dB. Two milliwatts represents a level increase of 3 dB, and from 2 to 4 milliwatts there is an additional 3 dB level increase. Thus:

–30 + 3 + 3 = –24 dB

4. What is the level difference between 40 and 100 watts? Note from the table that the level corresponding to 4 watts is 6 dB, and the level corresponding to 10 watts is 10 dB, a difference of 4 dB. Since the level of 40 watts is 10 dB greater than for 4 watts, and the level of 80 watts is 10 dB greater than for 8 watts, we have:

6 – 10 + 10 – 10 = –4 dB

We have done this last example the long way, just to show the rigorous approach. However, we could simply have stopped with our first observation, noting that the dB level difference between 4 and 10 watts, .4 and 1 watt, or 400 and 1000 watts will always be the same, 4 dB, because they all represent the same power ratio.

The level difference in dB can be converted back to a power ratio by means of the following equation:

Power ratio = 10

dB/10

For example, find the power ratio of a level difference of 13 dB:

Power ratio = 10

13/10

= 10

1.3

= 20

Voltage, Current, and Pressure Relationships

The decibel fundamentally relates to power ratios, and we can use voltage, current, and pressure ratios as they relate to power. Electrical power can be represented as:

P = EI

P = I

P = E2/Z

Because power is proportional to the square of the voltage, the effect of doubling the voltage is to quadruple the power:

(2E)2/Z = 4(E)2/Z

As an example, let E = 1 volt and Z = 1 ohm. Then, P = E2/Z = 1 watt. Now, let E = 2 volts; then, P = (2)2/1 = 4 watts.

The same holds true for current, and the following equations must be used to express power levels in dB using voltage and current ratios:

dB level = 10 log





20 log













20 log













, and





















The reader should acquire a reasonable skill in dealing with power ratios expressed as level differences in dB. A good “feel” for decibels is a qualification for any audio engineer or sound contractor. An extended nomograph for converting power ratios to level differences in dB is given in Figure 2-1.

Figure 2-1. Nomograph for determining power ratios directly in dB

2-2

Sound pressure is analogous to voltage, and

levels are given by the equation:





dB level = 20 log









Sound System Design Reference Manual

The normal reference level for voltage, E0, is one volt. For sound pressure, the reference is the extremely low value of 20 x 10

-6

newtons/m2. This reference pressure corresponds roughly to the minimum audible sound pressure for persons with normal hearing. More commonly, we state pressure in pascals (Pa), where 1 Pa = 1 newton/m2. As a convenient point of reference, note that an rms pressure of 1 pascal corresponds to a sound pressure level of 94 dB.

We now present a table useful for determining levels in dB for ratios given in voltage, current, or sound pressure:

Voltage, Current or

Pressure Ratios Level in dB

1.25 2

1.60 4 26

2.5 8

3.15 10 412 514

6.3 16 818

10 20

This table may be used exactly the same way as the previous one. Remember, however, that the reference impedance, whether electrical or acoustical, must remain fixed when using these ratios to determine level differences in dB. A few examples are given:

If we simply compare input and output voltages, we still get 0 dB as our answer. The voltage gain is in fact unity, or one. Recalling that decibels refer primarily to power ratios, we must take the differing input and output impedances into account and actually compute the input and output powers.

Input power =

Output power =

T 10 log

  

600



= 10 log 40 = 16 dBhus,

 

600

watt

Fortunately, such calculations as the above are not often made. In audio transmission, we keep track of operating levels primarily through voltage level calculations in which the voltage reference value of

0.775 volts has an assigned level of 0 dBu. The value of 0.775 volts is that which is applied to a 600ohm load to produce a power of 1 milliwatt (mW). A power level of 0 dBm corresponds to 1 mW. Stated somewhat differently, level values in dBu and dBm will have the same numerical value only when the load impedance under consideration is 600 ohms.

The level difference in dB can be converted back to a voltage, current, or pressure ratio by means of the following equation:

Ratio = 10

dB/20

1. Find the level difference in dB between 2

volts and 10 volts. Directly from the table we observe

20 – 6 = 14 dB.

2. Find the level difference between 1 volt and 100 volts. A 10-to-1 ratio corresponds to a level difference of 20 dB. Since 1-to-100 represents the product of two such ratios (1-to-10 and 10-to-100), the answer is

20 + 20 = 40 dB.

3. The signal input to an amplifier is 1 volt, and the input impedance is 600 ohms. The output is also 1 volt, and the load impedance is 15 ohms. What is the gain of the amplifier in dB? Watch this one carefully!

For example, find the voltage ratio

corresponding to a level difference of 66 dB:

voltage ratio = 10

66/20

= 10

3.3

= 2000.

2-3

Sound System Design Reference Manual

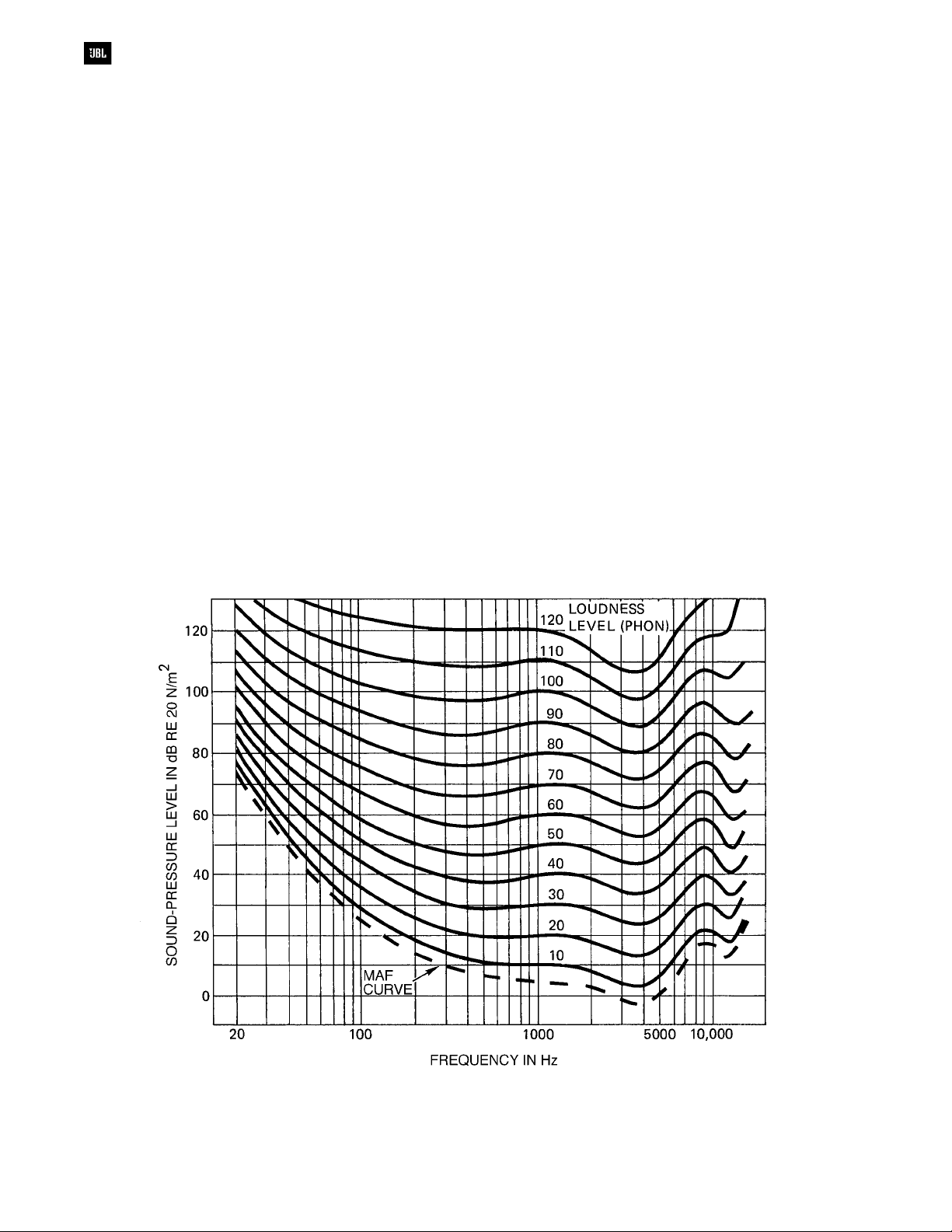
Sound Pressure and Loudness Contours

We will see the term dB-SPL time and again in professional sound work. It refers to sound pressure levels in dB above the reference of 20 x 10-6 N/m2. We commonly use a sound level meter (SLM) to measure SPL. Loudness and sound pressure obviously bear a relation to each other, but they are not the same thing. Loudness is a subjective sensation which differs from the measured level in certain important aspects. To specify loudness in scientific terms, a different unit is used, the phon. Phons and decibels share the same numerical value only at 1000 Hz. At other frequencies, the phon scale deviates more or less from the sound level scale, depending on the particular frequency and the sound pressures; Figure 2-2 shows the relationship between phons and decibels, and illustrates the well-known Robinson-Dadson equal loudness contours. These show that, in general, the ear becomes less sensitive to sounds at low frequencies as the level is reduced.

When measuring sound pressure levels, weighted response may be employed to more closely approximate the response of the ear. Working with sound systems, the most useful scales on the sound level meter will be the A-weighting scale and the linear scale, shown in Figure 2-3. Inexpensive sound level meters, which cannot provide linear response over the full range of human hearing, often have no linear scale but offer a C-weighting scale instead. As can be seen from the illustration, the C-scale rolls off somewhat at the frequency extremes. Precision sound level meters normally offer A, B, and C scales in addition to linear response. Measurements made with a sound level meter are normally identified by noting the weighting factor, such as: dB(A) or dB(lin).

Typical levels of familiar sounds, as shown in Figure 2-4, help us to estimate dB(A) ratings when a sound level meter is not available. For example, normal conversational level in quiet surrounds is about 60 dB(A). Most people find levels higher than 100 dB(A) uncomfortable, depending on the length of exposure. Levels much above 120 dB(A) are definitely dangerous to hearing and are perceived as painful by all except dedicated rock music fans.

2-4

Figure 2-2. Free-field equal loudness contours

+ 40 hidden pages