intersil HSP50210 DATA SHEET

www.BDTIC.com/Intersil

HSP50210

Data Sheet July 2, 2008

Digital Costas Loop

The Digital Costas Loop (DCL) performs many of the baseband processing tasks required for the demodulation of BPSK, QPSK, 8-PSK, OQPSK, FSK, AM and FM waveforms. These tasks include matched filtering, carrier tracking, symbol synchronization, AGC, and soft decision slicing. The DCL is designed for use with the HSP50110 Digital Quadrature Tuner to provide a two chip solution for digital down conversion and demodulation.

The DCL processes the In-phase (I) and Quadrature (Q) components of a baseband signal which have been digitized to 10 bits. As shown in the block diagram, the main signal path consists of a complex multiplier, selectable matched filters, gain multipliers, cartesian-to-polar converter, and soft decision slicer. The complex multiplier mixes the I and Q inputs with the output of a quadrature NCO. Following the mix function, selectable matched filters are provided, which perform integrate and dump or root raised cosine filtering (α ~ 0.40). The matched filter output is routed to the slicer, which generates 3-bit soft decisions, and to the cartesian-topolar converter, which generates the magnitude and phase terms required by the AGC and Carrier Tracking Loops.

The PLL system solution is completed by the HSP50210 error detectors and second order Loop Filters that provide carrier tracking and symbol synchronization signals. In applications where the DCL is used with the HSP50110, these control loops are closed through a serial interface between the two parts. To maintain the demodulator performance with varying signal power and SNR, an internal AGC loop is provided to establish an optimal signal level at the input to the slicer and to the cartesian-to-polar converter.

FN3652.5

Features

• Clock Rates Up to 52MHz

• Selectable Matched Filtering with Root Raised Cosine or Integrate and Dump Filter

• Second Order Carrier and Symbol Tracking Loop Filters

• Automatic Gain Control (AGC)

• Discriminator for FM/FSK Detection and Discriminator Aided Acquisition

• Swept Acquisition with Programmable Limits

• Lock Detector

• Data Quality and Signal Level Measurements

• Cartesian-to-Polar Converter

• 8-Bit Microprocessor Control - Status Interface

• Designed to Work With the HSP50110 Digital Quadrature Tuner

• 84 Lead PLCC

• Pb-Free Available (R oH S compliant)

Applications

• Satellite Receivers and Modems

• BPSK, QPSK, 8-PSK, OQPSK, FSK, AM and FM Demodulators

• Digital Carrier Tracking

• Related Products: HSP50110 Digital Quadrature Tuner, D/A Converters HI5721, HI5731, HI5741

• HSP50110/210EVAL Digital Demod Evaluation Board

Block Diagram

CARRIER

TRACK

CONTROL

HI/LO

I SER OR

(9-0)

SERCLK

OR CLK

Q SER OR

(9-0)

SYMBOL

TRACK

CONTROL

CONTROL/

STATUS

BUS

(COF)

LEVEL

DETECT

(SOF)

COS

NCO

SIN

SYMBOL

TRACKING

LOOP FILTER

CARRIER ACQ/TRK

LOOP FILTER

RRC

FILTER

RRC

FILTER

CONTROL

INTERFACE

CARRIER PHASE

ERROR DETECT

LOOP

FILTER

INTEGRATE/

DUMP

INTEGRATE/

DUMP

SYMBOL

PHASE ERROR

DETECT

CAUTION: These devices are sensitive to electrostatic discharge; follow proper IC Handling Procedures.

1-888-INTERSIL or 1-888-468-3774

LEVEL

DETECT

CARTESIAN

| Intersil (and design) is a registered trademark of Intersil Americas Inc.

All other trademarks mentioned are the property of their respective owners.

LOCK

DETECT

MAGNITUDE

PHASE

POLAR

SLICER

DATA PATH MULTIPLEXER

LKINT

THRESH A

OUT(9-0)

B OUT(9-0)

SMBLCLK

OEA

OEB

Pinout

www.BDTIC.com/Intersil

IIN6

IIN7

IIN8

IIN9

SERCLK

GND

SSYNC

HSP50210

(84 LD PLCC)

TOP VIEW

HI/LO

ISER

QSER

VCC

THRESH

SLOCLK

OEA

AOUT8

AOUT9

GND

AOUT7

AOUT5

AOUT6

AOUT4

757677787980818283841234567891011

IIN5 IIN4 IIN3 IIN2

GND

IIN1 IIN0

SYNC

QIN9 QIN8 QIN7

QIN6 QIN5 QIN4

VCC QIN3 QIN2 QIN1 QIN0

SOFSYNC

SOF

12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

COF

COFSYNC

GND

VCC

FZ-ST

FZ-CT

LKINT

535251504948474645444342414039383736353433

GND

74 73 72 71 70 69 68 67 66 65

64 63 62 61 60 59 58 57 56 55 54

AOUT3 AOUT2 AOUT1 AOUT0 SMBLCLK VCC CLK GND BOUT9 BOUT8

BOUT7 BOUT6 BOUT5 GND BOUT4 BOUT3 BOUT2 BOUT1 BOUT0

OEB

VCC

Ordering Information

PART NUMBER PART MARKING TEMP. RANGE (°C) PACKAGE PKG. DWG. #

HSP50210JC-52 HSP50210JC-52 0 to +70 84 Ld PLCC N84.1.15 HSP50210JC-52Z (Note) HSP50210JC-52Z 0 to +70 84 Ld PLCC (Pb-free) N84.1.15 HSP50210JI-52 HSP50210JI-52 -40 to +85 84 Ld PLCC N84.1.15 HSP50210JI-52Z (Note) HSP50210JI-52Z -40 to +85 84 Ld PLCC (Pb-free) N84.1.15

NOTE: These Intersil Pb-free plastic packaged products employ special Pb-free material sets, molding compounds/die attach materials, and 100% matte tin plate plus anneal (e3 termination finish, which is RoHS compliant and compatible with both SnPb and Pb-free soldering operations). Intersil Pb-free products are MSL classified at Pb-free peak reflow temperatures that meet or exceed the Pb-free requirements of IPC/JEDEC J STD-020.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

Pin Description

NAME TYPE DESCRIPTION

VCC - +5V Power Supply.

GND - Ground.

IIN9-0 I In-Phase Parallel Input. Data may be two’s complement or offset binary format (see Table 15). These inputs are

sampled by CLK when the SYNC

QIN9-0 I Quadrature Parallel Input. Data may be two’s complement or offset binary format (see Table 15). These inputs are

sampled by CLK when the SYNC

SYNC

COF O Carrier Offset Frequency. The frequency term generated by the Carrier Tracking Loop Filter is output serially via this

COFSYNC O Carrier Offset Frequency Sync. This signal is asserted one CLK or SLOCLK cycle before the MSB of the serial data

SOF O Sampler Offset Frequency. Sample frequency correction term generated by the Symbol Tracking Loop Filter is

SOFSYNC O Sampler Offset Frequency Sync. This signal is asserted one CLK or SLOCLK cycle before the MSB of the serial data

A2-0 I Address Bus. The address on these pins specify a target register for reading or writing (see “Microprocessor

C7-0 I/O Microprocessor Interface Data Bus. This bi-directional bus is used for reading and writing to the processor interface.

I Data Sync. When SYNC is asserted “Low”, data on IIN9-0 and QIN9-0 is clocked into the processing pipeline by the

rising edge of CLK.

pin. The new offset frequency is shifted out MSB first by CLK or SLOCLK starting with the clock cycle after the assertion of COFSYNC.

word. (Programmable Polarity, see Table 42 on page 42, Bit 11).

output serially via this pin. The frequency word is shifted out MSB first by CLK or SLOCLK starting with the clock cycle after assertion of SOFSYNC.

word. (Programmable Polarity, see Table 42 on page 42, Bit 12).

Interface” on page 27). A0 is the LSB.

These are the data I/O pins for the processor interface. C0 is the LSB. I Write. This is the write strobe for the processor interface (see “Microprocessor Interface” on page 27). I Read. This is the read enable for the processor interface (see “Microprocessor Interface” on page 27).

signal is active Low. IIN9 is the MSB. See “Input Controller” on page 6.

signal is active Low. QIN9 is t heMSB. “Input Controller” on page 6.

FZ_ST I Freeze Symbol Tracking Loop. Asserting this pin “high” zeroes the sampling error into the Symbol Tracking Loop

FZ_CT I Freeze Carrier Tracking Loop. Asserting this pin “high” zeroes the carrier Phase Error input to the Carrier Tracking

LKINT O Lock Detect Interrupt. This pin is asserted “high” for at least 4 CLK cycles when the Lock Detector Integration cycle

THRESH

SLOCLK O Slow Clock. Optional serial clock used for outputting data from the Carrier and Symbol Tracking Loop Filters. The

ISER I In-Phase Serial Input. Serial data input for In-Phase Data. Data on this pin is shifted in MSB first and is synchronous

QSER I Quadrature Serial Input. Serial data input for Quadrature Data. Data on this pin is shifted in MSB first and is

SSYNC I Serial Word Sync. This input is asserted “high” one CLK before the first data bit of the serial word (see Figure 2). SERCLK I Serial Clock. May be asynchronous to other clocks. Used to clock in serial data (see “Input Controller” on page 6). AOUT9 -0 O A Output. Data on this output depend on the configuration of Output Selector. AOUT9 is the MSB (see Table 43 on

BOUT9-0 O B Output. Data on this output depend on the configuration of Output Selector. BOUT9 is the MSB (see T able 43 page 44).

SMBLCLK O Symbol Clock. 50% duty cycle clock aligned with soft bit decisions (see Figure 19).

Filter (see “Symbol Tracking Loop Filter” on page 17).

Loop Filter.

is finished (see “Lock Detector” on page 23). Used as an interrupt for a pr ocessor. The Lock Detect Interrupt may be asserted “high” longer than 4 CLK cycles, depending on the Lock Detector mode.

O Threshold Exceeded. This output is asserted “low” when the magnitude out of the Cartesian to Polar converter

exceeds the programmable Power Detect Threshold (see Table 16 on page33 and “AGC” on page 10).

clock is programmable and has a 50% duty cycle. Note: Not used when the HSP50110 is used with the HSP50210 (see Table 42 page 42).

to SERCLK (see “Input Controller” on page 6).

synchronous to SERCLK (see “Input Controller” on page 6).

page 44).

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

Pin Description (Continued)

NAME TYPE DESCRIPTION

OEA I A Output Enable. This pin is the three-state control pin for the AOUT9-0. When OEA is high, the AOUT9-0 is high

impedance.

OEB

HI/LO

CLK I System Clock. Asynchronous to the processor interface and serial inputs.

I B Output Enable. This pin is the three-state control pin for the BOUT9-BOUT0. When OEB is high, the AOUT9-0 is

high impedance.

0 HI/LO. The output of the Input Level Detector is provided on this pin (see “Input Level Detector” o n page 6). This

signal can be externally averaged and used to control the gain of an amplifier to close an AGC loop around the A/D converter. This type of AGC sets the level based on the median value on the input.

FN3652.5

July 2, 2008

AGC

www.BDTIC.com/Intersil

LOOP

HI/LO

SYNC

IIN9-0

QIN9-0

SSYNC

SERCLK

ISER

QSER

LEVEL

DETECT

INPUT CONTROLLER

SYNTHESIZER/

MIXER

COS

NCO

MATCHED FILTERING

M U X

SIN

RRC

M U X

FILTER

I AND D

GAIN ERROR

DETECT

M U X

CARTESIAN

POLAR

I2+Q

TAN-1( )

SLICER

THRESH

SMBLCLK

SYMBOL TRACKING

SOFSYNC

SOF

COFSYNC

COF

SLOCLK

C7-0

A2-0

CLK

FRZ_ST FRZ_CT

July 2, 2008

FN3652.5

SERIAL

OUTPUT

FORMATTER

MICROPROCESSOR

INTERFACE

FROM LOCK

DETECTOR

ACQUISITION

CONTROL

FIGURE 1. FUNCTIONAL BLOCK DIAGRAM OF THE HSP50210

2ND ORDER LOOP

FILTER

CARRIER TRACKING

2ND ORDER LOOP

FILTER

SYMBOL PHASE ERROR DETECT

CARRIER PHASE

ERROR DETECT

DISCRIMINATOR

FREQUENCY

ERROR DETECT

LOCK

DETECT

AOUT9-0

BOUT9-0

OEA

OEB

LKINT

HSP50210

www.BDTIC.com/Intersil

Functional Description

The HSP50210 Digital Costas Loop (DCL) contains most of the baseband processing functions needed to implement a digital Costas Loop Demodulator. These functions include LO generation/mixing, matched filtering, AGC, carrier phase and frequency error detection, timing error detection, carrier loop filtering, bit sync loop filtering, lock detection, acquisition/tracking control, and soft decision slicing for forward error correction algorithms. While the DCL is designed to work with the HSP50110 Digital Quadrature Tuner (DQT) as a variable rate PSK demodulator for satellite demodulation, functions on the chip are common to many communications receivers.

The DCL provides the processing blocks for the three tracking loops commonly found in a data demodulator: the Automatic Gain Control (AGC) loop, the Carrier Tracking Loop, and a Symbol Tracking Loop. The AGC loop adjusts for input signal power variations caused by path loss or signal-to-noise variations. The carrier tracking loop removes the frequency and phase uncertainties in the carrier due to oscillator inaccuracies and doppler. The symbol tracking loop removes the frequency and phase uncertainties in the data and generates a recovered clock synchronous with the received data. Each loop consists of an error detector , a loop filter, and a frequency or gain adjustment/control. The AGC loop is internal to the DCL, while the symbol and carrier tracking loops are closed external to the DCL. When the DCL is used together with the HSP50110, the tracking loops are closed around the baseband filtering to center the signal in the filter bandwidth. In addition, the AGC function is divided between the two chips with the HSP50110 providing the coarse AGC, and the HSP50210 providing the fine or final AGC.

A top level block diagram of the HSP50210 is shown in Figure 1. This diagram shows the major blocks and the multiplexers used to reconfigure the data path for various architectures.

Input Controller

In-Phase (I) and Quadrature (Q) data enters the part through the Input Controller. The 10-bit data enters in either serial or parallel fashion using either two’s complement or offset binary format. The input mode and binary format is set in the Data Path Configuration Control Register, bits 14 and 15 (see Table 15 on page 32).

If Parallel Input mode is selected, I and Q data are clocked into the part through IIN0-9 and QIN0-9 respectively. Data enters the processing pipeline when the input enable (SYNC

) is sampled “low” by the processing clock (CLK). The enable signal is pipelined with the data to the various processing elements to minimize pipeline delay where possible. As a result, the pipeline delay through the AGC, Carrier Tracking, and Symbol Tracking Loop Filters is measured in CLKs; not input data samples.

If serial input mode is selected, the I and Q data enters via the ISER and QSER pins using SERCLK and SSYNC. The beginning of a serial word is designated by asserting SSYNC ‘high’ one SERCLK prior to the first data bit, as shown in Figure 2. On the following SERCLKs, data is shifted into the register until all 10 bits have been input. Data shifting is then disabled and the contents of the register are held until the next assertion of SSYNC. The assertion of a SSYNC transfers data into the processing pipeline, and the Shift Register is enabled to accept new data on the following SERCLK. When data is transferred to the processing pipeline by SSYNC, a processing enable is generated which follows the data through the pipeline. This enable allows the delay through processing elements (like the loop filters) to be minimized since their pipeline delay is expressed in CLKs not SSYNC periods. Note: SSYNC should not be asserted for more than one SERCLK cycle.

SERCLK

SSYNC

ISER/QSER

NOTE: Data must be loaded MSB first.

FIGURE 2. SERIAL INPUT TIMING FOR ISER AND QSER INPUTS

MSB

SSYNC LEADS 1st DATA BIT

MSB

Input Level Detector

The Input Level Detector generates a one-bit error signal for an external IF AGC filter and amplifier. The error signal is generated by comparing the magnitude of the input samples to a user programmable threshold. The HI/LO pin is then driven “high” or “low” depending on the relationship of its magnitude to the threshold. The sense of the HI/LO pin is programmable so that a magnitude exceeding the threshold can either be represented as a “high” or “low” logic state. The Input Level Detector (HI/LO output) threshold and the sense are set by the Data Path Configuration Control Register bits 16 to 23 and 13 (see Table 15 page 32).

Note: The Inpu t Level Detector is typically not used in applications which use the HSP50210 with the HSP50110.

The high/low outputs can be integrated by an external loop filter to close an AGC loop. Using this method, the gain of the loop forces the median magnitude of the input samples to the threshold. When the magnitude of half of the samples is above the threshold (and half is below), the error signal is integrated to zero by the loop filter. The magnitude of the complex input is estimated using Equation 1:

Mag (I, Q) I 0.375 Q if I Q and>×+= Mag (I, Q) Q 0.375 I if Q I>×+=

(EQ. 1)

FN3652.5

July 2, 2008

www.BDTIC.com/Intersil

@ = SYNC RATE

= TWICE SYMBOL RATE

! = SYMBOL RATE

BLANK = CLK RATE

MID AND END

SYMBOL SAMPLES

TO SYMBOL TRACKING

MID

END

MID

END

HI/LO

MATCHED FILTERING

REG REG

DETECT

LEVEL

IIN9-0QIN9-0

NCO MIXER

COMPLEX

MULTIPLY

BYPASS

MIXER

BYPASS

R E G

R E

U X

G R

RRC

15 TAP RRC

M U

G R

DUMP

M U X

DATA DE-SKEW

OQPSK

“0”

M U

R E G

M U X

SIN

COS REG REG REG REG

SIN/COS

ROM

REG

CF REGISTER

ROOT RAISED COSINE

(RRC)

AGC LOOP FILTER

UPPER

GAIN LIMIT

LOWER GAIN LIMIT

@ OR !

INTEGRATE AND DUMP

R E

LOOP GAIN EXPONENT

FALSE LOCK

COMPARE

S H

I F T

TWO SAMPLE

SUMMER

S H

F T

R E

F T

LOOP GAIN

MANTISSA

REG

R E G

BYPASS

I AND D

M U

HOLD AGC

U X

E M U X

D E M U X

M U X

AGC ERROR DETECT

“0”

AGC THRESHOLD

GAIN ERROR

POWER THRESHOLD

CARTESIAN TO

POLAR

DELAY

I2+Q

-1

TAN

( )

DELAY

PHASE OUT AT

MAG OUT AT

COMPARE

SOFT

DECISION

SLICER

TEST

M U X

REG

@ OR

@ OR !

R E G

! OR ! OR

S E L E

C T

AOUT9-0 BOUT9-0

R E G

HSP50210

TO CARRIER TRACKING AND DISCRIMINATOR

THRESH

R E G

FROM CARRIER TRACKING

LOOP FILTER

July 2, 2008

FN3652.5

FIGURE 3. MAIN DATA PATH

HSP50210

www.BDTIC.com/Intersil

NCO/Mixer

The NCO/Mixer performs a complex multiply between the baseband input and the output of a quadrature NCO (Numerically Controlled Oscillator). When the HSP50210 (DQT) is used with the HSP50110 (DCL), the NCO/Mixer shortens the Carrier Tracking Loop (i.e., minimizes pipeline delay around the loop) while providing wide loop bandwidths. This becomes important when operating at symbol rates near the maximum range of the part.

There are three configurations possible for closing the Carrier Tracking Loop when the DQT and the DCL are used together. The first configuration utilizes the NCO on the DQT and bypasses the NCO in the DCL. The Data Path Configuration Control Register (see Table 15 on page 32), Bit 10, and Carrier Loop Filter Control Register #1 (see Table 21 on page 34), Bit 6, are used to bypass the DCL NCO/Mixer and route the Loop filter outputs, respectively. The DQT provides maximum flexibility in NCO control with respect to frequency and phase offsets.

The second configuration feeds the lead Carrier Loop filter term to the DCL NCO/Mixer, and the lag Loop filter Term to the DQT NCO. This reduces the loop transport delay while maintaining wide loop bandwidths and reasonable loop damping factors. This configuration is especially useful in SATCOM applications with medium to high symbol rates. The Carrier Loop Filter Control Register #1, Bit 5 is where the lead/lag destination is set.

The final configuration feeds both the lead and lag Carrier Loop Filter terms back to the DCL NCO/Mixer. This provides the shortest transport delay. The DCL NCO/Mixer provides only for frequency/phase control from the Carrier Loop filter. The center frequency of this NCO/Mixer is set to the average of the Upper and Lower Carrier Loop Limits programmable parameters. These parameters are set in the two control registers bearing their names (see Tables 23 and 24 on page 35).

The NCO/Mixer uses a complex multiplier to multiply the baseband input by the output of a quadrature NCO. This operation is represented by Equations 2 and 3:

OUTIIN

Equation 3 illustrates how the complex multiplier implicitly performs the summing function when the DCL is configured as a modulator. The quadrature outputs of the NCO are generated by driving a sine/cosine look-up table with the output of a phase accumulator, as shown in Figure 3 on page 7. Each time the phase accumulator is clocked, its sum is incremented by the contents of the Carrier Frequency (CF) Register. As the accumulator sum increments from 0 to 2 the SIN/COS ROM produces quadrature outputs whose phase advances from 0 to 360°. The CF Register contains a

ωC()cos Q

ωC()sin Q

ωC()sin–=

ωC()cos+=

(EQ. 2)

(EQ. 3)

32-bit phase increment, which is updated with the output of Carrier Tracking Loop. Large phase increments take fewer clocks to step through the sine wave cycle, which results in a higher frequency NCO output.

The CF Register sets the NCO frequency using Equation 4:

CfCLK

CF INT F

where f complement hexadecimal value loaded into the Carrier Frequency Register. As an example, if the CF Register is loaded with a value of 4000 0000 (Hex), and the CLK frequency is 40MHz, the NCO would produce quadrature terms with a frequency of 10MHz. When CF is a negative value, a clockwise cos/sin vector rotation is produced. When CF is positive, a counterclockwise vector rotation is produced.

Note: The NCO is set to a fixed frequency by programming the upper and lower limits of the Carrier Tracking Loop Filter to the same value and zeroing the lead gain.

×=

⁄()2

[]H=

CfCLK

is the CLK frequency, and CF is the 32-bit two’s

CLK

CF()2⁄

(EQ. 4)

Matched Filtering

The HSP50210 provides two selectable matched filters: a Root Raised Cosine Filter (RRC) and an Integrate and Dump (I and D) filter. These are shown in Figure 3. The RRC filter is provided for shaped data pulses and the I and D filter is provided for square wave data. The filters may be cascaded for better adjacent channel rejection for square wave data. If these two filters do not meet baseband filtering requirements, then they can be bypassed and an external digital filter (such as the HSP43168 Dual FIR Filter or the HSP43124 Serial I/O Filter) used to implement the desired matched filter. The desired filter configuration is set in the Data Path Configuration Control Register, bits 1 through 7 (see Table 15 on page 32).

The sample rate of the baseband input depends on the symbol rate and filtering configuration chosen. In configurations which bypass both filters or use only the RRC Filter, the input sample rate must be twice the symbol rate. In configurations which use the I and D Filter, the input sample rate is decimated by the I and D Filter, down to two samples per symbol. I and D configurations support input sample rates up to 32x the input symbol rate.

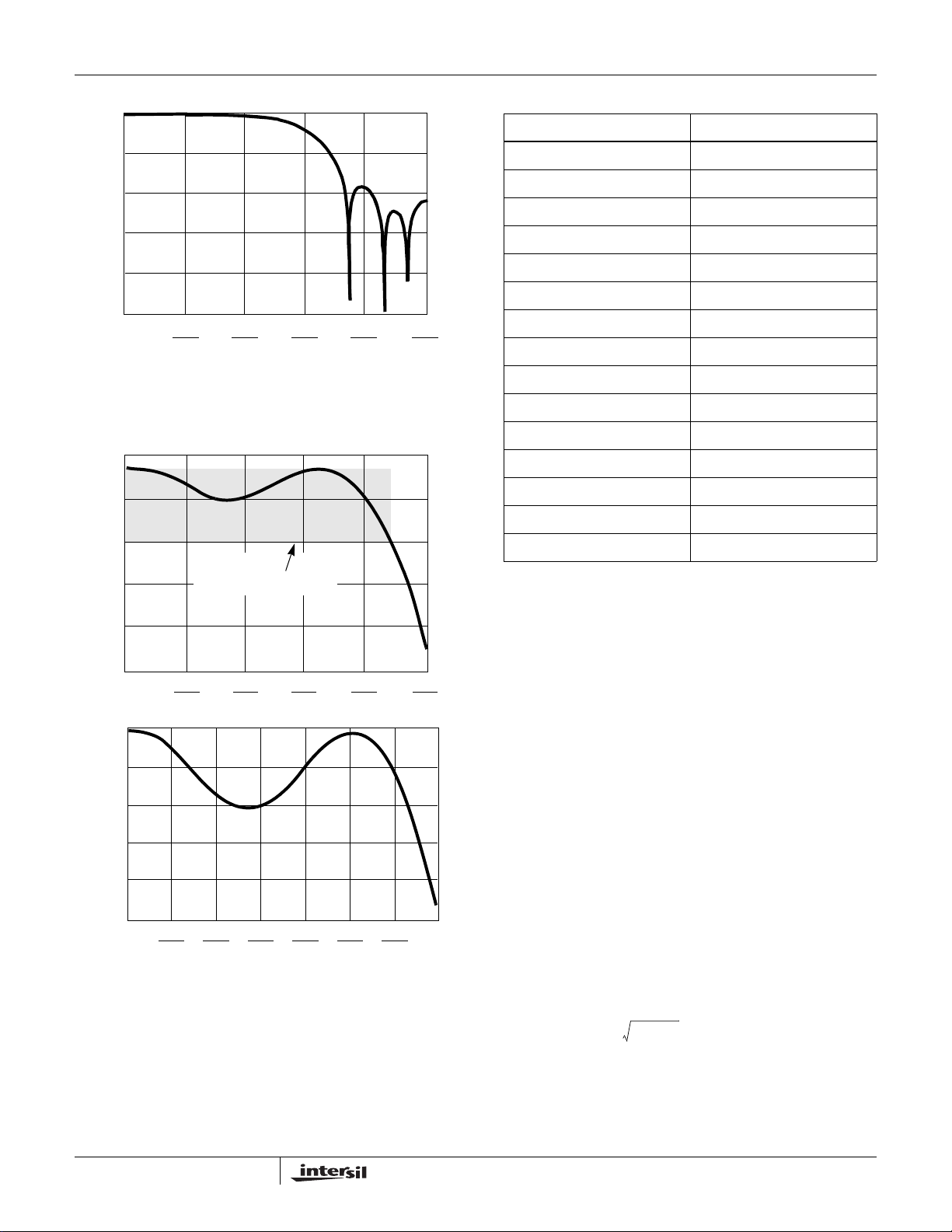
The RRC filter is a fixed coefficient 15 Tap FIR filter. It has ~40% excess bandwidth beyond Nyquist, which equates to α = ~0.4 shape factor. The filter frequency response is shown in Figures 4 and 5. In addition, the 9-bit filter coefficients are listed as integer values in Table 1. The noise

equivalent bandwidth of the RRC filter and other filter configurations possible with the HSP50110/210 chipset are given in Appendix A.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

-20

-40

-60

-80

NORMALIZED MAGNITUDE (dB)

-100 0

CLK

FREQUENCY (NORMALIZED TO INPUT SAMPLE RATE)

CLK

FIGURE 4. RRC FILTER IN HSP50210

-0.18

-0.36 SHOWN BELOW

-0.54

-0.72

NORMALIZED MAGNITUDE (dB)

-0.90

-0.07

-0.14

-0.21

-0.28

NORMALIZED MAGNITUDE (dB)

-0.35 0

FREQUENCY (NORMALIZED TO INPUT SAMPLE RATE)

ENLARGED FOR CLARITY

CLK

FIGURE 5. PASSBAND RIPPLE OF RRC FILTER IN HSP50210

TABLE 1. ROOT RAISED COSINE COEFFICIENTS

COEFFICIENT INDEX COEFFICIENT

02 1-2 21 38 4-16 5-14 686 7 160 886

9-14 10 -16 11 8 12 1 13 -2 14 2

The I and D filter consists of an accumulator, a programmable shifter and a two sample summer, as shown in Figure 3. The programmable shifter is provided to compensate for the gain introduced by the accumulator (see Table 15). The accumulator provides Integrate and Dump Filtering for decimation factors up to 16. The two sample summer provides the moving average required for an additional decimation factor of 2. A decimation factor of 1 (bypass), 2, 4, 8, 16, or 32 may be selected. At the maximum decimation rate, a baseband signal sampled at 32x the symbol rate can be filtered.

The output of the two sample summer is demultiplexed into two sample streams at the symbol rate. The demultiplexed data streams from the I and Q processing paths are fed to the Symbol Tracking Block and Soft decision slicer. The multiplexed data streams on I and Q are provided as one of the selectable inputs for the Cartesian-to-Polar Converter.

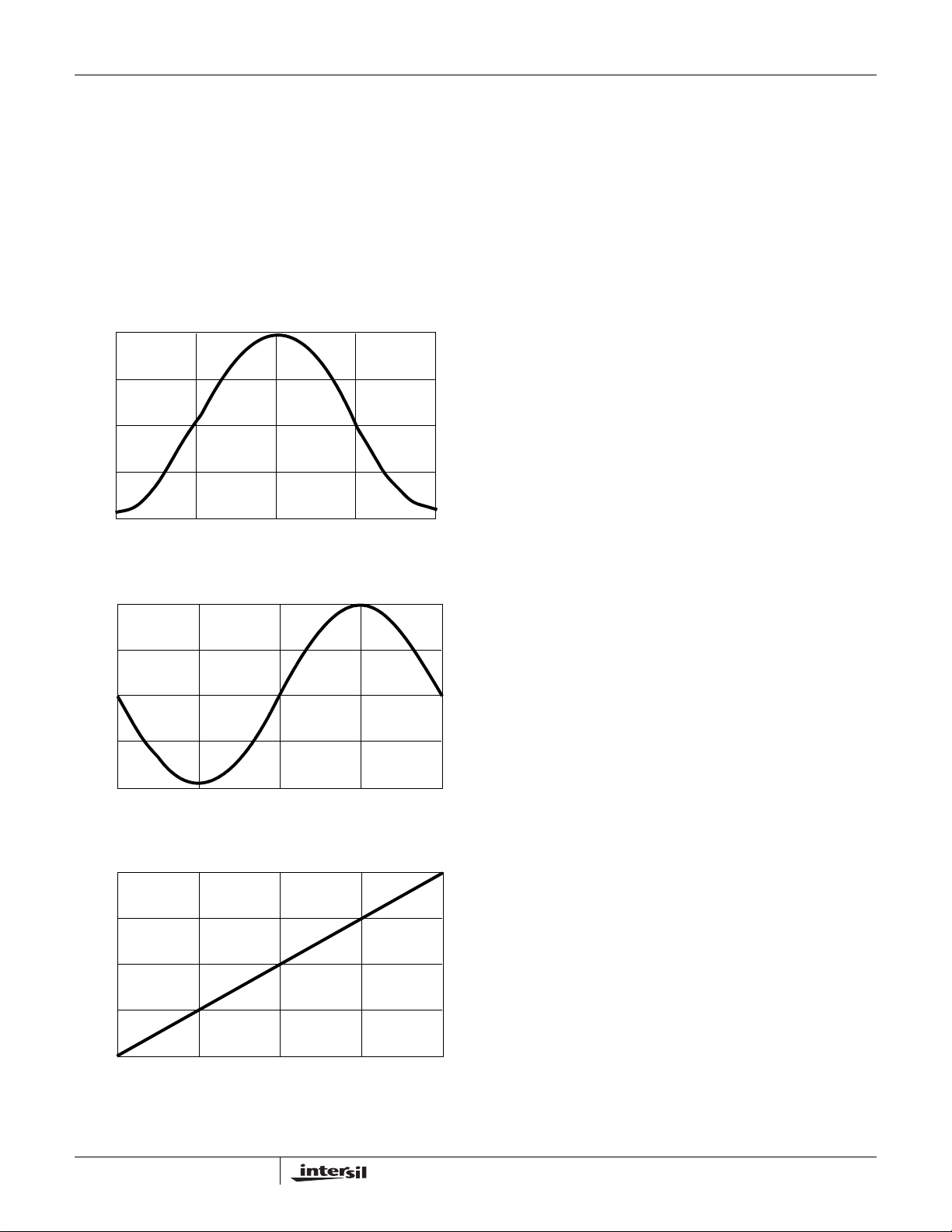
Cartesian/Polar Converter

The Cartesian/Polar Converter maps samples on the I and Q processing paths to their equivalent phase/magnitude representation. The magnitude conversion is equivalent to Equation 5:

Mag (I, Q) 0.81()∗I2Q2+()=

where 0.81 is the gain of the conversion process. The magnitude output is an 8-bit unsigned value ranging from 0.0 to 1.9922.

(EQ. 5)

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

The phase conversion is equivalent to Equation 6:

Phase (I, Q) tan

-1

where tan

( ) is the arctangent function. The phase

1–

QI⁄(),=

(EQ. 6)

conversion output is an 8-bit two’s complement output, which ranges from -1.0 to 0.9922 (80 to 7f HE X, respectively). The -1 to almost 1 range of the phase output represents phase values from -π to π, respectively. An example of the I/Q to phase mapping is shown in Figures 6A through 6C. The phase and magnitude values may be output via the Output Selector bits 0 through 3 (see Tab le 43).

1.0

0.5

MAGNITUDE

-0.5

-1.0

-π

FIGURE 6A. I INPUT TO CARTESIAN/POLAR CONVERTER

1.0

0.5

MAGNITUDE

-0.5

-1.0

-π

FIGURE 6B. Q INPUT TO CARTESIAN/POLAR CONVERTER

1.0

INPUT PHASE

π/2 π-π/2

The I/Q data path selected for input to the Cartesian-to-Polar converter determines the input data rate of the AGC and carrier tracking loops. If the I/Q data path out of the Integrate and Dump Filter is selected, the AGC is fed with magnitude values produced by the end-symbol samples. Magnitude values produced by midsymbol samples are not used because these samples occur on symbol transitions, resulting in poor signal magnitude estimates. The Carrier Tracking block is fed with phase values generated from both the end and mid-symbol samples. The carrier tracking loop filte r, however, is only fed with Ph ase Erro r terms gen erate d by the end symbol samples. If the input of the I and D is selected for input to the coordinate converter , the control loops are fed with data at the I/Q data rate. The desired dat a p a th input to the Cartesian to Polar converter is specified in the Data Path Configuration Control Register , Bit 8 (see Table 15 on page 32).

AGC

The AGC loop operates on the main data path (I and Q) and performs three signal level adjusting functions:

1. Maximizing dynamic range

2. Compensating for SNR variations

3. Maintaining an optimal level into the Soft Decision Slicer.

The AGC Loop Block Diagram, shown in Figure 7, consists of an Error Detector, a Loop Filter, and Signal Gain Adjusters (multipliers). The AGC Error Detector generates an error signal by subtracting the programmable AGC threshold from the magnitude output of the Cartesian to Polar Converter. This difference signal is scaled (gain adjusted via multiplier and shifter), then filtered (integrated) by the AGC Loop Filter to generate the gain correction to the I and Q signals at the multipliers. If a fixed gain is desired, set the upper and lower limits equal.

The AGC responds to the magnitude of the sum of all the signals in the bandpass of the narrowest filter preceding the Cartesian to Polar Coordinate Converter. This filter may be the Integrate and Dump filter shown in Figure 7 on page 12, the RRC filter upstream in the HSP50210 data path, or some other filter outside the DCL chip. The magnitude signal usually contains several components:

0.5

2. The noise comp onent, and

3. Interfering signals component.

1. The signal of interest component,

At high SNR’s the signal of interest is significantly greater than the other components. At lower SNR’s, components 2

-0.5

OUTPUT VOLTAGE

or 3 may become greater than the signal of interest. Narrowing the filter bandwidth is the primary technique

-1.0

-π

INPUT PHASE

π/2 π-π/2

used to mitigate magnitude contributions of component 3. This will also improve the SNR by reducing the magnitude contributions of element 2. Consideration of the range of signal amplitudes expected into the HSP50210, in

FIGURE 6C. CARTESIAN/POLAR CONVERTER PHASE OUTPUT

conjunction with a gain distribution analysis, will provide the

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

necessary insight to set the signal level into the Soft Decision Slicer to yield opti mum perf or ma nce .

Note: Failure to consider the variations due to noise or interfering signals, can result in signal limiting in the HSP50210 processing algorithms, which will degrade the system Bit Error Rate performance.

The AGC Loop is configured by the Power Detect Threshold and AGC Loop Parameters Control Registers (see Tables 16 and 17 on page 33). Seven programmable parameters must be set to configure the AGC Loop and its status outputs. Two parameters, the Power Threshold and the AGC Threshold are associated with the Error Detector and are represented in 8-bit fractional unsigned binary format: 2

02-12-22-32-42-52-62-7

. While the format provides a range from 0 to 1.9961 for the thresholds, the Cartesian-to-Polar Converter scales the I and Q input magnitudes by 0.81. Thus, if a full scale (±1) complex (I and Q) input signal is presented to the converter, the output will be √(0.81)

+ (0.81)2 = 1.1455. The AGC Threshold parameter value is the desired magnitude of the signal as it enters the Soft Decision Slicer. It is the parameter that will determine the error signal in the AGC loop. The Power Threshold, on the other hand, determines only the power threshold at which the THRESH

signal is asserted. If the signal magnitude exceeds the threshold, then the THRESH

is asserted. This may be used for signal detection, power detection or external AGC around the A/D converter. The AGC Threshold parameter is set in the AGC Loop Parameters Control Register, Bits 16 through 23 (see Table 17 on page 33). The Power Threshold parameter is set in the Power Detect Threshold Control Register, Bits 0 through 7 (see Table 16 on page 33). Note that these two threshold parameters are not required to be set to identical or even related values, since they perform independent functions.

The Enable AGC parameter sets the AGC Error Detector output to zero if asserted and to normal error detection output when not asserted. This control bit is set in the AGC Loop Parameter Control Register, Bit 31 (see Tables 17 on page 33). This bit is used to disable the AGC loop.

The remaining AGC parameters determine the AGC loop characteristics: gain tracking, tracking rate and tracking limits. The AGC Loop gain is set via two parameters: AGC Loop Gain Exponent and AGC Loop Gain Mantissa. In general, the higher the loop gain, the faster signal level acquisition and tracking, but this must be tempered by the specific signal characteristics of the application and the remaining programmable loop parameters. For the HSP50210, the AGC Loop Gain provides for a variable attenuation of t he input to the loop filter. The AGC gain mantissa is a 4-bit value which provides error signal scaling from 0.000 to 0.9375, with a resolution of 0.0625. Table 2 on page 11 details the discrete set of decimal values possible for the AGC Loop Gain mantissa. The exponent

-7

provides a shift factor scaling from 2

to 2

-14

. Table 3 on

page 11 details the discrete set of decimal values possible for

the AGC Loop Gain Exponent. When combined, the exponent and mantissa provide a loop gain defined as Equation 7:

GC Loop Gain: G

AGC

M()24–()[]2

7E+()–

()[]=

(EQ. 7)

where M is a binary number with a range from 0 to 15 and E is a 3-bit binary value from 0 to 7. M and E are the parameters set in the AGC Loop Parameters Control Register, Bits 24 through 30 (see Table 17 on page 33). The composite range of the AGC loop Gain is 0.0000 to [0.9375][2 to 7]. This will scale the AGC error signal to a range of 0.000 to (1.1455)(0.9375)(2 to 7) = 1.07297(2 to 7).

TABLE 2. AGC LOOP GAIN BINARY MANTISSA TO DECIMAL

SCALED MANTISSA MAPPING

BINARY

CODE

(MMMM)

0000 0.0000 1000 0.5000 0001 0.0625 1001 0.5625 0010 0.1250 1010 0.6250 0011 0.1875 1011 0.6875 0100 0.2500 1100 0.7500 0101 0.3125 1101 0.8125 0110 0.3750 1110 0.8750 0111 0.4375 1111 0.9375

TABLE 3. AGC LOOP BINARY EXPONENT TO SCALED

BINARY CODE

(EEE)

000 0 2 001 1 2 010 2 2 011 3 2 100 4 2 101 5 2 110 6 2 111 7 2

DECIMAL

SCALED

MANTISSA

DECIMAL EXPONENT MAPPING

DECIMAL/HEX

EXPONENT

BINARY

CODE

(MMMM)

DECIMAL SCALED

DECIMAL

SCALED

MANTISSA

EXPONENT

-7

-8

-9

-10

-11

-12

-13

-14

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

READ

REG

AGC GAIN = (1.0 + M) x 2

GAIN

ADJUST

AGC

AGC LOOP FILTER

AGC

UPPER

LOWER

LIMIT †

1.0000 TO 15.8572 = G

(0 TO 24dB)

AGC LOOP

GAIN

MANTISSA †

-7

TO 2

0.000 TO 1.07297(2

AGC

CART/POLAR INPUT SELECT†

AGC LOOP

EXPONENT †

-14

(0.000 TO 0.9375)

)

-7

)

I AND D FILTER

FIGURE 7. AGC LOOP BLOCK DIAGRAM

The AGC Loop Filter integrates the scaled error signal to provide a correction control term to the multipliers in the I and Q path. The loop filter accumulator has internal upper and lower limiters. The upper eight bits of the accumulator output map to an exponent and mantissa format that is used to set these upper and lower limits. The format, illustrated in Figure 8, is used for the AGC Upper Limit, AGC Lower Limit and the Correction Control Term (AGC output). This format should not be confused with the similar format used for the AGC Loop Gain. The input to the AGC Loop Filter is included in Figure 8 to show the relative weighting of the input to output of the loop filter. The loop filter input is represented as the eleve n letter “G”s. Lower case “e” and “m” detail the format for the AGC Upper and Lower Limits. This change in type case should help keep the AGC Limits and AGC Gain formats from being confused. The AGC Upper and Lower Limits are set in the AGC Loop Parameters Control Register, Bit s 0 throu gh15, (see Table 17). This 6-bit unsigned mantissa format provides for an AGC output control range from 0.0000 to 0.9844, with a resolution of 0.015625. The 2-bit exponent format provides an AGC output control range from 1 to 8. The decimal values for each of the 64 binary mantissa values is detailed in Table 4, while Table 5 details the decimal value for the 4 exponent values.

GAIN

M U X

“0”

ENABLE AGC †

The AGC Output is implemented in the multiplier according to Equations 8 and 9.

where m and e are the binary values for mantissa and exponent found in Ta bles 4 and 5.

Note: This format is identical to the format used to program the AGC Upper and Lower Limits, but in this usage it is not a programmed value. It is a representation of the digital AGC output number, which is presented to the Gain Adjuster (multipliers) to correct the gain of the I and Q data signals in the main data path.

These equations yield a composite (mantissa and exponent) AGC output range of 0.0000 to 1.9844(2 is a logarithmic range from 0dB to 24dB. Figure 9 has graphed the results of Equations 8 and 9 for both the linear and logarithmic equations. Figure 9 also has a linear estimate of the logarithmic equation. This linear approximation will be used in calculating the AGC response time.

M U

Out

AGC ERROR DETECT

COMPARE

POWER

THRSHLD †

GAIN ERROR

AGC THRSHLD †

CARTESIAN TO POLAR

1.0

AGC linear–

AGC dB–

I2+Q

TAN

20 log 1.0 m

R E

THRESH

1.64

-----------=

-1

( )

dcloutlvl agc thresh

where dcloutlvl is the

Q I

magnitude output expressed in dB from Full Scale (dBFS)

0.8 MAGNITUDE

(0 TO 1.1455)

PHASE

† Indicates a microprocessor control signal.

1.0 m

+()2e()=

AGC

+()2e()[]=

AGC

) which

1.64

⎛⎞

------------

⎝⎠

(EQ. 8)

(EQ. 9)

1 20 .2-1 2-2 2-3 2-4 2-5 2-6 2-7 2-8 2-9 2-10 2-11 2-12 2-13 2-14 2-15 2-16 2-17 2-18

2 ee.mmmmmm

GGGG GGGGGG G

FIGURE 8. AGC OUTPUT AND AGC LIMITS BIT WEIGHTING

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 4. AGC GAIN MANTISSA TO DECIMAL MAPPING

DECIMAL

VALUE

BINARY CODE

(MMMMMM

TABLE 5. AGC GAIN EXPONENT TO DECIMAL MAPPING

BINARY CODE

AGC

000000 0.000000 100000 0.500000 000001 0.015625 100001 0.515625 000010 0.031250 100010 0.531250 000011 0.046875 100011 0.546875 000100 0.062500 100100 0.562500 000101 0.078125 100101 0.578125 000110 0.093750 100110 0.593750 000111 0.109375 100111 0.609375 001000 0.125000 101000 0.625000 001001 0.140625 101001 0.640625 001010 0.156250 101010 0.656250 001011 0.171875 101011 0.671875 001100 0.187500 101100 0.687500 001101 0.203125 101101 0.703125 001110 0.218750 101110 0.718750

001111 0.234375 101111 0.734375 010000 0.250000 110000 0.750000 010001 0.265625 110001 0.765625 010010 0.281250 110010 0.781250 010011 0.296875 110011 0.796875 010100 0.312500 110100 0.812500 010101 0.328125 110101 0.828125 010110 0.343750 110110 0.843750 010111 0.359375 110111 0.859375 011000 0.375000 111000 0.875000 011001 0.390625 111001 0.890625 011010 0.406250 111010 0.906250 011011 0.421875 111011 0.921875 011100 0.437500 111100 0.937500 011101 0.453125 111101 0.953125

011110 0.468750 111110 0.968750

011111 0.484375 111111 0.984375

00 0 2 01 1 2 10 2 2 11 3 2

OF AGC

)

MANTISSA

BINARY CODE

(MMMMMM

DECIMAL/HEX

EXPONENT

AGC

DECIMAL SCALED

DECIMAL

VALUE

OF AGC

)

MANTISSA

EXPONENT

0 1 2 3

224

240

256

LINEAR ESTIMATE IN dB

DATA PATH GAIN (LINEAR)

1 0

1632486480

(8 MSBs OF LOOP FILTER ACCUMULATOR)

FIGURE 9. GAIN CONTROL TRANSFER FUNCTION

GAIN dB

112

128

144

GAIN CONTROL WORD

160

176

192

GAIN

LINEAR

208

There are two techniques for setting a fixed gain for the AGC. The first is to set Control Word 2 Bit 31 = 1. This precludes any error update of present AGC gain value. The second is to set the upper and lower AGC limits to the desired gain using Figure 9. The upper and lower limits have the same value for this case.

The HSP50210 provides two mechanisms for monitoring signal strength. The first, which involved the THRESH signal, has already been described. The second mechanism is via the Microprocessor Interface. The 8 most significant bits of the AGC loop filter output can be read by a microprocessor. Refer to the “Microprocessor Interface” on page 27 for details of how to read this value. This AGC value has the format describ ed i n Fi gur e 8.

AGC Bit Weighting and Loop Response

The AGC loop response is a function of the programmable gain, the bit weightings inherent in the connection of each element of the loop, the AGC Loop filter limits and the magnitude of the input gain error step. Table 6 on page 14 details the bit weighting between each element of the AGC Loop from the error detector through the weighting at the gain adjuster in the signal path. The AGC Loop Gain sets the growth rate of the sum in the loop filter accumulator. The Loop filter output growth rate determines how quickly the AGC loop traces the transfer function shown previously in Figure 9. To calculate the rate at which the AGC can adjust over a given period of time, a gain step is introduced to the gain error detector and the amount of change that is observed between clocks at the AGC Level Adjusters (multipliers) is the AGC response time in dB per symbol. This AGC loop will respond immediately with the greatest correction term, then asymptotically approach zero correction.

We begin calculation of the loop response with a full scale error detector input of ±1. This error input is scaled by the Cartesian to Polar converter, the error detecto r and th e AGC

GAIN (dB)

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

Loop Gain, accumulated in the loop filter , limited and output to the gain adjusters. The AGC loop tries to make the error correction as quickly as possible, but is limited by the AGC Loop Gain and potentially, the AGC limits. The maximum AGC response is the maximum gain adjustment made in any given clock cycle. This involves applying maximum Loop gain

TABLE 6. AGC BIT WEIGHTING

AGC

ACCUM

BIT

POSITION

22 Shifter → E1 12 21 Shifter → E0 6 20 Multiplier → M-1 3 19 M-2 1.5 18 M-3 0.75 17 M -4 0.375 16 M -5 0.1875 15 Multiplier → 1 M -6 0.09375 14 13 1 G -8 0.02344 12 2 G -9 0.01172 11 3 G -10 0.00586 10 4 G -11 0.00293

9 5 G -12 0.00146 8 8(S) = 1(S) 0. 12(S) 12(S) = 1 1 6 G -13 0.000732 77= 0• x1111= 0• 6 6 = 1 x 10 10 = 1 1 G -15 0.000183 5 5 = 2 x 9 9 = 2 2 G -16 0.0000916 4 4 = 3 x 8 8 = 3 3 G -17 0.0000458 3 3 = 4 7 7 = 4 4 G -18 0.0000229 2 2 = 5 6 6 = 5 5 -19 0.0000114 1 1 = 6 5 5 = 6 6 -20 0.00000572 0 0 = 7 4 -21 0.00000286

GAIN

ERROR

INPUT

GAIN

ERROR

BIT

WEIGHT

AGC LOOP

FILTER GAIN

(MANTISSA)

AGC LOOP

FILTER

GAIN

MULTIPLIER

(OUTPUT)

3 2 1 0

and setting the AGC limits as wide as possible. A calculation using only exponent terms of the various gains will be sufficient to yield a rough order of magnitude of the range of the AGC Loop response. The results are shaded in the last column of Table 6 on page 14 and provided in detail in Equations 10 and 11.

AGC

LOOP

FILTER

GAIN BITS

KEPT

(rnd) SHIFT = 0 SHIFT = 7

0• • 0-7 0.04688

0• G -14 0.000366

AGC

OUTPUT

AND AGC

LIMITS BIT

WEIGHT

RESOLUTION

AGC GAIN

(dB)

AGC Response

where (0.5) is the MSB of the 0.81 scaling in the Cartesian-to-Polar Coo rdinate Con verter, (0.5) is the MSB of the mantissa of the Loop Gain, (2

= Input (Cartesian to Polar Converter Gain)(Error Detector Gain)(AGC Loop Gain)(AGC Output Weighting)

MAX

-7)

10.5()± 0.5()27–()24() 129–()24()± 0.04688dB symbol time⁄===

is the maximum shift gain, and 24 is the maximum loop filter gain.

A similar procedure is used to calculate the minimum AGC response rate.

AGC Response

MIN

10.5()± 0.5()2

14–

()24() 12

16–

()24()± 0.000366dB symbol time⁄===

Thus, the expected range for the AGC rate is approximately 0.0004 to 0.0469dB/symbol time.

(EQ. 10)

(EQ. 11)

FN3652.5

July 2, 2008

SYNTHESIZER/

www.BDTIC.com/Intersil

MIXER

G = 1.0, 0.5 (NOTE 1)

PART

INPUT

(NOTE 4)

BINARY

POINT

-2

-1

AGC GAIN

MANTISSA

1.0 TO 1.9844

(0.0156 STEPS)

G = 1.0 - 1.9844*2

RRC

FILTER

G = 1.0, 1.13 (NOTE 2)

-2

-1

-2

-1

AGC

HSP50210

EXPONENT

TO 2

ACCUMULATOR

G = 1 TO 16

-2

-1

INT/DUMP

-2

-1

INTEGRATE AND

DUMP FILTER

INT/DUMP

SHIFTER

0 TO 2-4

G = 2

-2

-1

SAMPLE PAIR

SUMMER

G = 0.5, 1.0 (NOTE 3)

-2

-1

-2

-1

INPUT TO SOFT DECISION SLICER AND SYMBOL TRACKING BLOCK

-2

-1

-9

INPUT TO CARTESIAN-TO-POLAR CONVERTER

-10

RND

IF AGC OUTPUT SELECTED

-10

2 RND

-9

-7

RND

INPUT TO CARTESIAN-TO-POLAR CONVERTER

-7

IF INT/DUMP OUTPUT SELECTED

-11

-6

-7

NOTES:

1. If the Mixer is enabled, the result of the complex multiply is scaled by two (G = 0.5). If the mixer is bypassed, the data passes unmodified (G = 1.0).

2. If the Root Raised Cosine Filter is enabled, a gain of G = 1.13 is introduced. If the RRC filters bypassed, the gain is unity.

-7

3. If the integrate and Dump Filter is bypassed the Sample Pair summer has a gain of G = 1.0 and the 2

-bit position is set to 1. If the integrate

and dump is enabled, the sample pair sum is scaled by one half (G = 0.5).

4. The negative sign on the MSBs indicates use of 2’s complement data format.

FIGURE 10. GAIN DISTRIBUTION AND INTERMEDIATE BIT WEIGHTINGS

Gain Distribution

The gain distribution in the DCL is shown in Figure 10. These gains consist of a combination of fixed, programmable, and adaptive gains. The fixed gains are introduced by processing elements such as the Mixer and Square Root of Root Raised Cosine Filter. The adaptive gains are set to compensate for variations in input signal strength.

The main signal path, with processing block gains and path bit weightings, is shown in Figure 10. The quadrature inputs to the HSP50210 are 10-bit fractional two’s complement numbers with relative bit weightings, as shown in Figure 10.

Following the AGC, the signal path is limited to 8 bits and passed through the Integrate and Dump Filter en route to the Soft Decision Slicer and Symbol Tracking Block. The I and D Filter uses an accumulator together with a sample pair summer to achieve the desired decimation rate. The I and D shifter is provided to compensate for the gain introduced by the I and D Accumulator. The accumulator introduces gain equal to the decimation factor R, and the shifter gain can be set to 1/R. For example, if the I and D Filter decimation of 16 is chosen, the I and D Accumulator will accumulate 8 samples before dumping, which produces a gain of 8. Thus, for unity gain, the I and D Shifter would be set for a gain of 2

-3

. The Sample Pair Summer

is unity gain since its output is scaled by one-half.

The first element in the processing chain is the Mixer, which scales the quadrature outputs of the complex multiplier by 1/2 providing a gain of G = 0.5. If the Mixer is bypassed, the signal is passed unmodified with a gain of 1.0. Following the mixer, the quadrature signal is passed to the fixed coefficient RRC filtering block, which has a gain of 1.13 if enabled and

1.0 if bypassed. Next, the AGC supplies gain to maintain an optimal signal level at the input to the Soft Decision Slicer, Cartesian-to-Polar Converter, and the Symbol Tracking Loop. The gain supplied by the AGC ranges from 1.0 to

1.9844*2

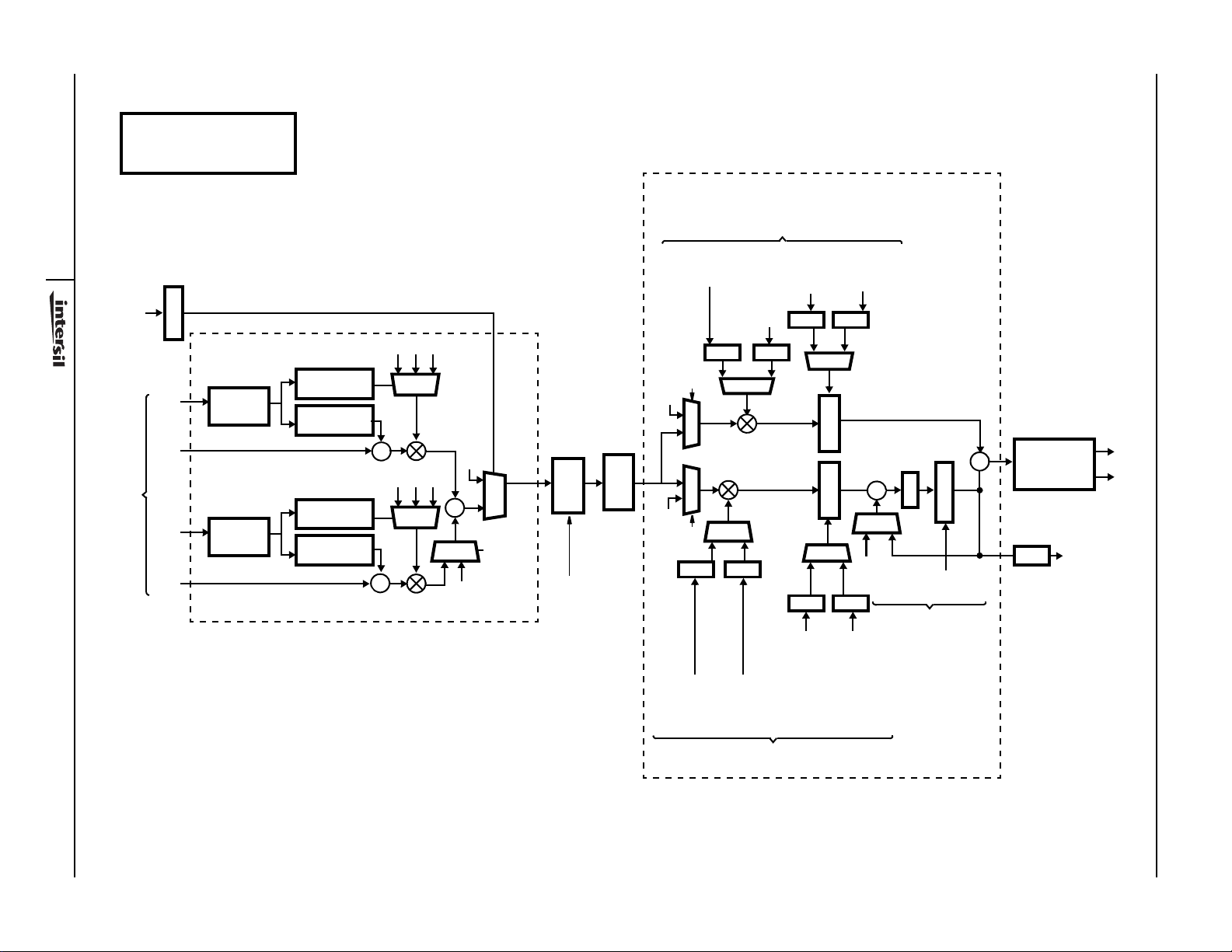
Symbol Tracking

The symbol tracking loop adjusts the baseband sampling frequency to force sampling of the baseband waveform at optimal points for data decisions. The key elements of this loop are the Sampling Error Detector and Symbol Tracking Loop Filter shown in Figure 11. The output of these two blocks is a frequency correction term which is used to adjust the baseband sample frequency external to the HSP50210. In typical applications, the frequency correction term is fed back to the HSP50110 to adjust baseband sampling via the Resampling NCO (see HSP501 10 Datasheet).

FN3652.5

July 2, 2008

www.BDTIC.com/Intersil

! = SYMBOL RATE

BLANK = CLK RATE

SYMBOL TRACK LOOP FILTER

LEAD GAIN

FRZ_ST

MID AND END

SYMBOL SAMPLES

END

MID

END

MID

R E G

SAMPLING ERROR DETECTOR

DATA

DECISION

MID-SYMBOL

DATA

DECISION

MID-SYMBOL

TRANSITION

DETECT

TRANSITION

MID-POINT

TRANSITION

DETECT

TRANSITION

MID-POINT

LEAD

MANTISSA

‘0’ ‘-1’‘1’

MUX

ACQ

ZERO

LEAD

“0”

LEAD

MANTISSA

TRACK

REG REG

MUX

“0”

‘0’ ‘-1’‘1’

‘0’

MUX

SINGLE/ DOUBLE

RAIL

SAMPLING

MUX

ERROR

INVERT

ERROR

ACCUM.

“0”

ZERO

LAG

REG REG

LAG

MANTISSA

ACQ

MUX MUX

MUX

LAG MANTISSA TRACK

LEAD

EXPONENT

ACQ

REG

REG REG

LAG

EXPONENT

ACQ

MUX

SHIFT SHIFT

MUX

LEAD EXPONENT TRACK

REG

MUX

LOAD ACC

LAG EXPONENT TRACK

REG

LIMIT

ACC LIMITS

UPPER/LOWER

LAG

ACCUMULATOR

SERIAL

OUTPUT

FORMATTER

SOFSYNC

REG

TO μP INTERFACE

SOF

HSP50210

July 2, 2008

FN3652.5

FIGURE 11. SYMBOL TRACKING

LAG GAIN

HSP50210

www.BDTIC.com/Intersil

Sampling Error Detector

The Sampling Error Detector is a decision based error detector which determines sampling errors on both the I and Q processing paths. The detector assumes that it is fed with samples of the baseband waveform taken in the middle of the symbol period (mid-symbol sample) and between symbols (end-symbol sample) as shown in Figure 12. The sampling error is a measure of how far the mid-symbol sample is from the symbol transition mid-point. The transition mid-point is half way between two symbol decisions. The detector makes symbol decisions by comparing the end-symbol samples against a selectable threshold set (see Modulation Order Select bits 9 through 10 in Table 29 on page 37). The error term is generated by subtracting the mid-symbol sample from the transition midpoint. The sign of the error term is negated for negatively sloped symbol transitions. If no symbol transitions are detected the error detector output is zeroed. Errors on both the I and Q processing paths are summed and divided by two if Double Rail error detection is selected (see Symbol Tracking Configuration Control Register, Bit 8: Table 29 on page 37).

The sampling Error Detector provides an error accumulator to compensate for the processing rate of the loop filter. The error detector generates outputs at the symbol rate, but the loop filter can only accept inputs every eight f Thus, if the symbol rate is faster than 1/8 CLK, the error accumulator should be used to accumulate the error until the loop filter is ready for a new input. If the error accumulator is not used when the symbol rate exceeds 1/8 CLK, some error outputs will be missed. For example, if f error accumulation is required for symbol rates greater than 5 MSPS (f be scaled accordingly if the accumulator is used.

/8). Note: The loop filter lead gain term must

CLK

MID-SYMBOL

SAMPLE

CLK

SAMPLING

ERROR

FIGURE 12. TRACKING ERROR ASSOCIATED WITH

BASEBAND SAMPLING ON EITHER I OR Q RAIL (BPSK/QPSK)

TRANSITION

MIDPOINT

clocks.

CLK

= 40MHz, then

END-SYMBOL SAMPLE

EXPECTED

SYMBOL

LEVELS

Symbol Tracking Loop Filter

The Symbol Tracking Loop Filter is a second order lead/lag filter. The sampling error is weighted by th e lag gain and accumulated to give the integral response (see Figure 11). The Lag Accumulator output is summed with the sampling error weighted by the Lead Gain. The result is a frequency term which is output serially, via the SOF output, to the NCO/VCO controlling the baseband sample rate (see “Serial Output Interfaces” on page 23). In basic configurations, the SOF output of the HSP50210 is connected to the SOF input of the HSP501 10.

Two sets of registers are provided to store the loop gain parameters associated with acquisition and tracking. The appropriate loop gain parameters are selected manually via the Microprocessor Interface or automatically via the Carrier Lock Detector. The loop filter’s lead and lag gain terms are represented as a mantissa and exponent. The mantissa is a 4-bit value which weights the loop filter input from 1.0 to

1.9375. The exponent defines a shift factor that provides additional weighting from 2 mantissa and exponent provide a gain range between 2 and

~1.0 as given by Equation 10.

Lead/Lag Gain = (1.0+M*2-4)*2

where M = a 4-bit binary number from 0 to 15, and E is a 5-bit binary value ranging from 0 to 31. For example, if M = 0101 and E = 001 10, the Gain = 1.3125*2 Control Registers described in Tables 32 and 33 beginning on page 38.

A limiter is provided on the lag accumulator output to keep the baseband sample rate within a user defined range (see Tables 30 and 31 on page 38). If the lag accumulator exceeds either the upper or lower limit, the accumulator is loaded with the limit. For additional loop filter control, the loop filter output can be frozen by asserting the FZ_ST pin which null the sampling error term into the loop filter. The lag accu mulator can be initialized to a particular value and can be rea d via the microprocessor interface as described in “Reading from the Microprocessor Interface” on page 27, and Table 34 on page 39. The symbol tracking loop filter bit weighting is identical to the carrier tracking loop bit weighting, shown in Figures 9 and 10.

-1

-32

to 2

. Together the loop gain

-(32 -E)

-26

. They are stored in the

-32

(EQ. 10)

Soft Decision Slicer

The Soft Decision Slicer encodes the I/Q end-symbol samples into 3-bit soft decisions. The input to the slicer is assumed to be a bipolar (2ary) baseband signal representing encoded values of either ‘1’ or ‘0’. The most significant bit of the 3-bit soft decision represents a hard decision with respect to the mid-point between the expected symbol values. The 2 LSBs represent a level of confidence in the decision. They are determined by comparing the magnitude of the slicer input to multiples (1x, 2x, and 3x) of a programmable soft decision threshold (see Figure 13).

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

HARD DECISION

THRESHOLD

‘1’ DECISION

STRONGER WEAKER STRONGERWEAKER

-0.5

THRESHOLD

2x THRESHOLD

3x THRESHOLD

1/2

MSB

1/3

MSB

1/2

-FS

FIGURE 13. OVERLAY OF THE HARD/SOFT DECISION

THRESHOLDS ON THE SYMBOL PROBABILITY DENSITY FUNCTIONS (PDFs) FOR BPSK/QPSK SIGNALS)

0.0

MSB-1

‘0’ DECISION

‘0’‘1’

0.5

THRESHOLD

2x THRESHOLD

3x THRESHOLD

PROBABILITY

DENSITY

FUNCTION

THRESHOLD

The soft decision threshold represents a range of magnitude values from 0.0 to ~0.5. Note: Since the input to the slicer has a range of 0.0 to

~1.0, the threshold setting

should be set to less than 1.0/3 = 0.33. This avoids saturation. The slicer decisions are output in either a two’s complement or sign/magnitude format (see Soft Decision Slicer Configuration Control Register, Bit 7: Table 41 on page 42). The slicer input to output mapping for a range of input magnitudes is given in Table 7. For example, a negative input to the slicer whose magnitude is greater than twice the programmable threshold but less than 3x the threshold would produce a sign/magnitude output of 110 (BINARY). The I and Q inputs to the slicer are encoded i nto 3-bit soft decisions ISOFT(2-0) and QSOFT(3-0). These signals are routed to the OUTA(9-4) outputs by the Output Configuration Control Register Selector bits 0-3 (see Table 43 on page 44).

TABLE 7. SLICER INPUT TO OUTPUT MAPPING

SLICER INPUT MAGNITUDE

RELATIVE TO

SIGNAL

+>>>011011 +>>≤ 010 010 +>≤ < 001 001 + ≤ < < 000 000

- ≤ < < 100 111

->≤ < 101 110

->>≤ 110 101

->>>111100

INPUT POLARITY

THRESHOLD2xTHRESHOLD

THRESHOLD

SIGN/MAGNITUDE

OUTPUT

TWO’S

OUTPUT

COMPLEMENT

Carrier Phase Error Detector

The Carrier Phase Error is computed by removing the phase modulation from the phase output of the Cartesian-to-Polar Converter. To remove the modulation, the phase term is rotated and multiplied (modulo 2π) to fold the Phase Error into an arc centered about 0° but encompasses the whole plane, as shown in Figure 14. The phase rotation is performed by adding a 4-bit two’s complement phase offset (resolution 22.5°) to the 4 MSBs of the 8-bit phase term. The multiplication is performed by left shifting the result from 0 to 3 positions with the MSBs discarded and zeros inserted into the LSBs. For example, Carrier Phase Error produces I/Q constellation points which are rotated from the expected constellation points as shown in Figure 14. By adding an offset of 45° (0010 0000 binary) and multiplying by 4 (left shift by two positions) the phase modulation is removed, and the error is folded into a 90° arc centered at 0°. The left axis represents a decision boundary of ±45°C, implying the vertical axis is ±22.5° as shown in Figure 15. The phase offset and shift factors required for different PSK orders is given in Table 9 on page 21. Configuration of the Carrier Phase Error Detector is done via the Carrier Phase Error Detector Control Register, bit s 0 to 5, (see Table 18 on page 33). The Phase Error term may be selected for output via the Output Selector Configuration Control Register, bits 0 to 3 (see Table 43 on page 44).

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

In applications where Phase Error terms are generated faster than the processing rate of the Carrier Loop Filter, an error accumulator is provided to accumulate errors until the loop filter is ready for a new input. Phase Error terms are generated at the rate I/Q samples are input to the Cartesian to Polar Converter. However, the Carrier Loop Filter cannot accept new input faster than CLK/6 since six CLK(f

CLK

) clock edges are required to complete its processing cycle. If the error accumulator is not used and the I/Q sample rate exceeds CLK/6, error terms will be missed.

Note: The carrier Phase Error terms input to the loop filter are only generated from the end-symbol samples when the output of the I and D filter is selected for input to the Cartesian-to-Polar converter.

Note: The loop filter lead gain term must be scaled accordingly if the accumulator is used.

90°

45°

0°±180°

-90°

DECISION

REGION

BOUNDARY

SHIFT

FACTOR

ACTUAL

CONSTELLATION

DECISION

REGION

BOUNDARY

FIGURE 14. PHASE ERROR DETECTOR OPERATION (QPSK)

MODULA TION

POINT

INPUT TO CARTESIAN/POLAR CONVERTER

90°

PHASE ROTATION BY 45°

TABLE 8. BASIC PHASE ERROR DETECTOR SETTINGS

TYPE

CW 0 BPSK 0 QPSK 45

8-PSK 22.5

-90°

PROJECTION OF PHASE ERROR (θ

PHASE

OFFSET

° (00 HEX) 0 (no shift) ±180 ° (00 HEX) 1 (left shift 1) ±90

° (20 HEX) 2 (left shift 2) ±45

° (10 HEX) 3 (left shift 3) ±22

EXPECTED CONSTELLATION POINT

0°±180°

DECISION

REGION

BOUNDARY

22.5°

-22.5°

MULTIPLICATION BY 4

(MODULO 2π)

) ABOUT 0°

PHASE ERROR

RANGE

0°±45°

Carrier Loop Filter

The Carrier Loop Filter is second order lead/lag filter as shown in Figure 14. The loop filter is similar to the Symbol Tracking Loop Filter except for the additional terms from the AFC Loop Filter and the Frequency Sweep Block. The output of the Lag Accumulator is summed with the weighted Phase Error term on the lead path to produce a frequency control term. The Carrier Loop Filter is configured for

operation by the Control Registers described in Tables 21 through 28 beginning on page 34.

The Carrier Tracking Loop is closed by using the loop filter output to control the NCO or VCO used to down convert the channel of interest. In basic configurations, the frequency correction term controls the Synthesizer NCO in the HSP50110 Digital Quadrature Tuner via the COF and COFSYNC pins of the HSP50210’s serial interface (see “Serial Output Interfaces” on page 23). In applications where the carrier tracking is performed using the NCO on board the HSP50210, the loop filter output is fed to the on-board NCO as a frequency control.

The gain for the lead and lag paths of the Carrier Loop Filter are set through a programmable mantissa and exponent. The mantissa is a 4-bit value which weights the loop filter input from 1.0 to 1.9375. The exponent defines a shift factor

-1

that provides additional weighting from 2

to 2

-32

. Together the loop gain mantissa and exponent provide a gain range between 2

Lead/Lag Gain = (1.0+M*2-4)*2

-32

and ~1.0 as given by Equation 11.

-(32 -E)

(EQ. 11)

where M = a 4-bit binary number from 0 to 15, and E is a 5-bit binary value ranging from 0 to 31. For example, if M = 0101 and E = 00110, the Gain = 1.3125*2

-26

. The loop gain mantissa and exponent are set in the Carrier Loop Gain Control Registers (see T ables 25 through 26 on page 36).

The Phase Error input to the Carrier Loop Filter is an 8-bit fractional two’s complement number between ~1.0 to -1.0 (Format -2

. 2-12-22-32-42-52-62-7). Some LSBs are zero for BPSK, QPSK and 8-PSK. If minimum loop gain is used, the Phase Error is shifted in significance by 2

-32

. With maximum loop gain, the Phase Error is passed almost unattenuated. The output of the Carrier Loop filter is a 40-bit fractional two’s complement number between ~1.0 and -1.0 (Format -

. 2-12-22-3..... 2

-392-40

). In typical applications, the 32 MSBs of the loop filter output represent the frequency control word needed to adjust the down converting NCO for phase lock. Tables 9 and 10 beginning on page 21 illustrate the bit weighting of the Carrier Loop Filter into the NCO for both tracking and acquisition sweep modes.

A limiter is provided on the Carrier lag accumulator output to keep frequency tracking within a user defined range (see Tables 23 and 24 on page 35). If the lag accumulator exceeds either the upper or lower limit the accumulator is loaded with the limit. For additional loop filter control, the Carrier Loop Filter output can be frozen by asserting the FZ_CT pin which nulls the Phase Error term into the loop filter. Also, the lag accumulator can be initialized to a particular value via the Microprocessor Interface as described in Tab le 28 on page 37 and can be read via the microprocessor interface as described in “Reading from t he Microprocessor Interface” on page 27.

FN3652.5

July 2, 2008

www.BDTIC.com/Intersil

FRZ_CT

TO POLAR

CONVERTER

PHASE OUTPUT

FROM CARTESIAN

DETECT

TO LOCK

TO OUTPUT

SELECT BLOCK

REG

CARRIER PHASE

ERROR DETECT

PHASE

OFFSET

SHIFT

REG

PHASE ERROR

)

(

DELAY

(1, 2, 4, 8, 16)

DISCRIMINATOR

SHIFT LEFT 0, 1, 2, 3

“0”

@ OR

MUX

ERROR

INVERT

PHASE

ERROR

@ = SYNC RATE

CARRIER

LOOP FILTER

MANTISSA

ZERO LEAD

“0”

@ OR !

INVERT

ERROR

ACCUM.

“0”

ZERO

LAG

MANTISSA

CARRIER LEAD GAIN

LEAD

ACQ

MUX

MUXMUX

MUX

LAG ACQ

CARRIER LAG GAIN

EXPONENT

LEAD MANTISSA TRACK

LAG MANTISSA TRACK

EXPONENT

LEAD

ACQ

LAG ACQ

LEAD EXPONENT TRACK

MUX

SHIFT SHIFT

MUX

LAG EXPONENT TRACK

MUX

LOAD ACC

FROM MICROPROCESSOR INTERFACE

UPPER/LOWER

LAG

ACCUMULATOR

REG

LIMIT

ACC LIMITS

LEAD/LEAD + LAG

LAG/LEAD + LA G

= TWICE SYMBOL

! = SYMBOL RATE

BLANK = CLK RATE

REG

MUX

REG

SERIAL

OUTPUT

FORMATTER

TO μP INTERFACE

TO NCO

COF

COFSYNC

HSP50210

ERROR

ACCUM.

“0”

ZERO

AFC LOOP FILTER

MUX

AFC

MANTISSA

ACQ

@ OR !

ERROR

FREQUENCY

SHIFT

FREQUENCY

SHIFT

SHIFT LEFT

0, 1, 2, 3

July 2, 2008

FN3652.5

“0”

REG

CARRIER

FREQUENCY

ERROR DETECT

MUX

ERROR

INVERT

FREQUENCY

ERROR

FIGURE 15. CARRIER ACQUISITION/TRACKING LOOP BLOCK DIAGRAM

MANTISSA

TRACK

AFC GAIN

MUX

EXPONENT

ACQ

SHIFT

EXPONENT

TRACK

FREQUENCY SWEEP

SHIFT

MUX

SWEEP RATE MANTISSA

ACQ

“0” TRACK

SWEEP RATE EXPONENT

ZERO SWEEP

HSP50210

www.BDTIC.com/Intersil

TABLE 9. BIT WEIGHTING IN THE CARRIER LOOP FILTER TO THE NCO - TRACKING

OUTPUT

FREQUENCY

RESOLUTION

CLK

/16

CLK

/32

CLK

/64

CLK

/128

CLK

/256

CLK

/512

CLK

/1024

CLK

/2048

CLK

/4096

CLK

/8192

CLK

BIT

WEIGHT

φe

(AND

ACCOM.)

MANTISSA

GAIN

MULT

OUT

BITS

KEPT

(RND) SHIFT = 0 SHIFT

≅ 32

SHIFT

COUNTS

NCO BIT WEIGHT

40 0f 39 Obtained with a shift of 31 and a Gain of 01.1111 (~2) → (8) - shift31 1 f 38 7. - shift31 2 f 37 6 - shift30 3 f 36 5 - shift29 4 f 35 4 - shift28 5 f 34 3 - shift27 6 f 33 2 - shift26 7 f 32 1 - shift25 8 f 31 0 - shift24 9 f 30 - shift23 10 f 29 - shift22 11 f 28 - shift21 12 f 27 - shift20 13 f 26 - shift19 14 f 25 - shift18 15 f 24 - shift17 16 f 23 - shift16 17 f 22 - shift15 18 f 21 - shift14 19 f 20 - shift13 20 f 19 - shift12 21 f 18 - shift11 22 f 17 - shift10 23 f 16 - shift9 24 f 15 - shift8 25 f 14 - shift7 26 f 13 17 - shift6 27 f 12 (12) 16 17 = (12) (12) - shift5 28 f

11 (11) 15 16 = (11) (11) - shift4 29 f

10 (10) 14 15 = (10) (10) - shift3 30 f

9 (9) 13 14 = (9) (9) - shift2 31 f 8 (8) 0 12 13 = (8) (8) - shift1 32 f 7 7. 1. 11. 12. = 7. 7. - shift0 33 f 66 x1011= 66 34f 55 x910= 55 35f 44 x89= 44 36f 33 x78= 33 37f 22 67= 22 38f 11 56= 11 39f 00 45= 00 40f

3 (RND) 2 1 0

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 10. BIT WEIGHTING IN THE CARRIER LOOP FILTER TO THE NCO - SWEEP

OUTPUT

BIT

WEIGHT

φe

SWEEP

MANTISSA GAIN SHIFT = 0 SHIFT = 32 SHIFT COUNTS NCO BIT WEIGHT

40 0f 39 Shift 27 and Gain = 01.1111 → (8) - shift28 1 f 38 7. - shift27 2 f 37 6 - shift26 3 f 36 5 - shift25 4 f 35 4 - shift24 5 f 34 3 - shift23 6 f 33 2 - shift22 7 f 32 1 - shift21 8 f 31 0 - shift20 9 f 30 - shift19 10 f 29 - shift18 11 f 28 - shift17 12 f 27 - shift16 13 f 26 - shift15 14 f 25 - shift14 15 f 24 - shift13 16 f 23 - shift12 17 f 22 - shift11 18 f 21 - shift10 19 f 20 - shift9 20 f 19 - shift8 21 f 18 - shift7 22 f 17 - shift6 23 f 16 - shift5 24 f 15 - shift4 25 f 14 - shift3 26 f 13 - shift2 27 f 12 (12) 0 5 - shift1 28 f

11 (11) 1. 4. - shift0 29 f

10 (10) x 3 30 f

9(9) x 2 31 f 8(8) x 1 32 f

77. x 0 33 f 66 z 34 f 55 z 35 f 44 z 36 f 33 z 37 f 22 z 38 f 11 z 39 f 00 z 40 f

NOTE:

min

= 2

-29

at 1% FLB, 4M

, 0.075Hz/Baud = 12Kbps.

clk

5. SW

FREQUENCY

RESOLUTION

CLK

/16

CLK

/32

CLK

/64

CLK

/128

CLK

/256

CLK

/512

CLK

/1024

CLK

/2048

CLK

/4096

CLK

/8192

CLK

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

Frequency Sweep Block

The Frequency Sweep Block is used during carrier acquisition to sweep the range of carrier uncertainty. The Sweep Block is loaded with a programmable value which is input to the lag path of the Carrier Tracking Loop Filter when frequency sweep is enabled. The sweep value is accumulated by the loop filter’s lag accumulator which causes a frequency sweep between the accumulator’s upper and lower limits. When one of the limits is reached, the sweep value is inverted to sweep the frequency back toward the other limit. The Frequency Sweep Block is controlled by the Lock Detector and is only enabled during carrier acquisition (see “Lock Detector Control” on page 24).

A stepped acquisition mode is provided for microprocessor controlled acquisition. In the stepped acquisition mode, the lag accumulator is incremented or decremented by the programmed sweep value each time the lock detector is restarted during acquisition. This technique prevents the loop from sweeping past the lock point before the microprocessor can respond. Typically in stepped acquisition mode, the step value is set to a percentage of the loop bandwidth. A dwell counter is also provided for stepped acquisition. This counter holds off the lock detector integration from 1 to 129 symbols to allow the loop to settle before starting the integration.

The sweep value is set via a programmable mantissa and exponent. The format is 01.MMMM * 2 MMMM is the 4-bit mantissa and EEEEE is the 5-bit exponent and the weighting is relative to the MSB of the NCO control word. In swept acquisition mode, the sweep value is the amount that the carrier lag accumulator is incremented or decremented each time a new filter output is calculated (sweep rate/N). In stepped acquisition mode, it is the amount the lag accumulator is incremented or decremented each time that the lock detector is restarted. (See Frequency Sweep/AFC Control Loop Control Register, Table 27.)

-(28 - EEEEE)

where

Error Detector. For PSK demodula tion, this block is byp assed by setting the offset and shift terms to zero (see Frequency Error Detector Control Register; Table 20 on page 34). The frequency error term may be selected for output via the Output Select Block. (See Serial Output Configuration Control Register, Table 42 on page 42).

Automatic Frequency Control (AFC) Loop Filter

The AFC Loop Filter supplies a frequency correction term to the lag path of the Carrier Loop filter . The frequency correction term is generated by weighting the output of the Frequency Error Detector by a user programmable weight (see Sweep/AFC Control Register; Table 27 ). Note: If AFC is n ot desired, the frequency error term to the loop filter is nulled via the Carrier Tracking Configuration Control Register #2 (see Table 22 on page 35).

Serial Output Interfaces

Frequency control data for Carrier and Symbol Tracking is output from the DCL through two separate serial interfaces. The Carrier Offset frequency control is output via the COF and COFSYNC pins. The Symbol Tracking Offset frequency control is output via the SOF and SOFSYNC pins. A SLOCLK is provided to allow for reduced serial rate data exchanges. The timing relationship of these signals is shown in Figure 16.

CLK

COFSYNC/

SOFSYNC

COF/SOF

Note: Data must be loaded MSB first.

MSB

LSB

MSB

Carrier Frequency Detector

The Frequency Detector generates a frequency term for use in Automatic Frequency Control (AFC) configurations. The Frequency Detector (discriminator) subtracts a previous Phase Error sample from the current one (d/dt) to produce a term proportional to the carrier frequency. The discriminator gain is adjusted by programming a variable delay (1-16) between the samples subtracted (see Frequency Detector Control Register; Table19).

Note: The input to the discriminator corresponds to phase terms taken from baseband samples at either the SYNC rate or twice symbol rate depending on the input source chosen for the Cartesian-to-Polar converter.

Carrier Frequency Error Detector

The Frequency Error Detector is used to generate a frequency error term for FSK modulated waveforms. The error is computed by adding an offset and shifting the frequency detector output in a manner similar to that used by the Phase

FIGURE 16. SERIAL OUTPUT TIMING FOR COF AND SOF

OUTPUTS

Each serial word has a programmable word width of either 8, 12, 16, 20, 24, 28, 32, or 40 bits (see Table 42, CW27, bits 4 through 6 for COF and bits 0 through 2 for SOF). The polarity of the sync signals is programmable and is set in CW27 Bit 12 for SOF and Bit 11 for COF. The polarity of the serial clock to the serial data is programmed via CW27 Bit 10. If reduced rate frequency updates is required, the SLOCLK rate is selected via CW27 Bit 7 and the rate is set via CW27 bits 8 through 9, to be either CLK/2, CLK/4, CLK/8 or CLK/16. Note that if the DCL is used with the HSP50110 DQT, then the SLOCLK cannot be used, i.e., the serial clock must be set to be CLK.

Lock Detector

The Lock Detector consists of the Dwell Counter, Integration Counter, Phase Error Accumulator, False Lock/Frequency Accumulator, Gain Error Accumulator and the Lock Detect

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

State Machine (see Figure 16). The function of the Lock Detector is to monitor the baseband symbols and to decide whether the Carrier Tracking Loop is locked to the input signal. Note: The Symbol Tracking Loop locks independently; under most circumstances, it will lock before the Carrier Tracking Loop locks up. Based on the in-lock/out-of-lock decision, either the Acquisition or Tracking parameters are selected in the Carrier Tracking Loop, the Symbol Tracking Loop and in the Lock Detector itself. The Lock Detector can be configured either to make the “lock” decision automatically using the State Machine Control Mode, or to collect the necessary data so that an external microprocessor can control the acqui s iti on /tracking process via the Microprocessor Control Mode (see Figure 22).

In State Machine Control Mode, the Lock Detector State Machine monitors the outputs of the Phase Error Accumulator and the False Lock Accumulator to determine the Lock Detector state. Accumulation effectively averages the Phase Error and false lock count, reducing their variance. Lock is detected by accumulating the magnitude of the Phase Error over a predetermined interval up to 1025 symbols (the Integration Time). When the Carrier Loop is locked, the Integration Period will end before an overflow occurs in the Phase Error Accumulator. At the beginning of a lock detection cycle, the Phase Error Accumulator and the Integration Counter are loaded with their respective pre-load values. With each end bit sample, the Phase Error Accumulator adds the magnitude of the current Phase Error to its accumulated sum, while the Integration Counter decrements one count. The Lock Detector State Machine monitors the overflow bit of the Phase Error Accumulator and the output of the Integration Counter . If the Phase Error Accumulator overflows before the Integration Counter reaches zero, then the accumulated Phase Error is too large for the Carrier Tracking Loop to be in lock and the Lock Detector State Machine goes into the Search state (see Lock Detector State Machine in Figure 17). In the search state, the loop parameters are reloaded with “Acquisition” rather than “Tracking” values. When the Phase Accumulator overflows or when the Integration Counter reaches zero, the Integration Counter and the accumulators are re-initialized and the process begins again. The Integration Counter Pre-load corresponds to the number of symbols over which to integrate. The Phase Error Preload corresponds to the distance the Phase Error Accumulator starts away from overflow. This dist ance divided by the Integration Period equals the average Phase Error. The pre-load value is calculated using Equation 12:

Preload = Full Scale

where Full scale = 2 Full scale phase = 180° for CW, 90° for BPSK, 45° for QPSK,

etc;

Lock Threshold

⎛⎞

----------------------------------------------

–

⎝⎠

Full Scale Phase

-1

x 128 x Integration Count

(EQ. 12)

Lock Threshold <45° for BPSK, <22.5° for QPSK, etc. (typical after shift); and Integration Count = Integration Period measured in symbol times.

The False Lock Detector is used to indicate false lock on square wave data in a high SNR environment. A false lock condition is detected by monitoring the final integration stage in the Q branch of the Integrate and Dump Filter (see Figure 3 on page 7). If the magnitude of the integration over the symbol period is less than the integration over half a symbol period, a possible false lock condition is detected; (integration over a symbol period has gone from end-bit to end-bit, while integration over half the symbol period has gone from the previous end-bit to mid-bit). By accumulating the number of these occurrences over the Integration Period, the Lock Detector State Machine determines whether a false lock condition exists. The False Lock Accumulator is used to accumulate the number of possible false lock occurrences over the Integration Period. The False Lock Accumulator can also be configured to accumulate the output of the Frequency Error Detector (see Lock Detection Configuration Control Register Bit 27: Table 35 on page 40).

The Gain Error Accumulator provides a mechanism to estimate data quality (E the magnitude of the gain error of the end-bit samples, over the Integration Period. Note: The Gain Error end-bit data is valid only after lock has been declared, and the demod is the tracking mode. The accumulated value gives an indication of the variance about the ideal constellation points. The accumulator output is read via the Microprocessor Interface. The Gain E rror Acc umu lator is always pre-loaded with zero.

For applications where stepped acquisition is used, a Dwell Counter is provided. In this mode, the lag accumulator in the Carrier Loop Filter is stepped to a new frequency after each Lock Detector integration. The Dwell Counter is used to hold off Lock Accumulator integration until the loop has a chance to settle.

). The accumulator integrates

s/No

Lock Detector Control

The selection of acquisition and tracking modes is controlled by either the internal state machine or an external microprocessor. The internal state machine monitors the rollover of the Phase Error Accumulator and the False Lock Accumulator relative to the Integration Counter. Depending on whether the accumulators or counter roll over first, the acquisition or tracking parameters are selected for the Loop Filters and the Lock Detector Accumulators. In addition, the state machine controls the frequency sweep input to the Carrier Tracking Loop.

The flow of the acquisition control is shown in the State Diagram in Figure 18 on page 26. The state machine controls the acquisition process described as follows:

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

Search. The frequency uncertainty is swept by enabling the Frequency Sweep Block to the lag path of the Carrier Tracking Loop Filter. The acquisition parameters are enabled to the Loop Filters and the Lock Detector Accumulators. Phase lock is obtained when the Lock Counter rolls over before the Phase Error Accumulator (average Phase Error is less than the lock threshold).

Verify. Once phase lock is obtained, the frequency sweep is disabled and the tracking parameters are enabled. Lock is verified if the accumulated Phase Error is below the threshold for a programmable number of Integration Periods. False lock conditions are also monitored by comparing the roll over of the False Lock Accumulator to that of the Integration Counter. If the False Lock Accumulator rolls over before the Integration Counter, a false lock condition exists.

False Lock. Once a false lock has been determined, the Frequency Sweep block is enabled to move the carrier tracking beyond the false lock region. The Frequency Sweep is performed for a programmable number of Integration Periods before returning to the search state.

Lock. When phase lock has been verified, the Lock status output is asserted and the False Lock Detector is disabled.

The lock state is maintained as long as the Integration Counter rolls over before the Phase Error Accumulator.

If the acquisition and tracking process is controlled externally, the Phase Error Accumulator and False Lock Accumulators are monitored by an external processor to determine when lock has been achieved. In this mode the accumulator pre-loads are typically set to zero and the accumulator output is compared in the processor against a threshold equal to th e maximum Phase Error per sample times the number of samples per Integration Period. The accumulators stop after each Integration Period to hold their outputs for reading via the Microprocessor Interface (see Read Enable Address Map; Table 13 on page 28). The accumulators are restarted by writing the Initialize Lock Detector Control address (see Initialize Lock Detector Control Register: Table 45 on page 46). To simplify the processor interface, the LKIN T output is provided to interrupt the processor when the accumulator integration period is complete. The processor controls the use of the acquisition/tracking parameters and lock status line by setting the appropriate bits in the Acquisition/Tracking Configuration Control Register (see Table 38 on page 41). In addition, the frequency sweep function is enabled via the Microprocessor Interface.

DWELL COUNT

ACQ

COUNTER

“0”

TRACK

DWELL

TC START TC

SWEPT

INT

PERIOD

ACQ

MUXMUX

INTEGRATION

COUNTER

INT

PERIOD

TRACK

PHASE ERROR

PRELOAD

ACQ

PHASE

ERROR

PRELOAD

TRACK

MUX

LOCK DETECTOR STATE MACHINE

PRELOAD

PHASE ERROR

|X|

REG

OVERFLOW OVERFLOW

ACQUIRE/ TRACK

FALSE

LOCK

ACQ

FALSE

LOCK

PRELOAD

TRACK

MUX

FALSE LOCK/

FREQUENCY

ERROR

“0”

|X|

MUX

REG REG

MUX

GAIN

ERROR

|X|

FIGURE 17. LOCK DETECTOR BLOCK DIAGRAM

FN3652.5

July 2, 2008

PHASE ERROR

www.BDTIC.com/Intersil

ACCUMULATOR

FINISHES BEFORE

INTEGRATION COUNTER

INTEGRATION

COUNTER FINISHES

BEFORE

PHASE ERROR

ACCUMULATOR

LOCK COUNTER

FALSE

DONE

HSP50210

PHASE ERROR ACCUMULATOR FINISHES BEFORE INTEGRATION COUNTER

PHASE ERROR

ACCUMULATOR

FINISHES BEFORE

INTEGRATION

COUNTER

INTEGRATION

COUNTER

FINISHES BEFORE

PHASE ERROR

ACCUMULATOR

AND VERIFY

COUNTER DONE

FALSE LOCK

ACCUMULATOR

BEFORE

LOCK COUNTER

FALSE

LOCK

INTEGRATION COUNTER FINISHES BEFORE PHASE ERROR ACCUMULATOR

VERIFYLOCK

FALSE LOCK COUNTER NOT DONE

INTEGRATION COUNTER FINISHES BEFORE PHASE ERROR ACCUMULATOR AND VERIFY COUNTER NOT DONE

FIGURE 18. ACQUISITION/TRACKING STATE DIAGRAM

Serial Output Controller

The frequency correction terms generated by the Symbol and Carrier Loop Filters are output through two separate serial interfaces. The symbol frequency offset used to close the symbol Tracking Loop is output via the SOF and SOFSYNC outputs. The carrier offset frequency used to close the Carrier Tracking Loop is output via the COF and COFSYNC outputs.

The serial output timing, identical for both of the loop filter outputs, is shown in Figure 19. The data word is output MSB first starting with the first rising edge of either CLK or SLOCLK that follows the assertion of sync (COFSYNC or SOFSYNC). The HSP50210 is configured to output the serial data with either CLK or SLOCLK (see Serial Output Configuration Control Registers Bit 7, Table 42 on page 42). The SLOCLK output is a programmable sub-multiple of CLK which is provided for applications requiring a slower serial clock. In applications where the HSP50210 is used with the HSP50110, both parts must be supplied with the same CLK and the HSP50210 is configured to use CLK as the serial clock. The serial output can be configured for word containing from 8 to 40 bits.

CLK/

SLOCLK

COFSYNC/

SOFSYNC

COF/

SOF

MSB MSB

Note: COFSYNC and SOFSYNC shown Configured as active “High”.

FIGURE 19. SERIAL OUTPUT TIMING FOR COF AND SOF

OUTPUTS

Output Selector

The output selector determines which internal signals are multiplexed to the AOUT9-0 and BOUT9-0 outputs. Fifteen different output options are provided: ISOFT(2:0), QSOFT(2:0), IEND(7:1), QEND(7:1), AGC(7:1), MAG(7:0), Phase(7:0), FREQERR(7:1), GAINERR(7:1), BITPHERR(7:1), CARPHERR(7:1), LKACC(6:0), LKCNT(6:0), NCOCOS(9:0), and STATUS (6:0). These are detailed in the Output Selector Configuration Control Register, bits 0 through3 (see Table 43 on page 44).

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

The status bit definition is shown in Table 11:

TABLE 11. STATUS BIT DEFINITIONS

STATUS BIT DEFINITION

6 Carrier Tracking Loop Lock 5Acq/Trk 4 Frequency Sweep Direction 3 High Power 2 Low Power 1 Data Rdy

To simplify the output interface, a symbol clock (SMBLCLK) is output which is synchronous to the soft bit decisions produced by the Slicer. The SMBLCLK is a 50% duty cycle clock whose rising edge is centered in the middle of the output data period for both the soft bit decisions and the end-symbol samples, as shown in Figure 20.

SMBLCLK

ISOFT2-0/

QSOFT2-0/

IEND7-1/

QEND7-1

FIGURE 20. OUTPUT DATA CLOCK TIMING

Microprocessor Interface

The Microprocessor Interface is used to write the HSP50210’s Control Registers and monitor various read points within the demodulator. Dat a written to the interface is loaded into a set of four 8-bit holding registers, on e Write Address Register, or one Read Address Register. These registers are accessed via the 3-bit address bus (A0-2) and an 8-bit data bus (C0-7) as shown in Table 12. The R/W column indicates whether the data is read from or written to the given address.

TABLE 12. READ/WRITE ADDRESS MAP FOR

MICROPROCESSOR INTERFACE

R/W A2-0 DESCRIPTION

W 000 Input Holding Register 0. Transfers to bits 7-0 of the

target control register. Bit 0 is the LSB of the target register.

W 001 Input Holding Register 1. Transfers to bits 15-8 of the

target control register.

W 010 Input Holding Register 2. Transfers to bits 23-16 of a

32-bit target control register.

W 011 Input Holding Register 3. Transfers to bits 31-24 of the

target control register. Bit 31 is the MSB of the 32-bit register.

W 100 Write Address Register. The register is loaded with the

address of the control register targeted for update. The address map for the control registers is given in Tables 1C-32C. Note: Addresses outside the range 0-31 are invalid.

TABLE 12. READ/WRITE ADDRESS MAP FOR

R/W A2-0 DESCRIPTION

W 101 Read Address Register. The address loaded into this

R 000 Selects output holding register bits 7-0 for output on

R 001 Selects output holding register bits 15-8 for output on

R 010 Selects output holding register bits 23-16 for output on

R 011 Selects output holding register bits 31-24 for output on

R 100 Multiplexes 8 bits of internal status out on C7-0. See

MICROPROCESSOR INTERFACE (Continued)

register specifies an internal read point as given the by address map in Table 12. Addresses outside the range 0-4 are invalid.

C7-0 respectively. Bit 0 is the LSB of the internal holding register.

C7-0, respectively.

C7-0, respectively. Bit 31 is the MSB.

Table 14 for bit map.

Data is read from an Internal Status Register and a series of output holding registers. The output holding registers range in size from 8 to 32 bits, and their contents are multiplexed out a byte at a time on C7-0 by controlling A2-0 and asserting RD

. The addresses listed in Table 11 with the R indicator provide the address map used for reading data from the Microprocessor Interface.

Writing to the Microprocessor Interface

The HSP50210 is configured for operation by loading a set of thirty-two control registers which range in size from 0 to 32 bits. They are loaded by first writing the configuration data to the Microprocessor interface’s four holding regi sters and then writing the target address to the Write Address Register as shown in Figure 21. The Control Register Address Map and bit definitions are given in Tables 14 through 45. The configuration data is transferred from the holding registers to the target control register on the fourth clock following a write to the address register. As a result, the holding registers should not be updated any sooner than 4 CLKs after an address register write (see Figure 21).

Note: The holding registers which map to the unused bits of a particular control register do not have to be loaded.

Reading from the Microprocessor Interface

The Microprocessor Interface is used to monitor demodulator operation by providing the ability to read the accumulator contents in the Lock Detector and Loop Filters. In addition, the interface is used to monitor the HSP50210’s Internal Status Register. More clearly, the following data is available to be read:

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

REGISTERS DEFINITION

(4) 32-bit Carrier Loop Letter Lag Acc. Output (4) 32-bit Symbol T racking Loop Letter Lag Acc. Output (1) 8-bit AGC Loop Letter Output (2) 16-bit Lock Detector φe Acc. Output (2) 16-bit Lock Detector GE Acc. Output (2) 16-bit Lock Detector FL/FE Acc. Output (1) 8-bit Internal Status

Total = 16

A different read procedure is required depending on whether the Lock Detector Accumulators, loop filter accumulators, or the Status Register is to be read. The read procedures are summarized in Figures 21 through 23.

The accumulators in the AGC Loop Filter, Carrier Loop Filter and Symbol Tracking Loop can be read via the Microprocessor Interface. Since these accumulator s are free running, their contents must be loaded into output holding registers before they can be read. Each accumulator has its own output holding register. The three holding registers are updated by loading 29 (decimal) into the Write Address Register of the Microprocessor Interface. The output of a particular holding register is then enabled for reading by loading its address into the Read Address Register (see Tables 12 and 13). The holding register addresses for the loop filter accumulators range from 0 to 4 as given in Table 13. The contents of the output holding registers are multiplexed out a byte at a time on C7-0 by changing A2-0 and asserting RD (see Read/Write Address Map in Table 12).

TABLE 13. READ ENABLE ADDRESS MAP

ADDRESS HOLDING REGISTER ENABLE

0 Carrier Loop Filter Lag Accumulator. Enables output

of holding register containing 32 MSBs of the lag accumulator.

1 Symbol Tracking Loop Filter Lag Accumulator.

Enables output of holding register containing 32 MSBs of the lag accumulator.

2 AGC GAIN. Enables output of holding register

containing 8 MSBs of the AGC accumulator.

3 Lock Detector 1. The 16 MSBs of the Lock Detector’s

Phase Error Accumulator and the 16 MSBs of the False Lock Accumulator are enabled for output. The accumulator contents are selected for output as follows, A2-0 = 3 (decimal) selects MSByte of the Phase Error Accumulator, A2-0 = 2 (decimal) selects LSByte of the Phase Error Accumulator, A2-0 = 1 (decimal) selects MSByte of the False Lock Accumulator, and A2-0 = 0 (decimal) selects LSByte of the False Lock Accumulator.

4 Lock Detector 2. Enables th e 16 MSBs of the Lock

Detector’s Gain Error Accumulator for output. The MSByte of the accumulator is selected for output by setting A2-0 = 1, and the LSByte is selected by A2-0 = 0.

The contents of the three accumulators in the Lock Detector can also be read via the Microprocessor Interface. However, the Lock Detector must be stopped before a read can be performed. In State Machine Control Mode, the Lock Detector is stopped by loading 24 (decimal) into the Write Address Register. In Microprocessor Control Mode, the Lock Detector stops after each Integration Period. To determine when the Lock Detector has stopped and is ready for reading, bits 7 and 6 of the Internal Status Register (SR7 and 6) must be monitored (see Table 14 on page 30). The control sequence for reading a Lock Detector Accumulator is shown in Figure 23. The control sequence for reading a Lock Detector Accumulator using the LKINT signal is shown in Figure 24.

An 8-bit Internal Status Register (SR7-0) can also be monitored via the Microprocessor interface. The Status Register indicates loop filter and Lock Detector status as listed in Table 14 on page 30. The St atus Registe r content s are output on C7-0 by setting A2-0 to 100 (binary) an asserting RD as shown in Figure 25 on page 31. The register contents are updated each CLK.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

DON’T CARE

A0-2

SIGNALS

PROCESSOR

C0-7

CLK

EARLIEST TIME ANOTHER

NOTE: These processor signals are meant to be representative. The actual shape of the waveforms will be set by the microprocessor used. Verify that the processor waveforms meet the parameters in “Waveforms” on page 50 to ensure proper operation. The Processor waveforms are not required to be synchronous to CLK. They are shown that way to clarify the illustration.

FIGURE 21. CONTROL REGISTER LOADING SEQUENCE

DON’T CARE

PROCESSOR

SIGNALS

A0-2

C0-7

CLK

1234

5 6

3154 02

MSB LSB029

43210 01

1234

LOAD CAN BEGIN

ADDRESS IS ASYNCHRONOUS TO CLK

DATA IS

ASYNCHRONOUS TO CLK

1 2 3 4 5

LOAD OUTPUT HOLDING REG

ENABLE

HOLDING

REG

FOR

READ

WAIT

6 CLKs

DELAY

TO RD

ASSERT

READ READ READ READ

1. Load the Write Address Register with 29

to load the output holding registers.

dec

2. Enable Carrier Loop Filter Lag Accumulator holding register for reading.

3. Select the MSByte of the output holding register for output.

4. Assert RD

5. Select other bytes of holding register by changing A0-2 and asserting RD

low to output data on C0-7. (Must wait for 6 CLKs after loading the holding registers).

FIGURE 22. LOOP FILTER ACCUMULATOR READ SEQUENCE

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

A0-2

SIGNALS

PROCESSOR

C0-7

CLK

DCL

SR-7

SIGNALS

SR7=0

1 2 3 5 6 8 6 8 6 8

HALT LD

AT END OF

CYCLE

ENABLE LD REG.

FOR READING

4254 13

SR7=1

STATUS READS

MSW

8 6

LOCK DETECTION STATUS READSINTERNAL

LSW

MSW

1. Load the Write Address Register with 24 counter in the lock detector. The verify counter is not reset and will resume at the stopped value when the lock detector is restarted.

2. Load the Read Address Register with 3

to halt the Lock Detector after the current integration cycle. This disables the reload of the integration

dec

to enable the Lock Detector Phase Error Accumulator for reading.

dec

3. Read Internal Status Register to monitor SR-7 to determine when the Lock Detector is stopped and ready to be read.

4. SR-7 goes high, indicating the Lock Detector integration cycle is complete, and ready to be read.

5. Read Internal Status Register and find SR-7 = 1; the Lock Detector is ready to be read.

6. Change Read address to (3; 2; 1; 0) for (Phase Error MSW; PE LSW; False Lock MSW; FL LSW) read.

7. End of Internal Status Valid Data.

8. Assert RD

9. Load The Write Address Register with 30 machine mode).

10. Load the Write Address Register with 25

to Read Lock Detector Status

to initialize Lock Detector Accumulators and Reset the Integration counters. (Not needed for state

dec

to restart the Lock Detector.

dec

FIGURE 23. PROCESSOR MONITORING INTERNAL STATUS/READING LOCK DETECTOR

LSW

RESET

DETECTOR

3024

LOCK

RESTART

LOCK

DETECTOR

TABLE 14. INTERNAL STATUS REGISTER (SR7-0) BIT MAP

BIT BIT DESCRIPTION

7 Lock Detector Stopped and Ready for Reading

(State Machine Control Mode). 0 = Lock Detector not stopped. 1 = Lock Detector stopped, ready for read.

6 Lock Detector Stopped and Ready for Reading

(Microprocessor Control Mode). 0 = Lock Detector not stopped. 1 = Lock Detector stopped, ready for read.

5 Carrier Loop Filter Lag Accumulator Load Complete. This bit

is used to determine when a 32-bit load of Carrier Lag Accumulator is complete. The accumulator load is initialized by loading the Write Address Register with 13 (decimal) as described in Table 28. 0 = Load not complete. 1 = Load complete.

4 Symbol Tracking Loop Filter Lag Accumulator Load

Complete. This bit is used to determine when a 32-bit load of Symbol Track Lag Accumulator is complete. The accumulator load is initialized by loading the Write Address Register with 19 (decimal) as described in Table 34. 0 = Load not complete. 1 = Load complete.

BIT BIT DESCRIPTION (Continued)

3 Lock. Carrier Lock state achieved by Lock Detector.

0 = Not locked. 1 = Locked.

2 Acquisition/Track. Indicates whether the Lock Detector is in

acquisition or tracking mode. 0 = Tracking Mode.

1 = Acquisition Mode. 1 Reserved. 0 Frequency Sweep Direction, defined for upper sideband

signals.

0 = UP.

1 = DOWN.

FN3652.5

July 2, 2008

www.BDTIC.com/Intersil

HSP50210

A0-2

SIGNALS

PROCESSOR

C0-7

CLK

SR-7

DCL

SIGNALS

LKINT

1 2

3 4 5 6 5 6 5 7 8 9 10

MSW

2035 41

LSW

MSW

5 6

LSW

1. LKINT Asserts Indicating End of Lock Detector Accumulation Cycle; Accumulators Ready to Read.

2. Set A0-2 to 5 for Reading Lock Detector.

3. Load Read Address Register with 3

to enable the Lock Detector Phase Error Accumulator for Reading.

dec

4. Set A0-2 to 3 for Phase Error (PE) Read.

5. Assert RD

and read (Phase Error (PE) MSW; PE LSW; False Lock (FL) MSW; FL LSW).

6. Change Read Address to (2; 1; 0) to read various Lock Detection values.

7. Change Address to 4 to Initialize the Lock Detector.

8. Load Write Address Register with 30

to initialize the Lock Detector Accumulators and Reset Integration Counters. (Only has

dec

an effect in µP mode).

9. Keep Address to 4 to Restart the Lock Detector.

10. Load Write Address Register with 25

FIGURE 24. PROCESSOR INTERRUPT MONITOR/LOCK DETECTOR READ

to restart the Lock Detector. (Only necessary if not in the µP mode).

dec

CLK

A0-2

C7-0

STATUS CAN CHANGE EVERY CLK

FIGURE 25. INTERNAL STATUS REGISTER READ

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 15. DATA PATH CONFIGURATION CONTROL REGISTER

DESTINATION ADDRESS = 0

BIT

POSITION FUNCTION DESCRIPTION

31-27 Reserved Reserved. Set to 0 for proper operation. 26-24 Integrate/Dump Shifter

Gain

23-16 Input Level Detector

Threshold

15 Input Data Format Select 0 = Two’s Complement Input.

14 Serial/Parallel Input

Select

13 Input Level Detector

Output Select

12 Q Input to Complex

Multiplier

11 I Input to Complex

Multiplier

10 Complex Multiplier

Bypass

9 Demodulation/Loop

Filter Mode Select

8 Cartesian/Polar Input

Select

7 RRC Filter Enable 0 = Enable RRC filter.

6 Integrate and Dump

Filter Test Mode

5 Integrate and Dump

Input Select

4-1 Integrate and Dump

Decimation Select

0 OQPSK Data

De-Skew Select

These bits set the shifter attenuation in the Integrate/Dump Filter. 000 = No Shift (Gain = 2 001 = Right Shift 1 (Gain = 2 010 = Right Shift 2 (Gain = 2 011 = Right Shift 3 (Gain = 2 100 = Right Shift 4 (Gain = 2 Other Codes are invalid.

This register sets the magnitude threshold for the Input Level Detector (see “Input Level Detector” on page 6). This 8-bit value is a fractional unsigned number whose format is given by:

. 2-1 2-2 2-3 2-4 2-5 2-6 2-7.

2 The possible threshold values range from 0 to 1.9961 (00 - FF hex). The magnitude range for complex inputs is 0.0 to 1.4142 while that for real inputs range is 0.0 to 1.0. Note: The algorithm used to estimate threshold produces a maximum output of 1.375, therefore a threshold of greater than 1.375 will never be exceeded.

1 = Offset binary Input. 0 = Parallel Input.

1 = Serial Input. 0 = HI/LO output of 1 means input ≤ threshold.

1 = HI/LO output of 1 means input > threshold. 0 = QIN9-0 enabled to Complex Multiplier.

1 = Q input to Complex Multiplier zeroed. 0 = IIN9-0 enabled to Complex Multiplier.

1 = I input to complex multiplier set to negative full scale (200 Hex). 0 = Data enabled to Complex Multiplier (Multiplied by output of NCO).

1 = Complex Multiplier Bypassed. 0 = Error detector outputs routed to Loop Filters (Normal Mode of Operation).

1 = Part functions as dual Loop Filters. The IIN9-0 input is routed to the Symbol Loop Filter; the QIN9-0 input is routed to the Carrier Loop Filter. Data is gated into the Loop Filters with the assertion of SYNC

0 = Enable output of AGC Multiplier to Cartesian to Polar Converter. 1 = Enable output of Integrate and Dump Filter to the Cartesian to Polar Converter.

1 = Bypass RRC filter. 0 = End-Symbol Samples routed to Output Formatter.

1 = Both End and Mid Symbol routed to Output Formatter: End-symbol samples occur when

0 = Input taken from output of Frequency Discriminator (FSK routing). 1 = Input taken from output of AGC Multiplier (Select this setting for PSK demodulation).

Bit 4 is the MSB. 1000 = No Decimation (no accumulation, no sample pair summing). 0000 = Decimation by 2 (no accumulation, sample pair summing). 0001 = Decimation by 4 (accumulate 2 samples, sample pair summing). 0010 = Decimation by 8 (accumulate 4 samples, sample pair summing). 0011 = Decimation by 16 (accumulate 8 samples, sample pair summing). 0100 = Decimation by 32 (accumulate 16 samples, sample pair summing). All other codes are invalid.

0 = Disables Q channel data delay. 1 = Delays Q Channel by 1/2 Symbol time to remove OQPSK stagger.

SMBLCLK is high; Mid-Symbol samples occur when SMBLCLK is low.

-1

-2

-3

-4

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 16. POWER DETECT THRESHOLD CONTROL REGISTER

DESTINATION ADDRESS = 1

BIT

POSITION FUNCTION DESCRIPTION

31-8 Not Used No programming required.

7-0 Power Threshold The THRESH

exceeds the threshold programmed here. The threshold is represented as an 8-bit fractional unsigned value with the following format:

. 2-1 2-2 2-3 2-4 2-5 2-6 2-7.

2 Using this format, the possible range of threshold values is between 0 to 1.9961. Bit position 7 is the MSB.

TABLE 17. AGC LOOP PARAMETERS CONTROL REGISTER

BIT

POSITION FUNCTION DESCRIPTION

31 Enable AGC 0 = Gain error enabled to AGC Loop Filter.

1 = Gain error into AGC Loop Filter set to zero.

30-28 AGC Loop Gain

Exponent (E)

27-24 AGC Loop Gain

Mantissa (M)

23-16 AGC Threshold The AGC gain error is generated by subtracting the threshold value programmed here from the

These bits set the loop gain exponent as given by: AGC Loop Gain Exponent = 2

where EEE corresponds to the 3-bit binary value programmed here. Thus, a gain range from 2-7 to 2 may be achieved for EEE = 000 to 111 Binary. Bit position 30 is the MSB. See Table 3 on page 11.

The loop gain mantissa is represented as a 4-bit unsigned value with the following format: AGC Loop Gain Mantissa = 0. 2

This format provides a mantissa range from 0.0 to 0.9375 for mantissa settings from 0000 to 11 1 1 Binary . Bit position 27 is the MSB. Mantissa resolution = 0.0625. See Table 2 on page 11.

magnitude value out of the Cartesian-to-Polar Converter. The binary format for the AGC Threshold is the same as that for the Power Threshold given in Table 15 on page 32.

output is driven low when the magnitude output of the Cartesian-to-Polar Converter

DESTINATION ADDRESS = 2

-(7 + EEE)

-12-22-32-4

; 0.MMMM.

-14

AGC THRESHOLD

VALUE

1.1453 (42h) 0

0.8108 (67h) -3

0.5740 (49h) -6

0.4064 (34h) -9

0.2877 (24h) -12

15-8 AGC Upper Limit The upper 8 bits of the AGC Accumulator set the AGC gain. The v alue p ro gr amm ed here sets upper limit

for AGC gain by specifying a limit for the upper 8 bit s of the AGC accumulator. If the accumulated sum exceeds the upper limit, the accumulator is loaded with the limit. These bits are packed as eemmmmmm where the e’s correspond to the exponent bits an d th e m’s correspond to the mantissa bits of Equation 8 (see also Figure 8). Bit position 15 is the MSB. By setting the AGC upper and lower limits to the same value , the AGC can be set to a fixed gain.

7-0 AGC Lower Limit The value programmed here sets the lower limit for the upper 8 bits of the AGC accumulator in a manner

similar to that described for the upper limit. If the accumulated sum falls below the lower limit, the accumulator is loaded with the limit. The format for these bits is as described for the upp er limit. By settin g the AGC upper and lower limits to the same value , t he A GC ca n be set to a fixed gain.

TABLE 18. CARRIER PHASE ERROR DETECTOR CONTROL REGISTER

DESTINATION ADDRESS = 3

BIT

POSITION FUNCTION DESCRIPTION

31-8 Not Used No programming required.

7-6 Reserved Reserved. Set to 0 for proper operation.

RESULTING OUTPUT

LEVEL (dBFS)

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 18. CARRIER PHASE ERROR DETECTOR CONTROL REGISTER (Continued)

DESTINATION ADDRESS = 3

BIT

POSITION FUNCTION DESCRIPTION

5-2 Phase Offset These bits set the phase offset added (modulo 2π) to the phase output of the Cartesian-to-Polar

Converter. The phase offset is represented as a 4-bit fractional 2’s Complement value with the following binary format:

Phase Offset = -2 This format provides a range from 0.875 to -1 (0111 to 1000) which corresponds to phase offset settings

π/8 to -π respectively. Resolution of 22.5° is provided. Bit position 5 is the MSB.

from 7

1-0 Shift Factor The bits set the left shift required by the Carrier Phase Error Detector. These two bits specify a left shift

BIT

POSITION FUNCTION DESCRIPTION

31-8 Not Used No programming required.

7-3 Reserved Reserved. Set to 0 for proper operation. 2-0 Discriminator Delay The frequency detector (discriminator) computes frequency by subtracting a delayed phase term from

of 0, 1, 2 or 3 places. MSBs are discarded and LSBs are zero-filled. Bit 1 is the MSB.

TABLE 19. FREQUENCY DETECTOR CONTROL REGISTER

the current phase term (d set the delay as given by:

Delay = 2 where K is the 3-bit value programmed here. Delays of 1, 2, 4, 8, and 16 are possible.

. 2-12-22

DESTINATION ADDRESS = 4

-3.

θ/dt). A programmable delay is used to set the discriminator gain. These bits

TABLE 20. FREQUENCY ERROR DETECTOR CONTROL REGISTER

DESTINATION ADDRESS = 5

BIT

POSITION FUNCTION DESCRIPTION

31-8 Not Used No programming required.

7-3 Frequency Offset The s e b i ts set th e f r equency of fset added (modulo) to the frequency output of the discriminator. The frequency

2-0 Shift Factor These bits set the left shift required by the Frequency Error Detector. These two bits set a left shift of 0,

BIT

POSITION FUNCTION DESCRIPTION

31-8 Not Used No programming required.

7 Reserved Reserved. Set to 0 for proper operation. 6 Lead/Lag to Serial

Output Routing

offset is represented as a 5-bit fractional 2’s complement value with the following binary format: Frequency Offset = -2

This format provides a range from 0.9375 to -1.0 (0111 to 1000). The range and resolution of the frequency offset depend on the discriminator delay and input rate. The frequency offset is added to the 5 MSBs of the discriminator output. Note: Set the frequency offset to 0 when using frequency aided acquisition with PSK waveforms.

1, 2, 3, or 4 places. Bit 2 is the MSB. Values greater than 4 are invalid. Note: Set the shift factor to 0 when using frequency aided acquisition with PSK waveforms.

TABLE 21. CARRIER LOOP FILTER CONTROL REGISTER #1

0 = The Carrier Loop Filter’s Lag Accumulator is routed to the Serial Output Controller. 1 = The lead and lag paths in the Carrier Loop Filter are summed and routed to the Serial Output

Controller.

. 2-12-22-32

DESTINATION ADDRESS = 6

-4.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 21. CARRIER LOOP FILTER CONTROL

DESTINATION ADDRESS = 6

BIT

POSITION FUNCTION DESCRIPTION

5 Lead/Lag to Internal

NCO Routing

4-0 Error Accumulation These bits set the number of phase and frequency error measurements that are accumulated before the

BIT

POSITION FUNCTION DESCRIPTION

31-8 Not Used No programming required.

7-6 Reserved Reserved. Set to 0 for proper operation.

5 Lead Phase Error

Enable

4 Lag Phase Error

Enable

3 AFC Enable 0 = Frequency error enabled to lag processing path of Carrier Loop Filter.

2 Carrier Sweep Enable 0 = Frequency sweep input to the lag path of the Carrier Loop Filter enabled.

1 Invert Carrier Phase

Error

0 Invert Carrier

Frequency Error

0 = Sum of lead and lag paths routed to the internal NCO. (32 MSBs of sum are routed). 1 = The lead term is routed to the internal NCO. (32 MSBs of lead term are routed).

Carrier and AFC Loop Filters are run. Since the Loop Filters can only accept new inputs every 6 CLKs (normally at the symbol rate), the error accumulation is required to ensure that no phase or frequency error outputs are missed when error terms are generated at a rate greater than 1/6 CLK (see “Carrier Phase Error Detector” on page 18). The 5-bit value programmed here should be set to one less than the desired number of error terms to accumulate. For example, setting these bits to 0011 (BINARY) would cause 4 error terms to be accumulated. A total range from 1 to 32 is provided.

When error accumulation is used, divide the Lead Gain by the number of errors accumulated. Note that the LAG Gain does not need to be scaled since it increases to compensate for the delay, since it is an accumulator.

TABLE 22. CARRIER LOOP FILTER CONTROL REGISTER #2

DESTINATION ADDRESS = 7

0 = Carrier Phase Error enabled to lead processing path of loop filter. 1 = Carrier Phase Error to lead processing path of loop filter zeroed.

0 = Carrier Phase Error enabled to lag processing path of loop filter. 1 = Carrier Phase Error to lag processing path of loop filter zeroed (First Order Loop).

1 = Frequency error zeroed.

1 = Sweep input to Carrier Loop Filter zeroed. 0 = Carrier Phase Error is normal into Carrier Loop Filter.

1 = Carrier Phase Error is inverted into Carrier Loop Filter. 0 = Carrier Frequency Error is normal into AFC loop filter.

1 = Carrier Frequency Error is inverted into AFC Loop filter.

TABLE 23. CARRIER LOOP FILTER UPPER LIMIT CONTROL REGISTER

DESTINATION ADDRESS = 8

BIT

POSITION FUNCTION DESCRIPTION

31-0 Carrier Loop Filter

Upper limit

BIT

POSITION FUNCTION DESCRIPTION

31-0 Carrier Loop Filter

Lower limit

The 32-bit two’s complement value pr ogramme d here set s the up per sweep an d tracking limit of the Carrie r Loop Filter by setting the upper limit of the loop filter’s lag accumulator. If the limit is exceeded, the upper 32 bits of the 40-bit accumulator are set to the limit, and the 8 LSBs are set to zero.

TABLE 24. CARRIER LOOP FILTER LOWER LIMIT CONTROL REGISTER

DESTINATION ADDRESS = 9

The 32-bit two’s complement value programmed here sets the Lower sweep and tracking limit of the Carrier Loop Filter by setting the lower limit of the loop filter’s lag accumulator. If the running sum falls below the limit, the upper 32 bits of the 40-bit accumulator are set to the limit, and the 8 LSBs are set to zero.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 25. CARRIER LOOP FILTER GAIN (ACQ) CONTROL REGISTER

DESTINATION ADDRESS = 10

BIT

POSITION FUNCTION DESCRIPTION

31-24 Not Used No programming required. 23-18 Reserved Reserved. Set to 0 for proper operation. 17-14 Carrier Lead Gain

Mantissa (Acquisition)

13-9 Carrier Lead Gain

Exponent (Acquisition)

8-5 Carrier Lag Gain

Mantissa (Acquisition)

4-0 Carrier Lag Gain

Exponent (Acquisition)

These bits are the 4 fractional bits of the lead gain mantissa shown as follows. Lead Gain Mantissa = 0 1. 2 This format provides a mantissa range from 1.0 to 1.9375 for mantissa settings from 0000 to 11 1 1 Binary . Bit position 17 is the MSB.

These bits set the lead gain exponent as given by: Carrier Lead Gain Exponent = 2

where E corresponds to the 5-bit binary value programmed here. Thus, a gain range from

-1

-32

to 2

(relative to the MSB position of the NCO control word) may be achieved for E = 11 1 1 1 to 00000

Binary. Bit position 13 is the MSB. Format same as lead gain mantissa. Bit position 8 is the MSB.

Format same as lead gain exponent. Bit position 4 is the MSB.

-12-22-32-4.

-(32-E).

TABLE 26. CARRIER LOOP FILTER GAIN (TRK

DESTINATION ADDRESS = 11

BIT

POSITION FUNCTION DESCRIPTION

31-24 Not Used No Programming required. 23-18 Reserved Reserved. Set to 0 for proper operation. 17-14 Carrier Lead Gain

Mantissa (Track)

13-9 Carrier Lead Gain

Exponent (Track)

8-5 Carrier Lag Gain

Mantissa (Track)

4-0 Carrier Lag Gain

Exponent (Track)

BIT

POSITION FUNCTION DESCRIPTION

31-27 Reserved Reserved. Set to 0 for proper operation.

Format same as lead gain mantissa (see Table 25). Bit position 17 is the MSB.

Format same as lead gain exponent (see Table 25). Bit position 13 is the MSB.

Format same as lead gain mantissa (see Table 25). Bit position 8 is the MSB.

Format same as lead gain exponent (see Table 25). Bit position 4 is the MSB.

TABLE 27. FREQUENCY SWEEP/ AFC LOOP CONTROL REGISTER

DESTINATION ADDRESS = 12

) CONTROL REGISTER

26-23 Sweep Rate Mantissa

(Acquisition)

22-18 Sweep Rate Exponent

(Acquisition)

17-14 AFC Gain Mantissa

(Acquisition)

13-9 AFC Gain Exponent

(Acquisition)

Sets carrier track sweep rate used during acquisition (see “Frequency Sweep Block” on page 23). Format same as lead gain mantissa (see Table 25). Bit position 22 is the MSB.

Sets carrier track sweep rate used during acquisition (see “Frequency Sweep Block” on page 23). Format same as lead gain exponent (see Table 25). Bit position 22 is the MSB. M = 0000, E = 00000 is 2

Sets Frequency Error Gain. Format same as lead gain mantissa (see Table 25). Bit position 11 is the MSB.

Sets Frequency Error Gain. Format same as lead gain exponent (see Table 25). Bit position 4 is the MSB.

-28

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 27. FREQUENCY SWEEP/ AFC LOOP CONTROL REGISTER (Continued)

DESTINATION ADDRESS = 12

BIT

POSITION FUNCTION DESCRIPTION

8-5 AFC Gain Mantissa

(Track)

4-0 AFC Gain Exponent

(Track)

TABLE 28. CARRIER LAG ACCUMULATOR INITIALIZATION CONTROL REGISTER

BIT

POSITION FUNCTION DESCRIPTION

N/A Carrier Lag

Accumulator Initialization

Sets Frequency Error Gain. Format same as lead gain mantissa (see Table 25). Bit position 11 is the MSB.

Sets Frequency Error Gain. Format same as lead gain exponent (see Table 25). Bit position 4 is the MSB.

DESTINATION ADDRESS = 13

Writing this address initializes the lag accumulator with the contents of the 4 Microprocessor Interface Holding Registers at the start of the next Carrier Loop Filter Computation cycle. The contents of the holding registers should not be changed until after the start of a new compute cycle, since the current contents of the holding registers are loaded at the compute cycle start. The Microprocessor Interface can be used to read an Internal Status Register which signals when the lag accumulator load is complete (see “Microprocessor Interface” on page 27). The contents of the holding registers are loaded into the 32 MSBs of the lag accumulator and the 8 LSBs are zeroed.

It is good practice to load the LAG Accumulators at the very end of a configuration load sequence.

TABLE 29. SYMBOL TRACKING LOOP CONFIGURATION CONTROL REGISTER

DESTINATION ADDRESS = 14

BIT

POSITION FUNCTION DESCRIPTION

31-16 Not Used No programming required. 15-13 Reserved Reserved. Set to 0 for proper operation.

12-11 Sampling Error Shift

Factor

10-9 Modulation Order

Select

The sampling error shifter is provided to left shift the sampling error to full scale before input to the Symbol Tracking Loop Filter . The magnitude of the sampling error varies with the number of symbol decision levels, and a left shift of 1 to 4 places is provided as required by modulation order . Suggested settings are provided in the following: 00 = x2 2 levels on each rail (BPSK, QPSK). 01 = x4 4 levels on each rail (8 PSK). 10 = x8 8 levels on each rail. 11 = x16 16 levels on each rail. Note: Saturation is provided in case of overflow.

These bits set the threshold levels used by the symbol decision blocks in the Sampling Error detector. The end-symbol samples on either the I or Q processing path are compared against the selected threshold set to determine the expected symbol value used in calculating the transition midpoint. The threshold levels can be set for up to 16ary signals on both the I and Q processing path. The decision thresholds are set as as follows. 00 = 2ary signal (Use this setting for BPSK, QPSK, and OQPSK signals). 01 = 4ary signal. 10 = 8ary signal. 11 = 16ary signal. The threshold levels are determined by equally dividing up the signal range by the order of the signal. For example, a 2ary signal would divide the signal would have thresholds at:

-0.5, 0, and +0.5.

~1.0 to -1.0 signal range by two forcing threshold at 0.0. A 4ary

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 29. SYMBOL TRACKING LOOP CONFIGURATION CONTROL REGISTER (Continued)

DESTINATION ADDRESS = 14

BIT

POSITION FUNCTION DESCRIPTION

8 Single/Double Rail

Sampling Error

7-3 Sampling Error

Accumulation

2 Lead Sampling Error

Enable

1 Lag Sampling Error

Enable

0 Invert Sampling Error 0 = Sampling error normal.

TABLE 30. SYMBOL TRACKING LOOP FILTER UPPER LIMIT CONTROL REGISTER

BIT

POSITION FUNCTION DESCRIPTION

31-0 Symbol Tracking

Loop Filter Upper Limit

This bit sets whether sampling error is derived from symbol transitions on just the I rail (single rail) or both the I and Q rails (dual rail). In single rail operation sampling error from the Q rail is nulled and only the I rail is used. In dual rail operation the sampling error from both the I an Q rails is summed and then scaled by one half. 0 = Dual Rail Operation. 1 = Single Rail Operation. Note: Set to 1 for BPSK operation and 0 for QPSK operation.

These bits set the number of sampling error measurements to accumulate before running the Symbol Loop Filter. The loop filter requires 8 CLKs to compute an output. The sampling error detector generates error terms at the symbol rate. Thus, the error accumulator must be used if the symbol rate exceeds 1/8 CLK to ensure that no error terms are missed (see “Sampling Error Detector” on page 17). The 5-bit value programmed here is set to one less than the desired number of error terms to accumulate. For example, setting these bits to 00011 (BINARY ) would cause 4 error terms to be accumulated. A total range from 1 to 32 is provided.

0 = Sampling error enabled to lead path of loop filter. 1 = Sampling error to lead path of loop filter zeroed.

Sampling error enabled to lag path of loop filter.

0 = 1 = Sampling error to lag path of loop filter zeroed (First Order Loop).

1 = Sampling error inverted.

DESTINATION ADDRESS = 15

The 32-bit two’s complement value programmed here sets the upper tracking limit of the Symbol Tracking Loop Filter by setting the upper limit of the loop filter’s lag accumulator. If the limit is exceeded, the upper 32 bits of the 40-bit accumulator are set to the limit, and the 8 LSBs are set to zero.

TABLE 31. SYMBOL TRACKING LOOP FILTER LOWER LIMIT CONTROL REGISTER

DESTINATION ADDRESS = 16

BIT

POSITION FUNCTION DESCRIPTION

31-0 Symbol Tracking

Loop Filter Lower Limit

TABLE 32. SYMBOL TRACKING LOOP FILTER GAIN (ACQ) CONTROL REGISTER

BIT

POSITION FUNCTION DESCRIPTION

31-24 Not Used No programming required. 23-18 Reserved Reserved. Set to 0 for proper operation. 17-14 Symbol Tracking

Lead Gain Mantissa (Acquisition)

The 32-bit two’s complement value programmed here sets the Lower tracking limit of the Symbol Tracking Loop Filter by setting the lower limit of the loop filter’s lag accumulator. If the running sum falls below the limit, the upper 32 bits of the 40-bit accumulator are set to the limit, and the 8 LSBs are set to zero.

DESTINATION ADDRESS = 17

These bits are the 4 fractional bits of the lead gain mantissa shown as follows: Symbol Tracking Lead Gain Mantissa = 01. 2

This format provides a mantissa range from 1.0 to 1.9375 for mantissa settings from 0000 to 1111 Binary. Bit position 17 is the MSB.

-12-22-32-4.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 32. SYMBOL TRACKING LOOP FILTER GAIN (ACQ) CONTROL REGISTER (Continued)

DESTINATION ADDRESS = 17

BIT

POSITION FUNCTION DESCRIPTION

13-9 Symbol Tracking

Lead Gain Exponent (Acquisition)

8-5 Symbol Tracking Lag

Gain Mantissa (Acquisition)

4-0 Symbol Tracking Lag

Gain Exponent (Acquisition)

TABLE 33. SYMBOL TRACKING LOOP FILTER GAIN (TRK) CONTROL REGISTER

BIT

POSITION FUNCTION DESCRIPTION

31-24 Not Used No programming required. 23-18 Reserved Reserved. Set to 0 for proper operation. 17-14 Symbol Tracking Lead Gain Mantissa

(Track)

13-9 Symbol Tracking Lead Gain Exponent

(Track)

8-5 Symbol Tracking Lag Gain Mantissa

(Track)

4-0 Symbol Tracking Lag Gain Exponent

(Track)

These bits set the lead gain exponent as given by: Symbol Tracking Lead Gain Exponent = 2

where E corresponds to the 5-bit binary value programmed here. Thus, a gain range from

-1

-32

to 2

2 Binary. Bit position 13 is the MSB.

Format same as lead gain mantissa. Bit position 8 is the MSB.

Format same as lead gain exponent. Bit position 4 is the MSB.

relative to the MSB position of the NCO control word may be achieved for E = 11111 to 00000

DESTINATION ADDRESS = 18

Format same as lead gain mantissa (see Table 32). Bit position 17 is the MSB.

Format same as lead gain exponent (see Table 32). Bit position 13 is the MSB.

Format same as lead gain mantissa (see Table 32). Bit position 8 is the MSB.

Format same as lead gain exponent (see Table 32). Bit position 4 is the MSB.

-(32-E),

TABLE 34. SYMBOL TRACKING LOOP FILTER LAG ACCUMULATOR INITIALIZATION CONTROL REGISTER

DESTINATION ADDRESS = 19

BIT

POSITION FUNCTION DESCRIPTION

N/A Symbol Tracking Loop

Filter Lag Accumulator Initialization

Writing to this address initializes the lag accumulator with the contents of the four Microprocessor Interface Holding Registers at the start of the next loop filter computation cycle. The contents of the holding registers should not be changed until after the start of a new compute cycle since the current contents of the holding registers are loaded at the compute cycle start. At a slow rate, it could take 1 low rate symbol time to change. The Microprocessor Interface should be used to read an internal status register which signals when the lag accumulator load is complete (see Table 13 in the “Microprocessor Interface” on page 27). The contents of the holding registers are loaded into the 32 MSBs of the lag accumulator and the 8 LSBs are zeroed.

It is a good practice to load the LAG accumulators at the very end of a configuration load sequence.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 35. LOCK DETECTOR CONFIGURATION CONTROL REGISTER

DESTINATION ADDRESS = 20

BIT

POSITION FUNCTION DESCRIPTION

31-28 Reserved Reserved. Set to 0 for proper operation.

27 False Lock

Accumulator Operation

26-20 Dwell Counter

Pre-load

19-10 Integration Counter

Pre-Load (Acquisition)

9-0 Integration Counter

Pre-Load (Track)

BIT

POSITION FUNCTION DESCRIPTION

31-16 Lock Accumulator Pre-

Load (Acquisition)

This bit selects the input to the False Lock Accumulator. 0 = Frequency Error input enabled to accumulator. 1 = False Lock Bit enabled to accumulator.

The Dwell Counter holds off the Lock Accumulator integration for the number of integration cycles programmed here. The length of the integration cycle is set in the bit positions 19-10. The 7-bit value programmed here should be set to 1 less than the desired hold off time in integration cycles. The pre-load is zeroed during Track Mode. Only used during stepped acquisition mode.

The Integration Counter controls the number Phase Error samples accumulated by the Lock Accumulator. The 10-bit number loaded here is set to two less than the number of Phase Error samples desired in the Integration Period. Total Range 2 to 1025. Bit 19 is the MSB.

Function is identical to Acquisition Integration Counter Pre-Load. See previous.

TABLE 36. LOCK ACCUMULATOR PRE-LOADS CONTROL REGISTER

DESTINATION ADDRESS = 21

The lock threshold is set by an accumulator pre-load which is backed off from the accumulator full scale by the threshold amount. The Lock Accumulator is 18 bits and the accumulator bit weightings relative to the magnitude of the Phase Error input and the pre-load is as follows:

BIT WEIGHTING OF ACCUMULATOR PRE-LOAD

210 29 28 27......2

-12-2 2-3 2-4 2-5 2-6 2-7

. 2

BINARY POINT

The accumulator roll over is at the 2

15-0 Lock Accumulator Pre-

Load (Track)

TABLE 37. FALSE LOCK ACCUMULATOR PRE-LOAD CONTROL REGISTER

BIT

POSITION FUNCTION DESCRIPTION

31-16 False Lock

Accumulator Pre-Load (Acquisition)

15-0 False Lock

Accumulator Pre-Load (Track)

Function is identical to Acquisition Lock Accumulation Pre-Load. See previous.

DESTINATION ADDRESS = 22

Depending on configuration, the input to the False Lock Accumulator is either the false lock indicator bit or the magnitude of the frequency error detector output. Like the Lock Accumulator, the threshold is set by an accumulator pre-load that is backed off from accumulator full scale. The False Lock Accumulator can accumulate sums up to 18 bits, and the bit weightings of the false lock indicator bit and the frequency error input relative to accumulator full scale are shown as follows.

BIT WEIGHTING OF ACCUMULATOR PRE-LOAD

210 29 28 27......2

BINARY POINT

The accumulator roll over is at the 2 See previous. The Lock Detector State Machine only uses the accumulator during the verify state during

which the Track parameters are used.

bit position.

-12-2 2-3 2-4 2-5 2-6 2-7

. 2

BIT WEIGHTING OF

FREQUENCY ERROR MAGNITUDE

bit position.

BIT WEIGHTING OF

PHASE ERROR MAGNITUDE

BIT WEIGHTING OF

FALSE LOCK INDICATOR BIT

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 38. ACQUISITION/TRACKING CONTROL REGISTER

DESTINATION ADDRESS = 23

BIT

POSITION FUNCTION DESCRIPTION

31-16 Not Used No programming required.

15 Reserved Set to 0 for proper operation. 14 False Lock Detect

Enable

13 Frequency Sweep

Mode

12-9 Verify State Length These bits set the number of integration cycles over which carrier lock must be maintained before the

8-5 False Lock Sweep These bits set the duration of forced frequency sweep before returning to the acquisition state.

4 Lock Detector Control This bit selects whether the acquisition/tracking process is controlled externally by a microprocessor or

This bit enables the false lock detection during the verify state of state machine controlled acquisition. The overflow of the False Lock Accumulator before the Integration Counter forces the false lock state. If disabled, the overflow of the False Lock Accumulator has no effect on state machine operation. 0 = Disable False Lock. 1 = Enable False Lock. Note: The false Lock Detector is designed for false lock detection on square wave data. For shaped waveforms false lock detection should be disabl ed or freque ncy error shou ld be used.

This bit selects whether stepped or continuous frequency sweep mode is used (see “Lock Detector” on page 23). 0 = Stepped Frequency Sweep (provided for microprocessor controlled acquisition mode). 1 = Continuous Frequency Sweep.

Lock State is declared. The verify state is used to make sure that lock detection was not the result of noise or false lock. The 4-bit value programmed here sets the verify state from 0 to 15 Integration Periods.

When

continuous frequency sweep mode is selected, the programmed number represents the number of Lock Accumulator integration cycles to sweep before returning to the acquisition state. In stepped frequency sweep mode, the number represents the number of loop filter compute cycles over which to enable the sweep input to the lag accumulator.

internally by the state machine. If microprocessor control is chosen, the lock detect accumulator integrates for the programmed period of time and ignores accumulator roll over, if any. The Lock Detector Accumulator halts after each Integration Period and waits to be restarted by the microprocessor. In addition, the microprocessor must select the acquisition/tracking parameters, as well as enable the Frequency Sweep Block. 0 = Microprocessor Control. 1 = Internal State Machine Control.

3 Microprocessor

Acquisition/Track Select

2 Microprocessor Lock This bit controls the state of the lock bit (STATUS6) in the status output STATUS6-0 (see “Output

1 Reserved Set to zero for proper operation. 0 Microprocessor

Frequency Sweep Enable

0 = Track Parameters Chosen. 1 = Acquisition Parameters Chosen.

Selector” on page 26). In addition, this bit sets the internal state machine to the locked state when Lock Detector Control is switched from microprocessor control to state machine control. See Table 47 for the STATUS bit information.

This bit is used to enable the output of the Frequency Sweep Block to the lag path of the Symbol Tracking Loop Filter. This bit is only used under microprocessor control of the Lock Detector.

July 2, 2008

FN3652.5

HSP50210

www.BDTIC.com/Intersil

TABLE 39. HALT LOCK DETECTOR FOR READING CONTROL REGISTER

DESTINATION ADDRESS = 24

BIT

POSITION FUNCTION DESCRIPTION

N/A Stop Lock Detector for

Reading

BIT

POSITION FUNCTION DESCRIPTION

N/A Restart Lock Detector Writing this location restarts the Lock Detector State Machine following a read of the Lock Detector . Note:

TABLE 41. SOFT DECISION SLICER CONFIGURATION CONTROL REGISTER

BIT

POSITION FUNCTION DESCRIPTION

31-8 Not Used No programming required.

7 Slicer Output Format 0 = Soft decision outputs are in sign/magnitude format.

Writing this location halts the Lock Detector State Machine at the end of t he curr ent L ock De tect or Accumulator integration cycle. This function is provided so that the Lock Detector integrators can be stopped for reading via the microprocessor interface (only useful when the Lock Detector is under internal state machine control). Bit 7 of t he int erna l status r egist er ca n b e mon ito re d via t he Microprocessor Interface to determine when the Lo ck Detector has stoppe d and is read y for read ing. See Table 14 for information on the internal status bits. The Lock Detector will remain stopped until restarted (see Restart Lock Detector Contro l Re gister : Table 40).

TABLE 40. RESTART LOCK DETECTOR CONTROL REGISTER

DESTINATION ADDRESS = 25

Stopping the Lock Detector for reading is not required in Microprocessor Control Mode since the Lock Detector Accumulators stop at the end of each integration cycle. See also Table 45.

DESTINATION ADDRESS = 26

1 = Soft decision outputs are in two’s complement format.

6-0 Soft Decision

Threshold

BIT

POSITION FUNCTION DESCRIPTION

31-16 Not Used No programming required. 15-13 Reserved Set to zero for proper operation.

12 Serial Data Sync

Polarity (SOF output)

11 Serial Data Sync

Polarity (COF output)

The input to the slicer is compared against thresholds which are 1x, 2x and 3x the value programmed here. The slicer output depends on the relationship of the I or Q magnitude to the 3 soft thresholds as given in Table 9. The threshold is programmed as a fractional unsigned value with the following bit weightings:

-12-2 2-3 2-4 2-5 2-6 2-7

0. 2 Note: Since the signal magnitude on either the I or Q path ranges between 0.0 and value should not exceed 1.0/3 = 0.33. Bit position 6 is the MSB.

TABLE 42. SERIAL OUTPUT CONFIGURATION CONTROL REGISTER

DESTINATION ADDRESS = 27

0 = SOFSYNC pulses “High” one serial clock before data word on SOF. 1 = SOFSYNC pulses “Low” one serial clock before data word on SOF. Set to 0 for use with the HSP50110.

0 = COFSYNC pulses “High” one serial clock before data word on COF. 1 = COFSYNC pulses “Low” one serial clock before data word on COF. Set to 0 for use with the HSP50110.

~1.0, the threshold

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 42. SERIAL OUTPUT CONFIGURATION CONTROL REGISTER (Continued)

DESTINATION ADDRESS = 27

BIT

POSITION FUNCTION DESCRIPTION

10 Serial Clock Phase

Relative to Data

9-8 Serial Clock Divider These bits set the clock rate of SLOCLK.

7 Serial Clock Select for

COF Output

6-4 Serial Word Length for

COF Output

3 Serial Clock Select for

SOF Output

2-0 Serial Word Length for

SOF Output

0 = Rising edge of serial clock at center of data bit. 1 = Falling edge of serial clock at center of data bit. Set to 0 for use with the HSP50110.

00 -> SLOCLK = CLK/2. 01 -> SLOCLK = CLK/4. 10 -> SLOCLK = CLK/8. 11 -> SLOCLK = CLK/16.

0 = CLK is used as the serial clock. 1 = SLOCLK is used as the serial clock. Note: If the HSP50210 is used together with the HSP50110, CLK must be selected as the serial clock for the SOF and COF outputs, and the same CLK must be used by both chips.

000 = 8 Bits 001 = 12 Bits 010 = 16 Bits 011 = 20 Bits 100 = 24 Bits 101 = 28 Bits 110 = 32 Bits 111 = 40 Bits

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

BIT POSITION FUNCTION DESCRIPTION

31-8 Not Used No programming required.

7-4 Reserved Set to zero for proper operation. 3-0 Output Select These bits select which input signals are routed to the 20 output pins AOUT9-0 and BOUT9-0. The signal

TABLE 43. OUTPUT SELECTOR CONFIGURATION CONTROL REGISTER

DESTINATION ADDRESS = 28

selections are listed below in Tables 43A and 43B.

Definition of Signal Bus Names

DATA SIGNAL BUSSES

ISOFT(2:0) This bus is the I channel soft decision slicer output data, expressed in the data format set

QSOFT(2:0) This bus is the Q channel soft decision slicer output data, expressed in the data format set

IEND(7:1) This bus is the 7 MSBs of I end symbol sample into the soft decision slicer, in 2’s

QEND(7:1) This bus is the 7 MSBs of Q end symbol sample into the soft decision slicer, in 2’s

STATUS SIGNAL PARAMETER BUSSES

AGC(7:1) . . . . . .This bus is the 7 MSBs of the AGC Accumulator Register. (MSB = AGC7).

MAG (7:0) . . . . .This bus is the 8-bit magnitude output of the Cartesian to Polar converter, in unsigned

PHASE (7:0) . . .This bus is the 8-bit phase output of the Cartesian to Polar converter, in unsigned binary

FE(7:1) . . . . . . .This bus is the seven MSBs of the Frequency Error Detector Output Register, in 2’s

GE (7:1) . . . . . .This bus is the seven MSBs of the Gain Error (AGC) Accumulator Register, in 2’s

TE (7:1) . . . . . .This bus is the seven MSBs of the Bit Phase Error Detector Output Register, in 2’s

CARPE (7:1) . . .This bus is the seven MSBs of the Carrier Phase Error Detector Output Register, in 2’s

LKACC(6:0) . . .This bus is the seven LSBs of the Phase Error Accumulator Register in the Lock Detector,

LKCNT(6:0) . . .This bus is the seven LSBs of the Integration Counter in the Lock Detector, in one’s

NCOCOS(9:0) . .This bus is the 10-bit two’s complement output of the DCL NCO, in 2’s complement

by CW26 bit 7, with one sign bit (ISOFT2) and two soft decision bits.

by CW26 bit 7, with one sign bit (QSOFT2) and two soft decision bits.

complement format. (MSB = Iend7).

complement format. (MSB = Qend7).

binary format. (MSB = MAG7).

format. (MSB = PHASE7).

complement format. (MSB = FE7).

complement format. (MSB = GE7).

complement format. (MSB = TE7).

complement format. (MSB = PE7).

in unsigned offset binary format. (MSB = LKA CC6) I f accumu la tion Bi ts 14-17 = 1, then Bits 7-13 are output as LKACC(6.0). These output s a re zero otherwise.

complement format. (MSB = LKCNT6) If Bits 7-9 of the accumulator are zero, then Bits 0-6 are output as LKCNT(6-0). These outputs are zero otherwise.

format. (MSB = NCOCOS7).

Applications for the Various Output Signals

ISOFT(2:0) and QSOFT(2:0)

These signals provide a simple interface to a FEC decoder. As the mo st likely to be used output bus, these signals are included in all but one of the programmable multiplexer outpu t conf ig urations.

IEND(7:1) and QEND(7:1)

These signals are useful when input to a D/A converter and displayed on a n oscilloscope in the X-Y plot . This will yield the constellation signal display with which analog modem designers are familiar.

STATUS(6:0)

These signals can be used in fault detection for use in BIT/BITE applications and are useful during system debug.

AGC(7:1)

This signal is useful in monitoring the AGC operation, signal detection and antenna tracking applications. Other single bit signals are provided for direct use in external AGC.

MAG(7:0) and PHASE(7:0)

These signals are useful in signal detection applications, where presence of a signal is represented by a particular signal magnitude or phase.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 43. OUTPUT SELECTOR CONFIGURATION CONTROL REGISTER (Continued)

DESTINATION ADDRESS = 28

BIT POSITION FUNCTION DESCRIPTION

FREQERR(7:1), GAINERR(7:1), BITPHERR(7:1), and CARPHERR(7:1)

These signals are useful in applications that need these signals output at the symbol rate and available for hardwiring, rather than at the processor access rate. Configurations that use the DCL as a stand alone demodulator and matched filter are examples of such applications.

LKACC(6:0) and LKCNT(6:0)

These signals are provided for applications which require a lock detection interface that is not processor dependent. These signals are also useful in fault detection in BIT/BITE applications.

NCOCOS(9:0)

This signal is provided for use when the DCL is configured as a stand alone Loop Filter and NCO. This signal can be useful in fault detection in BIT/BITE applications.

TABLE 43A. AOUT BIT DEFINITIONS

OUTPUT

SELECTAOUT 9AOUT 8AOUT 7AOUT 6AOUT 5 AOUT 4 AOUT 3 AOUT 2 AOUT 1 AOUT 0

0000 ISOFT2 ISOFT1 ISOFT0 QSOFT2 QSOFT1 QSOFT0 STATUS6 STATUS5 STATUS4 STATUS3 0001 ISOFT2 QSOFT2 MAG7 MAG6 MAG5 MAG4 MAG3 MAG2 MAG1 MAG0 0010 ISOFT2 ISOFT1 ISOFT0 QSOFT2 QSOFT1 QSOFT0 STATUS6 STATUS5 STATUS4 STATUS3 0011 ISOFT2 ISOFT1 ISOFT0 QSOFT2 QSOFT1 QSOFT0 STATUS6 STATUS5 STATUS4 STATUS3 0100 ISOFT2 ISOFT1 ISOFT0 QSOFT2 QSOFT1 QSOFT0 STATUS6 STATUS5 STATUS4 STATUS3 0101 ISOFT2 ISOFT1 ISOFT0 QSOFT2 QSOFT1 QSOFT0 STATUS6 STATUS5 STATUS4 STATUS3 0110 ISOFT2 ISOFT1 ISOFT0 QSOFT2 QSOFT1 QSOFT0 LKACC6 LKACC5 LKACC4 LKACC3

0111 ISOFT2 ISOFT1 ISOFT0 QSOFT2 QSOFT1 QSOFT0 Iend7 Iend6 Iend5 Iend4

1000 RSRVD7 RSRVD6 RSRVD5 RSRVD4 RSRVD3 RSRVD2 RSRVD1 RSRVD0 STATUS5 STATUS6

TABLE 43B. BOUT BIT DEFINITION

OUTPUT

SELECT BOUT 9 BOUT 8 BOUT 7 BOUT 6 BOUT 5 BOUT 4 BOUT 3 BOUT 2 BOUT 1 BOUT 0

0000 STATUS2 STATUS1 STATUS0 AGC7 AGC6 AGC5 AGC4 ACG3 AGC2 AGC1 0001 STATUS6 STATUS0 PHASE7 PHASE6 PHASE5 PHASE4 PHASE3 PHASE2 PHASE1 PHASE0 0010 STATUS2 STATUS1 STATUS0 FE7 FE6 FE5 FE4 FE3 FE2 FE1 0011 STATUS2 STATUS1 STATUS0 GE7 GE6 GE5 GE4 GE3 GE2 GE1 0100 STATUS2 STATUS1 STATUS0 TE7 TE6 TE5 TE4 TE3 TE2 TE1 0101 STATUS2 STATUS1 STATUS0 CARPE7 CARPE6 CARPE5 CARPE4 CARPE3 CARPE2 CARPE1 0110 LKACC2 LKACC1 LKACC0 LKCNT6 LKCNT5 LKCNT4 LKCNT3 LKCNT2 LKCNT1 LKCNT0

0111 Iend3 Iend2 Iend1 Qend7 Qend6 Qend5 Qend4 Qend3 Qend2 Qend1

1000 NCOCOS9 NCOCOS8 NCOCOS7 NCOCOS6 NCOCOS5 NCOCOS4 NCOCOS3 NCOCOS2 NCOCOS1 NCOCOS0

TABLE 44. UPDATE READ REGISTER CONFIGURATION CONTROL REGISTER

DESTINATION ADDRESS = 29

BIT

POSITION FUNCTION DESCRIPTION

N/A Load Output Holding

Loading the Address Register with this destination address samples the contents of the Carrier Loop Filter Lag Accumulator, Symbol Tracking Loop Filter Lag Accumulator, and the AGC Accumulator. The sampled accumulator values are loaded into the output holding registers for reading via the Microprocessor Interface. Allow 6 CLKs until the output holding register is stable for reading.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

TABLE 45. INITIALIZE LOCK DETECTOR (μP CONTROL MODE) CONTROL REGISTER

DESTINATION ADDRESS = 30

BIT

POSITION FUNCTION DESCRIPTION

N/A Initialization of Lock

Detector Accumulators

BIT

POSITION FUNCTION DESCRIPTION

31-16 Not Used No programming required.

15-6 Reserved Set to 0 for proper operation.

5 Initialize NCO This bit is used to zero the feed back in the NCO’s phase accumulator . This is useful in setting the output

4 Zero Symbol Tracking

Loop Filter Accumulator

3 Zero Carrier Loop Filter

Accumulator

2-0 Reserved Set to 0 for proper operation.

Loading the address register with this destination address pre-loads all of the Lock Detector Accumulators and resets the Integration Counters to restart the integration process. Note: A write to this address only initializes the Lock Detector when it is in microprocessor control mode (see Acquisition/Tracking Control Register; Table 38 on page 41).

TABLE 46. TEST CONFIGURATION CONTROL REGISTER

DESTINATION ADDRESS = 31

of the NCO to a known value. 0 = Enable normal NCO operation. 1 = Zero phase accumulator feedback for test.

This bit is used to zero the lag accumulator in the Symbol Tracking Loop Filter. 0 = Enable normal loop filter operation. 1 = Zero Lag Accumulator.

This bit is used to zero the lag accumulator in the Carrier Loop Filter. 0 = Enable normal loop filter operation. 1 = Zero Lag Accumulator.

TABLE 47. STATUS 6-0 SIGNAL DESCRIPTIONS

BIT

POSITION FUNCTION DESCRIPTION

6 Carrier Lock 0 = Lock Detector is not in locked state (Carrier Tracking Loop is not locked).

1 = Lock Detector has achieved the locked state (Carrier lock has been achieved).

5 Acquisition/Track

indicator 4 Reserved N/A. 3 Frequency Sweep

Direction

2 High Power This bit is one clock cycle long and indicates when the AGC is at its lower limit (see “AGC” on page 10

1 Low Power This bit is one clock cycle long and indicates when the AGC is at its upper limit (see “AGC” on page 10

0 Data Ready Strobe This bit pulses “High” for one CLK synchronous with a new signal output on OUTB6-0 (see Output

0 = Tracking Parameters currently being used by Tracking Loops. 1 = Acquisition Parameters currently being used by Tracking Loops.

This bit indicates the direction of the frequency sweep selected by the Frequency Sweep input to the lag path of the Carrier Tracking Loop Filter (Defined for upper sideband signals). 0 = Up (Sweep increasing in frequency). 1 = Down (Sweep decreasing in frequency).

and Table 17 on page 33). 0 = AGC above lower limit. 1 = AGC at lower limit.

and Table 17 on page 33). 0 = AGC is at or below its upper limit. 1 = AGC is above its upper limit.

Selector Control Register: Table 43 on page 44). For example if the lower 4 bits of the Output Selector Register are set to 0010 (BINARY), This bit will pulse active on the same CLK that new FE7-1 data is output.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

Appendix A

Noise Bandwidth Summary

For a given decimation rate, the double-sided noise equivalent bandwidth is shown using various combinations of the CIC filter and the compensation filters in the HSP50110. Each combination of filters is also shown with

TABLE 48. TABLE A

INTE-

GRATE/

DEC

2 1.0000 1.3775 0.492771 0.5348 0.6250 1.3937 0.420829 0.531055 10 1.0000 1.3775 0.492771 0.5348 0.5525 1.0785 0.402135 0.501525 18 1.0000 1.3775 0.492771 0.5348 0.5508 1.0714 0.401628 0.500731 26 1.0000 1.3775 0.492771 0.5348 0.5504 1.0698 0.401510 0.500547 34 1.0000 1.3775 0.492771 0.5348 0.5502 1.0691 0.401465 0.500477 42 1.0000 1.3775 0.492771 0.5348 0.5501 1.0688 0.401443 0.500443 50 1.0000 1.3775 0.492771 0.5348 0.5501 1.0687 0.401431 0.500424

DUMP

INTEGRATE/

DUMP

W/COMP

INT/DUMP

AND RRC

INT/DUMP

W/COMP

AND RRC

and without the root raised cosine filter in the HSP50210. The noise bandwidth (Note 6) is measured relative to the output sample rate.

3RD

ORDER CIC

3RD ORDER

CIC W/COMP

3RD ORDER CIC

AND RRC

3RD ORDER

CIC W/COMP

AND RRC

58 1.0000 1.3775 0.492771 0.5348 0.5501 1.0686 0.401424 0.500410 66 1.0000 1.3775 0.492771 0.5348 0.5501 1.0685 0.401424 0.500404 74 1.0000 1.3775 0.492771 0.5348 0.5500 1.0684 0.401415 0.500408 82 1.0000 1.3775 0.492771 0.5348 0.5500 1.0684 0.401462 0.500215 90 1.0000 1.3775 0.492771 0.5348 0.5500 1.0684 0.401598 0.501272 98 1.0000 1.3775 0.492771 0.5348 0.5500 1.0684 0.400708 0.499348

106 1.0000 1.3775 0.492771 0.5348 0.5500 1.0684 0.400933 0.497418 114 1.0000 1.3775 0.492771 0.5348 0.5500 1.0683 0.403557 0.501420

122-4096 1.0000 1.3775 0.492771 0.5348 0.5500 1.0683 - -

NOTE:

6. Noise Bandwidth of RRC Filter is 0.492676.

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

Absolute Maximum Ratings Thermal Information

Supply Voltage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . +7.0V

Input, Output Voltage. . . . . . . . . . . . . . . . .GND -0.5V to V

ESD . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .Class 3

+0.5V

Operating Conditions

Voltage Range. . . . . . . . . . . . . . . . . . . . . . . . . . . .+4.75V to +5.25V

Temperature Range

HSP50210JC (Commercial). . . . . . . . . . . . . . . . . . . 0°C to +70°C

HSP50210JI (Industrial). . . . . . . . . . . . . . . . . . . . .-40°C to +85°C

CAUTION: Do not operate at or near the maximum ratings listed for extended periods of time. Exposure to such conditions may adversely impact product reliability and result in failures not covered by warranty.

NOTE:

7. θ

is measured in free air with the component mounted on a high effective thermal conductivity test board with “direct attach” features. See

Tech Brief TB379.

Thermal Resistance (Typical, Note 7) θ

PLCC Package. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

Maximum Storage Temperature. . . . . . . . . . . . . . . .-65°C to +150°C

Maximum Junction Temperature PLCC . . . . . . . . . . . . . . . . .+150°C

Pb-Free Reflow Profile. . . . . . . . . . . . . . . . . . . . . . . . .see link below

http://www.intersil.com/pbfree/Pb-FreeReflow.asp

Die Characteristics

Gate Count . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45,000

°C/W

DC Electrical Specifications V

PARAMETER SYMBOL TEST CONDITIONS MIN MAX UNITS

Power Supply Current I

Standby Power Supply Current I Input Leakage Current I Output Leakage Current I Clock Input High V Clock Input Low V Logical One Input Voltage V Logical Zero Input Voltage V Logical One Output Voltage V Logical Zero Output Voltage V Input Capacitance C Output Capacitance C

NOTES:

8. Power supply current is proportional to frequency. Typical rating is 4mA/MHz.

9. Output load per test circuit and C

10. Not tested, but characterized at initial design and at major process/design changes.

= 5.0V ±5%, TA = 0°C to +70°C (Commercial), TA = -40°C to +85°C (Industrial). Parameters with

MIN and/or MAX limits are 100% tested at +25°C, unless otherwise specified. Temperature limits established by characterization and are not production tested.

VCC = Max, CLK = 52.6MHz (Notes 8, 9)

VCC = Max, Outputs Not Loaded - 500 µA VCC = Max, Input = 0V or V VCC = Max, Input = 0V or V VCC = Max, CLK 3.0 - V VCC = Min, CLK - 0.8 V VCC = Max 2.0 - V VCC = Min - 0.8 V IOH = -400µA, VCC = Min 2.6 - V IOL = 2mA, VCC = Min - 0.4 V f

= SCLK = 1MHz

CLK

All measurements referenced to GND.

= +25°C (Note 10)

= 40pF.

CCOP

CCSB

O IHC ILC

OUT

CC CC

- 225 mA

-10 10 µA

-10pF

Electrical Specifications V

PARAMETER SYMBOL

CLK Period t CLK High t CLK Low t SERCLK High t SERCLK Low t

= 5.0V ±5% , TA = 0°C to +70°C (Commercial), TA = -40°C to +85°C (Industrial), (Note 11) Parameters with

MIN and/or MAX limits are 100% tested at +25°C, unless otherwise specified. Temperature limits established by characterization and are not production tested.

CP CH

52MHz

UNITSMIN MAX

19 - ns

7-ns 7-ns 7-ns 7-ns

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

Electrical Specifications V

PARAMETER SYMBOL

Setup Time IIN9-0, QIN9-0, SYNC Hold Time IIN9-0, QIN9-0, SYNC Setup Time ISER, QSER, SSYNC to SERCLK t Hold Time ISER, QSER, SSYNC FROM SERCLK t Setup Time A0-2, C0-7 to Rising Edge of WR Hold Time A0-2, C0-7 from Rising Edge of WR

to CLK t

WR SERCLK to CLK t CLK to AOUT9-0, BOUT9-0, COF , COFSYNC, SOF, SOFSYNC,

SMBLCLK, HI/LO Read Address Low to Data Valid t CLK to Status Out on C0-7 t

High t

Low t

LOW to Data Valid t

HIGH to Output Disable t

RD Output Enable t Output Disable Time t Output Rise, Fall Time t

NOTES:

11. A C tests performed with C Test V

12. Controlled via design or process parameters and not directly tested. Characterized upon initial design and after major process and/or design changes.

13. Set-up time required to ensure action initiated by WR

, SLOCLK, LKINT, THRES

= 3.0V, V

= 4.0V, VIL = 0V.

IHC

= 5.0V ±5% , TA = 0°C to +70°C (Commercial), TA = -40°C to +85°C (Industrial), (Note 11) Parameters with

MIN and/or MAX limits are 100% tested at +25°C, unless otherwise specified. Temperature limits established by characterization and are not production tested. (Continued)

52MHz

, FZ_CT, FZ_ST to CLK t

, FZ_CT, FZ_ST FROM CLK t

= 40 pF, IOL = 2mA, and IOH = -400mA. Input reference level for CLK is 2.0V, all other inputs 1.5V.

or SERCLK will be seen by a particular CLK.

DSS

DSH

WH WC

ADO CDO WRH WRL

RL RDO ROD

OE OD

8-ns 1-ns 8-ns 0-ns

15 - ns

0-ns 15 - ns (Note 13) 10 - ns (Note 13)

-8ns

-26ns

-15ns 16 - ns 16 - ns 16 - ns

-15ns

- 10 ns (Note 12)

-8ns

- 8 ns (Note 12)

- 5 ns (Note 12)

UNITSMIN MAX

AC Test Load Circuit

AND I

†

CCOP

IOH 1.5V IOL

EQUIVALENT CIRCUIT

† Test head capacitance.

DUT

SWITCH S1 OPEN FOR I

CCSB

FN3652.5

July 2, 2008

Waveforms

www.BDTIC.com/Intersil

C0-7, A0-2

FIGURE 26. TIMING RELATIVE TO WR FIGURE 27. OUTPUT RISE AND FALL TIMES

CLK

WRL

HSP50210

WRH

OUTA9-0, OUTB9-0

OEA

OEB

2.0V

0.8V

1.5V

1.7V

1.3V

1.5V

IIN9-0, QIN9-0,

SYNC,

FZ_CT, FZ_ST

AOUT9-0, BOUT9-0,

COF, COFSYNC,

SOF, SOFSYNC,

, SMBLCLK,

HI/LO

SLOCLK, LKINT, THRES

SERCLK, WR

C7-0

FIGURE 28. TIMING RELATIVE TO CLK

tSC; t

CDO

A2-0

C0-7

FIGURE 29. OUTPUT ENABLE/DISABLE

RDO

ROD

ADO

FIGURE 30. TIMING RELATIVE TO READ

SERCLK

DSS

DSH

ISER, QSER, SSYNC

FIGURE 31. SERCLK TIMING

FN3652.5

July 2, 2008

HSP50210

www.BDTIC.com/Intersil

Plastic Leaded Chip Carrier Packages (PLCC)

0.042 (1.07)

0.048 (1.22)

PIN (1) IDENTIFIER

0.020 (0.51) MAX

3 PLCS

0.026 (0.66)

0.032 (0.81)

0.045 (1.14)

MIN

0.042 (1.07)

0.056 (1.42)

0.050 (1.27) TP

VIEW “A” TYP.

EE1

0.013 (0.33)

0.021 (0.53)

0.025 (0.64) MIN

0.004 (0.10) C

0.025 (0.64)

0.045 (1.14)

D2/E2

-C-

VIEW “A”

0.020 (0.51)

MIN

SEATING PLANE

N84.1.15 (JEDEC MS-018AF ISSUE A)

84 LEAD PLASTIC LEADED CHIP CARRIER PACKAGE

SYMBOL

A 0.165 0.180 4.20 4.57 -

A1 0.090 0.120 2.29 3.04 -

D 1.185 1.195 30.10 30.35 -

D1 1.150 1.158 29.21 29.41 3

D2 0.541 0.569 13.75 14.45 4, 5

E 1.185 1.195 30.10 30.35 -

E1 1.150 1.158 29.21 29.41 3

E2 0.541 0.569 13.75 14.45 4, 5

N84 846

INCHES MILLIMETERS

NOTESMIN MAX MIN MAX

Rev. 2 11/97

NOTES:

1. Controlling dimension: INCH. Converted millimeter dimensions are not necessarily exact.

2. Dimensions and tolerancing per ANSI Y14.5M-1982.

3. Dimensions D1 and E1 do not include mold protrusions. Allowable mold protrusion is 0.010 inch (0.25mm) per side. Dimensions D1 and E1 include mold mismatch and are measured at the extreme material condition at the body parting line.

4. To be measured at seating plane contact point.

-C-

5. Centerline to be determined where center leads exit plastic body.

6. “N” is the number of terminal positions.

All Intersil U.S. products are manufactured, assembled and tested utilizing ISO9000 quality systems.

Intersil Corporation’s quality certifications can be viewed at www.intersil.com/design/quality

Intersil products are sold by description only. Intersil Corporation reserves the right to make changes in circuit design, software and/or specifications at any time without notice. Accordingly, the reader is cautioned to verify that data sheets are current before placing orders. Information furnished by Intersil is believed to be accurate and reliable. However, no responsibility is assumed by Intersil or its subsidiaries for its use; nor for any infringements of patents or other rights of third parties which may result from its use. No license is granted by implic atio n or other wise u nde r any p a tent or patent rights of Intersil or its subsidiaries.

For information regarding Intersil Corporation and its products, see www.intersil.com

FN3652.5

July 2, 2008

intersil HSP50210 DATA SHEET

Specifications and Main Features

Frequently Asked Questions

User Manual