Page 1

i
IBM SPSS Complex Samples 19
Page 2

Note: Before using this information and the product it supports, read the general information
under Notices on p. 267.
This document contains proprietary information of S PSS Inc, an IBM Company. It is provided
under a license agreement and is protected by copyright law. The information contained in this
publication does not include any product warranties, and any statements provided in this manual
should not be interpreted as such.
When you send information to IBM or SPSS, you grant IBM and SPSS a nonexclusive right
to use or distribute the information in any way it believes appropriate without incurring any
obligationtoyou.
© Copyright SPSS Inc. 1989, 2010.
Page 3

IBM® SPSS ® Statistics is a comprehensive system for analyzing data. The Complex Samples
optional add-on module provides the additional analytic techniques described in this manual. The
Complex Samples add-on module must be used with the SPSS Statistics Core system and is
completely integrated into that system.
About SPSS Inc., an IBM Company
SPSS Inc., an IBM Company, is a leading global provider of predictive analytic software
and solutions. The company’s complete portfolio of products — data collection, statistics,
modeling and deployment — captures people’s attitudes and opinions, predicts outcomes of
future customer interactions, and then acts on these insights by embedding analytics into business
processes. SPSS Inc. solutions address interconnected business objectives across an entire
organization by focusing on the convergence of analytics, IT architecture, and business processes.
Commercial, government, and academic customers worldwide rely on SPSS Inc. technology as
a competitive advantage in attracting, retaining, and growing customers, while reducing fraud
and mitigating risk. SPSS Inc. was acquired by IBM in October 2009. For more information,
visit http://www.spss.com.
Preface
Technical support
Technical support is available to maintenance cus
Technical Support for assistance in using SPSS Inc. products or for installation help
for one of the supported hardware environments. To reach Technical Support, see the
SPSS Inc. web site at http://support.spss.com or fi
http://support.spss.com/default.asp?refpage=contactus.asp. Be prepared to identify yourself, your
organization, and your support agreement when requesting assistance.
Customer Service
If you have any questions concerning your shipment or account, contact your local office, listed
on the Web site at http://www.spss.com/worldwide. Please have your serial number ready for
identification.
Training Seminars
SPSS Inc. provides both public and onsite training seminars. All seminars feature hands-on
workshops. Seminars will be offered in major cities on a regular basis. For more information on
these seminars, contact your local office, listed on the Web site at http://www.spss.com/worldwide.
© Copyright SPSS Inc. 1989, 2010
tomers. Customers may contact
nd your local office via the web site at
iii
Page 4

Additional Publications
The SPSS Statistics: Guide to Data Analysis, SPSS Statistics: Statistical Procedures Companion,
and SPSS Statistics: Advanced Statistical Procedures Companion, written by Marija Norušis and
published by Prentice Hall, are available as suggested supplemental material. These publications
cover statistical procedures in the SPSS Statistics Base module, Advanced Statistics module
and Regression module. Whether you are just getting starting in data analysis or are ready for
advanced applications, these books will help you make best use of the capabilities found within
the IBM® SPSS® Statistics offering. For additional information including publication contents
and sample chapters, please see the author’s website: http://www.norusis.com
iv
Page 5

Contents
Part I: User’s Guide
1 Introduction to Complex Samples Procedures 1
PropertiesofComplexSamples .................................................. 1
UsageofComplexSamplesProcedures............................................ 2
PlanFiles................................................................ 2
FurtherReadings ............................................................. 3
2 Sampling from a Complex Design 4
Creating a Ne
Sampling Wiz
Tree Control
SamplingWizard:SamplingMethod............................................... 8
SamplingWizard:SampleSize...................................................10
DefineUnequalSizes.......................................................11
SamplingWizard:OutputVariables................................................12
SamplingWizard:PlanSummary .................................................13
SamplingWizard:DrawSampleSelectionOptions....................................14
SamplingWizard:DrawSampleOutputFiles.........................................15
SamplingWizard:Finish........................................................16
ModifyinganExistingSamplePlan................................................16
SamplingWizard:PlanSummary .................................................17
RunninganExistingSamplePlan ................................................. 18
CSPLANandCSSELECTCommandsAdditionalFeatures................................ 18
wSamplePlan .................................................... 4
ard:DesignVariables ............................................... 6
sforNavigatingtheSamplingWizard................................. 7
3 Preparing a Complex Sample for Analysis 19
CreatingaNewAnalysisPlan....................................................20
AnalysisPreparationWizard:DesignVariables.......................................20
TreeControlsforNavigatingtheAnalysisWizard..................................21
v
Page 6

AnalysisPreparationWizard:EstimationMethod.....................................22
AnalysisPreparationWizard:Size ................................................23
DefineUnequalSizes.......................................................24
AnalysisPreparationWizard:PlanSummary ........................................ 25
AnalysisPreparationWizard:Finish............................................... 26
ModifyinganExistingAnalysisPlan...............................................26
AnalysisPreparationWizard:PlanSummary ........................................ 27
4 Complex Samples Plan 28
5 Complex Samples Frequencies 29
Complex Sampl
Complex Sample
Complex Sample
6 Complex Sampl
ComplexSamplesDescriptivesStatistics...........................................34
ComplexSamplesDescriptivesMissingValues.......................................35
ComplexSamplesOptions ......................................................36
esFrequenciesStatistics ...........................................30
sMissingValues.................................................31
sOptions ......................................................32
es Descriptives 33
7 Complex Samples Crosstabs 37
ComplexSamplesCrosstabsStatistics............................................. 39
ComplexSamplesMissingValues.................................................40
ComplexSamplesOptions ......................................................41
8 Complex Samples Ratios 42
ComplexSamplesRatiosStatistics................................................ 43
ComplexSamplesRatiosMissingValues ...........................................44
ComplexSamplesOptions ......................................................44
vi
Page 7

9 Complex Samples General Linear M odel 45
ComplexSamplesGeneralLinearModelStatistics....................................48
ComplexSamplesHypothesisTests ...............................................49
ComplexSamplesGeneralLinearModelEstimatedMeans..............................50
ComplexSamplesGeneralLinearModelSave ....................................... 51
ComplexSamplesGeneralLinearModelOptions .....................................52
CSGLMCommandAdditionalFeatures.............................................53
10 Complex Samples Logistic Regression 54
ComplexSamplesLogisticRegressionReferenceCategory ............................. 55
ComplexSamplesLogisticRegressionModel........................................56
ComplexSamplesLogisticRegressionStatistics......................................57
ComplexSamplesHypothesisTests ...............................................59
ComplexSamplesLogisticRegressionOddsRatios....................................60
ComplexSamplesLogisticRegressionSave......................................... 61
ComplexSamplesLogisticRegressionOptions.......................................62
CSLOGISTICCommandAdditionalFeatures ......................................... 63
11 Complex Samples Ordinal Regression 64
Complex Samples Ordinal Regression Response Probabilities. . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
ComplexSamplesOrdinalRegressionModel ........................................66
ComplexSamplesOrdinalRegressionStatistics......................................68
ComplexSamplesHypothesisTests ...............................................69
ComplexSamplesOrdinalRegressionOddsRatios....................................70
ComplexSamplesOrdinalRegressionSave ......................................... 71
ComplexSamplesOrdinalRegressionOptions ....................................... 72
CSORDINALCommandAdditionalFeatures..........................................73
12 Complex Samples Cox Regression 74
DefineEvent ................................................................77
vii
Page 8

Predictors ..................................................................78
DefineTime-DependentPredictor............................................. 79
Subgroups..................................................................80
Model ..................................................................... 81
Statistics ................................................................... 82
Plots ...................................................................... 84
HypothesisTests .............................................................85
Save ...................................................................... 86
Export ..................................................................... 88
Options ....................................................................90
CSCOXREGCommandAdditionalFeatures .......................................... 91
Part II: Examples
13 Complex Samples Sampling Wizard 93
ObtainingaSamplefromaFullSamplingFrame......................................93
UsingtheWizard .........................................................93
PlanSummary........................................................... 103
SamplingSummary....................................................... 103
SampleResults.......................................................... 104
ObtainingaSamplefromaPartialSamplingFrame................................... 105
UsingtheWizardtoSamplefromtheFirstPartialFrame ........................... 105
SampleResults.......................................................... 118
UsingtheWizardtoSamplefromtheSecondPartialFrame......................... 118
SampleResults.......................................................... 123
Sampling with Probability Proportional to Size (PPS) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123
UsingtheWizard ........................................................ 123
PlanSummary........................................................... 135
SamplingSummary....................................................... 135
SampleResults.......................................................... 137
RelatedProcedures.......................................................... 139
14 Complex Samples Analysis Preparation Wizard 140
Using the Complex Samples Analysis Preparation Wizard to Ready NHIS Public Data . . . . . . . . . 140
UsingtheWizard......................................................... 140
Summary............................................................... 143
viii
Page 9

PreparingforAnalysisWhenSamplingWeightsAreNotintheDataFile................... 143
Computing Inclusion Probabilities and Sampling Weights . . . . . . . . . . . . . . . . . . . . . . . . . . 143
UsingtheWizard......................................................... 146
Summary............................................................... 154
RelatedProcedures.......................................................... 154
15 Complex Samples Frequencies 155
Using Complex Samples Frequencies to Analyze Nutritional Supplement Usage . . . . . . . . . . . . . 155
RunningtheAnalysis...................................................... 155
FrequencyTable ......................................................... 158
FrequencybySubpopulation................................................ 158
Summary............................................................... 159
RelatedProcedures.......................................................... 159
16 Complex Samples Descriptives 160
UsingComplexSamplesDescriptivestoAnalyzeActivityLevels......................... 160
RunningtheAnalysis...................................................... 160
UnivariateStatistics....................................................... 163
Univariate Sta
Summary............................................................... 164
Related Proced
tisticsbySubpopulation......................................... 163
ures .......................................................... 164
17 Complex Sample
Using Complex Samples Crosstabs to Measure the Relative Risk of an Event . . . . . . . . . . . . . . . 165
RunningtheAnalysis...................................................... 165
Crosstabulation.......................................................... 168
RiskEstimate ........................................................... 169
RiskEstimatebySubpopulation.............................................. 170
Summary............................................................... 170
RelatedProcedures.......................................................... 170
s C rosstabs 165
ix
Page 10

18 Complex Samples Ratios 171
UsingComplexSamplesRatiostoAidPropertyValueAssessment....................... 171
RunningtheAnalysis...................................................... 171
Ratios................................................................. 174
PivotedRatiosTable ...................................................... 174
Summary............................................................... 175
RelatedProcedures.......................................................... 175
19 Complex Samples General Linear Model 176
Using Complex S
Running the Ana
ModelSummary ......................................................... 181
TestsofModelEffects..................................................... 181
Parameter Esti
EstimatedMarginalMeans ................................................. 183
Summary .............................................................. 185
RelatedProcedures.......................................................... 185
amples General Linear Model to Fit a Two-Factor ANOVA . . . . . . . . . . . . . . . . . 176
lysis...................................................... 176
mates...................................................... 182
20 Complex Samples Logistic Regression 186
UsingComplexSamplesLogisticRegressiontoAssessCreditRisk....................... 186
RunningtheAnalysis...................................................... 186
PseudoR-Squares........................................................ 190
Classification............................................................ 191
TestsofModelEffects..................................................... 191
ParameterEstimates...................................................... 192
OddsRatios............................................................. 193
Summary............................................................... 194
RelatedProcedures.......................................................... 194
21 Complex Samples Ordinal Regression 195
UsingComplexSamplesOrdinalRegressiontoAnalyzeSurveyResults.................... 195
RunningtheAnalysis...................................................... 195
PseudoR-Squares........................................................ 200
TestsofModelEffects..................................................... 200
x
Page 11

ParameterEstimates...................................................... 201
Classification............................................................ 202
OddsRatios............................................................. 203
GeneralizedCumulativeModel .............................................. 204
DroppingNon-SignificantPredictors.......................................... 205
Warnings............................................................... 207
ComparingModels ....................................................... 208
Summary............................................................... 209
RelatedProcedures.......................................................... 209
22 Complex Samples Cox Regression 210
Using a Time-Dependent Predictor in Complex Samples Cox R egressio n. . . . . . . . . . . . . . . . . . . 210
PreparingtheData ....................................................... 210
RunningtheAnalysis...................................................... 216
SampleDesignInformation................................................. 221
TestsofModelEffects..................................................... 222
TestofProportionalHazards................................................ 222
AddingaTime-DependentPredictor .......................................... 222
MultipleCasesperSubjectinComplexSamplesCoxRegression ........................ 226
PreparingtheDataforAnalysis.............................................. 227
CreatingaSimpleRandomSamplingAnalysisPlan ............................... 242
RunningtheAnalysis...................................................... 246
SampleDesignInformation................................................. 254
TestsofModelEffects..................................................... 255
ParameterEstimates...................................................... 255
PatternValues........................................................... 256
Log-Minus-LogPlot....................................................... 257
Summary............................................................... 257
xi
Page 12

Appendices
A Sample Files 258
B Notices 267
Bibliography 269
Index 271
xii
Page 13

Part I:
User’s Guide
Page 14

Page 15

Introduction to Complex Samples Procedures
An inherent assumption of analytical procedures in traditional software packages is that the
observations in a data file represent a simple random sample from the population of interest. This
assumption is untenable for an increasing number of companies and researchers who find it both
cost-effective and convenient to obtain samples in a more structured way.
The Complex Samples option allows you to select a sample according to a complex design and
incorporate the design specifications into the data analysis, thus ensuring that your results are valid.
Properties of Complex Samples
Chapter
1
A complex sample can differ from a simple random sample in many ways. In a simple random
sample, individual sampling units are selected at random with equal probability and without
replacement (WOR) directly from the entire population. By contrast, a given complex sample
can have some or all of the following features:
Stratification. Stratified sampling involves selecting samples independently within
non-overlapping subgroups of the population, or strata. For example, strata may be socioeconomic
groups, job categories, age groups, or ethnic groups. With stratification, you can ensure adequate
sample sizes for subgroups of interest, improve the precision of overall estimates, and use different
sampling methods from stratum to stratum.
Clustering. Cluster sampling involves the selection of groups of sampling units, or clusters. For
example, clusters may be schools, hospitals, or geographical areas, a nd sampling units may be
students, patients, or citizens. Clustering is common in multistage designs and area (geographic)
samples.
Multiple stages. In multistage sampling, you select a first-stage sample based on clusters. Then
you create a second-stage sample by drawing subsamples from the selected clusters. If the
second-stage sample is based on subclusters, you can then add a third stage to the sample. For
example, in the first stage of a survey, a sample of cities could be drawn. Then, from the selected
cities, households could be sampled. Finally, from the selected households, individuals could be
polled. The Sampling and Analysis Preparation wizards allow you to specify three stages in
adesign.
Nonrandom sampling. When selection a t random is difficult to obtain, units can be sampled
systematically (at a fixed interval) or sequentially.
© Copyright SPSS Inc. 1989, 2010
1
Page 16

2
Chapter 1
Unequal selection probabilities. When sampling clusters that contain unequal numbers of units,
you can use probability-proportional-to-size (PPS) sampling to make a cluster’s selection
probability equal to the proportion of units it contains. PPS sampling can also use more general
weighting schemes to select units.
Unrestricted sampling. Unrestricted sampling selects units with replacement (WR). Thus, an
individual unit can be selected for the sample more than once.
Sampling weights. Sampling weights are automatically computed while drawing a complex
sample and ideally correspond to the “frequency” that each sampling unit represents in the target
population. Therefore, the sum of the weights over the sample should estimate the population
size. Complex Samples analysis procedures require sampling weights in order to properly analyze
a complex sample. Note that these weights shouldbeusedentirelywithintheComplexSamples
option and should not be used with other analytical procedures via the Weight Cases procedure,
which treats weights as case replications.
Usage of Complex Samples Procedures
Your usage of Complex Samples procedures depends on your particular needs. The primary
types of users are those who:
Plan and carry out surveys according to complex designs, possibly analyzing the sample later.
The p rimary tool for surveyors is the Sampling Wizard.
Analyze sample data files previously obtained according to complex designs. Before using the
Complex Samples analysis procedures, you may need to use the Analysis Preparation Wizard.
Plan Files
Regardless of which type of user you are, you need to supply design information to Complex
Samples procedures. This information is stored in a plan file for easy reuse.
Aplanfile contains complex sample specifications. There are two types of plan files:
Sampling plan. The specifications given in the Sampling Wizard defineasampledesignthat
is used to draw a complex sample. The sampling plan file contains those specifications. The
sampling plan file also contains a default analysis plan that uses estimation methods suitable for
the specified sample design.
Analysis plan. This plan file contains information needed by Complex Samples analysis procedures
to properly compute variance estimates for a complex sample. The plan includes the sample
structure, estimation methods for each stage, and references to required variables, such as sample
weights. The Analysis Preparation Wizard allows you to create and edit analysis plans.
There are several advantages to saving your specifications in a plan file, including:
A surveyor can specify the first stage of a multistage sampling plan and draw first-stage
units now, collect information on sampling units for the second stage, and then modify the
sampling plan to include the second stage.
Page 17

An analyst who doesn’t have access to the sampling plan file can specify an analysis plan and
refer to that plan from each Complex Samples analysis procedure.
A designer of large-scale public use samples can publish the sampling plan file, which
simplifies the instructions for analysts and avoids the need for each analyst to specify his
or her own analysis plans.
Further Readings
For more information on sampling techniques, see the following texts:
Cochran, W. G. 1977. Sampling Techniques, 3rd ed. New York: John Wiley and Sons.
Kish,L.1965. Survey Sampling. New York: John Wiley and Sons.
Kish, L. 1987. Statistical Design for Research. New York: John Wiley and Sons.
Murthy, M. N. 1967. Sampling Theory and Methods. Calcutta, India: Statistical Publishing
Society.
Särndal, C., B. Swensson, and J. Wretman. 1992. Model Assisted Survey Sampling.NewYork:
Springer-Verlag.
3
Introduction to Complex Sample s Procedures
Page 18
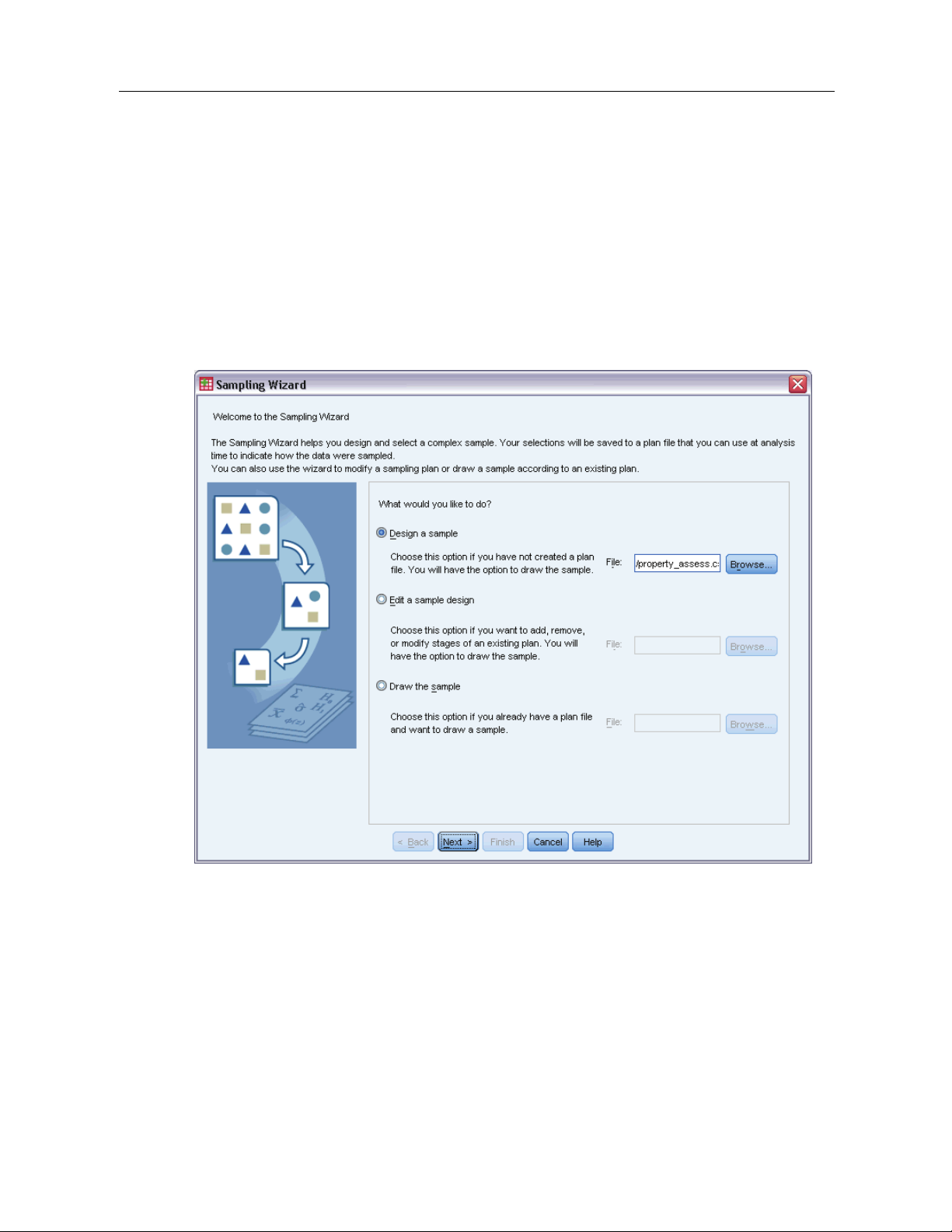
Sampling from a Complex Design
Figure 2-1
Sampling Wizard, Welcome step
Chapter
2
The Sampling Wizard guides you through the steps for creating, modifying, or executing a
sampling plan file. Before using the Wizard, you should have a well-defined target population, a
list of sampling units, and an appropriate sample design in mind.
Creating a New Sample Plan
E From the menus choose:
Analyze > Complex Samples > Select a Sample...
Select Design a sample and choose a plan filename to save the sample plan.
E
© Copyright SPSS Inc. 1989, 2010
4
Page 19

Sampling from a Complex Design
E
Click Next to continue through the Wizard.
E Optionally, in the Design Variables step, you can define strata, clusters, and input sample weights.
After you define these, click
E Optionally, in the Sampling Method step, you can choose a method for selecting items.
Next.
5
If you select
PPS Brewer or PPS Murthy, you can click Finish to draw the sample. Otherwise,
click Next and then:
E In the Sample Size step, specify the number or proportion of units to sample.
E You can now click Finish to draw the sample.
Optionally, in further steps you can:
Choose output variables to save.
Add a second or third stage to the design.
Set various selection options, including which stages to draw samples from, the random
number seed, and whether to treat user-missing values as valid values of design variables.
Choose where to save output data.
Paste your selections as command syntax.
Page 20
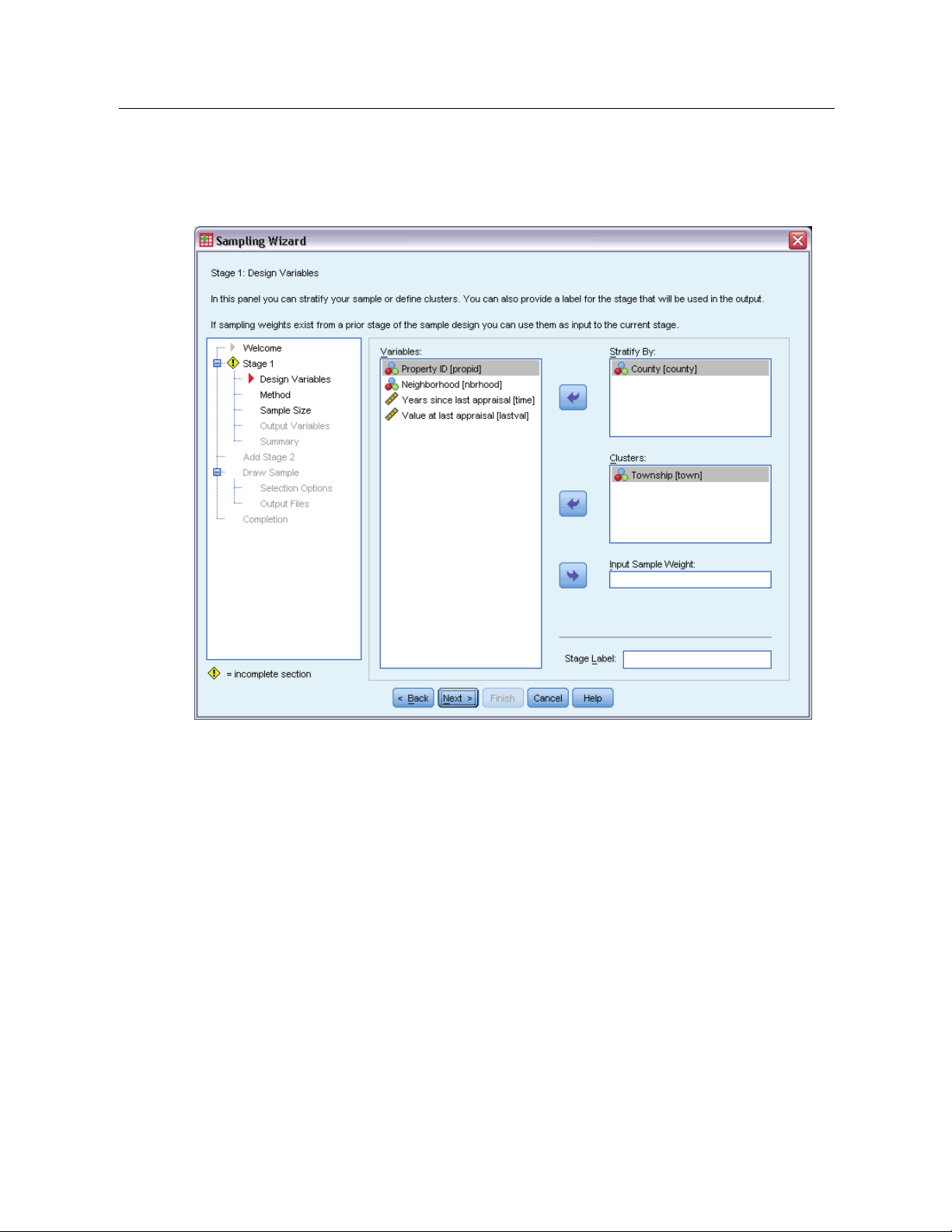
6
Chapter 2
Sampling Wizard: Design Variables
Figure 2-2
Sampling Wizard, Design Variables step
This step allows you to select stratification and clustering variables and to define input sample
weights. You can also specify a label for the stage.
Stratify By. The cross-classification of stratification variables defines distinct subpopulations, or
strata. Separate samples are obtained for each stratum. To improve the precision of your estimates,
units within strata should be as homogeneous as possible for the characteristics of interest.
Clusters. Cluster variables define groups of observational units, or clusters. Clusters are useful
when directly sampling observational units from the population is expensive or impossible;
instead, you can sample clusters from the population and then sample observational units from
the selected clusters. However, the use of clusters can introduce correlations among sampling
units, resulting in a loss of precision. To minimize this effect, units within clusters should be as
heterogeneous as possible for the characteristics of interest. You must define at least one cluster
variable in order to plan a multistage design. Clusters are also n ecessary in the use of several
different sampling methods. For more information, see the topic Sampling Wizard: Sampling
Method on p. 8.
Page 21

Input Sample Weight. If the current sample design is part of a larger sample design, you may have
sample weights from a previous stage of the larger design. You can specify a n umeric variable
containing these weights in the first stage of the current design. Sample weights are computed
automatically for subsequent stages of the current design.
Stage Label. Youcanspecifyanoptionalstringlabelforeachstage. Thisisusedintheoutputto
help identify stagewise information.
Note: The source variable list has the same content across steps of the Wizard. In other words,
variables removed from the source list in a particular step are removed from the list in all steps.
Variables returned to t he source list appear in the list in all steps.
Tree Controls for Navigating the Sam pling Wizard
On the left side of each step in the Sampling Wizard is an outline of all the steps. You can navigate
theWizardbyclickingonthenameofanenabled step in the outline. Steps are enabled as
long as all previous steps are valid—that is, if each previous step has been given the minimum
required specifications for that step. See the Help for individual steps for more information on
whyagivenstepmaybeinvalid.
7
Sampling from a Complex Design
Page 22
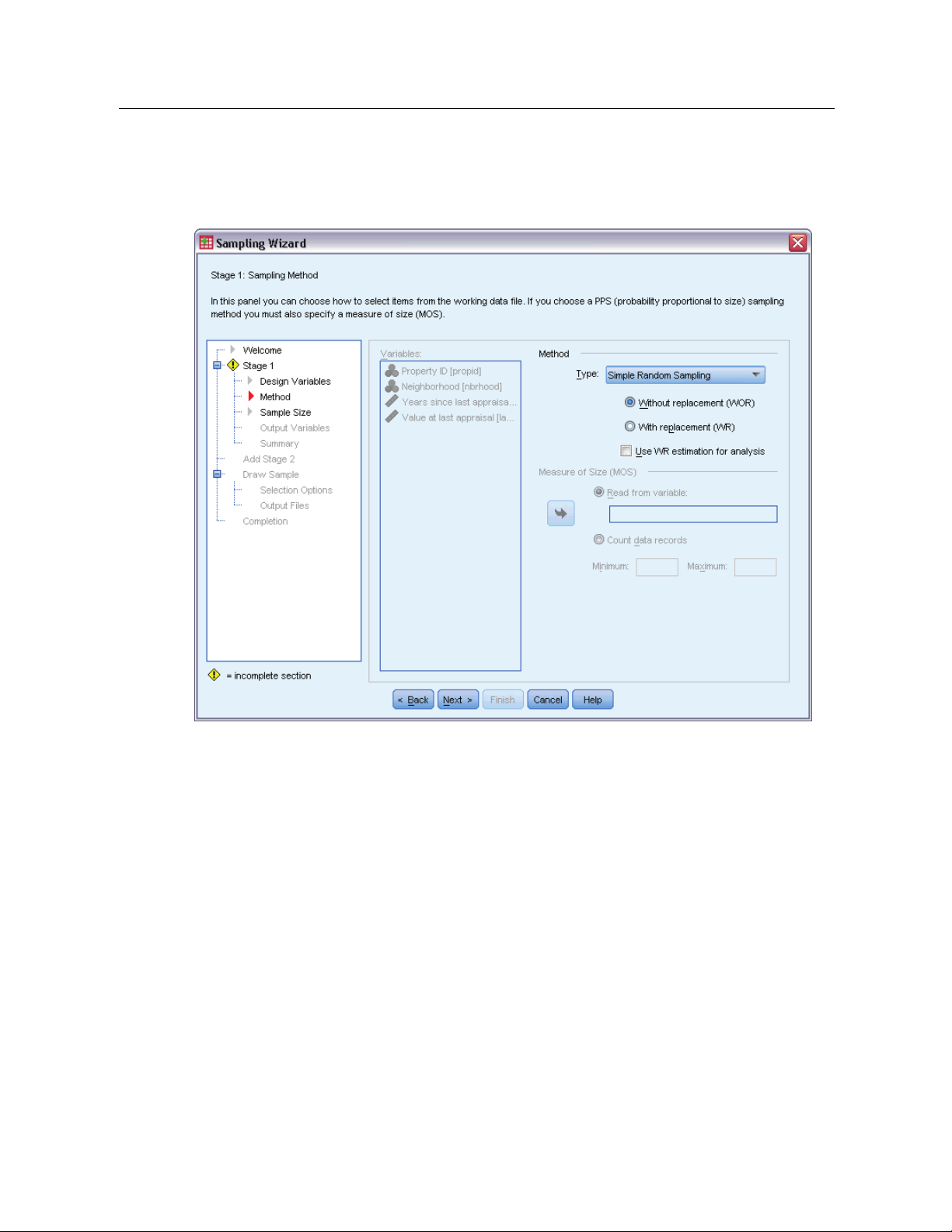
8
Chapter 2
Sampling Wizard: Sampling Method
Figure 2-3
Sampling Wizard, Sampling Method step
This step allows you to specify how to select cases from the active dataset.
Method. Controls in this group are used to choose a selection method. Some sampling types allow
you to choose whether to sample with replacement (WR) or w ithout replacement (WOR). See the
type descriptions for more information. Note that some probability-proportional-to-size (PPS)
types are available only when clusters have been defined and that all PPS types are available only
in the first stage of a design. Moreover, WR methods are available only in the last stage of a design.
Simple Random Sampling. Units are selected with equal probability. They can be selected
with or without replacement.
Simple Systematic. Units are selected at a fixed interval throughout the sampling frame (or
strata, if they have been specified) and extracted without replacement. A randomly selected
unit within the first interval is chosen as the starting point.
Simple Sequential. Units are selected sequentially with equal probability and without
replacement.
PPS. This is a first-stage method that selects units at random with probability proportional
to size. Any units can be selected with replacement; only clusters can be sampled without
replacement.
Page 23

Sampling from a Complex Design
PPS Systematic. This is a first-stage method that systematically selects units with probability
proportional to size. They are selected without replacement.
PPS Sequential. This is a first-stage method that sequentially selects units with probability
proportional to cluster size and without replacement.
PPS Brewer. This is a first-stage method that selects two clusters from each stratum with
probability proportional to cluster size and without replacement. A cluster variable must be
specified to use this method.
PPS Murthy. This is a first-stage method that selects two clusters from each stratum with
probability proportional to cluster size and without replacement. A cluster variable must be
specified to use this method.
PPS Sampford. This is a first-stage method that selects more than two clusters from each
stratum with probability proportional to cluster size and without replacement. It is an
extension of Brewer’s method. A cluster variable must be specified to use this method.
Use WR estimation f or analysis. By default, an estimation method is specified in the plan file
that is consistent with the selected sampling method. This allows you to use with-replacement
estimation even if the sampling method implies WOR estimation. This option is available
only in stage 1.
Measure of Size (MOS). If a PPS method is selected, you must specify a measure of size that defines
the size of each unit. These sizes can be explicitly defined in a variable or they can be computed
from the data. Optionally, you can set lower and upper bounds on the MOS, overriding any values
found in the MOS variable or computed from the data. These options are available only in stage 1.
9
Page 24
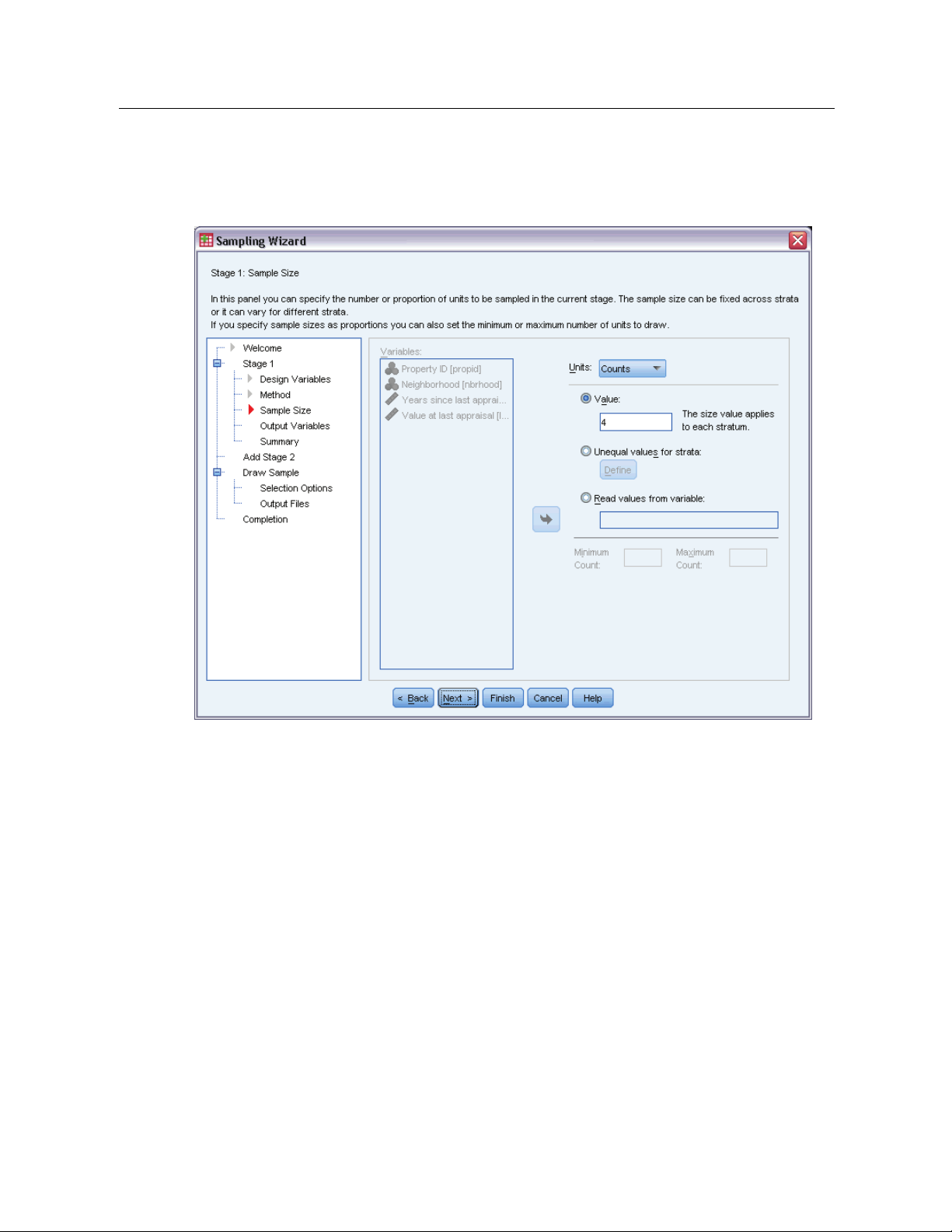
10
Chapter 2
Sampling Wizard: Sample Size
Figure 2-4
Sampling Wizard, Sample Size step
This step allows you to specify the number or proportion of units to sample within the current
stage. The sample size can be fixed or it can vary across strata. For the purpose of specifying
sample size, clusters chosen in previous stages can be used to define strata.
Units. You can specify an exact sample size or a proportion of units to sample.
Value. A single value is applied to all strata. If Counts is selected as the unit metric, you should
enter a positive integer. If
Proportions is selected, you should enter a non-negative value.
Unless sampling with replacement, proportion values should also be no greater than 1.
Unequal values for strata. Allows you to enter size values on a per-stratum basis via the Define
Unequal Sizes dialog box.
Read values from variable. Allows you to select a numeric variable that contains size values
for strata.
If Proportions is selected, you have the option to set lower and upper bounds on the number of
units sampled.
Page 25
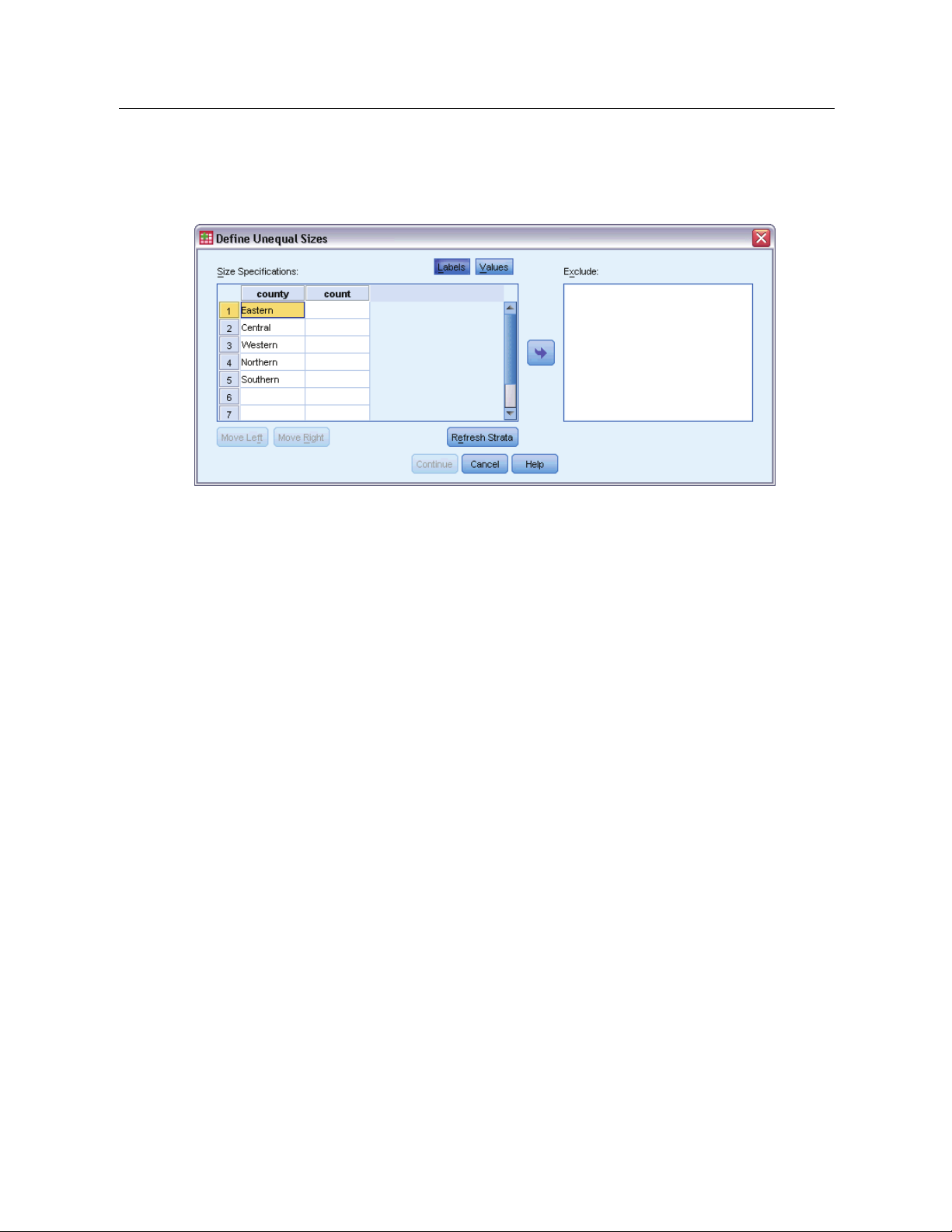
Define Unequal Sizes
Figure 2-5
Define Unequal Sizes dialog box
11
Sampling from a Complex Design
The Define U
Size Specifications grid. The grid displays the cross-classifications of up to five strata or
nequal Sizes dialog box allows you to enter sizes on a per-stratum basis.
cluster variables—one stratum/cluster combination per row. Eligible grid variables include all
stratifica
tion variables from the current and previous stages and all cluster variables from previous
stages. Variables can be reordered within the grid or moved to the Exclude list. Enter sizes in the
rightmost column. Click
stratific
ation and cluster variables in the grid cells. Cells that contain unlabeled values always
show values. Click
Labels or Va lues to toggle the display of value labels and data values for
Refresh Strata to repopulate the grid with each combination of labeled data
values for variables in the grid.
Exclude.
To specify sizes for a subset of stratum/cluster combinations, move one or more variables
to the Exclude list. These variables are not used to define sample sizes.
Page 26
12
Chapter 2
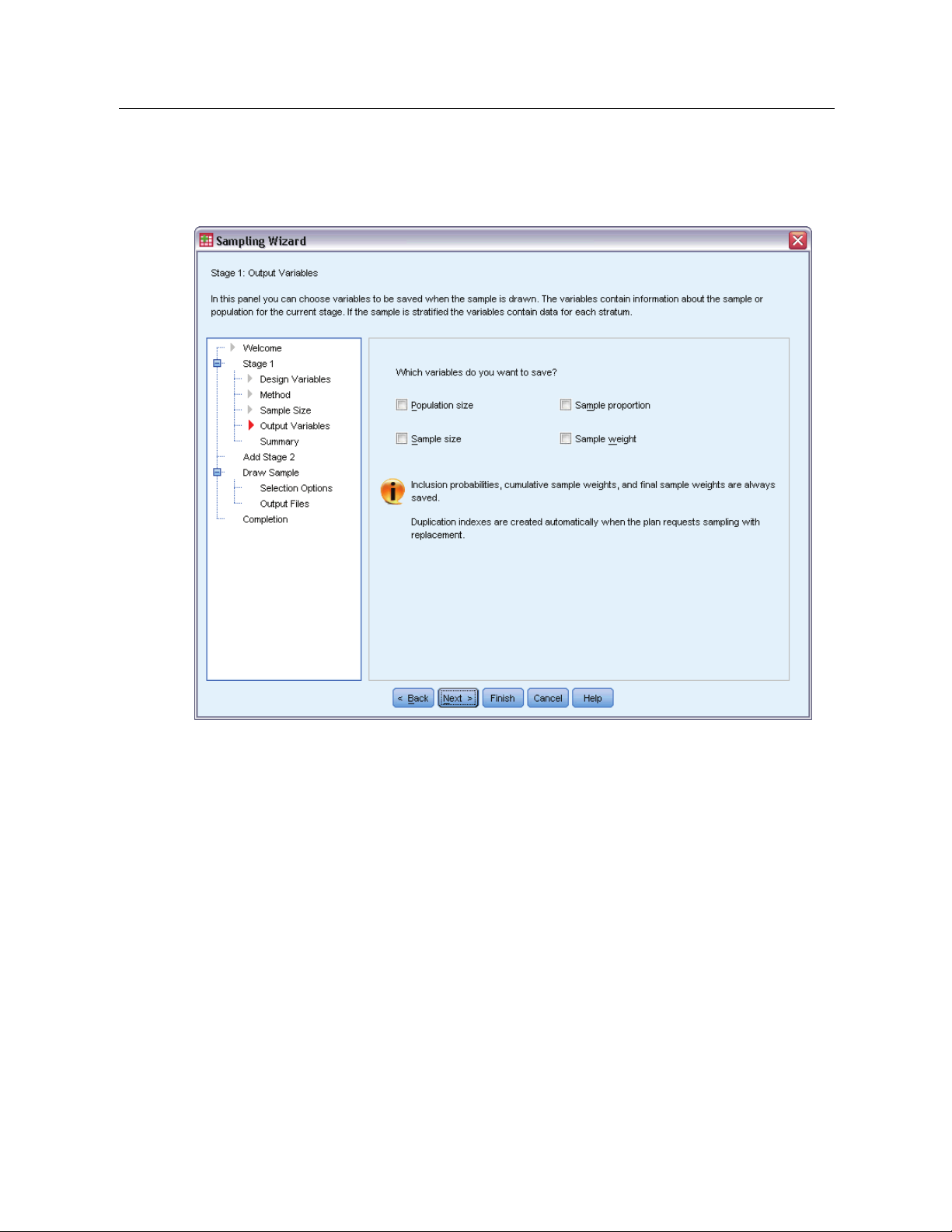
Sampling Wizard: Output Variables
Figure 2-6
Sampling Wizard, Output Variables step
This step allows you to choose variables to save when the sample is drawn.
Population size. The estimated number of units in the population for a given stage. The rootname
for the saved variable is PopulationSize_.
Sample proportion. The sampling rate at a given stage. The rootname for the saved variable is
SamplingRate_.
Sample size. The number of units drawn at a given stage. The rootname for the saved variable
is SampleSize_.
Sample weight. The inverse of the inclusion probabilities. The rootname for the saved variable is
SampleWeight_.
Some stagewise variables are generated automatically. These include:
Inclusion probabilities. The proportion of units drawn at a given stage. The rootname for the saved
variable is InclusionProbability_.
Cumulative weight. The cumulative sample weight over stages previous to and including the
current one. The rootname for the saved variable is SampleWeightCumulative_.
Page 27
Index. Identifies units selected multiple times within a given stage. The rootname for the saved
variable is Index_.
Note: Saved variable rootnames include an integer suffixthatreflects the stage number—for
example, PopulationSize_1_ for the saved population size for stage 1.
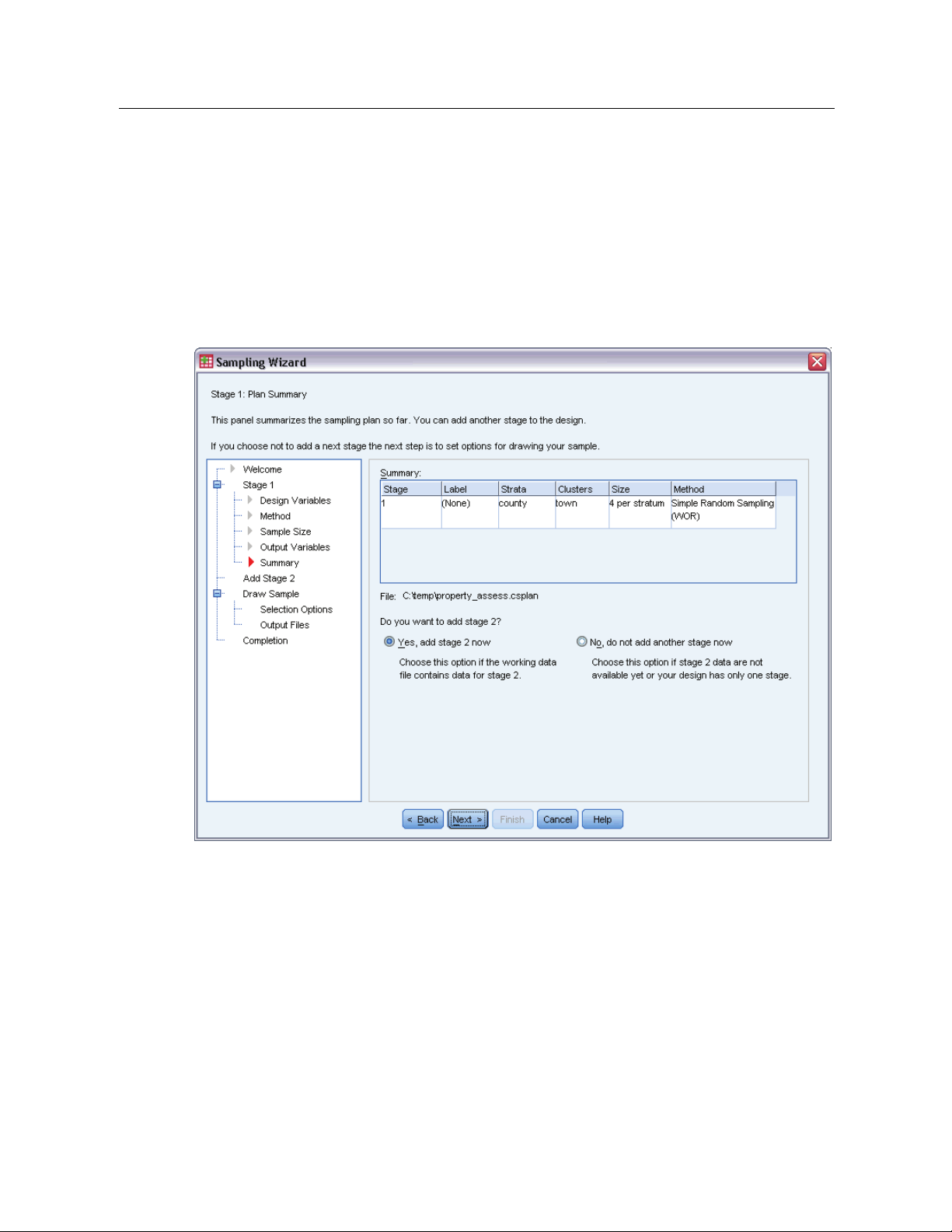
Sampling Wizard: Plan Summary
Figure 2-7
Sampling Wizard, Plan Summary step
13
Sampling from a Complex Design
This is the last step within each stage, providing a summary of the sample design specifications
through the current stage. From here, you can either proceed to the next stage (creating it, if
necessary) or set options for drawing the sample.
Page 28
14
Chapter 2
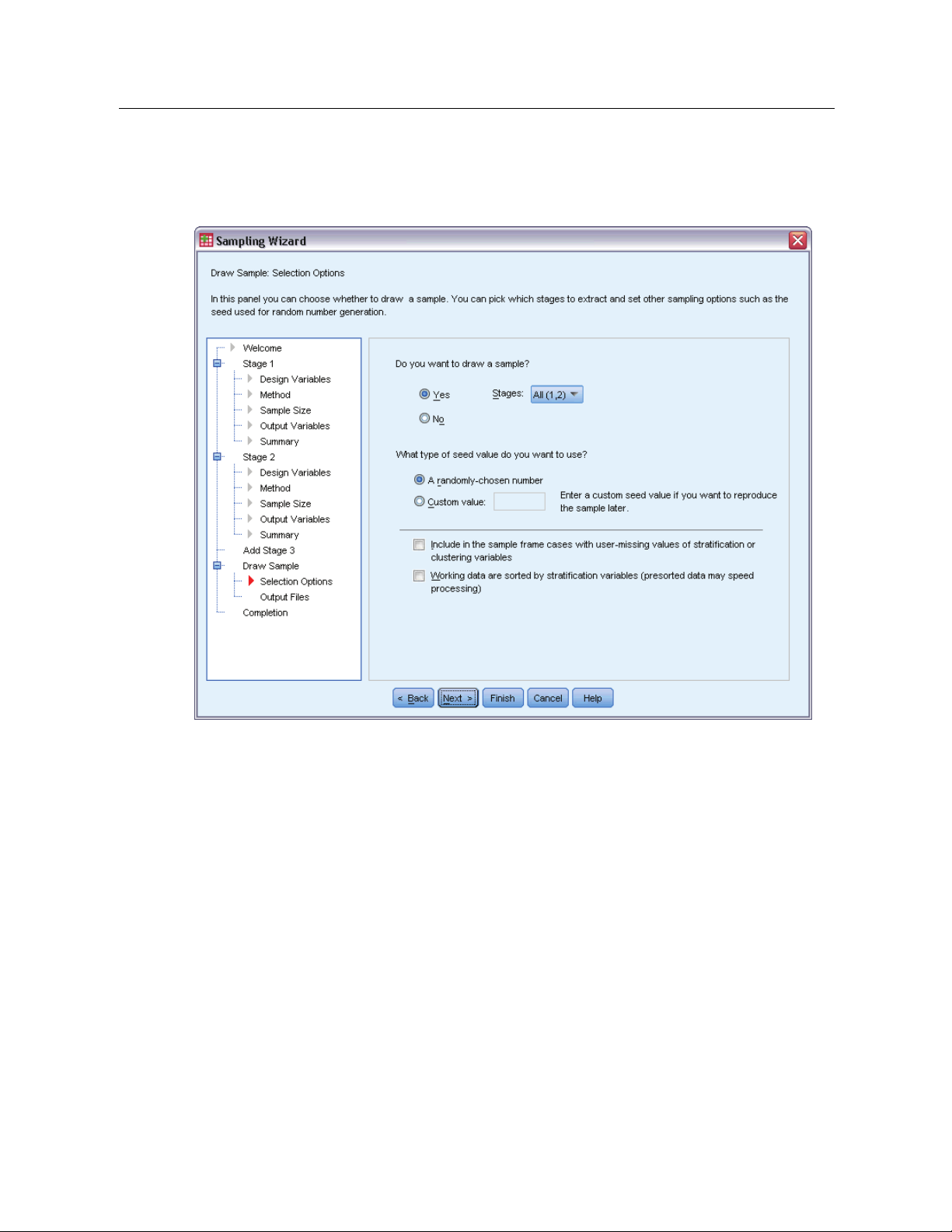
Sampling Wizard: Draw Sample Selection Options
Figure 2-8
Sampling Wizard, Draw Sample Selection Options step
This step allows you to choose whether to draw a sample. You can also control other sampling
options, such as the random seed and missing-value handling.
Draw sample. In addition to choosing whether to draw a sample, you can also choose to execute
part of the sampling design. Stages must be drawn in order—that is, stage 2 cannot be drawn
unless stage 1 is also drawn. When editing or executing a plan, you cannot resample locked stages.
Seed. This allows you to choose a seed value for random number generation.
Include user-missing values. This determines whether user-missing values are valid. If so,
user-missing values are treated as a separate category.
Data already sorted. If your sample frame is presorted by the values of the stratification variables,
this option allows you to speed the selection process.
Page 29
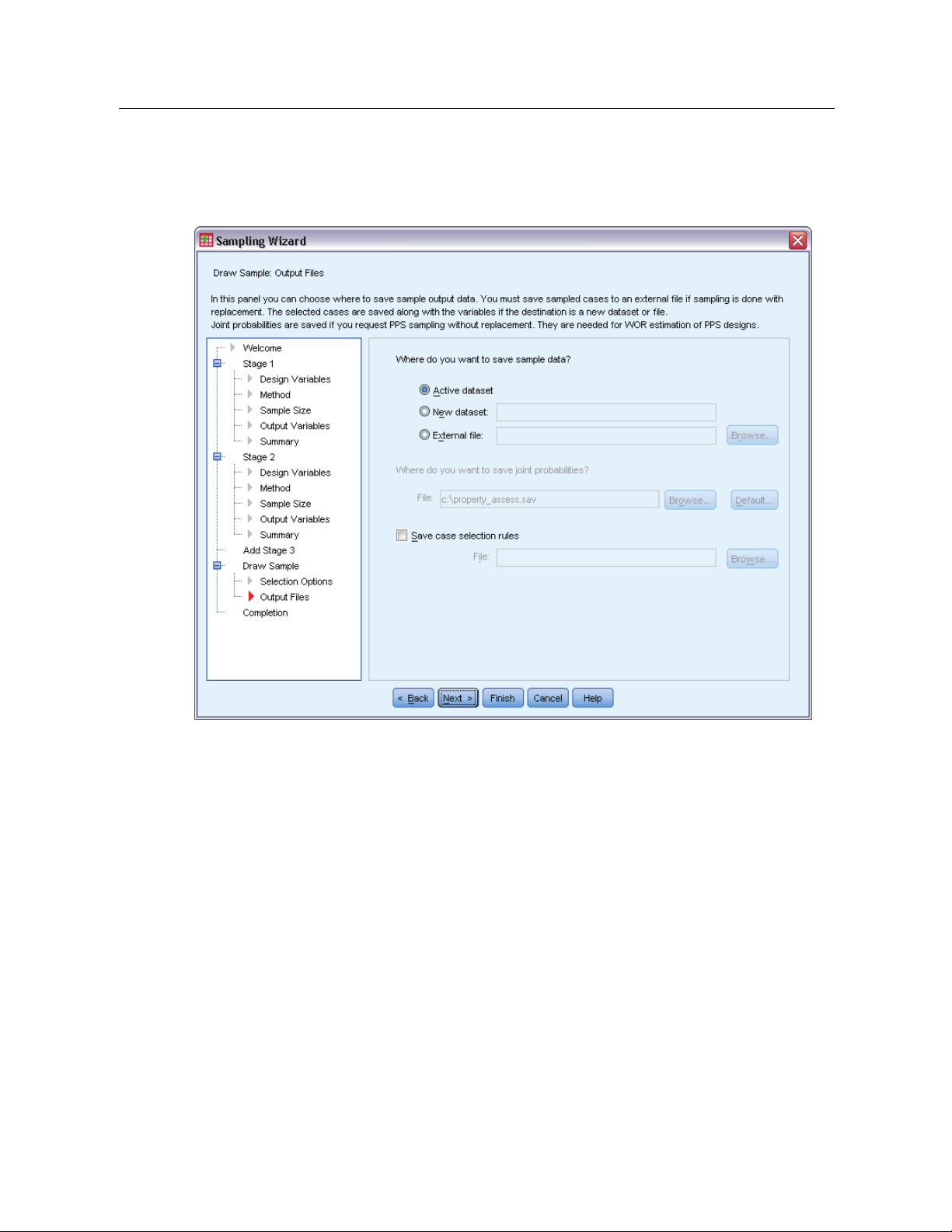
Sampling Wizard: Draw Sample Output Files
Figure 2-9
Sampling Wizard, Draw Sample Output Files step
15
Sampling from a Complex Design
This step allows you to choose where to direct sampled cases, weight variables, joint probabilities,
and case selection rules.
Sample data. These options let you determine where sample output is written. It can be added to
the active dataset, written to a new dataset, or saved to an external IBM® SPSS® Statistics data
file. Datasets are available during the current session but are not available in subsequent sessions
unless you explicitly save them as data files. Dataset names must adhere to variable naming rules.
If an external file or new dataset is specified, the sampling output variables and variables in the
active dataset for the selected cases are written.
Joint probabilities. These options let you determine where joint probabilities are written. They are
saved to an external SPSS Statistics data file. Joint probabilities are produced if the PPS WOR,
PPS Brewer, PPS Sampford, or PPS Murthy method is selected and WR estimation is not specified.
Case selection rules. If you are constructing your sample one stage at a time, you may want to
save the case selection rules to a text file. They are useful for constructing the subframe for
subsequent stages.
Page 30
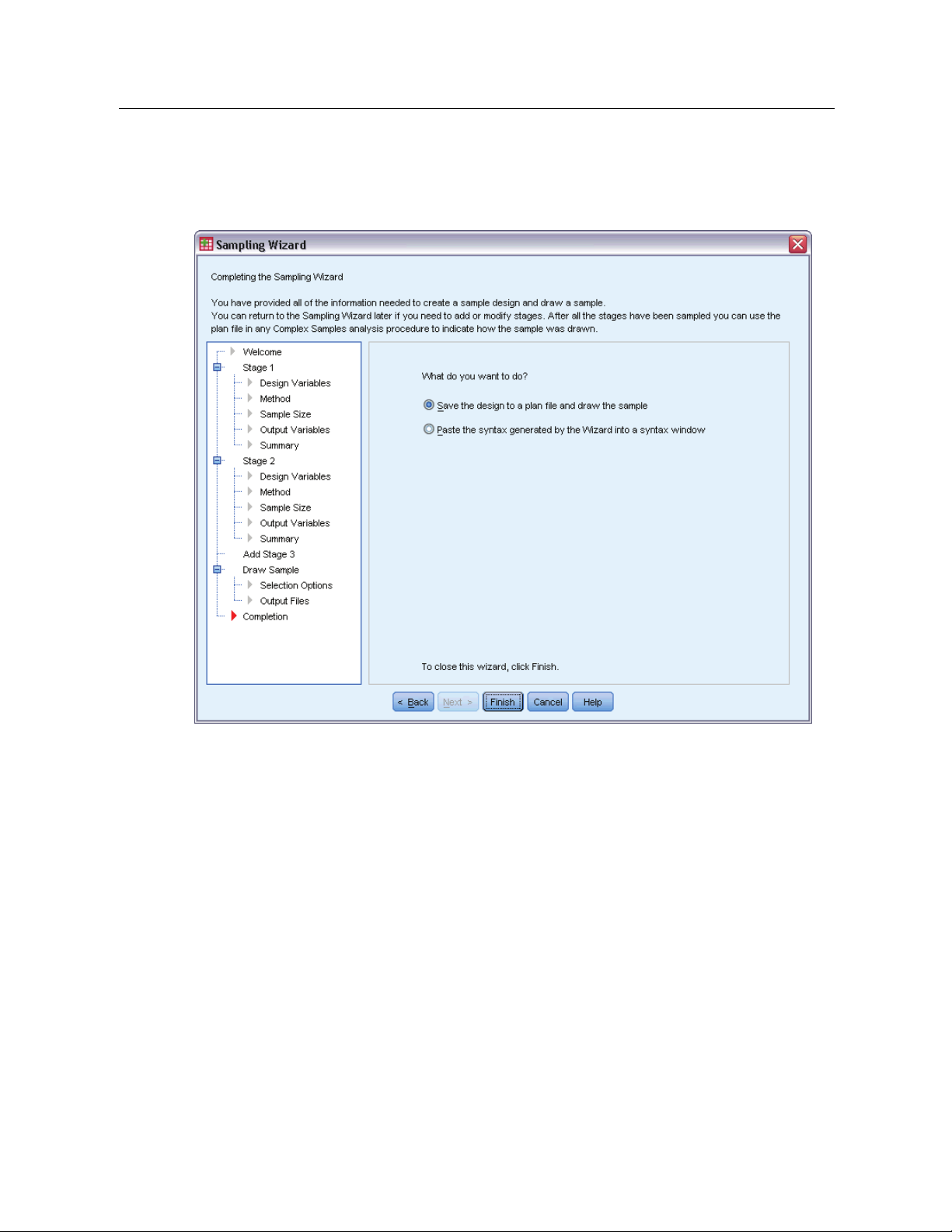
16
Chapter 2
Sampling Wizard: Finish
Figure 2-10
Sampling Wizard, Finish step
This is the final step. You can save the plan file and draw the sample now or paste your selections
into a syntax window.
When making changes to stages in the existing plan file, you can save the edited plan to a
new file or overwrite the existing file. When adding stages without making changes to existing
stages, the Wizard automatically overwrites the existing plan file. If you want to save the plan
to a new file, select
Paste the syntax generated by the Wizard into a syntax window and change the
filename in the syntax commands.
Modifying an Existing Sample Plan
E From the menus choose:
Analyze > Complex Samples > Select a Sample...
E
Select Editasampledesignand choose a plan file to edit.
E Click Next to continue through the Wizard.
Page 31

E
ReviewthesamplingplaninthePlanSummarystep,andthenclickNext.
Subsequent steps are largely the same as for a new design. See the Help for individual steps
for more information.
E Navigate to the Finish step, and specify a new name for the edited plan file or choose to overwrite
the existing plan file.
Optionally, you can:
Specify stages that have already been sampled.
Remove stages from the plan.
Sampling Wizard: Plan Summary
Figure 2-11
Sampling Wizard, Plan Summary step
17
Sampling from a Complex Design
This step allows you to review the sampling plan and indicate stages that have already been
sampled. If editing a plan, you can also remove stages from the plan.
Previously sampled stages. If an extended sampling frame is not available, you will have to execute
a multistage sampling design one stage at a time. Select which stages have already been sampled
from the drop-down list. Any stages that have been executed are locked; they are not available in
the Draw Sample Selection Options step, and they cannot be altered when editing a plan.
Page 32

18
Chapter 2
Remove stages. You can remove stages 2 and 3 from a multistage design.
Running an Existing Sample Plan
E From the menus choose:
Analyze > Complex Samples > Select a Sample...
Select Draw a sample and choose a plan file to run.
E
E Click Next to continue through the Wizard.
E ReviewthesamplingplaninthePlanSummarystep,andthenclickNext.
E The individual steps containing stage information are skipped when executing a sample plan. You
can now go on to the Finish step at any time.
Optionally, you can specify stages that have already been sampled.
CSPLAN and CSSELECT Commands Additional Features
The command syntax language also allows you to:
Specify custom names for output variables.
Control the output in the Viewer. For example, you can suppress the stagewise summary of
the plan that is displayed if a sample is designed or modified, suppress the summary of the
distribution of sampled cases by strata that is shown if the sample design is executed, and
request a case processing summary.
Choose a subset of variables in the active dataset to write to an external sample file or to
a different dataset.
See the Command Syntax Reference for complete syntax information.
Page 33

Preparing a Complex Sample for Analysis
Figure 3-1
Analysis Preparation Wizard, Welcome step
Chapter
3
The Analysis Preparation Wizard guides you through the steps for creating or modifying an
analysis plan for use with the various Complex Samples analysis procedures. Before using the
rd, you should have a sample drawn according to a complex design.
Wiza
Creating a new plan is most useful when you do not have access to the samp ling plan file used
to draw the sample (recall that the sampling plan contains a default analysis plan). If you do
access to the sampling plan file used to draw the sample, you can use the default analysis
have
plan contained in the sampling plan file or override the default analysis specifications and save
your changes to a new file.
© Copyright SPSS Inc. 1989, 2010
19
Page 34

20
Chapter 3
Creating a New Analysis Plan
E From the menus choose:
Analyze > Complex
Select Createaplanfile,andchooseaplanfilename to which you will save the analysis plan.
E
Samples > Prepare for Analysis...
E Click Next to continue t
E Specify the variable containing sample weights in the Design Variables step, optionally defining
hrough the Wizard.
strata and clusters.
E You can now click Finish to save the plan.
Optionally, in further steps you can:
Select the method for estimating standard errors in the Estimation Method step.
Specify the number of units sampled or the inclusion probability per unit in the Size step.
Add a second or third stage to the design.
Paste your selections as command syntax.
Analysis Preparation Wizard: Design Variables
Figure 3-2
Analysis Preparation Wizard, Design Variables step
Page 35

21
Preparing a Compl ex Sample for Analysis
This step allows you to identify t he stratification and clustering variables and define sample
weights. You can also provide a label for the stage.
Strata. The cross-classification of stratification variables defines distinct subpopulations, or strata.
Your total sample represents the combination of independent samples from each stratum.
Clusters. Cluster variables define groups of observational units, or clusters. Samples drawn in
multiple stages select clusters in the earlier stages and then subsample units from the s elected
clusters. When analyzing a data file obtained by sampling clusters with replacement, you should
include the duplication index as a cluster variable.
Sample Weight. You must provide sample weights in the first stage. Sample weights are computed
automatically for subsequent stages of the current design.
Stage Label. Youcanspecifyanoptionalstringlabelforeachstage. Thisisusedintheoutputto
help identify stagewise information.
Note: The source variable list has the same contents across steps of the Wizard. In other words,
variables removed from the source list in a particular step are removed from the list in all steps.
Variables returned to the source list show up in all steps.
Tree Controls for Navigating the Analysis Wizard
At the left side of each step of the Analysis Wizard is an outline of all the steps. You can navigate
the Wizard by clicking on the name of an enabled step in the outline. Steps are enabled as long as
all previous steps are valid—that is, as long as each previous step has b een given the minimum
required specifications for that step. For more information on why a given step may be invalid,
see the Help for individual steps.
Page 36

22
Chapter 3
Analysis Preparation Wizard: Estimation Method
Figure 3-3
Analysis Preparation Wizard, Estimation Method step
This step allows you to spec
WR (sampling with replacement). WR estimation does not include a correction for sampling from a
ify an estimation method for the stage.
finite population (FPC) when estimating the variance under the complex sampling design. You
can choose to include or exclude the FPC when estimating the variance under simple random
sampling (SRS).
Choosing not to include the FPC for SRS variance estimation is recommended when the
analysis weights have been scaled so that they do not add up to the population size. The SRS
variance estimate is used in computing statistics like the design effect. WR estimation can be
specified only in the final stage of a design; the Wizard will not allow you to add another stage if
you select WR estimation.
Equal WOR (equal probability sampling without replacement). Equal WOR estimation includes the
finite population correction and assumes that units are sampled with equal probability. Equal
WOR can be specified in any stage of a design.
Unequal WOR (unequal probability sampling without replacement). In addition to using the finite
population correction, Unequal WOR accounts for sampling units (usually clusters) selected with
unequal probability. This estimation method is available only in the first stage.
Page 37

Analysis Preparation Wizard: Size
Figure 3-4
Analysis Preparation Wizard, Size step
23
Preparing a Compl ex Sample for Analysis
This step is used to specify inclusion probabilities or population sizes for the current stage. Sizes
can be fixed or can vary across strata. For the purpose of specifying sizes, clusters specified in
us stages can be used to define strata. Note that this step is necessary only when Equal
previo
WOR is chosen as the Estimation Method.
Units. You can specify exact population sizes or the probabilities with which units were sampled.
Value. A single value is applied to all strata. If Population Sizes is selected as the unit metric,
you should enter a non-negative integer. If
avalue
Unequ
between 0 and 1, inclusive.
al values for strata.
Allows you to enter size values on a per-stratum basis via the Define
Inclusion Probabilities is selected, you should enter
Unequal Sizes dialog box.
Read values from variable. Allows you to select a numeric variable that contains size values
for strata.
Page 38

24
Chapter 3
Define Unequal Sizes
Figure 3-5
Define Unequal Sizes dialog box
The Define U
Size Specifications grid. The grid displays the cross-classifications of up to five strata or
nequal Sizes dialog box allows you to enter sizes on a per-stratum basis.
cluster variables—one stratum/cluster combination per row. Eligible grid variables include all
stratifica
tion variables from the current and previous stages and all cluster variables from previous
stages. Variables can be reordered within the grid or moved to the Exclude list. Enter sizes in the
rightmost column. Click
stratific
ation and cluster variables in the grid cells. Cells that contain unlabeled values always
show values. Click
Labels or Va lues to toggle the display of value labels and data values for
Refresh Strata to repopulate the grid with each combination of labeled data
values for variables in the grid.
Exclude.
To specify sizes for a subset of stratum/cluster combinations, move one or more variables
to the Exclude list. These variables are not used to define sample sizes.
Page 39

Analysis Preparation Wizard: Plan Summary
Figure 3-6
Analysis Preparation Wizard, Plan Summary step
25
Preparing a Compl ex Sample for Analysis
This is the last step within each stage, providing a summary of the analysis design specifications
through the current stage. From here, you can either proceed to the next stage (creating it if
ary) or save the analysis specifications.
necess
If you cannot add another stage, it is likely because:
No cluster variable was specified in the Design Variables step.
You selected WR estimation in the Estimation Method step.
This is the third stage of the analysis, and the Wizard supports a maximum of three stages.
Page 40

26
Chapter 3
Analysis Preparation Wizard: Finish
Figure 3-7
Analysis Preparation Wizard, Finish step
This is t
he final step. You can save the plan file now or paste your selections to a syntax window.
When making changes to stages in the existing plan file,youcansavetheeditedplantoanew
file or overwrite the existing file. When adding stages without making changes to existing stages,
the Wiza
new file, choose to
rd automatically overwrites the existing plan file. If you want to save the plan to a
Paste the syntax generated by the Wizard into a syntax window and change the
filename in the syntax commands.
Modifying an Existing Analysis Plan
E From the menus choose:
Analyze > Complex Samples > Prep are for Analysis...
Select Edit a plan file, and choose a plan filename to which you will save the analysis plan.
E
E Click Next to continue through the Wizard.
Page 41

E
Review the analysis plan in the Plan Summary step, and then click Next.
Subsequent steps are largely the same as for a new design. For more information, see the Help
for individual steps.
E Navigate to the Finish step, and specify a new name for the edited plan file, or choose to overwrite
the existing plan file.
Optionally, you can remove stages from the plan.
Analysis Preparation Wizard: Plan Summary
Figure 3-8
Analysis Preparation Wizard, Plan Summary step
27
Preparing a Compl ex Sample for Analysis
This step allows you to review the analysis plan and remove stages from the plan.
Remove Stages. You can remove stages 2 and 3 from a multistage design. Since a plan must have
at least one stage, you can edit but not remove stage 1 from the design.
Page 42
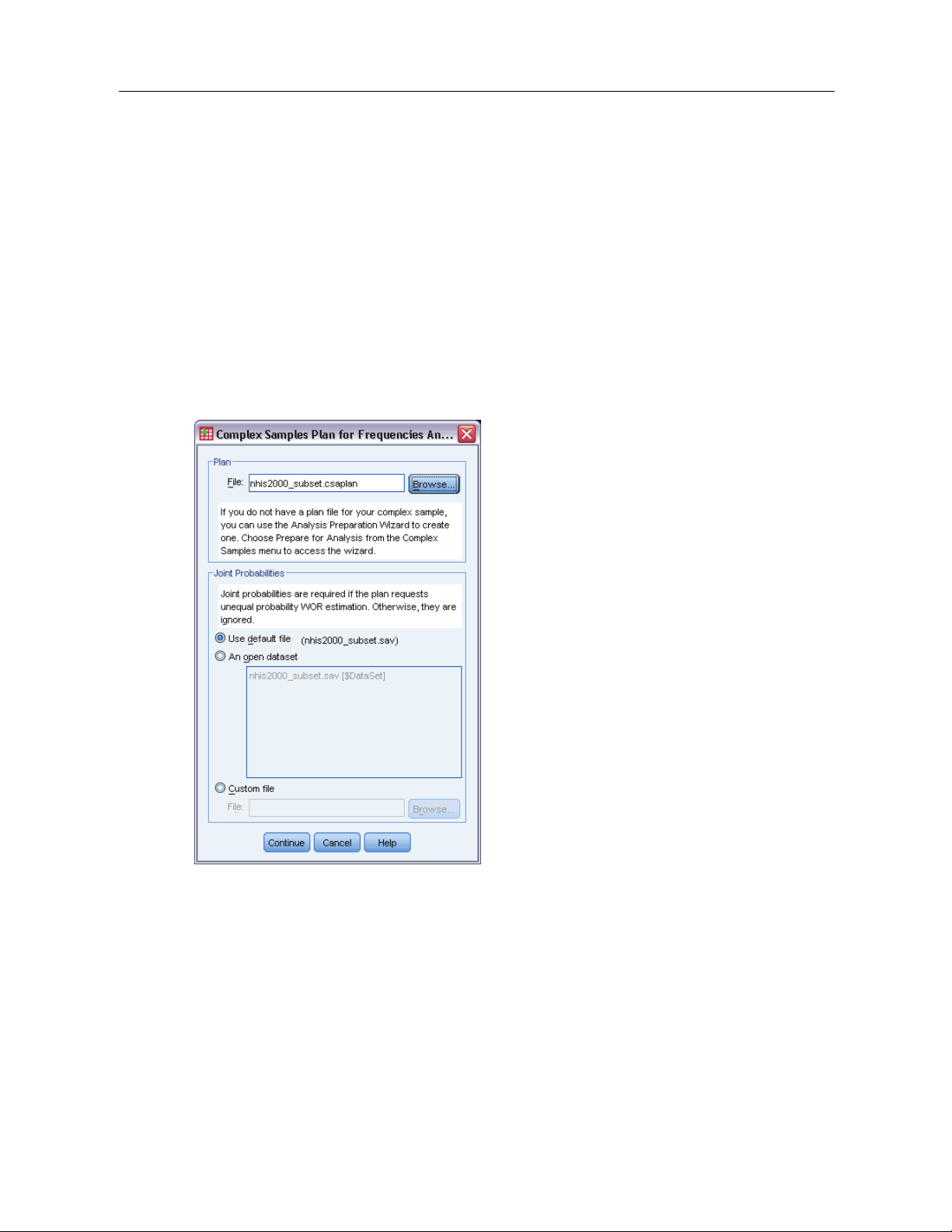
Complex Samples Plan
Complex Samples analysis procedures require analysis specifications from an analysis or sample
plan file in order to provide valid results.
Figure 4-1
Complex Samples Plan dialog box
Chapter
4
Plan. Specify the path of an analysis or sample plan file.
Joint Probabilities. In order to use Unequal WOR estimation for clusters drawn using a PPS WOR
method, you need to specify a separate file or an open dataset containing the joint probabilities.
This file or dataset is created by the Sampling Wizard during sampling.
© Copyright SPSS Inc. 1989, 2010
28
Page 43

Complex Samples Frequencies
The Complex Samples Frequencies procedure produces frequency tables for selected variables
and displays univariate statistics. Optionally, you can request statistics by subgroups, defined by
one or more categorical variables.
Example. Using the Complex Samples Frequencies procedure, you can obtain univariate tabular
statistics for vitamin usage among U.S. citizens, based on the results of the National Health
Interview Survey (NHIS) and with an appropriate analysis plan for this public-use data.
Statistics. The procedure produces estimates of cell population sizes and table percentages,
plus standard errors, confidence intervals, coefficients of variation, design effects, square roots
of design effects, cumulative values, and unweighted counts for each estimate. Additionally,
chi-square and likelihood-ratio statistics are computed for the test of equal cell proportions.
Chapter
5
Data. Variables for which frequency tables are produced should be categorical. Subpopulation
variables can be string or numeric but should be categorical.
Assumptions. The cases in the data file represent a sample from a complex design that should
be analyzed according to the specifications in the file selected in the Complex Samples Plan
dialog box.
Obtaining Complex Samples Freq uen cies
E From the menus choose:
Analyze > Complex Samples > Frequencies...
Select a plan file. Optionally, select a custom joint probabilities file.
E
E Click Continue.
© Copyright SPSS Inc. 1989, 2010
29
Page 44
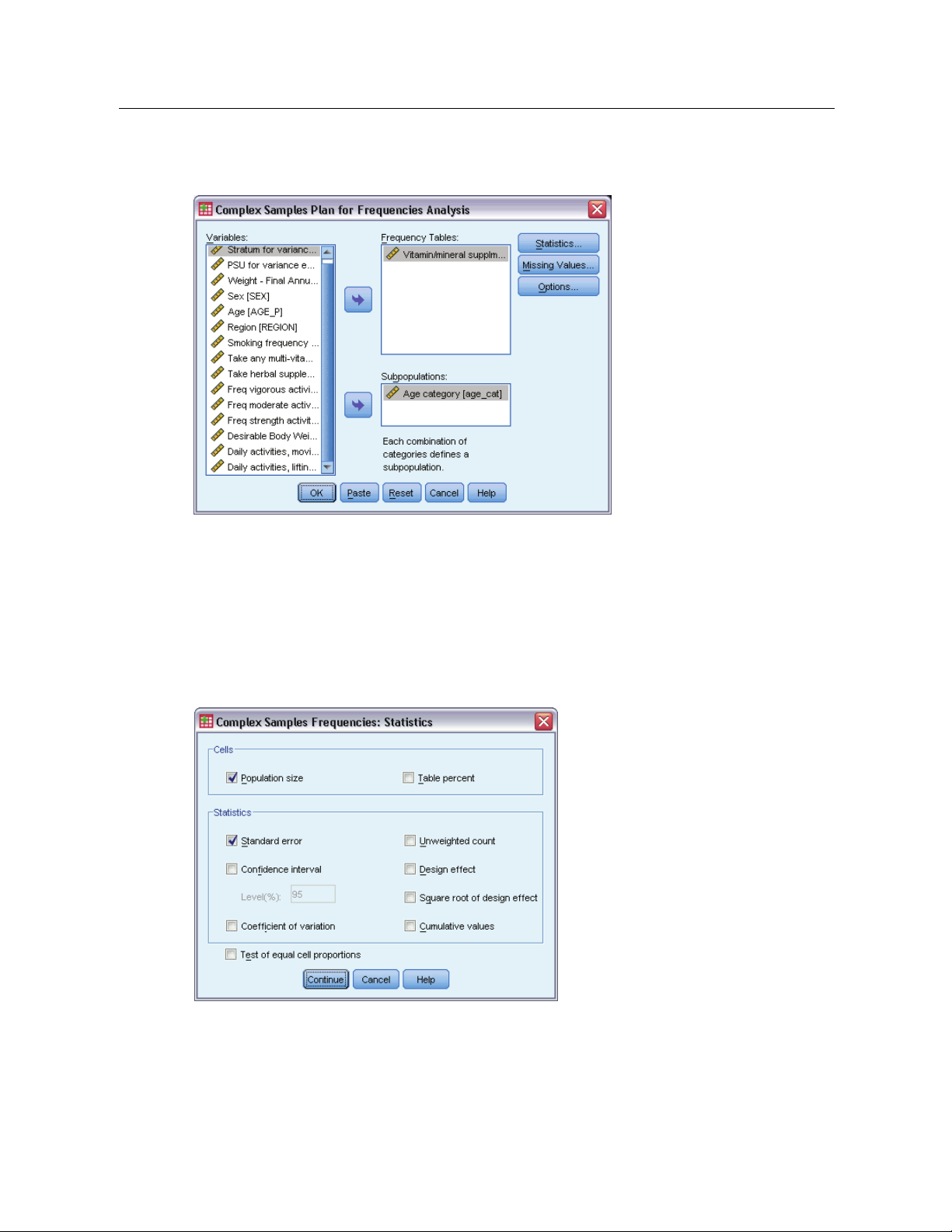
30
Chapter 5
Figure 5-1
Frequencies dialog box
E Select at least one frequency variable.
Optionally, you can specify variables to define subpopulations. Statistics are computed separately
for each subpopulation.
Complex Samples Frequencies Statistics
Figure 5-2
Frequencies Statistics dial og box
Cells. This group allows you to request estimates of the cell population sizes and table percentages.
Statistics. This group produces statistics associated with the population size or table percentage.
Standard error. The standard error of the estimate.
Page 45

Confidence interval. Aconfidence interval for the estimate, using the specified level.
Coefficient of variation. The ratio of the standard error of the estimate to the estimate.
Unweighted count. The number of units used to compute the estimate.
Design effect. The ratio of the variance of the estimate to the variance obtained by assuming
that the sample is a simple random sample. This is a measure of the effect of specifying a
complex design, where values further from 1 indicate greater effects.
Square root of design effect. This is a measure of the effect of specifying a complex design,
where values further from 1 indicate greater effects.
Cumulative values. The cumulative estimate through each value of the variable.
Test of equal cell proportions. This produces chi-square and likelihood-ratio tests of the hypothesis
that the categories of a variable have equal fre quencies. Separate tests are performed for each
variable.
Complex Samples Missing Values
Figure 5-3
Missing Values dialog box
31
Complex Samples Frequencies
Tables. This group determines which cases are used in the analysis.
Use all available data. Missing values are determined on a table-by-table basis. Thus, the cases
used to compute statistics may vary across frequency or crosstabulation tables.
Use consistent case base. Missing values are determined across all variables. Thus, the cases
used to compute statistics are consistent across tables.
Categorical Design Variables. This group determines whether user-missing values are valid
or invalid.
Page 46

32
Chapter 5
Complex Samples Options
Figure 5-4
Options dialog box
Subpopulation Display. You can choose to have subpopulations displayed in the same table or in
separate tables.
Page 47

Complex Samples Descriptives
The Complex Samples Descriptives procedure displays univariate summary statistics for several
variables. Optionally, you can request statistics by subgroups, defined by one or more categorical
variables.
Example. Using the Complex Samples Descriptives procedure, you can obtain univariate
descriptive statistics for the activity levels of U.S. citizens, based on the results of the National
Health Interview Survey (NHIS) and with an appropriate analysis plan for this public-use data.
Statistics. The procedure produces means and sums, plus t tests, standard errors, confidence
intervals, coefficients of variation, unweighted counts, population sizes, design effects, and square
roots of design effects for each estimate.
Data. Measures should be scale variables. Subpopulation variables can be string or numeric
but should be categorical.
Chapter
6
Assumptions. The cases in the data file represent a sample from a complex design that should
be analyzed according to the specifications in the file selected in the Complex Samples Plan
dialog box.
Obtaining Complex Samples Descriptives
E From the menus choose:
Analyze > Complex Samples > Descriptives...
Select a plan file. Optionally, select a custom joint probabilities file.
E
E Click Continue.
© Copyright SPSS Inc. 1989, 2010
33
Page 48

34
Chapter 6
Figure 6-1
Descriptives dialog box
E Select at least one measure variable.
Optionally, you can specify variables to define subpopulations. Statistics are computed separately
for each subpopulation.
Complex Samples Descriptives Statistics
Figure 6-2
Descriptives Statistics dialog box
Page 49

Summaries. This group allows you to request estimates of the means and sums of the measure
variables. Additionally, you can request t tests of the estimates against a specified value.
Statistics. This group produces statistics associated with the mean or sum.
Standard error. The standard error of the estimate.
Confidence interval. Aconfidence interval for the estimate, using the specified level.
Coefficient of variation. The ratio of the standard error of the estimate to the estimate.
Unweighted count. The number of units used to compute the estimate.
Population size. The estimated number of units in the population.
Design effect. The ratio of the variance of the estimate to the variance obtained by assuming
that the sample is a simple random sample. This is a measure of the effect of specifying a
complex design, where values further from 1 indicate greater effects.
Square root of design effect. This is a measure of the effect of specifying a complex design,
where values further from 1 indicate greater effects.
Complex Samples Descriptives Missing Values
Figure 6-3
Descriptives Missing Values dialog box
35
Complex Samples Descriptives
Statistics for Measure Variables. This group determines which cases are used in the analysis.
Use all available data. Missing values are determined on a variable-by-variable basis, thus the
cases used to compute statistics may vary across measure variables.
Ensure consistent case base. Missing values are determined across all variables, thus the
cases used to compute statistics are consistent.
Categorical Design Variables. This group determines whether user-missing values are valid
or invalid.
Page 50
36
Chapter 6
Complex Samples Options
Figure 6-4
Options dialog box
Subpopulation Display. You can choose to have subpopulations displayed in the same table or in
separate tables.
Page 51

Complex Samples Crosstabs
The Complex Samples Crosstabs procedure produces crosstabulation tables for pairs of selected
variables and displays two-way statistics. Optionally, you can request statistics by subgroups,
defined by one or more categorical variables.
Example. Using the Complex Samples Crosstabs procedure, you can obtain cross-classification
statistics for smoking frequency by vitamin usage of U.S. citizens, based on the results of the
National Health Interview Survey (NHIS) and with an appropriate analysis plan for this public-use
data.
Statistics. The procedure produces estimates of cell population sizes and row, column, and table
percentages, plus standard errors, confidence intervals, coefficients of variation, expected values,
design effects, square roots of design effects, residuals, adjusted residuals, and unweighted counts
for each estimate. The odds ratio, relative risk, and risk difference are computed for 2-by-2 tables.
Additionally, Pearson and likelihood-ratio statistics are computed for the test of independence of
the row and column variables.
Chapter
7
Data. Row and column variables should be categorical. Subpopulation variables can be string or
numeric but should be categorical.
Assumptions. The cases in the data file represent a sample from a complex design that should
be analyzed according to the specifications in the file selected in the Complex Samples Plan
dialog box.
Obtaining Complex Samples Crosstabs
E From the menus choose:
Analyze > Complex Samples > Crosstabs...
Select a plan file. Optionally, select a custom joint probabilities file.
E
E Click Continue.
© Copyright SPSS Inc. 1989, 2010
37
Page 52

38
Chapter 7
Figure 7-1
Crosstabs dialog box
E Select at least one row variable and one column variable.
Optionally, you can specify variables to define subpopulations. Statistics are computed separately
for each subpopulation.
Page 53

Complex Samples Crosstabs Statistics
Figure 7-2
Crosstabs Statistics dialog box
39
Complex Samples Crosstabs
Cells. This group allows you to request estimates of the cell population size and row, column,
and table percentages.
Statistics. This group produces statistics associated with the population size and row, column,
and table percentages.
Standard error. The standard error of the estimate.
Confidence interval. Aconfidence interval for the estimate, using the specified level.
Coefficient of variation. The ratio of the standard error of the estimate to the estimate.
Expected values. The expected value of the estimate, under the hypothesis of independence
of the row and column variable.
Unweighted count. The number of units used to compute the estimate.
Design effect. The ratio of the variance of the estimate to the variance obtained by assuming
that the sample is a simple random sample. This is a measure of the effect of specifying a
complex design, where values further from 1 indicate greater effects.
Square root of design effect. This is a measure of the effect of specifying a complex design,
where values further from 1 indicate greater effects.
Residuals. The expected value is the number of cases that you would expect in the cell if there
were no relationship between the two variables. A positive residual indicates that there are
more cases in the cell than there would be if the row and column variables were independent.
Adjusted residuals. The residual for a cell (observed minus expected value) divided by an
estimate of its standard error. The resulting standardized residual is expressed in standard
deviation units above or below the mean.
Page 54

40
Chapter 7
Summaries for 2-by-2 Tables. This group produces statistics for tables in which the row and column
variable each have two categories. Each is a measure of the strength of the association between
the presence of a factor and the occurrence of an event.
Odds ratio. The odds ratio can be u sed as an estimate of relative risk when the occurrence
of the factor is rare.
Relative risk. The ratio of the risk of an event in the presence of the factor to the risk of the
event in the absence of the factor.
Risk difference. The difference between the risk of an event in the presence of the factor and
the risk of the event in the absence of the factor.
Test of independence of rows and columns. This produces chi-square and likelihood-ratio tests of
the hypothesis that a row and column variable are independent. Separate tests are performed
for each pair of variables.
Complex Samples Missing Values
Figure 7-3
Missing Values dialog box
Tables. This group determines which cases are used in the analysis.
Use all available data. Missing values are determined on a table-by-table basis. Thus, the cases
used to compute statistics may vary across frequency or crosstabulation tables.
Use consistent case base. Missing values are determined across all variables. Thus, the cases
used to compute statistics are consistent across tables.
Categorical Design Variables. This group determines whether user-missing values are valid
or invalid.
Page 55

Complex Samples Options
Figure 7-4
Options dialog box
Subpopulation Display. You can choose to have subpopulations displayed in the same table or in
separate tables.
41
Complex Samples Crosstabs
Page 56

Complex Samples Ratios
The Complex Samples Ratios procedure displays univariate summary statistics for ratios of
variables. Optionally, you can request statistics by subgroups, defined by one or more categorical
variables.
Example. Using the Complex Samples Ratios procedure, you can obtain descriptive statistics for
the ratio of current property value to last assessed value, based on the results of a statewide survey
carried out according to a complex design and with an appropriate analysis plan for the data.
Statistics. The procedure produces ratio estimates, t tests, standard errors, confidence intervals,
coefficients of variation, unweighted counts, population sizes, design effects, and square roots of
design effects.
Data. Numerators and denominators should be positive-valued scale variables. Subpopulation
variables can be string or numeric but should be categorical.
Chapter
8
Assumptions. The cases in the data file represent a sample from a complex design that should
be analyzed according to the specifications in the file selected in the Complex Samples Plan
dialog box.
Obtaining Complex Samples Ratios
E From the menus choose:
Analyze > Complex Samples > Ratios...
Select a plan file. Optionally, select a custom joint probabilities file.
E
E Click Continue.
© Copyright SPSS Inc. 1989, 2010
42
Page 57

Figure 8-1
Ratios dialog box
E Select at least one numerator variable and denominator variable.
43
Complex Samples Ratios
Optionally, you can specify variables to define subgroups for which statistics are produced.
Complex Samples Ratios Statistics
Figure 8-2
Ratios Statistics dialog box
Statistics. This group produces statistics associated with the ratio estimate.
Standard error. The standard error of the estimate.
Confidence interval. Aconfidence interval for the estimate, using the specified level.
Coefficient of variation. The ratio of the standard error of the estimate to the estimate.
Unweighted count. The number of units used to compute the estimate.
Population size. The estimated number of units in the population.
Page 58

44
Chapter 8
Design effect. The ratio of the variance of the estimate to the variance obtained by assuming
that the sample is a simple random sample. This is a measure of the effect of specifying a
complex design, where values further from 1 indicate greater effects.
Square root of design effect. This is a measure of the effect of specifying a complex design,
where values further from 1 indicate greater effects.
Ttest. You can request t tests of the estimates against a specifi
Complex Samples Ratios Missing Values
Figure 8-3
Ratios Missing Values dialog box
Ratios. This group determines which cases are used in the analysis.
Use all available data. Missing values are determined on a ratio-by-ratio basis. Thus, the cases
used to compute statistics may vary across numerator-denominator pairs.
Ensure consistent case base. Missing values are determined across all variables. Thus, the
cases used to compute statistics are consistent.
ed value.
Categorical Design Variables. This group determines whether user-missing values are valid
or invalid.
Complex Samples Options
Figure 8-4
Options dialog box
Subpopulation Display. You can choose to have subpopulations displayed in the same table or in
separate tables.
Page 59

Complex Samples General Linear Model
The Complex Samples General Linear Model (CSGLM) procedure performs linear regression
analysis, as well as analysis of variance and covariance, for samples drawn by complex sampling
methods. Optionally, you can request analyses for a subpopulation.
Example. A grocery store chain surveyed a set of customers concerning their purchasing habits,
according to a complex design. Given the survey results and how much e ach customer spent in the
previous month, the store wants to see if the frequency with which customers shop is related to
the amount they spend in a month, controlling for the gender of the customer and incorporating
the sampling design.
Chapter
9
Statistics. The procedure produces estimates, standard errors, confidence intervals, t tests, design
effects, and square roots of design effects for model parameters, as well as the correlations and
covariances between parameter estimates. Measures of model fit and descriptive statistics for the
dependent and independent variables are also available. Additionally, you can request estimated
marginal means for levels of model factors and factor interactions.
Data. The dependent variable is quantitative. Factors are categorical. Covariates are quantitative
variables that are related to the dependent variable. Subpopulation variables can b e string or
numeric but should be categorical.
Assumptions. The cases in the data file represent a sample from a complex design that should
be analyzed according to the specifications in the file selected in the Complex Samples Plan
dialog box.
Obtaining a Complex Samples General Linear M odel
From the menus choose:
Analyze > Complex Samples > General Linear Model...
Select a plan file. Optionally, select a custom joint probabilities file.
E
E Click Continue.
© Copyright SPSS Inc. 1989, 2010
45
Page 60

46
Chapter 9
Figure 9-1
General Linear Model dialog box
E Select a dependent variable.
Optionally, you can:
Select variables for factors and covariates, as appropriate for your data.
Specify a variable to define a subpopulation. The analysis is performed only for the selected
category of the subpopulation variable.
Page 61
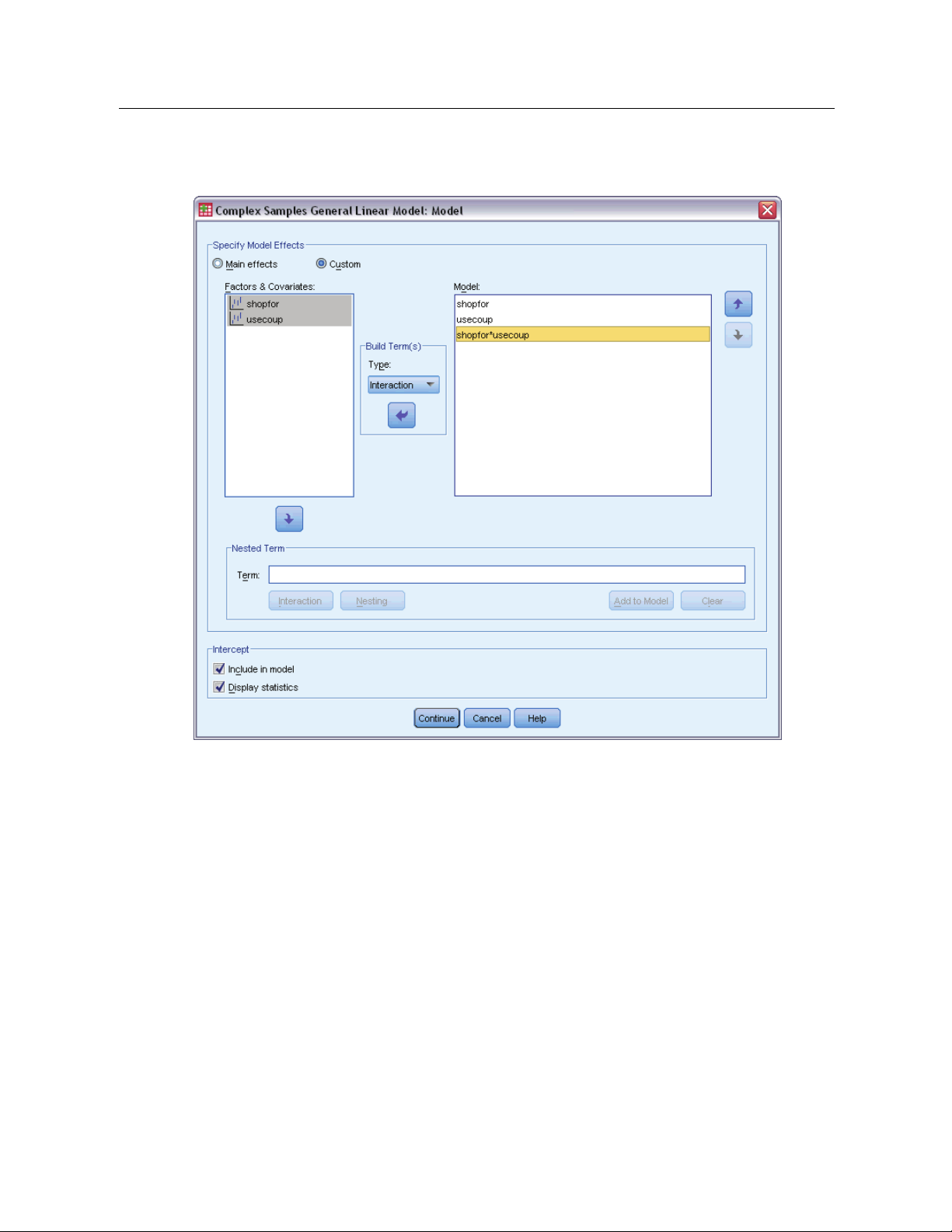
Figure 9-2
Model dialog box
47
Complex Samples Ge neral Linear Model
Specify Model Effects. By default, the procedure builds a main-effects model using the factors
and covariates specified in the main dialog box. Alternatively, you can build a custom model that
includes interaction effects and nested terms.
Non-Nested Terms
For the selected factors and covariates:
Interaction. Creates the highest-level interaction term for all selected variables.
Main effects. Creates a main-effects term for each variable selected.
All 2-way. Creates all possible two-way interactions of the selected variables.
All 3-way. Creates all possible three-way interactions of the selected variables.
All 4-way. Creates all possible four-way interactions of the selected variables.
All 5-way. Creates all possible five-way interactions of the selected variables.
Page 62

48
Chapter 9
Nested Terms
You can build nested terms for your model in this procedure. Nested terms are useful for modeling
the effect of a factor or covariate whose values do not interact with the levels of another factor.
For example, a grocery store chai
n may follow the spending habits of its customers a t several store
locations. Since each customer frequents only one of these locations, the Customer effect can be
said to be nested within the Store location effect.
Additionally, you can include in
teraction effects, such as polynomial terms involving the same
covariate, or add multiple levels of nesting to the nested term.
Limitations. Nested terms have the following restrictions:
All factors within an interaction must be unique. Thus, if A is a factor, then specifying A*A
is invalid.
All factors within a nested effect must be unique. Thus, if A is a factor, then specifying A(A)
is invalid.
No effect can be nested within a covariate. Thus, if A is a factor and X is a covariate, then
specifying A(X) is invalid.
Intercept. The intercept is usually included in the model. If you can assume the data pass through
the origin, you can exclude the intercept. Even if you include the intercept in the model, you
can choose to suppress statistics related to it.
Complex Samples General Linear Model Statistics
Figure 9-3
General Linear Model Statistics dialog box
Model Parameters. This group allows you to control the display of statistics related to the model
parameters.
Estimate. Displays estimates of the coefficients.
Standard error. Displays the standard error for each coefficient estimate
Confidence interval. Displays a confidence interval for each coefficient e
confidence level for the interval is set in the Options dialog box.
Ttest. Displays a t test of each coefficient estimate. The null hypothesis for each test is that
thevalueofthecoefficient is 0.
.
stimate. The
Page 63

Complex Samples Ge neral Linear Model
Covariances of parameter estimates. Displays an estimate of the covariance matrix for the
model coefficients.
Correlations of parameter estimates. Displays an estimate of the correlation matrix for the
model coefficients.
Design effect. The ratio of the variance of the estimate to the variance obtained by assuming
that the sample is a simple random sample. This is a measure of the effect of specifying a
complex design, where values further from 1 indicate greater effects.
Square root of design effect. This is a measure of the effect of specifying a complex design,
where values further from 1 indicate greater effects.
49
Model fit. Displays R
Population means of dependent variable and covariates. Displays summary information about the
2
and root mean squared error statistics.
dependent variable, covariates, and factors.
Sample design information. Displays summary information about the sample, including the
unweighted count and the population size.
Complex Samples Hypothesis Tests
Figure 9-4
Hypothesis Tests dialog box
Test Statistic. This group allows you to select the type of statistic used for testing hypotheses. You
can choose between F,adjustedF, chi-square, and adjusted chi-square.
Sampling Degrees of Freedom. This group gives you control over the sampling design degrees of
freedomusedtocomputep values for all test statistics. If based on the sampling design, the value
is the difference between the number of primary sampling units and the number of strata in the
Page 64

50
Chapter 9
first stage of sampling. Alternatively, you can set a custom degrees of freedom by specifying a
positive integer.
Adjustment for Multiple Comparisons. When performing hypothesis tests with multiple contrasts,
the overall significance level can be adjusted from the significance levels for the included
contrasts. This group allows you to choose the adjustment method.
Least significant difference. This method does not control the overall probability of rejecting
the hypotheses that some linear contrasts are different from the null hypothesis values.
Sequential Sidak. This is a sequentially step-down rejective Sidak procedure that is much
less conservative in terms of rejecting individual hypotheses but maintains the same overall
significance level.
Sequential Bonferroni. This is a sequentially step-down rejective Bonferroni procedure that is
much less conservative in terms of rejecting individual hypotheses but maintains the same
overall significance level.
Sidak. This method provides tighter bounds than the Bonferroni approach.
Bonferroni. This method adjusts the observed significance level for the fact that multiple
contrasts are being tested.
Complex Samples General Linear Model Estimated Means
Figure 9-5
General Linear Model Estimated Means dialog box
Page 65

51
Complex Samples Ge neral Linear Model
The Estimated Means dialog box allows you to display the model-estimated marginal means for
levels of factors and factor interactions specified in the Model subdialog box. You can also request
that the overall population mean be displayed.
Term. Estimated means are computed for the selected factors and factor interactions.
Contrast. The contrast determines how hypothesis tests are set up to compare the estimated means.
Simple. Compares the mean of each level to the mean of a specified level. This type of contrast
is useful when there is a control group.
Deviation. Compares the mean of each level (except a reference category) to the mean of all of
the levels (grand mean). The levels of the factor can be in any order.
Difference. Compares the mean of each level (except the first) to the mean of previous levels.
They are sometimes called reverse Helmert contrasts.
Helmert. Compares the mean of each level of the factor (except the last) to the mean of
subsequent levels.
Repeated. Compares the mean of each level (except the last) to the mean of the subsequent
level.
Polynomial. Compares the linear effect, quadratic effect, cubic effect, and so on. The
first degree of freedom contains the linear effect across all categories; the second degree
of freedom, the quadratic effect; and so on. These contrasts are often used to estimate
polynomial trends.
Reference Category. The simple and deviation contrasts require a reference category or factor
level against which the others are compared.
Complex Samples General Linear Model Save
Figure 9-6
General Linear Model Save dialog box
Save Variables. This group allows you to save the model predicted values and residuals as new
variables in the working file.
Page 66

52
Chapter 9
Export model as SPSS Statistics data. Writes a dataset in IBM® SPSS® Statistics format containing
the parameter correlation or covariance matrix with parameter estimates, standard errors,
significance values, and degrees of freedom. The order of variables in the matrix fi le is as follows.
rowtype_. Takes values (and value labels), COV (Covariances), CORR (Correlations), EST
(Parameter estimates), SE (Standard errors), SIG (Significance levels), and DF (Sampling
design degrees of freedom). There is a separate case with row type COV (or CORR) for each
model parameter, plus a separate case for each of the other row types.
varname_. Takes values P1, P2, ..., corresponding to an ordered list of all model parameters,
for row types COV or CORR, with value labels corresponding to the parameter strings shown
in the parameter estimates table. The cells are blank for other row types.
P1, P2, ... These variables correspond to an ordered list of all model parameters, with variable
labels corresponding to the parameter strings shown in the parameter estimates table, and
take values according to the row type. For redundant parameters, all covariances are set
to zero; correlations are set to the system-missing value; all parameter estimates are set at
zero; and all standard errors, significance levels, and residual degrees of freedom are set to
the system-missing value.
Note:Thisfile is not immediately usable for further analyses in other procedures that read a matrix
file unless those procedures accept all the row types exported here.
Export Model as XML. Saves the parameter estimates and the parameter covariance matrix, if
selected, in XML (PMML) format. You can use this model file to apply the model information to
other data files for scoring purposes.
Complex Samples General Linear Model Options
Figure 9-7
General Linear Model Options dialog box
User-Missing Values. All design variables, as well as the dependent variable and any covariates,
must have valid data. Cases with invalid data for any of these variables are deleted from the
analysis. These controls allow you to decide whether user-missing values are treated as valid
among the strata, cluster, subpopulation, and factor variables.
Confidence Interval. This is the confidence interval level for coefficient estimates and estimated
marginal means. Specify a value greater than or equal to 50 and less than 100.
Page 67

CSGLM Command Additional Features
The command syntax language also allows you to:
Specify custom tests of effects versus a linear combination of effects or a value (using the
CUSTOM subcommand).
Fix covariates at values other than their means when computing estimated marginal means
(using the
Specify a metric for polynomial contrasts (using the EMMEANS subcommand).
Specify a tolerance value for checking singularity (using the CRITERIA subcommand).
Create user-specified names for saved variables (using the SAVE subcommand).
Produce a general estimable function table (using the PRINT subcommand).
See the Command Syntax Reference for complete syntax information.
EMMEANS subcommand).
53
Complex Samples Ge neral Linear Model
Page 68

Chapter
10
Complex Samples Logistic Regression
The Complex Samples Logistic Regression procedure performs logistic regression analysis on
a binary or multinomial dependent variable for samples drawn by complex sampling methods.
Optionally, you can request analyses for a subpopulation.
Example. Aloanofficer has collected past records of customers given loans at several different
branches, according to a complex design. While incorporating the sample design, the officer
wants to see if the probability with which a customer defaults is related to age, employment
history, and amount of credit debt.
Statistics. The procedure produces estimates, exponentiated estimates, standard errors, confidence
intervals, t tests, design effects, and square roots of design effects for model parameters, as well as
2
the correlations and covariances between parameter estimates. Pseudo R
tables, and descriptive statistics for the dependent and independent variables are also available.
statistics, classification
Data. The dependent variable is categorical. Factors are categorical. Covariates are quantitative
variables that are related to the dependent variable. Subpopulation variables can b e string or
numeric but should be categorical.
Assumptions. The cases in the data file represent a sample from a complex design that should
be analyzed according to the specifications in the file selected in the Complex Samples Plan
dialog box.
Obtaining Complex Samples Logistic Regression
From the menus choose:
Analyze > Complex Samples > Logistic Regression...
Select a plan file. Optionally, select a custom joint probabilities file.
E
E Click Continue.
© Copyright SPSS Inc. 1989, 2010
54
Page 69

Figure 10-1
Logistic Regression dialog box
55
Complex Samples Logistic Regression
E Select a dependent variable.
Optionally, you can:
Select variables for factors and covariates, as appropriate for your data.
Specify a variable to define a subpopulation. The analysis is performed only for the selected
category of the subpopulation variable.
Complex Samples Logistic Regression Reference Category
Figure 10-2
Logistic Regression Reference Category dialog box
Page 70

56
Chapter 10
By default, the Complex Samples Logistic Regression procedure makes the highest-valued
category the reference category. This dialog box allows you to specify the highest value, the
lowest value, or a custom category as the reference category.
Complex Samples Logistic Regression Model
Figure 10-3
Logistic Regression Model dialog box
Specify Model Effects. By default, the procedure builds a main-effects model using the factors
and covariates specified in the main dialog box. Alternatively, you can build a custom model that
includes interaction effects and nested terms.
Non-Nested Terms
For the selected factors and covariates:
Interaction. Creates the highest-level interaction term for all selected variables.
Main effects. Creates a main-effects term for each variable selected.
All 2-way. Creates all possible two-way interactions of the selected variables.
Page 71

57
Complex Samples Logistic Regression
All 3-way. Creates all possible three-way interactions of the selected variables.
All 4-way. Creates all possible four-way interactions of the selected variables.
All 5-way. Creates all possible five-way interactions of the selected variables.
Nested Terms
You can build nested terms for your model in this procedure. Nested terms are useful for modeling
the effect of a factor or covariate whose values do not interact with the levels of anoth
er factor.
For example, a grocery store chain may follow the spending habits of its customers at several store
locations. Since each customer frequents only one of these locations, the Customer effect can be
said to be nested within the Store location effect.
Additionally, you can include interaction effects, such as polynomial terms involving the same
covariate, or add multiple levels of nesting to the nested term.
Limitations. Nested terms have the following restrictions:
All factors within an interaction must be unique. Thus, if A is a factor, then specifying A*A
is invalid.
All factors within a nested effect must be unique. Thus, if A is a factor, then specifying A(A
)
is invalid.
No effect can be nested within a covariate. Thus, if A is a factor and X is a covariate, then
specifying A(X) is invalid.
Intercept. The intercept is usually included in the model. If you can assume the data pass through
the origin, you can exclude the intercept. Even if you include the intercept in the model, you
can choose to suppress statistics related to it.
Complex Samples Logistic Regression Statistics
Figure 10-4
Logistic Regression Statistics dialog box
Model Fit. Controls the display of statistics that measure the overall model performance.
Page 72

58
Chapter 10
Pseudo R-square. The R
2
statistic from linear regression does not have an exact counterpart
among logistic regression models. There are, instead, multiple measures that attempt to mimic
2
the properties of the R
Classification table. Displays the tabulated cross-classifications of the observed category by
statistic.
the model-predicted category on the dependent variable.
Parameters. This group allows you to control the display of statistics related to the model
parameters.
Estimate. Displays estimates of the coefficients.
Exponentiated estimate. Displays the base of the natural logarithm raised to the power of the
estimates of the coefficients. While the estimate has nice properties for statistical testing, the
exponentiated estimate, or exp(B), is easier to interpret.
Standard error. Displays the standard error for each coefficient estimate.
Confidence interval. Displays a confidence interval for each coefficient estimate. The
confidence level for the interval is set in the Options dialog box.
Ttest. Displays a t test of each coefficient estimate. The null hypothesis for each test is that
thevalueofthecoefficient is 0.
Covariances of parameter estimates. Displays an estimate of the covariance matrix for the
model coefficients.
Correlations of parameter estimates. Displays an estimate of the correlation matrix for the
model coefficients.
Design effect. The ratio of the variance of the estimate to the variance obtained by assuming
that the sample is a simple random sample. This is a measure of the effect of specifying a
complex design, where values further from 1 indicate greater effects.
Square root of design effect. This is a measure of the effect of specifying a complex design,
where values further from 1 indicate greater effects.
Summary statistics for model variables. Displays summary information about the dependent
variable, covariates, and factors.
Sample design information. Displays summary information about the sample, including the
unweighted count and the population size.
Page 73

Complex Samples Hypothesis Tests
Figure 10-5
Hypothesis Tests dialog box
59
Complex Samples Logistic Regression
Test Statistic. This group allows you to select the type of statistic used for testing hypotheses. You
can choose between F,adjustedF, chi-square, and adjusted chi-square.
Sampling Degrees of Freedom. This group gives you control over the sampling design degrees of
freedomusedtocomputep values for all test statistics. If based on the sampling design, the value
is the difference between the number of primary sampling units and the number of strata in the
first stage of sampling. Alternatively, you can set a custom degrees of freedom by specifying a
positive integer.
Adjustment for Multiple Comparisons. When performing hypothesis tests with multiple contrasts,
the overall significance level can be adjusted from the significance levels for the included
contrasts. This group allows you to choose the adjustment method.
Least significant difference. This method does not control the overall probability of rejecting
the hypotheses that some linear contrasts are different from the null hypothesis values.
Sequential Sidak. This is a sequentially step-down rejective Sidak procedure that is much
less conservative in terms of rejecting individual hypotheses but maintains the same overall
significance level.
Sequential Bonferroni. This is a sequentially step-down rejective Bonferroni procedure that is
much less conservative in terms of rejecting individual hypotheses but maintains the same
overall significance level.
Sidak. This method provides tighter bounds than the Bonferroni approach.
Bonferroni. This method adjusts the observed significance level for the fact that multiple
contrasts are being tested.
Page 74

60
Chapter 10
Complex Samples Logistic Regression Odds Ratios
Figure 10-6
Logistic Regression Odds Ratios dialog box
The Odds Ratios dialog box allows you to display the model-estimated odds ratios for specified
factors and covariates. A separate set of odds ratios is computed for each category of the
dependent variable except the reference category.
Factors. For each selected factor, displays the ratio of the odds at each category of the factor to
the odds at the specified reference category.
Covariates. For each selected covariate, displays the ratio of the odds at the covariate’s mean value
plus the specified units of change to the odds at the mean.
When computing odds ratios for a factor or covariate, the procedure fixes all other factors at their
highest levels and all other covariates at their means. If a factor or covariate interacts with other
predictors in the model, then the odds ratios depend not only on the change in the specified
variable but also on the values of the variables with which it interacts. If a specified covariate
interacts with itself in the model (for example, age*age), then the odds ratios depend on both the
change in the covariate and the value of the covariate.
Page 75

Complex Samples Logistic Regression Save
Figure 10-7
Logistic Regression Save dialog box
61
Complex Samples Logistic Regression
Save Variables. This group allows you to save the model-predicted category and predicted
probabilities as new variables in the active d ataset.
Export model as SPSS Statistics data. Writes a dataset in IBM® SPSS® Statistics format containing
the parameter
correlation or covariance matrix with parameter estimates, standard errors,
significance values, and degrees of freedom. The order of variables in the matrix fi le is as follows.
rowtype_. Takes values (and value labels), COV (Covariances), CORR (Correlations), EST
(Parameter e
stimates), SE (Standard errors), SIG (Significance levels), and DF (Sampling
design degrees of freedom). There is a separate case with row type COV (or CORR) for each
model parameter, plus a separate case for each of the other row types.
varname_. Takes values P1, P2, ..., corresponding to an ordered list of all model parameters,
for row types
COV or CORR, with value labels corresponding to the parameter strings shown
in the parameter estimates table. The cells are blank for other row types.
P1, P2, ... These variables correspond to an ordered list of all model parameters, with variable
labels corresponding to the parameter strings shown in the parameter estimates table, and
take values
according to the row type. For redundant parameters, all covariances are set
to zero; correlations are set to the system-missing value; all parameter estimates are set at
zero; and all standard errors, significance levels, and residual degrees of freedom are set to
the system
-missing value.
Note:Thisfile is not immediately usable for further analyses in other procedures that read a matrix
file unless those procedures accept all the row types exported here.
Export Model as XML. Saves the parameter estimates and the parameter covariance matrix, if
selected, in XML (PMML) format. You can use this model file to apply the model information to
other data files for scoring purposes.
Page 76

62
Chapter 10
Complex Samples Logistic Regression Options
Figure 10-8
Logistic Regression Options dialog box
Estimation. This group gives you control of various criteria used in the model estimation.
Maximum Iterations. The maximum number of iterations the algorithm will execute. Specify a
non-negative integer.
Maximum Step-Halving. At each iteration, the step size is reduced by a factor of 0.5 until the
log-likelihood increases or maximum step-halving is reached. Specify a positive integer.
Limit iterations b ased on change in parameter estimates. When selected, the algorithm stops
after an iteration in which the absolute or relative change in the parameter estimates is less
than the value specified, which must be non-negative.
Limit iterations based on chang e in log-likelihood. When selected, the algorithm stops after an
iteration in which the absolute or relative change in the log-likelihood function is less than the
value specified, which must be non-negative.
Check for complete separation of data points. When selected, the algorithm performs tests to
ensure that the parameter estimates have unique values. Separation occurs when the procedure
can produce a model that correctly classifies every case.
Display iteration history. Displays parameter estimates and statistics at every n iterations
beginning with the 0
th
iteration (the initial estimates). If you choose to print the iteration
history, the last iteration is always printed regardless of the value of n.
User-Missing Values. All design variables, as well as the dependent variable and any covariates,
must have valid data. Cases with invalid data for any of these variables are deleted from the
analysis. These controls allow you to decide whether user-missing values are treated as valid
among the strata, cluster, subpopulation, and factor variables.
Page 77

Confidence Interval. This is the confidence interval level for coefficient e stimates, exponentiated
coefficient estimates, and odds ratios. Specify a value greater than or equal to 50 and less than 100.
CSLOGISTIC Command Additional Features
The command syntax language also allows you to:
Specify custom tests of effects versus a linear combination of effects or a value (using the
CUSTOM subcommand).
Fix values of other model variables when computing odds ratios for factors and covariates
(using the
Specify a tolerance value for checking singularity (using the CRITERIA subcommand).
Create user-specified names for saved variables (using the SAVE subcommand).
Produce a general estimable function table (using the PRINT subcommand).
See the Command Syntax Reference for complete syntax information.
ODDSRATIOS subcommand).
63
Complex Samples Logistic Regression
Page 78

Chapter
11
Complex Samples Ordinal Regression
The Complex Samples Ordinal Regression procedure performs regression analysis on a binary
or ordinal dependent variable for s amples drawn by complex sampling methods. Optionally,
you can request analyses for a subpopulation.
Example. Representatives considering a bill before the legislature are interested in whether there
is public support for the bill and how support for the bill is related to voter demographics.
Pollsters design and conduct interviews accordingtoacomplexsamplingdesign.UsingComplex
Samples Ordinal Regression, you can fit a model for the level of support for the bill based upon
voter demographics.
Data. The dependent variable is ordinal. Factors are categorical. Covariates are quantitative
variables that are related to the dependent variable. Subpopulation variables can b e string or
numeric but should be categorical.
Assumptions. The cases in the data file represent a sample from a complex design that should
be analyzed according to the specifications in the file selected in the Complex Samples Plan
dialog box.
Obtaining Complex Samples Ordinal Regressi on
From the menus choose:
Analyze > Complex Samples > Ordinal Regression...
Select a plan file. Optionally, select a custom joint probabilities file.
E
E Click Continue.
© Copyright SPSS Inc. 1989, 2010
64
Page 79

Figure 11-1
Ordinal Regression dialog box
65
Complex Samp les O rdinal Regression
E Select a dependent variable.
Optionally, you can:
Select variables for factors and covariates, as appropriate for your data.
Specify a variable to define a subpopulation. The analysis is performed only for the selected
category of the subpopulation variable, although variances are still properly estimated based
on the entire dataset.
Select a link function.
Link function. The link function is a transformation of the cumulative probabilities that allows
estimation of the model. Five link functions are available, summarized in the following table.
Function
Logit log( ξ /(1−ξ) ) Evenly distributed categories
Complementary log-log log(−log(1−ξ)) Higher categories more probable
Negative log-log −log(−log(ξ)) Lower categories more probable
Probit Φ−1(ξ) Latent variable is normally
Cauchit (inverse Cauchy) tan(π(ξ−0.5)) Latent variable ha s many extreme
Form
Typical application
distributed
values
Page 80

66
Chapter 11
Complex Samples Ordinal Regression Response Probabilities
Figure 11-2
Ordinal Regression Response Probabilities dialog box
The Response Probabilities dialog box allows you to specify whether the cumulative probability
of a response (that is, the probability of belonging up to and including a particular category of the
dependent variable) increases with increasing or decreasing values of the dependent variable.
Complex Samples Ordinal Regression Model
Figure 11-3
Ordinal Regression Model dialog box
Specify Model Effects. By default, the procedure builds a main-effects model using the factors
and covariates specified in the main dialog box. Alternatively, you can build a custom model that
includes interaction effects and nested terms.
Page 81

67
Complex Samp les O rdinal Regression
Non-Nested Terms
For the selected factors and covariates:
Interaction. Creates the highest-level interaction term for all selected variables.
Main effects. Creates a main-effects term for each variable selected.
All 2-way. Creates all possible two-way interactions of the selected variables.
All 3-way. Creates all possible three-way interactions of the selected variables.
All 4-way. Creates all possible four-way interactions of the selected variables.
All 5-way. Creates all possible five-way interactions of the selected variables.
Nested Terms
You can build nested terms for your model in this procedure. Nested terms are useful for modeling
the effect of a factor or covariate whose values do not interact with the levels of another factor.
For example, a grocery store chain may follow the spending habits of its customers at several store
locations. Since each customer frequents only one of these locations, the Customer effect can be
said to be nested within the Store location effect.
Additionally, you can include interaction effects, such as polynomial terms involving the same
covariate, or add multiple levels of nesting to the nested term.
Limitations. Nested terms have the following restrictions:
All factors within an interaction must be unique. Thus, if A is a factor, then specifying A*A
is invalid.
All factors within a nested effect must be unique. Thus, if A is a factor, then specifying A(A)
is invalid.
No effect can be nested within a covariate. Thus, if A is a factor and X is a covariate, then
specifying A(X) is invalid.
Page 82

68
Chapter 11
Complex Samples Ordinal Regression Statistics
Figure 11-4
Ordinal Regression Statistics dialog box
Model Fit. Controls the display of statistics that measure the overall model performance.
Pseudo R-square. The R
2
statistic from linear regression does not have an exact counterpart
among ordinal regression models. There are, instead, multiple measures that attempt to mimic
2
the properties of the R
Classification table. Displays the tabulated cross-classifications of the observed category by
statistic.
the model-predicted category on the dependent variable.
Parameters. This group allows you to control the display of statistics related to
the model
parameters.
Estimate. Displays estimates of the coefficients.
Exponentiated estimate. Displays the base of the natural logarithm raised to the power of the
estimates of the coefficients. While the estimate has nice properties for stati
stical testing, the
exponentiated estimate, or exp(B), is easier to interpret.
Standard error. Displays the standard error for each coefficient estimate.
Confidence interval. Displays a confidence interval for each coefficient estimate. The
confidence level for the interval is set in the Options dialog box.
Ttest. Displays a t test of each coefficient estimate. The null hypothesis for each test is that
thevalueofthecoefficient is 0.
Covariances of parameter estimates. Displays an estimate of the covariance
matrix for the
model coefficients.
Correlations of parameter estimates. Displays an estimate of the correlation matrix for the
model coefficients.
Page 83

69
Complex Samp les O rdinal Regression
Design effect. The ratio of the variance of the estimate to the variance obtained by assuming
that the sample is a simple random sample. This is a measure of the effect of specifying a
complex design, where values further from 1 indicate greater effects.
Square root of design effec t. This is a measure, expressed in units comparable to those of
the standard error, of the effect of specifying a complex design, where values further from
1 indicate greater effects.
Parallel Lines. This group allows you to request statistics associated with a model with nonparallel
lines where a separate regression line is fitted for each response category (except the last).
Wald test. Produces a test of the null hypothesis that regression parameters are equal for all
cumulative responses. The model with nonparallel lines is estimated and the Wald test of
equal parameters is applied.
Parameter estimates. Displays estimates of the coefficients and standard errors for the model
with nonparallel lines.
Covariances of parameter estimates. Displays an estimate of the covariance matrix for the
coefficients of the model with nonparallel lines.
Summary statistics for model variables. Displays summary information about the dependent
variable, covariates, and factors.
Sample design information. Displays summary information about the sample, including the
unweighted count and the population size.
Complex Samples Hypothesis Tests
Figure 11-5
Hypothesis Tests dialog box
Page 84

70
Chapter 11
Test Statistic. This group allows you to select the type of statistic used for testing hypotheses. You
can choose between F,adjustedF, chi-square, and adjusted chi-square.
Sampling Degrees of Freedom. This group gives you control over the sampling design degrees of
freedomusedtocomputep values for all test statistics. If based on the sampling design, the value
is the difference between the number of primary sampling units and the number of strata in the
first stage of sampling. Alternatively, you can set a custom degrees of freedom by specifying a
positive integer.
Adjustment for Multiple Comparisons. When performing hypothesis tests with multiple contrasts,
the overall significance level can be adjusted from the significance levels for the included
contrasts. This group allows you to choose the adjustment method.
Least significant difference. This method does not control the overall probability of rejecting
the hypotheses that some linear contrasts are different from the null hypothesis values.
Sequential Sidak. This is a sequentially step-down rejective Sidak procedure that is much
less conservative in terms of rejecting individual hypotheses but maintains the same overall
significance level.
Sequential Bonferroni. This is a sequentially step-down rejective Bonferroni procedure that is
much less conservative in terms of rejecting individual hypotheses but maintains the same
overall significance level.
Sidak. This method provides tighter bounds than the Bonferroni approach.
Bonferroni. This method adjusts the observed significance level for the fact that multiple
contrasts are being tested.
Complex Samples Ordinal Regression Odds Ratios
Figure 11-6
Ordinal Regression Odds Ratios dialog box
The Odds Ratios dialog b ox allows you to display the model-estimated cumulative odds ratios for
specified factors and covariates. This feature is only available for models using the Logit link
function. A single cumulative odds ratio is computed for all categories of the dependent variable
except the last; the proportional odds model postulates that they are all equal.
Page 85

Factors. For each selected factor, displays the ratio of the cumulative odds at each category o f the
factor to the odds at the specified reference category.
Covariates. For each selected covariate, displays the ratio of the cumulative odds at the covariate’s
mean value plus the specified units of change to the odds at the mean.
When computing odds ratios for a factor or covariate, the procedure fixes all other factors at their
highest levels and all other covariates at their means. If a factor or covariate interacts with other
predictors in the model, then the odds ratios depend not only on the change in the specified
variable but also on the values of the variables with which it interacts. If a specified covariate
interacts with itself in the model (for example, age*age), then the odds ratios depend on both the
change in the covariate and the value of the covariate.
Complex Samples Ordinal Regression Save
Figure 11-7
Ordinal Regression Save dialog box
71
Complex Samp les O rdinal Regression
Save Variables. This group allows you to save the model-predicted category, probability of
predicted category, probability
of observed category, cumulative probabilities, and predicted
probabilities as new variables in the active d ataset.
Export model as SPSS Statistics data. Writes a dataset in IBM® SPSS® Statistics format containing
the parameter correlation or covariance matrix with parameter estimates, standard errors,
significance values, and degrees of freedom. The order of variables in the matrix fi le is as follows.
Page 86

72
Chapter 11
rowtype_. Takes values (and value labels), COV (Covariances), CORR (Correlations), EST
(Parameter estimates), SE (Standard errors), SIG (Significance levels), and DF (Sampling
design degrees of freedom). There is a separate case with row type COV (or CORR) for each
model parameter, plus a separate case for each of the other row types.
varname_. Takes values P1, P2, ..., corresponding to an ordered list of all model parameters,
for row types COV or CORR, with value labels corresponding to the parameter strings shown
in the parameter estimates table. The cells are blank for other row types.
P1, P2, ... These variables correspond to an ordered list of all model parameters, with variable
labels corresponding to the parameter strings shown in the parameter estimates table, and
take values according to the row type. For redundant parameters, all covariances are set
to zero; correlations are set to the system-missing value; all parameter estimates are set at
zero; and all standard errors, significance levels, and residual degrees of freedom are set to
the system-missing value.
Note:Thisfile is not immediately usable for further analyses in other procedures that read a matrix
file unless those procedures accept all the row types exported here.
Export model as XML. Saves the parameter estimates and the parameter covariance matrix, if
selected, in XML (PMML) format. You can use this model file to apply the model information to
other data files for scoring purposes.
Complex Samples Ordinal Regression Options
Figure 11-8
Ordinal Regression Options dialog box
Page 87

73
Complex Samp les O rdinal Regression
Estimation M ethod. You can select a parameter estimation method; choose between
Newton-Raphson, Fisher scoring, or a hybrid method in which Fisher scoring iterations are
performed before switching to the Newton-Raphson method. If convergence is achieved during
the Fisher scoring phase of the hybrid method before the maximum number of Fisher iterations is
reached, the algorithm continues with the Newton-Raphson method.
Estimation. This group gives you control of various criteria used in the model estimation.
Maximum Iterations. The maximum number of iterations the algorithm will execute. Specify a
non-negative integer.
Maximum Step-Halving. At each iteration, the step size is reduced by a factor of 0.5 until the
log-likelihood increases or maximum step-halving is reached. Specify a positive integer.
Limit iterations b ased on change in parameter estimates. When selected, the algorithm stops
after an iteration in which the absolute or relative change in the parameter estimates is less
than the value specified, which must be non-negative.
Limit iterations based on chang e in log-likelihood. When selected, the algorithm stops after an
iteration in which the absolute or relative change in the log-likelihood function is less than the
value specified, which must be non-negative.
Check for complete separation of data points. When selected, the algorithm performs tests to
ensure that the parameter estimates have unique values. Separation occurs when the procedure
can produce a model that correctly classifies every case.
Display iteration history. Displays parameter estimates and statistics at every n iterations
beginning with the 0
th
iteration (the initial estimates). If you choose to print the iteration
history, the last iteration is always printed regardless of the value of n.
User-Missing Values. Scale design variables, as well as the dependent variable and any covariates,
should have valid data. Cases with invalid data for any of these variables are deleted from the
analysis. These controls allow you to decide whether user-missing values are treated as valid
among the strata, cluster, subpopulation, and factor variables.
Confidence Interval. This is the confidence interval level for coefficient e stimates, exponentiated
coefficient estimates, and odds ratios. Specify a value greater than or equal to 50 and less than 100.
CSORDINAL Command Additional Features
The command syntax language also allows you to:
Specify custom tests of effects versus a linear combination of effects or a value (using the
CUSTOM subcommand).
Fix values of other model variables at values other than their means when computing
cumulative odds ratios for factors and covariates (using the
Use unlabeled values as custom reference categories for factors when odds ratios are requested
(using the
Specify a tolerance value for checking singularity (using the CRITERIA subcommand).
Produce a general estimable function table (using the PRINT subcommand).
Save more than 25 probability variables (using the SAVE subcommand).
See the Command Syntax Reference for complete syntax information.
ODDSRATIOS subcommand).
ODDSRATIOS subcommand).
Page 88

Complex Samples Cox Regression
The Complex Samples Cox Regression procedure performs survival analysis for samples drawn
by complex sampling methods. Optionally, you can request analyses for a subpopulation.
Examples. A government law enforcement agency is concerned about recidivism rates in their area
of jurisdiction. One of the measures of recidivism is the time until second arrest for offenders. The
agency would like to model time to rearrest using Cox Regression but are worried the proportional
hazards assumption is invalid across age categories.
Medical researchers are investigating survival times for patients exiting a rehabilitation program
post-ischemic stroke. There is the potential for multiple cases per subject, since patient histories
change as the occurrence of significant nondeath events are noted and the times of these events
recorded. The sample is also left-truncated in the sense that the observed survival times are
“inflated” by the length of rehabilitation, because while the onset of risk starts at the time of the
ischemic stroke, only patients who survive past the rehabilitation program are in the sample.
Chapter
12
Survival Time. The procedure applies Cox regression to analysis of survival times—that is, the
length of time before the occurrence of an event. There are two ways to specify the survival time,
depending upon the start time of the interval:
Time=0. Commonly, you will have complete information on the start of the interval for each
subject and will simply have a variable containing end times (or create a single variable with
end times from Date & Time variables; see below).
Varies by subject. This is appropriate when you have left-truncation, also called delayed
entry; for example, if you are analyzing survival times for patients exiting a rehabilitation
program post-stroke, you might consider that their onset of risk starts at the time of the stroke.
However, if your sample only includes patients who have survived the rehabilitation program,
then your sample is left-truncated in the sense that the observed survival times are “inflated”
by the length of rehabilitation. You can account for this by specifying the time at which they
exited rehabilitation as the time of entry into the study.
Date & Time Variables. Date & Time variables cannot be used to directly define the start and
end of the interval; if you have Date & Time variables, you should use them to create variables
containing survival times. If there is no left-truncation, simply create a variable containing end
times based upon the difference between the date of entry into the study and the observation date.
If there is left-truncation, create a variable containing start times, based upon the difference
between the date of the start of the study and the date of entry, and a variable containing end times,
based upon the difference between the date of the start of the study and the date of observation.
Event Status. You need a variable that records whether the subject experienced the event of interest
within the interval. Subjects for whom the event has not occurred are right-censored.
© Copyright SPSS Inc. 1989, 2010
74
Page 89

75
Complex Samples Cox Regression
Subject Identifier. You can easily incorporate piecewise-constant, time-dependent predictors by
splitting the observations for a single subject across multiple cases. For example, if you are
analyzing survival times for patients post-stroke, variables representing their medical history
should be useful as predictors. Over time, they may experience major medical events that alter
their medical history. The following table shows how to structure such a dataset: Patient ID is the
subject identifier, End time defines the observed intervals, Status records major medical events,
and Prior history of heart attack and Prior history of hemorrhaging are piecewise-constant,
time-dependent predictors.
Patient ID End time Status Prior history of
heart attack
1
1
18
224
38
315
5
7
Heart Attack
Hemorrhaging
Died
Died
Heart Attack
Died
No No
Yes No
Yes Yes
No No
No No
Yes No
Prior history of
hemorrhaging
Assumptions. The cases in the data file represent a sample from a complex design that should
be analyzed according to the specifications in the file selected in the Complex Samples Plan
dialog box.
Typically, Cox regression models assume proportional hazards—that is, the ratio of hazards
from one case to another should not vary over time. If this assumption does not hold, you may
need to add time-dependent predictors to the model.
Kaplan-Meier Analysis. If you do not select any predictors (or do not enter any selected predictors
into the model) and choose the product limit method for computing the baseline survival curve on
the Options tab, the procedure performs a Kaplan-Meier type of survival analysis.
To Obtain Complex Samples Cox Regression
E From the menus choose:
Analyze > Complex Samples > Cox Regression...
Select a plan file. Optionally, select a custom joint probabilities file.
E
E Click Continue.
Page 90

76
Chapter 12
Figure 12-1
Cox Regression dialog box, Time and Event tab
E Specify the survival time by selecting the entry and exit times from the study.
E Select an event status variable.
E Click Define Event and define at least one event value.
Optionally, you can select a subject identifier.
Page 91

Define Event
Figure 12-2
Define Event dialog box
77
Complex Samples Cox Regression
Specify the values that indicate a terminal event has occurred.
Individual value(s). Specify one or more values by entering them into the grid or selecting them
from a lis
Range of
tofvalueswithdefined value labels.
values.
Specify a range of values by entering the minimum and maximum values or
selecting values from a list with defined value labels.
Page 92

78
Chapter 12
Predictors
Figure 12-3
Cox Regression dialog box, Predictors tab
The Predictors tab allows you to specify the factors and covariates used to build model e ffects.
.
Factors
Covariates. Covariates are scale predictors; they must be numeric.
Time-Dependent Predictors. There are certain situations in which the proportional hazards
assump
Factors are categorical predictors; they can be numeric or string.
tion does not hold. That is, hazard ratios change across time; the values of one (or more)
of your predictors are different at different time points. In such cases, you need to specify
time-dependent predictors. For more information, see the topic Define Time-Dependent Predictor
on p. 79. T
ime-dependent predictors can be selected as factors or covariates.
Page 93

Define Time-Dependent Predictor
Figure 12-4
Cox Regression Define Time-Dependent Predictor dialog box
79
Complex Samples Cox Regression
The Define Time-Dependent Predictor dialog box allows you to create a predictor that is
dependent upon the built-in time variable, T_. You can use this variable to define time-dependent
covariates in two general ways:
If you want to estimate an extended Cox regression model that allows nonproportional
hazards, you can do so by defining your time-dependent predictor as a function of the time
variable T_ and the covariate in question. A common example would be the simple product of
the time variable and the predictor, but more complex functions can be specified as well.
Some variables may have different values at different time periods but aren’t systematically
relatedtotime. Insuchcases,youneedtodefine a segmented time-dependent predictor,
which can be done using logical expressions. Logical expressions take the value 1 if true
and 0 if false. Using a series of logical expressions, you can create your time-dependent
predictor from a set of measurements. For example, if you have blood pressure measured
once a week for the four weeks of your study (identified as BP1 to BP4), you can define your
time-dependent predictor as (T_ <1)*BP1 +(T_ >= 1 & T_ <2)*BP2 +(T_ >= 2 & T_ <3)
* BP3 +(T_ >= 3 & T_ <4)*BP4. Notice that exactly one of the terms in parentheses will
be equal to 1 for any given case and the rest will all equal 0. In other words, this function
meansthatiftimeislessthanoneweek,useBP1; if it is more than one week but less than
two weeks, use BP2; and so on.
Page 94

80
Chapter 12
In the Define Time-Dependent Predictor dialog box, you can use the function-building controls
to build the expression for the time-dependent covariate, or you can enter i t directly in the
Numeric Expression text area. Note that string constants must be enclosed in quotation marks
or apostrophes, and numeric constants must be typed in American format, with the dot as the
decimal delimiter. The resulting variable is given the name you specify and should be included
as a factor or covariate on the Predictors tab.
Subgroups
Figure 12-5
Cox Regression dialog box, Subgroups tab
Note: If your segmented, time-dependent predictor is constant within segments, as in the blood
pressure example given above, it may be easier for you to specify the piecewise-constant,
time-dependent predictor by splitting subjects across multiple cases. See the discussion on
Subject Identifiers in Complex Samples Cox Regression on p. 74 for more information.
Baseline Strata. A separate b aseline hazard and survival function is computed for each value of
this variable, while a single set of model coefficients is estimated across strata.
Subpopulation Variable. Specify a variable to define a subpopulation. The analysis is performed
only for the selected category of the subpopulation variable.
Page 95

Model
81
Complex Samples Cox Regression
Figure 12-6
Cox Regression dialog box, Model t a b
Specify Model Effects. By default, the procedure builds a main-effects model using the factors
and covariates specified in the main dialog box. Alternatively, you can build a custom model that
includes interaction effects and nested terms.
Non-Nested Terms
For the selected factors and covariates:
Interaction. Creates the highest-level interaction term for all selected variables.
Main effects. Creates a main-effects term for each variable selected.
All 2-way. Creates all possible two-way interactions of the selected variables.
All 3-way. Creates all possible three-way interactions of the selected variables.
All 4-way. Creates all possible four-way interactions of the selected variables.
All 5-way. Creates all possible five-way interactions of the selected variables.
Page 96

82
Chapter 12
Nested Terms
You can build nested terms for your model in this procedure. Nested terms are useful for modeling
the effect of a factor or covariate whose values do not interact with the levels of another factor.
For example, a grocery store chain may follow the spending habits of its customers at several store
locations. Since each customer frequents only one of these locations, the Customer effect can be
said to be nested within the Store location effect.
covariate, or add multiple levels of nesting to the nested term.
Limitations. Nested terms have the following restrictions:
All factors within an interaction must be unique. Thus, if A is a factor, then specifying A*A
All factors within a nested effect must be unique. Thus, if A is a factor, then specifying A(A)
No effect can be nested within a covariate. Thus, if A is a factor and X is a covariate, then
Statistics
Additionally, you can include interaction effects, such as polynomial terms involving the same
is invalid.
is invalid.
specifying A(X) is invalid.
Figure 12-7
Cox Regression dialog box, Statistics tab
Page 97

83
Complex Samples Cox Regression
Sample design information. Displays summary information about the sample, including the
unweighted count and the population size.
Event and censoring summary. Displays summary information about the number and percentage of
censored cases.
Risk set at event times. Displays number of events and number at risk for each event time in
each baseline stratum.
Parameters. This group allows you to control the display of statistics related to the model
parameters.
Estimate. Displays estimates of the coefficients.
Exponentiated estimate. Displays the base of the natural logarithm raised to the power of the
estimates of the coefficients. While the estimate has nice properties for statistical testing, the
exponentiated estimate, or exp(B), is easier to interpret.
Standard error. Displays the standard error for each coefficient estimate.
Confidence interval. Displays a confidence interval for each coefficient estimate. The
confidence level for the interval is set in the Options dialog box.
t-test. Displays a t test of each coefficient estimate. The null hypothesis for each test is that the
value of the coefficient is 0.
Covariances of parameter estimates. Displays an estimate of the covariance matrix for the
model coefficients.
Correlations of parameter estimates. Displays an estimate of the correlation matrix for the
model coefficients.
Design effect. The ratio of the variance of the estimate to the variance obtained by assuming
that the sample is a simple random sample. This is a measure of the effect of specifying a
complex design, where values further from 1 indicate greater effects.
Square root of design effect. This is a measure of the effect of specifying a complex design,
where values further from 1 indicate greater effects.
Model Assumptions. This group allows you to produce a test of the proportional hazards
assumption. The test compares the fittedmodeltoanalternative model that includes
time-dependen
Time Function
_TF=T_.Forthelog function, _TF=log(T_). For Kaplan-Meier, _TF=1−S
S
KM
of T_ among the o
Parameter est
tpredictorsx*_TF for each predictor x,where_TF is the specified time function.
.
Specifies the form of _TF for the alternative model. For the identity function,
(T_), where
KM
(.) is the Kaplan-Meier estimate of the survival function. For rank, _TF is the rank-order
bserved end times.
imates for alternative model.
Displays the estimate, standard error, and confidence
interval for each parameter in the alternative model.
Covariance matrix for alte rnative model. Displays the matrix of estimated covariances between
parameters in the alternative model.
Baseline survival and cumulative hazard functions. Displays the baseline survival function and
baseline cumulative hazards function along with their standard errors.
Note: If time-dependent predictors defined on the Predictors tab are included in the model, this
option is not available.
Page 98

84
Chapter 12
Plots
Figure 12-8
Cox Regression dialog box, Plots tab
The Plots tab allows you to request plots of the hazard function, survival function, log-minus-log
of the survival function, and one minus the survival function. You can also choose to plot
confidence intervals along the specified functions; the confidence level is set on the Options tab.
Predictor patterns. You c an specify a pattern of predictor values to be used for the requested plots
and the exported survival file on the Export tab. Note that these options are not available if
time-dependent predictors defined on the Predictors tab are included in the model.
Plot Factors at. By default, each factor is evaluated at its highest level. Enter or select a
different level if desired. Alternatively, you can choose to plot separate lines for each level
of a single factor by selecting the check box for that factor.
Plot Covariates at. Each covariate is evaluated at its mean. Enter or select a different value
if desired.
Page 99

Hypothesis Tests
Figure 12-9
Cox Regression dialog box, Hypothesis Tests tab
85
Complex Samples Cox Regression
Test Statistic. This group allows you to select the type of statistic used for testing hypotheses. You
can choose between F,adjustedF, chi-square, and adjusted chi-square.
Sampling Degrees of Freedom. This group gives you control over the sampling design degrees of
freedomusedtocomputep values for all test statistics. If based on the sampling design, the value
is the difference between the number of primary sampling units and the number of strata in the
first stage of sampling. Alternatively, you can set a custom degrees of freedom by specifying a
positive integer.
Adjustment for Multiple Comparisons. When performing hypothesis tests with multiple contrasts,
the overall significance level can be adjusted from the significance levels for the included
contrasts. This group allows you to choose the adjustment method.
Least significant difference. This method does not control the overall probability of rejecting
the hypotheses that some linear contrasts are different from the null hypothesis values.
Sequential Sidak. This is a sequentially step-down rejective Sidak procedure that is much
less conservative in terms of rejecting individual hypotheses but maintains the same overall
significance level.
Page 100

86
Chapter 12
Save
Sequential Bonferroni. This is a sequentially step-down rejective Bonferroni procedure that is
much less conservative in terms of rejecting individual hypotheses but maintains the same
overall significance level.
Sidak. This method provides tighter bounds than the Bonferroni approach.
Bonferroni. This method adjusts the observed significance level for the fact that multiple
contrasts are being tested.
Figure 12-10
Cox Regression dialog box, Save tab
Save Variables. This group allows you to save model-related variables to the active dataset for
further use in diagnostics and reporting of results. Note that none of these are available when
time-dependent predictors are included in the model.
Survival function. Saves the probability of survival (the value of the survival function) at the
observed time and predictor values for each case.
Lower bound of confidence interval for survival function. Saves the lower bound of the
confidence interval for the survival function at the observed time and predictor values for
each case.
 Loading...
Loading...