Page 1

i
IBM SPSS Ad
19
vanced Statistics
Page 2

Note: Before using this information and the product it supports, read the general
information under Notices第 143 页码.
This document contains proprietary information of SPSS Inc, an IBM Company. It
is provided under a license agreement and is protected by copyright law. The
information contained in this publication does not include any product warranties,
and any statements provided in this manual should not be interpreted as such.
When you send information to IBM or SPSS, you grant IBM and SPSS a nonexclusive
right to use or distribute the information in any way it believes appropriate
without incurring any obligation to you.
© Copyright SPSS Inc. 1989, 2010.
Page 3

IBM® SPSS® Statistics 是一种用于分析数据的综合系统。Advanced Statistics 可选附
加模块提供本手册中描述的其他分析方法。此 Advanced Statistics 附加模块必须与
SPSS Statistics Core 系统一起使用,并已完全集成到了该系统中。
关于 SPSS Inc.,IBM 下属公司
SPSS Inc. 是一家 IBM 下属公司,它也是全球领先的预测分析软件和解决方案提供商。
该公司拥有全面的产品系列,涵盖数据收集、统计量、建模和部署,通过在业务流程
中嵌入分析技术,收集人们的态度与看法,预测未来客户交互结果,然后针对这些深
入见解采取相应行动。SPSS Inc. 解决方案着眼于整合分析技术、IT 基础设施和业务
流程,以帮助达成整个企业内相互关联的业务目标。全球各地的众多企业、政府和学
术机构客户依靠 SPSS Inc. 技术在吸引、留住和发展客户方面取得竞争优势,同时减
少欺诈并缓解风险。SPSS Inc. 在 2009 年 10 月被 IBM 并购。有关更多信息,请访问
http://www.spss.com。
前言
技术支持
客户服务
培训讲座
我们提供有“技术支持”以维护客户。客户可就 SPSS Inc. 产品使
用或某一受支持硬件环境的安装帮助寻求技术支持。要获得“技术支
持”,请访问 SPSS Inc. 网站 http://support.spss.com,或通过网站
http://support.spss.com/default.asp?refpage=contactus.asp 找到当地办事处。在请
求协助时,请准备好您和您组织的 ID 以及支持协议。
如果对发货或帐户存在任何问题,请联系您当地的办事处,联系方式列在 Web 站点中,
网址为 http://www.spss.com/worldwide。请先准备好您的序列号以供识别。
SPSS Inc. 提供公开的以及现场的培训讲座。所有讲座都是以实践小组为特色的。讲座
将定期在各大城市开展。关于这些讲座的更多信息,请联系您本地的办事处,联系方式
列在 Web 站点上,网址为 http://www.spss.com/worldwide。
© Copyright SPSS Inc. 1989, 2010
iii
Page 4

附加出版物
SPSS Statistics:数据分析指南、SPSS Statistics:Statistical Procedures Companion
和 SPSS Statistics:Advanced Statistical Procedures Companion(由 Marija Norušis
编写,并已由 Prenti
Statistics Base 模块、Advanced Statistics 模块和 回归模块中的统计过程。无论您是
刚开始从事数据分析工作,还是已准备好使用高级应用程序,这些书籍都将帮助您最有
效地利用在 IBM® SP
内容和示例章节,请参阅作者的网站: http://www.norusis.com
ce Hall 出版)作为建议的补充材料提供。这些出版物涵盖 SPSS
SS® Statistics 产品中找到的功能。有关其他信息,包括出版物的
iv
Page 5

1
Advanced Statistics 简介 1
2
GLM 多变量分析 2
GLM多变量:模型 ................................ 4
构建项 ................................... 4
平方和 ................................... 5
GLM多变量:对比 ................................ 6
对比类型 .................................. 6
GLM 多变量:轮廓图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
GLM 多变量:两两比较 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
GLM:保存 .................................... 9
GLM多变量:选项 ............................... 11
GLM 命令的附加功能 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
内容
3
GLM 重复测量 13
GLM 重复测量定义因子 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
GLM 重复测量:模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
构建项 .................................. 17
平方和 .................................. 18
GLM 重复测量:对比 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
对比类型 ................................. 19
GLM 重复测量:轮廓图 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
GLM 重复测量:两两比较 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
GLM 重复测量:保存 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
GLM 重复测量:选项 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
GLM 命令的附加功能 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
4
方差成分分析 26
方差成分:模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
构建项 .................................. 28
v
Page 6

方差成分:选项 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
平方和(方差成分) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
方差成分:保存到新文件 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
VARCOMP 命令的附加功能 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
5
线性混合模型 31
线性混合模型:选择主体/重复变量 . . . . . . . . . . . . . . . . . . . . . . . 33
线性混合模型:固定效应 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
构建非嵌套项 ............................... 34
建立嵌套项 ................................ 35
平方和 .................................. 35
线性混合模型:随机效果 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
线性混合模型:估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
线性混合模型:统计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
线性混合模型:EM 均值 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
线性混合模型:保存 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
MIXED 命令的附加功能 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
6
广义线性模型 42
广义线性模型响应 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
广义线性模型:参考类别 . . . . . . . . . . . . . . . . . . . . . . . . . . 47
广义线性模型:预测变量
广义线性模型:选项 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
广义线性模型:模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
广义线性模型:估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
广义线性模型:初始值 . . . . . . . . . . . . . . . . . . . . . . . . . . . 53
广义线性模型:统计量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
广义线性模型:EM 均值 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
广义线性模型:保存 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
广义线性模型:导出 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
GENLIN 命令的附加功能. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
7
广义估计方程 62
广义估计方程:模型类型
............................ 48
............................ 65
vi
Page 7

广义估计方程:响应 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
广义估计方程:参考类别 . . . . . . . . . . . . . . . . . . . . . . . . . . 69
广义估计方程:预测变量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
广义估计方程:选项 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
广义估计方程:模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
广义估计方程:估计 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
广义估计方程:初始值 . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
广义估计方程:统计量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
广义估计方程:EM 均值 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
广义估计方程:保存 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
广义估计方程:导出 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
GENLIN 命令的附加功能. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
8
广义线性混合模型 84
获取广义线性混合模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
目标 ..................................... 87
固定效应 ................................... 89
添加自定义项 ............................... 90
随机效应 ................................... 91
随机效应块 ................................ 92
权重和偏移量 ................................. 94
构建选项 ................................... 95
估算的均值 .................................. 96
保存 ..................................... 98
模型视图 ................................... 99
模型摘要 ................................. 99
数据结构 ................................. 99
按已观测进行预测 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
分类.................................... 99
固定效应 ................................. 100
固定系数 ................................. 100
随机效应协方差 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
协方差参数 ................................ 101
估算的均值:显著效应 . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
估算的均值:自定义效应 . . . . . . . . . . . . . . . . . . . . . . . . . . 102
vii
Page 8

9
模型选择对数线性分析 103
对数线性分析:定义范围 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
对数线性分析:模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
构建项 .................................. 105
模型选择对数线性分析:选项 . . . . . . . . . . . . . . . . . . . . . . . . . 106
HILOGLINEAR 命令的附加功能 . . . . . . . . . . . . . . . . . . . . . . . . . . 106
10
一般对数线性分析 107
一般对数线性分析模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
构建项 .................................. 109
一般对数线性分析:选项 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
一般对数线性分析:保存 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
GENLOG 命令的附加功能. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
11
Logit 对数线性分析
Logit 对数线性分析:模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
构建项 .................................. 114
Logit 对数线性分析:选项 . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
Logit 对数线性分析:保存 . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
GENLOG 命令的附加功能. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
12
寿命表 117
寿命表:为状态变量定义事件 . . . . . . . . . . . . . . . . . . . . . . . . . 118
寿命表:定义范围 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
寿命表:选项 ................................. 119
SURVIVAL 命令的附加功能 . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
13
Kaplan-Meier 生存分析 121
Kaplan-Meier:为状态变量定义事件 . . . . . . . . . . . . . . . . . . . . . . 122
Kaplan-Meier:比较因子水平 . . . . . . . . . . . . . . . . . . . . . . . . . . 123
112
viii
Page 9

Kaplan-Meier:保存新变量........................... 123
Kaplan-Meier:选项 .............................. 124
KM 命令的附加功能 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
14
Cox 回归分析 126
Cox 回归:定义分类变量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
Cox回归:图 ................................. 129
Cox 回归:保存新变量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 130
Cox回归:选项 ................................ 131
Cox 回归:为状态变量定义事件 . . . . . . . . . . . . . . . . . . . . . . . . . 131
COXREG 命令的附加功能. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
15
计算依时协变量 133
计算依时协变量 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133
带依时协变量的 Cox 回归的附加功能 . . . . . . . . . . . . . . . . . . . . 134
附录
A
分类变量编码设计 135
偏差 ..................................... 135
简单散点图 .................................. 136
Helmert.................................... 136
差分 ..................................... 137
多项式 .................................... 137
重复 ..................................... 138
特殊 ..................................... 138
指示符 .................................... 139
ix
Page 10

B
协方差结构 140
C Notices 143
索引 146
x
Page 11

Advanced Statistics 简介
Advanced Statistics 选项提供的过程可以提供比 Statistics Base 选项更高级的建
模选项。
“GLM 多变量”对“GLM 单变量”提供的一般线性模型进行了扩展,以允许使用多个
因变量。更进一步的扩展“GLM 重复测量”允许重复度量多个因变量。
“方差成分分析”是将因变量的变异性分解为固定和随机成分的特定工具。
“线性混合模型”对一般线性模型进行了扩展,因此允许数据表现出相关的和不
恒定的变异性。因此,线性混合模型提供了不仅能够就数据的均值还能够就其
方差和协方差建模的灵活性。
“广义线性模型”(GZLM) 放宽了误差项的正态假设,仅要求因变量通过转换或关
联函数与预测变量线性相关。“广义估计方程”(GEE) 对 GZLM 进行了扩展,以允
许重复度量。
“一般对数线性分析”允许您为交叉分类计数数据拟合模型,“模型选择对数
线性分析”可帮助您在模型间选择。
“Logit 对数线性分析”允许您拟合对数线性模型来分析分类因变量与一个或多
个分类预测变量之间的关系。
“生存”分析通过“寿命表”提供,用于检查时间事件变量的分布,可能按因子变
量水平分析;“Kaplan-Meier”生存分析用于检查时间事件变量的分布,可能按因
子变量水平分析,或按分层变量水平产生单独的分析;“Cox 回归”用于根据给定
协变量的值对指定事件的时间建模。
章
1
© Copyright SPSS Inc. 1989, 2010
1
Page 12

GLM 多变量分析
“GLM 多变量”过程通过一个或多个因子变量或协变量为多个因变量提供回归分析和
方差分析。因子变量将总体划分成组。通过使用此一般线性模型过程,您可以检验关
于因子变量对因变量联合分布的各个分组的均值的效应的原假设。可以调查因子之间
的交互以及单个因子的效应。另外,还可以包含协变量的效应以及协变量与因子的交
互。对于回归分析,自变量(预测变量)指定为协变量。
平衡与非平衡模型均可进行检验。如果模型中的每个单元包含相同的个案数,则设计
是平衡的。在多变量模型中,模型中的效应引起的平方和以及误差平方和以矩阵形式表
示,而不是以单变量分析中的标量形式表示。这些矩阵称为 SSCP(平方和与叉积)矩
阵。如果指定了多个因变量,则提供使用 Pillai 的轨迹、Wilks 的 lambda、Hotelling
的轨迹、Roy 的最大根条件以及近似 F 统计量的多变量方差分析,同时还提供每个因变
量的单变量方差分析。除了检验假设,“GLM 多变量”过程还生成参数估计。
常用的先验对比可用于执行假设检验。另外,在整体的 F 检验已显示显著性之后,可
以使用两两比较检验评估指定均值之间的差值。估计边际均值为模型中的单元提供了预
测均值估计值,且这些均值的轮廓图(交互图)允许您轻松对其中一些关系进行可视
化。单独为每个因变量执行两两多重比较检验。
残差、预测值、Cook 距离以及杠杆值可以另存为数据文件中检查假设的新变量。另外
还提供残差 SSCP 矩阵(残差的平方和与叉积的方形矩阵)、残差协方差矩阵(残差
SSCP 矩阵除以残差的自由度)和残差相关矩阵(残差协方差矩阵的标准化形式)。
WLS 权重允许您指定一个变量,用来针对加权最小平方 (WLS) 分析为观察值赋予不同
权重,这样也许可以补偿测量的不同精确度。
章
2
示例。 某塑料制造商要测量塑料膜的三种属性:抗扯强度、光泽度和不透明度。厂商
使用两种挤出速度和添加剂量进行了尝试,并对挤出速度和添加剂量的各种组合度量
了这三种属性。厂商发现挤出速度和添加剂量单独产生的结果很明显,但这两种因子
的交互作用并不明显。
方法。类型 I、类型 II、类型 III 和类型 IV 的平方和可用来评估不同的假设。类
型 III 是缺省值。
统计量。两两比较范围检验和多重比较:最小显著性差异、Bonferroni、Sidak、
Scheffé、Ryan-Einot-Gabriel-Welsch 多重 F、Ryan-Einot-Gabriel-Welsch 多范围、
Student-Newman-Keuls、Tukey’s 真实显著性差异、Tukey 的 b、Duncan、Hochberg’s
GT2、Gabriel、Waller-Duncan t 检验、Dunnett(单侧和双侧)、Tamhane’s T2、
Dunnett’s T3、Games-Howell 和 Dunnett’s C。描述统计:所有单元中所有因变量的
观察均值、标准差和计数;Levene 的方差齐性检验;对因变量协方差矩阵的齐性 Box
的 M 检验以及 Bartlett 的球形度检验。
图。分布-水平图、残差图以及轮廓图(交互)。
数据。因变量应是定量的。因子应是分类因子,可以具有数
是与因变量相关的定量变量。
© Copyright SPSS Inc. 1989, 2010
字值或字符串值。协变量
2
Page 13
GLM 多变量分析
假设。对于因变量,数据是来自多变量正态总体的随机向量样本;在总体中,所有单
元的方差-协方差矩阵均相同。尽管数据应对称,但方差分析对于偏离正态性是稳健
的。要检查假设,您可以使用方差齐性检验(包括 Box 的 M 检验)和分布-水平图。
您还可以检查残差和残差图。
相关过程。在进行方差分析之前使用“探索”过程来检查数据。对于单个因变量,
请使用“GLM 单变量”。如果您针对每个主体的多种情况度量相同的因变量,请使
用“GLM 重复测量”。
获取 GLM 多变量表
E 从菜单中选择:
分析 > 一般线性模型 > 多变量...
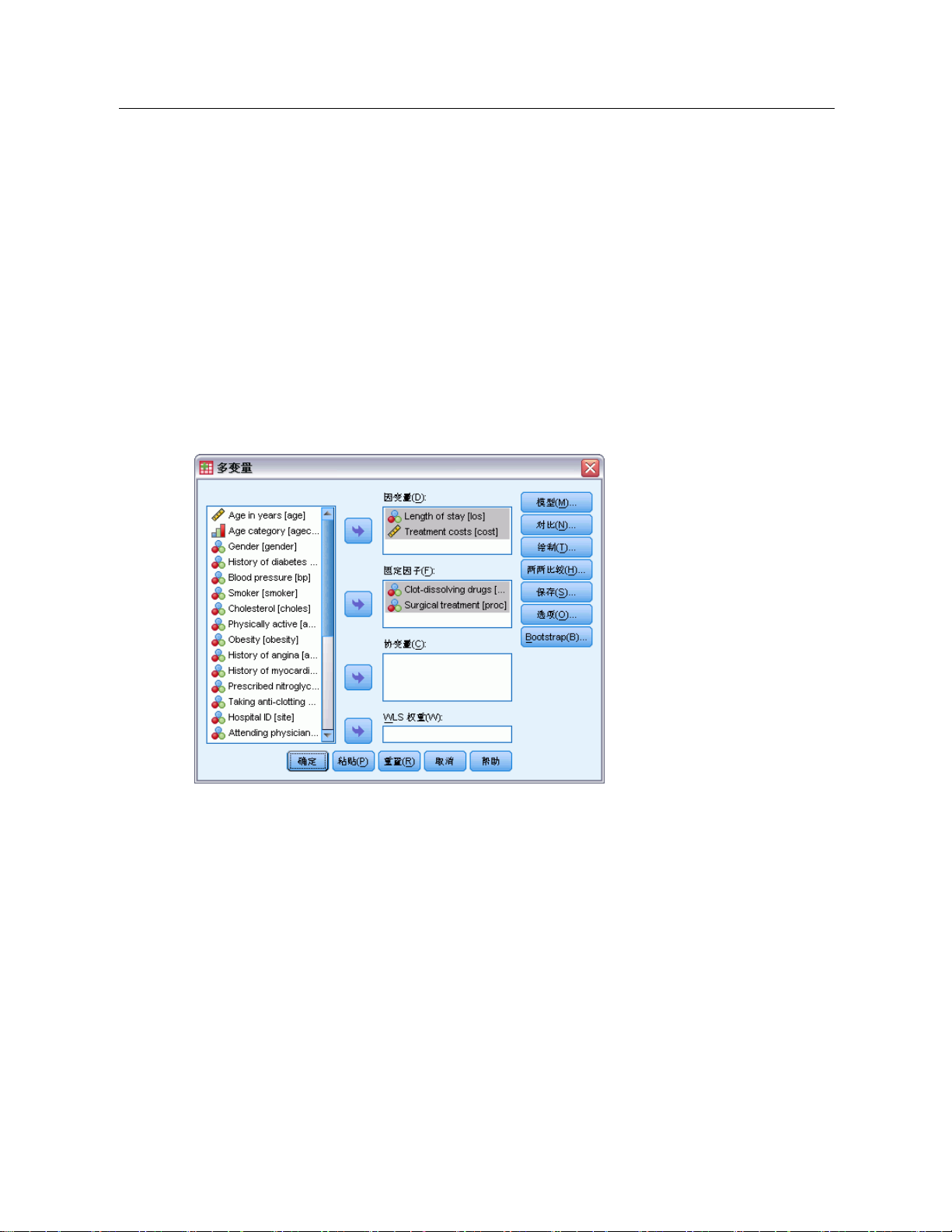
图片 2-1
“多变量”对话框
3
E 请选择至少两
个因变量。
或者,您也可以指定“固定因子”、“协变量”和“WLS 权重”。
Page 14
4
章2
GLM 多变量:模型
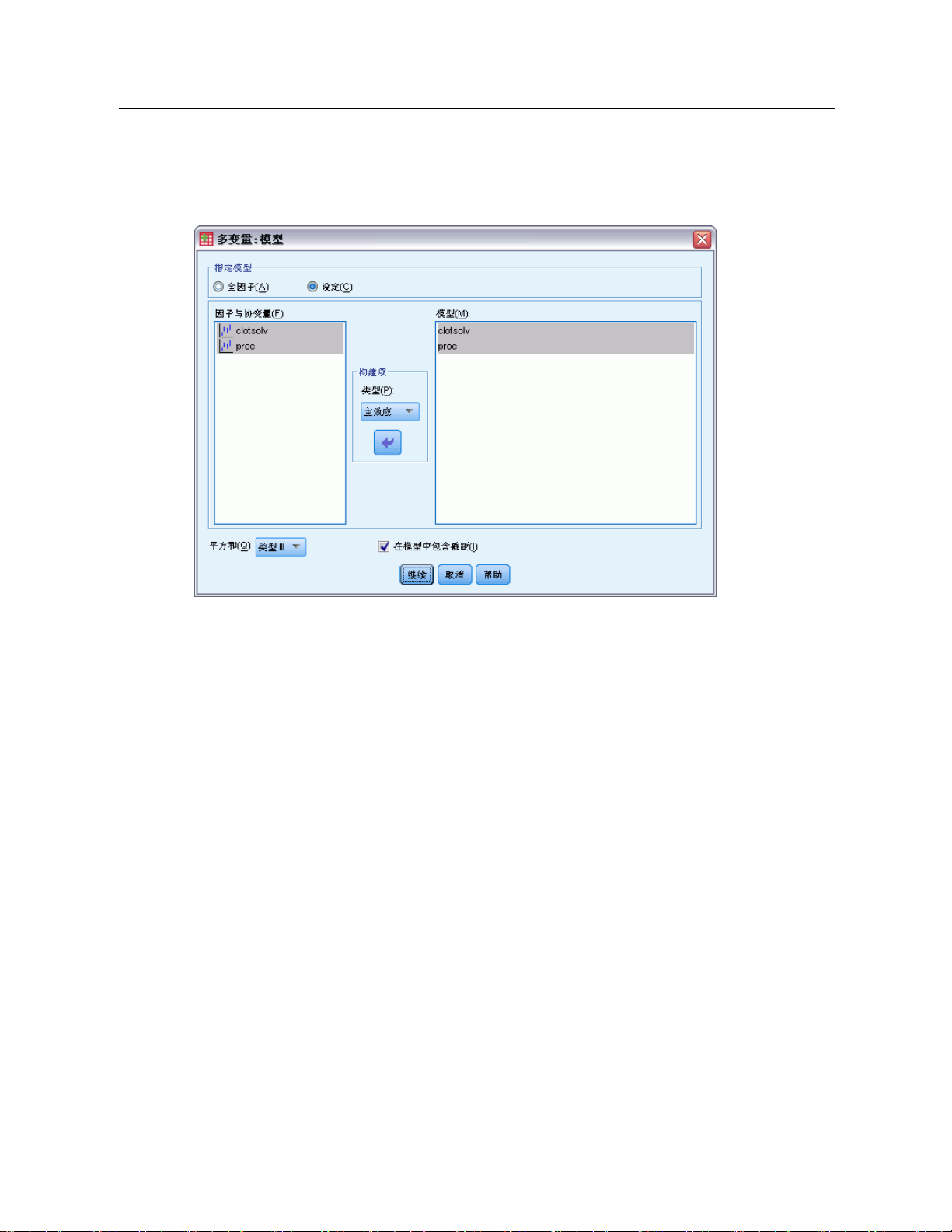
图片 2-2
“多变量:模型”对话框
构建项
指定模型。全因子模型包含所有因子主效应、所有协变量主效应以及所有因子间交互。
它不包含协变量交互。选择
定制可以仅指定其中一部分的交互或指定因子协变量交
互。必须指定要包含在模型中的所有项。
因子与协变量。列出因子与协变量。
模型。模型取决于数据的性质。选择定制之后,您可以选择分析中感兴趣的主效应
和交互效应。
平方和。计算平方和的方法。对于没有缺失单元的平衡或非平衡模型,类型 III 平
方和方法最常用。
在模型中包含截距。模型中通常包含截距。如果您可以假设数据穿过原点,则可以排
除截距。
对于选定因子和协变量:
交互。创建所有选定变量的最高级交互项。这是缺省值。
主效应。为每个选定的变量创建主效应项。
所有二阶。创建选定变量的所有可能的二阶交互。
所有三阶。创建选定变量的所有可能的三阶交互。
所有四阶。创建选定变量的所有可能的四阶交互。
所有五阶。创建选定变量的所有可能的五阶交互。
Page 15

平方和
5
GLM 多变量分析
对于该模型,您可以选择平方和类型。类型 III 最常用,并且是缺省类型。
类型 I。此方法也称为平方和分级解构法。在模型中,每一项只针对它前面的那项进行
调整。类型 I 平方和常用于:
平衡 ANOVA 模型,其中任何主效应在任何一阶交互效应之前指定,任何一阶交互效
应在任何二阶交互效应之前指定,依此类推。
多项式回归模型,其中任何低阶项在任何高阶项之前指定。
纯嵌套模型,其中第一个指定的效应嵌套在第二个指定的效应中,第二个指定的效应
嵌套在第三个指定的效应中,依此类推。(此嵌套形式只能通过使用语法来指定。)
类型 II。此方法在为所有其它“相应的”效应进行调节的模型中计算某个效应的平
方和。相应的效应是指,与所有效应(不包含正被检查的效应)相对应的效应。类型
II 平方和方法常用于:
平衡 ANOVA 模型。
任何只有主要因子效应的模型。
任何回归模型。
纯嵌套设计。(此嵌套形式能通过使用语法来指定。)
类型 III。缺省类型。此方法在设计中通过以下形式计算某个效应的平方和:为任何
不包含该效应的其他效应,以及任何与包含该效应正交的效应(如果存在)调整的平
方和。类型 III 平方和具有一个主要优点,那就是只要可估计性的一般形式保持不
变,平方和对于单元频率就保持不变。因此,我们常认为此类平方和对于不带缺失单元
格的不平衡模型有用。在不带缺失单元的因子设计中,此方法等同于 Yates 加权均值
平方方法。类型 III 平方和法常用于:
任何在类型 I 和类型 II 中列出的模型。
任何不带空白单元的平衡或非平衡模型。
类型 IV。此方法针对存在缺失单元的情况设计。对于设计中的任何效应 F,如果任何
其它效应中不包含 F,则类型 IV = 类型 III = 类型 II。当 F 包含在其它效应中时,
则类型 IV 将 F 中的参数中正在进行的对比相等地分配到所有较高水平的效应。类
型 IV 平方和法常用于:
任何在类型 I 和类型 II 中列出的模型。
任何带有空白单元的平衡或非平衡模型。
Page 16
6
章2
GLM 多变量:对比
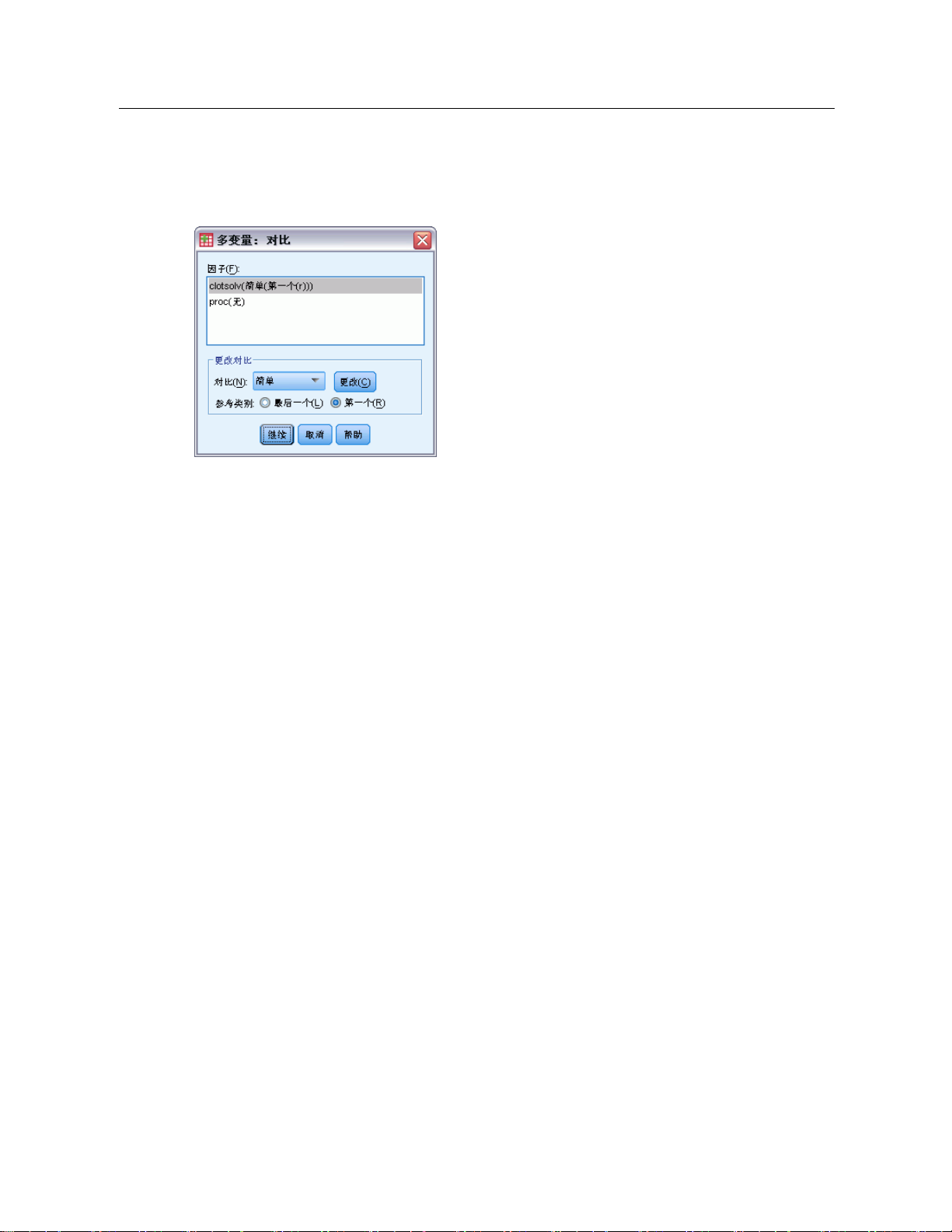
图片 2-3
“多变量: 对比”对话框
“对比”用于检验效应水平之间是否存在显著性差异。您可以为模型中的每个因子指定
一个对比。对比代表参数的线性组合。
假设检验基于原假设 LBM = 0,其中 L 是对比系数矩阵,M 是恒等矩阵,该矩阵的维数
等于因变量的个数,B 是参数矢量。当指定对比之后,创建一个 L 矩阵,使得与因子对
应的列与对比匹配。对剩余的列进行调整,使 L 矩阵可以估计。
除了使用 F 统计量的单变量检验和基于跨所有因变量的对比差分的 Student 的 t 分布
的 Bonferroni 型同时置信区间以外,还提供使用 Pillai 的轨迹、Wilks 的 lambda、
Hotelling 的轨迹以及 Roy 的最大根条件的多变量检验。
可用对比有偏移对比、简单对比、差分对比、Helmert 对比、重复对比和多项式对
比。对于偏移对比和简单对比,您可以选择参考类别是最后一个类别还是第一个类别。
对比类型
偏差。将每个水平(参考类别除外)的均值与所有水平的均值(总均值)进行比较。
因子的水平可以为任何顺序。
简单。将每个水平的均值与指定水平的均值进行比较。当存在控制组时,此类对比很
有用。可以选择第一个或最后一个类别作为参考类别。
差分。将每个水平的均值(第一个水平除外)与前面水平的均值进行比较。(有时候称
为逆 Helmert 对比。)
Helmert。将因子的每个水平的均值(最后一个水平除外)与后面水平的均值进行比较。
重复。将每个水平的均值(最后一个水平除外)与后一个水平的均值进行比较。
多项式。比较线性作用、二次作用、三次作用等等。第一自由度包含跨所有类别的线性
效应;第二自由度包含二次效应,依此类推。这些对比常常用来估计多项式趋势。
Page 17
GLM 多变量:轮廓图
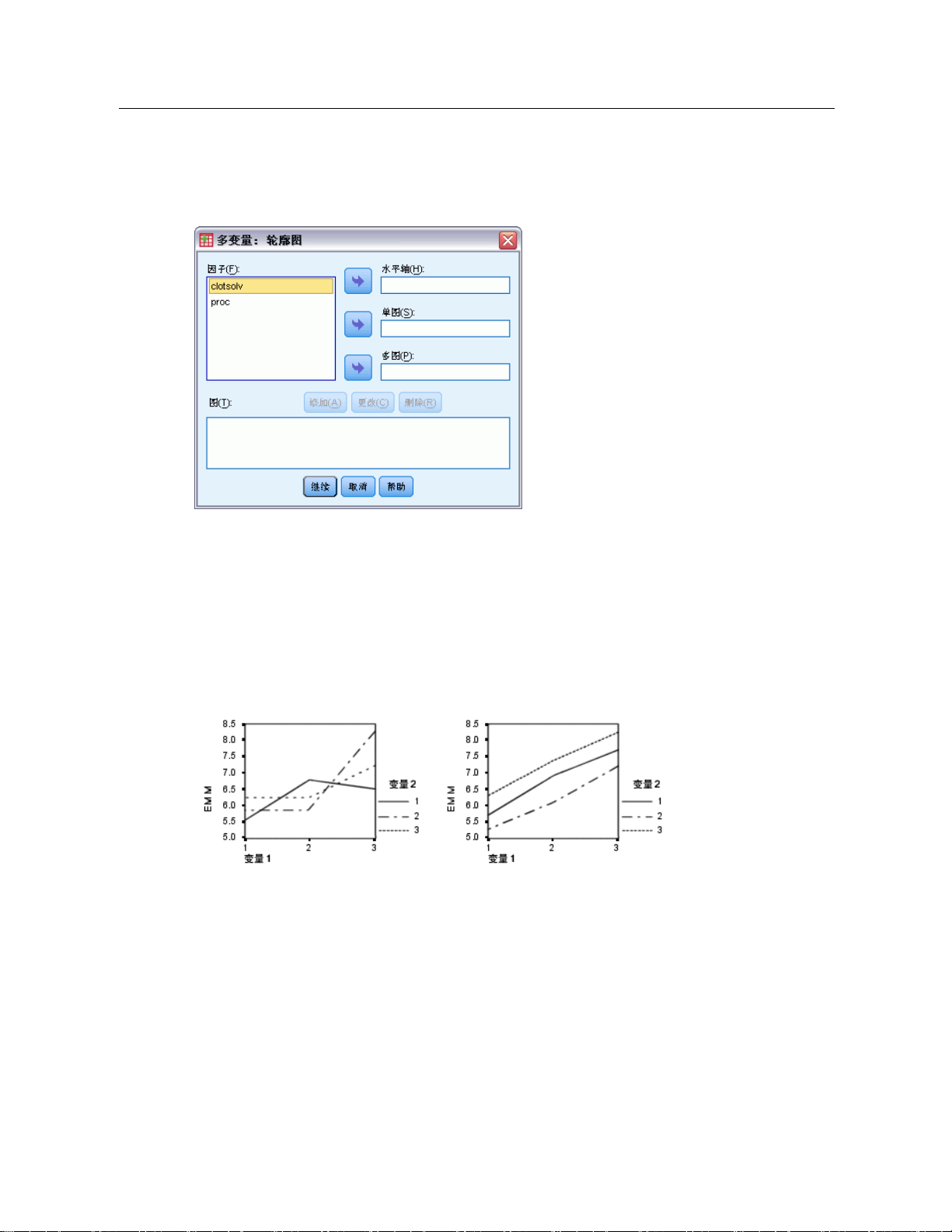
图片 2-4
“多变量: 轮廓图”对话框
7
GLM 多变量分析
轮廓图(交互图)对
于比较模型中的边际均值是有用的。轮廓图是一个线图,其中每个
点表示因子的一个水平上的估计因变量边际均值(已针对任何协变量进行调整)。第二
个因子的水平可用来绘制分离线。第三个因子中的每个水平可用来创建分离图。所有因
子都可用于图。为
每个因变量创建轮廓图。
单因子的轮廓图显示估计边际均值是沿水平增加还是减小。对于两个或更多因子,
平行线表示因子之间没有交互,这意味着您只能调查一个因子的水平。不平行的线
则表示交互。
图片 2-5
不平行图(左)和平行图(右)
在通过为水平
轴选择因子,以及通过为分离线和分离图选择因子(后者可选)指定了图
之后,该图必须添加到“图”列表中。
Page 18
8
章2
GLM 多变量:两两比较
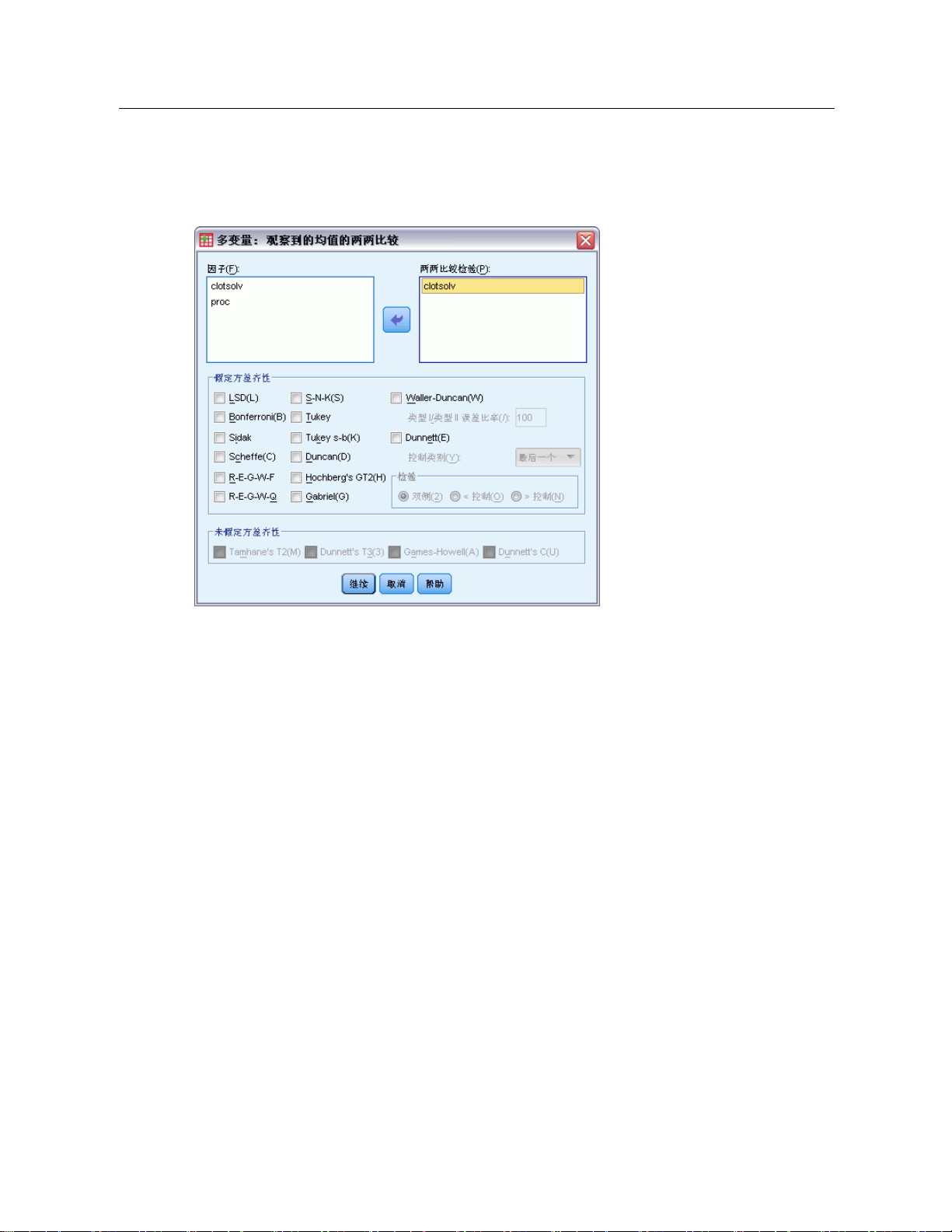
图片 2-6
“多变量:观察到的均值的两两比较”对话框
两两比较检验。 一旦确定均值间存在差值,两两范围检验和成对多重比较就可以确定哪
些均值存在差值了。对未调整的值进行比较。单独为每个因变量执行两两比较检验。
Bonferroni 和 Tukey’s 真实显著性差异检验是常用的多重比较检验。Bonferroni 检
验基于 Student 的 t 统计量,它针对已进行多重比较这一事实调整观察的显著性水平。
Sidak 的 t 检验也调整显著性水平,并提供比 Bonferroni 检验更严密的界限。Tukey’s
真实显著性差异检验使用 Student 化的范围统计量在组之间进行所有成对比较,并将试
验误差率设置为所有成对比较的集合的误差率。当检验大量均值对时,Tukey’s 真实显
著性差异检验比 Bonferroni 检验更有效。对于少量的对,Bonferroni 更有效。
Hochberg’s GT2 类似于 Tukey’s 真实显著性差异检验,但使用了 Student 化的最大
值模数。通常 Tukey 的检验更有效。Gabriel 的成对比较检验也使用 Student 化的最大
值模数,在单元格尺寸不等的情况下通常比 Hochberg’s GT2 更有效。当单元大小变化
过大时,Gabriel 检验可能会变得随意。
Dunnett 的成对多重比较 t 检验将一组处理与单个控制均值进行比较。最后一个类别
是缺省的控制类别。另外,您还可以选择第一个类别。您还可以选择双侧或单侧检验。
要检验因子的任何水平(控制类别除外)的均值是否不等于控制类别的均值,请使用双
侧检验。要检验因子的任何水平的均值是否小于控制类别的均值,请选择
地,要检验因子的任何水平的均值是否大于控制类别的均值,请选择
<控制。类似
>控制。
Ryan、Einot、Gabriel 和 Welsch (R-E-G-W) 开发了两个多重逐步降低范围检验。多
重逐步降低过程首先检验所有均值是否相等。如果不是所有的均值均相等,则检验一
部分均值的相等性。R-E-G-W F 基于 F 检验,而 R-E-G-W Q 基于 Student 化的范围。
这些检验要比 Duncan 的多范围检验和 Student-Newman-Keuls(也是多重逐步下降过
程)有效,但对于不相等的单元大小则不推荐使用它们。
Page 19
GLM 多变量分析
当方差不等时,使用 Tamhane’s T2(基于 t 检验的保守成对比较检验)、Dunnett’s
T3(基于 Student 化的最大模数的成对比较检验)、Games-Howell 成对比较检验(有时
是随意的)或者 Dunnett’s C(基于 Student 化的范围的成对比较检验)。
Duncan 的多范围检验、Student-Newman-Keuls (S-N-K)和Tukey 的 b 是排列组均值等
级的范围检验,并计算范围值。这些检验的使用频率不如先前讨论的检验。
Waller-Duncan t 检验使用 Bayesian 方法。当样本大小不相等时,此范围检验使用
样本大小的调和均值。
Scheffé 检验的显著性水平可允许要检验的组均值的所有可能的线性组合,而不仅仅
是此功能中可用的成对比较。其结果是,Scheffé 检验常常比其他检验更保守,这意味
着对于显著性,需要均值之间有更大的差别。
最小显著性差异 (LSD) 成对多重比较检验等同于所有组对之间的多重个别 t 检验。此
检验的缺点是,不进行任何尝试来为多重比较调整观察到的显著性水平。
显示的检验。为 LSD、Sidak、Bonferroni、Games-Howell、Tamhane’s T2 和 T3、
Dunnett’s C 以及 Dunnett’s T3 提供成对比较。为 S-N-K、Tukey 的 b、Duncan、
R-E-G-W F、R-E-G-W Q 以及 Waller 提供范围检验的均一子集。Tukey’s 真实显著性差
异检验、Hochberg’s GT2、Gabriel 的检验以及 Scheffé 的检验既是多重比较检验,
同时也是多范围检验。
9
GLM: 保存
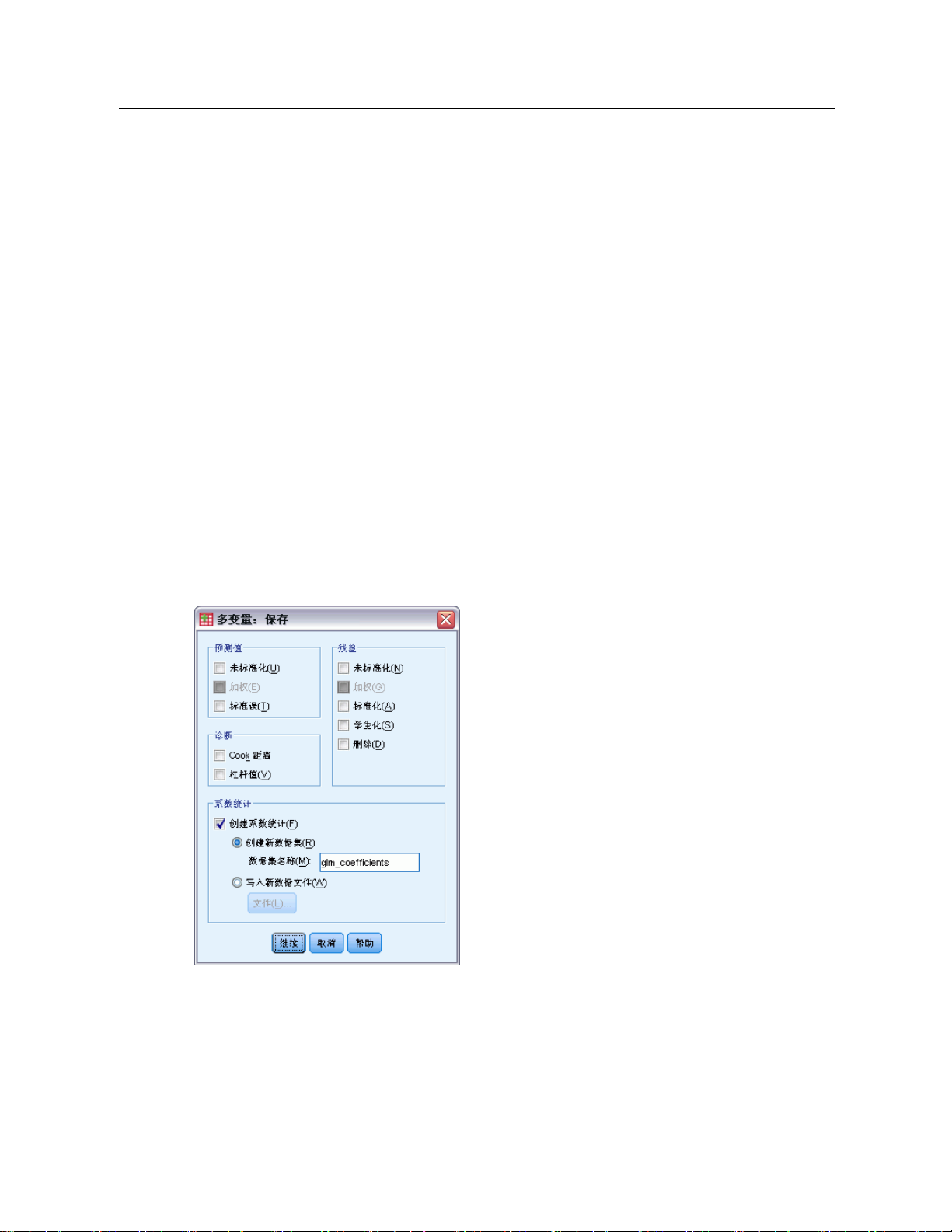
图片 2-7
保存对话框
您可以在数据编辑器中将模型预测的值、残差和相关测量另存为新变量。这些变量中
有许多可用于检查关于数据的假设。要保存供另一 IBM® SPSS® Statistics 会话中
使用的值,您必须保存当前数据文件。
预测值。模型为每个个案预测的值。
未标准化. 模型为因变量预测的值。
Page 20

10
章2
加权. 加权未标准化预测值。仅在之前已选择了 WLS 变量的情况下可用。
标准误. 对于自变量具有相同值的个案所对应的因变量均值标准差的估计。
诊断。标识以下个案的测量:自变量的值具有不寻常组合的个案,以及可能对模型
产生很大影响的个案。
Cook 距离. 在特定个案从回归系数的计算中排除的情况下,所有个案的残差变化
幅度的测量。较大的 Cook 距离表明从回归统计量的计算中排除个案之后,系数
会发生根本变化。
杠杆值. 未居中的杠杆值。每个观察值对模型拟合的相对影响。
残差。未标准化残差是因变量的实际值减去由模型预测的值。还提供标准化残差、
Student 化的残差以及剔除残差。如果选择了 WLS 变量,则提供加权的未标准化残差。
未标准化. 观察值与模型预测值之间的差。
加权. 加权未标准化残差。仅在之前已选择了 WLS 变量的情况下可用。
标准化. 残差除以其标准差的估计。标准化残差也称为 Pearson 残差,它的均
值为 0,标准差为 1。
学生化. 残差除以其随个案变化的标准差的估计,这取决于每个个案的自变量
值与自变量均值之间的距离。
删除. 当某个案从回归系数的计算中排除时,该个案的残差。它是因变量的值和
调整预测值之间的差。
系数统计。将模型中的参数估计值的协方差矩阵写入当前会话中的新数据集,或写入外
部 SPSS Statistics 数据文件。而且,对于每个因变量,将存在一行参数估计值、一行
与参数估计值对应的 t 统计量的显著性值以及一行残差自由度。对于多变量模型,每一
个因变量都存在类似的行。您可以在读取矩阵文件的其他过程中使用此矩阵文件。
Page 21
GLM 多变量:选项
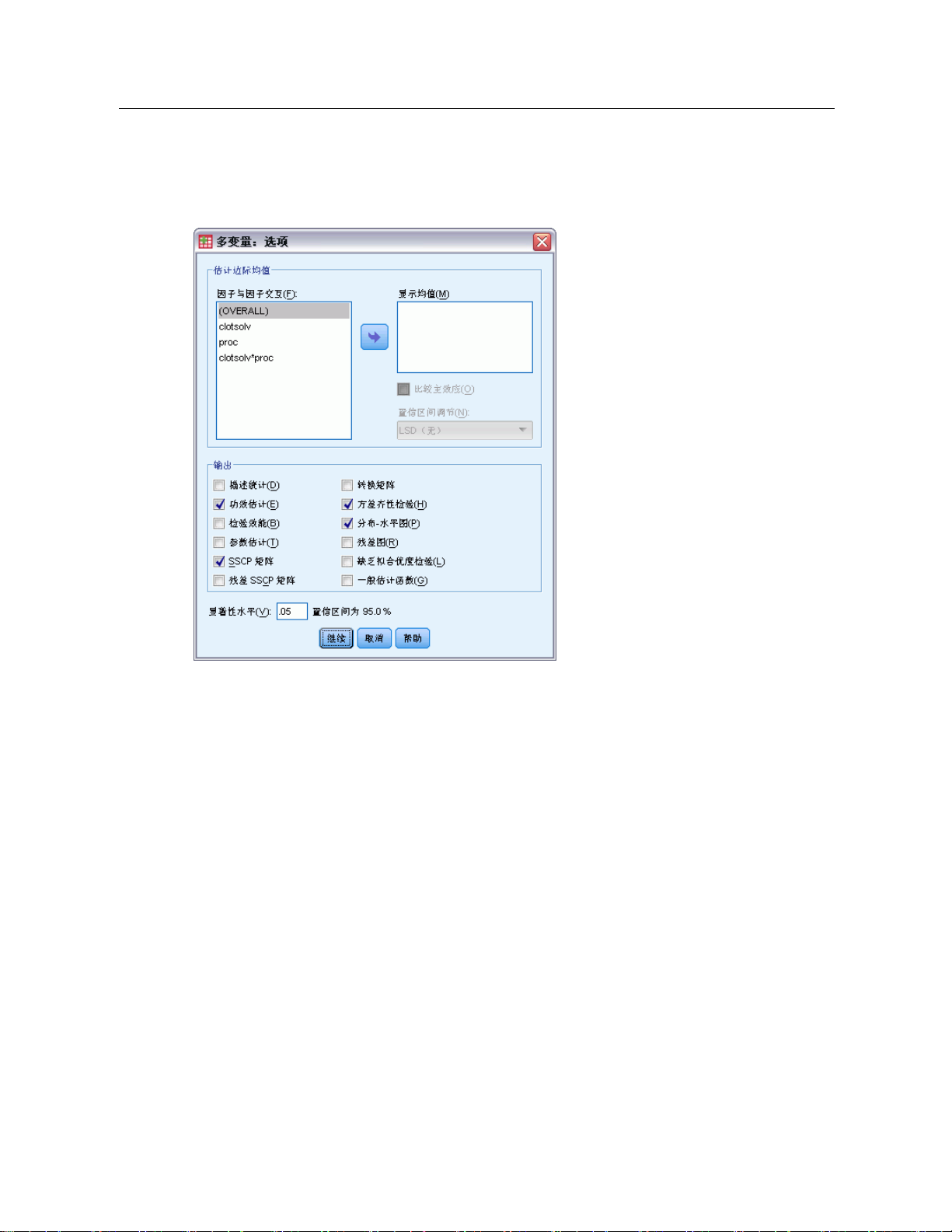
图片 2-8
“多变量:选项”对话框
11
GLM 多变量分析
此对话框中有一些可选统计量。统计量是使用固定效应模型计算的。
估计边际均值。选择您需要的单元中的总体边际均值估计的因子和交互作用。为协变量
(如果存在)调整这些均值。仅当指定了定制模型时交互才可用。
比较主效应。对于主体间和主体内因子,为模型中的任何主效应提供估计边际均
值未修正的成对比较。只有在“显示以下项的均值”列表中选择了主效应的情况
下,此项才可用。
置信区间调节。选择最小显著性差异 (LSD)、Bonferroni 或对置信区间和显著性的
Sidak 调整。此项只有在选择了
输出。选择描述统计以生成所有单元中的所有因变量的观察到的均值、标准差和计数。
功效估计给出了每个作用和每个参数估计值的偏 eta 方值。eta 方统计量描述总变异
比较主作用的情况下才可用。
性中可归因于某个因子的部分。当基于观察到的值设置备用假设时,选择检验效能可
获取检验的效能。选择
参数估计可为每个检验生成参数估计值、标准误、t 检验、置
信区间和检验效能。可以显示假设和误差 SSCP 矩阵以及残差 SSCP 矩阵加上残差协方差
矩阵的 Bartlett 球形度检验。
齐性检验为跨主体间因子所有水平组合的每个因变量生成 Levene 的方差齐性检验(仅
对于主体间因子)。另外,齐性检验包含对因变量协方差矩阵的齐性 Box M 检验,这些因
变量跨主体间因子的所有水平组合。分布-水平图和残差图选项对于检查关于数据的假设
很有用。如果不存在任何因子,则禁用此项。选择
准化残差图。这些图对于调查方差相等的假设很有用。选择
残差图为每个因变量生成观察-预测-标
缺乏拟合优度检验以检查因变
Page 22

12
章2
量和自变量之间的关系是否能由模型充分地描述。常规可估计函数允许您基于常规可估计
函数构造定制的假设检验。任何对比系数矩阵中的行均是常规可估计函数的线性组合。
显著性水平。您可能想要调整用在两两比较检验中的显著性水平,以及用于构造置信
区间的置信度。指定的值还用于计算检验的检验效能。如果指定了显著性水平,则相
关联的置信区间度会显示在对话框中。
GLM 命令的附加功能
这些功能可以适用于单变量、多变量或重复测量分析。使用命令语法语言还可以:
在设计中指定嵌套效应(使用 DESIGN 子命令)。
指定效应对比效应的线性组合或一个值的检验(使用 TEST 子命令)。
指定多个对比(使用 CONTRAST 子命令)。
包括用户缺失值(使用 MISSING 子命令)。
指定 EPS 标准(使用 CRITERIA 子命令)。
构造定制的 L 矩阵、M 矩阵或 K 矩阵(使用 LMATRIX、MMATRIX 或 KMATRIX 子命令)。
为偏移对比或简单对比指定中间参考类别(使用 CONTRAST 子命令)。
为多项式对比指定矩阵(使用 CONTRAST 子命令)。
为两两比较指定误差项(使用 POSTHOC 子命令)。
为因子列表中的任何因子或因子之间的因子交互计算估计边际均值(使用 EMMEANS 子
命令)。
为临时变量指定名称(使用 SAVE 子命令)。
构造相关矩阵数据文件(使用 OUTFILE 子命令)。
构造包含主体间 ANOVA 表中的统计量的矩阵数据文件(使用 OUTFILE 子命令)。
将设计矩阵保存到新的数据文件(使用 OUTFILE 子命令)。
请参见命令语法参考以获取完整的语法信息。
Page 23

GLM 重复测量
“GLM 重复测量”过程在对每个主体或个案多次执行相同的测量时提供方差分析。如果
指定了主体间因子,这些因子会将总体划分成组。通过使用此一般线性模型过程,您可
以检验关于主体间因子和主体内因子的效应的原假设。可以调查因子之间的交互以及单
个因子的效应。另外,还可以包含常数协变量的效应以及协变量与主体间因子的交互。
在双重多变量重复测量设计中,因变量表示主体内因子不同水平的多个变量的测量。
例如,您可能在三个不同的时间对每个主体同时测量了脉搏和呼吸。
“GLM 重复测量”过程提供了对重复测量数据的单变量和多变量分析。平衡与非平
衡模型均可进行检验。如果模型中的每个单元包含相同的个案数,则设计是平衡的。
在多变量模型中,模型中的效应引起的平方和以及误差平方和以矩阵形式表示,而不
是以单变量分析中的标量形式表示。这些矩阵称为 SSCP(平方和与叉积)矩阵。除
了检验假设,“GLM 重复测量”过程还生成参数估计。
常用的先验对比可用于对主体间因子执行假设检验。另外,在整体的 F 检验已显示
显著性之后,可以使用两两比较检验评估指定均值之间的差值。估计边际均值为模型
中的单元提供了预测均值估计值,且这些均值的轮廓图(交互图)允许您轻松对其中
一些关系进行可视化。
残差、预测值、Cook 距离以及杠杆值可以另存为数据文件中检查假设的新变量。另外
还提供残差 SSCP 矩阵(残差的平方和与叉积的方形矩阵)、残差协方差矩阵(残差
SSCP 矩阵除以残差的自由度)和残差相关矩阵(残差协方差矩阵的标准化形式)。
WLS 权重允许您指定一个变量,用来针对加权最小平方 (WLS) 分析为观察值赋予不同
权重,这样也许可以补偿测量的不同精确度。
章
3
示例。根据学生的焦虑程度检验的得分将十二个学生分配到高或低焦虑程度组。焦虑
等级被认为是主体间因子,因为它会将主体划分成组。让每个学生进行四个学习任务
试验,并记录每次试验中所犯错误的个数。每次试验的错误都记录在单独的变量中,
并使用四个试验的四个水平定义主体内因子(试验)。试验的效果很明显,而试验与
焦虑的交互则不明显。
方法。类型 I、类型 II、类型 III 和类型 IV 的平方和可用来评估不同的假设。类
型 III 是缺省值。
统计量。两两比较范围检验和多重比较(对于主体间因子):最小显著性
差异、Bonferroni、Sidak、Scheffé、Ryan-Einot-Gabriel-Welsch 多重 F、
Ryan-Einot-Gabriel-Welsch 多范围、Student-Newman-Keuls、Tukey’s 真实显著性差
异、Tukey 的 b、Duncan、Hochberg’s GT2、Gabriel、Waller-Duncan t 检验、Dunnett
(单侧和双侧)、Tamhane’s T2、Dunnett’s T3、Games-Howell 和 Dunnett’s C。描
述统计:所有单元中所有因变量的观察均值、标准差和计数;Levene 的方差齐性检验;
对因变量协方差矩阵的齐性 Box 的 M 检验以及 Mauchly 球形度检验。
图。分布-水平图、残差图以及轮廓图(交互)。
© Copyright SPSS Inc. 1989, 2010
13
Page 24

14
章3
数据。因变量应是定量的。主体间因子将样本划分为离散的子组,例如男性和女性。这
些因子应是分类因子,可以具有数字值或字符串值。主体内因子是在“重复测量定义因
子”对话框中定义的。协变量是与因变量相关的定量变量。对于重复测量分析,这些数
据在每个主体内变量水平都应该保持不变。
数据文件中应该为主体的每组测量包含一组变量。该组变量为组中的每次重复测
量包含一个变量。为水平数等于重复次数的组定义一个主体内因子。例如,进行权重
测量可能需要不同的天数。如果在五天内测量相同的属性,则主体内因子可以指定为
day,并且该因子具有五个水平。
对于多个主体内因子,每个主体的测量次数均等于每个因子的水平数的乘积。例
如,如果四天内在每天的三个不同时间进行测量,则每个主体的总测量次数为 12。主
体内因子可指定为 day(4) 和 time(3)。
假设。重复测量分析可通过两种方式完成,即单变量和多变量。
单变量方法(也称为分割图或混合模型方法)将因变量视为对主体内因子的水平的
响应。主体测量应为来自多变量正态分布的样本,方差-协方差矩阵在主体间效应形
成的单元内应该都相同。有些假设是针对因变量的方差-协方差矩阵的。如果方差-协
方差矩阵是圆形的,单变量方法中使用的 F 统计量的有效性就可以得到保证(Huynh
and Mandeville,1979 年)。
要检验此假设,可以使用 Mauchly 球形度检验,该方法会对进行了正交标准化转换的
因变量的方差-协方差矩阵执行球形度检验。对于重复测量分析,Mauchly 检验会自动显
示。对于较小的样本,此检验表现的功能并不十分强大。对于较大的样本,此检验的效
果可能显而易见,即使是在偏差对结果的影响很小的情况下也不例外。如果检验的显著
性很大,则可采用球形度假设。不过,在显著性不大并且似乎违反了球形度假设的情况
下,可以对分子和分母自由度进行一定的调整,以便验证单变量 F 统计量。“GLM 重复
测量”过程中存在三个对此调整的估计值,称为 epsilon。分子和分母自由度都必须
乘以 epsilon,并使用新的自由度估计 F 比的显著性。
多变量方法将主体测量视为来自多变量正态分布的样本,方差-协方差矩阵在主体间
效应形成的单元内应该都相同。要检验方差-协方差矩阵是否在所有单元内都相同,
可以使用 Box M 检验。
相关过程。在进行方差分析之前使用“探索”过程来检查数据。如果不 存在对每个
主体的重复测量,则请使用“GLM 单变量”或“GLM 多变量”。如果每个主体仅存在
两个测量(例如检验前和检验后测量),并且不存在主体间因子,则可以使用“配
对样本 T 检验”过程。
获取 GLM 重复测量
E 从菜单中选择:
分析 > 一般线性模型 > 重复测量...
Page 25
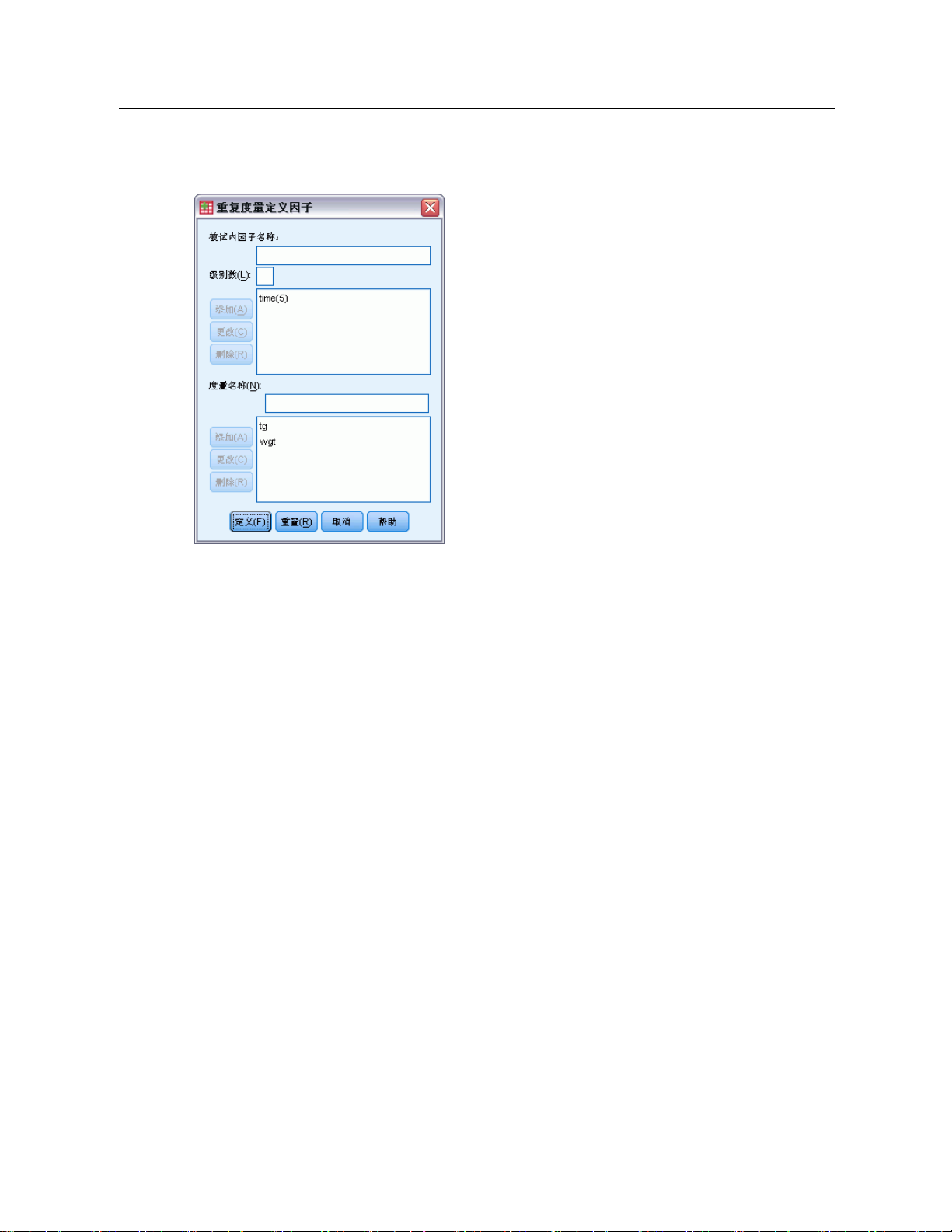
图片 3-1
“重复测量定义因子”对话框
15
GLM 重复测量
E 群体内部因子名称及其级别数。
E 单击添加。
E 对每个主体内因子重复这些步骤。
为双重多变量重复测量设计定义测量因子:
E 键入测量名称。
E 单击添加。
在定义完所有因子
E 单击定义。
和测量后:
Page 26

16
章3
图片 3-2
“重复测量”对话框
E 在列表上选择一个与群体内部因子(也可能是测量)的每个组合对应的因变量。
要更改变量位置,请使用向上和向下箭头。
要更改群体内部因子,可在不关闭主对话框的情况下重新打开“重复测量定义因
子”对话框。或者,您也可以指定主体间因子和协变量。
GLM 重复测量定义因子
“GLM 重复测量”可分析表示相同属性的不同测量的相关因变量的分组。此对话框使
您可以定义一个或多个主体内因子以便在“GLM 重复测量”中使用。请参阅第 15 页
码中的图片 3-1. 注意,指定主体内因子的顺序非常重要。每个因子都构成前一个因
子内的一个水平。
要使用“重复测量”,必须正确设置数据。您必须在此对话框中定义主体内因子。注
意,这些因子不是数据内的现有变量,而是在这里定义的因子。
示例。在减肥研究中,假设要连续五周每周测量几个人的体重。在数据文件中,每个人
就是一个主体或者个案。每周测量到的体重都记录在 weight1、weight2 等变量中。每
个人的性别则记录在其他变量中。通过定义主体内因子可以将为每个主体重复测量的体
重分组。该因子可命名为 week,并将其定义为具有五个水平。在主对话框中,变量
weight1 到 weight5 用于指定 week 的五个水平。数据文件中将女性和男性分组的变量
(gender) 可以指定为主体间因子以便研究男性和女性的差别。
测量。如果每次就多个测量对主体进行检验,请定义测量。例如,可以在一周的每一天
对每个主体的脉搏和呼吸比率进行测量。这些测量不作为变量保存在数据文件中,但是
在此处定义。具有多个测量的模型有时称为双重多变量重复测量模型。
Page 27
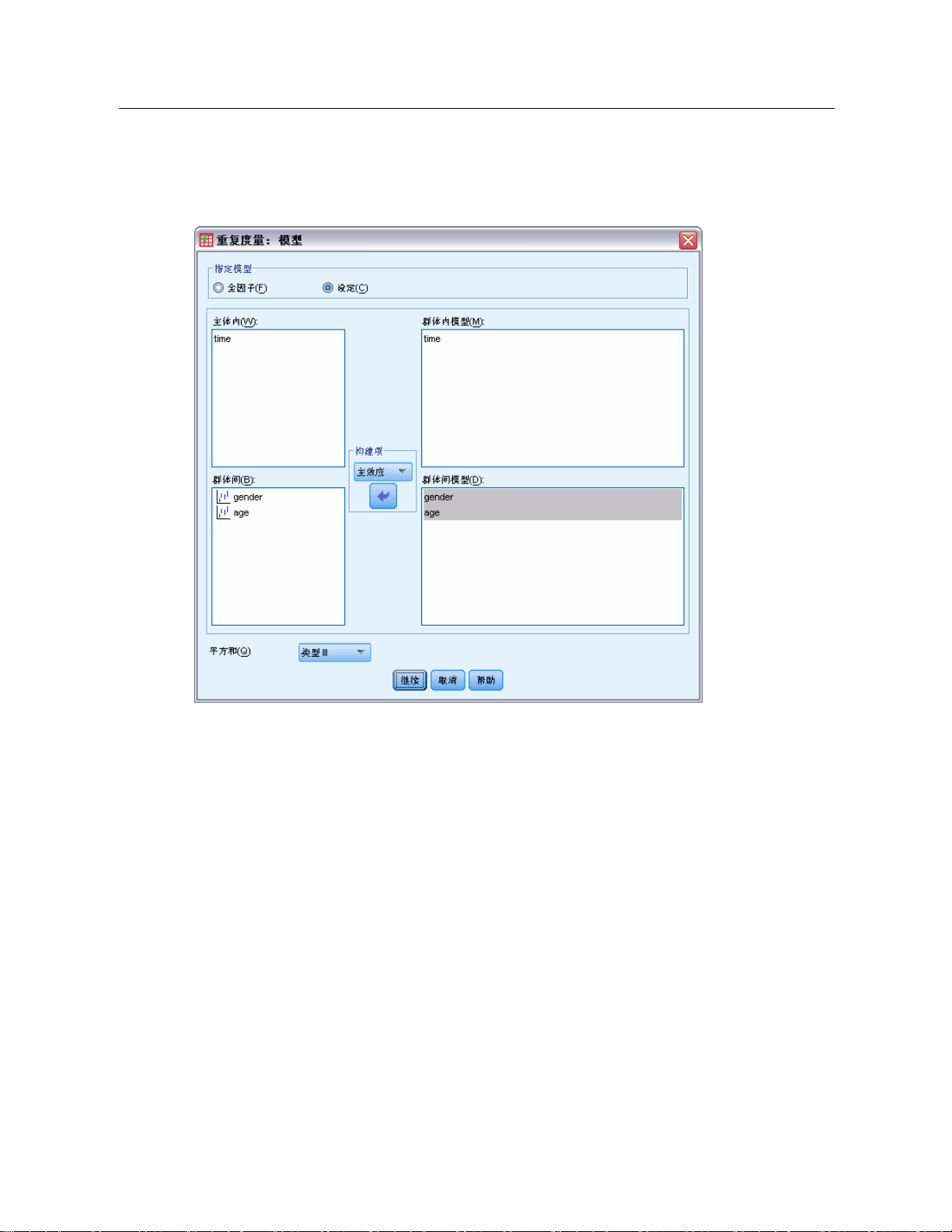
GLM 重复测量:模型
图片 3-3
“重复测量:模型”对话框
17
GLM 重复测量
构建项
指定模型。全因子模型包含所有因子主效应、所有协变量主效应以及所有因子间交互。
它不包含协变量交互。选择定制可以仅指定其中一部分的交互或指定因子协变量交
互。必须指定要包含在模型中的所有项。
主体间。列出主体间因子与协变量。
模型。模型取决于数据的性质。选择定制后,您可以选择分析中感兴趣的主体内效应和
交互以及主体间效应和交互。
平方和。计算主体间模型的平方和的方法。对于没有缺失单元的平衡或非平衡主体间模
型,类型 III 平方和法最常用。
对于选定因子和协变量:
交互。创建所有选定变量的最高级交互项。这是缺省值。
主效应。为每个选定的变量创建主效应项。
所有二阶。创建选定变量的所有可能的二阶交互。
Page 28

18
章3
平方和
所有三阶。创建选定变量的所有可能的三阶交互。
所有四阶。创建选定变量的所有可能的四阶交互。
所有五阶。创建选定变量的所有可能的五阶交互。
对于该模型,您可以选择平方和类型。类型 III 最常用,并且是缺省类型。
类型 I。此方法也称为平方和分级解构法。在模型中,每一项只针对它前面的那项进行
调整。类型 I 平方和常用于:
平衡 ANOVA 模型,其中任何主效应在任何一阶交互效应之前指定,任何一阶交互效
应在任何二阶交互效应之前指定,依此类推。
多项式回归模型,其中任何低阶项在任何高阶项之前指定。
纯嵌套模型,其中第一个指定的效应嵌套在第二个指定的效应中,第二个指定的效应
嵌套在第三个指定的效应中,依此类推。(此嵌套形式只能通过使用语法来指定。)
类型 II。此方法在为所有其它“相应的”效应进行调节的模型中计算某个效应的平
方和。相应的效应是指,与所有效应(不包含正被检查的效应)相对应的效应。类型
II 平方和方法常用于:
平衡 ANOVA 模型。
任何只有主要因子效应的模型。
任何回归模型。
纯嵌套设计。(此嵌套形式能通过使用语法来指定。)
类型 III。缺省类型。此方法在设计中通过以下形式计算某个效应的平方和:为任何
不包含该效应的其他效应,以及任何与包含该效应正交的效应(如果存在)调整的平
方和。类型 III 平方和具有一个主要优点,那就是只要可估计性的一般形式保持不
变,平方和对于单元频率就保持不变。因此,我们常认为此类平方和对于不带缺失单元
格的不平衡模型有用。在不带缺失单元的因子设计中,此方法等同于 Yates 加权均值
平方方法。类型 III 平方和法常用于:
任何在类型 I 和类型 II 中列出的模型。
任何不带空白单元的平衡或非平衡模型。
类型 IV。此方法针对存在缺失单元的情况设计。对于设计中的任何效应 F,如果任何
其它效应中不包含 F,则类型 IV = 类型 III = 类型 II。当 F 包含在其它效应中时,
则类型 IV 将 F 中的参数中正在进行的对比相等地分配到所有较高水平的效应。类
型 IV 平方和法常用于:
任何在类型 I 和类型 II 中列出的模型。
任何带有空白单元的平衡或非平衡模型。
Page 29
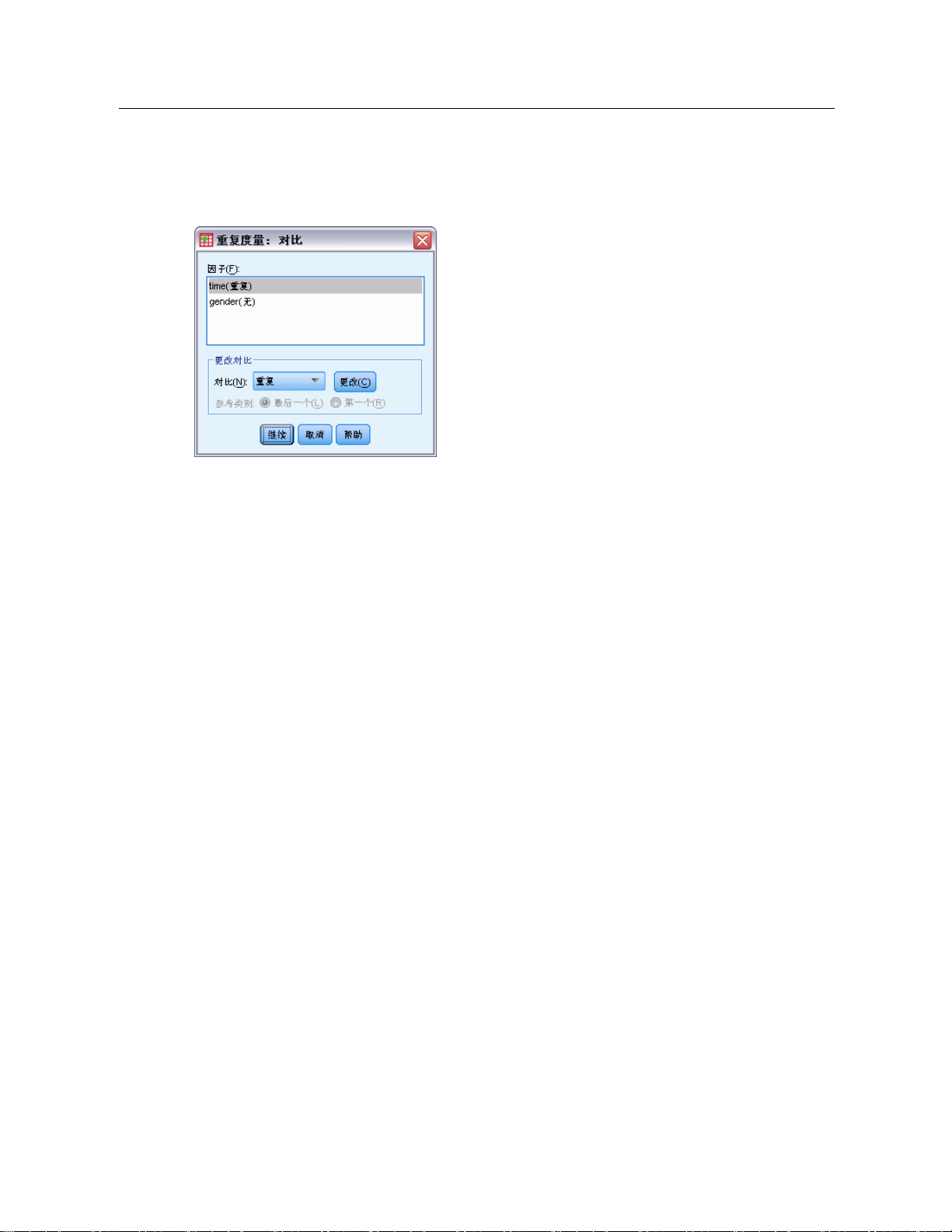
GLM 重复测量:对比
图片 3-4
“重复测量:对比”对话框
使用对比可以检验主体间因子的水平之间的差别。您可以为模型中的每个主体间因子指
定一个对比。对比代表参数的线性组合。
假设检验基于原假设 LBM =0,其中L 是对比系数矩阵,B 是参数矢量,M 是对应
于因变量的平均转换的平均矩阵。可以通过选择“重复测量: 选项”对话框中的
显示此转换矩阵。例如,如果有四个因变量和四个水平的主体内因子,且多项式
矩阵
对比(缺省值)用于主体内因子,则 M 矩阵将为 (0.5 0.5 0.5 0.5)’。当指定对
比之后,创建一个 L 矩阵,使得与主体间因子对应的列与对比匹配。对剩余的列进
行调整,使 L 矩阵可以估计。
可用对比有偏移对比、简单对比、差分对比、Helmert 对比、重复对比和多项式对
比。对于偏移对比和简单对比,您可以选择参考类别是最后一个类别还是第一个类别。
必须为主体内因子选择一个除
19
GLM 重复测量
转换
无之外的对比系数。
对比类型
偏差。将每个水平(参考类别除外)的均值与所有水平的均值(总均值)进行比较。
因子的水平可以为任何顺序。
简单。将每个水平的均值与指定水平的均值进行比较。当存在控制组时,此类对比很
有用。可以选择第一个或最后一个类别作为参考类别。
差分。将每个水平的均值(第一个水平除外)与前面水平的均值进行比较。(有时候称
为逆 Helmert 对比。)
Helmert。将因子的每个水平的均值(最后一个水平除外)与后面水平的均值进行比较。
重复。将每个水平的均值(最后一个水平除外)与后一个水平的均值进行比较。
多项式。比较线性作用、二次作用、三次作用等等。第一自由度包含跨所有类别的线性
效应;第二自由度包含二次效应,依此类推。这些对比常常用来估计多项式趋势。
Page 30
20
章3
GLM 重复测量:轮廓图
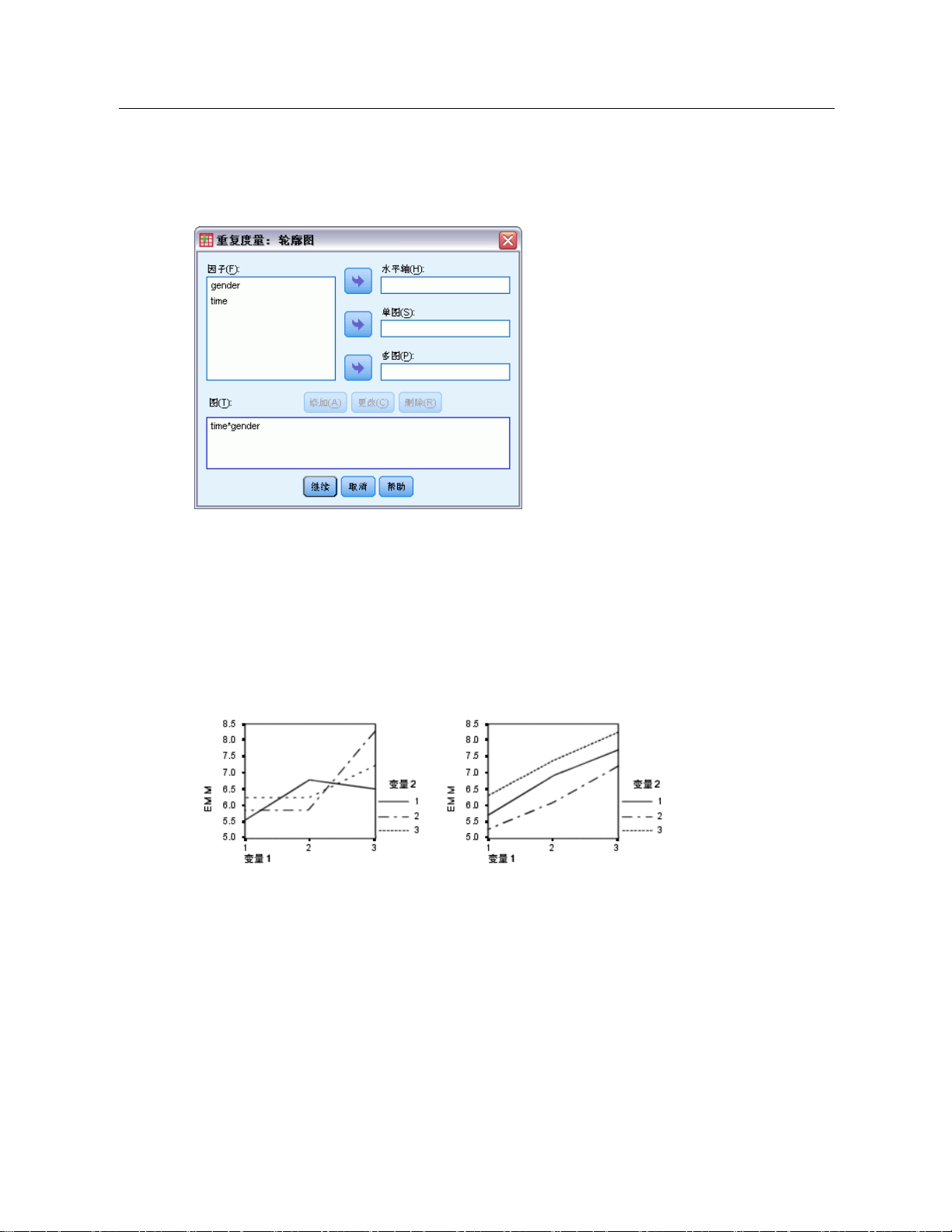
图片 3-5
“重复测量: 轮廓图”对话框
轮廓图(交互图)对
于比较模型中的边际均值是有用的。轮廓图是一个线图,其中每个点
表示因子的一个水平上的估计因变量边际均值(已针对任何协变量进行调整)。第二个
因子的水平可用来绘制分离线。第三个因子中的每个水平可用来创建分离图。所有因子
都可用于图。为每
个因变量创建轮廓图。主体间因子和主体内因子都可用在轮廓图中。
单因子的轮廓图显示估计边际均值是沿水平增加还是减小。对于两个或更多因子,
平行线表示因子之间没有交互,这意味着您只能调查一个因子的水平。不平行的线
则表示交互。
图片 3-6
不平行图(左)和平行图(右)
在通过为水平
轴选择因子,以及通过为分离线和分离图选择因子(后者可选)指定了图
之后,该图必须添加到“图”列表中。
Page 31

GLM 重复测量:两两比较
图片 3-7
“重复测量:观察到的均值的两两比较”对话框
21
GLM 重复测量
两比较检验。
两
一旦确定均值间存在差值,两两范围检验和成对多重比较就可以确定哪
些均值存在差值了。对未调整的值进行比较。如果没有主体间因子,则这些检验不可
用,并为跨主体内因子的水平的均值执行两两比较检验。
onferroni 和 Tukey’s 真实显著性差异检验是常用的多重比较检验。Bonferroni 检
B
验基于 Student 的 t 统计量,它针对已进行多重比较这一事实调整观察的显著性水平。
Sidak 的 t 检验也调整显著性水平,并提供比 Bonferroni 检验更严密的界限。Tukey’s
真实显著性差异检验使用 Student 化的范围统计量在组之间进行所有成对比较,并将试
验误差率设置为所有成对比较的集合的误差率。当检验大量均值对时,Tukey’s 真实显
著性差异检验比 Bonferroni 检验更有效。对于少量的对,Bonferroni 更有效。
Hochberg’s GT2 类似于 Tukey抯 真实显著性差异检验,但使用了 Student 化的最大
值模数。通常 Tukey 的检验更有效。Gabriel 的成对比较检验也使用 Student 化的最大
值模数,在单元格尺寸不等的情况下通常比 Hochberg’s GT2 更有效。当单元大小变化
过大时,Gabriel 检验可能会变得随意。
Dunnett 的成对多重比较 t 检验将一组处理与单个控制均值进行比较。最后一个类别
是缺省的控制类别。另外,您还可以选择第一个类别。您还可以选择双侧或单侧检验。
要检验因子的任何水平(控制类别除外)的均值是否不等于控制类别的均值,请使用双
侧检验。要检验因子的任何水平的均值是否小于控制类别的均值,请选择
地,要检验因子的任何水平的均值是否大于控制类别的均值,请选择
<控制。类似
>控制。
Ryan、Einot、Gabriel 和 Welsch (R-E-G-W) 开发了两个多重逐步降低范围检验。多
重逐步降低过程首先检验所有均值是否相等。如果不是所有的均值均相等,则检验一
部分均值的相等性。R-E-G-W F 基于 F 检验,而 R-E-G-W Q 基于 Student 化的范围。
这些检验要比 Duncan 的多范围检验和 Student-Newman-Keuls(也是多重逐步下降过
程)有效,但对于不相等的单元大小则不推荐使用它们。
Page 32

22
章3
当方差不等时,使用 Tamhane’s T2(基于 t 检验的保守成对比较检验)、Dunnett’s
T3(基于 Student 化的最大模数的成对比较检验)、Games-Howell 成对比较检验(有时
是随意的)或者 Dunnett’s C(基于 Student 化的范围的成对比较检验)。
Duncan 的多范围检验、Student-Newman-Keuls (S-N-K)和Tukey 的 b 是排列组均值等
级的范围检验,并计算范围值。这些检验的使用频率不如先前讨论的检验。
Waller-Duncan t 检验使用 Bayesian 方法。当样本大小不相等时,此范围检验使用
样本大小的调和均值。
Scheffé 检验的显著性水平可允许要检验的组均值的所有可能的线性组合,而不仅仅
是此功能中可用的成对比较。其结果是,Scheffé 检验常常比其他检验更保守,这意味
着对于显著性,需要均值之间有更大的差别。
最小显著性差异 (LSD) 成对多重比较检验等同于所有组对之间的多重个别 t 检验。此
检验的缺点是,不进行任何尝试来为多重比较调整观察到的显著性水平。
显示的检验。为 LSD、Sidak、Bonferroni、Games-Howell、Tamhane’s T2 和 T3、
Dunnett’s C 以及 Dunnett’s T3 提供成对比较。为 S-N-K、Tukey 的 b、Duncan、
R-E-G-W F、R-E-G-W Q 以及 Waller 提供范围检验的均一子集。Tukey抯 真实显著性差
异检验、Hochberg’s GT2、Gabriel 的检验以及 Scheffé 的检验既是多重比较检验,
同时也是多范围检验。
GLM 重复测量:保存
图片 3-8
“重复测量:保存”对话框
您可以在数据编辑器中将模型预测的值、残差和相关测量另存为新变量。这些变量中
有许多可用于检查关于数据的假设。要保存供另一 IBM® SPSS® Statistics 会话中
使用的值,您必须保存当前数据文件。
预测值。模型为每个个案预测的值。
Page 33

GLM 重复测量
未标准化. 模型为因变量预测的值。
标准误. 对于自变量具有相同值的个案所对应的因变量均值标准差的估计。
诊断。标识以下个案的测量:自变量的值具有不寻常组合的个案,以及可能对模型产生
很大影响的个案。可用的有 Cook 距离以及不居中的杠杆值。
Cook 距离. 在特定个案从回归系数的计算中排除的情况下,所有个案的残差变化
幅度的测量。较大的 Cook 距离表明从回归统计量的计算中排除个案之后,系数
会发生根本变化。
杠杆值. 未居中的杠杆值。每个观察值对模型拟合的相对影响。
残差。未标准化残差是因变量的实际值减去由模型预测的值。还提供标准化残差、
Student 化的残差以及剔除残差。
未标准化. 观察值与模型预测值之间的差。
标准化. 残差除以其标准差的估计。标准化残差也称为 Pearson 残差,它的均
值为 0,标准差为 1。
学生化. 残差除以其随个案变化的标准差的估计,这取决于每个个案的自变量
值与自变量均值之间的距离。
删除. 当某个案从回归系数的计算中排除时,该个案的残差。它是因变量的值和
调整预测值之间的差。
23
系数统计。将参数估计值的方差-协方差矩阵保存到数据集或数据文件。而且,对于每个
因变量,将存在一行参数估计值、一行与参数估计值对应的 t 统计量的显著性值以及一
行残差自由度。对于多变量模型,每一个因变量都存在类似的行。您可以在读取矩阵文件
的其他过程中使用此矩阵数据。可以在同一会话中继续使用数据集,但不会将其另存为
文件,除非在会话结束之前明确将其保存为文件。数据集名称必须符合变量命名规则。
Page 34

24
章3
GLM 重复测量:选项
图片 3-9
“重复测量: 选项”对话框
此对话框中有一些可选统计量。统计量是使用固定效应模型计算的。
估计边际均值。选择您需要的单元中的总体边际均值估计的因子和交互作用。为协变量
(如果存在)调整这些均值。可以选择主体内因子和主体间因子。
比较主效应。对于主体间和主体内因子,为模型中的任何主效应提供估计边际均
值未修正的成对比较。只有在“显示以下项的均值”列表中选择了主效应的情况
下,此项才可用。
置信区间调节。选择最小显著性差异 (LSD)、Bonferroni 或对置信区间和显著性的
Sidak 调整。此项只有在选择了
输出。选择描述统计以生成所有单元中的所有因变量的观察到的均值、标准差和计数。
功效估计给出了每个作用和每个参数估计值的偏 eta 方值。eta 方统计量描述总变异
比较主作用的情况下才可用。
性中可归因于某个因子的部分。当基于观察到的值设置备用假设时,选择检验效能可
获取检验的效能。选择
参数估计可为每个检验生成参数估计值、标准误、t 检验、置
信区间和检验效能。可以显示假设和误差 SSCP 矩阵以及残差 SSCP 矩阵加上残差协方差
矩阵的 Bartlett 球形度检验。
齐性检验为跨主体间因子所有水平组合的每个因变量生成 Levene 的方差齐性检验(仅
对于主体间因子)。另外,齐性检验包含对因变量协方差矩阵的齐性 Box M 检验,这些因
变量跨主体间因子的所有水平组合。分布-水平图和残差图选项对于检查关于数据的假设
很有用。如果不存在任何因子,则禁用此项。选择
准化残差图。这些图对于调查方差相等的假设很有用。选择
残差图为每个因变量生成观察-预测-标
缺乏拟合优度检验以检查因变
Page 35

量和自变量之间的关系是否能由模型充分地描述。常规可估计函数允许您基于常规可估计
函数构造定制的假设检验。任何对比系数矩阵中的行均是常规可估计函数的线性组合。
显著性水平。您可能想要调整用在两两比较检验中的显著性水平,以及用于构造置信
区间的置信度。指定的值还用于计算检验的检验效能。如果指定了显著性水平,则相
关联的置信区间度会显示在对话框中。
GLM 命令的附加功能
这些功能可以适用于单变量、多变量或重复测量分析。使用命令语法语言还可以:
在设计中指定嵌套效应(使用 DESIGN 子命令)。
指定效应对比效应的线性组合或一个值的检验(使用 TEST 子命令)。
指定多个对比(使用 CONTRAST 子命令)。
包括用户缺失值(使用 MISSING 子命令)。
指定 EPS 标准(使用 CRITERIA 子命令)。
构造定制的 L 矩阵、M 矩阵或 K 矩阵(使用 LMATRIX、MMATRIX 和 KMATRIX 子命令)。
为偏移对比或简单对比指定中间参考类别(使用 CONTRAST 子命令)。
为多项式对比指定矩阵(使用 CONTRAST 子命令)。
为两两比较指定误差项(使用 POSTHOC 子命令)。
为因子列表中的任何因子或因子之间的因子交互计算估计边际均值(使用 EMMEANS 子
命令)。
为临时变量指定名称(使用 SAVE 子命令)。
构造相关矩阵数据文件(使用 OUTFILE 子命令)。
构造包含主体间 ANOVA 表中的统计量的矩阵数据文件(使用 OUTFILE 子命令)。
将设计矩阵保存到新的数据文件(使用 OUTFILE 子命令)。
25
GLM 重复测量
请参见命令语法参考以获取完整的语法信息。
Page 36

方差成分分析
对于混合效应模型,“方差成分”过程估计每种随机效应对因变量方差的贡献。此过程
对于混合模型的分析尤其有趣,例如分割图、单变量重复度量以及随机区组设计。通过
计算方差成分,可以确定减小方差时的重点关注对象。
有四种不同的方法可用来估计方差成分:最小范数二次无偏估计 (MINQUE)、方差
分析 (ANOVA)、最大似然 (ML) 和受约束的最大似然 (REML)。不同的方法具有各种
不同的指定可供使用。
所有方法的缺省输出都包含方差成分估计。如果使用 ML 方法或 REML 方法,则还会
显示一个渐近协方差矩阵表。对于 ANOVA 方法,其他可用的输出包括 ANOVA 表和期
望均方,对于 ML 和 REML 方法,其他可用的输出包括迭代历史记录。“方差成分”
过程与“GLM 单变量”过程完全兼容。
WLS 权重允许您指定一个变量,用来针对加权分析为观察值赋予不同权重,这样
也许可以补偿不同的测量精确度偏差。
章
4
示例。某一农业学校测量六个不同猪栏中的猪一个月的重量增加量。猪栏这个变量是具
有六个水平的随机因子。(进行研究的六个猪栏是来自大的猪栏总体的随机样本。)调
查发现重量增长的方差更大程度上归因于猪栏的不同而不是猪栏中的猪的不同。
数据。因变量是定量变量。因子是分类变量。它们可以具有数字值或最多 8 个字节的字
符串值。至少必须有一个因子是随机的。也就是说,因子的水平必须是可能的水平的随
机样本。协变量是与因变量相关的定量变量。
假设。所有方法均假设随机效应的模型参数均值为零,方差为有限常数,并且模型参
数互不相关。来自不同随机效应的模型参数也不相关。
残差项的均值也为零,方差也为有限常数。它与任何随机效应的模型参数都不相关。
来自不同观察值的残差项被认为是不相关的。
基于这些假设,来自某一随机因子的相同水平的观察值是相关的。这就使得方差成分
模型与一般线性模型区分开来。
ANOVA 和 MINQUE 不需要正态假设。它们对于对正态假设的适度偏差来说是稳健的。
ML 和 REML 要求模型参数和残差项服从正态分布。
相关过程。在进行方差成分分析之前使用“探索”过程来检查数据。对于假设检验,使
用“GLM 单变量”、“GLM 多变量”和“GLM 重复测量”。
获取方差成分表
E 从菜单中选择:
分析 > 一般线性模型 > 方差成分...
© Copyright SPSS Inc. 1989, 2010
26
Page 37

图片 4-1
“方差成分”对话框
E 选择一个因变量。
27
方差成分分析
E 为“固定因子”、“随机因子”和“协变量”选择变量(如果适用于您的数据)。要
指定权重变量,请使用“WLS 权重”。
方差成分:模型
图片 4-2
“方差成分: 模型”对话框
Page 38

28
章4
构建项
指定模型。全因子模型包含所有因子主效应、所有协变量主效应以及所有因子间交互。
它不包含协变量交互。选择
定制可以仅指定其中一部分的交互或指定因子协变量交
互。必须指定要包含在模型中的所有项。
因子与协变量。列出因子与协变量。
模型。模型取决于数据的性质。选择定制之后,您可以选择分析中感兴趣的主效应和
交互效应。模型中必须包含随机因子。
在模型中包含截距。模型中通常包含截距。如果您可以假设数据穿过原点,则可以排
除截距。
对于选定因子和协变量:
交互。创建所有选定变量的最高级交互项。这是缺省值。
主效应。为每个选定的变量创建主效应项。
所有二阶。创建选定变量的所有可能的二阶交互。
所有三阶。创建选定变量的所有可能的三阶交互。
所有四阶。创建选定变量的所有可能的四阶交互。
所有五阶。创建选定变量的所有可能的五阶交互。
方差成分:选项
图片 4-3
“方差成分: 选项”对话框
方法。您可以选择四种方法中的一种估计方差成分。
MINQUE(最小范数二次无偏估计)可生成相对于固定效应不变的估计值。如果数
服从正态分布并且估计值是正确的,则此方法可生成所有无偏估计的最小方差。
您可以为随机效应优先选择一种法。
据
Page 39

29
方差成分分析
ANOVA
(方差分析)使用每种效应的类型 I 或类型 III 平方和计算无偏估计。ANOVA
方法有时会生成负数方差估计,这可指示模型不正确、估计方法不合适或需要更
多数据。
最大似然性 (ML) 使用迭代生成与实际观察到的数据最一致的估计值。这些估计值可能
存在偏差。此方法是渐近正态分布。ML 和 REML 估计值在转换时保持不变。此方法
不考虑估计固定效应时使用的自由度。
约束最大似然法 (REML) 估计在大多数(如果不是全部)平衡数据的情况下均可减少
ANOVA 估计值。由于此方法要针对固定效应进行调整,因此其标准误应比 ML 方法的
标准误要小。此方法考虑估计固定效应时使用的自由度。
随机效果优先。统一意味着所有随机效应以及残差项对观察值具有相同的影响。零方案等
同于假设随机效应方差为零。仅对 MINQUE 方法可用。
平方和。类型 I 平方和用于分层模型,分层模型常用于与方差成分有关的情况。如果选
择 GLM 中的缺省选项类型 III,则方差估计值可用在“GLM 单变量”中,进行具有类型
III 平方和的假设检验。仅对 ANOVA 方法可用。
标准。您可以指定收敛标准和最大迭代次数。仅对 ML 或 REML 方法可用。
显示。对于 ANOVA 方法,您可以选择显示平方和与期望均值平方。如果选择了最大似然性
或约束最大似然法,则可以显示迭代历史记录。
平方和(方差成分)
对于该模型,您可以选择一种平方和类型。类型 III 最常用,并且是缺省类型。
类型 I。此方法也称为平方和分级解构法。在模型中,每一项只针对它前面的那项进行
调整。类型 I 平方和法常用于:
平衡 ANOVA 模型,其中任何主效应在任何一阶交互效应之前指定,任何一阶交互效
应在任何二阶交互效应之前指定,依此类推。
多项式回归模型,其中任何低阶项在任何高阶项之前指定。
纯嵌套模型,其中第一个指定的效应嵌套在第二个指定的效应中,第二个指定的效应
嵌套在第三个指定的效应中,依此类推。(此嵌套形式只能通过使用语法来指定。)
类型 III。缺省类型。此方法在设计中通过以下形式计算某个效应的平方和:为任何
不包含该效应的其他效应,以及任何与包含该效应正交的效应(如果存在)调整的平
方和。类型 III 平方和具有一个主要优点,那就是只要可估计性的一般形式保持不
变,平方和对于单元频率就保持不变。因此,此类平方和常被认为对不带缺失单元的不
平衡模型有用。在不带缺失单元的因子设计中,此方法等同于 Yates 加权均值平方方
法。类型 III 平方和法常用于:
“类型 I”中列出的所有模型。
任何不带空白单元的平衡或非平衡模型。
Page 40

30
章4
方差成分:保存到新文件
图片 4-4
“方差成分: 保存到新文件”对话框
您可以将此过程的一些结果保存到新的 IBM® SPSS® Statistics 数据文件。
方差成分估计。将方差成分估计值和估计标签保存到数据文件或数据集。这些数据
可用于计算更多统计
置信区间或检验假设。
量或 GLM 过程的进一步分析。例如,您可以使用这些数据计算
成分共变。将方差-协方差矩阵或相关矩阵保存到数据文件或数据集。仅当指定了最大似
时才可用。
或受约束的最大
然
创建值的目的文件。允许您为包含方差成分估计值和/或矩阵的文件指定数据文件名称或
似然
外部文件名。可以在同一会话中继续使用数据集,但不会将其另存为文件,除非在会话
结束之前明确将其
可以使用
MATR
保存为文件。数据集名称必须符合变量命名规则。
IX
命令从数据文件抽取需要的数据,然后计算置信区间或执行检验。
VARCOMP 命令的附加功能
使用命令语法语言还可以:
在设计中指定嵌套效应(使用 DESIGN 子命令)。
包括用户缺失值(使用 MISSING 子命令)。
指定 EPS 标准(使用 CRITERIA 子命令)。
请参见命令语法参
考以获取完整的语法信息。
Page 41

线性混合模型
“线性混合模型”过程扩展了一般线性模型,因此允许数据表现出相关的和不恒定的
变异性。因此,线性混合模型提供了不仅能够就数据的均值还能够就其方差和协方
差建模的灵活性。
此外,“线性混合模型”过程也是用于拟合可作为混合线性模型构建的其他模型的灵
活工具。这些模型包括多变量模型、分层线性模型以及随机系数模型。
示例。有一家杂货连锁店想知道各种优惠券对客户消费的影响。通过抽取老客户的随机
样本,他们记录了每个客户在过去 10 周内的消费情况。该公司每周向这些客户邮寄一
种不同的优惠券。“线性混合模型”用于估计不同的优惠券对消费的影响,同时调整在
10 周内重复观察每个主体导致的相关性。
方法。最大似然 (ML) 和受约束的最大似然 (REML) 估计。
章
5
统计量。描述统计:各个不同的因子水平组合的因变量和协变量的样本大小、均值和标
准差。因子水平信息:每个因子水平及其频率的排序值。此外,还有固定效应的参数
估计值和置信区间,协方差矩阵的参数的 Wald 检验和置信区间。类型 I 和类型 III
的平方和可用于评估不同的假设。类型 III 是缺省值。
数据。因变量应是定量的。因子应是分类因子,可以具有数字值或字符串值。协变量和
权重变量应是定量的。主体和重复变量可为任意类型。
假设。假设因变量与固定因子、随机因子和协变量线性相关。固定效应就因变量的均值
建模。随机效应则就因变量的协方差结构建模。多个随机效应之间被认为是彼此独立
的,并且会为每个效应计算一个单独的协方差矩阵;不过,针对同一随机效应指定的模
型项可能是相关的。重复度量就残差的协方差结构建模。假定因变量也来自正态分布。
相关过程。在运行分析之前使用“探索”过程来检查数据。如果不怀疑相关的和不恒定
的变异性的存在,则可改为使用“GLM 单变量”或“GLM 重复测量”过程。如果随机效
应具有方差成分协方差结构,并且不存在重复度量,则可改用“方差成分分析”过程。
获取线性混合模型分析
E 从菜单中选择:
分析 > 混合模型 > 线性...
© Copyright SPSS Inc. 1989, 2010
31
Page 42

32
章5
图片 5-1
“线性混合模型: 指定主体和重复变量”对话框
E (可选)选择一个或多个群体变量。
E (可选)选择一个或多个重复变量。
E (可选)选择重复协方差类型。
E 单击继续。
图片 5-2
“线性混合模型”对话框
E 选择一个因变量。
Page 43

E
至少选择一个因子或协变量。
E 单击固定或随机并至少指定一个固定效应或随机效应模型。
根据需要,选择一个加权变量。
线性混合模型:选择主体/重复变量
此对话框允许选择定义主体和重复观察值的变量,也允许选择残差的协方差结构。 请
参阅第 32 页码中的图片 5-1.
主体。主体是可视为独立于其他主体的观察单元。例如,在医学研究中可以认为某患者
的血压读数独立于其他患者的读数。如果存在对每个主体的重复度量,而且您想要对这
些观察值之间的相关性建模,定义主体就非常重要。例如,您可能期望同一个患者在连
续多次就医时得到的血压读数是相关的。
主体也可由多个变量的因子水平组合进行定义;例如,您可以指定性别和年龄类
别作为主体变量,就 males over the age of 65 相互类似但独立于 males under 65
和 females 的可信度进行建模。
主体列表中指定的所有变量都可用于定义残差协方差结构的主体。可以使用部分或者
全部变量定义随机效应协方差结构的主体。
33
线性混合模型
重复。在此列表中指定的变量用于标识重复观察值。例如,单个变量周可以标识医学研
究中 10 周内的观察值,而月和天可共同用于标识一年内的每一天的观察值。
重复协方差类型。这指定残差的协方差结构。可用的结构如下:
前因:一阶。
AR(1)
AR(1):异质
ARMA(1,1)
复合对称
复合对称:相关性度规。
复合对称:异质
对角线
因子分析:一阶。
因子分析:一阶、异质
Huynh-Feldt
已标度的恒等
Toeplitz
Toeplitz:异质
未结构化
未结构化:相关
Page 44

34
章5
线性混合模型:固定效应
图片 5-3
“线性混合模型: 固定效应”对话框
固定效应。没有缺省模型,因此必须显式指定固定效应。还可以构建嵌套或非嵌套项。
包括截距。模型中通常包含截距。如果您可以假设数据穿过原点,则可以排除截距。
平方和。计算平方和的方法。对于不带缺失单元的模型,类型 III 方法最常用。
构建非嵌套项
对于选定因子和协变量:
因子。创建选定变量的所有可能的交互和主效应。这是缺省值。
交互。创建所有选定变量的最高级交互项。
主效应。为每个选定的变量创建主效应项。
所有二阶。创建选定变量的所有可能的二阶交互。
所有三阶。创建选定变量的所有可能的三阶交互。
所有四阶。创建选定变量的所有可能的四阶交互。
所有五阶。创建选定变量的所有可能的五阶交互。
Page 45

建立嵌套项
在此过程中,可为您的模型建立嵌套项。嵌套项有助于对其值不与另一个因子的水平
交互作用的因子或协变量的效应进行建模。例如,杂货连锁店可能在不同商店位置迎
合客户的消费习惯。由于每位客户只频繁光顾某一位置的商店,因此客户效应可以
说是嵌套在商店位置效应中。
此外,还可以包含交互效应或将多层嵌套添加到嵌套项。
限制。嵌套项有以下限制:
一次交互内的所有因子必须是唯一的。因此,如果 A 是因子,则指定 A*A 是无效的。
嵌套效应内的所有因子必须是唯一的。因此,如果 A 是因子,则指定 A(A) 是无效的。
效应不可嵌套在协变量中。因此,如果 A 是因子且 X 是协变量,则指定 A(X) 是
平方和
对于该模型,您可以选择平方和类型。类型 III 最常用,并且是缺省类型。
类型 I。此方法也称为平方和分级解构法。在模型中,每一项只针对它前面的那项进行
调整。类型 I 平方和常用于:
平衡 ANOVA 模型,其中任何主效应在任何一阶交互效应之前指定,任何一阶交互效
多项式回归模型,其中任何低阶项在任何高阶项之前指定。
纯嵌套模型,其中第一个指定的效应嵌套在第二个指定的效应中,第二个指定的效应
35
线性混合模型
无效的。
应在任何二阶交互效应之前指定,依此类推。
嵌套在第三个指定的效应中,依此类推。(此嵌套形式只能通过使用语法来指定。)
类型 III。缺省类型。此方法在设计中通过以下形式计算某个效应的平方和:为任何
不包含该效应的其他效应,以及任何与包含该效应正交的效应(如果存在)调整的平
方和。类型 III 平方和具有一个主要优点,那就是只要可估计性的一般形式保持不
变,平方和对于单元频率就保持不变。因此,我们常认为此类平方和对于不带缺失单元
格的不平衡模型有用。在不带缺失单元的因子设计中,此方法等同于 Yates 加权均值
平方方法。类型 III 平方和法常用于:
“类型 I”中列出的所有模型。
任何不带空白单元的平衡或非平衡模型。
Page 46

36
章5
线性混合模型:随机效果
图片 5-4
“线性混合模型: 随机效果”对话框
协方差类型。允许您为随机效应模型指定协方差结构。会为每个随机效应估计一个
单独的协方差矩阵。可用的结构如下:
前因:一阶。
AR(1)
AR(1):异质
ARMA(1,1)
复合对称
复合对称:相关性度规。
复合对称:异质
对角线
因子分析:一阶。
因子分析:一阶、异质
Huynh-Feldt
已标度的恒等
Page 47

Toeplitz
Toeplitz:异质
未结构化
未结构化:相关性度规。
Variance Components
随机效应。没有缺省模型,因此必须显式指定随机效应。还可以构建嵌套或非嵌套项。
也可以选择在随机效应模型中包括截距项。
可以指定多个随机效应模型。构建完第一个模型后,可以单击下一个构建下一个模
型。单击
上一个可以回滚现有模型。每个随机效应模型都被认为独立于所有其他随机
效应模型;也就是说,会为每个随机效应模型计算一个单独的协方差矩阵。在同一随
机效应模型中指定的项可以是相关的。
主体组。列出的变量就是您在“选择主体/重复变量”对话框中选择用作主体变量的变
量。请选择这些变量的部分或全部来定义随机效应模型的主体。
线性混合模型:估计
37
线性混合模型
图片 5-5
“线性混合模型: 估计”对话框
Page 48

38
章5
方法。选择最大似然性或约束最大似然性。
迭代:
最大迭代次数。指定一个非负整数。
最大步长对分。每次迭代时,步长都会减去因子 0.5,直到对数似然估计增加或者达
到最大步骤对分。指定一个正整数。
每隔 n 步打印迭代历史记录。显示一个表,其中包含对数似然估计函数值和从第 0 次
迭代(初始估计)开始每 n 次迭代的参数估计值。如果选择打印迭代历史记录,则
无论 n 值为多少,将总是打印最后一次迭代。
对数似然性收敛性。如果对数似然函数的绝对变化或相对变化小于指定的非负值,则假
定收敛。如果指定的值为 0,则不使用该标准。
参数收敛性。如果参数估计值的最大绝对变化或最大相对变化小于指定的非负值,则假
定收敛。如果指定的值为 0,则不使用该标准。
Hessian 收敛性。对于绝对指定,如果基于 Hessian 的统计量小于指定的值,则假定收
敛。对于
相对指定,如果统计量小于指定值与对数似然估计的绝对值的乘积,则假定收
敛。如果指定的值为 0,则不使用该标准。
最大得分步长。请求使用 Fisher 评分算法达到迭代次数 n。指定一个正整数。
奇异性容许误差。这是在检查奇异性时用作容差的值。指定一个正值。
线性混合模型:统计
图片 5-6
“线性混合模型: 统计量”对话框
摘要统计量。为以下项目生成表:
描述统计。显示因变量和协变量(如果已指定)的样本大小、均值和标准差。将为各
个不同的因子水平组合显示这些统计量。
个案处理摘要。显示因子、重复测量变量、重复度量主体以及随机效应主体及其频
率的排序值。
Page 49

模型统计量。为以下项目生成表:
参数估计。显示固定效应和随机效应参数估计值及其近似标准误。
协方差参数检验。显示协方差参数的渐近标准误和 Wald 检验。
参数估值的相关性。显示固定效应参数估计值的渐近相关矩阵。
参数估值协方差。显示固定效应参数估计值的渐近协方差矩阵。
随机效果的协方差。显示随机效应的估计的协方差矩阵。此选项仅当指定了至少一个
随机效应时才可用。如果为随机效应指定了主体变量,则显示通用区组。
残差的协方差。显示估计的残差协方差矩阵。此选项仅当指定了重复变量时才可用。
如果指定了主体变量,则显示通用区组。
对比系数矩阵。此选项显示用于检验固定效应和定制假设的可估计函数。
置信区间。只要构造了置信区间,就要使用此值。指定一个大于等于 0 且小于 100 的
值。缺省值为 95。
线性混合模型:EM 均值
图片 5-7
“线性混合模型: EM 值”对话框
39
线性混合模型
拟合模型的估计边际均值。此组允许您请求单元中因变量的模型预测的估计边际均值及其
对于指定因子的标准误。此外,您还可以请求比较主效应的因子水平。
因子与因子交互。此列表包含“固定”对话框中指定的因子与因子交互作用,以及一
OVERALL 项。此列表中不包含根据协变量构建的模型项。
个
Page 50

40
章5
显示均值。该过程将计算选入此列表的因子与因子交互作用的估计边际均值。如
果选择了
OVERALL,则会显示因变量的估计边际均值,并会折叠所有因子。注意,
选择的任何因子或因子交互作用都会一直选中,除非在主对话框中的“因子”列
表中移去了关联变量。
比较主效应。此选项允许您请求所选主效应水平的成对比较。“置信区间调整”允
许调整置信区间和显著性值以便进行多重比较。可用的方法为 LSD(无调整)、
Bonferroni 和 Sidak。最后,对于每个因子,您都可以选择进行比较的参考类别。
如果不选择参考类别,则将构造所有成对比较。参考类别的选项可以首先指定、最
后指定,也可以定制(在这种情况下,您需要输入参考类别的值)。
线性混合模型:保存
图片 5-8
“线性混合模型: 保存”对话框
此对话框允许将各种模型结果保存到工作文件中。
混合预测值。保存与不具有这些效应的回归均值相关的变量。
预测值。不具有随机效应的回归均值。
标准误。估计值的标准误。
自由度。与估计值相关联的自由度。
预测值和残差。保存与模型拟合值相关的变量。
预测值。模型拟合值。
标准误。估计值的标准误。
自由度。与估计值相关联的自由度。
残差。数据值减去预测值。
MIXED 命令的附加功能
使用命令语法语言还可以:
指定效应对比效应的线性组合或一个值的检验(使用 TEST 子命令)。
包括用户缺失值(使用 MISSING 子命令)。
Page 51

计算协变量的指定值的估计边际均值(使用 EMMEANS 子命令的 WITH 关键字)。
比较交互的简单主效应(使用 EMMEANS 子命令)。
请参见命令语法参考以获取完整的语法信息。
41
线性混合模型
Page 52

广义线性模型
广义线性模型对一般线性模型进行了扩展,这样因变量通过指定的关联函数与因子和
协变量线性相关。另外,该模型允许因变量呈非正态分布。它涵盖广泛使用的统计模
型,例如用于正态分布响应的线性回归、用于二分类数据的 Logistic 模型、用于计
数数据的对数线性模型、用于间隔检查生存数据的互补双对数模型,以及许多其他通
过其非常通用的模型规划的统计模型。
示例。 运输公司可以使用广义线性模型,对在不同期间建造的一些轮船类型的损坏统计
采用泊松回归,其结果模型可帮助确定哪些轮船类型最容易损坏。
汽车保险公司可以使用广义线性模型,对汽车损坏理赔采用 gamma 回归,其结果模型可
帮助确定对理赔额度贡献最大的因素。
医疗研究人员可以使用广义线性模型,对间隔检查生存数据采用互补双对数回归,以预
测医疗条件再次出现的时间。
章
6
数据。响应可以是尺度数据、计数数据、二分类数据或试验事件数据。假设因子是分
类型的。假设协变量、尺度权重和偏移量是尺度型的。
假设。假设个案为独立观察值。
获取广义线性模型
从菜单中选择:
分析 > 广义线性模型 > 广义线性模型...
© Copyright SPSS Inc. 1989, 2010
42
Page 53

图片 6-1
“广义线性模型: 模型类型”选项卡
43
广义线性模型
E 指定分布和关联函数(请参见下文获得有关各种选项的详细信息)。
E 在响应选项卡上选择一个因变量。
E 在预测选项卡上,选择用于预测因变量的因子和协变量。
E 在模型选项卡上,使用所选因子和协变量指定模型效应。
“模型类型”选项卡允许您为模型指定分布和关联函数,它为按响应类型分类的几种常
用模型提
供了快捷键。
模型类型
尺度响应。
线性。 将正态指定为分布,将恒等指定为关联函数。
具有对数链接的 Gamma。 将 Gamma 指定为分布,将对数指定为关联函数。
有序响应。
Page 54

44
章6
有序 logistic。将多项(序数)指定为分布,将累积 logit 指定为关联函数。
有序 probit。将多项(序数)指定为分布,将累积 probit 指定为关联函数。
计数。
泊松对数线性。 将泊松指定为分布,将对数指定为关联函数。
具有对数链接的负二项式。 将负二项式(拥有值为 1 的辅助参数)指定为分布,将对
数指定为关联函数。要使过程估计辅助参数的值,指定一个拥有负二项式分布的
定制模型,并在参数组中选择
估计值。
二元响应或事件/试验数据。
二元 logistic。 将二项式指定为分布,将 Logit 指定为关联函数。
二元 probit。 将二项式指定为分布,将 Probit 指定为关联函数。
间隔检查生存。 将二项式指定为分布,将互补双对数指定为关联函数。
混合。
具有对数链接的 Tweedie。 将 Tweedie 指定为分布,将对数指定为关联函数。
具有恒等式链接的 Tweedie。 将 Tweedie 指定为分布,将恒等指定为关联函数。
定制。指定您自己的分布和关联函数的组合。
分布
此选项指定因变量的分布。指定非正态分布和非恒等关联函数的功能是广义线性模型相
对一般线性模型的重要改进。分布-关联函数可能存在多种组合,其中一些适合任何给
定的数据集,因此可以根据先验理论的要求进行选择,或选择最合适的组合。
二项式。此分布仅适合表示二元响应或事件数量的变量。
Gamma。该分布适用于具有正尺度值并向更大的正值偏度的变量。如果数据值小于
等于 0 或缺失,那么分析中不会使用相应的个案。
逆高斯。该分布适用于具有正尺度值并向更大的正值偏度的变量。如果数据值小于
等于 0 或缺失,那么分析中不会使用相应的个案。
负二项式。该分布可以视为观察 k 成功所需的试验次数,适合具有非负整数值的变
量。如果数据值是非整数、小于 0 或缺失,那么分析中不会使用相应的个案。负二
项式分布辅助参数的固定值可以是大于等于 0 的任何值。您可将其设为固定值,或
允许过程对其进行估计。辅助参数设置为 0 时,使用此分布相当于使用泊松分布。
正态。该分布适合围绕某个中间值(均值)呈对称钟型分布的刻度变量。因变
量必须是数值型变量。
泊松。该分布可视为被观察事件在固定时间段内发生的次数,适合具有非负整数值的
变量。如果数据值是非整数、小于 0 或缺失,那么分析中不会使用相应的个案。
Tweedie。 此分布适合由 gamma 分布泊松混合表示的变量;之所以称为?混合?分布,
是因为它兼具连续(取非负实数值)和离散分布(在单个值 0 处为正概率质量)
的属性。因变量必须是数值型变量,数据值大于或等于零。如果数据值小于零或
Page 55

广义线性模型
缺失,那么分析中不会使用相应的个案。Tweedie 分布参数的固定值可以是任
何大于 1 且小于 2 的数字。
多项式。此分布适合表示序数响应的变量。因变量可以是数值或字符串,它必须
至少有两个不同有效数据值。
关联函数
联接函数是允许模型估计的因变量的转换。可用函数有:
恒等。f(x)=x。因变量不转换。该关联可用于任何分布。
互补双对数。f(x)=log( log(1 x))。该函数只适用于二项式分布。
累积 Cauchit。f(x) = tan(π (x – 0.5)),适用于每个响应类别的累积概率。
该函数只适用于多项式分布。
累积互补双对数。f(x)=ln( ln(1 x)),适用于每个响应类别的累积概率。该函数
只适用于多项式分布。
累积 logit。f(x)=ln(x / (1 x)),适用于每个响应类别的累积概率。该函数只适
用于多项式分布。
累积负双对数。f(x)= ln( ln(x)),适用于每个响应类别的累积概率。该函数
只适用于多项式分布。
累积 probit。f(x)=Φ
1
(x),适用于每个响应类别的累积概率,其中 Φ1是逆标
准正态累积分布函数。该函数只适用于多项式分布。
对数。f(x)=log(x)。该关联可用于任何分布。
对数补数。f(x)=log(1 x)。该函数只适用于二项式分布。
Logit。f(x)=log(x / (1 x))。该函数只适用于二项式分布。
负二项式。f(x)=log(x / (x+k
1
)),其中 k 是负二项式分布的辅助参数。该函数只
适用于负二项式分布。
负双对数。f(x)= log( log(x))。该函数只适用于二项式分布。
奇数幂。f(x)=[(x/(1 x))
α
1]/α,如果 α ≠ 0. f(x)=log(x),如果 α=0. α 为
必需的数字指定,且必须为实数。该函数只适用于二项式分布。
Probit。f(x)=Φ
1
(x),其中 Φ1是逆标准正态累积分布函数。该函数只适用于
二项式分布。
幂。f(x)=x
α
,如果 α ≠ 0. f(x)=log(x),如果 α=0. α 为必需的数字指定,且必
须为实数。该关联可用于任何分布。
45
Page 56

46
章6
广义线性模型响应
图片 6-2
“广义线性
模型”对话框
在许多情况下,您可以只指定一个因变量;但是,仅采用两个值的变量和记录试验
中事件的响应需要额外注意。
二元响应。如果因变量仅采用两个值,可以为参数估计指定参考类别。二元响
应变量可以是字符串或数值。
一组试验中发生的事件数量。当响应是一系列试验中发生的事件数时,因变量包含事
件数,您可以额外选择一个包含试验数的变量。或者,如果试验数在所有主体中
都相同,则可以使用固定值指定试验。试验数应大于等于每个个案的事件数。事
件应为非负整数,试验应为正整数。
对于有序多项模型,可以指定响应的类别顺序:升序、降序或数据(数据顺序意味着在
数据中遇到的第一个值定义第一个类别,遇到的最后一个值定义最后一个类别。)
刻度权重。尺度参数是与响应方差相关的估计模型参数。尺度权重是“已知”值,可能因
观察值的不同而异。如果指定了刻度权重变量,则对每个观察值,都会用与响应方差相关
的尺度参数除以该尺度权重变量。分析中不使用尺度权重值小于等于 0 或缺失的个案。
Page 57

广义线性模型:参考类别
图片 6-3
“广义线性模型: 参考类别”对话框
对于二元响应,可以为因变量选择参考类别。这会影响某些输出,如参数估计值和保存
的值,但不应更改模
缺省情况下,此过
下,模型保存的概率估计给定个案取值 0 的概率,参数估计值应解释为与类别 0
的似然估计相关。
如果您指定第一个值(最低值)或 0 作为参考类别,则模型保存的概率估计给
定个案取值 1 的概率
如果您指定定制值
别。在指定模型的过程中并不确定某一特定变量的编码方式时,这种方法非常方便。
47
广义线性模型
型拟合。例如,如果您的二元响应取值 0 和 1:
程将最后一个值(最高值)或 1 作为参考类别。在这种情况
。
并且变量已定义了标签,则可以通过从列表中选择值来设置参考类
Page 58

48
章6
广义线性模型:预测变量
图片 6-4
Generalized Linear Models:“预 测变量”选项卡
在“预测”选项卡中可以指定用于生成模型效应的因子和协变量并指定可选偏移。
因子。因子是分类预测变量,可以是数值或字符串。
协变量。协变量为刻度预测变量,必须为数值。
注意:当响应为二元格式的二项式时,该过程通过子体来计算偏差和卡方拟合优度统计
量,这些子体基于对所选因子和协变量观察值的交叉分类。您应在过程的多次运行中保
持相同的预测变量集,以确保一致的子体数量。
偏移量。偏移项是“结构化”预测变量。模型不估计该预测变量的系数,但假定其值为
1;因此,偏移值只是简单地加到因变量的线性预测变量中。这在每个个案对于被观察
事件都可能具有不同显现水平的泊松回归模型中尤其有用。例如,当对各个驾驶员事故
率进行建模时,3 年驾驶经历出现 1 次事故和 25 年出现 1 次事故的驾驶员之间有着重
大的差别!如果将驾驶员经历纳入偏移项,则事故数可以建模为泊松响应。
Page 59

广义线性模型:选项
49
广义线性模型
图片 6-5
“广义线性模型:选项”对
话框
这些选项适用于“预测”选项卡上指定的所有因子。
用户缺失值。要在分析中包含个案,因子必须具有有效值。通过这些控制可以决定是否
将用户缺失值在因子变量中视为有效值。
类别顺序。该选项与确定因子的最终水平有关,该水平可能与估计算法中的冗余参数相
关。更改类别顺序可更改因子水平效应的值,因为这些参数估计值相对于“最终”水平
进行计算。因子可以按从最低值到最高值的升序排序,按从最高值到最低值的降序排
序,或者按“数据顺序”排序。这意味着在数据中遇到的第一个值定义第一个类别,遇
到的最后一个唯一值定义最后一个类别。
Page 60

50
章6
广义线性模型:模型
图片 6-6
Generalized Linear Models:“模型”选项卡
指定模型效应。缺省模型是仅截距模型,因此必须明确指定其他模型效应。还可以
构建嵌套或非嵌套项。
非嵌套项
对于选定因子和协变量:
主效应。为每个选定的变量创建主效应项。
交互。为所有选定变量创建最高级交互项。
因子。创建选定变量的所有可能的交互和主效应。
所有二阶。创建选定
所有三阶。创建选定变量的所有可能的三阶交互。
所有四阶。创建选定变量的所有可能的四阶交互。
所有五阶。创建选定变量的所有可能的五阶交互。
变量的所有可能的二阶交互。
Page 61

51
广义线性模型
嵌套项
在此过程中,可为您的模型建立嵌套项。嵌套项有助于对其值不与另一个因子的水平交
互作用的因子或协变量的效应进行建模。例如,杂货连锁店可能在不同商店位置迎合顾
客的不同消费习惯。由于每位顾客只频繁光顾某一位置的商店,因此 Customer 效应可
以说是嵌套在 Store location 效应中。
此外,还可以包含交互效应,例如包含相同协变量的多项式项,或将多层嵌套添
加到嵌套项。
限制。嵌套项有以下限制:
一次交互内的所有因子必须是唯一的。因此,如果 A 是因子,则指定 A*A 是无效的。
嵌套效应内的所有因子必须是唯一的。因此,如果 A 是因子,则指定 A(A) 是无效的。
效应不可嵌套在协变量中。因此,如果 A 是因子且 X 是协变量,则指定 A(X) 是
无效的。
截距。模型中通常包含截距。如果您可以假设数据穿过原点,则可以排除截距。
多项有序分布的模型没有单个截距项;而包含定义相邻类别之间转换点的阈值参
数。模型中通常包含有阈值。
Page 62

52
章6
广义线性模型:估计
图片 6-7
Generalized Linear Models:“估计”选项卡
参数估计。该组中的控件允许指定估计方法并提供参数估计值的初始值。
方法。可以选择参数估计方法。可以选择的方法包括 Newton-Raphson、Fisher 评分
方法以及先执行 Fisher 评分迭代再切换为 Newton-Raphson 方法的混合方法。如果
在混合方法的 Fisher 评分方法阶段期间,在达到 Fisher 迭代的最大次数之前实现
了收敛,则算法将继续执行 Newton-Raphson 方法。
刻度参数方法。可以选择尺度参数估计方法。最大似然法可联合估计尺度参数和
模型效应;请注意,如果响应具有负二项式、泊松、二项式或多项式分布,则此
选项无效。偏差和 Pearson 卡方选项从这些统计量的值估计尺度参数。或者,
可以为尺度参数指定固定值。
初始值。该过程将自动计算参数的初始值。也可以指定参数估计值的初始值。
协方差矩阵。基于模型的估计是 Hessian 矩阵的广义逆负矩阵。健壮性(也称为
Huber/White/sandwich)估计是“改正”的基于模型的估计,即使错误地指定了方
差和关联函数,也能提供对协方差的一致估计。
迭代。
Page 63

53
广义线性模型
最大迭代次数。算法将执行的最大迭代次数。指定一个非负整数。
最大步骤对分。每次迭代时,步长都会减去因子 0.5,直到对数似然估计增加或者达
到最大步骤对分。指定一个正整数。
检查数据点的完整分隔。如果选择此项,算法将执行检验以确保参数估计值具有唯一
值。当过程可生成一个正确对每个个案进行分类的模型时,将发生分离。此选项可
用于二元格式的多项式响应和二项式响应。
收敛性准则。
参数收敛。如果选择此项,算法将在参数估计值的绝对或相对更改小于指定值(必
须为正值)的迭代之后停止。
对数似然估计收敛。如果选择此项,算法将在对数似然估计函数的绝对或相对更改小
于指定值(必须为正值)的迭代之后停止。
Hessian 收敛性。对于“绝对值”指定,如果基于 Hessian 收敛的统计量小于指定的
正值,则假定收敛。对于“相对”指定,如果统计量小于指定的正值和对数似然
估计的绝对值的乘积,则假定收敛。
奇异性容许误差。奇异(非可逆)矩阵具有线性相关列,对估计算法可能产生严重问
题。即使近似奇异的矩阵也可导致不良结果,因此该过程会将行列式小于容许误差的矩
阵作为奇异矩阵对待。指定一个正值。
广义线性模型:初始值
图片 6-8
“广义线性模型: 初始值”对话框
如果指定了初始值,则必须为模型中的所有参数(包括冗余参数)提供初始值。在数据
集中,变量从左到右的顺序必须为:RowType_、VarName_、P1、P2、…,其中 RowType_
和 VarName_ 是字符串变量,P1、P2、… 是对应于已排序参数列表的数值变量。
初始值在变量 RowType_ 具有值 EST 的记录上提供;实际初始值在变量 P1、P2、…
下提供。该过程忽略 RowType_ 具有非 EST 值的所有记录以及 RowType_ 的第一
次等于 EST 以外的所有记录。
截距(如果模型中包含)或阈值参数(如果响应具有多项式分布)必须是列出
的第一个初始值。
Page 64

54
章6
尺度参数和负二项式参数(如果响应具有负二项式分布)必须是指定的最后一个
初始值。
如果“拆分文件”有效,则变量必须以拆分文件变量开始(以创建“拆分文件”时
指定的顺序),后跟 RowType_、VarName_、P1、P2、…,如上所述。拆分在指定数
据集中的发生顺序必须与原始数据集中的顺序相同。
注意:变量名 P1、P2、… 不是必需的;过程接受参数的任何有效变量名,因为变量与
参数的映射基于变量位置,而不是变量名。超过最后一个参数的所有变量都会被忽略。
初始值的文件结构与将模型导出为数据时使用的结构相同;因此,可以使用一次过程
运行的最终值作为下一次运行的输入。
广义线性模型:统计量
图片 6-9
Generalized Linear Models:“统计量”选项卡
模型作用。
分析类型。指定要生成的分析
类型。类型 I 分析通常适合于对模型中预测变量的
排序具有先验理由的情况,而类型 III 应用范围更广。根据在“卡方统计量”组
中的选择,计算 Wald 或似然比统计。
Page 65

55
广义线性模型
置信区间。指定一个大于 50 且小于 100 的置信度。Wald 区间基于参数呈渐近正态分
布的假设之上;截面似然区间更加准确但需要进行大量的计算。截面似然区间的容
差水平可作为标准,用以停止在区间计算所采用的迭代算法。
对数似然函数。它控制对数似然函数的显示格式。整个函数包含一个相对于参数估计
恒定的额外项;它对参数估计没有任何影响,并且在某些软件产品中不会显示。
打印。可用输出如下:
个案处理摘要。显示分析和“相关数据摘要”表中包含的个案和从中排除的个案
的数量和百分比。
描述统计。显示有关因变量、协变量和因子的描述统计和摘要信息。
模型信息。显示数据文件名称、因变量或事件和试验变量、偏移变量、尺度权重
变量、概率分布和关联函数。
拟合度统计。显示离差和尺度化离差、Pearson 卡方和尺度化 Pearson 卡方、对数似
然估计、AIC 准则 (AIC)、有限样本校正 AIC (AICC)、BIC 准则 (BIC) 以及 CAIC 准
则 (CAIC)。
模型摘要统计。显示模型拟合检验,包括用于模型拟合 Omnibus 检验的似然比统计
量,以及每种效应的类型 I 或 III 对比的统计量。
参数估计。显示参数估计值和相应的检验统计和置信区间。除了显示原始参数估计值
之外,还可以选择显示取幂参数估计值。
参数估计的协方差矩阵。显示估计参数协方差矩阵。
参数估计的相关性矩阵。显示估计参数相关矩阵。
对比系数 (L) 矩阵。为缺省效应和估计边际均值显示对比系数(如果“EM 均值”
选项卡上要求)。
常规可估计函数。显示生成对比系数 (L) 矩阵的矩阵。
迭代历史记录。显示参数估计值和对数似然估计的迭代历史记录,并打印对梯度矢量
和 Hessian 矩阵的最后一次评估。迭代历史记录表从第 0 次迭代(初始估计值)开
始为每 n 次迭代显示参数估计值,其中,n 代表打印区间的值。如果请求迭代历史
记录,那么无论 n 的值是多少,都会显示最后一次迭代。
Lagrange 乘数检验。显示 Lagrange 乘数检验统计量,用于为正态、gamma、逆高斯和
Tweedie 分布评估使用离差或 Pearson 卡方计算或者设置为固定值的尺度参数的
有效性。对于负二项式分布,它检验固定辅助参数。
Page 66

56
章6
广义线性模型:EM 均值
图片 6-10
Generalized Linear Models:“EM 均 值”选 项卡
此选项卡用于显示因子水平和因子交互的估计边际均值。您还可以要求显示整体估计均
值。估计边际均值对有序多项模型不可用。
因子和交互。此列表包含“预测变量”选项卡上指定的因子和“模型”选项卡上指定的
因子交互。此列表中不包含协变量。可以直接从此列表选择项,或者使用
依据 * 按钮
将项组合到交互项中。
显示以下项的均值。计算所选因子和因子交互的估计均值。对比决定如何设定假设检验
以比较估计均值。简单对比需要一个用于比较其他项的参考类别或因子水平。
配对方式。为指定或默示的因子的所有水平组合计算成对比较。这是因子交互
的唯一可用对比方法。
简单散点图. 将每个水平的均值与指定水平的均值进行比较。当存在控制组时,
此类对比很有用。
偏差。因子的每个水平与总均值比较。偏移对比不是正交的。
Page 67

57
广义线性模型
差分. 将每个水平(第一个除外)的均值与先前水平的均值进行比较。有时候将其
称为逆 Helmert 对比。
Helmert. 将因子的每个水平的均值(最后一个水平除外)与后续水平的均值进
行比较。
重复. 将每个水平的均值(最后一个水平除外)与后续水平的均值进行比较。
多项式. 比较线性作用、二次作用、三次作用等等。第一自由度包含跨所有类别的线
性效应;第二自由度包含二次效应,依此类推。这些对比常常用来估计多项式趋势。
标度。对于响应,可根据因变量的原始刻度计算估算边际均值;对于线性预测变量,根
据关联函数变换的因变量计算估计边际均值。
调整的多重比较。在执行包含多重比较的假设检验时,总体显著性水平可从所包含的比
较的显著性水平进行调节。使用此组可以选择调节方法。
显著性最低的差异。此方法并不控制拒绝某些线性对比不同于原假设值这一假设
的总体概率。
Bonferroni. 此方法针对检验多个对比这一事实调整观测的显著性水平。
连续 Bonferroni. 这是按顺序逐步降低的拒绝 Bonferroni 过程,在拒绝个别假设方
面不保守,但维持相同的总体显著性水平。
Sidak. 此方法提供比 Bonferroni 方法更严密的界限。
连续 Sidak. 这是按顺序逐步降低的拒绝 Sidak 过程,在拒绝个别假设方面不保
守,但维持相同的总体显著性水平。
Page 68

58
章6
广义线性模型:保存
图片 6-11
Generalized Linear Models:“保存”选项卡
选中的项以指定的名称保存;可以选择用新变量覆盖现有的同名变量,或为新变量名添
加后缀使其成为唯一名称以避免名称冲突。
响应均值的预测值。以初始响应度规保存每个个案的模型预测值。当响应分布是二项
式,并且因变量为二元时,过程会保存预测概率。当响应分布是多项式时,项目
标签变成
累积预测概率,并且过程保存响应每个类别的累积预测概率(最后一个除
外),直至达到要保存的指定类别数量。
响应均值的置信区间下限保存响应均值置信区间的下限。当响应分布是多项式时,项
目标签变成
累积预测概率的置信区间下限,并且过程保存响应每个类别的下限(最后一
个除外),直至达到要保存的指定类别数量。
响应均值的置信区间上限。保存响应均值置信区间的上限。当响应分布是多项式时,
项目标签变成
累积预测概率的置信区间上限,并且过程保存响应每个类别的上限(最后
一个除外),直至达到要保存的指定类别数量。
预测类别。对于具有二项式分布和二元因变量或多项式分布的模型,该过程保存每个
个案的预测响应类别。此选项不支持其他响应分布。
Page 69

59
广义线性模型
线性预测器的预测值。以线性预测变量的度规保存每个个案的模型预测值(通过指定
的关联函数转换的响应)。当响应分布是多项式时,过程保存响应每个类别的预测
值(最后一个除外),直至达到要保存的指定类别数量。
线性预测变量的预测值的估计标准误。当响应分布是多项式时,过程保存响应每个类
别的估计标准误(最后一个除外),直至达到要保存的指定类别数量。
如果响应分布是多项式,则以下各项不可用。
Cook 距离. 在特定个案从回归系数的计算中排除的情况下,所有个案的残差变化
幅度的测量。较大的 Cook 距离表明从回归统计量的计算中排除个案之后,系数
会发生根本变化。
杠杆值. 度量某个点对回归拟合的影响。集中的杠杆值范围为从 0(对拟合无影
响)到 (N-1)/N。
原始残差. 观察值与模型预测值之间的差。
Pearson 残差。个案对 Pearson 卡方统计量的贡献的平方根(带原始残差的符号)。
标准化 Pearson 残差。尺度参数与 1 (个案的杠杆)的乘积的逆的平方根乘以
Pearson 残差。
偏差残差。个案对偏差统计量的贡献的平方根(带原始残差的符号)。
标准化偏差残差。尺度参数与 1 (个案的杠杆)的乘积的逆的平方根乘以偏差残差。
似然残差。标准化 Pearson 和标准化偏差残差的平方的加权平均值(基于个案杠
杆)的平方根,带原始残差的符号。
Page 70

60
章6
广义线性模型:导出
图片 6-12
Generalized Linear Models:“导出”选项卡
将模型导出为数据。写入一个 IBM® SPSS® Statistics 格式的数据集,包含具有参数估计
值、标准误、显著性值和自由度的参数相关性或协方差矩阵。矩阵文件中变量顺序如下。
拆分变量。定义拆分的任何变量(如果使用)。
RowType_。 取值(或值标签)为 COV(协方差)、CORR(相关性)、EST(参数估
计)、SE(标准误)、SIG (显著性水平)和 DF(抽样设计自由度)。存在每个模
型参数的 COV(或 CORR)行类型的单独个案,以及每个其他行类型的单独个案。
VarName_。 对于行类型 COV 或 CORR,取值为 P1、P2、...,对应于所有估计模型
参数(除尺度或负二项式参数外)的有序列表,值标签对应于在参数估计值表中
显示的参数字符串。对于其他行类型,单元格为空。
P1、P2、...这些变量对应于所有模型参数(必要时可包括尺度或负二项式参数)
的有序列表,值标签对应于在参数估计值表中显示的参数字符串,这些变量根据
行类型取值。
对于冗余参数,所有协方差设为零,相关性设为系统缺失值;所有参数估计值设为
零;并且所有标准误、显著性水平和残差自由度设为系统缺失值。
Page 71

对于尺度参数,协方差、相关性、显著性水平和自由度均设为系统缺失值。如果尺
度参数通过最大似然进行估计,则给出标准误;否则,它被设为系统缺失值。
对于负二项式参数,协方差、相关性、显著性水平和自由度均设为系统缺失值。如果
负二项式参数通过最大似然进行估计,则给出标准误;否则,它被设为系统缺失值。
如果存在拆分,则参数列表必须在所有拆分之间进行累积。在给定拆分中,某些参
数可能是无关的;但这不同于冗余。对于无关参数,所有协方差或相关性、参数估
计值、标准误、显著性水平和自由度均设为系统缺失值。
可以使用此矩阵文件作为进一步进行模型估计的初始值;注意,该文件不能立即用于
在其他读取矩阵文件的过程中执行进一步分析,除非这些过程接受在此导出的所有行
类型。尽管如此,您必须注意,在该矩阵文件中的所有参数对于读取此文件的过程
具有相同的含义。
将模型导出为 XML。将参数估计值和参数协方差矩阵(如果选择)以 XML (PMML) 格式保
存。您可以使用该模型文件以应用模型信息到其他数据文件用于评分目的。
GENLIN 命令的附加功能
使用命令语法语言还可以:
将参数估计值的初始值指定为数字列表(使用 CRITERIA 子命令)。
在计算估计边际均值时修正值不同于其均值的协变量(使用 EMMEANS 子命令)。
指定估计边际均值的定制多项式对比(使用 EMMEANS 子命令)。
指定因子的一个子集,以显示该子集的估计边际均值,并使用指定的对比类型对其
进行比较(使用
EMMEANS 子命令的 TABLES 和 COMPARE 关键字)。
61
广义线性模型
请参阅命令语法参考以获取完整的语法信息。
Page 72

广义估计方程
广义估计方程过程对广义线性模型进行了扩展,以允许分析重复的测量或其他相关观察
数据,例如聚类数据。
示例。公共卫生官员可以使用广义估计方程,在空气污染对儿童影响研究中采用重复度
量 Logistic 回归模型。
数据。响应可以是尺度数据、计数数据、二分类数据或试验事件数据。假设因子是分类
型的。假设协变量、尺度权重和偏移量是尺度型的。用于定义主体或主体内重复度量的
变量不能用于定义响应,但可以在模型中发挥其他作用。
假设。假设各个个案在主体内部是相关的,在主体之间是独立的。表示主体内相关性的
相关矩阵作为模型的一部分进行估计。
章
7
获得广义估计方程
从菜单中选择:
分析 > 广义线性模型 > 广义估计方程...
© Copyright SPSS Inc. 1989, 2010
62
Page 73

图片 7-1
广义估计方程:“重复”选项卡
63
广义估计方程
E 选择一个或多个主体变量(参见下文了解更多选项)。
指定变量的值组合应唯一定义数据集中的主体。例如,单个病人 ID 变量应足以定义
一个医院内的主体,但如果病人标识号在医院间不唯一,则需要使用医院 ID 和病人
ID 的组合。在重复度量设置中,将为每个主体记录多个观察数据,因此每个主体可
能在数据集中占用多个个案。
E 在模型类型选项卡上,指定分布和关联函数。
E 在响应选项卡上选择一个因变量。
E 在预测选项卡上,选择用于预测因变量的因子和协变量。
E 在模型选项卡上,使用所选因子和协变量指定模型效应。
或者,可以在“重复”选项卡上指定:
Page 74

64
章7
主体内变量。主体内变量值的组合定义主体中度量的顺序;因此,主体内变量和主体
变量的组合唯一定义每个度量。例如,时间、医院 ID 和病人 ID 的组合为每个个案
定义特定医院中特定病人的一次就诊。
如果数据集已经排序,每个主体的重复度量因而按正确顺序在连续个案段中发生,则
并不严格要求必须指定主体内变量,并且您可以取消选择
案进行排序
并保存执行(临时)排序所需的处理时间。通常,利用主体内变量确保度
按个体变量和主体内变量对个
量的正确顺序是很好的方法。
主体变量和主体内变量不能用于定义响应,但它们可以在模型中执行其他功能。例如,
医院 ID 可用作模型中的因子。
协方差矩阵。基于模型的估计是 Hessian 矩阵的广义逆负矩阵。健壮性估计(也称为
Huber/White/sandwich 估计)是“改正”的基于模型的估计,即使错误地指定了工作相
关矩阵,也能提供对协方差的一致估计。该规范适用于广义估计方程的线性模型部分中
的参数,而估计选项卡上的规范只适用于初始广义线性模型。
工作相关性矩阵。此相关矩阵表示主体内相关性。其大小由度量数决定,因此也由主体
内变量的值组合决定。您可以指定以下结构之一:
独立。重复度量不相关。
AR(1)。重复度量具有一阶自回归关系。任意两个元素之间的相关性对于相邻元素为
ρ,对于由第三个元素分隔的元素为 ρ
可交换。此结构在元素之间具有同质相关性。又称为复合对称结构。
依 M 协变量。连续的测量具有共同的相关系数,由第三个度量分隔的测量对具有共同
的相关系数,依此类推,直到由 m
2
,依此类推。ρ 受到约束,以使 –1<ρ<1。
1 个其他度量分隔的测量对。具有更多分隔的测
量假设为不相关。选择此结构时,请指定小于工作相关矩阵的阶的 m 值。
未结构化。这是一个非常一般的相关矩阵。
缺省情况下,过程将根据非冗余参数的数目调节相关估计值。如果希望估计值不会随着
数据中的主体级重复变化而发生变化,则可能需要去掉此调节功能。
最大迭代次数。广义估计方程算法将执行的最大迭代次数。指定一个非负整数。
该规范适用于广义估计方程的线性模型部分中的参数,而估计选项卡上的规范
只适用于初始广义线性模型。
更新矩阵。工作相关矩阵中的元素将根据参数估计值进行估计,参数估计值在算法
的每次迭代中更新。如果工作相关矩阵完全没有更新,则在整个估计过程中将使
用初始工作相关矩阵。如果该矩阵进行了更新,则可以指定更新工作相关矩阵元
素的迭代间隔。指定大于 1 的值可缩短处理时间。
收敛性准则。这些规范适用于广义估计方程的线性模型部分中的参数,而估计选项卡
上的规范只适用于初始广义线性模型。
参数收敛。如果选择此项,算法将在参数估计值的绝对或相对更改小于指定值(必
须为正值)的迭代之后停止。
Hessian 收敛性。如果基于 Hessian 的一个统计量小于指定值(必须为正值),
则认为收敛。
Page 75

广义估计方程:模型类型
图片 7-2
广义估计方程:“模型类型”选项卡
65
广义估计方程
“模型类型”选项卡允许您为模型指定分布和关联函数,它为按响应类型分类的几种常
用模型提供了快捷键。
模型类型
尺度响应。
线性。 将正态指定为分布,将恒等指定为关联函数。
具有对数链接的 Gamma。 将 Gamma 指定为分布,将对数指定为关联函数。
有序响应。
有序 logistic。将多项(序数)指定为分布,将累积 logit 指定为关联函数。
有序 probit。将多项(序数)指定为分布,将累积 probit 指定为关联函数。
Page 76

66
章7
计数。
泊松对数线性。 将泊松指定为分布,将对数指定为关联函数。
具有对数链接的负二项式。 将负二项式(拥有值为 1 的辅助参数)指定为分布,将对
数指定为关联函数。要使过程估计辅助参数的值,指定一个拥有负二项式分布的
定制模型,并在参数组中选择
估计值。
二元响应或事件/试验数据。
二元 logistic。 将二项式指定为分布,将 Logit 指定为关联函数。
二元 probit。 将二项式指定为分布,将 Probit 指定为关联函数。
间隔检查生存。 将二项式指定为分布,将互补双对数指定为关联函数。
混合。
具有对数链接的 Tweedie。 将 Tweedie 指定为分布,将对数指定为关联函数。
具有恒等式链接的 Tweedie。 将 Tweedie 指定为分布,将恒等指定为关联函数。
定制。指定您自己的分布和关联函数的组合。
分布
此选项指定因变量的分布。指定非正态分布和非恒等关联函数的功能是广义线性模型相
对一般线性模型的重要改进。分布-关联函数可能存在多种组合,其中一些适合任何给
定的数据集,因此可以根据先验理论的要求进行选择,或选择最合适的组合。
二项式。此分布仅适合表示二元响应或事件数量的变量。
Gamma。该分布适用于具有正尺度值并向更大的正值偏度的变量。如果数据值小于
等于 0 或缺失,那么分析中不会使用相应的个案。
逆高斯。该分布适用于具有正尺度值并向更大的正值偏度的变量。如果数据值小于
等于 0 或缺失,那么分析中不会使用相应的个案。
负二项式。该分布可以视为观察 k 成功所需的试验次数,适合具有非负整数值的变
量。如果数据值是非整数、小于 0 或缺失,那么分析中不会使用相应的个案。负二
项式分布辅助参数的固定值可以是大于等于 0 的任何值。您可将其设为固定值,或
允许过程对其进行估计。辅助参数设置为 0 时,使用此分布相当于使用泊松分布。
正态。该分布适合围绕某个中间值(均值)呈对称钟型分布的刻度变量。因变
量必须是数值型变量。
泊松。该分布可视为被观察事件在固定时间段内发生的次数,适合具有非负整数值的
变量。如果数据值是非整数、小于 0 或缺失,那么分析中不会使用相应的个案。
Tweedie。 此分布适合由 gamma 分布泊松混合表示的变量;之所以称为?混合?分布,
是因为它兼具连续(取非负实数值)和离散分布(在单个值 0 处为正概率质量)
的属性。因变量必须是数值型变量,数据值大于或等于零。如果数据值小于零或
缺失,那么分析中不会使用相应的个案。Tweedie 分布参数的固定值可以是任
何大于 1 且小于 2 的数字。
多项式。此分布适合表示序数响应的变量。因变量可以是数值或字符串,它必须
至少有两个不同有效数据值。
Page 77

广义估计方程
联接函数
联接函数是允许模型估计的因变量的转换。可用函数有:
恒等。f(x)=x。因变量不转换。该关联可用于任何分布。
互补双对数。f(x)=log( log(1 x))。该函数只适用于二项式分布。
累积 Cauchit。f(x) = tan(π (x – 0.5)),适用于每个响应类别的累积概率。
该函数只适用于多项式分布。
累积互补双对数。f(x)=ln( ln(1 x)),适用于每个响应类别的累积概率。该函数
只适用于多项式分布。
累积 logit。f(x)=ln(x / (1 x)),适用于每个响应类别的累积概率。该函数只适
用于多项式分布。
累积负双对数。f(x)= ln( ln(x)),适用于每个响应类别的累积概率。该函数
只适用于多项式分布。
累积 probit。f(x)=Φ
1
(x),适用于每个响应类别的累积概率,其中 Φ1是逆标
准正态累积分布函数。该函数只适用于多项式分布。
对数。f(x)=log(x)。该关联可用于任何分布。
对数补数。f(x)=log(1 x)。该函数只适用于二项式分布。
Logit。f(x)=log(x / (1 x))。该函数只适用于二项式分布。
负二项式。f(x)=log(x / (x+k
1
)),其中 k 是负二项式分布的辅助参数。该函数只
适用于负二项式分布。
负双对数。f(x)= log( log(x))。该函数只适用于二项式分布。
奇数幂。f(x)=[(x/(1 x))
α
1]/α,如果 α ≠ 0. f(x)=log(x),如果 α=0. α 为
必需的数字指定,且必须为实数。该函数只适用于二项式分布。
Probit。f(x)=Φ
1
(x),其中 Φ1是逆标准正态累积分布函数。该函数只适用于
二项式分布。
幂。f(x)=x
α
,如果 α ≠ 0. f(x)=log(x),如果 α=0. α 为必需的数字指定,且必
须为实数。该关联可用于任何分布。
67
Page 78

68
章7
广义估计方程:响应
图片 7-3
广义估计方程:“响应”选项卡
在许多情况下,您可以只指定一个因变量;但是,仅采用两个值的变量和记录试验
中事件的响应需要额外注意。
二元响应。如果因变量仅采用两个值,可以为参数估计指定参考类别。二元响
应变量可以是字符串或数值。
一组试验中发生的事件数量。当响应是一系列试验中发生的事件数时,因变量包含事
件数,您可
以额外选择一个包含试验数的变量。或者,如果试验数在所有主体中
都相同,则可以使用固定值指定试验。试验数应大于等于每个个案的事件数。事
件应为非负整数,试验应为正整数。
对于有序多项模型,可以指定响应的类别顺序:升序、降序或数据(数据顺序意味着在
数据中遇到的第一个值定义第一个类别,遇到的最后一个值定义最后一个类别。)
Page 79

刻度权重。尺度参数是与响应方差相关的估计模型参数。尺度权重是“已知”值,可能因
观察值的不同而异。如果指定了刻度权重变量,则对每个观察值,都会用与响应方差相关
的尺度参数除以该尺度权重变量。分析中不使用尺度权重值小于等于 0 或缺失的个案。
广义估计方程:参考类别
图片 7-4
“广义估计方程: 参考类别”对话框
69
广义估计方程
对于二元响应,可以为因变量选择参考类别。这会影响某些输出,如参数估计值和保存
的值,但不应更改模型拟合。例如,如果您的二元响应取值 0 和 1:
缺省情况下,此过程将最后一个值(最高值)或 1 作为参考类别。在这种情况
下,模型保存的概率估计给定个案取值 0 的概率,参数估计值应解释为与类别 0
的似然估计相关。
如果您指定第一个值(最低值)或 0 作为参考类别,则模型保存的概率估计给
定个案取值 1 的概率。
如果您指定定制值并且变量已定义了标签,则可以通过从列表中选择值来设置参考类
别。在指定模型的过程中并不确定某一特定变量的编码方式时,这种方法非常方便。
Page 80

70
章7
广义估计方程:预测变量
图片 7-5
广义估计方程:“预测变量”选项卡
在“预测”选项卡中可以指定用于生成模型效应的因子和协变量并指定可选偏移。
因子。因子是分类预测变量,可以是数值或字符串。
协变量。协变量为刻度预测变量,必须为数值。
注意:当响应为二元格式的二项式时,该过程通过子体来计算偏差和卡方拟合优度统计
量,这些子体基于对所选因子和协变量观察值的交叉分类。您应在过程的多次运行中保
持相同的预测变量集,以确保一致的子体数量。
偏移量。偏移项是“结构化”预测变量。模型不估计该预测变量的系数,但假定其值为
1;因此,偏移值只是简单地加到因变量的线性预测变量中。这在每个个案对于被观察
事件都可能具有不同显现水平的泊松回归模型中尤其有用。例如,当对各个驾驶员事故
率进行建模时,3 年驾驶经历出现 1 次事故和 25 年出现 1 次事故的驾驶员之间有着重
大的差别!如果将驾驶员经历纳入偏移项,则事故数可以建模为泊松响应。
Page 81

广义估计方程:选项
71
广义估计方程
图片 7-6
“广义估计方程: 选项”对
这些选项适用于“
预测”选项卡上指定的所有因子。
话框
用户缺失值。要在
分析中包含个案,因子必须具有有效值。通过这些控制可以决定是否
将用户缺失值在因子变量中视为有效值。
类别顺序。该选项与确定因子的最终水平有关,该水平可能与估计算法中的冗余参数相
关。更改类别顺序可更改因子水平效应的值,因为这些参数估计值相对于“最终”水平
进行计算。因子
可以按从最低值到最高值的升序排序,按从最高值到最低值的降序排
序,或者按“数据顺序”排序。这意味着在数据中遇到的第一个值定义第一个类别,遇
到的最后一个唯一值定义最后一个类别。
Page 82

72
章7
广义估计方程:模型
图片 7-7
广义估计方程:“模型”选项卡
指定模型效应。缺省模型是仅截距模型,因此必须明确指定其他模型效应。还可以
构建嵌套或非嵌套项。
非嵌套项
对于选定因子和协变量:
主效应。为每个选定的变量创建主效应项。
交互。为所有选定变量创建最高级交互项。
因子。创建选定变量的所有可能的交互和主效应。
所有二阶。创建选定变量的所有可能的二阶交互。
所有三阶。创建选定变量的所有可能的三阶交互。
Page 83

73
广义估计方程
所有四阶。创建选定变量的所有可能的四阶交互。
所有五阶。创建选定变量的所有可能的五阶交互。
嵌套项
在此过程中,可为您的模型建立嵌套项。嵌套项有助于对其值不与另一个因子的水平交
互作用的因子或协变量的效应进行建模。例如,杂货连锁店可能在不同商店位置迎合顾
客的不同消费习惯。由于每位顾客只频繁光顾某一位置的商店,因此 Customer 效应可
以说是嵌套在 Store location 效应中。
此外,还可以包含交互效应或将多层嵌套添加到嵌套项。
限制。嵌套项有以下限制:
一次交互内的所有因子必须是唯一的。因此,如果 A 是因子,则指定 A*A 是无效的。
嵌套效应内的所有因子必须是唯一的。因此,如果 A 是因子,则指定 A(A) 是无效的。
效应不可嵌套在协变量中。因此,如果 A 是因子且 X 是协变量,则指定 A(X) 是
无效的。
截距。模型中通常包含截距。如果您可以假设数据穿过原点,则可以排除截距。
多项有序分布的模型没有单个截距项;而包含定义相邻类别之间转换点的阈值参
数。模型中通常包含有阈值。
Page 84

74
章7
广义估计方程:估计
图片 7-8
广义估计方程:“估计”选项卡
参数估计。该组中的控件允许指定估计方法并提供参数估计值的初始值。
方法。可以选择参数估计方法;其中包括:Newton-Raphson、Fisher 评分方法以及
先执行 Fisher 评分迭代再切换为 Newton-Raphson 方法的混合方法。如果在混合方
法的 Fisher 评分方法阶段期间,在达到 Fisher 迭代的最大次数之前实现了收敛,
则算法将继续执行 Newton-Raphson 方法。
刻度参数方法。可以选择尺度参数估计方法。
最大似然法可联合估计尺度参数和模型效应;请注意,如果响应具有负二项式、泊
松或二项式分布,则此选项无效。因为广义估计方程没有纳入似然这一概念,所以
此规范仅适用于初始广义线性模型;该尺度参数估计值传递给广义估计方程,后
者通过 Pearson 卡方与其自由度的商更新尺度参数。
偏差和 Pearson 卡方选项从初始广义线性模型中统计量的值估计尺度参数;然后,
此尺度参数估计值传递给广义估计方程,后者将其作为固定值处理。
Page 85

75
广义估计方程
或者,可为尺度参数指定固定值。在估计初始广义线性模型和广义估计方程时,该
参数将作为固定值处理。
初始值。该过程将自动计算参数的初始值。也可以指定参数估计值的初始值。
此选项卡上指定的迭代和收敛标准仅适用于初始广义线性模型。有关用于拟合广义估计
方程的估计标准,请参见重复选项卡。
迭代。
最大迭代次数。算法将执行的最大迭代次数。指定一个非负整数。
最大步骤对分。每次迭代时,步长都会减去因子 0.5,直到对数似然估计增加或者达
到最大步骤对分。指定一个正整数。
检查数据点的完整分隔。如果选择此项,算法将执行检验以确保参数估计值具有唯一
值。当过程可生成一个正确对每个个案进行分类的模型时,将发生分离。此选项可
用于二元格式的多项式响应和二项式响应。
收敛性准则。
参数收敛。如果选择此项,算法将在参数估计值的绝对或相对更改小于指定值(必
须为正值)的迭代之后停止。
对数似然估计收敛。如果选择此项,算法将在对数似然估计函数的绝对或相对更改小
于指定值(必须为正值)的迭代之后停止。
Hessian 收敛性。对于“绝对值”指定,如果基于 Hessian 收敛的统计量小于指定的
正值,则假定收敛。对于“相对”指定,如果统计量小于指定的正值和对数似然
估计的绝对值的乘积,则假定收敛。
奇异性容许误差。奇异(非可逆)矩阵具有线性相关列,对估计算法可能产生严重问
题。即使近似奇异的矩阵也可导致不良结果,因此该过程会将行列式小于容许误差的矩
阵作为奇异矩阵对待。指定一个正值。
广义估计方程:初始值
该过程估计初始广义线性模型,从此模型得到的估计值用作广义估计方程的线性模型部
分中参数估计值的初始值。处理相关矩阵无需初始值,因为矩阵元素基于参数估计值。
此对话框上指定的初始值用作初始广义线性模型而不是广义估计方程的起始点,除非估
计选项卡上的“最大迭代次数”设置为 0。
Page 86

76
章7
图片 7-9
“广义估计方程: 初始值”对话框
如果指定了初始值,则必须为模型中的所有参数(包括冗余参数)提供初始值。在数据
集中,变量从左到右
的顺序必须为:RowType_、VarName_、P1、P2、…,其中 RowType_
和 VarName_ 是字符串变量,P1、P2、… 是对应于已排序参数列表的数值变量。
初始值在变量 RowType_ 具有值 EST 的记录上提供;实际初始值在变量 P1、P2、…
下提供。该过程忽略
RowType_ 具有非 EST 值的所有记录以及 RowType_ 的第一
次等于 EST 以外的所有记录。
截距(如果模型中包含)或阈值参数(如果响应具有多项式分布)必须是列出
的第一个初始值。
尺度参数和负二项式参数(如果响应具有负二项式分布)必须是指定的最后一个
初始值。
如果“拆分文件
”有效,则变量必须以拆分文件变量开始(以创建“拆分文件”时
指定的顺序),后跟 RowType_、VarName_、P1、P2、…,如上所述。拆分在指定数
据集中的发生顺序必须与原始数据集中的顺序相同。
注意:变量名 P1、P2、… 不是必需的;过程接受参数的任何有效变量名,因为变量与
参数的映射基于变
量位置,而不是变量名。超过最后一个参数的所有变量都会被忽略。
初始值的文件结构与将模型导出为数据时使用的结构相同;因此,可以使用一次过程
运行的最终值作为下一次运行的输入。
Page 87

广义估计方程:统计量
图片 7-10
广义估计方程:“统计量”选项卡
77
广义估计方程
模型作用。
分析类型。指定要模型效应检验生成的分析类型。类型 I 分析通常适合于对模型中预
测变量的排序具有先验理由的情况
,而类型 III 应用范围更广。根据在“卡方统
计量”组中的选择,计算 Wald 或一般化分数统计。
置信区间。指定一个大于 50 且小于 100 的置信度。无论选择哪种卡方统计量类型,
总是生成 Wald 区间,并且基于参数呈渐近正态分布的假设之上。
对数准似然函数。它控制对数准似然函数的显示格式。整个函数包含一个相对于参数
估计恒定的额外项;它对参数估计
打印。显示下面的输出。
个案处理摘要。显示分析和“相关数据摘要”表中包含的个案和从中排除的个案
没有任何影响,并且在某些软件产品中不会显示。
的数量和百分比。
描述统计。显示有关因变量、协变量和因子的描述统计和摘要信息。
Page 88

78
章7
模型信息。显示数据文件名称、因变量或事件和试变量、偏移变量、尺度权重
变量、概率分布和关联函数。
拟合度统计。 显示用于模型选择的 AIC 准则的两项扩展:用于选择最佳相关结构的
QIC 准则和用于选择最佳预测变量子集的另一个 QIC 度量。
模型摘要统计。显示模型拟合检验,包括用于模型拟合 Omnibus 检验的似然比统计
量,以及每种效应的类型 I 或 III 对比的统计量。
参数估计。显示参数估计值和相应的检验统计和置信区间。除了显示原始参数估计值
之外,还可以选择显示取幂参数估计值。
参数估计的协方差矩阵。显示估计参数协方差矩阵。
参数估计的相关性矩阵。显示估计参数相关矩阵。
对比系数 (L) 矩阵。为缺省效应和估计边际均值显示对比系数(如果“EM 均值”
选项卡上要求)。
常规可估计函数。显示生成对比系数 (L) 矩阵的矩阵。
迭代历史记录。显示参数估计值和对数似然估计的迭代历史记录,并打印对梯度矢量
和 Hessian 矩阵的最后一次评估。迭代历史记录表从第 0 次迭代(初始估计值)开
始为每 n 次迭代显示参数估计值,其中,n 代表打印区间的值。如果请求迭代历史
记录,那么无论 n 的值是多少,都会显示最后一次迭代。
工作相关性矩阵。显示表示主体内相关性的矩阵值。其结构取决于重复选项卡中
的规格。
Page 89

广义估计方程:EM 均值
图片 7-11
广义估计方程:“EM 均值”选项卡
79
广义估计方程
此选项卡用于显示因子水平和因子交互的估计边际均值。您还可以要求显示整体估计均
值。估计边际均值对有序多项模型不可用。
因子和交互。此列表包含“预测变量”选项卡上指定的因子和“模型”选项卡上指定的
因子交互。此列表中不包含协变量。可以直接从此列表选择项,或者使用
依据 * 按钮
将项组合到交互项中。
显示以下项的均值。计算所选因子和因子交互的估计均值。对比决定如何设定假设检验
以比较估计均值。简单对比需要一个用于比较其他项的参考类别或因子水平。
配对方式。为指定或默示的因子的所有水平组合计算成对比较。这是因子交互
的唯一可用对比方法。
简单散点图. 将每个水平的均值与指定水平的均值进行比较。当存在控制组时,
此类对比很有用。
Page 90

80
章7
偏差。因子的每个水平与总均值比较。偏移对比不是正交的。
差分. 将每个水平(第一个除外)的均值与先前水平的均值进行比较。有时候将其
称为逆 Helmert 对比。
Helmert. 将因子的每个水平的均值(最后一个水平除外)与后续水平的均值进
行比较。
重复. 将每个水平的均值(最后一个水平除外)与后续水平的均值进行比较。
多项式. 比较线性作用、二次作用、三次作用等等。第一自由度包含跨所有类别的线
性效应;第二自由度包含二次效应,依此类推。这些对比常常用来估计多项式趋势。
标度。对于响应,可根据因变量的原始刻度计算估算边际均值;对于线性预测变量,根
据关联函数变换的因变量计算估计边际均值。
调整的多重比较。在执行包含多重比较的假设检验时,总体显著性水平可从所包含的比
较的显著性水平进行调节。使用此组可以选择调节方法。
显著性最低的差异。此方法并不控制拒绝某些线性对比不同于原假设值这一假设
的总体概率。
Bonferroni. 此方法针对检验多个对比这一事实调整观测的显著性水平。
连续 Bonferroni. 这是按顺序逐步降低的拒绝 Bonferroni 过程,在拒绝个别假设方
面不保守,但维持相同的总体显著性水平。
Sidak. 此方法提供比 Bonferroni 方法更严密的界限。
连续 Sidak. 这是按顺序逐步降低的拒绝 Sidak 过程,在拒绝个别假设方面不保
守,但维持相同的总体显著性水平。
Page 91

广义估计方程:保存
图片 7-12
广义估计方程:“保存”选项卡
81
广义估计方程
选中的项以指定的名称保存;可以选择用新变量覆盖现有的同名变量,或为新变量名添
加后缀使其成为唯一名称以避免名称冲突。
响应均值的预测值。以初始响应度规保存每个个案的模型预测值。当响应分布是二项
式,并且因变量为二元时,过程会保存预测概率。当响应分布是多项式时,项目
标签变成
积预测概率
累
,并且过程保存响应每个类别的累积预测概率(最后一个除
外),直至达到要保存的指定类别数量。
响应均值的置信区间下限保存响应均值置信区间的下限。当响应分布是多项式时,项
目标签变成
个除外)
响应均
项目标签变成
累积预测概率的置信区间下限,并且过程保存响应每个类别的下限(最后一
,直至达到要保存的指定类别数量。
值的置信区间上限。
累积预测概率的置信区间上限,并且过程保存响应每个类别的上限(最后
保存响应均值置信区间的上限。当响应分布是多项式时,
一个除外),直至达到要保存的指定类别数量。
Page 92

82
章7
预测类别。对于具有二项式分布和二元因变量或多项式分布的模型,该过程保存每个
个案的预测响应类别。此选项不支持其他响应分布。
线性预测器的预测值。以线性预测变量的度规保存每个个案的模型预测值(通过指定
的关联函数转换的响应)。当响应分布是多项式时,过程保存响应每个类别的预测
值(最后一个除外),直至达到要保存的指定类别数量。
线性预测变量的预测值的估计标准误。当响应分布是多项式时,过程保存响应每个类
别的估计标准误(最后一个除外),直至达到要保存的指定类别数量。
如果响应分布是多项式,则以下各项不可用。
原始残差. 观察值与模型预测值之间的差。
Pearson 残差。个案对 Pearson 卡方统计量的贡献的平方根(带原始残差的符号)。
广义估计方程:导出
图片 7-13
广义估计方程:“导出”选项卡
Page 93

83
广义估计方程
将模型导出为数据。写入一个 IBM® SPSS® Statistics 格式的数据集,包含具有参数估计
值、标准误、显著性值和自由度的参数相关性或协方差矩阵。矩阵文件中变量顺序如下。
拆分变量。定义拆分的任何变量(如果使用)。
RowType_。 取值(或值标签)为 COV(协方差)、CORR(相关性)、EST(参数估
计)、SE(标准误)、SIG (显著性水平)和 DF(抽样设计自由度)。存在每个模
型参数的 COV(或 CORR)行类型的单独个案,以及每个其他行类型的单独个案。
VarName_。 对于行类型 COV 或 CORR,取值为 P1、P2、...,对应于所有估计模型
参数(除尺度或负二项式参数外)的有序列表,值标签对应于在参数估计值表中
显示的参数字符串。对于其他行类型,单元格为空。
P1、P2、...这些变量对应于所有模型参数(必要时可包括尺度或负二项式参数)
的有序列表,值标签对应于在参数估计值表中显示的参数字符串,这些变量根据
行类型取值。
对于冗余参数,所有协方差设为零,相关性设为系统缺失值;所有参数估计值设为
零;并且所有标准误、显著性水平和残差自由度设为系统缺失值。
对于尺度参数,协方差、相关性、显著性水平和自由度均设为系统缺失值。如果尺
度参数通过最大似然进行估计,则给出标准误;否则,它被设为系统缺失值。
对于负二项式参数,协方差、相关性、显著性水平和自由度均设为系统缺失值。如果
负二项式参数通过最大似然进行估计,则给出标准误;否则,它被设为系统缺失值。
如果存在拆分,则参数列表必须在所有拆分之间进行累积。在给定拆分中,某些参
数可能是无关的;但这不同于冗余。对于无关参数,所有协方差或相关性、参数估
计值、标准误、显著性水平和自由度均设为系统缺失值。
可以使用此矩阵文件作为进一步进行模型估计的初始值;注意,该文件不能立即用于
在其他读取矩阵文件的过程中执行进一步分析,除非这些过程接受在此导出的所有行
类型。尽管如此,您必须注意,在该矩阵文件中的所有参数对于读取此文件的过程
具有相同的含义。
将模型导出为 XML。将参数估计值和参数协方差矩阵(如果选择)以 XML (PMML) 格式保
存。您可以使用该模型文件以应用模型信息到其他数据文件用于评分目的。
GENLIN 命令的附加功能
使用命令语法语言还可以:
将参数估计值的初始值指定为数字列表(使用 CRITERIA 子命令)。
指定固定工作相关矩阵(使用 REPEATED 子命令)。
在计算估计边际均值时修正值不同于其均值的协变量(使用 EMMEANS 子命令)。
指定估计边际均值的定制多项式对比(使用 EMMEANS 子命令)。
指定因子的一个子集,以显示该子集的估计边际均值,并使用指定的对比类型对其
进行比较(使用
请参阅命令语法参考以获取完整的语法信息。
EMMEANS 子命令的 TABLES 和 COMPARE 关键字)。
Page 94

广义线性混合模型
广义线性混合模型扩展了线性模型,使得:
目标通过指定的关联函数与因子和协变量线性相关
目标可以有非正态分布
观测可能相关。
广义线性混合模型涵盖了从简单线性回归到复杂的非正态纵向数据多变量模型的各
种模型。
图片 8-1
“数据结构”选项卡
章
8
“数据结构”选项卡用于在观察值相关时指定数据集中记录间的结构关系。如果数据集
中的记录代表独立的观察值,则无需在此选项卡上指定任何设置。
© Copyright SPSS Inc. 1989, 2010
84
Page 95

85
广义线性混合模型
主体。 指定分类字段的值组合应唯一定义数据集中的主体。例如,单个病人 ID 字段
应足以定义一个医院内的主体,但如果病人标识号在医院间不唯一,则需要使用医院
ID 和病人 ID 的组合。在重复度量设置中,将为每个主体记录多个观察数据,因此每
个主体可能在数据集中占用多个记录。
主体是可视为独立于其他主体的观察单元。例如,在医学研究中可以认为某患者的血
压读数独立于其他患者的读数。如果存在对每个主体的重复度量,而且您想要对这些观
察值之间的相关性建模,定义主体就非常重要。例如,您可能期望同一个患者在连续
多次就医时得到的血压读数是相关的。
“数据结构”选项卡上被指定为主体的所有字段用于定义残差协方差结构的主体,并
提供定义随机效应块上的随机效应协方差结构主体的可能字段列表。
重复度量。 这里指定的字段用于识别重复观测。例如,单个变量周可以标识医学研究中
10 周内的观察值,而月和天可共同用于标识一年内的每一天的观察值。
定义协方差组。这里指定的字段定义独立重复效应协方差参数组;每个类别各有一个
参数组由分组字段的交叉分类定义。所有主体具有相同的协方差类型;相同协方差组
内的主体具有相同的参数值。
重复协方差类型。这指定残差的协方差结构。可用的结构是:
一阶自回归 (AR1)
自回归移动平均 (1,1) (ARMA11)
复合对称
对角线
已标度的恒等
Toeplitz
未结构化
方差成分
获取广义线性混合模型
此功能需要“高级回归”选项。
从菜单中选择:
分析 > 混合模型 > 广义线性...
定义数据结构选项卡上数据集的主体结构。
E
E 在字段和效应选项卡上,必须有一个可具有任何测量级别的单个目标,或者是一个必
须为连续的事件/试验指定。还可以指定其分布和关联函数、固定效应和任何随机
效应块、偏移量或分析权重。
E 单击构建选项以指定可选的构建设置。
E 单击模型选项以保存得分到活动数据集并导出模型到外部文件。
E 单击运行以运行过程并创建模型对象。
Page 96

86
章8
具有未知测量级别的字段
当数据集中的一个或多个变量(字段)的测量级别未知时,将显示测量级别警告。由于
测量级别会影响该过程的计算结果,因此所有变量必须都定义有测量级别。
图片 8-2
测量级别警报
扫描数据。 读取活动数据集中的数据,并分配默认测量级别给任何具有当前未知测
量级别的字段。如果数据集较大,该过程可能需要一些时间。
手动分配。 打开列出了所有具有未知测量级别的字段的对话框。您可以使用该对话框
将测量级别分配给这些字段。您也可以在数据编辑器的变量视图中分配测量级别。
由于测量级别对该过程很重要,因此您无法访问运行该过程的对话框,除非所有字
段均定义了测量级别。
Page 97

目标
87
广义线性混合模型
图片 8-3
目标设置
这些设置通过关联函数定义目标、其分布以及其到预测变量的关系。
目标。 需要目标。它可具有任何测量级别,同时目标的测量级别可限制适当的分布
和关联函数。
使用试验数作为分母。 当目标响应是一系列试验中发生的事件数时,目标字段包含事
件数,您可以额外选择一个包含试验数的字段。例如,在试验新型杀虫剂时,可以
对蚂蚁样本施用不同浓度的杀虫剂,然后记录每个样本中杀灭的蚂蚁数量以及被施
用杀虫剂的蚂蚁数量。在本例中,记录杀灭的蚂蚁数量的字段应指定为目标(事
件)字段,记录每个样本中蚂蚁数量的字段应指定为试验字段。如果在每个样本
中蚂蚁数量都相同,则可以将试验数指定为固定值。
试验数应大于等于每个记录的事件数。事件应为非负整数,试验应为正整数。
自定义参考类别。 对于分类目标,您可以选择参考类别。这会影响某些输出,如参数
估计值,但不应更改模型拟合。例如,如果您的目标使用 0、1 和 2 的值,默认情况
下,过程将最后(最高值)的类别或 2 作为参考类别。在这种情况下,参数估计应
被解释为与类别 0 或 1 的似然相对于类别 2 的似然相关。如果您指定一个自定义类
别,同时您的目标已定义标签,则可以通过从列表中选择一个值来设置参考类别。
在指定模型的过程中并不确定某一特定字段的编码方式时,这种方法非常方便。
Page 98

88
章8
目标的分布以及与线性模型的关系 (关联)。 给定预测变量的值,该模型将预期目标的值
分布会遵循指定的形状,同时目标值通过指定关联函数与预测变量线性相关。可以使用
现有的一些通用模型的快捷方式,或者如果您要拟合的特殊分布与关联函数组合不在此
快捷列表上,还可以选择
线性模型。 指定恒等关联的正态分布,在可使用线性回归或 ANOVA 模型预测目标
自定义设置。
时非常有用。
Gamma 回归。 指定对数关联的 Gamma 分布,应在目标包含所有正值并偏斜到更
大值时使用。
对数线性模型。 指定对数关联的泊松分布,应在目标表示固定时间段内的发生
计数时使用。
负二项式回归。 指定对数关联的负二项式回归,应在目标和分母表示观察 k 次成功
所需试验次数时使用。
多项 Logistic 回归。 指定广义 Logit 关联的多项分布,应在目标是多类别响应
时使用。
二元 logistic 回归。 指定 logit 关联的二元分布,应在目标是通过 logistic 回归
模型预测的二元响应时使用。
二元 probit。 指定 probit 关联的二元分布,应在目标是基础正态分布的二元
响应时使用。
间隔检查生存。 指定互补双对数关联的二项式分布,在一些观测没有终止事件的
生存分析中有用。
分布
此选项指定目标的分布。指定非正态分布和非恒等关联函数的功能是广义线性混合模型
相对线性混合模型的重要改进。分布-关联函数可能存在多种组合,其中一些适合任何
给定的数据集,因此可以根据先验理论的要求进行选择,或选择最合适的组合。
二项式。 此分布仅适合表示二元响应或事件数量的目标。
Gamma。 该分布适用于具有正尺度值并向更大的正值偏度的目标。如果数据值小于
等于 0 或缺失,那么分析中不会使用相应的个案。
逆高斯。 该分布适用于具有正尺度值并向更大的正值偏度的目标。如果数据值小于
等于 0 或缺失,那么分析中不会使用相应的个案。
多项式。该分布适用于表示多类别响应的目标。
负二项式。 负二项回归使用带对数关联的二项分布,它用在目标代表具有较高方差
的出现次数的情况下。
正态。 该分布适合围绕某个中间值(均值)呈对称钟型分布的连续目标。
泊松。该分布可视为被观察事件在固定时间段内发生的次数,适合具有非负整数值的
变量。如果数据值是非整数、小于 0 或缺失,那么分析中不会使用相应的个案。
关联函数
关联函数是目标的转换形式,可用于模型估计。可用函数有:
恒等。f(x)=x。不转换目标。该关联可用于除多项式以外的任何分布。
互补双对数。f(x)=log( log(1 x))。该函数只适用于二项式分布。
Page 99

对数补数。f(x)=log(1 x)。该函数只适用于二项式分布。
Logit。f(x)=log(x / (1 x))。该函数只适用于二项式或多项式分布,它也是多项
负双对数。f(x)= log( log(x))。该函数只适用于二项式分布。
Probit。f(x)=Φ
幂。f(x)=x
固定效应
图片 8-4
固定效应设置
对数。f(x)=log(x)。该关联可用于除多项式以外的任何分布。
式分布的唯一有效关联函数。
1
(x),其中 Φ1是逆标准正态累积分布函数。该函数只适用于
二项式分布。
α
,如果 α ≠ 0. f(x)=log(x),如果 α=0. α 为必需的数字指定,且必
须为实数。该关联可用于除多项式以外的任何分布。
89
广义线性混合模型
固定效应因子通常被视为字段,其所需的值都表示在数据集中,同时可用于评分。默认
情况下,在模型固定效应部分输入未在对话框中指定的具有预定义输入角色的字段。分
类(名义、有序)字段用作模型中的因子,同时连续字段用作协变量。
通过在源列表中选择一个或多个字段并拖到效应列表来将效应输入至模型。所创建
的效应类型取决于您放置选择的热区。
Page 100

90
章8
主。 放置的字段在效应列表底部显示为单独的主效应。
二阶。 放置字段的所有可能对在效应列表底部显示为二阶交互。
三阶。 放置字段的所有可能三元在效应列表底部显示为三阶交互。
*。 所有放置字段的组合在效应列表底部显示为单个交互。
效应构建器右侧的按钮可用于:
通过选择您要删除的项并单击删除按钮,可以从固定效应模型中删除项,
通过选择您要重新排序的项并单击向上或向下箭头,可以在固定效应模
型中重新排序项,并
通过单击“添加自定义项”按钮,使用 添加自定义项 对话框向模型添
加嵌套项。
包括截距。模型中通常包含截距。如果您可以假设数据穿过原点,则可以排除截距。
添加自定义项
图片 8-5
添加“自定义项”对话框
在此过程中,可为您的模型建立嵌套项。嵌套项有助于对其值不与另一个因子的水平交
互作用的因子或协变量的效应进行建模。例如,杂货连锁店可能在不同商店位置迎合顾
客的不同消费习惯。由于每位顾客只频繁光顾某一位置的商店,因此 Customer 效应可
以说是嵌套在 Store location 效应中。
此外,还可以包含交互效应,例如包含相同协变量的多项式项,或将多层嵌套添
加到嵌套项。
限制。嵌套项有以下限制:
一次交互内的所有因子必须是唯一的。因此,如果 A 是因子,则指定 A*A 是无效的。
 Loading...
Loading...