Page 1

Choosing a Phase Noise
Measurement Technique
Concepts and Implementation
Terry Decker • Bob Temple
RF & Microwave Measurement
Symposium and Exhibition
Page 2

2
Terry Decker, received her BA in Physics from Carleton College in Northfield, Minnesota in 1980 and a BSEE from the
University of Arizona in 1981. She worked as a microwave engineer for Hughes Aircraft Company on the Phoenix and
AMRAAM programs for 4 years. She is currently a product marketing engineer responsible for phase-noise measurement systems at the Spokane Division of Agilent Technologies.
Bob Temple, received his BA in Physics from Harvard University in 1961, and his MSEE in 1965, and PhD EE in 1971
from the University of Colorado in Boulder. Thesis topic was The Operation and Frequency Stability Measurement
of a Hydrogen Cyanide Beam Type Maser at 88.6 GHz.
His career with Hewlett-Packard began in December 1969 at the Loveland Division designing the frequency synthesis
loops for the 3320 and 3330 Frequency Synthesizers. He was co-project manager for the 3585A Spectrum Analyzer and
the inventor and project manager for the 3047A Spectrum Analyzer System for making comprehensive phase noise and
spectral purity measurements. He transferred to the Spokane Division in 1981 and supported phase noise measurements using the 3047A/11740A Phase Noise Measurement Systems working both within the Company and with customers. He is currently the Project Manager for the Agilent 3048A Phase Noise System.
Page 3

3
Slide 1
There are many techniques for measuring the phase noise from a source or added by a device. How well each of these
methods works depends on both the technique and the characteristics of what is being measured. This presentation
will examine the advantages and disadvantages of using several of the most prevalent methods when measuring the
phase noise of typical devices. One technique using a phase detector to demodulate the phase noise from the carrier
signal will be covered in detail along with a hardware implementation based on this method.
Agenda
* Basic Phase Noise Measurement Concepts
Direct Spectrum Measurement
Demodulation Techniques
Phase Demodulator
Residual or Added Noise Measurements
Single Source Measurements
Phase Detector with Two Sources
Reference Source
Voltage Controlled Source Tuning Requirements
Measurement Optimization
Measurement Examples
Page 4
4
Slide 2
There would be no need to discuss the measurement of phase noise if all sources produced perfect sinewave signals
and if two-port devices were not capable of adding phase noise to a signal. The deviations from the pure sinewave
signal need to be quantified as a first step to determining their effect on the end results. In this equation, representing
the signal voltage with respect to time, e(t) represents amplitude variations or amplitude modulation of the signal
and ø(t) represents the phase fluctuations modulating the ideal linear phase change of the signal. There are two
fundamental ways to measure these perturbations of the signal: the first is to look at the signal directly on a spectrum
analyzer and the second is to demodulate the f luctuations of the carrier for analysis at baseband.
On a spectrum analyzer, the sum total of all the instabilities of a signal appear as sidebands on either side of the carrier.
The spectral density of these sidebands, S
v(vo
±f), can be read directly for a given offset. Demodulating the amplitude,
phase or frequency fluctuations produces a time-domain voltage analog of these fluctuations for measurement and
analysis. The analysis of this baseband signal can produce the spectral density of the amplitude fluctuations, S
A
(f), of
the phase fluctuations, S
ø
(f), or of the frequency fluctuations, Sv(f). Note that the spectral densities of phase and fre-
quency fluctuations are directly related by the square of the offset frequency.
Basic Phase Noise Measurement Concepts
V (t) = V
O
[ 1+
e(t)
] sin [2π v
O
t + ø (t)]
II
A(t) v (t) = v
O
+
1 dø (t)
Direct Spectrum Demodulate, then analyze
S
v (v
O
± f) SA (f) Sø(f) Sv (f) = f 2 Sø(f)
V
O
2π dt
Page 5

Direct Spectrum Analysis
If AM << Pm L(f) = SV(v0±f)
Po
Agilent 3561A/62A Dynamic Signal Analyzer
Agilent 3582A Spectrum Analyzer
Agilent 3585A Spectrum Analyzer
Agilent 8566A/B Spectrum Analyzer
Agilent 8568A/B Spectrum Analyzer
5
Slide 3
The quantity that is usually measured in phase noise analysis is L(f), the single sideband phase noise of a signal.
This quantity is the noise power due to the phase fluctuations of the signal in a 1 Hz bandwidth at an offset f Hz
from the carrier normalized to the total signal power. If the AM noise is much less than the PM noise, L (f) is read
directly from the CRT of the spectrum analyzer as the relative level of the noise sidebands compared to the carrier
power. Corrections are necessary to normalize the results for a 1 Hz bandwidth and to account for the logarithmic
scaling of the spectrum analyzer. In addition, for a measurement of only the signal’s noise, the phase noise sidebands
to be measured must be greater than the spectrum analyzer’s own noise sidebands by about 10 dB. The spectrum
analyzers listed here are commonly used for a direct spectrum measurement of phase noise because they have
synthesized local oscillators (except the 3582A and 3561A which perform a Fourier conversion of the signal) to
prevent their own drift from affecting the result.
Page 6

Demodulate, Then Analyze
If (ø2(t))<< 1 L(f) = Sø (f)
2
Agilent 5390A Frequency Stability Analyzer
Agilent 8901A/B Modulation Analyzer
Agilent 8902A Measuring Receiver
Agilent 3047A/11740A Spectrum Analyzer System
Agilent 3048A Phase Noise Measurement System
Agilent 11729C Carrier Noise Test Set
6
Slide 4
The phase noise on a carrier can be demodulated for analysis with a baseband spectrum analyzer to get the spectral
density of the phase modulation S
ø
(f). The single sided phase noise, L (f), can be calculated from the spectral density of
the phase fluctuations, S
ø
(f), (or frequency fluctuations, Sv(f) = f2x Sø(f) ) if the mean square phase fluctuations <ø2(t)>
are small relative to one radian. Listed here are some of the instruments that are used to do this demodulation and
analysis of phase noise.
Page 7
7
Slide 5
Caution must be exercised when L(f) is calculated from the spectral density of the phase fluctuations, S
ø
(f), because
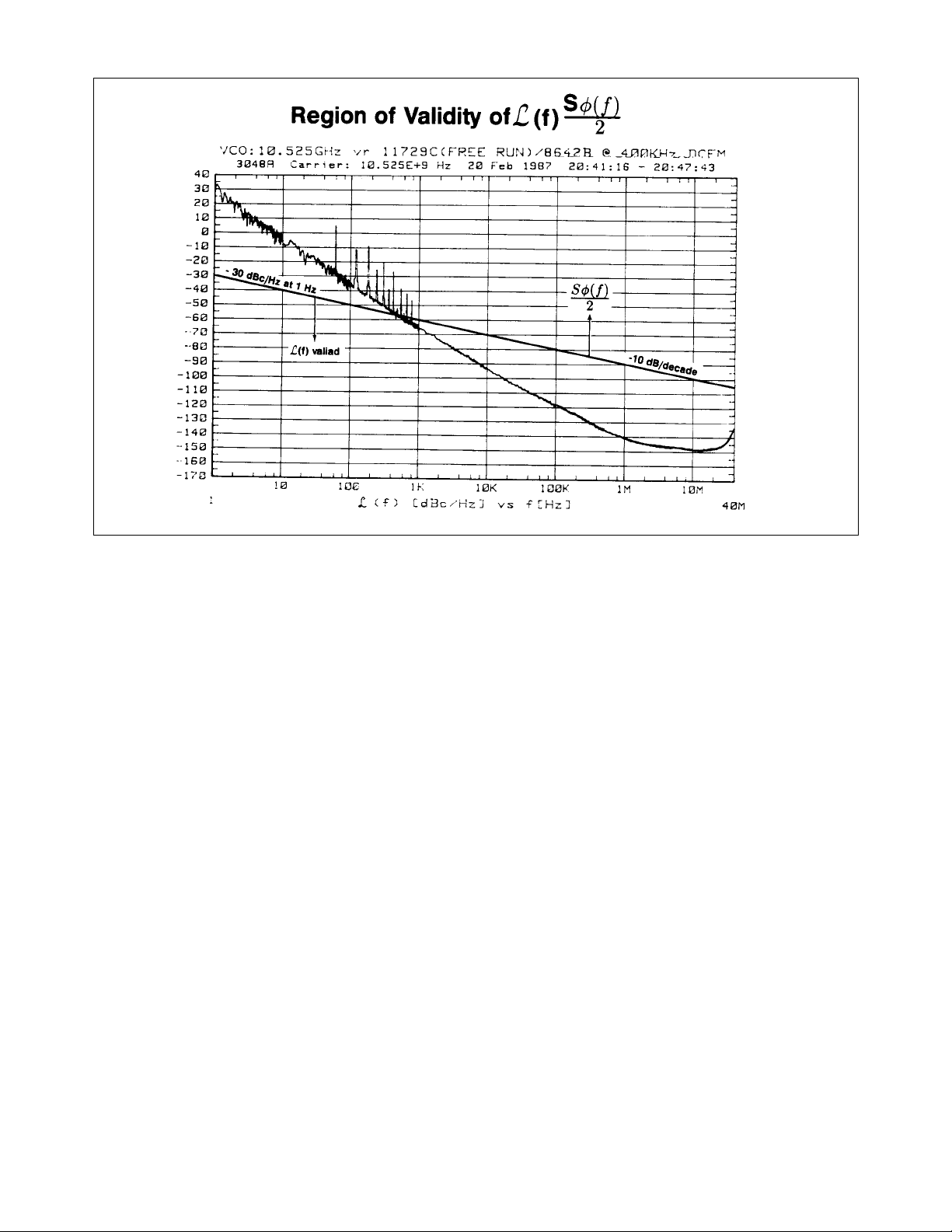
of the small angle criterion. This plot of L(f) resulting from the phase noise of a free-running VCO illustrates the
error that can occur if the instantaneous phase modulation exceeds a small angle. Approaching the carrier, L(f) is
obviously an invalid approximation of the actual phase noise as it reaches a relative level of +35 dBc/Hz at a 1 Hz
offset (35 dB more noise power at a 1 Hz offset in a 1 Hz bandwidth than the total power in the signal).
The –10 dB/decade line is drawn on the plot for an instantaneous phase deviation of 0.2 radians integrated over any
one decade of offset frequency. At approximately 0.2 radians the power in the higher order sidebands of the phase modulation is still insignificant compared to the power in the first order sideband, which ensures the calculation of L(f) is
still valid. Below the line the plot of L(f) is correct; above the line L(f) is increasingly invalid and S
ø
(f) must be used to
represent the phase noise of the signal.
Page 8
8
Slide 6
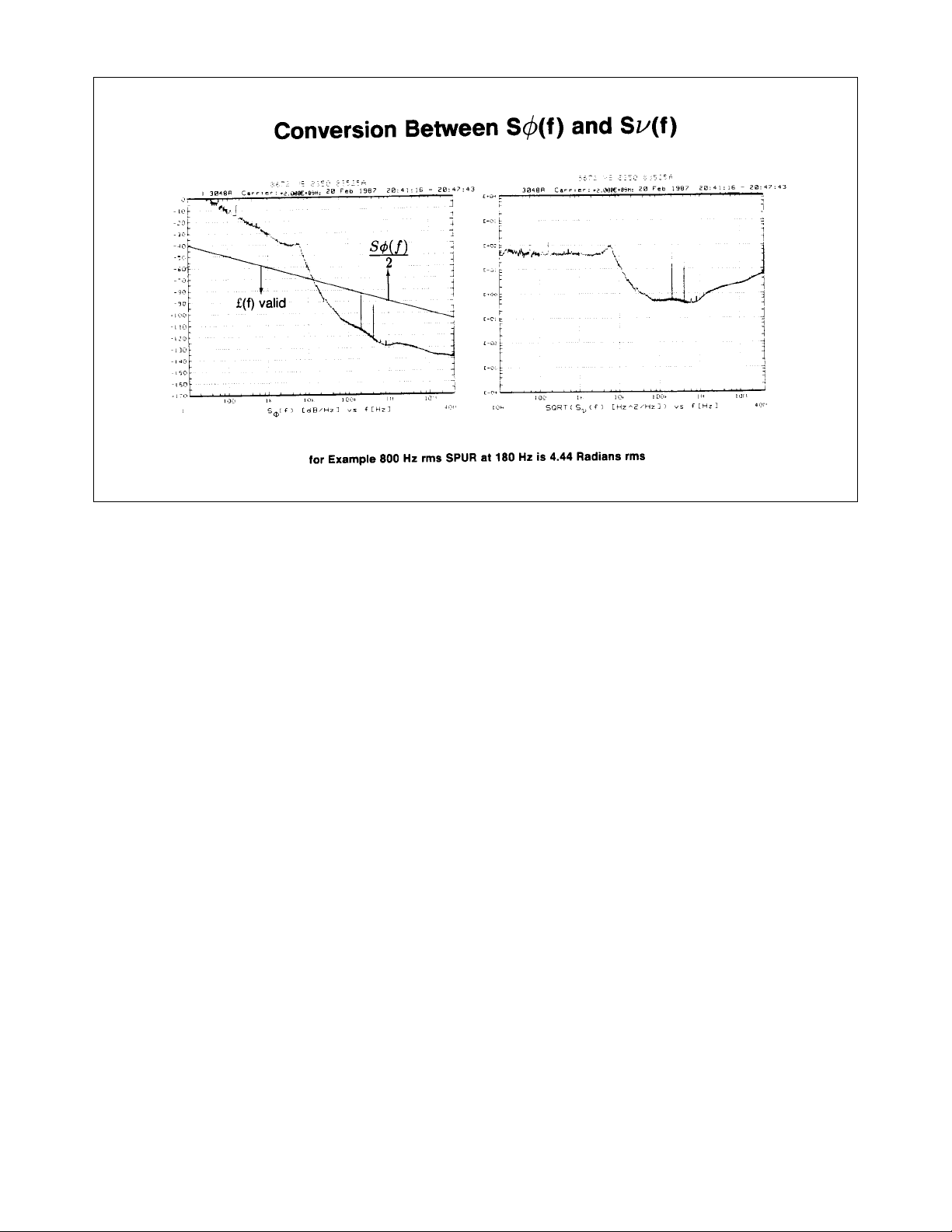
Another way to represent the instability of a signal besides S
ø
(f) or L(f) is with a plot of the spectral density of
frequency fluctuations, S
v
(f). As illustrated before, Sv(f) is equal to f2x Sø(f) because v(t) is the derivative of ø(t). These
two graphs are from the same data with the left one a plot of S
ø
(f) and the right one a plot of the square root of
S
v
(f). The graph of the square root of Sv(f) indicates the power spectral density of the frequency modulation (FM)
noise the signal has on it. A measure of the spectral density of the FM noise versus the offset from the carrier would
be important in the design of an FM system, for example.
Page 9

9
Slide 7
Let’s take a look at the direct spectrum method of measuring phase noise with a variety of spectrum analyzers.
Agenda
Basic Phase Noise Measurement Concepts
* Direct Spectrum Measurement
Demodulation Techniques
Phase Demodulator
Residual or Added Noise Measurements
Single Source Measurements
Phase Detector with Two Sources
Reference Source
Voltage Controlled Source Tuning Requirements
Measurement Optimization
Measurement Examples
Page 10

10
Slide 8
As listed previously, there are a number of spectrum analyzers that will display the single sideband phase noise, L(f),
of a signal. With the exception of the Agilent Technologies 3582A and 3561A which perform a Fourier conversion, the
spectrum analyzers listed here have synthesized local oscillators to prevent the drift of the analyzer from affecting the
measurement of the phase noise sidebands. The Agilent 3048A is a phase noise measurement system that consists of an
interface box for frequency conversion and amplification, the Agilent 3561A Dynamic Signal Analyzer, a controller, and
software to run the measurement and produce the resulting graphs.
The 3048A system software provides direct spectrum measurements with the sub-Hz resolution of the 3561A
for carrier frequencies <100 kHz. It will set up the 3561A, measure and plot the resulting noise voltage.
Page 11
11
Slide 9
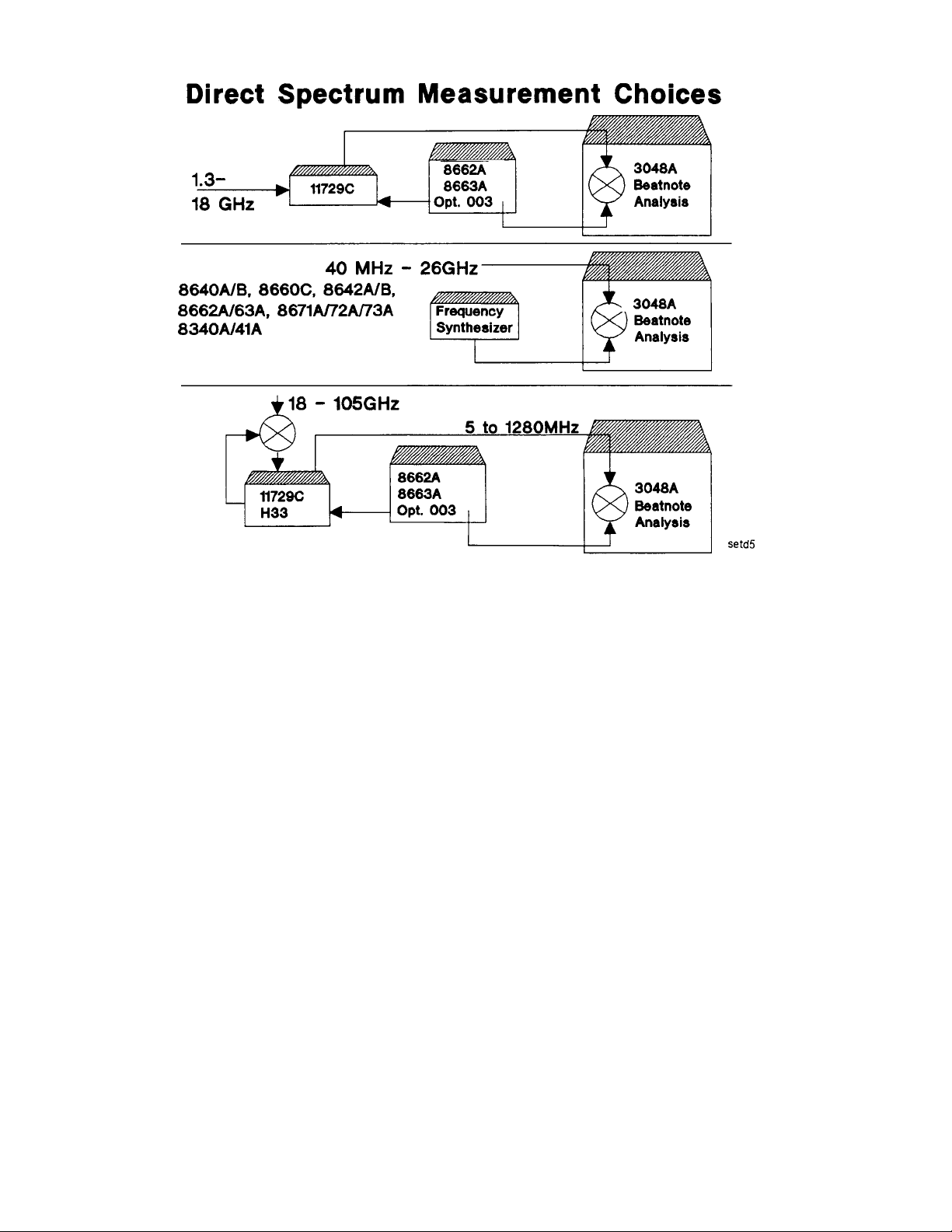
One important criterion for choosing a local oscillator for the downconversion of signals to baseband frequency for
analysis is that the LO should not drift. The local oscillators listed here are synthesized to reduce their frequency
drift to a multiple of a highly-stable crystal reference oscillator. An alternative to the single conversion to baseband
using the mixer in the 3048A interface box is to do a preliminary downconversion using the Agilent 11729C Carrier
Noise Test Set. As explained later, this dual conversion method can produce better sensitivity when measuring the
phase noise of signals in the frequency range of 1.3 to 18 GHz. For signals above 18 GHz there is a millimeter version,
Option H33 to the 11729C. This option allows access to a very clean mm signal to downconvert the test signal to
the nominal range of the 11729C.
Page 12
12
Slide 10
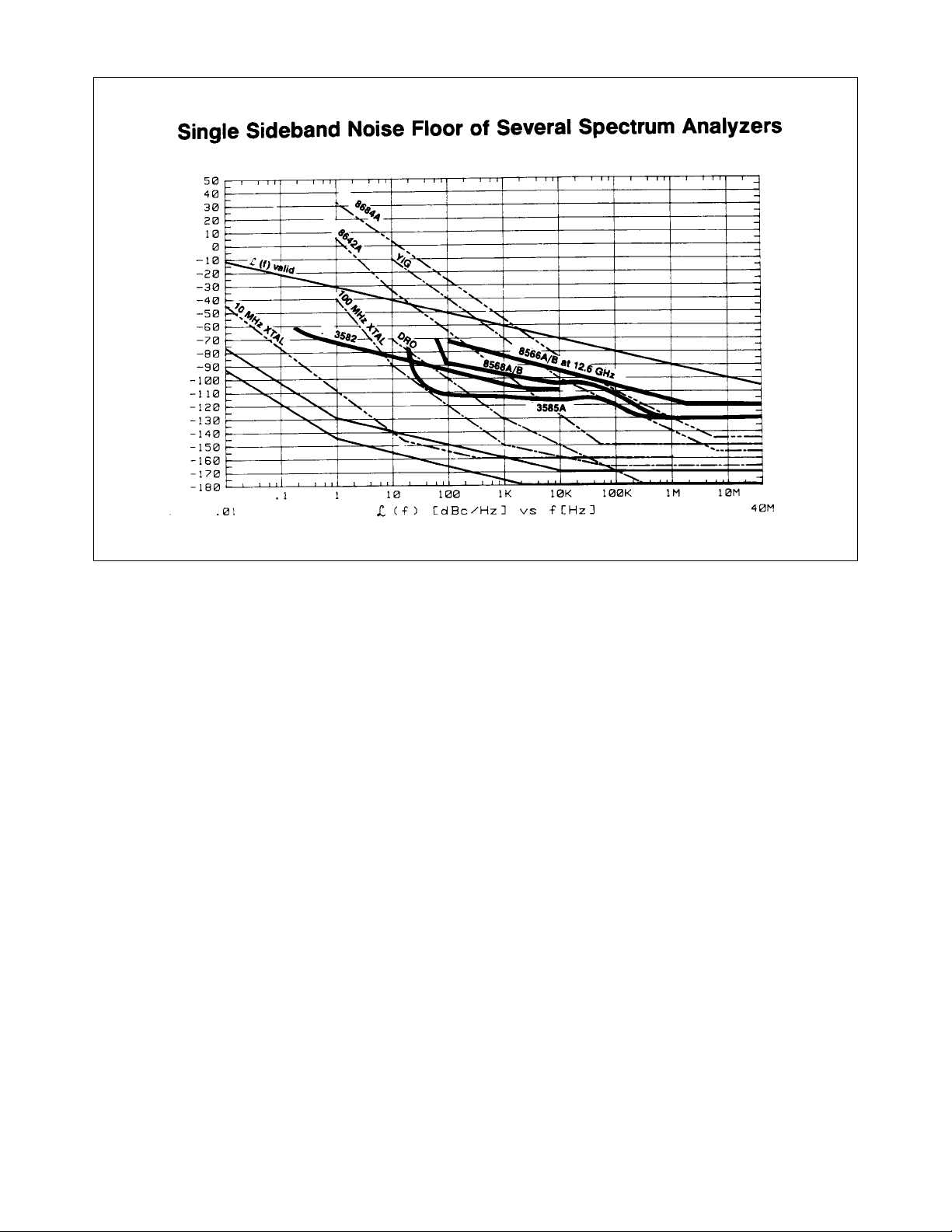
Throughout this presentation are a series of graphs illustrating the single sideband phase noise, L(f), of various sources
on plots covering an offset frequency range of 0.01 Hz to 40 MHz and down to a relative amplitude level of –180 dBc/Hz.
These graphs will provide a common format for comparing measurement techniques to the typical types of sources that
are measured. On the graph given here, L(f) is plotted for several types of oscillators ranging from a free-running VCO
(Agilent 8684A) to a highly-stable 10 MHz crystal oscillator used as the reference oscillator in many synthesized signal
generators. L(f) for the spectrum analyzers is overlayed on the graph to indicate which analyzer could be used to display the phase noise of typical sources.
Two measurement limitations for each spectrum analyzer are illustrated on this graph. The first is the analyzer’s internally generated noise floor. For the superheterodyne spectrum analyzers (Agilent 8566A/B, 8568A/B, and 3585A), the
phase noise of the analyzer’s synthesized local oscillator determines its sensitivity at offsets of less than approximately
1 MHz. Beyond a 1 MHz offset the noise of the analyzer’s IF circuitry sets its noise floor. The resolution of the Fourier
conversion and internal amplifiers determines the sensitivity of the 3582A. The second measurement limitation illustrated here is the minimum offset frequency specified by the analyzer. The superheterodyne spectrum analyzers are limited by their internal LO feedthrough to the IF Circuitry to a minimum offset of approximately 20 to 100 Hz. The 3582A
has measurement capability to within 0.2 Hz of the carrier due to the high resolution of its Fourier conversion process.
Page 13
13
Slide 11
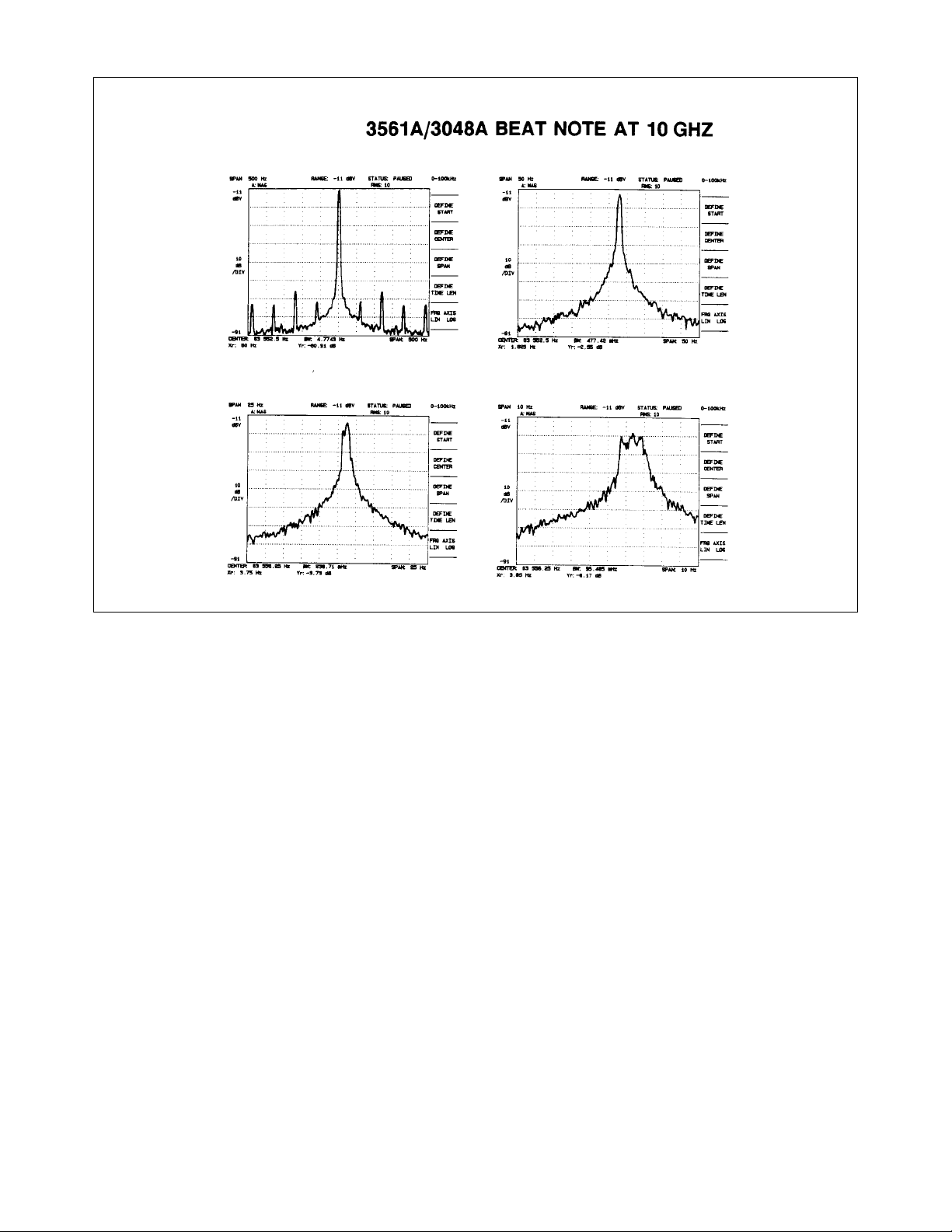
This is an example of the benefits of analyzing a microwave signal downconverted by the 11729C to an IF that is
then input for measurement on the 3561A Dynamic Signal Analyzer within the 3048A System. The measurement at the
upper left covers a 500 Hz span at 10.0 GHz and took approximately 1 second to complete on the 3561A. Sweeping the
8566A/B over the same range with a 10 Hz bandwidth would require 15 seconds during which any signal drift could
affect the results, and the resolution of low-level sidebands would be much more limited. Discrete sidebands are clearly
resolved with this technique. The frequency span can be decreased for better resolution until, as in the 10 Hz span of
the lower right plot, the carrier frequency is changing too much for this measure of single sideband phase noise to be
valid. The carrier instability exceeds the small angle criterion that L(f) depends on and a different measurement technique is required; one that determines the spectral density of the phase fluctuations rather than the power in the phase
noise sidebands.
Agilent
Page 14

14
Slide 12
This list summarizes the limitations of using the direct spectrum measurement technique to measure phase noise.
Spectrum analyzers are valuable tools and widely used for fast, qualitative looks at the stability of a signal.
Direct Spectrum
Measurement Limitations
• Cannot separate AM and PM noise
• AM noise must be << PM noise
• Inadequate dynamic range for many sources
• Cannot measure close in to a drifting carrier
• Valuable for qualitative quick evaluation
Page 15

15
Slide 13
Next let’s take a look at several measurement techniques that demodulate the phase fluctuations of the signal for
measurement and analysis.
Agenda
Basic Phase Noise Measurement Concepts
Direct Spectrum Measurement
* Demodulation Techniques
Phase Demodulator
Residual or Added Noise Measurements
Single Source Measurements
Phase Detector with Two Sources
Reference Source
Voltage Controlled Source Tuning Requirements
Measurement Optimization
Measurement Examples
Page 16

16
Slide 14
Listed here are several systems that demodulate the phase noise of the signal in different ways. The 5390A Frequency
Stability Analyzer translates counter readings of the frequency of a signal over a period of time into the equivalent level
of phase noise. The 8901A/B Modulation Analyzer and 8902A Measuring Receiver employ an FM discriminator to demodulate the phase noise of a signal. The 3048A Phase Noise Measurement System can be used in several ways to analyze
phase noise, one of which is with an internal phase detector to mix the signal under test with synthesized oscillator.
Demodulation Techniques Related
to Specific Instruments or Systems
Agilent 5390A Frequency Stability Analyzer
Agilent 8901A/B Modulation Analyzer
Agilent 8902A Measuring Receiver
Agilent 3048A Phase Noise Measurement System
Page 17

17
Slide 15
Although this system is now obsolete and cannot be ordered, it is instructive to examine the approach that was used
to measure phase noise. The counter in the system was used to measure the difference frequency of the signal under
test and a reference source. If the reference source is sufficiently more stable than the test signal and the test signal
does not drift during the measurement, variations of the difference frequency represent frequency (or phase) instability of the test signal. The system software compiles a series of readings of this difference frequency and calculates
the Allen or the Hadamard variance to determine the phase noise of the signal. This measurement approach can
yield phase noise data very close to the carrier with very good sensitivity if a low frequency beatnote is used.
Several significant limitations are inherent with this measurement technique. One is that the two sources used must be
offset to produce the beatnote to be counted. To overcome this problem, an option to the system was created to add a
second mixer such that the two oscillators of the same frequency to be compared were mixed with a third source at a
different frequency. With this variation the difference in period of the two beatnotes is measured and translated into
the corresponding phase noise. If the sources were of equal stability the result would be the combined phase noise of
both sources (the instability of the third source cancels out with this method).
To produce a valid phase noise measurement this system required a nondrifting signal to measure. Also, as this is
essentially a digital form of phase noise measurement with a series of discrete readings, aliasing is encountered such
that data at high offset frequencies is folded down to lower offsets according to the measurement rate. This aliasing of
the high offset phase noise would increase the phase noise readings at low offsets. This produced a requirement that
the phase noise of the signal under test be decreasing rapidly as the offset frequency increases so that the phase noise
power folded over to the lower offsets would not be significant.
Agilent
Agilent
Agilent
Agilent
Agilent
Page 18
18
Slide 16
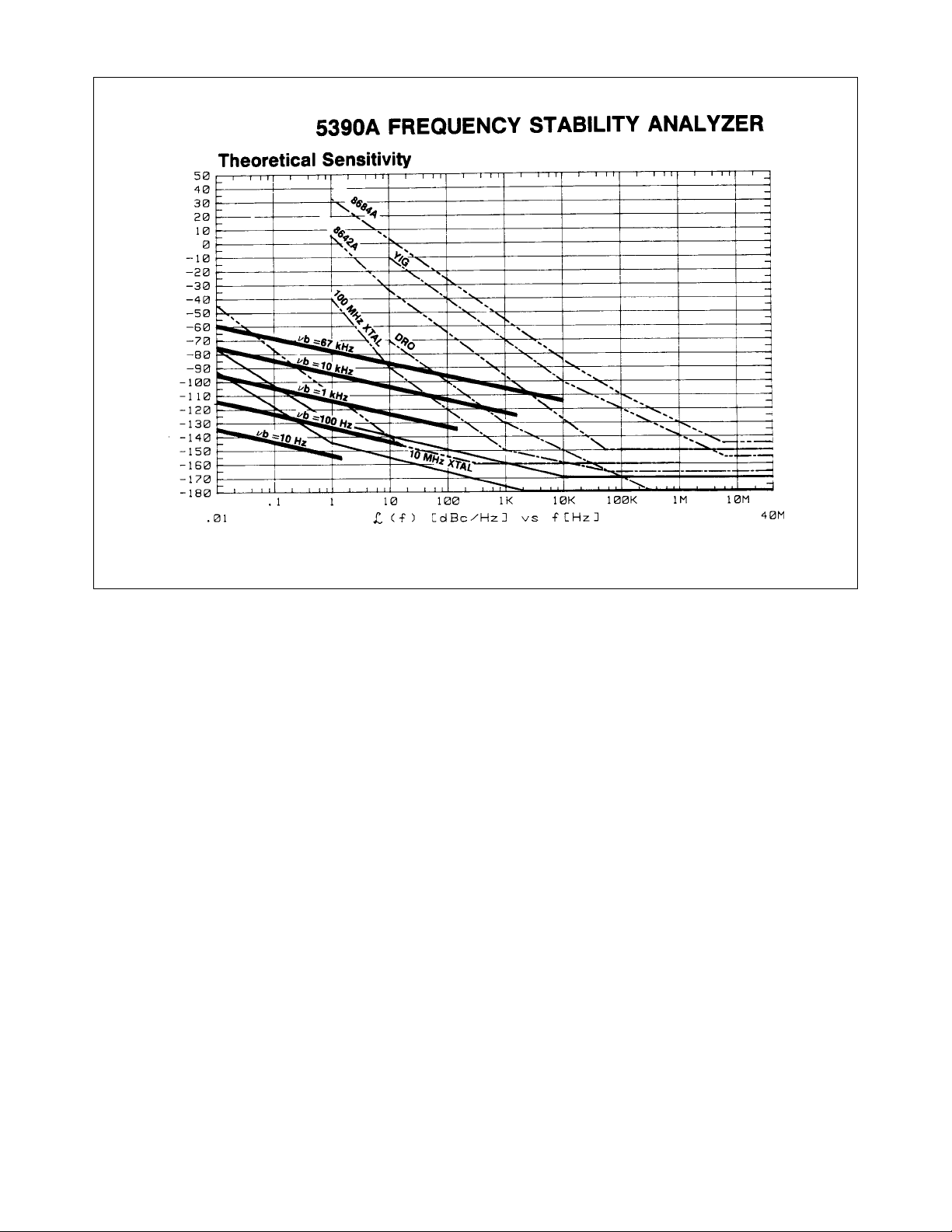
The sensitivity of the 5390A System and the offset range that could be measured were a function of the beatnote
frequency that was used. Excellent sensitivity was available with a beatnote of 10 Hz but the offset range was limited
to less than 1.6 Hz. This limitation is acceptable for measuring precision frequency oscillators used as time standards.
With increasing beatnote frequency, the 5390A System had a range of usefulness for measuring various sources but in
general could not produce a phase noise measurement out to the noise f loor of the oscillator under test.
Agilent
Page 19
19
Slide 17
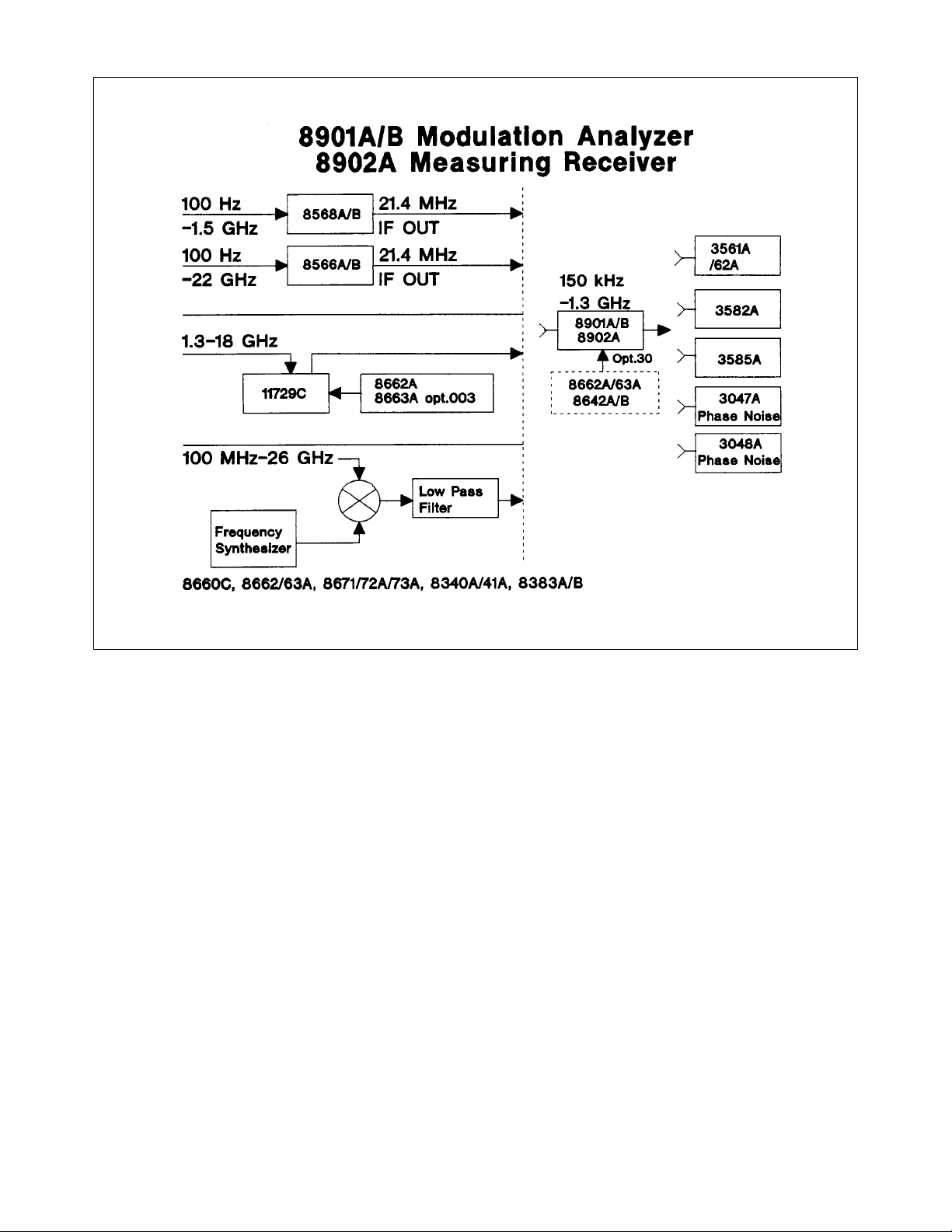
The 8901A/B Modulation Analyzer and 8902A Measuring Receiver convert the frequency fluctuations of a signal into
voltage variations with a frequency discriminator. The discriminator output can be connected to a spectrum analyzer
for a display of the spectral density of the phase noise over a range of offset frequencies or the noise can be integrated
over a bandwidth. A correction is made for the calibration constant of the discriminator to achieve calibration. This
calibration constant can be entered into the Agilent 3047A or 3048A System software for an automatically calibrated
output. The phase noise of the 8901A/B or 8902A Internal Local Oscillator is lowest for an input frequency below
300 MHz. For signals below 300 MHz the 8901A/B or 8902A sensitivity is maximized as is indicated on the next slide
of system sensitivity. An advantage of using a frequency discriminator approach as with the 8901A/B or 8902A is that
a certain amount of signal drift can be tolerated in making a valid measurement of the spectral density of phase noise.
Shown here are several methods for downconverting signals into the range of the 8901A/B or 8902A.
Page 20
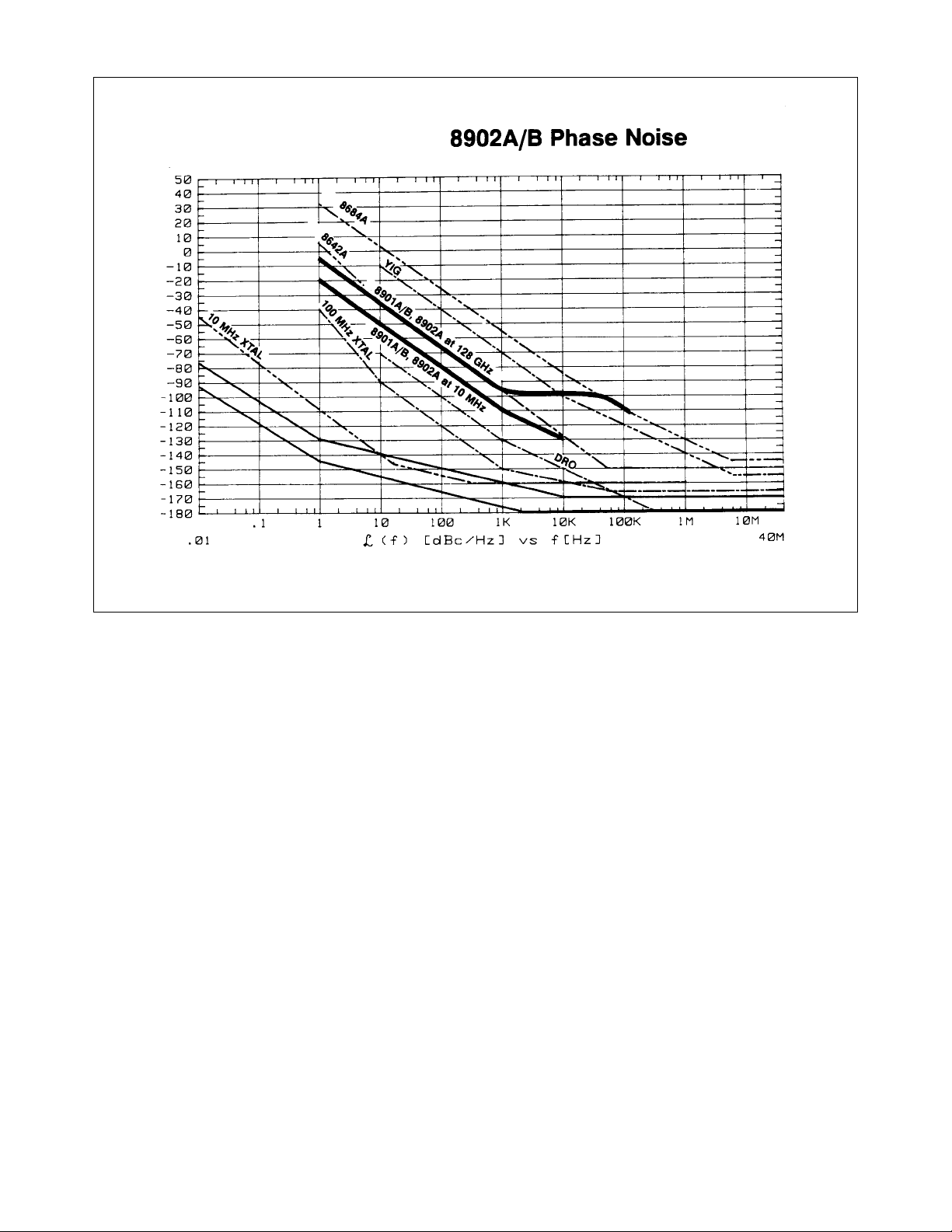
20
Slide 18
The curve for the 8901A/B or 8902A at 10 MHz on this graph is the sensitivity of the discriminator used in the analyzer
and actually extends to an offset of approximately 200 kHz for input signals above 10 MHz. At 1.28 GHz the phase noise
of the internal local oscillator of the 8901A/B or 8902A limits the sensitivity. This sensitivity is sufficient to measure
the phase noise of some free-running oscillators as indicated.
Agilent
Page 21

21
Slide 19
Now we’ll take a look at the phase demodulator technique used by the Agilent 3048A Phase Noise Measurement System.
Whereas the previous phase noise measurement techniques were useful within certain limits of signal stability, offset
ranges, and sensitivity levels, the phase demodulation technique used by the 3048A System has the broadest range of
applications of any system available today.
Agenda
Basic Phase Noise Measurement Concepts
Direct Spectrum Measurement
Demodulation Techniques
* Phase Demodulator
Residual or Added Noise Measurements
Single Source Measurements
Phase Detector with Two Sources
Reference Source
Voltage Controlled Source Tuning Requirements
Measurement Optimization
Measurement Examples
Page 22

22
Slide 20
A doubly balanced mixer is used as a phase detector as diagramed in this slide. The two signals are input to the mixer
at the same frequency but with 90° of phase difference. Any phase fluctuation that is not common to both signals,
i.e., ø(t), results in a voltage fluctuation from the mixer proportional to the phase difference if the phase f luctuations
are less than approximately 0.2 radian. This voltage output, V
n
(t), is equal to the difference phase fluctuation multiplied
by a constant, here labeled K
ø
, that is the phase slope of the mixer in units of volts per radian. The spectral density of
the phase fluctuations, S
ø
(f), is calculated by measuring the spectral density of the voltage f luctuations, Sn(f), and
dividing it by the square of the phase detector constant (squared due to the power relationship of spectral density).
The spectral density of the frequency fluctuations, S
v
(f), and the single sideband phase noise power, L(f), can be calcu-
lated as previously explained.
L
Page 23

23
Slide 21
An advantage of the phase detector method of measuring phase noise is the ease of determining the system’s noise
floor. By dividing a test signal with a power splitter and phase shifting the signal in one path by 90°, the signal from
each path enters the mixer in quadrature with each signal’s phase f luctuations correlated to the other. The output of
the mixer will remain 0 volts and the noise that is measured by the system’s analyzers is the system’s own internal
noise. This method of determining the system’s sensitivity supplies the phase detector mixer with the high level signals
that are present during normal operation without adding any noise.
Several cautions must be observed when performing this system noise floor measurement. One is that the AM noise of
the source may not be rejected sufficiently by the double-balanced mixer. The low frequency mixer of the 3048A system
has approximately 30 dB of AM noise rejection. Wide frequency range microwave mixers such as the high frequency
mixer of the 3048A are not as well balanced and the AM rejection can be much less than expected. A measurement of
the AM noise of the source and comparison to the phase noise measured can verify the AM rejection of the mixer.
Another caution that should be heeded is that the delay difference of the two signal paths be minimized to ensure the
noise through each remains as correlated as possible. At high offset frequencies even a minimal amount of delay difference will decorrelate the source’s noise and mask the system’s noise floor.
Page 24

24
Slide 22
This graph of the resulting noise floor of the phase detector method of the 3048A System demonstrates why this
method has the most usefulness for measuring the widest range of sources. The system’s typical sensitivity allows
measurement of even the cleanest of reference oscillators.
Agilent
Page 25

25
Slide 23
One application of the phase detector method of phase noise measurement is to quantify the amount of noise added to
a signal as it passes through a device. This added noise is referred to as residual noise.
Agenda
Basic Phase Noise Measurement Concepts
Direct Spectrum Measurement
Demodulation Techniques
Phase Demodulator
* Residual or Added Noise Measurements
Single Source Measurements
Phase Detector with Two Sources
Reference Source
Voltage Controlled Source Tuning Requirements
Measurement Optimization
Measurement Examples
Page 26

26
Slide 24
Using almost the same technique that was used to determine the system noise f loor, the noise added to a signal by a
device can be measured. A single frequency signal processor (i.e., an amplifier), a surface acoustic wave (SAW) delay
line, a ferrite phase shifter, etc., is inserted in one path to the phase detector and an adjustable phase shifter is placed
in the other. The phase shifter is adjusted to bring the two signals into quadrature. The noise measured by the
system will be the added noise of the device if it is above the system noise f loor.
Care must be taken that the delay of the device under test (DUT) is not so long that the phase noise of the source in that
path is decorrelated from the other path. Longer delay lines will decrease the maximum offset the phase noise can be
measured to or require a quieter source. Another thing to keep in mind is that any filtering of noise by the DUT will
affect the results of the measurement.
Page 27

27
Slide 25
If the device that is measured performs a translation of the input frequency to another frequency (i.e., a mixer), multiplier or divider, etc., two of the devices must be used with one placed in each signal path. The resulting noise that is
measured will be the RMS sum of the noise added by both devices. Although the noise of one device cannot be separated from that of the other device with a single measurement, important information is revealed by the measurement.
The measured noise will be the maximum noise of either device, and at any particular offset frequency the noise of one
of the devices will be at least 3 dB lower. If three of these devices with similar noise performance are available, the
three source comparison mode of the Agilent 3048A software will separate the noise of each device for individual
analysis. If one of the devices is appreciably lower (approximately 3 to 6 dB lower) than the others, its lower noise performance will still be indicated although its added noise cannot be accurately separated from the higher noise of the
other devices.
Page 28

28
Slide 26
Another application of the phase detector method is in combination with a delay line to form a frequency discriminator. This approach permits the measurement of the noise of a source without a separate lower noise source to serve
as a reference. It is also useful for measuring sources that have a high amount of drift and therefore may not be readily
tracked by a phase-lock-loop to maintain quadrature with a reference source.
Agenda
Basic Phase Noise Measurement Concepts
Direct Spectrum Measurement
Demodulation Techniques
Phase Demodulator
Residual or Added Noise Measurements
* Single Source Measurements
Phase Detector with Two Sources
Reference Source
Voltage Controlled Source Tuning Requirements
Measurement Optimization
Measurement Examples
Page 29

29
Slide 27
In the previous example of measuring the residual noise of devices, it was important to keep the delay in both signalpaths as equal as possible so the source noise would remain correlated and cancel at the phase detector. By adding a
device causing a transmission delay in one path to uncorrelate the noise, we can measure the phase noise of the
source. The delay line converts frequency fluctuations of the source into phase fluctuations relative to the signal at
the other port of the phase detector. The phase detector then converts the phase f luctuations into their voltage equivalent for measurement and analysis. The discriminator constant, K
d
, of the combination of the delay line and the
phase detector is calculated from the phase slope constant of the phase detector, K
ø
, and amount of delay, τ, that was
added. Note that the discriminator constant K
d
is independent of offset frequency f for f ≤1/2 πτ. Measurement at
higher offset frequencies requires correction for the sin(πfτ)/πfτ term.
Page 30

30
Slide 28
The frequency discriminator constant, K
d,
is used to calibrate the system for the spectral density of the frequency
fluctuations, S
v
(f), that the measured spectral density of the voltage fluctuations Sn(f) represents. The conversion to
the spectral density of the phase fluctuations, S
ø
(f), and the single sideband phase noise, L(f), is straightforward and
indicates the sensitivity a frequency discriminator system will have. The offset frequency squared term, f
2
, in the
denominator indicates the system sensitivity will increase by 20 dB per decade as the offset frequency of the measurement increases. The sensitivity gets better until it equals the sensitivity of the phase detector at an offset frequency of
1
/2 πτ. The calibration of the system from the frequency discriminator constant, K
d,
is valid up to an offset frequency of
one-half the inverse of the delay if the phase noise cancellation between the two paths is corrected for.
L
Page 31

31
Slide 29
The dependence of a frequency discriminator’s sensitivity on the offset frequency is obvious from this graph of
systems with different delays. By comparing the sensitivity specified for the phase detector of the 3048A System
to the delay line sensitivity, it is apparent the delay line sensitivity is “tipped up” by 20 dB/decade beginning at an
offset of
1
/2 πτ. For a 10 nanosecond delay, the offset frequency where the sensitivity equals that of the phase detector
is one-half the inverse of 10 x 10
-9
x π or approximately 16 MHz. At an offset of 16 kHz or three decades less, the
10 nanosecond delay line sensitivity is 60 dB (20 dB/decade) less than that of the phase detector or approximately
–110 dBc/Hz.
The sensitivity graphs indicate the delay line frequency discriminator can be used to measure some types of sources
with useful sensitivity. Longer delay lines will improve the sensitivity, but eventually the loss in the delay line will
exceed the source power available and cancel any further improvement. Also, longer delay lines limit the maximum
offset frequency that can be measured.
Page 32

32
Slide 30
To utilize the full sensitivity of the phase detector method of phase noise measurements, two sources at the same frequency are needed to demodulate the phase noise for baseband analysis. This is the next technique that is examined.
Agenda
Basic Phase Noise Measurement Concepts
Direct Spectrum Measurement
Demodulation Techniques
Phase Demodulator
Residual or Added Noise Measurements
Single Source Measurements
* Phase Detector with Two Sources
Reference Source
Voltage Controlled Source Tuning Requirements
Measurement Optimization
Measurement Examples
Page 33

33
Slide 31
The simplest configuration for measuring the phase noise of a signal using two sources is diagrammed on this slide.
The two signals are set to the same frequency and 90° out of phase with respect to one another. The reference signal
should have less noise than the signal under test, otherwise the sum of the noise of the two sources will be measured.
The range of offset frequencies that can be measured is only limited by the low-pass filter and the analyzer that is used.
The usefulness of this configuration is limited, however, as very few sources have the stability to remain in quadrature
for the duration of the measurement.
Agilent
Page 34

34
Slide 32
Adding a phase-lock-loop to the previous configuration provides the necessary feedback to one of the sources in order
to maintain quadrature. Either source can be controlled by the loop as the effect on the measurement is the same. Since
a phase-lock-loop suppresses the phase noise within the loop bandwidth, measurements are limited to offsets greater
than the loop bandwidth or the results must be corrected to remove the effect of the phase-lock-loop.
Agilent
Page 35

35
Slide 33
The 3048A System sets up a phase-lock-loop based on the parameters that are entered for the tuning range and sensitivity of the source that is controlled, and the sensitivity of the phase detector that is used. A theoretical response is calculated from the entered parameters and used to correct for the response of the loop bandwidth.
The dynamic response of the loop can also be verified by injecting a signal from the noise source of the Agilent 3561A
Dynamic Signal Analyzer and measuring the control voltage from the loop as it compensates for the injected voltage.
This measured data can be compared to the calculated loop response at several points. If differences between the calculated and measured response are beyond a specified limit an estimate of the accuracy spec degradation is made to
advise the system operator. The operator can then decide to proceed with the calculated or corrected response, or abort
the measurement and correct any problems.
With the system correcting for the response of the loop bandwidth, the range of offset frequencies that phase noise
can be measured over extends from 0.01 Hz to 40 MHz. The independence of the offset range to be measured from the
effects of the phase-lock-loop necessary to stabilize the source allows the system to measure a wide variety of sources
with excellent accuracy.
Page 36

36
Agenda
Basic Phase Noise Measurement Concepts
Direct Spectrum Measurement
Demodulation Techniques
Phase Demodulator
Residual or Added Noise Measurements
Single Source Measurements
Phase Detector with Two Sources
* Reference Source
Voltage Controlled Source Tuning Requirements
Measurement Optimization
Measurement Examples
Slide 34
As the reference oscillator is a key element of the two source configuration of the phase detector method, its required
characteristics will be examined next. Also, several possible variations of the downconversion process to produce the
demodulated voltage output from the phase detector are presented.
Page 37

37
Slide 35
The most important (and obvious) criterion for choosing a reference source is that its phase noise be less than what
is being measured. A margin of 10 dB is sufficient to ensure the measurement results are not significantly affected.
If a reference source with low enough phase noise to measure the full offset range is not available, several alternatives
are available. One option is to use several reference sources with sufficiently low noise at specific offset ranges.
Another method would be to use a reference source comparable to the source under test so that the measurement
results can be attributed to the noise from both sources. With three comparable sources, the software of the Agilent
3048A System will separate the phase noise from each source based on the results of three dependent measurements.
Whatever the hardware configuration, at least one of the sources must be tunable so that phase lock can be achieved
and maintained. The only exception to this rule is when an interpolation oscillator is used to demodulate the phase
noise of the test signal as explained next.
Reference Source Considerations
Ideally phase noise 10 dB below source under test
for all f of interest.
Practical Alternatives:
Different reference sources for different f.
Reference source comparable to source under test.
Three comparable sources and three source comparison
software.
Either source under test or reference source must be
tunable with one exception, phase locked interpolation
oscillator.
Page 38

38
Slide 36
Using an interpolation oscillator as diagramed on this slide simplifies the measurement of low-noise microwave signals
that cannot be tuned or where tuning would increase the phase noise of the signal. A reference source downconverts
the signal under test to an IF. At this lower frequency an interpolation oscillator set to the IF is phase locked by the
system to demodulate the phase noise on the downconverted signal. Several advantages are present with this configuration. The most important is the increased availability of appropriate sources for the downconversion and demodulation
functions of the process. The reference source can be a very clean, filtered multiple of the low frequency, low-noise
oscillator without any phase noise degradation due to a dc FM capability. This translates the phase noise of the signal
under test to the IF without adding reference noise. Then an interpolation oscillator is chosen for a combination of
sufficiently low noise and dc FM capability to track the source under test at an RF instead of a microwave frequency.
This approach using an interpolation oscillator can be used at any frequency extending into the millimeter region
depending on the availability of a mixer for the downconversion. The Agilent 11729C was developed to specifically provide the low-noise reference signal and the downconversion for signals up to 18 GHz, 11729C Option H33 provides a
downconversion process for signals up to 105 GHz.
Page 39

39
Slide 37
This is a block diagram of the 11729C Carrier Noise Test Set. A step recovery diode within the harmonic generator
creates multiples of a very low noise 640 MHz signal available from an Agilent 8662A or 8663A Option 003 Signal Generator (or from its internal SAW oscillator). These multiples are further filtered before entering a 2 to 18 GHz microwave mixer for downconverting the signal under test. The resulting IF signal is mixed with the interpolation signal from
the front panel output of the 8662A or 8663A. At this RF frequency the signal from the 8662A or 8663A usually has
lower phase noise than the downconverted microwave signal. Quadrature can be maintained through the use of a dc FM,
electronic frequency control (EFC), or an external 10 MHz timebase with wide tuning range available from the 3048A
interface. The phase demodulation of the IF can be done in the 3048A for fully automatic measurements over
an offset range of 0.01 Hz to 40 MHz from the carrier.
Page 40

40
Slide 38
This graph indicates the level of phase noise that has been measured for several potential reference sources.
Depending on the sensitivity that is required at the offset to be measured, a single reference source may suffice or
several different references may be needed to achieve the necessary sensitivity at different offsets.
Page 41

41
Slide 39
There are several considerations that need to be made concerning phase locking of various sources. The next section
covers the drift limits, phase-lock-loop bandwidths, and the tuning range required of the source by the Agilent 3048A
System.
Agenda
Basic Phase Noise Measurement Concepts
Direct Spectrum Measurement
Demodulation Techniques
Phase Demodulator
Residual or Added Noise Measurements
Single Source Measurements
Phase Detector with Two Sources
Reference Source
* Voltage Controlled Source Tuning Requirements
Measurement Optimization
Measurement Examples
Page 42

42
Slide 40
The maximum tuning voltage and the tuning slope of the source to be controlled by the phase-lock-loop determines
the characteristics of the loop set up by the system. After the user’s entry of the maximum tuning voltage, the system
measures the source tuning characteristic to ensure the phase-lock-loop can be set up and maintained during the
measurement. The system software also determines the correction factor needed to remove the effects of the phaselock-loop on the amplitude of the measured noise. When the maximum tuning voltage and the tuning slope of the
source are known, the peak tuning range, PTR, of the source is calculated. The system was designed to work with
peak tuning ranges of 0.1 Hz to 200 MHz to accommodate sources ranging from crystal reference oscillators to freerunning VCO’s.
The tuning range the system actually uses to maintain quadrature is limited to a fraction of the peak tuning range to
ensure the tuning slope is well behaved and the correction factor that was calibrated remains accurate. After phase
lock is established, the system monitors the tuning voltage required to maintain lock during calibration and measurement. If the tuning voltage has exceeded 10% of the peak tuning range when system calibration is done and the measurement is to begin, the system stops the procedure and informs the user that the source needs to be retuned before
the measurement can begin. If the tuning voltage exceeds 20% of the peak tuning range before the measurement is completed, the system again informs the user and requests the oscillator be retuned or the problem be otherwise corrected
before proceeding with the measurement. These limits have been found to guarantee good results even for sources with
very wide or complex tuning voltages.
(I)
Page 43

43
Slide 41
This graph outlines the voltage tuning range the system can provide for a given center voltage. The range of maximum
tuning voltage decreases as the absolute value of the center voltage increases due to hardware limitations of the system. As an example, for a source needing a bias voltage of 2 volts the system cannot provide a maximum tuning range
of less than ±1 volt or more than ±10 volts.
Page 44

44
Slide 42
The closed loop bandwidth of the phase-lock-loop, here labeled PLL BW, is determined from the peak tuning range,
PTR, that the system has calculated. A closed loop bandwidth can be set up by the system with a 3 dB bandwidth of
between 0.1 Hz and 160 kHz depending on the maximum tuning range that is available. For the phase-lock-loop to
be stable, the bandwidth of the tuning port of the source must be greater than the closed phase-lock-loop bandwidth.
Another criterion that must be met for a usable phase-lock-loop to be created is that there must be adequate source
isolation between the two sources to prevent injection locking of one source to the other. Adding buffer amplifiers
between one source and the mixer will generally provide sufficient isolation.
Voltage Controlled Source Tuning
Requirements (II)
For .1 Hz ≤ PTR ≤ 200 MHz
.1 Hz ≤ PLL BW ≤ 160 kHz
where PLL BW = closed phase-lock-loop
bandwidth
For a stable phase-lock-loop:
voltage controlled source tuning
port bandwidth > PLL BW
Source isolation such that
injection locking bandwidth << PLL BW
Page 45

45
Slide 43
This graph illustrates the closed phase-lock-loop bandwidth chosen by the system as a function of the peak tuning
range of the source. Knowing the approximate closed phase-lock-loop bandwidth allows the user to verify that there is
sufficient bandwidth on the tuning port and whether sufficient source isolation is present to prevent injection locking.
Page 46

46
Slide 44
Meeting the requirements for the tuned source that were just covered will result in a stable phase-lock-loop for measuring most sources, particularly free-running oscillators. An additional requirement is necessary when the source
has a high phase-noise pedestal that may extend beyond the closed bandwidth of the phase-lock-loop. As the bandwidth of the phase-lock-loop is determined by the tuning range that is entered, this high phase-noise pedestal may
determine the tuning range that is necessary to enable a stable phase-lock-loop.
Voltage Controlled Source Tuning
Requirements (III)
For almost all sources without a high
phase noise pedestal, satisfying the
preceding requirements will result in
a stable phase-lock-loop.
The allowable phase noise pedestal is
primarily a function of the peak tuning
range, PTR, and therefore may set the
source tuning range requirements.
Page 47

47
Tuning Characteristics of Various VCO Source Options
Carrier Tuning Center Voltage Input Calibration
VCO Source Freq. Constant Voltage Tuning Resistance Method
(Hz/V) (V) Range (±V) (ohms)
8662/3A
EFC v
o
5 x 10-9x v
o
0 10 1 E 6 Measure
DCFM FM Deviation 0 10 1k/600 Use Entered
8642A/B FM Deviation 0 10 600 Use Entered
8640B FM Deviation 0 10 600 Use Entered
8656B FM Deviation 0 10 600 Use Entered
Other Signal Generator
DCFM Calibrated FM Deviation 0 10 R
in
Use Entered
to ±1V
10 MHz Source A
Direct 10 0 10 1 E 6
Multiplied v
o
10 x vo÷ 10 E 6 0 10 1 E 6
As a Timebase: Measure
To 8662/3A v
o
10 x vo÷ 10 E 6 0 1010÷ v
o
1 E6
To other VCO
(PTR known) v
o
10 x vo÷ 10 E 6 0 106x PTR ÷ v
o
1 E6
10 MHz Source B
Direct 100 0 10 1 E 6
Multiplied v
o
100 x vo÷ 10 E 6 0 10 1 E 6
As a Timebase: Measure
To 8662/3A v
o
100 x vo÷ 10 E 6 0 109÷ vo, 2.5 1 E 6
To other VCO
(PTR known) v
o
100 x vo÷ 10 E 6 105x PTR ÷ v
o
350-500 MHz Source 12 E 6 0 2 1 E 6 Measure
Estimated –10
Other User VCO Source within a factor of 2 to +10 See Slide 41. 1 E 6 Measure
Slide 45
This table lists the tuning parameters for several VCO source options. If a 10 MHz oscillator from the Agilent 3048A
interface is used as an external, tunable timebase to an Agilent 8662A or 8663A, the tuning constant (Hz/volt) and the
voltage tuning range must be calculated to account for multiplication to the front panel frequency.
Page 48

48
Slide 46
This graph provides a comparison between the typical phase noise expected of a variety of sources and the minimum
tuning range that is necessary for the system to create a phase-lock-loop of sufficient bandwidth to make the
measurement. In general, the sources with higher phase noise that require a wider tuning range are usually designed
to provide the necessary tuning range due to the application for which they are intended.
Page 49

49
Slide 47
While the Agilent 3048A System will make measurements of the phase noise of sources with a wide variety of characteristics, there are techniques to optimize the measurements for better results, as are explained next.
Agenda
Basic Phase Noise Measurement Concepts
Direct Spectrum Measurement
Demodulation Techniques
Phase Demodulator
Residual or Added Noise Measurements
Single Source Measurements
Phase Detector with Two Sources
Reference Source
Voltage Controlled Source Tuning Requirements
* Measurement Optimization
Measurement Examples
Page 50

50
Slide 48
The sensitivity of the Agilent 3048A System can be improved by increasing the signal power at the R port of the phase
detector. This graph illustrates the approximate noise floor of the system for a range of R port signal levels from –15 dBm to
+15 dBm. The diagonal line on the left side indicates the approximate sensitivity for offsets greater than 10 kHz without
the system’s low noise amplifier in the signal path. The right diagonal line indicates the sensitivity with the amplifier
in. These estimates of sensitivity assume the signal level at the L port is appropriate for either the microwave or the RF
mixer that is used (+7 dBm or +15 dBm, respectively). The approximate calibration constant, K
ø
, that results from the
input signal level at the R port is also given.
Page 51

51
Slide 49
As the tuning port of an oscillator is a very sensitive input for adding noise to its signal, it is important to know the
level of noise that could be added by the 3048A System from the phase-lock-loop control voltage. The dark lines of this
graph are the equivalent phase noise due to the internal noise of the system at the tuning voltage control port for the
maximum tuning range entered for the source. A tuning voltage of ±10 volts and phase slope calibration constant
of 0.2V/rad is assumed. By comparing the noise caused by the system to the maximum noise level that the phase-lockloop can tolerate (as plotted in the upper part of the graph), a usable measurement range can be determined. As an
example, should the source to be tested require a tuning range of 125 kHz, the dark line labeled 125 kHz is the minimum phase noise that can be measured due to the system-induced noise at the tuning port of the source.
Agilent
Page 52

52
Slide 50
This graph plots the typical phase noise of various sources on the previous graph for comparison with the system’s
measurement limits of tuning range for the phase-lock-loop and system-added noise on the tuning line. In almost all
cases, as is illustrated here, the system’s added noise is significantly less than the phase noise expected of an oscillator
from its maximum tuning range that is used to create a stable phase-lock-loop. Looking at the 8684A with a tuning
range ±10 MHz as an example, its typical phase noise at 10 kHz is approximately –76 dBc/Hz. The system would set a
peak tuning range, PTR, of between 5 to 10 MHz to maintain phase lock with this source. For a PTR of 5 MHz the system-added noise will be approximately –132 dBc/Hz which is 56 dB less than the level to be measured.
Page 53

53
Slide 51
This graph provides a comparison of the sensitivity that can be achieved with a delay line discriminator versus the
noise floor set by the system noise on the VCO control port. The sensitivity plotted for delay line lengths of 10 nanoseconds, 100 nanoseconds, and 1 microsecond assumes the use of the phase detector of the 3048A System with the
delay line. Using the delay line avoids the addition of noise on the source tuning port but, as the graph indicates, the
measurement sensitivity is about the same in either case.
Page 54

54
Slide 52
A few measurement examples that illustrate the various measurement techniques follow.
Agenda
Basic Phase Noise Measurement Concepts
Direct Spectrum Measurement
Demodulation Techniques
Phase Demodulator
Residual or Added Noise Measurements
Single Source Measurements
Phase Detector with Two Sources
Reference Source
Voltage Controlled Source Tuning Requirements
Measurement Optimization
* Measurement Examples
Page 55

55
Slide 53
This is a measurement of the Agilent 3048A System noise floor. Quadrature was established by adding a short piece of
coax to one signal path and fine-tuning the source frequency. The calibration constant was determined from the input
signal levels to the mixer.
Page 56

56
Slide 54
This is an example of the residual or added noise of an amplifier. There are a number of ways to calibrate residual
measurements; in this case a single sided spur was injected with known amplitude and offset for the system to measure
and reference the measured noise to. Notice the slight decorrelation of source noise beyond 10 MHz.
Page 57

57
Slide 55
This is an example of frequency discriminator measurement of the phase noise of an Agilent 8640B Signal Generator.
Three modes are available to calibrate the 3048A System for the delay line that is used. If the source can be modulated,
the system will calibrate from the known level of modulation. Alternately, it can be derived by the system from the
injection of a double-sided spur of known amplitude and offset, or the user can enter the discriminator constant, K
d
,
resulting from the combination of the delay line length and the phase detector constant. The maximum offset for a valid
measurement without correction is f = 1/(2) = 1/(2 x 109 nsec) = 1.46 MHz. At these offsets the noise on the two signals entering the two ports of the phase detector is exactly correlated and therefore cancels.
Page 58

58
Slide 56
Two 8663’s were measured against each other using a phase-lock-loop to maintain quadrature. The lower curve
was measured using the 8663A EFC control as the VCO tune port, the other using the dc FM input as the VCO tune
port. When dc FM is enabled, low close-in phase noise is traded for wide tuning range. The noise plotted here is
the sum of the noise of two 8663’s.
Agilent
Page 59

59
Slide 57
In this measurement an 8642B was measured against the rear panel 640 MHz signal from an Agilent 8663A. In the
lower curve the 8663A with the 10 MHz “A” timebase from the system interface was tuned to maintain quadrature;
dc FM on the 8642B was used in the other. Since the 640 MHz reference of the 8663A is much lower in phase noise
than the 8642B, this graph is a plot of the 8642B only.
Agilent
B
Page 60

60
Slide 58
This measurement was made of an 8673B Microwave Synthesizer that was initially downconverted with the Agilent
11729C Carrier Noise Test Set. An 8663A tuned using EFC was used to track and demodulate the resulting IF.
Agilent
Page 61

61
Slide 59
This measurement was made of a free-running GUNN Diode without voltage tuning capability. The signal was initially
downconverted using the 11729C. An 8663A tuned using dc FM was used to track and demodulate the resulting IF.
Page 62

62
Slide 60
The Agilent 3048A will measure the AM noise of a signal. Calibration is accomplished by injecting a modulation sideband of a known level for the system to measure and reference the measured noise to or by entering the detector
constant. An external diode detector is used to demodulate the noise from the signal for input directly to the lownoise amplifier of the system.
Page 63

63
REFERENCES
1) Ashley, R.J., et al., “The Measurement of Noise in Microwave Transmitters,” IEEE Transactions on Microwave
Theory and Techniques, Vol. MTT-25, No. 4, pp. 294-318 (April 1977).
2) Fischer, M., “An Overview of Modem Techniques for Measuring Spectral Purity,” Microwaves, Vol. 18, No. 7,
pp. 66-75, July 1979.
3) Hewlett-Packard staff, “Understanding and Measuring Phase Noise in the Frequency Domain,” Application Note
207, October 1976.
4) Hewlett-Packard staff, “Measuring Phase Noise with the HP 3585A Spectrum Analyzer,” Application Note 246-2,
May 1981.
5) Hewlett-Packard staff, “Low Phase Noise Applications of the HP 8662A and 8663A Synthesized Signal
Generators,” Application Note 283-3, December 1986.
6) Howe, D.A., “Frequency Domain Stability Measurements: A Tutorial Introduction,” NBS Technical Note 679,
March 1976.
7) Lance, A.L., Seal, W.D., Hudson, N.W., Mendoza, F.G., and Donald Halford, “Phase Noise Measurements Using
Cross-Spectrum Analysis,” Conference on Precision Electromagnetic Measurements, Ottawa, Canada, June 1978.
8) Ondria F.G., “A Microwave System for Measurements of AM and FM Noise Spectra,” IEEE Transactions on
Microwave Theory and Techniques, Vol. MTT-16, pp. 767-781, September 1968.
9) Scherer, Dieter, “Design Principles and Test Methods for Low Phase Noise RF and Microwave Sources,”
Hewlett-Packard RF and Microwave Measurement Symposium, October 1978. (Also edited version in Microwaves,
“Today's Lesson—Learn About Low-Noise Design,” part 1, pp. 116-122, April 1979, part 2, pp. 72-77, May 1979.)
10) Shoaf, J.H., Halford, D., Risley, A.S., “Frequency Stability Specification and Measurement: High Frequency and
Microwave Signals,” NBS Technical Note 632, January 1973.
11) Hewlett-Packard staff, “Phase Noise Characterization of Microwave Oscillators, Phase Detector Method,”
Product Note 11729B-1, March 1984.
12) Hewlett-Packard staff, “Phase Noise Characterization of Microwave Oscillators, Frequency Discriminator Method,”
Product Note 11729C-2, September 1985.
13) Kroupa, V.F., “Frequency Stability: Fundamentals and Measurement,” IEEE Press, (Order Number: PC 01644),1983.
14) Barnes, J.A., et al., “Characterization of Frequency Stability,” NBS Technical Note 394, October 1970.
15) Lesson, D.B., Johnson, G.F., “Short-Term Stability for a Doppler Radar. Requirements, Measurements and
Techniques,” Proceedings of the IEEE, Vol. 54, No. 2, pp. 244-248, (February 1966).
16) Gibbs, J., Prouty B., “Using Phase Noise Measurements to Improve Performance,” Microwave Journal, Vol. 24,
No. 12, pp. 47-54, December 1981.
17) Barnes, J.A., Chic, A.R., Cutter, L.S., et al., “Characterization of Frequency Stability,” IEEE Transactions on
Instrumentation and Measurement, Vol. IN-20, No. 2, pp. 105-20, May 1971.
18) Keshner, Marvin S., “L/f Noise,” Proceedings of the IEEE, Vol. 70, No. 3, pp. 212-218, March 1982.
19) Rutman, J., “Characterization of Phase and Frequency Instabilities in Precision Frequency Sources:
Fifteen Years of Progress,” Proceedings of the IEEE, Vol. 66, No. 9, pp. 1048-1075, September 1978.
20) McNamee, M. “Automate for Improved Phase-Noise Measurement,” Microwaves, pp. 80-85, May 1979.
21) Fischer, M., “Frequency Stability Measurement Procedures,” Hewlett-Packard Co., presented at the Eighth
Annual Precision Time and Time Interval Meeting, December 1976.
22) Burgoon, R., “Conversion Between Time and Frequency Domain of Intersection Points of Slopes of Various Noise
Processes,” Thirty-second Annual Frequency Control Symposium, pp. 514-519, May 1978.
23) Scherer, D., “The ‘Art’ of Phase Noise Measurements,” Hewlett-Packard RF and Microwave Symposium, May 1983.
24) Muat, R., Upham, A., “Low Noise Oscillator Design,” Hewlett-Packard RF and Microwave Symposium, March 1986.
25) Moulton, G., “Analysis and Prediction of Phase Noise in Resonators and Oscillators,” Hewlett-Packard RF and
Microwave Symposium, September 1985.
Page 64

By internet, phone, or fax, get assistance
with all your test and measurement needs.
Online Assistance
www.agilent.com/find/assist
Phone or Fax
United States:
(tel) 1 800 452 4844
Canada:
(tel) 1 877 894 4414
(fax) (905) 206 4120
Europe:
(tel) (31 20) 547 2323
(fax) (31 20) 547 2390
Japan:
(tel) (81) 426 56 7832
(fax) (81) 426 56 7840
Latin America:
(tel) (305) 269 7500
(fax) (305) 269 7599
Australia:
(tel) 1 800 629 485
(fax) (61 3) 9210 5947
New Zealand:
(tel) 0 800 738 378
(fax) (64 4) 495 8950
Asia Pacific:
(tel) (852) 3197 7777
(fax) (852) 2506 9284
Product specifications and descriptions in this
document subject to change without notice.
Copyright © 1999, 2000 Agilent Technologies
Printed in U.S.A. 9/00
1000-1118
 Loading...
Loading...