HIT HD74ACT283, HD74AC283 Datasheet
HD74AC283/HD74ACT283
4-bit Binary Full Adder with Fast Carry
Description
The HD74AC283/HD74ACT283 high-speed 4-bit binary full adder with internal carry lookahead accepts
two 4-bit binary works (A0 – A3, B0 – B3) and a Carry input (C0). It generates the binary Sum outputs (S0 –
S3) and the Carry output (C4) from the most significant bit. The HD74AC283/HD74ACT283 will operate
with either active High or active Low operands (positive or negative logic).
Features
• Outputs Source/Sink 24 mA
• HD74ACT283 has TTL-Cmpatible Inputs
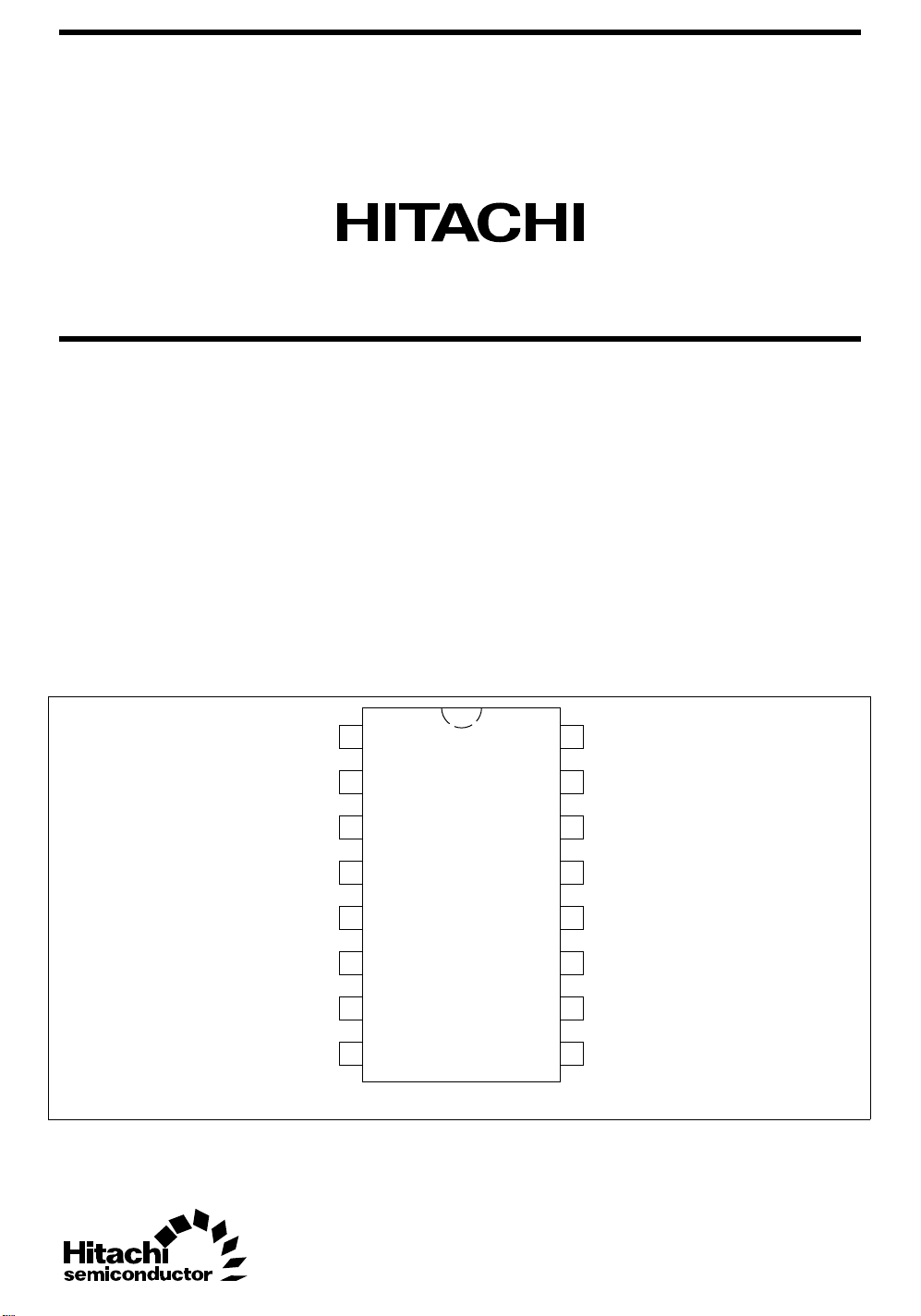
Pin Arrangement
S
B1
A1
S0
A0
B0
C0
GND
1
1
2
3
4
5
6
7
8
(Top view)
16
15
14
13
12
11
10
CC
V
B2
A2
S2
A3
B3
S3
9
C4
HD74AC283/HD74ACT283
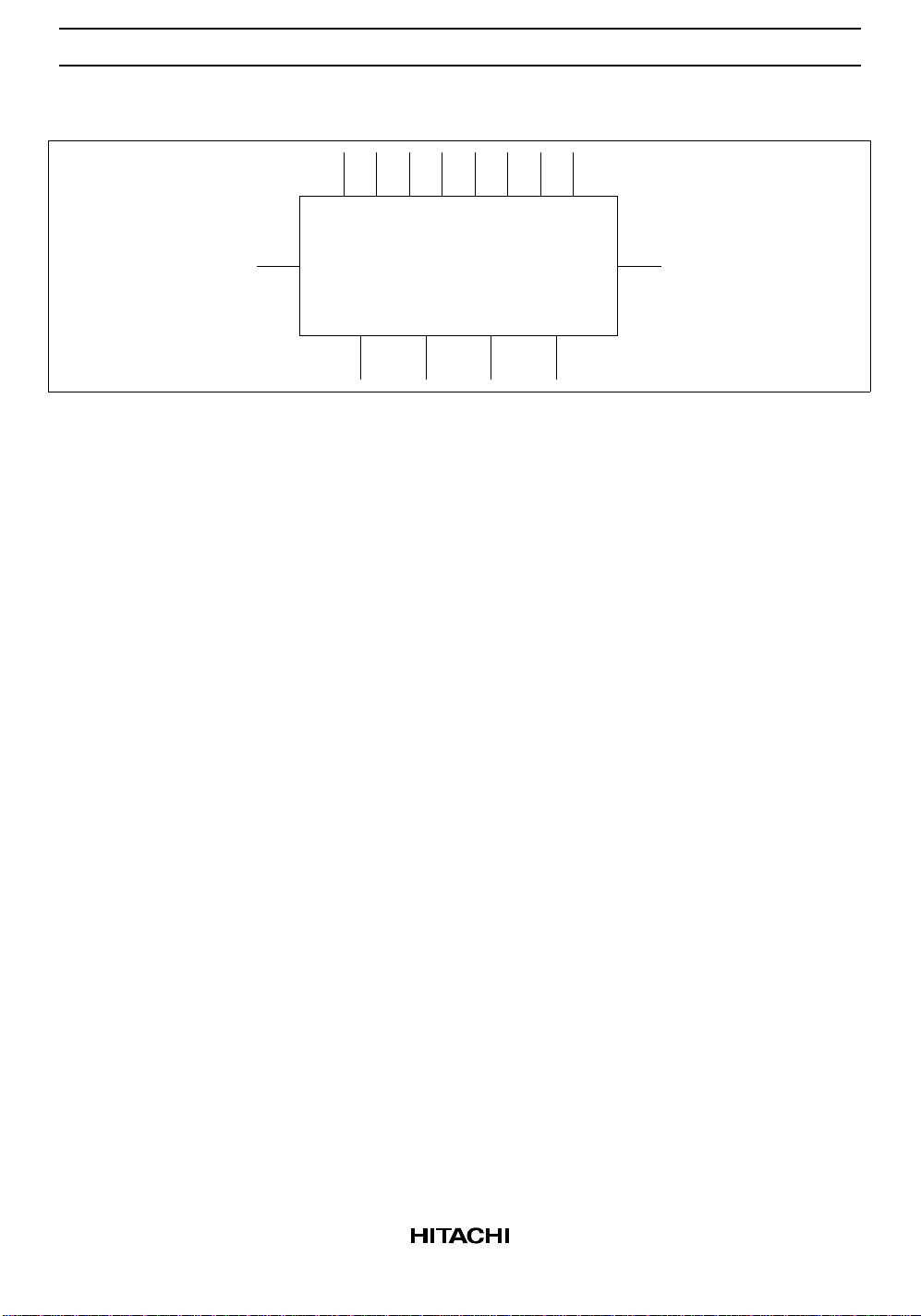
Logic Symbol
A0
C0 C4
A1
B0
S0 S1 S2 S3
B1
A2 A3
B2 B3
Pin Names
A0 – A3A Operand Inputs
B0 – B3B Operand Inputs
C
0
Carry Input
S0 – S3Sum Outputs
C
4
Carry Output
Functional Description
The HD74AC283/HD74ACT283 adds two 4-bit binary words (A plus B) plus the incoming Carry (C0).
The binary sum appears on the Sum (S0 – S3) and outgoing carry (C4) outputs. The binary weight of the
various inputs and outputs is indicated by the subscript numbers, representing powers of two.
20 (A0 + B0 + C0) + 21 (A1 + B1) + 22 (A2 + B2) + 23 (A3 + B3) = S0 + 2S1 + 4S2 + 8S3 + 16C
4
Where (+) = plus
Interchanging inputs of equal weight does not affect the operation. Thus C0, A0, B0 can be arbitrarily
assigned to pins 5, 6 and 7 for DIPS. Due to the symmetry of the binary add function, the
HD74AC283/HD74ACT283 can be used either with all inputs and outputs active High (positive logic) or
with all inputs and outputs active Low (negative logic). See Figure a. Note that if C0 is not used it must be
tied Low for active High logic or tied High for active Low logic.
Due to pin limitations, the intermediate carries of the HD74AC283/HD74ACT283 are not brought out for
use as inputs or outputs. However, other means can be used to effectively insert a carry into, or bring a
carry out from, an intermediate stage. Figure b shows how to make a 3-bit adder. Tying the operand inputs
of the fourth adder (A3, B3) Low makes S3 dependent only on, and equal to, the carry from the third adder.
Using somewhat the same principle Figure c shows a way of dividing the HD74AC283/HD74ACT283 into
a 2-bit and a 1-bit adder. The third stage adder (A2, B2, S2) is used merely as a means of getting a carry
(C10) signal into the fourth stage (via A2 and B2) and bringing out the carry from the second stage on S2.
Note that as long as A2 and B2 are the same, whether High or Low, they do not influence S2. Similarly,
when A2 and B2 are the same the carry into the third stage does not influence the carry out of the third
2
HD74AC283/HD74ACT283
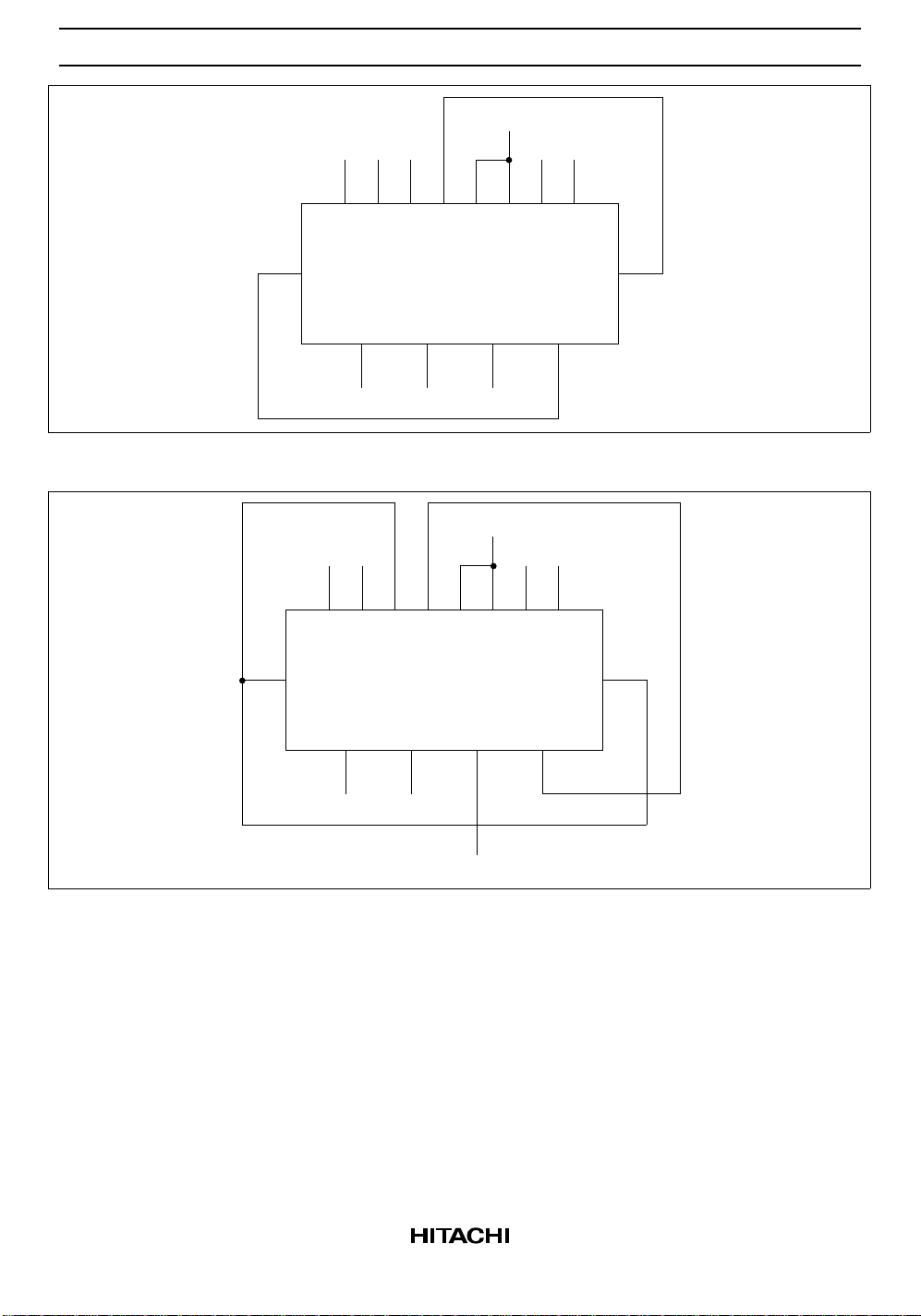
stage. Figure d shows a method of implementing a 5-input encoder, where the inputs are equally weighted.
The outputs S0, S1 and S2 present a binary number equal to the number of inputs I1 – I5 that are true. Figure
e shows one method of implementing a 5-input majority gate. When three or more of the inputs I1 – I5 are
true, the output M5 is true.
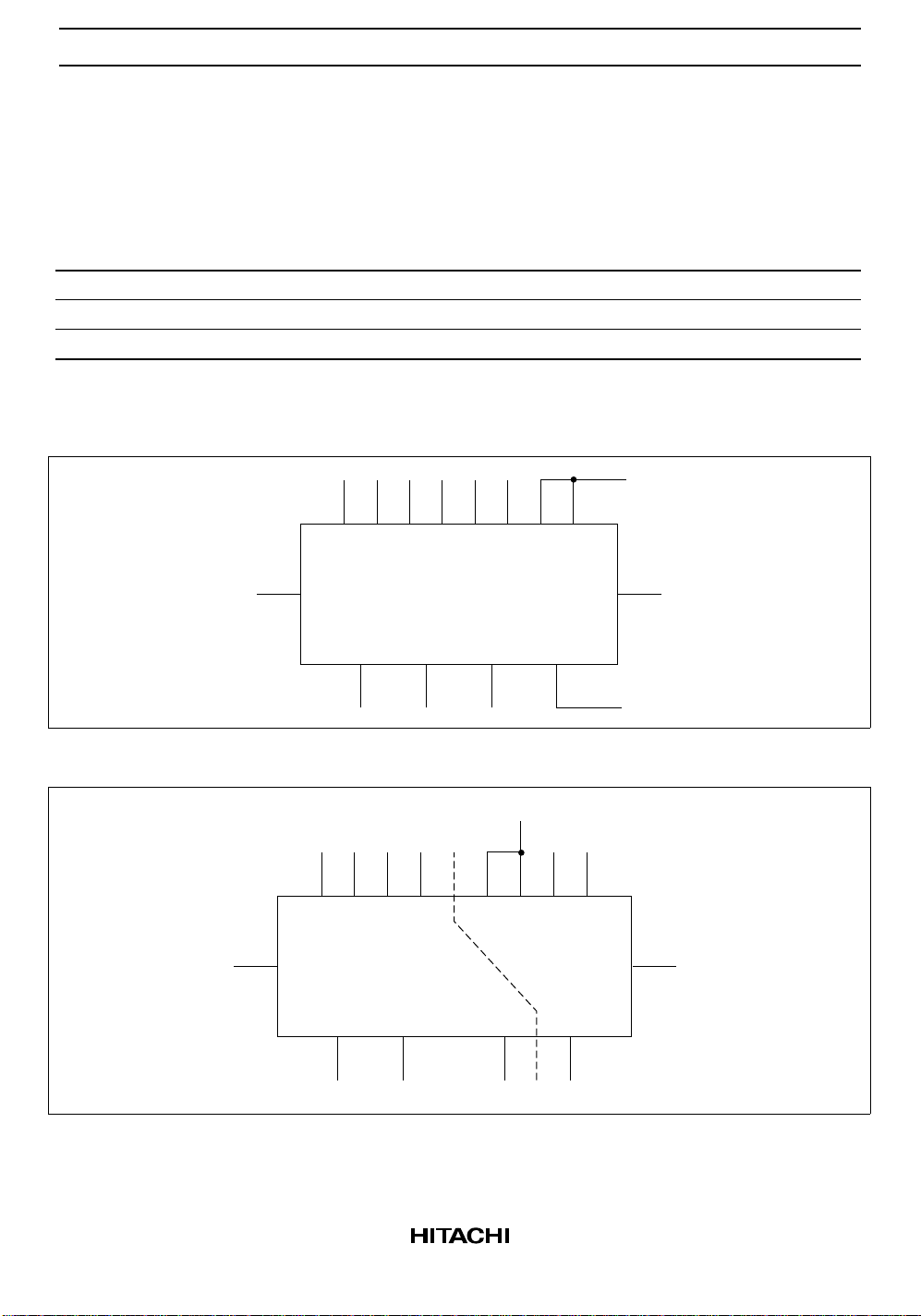
Fig. a Active HIGH varsus Active LOW Interpretation
C0A0A1A2A3B0B1B2B3S0S1S2S3C
Logic levels L L H L H H L L HHHLLH
Active HIGH 00101100111001
Active LOW 11010011000110
Active HIGH: 0 + 10 + 9 = 3 + 16
Active LOW: 1 + 5 + 6 = 12 + 0
L
A0
C0
A1
B0
S0 S1 S2 S3
B1
A2 A3
B2 B3
C4
C3
4
Fig. b 3-bit Adder
C10
A0 A1
B0
A0
C0C0 C4 C11
A1
B0
S0 S1 S2 S3
S0 S1 C2 S10
B1
A2 A3
B2
A10B1B10
B3
Fig. c 2-bit and 1-bit adders
3
HD74AC283/HD74ACT283
I1 I2 LI4I5
I3
A0
C0 C4
A1A2A3B1B2B3B0
S0
2
S1S2S3
0
1
2
2
2
Fig. d 5-Input Encoder
I3
I1 I2 I4 I5
A0
C0 C4
A1 A2 A3B1 B2 B3B0
S0 S1 S2
S3
M5
Fig. e 5-Input Majority Gate
4
 Loading...
Loading...