Heath Heathkit EC-1 Operation Manual
OPERATIONAL MANUAL FOR THE HEATH
EDUCATIONAL ANALOG COMPUTER
MODEL EC-1
PREFACE
The purpose of this manual is threefold: first, to present, in elementary form, the fundamental
mathematical theory of analog computers; second, to provide instructions for operation of the
Heath Educational Analog Computer; and third, to show some illustrative examples of problems
which can be solved on the Computer.
This manual is not intended to be exhaustive but rather to be a guide in the operation of the
computer. For this reason frequent references are made to the available literature. Several
excellent books as well as many articles are available. Some of these are listed in the references at
the end of the manual. These should be available to and used by anyone with a serious interest in
analog computers.
3/20/59
CONTENTS
Preface ...........................................................................................................1
Introduttion ................................................................................................... 3
Theory ............................................................................................................4
Circuit Description
DC Operational Amplifier .....................................................................13
Amplifier Powe r Supply ........................................................................14
Initial Co ndition Power Supplies .........................................................15
Control Circuit ......................................................................................15
Repetitive Oscillator ..............................................................................15
General Operating Instructions .................................................................16
Basic Mathematical Operations
Addition .................................................................................................17
Multiplication ........................................................................................19
Integration .............................................................................................19
Illustrative Problems
Falling Body ...........................................................................................21
Spring-Mass System .............................................................................24
Simultaneous Algebraic Equations ......................................................26
Proje ctile ................................................................................................27
Bouncing Ball ........................................................................................28
Reference s .......................................................................................................
....................................................................................................... 31
Specifications ..............................................................................................32
Parts List .....................................................................................................34
Page 2
Schematic ....................................................................................................38
INTRODUCTION
One of the wonders of the modern Electronic Age is the computer or "Giant Brain", as it is
sometimes called. Actually, the computer is not a "Brain" at all, since it does not think but must
be "told" what to do. It is capable of doing mathematical operations at much greater speed and with
greater accuracy than human beings.
A computer is a machine which performs physical operations that can be described by mathematical operations. In general, computers may be classified as digital or analog. Digital computers
operate by discrete steps, that is, they actually count. Common examples of digital computers are
the abacus, desk calculator, punched-card machine, and the modern electronic digital computer.
The fundamental operations performed by the digital computer are usually addition and
subtraction. Multiplication, for example, is accomplished by repeated additions.
Analog computers operate continuously, that is, they measure. Examples of analog computers are
the slide rule (which measures lengths), the mechanical differential analyzer, the electromechanical analog computer and the all-electronic analog computer. The last three generally
measure electrical voltages or shaft rotations. Physical quantities such as weight, temperature or
area are represented by voltages. Voltage
Arbitrary scale factors are set up to relate the voltages in the computer to the variables in the
problem being solved. For example, 1 volt equals 5 feet or 10 volts equals 1 pound. The name
"analog" comes from the fact that the computer solves by analogy by using physical quantities to
represent numbers.
The fact that the analog computer operates continuously makes it very useful in such operations
as integration; for this reason computers used this way are sometimes known as Differential
Analyzers.
One of the most powerful applications of analog computers is simulation in which physical
properties, not easily varied, are represented by voltages which are easily varied. Thus the "knee
action" of an automobile front wheel suspension can be simulated on an analog computer in which
the weight of the automobile, the constant of the spring, the damping of the shock absorber, the
nature of the road surface, the tire pressure and other conditions can be represented by voltages.
In practice these factors cannot be readily changed, but on the computer any one or all of these
may be varied at will and the results observed as the changes are made.
Analog computers are especially useful in solving dynamic problems in which the motion can be
expressed in the form of a differential equation.
All mathematical operations necessary to the solution of ordinary differential equations can be
built up from addition, multiplication by a constant, and integration. * As will be shown later, the
analog computer can perform these operations and thus is a convenient device for the solution of
differential equations.
The combination of the six basic computer operations will perform any continuous function.
Some of the types of problems which can be solved by these methods are radioactive decay,
chemical reaction, beam oscillation and heat flow. With the addition of crystal diodes and re-lays,
simulation of discontinuous functions is possible. This makes possible solution of problems
involving saturation, backlash, hysteresis, friction, limit stops, vacuum tube characteristics, and
different modes of operation such as sonic vs. subsonic flow.
is the electrical analog of the variable being analyzed.
* Shannon, C. , JOURNAL MATH. AND PHYSICS, Vol. 20, Pages 337-354, 1941.
Page 3
With the addition of special devices such as function generator and function multiplier, additional operations may be performed such as multiplication of variables, computation of trigonometric, exponential and logarithmic functions and generation of discontinuous functions. *
THEORY
In order to solve differential equations on an analog computer, it is necessary to have:
1. DC amplifiers (also called operational amplifiers) capable of performing the operation of
a. Integration
b. Addition (or summation)
c. Multiplication by a constant
d. Multiplication by -1(inversion)
2. A means of setting coefficients in a problem. This may be done by means of
a. Potentiometers
b. Changing the ratio of feedback resistance to input resistance.
3. A control system for starting and stopping solution of the problem, as well as resetting the
initial conditions so as to be ready for running a new solution with the same or new
coefficients and initial conditions.
The general procedure in solving a problem is to:
1. Set the machine variables (voltages) to the correct initial conditions.
2. Make the computing elements operative and force the voltages to vary in the manner
prescribed by the differential equations.
3. Observe and/or record the voltage variations, with respect to time, which constitute the
solution of the given problem.
4. Stop the machine and reset for a new run.
The heart of the analog computer is the DC operational amplifier which performs the basic
mathematical operations necessary for the solution of problems.
The amplifier used in the analog computer
feedback and is represented by a triangle with the base at the input end and the apex at the output end, as shown in Figure 1.
is a high gain direct-coupled amplifier with negative
Figure 1
AMPLIFIER SYMBOL
* Clarence L. Johnson, ANALOG COMPUTER TECHNIQUES (McGraw-Hill Book Company, Inc.,
New York 1956) Chapter 8, Pages 13 6-164.
Korn and Korn, ELECTRONIC ANALOG COMPUTERS (McGraw-Hill. Book Company, Inc. , New
York 1956) Second Edition, Chapter 6, Pages 251-344.
Page 4
In use, resistors and capacitors are connected as input and feedback elements in such a way as to
perform various mathematical operations. For use as a multiplier, resistors are used as input
and feedback elements, as shown in Figure 2.
AMPLIFIER AS MULTIPLIER AND INVERTER
In this Figure, e
represents the input voltage, eg the grid voltage, eo the output voltage, Ri the
i
input resistor and Rf the feedback resistor.
The gain of an amplifier is given by
From this it can be seen that eg approaches zero as A approaches infinity. In practice, A is made
large with respect to e
by using high gain amplifiers so that eg becomes very small, and for
o
practical purposes eg can be considered to be at ground potential.
Since the input to the amplifier is the grid of a tube, the current through the amplifier from the
input can be considered to be zero, with the result that the current ii through the resistor Ri is, for
all practical purposes, equal to the current i
through the resistor Rf, with the result that
f
*For a more rigorous approach, see Korn and Korn, ELECTRONIC ANALOG COMPUTERS
(McGraw-Hill Book Company, Inc. , New York, 1956), Second Edition, Page 12.
Page 5
The approximation which results from considering e = 0 will be used in the further discussion of
"
the DC amplifier but the "approximately equal to
considered to be equal to i
.
f
sign will not be used, that is, ii will be
In practice, the gain of DC computer amplifiers will vary from approximately 1000 for repetitive
computers to as high as 10 for a large commercial installation. Since the maximum output of an
amplifier is generally 100 volts, the value of eg will vary from about 0.1 volt to 1 micro-volt,
depending on the gain of the amplifier. Thus the amplifier gain is one factor in the accuracy of an
analog computer.
which is, in effect, multiplication by a constant. Since, in most cases, the output voltage is of the
opposite sign to the input voltage, the amplifier also acts as an inverter or sign changer.
To change the value of the constant K, it is necessary only to change R
at 1 megohm and R
is changed. This may be done by using a different value fixed resistor or by
i
using a potentiometer as shown in Figure 3.
or Rf. Generally, Rf is kept
i
Suppose, for example, a ratio of 3.7 is desired. If is made equal to 0.37 and Rf/Ri = 10 (Rf = 1
megohm and R
= 100 K ohm), then eo = -3.7 ei. Generally this method is to be preferred over that
i
shown in Figure 3.
In actual practice, the ratio Rf/Ri is generally greater than unity, since the amplifiers tend to
become unstable for values less than unity. Also the ratio Rf/R
is 100 or less, as values greater
i
than 100 introduce inaccuracies in the solution of the problem.
If, instead of the one input resistor shown in Figure 2, two or more resistors are used as shown in
Figure 5, the operational amplifier becomes an adder.
Figure 5 AMPLIFIER AS ADDER
Again making use of eg 0, the sum of the currents in the input resistors equals the current
through the feedback resistor.
The operational amplifier can thus be used to add and at the same time multiply any of its in-puts
by constants. Any number of inputs can be used as long as the output voltage does not exceed the
nominal range of the amplifier.
Page 7
Since subtraction can be considered to be the addition of negative numbers, subtraction can be
performed by using negative voltages for those quantities to be subtracted. The circuit shown in
g
Figure 6 would
ive the result
Figure 6
OPERATIONAL AMPLIFIER CIRCUIT USED FOR SUBTRACTION
Page 8
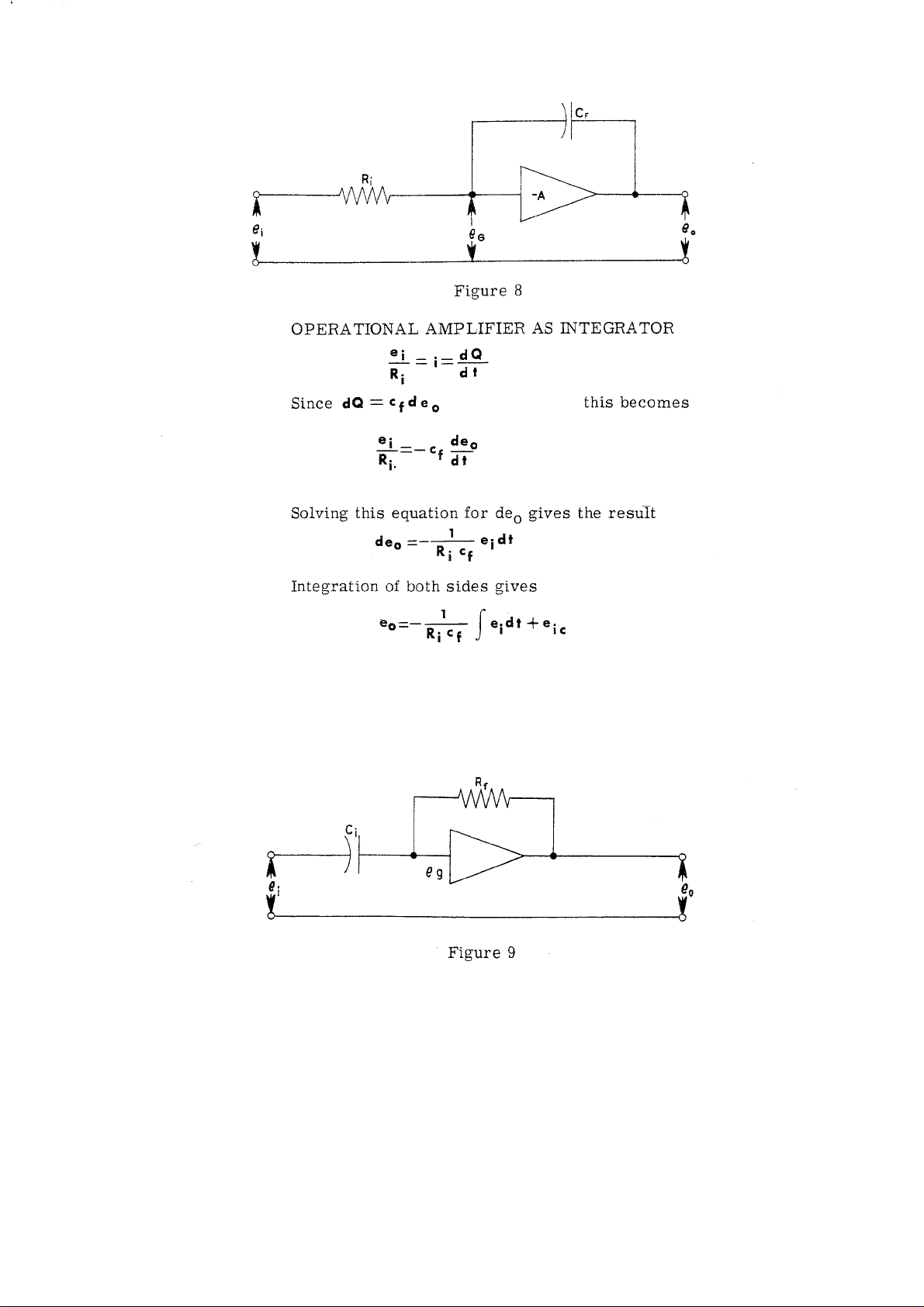
Where e
is the constant of integration
ic
(initial condition) and is the voltage
across the capacitor Cf at time t = o.
Thus the operational amplifier can integrate.
AMPLIFIER AS DIFFERENTIATOR
It is possible to show, by a similar analysis, that the operational amplifier can be used to
differentiate. The amplifier is used very seldom for this purpose, however, since noise in the input
tends to be magnified by differentiation, whereas it tends to cancel out in integration. Such
circuits also tend to be unstable.
In practice, the value of the feedback resistor Rf, when used, is generally 1 megohm and the value
of the feedback capacitor Cf, when used, is generally 1 microfarad. The value of the input resistor
usually varies from 0.1 megohm to 1.0 megohm, although in certain problems the values may be
different from these values.
g
e 10
Pa
A combination of simple operations forms a complex operation. In general, an analog computer is
not used for addition alone or for multiplication by a constant as a single operation. These can be
better performed by other means. The value of the computer lies in its ability to combine these
simple operations into a complex operation.
An example of a complex operation is indicated by the circuit shown in Figure 10.
where eo (o) is the output voltage at time t = o (start of problem solution). Amplifier A is used for
sign inversion. It can be omitted if a minus result is acceptable.
Another example of a simple type of problem involving complex operation is that of an object
falling due to the force of gravity. The acceleration which the body experiences is constant near
the surface of the earth and due to the force exerted on the object by the gravitational field of the
earth. This may be written as an equation,
where y is the distance the object falls in time t, and g is the acceleration given the object by the
earth's gravitational field. By integrating twice, it is possible to obtain an expression for y in terms
of g and the time t during which the body has fallen. This can easily be set up on the computer,
using two amplifiers as shown in Figure 11.
Figure 11
AMPLIFIER CONNECTIONS FOR SOLVING "FALLING BODY PROBLEM"
The input voltage e
is supplied by a suitable power supply and the value of ei is chosen so that eo
i
does not exceed the output capacity of amplifier 2. Instructions for setting up this problem are
given on Page 21. It is suggested, however, that the actual setup and solution of the problem be
withheld until the CIRCUIT DESCRIPTION and OPERATION sections of this manual have been
thoroughly reviewed and are generally understood.
Page 11
Other examples of the application of complex operation to the solution of problems are given in
the section on OPERATION.
SCALE FACTORS
In the operation of the analog computer two factors must be considered. The first of these is the
amplitude factor. In general, the output of each amplifier must be kept within the range ±100 volts,
the actual value depending on the amplifier used in the computer. In order to keep the output
within the specified limits, it is generally necessary to scale down the input voltages. It is not
always possible to determine before hand the range of the voltages, in which case a trial run can be
made and after the voltages are observed, the proper amplitude scale factors can be chosen.
Sometimes it is possible to estimate the range of voltages from the physics of the problem.
The other factor is time. If the product RiCf = 1 when Ri is measured in ohms and Cf is measured
in farads, the computation is said to be in real time. This is so, for example, when Ri = 1 megohm
6
and Cf = 1 µfd. (RiCf = 10
ohms x 10-6 farad = 1) If the computer is operated such that the
solution is obtained in less time than is required for the physical solution to occur, the operation is
said to be faster than real time. This is very useful if the physical occurrence which is being
simulated requires considerable time. Time is also saved, permitting the solution of more problems
in the same length of machine time.
Another advantage is that machine error is decreased, especially the error due to the leakage
resistance of the feedback capacitors. In general, the solution of a problem on the computer should
not require more than 1 to 5 minutes. Longer solution times require special precautions.*
REPETITIVE OPERATION
It is desirable, for many problems, to repeat the solution and observe the effect on the solution of
changing the various parameters of the problem. This is made possible by repetitive operation.
Some means is provided for automatically resetting the computer and re-running the problem. A
cathode ray oscilloscope is convenient for observing the solution in this case. Generally, one of the
computer amplifiers is used to provide the sweep for the oscilloscope . Details of operation will be
discussed in the section on OPERATION.
ACCURACY
As was shown previously, the higher the amplifier gain the less will be the error in each computing
operation. Thus the accuracy depends in part on the gain of the operational amplifier. Accuracy
also depends on the precision of the computing components, such as resistors and capacitors.
Time is also a factor in accuracy. In general, long runs introduce errors due to amplifier drift and
capacitor leakage.
* Goode and Machol, SYSTEM ENGINEERING (McGraw-Hill Book Company, Inc., New York, 1957),
Pages 278-283.
Clarence L. Johnson, ANALOG COMPUTER TECHNIQUES (McGraw-Hill Book Company, Inc. , New
York, 1956), Chapter 3, Pages 20-44.
Korn and Korn, ELECTRONIC ANALOG COMPUTERS (McGraw-Hill Book Company, Inc., New
York, 1956), Pages 30-35.
James B. Resnick, "Scale Factors for Analog Computers", Product Engineering, March, 1954.
Page 12
Any variations in voltages in any part of the circuit of a direct-coupled amplifier cause variations
in the output voltage which in turn introduce errors in the solution. With constant input the
output will vary, resulting in "drift", which increases with amplifier gain. This introduces a
paradox since, as has been shown, error is reduced by increasing amplifier gain but this in turn
increases drift which increases errors. For this reason, very high gain amplifiers generally use
some means of stabilization in order to reduce drift. *
READ-OUT
For arithmetic problems in which a single numerical answer is obtained, the result can be read on
the meter. In problems having a continuous solution (changing with time) an oscilloscope is
desirable. It is possible in this case to watch the effect on the solution of varying the various
problem parameters. This is especially true when repetitive operation is used. In this case one of
the computer amplifiers is used to provide the sweep. The oscilloscope must be a DC scope.
If a permanent record of the solution is desired, a photograph of the oscilloscope trace may be
made or a recording galvanometer may be used. Examples of both methods are shown in the
illustrative problems.
NON-LINEAR OPERATION
A discussion of non-linear operation is beyond the scope of this manual. An excellent treatment of
non-linear operation can be found in ANALOG COMPUTER TECHNIQUES by Clarence L.
Johnson, Chapter 7, _Pages 107-127.
CIRCUIT DESCRIPTION
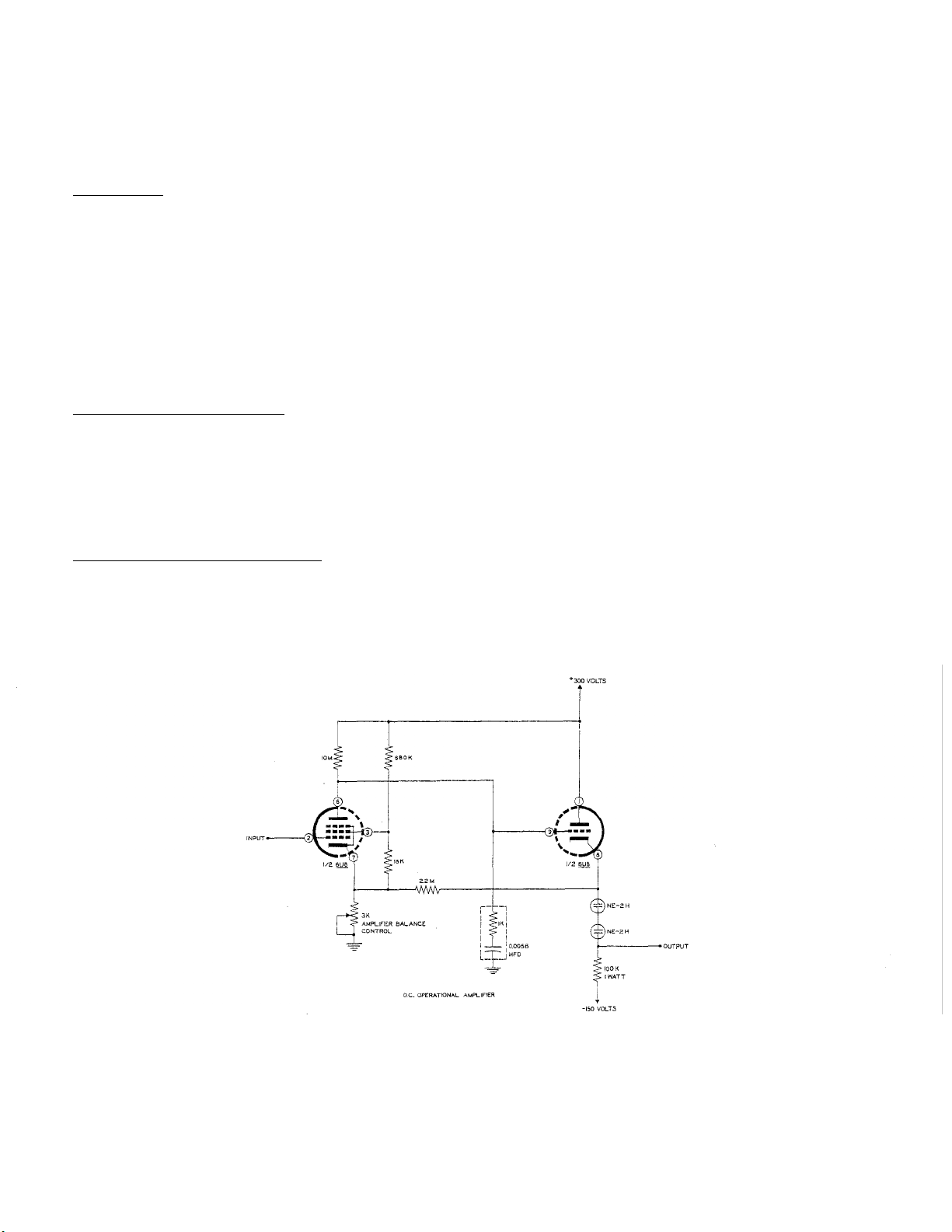
DC OPERATIONAL AMPLIFIER
The general requirements for a DC amplifier for computer use are high gain, high input impedance, low output impedance, good linearity and stability (low drift). The circuit of the amplifier
used in the Heath Analog Computer is shown in Figure
'
12.
Figure 12
DC OPERATIONAL AMPLIFIER FOR EC-1
* Korn and Korn, ELECTRONIC ANALOG COMPUTERS (McGraw-Hill Book Company, Inc., New
York, 1056) Second Edition, Pages 191-196 and 231-239.
Page 13
Loading...