Page 1

Freescale Semiconductor, Inc.
White Paper
Thermal Analysis of
Semiconductor Systems
Page 2

Contents
1 Introduction ................................................................................................................................ 2
2 Definitions and Basic Principles ................................................................................................. 3
2.1 Definitions ............................................................................................................................ 3
2.2 Basic Principles ................................................................................................................... 3
2.3 Transient Thermal Response ............................................................................................... 5
2.4 Convection and Radiation ................................................................................................... 6
3 Differences between Electrical and Thermal Domains .............................................................. 8
4 Thermal Rating ........................................................................................................................... 9
4.1 Thermal Resistance Ratings ................................................................................................ 9
4.2 JEDEC Test Methods and Ratings .................................................................................... 10
4.3 Thermally Enhanced Circuit Boards .................................................................................. 12
4.4 Transient Thermal Response Ratings ................................................................................ 15
5 Ramifications of High Operating Temperature ......................................................................... 18
6 Thermal Circuits ....................................................................................................................... 20
7 Thermal Modeling Software ..................................................................................................... 24
7.1 Uses of Thermal Modeling Software ................................................................................. 24
7.2 Thermal Modeling Software Options ................................................................................. 26
8 Empirical Analysis Techniques ................................................................................................. 28
9 Optimizing the Thermal Environment ....................................................................................... 30
10 Appendices............................................................................................................................. 32
10.1 Appendix A—List of JESD51 Series Publications ........................................................... 32
10.2 Appendix B—Thermal Properties of Common Semiconductor Packaging Materials .... 33
11 References.............................................................................................................................. 34
1 Introduction
Designing a cost competitive power electronics system requires careful
consideration of the thermal domain as well as the electrical domain.
Over designing the system adds unnecessary cost and weight; under
designing the system may lead to overheating and even system failure.
Finding an optimized solution requires a good understanding of how to
predict the operating temperatures of the system’s power components
and how the heat generated by those components affects neighboring
devices, such as capacitors and microcontrollers.
No single thermal analysis tool or technique works best in all
situations. Good thermal assessments require a combination of
analytical calculations using thermal specifications, empirical analysis
and thermal modeling. The art of thermal analysis involves using all
available tools to support each other and validate their conclusions.
This white paper first presents the basic principles of thermal systems
and then describes some of the techniques and tools needed to
complete such an analysis. Power devices and low lead count
packages are the primary focus, but the concepts herein are general
and can be applied to lower power components and higher lead count
devices such as microcontrollers.
Page 3

2 Definitions and Basic Principles
2.1. Definitions
A good way to begin a study of a domain is to familiarize oneself
with its definitions, nomenclature and notations. The terms used for
thermal analysis vary somewhat throughout the industry. Some of
the most commonly used thermal definitions and notations are:
T
Temperature at reference point “A”
A
Junction temperature, often assumed to be
T
J
constant across the die surface
T
or T
C
Package temperature at the interface between the
Case
package and its heatsink; should be the hottest
spot on the package surface and in the dominant
thermal path
ΔT
Temperature difference between reference points
AB
“A” and “B”,
q Heat transfer per unit time (Watts)
Power dissipation, source of heat flux (Watts)
P
D
The term “Junction Temperature”
The term junction temperature became commonplace in the early
days of semiconductor thermal analysis when bipolar transistors and
rectifiers were the prominent power technologies. Presently the term is
reused for all power devices, including gate isolated devices like power
MOSFETs and IGBTs.
Using the concept “junction temperature” assumes that the die’s
temperature is uniform across its top surface. This simplification
ignores the fact that x-axis and y-axis thermal gradients always exist
and can be large during high power conditions or when a single die has
multiple heat sources. Analyzing gradients at the die level almost always
requires modeling tools or very special empirical techniques.
H Heat flux, rate of heat flow across a unit area (J·m-
2
·s-1)
Thermal resistance between reference points “A” and
R
QAB
“B”, or R
R
Junction to moving air ambient thermal resistance
QJMA
Junction to case thermal resistance of a packaged
R
QJC
THAB
component from the surface of its silicon to its
thermal tab, or R
Junction to ambient thermal resistance, or R
R
QJA
C
Thermal capacitance between reference points “A”
QAB
and “B”, or C
THAB
THJC
THJA
ºC or K Degrees Celsius or degrees Kelvin
Transient thermal impedance between reference
Z
QAB
points “A” and “B”, or Z
THAB
Most of the die’s thickness is to provide mechanical support for the
very thin layer of active components on its surface. For most thermal
analysis purposes, the electrical components on the die reside at the
chip’s surface. Except for pulse widths in the range of hundreds of
microseconds or less, it is safe to assume that the power is generated
at the die’s surface.
3Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 4
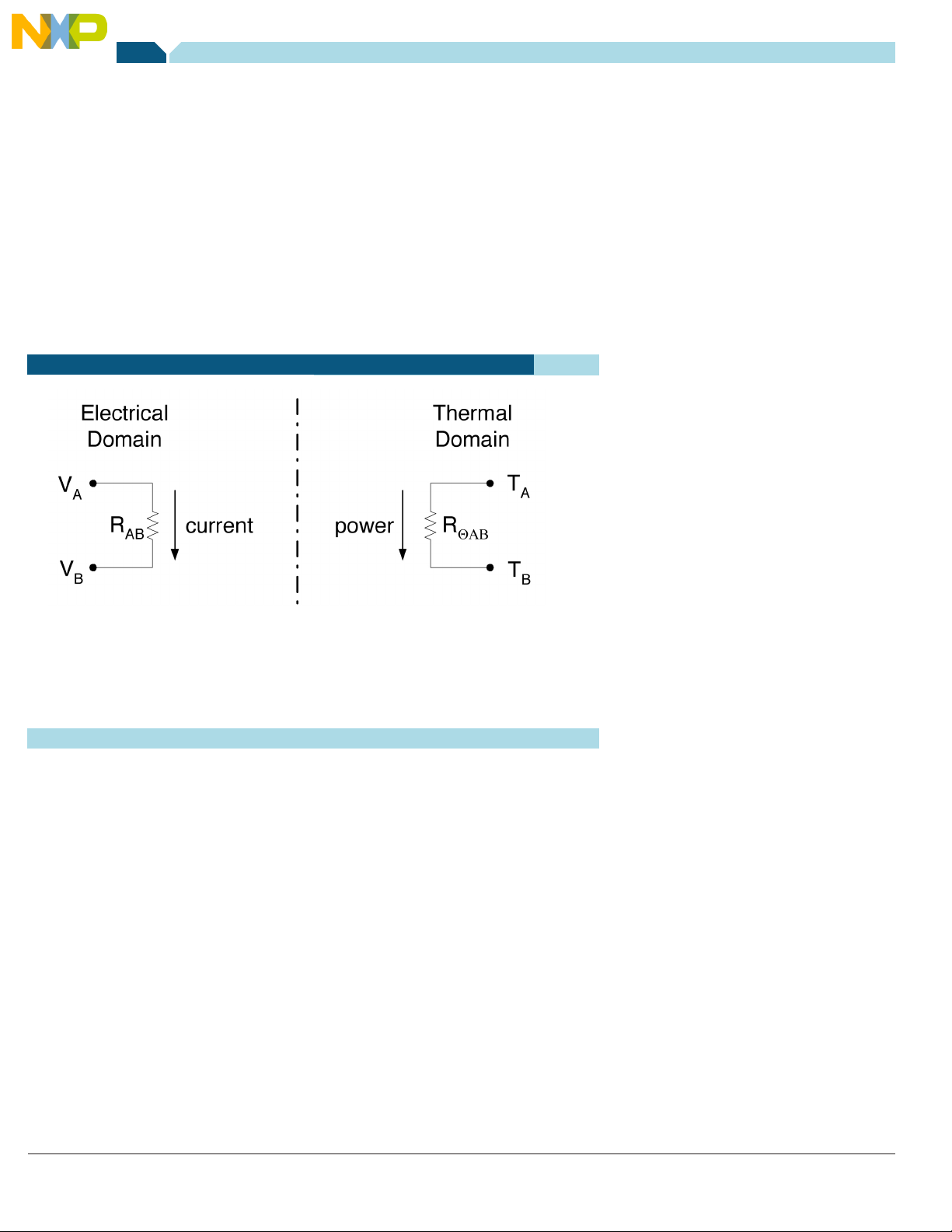
2.2. Basic Principles
The basic principles of thermal analysis are similar to those in the
electrical domain. Understanding one domain simplifies the task
of becoming proficient in the other. This is especially clear when
we consider thermal conduction. The two other thermal transport
mechanisms are discussed later.
Each domain has a “through” and an “across” variable, as shown in
Figure 1 and Table 1. The through variable can be thought of as the
parameter that flows from one reference point to another. Current is
the through variable for the electrical domain and power is the through
variable in the thermal domain.
The across variable can be thought of as the variable that forces
the flow of current or heat. In each domain the forcing function is a
difference in potential; in one domain it’s temperature and in the other
it’s voltage.
Both systems have a resistance that impedes the flow of the through
variable.
Given the duality of the two systems, it is no surprise that the
fundamental equations of the domains are similar. This is illustrated
most clearly when we see that each system has an “Ohm’s Law”, as is
shown in Table 1.
Figure 1—Fundamental Relationships in the Electrical and Thermal Domains
4 Freescale Semiconductor, Inc.Thermal Analysis of Semiconductor Systems
Page 5
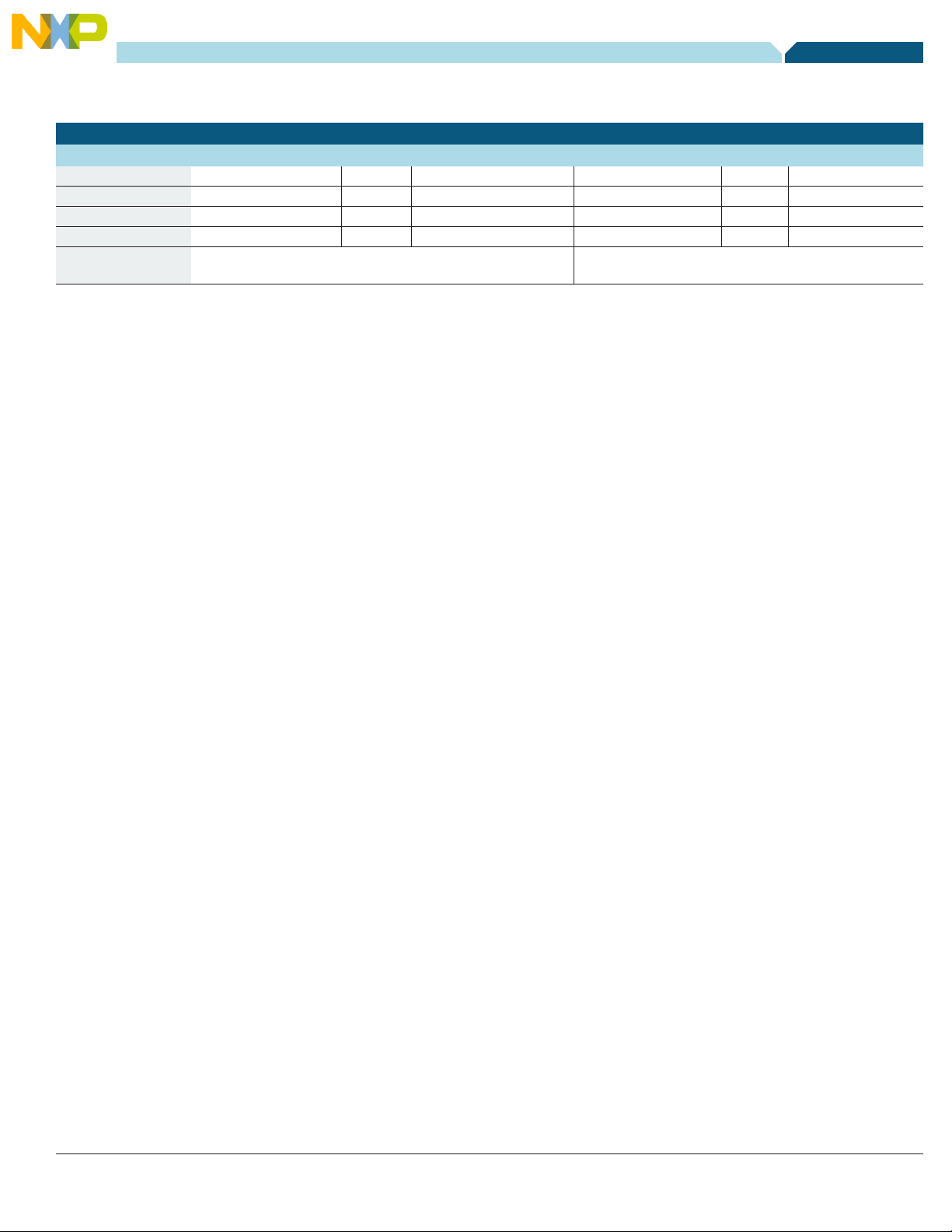
Table 1—Basic Relationships in the Electrical and
Thermal Domains
Electrical Domain Thermal Domain
Variable Symbol Units Variable Symbol Units
Through Variable Current I Amperes or Coulombs/s Power or Heat Flux P
D
Watts or Joules/s
Across Variable Voltage V Volts Temperature T ºC or K
Resistance Electrical Resistance R Ohms Thermal Resistance R
Capacitance Electrical Capacitance C Farads or Coulombs/V Thermal Capacitance C
“Ohm’s Law” ΔV
= VA – VB = I * R
AB
AB
ΔTAB = TA – TB = PD * R
(derived from Fourier’s Law)
QAB
Q
ºC/W or K/W
Joules/ºC
QAB
From the relationships above,
ΔT
= (TJ – TA) = PD R
JA
QJA
we can easily derive the often used equation for estimating junction
temperature:
T
= TA + (PD R
J
) (Eq. 1)
QJA
For example, let’s assume that:
R
P
T
= 30ºC/W
QJA
= 2.0W
D
= 75ºC
A
Then, by substitution:
T
= TA + (PD R
J
T
= 75ºC + (2.0W * 30ºC/W)
J
T
= 75ºC + 60ºC
J
T
= 135ºC
J
QJA
)
A cautionary note is in order here. The thermal conductivities of some
materials vary significantly with temperature. Silicon’s conductivity, for
example, falls by about half over the min-max operating temperature
range of semiconductor devices. If the die’s thermal resistance is
a significant portion of the thermal stackup, then this temperature
dependency needs to be included in the analysis.
2.3. Transient Thermal Response
Of course, the duality extends to transient as well as steady state
conditions. The existence of capacitance in both domains results in
thermal RC responses like those we are familiar with in the electrical
domain. The basic relationships follow.
Thermal time constant is equal to the thermal R-C product, that is:
t
= RQ CQ (Eq. 2)
Q
Thermal capacitance is a function of the temperature rise associated with
a given quantity of applied energy. The equation for thermal capacitance
is:
CQ = q t/ΔT (Eq. 3)
where:
q = heat transfer per second (J/s)
t = time (s)
ΔT = the temperature increase (ºC)
Thermal capacitance is also a function of mechanical properties. It is
the product of a material’s specific heat, density, and volume:
C
= c d V (Eq. 4)
Q
where:
c = specific heat (J kg
d = density (kg/m
V = volume (m
-1 K-1
)
3
)
3
)
Furthermore, the temperature of a thermal RC network responds to a
step input of power according to:
ΔT
AB
= R
QAB PD
(1 - e
(-t/t)
) (Eq. 5)
5Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 6

2.4. Convection and Radiation
Conduction is only one of three possible thermal transport
mechanisms. In addition to conduction, the other mechanisms are
radiation and convection. In fact, these other transport mechanisms
often become the predominant ones as heat exits a module.
Radiation and convection are clearly more complex thermal transport
mechanisms than conduction, and we will see that in their governing
equations. Consider first convection, which occurs when a solid
surface is in contact with a gas or liquid at a different temperature. The
fluid’s viscosity, buoyancy, specific heat and density affect the heat
transfer rate from the solid’s surface to the fluid. The surface’s area and
its orientation (i.e., horizontal or vertical) as well as the shape of the
volume in which the fluid is free to circulate are additional factors. And,
having the greatest effect is whether the system uses forced air (fan
cooling) or natural convection.
Although convective behavior is quite complex, its descriptive equation
is relatively simple and can be expressed as:
q = k A ΔT (Eq. 6)
where:
q = heat transferred per unit time (J/s)
k (or h) = convective heat transfer coefficient of the process
-2
(W m
ºC-1)
A = heat transfer area of the surface (m
2
)
ΔT = temperature difference between the surface and the bulk
fluid (ºC)
mechanism. But at the module level, because of the much larger
surface area and the heat transfer’s dependence on the 4th power
of temperature, radiation can play a much more important role.
Nevertheless, for larger objects thermal radiation is often accounted for
by including its effect in a general thermal resistance value. But since
radiation is a strong function of temperature, this practice is acceptable
only over a modest range of module and ambient temperatures or
when the module and ambient temperatures are nearly the same.
Applying three different and sometimes complex thermal transport
mechanisms to a complex thermal circuit creates a system that cannot
be evaluated by simple and inexpensive tools. Often the only feasible
approach is to model a thermal circuit with tools created for that
purpose and validate that model with empirical testing.
The convection coefficient, k, can be determined empirically, or it can
be derived from some thermal modeling programs. It changes, for
example, with air speed when a fan is used, with module orientation or
with fluid viscosity.
Radiation is a completely different process and augments the other
two transport mechanisms. Quantifying heat transferred by radiation
is complicated by the fact that a surface receives as well as emits
radiated heat from its environment. “Gray Body” (vs. “Black Body”)
radiation is the more general condition and its governing formula is:
4
q = e s A (T
4
- T
) (Eq. 7)
h
c
where:
q = heat transfer per unit time (W)
e = emissivity of the object (one for a black body)
s = Stefan-Boltzmann constant = 5.6703*10
A = area of the object (m
T
= hot body absolute temperature (K)
h
T
= cold surroundings absolute temperature (K)
c
2
)
-8
(W m-2 K-4)
Exercising Equation 7 shows that for geometries and temperatures
typical of semiconductor packages, radiation is not a primary transport
6 Freescale Semiconductor, Inc.Thermal Analysis of Semiconductor Systems
Page 7

3 Differences between Electrical and Thermal Domains
Leadframe
Exposed Pad
Standard SOIC
Thermally Enhanced
Considering how the electrical and thermal domains differ is a good
way to avoid some common misconceptions and misunderstandings.
One key difference between the domains is that in the electrical
domain the current is constrained to flow within specific circuit
elements, whereas in the thermal domain heat flow is more diffuse,
emanating from the heat source in three dimensions by any or all of
the three thermal transport mechanisms. In electrical circuit analysis
current is limited to defined current paths and that allows us to use
lumped circuit elements, such as resistors, capacitors, etc. But in
the thermal domain the thermal path is not so constrained, so using
lumped elements is not as appropriate. Even in relatively simple
mechanical systems, defining lumped thermal components is often an
exercise in estimation, intuition and tradeoffs. We want to use lumped
elements to model our thermal systems, but we must remember that to
do so we’ve made many simplifying assumptions.
A second major difference is that coupling between elements is usually
a more prominent behavior in the thermal domain. Isolating devices in
electrical circuits is usually easier than isolating elements in thermal
4 Thermal Ratings
4.1. Thermal Resistance Ratings
Now let’s investigate how these basic thermal relationships affect
manufacturers’ thermal resistance specifications. For a given package
style, for example the SOIC, thermal performance can vary substantially
depending on the package’s internal construction and how the system
extracts heat from the package leads or its body. Figure 2 shows
that the standard SOIC’s leadframe floats within the package’s mold
compound, so there is no direct low impedance thermal path from the
die to that package’s surface. Heat generated in the die readily travels
into the leadframe, but then it struggles to move through the mold
compound to the package surface and through the wirebonds to its
leads. Even though heat travels only a short distance, the package’s
thermal resistance is high due to the mold compound’s high thermal
resistivity and the wirebonds’ very small cross sectional area.
The portion of the leadframe on which the die is placed is called
the “die paddle,” or “flag.” The package’s thermal performance can
be enhanced substantially by improving the thermal path from the
paddle to the package’s surface. One way to do this is to stamp the
networks. Therefore, good thermal models usually employ thermal
coupling elements, while many electrical circuits do not require them.
The tools to model complex systems are quite different between
the domains. Electrical circuit analysis tools, such as SPICE, can be
used for thermal circuits of lumped elements, but such tools are not
appropriate for assessing how heat flows in a complex mechanical
assembly.
The test and evaluation tools differ as well. You can’t clamp a “heat flux
meter” around a thermal element to monitor how much power passes
through it. For thermal analysis infrared cameras and thermocouples
replace oscilloscopes and voltage probes.
Even though the domains have their differences, they are likely to
be interdependent. A prime example is the temperature dependence
of a power MOSFET’s on-resistance, which increases by 70 to 100
percent as the temperature increases from 25ºC to 150ºC. The higher
on-resistance increases power dissipation, which elevates temperature,
which increases on-resistance, and so on.
leadframe so that some of the leads are directly connected to the die
paddle (flag). This allows heat to flow relatively unimpeded through the
“thermally enhanced” leads and onto the PCB. Another approach is
to expose the die paddle at the bottom (or top) of the package. This
structure yields a much more direct thermal path and vastly improves
the device’s thermal performance.
Since the primary thermal path differs with modifications in the
package construction, each variation merits its own thermal reference
points and, therefore, its unique thermal resistance specifications.
Table 2 contains thermal resistance ratings of two devices with
essentially the same die. Both use a version of the 32-lead, fine-pitch,
wide-body SOIC. One version has an enhanced leadframe (the two
centermost leads on each side of the package are directly connected
to the die pad), and the other has an exposed pad on the IC’s belly.
Their internal construction and how they are typically mounted on a
PCB are shown in Figure 3.
Figure 2—Cross Sections of standard and exposed pad SOICs
7Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 8
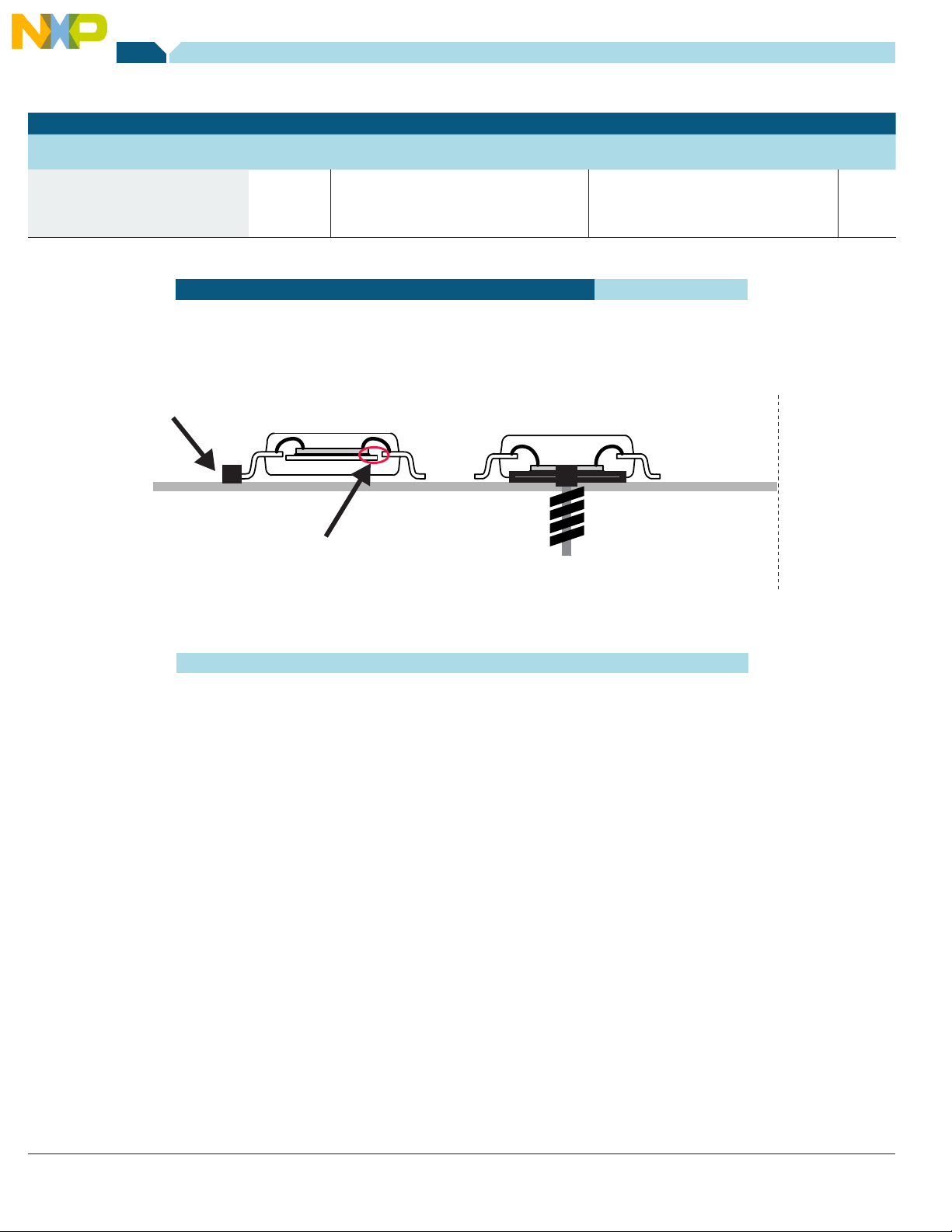
Table 2—Typical Thermal Resistance Specifications
Standard
Optimum T
lead
reference
Some leads may be
attached to the leadframe
Exposed Pad
Optimum T
case
reference point
circuit board
Thermal Ratings Symbol Value Unit
Thermal Resistance
Junction to Case
Junction to Lead
Junction to Ambient
32 lead SOIC Case 1324-02
R
QJC
R
QJL
R
QJA
Standard
18
70
Exposed pad
32 lead SOIC Case 1437-02
1.2
-
71
ºC/W
Figure 3—Cross Sections of standard and exposed pad SOICs
For the standard SOIC the primary path for heat flux is laterally through
the wirebonds and the mold compound, into the leads and then
vertically into the board. For the exposed pad package the path is
much more direct; heat passes vertically through a broad cross section
from the top of the die through the silicon, through the die attach
are most appropriate for devices whose primary thermal path is
through an exposed thermal tab, not through the leads. The moral of
the story is that the user should carefully note the reference points
used for a device’s thermal resistance specifications and correctly
apply those specifications to the application.
material, through a leadframe and another solder layer then into the
circuit board. The difference in thermal paths between the two options
is in the tens of ºC/W.
Semiconductor manufacturers are adept at specifying their devices’
thermal performance. But users want more. They want to know
what performance they can expect when the device is used as
However, the alert reader will note that the junction to ambient thermal
resistances of the two SOIC package options is essentially the same
even though one is clearly thermally superior. How is this possible? The
reason is that each device is characterized on a worst case board, that
is, one that has minimum heatsinking on the board. Without measures
to disperse heat, the advantage of the exposed pad package is lost.
But the important point here is that each device merits its own thermal
rating based on its primary thermal path. The standard SOIC merits
intended, that is, mounted to a board and possibly attached to a
heatsink. Unfortunately, thermal performance depends strongly on
how the device is mounted and used, and there is a vast array of
possibilities. So there is no single set of test conditions for a universally
applicable characterization. In order to provide some characterization,
manufacturers specify thermal behavior for worst case mounting
conditions or conditions typical of the application. Users must relate
the test data and specifications to their particular thermal environment.
a junction-to-lead specification, whereas the exposed pad device
requires a junction-to-case rating. Junction-to-case ratings, therefore,
8 Freescale Semiconductor, Inc.Thermal Analysis of Semiconductor Systems
Page 9

4.2. JEDEC Test Methods and Ratings
3 8 .1 m m , 38 .1 m m
2 5 m m
2 .54 m m
The rmoc oup le
Su pp ort Tu be
12 inch es
12 inch es
Ed ge
Co nn ecto r
De vice
Un der T es t
No n-
co ndu cti ve
su pp ort
No n-c on duc tive
ba se
Tes t
Ch amb er
12 inch es
JEDEC Solid State Technology Association (once known as the
Joint Electron Device Engineering Council) is the semiconductor
engineering standardization body of the Electronics Industries Alliance
(EIA). They have published thermal characterization test methods and
standards that apply to a wide variety of semiconductor packages,
mountings and usages. The recommendations in their JESD51
series of publications underpin many of the manufacturers’ thermal
specifications. A list of the JESD51 publications is provided in
Appendix A
Among their many contributions, several stand out for the thermal
characterization of power electronic devices:
1. Created a standard for electrically measuring thermal resistance
using a temperature sensitive parameter (TSP). This method can
be used to determine steady state behavior or transient response.
(JESD51-1)
2. Defined a test method for J-A measurement for still air. This
method tests the device on a PCB suspended in a one cubic foot
chamber, shown in Figure 4. (JESD51-2)
Figure 4—Test chamber as recommended in JESD51-2
5. Specified standards for “low” and “high” thermal conductivity
boards. Popularized usage of the terms “1s” and “2s2p” printed
circuit boards. (JESD51-3, 7)
Figure 5—JEDEC specified PCB for J-A thermal characterization
Figure 5 shows the PCB layout of a low thermal conductivity board.
The intent is to characterize the J-A resistance under conditions of a
worst case layout.
3. Identified and standardized the thermally relevant features of circuit
boards used in J-A characterization. Defined features including
board material, dimensions, trace design, via features, etc., as
shown in Figure 5. (JESD51-3)
4. Defined standards for forced convection testing (moving air)
and standardized the term Θ
resistance. (JESD51-6)
, junction to moving air thermal
JMA
The 1s board has signal traces on the component side of the board,
70µm copper thickness and no internal power or ground planes. The
JEDEC specification contains details of the board size and thickness,
trace width and length, etc. The board is allowed to have some traces
on the second side, but only if they are outside the fan-out area of the
topside traces.
The 2s2p board has 70µm signal traces on the component side of the
board and two internal planes with 35µm copper.
6. Created specifications for thermally enhanced circuit boards.
(JESD51-7)
7. Specified thermocouple probe placement to match a particular test
method and specification.
8. Standardized the terms for YJT (Psi-junction to top of package)
and YJB (Psi-junction to board) to estimate the junction
temperature based on the temperature at the top of the package.
These are “thermal characterization parameters” and not true
thermal resistances. (JESD51-2, 8, 10, 12)
From JESD51-12 we read, “Y
characterization parameter where T
is the junction to board thermal
JB
is the temperature measured
Board
on or near the component lead.” And, “Thermal characterization
parameters are not thermal resistances. This is because when the
parameter is measured, the component power is flowing out of the
component through multiple paths.”
9. Posted usage guidelines and identified limitations of applying
thermal specifications to actual thermal systems. (JESD51-12)
9Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 10

4.3. Thermally Enhanced Circuit Boards
A
33996DWB Terminal Connections
32-Terminal SOICW EP
0.65 mm Pitch
11.0 mm x 7.5 mm Body
4.6 x 5.7 mm exposed pad
80
100
10
Some commonly used techniques to improve thermal performance are
not addressed in the JEDEC51 specifications. As illustrated in Figure
6, dedicated copper islands may be placed near heat generating
components to conduct heat from the IC and to convect and radiate
heat from the PCB’s surface. Also, designers may attach a heatsink to
the backside of the PCB or even the top of the package. PCB traces
that conduct high current to power devices are commonly made as
large as allowable so as to minimize ohmic heating and enhance heat
flow. Heat generating devices are sometimes placed near other cooler
components, such as connectors, transformers or capacitors,
Figure 6—Thermal resistance test board with dedicated thermal pad
to improve dispersion. Modules designed for high power may very well
have heavy copper cladding with vias to the back of the board or to
internal copper planes. These measures and others can yield thermal
resistances substantially lower than those obtained from the JEDEC
specified tests.
The board illustrated in Figure 6 shows how a PCB might be modified
to reduce thermal impedance. To help users optimize thermal layouts,
many manufacturers specify thermal resistance with such thermally
enhanced boards. These ratings usually include a curve of thermal
resistance versus pad area, as shown in Figure 7.
10 Freescale Semiconductor, Inc.Thermal Analysis of Semiconductor Systems
Page 11

Figure 7—Junction to ambient thermal resistance decreases with dedicated thermal pad area
Another style of exposed pad package is the PQFN (power QFN). It
is a relatively new leadless power package and the 12mm by 12mm,
24-terminal version is shown in Figure 8. The power die is soldered to
the largest pad. The figure also shows a cross section of the PQFN
package mounted on a 0.062” PCB. The illustrated 2s2p board has
2 ounce/ft2 copper on the top and bottom layers (70µm thick) and 1
ounce/ft 2 copper (35µm) on the two inner layers. This figure illustrates
why layout is so important to thermal behavior.
Imagine two cases, each related to the top copper layer. The first uses
continuous topside copper to draw heat from IC’s exposed leadframe
to the surrounding board area. You can also imagine vias connecting
the topside copper to the other three layers. The second case has
copper only beneath the PQFN’s leadframe with no provision to
Figure 8 —Cross section of a PCB and a PQFN package
conduct heat laterally. This results in a thermal barrier at the copper to
PCB laminate interface. In the second case the thermal benefit of the
exposed thermal pad is almost completely lost.
The figure also illustrates which structures of the thermal stackup
contribute to thermal capacitance. The die, die attach, leadframe,
solder and even the package’s mold compound and the circuit board
provide a reservoir for thermal transients. (Appendix B shows the
thermal properties of common packaging materials.) These structures
can absorb energy transients, but like electrical capacitance, their
effectiveness drops to zero for steady state conditions. Since systems
are commonly subjected to power transients, designers need to
understand their system’s dynamic as well as static thermal behavior.
11Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 12
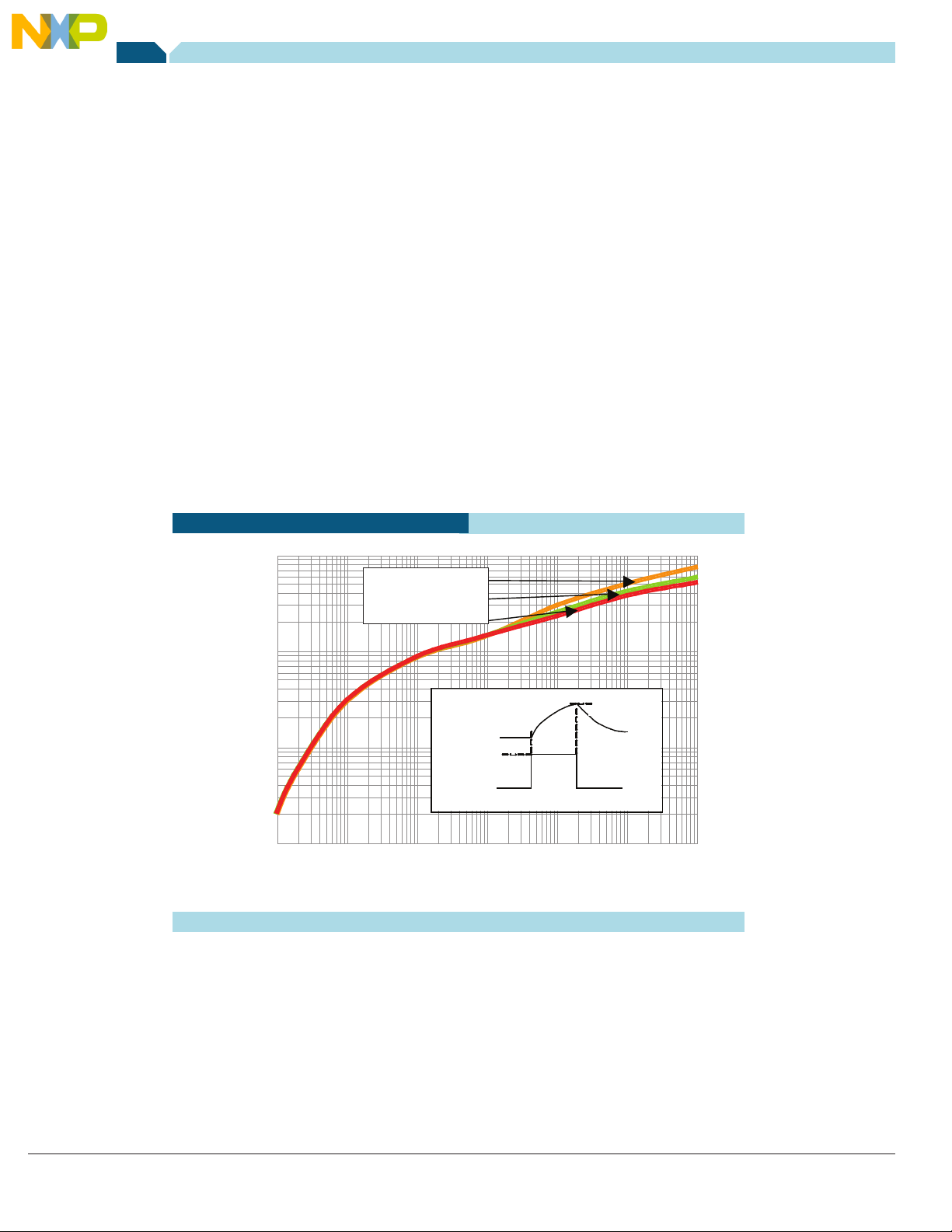
4.4. Transient Thermal Response Ratings
0.001
0.01
0.1
1.0
10
100
1000
1.0
10
100
0.1
Single Pulse Width, tp (seconds)
Z
JC
[K /W]
T
J initial
T
J peak
Pulse Width
P
D
Minimum footprint
A = 300mm
2
A = 600mm
2
In many systems the worst case conditions occur during a transient
condition, such as when inrush current flows into a cold lamp filament,
startup or stall currents appear in a motor or a short circuit causes fault
current. The duration of such a transient could very well be far shorter
than the system’s thermal time constant, especially since we often
use intelligent power devices to manage such events. If the system is
designed to meet worst case transient conditions for an unnecessarily
long time, the system will be over designed. Knowing how the system
responds to thermal transients helps the designer size components
and provide adequate, but not unnecessary, heatsinking.
When you include characterization in the time domain to the many
possible ways to characterize a device in steady state, the possible
options are too large to manage. To provide the most universally
useful data, the industry has adopted and promoted a concept called
“transient thermal response.”
Transient thermal response is a device’s or a system’s thermal
response to a step input of power. Note that the step input starts at
Figure 9—Transient thermal response curve
zero power, steps to some amplitude, then remains at that amplitude
forever. A transient thermal response curve is a plot of the junction
temperature rise as a function of time. As such, the curve incorporates
the thermal effects of a device’s entire structure. Manufacturers usually
create these curves empirically, but they can create them with models
as well.
Each point on the curve shows the die’s maximum temperature versus
how long the power pulse has been present. Transient response curves
can be referenced to case or ambient temperature.
It is important to note that the specific shape of the power pulse used
in the characterization may not match the shape of the pulse of interest
in the application. Therefore, it is important to remember what the
thermal response curves represent and to use them accordingly.
Figure 9 shows the transient thermal response curve of a transistor in a
28-pin SOIC. The far right side of the curve shows the device’s steady
state thermal resistance. In this case the three possible values are for
variously sized thermal pads.
Transient Thermal
Response [C/W]
12 Freescale Semiconductor, Inc.Thermal Analysis of Semiconductor Systems
Page 13

At narrow pulse widths the thermal impedance is far less than its
steady state value. For example, at one millisecond (ms) the thermal
impedance is only 0.2ºC/W, about 100 times less than the steady state
R
value.
QJA
Near the center of the graph the three curves diverge, implying that
for transients of less than one or two seconds in duration the device’s
heatsinking does not affect the peak temperature. Of course, this
is true because the heat wave front begins to exit the package after
those narrow pulse durations.
Part of the beauty of the transient thermal response curves is their
ease of use. Replacing R
QJA
with Z
in the basic thermal equation we
QJA
get:
T
= TA + (PD Z
Jpk
) (Eq. 8)
QJA
Now let’s assume that a system experiences a power transient with the
following characteristics and ambient temperature:
Power pulse width, tp = 1ms
P
= 50W
D
T
= 75ºC
A
To clarify understanding further and illustrate the importance of using
such curves properly, consider the initial junction temperature of this
example. It was not explicitly defined, but the use of the method sets
its value. Transient response curves apply only to systems that have
no initial power dissipation and that are thermally at equilibrium at time
zero. Therefore, in this example the initial junction temperature must be
the ambient temperature, or 75ºC.
Clever ways have been devised to use the transient response curves
for repetitive pulses of the same magnitude, alternate pulse shapes
and pulse trains of varying pulse widths and magnitudes. The basic
concept used to achieve the broader usage is the “Superposition
Principle.” This principle states that for linear systems the net effect
of several phenomena can be found by summing the individual effects
of the several phenomena. References 1, 2 and 8 explain these
techniques in detail.
From Figure 9 we can estimate Z
Z
@ 1ms = 0.2ºC/W
QJA
for a 1ms pulse width:
QJA
then,
ΔT
T
T
T
T
= (T
JApk
= TA + (PD Z
Jpk
= 75ºC + (50W * 0.2ºC/W)
Jpk
= 75ºC + 10ºC
Jpk
= 85ºC
Jpk
– TA) = PD Z
Jpk
)
QJA
QJA
5 Ramifications of High Operating Temperature
Motivation to conduct thermal assessments arises from an
understanding of how high operating temperature affects circuit
assemblies and their reliability. Some of the effects are well known;
others are much more subtle. Only a few can be briefly
mentioned here.
One interesting effect relates to all P-N junctions on a die. A graph
of diode forward voltage, Vf, as a function of temperature is shown
in Figure 10. It contains no surprises, showing the well-known and
well-behaved decrease in diode forward voltage with increasing
temperature. Extrapolating the curve to an even higher temperature
reveals that the forward voltage approaches 0V at about 325ºC.
The same relationship applies to the base-emitter junctions of a
device’s bipolar transistors, whether they are parasitic or not. The
result is that at a very high temperature even modest base-emitter
voltage can begin to turn on a transistor even though its base drive
circuit is trying to keep the BJT off. A similar phenomenon occurs
with MOSFETs because their gate-source threshold voltages fall with
temperature. Consequently, if a severe electrical transient generates a
hotspot, a BJT or MOSFET could reach a point of uncontrolled turn on.
Its temperature may continue to increase, and permanent damage
may ensue.
13Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 14

Figure 10—Diode forward voltage vs. operating temperature
.065
0.60
0.55
0.50
0.45
0.40
0.35
0.30
0.25
0.20
Tj, Junction Temperature [ºC]
0 25 50 75 100 125 150 175
Diode Forward
Voltage [V]
High junction temperature has many other electrical and mechanical effects. Among them are:
• Leakagecurrentsincrease
• Gateoxidesdegrademorequickly
• Ionicimpuritiesmovemorereadily
• Mechanicalstressesincrease
• Diodeforwardvoltagefalls
• MOSFETon-resistanceincreases
• MOSFETthresholdvoltagefalls
• Bipolartransistorswitchingspeedsslows
• Bipolartransistorgainstendtofall
• Breakdownvoltagestendtoincrease
• TransistorSafeOperatingAreasdecrease
Knowing some of the critical temperature milestones and thresholds is helpful in selecting the appropriate temperature ratings of other
components and for conducting forensic activity.
-55ºC Minimum semiconductor storage temperature
-40ºC Minimum automotive operating temperature
60ºC Metal surfaces are painfully hot
85ºC Maximum temperature of many electrolytic capacitors
125ºC Maximum operating temperature of many digital circuits
130ºC Common FR4 circuit board maximum temperature rating
150ºC Typical maximum junction temperature rating
165ºC to 185ºC Typical power transistor over temperature shutdown
155ºC to 190ºC Mold compound’s glass transition temperature*
183ºC Melting point of Sn
188ºC Melting point of Sn
217 to 220°C Melting point of Sn
280ºC Typical melting point of die attach solder
~350ºC Diode Vf approaches 0V
660ºC Melting point of pure aluminum (wirebonds and metallization are often aluminum)
1400ºC Melting point of silicon
*Glass transition temperature is the mid-point of a temperature range in which a solid plastic material, which does not melt, softens and the coefficient of thermal expansion increases.
Figure 11 shows a common model used for a single power transistor and its heatsinking. The electrical behavior is accounted for by an electrical
model on the far left side of the figure. Heat is transferred from the electrical to the thermal domain and is represented by a heat source, PD. The
14 Freescale Semiconductor, Inc.Thermal Analysis of Semiconductor Systems
solder (63% tin, 37% lead, eutectic)
63Pb37
solder
60Pb40
96.5Ag3.0Cu0.5
(96.5% tin, 3% silver, 0.5% copper)
Page 15

6 Thermal Circuits
R
thj-c
P
d
T
junction
C
thj-c
R
thc-hs
C
thc-hs
R
thhs-a
C
thhs-a
Ambient
Temperature
T
case
Power
Transistor
T
heatsink
Thermal
Domain
Electrical
Domain
Device Device to
Heatsink
Heatsink to
Ambient
symbol for the electrical current source is reused in the thermal domain
to denote the through variable. The heat source feeds successive RC
networks that model the behavior of the actual mechanical assembly.
Figure 11 shows three RC pairs, but a larger number could be used
to more accurately model a complex system, or a smaller number
could be used for a simple thermal network. The values of the R’s
and C’s can be estimated using the system’s material properties and
physical dimensions, or they can be extracted from empirical tests.
Figure 11—Electrical and Thermal Domain Circuits
the capacitor values are selected accordingly. The disadvantage of
the parallel RC configuration is that the capacitance values do not
directly relate to the system’s physical features, that is, they cannot be
calculated from the material’s density, capacity and volume.
The model shown in Figure 11 is of a single transistor and
consequently lacks any provision for thermal coupling between
neighboring components. For circuits with multiple power dissipating
For example, when the system is powered and is in steady state, the
thermal resistances can easily be derived from the power dissipation
and the temperatures at the three thermal nodes. Characterizing the
transient response requires monitoring temperature response to a step
input of power.
A good engineer will want to consider several aspects of this
representation. First is the meaning of the reference, or ground,
connection in the thermal domain. Since it is a node within the
thermal domain, it is an across variable and must represent some
reference temperature. There are two natural choices for this reference
temperature: ambient temperature or absolute zero. A simple
representation is to use absolute zero as the reference temperature
then use a temperature source for ambient temperature.
The second consideration is how to terminate the thermal
capacitances. The representation in Figure 11 connects the capacitor
to the reference terminal. However, a circuit with an equivalent thermal
response can be created with each of the capacitors in parallel with
their respective thermal resistors. Some tools used to extract the RC
thermal “ladder” more readily provide a circuit with the capacitors
in parallel with the resistors. Either capacitor arrangement suffices if
elements the components in Figure 11 are replicated for each heat
generating device, and thermal coupling resistors are placed between
each combination of nodes. Obviously, the thermal schematic
becomes more complex, but perhaps worse, the values of the new
components must be determined, most commonly through empirical
testing.
The thermal circuit shown in Figure 12 is a popular way of roughly
assessing multiple device behavior within a module. This method is not
used for transient conditions, so Figure 12 does not include thermal
capacitors. Each power dissipating device is treated independently of
the others and is assigned a junction to ambient thermal resistance
based on datasheet characterization and allotted circuit board area.
The designer estimates the module’s internal air temperature rise
above ambient based on experience and adjusted to account for
the module’s size and its other thermally significant features. Finally,
device junction temperatures are estimated from the device’s R
power dissipation and the module’s internal air temperature, which is
the “ambient” temperature for the power device.
This method has the following three key weaknesses:
QJA
, its
15Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 16
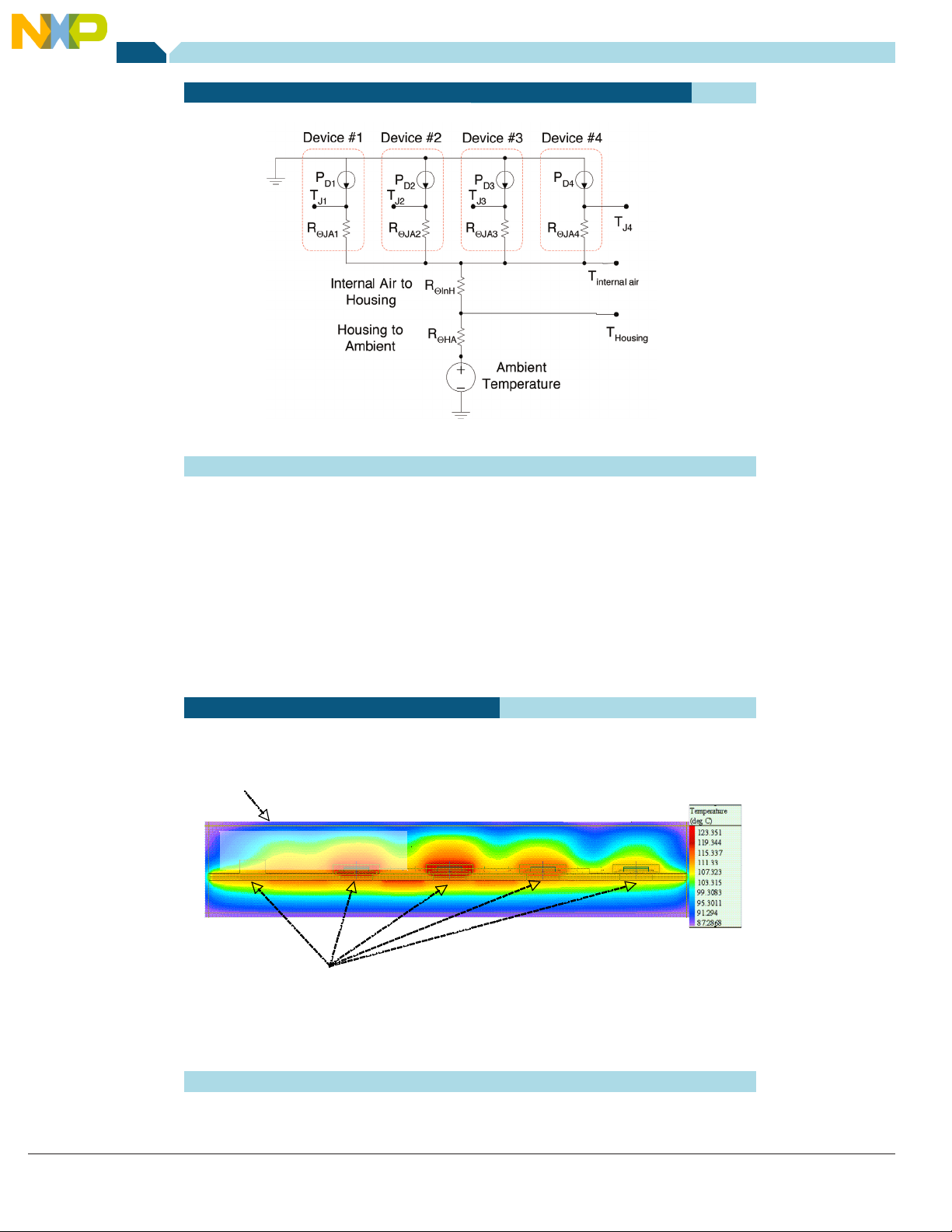
Figure 12—Popular thermal model for a module with multiple power devices
Module Housing
Power Gene rating Devices
internal “ ambient” tempe rature
Ta = 85ºC
1. It does not account for thermal coupling between devices on the
PCB. For this method devices affect one another only through their
effect on the internal ambient temperature.
2. It assumes a constant internal air temperature even though we
know “ambient” temperature within a module varies substantially
with distance from the heat sources. Figure 13 illustrates the
difficulty of selecting a single value for internal “ambient”
temperature.
Figure 13—Thermal gradients within a module.
3. Conditions existing in a module differ considerably from the
conditions used to specify the rated junction to ambient thermal
resistance. The PCB’s thermal characteristics differ and module’s
small volume constricts the flow of convective currents.
In spite of its clear drawbacks, this method is popular because it
quickly yields a rough estimate of operating temperature.
Other approaches are used, but all have limitations because each
inherently attempts to simplify a complex thermal circuit using a few
16 Freescale Semiconductor, Inc.Thermal Analysis of Semiconductor Systems
Page 17

lumped components. One alternate approach accounts for thermal
coupling between devices and is practical for systems with up to four
or five power devices. The improved accuracy comes at the cost of
additional empirical characterization and the need to solve several
or even many simultaneous equations. As the number of power
components increases, this rapidly becomes more difficult.
After taking the first round of measurements, individually power all
other devices in sequence and measure the temperature increases
each device induces in all other devices. Once these thermal coupling
coefficients are known the junction temperature of each device can be
estimated by solving simultaneous equations. Their equations can be
represented in matrix form as:
The first step of this method is to measure the junction to ambient
thermal resistance of each device when all other devices are not
generating power. Such a direct measurement gives the designer
an accurate value for the thermal resistance of that device in that
application. As a check, the calculated value should be compared to
the thermal resistance specifications.
The next step is to determine how each device heats its neighbors,
that is, the thermal coupling coefficients between devices. Use either
a thermal mock-up or a module prototype to determine these thermal
coupling factors. You can determine the coupling factors by powering
only a single device and measuring the temperature rise at every other
critical device. The coupling coefficient is the ratio of the induced
temperature rise in the unpowered device and temperature rise in the
powered device caused by self heating.
7 Thermal Modeling Software
loading and operating conditions. Given there are many, many ways
to implement a system, the designer needs an efficient way to search
for the workable solutions among the vast number of possible ones.
Furthermore, the task also requires converging on the final design as
quickly and efficiently as possible. Cost and time constraints prohibit
searching for the optimum design by redesigning and testing many
successive hardware variations. You may be restricted to just a few
cycles of building, testing and modifying a module because respinning
PCBs takes time, and modifying the module’s housing or connector is
particularly expensive. Thermal analysis software can speed design by
providing critical guidance during the search process.
T
J1
T
J2
T
J3
T
J4
c
11c21c31c41
c12c22c32c
=
c13c23c33c
c14c24c34c
42
43
44
P
1 R_JA1
P2 R
P3 R
P4 R
_JA2
_JA3
_JA4
x
T
A
T
A
+
T
A
T
A
where cmn is the coupling coefficient between Device m and Device n,
R
is the junction to ambient thermal resistance of Device m, and Pm
QJCm
is the power dissipated by Device m. By the way, do not assume that
c
is equal to cnm.
mn
For systems with many power dissipating sources the characterizations
and calculations become unmanageable. This is when commercially
available thermal modeling software tools can be used.
7.1. Uses of Thermal Modeling Software
A designer’s primary thermal concern is that his module must
economically meet all the system’s requirements under worst case
• Howmuchpowerwillmysystemdissipate?
• Howmuchpowercanmysystemdissipatewithoutoverheating?
• Whatisthesystem’sprimarythermalpath?
• Whatarethemosteffectivemeansofimprovingthatpath?
• Howmuchwilloneelementheatitsneighbor?…andsoon
If you are designing a system that has no predecessor, you will
immediately face basic questions, such as:
17Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 18

Three analysis tools can be used in combination to answer these and
other questions:
1. Analysis using manufacturers’ thermal ratings and characterizations
2. Empirical testing of a prototype or of a thermal mock-up
3. Thermal modeling
Before using a set of thermal modeling tools, it’s appropriate to
consider the purpose of the modeling, the characterization data
available to support those models and what a particular software tool
can and cannot provide. These are some of the best uses of thermal
analysis software:
Provide tradeoff assessments before any hardware is built
A model of a proposed implementation is a fast and low-cost way of
assessing if that implementation can potentially meet the system’s
requirements. However, you should expect that a first pass thermal
model will likely require refinements or even major revisions after you
compare the model’s simulation results to empirical test results of
actual hardware.
Uncover poorly understood thermal phenomena
After you decide on the first pass hardware, based on an initial thermal
model, the next steps are to build the hardware, characterize it and
compare empirical test results to the model’s predictions. Implicit in
this discovery process is that the designer must calibrate and validate
the model by empirically testing hardware.
More than likely there will be mismatches between the empirical and
modeled results. These incongruities identify thermal behaviors that
were not modeled properly, most likely because they were poorly
understood, thought to be unimportant or simply overlooked. Perhaps
the best use of modeling is to identify critical module characteristics
that were misrepresented in the model and to use that information to
improve your understanding of the module.
A model can be used to assess test conditions that are
difficult to create
Testing a module under some conditions is difficult or impractical. In
these cases a calibrated thermal model can be used instead.
Testing under worst case conditions is a good example of a set of
system conditions that are difficult to create. Let’s assume that you
would like to test the system with power transistors that have worst
case on resistances. You are not likely to find such devices for
empirical testing, but modifying the transistor’s power dissipation in the
model is easy. Or, you may have hardware limitations, such as oven
volume or temperature range, that prohibit certain tests. These could
be explored in the simulated domain instead.
Thermal models accurately simulate behavior of simple
structures
A thermal model of a simple structure can be quite accurate because
we can precisely describe simple structures mathematically. This
strength of thermal modeling gives it a special advantage for simple
structures that are difficult to empirically test, such as a power die
on a leadframe. Empirical testing is not likely to help map junction
temperature variations across a die, especially during transients. A
calibrated model is a handy tool for these situations.
Thermal models provide a means to estimate a system’s
response to power transients
A system’s worst case operating conditions are often transient, so
dynamic conditions often dictate the system’s required capability. It’s
difficult enough to envision how heat flows in a system under steady
state conditions let alone estimating how temperatures change during
a transient condition. Models can provide badly needed guidance in
these situations. Some allow you to create movies of the temperature
during transients, providing the designer with a more intuitive sense of
how the system is performing.
A calibrated thermal model speeds development
Once a thermal model is calibrated it becomes a powerful tool to
explore potential variations in the next layout iteration. Altering the
model and rerunning simulations is usually much faster and less
expensive than modifying the layout and retesting the hardware.
Once you create a validated thermal model it can, of course, be used
as a starting point for future modules of similar design.
18 Freescale Semiconductor, Inc.Thermal Analysis of Semiconductor Systems
Page 19

7.2. Thermal Modeling Software Options
There are quite a few commercially available thermal modeling software
packages. Each package claims its niche. Whether you are selecting
a package or using one that your company already has, it is good to
understand how they differ. Some of the differentiating features are:
• Cost,includinghardwareandmaintenancefees
• Simulationspeed
• Trainingrequiredforcompetency
• Abilitytomodelallthreemodesofheattransfer,whichfor
convection requires the ability to model fluid flow
• Abilitytomodelresponsestotimevaryingpowerwaveforms
• AbilitytoimportfilesfromotherCADpackages
• Methodofmanagingboundaryconditions
• Abilitytouseamulti-levelnestedmesh
• Abilitytolinkthermalmodelstomodelsinotherdomains(e.g.,
electrical models)
• Inclusionofasoftwarelibrarythatcontainscommonthermal
elements, such as heatsinks, enclosures, PCBs, etc.
• Abilitytoviewandexportasimulation’sresults
• Customersupport,includingtechnicalliterature
• Numericalmethodusedtosolvethegoverning
mathematical equations
ANSYS is one well known CFD thermal analysis software supplier that
offers CFX, Fluent, Iceboard and Icepak. Flomerics is another well
respected vendor and provides Flowtherm, which is the simulation
software used to create the image in Figure 13. CFD programs provide
the ability to view and export images of fluid speed and direction. This
feature helps to clearly illustrate the size and effectiveness of thermal
plumes, which are likely to form above hot surfaces.
When convection is not a significant thermal transport mechanism, a
program capable of modeling fluid flow is not necessary. An example
of such a system is a semiconductor package mounted to a heatsink
that is at a fixed or known temperature. A software package optimized
for conductivity might simulate faster or give more accurate results,
such as one using the Boundary Element Method. Instead of breaking
the modeled volume into a mesh of much smaller units, the BEM
creates a mesh on the surface of a solid. From the conditions at the
surface, it predicts the temperature and heat flux within the solid.
Because the BEM does not discretize the volume, it does not suffer
from the problems associated with having a mesh size that is too small
(excessively long simulation times) or too large (reduced accuracy). For
simple structures, such as a die in a package, the BEM is a fast and
accurate numerical method. Freescale engineers have successfully
used Rebeca 3D, a BEM package supplied by Epsilon Ingénierie, to
evaluate hotspot temperature of power die in a multi-die package.
A program’s numerical method, the last item in the above list, is the
most fundamental feature of each program. The numerical method is
the means by which the software resolves the governing
mathematical equations.
Numerical methods used in thermal analysis software include the
Boundary Element Method, Finite Difference Method, Finite Element
Method and Finite Volume Method. The latter is the method most often
used in computational fluid dynamics (CFD) software.
The particular numerical method a program uses makes it more or
less suitable for specific modeling tasks. The most obvious example
is CFD software. Like all viable thermal analysis software, it accounts
for conduction and radiation. But CFD also predicts fluid flow, which
is necessary to model convection. Therefore, if convection is a primary
transport method in your systems, you will likely require CFD software.
Even the most sophisticated thermal analysis software package is
not a panacea. Obviously, the quality of its predictions depends on
the model’s inputs, such as the system’s physical dimensions and
material properties. The results also improve with the detail included
in the model, but the simulation times increase accordingly. Therefore,
regardless of which modeling software is used, to obtain the most
value from a simulation you should carefully discuss the system’s
pertinent features with the engineer creating the model, including: the
mechanical features of the system; heat source sizes and locations;
potential thermal paths; all material characteristics; system orientation;
physical boundary to be modeled, etc. The engineer creating the
model should carefully explain the simplifying assumptions he/she
plans to make.
Appendix B contains a table of thermal properties of materials used in
typical semiconductor packages.
19Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 20

8 Empirical Analysis Techniques
The tools used for empirical thermal analysis are fairly well known.
The most common tool, of course, is the thermocouple. A few
guidelines to their use are:
1. Make sure your thermocouple type (J, K, T or E) matches your
meter setting.
2. Use small gauge thermocouple wires. This reduces the heatsinking
effect the leads have on the device under test.
3. Monitor as many points as practical to improve your overall
understanding of the circuit and to enhance your chance of
detecting unexpected hot spots.
4. Place probes at nodes as close as practical to the die of interest.
This measurement location need not be in the primary thermal
path. For instance, the temperature at the top of the package or
at an exposed tab may be very close to the die temperature even
though the measurement location is not in the primary
thermal path.
Infrared scanning is a very helpful technique because it provides
information about the entire scanned area. Discovering unexpected
hot spots, such as undersized PCB traces or connector pins, with
an infrared scan is not uncommon. This can be very helpful during
prototyping where assembly problems might otherwise go unnoticed. A
disadvantage of thermal imaging is that the camera must have access
to the device or PCB under test. Opening a module to provide such
access significantly alters the behavior you are trying to measure.
Handheld, infrared, contactless thermometers are inexpensive and
easy-to-use tools for taking spot measurements.
It’s possible to measure a device’s junction temperature by monitoring
a temperature sensitive parameter (TSP) of one of its components. A
diode’s forward voltage, Vf, is one the most commonly used TSPs, and
diodes may be readily accessible as ESD structures on a logic pin, for
example. The body diode of a power MOSFET is another often used
component, but using that diode requires reversing the current in the
MOSFET, which requires a bit of circuit gymnastics. Over temperature
shutdown (if available), MOSFET on-resistance and MOSFET
breakdown voltage are also options. Using a TSP requires establishing
the TSP’s variation over temperature, which must be done at near
zero power.
When making thermal resistance measurements, you should try to
use power levels that will generate easily measurable temperature
increases. A larger junction to ambient temperature differential
increases the quantity you are attempting to measure (temperature rise)
relative to any potential measurement errors in the system.
A common system requirement is that a module must operate at a
certain ambient temperature in still air. These conditions sound simple
enough to create, but the high test temperature will require an oven
and an oven often uses circulating air to control the temperature. Its
fan ensures the oven’s air is not still. To circumvent this problem
you can place a box in the oven and place the module in that box.
Of course, the box reduces the air speed around the module. With
this arrangement the oven temperature can be adjusted to attain the
specified “ambient” temperature in the box.
If you are designing a system that has a predecessor, use data from
that module as a starting point. If the system has no predecessor, then
consider building a thermal mock-up that will mimic the final module’s
behavior. Such a mock-up might have little or no electrical similarity
to the intended module, but it should have mechanical and thermal
similarity. Because an electrical circuit does not have to be built,
programmed and debugged, you might be able to create a thermal
prototype of your module very quickly to assess total module power
budget, thermal coupling, affects in changes to the primary thermal
path, etc.
Finally, plan to use empirical testing in conjunction with thermal
resistance ratings and thermal models to enhance your understanding
of the system.
20 Freescale Semiconductor, Inc.Thermal Analysis of Semiconductor Systems
Page 21

9 Optimizing the Thermal Environment
There are many ways to reduce the operating temperature of
semiconductor devices. Some of the techniques add little or no
additional cost to the module. Below are some suggestions:
Reduce the module’s or IC’s thermal load.
The most direct way to deal with excessive heat is to not generate it in
the first place. Portions of the circuit may be turned off. Load shedding
(if allowed), careful fault management, using oversized power
transistors or using ICs with power saving features are some of the
ways to cut
a module’s total dissipation. Carefully defining the module’s worst case
operating conditions is sometimes the most effective way to reduce
power dissipation.
Reduce thermal impedance in the IC’s immediate vicinity.
Semiconductor die are quite small compared to the size of a typical
module, and this results in very high heat flux in the die, the package
and its immediate vicinity. Therefore, thermal resistance encountered
early in the thermal path causes a large temperature gradient. That is
why temperature often falls rapidly as you move from the die into its
package and then into rest of the system. The most effective place
to focus resources to reduce thermal resistance is where the thermal
gradient is highest. So, be especially mindful of how the package is
attached to the PCB or heatsink and how thermal energy is transferred
and spread in that area. Spreading the heat at the beginning of the
thermal path not only reduces the thermal resistance near the IC, but it
also provides a broader area to further disseminate the heat. Reducing
the thermal impedance close to the die and package is mandatory for
good thermal performance.
Use a continuous low impedance path from the IC
to ambient.
Around the IC, provide an uninterrupted copper path to a large pad to
radiate heat, a heatsink, the module’s harness, etc. Any small break
in low impedance material is highly detrimental. Provide redundant
thermal paths where possible.
Separate heat generating components.
Place heat generating components as far apart as possible to reduce
thermal coupling effects. The thermal gradient is high near a power
dissipating device, so even small amounts of separation help reduce
thermal coupling.
Use thick copper cladding, if allowable.
The cross sectional area of a trace is quite small and can constrict
heat flow. Using heavier copper cladding reduces this effect. However,
if fine pitch ICs are used on the board, using heavier copper cladding
may violate manufacturing guidelines.
Beware of PCB trace and connector pin heating.
Modern power electronics devices can have very low on-resistances.
It’s quite possible that the PCB traces and connector pins that feed
current to these devices contribute more ohmic losses to the system
than the power transistors do. Such heating may be avoidable if
traces are upsized. Reducing trace ohmic losses may be the least
expensive way to reduce the module’s total power dissipation. Trace
width calculators, which also predict trace temperature rise, are readily
available on the internet.
Consider the effects of PCB and module orientation.
Heat convection is more efficient for a vertically mounted board.
Remember that components above heat producing devices run hotter
than those below.
If the board is to be horizontally mounted, place heat generating
devices on the PCB’s topside, if possible. A thermal plume forms more
readily on a board’s topside and it helps disperse heat.
Increase the surface area from which the heat exits
the module.
Ultimately, some surface will radiate the module’s heat or disperse it
by convection. Use all available features, such as the harness as well
as the housing. The utility of the harness depends on the number and
gauges of its wires, its insulation, its own ohmic losses and how well
heat can flow from the PCB through the connector and into
the harness.
21Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 22

Take advantage of thermal capacitance, if possible.
Worst case conditions are often briefer than the module’s thermal time
constant. Upon a change in operating conditions, a module can easily
take more than 10 minutes to stabilize thermally. The system may be
able to store the energy from the worst case conditions in the module’s
thermal capacitance. Heat sinks, heavy copper and multi-layered
boards all add to the module’s thermal capacitance.
Remember, too, that even when a device is mounted to a worst case
board, the device itself has some ability to absorb energy. If a device
has fast fault detection circuitry, it may be able to absorb the energy
and manage the fault without harm to the device, the PCB or the load.
Expect surprises.
Because we have a limited innate ability to sense thermal phenomena,
we lack an intuitive feel for how thermal systems behave. This makes
it advisable to monitor temperature at many points on a PCB or, better
yet, photograph the module, its PCB, and its harness with an infrared
camera. Any unexpected temperatures you find point you to aspects
of the thermal circuit that you do not completely understand. Finding
these surprises provides valuable clues that can lead to a better
understanding of the module’s thermal behavior.
10 Appendices
10.1. Appendix A—List of JESD51 Series Publications
JESD51 “Methodology for the Thermal Measurement of Component Packages (Single Semiconductor Device)”
JESD51-1 “Integrated Circuit Thermal Measurement Method—Electrical Test Method (Single Semiconductor Device)”
JESD51-2 “Integrated Circuit Thermal Test Method Environmental Conditions—Natural Convection (Still Air)”
JESD51-3 “Low Effective Thermal Conductivity Test Board for Leaded Surface Mount Packages”
JESD51-4 “Thermal Test Chip Guideline (Wire Bond Type Chip)”
JESD51-5 “Extension of Thermal Test Board Standards for Packages with Direct Thermal Attachment Mechanisms”
JESD51-6 “Integrated Circuit Thermal Test Method Environmental Conditions—Forced Convection (Moving Air) ”
JESD51-7 “High Effective Thermal Conductivity Test Board for Leaded Surface Mount Packages”
JESD51-8 “Integrated Circuit Thermal Test Method Environmental Conditions—Junction-to-Board”
JESD51-9 “Test Boards for Area Array Surface Mount Package Thermal Measurements”
JESD51-10 “Test Boards for Through-Hole Perimeter Leaded Package Thermal Measurements”
JEDEC51-12 “Guidelines for Reporting and Using Electronic Package Thermal Information”
10.2. Appendix B—Thermal Properties of Common Semiconductor Packaging Materials
Material Conductivity K
(W/m K) – (J/kg K) (kg/m3) (J/K m3) –
Epoxy Mold
Compound
Silicon (at 25C) 148 0.41111 712 2328.9 1658177 0.4908
SnPb Solder 50 0.13889 150 8500 1275000 0.3774
Silver Filled Die
Attach
CU Lead Frame 360 1.00000 380 8890 3378200 1.0000
FR-4 0.35 0.00097 878.6 1938 1702727 0.5040
Air 0.03 0.00008 1007 1.16 1170 0.0003
Values may vary with specific type of material, temperature
0.72 0.00200 794 2020 1603880 0.4748
2.09 0.00581 714 3560 2541840 0.7524
Relative
Conductivity
Thermal
Capacity CP
Density
Volumetric Heat
Capacity
Relative
Volumetric Heat
Capacity
22 Freescale Semiconductor, Inc.Thermal Analysis of Semiconductor Systems
Page 23

11 References
1. “MC33742DW Thermal Datasheet,” Freescale Semiconductor, April 2007, http://www.freescale.com
2. “MC33996 Datasheet”, Freescale Semiconductor, June 2007, http://www.freescale.com
3. Roger Stout, “Linear Superposition Speeds Thermal Modeling”, Part 1, pp20-25, Power Electronics Technology, January 2007
4. Roger Stout, “Linear Superposition Speeds Thermal Modeling”, Part 2, pp28-33, Power Electronics Technology, February 2007
5. T. Hopkins, et al, “Designing with Thermal Impedance”, SGS-Thompson Application Note AN261/0189, reprinted from Semitherm
Proceeding 1988
6. “Understanding the JEDEC Integrated Thermal Test Standards”, Advanced Thermal Solutions, Inc., http://www.QATS.com
7. JESD51-1 through JESD51-12 specifications, JEDEC Solid State Technology Association, http://www.jedec.org
8. REBECA-3D, http://www.rebeca3d.com
9. Roehr, Bill and Bryce Shiner, “Transient Thermal Resistance - General Data and Its Use,” AN569 in Motorola Power Applications
Manual, 1990, pp. 23-38 or http://www.bychoice.com/motorolaApps.htm
10. R. Behee, “Introduction to Thermal Modeling Using SINDA/G,” Network Analysis, Inc., http://www.sinda.com
11. “Thermocouples – An Introduction”, Omega Engineering website, http://www.omega.com
12. PCB Trace Width Calculator, http://circuitcalculator.com/wordpress/2006/01/31/pcb-trace-width-calculator/
13. “Important Questions to Ask When Evaluating Thermal Analysis Software for Electronics”, Stokes Research Institute,
http://www.stokes.ie/pdf/Questionnaire.pdf
14. M. Goosey and M. Poole, “An Introduction to High Performance Laminates and the Importance of Using Chemical Processes
in PCB Fabrication”, Rohm and Haas Electronic Materials, http://electronicmaterials.rohmhaas.com
23Thermal Analysis of Semiconductor SystemsFreescale Semiconductor, Inc.
Page 24

How to Reach Us:
Home Page:
www.freescale.com
Power Architecture Information:
www.freescale.com/powerarchitecture
e-mail:
support@freescale.com
USA/Europe or Locations Not Listed:
Freescale Semiconductor
Technical Information Center, CH370
1300 N. Alma School Road
Chandler, Arizona 85224
1-800-521-6274
480-768-2130
support@freescale.com
Europe, Middle East, and Africa:
Freescale Halbleiter Deutschland GmbH
Technical Information Center
Schatzbogen 7
81829 Muenchen, Germany
+44 1296 380 456 (English)
+46 8 52200080 (English)
+49 89 92103 559 (German)
+33 1 69 35 48 48 (French)
support@freescale.com
Japan:
Freescale Semiconductor Japan Ltd.
Headquarters
ARCO Tower 15F
1-8-1, Shimo-Meguro, Meguro-ku,
Tokyo 153-0064, Japan
0120 191014
+81 3 5437 9125
support.japan@freescale.com
Information in this document is provided solely to enable system and software implementers to use Freescale
Semiconductor products. There are no express or implied copyright license granted hereunder to design or
fabricate any integrated circuits or integrated circuits based on the information in this document.
Freescale Semiconductor reserves the right to make changes without further notice to any products herein.
Freescale Semiconductor makes no warranty, representation or guarantee regarding the suitability of its products
for any particular purpose, nor does Freescale Semiconductor assume any liability arising out of the application
or use of any product or circuit, and specifically disclaims any and all liability, including without limitation
consequential or incidental damages. “Typical” parameters which may be provided in Freescale Semiconductor
data sheets and/or specifications can and do vary in different applications and actual performance may vary
over time. All operating parameters, including “Typicals” must be validated for each customer application by
customer’s technical experts. Freescale Semiconductor does not convey any license under its patent rights nor
the rights of others. Freescale Semiconductor products are not designed, intended, or authorized for use as
components in systems intended for surgical implant into the body, or other applications intended to support or
sustain life, or for any other application in which the failure of the Freescale Semiconductor product could create
a situation where personal injury or death may occur. Should Buyer purchase or use Freescale Semiconductor
products for any such unintended or unauthorized application, Buyer shall indemnify and hold Freescale
Semiconductor and its officers, employees, subsidiaries, affiliates, and distributors harmless against all claims,
costs, damages, and expenses, and reasonable attorney fees arising out of, directly or indirectly, any claim of
personal injury or death associated with such unintended or unauthorized use, even if such claim alleges that
Freescale Semiconductor was negligent regarding the design or manufacture of the part.
Asia/Pacific:
Freescale Semiconductor Hong Kong Ltd.
Technical Information Center
2 Dai King Street
Tai Po Industrial Estate,
Tai Po, N.T., Hong Kong
+800 2666 8080
support.asia@freescale.com
For Literature Requests Only:
Freescale Semiconductor
Literature Distribution Center
P.O. Box 5405
Denver, Colorado 80217
1-800-441-2447
303-675-2140
Fax: 303-675-2150
LDCForFreescaleSemiconductor@hibbertgroup.com
Learn More:
Freescale and the Freescale logo are trademarks or registered trademarks of Freescale Semiconductor, Inc.
in the U.S. and other countries. All other product or service names are the property of their respective owners.
© Freescale Semiconductor, Inc. 2008
Document Number: BASICTHERMALWP/ REV 0
For current information about Freescale
products and documentation, please visit
www.freescale.com.
 Loading...
Loading...