Page 1

How to calibrate an RTD
or Platinum Resistance
Thermometer (PRT)
Topics Covered
●
Calibration by characterization
ITS-90
Callendar-Van Dusen
Polynomial
●
Tolerance testing
ASTM 1137
IEC 60751
Application Note
Introduction
There are two types of calibrations applicable to PRTs—characterization and tolerance
testing. The type of calibration to perform is determined by the way in which the UUT is
to be used and the accuracy required by the user. Characterization is the type of calibration in which the unit under test (UUT) resistance is determined at several temperature
points and the data are fitted to a mathematical expression. Tolerance testing on the
other hand is a calibration in which the UUT resistance is compared to defined values at
specific temperatures. No data fitting is performed. In the laboratory, we are required to
perform both types of calibration depending upon our customer’s needs.
Calibration Procedures
Characterization
Characterization is the method that is most often used for medium to high accuracy PRT
calibration. With this method, a new resistance vs. temperature relationship is determined anew with each calibration. Generally, with this type of calibration, new calibration coefficients and a calibration table are provided as a product of the calibration.
There are five basic steps to perform as listed below:
1. Place the reference probe and the UUTs in the temperature source in close proximity to one another.
2. Connect the leads to the readout(s) ensuring proper 2-, 3-, or 4-wire connection.
3. Measure the reference probe and determine the temperature.
4. Measure and record the resistance of the UUT(s).
5. Fit the data.
Some readouts simplify the technique by combining or eliminating some of the steps.
In the following discussion, we will consider an application involving PRT characterization by comparison to an SPRT.
Step 1: Probe Placement
All temperature sources have instabilities and gradients. These translate into calibration errors and/or uncertainties. To minimize the effects, the probes should be placed
as close together as practical. In baths the probes to be calibrated should be placed
in a radial pattern with the reference probe in the center (focus) of the circle. This
ensures an equal distance from the reference probe to each of the UUTs. In dry-well
temperature sources, the reference probe and probes to be calibrated should all be
placed the same distance from the center for best results, but the reference may be
placed in the center if needed.
Also, the sensing elements should be on the same horizontal plane. Even though
sensing elements are different lengths, having the bottoms of the probes at the same
level is sufficient. Sufficient immersion must be achieved so that stem losses do not
occur. Generally, sufficient immersion is achieved when the probes are immersed
to a depth equal to 20 times the probe diameter plus the length of the sensing element. For example, consider a 3/16 inch diameter probe with a 1 inch long sensing
element. Using the rule of thumb, 20 x 3/16 in + 1 in = 3 3/4 in + 1 in = 4 3/4 in.
In this example, minimum immersion is achieved at 4 3/4 inches. This rule of thumb
is generally correct with thin wall probe construction and in situations of good heat
transfer. If the probe has thick wall construction and/or poor heat transfer is present
(such as in the case of a dry-well with incorrectly sized holes), more immersion is
required.
F r o m t h e F l u k e D i g i t a l L i b r a r y @ w w w . f l u k e . c o m / l i b r a r y
Page 2
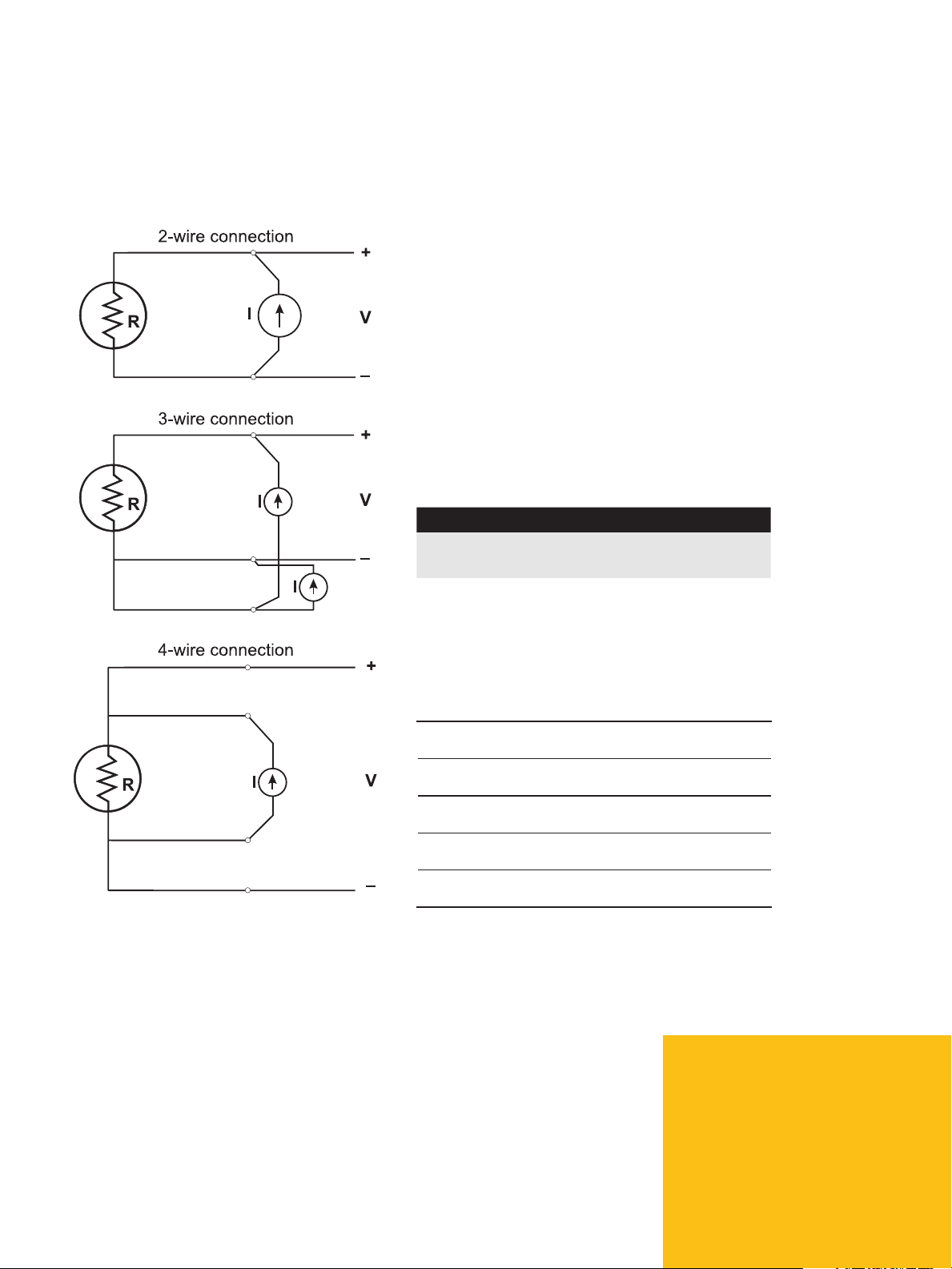
Step 2: Connection to Readout
This step is straightforward. Connections must be
tight and in proper 2-, 3-, or 4-wire configuration. If
using 4-wire configuration, ensure that the current
and voltage connections are correct. See Figure 1.
temperature data is available in real time. Some
modern readouts also display the data in graphical
format, allowing the operator to determine stability at a glance. Both of these features speed up the
process and eliminate possible operator error due to
incorrect table interpolation.
The second method is used when the readout
does not provide for proper temperature calculation.
(Some readouts, particularly DMMs, have some of
the more popular temperature conversions built in.
These typically do not allow use of unique calibration coefficients and cannot be used for accurate
temperature calibration.) In this case, the resistance
is measured and the temperature is determined
from either a calibration table or from a computer or
calculator program.
Since the temperature must be calculated after
the resistance is measured, the process is slower
and does not provide immediate, real time temperature data. See Tables 1 and 2 below.
Table 1. Interpolation from an RTD calibration table
(resistance vs. temperature).
t( °C) R(t) (W) dR/dt(t) W/°C
400 249.8820 0.3514
401 250.2335 0.3513
402 250.5848 0.3512
403 250.9360 0.3511
450 267.3108 0.3456
451 267.6564 0.3455
452 268.0019 0.3454
453 268.3472 0.3452
Figure 1. Thermometer readout connection schematics
Step 3: Measurement of Reference Probe
and Temperature Determination
There are two ways to measure the reference probe
and determine the temperature. Both techniques
have the same potential accuracy. That is, if done
correctly, neither technique is inherently more
accurate than the other.
The first and best method is used with sophisticated readouts designed for temperature work.
The resistance is measured and the temperature
calculated from calibration coefficients which were
entered into the readout previously. Once these
calibration coefficients have been entered, the temperature calculations are accomplished internally
and the readout displays in temperature units. The
1. Measure the reference
probe resistance
2. Locate where it falls on
the table
3. Subtract lower table value
from measured value
4. Divide by dR/dT(t) (slope
of curve)
5. Add fractional
temperature to table value
249.9071 W
between 249.8820 W and
250.2335 W
249.9071 W – 249.8820 W =
0.0251 W
0.0251 / 0.3514 = 0.0714 °C
0.0714 ’C + 400 =
400.0714 °C
Tech Tip
Manual calculation is more
prone to human error and
is more time consuming than using a readout
designed for temperature
work.
2 Fluke Corporation, Hart Scientific Division How to calibrate an RTD or Platinum Resistance Thermometer (PRT)
Page 3
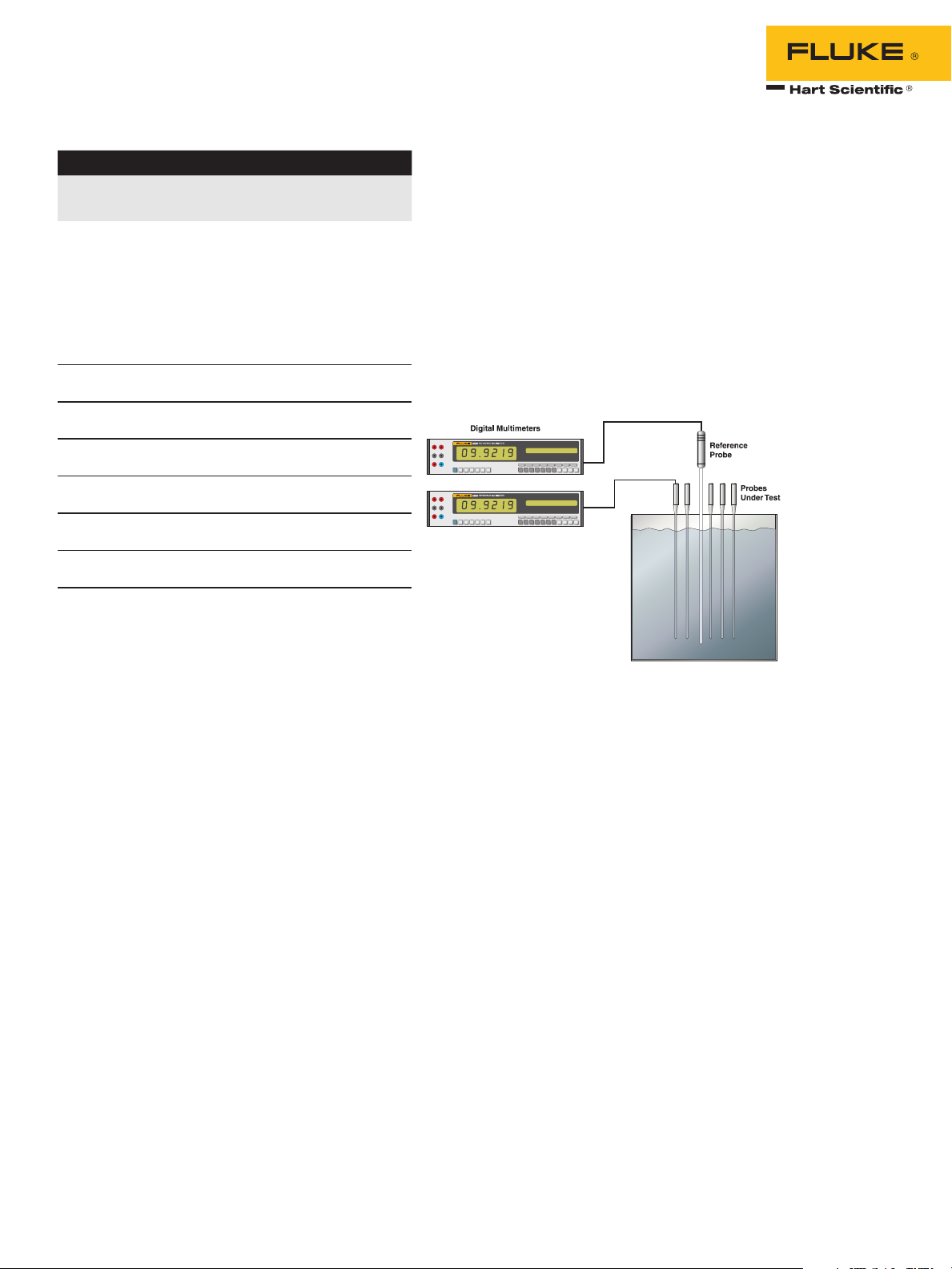
Table 2. Interpolation from an RTD calibration
(resistance ratio (W) table).
t( °C) W(t) dt/dW(t)
300 2.1429223 275.2199
301 2.1465557 275.3075
302 2.1501880 275.3951
303 2.1538192 275.4827
350 2.3231801 279.6655
351 2.3267558 279.7559
352 2.3303304 279.8464
353 2.3339037 279.9369
1. Measure reference probe
resistance
2. Calculate W (Rt/R
= 25.54964)
3. Locate where it falls on
the table
4. Subtract lower table value
from measured value
5. Multiply by dt/dW(t)
(inverse slope of curve)
6. 6) Add fractional
temperature to table value
) (R
tpw
54.75258 W
54.75258 W / 25.54964 W =
tpw
2.1429883
between 2.1429223 and
2.1465557
2.1429883 – 2.1429223 =
0.000066
0.000066 • 275.2199 =
0.0182 °C
0.01821 °C + 300 °C =
300.0182 °C
Number of readouts - will the reference probe
•
and UUTs be measured with the same readout or
different readouts?
Type of readout - a readout designed for temper-
•
ature calibration often has features which allow
flexibility in the measurement scheme.
UUT characteristics - self-heating time, source
•
current requirements, stability, and overall quality influence the measurement process.
It is not possible for us to anticipate all of the
variables and discuss the optimum solutions here.
However, in the following examples, we will consider some typical calibration scenarios and suggested measurement schemes.
Example 1: 2 DMM readouts, 1 reference
probe and 5 UUTs
Step 4: Measurement of Units Under Test
(UUTs)
Since the UUTs are resistance thermometers similar to the reference probe, they are measured in
a similar manner. If several UUTs are undergoing
calibration, ensure that when they are connected
or switched in, sufficient time is allowed for selfheating to occur before the data is recorded. Also,
ensure that the readout is set to the correct range
to provide the proper source current and to prevent
range changes between the measurements at different temperatures. Typically, the measurements
are conducted starting at the highest temperature
of calibration and working down. Additionally, it
increases the precision of the calibration to use
a mean (average) value calculated from multiple
measurements at the same temperature. Often, the
readout is designed with statistical features to facilitate this practice. It is also a good practice to close
the process with an additional measurement of the
reference probe. The sequence in which the probes
(reference and UUT) are measured is referred to as a
measurement scheme. There are many variables to
consider when designing a measurement scheme.
Some points to consider are:
Accuracy - the higher the accuracy desired, the
•
more all of the following must be considered.
Temperature source stability - the more stable
•
the source, the more time exists to conduct
the measurements before temperature changes
cause unwanted error.
Number of UUTs - the higher the number, the
•
longer it takes to cycle through all UUTs.
The reference probe is connected to one readout
and the first UUT is connected to the second readout. This places the probes to be measured under
current at all times, thus, eliminating self-heating
errors caused by changing current conditions. The
UUTs will be connected and measured individually.
The scheme is as follows:
REF(1)-UUT (1) - REF(2)-UUT (2) - REF(3)-UUT (3) -
REF(4)-UUT (4) - REF(5)-UUT (5)
This provides 5 readings each of the reference
and the UUT. Take the average of the readings and
use it for the data fit. If the reference probe readings are in resistance, the temperature will have to
be computed. After completion, repeat the process
for the additional UUTs.
Fluke Corporation, Hart Scientific Division How to calibrate an RTD or Platinum Resistance Thermometer (PRT) 3
Page 4
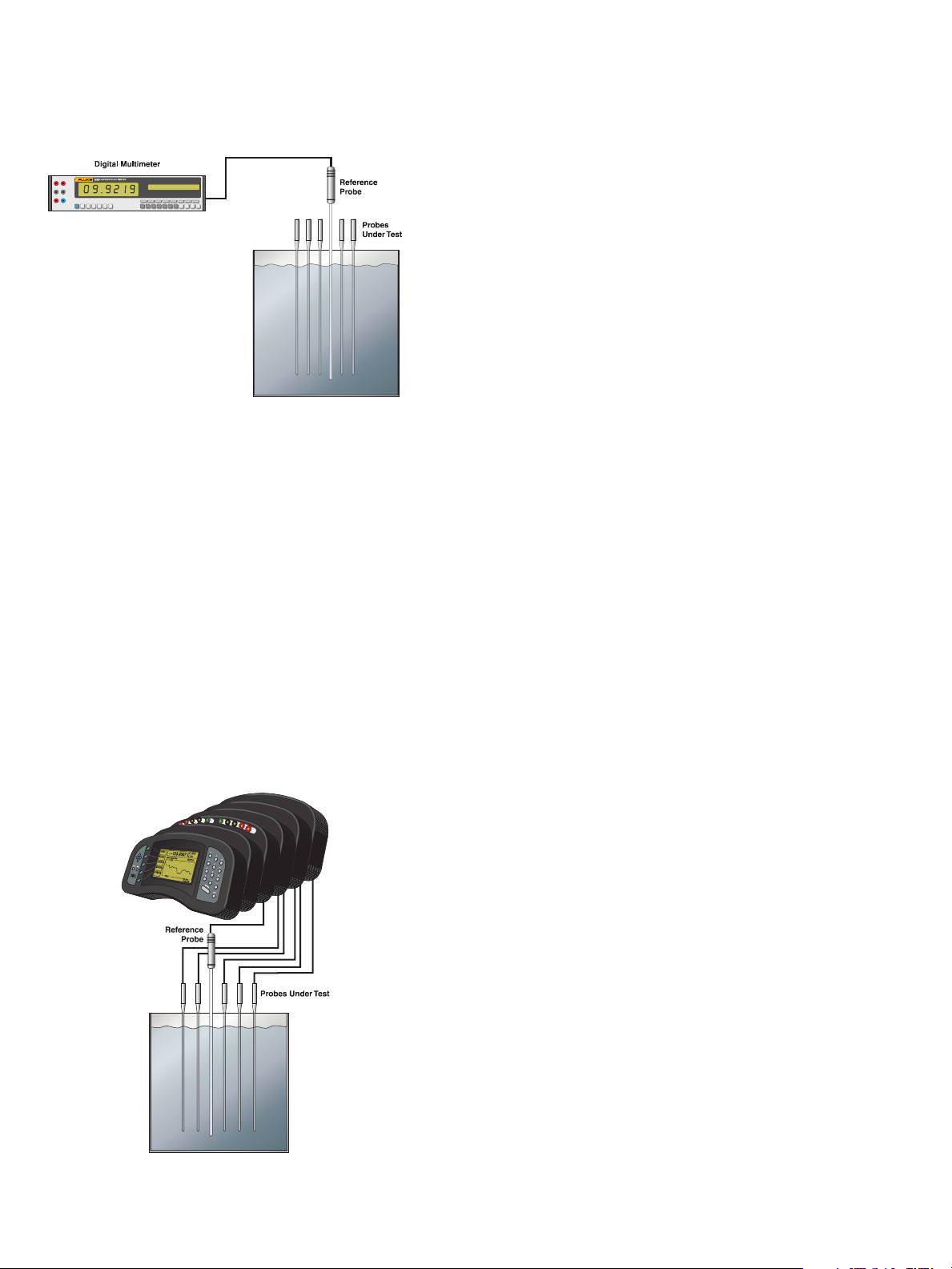
Example 2: 1 DMM readouts, 1 reference
probe and 5 UUTs
This example is similar to the first except that the
reference probe and UUT must be measured by the
same readout. The same scheme can be followed
but more time must be allowed between readings to
allow for self-heating. Since more time is involved,
it might be beneficial to reduce the number of readings from five to three unless the heat source is
extremely stable. Each probe will be connected and
measured individually
The scheme is as follows:
wait-REF(1)-wait-UUT (1) - wait-REF(2)-wait-
UUT(2) - wait-REF(1)-wait-UUT(3)-done
This provides 3 readings each of the reference
and the UUT. Take the average of the readings and
use it for the data fit. Again, the reference probe
readings are in resistance so the temperature will
have to be computed. After completion, repeat the
process for the additional UUTs.
Example 3: 1 multi-channel thermometer
readout, 1 reference probe and 5 UUTs
In this example, all of the probes are connected
directly to the thermometer readout, a Hart Scien-
tific 1560 Black Stack. The readout controls the
measurement and scans through all probes performing statistics in real time. Current may or may not
be supplied at all times depending on the type of
thermometer readout. If current is supplied at all
times, there will be no self-heating errors. If current
is not supplied at all times, ensure that the switching is done rapidly enough to reduce self-heating
errors to a negligible level.
The scheme is as follows
REF - UUT 1 - UUT 2 - UUT 3 - UUT 4 - UUT 5 -
repeat 10 or more times
This provides many readings each of the reference and all of the UUTs. The average can be calculated and displayed directly by the readout. Also,
the reference probe readings are in temperature
so no further computation is required - the data is
ready to fit.
Step 5: Thermometer calibration
curve fitting
Data fitting is simple in concept but can be complicated in practice. Essentially it is a process of solving a set of simultaneous equations which contain
the calibration data to arrive at a set of coefficients
unique to the PRT and calibration. There are several
commercial software programs available specifically
written to accomplish this task. Some are limited
in function and do no more than solve the basic
temperature functions. Others are more flexible and
allow options regarding the number and location
of calibration points and provide analysis regarding
the precision of the resultant fit. The latter type of
program is preferred. For metrologists who wish to
tackle the algorithms themselves, a good mathematics application software like Mathcad or Mathematica or even a spreadsheet like Excel is extremely
helpful. Hart Scientific offers two programs:
TableWare for calculating calibration coefficients
and MET/TEMP II for automating calibration tasks
and calculating calibration coefficients. Of course,
programs can be written in any of the modern computer languages (with double precision or better
floating point capability) to perform the calculations
with equal accuracy.
There are several equations which are used for
PRT characterization. Among the most common
are the International Temperature Scale of 1990
(ITS-90) series, the Callendar-Van Dusen, and
third through fifth order polynomials. Obviously,
with more than one model available to describe
the behavior of a physical system, we must choose
which one is best for our situation. The following
discussion covers the features and purpose of each
of these models and describes the form of the equations. The steps necessary to actually fit the data
will be discussed in the section on mathematics
later in this manual.
ITS-90: The ITS-90 series of functions were
developed through a concerted effort from the
international metrology community’s leading temperature experts. These functions are intended to
describe how the behavior of the SPRT relates, with
a very high degree of precision, to the fixed points
4 Fluke Corporation, Hart Scientific Division How to calibrate an RTD or Platinum Resistance Thermometer (PRT)
Page 5

on which the scale is based. It does this extremely
well SPRTs and with high quality PRTs. The ITS90 uses a reference function - deviation function
structure that has many advantages over traditional
polynomials and is the preferred model for high
accuracy applications. In the equations below, capital T refers to ITS-90 temperatures expressed in
Kelvin units.
Equation 1. ITS-90 resistance ratio
R T
( )
W T
( )
90
90
=
R
TPW
Where: W(T90) = resistance ratio at temperature T
R(T90) = measured resistance at temperature T
RTPW = measured resistance at the triple
point of water
Equation 2. Deviation from ITS-90 reference function.
∆W T W T W T
( ) ( ) ( )
= −
90 90 90
r
Where: ∆W(T90) = deviation of calculated W from
reference function at temperature T
W(T90) = calculated resistance ratio at temperature T (from equation (1))
Wr(T90) = reference function value at temperature T
Equation 3. Reference function for the range
13.8033 K to 273.16 K (–259.3467 °C to 0.01 °C):
i
.
1 5
+
12
ln W T A A
( ( ))
= +
r i
90 0
∑∑
i
=
1
T
ln
90
.
273 16
.
1 5
Where: Wr(T90) = reference function value at tem-
perature T
Ai = reference function coefficients from
definition
Equation 4. Deviation function for the subrange
83.8058 K to 273.16 K (–189.3442 °C to 0.01 °C):
∆W T a W T b W T W T
4 90 4 90 4 90 90
1 1( ) ( ( ) ) ( ( ) ) ln( ( ))= ⋅ − + ⋅ − ⋅
Where: ∆W(T90) = calculated deviation value at
temperature T (from equation (2))
W(T90) = calculated resistance ratio at
temperature T (from equation (1))
a4, b4 = resulting calibration coefficients
Where: Wr(T90) = reference function value at tem-
perature T
Ci = reference function coefficients from
definition
Equation 6. Deviation function for the subrange
273.15 K to 692.677 K (0.00 °C to 419.527 °C):
∆W T a W T b W T
8 90 8 90 8 90
1 1( ) ( ( ) ( ( ) )= ⋅ − + ⋅ −
2
Where: ∆W(T90) = calculated deviation value at tem-
perature T (from equation (2))
W(T90) = calculated resistance ratio at temperature T (from equation (1))
a8, b8 = resulting calibration coefficients
The designations 4 and 8 in the deviation functions, equations (4) and (6) were inserted by NIST
for identification of specific subranges. The values
for the coefficients Ai and Ci in the reference functions, equations (3) and (5) are given in Table 3.
Table 3. ITS-90 Reference Function Coefficients
Coefficient Value
A
0
A
1
A
2
A
3
A
4
A
5
A
6
A
7
A
8
A
9
A
10
A
11
A
12
C
0
C
1
C
2
C
3
C
4
C
5
C
6
C
7
C
8
C
9
–2.135 347 29
3.183 247 20
–1.801 435 97
0.717 272 04
0.503 440 27
–0.618 993 95
–0.053 323 22
0.280 213 62
0.107 152 24
–0.293 028 65
0.044 598 72
0.118 686 32
–0.052 481 34
2.781 572 54
1.646 509 16
–0.137 143 90
–0.006 497 67
–0.002 344 44
0.005 118 68
0.001 879 82
–0.002 044 72
–0.000 461 22
0.000 457 24
Equation 5. Reference function for the range
273.15 K to 1234.93 K (0.00 °C to 961.78 °C):
i
.
Fluke Corporation, Hart Scientific Division How to calibrate an RTD or Platinum Resistance Thermometer (PRT) 5
9
W T C C
( )
= +
r i
90 0
∑
i
=
1
T
90
754 15
−
K
481
Page 6

Callendar-Van Dusen: The Callendar-Van
Dusen (CVD) equation has a long history. It was the
main equation for SPRT and PRT interpolation for
many years. It formed the basis for the temperature
scales of 1927, 1948, and 1968. This equation is
far simpler than the ITS-90 equations but has serious limitations in the precision of fit. As a result, it
is not suitable for high accuracy applications but
is perfectly suited to modest accuracy applications.
Partly due to its history and simplicity, but mostly
due to its continued suitability, it continues to be
the preferred model for industrial platinum resistance thermometers today. In the equations below,
lower case t refers to ITS-90 temperature in Celsius
units.
Equation 7. Callendar-Van Dusen resistance ratio
R t
( )
( )
=
R
0
W t
Where: W(t) = resistance ratio at temperature t
R(t) = measured resistance at temperature t
R0 = measured resistance 0 °C
And...
Equation 8. Callendar-Van Dusen equation
W t At Bt Ct t( ) ( )= + + + ⋅ −1 100
2 3
Where: W(t) = resistance ratio at temperature t (ref-
erence 0 °C)
A,B,C = calibration coefficients (C is = 0
for temperatures above 0 °C)
NOTE: All temperatures are expressed in °C and
the resistance ratio (W) is referenced to
0 °C rather than the triple point of water
(0.010 °C) as with the ITS-90.
Polynomials: Polynomials are frequently used
to model physical phenomena from all fields of science. They have limited use with PRTs because of
the high order required to achieve a suitable fit.
(Recall that the reference functions for the ITS-90
are 9th and 12th order polynomials for the ranges
above 0 °C and below 0 °C.) Additionally, the previous models use resistance ratio as the variable to fit.
Most polynomials in use fit the resistance directly.
Since resistance is not as stable as the resistance
ratio, these models have serious limitations. That
having been said, polynomials can be very useful
over limited ranges and in applications where accuracy requirements are very modest.
Equation 9. Typical RTD polynomial equation
t a bR cR dR eR= + + + +
2 3 4
Tolerance Testing Method
PRT calibrations involving tolerance testing are
reserved for low accuracy applications. With this
type of calibration the UUT resistance is compared
to defined values at specific temperatures. The
values are defined by one of the common models
such as the ASTM 1137 or IEC 60751 curve. PRTs
calibrated in this way are generally used in industrial style applications where the readout is unable
to accept unique coefficients but is pre-programmed
with a common PRT curve. The probe must be
tested to ascertain its compliance to the curve of
interest. There are accuracy classes defined that
probes are intended to fit.
The two common accuracy classes are class A
and class B::
IEC 60751 ASTM 1137
Class A
Class B
± [0.15 + (0.002 · t)] °C ± [0.13 + (0.0017 · t)] °C
± [0.30 + (0.005 · t)] °C ± [0.25 + (0.0042 · t)] °C
These include errors arising from deviations in
R0 and from errors in slope. Frequently, we will see
probes rated at a fraction of Class A. For example,
0.1 ASTM Class A. Fractional accuracy is achievable
in sensors alone, but are very difficult to achieve in
probes. The calculations are straightforward. See
below:
Example 4: Calculate the accuracy of a 0.1
ASTM Class A probe at 100 °C
1. = (0.13 + (0.0017 · t)) · 0.1
2. = (0.13 + (0.0017 · 100)) · 0.1
3. = (0.13 + 0.17) · 0.1 = 0.03
PRTs that conform to a standard specification
such as ASTM 1137 or IEC 60751 are expected to
be within tolerances of defined resistance values
for any given temperature. The resistance values
are defined by a form of the Callendar-Van Dusen
(CVD) equation and specified values for coefficients
A,B and C (see table 4). These values may be determined using a published table or calculated by solving the equations.
Measurements for tolerance testing are carried
out in the same manner as measurements for characterization. ITS-90 temperature is determined by
the reference thermometer. The resistance of the
UUT is then compared to the defined resistance values, and pass or fail status is determined based on
the specified tolerances (i.e. Class A or Class B).
Where: t = temperature
R = resistance
a,b,c,d,e = calibration coefficients
6 Fluke Corporation, Hart Scientific Division How to calibrate an RTD or Platinum Resistance Thermometer (PRT)
Page 7

Table 4. Equations for ASTM 1137 and IEC 60751
− ° ≤ < °200 0 C Ct
0 650 ° ≤ ≤ °C Ct
Range Callendar-Van Dusen Equation
R R At Bt C t t
= + + + −
1 100[ ( ) ]
t
0
R R At Bt
= + +
1[ ]
t
0
ASTM 1137 and IEC 60751 coefficient values
A = 3.9083 X 10–3
B = –5.775 X 10–7
C = –4.183 X 10–12
2 3
2
Example 5: Calculate the tolerance of a 0.1
ASTM Class A probe at 100 °C
Measure the reference probe
temperature
Measure the indicated
UUT temperature using
ASTM 1137 equation and
coefficients
Calculate the error 0.05 °C
Calculate the tolerance at
100.00 °C
Determine tolerance status Fail (0.05 °C > 0.03 °C)
100.00 °C
100.05 °C (Given)
0.03 °C (See example 4)
To be certain of the tolerance status of a calibrated instrument it is necessary to have calibration uncertainties that are significantly better than
the tolerance of the instrument being calibrated.
Typically a ratio of 4:1 or four times better than
the tolerance of the instrument being calibrated is
required. When this is not the case the risk may be
unacceptably high that out of tolerance instruments
will be falsely accepted or that in tolerance instruments will be falsely rejected. As the magnitude of
the detected error approaches the tolerance of the
calibrated instrument, the risk of incorrectly assigning a tolerance status increases. Guard bands may
be helpful in these circumstances. For example if
a guard band is 80% of the tolerance then instruments found within 80% of their tolerance will
pass, instruments outside of the tolerance will fail
and instruments that are in between will be indeterminate. The better the calibration uncertainties
the tighter the guard band can be.
Conclusion
Platinum Resistance Thermometer calibration procedures are similar whether the method selected
is characterization or tolerance testing. For best
accuracy with modern equipment choose characterization. For equipment that does not allow characterization, tolerance testing may be your only choice
and this is a common situation in industry today.
When conducting tolerance testing it is important to
use equipment and procedures with sufficient accuracy to determine the tolerance status confidently.
Fluke Corporation, Hart Scientific Division How to calibrate an RTD or Platinum Resistance Thermometer (PRT) 7
Page 8

8 Fluke Corporation, Hart Scientific Division How to calibrate an RTD or Platinum Resistance Thermometer (PRT)
Fluke. Keeping your world
up and running.
Fluke Corporation
Hart Scientific Division
799 E Utah Valley Drive
American Fork, UT 84003
Tel: 801.763.1600
Fax: 801.763.1010
E-Mail: info@hartscientific.com
www.hartscientific.com
Fluke Eurpoe B. V.,
Hart Scientific Division
PO Box 1186, 5602 BD Eindhoven
The Netherlands
Tel: +31 (0)40 2675 403
Fax: +31 (0)40 2675 404
E-mail: Hart.Logistics@Fluke.NL
All other countries:
Tel: +1 801.763.1600
Fax: +1 801.763.1010
©2009 Fluke Corporation. All rights reserved.
Specifications subject to change without notice.
6/2009 3498460 A-EN-Rev A
®
 Loading...
Loading...