DBX Advanced Feedback Suppression White Paper

dbx ADVANCED FEEDBACK SUPPRESSION™ (AFS™)

Aaron Hammond

DSP Engineer, dbx Professional Products

INTRODUCTION

Feedback is the bane of almost all PA systems. It can take a great performance
and turn it into a painful and embarrassing experience for the performer, audience,
and the sound operator. Up until a few years ago there was little that could be
done electronically about feedback except rudimentary efforts using EQ. With
the advent of Digital Signal Processing (DSP), automatic feedback elimination
has been made possible. Unfortunately, many of these earlier products did not
maintain the sonic integrity of the audio signal because they required wide notch
filters to suppress feedback. The dbx® AFS™ algorithm solves this problem by
using Precision Frequency Detection
minimum number of very narrow notch filters, which will stop the feedback
without degrading the audio signal.

HOW ACOUSTIC FEEDBACK OCCURS

™

with adaptive filter bandwidth to place the

Acoustic feedback occurs in a sound re-enforcement system when the signal
output from the speaker is picked up by the microphone and amplified, creating a
feedback loop. What results is an audible “squealing” or “howling” of the
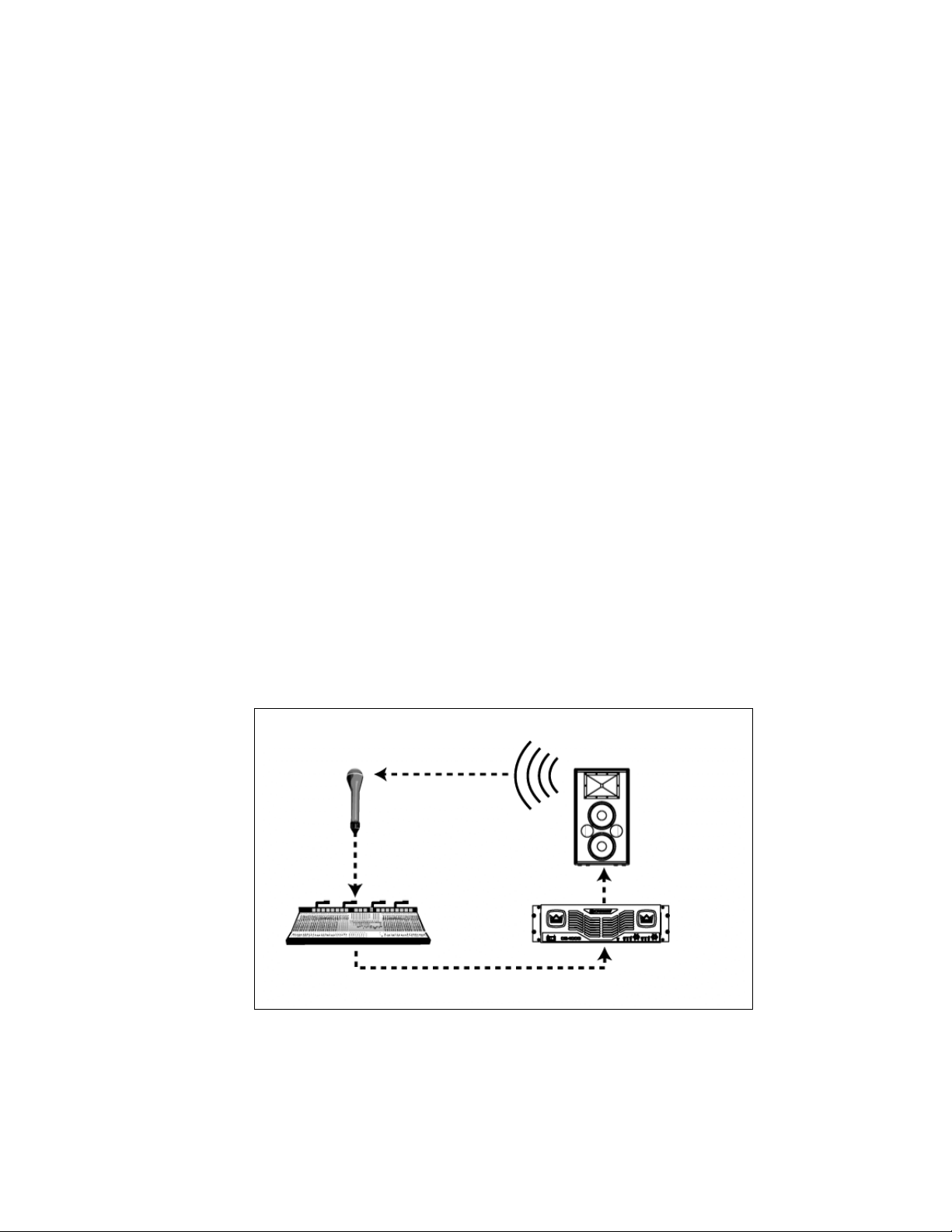
system. Figure 1 illustrates a typical system setup with a microphone, mixer,
amplifier, and speaker.

Figure 1

The loop gain consists of the gains in the mixer (
(

), as well as the losses in the system (

ampG _

) and amplifier

mixG _

), as illustrated in Figure 2.

sysL _

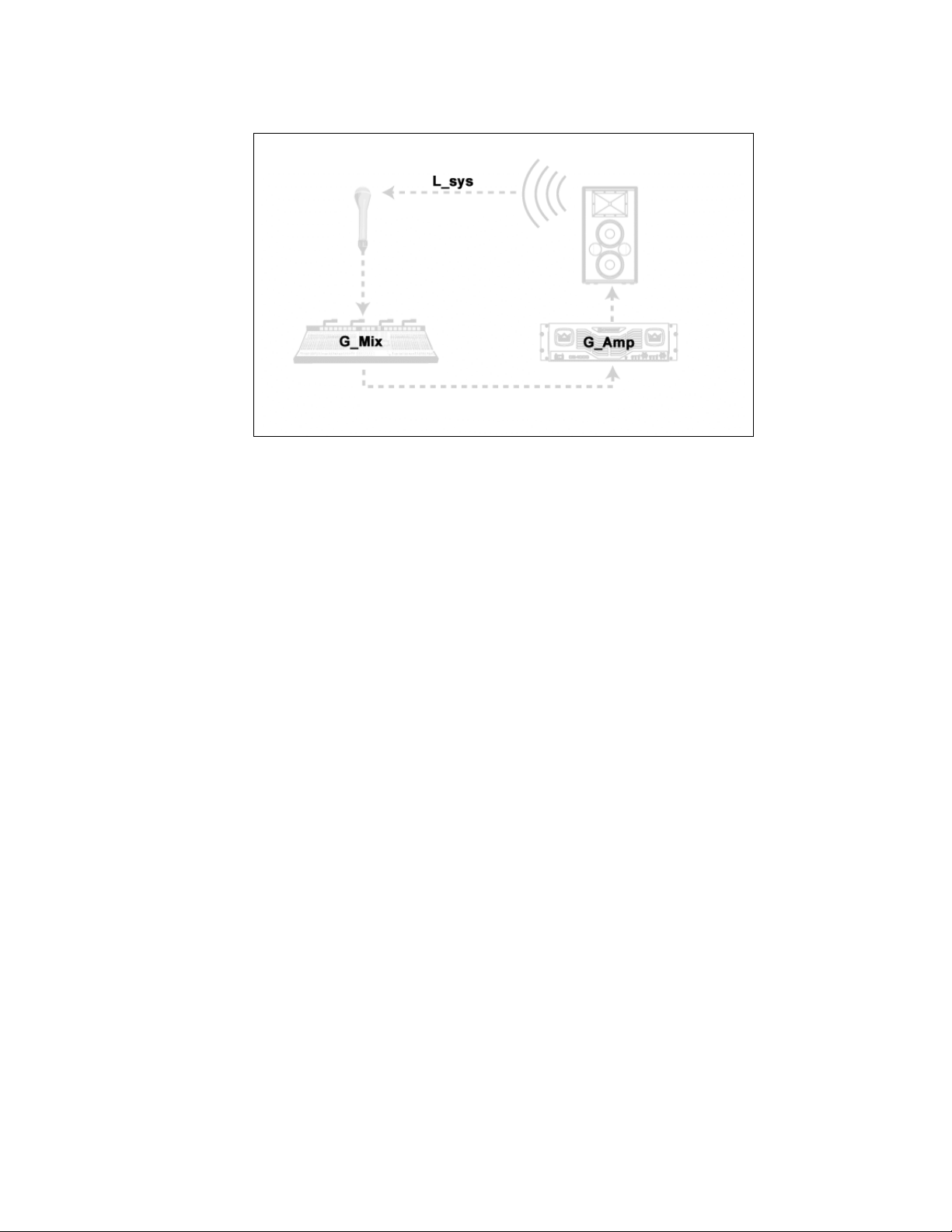
Figure 2

includes the losses from microphone to mixer, speaker to microphone,

sysL _

and any other losses in the loop. Therefore, the loop gain of the system can be
represented mathematically as

.___ sysLampGmixGLoopGain ∗∗=

This equation can be represented in dB as

.___

sysLampGmixGLoopGain ++=

dBdBdBdB

For feedback to occur, the loop gain must be greater than unity (or greater than 0
dB) and in phase at a particular frequency. When this occurs, the loop gain at the
feedback frequency must be reduced below unity to remove the feedback. This
gives us

,0___

dBattendBdBdB

where

LoopGain

G

represents the necessary amount of attenuation required to pull the

atten

=

dB

GsysLampGmixG <+++

loop gain at that frequency below 0 dB.

dbx ADVANCED FEEDBACK SUPPRESSION™ (AFS™)

The dbx Advanced Feedback Suppression™ (AFS™) algorithm eliminates
feedback by placing a very narrow notch filter at the frequency feeding back.
When the loop gain at that frequency is pushed below unity, the feedback

disappears. Using our patent pending Precision Frequency Detection™ with
adaptive filter bandwidth, we are able to place the minimum number of very

narrow notch filters (Q = 116, bandwidth = 1/80 octave1). Utilizing very narrow
notch filters preserves the sonic quality of the system.

Historically (before automatic feedback elimination), feedback was removed
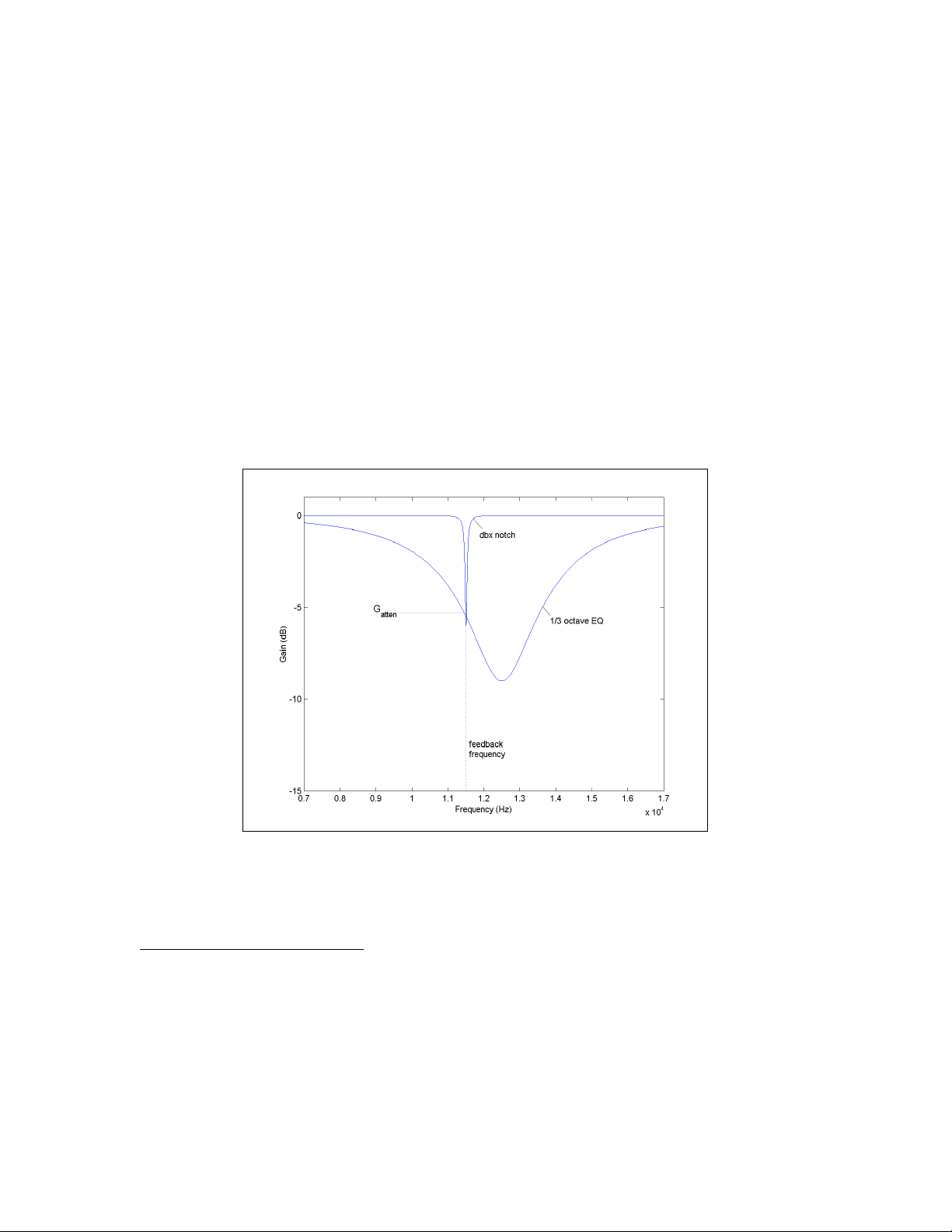
manually using a 1/3 octave graphic or parametric EQ. When feedback occurred,
the sound engineer would guess where the feedback was located, and pull down a
fader to decrease the gain at that frequency. This method unnecessarily cuts out

large portions of the spectrum. The dbx Advanced Feedback Suppression

™

(AFS) algorithm uses a very narrow notch filter to reduce the gain at the feedback
frequency. Figure 3 compares a 1/3 octave graphic EQ with the dbx AFS
narrow notch filter. Again,

G

represents the necessary cut required to

atten

™

very

guarantee that the feedback is removed. It is easy to see the limitations of the
manual approach.

Figure 3

1

The bandwidth of a filter can be stated as Q or in octaves. The Q is computed by dividing the center

frequency by the bandwidth of the filter. For dbx feedback notch filters, the bandwidth is measured at the

-3dB point (from 0 dB). That means that no matter how deep the notch filter cuts, its bandwidth will be
measured from –3 dB. This is important because many competitors will claim to have narrow notch filters,
but they measure their bandwidth 3dB above the peak cut depth. In other words, for a cut depth of –18 dB,
some of our competitors measure the bandwidth at –15 dB, which results in a significantly wider bandwidth
filter (this will be explained graphically in the next section). The other way to measure filter width is in
octaves. This means that the number stated (say 1/10 octave) is the bandwidth of the filter, which varies
depending on the center frequency.