Datasheet LP2975IMMX-5.0, LP2975IMMX-12, LP2975IMM-5.0, LP2975IMM-12, LP2975AIMMX-3.3 Datasheet (NSC)

LP2975
MOSFET LDO Driver/Controller

LP2975 MOSFET LDO Driver/Controller

September 1997

General Description

A high-current LDO regulator is simple to design with the
LP2975 LDO Controller. Using an external P-FET, the
LP2975 will deliver an ultra low dropout regulator with ex­tremely low quiescent current.

High open loop gain assures excellent regulation and ripple
rejection performance.

The trimmed internal bandgap reference provides precise
output voltage over the entire operating temperature range.

Dropout voltage is “user selectable” by sizing the external
FET: the minimum input-output voltage required for opera­tion is the maximum load current multiplied by the R
of the FET.

Overcurrent protection of the external FET is easily imple­mented by placing a sense resistor in series with V
57 mV detectionthresholdof the current sense circuitry mini­mizes dropout voltage and power dissipation in the resistor.

The standard product versions available provide output volt­ages of 12V, 5V, or 3.3V with guaranteed 25˚C accuracy of

1.5%(“A” grade) and 2.5%(standard grade).

DS

IN

Features

n Simple to use, few external components
n Ultra-small mini SO-8 package
n 1.5%(A grade) precision output voltage
n Low-power shutdown input

<

n

1 µA in shutdown

n Low operating current (180 µA typical
n Wide supply voltage range (1.8V to 24V)
n Built-in current limit amplifier
n Overtemperature protection
n 12V, 5V, and 3.3V standard output voltages

(ON)

n Can be programmed using external divider
n −40˚C to +125˚C junction temperature range

. The

Applications

n High-current 5V to 3.3V regulator
n Post regulator for switching converter
n Current-limited switch

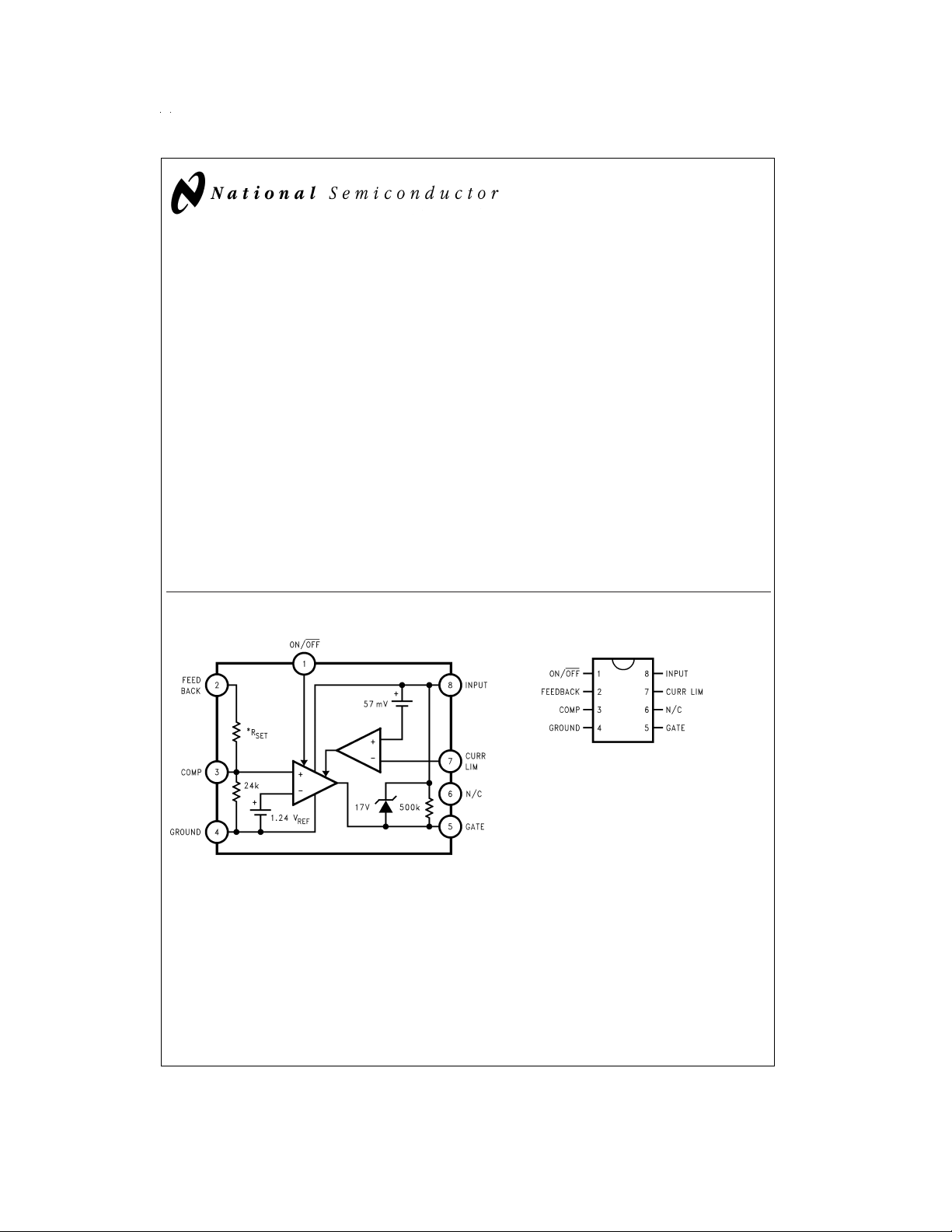
Block Diagram Connection Diagram

Surface Mount Mini SO-8 Package

Top View

For Order Numbers

See

Table 1

See NS Package Number MUA08A

of this Document

@

VIN= 5V)

DS100034-2

*R

values are: 208k for 12V part, 72.8k for 5V part, and 39.9k for 3.3V

SET

part.

© 1999 National Semiconductor Corporation DS100034 www.national.com

DS100034-1

Ordering Information

TABLE 1. Package Marking and Ordering Information

Output Voltage Grade Order Information Package Marking Supplied As:

12 A LP2975AIMMX-12 L47A 3.5k Units on Tape and Reel
12 A LP2975AIMM-12 L47A 250 Units on Tape and Reel
12 STD LP2975IMMX-12 L47B 3.5k Units on Tape and Reel
12 STD LP2975IMM-12 L47B 250 Units on Tape and Reel

5.0 A LP2975AIMMX-5.0 L46A 3.5k Units on Tape and Reel

5.0 A LP2975AIMM-5.0 L46A 250 Units on Tape and Reel

5.0 STD LP2975IMMX-5.0 L46B 3.5k Units on Tape and Reel

5.0 STD LP2975IMM-5.0 L46B 250 Units on Tape and Reel

3.3 A LP2975AIMMX-3.3 L45A 3.5k Units on Tape and Reel

3.3 A LP2975AIMM-3.3 L45A 250 Units on Tape and Reel

3.3 STD LP2975IMMX-3.3 L45B 3.5k Units on Tape and Reel

3.3 STD LP2975IMM-3.3 L45B 250 Units on Tape and Reel

www.national.com 2

Absolute Maximum Ratings (Note 1)

If Military/Aerospace specified devices are required,
please contact the National Semiconductor Sales Office/
Distributors for availability and specifications.

Storage Temperature Range −65˚C to +150˚C
Operating Junction Temperature

Range −40˚C to +125˚C

Lead Temp. (Soldering, 5 seconds) 260˚C

Input Supply Voltage (Survival) −0.3V to +26V
Input Supply Voltage (Operating) +1.8V to +24V
Current Limit Pins (Survival) −0.3V to +V
Comp Pin (Survival) −0.3V to +2V
Gate Pin (Survival) −0.3V to +V
ON/OFF Pin (Survival) −0.3V to +20V
Feedback Pin (Survival) −0.3V to +24V

ESD Rating 2 kV
Power Dissipation

(Note 2) Internally Limited

Electrical Characteristics

Limits in standard typeface are for TJ= 25˚C, and limits in boldface type apply over the full operating temperature range. Un­less otherwise specified; V

Symbol Parameter Conditions Typ

V

REG

Regulation Voltage
(12V Versions)

Regulation Voltage
(5V Versions)

Regulation Voltage
(3.3V Versions)

V

COMP

I

Q

V

CL

V

ON/OFF

I

ON/OFF

I

G

Comp Pin Voltage V

Quiescent Current VIN= 5V 180 240 240

Current Limit
Sense Voltage

ON/OFF Threshold Output = ON

ON/OFF
Input Bias Current

Gate Drive Current (Sourcing) VG= 7.5V

Gate Drive Current (Sinking) V

V

R(V

G(MIN)

IN

Gate Clamp Voltage VIN= 24V

-G) Resistance from
Gate to V

IN

Open Loop
Voltage Gain

= 1.5V, VIN= 15V.

ON/OFF

LM2975AI-X.X

(Note 3)

LM2975I-X.X

(Note 3)

Min Max Min Max

IN

- 0.5V)>V

IN

(VIN- 5V)

<

<

V

IN

- 0.5V)>V

IN

(VIN- 4.5V)

<

<

V

IN

- 0.5V)>V

IN

(VIN- 3.3V)

<

V

IN

<

24V 12.0 11.820 12.180 11.700 12.300

GATE

11.640 12.360 11.520 12.480

24V 5.0 4.925 5.075 4.875 5.125

GATE

4.850 5.150 4.800 5.200

24V 3.3 3.250 3.350 3.217 3.383

GATE

<

24V 1.240 1.215 1.265 1.203 1.277

3.201 3.399 3.168 3.432

12.5<V
(V

>

5.5
(V

>

3.8
(V

>

REG

1.209 1.271 1.196 1.284

V

= 0V 0.01 11

ON/OFF

VIN= 15V

=0.9XV

V

FB

Output = OFF

V

= 1.5V

ON/OFF

REG

57 45 69 45 69

39 72 39 72

0.94

0.87

1.10 1.10

1.20 1.20

34

0.70 0.70

0.40 0.40

50 50 µA

75 75

3.5 1.3 1.3

=1.1XV

V

V

FB

G
FB

= 7.5V

=0.9XV

REG

REG

0.3 0.3

1100 350 350

40 40

17 15 19 15 19 V

=0.9XV

V

FB

VIN= 24V
V

ON/OFF

VIN= 15V

0.5V ≤ V

=0

GATE

REG

500 kΩ

5000 V/V

≤ 13

IN

IN

Units

V

V

µA320 320

mV

V

mA

µA

Note 1: Absolute maximum ratings indicate limits beyond which damage to the component may occur. Electrical specifications do not apply when operating the de­vice outside of its rated operating conditions.

Note 2: The LP2975 has internal thermal shutdown which activates at a die temperature of about 150˚C. It should be noted that the power dissipated within the
LP2975 is low enough that this protection circuit should never activate due to self-heating, even at elevated ambient temperatures.

www.national.com3

Electrical Characteristics (Continued)

Note 3: Limits are 100%production tested at 25˚C. Limits over the operating temperature range are guaranteed through correlation using Statistical Quality Control

(SQC) methods. The limits are used to calculate National’s Average Outgoing Quality Level (AOQL).

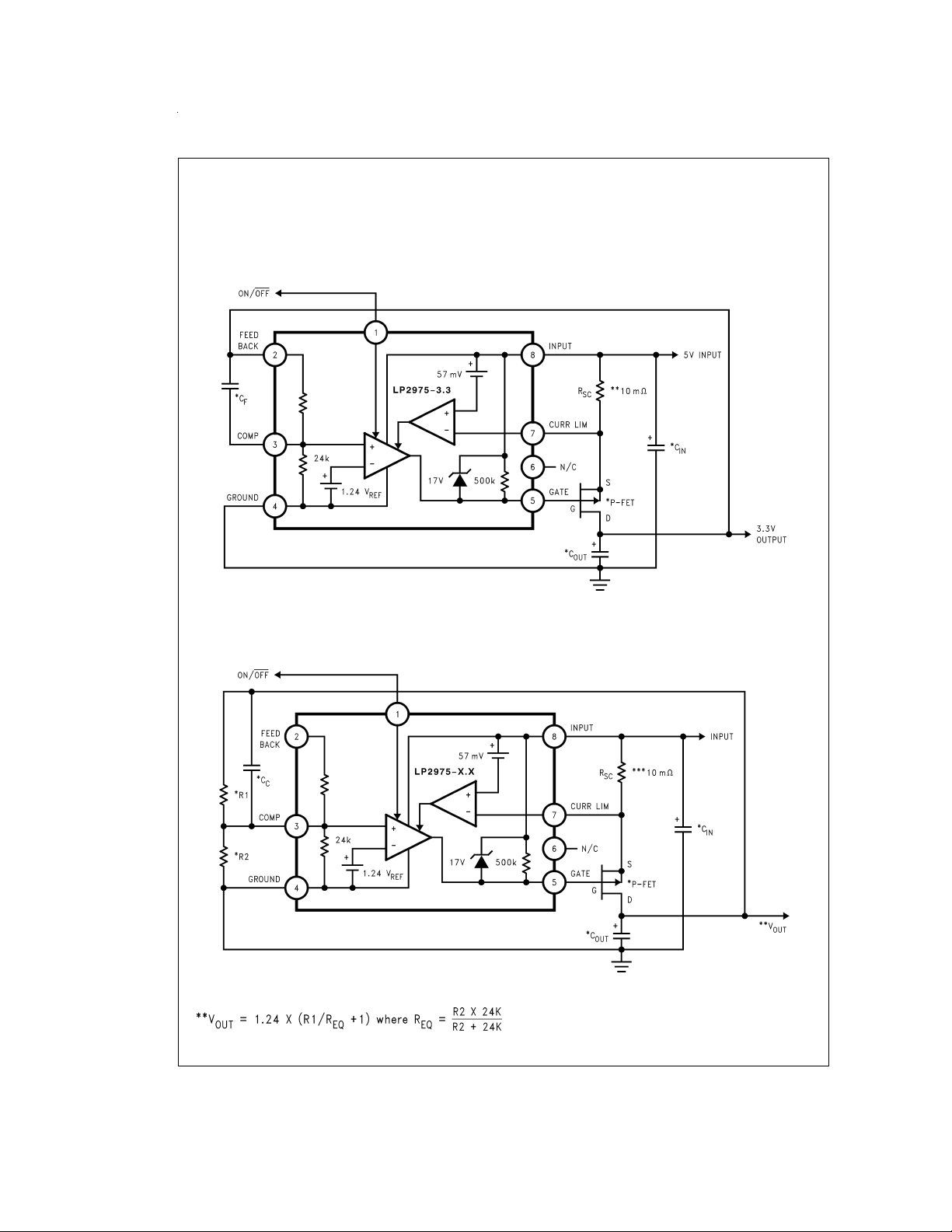
Typical Application Circuits

5V - 3.3V@5A LDO Regulator

*See Application Hints.
**If current limiting is not required, short out this resistor.

*See Application Hints.

***If current limiting is not required, short out this resistor.

DS100034-3

Adjustable Voltage 5A LDO Regulator

DS100034-4

www.national.com 4

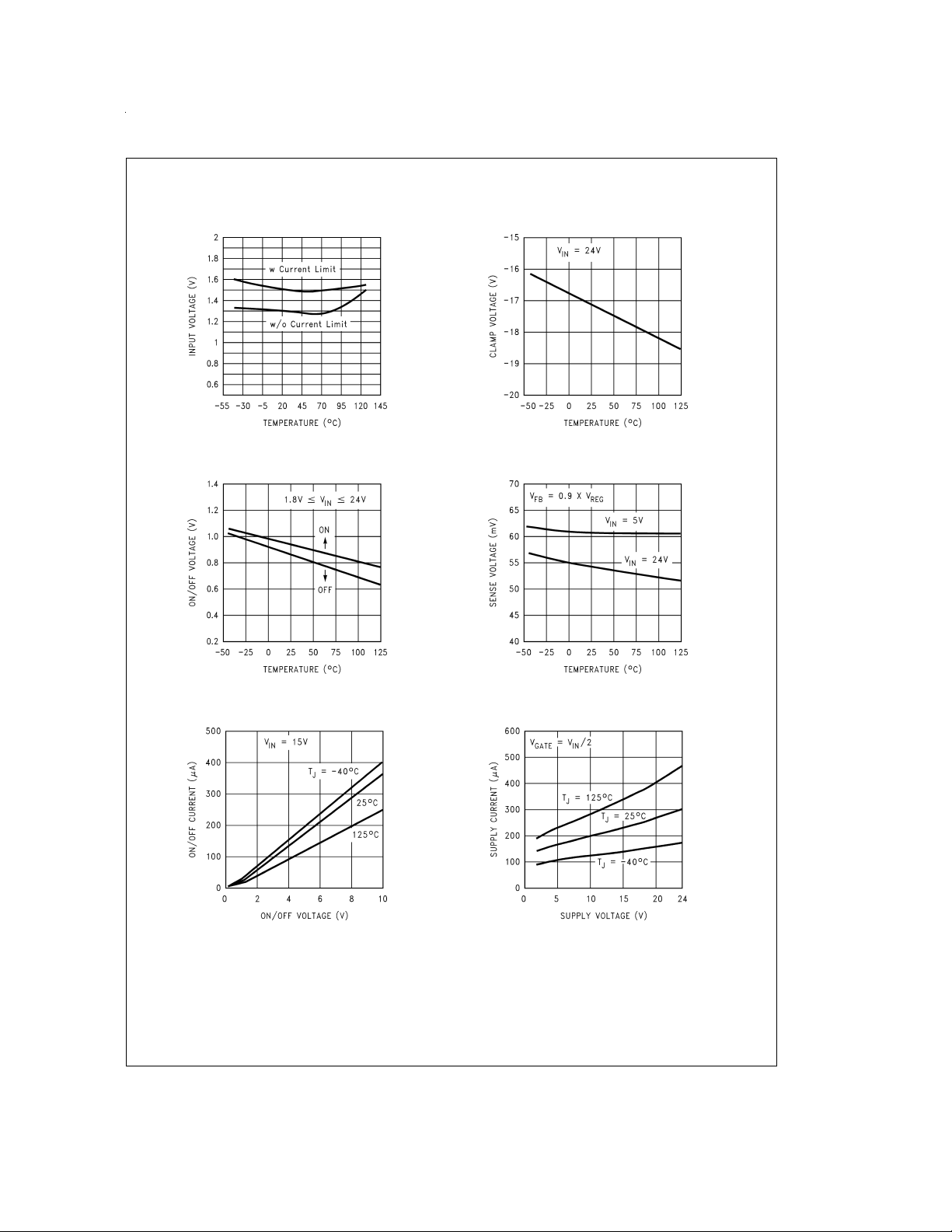
Typical Performance Characteristics Unless otherwise specified: T

is tied to 1.5V.

= 25˚C, CIN= 1 µF, ON/OFF pin

A

Minimum Operating Voltage

ON/OFF Threshold

DS100034-5

VINReferred Gate Clamp Voltage

DS100034-6

Current Limit Sense Voltage

ON/OFF Pin Current

DS100034-7

DS100034-9

DS100034-8

Supply Current

DS100034-10

www.national.com5

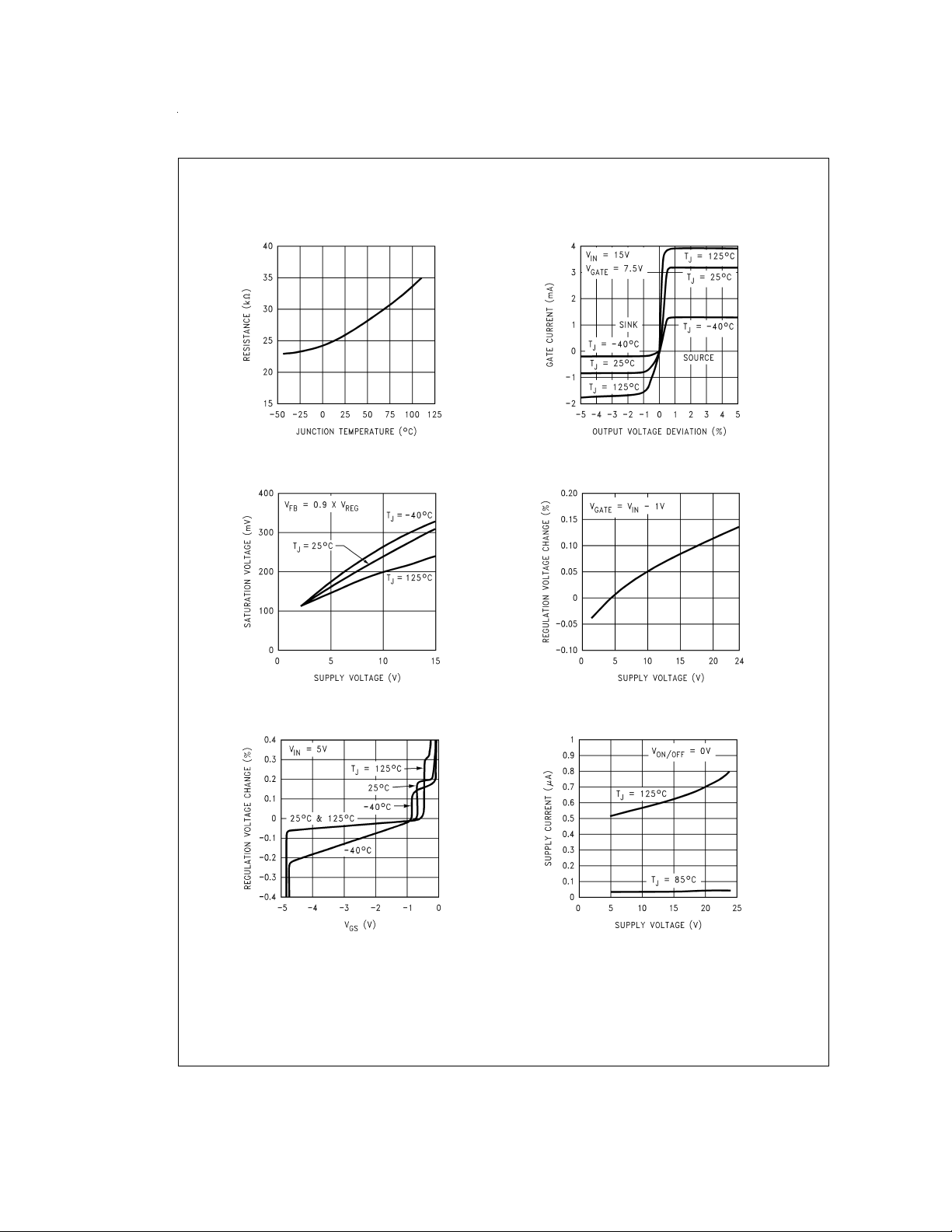
Typical Performance Characteristics Unless otherwise specified: T

is tied to 1.5V. (Continued)

= 25˚C, CIN= 1 µF, ON/OFF pin

A

ON/OFF Input Resistance

Gate-Ground Saturation

DS100034-11

Gate Current

DS100034-34

Line Regulation

DS100034-13

Load Regulation

DS100034-15

www.national.com 6

DS100034-14

Leakage Current

DS100034-35

Typical Performance Characteristics Unless otherwise specified: T

is tied to 1.5V. (Continued)

Controller Gain and Phase Response

DS100034-36

Reference Designs

The LP2975 controller can be used with virtually any
P-channel MOSFET to build a wide variety of linear voltage
regulators.

Since it would be impossible to document all the different
voltage and current combinations that could be built, a num­ber of reference designs will be presented along with perfor­mance data for each.

THE PERFORMANCE DATA SHOWN IS ACTUAL TEST
DATA, BUT IS NOT GUARANTEED.

#

DESIGN

Circuits)

COMPONENTS:

C
C
C
R
P-FET = NDP6020P
Heatsink: (assuming V

against a

θ

S-A

circuit survivability is not needed, a heatsink with θ
6 ˚C/W is adequate.

PERFORMANCE DATA:

Dropout Voltage

Dropout voltage

differential voltage required by the regulator to keep the out­put in regulation. It is measured by reducing V
put voltage drops below the nominal value (the nominal
value is the output voltage measured with V
5A for this test.

Load Regulation

Load regulation

voltage as the load current is varied. It is measured by
changing the load resistance and recording the minimum/

1: V

=5V@5A (Refer to Typical Application

OUT

= 82 µF Aluminum Electrolytic

IN

= 120 µF Aluminum Electrolytic

OUT

= 220 pF

F

=10mΩ

SC

≤ 7V and TA≤ 60˚C) if protection

continuous

IN

short-circuit is required, a heatsink with

≤ 1.5 ˚C/W must be used. However, if continuous short-

is defined as the minumum input-to-output

until the out-

IN

= 5.5V). IL=

IN

DROPOUT VOLTAGE = 323 mV

is defined as the maximum change in output

S-A

maximum output voltage. The measured change in output
voltage is divided by the nominal output voltage and ex­pressed as a percentage. V

5mA≤I

≤5A: LOAD REGULATION = 0.012

L

≤ 5A: LOAD REGULATION = 0.135

0 ≤ I

L

Line Regulation

Line regulation

is defined as the maximum change in output
voltage as the input voltage is varied. It is measured by
changing the input voltage and recording the minimum/
maximum output voltage. The measured change in output
voltage is divided by the nominal output voltage and ex­pressed as a percentage. I

5.4V ≤ V

≤ 10V: LINE REGULATION = 0.03

IN

Output Noise Voltage

Output noise voltage was measured by connecting a wide­band AC voltmeter (HP 400E) directly across the output ca­pacitor. V

= 6V and IL= 5A for this test.

IN

NOISE = 75 µV (rms)

Transient Response

Transient response

is defined as the change in output volt­age which occurs after the load current is suddenly changed.
V

≤

= 5.6V for this test.

IN

The load resistor is connected to the regulator output using a
switch so that the load current increases from 0 to 5A
abruptly.The change in output voltage is shown in the scope
photo below (the vertical scale is 200 mV/division and the
horizontal scale is 10 µs/division). The regulator nominal out­put (5V) is located on the center line of the photo.

The output shows a maximum change of about −600 mV
compared to nominal. This is due to the relatively small out­put capacitor chosen for this design. Increasing C
improves transient response (see Designs

= 25˚C, CIN= 1 µF, ON/OFF pin

A

= 5.6V for this test.

IN

%

%

= 5A for this test.

L

%

greatly

OUT

#

2 and#3).

www.national.com7

Reference Designs (Continued)

DS100034-37

Transient Response for 0–5A Load Step

#

2: V

DESIGN

Application Circuits, Adjustable Voltage Regulator)

COMPONENTS:

C

= 68 µF Tantalum

IN

=2X68µFTantalum

C

OUT

= 470 pF

C

C

R1 = 237 kΩ,1
R2 = NOT USED

= 0.1Ω

R

SC

Tie feedback pin to V
P-FET = NDT452P
Heatsink: Tab of N-FET is soldered down to 0.6 in

area on PC board.
Output Voltage Adjustment: For this application, a 3.3V part

is “trimmed” down to 3V by using a single external 237 kΩ re­sistor at R1, which parallels the internal 39.9 kΩ resistor (re­ducing the effective resistance to 34.2 kΩ).

Because the tempco of the external resistor will not match
the tempco of the internal resistor (which is typically 3000
ppm), this method of adjusting V
tor is only recommended in cases where the output voltage
is adjusted ≤ 10%away from the nominal value.

PERFORMANCE DATA:

Dropout Voltage

Dropout voltage

differential voltage required by the regulator to keep the out­put in regulation. It is measured by reducing V
put voltage drops below the nominal value (the nominal
value is the output voltage measured with V

0.5A for this test.

Load Regulation

Load regulation

voltage as the load current is varied. It is measured by
changing the load resistance and recording the minimum/

www.national.com 8

=3V@0.5A (Refer to Typical

OUT

%

OUT

2

by using a single resis-

OUT

is defined as the minimum input-to-output

until the out-

IN

= 5V). IL=

IN

DROPOUT VOLTAGE = 141 mV

is defined as the maximum change in output

copper

maximum output voltage. The measured change in output
voltage is divided by the nominal output voltage and ex­pressed as a percentage. V

≤ 0.5A: LOAD REGULATION = 0.034

0 ≤ I

L

= 3.5V for this test.

IN

%

Line Regulation

Line regulation

is defined as the maximum change in output
voltage as the input voltage is varied. It is measured by
changing the input voltage and recording the minimum/
maximum output voltage. The measured change in output
voltage is divided by the nominal output voltage and ex­pressed as a percentage. I

3.5V ≤ V

≤ 6V: LINE REGULATION = 0.017

IN

= 0.5A for this test.

L

%

Output Noise Voltage

Output noise voltage

was measured by connecting a wide­band AC voltmeter (HP 400E) directly across the output ca­pacitor. V

= 5V and IL= 0.5A for this test.

IN

NOISE = 85 µV (rms)

Transient Response

Transient response

is defined as the change in output volt­age which occurs after the load current is suddenly changed.
V

= 3.5V for this test.

IN

The load resistor is connected to the regulator output using a
switch so that the load current increases from 0 to 0.5A
abruptly.The change in output voltage is shown in the scope
photo (the vertical scale is 20 mV/division and the horizontal
scale is 50 µs/division). The regulator nominal output (3V) is
located on the center line of the photo. A maximum change
of about −50 mV is shown.

DS100034-38

Transient Response for 0–0.5A Load Step

Minimizing C

It is often desirable to decrease the value of C
cost and reduce size. The design guidelines suggest select­ing C

put Capacitor

OUT

to set the first pole ≤ 200 Hz (see later section

OUT

), but this is not an absolute requirement in all

OUT

to save

Out-

cases.
The effect of reducing C

phase margin is decreased, the output ringing will increase
when a load step is applied to the output. Eventually, if C
is made small enough, the regulator will oscillate.

To demonstrate these effects, the value of C

#

design

2 is halved by removing one of the two 68 µF output

is to decrease phase margin. As

OUT

in reference

OUT

OUT

capacitors and the transient response test is repeated (see

Reference Designs (Continued)

photo below). The total overshoot increases from −50 mV to
about −75 mV, and the second “ring” on the transient is no­ticeably larger.

DS100034-39

Transient Response with Output Capacitor Halved

The design is next tested with only a 4.7 µF output capacitor
(see scope photo below). Observe that the vertical scale has
been increased to 100 mV/division to accommodate the

−250 mV undershoot. More important is the severe ringing
as the transient decays. Most designers would recognize
this immediately as the warning sign of a marginally stable
design.

DS100034-40

Transient Response with Only 4.7 µF Output Cap

The reason this design is marginally stable is that the 4.7 µF
output capacitor (along with the 6Ω output load) sets the pole

at 5 kHz. Analysis shows that the unity-gain frequency of

f

p

the loop is increased to about 100 kHz, allowing the FET’s
gate capacitance pole f
fore the loop gain goes below unity. Also, because of the low
output voltage, the feedforward capacitor provides less than
10˚ of positive phase shift. For good stability, the output
capcitor needs to be larger than 4.7 µF.

For detailed information on stability and phase margin, see
the

Application Hints

to cause significant phase shift be-

pg

section.

#

DESIGN

Application Circuits, Adjustable Voltage Regulator)

3: V

= 1.5V@6A. (Refer to Typical

OUT

COMPONENTS:

C

= 1000 µF Aluminum Electrolytic

IN

= 4 X 330 µF OSCON Aluminum Electrolytic

C

OUT

= NOT USED

C

C

R1 = 261Ω,1
R2 = 1.21 kΩ,1
R

SC

%

%

=6mΩ
P-FET = NDP6020P
Heatsink: (Assuming V

against a

continuous

<

θ

2.5 ˚C/W must be used. However,if continuous short-

S-A

circuit survivability is not needed, a heatsink with θ
7 ˚C/W is adequate.

≤ 3.3V and TA≤ 60˚C) if protection

IN

short-circuit is required, a heatsink with

S-A

PERFORMANCE DATA:

Dropout Voltage

Dropout voltage

is defined as the minimum input-to-output
differential voltage required by the regulator to keep the out­put in regulation. It is measured by reducing V
put voltage drops below the nominal value (the nominal
value is the output voltage measured with V
6A for this test.

until the out-

IN

= 3.3V). IL=

IN

DROPOUT VOLTAGE = 0.68V

Load Regulation

Load regulation

is defined as the maximum change in output
voltage as the load current is varied. It is measured by
changing the load resistance and recording the minimum/
maximum output voltage. The measured change in output
voltage is divided by the nominal output voltage and ex­pressed as a percentage. V

≤ 6A: LOAD REGULATION = 0.092

0 ≤ I

L

= 3.3V for this test.

IN

%

Line Regulation

Line regulation

is defined as the maximum change in output
voltage as the input voltage is varied. It is measured by
changing the input voltage and recording the minimum/
maximum output voltage. The measured change in output
voltage is divided by the nominal output voltage and ex­pressed as a percentage. I

3.3V ≤ V

≤ 5V: LINE REGULATION = 0.033

IN

= 6A for this test.

L

%

Output Noise Voltage

Output noise voltage was measured by connecting a wide­band AC voltmeter (HP 400E) directly across the output ca­pacitor. V

= 3.3V and IL= 6A for this test.

IN

NOISE = 60 µV (rms)

Transient Response

Transient response

is defined as the change in output volt­age which occurs after the load current is suddenly changed.
V

= 3.3V for this test.

IN

The load resistor is connected to the regulator output using a
switch so that the load current increases from 0 to 6A
abruptly.The change in output voltage is shown in the scope
photo (the vertical scale is 50 mV/division and the horizontal
scale is 20 µs/division. The regulator nominal output (1.5V)
is located on the center line of the photo. A maximum change
of about −80 mV is shown.

<

www.national.com9

Reference Designs (Continued)

DS100034-41

Transient Response for 0–6A Load Step

Application Hints

SELECTING THE FET

The best choice of FET for a specific application will depend
on a number of factors:

VOLTAGE RATING: The FET must have a Drain-to-Source
breakdown voltage (sometimes called BV
greater than the input voltage.

DRAIN CURRENT: On-state Drain current must be specified
to be greater than the worst-case (short circuit) load current
for the application.

TURN-ON THRESHOLD: The Gate-to-Source voltage
where the FET turns on (called the Gate Threshold Voltage)
is very important. Many FET’s are intended for use with
G-to-S voltages in the 5V to 10V range. These should only
be used in applications where the input voltage is high
enough to provide

>

5V of drive to the Gate.

Newer FET’s are becoming available with lower turn-on
thresholds (Logic-Level FET’s) which turn on fully with a gate
voltage of only 3V to 4V. Low threshold FET’s should be
used in applications where the input voltage is ≤ 5V.

ON RESISTANCE: FET on resistance (often called R
is a critical parameter since it directly determines the mini­mum input-to-output voltage required for operation at a given
load current (also called dropout voltage).

R

ON is highly dependent on the amount of Gate-to-

DS

Source voltage applied. For example, the R
with V
V
dent, increasing at higher temperatures.

= 5V will typically decrease by about 25%as the

G-S

is increased to 10V. RDSON is also temperature depen-

G-S

The dropout voltage of any LDO design is directly related to
R

ON, as given by:

DS

Where R
Application Circuit).

V

DROPOUT=ILOAD

is the short-circuit current limit set resistor (see

SC

x(RDSON+RSC)

GATECAPACITANCE: Selecting a FET with the lowest pos­sible Gate capacitance improves LDO performance in two
ways:

1) The

Gate

pin of the LP2975 (which drives the Gate of the

FET) has a limited amount of current to source or sink. This

) which is

DSS

ON of a FET

DS

ON)

DS

means faster changes in Gate voltage (which corresponds to
faster transient response) will occur with a smaller amount of
Gate capacitance.

2) The Gate capacitance forms a pole in the loop gain which
can reduce phase margin. When possible, this pole should
be kept at a higher frequency than the cross-over frequency
of the regulator loop (see later section

QUENCY AND PHASE MARGIN

CROSS-OVER FRE-

).

A high value of Gate capacitance may require that a feedfor­ward capacitor be used to cancel some of the excess phase
shift (see later section

FEED-FORWARD CAPACITOR

)to

prevent loop instability.
POWER DISSIPATION: The maximum power dissipated in

the FET in any application can be calculated from:

P

=(VIN−V

Where the term I
should be noted that if the regulator is to be designed to with-

MAX

is the maximum output current. It

MAX

OUT

)xI

MAX

stand short-circuit, a current sense resistor must be used to
limit I

CURRENT LIMITING

to a safe value (refer to section

MAX

).

SHORT-CIRCUIT

The power dissipated in the FET determines the best choice
for package type. A TO-220 package device is best suited for
applications where power dissipation is less than 15W.
Power levels above 15W would almost certainly require a
TO-3 type device.

In low power applications, surface-mount package devices
are size-efficient and cost-effective, but care must be taken
to not exceed their power dissipation limits.

POWER DISSIPATION AND HEATSINKING

Since the LP2975 controller is suitable for use with almost
any external P-FET, it follows that designs can be built which
have very high power dissipation in the pass FET. Since the
controller can not protect the FET from overtemperature
damage, thermal design must be carefully done to assure a
reliable design.

THERMAL DESIGN METHOD: The temperature of the FET
and the power dissipated is defined by the equation:

T

J

=(θ

J-AxPD

)+T

A

Where:

is the junction temperature of the FET.

T

J

is the ambient temperature.

T

A

is the power dissipated by the FET.

P

D

is the junction-to-ambient thermal resistance.

θ

J-A

To ensure a reliable design, the following guidelines are rec­ommended:

1) Design for a maximum (worst-case) FET junction tem­perature which does not exceed 150˚C.

2) Heatsinking should be designed for worst-case (maxi­mum) values of T

and PD.

A

3) In designs which must survive a short circuit on the output,
the maximum power dissipation must be calculated assum­ing that the output is shorted to ground:

P

(MAX) = VINxI

D

SC

Where ISCis the short-circuit output current.

4) If the design is not intended to be short-circuit proof, the
maximum power dissipation for intended operation will be:

P

Where I

is the maximum output current.

MAX

LOW POWER (

(MAX) = (VIN−V

D

<

2W) APPLICATIONS: In most cases,

OUT

)xI

MAX

some type of small surface-mount device will be used for the

www.national.com 10

Application Hints (Continued)

FET in low power designs. Because of the increased cell
density (and tiny packages) used by modern FET’s, the cur­rent carrying capability may easily exceed the power dissipa­tion limits of the package. It is possible to parallel two or
more FET’s, which divides the power dissipation among all
of the packages.

It should be noted that the “heatsink” for a surface mount
package is the copper of the PC board and the package itself
(direct radiation).

Surface-mount devices have the value of θ
typical PC board mounting on their data sheet. In most cases
it is best to start with the known data for the application (P
T

) and calculate the required value of θ

A,TJ

value will define the type of FET and, possibly, the heatsink
required for cooling.

θ

=(TJ−TA)/PD(MAX)

DESIGN EXAMPLE:

and V

OUT

Based on these conditions, power dissipation in the FET dur-

J-A

A design is to be done with VIN=5V

= 3.3V with a maximum load current of 300 mA.

ing normal operation would be:

P

=(VIN−V

D

OUT

)xI

Solving, we find that PD= 0.51W. Assuming that the maxi­mum allowable value of T
70˚C, the value of θ

is 150˚C and the maximum TAis

J

is found to be

J-A

However, if this design must survive a continuous short on
the output, the power dissipated in the FET is higher:

P

(SC) = VINxISC= 5 x 0.33 = 1.65W

D

(This assumes the current sense resistor is selected for an
I

value that is 10%higher than the required 0.3A).

SC

The value of θ
is calculated to be

required to survive continuous short circuit

J-A

49˚C/W.

Having solved for the value(s) of θ
lected. It should be noted that a FET must be used with a

θ

value

J-A

less than or equal to the calculated value.

HIGH POWER (≥2W) APPLICATIONS: As power dissipa­tion increases above 2W, a FET in a larger package must be
used to obtain lower values of θ
rived in the previous section are used to calculate P

θ

.

J-A

Having found θ
value of θ
that a heatsink can be selected:

, it becomes necessary to calculate the

J-A

(the heatsink-to-ambient thermal resistance) so

S-A

θ

= θ

S-A

J-A

. The same formulae de-

J-A

−(θ

+ θ

J-C

Where:

is the junction-to-case thermal resistance. This pa-

θ

J-C

rameter is the measure of thermal resistance between the
semiconductor die inside the FET and the surface of the
case of the FET where it mounts to the heatsink (the value of

θ

can be found on the data sheet for the FET). A typical

J-C

FET in a TO-220 package will have a θ
mately 2–4˚C/W, while a device in a TO-3 package will be
about 0.5–2˚C/W.

θ

is the case-to-heatsink thermal resistance, which

C-S

measures how much thermal resistance exists between the
surface of the FET and the heatsink. θ
the package type and mounting method. A TO-220 package
with mica insulator and thermal grease secured to a heatsink
will have a θ
package mounted in the same manner will have a θ

value in the range of 1–1.5˚C/W. A TO-3

C-S

specified for a

J-A

needed. This

J-A

LOAD

157˚C/W.

, a FET can be se-

J-A

)

C-S

value of approxi-

J-C

is dependent on

C-S

C-S

and

D

value

of 0.3–0.5˚C/W. The best source of information for this is
heatsink catalogs (Wakefield, AAVID, Thermalloy) since they
also sell mounting hardware.

θ

is the heatsink-to-ambient thermal resistance, which

S-A

defines how well a heatsink transfers heat into the air. Once
this is determined, a heatsink must be selected which has a
value which is less than or equal to the computed value. The
value of θ
sheet for a heatsink, but the information is sometimes given

is usually listed in the manufacturer’s data

S-A

in a graph of temperature rise vs. dissipated power.

DESIGN EXAMPLE:

A design is to be done which takes

3.3V in and provides 2.5V out at a load current of 7A. The
power dissipation will be calculated for both normal opera-

,

D

tion and short circuit conditions.
For normal operation:

P

=(VIN−V

D

OUT

)xI

LOAD

= 5.6W

If the output is shorted to ground:

(SC) = VINxISC= 3.3 x 7.7 = 25.4W

P

D

(Assuming that a sense resistor is selected to set the value
of I

10%above the nominal 7A).

SC

will be calculated assuming a maximum TAof 70˚C and

θ

J-A

a maximum T

of 150˚C:

J

=(TJ−TA)/PD(MAX)

θ

J-A

For normal operation:

= (150 − 70) / 5.6 = 14.3˚C/W

θ

J-A

For designs which must operate with the output shorted to
ground:

θ

= (150 − 70) / 25.4 = 3.2˚C/W

J-A

The value of 14.3˚C/W can be easily met using a TO-220 de­vice. Calculating the value of θ
value of θ

= 3˚C/W and θ

J-C

= θ

θ

S-A

J-A

=14.3−(3+1)=10.3˚C/W

θ

S-A

required (assuming a

S-A

= 1˚C/W):

C-S

−(θ

+ θ

J-C

)

C-S

Any heatsink may be used with a thermal resistance ≤

10.3˚C/W

@

5.6W power dissipation (refer to manufacturer’s
data sheet curves). Examples of suitable heatsinks are Ther­malloy #6100B and IERC #LATO127B5CB.

However, if the design must survive a sustained short on the
output, the calculated θ
possibility of using a TO-220 package device.

Assuming a TO-3 device is selected with a θ

1.5˚C/W and θ
value of θ

C-S

:

S-A

θ

= 3.2 − (1.5 + 0.4) = 1.3˚C/W

θ

S-A

value ≤1.3˚C/W would require a relatively large heat-

A θ

S-A

sink, or possibly some kind of forced airflow for cooling.

value of 3.2˚C/W eliminates the

J-A

value of

= 0.4˚C/W, we can calculate the required

= θ

−(θ

S-A

J-A

+ θ

J-C

J-C

)

C-S

SHORT-CIRCUIT CURRENT LIMITING

Short-circuit current limiting is easiliy implemented using a
single external resistor (R
culated from:

). The value of RSCcan be cal-

SC

R

SC=VCL/ISC

Where:

is the desired short circuit current.

I

SC

is the current limit sense voltage.

V

CL

The value of V
listed in the Electrical Characteristics section. When doing a

is 57 mV (typical), with guaranteed limits

CL

worst-case calculation for power dissipation in the FET, it is
important to consider both the tolerance of V
ance (and temperature drift) of R

.

SC

and the toler-

CL

www.national.com11

Application Hints (Continued)

For maximum accuracy, the
pins must be Kelvin connected to RSC, to avoid errors
caused by voltage drops along the traces carrying the cur­rent from the input supply to the

EXTERNAL CAPACITORS

The best capacitors for use in a specific design will depend
on voltage and load current (examples of tested circuits for
several different output voltages and currents are provided in
a previous section.)

Information in the next sections is provided to aid the de­signer in the selection of the external capacitors.

INPUT CAPACITOR: Although not always required, an input
capacitor is recommended. Good bypassing on the input as­sures that the regulator is working from a source with a low
impedance, which improves stability. A good input capacitor
can also improve transient response by providing a reservoir
of stored energy that the regulator can utilize in cases where
the load current demand suddenly increases. The value
used for C
erence Designs section for examples of input capacitors.

may be increased without limit. Refer to the Ref-

IN

OUTPUT CAPACITOR: The output capacitor is required for
loop stability (compensation) as well as transient response.
During sudden changes in load current demand, the output
capacitor must source or sink current during the time it takes
the control loop of the LP2975 to adjust the gate drive to the
pass FET.As a general rule, a larger output capacitor will im­prove both transient response and phase margin (stability).
The value of C

may be increased without limit.

OUT

OUTPUT CAPACITOR AND COMPENSATION:

pensation for the LP2975 is derived from C
cases, the feed-forward capacitor C

forms a pole (referred to as fp) in conjuction with the

C

OUT

load resistance which causes the loop gain to roll off (de­crease) at an additional −20 dB/decade. The frequency of
the pole is:

f

=0.16/[(RL+ESR)xC

p

Where:

is the load resistance.

R

L

is the value of the output capacitor.

C

OUT

ESR is the equivalent series resistance of C

As a general guideline, the frequency of f
Hz. It should be noted that higher load currents correspond
to lower values of R
to keep f

p

L

at a given frequency.

DESIGN EXAMPLE:

capacitance for a design whose output specifications are 5V

@

1A:

=0.16/[(RL+ESR)xC

f

p

Re-written:

=0.16/[fpx(RL+ ESR) ]

C

OUT

Values used for the calculation:

= 200 Hz, RL=5Ω, ESR = 0.1Ω (assumed).

f

p

Solving for C
would be 180 µF).

OUT

,weget

The ESR of the output capacitor is very important for stabil­ity,as it creates a zero (f
shift resulting from one of the poles present in the loop. The
frequency of the zero is calculated from:

f

= 0.16 / (ESR x C

z

www.national.com 12

INPUT

and

CURRENT LIMIT

Source

pin of the FET.

Loop com-

and, in some

OUT

(see next section).

F

]

OUT

.

OUT

should be ≤ 200

p

, which requires that C

be increased

OUT

Select the minimum required output

]

OUT

157 µF

(nearest standard size

) which cancels much of the phase

z

)

OUT

For best results in most designs, the frequency of f
fall between 5 kHz and 50 kHz. It must be noted that the val­ues of C
verely in the case of aluminum electrolytics), and this must

and ESR usually vary with temperature (se-

OUT

should

z

be taken into consideration.
For the design example (V

which meets the f
ESR yields:

requirements. Solving the equation for

z

ESR = 0.16 / (f

Assuming f
for the 180 µF capacitor are found to be:

= 5 kHz and 50 kHz, the limiting values of ESR

z

=5V@1A), select a capacitor

OUT

)

zxCOUT

18 mΩ≤ESR ≤ 0.18Ω

A good-quality, low-ESR capacitor type such as the Pana­sonic HFQ is a good choice. However, the 10V/180 µF ca­pacitor (#ECA-1AFQ181) has an ESR of 0.3Ω which is not in
the desired range.

To assure a stable design, some of the options are:

1) Use a different type capacitor which has a lower ESR
such as an organic-electrolyte OSCON.

2) Use a higher voltage capacitor. Since ESR is inversely
proportional to the physical size of the capacitor, a higher
voltage capacitor with the same C value will typically have a
lower ESR (because of the larger case size). In this ex­ample, a Panasonic ECA-1EFQ181 (which is a 180 µF/25V
part) has an ESR of 0.17Ω and would meet the desired ESR
range.

3) Use a feed-forward capacitor (see next section).
FEED-FORWARD CAPACITOR: Although not required in

every application, the use of a feed-forward capacitor (C
can yield improvements in both phase margin and transient
response in most designs.

The added phase margin provided by C
lations in cases where the required value of C
can not be easily obtained (see previous section).

C

can also reduce the phase shift due to the pole resulting

F

from the Gate capacitance, stabilizing applications where

can prevent oscil-

F

OUT

and ESR

this pole occurs at a low frequency (before cross-over) which
would cause oscillations if left uncompensated (see later
section

GATE CAPACITANCE POLE FREQUENCY).

Even in a stable design, adding CFwill typically provide more
optimal loop response (faster settling time). For these rea­sons,

the use of a feed-forward capacitor is always rec-

ommended.

CFis connected across the top resistor in the divider used to
set the output voltage (see Typical Application Circuit). This
forms a zero in the loop response (defined as f
quency is:

f

=6.6x10−6/[CFx(V

zf

When solved for C

C

, the fzfequation is:

F

=6.6x10−6/[fzfx(V

F

For most applications, f
50 kHz.

zf

OUT

OUT

should be set between 5 kHz and

), whose fre-

zf

/1.24−1)]

/1.24−1)]

ADJUSTING THE OUTPUT VOLTAGE

If an output voltage is required which is not available as a
standard voltage, the LP2975 can be used as an adjustable
regulator (see Typical Application circuit). The external resis­tors R1 and R2 (along with the internal 24 kΩ resistor) set
the output voltage.

It is important to note that R2 is connected in parallel with the
internal 24 kΩ resistor. If we define R

tance between the COMP pin and ground, then its value

as the total resis-

EQ

will be the parallel combination of R2 and 24 kΩ:

)

F

Application Hints (Continued)

R

= (R2 x 24k) / (R2 + 24k)

It follows that the output voltage will be:

Some important considerations for an adjustable design:
The tolerance of the internal 24 kΩ resistor is about

Also, its temperature coefficient is almost certainly different
than the TC of the external resistor that is used for R2.

For these reasons, it is recommended that R2 be set at a
value that is not greater than 1.2k. In this way, the value of
R2 will dominate R
nal 24k resistor will have a negligible effect on output voltage
accuracy.

To determine the value for R1:

External Capacitors (Adjustable Application)

All information in the previous section

TORS

tion of how to select the value of the feed-forward capacitor.
The feed-forward capacitor C

(see Typical Application Circuit) performs exactly the same
function as described in the previous section

WARD CAPACITOR.

selected, a different formula must be used to determine the
value of C

As stated previously, the optimal frequency at which to place
the zero f

OPTIMIZING DESIGN STABILITY

Because the LP2975 can be used with a variety of different
applications, there is no single set of components that are
best suited to every design. This section provides informa­tion which will enable the designer to select components that
optimize stability (phase margin) for a specific application.

Gate Capacitance

An important consideration of a design is to identify the fre­quency of the pole which results from the capacitance of the
Gate of the FET (this pole will be referred to as f
gets closer to the loop crossover frequency, the phase mar­gin is reduced. Information will now be provided to allow the
total Gate capacitance to be calculated so that f
proximated.

The first step in calculating fp is to determine how much ef-

fective Gate capacitance (C

calculating C

Where:

is the Gate-to-Source capacitance, which is found

C

GS

from the values (refer to FET data sheet for values of C
and C

RSS

GGDis the Gate-to-Drain capacitance, which is equal to:

Gmis the transconductance of the FET. The FET data

sheet specifies forward transconductance (G
value of drain current (defined as I
sired value of load current (defined as I

EQ

=1.24[(R1/REQ)+1]

V

OUT

±

20%.

, and the tolerance and TC of the inter-

EQ

R1=R

[(V

OUT

/ 1.24) − 1]

EQ

EXTERNAL CAPACI-

applies to the adjustable application with the excep-

in the adjustable application

C

FEEDFOR-

However, because R1 is user-

:

C

is usually between 5 kHz and 50 kHz.

zf

C

EFF=CGS+CGD

):

=1/(2πxR1xfzf)

C

C

is:

EFF

C

GS=CISS−CRSS

G

m=Gfs

) is present. The formula for

EFF

[1+Gm(RL/ / ESR) ]

C

GD=CRSS

). To find Gm at the de-

D

L

1/2

x(IL/ID)

). As f

pg

can be ap-

pg

) at some

fs

), use the formula:

ISS

Where:

is the load resistance.

R

L

ESR is the equivalent series resistance of the output ca-

pacitor.
The term R

It can be seen from these equations that C
To get the worst-case (maximum) value for C
maximum value of load current, which also means the mini­mum value of load resistance R
most cases, the ESR is the dominant term which determines
the value of R

/ / ESR is defined as:

L

xESR)/(RL+ ESR)

(R

L

/ / ESR.

L

varies with RL.

EFF

, use the

EFF

. It should be noted that in

L

Gate Pin Output Impedance

DS100034-20

Gate Capacitance Pole Frequency (f

)

pg

The pole frequency resulting from the Gate capacitance
C

is defined as fpgand can be approximated from:

EFF

≅

0.16 / (ROxC

f

pg

EFF

)

Where:

is the output impedance of the LP2975 Gate pin which

R

O

drives the Gate of the FET. It is important to note that R
a function of input supply voltage (see graph

OUTPUT IMPEDANCE).

R

is about 550Ω@VIN= 24V, increasing to about 1.55 kΩ

O

@

VIN=3V.

pg

Using the equation for f
showing how f
(see graph

pg

fpgvs. C

As shown, the minimum value of

, a family of curves are provided

pg

varies with C

):

EFF

fpgvs. C

for several values of R

EFF

EFF

DS100034-21

O

GATE PIN

is

O

www.national.com13

Application Hints (Continued)

As can be seen in the graph, values of C
500 pF–2500 pF range produce values for f
40 kHz and 700 kHz. To determine what effect f
on stability, the bandwidth of the regulator loop must be cal­culated (see next section

PHASE MARGIN

CROSSOVER FREQUENCY AND

).

Crossover Frequency and Phase Margin

The term f
the regulator loop (which is the frequency where the gain

will be used to define the crossover frequency of

c

curve crosses the 0 dB axis). The importance of this fre­quency is that it is the point where the loop gain goes below
unity, which marks the usable bandwidth of the regulator
loop.

It is the phase margin (or lack of it) at f
whether the regulator is stable. Phase margin is defined as

c

the total phase shift subtracted from 180˚. In general, a
stable loop requires at least 20˚-30˚ of phase margin at f

can be approximated by the following equation (all terms

f

c

have been previously defined):

DS100034-23

This equation assumes that no C

is used and fpg/f

F

If the frequency of the Gate capacitance pole f
calculated (previous section), the amount of added phase
shift may now be determined. As shown in the graph below
(see graph
added phase shift increases as f

The amount of phase shift due to f
oscillation takes place depends on how much added phase
shift is present as a result of the C
section

PHASE SHIFT DUE TO fpg),

OUTPUT CAPACITOR).

Phase Shift Due to f

approaches fc.

pg

that can occur before

pg

pole (see previous

OUT

pg

DS100034-22

Because of this, there is no exact number for fpg/fcthat can
be given as a fixed limit for stable operation. However, as a
general guideline, it is recommended that f

pg

If this is not found to be true after inital calculations, the ratio
of f

can be increased by either reducing C

pg/fc

a different FET) or using a larger value of C
Along with these two methods, another technique for improv-

ing loop stability is the use of a feed-forward capacitor (see

in the

EFF

between

pg

will have

pg

that determines

c

>

1.

c

has been

pg

the amount of

≥ 3fc.

(selecting

EFF

.

OUT

next section

FEED-FORWARD COMPENSATION).

improve phase margin by cancelling some of the excess
phase shift.

Feed-Forward Compensation

Phase shift in the loop gain of the regulator results from f
(the pole from the output capacitor and load resistance), f
(the pole from the FET gate capacitance), as well as the IC’s
internal controller pole (see typical curve). If the total phase
shift becomes excessive, instability can result.

The total phase shift can be reduced using feed-forward
compensation, which places a zero in the loop to reduce the
effects of the poles.

The feed-forward capacitor C
it is selected to set the zero at the correct frequency. It is im-

can accomplish this, provided

F

portant to point out that the feed-forward capacitor produces

both a zero and a pole

will be defined as f
defined as f

.

are:

f

zf

f

pf

. The frequency where the zero occurs

, and the frequency of the pole will be

zf

. The equations to calculate the frequencies

pf

6.6x10

6.6x10

-6

/[CFx(V

-6

OUT

/[CFx (1 − 1.24/V

=

=

In general, the feed-forward capacitor gives the greatest im­provement in phase margin (provides the maximum reduc­tion in phase shift) when the zero occurs at a frequency
where the loop gain is

>

1 (before the crossover frequency).
The pole must occur at a higher frequency (the higher the
better) where most of the phase shift added by the new pole
occurs beyond the crossover frequency. For this reason, the
pole-zero pair created by C
proving loop stability as they get farther apart in frequency.

In reviewing the equations for f
they get closer together in frequency as V
For this reason, the use of C
output voltages, declining as V
(where C

has no effect at all).

F

become more effective at im-

F

and fpf, it can be seen that

zf

gives greatest benefit at higher

F

OUT

In selecting a value of feed-forward capacitor, the crossover
frequency f
quency of the zero (f
range:

must first be calculated. In general, the fre-

c

) set by this capacitor should be in the

zf

0.2 f

≤ fzf≤ 1.0 f

c

The equation to determine the value of the feed-forward ca­pacitor in fixed-voltage applications is:

=

C

F

6.6x10

-6

/[fzfx(V

OUT

In adjustable applications (using an external resistive di­vider) the capacitor is found using:

=

C

1/(2 π xR1xf

C

SUMMARY OF STABILITY INFORMATION

This section will present an explanation of theory and termi­nology used to analyze loop stability, along with specific in­formation related to stabilizing LP2975 applications.

BODE PLOTS AND PHASE SHIFT

Loop gain information is most often presented in the form of
a Bode Plot, which plots Gain (in dB) versus Frequency (in
Hertz).

A Bode Plot also conveys phase shift information, which can
be derived from the locations of the poles and zeroes.

POLE: A pole causes the slope of the gain curve to de­crease by an additional −20 dB/decade, and it also causes
phase lag (defined as negative phase shift) to occur.

A single pole will cause a maximum −90˚ of phase lag (see
graph

EFFECTS OF A SINGLE POLE

This can

/1.24 − 1) ]

)]

OUT

decreases.

OUT

approaches 1.24V

c

/1.24 − 1) ]

)

zf

). It should be noted

p

pg

www.national.com 14

Application Hints (Continued)

that when the total phase shift at 0 dB reaches (or gets close
to) −180˚, oscillations will result. Therefore, it can be seen
that at least two poles in the gain curve are required to
cause instability.

ZERO:A zero has an effect that is exactly
A zero will add a maximum +90˚ of phase lead (defined as
positive phase shift). Also, a zero causes the slope of the
gain curve to increase by an additional +20 dB/decade (see
graph

EFFECTS OF A SINGLE ZERO

Effects of a Single Pole

TOTAL PHASE SHIFT: The actual test of whether or not a

regulator is stable is the amount of phase shift that is present
when the gain curve crosses the 0 dB axis (the frequency
where this occurs was previously defined as f

The phase shift at f
poles and zeroes on the Bode plot and adding up the contri-

can be estimated by looking at all of the

c

butions of phase lag and lead from each one. As shown in
the graphs, most of the phase lag (or lead) contributed by a
pole (or zero) occurs within one decade of the frequency of
the pole (or zero).

In general, a phase margin (defined as the difference be­tween the total phase shift and −180˚) of at least 20˚ to 30˚
is required for a stable loop.

Effects of a Single Zero

opposite to a pole

).

DS100034-25

).

c

STABILITY ANALYSIS OF TYPICAL APPLICATIONS

The first application to be analyzed is a fixed-output voltage
regulator with no feed-forward capacitor (see graph

PLOT WITHOUT FEED-FORWARD

.

Stable Plot without Feed-Forward

In this example, the value of C
pole formed by C
at 200 Hz. The ESR of C
by the ESR and C
selections follow the general guidelines stated previously in

and RL(previously defined as fp)isset

OUT

OUT

(defined as fz) is set at 5 kHz (these

OUT

).

is selected so that the

OUT

is selected so that zero formed

this document). Note that the gate capacitance is assumed
to be moderate, with the pole formed by the C
as f

) occurring at 100 kHz.

pg

To estimate the total phase margin, the individual phase shift
contributions of each pole and zero will be calculated assum­ing f

=

p

200 Hz, f

z

=

5 kHz, f

=

10 kHz and f

c

Controller pole shift=−90˚

shift=−arctan (10k/200)=−89˚

f

p

shift=arctan (10k/5k)=+63˚

f

z

shift=−arctan (10k/100k)=−6˚

f

pg

Summing the four numbers, the estimate for the total phase
shift is −122˚, which corresponds to a phase margin of 58˚.
This application is stable, but could be improved by using a
feed-forward capacitor (see next section).

EFFECT OF FEED-FORWARD: The example previously
used will be continued with the addition of a feed-forward ca­pacitor C

FEED-FORWARD

fined as f
viously defined as f
corresponds to V

(see graph

F

) is set at 10 kHz and the pole formed by CF(pre-

zf

IMPROVED PHASE MARGIN WITH

). The zero formed by CF(previously de-

) is set at 40 kHz (the 4X ratio of fpf/f

pf

=

5V).

OUT

DS100034-27

GATE

pg

STABLE

(defined

=

100 kHz:

zf

DS100034-26

www.national.com15

Application Hints (Continued)

Improved Phase Margin with Feed-Forward

DS100034-28

To estimate the total phase margin, the individual phase shift
contributions of each pole and zero will be calculated assum-

=

200 Hz, f

ing f

p

=

f

50 kHz, and f

c

Controller pole shift=−90˚

shift=−arctan (50k/200)=−90˚

f

p

shift=arctan (50k/5k)=+84˚

f

z

shift=arctan (50k/100k)=+79˚

f

zf

shift=−arctan (50k/40k)=−51˚

f

pf

shift=−arctan (50k/100k)=−27˚

f

pg

Summing the six numbers, the estimate for the total phase
shift is −95˚, which corresponds to a phase margin of 85˚
(a 27˚ improvement over the same application without the
feed-forward capacitor).

For this reason, a feed-forward capacitor is recommended in
all applications. Although not always required, the added
phase margin typically gives faster settling times and pro­vides some design guard band against C
tions with temperature.

CAUSES AND CURES OF OSCILLATIONS

The most common cause of oscillations in an LDO applica­tion is the output capacitor ESR. If the ESR is too high or too
low, the zero (f

HIGH ESR: To illustrate the effect of an output capacitor with
high ESR, the previous example will be repeated except that
the ESR will be increased by a factor of 20X. This will cause
the frequency of the zero f
moves it from 5 kHz down to 250 Hz (see graph

UNSTABLE WITHOUT FEED-FORWARD

=

5 kHz, f

z

=

100 kHz:

pg

) does not provide enough phase lead.

z

=

10 kHz, f

zf

to decrease by 20X, which

z

pf

and ESR varia-

OUT

=

HIGH ESR

).

40 kHz,

High ESR Unstable without Feed-Forward

DS100034-29

As shown, moving the location of f
tends the bandwidth, pushing the crossover frequency f
to about 200 kHz. In viewing the plot, it can be seen that f

lower in frequency ex-

z

out

c

and fzessentially cancel out, leaving only the controller pole
and f

. However, since fpgnow occurs well before fc, it will

pg

cause enough phase shift to leave very little phase margin.
This application would either oscillate continuously or be
marginally stable (meaning it would exhibit severe ringing on
transient steps).

This can be improved by adding a feed-forward capacitor C
which adds a zero (f
graph

HIGH ESR CORRECTED WITH FEED-FORWARD

In this case, C
quency as f
to f
frequency, it will add<45˚ of phase lag, leaving a phase
margin of

pg

). Assuming the added pole fpfis near or beyond the f

pg

>

) and a pole (fpf) to the gain plot (see

zf

is selected to place fzfat about the same fre-

F

(essentially cancelling out the phase shift due

45˚ (adequate for good stability).

High ESR Corrected with Feed-Forward

DS100034-31

LOW ESR: To illustrate how an output capacitor with low
ESR can cause an LDO regulator to oscillate, the same ex­ample will be shown except that the ESR will be reduced suf­ficiently to increase the original f

The plot now shows (see graph

WITHOUT FEED-FORWARD

f

has moved down to about 8 kHz. Since fzis 6X fc, it means

c

that the zero f
which is not sufficient for stability.

can only provide about 9˚ of phase lead at fc,

z

from 5 kHz to 50 kHz.

z

LOW ESR UNSTABLE

) that the crossover frequency

p

,

F

).

c

www.national.com 16

Application Hints (Continued)

Low ESR Unstable without Feed-Forward

DS100034-30

This application can also be improved by adding a feed­forward capacitor. C
the gain plot (see graph

FEED-FORWARD

The crossover frequency f
lected so that f
(which means V
erably improved. Calculating out all the poles and zeroes,
the phase margin is increased from 9˚ to 43˚ (adequate for
good stability).

Low ESR Corrected with Feed-Forward

will add both a zero fzfand pole fpfto

F

LOW ESR CORRECTED WITH

).

is now about 10 kHz. If CFis se-

c

is about 5 kHz, and fpfis about 20 kHz

zf

=

5V), the phase margin will be consid-

OUT

The use of a feed-forward capacitor C
cess phase shift due to f
output voltage (see next section).

, but its effectiveness depends on

pg

LOW OUTPUT VOLTAGE AND C

will help reduce ex-

F

F

The feed-forward capacitor CFwill provide a positive phase
shift (lead) which can be used to cancel some of the excess
phase lag from any of the various poles present in the loop.
However, it is important to note that the effectiveness of C
decreases with output voltage.

This is due to the fact that the frequencies of the zero f
pole f

get closer together as the output voltage is reduced

pf

(see equations in section

TION

).

is more effective when the pole-zero pair are farther

C

F

apart, because there is less self cancellation. The net benefit
in phase shift provided by C
lead (positive phase shift) from f
phase shift) from f
quency f

. As the pole and zero frequency approach each

c

other, that difference diminishes to nothing.
The amount of phase lead at f

both on the f
To illustrate this more clearly, a graph is provided which

ratio and the location of fzwith respect to fc.

zf/fpf

FEED-FORWARD COMPENSA-

is the difference between the

F

and the lag (negative

which is present at the crossover fre-

pf

zf

provided by CFdepends

C

shows how much phase lead can be obtained for V
12V,5V,and 3.3V (see graph

C

).

F

Phase Lead Provided by C

PHASE LEAD PROVIDED BY

F

zf

OUT

and

F

=

DS100034-32

EXCESSIVE GATE CAPACITANCE: Higher values of gate
capacitance shift the pole f
cause stability problems (see previous section

PACITANCE POLE FREQUENCY
fpgvs. C

40 kHz and 500 kHz. How much phase shift this adds de-

, the pole fpgwill likely fall somewhere between

EFF

pends on the crossover frequency f

to lower frequencies, which can

pg

GATE CA-

). As shown in the graph

.

c

The effect of gate capacitance becomes most important at
high values of ESR for the output capacitor (see graph

ESR UNSTABLEWITHOUT FEED-FORWARD

ues of ESR increase f
tive gain portion of the curve. As f
quency (corresponding to higher values of gate

, which brings fpgmore into the posi-

c

moves to a lower fre-

pg

HIGH

). Higher val-

capacitance), this effect becomes even worse.
This points out why FET’s should be selected with the lowest

possible gate capacitance: it makes the design more tolerant
of higher ESR values on the output capacitor.

DS100034-33

The most important information on the graph is the fre­quency range of f
(most positive phase shift):

OUT
OUT
OUT

=
=
=

For V
For V
For V

which will provide the maximum benefit

zf

<

<

f

12V: 0.1 f
5V: 0.2 f

3.3V: 0.2 f

c

1.0 f

c

z

<

f

z

<

c

c

<

1.2 f

c

<

f

1.3 f

z

c

It’s also important to note how the maximum available phase
shift that C
than 50˚ can be obtained, but at 3.3V less than 30˚ is pos-

can provide drops off with V

F

. At 12V, more

OUT

sible. The lesson from this is that higher voltage designs are
more tolerant of phase shifts from both f
tance pole) and incorrect placement of f
output capacitor ESR is not at its nominal value). At lower
values of V
selected since C

, these parameters must be more precisely

OUT

can not provide as much correction.

F

(the gate capaci-

pg

(which means the

z

GENERAL DESIGN PROCEDURE

Assuming that V

, and RLare defined:

IN,VOUT

www.national.com17

Application Hints (Continued)

1) Calculate the required value of capacitance for C
that the pole f

PACITOR

≤ 200 Hz (see previous section

p

). For this calculation, an ESR of about 0.1Ω can

be assumed for the purpose of determining C
IMPORTANT: If a smaller value of output capacitor is used

(so that the value of f
control loop will be reduced. This will result in increased ring-

>

200 Hz), the phase margin of the

p

ing on the output voltage during a load transient. If the output
capacitor is made extremely small, oscillations will result.

To illustrate this effect, scope photos have been presented
showing the output voltage of reference design
output capacitor is reduced to approximately 1/30 of the
nominal value (the value which sets f
the effect of deviating from the nominal value is gradual and

= 200 Hz). As shown,

p

the regulator is quite robust in resisting going into oscilla­tions.

2) Approximate the crossover frequency f
tion in the previous section

AND PHASE MARGIN

CROSSOVER FREQUENCY

.

c

3) Calculate the required ESR of the output capacitor so that
the frequency of the zero f
tion

OUTPUT CAPACITOR

is set to 0.5 fc(see previous sec-

z

).

4) Calculate the value of the feed-forward capacitor C
that the zero f

occurs at the frequency which yields the

zf

OUT

OUTPUT CA-

.

OUT

#

2asthe

using the equa-

F

maximum phase gain for the output voltage selected (see

so

formula for calculating C

FORWARD CAPACITOR

previous section

LOW OUTPUT VOLTAGE AND C

is in the previous section

F

.

). The

F

FEED-

Lower ESR electrolytics are available which use organic
electrolyte (OSCON types), but are more costly than typical
aluminum electrolytics.

If the calculated value of ESR is higher than what is found in
the selected capacitor, an external resistor can be placed in
series with C

OUT

.

LOW VOLTAGE DESIGNS: Designs which have a low out­put voltage (where the positive effects of C
may be marginally stable if the C
carefully selected.

OUT

are very small)

F

and ESR values are not

Also, if the FET gate capacitance is large (as in the case of
a high-current FET), the pole f
enough in frequency to cause a problem.

could possibly get low

pg

The solution in both cases is to increase the amount of out­put capacitance which will shift f
reduce overall loop bandwidth). The ESR and C
tions should be repeated, since this changes the crossover
frequency f

.

c

to a lower frequency (and

p

calcula-

F

so

www.national.com 18

Physical Dimensions inches (millimeters) unless otherwise noted

LP2975 MOSFET LDO Driver/Controller

Surface Mount Mini SO-8 Package

NS Package Number MUA08A

LIFE SUPPORT POLICY

NATIONAL’S PRODUCTS ARE NOT AUTHORIZED FOR USE AS CRITICAL COMPONENTS IN LIFE SUPPORT
DEVICES OR SYSTEMS WITHOUT THE EXPRESS WRITTEN APPROVAL OF THE PRESIDENT AND GENERAL
COUNSEL OF NATIONAL SEMICONDUCTOR CORPORATION. As used herein:

1. Life support devices or systems are devices or
systems which, (a) are intended for surgical implant
into the body, or (b) support or sustain life, and
whose failure to perform when properly used in
accordance with instructions for use provided in the

2. A critical component is any component of a life
support device or system whose failure to perform
can be reasonably expected to cause the failure of
the life support device or system, or to affect its
safety or effectiveness.

labeling, can be reasonably expected to result in a
significant injury to the user.

National Semiconductor
Corporation

Americas
Tel: [phone]
Fax: [phone]
Email: [e-mail]

www.national.com

National does not assume any responsibility for use of any circuitry described, no circuit patent licenses are implied and National reserves the right at any time without notice to change said circuitry and specifications.

National Semiconductor
Europe

Fax: [phone]

Email: [e-mail]
Deutsch Tel: [phone]
English Tel: [phone]
Français Tel: [phone]
Italiano Tel: [phone]

National Semiconductor
Asia Pacific Customer
Response Group

Tel: [phone]
Fax: [phone]
Email: [e-mail]

National Semiconductor
Japan Ltd.

Tel: [phone]
Fax: [phone]