Page 1
TL/W/12459
LMX2305 PLLatinum 550 MHz Frequency Synthesizer
for RF Personal Communications
PRELIMINARY
August 1996
LMX2305
PLLatinum
TM
550 MHz Frequency Synthesizer
for RF Personal Communications
General Description
The LMX2305 is a high performance frequency synthesizer
with an integrated prescaler designed for RF operation up to
550 MHz. It is fabricated using National’s ABiC IV BiCMOS
process.
The LMX2305 contains a dual modulus prescaler which can
select either a 64/65 or a 128/129 divide ratio at input frequencies of up to 550 MHz. LMX2305, which employs the
digital phase lock loop technique, combined with a high
quality reference oscillator and a loop filter, provides the
tuning voltage for the voltage controlled oscillator to generate a very stable, low noise local oscillator signal.
Serial data is transferred into the LMX2305 via a three line
MICROWIRE
TM
interface (Data, Enable, Clock). Supply voltage can range from 2.65V to 5.5V. The LMX2305 features
very low current consumption, typically 4.0 mA at 2.75V.
The LMX2305 is available in a TSSOP 20-pin surface mount
plastic package.
Features
Y
RF operation up to 550 MHz
Y
2.65V to 5.5V operation
Y
Low current consumption:
I
CC
e
4.0 mA (typ) at V
CC
e
2.75V
Y
Dual modulus prescaler: 64/65 or 128/129
Y
Internal balanced, low leakage charge pump
Y
Small-outline, plastic, surface mount TSSOP,
0.173
×
wide package
Applications
Y
Analog Cellular telephone systems
(AMPS, ETACS, NMT)
Y
Portable wireless communications
(PCS/PCN, cordless)
Y
Wireless local area networks (WLANs)
Y
Other wireless communication systems
Y
Pagers
Block Diagram
TL/W/12459– 1
TRI-STATEÉis a registered trademark of National Semiconductor Corporation.
MICROWIRE
TM
and PLLatinumTMare trademarks of National Semiconductor Corporation.
C
1996 National Semiconductor Corporation RRD-B30M126/Printed in U. S. A.
http://www.national.com
Page 2

Connection Diagram
LMX2305
TL/W/12459– 2
20-Lead (0.173×Wide) Thin Shrink
Small Outline Package (TM)
Order Number LMX2305TM or LMX2305TMX
See NS Package Number MTC20
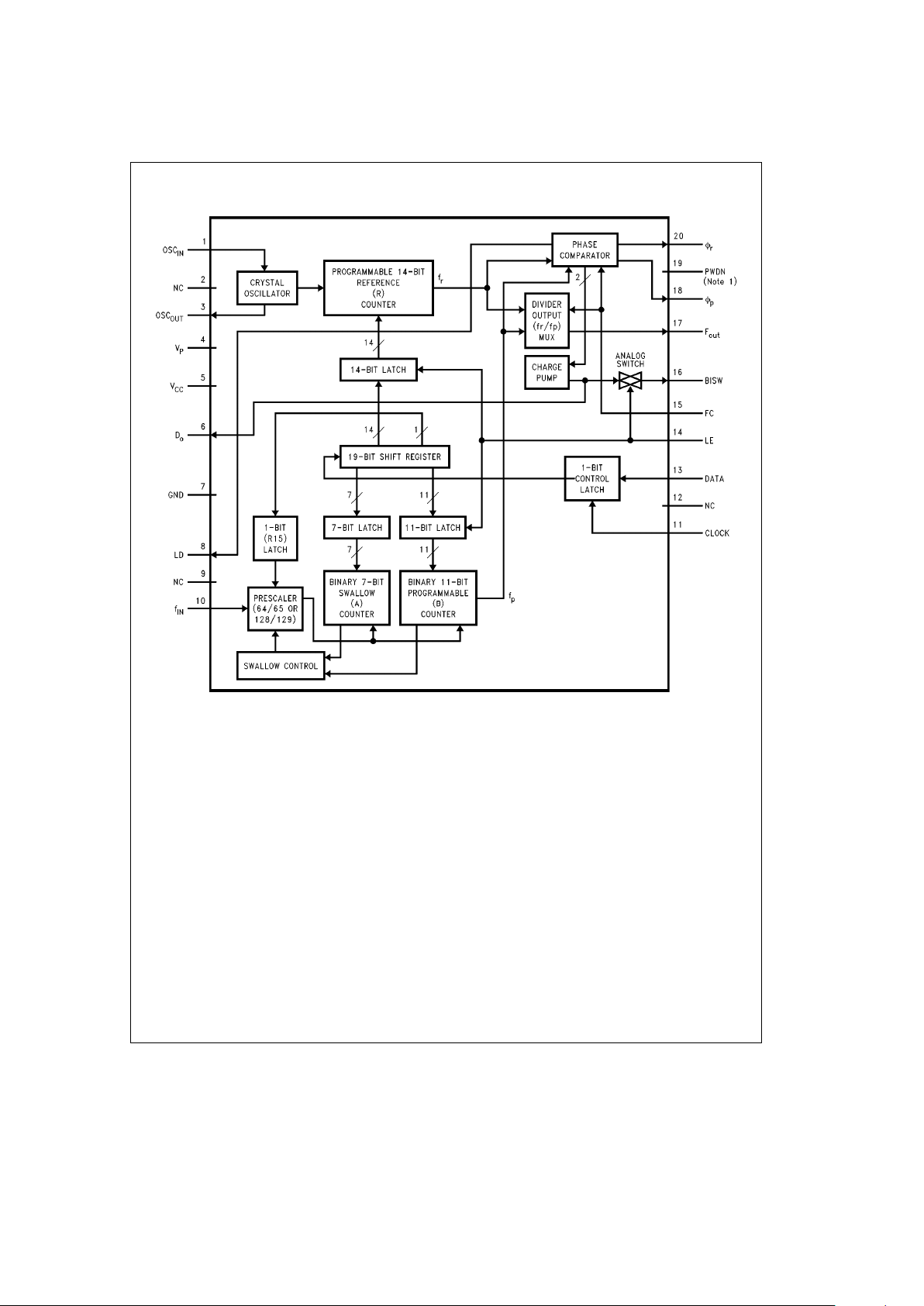
Pin Descriptions
Pin No. Pin Name I/O Description
1 OSC
IN
I Oscillator input. A CMOS inverting gate input intended for connection to a crystal resonator for
operation as an oscillator. The input has a V
CC
/2 input threshold and can be driven from an
external CMOS or TTL logic gate. May also be from a reference oscillator.
3 OSC
OUT
O Oscillator output.
4V
P
Power supply for charge pump. Must betVCC.
5V
CC
Power supply voltage input. Input may range from 2.65V to 5.5V. Bypass capacitors should be
placed as close as possible to this pin and be connected directly to the ground plane.
6D
o
O Internal charge pump output. For connection to a loop filter for driving the input of an external
VCO.
7 GND Ground.
8 LD O Lock detect. Output provided to indicate when the VCO frequency is in ‘‘lock’’. When the loop is
locked, the pin’s output is HIGH with narrow low pulses.
10 f
IN
I Prescaler input. Small signal input from the VCO.
11 CLOCK I High impedance CMOS Clock input. Data is clocked in on the rising edge, into the various
counters and registers.
13 DATA I Binary serial data input. Data entered MSB first. LSB is control bit. High impedance CMOS input.
14 LE I Load enable input (with internal pull-up resistor). When LE transitions HIGH, data stored in the
shift registers is loaded into the appropriate latch (control bit dependent). Clock must be low
when LE toggles high or low. See Serial Data Input Timing Diagram.
15 FC I Phase control select (with internal pull-up resistor). When FC is LOW, the polarity of the phase
comparator and charge pump combination is reversed.
16 BISW O Analog switch output. When LE is HIGH, the analog switch is ON, routing the internal charge
pump output through BISW (as well as through D
o
).
17 f
OUT
O Monitor pin of phase comparator input. CMOS output.
18 w
p
O Output for external charge pump. wpis an open drain N-channel transistor and requires a pull-up
resistor.
19 PWDN I Power Down (with internal pull-up resistor).
PWDN
e
HIGH for normal operation.
PWDNeLOW for power saving.
Power down function is gated by the return of the charge pump to a TRI-STATE condition.
20 w
r
O Output for external charge pump. wris a CMOS logic output.
2,9,12 NC No connect.
http://www.national.com 2
Page 3
Functional Block Diagram
TL/W/12459– 3
Note 1: The power down function is gated by the charge pump to prevent any unwanted frequency jumps. Once the power down pin is brought low the part will go
into power down mode when the charge pump reaches a TRI-STATE condition.
http://www.national.com3
Page 4

Absolute Maximum Ratings (Notes 1 and 2)
If Military/Aerospace specified devices are required,
please contact the National Semiconductor Sales
Office/Distributors for availability and specifications.
Power Supply Voltage
V
CC
b
0.3V toa6.5V
V
P
b
0.3V toa6.5V
Voltage on Any Pin
with GND
e
0V (VI)
b
0.3V to V
CC
a
0.3V
Storage Temperature Range (TS)
b
65§Ctoa150§C
Lead Temperature (TL) (solder, 4 sec.)
a
260§C
Recommended Operating
Conditions
Power Supply Voltage
V
CC
2.65V to 5.5V
V
P
VCCtoa5.5V
Operating Temperature (TA)
b
40§Ctoa85§C
Note 1: Absolute Maximum Ratings indicate limits beyond which damage to
the device may occur. Operating Ratings indicate conditions for which the
device is intended to be functional, but do not guarantee specific performance limits. For guaranteed specifications and test conditions, see the Electrical Characteristics. The guaranteed specifications apply only for the test
conditions listed.
Note 2: This device is a high performance RF integrated circuit with an ESD
rating
k
2 keV and is ESD sensitive. Handling and assembly of this device
should only be done at ESD workstations.
Electrical Characteristics V
CC
e
2.75V, V
P
e
2.75V;b40§CkT
A
k
85§C, except as specified
Symbol Parameter Conditions Min Typ Max Units
I
CC
Power Supply Current 4 6 mA
I
CC-PWDN
Power Down Current 30 180 mA
f
IN
RF Input Operating Frequency 45 550 MHz
f
OSC
Oscillator Input Operating Frequency 5 22 MHz
f
w
Phase Detector Frequency 10 MHz
Pf
IN
Input Sensitivity V
CC
e
2.65V to 5.5V
b
10
a
6 dBm
V
OSC
Oscillator Sensitivity OSC
IN
0.5 V
PP
V
IH
High-Level Input Voltage * 0.7 V
CC
V
V
IL
Low-Level Input Voltage * 0.3 V
CC
V
I
IH
High-Level Input Current (Clock, Data) V
IH
e
V
CC
e
5.5V
b
1.0 1.0 mA
I
IL
Low-Level Input Current (Clock, Data) V
IL
e
0V, V
CC
e
5.5V
b
1.0 1.0 mA
I
IH
Oscillator Input Current V
IH
e
V
CC
e
5.5V 100 mA
I
IL
V
IL
e
0V, V
CC
e
5.5V
b
100 mA
I
IH
High-Level Input Current (LE, FC) V
IH
e
V
CC
e
5.5V
b
1.0 1.0 mA
I
IL
Low-Level Input Current (LE, FC) V
IL
e
0V, V
CC
e
5.5V
b
100 1.0 mA
*Except fINand OSC
IN
http://www.national.com 4
Page 5

Electrical Characteristics V
CC
e
2.75V, V
P
e
2.75V;b40§CkT
A
k
85§C, except as specified (Continued)
Symbol Parameter Conditions Min Typ Max Units
I
Do-source
Charge Pump Output Current V
D
o
e
VP/2
b
2.5
b
1.0 mA
I
Do-sink
V
D
o
e
VP/2 1.0 2.5 mA
I
Do-Tri
Charge Pump TRI-STATEÉCurrent 0.5VsV
D
o
s
V
P
b
0.5V
b
5.0 5.0 nA
T
A
eb
40§CkT
A
k
85§C
V
OH
High-Level Output Voltage I
OH
eb
1.0 mA** V
CC
b
0.8 V
V
OL
Low-Level Output Voltage I
OL
e
1.0 mA** 0.4 V
V
OH
High-Level Output Voltage (OSC
OUT
)I
OH
eb
200 mAV
CC
b
0.8 V
V
OL
Low-Level Output Voltage (OSC
OUT
)I
OL
e
200 mA 0.4 V
I
OL
Open Drain Output Current (wp)V
OL
e
0.4V 1.0 mA
I
OH
Open Drain Output Current (wp)V
OH
e
2.75V 100 mA
t
CS
Data to Clock Set Up Time See Data Input Timing 50 ns
t
CH
Data to Clock Hold Time See Data Input Timing 10 ns
t
CWH
Clock Pulse Width High See Data Input Timing 50 ns
t
CWL
Clock Pulse Width Low See Data Input Timing 50 ns
t
ES
Clock to Enable Set Up Time See Data Input Timing 50 ns
t
EW
Enable Pulse Width See Data Input Timing 50 ns
**Except OSC
OUT
http://www.national.com5
Page 6

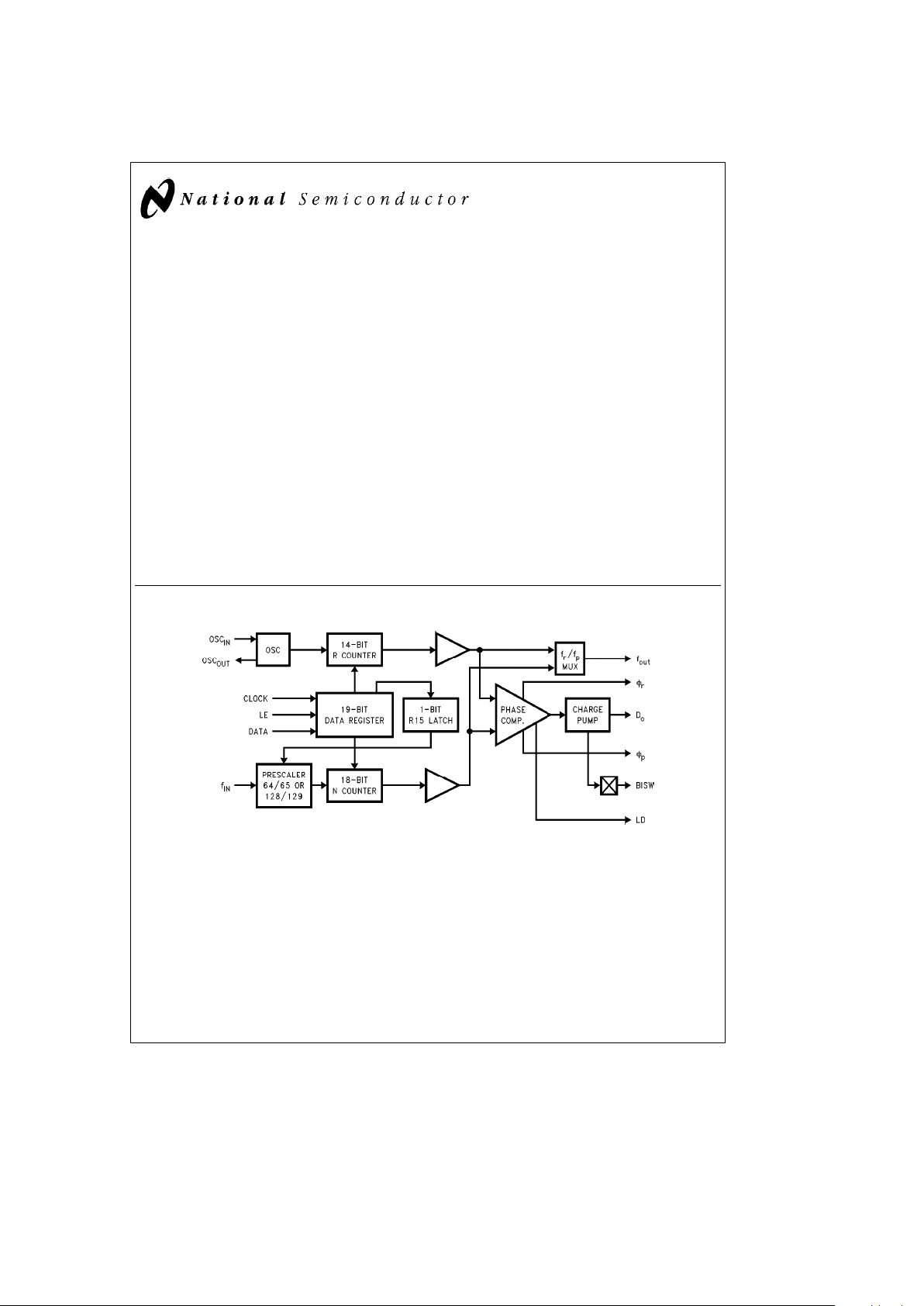
Functional Description
The simplified block diagram below shows the 19-bit data register, the 14-bit R Counter and the R15 Latch, and the 18-bit
N Counter (intermediate latches are not shown). The data stream is clocked (on the rising edge) into the DATA input, MSB first.
If the Control Bit (last bit input) is HIGH, the DATA is transferred into the R Counter (programmable reference divider) and the
S Latch (prescaler select: 64/65 or 128/129). If the Control Bit (LSB) is LOW, the DATA is transferred into the N Counter
(programmable divider).
TL/W/12459– 1
PROGRAMMABLE REFERENCE DIVIDER (R COUNTER) AND PRESCALER SELECT (R15 LATCH)
If the Control Bit (last bit shifted into the Data Register) is HIGH, data is transferred from the 19-bit shift register into a 14-bit
latch (which sets the 14-bit R Counter) and the 1-bit R15 Latch, which sets the prescaler: 64/65 or 128/129. Serial data format
is shown below.
TL/W/12459– 14
14-BIT PROGRAMMABLE REFERENCE DIVIDER RATIO
(R COUNTER)
Divide
14R13R12R11R10
RR9R8R7R6R5R4R3R2R
1
Ratio
R
3 0 0 0 0 0 000000011
4 0 0 0 0 0 000000100
# # # # # # #########
16383 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Notes: Divide ratios less than 3 are prohibited.
Divide ratio: 3 to 16383
R1 to R14: These bits select the divide ratio of the programmable
reference divider.
C: Control bit (set to HIGH level to load R counter and R15 Latch)
Data is shifted in MSB first.
1-BIT PRESCALER SELECT
(R15 LATCH)
Prescaler
15
R
Select
P
128/129 0
64/65 1
http://www.national.com 6
Page 7

Functional Description (Continued)
PROGRAMMABLE DIVIDER (N COUNTER)
The N counter consists of the 7-bit swallow counter (A counter) and the 11-bit programmable counter (B counter). If the Control
Bit (last bit shifted into the Data Register) is LOW, data is transferred from the 19-bit shift register into a 7-bit latch, which sets
the 7-bit Swallow (A) Counter, and an 11-bit latch, which sets the 11-bit programmable (B) Counter. Serial data format is shown
below.
TL/W/12459– 15
Note: S8 to S18: Programmable counter divide ratio control bits (3 to 2047)
7-BIT SWALLOW COUNTER DIVIDE RATIO
(A COUNTER)
Divide
N7N6N5N4N3N2N
1
Ratio
A
0 0000000
1 0000001
# #######
127 1111111
Note: Divide ratio: 0 to 127
B
t
A
11-BIT PROGRAMMABLE COUNTER DIVIDE RATIO
(B COUNTER)
Divide
18N17N16N15N14N13N12N11N10
NN9N
8
Ratio
B
3 00000000011
4 00000000100
# ###########
2047 1 1 1 1 1 1 1 1 1 1 1
Note: Divide ratio: 3 to 2047 (Divide ratios less than 3 are prohibited)
B
t
A
PULSE SWALLOW FUNCTION
f
VCO
e
[
(P
c
B)aA
]
c
f
OSC
/R
f
VCO
: Output frequency of external voltage controlled oscil-
lator (VCO)
B: Preset divide ratio of binary 11-bit programmable
counter (3 to 2047)
A: Preset divide ratio of binary 7-bit swallow counter
(0
sAs
127, AsB)
f
OSC
: Output frequency of the external reference frequency
oscillator
R: Preset divide ratio of binary 14-bit programmable ref-
erence counter (3 to 16383)
P: Preset modulus of dual modulus prescaler (64 or 128)
http://www.national.com7
Page 8

Functional Description (Continued)
SERIAL DATA INPUT TIMING
TL/W/12459– 16
Notes: Parenthesis data indicates programmable reference divider data.
Data shifted into register on clock rising edge.
Data is shifted in MSB first.
Test Conditions: The Serial Data Input Timing is tested using a symmetrical waveform around V
CC
/2. The test waveform has an edge rate of 0.6 V/ns with
amplitudes of 2.2V
@
V
CC
e
2.7V and 2.6V@V
CC
e
5.5V.
Phase Characteristics
In normal operation, the FC pin is used to reverse the polarity of the phase detector. Both the internal and any external
charge pump are affected.
Depending upon VCO characteristics, FC pin should be set
accordingly:
When VCO characteristics are like (1), FC should be set
HIGH or OPEN CIRCUIT;
When VCO characteristics are like (2), FC should be set
LOW.
When FC is set HIGH or OPEN CIRCUIT, the monitor pin of
the phase comparator input, f
out
, is set to the reference
divider output, f
r
. When FC is set LOW, f
out
is set to the
programmable divider output, f
p
.
VCO Characteristics
TL/W/12459– 17
PHASE COMPARATOR AND INTERNAL CHARGE PUMP CHARACTERISTICS
TL/W/12459– 18
Notes: Phase difference detection range:b2q toa2q
The minimum width pump up and pump down current pulses occur at the Dopin when the loop is locked.
FC
e
HIGH
http://www.national.com 8
Page 9

Analog Switch
The analog switch is useful for radio systems that utilize a frequency scanning mode and a narrow band mode. The purpose of
the analog switch is to decrease the loop filter time constant, allowing the VCO to adjust to its new frequency in a shorter
amount of time. This is achieved by adding another filter stage in parallel. The output of the charge pump is normally through the
D
o
pin, but when LE is set HIGH, the charge pump output also becomes available at BISW. A typical circuit is shown below. The
second filter stage (LPF-2) is effective only when the switch is closed (in the scanning mode).
TL/W/12459– 19
Typical Crystal Oscillator Circuit
A typical circuit which can be used to implement a crystal
oscillator is shown below.
TL/W/12459– 20
Typical Lock Detect Circuit
A lock detect circuit is needed in order to provide a steady
LOW signal when the PLL is in the locked state. A typical
circuit is shown below.
TL/W/12459– 21
http://www.national.com9
Page 10

Typical Application Example
Operational Notes:
TL/W/12459– 22
* VCO is assumed AC coupled.
** R
IN
increases impedance so that VCO output power is provided to the load rather than the PLL. Typical values are 10X to 200X depending on the VCO power
level. f
IN
RF impedance ranges from 40X to 100 X.
*** 50X termination is often used on test boards to allow use of external reference oscillator. For most typical products a CMOS clock is used and no terminating
resistor is required. OSC
IN
may be AC or DC coupled. AC coupling is recommended because the input circuit provides its own bias. (See
Figure
below)
TL/W/12459– 23
Application Hints:
Proper use of grounds and bypass capacitors is essential to achieve a high level of performance.
Crosstalk between pins can be reduced by careful board layout.
This is an electrostatic sensitive device. It should be handled only at static free work stations.
http://www.national.com 10
Page 11

Application Information
LOOP FILTER DESIGN
A block diagram of the basic phase locked loop is shown.
TL/W/12459– 24
FIGURE 1. Basic Charge Pump Phase Locked Loop
An example of a passive loop filter configuration, including
the transfer function of the loop filter, is shown in
Figure 2
.
TL/W/12459– 25
Z(s)
e
s (C2#R2)a1
s2(C1#C2#R2)asC1asC2
FIGURE 2. 2nd Order Passive Filter
Define the time constants which determine the pole and
zero frequencies of the filter transfer function by letting
T2
e
R2#C2 (1a)
and
T1
e
R2
#
C1#C2
C1aC2 (1b)
The PLL linear model control circuit is shown along with the
open loop transfer function in
Figure 3
. Using the phase
detector and VCO gain constants[Kw and K
VCO
]
and the
loop filter transfer function[Z(s)], the open loop Bode plot
can be calculated. The loop bandwidth is shown on the
Bode plot (
0p) as the point of unity gain. The phase margin
is shown to be the difference between the phase at the unity
gain point and
b
180§.
TL/W/12459– 27
Open Loop Gaineii/i
e
e
H(s) G(s)
e
Kw Z(s) K
VCO
/Ns
Closed Loop Gaineio/i
i
e
G(s)/[1aH(s) G(s)
]
TL/W/12459– 26
FIGURE 3. Open Loop Transfer Function
Thus we can calculate the 3rd order PLL Open Loop Gain in
terms of frequency
G(s)
#
H(s)
l
sej
#
0
e
b
Kw#K
VCO
(1aj0#T2)
0
2
C1#N(1aj0#T1)
#
T1
T2 (2)
From equation 2 we can see that the phase term will be
dependent on the single pole and zero such that
w(
0)
e
tan
b
1
(0#T2)btan
b
1
(0#T1)a180§(3)
By setting
dw
d0
e
T2
1a(0#T2)
2
b
T1
1a(0#T1)
2
e
0
(4)
we find the frequency point corresponding to the phase inflection point in terms of the filter time constants T1 and T2.
This relationship is given in equation 5.
0
p
e
1/0T2#T1 (5)
For the loop to be stable the unity gain point must occur
before the phase reaches
b
180 degrees. We therefore
want the phase margin to be at a maximum when the magnitude of the open loop gain equals 1. Equation 2 then gives
C1
e
Kw#K
VCO
#
T1
0
p
2
#N#
T2
Ó
(1aj0
p
#
T2)
(1aj0
p
#
T1)
Ó
(6)
http://www.national.com11
Page 12

Application Information (Continued)
Therefore, if we specify the loop bandwidth,
0
p
, and the
phase margin, w
p
, Equations 1 through 6 allow us to calculate the two time constants, T1 and T2, as shown in equations 7 and 8. A common rule of thumb is to begin your
design with a 45
§
phase margin.
T1
e
secw
p
b
tanw
p
0
p
(7)
T2
e
1
0
p
2
#
T1 (8)
From the time constants T1, and T2, and the loop bandwidth,
0
p
, the values for C1, R2, and C2 are obtained in
equations 9 to 11.
C1
e
T1
T2
#
Kw#K
VCO
0
p
2
#
N
0
1a(0
p
#
T2)
2
1a(0
p
#
T1)
2
(9)
C2
e
C1
#
#
T2
T1
b
1
J
(10)
R2
e
T2
C2 (11)
K
VCO
(MHz/V) Voltage Controlled Oscillator (VCO)
Tuning Voltage constant. The frequency vs voltage tuning ratio.
Kw (mA) Phase detector/charge pump gain
constant. The ratio of the current output to the input phase differential.
N Main divider ratio. Equal to RF
opt/fref
RF
opt
(MHz) Radio Frequency output of the VCO at
which the loop filter is optimized.
f
ref
(kHz) Frequency of the phase detector in-
puts. Usually equivalent to the RF
channel spacing.
In choosing the loop filter components a trade off must be
made between lock time, noise, stability, and reference
spurs. The greater the loop bandwidth the faster the lock
time will be, but a large loop bandwidth could result in higher
reference spurs. Wider loop bandwidths generally improve
close in phase noise but may increase integrated phase
noise depending on the reference input, VCO and division
ratios used. The reference spurs can be reduced by reducing the loop bandwidth or by adding more low pass filter
stages but the lock time will increase and stability will decrease as a result.
THIRD ORDER FILTER
A low pass filter section may be needed for some applications that require additional rejection of the reference sidebands, or spurs. This configuration is given in
Figure 4
.In
order to compensate for the added low pass section, the
component values are recalculated using the new open
loop unity gain frequency. The degradation of phase margin
caused by the added low pass is then mitigated by slightly
increasing C1 and C2 while slightly decreasing R2.
The added attenuation from the low pass filter is:
ATTEN
e
20 log[(2qf
ref
#R3#
C3)
2
a
1](12)
Defining the additional time constant as
T3eR3#C3 (13)
Then in terms of the attenuation of the reference spurs added by the low pass pole we have
T3
e
0
10
ATTEN/20
b
1
(2q#f
ref
)
2
(14)
We then use the calculated value for loop bandwidth
0
c
in
equation 11, to determine the loop filter component values
in equations 15 –17.
0
c
is slightly less than 0p, therefore
the frequency jump lock time will increase.
T2
e
1
0
c
2
#
(T1aT3) (15)
0
c
e
tanw#(T1aT3)
[
(T1
a
T3)
2
a
T1#T3
]
#
Ð0
1
a
(T1aT3)
2
a
T1#T3
[
tanw
#
(T1aT3)
]
2
b
1
(
(16)
C1
e
T1
T2
#
Kw#K
VCO
0
c
2
#
N
#
Ð
(1
a
0
c
2
#
T22)
(1
a
0
c
2
#
T12)(1
a
0
c
2
#
T32)
(
(/2
(17)
http://www.national.com 12
Page 13

Application Information (Continued)
EXTERNAL CHARGE PUMP
The LMX PLLatinum series of frequency synthesizers are
equipped with an internal balanced charge pump as well as
outputs for driving an external charge pump. Although the
superior performance of NSC’s on board charge pump eliminates the need for an external charge pump in most applications, certain system requirements are more stringent. In
these cases, using an external charge pump allows the designer to take direct control of such parameters as charge
pump voltage swing, current magnitude, TRI-STATE leakage, and temperature compensation.
One possible architecture for an external charge pump current source is shown in
Figure 9
. The signals wpand wrin
the diagram, correspond to the phase detector outputs of
the LMX2305 frequency synthesizer. These logic signals are
converted into current pulses, using the circuitry shown in
Figure 9
, to enable either charging or discharging of the
loop filter components to control the output frequency of the
PLL.
Referring to
Figure 9
, the design goal is to generatea5mA
current which is relatively constant to within 0.5V of the
power supply rail. To accomplish this, it is important to establish as large of a voltage drop across R5, R8 as possible
without saturating Q2, Q4. A voltage of approximately 300
mV provides a good compromise. This allows the current
source reference being generated to be relatively repeatable in the absence of good Q1, Q2/Q3, Q4 matching.
(Matched transistor pairs is recommended.) The wp and wr
outputs are rated for a maximum output load current of 1
mA while 5 mA current sources are desired. The voltages
developed across R4, 9 will consequently be approximately
258 mV, or 42 mV
k
R8, 5, due to the current density differ-
ences
À
0.026*1n (5 mA/1 mA)Óthrough the Q1, Q2/Q3, Q4
pairs.
In order to calculate the value of R7 it is necessary to first
estimate the forward base to emitter voltage drop (Vfn,p) of
the transistors used, the V
OL
drop of wp, and the VOHdrop
of wr’s under 1 mA loads. (wp’s V
OL
k
0.1V and wr’s
V
OH
k
0.1V.)
Knowing these parameters along with the desired current
allow us to design a simple external charge pump. Separating the pump up and pump down circuits facilitates the nodal analysis and give the following equations.
R
4
e
V
R5
b
V
T
#
ln
#
i
source
i
p max
J
i
source
R
9
e
V
R8
b
V
T
#
ln
#
i
sink
i
n max
J
i
sink
R
5
e
V
R5
i
p max
R
8
e
V
R8
i
r max
R
6
e
(V
p
b
V
VOLwp
)b(V
R5
a
Vfp)
i
p max
R
7
e
(V
P
b
V
VOHwr
)b(V
R8
a
Vfn)
i
max
EXAMPLE
Typical Device Parameters b
n
e
100, b
p
e
50
Typical System Parameters V
P
e
5.0V;
V
cntl
e
0.5Vb4.5V;
V
wp
e
0.0V; V
wr
e
5.0V
Design Parameters I
SINK
e
I
SOURCE
e
5.0 mA;
V
fn
e
V
fp
e
0.8V
I
rmax
e
I
pmax
e
1mA
V
R8
e
V
R5
e
0.3V
V
OLwp
e
V
OHwr
e
100 mV
TL/W/12459– 28
FIGURE 9
Therefore select
R
4
e
R
9
e
0.3Vb0.026#1n(5.0 mA/1.0 mA)
5mA
e
51.6X
R
5
e
0.3V
1.0 mA
e
300X
R
8
e
0.3V
1.0 mA
e
300X
R
6
e
R
7
e
(5Vb0.1V)b(0.3Va0.8V)
1.0 mA
e
3.8 kX
http://www.national.com13
Page 14

LMX2305 PLLatinum 550 MHz Frequency Synthesizer
for RF Personal Communications
Physical Dimensions inches (millimeters) unless otherwise noted
NS Package Number MTC20
20-Lead (0.173
×
Wide) Thin Shrink Small Outline Package (TM)
Order Number LMX2305TM
For Tape and Reel Order Number LMX2305TMX (2500 Units per Reel)
LIFE SUPPORT POLICY
NATIONAL’S PRODUCTS ARE NOT AUTHORIZED FOR USE AS CRITICAL COMPONENTS IN LIFE SUPPORT
DEVICES OR SYSTEMS WITHOUT THE EXPRESS WRITTEN APPROVAL OF THE PRESIDENT OF NATIONAL
SEMICONDUCTOR CORPORATION. As used herein:
1. Life support devices or systems are devices or 2. A critical component is any component of a life
systems which, (a) are intended for surgical implant support device or system whose failure to perform can
into the body, or (b) support or sustain life, and whose be reasonably expected to cause the failure of the life
failure to perform, when properly used in accordance support device or system, or to affect its safety or
with instructions for use provided in the labeling, can effectiveness.
be reasonably expected to result in a significant injury
to the user.
National Semiconductor National Semiconductor National Semiconductor National Semiconductor
Corporation Europe Southeast Asia Japan Ltd.
Fax:
a
49 (0) 180-530 85 86 Fax: (852) 2376 3901 Tel: 81-3-5620-7561
Americas
Email: europe.support
@
nsc.com Email: sea.support@nsc.com Fax: 81-3-5620-6179
Tel: 1(800) 272-9959
Deutsch Tel:
a
49 (0) 180-530 85 85
Fax: 1(800) 737-7018
English Tel:
a
49 (0) 180-532 78 32
Email: support
@
nsc.com
Fran3ais Tel:
a
49 (0) 180-532 93 58
Italiano Tel:
a
49 (0) 180-534 16 80
http://www.national.com
National does not assume any responsibility for use of any circuitry described, no circuit patent licenses are implied and National reserves the right at any time without notice to change said circuitry and specifications.
 Loading...
Loading...