How it Works
Datasheet
Loading...
LM629N-6
Datasheet (NSC)
24 pgs669.37 Kb0

Datasheet LM629N-8, LM629N-6, LM629MX-8, LM629M-8, LM629M-6 Datasheet (NSC)

Download
Page 1
LM628/LM629 Precision Motion Controller
General Description
The LM628/LM629 are dedicated motion-control processors designed for use with a variety of DC and brushless DC servo motors, and other servomechanisms which provide a quadrature incremental position feedback signal. The parts perform theintensive, real-time computational tasks required for high performance digital motion control. The host control software interface is facilitated by a high-level command set. The LM628 has an 8-bit output which can drive either an 8-bit or a 12-bit DAC. The components required to build a servo system are reduced to the DC motor/actuator, an in­cremental encoder, a DAC, a power amplifier, and the LM628. An LM629-based system is similar, except that it provides an 8-bit PWM output for directly driving H-switches. The parts are fabricated in NMOS and packaged in a 28-pin dual in-line package or a 24-pin surface mount package (LM629 only). Both 6 MHz and 8 MHz maximum frequency versions are available with the suffixes -6 and -8, respec­tively, used to designate the versions. They incorporate an SDA core processor and cells designed by SDA.
Features
n 32-bit position, velocity, and acceleration registers n Programmable digital PID filter with 16-bit coefficients n Programmable derivative sampling interval n 8- or 12-bit DAC output data (LM628) n 8-bit sign-magnitude PWM output data (LM629) n Internal trapezoidal velocity profile generator n Velocity, target position, and filter parameters may be
changed during motion
n Position and velocity modes of operation n Real-time programmable host interrupts n 8-bit parallel asynchronous host interface n Quadrature incremental encoder interface with index
pulse input
n Available in a 28-pin dual in-line package or a 24-pin
surface mount package (LM629 only)
TRI-STATE®is a registered trademark of National Semiconductor Corporation.
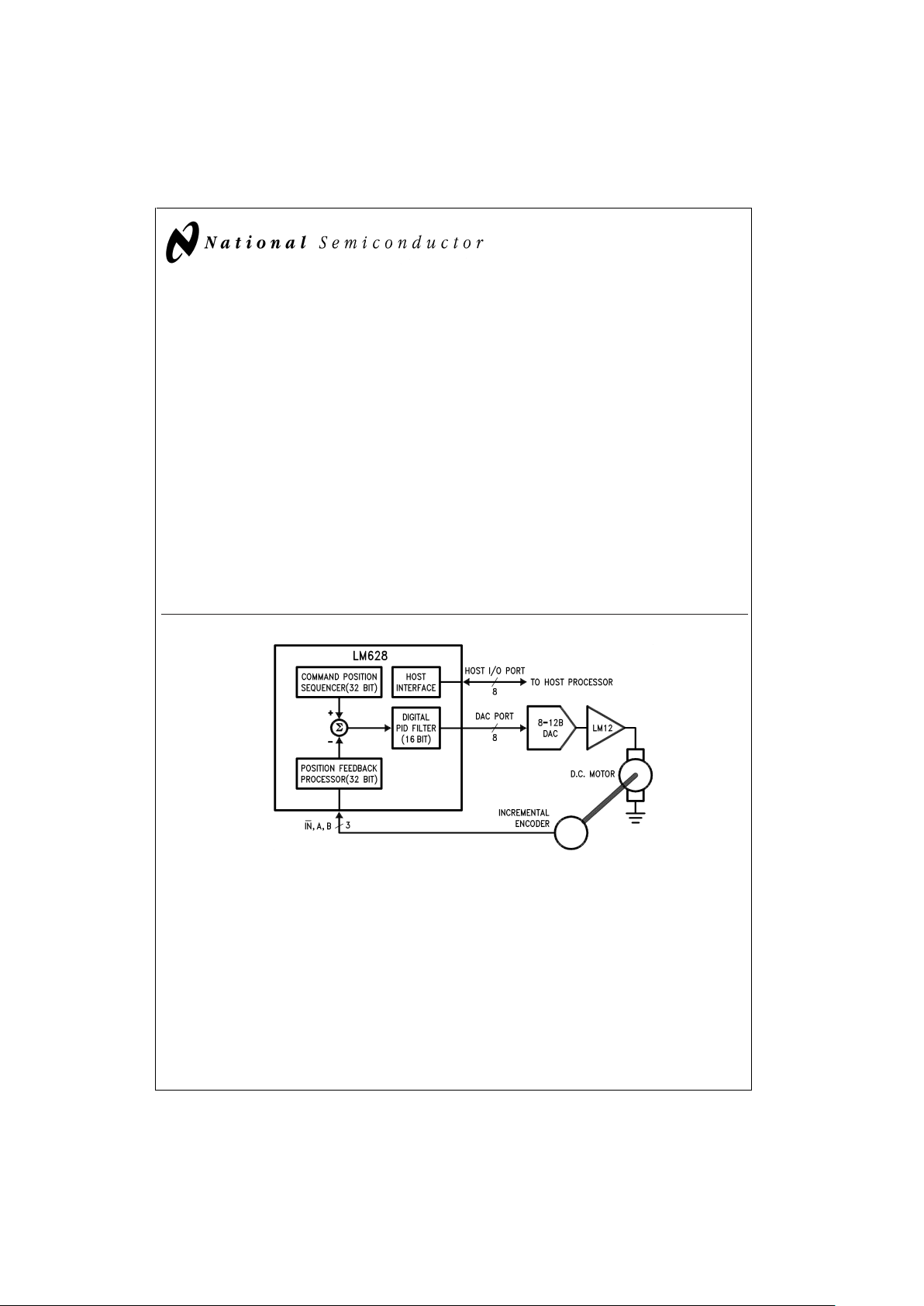
DS009219-1
FIGURE 1. Block Diagram
November 1999
LM628/LM629 Precision Motion Controller
© 1999 National Semiconductor Corporation DS009219 www.national.com
Page 2
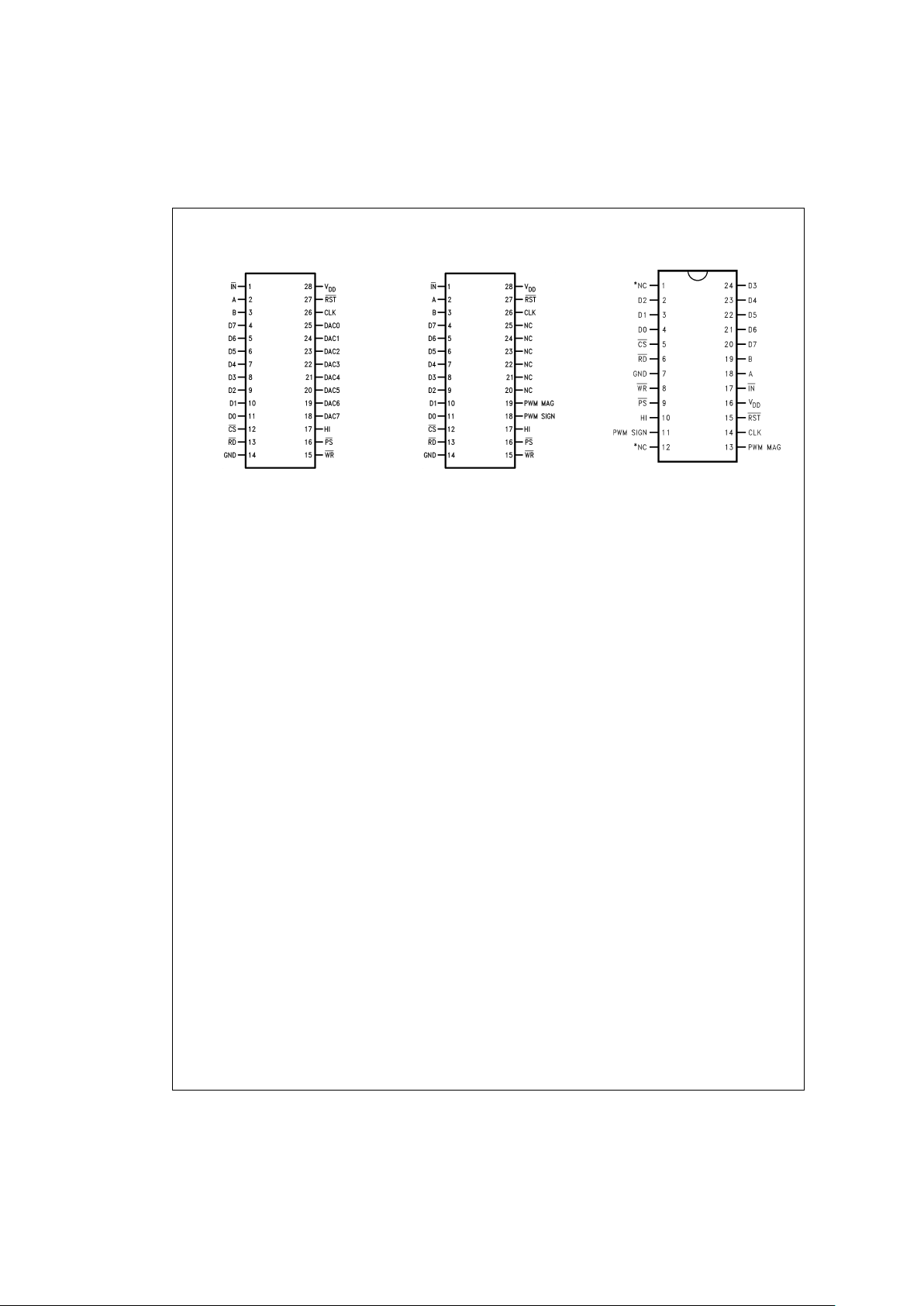
Connection Diagrams
LM628N
DS009219-2
LM629N
DS009219-3
LM629M
DS009219-21
*Do not connect.
Order Number LM629M-6, LM629M-8, LM628N-6, LM628N-8, LM629N-6 or LM629N-8
See NS Package Number M24B or N28B
LM628/LM629
www.national.com 2
Page 3
Absolute Maximum Ratings (Note 1)
If Military/Aerospace specified devices are required, please contact the National Semiconductor Sales Office/ Distributors for availability and specifications.
Voltage at Any Pin with
Respect to GND −0.3V to +7.0V Ambient Storage Temperature −65˚C to +150˚C Lead Temperature
28-pin Dual In-Line
Package (Soldering, 4 sec.) 260˚C
24-pin Surface Mount
Package (Soldering, 10 sec.) 300˚C Maximum Power Dissipation
(T
A
≤ 85˚C, (Note 2) 605 mW
ESD Tolerance
(C
ZAP
=
120 pF, R
ZAP
=
1.5k) 2000V
Operating Ratings
Temperature Range −40˚C<T
A
<
+85˚C
Clock Frequency:
LM628N-6, LM629N-6, LM629M-6 1.0 MHz
<
f
CLK
<
6.0 MHz LM628N-8, LM629N-8, LM629M-8 1.0 MHz
<
f
CLK
<
8.0 MHz
V
DD
Range 4.5V<V
DD
<
5.5V
DC Electrical Characteristics
(VDDand TAper Operating Ratings; f
CLK
=
6 MHz)
Symbol Parameter Conditions Tested Limits Units
Min Max
I
DD
Supply Current Outputs Open 110 mA
INPUT VOLTAGES
V
IH
Logic 1 Input Voltage 2.0 V
V
IL
Logic 0 Input Voltage 0.8 V
I
IN
Input Currents 0 ≤ VIN≤ V
DD
−10 10 µA
OUTPUT VOLTAGES
V
OH
Logic 1 I
OH
=
−1.6 mA 2.4 V
V
OL
Logic 0 I
OL
=
1.6 mA 0.4 V
I
OUT
TRI-STATE®Output Leakage Current 0 ≤ V
OUT
≤ V
DD
−10 10 µA
AC Electrical Characteristics
(VDDand TAper Operating Ratings; f
CLK
=
6 MHz; C
LOAD
=
50 pF; Input Test Signal t
r
=
t
f
=
10 ns)
Timing Interval T
#
Tested Limits Units
Min Max
ENCODER AND INDEX TIMING (See
Figure 2
)
Motor-Phase Pulse Width T1
µs
Dwell-Time per State T2
µs
Index Pulse Setup and Hold T3 0 µs (Relative to A and B Low) CLOCK AND RESET TIMING (See
Figure 3
)
Clock Pulse Width
LM628N-6, LM629N-6, LM629M-6 T4 78 ns LM628N-8, LM629N-8, LM629M-8 T4 57 ns
Clock Period
LM628N-6, LM629N-6, LM629M-6 T5 166 ns LM628N-8, LM629N-8, LM629M-8 T5 125 ns
Reset Pulse Width T6
µs
LM628/LM629
www.national.com3
Page 4
AC Electrical Characteristics (Continued)
(VDDand TAper Operating Ratings; f
CLK
=
6 MHz; C
LOAD
=
50 pF; Input Test Signal t
r
=
t
f
=
10 ns)
Timing Interval T
#
Tested Limits Units
Min Max
STATUS BYTE READ TIMING (See
Figure 4
) Chip-Select Setup/Hold Time T7 0 ns Port-Select Setup Time T8 30 ns Port-Select Hold Time T9 30 ns Read Data Access Time T10 180 ns Read Data Hold Time T11 0 ns RD High to Hi-Z Time
T12 180 ns
COMMAND BYTE WRITE TIMING (See
Figure 5
) Chip-Select Setup/Hold Time T7 0 ns Port-Select Setup Time T8 30 ns Port-Select Hold Time T9 30 ns Busy Bit Delay T13 (Note 3) ns WR Pulse Width
T14 100 ns Write Data Setup Time T15 50 ns Write Data Hold Time T16 120 ns DATA WORD READ TIMING (See
Figure 6
) Chip-Select Setup/Hold Time T7 0 ns Port-Select Setup Time T8 30 ns Port-Select Hold Time T9 30 ns Read Data Access Time T10 180 ns Read Data Hold Time T11 0 ns RD High to Hi-Z Time
T12 180 ns Busy Bit Delay T13 (Note 3) ns Read Recovery Time T17 120 ns DATA WORD WRITE TIMING (See
Figure 7
) Chip-Select Setup/Hold Time T7 0 ns Port-Select Setup Time T8 30 ns Port-Select Hold Time T9 30 ns Busy Bit Delay T13 (Note 3) ns WR Pulse Width
T14 100 ns Write Data Setup Time T15 50 ns Write Data Hold Time T16 120 ns Write Recovery Time T18 120 ns
Note 1: Absolute Maximum Ratings indicate limits beyond which damage to the device may occur. DC and AC electrical specifications do not apply when operating the device beyond the above Operating Ratings.
Note 2: When operating at ambient temperatures above 70˚C, the device must be protected against excessive junction temperatures. Mounting the package on a printed circuit board having an area greater than three square inches and surrounding the leads and body with wide copper traces and large, uninterrupted areas of copper, such as a ground plane, suffices. The 28-pin DIP (N) and the 24-pin surface mount package (M) are molded plastic packages with solid copper lead frames. Most of the heat generated at the die flows from the die, through the copper lead frame, and into copper traces on the printed circuit board. The copper traces act as a heat sink. Double-sided or multi-layer boards provide heat transfer characteristics superior to those of single-sided boards.
Note 3: In order to read the busy bit, the status byte must first be read. The time required to read the busy bit far exceeds the time the chip requires to set the busy bit. It is, therefore, impossible to test actual busy bit delay. The busy bit is guaranteed to be valid as soon as the user is able to read it.
LM628/LM629
www.national.com 4
Page 5
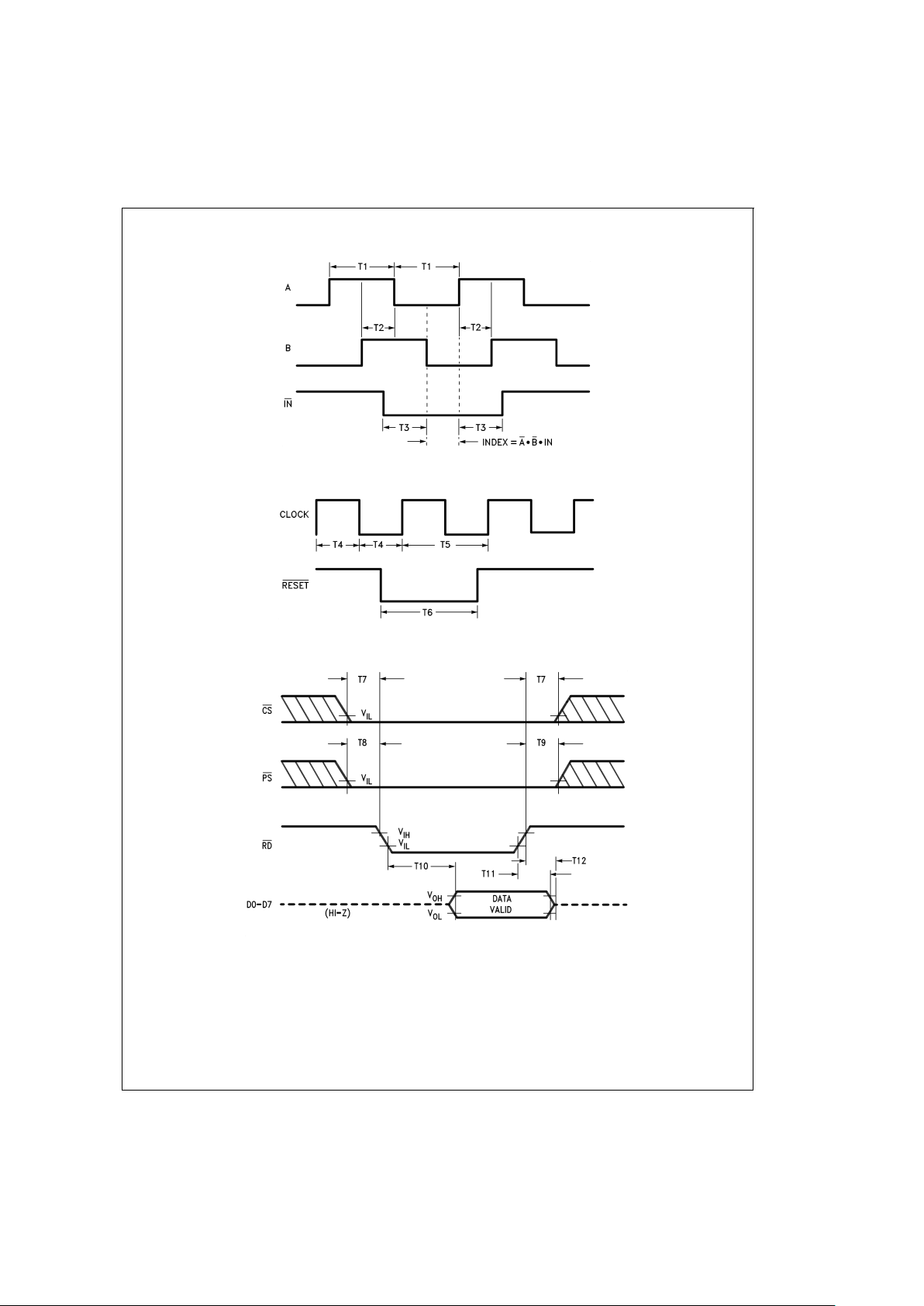
AC Electrical Characteristics (Continued)
DS009219-4
FIGURE 2. Quadrature Encoder Input Timing
DS009219-5
FIGURE 3. Clock and Reset Timing
DS009219-6
FIGURE 4. Status Byte Read Timing
LM628/LM629
www.national.com5
Page 6
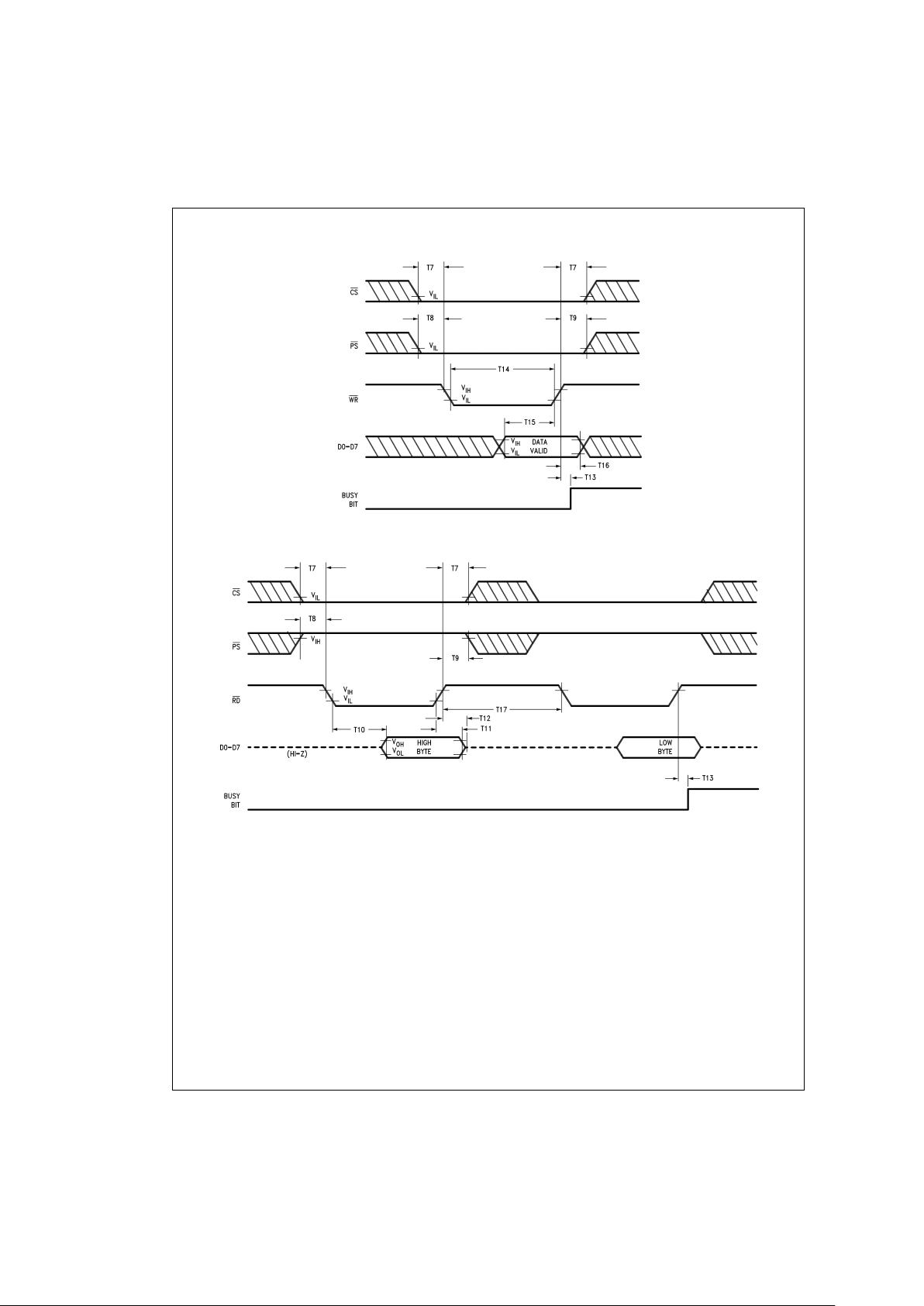
AC Electrical Characteristics (Continued)
DS009219-7
FIGURE 5. Command Byte Write Timing
DS009219-8
FIGURE 6. Data Word Read Timing
LM628/LM629
www.national.com 6
Page 7
AC Electrical Characteristics (Continued)
Pinout Description
(See Connection Diagrams) Pin numbers for the 24-pin sur­face mount package are indicated in parentheses.
Pin 1 (17), Index (IN) Input: Receives optional index pulse from the encoder. Must be tied high if not used. The index position is read when Pins 1, 2, and 3 are low.
Receive the two-phase quadrature signals provided by the incremental encoder. When the motor is rotating in the posi­tive (“forward”) direction, the signal at Pin 2 leads the signal at Pin 3 by 90 degrees. Note that the signals at Pins 2 and 3 must remain at each encoder state (See
Figure 9
) for a mini­mum of 8 clock periods in order to be recognized. Because of a four-to-one resolution advantage gained by the method of decoding the quadrature encoder signals, this corre­sponds to a maximum encoder-state capture rate of 1.0 MHz (f
CLK
=
8.0 MHz) or 750 kHz (f
CLK
=
6.0 MHz). For other clock frequencies the encoder signals must also remain at each state a minimum of 8 clock periods.
Pins 4 to 11 (20 to 24 and 2 to 4), Host I/O Port (D0 to D7):
Bi-directional data port which connects to host computer/ processor. Used for writing commands and data to the LM628, and for reading the status byte and data from the LM628, as controlled by CS (Pin 12), PS (Pin 16), RD (Pin
13), and WR (Pin 15). Pin 12 (5), Chip Select (CS ) Input: Used to select the
LM628 for writing and reading operations.
Pin 13 (6), Read (RD ) Input: Used to read status and data. Pin 14 (7), Ground (GND): Power-supply return pin. Pin 15 (8), Write (WR ) Input: Used to write commands and
data. Pin 16 (9), Port Select (PS ) Input: Used to select com-
mand or data port. Selects command port when low, data port when high. The following modes are controlled by Pin 16:
1. Commands are written to the command port (Pin 16
low),
2. Status byte is read from command port (Pin 16 low), and
3. Data is written and read via the data port (Pin 16 high). Pin 17 (10), Host Interrupt (HI) Output: This active-high
signal alerts the host (via a host interrupt service routine) that an interrupt condition has occurred.
Pins 18 to 25, DAC Port (DAC0 to DAC7): Output port which is used in three different modes:
1. LM628 (8-bit output mode): Outputs latched data to the DAC. The MSB is Pin 18 and the LSB is Pin 25.
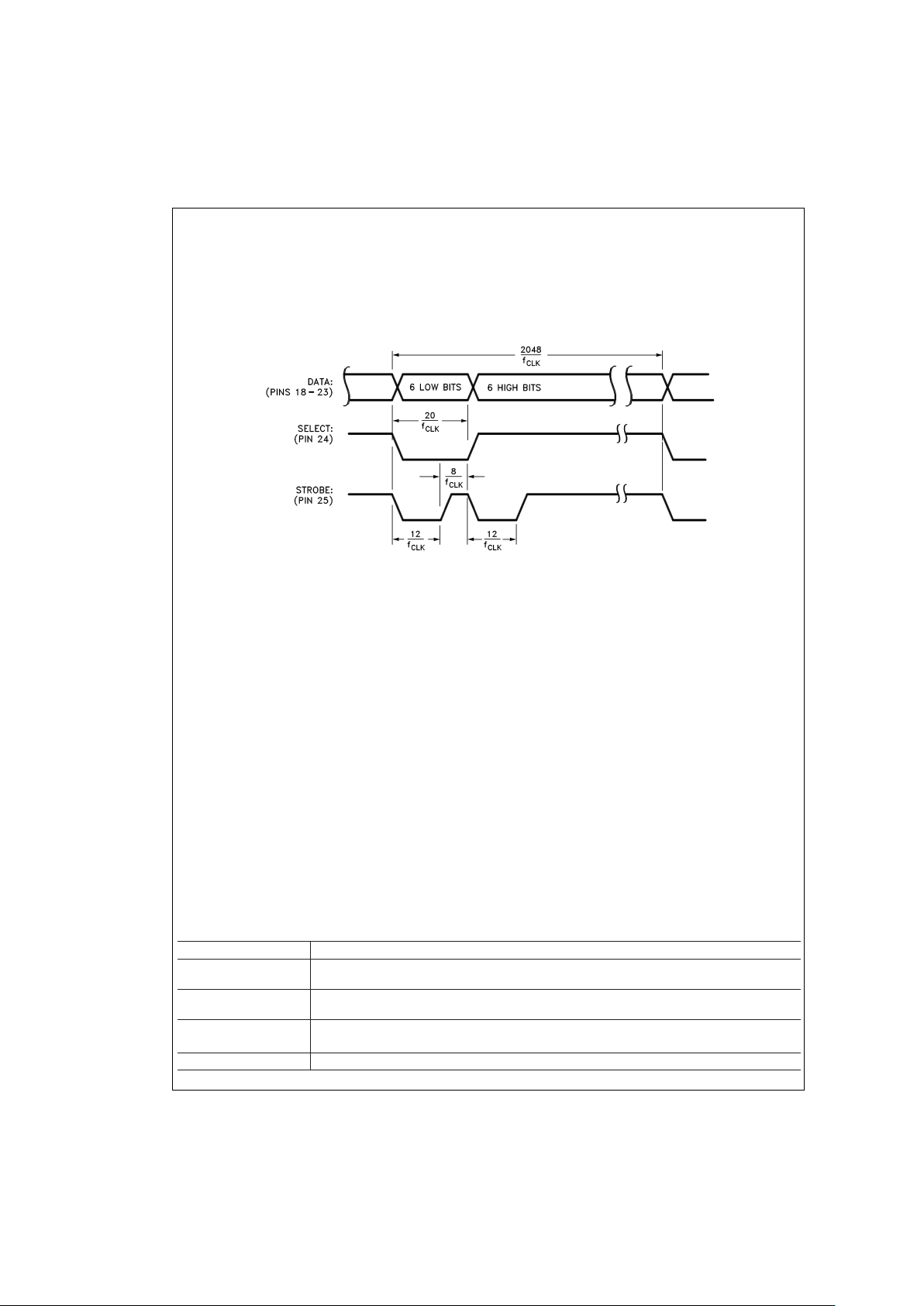
2. LM628 (12-bit output mode): Outputs two, multiplexed 6-bit words. The less-significant word is output first. The MSB is on Pin 18 and the LSB is on Pin 23. Pin 24 is used to demultiplex the words; Pin 24 is low for the less-significant word. The positive-going edge of the sig­nal on Pin 25 is used to strobe the output data.
Figure 8
shows the timing of the multiplexed signals.
3. LM629 (sign/magnitude outputs): Outputs a PWM sign signal on Pin 18 (11 for surface mount), and a PWM magnitude signal on Pin 19 (13 for surface mount). Pins 20 to 25 are not used in the LM629.
Figure 11
shows the
PWM output signal format.
Pin 26 (14), Clock (CLK) Input: Receives system clock. Pin 27 (15), Reset (RST) Input: Active-low, positive-edge
triggered, resets the LM628 to the internal conditions shown below. Note that the reset pulse must be logic low for a mini­mum of 8 clock periods. Reset does the following:
1. Filter coefficient and trajectory parameters are zeroed.
2. Sets position error threshold to maximum value (7FFF hex), and effectively executes command LPEI.
3. The SBPA/SBPR interrupt is masked (disabled).
4. The five other interrupts are unmasked (enabled).
5. Initializes current position to zero, or “home” position.
6. Sets derivative sampling interval to 2048/f
CLK
or 256 µs
for an 8.0 MHz clock.
7. DAC port outputs 800 hex to “zero” a 12-bit DAC and then reverts to 80 hex to “zero” an 8-bit DAC.
DS009219-9
FIGURE 7. Data Word Write Timing
LM628/LM629
www.national.com7
Page 8
Pinout Description (Continued)
Immediately after releasing the reset pin from the LM628, the status port should read “00”. If the reset is successfully completed, the status word will change to hex “84” or “C4” within 1.5 ms. If the status word has not changed from hex “00” to “84” or “C4” within 1.5 ms, perform another reset and repeat the above steps. To be certain that the reset was
properly performed, execute a RSTI command. If the chip has reset properly, the status byte will change from hex “84” or “C4” to hex “80” or “C0”. If this does not occur, perform an­other reset and repeat the above steps.
Pin 28 (16), Supply Voltage (V
DD
): Power supply voltage
(+5V).
Theory of Operation
INTRODUCTION
The typical system block diagram (See
Figure 1
) illustrates a servo system built using the LM628. The host processor communicates with the LM628 through an I/O port to facili­tate programming a trapezoidal velocity profile and a digital compensation filter. The DAC output interfaces to an exter­nal digital-to-analog converter to produce the signal that is power amplified and applied to the motor.An incremental en­coder provides feedback for closing the position servo loop. The trapezoidal velocity profile generator calculates the re­quired trajectory for either position or velocity mode of opera­tion. In operation, the LM628 subtracts the actual position (feedback position) from the desired position (profile genera­tor position), and the resulting position error is processed by the digital filter to drive the motor to the desired position.
Table1
provides a brief summary of specifications offered by
the LM628/LM629:
POSITION FEEDBACK INTERFACE
The LM628 interfaces to a motor via an incremental encoder. Three inputs are provided: two quadrature signal inputs, and an index pulse input. The quadrature signals are used to
keep track of the absolute position of the motor. Each time a logic transition occurs at one of the quadrature inputs, the LM628 internal position register is incremented or decre­mented accordingly. This provides four times the resolution over the number of lines provided by the encoder. See
Fig-
ure 9
. Each of the encoder signal inputs is synchronized with
the LM628 clock. The optional index pulse output provided by some encoders
assumes the logic-low state once per revolution. If the LM628 is so programmed by the user, it will record the abso­lute motor position in a dedicated register (the index register) at the time when all three encoder inputs are logic low.
If the encoder does not provide an index output, the LM628 index input can also be used to record the home position of the motor. In this case, typically,the motor will close a switch which is arranged to cause a logic-low level at the index in­put, and the LM628 will record motor position in the index register and alert (interrupt) the host processor. Permanently grounding the index input will cause the LM628 to malfunc­tion.
TABLE 1. System Specifications Summary
Position Range −1,073,741,824 to 1,073,741,823 counts Velocity Range 0 to 1,073,741,823/2
16
counts/sample; ie, 0 to 16,383 counts/sample, with a resolution of 1/2
16
counts/sample
Acceleration Range 0 to 1,073,741,823/2
16
counts/sample/sample; ie, 0 to 16,383 counts/sample/sample, with a
resolution of 1/2
16
counts/sample/sample
Motor Drive Output LM628: 8-bit parallel output to DAC, or 12-bit multiplexed output to DAC
LM629: 8-bit PWM sign/magnitude signals
Operating Modes Position and Velocity
DS009219-10
FIGURE 8. 12-Bit Multiplexed Output Timing
LM628/LM629
www.national.com 8
Page 9
Theory of Operation (Continued)
TABLE 1. System Specifications Summary (Continued)
Feedback Device Incremental Encoder (quadrature signals; support for index pulse) Control Algorithm Proportional Integral Derivative (PID) (plus programmable integration limit) Sample Intervals Derivative Term: Programmable from 2048/f
CLK
to (2048*256)/f
CLK
in steps of 2048/f
CLK
(256
to 65,536 µs for an 8.0 MHz clock). Proportional and Integral: 2048/f
CLK
VELOCITY PROFILE (TRAJECTORY) GENERATION
The trapezoidal velocity profile generator computes the de­sired position of the motor versus time. In the position mode of operation, the host processor specifies acceleration, maxi­mum velocity, and final position. The LM628 uses this infor­mation to affect the move by accelerating as specified until the maximum velocity is reached or until deceleration must begin to stop at the specified final position. The deceleration rate is equal to the acceleration rate. At any time during the move the maximum velocity and/or the target position may be changed, and the motor will accelerate or decelerate ac­cordingly.
Figure 10
illustrates two typical trapezoidal veloc-
ity profiles.
Figure 10
(a) shows a simple trapezoid, while
Fig-
ure 10
(b) is an example of what the trajectory looks like when velocity and position are changed at different times during the move.
When operating in the velocity mode, the motor accelerates to the specified velocity at the specified acceleration rate and maintains the specified velocity until commanded to stop. The velocity is maintained by advancing the desired position at a constant rate. If there are disturbances to the motion during velocity mode operation, the long-time average veloc­ity remains constant. If the motor is unable to maintain the specified velocity (which could be caused by a locked rotor, for example), the desired position will continue to be in­creased, resulting in a very large position error. If this condi-
DS009219-11
FIGURE 9. Quadrature Encoder Signals
DS009219-12
FIGURE 10. Typical Velocity Profiles
LM628/LM629
www.national.com9
Page 10
Theory of Operation (Continued)
tion goes undetected, and the impeding force on the motor is subsequently released, the motor could reach a very high velocity in order to catch up to the desired position (which is still advancing as specified). This condition is easily de­tected; see commands LPEI and LPES.
All trajectory parameters are 32-bit values. Position is a signed quantity. Acceleration and velocity are specified as 16-bit, positive-only integers having 16-bit fractions. The in­teger portion of velocity specifies how many counts per sam­pling interval the motor will traverse. The fractional portion designates an additional fractional count per sampling inter­val. Although the position resolution of the LM628 is limited to integer counts, the fractional counts provide increased av­erage velocity resolution. Acceleration is treated in the same manner. Each sampling interval the commanded accelera­tion value is added to the current desired velocity to generate a new desired velocity (unless the command velocity has been reached).
One determines the trajectory parameters for a desired move as follows. If, for example, one has a 500-line shaft en­coder,desires that the motor accelerate at one revolution per second per second until it is moving at 600 rpm, and then de­celerate to a stop at a position exactly 100 revolutions from the start, one would calculate the trajectory parameters as follows:
let P=target position (units=encoder counts) let R=encoder lines
*
4 (system resolution)
then R=500
*
4=2000
and P=2000
*
desired number of revolutions
P=2000
*
100 revs=200,000 counts (value to load)
P (coding)=00030D40 (hex code written to LM628) let V=velocity (units=counts/sample) let T=sample time (seconds)=341 µs (with 6 MHz
clock) let C=conversion factor=1 minute/60 seconds then V=R
*T*C*
desired rpm
and V=2000
*
341E−6*1/60*600 rpm V=6.82 counts/sample V (scaled)=6.82
*
65,536=446,955.52 V (rounded)=446,956 (value to load) V (coding)=0006D1EC (hex code written to LM628)
let A=acceleration (units=counts/sample/sample)
A=R
*T*T*
desired acceleration (rev/sec/sec)
then A=2000
*
341E−6*341E-6*1 rev/sec/sec
and A=2.33E−4 counts/sample/sample
A (scaled)=2.33E−4
*
65,536=15.24 A (rounded)=15 (value to load) A (coding)=0000000F (hex code written to LM628)
The above position, velocity, and acceleration values must be converted to binary codes to be loaded into the LM628. The values shown for velocity and acceleration must be mul­tiplied by 65,536 (as shown) to adjust for the required integer/fraction format of the input data. Note that after scal­ing the velocity and acceleration values, literal fractional data cannot be loaded; the data must be rounded and converted to binary. The factor of four increase in system resolution is due to the method used to decode the quadrature encoder signals, see
Figure 9
.
PID COMPENSATION FILTER
The LM628 uses a digital Proportional Integral Derivative (PID) filter to compensate the control loop. The motor is held at the desired position by applying a restoring force to the motor that is proportional to the position error, plus the inte­gral of the error, plus the derivative of the error.The following discrete-time equation illustrates the control performed by the LM628:
(1)
where u(n) is the motor control signal output at sample time
n, e(n) is the position error at sample time n, n' indi­cates sampling at the derivative sampling rate, and kp, ki, and kd are the discrete-time filter parameters loaded by the users.
The first term, the proportional term, provides a restoring force porportional to the position error, just as does a spring obeying Hooke’s law. The second term, the integration term, provides a restoring force that grows with time, and thus en­sures that the static position error is zero. If there is a con­stant torque loading, the motor will still be able to achieve zero position error.
The third term, the derivative term, provides a force propor­tional to the rate of change of position error. It acts just like viscous damping in a damped spring and mass system (like a shock absorber in an automobile). The sampling interval associated with the derivative term is user-selectable; this capability enables the LM628 to control a wider range of in­ertial loads (system mechanical time constants) by providing a better approximation of the continuous derivative. In gen­eral, longer sampling intervals are useful for low-velocity op­erations.
derivative
sam­pling interval, the previous error is subtracted from it (to form the derivative signal). All filter multiplications are 16-bit op­erations; only the bottom 16 bits of the product are used.
The integral signal is maintained to 24 bits, but only the top 16 bits are used. This scaling technique results in a more us­able (less sensitive) range of coefficient ki values. The 16 bits are right-shifted eight positions and multiplied by filter coefficient ki to form the term which contributes to the motor control output. The absolute magnitude of this product is compared to coefficient il, and the lesser, appropriately signed magnitude then contributes to the motor control sig­nal.
The derivative signal is multiplied by coefficient kd each
de-
rivative
sampling interval. This product contributes to the mo-
tor control output
every
sample interval, independent of the
user-chosen
derivative
sampling interval.
The kp, limited ki, and kd product terms are summed to form a 16-bit quantity.Depending on the output mode (wordsize), either the top 8 or top 12 bits become the motor control out­put signal.
LM628/LM629
www.national.com 10
Page 11
Theory of Operation (Continued)
LM628 READING AND WRITING OPERATIONS
The host processor writes commands to the LM628 via the host I/O port when Port Select (PS ) input (Pin 16) is logic low. The desired command code is applied to the parallel port line and the Write (WR ) input (Pin 15) is strobed. The command byte is latched into the LM628 on the rising edge of the WR input. When writing command bytes it is neces­sary to first read the status byte and check the state of a flag called the “busy bit” (Bit 0). If the busy bit is logic high, no command write may take place. The busy bit is never high longer than 100 µs, and typically falls within 15 µs to 25 µs.
The host processor reads the LM628 status byte in a similar manner: by strobing the Read (RD ) input (Pin 13) when PS (Pin 16) is low; status information remains valid as long as RD is low.
Writing and reading data to/from the LM628 (as opposed to writing commands and reading status) are done with PS (Pin
16) logic high. These writes and reads are always an integral number (from one to seven) of two-byte words, with the first byte of each word being the more significant. Each byte re­quires a write (WR ) or read (RD ) strobe. When transferring data words (byte-pairs), it is necessary to first read the status byte and check the state of the busy bit. When the busy bit is logic low, the user may then sequentially transfer both bytes comprising a data word, but the busy bit must again be checked and found to be low before attempting to transfer
the next byte pair (when transferring multiple words). Data transfers are accomplished via LM628-internal interrupts (which are not nested); the busy bit informs the host proces­sor when the LM628 may not be interrupted for data transfer (or a command byte). If a command is written when the busy bit is high, the command will be ignored.
The busy bit goes high immediately after writing a command byte, or reading or writing a second byte of data (See
Figure
5
thru
Figure 7
).
MOTOR OUTPUTS
The LM628 DAC output port can be configured to provide ei­ther a latched eight-bit parallel output or a multiplexed 12-bit output. The 8-bit output can be directly connected to a flow-through (non-input-latching) D/A converter; the 12-bit output can be easily demultiplexed using an external 6-bit latch and an input-latching 12-bit D/A converter. The DAC output data is offset-binary coded; the 8-bit code for zero is 80 hex and the 12-bit code for zero is 800 hex. Values less than these cause a negative torque to be applied to the mo­tor and, conversely, larger values cause positive motor torque. The LM628, when configured for 12-bit output, pro­vides signals which control the demultiplexing process. See for details.
The LM629 provides 8-bit, sign and magnitude PWM output signals for directly driving switch-mode motor-drive amplifi­ers.
Figure 11
shows the format of the PWM magnitude out-
put signal.
TABLE 2. LM628 User Command Set
Command Type Description Hex Data Note
Bytes
RESET Initialize Reset LM628 00 0 1 PORT8 Initialize Select 8-Bit Output 05 0 2 PORT12 Initialize Select 12-Bit Output 06 0 2 DFH Initialize Define Home 02 0 1 SIP Interrupt Set Index Position 03 0 1 LPEI Interrupt Interrupt on Error 1B 2 1 LPES Interrupt Stop on Error 1A 2 1 SBPA Interrupt Set Breakpoint, Absolute 20 4 1 SBPR Interrupt Set Breakpoint, Relative 21 4 1
DS009219-13
FIGURE 11. PWM Output Signal Format (Sign output (pin 18) not shown)
LM628/LM629
www.national.com11
Page 12
Theory of Operation (Continued)
TABLE 2. LM628 User Command Set (Continued)
Command Type Description Hex Data Note
Bytes
MSKI Interrupt Mask Interrupts 1C 2 1 RSTI Interrupt Reset Interrupts 1D 2 1 LFIL Filter Load Filter Parameters 1E 2 to 10 1 UDF Filter Update Filter 04 0 1 LTRJ Trajectory Load Trajectory 1F 2 to 14 1 STT Trajectory Start Motion 01 0 3 RDSTAT Report Read Status Byte None 1 1, 4 RDSIGS Report Read Signals Register 0C 2 1 RDIP Report Read Index Position 09 4 1 RDDP Report Read Desired Position 08 4 1 RDRP Report Read Real Position 0A 4 1 RDDV Report Read Desired Velocity 07 4 1 RDRV Report Read Real Velocity 0B 2 1 RDSUM Report Read Integration Sum 0D 2 1
Note 4: Commands may be executed “On the Fly” during motion. Note 5: Commands not applicable to execution during motion. Note 6: Command may be executed during motion if acceleration parameter was not changed. Note 7: Command needs no code because the command port status-byte read is totally supported by hardware.
User Command Set
GENERAL
The following paragraphs describe the user command set of the LM628. Some of the commands can be issued alone and some require a supporting data structure. As examples, the command STT (STarT motion) does not require additional data; command LFIL (Load FILter parameters) requires ad­ditional data (derivative-term sampling interval and/or filter parameters).
Commands are categorized by function: initialization, inter­rupt control, filter control, trajectory control, and data report­ing. The commands are listed in
Table2
and described in the following paragraphs. Along with each command name is its command-byte code, the number of accompanying data bytes that are to be written (or read), and a comment as to whether the command is executable during motion.
Initialization Commands
The following four LM628 user commands are used primarily to initialize the system for use.
RESET COMMAND: RESET the LM628
Command Code: 00 Hex Data Bytes: None Executable During Motion: Yes
This command (and the hardware reset input, Pin 27) results in setting the following data items to zero: filter coefficients and their input buffers, trajectory parameters and their input buffers, and the motor control output. A zero motor control output is a half-scale, offset-binary code: (80 hex for the 8-bit output mode; 800 hex for 12-bit mode). During reset, the DAC port outputs 800 hex to “zero” a 12-bit DAC and reverts to 80 hex to “zero” an 8-bit DAC. The command also clears five of the six interrupt masks (only the SBPA/SBPR interrupt
is masked), sets the output port size to 8 bits, and defines the current absolute position as home. Reset, which may be executed at any time, will be completed in less than 1.5 ms. Also see commands PORT8 and PORT12.
PORT8 COMMAND: Set Output PORT Size to 8 Bits
Command Code: 05 Hex Data Bytes: None Executable During Motion: Not Applicable
The default output port size of the LM628 is 8 bits; so the PORT8 command need not be executed when using an 8-bit DAC. This command must not be executed when using a 12-bit converter; it will result in erratic, unpredictable motor behavior. The 8-bit output port size is the required selection when using the LM629, the PWM-output version of the LM628.
PORT12 COMMAND: Set Output PORT Size to 12 Bits
Command Code: 06 Hex Data Bytes: None Executable During Motion: Not Applicable
When a 12-bit DAC is used, command PORT12 should be issued very early in the initialization process. Because use of this command is determined by system hardware, there is only one foreseen reason to execute it later: if the RESET command is issued (because an 8-bit output would then be selected as the default) command PORT12 should be imme­diately executed. This command must not be issued when using an 8-bit converter or the LM629, the PWM-output ver­sion of the LM628.
DFH COMMAND: DeFine Home
Command Code: 02 Hex Data Bytes: None Executable During Motion: Yes
LM628/LM629
www.national.com 12
Page 13
Initialization Commands (Continued)
This command declares the current position as “home”, or absolute position 0 (Zero). If DFH is executed during motion it will not affect the stopping position of the on-going move unless command STT is also executed.
Interrupt Control Commands
The following seven LM628 user commands are associated with conditions which can be used to interrupt the host com­puter. In order for any of the potential interrupt conditions to actually interrupt the host via Pin 17, the corresponding bit in the interrupt mask data associated with command MSKI must have been set to logic high (the non-masked state).
The identity of all interrupts is made known to the host via reading and parsing the status byte. Even if all interrupts are masked off via command MSKI, the state of each condition is still reflected in the status byte. This feature facilitates poll­ing the LM628 for status information, as opposed to interrupt driven operation.
SIP COMMAND: Set Index Position
Command Code: 03 Hex Data Bytes: None Executable During Motion: Yes
After this command is executed, the absolute position which corresponds to the occurrence of the next index pulse input will be recorded in the index register, and bit 3 of the status byte will be set to logic high. The position is recorded when both encoder-phase inputs and the index pulse input are logic low. This register can then be read by the user (see de­scription for command RDIP) to facilitate aligning the defini­tion of home position (see description of command DFH) with an index pulse. The user can also arrange to have the LM628 interrupt the host to signify that an index pulse has occurred. See the descriptions for commands MSKI and RSTI.
LPEI COMMAND: Load Position Error for Interrupt
Command Code: 1B Hex Data Bytes: Two Data Range: 0000 to 7FFF Hex Executable During Motion: Yes
An excessive position error (the output of the loop summing junction) can indicate a serious system problem; e.g., a stalled rotor. Instruction LPEI allows the user to input a threshold for position error detection. Error detection occurs when the absolute magnitude of the position error exceeds the threshold, which results in bit 5 of the status byte being set to logic high. If it is desired to also stop (turn off) the mo­tor upon detecting excessive position error, see command LPES, below. The first byte of threshold data written with command LPEI is the more significant. The user can have the LM628 interrupt the host to signify that an excessive po­sition error has occurred. See the descriptions for com­mands MSKI and RSTI.
LPES COMMAND: Load Position Error for Stopping
Command Code: 1A Hex Data Bytes: Two Data Range: 0000 to 7FFF Hex Executable During Motion: Yes
Instruction LPES is essentially the same as command LPEI above, but adds the feature of turning off the motor upon de­tecting excessive position error. The motor drive is not actu­ally switched off, it is set to half-scale, the offset-binary code for zero. As with command LPEI, bit 5 of the status byte is also set to logic high. The first byte of threshold data written with command LPES is the more significant. The user can have the LM628 interrupt the host to signify that an exces­sive position error has occurred. See the descriptions for commands MSKI and RSTI.
SBPA COMMAND:
Command Code: 20 Hex Data Bytes: Four Data Range: C0000000 to 3FFFFFFF Hex Executable During Motion: Yes
SBPR COMMAND:
Command Code: 21 Hex Data Bytes: Four Data Range: See Text Executable During Motion: Yes
MSKI COMMAND: MaSK Interrupts
Command Code: 1C Hex Data Bytes: Two Data Range: See Text Executable During Motion: Yes
The MSKI command lets the user determine which potential interrupt condition(s) will interrupt the host. Bits 1 through 6 of the status byte are indicators of the six conditions which are candidates for host interrupt(s). When interrupted, the host then reads the status byte to learn which condition(s) occurred. Note that the MSKI command is immediately fol­lowed by two data bytes. Bits 1 through 6 of the second (less significant) byte written determine the masked/unmasked status of each potential interrupt. Any zero(s) in this 6-bit field will mask the corresponding interrupt(s); any one(s) en­able the interrupt(s). Other bits comprising the two bytes have no effect. The mask controls only the host interrupt pro­cess; reading the status byte will still reflect the actual condi­tions independent of the mask byte. See
Table 3
.
LM628/LM629
www.national.com13
Page 14
Interrupt Control Commands
(Continued)
TABLE 3. Mask and Reset Bit Allocations for Interrupts
Bit Position Function
Bits 15 thru 7 Not Used Bit 6 Breakpoint Interrupt Bit 5 Position-Error Interrupt Bit 4 Wrap-Around Interrupt Bit 3 Index-Pulse Interrupt Bit 2 Trajectory-Complete Interrupt Bit 1 Command-Error Interrupt Bit 0 Not Used
RSTI COMMAND: ReSeT Interrupts
Command Code: 1D Hex Data Bytes: Two Data Range: See Text Executable During Motion: Yes
When one of the potential interrupt conditions of
Table3
oc­curs, command RSTI is used to reset the corresponding in­terrupt flag bit in the status byte. The host may reset one or all flag bits. Resetting them one at a time allows the host to service them one at a time according to a priority pro­grammed by the user. As in the MSKI command, bits 1 through 6 of the second (less significant) byte correspond to the potential interrupt conditions shown in
Table 3
. Also see description of RDSTAT command. Any zero(s) in this 6-bit field reset the corresponding interrupt(s). The remaining bits have no effect.
Filter Control Commands
The following two LM628 user commands are used for set­ting the derivative-term sampling interval, for adjusting the filter parameters as required to tune the system, and to con­trol the timing of these system changes.
LFIL COMMAND: Load FILter Parameters
Command Code: 1E Hex Data Bytes: Two to Ten Data Ranges…
Filter Control Word: See Text Filter Coefficients: 0000to 7FFF Hex (Pos Only) Integration Limit: 0000 to 7FFF Hex (Pos Only)
Executable During Motion: Yes
The filter parameters (coefficients) which are written to the LM628 to control loop compensation are: kp, ki, kd, and il (in­tegration limit). The integration limit (il) constrains the contri­bution of the integration term
tude of the integration term; when the magnitude of integra­tion term value exceeds il, the il value (with appropriate sign) is substituted for the integration term value.
The derivative-term sampling interval is also programmable via this command. After writing the command code, the first two data bytes that are written specify the derivative-term sampling interval and which of the four filter parameters is/ are to be written via any forthcoming data bytes. The first byte written is the more significant. Thus the two data bytes constitute a filter control word that informs the LM628 as to the nature and number of any following data bytes. See
Table 4
.
TABLE 4. Filter Control word Bit Allocation
Bit Position Function
Bit 15 Derivative Sampling Interval Bit 7 Bit 14 Derivative Sampling Interval Bit 6 Bit 13 Derivative Sampling Interval Bit 5 Bit 12 Derivative Sampling Interval Bit 4 Bit 11 Derivative Sampling Interval Bit 3 Bit 10 Derivative Sampling Interval Bit 2 Bit 9 Derivative Sampling Interval Bit 1 Bit 8 Derivative Sampling Interval Bit 0 Bit 7 Not Used Bit 6 Not Used Bit 5 Not Used Bit 4 Not Used Bit 3 Loading kp Data Bit 2 Loading ki Data Bit 1 Loading kd Data Bit 0 Loading il Data
Table 5
. The user must locally save and restore
these bits during successive writes of the filter control word. Bits 4 through 7 of the filter control word are not used. Bits 0 to 3 inform the LM628 as to whether any or all of the
The data bytes specified by and immediately following the fil­ter control word are written in pairs to comprise 16-bit words. The order of sending the data words to the LM628 corre­sponds to the descending order shown in the above descrip­tion of the filter control word; i.e., beginning with kp, then ki, kd and il. The first byte of each word is the more-significant byte. Prior to writing a word (byte pair) it is necessary to check the busy bit in the status byte for readiness. The re­quired data is written to the primary buffers of a double-buffered scheme by the above described operations; it is not transferred to the secondary (working) registers until the UDF command is executed. This fact can be used ad­vantageously; the user can input numerous data ahead of their actual use. This simple pipeline effect can relieve po­tential host computer data communications bottlenecks, and facilitates easier synchronization of multiple-axis controls.
UDF COMMAND: UpDate Filter
Command Code: 04 Hex Data Bytes: None
LM628/LM629
www.national.com 14
Page 15
Filter Control Commands (Continued)
Executable During Motion: Yes
The UDF command is used to update the filter parameters, the specifics of which have been programmed via the LFIL command. Any or all parameters (derivative-term sampling interval, kp, ki, kd, and/or il) may be changed by the appro­priate command(s), but command UDF must be executed to affect the change in filter tuning. Filter updating is synchro­nized with the calculations to eliminate erratic or spurious behavior.
Trajectory Control Commands
The following two LM628 user commands are used for set­ting the trajectory control parameters (position, velocity, ac­celeration), mode of operation (position or velocity), and di­rection (velocity mode only) as required to describe a desired motion or to select the mode of a manually directed stop, and to control the timing of these system changes.
LTRJ COMMAND: Load TRaJectory Parameters
Command Code: 1F Hex Data Bytes: Two to Fourteen Data Ranges…
Trajectory Control
Word: See Text Position: C0000000 to 3FFFFFFF Hex Velocity: 00000000 to 3FFFFFFF Hex
(Pos Only)
Acceleration: 00000000 to 3FFFFFFF Hex
(Pos Only)
Executable During
Motion: Conditionally, See Text
TABLE 5. Derivative-Term Sampling Interval Selection Codes
Bit Position Selected Derivative
15 14 13 12 11 10 9 8 Sampling Interval
00000000256µs 00000001512µs 00000010768µs 000000111024 µs, etc…
thru 1111111165,536 µs
Note 8: Sampling intervals shown are when using an 8.0 MHz clock. The 256 corresponds to 2048/8 MHz; sample intervals must be scaled for other clock frequen­cies.
The trajectory control parameters which are written to the LM628 to control motion are: acceleration, velocity, and po­sition. In addition, indications as to whether these three pa­rameters are to be considered as absolute or relative inputs, selection of velocity mode and direction, and manual stop­ping mode selection and execution are programmable via this command. After writing the command code, the first two data bytes that are written specify which parameter(s) is/are being changed. The first byte written is the more significant. Thus the two data bytes constitute a trajectory control word that informs the LM628 as to the nature and number of any following data bytes. See
Table 6
.
TABLE 6. Trajectory Control Word Bit Allocation
Bit Position Function
Bit 15 Not Used Bit 14 Not Used Bit 13 Not Used Bit 12 Forward Direction (Velocity Mode Only) Bit 11 Velocity Mode Bit 10 Stop Smoothly (Decelerate as
Programmed) Bit 9 Stop Abruptly (Maximum Deceleration) Bit 8 Turn Off Motor (Output Zero Drive) Bit 7 Not Used Bit 6 Not Used
Bit Position Function
Bit 5 Acceleration Will Be Loaded Bit 4 Acceleration Data Is Relative Bit 3 Velocity Will Be Loaded Bit 2 Velocity Data Is Relative Bit 1 Position Will Be Loaded Bit 0 Position Data Is Relative
Bit 12 determines the motor direction when in the velocity mode.A logic one indicates forward direction. This bit has no effect when in position mode.
Bit 11 determines whether the LM628 operates in velocity mode (Bit 11 logic one) or position mode (Bit 11 logic zero).
Bits 8 through 10 are used to select the method of
manually
stopping
the motor. These bits are
not
provided for one to
merely specify the desired
mode
of stopping, in position mode operations, normal stopping is always smooth and oc­curs automatically at the end of the specified trajectory. Un­der exceptional circumstances it may be desired to manually intervene with the trajectory generation process to affect a premature stop. In velocity mode operations, however, the normal means of stopping
is
via bits 8 through 10 (usually bit
10). Bit 8 is set to logic one to stop the motor by turning off motor drive output (outputting the appropriate offset-binary code to apply zero drive to the motor); bit 9 is set to one to stop the motor abruptly (at maximum available acceleration, by setting the target position equal to the current position); and bit 10 is set to one to stop the motor smoothly by using
LM628/LM629
www.national.com15
Page 16
Trajectory Control Commands
(Continued)
the current user-programmed acceleration value. Bits 8 through 10 are to be used
exclusively;
only one bit should be
a logic one at any time. Bits 0 through 5 inform the LM628 as to whether any or all of
the trajectory controlling parameters are about to be written, and whether the data should be interpreted as absolute or relative. The user may choose to update any or all (or none) of the trajectory parameters. Those chosen for updating are so indicated by logic one(s) in the corresponding bit posi­tion(s). Any parameter may be changed while the motor is in motion; however, if acceleration is changed then the next STT command must not be issued until the LM628 has com­pleted the current move or has been manually stopped.
The data bytes specified by and immediately following the trajectory control word are written in pairs which comprise 16-bit words. Each data item (parameter) requires two 16-bit words; the word and byte order is most-to-least significant. The order of sending the parameters to the LM628 corre­sponds to the descending order shown in the above descrip­tion of the trajectory control word; i.e., beginning with accel­eration, then velocity, and finally position.
Acceleration and velocity are 32 bits, positive only, but range only from 0 (00000000 hex) to [2
30
]−1 (3FFFFFFF hex). The bottom 16 bits of both acceleration and velocity are scaled as fractional data; therefore, the least-significant integer data bit for these parameters is bit 16 (where the bits are num­bered 0 through 31). Todetermine the coding for a given ve­locity, for example, one multiplies the desired velocity (in counts per sample interval) times 65,536 and converts the result to binary. The units of acceleration are counts per sample per sample. The value loaded for acceleration must not exceed the value loaded for velocity.Position is a signed, 32-bit integer, but ranges only from −[2
30
] (C0000000 hex) to
[2
30
]−1 (3FFFFFFF Hex).
The required data is written to the primary buffers of a double-buffered scheme by the above described operations; it is not transferred to the secondary (working) registers until the STT command is executed. This fact can be used advan­tageously; the user can input numerous data ahead of their actual use. This simple pipeline effect can relieve potential host computer data communications bottlenecks, and facili­tates easier synchronization of multiple-axis controls.
STT COMMAND: STarT Motion Control
Command Code: 01 Hex Data Bytes: None Executable During Motion: Yes, if acceleration has not
been changed
The STT command is used to execute the desired trajectory, the specifics of which have been programmed via the LTRJ command. Synchronization of multi-axis control (to within one sample interval) can be arranged by loading the re­quired trajectory parameters for each (and every) axis and then simultaneously issuing a single STT command to all axes. This command may be executed at any time, unless the acceleration value has been changed and a trajectory has not been completed or the motor has not been manually stopped. If STT is issued during motion and acceleration has been changed, a command error interrupt will be generated and the command will be ignored.
Data Reporting Commands
The following seven LM628 user commands are used to ob­tain data from various registers in the LM628. Status, posi­tion, and velocity information are reported. With the excep­tion of RDSTAT, the data is read from the LM628 data port after first writing the corresponding command to the com­mand port.
RDSTAT COMMAND: ReaD STATus Byte
Command Code: None Byte Read: One Data Range: See Text Executable During Motion: Yes
The RDSTATcommand is really not a command, but is listed with the other commands because it is used very frequently to control communications with the host computer. There is no identification code; it is directly supported by the hard­ware and may be executed at any time. The single-byte sta­tus read is selected by placing CS , PS and RD at logic zero. See
Table 7
.
TABLE 7. Status Byte Bit Allocation
Bit Position Function
Bit 7 Motor Off Bit 6 Breakpoint Reached [Interrupt] Bit 5 Excessive Position Error [Interrupt] Bit 4 Wraparound Occurred [Interrupt] Bit 3 Index Pulse Observed [Interrupt] Bit 2 Trajectory Complete [Interrupt] Bit 1 Command Error [Interrupt] Bit 0 Busy Bit
Bit 7, the motor-off flag, is set to logic one when the motor drive output is off (at the half-scale, offset-binary code for zero). The motor is turned off by any of the following condi­tions: power-up reset, command RESET, excessive position error (if command LPES had been executed), or when com­mand LTRJ is used to manually stop the motor via turning the motor off. Note that when bit 7 is set in conjunction with command LTRJ for producing a manual, motor-off stop, the actual setting of bit 7 does not occur until command STT is issued to affect the stop. Bit 7 is cleared by command STT, except as described in the previous sentence.
Bit 6, the breakpoint-reached interrupt flag, is set to logic one when the position breakpoint loaded via command SBPAor SBPR has been exceeded. The flag is functional indepen­dent of the host interrupt mask status. Bit 6 is cleared via command RSTI.
Bit 5, the excessive-position-error interrupt flag, is set to logic one when a position-error interrupt condition exists. This occurs when the error threshold loaded via command LPEI or LPES has been exceeded. The flag is functional in­dependent of the host interrupt mask status. Bit 5 is cleared via command RSTI.
Bit 4, the wraparound interrupt flag, is set to logic one when a numerical “wraparound” has occurred. To “wraparound” means to exceed the position address space of the LM628, which could occur during velocity mode operation. If a wrap­around has occurred, then position information will be in er­ror and this interrupt helps the user to ensure position data integrity.The flag is functional independent of the host inter­rupt mask status. Bit 4 is cleared via command RSTI.
LM628/LM629
www.national.com 16
Page 17
Data Reporting Commands (Continued)
Bit 3, the index-pulse acquired interrupt flag, is set to logic one when an index pulse has occurred (if command SIP had been executed) and indicates that the index position register has been updated. The flag is functional independent of the host interrupt mask status. Bit 3 is cleared by command RSTI.
Bit 2, the trajectory complete interrupt flag, is set to logic one when the trajectory programmed by the LTRJ command and initiated by the STT command has been completed. Be­cause of overshoot or a limiting condition (such as com­manding the velocity to be higher than the motor can achieve), the motor may not yet be at the final commanded position. This bit is the logical OR of bits 7 and 10 of the Sig­nals Register, see command RDSIGS below. The flag func­tions independently of the host interrupt mask status. Bit 2 is cleared via command RSTI.
Bit 1, the command-error interrupt flag, is set to logic one when the user attempts to read data when a write was ap­propriate (or vice versa). The flag is functional independent of the host interrupt mask status. Bit 1 is cleared via com­mand RSTI.
Bit 0, the busy flag, is frequently tested by the user (via the host computer program) to determine the busy/ready status prior to writing and reading any data. Such writes and reads may be executed only when bit 0 is logic zero (not busy). Any command or data writes when the busy bit is high will be ig­nored. Any data reads when the busy bit is high will read the current contents of the I/O port buffers, not the data ex­pected by the host. Such reads or writes (with the busy bit high) will not generate a command-error interrupt.
RDSIGS COMMAND: ReaD SIGnalS Register
Command Code: 0C Hex Bytes Read: Two Data Range: See Text Executable During Motion: Yes
The LM628 internal “signals” register may be read using this command. The first byte read is the more significant. The less significant byte of this register (with the exception of bit
0) duplicates the status byte. See
Table 8
.
TABLE 8. Signals Register Bit Allocation
Bit
Position
Function
Bit 15 Host Interrupt Bit 14 Acceleration Loaded (But Not Updated) Bit 13 UDF Executed (But Filter Not yet Updated) Bit 12 Forward Direction Bit 11 Velocity Mode Bit 10 On Target Bit 9 Turn Off upon Excessive Position Error Bit 8 Eight-Bit Output Mode Bit 7 Motor Off Bit 6 Breakpoint Reached [Interrupt] Bit 5 Excessive Position Error [Interrupt] Bit 4 Wraparound Occurred [Interrupt] Bit 3 Index Pulse Acquired [Interrupt] Bit 2 Trajectory Complete [Interrupt]
Bit
Position
Function
Bit 1 Command Error [Interrupt] Bit 0 Acquire Next Index (SIP Executed)
Bit 15, the host interrupt flag, is set to logic one when the host interrupt output (Pin 17) is logic one. Pin 17 is set to logic one when any of the six host interrupt conditions occur (if the corresponding interrupt has not been masked). Bit 15 (and Pin 17) are cleared via command RSTI.
Bit 13, the UDF-executed flag, is set to logic one when the UDF command is executed. Because bit 13 is cleared at the end of the sampling interval in which it has been set, this sig­nal is very short-lived and probably not very profitable for monitoring.
Bit 11, the velocity mode flag, is set to logic one to indicate that the user has selected (via command LTRJ) velocity mode. Bit 11 is cleared when position mode is selected (via command LTRJ). The actual setting and clearing of bit 11 does not occur until command STT is executed.
Bit 9, the turn-off on-error flag, is set to logic one when com­mand LPES is executed. Bit 9 is cleared by command LPEI.
Bit 8, the 8-bit output flag, is set to logic one when the LM628 is reset, or when command PORT8 is executed. Bit 8 is cleared by command PORT12.
Bits 0 through 7 replicate the status byte (see ), with the ex­ception of bit 0. Bit 0, the acquire next index flag, is set to logic one when command SIP is executed; it then remains set until the next index pulse occurs.
RDIP COMMAND: ReaD Index Position
Command Code: 09 Hex Bytes Read: Four Data Range: C0000000 to 3FFFFFFF Hex Executable During Motion: Yes
This command reads the position recorded in the index reg­ister. Reading the index register can be part of a system er­ror checking scheme. Whenever the SIP command is ex­ecuted, the new index position minus the old index position, divided by the incremental encoder resolution (encoder lines times four), should always be an integral number. The RDIP command facilitates acquiring these data for host-based cal­culations. The command can also be used to identify/verify home or some other special position. The bytes are read in most-to-least significant order.
RDDP COMMAND: ReaD Desired Position
Command Code: 08 Hex Bytes Read: Four Data Range: C0000000 to 3FFFFFFF Hex Executable During Motion: Yes
LM628/LM629
www.national.com17
Page 18
Data Reporting Commands (Continued)
This command reads the instantaneous desired (current
temporal
) position output of the profile generator. This is the “setpoint” input to the position-loop summing junction. The bytes are read in most-to-least significant order.
RDRP COMMAND: ReaD Real Position
Command Code: 0A Hex Bytes Read: Four Data Range: C0000000 to 3FFFFFFF Hex Executable During Motion: Yes
This command reads the current actual position of the motor. This is the feedback input to the loop summing junction. The bytes are read in most-to-least significant order.
RDDV COMMAND: ReaD Desired Velocity
Command Code: 07 Hex Bytes Read: Four Data Range: C0000001 to 3FFFFFFF Executable During Motion: Yes
This command reads the integer and fractional portions of the instantaneous desired (current
temporal
) velocity, as used to generate the desired position profile. The bytes are read in most-to-least significant order. The value read is properly scaled for numerical comparison with the user-supplied (commanded) velocity; however, because the two least-significant bytes represent
fractional
velocity, only the two most-significant bytes are appropriate for compari­son with the data obtained via command RDRV (see below). Also note that, although the velocity
input
data is constrained to positive numbers (see command LTRJ),the data returned by command RDDV represents a
signed
quantity where negative numbers represent operation in the reverse direc­tion.
RDRV COMMAND: ReaD Real Velocity
Command Code: 0B Hex Bytes Read: Two Data Range: C000 to 3FFF Hex, See Text Executable During Motion: Yes
This command reads the
integer
portion of the instanta­neous actual velocity of the motor. The internally maintained fractional portion of velocity is not reported because the re­ported data is derived by reading the incremental encoder, which produces only integer data. For comparison with the result obtained by executing command RDDV (or the user-supplied input value), the value returned by command RDRV must be multiplied by 2
16
(shifted left 16 bit positions). Also, as with command RDDV above, data returned by com­mand RDRV is a
signed
quantity,with negative values repre-
senting reverse-direction motion.
RDSUM COMMAND: ReaD Integration-Term SUMmation Value
Command Code: 0D Hex Bytes Read: Two Data Range: 00000 Hex to
±
the Current
Value of the Integration Limit
Executable During Motion: Yes
This command reads the value to which the integration term has accumulated. The ability to read this value may be help­ful in initially or adaptively tuning the system.
Typical Applications
Programming LM628 Host Handshaking (Interrupts)
A few words regarding the LM628 host handshaking will be helpful to the system programmer. As indicated in various portions of the above text, the LM628 handshakes with the host computer in two ways: via the host interrupt output (Pin
17), or via polling the status byte for “interrupt” conditions. When the hardwired interrupt is used, the status byte is also read and parsed to determine which of six possible condi­tions caused the interrupt.
When using the hardwired interrupt it is very important that the host interrupt service routine does not interfere with a command sequence which might have been in progress when the interrupt occurred. If the host interrupt service rou­tine were to issue a command to the LM628 while it is in the middle of an ongoing command sequence, the ongoing com­mand will be aborted (which could be detrimental to the ap­plication).
Typical Host Computer/Processor Interface
The LM628 is interfaced with the host computer/processor via an 8-bit parallel bus.
Figure 12
shows such an interface
and a minimum system configuration. As shown in
Figure 12
, the LM628 interfaces with the host data, address and control lines. The address lines are de­coded to generate the LM628 CS input; the host address LSB directly drives the LM628 PS input.
Figure 12
also shows an 8-bit DAC and an LM12 Power Op Amp interfaced to the LM628.
LM628 and High Performance Controller (HPC) Interface
Figure 13
shows the LM628 interfaced to a National HPC High Performance Controller.The delay and logic associated with the WR line is used to effectively increase the write-data hold time of the HPC (as seen at the LM628) by causing the WR pulse to rise early. Note that the HPC CK2 output pro­vides the clock for the LM628. The 74LS245 is used to de­crease the read-data hold time, which is necessary when in­terfacing to fast host busses.
Interfacing a 12-Bit DAC
Figure 14
illustrates use of a 12-bit DAC with the LM628. The 74LS378 hex gated-D flip-flop and an inverter demultiplex the 12-bit output. DAC offset must be adjusted to minimize DAC linearity and monotonicity errors. Twomethods exist for making this adjustment. If the DAC1210 has been socketed, remove it and temporarily connect a 15 kΩ resistor between Pins 11 and 13 of the DAC socket (Pins 2 and 6 of the LF356) and adjust the 25 kΩ potentiometer for 0V at Pin 6 of the LF356.
If the DAC is not removable, the second method of adjust­ment requires that the DAC1210 inputs be presented an all-zeros code. This can be arranged by commanding the ap-
LM628/LM629
www.national.com 18
Page 19
Typical Applications (Continued)
propriate move via the LM628, but with no feedback from the system encoder. When the all-zeros code is present, adjust the pot for 0V at Pin 6 of the LF356.
A Monolithic Linear Drive Using LM12 Power Op Amp
Figure 15
shows a motor-drive amplifier built using the LM12 Power Operational Amplifier. This circuit is very simple and can deliver up to 8A at 30V (using the LM12L/LM12CL). Re­sistors R1 and R2 should be chosen to set the gain to pro­vide maximum output voltage consistent with maximum input voltage. This example provides a gain of 2.2, which allows for amplifier output saturation at
±
22V with a±10V input, as-
suming power supply voltages of
±
30V. The amplifier gain should not be higher than necessary because the system is non-linear when saturated, and because gain should be con­trolled by the LM628. The LM12 can also be configured as a current driver, see 1987 Linear Databook, Vol. 1, p. 2–280.
Typical PWM Motor Drive Interfaces
Figure 16
shows an LM18298 dual full-bridge driver inter­faced to the LM629 PWM outputs to provide a switch-mode power amplifier for driving small brush/commutator motors.
Incremental Encoder Interface
The incremental (position feedback) encoder interface con­sists of three lines: Phase A (Pin 2), Phase B (Pin 3), and In­dex (Pin 1). The index pulse output is not available on some
encoders. The LM628 will work with both encoder types, but commands SIP and RDIP will not be meaningful without an index pulse (or alternative input for this input … be sure to tie Pin 1 high if not used).
Some consideration is merited relative to use in high Gaussian-noise environments. If noise is added to the en­coder inputs (either or both inputs) and is such that it is not sustained until the next encoder transition, the LM628 de­coder logic will reject it. Noise that mimics quadrature counts or persists through encoder transitions must be eliminated by appropriate EMI design.
Simple digital “filtering” schemes merely reduce susceptibil­ity to noise (there will always be noise pulses longer than the filter can eliminate). Further, any noise filtering scheme re­duces decoder bandwidth. In the LM628 it was decided (since simple filtering does not eliminate the noise problem) to not include a noise filter in favor of offering maximum pos­sible decoder bandwidth.Attempting to drive encoder signals too long a distance with simple TTL lines can also be a source of “noise” in the form of signal degradation (poor rise­time and/or ringing). This can also cause a system to lose positional integrity. Probably the most effective countermea­sure to noise induction can be had by using balanced-line drivers and receivers on the encoder inputs.
Figure 17
shows circuitry using the DS26LS31 and DS26LS32.
DS009219-14
Note:
FIGURE 12. Host Interface and Minimum System Configuration
LM628/LM629
www.national.com19
Page 20
Typical Applications (Continued)
DS009219-15
FIGURE 13. LM628 and HPC Interface
LM628/LM629
www.national.com 20
Page 21
Typical Applications (Continued)
DS009219-16
*
DAC offset must be adjusted to minimize DAC linearity and monotonicity errors. See text.
FIGURE 14. Interfacing a 12-Bit DAC and LM628
LM628/LM629
www.national.com21
Page 22
Typical Applications (Continued)
DS009219-17
FIGURE 15. Driving a Motor with the LM12 Power Op Amp
DS009219-18
FIGURE 16. PWM Drive for Brush/Commutator Motors
DS009219-20
FIGURE 17. Typical Balanced-Line Encoder Input Circuit
LM628/LM629
www.national.com 22
Page 23
Physical Dimensions inches (millimeters) unless otherwise noted
24-Lead Small Outline Package (M)
Order Number LM629M-6 or LM629M-8
NS Package Number M24B
28 Lead Molded Dual-In-Line Package (N)
Order Number LM628N-6, LM628N-8, LM629N-6 or LM629N-8
NS Package Number N28B
LM628/LM629
www.national.com23
Page 24
Notes
LIFE SUPPORT POLICY
NATIONAL’S PRODUCTS ARE NOT AUTHORIZED FOR USE AS CRITICAL COMPONENTS IN LIFE SUPPORT
DEVICES OR SYSTEMS WITHOUT THE EXPRESS WRITTEN APPROVAL OF THE PRESIDENT AND GENERAL
COUNSEL OF NATIONAL SEMICONDUCTOR CORPORATION. As used herein:
1. Life support devices or systems are devices or systems which, (a) are intended for surgical implant into the body, or (b) support or sustain life, and whose failure to perform when properly used in accordance with instructions for use provided in the labeling, can be reasonably expected to result in a significant injury to the user.
2. A critical component is any component of a life support device or system whose failure to perform can be reasonably expected to cause the failure of the life support device or system, or to affect its safety or effectiveness.
National Semiconductor Corporation
Americas Tel: 1-800-272-9959 Fax: 1-800-737-7018 Email: support@nsc.com
National Semiconductor Europe
Fax: +49 (0) 1 80-530 85 86
Email: europe.support@nsc.com Deutsch Tel: +49 (0) 1 80-530 85 85 English Tel: +49 (0) 1 80-532 78 32 Français Tel: +49 (0) 1 80-532 93 58 Italiano Tel: +49 (0) 1 80-534 16 80
National Semiconductor Asia Pacific Customer Response Group
Tel: 65-2544466 Fax: 65-2504466 Email: sea.support@nsc.com
National Semiconductor Japan Ltd.
Tel: 81-3-5639-7560 Fax: 81-3-5639-7507
www.national.com
LM628/LM629 Precision Motion Controller
National does not assume any responsibility for use of any circuitry described, no circuit patent licenses are implied and National reserves the right at any time without notice to change said circuitry and specifications.
Loading...
Buy Points How it Works FAQ Contact Us Questions and Suggestions Privacy Policy Cookie Policy Terms of Use