Datasheet CS8164 Datasheet (CHERRY Semiconductor)

1

Features

■ Two Regulated Outputs

Primary Output

8V ±5%; 750mA

Secondary Output

5V ±2%; 100mA

■ Low Dropout Voltage

■ ON/OFF Control

Option

■ Standby Quiescent Drain

(<2mA)

■ Protection Features

Reverse Battery
60V Peak Transient
Voltage

-50V Reverse Transient
Short Circuit

Thermal Shutdown

Package Options

5 Lead TO-220

Tab (Gnd)

1

CS8164

8V/5V Low Dropout Dual Regulator

with ENABLE

CS8164

Description

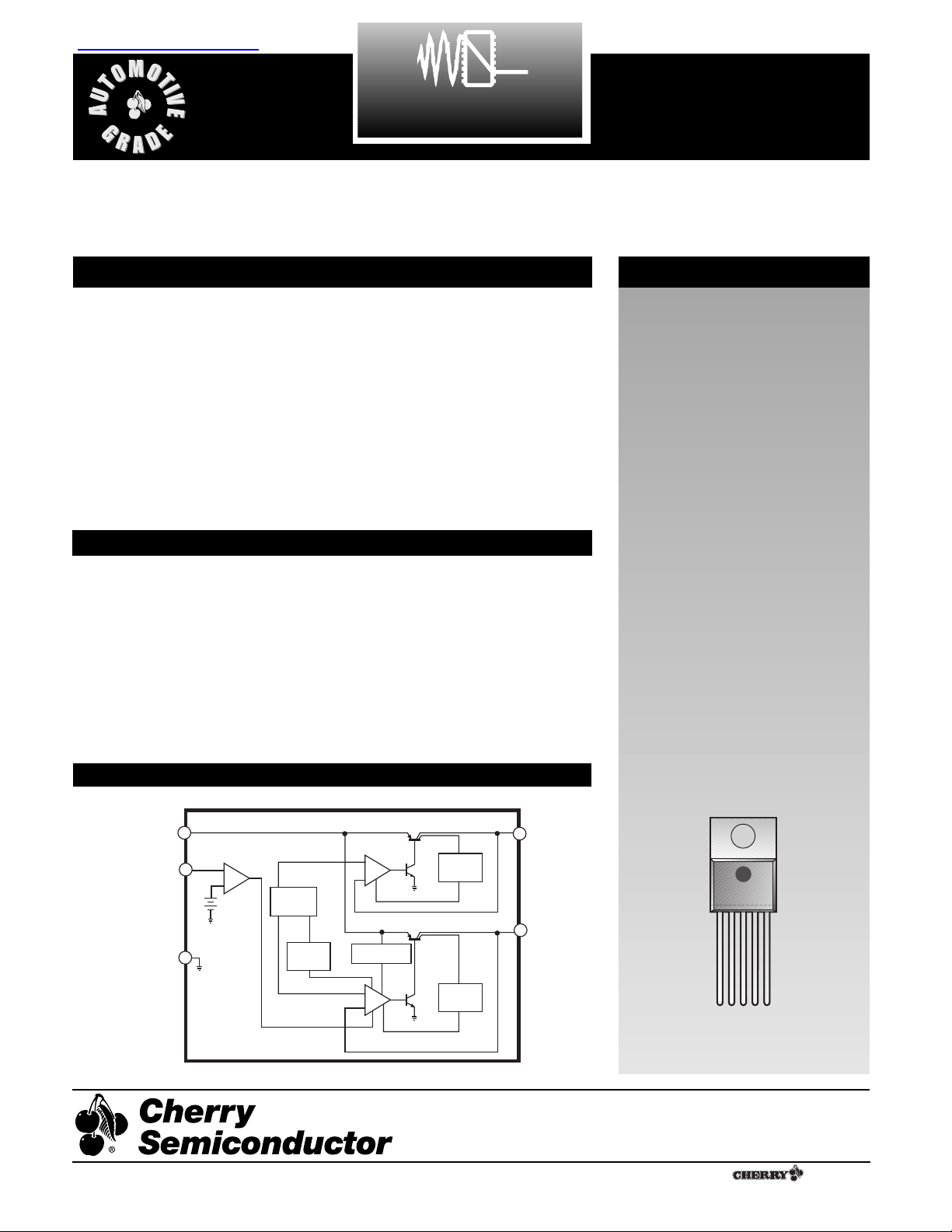
Block Diagram

Absolute Maximum Ratings

DC Input Voltage.............................................................................-0.5V to 26V

Transient Peak Voltage (46V Load Dump).................................................60V

Internal Power Dissipation..................................................Internally Limited

Operating Temperature Range................................................-40¡C to +125¡C

Junction Temperature Range...................................................-40¡C to +150¡C

Storage Temperature Range ....................................................-65¡C to +150¡C

Reverse Polarity V

OUT1

Input Voltage, DC ................................................-18V

Reverse Polarity Input Voltage, Transient ................................................-50V

Lead Temperature Soldering

Wave Solder (through hole styles only)..........10 sec. max, 260¡C peak

The CS8164 is a low dropout, dual
8V/5V linear regulator. The secondary
5V/100mA output is used for powering
systems with standby memory.
Quiescent current drain is less than
2mA when supplying 10mA loads from
the standby regulator.

In automotive applications, the CS8164
and all regulated circuits are protected
from reverse battery installations, as
well as high voltage transients. During
line transients, such as a 60V load
dump, the 750mA output will automat-

ically shutdown to protect both internal
circuits and the load, while the sec­ondary regulator continues to power
any standby load.

The on board ENABLE function con­trols the regulator's primary output.
When ENABLE is in the low state, the
regulator is placed in STANDBY mode
where it draws 2mA (typ) quiescent
current.

The CS8164 is packaged in a 5-lead
TO-220, with copper tab for connection
to a heat sink, if necessary.

1V

IN

2V

OUT1

3 Gnd
4 ENABLE
5V

OUT2

A Company

¨

Rev. 2/17/98

Cherry Semiconductor Corporation

2000 South County Trail, East Greenwich, RI 02818

Tel: [phone] Fax: [phone]

Email: [e-mail]

Web Site: www.cherry-semi.com

查询CS8164YT5供应商

V

ENABLE

Gnd

IN

+

­Bandgap

Reference

Thermal

Shutdown

Standby Output

+

-

Primary Output

Over Voltage

Shutdown

+

-

Output

Current

Limit

Output

Current

Limit

V

V

OUT2

OUT1

2

CS8164

PARAMETER TEST CONDITIONS MIN TYP MAX UNIT

Electrical Characteristics for V

OUT

: VIN= 14V, I

OUT

= 500mA, -40¡C ² TJ² +150ûC unless otherwise specified

Package Lead Description

PACKAGE LEAD # LEAD SYMBOL FUNCTION

5 Lead TO-220

1V

IN

Supply voltage, usually direct from battery.

2V

OUT1

Regulated output 8V, 750mA (typ).

3 Gnd Ground connection.

4 ENABLE CMOS compatible input lead; switches V

OUT1

on and off. When

ENABLE is high, V

OUT1

is active.

5V

OUT2

Standby output 5V, 100mA (typ); always on.

■ OUTPUT STAGE (V

OUT1

)

Output Voltage, V

OUT1

13V ² VIN² 26V, I

OUT1

² 500mA, 7.6 8.0 8.4 V

13V ² VIN² 16V, I

OUT1

² 750mA 7.6 8.0 8.4 V

Dropout Voltage I

OUT1

= 500mA 0.60 V

Line Regulation 13V ² VIN² 16V, I

OUT1

= 5mA 15 80 mV

Load Regulation 5mA ² I

OUT1

² 500mA 15 80 mV

Quiescent Current I

OUT1

² 10mA, No Load on Standby 3 7 mA

I

OUT1

= 500mA, No Load on Standby 40 100 mA

I

OUT1

= 750mA, No Load on Standby 90 mA
Ripple Rejection f = 120Hz 53 dB
Current Limit 0.75 1.40 2.50 A
Long Term Stability 50 mV/khr
Output Impedance 500mA DC and 10mA rms, 200 m½

100Hz - 10kHz
Thermal Shutdown 150 190 ¡C
Overvoltage Shutdown 26 40 V

■ Standby Output (V

OUT2

)

Output Voltage, (V

OUT2

) 6V ² VIN² 26V 4.75 5.00 5.25 V

Dropout Voltage I

OUT2

² 100mA 0.55 0.70 V
Line Regulation 6V ² VIN² 26V 4 50 mV
Load Regulation 1mA ² I

OUT2

² 100mA 10 50 mV

Quiescent Current I

OUT2

² 10mA, -40ûC ² TJ² +125ûC 2 3 mA

V

OUT1

OFF
Ripple Rejection f = 120Hz 66 dB
Current Limit 200 mA
Long Term Stability 20 mV/khr
Output Impedance 10mA DC and 1mA rms, 100Hz - 10kHz 1 ½

■ ENABLE Function (ENABLE)

Input ENABLE Threshold V

OUT1

Off 1.25 0.80 V

V

OUT1

On 2.00 1.25 V
Input ENABLE Current V

ENABLE²VTHRESHOLD

-10 10 µA

3

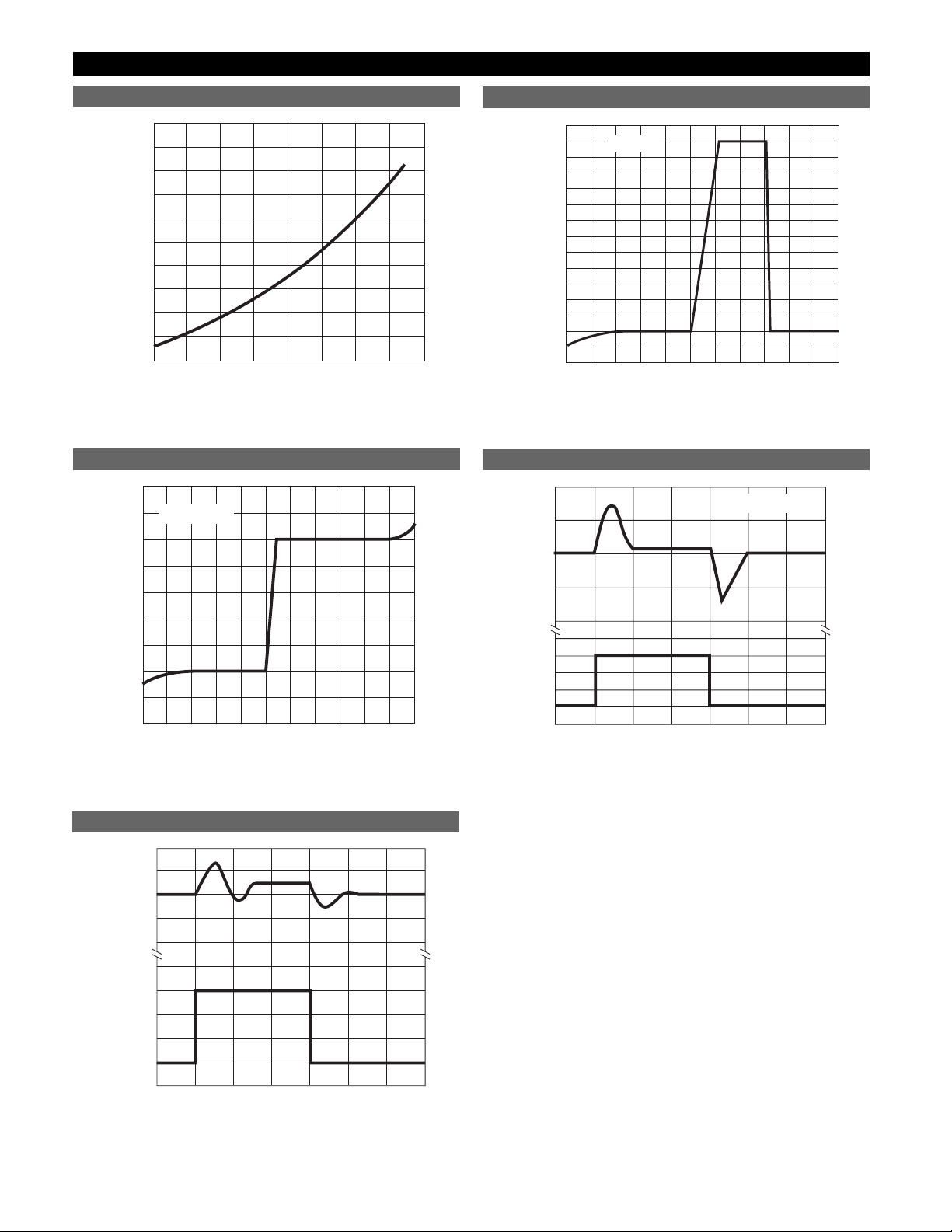
Typical Performance Characteristics

CS8164

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

INPUT-OUTPUT DIFFERENTIAL VOLTAGE (V)

OUTPUT CURRENT (mA)

0 200 400 600 800

Dropout Voltage vs. Output Current

7
6
5
4
3
2
1
0

-1

-2

INPUT VOLTAGE (V)

OUTPUT VOLTAGE (V)

8

9

10

11

12

13

-40 -20 0 20 40 60

RL=10W

Output Voltage vs. Input Voltage

7

6

5

4

3

2

1

0

-1

-2

INPUT VOLTAGE (V)

OUTPUT VOLTAGE (V)

-40 -20 0 20 40 60

RL= 500W

Standby Output Voltage vs. Input Voltage

20

10

0

-10

-20

3
2
1

0

TIME (ms)

INPUT VOLTAGE

CHANGE (V)

OUTPUT VOLTAGE

DEVIATION (mV)

I

OUT1

= 500mA

0 102030405060

Line Transient Response (V

OUT1

)

10

TIME (ms)

INPUT VOLTAGE

CHANGE (V)

OUTPUT VOLTAGE

DEVIATION (mV)

5

0

-5

-10

3

2

1

0

0 1020 3040 5060

Line Transient Response (V

OUT2

)

4

CS8164

Typical Performance Characteristics

OUTPUT CURRENT (mA)

QUIESCENT CURRENT (mA)

120

100

80

60

40

20

0

0

200 400 600 800

I

STBY

=10mA

Quiescent Current vs. Output Current

150

TIME (ms)

STANDBY LOAD

CURRENT (mA)

STANDBY

OUTPUT VOLTAGE

DEVIATION (mV)

100

50

0

-50

-100

-150

20

15

10

5

0

0 102030405060

Load Transient Response (V

OUT2

)

AMBIENT TEMPERATURE (°C)

POWER DISSIPATION (W)

20

18

16

14

12

10

8

6

4

2

0

0 10 20 30 40 50 60 70 80 90

INFINITE

HEAT SINK

10°C/W HEAT SINK

NO HEAT SINK

Maximum Power Dissipation (TO-220)

150

TIME (ms)

LOAD

CURRENT (A)

OUTPUT VOLTAGE

DEVIATION (mV)

100

50

0

-50

-100

-150

0.8

0.6

0.4

0.2

0

0 102030405060

Load Transient Response (V

OUT1

)

5

The CS8164 is equipped with two outputs. The second
output is intended for use in systems requiring standby
memory circuits. While the high current primary output
can be controlled with the ENABLE lead described below,
the standby output remains on under all conditions as long
as sufficient input voltage is applied to the IC. Thus, mem­ory and other circuits powered by this output remain unaf­fected by positive line transients, thermal shutdown, etc.

The standby regulator circuit is designed so that the quies­cent current to the IC is very low (<2mA) when the other
regulator output is off.

In applications where the standby output is not needed, it
may be disabled by connecting a resistor from the standby
output to the supply voltage. This eliminates the need for
a capacitor on the output to prevent unwanted oscilla­tions. The value of the resistor depends upon the mini­mum input voltage expected for a given system. Since the
standby output is shunted with an internal 6.0V Zener, the
current through the external resistor should be sufficient

Standby Output

CS8164

V

IN

ENABLE

V

OUT1

System

Condition

60V

3V

2.4V

8V

0V

Turn

On

Load

Dump

Low V

IN

Line Noise, Etc. V

OUT2

Short

Circuit

Thermal

Shutdown

Turn

Off

5V

0V

14V

5V

2.0V

0.8V

14V

26V

31V

8V 8V

2.4V

8V8V

5V

0V

V

OUT2

Typical Circuit Waveform

Dropout Voltage

The input-output voltage differential at which the circuit
ceases to regulate against further reduction in input volt­age. Measured when the output voltage has dropped
100mV from the nominal value obtained at 14V input,
dropout voltage is dependent upon load current and junc­tion temperature.

Input Voltage

The DC voltage applied to the input terminals with respect
to ground.

Input Output Differential

The voltage difference between the unregulated input
voltage and the regulated output voltage for which the
regulator will operate.

Line Regulation

The change in output voltage for a change in the input
voltage. The measurement is made under conditions of
low dissipation or by using pulse techniques such that the
average chip temperature is not significantly affected.

Load Regulation

The change in output voltage for a change in load current
at constant chip temperature.

Long Term Stability

Output voltage stability under accelerated life-test condi­tions after 1000 hours with maximum rated voltage and
junction temperature.

Output Noise Voltage

The rms AC voltage at the output, with constant load and
no input ripple, measured over a specified frequency
range.

Quiescent Current

The part of the positive input current that does not con­tribute to the positive load current. i.e., the regulator
ground lead current.

Ripple Rejection

The ratio of the peak-to-peak input ripple voltage to the
peak-to-peak output ripple voltage.

Temperature Stability of V

OUT

The percentage change in output voltage for a thermal
variation from room temperature to either temperature
extreme.

Current Limit

Peak current that can be delivered to the output.

Definition of Terms

Circuit Description

6

CS8164

to bias V

OUT2

up to this point. Approximately 60µA will
suffice, resulting in a 10k½ external resistor for most appli­cations.

Unlike the standby regulated output, which must remain
on whenever possible, the high current regulated output is
fault protected against overvoltage and also incorporates
thermal shutdown. If the input voltage rises above
approximately 30V (e.g., load dump), this output will
automatically shutdown. This protects the internal circuit­ry and enables the IC to survive higher voltage transients
than would otherwise be expected. Thermal shutdown is
effective against die overheating since the high current out­put is the dominant source of power dissipation in the IC.

The enable function controls V

OUT1

When ENABLE is high

(5V), V

OUT1

is on. When ENABLE is low, V

OUT1

is off.

ENABLE

High Current Output

Circuit Description: continued

Disabling V

OUT2

when it is not needed. C3 is no longer needed.

CS8164

C1*

0.1 mF

ENABLE

V

IN

V

OUT1

Gnd

C

3

**

10mF

+

+

10mF

C2**

V

OUT2

Test & Application Circuit

Application Notes

NOTES:

* C1 required if regulator is located far from power
supply filter.

** C

2

, C3required for stability.

The output or compensation capacitor helps determine
three main characteristics of a linear regulator: start-up
delay, load transient response and loop stability.

The capacitor value and type should be based on cost,
availability, size and temperature constraints. A tantalum
or aluminum electrolytic capacitor is best, since a film or
ceramic capacitor with almost zero ESR can cause instabil­ity. The aluminum electrolytic capacitor is the least expen­sive solution, but, if the circuit operates at low tempera­tures (-25¡C to -40¡C), both the value and ESR of the
capacitor will vary considerably. The capacitor manufac­turers data sheet usually provides this information.

The value for each output capacitor shown in the test and
applications circuit should work for most applications,
however it is not necessarily the optimized solution.

To determine acceptable values for C

2

and C3a particular
application, start with a tantalum capacitor of the recom­mended value and work towards a less expensive alterna­tive part for each output.

Step 1: Place the completed circuit with the tantalum
capacitors of the recommended values in an environmen­tal chamber at the lowest specified operating temperature
and monitor the outputs with an oscilloscope. A decade
box connected in series with the capacitor C2will simulate
the higher ESR of an aluminum capacitor. Leave the
decade box outside the chamber, the small resistance
added by the longer leads is negligible.

Step 2: With the input voltage at its maximum value,
increase the load current slowly from zero to full load on
the output under observation. look for oscillations on the
output. If no oscillations are observed, the capacitor is
large enough to ensure a stable design under steady state
conditions.

Stability Considerations

V

IN

R

D

10kW

V

OUT2

V

OUT2

+

C3

7

CS8164

Application Notes: continued

Step 3: Increase the ESR of the capacitor from zero using

the decade box and vary the load current until oscillations
appear. Record the values of load current and ESR that
cause the greatest oscillation. This represents the worst
case load conditions for the output at low temperature.

Step 4: Maintain the worst case load conditions set in step
3 and vary the input voltage until the oscillations increase.
This point represents the worst case input voltage condi­tions.

Step 5: If the capacitor is adequate, repeat steps 3 and 4
with the next smaller valued capacitor. A smaller capacitor
will usually cost less and occupy less board space. If the
output oscillates within the range of expected operating
conditions, repeat steps 3 and 4 with the next larger stan­dard capacitor value.

Step 6: Test the load transient response by switching in
various loads at several frequencies to simulate its real
working environment. Vary the ESR to reduce ringing.

Step 7: Remove the unit from the environmental chamber
and heat the IC with a heat gun. Vary the load current as
instructed in step 5 to test for any oscillations.

Once the minimum capacitor value with the maximum
ESR is found for each output, a safety factor should be
added to allow for the tolerance of the capacitor and any
variations in regulator performance. Most good quality
aluminum electrolytic capacitors have a tolerance of +/­20% so the minimum value found should be increased by
at least 50% to allow for this tolerance plus the variation
which will occur at low temperatures. The ESR of the
capacitors should be less than 50% of the maximum allow­able ESR found in step 3 above.

Repeat steps 1 through 7 with the capacitor on the other
output, C3.

The maximum power dissipation for a dual output regula­tor (Figure 1) is:

P

D(max)

= {V

IN(max)

- V

OUT1(min)}IOUT1(max)

+

{V

IN(max)

- V

OUT2(min)}IOUT2(max)+VIN(max)IQ

(1)

where:

V

IN(max)

is the maximum input voltage,

V

OUT1(min)

is the minimum output voltage from V

OUT1

,

V

OUT2(min)

is the minimum output voltage from V

OUT2

,

I

OUT1(max)

is the maximum output current for the applica-

tion,

I

OUT2(max)

is the maximum output current for the applica-

tion, and

IQis the quiescent current the regulator consumes at
I

OUT(max)

.

Figure 1: Dual output regulator with key performance parameters
labeled.

Once the value of P

D(max)

is known, the maximum permis-

sible value of R

QJA

can be calculated:

R

QJA

=

(2)

The value of R

QJA

can then be compared with those in the
package section of the data sheet. Those packages with
R

QJA

's less than the calculated value in equation 2 will keep

the die temperature below 150¡C.

In some cases, none of the packages will be sufficient to
dissipate the heat generated by the IC, and an external
heatsink will be required.

A heat sink effectively increases the surface area of the
package to improve the flow of heat away from the IC and
into the surrounding air.

Each material in the heat flow path between the IC and the
outside environment will have a thermal resistance. Like
series electrical resistances, these resistances are summed
to determine the value of R

QJA

:

R

QJA

= R

QJC

+ R

QCS

+ R

QSA

(3)

where:

R

QJC

= the junction-to-case thermal resistance,

R

QCS

= the case-to-heatsink thermal resistance, and

R

QSA

= the heatsink-to-ambient thermal resistance.

R

QJC

appears in the package section of the data sheet. Like

R

QJA

, it too is a function of package type. R

QCS

and R

QSA

are functions of the package type, heatsink and the inter­face between them. These values appear in heat sink data
sheets of heat sink manufacturers.

Heat Sinks

150¡C - T

A

P

D

Calculating Power Dissipation

in a Dual Output Linear Regulator

I

V

IN

IN

Smart

I

OUT1

Regulator

I

OUT2

Control
Features

}

I

Q

V

V

OUT1

OUT2

8

Part Number Description

CS8164YT5 5 Lead TO-220 Straight
CS8164YTVA5 5 Lead TO-220 Vertical
CS8164YTHA5 5 Lead TO-220 Horizontal

CS8164

Ordering Information

Rev. 2/17/98

Package Specification

Thermal Data 5 Lead TO-220

R

QJC

typ 2.0 ûC/W

R

QJA

typ 50 ûC/W

PACKAGE THERMAL DATA

PACKAGE DIMENSIONS IN mm (INCHES)

© 1999 Cherry Semiconductor Corporation

Cherry Semiconductor Corporation reserves the
right to make changes to the specifications without
notice. Please contact Cherry Semiconductor
Corporation for the latest available information.

5 Lead TO-220 (T) Straight

2.87 (.113)

2.62 (.103)

6.93(.273)

6.68(.263)

9.78 (.385)

10.54 (.415)

1.02(.040)

0.63(.025)

1.83(.072)

1.57(.062)

0.56 (.022)

0.36 (.014)

2.92 (.115)

2.29 (.090)

1.40 (.055)

1.14 (.045)

4.83 (.190)

4.06 (.160)

6.55 (.258)

5.94 (.234)

14.22 (.560)

13.72 (.540)

1.02 (.040)

0.76 (.030)

3.71 (.146)

3.96 (.156)

14.99 (.590)

14.22 (.560)

5 Lead TO-220 (TVA) Vertical

1.68
(.066) typ

1.70 (.067)

7.51 (.296)

1.78 (.070)

4.34 (.171)

0.56 (.022)

0.36 (.014)

1.40 (.055)

1.14 (.045)

4.83 (.190)

4.06 (.160)

14.99 (.590)

14.22 (.560)

2.92 (.115)

2.29 (.090)

.94 (.037)
.69 (.027)

8.64 (.340)

7.87 (.310)

6.80 (.268)

10.54 (.415)

9.78 (.385)

2.87 (.113)

2.62 (.103)

6.55 (.258)

5.94 (.234)

3.96 (.156)

3.71 (.146)

5 Lead TO-220 (THA) Horizontal

0.81(.032)

1.70 (.067)

6.81(.268)

1.40 (.055)

1.14 (.045)

5.84 (.230)

6.60 (.260)

6.83 (.269)

0.56 (.022)

0.36 (.014)

10.54 (.415)

9.78 (.385)

6.55 (.258)

5.94 (.234)

3.96 (.156)

3.71 (.146)

1.68

(.066)

TYP

14.99 (.590)

14.22 (.560)

2.77 (.109)

2.29 (.090)

2.92 (.115)

4.83 (.190)

4.06 (.160)

2.87 (.113)

2.62 (.103)