Datasheet AN-501 Datasheet (ANALOG DEVICES)

AN-501

()(

π

=

(

)

(

π

=

One Technology Way • P.O. Box 9106 • Norwood, MA 02062-9106, U.S.A. • Tel: [phone] • Fax: [phone] • www.analog.com

APPLICATION NOTE

Aperture Uncertainty and ADC System Performance

by Brad Brannon and Allen Barlow

APERTURE UNCERTAINTY

Aperture uncertainty is a key ADC concern when performing
IF sampling. The terms aperture jitter and aperture uncertainty
are synonymous and are frequently interchanged in the
literature. Aperture uncertainty is the sample-to-sample
variation in the encoding process. It has three distinct effects on
system performance. First, it can increase system noise. Second,
it can contribute to the uncertainty in the actual phase of the
sampled signal itself giving rise to increases in error vector
magnitude. Third, it can heighten intersymbol interference
(ISI). However, in typical communications applications, an
aperture uncertainty that is sufficiently small to meet system
noise constraints results in negligible impact on phase
uncertainty and ISI. For example, consider the case of sampling
an IF of 250 MHz. At that speed, even 1 ps of aperture jitter can
limit any ADC’s SNR to only 56 dB, while for the same
conditions, the phase uncertainty error is only 0.09 degrees rms
based on a 4 ns period. This is quite acceptable even for a
demanding specification such as GSM. The focus of this
analysis is, therefore, on overall noise contribution due to
aperture uncertainty.

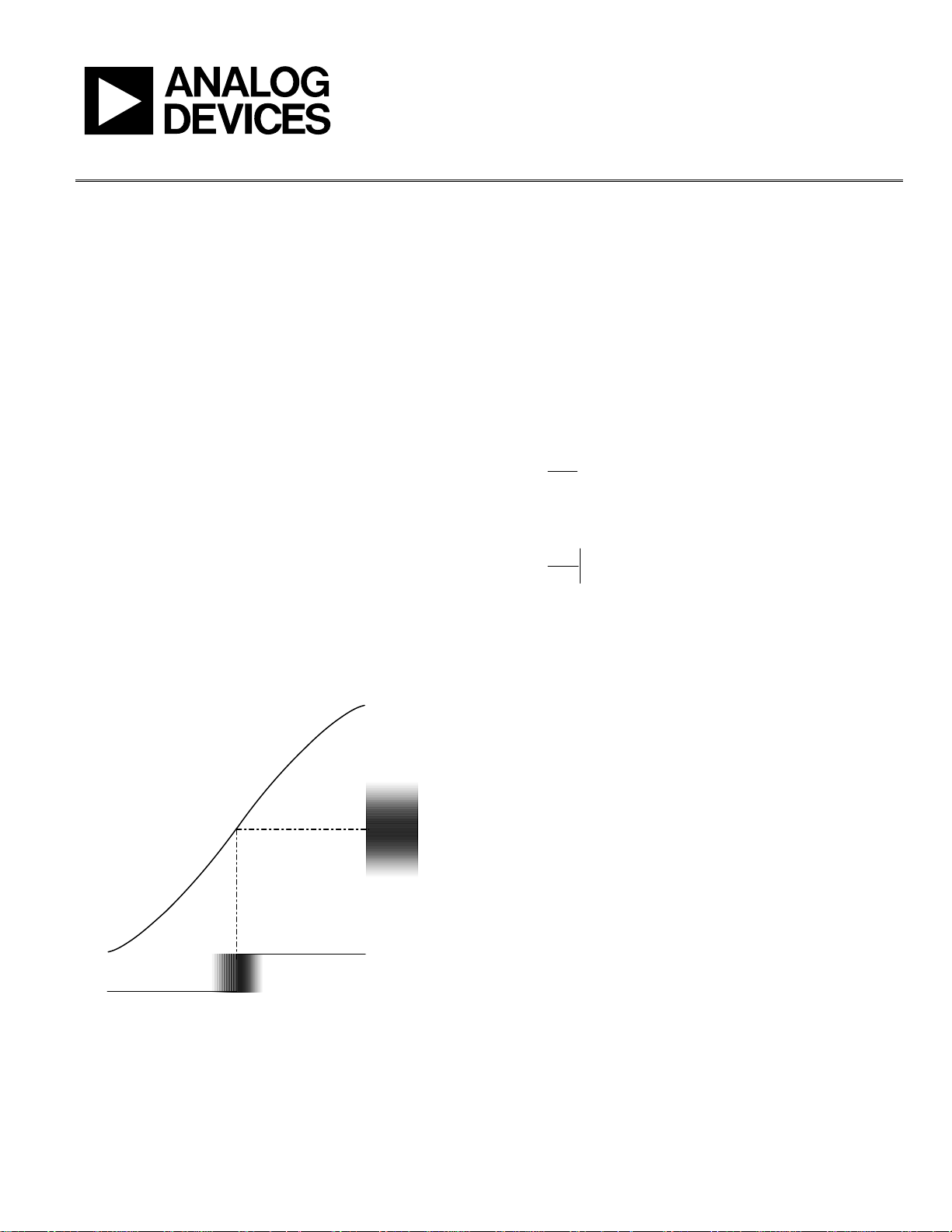
Figure 1 illustrates how an error in the sampling instant results
in an error in the sampled voltage. Mathematically, the
magnitude of the sampled voltage error is defined by the time
derivative of the signal function. Consider a sine wave input
signal

(1)

)

ftAtv

2sin

The derivative is

tdv

dt

The maximum error occurs when the cosine function equals 1,
that is, at t = 0.

)

dv

0

dt

max

We s e e fr o m
corresponding to the jitter dt. For conceptual clarity, if we
relabel dv as V
factors, we get

fA

π

2

=

Figure 1 that dv is the error in the sampled voltage

and dt as ta (aperture error) and rearrange the

err

(4)

ftAV

2

aerr

(2)

(

)

ftfA

ππ

2cos2=

(3)

ENCODE

dt

Figure 1. RMS Jitter vs. RMS Noise

ERROR VOLTAGE

dv

01399-001

Rev. A | Page 1 of 4

If t

is given as an rms value, the derived V

a

Although this is the error at maximum input slew and
represents an upper bound rather than a nominal, this simple
model proves surprisingly accurate and useful for estimating
the degradation in SNR as a function of sample clock jitter.

is also rms.

err

JITTER AND SNR

As Equation 4 indicates, the error in the sampled voltage
increases linearly with input frequency, so at high frequencies,
for example, in IF sampled receiver applications, clock purity
becomes extremely important. Sampling is a mixing operation:
the input signal is multiplied by a local oscillator or in this case,
a sampling clock. Because multiplication in time is convolution
in the frequency domain, the spectrum of the sample clock is
convolved with the spectrum of the input signal. Considering
that aperture uncertainty is wideband noise on the clock, it
shows up as wideband noise in the sampled spectrum, periodic
and repeated around the sample rate.

AN-501

W

A

Because ADC encode inputs have very high bandwidth, the
effects of clock input noise can extend out many times the
sample rate itself and alias back into the baseband of the
converter. Therefore, this wideband noise degrades the noise
floor performance of the ADC. Consider a sinusoidal input
signal of amplitude A. Utilizing Equation 4, the SNR for an
ADC limited by aperture uncertainty is

SNR

A

V

err

(5)

(

ft

π

2log20log20 −==

)

a

Equation 5 illustrates why systems that require high dynamic
range and high analog input frequencies also require a low jitter
encode source. For an analog input of 200 MHz and only
300 femtoseconds rms clock jitter, SNR is limited to only

68.5 dB, well below the level commonly achieved at lower
speeds by 12-bit converters. Note in Equation 5 that the jitter
limit of SNR is independent of the converter resolution. (For
the case just mentioned, a 14-bit converter would do no better.)

Aperture jitter is not always the performance limiter. Equation 6
shows its effect in superposition with other noise sources. The
first term in the brackets is the jitter from Equation 5. To that,
we must add terms for quantization noise, DNL, and thermal
noise. For other analytic purposes, each of these could be
broken out separately, but for simplicity in isolating the effect of
jitter, we combine them here in a single additional term.

2/1

2

⎡

2

()

tfSNR

2log20

π

⎢
⎢

⎣

+−=

a

⎤

1

ε

+

⎛
⎜

2

⎝

(6)

⎞
⎟

⎥

N

⎠

⎥

⎦

where:

f = analog input frequency.
t

= aperture uncertainty (jitter).

a

ε = “composite rms DNL” in LSBs, including thermal noise.

N = number of bits.

This simple equation provides considerable insight into the
noise performance of a data converter.

MEASURING SUBPICOSECOND JITTER

Aperture uncertainty is readily determined by examining SNR
without harmonics as a function of analog input frequency. Two
measurements are required for the calculation. The first
measurement is done at a sufficiently low analog input
frequency that the effects of aperture uncertainty are negligible.
Since jitter is negligible, Equation 6 can be simplified and
rearranged to solve for ε, the “composite DNL.”

−SNR

N

20

1102

−×=ε

(7)

Next, an FFT is done at high (IF) frequency. The high frequency
chosen should be as high as possible. Again, the SNR value
without harmonics is measured. This time jitter is a contributor
to noise and solving Equation 6 for t

2

SNR

−

10

⎞

20

⎟
⎟
⎠

π

2

ε

1

+

⎛

−

⎜

N

2

⎝

f

⎛
⎜
⎜
⎝

t

=

a

yields

a

2

⎞
⎟

⎠

(8)

where:

SNR = the high frequency SNR just measured

ε = the value determined in the low frequency measurement.

EXAMPLE: JITTER AND THE AD9246

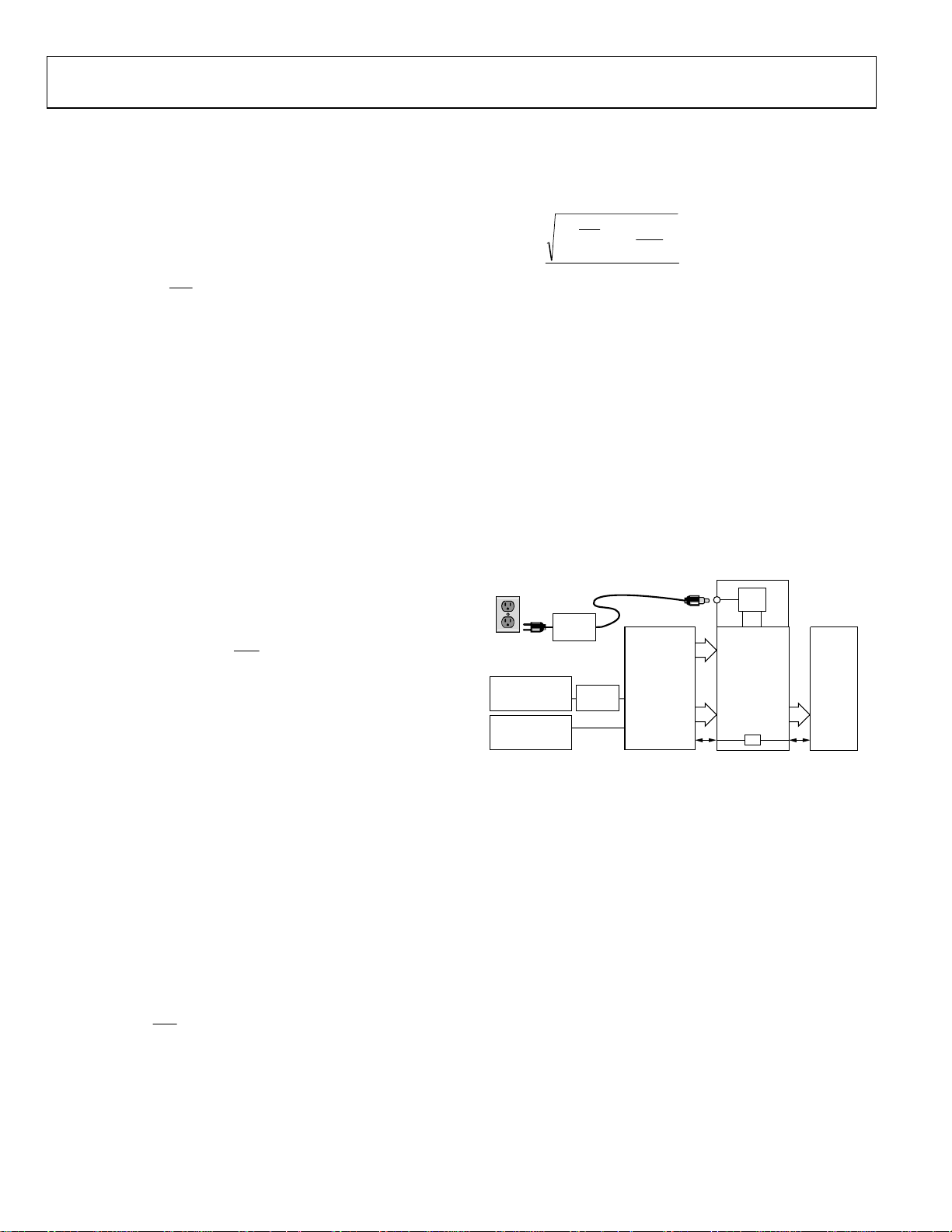
The example shown here utilizes the AD9246 evaluation board,
a 14-bit, 125 MSPS ADC. An external clock oscillator such as a
Wenzel Sprinter or Ultra-Low Noise provides a suitable encode
source. A mainstream RF synthesizer from Rohde & Schwarz or
Agilent can be used for the analog source. Typically, these
generators have insufficient phase noise performance for use as
the encode source. For more information about configuring
Analog Devices evaluation boards, please consult the individual
product data sheet.

LL OUTLET
100V TO 240V AC
47Hz TO 63Hz

6V DC

PARALLEL

BOARD

PARALLEL

CHB

CMOS

OUTPUTS

CHA

CMOS

OUTPUTS

2A MAX

ROHDE & SCHWARZ,

SMHU,
2V p-p SIGNAL
SYNTHESIZER

ROHDE & SCHWARZ,

SMHU,
2V p-p SIGNAL
SYNTHESIZER

SWITCHING

POWER
SUPPLY

BAND-PASS

FILTER

EVALUATION

XFMR
INPUT

CLK

Figure 2. Aperture Uncertainty Measurement Setup with AD9246 Customer

Evaluation Board

Figure 3 is a 5 average, 64 K FFT of the AD9246 sampling a 2.3
MHz sine wave at 125 MSPS. Analog Devices’ ADC Analyzer
Software (

www.analog.com/fifo) collects and processes the data

to report SNR without harmonics. From the plots, the SNR is

72.05 dBFS.

3.3V

–+

VCC

GND

HSC-ADC-EVALB-DC

FIFO DATA

CAPTURE

BOARD

USB

CONNECTION

SPI

PC

RUNNING

ADC

ANALYZER

SPISPI

TM

01399-002

Here, SNR is the low frequency value just measured.

Rev. A | Page 2 of 4

AN-501

Device: AD9246

Device No.: 1

Avcc: 1.8 Volts

Dvcc: 1.8 Volts

Encode: 125. MSPS

Analog: 2.3 MHz

SNR: 71.06 dB

SNRFS: 72.05 dBFS

UDSNR: 96.62 dB

NF: 30.69 dB

SINAD: 70.87 dB

Fund: –0.999 dBfs

2nd: –90.62 dBc

3rd: –86.59 dBc

4th: –104.15 dBc

5th: –108.51 dBc

6th: –94.04 dBc

WoSpur: –90.53 dBc +

THD: –84.55 dBc

SFDR: 86.59 dBc

Noise Floor: –117.21 dBFS

Samples: 65536

Windowing: None

Using this value for SNR in Equation 7 gives a “composite DNL
(ε)” for this converter of 3.09 LSB.

Next, the degradation in SNR as a function of analog input
frequency is found.
clock, but using an analog input frequency of 201 MHz. Here, the
noise floor has risen and the resulting SNR is 69.05 dBFS.

Device: AD9246

Device No.: 1

Avcc: 1.8 Volts

Dvcc: 1.8 Volts

Encode: 125. MSPS

Analog: 49.004 MHz

SNR: 67.98 dB

SNRFS: 69.05 dBFS

UDSNR: 93.4 dB

NF: 33.69 dB

SINAD: 66.75 dB

Fund: –1.069 dBfs

2nd: –78.21 dBc

3rd: –74.41 dBc

4th: –103.12 dBc

5th: –104.29 dBc

6th: –93.26 dBc

WoSpur: –90.65 dBc +

THD: –72.85 dBc

SFDR: 74.41 dBc

Noise Floor: –114.2 dBFS

Samples: 65536

Windowing: None

Using this SNR and the previous solution for ε, Equation 8 gives

t

a

This value, 197 fs, is the combined aperture uncertainty for the
AD9246 plus the clock oscillator. Since total noise squared is the
sum of the squares of individual contributors, the jitter of the
ADC itself is readily determined if the jitter of the source clock
is known. Here a Wenzel ULN clock oscillator with about 50 fs
jitter is used, giving a jitter for the ADC of about 190
simple measurements confirm that it is possible to measure very
small aperture uncertainty numbers using readily available
hardware and simple numeric calculations.

0

–10

–20

–30

–40

–50

–60

–70

–80

3

2

–90

–100

–110

–120

–130

010

6

4

5

5 1520253035404550 5560

+

FREQUENC Y (MHz)

Figure 3. 2.3 MHz FFT

Figure 4 shows data from the same setup and

01399-003

Figure 5 overlays plots of Equation 5 for various jitter values
(the sloped lines) with ideal, quantization noise limited
performance at various resolutions (the horizontal lines), and is
a useful guide for quickly determining jitter limits based on
analog input frequency and SNR requirements.

100

90

0

0

.

.2

80

2

p

s

SNR (dB)

70

60

50

10 100 1000

0

.5

1

p

p

s

s

INPUT (MHz)

1

2

5

5

p

p

s

s

Figure 5. Signal-to-Noise Ratio Due to Aperture Jitter

16 BITS

14 BITS

12 BITS

10 BITS

01399-005

CLOCK DISTRIBUTION

System clocks commonly must be distributed to multiple

0

–10

–20

–30

–40

–50

–60

–70

–80

–90

–100

5

–110

–120

–130

5 1520 2530354045505560

010

3

2

+

FREQUENC Y (MHz)

6

4

01399-004

Figure 4. 201 MHz FFT

2

−

05.69

⎛
⎜

10

⎜
⎝

=

⎞

+

20

⎛

⎟

−

⎜

⎟

⎝

⎠

π

102012

×

2

092.31

⎞
⎟

14

2

⎠

6

=

(9)

rmsfs197

. These

fs

converters, and additionally to the FPGAs, ASICs, and DSPs
included in the signal chain. There are several ways to distribute
clocks with the low jitter demanded by the converters.

If the sample clock is generated as a sinewave, it can be
distributed using power dividers and delivered to the ADC with
a transformer as shown in

Figure 6. This solution is simple and
works well for many applications, especially in situations
involving single-ended to differential conversion.

However, more often than not the clock is a logic signal sourced
directly from a PLL, VCO, or VCXO. In these cases, it is
advantageous to use logic gates to fan out the signal and to drive the
data converters.

Table 1 summarizes the typical jitter that can be
achieved with a variety of logic families. It should be noted that
many of the older families, and even current FPGAs, cannot deliver
acceptable performance. Some newer, high-speed devices do
provide acceptable jitter and have the ability to translate single­ended signals into differential signals as shown in

Figure 7.

Table 1.

Gate Type Jitter

1

FPGA

33 to 50 ps
74LS00 4.94 ps
74HCT00 2.20 ps
74ACT00 0.99 ps
MC100EL16 (PECL) 0.70 ps
AD9510 Clock Synthesis and Distribution 0.22 ps
NBSG16 (Reduced Swing ECL) 0.20 ps

1

Does not include the jitter introduced by input structure or internal routing

gates, or the jitter associated with the use of internal DLL/PLL structures.
Based on product data sheet peak-to-peak values ranging from ±100 ps to
±300 ps peak.

Rev. A | Page 3 of 4

AN-501

S

VSV

V

CLOCK
OURCE

0.1µF

ADT1–1WT

HSMS2812

DIODES

CLK+

AD9444

CLK–

1399-006

Figure 6. Distribution and Differential Encode Options

T

0.1µF

ECL/

PECL

VT

0.1µF

ENCODE

AD9444

ENCODE

01399-007

Figure 7. Active Differential Drive Circuit

Clock trees employing cascaded gates are commonly used in
digital circuits (see

Figure 8), but jitter accumulates as the clock

progresses down the tree.

ADC ENCODE INPUT

SYSTEM CLOCK

(A)

SYSTEM CLOCK

(B)

Figure 8. Clock Distribution Chains

ADC DATA LATCH

DAC CLOCK INPUT

DACDATALATCH

ADC ENCODE INPUT

In addition, the AD9510 includes many other features not
available in discrete logic such as selectable output types (LVDS,
PECL, and CMOS) and programmable fine delays.

Figure 10
shows how the AD9510 can be used in a typical low jitter
solution.

RSET

GND

DISTRIBUTION

REFIN

REFINB

SYNCB,

FUNCTION

CLK1

CLK1B

SCLK

SDIO

SDO

CSB

01399-008

RESETB

PDB

SERIAL

CONTROL

PORT

REF

R DIVIDER

N DIVIDER

PROGRAMM ABLE

AD9510

FREQUENCY

DETECTOR

DIVIDERS AND

PHASE ADJUST

/1, /2, /3... /31, /32

/1, /2, /3... /31, /32

/1, /2, /3... /31, /32

/1, /2, /3... /31, /32

/1, /2, /3... /31, /32

/1, /2, /3... /31, /32

/1, /2, /3... /31, /32

/1, /2, /3... /31, /32

PHASE

Figure 9. AD9510 Clock Synthesis and Distribution

CPRSET

CP

PLL
REF

CHARGE

PUMP

PLL

SETTINGS

LVPECL

LVPECL

LVPECL

LVPECL

LVDS /C MOS

LVDS /C MOS

ΔT

LVDS /C MOS

ΔT

LVDS /C MOS

CP

STATUS

CLK2

CLK2B

OUT0

OUT0B

OUT1

OUT1B

OUT2

OUT2B

OUT3

OUT3B

OUT4

OUT4B

OUT5

OUT5B

OUT6

OUT6B

OUT7

OUT7B

01399-009

In a cascade of just three NBSG16 gates (one of the better
performers), the cumulative rms jitter increases to 350 fs, which
is a significant impact on system performance of an IF sampling
system. It is better to avoid conventional clock trees altogether,
and instead, approach clock generation and distribution as a
system level function.

Devices such as the AD9510 have optimized the clock paths to
minimize total rms noise. By comparing

Figure 8 and Figure 9,
it is clear that the AD9510 offers the same function for clock
distribution as that in

Figure 8, but with an additive jitter of
only 220 fs. In addition, this part includes an ultra low noise
PLL similar to the ADF4106 that allows complete clock cleanup,
synthesis, and distribution in a single package.

©2006 Analog Devices, Inc. All rights reserved. Trademarks and
registered trademarks are the property of their respective owners.
AN01399-0-3/06(A)

Rev. A | Page 4 of 4

DSP

16

IF = ~190MHz

491.52MHz

LOOP FILTER

VCXO

IF = ~190MHz

IF = ~190MHz

32.768MHz

REFERENCE

92.16MHz

92.16MHz

92.16MHz

AD9510

92.16MHz

14

92.16MHz

14

Figure 10. Typical Clock Distribution Application

TXAD9786AD6633

MAIN TX

RXAD9246AD6636

MAIN RX

RXAD9246AD6636

DIVERSITY

RX

01399-010