Datasheet ALD500RAU-20SEI, ALD500RAU-20SE, ALD500RAU-20QEI, ALD500RAU-20QE, ALD500RAU-20PEI Datasheet (Advanced Linear Devices Inc)

ADVANCED
LINEAR
DEVICES, INC.

ALD500RAU/ALD500RA/ALD500R

PRECISION INTEGRATING ANALOG PROCESSOR

WITH PRECISION VOLTAGE REFERENCE

APPLICATIONS

• 4 1/2 digits to 5 1/2 digits plus sign measurements

• Precision analog signal processor

• Precision sensor interface

• High accuracy DC measurement functions

• Portable battery operated instruments

• Computer peripheral

• PCMCIA

FEATURES

• Resolution up to 18 bits plus sign bit and over-range bit

• Accuracy independent of input source impedances

• Accurate on-chip voltage reference

• Tempco as low as 10 ppm/°C guaranteed

• Chip select - power down mode

• High input impedance of 10

12

Ω

• Inherently filters and integrates any external noise spikes

• Differential analog input

• Wide bipolar analog input voltage range ±3.5V

• Automatic zero offset compensation

• Low linearity error - as low as 0.001% typical

• Fast zero-crossing comparator - 1µs

• Low power dissipation - 6mW typical

• Automatic internal polarity detection

• Low input current - 2pA typical

• Optional digital control from a microcontroller, an ASIC, or
a dedicated digital circuit

• Flexible conversion speed vs. resolution trade-off

BENEFITS

• Low cost, simple functionality

• Wide dynamic signal range

• Very high noise immunity

• Automatic compensation and cancellation
of error sources

• Easy to use to acquire bipolar signals

• Up to 19 bit (18 bit + sign bit) single conversion
or 21 bit (20 bit + sign bit) multiple conversion
and noise performance

• Inherently linear and stable with temperature
and component variations

PIN CONFIGURATION

ALD500R

I

1

B

C

2

INT

-

3

V

4

C

AZ

5

B

UF

6

AGND

-

7

C

REF

+

8

C

REF

9

N/C

10

N/C

QE, PE, SE PACKAGE

* N/C pin is connected internally. Connect to V

20

C

S

+

19

V
DGND

18
17

C

OUT

16

B

15

A

+

14

V

IN

-

V

13

IN

+

12

V

REF

-

11

V

REF

-

.

Ordering Information

Resolution Endpoint Voltage Reference Package Type Operating

16 bit 0.015% 0.5% 50ppm/C ALD500R-50PE ALD500R-50SE ALD500R-50QE 0°C to 70°C
17 bit 0.01% 0.3% 20ppm/C ALD500RA-20PE ALD500RA-20SE ALD500RA-20QE 0°C to 70°C
18 bit 0.005% ALD500RAU-20PE ALD500RAU-20SE ALD500RAU-20QE
17 bit 0.01% 0.2% 10ppm/C ALD500RA-10PE ALD500RA-10SE ALD500RA-10QE 0°C to 70°C
18 bit 0.005% ALD500RAU-10PE ALD500RAU-10SE ALD500RAU-10QE
17 bit 0.01% 0.3% 20ppm/C ALD500RA-20PEI ALD500RA-20SEI ALD500RA-20QEI -40°C to +85°C
18 bit 0.005% ALD500RAU-20PEI ALD500RAU-20SEI ALD500RAU-20QEI
18 bit 0.005% 0.3% 20ppm/C ALD500RAU-20DE -55°C to +125°C

Linearity Accuracy/Tempco Temperature

20L PDIP 20L SOIC 20L QSOP 20LCDIP

* Contact factory for customized voltage reference voltage levels, accuracy and tempco specifications.

Rev. 1.01 © 1999 Advanced Linear Devices, Inc., 415 Tasman Drive, Sunnyvale, California 94089-1706 Tel: [phone], Fax: [phone]

http://www.aldinc.com

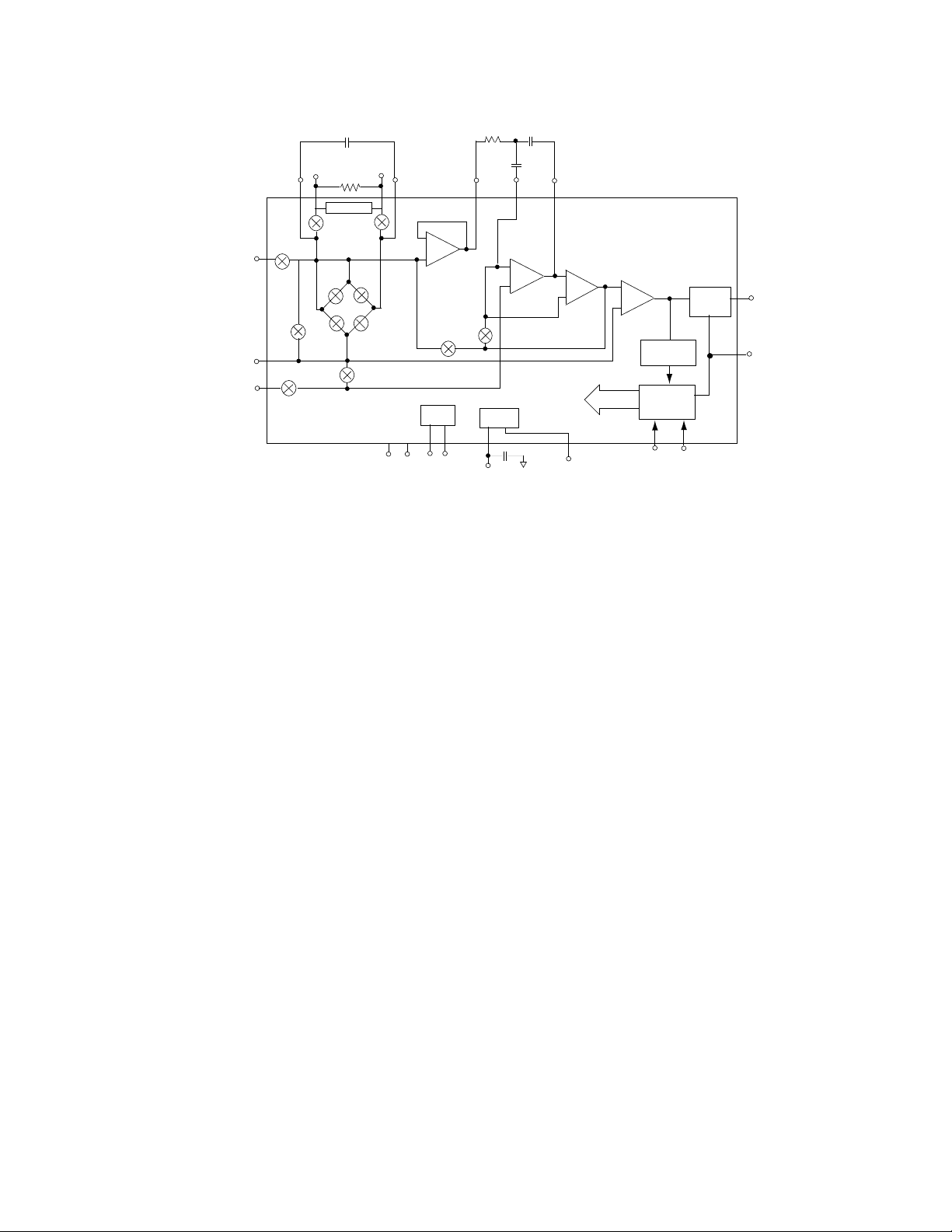
R

= 100KΩ

REF

CB = 0.1µF

+

V

(14)

AGND

(6)



V

(13)

FIGURE 1. ALD500R Functional Block Diagram

C

N/C

SW

BUF

R

INT

INT

C

AZ

(5)

Integrator

­+

AZ

Bias

C

B

I

B

(1)

C

INT

C

AZ

(2)

(4)

Comp1

Analog
Switch
Control
Signals

C
(20)

+

-

S

-

Comp2

+

Polarity
Detection


Phase
Decoding
Logic


A

B

(16)(15)

Control Logic

Level 
Shift

C

OUT

(17)

DGND

(18)

C

REF

-

R

REF

REF

INT

SWRSW

-

SW

R

+

R

V

REF

(11)

R

+

R

-

SW

R

SW

G

SS

(3) (19) (10) (9)

-

C

REF

(7)

-

Buffer

+

SW

S

REF

Control

N/CVDDV

+

V

REF

(12)

+

C

REF

(8)

SW

IN

IN

SW

SW

Az

SW

SW

IN

-

IN

GENERAL DESCRIPTION

The ALD500RAU/ALD500RA/ALD500R are integrating
dual slope analog processors, designed to operate on ±5V
power supplies for building precision analog-to-digital
converters. The ALD500RAU/ALD500RA/ALD500R
feature specifications suitable for 18 bit/17 bit/16 bit
resolution conversion, respectively. Together with three
capacitors, two resistors, and a digital controller, a precision
Analog to Digital converter with auto zero can be
implemented. The digital controller can be implemented
by an external microcontroller, under either hardware
(fixed logic) or software control. For ultra high resolution
applications, up to 23 bit conversion can be implemented
with an appropriate digital controller and software.

The ALD500R series of analog processors accept
differential inputs and the external digital controller first
counts the number of pulses at a fixed clock rate that a
capacitor requires to integrate against an unknown analog
input voltage, then counts the number of pulses required
to deintegrate the capacitor against a known internal
reference voltage. This unknown analog voltage can then
be converted by the microcontroller to a digital word, which
is translated into a high resolution number, representing
an accurate reading. This reading, when ratioed against
the reference voltage, yields an accurate, absolute voltage
measurement reading.

The ALD500R analog processors consist of on-chip digital
control circuitry to accept control inputs, integrating buffer
amplifiers, analog switches, and voltage comparators and
a highly accurate, ultra-stable voltage reference. It
functions in four operating modes, or phases, namely auto
zero, integrate, deintegrate, and integrator zero phases.
At the end of a conversion, the comparator output goes
from high to low when the integrator crosses zero during
deintegration. ALD500R analog processors also provide
direct logic interface to CMOS logic families.

GENERAL THEORY OF OPERATION
Dual-Slope Conversion Principles of Operation

The basic principle of dual-slope integrating analog to digital
converter is simple and straightforward. A capacitor, C
charged with the integrator from a starting voltage, V

INT

, for a

X

, is

fixed period of time at a rate determined by the value of an
unknown input voltage, which is the subject of measurement.
Then the capacitor is discharged at a fixed rate, based on an
external reference voltage, back to V

where the discharge

X

time, or deintegration time, is measured precisely. Both the
integration time and deintegration time are measured by a
digital counter controlled by a crystal oscillator. It can be
demonstrated that the unknown input voltage is determined
by the ratio of the deintegration time and integration time, and
is directly proportional to the magnitude of the external reference
voltage.

The major advantages of a dual-slope converter are:

a. Accuracy is not dependent on absolute values of

integration time t

and deintegration time t

INT

DINT

, but is
dependent on their relative ratios. Long-term clock frequency
variations will not affect the accuracy. A standard crystal
controlled clock running digital counters is adequate to generate
very high accuracies.

b. Accuracy is not dependent on the absolute values of

R

INT and CINT

, as long as the component values do not vary
through a conversion cycle, which typically lasts less than 1
second.

c. Offset voltage values of the analog components, such

as VX, are cancelled out and do not affect accuracy.

d. Accuracy of the system depends mainly on the accuracy

and the stability of the voltage reference value.

2 Advanced Linear Devices ALD500RAU/ALD500RA/ALD500R

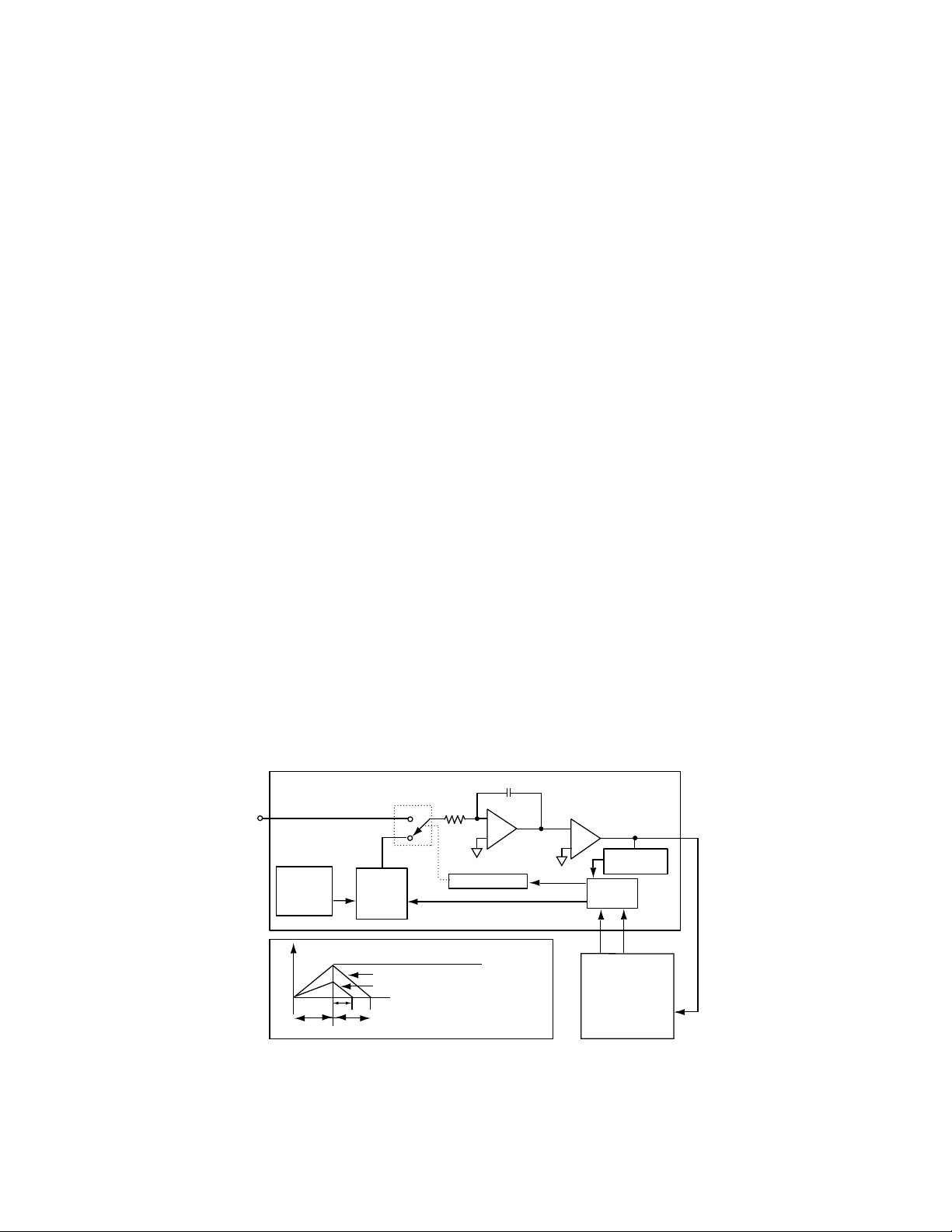
e. Very high resolution, high accuracy measurements

can be achieved simply and at very low cost.
An inherent benefit of the dual slope converter system is noise

immunity. The input noise spikes are integrated (averaged to
near zero) during the integration periods. Integrating ADCs
are immune to the large conversion errors that plague
successive approximation converters and other high resolution
converters and perform very well in high-noise environments.

The slow conversion speed of the integrating converter provides
inherent noise rejection with at least a 20dB/decade attenuation
rate. Interference signals with frequencies at integral multiples
of the integration period are, theoretically, completely removed.
Integrating converters often establish the integration period to
reject 50/60Hz line frequency interference signals.

The relationship of the integrate and deintegrate (charge
and discharge) of the integrating capacitor values are
shown below:

.

V

INT

= VX - (V

IN

t

/ R

. C

INT

INT

INT

)

(integrate cycle) (1)

.

= V

INT

- (V

V

X

REF

t

DINT

/ R

INT

.

C

)

INT

(deintegrate cycle) (2)

Combining equations 1 and 2 results in:

V

/ V

REF

= -t

IN

DINT

/ t

INT

(3)

V

= Reference Voltage

REF

C

= Integrating Capacitor value

INT

R

= Integrating Resistor value

INT

Actual data conversion is accomplished in two phases: Input
Signal Integration Phase and Reference Voltage Deintegration
Phase.

The integrator output is initialized to 0V prior to the start of
Input Signal Integration Phase. During Input Signal Integration

reference voltage is integrated

Phase, internal analog switches connect V

to the buffer

IN

input where it is maintained for a fixed integration time period
(t

). This fixed integration period is generally determined by

INT

a digital counter controlled by a crystal oscillator. The
application of V
a rate determined by V
polarity of V

causes the integrator output to depart 0V at

IN

.

IN

and a direction determined by the

IN

The Reference Voltage Deintegration Phase is initiated
immediately after t

, within 1 clock cycle. During

INT

ReferenceVoltage Deintegration Phase, internal analog
switches connect a reference voltage having a polarity opposite
that of V

to the integrator input. Simultaneously the same

IN

digital counter controlled by the same crystal oscillator used
above is used to start counting clock pulses. The Reference
Voltage Deintegration Phase is maintained until the comparator
output inside the dual slope analog processor changes state,
indicating the integrator has returned to 0V. At that point the
digital counter is stopped. The Deintegration time period

), as measured by the digital counter, is directly

(t

DINT

proportional to the magnitude of the applied input voltage.

where:

V

x

V

INT

V

IN

t

INT

t

DINT

= An offset voltage used as starting voltage
= Voltage change across C

during t

(equal in magnitude)

DINT

during t

INT

INT

and

= Average, or an integrated, value of input voltage

to be measured during t

(Constant VIN)

INT

= Fixed time period over which unknown voltage is

integrated

= Unknown time period over which a known

R

INT

ANALOG

INPUT

(V

)

IN

VOLTAGE

REFERENCE

OUTPUT

INTEGRATOR

t

INT

t

DINT

t

DINT

SWITCHES

S1

REF

V

IN ≈ VFULL SCALE

V

IN ≈ 1/2VFULL SCALE

V

≈

0

x



After the digital counter value has been read, the digital
counter, the integrator, and the auto zero capacitor are all
reset to zero through an Integrator Zero Phase and an Auto
Zero Phase so that the next conversion can begin again. In
practice, this process is usually automated so that analog-to­digital conversion is continuously updated. The digital control
is handled by a microprocessor or a dedicated logic controller.
The output, in the form of a binary serial word, is read by a
microprocessor or a display adapter when desired.

C

INT

INTEGRATOR

-

+

SWITCH DRIVER



POLARITY CONTROL

V

INT

= 4.1V MAX

V

INT

PHASE

CONTROL

COMPARATOR

-

+

POLARITY

DETECTION



CONTROL

LOGIC

AB

MICROCONTROLLER

(CONTROL LOGIC

+ COUNTER)

C

OUT

Figure 2. Basic Dual-Slope Converter

ALD500RAU/ALD500RA/ALD500R Advanced Linear Devices 3

ABSOLUTE MAXIMUM RATINGS

Supply voltage, V
Differential input voltage range -0.3V to V+ +0.3V
Power dissipation 600 mW
Operating temperature range PE, SE package 0°C to +70°C
Operating temperature range QE package -55°C to +125°C
Storage temperature range -65°C to +150°C
Lead temperature, 10 seconds +260°C

+

13.2V

OPERATING ELECTRICAL CHARACTERISTICS
T

= 25°C V

A

+

= +5V V- = -5V (V supply ± 5V) unless otherwise specified; CAZ = C

REF

= 0.47µf

500RAU 500RA 500R

Parameter Symbol Min Typ Max Min Typ Max Min Typ Max Unit Test Conditions

Resolution 15 30 60 µV Notes 1, 7

Zero-Scale Z
Error 0.003 0.005 0.008 %

End Point E
Linearity 0.007 0.015 0.020 0°C to +70°C

Best Case N
Straight Line

SE

NL

L

0.0025 0.003 0.005 % 0°C to 70°C

0.001 0.005 0.003 0.010 0.005 0.015 % Notes 1, 2

0.0025 0.003 0.005 0.003 0.008 % Notes 1, 2

Linearity 0.004 0.008 0.015 0°C to +70°C

Zero-Scale TC
Temperature

ZS

0.3 0.6 0.3 0.7 0.3 0.7 µV/°C0°C to +70°C

Coefficient 0.15 0.3 0.15 0.35 0.15 0.35 ppm/°C Notes 1, 7

Full-Scale S
Symmetry Error

YE

0.005 0.008 0.01 % 0°C to 70°C

(Rollover Error) 0.008 0.010 0.012 %

Full-Scale TC
Temperature Note 7

FS

1.3 1.3 1.3 ppm/°C0°C to +70°C

Coefficient

Input I
Current

IN

222pAV

= 0V

IN

Common-Mode CMVR V
Voltage Range

Integrator V
Output Swing

INT

Analog Input VINV
Signal Range

Voltage V
Reference

REF

+1.5

SS

V

+0.9

SS

+1.5

SS

V

+1

SS

V

-1.5 VSS+1.5

DD

V

-0.9 VSS+0.9

DD

V

-1.5 VSS+1.5

DD

VDD-1 V

+1 V

SS

V

V

-1.5

-0.9

-1.5

+1.5

SS

V

+0.9

SS

V

+1.5

SS

V

-1

+ 1

SS

DD

V

DD

V

DD

DD

V

DD

V

DD

V

DD

V

V

-1.5

V

-0.9

V AGND = 0V

-1.5

V

-1

DD

Range

4 Advanced Linear Devices ALD500RAU/ALD500RA/ALD500R

DC & AC ELECTRICAL CHARACTERISTICS

= 25°C V supply = ±5.0V unless otherwise specified; CAZ = C

T

A

500RAU 500RA 500R

Parameter Symbol Min Typ Max Min Typ Max Min Typ Max Unit Test Conditions

Supply Current I

Power Dissipation P

Positive Supply Range V

S

D

4.5 5.5 4.5 5.5 4.5 5.5 V Note 4

+S

0.6 1.0 0.6 1.0 0.6 1.0 mA V+ = 5V , A =1,B=1

10 10 10 mW V supply= ±5V

REF

= 0.47µf

Negative Supply Range V

Comparator Logic 1, V
Output High

Comparator Logic 0, V
Output Low

Logic 1, Input High V
Voltage

Logic 0, Input Low V
Voltage

Logic Input Current I

Comparator Delay t

1.8432 MHz Clock

A INPUT

B INPUT

C

C

START
CONVERSION
CYCLE

OUT

OUT

Positive Input Signal

Negative Input Signal

-4.5 -5.5 -4.5 -5.5 -4.5 -5.5 V Note 4

-S

OH

44 4VI

OL

3.5 3.5 3.5 V

IH

IL

L

0.01 0.01 0.01 µA

D

Figure 3. ALD500R TIMING DIAGRAM

~

66.667 msec.

~

~

~

NOT VALID

NOT VALID

Auto Zero

Phase

Clock data in

as needed.

0.5416 µs

START DEINTEGRATION CYCLE

123,093
Clock Pulses

~

~

or clock data out

of counters within the

the microcontroller

or fixed logic controller,

START INTEGRATION CYCLE

SOURCE

0.4 0.4 0.4 V I

SINK

111V

111µsec Note 5

1 Conversion Cycle

123,093
Clock Pulses

~

~

66.667 msec.

~

~

Input Signal

Integration

Phase

~

~

Reference

Voltage

Deintegration

~

~

~

~

~

~

Integrator Zero

Phase

Auto Zero

Phase

Phase

Fixed number

of clock pulses

by design.

Variable

number of

clock pulses.

At VIN MAX,
max. number of
clock pulses

~

= 246,185

Fixed period of

approx.1 msec.

Stop counter upon
detection of comparator
output going from high
to low state.

START INTEGRATOR ZERO CYCLE

REPEAT
CONVERSION
CYCLE

= 400µA

= 1.1mA

ALD500RAU/ALD500RA/ALD500R Advanced Linear Devices 5

DC ELECTRICAL CHARACTERISTICS

= 25°C V supply = +5.0V unless otherwise specified; CAZ = C

T

A

Parameter Symbol 500RAU-10 500RAU-20 500RAU-50 Unit Test Conditions

500RA-10 500RA-20 500RA-50

Min Typ Max Min Typ Max Min Typ Max

Voltage Reference V

Supply Voltage V
Rejection Ratio

R

RSR

0.998 1.000 1.002 0.997 1.000 1.003 0.995 1.000 1.005 V

95 95 95 dB

REF

= 0.47µf, R

500R-50

= 100KΩ (1% metal film)

REF

Temperature V
Coefficient

Long Term Drift ∆V

Warm Up Time 10 10 10 min. Note 7

Positive Supply V+ 4.5 5.5 4.5 5.5 4.5 5.5 V
Operating Voltage Range

Negative Supply V- -5.5 -4.5 -5.5 -4.5 -5.5 -4.5 V
Operating Voltage Range

Power Down Supply I
Current

NOTES:

1. Integrate time ≥ 66 msec., Auto Zero time ≥ 66 msec., V
Resolution = V

2. End point linearity at ±1/4, ±1/2, ±3/4 Full Scale after Full Scale adjustment.

3. Rollover Error also depends on C

4. Contact factory for other power supply operating voltage ranges, including Vsupply = ±3V or Vsupply = ±2.5V.

5. Recommended selection of clock periods of one of the following:
t clk = 0.27µsec, 0.54µsec, or 1.09µsec
which corresponds to clock frequencies of 3.6864 MHz, 1.8432 MHz, 0.9216 MHz respectively.

6. R

REF

7. Sample tested parameter.

INT

is 100K Ω 1% metal film, 50 ppm/C.

RTC

/ -0.08 -0.08 -0.08 ppm/ Note 7

REF

∆t 1000hrs

PD

/integrate time/clock period

, C

INT

REF

3 10 7 20 15 50 ppm/C°

25 25 25 µA Note 7

= 4V, VIN = 2.0V Full Scale

INT

, C

characteristics.

AZ

~

6 Advanced Linear Devices ALD500RAU/ALD500RA/ALD500R

PIN DESCRIPTION

Pin No. Symbol Description

1I
2C
3V
4C
5 BUF The Integrator resistor buffer connection.
6 AGND This pin is analog ground.
7C
8C
9 N/C Internally connected. Connect to V- for normal operation.
10 N/C Internally connected. Connect to V- for normal operation.
11 V
12 V
13 V
14 V
15 A Converter phase control MSB Input.
16 B Converter phase control LSB Input.
17 C

18 DGND Digital ground.
19 V
20 C

B

INT

-

AZ

-

REF

+

REF

-

REF

+

REF

-

IN

+

IN

OUT

+

S

Bias circuit pin. Connect a 0.1µF capacitor from this pin to V- to minimize noise.
Integrator capacitor connection.
Negative power supply.
The Auto-zero capacitor connection.

Negative reference capacitor connection.
Positive reference capacitor connection.

External voltage reference (-) connection. High impedance load (≥100MΩ) only.
External voltage reference (+) connection. High impedance load (≥100MΩ) only.
Negative analog input.
Positive analog input.

Comparator output. C
is LOW when a negative input voltage is being integrated. A HIGH-to-LOW transition on C
that the Deintegrate phase is completed. C
time the Integrator Zero phase.

Positive power supply.
Chip select - power down pin. Logic 1 = power on. Logic 0 = power down.

is HIGH during the Integration phase when a positive input voltage is being integrated and

OUT

is undefined during the Auto-Zero phase. It should be monitored to

OUT

signals the processor

OUT

Table 1. Conversion Phase and Control Logic Internal Analog Switch Functions

Switch Functions

Input Reference Input Auto Zero Reference VIN=AGND System

Connect Polarity Sample Offset

Conversion Control
Phase Logic

SW

IN

Auto Zero A = 0, B = 1 Open Open Closed Closed Closed Open

Input Signal A = 1, B = 0 Closed Open Open Open Open Open
Integration

Reference Voltage A = 1, B = 1 Open Closed* Open Open Closed Open
Deintegration

Integrator A = 0, B = 0 Open Open Open Closed Closed Closed
Output Zero

+

would be closed for a positive input signal. SW

*SW

R

+

SW

R or

-

would be closed for a negative input signal.

R

ALD500RAU/ALD500RA/ALD500R Advanced Linear Devices 7

SW

-

SW

R

AZ

SW

R

SW

G

SW

S

ALD500RAU/ALD500RA/ALD500R CONVERSION CYCLE

The ALD500RAU/ALD500RA/ALD500R conversion cycle
takes place in four distinct phases, the Auto Zero Phase, the
Input Signal Integration Phase, the Reference Voltage
Deintegration Phase, and the Integrator Zero Phase. A typical
measurement cycle uses all four phases in an order sequence
as mentioned above. The internal analog switch status for
each of these phases is summarized in Table 1.

The following is a detailed description of each one of the four
phases of the conversion cycle.

Auto Zero Phase (AZ Phase)

The analog-to-digital conversion cycle begins with the Auto
Zero Phase, when the digital controller applies low logic level
to input A and high logic level to input B of the analog
processor. During this phase, the reference voltage is stored
on reference capacitor C

, comparator offset voltage and

REF

the sum of the buffer and integrator offset voltages are stored
on auto zero capacitor C

. During the Auto Zero Phase, the

AZ

comparator output is characterized by an indeterminate
waveform.

During the Auto Zero Phase, the external input signal is
disconnected from the internal circuitry of the ALD500RAU/
ALD500RA/ALD500R by opening the two SW

analog

IN

switches and connecting the internal input nodes internally to
analog ground. A feedback loop, closed around the integrator
and comparator, charges the C
compensate for buffer amplifier, integrator and comparator

capacitor with a voltage to

AZ

offset voltages.
This is the system initialization phase, when a conversion is

ready to be initiated at system turn-on. In practice the
converter can be operated in continuous conversion mode,
where AZ phase must be long enough for the circuit conditions
to settle out any system errors. Typically this phase is set to
be equal to t

INT

.

Input Signal Integration Phase (INT Phase)

During the Input Signal Integration Phase (INT), the
ALD500RAU/ALD500RA/ALD500R integrates the differential
voltage across the (V

+

) and (V

IN

-

) inputs. The differential

IN

voltage must be within the device's common-mode voltage
range CMVR. The integrator charges C

for a fixed period

INT

of time, or counts a fixed number of clock pulses, at a rate
determined by the magnitude of the input voltage. During this
phase, the analog inputs see only the high impedance of the
noninverting operational amplifier input of the buffer. The
integrator responds only to the voltage difference between the
analog input terminals, thus providing true differential analog
inputs.

The input signal polarity is determined by software control at
the end of this phase: C
C

= 0 for negative input polarity. The value is, in effect, the

OUT

= 1 for positive input polarity;

OUT

sign bit for the overall conversion result.

time and depends on system parameters and component
value selections. The total number of clock pulses or clock
counts, during integration phase determine the resolution of
the conversion. For high resolution applications, this total
number of clock pulses should be maximized. The basic unit
of resolution is in µV/count. Before the end of this phase,
comparator output is sampled by the microcontroller. This
phase is terminated by changing logic inputs AB from 10 to 11.

Reference Voltage Deintegration Phase (D

Phase)

INT

At the end of the Input Signal Integration Phase, Reference
Voltage Deintegration Phase begins. The previously charged
reference capacitor is connected with the proper polarity to
ramp the integrator output back to zero. The ALD500RAU/
ALD500RA/ALD500R analog processors automatically selects
the proper logic state to cause the integrator to ramp back
toward zero at a rate proportional to the reference voltage
stored on the reference capacitor. The time required to return
to zero is measured by the counter in the digital processor
using the same crystal oscillator. The phase is terminated by
the comparator output after the comparator senses when the
integrator output crosses zero. The counter contents are then
transferred to the register. The resulting time measurement
is proportional to the magnitude of the applied input voltage.

The duration of this phase is precisely measured from the
transition of AB from 10 to 11 to the falling edge of the
comparator output, usually with a crystal controlled digital
counter chain. The comparator delay contributes some error
in this phase. The typical comparator delay is 1µ

sec

. The
comparator delay and overshoot will result in error timing,
which translates into error voltages. This error can be zeroed
and minimized during Integrator Output Zero Phase and
corrected in software, to within ±1 count of the crystal clock
(which is equivalent to within ± 1 LSB, when 1 clock pulse = 1
LSB).

Integrator Zero Phase ( I

NTZ

Phase)

This phase guarantees the integrator output is at 0V when the
Auto Zero phase is entered, and that only system offset
voltages are compensated. This phase is used at the end of
the reference voltage deintegration and is used for applications
with high resolutions. If this phase is not used, the value of the
Auto-Zero capacitor (C
value of the integration capacitor (C

) must be much greater than the

AZ

) to reduce the effects

INT

of charge-sharing. The Integrator Zero phase should be
programmed to operate until the Output of the Comparator
returns "HIGH". A typical Integrator Zero Phase lasts 1msec.

The comparator delay and the controller's response latency
may result in Overshoot causing charge buildup on the
integrator at the end of a conversion. This charge must be
removed or performance will degrade. The Integrator Output
Zero phase should be activated (AB = 00) until C

OUT

goes
high. At this point, the integrator output is near zero. Auto Zero
Phase should be entered (AB = 01) and the ALD500RAU/
ALD500RA/ALD500R is held in this state until the next
conversion cycle.

The duration of this phase is selected by design to be a fixed

8 Advanced Linear Devices ALD500RAU/ALD500RA/ALD500R

+

Differential Inputs (V

-

,V

IN

IN)

The ALD500RAU/ALD500RA/ALD500R operates with
differential voltages within the input amplifier common-mode
voltage range. The amplifier common-mode range extends
from 1.5V below positive supply to 1.5V above negative
supply. Within this common-mode voltage range, common­mode rejection is typically 95dB.

The integrator output also follows the common-mode voltage.
When large common-mode voltages with near full-scale
differential input voltages are applied, the input signal drives
the integrator output to near the supply rails where the
integrator output is near saturation. Under such conditions,
linearity of the converter may be adversely affected as the
integrator swing can be reduced. The integrator output must
not be allowed to saturate. Typically, the integrator output can
swing to within 0.9V of either supply rails without loss of
linearity.

Analog Ground

Analog Ground is V
Voltage Deintegration Phase. If V

-

during Auto Zero Phase and Reference

IN

-

is different from analog

IN
ground, a common-mode voltage exists at the inputs. This
common mode signal is rejected by the high common mode

-

rejection ratio of the converter. In most applications, V

IN

is
set at a fixed known voltage (i.e., power supply ground). All
other ground connections should be connected to digital
ground in order to minimize noise at the inputs.

+

Differential Reference (V

REF

, V

-

REF

)

The reference voltage can be anywhere from 1V of the power
supply voltage rails of the converter. Roll-over error is caused
by the reference capacitor losing or gaining charge due to the
stray capacitance on its nodes. The difference in reference for

(+) or (-) input voltages will cause a roll-over error. This error
can be minimized by using a large reference capacitor in
comparison to the stray capacitance.

Phase Control Inputs (A, B)

The A and B logic inputs select the ALD500RAU/ALD500RA/
ALD500R operating phase. The A and B inputs are normally
driven by a microprocessor I/O port or external logic, using
CMOS logic levels. For logic control functions of A and B logic
inputs, see Table 1.

Comparator Output (C

OUT

)

By monitoring the comparator output during the Input Signal
Integration Phase, which is a fixed signal integrate time
period, the input signal polarity can be determined by the
microcontroller controlling the conversion. The comparator
output is HIGH for positive signals and LOW for negative
signals during the Input Signal Integration Phase. The state of
the comparator should be checked by the microcontroller at
the end of the Input Signal Integration Phase, just before
transition to the Reference Voltage Deintegration Phase. For
very low level input signals noise may cause the comparator
output state to toggle between positive and negative states.
For the ALD500RAU/ALD500RA/ALD500R, this noise has
been minimized to typically within one count.

At the start of the Reference Voltage Deintegration Phase,
comparator output is set to HIGH state. During the Reference
Voltage Deintegration Phase, the microcontroller must monitor
the comparator output to make a HIGH-to-LOW transition as
the integrator output ramp crosses zero relative to analog
ground. This transition indicates that the conversion is
complete. The microcontroller then stops and records the
pulse count. The internal comparator delay is 1µsec, typically.
The comparator output is undefined during the Auto Zero
Phase.

)

IN

REFERENCE
DEINTEGRATE

ZERO
CROSSING

Negative Input Signal (VIN)

ANALOG INPUT

INTEGRATE

INTEGRATOR

OUTPUT

)

(V

INT

EXTERNAL INPUT
POLARITY DETECTION

COMPARATOR

OUTPUT

)

(C

OUT

0V

REFERENCE
DEINTEGRATE

ZERO
CROSSING

ANALOG INPUT

INTEGRATE

INTEGRATOR

OUTPUT

)

(V

INT

EXTERNAL INPUT
POLARITY DETECTION

COMPARATOR

OUTPUT

)

(C

OUT

Positive Input Signal (V

Figure 4. Comparator Output

ALD500RAU/ALD500RA/ALD500R Advanced Linear Devices 9

APPLICATIONS AND DESIGN NOTES
Determination and Selection of System Variables

The procedure outlined below allows the user to determine the
values for the following ALD500RAU/ALD500RA/ALD500R
system design variables:

where:

V

MAX = Maximum input voltage desired

IN

(full count voltage)

R

INT

= Integrating Resistor value

For minimum noise and maximum linearity, R
the range of between 50kΩ to 150kΩ .

should be in

INT

(1) Determine Input Voltage Range
(2) Clock Frequency and Resolution Selection
(3) Input Integration Phase Timing

, C

(4) Integrator Timing Components (R

INT

INT

)
(5) Auto Zero and Reference Capacitors
(6) Voltage Reference

System Timing

Figure 3 and Figure 4 show the overall timing for a typical
system in which ALD500RAU/ALD500RA/ALD500R is
interfaced to a microcontroller. The microcontroller drives the
A, B inputs with I/O lines and monitors the comparator output,
C

, using an I/O line or dedicated timer-capture control pin.

OUT

It may be necessary to monitor the state of the comparator
output in addition to having it control a timer directly during the
Reference Deintegration Phase.

There are four critical timing events: sampling the input
polarity; capturing the deintegration time; minimizing overshoot
and properly executing the Integrator Output Zero Phase.

Selecting Input Integration Time

For maximum 50/60 cycle noise rejection, Input Integration
Time must be picked as a multiple of the period of line
frequency. For example, t

times of 33msec, 66msec and

INT

100 msec maximize 60Hz line rejection, and 20msec, 40
msec, 80msec, and 100 msec maximize 50Hz line rejection.
Note that t

of 100 msec maximizes both 60 Hz and 50Hz

INT

line rejection.

INT and D

Phase Timing

INT

Integrating Capacitor (C

INT

)

The integrating capacitor should be selected to maximize
integrator output voltage swing V

, for a given integration

INT

time, without output level saturation. For +/-5V supplies,
recommended V

range is between +/- 3 Volt to +/-4 Volt.

INT

Using the 20µA buffer maximum output current, the value of
the integrating capacitor is calculated as follows:

= (t

) . (20 x 10-6) / V

INT

INT

= Input Integration Phase Period
= Maximum integrator output

where: t

C

INT

INT

V

INT

voltage swing

It is critical that the integrating capacitor must have a very low
dielectric absorption, as charge loss or gain during conversion
directly converts into an error voltage. Polypropylene capacitors
are recommended while Polyester and Polybicarbonate
capacitors may also be used in less critical applications.

Reference (C

and CAZ must be low leakage capacitors (e.g.

C

REF

) and Auto Zero (CAZ) Capacitors

REF

polypropylene types). The slower the conversion rate, the
larger the value C
values for C

and C

C

AZ

Calculate V

REF

may also be used to limit roll-over errors.

REF

REF

must be. Recommended capacitor

REF

and CAZ are equal to C

. Larger values for

INT

The reference deintegration voltage is calculated using:

= (V

V

REF

INT

) . (C

INT

) . (R

INT

) / 2(t

INT

)

The duration of the Reference Deintegrate Phase (D
function of the amount of voltage charge stored on the
integrator capacitor during INT phase, and the value of V
The D

phase must be initiated immediately following INT

INT

INT)

is a

R

in order to operate properly. This R

REF

metal film 100KΩ resistor, 50 ppm/C. Any other loading must

.

REF

REF

be high impedance (≥100MΩ).

should be a 1%

The ALD500RAU/ALD500RA/ALD500R requires an external

phase and terminated when an integrator output zero-crossing
is detected. In general, the maximum number of counts
chosen for D
with V

REF

example, V

phase is twice to three times that of INT phase

INT

chosen as a maximum voltage relative to VIN. For

= VIN(max)/2 would be a good reference

REF

voltage.

Converter Noise

The converter noise is the total algebraic sum of the integrator
noise and the comparator noise. This value is typically 14 µV
peak to peak. The higher the value of the reference voltage,
the lower the converter noise. Such sources of noise errors

Integrating Resistor (R

INT

)

The desired full-scale input voltage and amplifier output
current capability determine the value of R

. The buffer and

INT

integrator amplifiers each have a full-scale current of 20µA.
The value of R

R

INT

is therefore directly calculated as follows:

INT

=VIN MAX / 20 µA

can be reduced by increased integration times, which effectively
filter out any such noise. If the integration time periods are
selected as multiples of 50/60Hz frequencies, then 50/60Hz
noise is also rejected, or averaged out. The signal-to-noise
ratio is related to the integration time (t
time constant (R

S/N (dB) = 20 Log ((V

INT

) (C

) as follows:

INT

/ 14 x 10-6) . t

INT

) and the integration

INT

/(R

INT

INT

This converter noise can also be reduced by using multiple
samples and mathematically averaged. For example, taking
16 samples and averaging the readings result in a mathematical
(by software) filtering of noise to less than 4µV.

10 Advanced Linear Devices ALD500RAU/ALD500RA/ALD500R

. C

INT

))

EQUATIONS AND DERIVATIONS
Dual Slope Analog Processor equations and derivations
are as follows:

t

INT

(t) = V

INT

= V

REF

t

INT

V

V

IN

I

B

INT

∫

0

(constant):

IN

t

INT

.

.

I

INT

value:

INT

=

VIN(t)dt =

.

V

t

DINT

t

INT

B

VINMAX

IBMAX

IN

V

REF

=

R

INT

1

.

C

R

INT

For V

IN

1

.

C

R

INT

...

V

IN

C

=

INT

MAX, the current IB is also at a maximum level,

At V

IN

for a given R

R

=

INT

V

R

.
.

REF

INT

t

DINT

C

INT

.
.

t

DINT

C

(1)

INT

(2)

(2a)

(3)

(4)

From equation (2a),


OR




V


V


REF

REF

.

V

t

IN

=

=

INT

t

DINT

.

MAX

DINT



t

MAX

INT

V

IN

t

(5a)

(5b)

Rearranging equations (3) and (4):




and




At V




t

I

INT = VINT

t

INT

MAX =

B

INT

C

INT . VINT

=

I

B

MAX

V

IN



R

INT

MAX, equation (6) becomes:

C

=

INT . VINT

MAX

IBMAX

(6)

(7)

(6a)


Combining (6a) and (7):


...

t

INT



In equation (5b), substituting equation (8) for t




V

=

REF







=

.

V

C

INT

V

C

IN





INT



VINMAX

MAX

.

V

t

DINT

INT

INT

=

.

MAX

C

t

DINT

MAX

MAX

INT

.

R

.

V
V

IN

MAX

.

R

INT

INT

INT

MAX

MAX

(8)

:

INT

.

R

INT

(9)


For t

MAX = 2 x t

DINT

INT

,

equation (9) becomes:

V

REF

.

V

C

INT

=

INT

2t

INT

MAX

.

R

INT

(10)





DESIGN EXAMPLES
We now apply these equations in the following 
design examples.


Design Example 1:



1. Pick resolution = 16 bit. 


2. Pick t




INT

1

= 4x = 4 x 16.6667 msec.

60Hz

= 66.6667ms


= 0.0666667 sec.

3. Pick clock period = 1.08507 µs and number of counts


over t




INT



4. Pick V

I

B



5. Applying equation (3) to calculate C


C




6. Pick C

0.0666667

=

1.08507x10

MAX value, e.g., VINMAX = 2.0 V

IN

MAX = 20µA R

= (0.0666667)(20x10-6)/4 where V

INT

~

0.33 µF

=

and CAZ ≥ C

REF

= 61440

-6

2.0

= = 100 kΩ

INT

20x10

: C

INT

CAZ 0.33 µF

REF

INT:

~

=

-6

= 4.0V

INT

~

=



7. Pick t


8. Calculate V


DINT

= 2 x t

REF

= 133.3333 msec

INT

V

MAX

INT



=

=

t

DINT

4 x 0.33 x 10

133.3333 x 10

~

1.00V

=

.

C
MAX

.

R

INT

-6

x 100 x 10

-3

INT

V

3

V

Design Example 2:



1. Select resolution of 17 bit. Total number of
counts during t

is131,072.

INT



2. We can pick t
 or alternately, pick t

of 16.6667 msec. x 5 = 83.3333 msec.

INT

INT

equal 

 16.6667 msec. x 6 = 100.00 msec.



 (for 60 Hz rejection)
 which is t
  

 Therefore, using t

= 20.00 msec. x 5 

INT

= 100.00 msec. (for 50 Hz rejection)


= 100 msec. would achieve

INT

 both 50 Hz and 60 Hz cycle noise rejection. For this
 example, the following calculations would assume
t

of 100 msec. Now select period equal to 

INT

 0.5425 µsec. (clock frequency of 1.8432 MHz)



ALD500RAU/ALD500RA/ALD500R Advanced Linear Devices 11

3. Pick VINMAX = ±2V

 For IBMAX = 20µA, applying equation (4),

R

INT

4. Calculate, using equation (3) for C


Use C

5. Pick C

6. Pick t

= (0.1) x (20 x 10-6/4)

C

INT

 ~

= 0.5 µF

0.47µF as the closest practical value.

INT

and CAZ = 0.47 µF

REF

= 2 x t

DINT

7. Calculate the value for V

2

= = 100 K Ω

20x10

-6

INT

(assume V

= 200 msec.

INT

, from equation (10):

REF

:

INT

MAX = 4V)

V

REF

=

=

.

C

INT

t

0.5 x 10

V

INT

DINT

-6

200 x 10

.

MAX

R

INT

MAX

x 4 x 100 x 10

-3

3

= 1.00V

Design Example 3:

1. Pick resolution of 18 bit. Total number of counts during
t

is 262,144.

INT

Design Example 4:

Objective: 5 1/2 digit + sign +over-range measurement.

1. Pick t

= 133.333 msec. for 60Hz noise rejection.

INT

(16.6667 msec. x 8 cycles)
Frequency = 1.8432 MHz
clock period = 0.5425 µsec.

During Input Integrate Phase,

total count =

133.333 x 10-3

0.5425 x 10

-6

= 245776

For V

For V

2. Pick V

For IB = 20 µA, R

3. Calculate C

4. Pick C

5. Select t

= 4.0V, the basic resolution is

INT

4

245776

IN

16.276 x

IN

REF

or 16.276 µV/count

MAX = 2.00V, the input resolution is

V

MAX

IN

V

INT

= 8.138 µV/count

MAX

range = ± 2V

2

=

INT

20 x 10

= (0.133333) x (20 x 10-6)/4 = 0.67 µF

INT

= 100 KΩ

-6

= CAZ = 0.67 µF

DINT

= 2 x t

= 266.667 msec.

INT

~

2. Pick t

= 16.66667 msec. x 10 cycles

INT

= 0.1666667 sec.

 This t

allows clock period of 0.5425 µsec.

INT

 and still achieve 18 bits resolution.

3. Again, as shown from previous example, pick VINMAX = ±2V

 For IBMAX = 20 µA, R

4. Next, we calculate C

C


= (0.1666667) x (20 x 10-6)/4

INT

~

= 0.83 µF

INT:

INT =

20x10

(V

INT

2

= 100 KΩ

-6

MAX = 4.0V)

 In this case, use CINT = 1.0 µF to keep
V

5. Pick C

6. Select t

7. Calculate V
and V

< 4.0V

INT

and CAZ = 1.0 µF

REF

= 2 x t

DINT

as shown in the previous examples

REF

= 1.00V

REF

= 333.333 msec.

INT

6. Calculate V

as shown in Design Example 1,

REF

substituting the appropriate values:

V

REF

C

INT

=

~

= 1.005V

.

V

t

DINT

INT

MAX

MAX

.

R

INT

12 Advanced Linear Devices ALD500RAU/ALD500RA/ALD500R