Datasheet AD8139 Datasheet (Analog Devices)

Low Noise Rail-to-Rail

FEATURES

Fully differential
Low noise

2.25 nV/√Hz

2.1 pA/√Hz
Low harmonic distortion
98 dBc SFDR @ 1 MHz
85 dBc SFDR @ 5 MHz
72 dBc SFDR @ 20 MHz
High speed

410 MHz, 3 dB BW (G = 1)
800 V/µs slew rate

45 ns settling time to 0.01%
69 dB output balance @ 1 MHz
80 dB dc CMRR
Low offset: ±0.5 mV max
Low input offset current: 0.5 µA max
Differential input and output
Differential-to-differential or single-ended-to-differential

operation
Rail-to-rail output
Adjustable output common-mode voltage
Wide supply voltage range: 5 V to 12 V
Available in small SOIC package

GENERAL DESCRIPTION

The AD8139 is an ultralow noise, high performance differential
amplifier with rail-to-rail output. With its low noise, high SFDR,
and wide bandwidth, it is an ideal choice for driving ADCs with
resolutions to 18 bits. The AD8139 is easy to apply, and its in­ternal common-mode feedback architecture allows its output
common-mode voltage to be controlled by the voltage applied
to one pin. The internal feedback loop also provides out­standing output balance as well as suppression of even-order
harmonic distortion products. Fully differential and single­ended-to-differential gain configurations are easily realized by
the AD8139. Simple external feedback networks consisting of a
total of four resistors determine the amplifier’s closed-loop gain.

The AD8139 is manufactured on ADI’s proprietary second gen­eration XFCB process, enabling it to achieve low levels of distor­tion with input voltage noise of only 1.85 nV/√Hz.

Differential ADC Driver

AD8139

APPLICATIONS

ADC drivers to 18 bits
Single-ended-to-differential converters
Differential filters
Level shifters
Differential PCB board drivers
Differential cable drivers

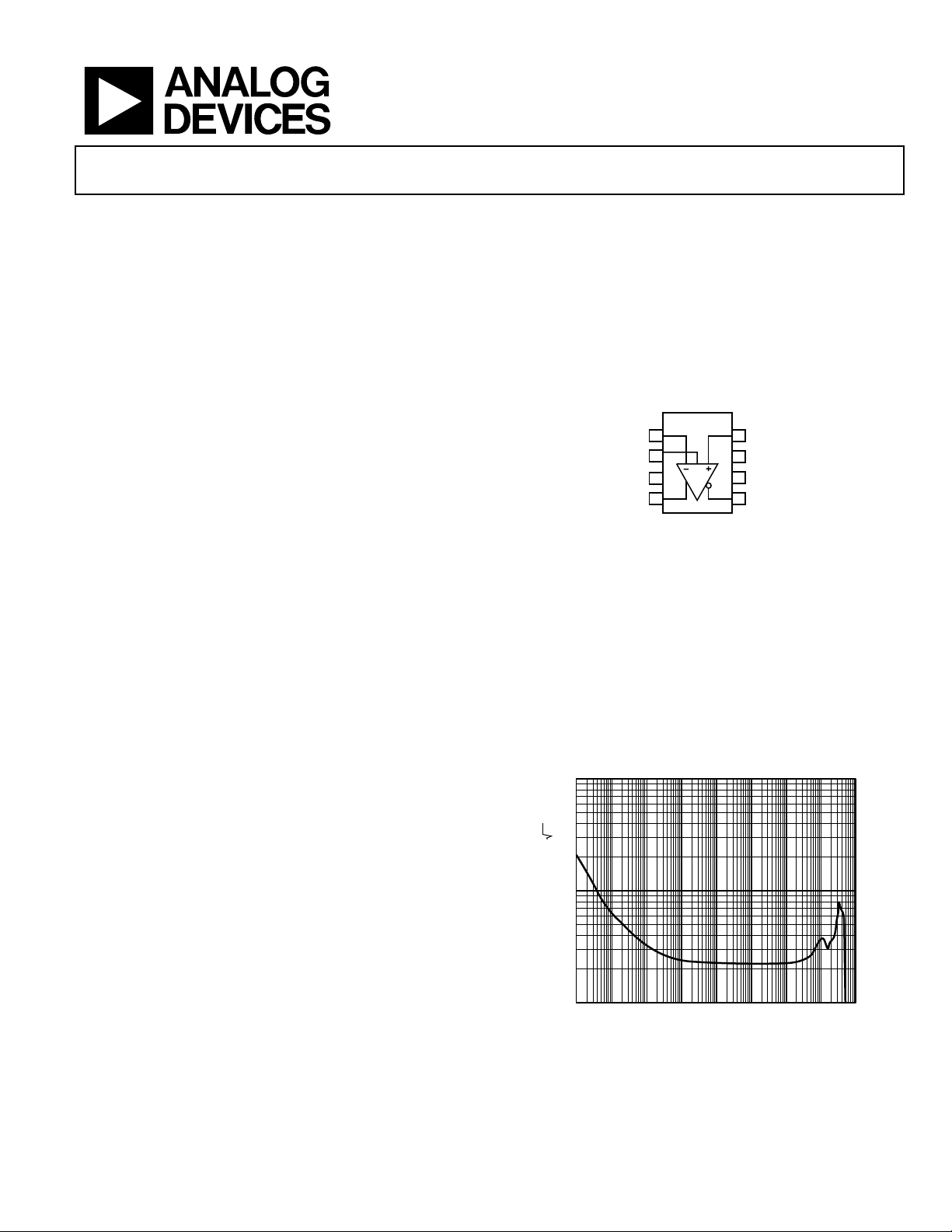
FUNCTIONAL BLOCK DIAGRAM

AD8139

–IN 1

2

V

OCM

V+ 3

+OUT 4

NC = NO CONNECT

Figure 1.

The AD8139 is available in an 8-lead SOIC package with an
exposed paddle (EP) on the underside of its body and a 3 mm ×
3 mm LFCSP. It is rated to operate over the temperature range
of −40°C to +125°C.

100

10

INPUT VOLTAGE NOISE (nV/ Hz)

1

10 100 1k 10k 100k 1M 10M 1G100M

Figure 2. Input Voltage Noise vs. Frequency

FREQUENCY (Hz)

+IN8
NC7
V–6
–OUT5

04679-0-001

04679-0-078

Rev. A

Information furnished by Analog Devices is believed to be accurate and reliable.
However, no responsibility is assumed by Analog Devices for its use, nor for any
infringements of patents or other rights of third parties that may result from its use.
Specifications subject to change without notice. No license is granted by implication
or otherwise under any patent or patent rights of Analog Devices. Trademarks and
registered trademarks are the property of their respective owners.

One Technology Way, P.O. Box 9106, Norwood, MA 02062-9106, U.S.A.
Tel: [phone]
Fax: [phone] © 2004 Analog Devices, Inc. All rights reserved.

www.analog.com

AD8139

TABLE OF CONTENTS

VS = ±5 V, V

= 0 V Specifications.............................................. 3

OCM

Typical Connection and Definition of Terms ........................ 18

VS = 5 V, V

= 2.5 V Specifications............................................. 5

OCM

Absolute Maximum Ratings............................................................ 7

Thermal Resistance ......................................................................7

ESD Caution.................................................................................. 7

Pin Configuration and Function Descriptions............................. 8

Typical Performance Characteristics............................................. 9

Theory of Operation ...................................................................... 18

REVISION HISTORY

8/04—Data Sheet Changed from a Rev. 0 to Rev. A.

Added 8-Lead LFCSP.........................................................Universal

Changes to General Description .................................................... 1

Changes to Figure 2.......................................................................... 1

Changes to V
Changes to V

= ±5 V, V

S

= 5 V, V

S

= 0 V Specifications......................... 3

OCM

= 2.5 V Specifications......................... 5

OCM

Changes to Table 4............................................................................ 7

Changes to Maximum Power Dissipation Section....................... 7

Changes to Figure 26 and Figure 29............................................. 12

Inserted Figure 39 and Figure 42.................................................. 14

Changes to Figure 45 to Figure 47................................................ 15

Inserted Figure 48........................................................................... 15

Changes to Figure 52 and Figure 53............................................. 16

Changes to Figure 55 and Figure 56............................................. 17

Changes to Table 6.......................................................................... 19

Changes to Voltage Gain Section.................................................. 19

Changes to Driving a Capacitive Load Section ..........................22

Changes to Ordering Guide.......................................................... 24

Updated Outline Dimensions....................................................... 24

Applications..................................................................................... 19

Estimating Noise, Gain, and Bandwidth with Matched
Feedback Networks

.................................................................... 19

Outline Dimensions....................................................................... 24

Ordering Guide .......................................................................... 24

5/04—Revision 0: Initial Version

Rev. A | Page 2 of 24

AD8139

VS = ±5 V, V

@ 25°C, Diff. Gain = 1, R

= 0 V SPECIFICATIONS

OCM

= 1 kΩ, RF = RG = 200 Ω, unless otherwise noted. T

L, dm

MIN

to T

= −40°C to +125°C.

MAX

Table 1.

Parameter Conditions Min Typ Max Unit

DIFFERENTIAL INPUT PERFORMANCE
DYNAMIC PERFORMANCE

−3 dB Small Signal Bandwidth V

−3 dB Large Signal Bandwidth V
Bandwidth for 0.1 dB Flatness V
Slew Rate V
Settling Time to 0.01% V
Overdrive Recovery Time G = 2, V

= 0.1 V p-p 340 410 MHz

O, dm

= 2 V p-p 210 240 MHz

O, dm

= 0.1 V p-p 45 MHz

O, dm

= 2 V Step 800 V/µs

O, dm

= 2 V Step, CF = 2 pF 45 ns

O, dm

= 12 V p-p Triangle Wave 30 ns

IN, dm

NOISE/HARMONIC PERFORMANCE

SFDR V
V
V
Third-Order IMD V

= 2 V p-p, fC = 1 MHz 98 dB

O, dm

= 2V p-p, fC = 5 MHz 85 dB

O, dm

= 2 V p-p, fC = 20 MHz 72 dB

O, dm

= 2 V p-p, fC = 10.05 MHz ± 0.05 MHz −90 dBc

O, dm

Input Voltage Noise f = 100 KHz 2.25 nV/√Hz
Input Current Noise f = 100 KHz 2.1 pA/√Hz

DC PERFORMANCE

Input Offset Voltage VIP = VIN = V
Input Offset Voltage Drift T
Input Bias Current T

MIN

MIN

to T
to T

MAX

MAX

OCM

= 0 V

−500 ±150 +500 µV

1.25 µV/ºC

2.25 8.0 µA
Input Offset Current 0.12 0.5 µA
Open-Loop Gain 114 dB

INPUT CHARACTERISTICS

Input Common-Mode Voltage Range −4 +4 V
Input Resistance Differential 600 kΩ
Common Mode 1.5 MΩ
Input Capacitance Common Mode 1.2 pF
CMRR V

= ±1 V dc, RF = RG = 10 kΩ 80 84 dB

ICM

OUTPUT CHARACTERISTICS

Output Voltage Swing Each Single-Ended Output, RF = RG = 10 kΩ −VS + 0.20 +VS – 0.20 V

Each Single-Ended Output,

= Open Circuit, RF = RG = 10 kΩ

R

L, dm

+ 0.15 +VS – 0.15 V

−V

S

Output Current Each Single-Ended Output 100 mA
Output Balance Error f = 1 MHz −69 dB

V

to V

OCM

V

OCM

−3 dB Bandwidth V
Slew Rate V

PERFORMANCE

O, cm

DYNAMIC PERFORMANCE

= 0.1 V p-p 515 MHz

O, cm

= 2 V p-p 250 V/µs

O, cm

Gain 0.999 1.000 1.001 V/V

V

INPUT CHARACTERISTICS

OCM

Input Voltage Range −3.8 +3.8 V
Input Resistance 3.5 MΩ
Input Offset Voltage V

OS, cm

= V

O, cm

− V

; VIP = VIN = V

OCM

= 0 V −900 ±300 +900 µV

OCM

Input Voltage Noise f = 100 kHz 3.5 nV/√Hz
Input Bias Current 1.3 4.5 µA
CMRR V

/V

, V

OCM

O, dm

= ±1 V 74 88 dB

OCM

Rev. A | Page 3 of 24

AD8139

Parameter Conditions Min Typ Max Unit

POWER SUPPLY

Operating Range 4.5 ±6 V
Quiescent Current 24.5 25.5 mA
+PSRR Change in +VS = ±1V 95 112 dB

−PSRR Change in −VS = ±1V 95 109 dB

OPERATING TEMPERATURE RANGE −40 +125 °C

Rev. A | Page 4 of 24

AD8139

VS = 5 V, V

@ 25°C, Diff. Gain = 1, R

= 2.5 V SPECIFICATIONS

OCM

= 1 kΩ, RF = RG = 200 Ω, unless otherwise noted. T

L, dm

MIN

to T

= −40°C to +125°C.

MAX

Table 2.

Parameter Conditions Min Typ Max Unit

DIFFERENTIAL INPUT PERFORMANCE
DYNAMIC PERFORMANCE

−3 dB Small Signal Bandwidth V

−3 dB Large Signal Bandwidth V
Bandwidth for 0.1 dB Flatness V
Slew Rate V
Settling Time to 0.01% V
Overdrive Recovery Time G = 2, V

= 0.1 V p-p 330 385 MHz

O, dm

= 2 V p-p 135 165 MHz

O, dm

= 0.1 V p-p 34 MHz

O, dm

= 2 V Step 540 V/s

O, dm

= 2 V Step 55 ns

O, dm

= 7 V p-p Triangle Wave 35 ns

IN, dm

NOISE/HARMONIC PERFORMANCE

SFDR V
V
V
Third-Order IMD V

= 2 V p-p, fC = 1 MHz 99 dB

O, dm

= 2 V p-p, fC = 5 MHz, (RL = 800 Ω) 87 dB

O, dm

= 2 V p-p, fC = 20 MHz, (RL = 800 Ω) 75 dB

O, dm

= 2 V p-p, fC = 10.05 MHz ± 0.05 MHz −87 dBc

O, dm

Input Voltage Noise f = 100 kHz 2.25 nV/√Hz
Input Current Noise f = 100 kHz 2.1 pA/√Hz

DC PERFORMANCE

Input Offset Voltage VIP = VIN = V
Input Offset Voltage Drift T
Input Bias Current T

MIN

MIN

to T
to T

MAX

MAX

OCM

=0 V

−500 ±150 +500 µV

1.25 µV/ºC

2.2 7.5 A
Input Offset Current 0.13 0.5 µA
Open-Loop Gain 112 dB
INPUT CHARACTERISTICS
Input Common-Mode Voltage Range 1 4 V
Input Resistance Differential 600 KΩ
Common-Mode 1.5 MΩ
Input Capacitance Common-Mode 1.2 pF
CMRR ∆V

= ±1 V dc, RF = RG = 10 kΩ 75 79 dB

ICM

OUTPUT CHARACTERISTICS

Output Voltage Swing Each Single-Ended Output, RF = RG = 10 kΩ −VS + 0.15 +VS − 0.15 V

Each Single-Ended Output,

= Open Circuit, RF = RG = 10 kΩ

R

L, dm

+ 0.10 +VS − 0.10 V

−V

S

Output Current Each Single-Ended Output 80 mA
Output Balance Error f = 1 MHz −70 dB

V

to V

OCM

V

OCM

−3 dB Bandwidth V
Slew Rate V

PERFORMANCE

O, cm

DYNAMIC PERFORMANCE

= 0.1 V p-p 440 MHz

O, cm

= 2 V p-p 150 V/s

O, cm

Gain 0.999 1.000 1.001 V/V

V

INPUT CHARACTERISTICS

OCM

Input Voltage Range 1.0 3.8 V
Input Resistance 3.5 MΩ
Input Offset Voltage V

OS, cm

= V

O, cm

− V

; VIP = VIN = V

OCM

= 2.5 V −1.0 ±0.45 +1.0 mV

OCM

Input Voltage Noise f = 100 KHz 3.5 nV/√Hz
Input Bias Current 1.3 4.2 A
CMRR ∆V

/∆VO(dm), ∆V

OCM

= ±1 V 67 79 dB

OCM

Rev. A | Page 5 of 24

AD8139

Parameter Conditions Min Typ Max Unit

POWER SUPPLY

Operating Range +4.5 ±6 V
Quiescent Current 21.5 22.5 mA
+PSRR Change in +VS = ±1 V 86 97 dB

−PSRR Change in −VS = ±1 V 92 105 dB

OPERATING TEMPERATURE RANGE −40 +125 °C

Rev. A | Page 6 of 24

AD8139

ABSOLUTE MAXIMUM RATINGS

Table 3.

Parameter Rating

Supply Voltage 12 V
V

OCM

±V

S

Power Dissipation See Figure 3
Input Common-Mode Voltage ±V

S

Storage Temperature –65°C to +125°C
Operating Temperature Range –40°C to +125°C
Lead Temperature Range

300°C

(Soldering 10 sec)
Junction Temperature 150°C

Stresses above those listed under Absolute Maximum Ratings
may cause permanent damage to the device. This is a stress rat­ing only; functional operation of the device at these or any
other conditions above those indicated in the operational sec­tion of this specification is not implied. Exposure to absolute
maximum rating conditions for extended periods may affect
device reliability.

THERMAL RESISTANCE

θJA is specified for the worst-case conditions, i.e., θJA is specified
for device soldered in circuit board for surface-mount packages.

Table 4. Thermal Resistance

Package Type θ

JA

SOIC-8 with EP/4-Layer 70 °C/W
LFCSP/4-Layer 70 °C/W

Maximum Power Dissipation

The maximum safe power dissipation in the AD8139 package is
limited by the associated rise in junction temperature (T
die. At approximately 150°C, which is the glass transition tem­perature, the plastic will change its properties. Even temporarily
exceeding this temperature limit may change the stresses that the
package exerts on the die, permanently shifting the parametric

Unit

) on the

J

The power dissipated in the package (P
quiescent power dissipation and the power dissipated in the
package due to the load drive for all outputs. The quiescent
power is the voltage between the supply pins (V
quiescent current (I
and common-mode currents flowing to the load, as well as
currents flowing through the external feedback networks and
the internal common-mode feedback loop. The internal resistor
tap used in the common-mode feedback loop places a 1 kΩ
differential load on the output. RMS output voltages should be
considered when dealing with ac signals.

Airflow reduces θ
the package leads from metal traces, through holes, ground, and
power planes will reduce the θ

Figure 3 shows the maximum safe power dissipation in the
package versus the ambient temperature for the exposed paddle
(EP) SOIC-8 (θ
70°C/W) on a JEDEC standard 4-layer board. θ
approximations.

4.0

3.5

3.0

2.5

2.0

1.5

1.0

MAXIMUM POWER DISSIPATION (W)

0.5

0

–40 –20 0 20 40 60 80 100 120

performance of the AD8139. Exceeding a junction temperature of
175°C for an extended period of time can result in changes in the
silicon devices potentially causing failure.

Figure 3. Maximum Power Dissipation vs. Temperature for a 4-Layer Board

). The load current consists of differential

S

. Also, more metal directly in contact with

JA

.

JA

= 70°C/W) package and LFCSP (θJA =

JA

SOIC

AND LFCSP

AMBIENT TEMPERATURE (°C)

) is the sum of the

D

) times the

S

values are

JA

04679-0-055

ESD CAUTION

ESD (electrostatic discharge) sensitive device. Electrostatic charges as high as 4000 V readily accumulate on the
human body and test equipment and can discharge without detection. Although this product features proprie­tary ESD protection circuitry, permanent damage may occur on devices subjected to high energy electrostatic
discharges. Therefore, proper ESD precautions are recommended to avoid performance degradation or loss of
functionality.

Rev. A | Page 7 of 24

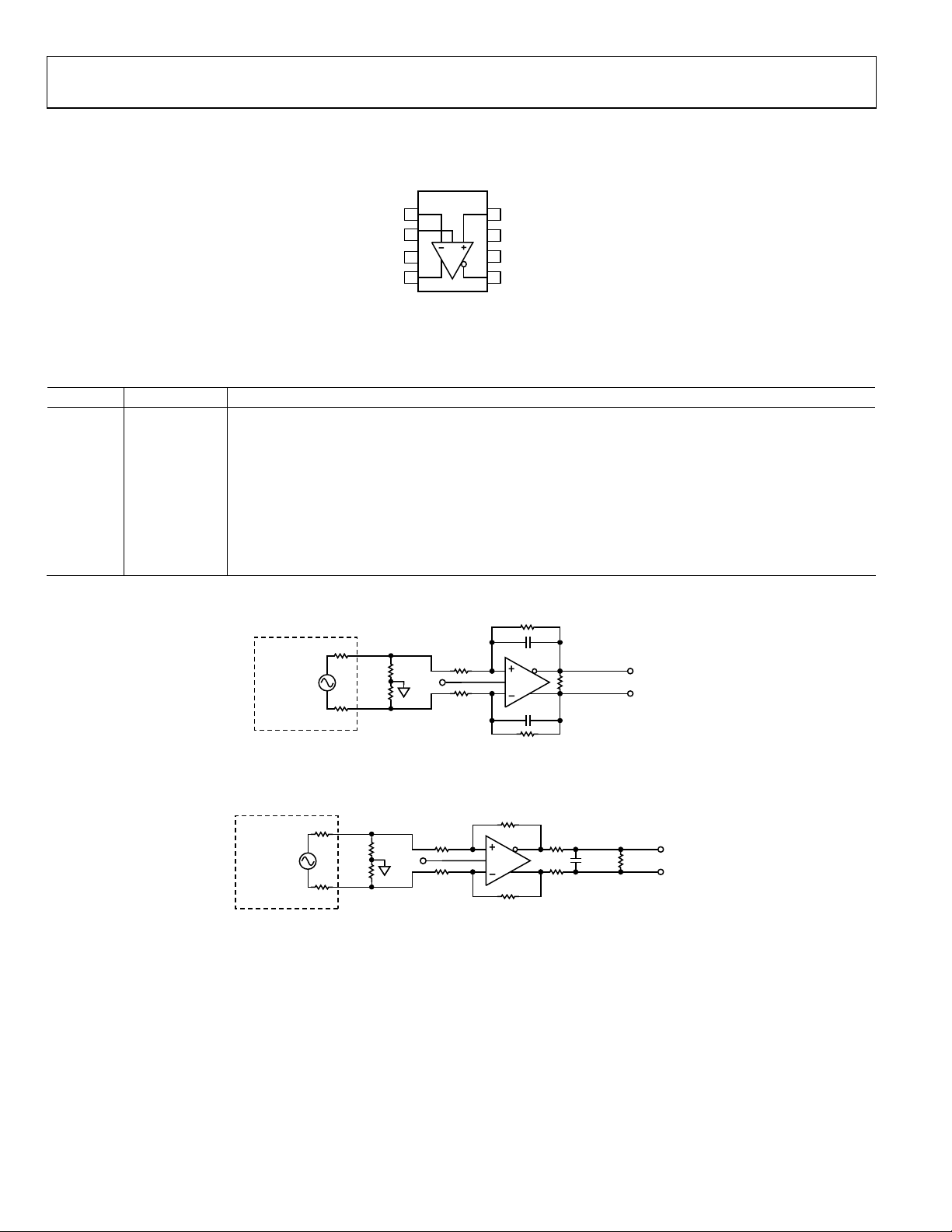
AD8139

PIN CONFIGURATION AND FUNCTION DESCRIPTIONS

AD8139

–IN

1

2

V

OCM

V+

3

+OUT

4

NC = NO CONNECT

Figure 4. Pin Configuration

Table 5. Pin Function Descriptions

Pin No. Mnemonic Description

1 −IN Inverting Input.
2 V

OCM

An internal feedback loop drives the output common-mode voltage to be equal to the
voltage applied to the V

pin, provided the amplifier’s operation remains linear.

OCM

3 V+ Positive Power Supply Voltage.
4 +OUT Positive Side of the Differential Output.
5 −OUT Negative Side of the Differential Output.
6 V− Negative Power Supply Voltage.
7 NC No Internal Connection.
8 +IN Noninverting Input.

8

7

6

5

+IN
NC
V–
–OUT

R

F

04679-0-003

TEST
SIGNAL
SOURCE

V

TEST
SIGNAL
SOURCE

TEST

V

TEST

50Ω

60.4Ω

60.4Ω

50Ω

V

OCM

RG= 200Ω

RG= 200Ω

Figure 5. Basic Test Circuit

50Ω

60.4Ω

60.4Ω

50Ω

V

RG= 200Ω

OCM

RG= 200Ω

Figure 6. Capacitive Load Test Circuit, G = +1

AD8139

= 200Ω

R

F

AD8139

RF= 200Ω

C

F

R

L, dm

C

F

R

F

R

S

C

R

S

–

V

= 1kΩ

O, dm

+

L, dmRL, dm

04679-0-072

–

V

O, dm

+

04679-0-075

Rev. A | Page 8 of 24

AD8139

TYPICAL PERFORMANCE CHARACTERISTICS

Unless otherwise noted, Diff. Gain = +1, RG = RF = 200 Ω, R
Figure 5 for the definition of terms.

2
1

0
–1
–2
–3
–4
–5
–6
–7
–8
–9

–10
–11

NORMALIZED CLOSED-LOOP GAIN (dB)

RG = 200Ω

–12
–13

= 0.1V p-p

V

O, dm

1 10 100 1000

G = 10

FREQUENCY (MHz)

Figure 7. Small Signal Frequency Response for Various Gains

5

4

3

2

1

0
–1
–2
–3
–4
–5
–6

CLOSED-LOOP GAIN (dB)

–7
–8
–9

V

= 0.1V p-p

O, dm

–10

10 100 1000

FREQUENCY (MHz)

VS =±5V

Figure 8. Small Signal Frequency Response for Various Power Supplies

3

2

1

0
–1
–2
–3
–4
–5
–6
–7
–8

CLOSED-LOOP GAIN (dB)

–9

–10
–11

V

= 0.1V p-p

O, dm

–12

10 100 1000

FREQUENCY (MHz)

Figure 9. Small Signal Frequency Response at Various ΩTemperatures

G = 2

G = 5

V

S

+125°C

+25°C

G = 1

= +5V

+85°C

–40°C

= 1 kΩ, VS = ±5 V, TA = 25°C, V

L, dm

2
1

0
–1
–2
–3
–4
–5
–6
–7
–8
–9

–10
–11

RG = 200Ω

NORMALIZED CLOSED-LOOP GAIN (dB)

–12

04679-0-004

V

–13

1 10 100 1000

Figure 10. Large Signal Frequency Response for Various Gains

3

2

1

0
–1
–2
–3
–4
–5
–6
–7
–8

CLOSED-LOOP GAIN (dB)

–9

–10
–11

04679-0-005

V

–12

10 100 1000

Figure 11. Large Signal Frequency Response for Various Power Supplies

3

2

1

0
–1
–2
–3
–4
–5
–6
–7
–8

CLOSED-LOOP GAIN (dB)

–9

–10
–11

04679-0-006

V

–12

10 100 1000

Figure 12. Large Signal Frequency Response at Various Temperatures

O, dm

O, dm

O, dm

OCM

= 2.0V p-p

= 2.0V p-p

= 2.0V p-p

= 0 V. Refer to the basic test circuit in

G = 1

G = 2G = 5

G = 10

04679-0-007

FREQUENCY (MHz)

VS =±5V

= +5V

V

S

04679-0-008

FREQUENCY (MHz)

+125°C +85°C

–40°C

FREQUENCY (MHz)

+25°C

04679-0-009

Rev. A | Page 9 of 24

AD8139

3
2
1

0
–1
–2
–3
–4
–5
–6
–7
–8

CLOSED-LOOP GAIN (dB)

–9

–10
–11

V

= 0.1V p-p

O, dm

–12

10 100 1000

Figure 13. Small Signal Frequency Response for Various Loads

3

2

1

0
–1
–2
–3
–4
–5
–6
–7
–8

CLOSED-LOOP GAIN (dB)

–9

–10
–11

V

= 0.1V p-p

O, dm

–12

10 100 1000

Figure 14. Small Signal Frequency Response for Various C

6

5

4

3

2

1

0
–1
–2
–3
–4
–5

CLOSED-LOOP GAIN (dB)

–6
–7
–8

V

= 0.1V p-p

O, dm

–9

10 100 1000

Figure 15. Small Signal Frequency Response at Various V

= 200Ω

R

L

FREQUENCY (MHz)

C

= 2pF

F

FREQUENCY (MHz)

V

= +4.3V

OCM

= –4.3V

V

OCM

V

OCM

FREQUENCY (MHz)

RL = 1kΩ

= 0V

RL = 100Ω

= 0pF

C

F

CF = 1pF

V

= +4V

OCM

V

OCM

R

L

= –4V

= 500Ω

OCM

2
1
0

–1

RL = 100Ω

R

L

= 500Ω

–2
–3
–4
–5
–6
–7
–8
–9

CLOSED-LOOP GAIN (dB)

–10

R

= 1kΩ

L

–11

04679-0-040

O, dm

–13

10 100 1000

FREQUENCY (MHz)

R

L

= 200Ω

04679-0-041

–12

V

= 2.0V p-p

Figure 16. Large Signal Frequency Response for Various Loads

2
1

0
–1
–2
–3
–4
–5
–6
–7
–8
–9

CLOSED-LOOP GAIN (dB)

–10
–11
–12

V

= 2.0V p-p

04679-0-011

O, dm

–13

10 100 1000

F

04679-0-012

Figure 17. Large Signal Frequency Response for Various C

0.5

0.4

0.3

0.2

0.1

0

–0.1

–0.2

–0.3

NORMALIZED CLOSED-LOOP GAIN (dB)

–0.4

–0.5

1 10 100

CF = 0pF

C

= 2pF

F

FREQUENCY (MHz)

(V

O, dm

R

L

= 2.0V p-p)

(V

O, dm

R

= 2.0V p-p)

(V

O, dm

FREQUENCY (Hz)

C

= 1pF

F

RL = 100Ω

= 0.1V p-p)

= 100Ω

= 1kΩ

L

(V

O, dm

RL = 1kΩ

= 0.1V p-p)

04679-0-014

F

04679-0-042

Figure 18. 0.1 dB Flatness for Various Loads and Output Amplitudes

Rev. A | Page 10 of 24

AD8139

–30

V

= 2.0V p-p

O, dm

–40

–50

–60

–70

–80

–90

DISTORTION (dBc)

–100

–110

–120

–130

0.1 1 10 100
FREQUENCY (MHz)

V

=±5V

S

VS = +5V

04679-0-015

Figure 19. Second Harmonic Distortion vs. Frequency and Supply Voltage

–30

V

= 2.0V p-p

O, dm

–40
–50
–60
–70
–80
–90

–100

DISTORTION (dB)

–110
–120
–130
–140

0.1 1 10 100

G = 5

FREQUENCY (MHz)

G = 1

G = 2

04679-0-016

Figure 20. Second Harmonic Distortion vs. Frequency and Gain

–30

V

= 2.0V p-p

O, dm

–40

–50

–60

–70

–80

–90

DISTORTION (dBc)

–100

–110

–120

–130

0.1 1 10 100

RL = 100Ω

= 200Ω

R

L

R

= 1kΩ

L

FREQUENCY (MHz)

R

L

= 500Ω

04679-0-017

Figure 21. Second Harmonic Distortion vs. Frequency and Load

–30

V

= 2.0V p-p

O, dm

–40

–50

–60

–70

–80

–90

DISTORTION (dBc)

–100

–110

–120

–130

0.1 1 10 100
FREQUENCY (MHz)

VS = +5V

V

=±5V

S

04679-0-018

Figure 22. Third Harmonic Distortion vs. Frequency and Supply Voltage

–30

V

= 2.0V p-p

O, dm

–40
–50
–60
–70
–80
–90

–100

DISTORTION (dB)

–110
–120
–130
–140

DISTORTION (dBc)

–100

–110

–120

–130

G = 1

0.1 1 10 100

G = 2

G = 5

FREQUENCY (MHz)

Figure 23. Third Harmonic Distortion vs. Frequency and Gain

–30

V

= 2.0V p-p

O, dm

–40

–50

–60

–70

–80

–90

0.1 1 10 100
FREQUENCY (MHz)

R

L

R

L

RL = 100Ω

= 200Ω

= 1kΩ

R

L

= 500Ω

04679-0-019

04679-0-020

Figure 24. Third Harmonic Distortion vs. Frequency and Load

Rev. A | Page 11 of 24

AD8139

–30

V

= 2.0V p-p

O, dm

–40

–50

–60

–70

–80

–90

DISTORTION (dBc)

–100

–110

–120

–130

0.1 1 10 100

Figure 25. Second Harmonic Distortion vs. Frequency and R

–80

FC = 2MHz

–90

–100

–110

RF = 200Ω

R

= 500Ω

F

R

= 1kΩ

F

FREQUENCY (MHz)

V

S

V

=±5V

= +5V

S

F

04679-0-021

–30

V

= 2.0V p-p

O, dm

–40

–50

–60

–70

–80

–90

DISTORTION (dBc)

–100

–110

–120

–130

0.1 1 10 100

RF = 200

Ω

RF = 1k

Ω

FREQUENCY (MHz)

RF = 500

Ω

Figure 28. Third Harmonic Distortion vs. Frequency and R

–80

FC = 2MHz

–90

–100

–110

VS = +5V

VS =±5V

04679-0-024

F

–120

DISTORTION (dBc)

–130

–140

–150

012345678

V

O, dm

(V p-p)

Figure 26. Second Harmonic Distortion Vs. Output Amplitude

–60

–70

–80

–90

–100

DISTORTION (dBc)

–110

–120

–130

0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0

Figure 27. Harmonic Distortion vs. V

V
F

O, dm
C

= 2MHz

= 2V p-p

SECOND HARMONIC

THIRD HARMONIC

V

(V)

OCM

, VS = +5 V

OCM

04679-0-022

04679-0-023

–120

DISTORTION (dBc)

–130

–140

–150

087654321

V

O, dm

(V p-p)

Figure 29. Third Harmonic Distortion vs. Output Amplitude

–60

–70

–80

–90

–100

DISTORTION (dBc)

–110

–120

–130

–5 –4 –3 –2 –0 0 1 2 3 4 5

V

O, dm

= 2MHz

F

C

= 2V p-p

SECOND HARMONIC

THIRD HARMONIC

V

OCM

(V)

Figure 30. Harmonic Distortion vs. V

, VS = ±5 V

OCM

04679-0-025

04679-0-026

Rev. A | Page 12 of 24

AD8139

100

V

= 100mV p-p

O, dm

75

50

(V)

O, dm

V

–100

–25

–50

–75

CF = 0pF

= 0pF,

(C

F

25

V

=±5V)

S

0

V

O, dm

(CF = 2pF, VS =±5V)

TIME (ns)

5ns/DIV

Figure 31. Small Signal Transient Response for Various C

(V)

O, dm

V

–0.025

–0.050

–0.075

–0.100

0.100

0.075

0.050

0.025

0

RS = 31.6
C

= 30pF

L, dm

= 63.4

R

S

C

= 15pF

L, dm

Ω

Ω

5ns/DIV

TIME (ns)

Figure 32. Small Signal Transient Response for Capacitive Loads

5

V

= 2V p-p

O, dm

0

1 = 10MHz

F

C

–5

2 = 10.1MHz

F

C

–10
–15
–20
–25
–30
–35
–40
–45
–50
–55
–60
–65
–70
–75

NORMALIZED OUTPUT (dBc)

–80
–85
–90
–95

–100

9.55 9.65 9.75 9.85 9.95 10.05 10.15 10.25 10.35 10.45 10.55
FREQUENCY (MHz)

Figure 33. Intermodulation Distortion

04679-0-043

F

04679-0-064

04679-0-027

2.5

(V)

O, dm

V

–0.5

–1.0

–1.5

–2.0

–2.5

2.0

1.5

1.0

0.5

CF = 0pF

C

= 2pF

F

C

= 0pF

F

= 2pF

C

F

0

4V p-p

2V p-p

5ns/DIV

TIME (ns)

Figure 34. Large Signal Transient Response For C

(V)

O, dm

V

1.5

1.0

0.5

0

–0.5

–1.0

–1.5

RS = 63.4
C

L, dm

= 31.6

R

S

C

L, dm

Ω

= 15pF

Ω

= 30pF

TIME (ns)

5ns/DIV

Figure 35. Large Signal Transient Response for Capacitive Loads

1.5

1.0

0.5

0

AMPLITUDE (V)

–0.5

–1.0

–1.5

V

O, dm

V

IN

TIME (ns)

CF = 2pF
V

O, dm

ERROR

= 2.0V p-p

35ns/DIV

Figure 36. Settling Time (0.01%)

04679-0-044

F

04679-0-065

600

400

200

0

–200

ERROR (µV) 1DIV = 0.01%

–400

04679-0-034

–600

Rev. A | Page 13 of 24

AD8139

1.5

1.0

0.5

(V)

0

OCM

V

–0.5

–1.0

–1.5

0

V
INPUT CMRR =

–10

–20

–30

–40

–50

CMRR (dB)

–60

–70

–80

–90

1 10 100 500

100

±

5V

V

O, cm

V

IN, dm

Figure 37. V

= 0.2V p-p

IN, cm

Large Signal Transient Response

OCM

∆

V

O, cm

RF = RG = 10k

FREQUENCY (MHz)

Figure 38. CMRR vs. Fre quency

+5V

= 2V p-p

= 0V

TIME (ns)

/∆V

IN, cm

Ω

RF = RG = 200

6
5
4
3
2
1

0
–1
–2
–3

V

= 2.0V p-p

O, cm

–4
–5

CLOSED-LOOP GAIN (dB)

–6

10ns/DIV

04679-0-069

–7
–8
–9

10 100 1000

Figure 40. V

0

V
V

–10

–20

–30

–40

–50

CMRR (dB)

OCM

V

–60

Ω

04679-0-066

–70

–80

–90

1 10 100 500

O, cm

CMRR =∆V

OCM

VS = +5V

Frequency Response for Various Supplies

OCM

= 0.2V p-p

O, dm

Figure 41. V

100

VS = +5V

V

O, cm

V

=±5V VS =±5V

S

FREQUENCY (MHz)

/∆V

O, cm

FREQUENCY (MHz)

CMRR vs. Frequency

OCM

= 0.1V p-p

04679-0-038

04679-0-045

10

INPUT VOLTAGE NOISE (nV/ Hz)

1

10 100 1k 10k 100k 1M 10M 1G100M

FREQUENCY (Hz)

Figure 39. Input Voltage No ise vs. Frequency

04679-0-079

Rev. A | Page 14 of 24

10

NOISE (nV/ Hz)

OCM

V

1

10 100 1k 10k 100k 1M 10M 1G100M

Figure 42. V

FREQUENCY (Hz)

Voltage Noise vs. Frequency

OCM

04679-0-080

AD8139

0

R

= 1k

Ω

L, dm

PSRR =∆V

–10

–20

–30

–40

–50

–60

PSRR (dB)

–70

–80

–90

–100

1 10 100 500

O, dm

/∆V

S

–PSRR

+PSRR

FREQUENCY (MHz)

Figure 43. PSRR v s. Frequency

100

VS = +5V

04679-0-047

14

G = 2

12
10

8
6
4
2
0

–2

VOLTAGE (V)

–4
–6

–8
–10
–12
–14

0

V

O, dm

OUTPUT BALANCE =

–10

TIME (ns)

Figure 46. Overdrive Recovery

= 1V p-p

∆

V

/∆V

O, cm

2× V

O, dm

IN, dm

V

O, dm

50ns/DIV

04679-0-046

10

)

Ω

V

1

OUTPUT IMPEDANCE (

0.1

0.01

0.1 1 10 100 1000
FREQUENCY (MHz)

Figure 44. Single-Ended Output Impedance vs. Frequency

700
600
500
400
300
200
100

0

V

=±5V

S

–100
–200
–300
–400
–500
–600

SINGLE-ENDED OUTPUT SWING FROM RAIL (mV)

–700

100 1k 10k

VS = +5V

RESISTIVE LOAD (Ω)

VS+– V

VON– V

OP

S–

Figure 45. Output Saturation Voltage vs. Output Load

=±5V

S

04679-0-028

04679-0-068

–20

–30

–40

–50

OUTPUT BALANCE (dB)

–60

–70

–80

1 10 100 500

FREQUENCY (MHz)

Figure 47. Output Balance vs. Frequency

300

VS = ±5V
G = 1 (RF = RG = 200Ω)

= 1kΩ

R

L, dm

250

200

150

SWING FROM RAIL (mV)

OP

V

100

50

–40 120100806040200–20

VS+– V

OP

VON– V

TEMPERATURE (°C)

S–

Figure 48. Output Saturation Voltage vs. Temperature

04679-0-067

–50

–100

–150

–200

SWING FROM RAIL (mV)

ON

V

–250

04679-0-077

–300

Rev. A | Page 15 of 24

AD8139

3.0

(µA)

2.0

BIAS

I

1.5

I

BIAS

170

I

OS

1452.5

120

(nA)

OS

I

95

26

25

24

23

22

SUPPLY CURRENT (mA)

21

VS =±5V

VS = +5V

1.0
–40 –20 0 20 40 60 80 100 120

TEMPERATURE (°C)

Figure 49. Input Bias and Offset Current vs. Temperature

10

8

6

VS =±5V

4

2

0

–2

–4

INPUT BIAS CURRENT (µA)

–6

–8

–10

–5 –4 –3 –2 –1 0 1 2 3 4 5

V

ACM

(V)

V

= +5V

S

Figure 50. Input Bias Current vs.

Input Common-Mode Voltage

5

(V)

OUT, cm

V

4

3

2

1

0

–1

–2

–3

–4

–5

–5 543210–1–2–3–4

Figure 51. V

O, cm

vs. V

V

(V)

OCM

OCM

VS =±2.5V

Input Voltage

V

=±5V

S

70

04679-0-062

04679-0-073

04679-0-048

20

–40 –20 0 20 40 60 80 100 120

TEMPERATURE (°C)

Figure 52. Supply Current vs. Temperature

300

V

V

OS, dm

OS, cm

TEMPERATURE (°C)

250

200

(µV)

150

OS, dm

V

100

50

0

–40 –20 0 20 40 60 80 100 120

Figure 53. Offset Voltage vs. Temperature

50

COUNT = 350
MEAN = –50µV

45

STD DEV = 100µV

40

35

30

25

20

FREQUENCY

15

10

5

0

–500

–450

–400

–350

–300

–250

–200

Figure 54. V

–150

–50

–100

V

OS, dm

Distribution

OS, dm

0

50

(µV)

100

150

200

250

300

350

400

450

600

400

200

0

–200

–400

–600

500

04679-0-060

(µV)

OS, cm

V

04679-0-061

04679-0-071

Rev. A | Page 16 of 24

AD8139

1.7

1.6

1.5

1.4

1.3

(µA)

1.2

VOCM

I

1.1

1.0

0.9

0.8

0.7
–40 –20 0 20 40 60 80 100 120

Figure 55. V

TEMPERATURE (°C)

Bias Current vs. Temperature

OCM

04679-0-063

6

4

VS =±5V

–5 –4 –3 –2 –1 0 1 2 3 4 5

Figure 56. V

OCM

V

(V)

OCM

Bias Current vs. V

CURRENT (µA)

OCM

V

2

0

–2

–4

–6

V

= +5V

S

Input Voltage

OCM

04679-0-074

Rev. A | Page 17 of 24

AD8139

V

=

V

THEORY OF OPERATION

The AD8139 is a high speed, low noise differential amplifier
fabricated on the Analog Devices second generation eXtra Fast
Complementary Bipolar (XFCB) process. It is designed to
provide two closely balanced differential outputs in response to
either differential or single-ended input signals. Differential
gain is set by external resistors, similar to traditional voltage­feedback operational amplifiers. The common-mode level of the
output voltage is set by a voltage at the V
pendent of the input common-mode voltage. The AD8139 has
an H-bridge input stage for high slew rate, low noise, and low
distortion operation and rail-to-rail output stages that provide
maximum dynamic output range. This set of features allows for
convenient single-ended-to-differential conversion, a common
need to take advantage of modern high resolution ADCs with
differential inputs.

TYPICAL CONNECTION AND DEFINITION OF TERMS

Figure 57 shows a typical connection for the AD8139, using
matched external R
terminals of the AD8139, V
junctions. An external reference voltage applied to the V
terminal sets the output common-mode voltage. The two
output terminals, V
balanced fashion in response to an input signal.

networks. The differential input

F/RG

and VAN, are used as summing

AP

and VON, move in opposite directions in a

OP

C

F

pin and is inde-

OCM

OCM

balanced differential outputs of identical amplitude and exactly
180 degrees out of phase. The output balance performance does not
require tightly matched external components, nor does it require
that the feedback factors of each loop be equal to each other. Low
frequency output balance is limited ultimately by the mismatch
of an on-chip voltage divider, which is trimmed for optimum
performance.

Output balance is measured by placing a well matched resistor
divider across the differential voltage outputs and comparing
the signal at the divider’s midpoint with the magnitude of the
differential output. By this definition, output balance is equal to
the magnitude of the change in output common-mode voltage
divided by the magnitude of the change in output differential­mode voltage:

Δ

V

BalanceOutput

cmO,

= (3)

Δ

V

dmO,

The block diagram of the AD8139 in Figure 58 shows the
external differential feedback loop (R
differential input transconductance amplifier, G

networks and the

F/RG

DIFF

) and the
internal common-mode feedback loop (voltage divider across
V

and VON and the common-mode input transconductance

OP

amplifier, G
voltages at the summing junctions V

). The differential negative feedback drives the

CM

and VAP to be essentially

AN

equal to each other.

R

V

OCM

V

R

G

IP

R

G

IN

V

V

AP

AN

F

+

AD8139

–

R

F

C

F

V

ON

R

L, dm

V

OP

V

O, dm

–

+

04679-0-050

Figure 57. Typical Connection

The differential output voltage is defined as

(1)

VVV −=

dmO,

ONOP

Common-mode voltage is the average of two voltages. The
output common-mode voltage is defined as

VVV+

ONOP

=

cmO,

(2)

2

Output Balance

Output balance is a measure of how well VOP and VON are
matched in amplitude and how precisely they are 180 degrees
out of phase with each other. It is the internal common-mode
feedback loop that forces the signal component of the output
common-mode towards zero, resulting in the near perfectly

VV

(4)

APAN

The common-mode feedback loop drives the output common­mode voltage, sampled at the midpoint of the two 500 Ω resistors,
to equal the voltage set at the V

V

VV +=

OCMOP

dmO,

2

terminal. This ensures that

OCM

(5)

and

V

VV −=

OCMON

R

G

IN

V

AN

V

AP

V

IP

R

G

dmO,

(6)

2

+

G

DIFF

MIDSUPPLY

+

Figure 58. Block Diagram

10pF

G

G

G

10pF

R

F

O

CM

O

R

F

500Ω

500Ω

V

OP

V

OCM

V

ON

04679-0-051

Rev. A | Page 18 of 24

AD8139

−=−

===

APPLICATIONS

R

ESTIMATING NOISE, GAIN, AND BANDWIDTH
WITH MATCHED FEEDBACK NETWORKS

Estimating Output Noise Voltage

The total output noise is calculated as the root-sum-squared
total of several statistically independent sources. Since the
sources are statistically independent, the contributions of each
must be individually included in the root-sum-square calcula­tion. Table 6 lists recommended resistor values and estimates of
bandwidth and output differential voltage noise for various
closed-loop gains. For most applications, 1% resistors are
sufficient.

Table 6. Recommended Values of Gain-Setting Resistors and
Voltage Noise for Various Closed-Loop Gains

3 dB
Bandwidth

Gain RG (Ω) RF (Ω)

(MHz)

1 200 200 400 5.8
2 200 400 160 9.3
5 200 1 k 53 19.7
10 200 2 k 26 37

The differential output voltage noise contains contributions
from the AD8139’s input voltage noise and input current noise
as well as those from the external feedback networks.

The contribution from the input voltage noise spectral density
is computed as

Total Output
Noise (nV/√Hz)

The contribution from each

kTRnVo 44_ = (10)

F

Voltage Gain

The behavior of the node voltages of the single-ended-to­differential output topology can be deduced from the previous
definitions. Referring to Figure 57, (C
one can write

VV

IP

AP

R

G

R

⎡

==

VVV

OPAPAN

⎢
⎣

Solving the above two equations and setting VIP to Vi gives the
gain relationship for V

ONOP

O, dm/Vi

VVV ==−

dmO,

An inverting configuration with the same gain magnitude can
be implemented by simply applying the input signal to V
setting V

V

IN, dm

= 0. For a balanced differential input, the gain from

IP

to V

is also equal to RF/RG, where V

O, dm

Feedback Factor Notation

When working with differential amplifiers, it is convenient to
introduce the feedback factor β, which is defined as

is computed as

F

= 0) and setting VIN = 0

F

VV

ONAP

(11)

F

R

⎤

G

(12)

⎥

+

RR

F

G

⎦

.

R

F

V

(13)

i

R

G

and

IN

= VIP − VIN.

IN, dm

R

⎞

F

+=

, or equivalently, vn/β (7)

⎟

R

G

⎠

where

⎛

vVo_n 11

⎜

n

⎝

v

is defined as the input-referred differential voltage

n

noise. This equation is the same as that of traditional op amps.

The contribution from the input current noise of each input is
computed as

()

RiVo_n =2 (8)

n

F

where

i

is defined as the input noise current of one input. Each

n

input needs to be treated separately since the two input currents
are statistically independent processes.

The contribution from each

=

kTRVo_n 43

R

is computed as

G

R

⎞

⎛

F

(9)

⎟

⎜

G

R

G

⎠

⎝

This result can be intuitively viewed as the thermal noise of
each

R

multiplied by the magnitude of the differential gain.

G

Rev. A | Page 19 of 24

R

G

=β (14)

RR

+

F

G

This notation is consistent with conventional feedback analysis
and is very useful, particularly when the two feedback loops are
not matched.

Input Common-Mode Voltage

The linear range of the VAN and VAP terminals extends to within
approximately 1 V of either supply rail. Since V

and VAP are

AN

essentially equal to each other, they are both equal to the ampli­fier’s input common-mode voltage. Their range is indicated in
the Specifications tables as input common-mode range. The
voltage at V

and VAP for the connection diagram in Figure 57

AN

can be expressed as

VVV

ACMAPAN

where

R

⎛

F

⎜

+

RR

F

⎝

G

V

is the common-mode voltage present at the

ACM

+

)(

×

INIP

2

RVV

⎞

⎛

G

+

⎟

⎜

+

RR

F

⎠

⎝

G

⎞

×

V

(15)

⎟

OCM

⎠

amplifier input terminals.

AD8139

(

)

β−+β

(

)

β

G

Using the β notation, Equation 15 can be written as

= 1 (16)

or equivalently,

+= (17)

V

where

ICM

is the common-mode voltage of the input signal, i.e.,

ICM

VVV+

INIP

=

.

2

For proper operation, the voltages at V
within their respective linear ranges.

Calculating Input Impedance

The input impedance of the circuit in Figure 57 will depend on
whether the amplifier is being driven by a single-ended or a
differential signal source. For balanced differential input signals,
the differential input impedance (

(18)

RR 2=

dmIN,

G

VVV

ICMOCMACM

VVVV −

ICMOCMICMACM

and VAP must stay

AN

R

) is simply

IN, dm

For a single-ended signal (for example, when V
and the input signal drives V

R

R

=

IN

G

R

1

F

−

RR

+

), the input impedance becomes

IP

(19)

)(2

F

is grounded

IN

The input impedance of a conventional inverting op amp
configuration is simply R

, but it is higher in Equation 19

G

because a fraction of the differential output voltage appears at
the summing junctions, V

and VAP. This voltage partially

AN

bootstraps the voltage across the input resistor RG, leading to
the increased input resistance.

Input Common-Mode Swing Considerations

In some single-ended-to-differential applications, when using a
single-supply voltage attention must be paid to the swing of the
input common-mode voltage, V

Consider the case in Figure 59, where
about a baseline at ground and

.

ACM

V

is 5 V p-p swinging

IN

V

is connected to ground.

REF

5V

+2.5V
GND
–2.5V

0.1µF 0.1µF 0.1µF

200Ω

V

OCM

2.5V

V

IN

V

REF

200Ω 324Ω

V

ACM

WITH V

REF

= 0

8

+

2

AD8139

1

–

324Ω

15Ω

3

5

4

6

+1.7V
+0.95V
+0.2V

15Ω

2.7nF

2.7nF

AVDD

IN–

IN+

DGND AGND REFGND REF REFBUFIN PDBUF

20Ω

DVDD

AD7674

0.1µF

Figure 59. AD8139 Driving AD7674, 18-Bit, 800 kSPS A/D Converter

47µF

ADR431

2.5V

REFERENCE

04679-0-052

Rev. A | Page 20 of 24

AD8139

0

×∆=

The circuit has a differential gain of 1.6 and β = 0.38. V

ICM

has
an amplitude of 2.5 V p-p and is swinging about ground. Using
the results in Equation 16, the common-mode voltage at the

V

AD8139’s inputs,
baseline of 0.95 V. The maximum negative excursion of

, is a 1.5 V p-p signal swinging about a

ACM

V

in

ACM

this case is 0.2 V, which exceeds the lower input common-mode
voltage limit.

One way to avoid the input common-mode swing limitation is
to bias V
swinging about a baseline at 2.5 V and V
low-Z 2.5 V source. V
is swinging about 2.5 V. Using the results in Equation 17, V
calculated to be equal to

V

ACM

and V

IN

at midsupply. In this case, VIN is 5 V p-p

REF

is connected to a

REF

now has an amplitude of 2.5 V p-p and

ICM

V

because V

ICM

OCM

= V

. Therefore,

ICM

swings from 1.25 V to 3.75 V, which is well within the

ACM

is

input common-mode voltage limits of the AD8139. Another
benefit seen in this example is that since

V

= V

= V

OCM

ACM

ICM

no
wasted common-mode current flows. Figure 60 illustrates how
to provide the low-Z bias voltage. For situations that do not
require a precise reference, a simple voltage divider will suffice
to develop the input voltage to the buffer.

5V

This estimate assumes a minimum 90 degree phase margin for
the amplifier loop, which is a condition approached for gains
greater than 4. Lower gains will show more bandwidth than
predicted by the equation due to the peaking produced by the
lower phase margin.

Estimating DC Errors

Primary differential output offset errors in the AD8139 are due
to three major components: the input offset voltage, the offset
between the V

and VAP input currents interacting with the

AN

feedback network resistances, and the offset produced by the dc
voltage difference between the input and output common-mode
voltages in conjunction with matching errors in the feedback
network.

The first output error component is calculated as

RR

+

⎞

F

G

, or equivalently as VIO/β (21)

⎟

R

G

⎠

where V

⎛

VeVo 1_

=

⎜

IO

⎝

is the input offset voltage. The input offset voltage of the

IO

AD8139 is laser trimmed and guaranteed to be less than 500 μV.

The second error is calculated as

V

V TO 5V

0.1µF

10µF

0.1µF

200Ω

V

IN

OCM

200Ω 324Ω

0.1µF

+

Figure 60. Low-Z 2.5 V Buffer

8

+

2

AD8139

1

–

AD8031

324Ω

3

5

4

6

5V

+

–

TO AD7674 REFBUFIN

ADR431

2.5V

REFERENCE

04679-0-053

Another way to avoid the input common-mode swing limita­tion is to use dual power supplies on the AD8139. In this case,
the biasing circuitry is not required.

Bandwidth Versus Closed-Loop Gain

The AD8139’s 3 dB bandwidth decreases proportionally to
increasing closed-loop gain in the same way as a traditional
voltage feedback operational amplifier. For closed-loop gains
greater than 4, the bandwidth obtained for a specific gain can be
estimated as

R

G

VdBf

=−

dmOUT

,

×

RR

+

F

G

)300(,3

MHz

(20)

or equivalently, β(300 MHz).

where I

+

RR

⎛

F

=2_

IeVo =

⎜

IO

⎝

is defined as the offset between the two input bias

IO

G

R

G

RR

⎞

⎛

⎟

⎜

⎠

⎝

⎞

F

G

+

RR

F

G

()

RI

⎟
⎠

(22)

F

IO

currents.

The third error voltage is calculated as

)(3_

VVenreVo −

(23)

OCMICM

where Δ

enr is the fractional mismatch between the two

feedback resistors.

The total differential offset error is the sum of these three error
sources.

Other Impact of Mismatches in the Feedback Networks

The internal common-mode feedback network will still force
the output voltages to remain balanced, even when the R

F/RG

feedback networks are mismatched. The mismatch will,
however, cause a gain error proportional to the feedback
network mismatch.

Ratio-matching errors in the external resistors will degrade the
ability to reject common-mode signals at the V

and VIN input

AN

terminals, much the same as with a four-resistor difference
amplifier made from a conventional op amp. Ratio-matching
errors will also produce a differential output component that is
equal to the V

input voltage times the difference between the

OCM

feedback factors (βs). In most applications using 1% resistors,
this component amounts to a differential dc offset at the output
that is small enough to be ignored.

Rev. A | Page 21 of 24

AD8139

Driving a Capacitive Load

A purely capacitive load will react with the bondwire and pin
inductance of the AD8139, resulting in high frequency ringing
in the transient response and loss of phase margin. One way to
minimize this effect is to place a small resistor in series with
each output to buffer the load capacitance, see Figure 6 and
Figure 61. The resistor and load capacitance will form a first­order low-pass filter; therefore, the resistor value should be as
small as possible. In some cases, the ADCs require small series
resistors to be added on their inputs.

5
4
3
2
1

0
–1
–2
–3
–4
–5
–6
–7
–8

CLOSED LOOP GAIN (dB)

–9

VS =±5V

–10

V

= 0.1V p-p

O, dm

–11

G = 1 (R

= RG = 200Ω)

–12
–13

10M 100M 1G

F

R

= 1kΩ

L, dm

Figure 61. Frequency Response for

Various Capacitive Load and Series Resistance

RS = 30.1Ω
C

= 15pF

L

R

= 60.4Ω

S

C

= 15pF

L

= 60.4Ω

R

S

C

= 5pF

L

FREQUENCY (MHz)

The Typical Performance Characteristics that illustrate transient
response versus the capacitive load were generated using series
resistors in each output and a differential capacitive load.

Layout Considerations

Standard high speed PCB layout practices should be adhered to
when designing with the AD8139. A solid ground plane is recom­mended and good wideband power supply decoupling networks
should be placed as close as possible to the supply pins.

To minimize stray capacitance at the summing nodes, the
copper in all layers under all traces and pads that connect to the
summing nodes should be removed. Small amounts of stray
summing-node capacitance will cause peaking in the frequency
response, and large amounts can cause instability. If some stray
summing-node capacitance is unavoidable, its effects can be
compensated for by placing small capacitors across the feedback
resistors.

Terminating a Single-Ended Input

Controlled impedance interconnections are used in most high
speed signal applications, and they require at least one line
termination. In analog applications, a matched resistive
termination is generally placed at the load end of the line. This
section deals with how to properly terminate a single-ended
input to the AD8139.

= 30.1Ω

R

S

C

= 5pF

L

R
C

= 0Ω

S
L, dm

= 0pF

04679-0-076

The input resistance presented by the AD8139 input circuitry is
seen in parallel with the termination resistor, and its loading
effect must be taken into account. The Thevenin equivalent
circuit of the driver, its source resistance, and the termination
resistance must all be included in the calculation as well. An
exact solution to the problem requires the solution of several
simultaneous algebraic equations and is beyond the scope of
this data sheet. An iterative solution is also possible and simpler,
especially considering the fact that standard 1% resistor values
are generally used.

Figure 62 shows the AD8139 in a unity-gain configuration
driving the AD6645, which is a 14-bit high speed ADC, and
with the following discussion, provides a good example of how
to provide a proper termination in a 50 Ω environment.

The termination resistor, R

, in parallel with the 268 Ω input

T

resistance of the AD8139 circuit (calculated using Equation 19),
yields an overall input resistance of 50 Ω that is seen by the
signal source. In order to have matched feedback loops, each
loop must have the same R

if they have the same RF. In the

G

input (upper) loop, RG is equal to the 200 Ω resistor in series
with the (+) input plus the parallel combination of RT and the
source resistance of 50 Ω. In the upper loop, RG is therefore
equal to 228 Ω. The closest standard 1% value to 228 Ω is 226 Ω
and is used for R

in the lower loop. Greater accuracy could be

G

achieved by using two resistors in series to obtain a resistance
closer to 228 Ω.

Things get more complicated when it comes to determining the
feedback resistor values. The amplitude of the signal source
generator V

is two times the amplitude of its output signal

S

when terminated in 50 Ω. Thus, a 2 V p-p terminated amplitude
is produced by a 4 V p-p amplitude from V
equivalent circuit of the signal source and R

. The Thevenin

S

must be used

T

when calculating the closed-loop gain because in the upper loop

is split between the 200 Ω resistor and the Thevenin resis-

R

G

tance looking back toward the source. The Thevenin voltage of
the signal source is greater than the signal source output voltage
when terminated in 50 Ω because R

must always be greater

T

than 50 Ω. In this case, it is 61.9 Ω and the Thevenin voltage
and resistance are 2.2 V p-p and 28 Ω, respectively. Now the
upper input branch can be viewed as a 2.2 V p-p source in series
with 228 Ω. Since this is a unity-gain application, a 2 V p-p
differential output is required, and R

must therefore be 228 ×

F

(2/2.2) = 206 Ω. The closest standard value to this is 205 Ω.

When generating the Typical Performance Characteristics data,
the measurements were calibrated to take the effects of the
terminations on closed-loop gain into account.

Rev. A | Page 22 of 24

AD8139

Since this is a single-ended-to-differential application on a
single supply, the input common-mode voltage swing must be
checked. From Figure 62, β = 0.52, V

1.1 V p-p swinging about ground. Using Equation 16,

= 2.4 V, and V

OCM

V

ICM

ACM

is

is
calculated to be 0.53 V p-p swinging about a baseline of 1.25 V,
and the minimum negative excursion is approximately 1 V.

Exposed Paddle (EP)

The SOIC-8 and LFCSP packages have an exposed paddle on
the underside of its body. In order to achieve the specified
thermal resistance, it must have a good thermal connection to one
of the PCB planes. The exposed paddle must be soldered to a pad
on top of the board that is connected to an inner plane with several
thermal vias.

5V 3.3V

0.01µF
205Ω 25Ω

2V p-p

50Ω

V

S

SIGNAL
SOURCE

R

61.9Ω

200Ω

V

T

OCM

226Ω

2.4V

Figure 62. AD8139 Driving AD6645,

3

8

+

2

AD8139

1

–

6

5

4

205Ω

25Ω

14-Bit, 80 MSPS/105 MSPS A/D Converter

AIN

AIN

AV

GND C1

0.01µF 0.01µF

CC

AD6645

C2 VREF

0.1µF

0.1µF

DV

CC

04679-0-054

Rev. A | Page 23 of 24

AD8139

Y

R

OUTLINE DIMENSIONS

4.00 (0.157)

3.90 (0.154)

3.80 (0.150)

5.00 (0.197)

4.90 (0.193)

4.80 (0.189)

85

TOP VIEW

41

6.20 (0.244)

6.00 (0.236)

5.80 (0.228)

BOTTOM VIEW

(PINS UP)

2.29 (0.092)

2.29 (0.092)

1.27 (0.05)
BSC

0.25 (0.0098)

0.10 (0.0039)

COPLANARIT

0.10

CONTROLLING DIMENSIONS ARE IN MILLIMETERS; INCH DIMENSIONS
(IN PARENTHESES) ARE ROUNDED-OFF MILLIMETER EQUIVALENTS FOR
REFERENCE ONLY AND ARE NOT APPROPRIATE FOR USE IN DESIGN

SEATING

PLANE

COMPLIANT TO JEDEC STANDARDS MS-012

1.75 (0.069)

1.35 (0.053)

0.51 (0.020)

0.31 (0.012)

0.25 (0.0098)

0.17 (0.0068)

0.50 (0.020)

0.25 (0.010)

8°

1.27 (0.050)

0°

0.40 (0.016)

× 45°

Figure 63. 8-Lead Standard Small Outline Package with Exposed Pad [SOIC/EP], Narrow Body (RD-8-1)—Dimensions shown in millimeters and (inches)

0.50

0.40

PAD

0.30

4

1

1.60

1.45

1.30

1.50
REF

PIN 1
INDICATOR

1.90

1.75

1.60

PIN 1

INDICATO

0.90

0.85

0.80

SEATING

PLANE

12° MAX

3.00

BSC SQ

TOP

VIEW

0.30

0.23

0.18

0.80 MAX

0.65TYP

2.75

BSC SQ

0.20 REF

0.05 MAX

0.02 NOM

0.45

0.50

BSC

0.60 MAX

0.25
MIN

8

EXPOSED

(BOTTOMVIEW)

5

Figure 64. 8-Lead Lead Frame Chip Scale Package [LFCSP], 3 mm × 3 mm Body (CP-8-2)—Dimensions shown in millimeters

ORDERING GUIDE

Model Temperature Range Package Description Package Option Branding

AD8139ARD –40°C to +125°C 8-Lead Small Outline Package (SOIC) RD-8-1
AD8139ARD-REEL –40°C to +125°C 8-Lead Small Outline Package (SOIC) RD-8-1
AD8139ARD-REEL7 –40°C to +125°C 8-Lead Small Outline Package (SOIC) RD-8-1

AD8139ARDZ
AD8139ARDZ-REEL1 –40°C to +125°C 8-Lead Small Outline Package (SOIC) RD-8-1
AD8139ARDZ-REEL71 –40°C to +125°C 8-Lead Small Outline Package (SOIC) RD-8-1
AD8139ACP-R2 –40°C to +125°C 8-Lead Lead Frame Chip Scale Package (LFCSP) CP-8-2 HEB
AD8139ACP-REEL –40°C to +125°C 8-Lead Lead Frame Chip Scale Package (LFCSP) CP-8-2 HEB
AD8139ACP-REEL7 –40°C to +125°C 8-Lead Lead Frame Chip Scale Package (LFCSP) CP-8-2 HEB
AD8139ACPZ-R21 –40°C to +125°C 8-Lead Lead Frame Chip Scale Package (LFCSP) CP-8-2 HEB
AD8139ACPZ-REEL1 –40°C to +125°C 8-Lead Lead Frame Chip Scale Package (LFCSP) CP-8-2 HEB
AD8139ACPZ-REEL71 –40°C to +125°C 8-Lead Lead Frame Chip Scale Package (LFCSP) CP-8-2 HEB

1

Z = Pb-free part.

© 2004 Analog Devices, Inc. All rights reserved. Trademarks and regis­tered trademarks are the property of their respective owners.

D04679–0–8/04(A)

1

–40°C to +125°C 8-Lead Small Outline Package (SOIC) RD-8-1

Rev. A | Page 24 of 24