Danfoss Hydraulic Fan Drive Systems Application guide

Download

Design Guidelines

Hydraulic Fan Drive Systems

www.danfoss.com

Design Guidelines

Hydraulic Fan Drive Systems

Revision history Table of revisions

Date Changed Rev

January 2020 Updated Appendix H with new graphs for all frame sizes 0401

July 2018 Appendix H - new graphs for some frame sizes 0303

May 2018 add notes: H1 pumps with fan drive control 0302

April 2017 Updated Appendix H chapter 0301

July 2015 Danfoss layout - Add Appendix I - RDM Fan Drives 0201

2006 - 2013 Various changes. AA up to BC

2 | © Danfoss | January 2020 AB00000019en-000401

Design Guidelines

Hydraulic Fan Drive Systems

Introduction

Abstract................................................................................................................................................................................................5

Overview..............................................................................................................................................................................................5

Principles of Operation...................................................................................................................................................................5

Power Savings ...................................................................................................................................................................................6

Modulation Preferred Over on/off Fan Speed Control....................................................................................................... 6

Fan Drive Design

Design Considerations....................................................................................................................................................................7

Fan Drive Components

Fan Drive Element Selection........................................................................................................................................................ 8

Estimate of Maximum Input Torque to the Pump................................................................................................................8

System Design Parameters

Sizing.................................................................................................................................................................................................. 10

Sizing Equations............................................................................................................................................................................. 12

Equations.....................................................................................................................................................................................12

Variables.......................................................................................................................................................................................12

Axial Flow Fan Power Formula..................................................................................................................................................13

System Design Data Form...........................................................................................................................................................14

Engine details.............................................................................................................................................................................14

Power steering...........................................................................................................................................................................14

Fan information.........................................................................................................................................................................15

Control preference...................................................................................................................................................................15

Reservoir...................................................................................................................................................................................... 15

Fluid...............................................................................................................................................................................................16

Filtration.......................................................................................................................................................................................16

Technical Features.........................................................................................................................................................................17

Shaft Loads and Bearing Life......................................................................................................................................................17

Maximum Pump Speed............................................................................................................................................................... 17

Minimum Pump and Motor Speed..........................................................................................................................................17

Motor Starting Pressure (open circuit motors)....................................................................................................................17

Motor Free Run Pressure.............................................................................................................................................................17

Input Torque Ratings....................................................................................................................................................................18

Pump Drive Conditions................................................................................................................................................................18

Tapered Shaft and Hub Connections......................................................................................................................................18

Pump Suction..................................................................................................................................................................................18

Case Drain Pressure.......................................................................................................................................................................19

Filtration............................................................................................................................................................................................ 19

Operating Temperatures.............................................................................................................................................................19

Fluids.................................................................................................................................................................................................. 19

Mounting.......................................................................................................................................................................................... 20

Axial Thrust Motors....................................................................................................................................................................... 20

Piping................................................................................................................................................................................................. 21

Reservoir............................................................................................................................................................................................21

Cavitation and Aeration Damage.............................................................................................................................................21

Cooling...............................................................................................................................................................................................22

Pressure Protection and Ratings...............................................................................................................................................22

Bearing Life Expectancy...............................................................................................................................................................22

Glossary

Terminology.....................................................................................................................................................................................23

Appendix A-Fan Performance

Fans.....................................................................................................................................................................................................24

Fan Performance............................................................................................................................................................................24

Axial Thrust.......................................................................................................................................................................................25

Fan Laws............................................................................................................................................................................................26

Example 1.................................................................................................................................................................................... 28

Example 2.................................................................................................................................................................................... 28

Danfoss | January 2020 AB00000019en-000401 | 3

Design Guidelines

Hydraulic Fan Drive Systems

Contents

Example 3.................................................................................................................................................................................... 28

Example 4.................................................................................................................................................................................... 29

Appendix B-Fan Drive Sizing Equations

Fan Drive Sizing Equations and Derivations........................................................................................................................ 30

Hydraulic System Comparisons................................................................................................................................................32

Appendix C-Fan Drive Sizing Equations, using Variable Displacement Motors

Hydraulic Systems with 2 Position, Variable Displacement Motors, Equations and Derivations..................... 34

Spreadsheet to Calculate the Optimum Minimum Displacement for 2 Position Variable Motor.................... 35

Appendix D-Pressure change due to transient flow in a passage

Pressure Change due to Transient Flow in a Passage, Equations and Derivations................................................37

Appendix E-Influence of Bypass Valve Pressure Drop in Open Circuit Systems Appendix F1-Influence of temperature, pressure and relative humidity on specific weight of air

Influence of Temperature, Pressure and Relative Humidity on Specific Weight of Air........................................ 43

Appendix F2-Influence of Altitude on Atmospheric Pressure

Influence of Altitude on Atmospheric Pressure..................................................................................................................45

Appendix F3-Influence of generic altitude on atmospheric pressure

Influence of Generic Altitude on Atmospheric Pressure................................................................................................. 46

Appendix G-Influence of reversed fan rotation on system performance Appendix H-System considerations for H1 fan drives with reversed fan rotation

System Considerations for H1 Fan Drives with Reversed Fan Rotation.....................................................................54

Pressure Limiter Adjusting Procedure....................................................................................................................................54

Additional Information concerning the H1 Fan Drive Controller Option..................................................................55

FDC Start and End Current..........................................................................................................................................................55

Operating Envelope for H1 Pumps with Fan Drive Control............................................................................................56

Sensitivity to Prime Mover Speed Changes (Load Sensitivity) - (J Frame as example).........................................63

H1 FDC Response Time (with Typical Fan Drive System Loading)...............................................................................66

Application startup method (to account for PL offset).................................................................................................... 66

Appendix I-System Considerations for RDM Fan Drives

System Considerations for RDM Fan Drives.........................................................................................................................68

Reversing Sequence................................................................................................................................................................ 68

Shift Rate Control......................................................................................................................................................................69

System Considerations...........................................................................................................................................................71

Zero RPM Motor Output.........................................................................................................................................................75

Reference Literature

Open Circuit Axial Piston Pumps..............................................................................................................................................76

Open/Closed Circuit Axial Piston Motors..............................................................................................................................76

Controllers........................................................................................................................................................................................ 76

System Guidelines......................................................................................................................................................................... 76

Closed Circuit Axial Piston Pumps........................................................................................................................................... 76

4 | © Danfoss | January 2020 AB00000019en-000401

205

200

400

600

800

1000

1200

1400

1600

1800

2000

170(F) 175 180 185 190 195 200

an speed (rpm)

Engine temperatur e

9580(C) 85 90

P101 276E

Design Guidelines

Hydraulic Fan Drive Systems

Introduction

Abstract

Fan drive system sizing relies heavily on the input received from the customer. All system sizing calculations are based on the required fan power @ trim speed data given to the hydraulic system design engineer. This data is a statement of the fan drive motor shaft power that is required to turn a fan at the required speed to push, or pull, a required volume of air across coolers/radiators. The usual sequence of events is:

•

Overview

One goal of this document is to provide the reader with the equations and formulae needed to size a hydraulic fan drive, given that they are provided with the following information:

•

The engine manufacturer advises the customer, or cooling system designer, of the heat dissipation required from the cooling system, charge air cooler etc. This information is combined with the heat rejection data for any accessories and work functions on the machine (such as : transmission cooler, hydraulic cooler, and A/C condenser) to determine the maximum heat rejection profile for the system.

The customer’s cooling pack manufacturer uses this data to size the cooling package and generally recommends a fan to suit this need, providing the rated fan power, rated fan speed, and the fan speed and static pressure required to satisfy the cooling needs of the system.

With this information, knowing the minimum engine speed at which maximum fan speed needs to occur, the hydraulic system designer can size the hydraulic fan drive system.

Rated fan power. Rated fan speed. Fan speed required to meet the maximum cooling needs of the cooling system. Engine speed at which maximum system cooling is required.

This document also provides an explanation of the terms and factors used in the derivation of the sizing equations. In addition, the reader is provided with recommendations of simple system design solutions that will help provide a viable system with satisfactory performance.

Principles of Operation

The vehicle’s cooling fan is driven by a hydraulic motor, which in turn, is driven by a hydraulic pump. The hydraulic pump can be driven directly off of the engine supplied PTO (Power Take Off), or with a belt drive. An electrically controlled proportional pressure control valve modulates the fan speed depending on a temperature reading. In a cold condition, the fan idles with very low power consumption. During the hot condition, the maximum fan speed is controlled by a pressure control valve, which adjusts the fan speed to meet the cooling needs of the total system. Every system has a temperature, which allows for the most efficient performance. The electronic control system, attempts to maintain the coolant at the optimum design temperature, which the “system integrator” selects during the design phase of the project.

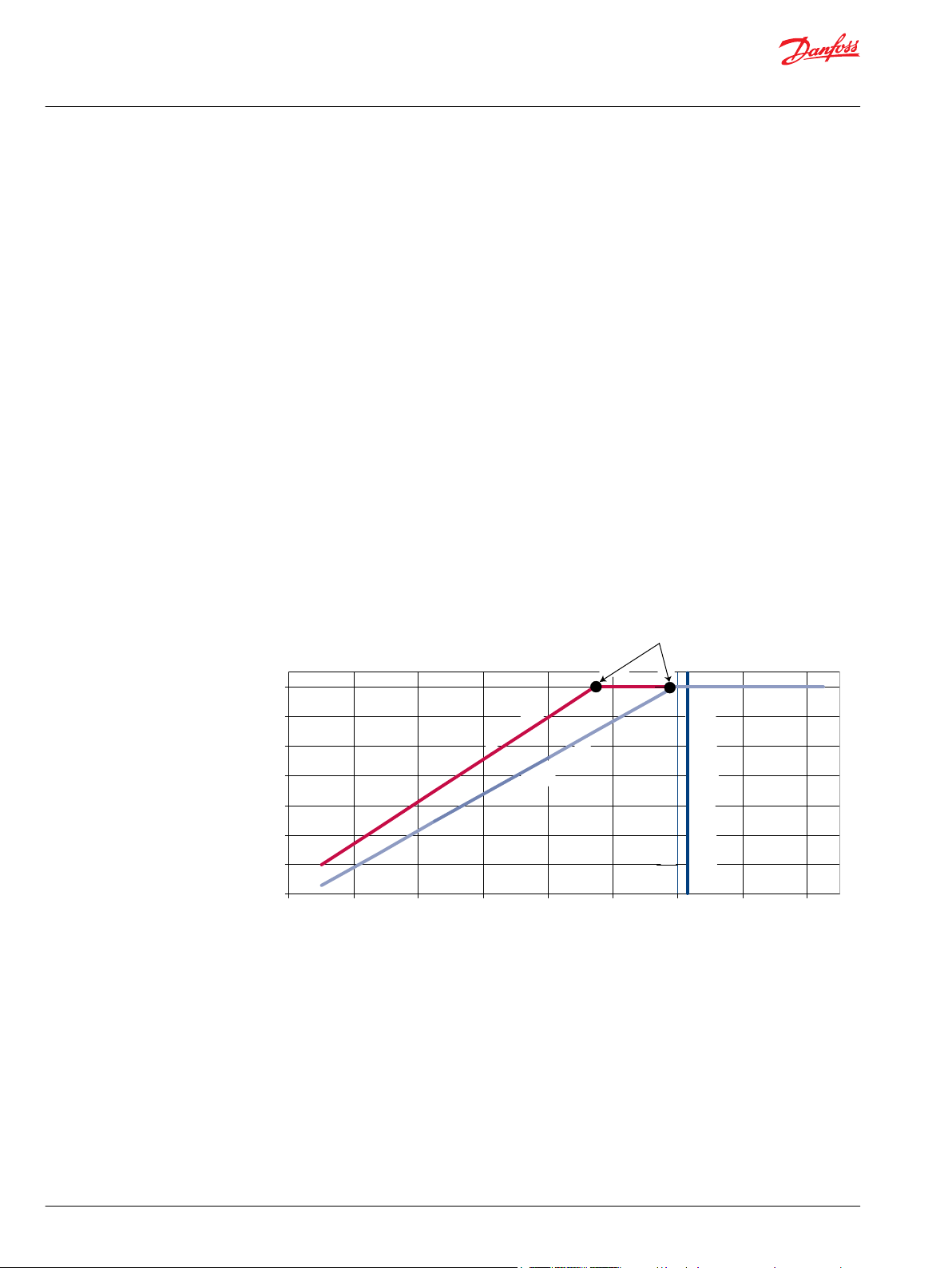
Fan speed vs engine temperature

To optimize the cooling system operation in various environmental conditions and to minimize parasitic losses, the Danfoss modulating fan drive system enables the fan cycle to be designed to specific heat

Danfoss | January 2020 AB00000019en-000401 | 5

Design Guidelines

Hydraulic Fan Drive Systems

Introduction

rejection requirements for a wide range of environmental conditions. Vehicle manufacturers have complete control of the fan cycle by choosing the appropriate temperature limits.

The Danfoss modulating fan drive system remains at idle speed until conditions require increased fan speeds. By regulating the pressure drop across the hydraulic motor, modulation of fan speed occurs, and over-cooling is prevented.

Power Savings

In the fan off condition, the fan may idle at approximately 30% of rated speed, but it will only consume about 3% of rated power. The Danfoss modulating fan drive system allows the system designer to size the fan for the engine speed at which maximum heat rejection occurs. The fan speed will remain essentially constant at all higher engine speeds. Consequently, the fan will not require excessive parasitic losses as engine speed increases. In systems where the engine speed at maximum heat rejection is 80% of the governed speed, the power savings compared to over-speeding a mechanically driven fan can be as high as 95%.

Modulation Preferred Over on/off Fan Speed Control

Fan speed modulation occurs over a temperature range chosen by the system’s designer. This eliminates the sudden changes in speed that cause dramatic changes in noise levels. Similarly, large accelerations of components, which may limit the reliability for long-term operation, are eliminated. Modulation also allows intermediate levels of cooling without unnecessary cycling of the fan between minimum and maximum speed. The calibration temperature, operating range, and ramp times can be varied independently by the system designer to achieve the desired level of temperature control.

6 | © Danfoss | January 2020 AB00000019en-000401

Design Guidelines

Hydraulic Fan Drive Systems

Fan Drive Design

Design Considerations

•

Hydraulic fan drive system designers select components for unique combinations of engine, fan, and application parameters. Do not exchange/change fan system components indiscriminately. Design factors which determine the selection of the fan drive system for a particular engine, or vehicle, include:

•

Parasitic losses from excessive fan speed are high. Power consumed by a fan is proportional to fan speed cubed (speed3).

Heat rejection to the atmosphere does not increase linearly with engine speed. Overheating and/or over cooling the system will result in loss of efficiency and productivity. Overheating, and/or over cooling the engine can result in increased emissions to the environment. The proportion of operating time during which full fan speed (maximum fan power) is needed is

typically about 20% and can be as low as 5%. Mounting the fan directly to the engine requires large fan blade tip clearances due to normal engine

vibration and movement. This leads to loss of fan performance. Mounting the fan directly to a hydraulic motor can minimize tip clearance and boost fan performance significantly.

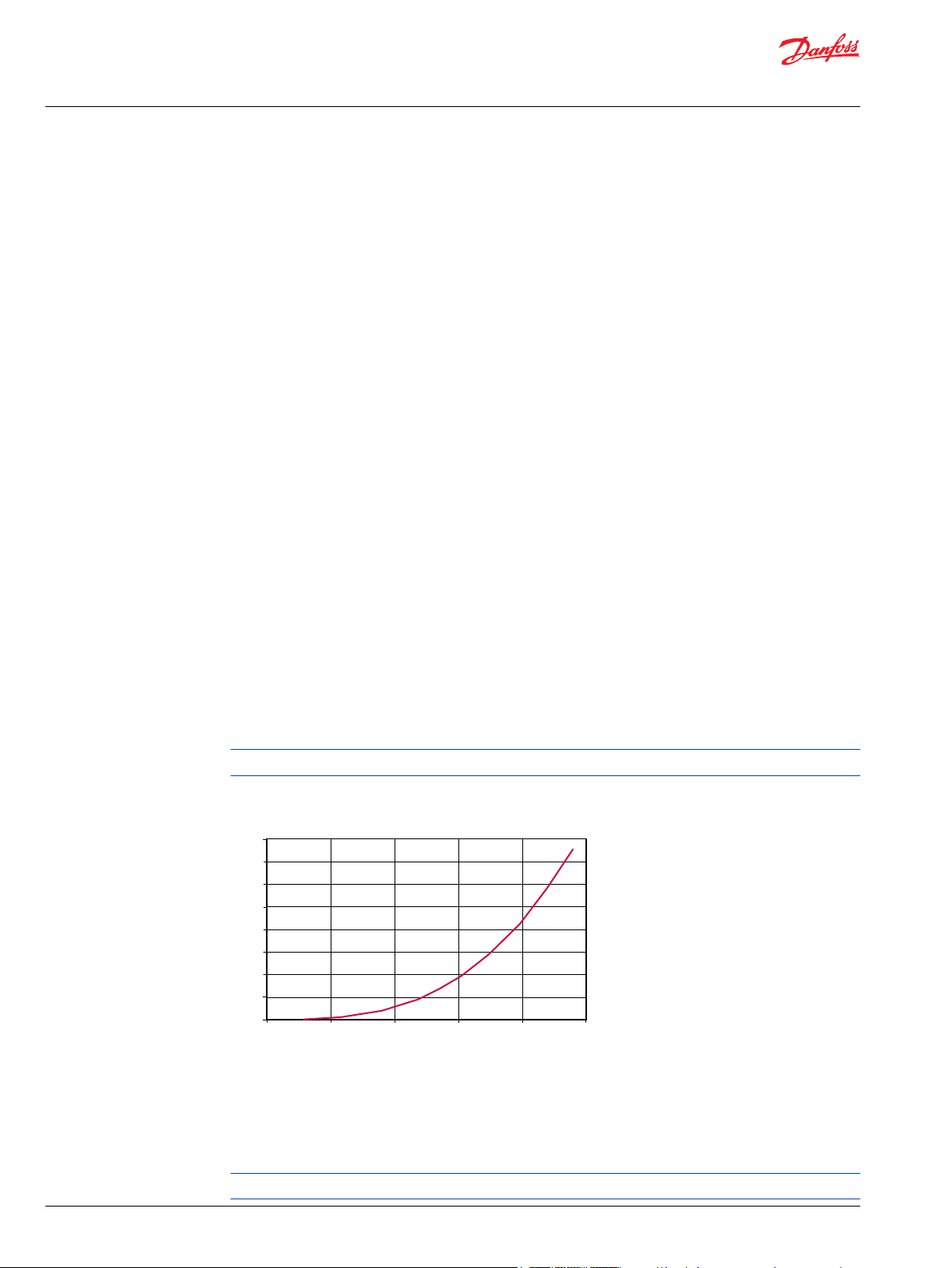
Engine set point and maximum heat rejection Pump rotation Pump input torque limitations Maximum applied pressure and speed limits for the individual components Fit-up and available installation space Pump support structure requirements for individual engine mounting combinations Specific engine and accessory temperature control limits

Fan drive element selection

Fan drive Element Design parameter Design flexibility Design champion

Engine & accessories Power, speed, total heat rejection and duty cycle Yes OEM PTO & Gearing Engine to pump gear ratio Sometimes OEM’s choice of engine

supplier

Pump(s) Displacement, pressure, speed, fixed pump or variable pump, mounting

& drive line

Fan drive control Sensor input(s), control output, number of control elements Yes Danfoss technical

Motor(s) Displacement, pressure, speed, fixed motor or variable motor, mounting

& coupling

Fan(s) Fan rated power @ rated speed, fan diameter, number of blades, blade

pitch, proximity of blades to heat exchanger, direction of air flow

Shroud(s) Type of shroud (flat plate, short duct, venturi), blade axial position in

shroud, tip clearance

Air flow stream(s) Air flow rate & static pressure across heat exchanger(s), maximum

ambient air temperature, minimum atmospheric pressure, hot air recirculation, baffles, louvres & obstructions

Heat exchangers Physical size, height & width, number of heat exchangers in air flow

stream, side-by-side, axial stack, materials selected, construction, number and types of tubes, tube configuration, fin density

Yes Danfoss technical

representative, & OEM

Yes Danfoss technical

representative, & OEM

Yes OEM & cooling specialists

Sometimes OEM & cooling specialists

Yes OEM & cooling specialists

Danfoss | January 2020 AB00000019en-000401 | 7

Engine speed (rpm )

n S

peed

pm)

Engine set point

800

1000

1200

1400

1600

1800

2000

2200

600 800 1000 1200 1400 1600 1800 2000 2200

Ma x

e n g i

n e

h e a t r

e j

e c t

o n

pe e

P106 107E

(Fan Trim Speed)

Design Guidelines

Hydraulic Fan Drive Systems

Fan Drive Components

Fan Drive Element Selection

Optimizing the size of fan drive elements depends on selecting the correct components and gear ratios. By matching these components to the fan power requirements, the required unit sizes can be quickly determined. The pump and motor displacements, input gear ratios, engine set point, and pressure limits can be adjusted to provide some optimization of component size. Along with the sizing equations presented in this article, a Danfoss fan drive sizing computer tool is available to assist with sizing the hydraulic components.

Many modulating hydraulic fan drives rely on dedicated pumps to provide flow to the fan circuit for optimum sizing. Other circuits are available that provide additional flow for power assisted steering and other accessory systems. In these, and many other circuits, the sizing equations and fan drive sizing tool may still be used to select the required components. Note that the design limits for associated design elements are not identified in this article. They may be reviewed by referring to the Danfoss technical information for the components being considered. Machine designers should verify that all design parameters are met for all drive line components.

While the methods described in this article may be useful, they do not represent the only approach to sizing hydraulic components. Contact your Danfoss representative if questions of interpretation exist.

Collect the application sizing parameters as identified in the System Design Parameters chapter of this document. Pay particular attention to the minimum engine speed at which maximum heat rejection to the atmosphere is required. When sizing the pump for the application, the system designer should ensure that the engine set point under hot oil condition is less than the engine speed at which maximum heat rejection occurs. Failure to do this can result in a condition where the cooling system may not provide adequate cooling when maximum work loading and maximum ambient conditions occur simultaneously.

Sample graph, performance prediction will vary depending on choice of input parameters.

Estimate of Maximum Input Torque to the Pump

One of the first things that the systems designer should consider is whether the maximum pump torque needed will exceed the input torque limitation of the pump drive. One way to calculate this is to divide the fan power requirement by an estimate of the hydraulic system’s overall efficiency and then determine the input torque requirement at the pump speed that is equivalent to the maximum heat rejection speed of the engine.

Compare the estimated maximum input torque to the maximum available input torque at the pump drive; this will determine the design margin that is available to the designer. The hydraulic system designer should consult with the vehicle system’s designer, and/or the prime mover’s technical support staff for assistance, if required.

8 | © Danfoss | January 2020 AB00000019en-000401

English system

SI system

Pump torque, Tp

(lbf•in)

≈ (lbf • in)

Pfhp

0.7

•

(Ne • R)

(63025)

( )

]

[

Pump torque, Tp

(N•m)

≈ (N•m)

PfkW

0.7

•

(Ne • R)

(9549.0)

(

)

]

[

Where: Pf

(Ne • R) R Ne

0.7

= Max fan power, kW [hp] = Pump speed, rpm = Pump/Engine ratio = Engine speed, rpm = ηt for hydraulic system (pump and motor)

(lbf•in)

8.8507

( )

Pump torque, Tp

(N•m)

= (N•m)

(lbf•in)

12.0

(

)

Pump torque, Tp

(lbf•ft)

= (lbf•ft)

(N•m)

0.7376 •

Pump torque, Tp

(lbf•ft)

= (lbf•ft)

(N•m)

8.8507

•Pump torque, Tp

(lbf•in)

= (lbf•in)

Converting terms

Design Guidelines

Hydraulic Fan Drive Systems

Fan Drive Components

Danfoss | January 2020 AB00000019en-000401 | 9

P106 108E

an power (kW

)

Fan speed (RPM)

40 35 30 25 20 15 10

5 0

500

1000

1500

2000

2500

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

Sizing

•

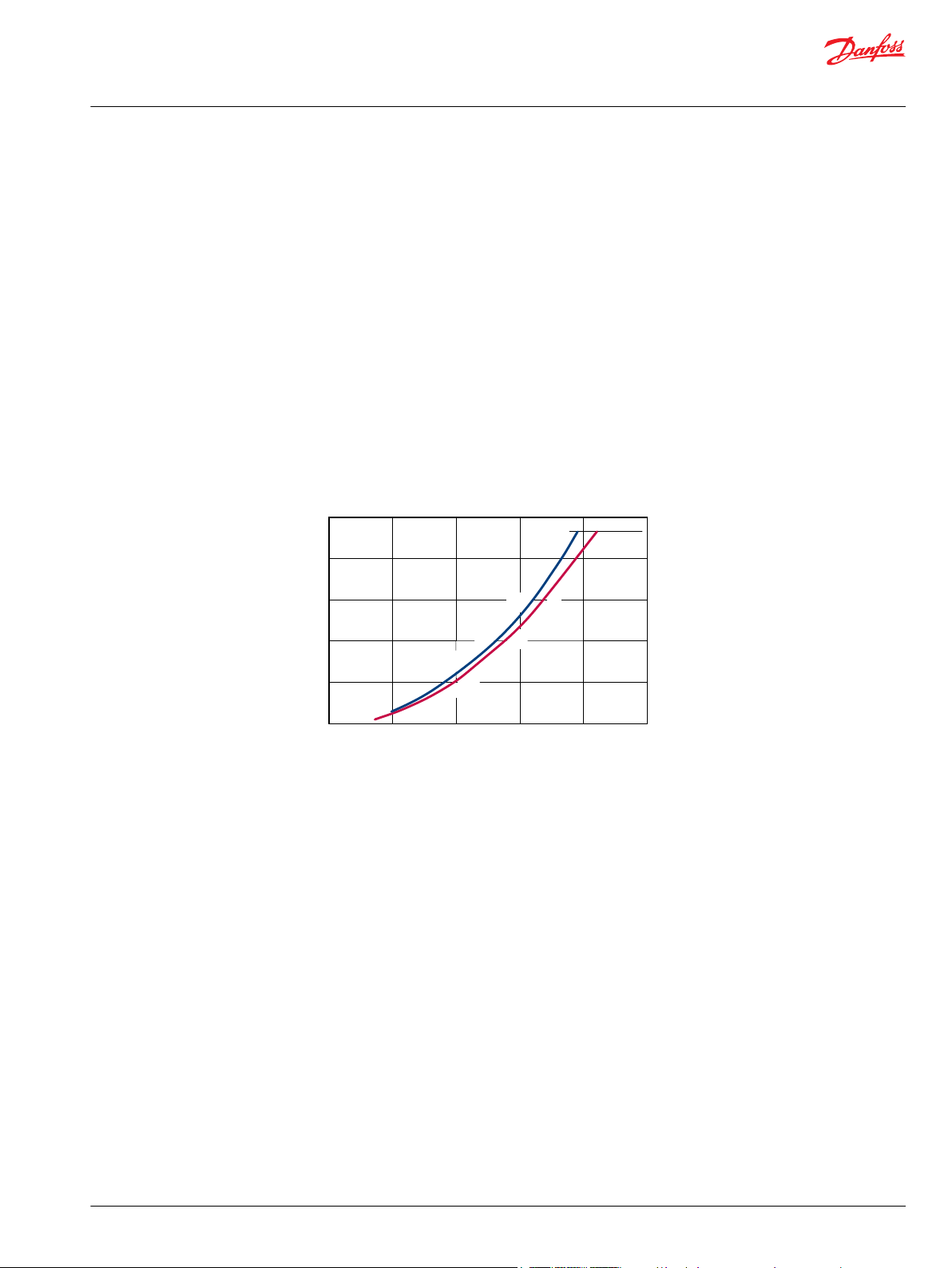
To completely understand any fan drive system is to understand the fan load characteristics. Fans are unique in that the power to drive the fan changes with the cube of the fan speed, as follows:

Pf=k•(Nf) Pf1 / Pf2 = (Nf1 / Nf2) Where: Pf = fan power (kW, hp) Nf = fan speed (rpm) 1,2 = subscripts for two different conditions k = Fan power coefficient Fan power is defined as the power required to drive the shaft connected to the fan and is equal to the

output power of the motor.

The customer’s cooling pack manufacturer will then use this data to size the cooling package and will generally recommend a fan to suit this need, providing the rated fan power, rated fan speed, and the fan speed required to satisfy the cooling needs of the system.

With this information, knowing the minimum engine speed at which maximum fan speed needs to occur, the hydraulic system designer can size the hydraulic fan drive system.

When a given fan speed is doubled; the required power to drive the fan increases by a factor of 8.

Fan power requirements (Example) Fan rating = 22 kW @ 2000 rpm

10 | © Danfoss | January 2020 AB00000019en-000401

Since fan power is a function of both pressure and flow (fan speed), it follows that the relationship between fan speed and system pressure is

∆P1 / ∆P2 = (Nf1 / Nf2 )

Where: ΔP = delta pressure across the hydraulic motor (bar, psid)

An accurate value of the fan rating is critical to the correct selection of components and their settings.

P106 109E

2500

2000

1500

1000

500

1000

1500

2000

2500

System pressure (psi)

System pressure (bar)

Fan speed min-1(rpm)

160 bar

2300 psi

120

150

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

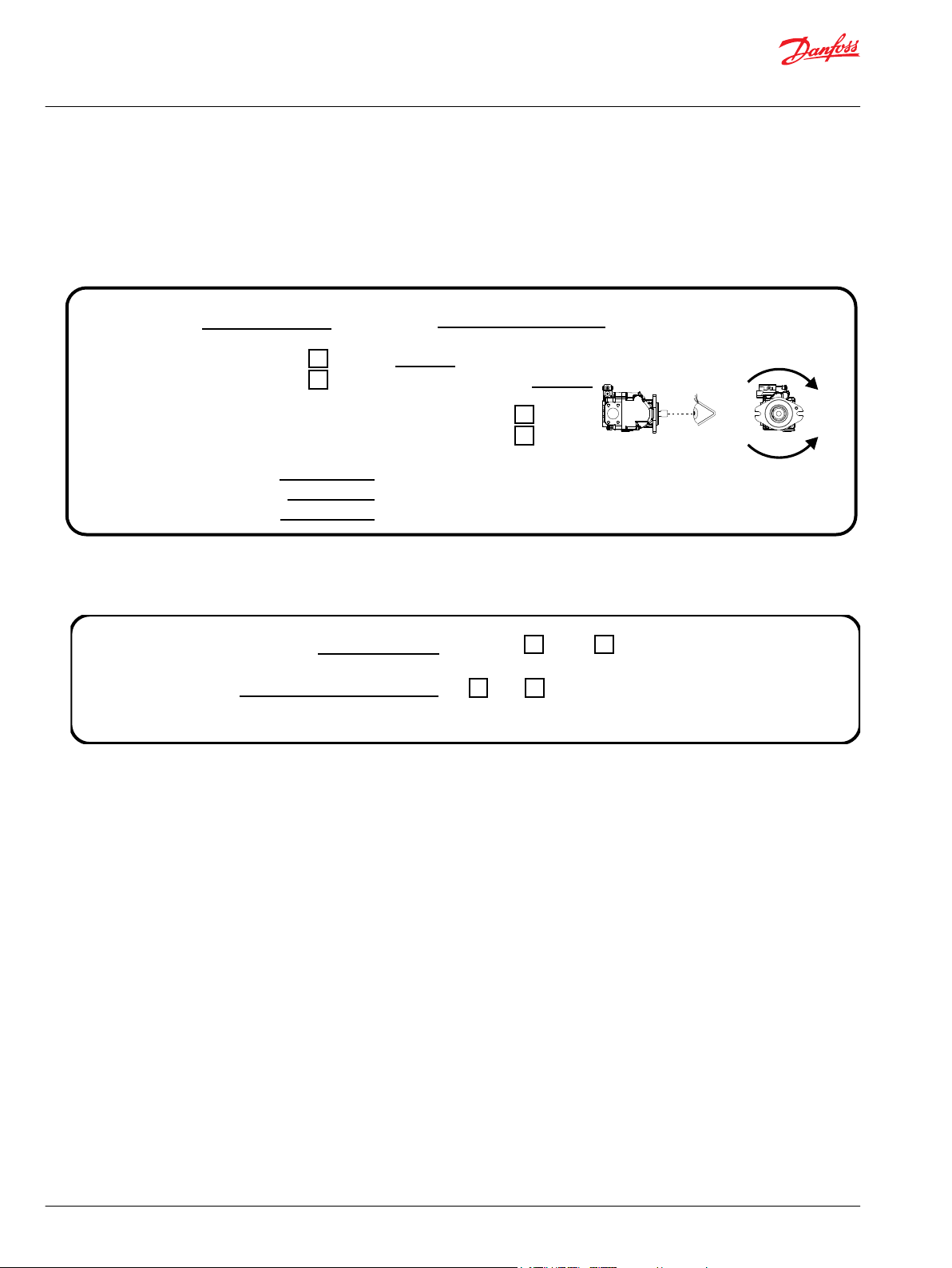
Although the cubic relationship between fan power and fan speed has been consistently verified experimentally, it is still an approximation of the fan behavior. Therefore, to avoid significant errors in predicting power requirements, the fan power rating should be taken at a speed representative of typical fan operation.

For example, for a system in which the fan usually operates in a speed range of 1800-2200 rpm, a fan rating specified at 2000 rpm will yield more accurate results than a rating specified at, say, 1500 or 2500 rpm.

Fan curves provided by the fan manufacturer are often developed under ideal conditions. It is unlikely that a fan will exhibit exactly the same performance in an actual application (because of: shrouding, heat exchange airflow characteristics, and air density). Only through test data taken on the actual vehicle can a fan’s performance characteristics be accurately determined. The curve below illustrates the differences between predicted performance and actual performance of a fan installed in a vehicle. The system designer/integrator is encouraged to confirm their performance predictions via test over the entire operating speed range of the engine, and to refine their prediction model with a revised fan power coefficient when they rerun the sizing calculations.

Fan power requirements (example) Fan rating = 22 kW @ 2000 rpm

Danfoss | January 2020 AB00000019en-000401 | 11

Based on SI units

= (l/min)

Input torque M = (N•m)

Input power P = (kW)

Motors

Based on SI units

Output torque M = (N•m)

Output power P = (kW)

Based on English units

= (US gal/min)

Input torque M = (lbf•in)

Input power P = (hp)

Based on English units

Output torque M = (lbf•in)

Output power P = (hp)

Vg • n • η

1000

Vg • ∆p

20 • π • η

Vg• n• ∆p 600 000 • η

Vg • n • η

231

Vg • ∆p

2 • π • η

Vg • ∆p • η

20 • π

Q • ∆p • ηt

600

Vg • ∆p • η

2 • π

Q • ∆p • η

1714

Pumps

Vg• n• ∆p

396 000 • η

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

Sizing Equations

Equations

Variables

SI units [English units]

Vg = Displacement per revolution cm3/rev [in3/rev] pO = Outlet pressure bar [psi] pi = Inlet pressure bar [psi] ∆p = pO - pi (system pressure) bar [psi] n = Speed min-1 (rpm) ηv = Volumetric efficiency ηm = Mechanical efficiency ηt = Overall efficiency (ηv • ηm)

SI unit formulas are based on cm3, bar, N, N•m, W. English formulas are based on in3, psi, lbf•in, hp.

12 | © Danfoss | January 2020 AB00000019en-000401

(N2)3 • (D2)5 • ν

(N1)3 • (D1)5 • ν

•

(

)

•

(

)

•

(

)

•

(

)

(

)

•

(

)

∆P

•

(

)

•

(

)

•

(

)

•

(

)

•

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

Axial Flow Fan Power Formula

Power to system parameter relationships

Pf1 = Power of fan at known condition #1 Pf2 = Power of fan at condition #2 N1 = Fan speed at condition #1 N2 = Fan speed at condition #2 D1 = Fan diameter at condition #1 D2 = Fan diameter at condition #2 ν1 = Specific weight of air at condition #1 ν2 = Specific weight of air at condition #2 r 1 = Density of air at condition #1 r 2 = Density of air at condition #2 ∆P1 = Hydraulic and/or Static Pressure at condition #1 ∆P2 = Hydraulic and/or Static Pressure at condition #2 V1 = Flow rate of air at condition #1 V2 = Flow rate of air at condition #2

Danfoss | January 2020 AB00000019en-000401 | 13

P106110

Model or Series

Belt Drive

(engine to pump)

Clockwise, Right hand Counterclockwise, Anti-clockwise, Left hand

Manufacturer

Pump Drive

Pump Rotation

Speeds

Engine PTO

Ratio

Low Idle Governed High Idle

RPM (rated) RPM (rated) RPM (max speed)

Input torque limit:

P104 376E

US gal/min

bar

(maximum)

Controlled Flow Requirement

Steering Pressure

psi

l/min

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

System Design Data Form

Print this form. Fill in all the fields and check the appropriate check boxes. Fax the filled out form to your Danfoss Power Solutions Technical Sales Representative.

Engine details

Power steering

(if applicable)

14 | © Danfoss | January 2020 AB00000019en-000401

P101 344E

Model or Series

Manufacturer

Fan Diameter

At speed

Fan Input Power

rpm

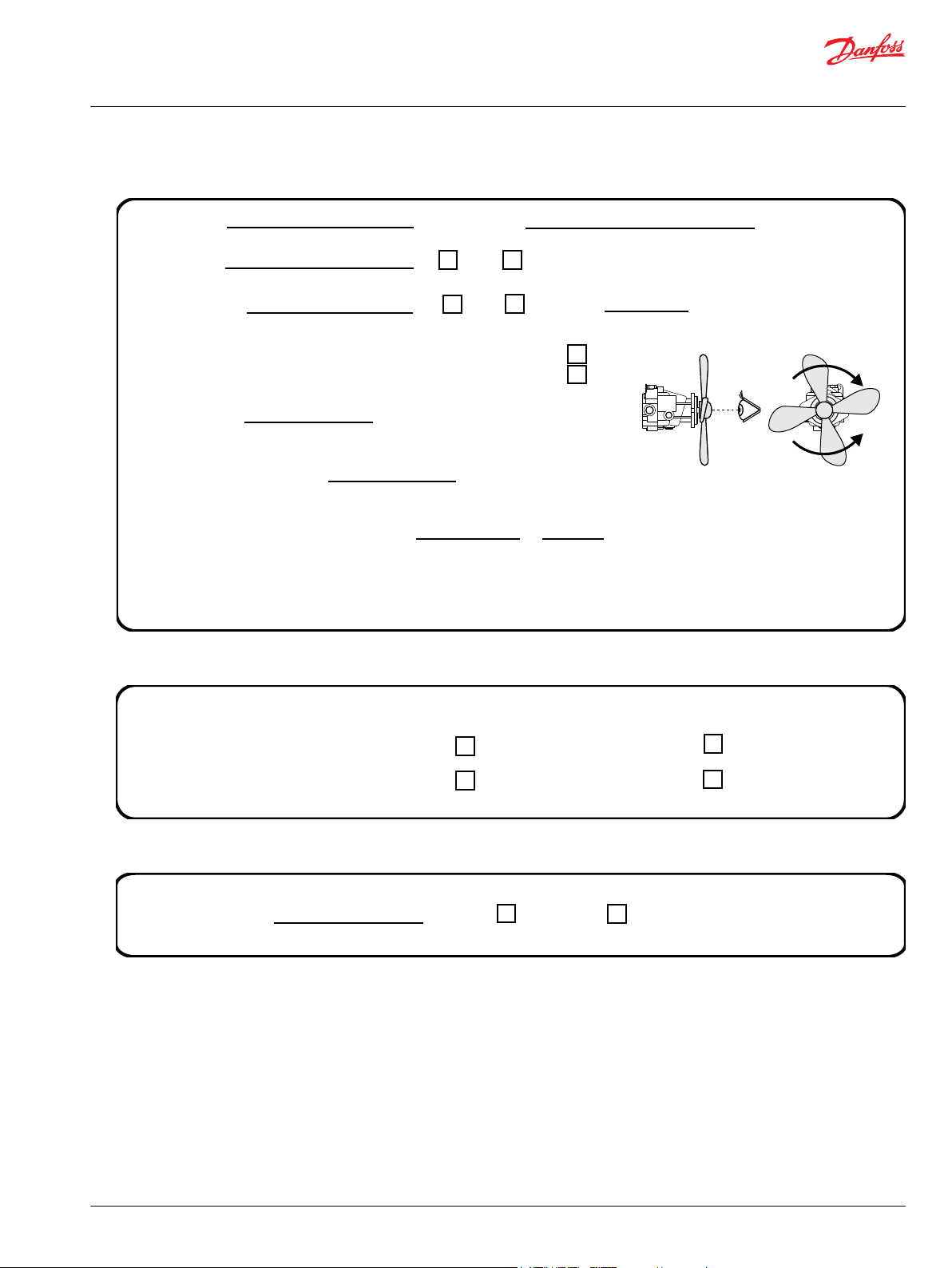
Fan Rotation

(viewed on motor shaft, see illustration)

Clockwise Counterclockwise

Fan Trim Speed

rpm

Set Point at Fan Trim Speed

(engine speed where max heat load occurs)

rpm

Coolant Temperature at Fan Trim Speed

(coolant temp where max fan speed is required)

°F

°C

Note: To properly size and specify a fan drive system, fan power requirements must be stated as accurately as possible. Fan power requirements can be determined from fan curves supplied by the manufacturer. Radiator and cooler manufacturers will supply air flow requirements based on heat loads. Air flow information must include accurate air flow and static pressure to determine correct fan power requirements.

P104 377E

Single Input

Electro-Hydraulic Modulating Electro-Hydraulic ON/OFF

Multiple Inputs

P104 378E

US gal

Reservoir Capacity

liter

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

Fan information

Control preference

Reservoir

Danfoss | January 2020 AB00000019en-000401 | 15

P104 379E

at 40° C [104°F]

Hydraulic Fluid Type

Viscosity

cSt

Maximum Fluid Temperature

°F

°C

SUS

at 100° C [212°F]

P104 380E

Inlet Line

Filter Position

Pressure Line

(recommended)

Return Line

Filter Rating

Full Flow

Filter Flow

Partial Flow

micron

x ratio

Note: Do not locate the filter cartridge inside the reservoir. This reduces the reservoir capacity and reduces the dwell time (the time the oil spends in the resrevoir). It also increases the potential for damage to the hydraulic components due to aeration of the oil.

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

Fluid

Filtration

16 | © Danfoss | January 2020 AB00000019en-000401

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

Technical Features

In this document, we introduce the equations that are used to size the components of a modulating fan drive system. In addition to these principles, there are several other factors to consider to ensure that the hydraulic system performs to expectations. Following are some considerations you are encouraged to address during the design phase.

Shaft Loads and Bearing Life

For information on shaft loads and bearing life, refer to:

•

Maximum Pump Speed

Pump displacement, and centrifugal filling of the pumping chambers, limit maximum pump speed. Unless otherwise specified, maximum rated pump speeds are based on operation at sea level with hydraulic fluids having a specific gravity of 0.9 and a viscosity of 58 SUS (9 cSt) at 180° F (80° C). Speed limits for a particular application depend on the absolute pressure and oil viscosity. Speed limits for individual products may be found in their respective technical information bulletins. Consult a Danfoss representative for operation outside of these published limits.

Series 45 Technical Information 520L0519 Series 40 Motors Technical Information 520L0636 Series 42 Pumps Technical Information 11022637 H1 Pumps Technical Information Manuals (see Reference Literature at the back of this manual)

Minimum Pump and Motor Speed

Volumetric efficiency limits minimum pump speed. If lower than recommended starting or operating speeds are required, contact a Danfoss representative for assistance. Piston motors are designed for continuous operation at low speed, and at rated pressure. Motors may be started from zero speed on fan drives, and torque will increase with speed.

Motor Starting Pressure (open circuit motors)

No-load motor start-up pressures may range from 100 to 725 psid (7 to 50 dbar), depending on displacement. This property of the motor is dependent on motor design parameters, the CSF (Coefficient of Static Friction), and it is inversely proportional to motor displacement. For example: The starting torque for any given motor is largely dependent on the pitch diameter of the pistons and the CSF. Since torque is dependent on the product of pressure and displacement, and starting torque is essentially constant for any given frame size; starting pressure will be dependent on displacement, in an inverse relationship. To minimize starting pressure, select the smallest frame size for the required motor displacement.

Besides displacement, there are several factors which also effect motor starting pressure. They include: pressure rise rate (pressure gradient), temperature, fluid viscosity, motor return pressure (back pressure), fan inertia, pump flow rate, and piece-to-piece variation between motors.

Motor Free Run Pressure

Free run pressure is the minimum delta pressure across the motor that is required to keep the motor

turning when there is no cooling demand. Free run pressure is dependent on motor displacement and shaft speed.

If the delta pressure across the motor is allowed to fall below the free run pressure; the motor will stop, and it will be necessary for the motor to go through the starting condition (start-up procedure) when cooling is needed again. In most applications, it is desirable to initiate fan rotation when the engine starts and prevent the motor from stopping, while the engine is running.

Danfoss | January 2020 AB00000019en-000401 | 17

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

Input Torque Ratings

When applying pumps in multiple configurations, ensure the input torque limitations are met for each section and for cumulative sections. Refer to individual product technical information bulletins for specific product torque limits. Always ensure that any individual pump in a multiple unit does not exceed its respective torque rating.

Torques in excess of recommended values may cause premature input shaft, or unit, failure.

Pump Drive Conditions

Most Danfoss products are available with SAE and metric, standard spline, tapered key, or cylindrical keyed drive shafts for direct or indirect drive applications. An intermediate coupling is the preferred method for direct drives, thereby eliminating radial and axial loading. Direct Drive (or plug-in or rigid) spline drives can impose severe radial loads on the pump shaft when the mating spline is rigidly supported. Increased spline clearance does not alleviate this condition. Both concentricity and angular alignment of shafts are important to pump life. Misalignment can induce excessive side loads on bearings and seals, causing premature failure.

Overhung load drives (chain, belt, or gear) are permissible. Contact Danfoss for assistance. The allowable radial shaft loads are a function of the load magnitude, the load position, the load orientation, and the operating pressure of the hydraulic pump. All external shaft loads will have an effect on bearing life and may affect pump performance. In applications where external shaft loads cannot be avoided; optimizing the position, orientation, and magnitude of the radial load can minimize their influence on the pump. A tapered input shaft is recommended for applications where radial shaft loads are present. (Spline shafts are not recommended for belt or gear drive applications, the clearance between the mating splines will prevent accurate alignment of the drive elements and will contribute to excessive wear of the spline.) For belt drive applications, a spring loaded belt-tensioning device is recommended to avoid excessive radial loads on the input shaft.

Caution

Note for H1 pump with an FDC: Due to the failsafe functionality of the H1P FDC control the pump will stroke to max. displacement in case the input signal to the pump control and the Diesel engine will be switched off at the same time. In this situation a low loop event can occur which may damage the pump. Therefore, it’s strictly recommended to keep the input signal to the pump control alive while switching off the engine.

For further information please contact your Danfoss representative

Tapered Shaft and Hub Connections

Tapered shaft/hub connections provide excellent control of both axial and radial position of the drive coupling or fan assembly. When using the tapered connection, additional effort should be used to insure that there is adequate axial clamping load between the hub and the shaft. The designer is encouraged to establish that there is:

Adequate clearance under the bolt/nut to insure full axial load may be applied to the taper without

•

bottoming out. Adequate clearance between the top of the key and the bottom of the keyway in the hub.

•

Interference between the top of the key and the bottom of the keyway will prevent the hub from seating onto the taper of the shaft. This will compromise the ability of the shaft to transmit its full torque capacity, and may result in failure of the shaft.

Pump Suction

For maximum pump life, the inlet pressure should not drop below 0.8 bar absolute [6 in. Hg vac.] at the pump inlet port.

For cold start conditions, inlet pressure down to 0.6 bar absolute [12 in. Hg vac.] is acceptable for short durations. The possibility of damage due to fluid cavitation and aeration is proportional to decreases in

18 | © Danfoss | January 2020 AB00000019en-000401

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

inlet pressure. In addition, oil film lubrication may be disrupted by low inlet pressure. These factors, either singularly or combined, may contribute to a decrease in pump life. Multiple changes in either diameter or direction can have a significant effect on the resistance to flow in inlet passages and can result in a substantial increase in the effective length of the inlet line. For this reason, Danfoss recommends that the inlet line contain a minimum number of adaptor fittings, tees, and elbows; as each are a source of additional restriction and, potentially, a source of leakage.

Continuous operation with inlet pressures below 0.8 bar absolute [6 in. Hg vac.] can cause premature unit failure. Ensure adequate flow/pressure head at the pump inlet at all times.

Case Drain Pressure

Maximum pressure limitations for both case drain and inlet passages are available by consulting the appropriate technical information bulletin for the products being applied. Both line length and diameter influence the pressure drop of the fluid in these passages as it flows to/from the reservoir. In addition, both steady state flow velocity and transient conditions, which can accelerate the fluid in these passages, must be considered when determining their correct size. Of the two design parameters: line length and diameter, diameter has the most influence on the success of the design. Increasing line diameter can decrease both the steady state and the transient pressure drops exponentially. For additional information on steady state pressure drops in hydraulic passages, the reader is encouraged to consult any good text on basic hydraulic design. For additional information on transient pressure drops, refer to Appendix D.

Introducing additional flow from external sources into these return lines can also result in transient pressure pulses that may exceed the drain, or case pressure limits of these products. Danfoss recommends that the bearing drain and case drain lines return directly to the reservoir and remain dedicated to their intended function without connecting them to additional flow sources.

Caution

Filtration

Operating Temperatures

Fluids

To prevent premature wear, it is imperative that only clean fluid enters the pump and hydraulic circuit. A filter capable of controlling the fluid cleanliness to class 22/18/13 (per ISO 4406-1999) or better, under normal operating conditions, is recommended. At initial start up, the system can be at Class 25/22/17 but should not be run at high speed or pressure until the Class 22/18/13 is achieved through filtration. Since the filter must be changed at regular intervals, the filter housing should be located in an accessible area. Appropriate filter change intervals may be determined by test or by gauges indicating excessive pressure drop across the filter element.

For more information refer to Design Guideline for Hydraulic Fluid Cleanliness, Technical Information 520L0467.

With Buna seals and normal operating conditions, the system temperature should not exceed 82 °C [180 °F] except for short periods to 93 °C [200 °F]. With optional Viton elastomer, the system may be operated at continuous temperatures up to 107°C [225°F] without damage to the hydraulic components.

Caution

Operation in excess of 107 °C [225 °F] may cause external leakage or premature unit failure.

A mineral based fluid is recommended that includes additives to resist corrosion, oxidation and foaming. The oil should have a maximum viscosity commensurate with system pressure drop and pump suction pressures. Since the fluid serves as a system lubricant, as well as transmitting power, careful selection of the fluid is important for proper operation and satisfactory life of the hydraulic components. Hydraulic

Danfoss | January 2020 AB00000019en-000401 | 19

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

fluids should be changed at appropriate intervals determined by test, supplier, or by change in color, or odor, of the fluid.

Every 10°C [18°F] rise in continuous reservoir temperature over 80°C [176 °F] decreases the life of the oil by ½.

For additional technical information on hydraulic fluids refer to Hydraulic Fluids and Lubricants 520L0463 Technical Information Bulletin and specific product technical bulletins.

For information relating to biodegradable fluids, see Danfoss publication Experience with Biodegradable

Hydraulic Fluids 520L0465 or consult the Danfoss Technical Services Department.

Mounting

The pump mount/drive should be designed to minimize axial and radial loads on the shaft. When using an indirect (chain, belt, or gear) drive, contact Danfoss to determine permissible load limits and orientation of the installation.

The motor mount should be designed to position the motor/fan assembly within the shroud for optimum fan performance and to locate the leading edge of the fan blades relative to the adjacent surface of the heat exchanger. The support structure should be constructed so that it will be robust against forces and deflections due to shock and vibration as well as the loads applied to it by the fan and the hydraulic plumbing that will be connected to the motor.

Axial Thrust Motors

When a fan is directly mounted onto the drive shaft of a hydraulic motor, it imparts both a radial and an axial thrust load onto the shaft. In general, the weight of the fan is insignificant when compared to the radial load capacity of the bearings in the motor. But, the axial thrust load must be considered carefully. Under normal operating conditions, Danfoss motors have adequate axial thrust capacity for most fans that are applied in the industry, but they do have limitations. It is recommended that the system designer determine the axial thrust force that will be produced by the fan and compare it to the values listed below:

Series 40 motors external shaft load limits

Unit M25 M35/44 M46

T N [lbf] 848 [190] 966 [217] 1078 [242]

N•m [lbf•in] 29 [256] 25 [221] 24 [212]

L and K motors external shaft load limits

Frame L K Mounting configuration SAE Cartridge SAE Cartridge Maximum allowable external moment (Me) N•m 7.7 21.7 13.3 37.5

[lbf•in] 68 192 118 332

Maximum allowable thrust load (T) N 750 1100

lbf 169 247

Refer to Appendix-A for equations that will assist in calculating the axial thrust loads from the fan. Calculated loads should be confirmed by test.

For shaft load limit calculations on Series 90 motors and H1B motors, contact your Danfoss representative.

20 | © Danfoss | January 2020 AB00000019en-000401

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

Piping

The choice of piping size and installation should always be consistent with minimizing maximum fluid velocity. This will reduce system noise, pressure drops and overheating, thereby adding to cost savings for the operation of the system. Inlet piping should be designed to prevent continuous pump inlet pressures below 0.8 bar abs. [6 in. Hg vac.] or 0.6 bar abs. [12 in. Hg vac.] during start-up. When selecting pipe sizing, recognize pressure drops are related to flow velocity. Danfoss recommends limiting the maximum average mean flow velocity to 5 m/sec [15 ft/sec.] in pressure lines, and 2.5 m/sec [7 ft/sec.] in suction lines.

In addition to limiting maximum flow velocity, it is recommended that the designer select the hoses, fittings and integral valve elements to be compatible with the desired working pressure of the hydraulic system. The following documents may be used to determine the working pressure ratings for the respective system elements:

•

SAE J514: for working pressure ratings and fitting installation torques for - O-ring boss fittings/ports and JIC 37º flared tubing connections

SAE J518: for working pressure ratings and bolt installation torques for SAE code 61 4-Bolt flange fittings/ports,

SAE J517: for working pressure ratings for SAE hydraulic hose SAE J1453: for working pressure ratings for flat face O-ring fittings.

Reservoir

The reservoir should be designed to accommodate expected maximum volume exchange during all system operating modes and to prevent aeration of the fluid as it passes through the reservoir. Return and inlet lines should be positioned below the reservoir low oil level and be located as far as possible from each other. A diffuser and a baffle plate located between the pump inlet and return line is desirable to reduce turbulence and to allow the oil to de-aerate before it re-enters the pump.

Reservoirs must be sized to ensure de-aeration of the oil before it re-enters the pump. For dwell times of less than 90 seconds, the system designer is encouraged to verify that entrained air (bubbles) are not included in the oil that is being transmitted from the reservoir to the pump. This may be accomplished by placing a sight gage into the inlet line between the reservoir and the pump. Placing a variable frequency strobe light source behind the sight gage will improve the observer’s ability to see air bubbles present in the fluid as it passes through the inlet line.

Danfoss encourages system designers to locate the reservoir so that the oil level in the reservoir will remain above the level of the inlet port of the pump under all conditions. By doing this, a positive head is produced that can offset the effects of line losses and altitude on the inlet pressure available at the pump.

Danfoss also encourages system designers to consider the potential for air to be introduced into the inlet line within the reservoir via the introduction of a vortex or whirlpool, between the surface of the oil and the inlet port. One way to discourage a vortex is to locate a baffle between the inlet passage, or suction strainer, and the surface of the oil. The system designer should consider the design parameters of size and position for the baffle to ensure that a vortex cannot form if the reservoir attitude is at its extremes, the oil level is at or below the minimum recommended capacity, or if sloshing occurs due to operation of the machine.

Cavitation and Aeration Damage

Hydraulic oil used in the majority of systems contains about 10% dissolved air by volume. This air, under certain conditions of vacuum within the system, is released from the oil causing air bubbles. These entrained air bubbles collapse if subjected to pressure, and this collapse creates erosion of the adjacent metal surfaces and degradation of the oil. Because of this, it becomes obvious that the greater the air content within the oil, or the greater the vacuum in the inlet line, the more severe will be the resultant damage. The main causes of over-aeration of the oil are air leaks, particularly on the inlet side of the pump, and flow line restrictions such as inadequate pipe sizes, elbow fittings and sudden changes in flow passage cross-sectional area. To avoid cavitation problems when using Danfoss pumps and motors, avoid defects in plumbing and construction, maintain pump inlet pressure and rated speed requirements, and ensure reservoir size and follow recommended guidelines.

Danfoss | January 2020 AB00000019en-000401 | 21

Design Guidelines

Hydraulic Fan Drive Systems

System Design Parameters

When entrained air entering the pump is pressurized at the pump outlet, it is forced into solution in the oil as the bubbles collapse. This super-saturated solution of dissolved air and oil will release its air when the pressure is released. Symptoms of this condition can be observed by oil / foam escaping from the fill port of the reservoir when the system is shut down.

Cooling

Depending on duty cycle and reservoir/line construction, an oil-cooler may be required. The oil-cooler size is based on typical power losses in the hydraulic circuit. The oil cooler is usually placed in the return line to the reservoir.

Pressure Protection and Ratings

The pump, as well as other system components, has pressure limitations. Thus a relief valve, or pressure limiting device, must be installed in the system, and its setting must be consistent with the product ratings. Refer to the relevant Danfoss technical bulletins for this information.

Failure to install a relief valve or over-pressure protection may result in premature unit failure.

Caution

Bearing Life Expectancy

All Danfoss piston pumps and motors utilize anti-friction, rolling element bearings, and journal bearings, which have an oil film maintained at all times between the bearing surfaces. If this oil film is sufficiently sustained through proper system maintenance and the product’s operating limits are adhered to, a long bearing life can be expected.

A B10 type life expectancy number is generally associated with rolling element bearings. Bearing life is a function of speed, system pressure, and other system parameters such as oil viscosity and oil cleanliness.

22 | © Danfoss | January 2020 AB00000019en-000401

Design Guidelines

Hydraulic Fan Drive Systems

Glossary

Terminology

Trim speed is the maximum fan speed required at the full-on condition. This is equal to, or greater than,

the fan speed required to meet the maximum cooling needs of the cooling system. Engine set point is the engine speed at which trim speed should occur, and is provided by the cooling

system designer. This is equal to, or less than, the engine speed at which maximum system cooling is required.

Fan power at trim is the power that needs to be generated at the motor shaft to drive the fan at trim speed.

Fan rating is the value by which different types of fans can be compared. Usually designated as X power @ Y rpm and equates back to an air volume (mass flow rate) that can be moved per minute at the Y rpm.

To assist with the sizing exercise, Danfoss has developed a sizing tool to perform the necessary calculations. Within the sizing tool, worksheets are provided for both fixed displacement pump/fixed displacement motor, and variable displacement pump/fixed displacement motor hydraulic systems. The sizing tool has been provided to your Danfoss representative.

Refer to the data sheets on pages in the System Design Parameters chapter. When the data on these sheets is complete, calculations can be made to determine the most suitable pump/motor/controller combination for the application based on:

•

Pump drive available (torque, shaft, mounting flange, overall space envelope) System pressure required Additional flow/pressure required from the pump, (for example: steering flow) Control type requested by the customer Limiting operating parameters of the fan drive family products Fit (space envelope)

Contact your Danfoss representative for a report of the performance prediction generated by the fan drive sizing tool.

For systems using axial piston pumps, refer to AE Note 2010-02 for sizing calculations. Contact your Danfoss representative for access to AE Note 2010-02.

Danfoss | January 2020 AB00000019en-000401 | 23

English system

Theoretical hp = [hp]

ft3

min

( )

•

(Total pressure, [in H20])

(6356)

Theoretical power = [watts]

sec

( )

•

(Total pressure, [Pa],

(1.0)

[

]

)

SI system

Design Guidelines

Hydraulic Fan Drive Systems

Appendix A-Fan Performance

Fans

Fans are generally divided into two classifications:

•

The typical axial flow fan is commonly referred to as a propeller fan, and is customarily used for free delivery, or against low resistance. They are usually mounted within a circular ring or shroud with a circular opening.

Fan Performance

Fan performance is a measure of volume, total pressure, static pressure, speed, power input, mechanical efficiency, and static efficiency, at a stated density. Some useful definitions are:

Volume delivered by a fan is the number of cubic feet of air per minute (or, cubic meters per second), expressed at fan inlet conditions.

Total pressure is the rise of pressure from fan inlet to fan outlet. Velocity pressure is the pressure corresponding to the average velocity, determined from the volume of

airflow at the fan outlet area. Static pressure is the total pressure diminished by the fan’s velocity pressure. Static pressure is a

measure of the fan’s performance and is reported by the fan manufacturer in their technical literature. Static pressure is also a measure of the resistance to the flow of air thru the heat exchanger.

Power output is expressed in horsepower (or, kilowatts) and is based on fan volume and fan total pressure.

Power input is expressed in horsepower (or, kilowatts) and is the measured power delivered to the fan shaft.

Mechanical efficiency of a fan is the ratio of power output to power input. Static efficiency of a fan is the mechanical efficiency multiplied by the ratio of static pressure to the total

pressure. The theoretical power required to move a quantity of air may be determined by the following formula:

Centrifugal or radial flow - in which the air flows radially thru the impeller within a scroll type of housing

Axial flow - in which the air flows axially thru the impeller within a cylinder or ring.

Pressure and power both vary with air density.

Fan efficiencies may be determined by the following formulae:

24 | © Danfoss | January 2020 AB00000019en-000401

English system

ft3

min

•

(Total pressure, [in H20])

(6356.0)

sec

•

(Total pressure, [Pa],

(Power input, [watts])

)

SI system

(Horsepower input)

(

)

[ ]

[

]

(

)

English system

ft3

min

•

(Static pressure, [in H20])

(6356.0)

sec

•

(Static pressure, [Pa],

(Power input, [watts])

N m2

)

SI system

(Horsepower input)

(

)

[ ]

( )

[ ]

English system

ft3

min

•

(Static pressure, [in H20])

(6356.0)

sec

•

(Static pressure, [Pa],

(Power input, [watts])

N m2

)

SI system

(Horsepower input)

(

)

[ ]

( )

[ ]

Design Guidelines

Hydraulic Fan Drive Systems

Appendix A-Fan Performance

Mechanical efficiency, based on total pressure is applicable for fans operating with high outlet velocity pressure relative to the static pressure, typical of centrifugal fans.

Axial Thrust

Static efficiency, based on static pressure is applicable to fans with high static pressure relative to the velocity pressure. Static pressure and static efficiency are used more often than mechanical efficiency and total pressure. When a fan operates against no resistance, the static efficiency becomes zero and is meaningless.

Total pressure = static pressure + velocity pressure Velocity pressure is proportional to air velocity.

Danfoss | January 2020 AB00000019en-000401 | 25

English system

Velocity pressure =

V =

min

4005

)2,

(

[in H20]

[

]

Velocity pressure =

Pa,

(V2 • )

SI system

V =

sec

= Density of air,

[

]

[

]

[ ]

English system

Axial thrust = , [N]

π • Total pressure • (Fan diameter)

SI system

Total pressure,

Pa,

Fan diameter, [m]

Axial thrust =

π • Total pressure • (Fan diameter)

Total pressure,

(27.68)•4

Fan diameter, [inches]

[in H20]

[

]

[

]

[

]

, [lbf ]

Design Guidelines

Hydraulic Fan Drive Systems

Appendix A-Fan Performance

Four inches H2O = 1000 Pa

Fan Laws

The performance characteristics of fans of all types follow certain laws, which are useful in predicting the effect upon performance of certain changes in the conditions of operation, or the size of the equipment due to limitations of space, power, and/or speed. In the following categories, Q = air flow, and Pres. = static, velocity, or total pressure. The categories pertaining to fan size apply only to fans, which are geometrically similar, i.e., those in which all of the dimensions are proportional to some linear dimension identified as size.

Variation in fan speed:

26 | © Danfoss | January 2020 AB00000019en-000401

Constant air density – Constant system

Q: Varies as fan speed

Pres: Varies as square of fan speed

Power: Varies as cube of fan speed

Variation in fan size: Constant tip speed – Constant air density Constant fan proportions – Fixed point of rating

Design Guidelines

Hydraulic Fan Drive Systems

Appendix A-Fan Performance

Q: Varies as square of fan diameter

Pres: Remains constant

rpm: Varies inversely as fan diameter

Power: Varies as square of fan diameter

Variation in fan size: At constant rpm – Constant air density Constant fan proportions – fixed Point of rating

Q: Varies as cube of fan diameter

Pres: Varies as square of fan diameter

Tip speed: Varies as fan diameter

Power Varies as fifth power of diameter

Variation in air density: (Refer to Appendix F) Constant volume – Constant system Fixed fan size – Constant fan speed

Q: Constant

Pres: Varies as density (SI), specific weight (English)

Power: Varies as density (SI), specific weight (English)

Variation in air density: (Refer to Appendix F) Constant pressure – Constant system Fixed fan size – Variable fan speed

Q: Varies inversely as square root of density (SI), specific weight (English)

Pres: Constant

rpm: Varies inversely as square root of density (SI), specific weight (English)

Power: Varies inversely as square root of density (SI), specific weight (English)

Variation in air density: (Refer to Appendix F) Constant weight of air – Constant system Fixed fan size – Variable fan speed

Q: Varies inversely as density (SI), specific weight (English)

Pres: Varies inversely as density (SI), specific weight (English)

rpm: Varies inversely as density (SI), specific weight (English)

Power: Varies inversely as square of density (SI), specific weight (English)

Fan laws at a glance

Variation in fan speed Variation in fan size Variation in air density

Fan laws Fan law #1 Fan law #2 Fan law #3 Fan law #4 Fan law #5 Fan law #6

Parameters Constant air density &

constant system

Q, Air volume, (flow rate) Varies as fan speed Varies as square of

Danfoss | January 2020 AB00000019en-000401 | 27

Constant tip speed & constant air density

Constant tip proportions & fixed point of rating

fan diameter

Constant rpm & constant air density

Constant fan proportions & fixed point of rating

Varies as cube of fan diameter

Constant volume & constant system

Fixed fan size & constant fan speed

Constant Varies

Constant pressure & constant system

Fixed fan size & variable fan speed

inversely as square root of density or specific weight

Constant weight of air & constant system

Fixed fan size & variable fan speed

Varies inversely as density or specific weight

Design Guidelines

Hydraulic Fan Drive Systems

Appendix A-Fan Performance

Fan laws at a glance (continued)

Variation in fan speed Variation in fan size Variation in air density

Fan laws Fan law #1 Fan law #2 Fan law #3 Fan law #4 Fan law #5 Fan law #6

Pressure Varies as square of fan

speed

rpm Constant Varies inversely as

Power Varies as cube of fan

speed

Tip Speed N/A N/A Varies as fan

Remains constant Varies as square of

fan diameter

Constant Constant Varies

fan diameter

Varies square of fan diameter

Varies as 5th power of diameter

diameter

Varies as density or specific weight

Varies as density or specific weight Varies inversely as 4th power of diameter

N/A

Constant Varies inversely as

density or specific weight

Varies inversely as inversely as square root of density or specific weight

Varies as inversely as square root of density or specific weight

density or specific

weight

Varies as inversely

as square of density

or specific weight

Example 1

A fan delivers 12,000 cfm at a static pressure of 1 in. H2O when operating at a speed of 400 rpm and requires an input of 4 hp. If in the same installation, 15,000 cfm are required, what will be the speed, static pressure, and power?

Using fan law 1: Speed = 400 * {15,000/12,000} = 500 rpm Static pressure = 1 * {500/400}2 = 1.56 in. H2O Power = 4 * {500/400}3 = 7.81 hp

Example 2

A fan delivers 12,000 cfm at 70 °F and normal barometric pressure (density = 0.075 lb per cubic foot) at a static pressure of 1 in. H2O when operating at 400 rpm, and requires 4 hp. If the air temperature is increased to 200 °F (density = 0.0602 lb per cubic foot) and the speed of the fan remains the same, what will be the static pressure and power?

Using fan law 4: Static pressure = 1 * {0.0602/0.075} = 0.80 in. H2O Power = 4 * {0.0602/0.075} = 3.20 hp

Example 3

If the speed of the fan in example 2 is increased to produce a static pressure of 1 in. H2O at 200 °F, as at 70 °F, what will be the speed, capacity, and static power?

Using fan law 5: Speed = 400 * SQRT {0.0705/0.0602} = 446 rpm Capacity = 12,000 * SQRT {0.075/0.0602} = 13,392 cfm (measured at 200°F) Power = 4 * SQRT {0.075/0.0602} = 4.46 hp

28 | © Danfoss | January 2020 AB00000019en-000401

Design Guidelines

Hydraulic Fan Drive Systems

Appendix A-Fan Performance

Example 4

If the speed of the fan in the previous examples is increased to deliver the same weight of air (same cooling capacity) at 200°F as at 70°F, what will be the speed, capacity, static pressure, and power?

Heat transfer is determined by the mass, or weight, of the air presented to the heat exchanger, or radiator.

Using fan law 6: Speed = 400 * {0.075/0.0602} = 498 rpm Capacity = 12,000 * {0.075/0.0602} = 14,945 cfm (measured at 200 F) Static Pressure = 1 * {0.075/0.0602} = 1.25 in. H2O Power = 4 * {0.075/0.0602}2 = 6.20 hp

The fan laws may be combined to give other overall values. One useful combination is the product of Laws 1 and 3, which gives the following relationships:

•

Capacity (flow rate of air) varies as the ratio of size cubed, times the ratio of the rpm. Pressure varies as the ratio of size squared, times the ratio of the rpm squared. Power varies as the ratio of the size to the fifth power, times the ratio of the rpm cubed.

Centrifugal fans produce pressure from two independent sources: from the centrifugal force created by rotating the enclosed air column, and from the kinetic energy imparted to the air by virtue of its velocity leaving the impeller. The energy imparted to the air depends on the velocities and is dependent on the curvature of the fan blades. Therefore, for fans with forward curved blades, the energy per pound of air rises rapidly with an increase of air delivery. For fans with backward curved blades, the energy per pound of air may decrease with air delivery (flow rate). For fans with straight blades, the energy per pound of air is roughly constant, regardless of air delivery (flow rate). A unique characteristic of centrifugal fans is that the maximum power required by the fan is found at maximum delivery. Or, otherwise stated, the minimum power required by the fan is found at zero delivery, or under stall conditions.

Axial-flow fans develop none of their static pressure by centrifugal force; all of the static pressure is derived from the change in velocity in passing thru the impeller and its conversion into static pressure. They are inherently high velocity fans and are very dependent on the shape of the blade. Since any particular shape of blade can only be correct for a narrow range of capacity at constant speed, the performance curves for individual fan blade shapes are unique and vary significantly from manufacturer, to manufacturer. To absorb energy, the air must be given a tangential motion in passing thru the impeller; as with the centrifugal fan, the pressure rises generally from free delivery to no delivery, but may drop significantly when the capacity decreases below a certain volume. The drop in pressure is indicative that a stall condition occurs and the blades cease to function in the normal manner.

Fan manufacturers generally agree that the tip clearance around the fan’s blades is significant and will contribute to the performance, delivery, and operating efficiency of the fan. Likewise, the type of shroud that surrounds the fan, the axial position of the fan within the shroud, and the clearance between the leading edge of the fan and the cooler can contribute significantly to the performance, operating efficiency, and noise of operation of the fan. The system designer is advised to consult with both the fan and cooler manufacturer for these specific design elements for the system under consideration.

Danfoss | January 2020 AB00000019en-000401 | 29

Pf = Rated fan power, [kW] Nr = Rated fan speed, [rpm] Nfr = Fan speed, [rpm]

1. Pf ≡ Cf • Nfr3 ≡ , [kW]

Tfr • Nfr

9549

2. Tfr = , [N•m]

∆P = Pressure drop across hydraulic motor, [bar]

∆P • Dm • ntm

20π

Tfr = Rated fan torque, [N•m]

Dm ≡ Motor displacement,

cm3

rev

Dm = (Motor displacement,

in3 rev

• (2.54

)

cm3

rev

rpm

3. Pf = , [kW]

(∆P • Nf • Dm • ηtm)

(20π •9549)

4. Qm =

Nf • Dm

(1000.0 • ηvm)

min

5. Nf • Dm =

(20π • 9549.0)

(∆P • ηtm)

min

(Cf • Nf3) •

6. Qm =

(20π •9549.0)

(∆P • ηtm • 1000 • ηvm)

(Cf • Nf3) •

min

Re-arranging #5. above,

7. Nf = , [rpm]

(600,000 • Cf)

∆P • Dm • ηtm

√

And also,

8. Qm =

(600,000 • Cf)

∆P • Dm3 • ηtm

√

(1,000 • ηvm)

min

Likewise,

9. Dm =

Nf2 • 600,000 • Cf

∆P • n

cm3

rev

[

]

[

]

[

]

[

]

[

]

[

]

[

]

[

]

[ ]

[

]

(

10. ∆P =

Cf • Nf2 • 600,000

Dm • η

[ ]

and,

, [bar]

Design Guidelines

Hydraulic Fan Drive Systems

Appendix B-Fan Drive Sizing Equations

Fan Drive Sizing Equations and Derivations

Fan drive sizing equations - SI system

30 | © Danfoss | January 2020 AB00000019en-000401

Pf = Rated fan power, [hp] Nfr = Rated fan speed, [rpm] Nf = Fan speed, [rpm]

1. Pf ≡ Cf • Nfr3 ≡

Tfr • Nfr

63,025

2. Tfr = , [lbf•in]

∆P = Pressure drop across hydraulic motor, [psid]

∆P • Dm • ηtm

2π

Tfr = Rated fan torque, [lbf • in]

Dm = Motor displacement,

in3

rev

Dm ≡

in3

rev

rpm

3. Pf = , [hp]

(∆P • Nf • Dm • ηtm)

(2π • 63025)

4. Qm = , [US gal/min]

Nf • Dm

(231 • ηvm)

5. Nf • Dm =

(2π • 63,025)

(∆P • ηtm)

min

(Cf • Nf3) •

6. Qm =

(2π • 63,025)

(∆P • ηtm • 231 • ηvm)

(Cf • Nf3) •

Re-arranging #5. above,

7. Nf = , [rpm]

(396,000 • Cf)

∆P • Dm • ηtm

√

And also,

8. Qm = , [US gal/min]

(396,000 • Cf)

∆P • Dm3 • ηtm

√

(231 •ηvw)

[

]

, [

]

[

]

[

]

[ ]

(Motor Displacement,

(2.54

cm3 rev

[

]

)

[

]

)

, [hp]

, [US gal/min]

Likewise,

9. Dm = ,

Nf2 • 396,000 • Cf

∆P • η

in3

[

]

rev

[ ]

10. ∆P = , [psid]

Cf • Nf2 • 396,000

Dm • η

[ ]

and,

Design Guidelines

Hydraulic Fan Drive Systems

Appendix B-Fan Drive Sizing Equations

For charge pump sizing equations, refer to the product specific Technical Information manuals, and Systems Applications manuals.

Fan drive sizing equations - English system

Danfoss | January 2020 AB00000019en-000401 | 31

SI system

From equ ation 7,

Nf2 =

(600,000 • Cf)

∆P • Dm • η

Therefore at condition 1:

Nf2 =

(600,000 • Cf)

∆P1 • Dm • η

and at condition 2:

Nf2 =

(600,000 • Cf)

∆P2 • Dm • η

Then,

∆P

Nf2 = Nf

• √

∆P

English system

From equ ation 7,

Nf2 =

(396,000 • Cf)

∆P • Dm • η

Therefore at condition 1:

Nf2 =

(396,000 • Cf)

∆P1 • Dm • η

and at condition 2:

Nf2 =

(396,000 • Cf)

∆P2 • Dm • η

Then,

∆P

Nf2 = Nf

• √

∆P

[

]

[

]

[

]

[

]

[

]

[

]

Nf2 = Nf

• √

∆P

Nf2 = 2000

• = 663 rpm √

310

2822

Nf2 = Nf

• √

∆P

Nf2 = 663

• = 753 rpm √

400 310

Design Guidelines

Hydraulic Fan Drive Systems

Appendix B-Fan Drive Sizing Equations

For charge pump sizing equations, refer to the product specific Technical Information manuals, and Systems Applications manuals.

Therefore, comparing equations 7 thru 10 on the previous pages, for any given combination of fan configuration and motor displacement, there is a unique relationship between system pressure, motor flow, and motor speed.

Hydraulic System Comparisons

One application of the sizing equations is to use them to relate the fan speed/pressure relationship from one condition to another.

If the theoretical trim pressure is 2822 psid at a fan speed of 2000 rpm, what is the fan speed at a minimum standby pressure of 310 psid?

If the minimum standby pressure suddenly changes from 310 psid, to 400 psid, due to the external circuit, what is the resulting fan speed?

32 | © Danfoss | January 2020 AB00000019en-000401

The graph below illustrates this quadratic relationship between fan system delta pressure and fan speed. The graph is normalized by dividing the individual operating parameters of pressure and speed by the trim pressure and trim speed of the fan so that the curve is representative of all fan systems.

0.0000

0.2000

0.4000

0.6000

0.8000

1.0000

1.2000

1.4000

1.6000

1.8000

2.0000

0.0000 0.2000 0.4000 0.6000 0.8000 1.0000 1.2000 1.4000 1.6000

Fan speed ratio (dimensionless)

Press.Ratio

y = x

essure

tio

(dimensionless)

P106 119E

0.0000

0.2000

0.4000

0.6000

0.8000

1.0000

1.2000

1.4000

1.6000

1.8000

2.0000

0.0000 0.2000 0.4000 0.6000 0.8000 1.0000 1.2000 1.4000 1.6000

Fan speed ratio (dimensionless)

Power Ratio

wer

tio

(dimensionless)

P106 120E

Design Guidelines

Hydraulic Fan Drive Systems

Appendix B-Fan Drive Sizing Equations

Consequently, the curve converges on the coordinates of (1.000, 1.000) for both the fan pressure ratio and the fan speed ratio.

Pressure ratio vs fan speed ratio

Power ratio vs fan speed ratio

On examination of the curve, one can see:

To increase fan speed 10% above the trim speed we would need to increase the delta pressure across

•

the motor by 21% To reduce fan speed below 32% of the trim speed we would need to reduce the delta pressure across

•

the motor by more than 90%.

Danfoss | January 2020 AB00000019en-000401 | 33

SI system

Assume Qm = Qp,

Nf • Dm

Np • Dp • η

Therefore:

11. Nf =

Np • Dp • ηvp • η

(Ne • R) • Dp • η

• η

Ne = Engine spee d, rpm (In this case, Ne = engine low idle speed.) R = Engine-pump gear ratio, no dimension. Combining e q. 1. and eq. 11.,

12. Pf = Cf • Nf3 =

∆P • Dm • η

600,000

•

Ne • R • Dp • η

• η

, [kW]

13. Nf =

∆P • Ne • R • Dp • η

tm • ηvp • ηvm

600,000 • Cf

, [rpm]

1/3

14.

Ne • R • Dp • η

vp • ηvm

Combining equ ation 11 and equ ation 13,

∆P • Ne • R • Dp • η

tm • ηvp • ηvm

600,000 • Cf

Solving for Dm,

15. Dm =

• (Ne • R • Dp • η

vp • ηvm

)

∆P •η

600,000 • Cf

1/3

in3

rev

[

]

[

]

[

]

[

]

[

]

[

]

Design Guidelines

Hydraulic Fan Drive Systems

Appendix C-Fan Drive Sizing Equations, using Variable Displacement Motors

Hydraulic Systems with 2 Position, Variable Displacement Motors, Equations and Derivations

Some systems may require additional cooling when the engine is at the low idle speed. A system with a fixed displacement motor may require additional pump flow to accomplish this. If the pump flow is limited, there is the possibility of providing additional cooling by utilizing a variable displacement motor in the hydraulic circuit. For normal operation, the variable displacement motor is held in the maximum displacement position in order to minimize the operating pressure for any given cooling requirement. But, when the engine is at the low idle speed, the control system can command the motor to its minimum displacement position to take full advantage of the flow that is available from the pump. In both conditions, the fan speed is modulated in response to the temperature of the coolant to satisfy the cooling needs of the system.

If you would like to determine the optimum minimum displacement for a variable motor, which would provide the maximum fan speed when, the engine speed is at low idle and the system pressure is at the trim pressure setting:

The following analysis assumes that the bypass flow around the motor is zero.

SI system

34 | © Danfoss | January 2020 AB00000019en-000401

English system

Assume Qm = Qp,

Nf • Dm

Np • Dp • η

Therefore:

11. Nf =

Nf • Dp • ηvp • η

(Ne • R) • Dp • η

• η

Ne = Engine spee d, rpm (In this case, Ne = engine low idle speed.) R = Engine/pump gear ratio, no dimension. Combining e q. 1. and eq. 11.,

12. Pf = Cf • Nf3 =

∆P • Dm • η

396,000

•

Ne • R • Dp • η

• η

, [hp]

13. Nf =

∆P • Ne • R • Dp • η

tm • ηvp • ηvm

396,000 • Cf

, [rpm]

1/3

14.

Ne • R • Dp • η

vp • ηvm

Combining e q. 11. and eq. 13.,

∆P • Ne • R • Dp • η

tm • ηvp • ηvm

396,000 • Cf

Solving for Dm,

15. Dm =

• (Ne • R • Dp • η

vp • ηvm

)

∆P •η

396,000 • Cf

1/3

in3

rev

[

]

[

]

[

]

[

]

[ ]

[

]

[

]

Design Guidelines

Hydraulic Fan Drive Systems

Appendix C-Fan Drive Sizing Equations, using Variable Displacement Motors

English system

This is the optimum minimum motor displacement at which the fan speed will be maximum for the given pump flow at engine idle and at the system’s trim pressure. An ExcelTM spreadsheet has been developed to calculate the optimum minimum displacement for the variable displacement motor. Consult your Danfoss representative for assistance.

Spreadsheet to Calculate the Optimum Minimum Displacement for 2 Position Variable Motor

Spreadsheet calculator tool (example)

Rated fan power, hp 40 Input data only in second column: Rated fan speed, rpm 2400 Optimum displ.

Desired fan trim speed, rpm 2600 Trim pressure, Psig 3205 Motor displ., cc/rev 44 Motor torque eff 90% Cf = hp_fan/Nf^3 2.89E-09 Engine idle speed, rpm 700 Engine: pump ratio, _:1 1 Pump displ, cc/rev 55 Pump displ, In^3/rev 3.36

Dm =

In^3/rev

1.230

cc/rev

20.15

Danfoss | January 2020 AB00000019en-000401 | 35

Fan rated power = 40 hp

Fan rated speed = 2400 rpm

500

1000

1500

2000

2500

3000

3500

4000

4500

5000

44 42 40 38 36 34 32 30 28 26 24 22 20 18 16 14 12 10 8

Motor displacement, cm³/rev

tor shaf

t speed

, ( rp m )

Free shaf t speed at eng .idle,RPM

Fan trim speed at max trim press , RPM

Optimum minimum displacemen t for variable motor is defined at the intersec tion of the two cur ves.

Fan speed for fan motor operating at maximum displacement with the pump speed at engine idle .

Fan speed for fan motor operatin g at optimum displacement with th e pump speed at engine idle .

P106121

Design Guidelines

Hydraulic Fan Drive Systems

Appendix C-Fan Drive Sizing Equations, using Variable Displacement Motors

Spreadsheet calculator tool (example) (continued)

Motor vol eff 96% Pump vol eff 96%

This relationship is illustrated in the graph below.

The curve described by the square data points represents the speed of the motor shaft as a function

•

of motor displacement when the pump’s displacement is constant, and the pump’s input speed is at the engine idle speed.

The curve described by the triangular data points represents the speed of the motor shaft as a

•

function of the fan power coefficient, the trim pressure and the motor’s displacement. For the system parameters that have been chosen, the optimum minimum motor displacement for

•

the variable motor will be found at the intersection of these two curves.

Variable motor shaft speed vs. displacement

36 | © Danfoss | January 2020 AB00000019en-000401

P106 118E

∆P = (P1 – P2), psid

a , in/sec

Fluid acceleration in L length of conduit

L = 1 ft Length of conduit

A, in

Area of conduit

m, lbf-sec2/in

Fluid mass within the L length of conduit

S.G. = 0.861

Q = V • A, in3/sec Flow rate (in3/sec = GPM x 3.85)

V, ft/sec

D, in Diameter of the conduit

F, lbf Force

g Acceleration of gravity γ

γ/g = r

t Time interval, seconds

D Pump displa ceme nt

F = ∆P • A, lbf = m • a = rf • Q • V,

∆P • A = rf • Q • V = r •

L • A

• V

∆P • A = rf •

L • A

•

∆P = rf •

L • Q

t • A

and, rf = S.G. • r

H20

(

)

(

)

(

)

Therefore:

∆P =

1.43 E-3 t • d

(

)

S.G.

(

)

(

)

(

)

, Psid

Design Guidelines

Hydraulic Fan Drive Systems

Appendix D-Pressure change due to transient flow in a passage

Pressure Change due to Transient Flow in a Passage, Equations and Derivations

Flow passage

Danfoss | January 2020 AB00000019en-000401 | 37

SI system

∆P

, = (2.122E - 7) •

S.G. • Q

t • d

bar

meter

min

L = length, [m]

d = diame ter, [m]

and,

∆P

, = (0.2122) •

S.G. • Q

t • d

bar

meter

when:

d = diame ter, [mm]

also,

∆P

, = (2.122E - 4) •

S.G. • N • D

t • d

bar

meter

when:

d = diame ter, [mm]

D = displaceme nt,

Rev

∆N

, average ac celerationa =

rpm

sec

English system

∆P

, = (5.4996E - 3) •

S.G. • Q

t • d

psid

L = length, [ft]

d = diame ter, [in]

∆P

, = (3.7189E - 3) •

psid

when:

S.G. = 0.861

∆N

, a =

rpm

sec

when:

D = displaceme nt,

rev

A = 1 in

∆P

• a, = (2.3808E - 3) •

S.G. • D

psid

meter

= average ac celeration

(

)

[

]

[ ]

(

)

[

]

(

)

[

]

[

]

[

]

[

]

[

]

[

]

(

)

[

]

(

)

[

]

(

)

N = speed, [rpm]

and,

∆P

, = (2.122E - 4) •

S.G. • D • a

bar

meter

(

)

[

]

when:

d = diame ter, [mm]

D = displaceme nt,

Rev

[

]

Design Guidelines

Hydraulic Fan Drive Systems

Appendix D-Pressure change due to transient flow in a passage

38 | © Danfoss | January 2020 AB00000019en-000401

Motor

Inlet

Motor Outlet

tor

Drain

P103122

PV=

+ δP

QM+δ

PM= + δP

QΣ+ δ

+δ

P106 123E

Design Guidelines

Hydraulic Fan Drive Systems

Appendix E-Influence of Bypass Valve Pressure Drop in Open Circuit Systems

In applications where the system is sized close to the maximum limits of fan speed, motor speed, or component pressure ratings, it may be necessary to determine the influence of the bypass valve’s pressure-flow characteristics on the system. In a typical circuit, there will be a rise in pressure across a component with an increase in flow. This is normal, and the system’s designer is encouraged to check whether this characteristic will have an adverse effect on the system and its components.

In this section, we will determine the effect of the pressure rise with flow characteristic of the bypass valve on the change in trim speed of the fan and the trim pressure across the hydraulic motor. In most pressure regulating valves there is a range of flows where the pressure rise is either linear, or nearly linear, with increases in flow. This is illustrated below for an electro-hydraulic proportional pressure control. Adjacent to each of the characteristic curves is a coefficient, which is the nominal slope of each curve. With this coefficient and other system parameters that are described below: the system designer can determine the change in trim speed and trim pressure with increases in engine speed above the engine set point that has been selected.

For the purposes of this derivation, the basic modulating fan drive circuit may be simplified as shown below:

Basic modulating fan drive circuit

As can be seen in the simplified schematic, all of the pump flow, QS goes thru either the bypass valve, QV,

Danfoss | January 2020 AB00000019en-000401 | 39

or the fan motor, QM. At the initial condition for our derivation, the flow thru the bypass valve is zero and all of the pump flow is passing thru the motor. This is the trim point, when the engine is at the engine set point. Above the trim point, a portion of the flow will pass thru the motor and the remaining flow will pass thru the bypass valve. The proportion of the flow going thru each will be determined by the pressure-flow characteristics of the valve and the pressure-flow relationship of the motor-fan that is determined by the fan laws.

QS0 = QV0 + Q

@t = 0, QV0 = 0.0

\QS0 = Q

\dQS = dQV + dQ

QS0 + dQS = Q

+ dQV + QM0 + dQ

From the g raph of ∆Pv vs ∆Qv,

PV = P0 + Kp • dQ

Kp ≡

From the fan l aws,

∆Pv ∆Qv

Therefore, dPm = ,

+ dQ

- P

dPm ≡ dPV, therefore:

dPV = P0 • ,

+ dQ

- 1

= ,

+ dQ

- 1

Expanding the right side of the equ ation,

1 + 2

- 1

= +

If «

Then,

= , 2

Since, dPV =Kp • dQV = Kp • (dQS - dQM),

Therefore,

(dQS - dQM) = 2

Expanding,

Kp • dQS = P0 • + Kp • dQM, 2

Kp • dQS = • {2P0 + Kp • QM0},

Then , dQM =

Kp • dQS • Q

(2P0 + Kp • QM0)

Therefore, dNM =

Likewise;

(dQV) = (dQS - dQM),

dQV = dQS •

Kp • Q

(2P0 + Kp • QM0)

, 1-

Then ,

dPV = Kp • dQS •

Kp • Q

(2P0 + Kp • QM0)

Summarizing then:

thru the mo tor at the engine set point, QM0, the mo tor displaceme nt, DM, the initial trim pressure, P0, and the bypass

we can de termine the inc rease in fan speed, dNM, above the theo retical trim speed, NM0.

dNM =

Kp • dQS • Q

DM • (2P0 + Kp • QM0)

Likewise, we can de termine the change in pressu re across the fan mo tor, dPV, as shown.

This is valid for dQM ≤ 0.5 • dQ

(

)

(

)

( ) (

)

[

]

(

)

[

]

(

)

(

)

(

)

(

)

[ ]

[

]

(

)

(

)

(

)

[

]

[

]

(

)

(

)

{

}

{

}

{

}

{

}

[

]

dPV = Kp • dQS •

Kp • Q

(2P0 + Kp • QM0)

[

]

{

}

N = R • Ne

δQ

Bypass valve and fan motor ﬂow vs. pump ﬂow

Design Guidelines

Hydraulic Fan Drive Systems

Appendix E-Influence of Bypass Valve Pressure Drop in Open Circuit Systems

40 | © Danfoss | January 2020 AB00000019en-000401

100

110

120

130

140

150

160

170

180

190

200

210

220

230

240

250

260

270

0 10 2 0 30 40 50 60 70

Bypass Flow (l/min)

P106 124E

essure (bar)

Design Guidelines

Hydraulic Fan Drive Systems

Appendix E-Influence of Bypass Valve Pressure Drop in Open Circuit Systems

Pressure vs. flow diagram for Comatrol PRV10 valve identification

Y, W, U, etc. - Refer to electro-hydraulic proportional valve nomenclature code in 520L0588 Comatrol Cartridge Valves Technical Information.

Danfoss | January 2020 AB00000019en-000401 | 41

100

110

120

130

140

150

160

170

180

190

200

210

220

230

240

250

260

270

0 10 20 30 40 50 60

100

Bypass Flow (l/min)

P106 125E

essure (bar)

Design Guidelines

Hydraulic Fan Drive Systems

Appendix E-Influence of Bypass Valve Pressure Drop in Open Circuit Systems

Pressure vs. flow diagram for Comatrol PRV12 valve identification

W, U, S, etc. - Refer to electro-hydraulic proportional valve nomenclature code in 520L0588 Comatrol Cartridge Valves Technical Information.

42 | © Danfoss | January 2020 AB00000019en-000401

0 50 100 150

Ambientt emperature, ºF

Satur

ated

por

essur

In.

P106 155E

Design Guidelines

Hydraulic Fan Drive Systems

Appendix F1-Influence of temperature, pressure and relative humidity on specific weight of air

Influence of Temperature, Pressure and Relative Humidity on Specific Weight of Air

Where: ν = Specific Weight of Air, lbf/ft3 P = Standard Barometric Pressure, in Hg RH = Relative Humidity, (%/100) Pvs = Saturation Water-Vapor Pressure, in Hg T = Temperature, °F H = Altitude, ft.

Standard barometric pressure varies with altitude

P = (1.34955E-8)H2 - (1.07145E-3)H + 29.92, In. Hg Accurate within +0.0/- 0.5 In. Hg from - 1000 to 15000 ft

Saturated water vapor pressure vs ambient temperature, ºF

y = 4E-06x3 - 0.0005x2 + 0.0343x - 0.5782

Temperature, vs pressure (in. Hg)

Temp., ºF Pvs, in. Hg

40 0.2478 42 0.2671 44 0.2891

Danfoss | January 2020 AB00000019en-000401 | 43

46 .03119 48 0.3363 50 0.3624 52 0.3905 54 0.42 56 0.4518 58 0.4854

Design Guidelines

Hydraulic Fan Drive Systems

Appendix F1-Influence of temperature, pressure and relative humidity on specific weight of air

Temp., ºF Pvs, in. Hg

60 0.5214 62 0.5597 64 0.6004 66 0.6438 68 0.6898 70 0.7387 72 0.7906 74 0.8456 76 0.904 78 0.9657

Temp., ºF Pvs, in. Hg

80 1.032 82 1.101 84 1.175 86 1.253 88 1.335 90 1.421 92 1.513 94 1.609 96 1.711 98 1.818

Temp., ºF Pvs, in. Hg

100 1.932 102 2.0528 104 2.1786 106 2.3109 108 2.4502 110 2.5966 112 2.7505 114 2.9123 116 3.0821 118 3.3606

Temp., ºF Pvs, in. Hg

120 3.4474 122 3.6436 124 3.8492 126 4.0649 128 4.2907 130 4.5272

44 | © Danfoss | January 2020 AB00000019en-000401

Design Guidelines

Hydraulic Fan Drive Systems

Appendix F2-Influence of Altitude on Atmospheric Pressure

Influence of Altitude on Atmospheric Pressure

Atmospheric Properties:

Altitude Atmospheric

Meters Feet

0 0 14.696 29.92 760 30 98 14.64 29.80 757 60 197 14.58 29.69 754 90 295 14.52 29.57 751 120 394 14.47 28.45 748 150 492 14.41 29.34 745 180 591 14.35 29.22 742 210 689 14.30 29.11 739 240 787 14.24 28.99 736 270 886 14.18 28.88 734 300 984 14.13 28.76 731 330 1083 14.07 28.65 728 360 1181 14.02 28.54 725 390 1280 13.96 28.43 722 420 1378 13.91 28.32 719 450 1476 13.85 28.20 716 480 1575 13.80 28.09 714 510 1673 13.74 27.98 711 540 1772 13.69 27.87 708 570 1870 13.64 27.76 705 600 1969 13.58 27.65 702 900 2953 13.06 26.59 675 1200 3937 12.55 25.56 649 1500 4921 12.07 24.57 624 1800 5906 11.60 23.63 600 2100 6890 11.16 22.71 577 2400 7874 10.73 21.84 555 2700 8858 10.31 20.99 533 3000 9843 9.91 20.18 513 3300 10827 9.53 19.40 493 3600 11811 9.16 18.65 474 3900 12795 8.81 17.93 456 4200 13780 8.47 17.24 438 4500 14764 8.14 16.58 421 6000 19685 6.69 13.61 346

pressure, Psia @ 32 deg F

Absolute pressure Inches Mercury

Absolute pressure millimeters Mercury

Danfoss | January 2020 AB00000019en-000401 | 45

Atmospher

essur

In.

Altitude,ft

5000

10000

15000

20000

25000

30000

35000

y = 30.262e

-4E-05x

R = 0.999

)

(

P106 154E

Design Guidelines

Hydraulic Fan Drive Systems

Appendix F3-Influence of generic altitude on atmospheric pressure

Influence of Generic Altitude on Atmospheric Pressure

Atmospheric pressure vs altitude

Data showing atmospheric pressure vs altitude

Data from ASHRAE Guide: Calculated

Altitude, ft. Pressure in. Hg

pressure in. Hg

-1000 31.02 31.50 0.48

-500 30.47 30.87 0.40 0 29.921 30.26 0.34 500 29.38 29.66 0.28 1000 28.86 29.08 0.22 5000 24.89 24.78 -0.11 10000 20.58 20.29 -0.29 15000 16.88 16.61 -0.27 20000 13.75 13.60 -0.15 25000 11.1 11.13 0.03 30000 8.88 9.11 0.23 35000 7.04 7.46 0.42 40000 5.54 6.11 0.57 45000 4.36 5.00 0.64 50000 3.436 4.10 0.66

Error = calculated - given pressure in. Hg

46 | © Danfoss | January 2020 AB00000019en-000401

Do you need a reversing fan?

Yes

Acceptable

Not Acceptable

Input fan & engine data into Fan Drive Sizing Tool

Output pump and motor displacement and pressure setting

Will complete

reverse cycle last

longer than 30

seconds?

Determine fan performance data in both forward and reverse directions of operation

Fans operating in reverse may produce significantly different results than those operating in the forward direction

If the fan speed in reverse is equal to the forward speed, the fan flow rate through the cooler will be reduced

* Use the original output from the Fan Sizing Tool

* Calculate “New” max. ambient temperature for max. heat rejection in reverse fan direction

If the desired fan power in reverse is equal to the power in the forward direction; the fan speed will increase, the air flow rate will increase, but the heat rejection will be less than the forward direction of rotation

If the desired heat rejection and max. ambient temperature for reverse rotation is equal to the forward direction, the air flow will be the same. The fan speed will increase and the power required to rotate the fan may increase significantly.

* Determine the new fan performance data for reverse rotation and input into the Fan Drive Sizing Tool. * Determine new pump and motor displacement and/or pump drive ratio, and pressure settings for both forward and reverse directions of rotation. * Use new pump and motor displacements in the Fan Drive Sizing Tool, recalculate fan drive system performance in the forward direction.

* Determine the new fan performance data for reverse rotation and input into the Fan Drive Sizing Tool. * Determine new pump and motor displacement and/or pump drive ratio. *Use new pump and motor displacements in the Fan Drive Sizing Tool, recalculate fan drive system performance in the forward direction. * Calculate “New” max. ambient temperature for max. heat rejection in reverse fan direction.

P108 352E

Design Guidelines

Hydraulic Fan Drive Systems

Appendix G-Influence of reversed fan rotation on system performance

In applications where it is necessary to change the direction of fan rotation, most fans will have reduced performance. Some fans are designed for equal, or similar, performance in the reverse direction, but this is not typical of many axial flow fans that are installed in vehicles today. Some fan blade designs have significantly different efficiencies depending on their direction of rotation and pitch angle (angle of attack). In this instance, we’re using the term “efficiency” to indicate that the fan does not produce the same amount of air flow at the same speed; and/or it requires more power to produce the same amount of air flow as in the forward direction of rotation.

The cooling system designer is encouraged to consult with their fan supplier for performance characteristics specific to their fan; based on the speed of operation, static pressure drop, and direction of rotation. Using this information, it is possible to validate whether the fan will meet the specific needs of the cooling system. Given this information, the system designer can investigate the effect of these changes and determine if corrective actions need to be introduced.

The following is a guide to some of the characteristics that one could encounter when reversing the direction of a fan. For these purposes, the fan is assumed to be operating at its design “trim” speed and at the desired maximum “static” operating pressure across the cooler when in the forward direction.

Danfoss | January 2020 AB00000019en-000401 | 47

Design Guidelines

Hydraulic Fan Drive Systems

Appendix G-Influence of reversed fan rotation on system performance

Baseline: Fan operating in Forward Direction at 2600 RPM

The Flow Rate for a given fan speed is determined by the intersection of the Fan’s Flow/StaticPressure Curve for that speed and the Cooler’s Resistance Pressure vs Airflow characteristic curve.

The power required to turn the fan at that speed (airflow & static pressure) is located directly above this intersection point on the Fan Flow Rate vs Fan Power Curve at constant RPM. The magnitude of the fan power is determined by the secondary Y-Axis in the upper right hand corner of the graph.

Condition 1: Fan operating in Reverse Direction at 2600 RPM

The Flow Rate for 2600 RPM in the reverse direction is less than that produced by the fan at 2600 RPM in the forward direction of rotation. Since the air flow rate is less, the static pressure across the cooler is also reduced.

The power required to turn the fan at the same speed, but in reverse direction, is less than that required in the forward direction of rotation. The fan is producing less flow at a lower static pressure; thus a lower power requirement.

48 | © Danfoss | January 2020 AB00000019en-000401

Design Guidelines

Hydraulic Fan Drive Systems

Appendix G-Influence of reversed fan rotation on system performance

Condition 2: Fan operating in Reverse Direction at approximately the same input power level (by increasing the fan speed in reverse)

The fan is producing less flow, even though the fan speed is now 2810 RPM in the reverse direction of rotation.

The power required to turn the fan at 2810 RPM, in reverse direction, is approximately the same as that required to turn the fan at 2600 RPM in the forward direction of rotation. The fan is still producing less flow at a lower static pressure. (Fan efficiency is reduced in the reverse direction.)

Condition 3: Fan operating in Reverse Direction at approximately the same flow rate (by increasing the fan speed in reverse)

The fan is producing approximately the same flow rate, even though the fan speed is now 3060 RPM in the reverse direction of rotation.

The fan requires more power at the same flow rate and static pressure, because the fan is less efficient in the reverse direction of rotation.

Danfoss | January 2020 AB00000019en-000401 | 49

Design Guidelines

Hydraulic Fan Drive Systems

Appendix G-Influence of reversed fan rotation on system performance

System Response to Reversed Fan Rotation:

“Cooling Effectiveness” is proportional to the cooling capacity of the cooler; i.e., the ratio is greater

•

than one when the Temperature (System Design Temperature). When the ratio is greater than 1.0, the cooler will not require as much air flow to satisfy the cooling needs of the system. Therefore, the Fan Power requirement will be less than at the “design” maximum ambient temperature.

At the “design” Maximum Ambient Temperature, reducing the air flow rate thru the cooler has an

•

equivalent effect of reducing the “Cooling Effectiveness” of the cooler; as such, the two concepts may be equated.

Therefore, as the air flow rate thru the cooler is reduced (Cooling Effectiveness ≤ 1.0); a new “T

•

” can be calculated, which will define a new upper limit of ambient temperature where the cooler

Amb

will still satisfy the maximum heat load.

The new “T Temperature.

Actual Amb

” temperature will be lower than the original Design Maximum Ambient

ient Temperature is less than the original design Maximum Ambient

Actual

50 | © Danfoss | January 2020 AB00000019en-000401

( )

( ) ( )

( )

CCCCT

Therefore

Let

and

then

TTQ

TTCm

and

TTCm

Coolant

Maximum

Coolant

MaxAmbient

Coolant

Maximum

MaxAmbient

MaxAmbientCoolant

ActualAmbCoolant

Maximum

CoolantMaximum

CoolantA

Coolant

º65.40º50º1001

8424.0

º100*

8424.0

º50

º100

,0.1

tionHeat Rejec

: LetAnd

rd RPM Forwa2600at Flow

se RPM Rever2600at Flow

8424.0

bemust Tnew the therefore1.0,bemust

,0.1

and ,0.1

tionHeat Rejec

**tionHeat Rejec

Revin Amb ActualNew

Actual

Ambient Actual Maximum

Maximum

ctual

Actual

Revin ActualAmb

Actual

Maximum

ctual

Ambient Actual Maximum

Amb ActualActual

Maximum

ctual

Ambient Actual MaximumMaximumMaximum

Amb ActualActualctual

=−−−=

−=−

≡

≤≥

−

≤

≤≡

−

−=

Design Guidelines

Hydraulic Fan Drive Systems

Appendix G-Influence of reversed fan rotation on system performance

Derivation:

Danfoss | January 2020 AB00000019en-000401 | 51

Suggested Guidelines for Reversing Fan Drive Systems: IF the desire is to keep the fan speed in the reverse direction the same as in the forward direction:

This will occur automatically, IF the fan drive system is flow limited by pump speed, or displacement; but not IF the system is pressure limited.

Design Guidelines

Hydraulic Fan Drive Systems

Appendix G-Influence of reversed fan rotation on system performance

The heat rejected by the cooling system will be less than in the forward direction of rotation,

•

The power to drive the fan in reverse will be less than in the forward direction,

•

The Torque to turn the fan, and therefore the delta pressure across the hydraulic motor, will be

•

proportional to the power ratio, since the fan speed is the same.

IF the desire is to keep the fan power in the reverse direction the same as in the forward direction:

The Heat Rejection by the system will still be less than in the forward direction, but better than when

•

maintaining constant fan speed, (HR α Speed Ratio) The fan speed in reverse will be greater than in the forward direction. The Torque to turn the fan (and

•

hydraulic delta pressure) will be less than in the forward direction, (Power to turn the fan is the same, but the speed is greater.)

This condition may define the maximum pump displacement or speed required to satisfy the flow

•

requirements of the fan system, since the flow required to rotate the fan will be larger in the reverse direction than in the forward direction.

Be sure to validate these conditions with the fan supplier. The new speed requirement may exceed

•

the maximum speed limit.

Tip speed is proportional to the fan rotational speed and internal stresses in the fan are proportional to the square of the fan speed.

IF the desire is to keep the fan flow rate in the reverse direction the same as in the forward direction:

The Heat Rejection by the system will be the same as in the forward direction,

•

The Power required to rotate the fan in the reverse direction will be greater than in the forward

•

direction of rotation, because the fan is less efficient in the reverse direction of rotation, The fan speed in reverse will be greater than in the forward direction. The Torque to turn the fan (and

•

hydraulic delta pressure) may be greater than in the forward direction, (Power to turn the fan is greater, and the speed is greater.)

This condition may define the maximum pump displacement required to satisfy the flow

•

requirements of the fan system, since the flow required to rotate the fan will be larger in the reverse direction than in the forward direction.

Be sure to validate these conditions with the fan supplier. The new speed requirement may exceed

•

the maximum speed limit.

Tip speed is proportional to the fan rotational speed and internal stresses in the fan are proportional to the square of the fan speed.

52 | © Danfoss | January 2020 AB00000019en-000401

Design Guidelines

Hydraulic Fan Drive Systems

Appendix G-Influence of reversed fan rotation on system performance

Performance Summary: (For Reference Only)

Danfoss | January 2020 AB00000019en-000401 | 53

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

System Considerations for H1 Fan Drives with Reversed Fan Rotation

As stated in Appendix G, in applications where it is necessary to change the direction of fan rotation, most fans will have reduced performance. For fan systems using H1 pumps with the H1 Fan Drive Control Valve, the control valve receives a command from the PLUS+1® Controller to regulate fan speed by changing pump displacement. When the pump speed is at the design set point, fan speed required for the desired cooling capacity is determined by the pump’s displacement.

In many systems, the fan’s speed at this condition may be close to its maximum design speed. If the pump speed increases beyond the set point and the pump is commanded to maximum displacement; then the fan speed will increase in proportion to the pump speed ratio and the delta pressure across the fan motor will increase in proportion to the square of the pump speed ratio.

To prevent this from happening, the system designer is encouraged to limit the maximum fan speed in each direction of rotation by adjusting the set pressure of the Pressure Limiters for both directions of rotation.

Pressure Limiter Adjusting Procedure

For the forward direction of rotation, determine the delta pressure across the fan motor when it’s at the maximum desired fan speed and power; this is the forward design pressure. Adjust the pressure limiter setting to be equal to the forward design pressure plus 20 bar (to account for piece-to-piece variation within the cooling system) for the forward direction of rotation.

For the reverse direction of rotation, determine the delta pressure across the fan motor when it’s at the maximum desired fan speed and power; this is the reverse design pressure, (consult with the fan and cooler manufacturer to determine the desired fan speed and power for the fan when it is rotating in the reverse direction, reference Appendix G). Adjust the pressure limiter setting to be equal to the reverse design pressure plus 20 bar (to account for piece-to-piece variation within the cooling system) for the reverse direction of rotation.

When the pump arrives at the OEM’s production line, it will have a nominal PL setting of 150 bar and may have a High Pressure Relief Valve setting of 250 bar, 300 bar, 350 bar, or 400 bar. depending on order code selected. The PL must be re-adjusted to ensure that the fan reaches the desired fan speed to satisfy the cooling needs of the system. It may be necessary to replace the HPRV with a valve that has a higher pressure setting. To replace the valves, follow the recommended procedures that are available in Service Documents 520L0848 or 520L0958.

The HPRV setting must be greater than the PL setting by at least 30 bar after the PL has been re-adjusted. When adjusting the pressure limiters, follow the recommended adjustment procedure that is available in

Service Document 520L0848 or 520L0958, or after stopping the prime mover and ensuring that the fan has stopped rotating.

Verify that the pressure limiter settings will not cause the fan speed to exceed the manufacturer’s maximum speed limitation when the engine’s speed is at its No Load High Idle (NLHI) condition and during periods of positive acceleration between the design set point and NLHI. Make adjustments accordingly. Refer to the graphs on pages 58-59 for typical representative behavior of fan speed changes when the engine is accelerating.

In the event of sudden engine speed increases, when the fan is operating close to the Pressure Limiter and High Pressure Relief Valve settings, then it is possible for the fan speed to exceed the design trim speed by approximately 10% (System delta pressure will exceed the setting of the High Pressure RV by approximately 20%.) Consequently, the system integrator needs to take this into consideration when sizing the fan and hydraulic components.

Pump and motor life are influenced by both speed and pressure. Contact your Danfoss technical representative for an analysis of the systems’ duty cycle to determine if it will meet the desired life goals.

54 | © Danfoss | January 2020 AB00000019en-000401

M14

F00B

F00A

P108 684E

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

Additional Information concerning the H1 Fan Drive Controller Option

H1 Pump with FDC Control - Schematic

Flow Direction vs. Signal

Pump Rotation Clockwise (CW) as seen from shaft

Forward fan rotation Reverse fan rotation

Control current Less than 1050 mA for 12 Vdc

Less than 550 mA for 24 Vdc

System port A flow

System port B flow

Servo gauge port high pressure

In (Low) Out (High) Out (High) In (Low)

Out (High) In (Low) In (Low) Out (High)

M5 M4 M5 M4

FDC Start and End Current

Typical FDC control curve in Fan Drive System, overlaid on FDC constant pressure control curves from a representative NFP Load Valve test. In the FDC Control test, a fixed orifice is placed in the flow stream between the A and B ports of the pump and it is sized to be equivalent to the flow/pressure relationship of a fixed displacement motor driving a fan.

(radiator cleaning) More than 1050 mA for 12 Vdc

More than 550 mA for 24 Vdc

Pump Rotation Counterclockwise (CCW) as seen from shaft

Forward fan rotation Reverse fan rotation

Less than 1050 mA for 12 Vdc Less than 550 mA for 24 Vdc

(radiator cleaning) More than 1050 mA for 12 Vdc

More than 550 mA for 24 Vdc

Danfoss | January 2020 AB00000019en-000401 | 55

-2

-4

-6

-8

-10

-12

-14

-16

-18

-20

Degrees

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

2.0

Amps

P108 678E

tc1_hyst_12volt_1800 rpm_ 360dbar_50secrmp: Swangle

tc1_hyst_12volt_1800 rpm_ 250dbar_50secrmp: Swangle

tc2_hyst_12volt_1800 rpm_

154.8lpm_50secrmp: Swangle

tc1_hyst_12volt_1800 rpm_ looped hoses_50secrmp: Swangle

tc1_hyst_12volt_1800 rpm_ 50dbar_50secrmp: Swangle

tc1_hyst_12volt_1800 rpm_ 150dbar_50secrmp: Swangle

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

Start and End Current

Typical, representative points on the curve are shown in the following table.

Start and End Current

Control Parameter Forward Current (mA)

(decreasing current direction)

12Vdc Start Current (typical) 780 1300

End Current Dependent on Fan Drive System Pressure Tolerance of End Current Nominal Range

Operating Envelope for H1 Pumps with Fan Drive Control

24Vdc Start Current (typical) 400 680

The Fan Drive Control (FDC) has limitations on the maximum servo delta pressure developed, compared to other types of controls, and so there are limitations to the operating conditions which can be achieved in the various frame size H1 pumps. Typical fan drive systems are unusual in that they achieve peak pressure only at high flows, so it is important that FDC equipped pumps not be applied beyond the limits defined below.

Typical limits for the operating envelope of the H1 pump family with the Fan Drive Control are shown in the following figures. There is one figure for each H1 pump displacement. Note that the constant pressure values are not the same for each displacement, as all are not necessarily applicable for each displacement.

Max Current Allowed 1800

End Current Dependent on Fan Drive System Pressure Tolerance of End Current Nominal Range Max Current Allowed 920

Reverse Current (mA) (increasing current direction)

100

120

0 500 1000 1500 2000 2500 3000 3500 4000

Stroke (%)

Pump RPM

290 Bar Delta Pressure 360 Bar Delta Pressure 385 Bar Delta Pressure 400 Bar Delta Pressure

100

120

0 500 1000 1500 2000 2500 3000 3500 4000

Stroke (%)

Pump RPM

280 Bar Delta Pressure 300 Bar Delta Pressure 350 Bar Delta Pressure

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

In the following figures, the area underneath each curve represents the appropriate operating envelope for a given system delta pressure:

H1P045 pump with CP8 valve plate and FDC

H1P053 pump with CP8 valve plate and FDC

Danfoss | January 2020 AB00000019en-000401 | 57

100

120

0 500 1000 1500 2000 2500 3000 3500 4000

Stroke (%)

Pump RPM

290 Bar Delta Pressure 405 Bar Delta Pressure 425 Bar Delta Pressure 450 Bar Delta Pressure

100

120

0 500 1000 1500 2000 2500 3000 3500 4000

Stroke (%)

Pump RPM

235 Bar Delta Pressure 350 Bar Delta Pressure 360 Bar Delta Pressure 450 Bar Delta Pressure

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

H1P060 pump with CP17 valve plate and FDC

H1P068 pump with CP17 valve plate and FDC

100

120

0 500 1000 1500 2000 2500 3000 3500 4000

Stroke (%)

Pump RPM

300 Bar Delta Pressure 380 Bar Delta Pressure 395 Bar Delta Pressure 450 Bar Delta Pressure

100

120

0 500 1000 1500 2000 2500 3000 3500 4000

Stroke (%)

Pump RPM

320 Bar Delta Pressure 380 Bar Delta Pressure 450 Bar Delta Pressure

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

H1P069 pump with CP17 valve plate and FDC

H1P078 pump with CP17 valve plate and FDC

Danfoss | January 2020 AB00000019en-000401 | 59

100

120

0 500 1000 1500 2000 2500 3000 3500

Stroke (%)

Pump RPM

305 Bar Delta Pressure 325 Bar Delta Pressure 380 Bar Delta Pressure 385 Bar Delta Pressure 450 Bar Delta Pressure

100

120

0 500 1000 1500 2000 2500 3000 3500

Stroke (%)

Pump RPM

280 Bar Delta Pressure 305 Bar Delta Pressure 340 Bar Delta Pressure 350 Bar Delta Pressure 450 Bar Delta Pressure

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

H1P089 pump with CP17 valve plate and FDC

H1P100 pump with CP17 valve plate and FDC

100

120

0 500 1000 1500 2000 2500 3000 3500

Stroke (%)

Pump RPM

355 Bar Delta Pressure 380 Bar Delta Pressure 410 Bar Delta Pressure 450 Bar Delta Pressure

100

120

0 500 1000 1500 2000 2500 3000 3500

Stroke (%)

Pump RPM

340 Bar Delta Pressure 390 Bar Delta Pressure 450 Bar Delta Pressure

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

H1P115 pump with CP17 valve plate and FDC

H1P130 pump with CP17 valve plate and FDC

Danfoss | January 2020 AB00000019en-000401 | 61

100

120

0 500 1000 1500 2000 2500 3000 3500

Stroke (%)

Pump RPM

240 Bar Delta Pressure 340 Bar Delta Pressure 415 Bar Delta Pressure 435 Bar Delta Pressure 450 Bar Delta Pressure

100

120

0 500 1000 1500 2000 2500 3000 3500

Stroke (%)

Pump RPM

330 Bar Delta Pressure 350 Bar Delta Pressure 390 Bar Delta Pressure 410 Bar Delta Pressure 450 Bar Delta Pressure

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

H1P147 pump with CP17 valve plate and FDC

H1P165 pump with CP17 valve plate and FDC

100

120

0 500 1000 1500 2000 2500 3000

Stroke (%)

Pump RPM

325 Bar Delta Pressure 385 Bar Delta Pressure 450 Bar Delta Pressure

100

120

0 500 1000 1500 2000 2500 3000

Stroke (%)

Pump RPM

320 Bar Delta Pressure 350 Bar Delta Pressure 450 Bar Delta Pressure

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

H1P210 pump with CP17 valve plate and FDC

H1P250 pump with CP17 valve plate and FDC

Sensitivity to Prime Mover Speed Changes (Load Sensitivity) - (J Frame as example)

The natural NFPE behavioral characteristic of the pump tends to correct for engine/pump speed variations which occur as a normal part of operation, and maintain the fan speed near to the level which was produced before the engine speed change. Of course, this can only occur to the extent that the pump can achieve its maximum displacement; beyond that, significant fan speed change will occur.

In the conditions representing an engine lugging condition (engine speed reduction less than 20%), there was no significant reduction in fan speed; the lower pump moments at the lower pump speed allowed the pump to increase stroke to maintain a relatively constant output flow.

In all conditions representing a throttle down condition (engine speed reduction greater than 50%), the percent of fan speed drop was lower than the percent of pump speed drop.

Danfoss | January 2020 AB00000019en-000401 | 63

Curves shown below are from J frame testing, and are representative of the behavior which will be seen on other frame sizes.

3.0

RPM x 10

Input speed

2.9

2.8

2.7

2.6

2.5

2.4

2.3

2.2

2.1

2.0

1.9

1.8

1.7

1.6

1.5

1.4

1.3

1.2

1.1

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

120

160

200

240

280

320

360

400

-40

-80

-120

-160

-200

-240

-280

-320

-360

-400

Bar

Degrees

-2

-4

-6

-8

-10

-12

-14

-16

-18

-20

3 4 5

12 13

19 20

Fan drive speed

Swangle

MA_MB_System_Press

M4_M5_Servo_Press

P108 679E

DBar

-14

-18

-2

-6

-10

-22

-26

-30

-4

-8

-12

-16

-20

-24

-28

Seconds

3.0

RPM x 10

Input speed

2.9

2.8

2.7

2.6

2.5

2.4

2.3

2.2

2.1

2.0

1.9

1.8

1.7

1.6

1.5

1.4

1.3

1.2

1.1

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

120

160

200

240

280

320

360

400

-40

-80

-120

-160

-200

-240

-280

-320

-360

-400

Bar

Degrees

-2

-4

-6

-8

-10

-12

-14

-16

-18

-20

3 4 5

12 13

19 20

Fan drive speed

Swangle

M4_M5_Servo_Press

P108 680E

MA_MB_System_Press

DBar

-14

-18

-2

-6

-10

-22

-26

-30

-4

-8

-12

-16

-20

-24

-28

Seconds

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

Prime Mover Speed Change (2500 - 2000 - 2500 rpm)

Prime Mover Speed Change (2500 - 1000 - 2500 rpm)

3.0

RPM x 10

Input speed

2.9

2.8

2.7

2.6

2.5

2.4

2.3

2.2

2.1

2.0

1.9

1.8

1.7

1.6

1.5

1.4

1.3

1.2

1.1

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

120

160

200

240

280

320

360

400

-40

-80

-120

-160

-200

-240

-280

-320

-360

-400

Bar

Degrees

-2

-4

-6

-8

-10

-12

-14

-16

-18

-20

3 4 5

12 13

19 20

Fan drive speed

Swangle

M4_M5_Servo_Press

P108 681E

MA_MB_System_Press

DBar

-14

-18

-2

-6

-10

-22

-26

-30

-4

-8

-12

-16

-20

-24

-28

Seconds

3.0

RPM x 10

Input speed

2.9

2.8

2.7

2.6

2.5

2.4

2.3

2.2

2.1

2.0

1.9

1.8

1.7

1.6

1.5

1.4

1.3

1.2

1.1

1.0

0.9

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

0.0

120

160

200

240

280

320

360

400

-40

-80

-120

-160

-200

-240

-280

-320

-360

-400

Bar

Degrees

-2

-4

-6

-8

-10

-12

-14

-16

-18

-20

3 4 5

12 13

19 20

Fan drive speed

Swangle

M4_M5_Servo_Press

P108 682E

MA_MB_System_Press

DBar

-14

-18

-2

-6

-10

-22

-26

-30

-4

-8

-12

-16

-20

-24

-28

Seconds

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

Prime Mover Speed Change (2500 - 1600 - 2500 rpm)

Prime Mover Speed Change (2500 - 800 - 2500 rpm)

Danfoss | January 2020 AB00000019en-000401 | 65

P108 683E

9 8

7 6 5 4 3 2 1 0

10% displacement to 90% displacement response time

Destroke from maximum forward to neutral

Maximum forward to maximum reverse

Pump Frame

Response time in seconds

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

J Frame is used as an example only In the event of sudden engine speed increases, when the fan is operating close to the Pressure Limiter

and High Pressure Relief Valve settings, then it is possible for the fan speed to exceed the design trim speed by approximately 10% (System delta pressure will exceed the setting of the High Pressure RV by approximately 20%.) Consequently, the system integrator needs to take this into consideration when sizing the fan and hydraulic components.

Due to the failsafe functionality of the FDC control the pump will stroke to max. displacement in case the input signal to the pump control and the Diesel engine will be switched off at the same time. In this situation a low loop event can occur which may damage the pump. Therefore, it’s strictly recommended to keep the input signal to the pump control alive while switching off the engine.

For further information please contact your Danfoss representative

H1 FDC Response Time (with Typical Fan Drive System Loading)

Warning

This control is for Fan Drive Systems only!

Use in other systems could result in unintended movement of the machine or its elements. Loss of the input signal to this control will cause the pump to produce maximum flow. Contact Danfoss or an authorized distributor with questions regarding the use of this product.

Application startup method (to account for PL offset)

The Pressure Limiter (PL) setting at high swashplate angles can be significantly (30 to 50 bar) lower than the setting on the Danfoss production test stand, which is done with system ports blocked.

This effect has a strong impact on Fan Drive applications; these applications are unique in that they always reach their peak pressure at a high swashplate angle (due to the typical fan speed/torque curve). Since the PL is needed to limit the peak system pressure, and therefore fan speed, in a particular application, this reduction in PL setting due to the standard factory test procedure will cause less than

optimum cooling. Because of this behavior, the following procedure should be used to determine the nominal value for the factory PL adjustment (nomenclature) for a new fan drive application. This will be required if there is a desire to pre-set the Pressure Limiters at a test facility without a working fan assembly, and prior to installing the pump onto a machine:

1. Order the FDC pump with the standard PL settings of 150 bar. Standard pump configurations are

provided with 150 bar PL settings and with the HPRV settings at 250 bar, 300 bar, 350 bar, and 400 bar.

2. Start the machine with a neutral signal to the FDC control and with the engine at its rated operating

speed. Gradually change the signal to the FDC to increase the fan speed; if the fan begins to exceed its maximum operating speed limit, use the procedure mentioned in paragraph above or shut off the

Design Guidelines

Hydraulic Fan Drive Systems

Appendix H-System considerations for H1 fan drives with reversed fan rotation

machine and adjust the PLs to a lower pressure setting. Repeat this for forward and reverse directions of fan rotation; until it is assured that the PLs are limiting fan speed within acceptable levels. This step is to ensure that the fan cannot operate above its maximum speed limit in subsequent steps. It may be necessary to increase the pressure setting of the HPRVs. Verify that the Pressure Limiter settings are at least 30 bar below the pump’s High Pressure Relief Valves following the recommended installation procedure provided within Service Bulletin 520L0848 or 520L0958.

3. Adjust the PL settings to the value determined during the sizing process by following the recommended adjustment procedure provided within Service Bulletin 520L0848 or 520L0958, or stop the machine and ensure that the fan has stopped.

This will be a mid-range current level, not zero amps.

4. Operate the engine at its rated operating speed, and with a maximum command to the FDC. If necessary, adjust the PLs to achieve the desired peak fan speed as above following the recommended adjustment procedure provided within Service Bulletin 520J0848 or 520L0958 (do this for forward and then for reverse directions of fan rotation).

5. During the Application Review process, or at “Initial Application Start” follow the instructions in steps 2 through 4. Stop the machine, then disconnect the pump system hoses from the fan drive circuit, and block the system ports to simulate the factory test stand -“no flow” condition.

6. Start the machine with a neutral signal to the FDC, and operate at the following conditions to simulate the factory test stand conditions: 1775 rpm pump speed, 50C - 80C oil temperature, and at zero and full flow current to the FDC solenoid. Record the System Delta Pressure achieved for the forward and reverse flow directions.

7. Verify that these system delta pressure settings are at least 30 bar below the pump’s High Pressure Relief Valves (if not, stop the machine, consult Danfoss technical sales and then install the next highest pressure level HPRVs, and repeat this test) following the recommended installation procedure provided within Service Bulletin 520L0848 or 520L0958

The PL setting must be less than the HPRV setting.

Danfoss | January 2020 AB00000019en-000401 | 67

P108918

Design Guidelines

Hydraulic Fan Drive Systems

Appendix I-System Considerations for RDM Fan Drives

System Considerations for RDM Fan Drives

These application guidelines are for open circuit systems which are equipped with the Reverse Displacement Motor (RDM) to allow reversing of the load output direction without a directional control valve and the system losses that go with a DCV. The RDM should only be used in open circuit systems that regulate load speed by controlling system pressure based on the input command. A displacement, or flow controlled pump should not be used with the RDM; due to the risk of over speeding the motor and/or load as the direction changes. This is because the motor displacement goes from full forward through zero to full reverse.

Reversing Sequence

The recommended reversing sequence is shown below. The load is first decelerated to the minimum normal system speed by commanding the system to the lowest normal system pressure (low pressure standby) and allowing the load’s speed to slow down. The RDM is then shifted to reverse and the system pressure is then increased to achieve the desired speed. The same process is then used to return the load to the original direction. The primary purpose of decelerating the load prior to shifting the motor is to reduce the “flywheel” affect inherent in reversing a spinning load. This will minimize pressure spikes and other disturbances in the system caused by feeding the energy of the rotating load back into the hydraulic system. It will also minimize the potential for requiring oil to flow through the motor system return line in a direction opposite that of the normal flow.

Another reason for reducing the speed and pressure in the system prior to initiating a motor reversal is to minimize the impact of the shifting process on the life of the motor. The higher the system pressure and/or speed is when the reversal is started, the greater the risk of wear in the swashplate bearings and a reduction in the life of those bearings.

Reversing Sequence

If, for some reason, this ideal process can’t be achieved, based on the system requirements for a faster load deceleration; the minimum requirement is that the system pressure setting be reduced prior to the reversal to minimize and delay the pressure spikes in the system while the fan is reversing. The delay in this step, between the pressure reduction signal and the reversing signal should be long enough to ensure the pressure control responds and the fan decelerates to the minimum speed condition. Experience to date would suggest that a 1 second delay is sufficient, but this should be verified by test. Once the fan reversal is accomplished, the pressure can be increased to achieve the desired fan speed, or fan acceleration time.

Since the unrestricted response time of the motor to shift from forward to reverse is approximately 350 ms, the delay required between sending the reversing signal and sending the signal to increase the

Design Guidelines

Hydraulic Fan Drive Systems

Appendix I-System Considerations for RDM Fan Drives

system pressure should be greater than 500 ms. A command to increase system pressure before the motor reaches full displacement will result in higher system pressures while the fan is accelerating. A longer delay will allow the fan to decelerate more and will minimize the pressure to fully stop the fan and reverse its direction; but will also lead to reduced cooling capacity during the shift sequence. Likewise, when the motor is returning to the forward direction, the minimum delay time between these two events is 1 second, instead of the 500 ms interval above. This is because the natural shift response of the motor is slower when returning to the forward direction.

A duty cycle that follows these recommended guidelines will result in a reversing cycle “capability” of more than 60,000 cycles, because the motor is not actually shifting under high pressure. A duty cycle where the motor shifts before slowing down will see higher system pressures because the load energy is being dissipated more quickly. This will have an impact on the life of the motor kit, swashplate bearings and shaft bearings.

Shift Rate Control

In general, the best option is to allow the motor to shift as quickly as possible when the motor is at minimum speed. This will reduce the risk of the motor shifting under load, thus impacting the life of the swashplate bearings. There may be systems, however, where it is desired to control the shift rate of the motor. One example might be in systems with very high inertia loads.

If required, the reversal rate of the RDM can be controlled. The motor is equipped with an integrated shift valve, by controlling the input signal to the motor; the rate of reversal can be controlled. The shifting of the motor from forward to reverse happens through the range of 300-750 mA input for a 12 volt valve and 150-375 mA for a 24 volt valve. The input current should be ramped through this range based on the desired shift time of the motor. The return to the forward direction will happen through the range of 550-150 mA for a 12 volt valve and 275-75 mA for a 24 volt valve.

For motors with an integral shift valve, if the electrical input to the motor control can’t be regulated as described above; there is an option to install an orifice, either in front of the shift valve, or between the shift valve and the servo cavity. The first orifice will impact the forward-to-reverse shift without influencing the return-to-forward shift; the second will impact both reversals.

The “non-orifice” shift time of the motor with 12 bar or greater system pressure is approximately 350 msec. An orifice of 0.8mm (0.032”) in the supply position, or an orifice of 1.3mm (0.051”) between the control valve and servo piston, will approximately double this time. Slowing the motor’s shift rate will reduce, if not eliminate, the initial pressure spike during the shaft reversal and will allow the load to slow down some before the motor actually reverses into pumping mode. The pressure during the rest of the load deceleration will be similar to the “non-orifice” system interval. The addition of either orifice will result in a longer deceleration time interval.

The process of returning to forward is not affected by a supply orifice, but will be affected by an orifice between the control valve orifice and the servo piston. The total time to stop the fan in this direction is nearly the same but more time is spent at high pressure if an orifice after the control valve is used.

The preference would be to apply the motor without the orifice since this allows the motor itself to shift at lower system pressures. If high pressure spikes, or system instability, are seen during the forward to reverse step, the best option is introduce a supply orifice into the control circuit.

Danfoss | January 2020 AB00000019en-000401 | 69

200

400

600

800

1000

1200

1400

1600

1800

100

150

200

250

300

2 2.5 3 3.5 4 4.5 5 5.5 6 6.5 7

RPM

Flow (lpm)

Time (sec)

P_System_A (bar) - No Orifice P_System_A (bar) - Orifice

n_RDM (LPM)-No Orifice n_RDM (LPM)-Orifice

P108919

Design Guidelines

Hydraulic Fan Drive Systems

Appendix I-System Considerations for RDM Fan Drives

Control Orifice Impact Forward to Reverse

RPM

Flow (lpm)

secTime ( )

P108920

200

400

600

800

1000

1200

1400

1600

1800

100

150

200

250

300

17 18 19 20 21 22 23 24 25

P_System_A (bar) - No Orifice

P_System_A (bar) - Orifice

n_RDM (LPM)-No Orifice

n_RDM (LPM)-Orifice

Design Guidelines

Hydraulic Fan Drive Systems

Appendix I-System Considerations for RDM Fan Drives

Control Orifice Impact Reverse to Forward

System Considerations

There are some system considerations that need to be taken into account when applying an RDM motor.

1. Anytime the RDM is used in a typical system, as shown in the schematic, a displacement reversal command will cause the RDM to turn into a pump until the load is stopped. This will cause oil to flow from the motor toward the pump (opposite the normal direction) with the amount of flow and length of time depending on system parameters such as the fan inertia, fan speed at command initiation, and reversing rate. When this happens, the motor (now operating as a pump) must be able to draw oil in through what is normally the return flow portion of the system.

Danfoss | January 2020 AB00000019en-000401 | 71

P108921

RDM Motor Cartridge

Reverse

CV #3

CV #1

CV #2

Return portion of system

Design Guidelines

Hydraulic Fan Drive Systems

Appendix I-System Considerations for RDM Fan Drives

RDM System Schematic

The amount of flow is a function of the motor displacement and speed so a system operating using the recommended reversing cycle will have only a very small amount of flow in the reverse direction, since the reversal starts at a much lower motor speed. A cycle with a high deceleration rate however, as shown in Control Orifice Impact graphs above, will require much greater amounts of flow, since the motor displacement is reversed at a much higher speed. Any filters, coolers, or other components that are in the return line could cause a restriction leading to cavitation in the motor. In addition to adding to any noise during the reversal, this could eventually lead to damage to the filter, heat exchanger, motor, or pump - causing reduced performance, or life, of the system.

One way to reduce this concern is to have a by-pass check valve in parallel to the filter and heat exchanger to allow free flow of oil into the motor when required. This is identified as CV #2 in the above schematic. This would also reduce the risk of this oil flow pulling contamination from the filter or damaging either of these components. This risk can be further minimized by adding a second check valve, shown as CV #1 in the schematic.

Motor Flow Requirements in Pumping Mode on page 73, below, shows an example in one system of

the impact of such a by-pass valve. When comparing the “Standard Schematic” data to the “Includes CV#2 only” data, during the first 250 msec after the motor displacement is reversed, the system without the by-pass valve shows a much greater deficiency in make-up flow into the motor than did the system with the by-pass valve.

100

150

200

250

300

2 2.5 3 3.5 4 4.5 5 5.5 6

low

(

pm)

Time (sec)

Motor System Flow Requirements

Forward to Reverse

-Q_System (LPM) Standard Schematic

Q_System (LPM) - Includes CV #2 only

tQ_Sys em (LPM) - Includes CV #3 only

Pred Motor Flow (lpm) - Standard Schematic

dPre Motor Flow (lpm) - Includes CV #2 only

Motor displacement is fully reversed at this point

Gap between blue lines gives a measure of the flow defficiency between flow going from the motor to the pump (predicted flow) and the make-up flow the motor is able to pull through the return system, with the standard schematic.

A much lower return flow is required if using check valve

CV #3 since the only flow required is to make up leakage,

once the system is pressurized.

P108916

Design Guidelines

Hydraulic Fan Drive Systems

Appendix I-System Considerations for RDM Fan Drives

Motor Flow Requirements in Pumping Mode

2. The peak value, and duration, of any pressure spike in the high pressure line will be controlled by how quickly the load energy is put into the system and by the avenues available to the system to drain this energy out. The avenues in a typical open circuit system would be;

Pump and motor control leakage flow

•

Pump and motor kit leakage flow

•

Pump’s ability to absorb oil by going over-center

•

Relief valves in the system

•

The characteristics of each of the above items are discussed in more detail below. By looking at the energy in the load during the reversal initiation, the power level required to reverse the load in the desired time and the paths available for energy dissipation; the system designer can determine if any other actions might be required.

3. Another system consideration is the impact on the case drain system. During the time interval of the reversal, the output flow at the motor case drain is significantly higher than under normal conditions during the reversal process. The servo piston will force approximately 53 cc’s (3.2 in^3) of oil into the motor case. Introducing 53 cc’s of fluid in 350ms equates to a nearly instantaneous change in the average case flow rate of approximately 9 lpm (2.4 gpm).

Also, in a system set-up like the schematic above, there may be a surge of oil through the pump control resulting in higher case flow leaving the pump. [Experience to date has not shown a problem with this on S45 pumps but this should be investigated during prototype testing to ensure there are no issues.]

4. Another system consideration is the impact on the system downstream of the motor outlet. During the motor reversal, the flow out of the motor will quickly reduce to zero (the motor’s at zero

Danfoss | January 2020 AB00000019en-000401 | 73

100

150

200

250

300

3 3.5 4 4.5 5 5.5 6 6.5 7 7.5 8

P_System_A (bar)

Standard Setup

Addition of Bypass only

Addition of Check only

P108917

Time (sec)

System Pressure (bar)

Design Guidelines

Hydraulic Fan Drive Systems

Appendix I-System Considerations for RDM Fan Drives

displacement) and then reverse direction (as discussed above). This has been shown to result in the motor outlet pressure cycling from normal - to a vacuum - to a high level spike. The main concern for the RDM itself is if the case-pressure rise (discussed directly above) and the outlet pressure drop - are too severe; such that added together they may cause a problem.

Laboratory tests following the recommended reversing cycle have shown that the RDM is more capable of handling a (“case minus return”) delta pressure pulse higher than the catalog rating, but this value should be kept below 3 bar.

For example, a test was performed with a a S45 J open circuit pump, a K-Frame RDM motor, and a fan inertia of 2kgm^2. System Pressure Response Characteristic on page 74 below shows a typical system pressure response. The blue line, or “Standard Setup”, would be the base system described in the schematic above. The red line, or “Addition of Bypass valve”, reflects adding the bypass valve, CV #2, into the circuit. The system builds pressure more quickly and, as a consequence, slows the fan more quickly; this brings the pressure down sooner. [This is because the RDM is able to draw more oil in during its pumping mode, allowing the fan energy to be dissipated more quickly.]

The data in System Pressure Response Characteristic on page 74 shown by the green line represents the “addition of check valve, CV#3”, (by itself) into the circuit between the pump and motor. It prevents the reverse flow from going into the pump. This system then utilizes only the motor leakage and integrated relief valve to dissipate the fan energy. As can be seen here, this results in a higher pressure and takes the longest time to reverse the fan.

System Pressure Response Characteristic

Design Guidelines

Hydraulic Fan Drive Systems

Appendix I-System Considerations for RDM Fan Drives

Zero RPM Motor Output

The RDM has the ability to reach and maintain a zero shaft speed condition. This could be beneficial for the purpose of reducing the time required for an engine to reach operating temperature, or for power savings - when cooling is not required.

A limited amount of tests have been performed in the laboratory to verify that this condition if is “possible”; but additional testing in the laboratory and on prototype vehicles under field conditions will be needed to verify whether a production solution on an individual vehicle system is feasible.

Warning

With regard to the swashplate bearings, at some point in the life of the motor, there is a potential that the motor will not return to the forward direction when the reverse command is removed. This is caused by excessive wear of the journal bearing and there are a number of factors that influence this life. Testing to date using the standard reversing cycle and schematic has shown have demonstrated a swashplate bearing life exceeding 60,000 reversals. This is believed to be satifactory for most applications.

Warning

With regard to the standard reversing cycle, a loss of control signal to the pump (due to a broken wire, corroded connection, etc.) would cause the pump to maintain maximum system pressure and motor speed. In this instance, the RDM will be able to reverse direction, but it may not be able to return to the forward direction, due to the high pressure and speed. As long as this does not become a standard operating mode, it will not damage the motor. Once the pressure and speed are reduced to their normal low pressure settings, the motor will return to the forward direction.

Danfoss | January 2020 AB00000019en-000401 | 75

Design Guidelines

Hydraulic Fan Drive Systems

Reference Literature

Fan drive systems may consist of a variety of pump, motor, valve and control combinations. The product codes shown below are for components that have been designed specifically for fan drive systems. Refer to the literature listed below for product code information and specifications for other Danfoss components that may be utilized in a fan drive system.

Open Circuit Axial Piston Pumps

Series 45 Axial Piston Pumps 520L0519

•

Open/Closed Circuit Axial Piston Motors

L and K Frame Variable Motors 520L0627

•

Series 40 Axial Piston Motors 520L0636

•

Series 90 Axial Piston Motors 520L0604

•

H1B Axial Piston Motors 11037153

•

Controllers

Fan Drive Control Temperature Sensors BLN-95-9063

•

Electronic Fan Drive Controller (FDC) 11005336

•

Electronic Fan Drive Controller Assembly (FDCA) 11005337

•

PLUS+1TM Controller Family 520L0719

•

System Guidelines

•

Closed Circuit Axial Piston Pumps

•

Design Guidelines for Hydraulic Fluid Cleanliness 520L0467 Design Guidelines for Hydraulic Fan Drive Systems 520L0926

H1 Axial Piston Pumps Basic Information 11062168 Series 42 Axial Piston Pumps 11022637

H1 045/053 Tandem Axial Piston Pumps Technical Information 11063345

H1 045/053 Single Axial Piston Pumps Technical Information 11063344

H1 089/100 Single Axial Piston Pumps Technical Information 11069970

H1 069/078 Single Axial Piston Pumps Technical Information 11062169

H1 147/165 Single Axial Piston Pumps Technical Information 11063347

H1 210/250 Single Axial Piston Pumps Technical Information L1208737

H1 115/130 Single Axial Piston Pumps Technical Information 11063346

Danfoss Power Solutions GmbH & Co. OHG

Krokamp 35 D-24539 Neumünster, Germany Phone: +49 4321 871 0

Danfoss Power Solutions ApS

Nordborgvej 81 DK-6430 Nordborg, Denmark Phone: +45 7488 2222

Danfoss Power Solutions (US) Company

2800 East 13th Street Ames, IA 50010, USA Phone: +1 515 239 6000

Danfoss Power Solutions Trading (Shanghai) Co., Ltd.

Building #22, No. 1000 Jin Hai Rd Jin Qiao, Pudong New District Shanghai, China 201206 Phone: +86 21 2080 6201

Products we offer:

Hydro-Gear

www.hydro-gear.com

Daikin-Sauer-Danfoss

www.daikin-sauer-danfoss.com

DCV directional control

•

valves Electric converters

•

Electric machines

•

Electric motors

•

Gear motors

•

Gear pumps

•

Hydrostatic motors

•

Hydrostatic pumps

•

Orbital motors

•

PLUS+1® controllers

•

PLUS+1® displays

•

PLUS+1® joysticks and

•

pedals PLUS+1® operator

•

interfaces PLUS+1® sensors

•

PLUS+1® software

•

PLUS+1® software services,

•

support and training Position controls and

•

sensors PVG proportional valves

•

Steering components and

•

systems Telematics

•

Danfoss Power Solutions is a global manufacturer and supplier of high-quality hydraulic and electric components. We specialize in providing state-of-the-art technology and solutions that excel in the harsh operating conditions of the mobile off-highway market as well as the marine sector. Building on our extensive applications expertise, we work closely with you to ensure exceptional performance for a broad range of applications. We help you and other customers around the world speed up system development, reduce costs and bring vehicles and vessels to market faster.

Danfoss Power Solutions – your strongest partner in mobile hydraulics and mobile electrification.

Go to www.danfoss.com for further product information.

We offer you expert worldwide support for ensuring the best possible solutions for outstanding performance. And with an extensive network of Global Service Partners, we also provide you with comprehensive global service for all of our components.

Local address:

Danfoss can accept no responsibility for possible errors in catalogues, brochures and other printed material. Danfoss reserves the right to alter its products without notice. This also applies to products already on order provided that such alterations can be made without subsequent changes being necessary in specifications already agreed. All trademarks in this material are property of the respective companies. Danfoss and the Danfoss logotype are trademarks of Danfoss A/S. All rights reserved.

Danfoss | January 2020 AB00000019en-000401

Danfoss Hydraulic Fan Drive Systems Application guide

Specifications and Main Features

Frequently Asked Questions

User Manual

Contents

Introduction

Abstract

Overview

Principles of Operation

Power Savings

Modulation Preferred Over on/off Fan Speed Control

Fan Drive Design

Design Considerations

Fan Drive Components

Fan Drive Element Selection

Estimate of Maximum Input Torque to the Pump

System Design Parameters

Sizing

Sizing Equations

Equations

Variables

Axial Flow Fan Power Formula

System Design Data Form

Engine details

Power steering

Fan information

Control preference

Reservoir

Fluid

Filtration

Technical Features

Shaft Loads and Bearing Life

Maximum Pump Speed

Minimum Pump and Motor Speed

Motor Starting Pressure (open circuit motors)

Motor Free Run Pressure

Input Torque Ratings

Pump Drive Conditions

Tapered Shaft and Hub Connections

Pump Suction

Case Drain Pressure

Filtration

Operating Temperatures

Fluids

Mounting

Axial Thrust Motors

Piping

Reservoir

Cavitation and Aeration Damage

Cooling

Pressure Protection and Ratings

Bearing Life Expectancy

Glossary

Terminology

Appendix A-Fan Performance

Fans

Fan Performance

Axial Thrust

Fan Laws

Example 1

Example 2

Example 3

Example 4

Appendix B-Fan Drive Sizing Equations

Fan Drive Sizing Equations and Derivations

Hydraulic System Comparisons

Appendix C-Fan Drive Sizing Equations, using Variable Displacement Motors

Hydraulic Systems with 2 Position, Variable Displacement Motors, Equations and Derivations

Spreadsheet to Calculate the Optimum Minimum Displacement for 2 Position Variable Motor

Appendix D-Pressure change due to transient flow in a passage

Pressure Change due to Transient Flow in a Passage, Equations and Derivations

Appendix E-Influence of Bypass Valve Pressure Drop in Open Circuit Systems

Appendix F1-Influence of temperature, pressure and relative humidity on specific weight of air

Influence of Temperature, Pressure and Relative Humidity on Specific Weight of Air

Appendix F2-Influence of Altitude on Atmospheric Pressure

Influence of Altitude on Atmospheric Pressure

Appendix F3-Influence of generic altitude on atmospheric pressure

Influence of Generic Altitude on Atmospheric Pressure

Appendix G-Influence of reversed fan rotation on system performance

Appendix H-System considerations for H1 fan drives with reversed fan rotation