Commodore CBM 2001, CBM 3001 User Manual

Download

commodore -

Bedienungshandbuch

Computer

Dieses Handbuch wurde gescannt, bearbeitet und ins PDF-Format konvertiert von

Einleitung

Diese Einleitung befaßt sich mit dem grundsätzlichen Kennenlernen Ihres Computers.

Sollten Sie mit dessen Bedienung schon etwas vertraut sein, so dürfte diese Anleitung für Sie kaum etwas Neues bieten. Wir halten es jedoch für unerläßlich, Sie mit der Grundbedienung vertraut zu machen. Meist ist es ja so, daß der Neuling an Kleinigkeiten verzweifelt, die dem Erfahrenen nur ein müdes Lächeln abringen.

Stecken Sie also den Schukostecker in die Steckdose und schalten das Gerät einmal ein. Der Einschalter befindet sich auf der Rückseite des Rechners links unten. Nach kurzer Zeit haben Sie ersten Kontakt; der Rechner meldet sich auf dem Bildschirm mit der Meldung:

# # # COMMODORE BASIC # # # 7167 BYTES FREE READY.

Die Zahl 7167 (oder 15359 bei den Geräten der Serie 3016 bzw. 31743 beim 3032) sagt Ihnen übrigens, wie groß der Schreib-Lese-Speicher Ihres Computers ist.

Die Meldung # # # COMMODORE BASIC# # # sagt Ihnen, in welcher Sprache der Rechner program miert werden kann. Auf die Sprache BASIC kommen wir ausführlich in Kapitel 1 zu sprechen.

Sollte wider Erwarten der Einschaltvorgang nicht korrekt ablaufen, so versuchen Sie bitte folgendes:

1. Drehen Sie den Helligkeitsregler für den Bildschirm entgegen dem Uhrzeigersinn bis zum Anschlag. Sollte die Meldung des Rechners jetzt sichtbar sein, so drehen Sie den Regler wieder soweit zurück, bis die Schrift normal hell sichtbar ist.

2. Schalten Sie den Rechner wieder aus. Ziehen Sie den Netzstecker aus der Steckdose. Überprüfen Sie die Sicherung, die Sie mit einem Schraubenzieher herausdrehen können (die Siche

rung befindet sich direkt neben dem Einschalter). Sollte die Sicherung noch in Ordnung sein, so bleibt Ihnen nichts anderes übrig, als Ihren Fachhändler aufzusuchen.

Nachdem Sie nun den Rechner eingeschaltet haben, wollen wir kurz einmal den Begriff der Dialogfähig keit des Rechners erläutern. Die Dialogfähigkeit des Rechners besagt nichts anderes, als daß:

1. Sowohl eine Eingabemöglichkeit, als auch eine Ausgabemöglichkeit des Rechners in Sicht- und Griff weite des Bedieners sein müssen (bei Ihrem Gerät sind das der Bildschirm und die Tastatur).

2. Daß sowohl der Rechner fragen kann und Sie antworten als auch Sie Fragen oder Aufgaben stellen können und der Rechner antwortet.

3. Der Rechner Ihnen offensichtliche Fehler, die Sie bei der Programmierung gemacht haben, möglichst genau lokalisiert, so daß eine Korrektur leicht und schnell möglich ist.

Alle diese Möglichkeiten bietet Ihnen der Computer. Er kann somit ohne Einschränkungen als dialogfähig bezeichnet werden.

Sehen wir uns einmal die Tastatur genauer an. Grundsätzlich gliedert sich die Tastatur in sieben Unter gruppen:

1. Die alphabetischen Tasten

Drücken Sie einmal leicht auf die Taste Q. Wie zu erwarten, erscheint auf dem Bildschirm an der Stelle, wo sich das blinkende Quadrat gerade noch befand, ein Q und das Quadrat wandert eine Stelle weiter nach rechts (es nennt sich übrigens CURSOR).

Der Computer reagiert natürlich auf alle Buchstaben, Zahlen und Sonderzeichen genauso, wie auf dasQ.

2. Die numerischen Tasten

An sich ist eine Trennung dieser Tasten von den anderen nicht nötig. Da in einem Computer sehr oft Zahlen eingegeben werden, ist es aber sinnvoll, die Zifferntasten zusammenfassen, damit Sie ohne große Handbewegung schnell hintereinander erreichbar sind.

Erstaunen mag Sie als EDV-Neuling wohl, was der Punkt in diesem Block zu suchen hat, während das Komma, bei jeder Zahl mit Nachkommastellen unerläßlich, ganz wo anders angebracht ist.

Doch das ist schnell erklärt.

In den U.S. A., wo auch Ihr Computer herkommt, gibt es kein Dezimalkomma, sondern ein Punkt trennt Vor- und Nachkommastellen. Wenn Sie sich diese Besonderheit schon jetzt einprägen, werden Sie später viele Eingabefehler an Ihrem Rechner umgehen können.

3. Die grafischen Zeichen (Siehe Anhang VIII für die -2-Tastatur)

Bestimmt haben Sie die seltsamen Hieroglyphen auf der Tastatur schon verwundert. Das sind gra fische Zeichen, mit denen man z. B. Tabellen oder einfache Bilder herstellen kann. Um diese Zeichen auf dem Bildschirm darzustellen, machen Sie folgendes:

A) Drücken Sie eine der beiden SHIFT-Tasten (im alphabetischen Tastenblock untere Reihe links und

rechts).

B) Halten Sie diese Taste gedrückt und drücken Sie gleichzeitig beispielsweise die Taste Q. Auf dem

Bildschirm erscheint das zugehörige Sonderzeichen (statt eines Q beispielsweise ein weißer Kreis). Siehe auch 1.2.36.

4. Die CURSOR-Steuertasten

Was der Cursor (sprich Körser) ist, haben wir bereits einmal kurz angesprochen. Wir wollen an dieser Stelle jedoch einmal genauer darauf eingehen.

Prinzipiell hat der Cursor 2 Funktionen:

Erstens teilt der Computer Ihnen dadurch mit, daß er auf eine Eingabe per Tastatur von Ihnen wartet. Zweitens zeigt er Ihnen an, wo auf dem Bildschirm diese Eingabe angezeigt wird. Das durch die Ta

statur gewählte Zeichen erscheint genau an der Stelle, wo sich der Cursor gerade befindet. Nun ist es oftmals nötig, den Cursor zu bewegen, ohne daß ein Zeichen geschrieben wird, oder Sie

haben sich verschrieben und wollen ein Zeichen nachträglich einfügen, ändern oder löschen. Dazu dienen die Cursor-Steuertasten.

Diese befinden sich in der oberen Reihe des numerischen Tastaturblocks.

Sehen wir uns ein Beispiel an: Drücken Sie gleichzeitig

SHIFT

CLR

HOME

Der gesamte Bildschirminhalt wird gelöscht und der Cursor steht in der oberen Zeile links.

Geben Sie nun einen beliebigen Text ein, z. B.: DER cbm IST EIN COMPUTER

Nach jedem Buchstaben bewegt sich der Cursor eine Stelle weiter nach rechts und steht zum Schluß hinter dem R von Computer.

Wir wollen nun den Text ändern, daß er zum Schluß heißt:

DER cbm - MEIN COMPUTER

Zuerst löschen wir das IST und ersetzen es durch -. Drücken Sie dazu die Tasten

SHIFT

CRSR

—»

Wie Sie sehen, bewegt sich der Cursor um eine Stelle nach links. Er steht jetzt auf dem R von Com puter. Wiederholen Sie den Vorgang, bis der Cursor auf dem T von IST steht.

Nun drücken Sie zweimal die Taste

INST

DEL

Nach jedem Tastendruck verschwindet das sich jeweils links neben dem Cursor befindliche Zei chen und der Rest der Zeile wird, einschließlich dem Cursor, um eine Stelle nach links nachgeführt.

Geben Sie jetzt einfach das Zeichen - ein; es überschreibt das vom IST übrig gebliebene T. Mit der Taste

CRSR (aber ohne SHIFT

Mit den Tasten

) bewegen Sie jetzt den Cursor auf das E von EIN.

machen Sie nun Platz für das noch fehlende M. Dabei wird der Rest der Zeile ab dem Cursor um eine Stelle nach rechts verschoben. Zum Schluß gehen Sie mit der Taste

wieder an das Ende des Satzes.

In diesem Beispiel haben wir den Cursor in einer Zeile hin- und her bewegt. Genauso leicht ist es aber

auch möglich, in die darunter liegende Zeile

CRSR

oder darüber liegende Zeile

SHIFT +

CRSR

zu springen. Zwei Besonderheiten an dieser Stelle noch zu dem Bildschirm: wenn beim Einfügen mit den Tasten

SHIFT

der Rest der Eingabe das Ende der Zeile erreicht hat, so wird er in die nächste tiefere Zeile schreibrich tig übertragen. Über mehr als eine Zeile ist das aber nicht möglich. Das Einfügen von Zeichen wird dann blockiert. Das geschieht aus folgendem Grund:

In seinem Speicher behandelt der Rechner zwei Bildschirmzeilen â 40 Zeichen wie eine Zeile â 80 Zei chen. Mehr als 80 Zeichen können also nicht gleichzeitig behandelt werden. Die zweite Besonderheit stellen Sie fest, wenn Sie mit dem Cursor in die unterste Zeile »fahren«. An sich müßte der Cursor jetzt

bei weiteren Versuchen, noch tiefer zu fahren, stehen bleiben. Z. B. am oberen Rand, wenn Sie noch

höher fahren wollen. Das geschieht zwar auch, der Bildschirminhalt wird um eine Zeile nach oben ge

schoben und die oberste Zeile des Bildes verschwindet. Man nennt das »der Bildschirm rollt« oder

auch

ROLL MODE

im Gegensatz zum stehenden Bild, das man

BLOCK MODE

nennt.

Die verschwundene Zeile ist endgültig gelöscht, da der Roll Mode nur in einer Richtung arbeitet und

zwar nur von unten nach oben.

Sie selber haben gesehen, welche Vorteile die Cursor-Steuertasten haben. Ihr Gebrauch wird Ihnen

schnell zur Gewohnheit werden.

INST

DEL

Daher noch einmal eine Zusammenfassung

CURSOR RIGHT (Cursor nach rechts)

: Der Cursor bewegt sich eine Stelle nach rechts;

SHIFT CRSR

CRSR

SHIFT

INST

DEL

SHIFT

CLR

HOME

CRSR

INST

DEL

CURSOR LEFT (Cursor nach links) Der Cursor bewegt sich eine Stelle nach links;

CURSOR DOWN (Cursor nach unten) Der Cursor bewegt sich um eine Zeile nach unten;

CURSOR UP (Cursor nach oben) Der Cursor bewegt sich um eine Zeile nach oben;

DELETE (Zeichen löschen) Das links von dem Cursor befindliche Zeichen wird gelöscht. Gleichzeitig wird der

gesamte rechte Teil der Zeile zusammen mit dem Cursor um ein Zeichen nach links versetzt.

INSERT (Zeichen einfügen)

Ab der Position des Cursors wird der rechte Teil der Zeile um eine Stelle nach rechts verschoben. Der Cursor bleibt an der gleichen Stelle stehen, wo sich nun ein Leer zeichen befindet.

HOME (Cursor in Grundstellung) Der Cursor wird in seine Grundstellung nach links oben versetzt.

SHIFT

CLR

HOME

CLEAR (löschen des Bildschirms) Zusätzlich zu der Home-Funktion wird der gesamte Bildschirminhalt gelöscht.

5. Die RVS-Taste

(Reverse = umgekehrt)

RVS

Mit dieser Taste können Sie alle Zeichen auf dem Bildschirm dunkel auf hellem Untergrund stellen. Man nennt das

INVERSE VIDEO (umgekehrter Bildschirm) Diese Darsteilungsart wird bevorzugt, um besonders wichtige Meldungen auf dem Bildschirm hervor

zuheben. Die RVS-Taste hat drei Bedeutungen:

OFF RVS

SHIFT

OFF

RVS

OFF

RVS

Nach Drücken dieser Taste erscheinen alle folgenden Zeichen invertiert, bis die Funktion ausgeschaltet, oder die Taste »RETURN« gedrückt wird.

Nach Drücken dieser Taste wird inverse video wieder abgeschaltet und

alle weiteren Zeichen erscheinen wieder normal.

Sollten Sie einmal Informationen auf dem Bildschirm nicht lesen kön nen, weil im Roll-Mode die Zeilen zu schnell »vorbeilaufen«, so kann durch Drücken der Taste »OFF RVS« die Ausgabe so weit verlangsamt werden, daß ein Lesen in Ruhe erfolgen kann.

6. Die RETURN-Taste

Diese Taste (Alpha -Tastenblock, 2. + 3. Zeile rechts, rot) beendet eine Eingabe in den Rechner (nicht zu verwechseln mit dem Bildschirm, der ist nur ein Teil des Rechners). Ihr Computer kann nämlich nicht ahnen, wann die Information (man sagt in Fachkreisen dazu DATEN; auch wir werden uns jetzt daran halten) vollständig sind. Wenn Sie z. B. eine 1 eingegeben haben, weiß der Rechner nicht, ob vielleicht noch eine 6 folgt. Dazu beenden Sie alle Dateneingaben mit der Taste RETURN:

Z.B.:

1 RETURN

(Eingabe der Zahl 1).

RETURN

(Eingabe der Zahl 16).

7. Die RUN/STOP-Taste

Auch die RUN/STOP-Taste hat zwei Bedeutungen. Zum einen können Sie mit dieser Taste ein laufen des Programm an jeder beliebigen Stelle abbrechen. Das ist dann sinnvoll, wenn Sie in einem laufenden

Programm gewisse Daten überprüfen wollen, die nicht von selber ausgegeben werden. Beispiele dafür

geben wir Ihnen später.

Zum anderen können Sie auf einer Kassette gespeichertes Programm mit

SHIFT

RUN

STOP

in den Speicher des Computers einladen und automatisch starten.

1. DER COMPUTER UND SEINE SPRACHE

BASIC, die Sprache in der Ihr Computer arbeitet, ist eine leicht erlernbare, zum Teil aus englischen

Worten, zum Teil aus mathematischen Zeichen bestehende Folge von Befehlen. Obwohl es eine der

leichtesten Programmiersprachen ist, ist sie ungeheuer vielseitig und flexibel. Ursprünglich an der Dartmouth University entwickelt um Studenten die Möglichkeit zu geben, schnell und leicht Pro bleme an einem Computer zu bearbeiten, breitete sich diese Sprache sehr schnell in der ganzen Welt aus. Heute existiert BASIC in unzähligen Versionen auf fast jedem größeren Computer.

Bei unserem COMMODORE-BASIC stand auch das DARTMOUTH-BASIC Pate; gleichzeitig ist das COMMODORE-BASIC größer und leistungsfähiger geworden.

1.1. Die Komponenten der BASIC-Programmiersprache

Bevor wir uns mit der eigentlichen Sprache BASIC befassen, müssen wir uns zuvor über einige Schreibregeln einigen. Nachfolgend eine Liste der Konventionen und Ausdrücke, die wir in diesem Buch zu unserer und Ihrer Erleichterung einführen:

Eckige Klammern [ ] - Ausdrücke in eckigen Klammern können, müssen aber nicht angegeben

werden.

Zeichen - Ein Buchstabe, eine Zahl oder ein beliebiges Sonderzeichen.

Konstante - Eine Zahl innerhalb der Rechengrenzen Ihres Computers (siehe 1.1.1 ).

Formel - Eine Konstante, eine Variable oder ein Ausdruck, bestehend aus Konstanten

und /oder Variabaien (z. B. 8 + 3* %).

Buchstabe Zeilennummer Text Variable

Integer

Byte Geschweifte Klammer O

Ein alphabetisches Zeichen von A - Z. Eine ganze Zahl von 0 bis 63999. Eine Folge von 0 bis 255 beliebigen Zeichen.

Siehe 1.1.2. Eine ganzzahlige Konstante oder Variable im Bereich von - 32768 bis 32767. Eine ganzzahlige Konstante oder Variable im Bereich von 0 bis 255. Genau einer der in geschweiften Klammern angegebenen Ausdrücke muß

benutzt werden.

1.1.1 Die Konstanten

Die Grundform einer Konstanten ist eine Dezimalzahl zwischen 1.7*1038 und 2.93*1 CT39.

Bis zu 9 Stellen einer Zahl können gespeichert werden und es kann damit gerechnet werden.

Beispiele für Konstanten: 25,15.75, -87, 0, 3255, 45E7.14.2E-6,13.12345678

In zwei der Konstanten tauchte der Buchstabe E auf. Der Buchstabe E besagt, daß die nach

folgenden Zahlen den Exponenten zur Basis 10 darstellen.

1.5E3 bedeutet 1.5*103=1.5*10*10*10 = 1.5*1000 = 1500

1.27E-2 bedeutet 1.27*10“2 = 1.27/10/10 = 1.27/100 = 0.0127. Das Vorzeichen wird nur bei negativen Zahlen geschrieben.

Konstanten werden verwendet, um feste Werte zu fixieren.

Da der Computer nicht nur numerische Werte verarbeiten kann, sondern auch Textverarbeitung

zuläßt, gibt es genauso wie numerische Konstanten auch Textkonstanten:

”A”, ’’PETER IST LIEB”, ’’ICH BIN EIN CBM”, ”125 LAMPEN”.

Die Textkonstanten erkennt man daran, daß sie in Anführungszeichen eingebettet sind. Die Anfüh

rungszeichen selber gehören jedoch nicht zur eigentlichen Textkonstante.

1.1.2. Die Variablen

Eine Variable ist ein Symbol, dessen Wert sich ändern kann. Der Name einer Variablen besteht aus

entweder einem Buchstaben z. B.: A, G, Z oder einem Buchstaben und einer Zahl z. B.: A1, F6,V9 oder zwei Buchstaben z. B.: AX, PE, UT, UX plus (wahlweise) der Kennzeichnung % oder $.

Eine Variable kann aus mehr als zwei Zeichen bestehen, es werden aber nicht mehr als zwei Zei chen abgefragt. Wenn Sie zum Beispiel zwei Variablen HANS und HABEL nennen, so werden diese wie eine Variable behandelt, da beide mit HA anfangen.

Die Variable kann innerhalb eines BASIC-Programms verschiedene Funktionen annehmen:

- Variablen repräsentieren numerische Werte z. B.: A=10 , A5=-5.6E-3 , XY=3.14

- Variablen können in den Rechner eingegeben werden z. B. 10 INPUT A,B,C1,XY

~T~ P- I

___________________________________________

____________________________________________________ Zeilennummer

- Variablen können gleich gesetzt werden z. B. A = B, A5= XY, XY = B (A wird gleich B gesetzt, usw.)

_____________________________

Variablenliste

Eingabebefehl

Variablen können ausgedruckt werden

Z. B. 20 PRINT A. B. C1.XY

Variablenliste Ausgabebefehl Zeilennummer

Es gibt drei Arten von Variablen:

1. Fließkommavariablen

Diese Variablen können jeden beliebigen Wert innerhalb der Rechengrenzen des Computers an nehmen.

Jede Variable, deren Name das Kennzeichen % oder$ nicht enthält, ist eine Fließkommavariable.

Beispiel: A = 7

B8 = 1.5E3 ZY = 9E9 X1 =-0.52187

2. Festkommavariablen

Diese Variablen können als Wert ganze Zahlen zwischen (einschließlich) -32767 und +32767 an nehmen. Sie haben am Ende des Namens das Zeichen % stehen.

Beispiel: A% = 7

L1 % = 4528 X0% =0

3. Stringvariablen (Strings, Textvariablen)

Diese Variablen haben als Wert einen beliebigen Text aus 0 bis 255 Zeichen. Sie werden mit ange hängtem $ gekennzeichnet.

Beispiel: A$ = ’’TEXT”

B$ = ”55” C$ = ’’DIES IST EIN STRING”

X1 $ = ’’COMPUTER 3001 ”

N$ = ” ” (Bemerkung: dieser String besteht aus keinem Zeichen.)

Alle drei Variablenarten können noch indiziert werden. Man spricht dann von dimensionierten Variablen, Matrizen, Feldern oder Arrays. Siehe 1.2.18.

1.1.3. Arithmetische Operationen Zu den arithmetischen Operationen gehören zunächst einmal die vier Grundrechenarten, die auf dem Computer eine etwas andere Darstellungsform besitzen als Sie es vielleicht von anderen

Geräten oder Beschreibungen her kennen.

Nachfolgend die Darstellung dieser Zeichen:

Addition + Subraktion Multiplikation *

Division /

Darüberhinaus existieren eine Vielzahl von mathematischen Funktionen, die standardmäßig vor handen sind.

Betrachten wir diese Funktionen im einzelnen.

• SGN Die SIGNUM (Vorzeichen)-Funktion. Der Funktionswert ist:

für negative Zahlen -1 für positive Zahlen +1 für Null 0

Syntax: SGN ({Variable, Konstante, arithm. Ausdruck }) Beispiel: A = SGN (B)

PRINT SGN (-45) PRINT SGN (A + 7T *2)

Den Wert in der Klammer bezeichnet man als Argument.

Anstelle von PRINT kann auch das Fragezeichen gesetzt werden.

Anwendung:

Auf sehr einfache Weise bestimmen, ob eine Zahl negativ, positiv oder 0 ist.

• INT Die INTEGER-Funktion Sie bildet bei positiven Zahlen die kleinste ganze Zahl, d.h. alle Nachkommastellen werden zu 0 gesetzt.

Bei negativen Zahlen bildet sie die kleinste negative Zahl, d. h. alle Nachkommastellen werden bis zur nächsten ganzen Zahl abgerundet.

Syntax: INT ({Variable, Konstante arithm. Ausdruck })

Beispiel: A = INT (B)

? INT (B) ? INT (-2.5) ?INT(X-Y)

Anwendungsbeispiel:

Auf- oder Abrunden eines Ergebnisses, wenn nur eine ganzzahlige Größe erlaubt ist, z. B. bei der

rechnerischen Ermittlung einer Zahl von Schrauben in einem Behälter.

• ABS Die ABSOLUTWERT-Funktion

Sie schneidet das Vorzeichen ab und bildet nur den absoluten Wert.

Syntax: ABS ({Variable, Konstante, arithm. Ausdruck })

Beispiel: A = ABS (B)

? ABS (-145)

Anwendungsbeispiel:

Berechnung einer Wurzel aus einer unbekannten Zahl. Da es mathematisch nicht möglich ist, aus

einer negativen Zahl eine Wurzel zu ziehen, kann man zuvor den Absolutwert bilden.

• SQR Die SQUARE ROOT (Quadratwurzel)-Funktion

Sie bildet die Quadratwurzel aus dem Argument.

Syntax: SQR ({Variable, Konstante, arithm. Ausdruck })

Beispiel: A = SQR (B) ? SQR (16)

Anwendung:

Im Bereich der Mathematik.

• SIN Die SINUS-Funktion Sie berechnet den Sinuswert des Arguments im Bogenmaß. (Die mathematische Be deutung der trigonometrischen Funktionen wird als bekannt vorausgesetzt.)

Syntax: SIN ({Variable, Konstante, arithm. Ausdruck })

Beispiel: A = SIN (B)

? SIN (30)

Anwendung:

Im Bereich der Mathematik. Ist das Argument in GRAD gegeben, muß es durch eine Umrechnung modifiziert werden.

Beispiel: A = SIN (30 * 7r /180)

Ist das Argument in NEUGRAD gegeben, so lautet die Umrechnung:

Beispiel: A = SIN (30 * tt / 200)

• COS Die COSINUS-Funktion Sie wird genauso behandelt wie die SIN-Funktion.

• TAN DieTANGENS-Funktion Sie wird behandelt wie die SIN-Funktion.

Die COTANGENS-Funktion existiert bei Ihrem Rechner nicht, da sie sehr einfach durch dieTANFunktion gebildet werden kann. Die Beziehung lautet:

COT (X) =

TAh

S (X)

Beispiel: Y = 1 / TAN (X)

Von den Umkehrfunktionen zu den bisher behandelten trigonometrischen Funktionen existiert

lediglich die

• ATN ARCUSTANGENS-Funktion. Sie bildet die Umkehr-Funktion des TANGENS.

Syntax: ATN ({Variable, Konstante, arithm. Ausdruck })

Beispiel: Y = ATN (X)

Anwendung:

Im Bereich der Mathematik.

Die Umkehrfunktionen zum SIN und COS lassen sich leicht mit dem ATN berechnen. Die Beziehungen lauten:

ARC SIN (X) = ATN (X / SQR (1 - X f 2))

ARC COS (X) = ATN (SQR (1 - X | 2) / X)

• LOG der NATÜRLICHE LOGARITHMUS ermittelt die Logarithmen zur BASIS e = 2,7182818

Syntax: LOG ({Variable, Konstante, arithm. Ausdruck }) Beispiel: Y = LOG (X)

• EXP der EXPONENT zur natürlichen Basis e ermittelt den Wert der Funktion y = e

Syntax: EXP ({Variable, Konstante, arithm. Ausdruck }) Beispiel: Y = EXP (X)

0 I die Potenzierung zu einer beliebigen Basis mit beliebigen Exponenten.

Syntax: {Variable, Konstante, arithm. Ausdruck} { {Variable, Konstante, arithm. Ausdruck}

Beispiel: Y = A { X

? 2 } 3

• RND die RANDOMIZE (Zufalls)-Funktion Sie bildet Pseudo-Zufallszahlen zwischen 0 und 1.

Syntax: RND ({ Variable, Konstante, arithm. Ausdruck })

Beispiel: ? RND (X)

a) X negativ

RND mit negativem Argument ergibt immer den gleichen Funktionswert. Dies kann beispielsweise für Fehlersuche oder während der Programmentwicklung nützlich sein.

b) X = 0

ergibt einen Wert, der nur von der Zeit seit dem Einschalten des Computers abhängt.

c) X positiv

liefert von der Zeit und von X abhängige Zufallsvariablen.

Beispiel: Es soll ein Würfel simuliert werden.

10 W = RND(-TI)

20 W = INT (6 * RND (1) + 1) 30? W

• is die Zahl PI. Sie ist fest gespeichert, tt = 3.14159265

1.1.4 OPERATOREN

zu den Operatoren zählen: a) die Vergleichsoperatoren

b) die logischen Operatoren

Vergleichsoperatoren

Sie dienen dazu, Zahlenwerte zu vergleichen. Dies bildet einen sehr wichtigen Bestandteil bei der Behandlung und Untersuchung von Zahlen.

Wenn z. B. aus einer Zahlenfolge alle Zahlen ermittelt werden sollen, die einen bestimmten Grenz wert überschreiten, wird ein Vergleichsoperator angewendet.

Die Frage lautet:

- Welcher Wert ist größer als der Grenzwert, bzw.

- Welcher Wert ist kleiner oder gleich dem Grenzwert.

Die mathematische Darstellungsform dieser Vergleichsoperatoren zeigt nachfolgende Tabelle:

BASIC SCHREIBWEISE BEDEUTUNG

< kleiner als > größer als

= < gleich oder kleiner als = > gleich oder größer als

<> oder ><

Einige Beispiele mögen die Anwendung und Bedeutung der Vergleichsoperatoren hervorheben. Dabei benutzen wir schon jetzt die im Rechner gebräuchliche Schreibweise.

IF A < B THEN ? A IF

A > B THEN ? B

A < > B (oder: IF A >< B) IF A >= B IF A <= B

A = B THEN ? ”A =

nicht gleich Gleichheit

wenn A kleiner als B, dann drucke A

Wenn A größer gleich B, dann ...

B” wenn A gleich B, dann drucke: A = B

LOGISCHE OPERATOREN

Sie sind der Booleschen Algebra entlehnt und finden unter anderem in der elektronischen Digital technik (also die Technik, in der der Rechner arbeitet) Anwendung.

In den Programmiersprachen haben sie ebenfalls eine sehr große Bedeutung. Man kann mit Ihnen

komplizierte Abfragen aufbauen. Der Rechner kennt drei logische Operatoren, nämlich AND (und -Bedingung)

OR (oder-Bedingung)

NOT (nicht- Bedingung)

Diese Operatoren können angewendet werden auf beliebige Variablen.

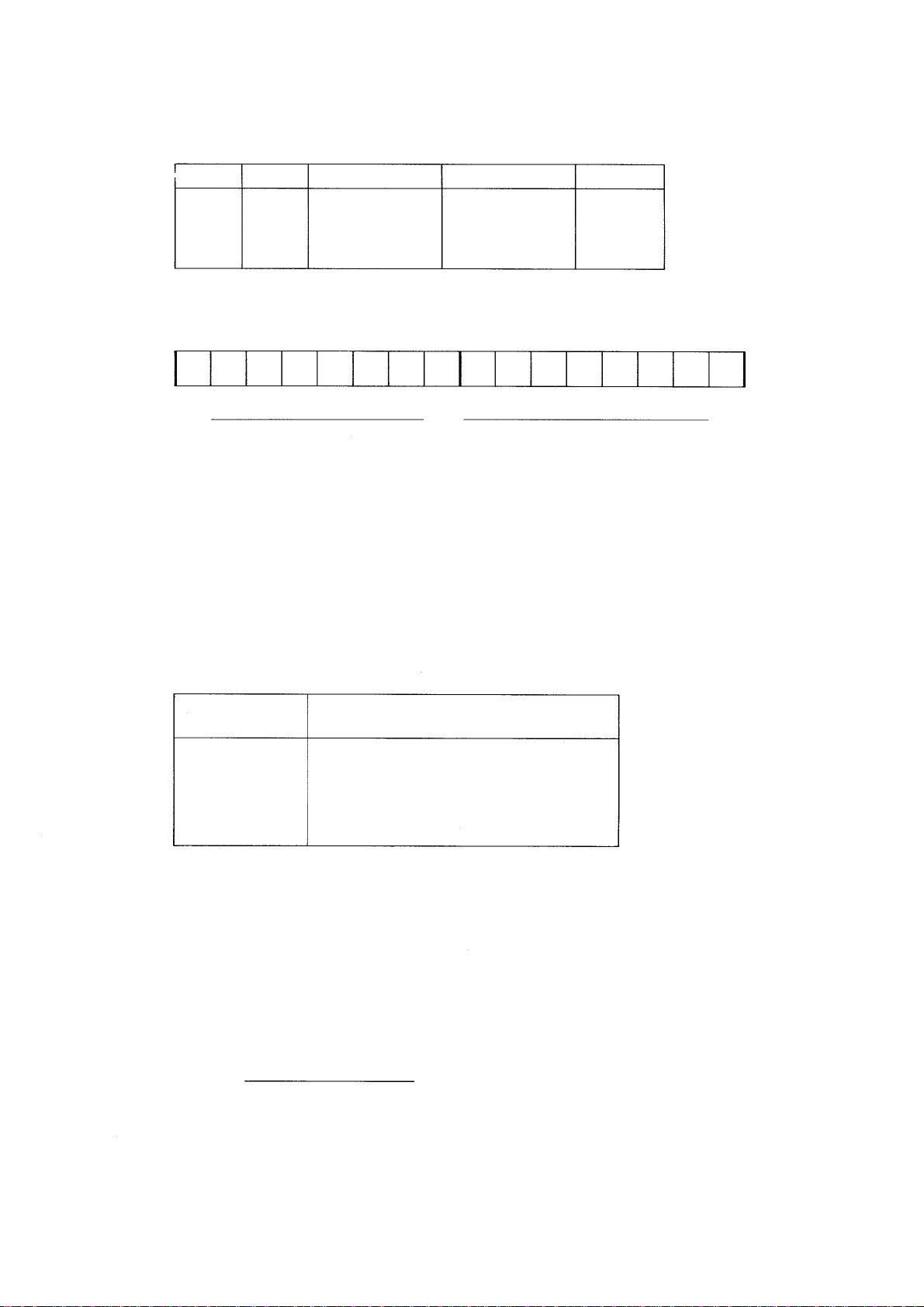
1. AND, OR und NOT bei Festkommavariablen:

Bei ganzen Zahlen zwischen — 32767 und 32767 arbeiten diese Funktionen bitweise in der folgen

den Art:

0 0 0 0 1

1 1 1 1

Alle Festkommazahlen (Integerzahlen) sind im Computer binär verschlüsselt. Sie bestehen aus 16 Bits, die jeweils den Zustand 0 oderl annehmen können.

X X X X X

____

Daraus folgt, daß 216 = 65536 verschiedene Integerzahlen darstellbar sind. Da wir aber bei ganzen Zahlen auch negative Zahlen darstellen wollen, wird Bit 15 als Vorzeichen

benutzt. Wenn dieses Bit Null ist, so ist die Zahl positiv, ist Bit 15 gleich Eins, so ist die Zahl negativ. Es bleiben damit 215 -1 = 32767 verschiedene Möglichkeiten, positiv oder negativ.

Positive Zahlen sind in der Weise codiert, daß Bit n der Wert 2n zugewiesen wird, wenn dieses Bit gleich 1 ist. Ansonsten hat Bit n den Wert 0. Die Werte aller Bits werden addiert, um die Zahl zu er halten.

Die Bitdarstellung einer negativen Zahl erhält man folgendermaßen: Man bildet die entsprechende positive Zahl in Binärdarstellung invertiert dann alle Bits und addiert 1.

Y XANDY

X OR Y NOT X

0 1

0 0 1

X X X X

12 11

Byte 2 Byte 1

9 8

_____

X X X X X

6 5

1 0 0

3 2 1

X X

_____

Beispiel:

Integer

- 1

- 2

- 100 1111 1111

- 119 1111 1111

- 127 1111

AND, OR und NOT bilden aus den Argumenten die neuen Werte durch bitweises Vorgehen ent

sprechend der Wahrheitstabelle.

1111 1111 1111 1111

Beispiel: ? 5000 AND -127

? 5000 OR -127 ? NOT 5000

wegen

00010011 10001000 ( 5000)

11111111 10000001 (-127)

00010011 10000000

11111111 10001001 11101100 01110111

1111

Binär

1111 1111 1111

1001 1000 1001 1000 0001

ergibt 4992 ergibt- 119 ergibt -5001

5000 AND -127 5000 OR -127 NOT 5000

1110 1100

2. „Wahr“ und „Falsch“

Jeder Aussage wird vom Computer ein Wert zugeordnet, und zwar der Wert -1 (alle Bits = 1), wenn

die Aussage trifft, und der Wert 0 (alle Bits = 0), wenn die Aussage nicht zutrifft.

Bit 15

Bit 14

12 4096 11 10

Beispiel:

Integer

10000

32767

Wert, wenn Bit = 1

negativ

16384

8192 0

2048 1024 0

7 128

5 4 3

512 0 256

64 0 32 0 16

2 1 0

0000

1 0000

4 0

2 1 0

0000 0000

Wert, wenn Bit = 0

Binär

100 0000 0000 0110

1000

5000

0000

0010

0111

0001

0011 0111

1111

0011

positiv

0 0

0000 0000 0000

0001

0100 1110 0001

1000

0000

1111 1111

1000

Beispiel: A$ = "AMEN” : ? A$ = ’’AMEN” : ? A$ = ’’AMENDE”

Hier wird der Variable A$ der String AMEN zugeordnet, dann soll der „Wert“ zweier Aussagen gedruckt werden. Da die erste Aussage „wahr“ und die zweite Aussage „falsch“ ist, erhält man als Antwort: -1 und0.

Beispiel: ? A = NOTB

? X > Y ? X$ = A$ + ”X”

usw.

3. AND, OR und NOT bei Aussagen

Die AND-Funktion ist dann wahr, wenn alle Einzelbedingungen wahr sind.

Beispiel: IF A = 1 AND B = 2 AND C = 3 THEN PRINT ’’FERTIG”

Der Computer wird das Wort FERTIG nur dann ausgeben, wenn die Variablen A, B und C die Werte 1, 2 bzw. 3 haben.

Beispiel: IF A$ = ”J” THEN ? ”JA”

Die OR-Funktion ist dann wahr, wenn mindestens eine der Einzelbedingungen wahr ist.

Beispiel: IF A$ = ”J” OR A$ = ”Y” THEN ? ”JA”

Der Computer wird nur dann JA ausgeben, wenn A$ vorher den String ”J” oder den String ”Y” zugewiesen erhielt.

Die NOT Funktion kann nicht auf Strings angewendet werden, sondern nur auf Festkomma

variabien, ist das Argument eine Dezimalzahl, so werden die Nachkommastellen nicht beachtet.

Liegt das Argument nicht innerhalb der Grenzen für eine Integerzahl, so erhält man eine ent sprechende Fehlermeldung (? ILLEGAL QUANTITY ERROR).

Beispiel: A = - 3 : B = -3.54 : ? NOTA, NOTB

ergibt: 2 2 A = - 5 : ? NOTA, NOT NOTA ergibt: 4 - 5 A = 123456 : ? NOTA ergibt: ? ILLEGAL QUANTITY ERROR (Argument zu groß)

BEISPIELE FÜR BOOLESCHE OPERATIONEN

63 AND 16 = 16 Da die binäre Schreibform von 63

111111, und von 16 10000 ist,

ergibt sich nach der AND-Verknüpfung

10000 oder 16.

15 AND 14 = 14 15 =

14 =

Resultat

-1 AND 8 = 8

-1 = 8 =

Resultat

10 OR 10 = 10

10 = 10 =

Resultat

-1 OR -2 = -1

-1 = 1111111111111111

-2 =

Resultat

NOT 0= -1

0 =

Komplement davon 1111111111111111 = —1

1111 1110

1110 =14

1111111111111111 0000000000001000

0000000000001000 = 8 1010

1010 1010 = 10

1111111111111110 1111111111111111 = -1

0000000000000000

1.1.5 PRIORITÄTEN bei Formeln

Da in der Rechnerschreibweise Formeln und Anweisungen in einer Zeile geschrieben werden, muß der Rechner ein Schema besitzen, diese Formeln der Reihe nach abzuarbeiten.

Diese PRIORITÄT zur Abarbeitung mathematischer Formeln kann man sehr einfach darstellen. Oberste Priorität haben immer die mathematischen Operatoren, gefolgt von den Vergleichs operatoren und den logischen Operatoren.

Im einzelnen läßt sich das wie folgt darstellen:

Mathem. Operatoren Höchste Priorität

Funktionen Î

+ -

VERGLEICHSOPERATOREN

<> (oder ><) > < > = < =

LOGISCHE OPERATOREN

NOT AND OR Niedrigste Priorität

Beispiel: ? 2 j 3 + 6 ergibt 14, weil 2 | 3 zuerst berechnet wird.

1.1.6 Besonderheiten des Gleichheitszeichens

Das Gleichheitszeichen hat in der EDV-Terminologie eine von der Algebra abweichende Bedeutung.

Es bedeutet:

„Ist der Wert von“

und ist nicht zu verwechseln mit der algebraischen Bedeutung:

„Ist gleich“

Die Rechenanweisung

X = X + 1

wäre in der Algebra falsch, da sie auf den Widerspruch 0 = 1 führt.

In der Programmiersprache BASIC ist diese Anweisung jedoch korrekt, sie besagt nämlich:

X „ist der Wert von“ alter Wert von X plus 1

oder

X = X * B X „ist der Wert von“ alter Wert von X mal dem Wert von B.

1.1.7 MATHEMATISCHE FORMELN ALS BEISPIEL FÜR RECHENANWEISUNGEN

Mathematische Formeln werden in BASIC etwas anders geschrieben als in der herkömmlichen

Schreibweise.

Den besten Vergleich erhält man, wenn man diese unterschiedlichen Schreibweisen anhand von Beispielen einander gegenüber stellt.

ALGEBRAISCH

a + b c + d

a + b

a • b

a b c

BASIC

(A + B) / (C + D)

(A + B) / C

A * B / C

A/B/C

a b c

A / (B / C)

(ab)N C

+ i

ba +1

5v^3

Die Rechenanweisung wird nun gebildet durch das Gleichheitszeichen, auf dessen Besonderheit bereits hingewiesen wurde.

Die Darstellung einer Rechenanweisung erfolgt genauso wie in der Algebra. z.B. X = A + B + C

-----------------------

-----------------------------------------------Eine Variable, der das

Diese Darstellungsform muß immer eingehalten werden und darf nicht verändert werden. So ist z. B. vorgeschrieben, daß links vom Gleichheitszeichen immer eine Variable stehen muß, während rechts entweder eine Variable oder eine mathematische Formel stehen muß. Es darf links kein mathematischer Ausdruck stehen.

A / (B * C) (A * B) î N * C

B t (A + 1) B f A + 1

A f 0.6 [| = 0.6]

A t (—0.5) [|=0.5]

mathem. Formel

Rechenergebnis zugewiesen wird.

1.1.8 Der Aufbau eines Programms in BASIC

Um ein Programm in BASIC zu erstellen, benutzt man die nachfolgend beschriebenen BASICAnweisungen.

Auch hierbei muß man sich an eine bestimmte Ordnung halten, ähnlich wie bei den Rechen anweisungen.

Eine BASIC-Programmzeile besteht immer aus einer bestimmten Zeilennummer, die man auch als Adresse bezeichnen könnte, der BASIC-Anweisung selbst, sowie (sofern vorhanden) der Variablenliste. Die Programmzeile kann maximal 80 Zeichen lang werden.

Eine einfache Anweisung, nämlich die Werte von 5 Variablen auszudrucken, sieht recht übersicht lich aus.

10 PRINT A, B, C, D, E

-------------------

---------------------------------------------

--------------------------------------------------------------Zeilennummer

Die Zeilennummer ist sozusagen der Fingerabdruck der BASIC-Anweisung. Sie gibt es nur einmal und ist daher unverwechselbar. Anhand dieser Zeilennummer finden wir die Anweisung immer wieder.

Sie ist immer ganzzahlig, in aufsteigender Reihenfolge und kann von

0 bis 63999

definiert sein.

Variablenliste

BASIC-Anweisung (Befehlswort)

Die Anweisung selbst sagt aus, was mit der nachfolgenden Variablenliste, die im Übrigen aus verschiedenen Informationen bestehen kann, passieren soll.

Möglich sind Texte, Konstanten und Variablen. Das normale Standard-BASIC sieht vor, daß mit diesen Informationen eine Programmzeile be

endet ist. Eine neue Zeile sollte beginnen. Bei Ihrem Computer ist es jedoch möglich, mehrere BASIC-Anweisungen getrennt durch einen

Doppelpunkt, in eine Zeile zu schreiben. Maximal kann diese Zeile 80 Zeichen aufnehmen. Bedingt durch die Begrenzung von 40 Zeichen pro Zeile auf dem Bildschirm, bildet sich der Rechner automatisch eine Doppelzeile.

Beispiel: 10 PRINT A, B, C, D, E: PRINT Y: GOTO 100

1.2.1 Der REM Befehl

Wichtig ohne etwas zu tun ... Sobald die Probleme, die Sie mit Ihrem Rechner lösen, komplexer werden, wird Ihr Programm

natürlich länger und damit meist unübersichtlicher. Ein gutes Hilfsmittel, um ein Programm gut überschaubar zu machen, ist der REMARK-Befehl:

n REM TEXT

Die REM-Anweisung ist eine Mitteilung an den Rechner, die nachfolgenden Ausführungen,

Anweisungen oder Bemerkungen beim Rechenvorgang nicht zu berücksichtigen. Sie hat auf den

Programmablauf keinen Einfluß, sondern wird nur beim Auflisten des Programms ausgegeben, um dem Programmierer die Arbeit zu erleichtern. Zu beachten ist, daß die REM-Anweisung Speicherplatz benötigt und der nachfolgende Text nicht länger ist, als es die Programmzeile erlaubt (insgesamt 80 Zeichen).

Wird REM gemeinsam mit anderen Befehlen in einer Zeile verwendet, so muß REM der letzte

Befehl der Zeile sein, da Befehle nach REM nicht ausgeführt werden.

n = Zeilennummer des Befehls

Text - beliebige Informationen

Bei- 100 REM Beginn des Unterprogramms

spiele: 5810 REM Schachprogramm

12 PRINT A: REM ERGEBNIS

1.2.2 Der END Befehl

Jetzt hört’s auf... Auch wenn das Programmieren noch soviel Spaß macht, einmal ist jedes Programm zu Ende.

Um das logische Ende des Programms zu kennzeichnen, benutzen wir den Befehl:

n END n = Zeilennummer des Befehls

Der Befehl END kann mehrmals in einem Programm benutzt werden, was vor allem bei Programm

verzweigungen sinnvoll sein kann. Dieser Befehl bewirkt das Anhalten des Programms, ohne

irgendwelche Daten zu verändern. Das Programm kann nach dem END durch den Befehl CONT (siehe 1.3.2) fortgesetzt werden.

Beispiel: 10 END

1.2.3 Der STOP Befehl

Das Programm kann verschnaufen ... Es soll ja Vorkommen, daß ein Programm nicht gleich so arbeitet wie sein Schöpfer gern hätte.

Dann sind oft einige Testläufe nötig. Bei diesen Tests kann man den Befehl

n STOP

n = Zeilennummer des Befehls

benutzen um das Programm anzuhalten und den Wert einiger Variablen zu erfragen. Der STOP-

Befehl unterscheidet sich vom END-Befehl dadurch, daß beim Beenden des Programms die

Meldung: BREAK IN ... (Zeilennummer) ausgegeben wird.

Auch nach dieser Unterbrechung kann das Programm mit CONT (siehe 1.3.2) fortgesetzt werden.

Beispiel: 120 STOP

1.2.4 Der LET Befehl

Man kann ihn auch vergessen ...

Bei Ihrem Rechner ist es genauso wie bei uns Menschen, seine Sprache ist älter als er. Bei älteren Rechnertypen war der Befehl

n LET Zuweisung

nötig um Werte einer Variablen zuzuordnen. Unseren Rechner stört diese Anweisung nicht, sie ist aber auch nicht nötig und man sollte sie möglichst fortlassen, da sie 1 Byte unseres Speicher platzes belegt.

n = Zeilennummer des Befehls

Beispiel: 130LETA = 10*B

besser 130A = 10*B

1.2.5 Der PRINT Befehl

So unterhalte ich mich ... Soll der Rechner seinen Benutzer während des Programmlaufs ansprechen, ihm Daten angeben

oder einen guten Morgen wünschen, benutzen wir den Befehl:

n { PRINT / ? } {Text / Variablenliste }

n = Zeilennummer des Befehls

Der PRINT-Befehl bewirkt das Ausgehen einer nachfolgenenden Text- und/oder Variablenliste.

Das Fragezeichen ist gleichbedeutend mit dem Wort PRINT und wird vom Rechner beim Listen des Programms durch PRINT ersetzt. Auszugebender Text muß in Anführungszeichen gesetzt werden.

Bei- 110 PRINT ’’LISTE-NR.”, A ; D $ spiele: 20 ? ’’PROGRAMMANFANG”, C $

Nach einem PRINT-Befehl erfolgt ein Wagenrücklauf und ein Zeilenvorschub, so daß jeder PRINTBefehl am Anfang einer neuen Zeile ausgeführt wird. Mit dem bloßen PRINT-Befehl erzeugt man

also eine Leerzeile auf dem Ausgabegerät. Der Computer läßt verschiedene Formatierungsarten zu; dabei ist zu beachten, daß ein String

genausoviel an Platz belegt, wie er Zeichen hat. Eine Zahl belegt soviele Plätze, wie sie Ziffern hat, plus eine Spalte für das Vorzeichen.

Das Komma:

Jede zehnte Druckposition ist intern im Computer vortabuliert. Das Komma in einem PRINT-

Befehl bewirkt, daß das folgende Zeichen in die nächste vortabulierte Position geschrieben wird. Zeilenvorschub und Wagenrücklauf werden unterdrückt.

Beispiel: ? , ”XY”, ”XY”

Î t

Beispiel: A = 3 : : B = - 4 : ?

Î Î

- 4

2 11

Das Semikolon:

Das Semikolon in einem PRINT-Befehl bewirkt, daß Zeilenvorschub und Wagenrücklauf unter

drückt werden (Ausgabe ohne Zwischenraum).

Beispiel: ? ”COM”; : ? ’’PUTER”

COMPUJIR

Beispiel: A = -3:B = -4:?A;B; ’’TEXT”; A

= 3_:4_IEXJ-3

Der SPC-Befehl:

Der SPC(n) bewirkt den Ausdruck von n Leerzeilen, n kann zwischen 0 und 255 liegen, n kann auch eine Variable oder ein berechneter Ausdruck sein. Nachkommastellen bleiben unbeachtet.

Beispiel: ? SPC(3) ’’DREI” SPC(1) ’’FUENF”

DREI FUENF

Beispiel: ? SPC(^) ’’DREI”

DREI

Siehe Anmerkung zum TAB-Befehl.

Der TAB-Befehl:

Er hat das Format TAB(n), wobei n eine Zahl oder ein berechneter Ausdruck zwischen 0 und 255 sein kann. Stellt n keine ganze Zahl dar, so werden die Nachkommastellen nicht beachtet.

Der Befehl TAB(n) bewirkt den Ausdruck des folgenden Zeichens n Freistellen vom linken Bildschirmrand (oder Papierrand) entfernt.

Beispiel: ? TAB (4) 4; TAB (8) ”X”

4 X

Ist die durch den TAB-Befehl spezifizierte Druckposition bereits belegt, so wird in die nächste freie Position geschrieben.

Beispiel: ? TAB(4) ”X” TAB(3) ”Y”

Anmerkung: Bei der Verwendung von TAB und SPC dürfen die Daten nur durch Semikolon ge

trennt werden, da das Komma eine höhere Priorität besitzt als die Befehle TAB und SPC.

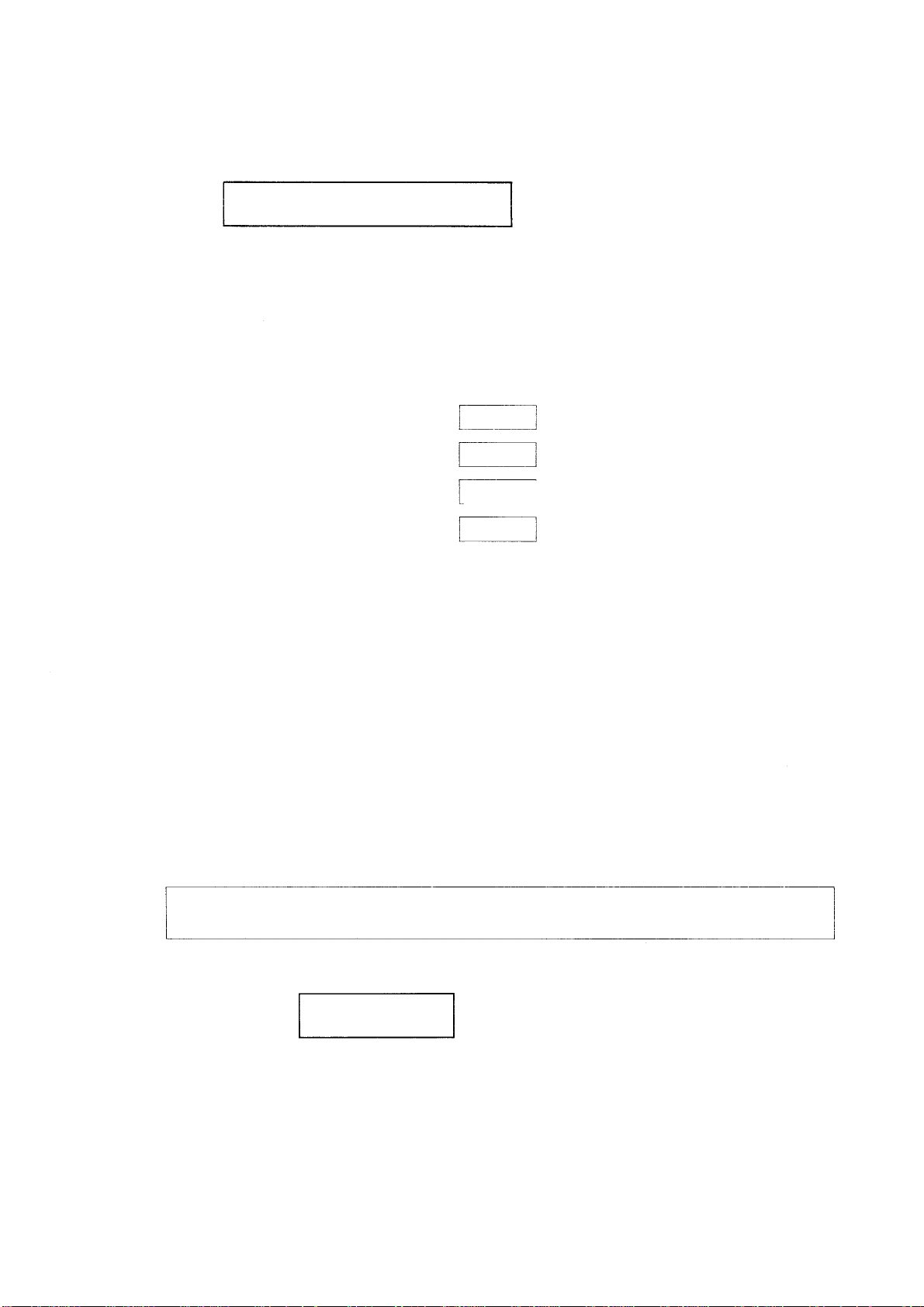
1.2.6. Der INPUT-Befehl

Und so verstehe ich Sie ... Um die Dialogfähigkeit des cbm zu verwirklichen, reicht der PRINT-Befehl nicht, wir benötigen

auch ein offenes Ohr, den INPUT-Befehl:

n INPUT [’TEXT” ;] Variablenliste

(n = Zeilennummer des Befehls)

Der INPUT-Befehl bewirkt einen Stop des Programms und ermöglicht eine Dateneingabe für die

Variablen, die hinter dem INPUT aufgeführt werden.

Stehen mehrere Variablen hinter dem INPUT, so müssen entweder alle Daten durch Komma getrennt werden und abschließend muß die RETURN-Taste gedrückt werden oder nach jeder einzelnen Eingabe muß die RETURN-Taste betätigt werden.

Beispiel: 20 INPUT A, C $, D

Eingabe : 2, KARO, 3

RETURN

oder : 2

KARO

3 RETURN

Das Programm zeigt die Bereitschaft zur Eingabe durch ein Fragezeichen oder durch Drucken des

Textes, den wir hinter dem INPUT in Anführungszeichen vermerkt haben, plus Fragezeichen an.

RETURN

__________

Beispiel: 30 INPUT A

Ausdruck: ?

40 INPUT ’’GEBEN SIE A EIN”; A Ausdruck: GEBEN SIE A EIN?

Als Variable können selbstverständlich auch Ganzzahl- und Textvariablen verwendet werden.

Beispiel: 10 INPUT ’’TEXTEINGABE”; B $

Geben Sie mehr als 80 Zeichen bei einem INPUT-Befehl ein, so ignoriert der Computer die ersten

80 Zeichen und speichert nur die nachfolgenden Zeichen ab. Weiter darf während der Eingabe für eine numerische Variable kein Komma oder Doppelpunkt

benutzt werden, da der Computer diese Zeichen als Eingabeende interpretiert.

Soll ein String eingegeben werden, der Komma oder Doppelpunkt enthält, so muß dieser String

in Anführungszeichen geschrieben werden.

1.2.7 Der GET Befehl

Für Leute die nicht mehr warten wollen ...

Der n GET Variable

Befehl ist ebenfalls ein Eingabebefehl. Im Gegensatz zum INPUT hält das Programm bei einem GET nicht an und es kann nur eine Variable

eingegeben werden. Es können Variablen oder Textvariablen eingegeben werden. Es wird nur ein Zeichen bzw. eine Ziffer übernommen.

n = Zeilennummer des Befehls

Beispiel: 10 GET C

30 GET B $

Da der Rechner in der Lage ist, bis zu 9 Tastenbetätigungen zu speichern, wird dasjenige Zeichen übernommen, das während des Programmlaufes vor Erreichen des GET-Befehls gedrückt wurde.

Soll der Rechner auf Eingabe eines Zeichens warten, so kann das mit einer Warteschleife erreicht werden. (Siehe 1.2.15).

Beispiel:

20 GET A $ 30 IF A $ = “ “ THEN 20

1.2.8 Der DATA Befehl

Mein Grundwissen ... Nun lernen wir einen Befehl kennen, mit dem man Daten speichern kann, auf die der Rechner im

Bedarfsfälle zurückgreift. Es ist der Befehl:

n DATA Liste n = Zeilennummer des Befehls

Die Daten werden hierbei an beliebiger Stelle im Programm hinter DATA aufgereiht und später der Reihe nach von links nach rechts mittels READ gelesen, (siehe 1.2.9) Die Daten werden unter einander durch Kommas getrennt und dürfen daher weder Komma noch Doppelpunkt enthalten. Sollen diese beiden Zeichen oder führende Leerzeichen mittels DATA in eine Textvariable gebracht

werden, so muß dieser Text in der DATA-Anweisung in Anführungszeichen stehen, was ansonsten

bei Texten hinter DATA nicht der Fall ist.

Beispiel: 100 DATA 15,3.7, 9,12

150 DATA "DER:”, COMPUTER

Die Daten hinter einem DATA können von verschiedenen READ-Anweisungen gelesen werden,

da sich ein Pointer (Zeiger) „merkt“, ab welchem Wert mit dem READ Befehl weiter gelesen wird.

Beispiel: 10 READ A, B, C

Pointer (READ noch nicht durchgelaufen)

Pointer (READ 1 x durchgelaufen)

| Pointer (READ 2 x durchlaufen)

100 DATA 4, 5, 7, 3.1,7, 9 I

1.2.9 Falls ich es vergessen habe

..........

DER RESTORE BEFEHL

Beim DATA-Befehl haben wir erfahren, daß der Computer die Daten hinter dem DATA der Reihe nach liest. Sollen, nachdem bereits Daten gelesen wurden, nicht die nachfolgenden, sondern die ersten Daten gelesen werden, so benutzen wir den

n RESTORE

n = Zeilennummer des Befehls

Befehl.

Mit anderen Worten, dieser Befehl setzt den Pointer vor das 1. Zeichen der Daten.

Beispiel: 30 RESTORE

1.2.10

------

und so komme ich daran

DER READ BEFEHL

Der

n READ Variablenliste

Befehl bezieht sich auf die DATA-An Weisung und kommt ohne diese nicht aus. Der READ-Befehl liest die Daten in der vorgegebenen Reihenfolge und ordnet sie den Variablen, die hinter ihm auf geführt sind, in der gleichen Reihenfolge zu.

n = Zeilennummer des Befehls

Beispiel: 10 READ A, B

20 DATA 102, 3, 5, 6 Wird der READ-Befehl zum ersten Mal durchlaufen so ist A = 102, B = 3;

beim zweiten Durchlauf von READ ist A = 5, B = 6.

Natürlich können auch Textvariablen gelesen werden. Falls der Pointer hinter dem letzten Zeichen

der DATA-Anweisung steht und ein READ erfolgt, erscheint die Fehlermeldung:

?OUT OF DATA ERROR IN . ..

(Sie wissen natürlich schon, daß man diese Fehlermeldung mit RESTORE (siehe 1.2.9) umgehen kann).

1.2.11 Ich kann auch springen

.........

DER GOTO BEFEHL

Dieser Sprungbefehl wird als unbedingter Sprungbefehl bezeichnet, da er immer ausgeführt wird, sobald das Programm auf einen derartigen Befehl stößt, oder sobald ein GOTO direkt eingegeben wird.

n GOTO m

n = Zeilennummer in der der Befehl steht m = Zeilennummer in die gesprungen wird

Dieses GOTO bewirkt, daß nicht der Befehl mit der nach n folgenden Zeilennummer bearbeitet wird, sondern daß das Programm seine Arbeit in der Zeilennummer m fortsetzt.

Beispiel: 10 PRINT’’ANFANG”

20 GOT0150

30 PRINT ’’ENDE”

150 PRINT ’’SPRUNG”

Eingabe von RUN (siehe 1.3.1) bewirkt folgende Ausgabe: ANFANG SPRUNG

Die Zeilennummer m muß vorhanden sein, sonst erfolgt eine Fehlermeldung. Variablen oder andere Zeichen als ganzzahlige positive Zahlen dürfen nicht benutzt werden.

Stehen in einer Programmzeile weitere Befehle hinter einer GOTO-Anweisung, so werden sie

nicht ausgeführt.

1.2.12 Gewußt wohin

........

DER ON ... GOTO BEFEHL

Hatte das Programm beim GOTO nur eine Möglichkeit zu springen, so kann beim ON ... GOTO Befehl der Sprung vom Wert einer Variablen abhängig gemacht werden.

n ON v GOTO m1, m2,

n = Zeilennummer des Befehls v = Formel, die den Sprung bestimmt

m1, m2 = Zeilennummern zu denen gesprungen werden soll

Beispiel: 10 ON F GOTO 50,100, 300

Ist F < 1 erfolgt kein Sprung Ist F = 1 erfolgt Sprung nach 50

Ist F = 2 erfolgt Sprung nach 100 Ist F = 3 erfolgt Sprung nach 300 Ist F > 3 erfolgt kein Sprung

Anstelle der Variablen kann auch ein mathematischer Ausdruck stehen. Das Ergebnis des er-

rechneten Ausdrucks wird vom Rechner zu einer ganzzahligen Größe umgewandelt, d. h. Nach kommastellen werden ignoriert.

Beispiel: 50 ON (A+B) - (C+D) GOTO 1000, 300, 700

Die Anzahl der Sprungadressen ist durch die maximale Zahl von 80 Zeichen pro Zeile begrenzt.

Als Alternative bei sehr umfangreichen ON ... GOTO-Befehlen bieten sich daher mehrere ON ...

GOTO’s an, bei denen die Variable im zweiten Befehl dem Programm entsprechend berechnet wird.

Beispiel: 10 ON K GOTO 100, 200, 300, 400

30 ON K-4 GOTO 500, 600, 700, 800

1.2.13 Jetzt geht es in die Unterwelt

.........

DER GOSUB BEFEHL

Der folgende Befehl sollte für die Programmteile benutzt werden, die wiederholt, auch von ver schiedenen Stellen des Programms aus, durchlaufen werden müssen. Diese Programmteile nennt man Unterprogramm oder auch Subroutine. Sie können an beliebiger Stelle im Programm stehen und werden mit dem Befehl

n GOSUB m

aufgerufen. Nach Bearbeitung des Unterprogramms kehrt der Rechner zu dem Befehl zurück, der hinter dem

GOSUB folgt, (siehe RETURN 1.2.16).

n = Zeilennummer des Befehls m = 1. Zeilennummer des Unterprogramms

Beispiel: 10 GOSUB 100

20 PRINT ’’HAUPTPROGRAMM” 50 END: REM ENDE DES HAUPTPROGRAMMS 100 PRINT ’’UNTERPROGRAMM” 110 RETURN: REM ENDE DES UNTERPROGRAMMS

Die Eingabe von RUN bewirkt die

Ausgabe: UNTERPROGRAMM

HAUPTPROGRAMM

Ein Unterprogramm kann wiederum ein anderes Unterprogramm aufrufen, und dieses dann das nächste

..........

Insgesamt können bis zu 26 Unterprogramme ineinander verschachtelt werden.

1.2.14 Verteiler für die Unterwelt

........

DER ON ... GOSUB BEFEHL

Der Befehl

n ON v GOSUB m1,m2...

n = Zeilennummer des Befehls v = Formel, die den Sprung bestimmt m1,m2... = Zeilennummern, zu denen gesprungen werden soll

entspricht dem ON . . . GOTO (siehe 1.2.12), nit dem Unterschied, daß hier keine einfachen Sprünge stattfinden, sondern zu Unterprogrammen verzweigt wird (siehe 1.2.13).

Beispiel: 10 ON Z GOSUB 1000,1500, 2000

20 STOP

Der Sprung erfolgt abhängig von der Variablen Z in eines der 3 Unterprogramme, die natürlich mit RETURN abgeschlossen werden müssen. Nach Abarbeitung des betreffenden Unterprogramms wird die Zeile 20 ausgeführt.

1.2.15 Nun fällt die Entscheidung ... DER IF... THEN BEFEHL

Um abhängig von einer logischen oder mathematischen Aufgabe eine Entscheidung zu fällen, gibt es die Befehlsgruppe IF ... THEN.

n IF Vergleich THEN {m, Befehl}

n = Zeilennummer des Befehls

Vergleich = Vergleich einer oder mehrerer Variablen oder Formeln

m = Zeilennummer deren Befehl ausgeführt werden soll

Befehl = Befehl der ausgeführt werden soll

Beim Vergleich können Variablen (Auch Textvariablen), Konstanten oder Formeln untereinander verglichen werden.

Beispiel: IF A = 1 ... / IF A$ = ”JA” ... / IF CC = 3 ...

IF 3> B*C + 3.../IFA <> C . .. / IF D% > E % . . .

Ist die Vergleichsbedingung erfüllt, so wird der Befehl hinter dem THEN ausgeführt oder nach der dort stehenden Zeilennummer verzweigt, ansonsten fährt das Programm mit der nächsten Zeilen nummer fort.

Beispiel: 10 IF A + B < = 150 THEN 30

20 PRINT ”A + B > 150”: GOTO 100

30 PRINT ”A + B < = 150”: GOTO 100

eleganter: 10 IF A + B < = 150 THEN PRINT ”A + B < = 150”: GOTO 100

20 PRINT ”A + B > 150”: GOTO 100

Wie in diesem Beispiel das PRINT, so können auch andere Befehle hinter dem THEN stehen. Als Besonderheit läßt das COMMODORE-BASIC mehrere IF-Abfragen in einer Zeile zu.

Beispiel: 10 IF A = C THEN IF A = 5 * B THEN ....

Ist hierbei bereits die erste Abfrage nicht erfüllt, wird sofort die nächst höhere Programmzeile aus geführt.

1.2.16 Zurück geht’s immer leichter DER RETURN BEFEHL

Wir haben mit GOSUB, ON . . . GOSUB die Möglichkeit kennengelernt ein Unterprogramm auf zurufen. Um nun wieder ins Hauptprogramm zurückzukehren, muß der letzte Befehl jedes Unter

programms:

n RETURN

sein. Diese Anweisung bewirkt, daß der dem Aufrufbefehl (GOSUB oder ON ... GOSUB) folgende Be

fehl als nächster ausgeführt wird (siehe 1.2.13,1.2.14).

Der Befehl RETURN muß Buchstabe für Buchstabe eingegeben werden und darf nicht mit derTaste

RETURN verwechselt werden.

Beispiel: 40 A = 5 : B = 10

50 GOSUB 1000 60 PRINT ’’ERGEBNIS” U

1000 REM UNTERPROGRAMM 1010 U = (A+B) * 3 1020 RETURN

READY RUN ERGEBNIS 45

Solange die Unterprogrammtechnik für uns noch ungewohnt ist, werden wir vielleicht die Fehler

meldung: 7RETURN WITHOUT GOSUB ERROR erhalten. Sie tritt auf, falls ein RETURN erreicht

wird, ohne daß ein GOSUB durchlaufen wurde. Dieser Fehler kann auftreten, wenn in ein Unter

programm mit einer GOTO-Anweisung gesprungen wurde. Auch dann, wenn ein Unterprogramm

ans Ende des Hauptprogramms geschrieben wird und am Ende des Hauptprogramms kein STOP oder END steht.

------

n = Zeilennummer des Befehls

Beispiel: 10 REM HAUPTPROGRAMM

50 GOSUB 1000

1000 REM UNTERPROGRAMM

1100 RETURN

Bei diesem Beispiel durchläuft das Programm die Subroutine nicht nur nach dem Befehl GOSUB

1000 sondern auch nach Ende des Hauptprogramms. Der Befehl:

990 END (etwa 10 Leerzeichen) verhindert diesen Fehler.

1.2.17 Immer wieder das Gleiche

DIE BEFEHLSGRUPPE - FOR NEXT STEP

Wollen Sie eine Schleife programmieren, d. h. eine Routine, die mehrmals mit einer veränderten Variablen durchlaufen wird, so benutzen Sie die Befehlsgruppe:

n, FOR {Laufvariable = Anfangswert} TO {Endwert} STEP {Schrittweite} n2 NEXT {Laufvariable}

n^ n2 = Zeilennummern der Befehle

.........

Laufvariable

Anfangswert

Endwert

Schrittweite

Die FOR-NEXT Befehlsfolge bewirkt, daß der Programmteil zwischen n, und n2 solange durch laufen wird bis die Laufvariable größer als der Endwert ist. Hiernach wird die Anweisung nach n2 be arbeitet. Bei jedem Durchlauf des NEXT wird die Laufvariable, die zuerst gleich dem Anfangswert ist, um die Schrittweite erhöht und das Programm bearbeitet die Befehle zwischen n, und n2.

muß eine Fließkommavariable sein (darf keine Integervariable sein) kann eine Konstante, eine Variable oder ein mathematischer Ausdruck sein kann eine Konstante, eine Variable oder ein mathematischer Ausdruck sein kann eine Konstante, eine Variable oder ein mathematischer Ausdruck sein. Unterbleibt die Angabe für die Schrittweite, so ist diese automatisch +1.

Beispiel: 10 FOR A = 1 TO 10 STEP 0.5

20 PRINT A 30 NEXT A 10 FOR K = 3*B TO C/5 STEP -1

100 NEXT K

Die Laufvariable muß beim Rechner nicht im NEXT-Befehl angegeben werden. Also ist folgende Befehlsfolge auch korrekt:

100 FOR J = 5 TO 100

200 NEXT

FOR-NEXT Schleifen können auch verschachtelt angeordnet werden.

Beispiel:

äußere

Schleife

Die Verschachtelung muß symmetrisch sein, d. h. die zuletzt eröffnete Schleife muß als erste wieder geschlossen werden. Die Befehle 100 und 110 können zu einem Befehl:

10 FOR A = 1 TO 100 20 FOR B = 1 TO 10

innere Schleife

100 NEXT B

—110 NEXT A

100 NEXT B,A zusammengefaßt werden.

Bei verschachtelten Schleifen müssen unterschiedliche Laufvariablen benutzt werden.

1.2.18 Wieviel soils denn sein ... DER DIM-BEFEHL

Im Kapitel 1.1.2 haben Sie drei Formen von Variablen (A, A%, A$) kennengelernt. Es gibt nun eine Möglichkeit Gruppen einer dieser 3 Variablensorten zu einem „Feld“ (Matrix, Array) zusammenzu fassen. Ein solches Feld besteht dann aus mehreren Variablen einer Sorte (z. B. Textvariable), die

indizierte Variablen genannt werden. Indizierte Variable, weil zu der normalen Variablen ein Index tritt. Während eine gewöhnliche Variable nur einen Speicherplatz repräsentiert, kennzeichnet man ein ganzes Feld von Speicherplätzen mit einer Variablen und unterscheidet die einzelnen Elemente durch Indizes. Das heißt indizierte Variablen aus einem Feld haben die gleiche Variable und unter scheiden sich nur durch ihren Index.

Beispiel: Indizierte Variablen aus einem Feld

A$(1), A$(9), A$(12), A$(21)

Variable, die das

Feld kennzeichnet

Index, nach dem die Elemente eines Feldes unterschieden werden

__________

Indizierte Variablen aus verschiedenen Feldern: B1$(3), C%(5), A(12), A3(5), D3%(2)

Die im Beispiel gezeigten Variablen haben alle nur einen Index, deshalb nennt man diese Felder „eindimensionale Felder“. Im COMMODORE-BASIC können aber auch mehrdimensionale Felder

aufgebaut werden, d. h. Felder deren Elemente mehr als einen Index haben.

Diese Indizes werden innerhalb der Klammern durch Kommata getrennt.

Beispiel: Z%(1,0,2) X$(1,2) ZA(3,2,0,1)

Es kann auch jede Variable oder Formel deren Wert 3= 0 ist als Index benutzt werden. (Nachkomma stellen werden ignoriert!).

Beispiel: Y$(N,1) K%(A+2,B*3,0) KA(N|3)

Hierdurch erreicht man eine indirekte Adressierung von Variablen, die durch ein Beispiel veran schaulicht werden soll:

10 FORI = 0 TO 2 20 FOR J = 0 TO 2 40 FOR K = 0 TO 3 50 A(I,J,K) = RND (5) 60 NEXT K,J,I 70 STOP

Im Normalfall reserviert der Rechner pro Feld einen Speicherplatz für 11 indizierte Variablen pro Index. D.h., daß er für das im Beispiel benutzte dreidimensionale Feld Speicherplatz für 11 *11 *11 = 1331 Variablen reserviert. Das entspricht 6655 Bytes.

Diese Reservierung können wir jedoch mit dem folgenden Befehl ändern:

n DIM Name 1 (Zahl, Zahl,... ), Name2 (Zahl, Zahl,... )

n = Zeilennummer des Befehls Name = Variable durch die das Feld bezeichnet wird Zahl = höchster Index, der benutzt wird (kann Variable oder Formel sein).

Für unser letztes Beispiel lautet der Befehl:

5 DIM A (2,2,3)

Er bewirkt, daß nur Speicherplatz für 3*3*4* = 36 Variablen reserviert wird. Es ist auch möglich, mehr als 11 Speicherplätze zu reservieren:

Beispiel: 10 DIM A$(29)

Mit diesem Befehl wird ein Feld für 30 Textvariablen dimensioniert.

Weitere Beispiele:

DIM A% (2,N) DIM B (2,J+3,K*2) DIM C$ (1,BA,K|3)

1.2.19 Einmal gewußt - immer gewußt...

DIE BEFEHLSGRUPPE DEF FN. ( )

FN.( )

Soll eine bestimmte Berechnung mehrmals für verschiedene Zahlenwerte durchgeführt werden, so definieren wir eine Funktion durch den Befehl:

ni DEF FN Name (Variable) = Formel

n! = Zeilennummer des Befehls Name = eine Variable fungiert als Name der Funktion

Variable = die Variable, die bei jedem Funktionsaufruf

angegeben wird.

Formel = mathematischer Ausdruck.

Diese Funktion kann, nachdem sie definiert ist, beliebig oft direkt oder von verschiedenen Stellen des Programms durch den Befehl:

n2 FN Name (Variable)

aufgerufen werden.

n2 = Zeilennummer des Befehls (muß immer größer als ^ sein) Name = die Variable, die beim DEF-Befehl als Name gewählt wurde

Variable = die Variable oder die Konstante für die die Formel berechnet

werden soll.

Beispiel: 10 DEF FNQ (Y) = Y f 0.2

50 Z = FNQ (A)

Durch diese Befehle wird der Wert für die 5. Wurzel aus A im Speicherplatz Z abgespeichert.

Beispiel:

Soll in einem Programm mehrmals der Hyperbelsinus von verschiedenen Zahlen (X) berechnet

werden, so definieren wir die Funktion mit dem Namen „H“:

10 DEF FNH (X) = (EXP (X) - EXP (-X)) / 2

Wollen wir nun den Hyperbol-Sinus für 3 ausrechnen und ausdrucken so schreiben wir:

PRINT FNH (3)

Anmerkung: sinh (x) = e ~

1.2.20 Der Schlüssel nach draußen ...

DER OPEN BEFEHL

Wie sie vielleicht wissen, können sie an Ihrem Rechner die verschiedenartigsten „Peripherie geräte“ anschließen. Zum Beispiel einen Ausgabedrucker oder ein Floppy-Disk-Laufwerk.

Um diese Geräte ansprechen zu können, müssen Sie ein sogenanntes logisches FILE, d.h. eine DATEI eröffnen, in die Daten geschrieben oder aus der Daten gelesen werden. Sie eröffnen eine DATEI durch den Befehl:

OPEN m,, [m2, m3, ’’Name”]

rri! = die logische Datei-Nr., ganze Zahl zwischen 1 und 255. m2 = Geräte-Nr. des anzusprechenden Gerätes

(wird 1 gesetzt, falls Angabe fehlt)

0 = Tastatur

1 = # 1 Recorder 2 = # 2 Recorder 3 = Bildschirm

4-15 = externe Geräte

m3 = Art der Datenbewegung (wird 0 gesetzt, falls Angabe fehlt)

0 = lesen

1 = schreiben

2 = schreiben mit zusätzlichem END OF TAPE-Zeichen.

Name = kann angegeben werden um Dateien mit einem Namen direkt

anzusprechen. Der Name darf aus höchstens 16 Zeichen bestehen und darf nicht in anderen Namen enthalten sein.

Es dürfen höchstens 10 Dateien gleichzeitig geöffnet sein! Wird diese Zahl überschritten, erfolgt die Fehlermeldung: ?TOO MANY FILES ERROR.

Beispiele:

30 OPEN 1,2,1, ’’DAT 1”

Der Befehl bewirkt das öffnen der Datei 1 um auf der 2. Kassette Daten unter dem Namen DAT 1

abzuspeichern.

40 OPEN 2,1,0

Dieser Befehl öffnet Datei 2 zum Lesen vom Recorder # 1.

Kürzer: 40 OPEN 2

1.2.21 und so schließe ich ab ...

DER CLOSE BEFEHL

um zu verhindern, daß die maximale Anzahl der geöffneten Dateien (Files) überschritten wird, sollte

jede Datei geschlossen werden, sobald die Lese- oder Schreiboperationen ausgeführt sind. Dies geschieht durch:

n CLOSE rr^

n = Zeilennummer des Befehls nri! = die logische Datei-Nr. derzu schließenden Datei (ganzeZahl zwischen 1 und 255)

Beispiel: 100 CLOSE 2

Der Befehl bewirkt das Schließen der Datei-Nr. 2.

1.2.22 Ein Programm wird gespeichert...

DER SAVE BEFEHL

Das einmal in den Rechner eingegebene Programm kann auf einfache Weise gespeichert werden. Die einfachste Möglichkeit hierzu ist das Abspeichern des Programms mittels des Kassettenre corders.

Sie beginnen den Vorgang mit dem Befehl:

SAVE [’’Name”]

Name = höchstens 255 Zeichen können als Bezeichnung des Programms angegeben

werden. (Sinnvoll beim Speichern mehrerer Programme auf einer Kassette).

Beispiel: SAVE ’’ABRECHNUNG”

Nach der Eingabe des SAVE-Befehls erscheint der Satz: PRESS PLAY & RECORD ON TAPE # 1 auf dem Bildschirm des Rechners. Sie werden hierdurch

aufgefordert die Tasten

RECORD

des Kassettenrecorders gleichzeitig zu drücken. Sind die Tasten eingerastet, so erscheint OK WRITING gegebenenfalls die ersten 16 Zeichen des Namens des Programms. Nach Beendi gung der Aufzeichnung erscheint READY und der Kassettenrecorder hält an.

Bei der Namensgebung eines Programmes ist zu beachten, daß ein Name nicht bereits im Namen eines anderen Programmes enthalten sein sollte (z.B. PROG und PROG 1), um Verwechslungen auszuschließen.

und PLAY

1.2.23 ... und ein anderes geladen ... DER LOAD BEFEHL

Es gibt zwei Möglichkeiten ein auf der Kassette gespeichertes Programm in den Rechner zu laden.

Hier die erste:

Sie drücken gleichzeitig die Tasten:

SHIFT

und auf dem Bildschirm erscheint LOAD, PRESS PLAY ON TAPE # 1. Kommt man der Aufforde rung die Taste

RUN

STOP

PLAY

zu drücken nach, so kann man auf dem Bildschirm OK SEARCHING lesen. Sobald der Rechner den ersten Programmanfang nach der augenblicklichen Bandposition gefunden hat, zeigt der Bild schirm: FOUND bzw. FOUND Name, falls das gefundene Programm unter einem Namen abge speichert wurde, (siehe 1.2.22). Nach Beendigung des Ladens wird das Programm automatisch gestartet.

Die zweite Möglichkeit

Sie geben Buchstabe für Buchstabe den Befehl:

LOAD [’’Name”]

Name = muß nur eingegeben werden, falls sie ein bestimmtes Programm suchen.

Werden auf der Suche nach diesen Programmen andere Programme ge funden, so werden diese auf dem Bildschirm durch „FOUND Name“ registriert, jedoch nicht geladen.

Der Rechner beantwortet den LOAD-Befehl mit PRESS PLAY ON TAPE # 1 und dann das Drücken der Taste

PLAY

mit OK SEARCHING bzw. OK SEARCHING FOR Name. Hat er entweder das Programm mit dem gesuchten Namen oder, falls kein Name eingegeben wurde, den ersten Programmanfang ge funden, so erscheint: „FOUND Name“, „LOADING“ auf dem Bildschirm. Nach Beendigung des Ladevorganges erfolgt die Meldung „READY“ auf dem Bildschirm und das Programm kann durch den Befehl: „RUN“ (als Einzelbuchstaben) gestartet werden.

1.2.24 ... geprüft und für gut befunden ...

DER VERIFY-BEFEHL

Um zu kontrollieren, ob das Programm im Rechner mit dem abgespeicherten Programm identisch

ist, dient der Befehl

VERIFY [’’Name”]

Name = Name des abgespeicherten Programms (Falls Programm unter einem Namen

abgespeichert ist).

Nach Drücken der Taste

PLAY

(siehe 1.2.23) meldet der Rechner entweder „OK“, d.h. das Programm ist identisch oder aber

„7VERIFY ERROR“, d.h. das Programm ist nicht richtig abgespeichert und der Befehl SAVE muß

wiederholt werden. Soll ein Programm auf eine Kassette überspielt werden, die zum Beispiel schon zwei Programme

enthält, kann man folgendermaßen vorgehen: Kassette zurückspulen

VERIFY (es erscheint ? VERIFY ERROR) nochmals VERIFY (es erscheint ? VERIFY ERROR)

Nun steht der Aufnahmekopf hinter dem 2. Programm und es kann ein 3. Programm dahinter ge

speichert werden.

1.2.25 Mein Wissen wird zum Teil gelöscht...

DER CLR-BEFEHL

Der Befehl

CLR

löscht sämtliche Variablen einschließlich Dimensionierung (siehe 1.2.18) und beinhaltet den RESTORE-Befehl (siehe 1.2.9). Weiter werden auch die Zähler der FOR-NEXT Schleifen und der GOSUB auf Ausgangsstellung gesetzt.

Beispiel: 120 CLR

1.2.26 Die Länge wird geprüft...

DER LEN ( )-BEFEHL

Der folgende Befehl dient dazu die Länge einer Textvariablen (z. B. A$) zu errechnen.

LEN ({Textvariable, ’’Text”})

Textvariable = hier muß die Textvariable stehen, deren Länge errechnet werden soll,

oder der Text selbst (in Anführungszeichen).

Bei der Berechnung der Länge werden auch Leerzeichen (Blanks) mitgezählt.

Beispiel: 10 A$ = ’’COMPUTER”

20 PRINT LEN (A$)

READY RUN

READY

Die Länge einer Textvariablen kann als Zahlvariable benutzt werden, d. h. es sind folgende Befehle denkbar:

A = LEN (A$) *3

10 FORK = 1 TO LEN (A$).. .

1.2.27 Mit Texten kann man nicht rechnen ...

DER VAL ( )-BEFEHL

Wie die Überschrift schon besagt, kann man mit Textvariablen nicht rechnen, auch wenn sie Ziffern enthalten. Mit dem Befehl:

VAL ({Textvariable, ’’Text”})

können die führenden Ziffern einer Textvariable in eine Zahl umgeformt werden, falls ihre ersten Zeichen +, -, Dezimalpunkt oder Ziffern sind. Beginnt die Textvariable mit nichtnumerischen Zeichen, so ist VAL (Textvariable) = 0.

Beispiele:

? VAL (”1357 COMPUTER”)

Anzeige: 1357

B$ = 1.5E + 2DM” ? VAL (B$)

Anzeige: -150

C$ = ’’COMPUTER 12”

? VAL (C$)

Anzeige: 0

Nur die Ziffern, die als erste Zeichen der Textvariablen stehen, werden umgeformt.

1.2.28 Verwandeln kann man auch ...

DER STR$ ( )-BEFEHL

Wollen sie eine Zahl oder eine Variable in eineTextvariable umwandeln, so benutzen Sie den Befehl:

STR$ ({Variable, Zahl})

Beispiele: 10 A$ = STR$ (B)

20 C$ = STR$ (12.5)

1.2.29 So sieht ein ASCII-CODE aus ...

DER ASC ( )-BEFEHL

Da der Rechner intern nur Zahlen verarbeiten kann, ist jedem Zeichen ein Zahlenwert zugeordnet.

Diese Zuordnung geschieht nach dem ASCII (American Standard Code for Information Inter change), siehe Tabelle in 2.1.

Wollen wir kontrollieren welche Zahl dem ersten Zeichen einer Textvariablen im ASCII entspricht, so benutzen wir den Befehl:

ASC ({Textvariable, ’’Zeichen”})

Beispiel: 10A$ = ’’ASCII”

20 ?ASC (A$)

READY RUN 65 READY

Das obige Beispiel zeigt, daß dem Zeichen A die Zahl 65 im ASCII zugeordnet ist.

Beispiel: ?ASC(”3”)

1.2.30 ... die passende Umkehrung ...

DER CHR$ ( )-BEFEHL

Der CHR$-Befehl stellt die Umkehrung des ASC ( ) Befehls dar. Mit seiner Hilfe lassen sich aus den Zahlen 0 - 255 die dazugehörigen Zeichen ermitteln:

CHR$ ({Variable, Zahl})

Der CHR$ ( ) Befehl kann sich auf eine Zahl oder eine Variable beziehen.

Beispiel: A$ = CHR$ (65)

Das zum ASCII 65 gehörende Zeichen (A) wird ermittelt und in A$ gespeichert. Mittels dieses Befehls können sie sich leicht eine ASCII Tabelle selbst erstellen:

10 FOR I = 0 TO 255

20 IF I = 147 THEN PRINT: GOTO 40 30 PRINT CHR $ (I), I 40 NEXT I

Merke: Die ersten 32 Zeichen sind Sonderzeichen die vom Rechner nicht angezeigt werden. Das

Zeichen mit dem Code 147 entspricht Bildschirm löschen, es wird daher im obigen Programm übergangen.

1.2.31 Hätten Sie es gern links...

DER LEFT $ ( )-BEFEHL

Warum BASIC für seine leichte Textverarbeitung so gelobt wird, werden sie bei den folgenden vier

Befehlen schnell erkennen. Der erste Befehl

LEFT$ (Textvariable, Anzahl)

bewirkt, daß die im Befehl angegebene Anzahl von Zeichen, von links beginnend, abgespalten wird.

Die Ausgangstextvariable bleibt von diesem Befehl unberührt. Textvariable = Textvariable, auf die LEFT angewandt wird. Anzahl = Variable, Formel oder Konstante, die die Zahl der zu übernehmenden Zeichen

angibt. Hat die Textvariable weniger Zeichen als angegeben, so wird sie ganz übernommen.

Beispiel: 10 A$ = ’’COMPUTER”

20 B$ = LEFT$ (A$,3) 30 ? B$

READY RUN COM READY

weitere Beispiele:

30 B$ = LEFTS (DA$,3*C)

50 PRINT LEFTS (B$,2)

1.2.32 ... oder bevorzugen Sie rechts ...

DER RIGHTS ( )-BEFEHL

Der Befehl...

RIGHTS (Textvariable, Anzahl)

Textvariable = Textvariable auf die RIGHT angewandt wird. Anzahl = Variable, Formel oder Konstante, welche die Zahl der zu übernehmenden Zeichen

angibt. Hat die Textvariable weniger Zeichen als angegeben, so wird sie ganz übernommen.

... bewirkt, daß die im Befehl angegebene Anzahl von Zeichen, von rechts beginnend abgespalten wird. Die Ausgangstextvariable bleibt von diesem Befehl unberührt.

Beispiel: 10 A$ = ’’COMPUTER”

20 B$ = RIGHTS (AS,5) 30 ? B$

READY RUN PUTER

READY

1.2.33 ... und für Unentschlossene die ... Mitte ...

DER MIDS ( )-BEFEHL

Der Befehl...

MID $ (Textvariable, Zeichennr., Anzahl)

Textvariable = Textvariable, auf die MID angewandt wird. Zeichennr. = Variable, Formel oder Konstante als Zeiger Anzahl = Variable, Formel oder Konstante, die die Zahl der zu übernehmenden Zeichen

angibt.

... bewirkt, daß von einem gewissen Zeichen an (Zeichennr.) eine bestimmte Anzahl von Zeichen (Anzahl) übernommen wird.

Beispiele: 1 A$ = ’’COMPUTER”

2 B$ = MID$ (A$,4,4) 3 ?B$

READY RUN PUTER READY

10 D$ = MID$ (C$,I+2,D*3)

Eine kleine Spielerei:

10 A$ = ’’COMPUTER” 20 FOR I = 1 TO 8 30 PRINT MID$ (A$,1,l), I 40 NEXT

1.2.34 Der Schlüssel zur Maschinensprache, der SYS ( )-Befehl

Der SYS-Befehl dient dazu, innerhalb eines BASIC-Programmes Unterprogramme aufzurufen, die in der Maschinensprache geschrieben werden.

SYS (Startadresse)

Beispiel: 10 SYS (65490)

Hierbei ist die Zahl 65490 die Dezimaladresse des Speicherplatzes, zu dem die Programmaus

führung verzweigt. Die Startadresse muß eine positive Zahl und darf nicht größer als 65535 sein. Ab dieser Adresse wird der Inhalt als Maschinenprogramm verstanden und auch ausgeführt.

Das Maschinenprogramm wird beendet, sobald der Maschinenbefehl RTS gelesen wird. Die Programmausführung verzweigt wieder zurück zum BASIC-Programm, und zwar zu dem

Befehl, der hinter dem SYS-Befehl folgt. Die Logik ist also die gleiche, wie bei dem Aufruf von BASIC-Unterprogrammen mit dem Befehl GOSUB.

Um nun Programme in der Maschinensprache zu erstellen, ist es notwendig, die Befehle des Mikro prozessors 6502 zu kennen. Hier sei als Literatur die Programmierfibel zum 6502 empfohlen (er

hältlich über Ihren Commodore-Vertragshändler).

1.2.35 So geben Sie noch Daten mit... Der USR ( )-Befehl

Der USR-Befehl ist eine Erweiterung des SYS-Befehls. Er dient ebenfalls dazu, Unterprogramme aufzurufen, die in der Maschinensprache geschrieben sind. Als Erweiterung ist es mit dem USRBefehl jedoch möglich, eine beliebige Variable an das Unterprogramm zu übergeben.

USR (Variable)

Beispiel: A = USR (A)

Beispiel: 10 ON USR (SIN(X) / SQR(Y)) GOTO 100, 200,300

Bevor der USR-Befehl aufgerufen wird, sind jedoch einige Punkte unbedingt zu beachten.

1. Da aus dem USR-Befehl selbst nicht hervorgeht, wo das Unterprogramm steht, muß die Pro

grammanfangsadresse in die Speicherstelle 1 und 2 geschrieben werden.

Beispiel: Das Unterprogramm beginnt bei der Speicherstelle 7000. Die Speicherstellen 1 und 2

müssen daher zuerst wie folgt mit POKE belegt werden:

POKE 2, INT (7000/256) Höherwertiges Byte POKE 1,7000 AND 255 Niederwertiges Byte A = USR (10)

--------------

-------------------------------------Ergebnis vom Unterprogramm

2. Der Übergabebereich der Variablen liegt an den Speicherstellen 176 bis 183. Das ist nur wichtig für das Maschinenprogramm. Siehe Beschreibung des TIM-Monitorprogramms im Anhang.

3. Sind die Speicherstellen 1 und 2 einmal belegt worden, so brauchen sie nicht vor jedem weiteren USR-Befehl erneuert werden.

4. Grundsätzlich sollten Sie sehr vorsichtig mit den SYS- und USR-Befehlen umgehen, da ein falscher Sprung in ein Unterprogramm den Rechner zu nicht beeinflußbaren Operationen ver anlaßt.

Danach können Sie nur durch Aus- und Einschalten den Normalzustand erreichen.

Variable für das Unterprogramm

1.2.36 Ein Elixier für Starprogrammierer, die Befehlsgruppe POKE, PEEK ()

Die Befehle PEEK und POKE zählen zu den Sonderbefehlen, mit denen über das herkömmliche BASIC hinaus Speicherplatzoperationen durchgeführt werden können.

POKE - ermöglicht es, direkt in eine bestimmte Speicherstelle einen Wert hineinzuschreiben.

POKE Speicherstelle, Wert

Beispiel: POKE 59468,12

In die Speicherstelle (dezimal) 59468 wird hier der Zahlenwert 12 eingeschrieben. Dieses Beispiel ist gleichzeitig der Befehl für die Umschaltung von Grafikzeichen auf Kleinbuchstaben; d. h. die

Shift-Funktion der Tastatur erzeugt jetzt in Verbindung mit einer Taste den zugehörigen Kleinbuch staben, siehe Anhang VIII für die -2-Tastatur.

Dieser Zustand bleibt erhalten, bis entweder das Gerät ausgeschaltet wird oder bis der Umschalt befehl

POKE 59468,14 folgt.

PEEK - Liest den Inhalt einer Speicherstelle, die dezimal angegeben wird.

PEEK (Speicherstelle)

Beispiel: ? PEEK (59468) Anzeige: 14

1.3 DIE AUSFÜHRUNGSBEFEHLE

Diese Befehle kann man als Steuerbefehle für ein Programm auffassen; wir bestimmen damit, was mit dem Programm geschehen soll, ob es

- mit RUN gestartet werden soll,

- mit STOP gestoppt werden soll,

- ob es mit LIST ausgedruckt bzw. am Bildschirm dargestellt werden soll,

- mit NEW gelöscht werden soll,

- mit CONT (CONTINUE) nach einem STOP-Befehl

weitergestartet werden soll oder mit

- GOTO ab einer bestimmten Adresse gestartet werden soll, oder ob mit

- CLR alle Variablen gelöscht werden sollen.

Um diese Befehle kennenzulernen, müssen wir ein kleines Beispielprogramm in den Rechner

eingeben. Geben Sie bitte nachfolgendes Programm Zeile für Zeile in den Rechner ein. Nach jeder Zeile be

tätigen Sie die RETURN-Taste. Mit dieser RETURN-Taste wird die Programmzeile, die ja zunächst nur im Bildschirm steht, in den Arbeitsspeicher gebracht, wo sie später zur Ausführung gebracht werden kann.

10 INPUT A,B,C 20 PRINT A,B,C 30 STOP 40 PRINT „BEISPIEL“ 50 END

1.3.1 Das Programm wird gestartet

Mit dem Befehl

RUN (RETURN)

wird das gesamte Programm gestartet. In dem Beispielprogramm erkennt man das daran, daß im Bildschirm ein Fragezeichen erscheint. Dieses Fragezeichen ist typisch für die Input-Anweisung der Zeile 10.

Nach Eingabe von 3 numerischen Werten

z.B. 1 (RETURN)

2 (RETURN) 3 (RETURN)

setzt das Programm automatisch den Ablauf fort.

MERKE: Mit dem RUN-Befehl werden alle bereits im Rechner befindlichen Variablen gelöscht! Der RUN-Befehl kann auch modifiziert angewendet werden; z. B. wird mit

RUN Zeilennummer

das Programm ab der angegebenen Zeilennummer gestartet.

In dem Beispiel läßt sich dieses mit

RUN 40

testen.

1.3.2 Die Verschnaufpause wird beendet

Wird der Ablauf eines BASIC-Programms durch einen Stop-Befehl unterbrochen, so läßt sich das

Programm sehr einfach ab dieser Stelle fortsetzen durch

CONT (RETURN)

MERKE: Der CONT-Befehl verändert keine Variablen oder Werte eines Programms.

1.3.3 Und so sieht Ihr Programm aus

Möchten Sie sich das im Rechner befindliche BASIC-Programm einmal in seiner Gesamtheit an-

sehen, benutzen Sie die Befehlsfolge

LIST (RETURN)

Auf dem Bildschirm erscheint nun das gesamte BASIC-Programm, sortiert nach aufsteigenden Zeilennummern.

..........

____

Selbstverständlich lassen sich auch Teilbereiche des Programms ausgeben.

LIST 40 (RETURN) listet nur Zeile 40 LIST -30 (RETURN) listet bis Zeile 30 LIST 30- (RETURN) listet ab Zeile 30 LIST 20-30 (RETURN) listet von Zeile 20 bis 30 LIST 40-40 (RETURN) listet nur Zeile 40

1.3.4 Man muß nicht immer am Anfang starten

Sollte der Ablauf eines Programms einmal ab einer bestimmten Zeilennummer fortgesetzt werden

____

ohne die im Rechner befindlichen Werte zu löschen bzw. ohne die Anweisung STOP zu benutzen,

bietet sich die GOTO-Anweisung an.

Syntax: GOTO Zeilennummer

Beispiel: GOTO 40 (RETURN) MERKE: Die GOTO-Anweisung verändert keine Variablen oder Werte.

1.3.5 So kann man altes vergessen.........

Soll der Rechner in den sogenannten Einschaltzustand gebracht werden, benutzt man die Befehls folge

NEW (RETURN)

d.h. das gesamte Programm und sämtliche im Rechner befindlichen Variablen werden gelöscht.

Die in 1.3. aufgeführten Ausführungsbefehle sind außer CONT auch programmierbar. Sie können

also wie normale Befehle ins Programm geschrieben werden.

DIE BESONDERHEITEN DES 2001 UND DER 3001 -COMPUTER

2.1

Die graphischen Symbole (siehe Anhang VIII für die -2-Tastatur.)

Neben den großen Buchstaben auf der Tastatur existieren noch eine Vielzahl von Sonderzeichen,

nämlich die graphischen Symbole. Diese Symbole werden dargestellt, wenn gleichzeitig die SHIFT-Taste und eine weitere Taste mit

den dargestellten Sonderzeichen betätigt wird. Zusätzlich ist es möglich, auch in Kleinschrift zu schreiben.

Der Rechner besitzt 3 sogenannte Zeichensätze:

1. Großschrift und Sonderzeichen

2. Graphische Symbole

3. Kleinschrift Wobei 1. immer vorhanden ist und 2. oder 3. wahlweise einschaltbar sind. Der Befehl zum Umschalten zwischen 2. und 3. Zeichensatz lautet:

POKE 59468,12 (Kleinschrift gewählt) POKE 59468,14 (Graphische Symbole gewählt)

Bei der Umschaltung ist zu beachten, daß der gesamte Bildschirminhalt umgeschaltet wird.

Beispiel: 10

Nachfolgende Tabelle gibt den Zusammenhang zwischen Dezimal, Hexa-Dezimal, ASCII und Bildschirmcode wieder.

FOR I = 1 TO 255 IF I = 147 THEN PRINT: GOTO 40

PRINT CHR$(I);

30 40

NEXT POKE 59468,14: FOR I = 1 TO 999: NEXT

POKE 59468,12: FOR I = 1 TO 999: NEXT: GOTO 50

32 20

[

o Tl

—X X.

o m

r~ Tl

CD oao

Tl Tl

roCDfO

ESC

—X >

SUB

Ulru-p>

CAN m S

ruCOru

_k Si

ETB

SYC

Ul *>. CO ru o NAK

aoD

CO 00

O) Ul

DLE

o DD

_X O CD

O CDo00

•n

O s|

03 r~

Ul CO ru

O05oUlo

ENQ

ACK

p>.oCOoru EOT

ETX

STX

-m X

O o

HOS

o NULL

DEZIMAL HEXA

DEZIMAL

ASCII

[

♦

o> ru

-p>

CO CO

■p>. o

■o

•o

COSJCDo>CD

<J>

□

—

ro CO

CJ1

cnTIUl

's.

O) 05

CODCO

CD CD

127

si Tl

DEL

— N

OUlCO

OCODO

UlOUl

—

126

simsi

en00ai-gai

CO >

CO(UCD CD

UlDDUl

—

125

124

□

O)enen CO00COsiCO05CO

CO 00

ai CD

-< X

♦

□

123

122

□

■p>.

-sJ

05 Ul

000000sJ000500Ul00 00

UlsiUl05UlUlUl

120

siCO-Ni

00sisi

UlCOUl

119

ru COaCO

-P^ CO

E □

118

si05si

< C

Q B

•fc.

117

Ul o

CO ru

UlCOcnN)cn Ul

116 ;

-P00

CO CO COoru

115

114

si COSiru

—»

•P*si■fc.

00osi

■fc.

n S 0

□ I 113

112

si O05Tl

_Q TD

I“

-P.

-PUl

-P>-

IUDru

I - +

P».o•P*

-P>. m

110

C-

—

P*COP>

ruDDru

* —

si05siUlsi

I 108

109

O) Da>O

—

X o

P-oCOcoCO

__x

ruCOruoorusiru05rocnru

—

siCOsi

■P».

■p. ê

—

a S B

107

106

05DD05

—

O O

CO Si

p°

104

3" CO

sO o'-

o S

O) Tl

103

□

- e°

-P-00pksi-P*.

X o

I 105

a> CD0500

—

CO03CDenco

-p^ruco

11-

050005

-N

P>.

-P*

D o

□

102

05Ul05

> f9

co co

Pl.

ru ru

;

—

-P».

100

CD co

O) CD

Q. o

□

□ BILDSCHIRM

BILDSCHIRM

DEZIMAL

HEXA DEZIMAL

ASCII

BILDSCHIRM

DEZIMAL

HEXA DEZIMAL

ASCII

BILDSCHIRM

DEZIMAL

HEXA DEZIMAL

ASCII

IN HEXADEZIMAL; ASCII & BILDSCHIRMCODE

2.2. DIE EINGEBAUTE UHR .... ein Leckerbissen

Jeder Computer braucht, um seine Befehle auszuführen, einenTaktgenerator, der die Geschwindig

keit der Befehlsausführung bestimmt. Um die Genauigkeit des Generators zu erhöhen, verwenden manche Computerhersteller dazu Quarze, wie sie auch in Uhren verwendet werden. Bei Ihrem Rechner wird dieser Taktgenerator gleichzeitig als Uhr mit verwendet.

Diese Uhr kann in 2 Formen abgerufen werden. Geben Sie folgendes ein:

PRINT Tl$ (RETURN) Die Antwort sind 6 Ziffern die Ihnen die Zeit seit Einschalten des Rechners angeben. Die Ziffern bedeuten:

Ziffer 1+2: Stunden Ziffer 3 + 4: Minuten Ziffer 5 + 6: Sekunden

Geben Sie ein:

PRINT TI Die Antwort ist eine Zahl, die Ihnen die Anzahl von 1/60 Sekunden seit Einschalten des Rechners

angibt. Wenn Sie die Uhr auf eine bestimmte Zeit stellen wollen, so verändern Sie die Variable Tl$.

Beispiel: Tl$ = ”143000” (Die Uhr wird auf 14h.30 gestellt.)

Tl$ = ”080530” (Die Uhr wird auf 8h.05 u. 30 Sekunden gestellt.)

Ein Verändern der Variablen TI ist nicht möglich. Der Anwendungsbereich der Uhr ist sehr leicht erklärt:

Zeitgenaue Meßwerterfassung

Terminkalender für den Tag

Abbrechen von Programmen nach einer bestimmten Zeit

Überprüfung von Zeitabläufen Ein kleines Beispiel soll eine der Anwendungen der Uhr veranschaulichen.

100 INPUT ’’WIE SPÄT IST ES”; A$ 110 IF LEN (A$)< 6 THEN 100 120 B$ = ”” 130 FOR I = 1 TO LEN (A$) 140 IF MID$ (A$,l,1) <”0” or MID$ (A$,l,1)

> ”9”THEN 160

150 B$ = B$ + MID$(A$,I,1) 160 NEXT I 170 IF LEN (l$) <>6 THEN 100 180 Tl$ = B$ 190 PRINT ’’DRÜCKEN SIE [RETURN], WENN SIE” 200 PRINT ’’WISSEN WOLLEN, WIE SPÄT ES IST.” 210 GET IN$: IF IN$ = ” ’’THEN 210 220 IF ASC (IN$) >< 13 THEN 210 230 PRINT ”ES IST JETZT:”; 240 B$ = Tl$ 250 A$ = LEFTS (B$,2) + ”UHR”, + MID$ (B$,3,2)

+ ”MIN” + RIGHTS (B$,2) + ”SEK” 260 PRINT A$ 270 GOTO 210

2.4 Die Möglichkeiten Peripherie anzuschließen

Das nachfolgende Bild illustriert die Anschlußmöglichkeiten für externe Geräte.

Abb. 1 : Rückseite des Computers

1 = Anschluß für externen Recorder 2 = 8 Bit Parallel-Schnittstelle 3 = IEC-Bus-Schnittstelle 4 = Seriennummer 5 = 0,6 Amperé-Sicherung 6 = Netzkabel 7 = Netzschalter

2.4.1 DER RECORDER

Der externe Recorder wird über den vorhandenen Steckerkontakt auf der Rückseite des Rechners angeschlossen.

Die logische Behandlung des Kassettengerätes geschieht mittels der Anweisungen:

OPEN Kapitel 1.2.20 CLOSE SAVE

LOAD

VERIFY

PRINT # INPUT #

Soll ein Programm auf dem Recorder gespeichert werden, so lautet die Befehlsfolge

SAVE ’’NAME”,

oder

’’SAVE”,

Entsprechend:

LOAD ’’NAME”,

bzw.

’’LOAD”,

Der 2. Recorder wird innerhalb des Gerätes an der Platine angeschlossen. Beim Zugriff auf diesen

Recorder muß beim öffnen der Datei der Gerätenummer 2 angesprochen werden; desgleichen

beim Laden und beim Lesen.

bis

Sollen Daten auf den Recorder geschrieben oder vom Band gelesen werden, so verwendet man PRINT# bzw. INPUT# .

Beispiel: 10 OPEN 5,1,1 (Siehe Kapitel 1.2.20)

20 FOR K = 1 TO 50

30 PRINT # 5,K 40 NEXT K

50 CLOSE 5

Für den Lesevorgang sieht das Beispiel geringfügig anders aus.

Beispiel: 5 DIM A (50)

10 OPEN 5,1,0 20 FOR K = 1 TO 50 30 INPUT#5,A(K) 40 NEXT K 50 CLOSE 5

Anmerkung: Beim 2001-Computer ist es notwendig, vor jedem OPEN-Befehl, der sich auf einen

Recorder bezieht, folgende 2 Befehle einzufügen: POKE 243,122: POKE 244,2 vor OPEN für Recorder # 1

bzw. POKE 243,58: POKE 244,3 vor OPEN für Recorder # 2

Bei den Geräten der 3001-Serie dürfen diese Befehle nicht verwendet werden.

2.4.2 Der 8 Bit Parallelanschluß

Der Parallelanschluß, (Abb. 1, Pkt. 3), auch User-Port genannt, besteht aus 12 Doppelkontakten (Abstand Kontakt zu Kontakt: 0,156 inch) für die verschiedensten Möglichkeiten des Sendens und Empfangens von Informationen.

Die unteren Kontakte des Parallelanschlusses (CA1, PA0-7, CB2) sind direkt auf einen InterfaceAdapter VIA 6522 geführt und können hexadezimal ab $E840 bzw. dezimal ab 59456 ange sprochen werden.

Näheres siehe Anhang S (Schnittstellenbeschreibung).

Trägermaterial

(Isolierung)

Abb. 2 8 Bit Parallelanschluß

Sicht auf Rückseite Computer.

2.5. DATEIVERWALTUNGEN

Im Zusammenhang mit dem IEC-Bus ist die Behandlung von Dateien und das Wissen darüber unentbehrlich.

Dateien werden benutzt, um Daten oder Informationen abzuspeichem und/oder wiederzube schaffen. Das geschieht beispielsweise auch mit Programmen auf der Kassette. Eine Erweiterung dieser Erklärung ist es, jede Vorrichtung, die Daten empfangen oder erzeugen kann, als logische Datei zu benennen. Zum Beispiel kann ein Digitalvoltmeter auf Anfrage des Rechners seine Infor mationen über den IEC-Bus senden. Da aber verschiedene Geräte wie Kassette, Bildschirm, Tastatur, Voltmeter u. a. völlig verschieden aufgebaut sind, unterscheidet man bei diesen zwischen einer physikalischen und einer logischen Adresse dieses Gerätes.

a) Die physikalische Adresse eines Gerätes ist unabänderlich und vom Hersteller festgelegt. Bei

Ihrem Modell kann die physikalische Adresse von 0-15 gehen. Folgende Adressen sind bereits belegt:

physikalische Adresse

Als Geräte 4-15 sind lEC-Bus-Geräte nach Belieben anschließbar.

b) Die logische Adresse einer Datei ist von 1 bis 255 von Ihnen frei definierbar. Sie legen die Zu

weisung einer logischen Adresse beim Eröffnen dieser Datei fest. Diese Verknüpfung hat für

Sie den Vorteil, daß Sie beim Ändern eines physikalischen Gerätes nur angeben, um welches Gerät es sich handelt. In dem folgenden Beispiel sehen Sie, daß eine Tabelle, von dem selben Unterprogramm generiert, einmal auf dem Bildschirm ausgegeben wird und das zweite Mal auf der Kassette:

10 OPEN 1,3,1: REM Bildschirm

11 GOSUB 100: REM Sprung ins Unterprogramm 12 CLOSE 1 13 Open 1,1,1: REM Recorder 14 GOSUB 100 15 CLOSE 1 16 END

100 FOR I = TO 25: REM Unterprogramm 101 PRINT# 1,1; SQR(I) 102 NEXT I 103 RETURN

Gerät

Tastatur Recorder # 1 Recorder #2 Bildschirm

Zusätzlich zu der physikalischen und logischen Adresse können Sie beim Eröffnen eines Gerätes noch eine Zweitadresse angeben. Die Zweitadresse gibt einem intelligenten Peripheriegerät beim

Eröffnen zusätzlich noch an, in welcher Art es die Daten zu behandeln hat. Beim Drucker gibt es

beispielsweise 6 verschiedene Arten, die Daten zu drucken:

Zweitadresse Druckart

0 Normal drucken

1 Drucken unter Formatkontrolle 2 Übersetzen des Formates 3 Setzen variable Anzahl Zeilen/Seite 4 Benutzen der Fehlerdiagnose 5 Übertragen eines programmierbaren Zeichens

Bei der Kassettenstation gibt es 3 verschiedene Arten, Daten zu verwalten:

Zweitadresse Operation

0 Lesen von Daten

1 Schreiben von Daten 2 Schreiben von Daten und eine

Bandende-Kennung beim Schließen der Datei

Als letzte Information können Sie einen Dateinamen beim Eröffnen eines Gerätes mit angeben.

Das ist sinnvoll, wenn dieses Gerät verschiedene Dateien verwaltet. Bei Ihrer Kassette ist es bei

spielsweise so, daß Sie mehrere Dateien hintereinander ablegen können. Um nun eine bestimmte

Datei auf dieser Kassette abzuspeichern, können Sie diese mit einem Namen versehen. Dieser Name kann bis zu 128 Zeichen umfassen, es werden allerdings beim späteren Suchen dieser Datei nur die ersten 16 Zeichen abgefragt.

2.5.1. KOMMUNIKATION

Um nun Daten mit einem peripheren Gerät auszutauschen, gibt es 6 spezielle Kommunikations befehle. Diese sind zwar schon in Kapitel 2 beschrieben, sollen aber an dieser Stelle noch einmal vertieft werden.

a) OPEN logische Adresse [Physikalische Adresse [Zweitadresse [’’Dateiname”]]]

b) CLOSE logische Adresse

c) PRINT # logische Adresse [Beliebige Daten]

d) GET # logische Adresse, Variable [Variable, Kostante, arith. Ausdruck]

e) INPUT # logische Adresse, Variable [Variable, Konstante, arithm. Ausdruck]

f) CMD logische Adresse

Um jedem die Möglichkeit zu geben, die nachfolgenden Prozeduren nachzuvollziehen, be schränken wir uns dabei nur auf Kassette, Bildschirm und Tastatur. Es sei jedoch erwähnt, daß

jedes weitere an den IEC-Bus angeschlossene Gerät gleichartig arbeitet. Hierbei ist nur zu unter

scheiden, ob es sich um ein Eingabegerät (Tastatur), Ausgabegerät (Bildschirm) oder Mehrdatei gerät (Kassette) handelt.

2.5.2. DATEIVERWALTUNG PER KASSETTE

Die Kassettenstation Ihres Rechners ist prinzipiell identisch mit einem normalen Kassettenrecorder. Unterschiedlich ist lediglich das Sende-Empfangsteil für digitale Informationen und ein Schalter, der die Stellungen der Bedienungstasten kontrolliert. So kann der Rechner feststellen, ob die

PLAY, REWIND oder FAST FORWARD-Taste gedrückt ist, er kann aber nicht feststellen, um welche dieser drei Tasten es sich handelt.

Sobald dieTaste PLAY gedrückt ist, kann der Rechner den Motor ein- und ausschalten. Er nutzt dies aus, um Dateien in einzelne Blöcke zu unterteilen.

Die Struktur einer Datei auf der Kassette sichert Ihnen ein Minimum an Platzverbrauch, kombiniert mit einem Maximum an Schreibsicherheit. So werden beispielsweise alle Daten zweimal hinter einandergeschrieben, um bei einer Bandschwäche defekte Daten rekonstruieren zu können.

Geschwindigkeitsschwankungen des Bandes werden durch eine spezielle Anpassungstechnik ausgeglichen. So wird ein fester Ton zwischen jedem Datenblock und an den Anfang jeder Datei geschrieben. Durch die Länge dieses Tones stellt der Rechner fest, ob es sich um einen Dateikopf oder einen Dateiblock handelt.

Ein Dateikopf signalisiert dem Rechner, daß die Kassette an einem Dateianfang positioniert ist. Er enthält neben dem Dateinamen auch die Information, ob es sich um eine Datei oder ein Programm handelt.

Um nun den Zugriff auf die Information einer Datei zu beschleunigen, liest Ihr Rechner nicht nur die

gewünschte Information, sondern immer einen kompletten Block von insgesamt 192 Zeichen, da das Starten und Stoppen des Kassettenmotors nach jeder einzelnen Information zu Zeitaufwendig ist.

Dieser Block wird in einen Pufferbereich eingelesen und von dort je nach Bedarf in die gewünschten Variablen gebracht. Beim Schreiben ist das Verfahren umgekehrt. Es werden die Informationen, so lange in den Puffer gebracht, bis dieser voll ist. Der gesamte Puffer wird dann gemeinsam auf das Band geschrieben.

Der Pufferbereich befindet sich für Kassette 1 an den Speicherstellen 634 - 825, für die 2. Kas

settenstation von 826 - 1017. Für Programme werden diese Pufferbereiche nicht benutzt, da

Programme nicht in mehreren Blöcken geschrieben werden. Nachfolgend ein Schema, daß Ihnen

zeigt, wie eine Datei und ein Programm auf Kassette aufgezeichnet werden.

10 Sekunden Festton

192 Zeichen Dateikopf

2 Sekunden Festton

192 Zeichen Duplikat des Dateikopfes 2 Sekunden Festton

192 Zeichen 1. Datenblock 2 Sekunden Festton 192 Zeichen Duplikat 1. Datenblock

2 Sekunden Festton

192 Zeichen letzter Datenblock

2 Sekunden Festton

192 Zeichen Kopie des letzten Datenblocks

10 Sekunden Festton

192 Zeichen Programmkopf

2 Sekunden Festton

192 Zeichen Kopie des Programmkopfes

2 Sekunden Festton

10 - 32768 Byte Programm

* An diesen Stellen bleibt der Kassettenmotor stehen.

- Beispiel für eine Bandaufzeichnung -

2.5.3 EIN- AUSGABEOPERATIONEN BEI LOGISCHEN DATEIEN

Ein- Ausgaben teilen sich in 3 Schritte auf: * Eröffnen der Datei - Mitteilung aller Informationen über diese physikalische und logische Datei * Lesen oder

Schreiben der

Daten -

* Schließen der

Datei - Trennen der Verknüpfung von logischer und physikalischer Datei

Die 3 Teile wollen wir im folgenden beschreiben:

* ERÖFFNEN DER DATEI

Die Eröffnung einer Datei dient dazu, dem Rechner alle Informationen über diese Datei mitzuteilen. Der Rechner selbst speichert diese Informationen in speziell dafür vorgesehene Tabellen, errichtet ggf. Pufferbereiche für diese Datei und sorgt dafür, daß diese Datei anhand der angegebenen lo gischen Adresse zukünftig angesprochen werden kann. Gleichzeitig sendet er Test- und Infor mationssignale an diese Datei, um ihre Funktionsfähigkeit zu prüfen und um sie auf Empfangsbzw. Sendebereitschaft zu schalten.

Programmdateien, egal ob auf der Kassette oder auf anderen Geräten halten sich nicht an die Ein- Ausgabeschritte 1 - 3.

Um ein Programm in den Rechner einzuladen oder vom Rechner wegzuspeichern brauchen Sie

jeweils nur einen einzigen Befehl,

zum Einladen:

LOAD ’’Programmname”, physikalische Adresse

zum Abspeichern: SAVE ’’Programmname”, physikalische Adresse

* LESEN ODER SCHREIBEN

a) LESEN

Für das Lesen von Informationen einer Datei gibt es 2 Befehle:

INPUT # logische Adresse, Eingabevariable(n)

GET # logische Adresse, Eingabevariable

Der INPUT-Befehl veranlaßt den Rechner, solange zu warten, bis alle angegebenen Eingabe

variablen von der Datei gesandt worden sind.

Im Gegensatz dazu holt der GET-Befehl lediglich ein Zeichen. Sofern kein Zeichen gemeldet ist, enthält die Eingabevariable eine 0 oder ein Null-Zeichen, je nachdem ob es sich um eine nu merische oder eine Textvariable handelt. In jedem Fall wird das Programm ohne Pause fort gesetzt.

b) SCHREIBEN

Das Schreiben von Daten vom Rechner in eine Datei geschieht mit folgendem Befehl:

PRINT Alogische Adresse, Variable(n)

Der PRINT-Befehl veranlaßt den Rechner, die angegebenen Variablen in der Reihenfolge ihres Auftretens an die Datei zu senden. Der Rechner wartet nach jedem gesandten Zeichen auf eine

Fertigmeldung der Datei. Bleibt diese aus, z. B. durch Defekt des angesprochenen Gerätes, so

„hängt“ der Rechner an dieser Stelle. Nur durch Aus- Einschalten ist eine Reaktivierung möglich.

Besonderheit für Ausgaben: Durch

CMD logische Adresse

ist es möglich, fast alle Bildschirmausgaben zu einer anderen Datei zu senden. Ausnahmen hierbei sind alle über Tastatur eingegebenen Zeichen, sowie Fehlermeldungen des Betriebs systems. Diese werden nach wie vor auf dem Bildschirm dargestellt. Vorteilhaft ist der CMDBefehl beispielsweise für Programmlisten auf einem angeschlossenen Drucker:

OPEN 1, Druckeradresse (physikalisch) CMD 1

LIST PRINT #

CLOSE 1

(Durch den Befehl PRINT # log. Adresse wird ein vorhergehender CMD-Befehl wieder auf gehoben.)

* SCHLIESSEN EINER DATEI

Geschlossen wird eine Datei durch den Befehl:

CLOSE logische Adresse

Der Pufferbereich des Rechners wird entleert und alle Tabelleneintragungen gelöscht. Die ange sprochene Datei ist nach dem CLOSE-Befehl logisch getrennt, d.h. die Kabelverbindung existiert zwar noch, alle Ein- Ausgabebefehle werden aber vom Betriebssystem verweigert.

2.5.4 FEHLERINFORMATION BEI EIN/AUSGABEN

Der Computer besitzt eine Variable ST, die nach einer Ein- Ausgabe eine Fehlerdiagnose bein haltet. Durch Abfragen dieser Variablen ist es möglich, Fehler rechtzeitig zu entdecken.

Die Variable ST besitzt 8 Bit-Positionen. Jedes Bit beinhaltet eine getrennte Fehlermeldung. Durch Verknüpfung ist eine Erkennung von mehreren Fehlern möglich.

Folgende Fehlerquellen sind bei angegebenem Gerät erkennbar:

Bit

0 1

1 2

2 4 Zu kurzer Block

3 8 Zu langer Block

5 32

6 64

Zahlenwert

16 nicht korrigierbarer

- 128

Recorder

eingelesen

Lesefehler

Prüfsummenfehler

Dateiende erreicht

Bandende erreicht

lEEE-Bus

Zeitüberschreitung beim Schreiben

Zeitüberschreitung beim Lesen

Eingabeende

Gerät nicht angeschlossen

Beispiel: Kassette: ST = 36 = 32 + 4

Es wurde ein zu kurzer Block eingelesen. Dadurch kam es zu einem Prüfsummenfehler.

Wie sie sehen, ist eine gleichzeitige Erkennung mehrerer Fehler möglich.

2.6. Der IEC-Bus (IEEE-BUS) Der IEC-Bus besteht aus 8 Datenleitungen, 3 Steuerleitungen und 5 Informationsleitungen.

Die Datenleitungen übertragen die eigentliche Information. Die Handshake-Leitungen sind zur Synchronisierung der Dateninformation zwischen Sender und Empfänger.

Der IEC-Bus benutzt ein Dreidraht-Handshake-Verfahren. Der Ablauf geschieht folgendermaßen:

Nicht größer als 64 msek.

empfangsbereit

nicht empfangsbereit

Daten nicht gültig Daten stehen an Daten empfangen

Daten (noch) nicht empfangen

Bit (Wert = 0) Hochohmig Bit (Wert = 1 )

Der Sender steht permanent auf Sendebereitschaft. Meldet der Empfänger, daß er empfangsbereit ist (1 ), so stellt der Sender die Daten auf dem Datenbus zur Verfügung (2). Er meldet diese Bereit

stellung durch die Meldung „Data valid“ (Daten gültig) (3). Sobald der Empfänger das DAV-Signal empfängt, nimmt er die Daten-Empfangsbereitschaft weg

und meldet damit dem Sender, daß er vorläufig noch keine neuen Daten gebrauchen kann (4). Nach

einer kurzen Verzögerungszeit, die vom inneren Aufbau des Empfängers abhängt, hat er diese

Daten übernommen und meldet über die NDAC-Leitung diese Tatsache (5) an den Sender zurück. Daraufhin kann der Sender die Daten und das DAV-Signal vom Bus wegnehmen (6) (8). Wenn

das DAV-Signal verschwunden ist, nimmt der Empfängerauch das NDAC-Signal weg (7); damit ist ein Übertragungszyklus beendet und der Bus ist in seinem Ruhestand.

Wenn der Empfänger jetzt die nächsten 8 bit aufnehmen kann, meldet er das über die NRFD-

Leitung und der nächste Zyklus kann beginnen.

Die 5 Informationsleitungen haben folgende Bedeutung:

- IFC-Interface clear

Über diese Leitung sendet Ihr Rechner beim Einschalten ein allgemeines Rücksetzsignal (100 msec), mit dem sich alle angeschlossenen Geräte ebenfalls in den Einschaltezustand ver

setzen können.

- REN - Remote enable Diese Leitung dient im allgemeinen dazu, Handbedienungen von angeschlossenen Geräten

zu verweigern. Bei Ihrem Computer ist diese Leitung gegen Masse kurzgeschlossen.

- SRQ - Service Request Über diese Leitungen können angeschlossene Geräte zu sendende Informationen anmelden.

Diese Leitung wird zwar vom Betriebssystem des Rechners nicht abgefragt, Sie jedoch können mit dem Befehl

? (PEEK(59427)AND128)/128

diese Leitung auf 0 oder 1 abfragen.

- ATN - Attention Der Rechner hält diese Leitung auf logisch 0, während er Adressen oder Befehl über die Daten

leitungen sendet. Ist diese Leitung logisch 1, so befinden sich Daten auf diesen Leitungen.

- EOI - End or Identify Das EOl-Signal hat, wie der Name sagt, zwei Funktionen: 1. wird mit ihm das Ende einer Block

übertragung angezeigt und 2. wird es bei der Identifizierung von Geräten benutzt. Die letztere

Anwendung ist allerdings bei Ihrem Computer nicht eingebaut.

Das „Ende“-Signal wird vom Rechner zusammen mit dem letzten Zeichen eines Datenblocks über

tragen und dient dazu, eine Geräteadressierung wieder aufzuheben.

Folgende Kombinationen von ATN und EOI können auftreten:

ATN

Alle Daten-, Handshake- und Informationsleitungen haben TTL-Pegel.

EOI

0 0 Normale Datenübertragung 0

1 1 1

Letztes Datenbyte eines Blockes

0 Übertragung einer Geräteadresse oder eines Gerätebefehls

Aufforderung zur Identifizierung nach einer SRQ-Anfrage (bei Ihrem Modell nicht verwendet)

3. Wieso versteht der Computer die Sprache BASIC

3.1 Die Sprache der Zentraleinheit

Die Zentraleinheit des Computers ist ein Mikroprozessor Typ 6502. Es ist einer der schnellsten zur

Zeit auf dem Markt befindlichen 8 Bit Prozessoren.

Der Befehlsvorrat dieses Prozessors ist jedoch nicht mit dem Befehlsvorrat von BASIC zu ver

wechseln. Eine BASIC-Zeile kann viele tausend Prozessorbefehle zur Folge haben.

BASIC nennt man eine höhere Programmiersprache. Zum Unterschied zur Maschinensprache versteht fast jeder Rechner BASIC, während die Maschinensprache speziell auf den Prozessor zu geschnitten ist. Der Computer interpretiert die BASIC-Befehle, er führt sie jedoch nicht direkt aus.

Ihr Rechner hat also einen BASIC-Interpreter. Zusätzlich ist es aber auch möglich, kleinere Pro gramme direkt in der Maschinensprache zu schreiben. Wir wollen Ihnen nachfolgend ein kleines

Beispiel dazu zeigen, ohne jedoch tiefer auf die Maschinensprache einzugehen.

Unser Maschinenprogramm soll uns eine beliebige Integerzahl in eine Binärzahl, so wie sie im Arbeitsspeicher steht, umwandeln und auf dem Bildschirm anzeigen.

3.2. Der innere Aufbau des cbm

Nachfolgend sehen Sie ein Blockdiagramm Ihres Computers. Alle Schnittstellen, auch für IEC-Bus, Kassette, Bildschirm, Tastatur sind mit dem Adressbus des

Prozessors verbunden. Es ist tatsächlich so, daß alle Schnittstellen im Rechnerwie Speicherstellen behandelt werden, d. h.

der IEC-Bus ist nicht hardware - sondern softwaremäßig realisiert. Ebenso wird die Dekodierung der Tastatur per Programm durchgeführt.

Zwar ist die Entwicklung des Betriebssystems für solch eine Lösung nicht gering, gleichzeitig ist aber ein solches System sehr flexibel, da lediglich eine Änderung des Programmes nötig ist, um z. B. eine völlig andere Tastatur an den Rechner anzuschließen.

MICROPROZESSOR

6502

(CPU)

Adress- und Datenbus

.•>

' • '.'

ROM

RAM

BILDSCHIRM-

RAM

TASTATUR

•

PERIPHERIE

BAUSTEINE

USER-PORT

IEEE-488

3.3. Der logische Aufbau des Speichers

Aufgebaut ist der Adressbereich des Rechners in 256 Blöcke von je 256 Byte. Das sind insgesamt 64 KB, die der Prozessor 6502 addressieren kann.

Die Unterteilung in 256 Blöcke, sogenannte Pages (Seiten) entsteht dadurch, daß der Adressbus in 2 getrennte Busse von je 8 bit aufgeteilt ist. Die Pages 0,1 und 255 nehmen in diesem Zusammen hang eine Sonderstellung ein.

Page 0 dient hauptsächlich zur schnellen Verarbeitung und Speicherung von Daten. Zur Speiche rung von Programmen ist sie weniger geeignet.

Page 1 ist prozessorbedingt zum Zwischenspeichern von Adressen und Registerdaten reserviert. In diesen Bereich sollten keine Daten willkürlich geschrieben werden, da der Rechner diesen Bereich permanent benötigt und verwaltet.

In Page 255 sind die letzten 6 Bytes als Sprungadressen für Unterbrechungen oder Einschalt

vorgänge reserviert. Da dieser Bereich jedoch ohnehin durch ein ROM belegt ist, haben Sie keiner

lei Einfluß auf diese Speicherstellen.

1024

Betriebssystem und Basic Interpreter

8192

16384

32767 32768 33792 34816

35840

36864

49152

59392

RAM

RAM 16K cbm

RAM 32K cbm

Basic Programm

_______________________

Variablen

Bildschirm

Images of TV RAM

12K ROM Erweiterung

ROM BASIC

61440

65536

I/O

ROM Betriebssystem

3.3.1 DER BILDSCHIRMBEREICH

Ab der Speicherstelle 32768 ist der Bildschirminhalt abgespeichert. Es gibt nun die verschiedensten

Möglichkeiten, eine Information anzuzeigen. Einige davon stellen wir Ihnen nachfolgend vor. Jede Möglichkeit hat ihre Vor- und Nachteile. Sie sollten sich je nach Aufgabenstellung für die eine oder andere Möglichkeit entscheiden, oder eine Kombination wählen.

a) Relative Steuerung durch Print und Cursorsteuertasten sowie TAB ( ) und SPC ( ).

Die Befehle TAB ( ) und SPC ( ) sind in Kapitel 1.2.5 beschrieben. Zusätzlich haben Sie die Möglichkeit, den Cursor per Programm genauso wie von Hand zu steuern.

Beispiel: 10 REM ” H ” = CURSOR CLR/HOME

12 REM ”Q ” = CURSOR NACH UNTEN 14 REM ”3 ” = CURSOR NACH RECHTS 16 PRINT QQJA” 18 END

Sie geben also nach dem Anführungszeichen die gleiche Tastenfolge vor wie von Hand und be enden die Zeichenfolge mit einem 2. Anführungszeichen.

Bemerkung:

Alle Steuertasten mit Ausnahme der DELETE-Taste werden innerhalb von Anführungszeichen

nicht ausgeführt sondern für eine spätere Ausführung abgespeichert.

b) Absolute Cursorsteuerung über Unterprogramm

Mit Hilfe des nachstehend aufgeführten Unterprogramms haben Sie die Möglichkeit, eine be stimmte Stelle im Bildschirm anzusteuern. Dazu geben Sie die Zeile invariablen Z und die Spalte in der Variablen S an. Anschließend springen Sie mit GOSUB an den Anfang des Unterpro grammes.

Unterprogramm:

100 REM UNTERPROGRAMM zur Cursor-Steuerung 110 POKE 198,S-1 120 POKE 215,Z-1 130 POKE 197, INT (40* (Z-1)/256) + 128 140 POKE 196, (40*(Z-1)) AND 255 150 RETURN

Beispiel: 10 PRINT

20 Z = 4 : S = 3 : GOSUB 100 30 PRINT ”A” 40 END

c) Direktes Schreiben in den Bildschirm

Die 1000 Plätze des Bildschirms entsprechen den RAM-Speicherplätzen 32768 (erstes Zeichen) bis 33767 (1000. Zeichen). Die restlichen 24 Plätze im RAM (33768 bis 33791) können vom Benutzer belegt werden, werden aber mit CLR (Bildschirm löschen) jedesmal mitgelöscht.

Mit dem POKE-Befehl ist es möglich, eine bestimmte Stelle im Bildschirm zu beschreiben oder mit

dem PEEK-Befehl zu lesen.

Beispiel: POKE 33111,160

Beachten Sie jedoch, daß der Code im Bildschirm nicht mit dem ASCII-Code identisch ist. Siehe 2.1. Zum Abschluß ein Vergleich der 3 aufgeführten Verfahren:

Verfahren 1

PRINT/SPC/Cursor

Steuertasten

Verfahren 2

Unterprogramm

Vorgabe Z/S

Verfahren 3 POKE-Befehl

Geschwindigkeit

Bildschirmgüte

CODE

Steuer

geschwindigkeit Ansprechen eines

best. Punktes

Anwendung:

mittel langsam

mittel gut

ASCII

langsam

Schreiben

ASCII + Zeile + Spalte

mittel

Einschreiben in

vorgegebene Formen

schnell

schlecht

Bildschirmcode

schnell

spez. Anwendungen

3.3.2 EIN- AUSGABEBEREICHE

Von Speicherstelle 59392 bis 61440 befinden sich die Ein-Ausgabebereiche für die Peripherie (Tastatur, Kassette, IEC-Bus, 8 Bit-Port sowie Steuerteile des Bildschirms), wobei bei manchen Bytes jedes Bit eine andere Funktion haben kann.

ACHTUNG:

Das willkürliche Beschreiben oder Lesen dieser Speicherstellen mit POKE oder PEEK kann un kontrollierbare Erscheinungen des Rechners zur Folge haben. Dieser Zustand kann nur durch Ausund Einschalten beendet werden.

CHIP: 6520

Registername

PIAL PIAL1 PIAK PIAS

Registername Hex. Adresse Dez. Adresse

IEEI $E820 59424 IEEIS IEEO IEEOS $E823

Hex. Adresse Dez. Adresse

$E810 59408 $E811 59409 $E812 $E813

$E821 $E822 59426

59410 59411

59425

59427

CHIP: 6522

Registername Hex. Adresse Dez. Adresse

PIA SYNC $E841 P2DB $E842 P2DA TIL $E844 Tl H TILL TILH T2L T2H SR $E84A ACR $E84B 59467 PCR $E84C 59468 IFR 1ER $E84E 59470 SYNC1 $E84F

Näheres siehe: cbm 3016 und 3032 ASSEMBLER LISTING (erhältlich beim Commodore-Vertrags-

händler).

$E840 59456

59457 59458

$E843 59459

59460 $E845 59461 $E846 59462 $E847 $E848 59464 $E849

$E84D

59463

59465

59466

59469

59471

3.3.3 DER BEREICH DES BETRIEBSSYSTEMS

Im Speicherbereich 61440—65535 befinden sich die Maschinensprachenprogramme für die spezielle Bedienung Ihrer Rechnerkonfiguration wie z. B. Anzeigen eines Zeichens im Bildschirm oder Empfangen eines Zeichens von der Tastatur.

Ebenfalls befinden sich in diesem Bereich gewisse Testroutinen, die die ordnungsgemäße Arbeit Ihres Rechners überprüfen.

Beispiel: SYS (65490)

(Drucken eines Zeichens im Bildschirm)

Beispiel: SYS (65487)

(Eingabe von Zeichen über Tastatur und Drucken dieser Zeichen im Bildschirm bis RETURN gedrückt wird.)

3.3.4 DER BEREICH DES BASIC INTERPRETERS

Der Basic-Interpreter ist das A und O Ihrer ganzen Anlage. Durch ihn erst ist es möglich, daß Sie einen Sinus berechnen können, oder bestimmte Werte abspeichern und jederzeit wiederfinden. Die Programme dieses Interpreters befinden sich an den Speicherstellen 49152 bis 57343. Diesen Bereich können Sie im Gegensatz zu dem restlichen Speicher mit PEEK nicht abfragen . . . ver ständlich, da Erstellungszeit und Kosten immens waren. Das Copyright für diesen Interpreter liegt bei der Firma Microsoft.

3.3.5 Dieser Interpreter braucht natürlich auch einen gewissen Bereich, wo er Daten und Informationen

Zwischenspeichern kann. Er benutzt dazu die Speicherstellen 0-1023. Dieser Bereich steht nicht frei zur Verfügung. Aus diesem Grunde haben Sie bei Ihrem Modell cbm auch nicht 32768 Bytes

frei, sondern 32768 -1025 = 31743 Bytes.

Im folgenden finden Sie eine Liste der Belegung der Speicherstellen 0-1023.

cbm SPEICHERBELEGUNG: PAGE 0

(Nicht aufgeführte Adressen werden gebraucht, haben aber keine eindeutige Funktion.) ! VORLÄUFIGE SPEZIFIKATION - ÄNDERUNGEN VORBEHALTEN!

1 2 3 5

Konstante $4C (JMP-Befehl in Maschinensprache) Vektor für USR-Funktion L,H

Anfang-Trennungszeichen

Hilfszähler für BASIC

6 7 8 9

10 11 12 13 14 Aktiver I/O-Kanal 15 Zeilenlänge des Terminals 16 17 19

20 21 22

30 31 32 33 34 39 40 42 43 44 45 46 48

50 51 52 54 54 55 # der gerade ausgeführten Zeile; L,H 56 57 Zeilen# fürCONT; L,H 58 59 Zeiger auf den nächsten Befehl; L,H 60 61 # der DATA-Zeile bei ERROR; L,H 62 64 65 Herkunft des Input; L,H 66 68 69 Zeiger auf die laufenden Variablen; L,H 70 71

Flag für dimensionierte Variablen

Flag für Variablenart (0 = numerisch; 1 = String) Flag für Integervariablen Flag für ” und REM Flag, ob Indizes erlaubt sind Flag für INPUT oder READ Flag für Vorzeichen von TAN Flag, ob OUTPUT unterdrückt wird

Maximale Anzahl Zeichen pro BASIC-Zeile

Zeilen# (Zwischenspeicher)

Zeigt auf nächsten Descriptor Zeiger auf den zuletzt benutzten String Tabelle der Descriptoren für Variablen (je 2 Bytes)

Indirekter Index # 1 ,L,H Indirekter Index # 2,L,H Pseudoregister für Operanden von Funktionen Zeiger auf den Beginn der BASIC-Befehle; L,H

Zeiger auf den Beginn der Variablentabelle; L,H Zeiger auf den Beginn der Array-Tabelle; L,H Zeiger auf das Ende der Variablentabelle; L,H

Zeiger auf Ende des letzten Strings; L,H

Zeiger auf den Beginn der Strings; L,H Zeiger auf höchste RAM-Adresse; L,H

ist 2, wenn ein direkter Befehl ausgeführt wird

Zeiger auf nächstes DATA; L,H

67 Name der laufenden Variablen (1. und 2. Zeichen)

Zeiger auf die laufende FOR-NEXT-Variable; L,H

73 Zeiger auf den laufenden Operator; L,H

75 77 79 80 81 82 84 90 92 94

100

101

102

108 109

110 112

118 119 136 141 144 146 148 150 151 152 153 155 157 158 159 160 167 168 169 170

171 174 175 176 177 178 186 187 189 190 193 194 195 196 198 199

201

203 205 206 209

210

Maske für laufenden Operator (>, = ,<) 76 Zeiger auf DEFFN; L,H 78 Zeiger auf den String-Descriptor; L,H

Länge des obigen Strings

Konstante

$2C (Konstante für INPUT) 83 Vektor für Funktionen; L,H 89 Fließkommaakkumulator #3 91 Zeiger #1 für Blocktransfer; L,H 93 Zeiger #2 für Blocktransfer; L,H 99 Fließkommaakkumulator #1 (u. a. für USR)

Vorzeichen der Mantisse aus Akku #1

Zählt die zum Normalisieren von Akku #1 nötigen Shifts

107 Fließkommaakkumulator #2

Overflowbytes des Arguments aus Akku #2

Vorzeichen der Mantisse aus Akku #2

111 Zeiger auf ASCII-Darstellung des Akku #2; L,H 135 CHRGET-Routine. Holt nächstes Zeichen des BASIC-Textes

Label CHRGOT

120 Zeiger auf nächstes Zeichen des BASIC-Textes 140 Nächste Zufallszahl 143 24h-Uhr in 1/60 Sekunden 145 IRQ-Vektor (interrupt request) für internen Interrupt 147 BRK-Vektor 149 NMI-Vektor (nicht maskierbarer Interrupt)

I/O-Status Letzte Taste Flag für SHIFT (1 bei gedrückter Taste, sonst 0)

154 Korrekturfaktor für die Uhr 156 *

Flag für VERIFY

Anzahl Bytes im Tastaturpuffer (ab 623)

RVS-Flag

166 *

Flag für Cursor ein/aus

Zähler für die Blinkdauer des Cursors

★

Zwischenspeicher für Zeichen während Blinken des Cursors

173 *

Zeiger in die Tabelle der logischen Files Ersatzparameter (Geräte# für INPUT) Ersatzparameter (Geräte# für OUTPUT) Paritätsbyte für Band

185 *

Zur Synchronisation beim Lesen

188 Zeiger auf den aktiven Recorder

192 Fehlerkorrektur

Flag für Lesen von Kassette Dauer der ’’shorts” vor dem Schreiben von Daten

197 Adresse der Position des Cursors

Cursorspalte 200 Startadresse für LOAD 202 Endadresse für LOAD 204 *

Flag für ” 208 *

Länge des laufenden Files

logische # des laufenden Files

211 212 213 218 219 220 221 222 223 224 249

Sekundäradresse des laufenden Files Primäradresse des laufenden Files

217

Adresse des laufenden Filenames *

Blockzähler für Recorder (Lesen)

248

Tabelle der LSB’s der Zeilenanfänge (Bildschirm)

255

cbm PAGE 1

256-317 (dezimal) werden zur Fehlerkorrektur beim Lesen vom Band benutzt, sowie als Puffer für Zeilenumwandlungen. Der Rest von Page 1 dient als Speicher im Zusammenhang mit GOSUB und FOR-NEXT, sowie als Hardware-Stack.

cbm PAGE 2

(Nicht aufgeführte Adressen werden gebraucht, haben aber keine eindeutige Funktion). ! VORLÄUFIGE SPEZIFIKATION - ÄNDERUNGEN VORBEHALTEN !

512 592 BASIC-Input-Puffer 512 513 Programmzähler des 6502 514 Statusregister des Prozessors 515 Akkumulatorinhalt 516 517 Y Register 518 Stapelzeiger 519 520 593 602 Tabelle der Filenummern 603 612 Tabelle der Gerätenummern 613 622 Tabelle der Sekundäradressen 623 633 634 826 1018 1023

X Register

IRQ-Vektor für externen Interrupt

Tastaturpuffer (Anzahl Zeichen steht in 158)

825 Puffer für Recorder# 1

1017

Puffer für Recorder#2

3.3.6 SPEICHERUNG VON PROGRAMMEN

Eine Programmzeile besteht aus Zeilennummer und Befehlen. Alle Programmzeilen werden in Reihenfolge der Zeilennummer von 1024 an aufwärts folgendermaßen gespeichert (n ist die

Zeilennummer, (n + x) ist die auf n folgende Zeilennummer):

Das erste Byte ist Null. (An).

Es folgen 2 Bytes (Bn; Cn). Sie stellen die Verbindung zur nächsten Programmzeile her. Der Wert Bn + 256 * Cn gibt die Adresse an, in der die Größe B

steht. Sind Bn und Cn beide Null, dann ist

n + x

n die letzte Zeilennummer des Programms.

Die nächsten zwei Bytes (Dn; En) geben die Zeilennummer an: Zeilennummer = Dn + 256 * En.

Es folgen die BASIC-Befehle (codiert in 1 Byte pro Befehl bzw. 1 Byte pro Zeichen. Die Codeliste steht im Anhang unter Interpretercode).

Beispiel: Das Programm

1000 PRINTX 2000 GOT01000

wird folgendermaßen gespeichert:

0 8

1024

1025

Verbindungsglied

1026

232

1027

Zeilen #

3 153 88

1028 1029

_E ,

PRINT X

1030

Inhalt

Speicherstelle Übersetzung

1031

1032

A B C , D E

Verbindungsglied

208

1033 1034 1035

Zeilen #

137 49

1036 1037

GOTO

48 48

1038 1039

0 0 0

1041 1042 1043

ABC

3.3.7 Es stellt sich nun die Frage, wie der Rechner die Variablen verwaltet, die Sie eingeben. Nehmen wir an, Sie haben den Rechner eingeschaltet und geben ein:

A$ = ’’ICH BIN DAS MODELL CBM”

Der Rechner meldet:

READY

Die Stelle, wo der Text „ICH BIN DAS MODELL CBM” steht, können Sie nun folgendermaßen

finden:

PRINT PEEK (42) + PEEK (43) *256 + 2 Antwort: 1029 An der Speicherstelle 1030 steht in diesem Fall, wie lang der eingegebene Text ist. Die beiden

nachfolgenden Speicherstellen geben an, wo der Text steht.

? PEEK (1029), PEEK (1030) + PEEK (1031) * 256

Antwort: 23 8169 Der Text ist also 23 Stellen lang und steht ab Speicherstelle 8169. Geben Sie ein:

FOR I = 8169 TO 8169 + 22: PRINT CHR$ (PEEK(I));:NEXTI

Antwort: ICH BIN DAS MODELL CBM Sie haben gesehen, welche Vorgänge der BASIC-Interpreter durchführt, um eine Variable wieder

zufinden.

In den Speicherstellen 124, 125 und 1031, 1032 stehen in unserem Beispiel sogenannte Pointer (Zeiger).

Pointer sind Informationen, die angeben, wo eine gesuchte Information steht. 1-Byte-Pointer können Werte von 0-255 annehmen. Um beispielsweise auf die Speicherstelle 8169

zeigen zu können, benötigt man 2-Byte-Pointer. 2-Byte-Pointer sind wie folgt verschlüsselt: Speicherstelle = X + 256 * (x + 1)

X und x + 1 sind die Inhalte zweier aufeinanderfolgender Speicherstellen. Nachfolgend eine Tabelle des Speicherplatzes und dessen Aufteilung mit Angabe der Pointer für

diese Aufteilung.

1040

RAM-ZUTEILUNG UND POINTER

Obergrenze

RAM

Beginn der Strings

CO ü)

"v—

‘<D

-Q

o o

f^.

N-

LU LU LU CL CL

* +

CD ID

■X .

o Tj-

CO ®

< 0

CD CD

M—

3.4 WIE EIN PROGRAMM ABLAUFT

Sobald Sie RUN eingegeben haben, beginnt der Rechner die Abarbeitung der Befehle in auf

steigender Reihenfolge. Einen Befehl erkennt der Rechner an seiner Abkürzung als Zahl von 128 bis 202 (siehe Interpretercode). Findet er einen solchen Befehl, so führt er diesen Befehl aus. Wenn er einen Befehl ausführen soll, so prüft er, ob weitere Informationen zu diesem Befehl nötig sind.

CM o

'o_

Wenn ja, so holt er sich diese Informationen aus dem Speicher. Wenn nein, so führt er den ange gebenen Befehl sofort aus. Sollte der Interpreter hierbei einen Fehler feststellen, so zeigt er diesen an und beendet seine Arbeit.

Stellt nun der Interpreter eine Variable fest, so sucht er diese in seiner Variablenliste. Findet er sie dabei nicht, so legt er sie neu an. Dabei verschiebt er mitunter seinen kompletten Speicher mehrere hundert Mal. Hat er einmal eine Variable angelegt, so findet er sie immer wieder. Auch nach Be endigung des Programms stehen die Variablen zur Verfügung, bis Sie entweder mit RUN das Programm neu starten oder das Programm ändern.

4. TIM: MONITOR FÜR DIE MASCHINENSPRACHE

TIM (Terminal Interface Monitor) wurde für die Mikroprozessoren der Serie 65xx entwickelt.

TIM BEFEHLE

M display memory;

R display register;

G begin execution; X exit to BASIC; L load; S save;

Anzeige des Speicherinhalts Anzeige der Registerinhalte Ausführung eines Programmes in Maschinensprache Rückkehr zu BASIC Laden eines Programms von Kassette Überspielen eines Programms auf Kassette

TIM UNTERPROGRAMME

JSR JSR JSR JSR JSR JSR JSR JSR

WRT RDT GET CRLF SPACE WROB

RDOB HEXIT

$FFD2 type a character; Ausgabe eines Zeichens $FFCF input a character; Eingabe eines Zeichens $FFE4 $FDD0 $FDCD $E775 $E7B6 $E7E0 ASCII to hex in A;

get a character; type a CR; type a space; type a byte; read a byte;

Holen eines Zeichens Schreibe CR = CHR$(13) Schreibe Zwischenraum = CHR$(32) Schreiben eines Bytes

Lesen eines Bytes Umwandlung ASCII-Code nach hexadezimal

TIM ZAHLENSYSTEM

Generell hexadezimale Ein- und Ausgabe.

ANZEIGE DES SPEICHERINHALTS .M XXXX YYYY

Anfangsadresse (XXXX) und Endadresse (YYYY) müssen vollständig (als vierziffrige HexZahlen) angegeben werden.

Um den Inhalt einer Speicherzelle zu verändern, wird der Cursor an die entsprechende Stelle

bewegt, dann die Korrektur vorgenommen und mit der Taste RETURN bestätigt.

Beispiel: . M C000, C010

0 C000 C008 C5 CA DF C010

2 3

C7 48 C6

CA 70 C7

5 6

EF C7 23

35 CC

74 C7 1F

CB C8

ANZEIGE DER REGISTERINHALTE .R

Die Inhalte der Register der CPU (Central processing unit, 6502) werden angezeigt: PC Programmzähler (program counter)

IRQ Interruptvektor SR Statusregister des Prozessors AC Akkumulator XR Indexregister X YR Indexregister Y SP Stapelzeiger (stack pointer)

Beispiel: .R

PC IRQ SR AC XR YR SP

0401 E62E 32 04 5E 00 EE

Änderungen können wie bei . M mit Hilfe des Cursors und der Taste RETURN vorgenommen werden. Bei jedem Eintritt (von BASIC nach TIM) werden die Registerinhalte gespeichert und bei der Rückkehr (von TIM nach BASIC) wiederhergestellt.

PROGRAMMAUSFÜHRUNG .G XXXX

Der Go-Befehl bewirkt einen Sprung zu der durch XXXX angegebenen Adresse. Wird XXXX nicht eingegeben, so dient der Inhalt des Programmzählers PC als Zieladresse.

Beispiel: . G C38B bewirkt Sprung nach C38B

EXIT-RÜCKKEHR ZU BASIC .X

. X bewirkt einen Rücksprung nach BASIC. Die Speicherinhalte bleiben dabei unverändert, und

BASIC befindet sich im selben Zustand wie vor dem Aufruf des Monitors.

LOAD - EINLESEN DES PROGRAMMS VON KASSETTE .L ’’NAME”, XX

XX steht für die Nummer des Peripheriegeräts, Gerätenummer und Filename müssen angegeben werden. Das OS (Operating system) reagiert wie bei BASIC. Die mit dem SAVE-Befehl definierten Speicheradressen werden geladen.

Unterprogramme in Maschinensprache können auch von BASIC geladen werden. Dabei ist aber zu beachten, daß der Variablenpointer auf das zuletzt geladene Byte plus eins zeigt. Daher dürfen BAS IC-Variablen nach LOAD nicht verwendet werden. Will man nach LOAD mit BASIC Weiter arbeiten, so muß zuerst ein erneuter Sprung zum TIM erfolgen, dann eine ordnungsgemäße Rückkehr (RUN, dann .X).

Beispiel: ,L”NAME”,01

PRESS PLAY ON TAPE # 1 OK SEARCHING FOR NAME

FOUND NAME

SAVE - SPEICHERN EINES PROGRAMMS .S ’’NAME”,XX, YYYY, ZZZZ

XX steht für die Nummer des Peripheriegeräts (siehe . L). YYYY ist die hexadezimale Anfangs adresse des aufzunehmenden Programms und ZZZZ die Endadresse plus eins.

Beispiel: .S ’’NAME”, 01, 033A, 076B

PRESS PLAY & RECORD ON TAPE # 1 OK WRITING NAME

076B ist Endadresse plus eins, das letzte Datenbyte befindet sich also in 076A.

BREAK UND INTERRUPTS

Der Maschinenbefehl BRK ($00) bewirkt einen Software-Interrupt. Dies bedeutet, daß der Pro zessor das gegenwärtige Programm unterbricht, (PC+2) und SR auf dem Stapel ablegt und dann an eine Stelle verzweigt, die durch den Vektor in $021B und $021C gegeben ist. TIM initialisiert diesen Vektor in der Weise, daß er auf TIM zeigt. Nach einem BRK-Befehl übernimmt TIM daher die Kontrolle, druckt B* aus (entry via breakpoint - im Gegensatz zu C*, entry via call), zeigt die Re gisterinhalte an und wartet auf Befehle vom Operator.

Der oben erwähnte Vektor kann auch verändert werden, etwa um auf eine spezielle Routine zu ver zweigen.

Beachten Sie: 1 ) Nach einem BRK, der auf TIM verzweigt, zeigt der PC auf das dem BRK-Befehl

folgende Byte.

2) Bei einem BRK, der nicht auf TIM verzweigt, zeigt der PC nach der Rückkehr (via RTI) auf das zweite Byte nach dem BRK-Befehl.

AUFRUF VON TIM

Nach dem Laden des Programms kann TIM entweder mit dem Befehl

SYS 64785

oder mit dem Befehl

SYS (1024)

aufgerufen werden. Der erste Fall stellt einen ’’entry by call” dar, der zweite einen ’’entry via break point”. (Die Speicherzelle 1024 enthällt Null).

BEISPIEL:

Das folgende Programm mit dem Namen CHSET schreibt 64 ASCII-Zeichen auf dem Bildschirm. Es soll im Puffer für Recorder # 2 gespeichert werden:

* = $33A CRLF = $FD00 WRT = $FFD2

33A 20 00 FD CHSET 33D A2 20 LDX # $20 33 F 8A LOOP

20 D2 FF JSR WRT

340

343 E8

344 E0 60 CPX #$60

D0F7

346

348 00

349

4C 3A 03

Um dieses Programm einzugeben, werden mit dem Befehl

.M 033A, 034B

die betreffenden Speicherinhalte zur Anzeige gebracht und geändert. Schließlich erhält man die Anzeige:

.M 033A, 034B . : 033A 00 FD 04 A2 20 8A 20 D2 . : 0342 FF E8 E0 60 D0 F7 00 4C .: 034A3A03

JSR CRLF

TXA

INX

BNELOOP BRK

JMP CHSET

Der Befehl:

. G 033A

bringt das Programm jetzt zur Ausführung:

!”H$%& ()|+,-. /0123456789 : ; <=>?§ABCDEFG HIJKLMNOPQRSTUVWXYZ[/]t<—!

Beachten Sie den Inhalt des Programmzählers (siehe BREAK und INTERRUPTS). Es ist jetzt möglich, ohne Angabe der Anfangsadresse das Programm mit dem Befehl:

.G nochmals zu starten. Um CHSET von BASIC aus aufrufen zu können, ersetzt man zunächst die BRK-Anweisung in

$348 durch ein RTS (return from subroutine). $348 wird also von 00 auf 60 geändert. CHSET kann nun von BASIC aus mit SYS826 aufgerufen werden.

Will man den Befehl USR verwenden, so ändert man den zugehörigen USR-Vektor in $1 und $2 dermaßen, daß er auf die Subroutine CHSET zeigt:

. M 0001, 0002

0 1 ....

0001 3A 03 ....

Nach der Rückkehr zu BASIC (. X) kann CHSET somit jederzeit mit SYS826 oder A = USR(0) auf gerufen werden.

RESIDENT

MONITOR......PAGE 0801

LINE • LOC

CODE

LINE

2517 FD 1 1 2518 2519 2520

FD 1 1 A 9 43 CALLE LD A» ' C F D 1 385 85

F D 1 5D 0 16

iCOMMODORE INTERNATIONAL LIMITED

NCMDS = 8

ST A

TMPC

BNE

83 252 1 FD 1 7 A 942 B R K E LD A* ' B 2522

FD 1 9 85 85

2523 FD 1 BD 8

2524 2525 2526

2527 2528 2529 2538

FD1C 4 A FD 1 D68

05 02

FD IE 8 D F D 2 1

F D 2 28 D F B 2 568

F D 2 68 D83 82 253 1 F D 2 968 2532 2533

2534

F D 2 A F D 2 D68 FD2E 69

8 D

2535 F D 3 08 D0 1 82 2536 2537 F D 3 4 2538

2539 2540 254 1 2542 F D 4 0 2543 2544 2545 F D 4 7 2546 2547

2548 2549 2550 255 1 FD 5 4

F D 3 368

69 F D 3 68 Ds e F D 3 9A 5 FD 3 B

8 D

82 STA

FD3E A 59 1

07 02 STA

8 D F D 4 38 A F D 4 48 E 06 02 S T XSP

F D 4 820 D 0 F D 4 BA 6B 5 FD 4 DA 9 F 0 4 F F D 3 2

2 A

84 E 7 JS R

A 9

52 LDA # ' R ; DISPLAY REGISTERS COMMAND

D 0 1 A BNE

B 3

FT B5 JS RC RL F ; PRINT ENTRY DATA

STA

TMPC

CL D

LS RA PLA STA YR PLA STA XR PLA STA

ACC PLA STA

F L G S ; S AVE FLAGS

PLA

A D C1 $ F F STA

PCL PLA AD C1 $F F

P CH

LDA C I H V ; S AV E C U U R E H T IRQ VECTOR STA

LDA

I N V L

C I N V + 1

I N V H

TSX ; S A V E CURRENT STACK POINTER

CL I

LDX LDA

TMPC

# ' *

y R T U 0

S 0

;CALL ENTRY

; BREAK ENTRY

;C SET FOR PC CORRECTION

; S A V E Y

/SAVE X

; S AVE ACCUMULATOR

; P C- 1 FOR BREAK

; CLEAR INTERRUPT DISABLE

; T Y P E OF ENTRY (B OR C>

; y R T T E '*C' OR '*B'

; S KIP TO INTERPRET COMMAND

2553 2554 2555

2556 2557 2558 2559

2560

2561 2562 2563 2564

F D 5 6 F D 5 885 FD5A A9

A 9

02 77 00

STRT LDA

STA TXTPTR LDA te

F D 5 C85DE STA y R a p FD 5 EA 2 0 D F D 6 0 FD 6 2 20

FD65

F D 6 8 FD6A F 0

A 9 2 E LDA » ' .

84 E 7 EB E7

2E CMP

C 9

F 9 FD6C C 920 FD6E F 0

F 5

STI

LDX

JS R JSR

BEQ CMP BEQ

• CR

U R T U 0

R DOC

i' .

STI

• 420

STI

; U SE R COMMAND INPUT

; COMING FROM TEXT BUFFER

; A D D R y RAP AROUND FLAG

; START PROMPT NITH CRLF ; A PROMPTING ' '

iINPUT COMMAND LINE

; IGNORE PROMPTING ' '

/SPAN BLANKS

RESIDENT MONITOR

...........

PAGE 0832

LINE

2566 F D ? 0 256? 2568 FD ? 5 D 0 2569 2 5 ? 0 2 5 ? 1 2572 2 5 ? 3F D 7 9 2574

2575 2576 257? 2578 2579 F D 8 3

2581

2583

2584

2585 FD8D 2586

258?

# LOC

A 2

F D 7 2DD

FD 7 7 86 FD 7 9 FD ? 9 FD ? 9

eD FD7C 48 FD7D BD F 0 FD 8 0 48 F D 8 I F D 8 2CA

FD 8 5 6 C

F D 8 8A 5 F D 8 A

FD 8 F FD92

1 0 ED

8 D A 5 8 D 60

CODE

07 E 0

FD 8 B 84

E 8

FB 01

02 FC 80

LINE

S0 LDX

SI CMP

; I ND I RE CT ; PUSHING ; THEN RTS

S2 DEX

P U T P

BHE

STX

LDA

PHA

LDA

PHA

RTS

BPL

JM P

LDA

ST A

LDA

ST A

RTS

tNCHDS-1 iLOOKUP COMMAND CHDS,X S 2

SAYX ; INDEX OF COMMAND IN TABLE

JM P FROM TABLE BY TARGET ADDRESS-l

ABRH,X

ADRL,X

SI /LOOP FOR ALL COMMANDS

CUSRCMD) ; ALLOW USER COMMANDS

T MP 0 PCL TMP0+1

P CH

2589 2590 2591 2592 2593 2594 2595 2596 2597 2598 2599 2660 2601 2682 2683

2665 2686 268? 2608 2609 2610 261 I 2612 2613 2614 2615 2616

F D 9 3 F D 9 3 F D 9 3 FD 9 3 FD9 3 FD 9 5 FD 9 7

FD 3 AB 1 FD9C FD9F FD A 2C 6

FD A4

FDA6 60

FDA7

FDA A

FD AC

FDAE 81

FBB0

FDB2

FDB4

FDB5

FDB6

FDB9

FDBC

FDBE

85 B 5 A 0

20 CD

D 5

D 0F 1

0 D

A 2

F 0

05 68 68 4 CF 7 20

D5 FD C 6

B5 60

; D I S P L A Y MEM SUBR. SET

/ 0F MEMORY

; T MP 0

E 7 FD

DM1

/READ

;NO STORE

BYTE

BY3

= ADR

JS R

RTS

AND

JS R

LDX

CMP

BYTES DISPLAYED

OF HEM DISPLAYED

ST A

TMPC

LD Y

«0 SPACE

LDA

( T H P 8 ) , Y

JS R

WROB INCTMP

DEC

TMPC

BHE

DM!

STORE BYTE. IF SPACE OR

RDOB

BCC

BY3 #0

STA

( « MP0. X> C TMP0Z X)

BEQ

BY3 PLA PLA JH P

ERROPR JSR

INCTMP DEC

TMPC RTS

AR=NUMBER

; UR N BYTES ; (TMP0)=A DR

TMPC = 0

; SPACE

i STORE BYTE

; VERIFY WRITE

; ERROR:CLEAR STACK

; INC TMP0 ADR

RESIDENT MONITOR

PAGE 0003

LINE

2 618

2619 2628 2621 2622 2623

2625 2626 262? 2628 2629

2631 2632 2633 2634 2635 2636 263?

1 LOC

FDBF A 9 FDC1 85 FDC3

A 9 FDC5 85 FDC7 A 9 FDC9

FDCA

20 FD C DA 9 FDCF FD D 8

2 C

A 9 FDD2 4 C D 2

FDD5

FDD7

FDD9 FDDB FDDD FD DF

E 6 F 8

D 006

E 6 FC

D 8 E 6 60

CODE

02 F 8 02

CD 20

8 D

82 DE

LINE

SE TR

LDA ST A LDA ST A LDA RTS

SPAC2

SPACE

JS R LDA

. BYT

CR LF

LDA JM P

/INCREMENT

INCTMP

INC

BNE

INC

BNE

INC

SETUR

RTS

KFLGS T MP 8 * >F LGS THP0+1 «5

SPACE

t S 2 8

$2 C #*D $ FFD2

< TM P 0/ T MP 0 SETUR TMP0+1 SETUR URAP

;S ET TO ACCESS REGS

;L OU BYTE

; H IGH BYTE

2639

264 1 2642 264 3 264 4 2645 2646 2647 2648

2549

2653 265 1 2 65 2 2653 2654 2655 2656 285? 2658 2659 2663 266 1 2662 2663 2654

F D E 0

FDE0 3 A F D E 13 B F D E 252 F DE3

F D E 4

4 D 47

FDE5 58

F D E 6

4 C FDE 7 53 F DE8 FDE 9 FD E A F D E B

-E FDE C FE F D £ DFF F D E E

FF F D E FFF F D F 0B 8 FD F 1

96 F DF2 22

FDF 3 57 F D F 4

CE F B F 586 FD F 6

F DF 7

1 0 10

/COMMAND AND

CM DS

.BYT . 8 Y T . BYT . BYT . BYT . BYT . BYT . BYT

AD RH

.BYT . BYT . BYT . BYT . BYT . BYT . BYT .BYT

ADRL

.BYT . BYT

. BYT . BYT . BYT . BYT . 8 Y T

. BYT

ADDRESS TABLE

/ é 4

> . 4

' R '

' M '

' G ' ' X ' ' L '

' S

; MODIFY MEMORY

; ALTER REGISTERS

/DISPLAY REGS

; DISPLAY MEMORY

; START EXECUTION

;UARM START BASIC

/LOAD MEMORY

;SAVE MEMORY >221 >222 >223 >224 >225 >226 >227

>228 <221

<222 <223

<224 <225 <226 <227 <228

RESIDENT MONITOR.

. . PAGE 0004

LINE t LOC

2666

FD F 8 0 D 2666 FDF 9 266?F D F D

2669 2 6 ? 0 26? 1

FE 1 5 FE 1 6

FEI 7

2672 FE IA

FE 1 B

2673 2674FE 1 D 2675

FE 2 0

2677F E 2 3 2678FE 2 5 8 D

2679 2680 2681 2682

FE 28

FE 2 8 E 8

FE 2 C E 0 ID

FE 2 E 2683F E 3 0 A 0 2684

FE 3 2 20 2685FE 3 5

CODE

20 20

98 48 20 D 0 68 A 2

2 E

4 C

A 2

80 F 8 FD

20 D 2FF

D 0F 5

38 1 5 FE

AD 00 82

2686FE 3 8 29 75

268?

FE 3B

01 2688 FE 3E 28 75 2689

FE 4 1 20 CD

2690

FE 4 4

269 1

F E 4 7

2692

F £ 4 A

2693FE 4 D

AD 20 75 AD 08 20 75 E 7

2694 FE20 2*33F

2695 F £53

2696FE 5 6 F 0 39

E 7 FD

E 7 02 E 7 FD 82 E 7 82

FD FD

LINE

RE GK

ALTRIT

.BYT CR* '

TY A PHA

JS R

PLA LD X

JS R JM P

D S P L Y R D2

LDX • 0

LDA

JS R

I N X CPX BHE LO Y JS R LDA P C H JS R LDA PCL JS R JS R

LDA

o S R LDA

JS R JS R

JS R

BEQ

BYT

'PC

C RL F

* ' . WRT «0

S P A C 2

REGK'X * FF D2

• 29 D 2

f ' ;

A L T R I T

U RO B

y ROB SPACE

I NV H y ROB I N V L y ROB SET R 3 :i SEBS 1

SR AC XR YR SP'

2698 2 69 9

2700 2791 2792

2 793 2704

2705

270? 2798 2 73 3 2710 271 1 2712 2713 2714 2715 2716 2717 2713

2719

FE 3 3

F £ 5 B

F E 5 E 90 34 F E 6 0

■r E 6 3

F E 6 6 20 A 7

FE 69 98 29

FE 6 B

FE6E 20

FE 7 i

FE 7 3

FE ? 5

FE 7 7 FE 7 8

F E ? A

FE7C FE 7 E FE 3 0 FE 8 2 FE 8 4

Ff. 3 7

29 EB £7

20 A?

2 9

9? E 8

E 7

E 7 E 7 E 7

E 7

8 1 F 3

F 3

A 6

1 A 38 A 5

E 5

A 5

£ 5

3F AB

3 A

6 A

FE E 7

2 3

DSPLYM

DSP 1

JS R

R DOC

J 3 R

R D 0 A

BCC

ERRS 1

Jn;

T 2 T 2 h A

JS t?

»\ V !.» O

JS R

R DO A

SCC ERRS 1 JS R

T 2 T 2

JS R

STOP 1

BEC

8 E S S 1

«RAP

LDX 8NE

8ESS1 SEC LDA

T MP 2 SBC T MP 0 LDA

THP2+1

SBC ïMP 0 + 1 BCC 3F.BS1

LD Y

1 ' :

JS R

ALTRIT

JS R

N RO A

; READ START ADR ;E RR IF NO SA ;SA TO TMP2 ; SKIP DELIMITER ; READ END ADR ; ERR IF NO EA

;SA TO TMP0, EA TO TMP

'TEST FOR STOP KEY

'DOUBLE BYTE COMPARE

;EA LESS THAN SA

RESIDENT MONITOR

.............

PAGE 0335

LINE

2700

2721

« LOC

FE 8ft ft 9

FE 8 C

20 93

2722 FE 8 F F 0

2724

2726

FE 9 1

F E 9 4

4 C

2728 FF. 9 7

2730 273 1 2732 2733

2734 FE A2 2 73 5 2736 2737 2738 2739 2740 2 7 4 : 2 74 2

F E 9 7 FE 9 ft FE 9 D FE 9 F

20 2B A 7 98 20

20 FE ft 5 FE ft 8 FE AA FE ft C

FE ft F

FE 8 1

A 5 F 8

8 D

A 5

8 D F E 6 420

F E B 7D 0

CODE

F B

F 7

E 7

B 6E 7

E 7 03 88 FD

FF A 7

E 7 0 A

82 FC 87

02 FD

ßF

0 A

LINE

BE QS 1

ERRS 1

; ALTER

AL TR

AL 2

AL 3

LDA JS R

BEQ

JH P

JHP

REG

ISTERS

J S R J S R BCC JS R J S R JS R

BCC

LDA STA LDA STA JS R 8 N E

98 DH DSP 1

S TR T

ERROPR

R DO B R DO A AL2 P U T P * F F C F R DO A A L 3

T HP 0 I HVL

T HP 9 + 1

I NV H SE IR A4

; DISPLAY 8, INCR TH PB

; S K I P 2 SPACES ; C Y = 0 IF SP

; SPACE

; ALTER PC

; S E T TO ALTER R'S

2744

2 74 6 274 7 274 8 2 7 4 9 2750 2751 2752 2753 2 75 4 2755

2756 2 757

2 75 8

2759 2760 2 76 1 2 76 2 2763 2764 2765 2766 276 7 2768 2769

2779 277 1

2772 2773

2774

FEB9

F E ß 9

FEBC

F E 8 F FECI F E C 3 F E C 5

f E C 8

FE CO

B 6

A 7

D 3

A 9 88 3 5

B 5 20 E 8 20

F 8

F F. CI) F 0 C 2

FECF

F ED 2 C 9 FE B4 FE D S FE D8 D 0 FE D A F £ 0 3 F E 5 F Ft E 2 FEE5 FEE6

FE E 7 FE E A FEEC FEEF

FE F i

FEF 4

FE F 5

FE F 8 FEF9

9 D

F 8

3 C

C 320

BA 23 A 7 98

83 20

AE 86 9 A 78 AD

9 1

AD 08

85 90

AD 99 92 48 AD

01 82 LDA

E 7 E 7

; ALTER

AL TH

HE H OR Y - READ

JS R

J S R BCC

LDA

E 7 FD

A4 A5

S f A JS R JSR B N £

A 9 CO

BEQ JS R cap ßEQ cap 9NE

JS R BCC

FD 02

G 1

JS RP U T P LD XSP TXS SEI

LDA STA

LDA STA LBA PHA

PHA

02 LDA

R LO B R DO A

ERRS I

f H?C

R DO C BYTE fi 5 BEÜS1 $FFCF i$8D G 1 #420 ERRS 1 R DO A G 1

I NV H CIHV+1 I N V L C IH V P CH

PCL

FLGS

ADR AND DATA

;SKIP 2 SPACES ;READ HEM ALTER ADR ; C Y=0, IF SPACE, ERR ; SET CNT = 8

; IF CR, EXIT

; IF NOT SPACE. ERR

;ORIG OR NEW SP VALUE

RESIDENT MONITOR

. . PAGE

08 3

LINE

2 7 ? 5FEFC 2 7 7 6FEFB AD

2??? 2 773 2 7 ? 9F F 0 6

2 73 1 F F 0 7 2732 FF 0 A 2783 F F 0 B

2785

2 78 7

2789

2791

2792 FF 1 3

2793 FF 1 5

2794

• LOC

CODE

83 FF 0 0 AE F F 0 3AC

04 05

86 9 A 4 C89 C 3

FF 0 E 4 CF 7 E 7

FF 1 1

FF i l

FF 1 1

A 0 01 84 D 4 88

FF 1 6 84

DI 2795 FF 1 8 84 9 D 2796 FF 1 A A 9

2797

2798

2799

2800

2801 2882

FF 1 C FF 1 E FF 20 85 FF 22 F F 2 5C 9

FF 27 F 0 2803 F F 2 9 2804 2805

FF 28

FF2D C 9 22 2806 FF 2 F 2807

FF 3 1 2808 FF 34 2809 2810 281 1 2812 2813

FF 3 6

FF 38

FF 3 A F 0

FF 3C 91

FF 3E

A 9

07 DA

20 CF

20 F 9

C 90 D

F 8

1 A

D 0

DD CF

C 9

F 0

C 90D

0 B

E 6

DI 2814 FF 4 0 C8 2815 2816 2817

2818 FF 4 7

2819 2820 FF 4 B

2821 2822 FF 5 0 2823 FF 5 3 2824 2825 FF 57 2826 2827 2828 2829

FF 4 1

C0 FF 4 3 F 0 FF 4 5 D 0

A 5 F F 4 9C 9

D 0 FF 4D

20 22 F 3

A 5 96 FF 5 5

D 0 FF 59 FF 5C

FF 5F

FF 6 1

4 C

C 9

F 0

1 0 C 9 EA 84 86 E 2

E 6

10 F 2 56 FD CF 0D E 4

02 02

F 8

LINE

PHA LDA

ACC LDX XR LD YYR RT I

EXIT

LDX

TXS

J H P

READY

ER RL

ZZZ1

/rtrtwHlNE LANGUAGE LUAD

JMP

E RR 0PR

= E'JF + 7

LD Y

« 1 STY

ROUTINE

; DEFAULT DEVICE »1

DEY

STY

FNLEN STY

VERCK

LDA

ST A LDA STA JS R

t>ZZZl

FNADR+1

#<ZZZ1

F NA DR

$ FF C F

; PLACE TO STORE NAME

CMP»'

L 2 L3

BEQ L 1 CMP

# CR

BEQ

ÿ / «

CM P BHE

E RR L

JS R

î FF C F

;SPAN BLANKS

; DEFAULT TO LOAD

;FILE NAME MUST BE NEXT

CMP* ' “ BEQ CMP

L 8

• CR

;E ND OF NAME /DEFAULT A LOAD

BEQ L 5 STA

(FHADR)Y

INC

FNLEN

I N Y

CP Y

»16

BEQ

E RR L

/FILE NAME TOO LONG

BHE L 3

LDA CMP BHE JS R JS R LDA AND BNE JMP JS R CMP BEQ

S AV X

«6

L 2

L D1 5

TUAIT

SATUS

»SPERR

L6 STRT *FFCF »CR L 5

;NOT A LOAD

/LOAD ERROR

/•DEFUALT LOAD

sIT ÏO 3 R 3 I C U A R Î1 START

RESIDENT MONITOR

PAGE 0807

LINE

2830 283 1 FF 6 5 2832 2833 F F 6 A29 2834 2835

2836 2837 2838

2839

2840

284 1 284 2 284 3 284 4 284 5 2 84 6 284 7 284 8 284 3 2850 F F 9 1 285 1 2852 F F 9 5 2853 F F 9 7 2854 2 855 2856 2857 2858 2853 2860 FF A 7 286 1 2862 2863

# LOC

FF 6 3

FF 6?

F F 6 C FF 6E FF 70

FF 7 2

FF74

F F 7 7

FF 79

F F 7 B FF ?B FF 7F F F 8 220 97 F F 8 520 F F 8 8C 9 FF 8 A D 0 F F 8 C F F 8F

F F 9 3

FF 9A F F 9 D FF 9F F F A 1 FF A3 FF A5

FF A9 FF AB F F A E4 C

C 9

D 0

F 0 C 9

F 0 85 20 C 90 D F 0 C 9

D 0

20 A 7

28 A 5 FB 85 A 5 85 20 20 C 9 F 0 F 9

C 9 D 0 A 5 B 4

C 9

D 0F 8

CODE

2 C F 0 B 6

E 7

D5 03 FA D 4 CF

CC 2 C E6

E 7

E 7 CF FF 2 C F 1

E 7

A 7

C 9 FC CA 97

E 7 CF

FF 20

0 D E 5

F 6

LINE

CMP I'.

L9 BNE L 7

JSR R DO8

AND tSF

L10 BEQ L4

CMP #3

LI 1 BEQ L 10

STA FA JSR $ FF C F

CMP t CR

BEQ L 5

CMP #',

L 1 2 BNE L 9

JSR R DO A JSR T2T2 JSR $FFCF CMP #'.

L13 BNE L12

JSR R DO A LDA T HP 0 STA EAL LDA TMP0+1 STA E AH JSR T2T2

L 2 0 JSR $ F F C F

CMP #$20

3EQ L 2 0 CMP # CR

L14 BNE L 1 3

LDA SAVX

CMP #7

BNE L14 JSR SV5 JMP S TR T

;BAD SYNTAX

; DEVICE 0

JDEVICE 3

;DEF AULT LOAD

; B A D SYNTAX

/MISSING END ADDR

/MISSING CR AT END

2865 FF B 1 2866 FF B 1

2867 2868

2869 2870 287 1 2872 FF B 1

FF B 1 F F B 1

FF B 1 FF 8 1 FF B 1

ZZ1 = ALTM- I ZZ2 = ALTR- 1 ZZ3=DSPLYR-1 ZZ4=DSPLYM-1 ZZ5 = GO- 1 ZZ6=EXTT-1 ZZ 7 = L D-i ZZ3 = L D- I

NOTIZEN

5. Programme, die Ihnen den Computer erklären

5.1. Übungs- und Beispielprogramme zu den Punkten 1.2.1-1.2.16

Der REM-Befehl

100 REM PROGRAMMANFANG 110 REM EINGABE VON 2 WERTEN 120 INPUT ’’GEBEN SIE WERT1 EIN” ; A 130 INPUT’’GEBEN SIE WERT 2 EIN” ;B 140 REM ADDITION DER BEIDEN WERTE 150 C = A + B 160 REM AUSGABE DES ERGEBNISSES AUF DEM BILDSCHIRM 170 PRINT ’’DAS ERGEBNIS IST” ; C: REM PROGRAMMENDE

Die hinter dem REM-Befehl stehenden Zeichen haben keinen Einfluß auf das Programm. Sie

dienen lediglich der besseren Übersicht beim Erstellen der Programme oder bei der Fehlersuche

in Programmen; siehe Zeile 100,110,140,160. Wird ein REM-Befehl mit anderen Befehlen in eine Zeile geschrieben, so muß er immer als letzter stehen, (siehe Zeile 170) da die Befehle, die hinter dem REM-Befehl stehen, nicht ausgeführt werden.

Die END-Anweisung

10 REM PROGRAMMANFANG 11 INPUT ’’ZAHL 1” ; A 12 INPUT ’’ZAHL 2” ; B 13 IF A > B THEN PRINT A ”IST GROSSER ALS” ; B 14 IF A < B THEN PRINT A ”IST KLEINER ALS” ; B 15 IF A = B THEN PRINT A ’’IST GLEICH” ; B 16 INPUT ’’WOLLEN SIE NOCH EINEN VERGLEICH DURCHFÜHREN”

; A$ : IFA$= ”JA” THEN 10

17 END

Die END-Anweisung in Zeile 17 beendet das Programm. Sie kann aber auch fortgelassen werden.

Eine END-Anweisung darf auch öfter im Programm verwendet werden. Sie beendet den Programm ablauf ohne Meldung ’’BREAK IN . . .” wie bei der STOP-Anweisung. Stattdessen erscheint die

Meldung READY im Bildschirm.

Der STOP-Befehl

110 PRINT ’’VON WELCHER ZAHL WOLLEN SIE DIE WURZEL ZIEHEN?” 120 INPUT A 130 B = SQR (A) 140 PRINT ’’DIE WURZEL DER ZAHL ”A” IST ”B” 150 STOP 160 GOT0110

Der STOP-Befehl in Zeile 150 bewirkt das Anhalten des Programmes und die Meldung ’’BREAK

IN 110”. Es können auch mehrere STOP-Befehle in einem Programm verwendet werden. Nach einem Programmhalt durch einen STOP-Befehl kann das Programm mittels ”CONT” fortgesetzt werden.

Der LET-Befehl

INPUT ’’ZAHL 1 ”

INPUT ’’ZAHL 2”

INPUT ’’ZAHL 3”

LET D = A + B + C

PRINT ”A” PLUS ”B” PLUS ”C” IST GLEICH ”D”

Der LET-Befehl in Zeile 14 war bei früheren BASIC-Versionen als Zuordnung nötig. Er kann bei

Ihrem Computer weggelassen werden. Zeile 14 sähe dann so aus:

14 D = A + B + C. Ältere Programme, in denen noch ein LET-Befehl steht, brauchen nicht modifiziert

werden, da er keine Fehlermeldung hervorruft.

100 REM PROGRAMMANFANG 110 FOR I = 1 TO 10 : INPUTTEXT”;A$(I) : NEXT

120 PRINT : PRINT’WELCHE AUSGABE (0 BIS 4; 0=PROGRAMMENDE)” 130 INPUT A 135 PRINT

140 ON A+1 GOTO 300, 220, 240, 260, 280 200 PRINT "EINGABE UNZULAESSIG” 210 GOTO 130 220 FOR I = 1 TO 10 : PRINT A$(l) : NEXT 230 GOTO 120 240 FOR I = 1 TO 10 : PRINT A$(l),: NEXT 250 GOTO 120 260 FOR I = 1 TO 10 : PRINT A$(l);: NEXT 270 GOTO 120 280 FOR 1=1 TO 10 : PRINT A$(l)” ”;:NEXT 290 GOTO 120

300 PRINT "ENDE” : END

Die PRINT-Befehle in den Zeilen 220, 240, 260, 280 bewirken die Darstellung von Zeichen

auf dem Bildschirm. In Zeile 220 werden die eingegebenen Werte untereinander geschrieben.

Setzt man ein Komma oder ein Semikolon hinter den PRINT-Befehl (wie in den Zeilen 240, 260),

so werden die Werte nebeneinander geschrieben. Nur die Abstände zwischen den einzelnen Werten ändern sich durch das Komma oder Semikolon. Man kann nun noch den Abstand ver

größern, indem man Leerstellen mit ausdrucken läßt (Zeile 280).

INPUT

100 INPUT A 110 INPUT "ZAHL 2”;B 120 INPUT A$ 130 FOR I = 1 TO 10 : INPUT "GEBEN SIE NAECHSTEN WERT EIN”;A$(I) : NEXT 140 PRINT A 150 PRINT B 160 PRINTA$ 170 FORI=1TO10:PRINTA$(I):NEXT

Der INPUT-Befehl ermöglicht die Eingabe von Werten über die Tastatur. Durch den INPUT-Befehl in Zeile 100 können Sie eine Zahl eingeben. Der Rechner meldet sich nur mit einem Fragezeichen. Für die Zeile 110 gilt das Gleiche wie für Zeile 100, außer daß der Rechner den Text innerhalb der

Anführungszeichen am Bildschirm darstellt. Es können neben Zahlen auch Buchstaben und gra

phische Zeichen eingegeben werden, wenn diese in einer Stringvariablen gespeichert werden (Zeile 120,130). Für die Stringvariablen gilt die gleiche Vorschrift wie für einfache Variablen.

GET

10 PRINT-B LOESCHT DEN BILDSCHIRM,”

20 PRINT’V LOESCHT ALLE VARIABLEN,”

30 PRINT’N LOESCHT DAS PROGRAMM.” 40 PRINT:PRINT”EINGABE?”

50 GET C$ : IF C$=” ” THEN 50 60 IF C$ = ”B” THEN PRINT CHR$ (147) : END 70 IF C$ = ”V” THEN CLR : END 80 IFC$ = ”N” THEN NEW 90 GOTO 50

Durch einen GET-Befehl wird ein einzelnes Zeichen vom Tastenfeld eingelesen, jedoch ohne das

Programm anzuhalten, wie es beim INPUT-Befehl ist. Der GET-Befehl in Zeile 50 bewirkt das Ein

lesen des Zeichens und speichert dieses in C$. Im zweiten Teil der Zeile 50 wird abgefragt, ob

überhaupt ein Zeichen eingelesen wurde. Ist dies der Fall, so wird das Programm mit der Zeile 60

fortgesetzt, ansonsten wird Zeile 50 wiederholt. Dies ist also eine Schleife, die das Programm

solange anhält, bis ein Zeichen eingelesen wurde.

DATA, READ und RESTORE

100 DATA ICH, DU, ER, SIE, ES, WIR, IHR, SIE, 1,2,3,4,5,6,7,8,9,10 110 PRINT "DRÜCKEN SIE JETZT 1 ODER 2”

115 PRINT "(1 = READ, 2 = RESTORE UND READ)” 120 GETA$ : IFA$ = ”1” OR A$ = ”2” THEN 140 130 GOTO 120 140 IFA$ = ”1” THEN 170 150 IFA$ = ”2” THEN 160 160 RESTORE 170 READ A$ 180 PRINT A$ 190 IFA$= ”10” THEN 210 200 GOTO 120

210 RESTORE

220 GOTO 120

Die Daten, die hinter der DATA-Anweisung im Programm stehen (Zeile 100) können mittels eines

READ-Befehls (Zeile 120) nacheinander gelesen werden. Versucht man, mehr Daten, als unter

DATA stehen, zu lesen, so erfolgt eine Fehlermeldung. Nach einem RESTORE-Befehl (Zeile 160) wird mit dem nächsten READ-Befehl wieder der erste Wert der DATA-Anweisung gelesen. So ist es

möglich, die Werte der Anweisung öfter zu benutzen.

GOTO, ON .. GOTO, IF ... THEN

10 REM TEXTAUSWAHL

15 PRINT

20 INPUT’WELCHES DER 5 TEXTMODULN”;X

30 IFX<1 OR X>5 THEN 160 40 ON X GOTO 60,80,100,120,140

50 GOTO 20

60 PRINT’FUER JEDES ’MODUL’ KOENNTE BELIEBIGER TEXT STEHEN”

70 GOTO 15

80 PRINT’’MODUL2”

90 GOTO 15

100 PRINT’’MODUL3”

110 GOTO 15

120 PRINT ’’MODUL4”

130 GOTO 15

140 PRINT’’MODUL5” 150 GOTO 15 160 PRINT”BITTE GEBEN SIE EINE ZAHL ZWISCHEN 1 UND 5 EIN!” 170 GOTO 15

Die Variable (oder Funktion) hinter ON .. gibt die Position in der nach GOTO folgenden Adressen

liste an. Die gefundene Adresse wird dann für den Sprungbefehl GOTO in der gleichen Zeile (40)

benutzt.

Ist bei ON ... GOTO die Variable 0, verzweigt der Programmablauf direkt zur nächsthöheren Programmzeile.

GOSUB, ON... GOSUB

10 INPUT’WUENSCHEN SIE EINE ERKLAERUNG”;X$ 20 IF X$=”JA”THEN GOSUB160 30 INPUT”IHRE ZAHL”;A 40 INPUT”IHREN CODE”;B:IFB<0ORB>3THEN10

50 ON B GOSUB70,100,130

60 GOTO30 70 REM UNTERPROGRAMM 1 80 PRINT’DIE WURZEL AUS IHRER ZAHL LAUTET”;SQR(A)

90 RETURN

100 REM UNTERPROGRAMM 2

110 PRINT’IHRE ZAHL ZUM QUADRAT LAUTET”;Af2

120 RETURN 130 REM UNTERPROGRAMM 3 140 PRINT’DIE ZUFALLSZAHL AUS IHRER ZAHL LAUTET”;RND(A) 150 RETURN 160 REM ERKLAERUNG 170 PRINT’GEBEN SIE EINE BELIEBIGE ZAHL EIN” 180 PRINT’MIT EINER CODE-ZAHL BESTIMMEN SIE EINE VORPROGRAMMIERTE

RECHENOP.”

190 PRINTTAB(10)”1=QUADRATWURZEL”

200 PRINTTAB(10)”2=POTENZIERUNG MIT 2”

210 PRINT TAB(10)”3=ZUFALLSZAHL 220 RETURN

Mit GOSUB 160 in Zeile 20 wird ein Unterprogramm angesprungen und automatisch ausgeführt. Hier wird nur eine Erklärung zum Programm ausgedruckt.

Mit ON .. GOSUB wird das gleiche Prinzip wie bei ON .. GOTO erfüllt. In Abhängigkeit von einer Variablen wird eine bestimmte Adresse für einen Unterprogrammsprung verwendet.

Durch RETURN in den Unterprogrammen verzweigt das Programm wieder zurück zu dem Befehl, der nach dem GOSUB-Befehl steht. Hier ist das immer der Befehl in der nächsten Zeile. Der nach folgende Befehl kann jedoch in der gleichen Zeile stehen. Ist bei ON .. GOSUB die Variable=0, so verzweigt das Programm direkt zur nächsthöheren Programmzeile.

5.2. Beispielprogramm zu 1.2.17 DIE BEFEHLSGRUPPE FOR, NEXT, STEP.

5 PRINT CHRS (147)

10 F0RI = 1T03 20 PRINT”VERSUCH”;J

30 NEXTI 40 PRINT

50 A=0:B=20:C=2 60 FORI=A TOB STEP C 70 PRINT”SCHRITT”;I 80 NEXT 85 PRINT” WARTESCHLEIFE”:FORI=1TO2000:NEXT 90 DIMA(3,8):PRINT” RANDOM GENERATOR 100 F0RI=1T03 110 FORJ=1T08

120 A(I,J)=RND(7t)

130 NEXTJ

140 NEXTI 150 END

In Zeile 10 und 30 wird ein einfacher Zähler gebildet, der von 1 bis 3 läuft, wobei die Schrittweite 1 ist,

da diese (mit STEP) nicht angegeben ist.

In Zeile 60 werden die Grenzwerte und die Schrittweite der Schleife in Form von einfachen Varia

blen (Zeile 50) vorgegeben. Hier wird eine Schrittweite von 2 vorgegeben.

In den Zeilen 100,110,130,140 wird eine „verschachtelte” FOR-NEXT-Schleife angegeben. Hier ist darauf zu achten, daß die Verschachtelung symmetrisch ist, d.h. die Schleife muß mit der Variablen beendet werden, mit der sie begonnen hat (Zeile 140 und 100).

Eine Besonderheit des Commodore-BASIC ist in Zeile 80 deutlich zu erkennen. In der NEXTAnweisung muß nicht zwingend die Laufvariable angegeben werden.

5.3. Beispielprogramm zu 1.2.18

10 DIMA(100),B(10,10),C(3,3,3),D%(100) 20 FORI=0TO100 30 A(I)=I:D%(I)=I|2 40 NEXTI

45 PRINT CHR$ (147)

50 FORJ=0TO10 60 FORK=0TO10 70 B(J,K)=RND(tt)

80 NEXTK 90 NEXTJ

100 FORI=0TO3 110 FORJ=0TO3 120 FORK=0TO3 130 C(I,J,K)=I*J*K 135 PRINT”ELEMENTC(”I;J;K”)=”C(I,J,K) 140 NEXTK 150 NEXTJ

160 NEXTI Der DIM-Befehl in Zeile 10 reserviert innerhalb des Speichers den notwendigen Platz für ein-, zwei-

oder mehrdimensionale Felder (Arrays). Wichtig ist, daß dieser Befehl vor Benutzung der Arrays mindestens einmal durch Starten des Programms mit RUN durchlaufen wird. RUN löscht ja be kanntlich alle Variablen und somit auch Arrays, die vorher vorhanden waren. Das Array D% (100) ist ein INTEGER-Array; d.h. die Zahlenwerte dürfen nicht größer als 32768 und nicht kleiner als

-32767 sein. Es ist darauf zu achten, daß Ihr Rechner mit der Basis-Null-Indizierung arbeitet; d.h. das erste

Element besitzt die Indizierung 0. Diese Besonderheit ist in den FOR Statements in Zeile 20,50,60, 100,110 und 120 Rechnung getragen. Die Laufvariablen beginnen dort mit0. Um die Darstellung auf dem Bildschirm zu verlangsamen, kann die Taste RVS betätigt werden.

5.4. Beispielprogramme zu 1.2.19-1.2.24 DEFFN... und FN...

20 DEFFNY(X)=A+A1 *X+A2*X|2+A3*X|3 30 INPUT”A,A1 ,A2,A3,X”;A,A1 ,A2,A3,X 40 PRINT:PRINT”FNY(”X”)=”FNY(X) 50 PRINT:GOTO20

In der Zeile 20 wird eine mathematische Funktion definiert. Daher auch DEFINE FUNCTION als Bezeichnung für dieses Statement. Die einmal mit RUN durchlaufene Formel kann innerhalb eines Programmes beliebig oft mit FNY aufgerufen werden.

Als Name für die Funktion (hier Y) können maximal 2 Zeichen (einfache Variablen, ausgenommen

INTEGER-Variablen) Verwendung finden.

OPEN, PRINT # , CLOSE und INPUT #

100 REM DATENEINGABE 110 FORI=1TO10 112 INPUT” ARTIKEL”;A$(I) 114 INPUT” PREIS”;B$(I) 116 NEXT 120 PRINT”BITTE DATENKASSETTE RUECKSPULEN, DANN ’S’ DRUECKEN!” 130 GETZ$:IFZ$O”S”THEN130 140 OPEN1,1,1 150 FORI=1TO10:PRINT#1,A$(I):NEXT 160 FORI=1TO10:PRINT# 1 ,B$(I):NEXT 170 CLOSE 1 180 CLR

190 PRINT”BITTE DATENKASSETTE RUECKSPULEN, DANN ’L’ DRUECKEN!” 200 GETZ$:IFZ$O”L”THEN200 210 OPEN3 220 FORI=1TO10:INPUT#3,A$(I):NEXT 230 FORI=1TO10:INPUT#3,B$(I):NEXT 240 CLOSE3 250 FORI=1 TOI0:PRINTA$(l)„B$(l):NEXT

260 END

Zur Ausgabe von Daten auf das Kassettengerät oder ein anderes Peripheriegerät muß zunächst ein logisches File eröffnet werden. Für das Kassettengerät steht dieser Befehl in Zeile 140. Danach könnten Daten mit dem Befehl (PRINT # 1, Variable) auf Band geschrieben werden (Zeile 150,

160). Sind alle Daten auf Band gespeichert, so muß das eröffnete File geschlossen werden. Dieses

geschieht mit dem Befehl in Zeile 170 (CLOSE 1 ). Wollen Sie nun Daten von der Kassette lesen, so müssen Sie wieder ein logisches File eröffnen,

beim Lesen der Kassette lautet der Befehl OPEN 3 (Zeile 210). Das eigentliche Einlesen geschieht durch den Befehl ’’INPUT # 3, Variable” (Zeile 220,230). Genau wie beim Schreiben, so muß auch nach dem Lesen der Daten das File wieder geschlossen werden. Dies geschieht durch CLOSE 3

(Zeile 240).

5.5. Beispielprogramme zu 1.2.25-1.2.36 DIE LEN-FUNKTION

10 INPUT’GEBEN SIE EINEN BELIEBIGEN TEXT EIN”;A$

20 PRINT”DIESER TEXT IST”LEN(A$)”ZEICHEN LANG” 30 FORI=1TOLEN(A$) 40 PRINTMID$(A$,I,1 ) 45 F0RU=1T0555:NEXT:REM * WARTE *

50 NEXT 60 PRINT’TEXTLAENGE HOCH ZWEI IST”;LEN(A$)f2

Die Funktion LEN ( ) ermittelt die Länge (Anzahl der Zeichen) einer Stringvariablen (Zeile 20). Sie kann darüber hinaus die Funktion einer normalen Variablen übernehmen (FOR-Statement in

Zeile 30). Mit ihr kann aber auch gerechnet werden (Zeile 60).

STR $ und VAL

10 INPUT”IRGENDEINE ZAHL”;A 20 A$=STR$(A)

30 PRINT”A=”A,”A$=”A$ 40 B=VAL(A$)

50 PRINT”B=”B,”A$=”A$ 60 PRINT:GOTO10

Mit STR$ ( ) läßt sich ein numerischer Wert in eine Stringvariable transferieren (Zeile 20). Die Umkehrfunktion dazu, die VAL ( ) Funktion, ermöglicht es, aus einer Stringvariablen den

numerischen Teil (incl. Vorzeichen) zu lesen. Der Inhalt der Stringvariablen bleibt bei dieser Opera

tion unverändert.

Befindet sich im String hinter dem numerischen Wert ein E, so wird dies als Exponent verstanden, und die nachfolgenden Zahlen werden als Exponent gelesen.

ASC und CHR$

10 PRINT” ASCII-TABELLE FUER A-P”:PRINT:PRINT

20 A$=”ABCDEFGHIJKLMNOP” 30 FORI=1T016 40 M$=MID$(A$,I,1)

50 PRINTM$” HAT CODE ”ASC(M$)

60 NEXT

70 PRINT’IRGENDEINE TASTE DRUECKEN-”

80 GETR$:IFR$=” "THEN80

90 INPUT’WELCHER CODE”;C

100 PRINT’ASC VON”C”= ”CHR$(C)

110 PRINT:GOTO90 Die ASC ( )-Funktion wandelt das in der Klammer angegebene Zeichen in den zugehörigen ASCII* um (Zeile 50), während die CHR$ ()-Funktion aus einem ASCII-Zeichen wiederum das alphanu merische Zeichen bildet. In Zeile 100 wird aus dem Code das zugehörige Zeichen gebildet.

ASCII = American Standard Code for Information Interchange

(standardisierter Code für Informationsaustausch)

RIGHTS, MID$, LEFTS

100 INPUT’WIE SPAET IST ES JETZT - HHMMSS”;Z$ 110 PRINT” ”:REM‘BILDSCHIRM LOESCHEN* 115 I FVAL(Z$) <0ORVAL(Z$) >240000THEN 100 116 TI$=Z$ 120 A$=RIGHT$(TI$,2):REM *DIE BEIDEN RECHTEN ZEICHEN * 130 B$=MID$(TI$, 3,2):REM ‘DIE BEIDEN MITTLEREN ZEICHEN AB DEM DRITTEN* 140 C$=LEFT$(TI$,2):REM ‘DIE BEIDEN LINKEN ZEICHEN * 150 PRINT” QQQQQQQQ ES IST JETZT”:PRINTC$” UHR, ”B$” MINUTEN, ”A$” SEKUNDEN 160 GOTO 120

Durch den Befehl A$ = RIGHTS (Tl$,2) in Zeile 120 werden von dem String Tl$, das die Uhrzeit HHMMSS enthält, von der rechten Seite an 2 Zeichen in A$ gespeichert. Durch den Befehl in

Zeile 130 werden aus der Mitte des Strings Tl$, vom 3. Zeichen beginnend, 2 Zeichen in B$ gespei

chert. Der Befehl in Zeile 140 bewirkt das Einlesen von 2 Zeichen von der linken Seite des Strings. Sollen mehr Zeichen als das String hat eingelesen werden, so wird der gesamte String dargestellt.

Durch die Printanweisung in Zeile 150 wird erst „Cursor home” programmiert, dann 10 mal „Cursor nach unten”. (Programmierte Cursorbewegungen erscheinen als Sonderzeichen auf dem Bild schirm.)

POKE, PEEK, SYS

Nachfolgendes Assemblerprogramm addiert die Inhalte zweier Speicher und legt sie in einem dritten Speicherplatz ab.

CLC

LDA ADC STA

RTS

Umgesetzt in die Maschinensprache erhält man

18 AD 47 03

6D 47 03 Hexadezimalcode 8D 47 03 60

Zunächst werden die Befehle nach Dezimal umgewandelt:

173 71 3

109 72 3 141 73 3

Mit einem BASIC-Programm wird dieses Programm in den Speicher geschrieben.

10 DATA 24,173, 71,3,109, 72, 3, 141,73, 3, 96

20 FOR M = 826 TO 836 30 READ A 40 POKE M, A

50 NEXT

Der Befehl SYS (826) kann dieses Maschinenprogramm aufrufen. Zuvor kann mit NEW der Hauptspeicher gelöscht werden, da ab Adresse 826 der Pufferspeicher

der Kassette # 2 beginnt, der mit NEW nicht gelöscht wird.

10 INPUT”1.ZAHL”;Z1 :POKE839,Z1

20 INPUT”2.ZAHL”;Z2: POKE840,Z2 30 SYS(826) 40 PRINTZ1 ” + ”=”PEEK(841)

Mit POKE (Zeile 40) wurde der Code unseres Maschinenprogramms direkt in die Speicherstellen 826 bis 836 geschrieben.

Bei der Abarbeitung des Unterprogramms (Zeile 30) wurde das Ergebnis in den Speicher 841 gebracht. PEEK (841) in Zeile 40 liest diesen Wert und druckt ihn aus.

$0347 Lade-Akku mit Inhalt von 839 $0348 Addiere zum Akku den Inhalt von 840 $0349 Speichere das Ergebnis in 841

Clear Carry-Flag

Return (Rückkehr aus der Subroutine)

Was tue ich, wenn der Computer mich nicht versteht?

Im allgemeinen wird es nötig sein, Ihr Gerät zum Service zu bringen. Ihr Computer enthält hoch komplexe Schaltungen, und wir empfehlen keinerlei Eingriffe, außer der unten ausdrücklich be schriebenen.

Beachten Sie besonders, daß der Bildschirmteil mit Hochspannung (mehrere Tausend Volt) arbei tet.

Trotzdem einige Fehlerhinweise für Hardware-Interessierte:

6.1. Der Bildschirm spinnt.

a) Der Bildschirmhintergrund ist zu hell.

Diagnose: Versuchen Sie, am Potentiometer (Regler) auf der Bildschirmrückseite das gesamte

Bild dunkler zu regeln. Sollte das keinen Erfolg haben, so ist der HF-Trafo im Bild schirmteil defekt.

b) Der Bildschirm zeigt nach dem Einschalten ein festes Bild mit diversen Zeichen und reagiert

nicht auf die Tastatur.

Diagnose: Der Einschaltzyklus des Rechners ist nicht einwandfrei (power-on-reset).

c) Der Bildschirm zeigt nach dem Einschalten weniger als 31743 bzw. 15359 bzw. 7167 Bytes an.

Diagnose:Eines der RAM’s ist defekt, sofern dieser Fehler wiederholt auftritt. Sie können trotz

dem noch mit dem verbliebenen Speicherrest arbeiten, sollten aber das defekte RAM irgendwann einmal austauschen lassen.

d) Im Bildschirm befindet sich eine Stelle, die nach ’’Clear Home” noch immer ein Zeichen beinhal

tet.

Diagnose: Eines der RAM für den Bildschirm ist defekt. Der Fehler ist nicht tragisch, sollte jedoch

behoben werden.

e) Gewisse Zeichen werden auf dem Bildschirm falsch angezeigt (z.B.: 7 anstatt A)

Diagnose: Der Zeichengenerator ist defekt.

f) Der Bildschirm ist vertikal gedrückt oder gedehnt.

Diagnose: Lassen Sie die Einstellung der Vertikalablenkung in einer Service-Werkstatt durch

führen.

g) Das Bild steht schräg.

Diagnose: Lassen Sie in Ihrer Werkstatt die Ablenkspulen justieren.

h) Die Zeichen sind verschwommen.

Diagnose:Lassen Sie die Fokussierung einstellen.

6.2. Die Tastatur reagiert nicht mehr.

a) Eine einzelne Taste funktioniert nicht.

Diagnose: Die Tastatur muß gereinigt werden. Durch normale Benutzung verunreinigen die Ta-

staturkontakte mit der Zeit. Die meisten Probleme treten bei den Tasten RETURN / SHIFT / HOME auf, da diese Tasten auch am meisten benutzt werden.

Hinweis: Es ist möglich, einzelne Tasten vorsichtig mit einem Schraubenzieher abzuheben.

b) Eine Gruppe von Tasten reagiert nicht. Diagnose: Eine Leitung an der Tastatur ist locker.

6.3. Die Kassette will nicht so wie ich.

a) Beim Einladen eines Programmes von Kassette wird nichts gefunden, obwohl ein Programm

vorhanden ist.

Diagnose:Haben Sie die Kassette vor Programmbeginn zurückgespult?

Wenn ja, so kann der Tonkopf am Rekorder falsch stehen. Lassen Sie das über

prüfen.

b) Sie speichern ein Programm auf Kassette. Anschließend stellen Sie fest, daß die Kassette feh

lerhaft beschrieben wurde. Diagnose: Reinigen Sie den Tonkopf des Rekorders mit einem handelsüblichen Tonkopfreini

ger. Sollte der Fehler danach wieder auftreten, so ist die Qualität der benutzten Kas sette schlecht.

Übrigens: Sie sollten den Tonkopf ca. alle 10 Spielstunden reinigen.

c) Der Rechner reagiert nicht auf Tastenbenutzung am Kassettenrekorder, wenn Sie darauf lesen

oder schreiben wollen.

Diagnose:Es kann sich hierbei um einen Kontaktfehler im Rekorder handeln. Suchen Sie die

Werkstatt auf.

d) Der Kassettenrekorder leiert.

Diagnose: Lassen Sie die Zugrollen im Rekorder reinigen.

6.4. Es tut sich gar nichts.

Diagnose: Überprüfen Sie die Sicherung auf der Rechnerrückseite (ziehen Sie unbedingt vorher

den Netzstecker). Sollte diese in Ordnung sein, so kann der Bildschirmstecker auf der

Hauptplatine lose sein, oder der Einschaltzyklus des Rechners ist nicht einwandfrei. Ihre Werkstatt wird in diesem Falle helfen können.

6.5. Der Computer meldet einen Fehler.

Grundsätzlich ist Ihr Computer so ausgelegt, daß er keinerlei Bauteildefekte lokalisieren kann. Fehlbedienungen durch Ihre Programmierung kann der Rechner allerdings in weitem Rahmen fest stellen, und meldet diese auch. Im Anhang finden Sie eine Anzahl von Meldungen, die auf dem Bild schirm angezeigt werden, wenn ein Programmierfehler entdeckt wurde.

An dieser Stelle ist jedoch zu erwähnen, daß ein Fehler erst in dem Augenblick gemeldet wird, wenn das Programm im Ablauf die Fehlerstelle erreicht hat. Sollte Ihr Programm umfangreicher sein, so müssen Sie alle Eventualitäten beim Testen des Programmes berücksichtigen, um auch tatsäch lich alle Fehler im Programm zu entdecken. So werden Sie bei dem Programm:

10 INPUT "GIB WERT A UND B”;A,B

20 PRINT "ERGEBNIS”; A/B nur dann Fehler entdecken, wenn Sie folgendes eingeben: a) für B den Wert 0. Der Rechner meldet dann DIVISION BY ZERO ERROR IN 20.

b) für A = 1E30 und B = E-25. Der Rechner stellt dann ? OVERFLOW ERROR IN 20 fest, da das

Ergebnis 1E55 größer als die größte abzuspeichernde Zahl 1.5E38 ist.

c) Geben Sie durch Kommata getrennt 3 anstatt der verlangten 2 Variablen ein.

Der Rechner bemerkt dazu

? EXTRA IGNORED.

Da dieser Fehler aber nicht tragisch ist, setzt der Rechner anschließend seine Arbeit fort und

vergißt die 3. Zahl.

6.6. Was sonst noch so passieren kann.

Wir können Ihnen im Rahmen dieses Handbuches verständlicherweise nicht alle möglicherweise auftretenden Fehler diagnostizieren.

Für diese Fälle haben wir ein Servicenetz in Deutschland aufgebaut, das sich sehen lassen kann. Bei jedem COMMODORE-Händler befindet sich gleichzeitig eine Reparatur-Werkstatt, die durch uns speziell auch für Ihren Rechnertyp geschulte Techniker hat. Dort wird man Ihre Probleme mit dem Rechner schnell und sicher beseitigen können. Während der Garantiezeit sind die Reparatur-

und evtl. Ersatzteile natürlich kostenlos. (Es sei denn, der Techniker kommt zu Ihnen ins Haus.) Aber auch danach wird für eine schnelle Instandsetzung gesorgt sein. Ein Verzeichnis unserer

Händler und Service-Werkstätten liegt diesem Handbuch bei.

7. Wie schnell ist eigentlich mein Rechner?

7.1. Die Geschwindigkeit des BASIC-Interpreters.

Ihnen eine Tabelle mit Zeiten für jeden Befehl zu geben, halten wir für unsinnig. Durch den jewei

ligen Aufbau des Programmes können sich nämlich erhebliche Geschwindigkeitsdifferenzen ergeben. Wir wollen Ihnen lieber ein Programm zeigen, mit dem Sie die Geschwindigkeit eines einzelnen Befehls genauso messen können wie die einer kompletten Programmroutine oder auch eines ganzen Programmes.

Von Zeile 1 bis Zeile 63995 kann Ihr zu testendes Programm stehen. In diesem dürfen TU, TV und TT nicht als Variablen Vorkommen. Starten Sie das komplette Programm mit RUN und warten Sie

mindestens 20 Sekunden. 0 TT=TI:FORTU=0TOTV

1 REM *** TESTANFANG *** 2 A=A

63996 REM *** TESTENDE 63997 NEXT:TT=TI—TT:IFTT(1000THENTV=TU*1000/TT:GOTO0

63998 PRINTINT(10000*(TT/(TU*60)))/10”MILLISEKUNDEN PRO DURCHLAUF”

63999 PRINT’GETESTET IN”TU”DURCHLAEUFEN”

7.2. Die Geschwindigkeit der Maschinensprache.

Die Taktfrequenz Ihres Rechners beträgt genau 1 MHz, die eigentlichen Maschinensprachen

befehle brauchen zwischen 2 und 7 Taktzyklen. Das bedeutet, daß 1 Maschinensprachenbefehl 2-7 ix sec braucht. Wenn man davon ausgeht, daß eine Addition zweier Integerzahlen mit ca. 20

Befehlen zu bewältigen ist, so dauert solch eine Addition im ungünstigsten Falle 140 fxsec.

7.3. Wie kommt es zu solchen Geschwindigkeitsdifferenzen ?

Wenn wir eine Integer-Addition in Basic programmieren und diese mit unserem Testprogramm zeit

lich erfassen, so erhalten wir eine Zeit von ca. 3 Millisekunden.

10 A% = A%+A%

Das vergleichbare Maschinenprogramm ist in diesem Falle rund 20 mal schneller.

Generell kann man sagen, daß Maschinenprogramme etwa zwanzig bis tausend mal schneller

sind als in Basic geschriebene Programme. Die Geschwindigkeitsdifferenz erklärt sich dadurch,

daß die Basicbefehle vom Rechner zusätzlich zur Ausführung noch interpretiert werden müssen.

Und das dauert halt seine Zeit. Für diejenigen unter Ihnen, die jetzt sagen: „Warum soll ich dann nicht generell in der Maschinensprache programmieren?” sei erwähnt, daß Programme in Maschi nensprache sich wesentlich schwerer programmieren lassen als in Basic und Ihnen keinerlei Möglichkeiten geben, Befehle einzufügen oder zu listen.

8. Wie schreibe ich ein Programm?

8.1 Am Anfang steht die Idee

Bevor Sie die Idee in die Tat umsetzen, sollten Sie sich natürlich einige Gedanken machen, ob der Computer überhaupt in der Lage ist, Ihr Problem zu lösen.

Zunächst gilt es, den erforderlichen Speicherbedarf zumindest überschlägig zu ermitteln, denn sehr oft ist dieses die kritischste Größe überhaupt. Die zu speichernden Daten werden meistens

in Tabellen (Arrays) innerhalb von DATA-Statements Ihres Programms abgelegt. Hier kann sehr einfach auf exakte Art der erforderliche Platzbedarf ermittelt werden. Beim Anlegen von Arrays gelten nachfolgende Speicherbedarf-Formeln:

Array mit voller Genauigkeit:

x = 5 + 2*Z + 5*7T (Zy + 1)

y = 1 • ■ ■ Z

Array mit Integer Genauigkeit:

x = 5 + 2*Z + 2*77 (Zy + 1)

y = 1...Z

Arrays mit String-Variablen:

x = 5 + 2*Z + 3*77 (Zy + 1)

y = 1...Z

dabei bedeuten:

x = gesamter Platzbedarf in Bytes Z = Anzahl der Dimensionen

Zi bis Z

= Größe der einzelnen Dimensionen, wie in DIM-Befehl angegeben

7j- = Alle Summen werden miteinander multipliziert.

Beispiel:

DIM A (5,6): REM hier ist Z = 2

X = 5 + 2*2 + 5 * (5 + 1) * (6 + 1) = 219 Bytes

DIM A % (3,4)

x = 5 + 2*2 + 2*(3 + 1)*(4 + 1) = 49 Bytes

DIM A (10,10,10)

x = 5 + 2 * 3 + 5 * (10 + 1) * (10 + 1) * (10 + 1) = 6666 Bytes

DIM A$ (5,6)

x = 5 + 2 * 2 + 3 * (5 + 1) * (6 + 1) = 135 Bytes

Sollen eventuelle Daten oder Texte innerhalb eines Programms in DATA Statements abgelegt werden, muß man wohl oder übel Zeichen für Zeichen zählen und so den erforderlichen Platz

bedarf ermitteln. Ein Zeichen entspricht dann einem Byte. Ferner könnte man die Ein- und Ausgabe-Intensität des zukünftigen Programms berücksichtigen.

Ihr Rechner bietet sehr viel Komfort für den Dialog mit dem Benutzer, den man selbstverständlich auch ausnutzen möchte. Dieser Komfort kostet andererseits auch viel Platz. Wenn man davon ausgeht, daß im allgemeinen ca. 30 % eines vollbeschriebenen Bildschirms für eine gut gestaltete

Ein-/Ausgabemaske benötigt werden, so erzielt man auch hier sehr schnell, je nach Anzahl der

Masken, den erforderlichen Platzbedarf.

Sind die Speicherbedarf-Kriterien geklärt, kann man sich mit dem Ablaufschema befassen.

8.2 Ein Schema wird erdacht (Flußdiagramm)

Um ein Flußdiagramm erstellen zu können, ist es natürlich notwendig, die dazu verwendeten

Symbole kennenzulernen.

Auch hier gibt es eine Norm. Die nachfolgende Liste zeigt die nach DIN 66001 zulässigen Symbole.

Symbole nach DIN 66001 für Programmablaufpläne

Eine allgemeine Operation, die etwas ausführt (Handlung)

Eine Verzweigung, wahlweise in eine von zwei Richtungen

(identisch mit unserer Fragestellung)

Ein Unterprogramm (Befehlsempfänger zur Durchführung einer bestimmten

Aufgabe)

\ Programmodifikation

Operation von Hand (Operationen, die der Rechner nicht ausführen kann, z. B. drücken einer Taste auf dem Kassettenrecorder)

Eingabe, Ausgabe (wenn z. B. am Anfang eines Programms Werte für eine Berechnung vorgegeben werden müssen)

Ablauflinie

Zusammenführung von Ablauflinien

Grenzstelle (z. B. Beginn oder Ende eines Programms)

Übergangsstelle oder Schnittstelle

Bemerkungen zum Ablaufplan können neben diesem Symbol vorgenommen werden

Im nachfolgenden Beispiel eines Ablaufplans wird ein einfacher Zähler, der bis zu einem bestimm

ten Grenzwert G laufen soll, dargestellt.

Dieses Flußdiagramm in die Sprache BASIC umzusetzen, ist nicht weiter schwierig:

20 INPUT’’EINGABE G”; G 30 N = 0

40 IF N = G THEN END 50 N = N + 1 60 ? N 70 GOTO 40

Die Schwierigkeit bei der Umsetzung eines Flußdiagramms in die jeweilige Programmiersprache

besteht darin, daß Programm möglichst effektiv aufzubauen. Und da hilft Ihnen - leider - ein Fluß diagramm kaum.

Das gleiche Programm sieht optimiert so aus:

20 INPUT’’EINGABE G”; G

30 FOR N = 0 TO G: ? N: NEXT: END Bei solchen Umwandlungen ist nur noch Ihre Erfahrung maßgebend, und die kommt erst mit der Zeit. Seien Sie nicht ungeduldig; irgendwann ist auch Ihre Programmierung schnell und kurz. Für den Anfang jedoch reicht auch die 1. Lösung, denn Sie wollen schließlich die ersten Ergebnisse sehen.

Und die Wirkung ist bei beiden Programmversionen gleich.

Doch kommen wir zum Thema zurück. Flußdiagramme sind heute bei der Programmierung kaum wegzudenken. In der Groß-EDV

dienen sie zur Dokumentation und Übersichtlichkeit der Programme, und Sie als Anfänger werden rasch die Vorteile erkennen. Auf einem Blatt Papier kann man grafisch (und natürlich mit Bleistift geschrieben, um Korrekturen zu vereinfachen) wesentlich mehr übersehen, als in einer Programm liste.

Gleichzeitig ist ein Ablaufdiagramm sprachenunabhängig. Ob Sie es in Maschinensprache oder BASIC oder sonst einer Programmiersprache ausführen, bleibt gleich.

Übrigens: Ob Sie sich an die genormten Symbole halten oder nicht:

Wichtig ist, daß Sie die Kästchen groß genug zeichnen, um alle Ausführungsbefehle einzuschreiben.

Zeichnen Sie ebenso möglichst viele Richtungspfeile an die Verbindungslinien. Sie geraten sonst leicht bei kompliziertem Aufbau auf den falschen „Pfad“. Lassen Sie genug Platz zwischen den einzelnen Kästchen um gegebenenfalls später ein oder zwei Symbole nachtragen zu können.

Gehen Sie genug ins Detail bei jedem Diagrammschritt. Es reicht nicht, wenn Sie nur 3 Symbole benutzen, wie z. B.:

Beispiel:

BERECHNUNG

FALSCH

ENDE

Verhaspeln Sie sich aber auch nicht, indem Sie versuchen, die Symbole den BASIC-

Befehlen gleichzustellen.

FALSCH

Versuchen Sie in Ihrer Sprache, das Problem zu unterteilen. Benutzen Sie dabei ruhig Begriffe, die eine für Sie geschlossene Einheit bilden, wie z. B.: EINGABE DER WERTE A UND B UND PRÜFEN AUF RICHTIGKEIT

Schreiben Sie Formeln so, wie sie im Mathematikbuch stehen:

X1/2 = - 2 ± 3-9

P P

8.3 Das Programm entsteht

Nachdem Sie nun die Vorarbeit geleistet haben und wissen, was Sie programmieren wollen, beginnt die eigentliche Arbeit am Rechner.

An dieser Stelle ein Tip, der Ihnen viel Ärger ersparen kann:

1. Geben Sie zu Beginn dem Programm einen Namen. Dieser Name sollte möglichst aus einem Wort mit nicht mehr als 12 Buchstaben bestehen.

2. Nehmen Sie sich 3 leere Kassetten, die Sie mit diesem Namen beschriften (Bleistift).

3. Speichern Sie auch schon während der Programmierung Ihr bisher erstelltes Programmteil auf jeweils die älteste Kassette ab (Reihenfolge: Kass 1, Kass 2, Kass 3, Kass 1, Kass 2 ...), so daß

Sie zumindest die letzten drei Arbeitsschritte nachvollziehen können, wenn Ihr Rechner durch Stromausfall o.ä. ausfällt.

4. Speichern Sie das Programm(-teil) immer mit seinem Namen ab.

Schreiben Sie hinter diesem Namen ein Kennzeichen, daß Ihnen sagt, um welche Version Ihres Programmes es sich handelt.

Wir empfehlen Ihnen folgende Kennzeichnung:

X YY

I I

Art Lfd. Nr. (00-99)

P = Programmteil

T = Testphase

R = Fertiges Programm

Beispiel: SAVE "HAUSHALT P01 ”

SAVE "HAUSHALT P02” SAVE "HAUSHALT P03” SAVE "HAUSHALT T01 ”

SAVE "HAUSHALT T02” SAVE "HAUSHALT R01 ”

Diese oben angegebene Vorgehensweise hat sich als sehr vorteilhaft erwiesen. Zum Einen sind Sie vor allen Defekten des Rechners gefeit, da Sie eine Kopie des letzten Programmschrittes immer auf Kassette haben. Zum Anderen ist durch die Kennzeichnung des Programmnamens gewährleistet, daß Sie mit den verschiedenen Kassetten (und das werden immer mehr) nicht durcheinanderkommen. Sobald Ihr Programm fehlerfrei läuft, speichern Sie es mindestens 2 Mal hintereinander auf der gleichen Kassette ab. Benutzen Sie dazu folgenden Befehl:

FORI = 0TO1: SAVE “PROGRAMMNAME R01“: NEXT

Überprüfen Sie die korrekte Abspeicherung durch

VERIFY Ist Ihr Programm fehlerfrei gespeichert, so löschen Sie alle vorherigen Versionen mit Pxx und Txx. Sollten Sie zu einem späteren Zeitpunkt Ihr Programm noch ändern und sei es auch nur die

kleinste Modifikation, so erhöhen Sie in jedem Fall die laufende Nummer um 1.

(Programmteil 1 ) (Programmteil 1 + 2) (Programmteil 1 +2 + 3) (Fertiges Programm Test 1 ) (Fertiges Programm Test 2) (Fertiges Programm getestet und o.k.)

Wenn Sie alle Punkte gewissenhaft beachten, wird Ihr Archiv stets auf dem neuesten Stand sein

und Sie werden wesentlich mehr Freude mit Ihrem Rechner haben.

8.4 Da stimmt doch was nicht (Fehlersuche und Beseitigung)

Sehr viel Zeit muß im allgemeinen in einem Testlauf investiert werden, nachdem das Programm, oder auch das Teilprogramm erstellt wurde.

Ein auf Anhieb fehlerfrei funktionierendes Programm gibt es wohl nicht, sobald es auch nur etwas komplizierter ist.

Bei der Testphase ist es dann angebracht, das Programm in Module (Teilprogramme) aufzuteilen und diese separat zu testen. Durch ein vorübergehendes STOP oder END am Ende eines Modules oder Unterprogramms läßt sich der Programmablauf teilen und die Ergebnisse können somit leichter kontrolliert werden. Bei rechenintensiven Programmen besteht oft Unsicherheit über die Richtigkeit der Ergebnisse.

Hier empfiehlt sich, auch wieder vorübergehend, einen PRINT-Befehl an der entscheidenden Stelle des Programms einzuflechten und damit die sonst im verborgenen ablaufenden Rechen

werte sichtbar zu machen und zu kontrollieren.

Das gleiche gilt natürlich auch bei komplexeren Dateienbehandlungen, wenn mit vielen Indizes gearbeitet wird.

Ein PRINT-Befehl zur Ausgabe der behandelten Elemente erhöht oft in starkem Maße die Über sichtlichkeit über den Programmablauf und dessen Ergebnisse.

8.5 Wie mache ich es schneller

Allgemein gibt es drei Verfahren, ein Programm schneller zu machen:

1. Verbessern des Ablaufgeschehens und der Berechnungsart. Hierbei können wir Ihnen keine Tips geben, da wir nicht wissen, welches Problem Sie lösen wollen. Solche Verfahren können jedoch die meiste Zeit einsparen.

2. Vermeiden von Unterprogrammen, Schleifen und Sprüngen. Grundsätzlich ist dieses Verfahren schneller. Seine Nachteile sind jedoch beträchtlich. Zum Einen wird Ihr Programm unverhältnismäßig groß und sprengt leicht die Grenzen Ihres Rechners. Zum Anderen verlieren Sie leicht die Übersicht über solche Programme. Auch sind solche Programme nur durch immensen Zeitaufwand zu verändern.

3. Syntaktische und Speicherungstechnische, rechnerbezogene Verbesserungen. Hierzu gehören eine Reihe von Punkten, die einzeln nicht sehr viel Zeit einsparen; summiert aber doch eine Menge ausmachen

a) entfernen Sie alle unnötigen Leerstellen und REM-Befehle aus Ihrem Programm; b) Verwenden Sie Variablen anstelle von Konstanten. Die Umwandlung einer Konstanten in das

rechnerinterne Format benötigt wesentlich mehr Zeit als der Zugriff auf den Wert einer Variablen.

c) Dimensionieren Sie Ihre Variablen und Felder stets als erstes im Programm. Gehen Sie dabei

in der Reihenfolge der Benutzungshäufigkeit vor.

d) Schreiben Sie NEXT ohne die Indexvariable. e) Schreiben Sie möglichst viele Statements in einer Zeile.

Beispiel: 5

RESTORE DATA 9,10

REM ungünstiges Beispiel

REM Berechnung der Kombination

GOT0100

P = 1

FORI = 1 TOX

P = P*l

NEXT I

RETURN READ X

100

110

GOSUB 40

120

A = P READ X

130

140 GOSUB 40 150 B = P 160 PRINT B/A

Zeit ungefähr 170 m.sec.

5 RESTORE: DATA 9,10

40 READX: GOSUB 100: A = P: READX: GOSUB 100: PRINT P/A: GOTO 63997

100 P = 1 : FORI = 1TOX: P = P * I: NEXT: RETURN

Zeit ungefähr 150 m.sec.

ANHANG I

LISTE der Befehle des COMMODORE-BASIC

Befehl

ABS AND A = B AND C

ASC B = ASC(“Q“)

ATN A = ATN (B) CHR$ B$ = CHR$ (49) CLOSE CMD CMD 3 COS

DATA DEFFN DIM DIM B%(9), C2$(3,3)

END END EXP

FN FOR . . . NEXT FORI = TO 100 STEP 2 FRE ?FRE(0)

GET GET# GOSUB GOTO

IF. . .THEN INPUT INPUT # INPUT# 1, A 45 INT

LEFTS LEN LET LET A = 5 * 6 LOAD

LOG MID$ NEXT NOT

ON . ..GOSUB ON . ..GOTO OR

OPEN

PEEK

POKE

Beispiel

B = ABS (A)

IF A = B AND C = 3 THEN . .

CLOSE 1

B = COS (A) DATA 9, “PETER“

DEFFNA(X) = SIN (X)/X

B = EXP(A) B = FNC/(Z)

GET INS

GET # 3, INS GOSUB 1000 GOTO 170

IF A = 5 THEN A = 6 INPUT “WERT“; A

B = INT (A)

AS = LEFTS (B$,3)

A = LEN (A$)

LOAD “KURVE“ 29 B = LOG (A)

A$ = MID$ (BS.2,2) siehe FOR ... NEXT B = NOT B ON A-5 GOSUB 10, 20, 30 ON A-6 GOTO 20, 30 A = AORC IF A = B OR C = 3 THEN . . . OPEN 1,1,1, “DATEN“

A = PEEK (B) POKE B, A

Erklärung Seite

10 10

27 25

27 24

19 45

32 31

10 23 22

23 27

35 35

10 19

PRINT PRINT A$; ”=”; B$ PRINT # PRINT # 5, AS; ”=”; B$

READ REM RESTORE RETURN RIGHTS

RND

SAVE

READ A, A$ REM ERKLAERUNG RESTORE RETURN

B$ = RIGHT$(A$,5) B = RND (Tl) SAVE “VERSUCH“, 2

17 19

20 16 20 24 33

Befehl

Beispiel

Erklärung Seite

SGN SIN

SQR STEP STOP

STR$ SYS

TAN THEN USR VAL

VERIFY

WAIT

77 A = 77

? î

B = SGN (A) B = SIN (A) B = SQR (A) siehe FOR ... NEXT STOP A$ = STR$ (A) SYS (64824)

A = TAN (B) siehe IF ... THEN A = USR (B) A = VAL (A$) VERIFY

WAIT A, B, C

A = A + B A = A - B A = A * B A = A/B

? A A = A 1 B

RESERVIERTE VARIABLEN

Tl interne Zeit in Sechzigstelsekunden

Tl$

ST Status

interne Zeit in Stunden, Minuten, Sekunden

8 8

16 31 34

34 31 30

133 14

14 14 14 14 17 14

39 39

122

CO N3

N> O

SUB

rocnN3

co 00

Pkrocororo

CAN

ETB

mao

DO03o

[

CDroviNS03

ESC

I\3

SYC

ro ro

cn NAK

o co

*>■

o o

O O

CD CD

mmL

OOTl DLE

-p» co o

■n

oao

3 3

Tl Tl

CD 00

o o

OCDo00OvlO03O

ACK

cn ENQ

Pk o

Pk EOT

co ocoo ETX

ro STX

o o

HOS

o NULL

DEZIMAL HEXA

DEZIMAL

ASCII

ANHANG II Umwandlungstabelle der Dezimalzahlen 1-127

[ a>

♦

t O

CT 0)

Î O)PkCD

-r» o

CO Vj

—

CO TCOm

•O

toCDCOcnCO

«1

□

CD a>o01cocn

CO OCOO

II A -•

CD maiO

127

vi TI

DEL

—

CO cocoro

—

126

□

co CD

-•

cn O

125

VIaV|

00 co

co co

CDCDcn

—

124

? cn

CD vl

O)cncn

co00co

00 ■Vl

o00co

cncoCD00cnvjcn

♦

□

123

122

-V N

□

< c

00 00

♦

covl00

CDPkcncocnrocn CD

00O)co

CD cn

00vj00

X Q □

120

119

vj vj

CO 33

coPkcocoCOroco CO

Pk co

00cn00

-N

c H co

118

vl CDvlCD

OPkCO

cnrocn

3 3

116

115

vlPkvlcovl

C/3 -Q

Pk00Pk

vl ro

00 00oVlCOV|00vl

□

pl14

113

vl vl

Pk CD cnA■Pk

roOro

ro m

-n

-fe

z 1“ X

□

112

~o o

E ffl

- +

-Pk

110

—

-pk co ro

ro co

■vl03Vlcnvl

■Pk

-Pk03•Pk

a a

109

108

—

oCOco

roCDro00NO

—

vlCOvl

■Pk

co 00

c__

— X

107

106

O)03CD

—

D O

CO 00covl

ro0)rocnro ro03ro

—I

e°

B°

Pk vl

B E

104

C O

Z T

0s-

vl O s

103

□

105

—

co 0303cn

4* cn

□

102

a>o03

■

> 0

coPkco

;

-H-

PkPkPk

D O

m B

□

100

03 Pk

Q_ O

□ □ BILDSCHIRM

co ro

—

03 03

CD CO

03 CO

BILDSCHIRM

DEZIMAL HEXA

DEZIMAL

ASCII

BILDSCHIRM

DEZIMAL

HEXA DEZIMAL

ASCII

BILDSCHIRM

DEZIMAL

HEXA DEZIMAL

ASCII

in Hexadezimal; ASCII und Bildschirmcode

ANHANG III. LISTE DER FEHLERMELDUNGEN

?BAD SUBSCRIPT

?BAD DATA

7CANT CONTINUE

7DIVISION BY ZERO Division durch 0 unzulässig.

7ILLEGAL DIRECT INPUT, GET und DEFFN kann nicht direkt, sondern nur im Pro

7NEXT WITHOUT FOR

70UT OF DATA

70UT OF MEMORY Vorhandener Speicherplatz reicht nicht aus.

70VERFL0W

Ansprache eines Matrix-Elementes, welches außerhalb der Dimensionierung der Matrix liegt, z.B. LET A (1,1,1,) = Z wenn A dimensioniert wurde: DIM A (2,29).

Versuch, Strings in normale Variable aus einem Peripherie-Gerät einzulesen.

Nach einer Fehlermeldung oder einer Programmänderung ist CONTINUE nicht möglich.

gramm ausgeführt werden.

Bei der Programmschleife fehlt das entscheidende FORSTATEMENT.

Mehr READ-Anweisungen als DATA-Anweisungen sind vor handen.

Ergebnis oder Zwischenergebnis einer Rechnung war größer als 10|38. Bei Underflow erscheint ”0” ohne einen Fehlerhinweis. Das Programm wird hierbei fortgesetzt.

7RETURN WITHOUT GOSUB Subroutine ohne GOSUB

?REDIM’D ARRAY

7STRING TO LONG

7SYNTAX

7TYPE MISMATCH

7UNDEFD STATEMENT

7UNDEFD FUNCTION

Fehlermeldung ohne Programmunterbrechung

7REDO FROM START

Ein Feld kann nicht zweimal dimensioniert werden.

Zeichenkette länger als 255 Zeichen.

SYNTAX-Fehler (der Befehl ist fehlerhaft oder existiert nicht). Klammer, Buchstaben bzw. Zeichen fehlen in einer Programm zeile.

Behandlung normaler Variablen als String oder umgekehrt.

GOTO, GOSUB oder THEN zu einer nicht existenten Zeilen

nummer.

Nicht definierte Funktion wurde aufgerufen.

Versuch, nichtnumerische Daten bei einer INPUT-Operation vom Tastenfeld in eine normale Variable einzulesen. Diese Fehler

meldung fordert Sie auf, die Eingabe zu wiederholen.

IV. Zeichenvorrat der Tastatur

V. Technische Daten des cbm

Höhe Breite

Tiefe

Gewicht Spannung Verbrauch

Bildschirm

Diagonale Zeilen Spalten Zeichenauflösung Darstellungsart

Sonderzeichen

Programmierung

Sprache Anzahl Befehle

Kapazität

Kassette Aufzeichnungsformat Anschlüsse

Prozessor

Taktfrequenz

ANHANG V

36 cm 42 cm 47 cm 20 kg 220V ±10%/50 Hz 250 W

: 22 cm : 25

: 40 : 8 * 8 Punktmatrix vorprogrammiert : Hell auf dunklem Grund

(programmierbar dunkel auf hellem Grund)

: 66 grafische Zeichen

: BASIC festgespeichert in 8 kB ROM : 64, davon 19 mathematisch, 8 Textverarbeitung,

11 Peripheriebefehle : 16 bzw. 32 kB : Rekorder für Standard Musikkassetten

: Einspur-Frequenzmodulation nach eigenem Standard

(1 * IEC-Bus)

5(1* 8bit Parallel mit 2-Draht Handshake)

(1*1. Kassettenrekorder) (1 * Speichererweiterungsausgang)

(1 * 2. Kassettenrekorder) : 6502 : 1 MHz

Commodore CBM 2001, CBM 3001 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual