Page 1

TV
AUDIO
VIDEO
TV
AUDIO
VIDEO
MICROPROCESADORES
MICROPROCESADORES
SSAABBEERR
EELLEECCTTRROONNIICCAA
EDICION ARGENTINA
ES UNA EDICION ESPECIAL DE
REP. ARG. EDICION ESPECIAL: 3005
LOS COMPONENTES
EN CORRIENTE ALTERNA
TIRISTORES
LOS COMPONENTES
EN CORRIENTE ALTERNA
TIRISTORES
Page 2
Enciclopedia
Enciclopedia
V
V
isual
isual
de la
de la
Electrónica
Electrónica
INDICE DEL
C
APITULO 5
MAGNETISMO E INDUCTANCIA
MAGNETICA
El efecto magnético......................................67
Campo eléctrico y campo magnético ......67
Propiedades magnéticas de la materia ....69
Cálculos con fuerzas magnéticas...............69
Dispositivos electromagnéticos....................70
Electroimanes y solenoides...........................70
Relés y Reed-relés..........................................70
Los galvanómetros .........................................71
Los inductores ................................................71
LOS COMPONENTES DE CORRIENTE ALTERNA
Corriente continua y corriente alterna.......72
Representación gráfica de la
corriente alterna ............................................75
Reactancia.....................................................75
Reactancia capacitiva.................................76
Fase en el circuito capacitivo......................77
Reactancia inductiva ...................................77
Fase en el circuito inductivo ........................78
¿Qué es una señal?.......................................78
TIRISTORES Y OTROS DISPOSITIVOS DE DISPARO
Los tiristores......................................................78
Rectificador controlado de silicio................78
Interruptor controlado de silicio...................79
FotoSCR...........................................................79
Diodo de cuatro capas................................79
SUS, TRIAC, DIAC, SBS, SIDAC, UJT ................80
Cupón Nº 5
Guarde este cupón: al juntar 3 de
éstos, podrá adquirir uno de los videos
de la colección por sólo $5
Nombre: ________________________
para hacer el canje, fotocopie este cupón y
entréguelo con otros dos.
Page 3
ELE
FECTO
M
AGN TICO
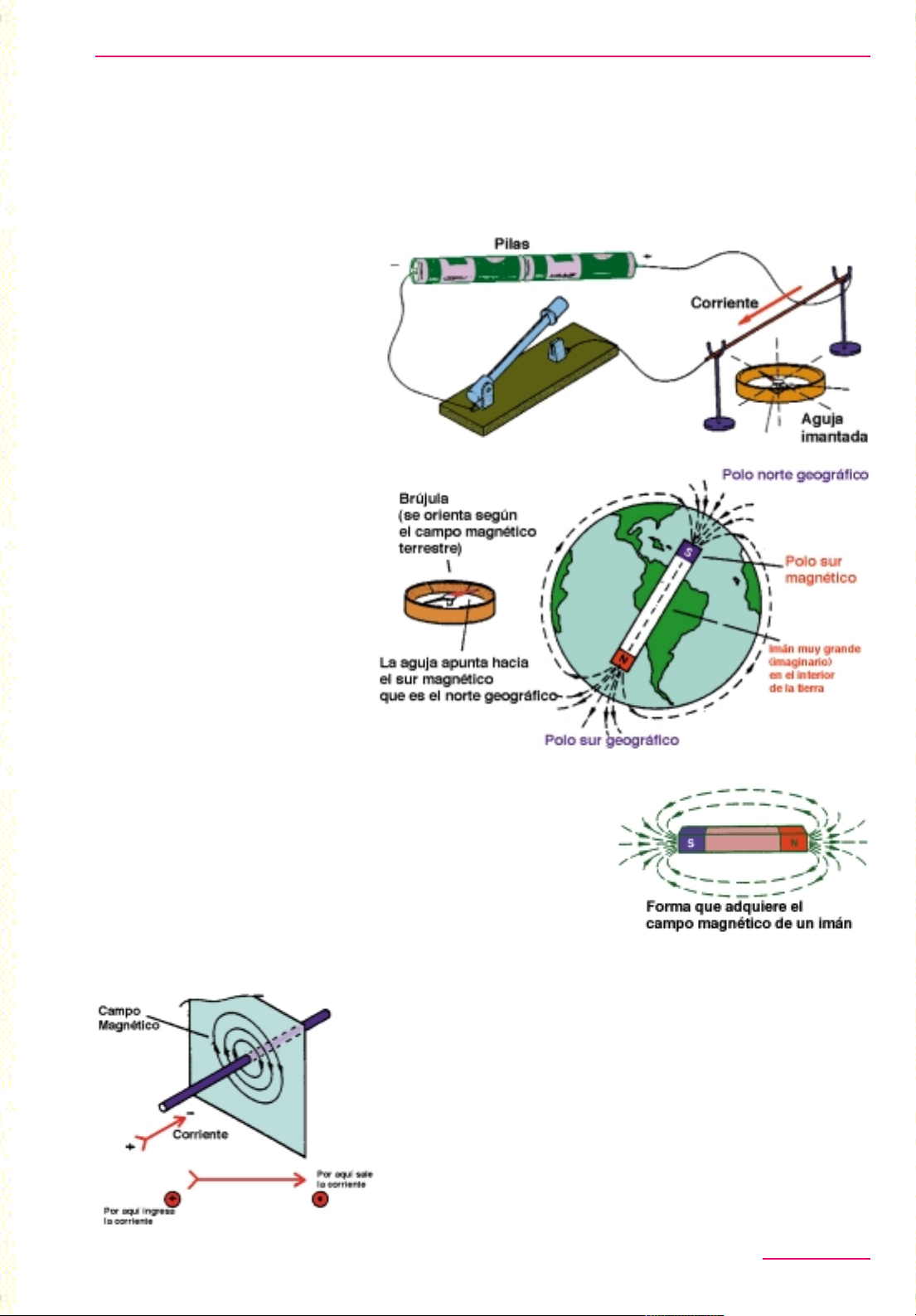
Un profesor dinamarqués de la
escuela secundaria llamado Hans
Chistian Oersted observó que colocando una aguja imantada cerca
de un alambre conductor, cuando
se establecía la corriente en el conductor, la aguja se desplazaba hacia una posición perpendicular al
alambre, como se muestra en la figura 1. Como seguramente sabrán
los lectores, las agujas imantadas
procuran adoptar una posición determinada según el campo magnético terrestre, dando origen a la brújula (figura 2).
El movimiento de la aguja imantada sólo revelaba que las corrientes
eléctricas producen campos magnéticos y también facilitaba el establecimiento exacto de la orientación de este campo, o sea su modo
de acción. Como en el caso de los
campos eléctricos, podemos representar los campos magnéticos por líneas de fuerza. En un imán, como se
muestra en la figura 3, esas líneas salen del polo norte (N) y llegan al polo sur (S).
Para la corriente eléctrica que
fluye en el conductor, verificamos
que las líneas de fuerza lo rodean, tal
como muestra la figura 4. Representando con una flecha la corriente
que fluye del positivo hacia el negativo, tenemos una regla que permite
determinar cómo se manifiesta el
campo. Con la flecha entrando en
la hoja (corriente entrando) las líneas son concéntricas, con orientación en el sentido horario (sentido
de las agujas del reloj). Para la corriente saliente, las líneas se orientan
en el sentido antihorario (figura 5).
El hecho importante es que dispo-
niendo conductores recorridos por corrientes de formas
determinadas, podemos obtener campos magnéticos
muy fuertes, útiles en la construcción de diversos dispositivos.
C
AMPOEL CTRICO Y
C
AMPOMAGN TICO
Si tenemos una carga
eléctrica, alrededor de esta
carga existe un campo eléc-
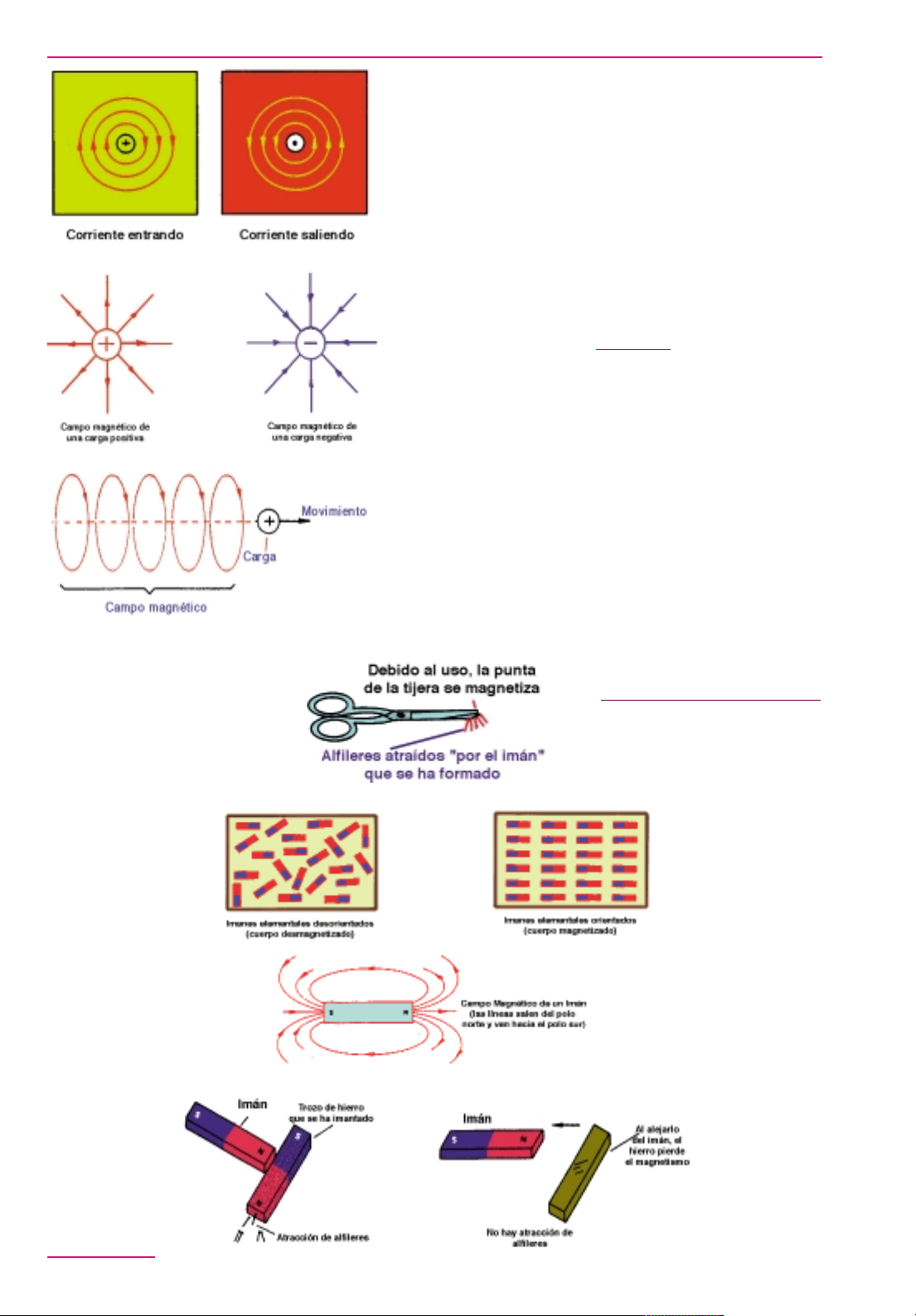
trico cuyas líneas de fuerza se orientan como muestra la figura 6. Una
carga eléctrica en reposo (detenida) posee sólo campo eléctrico. Sin
embargo, si se pone en movimiento
una carga eléctrica, lo que tendremos será una manifestación de fuerzas de naturaleza diferente: tendremos la aparición de un campo magnético. Este campo tendrá líneas de
fuerza que envuelven la trayectoria
de la carga, como muestra la figura
7. El campo eléctrico puede actuar
sobre cualquier tipo de objeto, provocará atracción o repulsión según
Capítulo 5
67
Capítulo 5
Magnetismo e Inductancia Magnética
Fig. 1
Fig. 2
Fig. 3
Fig. 4
Page 4
su naturaleza. El campo magnético
sólo actúa atrayendo o repeliendo,
sobre materiales de determinada
naturaleza de forma más eminente.
Teniendo en cuenta el origen del
campo magnético podemos explicar fácilmente por qué ciertos cuerpos son imanes y por qué una corriente puede actuar
sobre una aguja magnetizada.
En un cuerpo común los electrones que
se mueven alrededor
de los átomos lo hacen
de manera desordenada, de modo que el
campo producido no
aparece.
Sin embargo, podemos orientar estos movimientos de modo de
concentrar el
efecto de una manera determinada,
como muestra la figura 8.
Obtenemos,
entonces, "imanes
elementales", cuyos efectos suma-
dos dotan al material de
propiedades magnéticas. Tenemos así, cuerpos denominados imanes permanentes. Un
imán permanente tiene
dos polos, denominados
NORTE (N) y SUR (S), cuyas propiedades son semejantes a las de las cargas eléctricas.
Podemos decir que
polos de nombres diferentes se atraen (Norte
atrae a Sur y vicerversa).
Polos del mismo
nombre se repelen (Norte
repele a Norte y Sur repele a Sur).
Los imanes permanentes pueden ser naturales o artificiales. Entre
los naturales destacamos la magnetita, una
forma de mineral de hierro que ya se obtiene en
los yacimientos con las
propiedades que caracterizan un
imán.
Entre los artificiales destacamos
el Alnico, que es una aleación (mezcla) de aluminio, níquel y cobalto,
que no tiene magnetismo natural
hasta que es establecido por procesos que veremos posteriormente. Los
materiales que podemos convertir
en imanes son llamados materiales
magnéticos; podemos magnetizar
un material que lo admita orientando sus imanes elementales. Para ello
existen diversas técnicas:
a) Fricci n:
de tanto usar una herramienta, una tijera, por ejemplo, los
imanes elementales se orientan y ésta pasa a atraer pequeños objetos
de metal, o sea, se vuelve un imán
(figura 9). Frotando una aguja contra
un imán, orienta sus imanes elementales y retiene el magnetismo.
Advierta que existen cuerpos que
no retienen el magnetismo, como
por ejemplo el hierro.
Si apoyamos un imán contra un
hierro, éste se magnetiza, como
muestra la figura 10, pero en cuanto
lo separamos del imán, el hierro pier-
de la propiedad de atraer pequeños objetos, debido a que sus imanes elementales se desorientan.
b) Mediante un campo intenso:
colocando un objeto magnetizable
en presencia de un campo magnético fuerte, podemos orientar sus
imanes elementales y, de esta manera, convertirlos en un imán. El
campo de una bobina puede ser suficiente para esto. Del mismo modo que los materiales pueden retener magnetismo, también pueden perderlo
bajo ciertas condiciones.
Si calentamos un
trozo de magnetita, o
sea un imán permanente natural, a una
temperatura de
585°C, el magnetismo desaparece. Esta temperatura es conocida con el nombre
de Punto Curie y
varía de acuerdo
a los diferentes
materiales.
Magnetismo e Inductancia Magnética
68
Fig. 5
Fig. 10
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Page 5
P
ROPIEDADES
M
AGN TICAS
DE LA
M
ATERIA
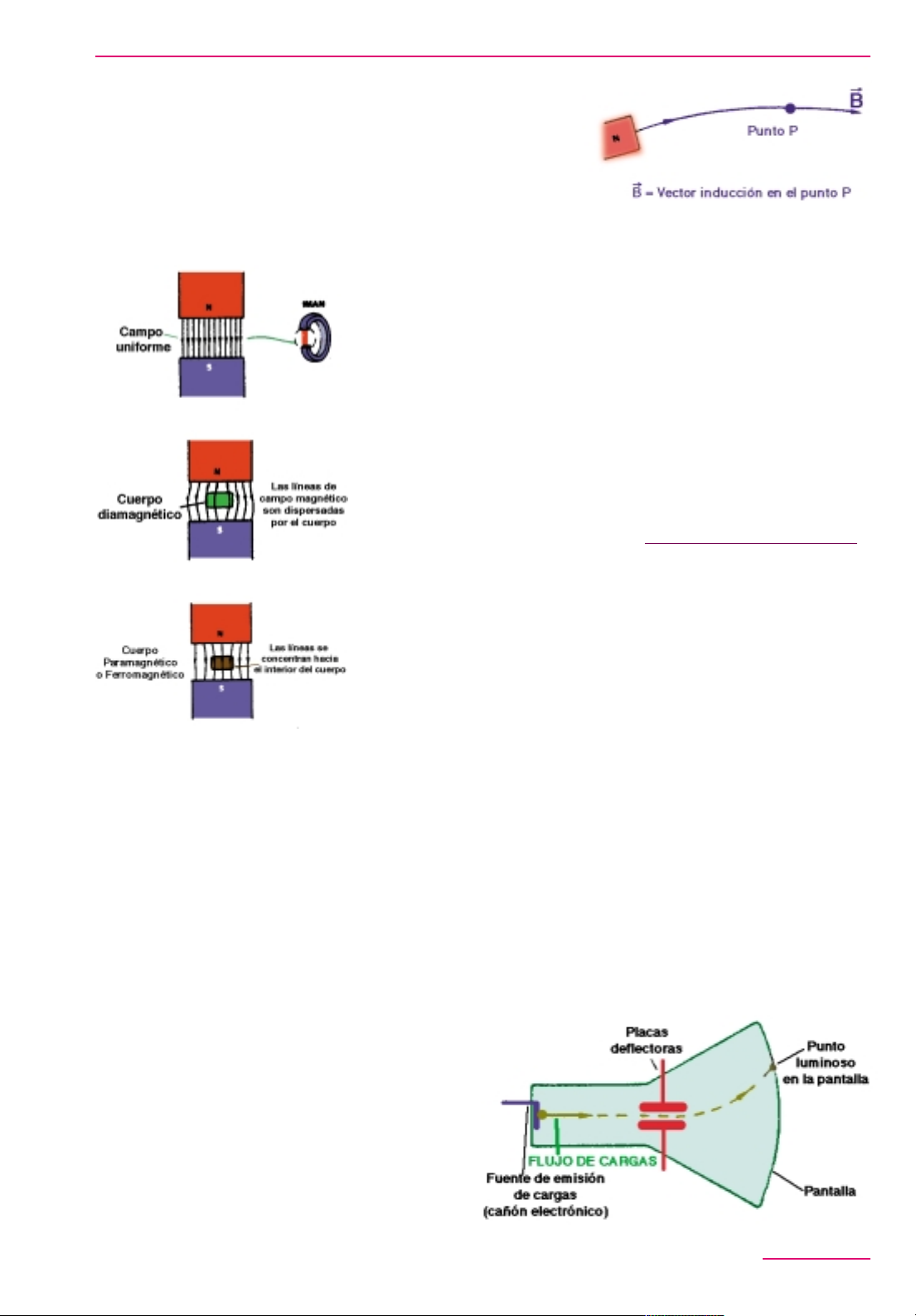
Imaginemos los polos de un imán
permanente, como muestra la figura
11. Tenemos un campo uniforme, dado que las líneas de fuerza son paralelas (dentro del espacio considerado). Pues bien, colocando diversos tipos de materiales entre los polos del
imán, podemos observar lo siguiente:
a) El material "dispersa" las l neas
de fuerza del campo magn tico, como
muestra la figura 12.
El material en cuestión se llama
"diamagnético", tiene una suscepti-
bilidad magnética menor que 1 y
presenta la propiedad de ser ligeramente repelido por los imanes (cualquiera de los dos polos). Entre los materiales diamagnéticos citamos el
COBRE, el VIDRIO y el BISMUTO.
b) El material concentra las l neas
de fuerza de un campo magn tico, como muestra la figura 13.
Si la concentración fuera pequeña (susceptibilidad ligeramente mayor que 1), diremos que la sustancia
es paramagnética, como por ejemplo el aluminio, el aire, el platino y el
tungsteno.
Si bien existe una fuerza de atracción de los imanes por estos materiales, la misma es muy pequeña para
ser percibida.
En cambio, si la concentración de las líneas de fuerza fuera muy grande (susceptibilidad
mucho mayor que 1), entonces
el material se denomina "ferro-
magnético", siendo atraído
fuertemente por el imán. El
nombre mismo nos está diciendo que el principal material de este
grupo es el hierro.
Los materiales ferromagnéticos
son usados para la fabricación de
imanes y para la concentración de
efectos de los campos magnéticos.
Los materiales diamagnéticos se
utilizan en la construcción de blindajes, cuando deseamos dispersar las líneas de fuerza de un campo magnético.
C
LCULOS CON
F
UERZASMAGN TICAS
Si colocamos una carga eléctrica bajo la acción de un campo
eléctrico, la misma queda sujeta a
una fuerza; esta fuerza puede ser
calculada mediante:
F = q . E
donde:
F es la intensidad de la fuerza (N).
q es el valor de la carga (C) y E es
la intensidad del campo (N/C).
Para el caso del campo magnético, podemos definir una magnitud
equivalente a E (Vector de intensidad de Campo), que se denomina
Vector de Inducción Magnética, el
cual es representado por la B (figura
14). La unidad más común para medir el Vector Inducción Magnética es
el Tesla (T), pero también encontramos el Gauss (G).
1 T = 104G
El lanzamiento de
una carga
eléctrica en
un campo
eléctrico o
en un campo magnético es la base de dispositivos electrónicos muy
importantes. Así, podemos dar como
ejemplo el caso de un tubo de rayos
catódicos, (tubo de rayos catódicos
de TV, por ejemplo) en el que la imagen está totalmente determinada
por fuerzas de naturaleza eléctrica y
magnética que determinan la trayectoria de los electrones que inciden en una pantalla fluorescente (figura 15). Es, por lo tanto, necesario
que el técnico electrónico sepa hacer algunos cálculos elementales relativos al comportamiento de cargas
en campos eléctricos y también
magnéticos.
a) Fuerza en un campo el ctrico
Suponiendo dos placas paralelas, como muestra la figura 16, sometidas a una tensión V (+Ve; -V), entre
ellas existe un campo eléctrico uniforme cuya intensidad es:
E = V/d
(V = Potencial y d = distancia)
Si entre las placas lanzamos una
carga eléctrica, un electrón, o una
carga, ésta quedará sujeta a una
fuerza que depende de dos factores: su polaridad y su intensidad. Si la
carga fuera positiva, la fuerza se
ejercerá en el sentido de empujarla
hacia la placa negativa y, si fuera
negativa, al contrario. La intensidad
de la fuerza estará dada por:
F = q . E
Donde:
Capítulo 5
69
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Page 6

F es la fuerza en Newtons.
q es la fuerza en Coulombs.
E es la intensidad de campo en
V/m o N/C.
En el caso de un campo magnético, el comportamiento de la carga
lanzada es un poco diferente.
De hecho, sólo existirá la fuerza si
la carga estuviera en movimiento.
Una carga estática no es influenciada por campos magnéticos.
b) Fuerza en campos magn ticos
La fuerza a que queda sometida
una carga eléctrica lanzada en un
campo magnético es denominada
Fuerza de Lorentz y tiene las siguientes características:
Dirección perpendicular al Vector B y al vector v (velocidad), la Intensidad está dada por la fórmula:
F = q . v . B sen ¿
Donde:
F = fuerza en Newtons
q = carga en Coulombs
v = velocidad en m/s
ø = ángulo entre V y B
Sentido dado por la regla de la
mano izquierda de Fleming, como
muestra la figura 17.
Representando el campo (B) con
el dedo índice y la velocidad (v) con
el dedo del medio, la fuerza que actuará sobre la carga estará dada
por la posición del pulgar (F).
Si la carga fuera negativa, se invierte el sentido de F. Observe que si
lanzamos una carga paralela a las líneas de fuerza del campo magnético (B paralelo a v), entonces, el seno
ø será nulo. En estas condiciones, no
habrá ninguna fuerza que actúe sobre la carga.
D
ISPOSITIVOS
E
LECTROMAGN TICOS
Sabemos que cuando una corriente recorre un conductor rectilíneo, el movimiento de las cargas es
responsable
de la aparición de un
campo magnético. Ese
campo magnético tiene la
misma natura-
leza que el
que se produce con
una barra de imán
permanente y puede
atraer o repeler objetos de metal.
En el caso del
campo producido por una corriente
en un conductor, no sólo tenemos el
control de su intensidad sino que
también podemos intervenir en la
"geometría" del sistema, darle formas
y disposiciones mediante las que se
puede aumentar, dirigir y difundir las
líneas de fuerza del campo según se
desee. Hay varias maneras de lograr
eso, lo que nos lleva a la elaboración
de distintos dispositivos de aplicación
en electrónica.
E
LECTROIMANES Y
S
OLENOIDES
El campo creado por una corriente que recorre un conductor rectilíneo es muy débil. Se necesita una
corriente relativamente intensa, obtenida de pilas grandes o de batería,
para que se observe el movimiento
de la aguja imantada. Para obtener
un campo magnético mucho más
intenso que éste, con menos corriente y a partir de alambres conductores, pueden enrollarse los alambres
para formar una bobina o solenoide,
como muestra la figura 18.
Cada vuelta de alambre se comporta como un conductor separado
y, entonces, el conjunto tiene como
efecto la suma de los efectos de las
corrientes. De esta manera, en el interior del solenoide tenemos la suma
de los efectos magnéticos.
En la figura 19 se grafica la forma
de obtener el sentido del campo
magnético generado cuando se conoce la polaridad de la corriente. Se
observa que la bobina se comporta
como un imán en forma de barra
con los polos en los extremos. Cualquier material ferroso, en las cercanías de la bobina, será atraído por el
campo magnético que ésta genera.
Si en el interior de la bobina coloco un núcleo de hierro, el campo
magnético se incrementa, y puede
atraer a otros objetos ferrosos más
pesados.
Al conjunto así formado se lo llama electroimán y posee innumerables aplicaciones, por ejemplo en
grúas, válvulas en lavarropas, maquinarias textiles, etc.
R
EL S YREED-REL S
La estructura de un relé se muestra en la figura 20. Se puede apreciar
que en las cercanías del electroimán
recién estudiado se coloca un juego
de contactos eléctricos. En el caso
Magnetismo e Inductancia Magnética
70
Fig. 17
Fig. 16
Fig. 18
Fig. 19
Fig. 20
Page 7

de la figura, cuando no circula corriente por el solenoide (bobina), los
contactos permanecen abiertos.
Cuando la bobina es energizada, el
campo magnético atrae el contador móvil que se "pega" con el fijo, y
cierra, de esta manera, algún circuito eléctrico.
En la figura 21 se da un ejemplo
de relé con 3 contactos; el principio
de funcionamiento es el mismo, sólo
que ahora existe un contacto normal cerrado (bobina sin energía) y
otro normal abierto. Otro tipo de relé
es el llamado "reed-rel ", cuyo aspecto funcional se ve en la figura 22.
Se tiene un interruptor de láminas
encerradas en un tubo de vidrio lleno de gas inerte. Con el gas inerte,
las chispas que se producen durante
el cierre y apertura de los contactos
no les causan daños (no se queman).
Con eso, contactos relativamente chicos pueden soportar corrientes
intensas y, además, la operación es
relativamente alta en relación con la
distancia que separa a los contactos
en la posición "abierto". El "reed-
switch", que es un interruptor de lámi-
nas, se acciona, en condiciones normales, por la aproximación del imán.
Una aplicación importante de este
componente está en los sistemas de
alarma, en los que la apertura de
una puerta o una ventana hace que
un imán abra o cierre los contactos
de una reed-switch activando la
alarma.
En el caso de un reed-relé, el accionamiento de los contactos lo
efectúa el campo magnético de un
solenoide que envuelve la ampolla.
Con muchas espiras de alambre barnizado pueden obtenerse relés ultra
sensibles, capaces de cerrar los contactos con corrientes de bobina de
pocos miliamperes. La corriente de
contacto depende exclusivamente
del "reed-switch" que se use, pero
son típicas las del orden de 100 a
1.000mA. La ventaja principal de este relé, además de la sensibilidad, es
la posibilidad de montaje en un espacio muy reducido, pues el componente es de pequeñas dimensiones.
L
OSGALVAN METROS
El galvanómetro de bobina móvil o de D'Arsonval
es un componente electrónico que utiliza el efecto
magnético de la corriente.
Se usa este dispositivo para
medir corrientes eléctricas
para aprovechar justamente el hecho de que el
campo magnético y, por
consiguiente, la fuerza que
actúa con el imán, es proporcional a la corriente
que pasa por la bobina. En
la figura 23, vemos este
componente en forma
simplificada. Entre los polos
de un imán permanente se
coloca una bobina que
puede moverse respecto
de dos ejes que sirven también de
contactos eléctricos. Resortes espiralados limitan el movimiento de la bobina, el que se hace más difícil cuando se acerca al final del recorrido.
En la bobina se coloca una aguja que se desplaza sobre una escala.
Cuando circula corriente por la bobina se crea un campo magnético
que interactúa con el campo del
imán permanente, surgiendo, entonces, una fuerza que tiende a mover
el conjunto. El movimiento será tanto
mayor cuanto más intensa sea la corriente.
Podemos, así, calibrar la escala
en función de la intensidad de la corriente. Son comunes los galvanómetros que tienen sus escalas calibradas con valores máximos, llamados
también "fondo de escala", entre
10µA (microamperes) y 1mA (miliampere). Los galvanómetros pueden
formar parte de diversos instrumentos que miden corrientes (miliamperímetros o amperímetros), que miden
tensiones (voltímetros, resistencias
ohmímetros), o que miden todas las
magnitudes eléctricas (multímetros).
L
OSINDUCTORES
Podemos reforzar en forma considerable el campo magnético creado por una corriente que circula en
Capítulo 5
71
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Page 8

un conductor, si enrollamos el conductor para formar una bobina. La
inductancia de una bobina es también mucho mayor que la de un
conductor rectilíneo. Tenemos, entonces, componentes llamados inductores (que aparecen en los diagramas representados por espirales
con letras "L") que presentan inductancias, o sea una inercia a las variaciones bruscas de la corriente (figura
24). Los inductores pueden tener diversas características de construcción según la aplicación a la que se
destinan. Tenemos, entonces, los inductores de pequeñas inductancias,
formados por pocas espiras de
alambre, con o sin un núcleo de material ferroso en su interior . La presencia del material ferroso aumenta la
inductancia, multiplicada por un
factor que puede ser bastante grande.
La unidad de inductancia es el
henry, H en forma abreviada.
El múltiplo más usado es:
-El milihenre (mH) que vale 0,001
henry, o mil sima parte del Henry.
Los pequeños inductores para
aplicaciones en frecuencias elevadas tienen inductancias que varían
entre pocos microhenry y milihenry,
mientras que los que se usan para
frecuencias medias y bajas pueden
tener inductancias hasta de algunos
henrys.
La oposición o inercia que presenta el inductor a las variaciones de
intensidad de la corriente depende
de la cantidad de líneas de fuerza
que cortan el conductor o espiras de
la bobina.
Denominamos flujo magnético,
representado por Ø, al número de líneas de fuerza que atraviesan una
cierta superficie (S). Calculamos el
flujo en una espira de la bobina mediante la fórmula:
Ø = B. S. cos α
En la que:
Ø es la intensidad del flujo mag-
nético que se mide en weber, cuyo
símbolo es Wb.
B es la intensidad de la inducción
magnética medida en Tesla (T).
S es la superficie rodeada por la
espira, en metros cuadrados.
Si tuviéramos una bobina con n
espiras, basta multiplicar el segundo
miembro de la fórmula por n:
Ø = n.B.S.cos α
Si en el interior del solenoide o
bobina se colocara un núcleo de
material ferroso, debemos multiplicar
la permeabilidad del material por el
resultado.
Partiendo de esta fórmula del flujo se puede, fácilmente, llegar a la
fórmula de la inductancia propiamente dicha, que será válida para
solenoides en los que la longitud no
sea mucho mayor que el diámetro.
Tenemos, entonces:
1,257 . n
2
. S . 10
-8
L =
______________________
I
En la que:
L es la inductancia en henry (H).
n es el número de espiras del so-
lenoide.
I es la longitud del solenoide en
centímetros.
S es la superficie rodeada por
una espira, en centímetros cuadrados.
Los valores 1,257 y 10
-8
son constantes que dependen de la permeabilidad magnética del medio, en este caso del aire, además de las unidades de longitud y superficie que
se utilicen.
Magnetismo e Inductancia Magnética
72
Los Componentes en Corriente Alterna
L
la corriente que tomamos de la
línea es alterna y es muy diferente de la que obtenemos de pilas
o baterías. Pero ¿cuál es la diferen-
cia y de qué modo influye en el
comportamiento de los distintos
componentes que estudiamos hasta el momento?
Si conectamos un resistor, un cable conductor o una lámpara a una
pila o batería, se establecerá una
corriente que es un flujo de electrones libres. Esos electrones van a dirigirse del polo negativo (que los tiene en exceso) al polo positivo (que
los tiene en defecto).
Suponiendo que la resistencia
del resistor, conductor o lámpara no
varíe en el transcursor del tiempo, el
flujo de electrones será constante
como ilustra el gráfico de la figura 1.
Esta es una corriente continua
porque: "Circula siempre en el mis-
mo sentido y tiene intensidad cons-
tante". Una corriente continua se re-
presenta en forma abreviada por
CC (corriente continua) o DC (direct
current). Pero existe otro tipo de corriente.
Vamos a suponer que se establezca una corriente en un conductor, resistor u otra clase de carga, de
manera que su intensidad no es
constante sino
que varía cíclicamente, es decir,
siempre de la misma manera. Una
corriente que
cambia en forma
constante su sentido de circulación
y varía su intensidad es una corriente alterna.
A nosotros va a interesarnos al
principio la corriente alterna sinusoidal, que explicaremos enseguida.
Un conductor que corte las líneas de fuerza de un campo magnético, manifestará en sus extremos
una fuerza electromotriz que puede
calcularse mediante la expresión:
Fig. 1
Page 9

E = B x L x sen α
Donde:
E es la fuerza electromotriz
B es el vector inducción magnéti-
ca
L es la longitud del alambre
α es el ángulo en que el conduc-
tor corta las líneas del campo.
Vea que la inducción de una tensión será tanto mayor cuanto mayor
sea el ángulo según el que el conductor corta las líneas de fuerza del
campo magnético.
Partiendo de ese hecho, vamos
a suponer que montamos una espira
(una vuelta completa del alambre
conductor) de manera de girar dentro del campo magnético uniforme,
como se ve en la figura 2.
Un campo magnético uniforme
se caracteriza por tener la misma intensidad en todos sus puntos, lo que
nos lleva a representarlo por líneas
de fuerza paralelas. Vamos a representar esta espira vista desde arriba
para comprender con mayor facilidad los fenómenos que se producirán cuando la giramos, como muestra la figura 3.
Partiendo entonces de la posición de la figura 3, hacemos que la
espira gire 90° en el sentido indicado,
de modo que corte las líneas de
fuerza del campo magnético.
En estas condiciones, a medida
que la espira "entra" en el campo, el
ángulo se va acentuando de manera que al llegar a 90, el valor va desde cero hasta el máximo.
En esta posición, la espira corta el
campo en forma perpendicular aunque sólo sea por un instante. Como
la tensión inducida depende del ángulo, vemos que en este arco de 90°,
el valor va desde 0 hasta el máximo,
lo que puede representarse mediante el gráfico de la figura 4. Continuando la rotación de la espira, vemos que entre 90° y 180° tiende a
"salir" del campo y se va reduciendo
el ángulo según el cual corta las líneas de fuerza del campo magnético. La tensión inducida en estas condiciones cae hasta el mínimo en este
arco.
Vea que realmente la tensión
cae a cero pues a 180°, aunque sólo
por un instante, el movimiento de la
espira es paralelo a las líneas de fuer-
za y entonces no
hay inducción.
En la figura 5 se
tiene la representación gráfica de lo
que ocurre con el
valor de la tensión
en estos arcos de
90° (0° a 90° y 90° a
180°).
Recorriendo
ahora 90° más, de
180 a 270°, la espira
vuelve a "penetrar"
en el campo magnético en forma más
acentuada pero en
sentido opuesto al
del arco inicial. Así
ocurre la inducción
pero la polaridad de
tensión en los extremos de la espira se
ha invertido, es decir,
si tomamos una referencia inicial que lleve a una representación positiva en los 180 grados iniciales, a
partir de este punto la representación será negativa como
muestra la figura 6.
Igualmente, la tensión asciende, pero hacia valores negativos máximos, hasta llegar
en los 270 grados al punto de
corte, prácticamente perpendicular aunque sea por un breve instante. En los 90° finales de la
vuelta completa, de 270 a 360 grados, nuevamente el ángulo en el
que la espira corta las líneas de fuerza, disminuye y la tensión inducida
cae a cero.
El ciclo completo de representación de la tensión generada se ve en
la figura 7.
Si tuviéramos un circuito externo
para la circulación de la corriente y
si la resistencia fuera constante, la intensidad dependerá exclusivamente
de la tensión). La corriente circulante
tendrá entonces las mismas características de la tensión, es decir, variará
según la misma curva.
Como la tensión generada está
regida por la función seno (sen α)
que determina el valor según el ángulo, ya que B y L son constantes, la
forma de la onda recibe el nombre
de sinusoide. Se trata, por lo tanto de
Capítulo 5
73
Fig. 3
Fig. 2
Fig. 4
Fig. 5
Page 10

una corriente alterna sinusoidal. Para
generar esta corriente alterna sinusoidal se establece una tensión también sinusoidal. Esa tensión, también
alterna tiene la misma representación gráfica.
Podemos decir entonces:
"Una tensi n alterna produce una
corriente alterna que es aquella cuya
intensidad var a en forma constante
seg n una funci n peri dica y su
sentido se invierte constantemente."
Vea que una "función periódica"
es la que se repite continuamente
como la sinusoide que es la misma a
cada vuelta de espira (figura 8).
Una corriente alterna s lo puede
ser establecida por una tensi n alterna.
El tiempo que la espira tarda en
dar una vuelta completa determina
un valor muy importante de la corriente alterna, que podemos medir.
Este tiempo de una vuelta es el periodo que se representa con T y se
mide en segundos.
El número de vueltas que da la
espira en un segundo determina otra
magnitud importante que es la frecuencia, representada por f y medida en hertz (Hz).
Numéricamente, la frecuencia es
la inversa del período:
T = 1/f
Los alternadores de las usinas hidroeléctricas (y atómicas) que envían energía eléctrica a nuestras casas, operan con una frecuencia de
50 hertz (50Hz).
Decimos entonces que la corriente alterna obtenida en las tomas de
energía tiene una frecuencia de 50
hertz.
Esto significa que en cada segundo, la corriente es forzada a circular
50 veces en un sentido y 50 veces en
el opuesto, pues ése es el efecto de
la inversión de la polaridad (vea nuevamente la figura 8).
Alimentando una lámpara incandescente común, en cada segundo
existen 100 instantes en que la corriente se reduce a cero, pero la lámpara no llega a apagarse por la inercia del filamento que se mantiene
caliente. La tensión producida puede variar y es de 220V. No podemos
hablar de un valor fijo de tensión o
de corriente pues el cambio de la
polaridad y del valor es constante.
¿Qué significa entonces 220V?
Si tenemos en cuenta la tensión
sinusoidal de la toma de energía de
la red, vemos que lo cierto sería hablar de valores instantáneos, es decir: de la tensión que encontramos
en cada instante, que depende del
instante de cada ciclo considerado.
Podemos encontrar tanto un mínimo
negativo como un máximo positivo,
o cero, según el instante dado.
Es claro que a los efectos prácticos, eso no tiene mucho sentido. Es
así que, para medir tensiones y corrientes alternas es preciso establecer una manera que nos dé una
idea del efecto promedio o real obtenido. Esto puede entenderse de la
siguiente manera:
Si alimentamos una lámpara común con tensión alterna en los instantes en que la corriente circula por
el filamento, en un sentido o en otro,
se produce el calentamiento y la
lámpara se enciende. El efecto es el
mismo que tendríamos si la alimentáramos con una tensión continua de
determinado valor.
¿Cuál sería ese valor?
Si comparamos el gráfico que representa la circulación de corriente
continua por un circuito y el gráfico
que representa la circulación de una
corriente alterna, la superficie cu-
bierta en un intervalo se relaciona
con la cantidad de energía que tenemos a disposición. Entonces nos
basta hacer la pregunta siguiente
para tener la respuesta a nuestro
problema:
¿Cuál debe ser el valor de la tensión continua que nos produce el
mismo efecto que determinada tensión alterna?
En la figura 9 vemos que, si la tensión alterna llega a un valor máximo
X, el valor que la tensión continua
debe tener para producir el mismo
efecto se consigue dividiendo X por
la raíz cuadrada de 2, o sea: 1,4142.
El valor máximo alcanzado en un ciclo (el mínimo también) se llama valor de pico, mientras que el valor que
produce el mismo efecto, se llama
valor eficaz o r.m.s. ("root mean squa-
re"). Para la red de 220V, los 220V re-
presentan el valor r.m.s. Existen instantes en que la tensión de la red llega a 220V multiplicados por 1,4142 y
así obtenemos que el valor pico es
311,12V.
Este valor se logra dividiendo el
promedio de todos los valores en cada instante del semiciclo, o sea la mitad del ciclo completo, pues si entrasen en el cálculo valores negativos,
el resultado sería cero (figura 10). Podemos entonces resumir los "valores"
en la forma siguiente:
V
ALOR PICO
: es el valor máximo
que alcanza la tensión o la corriente
Magnetismo e Inductancia Magnética
74
Fig. 6
Fig. 7
Page 11

en un ciclo, pudiendo ser tanto negativo como positivo. Es un valor instantáneo, es decir, aparece en un
breve instante en cada ciclo de corriente o tensión alternada.
V
ALOR EFICAZ O R.M.S
.: es el valor
que debería tener la tensión o corriente si fuese continua para que se
obtuvieran los mismos efectos de
energía.
V
ALOR MEDIO
: obtenemos este va-
lor dividiendo la suma de los valores
instantáneos de un semiciclo por su
cantidad, o sea: sacamos la media
artimética de los valores instantáneos en un semiciclo.
No podemos hablar de polaridad
para una tensión alterna, ya que
cambia constantemente. Una corriente de cualquier carga conectada a un generador de corriente alterna invierte su sentido en forma
constante. En el caso de la red, sabemos que uno de los polos "produ-
ce shock" y el otro, no. Eso nos lleva
a las denominaciones de polo vivo y
polo neutro.
¿Qué sucede entonces?
Si tenemos en cuenta que el generador de energía de las compañías tiene uno de los cables conectado a tierra, que se usa como conductor de energía, resulta fácil entender lo que ocurre.
Al estar en contacto con la tierra,
cualquier objeto, en cualquier instante, tendrá el mismo potencial del
polo generador conectado a tierra
que es entonces la referencia. Este
es el polo neutro, que tocado por
una persona no causa shock porque
estando al mismo potencial no hay
circulación de corriente.
La tensión varía alrededor del valor del polo de referencia según la sinusoide del otro polo. Es así que en
relación al neutro, el otro polo, es decir el polo vivo, puede estar positivo
o negativo, 50 veces por segundo. Al
tocar el polo vivo (figura 11), habrá
una diferencia de potencial respecto de tierra (variará 50 veces por segundo), pero ella puede causar la
circulación de una corriente eléctrica y producir el shock eléctrico.
R
EPRESENTAC I N
G
R FICA
DE LA
C
ORRIENTEALTERNA
Los lectores deben acostumbrarse a la representación de fenómenos
de naturaleza diversa mediante gráficos.
Cuando se tiene un fenómeno
que ocurre de manera dinámica,
una magnitud varía en función de
otra; por ejemplo, en el caso de la
corriente alterna, la intensidad de la
corriente o la tensión son las que varían con el tiempo.
Para representar esas variaciones
hacemos un gráfico de tensión versus tiempo (V x t) como muestra la figura 12. Colocamos, entonces, en el
eje vertical (Y) los valores de tensión,
graduamos este eje en la forma
adecuada y en el eje horizontal (X)
colocamos los valores del tiempo (t),
graduamos también el eje en forma
adecuada. Después definimos cada
punto del gráfico como un par de
valores (X e Y), dado por el valor de
la tensión en un determinado instante. Para el caso de la tensión alterna,
si dividimos el tiempo de un ciclo
(1/50 de segundo) en 100 partes, por
ejemplo, podemos determinar 100
puntos que unidos darán la curva
que representa la forma de onda de
esta tensión.
Es claro que el gráfico ideal se
obtiene con infinitos puntos pero eso
no siempre es posible.
Mientras, por distintos procedimientos podemos tener una aproximación que haga continua la curva
y se obtenga así un gráfico (curva)
ideal. A partir de esta representación
podemos entonces obtener el valor
instantáneo de la tensión en cualquier momento y del mismo modo,
dado el valor podemos encontrar el
instante en que se produce.
R
EACTANCIA
Los capacitores e inductores presentarán una propiedad denomina-
Capítulo 5
75
Fig. 8
Fig. 10
Fig. 9
Fig. 11
Page 12

da "reactancia" cuando se los somete al paso de una corriente alterna
Si se conecta un capacitor a un
generador de corriente continua,
como una pila, por ejemplo, una vez
que cierta cantidad de cargas fluya
a sus armaduras y se cargue, desaparece cualquier movimiento de
esas cargas y la corriente en el circuito pasa a ser indefinidamente nula.
En esas condiciones, el capacitor
está totalmene cargado, posee una
resistencia infinita y no deja circular
la corriente.
Por otra parte, si conectamos al
mismo generador un inductor ideal
(que no presenta resistencia en el
alambre del cual está hecho) una
vez que la corriente se haya establecido y el campo magnético adquiera la intensidad máxima, no encontramos efecto alguno de inductancia. Las cargas podrán fluir con la intensidad máxima como si el inductor
no existiera.
La presencia del capacitor y del
inductor en un circuito de corriente
continua es importante sólo en el instante en que ocurren variaciones:
cuando la corriente se establece o
cuando la corriente se desconecta. Ya estudiamos
ampliamente los fen menos que se producen en
esos instanes.
Pero, ¿qué sucedería si
se conectara el inductor o
el capacitor a un circuito
de corriente alterna en el
que la tensión varía con rapidez, en forma repetitiva?
¿Qué fenómenos importantes se producirían?
R
EACTANCIACAPACITIVA
Vamos a empezar con
el capacitor, lo conectamos, por
ejemplo, a un circuito de corriente
alterna de 50 hertz, de la red. Durante el primer cuarto del ciclo, cuando
la tensión aumenta de cero a su valor máximo, el capacitor se carga
con la armadura A positiva y la B negativa. Eso sucede en un intérvalo
de 1/200 de segundo. En el segundo
cuarto, cuando la tensión cae a cero desde el valor máximo, se invierte
la corriente en el capacitor y se descarga. En el tercer cuarto se invierte
la polaridad de la red de manera
que la corriente de descarga continúa en el mismo sentido pero carga
positivamente la armadura B. El capacitor invierte su carga hasta un valor máximo. En el último cuarto,
cuando la tensión vuelve a caer a
cero, la corriente se invierte y la carga del capacitor cae a cero.
En la figura 13 tenemos la representación del proceso que ocurre en
un ciclo y que se repite indefinidamente en cada ciclo de alimentación. Como se tienen 50 ciclos en
cada segundo, el capacitor se carga y descarga positivamente primero y luego negativamente, 50 veces
por segundo.
Al revés de lo
que ocurre cuando la alimentación es con corriente continua,
en la que, una
vez cargado, cesa la circulación
de corriente; con
corriente alterna
ésta queda en
forma permanen-
te en circulación por el capacitor,
carga y descarga con la misma frecuencia de la red. La intensidad de
la corriente de carga y descarga va
a depender del valor del capacitor y
también de la frecuencia de la corriente alterna.
Cuanto mayor es la capacidad
del capacitor, mayor será la intensidad de la corriente (la corriente es
entonces directamente proporcional a la capacidad) y cuanto mayor
sea la frecuencia, mayor será la intensidad de la corriente (la corriente
también es proporcional a la frecuencia). Entonces se verifica que el
capacitor, alimentado con corriente
alterna, se comporta como si fuese
una "resistencia" y per mite mayor o
menor circulación de corriente en
función de los factores explicados
antes.
Como el término "resistencia" no
es el adecuado para el caso pues
no se trata de un valor fijo, como en
el caso de los resistores, sino que varía con la frecuencia y no es sólo inherente al componente, se prefiere
decir que el capacitor presenta una
"reactancia" y en el caso específico
del capacitor, una "reactancia capacitiva" (abreviada Xc).
Podemos, entonces, redefinir la
reactancia capacitiva así:
"Se denomina reactancia capacitiva (Xc) a la oposici n que un capacitor ofrece a la circulaci n de una corriente alterna."
Para calcular la reactancia capacitiva, se tiene la fórmula siguiente:
1
XC =
________________
(1)
2 . 3,114 . f . C
Donde,
Xc es la reactancia medida en
ohm.
3,14 es la constante pi (π)
f es la frecuencia de la corriente
alterna en hertz.
C es la capacidad del capacitor
en farad.
El valor "2 . 3,14 . f" puede representarse con la letra omega (ω) y este valor se llama "pulsaci n". La fórmula de la reactancia capacitiva
Magnetismo e Inductancia Magnética
76
Fig. 12
Fig. 13
Page 13

queda entonces:
1
Xc =
______
(2)
ω . C
* La reactancia capacitiva es
menor cuanto más alta es la frecuencia, para un capacitor de valor
fijo.
Puede decirse que los capacitores dejan pasar con más facilidad las
señales de frecuencias más altas.
* La reactancia capacitiva es
menor en los capacitores de mayor
valor, para una frecuencia constante. Puede decirse que los capacitores mayores ofrecen menos oposición al pasaje de las corrientes alternas.
Fase en un Circuito Capacitivo
=
Dos señales pueden estar en fa-
ses diferentes o en concordancia de
fase, conforme sus formas de onda
coincidan por superposición en un
instante dado y siempre que tengan
la misma frecuencia (figura 14).
Podemos hablar también de la
diferencia de fase entre dos señales
de corriente alterna y entre una corriente alterna y una tensión si llegaran a los puntos de máximo (o de mínimo) en distintos instantes.
Esta diferencia entre los instantes
nos da la diferencia de fase que
puede expresarse con un ángulo como muestra la figura 14.
Si dos señales estuvieran en concordancia de fase, es evidente que
la diferencia sería cero. Si la diferencia fuera de 90 grados, diremos que
las señales están en cuadratura y si
fuera de 180 grados, diremos que las
señales están en oposición
de fase.
Conectando un resistor
en un circuito de corriente
alterna, es evidente que
siendo la tensión la causa y
la corriente el efecto, deben estar en concordancia de fase, es decir, cuando la tensión aumenta, la
corriente debe aumentar
en la misma proporción .
Pero si conectamos un capacitor en un circuito de
corriente alterna, las cosas
no suceden de este modo.
Si consideramos un capacitor de capacidad C
conectado a un generador de corriente alterna cuya tension esté dada por E = Eo sen
ω
t, veremos que la
diferencia de potencial entre las placas del capacitor varía con el tiempo.
La corriente estar ADELANTADA
90 grados respecto de la tensi n .
R
EACTANCIAINDUCTIVA
Cuando conectamos un inductor
de inductancia L a un generador de
corriente alterna, durante el primer
cuarto del ciclo, la tensión sube a
cero hasta el valor máximo qe corresponde a una variación a la que
el inductor se opone. En estas condiciones, comienza a circular una corriente por el inductor que crea el
campo magnético, hasta su máximo. En el segundo cuarto, la tensión
cae a cero lo que también es una
variación a la que el inductor se opone. En estas condiciones, comienza
a circular una corriente por el inductor que crea el campo magnético,
hasta su máximo. En el segundo
cuarto, la tensión cae a
cero lo que también es
una variación a la que
el inductor se opone.
Pero aun así, el campo
magnético se contrae
hasta desaparecer. En
el tercer cuarto, la tensión invierte su polaridad y aumenta de valor hasta un máximo negativo; variación a la
que el inductor se opone pero lo hace esta-
bleciendo un campo magnético
que se expande. Finalmente, en el
último cuarto, encontramos oposición del inductor a la circulación de
la corriente. Las líneas de fuerza se
contraen durante este cuarto de ciclo.
En realidad, según veremos va a
existir un pequeño atraso en esta retracción de las líneas.
Lo importante es observar que
mientras en el circuito de corriente
continua, una vez establecido el
campo, la resistencia (oposición) desaparecía y la corriente circulaba libremente, en este caso la oposición
es permanente.
En la figura 15 se ve la representación de este proceso.
Vea entonces que se establece
un campo magnético alterno en el
inductor que varía constantemente
en intensidad y polarización.
La oposición constante manifestada por el inductor a las variaciones
de la tensión va a depender tanto
de la inductancia como de la frecuencia de la corriente.
Cuanto mayor sea la inductancia, mayor será la oposición a la circulación de la corriente.
El inductor también se comporta
como una "resistencia" a la circulación de la corriente alterna, pero el
término resistencia tampoco cabe
en este caso pues no es algo inherente sólo al componente sino también a las características de la tensión aplicada.
Nos referimos entonces a reac-
tancia inductiva, representada por
XL, como la oposición que un induc-
tor presenta a la circulación de una
corriente alterna. La reactancia inductiva se mide en ohms como la
reactancia capacitiva y puede calcularse mediante la siguiente fórmu-
Capítulo 5
77
Fig. 14
Fig. 15
Page 14

la:
XL = 2 . 3,14 . f . L (3)
Donde:
XL es la reactancia inductiva en
ohms
3,14 es la constante pi (π)
f es la frecuencia de la corriente
alterna en hertz.
L es la inductancia en henry.
Como la expresión "2 . 3,14 . f"
puede expresarse como "ω" (pulsa-
ción), podemos escribir:
XL = ω . L (4)
Tenemos finalmente las propiedades de los inductores en los circuitos de corriente alterna:
* La reactancia inductiva es tanto mayor cuanto mayor sea la fre-
cuencia. Puede decirse
que los inductores ofrecen
una oposición mayor a las
corrientes de frecuencias
más altas.
* la reactancia inductiva es mayor para los inductores de mayor valor para
una frecuencia determinada. Los inductores de mayor valor ofrecen una oposición mayor a la circulación de corrientes alternas.
Fase en el
Circuito Inductivo
Si conectamos un inductor a un
circuito de corriente alterna, la corriente no estará en fase con la tensión.
* La corriente tiene la misma frecuencia que la tensión.
* La corriente tiene su fase atrasada 90 grados (π/2) en relación a la
tensión.
El gráfico de la figura 16 muestra
lo que ocurre con la tensión respecto de la corriente .
Q
UE ES UNA SE AL
?
En los circuitos electrónicos aparecen corrientes de distintos tipos:
continuas puras, continuas pulsantes
y alternas con diversas formas de onda. En el caso específico de los aparatos de sonido, por ejemplo, las formas de onda son "retrasos" del sonido que debe reproducirse y que
aparecen en una amplia variedad
de formas de onda y de frecuencias.
Las corrientes con que trabajan
los circuitos —amplificadoras, productoras, reproductoras o captadoras— se denominan señales. Encontramos, en los circuitos electrónicos,
señales que pueden ser desde simples corrientes continuas hasta señales cuyas frecuencias pueden llegar
a centenas de millones de hertz.
¿Es importante conocer las fórmulas solamente o saber deducirlas?
La deducción de una fórmula se
hace para demostrar su validez, mediante la descripción de un fenómeno y de un raciocinio lógico. En la
deducción de algunas de las fórmulas que presentamos, utilizamos el
cálculo diferencial e integral, que el
lector no necesita conocer. En estos
casos, aunque la deducción no se
comprenda bien, bastará que el lector sepa la fórmula pues le será de
utilidad en cálculos futuros.
Sugerimos que los lectores que
Magnetismo e Inductancia Magnética
78
Fig. 16
Tiristores y Otros Dispositivos de Disparo
tengan dificultades con matemáticas y que deseen profundizar sus estudios de electrónica, estudien algo
más de esa ciencia importante.
LOS TIRISTORES
Los tiristores funcionan como
una especie de interruptor del control electrónico y se emplean precisamente para controlar grandes
corrientes de carga en motores,
calentadores, sistemas de iluminación y demás circuitos similares. Internamente están conformados
por cuatro capas de material semiconductor; algunas de sus secciones se conectan de manera externa a terminales conductoras.
R
ECTIFICADOR CONTROLADO DE SILI-
CIO
El SCR o Rectificador Controlado de Silicio, es un dispositivo semiconductor de cuatro capas con
tres terminales externas llamadas
c todo , nodo y compuerta ;
cada una de éstas se encuentra
conectada a una sección del semiconductor.
Un SCR se comporta como un
interruptor; al aplicarle la alimentación por primera vez, se encontrará abierto; pero si se aplica un pulso de disparo a la terminal compuerta, se cerrará (permitiendo así
que la corriente eléctrica lo atraviese). Esto es, si el SCR se conecta
en serie con una batería y un resistor, el dispositivo resultante será
considerado como un diodo en
polarización directa; esto significa
que se mantiene en estado de noconducción. Para que el dispositivo inicie la conducción, es necesario un pequeño pulso de tensión en
el terminal compuerta; esto lo
mantendrá en conducción, a menos que la corriente que lo atraviesa disminuya por debajo de un
cierto valor crítico (figura 1).
El circuito equivalente del SCR
se comporta como un interruptor
abierto, cuando se polariza con
una batería VCC y en serie con
una resistencia de carga RC. Como los transistores no están polarizados correctamente, no conducen; en consecuencia, no circula
corriente eléctrica a través del circuito. Para que la corriente fluya,
se necesita aplicar un pulso de dis-
Page 15

paro a la terminal compuerta; puede ser aplicado por medio de una
batería VP. La batería polariza di-
rectamente la unión Base-Emisor
del transistor T2, poniéndolo así
en estado de saturación. La corriente de colector de T2 ingresa
a la base del transistor T1, polarizando también la unión EmisorBase; esto provoca que T1 esté
en saturación (figura 2).
Si se dan las condiciones arriba señaladas, el voltaje de VP
ya no será necesario; por lo que
al retirar éste, el circuito se mantendrá en conducción. La corriente de colector de T2 mantiene polarizada directamente la
unión Base-Emisor de T1; a su vez,
la corriente de colector de T1
mantiene la polarización directa
de la unión Base-Emisor de T2.
Cuando esto sucede, el dispositi-
vo se comporta como un interruptor cerrado. Desconectando la alimentación de la fuente Vcc el SCR
va al estado de corte. Otra forma
de hacer que el circuito se “abra”,
consiste en aplicar un pulso negativo a la compuerta (base de T2).
INTERRUPTOR CONTROLADO DE SILICIO
El interruptor controlado de sili-
cio o SCS (Silicon Controlled
Switch), es una versión modificada
del SCR; está formado por cuatro
capas de material semiconductor
dopado, donde cada una de las
secciones se conecta a una terminal. Este dispositivo se comporta de
manera similar al SCR, con la diferencia de que puede ser disparado
por medio de cualquiera de las dos
compuertas (ánodo y cátodo);
además, está diseñado para trabajar con corrientes eléctricas pequeñas del orden de los miliampers (figura 3).
FotoSCR (fig. 4a)
Es un dispositivo con tres terminales; su encapsulado en la parte
superior dispone de una lente que
permite el paso de la luz, para iluminar el semiconductor que forma al
fotoSCR. La luz incidente en el semiconductor provoca la liberación de
los electrones en la compuerta. Estos electrones forman una corriente
eléctrica suficiente para lograr que
el fotoSCR conmute al estado de
conducción, si es que el dispositivo
se encuentra en polarización directa.
Diodo de Cuatro Capas (fig. 4b)
El diodo Shockley o diodo de
cuatro capas conduce la corriente
cuando se le aplica una tensión de
polarización en sentido directo. La
estructura de este dispositivo es de
cuatro capas de material semiconductor, en cuyos extremos se ha colocado un par de terminales externas. Se considera un diodo, porque
dispone de dos terminales (no confundir con el diodo Schottky); tam-
bién se le conoce como diodo
PNPN. La única forma de hacer que
el diodo deje de conducir, es reduciendo la corriente que lo atraviesa
hasta un valor inferior a la corriente
de mantenimiento (valor mínimo de
corriente requerido para que el dispositivo se mantenga en estado de
Capítulo 5
79
Fig. 1
Fig. 2
Fig. 4
Fig. 3
Page 16

conducción).
SUS (fig. 4.c)
El interruptor unilateral de silicio
o SUS (Silicon Unilateral Switch), es
un dispositivo que permite el paso
de la corriente eléctrica en un solo
sentido cuando la tensión aplicada
a sus terminales en sentido directo
supera cierto valor . Es muy parecido
al diodo Shockley, con la diferencia
que posee un terminal extra de disparo con la que se controla la condición de disparo en la que opera .
Un SUS opera con valores de tensión y corriente eléctrica bajos.
TRIAC
El TRIAC es un dispositivo semiconductor bidireccional con tres
terminales; o sea, puede conducir
la corriente eléctrica en ambos sentidos. Las terminales ánodo y cátodo se han cambiado por MT1 y MT2,
que es la abreviatura de Terminal
Principal 1 y Terminal Principal 2.
El circuito equivalente para el
TRIAC se puede formar con dos SCR
en paralelo, pero con sus polaridades invertidas (figura 5). Cuando se
aplica el pulso de activación en el
terminal compuerta, no importa la
polaridad aplicada a las terminales
MT; la razón, es que uno de los dos
SCR se encontrará polarizado directamente y conducirá.
Si el SCR1 se encuentra polarizado en forma inversa y el SCR2 en
forma directa cuando se aplica el
pulso a la compuerta G, solamente
este último conducirá. Si se invierte
la polaridad de la batería y se aplica el pulso de disparo nuevamente
en la compuerta G, sólo el SCR1
conducirá.
El efecto total del dispositivo es
el de permitir el paso de la corriente eléctrica, independientemente
de la polaridad de la tensión apli-
cada en las terminales
MT.
Los parámetros a considerar cuando se elige un
TRIAC, son iguales a los
utilizados para el SCR; la
única diferencia es que el
VRRM o voltaje inverso no
existe en el caso de los
TRIAC’s, debido a que no
importa la polaridad en
sus extremos.
DIAC
El DIAC o diodo bidireccional de
disparo (Diodo de Corriente Alterna, por su nombre en inglés) es un
dispositivo semiconductor muy parecido al diodo Shockley, con la di-
ferencia de que permite el paso de
la corriente eléctrica en ambos sentidos; también tiene un valor de voltaje de conducción (breakover)
que es el mismo en ambos sentidos.
El circuito equivalente del DIAC es
un par de diodos Shockley en paralelo, pero con polaridades opuestas. Cuando se aplica una tensión
en los extremos del DIAC, éste se
mantiene en estado de noconducción mientras no se supere la tensión nominal de conducción. Por ser
un dispositivo de tipo bidireccional,
es utilizado como disparador de
compuerta en los TRIAC’s.
SBS
Es un dispositivo de control para
el disparo de la compuerta en
TRIAC’s. Tiene la propiedad de conducir la corriente eléctrica en ambos sentidos; cuando la tensión alcanza el valor de conducción, a diferencia de un DIAC, el SBS adquiere un voltaje de conducción mucho
más pequeño. Está formado por un
conjunto de dispositivos discretos, y
se fabrica más bien como un circuito integrado; además, cuenta con
una terminal extra llamada com-
puerta que proporciona mayor fle-
xibilidad en el disparo.
SIDAC
El disparador bilateral de alto
voltaje o SIDAC, es un dispositivo
electrónico de reciente aparición.
Permite la manipulación de voltajes
altos de disparo, lo que amplía la
gama de aplicaciones de los dispositivos disparadores; de esta manera, se ahorran gastos en componentes extras que serían necesarios
para ciertas clases de circuitos.
UJT
El UJT o transistor uniunión (Unijunction Transistor), es utilizado co-
mo dispositivo de disparo. Se trata
de un elemento semiconductor de
conmutación por ruptura, muy utilizado en circuitos industriales, temporizadores, osciladores, generadores de onda y como circuitos de
control de compuerta para TRIAC y
SCR. La zona P del emisor está altamente dopada, mientras que la zona N del semiconductor tiene un
dopado pequeño. Cuando el emisor del transistor no se encuentra
conectado a ningún circuito externo, la resistencia entre las terminales Base 1 y Base 2 es de unos 4,000
a 10,000Ω. Este dispositivo tiene la
característica de presentar resistencia negativa; es decir, a un aumento de corriente se sucede una disminución de voltaje en las terminales del mismo. ******************
Magnetismo e Inductancia Magnética
Es una publicación de Editorial Quark, compuesta de 24 fascículos,
preparada por el Ing. Horacio D. Vallejo, contando con la colaboración
de docentes y escritores destacados en el ámbito de la electrónica internacional. Los temas de este capítulo fueron escritos por Horacio Vallejo
y Oscar Montoya Figueroa.
Editorial Quark SRL - Herrera 761, (1295), Bs. As. - Argentina - Director: H. D. Vallejo - Tel.: 4301-8804
Fig. 5
 Loading...
Loading...