How it Works
Campbell Scientific
Loading...
4WFBS350
User Manual
46 pgs1.62 Mb0
Table of contents
Loading...

Campbell Scientific 4WFBS120, 4WFBS350, 4WFBS1K User Manual

4WFBS120, 4WFBS350, 4WFBS1K
4 Wire Full Bridge Terminal
Input Modules
Revision: 3/12
Copyright © 1996-2010
Campbell Scientific, Inc.

Warranty

Assistance

Products may not be returned without prior authorization. The following contact information is for US and international customers residing in countries served by Campbell Scientific, Inc. directly. Affiliate companies handle repairs for customers within their territories. Please visit
www.campbellsci.com to determine which Campbell Scientific company serves
your country.
To obtain a Returned Materials Authorization (RMA), contact CAMPBELL SCIENTIFIC, INC., phone (435) 227-9000. After an applications engineer determines the nature of the problem, an RMA number will be issued. Please write this number clearly on the outside of the shipping container. Campbell Scientific's shipping address is:
CAMPBELL SCIENTIFIC, INC. RMA#_____ 815 West 1800 North Logan, Utah 84321-1784
For all returns, the customer must fill out a "Statement of Product Cleanliness and Decontamination" form and comply with the requirements specified in it. The form is available from our web site at www.campbellsci.com/repair. A completed form must be either emailed to repair@campbellsci.com or faxed to (435) 227-9106. Campbell Scientific is unable to process any returns until we receive this form. If the form is not received within three days of product receipt or is incomplete, the product will be returned to the customer at the customer's expense. Campbell Scientific reserves the right to refuse service on products that were exposed to contaminants that may cause health or safety concerns for our employees.
4WFBS120, 4WFBS350, 4WFBS1K Table of Contents
PDF viewers: These page numbers refer to the printed version of this document. Use the PDF reader bookmarks tab for links to specific sections.
1. Function........................................................................1
2. Specifications ..............................................................1
3. Measurement Concepts ..............................................2
4. Quarter Bridge Strain ..................................................4
4.1 Quarter Bridge Strain with 3 Wire Strain Element...................................4
4.1.1 Quarter Bridge Strain with 3 Wire Element Wiring .......................5
4.1.1.1 Quarter Bridge Strain with 3 Wire Element Wiring using
a multiplexer.......................................................................5
4.1.2 Quarter Bridge Strain with 3 Wire Element Calculations...............6
4.1.3 Quarter Bridge Strain with 3 Wire Program Examples ..................7
4.1.3.1 CRBasic Programming..........................................................7
4.1.3.2 Edlog ...................................................................................11
4.2 Quarter Bridge Strain with 2 Wire Element ...........................................17
4.2.1 Quarter Bridge Strain with 2 Wire Element Wiring .....................17
4.2.2 Two Wire ¼ Bridge use with Multiplexers and Equations...........18
4.3 Quarter Bridge Strain with Dummy Gage ..............................................18
4.3.1 Quarter Bridge Strain with Dummy Gauge Wiring Setup............20
4.3.2 Quarter Bridge Strain with Dummy Gauge Calculations..............21
4.3.3 Quarter Bridge Strain with Dummy Gauge Example Programs ...21
4.4 Quarter Bridge Strain Lead Resistance Compensation...........................21
4.4.1 Mathematical Lead Compensation for 3-Wire, ¼ Bridge Strain ..21
4.4.1.1 Mathematical Lead Compensation Circuit and Equations ..22
4.4.1.2 Mathematical Lead Compensation Programs......................23
4.4.2 Shunt Calibration Lead Compensation for 3-Wire, ¼ Bridge
Strain .........................................................................................30
4.4.2.1 Three Wire Gage Circuit with Shunt...................................30
4.4.2.2 Math for Shunt Calibration of 3-Wire, ¼ Bridge Strain
Circuits .............................................................................32
4.4.2.3 Example Programs for Shunt Calibration of 3-Wire,
¼ Bridge Strain Circuits...................................................34
4.4.3 Lead Compensation using Quarter Bridge Strain with 2 Wire
Element .....................................................................................35
4.5 Calculation of Strain for ¼ Bridge Circuits............................................37
i
4WFBS120, 4WFBS350, 4WFBS1K Table of Contents
Figures
1-1. Terminal Input Module with CR1000 .................................................... 1
2-1. Schematic................................................................................................ 2
3-1. Strain definition ...................................................................................... 2
4.1-1. Three wire quarter bridge strain circuit ............................................... 4
4.1-2. 3-wire ¼ bridge strain wiring .............................................................. 5
4.1-3. 3-wire ¼ bridge strain with multiplexer wiring................................... 5
4.2-1. Two wire quarter bridge strain circuit ............................................... 17
4.2-2. Wiring for 2-wire gauges................................................................... 18
4.3-1. Quarter bridge strain circuit with dummy gauge............................... 19
4.3-2. ¼ bridge strain with remote dummy gauge ....................................... 20
4.3-3. ¼ bridge strain with dummy gauge at datalogger.............................. 20
4.4-1. Three wire ¼ bridge strain circuit...................................................... 22
4.4-2. Shunting remotely across active gauge.............................................. 31
4.4-3. Circuit for shunting across dummy resistor....................................... 31
4.4-4. Wiring for shunt across dummy resistor............................................ 32
4.4-5. Two wire quarter bridge strain circuit ............................................... 35
4.5-1. Strain gage in full bridge ................................................................... 37
Table
4-1. Input Locations Used in CR10(X), 21X, and CR7 Examples .............. 11
ii

4WFBS120, 4WFBS350, 4WFBS1K 4 Wire Full Bridge Terminal Input Modules (TIM)

1. Function

The 4WFBS120, 4WFBS350, and 4WFBS1K Terminal Input Modules (TIM) complete a full Wheatstone bridge for a single strain gage or other sensor that acts as a single variable resistor. The difference between the three models is in the resistor that matches the nominal resistance of a 120 ohm, 350 ohm, or 1000 ohm quarter bridge strain gage. It can also be used to complete the back half of a Wheatstone bridge for use in a ¼ bridge strain circuit (1 active element) using a dummy gage, or in a ½ bridge strain circuit (2 active elements).
FIGURE 1-1. Terminal Input Module with CR1000

2. Specifications

2:1 Resistive Divider Resistors:
Ratio tolerance @ 25 °C: Ratio temperature coefficient:
Power rating per element:
Completion Resistor: 120, 350, or 1000 Ω Tolerance @ 25 °C: Temperature coefficient:
Power rating:
1 kΩ/1 kΩ ±0.01%
0.5 ppm/°C (-55°C to 85°C)
0.1 W @ 70°C
±0.01% ±0.8 ppm °C (-55°C to 85°C)
0.25 W @ 70°C
-1
1
4WFBS120, 4WFBS350, 4WFBS1K 4 Wire Full Bridge Terminal Input Modules (TIM)
ε
(
)
ε
με
=
Δ
Δ
FIGURE 2-1. Schematic

3. Measurement Concepts

Measuring strain is measuring a change in length. Specifically, the unit strain
is the change in length divided by the unstrained length
()
and thus is dimensionless.
,
LL /Δ=
LT + ΔL
T
L
T
L
PP
L + ΔL
FIGURE 3-1. Strain definition
As the subject is elongated in the longitudinal direction, the material will be narrowed or thinned down in the transverse direction. The ratio of the
transverse strain to the longitudinal strain is known as the Poisson ratio (
L
Δ
T
L
ν
=
3.1
This Poisson ratio is a known property for most materials and is used in some half bridge strain and full bridge strain circuits.
T
L
Δ
L
ν).
2
Strain is typically reported in microstrain
expressed in parts per million, i.e.: a change in length divided by one millionth of the length.
A metal foil strain gage is a resistive element that changes resistance as it is stretched or compressed. The strain gage is bonded to the object in which strain is measured. The gage factor,
resistance to the change in strain:
GF , is the ratio of the relative change in
GF R R l l
. Microstrain is strain
()
//
. For example, a
4WFBS120, 4WFBS350, 4WFBS1K 4 Wire Full Bridge Terminal Input Modules (TIM)
μ
Δ
(
−
=
(
)
⋅
gage factor of 2 means that if the length changes by one micrometer per meter of length
resistance. A more common method of portraying this equation is:
, the resistance will change by two micro-ohms per ohm of
()1
ε
=
ε
Or in terms of micro-strain:
με
=
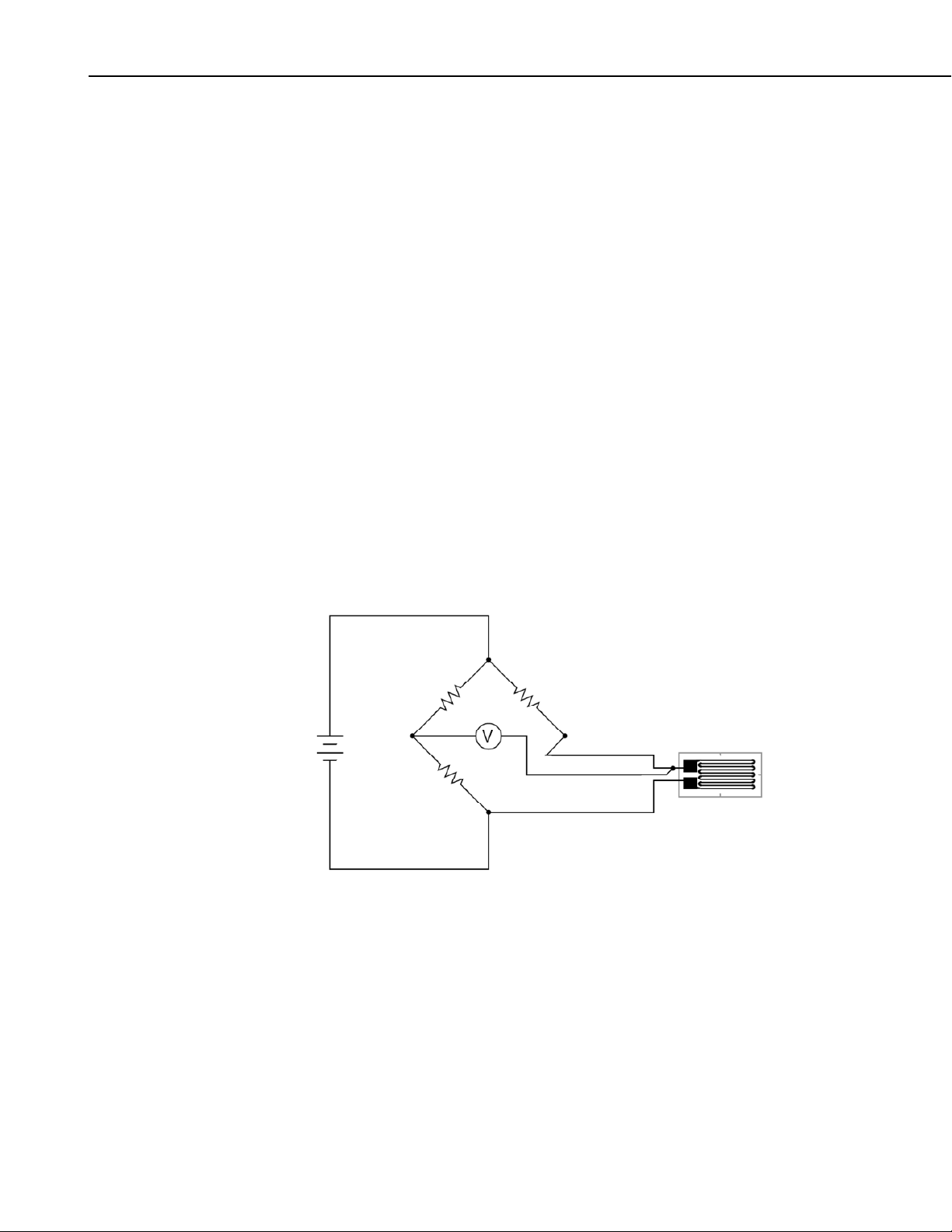
Because the actual change in resistance is small, a full Wheatstone bridge configuration is used to give the maximum resolution. The Wheatstone bridge can be set up with 1 active gage (Quarter bridge strain circuit), two active gages (Half bridge strain circuit), or 4 active gages (Full bridge strain circuit). For each of these Wheatstone bridge circuits there are multiple configurations.
The 4WFBS module provides three resistors that can be used for three of the arms of the Wheatstone Bridge (Figure 4-1). There are two 1000 ohm precision resistors for the back plane of the Wheatstone bridge, and a resistor matching the strain gage's resistance for the bridge arm opposite the gage. The inputs of the 4WFBS are configured so that this matching resistor can be bypassed if it is desired to utilize a dummy gauge, or to use two active gauges (Half Bridge Strain circuit).
For Full Bridge Strain circuits, as all four arms of the Wheatstone bridge are active gages, there is no need for completion resistors, and thus a 4WFBS module is not required.
G
RGFR•
G
3.2
6
)
101
RΔ×
G
RGF •
G
3.3
The resistance of an installed gage will differ from the nominal value. In addition, lead resistance imbalances can result in further unbalancing of the bridge. A zero measurement can be made with the gage installed. This zero measurement can be incorporated into the datalogger program such that subsequent measurements can report strain relative to this zero basis point. This removes the apparent strain resulting from the initial bridge imbalance.
Strain is calculated in terms of the result of the full bridge measurement. This result is the measured bridge output voltage divided by the bridge excitation voltage:
All of the various equations that are used to calculate strain use V in the bridge measurement from the zero state:
The result of the zero measurement,
the calculation of future strain measurements. Alternatively, the zero reading value can be left at 0 (zero measurement is neither recorded nor used).
It should be noted the actual result of the full bridge instruction (BrFull) is the millivolts output per volt of excitation (
V
outex
V
/
.
VVVVV )/()/(
ZeroexoutStrainedexoutr
, can be stored and used in
VV /⋅
exout
Zero
1000 VV
out ex
). The StrainCalc
/
, the change
r
3.4
3
4WFBS120, 4WFBS350, 4WFBS1K 4 Wire Full Bridge Terminal Input Modules (TIM)
function used in CRBasic uses this raw output as its input to calculate µstrain. See Section 4.5 Calculation of Strain for ¼ Bridge Circuits for a detailed derivation of the equations used.

4. Quarter Bridge Strain

A "quarter bridge strain circuit" is so named because an active strain gage is used as one of the four resistive elements that make up a full Wheatstone bridge. The other three arms of the bridge are composed of inactive elements. There are various circuits that use a single active element, including 2-Wire gauges, 3-Wire gauges, as well as a few circuits that utilize a dummy gauge for the arm opposite the arm holding the active gage instead of a resistor, R Figure 4.1.-1 (See Figures 4.3-1, 4.3-2, and 4.3-3). The 4WFBS TIM modules can support all types of these ¼ Bridge Strain circuits.

4.1 Quarter Bridge Strain with 3 Wire Strain Element

A 3-wire quarter bridge strain circuit is shown in figure 4.1-1. Strain gages are available in nominal resistances of 120, 350, and 1000 ohms. The 4WFBSXXX model must match the nominal resistance of the gage when using the 3-Wire circuit (e.g., the 4WFBS120 is used with a 120 ohm strain gage).
D
in
In Figure 4.1-1, R the Wheatstone bridge, as is done in the TIM design. R element, is the complementary resistor that has a nominal resistance of the un­strained gage. The 4
R2=1 KΩ
Excite V
R
and R2 are 1000 ohm resistors making up the back plane of
1
, the third resistive
D
th
resistive element is the active strain gage.
R
D
R
= Gauge
4
=1 KΩ
1
L
-
+
3
L
2
L
1
FIGURE 4.1-1. Three wire quarter bridge strain circuit
The 3-Wire gage alleviates many of the issues of the 2-Wire gage. As can be seen in Figure 4.1-1, lead wire L has the completion resistor while lead wire L gage. L
is tied back to the input channel of the datalogger that has an input
2
is in the arm of the Wheatstone bridge that
3
is in the arm that has the active
1
resistance greater than 1 Gohm, thus the current flow is negligible, negating effects of L
’s resistance. This circuit nulls temperature induced resistance
2
changes in the leads as well as reduces the sensitivity effect that the wires have on the gauge. See Section 4.4 for more on Lead resistance effects and methods to compensate for them.
4
4WFBS120, 4WFBS350, 4WFBS1K 4 Wire Full Bridge Terminal Input Modules (TIM)
A
A
X
4
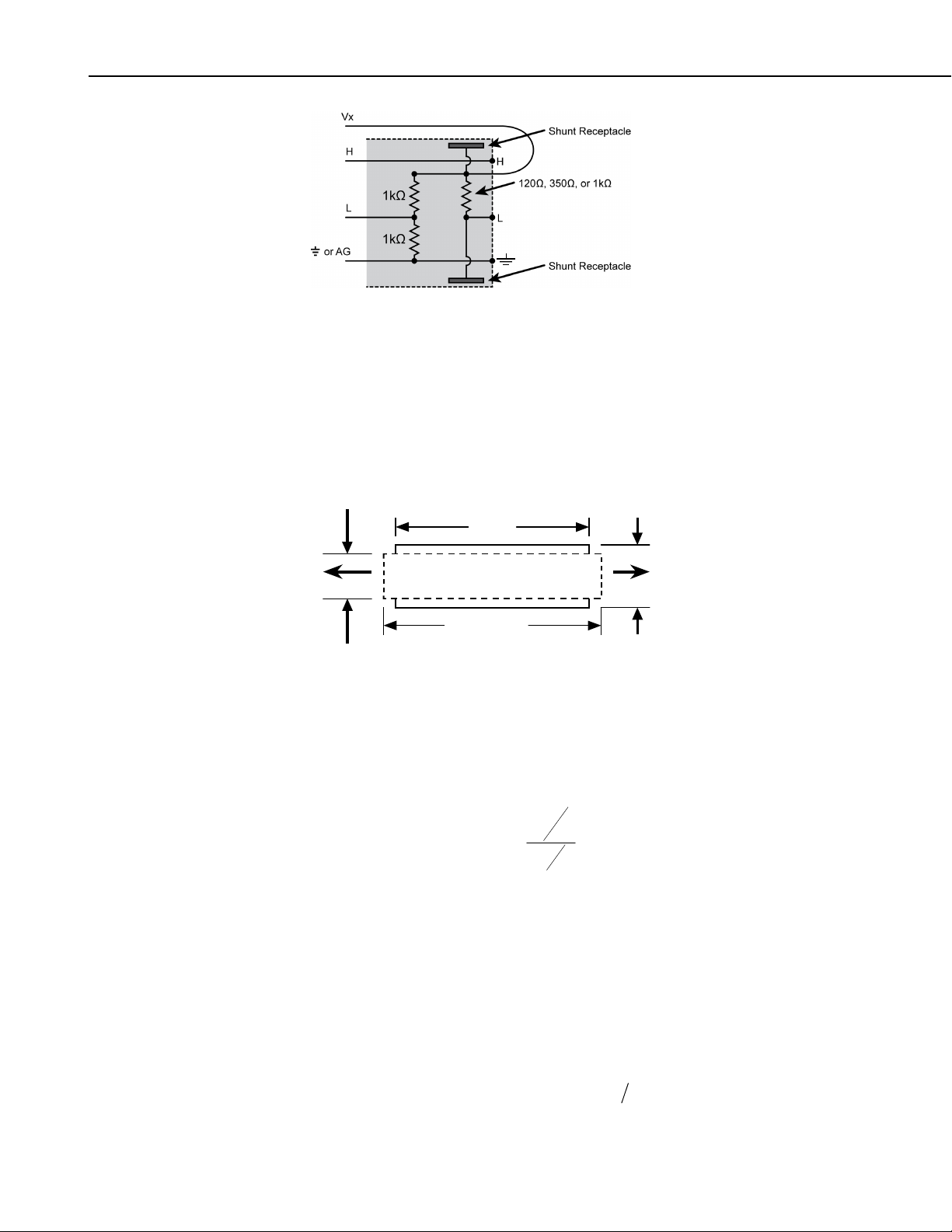
4.1.1 Quarter Bridge Strain with 3 Wire Element Wiring
Figure 4.1-2 illustrates the wiring of the strain gage to the 4WFBS module and the wiring of the module to the datalogger. It is important that the gage be wired as shown, and that the leads to the L and G terminals be the same length, diameter, and wire type. It is preferable to use a twisted pair for these two wires so that they will undergo the same temperature and electromagnetic field variations. With this configuration, changes in wire resistance due to temperature occur equally in both arms of the bridge with negligible effect on the output from the bridge.
Datalogger
VX or E
4WFBSXXX TIM
Shunt Receptacl e
H
R
2
R
=1KΩ R
D
L
1
=1KΩ
ctive Gauge
G
or G
Shunt Receptacle
FIGURE 4.1-2. 3-wire ¼ bridge strain wiring
4.1.1.1 Quarter Bridge Strain with 3 Wire Element Wiring using a multiplexer
When using a mechanical relay multiplexer such as the AM16/32B, the 4WFBS module should normally be placed on the face of the multiplexer similar as shown in Figure 4.1-3.
WFBS
2 345
H L H LH LHL
HLG
AM16/32B Relay Multiplexer
23
COM
ODD EVEN
H LHL H L
4X16
GND
CLK
RES
12V
N
1
O
2X32
11
21
LHLHLHLHL
H
12
22
23 24
7
13
13
25
Cable Shield
CR10X
AG
E1–E3
1L
1H
CR800 CR850
12 V
C1–C4
C1–C4
CR1000
EX1–EX3 or
VX1–VX3
1L
1H
CR23X
CR5000
12 V
G
C1–C8
C1–C8
CR3000 CR5000
VX1–VX4
1L
1H
21X
+12 V
EXCIT 1–4
C1–C6
21X
EXCITATION
1–4
1L
1H
CR7
12 V
EXCITATION
725 Card
Control
CR23X
EX1–EX4
1L
1H
CR10X CR1000 CR3000
G
G
12 V
G
G
C1–C8
C1–C8
CR7
SWITCHED
ANALOG OUT
1L
1H
CR800 CR850
EX1–EX2 or
VX10VX2
1L
1H
FIGURE 4.1-3. 3-wire ¼ bridge strain with multiplexer wiring
5
4WFBS120, 4WFBS350, 4WFBS1K 4 Wire Full Bridge Terminal Input Modules (TIM)
(
⋅
=
−
V
Although this requires a 4WFBS module for each strain gage, it is important because placing relays internal a Wheatstone bridge strain system is discouraged. Any change in resistance of the multiplexer’s relay contacts would result in a corresponding change in the bridge’s output voltage.
Changes in contact resistance can be induced by temperature fluctuations, oxidation, environmental conditions, and normal wear of contact surfaces. The specification for the relays that are used in our multiplexers state that initial contact resistance will be less than 100 milliohms (AM16/32B). There is not a specification for change in contact resistance for the relays because there are so many variables that affect contact resistance. Test reports exist for various test conditions that show contact resistance changing over time by 10 to 20 milli­Ohms. These tests were performed using static test temperatures, so it is safe to assume that real world conditions would result in larger resistance shifts.
When strain gauges are used in the Wheatstone bridge, small changes in contact resistance result in large apparent strains. To understand the error that can be introduced from allowing the relay contacts to be internal of the Wheatstone bridge, let us assume that the two relays carrying the current from the strain gage vary by 20 milliohms (40 milliohm total variance or ΔR mΩ ). Inserting this into equation 3.3, using a 120 ohm strain gage with a gage factor of 2 results in an apparent strain of about 167 με.
= 40
G
6
με
167
=
)
1202
Ω×× 04.0101
Ω×
4.1.2 Quarter Bridge Strain with 3 Wire Element Calculations
As noted in Section 3, in real life applications the Wheatstone bridge starts out unbalanced. The strain gauge is never perfectly at its nominal resistance even prior to installation. The installation process can lead to even more deviation from this nominal state. In addition, lead resistance can cause an initial apparent strain reading. To remove this initial offset, a zero measurement can be made with the gauge installed. This zero measurement can be incorporated into the datalogger program and subsequent measurements can report strain relative to this zero basis point.
Strain is calculated in terms of the result of the full bridge measurement. This result is the measured bridge output voltage divided by the bridge excitation voltage
V
out ex
millivolts output per volt of excitation, measurement, strain measurements. The change in the full bridge measurement from the zero
state, V
, is used in the calculation of the strain.
r
. (The actual result of the full bridge instruction is the
V
/
1000⋅V
1000
VV
out ex
VVV V V
r out ex out ex
can be stored and used to calculate future
/
0
(/)( /)
out
0
) The result of the zero
/ V
ex
4.1.1
Using V
4.1.2
from equation 4.1.1, the strain is calculated using equation 4.1.2.
r
ε
=
GF V
r
()
−412
r
The calculations are covered in more detail in Section 4.5.
6
4WFBS120, 4WFBS350, 4WFBS1K 4 Wire Full Bridge Terminal Input Modules (TIM)
4.1.3 Quarter Bridge Strain with 3 Wire Program Examples
This section is broken out into CRBasic programs and EDLOG programs. These programs are only to be used as examples. Besides adding additional measurement instructions, the programs will need to have the scan and data storage intervals altered for actual applications. Refer to the datalogger’s manuals and/or the CRBasic Editor’s help files for detailed information on the program instructions used as well as additional program examples.
4.1.3.1 CRBasic Programming
Dataloggers that use CRBasic include our CR800, CR850, CR1000, CR3000, CR5000, and CR9000(X). CRBasic uses the StrainCalc Instruction for calculating strain from the output of different full bridge configurations:
StrainCalc(Dest,Reps,Source,BrZero,BrConfig,GageFactor,PoissonRatio)
Source is the variable holding the current result from the full bridge
measurement
BrZero is the zero measurement; this parameter uses the results of a previous full bridge measurement instruction when the gage is at the zero condition (multiplier=1, offset=0, mV/V) directly.
BRCode for the Bridge Configuration used with the 4WFBS module should be set to -1 for a quarter bridge strain circuit.
Enter the actual gage factor in the GageFactor parameter.
Enter 0 for the Poisson ratio parameter, which is not used with ¼ Bridge strain circuits.
Example Program 4.1. CR9000X ¼ bridge Strain with 3 reps
This example program measures the output from the Wheatstone bridge using the BrFull instruction. The output from this instruction is input into the
StrainCalc instruction in order to calculate the raw µstrain value. This
program does not use a zero offset reading. See Example Program 4.2 for an example that performs a zero calibration.
' Program name: STRAIN.C9X
Public StrainMvperV(3) : Units StrainMvperV = mV_per_V 'Raw Strain dimensioned source Public Strain(3) : Units Strain = uStrain ‘uStrain dimensioned source Public GF(3) 'Dimensioned gauge factor
DataTable(STRAIN,True,-1) 'Trigger, auto size DataInterval(0,0,0,100) 'Synchronous, 100 lapses, autosize CardOut(0,-1) 'PC card , size Auto Sample (3,Strain(),IEEE4) '3 Reps, uStrain, Resolution Sample (3,StrainMvperV(),IEEE4) ‘3Reps,Stain mVolt/Volt, Resolution EndTable 'End of table STRAIN
BeginProg 'Program begins here
GF(1) = 2.1 : GF(2) = 2.2 : GF(3) = 2.3 'Initialize gauge factors for Strain( )
7
4WFBS120, 4WFBS350, 4WFBS1K 4 Wire Full Bridge Terminal Input Modules (TIM)
Scan(10,mSec,100,0) 'Scan once every 10 mSecs, non-burst BrFull(StrainMvperV(),3,mV50,4,1,5,7,1,5000,True,True,70,100,1,0) StrainCalc(Strain(),3,StrainMvperV(),0,-1,GF(),0) 'Strain calculation CallTable STRAIN Next Scan 'Loop up for the next scan
SlowSequence 'Slow sequence Scan to perform temperature
Scan(1,Sec,0,0) ' compensation on DAQ Calibrate 'Corrects ADC offset and gain BiasComp 'Corrects ADC bias current Next Scan EndProg 'Program ends here
Example Program 4.2. CR9000X ¼ bridge Strain with 3 reps and zero offset
This example program starts out with Example Program 4.1 and adds instructions (highlighted) to perform a zero calibration. As all strain circuits have a zero or initial imbalance that is related to the circuit rather than the member undergoing strain, a zero reading is often used to offset or remove this apparent strain. Again, see the manual and CRBasic editor’s Help file for more in-depth discussion on the instructions.
The FieldCalStrain instruction takes care of the underlying math for the zeroing using equation 4.1.2.
The LoadFieldCal instruction facilitates the reloading of the calibration factors when the logger is powered up. In addition, the programmer should create a DataTable (we have called this DataTable Calib in the example) to store the calibration factors each time a calibration is done.
The NewFieldCal is a Boolean flag variable that is only high during the Scan that a calibration has been completed. It is used in the DataTable instruction’s trigger parameter to trigger the table to record a record.
The SampleFieldCal output instruction is used to inform the logger to store all of the calibration factors that are controlled using the FieldCalStrain instruction.
Program name: STRAIN0.C9X
'
Public StrainMvperV(3) : Units StrainMvperV = mV_per_V 'Raw Strain dimensioned source Public Strain(3) : Units Strain = uStrain ‘uStrain dimensioned source Public GF(3) 'Dimensioned gauge factor Public ZeromV_V(3), ZeroStrain(3) Public ZReps, ZIndex, ModeVar
DataTable(STRAIN,True,-1) 'Trigger, auto size DataInterval(0,0,0,100) 'Synchronous, 100 lapses, autosize CardOut(0,-1) 'PC card , size Auto Sample (3,Strain(),IEEE4) '3 Reps, uStrain, Resolution Sample (3,StrainMvperV(),IEEE4) ‘3Reps,Stain mVolt/Volt, Resolution EndTable 'End of table STRAIN
DataTable (Calib,NewFieldCal,10) ‘Table for calibration factors from zeroing SampleFieldCal ‘User should collect these to his computer EndTable ‘for future reference
8
Loading...
+ 32 hidden pages
Buy Points How it Works FAQ Contact Us Questions and Suggestions Privacy Policy Cookie Policy Terms of Use